Kaon and pion parton distributions

Abstract

Beginning with results for the leading-twist two-particle distribution amplitudes of $\pi$- and K-mesons, each of which exhibits dilation driven by the mechanism responsible for the emergence of hadronic mass, we develop parameter-free predictions for the pointwise behaviour of all $\pi$ and K distribution functions (DFs), including glue and sea. The large-x behaviour of each DF meets expectations based on quantum chromodynamics; the valence-quark distributions match extractions from available data, including the pion case when threshold resummation effects are included; and at $\zeta _5=5.2\,$GeV, the scale of existing measurements, the light-front momentum of these hadrons is shared as follows: $\langle x_{\mathrm{valence}} \rangle ^\pi = 0.41(4)$, $\langle x_{\mathrm{glue}} \rangle ^\pi = 0.45(2)$, $\langle x_{\mathrm{sea}} \rangle ^\pi = 0.14(2)$; and $\langle x_{\mathrm{valence}} \rangle ^K = 0.42(3)$, $\langle x_{\mathrm{glue}} \rangle ^K = 0.44(2)$, $\langle x_{\mathrm{sea}} \rangle ^K = 0.14(2)$. The kaon’s glue and sea distributions are similar to those in the pion, although the inclusion of mass-dependent splitting functions introduces some differences on the valence-quark domain. This study should stimulate improved analyses of existing data and motivate new experiments sensitive to all $\pi$ and K DFs. With little known empirically about the structure of the Standard Model’s (pseudo-) Nambu-Goldstone modes and analyses of existing, limited data being controversial, it is likely that new generation experiments at upgraded and anticipated facilities will provide the information needed to resolve the puzzles and complete the picture of these complex bound states.

1 Introduction

The past decade saw discovery of the Higgs boson [1, 2], thereby completing the Standard Model (SM). Nevertheless, two concrete paths remain open: searching for an understanding of known phenomena whose explanation is not provided by the SM, e.g. dark energy, dark matter, the size of the matter-antimatter asymmetry in the known Universe, etc. [3]; and elucidating the complete content and range of consequences of the SM.

The first track needs no explanation. This is a typical mode for high-energy physics. On the other hand, the second might seem odd. Consider, therefore, that although the SM is remarkably successful, it is only understood at the level of perturbation theory; and even in this context, e.g. the computation of five-point two-loop diagrams is an open challenge [4]. Moreover, there are SM phenomena whose explanation cannot be found in perturbation theory. Primary amongst these is the source of nuclear-size mass. The Higgs boson produces the Lagrangian (current) masses of all fermions; but so far as the building blocks of known nuclei are concerned (protons and neutrons, i.e. nucleons), the current masses of the valence u- and d-quarks sum to just 1% of the nucleon mass. The remaining 99% is suspected to emerge as a consequence of dynamics within the SM’s strong interaction sector; namely, quantum chromodynamics (QCD).

Emergent hadronic mass (EHM) is the origin of the $m_N \approx 1\,$GeV scale that characterises and supports the bulk of visible matter; and any theoretical account should link EHM with an array of empirically verifiable consequences so that the explanation’s credibility can be established. This requires a nonperturbative analysis of QCD in its strong-coupling domain. Critically, given the necessary connection between EHM and dynamical chiral symmetry breaking (DCSB), one should preferably employ nonperturbative methods in quantum field theory which preserve the Ward–Green–Takahashi identities that connect symmetry-related Schwinger functions. With sufficient computer resources and careful analyses of the various necessary limits, numerical simulations of lattice-regularised QCD (lQCD) can meet this challenge [5,6,7]. An alternative approach is provided by continuum Schwinger function methods (CSMs); in particular, the Dyson-Schwinger equations (DSEs) [8,9,10,11], which provide a systematic, symmetry-preserving approach to solving the continuum bound-state problem for hadrons.

Significantly, where fair comparisons can be drawn, predictions from DSE analyses are practically identical to those obtained using lQCD; and whilst the lattice formulation maintains a tighter connection with the QCD Lagrangian, the range of observables currently accessible to DSE methods is greater. The approaches are complementary and the synergy between them can profitably be exploited to understand EHM.

The need for a symmetry preserving framework is acute when studying pseudoscalar mesons whose valence constituents are drawn exclusively from the set of lighter u-, d-, s-quarks and their antiquark partners, e.g. $\pi$ and K mesons.¹ These states are massless in the absence of a Higgs mechanism: they are the SM’s Nambu-Goldstone (NG) modes. As such, $\pi$ and K mesons express a peculiar dichotomy. Namely, they are hadron bound states defined, like all others, by their valence quark and/or antiquark content; yet, the mechanism(s) which give all other hadrons their roughly $1\,$GeV mass-scale are obscured in such systems. Hence, in exploring the origins of EHM, understanding the character of NG modes is of great importance [13]. These states are not pointlike; their internal structure is more complex than is usually imagined; and it can be argued that the properties of these nearly-massless strong-interaction composites provide the clearest windows onto EHM [14].

With the strong link to EHM in mind, in Sect. 2 we consider the simplest $\pi$ and K distribution amplitudes (DAs), explain how they may be calculated, and draw a connection between these DAs and the valence-quark distribution functions (DFs) of the $\pi$ and K. That connection is made through the light-front wave functions for these systems, which can be obtained via light-front projection of the appropriate Bethe–Salpeter wave functions. The key conjecture in Sect. 2 is that there exists a resolving scale, $\zeta _H$, at which the dressed quasiparticles emerging from the valence-quark and -antiquark degrees of freedom express all properties of the $\pi$ and K mesons; in particular, they carry all the hadron’s light-front momentum. (This feature is also typical of well-constructed models, e.g. Refs.  [15,16,17,18,19].)

Section 3 reviews a perspective on QCD’s running coupling, highlighting that the emergence of a gluon mass-scale [20,21,22,23,24,25,26,27,28,29,30,31,32,33] ensures QCD interactions can be described by a process-independent (PI) effective charge which saturates to a nonzero, finite value at infrared momenta [34,35,36,37,38]. Such behaviour may be associated with the opening of a conformal window at long wavelengths. The associated gauge sector screening mass then serves as a natural value for $\zeta _H$ because it marks the border between soft and hard physics. In having thus identified $\zeta _H$ at the outset, all DA and DF results obtained herein are unified predictions [39, 40].

Our approach fixes $\zeta _H<m_N$; hence, comparisons with typical extractions of DFs require evolution to $\zeta >\zeta _H$. Section 4 therefore explains why the PI effective charge provides a suitable starting point for integrating the DGLAP equations [41,42,43,44], leading to an all-orders evolution scheme that enables predictions to be made for $\pi$ and K DFs, i.e. valence, glue and sea. It also reiterates a longstanding prediction of the QCD-improved parton model [45,46,47,48], viz. in a $J=0$ hadron, M, the valence-quark DF has the following large-x behaviour:

(1)

where is independent of x. Eq. (1) is controversial because most analyses of extant data on imply $\beta (\zeta _H)<2$. The only analyses that agree with Eq. (1) are those at next-to-leading order (NLO) which include threshold resummation effects [49, 50]. Much of the discussion herein bears upon the validity of Eq. (1).

Section 5 presents our results for $\pi$ DFs, providing extensive comparisons, e.g.: with older [51] and more recent phenomenological analyses [52]; and with recent lQCD results for the moments [53, 54] and pointwise behaviour [55] of .

Our prediction for the kaon’s simplest DA is explained in Sect. 6. Building upon that, Sect. 7 describes predictions for all the kaon’s DFs. They include results for the host-dependence of valence, glue and sea DFs, i.e. $K/\pi$ ratios for all common DFs. It should be emphasised that within the SM’s strong interaction sector there can be no differences between $\pi$ and K mesons without a Higgs mechanism; but EHM modulates the observable effects of this mechanism in a variety of ways, many of which have not yet been elucidated. Finally, along with providing a summary, Sect. 8 presents a perspective on the potential for further studies of $\pi$ and K structure to deliver insights into EHM and the manner by which its effects are tempered by the Higgs boson.

2 Light front wave functions and parton distributions

If one seeks a description of a given hadron’s measurable properties in terms of the probability expressions typical of quantum mechanics, then the hadron’s light front wave function (LFWF), $\psi _H(x,\mathbf {k}_\perp ;P)$, where P is the hadron’s total momentum, takes a leading role. In approaching the problem of expressing $\psi$ from a partonic perspective with a connection to perturbative QCD, it is usual to employ a Fock-space decomposition of the LFWF. Each element in that expansion then represents the probability amplitude for finding n partons in the hadron with momenta $\{ (x_i,k_{\perp i}) \, |\, i=1,\ldots ,n\}$, always requiring conservation of total momentum.

The strength of this approach is exemplified by observing that the DAs which feature in formulae describing hard exclusive processes and the DFs that characterise hard inclusive reactions can both be expressed directly in terms of the LFWF [56], viz., respectively:

(2a)

(2b)

where $\zeta$ is the scale at which the hadron is being resolved. As indicated by this $\zeta$-dependence, considered as a problem in quantum field theory, the perceived character of any hadron depends upon the energy scale at which it is observed. That is not to say empirical cross-sections are affected; rather, this energy scale determines the optimal choice for the degrees of freedom needed to solve the problem and express an insightful interpretation.

In order to capitalise on Eq. (2), one must be able to compute a hadron’s LFWF. This might be achieved by constructing a sound approximation to QCD’s light-front Hamiltonian [57]. However, that path is complicated by, inter alia, the need to solve complex constraint equations along the way [58]. A different approach, applied elsewhere [59] to a local U$(N_c)$ gauge theory in two dimensions, with $N_c$ very large, is to: use the covariant DSEs; solve for Bethe–Salpeter wave functions; and subsequently project these quantities onto the light front, thereby obtaining the desired LFWFs. This scheme was shown to be practical for QCD in Ref.  [60]. We follow it herein.

In employing DSEs to solve the continuum bound state problem, one must specify a kernel. In most cases, a rainbow-ladder (RL) truncation is used, viz. leading order in the systematic, symmetry-preserving scheme formalised in Refs.  [61, 62]. For instance, RL studies have recently delivered predictions for the valence, glue and sea distributions within the pion [39, 40] and unified them with, e.g. electromagnetic pion elastic and transition form factors [63,64,65,66].

Experience and practice have shown that owing to cancellations between correction terms, RL truncation delivers sound predictions for diverse properties of systems constituted from (nearly) degenerate valence-parton degrees-of-freedom in which orbital angular momentum does not play a significant role, e.g. [67,68,69,70,71,72,73]: $\pi$ and $\rho$ mesons and the nucleon and $\varDelta$-baryon. However, in mesons with an imbalance between the current-masses of the valence-quark and -antiquark, straightforward implementation of RL truncation becomes increasingly unreliable as the difference between current masses increases. For instance, concerning the kaon, it yields a leading-twist DA, $\varphi _K(x)$, that is both too asymmetric around $x=1/2$ and too dilated [74, 75]. Many such defects are remedied by the dynamical-chiral-symmetry-breaking-improved (DB) truncation [76], whose development enabled a bridge to be built between studies of QCD’s gauge and matter sectors [28].

QCD is a renormalisable quantum field theory; hence, a renormalisation scheme and scale must be chosen when formulating and solving the continuum bound state problem. We use a mass-independent momentum subtraction procedure with scale $\zeta =\zeta _H$, i.e. the infrared “hadronic” scale at which the dressed quasiparticles obtained as solutions to the quark gap equation express all properties of the bound state under consideration, e.g. they carry all of the hadron’s momentum at $\zeta _H$. As explained elsewhere [39, 40, 64, 65, 77, 78], this approach ensures that parton splitting can properly be expressed through $\zeta$-evolution of hadron wave functions [79,80,81] thereby overcoming a known deficiency of truncated bound-state kernels. (This is elucidated in Sect. 5.1.)

Following the procedure just described, reviewed in Refs.  [8,9,10], one can obtain the Bethe–Salpeter wave functions for the $\pi$ and K described as bound states of a dressed u-quark and h-antiquark ($M=\pi$, $h=d$ and $M=K$, $h = s$):

$$\begin{aligned} \chi _M^P&(k_{\eta {\bar{\eta }}};\zeta _H) = S_{u}(k_\eta ;\zeta _H) \varGamma _M^P(k_{\eta {\bar{\eta }}};\zeta _H) S_{h}(k_{{\bar{\eta }}};\zeta _H), \end{aligned}$$

(3)

where P is the meson’s total momentum; $S_f(k;\zeta _H)$ is the dressed propagator for a quark with flavour f and renormalisation point invariant current-mass ${\hat{m}}_f$,

$$\begin{aligned} S_f(k;\zeta _H)&= Z_f(k^2;\zeta _H^2)/[i\gamma \cdot k + M_f(k^2)]\,; \end{aligned}$$

(4)

and the Bethe–Salpeter amplitude ($\ell = k_{\eta {\bar{\eta }}}$)

$$\begin{aligned} \varGamma _M^P&(\ell ;\zeta _H) = \gamma _5 \left[ i E_M(\ell ;P;\zeta _H) + \gamma \cdot P \, F_M(\ell ;P;\zeta _H) \right. \nonumber \\&\left. +\gamma \cdot \ell \, G_M(\ell ;P;\zeta _H) + \sigma _{\mu \nu } \ell _\mu P_\nu \, H_M(\ell ;P;\zeta _H) \right] . \end{aligned}$$

(5)

$E_M(\ell ;P;\zeta _H)$ is a scalar function of $\ell ^2$, $\ell \cdot P$; likewise, the other functions. Here, $k_{\eta {\bar{\eta }}}=[k_\eta + k_{{\bar{\eta }}}]/2$, $k_\eta = k+\eta P$, $k_{{\bar{\eta }}}=k-(1-\eta )P$, $\eta \in [0,1]$; and owing to Poincaré covariance, no observable depends on $\eta$, i.e. the definition of the relative momentum. (The analysis herein is predicated on the following current-quark mass values: ${\hat{m}}_u={\hat{m}}_d = 4.4\,$MeV, ${\hat{m}}_s = 90\,$MeV.)

It is worth highlighting that the matrix valued function $\chi _M^P(k_{\eta {\bar{\eta }}};\zeta _H)$, described above, yields a LFWF for the meson M whose Fock space expansion in terms of non-interacting parton eigenstates of the free light-front Hamiltonian contains a countable infinity of terms. In practice, the weighting of each one of the terms in the LFWF is determined by the truncation employed in the DSE calculation; and as the truncation is improved, these strengths more veraciously express QCD.

The leading-twist two-particle DA for the u-quark in the meson M can now be obtained by light-front projection of $\chi _M$:

$$\begin{aligned}&f_M \,\varphi ^u_{M}(x;\zeta _H)= \frac{1}{16\pi ^3}\int d^2 k_\perp \, \psi _{M_u}^{\uparrow \downarrow }(x,k_\perp ^2;\zeta _H) \end{aligned}$$

(6a)

$$\begin{aligned}&=N_c \mathrm{tr}Z_2(\zeta _H,\varLambda ) \int _{dk}^\varLambda \delta _n^x(k_\eta )\gamma _5 \gamma \cdot n \chi _M(k_{\eta {\bar{\eta }}};P ;\zeta _H), \end{aligned}$$

(6b)

where $N_c=3$; the trace is over spinor indices; $\int _{dk}^\varLambda$ is a symmetry-preserving regularisation of the four-dimensional integral, with $\varLambda$ the regularisation scale; $Z_2(\zeta _H,\varLambda )$ is the quark wave function renormalisation constant; $\delta _n^x(k_\eta ) = \delta (n\cdot k_\eta - x n\cdot P)$, n is a light-like four-vector, $n^2=0$, with $n\cdot P = -m_M$ in the meson rest frame; and $f_M$ is the meson’s leptonic decay constant, so

$$\begin{aligned} \int _0^1 dx\, \varphi ^u_{M}(x;\zeta _H) = 1. \end{aligned}$$

(7)

The companion DA for the h-antiquark is

$$\begin{aligned} \varphi _{M}^{{\bar{h}}}(x;\zeta _H) = \varphi _{M}^{u}(1-x;\zeta _H). \end{aligned}$$

(8)

In terms of the two-particle LFWF defined viaEq. (6a), the meson’s valence u-quark DF is

(9)

This can be demonstrated in many ways, one of which proceeds from analysis of pseudoscalar meson generalised parton distributions [82]. As explained above, since the meson M is constituted solely from dressed u and ${\bar{h}}$ degrees-of-freedom at $\zeta _H$, then

(10)

At this point we recall the analysis of $\pi$ and K distributions in Ref.  [83], which demonstrates that a factorised representation of $\psi _{M_u}^{\uparrow \downarrow }(x,k_\perp ^2;\zeta _H)$ is quantitatively reliable for integrated quantities. Namely, it is a good approximation to write

$$\begin{aligned} \psi _{M_u}^{\uparrow \downarrow }(x,k_\perp ^2;\zeta _H) = \varphi _{M}^{u}(x;\zeta _H) \psi _{M_u}^{\uparrow \downarrow }(k_\perp ^2;\zeta _H), \end{aligned}$$

(11)

where $\psi _{M_u}^{\uparrow \downarrow }(k_\perp ^2;\zeta _H)$ is some sensibly chosen function. Using Eq. (9), it follows with equal precision that²

(12)

where the constant of proportionality is fixed by baryon number conservation. Owing to parton splitting effects, Eq. (12) is not valid on $\zeta >\zeta _H$. Nevertheless, since the evolution equations for both DFs and DAs are known [41,42,43,44, 79,80,81], the connection changes in a traceable manner.

3 Process independent effective charge and the hadronic scale

In studies of DFs, the hadronic scale, $\zeta _H$, is typically used as a parameter [84]. A practitioner develops a DF model that is supposed to be valid at an unspecified scale, which is subsequently identified as $\zeta _H$. Then a target DF is identified, one that has typically been extracted through a phenomenological analysis of selected experimental data at $\zeta _E\gg \zeta _H$. The practitioner finally chooses a value of $\zeta _H$ so that, after DGLAP evolution $\zeta _H\rightarrow \zeta _E$, the model DF reproduces some property or properties of the target distribution.

We adopt a different approach, which delivers predictive power [39, 40]. It capitalises on the existence of a PI effective charge in QCD [38], ${\hat{\alpha }}(k^2)$, which, owing to the emergence of a nonzero gluon mass-scale [20], saturates in the infrared: ${\hat{\alpha }}(0)/\pi = 0.97(4)$. An interpolation of the numerical result is obtained by writing

(13)

$\gamma _m=4/\beta _0$, $\beta _0=11 - (2/3)n_f$, $n_f=4$, $\varLambda _{\mathrm{QCD}}=0.234\,$GeV, with (in $\hbox {GeV}^2$)

$$\begin{aligned} \begin{array}{c|c|c} a_0 &{} a_1 &{} b_0 \\ \hline 0.104(1) &{} 0.0975 &{} 0.121(1) \end{array}. \end{aligned}$$

(14)

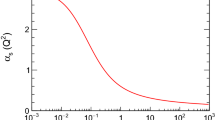
This interpolation is depicted in Fig. 1. Notably, ${{\hat{\alpha }}}(k^2)$ agrees to better than 0.1% with QCD’s one-loop perturbative running coupling on $k^2 > rsim (9\varLambda _{\mathrm{QCD}})^2$.

Fig. 1

Process-independent effective charge, ${\hat{\alpha }}(k^2)/\pi$, computed elsewhere [38] and interpolated using Eqs. (13), (14). (The band bracketing the solid blue curve expresses the uncertainty in ${\hat{\alpha }}(k^2=0)/\pi = 0.97(4)$. Details are provided in Ref.  [38].) The vertical dashed red line marks the screening mass $k=m_G=0.331(2)\,$GeV

The perturbative running coupling in QCD exhibits a Landau pole at $k^2=\varLambda _{\mathrm{QCD}}^2$. This singularity is eliminated from the PI effective charge by nonperturbative gauge sector dynamics. The effect of such dynamics is plain in Eq. (13), where $k^2/\varLambda _{\mathrm{QCD}}^2$ is replaced by as the argument of the logarithm. The value

(15)

thus defines a screening mass. As evident in Fig. 1, $m_G$ marks a boundary: the running coupling alters character at $k \simeq m_G$ so that modes with $k^2 \lesssim m_G^2$ are screened from interactions and the theory enters a conformal domain. This being so, then the line $k=m_G$ draws a natural border between soft and hard physics; hence, we identify

$$\begin{aligned} \zeta _H=m_G. \end{aligned}$$

(16)

4 Scale evolution of distribution functions

4.1 All-orders evolution hypothesis

The hadronic scale, $\zeta _H$, is not directly accessible in analyses of experiments capable of providing information about DFs because certain kinematic conditions need to be met in order for the data to be interpreted in such terms [85]. These conditions typically require experiments with momentum transfers squared $Q^2 \sim \zeta _E^2 > m_N^2$. Hence, any result for a DF at $\zeta _H$ must be evolved to $\zeta _E$ for comparison with experiment.

The usual evolution framework is provided by the DGLAP equations. However, an evolution prescription must still be specified because the DGLAP equations involve QCD’s running coupling. One may take a purely perturbative QCD (pQCD) perspective and implement evolution by using DGLAP kernels computed at a given order in perturbation theory. In this case, if the scale at which evolution begins is large enough, then leading-order (LO) evolution kernels may be sufficient, at least in practice. Failing that, then next-to-leading order can be implemented, and so on, in principle.

An alternative supposes that [86,87,88,89,90]: (i) in connection with a given process, a nonperturbative running coupling (effective charge) exists; (ii) being derived from experiment, this charge is free of a Landau pole; and (iii) using this charge, the associated leading-order DGLAP equations are exact. Notwithstanding the feature that effective charges from different observables can in principle be related via an expansion of one coupling in terms of the other, the process-dependence of such couplings may be unsettling because: (a) knowledge of one process-dependent (PD) charge does not usually enable global predictions to be made for another process; and (b) the connection between two such charges at infrared momenta can only be determined after both are independently constructed.

Following Refs.  [37,38,39,40], our approach is to refashion the PD-charge alternative and implement evolution by employing the PI effective charge described in Sect. 3, to integrate the one-loop DGLAP equations. Using this procedure, e.g. one has the following relationship between the Mellin moments of a meson’s valence-quark DF:

(17)

(18a)

(18b)

where $t=\ln k^2$ and

$$\begin{aligned} \gamma _0^n = -\frac{4}{3} \left[ 3 + \frac{2}{(n+1)(n+2)} - 4 \sum _{k=1}^{n+1}\frac{1}{k}\right] . \end{aligned}$$

(19)

Note that $\gamma _0^0=0$, so baryon-number does not change with $\zeta$, and $\gamma _0^1 = 32/9$.

Our reasons for adopting this scheme are manifold. For example, as illustrated in Fig. 1, ${{\hat{\alpha }}}(k^2)$ is monotonically decreasing on $k^2\ge 0$ and capable of marking the boundary between soft and hard physics. Moreover, it is known to unify many observables, inter alia: hadron static properties [72, 73, 91, 92]; parton distribution amplitudes of light- and heavy-mesons [74, 75, 93,94,95] and associated elastic and transition form factors [66, 77, 78, 96, 97]. In addition, ${{\hat{\alpha }}}(k^2)$ is pointwise (almost) identical to the PD effective charge, $\alpha _{g_1}$, defined via the Bjorken sum rule [98,99,100]. In possessing such an array of properties, ${{\hat{\alpha }}}(k^2)$ emerges as a strong candidate for that object which properly represents the interaction strength in QCD at any given momentum scale [87]. Hence, it is a suitable input for our procedure.³

4.2 Distribution functions on $x\simeq 1$

The Introduction reiterated one of the earliest predictions of the QCD-improved parton model [45,46,47,48]:

(20)

where is a constant, i.e. independent of x, and the exponent increases logarithmically with $\zeta$: $\beta (\zeta )>\beta (\zeta _H)$ for $\zeta >\zeta _H$. In fact, as shown in Appendix 1, an analysis of the large-n behaviour of Eqs. (17)–(19) yields ($\gamma _E=0.5772\ldots$ is Euler’s constant)

(21a)

(21b)

It is worth noting that although Eq. (21a), when expressed at one-loop order in pQCD, is a textbook result, e.g. Ref.  [85, Eq. (4.137)], it is often overlooked. Equation (21) establish a connection between the large-x exponent of a meson’s valence-quark DF at scale $\zeta$ and the momentum fraction carried by valence-quarks at this scale, viz. the exponent increases logarithmically with the decrease in valence-quark momentum fraction and the multiplicative coefficient decreases.

5 Pion distributions

5.1 Scale invariance

The DFs of valence-quarks, sea and glue in the pion were calculated using a symmetry-preserving implementation of RL truncation in Refs.  [39, 40]. In that study, the valence-quark DF was obtained using [101]:

(22)

This is a practicable approximation to the complete set of box diagrams necessary for a symmetry-preserving calculation of the valence-quark DFs. Using Eq. (22), it is straightforward to verify Eq. (10).

All existing continuum quantum field theory studies of meson valence-quark DFs begin with a formula in the same class as Eq. (22) – see Ref.  [48] and citations thereof. It is important, therefore, to highlight a particular feature of Eq. (22) that has hitherto been overlooked. Namely, computed using functions obtained in rainbow-ladder truncation or any kindred variant, the result is actually independent of $\zeta$.

The proof is straightforward. In a computational framework that preserves the multiplicative renormalisability of QCD:

$$\begin{aligned} S(k;\zeta _1) Z_2(\zeta _1^2,\varLambda ^2)&= S(k;\zeta _2) Z_2(\zeta _2^2,\varLambda ^2), \end{aligned}$$

(23a)

$$\begin{aligned} \varGamma ^P(k_{\eta {\bar{\eta }}};\zeta _1)/Z_2(\zeta _1^2,\varLambda ^2)&= \varGamma ^P(k_{\eta {\bar{\eta }}};\zeta _2)/Z_2(\zeta _2^2,\varLambda ^2). \end{aligned}$$

(23b)

Hence,

$$\begin{aligned} S(k;\zeta _1) \varGamma ^P(k_{\eta {\bar{\eta }}};\zeta _1) = S(k;\zeta _2) \varGamma ^P(k_{\eta {\bar{\eta }}};\zeta _2)\,; \end{aligned}$$

(24)

and, as defined by Eq. (22), . It should be noted that the same is true of $\varphi _M(x;\zeta )$ obtained from Eq. (6b).

This characteristic is good so far as baryon number conservation is concerned because it guarantees

(25)

However, it also imposes the same identity for all $n\ge 1$ moments (Eq. 17), i.e. it precludes DF evolution. Consequently, like Eq. (12), Eq. (22) can only be valid for $\zeta =\zeta _H$, whereat the meson is constituted solely from dressed u and ${\bar{h}}$ degrees-of-freedom.

If one analyses the derivations of formulae in the class of truncations which contains Eq. (22), the origin of the scale invariance becomes clear. In fact, it was identified in Ref.  [81]: diagrams with any number of longitudinally polarised gluons contribute at leading order in covariant gauges and they are neglected in deriving Eq. (22) and kindred expressions. Such contributions do not change power laws associated with scaling behaviour; but they do produce the anomalous dimensions necessary for scaling violations and parton splitting, i.e. the undressing of dressed quasiparticles as $\zeta$ is increased. Another way of understanding this is to recognise that any Wilson line is nonzero in calculations using covariant gauges; hence, the bare partial derivative in the light-front projection should be converted into the covariant derivative. It was to remedy precisely these weaknesses that Refs.  [64, 65, 77, 78] incorporated Bethe–Salpeter wave function evolution.

5.2 Connecting the pion’s DF and DA

In Refs.  [39, 40], the single mass-scale characterising the interaction used to define the RL truncation was chosen so as to deliver a realistic description of pseudoscalar mesons constituted from mass-degenerate valence-quark and -antiquark degrees-of-freedom over a wide range of current-quark masses [66]. It follows that implementing a DB kernel cannot bring material improvement because no realistic kernel can do better than reproduce experiment and the RL study was already tuned to that purpose.

Fig. 2

Comparison of pion leading-twist two-particle DAs: $\varphi _\pi (x;\zeta _H)$ computed using the DB kernel [60], solid blue curve; and Eq. (27), dashed green curve

The preceding claim and also the utility of Eq. (12) can be validated as follows. In Refs.  [39, 40] the valence-quark DF is

(26)

from which one obtains the unit-normalised square-root:

$$\begin{aligned}&\varphi _\pi ^\surd (x;\zeta _H) = 15.271\, x(1-x) \nonumber \\&\quad \times [1-2.9342 \sqrt{x(1-x)}+2.2911 x(1-x)]^{1/2}. \end{aligned}$$

(27)

According to Eq. (12), $\varphi _\pi ^\surd$ should be a fair approximation to the pion’s leading-twist two-particle DA; and this is verified by Fig. 2, which compares Eq. (27) with the result obtained from Eq. (6b) using the DB kernel [60]:

$$\begin{aligned}&\varphi _\pi ^{\mathrm{DB}} (x;\zeta _H) = 20.227\, x(1-x) \nonumber \\&\quad \times [1- 2.5088\, \sqrt{x(1-x)}+ 2.0250 \, x(1-x)]. \end{aligned}$$

(28)

It is necessary to remark here that Ref.  [60] chose to reconstruct the pion’s DA from its moments using an order-$\alpha$ Gegenbauer expansion. This is a useful first step because the procedure converges rapidly; hence, enables the qualitative feature of broadening driven by EHM in the SM to be exposed. Such broadening, however, need not and should not disturb the DA’s endpoint behaviour, which QCD predicts to be linear in the neighbourhoods $x\simeq 0, 1$. Therefore, as a second step, we re-expressed the result from Ref.  [60] as the function in Eq. (28). The first eleven moments agree at the level of 1.6(1.4)%, i.e. well within any sensible estimate of uncertainty in the computation of high-order moments.

Hereafter, we consider Eqs. (12), (28) to deliver the best founded prediction for the pion’s valence-quark DFs, viz.

(29)

with . Notably, even though it is plain that

(30)

is only realised on $x>0.98$ as a consequence of EHM-induced broadening.

5.3 Evolved pion DFs

5.3.1 GRS scale

Reference [51] (GRS) postulates that hadron DFs at a scale $\zeta$ can be computed by beginning with nonzero valence-like distributions for all partons at a scale $\zeta _0$ and then using pQCD DGLAP equations (at LO or NLO) to evolve these input distributions to the larger scale, $\zeta$, in the process of fitting a selected body of structure function data. There are similarities between this hypothesis and our approach, but also differences, e.g.: whilst Ref.  [51] uses $\zeta _0$ as a parameter, our value of $\zeta _H$ is fixed by ${{\hat{\alpha }}}(k^2=\varLambda _{\mathrm{QCD}}^2)$; and Ref.  [51] has nonzero distributions for all partons at the starting scale, $\zeta _0$, whereas we argue that glue and sea distributions are zero at $\zeta _H$. Notably, GRS use $\zeta _0^{\mathrm{LO}} =0.51\,$GeV or $\zeta _0^{\mathrm{NLO}}=0.63\,$GeV and we have $\zeta _H = 0.33\,$GeV$<\zeta _0^{\mathrm{LO}} <\zeta _0^{\mathrm{NLO}}$. Given this feature, we judge it worthwhile to begin with Eq. (29), employ the evolution procedure explained in Sect. 4.1, and compare our predictions for the pion’s valence-quark, glue and sea distributions at a GRS scale with the input distributions assumed in Ref.  [51]. Only the LO GRS distributions are reported. For all practical purposes, the comparison with NLO GRS is equivalent.

Our $\zeta _H \rightarrow \zeta _0^{\mathrm{LO}}$ evolved valence-quark DF is compared with the GRS Ansatz in Fig. 3a. Evidently, the GRS distribution is much harder than our prediction. Notwithstanding that, the valence-quark momentum fraction is comparable with ours, albeit 29(12)% smaller: we predict

(31)

whereas the GRS DF yields 0.56. We find once again that with our prediction is only realised on $x>0.99$.

Fig. 3

a Solid blue curve: valence-quark distribution in Eq. (29) evolved to the GRS-input scale, $\zeta _0^{LO}=0.51\,$GeV, using the procedure explained in Sect. 4.1. Dashed blue curve: GRS input distribution at this scale [51]. b Solid green curve, $p=g$—our prediction for the pion’s glue distribution; and dot-dashed red curve, $p=S$—predicted sea-quark distribution. The long-dashed green curve and dotted red curve are the GRS input distributions: $p=g$ and $p=S$, respectively. In our normalisation convention, . (The uncertainty bands bracketing our results are explained following Eq. (31))

Here and hereafter, following Refs.  [39, 40], we report results with an uncertainty determined by varying $\zeta _H \rightarrow (1\pm 0.1) \zeta _H$. Given that the precision of the infrared value of the PI coupling is 4%, the 10% variation in $\zeta _H$ produces a conservative uncertainty estimate.

Fig. 4

a Solid blue curve – valence-quark distribution in Eq. (29) evolved to $\zeta =\zeta _2$, using the procedure explained in Sect. 4.1; long-dashed black curve – result from Ref.  [102]; and short-dashed cyan – phenomenological result from Ref.  [52], also at $\zeta =\zeta _2$. b Solid green curve, $p=g$ – our prediction for the pion’s glue distribution; and dot-dashed red curve, $p=S$ – predicted sea-quark distribution. Phenomenological results from Ref.  [52] are plotted for comparison: $p=\,$glue – long-dashed dark-green; and $p=\,$sea – dashed brown. Normalisation convention: . Notably, on $x>0.2$, marking this as the valence domain within the pion. (The uncertainty bands bracketing our results are explained in the text)

Beginning with Eq. (29), we generate glue and sea distributions from their initial identically-zero inputs using singlet evolution equations developed in analogy with that for nonsinglet evolution described in Sect. 4.1. Our predictions at $\zeta =\zeta _0^{\mathrm{LO}}$ are displayed in Fig. 3b and compared therein with the GRS input distributions at this scale. Not unexpectedly, our results do not support the use of valence-like distributions for glue and sea at this scale. An explicit comparison of the momentum fractions is nevertheless revealing:

$$\begin{aligned} \begin{array}{l|cc} &{} \langle x g(x;\zeta _0^{\mathrm{LO}})\rangle &{} \langle x S(x;\zeta _0^{\mathrm{LO}}) \rangle \\ \hline \text{ herein } &{} 0.24(5) &{} 0.03(1) \\ \text{ GRS } &{} 0.29 &{} 0.15 \end{array}. \end{aligned}$$

(32)

The gluon momentum fractions are roughly comparable, but the sea contribution to the pion’s momentum expressed in the GRS Ansatz is five-times greater than our prediction.

The models built in Refs.  [101, 103] were constrained by the GRS values for the glue and sea momentum fractions; hence, very likely placed too little momentum in the valence-quarks at $\zeta _0^{\mathrm{LO}}$. On the other hand, Ref.  [102] estimated , compatible with our prediction.

Table 1 Coefficients and powers that reproduce the computed pion valence-quark distribution functions, depicted in Figs. 4, 5, when used in Eq. (33)

5.3.2 $\zeta = \zeta _2 = 2\,$GeV

Our prediction for is depicted in Fig. 4a. The solid curve and surrounding bands are described by the following function, a generalisation of Eq. (26):

(33)

where ensures Eq. (25) and the powers and coefficients are listed in Table 1. These interpolations express the large-x behaviour prescribed by Eq. (21); yet here is only realised on $x>0.99$. Plainly, subleading corrections to Eq. (21) play an important rôle at empirically accessible values of x. We therefore extract an “effective large-x exponent”, $\beta _{\mathrm{eff}}(\zeta )$ by plotting against $\ln (1-x)$ on $x\in [0.9,1.0]$ and computing the slope, with the result

$$\begin{aligned} \beta _{\mathrm{eff}}(\zeta _2) = 2.63(8). \end{aligned}$$

(34)

The uncertainty expresses that ascribed to $\zeta _H$. Notably, expanding the fitting domain to $x\in [0.85,1.0]$ and employing a jackknife analysis to obtain an array of slopes changes neither the central value nor the uncertainty at the quoted level of accuracy. For comparison, Refs.  [39, 40], which did not implement Eq. (21), determined $\beta (\zeta _2)=2.38(9)$ after evolution of in Eq. (26). It is worth remarking that Ref.  [102] found $\beta (\zeta _2)=2.43$ and made no effort at an uncertainty estimate.

Here it is also worth providing a comparison of our calculated low-order moments with those obtained in some recent lattice QCD (lQCD) simulations ($\zeta =\zeta _2$):

$$\begin{aligned} \begin{array}{l|lll} &{} \langle x \rangle _u^\pi &{} \langle x^2 \rangle _u^\pi &{} \langle x^3 \rangle _u^\pi \\ \hline \text{ lQCD }\, [53] &{} 0.21(1) &{} 0.16(3) &{} \\ \text{ lQCD }\, [54] &{} 0.254(03) &{} 0.094(12) &{} 0.057(04) \\ \hline \text{ Ref. }\, [102] &{} 0.24 &{} 0.098 &{} 0.049 \\ \text{ Refs. }\, [39,40] &{} 0.24(2) &{} 0.098(10) &{} 0.049(07)\\ \hline \mathrm{Herein} &{} 0.24(2) &{} 0.094(13) &{} 0.047(08) \end{array}. \end{aligned}$$

(35)

(We have simplified the notation: , with the scale specified separately.) Plainly, continuum and lQCD results agree on the light-front momentum fraction carried by valence-quarks in the pion at $\zeta =\zeta _2$:

(36)

(Ref.  [19, Table III] provides a larger array of comparisons, including model results.)

A similar valence-quark momentum fraction was obtained in Ref.  [52] by analysing data on $\pi$-nucleus Drell-Yan (DY) and leading neutron electroproduction [52]: at $\zeta =\zeta _2$. The associated phenomenological distribution is drawn as the short-dashed cyan curve in Fig. 4a. Even though this DF yields a compatible momentum fraction, its x-profile is different. In fact, the phenomenological DF conflicts with the QCD constraint (Eq. 20). Significantly, the Ref.  [52] analysis ignored threshold resummation effects, which are known to have a material impact at large x [50, 104]. (Similar remarks apply to the analysis in Ref.  [105].)

Table 2 Coefficients and powers that reproduce the computed pion’s glue and sea distribution functions, depicted in Figs. 4, 5, when used in Eq. (37)

In our approach, as highlighted in the paragraph preceding that containing Eq. (3), a hadron’s glue and sea distributions are identically zero at $\zeta _H$: they are generated by evolution on $\zeta >\zeta _H$. Employing the same procedure used in developing our comparison with the GRS distributions, Eq. (32), we obtained the $\zeta =\zeta _2$ glue and sea distributions depicted in Fig. 4b. Adopting functional forms from Ref.  [51], viz.

(37)

, these distributions are effectively interpolated using the coefficients in Table 2. The associated momentum fractions are ($\zeta =\zeta _2$):

$$\begin{aligned} \langle x\rangle ^\pi _g = 0.41(2), \quad \langle x\rangle ^\pi _{\mathrm{sea}} = 0.11(2). \end{aligned}$$

(38)

References [39, 40] obtained 0.41(2), 0.11(2), respectively, from in Eq. (26). (Although the model in Ref.  [19] produces a pion valence-quark DF that disagrees with Eq. (20), it yields momentum fractions at $\zeta _2$ that are consistent with our predictions, viz. [106]: $\langle 2 x \rangle _u^\pi =0.49$, $\langle x\rangle ^\pi _g =0.40$, $\langle x\rangle ^\pi _{\mathrm{sea}}=0.11$.)

It is worth remarking that the ordering of our predictions agrees with that in Ref.  [52]: 0.35(3), 0.16(1), but our gluon fraction is $\sim 20\%$ larger and the sea fraction is $\sim 30$% smaller. The associated DFs from Ref.  [52] are drawn, respectively, as the long-dashed dark-green and short-dashed brown curves in Fig. 4b. Regarding the glue DFs, our prediction and the phenomenological result agree semiquantitatively on $x > rsim 0.05$; but they are markedly different on the complementary domain. Moreover, both glue DFs in Fig. 4 disagree with those inferred in earlier analyses [51, 107]. These observations highlight the need for new experiments that are directly sensitive to the pion’s gluon content. This might be addressed through measurements of prompt photon and $J/\varPsi$ production [108, 109].

The sea DFs in Fig. 4 have markedly different profiles on the entire x-domain. Hence, if the pion’s gluon content is considered uncertain, then it is fair to describe the sea-quark distribution as empirically unknown. This is good motivation for the collection and analysis of DY data with $\pi ^\pm$ beams on isoscalar targets [108, 110].

Fig. 5

a Solid blue curve – valence-quark distribution in Eq. (29) evolved to $\zeta =\zeta _5=5.2\,$GeV, using the procedure explained in Sect. 4.1; and long-dashed black curve – result from Ref.  [102] at this scale. Dot-dot-dashed (grey) curve within shaded band – lQCD result [55]. Data (purple) from Ref.  [111], rescaled according to the analysis in Ref.  [50]. Comparing our central prediction with the plotted data, one obtains $\chi ^2/\mathrm{d.o.f.} = 1.66$. b Solid green curve, $p=g$ – our prediction for the pion’s glue distribution; and dot-dashed red curve, $p=S$ – predicted sea-quark distribution. Normalisation convention: . (The uncertainty bands bracketing our results are explained in the text)

5.3.3 $\zeta = \zeta _5 = 5.2\,$GeV

Drell-Yan data on the pion’s valence-quark DF was taken in the E615 experiment [111]. Although this is the most recent set, it is more than thirty years old. Our predictions for the pion DFs at a scale appropriate for the E615 experiment, i.e. $\zeta _5=5.2\,$GeV [49, 111], are depicted in Fig. 5. The solid blue curve and surrounding bands are described by the function in Eq. (33) with the powers and coefficients listed in Table 1. Again, these interpolations express the large-x behaviour prescribed by Eq. (21), but is only realised on $x>0.99$. Here,

$$\begin{aligned} \beta _{\mathrm{eff}}(\zeta _5) = 2.81(8), \end{aligned}$$

(39)

a result consistent with Refs.  [39, 40]: $\beta (\zeta _5) = 2.66(12)$.

Working with the lQCD results obtained in Ref.  [55], one finds $\beta _{\mathrm{lQCD}}(\zeta _5) = 2.45(58)$; and also the following comparison between low-order moments:

$$\begin{aligned} \begin{array}{l|lll} \zeta _5 &{} \langle x \rangle _u^\pi &{} \langle x^2 \rangle _u^\pi &{} \langle x^3 \rangle _u^\pi \\ \hline \text{ Ref. } \,[55] &{} 0.18(3) &{} 0.064(10) &{} 0.030(5)\\ \mathrm{Herein} &{} 0.20(2) &{} 0.074(10) &{} 0.035(6) \end{array} . \end{aligned}$$

(40)

Ref.  [102] predicted, respectively: 0.21, 0.076, 0.036. We find

(41)

i.e. only 40% of the pion’s momentum is carried by valence quarks at the E615 scale.

The data plotted in Fig. 5 is that reported inRef.  [111], rescaled according to the analysis in Ref.  [50], which is NLO and includes soft-gluon resummation. Our prediction agrees with the rescaled data. No parameters were varied in order to achieve this outcome. Moreover, the EHM-induced broadening of the pion DF described in Sect. 5.2 is crucial to the agreement.

The lQCD result for the pion valence-quark DF [55] evolved to the E615 scale is drawn in Fig. 5 as the dot-dot-dashed (grey) curve bracketed by grey bands: within errors, it agrees with our prediction. This is significant [39, 40]: two disparate treatments of the pion bound-state problem, one using continuum methods and the other using lQCD, have arrived at consistent results for the pion’s valence-quark DF.

Our predictions for the pion’s glue and sea DFs at $\zeta _5$ are displayed in Fig. 5b. From these DFs one obtains the following momentum fractions ($\zeta =\zeta _5$):

$$\begin{aligned} \langle x\rangle ^\pi _g = 0.45(2), \quad \langle x\rangle ^\pi _{\mathrm{sea}} = 0.14(2), \end{aligned}$$

(42)

in agreement with Refs. [39, 40]. The DFs are described by the function in Eq. (37) evaluated using the appropriate coefficients and powers in Table 2.

To highlight the importance of a complete next-to-leading-order treatment, which includes threshold resummation effects, in any analysis of data whose aim is extraction of a valence-quark DF, Fig. 6 compares our prediction for and that from Ref.  [55] with the results published in Ref.  [111]. The latter were obtained in a straightforward LO analysis; and disagree markedly with modern predictions on $x > rsim 0.5$.

Fig. 6

Solid blue curve – valence-quark distribution in Eq. (29) evolved to $\zeta =\zeta _5=5.2\,$GeV, using the procedure explained in Sect. 4.1; long-dashed black curve – result from Ref.  [102] at this scale; and dot-dot-dashed (grey) curve within shaded band – lQCD result [55]. Data (red) – DF as determined in a straightforward LO analysis [111]. Comparing our central prediction with the data plotted here, one obtains $\chi ^2/\mathrm{d.o.f.} = 19.4$. (The uncertainty bands bracketing our results are explained in the text)

In closing this section it is worth recalling another textbook result. Namely, on $\varLambda _{\mathrm{QCD}}^2/\zeta ^2 \simeq 0$, for any hadron [112]: $\langle x\rangle _q =0$, $\langle x\rangle _g = 4/7\approx 0.57$, $\langle x\rangle _S = 3/7\approx 0.43$. This means there is a scale beyond which DFs cannot provide information that enables distinctions to be drawn between different hadrons: for each one, the valence distribution is a $\delta$-function located at $x=0$ [113,114,115].

6 Kaon distribution amplitude

Calculations of the kaon’s leading twist DA, $\varphi _K(x)$, using Eq. (6b) are reported in Refs.  [74, 75]. They are complemented by related analyses of the kaon electromagnetic elastic form factor [65, 77] and lQCD results for the DA’s first two nontrivial moments [116,117,118]. These analyses reveal that whilst the pion’s DA is well constrained, the kaon’s is more uncertain. One can at most conclude the following: (i) $\varphi _K(x;\zeta _H)$ is somewhat less broadened than $\varphi _\pi (x;\zeta _H)$; and (ii) it is slightly asymmetric about $x=1/2$ owing to the significantly smaller role played by the Higgs mechanism of mass generation for u-quarks as contrasted with s-quarks, viz.  $M_u(k^2=0)/M_s(k^2=0)\approx f_\pi /f_K \approx 0.84$. Defining

$$\begin{aligned} \langle \xi ^n = (1-2x)^n \rangle ^{u_\zeta }_{M} = \int _0^1 dx\, (1-2x)^n\,\varphi _M^u(x;\zeta ) , \end{aligned}$$

(43)

these remarks can be stated quantitatively as follows:

$$\begin{aligned} \langle [\xi ,\xi ^2]\rangle _\pi ^{u_{\zeta _H}}&= [0,0.25], \end{aligned}$$

(44a)

$$\begin{aligned} \langle [\xi ,\xi ^2]\rangle _K^{u_{\zeta _H}}&= [0.035(5) , 0.24(1)]. \end{aligned}$$

(44b)

Table 3 Coefficients and powers that specify the kaon DA determined by Eq. (45). Upper, middle, lower refer to the values of $\langle \xi ^2\rangle _{K}^{u_{\zeta _H}}$ produced by the identified coefficients. The “upper” parameter values produce the curve in Fig. 7 with the smallest magnitude at $x=0.5$, etc

Following the procedures described in Ref.  [74] and Sect. 5.2 herein, Eq. (44b) can be used to determine the following pointwise form for the kaon’s DA:

(45)

where ensures unit normalisation, and the interpolation coefficients are listed in Table 3. Here “upper” indicates the curve that produces the largest value of $\langle \xi ^2\rangle _K^{u_{\zeta _H}}$ and lower, the smallest. $\varphi _K^{{\bar{s}}}(x;\zeta _H)$ is obtained using Eq. (8).

Fig. 7

Kaon DA, $\varphi _K^u(x;\zeta _H)$, described by Eq. (45) and the “middle” coefficients in Table 3 – solid blue curve. The associated band marks the domain bounded by the “upper” and “lower” coefficients in Table 3. Result obtained using the DB kernel in Ref.  [74] – dot-dashed red curve. Pion DA in Eq. (28) – dashed green curve

The DA family described by Eq. (45) and the coefficients in Table 3 is drawn in Fig. 7 as the solid blue curve within blue shading. For comparison, the dot-dashed red curve is the kaon DA obtained using the DB kernel in Ref.  [74]. The agreement between our curves and that result is good; especially since no uncertainty estimate was provided in Ref.  [74], yet that uncertainty cannot be entirely negligible because numerous interpolations and extrapolations of propagators and amplitudes were employed to complete the calculation. The level of agreement is further highlighted by a comparison between moments:

$$\begin{aligned} \begin{array}{l|cccc} &{} \langle \xi \rangle _K^{u_{\zeta _H}} &{} \langle \xi ^2\rangle _K^{u_{\zeta _H}} &{} \langle \xi ^3\rangle _K^{u_{\zeta _H}} &{}\langle \xi ^4\rangle _K^{u_{\zeta _H}} \\ \hline \text{ Ref. }\, [74] &{} 0.040 &{} 0.23 &{} 0.021 &{} 0.11 \\ \text{ herein } &{} 0.035(5) &{} 0.24(1) &{} 0.016(2) &{} 0.11(1) \end{array}. \end{aligned}$$

(46)

In order to provide immediately for a contrast between pion and kaon DAs, the pion DA in Eq. (28) is drawn as the dashed green curve in Fig. 7.

Fig. 8

A comparison between kaon and pion valence-quark DFs. Solid blue curve: calculated from Eq. (47). The associated band marks the domain bounded by the kaon DFs produced using Eqs. (12), (45) and the “upper” and “lower” rows in Table 3. Dashed green curve: in Eq. (29). Dotted grey curve: scale free form,

7 Kaon distribution functions

7.1 Hadron scale

Having established that the results for the kaon’s DA are sound, we identify Eq. (12) as our prediction for the kaon’s valence-quark DFs; viz., using the “middle” curve as representative:

(47)

with .

An instructive comparison between the kaon’s valence-quark DFs and that of the pion is depicted in Fig. 8, viz. vs. . The evident similarity between these curves is determined by Eqs. (10), (12), (44). Namely: (i) at $\zeta _H$, the dressed-valence quasiparticles express all properties of the bound state under consideration; and (ii) relative to the pion, the impact of EHM, as expressed in broadening of parton distributions, is only marginally less strong in the kaon. The broadening distinguishes physical light- and lighter-quark DFs from the scale free form: .

At this point, one more independent check is possible. Namely, working with the DB-kernel propagators and amplitudes reported in Ref.  [74], Eq. (22) can be used directly to calculate the lowest four nontrivial moments of the kaon DF. This procedure yields the following comparison:

(48)

This is a favourable comparison, especially since the DA in Ref.  [74] is similar to ours but not identical, being less dilated – see Fig. 7 and Eq. (46). Owing to Eq. (10),

(49)

(The uncertainty estimate in Row 1 of Eq. (48) is based on a $\pm 30$% variation in the strength of the skewing-term in the DB-kernel result for the Bethe–Salpeter amplitude. Such variation changes the calculated value of $f_K=0.11\,$GeV by $<0.2$%.)

Fig. 9

Kaon DFs, defined at $\zeta _H$ by Eqs. (12), (45) and Table 3, evolved $\zeta _H\rightarrow \zeta _5$: solid blue curve – ; and dot-dashed green curve – . The like-coloured bands surrounding each curve mark the domain between the “upper” and “lower” results from Table 3: “lower” produces the curve with greatest magnitude in the peak region and smallest magnitude at large x

Table 4 Coefficients and powers that provide interpolations for the computed kaon valence-quark distribution functions, depicted in Fig. 9, when used in Eq. (33): Rows 1–3 – u-quark; and Rows 4–6 – ${\bar{s}}$-quark

7.2 Evolved kaon DFs: massless splitting

Regarding kaon structure functions, the only available empirical information is the ratio , which was measured in the production of massive muon pairs forty years ago [119]. The mass-scale in this experiment is similar to that of E615, i.e. $\zeta \approx \zeta _5$. Thus, in order to deliver results for comparison with this DY data, our kaon valence-quark DFs must be evolved: $\zeta _H \rightarrow \zeta _5$.

It is straightforward to employ the approach explained in Sect. 4.1, used above for the pion, to evolve the kaon DFs defined at $\zeta _H$ by Eqs. (12), (45) and Table 3 to the E615 scale, $\zeta _5$. This procedure yields the curves plotted in Fig. 9, which may be interpolated using the functional form in Eq. (33) and the coefficients and powers in Table 4. The curves in Fig. 9 produce the following low-order moments:

(50)

Combining the results in column 1, one finds

(51)

hence, using mass-independent splitting functions, the valence-quark momentum fraction in the kaon at $\zeta _5$ is the same as that in the pion (Eq. 41). (The uncertainties listed here derive from the variation in kaon DAs, illustrated in Fig. 7.)

Using the $\zeta _H \rightarrow \zeta _5$ evolved kaon DFs, one obtains the ratio $u^K(x;\zeta _5)/u^\pi (x;\zeta _5)$ drawn in Fig. 10. Evidently, the uncertainty existing in the kaon DA is expressed in the behaviour of this ratio on $x > rsim 0.5$: a broader kaon DA yields a ratio closer to unity at $x=1$. The central curve is interpolated by the function:

$$\begin{aligned}&\frac{u^K(x;\zeta _5)}{u^\pi (x;\zeta _5)}\nonumber \\&\quad = \frac{1.04 - 2.54\, x+ 3.87 \,x^2+3.82 \, x^3 - 3.90\,x^4}{1 - 2.61\, x + 5.64\, x^2}. \end{aligned}$$

(52)

The best agreement with extant data [119] is delivered by the kaon DF written in Eq. (47). Thus, hereafter, we focus on the kaon DFs defined by this curve; and, just as we did above for the pion, consider the impact of varying $\zeta _H\rightarrow (1.0\pm 0.1)\zeta _H$, thereby providing a conservative estimate of the uncertainty arising from that in the infrared value of the PI coupling, Fig. 1. This process yields the DFs plotted in Fig. 11a, which can be interpolated using the functional form in Eq. (33) and the coefficients and powers in Table 5. These interpolations express the large-x behaviour indicated in Eq. (21), but is only realised on $x>0.95$. Here, consistent with Eq. (39):

$$\begin{aligned} \beta _{\mathrm{eff}}(\zeta _5) = 2.73(7). \end{aligned}$$

(53)

The kaon DFs just described produce the following low-order moments:

(54)

hence, accounting for $\zeta _H\rightarrow \zeta _H (1.0\pm 0.1)$,

(55)

reproducing the pion result (Eq. 41).

Fig. 10

$u^K(x;\zeta _5)/u^\pi (x;\zeta _5)$. Solid blue curve – result obtained after evolution of Eq. (29) [$\pi$] and Eq. (47) [K]. (Eq. (52) provides an interpolation for this curve.) The light-blue band marks the domain between the results obtained using Eqs. (12), (45), Table 3–upper and Eqs. (12), (45), Table 3–lower, with “lower” producing the smallest value at $x=1$. Data (orange) from Ref.  [119]

Table 5 Coefficients and powers that provide interpolations for the computed kaon valence-quark distribution functions, depicted in Fig. 11, when used in Eq. (33): Rows 1–3 – u-quark; and Rows 4–6 – ${\bar{s}}$-quark

Fig. 11

a Solid blue curve – kaon’s valence u-quark distribution, defined at $\zeta _H$ by Eq. (47), evolved $\zeta _H\rightarrow \zeta _5$ using the procedure explained in Sect. 4.1. Dot-dashed green curve – analogous result for the kaon’s valence ${\bar{s}}$ distribution. b Dashed grey curve within grey bands – kaon ${\bar{s}}$ valence-quark distribution obtained in a recent lQCD study [120]; otherwise, as in A. (In both panels, the bands bracketing our central DF curves reflect the uncertainty in ${{\hat{\alpha }}}(0)$, Fig. 1)

First lQCD results for the kaon’s valence-quark DFs are now available [120]. The study finds the following moments, listed here in the order of appearance in Eq. (54): u – 0.193(8), 0.080(7), 0.042(6); and ${\bar{s}}$ – 0.267(8), 0.123(7), 0.070(6). These values are systematically larger than our predictions, especially for the ${\bar{s}}$, viz. the excesses are: u – 0.6(4.8)%, 21(6)%, 40(4)%; and ${\bar{s}}$ – 24(7)%, 53(13)%, 84(16)%. This is because, when compared with our predictions, the lQCD DFs are much harder; a feature highlighted by Fig. 11b. In fact, the lQCD results are inconsistent with the QCD prediction in Eq. (20): on $x\simeq 1$, the lQCD DF behaves as $(1-x)^{\beta }$, $\beta = 1.13(16)$. We expect that future refinements of lQCD setups, algorithms and analyses will move the lattice results closer to ours.

It is interesting that even though the valence-quark DFs computed using the model Hamiltonian in Ref.  [19] are also harder than those in Fig. 11 and in conflict with the QCD constraint (Eq. 20), the pattern of comparison with the lQCD results [120] is similar. Namely, the valence-quark lQCD moments, especially those associated with the ${\bar{s}}$, are significantly larger than those produced by the model.

Figure 12 depicts the ratio obtained by evolving the pion and kaon DFs $\zeta _H\rightarrow \zeta _5$, accounting for a 10% uncertainty in $\zeta _H$. Evidently, the impact of $\zeta _H\rightarrow \zeta _H(1.0\pm 0.1)$ on both and is almost identical because the ratio exhibits practically no sensitivity. It is worth highlighting here that Eqs. (17)–(21) guarantee that the large-x power-law exponents of $u^{\pi }(x,\zeta )$ and $u^{\mathrm{K}}(x,\zeta )$ evolve at the same rate, in consequence of which the ratio $u^{\mathrm{K}}(x,\zeta _5)$ $/$ $u^{\pi }(x,\zeta _5)$ is nonzero and finite on $x\simeq 1$.

The first lQCD results for this ratio are also drawn in Fig. 12. The relative difference between the central lQCD result and our prediction is $\approx 5$% despite the fact that the individual lQCD DFs are qualitatively and quantitatively different from ours, drawn in Figs. 5, 9, 11. This feature highlights a long known characteristic, i.e. is quite forgiving of even large differences between the individual DFs used to produce the ratio, as may be seen by comparing, e.g. Refs.  [17, 19, 121,122,123]. More precise data is crucial if this ratio is to be used effectively to inform and test the modern understanding of SM NG modes; and results for , separately have greater discriminating power [108, 124, 125].

Fig. 12

$u^K(x;\zeta _5)/u^\pi (x;\zeta _5)$. Solid blue curve – result obtained for the ratio after $\zeta _H\rightarrow \zeta _5$ evolution of Eq. (29) [$\pi$] and Eq. (47) [K]. (Eq. (52) provides an interpolation for this curve.) The lighter-blue band bracketing the curve reveals the effect of $\zeta _H \rightarrow \zeta _H(1.0\pm 0.1)$: it is negligible. Dot-dashed grey curve within grey band – lQCD result [120]. Data (orange) from Ref.  [119]

7.3 Evolved kaon DFs: mass-dependent splitting

Hitherto, when implementing the evolution procedure described in Sect. 4.1, we have used textbook forms of the massless splitting functions. Consequently, given the results highlighted in Fig. 8, the glue and sea distributions in the kaon are practically identical to those in the pion. Indeed, any symmetry-preserving study that begins at $\zeta _H$ with a bound-state constituted solely from dressed quasiparticles and implements physical constraints on $\pi$ and K wave functions will deliver this outcome when using massless splitting functions. Of course, the s-quark is more massive than the u-quark. Hence, physically [126, 127]: valence ${\bar{s}}$-quarks must produce less gluons than valence u-quarks; and gluon splitting must produce less ${\bar{s}} s$-pairs than light-quark pairs. Such effects can be expressed in the splitting functions and we now illustrate their impact.

The integro-differential equations describing singlet evolution involve a splitting function kernel of the form

$$\begin{aligned} \left( \begin{array}{cc} P_{q\leftarrow q} &{} P_{q\leftarrow g}\\ P_{g\leftarrow q} &{} P_{g\leftarrow g} \end{array}\right) , \end{aligned}$$

(56)

where the $P_{a\leftarrow b}$ are splitting functions and the subscript indicates the direction of momentum transfer between participating partons. Momentum conservation imposes the following constraints:

$$\begin{aligned} 0&= \int _0^1dz\,z\left[ P_{q\leftarrow q}(z) + P_{g\leftarrow q}(z)\right] , \end{aligned}$$

(57a)

$$\begin{aligned} 0&= \int _0^1dz\,z\left[ 2 n_f P_{q\leftarrow g}(z) + P_{g\leftarrow g}(z)\right] , \end{aligned}$$

(57b)

$P_{g\leftarrow q}(z)=P_{q\leftarrow q}(1-z)$, $P_{q\leftarrow g}(z)=P_{q\leftarrow g}(1-z)$, $P_{g\leftarrow g}(z)$ $=P_{g\leftarrow g}(1-z)$. Moreover, baryon number conservation requires that the complete evolution kernel guarantees

(58)

Fig. 13

Solid green curve – kaon’s valence ${\bar{s}}$-quark distribution defined at $\zeta _H$ by Eqs. (10), (47), evolved $\zeta _H\rightarrow \zeta _5$ using the procedure explained in Sect. 4.1, including the splitting function modification in Eq. (59a) with $\sigma _{s}=1$. Dot-dashed blue curve – kaon’s valence u-quark distribution, unchanged from Fig. 11. Dashed black curve – central ${\bar{s}}$-quark distribution from Fig. 11, i.e. obtained with mass-independent evolution. (The bands bracketing the central DFs reflect the uncertainty in the $k^2=0$ value of the PI charge, Fig. 1 )

There are many prescriptions for introducing mass dependence into the splitting functions, e.g. Refs.  [128,129,130]; and a novel formulation will be presented elsewhere [131]. Herein, however, we implement a simple expedient for the purpose of illustrating the typical outcome. Namely, we identify and separate the quark flavours, modify the s-quark evolution kernel contributions as follows:

$$\begin{aligned} P_{s\leftarrow s}(z)&\rightarrow P_{q\leftarrow q}(z) - \varDelta _{s\leftarrow s} (z,\zeta ), \end{aligned}$$

(59a)

$$\begin{aligned} P_{s\leftarrow g}(z)&\rightarrow P_{s\leftarrow g}(z) + \varDelta _{s\leftarrow g}(z,\zeta ) , \end{aligned}$$

(59b)

and use the following Ansätze for the modifications

$$\begin{aligned} \varDelta _{s\leftarrow s}(z,\zeta )&= \sqrt{3} (1 - 2 z) \frac{ \sigma _{s} \, \delta ^2}{\delta ^2+(\zeta -\zeta _H)^2}, \end{aligned}$$

(60a)

$$\begin{aligned} \varDelta _{s\leftarrow g}(z,\zeta )&= \sqrt{5} (1-6 z+6 z^2)\frac{ \sigma _{s}\, \delta ^2 }{\delta ^2 +(\zeta -\zeta _H)^2}, \end{aligned}$$

(60b)

which, following Ref.  [101], are based on the simplest two nontrivial Gegenbauer polynomials that ensure the momentum conservation constraints, Eq. (57). Here, $\delta = 0.1\,\mathrm{GeV} \approx M_s(k^2=0)-M_u(k^2=0)\approx {\hat{m}}_s - {\hat{m}}_u$ and $\sigma _{s}>0$ is a strength parameter.

The impacts of these modifications are clear: Eq. (59a) serves to reduce the number of gluons emitted by ${\bar{s}}$-quarks; and Eq. (59b) suppresses the density of $s{\bar{s}}$ pairs produced by gluons. Both effects increase with the quark mass difference, $\delta$, and decrease as $\delta ^2/\zeta ^2$ with increasing resolving scale.

Table 6 Coefficients and powers that provide interpolations for the computed kaon valence-quark distribution functions, depicted in Fig. 13, when used in Eq. (33): Rows 1–3 – u-quark, unchanged from Table 5, included here to simplify comparisons; and Rows 4–6 – ${\bar{s}}$-quark, obtained using mass-dependent splitting functions, Eq. (59)

We plot the new results for in Fig. 13. Obtained with $\sigma _{s}=1$, these DFs produce the following low-order moments:

(61)

Naturally, the u-quark values are unchanged from Eq. (54), but those for the ${\bar{s}}$-quark are increased by 4.8(8)%. The choice $\sigma _{s}=1$ is practically maximal, i.e. if one chooses a value too much larger, then distortions begin to appear at very low x in .

The curves in Fig. 13 may be interpolated using the functional form in Eq. (33) and the coefficients and powers in Table 6. These interpolations express the large-x behaviour indicated in Eq. (21), but $>0.5$ is only realised on $x>0.96$. Here, a result unchanged from Eq. (53):

$$\begin{aligned} \beta _{\mathrm{eff}}(\zeta _5) = 2.73(8). \end{aligned}$$

(62)

Fig. 14

Prediction for – solid green curve within green shading; and for – dot-dashed red curve within red shading. (The uncertainty introduced by that in the $k^2=0$ value of the PI charge, Fig. 1, is indicated by the shaded band bracketing each curve. In both cases here, that band is no thicker than the width of the central line.) Data on (orange) from Ref.  [119] are included to guide comparisons

Our predictions for the kaon’s glue and sea DFs are best expressed by the following ratios:

(63a)

(63b)

which are depicted in Fig. 14. The results drawn therein are described by the curves:

(64a)

(64b)

The uncertainty in these ratios owing to that in ${{\hat{\alpha }}}(0)$ is negligible, i.e. no larger than the line width in either case.

Evidently, the kaon’s glue and sea distributions differ from those of the pion only on the valence region $x > rsim 0.2$. In hindsight, this is not surprising: mass-dependent splitting functions act primarily to modify the valence DF of the heavier quark; valence DFs are negligible at low-x, where glue and sea distributions are large, and vice versa; hence the biggest impact of a change in the valence DFs must lie at large-x. It is notable that each of the predicted ratios depicted in Fig. 14 is pointwise similar to the measured value of . On the flip side, the glue and sea DFs in the kaon and pion are practically identical on $x\lesssim 0.2$.

Using our computed DFs, we find ($\zeta =\zeta _5$):

$$\begin{aligned} \langle x\rangle ^K_g = 0.44(2), \quad \langle x\rangle ^K_{\mathrm{sea}} = 0.14(2), \end{aligned}$$

(65)

with , $\langle x\rangle ^K_{\mathrm{sea}_{s}} = 0.045(06)$, where denotes the light-quarks. Comparing these results with those in Eq. (42), then accounting for mass-dependent splitting functions and being careful to use the computed ratio functions, we find that the gluon light-front momentum fraction in the kaon is $\sim 1$% less than that in the pion and the sea fraction is $\sim 2$% less.

It is worth remarking that the impact of the $P_{s\leftarrow g}$ correction in Eq. (59b) is negligible. Eliminating this term changes no result by more than 0.01%. Thus, our analysis indicates that the primary effect of mass-dependent splitting functions is to suppress the transfer of momentum from the heavier valence-quark into glue; and with less glue, there is less sea. One may ignore the additional mass-dependent suppression on the subsequent splitting of gluons into heavier sea quarks introduced by $P_{s\leftarrow g}$.

A comparison with Ref.  [103] is now possible. Following Ref.  [101], that analysis used algebraic Ansätze for the quark propagators and Bethe–Salpeter amplitudes needed to compute $\pi$ and K valence-quark DFs. The pion analysis was informed by the GRS suggestion [51] that , a value $> rsim 20$% smaller than that we find herein (Eq. 31). The valence-quark momentum fraction in the kaon was then used as a parameter and fixed in a least-squares fit to the data in Ref.  [119]. The best fit to data was obtained with , leading to the conclusion that the valence-quark momentum fraction in the kaon is much larger than that in the pion, or, equivalently, the kaon’s glue$\,+$ sea content is much smaller.

Reviewing the Ref.  [103] analysis, our prediction for in Fig. 12 is best matched by the upper bound on kaon glue$\,+$ sea determined in Ref.  [103], i.e. 10%. Moreover, any repeat of the Ref.  [103] study would now be informed by our results; hence, begin with a significantly smaller glue$\,+$ sea content in the pion. Thus, one can expect that an update of the phenomenological analysis in Refs.  [101, 103] would produce results compatible with those described herein.

8 Summary and perspective

Working with information gained from solving the continuum meson bound-state problem using sophisticated scattering kernels that incorporate effects generated by the mechanism responsible for the emergence of hadronic mass, we described parameter-free predictions for the leading-twist two-particle distribution amplitudes (DAs) of the $\pi$- and K-mesons (Sects. 5.2, 6). Using properties of light-front wave functions, these DAs were then used to provide $\pi$ and K distribution functions (DFs) at the hadronic scale, $\zeta _H$ (Sects. 5.2, 7.1). The hadronic scale is fixed by properties of QCD’s infrared-finite process-independent effective charge (Sect. 3).

Building upon this foundation and employing an all-orders evolution hypothesis (Sect. 4.1), we subsequently delivered predictions for all $\pi$ and K DFs, viz. valence-quark, glue and sea. Focusing first on the pion, we provided comparisons with phenomenological analyses and results from lattice-QCD (lQCD) (Sect. 5.3) and arrived at a range of significant conclusions. (i) Amongst existing phenomenological studies of pion structure functions, only one [50] employs a next-to-leading-order analysis that includes threshold resummation and this study is unique in producing a valence-quark DF that is consistent with QCD and matches our prediction (Fig. 5). (ii) Our prediction for the pion’s valence-quark DF agrees with modern lQCD results for the pointwise behaviour of this function. (iii) The general disagreement between phenomenological results and theory predictions for the pion’s valence-quark DF feeds into the pion’s glue and sea distributions; hence, existing inferences of the pion’s gluon distribution disagree with our prediction on $x \lesssim 0.05$ and the pion’s phenomenologically determined sea-quark distribution disagrees with our result on the entire physical x-domain. A resolution of these conflicts must await improved phenomenological analyses that include threshold resummation and new data that constrains the pion’s glue and sea distributions.

Very little empirical information is available on K DFs; so there are no recent phenomenological inferences. Naturally, within QCD, in the absence of Higgs-generated current-quark mass differences, kaon DFs are identical to those of the pion, being entirely determined by the mechanism(s) responsible for emergent hadronic mass (EHM). Hence, all differences between K and $\pi$ DFs result from Higgs-induced modulations of EHM. Regarding kaon valence-quark distributions, there are model calculations and a single, recent lQCD study; but there are no results for the pointwise behaviour of the kaon’s glue and sea distributions. Hence, our predictions for the entire array of kaon DFs currently stand alone. The one piece of available experimental information is the valence-quark ratio , $\zeta _5=5.2\,$GeV [119]. Our prediction for this ratio is consistent with the data (Figs. 10, 12). However, given the large empirical errors, this ratio is very forgiving of even material differences between various calculations of the individual DFs used to produce the ratio. Modern, precise data is critical if this ratio is to be used as a path to understanding the Standard Model’s Nambu-Goldstone modes; and results for , separately would be better.

Regarding the kaon’s glue and sea distributions, we predicted that they are similar to those in the pion (Sects. 7.2, 7.3). The degree of similarity depends on the interplay between EHM and Higgs-generated current-quark mass differences. Consequently, a detailed comparison requires the use of mass-dependent splitting functions. We therefore introduced a one-parameter model for the relevant splitting functions in order to illustrate the potential impact on kaon DFs of the mass difference between u and s-quarks. This led to the following conclusions: (i) the light-front momentum fraction carried by s-quarks in the kaon increases by $\sim 5$%; and (ii) this is compensated by a commensurate decrease in the fractions carried by glue ($-1$%) and sea ($-2$%). Our predictions for the $K/\pi$ ratios of glue and sea distributions are presented in Fig. 14.

The analysis described herein can be improved in two ways: (a) one could further test the assumption of factorisation made for the meson light-front wave functions (Sect. 2); and (b) a more rigorous treatment of mass-dependence in splitting functions should be implemented (Sect. 7.3). Both improvements are underway.

The Standard Model’s (pseudo-) Nambu-Goldstone modes – pions and kaons – are basic to the formation of everything, from nucleons to nuclei, and on to neutron stars. Hence, new-era experiments capable of discriminating between the results and predictions discussed herein should have high priority. Naturally, the phenomenological methods needed to proceed from data to DFs must match modern experiments in precision. Concerning theory, continuum and lattice analyses of the pion’s valence-quark DF are converging on the same form, confirming the longstanding QCD expectation, Eq. (1); but given the predictions presented herein, lattice results for the pion’s glue and sea distributions would be very valuable. This is even more true for the kaon. With only one extant lattice study of kaon DFs, addressing solely the valence distributions, disagreeing in many ways with continuum predictions and also conflicting with Eq. (1), many opportunities are available.

Appendix A: Large x behaviour of meson distribution functions

In order to establish Eq. (21), consider that in some sufficiently compact neighbourhood $x\simeq 1$:

(A.1)

namely, has a regular Taylor expansion on this neighbourhood and

(A.2)

This being the case, then

(A.3a)

(A.3b)

(A.3c)

Consequently,

(A.4)

At this point, recall Eqs. (17)–(19), which yield

(A.5a)

(A.5b)

where $\gamma _E$ is the Euler constant.

Finally, equating like leading-s coefficients in Eqs. (A.4), (A.5b), one arrives at the anticipated results:

(A.6a)

(A.6b)

A similar derivation can be found in Ref.  [18, Sect. VIII].