1 Introduction

Einstein-dilaton theory, as an alternative gravity theory, is related to the scalar-tensor theory via conformal transformations [1,2,3,4,5]. The scalar-tensor gravity theory is a modified gravity theory which, despite the original Einstein theory, explains the accelerated expansion of Universe, successfully [6,7,8,9]. The scalar-tensor theory of gravity itself is originated from the fact that the low energy limit of superstring theory covers the Einstein theory which is coupled to a scalar field [10]. Nowadays, despite the original no-hair conjecture, it is well-known that the spacetime geometry is affected by the scalar field and, in the presence of scalar field, the asymptotic behavior of the spacetime is no longer flat or AdS [11,12,13]. Finding of the exact black hole solutions in the Einstein-dilaton theory has been the subject of many interesting papers in three- four- and higher-dimensional spacetimes [14,15,16,17]. Although, this theory has been studied extensively, it seems that there are many unknown issues to be studied yet.

It is a common believe that black holes, as the more interesting prediction of Einstein’s gravity theory, are thermodynamic systems with the well-defined thermodynamic quantities. Findings of Hawking et. al., as the more outstanding achievements of geometrical physics, showed that black holes posses a temperature, which is related to their surface gravity, and a pure geometrical entropy which is proportional to the horizon surface area [18,19,20]. Thermodynamic properties and, in particular, thermodynamic stability of the black holes is an interesting subject area which has attracted much attentions. This issue can be investigated from different approaches such as canonical and grand canonical ensembles, thermodynamic geometry and Hessian matrix . In the canonical ensemble method, thermal stability of the black holes is analyzed regarding the signature of the black hole heat capacity. Global stability of the black holes is studied based on the signature of Gibbs free energy. Thermodynamic geometry is a method based on which one can extract some information about phase transition points. In this method, by use of the Ricci scalar of a proposed thermodynamic metric one is able to determine the location of the phase transition points. The divergent points of Ricci scalar are the horizon radius of those black holes which experience type-one or type-two phase transition. Stability of the black holes is already studied by use of Hessian matrix. Positivity of determinant of this matrix guaranties stability of black holes [21,22,23,24,25,26,27,28,29,30,31].

In addition, study of P–V criticality and consideration of black hole quantum thermal fluctuations are other interesting issues in the context of black hole thermodynamics. The critical behavior of the black holes can be studied in the usual and extended phase spaces [32,33,34,35,36]. Also, the impacts of thermal fluctuations on the black hole thermodynamics have been studied extensively [37,38,39,40,41,42,43].

Although, singularities of Maxwell’s electrodynamics are removed by use of quantum electrodynamics techniques, but they are exist yet in classical electrodynamics. In addition to the appearance of infinite field and self-energies, violation of conformal symmetry, in three and higher-dimensional spacetimes, is the other failure of Maxwell’s classical electrodynamics [31]. The idea of nonlinear electromagnetic theory was initially proposed for solving the problems of Maxwell’s electrodynamics. Among the alternative proposed nonlinear electromagnetic models, the Born–Infeld, logarithmic, exponential, quadratically-extended and power-Maxwell theories have been studied extensively in the context of geometrical physics by obtaining the exact black hole solutions in the alternative models of modified gravity theory [44,45,46,47,48,49,50,51,52,53,54]. Lagrangian of the alternative models of nonlinear electrodynamics are functions of Maxwell’s Lagrangian. By expanding them one can show that they include higher powers of Maxwell Lagrangian. In the case of weak electromagnetic fields higher powers are negligible and Maxwell (or linear) electrodynamics is recovered. In this regards, nonlinear theory of electrodynamics is considered as the extension of Maxwell’s theory to the case of very strong electromagnetic fields [48, 55, 56].

The exact black hole solutions of the Einstein–Maxwell-dilaton gravity theory have been obtained and their thermodynamic properties have been studied in ref. [13]. The exponential and logarithmic charged dilaton black holes have been studied in refs. [47, 50]. Also, three-dimensional Einstein–Born–Infeld-dilaton black holes have been studied in ref. [45]. Now, we extend this study to the four-dimensional spacetimes by considering the Born–Infeld nonlinear electrodynamics instead of Maxwell’s linear electrodynamics. We believe that consideration of this theory can help to understand the properties of Einstein-dilaton gravity in the presence of nonlinear electromagnetic theory.

The main goal of the present work is to obtain the novel exact black hole solutions in the Einstein-dilaton gravity theory which is coupled to the Born–Infeld nonlinear electrodynamics, and to investigate their thermodynamic properties, and especially to perform a detail analysis of local and global stability of the black holes. Thus, we have organized the paper as follows: The explicit form of the field equations and their exact solutions have been obtained in Sect. 2. It has been shown that the solutions of the scalar field equation can be obtained as the liner combination of two Liouville-type potentials. Also, three classes of new black holes have been introduced as the exact solutions of the gravitational field equations. They recover the corresponding solutions in the Einstein–Maxwell-dilaton gravity theory, when the nonlinearity parameter is chosen very large. In Sect. 3, the thermodynamic and conserved quantities have been calculated, and it has been shown that they satisfy the first law of black hole thermodynamics. Also, it has been shown that the extreme, physical and unphysical black holes, in order, with zero, negative and positive temperatures can occur. Section 4 is devoted to study of the local stability or thermodynamic phase transition of the black holes. Making use of the canonical ensemble method and regarding the signature of black hole heat capacity, the type-one and type-two phase transition points as well as the ranges at which black holes are locally stable have been identified. In Sect. 5 the local stability of the black holes has already been studied by use of the thermodynamic geometry. It has been fund that the results of canonical ensemble and geometrical approaches are identical if the HEPM thermodynamic metric is utilized. In Sect. 6, global stability or Hawking–Page phase transition points have been studied based on the grand canonical ensemble method. By calculating the Gibbs free energy of the black holes we have determined the horizon radius of the black holes which undergo Hawking–Page phase transition. Also, we characterized the horizon radii of those black holes which are globally stable or are in the radiation phase. Section 7 is devoted to summarizing and discussing the results.

2 The action and field equations

We start with the proper action of the four-dimensional Einstein-dilaton gravity theory in the presence of the nonlinear electrodynamics. It can be written as [13, 14]

$$\begin{aligned} I=\frac{1}{16\pi }\int \sqrt{-g}\left[ \mathcal{{R}}-V(\phi )-2g^{\mu \nu }\partial _\mu \phi \partial _\nu \phi +L(\mathcal{{F}}, \phi )\right] d^4x. \end{aligned}$$
(2.1)

Here, \(\mathcal{{R}}\) is the Ricci scalar, \(\phi \) is a scalar field coupled to itself via the functional form \(V(\phi )\). The term \(L(\mathcal{{F}}, \phi )\) denotes the scalar coupled electromagnetic Lagrangian density. The Maxwell invariant \(\mathcal{{F}}\) is defined as \(\mathcal{{F}}=F^{\alpha \beta }F_{\alpha \beta }\), and \(F_{\alpha \beta }\) is the Faraday tensor which in terms of the electromagnetic potential \(A_\alpha \) is defined as \(F_{\alpha \beta }=\partial _\alpha A_\beta -\partial _\beta A_\alpha \). Here, we are interested on the Born–Infeld nonlinear electrodynamics. Therefore, we have [57]

$$\begin{aligned} L(\mathcal{{F}}, \phi )=4a^2e^{2\alpha \phi }\left( 1-\sqrt{1+Y}\right) ,\;\;\hbox {with}\;\;Y=\frac{\mathcal{{F}}}{2a^2}e^{-4\alpha \phi }. \end{aligned}$$
(2.2)

It can be expanded in the following form

$$\begin{aligned} L(\mathcal{{F}}, \phi )&=-\mathcal{{F}}e^{-2\alpha \phi }+\frac{\mathcal{{F}}^2}{8a^2}e^{-6\alpha \phi }\nonumber \\&\quad -\frac{\mathcal{{F}}^3}{32a^4}e^{-10\alpha \phi }+\frac{5\mathcal{{F}}^4}{512a^6}e^{-14\alpha \phi }+\mathcal{{O}}\left( \frac{1}{a^8} \right) .\nonumber \\ \end{aligned}$$
(2.3)

Noting Eq. (2.3), one can argue that in the limiting case \(a\rightarrow \infty \), the Born–Infeld electromagnetic Lagrangian reduces to \(L(\mathcal{{F}}, \phi )=-\mathcal{{F}}e^{-2\alpha \phi }\), which is noting but the coupled scalar-electromagnetic Lagrangian density in the Einstein–Maxwell-dilaton gravity theory [13]. Thus it is expected that our solutions recover those of Einstein–Maxwell-dilaton gravity theory in the limit \(a\rightarrow \infty \). A worth mentioning point is that if the electromagnetic fields are weak enough the higher powers of \(\mathcal{{F}}\) are negligible and Lagrangian of the nonlinear electrodynamics reduces to that of Maxwell (or linear) one.

Variation of the action (2.1), with respect to different fields, leads to the following field equations

$$\begin{aligned}&\nabla _\mu \left( \frac{e^{-2\alpha \phi } F^{\mu \nu }}{\sqrt{1+Y}}\right) =0,\;\;\;\hbox {with}\;\;\;\phi =\phi (r), \end{aligned}$$
(2.4)
$$\begin{aligned}&4\Box \phi (r)=\frac{d V(\phi )}{d\phi }-8\alpha a^2\left( 1-\frac{1}{\sqrt{1+Y}} \right) e^{2\alpha \phi }, \end{aligned}$$
(2.5)
$$\begin{aligned}&\mathcal{{R}}_{\mu \nu }-\frac{1}{2} g_{\mu \nu }V(\phi )=2 \nabla _\mu \phi \nabla _\nu \phi \nonumber \\&\quad -2a^2\left( 1-\frac{1}{\sqrt{1+Y}}\right) g_{\mu \nu }e^{2\alpha \phi }+\frac{F_{\mu \rho }F^{\;\;\rho }_{\nu }}{\sqrt{1+Y}}e^{-2\alpha \phi },\nonumber \\ \end{aligned}$$
(2.6)

for the electromagnetic, scalar and gravitational fields, respectively.

We solve the above field equations in a four-dimensional spherically symmetric geometry with the following line element [13, 47, 50]

$$\begin{aligned} ds^2=-W(r)dt^2+\frac{1}{W(r)}dr^2+r^2H^2(r)(d\theta ^2+\sin ^2\theta d\varphi ^2). \end{aligned}$$
(2.7)

The metric function W(r) and the dimensionless function H(r) are two unknown functions to be determined. H(r) can be considered as the impacts of dilaton field on the spcetime geometry. In the case \(H(r)=1\) the line element (2.7) reduces to the well-known metric of the Einstein-\(\Lambda \) gravity theory.

By use of the line element (2.7), for the tt, rr and \(\theta \theta (\varphi \varphi )\) components of the gravitational field equation (2.6), we have

$$\begin{aligned} C_{tt}&=W''(r)+2\left[ \frac{1}{r}+\frac{H'(r)}{H(r)}\right] W'(r)\nonumber \\&\quad +V(\phi )-4a^2e^{2\alpha \phi }\left( 1-\sqrt{1+Y}\right) =0, \end{aligned}$$
(2.8)
$$\begin{aligned} C_{rr}&=C_{tt}+4\left[ \frac{H''(r)}{H(r)}+\frac{2}{r}\frac{H'(r)}{H(r)}+\phi '^2(r)\right] W(r)=0,\nonumber \\ \end{aligned}$$
(2.9)
$$\begin{aligned} C_{\theta \theta }&=C_{\varphi \varphi }=2\left[ \frac{1}{r}+\frac{H'(r)}{H(r)}\right] W'(r)\nonumber \\&\quad + 2\left[ \frac{H''(r)}{H(r)}+\frac{1}{r^2}+\frac{4H'(r)}{rH(r)}+\frac{H'^2(r)}{H^2(r)}\right] W(r)\nonumber \\&\quad +V(\phi )+4a^2e^{2\alpha \phi }\left( \frac{1}{\sqrt{1+Y}}-1\right) -\frac{2}{r^2H^2(r)} =0.\nonumber \\ \end{aligned}$$
(2.10)

Noting Eqs. (2.8) and (2.9), we have

$$\begin{aligned} \frac{H''(r)}{H(r)}+\frac{2}{r}\frac{H'(r)}{H(r)}+\phi '^2(r)=0. \end{aligned}$$
(2.11)

Now, we can use an exponential solutions of the form \(H(r)=e^{\alpha \phi }\) in Eq. (2.11), and show that \(\phi =\phi (r)\) satisfies the following differential equation [45]

$$\begin{aligned} \alpha \phi ''+(1+\alpha ^2)\phi '^2+\frac{2\alpha }{r}\phi ' =0. \end{aligned}$$
(2.12)

The solution of (2.12) is easily written in terms of a positive constant b as

$$\begin{aligned} \phi (r)=\frac{\alpha }{1+\alpha ^2} \ln \left( \frac{b}{r}\right) . \end{aligned}$$
(2.13)

The scalar field equation (2.5) can be written in the following explicit form

$$\begin{aligned}&\frac{4\alpha }{(1+\alpha ^2) r}\left[ W'(r)+(1-2\gamma )\frac{W(r)}{r}\right] \nonumber \\&\quad +\frac{dV(\phi )}{d\phi }-8\alpha a^2 \left[ 1-\frac{1}{\sqrt{1+Y}} \right] e^{2\alpha \phi }=0. \end{aligned}$$
(2.14)

It must be noted that the only nonvanishing component of electromagnetic field is \(F_{tr}\). Assuming as a function of r, we have \(\mathcal{{F}}=-2(F_{tr}(r))^2\).

Making use of these solutions together with Eqs. (2.4) and (2.7), one can show that \(F_{tr}=A_t'(r)\), satisfies the following equation

$$\begin{aligned} \partial _r\left( r^2 H^2(r)\frac{F_{tr}e^{-2\alpha \phi }}{\sqrt{1+Y}}\right) =0, \end{aligned}$$
(2.15)

which can be solved in terms of the constant coefficient q, as

$$\begin{aligned} F_{tr}=\frac{q}{r^2}\left( 1+\frac{q^2e^{-4\alpha \phi }}{a^2r^4}\right) ^{-\frac{1}{2}}, \end{aligned}$$
(2.16)

which can be expanded as

$$\begin{aligned} F_{tr}=\frac{q}{r^2}\left[ 1-\frac{q^2e^{-4\alpha \phi }}{2a^2r^4}+\mathcal{{O}}\left( \frac{1}{a^{4}}\right) \right] . \end{aligned}$$
(2.17)

Equation (2.17) shows that for large values of the nonlinearity parameter a, \(F_{tr}\) reduces to its corresponding value in the Einstein–Maxwell-dilaton gravity theory [13].

Noting the \(\theta \theta \) (\(\varphi \varphi \)) component of the gravitational field equation (2.10) together with the scalar field equation (2.14), after some algebraic calculations, we have

$$\begin{aligned} \frac{dV(\phi )}{d\phi }-2\alpha V(\phi )+\frac{4\alpha }{ r^2}\left( \frac{r}{b}\right) ^{2\gamma }=0, \end{aligned}$$
(2.18)

where, \(\gamma =\alpha ^2(1+\alpha ^2)^{-1}\). Now, the solution to Eq. (2.18) can be written in the following form

$$\begin{aligned} V(\phi )=\left\{ \begin{array}{ll} 2\left( \Lambda -\frac{2}{b^2} \phi \right) e^{2\phi },\;\;\;\;\;\;\alpha =1,\\ \\ 2\Lambda e^{2\alpha \phi }+2\Lambda _0 e^{2\alpha _{_0}\phi },\;\;\;\;\;\;\alpha \ne 1, \end{array} \right. \end{aligned}$$
(2.19)

where

$$\begin{aligned} \Lambda _0=\frac{\alpha ^2}{b^2(\alpha ^2-1)},\;\;\;\;\;\;\;\;\alpha _{_0}=\frac{1}{\alpha }. \end{aligned}$$

Note that, in the absence of the dilaton field (e.i. \(\phi =0\) or equivalently \(\alpha =0\)) we have \(V(\phi =0)=2\Lambda \) and the action (2.1) reduces to the action of Einstein–Maxwell gravity with cosmological constant \(\Lambda =-3\ell ^{-2}\) [15, 16]. It is understood from Eq. (2.19) that the dilatonic potential can be written as the linear combination of two Liouville-type potentials.

Making use of Eq. (2.19) into Eq. (2.10), after some manipulations, we obtained the metric function W(r) as

$$\begin{aligned}&W(r)\nonumber \\&\quad =\left\{ \begin{array}{ll} -\frac{m}{r^{1-2\gamma }}+\frac{1+\alpha ^2}{1-\alpha ^2}\left( \frac{r}{b}\right) ^{2\gamma } -\frac{\Lambda b^2(1+\alpha ^2)^2}{3-\alpha ^2}\left( \frac{r}{b}\right) ^{2-2\gamma }\\ \quad +\frac{2a^2b^{4\gamma }(1+\alpha ^2)}{b}\left( \frac{r}{b}\right) ^{2\gamma -1}\varUpsilon (r),\;\;\;\;\alpha \ne 1,\;\sqrt{3},\;\;(a)\\ -mr^{\frac{1}{2}}-2\left( \frac{r}{b}\right) ^{\frac{3}{2}} -4\Lambda b^2\left( \frac{r}{b}\right) ^{\frac{1}{2}}\ln \left( \frac{r}{L}\right) \\ \quad +8a^2 b^2\left( \frac{r}{b}\right) ^{\frac{1}{2}}\varUpsilon _3(r),\;\;\;\;\;\;\alpha =\sqrt{3},\;\;\;\;(b)\\ -m+\frac{2r}{b}\left[ 2-\Lambda b^2+\ln \left( \frac{r}{b}\right) \right] \\ \quad +4a^2 b\varUpsilon _1(r),\;\;\;\;\;\alpha =1,\;\;\;\;(c) \end{array} \right. \end{aligned}$$
(2.20)

where, m is an integration constant related to the black hole mass, L is a dimensional parameter and

$$\begin{aligned}&\varUpsilon (r)=\frac{r^{3-4\gamma }}{3-4\gamma }-\int \frac{dr}{r^{4\gamma -2}}\sqrt{1+\frac{B^2}{r^{4-4\gamma }}}\nonumber \\&\quad =\frac{1+\alpha ^2}{3-\alpha ^2}r^{3-4\gamma }\nonumber \\&\qquad \times \left\{ 1-{\;_2}F_1\left[ \frac{\alpha ^2-3}{4},-\frac{1}{2}, \frac{\alpha ^2+1}{4};\frac{-B^2}{r^{4-4\gamma }}\right] \right\} , \end{aligned}$$
(2.21)
$$\begin{aligned}&\varUpsilon _1(r)=r-\int \sqrt{1+\frac{A^2}{r^2}}dr =r-r\sqrt{1+\frac{A^2}{r^2}}\nonumber \\&\quad -A\ln \left( \frac{r}{L} \right) +A\ln \left( 1+\sqrt{1+\frac{A^2}{r^2}} \right) , \end{aligned}$$
(2.22)
$$\begin{aligned}&\varUpsilon _3(r)=\ln r-\int \frac{dr}{r}{\sqrt{1+\frac{A^2}{rb}}}\nonumber \\&\quad =2\sqrt{1+\frac{A^2}{rb}}-\ln \left[ 2\left( 1+\sqrt{1+\frac{A^2}{rb}}\right) +\frac{A^2}{rb}\right] ,\nonumber \\ \end{aligned}$$
(2.23)

where, \(A=\frac{q}{ab}\) and \(B=\frac{q}{ab^{2\alpha \gamma }}\).

Now, the metric function (2.20) can be rewritten in the following form

$$\begin{aligned}&W(r)\nonumber \\&\quad =\left\{ \begin{array}{ll} \frac{-m}{r^{1-2\gamma }}+\frac{1+\alpha ^2}{1-\alpha ^2}\left( \frac{r}{b}\right) ^{2\gamma }+\frac{\Lambda b^2(1+\alpha ^2)^2}{\alpha ^2-3}\left( \frac{r}{b}\right) ^{2-2\gamma } \\ \quad +\frac{q^2(1+\alpha ^2)}{b^{2}}\left( \frac{b}{r}\right) ^{2-2\gamma } -\frac{q^4(1+\alpha ^2)}{4a^2b^{6}(5-4\gamma )}\left( \frac{b}{r}\right) ^{6-6\gamma } \\ \quad +\mathcal{{O}}\left( \frac{1}{a^{4}}\right) ,\;\;\;\;\alpha \ne 1,\;\sqrt{3},\;\;\;(a)\\ -mr^{\frac{1}{2}}-2\left( \frac{r}{b}\right) ^{\frac{3}{2}} -4\Lambda b^2\left( \frac{r}{b}\right) ^{\frac{1}{2}}\ln \left( \frac{r}{L}\right) +\frac{4q^2}{b^2}\left( \frac{b}{r}\right) ^{\frac{1}{2}}\\ \quad -\frac{q^4}{2a^2b^6}\left( \frac{b}{r}\right) ^{\frac{3}{2}}+\mathcal{{O}}\left( \frac{1}{a^{4}}\right) ,\;\alpha =\sqrt{3},\;(b)\\ -m+\frac{2r}{b}\left[ 2-\Lambda b^2+\ln \left( \frac{b}{r}\right) \right] \\ \quad +\frac{2q^2}{b^2}\left( \frac{b}{r}\right) -\frac{q^4}{6a^2b^6}\left( \frac{b}{r}\right) ^3+\mathcal{{O}}\left( \frac{1}{a^{4}}\right) , \alpha =1,\;\;\;(c) \end{array} \right. \nonumber \\ \end{aligned}$$
(2.24)

up to the first order corrections arisen from the application of nonlinear electrodynamics. It is clear that in the limits \(a\rightarrow \infty \) the solutions are compatible with the results of ref. [13]. Also, it must be noted that in the absence of dilaton field (i.e. \(\alpha =0\)), when the limit \(a\rightarrow \infty \) is taken, the metric function (2.20) reduces to that of Reissner–Nordström-A(dS).

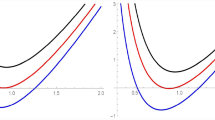
The plots of metric function (2.20) versus r, in terms of different dilatonic parameters, are shown in Figs. 1, 2 and 3. They show that one-horizon, two-horizon, multi-horizon, extreme, and naked singularity black holes can occur if the parameters are chosen, properly. Also, the plots indicate the impacts of different values of dilaton parameter \(\alpha \), nonlinearity parameter a, and black hole mass M.

Now, we consider the curvature singularities through consideration of the Ricci and Kretschmann scalars. It is a matter of calculation to show that the Ricci and Kretschmann scalars are finite for finite values of the radial coordinate r. Also, it is easily shown that

$$\begin{aligned}&\lim _{r\longrightarrow \infty }\mathcal{{R}}=0,\quad \hbox {and}\quad \lim _{r\longrightarrow 0}\mathcal{{R}}=\infty , \end{aligned}$$
(2.25)
$$\begin{aligned}&\lim _{r\longrightarrow \infty }\mathcal{{R}}^{\mu \nu \rho \lambda }\mathcal{{R}}_{\mu \nu \rho \lambda }=0,\quad \hbox {and}\quad \lim _{r\longrightarrow 0}\mathcal{{R}}^{\mu \nu \rho \lambda }\mathcal{{R}}_{\mu \nu \rho \lambda }=\infty .\nonumber \\ \end{aligned}$$
(2.26)

Therefore, there is an essential (not coordinate) singularity located at \(r=0\). Appearance of the singularities in the Ricci and Kretschmann scalars together with existence of black hole horizons are in favor of the solutions to be interpreted as black holes. Also, the asymptotic behavior of the solutions is neither flat nor A(dS). It means that the asymptotic behavior of the space times is affected by the coupled scalar field. As mentioned before, the direct impact of the scalar field, on the spacetime geometry, is given by the function H(r) in Eq. (2.7).

Fig. 1
figure 1

W(r) versus r for \(\Lambda =-3,\;b=1\), Eq. (2.20-a). Left: \(\alpha <1\), \(a=1,\;Q=1,\;M=1.5\) and \(\alpha =0.63\,\,(\hbox {black}),\;0.702\,\,(\hbox {blue}),\;0.76\,\,(\hbox {red}).\) Middle: \(\alpha <1\), \(\alpha =0.7,\;Q=1,\;M=1.5\) and \(a=0.8\,\,(\hbox {black}),\;1.01\,\,(\hbox {blue}),\;1.4\,\,(\hbox {red})\). Right: \(a=0.5,\;Q=1.2,\;M=2\) and \(\alpha =1.216\,\,(\hbox {black}),\;1.2179\,\,(\hbox {brown}),\;1.22\,\,(\hbox {blue}),\;1.223\,\,(\hbox {red}),\;1.2252(\hbox {green})\)

Full size image
Fig. 2
figure 2

W(r) versus r for \(\Lambda =-3,\;Q=1.75,\;b=1,\;L=0.8,\;\alpha =\sqrt{3}\), Eq. (2.20b). Left: \(M=2.5\) and \(a=0.9\,\,(\hbox {black}),\;1.075\,\,(\hbox {blue}),\;1.23\,\,(\hbox {red}),\;1.34\,\,(\hbox {green}),\;1.44\,\,(\hbox {brown}).\) Right: \(a=1.4\) and \(M=2.45\,\,(\hbox {black}),\;2.6\,\,(\hbox {blue}),\;2.8\,\,(\hbox {red}),\;3\,\,(\hbox {green}),\;3.15\,\,(\hbox {brown})\)

Full size image
Fig. 3
figure 3

W(r) versus r for \(\Lambda =-3,\;Q=1,\;b=1,\;\alpha =1\), Eq. (2.20c). Left: \(M=3\) and \(a=1\,\,(\hbox {black}),\;1.37\,\,(\hbox {blue}),\;1.7\,\,(\hbox {red}).\) Right: \(a=1\) and \(M=2.4\,\,(\hbox {black}),\;2.66\,\,(\hbox {blue}),\;3\,\,(\hbox {red})\)

Full size image

3 The first law of black hole thermodynamics

Now, we investigate the thermodynamic properties of the four-dimensional nonlinearly charged dilatonic black hole solutions, obtained in the previous section. The aim of this section is to seek for satisfaction of the first law of black hole thermodynamics. For this purpose we need to calculate the conserved and thermodynamic quantities of the black holes.

The black hole temperature T, associated with the black hole horizon, can be obtained by use of the concept of surface gravity \(\kappa \). Noting the relation \(\kappa =\sqrt{-\frac{1}{2}\left( \nabla _\mu \chi _\nu \right) \left( \nabla ^\mu \chi ^\nu \right) }\) and taking \(\chi ^\mu =(-1,0,0,0)\), after some algebraic calculations, one can show that

$$\begin{aligned}&T=\frac{\kappa }{2\pi }\nonumber \\&\quad =\left\{ \begin{array}{ll} \frac{1}{2\pi b}\left[ \frac{1+\alpha ^2}{2(1-\alpha ^2)}\left( \frac{r_{+}}{b}\right) ^{2\gamma -1}-\frac{\Lambda b^2\left( 1+\alpha ^2\right) }{2}\left( \frac{r_{+}}{b}\right) ^{1-2\gamma }\right. \\ \quad \left. +a^2 b^2 \left( 1+\alpha ^2\right) \left( \frac{r_{+}}{b}\right) ^{1-2\gamma }\left( 1-\sqrt{1+\frac{B^2}{r_{+}^{4-4\gamma }}}\right) \right] , \\ \quad \alpha \ne 1,\sqrt{3},\quad (a)\\ \frac{1}{2\pi b}\left( \frac{r_{+}}{b}\right) ^{\frac{1}{2}}\left[ -1-2\Lambda b^2\left( \frac{b}{r_{+}}\right) \right. \\ \quad \left. +4a^2b^2\left( \frac{b}{r_{+}}\right) \left( 1-\sqrt{1+\frac{A^2}{br_{+}}}\right) \right] ,\quad \alpha =\sqrt{3},\quad (b)\\ \frac{1}{2\pi b}\left[ 1-\Lambda b^2+\ln \left( \frac{b}{r_{+}}\right) +2a^2b^2 \left( 1-\sqrt{1+\frac{A^2}{r_{+}^2}}\right) \right] ,\quad \\ \quad \alpha =1,\quad (c), \end{array} \right. \nonumber \\ \end{aligned}$$
(3.1)

Here, \(r_+\) is the outer black hole horizon radius which can be determined as the largest real root(s) of equation \(W(r_+)=0\). By expanding the last terms, and taking the limit \(a\rightarrow \infty \), it is easily shown that Eq. (3.1) is consistent with its corresponding quantity in the Einstein–Maxwell-dilaton gravity theory.

It must be noted that the extreme black holes (i.e. black holes with zero temperature) can occur provided that the black hole charge and size are fixed such that \(T(r_+=r_{ext},q=q_{ext})=0\), or equivalently

$$\begin{aligned}&\frac{1}{1-\alpha ^2}\left( \frac{r_{+}}{b}\right) ^{4\gamma -2}-\Lambda b^2+2a^2 b^2 \left( 1-\sqrt{1+\frac{B^2}{r_{+}^{4-4\gamma }}}\right) =0,\nonumber \\&\quad \alpha \ne 1,\sqrt{3}, \end{aligned}$$
(3.2)
$$\begin{aligned}&1+2\Lambda b^2\left( \frac{b}{r_{+}}\right) -4a^2b^2\left( \frac{b}{r_{+}}\right) \left( 1-\sqrt{1+\frac{A^2}{br_{+}}}\right) =0,\nonumber \\&\quad \alpha =\sqrt{3}, \end{aligned}$$
(3.3)
$$\begin{aligned}&1-\Lambda b^2+\ln \left( \frac{b}{r_{+}}\right) +2a^2b^2 \left( 1-\sqrt{1+\frac{A^2}{r_{+}^2}}\right) =0, \nonumber \\&\quad \alpha =1. \end{aligned}$$
(3.4)

The nonlinear equations (3.2), (3.3) and (3.4) cannot be solved analytically. Thus, we use the plots for obtaining the roots. The plots of Figs. 4 and 5 show that for the black holes with \(\alpha < 1\) these equations have only one real root labeled by \(r_+=r_{ext}\), and the physical black holes, having positive temperature, are those with \(r_+>r_{ext}\). Otherwise the black holes have negative temperature and are not physically reasonable, which we call unphysical black holes throughout the paper. For the black holes with \(\alpha \ge 1\) Eqs. (3.2)–(3.4) have two real roots which we label by \(r_{1\;ext}\) and \(r_{2\;ext}\), and suppose that \(r_{1\;ext}<r_{2\;ext}\). The physical black holes occur only in the range \(r_{1\;ext}<r_+<r_{2\;ext}\).

The black hole entropy, as a pure geometrical quantity, is obtained by use of the well-known entropy-area law. It can be written as

$$\begin{aligned} S=\frac{A}{4}=\pi r_+^2\left( H(r_+)\right) ^2=\pi r_+^{2}\left( \frac{b}{r_+}\right) ^{2\gamma }, \end{aligned}$$
(3.5)

which is compatible with that of Reissner–Nordstr\(\ddot{\hbox {o}}\)m-A(dS) black holes in the absence of dilaton field (i.e. \(\alpha =0=\gamma \)). The electric potential \(\Phi \), measured with respect to a reference point at a large distance from the horizon, is defined by the following standard relation [14, 15, 52]

$$\begin{aligned} U(r_+)=A_\mu \chi ^\mu |_{\hbox {reference}}-A_\mu \chi ^\mu |_{r=r_+}, \end{aligned}$$
(3.6)

where, \(A_t\) is the temporal component of the electromagnetic four-potential, and \(\chi ^\mu \) is the null generator of the horizon.

Noting Eq. (2.16) and making use of the relation \(F_{tr}=A_t'(r)\), one is able to calculate the temporal component of the electromagnetic four-potential. That is

$$\begin{aligned} A_t(r)&=-\int \frac{q}{r^2}\left( 1+\frac{q^2e^{-4\alpha \phi }}{a^2r^4}\right) ^{-\frac{1}{2}}\nonumber \\ dr&=\frac{q}{r}{\;_2}F_1\left[ \frac{\alpha ^2+1}{4}, -\frac{1}{2}, \frac{\alpha ^2+5}{4};-\frac{q^2}{a^2r^4}\left( \frac{r}{b}\right) ^{4\gamma }\right] \nonumber \\ \end{aligned}$$
(3.7)

Note that the constant of integration is chosen equal to zero. For large values of the nonlinearity parameter a, one can expand the above relation and show that

$$\begin{aligned} A_t(r)=\frac{q}{r}\left[ 1-\frac{(\alpha ^2+1)q^2}{2(\alpha ^2+5)a^2r^4}\times \left( \frac{r_+}{b}\right) ^{4\gamma }+\mathcal{{O}}\left( \frac{1}{a^{4}}\right) \right] .\nonumber \\ \end{aligned}$$
(3.8)

This relation show that \(A_t(r)\) vanishes for large values of r (i.e. \(r\rightarrow \infty \)), and this is a physically reasonable property. Also, \(A_t(r)\) reduces to its corresponding value in the Einstein–Maxwell-dilaton gravity, in the limiting case \(a\rightarrow \infty \). Now, by substituting (3.7) into (3.6), we obtain the electric potential \(U(r_+)\), on the black hole horizon as

$$\begin{aligned} U(r_+)=\frac{q}{r_+}{\;_2}F_1\left[ \frac{\alpha ^2+1}{4},-\frac{1}{2}, \frac{\alpha ^2+5}{4};-\frac{q^2}{a^2r_+^4}\left( \frac{r_+}{b}\right) ^{4\gamma }\right] .\nonumber \\ \end{aligned}$$
(3.9)

The black hole electric charge, as a conserved quantity, can be obtained by calculating the flux of the electric field at infinity (i.e. \(r\rightarrow \infty \)). For this purpose we must use the Gauss’s electric law. It yields \( Q=q\) [13, 47, 50].

The asymptotic behavior of our solutions is not flat or AdS. Thus, for obtaining the black hole mass we use the method of refs. [58, 59]. As a matter of calculation one is able to show that [13, 45]

$$\begin{aligned} m=2M(1+\alpha ^2)b^{-2\gamma }. \end{aligned}$$
(3.10)

Note that the integration constant m is obtained by use of the condition \(W(r_+)=0\). In the absence of dilaton field the Eq. (3.10) reduces to \(m=2M\) which is just the mass of Reissner–Nordström-A(dS) black holes.

Here, we check the first law of thermodynamics for the quantities obtained in this subsection. At first we obtain the mass as a function of the extensive quantities S and Q. That is

$$\begin{aligned}&M(r_+(S),Q)\nonumber \\&\quad =\left\{ \begin{array}{ll} \frac{r_+}{2} \left[ \frac{1}{1-\alpha ^2}+\frac{\Lambda b^2(1+\alpha ^2)}{\alpha ^2-3}\left( \frac{r_+}{b}\right) ^{2-4\gamma } +\frac{2a^2}{r_+}b^{4\gamma }\varUpsilon (r=r_+)\right] ,\\ \quad \alpha \ne 1,\sqrt{3},\;(a),\\ \frac{-b}{4}\left[ \frac{r_+}{b}+2\Lambda b^2\ln \left( \frac{r_+}{L}\right) -4a^2 b^2\varUpsilon _3(r=r_+)\right] ,\\ \quad \alpha =\sqrt{3},\;\;\;(b),\\ \frac{r_+}{2}\left[ 2-\Lambda b^2+\ln \left( \frac{b}{r_+}\right) +\frac{2a^2b^2}{r_+}\varUpsilon _1(r=r_+)\right] ,\\ \quad \alpha =1,\;\;(c). \end{array} \right. \end{aligned}$$
(3.11)

where, Eqs. (2.20), (3.5) and (3.10) have been used. By treating Q and S as the thermodynamical extensive variables one can show that

$$\begin{aligned}&U(r_+) = \left( \frac{\partial M }{\partial Q}\right) _S,\nonumber \\&T(r_+) =\left( \frac{\partial M}{\partial S} \right) _Q,\quad \hbox {for all allowed values of}\;\alpha . \end{aligned}$$
(3.12)

Thus, we have

$$\begin{aligned} dM=TdS+U dQ,\quad \hbox {for all allowed values of}\;\alpha .\end{aligned}$$
(3.13)

It confirms the validity of the thermodynamical first law in its standard form. Therefore, the first law of black hole thermodynamics is valid for all the new black holes introduced here.

Fig. 4
figure 4

\(T(\hbox {dashed})\) and \(C_Q(\hbox {continues})\) versus \(r_+\) for \(\Lambda =-3,\;b=1\), Eqs. (3.1) and (4.1). Left: \(\alpha <1\), 4T and \(C_Q\): \(Q=2,\;a=1.22\) and \(\alpha =0.6\,\,(\hbox {black}),\;0.7\,\,(\hbox {blue})\). Middle: \(\alpha <1\), 4T and \(C_Q\): \(Q=2,\;\alpha =0.75\) and \(a=1\,\,(\hbox {black}),\;1.5\,\,(\hbox {blue})\). Right: \(\alpha >1\), 10T and \(0.5C_Q\): \(Q=1,\;b=1,\;a=1\) and \(\alpha =1.3\,\,(\hbox {black}),\;1.45\,\,(\hbox {blue})\)

Full size image

4 Local stability in the canonical ensemble

At this stage we explore the thermal stability or thermodynamic phase transition of the new AdS black holes identified here. It is well-known that the type-one and type-two phase transition points and the ranges at which the black holes remain stable can be extracted regarding the signature of the black hole heat capacity. In the canonical ensemble method the black hole heat capacity, with the black hole charge as a constant, can be calculated via the following relation [13, 31, 53, 60]

$$\begin{aligned} \mathcal{{C}}_Q =T\left( \frac{\partial S}{\partial T}\right) _Q=\frac{T}{M_{SS}}, \hbox {with}\;\;\;M_{SS}=\left( \frac{\partial ^2 M}{\partial S^2}\right) _Q. \end{aligned}$$
(4.1)

Noting Eq. (IV.1), the numerator of the black hole heat capacity is just the black hole temperature which is presented in Eq. (3.1). Thus, we need to calculate the denominator. It can be calculated by use of Eqs. (3.11) and (3.12). Now, we proceed to analysis the thermal stability or thermodynamic phase transitions for all of the new black hole solutions, separately.

4.1 The black holes with \(\alpha \ne 1,\;\sqrt{3}\)

Making use of the above mentioned equations, after some algebraic calculations, one is able to show that the denominator of the black hole heat capacity takes the following form

$$\begin{aligned}&M_{SS}= \frac{-(1+\alpha ^2)}{8\pi ^2b^2r_+} \left\{ \left( \frac{b}{r_+}\right) ^{2-4\gamma }+ b^2(1-\alpha ^2)\right. \nonumber \\&\quad \left. \times \left[ \Lambda -2a^2\left( 1-\sqrt{1+\frac{B^2}{r_+^{4-4\delta }}}\right) \right] \right. \nonumber \\&\quad \left. -\frac{4q^2\left( \frac{b}{r_+}\right) ^{4-4\gamma }}{b^2\sqrt{1+\frac{B^2}{r_+^{4-4\delta }}} }\right\} . \end{aligned}$$
(4.2)

It is well-known that the real roots of equation \(M_{SS}=0\) are the locations of type-two phase transition points. Evidently, these points cannot be determined analytically. Thus, In order to determine the points of type-one and type-two phase transitions and to characterize the ranges at which the black holes are stable, we have plotted \(\mathcal{{C}}_Q \) and T versus \(r_+\) in Figs.4 for \(\alpha <1\) and \(\alpha >1\) cases, separately. The plots show that, in the case \(\alpha <1\), there is only one point of type-one phase transition located at \(r_+=r_{ext}\). These black holes with the horizon radius equal to \(r_{ext}\) undergo type-one phase transition at the vanishing point of the black hole heat capacity, which is just the horizon radius of the extreme black holes. They are locally stable provided that the horizon radii are in the range \(r_+>r_{ext}\) (Fig. 4 left and middle). For the black holes with \(\alpha >1\) there are two points of type-one phase transition which coincide with the radii of extreme black holes (i.e. \(r_{1ext}\) and \(r_{2ext}\) with \(r_{1ext}<r_{2ext}\)). There is one points of type-two phase transition, which is labeled by \(r_{\infty }\). The black holes with horizon radii in the interval \(r_{1ext}<r_+< r_{\infty }\) are locally stable (Fig. 4 right).

4.2 The black holes with \(\alpha =1\) and \(\alpha =\sqrt{3}\)

As a matter of calculation, one is able to show that the denominator of the black hole heat capacity is given by the following equation

$$\begin{aligned}&M_{SS}\nonumber \\&\quad = \left\{ \begin{array}{ll} \frac{1}{2\pi ^2b^3}\Bigg \lbrace \frac{2b^3}{r_+}\Big [\Lambda -2a^2\Big ( 1-\sqrt{1+\frac{A^2}{r_+b}}\Big )\Big ]\\ \quad +\frac{4q^2}{b^2\sqrt{1+\frac{A^2}{r_+b}} }\Big (\frac{b}{r_+}\Big )^2-1\Bigg \rbrace ,\;\;\alpha =\sqrt{3},\;\;(a),\\ \frac{1}{2\pi ^2b^2r_+}\left( \frac{2q^2}{r_+^2\sqrt{1+\frac{A^2}{r_+^{2}}}}-1\right) ,\quad \alpha =1,\;\;(b). \end{array} \right. \end{aligned}$$
(4.3)

It is necessary to obtain the real roots of equations \(M_{SS}=0\) and \(C_Q=0\), for analyzing the thermal stability or thermodynamic phase transition of the black holes. As the equations are nonlinear, we use the plots for determining the real roots. The plots of T and \(C_Q\), versus \(r_+\), are given In Fig. 5 for the \(\alpha =1\) and \(\alpha =\sqrt{3}\) cases. The plots show that, for both classes of black holes, There two points of type-one phase transition, named as \(r_+=r_{1ext}\) and \(r_+=r_{2ext}\) which are the simultaneous vanishing points of T and \(C_Q\). There is only one type-two phase transition point located at the divergent point of the heat capacity labeled by \(r_+=r_{\infty }\). Both classes of black holes are locally stable if their horizon radii are in the interval

Fig. 5
figure 5

\(T(\hbox {dashed})\) and \(C_Q(\hbox {continues})\) versus \(r_+\) for \(\Lambda =-3\), Eqs. (3.1) and (IV.1). Left: \(100T,\;\alpha =\sqrt{3},\;Q=2,\;b=1,\) \(a=2(\hbox {black}),\;5\,\,(\hbox {blue})\). Right: \(200T,\;\alpha =1,\;a=2,\;b=0.75,\) \(Q=2\,\,(\hbox {black}),\;3\,\,(\hbox {blue})\)

Full size image

5 Thermodynamic geometry

Thermodynamic geometry is an interesting method for studying the thermodynamic stability, by use of which we can find the positions of the thermodynamic phase transition points. The thermodynamic phase transition points are identified as the divergent points of the thermodynamic Ricci scalar. Indeed, the information about thermodynamic phase transitions is extracted from Ricci scalar of a thermodynamic metric. Among the various proposed thermodynamic metrics, the Weinhold, Ruppeiner and Quevedo thermodynamic metrics have attracted more attention [61,62,63,64,65,66]. Recently, it has been demonstrated that the phase transition points of these metrics are not compatible with those of canonical ensemble method. The research group of Hendi, Panahiyan, Eslam Panah and Momennia (HPEM) have proposed a new thermodynamic metric which is written in the following form [27, 29, 30, 67]

$$\begin{aligned} ds^2=\frac{SM_S}{M^3_{QQ}}\left( -M_{SS}dS^2+M_{QQ}dQ^2\right) . \end{aligned}$$
(5.1)

The black hole mass M is a function of black hole charge and entropy, and the indices Q and S indicate the quantities with respect to which derivatives are taken. Making use of this thermodynamic metric, one can calculate the related Ricci scalar and show that its denominator takes the following form [28]

$$\begin{aligned} Den.[\mathcal{{R}}]=2S^3 M^3_S M^2_{SS}. \end{aligned}$$
(5.2)

In order to find the divergent points of the Ricci scalar, as the points of thermodynamic phase transitions, and to compare the results with the results of canonical ensemble method, we have plotted \(\mathcal{{R}}\) and \(C_Q\) versus S together, in Figs. 6 and 7. The plots show that: (i) For \(\alpha <1\) the Ricci scalar has only one divergent point which coincides with the vanishing point of the black hole heat capacity, and indicates the location of the only type-one phase transition point (Fig. 6 left).

Fig. 6
figure 6

\(\mathcal{{R}}\,\,(\hbox {red})\) and \(C_Q\,\,(\hbox {black})\) versus S for \(\Lambda =-3,\;b=1,\;Q=2\). Left: \(\mathcal{{R}}\) and \(2C_Q\), \(\alpha <1\), \(\alpha =0.75,\;a=2.\) Right: \(0.2\mathcal{{R}}\) and \(2C_Q\), \(\alpha >1\), \(\alpha =1.5,\;a=1.\)

Full size image
Fig. 7
figure 7

\(\mathcal{{R}}\,\,(\hbox {red})\) and \(C_Q\,\,(\hbox {black})\) versus S for \(\Lambda =-3,\;b=1,\;a=2\). Left: \(0.1\mathcal{{R}}\) and \(C_Q,\;\alpha =\sqrt{3},\;Q=2\). Right: \(300\mathcal{{R}}\) and \(0.1C_Q,\;\alpha =1,\;Q=4\)

Full size image

(ii) For \(\alpha \ge 1\) there are three points at which the thermodynamic Ricci scalar diverges. Two of them are located just on the vanishing points of heat capacity and indicate the points of type-one phase transition. The third one coincides with the divergent point of heat capacity and shows the type-two phase transition point (Figs. 6 right and 7). Therefore, by applying the HPEM metric, the results of thermodynamic geometry is fully compatible with those of canonical ensemble method.

6 Global stability in the grand canonical ensemble

The global stability of the black holes can be investigated with the help of Gibbs free energy of the black holes. It is well-known that the black holes are globally stable provided that their Gibbs free energy is positive. The real roots of \(G(r_+)=0\) are the locations of Hawking–Page phase transition points. The black holes with negative free energy are in the radiative phase [24, 25]. Therefore, in order to analyze the global stability and to characterize the Hawking–Page phase transition points, it is necessary to calculate the Gibbs free energy of the new black holes. The Gibbs free energy is defined through the following relation [26, 68]

$$\begin{aligned} G(r_+)=M(r_+)-S(r_+)T(r_+)-QU(r_+). \end{aligned}$$
(6.1)

Regarding Eqs. (3.1), (3.5), (3.9) and (3.11), as a matter of calculation, one can show that

$$\begin{aligned}&G(r_+)\nonumber \\&\quad = \left\{ \begin{array}{ll} \frac{r_+}{4}\left[ 1-2a^2b^2(1+\alpha ^2)\left( \frac{b}{r_+}\right) ^{4\gamma -2}\left( 1-\sqrt{1+\frac{B^2}{r_+^{4-4\delta }}}\right) \right. \\ \quad +\frac{4a^2b^{4\gamma }}{r_+}\varUpsilon (r_+) \\ \quad \left. +\frac{\Lambda b^2(1-\alpha ^4)}{3-\alpha ^2}\left( \frac{b}{r_+}\right) ^{4\gamma -2}\right] -QU(r_+) ,\;\;\;\;\alpha \ne 1,\;\sqrt{3},\;\;(a),\\ \frac{r_+}{4}\left\{ 1+\frac{2\Lambda b^3}{r_+}\left[ 2-\ln \left( \frac{r_+}{L}\right) \right] -\frac{8a^2 b^3}{r_+}\left( 1-\sqrt{1+\frac{A^2}{r_+b}}\right) \right. \\ \quad \left. +\frac{4a^2 b^3}{r_+}\varUpsilon _3(r_+)\right\} -QU(r_+),\;\;\alpha =\sqrt{3},\;\;(b),\\ \frac{r_+}{2}\left[ 1-2a^2b^2\left( 1-\sqrt{1+\frac{A^2}{r_+^{2}}}\right) +\frac{2a^2b^2}{r_+}\varUpsilon _1(r_+)\right] \\ \quad -QU(r_+) , \alpha =1,\;\;(c). \end{array} \right. \nonumber \\ \end{aligned}$$
(6.2)

Since, it is difficult to find the real roots of equation \(G(r_+)=0\) analytically, we plot the Gibbs free energy versus \(r_+\). The plots are shown in Figs. 8 and 9 by considering the cases \(\alpha \ne 1,\;\sqrt{3}\) (with \(\alpha <1\) and \(\alpha >1\)) and \(\alpha =1\) and \(\alpha =\sqrt{3}\), separately.

Fig. 8
figure 8

\(G(r_+)\) and \(T(r_+)\) versus \(r_+\) for \(\Lambda =-3,\;Q=1\), Eqs. (3.1) and (5.2). Left: \(2T\,\,(\hbox {dashed})\) and \(G\,\,(\hbox {continues})\), \(a=1,\;b=1.5,\;\alpha =0.65\,\,(\hbox {black}),\;0.8\,\,(\hbox {blue})\). Right: \(30T\,\,(\hbox {dashed})\) and \(G\,\,(\hbox {continues})\), \(a=1.5,\;b=1,\;\alpha =1.3\,\,(\hbox {black}),\;1.4\,\,(\hbox {blue})\)

Full size image
Fig. 9
figure 9

\(6T\,\,(\hbox {dashed})\) and \(G\,\,(\hbox {continues})\) versus \(r_+\) for \(\Lambda =-3,\;L=0.8\), Eqs. (3.1) and (5.2). Left: \(\alpha =\sqrt{3},\;Q=1.5,\;b=1,\) \(a=0.8\,\,(\hbox {black}),\;1\,\,(\hbox {blue})\). Right: \(\alpha =1,\;a=2,\;b=0.7,\) \(Q=1\,\,(\hbox {black}),\;1.22\,\,(\hbox {blue})\)

Full size image

Noting Fig. 8 one can argue that, in the case \(\alpha <1\) (Left panel), the Gibbs free energy vanishes at a point, say at \(r_+=r_0\), it is a point of Hawking–Page phase transition. The physical black holes with the horizon radii in the range \(r_{ext}<r_+<r_0\) are globally stable. Those with horizon radii greater than \(r_0\) are in the radiative phase. In the case \(\alpha >1\), Fig. 8-right show that there is no point of Hawking–Page phase transition. The black holes with horizon radii in the interval \(r_{1ext}<r_+<r_{2ext}\) are globally stable.

The plots of Fig. 9-left show that the Gibbs free energy vanishes at the points \(r_+=r_1\) and \(r_+=r_2\), and physical black holes with the horizon radius equal to \(r_2\), undergo Hawking–Page phase transition. The black holes with the horizon radii in the range \(r_{1ext}<r_+<r_2\) prefer the radiative phase. Those with the horizon radii in the interval \(r_{2}<r_+<r_{2ext}\) are globally stable. The right panel of Fig. 9 shows that for the physical black holes the Gibbs free energy has two vanishing points too. The black holes with the horizon radii in the range \(r_{1}<r_+<r_{2}\) are in the radiation phase. They undergo Hawking–Page phase transition at the points \(r_+=r_1\) and \(r_+=r_2\). The physical black holes with the horizon radii in the ranges \(r_{1ext}<r_+<r_1\) and \(r_{2}<r_+<r_{2ext}\) are globally stable.

7 Conclusion

Making use of the suitable four-dimensional action in which Einstein’s original action, in addition to a scalar dilatonic field, is coupled to the Lagrangian of Born–Infeld nonlinear electrodynamics. Variation of this action, with respect to various fields, leads to the coupled scalar, electromagnetic and gravitational field equations. We obtained the exact solutions in a static and spherically symmetric geometry. Existence of the event horizons and the singularities in curvature scalars confirms that the solutions are black holes. Three classes of novel Einstein–Born–Infeld-dilaton black holes have been introduced, with the non-flat and non-Ads asymptotic behavior. Also, the solutions can produce multi-horizon, two-horizon, one-horizon, extreme and naked singularity black holes provided that the parameters are chosen, suitably (Figs. 1, 2, 3). It must be noted that the black holes with \(\alpha =1\) and \(\alpha =\sqrt{3}\), as well as the multi-horizon black holes have been introduced here for the first time.

We calculated the black hole conserved and thermodynamic quantities such as mass, electric charge, temperature, entropy and electric potential, by use of the geometric and thermodynamic methods. Through a Smarr-type mass formula, we obtained the black hole mass as a function of black hole charge and entropy, as the extensive thermodynamic parameters. The calculations show that these quantities satisfy the first law of black hole thermodynamics in its standard form (Eq. 3.13). Also, we identified the black holes with zero temperature, named as extreme black holes, physically reasonable black holes, having positive temperature, and unphysical black holes with negative temperature (Figs. 4 and 5). The behavior of black hole temperature and heat capacity for the cases \(\alpha \ge 1\), which have been forgotten in all the previous works, are slightly different.

Thermodynamic local stability or phase transition of the new Einstein–Born–Infeld-dilaton black holes have been studied making use of the canonical ensemble method. The black hole heat capacity of the black holes have been calculated. Noting the signature of black hole heat capacity, the points of type-one and type-two phase transitions, and the ranges at which the physically reasonable black holes remain locally stable have been characterized, exactly. Thermal stability of the black holes has been investigated by applying the concept of geometrical thermodynamics too. In this approach, the phase transition points are identified noting the divergent points of the Ricci scalar of a thermodynamic metric. We showed that the results of this method are fully consistent with those of canonical ensemble method if HEPM thermodynamic metric is used (Figs. 6 and 7).

Global stability of the black holes has been investigated by use of the grand canonical ensemble and regarding the Gibbs free energies. By analyzing the Gibbs free energy of the black holes, the horizon radius of the black holes which experience Hawking–Page phase transition as well as the ranges for the horizon radii at which the black holes are globally stable or are in the radiative phase have been identified (Figs. 8 and 9).

Study of the P–V criticality and impacts of the quantum thermal fluctuations as well as consideration of dynamic stability of the novel black holes introduced in this work, are suggested for the subject of forthcoming papers.