Electrical neutrality and $\beta$-equilibrium conditions in dense quark matter: generation of charged pion condensation by chiral imbalance

Abstract

The phase diagram of dense quark matter with chiral imbalance is considered with the conditions of electric neutrality and $\beta$-equilibrium. It has been shown recently that chiral imbalance can generate charged pion condensation (PC) in dense quark matter. It was, therefore, interesting to verify that this phenomenon takes place in realistic physical scenarios such as electrically neutral quark matter in $\beta$-equilibrium, because a window of charged PC at dense quark matter phase diagram (without chiral imbalance) predicted earlier was closed by the consideration of these conditions at the physical current quark mass. In this paper it has been shown that the charged PC phenomenon is generated by chiral imbalance in the dense electric neutral quark/baryonic matter in $\beta$-equilibrium, i.e. matter in neutron stars. It has also been demonstrated that charged PC is an inevitable phenomenon in dense quark matter with chiral imbalance if there is nonzero chiral imbalance in two forms, chiral and chiral isospin one. It seems that in this case charged PC phase can be hardly avoided by any physical constraint on isospin imbalance and that this conclusion can be probably generalized from neutron star matter to the matter produced in heavy ion collisions or in neutron star mergers. The chiral limit and the physical point (physical pion mass) have both been considered and it was shown that the appearance of charged PC is not much affected by the consideration of nonzero current quark mass.

1 Introduction

It is expected that there exists a rich phase structure of QCD at finite temperature and baryon density. For example, lattice simulations from the first principles have revealed that the confined quarks will become released to quark-gluon plasma around the temperature $T_{c}=\Lambda _{QCD}$. The study of hot and dense QCD is not just pure academic research but is important for various physical applications ranging from the evolution of the early universe through neutron star physics to heavy-ion collisions. Hence why it is of interest to determine the behavior of quarks and gluons if the system is heated up or compressed. In heavy-ion collision there exist a fireball of very hot matter as a rule with small baryon chemical potential $\mu _B$.¹ The region of phase diagram with high $\mu _B$ and almost zero temperatures could be realized in nuclear/quark matter in the interior of compact stars.

In the last years lattice QCD as an ab initio approach has made enormous progress in describing the thermodynamics of QCD and has provided important contributions to the understanding of the QCD phase diagram. However, computer power is not the only limitation of the lattice approach. While it is a feasible method in the case of zero baryon chemical potential, it has a conceptual problem when calculating at $\mu _B\ne 0$. For finite chemical potential $\mu _B$ the fermion determinant, which is used as a probability weight in the Monte Carlo sampling, becomes complex and, thus, the method fails. This is known as the sign problem. Although there are ways to explore the region of small chemical potential $\mu _B$ on lattice, but up to now lattice calculations at intermediate (let alone the large) values of $\mu _B$ is not possible.

Therefore, effective QCD-like models, which exhibit the features of color confinement and spontaneous chiral symmetry breaking, are more feasible to be used in studies of the phase structure of QCD with nonzero density in addition to temperature. One of the most widely used effective model is the Nambu–Jona–Lasinio (NJL) model [1, 2] (see for review [3,4,5]). The degrees of freedom of this model are not hadrons, as in the chiral perturbation theory (ChPT), but rather self-interacting quarks and there are no gluons in considerations, they are integrated out. The most attractive feature of the NJL-like models is the dynamical breaking of the chiral symmetry (quarks acquirement of a comparatively large mass) and hence the possibility of using it as a basis model for constituent quark model. The main drawback is the absence of confinement in the model and it does not contain any baryons. The use of NJL-type models seem to be justified in cold deconfined quark matter where both, confinement and gluon degrees of freedom become less relevant. Also let us note that it has been claimed recently that different constraints seems to point to the existence of quark matter in the cores of most massive (closer to two solar mass) neutron stars [6]. Below we use NJL model for the description of pion condensation phenomenon in dense baryonic/quark matter at various baryon densities. As it will be shown the considered in the paper phenomena happen mostly at rather large baryon density, where quark matter can be expected and the use of NJL model is justified. Also one can mention that confinement is not always a decisive feature and sometimes it is less important. For example, NJL model gives a rather good description of the isospin asymmetric matter (including cold one) despite the fact that in this case the matter is confining. While one should always treat the results of the model calculation with the grain of salt, as obtained not from the first principles, they can be anyway quite helpful in understanding various features.

However, there are several additional parameters besides the temperature and the baryon density (or baryon chemical potential $\mu _B$) which also characterize the aforementioned real dense QCD matter. They are connected, for instance, with isospin and chiral imbalances of quark medium. Usually, in order to describe the first phenomenon the isospin $\mu _I$ chemical potential is used, which is thermodynamically conjugated to the isospin density $n_I=(n_u-n_d)/2$ of a system. While the second, chiral imbalance, is characterized, in general, by two different densities. One of them is the so-called chiral $n_5$ density. Here $n_5=n_L-n_R$ where $n_L$ and $n_R$ are the densities of left- and right-handed quarks. Another is the so-called chiral isospin $n_{I5}$ density, where $n_{I5}=(n_{u5}-n_{d5})/2$, and $n_{f5}=n_{fL}-n_{fR}$ is the chiral density of the quark flavor f. So in the most general case the chiral imbalance of dense quark matter can be described by two different chemical potentials, chiral $\mu _5$ and chiral isospin $\mu _{I5}$, which are conjugated to the above densities, $n_5$ and $n_{I5}$, correspondingly. There is a significant number of studies [7,8,9,10,11,12,13,14,15,16,17], in which the influence of the chiral imbalance on the phase structure was considered only in the form of the chiral chemical potential $\mu _{5}$. And it is thought that this form of chiral imbalance can be generated in the fireball after heavy-ion collision as a consequence of the famous chiral Adler–Bell–Jackiw anomaly and it plays an important role in the chiral magnetic effect phenomenon [18], etc. Moreover, chiral densities $n_5$ and $n_{I5}$ (and hence both $\mu _{5}\ne 0$ and $\mu _{I5}\ne 0$) can be produced in dense quark matter in the presence of external magnetic field due to the so-called chiral separation effect [19] (the corresponding simplistic argument for this fact is given in appendices to the papers [20,21,22,23], only for $\mu _{5}$ similar arguments were mentioned in [17]). Or in fast rotating dense matter due to the so-called chiral vortical effect [24]. Chiral density $n_5$ can also be produced in parallel electric and magnetic fields [25,26,27,28]. Due to the different quark electric charges, chiral isospin density $n_{I5}$ can also be produced equally well in parallel electric and magnetic fields [23] (in this case in principle it could be rather considerable). The influence of the chiral imbalance connected with $\mu _{I5}$ on the phase structure of dense quark matter has been considered in [20,21,22,23, 29,30,31,32,33,34,35,36,37,38,39]. Let us also note that the inclusion of chiral isospin chemical potential $\mu _{I5}$ is formally more rigorous [20,21,22,23] and does not have the same problems as with an introduction of $\mu _{5}$. However, it should also be noted that although, the appearance of nonzero chiral imbalance in neutron star cores is possible, i.e. there are several possible qualitative mechanisms leading to it, the in-depth quantitative investigations on the value of produced chiral imbalance (how considerable this value can be and if it is nonzero at all) are to be performed.

In connection with the physics of neutron star matter and experiments on heavy-ion collision, there has recently appeared an interest in the study of quark medium with isospin (isotopic) asymmetry. QCD phase diagram at nonzero values of the isotopic chemical potential $\mu _I$ has been studied in different approaches, e.g., in lattice QCD approach [40,41,42,43,44,45,46,47,48], in ChPT [49,50,51,52,53], in different QCD-like effective models such as NJL model [34, 38, 54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71], quark meson model [72, 73], also in perturbative QCD (with diagrams resummation) [74, 75], in effective theory at asymptotically high isospin density [76], in a random matrix model [77], in hadron resonance gas model [78]. It was shown in these papers that if there is an isospin imbalance then charged pion condensation (PC) phenomenon can be generated in quark matter. Recent review on meson condensation including pion condensation is [79]. Even idea of pion stars, a type of compact star whose main constituent is a Bose–Einstein condensate of charged pions, has been discussed [80, 81].

The possibility of PC in a nuclear medium was speculated a long time ago, in the early 1970s, by Migdal and others [82,83,84,85,86,87,88,89,90,91,92]. In Refs. [82,83,84,85,86,87,88] the neutral PC has been considered. Then the charged PC in neutron rich matter has been investigated for the first time in Refs. [89,90,91,92,93]. After that many efforts have been made to clarify these phenomena since a better insight into PC phenomena would lead to important advances in the physics of pionic atoms [94, 95], in the physics of neutron stars [96, 97], supernovae [98], and heavy-ion collisions [99]. In nuclear matter a crucial role in the study of pion condensations is played by the so-called Landau–Migdal parameters for nucleon-nucleon, nucleon-$\Delta$ and $\Delta$-$\Delta$ couplings. In most of the earlier calculations, universality was assumed (the Landau–Migdal parameters are equal) and a rather large value of the Landau–Migdal parameter was obtained, for which pion condensations are hardly expected even at high baryon densities [100, 101]. Then new information on the Landau–Migdal parameters has been obtained from the experiments on the giant Gamow–Teller resonances, and the results show that the critical baryon density of neutral PC in symmetric nuclear matter and that of charged PC in neutron matter have been estimated to be of the order or less than two normal nuclear density for both condensations [100,101,102]. Similar results have been obtained in the new experiments on Gamow–Teller resonances [103]. Nevertheless, the situation is still not clear and further studies on more neutron-rich nuclei are needed and planned [103].

All of the above refers to the p-wave pion condensation. In this case the pions of condensate have nonzero momentum. However, the possibility of the s-wave pion condensation (when condensed pions have zero momentum) in neutron stars has been explored in [104]. It has been shown there that s-wave PC is very unlikely to take place in neutron stars. Proton fraction and electron chemical potential in [104] was evaluated in the hadronic relativistic mean field models and, in general, all the studies discussed above was performed in hadronic models and were mostly concerned with pion-nucleon interaction, coupling between pions and baryons in the nuclear medium and considered the pion as an elementary point-like object. Then the possibility of the s-wave charged pion condensation was studied in a microscopic model built of quarks and composite pions (with quarks as the constituents), namely in the NJL model, which exhibits chiral symmetry restoration at some finite value of quark chemical potential or temperature [54,55,56,57,58,59,60,61]. It was also shown that there could be the s-wave charged PC (below throughout the paper it is simply denoted as charged PC) in baryonic matter with nonzero baryon density [60], and it was even shown in [61] that this phase is realized (in the chiral limit) in electrically neutral dense matter that is in the $\beta$-equilibrium. It was then demonstrated that charged PC found in [62, 63] is extremely fragile to explicit chiral symmetry breaking by a finite current quark mass. And at the physical point (when physical current quark mass is nonzero) it completely evaporates. So one can conclude that as in the framework of hadronic models as in the framework of quark models in a pure electrically neutral dense hadron/quark matter in $\beta$-equilibrium (without additional conditions such as, for example, chiral imbalance) there is no charged PC phenomenon at the physical point.

However, several external factors have recently been discovered, which promote the formation of the charged PC phase in dense quark matter (see, e.g., the review [34]).² One of them is chiral imbalance, or to be more precise, its two forms, described respectively by the chiral $\mu _{5}$ and the chiral isotopic $\mu _{I5}$ chemical potentials. The effect of chiral isospin imbalance, i.e. of $\mu _{I5}$, on dense quark medium was considered in the chiral limit both within the framework of a toy NJL$_2$ (in Refs. [31,32,33]) and in a more realistic NJL$_4$ (in Refs. [20,21,22,23, 29, 30]) models. The effect of chiral chemical potential $\mu _{5}$ has been considered in [29, 30]. It has been shown that chiral imbalance leads to generation of charged pion condensation in dense quark matter. But in these papers the influence of chiral imbalance on the formation of the charged PC phenomenon was considered without taking into account the possible electric neutrality and $\beta$-equilibrium of dense quark matter and the real nonzero values of $m_0$, i.e. the results of these studies are still not applicable to such astrophysical objects as neutron stars, etc.

In the present paper we fill this gap of our previous researches of charged PC phase in dense quark medium and study the phase diagram of QCD and charged PC phenomenon in the framework of (3 + 1)-dimensional NJL model with two quark flavors and in the presence of the chiral isospin $\mu _{I5}$, chiral $\mu _5$, etc chemical potentials under electric charge neutrality and $\beta$-equilibrium constraints and with physical-valued current quark mass $m_0$ at zero temperature. In particular, it is shown in the framework of the NJL model under consideration that in the mean-field approximation and under the above restrictions (electric charge neutrality, etc) the chiral imbalance leads to generation of the charged PC phase in quark matter with nonzero baryon density. For this, it is enough to have nonzero chiral isospin chemical potential, i.e. $\mu _{I5}\ne 0$. Moreover, the nonzero values of chiral chemical potential $\mu _{5}$ greatly facilitate this effect and lead to a rather large parameter space of dense quark matter occupied by charged PC phase. So one can say that charged pion condensation is inevitable phenomenon in dense quark matter with chiral imbalance of both forms, i.e. at $\mu _{I5}\ne 0$ and $\mu _{5}\ne 0$. And the regions of the charged PC phase in this case are rather large and located in such a way that it is hard to imagine how other physical constraints on isospin imbalance can avoid this phase. This conclusion can be probably generalized to the conditions realized in heavy-ion collisions or neutron star mergers. These conditions require a separate, detailed investigation, however, it has been revealed in [20,21,22] that PC phase is a rather robust phenomenon with respect to the thermal effects and can be realized even at temperatures up to several tens or even close to hundred MeV, these are around highest temperatures that can be reached in neutron star mergers [111]. The investigations have been performed both in the chiral limit and at physical value of current quark mass $m_0$ and it was shown that nonzero value of $m_0$ does not influence much the generation of charged pion condensation in dense quark matter with chiral imbalance.

The paper is organized as follows. First, in Sect. 2 a (3 + 1)-dimensional NJL model with two quark flavors (u and d quarks) that includes four kinds of chemical potentials, $\mu _B,\mu _I,\mu _{I5}$ and $\mu _{5}$, is introduced. Then, the conditions of electric charge neutrality and $\beta$-equilibrium are discussed and corresponding thermodynamic potential of the model is obtained in the mean-field approximation. The phase structure of the system is discussed in Sect. 3. Section 3.1 contains a study of the phase structure of the considered model without chiral imbalance. In Sect. 3.2.1 two cases, with $\mu _{I5}\ne 0$, $\mu _{5}=0$ and $\mu _{I5}=0$, $\mu _{5}\ne 0$, are considered and different phase portraits of the model are depicted in the chiral limit. Then in Sect. 3.2.2 this discussion is generalized to the case when $\mu _{I5}\ne 0$ and $\mu _{5}\ne 0$, also in the chiral limit. Finally, in Sect. 3.3 the influence of $m_0=5.5$ MeV on the phase structure of the system under consideration is discussed. In particular, it is shown in this paper that at rather high values of $\mu _{I5}$ and $\mu _{5}$, larger than the mass of $\pi$ meson, the nonzero $m_0$ does not influence significantly the results obtained in the chiral limit. Hence, in dense quark matter under electric charge neutrality and $\beta$-equilibrium constraints the charged PC phase can be realized, if there is chiral imbalance in the system (both at $m_0=0$ and $m_0\ne 0$), in addition. Section 4 contains summary and conclusions.

2 The model

As a starting point of our study, let us consider an auxiliary (3 + 1)-dimensional system, which is composed of u and d quarks and electrons and described by the following Lagrangian:

$$\begin{aligned}&L=\bar{q}\big [\gamma ^\nu \mathrm {i}\partial _\nu -m_0 \big ]q+ G\left[ (\bar{q}q)^2+(\bar{q}\mathrm {i}\gamma ^5\vec \tau q)^2 \right] \nonumber \\&\qquad +\bar{\psi }\big (\gamma ^\nu \mathrm {i}\partial _\nu -m_{e} \big )\psi . \end{aligned}$$

(1)

In Eq. (1) q(x) is the flavor doublet, $q=(q_u,q_d)^T$, where $q_u$ and $q_d$ are four-component Dirac spinors corresponding to u and d quarks, as well as a color $N_c$-plet, and $\psi (x)$ is also a Dirac spinor but of electrons (the summation in (1) over flavor and spinor indices is implied); $\tau _k$ ($k=1,2,3$) are Pauli matrices. For simplicity, we assume that quarks and electrons do not interact with each other and, in addition, we will assume in the following that the mass $m_e$ of electrons is equal to zero. Since the Lagrangian (1) is invariant with respect to the abelian $U_B(1)$, $U_{I_3}(1)$ and $U_{Q}(1)$ groups,

$$\begin{aligned}&U_B(1):~q\rightarrow \exp (\mathrm {i}\alpha /3) q;~ U_{I_3}(1):~q\rightarrow \exp \left( \mathrm {i}\alpha \tau _3/2\right) q; \nonumber \\&U_{Q}(1):~q\rightarrow \exp (\mathrm {i}\widetilde{Q} \alpha ) q,~~~\psi \rightarrow \exp (\mathrm {i}e \alpha )\psi , \end{aligned}$$

(2)

where $\widetilde{Q}=\mathrm{diag}(2|e|/3,-|e|/3)$ and e is the value of electric charge of an electron, there are three conserved charges (quantities) in the system (1), total baryon charge, third component of isotopic spin and total electric charge. The density operators $n_B$, $n_I$ and $n_Q$ of these conserved quantities have, respectively, the form

$$\begin{aligned}&n_B\equiv \frac{1}{3}\bar{q}\gamma ^0q=\frac{1}{3}(n_u+n_d),\nonumber \\&n_I\equiv \frac{1}{2}\bar{q}\gamma ^0\tau ^3 q=\frac{1}{2}(n_u- n_d),\nonumber \\&n_{Q}\equiv \bar{q}\widetilde{Q}\gamma ^0q-|e|\bar{\psi }\gamma ^0\psi =\frac{2|e|}{3} n_u-\frac{|e|}{3} n_d-|e| n_e,\nonumber \\ \end{aligned}$$

(3)

where $n_u=\bar{q}_u\gamma ^0q_u$, $n_d=\bar{q}_d\gamma ^0q_d$ and $n_e=\bar{\psi }\gamma ^0\psi$ are the operators of the particle number densities of u and d quarks and electrons, respectively. From now on we suppose that $|e|=1$. As a result, it is clear that in the framework of the model (1) it is possible to study some properties of dense matter, composed of u, d quarks and electrons. We also assume that it is in the state of thermodynamic equilibrium at zero temperature. It is well known that a consideration of this dense matter is more convenient to perform in terms of chemical potentials, which are the quantities, thermodynamically conjugated to corresponding densities $n_B$, $n_I$ and $n_Q$ presented in Eq. (3). Therefore, when studying such a dense medium, one could rely on the Lagrangian of the form

$$\begin{aligned} \bar{L}= & {} L+\mu _Bn_B+\mu _In_I+\mu _Qn_Q\nonumber \\= & {} L+\mu _un_u+\mu _dn_d+\mu _en_e, \end{aligned}$$

(4)

where L is presented in Eq. (1) and $\mu _B$, $\mu _I$ and $\mu _Q$ are baryon, isospin (isotopic) and electric charge chemical potentials of the system, respectively. Moreover, in the second line of Eq. (4) we introduce the particle number chemical potentials $\mu _u,\mu _d$ and $\mu _e$ of u and d quarks and electrons, respectively, where

$$\begin{aligned} \mu _u= & {} \frac{\mu _B}{3}+\frac{\mu _I}{2}+\frac{2\mu _Q}{3},~~\mu _d=\frac{\mu _B}{3}-\frac{\mu _I}{2}- \frac{\mu _Q}{3},\nonumber \\ \mu _e= & {} -\mu _Q. \end{aligned}$$

(5)

As it was noted above, we will study dense cold matter, described by the Lagrangian (4), under two constraints. The first is the reqiurement that matter remains in $\beta$-equilibrium, i.e., all $\beta$ processes such as $d\rightarrow u+e+\bar{\nu }_{e}$, $u+e\rightarrow d+\nu _{e}$, etc should go with equal rates in both directions. This means that there should hold the relation $\mu _d=\mu _u+\mu _e-\mu _{\nu }$ between chemical potentials of corresponding particles. Since all neutrinos ($\bar{\nu }_{e}$ and $\nu _{e}$) leave the system, we assume that their chemical potential $\mu _{\nu }$ is zero. So, as a consequence of $\beta$-equilibrium, we have the following relation

$$\begin{aligned} \mu _u+\mu _e=\mu _d. \end{aligned}$$

(6)

Taking into account the relations (5), we conclude from Eq. (6) that $\mu _I$ is equal to zero, i.e., the Lagrangian (4) describes dense quark matter in the $\beta$-equilibrium state only at $\mu _I=0$. In addition, we will also impose on the system under consideration the requirement of local electrical neutrality, $\langle n_Q\rangle =0$,³ thereby approximating its properties to the properties of such astrophysical objects as compact (neutron) stars, etc. (In spite of the fact that these objects are electrically neutral as a whole, we impose, for simplicity, a stronger demand. Namely, that the electric neutrality is observed at every point of these systems, i.e. locally.) Recall that dense quark matter restricted by $\beta$-equilibrium and electric charge neutrality requirements and described by the Lagrangian (4) with $\mu _I=0$ was investigated in Ref. [61] in the chiral limit. In this case, the existence of the charged PC phase is allowed. But if $m_0=5.5$ MeV, then charged PC phase cannot be realized in electrically neutral dense quark matter with $\beta$-equilibrium [62, 63].

However, it is interesting to note that there are arguments (see in the appendices to Refs. [20,21,22,23]), although simplistic and qualitative, in favor of the fact that chiral asymmetry can arise in dense quark medium inside compact stars. This phenomenon can be described using two new additional parameters, chiral $\mu _5$ and chiral isospin $\mu _{I5}$ chemical potentials. Moreover, it was shown in our previous papers [23, 29, 30] that chiral asymmetry, especially in the presence of $\mu _{I5}\ne 0$, is a reliable basis for the appearance of the charged PC effect in dense quark matter, described in the framework of the models (1)–(4). But in [23, 29, 30] we have used $m_0=0$ and did not take into account the property of electrical neutrality of the medium. Naturally, in the present paper, we fill this gap and investigate the phase structure of cold and dense quark matter in the framework of the Lagrangian

$$\begin{aligned}&\mathcal{L}=\bar{L}\big |_{\mu _I=0}+ \frac{\mu _{I5}}{2} \bar{q}\tau _3\gamma ^0\gamma ^5q+\mu _{5}\bar{q}\gamma ^0\gamma ^5q, \end{aligned}$$

(7)

where $\bar{L}$ is given in Eq. (4), under the requirement that in the ground state of the system, i.e. in the state of thermodynamic equilibrium, the density $n_Q$ of electric charge should be zero.⁴ Since $\mu _I=0$ in the Lagrangian (7), the corresponding system is in the $\beta$-equilibrium state.

Remember that the 2$\times$2 matrix $\widetilde{Q}$ of electric charge of quarks (see in Eqs.  (2)–(4)) can be presented in the following form $\widetilde{Q}=I_{3}+\frac{B}{2}$, where $I_{3}=\tau _{3}/2=\mathrm{diag}(1/2,-1/2)$ is the third component of isospin, $B=\mathrm{diag}(1/3,1/3)$. Using this relation one can obtain for initial Lagrangian (7) the following expression

$$\begin{aligned}&\mathcal{L}=\bar{q}\left[ \gamma ^\nu \mathrm {i}\partial _\nu -m_0 +\bar{\mu }\gamma ^0+\nu \tau _3\gamma ^0 \right. \nonumber \\&\qquad \left. +\nu _{5} \tau _3\gamma ^0\gamma ^5+\mu _{5}\gamma ^0\gamma ^5\right] q \nonumber \\&\qquad +G\left[ (\bar{q}q)^2+(\bar{q}\mathrm {i}\gamma ^5\vec \tau q)^2 \right] \nonumber \\&\qquad +\bar{\psi }\Big (\gamma ^\nu \mathrm {i}\partial _\nu -\mu _{Q}\gamma ^0 \Big )\psi , \end{aligned}$$

(8)

where

$$\begin{aligned} \bar{\mu }\equiv \mu +\frac{\mu _Q}{6},~~\mu \equiv \frac{\mu _B}{3},~~\nu \equiv \frac{\mu _Q}{2},~~\nu _5\equiv \frac{\mu _{I5}}{2}. \end{aligned}$$

(9)

We would like to emphasize once again that the Lagrangian (8), (9) describes a dense quark medium in a state of $\beta$-equilibrium. Phase structure of dense matter described by this Lagrangian is determined by the values of the so-called order parameters and their behavior vs chemical potentials. In turn, the order parameters are the coordinates of the global minimum point of the thermodynamic potential of the system. Moreover, the ground state expectation values $n_B$, $n_Q$, $n_5$ and $n_{I5}$ can be found by differentiating the thermodynamic potential of the model (8) with respect to the corresponding chemical potentials. The goal of the present paper is the investigation of the ground state properties (or phase structure) of the model (8) and clarification of the problem of the existence of a charged PC phase in electrically neutral cold and dense quark matter. Furthermore, a special attention will be paid to the influence of the chiral asymmetry on the fate of this phase.

To find the thermodynamic potential of the system, we use a semibosonized version of the Lagrangian (8), which contains composite boson fields $\sigma (x)$ and $\pi _a (x)$ $(a=1,2,3)$:

$$\begin{aligned} \widetilde{\mathcal{L}}\displaystyle= & {} \bar{q}Dq -\frac{1}{4G}\left( \sigma ^2+\pi _a\pi _a\right) + \bar{\psi }\left( \gamma ^\nu \mathrm {i}\partial _\nu -\mu _{Q}\gamma ^0 \right) \psi ,\nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned} D\equiv & {} \gamma ^\rho \mathrm {i}\partial _\rho +\bar{\mu }\gamma ^0 + \nu \tau _3\gamma ^0+\nu _{5}\tau _3\gamma ^0\gamma ^5 \nonumber \\&+\mu _5\gamma ^0\gamma ^5-m_{0}-\sigma -\mathrm {i}\gamma ^5\pi _a\tau _a. \end{aligned}$$

(11)

Note that D is a nontrivial operator in coordinate, spinor and flavor spaces, but it is proportional to a unit operator in the $N_c$-dimensional color space (below in our paper, in all numerical calculations we use $N_c=3$). In Eq. (10) and below the summation over repeated indices is implied. From the semibosonized Lagrangian (10) one gets the equations for the boson fields

$$\begin{aligned} \sigma (x)=-2 G(\bar{q}q);~~~\pi _a (x)=-2 G(\bar{q} \mathrm {i}\gamma ^5\tau _a q). \end{aligned}$$

(12)

Note that the composite boson field $\pi _3 (x)$ can be identified with the physical $\pi ^0(x)$-meson field, whereas the physical $\pi ^\pm (x)$-meson fields are the following combinations of the composite fields, $\pi ^\pm (x)=(\pi _1 (x)\mp i\pi _2 (x))/\sqrt{2}$. Obviously, the semibosonized Lagrangian $\widetilde{\mathcal{L}}$ is equivalent to the initial Lagrangian (8) when using the Eq. (12). Furthermore, it is clear from Eq. (2) that the composite boson fields (12) are transformed under the abelian isospin $U_{I_3}(1)$ group in the following manner:

$$\begin{aligned}&U_{I_3}(1):\quad ~\sigma \rightarrow \sigma ;~~\pi _3\rightarrow \pi _3;~~\pi _1\rightarrow \cos (\alpha )\pi _1\nonumber \\&\quad +\sin (\alpha )\pi _2; \,\pi _2\rightarrow \cos (\alpha )\pi _2-\sin (\alpha )\pi _1. \end{aligned}$$

(13)

Starting from the semibosonized Lagrangian (10), one can obtain in the mean-field approximation (i.e. in the one-fermion loop approximation) the following path integral expression for the effective action $\mathcal{S}_\mathrm{{eff}}(\sigma ,\pi _a)$ of the boson $\sigma (x)$ and $\pi _a (x)$ fields:

$$\begin{aligned} \exp (\mathrm {i}\mathcal{S}_\mathrm{{eff}}(\sigma ,\pi _a)) = N'\int [d\bar{q}][dq][d\bar{\psi }][d\psi ]\exp \left( \mathrm {i}\int \widetilde{\mathcal{L}}\,d^4 x\right) , \end{aligned}$$

where

$$\begin{aligned} \mathcal{S}_\mathrm{{eff}} (\sigma (x),\pi _a(x))=-\int d^4x\left[ \frac{\sigma ^2+\pi ^2_a}{4G} \right] +\tilde{\mathcal{S}}_\mathrm{{eff}}. \end{aligned}$$

(14)

The loop contribution to the effective action, i.e. the term $\tilde{\mathcal{S}}_\mathrm{{eff}}$ in (14), is given by:

$$\begin{aligned} \exp (\mathrm {i}\tilde{\mathcal{S}}_\mathrm{{eff}})= & {} N'\int [d\bar{q}][dq]\exp \left( \mathrm {i}\int \Big \{\bar{q} Dq\Big \}d^4 x\right) \nonumber \\&\times \int [d\bar{\psi }][d\psi ]\exp \left( \mathrm {i}\int \left\{ \bar{\psi }(\gamma ^\rho \mathrm {i}\partial _\rho -\mu _{Q}\gamma ^0 )\psi \right\} d^4 x\right) \nonumber \\= & {} [\mathop {\mathrm{Det}}\nolimits D]^{N_c}\mathop {\mathrm{Det}}\nolimits (\gamma ^\rho \mathrm {i}\partial _\rho -\mu _{Q}\gamma ^0), \end{aligned}$$

(15)

where $N'$ is a normalization constant. Using the general formula $\mathop {\mathrm{Det}}\nolimits D=\exp \mathrm{Tr}\ln D$, one obtains for the effective action (14) the following expression

$$\begin{aligned} \mathcal{S}_\mathrm{{eff}}(\sigma (x),\pi _a(x))= & {} -\int d^4x\left[ \frac{\sigma ^2(x)+\pi ^2_a(x)}{4G}\right] \nonumber \\&-\mathrm {i}N_c\mathrm{Tr}_{sfx}\ln D+\mathcal{S}_{e}, \end{aligned}$$

(16)

where the Tr-operation stands for the trace in spinor (s), flavor (f) as well as four-dimensional coordinate (x) spaces, respectively, and

$$\begin{aligned} \mathcal{S}_{e}=-i\mathrm{Tr}_{sx}\ln (\gamma ^\rho \mathrm {i}\partial _\rho -\mu _{Q}\gamma ^0) \end{aligned}$$

(17)

is the contribution of electrons to the effective action of a whole system.

The ground state expectation values $\langle \sigma (x)\rangle$ and $\langle \pi _a(x)\rangle$ of the composite boson fields are determined by the following saddle point equations,

$$\begin{aligned} \frac{\delta \mathcal{S}_\mathrm{{eff}}}{\delta \sigma (x)}=0,~~~~~ \frac{\delta \mathcal{S}_\mathrm{{eff}}}{\delta \pi _a (x)}=0,~~~~~ \end{aligned}$$

(18)

where $a=1,2,3$. Just the knowledge of $\langle \sigma (x)\rangle$ and $\langle \pi _a(x)\rangle$ and, especially, of their behavior vs chemical potentials supplies us with a phase structure of the model (8). It is clear from (13) that if $\langle \pi _1(x)\rangle \ne 0$ and/or $\langle \pi _2(x)\rangle \ne 0$, we have in the system a spontaneous breaking of the isospin $U_{I_3}(1)$ symmetry (2). Since in this case the ground state expectation values, or condensates, both of the field $\pi ^+(x)$ and of the field $\pi ^-(x)$ are not zero, this phase is usually called the charged PC phase. In addition, it is easy to see from (12) that the nonzero condensates $\langle \pi _{1,2}(x)\rangle$ (or $\langle \pi ^\pm (x)\rangle$) are not invariant with respect to the electromagnetic $U_Q(1)$ transformations (2) of the flavor quark doublet. Hence in the charged PC phase the electromagnetic $U_Q(1)$ invariance of the model (1) is also broken spontaneously, and superconductivity is an unavoidable property of the charged PC phase. It is also possible to show that at $m_0\ne 0$ the relations $\langle \pi _3(x)\rangle = 0$ and $\langle \sigma (x)\rangle \ne 0$ are fulfilled for arbitrary solution of the saddle point equations (18) (this fact has been proven, e.g., in Ref. [112], where the similar stationary equations with nonzero bare quark mass were investigated (see Eqs. (13) and (14) of [112]). As a result, the phase with $\langle \sigma (x)\rangle \ne 0$ and $\langle \pi _a(x)\rangle =0$ ($a=1,2,3$) we will call the phase of normal quark matter, i.e. the phase in which charged PC is absent.

In the present paper we suppose that in the ground state of the system, i.e. in the state of thermodynamic equilibrium, the ground state expectation values $\langle \sigma (x)\rangle$ and $\langle \pi _a(x)\rangle$ do not depend on spacetime coordinates, so

$$\begin{aligned} \langle \sigma (x)\rangle \equiv M-m_{0},~~~\langle \pi _a(x)\rangle \equiv \pi _a, \end{aligned}$$

(19)

where M and $\pi _a$ ($a=1,2,3$) are already constant quantities. In fact, they are coordinates of the global minimum point (GMP) of the thermodynamic potential (TDP) $\Omega (M,\pi _a)$. In the mean-field approximation it is defined by the following expression:

$$\begin{aligned} \int d^4x \Omega (M,\pi _a)=-\mathcal{S}_\mathrm{{eff}}\big (\sigma (x),\pi _a (x)\big )\Big |_{\sigma (x)=M-m_0,\pi _a(x)=\pi _a}, \end{aligned}$$

(20)

where $\mathcal{S}_\mathrm{{eff}}$ is introduced in Eq. (16). In what follows we are going to investigate the dependence of the global minimum point of the function $\Omega (M,\pi _a)$ vs chemical potentials. To simplify the task, let us note that due to a $U_{I_3}(1)$ invariance of the model, the TDP (20) depends on $\pi _1$ and $\pi _2$ through the combination $\pi _1^2+\pi _2^2$. In this case, without loss of generality, one can put $\pi _2=0$ in (20). Moreover, since at $m_0\ne 0$ we have $\langle \pi _3(x)\rangle =0$ (see the corresponding remark between Eqs. (18) and (19)), it is also possible to put $\pi _3=0$ in (20) and study the TDP as a function of only two variables, $M\equiv \sigma +m_0$ and $\Delta \equiv \pi _1$. In this case the TDP (20) reads

$$\begin{aligned} \Omega (M,\Delta )=\Omega _q (M,\Delta ;\bar{\mu },\nu ,\nu _5,\mu _5)+\Omega _e, \end{aligned}$$

(21)

where the contribution of electrons, $\Omega _e$, to the whole TDP has the form

$$\begin{aligned} \Omega _{e}= & {} \frac{i\mathrm{Tr}_{sx}\ln (\gamma ^\rho \mathrm {i}\partial _\rho -\mu _{Q}\gamma ^0)}{\int d^4x} \nonumber \\= & {} -\int _{0}^{\infty }\frac{d^{3}p}{(2\pi )^{3}}(|\mu _{Q}-|\vec p||+|\mu _{Q}+|\vec p||)=-\frac{\mu _{Q}^{4}}{12\pi ^2}\nonumber \\ \end{aligned}$$

(22)

(note that in the final expression (22) for the $\Omega _{e}$ we have ignored an inessential infinite constant). The quark contribution to the expression (21), $\Omega _q (M,\Delta ;\ldots )$, looks like

$$\begin{aligned}&\Omega _q (M,\Delta ;\bar{\mu },\nu ,\nu _5,\mu _5)\nonumber \\&\quad =\frac{(M-m_{0})^2+\Delta ^2}{4G}+\mathrm {i}N_c\frac{\mathrm{Tr}_{sfx}\ln D}{\int d^4x}\nonumber \\&\quad = \frac{(M-m_0)^2+\Delta ^2}{4G}+\mathrm {i}N_c\int \frac{d^4p}{(2\pi )^4}\ln \mathop {\mathrm{Det}}\nolimits \overline{D}(p), \end{aligned}$$

(23)

where

$$\begin{aligned} \overline{D}(p)=\not {p} +\bar{\mu }\gamma ^0 + \nu \tau _3\gamma ^0+\nu _{5}\tau _{3}\gamma ^0\gamma ^5+ \mu _{5}\gamma ^0\gamma ^5-M-\mathrm {i}\gamma ^5\Delta \tau _1 \end{aligned}$$

(24)

is the momentum space representation of the Dirac operator D (11) under the constraints $\sigma +m_0=M,\pi _1=\Delta ,\pi _{2,3}=0$. It should be noted that the parameters $\bar{\mu }$, $\nu$ and $\mu _Q$ are constrained by the relations (9), i.e. the TDP (21)–(24) describes the state of dense quark matter in $\beta$-equilibrium with electrons.

It is evident that the integral term in Eq. (23) is an ultraviolet divergent. So we regularize this expression, introducing a three-dimensional cutoff parameter $\Lambda$, and integrate in Eq. (23) over the region, for which $|\vec p|<\Lambda$. In the following we will study the behavior of the global minimum point of the TDP (21) vs chemical potentials for a special set of the model parameters,

$$\begin{aligned} G=5.01\, \mathrm{GeV}^{-2},~~~\Lambda =0.65\, \mathrm{GeV},~~~m_0=5.5\,\mathrm{MeV}, \quad N_c=3. \nonumber \\ \end{aligned}$$

(25)

In this case at zero chemical potentials one gets for constituent quark mass the value $M=301.58$ MeV. The same parameter set has been used, e.g., in Refs. [5, 60, 61]. Note also that the integration in Eq. (23) can be carried out analytically only at $\Delta =0$ or $M=0$ but the obtained expressions would be rather involved (see the technique elaborated in Refs. [23, 29, 30]). However, for the evaluation of the TDP (23) at $\Delta \ne 0$ and $M\ne 0$ it is necessary to use numerical calculations.

As a result, we see that in order to find the phase portrait of dense quark matter in $\beta$-equilibrium with electrons (in this case the system is described by the Lagrangian (7), (8)), it is necessary to find the GMP of the whole TDP (21)–(24) when the chemical potential parameters $\bar{\mu }$, $\nu$ and $\mu _Q$ are constrained by the Eq. (9). Then, if at some fixed values of the chemical potentials the GMP has the form $(M_0\ne 0,\Delta _0\ne 0)$, the charged PC phase is realized in the system. Whereas the GMP of the form $(M_0\ne 0,\Delta _0= 0)$ corresponds to a normal quark matter (NQM) phase, if $M_0\gg m_0$. However, if in the GMP we have $M_0\approx m_0$, the corresponding phase is called approximately symmetrical (ApprSYM).⁵ It is evident that the coordinates $M_0$ and $\Delta _0$ of the GMP depend on chemical potentials and satisfy to the following set of stationary equations

$$\begin{aligned} \frac{\partial \Omega (M,\Delta )}{\partial M}=0,~~~~~ \frac{\partial \Omega (M,\Delta )}{\partial \Delta }=0. \end{aligned}$$

(26)

In contrast to the bare quark mass $m_0$, in the mean-field approximation the quantity $M_0$ is usually called dynamical quark mass. Below, as a set of independent chemical potentials, which characterizes the $\beta$-equilibrium of the system under consideration, we will use, as a rule, the quantities $\mu ,\nu ,\nu _5$ and $\mu _5$ introduced in Eqs. (7)–(9). Then, if the GMP of the TDP (21) under the constraints (9) is found for each fixed set $(\mu ,\nu ,\nu _{5},\mu _5)$ of the chemical potentials, one can say that the most general $(\mu ,\nu ,\nu _{5},\mu _{5})$-phase portrait of the model (7) is established in the $\beta$-equilibrium state. It means that we have found the one-to-one correspondence between any point $(\mu ,\nu ,\nu _{5},\mu _{5})$ of the four-dimensional space of chemical potentials and possible model phases (NQM, charged PC or ApprSYM phases). However, it is clear that this four-dimensional general phase portrait is quite bulky and it is rather hard to imagine it as a whole. Thus, in order to obtain a more deep understanding of the phase diagram as well as gain a greater visibility of it, it is very convenient to consider different low-dimensional cross-sections of this general $(\mu ,\nu ,\nu _{5},\mu _{5})$-phase portrait, defined by the constraints of the form $\mu = const$ or $\mu _5=const$, etc.

Since one of the purposes of the present paper is to verify the possibility of the charged PC phenomenon in dense quark matter (at least in the framework of the NJL model (1)) under the $\beta$-equilibrium and electric neutrality conditions, the consideration of the physical quantities $\langle n_{B}\rangle$ and $\langle n_Q\rangle$, called baryon and electric charge densities in the ground state, respectively, are now in order. These quantities are very important characteristics of the ground state. So if the coordinates $M_0$ and $\Delta _0$ of the GMP of the TDP (21) is known, then

$$\begin{aligned} \langle n_B\rangle\equiv & {} n_B=-\frac{\partial \Omega (M_0,\Delta _0)}{\partial \mu _B} \nonumber \\= & {} -\frac{1}{3}\frac{\partial \Omega _q (M_0,\Delta _0;\bar{\mu },\nu ,\nu _5,\mu _5)}{\partial \bar{\mu }}, \end{aligned}$$

(27)

$$\begin{aligned} \langle n_{Q}\rangle\equiv & {} n_Q=-\frac{\partial \Omega (M_0,\Delta _0)}{\partial \mu _Q}\nonumber \\= & {} \frac{\mu _Q^3}{3\pi ^2} -\frac{1}{6}\frac{\partial \Omega _q (M_0,\Delta _0;\bar{\mu },\nu ,\nu _5,\mu _5)}{\partial \bar{\mu }}\nonumber \\&-\frac{1}{2}\frac{\partial \Omega _q (M_0,\Delta _0;\bar{\mu },\nu ,\nu _5,\mu _5)}{\partial \nu }, \end{aligned}$$

(28)

where $\Omega _q(M,\Delta ;\bar{\mu },\nu ,\nu _5,\mu _5)$ is the quark contribution (23) to the whole TDP (21), and the quantities $\bar{\mu },\nu ,\nu _5$ are introduced in Eq. (9).

The quantity $\mathop {\mathrm{Det}}\nolimits \overline{D}(p)$ from Eq. (23) is the eighth-order polynomial over $\eta =p_0+\bar{\mu }$. Its roots are $\eta _i\equiv \eta (M,\Delta ;\nu ,\nu _5,\mu _5)$, where $i=1,\ldots ,8$. The algorithm for finding the roots $\eta _i$ is presented in Refs. [29, 30]. There the details of the calculation of the $\Omega _q(M,\Delta ;\bar{\mu },\nu ,\nu _5,\mu _5)$ are also presented. So the final expression for the TDP (21) reeds (at $N_c=3$)

$$\begin{aligned} \Omega (M,\Delta )= & {} \frac{(M-m_0)^2+\Delta ^2}{4G} \nonumber \\&-\frac{3}{2}\sum _{i=1}^{8}\int \frac{d^3p}{(2\pi )^3}|\mu +\nu /3-\eta _{i}|-\frac{4\nu ^{4}}{3\pi ^2}. \nonumber \\ \end{aligned}$$

(29)

Recall that in Eq. (29) $\mu =\mu _B/3$ and $\nu =\mu _Q/2$, where $\mu _B$ and $\mu _Q$ are baryon and electric charge chemical potentials of the system, respectively. And the TDP $\Omega (M,\Delta )$ (29) describes only the $\beta$-equilibrium state of dense quark matter with electrons. But just this expression can also be used in order to obtain the phase structure of electrically neutral quark matter in $\beta$-equilibrium, when $m_0\ne 0$. Indeed, in this case one should (i) find on the basis of the TDP (29) the general $(\mu ,\nu ,\nu _5,\mu _5)$-phase portrait of the model (7), (8) and then (ii) select all those chemical potentials that obey to the equation $n_{Q}=0$. As a result, in the general $(\mu ,\nu ,\nu _5,\mu _5)$-phase diagram of the model (7), (8) we obtain a three-dimensional manifold of physically acceptable chemical potential values. Finally, we are going to show that among all these acceptable chemical potentials one can find those that corresponds to the charged PC phase with $n_B\ne 0$.

But in the chiral limit the task is simplified. Indeed, as it was discussed in Refs. [29, 30], in this case it is enough to study the projections $F_1(M)$ and $F_2(\Delta )$ of the TDP (29) on the M and $\Delta$ axes, respectively

$$\begin{aligned} F_{1}(M)\equiv & {} \Omega (M,0) =\frac{M^2}{4G}-\frac{3}{4\pi ^2} \nonumber \\&\times \sum _{i=1}^{8}\int _{0}^{\Lambda } d|\vec p||\vec p|^2 \left| \mu +\nu /3-\eta ^{M}_{i}\right| -\frac{4\nu ^{4}}{3\pi ^2},\nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned} F_{2}(\Delta )\equiv & {} \Omega (0,\Delta ) =\frac{\Delta ^2}{4G}-\frac{3}{4\pi ^2} \nonumber \\&\times \sum _{i=1}^{8}\int _{0}^{\Lambda } d|\vec p||\vec p|^2 |\mu +\nu /3-\eta ^{\Delta }_{i}|-\frac{4\nu ^{4}}{3\pi ^2},\nonumber \\ \end{aligned}$$

(31)

where the roots are

$$\begin{aligned}&\eta ^{M}_{1,2,3,4}=\nu \pm \sqrt{M^2+(|\vec p|\pm (\mu _5-\nu _{5}))^2}, \nonumber \\&\eta ^{M}_{5,6,7,8}=-\nu \pm \sqrt{M^2+(|\vec p|\pm (\mu _5+\nu _{5}))^2},\nonumber \\&\eta ^{\Delta }_{1,2,3,4}=\nu _{5} \pm \sqrt{\Delta ^2+(|\vec p|\pm (\mu _5-\nu ))^2}, \nonumber \\&\eta ^{\Delta }_{5,6,7,8}=-\nu _{5} \pm \sqrt{\Delta ^2+(|\vec p|\pm (\mu _5+\nu ))^2}. \end{aligned}$$

(32)

Then the GMP of the TDP (29) in the chiral limit can be found by comparing the least values of the functions (30) and (31).

3 Phase diagram

3.1 Charged pion condensation in dense quark matter with isospin imbalance only

Let us discuss the story of charged pion condensation penomenon in dense quark matter without chiral imbalance, i.e. at $\mu _{I5}=0$ and $\mu _5=0$. It started with the prediction of the possibility of the existence of the charged PC phase in dense quark matter with isospin asymmetry but without the requirements of its $\beta$-equilibrium and electrical neutrality. In the chiral limit, the investigation of such a quark matter was performed in Ref. [60] in the framework of the NJL model (1)–(4) at $\mu _B\ne 0$, $\mu _I\ne 0$, but at $\mu _Q=0$, i.e. in the case when the contribution of electrons are not taken into account in the model (1). It has been shown in this paper that at nonzero baryon density and not very large isospin chemical potential $\mu _I$ one can observe the charged PC phase in the system (see the $(\mu _I,\mu )$-phase portrait of Fig. 1 where $\mu =\mu _B/3$). Then it was shown in Ref. [61] that this prediction stays valid also under the conditions that are realized in neutron star matter, namely if one includes into consideration the electric neutrality and $\beta$-equilibrium requirements. In this case the investigation can be performed in terms of the NJL model (4) as well but under the $\beta$-equilibrium (6) and electric neutrality $\langle n_Q\rangle =0$ conditions, which implies the presence of electrons in the system. For simplicity, as very often is done in similar situations, the consideration in Ref. [61] has been also performed in the chiral limit.

Soon after that, it was shown in Refs. [62, 63] that if one accurately include into the NJL model (4) considerations the electric neutrality and $\beta$-equilibrium conditions, combined with the fact that the current quark mass $m_0$ is small but non-zero, the charged PC phase is completely evaporated from the phase diagram of quark matter. (And there is no any indication that this phenomenon, the charged pion condensation, can take place at least in the NJL model approach.) Indeed, in this case the $\beta$-equilibrium condition (6) makes the contribution of the isospin chemical potential $\mu _I$ vanish in the Lagrangian (4) (see the discussion in the previous section). As a result, only two chemical potentials, $\mu _B$ and $\mu _Q$, continue to exist in this model (or, equivalently, in the models (8)–(9) at $\mu _{I5}=0$ and $\mu _5=0$). It is then (i) possible to draw the $(\mu ,\mu _Q)$-phase diagram of such a truncated (by the condition $\mu _I=0$) NJL model (4) at the physical point, i.e. at $m_0=5.5$ MeV. (ii) After that, one can depict on the phase diagram the curve along which the density $\langle n_Q\rangle$ of electric charge is zero. The result of these two procedures, performed in Refs. [62, 63], is presented in Fig. 2 which shows the $(\mu ,\nu =\mu _Q/2)$-phase portrait of the system composed of dense quark matter in $\beta$-equilibrium with electrons. The “neutrality line” in the figure corresponds to the points $(\mu ,\nu =\mu _Q/2)$, for which the electric charge density $\langle n_Q\rangle$ is zero. Since this line does not intersect with PC-region of the phase diagram, one should conclude that in the system under consideration the existence of the charged PC phase is prohibited at the physical point.

Fig. 1

The $(\mu _I,\mu )$-phase diagram of the model (4) in the chiral limit at $\mu _Q=0$ and without charge neutrality and $\beta$-equilibrium conditions (and without chiral asymmetry). Here $\mu =\mu _B/3$, PC denotes the charged PC phase with zero baryon density, the PCd denotes the charged PC phase with nonzero baryon density. SYM corresponds to symmetrical phase of the model

Fig. 2

The $(\mu ,\nu \equiv \mu _{Q}/2)$-phase diagram of dense quark matter which is in the $\beta$-equilibrium with electrons at $\nu _{5}=0$, $\mu _{5}=0$ and $m_0=5.5$ MeV. PC denotes the phase with charged pion condensation. CSB and ApprSYM denote the phases where there is no pion condensation and dynamical quark mass is much greater or around the current quark mass value, respectively. A solid line corresponds to second order phase transitions. A dotted line corresponds to first order phase transitions between CSB and ApprSYM phases. Along the dashed “neutrality line” the density of electric charge $\langle n_Q\rangle$ equals to zero

Then several years after this consideration there have been found several external conditions that are rather realistic to be realized and that create or enhance the generation of the charged PC phase in the system (see, e.g., in the recent review on this topic [34]). In particular, it was shown in Refs. [108,109,110] that this phase can be realized in dense quark matter if we allow the possibility of the existence of spatially inhomogeneous condensates in it. Or take into account that real physical systems have finite sizes [105,106,107]. Moreover, it was recently argued that chiral imbalance also can lead to the generation of charged PC phase in dense baryonic (quark) matter, especially if there are two types of the chiral imbalances in it [23, 29,30,31,32,33] (in this case there is even no need for nonzero isospin chemical potential).

Hence, it would be interesting to check if the charged PC phenomenon can also be realized in electrically neutral and $\beta$-equilibrated dense quark matter with chiral imbalance, i.e. at $\mu _{I5}=2\nu _5\ne 0$ and $\mu _5\ne 0$, or the electric charge neutrality and $\beta$-equilibrium conditions would completely or partially destroy this effect.

3.2 Accounting for chiral imbalance in the chiral limit, $m_0=0$

To study the problem, it is more convenient to consider from the very beginning the case of zero current quark mass $m_0$. One of the motivations for such an approach is that in this case the expression for the TDP (29) is significantly simplified. Moreover, in Refs. [20,21,22] it was shown that the charged PC phase appears on the phase diagram of dense quark matter (without electric charge neutrality and $\beta$-equilibrium requirements) at rather high values of chiral isospin chemical potential $\mu _{I5}\equiv 2\nu _5$, and in this case the influence of the nonzero current quark mass $m_0$ on the location and sizes of the phase is negligible, i.e. in the region of $\nu _5$ that is larger than pion mass, the chiral limit is a good approximation. Below, we will demonstrate that it is also a viable approximation in the case of electrically neutral quark matter in $\beta$-equilibrium.

Fig. 3

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the models (7), (8)) at $\mu =300$ MeV and $\mu _{5}=0$ in the chiral limit, $m_0=0$. CSB is the notation for the chiral symmetry breaking phase. Along the dashed line the electric charge density is zero, $n_Q=0$. Other notations are the same as in Fig. 1

Fig. 4

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the models (7), (8)) at $\mu =400$ MeV and $\mu _{5}=0$ in the chiral limit, $m_0=0$. Other notations are the same as in Figs. 1, 2 and 3

Fig. 5

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the model (7), (8)) at $\mu =450$ MeV and $\mu _{5}=0$ in the chiral limit, $m_0=0$. All the notations are the same as in Figs. 1, 2 and 3

Fig. 6

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the model (7), (8)) at $\mu =500$ MeV and $\mu _{5}=0$ in the chiral limit, $m_0=0$. All the notations are the same as in Figs. 1, 2 and 3

3.2.1 Two particular cases: $\mu _{I5}\ne 0$, $\mu _{5}=0$ and $\mu _{I5}=0$, $\mu _{5}\ne 0$

Let us first consider dense baryon matter in which chiral imbalance is realized in the particular form, characterized by $\mu _{I5}\ne 0$, $\mu _{5}=0$. It means that in this case the $\beta$-equilibrium state of the system with Lagrangian (7), (8) can be described by three, $\mu \equiv \mu _B/3$, $\nu \equiv \mu _Q/2$ and $\nu _{5}\equiv \mu _{I5}/2$, independent chemical potentials. For simplicity, here the phase properties of this system are represented in terms of different ($\nu _{5},\nu$)-phase diagrams at some fixed values of $\mu$, i.e. we trace its evolution with respect to changing the quark number (or baryon) density of matter. One can see from the example of the ($\nu _{5},\nu$)-phase diagram at fixed $\mu =300$ MeV (see in Fig. 3) that at zero or rather small baryon densities (low values of $\mu$) the line of zero electric charge density $n_{Q}=0$ does not cross the charged PC phase at any values of chiral isospin chemical potential $\nu _{5}$. Hence, at $\mu _5=0$ but at $\nu _5\ne 0$ in the electrically neutral quark matter at zero or low quark number density (corresponding to $\mu \le 350$ MeV) in $\beta$-equilibrium state, only the CSB or symmetrical phase can be realized. At larger values of $\mu$, as one can see in Figs. 4, 5 and 6, the electric charge neutrality line $n_{Q}=0$ crosses the PC$_{d}$ phase (it is the notation for the charged PC phase with nonzero baryon density) at values of $\nu _5$ of several hundred MeV. Indeed, using numerical calculations it is possible to show that starting from the value of quark number chemical potential $\mu =380$ MeV the PC$_{d}$ phase crosses the $n_{Q}=0$ line, but the crossed region of the PC$_{d}$ phase is very tiny, and it is in a small vicinity around $\nu _5\sim 350$ MeV at $\mu =400$ MeV (see in Fig. 4). However, this region increases in size with increasing chemical potential $\mu$. For example, at the value of $\mu =450$ MeV the PC$_{d}$ phase of electrically neutral etc. medium is realized at values of chiral isospin chemical potential $\nu _{5}$ from 370 to 400 MeV (see in Fig. 5). And if $\mu =500$ MeV, then the region of the PC$_{d}$ phase on the line $n_Q=0$ spans in Fig. 6 from values of $\nu _{5}$ of 400 MeV up to 450 MeV (hence, the region is rather large and of order of 50 MeV). These values of chemical potentials are still less than the cut-off and in the scope of validity of the model.

As a result, we see that at $\nu _5\ne 0$ and $\mu _5=0$ the charged PC phase can be generated in dense and electrically neutral quark matter in $\beta$-equilibrium, if the quark number chemical potential $\mu \ge 380$ MeV (of course one should stay in the scope of validity of the model (7), (8)). The larger baryon density (the quark number chemical potential $\mu$), the larger chiral isospin imbalance (the value of the chiral isospin chemical potential $\nu _5$) we should have in order that the PC$_{d}$ phase to be realized in this electrically neutral system in $\beta$-equilibrium at $\mu _5=0$.

Let us now consider the case when the system under consideration is in the chiral imbalance of an opposite form, i.e. at $\nu _{5}=0$ but $\mu _{5}\ne 0$. Similar case, but without $\beta$-equilibrium and electric neutrality constraints, dense quark matter was investigated in Refs. [29, 30] where it was shown that the charged PC phase can be generated in the system for a not too large region of $\mu _5$ and only at not too large baryon densities. The same is valid for the models (7), (8) as such, i.e. in each of its $(\mu _5,\nu )$-phase diagram the PC$_{d}$ phase can appear at rather small region of $\mu _5$ and only at not too large values of $\mu$. However, if in addition to $\beta$-equilibrium the electric charge neutrality constraint is imposed on dense quark medium, then in each $(\mu _5,\nu )$-phase portrait of the models (7), (8) the line of zero electric charge density $n_{Q}=0$ does not cross this not too extensive region of PC$_{d}$ phase. So one can conclude that there is no charged pion condensation in electrically neutral dense quark matter in $\beta$-equilibrium state, if there is chiral imbalance in the form when $\mu _{I5}=0$ but $\mu _5\ne 0$.

3.2.2 The general case, $\mu _{I5}\ne 0$ and $\mu _{5}\ne 0$

We saw in Refs. [29, 30] that if there is a chiral imbalance in a form of both nonzero chiral isospin $\mu _{I5}$ and chiral $\mu _{5}$ chemical potentials, then the generation of PC$_{d}$ phase in dense quark matter (without requirement of electric neutrality, etc) is more common and happens in a rather wide region of the chemical potential space and can be realized at any value of isospin chemical potential $\mu _I$. It is evident that this conclusion is also valid in the framework of the models (7), (8) itself at any values of $\mu _{Q}$, i.e. in the case of only $\beta$-equilibrium of medium. Thus, one can expect to have a more pronounced generation of charged pion condensation in dense chirally asymmetric quark matter described by the Lagrangian (7), (8) with $\mu _{I5}\ne 0$ and $\mu _{5}\ne 0$, when electric neutrality condition is taken into account. Now the consideration of this general case is in order.

Fig. 7

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the models (7), (8)) at $\mu =350$ MeV and $\mu _{5}=150$ MeV in the chiral limit, $m_0=0$. All the notations are the same as in Figs. 1, 2 and 3

Fig. 8

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the models (7), (8)) at $\mu =500$ MeV and $\mu _{5}=150$ MeV in the chiral limit, $m_0=0$. All the notations are the same as in Figs. 1, 2 and 3

The results of this investigation at $m_0=0$ are still formulated in terms of the different $(\nu _5,\nu )$-phase portraits (this time at some fixed values of $\mu$ and $\mu _5$) of the models (7), (8)), in which the electric neutrality is taken into account using the curve $n_Q=0$ (see in Figs. 7, 8, 9 and 10).

One can see that if $\mu _{5}$ is nonzero, then it is possible to have a rather large region of PC$_{d}$ phase in dense and electrically neutral quark matter with $\beta$-equilibrium even for sufficiently small values of $\mu$, at which this phase is not realized at $\mu _5=0$. For example, in Fig. 7, corresponding to $\mu =350$ MeV and $\mu _5=150$ MeV, there is a rather voluminous region (it is of order 150 MeV in length) of the PC$_d$ phase in electrically neutral case, whereas at this value of $\mu$ and at $\mu _5=0$ the PC$_d$ phase is forbidden. Moreover, from these figures one can easily see from these figures that the chemical potential $\mu _5$ promotes a significant increase in the size (from several tens to several hundreds of MeV) of the region of the PC$_d$ phase, compared with the case when $\mu _5=0$. To verify this, it is enough to compare Figs. 6 and 8 for $\mu =500$ MeV with each other, or Figs. 4, 9 and 10 for $\mu =400$ MeV, etc.

Fig. 9

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the models (7), (8)) at $\mu =400$ MeV and $\mu _{5}=300$ MeV in the chiral limit, $m_0=0$. All the notations are the same as in Figs. 1, 2 and 3

Fig. 10

The $(\nu _{5},\nu )$-phase diagram of $\beta$-equilibrium quark matter (see the models (7), (8)) at $\mu =400$ MeV and $\mu _{5}=400$ MeV in the chiral limit, $m_0=0$. All the notations are the same as in Figs. 1, 2 and 3

The fact, that the PC$_d$ phase is realized at the phase diagram of neutral quark matter when there are both types of chiral imbalance (both $\mu _5$ and $\nu _5$ are nonzero), could be guessed from the results of the considerations without the $\beta$-equilibrium and electric charge neutrality constraints [29, 30]. Considering the behavior of the PC$_d$ phase regions with respect to the values of $\mu _5$ and $\nu _5$, it could be noted that it is quite hard to avoid this phase by any constraint on $\nu$, the $n_Q=0$, etc. Especially striking hint was that PC$_d$ phase is generated in this case even at $\mu _I=0$. Nevertheless, it was interesting to investigate explicitly what regions are occupied by PC$_d$ phase and how common this phase is in the phase diagram, what is done in this paper. But the general arguments of the PC$_d$ phase behavior with respect to the $\mu _5$ and $\nu _5$ show us that this phase can also be probably produced in different scenarios such as heavy-ion collisions or neutron star mergers. Of course, in general these situations require separate considerations, but one can at least note that there are several arguments in favor of such a condensation. First, let us discuss the conditions pertinent to these settings and elaborate a little bit more on why the PC is probable as in cold as well as in hot quark matter (heavy-ion collisions or neutron star mergers). Unlike here, in the case of heavy-ion collisions one should not include electrons into consideration and just require for electric charge density a physical value (for example, it can be easily shown that for the most common heavy-ion collisions of Au + Au and Pb + Pb $n_Q=0.4 \,n_{B}$ [116]). The above-mentioned general arguments of the behavior of the PC$_d$ phase are directly applied to this situation and tells us that in this case it is hard to avoid PC$_d$ phase by any constraint, including $n_Q=0.4 \,n_{B}$. In the case of neutron star mergers the consideration is similar to the paper at hand, although, one should include nonzero isospin chemical potential $\mu _I$ [117] (which in our case is equal to zero). But it was shown in [117] that its value is not that high and reaches values not higher than 15 MeV. Taking even a short look at Figs. 8, 9 and 10, one can see that it is not nearly enough to avoid the PC$_d$ phase. Besides all these arguments, it is clear that in the considered situations the temperature is rather high and could easily destroy the condensation. However, it was shown in [20,21,22] that in the case without any constraints on isospin asymmetry the thermal effects do not melt the pion condensate up to rather high temperatures of several tens or even hundred MeV. Hence, one can expect that with the electric neutrality and $\beta$-equilibrium constraints the situation would not be much different. Thus, one can probably conclude that, in general, charged PC is an inevitable phenomenon in dense quark matter with chiral imbalance.

Let us give some qualitative condensed matter type arguments for the charged pion condensation in dense electrically neutral quark matter in $\beta$-equilibrium. More specifically, why in this case chiral imbalance $\mu _{I5}$ leads to the generation of charged PC$_d$ phase and why chiral imbalance $\mu _5$ greatly facilitate this phenomenon. One could notice that in [29, 30] large chunk of the PC$_d$ phase was located in the region where $\mu \sim \nu _5$. The similar behavior can be observed in our case, one should only bear in mind that the $\beta$-equilibrium leads to the shift of $\mu$ (see in Eqs. (8), (9)). For example, take a look at Fig. 6, where one can see that charged PC$_d$ phase is realized for $\mu =500$ MeV at $\nu _5$ around 400 MeV (with the tilt towards 450 MeV if one look at the tip of the phase). In the case of quark matter without $\beta$-equilibrium the tip of the PC$_d$ phase coincides with the value $\nu _5=\mu$, so this is in principle the same PC$_d$ region but for the quark matter in $\beta$-equilibrium. Now let us try to argue why charged PC is promoted by chiral imbalance $\mu _{I5}$ (in the case of $\mu _5=0$). It is clear that particle number chemical potentials of the left- and right-handed u, d-quark fields can be expressed in terms of $\mu , \nu$ and $\nu _5$ chemical potentials as $\mu _{uL}=\mu +\nu -\nu _5$, $\mu _{dR}=\mu -\nu -\nu _5$, respectively (see, e.g., in Refs. [29, 30]). Let us note that if one considers the region of $\mu \approx \nu _5$ for the $q_{uL}$ and $q_{dR}$ quarks one has $\mu _{uL}\approx \nu$ and $\mu _{dR}\approx -\nu$. From here it is clear that at nonzero negative (rather high) $\nu$ there is a Fermi sea of $q_{dR}$ quarks with positive energies, but concerning $q_{uL}$ quarks there exists a Fermi sea of $\overline{q}_{uL}$ antiquarks, also with positive energies. Over the surfaces of these Fermi seas the $q_{dR}$ quark with some momentum $\vec p$ and $\overline{q}_{uL}$ antiquark with opposite momentum $-\vec p$ can be born. Then, due to attractive interaction they can form a $\overline{q}_{uL}q_{dR}\sim \pi ^{-}$ Cooper pair with quantum numbers of charged pion. And Bose–Einstein condensation of such Cooper pairs leads to the formation of the ground state of the charged PC phase. This mechanism can account for (having in mind the shift of $\mu$ that has been discussed above) the region of PC$_d$ phase in Figs. 4, 5 and 6, the value of isospin chemical potential $\nu$, which is determined by charge neutrality constraint $n_Q=0$, happens to be enough for this kind of condensation pattern, although one can see that for $\mu =400$ MeV it is barely enough. Let us also note that in case of $\mu =300$ MeV (Fig. 3) the isospin imbalance in the system happens to be not large enough and there is no charged PC in electrically neutral matter with $\beta$-equilibrium in this case.

Now let us qualitatively show why pion condensation in dense quark matter is largely facilitated if there is nonzero chiral imbalance in the form of $\mu _5$, in addition. The Fermi energies of $q_{uL}$ and $q_{dR}$ quarks are $\mu _{uL}=\mu +\nu -\nu _5-\mu _5$ and $\mu _{dR}=\mu -\nu -\nu _5+\mu _5$ and one can see that $\nu$ and $\mu _5$ chemical potentials play the same role. Hence, if there is nonzero $\mu _5>0$ in the system then one needs smaller isospin imbalance $\nu <0$ for charged PC phase to appear. For example, at $\mu =500$ MeV PC$_d$ phase is more easily generated at $\mu _5=400$ MeV (see in Fig. 9) if one compares with the case of $\mu _5=0$ (Fig. 4). Or one can see in Fig. 7 that PC$_d$ phase easily emerges at $\mu =350$ MeV and $\mu _5=150$ MeV, whereas if $\mu _5=0$ this does not happen at all. The striking feature that if $\mu _5\ne 0$ the PC$_d$ phase can appear even if there is no isospin imbalance at all, i. e. $\nu =0$. In this case $\mu _{uL}=-\mu _5$ and $\mu _{dR}=\mu _5$ (sure we consider the region $\mu \approx \nu _5$) and $\mu _5$ makes the same mechanism feasible, as $\nu$ in the discussion above. Moreover, it can be seen in Figs. 9 and 10 that in $\beta$-equilibrium quark matter (but without electrical neutrality requirement) the region of PC$_d$ phase goes up to the values of $\nu =0$. And if one has rather large $\mu _5$ then the PC$_d$ phase persists in a very wide (almost for every value) interval of $\nu$ (see Figs. 9 and 10). It can be accounted for by the same mechanism, if $\mu _5\ne 0$ it is rather hard to break the discussed above picture of the Fermi surfaces by varying the value of $\nu$ (For example, one can see that in Fig. 9 for the case of $\mu _5=300$ MeV PC$_d$ phase expands in a slightly narrower region along $\nu$ axis than in Fig. 10 for the case of larger value of $\mu _5=400$, where this region is greater in both directions). So this mechanism qualitatively explains why for generation of charged PC at zero baryon density ($\mu =0$) it is enough to have $\nu$ and/or $\mu _5$ (one does not have to compensate $\mu$ in the expressions for the Fermi energies) and shows that if $\mu \ne 0$ one needs $\nu _5$ to eliminate $\mu$. While $\mu$ is compensated by $\nu _5$, nonzero value of $\mu _5$ greatly facilitates the mechanism of charged pion condensation in dense quark matter making this phenomenon in a way inevitable.

3.3 The case of $m_{0}\ne 0$

Let us now show (for some fixed sets of chemical potentials $\mu$, $\nu _{5}$ and $\mu _5$) that in electrically neutral and chirally asymmetric dense quark matter with $\beta$-equilibrium the charged PC phenomenon can be realized not only in the chiral limit but at the physical point as well, i.e. when current quark mass $m_0=5.5$ MeV. Recall that if chiral asymmetry is absent, then in this case, as it was shown in Refs. [62, 63], the charged PC phenomenon is impossible. In contrast, in the chiral limit (and at $\nu _5=\mu _5=0$) this phenomenon takes place in dense quark medium under above-mentioned external conditions [61]. So one can ask a question whether the generation of the charged PC$_{d}$ phase by chiral imbalance is smothered by bare quark mass $m_0$ in dense quark matter with charge neutrality and $\beta$-equilibrium. As it was mentioned above (see at the beginning of the Sect. 3.2), the inclusion into consideration of a nonzero bare quark mass $m_0=5.5$ MeV does not significantly change neither the phase diagram and nor the behavior of condensates vs. chemical potentials, if chiral isospin chemical potential $\mu _{I5}\equiv 2\nu _5$ of quark matter is rather high in comparison with pion mass $m_\pi$ ($\approx 140$ MeV) [20,21,22]. Hence, in this case for a rather wide interval of $m_0$ values both the shape and the sizes of the charged PC$_d$ phase remain approximately the same as this phase has in the chiral limit. But in the paper [20,21,22] the possible electric charge neutrality and $\beta$-equilibrium properties of quark medium were not taken into account. Moreover, only the case $\nu _5\ne 0$, $\mu _5=0$ was studied in there.

In the paper under consideration we generalize the results of Refs. [20,21,22] to the case of chirally asymmetric (with $\nu _{5}\ne 0$ and $\mu _5\ne 0$) dense quark matter under electric neutrality and $\beta$-equilibrium constraints. But in this case, i.e. at $m_0\ne 0$, the dynamical quark mass $M_0$ (or chiral condensate) is nonzero in all possible phases of the models (7), (8). Moreover, there is a small chiral condensate $M_0$ even in the charged PC phase, and one cannot use the projections (30), (31) anymore in order to obtain the $(\nu _5,\nu )$-phase diagrams of the $\beta$-equilibrium quark matter described by the Lagrangians (7), (8) (recall that as in Eq. (9), here and below we use the notation $\nu =\mu _Q/2$). The calculations become more difficult. Therefore, we abandon the approach used in the previous sections and show numerically (see the examples below) that for each fixed set of chemical potentials $\mu ,\nu _5,\mu _5$, which are larger than $m_\pi$, there is a solution $\nu$ of the equation $n_Q=0$ such that the GMP of the TDP (29) corresponds to a charged PC phase. Furthermore, since in this case we have $n_B\ne 0$ in addition, one can conclude that the charged PC phase is easily generated by the chiral imbalance, i.e. at $\nu _{5},\mu _5\gg m_\pi$, in dense quark matter which is in the electrically neutral and $\beta$-equilibrium state even at the physical point ($m_0=5.5$ MeV). Recall once more that without chiral imbalance, i.e. at $\nu _{5}=\mu _5=0$, the existence of the charged PC phase is forbidden in such dense medium (see in Refs. [62, 63]).

To support the main conclusion of the paper we present here the relevant numerical investigations for some sets of the chemical potentials $\mu ,\nu _5,\mu _5$ considered in the previous sections, but in the case of the physical current quark mass.

As it has been mentioned above without electric charge neutrality and $\beta$-equilibrium conditions, both the phase diagram of the model and the behavior of condensates vs. chemical potentials are not significantly changed if values of chemical potentials are larger than pion mass $m_\pi$. And it is natural to expect that it is the case also with electric charge neutrality and $\beta$-equilibrium conditions, considering that PC phase is generated as a rule at chiral isospin chemical potential larger than pion mass. This has been also checked by direct numerical calculations and it was shown that current quark mass does not affect greatly the phase diagrams presented in the previous sections, especially the parts with PC condensation at nonzero baryon density. Since phase diagrams at the physical point would be essencially the same as the ones in the chiral limit, we decided not to overload the paper with similar plots, and present the difference between behavior of condensates. The difference (its absence) between physical point and the chiral limit is more clearly demonstrated if one sees the values of condensates in the same points of the phase diagram. Also, as we have not shown the condensates in the chiral limit, it is interesting to see which values they can reach in various phases and, especially, how large pion condensate can be in the PC$_d$ phase. Thus, the purpose of this section is twofold. First, to demonstrate that current quark mass does not influence the conclusions drawn in the chiral limit and, second, to show the values and behavior of corresponding condensates in the phase diagram.

Fig. 11

The condensates $\Delta _{0},M_{0}$ and electric charge density $n_{Q}$ as a function of $\nu$ in the ground state of $\beta$-equilibrium quark matter at $\mu =\mu _{5}=\nu _{5}=400$ MeV at the physical point, $m_{0}=5.5$ MeV. At $\nu <\nu _c\approx -225$ MeV the condensates (coordinates of the GMP of the TDP (29)) correspond to the ApprSYM phase, at $\nu >\nu _c$ the charged PC phase of $\beta$-equilibrium quark matter is realized. Note that at the point $\nu =\nu _0\approx -105$ MeV we have $n_{Q}=0$. It means that in this case, since $\nu _0>\nu _c$, $\beta$-equilibrium quark matter is electrically neutral and there the charged PC phase is realized

Fig. 12

The condensates $\Delta _{0},M_{0}$ and electric charge density $n_{Q}$ as a function of $\nu$ in the ground state of $\beta$-equilibrium quark matter at $\mu =\mu _{5}=\nu _{5}=400$ MeV in the chiral limit, $m_{0}=0$. At $\nu <\nu _c\approx -225$ MeV the condensates correspond to the symmetrical phase, at $\nu >\nu _c$ the charged PC phase of $\beta$-equilibrium matter is realized. Note that at the point $\nu _0>\nu _c$, where $\nu _0\approx -105$ MeV, we have $n_{Q}=0$, i.e. the realization of the charged PC phase in electrically neutral and $\beta$-equilibrium quark matter

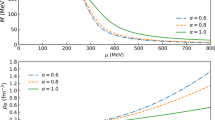
We present here the numerical investigations for some fixed sets of the chemical potentials $\mu ,\nu _5,\mu _5$ in the case of the physical current quark mass (at the physical point). For example, in Fig. 11 one can see the behaviors of the GMP coordinates (or condensates) $M_0$ and $\Delta _0$ of the TDP (29) vs $\nu$ at $\mu =\nu _5=\mu _5=400$ MeV and $m_0=5.5$ MeV in the $\beta$-equilibrium state. Moreover, the plot of the electric charge density $n_Q$ vs $\nu$ in the ground state is also depicted in this figure. The dashed vertical line of the figure corresponds to a value of $\nu =\nu _0\approx -105$ MeV at which $n_Q=0$. At this value of $\nu$ the condensates $M_0$ and $\Delta _0$ are nonzero. In addition, in this case we have $n_B\ne 0$. So, for this fixed set $\mu ,\nu _5,\mu _5$ of chemical potentials and only at $\nu =\nu _0\approx -105$ MeV the charged PC phase can be realized in electrically neutral dense quark matter with $\beta$-equilibrium. Hence, we see that nonzero $m_0$ cannot suppress the generation of the charged PC phase in this case. For comparison, in Fig. 12 the plots of the same quantities vs $\nu$ are presented at the same $\mu ,\nu _5,\mu _5$-chemical potential values, but in the chiral limit. Namely, Fig. 12 describes the changes of the condensates $M_0$ and $\Delta _0$ and electric charge density $n_Q$ vs $\nu$ in the ground state of $\beta$-equilibrium medium when one moves along a vertical line $\nu _5=400$ MeV on the phase diagram of Fig. 10. Comparing Figs. 11 and 12, one can see that in $\beta$-equilibrium there is almost no difference in $\Delta _{0}$ between $m_{0}=0$ and $m_{0}=5.5$ MeV cases (there is only small difference in $M_{0}$ in the charged PC phase). Moreover, it is clear that the boundary point $\nu _c\approx -225$ MeV of the charged PC phase (it is the critical point of the 1st order phase transitions from the charged PC to other phases) in both figures is almost the same, i.e. the size of the charged PC phase does not depend significantly on the bare quark mass $m_0$, thereby generalizing the conclusion of the paper [20,21,22] on the case of dense quark matter in $\beta$-equilibrium (at rather large values of $\mu$, $\nu _5$ and $\mu _5$). Furthermore, let us note in addition that, as it follows from Figs. 11 and 12, the charged pion condensate $\Delta _0$ of $\beta$-equilibrium medium (as well as of electrically neutral quark matter, when $n_Q=0$) reaches the value of 150 MeV, which is a comparatively high value and can have significant implications for the properties of dense quark matter.

Fig. 13

The condensates $\Delta _{0},M_{0}$ and electric charge density $n_{Q}$ as a function of $\nu$ in the ground state of $\beta$-equilibrium quark matter at $\mu =\nu _{5}=400$ MeV and $\mu _5=300$ MeV at the physical point, $m_{0}=5.5$ MeV. At $\nu <\nu _c\approx -235$ MeV the condensates correspond to the CSB phase. At $\nu >\nu _c$ the charged PC phase of $\beta$-equilibrium matter is realized. Note that at the point $\nu _0\approx -140$ MeV we have $n_{Q}=0$. It means that at $\nu =\nu _0$ the $\beta$-equilibrium quark matter is electrically neutral and there the charged PC phase is realized

Fig. 14

The condensates $\Delta _{0},M_{0}$ and electric charge density $n_{Q}$ as a function of $\nu$ in the ground state of $\beta$-equilibrium quark matter at $\mu =\nu _{5}=400$ MeV and $\mu _5=300$ MeV in the chiral limit, $m_{0}=0$. At $\nu <\nu _c\approx -240$ MeV the condensates correspond to the CSB phase. At $\nu >\nu _c$ the charged PC phase of $\beta$-equilibrium quark matter is realized. Note that at the point $\nu _0\approx -140$ MeV we have $n_{Q}=0$. It means that at $\nu =\nu _0$ the $\beta$-equilibrium quark matter is electrically neutral and there the charged PC phase is realized

In Figs. 13 and 14 the behavior of condensates $M_0$ and $\Delta _0$ as well as electric charge density $n_Q$ vs $\nu$ in the ground state of $\beta$-equilibrium quark matter are depicted for the same values of $\mu$ and $\nu _5$, i.e. for $\mu =400$ MeV, $\nu _5=400$ MeV, but for another value of $\mu _5$, for $\mu _5=300$ MeV, at the physical point and in the chiral limit, respectively. (In this case the plots of Fig. 14 show the behavior of the condensates $M_0$ and $\Delta _0$ and electric charge density $n_Q$ in $\beta$-equilibrium medium in the chiral limit, when one moves along a vertical line $\nu _5=400$ MeV in the phase diagram of Fig. 9.) And it is clear that for this particular choice of $\mu$, $\nu _5$ and $\mu _5$ and at $m_0=5.5$ MeV we can conclude that $n_Q=0$ at $\nu =\nu _0\approx -140$ MeV (see in Fig. 13), where $\Delta _0\ne 0$, i.e. the PC$_d$ phase is realized in electrically neutral quark matter with $\beta$-equilibrium. Moreover, the boundary critical point $\nu _c$ of the PC$_d$ phase of $\beta$-equilibrium quark matter at $m_0\ne 0$ (it is clear from Fig. 13 that $\nu _c\approx -235$ MeV) is practically the same, with a slight difference, as in the chiral limit, where $\nu _c\approx - 240$ MeV (see in Fig. 14 or in Fig. 9 at $\nu _5=400$ MeV). This situation can be easily understood. Notice that the chiral condensate $M_0$ takes clearly larger values in the case of physical current quark mass (Fig. 13) than in the chiral limit (Fig. 14). At the same time the charged pion condensate $\Delta _0$ does not change almost at all at each value of $\nu$ in both figures. So we see that in the region $\nu < -240$ MeV, where at $m_0=0$ the CSB is arranged, a rather noticeable enhancement of the chiral condensate $M_0$ occurs when the bare quark mass takes on a value of 5.5 MeV. As a result, this phase slightly increases in size by an amount proportional to $m_0$, i.e. its critical boundary point $\nu _c$ is shifted from the value $\nu _c\approx - 240$ MeV in the chiral limit (see Fig. 14) to $\nu _c\approx -235$ MeV at the physical point (see Fig. 13).

In the case of the transition between PC and symmetric phase at $m_0=0$ (see in Fig. 12) we see that the changes of the condensate $\Delta _0$ are negligible when $m_0\rightarrow 5.5$ MeV. Moreover, in the last case, i.e. at the physical point, instead of the SYM phase the ApprSYM phase appears in which chiral symmetry breaking is rather weak since $M_0\sim m_0$ (see in Fig. 11). As a result, the transition point $\nu _c$ between charged PC and SYM phases stays almost intact when $m_0$ becomes physical (compare Fig. 11 at the physical point and Fig. 12 in the chiral limit). The phase diagrams at the values of $\mu$ and $\mu _5$ presented in Figs. 9 and 10 would be very similar, more specifically, the regions occupied by PC$_d$ phase will almost not change at all if one considers the physical pion mass instead of the chiral limit considerations, the only change is that CSB phase will get slightly larger and eats some parts of the PC phase but not by a considerable degree. The phase structure of electrically neutral and $\beta$-equilibrium quark matter (the part corresponding to the line $n_{Q}=0$) in Figs. 9 and 10 will not experience almost any changes at all.

In a similar way, it is possible to show numerically that, e.g., at various values of $\mu$, $\nu _5$ and $\mu _5$ considered in the previous sections the charged PC$_d$ phase can be realized in electrically neutral and $\beta$-equilibrium quark matter at the physical point. For example, the phase diagram presented in the chiral limit in Fig. 8 would look absolutely the same at the physical point. This is due to the fact that there is no CSB phase at the phase diagram. The same is true for the case of $\mu _5=0$, Figs. 4, 5 and 6 would be very similar at the physical point, only in Figs. 4 and 5, where there is CSB phase, this phase will expand but will not cause any differences to PC$_d$ phase and the phase structure of neutral matter at the line $n_{Q}=0$. So the conclusions of the Sect. 3B 1 that chiral imbalance in the form of $\nu _5$ generates PC$_d$ phase stays intact when one considers physical pion mass (at the physical point). Let us also point out here that the conclusion of the Sect. 3B 2 that the $\mu _5$ greatly facilitates the generation of PC$_d$ phase is not affected by the value of the pion mass either. And one can note that the value of the current quark mass does not play a significant role in the conditions considered in this paper. So the chiral limit considerations of Sect. 3B are justified.

4 Summary and conclusions

In this paper the influence of isotopic, chiral and chiral isotopic imbalances on the phase structure of dense quark matter has been investigated in the framework of the mean-field approximation to the (3 + 1)-dimensional NJL model with two quark flavors under the electric charge neutrality and $\beta$-equilibrium conditions both with nonzero current quark mass, $m_0\ne 0$, and in the chiral limit, $m_0=0$. Dense matter means that our consideration also has been performed at nonzero baryon $\mu _B$ chemical potential. Isotopic imbalance in the system was accounted for by introducing isospin $\mu _I$ (see Lagrangian (1)) chemical potential, and chiral isospin and chiral imbalances in the system were accounted for by introducing chiral isospin $\mu _{I5}$ and chiral $\mu _{5}$ chemical potentials into the Lagrangian (7), (8).

Let us remind the story with the prediction of charged pion condensation (PC) in dense baryon matter. The first investigations and predictions that pion condensation could be observed in nuclear matter, such as neutron stars, appeared in the seventies [82,83,84,85,86,87,88]. But soon it was understood that in the framework of effective models for nuclear matter, in which pion is a point particle, the s-wave charged PC (in this case pions that form a condensate have zero momenta, and the PC is spatially homogeneous) is highly unlikely to be realized. And a possibility for charged p-wave pion condensation has been argued [113,114,115]. However, in the core of a neutron star the baryon density is several times higher than the ordinary nuclear density. At such densities, the hadrons can be so close to each other that the boundaries between them are not distinguishable, and in fact, we will deal with quark matter (with nonzero baryon density). In this case, to study the properties of a dense baryonic medium, it is more appropriate to use the QCD-like effective models such as the NJL model, etc. But in the NJL models, pions (and other hadrons) are not point particles. They are rather Nambu–Goldstone bosons (in the chiral limit) associated with spontaneous CSB. If there is an isospin imbalance in the system, then, as shown in Refs. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60, 64,65,66,67,68], the formation of s-wave Cooper $\bar{u}\gamma ^5 d$ pairs (with quantum numbers of charged pions) is possible, their condensation leads to spontaneous breaking of the isotopic $U_{I_3}(1)$ invariance (see in Eq. (2)) and the appearance of the charged (s-wave) PC phenomenon in dense quark matter even under electric charge neutrality and $\beta$-equilibrium conditions (in the chiral limit, $m_0=0$, but without chiral imbalance) [61]. However, in Refs. [62, 63] it was shown that in this case, i.e. at $\mu _5=\mu _{I5}=0$, and at the physical point, $m_0=5.5$ MeV, the charged PC phase cannot be realized in electrically neutral dense quark matter.

Then it has been found several conditions, including chiral imbalance at nonzero $m_0$, that can promote this phenomenon in dense baryonic matter [20,21,22,23, 29,30,31,32,33,34, 105,106,110]. So now it is interesting if the generation of the charged PC can survive rather strict requirements of electric neutrality and $\beta$-equilibrium. Here in this paper the fate of the charged PC phase of dense quark matter is investigated under influence of these external constraints. Let us summarize the central results of our paper.

• 1. It is established that charged pion condensation phenomenon is induced by chiral imbalance in dense (i.e. at $\mu _B\ne 0$ when baryon density in nonzero) and electrically neutral medium with $\beta$-equilibrium both at $m_0=0$ and $m_0\ne 0$. This matter exists, for example, inside neutron stars and generation of charged PC in its cores can lead to a number of potentially interesting physical implications.

• 2. The discussed generation of charged PC can be promoted even by only chiral isospin chemical potential $\mu _{I5}\equiv 2\nu _5$ at zero chiral chemical potential, $\mu _{5}=0$. In this case the generation of this phenomenon takes place in the region of the chemical potential $\nu _5$ which may be 50/70 MeV in size (see in Sect. 3B1), but perhaps it is not still so wide and could be easily spoiled by extreme conditions. For example, it is not guaranteed to survive in the environment appearing in heavy-ion collisions or neutron star mergers.

• 3. However, if there are both forms of chiral imbalance in the system (chiral $\mu _{5}$ and chiral isospin $\nu _{5}$ chemical potentials are nonzero), then the generation of charged PC in dense baryon matter, limited by electric charge neutrality, etc, conditions, is a quite inevitable phenomenon (see in Sect. 3B2). In this case it can be realized in a larger region of the parameter space. For example, even for rather small values of chiral chemical potential $\mu _5\in 50/150$ MeV the charged PC phase became much more common in the electrically neutral quark (baryon) matter (it could be in a range of $\nu _{5}$ as large as 150/200 MeV).

• 4. It is also can be observed that nonzero values of $\mu _{5}$ rather drastically change the position of the dense charged PC phase in such a way that it is quite hard to imagine that this phase can be evaded by any constraints (such as the electric charge neutrality). And this can be generalized to the conditions on isospin imbalance from heavy-ion collisions or neutron star mergers [117]. It is not even that important how the constraint in heavy-ion collisions looks like exactly, for example, for the most common heavy-ion collisions of Au+Au and Pb+Pb it is $n_Q=0.4 n_{B}$ [116]. In neutron star mergers $\beta$-equilibrium condition requires nonzero isospin chemical potential, but it cannot be larger than about 15 MeV [117] and it will not change the situation. Hence, one can say that charged PC is an unavoidable phenomenon in dense quark (baryon) matter with two types, $\mu _5\ne 0$ and $\nu _5\ne 0$, of chiral imbalances.

• 5. Although in dense and electrically neutral quark matter, which is in the $\beta$-equilibrium state but without chiral imbalance (i.e. at $\mu _5= 0$ and $\nu _5= 0$), the physical bare quark mass, $m_0=5.5$ MeV, destroys the charged PC phase observed in the chiral limit, $m_0=0$, [62, 63], the inclusion of the physical quark mass into consideration, when chiral imbalance is nonzero, does not spoil the generation of charged PC which is observed in the chiral limit, and even does not almost affect it at all (see the results of Sect. 3C). Because it happens as a rule at the values of chiral chemical potentials larger than the half of the pion mass. Hence, for these values of $\mu _5$ and $\nu _5$ the consideration in the chiral limit is justified.

It leads to interesting possible applications for physics of neutron stars since there are several mechanisms of generation of chiral isospin and chiral imbalances in dense quark matter especially under influence of external magnetic field (see, e.g., the discussion in [20,21,22,23], where some simple qualitative arguments in favor of this phenomenon are presented). In a view of the latest and forthcoming NICER results and the first observed and possibly new events of neutron star mergers, it is rather interesting to explore how possible chiral imbalance in neutron star can influence and change mass-radius relation, etc. Here we consider only physical condition pertinent to neutron stars physics, but it can be also an indirect indication that other various physical conditions do not destroy the charged PC phenomenon, and there can be a possibility that it happens also in moderate energy heavy-ion collision experiments such as NICA, RHIC and FAIR.