Layouts for fixed-target experiments and dipole moment measurements of short-lived baryons using bent crystals at the LHC

Abstract

Several studies are on-going at CERN in the framework of the Physics Beyond Collider study group, with main aim of broadening the physics research spectrum using the available accelerator complex and infrastructure. The possibility to design a layout that allows fixed-target experiments in the primary vacuum of the CERN Large Hadron Collider (LHC), without the need of a dedicated extraction line, is part of these studies. The principle of the layouts presented in this paper is to deflect beam halo protons on a fixed-target placed in the LHC primary vacuum, by means of the channeling process in bent crystals. Moreover, the presence of a second bent crystal adjacent to the target opens a unique opportunity for the first direct measurement of electric and magnetic dipole moments of short-lived baryons. Two possible layouts are reported, together with a thorough evaluation on their expected performance and impact on LHC operations.

1 Introduction

Fig. 1

Working principle of the double-crystal scheme for fixed-target experiments and dipole moment measurements at the LHC, and its integration in the collimation hierarchy

Several studies are on-going at CERN in the framework of the Physics Beyond Collider study group [1]. The main aim is to assess the potential of the CERN accelerator complex and infrastructure to expand the physics reach beyond high-energy colliders. A powerful probe for studies of physics beyond the Standard Model is the measurement of electric and magnetic dipole moments. Standard measurement techniques for unstable particles, consist of applying a dipolar magnetic field that induces a dipole moment precession. The angular distribution and energy spectrum of decay products depends on the induced precession. Thus, the dipole moment can be inferred by measuring such distribution and spectrum. However, it is impossible to use conventional magnets for short-lived baryons such as the $\Lambda _\mathrm {c}$, because the achievable magnetic field does not induce a measurable precession. A possible solution to overcome this problem is the use of bent crystals [2, 3]. The equivalent magnetic field acting on a particle trapped between bent crystalline planes can be several orders of magnitude higher than what is achievable using dipole magnets, inducing measurable precession over distances of a few cm. This technique has been proved by the E761 Collaboration, which used the extracted 800 GeV/c proton beam from the Fermilab Proton Center on copper target to produce ${\Sigma ^+}$ and measuring its magnetic moment precession in bent crystals [4].

A 6.5 TeV/c proton beam is nowadays available at the LHC, but no extraction lines are present. The experience gained with bent crystals for collimation of the circulating beam, triggered the idea of an in-vacuum fixed-target apparatus. Bent crystals can be used to deflect halo particles from the circulating beam onto a target placed in the LHC primary vacuum, allowing a unique opportunity for fixed-target experiments at such a high energy. The successful observation of crystal channeling with 6.5 TeV/c proton beams has been already achieved [5]. Heavier interaction products would become accessible at this energy, making possible to perform dipole moment measurements of the $\Lambda _\mathrm {c}$ and potentially of other heavy-flavoured positively charged baryons, as well as the $\tau$ lepton. The $\Lambda _\mathrm {c}$ magnetic moment is particularly interesting because it is closely related to the magnetic moment of the charm quark, which has never been directly measured. The main idea is to use a bent crystal to deflect halo particles of the circulating beam onto a target, where $\Lambda _\mathrm {c}$ are produced and channeled by a second bent crystal placed right after the target. This idea was firstly presented at the Physics Beyond Collider kickoff workshop [6, 7], where the $\Lambda _\mathrm {c}$ magnetic dipole moment measurement was proposed and gathered significant interest, motivating further studies to conceive optimised layouts. Similar investigations were later carried out in [8, 9], also proposing to measure the $\Lambda _\mathrm {c}$ electric dipole moment. The main scope of this paper is to assess the feasibility of this experiment from the accelerator physics side, comparing the expected performance of two possible layouts.

Further applications based on precession in bent crystals were proposed in [10, 11], for measuring the electromagnetic dipole moments of the $\tau$ lepton using double or triple crystal setups at LHC.

Very promising results towards a feasibility demonstration of the double-crystal concept were achieved by the UA9 Collaboration at the CERN Super Proton Synchrotron (SPS), where a complete test stand has been setup [12, 13]. In 2017, the double channeling was demonstrated for the first time, by placing a crystal into the halo channeled by a first crystal in a setup equivalent to that proposed for the LHC experiment, although still without target. In 2018, additional measurements were carried out in the SPS by adding to the setup a target upstream of the second crystal [14]. However, stored beams of 270 GeV/c are available at the SPS and the measurement of $\Lambda _\mathrm {c}$ magnetic moment produced in fixed target by sub-TeV protons would require a prohibitive data-taking time¹ [4, 15], while using multi-TeV beams at the LHC would make it feasible [16].

2 LHC layout and collimation system

The LHC demands a tight control of beam loss because of its cryogenic nature. Tens of $\mathrm {mJ/cm^3}$ deposited in superconducting magnets can cause an abrupt loss of their superconducting properties, i.e. a magnet quench. On the other hand, about 300 MJ are presently stored in the LHC circulating beam, which will increase to about 700 MJ in the High-Luminosity upgrade (HL-LHC) [17,18,19]. A highly-efficient collimation system is required in order to minimise the amount of deposited energy in the superconducting magnets by beam loss.

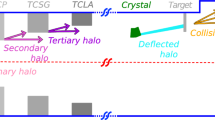
An illustrative picture of the working principle of the LHC collimation system is given in the left side of Fig. 1. The present LHC system [20] is composed of 44 movable ring collimators per beam, placed in a precise multi-stage hierarchy that must be maintained in any machine configuration to ensure optimal cleaning performance. Two LHC insertions (IRs) are dedicated to beam halo collimation: IR3 for momentum cleaning, i.e. removal of particles with a large energy offset (cut from $\delta p/p\sim 0.2\,\%$ for zero betatron amplitude); and IR7 for betatron cleaning, i.e. continuous controlled disposal of transverse halo particles. Each collimation insertion features a three-stage cleaning based on primary collimators (TCP), secondary collimators (TCSG) and absorbers (TCLA). In this scheme, the energy carried by the beam halo intercepted by TCPs is distributed over several collimators (e.g. 19 collimators are installed in the betatron cleaning insertion). Dedicated collimators for protection of sensitive equipment (such as TCTP for the inner triplets²), absorption of physics debris (TCL) and beam injection/dump protection (TDI/TCDQ-TCSP) are also present at specific locations of the ring. A detailed description of the system functionalities goes beyond the scope of this paper and can be found in [20].

The other IRs house the Radio Frequency system (RF) and the Beam Dump system (LBDS) in IR4 and IR6, respectively. The main physics detectors are placed in the remaining IRs: the multi-purposes physics ATLAS and CMS are placed in IR1 and IR5, respectively; the flavour physics LHCb is placed in IR8; the heavy ion physics ALICE is placed in IR2.

IR8 is a natural choice to deploy a layout that would allow fixed-target and dipole moment experiments, because of the presence of the LHCb detector that is suited for forward physics thanks to its asymmetric design. This option was originally studied in [6], where it was already clear that serious limitations could come from losses on superconducting magnets. In particular, a sort of mini collimation system would be needed around IR8 to handle losses of high-intensity beams.

As opposed to the choice of installing new collimators around an existing large detector, new studies have been performed to probe the feasibility of using an existing collimation insertion where a smaller and dedicated detector could be located. In this case, the natural choice is IR3 for different reasons illustrated in Sect. 5.

3 Design goals, constraints and tools

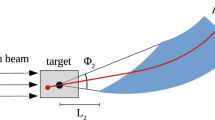
The schematic working principle of the layouts is shown in Fig. 1. The main goal is to maximise the number of protons on target (PoT) while keeping the losses on superconducting magnets below limits tolerable for operations.

It would be possible to design a dedicated beam optics with present magnet layout, in order to optimise the layout performance. However, the overhead would become too large if new optics needs to be commissioned. Moreover, a dedicated optics would imply dedicated running conditions that could affect standard LHC operations at the expenses of delivered luminosity to the other experiments. It was therefore decided to design optimised layouts for the existing and already commissioned optics. The same approach was used to design the crystal collimation layout currently installed in the LHC [21], which led to the successful observation of crystal channeling with 6.5 TeV/c protons beams [5].

3.1 Main constraints

Important constraints for the design, e.g., on longitudinal positions, come from space availability. Although this work does not include a dedicated integration study, all known constraints from the present space occupancy were taken into account in the layouts presented here.

Regarding the best location of the first crystal, once free locations are found they must be combined with optimal beam optics requirements in order to:

• Enhance the displacement due to a given deflection by maximizing the beam size (i.e. $\sigma (s)= \sqrt{\beta (s) \varepsilon }$).

• Improve the channeling efficiency of multi-turn halo by minimizing the beam divergence (i.e. $\sigma ^\prime (s)= \sqrt{\gamma (s) \varepsilon }$).

Thus, the following ratio must be maximised:

$$\begin{aligned} \frac{\sigma (s)}{\sigma ^\prime (s)}=\beta (s)\sqrt{\frac{1}{1+\alpha ^2(s)}}\,, \end{aligned}$$

(1)

where $\alpha$, $\beta$ and $\gamma$ are the Twiss parameters, while $\varepsilon$ is the physical beam emittance. This parameter is very important to minimise the required bending of the first crystal and to enhance the channeling efficiency of secondary and tertiary halo, i.e. halo protons emerging from primary and secondary collimators, respectively (see Fig. 1).

It is clear that absorbers need to be added to dispose of the channeled halo that emerges from the target and to dispose of out-scattered protons. Optimizing the location for such collimators calls for an installation at the closest location where the betatron phase advance from the first crystal is about $\pi /2$. Smaller beam sizes at the collimators are also favoured because allow closer settings for a better efficiency in intercepting particles emerging from crystal and target. These two parameters – phase advance and transverse settings – define the angular cut made by the absorber, as defined in Eq. (2). For convenience, this is typically expressed as the minimum kick for particles out-scattered at the crystal that are still intercepted by the downstream collimators. The optimization of this angular cut is one of the main differences between the layouts presented in Sects. 4 and 5.

The trajectory of channeled halo particles between the first crystal and the absorbers must remain at a safe distance from the machine geometrical aperture. An initial clearance of 4 mm is assumed, which can accomodate pessimistic orbit errors used in the LHC design phase [22]. Detailed aperture calculations, with a proper accounting of relevant errors on optics, aperture, orbit, etc., shall be performed in a later stage. A distance between the target and the circulating beam envelope of 4 mm is also required, which defines the minimum bending angle of the first crystal. This retraction ensures that the target is not intercepting significant beam halo. It can be demonstrated that, for the operational scenarios discussed below, approaching the target further does not bring significant benefits.

Furthermore, all the system must be placed in the vertical plane in order to relax constraints due to machine protection aspects. This because the beam is deflected in the horizontal plane and directed into the dump line when a beam dump is triggered. It can happen that the beam dump kickers are not fired synchronously with respect to the abort gap (range of the ring left empty) and dangerous portions of the beam are kicked wrongly. Thus, by placing the system in the vertical plane, the possibility to get hit by the beam during an asynchronous dump is removed. This opens the possibility to get closer to the beam with the first crystal, in principle down to the aperture of the primary collimators in IR7. Finally, crystals must be placed above the circulating beam, in order to provide the required space needed to fit the goniometers that hold and orient them [23, 24].

3.2 Simulation tools

Semi-analytical tools were developed to evaluate quickly the feasibility of each layout. The trajectory of particles experiencing an angular kick $\theta$ at $s_{1}$ can be described using the transfer matrix formalism. If a crystal is installed at $s_{1}$, and assuming $\alpha (s_{1})\sim 0$, the trajectory of a kicked particle is described by:

$$\begin{aligned} x(s)=&\sqrt{\frac{\beta (s)}{\beta (s_{1})}}\cos \left( \varDelta \mu _{s-s_{1}}\right) x(s_{1})\nonumber \\&+\theta \sqrt{\beta (s)\beta (s_{1})}\sin \left( \varDelta \mu _{s-s_{1}}\right) \,, \end{aligned}$$

(2)

where $\varDelta \mu _{s-s_{1}}=\intop _{s_{1}}^{s}\frac{ds'}{\beta \left( s'\right) }$ is the betatron phase advance between $s_{1}$ and s, and other parameters were defined above.

After a first identification of suitable installation locations based on space availability, a sub-set of possible locations, crystal parameters, and collimator settings is determined based on semi-analytical tools. Then, complete multi-turn tracking simulations are performed. They are made using SixTrack [25,26,27,28] that allows a symplectic, fully chromatic and 6D³ tracking along the magnetic lattice of the LHC, taking into account interactions with the ring collimators and the detailed aperture model of the entire machine. SixTrack has been successfully benchmarked with LHC data in [29,30,31]. The treatment of interactions between protons and bent crystals is carried out using a dedicated routine implemented in SixTrack. The details of this implementation and the physics models used can be found in [32,33,34], while its benchmarking in the energy range from 180 GeV/c to 6.5 TeV/c is reported in [33, 35,36,37,38]. This simulation setup allows estimation of the density of protons lost per metre with a resolution of 10 cm along the entire ring circumference.

Table 1 Installation position and main features of the proposed experimental layout in IR8. All the components act on the vertical plane

Fig. 2

Trajectory of channeled halo particles and mechanical aperture of the beam pipe (black) versus longitudinal position along the IR8 insertion. The first crystal, shown by the light orange line, sits on the $5~\sigma$ beam envelope shown by the red lines. The assembly of target plus second crystal, shown by the dark orange line, is placed at about 2.4 m upstream of IP8 in the Beam 1 direction and intercepts halo particles channeled by the first crystal (light magenta line). The trajectory followed by particles channeled also by the second crystal is shown by the dark magenta line. The TCSGs and TCLA used to intercept channeled halo particles are represented in cyan and green lines and are set at $10~\sigma$ and $13~\sigma$, respectively. The magnetic lattice is also reported on top, where blue and white boxes represent main superconducting quadrupoles and dipoles, respectively

4 IR8 layout design

The design of optimised layout in IR8 is shown in Fig. 2. It is placed on Beam 1 with clock-wise orientation due to the LHCb asymmetry and satisfies the constraints discussed in Sect. 3.1, in order to provide optimum operational performance. It consists of a first crystal (${\mathrm {Cry_1}}$) with bending $\theta _b^{{\mathrm {Cry_1}}}=150~\upmu \hbox {rad}$ that separates the halo particles from the primary beam sufficiently to impinge on a target, respecting the constrains of displacement of 4 mm with respect to the beam envelope at the target, and clearance between the geometrical machine aperture and the deflected halo of at least 4 mm along the entire trajectory.

The crystal length is $l^{\mathrm {Cry_1}}=1.2~\hbox {cm}$, which was chosen to have a bending radius $R=80~$m, as the present crystals installed in the LHC. This follows the parametric studies reported in [21] and ensures an optimum crystal channeling performance at LHC top energy, while keeping the nuclear interactions rate as low as possible.

Initial integration studies indicated that a position at a distance of 2.4 m from IP8 was available for the installation of the target assembly [6]. A later assessment showed that a closer position at 1.2 m from IP8 is actually also accessible. While that latter is used in the latest LHCb simulations [39], the former is still used for the loss studies presented here. This small shift is not expected to induce significant differences for the loss behaviour.

The optimal target length and material should be tuned to fulfill the physics requirements. A 5 mm long target of tungsten is presently assumed for the production of $\Lambda _\mathrm {c}$, in order to increase its production cross section while keeping low detrimental effects (i.e. decay and multiple coulomb scattering in the target volume) [40, 41].

A second crystal ($\mathrm {Cry_2}$) is placed adjacent to the target. The required bending is $\theta _b^{\mathrm {Cry_2}}=14~$mrad, which is needed to send $\Lambda _\mathrm {c}$ decay products inside the LHCb acceptance, while the length is $l^{\mathrm {Cry_2}}=7~\hbox {cm}$, as defined in [9]. Both $\mathrm {Cry_1}$ and $\mathrm {Cry_2}$ are presently considered to be made of silicon, because it is produced with high purity lattice and dislocations below $1/\mathrm {cm^{2}}$. Germanium crystals can feature a similar lattice quality and a deeper potential well, which could improve the single-pass channeling efficiency. However, R&D on bent silicon crystals is much more advanced and they are presently used in the LHC.

Beam halo particles that do not interact with the target+$\mathrm {Cry_2}$ assembly are intercepted by 4 double-sided LHC-type collimators. The first 3 are made of 1 m long carbon-fiber-carbon composite jaws (as the present TCSGs in the LHC), while the last one is made of 1 m long tungsten jaws (as the present TCLAs in the LHC). Nevertheless, this is a performance-oriented choice whose feasibility needs to be discussed later and the number of absorbers needed can be revised as a function of the operational scenario. Parametric studies have been performed by changing the number and material of these absorbers and this configuration has been found to have the best performance with a minimal number of collimators. Their longitudinal position has been defined to optimise the angular cut on protons out-scattered by $\mathrm {Cry_1}$. Protons that acquire an angular deflection $>60~\upmu \hbox {rad}$ by $\mathrm {Cry_1}$ are intercepted, if TCSGs are set at 10 $\sigma$. These local TCSGs cannot be set to tighter settings because of the collimation hierarchy introduced in Sect. 2 that must be respected, i.e. these local TCSGs must have larger aperture than collimators in IR7 (Table 4) to do not interfere with the multi-turn collimation process.

Fig. 3

Proposed experimental layout in IR3. Same notation as in Fig. 2. Normal conducting quadrupoles and dipoles are shown by the light blue and gray boxes, respectively

Table 2 Installation position and main features of the proposed experimental layout in IR3. All the components act on the vertical plane

It is noted that this setup is only on one side of the beam, as initially proposed in [6] and opposed to what proposed in [9]. Effects due to parity violation [42] that can lead to systematic uncertainties, can be addressed with a single crystal deflecting baryons under study. In particular, a single crystal can deflect two distinct fractions of $\Lambda _\mathrm {c}$ with positive and negative polarisation projection on the orthogonal crystallographic plane, as demonstrated in [43]. In any case, this choice has no critical impact on the studies described here and simplifies operational aspects and the overall complexity of the apparatus. Taking into account the multi-turn dynamics, our study indicates that the improvement from doubling the devices by installing them at both sides is minor. If $\mathrm {Cry_1}$ were to be used as primary collimator, it would intercept all particles diffusing out of the core so a second, symmetric apparatus would be useless. For retracted $\mathrm {Cry_1}$ settings the impact was minor for the optics of 2018 studied here. Anyhow, the layout can be easily duplicated if further experimental needs will require it, which can be done just installing mirrored $\mathrm {Cry_1}$+target+$\mathrm {Cry_2}$ without any change of the collimator setup downstream.

The main layout parameters are reported in Table 1.

5 IR3 layout design

The design of the optimised layout in IR3 is shown in Fig. 3. This layout satisfies the constraints discussed in Sect. 3.1, in order to provide optimum operational performance. The main motivation to look for an alternative layout comes from the need to overcome intrinsic limitations that are present in IR8, namely:

• Required bending of $\mathrm {Cry_1}$ and angular cut performed by the absorbers, due to the local optics in proximity of IP8.

• Required bending of $\mathrm {Cry_2}$ to send decay products into the LHCb acceptance.

The IR3 layout consists of a $\mathrm {Cry_1}$ with bending $\theta _b^{\mathrm {Cry_1}}=50~\upmu \hbox {rad}$ and length $l^{\mathrm {Cry_1}}=4~$mm (same parameters are used for crystals presently installed in IR7 for collimation studies [5, 21]). With respect to the layout in IR8, these parameters allow to reduce the nuclear interaction probability in the first crystal from the 1.6 % to the 0.7 %. Combining this reduction with the more effective absorber layout (introduced below), smaller settings of the $\mathrm {Cry_1}$ become accessible, leading to a larger rate of PoT achievable, as discussed in detail in Sect. 6.3.

Table 3 LHC operational parameters in 2018 at End of Squeeze

The same criteria as in IR8 has been used to design the absorber layout, which is made of the same elements. The reduced constraints on longitudinal space available and the smaller $\beta _y(s)$ function with respect to IR8, made possible to better optimise their performance. Using the same TCSGs settings of 10 $\sigma$ the angular cut performed is of about $20~\upmu \hbox {rad}$ (i.e. $\times 3$ smaller than in IR8). This is very important in terms of operational performance, as discussed in Sect. 6.3.

The bending of the second crystal can be significantly reduced, increasing the yield of channeled $\Lambda _\mathrm {c}$ that acquired the desired precession, as further discussed in Sect. 7.

Same considerations as in IR8 apply to the target choice, i.e. 5 mm long tungsten in case of $\Lambda _\mathrm {c}$ studies.

A drift space of about 70 m is present between target+$\mathrm {Cry_2}$ assembly and the first downstream magnet. Thus, a dedicated experimental apparatus could be designed and fit in this available space (with the reconstruction of the $\Lambda _\mathrm {c}$ decay products as main functionality needed).

Same considerations as in IR8 apply on the possibility of a mirrored $\mathrm {Cry_1}$+target+$\mathrm {Cry_2}$ assembly.

Another important difference with respect to the IR8 layout is that the magnets in this insertion are warm, as opposed to the superconducting magnets in IR8. Thus, reduced constraints on sustainable beam loss and relative magnet lifetime due to deposited energy are present in IR3.

A clock-wise orientation in Beam 1 of the layout is adopted because possible debris from the absorbers goes to IR4 (where the RF is placed) rather than to IR2 (where the ALICE experiment is located).

An additional feature of IR3 is that the two beams are in two separated vacuum pipes and do not interfere with each other. Thus, it could be considered to have a mirror layout in Beam 2 that shares a common detector in the 70 m drift space. This will require duplicating the hardware of crystals, target and absorbers but can open the possibility to either perform different studies in the two beams⁴ or double the statistics.

The main layout parameters are reported in Table 2.

6 Machine losses and achievable PoT

An extensive simulation study was carried out to assess comparatively the expected performance of the layouts proposed. Simulations were performed using the tools introduced in Sect. 3.2. The main goal is the evaluation of the loss pattern around the entire LHC ring, to be compared to the present operational configuration. This is very important in order to define a possible operational scenario. In particular, if the loss pattern is not affected by the insertion of the $\mathrm {Cry_1}$+target assembly, it would be possible to perform measurements during standard physics operations. This operational mode is defined as parasitic. On the other hand, if significant amount of losses are induced by the presence of these objects, the maximum loss rate (i.e. maximum stored intensity) that ensures safe and reliable machine operations must be estimated. This operational mode is defined as dedicated.

6.1 Machine configuration

The machine configuration “End of Squeeze” is used for the simulations reported here. At this point of the LHC cycle the optics of the machine is the same as in physics (with colliding beams), but the separation bumps are not yet collapsed. Thus, it is the most critical configuration in terms of available geometrical aperture. The 2018 operational optics and 6.5 TeV/c beams have been used, with main parameters reported in Table 3.

Operational settings for the entire collimation system were used and reported in Table 4.

6.2 Operational performance

An example of simulated loss maps with 2018 operational settings is shown in Fig. 4. Losses on superconducting magnets, warm elements and collimators are indicated as cold, warm and collimator, respectively. It is clearly visible that the Dispersion Suppressor in IR7 (IR7-DS) is the limiting location of the whole ring in terms of cleaning efficiency (i.e. where the highest losses on cold elements are present). Thus, parasitic operations can be envisaged if losses on cold magnets stays below present IR7-DS level after the insertion of the $\mathrm {Cry_1}$+target assembly.

Table 4 LHC collimation settings in 2018, which are expressed in units of RMS beam size ($\sigma$), assuming a gaussian beam distribution and normalised emittance $\varepsilon ^*=3.5~\mu$m

Fig. 4

Simulated beam-loss pattern at End of Squeeze, with 6.5 TeV/c beams in 2018 and operational settings. The whole LHC (a), zoom of the IR7 insertion (b) ($1~\hbox {p} = 1.8\times 10^{-6}~\mathrm {m^{-1}}$)

Fig. 5

Simulated beam-loss pattern for the IR3 layout with $\mathrm {Cry_1}$ at $5~\sigma$. The whole LHC (a), zoom of the IR3 insertion (b) ($1~\hbox {p} = 9.1\times 10^{-7}~\mathrm {m^{-1}}$)

Fig. 6

Simulated beam-loss pattern for the IR8 layout with $\mathrm {Cry_1}$ at $5~\sigma$. The whole LHC (a), zoom of the arc 81 (b) ($1~\hbox {p} = 6.2\times 10^{-7}~\mathrm {m^{-1}}$)

6.3 Expected layouts performance

The beam loss pattern obtained placing $\mathrm {Cry_1}$ at $5~\sigma$ (i.e. same aperture of the TCP in IR7) are shown in Figs. 5 and 6 for the IR3 and IR8 layouts, respectively. The aperture of the local TCSGs and TCLA is $10~\sigma$ and $13~\sigma$, respectively, in order to not interfere with the multi-turn betatron cleaning process.

In principle the IR3 layout would allow parasitic operations during standard LHC operations also with such a tight $\mathrm {Cry_1}$ setting, because the loss pattern in Fig. 5 do not show any peak of cold losses above the threshold defined by Fig. 4b. This is mainly due to the reduced bending and length needed for the $\mathrm {Cry_1}$ and the tighter angular cut performed by the TCSGs in IR3, with respect to the IR8 layout. Thus, less protons experience nuclear interactions in the $\mathrm {Cry_1}$ itself and are intercepted by the TCSGs more efficiently. Indeed, the IR8 layout shows an unacceptable loss pattern, as clearly visible from Fig. 6b, with very high cold losses in the arc 81 (much above the IR7-DS). Studies to understand the source of these losses were performed. Most of them are due to off-momentum protons generated by the interaction with the $\mathrm {Cry_1}$ (i.e. single diffractive events). These protons emerge from the $\mathrm {Cry_1}$ with a deflection that is not enough to be intercepted by the absorbers in IR8 and are lost at the first dispersive peaks because of the momentum offset acquired. Very high losses are also induced on the TCTPs placed in front of IP1 ($\sim \times 200$ larger than operational), with a possible impact on ATLAS background. Thus, it is not possible to use the IR8 layout with $\mathrm {Cry_1}$ at $5~\sigma$ for parasitic operations with full machine. The maximum peak in Fig. 6b is about 10 times larger than in Fig. 4b. Hence, the circulating intensity that would lead to comparable loads on cold elements with respect to standard physics operations, is about 10 times smaller. Meaning that this configuration could be used only in dedicated operations with a maximum of about 250 bunches of $1.1\times 10^{11}$ protons circulating in the machine. Simulations with settings of TCSGs-TCLA in IR8 down to 6–9 $\sigma$ were carried out and no significant changes in the loss pattern was observed. This is because the angular cut performed by the TCSGs in IR8 is not enough to intercept a significant fraction of single diffractive events coming from the $\mathrm {Cry_1}$. This limitation cannot be easily mitigated because of the proximity to IP8, which leads to large $\beta _y$ at the absorbers (i.e. large gap in mm that defines the angular cut). Simulations have been performed moving the absorbers in front of the main quadrupole in cell 6 right of IP8, which provides a much better angular cut thanks to the reduced $\beta _y$ value. However, losses on cold elements and TCTPs upstream of IP1 remain a substantial limitation. Further improvements could be achieved by installing a collimator in a region with enough dispersion to intercept off-momentum protons coming from the $\mathrm {Cry_1}$. This could be obtained by replacing a standard dipole in the IR8-DS with two shorter 11 T dipoles and a collimator between them, or installing a collimator in the empty cryostat of the missing dipole in the IR8-DS, similarly to what adopted in HL-LHC to mitigate losses in IR7 and IR2, respectively [44]. Nevertheless, detailed tracking simulations would be needed to evaluate the expected reduction of losses on cold elements, which are beyond the scope of this paper because either of the two solutions would require a major hardware change in the machine.

Fig. 7

Angular distribution (in the machine reference frame) of impacting protons for different settings of the $\mathrm {Cry_1}$ in IR3

Simulations with $\mathrm {Cry_1}$ settings from $6~\sigma$ to $8~\sigma$ in steps of $1~\sigma$ were also carried out. A significant reduction of losses is obtained with the IR8 layout and a similar loss pattern as standard operational performance, in terms of cold losses, is achieved when $\mathrm {Cry_1}$ is at $6~\sigma$. Thus, parasitic operations with $\mathrm {Cry_1}$ at $6~\sigma$ may be possible from collimation aspects, for the IR8 layout.

Of course, the larger the $\mathrm {Cry_1}$ aperture, the larger the angular distribution of impacting protons, as shown in Fig. 7. This reduces the steering performance of the $\mathrm {Cry_1}$ at increasing aperture. Thus, angular scans of the $\mathrm {Cry_1}$ were simulated in order to find the optimal orientation at each setting, which are reported in Fig. 8. The orientation leading to the maximum channeling efficiency (defined below) was adopted to produce all the results reported here.

Fig. 8

Channeling efficiency as a function of the crystal orientation (in the machine reference frame) for different settings of the $\mathrm {Cry_1}$ in IR3

Let us define the number of PoT as figure of merit to evaluate the system performance. The number of PoT can be estimated as:

$$\begin{aligned} PoT(t)=\frac{1}{2}\frac{I(t)}{\tau }\exp \left( -\frac{t}{\tau }\right) ~\frac{N_{\mathrm{{imp}}}^{\mathrm {Cry_1}}}{N_{\mathrm{{sim}}}}~\varepsilon _{CH}^{\mathrm {Cry_1}}\,, \end{aligned}$$

(3)

Table 5 Fraction of simulated protons that hit $\mathrm {Cry_1}$ in both layouts and relative channeling efficiency, together with integrated PoT in a 10 h fill with 200 h beam lifetime. A total injected intensity of 2556 bunches is considered for all cases, except for the IR8 layout with $\mathrm {Cry_1}$ at $5~\sigma$, where 256 bunches are used as discussed in Sect. 6.3

where $\frac{I(t)}{\tau }\exp (-\frac{t}{\tau })$ is the total beam loss rate for a certain beam lifetime $\tau$ and circulating intensity I(t), $\frac{1}{2}$ is the sharing of the total loss rate between the horizontal and vertical planes [45], $\frac{N_{\mathrm{{imp}}}^{\mathrm {Cry_1}}}{N_{\mathrm{{sim}}}}$ is the fraction of simulated protons that hit the $\mathrm {Cry_1}$, and $\varepsilon _{CH}^{\mathrm {Cry_1}}=\frac{N_{CH}^{\mathrm {Cry_1}}}{N_{\mathrm{{imp}}}^{\mathrm {Cry_1}}}$ is the channeling efficiency of $\mathrm {Cry_1}$ (i.e. fraction of impacting protons trapped between crystalline planes for the entire path in the crystal). In this formalism, the lifetime $\tau$ is used to measure primary beam losses that occur in IR7 (beam particles impinging on the primary collimators). This is a complex function of time that depends on various machine parameters and configuration changes during the collision process. The total intensity I(t) is dominated by the collisions in all experiments⁵ and we approximate it as:

$$\begin{aligned} I(t)=I_{\mathrm{{tot}}}\exp \left( -\frac{t}{\tau _{\mathrm{{BO}}}}\right) \,, \end{aligned}$$

(4)

where $I_{\mathrm{{tot}}}$ is the total stored intensity at the beginning of the fill, while $\exp (-\frac{t}{\tau _{\mathrm{{BO}}}})$ takes into account the intensity decay due to burn-off (with $\tau _{\mathrm{{BO}}}\sim 20$ h [46]). Assuming a conservative beam lifetime of $\tau \sim 200$ h according to usual operational values in 2018 [47], the achievable instantaneous and integrated PoT during one fill are shown in Fig. 9. More aggressive running conditions in terms of dynamic aperture can lead to a reduced beam lifetime and increased losses in IR7, which are normally avoided in order to maximise the number of protons lost by burn-off. The integrated PoT in 10 h (usual fill length during LHC operations) for different $\mathrm {Cry_1}$ settings are reported in Table 5. The maximum $I_{\mathrm{{tot}}}$ stored in 2018 was of 2556 bunches with about $1.1\times 10^{11}$ protons per bunch, which is equivalent to about $2.8\times 10^{14}$ protons injected [47]. This initial intensity is scaled down by a factor 10 for the IR8 layout with $\mathrm {Cry_1}$ setting of $5~\sigma$, as explained previously to allow dedicated operations.

Fig. 9

Instantaneous (a) and integrated (b) PoT in a 10 h fill, for different settings of $\mathrm {Cry_1}$. Expectations for the layouts in IR3 and IR8 are shown by the solid and dashed lines, respectively

In conclusion, the main gain of the IR3 layout is its potential use in parasitic operations for settings of the $\mathrm {Cry_1}$ down to the same aperture of primary collimators in IR7. The expected PoT rate with both layouts becomes similar as soon as the $\mathrm {Cry_1}$ is retracted in the shadow of collimators in IR7. This is because the $\mathrm {Cry_1}$ would intercept secondary halo (or even tertiary, see Fig. 1) that has an angular divergence much larger than the channeling acceptance (i.e. $\sim 2.5~\upmu \hbox {rad}$ at 6.5 TeV/c). Thus, these results could be generalised and represents the expected PoT for any layout that follows the design criteria defined in Sect. 3, and feature a $\mathrm {Cry_1}$ placed in the shadow of IR7 collimators.

7 $\Lambda _\mathrm {c}$ yield performance

Several considerations are required to optimise the yield of $\Lambda _\mathrm {c}$ channeled by $\mathrm {Cry_2}$ and the measurement of their precession. The spin precession angle ($\phi$) of $\Lambda _\mathrm {c}$ in bent crystals is proportional to their bending and energy [3]:

$$\begin{aligned} \phi =\left( 1 + \gamma \, \frac{g-2}{2} \right) \, \theta _b^{\mathrm {Cry_2}}\,, \end{aligned}$$

(5)

where $\gamma =\frac{E}{m}$ with E and m energy and rest mass of the particle, $\theta _b^{\mathrm {Cry_2}}$ is the bending angle of $\mathrm {Cry_2}$ and g the gyromagnetic factor (or dimensionless magnetic moment). Thus, the larger the crystal bending and the $\Lambda _\mathrm {c}$ energy, the larger the induced precession (i.e. the easier its measurement). Bending of the order of mrad is needed to obtain reasonable precision on $\phi$, and hence on the gyromagnetic factor g at LHC energy [9, 40].

Fig. 10

Distribution of $\Lambda _\mathrm {c}$ per 6.5 TeV/c protons on target, obtained using Pythia8.240

Such large bending angles require long crystals with large bending radius (R). Large bending radius are needed because of the critical bending radius $(R_c)$, which is the radius where the potential well between crystalline planes disappears and the channeling regime is no longer possible. In particular, $R_c$ depends linearly on the particle energy (pv) as [48, 49]:

$$\begin{aligned} R_{c}=\frac{pv}{U'_{max}}\,, \end{aligned}$$

(6)

where $U'_{max}$ is the maximum gradient of interplanar electric potential. For the plane (110) in silicon crystal $U'_{max}\approx 6$ GeV/cm, thus for 6.5 TeV/c positively charged particles $R_c\approx 11$ m. This implies an angular acceptance of the channeling process in bent crystals $(\theta _{c}^{b})$ of:

$$\begin{aligned} \theta _{c}^{b}=\theta _{c}\left( 1 -\frac{R_{c}}{R}\right) =\sqrt{\frac{2U_{max}}{pv}}\left( 1 -\frac{R_{c}}{R}\right) \,, \end{aligned}$$

(7)

where $\theta _{c}$ is the critical channeling angle in straight crystals [50] and $U_{max}\approx$ 21.3 eV in Si crystals [51] is the maximum of the potential well between crystalline planes.

On the other hand, the longer the crystal, the higher the probability to experience dechanneling. The dechanneling process can be described as an exponential decay of the initial population of channeled particles, with a decay constant that is linear in particle energy [48]. Thus, when the crystal length becomes comparable to the dechanneling length, a significant fraction on channeled particles will escape from the crystalline planes without acquiring the deflection (i.e. precession) required and will not be in the detector acceptance.

The combined effect of dechanneling and angular acceptance makes a bent crystal behaving as a spectrometer over the energy spectrum of impacting particles. Qualitatively, one can expect a linear increase of efficiency as a function of energy because of the growing dechanneling length, which is followed by a plateau and a new decrease of efficiency due to the reduction of $\theta _{c}^{b}$. Therefore, the smaller the bending angle, the larger the maximum channeling efficiency, while the longer the crystal, the larger the energy range with stable channeling efficiency.

Let us define the channeling efficiency of $\mathrm {Cry_2}$, without considering the $\Lambda _\mathrm {c}$ decay, as:

$$\begin{aligned} \varepsilon _{CH}^{\mathrm {Cry_2}}(E)=\frac{N_{CH}^{\Lambda _\mathrm {c}}(E)}{N_{\mathrm{{imp}}}^{\Lambda _\mathrm {c}}(E)}\,, \end{aligned}$$

(8)

where $N_{CH}^{\Lambda _\mathrm {c}}(E)$ is the number of $\Lambda _\mathrm {c}$ that remain in channeling for the full crystal length, and $N_{\mathrm{{imp}}}^{\Lambda _\mathrm {c}}(E)$ is the number of impacting $\Lambda _\mathrm {c}$.

The distribution of $N_{\mathrm{{imp}}}^{\Lambda _\mathrm {c}}(E)$ was obtained using the Pythia8.240 event generator, starting from the impacting distribution of protons on the target, coming from $\mathrm {Cry_1}$. The distribution of $\Lambda _\mathrm {c}$ obtained for 6.5 TeV/c protons on target is shown in Fig. 10.

Fig. 11

Particle distribution at the target location for the two layouts. Projections of both planes are also reported

Transverse dimensions of $\mathrm {Cry_2}$, compared to the impacting distribution of protons on target, are crucial in order to intercept the maximum number of produced $\Lambda _\mathrm {c}$ (i.e. $\mathrm {Cry_2}$ thickness must be larger than the impacting distribution on target). The particle distributions at the target location for the two layouts are shown in Fig. 11, where the spot due to channeled particles in the $\mathrm {Cry_1}$ is well visible, together with the dechanneled particles that populate the region of intermediate deflections down to the beam core. To be noted that for the IR8 layout, the distribution is shifted because of the local orbit distortion needed to make beams colliding at IP8. A uniform crystal curvature must be ensured for optimal steering performance, which can be achieved respecting the ratio of $\frac{R}{y}\sim 3000$ [52], where R and y are bending radius and crystal thickness, respectively. Thus, $y_\mathrm {{Cry_{2}}}^\mathrm {{IR8}}=2$ mm and $y_\mathrm {{Cry_{2}}}^\mathrm {{IR3}}=5$ mm.

This efficiency must be convoluted with the $\Lambda _\mathrm {c}$ decay inside the crystal. Thus, let us define efficiency of $\Lambda _\mathrm {c}$ channeled by the $\mathrm {Cry_2}$ as:

$$\begin{aligned} \varepsilon _{CH}^{\Lambda _\mathrm {c}}(E)=\varepsilon _{CH}^{\mathrm {Cry_2}} (E)\exp (-l_{\mathrm {Cry_2}}/c\gamma \tau _{\Lambda _\mathrm {c}})\,, \end{aligned}$$

(9)

where $l_{\mathrm {Cry_2}}$ is the length of $\mathrm {Cry_2}$ depending on the layout, while $c\tau _{\Lambda _\mathrm {c}}=59.9\,\, \upmu$m [53] is the decay length of the ${\Lambda _\mathrm{c}}$ baryon.

Fig. 12

Spectrum of $\Lambda _\mathrm {c}$ produced by 6.5 TeV/c protons on target

A further step towards the evaluation of expected $\Lambda _\mathrm {c}$ yield is the convolution with the expected number of PoT and production in the target. The number of $\Lambda _\mathrm {c}$ produced can be calculated as:

$$\begin{aligned} N_{\Lambda _\mathrm {c}}=N_A\rho _{\mathrm{{t}}} l_{\mathrm{{t}}} \sigma (\Lambda _\mathrm {c}) = 0.6\times 10^{-4} \Lambda _\mathrm {c}/p\,, \end{aligned}$$

(10)

where $N_A$, $\rho _{\mathrm{{t}}}$, $l_{\mathrm{{t}}}$ and $\sigma (\Lambda _\mathrm {c})$ are the Avogadro’s number, target density, target length, and total cross section, respectively. In particular $\sigma (\Lambda _\mathrm {c})=10.13~\,\,\upmu \mathrm {b}$ was used for 6.5 TeV impacting protons, as calculated using Pythia8.240. Note that the $\Lambda _\mathrm {c}$ production and decay in the target volume must be taken into account as:

$$\begin{aligned} P_t(E)=\frac{1}{l_{\mathrm{{t}}}}\int _{0}^{l_{\mathrm{{t}}}} \exp (-l/c\gamma \tau _{\Lambda _\mathrm {c}}) dl\,. \end{aligned}$$

(11)

The production spectrum of $\Lambda _\mathrm {c}$ $(S_{\Lambda _\mathrm {c}}(E))$ must be also taken into account and it is shown in Fig. 12.

In conclusion, the yield of $\Lambda _\mathrm {c}$ emerging from $\mathrm {Cry_2}$ that have acquired the desired precession can be expressed as:

$$\begin{aligned} Y_{\Lambda _\mathrm {c}}(E)= N_{\Lambda _\mathrm {c}}P_t(E) S_{\Lambda _\mathrm {c}}(E) \varepsilon _{CH}^{\Lambda _\mathrm {c}}(E)\int _{10h} PoT(t)dt\,. \end{aligned}$$

(12)

Finally, the $Y_{\Lambda _\mathrm {c}}(E)$ for the two layouts proposed and for different operational scenario are shown in Fig. 13, using $\int _{10h} PoT(t)dt$ reported in Table 5.

A factor in the range of 20–140 more integrated $\Lambda _\mathrm {c}$ over the available energy spectrum are expected using the IR3 layout with respect to IR8, with $\mathrm {Cry_1}$ settings from $8~\sigma$ to $5~\sigma$, respectively.

Fig. 13

Expected yield of $\Lambda _\mathrm {c}$ emerging from $\mathrm {Cry_2}$ that acquired the desired precession in 10 h LHC fill as defined in Eq. (12)

The parameters of $\mathrm {Cry_2}$ for the IR3 layout were chosen to ensure:

• Smallest bending angle that lead to measurable precession and clear separation of the expected physics signal with respect to the background [40].

• Largest length that increases as much as possible the energy range of stable channeling efficiency, but avoids channeling of 6.5 TeV/c protons coming from the $\mathrm {Cry_1}$.

The flexibility provided by the IR3 layout allows to optimise these parameters leading to a significant gain with respect to the IR8 layout in terms of $\Lambda _\mathrm {c}$ yield, for every operational configuration and $\mathrm {Cry_1}$ settings considered, as clearly visible from Fig. 13.

The parameters of the $\mathrm {Cry_2}$ for the IR3 layout are consistent with independent estimations of ideal parameters that are based on the minimisation of the uncertainty on the measurement, discussed in [9] and [40]. On the other hand, the work in [9] and [40] does not take into account the constraint of avoiding channeling of 6.5 TeV/c protons coming from the $\mathrm {Cry_1}$. Thus, the parameters defined here represents a compromise between the ideal case and constraints given by real operations in a particle accelerator. Detailed studies on expected uncertainty on measured precession using parameters defined in this paper are reported in [43].

The channeling efficiency of the $\mathrm {Cry_2}$ was also calculated using a parameterization based on the Monte-Carlo simulation of particle propagation through a crystalline lattice, taking into account incoherent scattering on electrons and thermal vibrations of the atoms at lattice nodes [54]. The results are in agreement at the level of few %. An agreement at the level of few % is also present between predictions reported in [55] and in [56], where the tools used in this paper and a yet different simulation approach are used, respectively. In particular, the latter is based on solving the equation of motion for a charged particle interacting with the electric field generated by crystalline lattice accounting also for multiple scattering [57,58,59].

8 Optimised operational scenario

Operations with $\mathrm {Cry_1}$ at $5~\sigma$ are likely to be excluded for both layouts, due to machine protection aspects. On the other hand, the larger the $\mathrm {Cry_1}$ setting, the smaller the expected rate of PoT. Thus, the best compromise between performance and machine protection constraints has to be found. Minimum setting of the $\mathrm {Cry_1}$ has to ensure that:

• 1. It is impossible that $\mathrm {Cry_1}$ becomes the primary collimation stage.

• 2. Local losses are always below safe limits even if the channeling orientation of $\mathrm {Cry_1}$ is lost.

• 3. Local losses are always below safe limits also in the occurrence of beam lifetime drops.

Margins to ensure item 1 are defined by optics errors and orbit stability. Optics corrections in the LHC ensure a peak $\delta \beta /\beta <10\%$ [60, 61], which corresponds to a $5\%$ error on beam size. Thus, $\mathrm {Cry_1}$ cannot be set below $5.5~\sigma$ if TCPs in IR7 are set at $5~\sigma$. However, this margin can be reduced by performing a beam-based alignment of the $\mathrm {Cry_1}$ with respect to the TCPs, because the eventual $\delta \beta /\beta$ will no longer change after optics correction are deployed. Nevertheless, fill-to-fill orbit stability and reproducibility are also in the range of $<100~\upmu$m [62, 63], which is also of the order of $0.5~\sigma$ at $\mathrm {Cry_1}$ locations. Thus, a lower limit of $5.5~\sigma$ for $\mathrm {Cry_1}$ setting is defined for the machine configuration taken into account.

Fig. 14

Expected instantaneous (a) and integrated (b) PoT for both layouts with $\mathrm {Cry_1}$ at $5.5~\sigma$ during a 10 h fill

Regarding item 2, losses around the ring are below safe limits for both layouts with $\mathrm {Cry_1}$ at $5.5~\sigma$. The reduced rate of primary protons on the $\mathrm {Cry_1}$ can make possible running with less absorbers (i.e. only one TCSG and one TCLA locally) for the IR3 layout. Thus, less collimators and relative infrastructure would be needed with a following cost reduction. However, energy deposition simulations are needed for a final assessment of loads on local collimators and magnets, which will be used to define the material budget needed to safely absorb the deflected halo by the $\mathrm {Cry_1}$. Simulations were carried out also with $\mathrm {Cry_1}$ in amorphous orientation, i.e. behaving as a scatterer made of silicon, which do not show any anomaly in the loss pattern.

Finally, item 3 is fulfilled by the fact that with $\mathrm {Cry_1}$ at $5.5~\sigma$, the load on crystal and absorbers ensures that local losses will be on the shadow of IR7 losses in the case of lifetime drops, without triggering spurious dumps or inducing a magnet quench. Nevertheless, thresholds on allowed local losses before triggering a beam dump request must be carefully evaluated based on energy deposition simulations.

In conclusion, no show-stopper has been identified for parasitic operations with full machine for both layouts with $\mathrm {Cry_1}$ at $5.5~\sigma$. Nevertheless, additional loss clusters with respect standard operations are visible for the layout in IR8 and will need to be addressed with energy deposition simulations, together with the expected increase of background to the ATLAS experiment due to a larger load on the upstream TCTPs.

Table 6 Fraction of simulated protons that hit the $\mathrm {Cry_1}$ at $5.5~\sigma$ in both layouts and relative channeling efficiency, together with integrated PoT in a 10 h fill with 200 h beam lifetime. A total injected intensity of 2556 bunches with $1.1\times 10^{11}$ protons per bunch is considered

The achievable instantaneous and integrated PoT during one fill are shown in Fig. 14. A summary is reported in Table. 6.

The expected $Y_{\Lambda _\mathrm {c}}(E)$ for parasitic operations of both layouts with full machine and $\mathrm {Cry_1}$ at $5.5~\sigma$ are shown in Fig. 15. About a factor 20 more integrated $\Lambda _\mathrm {c}$ over the available energy spectrum are expected using the IR3 layout with respect to IR8.

9 Margins for improvements and further constraints

Margins for improvements and further constraints are present, but are out of the scope of this paper and are reported as an overview of possible future studies.

An increased target length with the use of germanium crystals can lead to a larger production of $\Lambda _\mathrm {c}$ and channeling efficiency, respectively. Increasing the target length from 5 mm to 40 mm and using germanium crystals can reduce the data taking time by a factor 6 and 2.4, respectively, as discussed in [43]. This is mainly due to the increased total $\Lambda _\mathrm {c}$ production in the target while keeping low detrimental effects (i.e. $\Lambda _\mathrm {c}$ decay in the target and hadronic showers production), together with an increased $\mathrm {Cry_2}$ channeling efficiency due to the deeper potential well in germanium with respect to silicon. Local losses induced by the 5 mm long tungsten target considered in this paper are negligible, but the effect of thicker targets needs to be addressed.

A factor 2 in bunch intensity is expected if running in the HL-LHC scenario, which is directly translated in a factor 2 larger PoT rate with respect to what considered in previous sections. Moreover, the selective excitation of bunch trains in the vertical plane could lead to larger flux of particles on $\mathrm {Cry_1}$, thus increasing the PoT. However, this beam excitation is made through white noise [64] leading to an emittance blow up that will induce a reduction of luminosity in the main experiments. Thus, a compromise between the acceptable loss of luminosity and required increase of PoT will need to be found.

Fig. 15

Expected yield of $\Lambda _\mathrm {c}$ emerging from the $\mathrm {Cry_2}$ that acquired the desired precession in 10 h LHC fill with the $\mathrm {Cry_1}$ at $5.5~\sigma$

Additional constraints can come from failure scenarios and optics corrections in HL-LHC. For example, crab-cavities failures can induce large bunch oscillations/rotations [65]. Thus, a significant fraction of mis-kicked bunches can be intercepted and potentially channeled by $\mathrm {Cry_1}$. Hence, an additional safety margin with respect to TCPs in IR7 must be computed, which can be larger than the $0.5~\sigma$ considered above. Optics corrections in the HL-LHC are assumed to ensure a peak $\delta \beta /\beta <20\%$ [66], which corresponds to $\sim 10\%$ error on beam size. On the other hand, hollow electron lens (HEL) may be installed in HL-LHC [67,68,69], which will be used for an active control of beam tails. The presence of HEL will mitigate losses on the primary aperture during failure scenarios, possibly allowing for similar safety margin of $0.5~\sigma$. Nevertheless, the impact on the expected performance due to the reduced population and increased diffusion speed of the beam halo that is generated by the HEL must be evaluated.

Constraints can come also from possible damages to the detectors. The LHC collimation system is designed to withstand the failure scenario of beam lifetime drops down 0.2 h for 10 s. With LHC operational settings in 2018, $\mathrm {Cry_1}$ at $5.5~\sigma$ and 200 h of beam lifetime an average PoT rate of about $10^6$ p/s is expected, as shown in Fig. 14a. Thus, a lifetime of 0.2 h will directly translates in to PoT rate of about $10^9$ p/s. A beam dump request is triggered by LHCb if dangerous events rate are approached. Thus, no damages should be caused but energy deposition simulations are needed to asses this limit in LHCb, to set appropriate margins on sustainable PoT rate during operations and failure scenarios. The layout flexibility in IR3 may allows a detector design capable to withstand higher events rate.

The LHCb experiment is operated at leveled luminosity. The leveling is performed reducing the separation bump in steps. The separation plane in LHCb is vertical. All the components of the proposed layout are also in the vertical plane, and within the separation bump. Thus, dynamic changes of settings (in mm, not in $\sigma$) may be needed during the physics data taking to follow closed-orbit movements. As opposed to IR8, in IR3 everything is frozen once arrived at top energy and the data taking can be carried out in static conditions.

Last but not least, impedance aspects associated with the operation of the crystals at high intensity and with the presence of additional collimators around the ring need to be studied. In particular for the IR8 layout, where all the divices are installed near IP8 and beams share a common pipe.

10 Conclusions

Two possible layouts for fixed-target experiments and dipole moment measurements of short-lived baryons at the LHC were presented. They can provide the unique opportunity of having multi-TeV fixed-target experiments without the need for a new dedicated extraction line at the LHC, and would allow the first direct measurement of the charmed baryon electric and magnetic dipole moments.

Both designs were optimised in order to maximise the number of deliverable PoT, while keeping the losses on superconducting magnets below limits tolerable for standard LHC operations. IR8 would be a natural choice to place this experiment, to profit of the presence of the LHCb detector. On the other hand, the particular features of this insertion pose several constraints on the achievable rate of PoT that cannot be easily overcome. Thus, an alternative layout placed in the momentum cleaning insertion IR3 was studied, showing an increase of achievable yield of $\Lambda _\mathrm {c}$ of at least a factor 20 with respect to IR8. For this scenario, a dedicated detector should be built in IR3, for which about 70 m of longitudinal space are available.