On the importance of NNLO QCD and isospin-breaking corrections in $\varepsilon '/\varepsilon$

Abstract

Following the 1999 analysis of Gambino, Haisch and one of us, we stress that all the recent NLO analyses of $\varepsilon '/\varepsilon$ in the Standard Model (SM) suffer from the renormalization scheme dependence present in the electroweak penguin contributions as well as from scale uncertainties in them related to the matching scale $\mu _W$ and in particular to $\mu _t$ in $m_t(\mu _t)$. We also reemphasize the important role of isospin-breaking and QED effects in the evaluation of $\varepsilon '/\varepsilon$. Omitting all these effects, as done in the 2015 analysis by RBC-UKQCD collaboration, and choosing as an example the QCD penguin ($Q_6$) and electroweak penguin ($Q_8$) parameters $B_6^{(1/2)}$ and $B_8^{(3/2)}$ to be $B_6^{(1/2)}= 0.80 \pm 0.08$ and $B_8^{(3/2)}= 0.76 \pm 0.04$ at $\mu = m_c=1.3\,\, \text {GeV}$, we find $(\varepsilon '/\varepsilon )_\mathrm{SM} = (9.4 \pm 3.5) \times 10^{-4}$, whereas including them results in $(\varepsilon '/\varepsilon )_\mathrm{SM} = (5.6\pm 2.4)\times 10^{-4}$. This is an example of an anomaly at the $3.3\,\sigma$ level, which would be missed without these corrections. NNLO QCD contributions to QCD penguins are expected to further enhance this anomaly. We provide a table for $\varepsilon '/\varepsilon$ for different values of $B_6^{(1/2)}$ and the isospin-breaking parameter ${\widehat{\Omega }}_\text {eff}$, that should facilitate monitoring the values of $\varepsilon '/\varepsilon$ in the SM when the RBC-UKQCD calculations of hadronic matrix elements including isospin-breaking corrections and QED effects will improve with time.

1 Introduction

The direct CP-violation in $K\rightarrow \pi \pi$ decays, represented by the ratio $\varepsilon '/\varepsilon$, plays a very important role in the tests of the Standard Model (SM) and more recently in the tests of its possible extensions [1]. In the SM $\varepsilon '/\varepsilon$ is governed by QCD penguins (QCDP) but receives also an important contribution from the electroweak penguins (EWP), pointed out already in 1989 [2, 3], that entering $\varepsilon '/\varepsilon$ with the opposite sign to QCDP suppress this ratio significantly. The partial cancellation of these two contributions in addition to the significant uncertainties in the evaluation of the hadronic matrix elements of QCDP and EWP operators is the reason why until today a precise prediction for $\varepsilon '/\varepsilon$ in the SM is still missing.

The situation of $\varepsilon '/\varepsilon$ in the SM by the end of 2017 could be briefly summarized as follows:

• The analysis of $\varepsilon '/\varepsilon$ by the RBC-UKQCD lattice QCD (LQCD) collaboration based on their 2015 results for $K\rightarrow \pi \pi$ matrix elements [4, 5], as well as the analyses performed in [6, 7] that are based on the same matrix elements but also include isospin breaking effects [8, 9], found $\varepsilon '/\varepsilon$ in the ballpark of $(1-2) \times 10^{-4}$. This is by one order of magnitude below the experimental world average from NA48 [10] and KTeV [11, 12] collaborations,

  $$\begin{aligned} (\varepsilon '/\varepsilon )_\text {exp}&= (16.6 \pm 2.3) \times 10^{-4} \,. \end{aligned}$$

  (1)

  However, with an error in the ballpark of $5 \times 10^{-4}$ obtained in these analyses, one could talk about an $\varepsilon '/\varepsilon$ anomaly of at most $3\,\sigma$. Simultaneously, we note that the 2015 RBC-UKQCD result for the $\pi \pi$-strong-interaction phase $\delta _0$ of the isospin $I = 0$ amplitude is in almost $3\,\sigma$ conflict with the result from extrapolations in the chiral limit [13]. This suggests that there were methodical problems with the 2015 RBC-UKQCD calculation, which were meanwhile successfully addressed, as will be reported later. As a conclusion, one has to be aware that for $I = 0$ the $K\rightarrow \pi \pi$ matrix elements, represented mainly by the parameter $B_6^{(1/2)}$, and hence also the 2015 RBC-UKQCD result for $\varepsilon '/\varepsilon$ suffer from an unaccounted systematic uncertainty.

• An independent analysis based on hadronic matrix elements from the Dual QCD (DQCD) approach [14, 15] gave a strong support to the 2015 RBC-UKQCD result and moreover provided an upper bound on $\varepsilon '/\varepsilon$ in the ballpark of $6\times 10^{-4}$. However, in this approach the treatment of $\pi \pi$ strong interaction phases is presently problematic.

• Chiral perturbation theory (ChPT) together with large-N considerations¹ are used in [17], leading to a SM prediction of $\varepsilon '/\varepsilon = (15 \pm 7) \times 10^{-4}$. The uncertainties are larger than in [6, 7], reflecting in part the difficulties in matching long-distance and short-distance contributions in this framework, but are also of parametric origin due to low-energy constants. Consequently, the predicted central value is one order of magnitude larger compared to DQCD and lattice results of 2015, but with a small tension of $1.6\,\sigma$ in view of the large uncertainties.

Recently progress towards an improved estimate of $\varepsilon '/\varepsilon$ in the SM has been made:

• The RBC-UKQCD collaboration is expected to present this year new values of the $K\rightarrow \pi \pi$ hadronic matrix elements, most importantly the parameter $B_6^{(1/2)}$. In particular the discrepancy in the prediction of the $\pi \pi$-strong-interaction phase $\delta _0$ has been identified [18,19,20,21] in the form of excited-state contamination requiring the introduction of additional $\pi \pi$ operators in the simultaneous fits to allow for a better isolation of the ground state. It can be expected that the statistical errors will decrease, though less dramatically as assumed before due to the additional operators. Unfortunately, the inclusion of isospin-breaking and QED effects will still take more time.

• An improved estimate of isospin-breaking corrections to $\varepsilon '/\varepsilon$ has been presented in [22] increasing moderately the role of these corrections in suppressing $\varepsilon '/\varepsilon$. The updated ChPT analysis [22] resulted in the value

  $$\begin{aligned} (\varepsilon '/\varepsilon )_\text {ChPT}&= (14 \pm 5) \times 10^{-4} \,, \qquad (\text {ChPT}-2019), \end{aligned}$$

  (2)

  in full agreement with the experimental world average(1).

• The preliminary result on NNLO QCD corrections to QCDP contributions [23, 24] demonstrates significant reduction of various scale uncertainties, foremost of $\mu _c$, and indicates an additional modest suppression of $\varepsilon '/\varepsilon$.

In contrast to the expected RBC-UKQCD result, the ChPT analysis includes isospin-breaking and QED corrections but the known difficulties in matching long-distance and short-distance contributions in this approach imply a large uncertainty. In particular, the absence of the so-called meson evolution in ChPT that suppresses $\varepsilon '/\varepsilon$ within the DQCD approach [15, 16] is responsible for the poor matching and according to the latter authors responsible in part for the large value of $\varepsilon '/\varepsilon$ in (2). The DQCD analysis in [25] demonstrates through the example of BSM matrix elements in $K^0-{\overline{K}}^0$ mixing that the effects of meson evolution are included in the present LQCD calculations. As shown in [25], neglecting this evolution in the case of $K^0-{\overline{K}}^0$ mixing would miss the values of the relevant hadronic matrix elements by factors of $2-4$, totally misrepresenting their values obtained by three LQCD collaborations [26,27,28,29,30]. The fact that in $K^0-{\overline{K}}^0$ mixing the FSI are absent allows to study the impact of meson evolution better than it is possible in $K\rightarrow \pi \pi$ decays. Yet, as demonstrated in [14, 15] these important QCD dynamics must also be present in $K\rightarrow \pi \pi$ and is also required by the proper matching of long-distance and short-distance contributions. Therefore it is expected to suppress the result for $\varepsilon '/\varepsilon$ in (2).

Now all the 2015 analyses of $\varepsilon '/\varepsilon$ and the one in [22] used the known Wilson coefficients at the NLO level [31,32,33,34,35,36] in the naive dimensional regularization (NDR) scheme [37]. But already in [38] and recently in [16, 39] it has been pointed out that without NNLO QCD corrections to the EWP contribution the results for $\varepsilon '/\varepsilon$ are renormalization-scheme dependent and exhibit significant non-physical dependences on the scale $\mu _t$ at which the top-quark mass $m_t(\mu _t)$ is evaluated as well as on the matching scale $\mu _W$.

Fortunately, all these uncertainties have been significantly reduced in the NNLO matching at the electroweak scale performed in [38] and it is of interest to look at them again in the context of new analyses with the goal to improve the present estimate of $\varepsilon '/\varepsilon$. Additional importance in such an analysis is the finding in [38] that these corrections further suppress $\varepsilon '/\varepsilon$ relative to the NLO results performed in the NDR scheme.

In view of the fact that LQCD calculations contain both the meson evolution and FSI, the optimal strategy for the evaluation of $\varepsilon '/\varepsilon$ as of 2019 appears to be as follows:

• 1. Use future RBC-UKQCD results for hadronic matrix elements of the dominant QCDP ($Q_6$) and EWP ($Q_8$) operators, represented by the parameters $B_6^{(1/2)}$ and $B_8^{(3/2)}$, respectively—with improved values of $\pi \pi$-strong-interaction phases $\delta _{0,2}$—but determine hadronic matrix elements of $(V-A)\otimes (V-A)$ operators from the experimental data on the real parts of the $K\rightarrow \pi \pi$ amplitudes as done in [6, 34].

• 2. Use the result for isospin-breaking and QED corrections from [22], which are compatible with the ones obtained already 30 years ago in [40].

• 3. Use the NNLO QCD contributions to EWP in [38] in order to reduce the unphysical renormalization scheme and scale dependences.

• 4. Include NNLO QCD contributions to QCDP from [23, 24] in order to reduce left-over renormalization scale uncertainties.

In view of the fact that meson evolution and the remaining three effects tend to suppress $\varepsilon '/\varepsilon$, whereas the aforementioned systematic uncertainties in the 2015 RBC-UKQCD calculation of $B_6^{(1/2)}$ related to FSI effects discussed before in connection with $\delta _0$ could tend to increase it, as does FSI in the case of ChPT, it could well happen that future LQCD predictions of $\varepsilon '/\varepsilon$ in the SM increase only moderately to end up in or a bit above the ballpark $\varepsilon '/\varepsilon \approx (5\pm 2) \times 10^{-4}$ of the expectation based on the DQCD approach in [16].

The main goal of our paper is to illustrate how a future result from RBC-UKQCD would be affected by the inclusion of known isospin-breaking and QED corrections from [22] in point 2. and the NNLO QCD contributions to EWP in [38] in point 3. We also comment on the expected size of NNLO QCD contributions to QCDP from [23, 24] in point 4. leaving a detailed analysis of them to these authors.

Our paper is organized as follows. In Sect. 2 we recall a number of basic formulae that will be used in the rest of our paper. In Sect. 3 we address the issue of scale and renormalization scheme dependences at the NLO level resulting from the EWP sector. We illustrate the size of these unphysical effects present at the NLO level that would increase the errors quoted in the existing NLO analyses but are significantly reduced when NNLO QCD corrections to EWP contributions from [38] are taken into account. To this end we use first as an example particular values for the hadronic parameters $B_6^{(1/2)}$ and $B_8^{(3/2)}$ quoted in the abstract of our paper and quantify also the role of isospin-breaking and QED corrections from [22]. As the values of $B_6^{(1/2)}$ and the size of isospin-breaking corrections are expected to dominate the theoretical uncertainties in $\varepsilon '/\varepsilon$ for some time, we present in Sect. 4 a table of the SM values of $\varepsilon '/\varepsilon$ for different $B_6^{(1/2)}$ and the isospin-breaking parameter ${\widehat{\Omega }}_\text {eff}$ that should facilitate monitoring the SM estimates of $\varepsilon '/\varepsilon$ when the LQCD calculations of hadronic matrix elements including isospin-breaking corrections and QED effects will improve with time. A brief summary and an outlook are given in Sect. 5.

2 Basic formulae

2.1 An analytic formula

As in [6], our starting expression is the formula

$$\begin{aligned} \frac{\varepsilon '}{\varepsilon }&= -\,\frac{\omega _+}{\sqrt{2}\,|\varepsilon _K|} \left[ \, \frac{{{\,\mathrm{Im}\,}}A_0}{{{\,\mathrm{Re}\,}}A_0}\, (1 - {\widehat{\Omega }}_\text {eff}) - \frac{1}{a} \, \frac{{{\,\mathrm{Im}\,}}A_2}{{{\,\mathrm{Re}\,}}A_2} \,\right] , \end{aligned}$$

(3)

where [9, 22]

$$\begin{aligned} \omega _+&= a\,\frac{{{\,\mathrm{Re}\,}}A_2}{{{\,\mathrm{Re}\,}}A_0} = (4.53 \pm 0.02) \times 10^{-2}, \nonumber \\ a&= 1.017,{\widehat{\Omega }}_\text {eff}= (17.0\pm 9.1) \times 10^{-2} \,. \end{aligned}$$

(4)

Here a and ${\widehat{\Omega }}_\text {eff}$ summarize isospin-breaking corrections and include strong isospin violation $(m_u \ne m_d)$, the correction to the isospin limit coming from $\Delta I=5/2$ transitions and electromagnetic corrections as first summarized in [8, 9] and recently updated in [22]. Our ${\widehat{\Omega }}_\text {eff}$, defined by

$$\begin{aligned} {\widehat{\Omega }}_\text {eff}&\equiv \Omega _\text {IB} - \Delta _0|_{\alpha = 0} - f_{5/2} \,, \end{aligned}$$

(5)

differs from $\Omega _\text {eff}$ in [8, 9, 22] as in contrast to these papers it does not include EWP contributions to ${{\,\mathrm{Im}\,}}A_0$, summarized in these papers by $\Delta _0$. This is indicated here by $\Delta _0|_{\alpha = 0}$, which contains the remaining contributions only. We find it more natural to calculate ${{\,\mathrm{Im}\,}}A_0$ including both QCD and EWP contributions as this allows to keep track of NP contributions to ${{\,\mathrm{Im}\,}}A_0$. The dominant EWP contribution to $\varepsilon '/\varepsilon$ is of course present in ${{\,\mathrm{Im}\,}}A_2.$ In fact the RBC-UKQCD collaboration includes EWP contributions to ${{\,\mathrm{Im}\,}}A_0$ as well. We note also that the latest central value for $\Omega _\text {IB} = 0.25 \pm 0.08$ from [22] agrees perfectly with the one obtained already 30 years ago in [40].

The real parts of the isospin amplitudes $A_{0,2}$ in (3) are then extracted from the branching ratios on $K\rightarrow \pi \pi$ decays in the isospin limit. In the limit $a = 1$ and ${\widehat{\Omega }}_\text {eff}= 0$ the formula in (3) reduces to the one used in RBC-UKQCD [4, 5], where all isospin-breaking corrections except for EWP contributions at the NLO level have been set to zero.

Using the technology in [6] we arrive at the formula

$$\begin{aligned}&\frac{\varepsilon '}{\varepsilon } = {{\,\mathrm{Im}\,}}\lambda _t \cdot \left[ a (1 - {\widehat{\Omega }}_\text {eff}) \left( a_0^{(1/2)} + a_6^{(1/2)} B_6^{(1/2)}\right) \right. \nonumber \\&\quad \left. - a_0^{(3/2)} - a_8^{(3/2)} B_8^{(3/2)}\right] \,, \end{aligned}$$

(6)

with the coefficients $a_{0,6}^{(1/2)}$ and $a_{0,8}^{(3/2)}$ given in Table 1 at NLO and NNLO from EWPs as discussed below. Explicit formulae for $a_{0,6}^{(1/2)}$ and $a_{0,8}^{(3/2)}$ in terms of Wilson coefficients and ${{\,\mathrm{Re}\,}}A_{0,2}$ are given in [6]. The values of the Wilson coefficients used by us are collected in Appendix A, whereas $\lambda _t = V_{td}^{} V^*_{ts}$ is the relevant CKM combination.

Table 1 Coefficients entering the semi-numerical formula of (6)

2.2 The parameters $B_6^{(1/2)}$ and $B_8^{(3/2)}$

The $B_6^{(1/2)}$ and $B_8^{(3/2)}$ parameters, that enter the formula (6), are defined as follows

$$\begin{aligned} \langle Q_6(\mu ) \rangle _0&= -\,4 h \left[ \frac{m_K^2}{m_s(\mu ) + m_d(\mu )}\right] ^2 (F_K - F_\pi ) \,B_6^{(1/2)}\nonumber \\&= -0.473\, h B_6^{(1/2)}\, \text {GeV}^3 \,, \end{aligned}$$

(7)

$$\begin{aligned} \langle Q_8(\mu ) \rangle _2&= \sqrt{2} h \left[ \frac{m_K^2}{m_s(\mu ) + m_d(\mu )} \right] ^2 F_\pi \,B_8^{(3/2)}\,\nonumber \\&= 0.862\, h B_8^{(3/2)}\, \text {GeV}^3 \,, \end{aligned}$$

(8)

with [40, 41]

$$\begin{aligned} B_6^{(1/2)}&= B_8^{(3/2)}= 1\,, \end{aligned}$$

(9)

in the large-N limit. The dimensionful parameters entering (7), (8) have been calculated at $\mu = m_c$ using [42]

$$\begin{aligned} m_K&= 497.614 \, \text {MeV}, F_\pi = 130.41(20) \, \text {MeV}, \nonumber \\ \frac{F_K}{F_\pi }&= 1.194(5) \,, \end{aligned}$$

(10)

$$\begin{aligned} m_s(m_c)&= 109.1(2.8) \, \text {MeV}, \nonumber \\ m_d(m_c)&= 5.44(19) \, \text {MeV}\,. \end{aligned}$$

(11)

We have introduced the factor h in order to emphasize different normalizations of these matrix elements present in the literature. For instance RBC-UKQCD and [6] use $h=\sqrt{3/2}$, while [14, 15, 17, 22] use $h = 1$.

As an example we will first use the values

$$\begin{aligned} B_6^{(1/2)}(m_c)&= 0.80\pm 0.08 ,&B_8^{(3/2)}(m_c)&= 0.76\pm 0.04 , \end{aligned}$$

(12)

to be compared with the 2015 values $B_6^{(1/2)}(m_c) = 0.57 \pm 0.19$ and $B_8^{(3/2)}(m_c) = 0.76 \pm 0.05$ from RBC-UKQCD [4, 5].

While we do not expect significant modification of the RBC-UKQCD result for $B_8^{(3/2)}$ through the improvements on FSI, taking the arguments on the impact of FSI on $B_6^{(1/2)}$ from ChPT into account [22], we allow for an enhancement of $B_6^{(1/2)}$, which however is still consistent with the arguments in [15] that the suppression of $B_6^{(1/2)}$ by meson evolution below unity is stronger than its enhancement by FSI. We emphasize that the choice of $B_6^{(1/2)}$ in (12) is only an example. Other examples will be presented in Sect. 4, where also values of $B_6^{(1/2)}>1.0$, in the spirit of [22], are considered. We anticipate a significant reduction of the error on $B_6^{(1/2)}$ in the new results of RBC-UKQCD collaboration relative to its 2015 analysis so that the expectations from [15] and [22] will be tested.

3 Scale uncertainties at NLO

It should be emphasized that although the NLO QCD analyses of $\varepsilon '/\varepsilon$ in [31,32,33,34,35,36] reduced renormalization scheme dependence in the QCDP sector, the dependence of $\varepsilon '/\varepsilon$ on the choice of $\mu _t$ in $m_t(\mu _t)$ remained. This dependence can only be removed through the NNLO QCD calculations, but in the QCDP sector it is already weak at the NLO level because of the weak dependence of the QCDP contributions on $m_t$. On the other hand, as pointed out already in [38], the EWP contributions at the NLO level suffer from a number of unphysical dependences.

• First of all there is the renormalization-scheme dependence with $\varepsilon '/\varepsilon$ in the HV scheme, as used in [35, 36], generally smaller than in the NDR scheme used in [31,32,33,34]. In what follows we will consider only the NDR scheme as this is the scheme used by the RBC-UKQCD collaboration and other analyses listed above.

• The dependence on $\mu _t$, which is much larger than in the QCDP sector because the EWP contributions exhibit much stronger dependence on $m_t$. Increasing $\mu _t$ makes the value of $m_t$ smaller, decreasing the EWP contribution and thereby making $\varepsilon '/\varepsilon$ larger. At NLO there is no QCD correction that could cancel this effect.

• The dependence on the choice of the matching scale $\mu _W$. It turns out that with increasing $\mu _W$ in the EWP contribution, the value of $\varepsilon '/\varepsilon$ decreases.

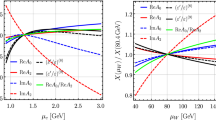
One should note that the scales $\mu _W$ and $\mu _t$ can be chosen to be equal or different and they could be varied independently in the ranges illustrated in Fig. 1 implying significant uncertainties in the NLO prediction for $\varepsilon '/\varepsilon$ as demonstrated in [38]. In obtaining the values in Table 1 we provide the two settings from [38]: i) $\mu _W = \mu _t = m_W$ as well as ii) $\mu _W = m_W$ and $\mu _t = m_t$. For example ii) has been used in [6]. Other choices of these scales would significantly change the NLO values of $\varepsilon '/\varepsilon$ with significantly reduced change when NNLO corrections to EWPs are included.

We next evaluate $\varepsilon '/\varepsilon$ for the values of $B_6^{(1/2)}$ and $B_8^{(3/2)}$ given in (12) and

• set $\mu _W = m_W$ and $\mu _t = m_t$ in the NLO formulae in the NDR scheme,

• set ${\widehat{\Omega }}_\text {eff}= 0.0$,

as done by RBC-UKQCD. This results at NLO in

$$\begin{aligned} (\varepsilon '/\varepsilon )_{\text {NLO},\, {\widehat{\Omega }}_\text {eff}= 0.0}&= (9.4 \pm 3.5) \times 10^{-4} \,, \end{aligned}$$

(13)

that is a value by a factor of 7 larger than the 2015 result from the RBC-UKQCD collaboration. The quoted error is a guess estimate based on the uncertainties in (12) and scale uncertainties as well as omission of isospin-breaking effects ignoring the known signs of these effects. But as we will see soon its precise size is irrelevant for the point we want to make. The result in (13) is compatible with experiment (1) with a tension of $1.7\,\sigma$.

At first sight it would appear that this result confirms the claims in [17] and [22] as (13) is quite consistent with (2). But such a conclusion would be false as we will illustrate now.

Indeed as stated above at the NLO level significant dependences on $\mu _W$ and $\mu _t$ are present and the impact of a non-vanishing ${\widehat{\Omega }}_\text {eff}$ is very significant. In order to exhibit these dependences we vary in Fig. 1 the matching scale $\mu _W$ independently of the scale $\mu _t$ at which the top-quark mass $m_t(\mu _t)$ is evaluated and plot $\varepsilon '/\varepsilon$ versus $\mu _t$ for the three values of $\mu _W = \{60,\, 80,\, 120\}\,$GeV. We show these dependences both for ${\widehat{\Omega }}_\text {eff}= 0.0$ [green] and ${\widehat{\Omega }}_\text {eff}= 0.17$ [blue]. They are very significant.

Fortunately all these uncertainties have been significantly reduced in the NNLO matching at the electroweak scale performed in [38]. In the NDR scheme, used in all recent analyses, these corrections enhance for (i) $\mu _W = \mu _t = m_W$ the EWP contribution by roughly $7\,\%$ and for (ii) $\mu _W = m_W$ and $\mu _t=m_t$ by $16\,\%$. Thereby they imply a negative shift in $\varepsilon '/\varepsilon$ that depends on $B_8^{(3/2)}$ and ${{\,\mathrm{Im}\,}}\lambda _t$ and in fact, as just stated and evident from Fig. 1 on the chosen values of $\mu _t$ and $\mu _W$ in the NLO expressions. Including NNLO QCD corrections in question and using ${\widehat{\Omega }}_\text {eff}$ in (4) the result in (13) is changed to

$$\begin{aligned} \varepsilon '/\varepsilon&\, = (5.6 \pm 2.4) \times 10^{-4} \,, \end{aligned}$$

(14)

which compared with the experimental value in (1) signals an anomaly at the level of $3.3\,\sigma$. In Table 2 below, we have set ${{\,\mathrm{Im}\,}}\lambda _t = 1.4 \times 10^{-4}$. For the result in (13) and (14) we have used ${{\,\mathrm{Im}\,}}\lambda _t = (1.43\pm 0.04) \times 10^{-4}$, based on recent analyses of the unitarity triangle by the bayesians (“UTfitter”) and frequentists (“CKMfitter”) that can be found in [43] and [44], respectively.

Fig. 1

The dependence of $\varepsilon '/\varepsilon$ for $B_6^{(1/2)}= 0.80$ on the scale $\mu _t$ of $m_t(\mu _t)$ for three values of the matching scale $\mu _W = \{60,\, 80,\, 120\}\,$GeV [dotted, red, dashed] for ${\widehat{\Omega }}_\text {eff}= 0.0$ [green] and ${\widehat{\Omega }}_\text {eff}= 0.17$ [blue]. The black dots show the NNLO result for ${\widehat{\Omega }}_\text {eff}= 0.17$ at these scales $\mu _t$ from [38] with interpolation shown by the dashed line. We set $B_8^{(3/2)}=0.76$

The error budget, discussed in Appendix B and summarized in Table 6, would imply the parametric theoretical error of $2.3\times 10^{-4}$. We increased it in order to take into account left-over scale uncertainties both in the EWP sector discussed here and in the QCDP sector analyzed at NNLO in [23, 24]. But one should keep in mind that the central value in (14) will be shifted down by NNLO QCD corrections to QCDP by about $0.5\times 10^{-4}$ as indicated in the preliminary plots in [23, 24] without modifying the error in (14). We are looking forward to the final results of these authors.

Table 2 The ratio $10^4 \times \varepsilon '/\varepsilon$ at NNLO for different values of the isospin corrections ${\widehat{\Omega }}_\text {eff}$ and the parameter $B_6^{(1/2)}(m_c)$ with more details in Appendix B and fixed value of $B_8^{(3/2)}= 0.76$ and ${{\,\mathrm{Im}\,}}\lambda _t = 1.4 \times 10^{-4}$. In the first three rows we provide for comparison the NLO result for $\mu _t = 300\,$GeV (A), $\mu _t = m_t$ (B) and $\mu _t = m_W$ (C), respectively

Our NNLO central value in (14), represented in Fig. 1 by the black points at $\mu _t = \{m_W,\, m_t,\, 300\,\, \text {GeV}\}$, is much less dependent on $\mu _t$. This exercise shows also the importance of isospin-breaking corrections. They are significantly larger than the NNLO QCD corrections to EWP contributions.

It should be emphasized that in [38] complete $\mathcal {O}(\alpha _W \alpha _s)$ and $\mathcal {O}(\alpha _W\alpha _s\sin ^2\theta _W m_t^2)$ corrections, with $\alpha _W = \alpha /\sin ^2\theta _W$, to the Wilson coefficients $C_{7-10}(\mu )$ of EWP operators at $\mu = m_c$ have been calculated. In particular as demonstrated in Sect. 3 of that paper no three-loop anomalous dimensions of involved operators are necessary to find these corrections. See formula (3.14) of that paper. In order to complete the NNLO analysis of EW contributions one should calculate $m_t$-independent $\mathcal {O}(\alpha _W\alpha _s\sin ^2\theta _W)$ corrections, which as argued in [38] are much smaller than the ones included here.

Much more difficult is the NNLO analysis of QCD penguin contributions which in addition to two-loop calculations requires three-loop anomalous dimension matrices [23, 24], obtained fortunately already in [45].

Table 3 Papers studying implications of the $\varepsilon '/\varepsilon$ anomaly

Inspection of the formulae in [6] together with the numbers in Table 1 shows that the NNLO matching corrections lead mainly to an enhancement of the coefficient $a_8^{(3/2)} \propto y_8(\mu )$ of $B_8^{(3/2)}$ by $1.07\, (1.16)$ due to $y_8(\mu )$, whereas the NNLO impact on $\varepsilon '/\varepsilon$ through $y_{7,9,10}$ is negligible due to the smaller matrix elements multiplying them. The size of the enhancement depends on the choice of the matching scale $\mu _W$ and the $\mu _t$ scale in $m_t(\mu _t)$ in the NLO expressions. The implications of these uncertainties for $\varepsilon '/\varepsilon$ are clearly seen in Fig. 1.

It should be added that the shift of including NNLO corrections in question on $\varepsilon '/\varepsilon$ is independent of the value of $B_6^{(1/2)}$, but its magnitude depends of course on ${{\,\mathrm{Im}\,}}\lambda _t$ and $B_8^{(3/2)}$ that we set to 0.76 in Fig. 1. It reads for the choice $\mu _W = m_W$

$$\begin{aligned} \Delta \varepsilon '/\varepsilon |_\text {NNLO'}&= -\frac{{{\,\mathrm{Im}\,}}\lambda _t}{1.4\cdot 10^{-4}} \times \left\{ \begin{array}{rl} 0.80 \; B_8^{(3/2)}&{} \qquad \mu _t = m_W \\ 1.81 \; B_8^{(3/2)}&{} \qquad \mu _t = m_t \end{array} \right. \,. \end{aligned}$$

(15)

For other choices of $\mu _W$ and $\mu _t$ the shifts can be read off from Fig. 1. The prime in (15) reminds us that small $\mathcal {O}(\alpha _W\alpha _s\sin ^2\theta _W)$ NNLO corrections have not been included in this formula.

In contrast to [6], in obtaining the result for $\varepsilon '/\varepsilon$ in (14) we anticipated that in a future analysis of $\varepsilon '/\varepsilon$ the LQCD values of matrix elements $\langle Q_6(m_c) \rangle _0$ and $\langle Q_8(m_c) \rangle _2$ and not the parameters $B_6^{(1/2)}(m_c)$ and $B_8^{(3/2)}(m_c)$ will be used, which avoids the uncertainties in (10) and (11) that enter the extraction of $B_6^{(1/2)}$ and $B_8^{(3/2)}$. Therefore, when calculating the error in (14) the uncertainties in (10) and (11) have not been included. Then the values of the matrix elements in question corresponding to $B_6^{(1/2)}(m_c)$ and $B_8^{(3/2)}(m_c)$ in (12) are given as follows

$$\begin{aligned} \langle Q_6(m_c) \rangle _0&= h\,(-0.38\pm 0.04)\, \text {GeV}^3 \,, \nonumber \\ \langle Q_8(m_c) \rangle _2&= h\,(0.66 \pm 0.03)\, \text {GeV}^3 \,. \end{aligned}$$

(16)

The error budget is discussed in Appendix B and summarized in Table 6.

What is still missing are NNLO QCD corrections to QCDPs which on the basis of [23, 24] are expected to further suppress $\varepsilon '/\varepsilon$, albeit the effect appears to be smaller than the one of NNLO QCD contributions to EWPs. One could in principle question the inclusion of the latter contributions while leaving out NNLO corrections to QCDPs. Yet these two different NNLO contributions do not have anything to do with each other. In particular while NLO QCD corrections to QCDPs remove already some scale and renormalization scheme dependences present at the LO, in the EWP sector these unphysical scheme dependences are first removed at the NNLO level [38].

4 Numerical analysis

Our analysis shows that the largest remaining uncertainties in the evaluation of $\varepsilon '/\varepsilon$ are present in the values of $\langle Q_6(m_c)\rangle _0$ (or $B_6^{(1/2)}$) and ${\widehat{\Omega }}_\text {eff}$. In Table 2 we give $\varepsilon '/\varepsilon$ as a function of these two parameters for $B_8^{(3/2)}=0.76$. This table should facilitate monitoring the values of $\varepsilon '/\varepsilon$ in the SM when the LQCD calculations of hadronic matrix elements including isospin-breaking corrections and QED effects will improve with time. We observe a large sensitivity of $\varepsilon '/\varepsilon$ to $B_6^{(1/2)}$, but for $B_6^{(1/2)}\ge 0.7$ also the dependence on ${\widehat{\Omega }}_\text {eff}$ is significant.

Finally, it is of interest to ask how large a central value of $B_6^{(1/2)}$ should be in order to reproduce the central experimental value in (1). It turns out to be $B_6^{(1/2)}= 1.40$, in total disagreement with (12). The central value in (2) is obtained for $B_6^{(1/2)}= 1.24$.

5 Summary and outlook

Our analysis and in particular the comparison of the results in (13) and (14) as well as the Table 2 demonstrates the importance of NNLO QCD corrections and of isospin-breaking effects. Anticipating that the new RBC-UKQCD analysis will find $B_6^{(1/2)}(m_c)< 1.0$ as hinted by DQCD, the values of $\varepsilon '/\varepsilon$ in the SM will be significantly below the data. Our example with $B_6^{(1/2)}(m_c)$ in the ballpark of $0.80 \pm 0.08$ illustrates a significant anomaly in $\varepsilon '/\varepsilon$ of about $3.3\,\sigma$. If confirmed by new RBC-UKQCD analysis this would turn out to be one of the largest anomalies in flavour physics present in a single observable and comparable to the anomaly in the flavour conserving $(g-2)_\mu$. Moreover, this would be presently the only significant anomaly as far as CP-violation is concerned with the possible exception of the one present in $B\rightarrow \pi K$ decays [46], as recently reviewed in [47,48,49,50].

However, even if our expectations for $\varepsilon '/\varepsilon$ in the SM would be confirmed by new RBC-UKQCD results, in order to obtain a better assessment which NP is responsible for this anomaly it is very important to perform a number of the following steps:

• Obtain satisfactory precision on $\langle Q_6(m_c)\rangle _0$ or $B_6^{(1/2)}$.

• Reduce the error on ${\widehat{\Omega }}_\text {eff}$. In particular isospin-breaking and QED effects should be taken into account in LQCD calculations.

• Even if the insight from DQCD allowed us to identify the dynamics (meson evolution) responsible for this anomaly, at least a second lattice QCD collaboration should calculate $K\rightarrow \pi \pi$ matrix elements and $\varepsilon '/\varepsilon$.

• Further reduce the short-distance uncertainties, in particular in the QCD penguin sector. But the subleading NNLO QCD contributions to the electroweak penguin sector should be also evaluated.

• Calculation of BSM $K\rightarrow \pi \pi$ hadronic matrix elements of four-quark operators by lattice QCD that presently are known only in the DQCD [51].

There have been numerous BSM analyses of $\varepsilon '/\varepsilon$ which we collect in Table 3. Here we just mention that the leptoquark models, with possible exception of the vector $U_1$ model, are not capable in explaining this anomaly because of the constraints from rare Kaon decays [52]. This shows how crucial correlations of $\varepsilon '/\varepsilon$ with other observables in a given NP scenario are. As indicated in Table 3, they have been analyzed in other NP scenarios. In particular, very recently, a correlation of hinted anomalies in $\varepsilon '/\varepsilon$ and $B\rightarrow \pi K$ decays has been pointed out in the context of models with $U(2)^3$ flavour symmetry in [53].

Also the lessons gained from the SMEFT analysis in [39] should be very helpful in identifying NP behind hinted $\varepsilon '/\varepsilon$ anomaly. Such a general analysis allows to take the constraints from other processes, in particular from electroweak precision tests and collider processes into account. To this end the master formula for $\varepsilon '/\varepsilon$ [54] valid in any extension of the SM should facilitate the search for the dynamics behind the anomaly in question.

Appendices

A Wilson coefficients

Here we summarize the $\Delta S = 1$ Wilson coefficients at the scale $\mu = m_c = 1.3\,$GeV in the NDR-${\overline{\text {MS}}}$ scheme using the NLO RG evolution from [34]. The numerical input is fixed to values in Table 4. The running of the couplings at the low-energy scale are $\alpha _s(m_c) = 0.3764$ and $1/\alpha _\text {em}(m_c) = 133.84$. The threshold crossings are at $\mu _4 = 4.2\,$GeV for $N_f = 5 \rightarrow 4$ and $\mu _3 = 1.3\,$GeV for $N_f = 4 \rightarrow 3$ quark flavours.

Table 4 Numerical input for Wilson coefficients

Table 5 The $\Delta S = 1$ Wilson coefficients at $\mu = m_c = 1.3\,$GeV in the NDR-${\overline{\text {MS}}}$ scheme for the renormalization scale $\mu _W = m_W$ and $\mu _t = m_W$ or $\mu _t = m_t$ using NLO and partial NNLO matching results for $y_{7,\ldots ,10}$. The symbol $\leftarrow$ indicates that there are now changes in the numerical value within the adapted approximation

We will use the results in [38] to demonstrate the numerical impact of the dominant NNLO matching corrections that resolve the NLO renormalization scheme ambiguities for the two choices $\mu _t = m_W$ and $\mu _t = m_t$. As given in Table 2 (Table 3) of [38] they lead to a rescaling of $y_{7, \ldots , 10}(\mu )$ at the low-energy scale² of about $1.07\,(0.92)$, $1.07\,(1.16)$, $0.89\,(0.98)$ and $0.76\,(0.85)$ for $\mu _t = m_W\, (m_t)$ to the NNLO’ values in Table 5, which we adapt in the numerics. The prime in this Table indicates that still small $m_t$-independent $\mathcal {O}(\alpha _W\alpha _s\sin ^2\theta _W)$ corrections are not included and NNLO corrections to $y_{3,4,5,6}$ are neglected as well.

B Error budget

We summarize the error budget leading to the result in (14) in Table 6. The scale uncertainties after the inclusion of NNLO corrections to both QCDP and EWP are not shown as they have negligible impact on the final error.

Table 6 Table of the absolute error of $\varepsilon '/\varepsilon$ for benchmark point (12) with input parameters from (4) and (12). The absolute error of $\varepsilon '/\varepsilon$ from these parametric uncertainties becomes $10^4 \times \delta (\varepsilon '/\varepsilon ) = 2.3$ when added in quadrature