Electromagnetic form factors of the baryon decuplet with flavor SU(3) symmetry breaking

Abstract

We investigate the electromagnetic form factors of the baryon decuplet within the framework of the $\mathrm {SU(3)}$ self-consistent chiral quark-soliton model, taking into account the $1/N_c$ rotational corrections and the effects of flavor $\mathrm {SU(3)}$ symmetry breaking. We first examine the valence- and sea-quark contributions to each electromagnetic form factor of the baryon decuplet and then the effects of the flavor SU(3) symmetry breaking. We also compute the charge radii, the magnetic radii, the magnetic dipole moments and the electric quadrupole moments, comparing their results with those from other theoretical works. We also make a chiral extrapolation to compare the present results with the lattice data in a more quantitative manner. The results show in general similar tendency to the lattice results. In particular, the results of the M1 and E2 form factors are in good agreement with those of lattice QCD.

1 Introduction

The $\Delta$ isobars are the first excited baryons with spin 3/2. Its electromagnetic (EM) structure and properties have been experimentally studied at a rather gradual pace over decades because of its ephemeral nature, the $\gamma ^* N\rightarrow \Delta$ transitions being mainly focused [1, 2]. By the turn of the new century, however, being equipped with a new generation of electron beam accelerators and detectors with high precision, one was able to take a better grasp of the EM transitions of $\Delta$ isobars [3, 4]. For example, various experimental groups have announced the results on the $\gamma ^* N\rightarrow \Delta$ excitation: the Laser Electron Gamms Source (LEGS) Collaboration at the National Synchrotron Light Source (NSLS) of Brookhaven National Laboratory [5,6,7], the CLAS Collaboration [8,9,10] at Jefferson Laboratory, and the A1 and A2 Collaborations [11,12,13,14,15,16] at MAMI. The EM structure of the strangeness members of the baryon decuplet has been also experimentally investigated at these experimental facilities. So far the static magnetic dipole moments have been only measured [18,19,20]. Future experiments will even provide the EM data on the $\Xi ^*$ and $\Omega ^-$ baryons [17] in detail. The EM structure of the baryon decuplet is more complicated than that of the baryon octet, since all the decuplet baryons have spin 3/2. Thus, a decuplet baryon has two more terms of the EM form factors than the baryon octet, i.e. the electric quadrupole (E2) form factor and the magnetic octupole (M3) form factors in addition to the electric monopole (E0) and magnetic dipole (M1) form factors.

The EM form factors of the $\Delta$ isobars and the other members of the baryon decuplet are still experimentally unknown. However, recently, a series of calculations in lattice quantum chromodynamics (QCD) was carried out. Alexandrou et al. reported the lattice results on the EM form factors of the $\Delta$ and $\Omega$ [21,22,23,24], which improved greatly the old lattice work [25]. The magnetic dipole moments of the $\Delta$ and $\Omega$ were examined also in lattice QCD [26,27,28]. Theoretically, the EM properties of the baryon decuplet have been studied within various different models and theoretical frameworks: for example, effective field theory and baryon chiral perturbation theories [29,30,31,32], $1/N_c$ expansions [33,34,35], various versions of the quark models [36,37,38,39], the Skyrme models [40, 41], QCD sum rules [42,43,44], and Bethe–Salpeter approaches [45,46,47], and holographic QCD [48].

In the present work, we will investigate the EM form factors of all the members in the baryon decuplet within the chiral quark-soliton model ($\chi$QSM), taking into account the effects of explicit flavor SU(3) symmetry breaking. The $\chi$QSM has been developed as a pion mean-field approach, based on the seminal papers by Witten [49, 50]. In the limit of the large number of colors ($N_c$), the nucleon mass is proportional to $N_c$, whereas its decay width is of order $\mathcal {O}(1)$. It implies that the meson-loop corrections can be suppressed in this limit. Then the nucleon arises as a state consisting of the $N_c$ valence quarks, which is bound by the pion mean fields [51,52,53,54]. The presence of the $N_c$ valence quarks brings about the vacuum polarization that produces effectively the pion mean fields. Then, they are again affected by these pion mean fields in a self-consistent manner. The $\chi$QSM has been successfully applied to the description of the SU(3) baryons. For example, the model explains very well various form factors of the lowest-lying SU(3) baryons such as electromagnetic structures [56,57,58,59], strange form factors [60,61,62,63], tensor charges and form factors [64,65,66,67,68,69], semileptonic decays [70,71,72], radiative decay [73,74,75] and the parton distributions [76,77,78,79,80], etc. Moreover it was shown that the $\chi$QSM can be extended to describing the singly heavy baryons by changing the pion mean fields arising from the $N_c-1$ valence quarks. With this extension, the model reproduces very well the observables of the singly heavy baryons such as mass splittings [81, 82], strong decays [83,84,85] and electromagnetic properties [86, 87].

In fact, The EM form factors of the $\Delta$ baryon have been already studied by Ref. [88] within the same framework, with flavor SU(3) symmetry assumed.¹ In this work, we want to investigate the EM form factors of all the members in the baryon decuplet, taking into account the $1/N_c$ rotational corrections and the effects of flavor SU(3) symmetry breaking. Since there exist in particular the lattice results of the $\Omega$ EM form factors [24], it is of great interest to compute and compare them with those from lattice QCD. Thus, we will present and discuss the results of the E0, M1, and E2 form factors of the baryon decuplet, emphasizing the comparison with the lattice data. Concerning the M3 form factors, any chiral soliton approach yields null results of the M3 form factors. It is consistent with the fact that the magnitudes of the M3 form factors are very small.

The structure of the present work is sketched as follows: in Sect. 2, we define the EM form factors of the baryon decuplet in terms of the matrix elements of the EM current. In Sect. 3, we briefly review the formalism of the $\chi$QSM in the context of the derivation of the EM form factors of the baryon decuplet. In Sect. 4 we present the numerical results of them. We discuss first the valence and sea contributions to the EM form factors, and then examine the effects of flavor SU(3) symmetry breaking. We also show the numerical results of the charge and magnetic radii, the magnetic dipole moments, and the electric quadrupole moments. In the last subsection of Sect. 4, we make a chiral extrapolation of the present work so that we can compare the numerical results with those from lattice QCD in a quantitative manner. In the final section, we summarize the present work and draw conclusions.

2 Electromagnetic multipole form factors of the baryon decuplet

The EM current is defined as

$$\begin{aligned} J_\mu (x) = \bar{\psi } (x) \gamma _\mu \hat{\mathcal {Q}} \psi (x), \end{aligned}$$

(1)

where $\psi (x)$ denotes the quark field $\psi =(u,\,d,\,s)$ in flavor space. The charge operator of the quarks $\hat{\mathcal {Q}}$ is written in terms of the flavor SU(3) Gell–Mann matrices $\lambda _3$ and $\lambda _8$

$$\begin{aligned} \hat{\mathcal {Q}} = \begin{pmatrix} \frac{2}{3} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\frac{1}{3} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\frac{1}{3} \end{pmatrix} = \frac{1}{2}\left( \lambda _3 + \frac{1}{\sqrt{3}} \lambda _8\right) . \end{aligned}$$

(2)

The matrix elements of the EM current between baryons with spin 3/2 can be parametrized by four real form factors $F_i^{B}$ ($i=1,\ldots ,4$) as follows:

$$\begin{aligned}&\langle B(p',s) | e_B J^{\mu }(0) | B(p,s) \rangle \nonumber \\&\quad = - e_B \overline{u}^{\alpha }(p',s) \left[ \gamma ^{\mu } \left\{ F^{B}_{1}(q^2) \eta _{\alpha \beta } + F^{B}_{3}(q^2) \frac{ q_{\alpha } q_{\beta } }{4M_{B}^{2}} \right\} \right. \nonumber \\&\qquad \left. + \,i\frac{\sigma ^{\mu \nu } q_{\nu }}{2M_{B}} \left\{ F^{B}_{2}(q^2) \eta _{\alpha \beta } + F^{B}_{4} (q^2)\frac{q_{\alpha } q_{\beta }}{4 M_{B}^2} \right\} \right] {u}^{\beta }(p,s), \end{aligned}$$

(3)

where $M_B$ denotes the mass of the corresponding baryon in the decuplet, and $e_B$ stands for the corresponding electric charge of the baryon B. The metric tensor $\eta _{\alpha \beta }$ of Minkowski space is expressed as $\eta _{\alpha \beta } =\mathrm {diag}(1,\,-1,\,-1,\,-1)$. $q_\alpha$ designates the momentum transfer $q_\alpha =p'_\alpha -p_\alpha$ and its square is given as $q^2=-Q^2$ with $Q^2 >0$. $u^\alpha (p,\,s)$ represents the Rarita–Schwinger spinor that describes the decuplet baryon with spin 3/2, carrying the momentum p and the spin component s projected along the direction of the momentum. $\sigma ^{\mu \nu }$ is the well-known antisymmetric tensor $\sigma ^{\mu \nu }=i[\gamma ^\mu ,\,\gamma ^\nu ]/2$.

It is often more convenient to introduce the multipole EM form factors, which can be expressed in terms of the $F_i^B$ given in Eq. (3)

$$\begin{aligned} G_{E0}^B(Q^{2})= & {} \left( 1 + \frac{2}{3} \tau \right) [F_{1}^{B}-\tau F_{2}^{B}] \nonumber \\&- \frac{1}{3} \tau (1+ \tau ) [F_{3}^{B} - \tau F_{4}^{B}], \nonumber \\ G_{E2}^B(Q^{2})= & {} [F_{1}^{B}-\tau F_{2}^{B}]- \frac{1}{2} (1+ \tau ) [F_{3}^{B} - \tau F_{4}^{B}] , \nonumber \\ G_{M1}^B (Q^{2})= & {} \left( 1+\frac{4}{5} \tau \right) [F^{B}_{1}+F^{B}_{2}] \nonumber \\&- \frac{2}{5} \tau (1+ \tau )[F^{B}_{3}+F^{B}_{4}], \nonumber \\ G_{M3}^B(Q^{2})= & {} [F^{B}_{1}+F^{B}_{2}] -\frac{1}{2}(1+\tau ) [F^{B}_{3}+F^{B}_{4}], \end{aligned}$$

(4)

where $\tau =Q^2/4M_B^2$. These four form factors are called, respectively, the electric or Coulomb monopole (E0), magnetic dipole (M1), electric quadrupole (E2), and magnetic octupole (M3) form factors. Each form factor at $Q^2=0$ has a clear physical meaning: $G_{E0}^B(0)$ is the normalized charge, i.e. the corresponding decuplet baryon B with positive or negative charge will have the value of $G_{E0}^B(0)=1$ or $G_{E0}^B=-1$, whereas the neutron one will have $G_{E0}^B(0)=0$. $G_{M1}^B(0)$ means the magnetic dipole moment $\mu _B$ for the corresponding baryon, whereas $G_{E2}^B(0)$ yields the corresponding electric quadrupole moment $Q_B$. $G_{M3}^B(0)$ will give us the magnetic octupole ($O_B$) moment of the corresponding decuplet baryon B [4]. Thus, these physical quantities can be written in terms of the charge and the form factors $F_i^{B}$

$$\begin{aligned} e_B&= e G_{E0}^B(0) = e F_1^{B}(0),\nonumber \\ \mu _B&= \frac{e}{2M_B} G_{M1}^B = \frac{e}{2M_B} \left[ e_B+F_2^{B}(0)\right] ,\nonumber \\ Q_B&= \frac{e}{M_B^2} G_{E2}^B(0) = \frac{e}{M_B^2} \left[ e_B -\frac{1}{2} F_3^{B}(0)\right] ,\nonumber \\ O_B&= \frac{e}{M_B^3} G_{M3}^B(0) \nonumber \\&= \frac{e}{M_B^3} \left[ e_B+F_2^{B}(0) - \frac{1}{2} (F_3^{B}(0) + F_4^{B}(0))\right] . \end{aligned}$$

(5)

If one chooses the Breit frame, i.e. $p'=-p=q/2$, then the EM multipole form factors can be explicitly expressed as

$$\begin{aligned} G_{E0}^B(Q^{2})&= \int \frac{d \Omega _{q}}{4 \pi }\langle B(p',3/2) | J^{0}(0) | B (p,3/2) \rangle , \nonumber \\ G_{E2}^B(Q^{2})&= -\int {d \Omega _{q}} \sqrt{\frac{5}{4\pi } }\frac{3}{2} \frac{1}{\tau }\nonumber \\&\quad \times \langle B(p',3/2) | Y^{*}_{20} (\Omega _{q}) J^{0}(0) | B (p,3/2) \rangle , \nonumber \\ G_{M1}^B(Q^{2})&= \frac{3 M_B}{4\pi }\int \frac{d\Omega _{q}}{ i |{\varvec{q}}|^{2}}q^{i}\epsilon ^{ik3}\nonumber \\&\quad \times \langle B (p',3/2) | J^{k}(0) | B (p,3/2) \rangle , \nonumber \\ G_{M3}^B(Q^{2})&=-\frac{35M_{B}}{8}\sqrt{\frac{5}{\pi }} \int \frac{d\Omega _{q}}{ i |{\varvec{q}}|^{2} \tau }q^{i}\epsilon ^{ik3} \left\langle \phantom {\left| \left( Y^{*}_{20}(\Omega _{q})+\sqrt{\frac{1}{5}}Y^{*}_{00}(\Omega _{q}) \right) J^{k}(0) \right| } B (p',3/2)\right. \nonumber \\&\quad \left. \times \left| \left( Y^{*}_{20}(\Omega _{q})+\sqrt{\frac{1}{5}}Y^{*}_{00}(\Omega _{q}) \right) J^{k}(0) \right| B (p,3/2) \right\rangle , \end{aligned}$$

(6)

where $J^0$ and $J^i$ denote the temporal and spatial components of the EM current, respectively. Thus, we can straightforwardly compute the matrix elements of the EM current in Eq. (6) within the $\chi$QSM.

3 Electromagnetic form factors in the chiral quark-soliton model

The $\chi$QSM is characterized by the effective chiral partition function

$$\begin{aligned} \mathcal {Z}_{\chi \mathrm {QSM}}&= \int \mathcal {D}\psi \mathcal {D} \psi ^\dagger \mathcal {D} \pi ^a \exp \left[ -\int d^4 x \psi ^\dagger i D(\pi ^a) \psi \right] \nonumber \\&= \int \mathcal {D} \pi ^a \exp (-S_{\mathrm {eff}}[\pi ^a]), \end{aligned}$$

(7)

where $\psi$ and $\pi ^a$ represent the quark and pseudo-Nambu–Goldstone (NG) boson fields, respectively. The $S_{\mathrm {eff}}$ denotes the effective chiral action given as a functional of $\pi ^a$

$$\begin{aligned} S_{\mathrm {eff}}[\pi ^a] \;=\; -N_{c}\mathrm {Tr}\ln D\,, \end{aligned}$$

(8)

where $\mathrm {Tr}$ stands for the trace running over space-time and all relevant internal spaces. The $N_c$ is the number of colors, and $D(\pi ^a)$ is the one-body Dirac differential operator defined by

(9)

We assume isospin symmetry, so the up and down current quark masses are set equal to each other, i.e. $m_{\mathrm {u}}=m_{\mathrm {d}}$. We define the average mass of the up and down current quarks by $\overline{m}=(m_{\mathrm {u}} + m_{\mathrm {d}})/2$. Then, the mass matrix of the current quark is written as $\hat{m} =\mathrm {diag}(\overline{m},\, \overline{m},\, m_{\mathrm {s}}) = \overline{m} +\delta m$. $\delta m$ contains the mass of the strange current quark, which can be decomposed in to the flavor singlet and octet parts

$$\begin{aligned} \delta m = \frac{-\overline{m} + m_{s}}{3}\gamma _{4}{\varvec{1}} + \frac{\overline{m} - m_{s}}{\sqrt{3}} \gamma _{4} \lambda ^{8} = m_{1}\gamma _{4} {\varvec{1}} + m_{8} \gamma _{4} \lambda ^{8}\,, \end{aligned}$$

(10)

where $m_1$ and $m_8$ designate respectively the singlet and octet components of the current quark masses. They are expressed as $m_1=(-\overline{m} +m_{\mathrm {s}})/3$ and $m_8=(\overline{m} -m_{\mathrm {s}})/\sqrt{3}$. The one-body Dirac operator multiplied by $\gamma _4$ can be written as

$$\begin{aligned} \gamma _4 D = -i\partial _{4} + h(U(\pi ^a)) - \delta m, \end{aligned}$$

(11)

where $\partial _4$ denotes the derivative with respect to the Euclidean time. The SU(3) single-quark Hamiltonian h(U) is defined as

$$\begin{aligned} h(U) = i\gamma _{4}\gamma _{i}\partial _{i}-\gamma _{4}MU^{\gamma _{5}} - \gamma _{4} \overline{m}\, , \end{aligned}$$

(12)

where $U^{\gamma _5}$ represents the SU(3) chiral field. Since it is well known that the isovector charge radii [89] diverge in the chiral limit, it is essential to include $\overline{m}$ in the Dirac Hamiltonian (12). Moreover, $\overline{m}$ in Eq. (12) produces the correct Yukawa tail of the pion field.

Since the pseudo-NG fields carry the flavor indices, the hedgehog ansatz is usually imposed, in which each pion field with $a=1,\,2,\,3$ is taken to be aligned along each three-dimensional spatial component

$$\begin{aligned} \pi ^a ({\varvec{x}}) = {n}^a P(r), \end{aligned}$$

(13)

where $n^a=x^a/r$ with $r=|{\varvec{x}}|$. P(r) is called the profile function of the chiral soliton. Then the flavor SU(2) chiral field is written as

$$\begin{aligned} U_{\mathrm {SU(2)}}^{\gamma _5}&= \exp (i\gamma ^{5}\hat{{\varvec{n}}}\cdot {\varvec{\tau }} P(r)) \nonumber \\&= \frac{1+\gamma ^{5}}{2}U_{\mathrm {SU(2)}} + \frac{1-\gamma ^{5}}{2}U_{\mathrm {SU(2)}}^{\dagger } \end{aligned}$$

(14)

with $U_{\mathrm {SU(2)}}=\exp (i\hat{{\varvec{n}}}\cdot {\varvec{\tau }} P(r))$. The flavor SU(3) chiral field is constructed by embedding the SU(2) soliton into SU(3) [50]

$$\begin{aligned} U^{\gamma _{5}}(x) \;=\; \left( \begin{array}{lr} U_{\mathrm {SU(2)}}^{\gamma _{5}}(x) &{} 0\\ 0 &{} 1 \end{array}\right) . \end{aligned}$$

(15)

Since we employ the pion mean-field approximation, we perform the integration over U in Eq. (7) around the saddle point, which yields $\delta S_{\mathrm {eff}}/\delta P(r) =0$. This saddle point approximation furnishes the classical equation of motion that can be solved self-consistently. The solution provides the pion mean field and consequently the self-consistent profile function P(r). For the detailed formalism of constructing the collective Hamiltonian, we refer to reviews [53, 54].

The matrix elements of the EM current (3) can be computed by considering the following functional integral

$$\begin{aligned}&\langle B,\,p'| J_\mu (0) |B,\,p\rangle \nonumber \\&\quad = \frac{1}{\mathcal {Z}} \lim _{T\rightarrow \infty } \exp \left( i p_4\frac{T}{2} - i p_4' \frac{T}{2}\right) \nonumber \\&\qquad \times \int d^3x d^3y \exp (-i {\varvec{p}}'\cdot {\varvec{y}} + i {\varvec{p}}\cdot {\varvec{x}}) \nonumber \\&\qquad \times \int \mathcal {D} \pi ^a \int \mathcal {D} \psi \int \mathcal {D} \psi ^\dagger J_{B}({\varvec{y}},\,T/2) \psi ^\dagger (0)\nonumber \\&\qquad \times \gamma _4\gamma _\mu \hat{Q} \psi (0) J_B^\dagger ({\varvec{x}},\,-T/2) \exp \left[ -\int d^4 z \psi ^\dagger iD(\pi ^a) \psi \right] , \end{aligned}$$

(16)

where the baryon states $|B,\,p\rangle$ and $\langle B,\,p'|$ are respectively defined by

$$\begin{aligned} |B,\,p\rangle&= \lim _{x_4\rightarrow -\infty } \exp (i p_4 x_4)\nonumber \\&\quad \times \frac{1}{\sqrt{\mathcal {Z}}} \int d^3 x \exp (i{\varvec{p}}\cdot {\varvec{x}}) J_B^\dagger ({\varvec{x}},\,x_4)|0\rangle ,\nonumber \\ \langle B,\,p'|&= \lim _{y_4\rightarrow \infty } \exp (-i p_4' y_4)\nonumber \\&\quad \times \frac{1}{\sqrt{\mathcal {Z}}} \int d^3 y \exp (-i{\varvec{p}}'\cdot {\varvec{y}}) \langle 0| J_B^\dagger ({\varvec{y}},\,y_4). \end{aligned}$$

(17)

The baryon current $J_B$ can be constructed as an Ioffe-type current in terms of $N_c$ valence quarks

$$\begin{aligned} J_B(x) = \frac{1}{N_c!} \epsilon _{i_1\cdots i_{N_c}} \Gamma _{JJ_3 TT_3 Y}^{\alpha _1\cdots \alpha _{N_c}} \psi _{\alpha _1 i_1} (x) \cdots \psi _{\alpha _{N_c} i_{N_c}}(x), \end{aligned}$$

(18)

where $\alpha _1\cdots \alpha _{N_c}$ and $i_1\cdots i_{N_c}$ denote spin-flavor indices and color ones, respectively. The matrices $\Gamma _{JJ_3 TT_3 Y}^{\alpha _1\cdots \alpha _{N_c}}$ will project out the baryon state with quantum numbers $JJ_3TT_3Y$. The creation current operator $J_B^\dagger$ can be expressed in a similar manner. As for the detailed formalism of the zero-mode quantization and the techniques of computing the baryonic correlation function given in Eq. (16), we refer to Refs. [53, 55]. See also Ref. [88].

Having performed the zero-mode quantization, we derive the collective Hamiltonian as

$$\begin{aligned} H_{\mathrm {coll}} = H_{\mathrm {sym}} + H_{\mathrm {sb}}, \end{aligned}$$

(19)

where

$$\begin{aligned} H_{\mathrm {sym}}&= M_{\mathrm {cl}} + \frac{1}{2I_1} \sum _{i=1}^3 J_i^2 + \frac{1}{2I_2} \sum _{p=4}^7 J_p^2,\nonumber \\ H_{\mathrm {sb}}&= \alpha D_{88}^{(8)} + \beta \hat{Y} + \frac{\gamma }{\sqrt{3}} \sum _{i=1}^3 D_{8i}^{(8)} \hat{J}_i. \end{aligned}$$

(20)

$I_1$ and $I_2$ denote the soliton moments of inertia. The parameters $\alpha$, $\beta$, and $\gamma$ for the part of explicit flavor SU(3) symmetry breaking are defined by

$$\begin{aligned}&\alpha =\left( -\frac{{\Sigma }_{\pi N}}{3\bar{m}}+\frac{ K_{2}}{I_{2}}{Y'} \right) m_{\mathrm {s}}, \;\;\; \beta =-\frac{ K_{2}}{I_{2}}m_{\mathrm {s}}, \nonumber \\&\gamma =2\left( \frac{K_{1}}{I_{1}}-\frac{K_{2}}{I_{2}} \right) m_{\mathrm {s}}, \end{aligned}$$

(21)

where that the three parameters $\alpha$, $\beta$, and $\gamma$ are expressed in terms of the moments of inertia $I_{1,\,2}$ and $K_{1,\,2}$.

The symmetry-breaking part of the collective Hamiltonian $H_{\mathrm {sb}}$ being considered as a perturbation, the states of the baryon decuplet are blended with other SU(3) representations as follows:

$$\begin{aligned} |B_{{{\varvec{1}}0}_{3/2}}\rangle = |{{\varvec{10}}}_{3/2},B\rangle + a^{B}_{{27}}|{{{\varvec{27}}}}_{3/2},B\rangle + a^{B}_{{35}}|{{{\varvec{35}}}}_{3/2},B\rangle , \end{aligned}$$

(22)

with the mixing coefficients

$$\begin{aligned} a_{{27}}^{B} = a_{{27}}\left[ \begin{array}{c} \sqrt{15/2}\\ 2 \\ \sqrt{3/2} \\ 0 \end{array}\right] ,&\quad a_{35}^{B} = a_{35}\left[ \begin{array}{c} 5/\sqrt{14}\\ 2\sqrt{{5}/{7}} \\ 3\sqrt{{5}/{14}} \\ 2\sqrt{{5}/{7}} \end{array}\right] , \end{aligned}$$

(23)

respectively, in the basis $\left[ \Delta ,\;\Sigma ^{*},\;\Xi ^{*},\;\Omega \right]$. The parameters $a_{{27}}$ and $a_{35}$ are given by

$$\begin{aligned} a_{27} = {\displaystyle -\frac{{I}_{2}}{8} \left( \alpha + \frac{5}{6}\gamma \right) },&\quad a_{35} \;=\; {\displaystyle -\frac{{I}_{2}}{24} \left( \alpha - \frac{1}{2}\gamma \right) }. \end{aligned}$$

(24)

The $a_{27}$ and the $a_{35}$ were derived in Ref. [82]: $a_{27}=0.126$ and $a_{35}=0.035$. The collective wavefunction of a baryon with flavor $F=(Y,T,T_3)$ and spin $S=(Y'=-N_{c}/3,J,J_3)$ in the representation $\nu$ is expressed in terms of a tensor with two indices, i.e. $\psi _{(\nu ;\, F),(\overline{\nu };\,\overline{S})}$, one running over the states F in the representation $\nu$ and the other one over the states $\overline{S}$ in the representation $\overline{\nu }$. Here, $\overline{\nu }$ denotes the complex conjugate of the $\nu$, and the complex conjugate of S is written by $\overline{S}=(N_{c}/3,\,J,\,J_3)$. Thus, the collective wavefunction is expressed as

$$\begin{aligned} \psi _{(\nu ;\, F),(\overline{\nu };\,\overline{S})}(R) = \sqrt{\mathrm {dim}(\nu )} (-1)^{Q_S} [D_{F\,S}^{(\nu )}(R)]^*, \end{aligned}$$

(25)

where $\mathrm {dim}(\nu )$ stands for the dimension of the representation $\nu$ and $Q_S$ a charge corresponding to the baryon state S, i.e. $Q_S=J_3+Y'/2$.

Having taken into account the rotational $1/N_c$ and linear $m_{\mathrm {s}}$ corrections, we obtain the final expression of the E0 form factors for the baryon B

$$\begin{aligned} {{G}}^{B}_{E0} (q^{2})= \int d^{3} z j_{0}(|{\varvec{q}}| |{\varvec{z}}|) {\mathcal {G}}_{E0}^B ({\varvec{z}}), \end{aligned}$$

(26)

where ${\mathcal {G}}^{B}_{E0} ({\varvec{z}})$ stands for the corresponding electric charge distribution

$$\begin{aligned} {{\mathcal {G}}}^{B}_{E0} ({\varvec{z}})&= \frac{1}{\sqrt{3}} \langle D^{(8)}_{Q8}\rangle _B \mathcal {B}({\varvec{z}}) - \frac{2}{I_{1}} \langle D^{(8)}_{Qi} \hat{J}_{i} \rangle _B {{\mathcal {I}}}_{1}({\varvec{z}}) \nonumber \\&\quad -\, \frac{2}{I_{2}} \langle D^{(8)}_{Qp} \hat{J}_{p} \rangle _B {{\mathcal {I}}}_{2}({\varvec{z}}) \nonumber \\&\quad -\,\frac{4 m_{8}}{I_{1}} \langle D^{(8)}_{8i} D^{(8)}_{Qi} \rangle _B (I_{1}{{\mathcal {K}}}_{1}(z) - K_{1}{{\mathcal {I}}}_{1}(z)) \nonumber \\&\quad -\,\frac{4 m_{8}}{I_{2}} \langle D^{(8)}_{8p} D^{(8)}_{Qp} \rangle _B (I_{2}{{\mathcal {K}}}_{2}(z) - K_{2}{{\mathcal {I}}}_{2}(z)) \nonumber \\&\quad -\,2\left( \frac{m_1}{\sqrt{3}}\langle D^{(8)}_{Q8} \rangle _B + \frac{m_8}{3}\langle D^{(8)}_{8 8}D^{(8)}_{Q8} \rangle _B \right) {{\mathcal {C}}}({\varvec{z}}), \end{aligned}$$

(27)

where the explicit expressions for the densities $\mathcal {B}({\varvec{z}})$, $\mathcal {I}_{1}({\varvec{z}})$, $\mathcal {I}_{2}({\varvec{z}})$, $\mathcal {K}_{1}({\varvec{z}})$, $\mathcal {K}_{2}({\varvec{z}})$ and $\mathcal {C}({\varvec{z}})$ can be found in Refs. [55, 75]. The indices i and p denote dummy ones running over $i=1,\ldots , 3$ and $p=4,\ldots , 7$, respectively. Since the integrations of the densities in Eq. (27) are given as

$$\begin{aligned}&\int d^3 z \,\mathcal {B}({\varvec{z}}) ={N_{c}},\;\;\; \frac{1}{I_i}\int d^3 z \,\mathcal {I}_i ({\varvec{z}}) = 1,\nonumber \\&\frac{1}{K_i}\int d^3 z \,\mathcal {K}_i ({\varvec{z}}) = 1,\;\;\; \int d^3 z \,\mathcal {C}({\varvec{z}}) = 0, \end{aligned}$$

(28)

we find that the electric charge is preserved by the relation

$$\begin{aligned} \mathcal {Q}_B&= \left\langle \hat{T}_3 + \frac{\hat{Y}}{2}\right\rangle _B \nonumber \\&= \frac{N_c}{\sqrt{3}} \langle D^{(8)}_{Q8}\rangle _B - 2 \langle D^{(8)}_{Qi} \hat{J}_{i} \rangle _B - 2 \langle D^{(8)}_{Qp} \hat{J}_{p} \rangle _B, \end{aligned}$$

(29)

where $\hat{T}_3$ and $\hat{Y}$ denote the operators for the third component of the isospin and the hypercharge, respectively. Thus, the electric form factor $G_{E0}^B$ at $Q^2=0$ is just the charge of the corresponding baryon. Note that we also have considered the symmetry-conserving quantization [90].

The expression for the magnetic dipole moment form factor of a baryon B is written as

$$\begin{aligned} {{G}}^{B}_{M1} (q^{2})=\frac{ M_{B}}{|{\varvec{q}}|} \int d^{3} z \frac{j_{1}(|{\varvec{q}}| |{\varvec{z}}|)}{ |{\varvec{z}}|} \mathcal {G}^{B}_{M1} ({\varvec{z}}), \end{aligned}$$

(30)

where the magnetic distribution $\mathcal {G}_{M1}^B$ is given by

$$\begin{aligned} \mathcal {G}^{B}_{M1}({\varvec{z}})&= \langle D^{(8)}_{Q3 } \rangle _B \left( {{\mathcal {Q}}}_{0} ({\varvec{z}}) + \frac{1}{I_{1}} {{\mathcal {Q}}}_{1} ({\varvec{z}}) \right) \nonumber \\&\quad - \frac{1}{\sqrt{3}} \langle D^{(8)}_{Q 8}J_{3} \rangle _B \frac{1}{I_{1}} {{\mathcal {X}}}_{1} ({\varvec{z}}) - \langle d_{pq3} D^{(8)}_{Qp} J_{q} \rangle _B \frac{1}{I_{2}} {{\mathcal {X}}}_{2} ({\varvec{z}}) \nonumber \\&\quad + \frac{2}{\sqrt{3}} m_{8} \langle D^{(8)}_{83} D^{(8)}_{Q8} \rangle _B \left( \frac{K_{1}}{I_{1}}{{\mathcal {X}}}_{1} ({\varvec{z}}) - {{\mathcal {M}}}_{1} ({\varvec{z}})\right) \nonumber \\&\quad +2 m_{8} \langle d_{pq3} D^{(8)}_{8p} D^{(8)}_{Qq} \rangle _B \left( \frac{K_{2}}{I_{2}}{{\mathcal {X}}}_{2} ({\varvec{z}}) - {{\mathcal {M}}}_{2} ({\varvec{z}})\right) \nonumber \\&\quad - 2 \left( m_{1} \langle D^{(8)}_{Q3} \rangle _B + \frac{1}{\sqrt{3}} m_{8} \langle D^{(8)}_{88} D^{(8)}_{Q3} \rangle _B \right) {{\mathcal {M}}}_{0} ({\varvec{z}}). \end{aligned}$$

(31)

Here the indices p and q are the dummy indices running over $4\cdots 7$. The explicit forms of the magnetic densities can be found in Refs. [55, 75]. The matrix elements of the collective operators are explicitly presented in Appendix A.

The expression for the electric quadrupole form factor of a baryon B is obtained as

$$\begin{aligned} G^{B}_{E{2}}(Q^{2})&= 6 \sqrt{{5} } M^{2}_{B} \int d^{3} z \frac{j_{2}(|{\varvec{q}}||{\varvec{z}}|)}{|{\varvec{q}}|^{2}} \mathcal {G}^{B}_{E2}({\varvec{z}}) , \end{aligned}$$

(32)

where $\mathcal {G}_{E2}^B$ is given by

$$\begin{aligned} \mathcal {G}^{B}_{E2}({\varvec{z}})&= -2 \left( \frac{3}{I_{1}} \langle \ D^{(8)}_{Q 3} J_{3} \rangle _{B} - \frac{1}{I_1} \langle D^{(8)}_{Q i} J_{i} \rangle _{B} \right) \mathcal {I}_{1E2} ({\varvec{z}}) \nonumber \\&\quad +\, 4 m_{8}\left( \frac{K_{1}}{I_{1}} \mathcal {I}_{1E2}({\varvec{z}}) - \mathcal {K}_{1E2}({\varvec{z}})\right) \nonumber \\&\quad \times \,\left( 3\langle D^{(8)}_{8 3} D^{(8)}_{Q 3}\rangle _{B} -\langle D^{(8)}_{8 i} D^{(8)}_{Q i} \rangle _{B} \right) . \end{aligned}$$

(33)

The expressions for the densities $\mathcal {I}_{1E2}$ and $\mathcal {K}_{1E2}$ can be found in Appendix B. Though we could also express the magnetic octupole form factors, we will not present them here, because they all vanish within the present model.

It is convenient to decompose the densities into the flavor SU(3) symmetric and explicit symmetry-breaking terms. In fact, there are two different contributions from the explicit symmetry-breaking terms: The one arises from the linear $m_{\mathrm {s}}$ term in the effective chiral action (8) and the other comes from the mixed collective wavefunctions (22). Thus, we can split the densities in terms of these three different terms

$$\begin{aligned} \mathcal {G}^{B}_{E0}({\varvec{z}})&= \mathcal {G}^{B(0)}_{E0}({\varvec{z}}) + \mathcal {G}^{B(\text {op})}_{E0}({\varvec{z}}) +\mathcal {G}^{B(\text {wf})}_{E0}({\varvec{z}}),\nonumber \\ \mathcal {G}^{B}_{M1}({\varvec{z}})&= \mathcal {G}^{B(0)}_{M1}({\varvec{z}}) +\mathcal {G}^{B(\text {op})}_{M1}({\varvec{z}}) +\mathcal {G}^{B(\text {wf})}_{M1}({\varvec{z}}),\nonumber \\ \mathcal {G}^{B}_{E2}({\varvec{z}})&= \mathcal {G}^{B(0)}_{E2}({\varvec{z}}) + \mathcal {G}^{B(\text {op})}_{E2}({\varvec{z}}) + \mathcal {G}^{B(\text {wf})}_{E2}({\varvec{z}}), \end{aligned}$$

(34)

where $\mathcal {G}_{E0,M1,E2}^{B(0)}$, $\mathcal {G}_{E0,M1,E2}^{B(\mathrm {op})}$, and $\mathcal {G}_{E0,M1,E2}^{B(\mathrm {wf})}$ represent the symmetric terms, the flavor SU(3) symmetry-breaking ones from the effective chiral action, and those from the mixed collective wavefunctions, respectively. They are written explicitly as

$$\begin{aligned}&{{\mathcal {G}}}^{B(0)}_{E0}({\varvec{z}}) = \left( \frac{1}{24}{\mathcal {B}}({\varvec{z}}) + \frac{5}{8I_{1}} {\mathcal {I}}_{1}({\varvec{z}})+\frac{1}{4I_{2}} {\mathcal {I}}_{2}({\varvec{z}}) \right) \mathcal {Q}_B, \end{aligned}$$

(35)

$$\begin{aligned}&{{\mathcal {G}}}^{B(\text {op})}_{E0}({\varvec{z}}) \nonumber \\&\quad = -\frac{1}{168\sqrt{3}}\left( \begin{array}{c} 13\mathcal {Q}_{\Delta } + 19 \\ 12 \mathcal {Q}_{\Sigma ^*} + 31 \\ 11 \mathcal {Q}_{\Xi ^*} + 43 \\ -45 \mathrm {Q}_{\Omega ^-} \end{array} \right) \frac{4m_{8}}{I_{1}}\bigg ( I_{1} {\mathcal {K}}_{1}({\varvec{z}}) - K_{1} {\mathcal {I}}_{1}({\varvec{z}})\bigg ) \nonumber \\&\qquad -\frac{1}{168\sqrt{3}}\left( \begin{array}{c} -10\mathcal {Q}_{\Delta } + 50\\ -6 \mathcal {Q}_{\Sigma ^*}+44 \\ -2 \mathcal {Q}_{\Xi ^*} + 38 \\ -30 \mathrm {Q}_{\Omega ^-} \end{array} \right) \frac{4m_{8}}{I_{2}} \bigg ( I_{2} {\mathcal {K}}_{2}({\varvec{z}})- K_{2} {\mathcal {I}}_{2}({\varvec{z}})\bigg )\nonumber \\&\qquad -2 \left( \frac{m_{1}}{24}+ \frac{m_{8}}{168\sqrt{3}}\left( \begin{array}{c} - \mathcal {Q}_{\Delta } + 5 \\ -2 \mathcal {Q}_{\Sigma ^*} + 3 \\ -3 \mathcal {Q}_{\Xi ^*} + 1 \\ -3 \mathcal {Q}_{\Omega ^-} \end{array} \right) \right) {\mathcal {C}} ({\varvec{z}}), \end{aligned}$$

(36)

$$\begin{aligned}&{{\mathcal {G}}}^{B(\text {wf})}_{E0}({\varvec{z}})\nonumber \\&\quad =+ a_{27}\left( \begin{array}{c c c} {\frac{5}{24}}(- \mathcal {Q}_{\Delta } + 2) \\ {\frac{1}{12}}(-3 \mathcal {Q}_{\Sigma ^*} + 2)\\ {\frac{1 }{24}}(-7 \mathcal {Q}_{\Xi ^*} - 2) \\ 0 \end{array} \right) \left( {\mathcal {B}}({\varvec{z}})-\frac{5}{I_{1}} {\mathcal {I}}_{1}({\varvec{z}})+\frac{2}{I_{2}}{\mathcal {I}}_{2}({\varvec{z}}) \right) \nonumber \\&\qquad +a_{35}\left( \begin{array}{c c c} {\frac{1}{56}}(-\mathcal {Q}_{\Delta } - 2) \\ {\frac{2}{56}}(-\mathcal {Q}_{\Sigma ^*} - 2) \\ {\frac{3}{56}}(-\mathcal {Q}_{\Xi ^*} - 2) \\ {\frac{4}{56}}(-\mathcal {Q}_{\Omega ^-} - 2) \end{array} \right) \left( -5 {\mathcal {B}}({\varvec{z}})-\frac{5}{I_{1}} {\mathcal {I}}_{1}({\varvec{z}})+\frac{10}{I_{2}}{\mathcal {I}}_{2}({\varvec{z}})\right) , \end{aligned}$$

(37)

for the electric monopole form factors,

Fig. 1

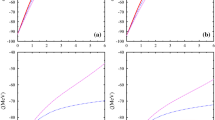
Contributions of the valence and sea quarks to the electric monopole form factors of the $\Delta ^+$ isobar and $\Omega ^-$ in the left and right panels, respectively. The dashed curves depict the valence-quark contributions, the short-dashed ones draw those of the sea quarks, and the solid ones show the total results. The lattice data are taken from Refs. [21, 23, 24]. The data of the EM from factors of the $\Delta ^{+}$ can be found in Ref. [23], and especially, the values of the physical extrapolation are taken from Ref. [21], whereas those of the EM form factors of $\Omega ^{-}$ can be found in Ref. [24]

$$\begin{aligned}&{{\mathcal {G}}}^{B_{10}(0)}_{M1}({\varvec{z}})\nonumber \\&\quad = -\frac{1}{8} \mathcal {Q}_B \left[ \left( {{\mathcal {Q}}}_{0} ({\varvec{z}}) + \frac{1}{I_{1}} {{\mathcal {Q}}}_{1} ({\varvec{z}}) \right) \right. \nonumber \\&\qquad \left. + \frac{1}{2} \frac{1}{I_{1}} {{\mathcal {X}}}_{1} ({\varvec{z}}) + \frac{1}{2} \frac{1}{I_{2}} {{\mathcal {X}}}_{2} ({\varvec{z}}) \right] , \end{aligned}$$

(38)

$$\begin{aligned}&{{\mathcal {G}}}^{B_{10}(\text {op})}_{M1}({\varvec{z}}) \nonumber \\&\quad = -\frac{m_{8}}{84\sqrt{3}}\left( \begin{array}{c} 5 \mathcal {Q}_{\Delta } - 4 \\ 3 \mathcal {Q}_{\Sigma ^*} - 1 \\ \mathcal {Q}_{\Xi ^{*}} + 2 \\ -6 \mathcal {Q}_{\Omega ^-} \end{array} \right) \left( \frac{K_{1}}{I_{1}}{{\mathcal {X}}}_{1} ({\varvec{z}}) - {{\mathcal {M}}}_{1} ({\varvec{z}})\right) \nonumber \\&\qquad + \frac{m_1}{4} \mathcal {Q}_B {\mathcal {M}}_{0} ({\varvec{z}}) -\frac{m_{8}}{84\sqrt{3}} \left( \begin{array}{c} 11 \mathcal {Q}_{\Delta } - 13 \\ 15 \mathcal {Q}_{\Sigma ^*} + 2 \\ 19 \mathcal {Q}_{\Xi ^*} + 17 \\ -9 \mathcal {Q}_{\Omega ^-} \end{array} \right) \nonumber \\&\qquad \times \left( \frac{K_{2}}{I_{2}}{{\mathcal {X}}}_{2} ({\varvec{z}}) - {{\mathcal {M}}}_{2} ({\varvec{z}})\right) + \frac{m_{8}}{84\sqrt{3}} \left( \begin{array}{c} 5\mathcal {Q}_{\Delta } - 4 \\ 3 \mathcal {Q}_{\Sigma ^*} - 1 \\ \mathcal {Q}_{\Xi ^*} +2 \\ -6 \mathcal {Q}_{\Omega ^-} \end{array} \right) \mathcal {M}_{0} ({\varvec{z}}), \end{aligned}$$

(39)

$$\begin{aligned}&{{\mathcal {G}}}^{B_{10}(\text {wf})}_{M1}({\varvec{z}}) \nonumber \\&\quad = a_{27}\left( \begin{array}{ccc} {\frac{5}{24}}(- \mathcal {Q}_{\Delta } + 2) \\ {\frac{1}{12}}(-3 \mathcal {Q}_{\Sigma ^*} + 2) \\ {\frac{1 }{24}}(-7 \mathcal {Q}_{\Xi ^*} - 2) \\ 0 \end{array} \right) \nonumber \\&\qquad \times \left[ \left( {{\mathcal {Q}}}_{0} ({\varvec{z}}) + \frac{1}{I_{1}} {{\mathcal {Q}}}_{1} ({\varvec{z}}) \right) - \frac{3}{2} \frac{1}{I_{1}} {{\mathcal {X}}}_{1} ({\varvec{z}}) - \frac{1}{2} \frac{1}{I_{2}} {{\mathcal {X}}}_{2} ({\varvec{z}}) \right] \nonumber \\&\qquad + a_{35}\left( \begin{array}{c c c} {\frac{1}{56}}(- \mathcal {Q}_{\Delta } - 2) \\ {\frac{2}{56}}(-\mathcal {Q}_{\Sigma ^*} - 2) \\ {\frac{3}{56}}(- \mathcal {Q}_{\Xi ^*} - 2) \\ {\frac{4}{56}}(-\mathcal {Q}_{\Omega ^-} - 2) \end{array} \right) \nonumber \\&\qquad \times \left[ \left( {{\mathcal {Q}}}_{0} ({\varvec{z}}) + \frac{1}{I_{1}} {{\mathcal {Q}}}_{1} ({\varvec{z}}) \right) + \frac{5}{2} \frac{1}{I_{1}} {{\mathcal {X}}}_{1} ({\varvec{z}}) - \frac{5}{2} \frac{1}{I_{2}} {{\mathcal {X}}}_{2} ({\varvec{z}}) \right] , \end{aligned}$$

(40)

for the magnetic dipole form factors, and

$$\begin{aligned} {{\mathcal {G}}}^{B_{10}(0)}_{E2}&= \frac{1}{2I_1} \mathcal {Q}_B {{\mathcal {I}}}_{1E2} ({\varvec{z}}), \nonumber \\ {{\mathcal {G}}}^{B_{10}(\text {op})}_{E2}&= \frac{4}{63\sqrt{3}}m_{8} \left( \frac{K_{1}}{I_{1}} \mathcal {I}_{1E2}({\varvec{z}}) - \mathcal {K}_{1E2}({\varvec{z}}) \right) \nonumber \\&\quad \times \left( \begin{array}{ccc} 4Q_{\Delta }+1 \\ -6Q_{\Sigma ^{*}}-5 \\ -16Q_{\Xi ^{*}}-11 \\ 9 \end{array} \right) , \nonumber \\ {{\mathcal {G}}}^{B_{10}(\text {wf})}_{E2}&= -\frac{4}{I_{1}} \left( a_{27}\left( \begin{array}{ccc}{\frac{5}{24}}(- \mathcal {Q}_{\Delta }+2) \\ {\frac{1}{12}}(-3 \mathcal {Q}_{\Sigma ^*} + 2) \\ {\frac{1}{24}}(-7 \mathcal {Q}_{\Xi ^*} - 2) \\ 0 \end{array} \right) \right. \nonumber \\&\quad \left. + a_{35}\left( \begin{array}{c c c} {\frac{1}{56}}(- \mathcal {Q}_{\Delta }-2) \\ {\frac{2}{56}}(-\mathcal {Q}_{\Sigma ^*}-2) \\ {\frac{3}{56}}(-\mathcal {Q}_{\Xi ^*}-2) \\ {\frac{4}{56}}(-\mathcal {Q}_{\Omega ^-} - 2) \end{array} \right) \right) {{\mathcal {I}}}_{1E2} ({\varvec{z}}) \end{aligned}$$

(41)

for the electric quadrupole form factors. Note that all the symmetric contributions to the EM form factors of a decuplet baryon are proportional to the corresponding charge. It indicates that all the EM form factors of the neutral baryons in the decuplet vanish in the chiral limit [58]. Moreover, the $m_{\mathrm {s}}$ corrections on the E2 form factors of the neutral decuplet baryons come from the collective operators and collective wavefunctions. It implies that the magnitudes of the E2 form factors of the neutral baryons in the decuplet are in particular small, compared to those of other members of the baryon decuplet.

In the $\chi$QSM, various sum rules for the magnetic dipole moments of the baryon decuplet can be derived, as already shown in Ref. [58]. If we examine the expressions for the E2 form factors of the baryon decuplet given in Eq. (41), then we can find that they have the same group structure as those of the M1 form factors (40). Thus, we can obtain the similar sum rules for the electric quadrupole moments. In the chiral limit, one can find the following relations [58]:

$$\begin{aligned} Q_{\Sigma ^{*0}}&= \frac{1}{2} (Q_{\Sigma ^{*+}} + Q_{\Sigma ^{*-}}), \nonumber \\ Q_{\Delta ^{-}} + Q_{\Delta ^{++}}&= Q_{\Delta ^{0}} + Q_{\Delta ^{+}}, \nonumber \\ \sum _{B\in \mathrm {decuplet}} Q_{B}&= 0. \end{aligned}$$

(42)

Even though the flavor SU(3) symmetry is broken, we still can find the following sum rules

$$\begin{aligned} -4 Q_{\Delta ^{++}} + 6 Q_{\Delta ^{+}} + 3 Q_{\Sigma ^{*+}} - 6 Q_{\Sigma ^{*0}} + Q_{\Omega ^{-}}&= 0, \nonumber \\ -2 Q_{\Delta ^{++}} + 3 Q_{\Delta ^{+}} + 2 Q_{\Sigma ^{*+}} - 4 Q_{\Sigma ^{*0}} + Q_{\Xi ^{*-}}&= 0, \nonumber \\ -Q_{\Delta ^{++}} + 2 Q_{\Delta ^{+}} - 2 Q_{\Sigma ^{*0}} + Q_{\Xi ^{*0}}&= 0, \nonumber \\ Q_{\Sigma ^{*+}} - 2 Q_{\Sigma ^{*0}} + Q_{\Sigma ^{*-}}&= 0, \nonumber \\ 2Q_{\Delta ^{++}} -3 Q_{\Delta ^{+}} + Q_{\Delta ^{-}}&= 0, \nonumber \\ Q_{\Delta ^{++}} -2 Q_{\Delta ^{+}} + Q_{\Delta ^{0}}&= 0. \end{aligned}$$

(43)

We also get the differences between the electric quadrupole moments of the baryon decuplet.

$$\begin{aligned} \frac{1}{3}(Q_{\Omega ^{-}}-Q_{\Delta ^{++}})&= \frac{1}{2}(Q_{\Xi ^{*-}}-Q_{\Delta ^{+})} \nonumber \\&= Q_{\Xi ^{*0}}-Q_{\Sigma ^{*+}} = Q_{\Sigma ^{*-}}-Q_{\Delta ^{0}}. \end{aligned}$$

(44)

4 Results and discussion

Before we present the numerical results of the present work, we first explain how to fix the parameters of the model. In the $\chi$QSM, the dynamical quark mass M is the only free parameter, which was already determined by computing various form factors of the nucleon in the previous works [53, 55]. The most preferable value is $M = 420$ MeV. We have already examined that the numerical results of all the EM form factors in this work are insensitive to the value of M. Thus, we adopt the same value of $M = 420$ MeV in the present work. The average mass of the current up and down quarks $\overline{m}$ is fixed by reproducing the pion mass in the mesonic sector. The strange current quark mass $m_{\mathrm {s}}$ is taken to be 180 MeV, which produces very well the mass splittings of the SU(3) baryons and singly heavy baryons [53, 82]. Since the divergences from the sea quarks or from the vacuum polarizations are tamed by introducing the regularization, we fix the cutoff parameter $\Lambda$ by reproducing the pion decay constant $f_\pi = 93$ MeV.

Fig. 2

Sea and valence contributions of the electric monopole form factors of the other members of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$ baryons. Notations are the same as in Fig. 1

Fig. 3

Contributions of the valence and sea quarks to the magnetic dipole form factors of the $\Delta ^+$ isobar and $\Omega ^-$ in the left and right panels, respectively. Notations are the same as in Fig. 1. The lattice data are taken from Refs. [21, 23, 24]

4.1 Contributions of the valence quarks and sea-quark polarization

Since there exist the lattice data on the $\Delta ^+$ isobar and $\Omega ^-$ hyperon EM form factors, we will first focus on those of the $\Delta ^+$ and $\Omega ^-$ and then will discuss the EM form factors of all the other members in the baryon decuplet. In Fig. 1, we draw the numerical results for the E0 form factors of the $\Delta ^+$ and $\Omega ^-$ in the left and right panels respectively, examining the valence-quark and sea-quark contributions. As shown in Fig. 1 explicitly, the valence-quark contributions are the dominant ones in general. The valence quarks contribute to the $\Delta ^+$ electric monopole form factor by about 75 % whereas the sea quarks provide approximately 25 % contribution to it. We also see that the general feature of each contribution seems very similar in the case of the $\Omega ^-$, except that the effect of the sea-quark polarization becomes slightly larger than that on the $\Delta ^+$ E0 form factor. Note that the sea-quark contribution to the proton electric monopole form factor is smaller than those to the $\Delta ^+$ and $\Omega ^-$ form factors.

Compared with the lattice data of the $\Delta ^+$ and $\Omega ^-$ electric monopole form factors, we find that the present results fall off faster than those of the lattice calculation as $Q^2$ increases. However, the lattice calculations tend to provide the results of the electric monopole form factor of the proton, which decrease more slowly than the experimental data, in particular, when the unphysical value of the pion mass is used [91,92,93,94]. Even though the physical pion mass is employed, the lattice results fall off still more slowly than the experimental data [95]. One can find the similar tendency in the case of the tensor and anomalous form factors of the nucleon. Compared with the lattice data on these form factors [96, 97] , the results of the $\chi$QSM again decrease more slowly [67, 68]. In this respect, it is natural for the present results to fall off faster than the lattice ones. We will discuss the comparison with the lattice data in detail in Sect. 4.4, considering the chiral extrapolation.

In Fig. 2, we present the results of the electric monopole form factors for all other baryons except for the $\Delta ^+$ and $\Omega ^-$ baryons, decomposing the valence and sea quark contributions. Those of the charged baryons show similar tendencies as the $\Delta ^+$ and $\Omega ^-$ form factors. However, when it comes to the electric monopole form factors of the neutral hyperons, the situation is very different. First of all, since the leading contributions and rotational $1/N_c$ corrections are proportional to the charge of the corresponding baryon, which is shown explicitly in Eq. (35), they do not contribute to the E0 form factors of the neutral baryon decuplet. Thus, the $m_s$ corrections become effectively the main contributions to them.

Fig. 4

Sea and valence contributions to the magnetic dipole form factors of the other members of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$ baryons. Notations are the same as in Fig. 1

Fig. 5

Contributions of the valence and sea quarks to the electric quadrupole form factors of the $\Delta ^+$ isobar and $\Omega ^-$ in the left and right panels, respectively. Notations are the same as in Fig. 1. The lattice data are taken from Refs. [21, 23, 24]

The contribution from the valence quarks is almost canceled by the sea-quark contribution in the case of the $\Delta ^0$ electric monopole form factor. This cancellation makes it possible to satisfy the charge conservation at $Q^2=0$. For the $\Sigma ^{*0}$, the cancellation is even stronger and complicated. While the valence-quark part wins the sea-quark contribution, it becomes weaker as $Q^2$ increases. When $Q^2$ grows more than $0.2\,\mathrm {GeV}^2$, the sea quarks takes control of the $\Sigma ^{*0}$ E0 form factor. Thus, its $Q^2$ dependence seems rather different from that of the $\Delta ^0$ form factor that looks similar to the neutron electric form factor (see Fig. 13 in Appendix C). The electric monopole form factor of the $\Xi ^{*0}$ baryon is even more interesting. The magnitude of the sea-quark contribution is larger than the valence part in lower $Q^2$ regions and the valence-quark contribution turns negative as $Q^2$ increases. As a result, the $\Xi ^{*0}$ E0 form factor is negative over all the $Q^2$ regions.

Before we compare the present results of the magnetic dipole form factors of the baryon decuplet with those of the lattice calculation, we want to mention that we follow the definition employed by the lattice calculation. In Refs. [21, 23, 24], the following definition for the magnetic dipole moment of the $\Delta ^+$ and $\Omega ^-$ was used

$$\begin{aligned}&\mu _{\Delta ^+} = G_{M1}^{\Delta ^+} (0) \left( \frac{e}{2M_\Delta }\right) = G_{M1}^{\Delta ^+}(0) \left( \frac{M_N}{M_\Delta }\right) \mu _N,\nonumber \\&\mu _{\Omega ^-} = G_{M1}^{\Omega ^-} (0) \left( \frac{e}{2M_\Omega }\right) = G_{M1}^{\Omega ^-} (0) \left( \frac{M_N}{M_\Omega }\right) \mu _N, \end{aligned}$$

(45)

where $M_N$, $M_\Delta$, and $M_{\Omega }$ denote the masses of the nucleon, the $\Delta$ isobar, and the $\Omega ^-$. $\mu _N$ stands for the nuclear magneton. Thus, the M1 form factors of the $\Delta ^+$ and $\Omega ^-$ in the lattice calculation are scaled by the mass of the corresponding baryon. In order to compare the present results with the lattice ones, we must use the same definition of the M1 form factors of the baryon decuplet. We want to note that the present values of the M1 form factors of the baryon decuplet do not give the corresponding magnetic dipole moments that are presented conventionally in unit of the nuclear magneton.

Figure 3 depicts the results of the magnetic dipole form factors of the $\Delta ^+$ and $\Omega ^-$ in the left and right panels, respectively. The sea-quark polarization contributes to the $\Delta ^+$ M1 form factor only by about 20 %, while it enhances the $\Omega ^-$ form factor by approximately 30 %. Thus, we find the similar tendency as in the case of the electric monopole form factors shown in Fig. 1. In comparison with the lattice data, the present results again fall off faster than the lattice ones.

In Fig. 4, we draw the contributions of the valence and sea quarks on the magnetic dipole form factors of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$ form factors. Being similar to the results of the $\Delta ^+$ and $\Omega ^-$ M1 form factors drawn in Fig. 3, those of the charged baryon decuplet exhibit similar $Q^2$ dependence. The sizes of the valence and sea quark contributions show the similar tendency. However, the M1 form factors of the charged baryon decuplet show rather different behaviors. While the sea-quark polarizations contribute to the $\Xi ^{*0}$ M1 form factor, they dominate over the valence-quark contributions for the $\Sigma ^{*0}$ one. On the other hand, the sea-quark effects are larger than the valence-quark ones only at the low $Q^2$ region and fall off faster than the valence-quark contributions.

Fig. 6

Contributions of the valence and sea quarks to the electric quadrupole form factors of the other members of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$ baryons. Notations are the same as in Fig. 1

We use the following definition of the electric quadrupole form factors of the baryon decuplet used in the lattice calculation

$$\begin{aligned} Q_{B_{10}} = G_{E2}^{B_{10}} (0) \left( \frac{|e|}{M_{B_{10}}^2}\right) , \end{aligned}$$

(46)

so that we are able to compare the present results with the lattice data. In Fig. 5, we draw the results of the E2 form factors of the $\Delta ^+$ and $\Omega ^-$ in the left and right panels, respectively. The contribution of the sea-quark polarization to the $\Delta ^+$ E2 form factor is dominant over that of the valence quarks in lower $Q^2$ regions ($0\le Q^2 \le 0.3\,\mathrm {GeV}^2$), which is opposite to the case of both the E0 and M1 form factors of the $\Delta ^+$, as already discussed in Ref. [88]. In particular, the sea-quark polarization gives more than 90 % contribution to the $\Delta ^+$ E2 form factor in the vicinity of $Q^2=0$. When $Q^2$ further increases ($Q^2 > 0.3 \,\mathrm {GeV}^2$), the valence-quark effects outdo the sea-quark contribution. Interestingly, though the sea-quark polarization contributes also dominantly to the $\Omega ^-$ E2 form factor but it provides approximately 70 %. The $Q^2$ dependence of the $\Omega ^-$ E2 form factor is similar to the case of the $\Delta ^+$ one. However, the sign of the $\Omega ^-$ E2 form factor is positive while that of the $\Delta ^+$ is negative. It indicates that the charge distribution of the $\Delta ^+$ is in an oblate shape ($Q_{\Delta ^+}<0$) whereas that of the $\Omega ^-$ looks prolate ($Q_{\Omega ^-}>0$). Though the absolute value of $G_{E2}^{\Omega ^-}(0)$ at $Q^2=0$ seems larger than that of $G_{E2}^{\Delta ^+}(0)$, the magnitude of the $\Omega ^-$ electric quadrupole moment is in fact slightly smaller than that of the $\Delta ^+$, as will be shown later in Table 4. The discussion given above has important physical implications. The sea-quark polarizations or the pion clouds in a conventional terminology are the main reason for the deformation of a decuplet baryon. It also indicates that the valence quarks sit on the inner part of a decuplet baryon whereas the pion clouds govern the charge distribution in the outer region of the baryon.

Fig. 7

Effects of the explicit flavor SU(3) symmetry breaking on the electric monopole form factors of the $\Delta ^+$ isobar and $\Omega ^-$ in the left and right panels, respectively. The dashed curves depict the E0 form factors without the effects of the explicit flavor SU(3) symmetry breaking, whereas the solid ones present those with the effects. The lattice data are taken from Refs. [21, 23, 24]

Fig. 8

Effects of the explicit flavor SU(3) symmetry breaking on the electric monopole form factors of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$ baryons. Notations are the same as in Fig. 7

In contrast to the cases of the E0 and M1 form factors, the lattice data [21, 23, 24] contain large numerical uncertainties for the E2 form factors of the $\Delta ^+$ and $\Omega ^-$. Moreover, there exist the lattice date only in relatively larger $Q^2$ regions. Nevertheless, the present results are in good agreement with them, as illustrated in Fig 5.

In Fig. 6, we draw the results of the electric quadrupole form factors of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$. As in the cases of the $\Delta ^+$ and $\Omega ^-$, the sea-quark contributions generally dominate over the valence-quark ones in lower $Q^2$ regions and fall off faster than the valence-quark ones, so that the sea-quark contributions becomes smaller than the valence-quark contributions in higher $Q^2$ regions. The positively charged baryon decuplet have in general negative values of the E2 form factors, while it is consistently other way around in the case of the negatively charged decuplet baryons. As discussed previously, the distributions of the positively charged baryon decuplet take an cushion shape ($Q_B<0$) whereas the negative ones look like a rugby-ball shape ($Q_B>0$).

The E2 form factors of the neutral baryon decuplet arise only from the contribution of the $m_s$ corrections. As expressed in Eq. (41), the leading-order contributions to the neutral E2 form factors vanish, because they are proportional to the corresponding charges. Thus, the $m_{s}$ corrections play the leading role.

4.2 Effects of flavor SU(3) symmetry breaking

We now examine the effects of the linear $m_s$ corrections on the E0 form factors of the $\Delta ^+$ and $\Omega ^-$ baryons. As shown explicitly in Fig. 7, the linear $m_s$ corrections are almost negligible in the case of the $\Delta ^+$ baryon. They also do not contribute much to the $G_{E0}^{\Omega ^-}$ form factor. In the case of the neutral E0 form factor, however, the leading contributions together with the rotational $1/N_c$ effects vanish, because they are proportional to the corresponding charge as shown in Eq. (35). In Fig. 8, we draw the E0 form factors of all the members in the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$. In general, the effects of the linear $m_s$ corrections are rather small on the E0 form factors of the charged baryons. However, it is of great interest to see the results of the neutral E0 form factors. In this case, the linear $m_s$ corrections become the leading-order contribution.

Fig. 9

Effects of the explicit flavor SU(3) symmetry breaking on the magnetic dipole form factors of the $\Delta ^+$ isobar and $\Omega ^-$ in the left and right panels, respectively. The dashed curves depict the E0 form factors without the effects of the explicit flavor SU(3) symmetry breaking, whereas the solid ones present the E0 form factors with the effects. The lattice data are taken from Refs. [21, 23, 24]. Notations are the same as in Fig. 7

Fig. 10

Effects of the explicit flavor SU(3) symmetry breaking on the magnetic dipole form factors of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$ baryons. Notations are the same as in Fig. 7

As depicted in Fig. 9, the effects of the flavor SU(3) symmetry breaking are also small on the $\Delta ^+$ and $\Omega ^-$ M1 form factors. However, the result of the magnetic dipole form factor of the $\Delta ^-$ is enhanced by almost $15~\%$ with the linear $m_s$ corrections included. The reason can be found easily by examining the expressions of the $m_s$ corrections written in Eqs. (39) and (40). In the case of $\Delta ^-$, the charge-dependent terms and other ones are constructively added, so that the $m_s$ corrections are strengthened. As for the M1 form factors of the neutral baryon decuplet, the leading-order and rotational $1/N_c$ contributions vanish, since they are proportional to the corresponding charge. Thus, the linear $m_s$ corrections again play the leading role in the case of the neutral form factors of the baryon decuplet (Fig. 10).

Fig. 11

Effects of the explicit flavor SU(3) symmetry breaking on the electric quadrupole form factors of the $\Delta ^+$ isobar and $\Omega ^-$ in the left and right panels, respectively. The dashed curves depict the E2 form factors without the effects of the explicit flavor SU(3) symmetry breaking, whereas the solid ones present the E2 form factors with the effects. The lattice data are taken from Refs. [21, 23, 24]. Notations are the same as in Fig. 7

Figure 11 shows the results of the electric quadrupole form factors of the $\Delta ^+$ and $\Omega ^-$ baryons. Interestingly, the $m_s$ corrections are quite sizable to the $\Delta ^+$ E2 form factor whereas they are marginal to the $\Omega ^-$ one. We can understand this difference from Eq. (41). In Fig. 12, we present the results of the E2 form factors of all other baryons with the effects of flavor SU(3) symmetry breaking shown.

4.3 Charge radii, magnetic dipole moments, magnetic radii, and electric quadrupole moments

In Table 1, we list the present results of the charge radii of the baryon decuplet in comparison with those from various theoretical approaches. The present results are in general larger than those of lattice data, which was already expected when we compared the results of the E0 form factors with those of the lattice QCD previously. The results of the form factors from the lattice calculation fall off more slowly than the present ones. The covariant versions of chiral perturbation theory [31, 32] yield systematically smaller values of the charge radii of the baryon decuplet, compared with the present ones. On the other hand, the large $N_c$ expansions give the results similar to the present ones [34, 35]. Wagner et al. [38] computed the various observables of the baryon decuplet based on a potential model including chiral residual interactions in addition to the confining potentials. Interestingly, the results of Ref. [38] are rather similar to the present ones. Berger et al. used the Goldstone-boson-exchange (GBE) constituent quark model (CQM). The GBE CQM is distinguished from that of Ref. [38]. The GBE CQM is a relativistic one though it also contains the chiral interactions for the Nambu–Goldstone bosons. The results are quite underestimated in comparison with the present ones but are comparable to those of Refs. [31, 32].

Table 1 Charge radii of the baryon decuplet in comparison with those from lattice QCD [21, 24, 27], the chiral constituent-quark model [39], the chiral quark model [38], large $N_{c}$ [34], combined chiral and $1/N_{c}$ expansion [35], covariant $\chi$PT [31] and $\chi$PT [32]

Comparing the results of the second row and those of the third one, we see that the effects of flavor SU(3) symmetry breaking are marginal on the electric monopole form factors of the baryon decuplet, as mentioned already. Note that the charge radii of the neutral decuplet baryons vanish when $m_s$ is set equal to zero, since the SU(3) symmetric parts of the expression for the electric monopole form factors are proportional to the corresponding charges. Thus, the main contributions arise from the linear $m_s$ corrections. As shown explicitly in Eq. (37), there are two different $m_s$ contributions, i.e. those from the collective operators and those from the wavefunction corrections. Interestingly, the charge densities of these two different contributions are oppositely polarized. That is, the contributions from the wavefunction corrections provide positive charge densities whereas the collective operator parts yield negative ones. It indicates that the charge radii of the neutral decuplet baryons should be even smaller than that of the neutron.

Table 2 lists the numerical results of the present model. Before we discuss them, we want to mention two important points related to the magnetic dipole moments within the $\chi$QSM. Firstly, it is well known that the results of the magnetic dipole moments of the baryon octet from any chiral solitonic approaches are underestimated in comparison with the experimental data. In order to improve them, Ref. [88] used the nuclear magneton in terms of the classical soliton mass instead of the physical nucleon mass. Thus, the results of the magnetic dipole moments were obtained by an additional mass factor 1.36. With this factor included, Ref. [88] reproduced nicely the experimental data on the magnetic dipole moment of the $\Omega ^-$ baryon. If we introduce this additional factor in the present work, of course we are able to reproduce almost the same results as in Ref. [88], which we list in the fourth row of Table 2.² However, we present also the results without this mass factor, since we want to concentrate on the physics of the $\chi$QSM as such. Secondly, the $\chi$QSM provides the SU(3) symmetric expressions of the magnetic dipole moments, which are proportional to the corresponding charges of the baryon decuplet, as shown in Eq. (38). Thus, all the magnetic moments of the neutral decuplet baryons vanish as listed in the third row of Table 2, when the $m_s$ corrections turned off. In general, the effects of the $m_s$ corrections are again small on those of the positively charged decuplet baryons. The results are also compared with those from various different theoretical approaches.

In Table 3, we present the results of the magnetic radii of the baryon decuplet. The magnetic radius of a baryon is defined as the derivative of its magnetic dipole form factor

$$\begin{aligned} \langle r^2 \rangle _{M1}^B = \left. -\frac{6}{G_{M1}^B(0)}\frac{d G_{M1}^{B}(Q^2)}{dQ^2}\right| _{Q^2=0}. \end{aligned}$$

(47)

Thus, the SU(3) symmetric results of the baryon decuplet are all the same. It means that the results of the magnetic radii exhibit effectively the effects of the flavor SU(3) symmetry breaking. The $\Delta ^-$ magnetic radius shows the strongest enhancement due to the $m_s$ corrections except for the case of the neutral baryons. However, the effects of the flavor SU(3) symmetry breaking are in general small on the magnetic radii of the positively charged decuplet baryons. Compared to the results of chiral perturbation theory [32] and the chiral quark-potential model [38], the present ones of the positively charged baryons are in good agreement with them, whereas those of the neutral baryons are rather different from each other. Note that the neutral baryons have the same magnetic radii as those of the charged baryons, since the denominator and numerator SU(3) D-functions are explicitly canceled out (see Eq. (47)).

Fig. 12

Effects of the explicit flavor SU(3) symmetry breaking on the electric quadrupole form factors of the baryon decuplet except for the $\Delta ^+$ and $\Omega ^-$ baryons. Notations are the same as in Fig. 7

Table 2 Magnetic dipole moments of the baryon decuplet in comparison with the results from lattice QCD [25,26,27,28], the relativistic quark model [37], next-to-leading-order HB$\chi$PT [30], large $N_{c}$ [33], QCD sum rules [42], the chiral quark model [38], covariant $\chi$PT [31], $\chi$PT [32] and the experimental data [13, 18, 19]

Table 3 Magnetic radii of the baryon decuplet in comparison with those of the chiral quark model [38], $\chi$PT [32]

Table 4 Electric quadrupole moments of the baryon decuplet in comparison with the quark model [36], HB$\chi$PT [30], the Skyrme model [40], large $N_{c}$ [34], the chiral quark model [38], the QCD sum rules [43, 44]

Fig. 13

Numerical results of the EM form factors of the $\Delta ^{+}$ and $\Omega ^{-}$ baryons with the different pion masses in the calculations of lattice QCD  [21, 23, 24] employed

Table 4 lists the results of the electric quadrupole moments in comparison with those from other theoretical works. Since $Q_B$ reveals how much the corresponding baryon is distorted from a spherical charge distribution, it is of great interest to examine it carefully. As we have already mentioned in the previous subsection, when $Q_B$ is negative the corresponding baryon takes an oblate shape (cushion shape), while when $Q_B>0$ it does a prolate one (rugby-ball shape). As shown in Table 4, the positively charged baryons all have negative values of $Q_B$, whereas the negatively charged ones get the positive values. This conclusion is shared by all other theoretical predictions. However, when it comes to the case of the neutral decuplet baryons, $Q_B$ are small but positive except for the $\Xi ^{*0}$. Note that heavy-baryon chiral perturbation theory [30], the nonrelativistic quark model (NQM) [36], and the chiral quark-potential model [38] give the negative values of $Q_{\Sigma ^{*0}}$.

4.4 Chiral extrapolation and comparison with the lattice data

To compare the present results of the EM form factors of the $\Delta ^+$ and $\Omega ^-$ baryons with those from lattice QCD, we made a chiral extrapolation as done in Ref. [98]. We first derived the profile functions of the soliton, which correspond to the values of the unphysical pion mass: $m_\pi =297$ MeV, 311 MeV, 353 MeV and 384 MeV. Using them, we computed the EM form factors of the $\Delta ^+$ and $\Omega ^-$.

The results are drawn in Fig. 13. In general, the larger values of the pion mass yield the EM form factors that fall off more slowly than those with the physical pion mass ($m_\pi =139$ MeV). In the case of the electric form factors, the present results get closer to the lattice ones with the value of $m_\pi$ increased. To compare the present results with the lattice data more closely, we have scaled the M1 form factors by introducing the corresponding numerical results of the $\Delta ^+$ and $\Omega ^-$ magnetic moments taken from a model-independent approach [99], which reproduces the experimental data very well. Then it is clearly seen that the $Q^2$ dependences of the M1 form factors become very similar to the lattice data. When it comes to the E2 form factors, the results are remarkable. The numerical results of the E2 form factors are very sensitive to the values of the pion mass. In particular, the present results of the $\Omega ^-$ E2 form factors are in good agreement with the lattice data when higher values of the pion mass are used.

5 Summary and conclusion

In the present work, we investigated the electromagnetic form factors of the baryon decuplet together with other related observables, based on the self-consistent SU(3) chiral quark-soliton model. We considered the $1/N_c$ rotational corrections and the linear $m_s$ corrections with the symmetry-conserving zero-mode quantization used. We first computed the electric monopole form factors of the $\Delta ^+$ and $\Omega ^-$ and compared the results with those from recent calculations of lattice QCD. Taking into account the fact that result of the E0 form factor of the proton from lattice QCD fall off more slowly than the experimental data, we find that the present results are comparable with the lattice data. We presented the results of the electric monopole form factors for all other members of the baryon decuplet. The contributions of the sea-quark polarization are stronger to the negatively charged decuplet baryons than to the positively charged ones. However, the valence quark contributions are almost canceled by the sea-quark ones. At $Q^2=0$, they are exactly canceled each other as they should be. The results of the magnetic dipole form factors show very similar $Q^2$ dependences in comparison with the lattice data. While the sea-quark contributions are smaller than the valence ones to the M1 form factors of both the positively and negatively charged baryons, they are dominant over the valence-quark contributions in the case of the neutral baryons except for the $\Xi ^{*0}$. We also computed the electric quadrupole form factors of the $\Delta ^+$ and $\Omega ^-$ and the results are in agreement with the lattice ones. The sea-quark contributions govern the form factor in smaller $Q^2$ regions and then yield to the valence-quark contributions as $Q^2$ increases. This tendency is general also for the E2 form factors of all other decuplet baryons. In the present framework, the magnetic octupole form factors vanish because of the hedgehog symmetry. It implies that the M3 form factors must be very small.

We also examined the effects of flavor SU(3) symmetry breaking. In fact, there are two different sources of the linear $m_s$ corrections: one from the effective chiral action and the other from the wavefunction corrections that arise from the mixing of the baryon decuplet wavefunctions with higher representations. Since all the form factors of the baryon decuplet are proportional to the corresponding charges when the $m_s$ corrections are switched off, the effects of the flavor SU(3) symmetry breaking are in particular important on the form factors of the neutral decuplet baryons. In fact, the linear $m_s$ corrections are the leading-order contributions to them. While the $m_s$ corrections are marginal to most of the form factors, their effects are nonnegligible on the electric quadrupole form factors. We also presented the charge radii, the magnetic radii, the magnetic dipole moments and the electric quadrupole moments of the baryon decuplet, discussed them in comparison with those from other theoretical works.

Finally, we used the values of the unphysical pion mass to compare the present results with the lattice data in a more quantitative manner. Indeed, larger values of the pion mass bring the present results closer to those of lattice QCD. In particular, the $Q^2$ dependence of the $\Delta ^+$ and $\Omega ^-$ M1 form factors are in good agreement with the lattice data. We also showed that the E2 form factors are rather sensitive to the values of the pion mass. As a result, the present result of the $\Omega ^-$ E2 form factor is in quantitative agreement with the lattice data, when larger values of the pion mass are employed.

It is also of great importance to study the electromagnetic transition form factors of the baryon decuplet to the baryon octet. Though there are previous works on the $\Delta \rightarrow N\gamma$ transitions within the same theoretical framework, Other decay channels were not investigated. However, it is indeed important to scrutinize the radiative decays such as $\Sigma ^*\rightarrow \Sigma \gamma$ and $\Xi ^*\rightarrow \Xi \gamma$, since they provide information not only on radiative decays but also on the vector-meson couplings to the baryon octet and decuplet. The corresponding investigation is under way.

Appendices

Appendix A: Matrix elements of the SU(3) Wigner D function

In the following we list the results of the matrix elements of the relevant collective operators for the EM form factors of the baryon decuplet in Tables 5, 6, 7, 8 9, 10, 11, 12. The collective operators for E2 form factors can be found in those for E0 and M1.

Table 5 The matrix elements of the collective operators of the leading terms and the $1/N_c$ rotational corrections to the electric monopole form factors

Table 6 The matrix elements of the collective operators of the $m_s$ corrections to the electric monopole form factors

Table 7 The relevant transition matrix elements of the collective operators coming from the 27plet component of the baryon wavefunctions for the electric monopole form factors

Table 8 The relevant transition matrix elements of the collective operators coming from the 35plet component of the baryon wave functions for the electric monopole form factors

Table 9 The matrix elements of the collective operators of the leading terms and the $1/N_c$ rotational corrections to the magnetic dipole form factors

Table 10 The matrix elements of the collective operators of the $m_s$ corrections to the magnetic dipole form factors

Table 11 The relevant transition matrix elements of the collective operators coming from the 27plet component of the baryon wave functions for the magnetic dipole form factors

Table 12 The relevant transition matrix elements of the collective operators coming from the 35plet component of the baryon wave functions for the magnetic dipole form factors

Appendix B: Densities of the electric quadrupole form factors

The densities of the electric quadrupole form factors are given as

$$\begin{aligned}&(-\sqrt{10})\frac{2}{N_{c}} {{\mathcal {I}} }_{1E2}({\varvec{z}})\nonumber \\&\quad = \sum _{n \ne \mathrm {val} }\frac{1}{E_{n}-E_{\mathrm {val}}}{\langle \mathrm {val} | {\varvec{\tau }} | n\rangle } \cdot {\langle n |{\varvec{z}} \rangle \{ \sqrt{4\pi }Y_{2} \otimes \tau _{1} \}_{1}\langle {\varvec{z}} | \mathrm {val}\rangle } \nonumber \\&\qquad + \frac{1}{2} \sum _{n,m} {{\mathcal {R}}}_{3}(E_n,E_m) {\langle n | {\varvec{\tau }} | m \rangle } \cdot {\langle m | {\varvec{z}} \rangle \{ \sqrt{4\pi } Y_{2} \otimes \tau _{1} \}_{1} \langle {\varvec{z}} | n \rangle } ,\nonumber \\&(-\sqrt{10})\frac{2}{N_{c}} {{\mathcal {K}} }_{1E2}({\varvec{z}})\nonumber \\&\quad = \sum _{n \ne \mathrm {val} } \frac{1}{E_{n}-E_{\mathrm {val}}} {\langle \mathrm {val} | \gamma ^{0} {\varvec{\tau }} | n \rangle } \cdot {\langle n | {\varvec{z}} \rangle \{ \sqrt{4\pi } Y_{2} \otimes \tau _{1} \}_{1} \langle {\varvec{z}} | \mathrm {val} \rangle } \nonumber \\&\qquad + \frac{1}{2} \sum _{n,m} {{\mathcal {R}}}_{5}(E_n,E_m) {\langle n | \gamma ^{0} {\varvec{\tau }} | m \rangle } \cdot {\langle m | {\varvec{z}} \rangle \{ \sqrt{4\pi } Y_{2} \otimes \tau _{1} \}_{1} \langle {\varvec{z}} | n \rangle }, \end{aligned}$$

(B1)

Fig. 14

Electric monopole form factors of the baryon decuplet in comparison with those of the nucleon

where the regularization functions are defined as

$$\begin{aligned} {{\mathcal {R}}}_{3}(E_{n},E_{m})&= \frac{1}{2 \sqrt{\pi }} \int ^{\infty }_{0} \phi (u) \frac{du}{\sqrt{u}} \left[ \frac{ e^{-u E_{m}^{2}}- e^{-u E_{n}^{2}}}{u(E^{2}_{n} - E^{2}_{m})} \right. \nonumber \\&\quad \left. -\frac{E_{m} e^{-u E_{m}^{2}}+E_{n} e^{-u E_{n}^{2}}}{E_{n} + E_{m}} \right] , \nonumber \\ {{\mathcal {R}}}_{5}(E_{n},E_{m})&= \frac{\mathrm {sign}(E_{n})-\mathrm {sign}(E_{m})}{2(E_{n}-E_{m})}. \end{aligned}$$

(2)

Here, $|\mathrm {val}\rangle$ and $|n\rangle$ denotes the state of the valence and sea quarks with the corresponding eigenenergies $E_{\mathrm {val}}$ and $E_n$ of the single-quark Hamiltonian $h(U_c)$, respectively.

Fig. 15

Magnetic dipole form factors of the baryon decuplet in comparison with those of the nucleon

Appendix C: Comparison with the nucleon EM form factors

The results on the nucleon form factors were computed with the same set of parameters within the same framework. In the left panel of Fig. 14, we compare the results of the E0 form factors of the positively singly charged baryon decuplet with those of the proton electric form factor, whereas in the right panel of Fig. 14, we do those of the neutral baryon decuplet with those of the neutron electric form factor. The charged baryon form factors behave in a way very similar to the proton one. On the other hand, the neutral E0 form factors are in general different from that of the neutron. For example, that of $\Xi ^{*0}$ becomes even negative.

The left panel of Fig. 15 presents the results of the M1 form factors of the positively singly charged baryon decuplet in comparison with those of the proton electric form factor, whereas in the right panel of Fig. 15, the right panel shows those of the neutral baryon decuplet being compared with those of the neutron electric form factor. The general tendency of the results on the M1 form factors of the charged baryon decuplet are similar to the proton one. However, those of the neutral baryons are rather different from these of the neutron. The magnitudes of the magnetic dipole moments of the neutral decuplet baryons are very small, compared to that of the neutron.