Revisiting $\Lambda _{b}\rightarrow \Lambda _{c}$ and $\Sigma _{b}\rightarrow \Sigma _{c}$ weak decays in the light-front quark model

Abstract

In this work, we study $\Lambda _{b}\rightarrow \Lambda _{c}$ and $\Sigma _{b}\rightarrow \Sigma _{c}$ weak decays in the light-front quark model. As is well known, the key point for such calculations is properly evaluating the hadronic transition matrix elements which are dominated by the non-perturbative QCD effect. In our calculation, we employ the light-front quark model and rather than the traditional diquark picture, we account the two spectator light quarks as individual ones. Namely during the transition, they retain their color indices, momenta and spin polarizations unchanged. Definitely, the subsystem composed of the two light quarks is still in a color-anti-triplet and possesses a definite spin, but we do not priori assume the two light quarks to be in a bound system–diquark. Our purpose is probing the diquark picture, via comparing the results with the available data, we test the validity and applicability of the diquark structure which turns a three-body problem into a two-body one, so greatly simplifies the calculation. It is indicated that the two approaches (diquark and a subsystem within which the two light quarks are free) lead to similar numerical results even though the model parameters in the two schemes might deviate slightly. Thus, the diquark approach seems sufficiently reasonable.

1 Introduction

The study on baryon physics is much behind that on mesons so far, because the structure of baryon is remarkably more complicated even though only one more quark gets involved. The case of $\Lambda _b$, $\Lambda _c$, $\Sigma _b$ and $\Sigma _c$ which contain one heavy quark is simpler than that with all light quarks, so that corresponding research attracts attention of both experimentalists and theorists of high energy physics. Thanks to the successful operation of LHC, plenty of data on baryons, especially those on heavy baryons have been collected. Thus researchers have a great opportunity to study heavy baryons via their production and decays to gain information of their structure and how the fundamental dynamics works for the baryon case. $\Lambda _b$ is the ground state of b baryons so it can only decay via weak interactions. Indeed besides study on the baryon structure, its weak decays may be valuable for determining the CKM parameter $V_{cb}$ as a compensation to the measurements on mesons and furthermore one can investigate the non-perturbative QCD effects in the heavy baryon system because of the existence of the heavy quark. $\Sigma _b$ is heavier than $\Lambda _b$ which would dominantly decay via the portal $\Lambda _b+\pi$, therefore a sizable branching ratio of its weak decays may imply a possible involvement of new physics, so can serve as an ideal laboratory for searching new physics beyond the standard model.

The weak decays of heavy baryons including $\Lambda _b$ and $\Sigma _b$ have been studied. For example: Korner and Kroll [1] explored the weak decays of baryons under the heavy quark limit [2, 3] where the quark–diquark picture was employed; in Ref. [4] Ebert et al. used their relativistic quark model to calculate the decay rates of several weak decay modes where baryons consist of a heavy quark and a light diquark; Singleton examined the semileptonic decays of spin-$\frac{1}{2}$ baryons in the spectator-quark model [5]; in Ref. [6] Ivanov et al. employed their relativistic three-quark model to study the weak decays of several baryons under the heavy quark limit; lately, Ivanov et al. [7] also studied heavy baryon decays in the Bethe–Salpeter approach under the heavy quark limit. By those works the properties of the weak decays of $\Lambda _b$ and $\Sigma _b$ have been investigated and the non-perturbative QCD effects for baryons (at least for heavy baryons) are partly understood or at least can be approximately handled.

We extended the light-front quark model to study the weak decays of $\Lambda _b$ and $\Sigma _b$ in the heavy-quark–light-diquark picture of baryon [8,9,10]. The light-front quark model (LFQM) is a relativistic quark model which has been applied to study transitions among mesons and the results agree with the data within reasonable error tolerance [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Our results presented in [8,9,10] are consistent with those given in literatures. The application of the extension of the light-front quark model to baryon has achieved a preliminary success [29,30,31]. Even though the baryon quark–diquark picture works well for dealing with the transition among heavy baryons, its reasonability and applicability are still not fully convincing yet.

There exists an acute dispute about the diquark structure of baryons yet. As is well known, the fundamental structure of baryons is determined by the Faddeev equations. However, that is an equation group for the three-body system whose solutions are difficult to gain. The diquark picture has been raised for a long while, even at the birth time of quark model [32]. In that picture two quarks are loosely bound into a subsystem which can be a vector, axial vector, scalar or pseudoscalar in color-anti-triplet. This approach definitely is an approximation which turns the three-body problem into a two-body problem, so greatly simplifies the calculation. In the earlier works as listed above where the diquark picture was employed, the diquark was treated as a point-like boson with a definite mass, spin and isospin. When it is involved in the concerned reaction [33], a form factor composed of a few free parameters which are fixed phenomenologically, is introduced. The picture is somehow in analog to the case of elastic electron-proton scattering where the inner structure of proton is manifested in the electric and magnetic form factors.

The assertion needs to be verified in some ways. To test the validity and applicability of the diquark approach, in this work, we treat the three quarks (one heavy and two light) as individual ones and possess their own color indices, spin polarizations(or helicities) and momenta, namely they share the total momentum of the baryon. During the transition, the two light quarks are spectators, i.e. maintain their all quantum numbers (spin, color) and momenta unchanged. In one word, we make a three-body calculation rather than a two-body one. Comparing the upcoming results with that obtained in terms of diquark, one can make a judgement whether the diquark picture indeed works well in the concerned processes where the light-quark subsystem is a spectator. Our results show that when the light quarks can be treated as spectators during the hadronic transitions, the point-like diquark picture is a good approximation, at least at the leading order.

In order to calculate the hadronic transition matrix element one needs to know the effective vertex functions. We construct them at first. Since the isospins of $\Lambda _b$ and $\Lambda _c$ are 0, the light ud subsystem must be an isospin-0 and color $\bar{3}$ state. To guarantee the total spin of $\Lambda _{b(c)}$ to be 1/2 and the spin of the ud system should be zero, i.e. the wavefunction of the ud subsystem is totally antisymmetric for spin$\times$color$\times$isospin. Instead, the isospin of $\Sigma _b$ or $\Sigma _c$ is 1, according to the same principle the spin of the light subsystem (ud) is determined to be 1. Thus the spin polarizations of the two quarks are not free, but correlated.

With the spin arrangements [34] we obtain the vertex function of $\Lambda _b$, $\Lambda _c$, $\Sigma _b$ and $\Sigma _c$ (denoting as $\mathcal {B}_{Q(')}$). Then following the common approach [8,9,10] we write down the transition matrix element and extract the form factors $f_1$, $f_2$, $g_1$ and $g_2$ which are defined for the transition(see the text for details). We compute these form factors $f_1$, $f_2$, $g_1$ and $g_2$ numerically.

Since the leptons do not participate in the strong interaction, the semileptonic decay is less contaminated by the non-perturbative QCD effect, therefore study on semileptonic decay might more help to test the employed model and/or constrain the model parameters. With the form factors we calculate the widths of the concerned semileptonic decays. Comparing the numerical result with the data the model parameters in the wave function are fixed. Moreover, moving one more step, using those parameters we write out the amplitude of the non-leptonic decay $\Sigma _{b}\rightarrow \Sigma _{c}+M$. In the case, we suppose that one can factorize out the meson current. Definitely, the factorization does not rigorously holds, but can be a good approximation at the leading order which was thoroughly investigated for the meson decays.

This paper is organized as follows: after the introduction, in Sect. 2 we construct the vertex functions of heavy baryons, then write down the transition amplitude for $\Lambda _b\rightarrow \Lambda _c$ and $\Sigma _{b}\rightarrow \Sigma _{c}$ in the light-front quark model and deduce the form factors, then we present our numerical results for $\Lambda _b\rightarrow \Lambda _c$ and $\Sigma _{b}\rightarrow \Sigma _{c}$ along with all necessary input parameters in Sect. 3. Section 4 is devoted to our conclusion and discussions.

2 $\Lambda _{b}\rightarrow \Lambda _{c}$ and $\Sigma _{b}\rightarrow \Sigma _{c}$ in the light-front quark model

2.1 the vertex functions of $\Lambda _{b}$, $\Lambda _{c}$, $\Sigma _{b}$ and $\Sigma _{c}$

In our previous work [8,9,10], we employed the quark–diquark picture to study the transitions. Instead, in this work we will estimate the transition rate by treating the three quarks as individual ones. It is noted, the transition occurs between heavy b and c quarks. Even though the other two light quarks are not bound together, the subsystem where they reside in, is still of definite spin, color and isospin and as the two quarks are spectators, all the quantum numbers of the subsystem keep unchanged. In analog to the references [35, 36] the vertex functions of a baryon $\mathcal {B}_Q$ ($Q=b,c$) with total spin $S=1/2$ and momentum P is

$$\begin{aligned}&|\mathcal {B}_{Q}(P,S,S_z)\rangle =\int \{d^3\tilde{p}_1\}\{d^3\tilde{p}_2\}\{d^3\tilde{p}_3\} \, 2(2\pi )^3\nonumber \\&\quad \times \delta ^3(\tilde{P}-\tilde{p_1}-\tilde{p_2}-\tilde{p_3}) \nonumber \\&\quad \times \sum _{\lambda _1,\lambda _2,\lambda _3}\Psi ^{SS_z}(\tilde{p}_1,\tilde{p}_2,\tilde{p}_3,\lambda _1,\lambda _2,\lambda _3) C^{\alpha \beta \gamma }\nonumber \\&\quad \times F_{Qdu}| Q_{\alpha }(p_1,\lambda _1)u_{\beta }(p_2,\lambda _2)d_{\gamma }(p_3,\lambda _3)\rangle , \end{aligned}$$

(1)

where $C^{\alpha \beta \gamma }$ and $F_{Qdu}$ are the color and flavor factors, $\lambda _i\,(i=1,2,3)$ and $p_i\,(i=1,2,3)$ are helicities and light-front momenta of the on-mass-shell quarks defined as

$$\begin{aligned}&\tilde{p_i}=(p_i^+,p_{i\perp }),\quad p_{i\perp }=(p_i^1,p_i^2),\quad p_i^-=\frac{m^2+p_{i\perp }^2}{p_i^+},\nonumber \\&\quad \{d^3p_i\}\equiv \frac{dp_i^+d^2 p_{i\perp }}{2(2\pi )^3}. \end{aligned}$$

(2)

In order to describe the motions of the constituents, one needs to introduce intrinsic variables $(x_i, k_{i\perp })$ ( $i=1,2$) through

$$\begin{aligned}&p^+_i=x_i P^+, \quad p_{i\perp }=x_i P_{\perp }+k_{i\perp } \quad x_1+x_2+x_3=1,\nonumber \\&\quad k_{1\perp }+k_{2\perp }+k_{3\perp }=0, \end{aligned}$$

(3)

where $x_i$ are the light-front momentum fractions constrained by $0<x_1, x_2, x_3<1$. The variables $(x_i, k_{i\perp })$ are independent of the total momentum of the hadron and thus are Lorentz-invariant. The invariant mass square $M_0^2$ is defined as

$$\begin{aligned} M_0^2=\frac{k_{1\perp }^2+m_1^2}{x_1}+ \frac{k_{2\perp }^2+m_2^2}{x_2}+\frac{k_{3\perp }^2+m_3^2}{x_3}. \end{aligned}$$

(4)

The invariant mass $M_0$ is in general different from the hadron mass M which obeys the physical mass-shell condition $M^2=P^2$. This is due to the fact that the baryon, heavy quark and the two-light-quark subsystem cannot be on their mass shells simultaneously. We define the internal momenta as

$$\begin{aligned} k_i= & {} (k_i^-,k_i^+,k_{i\bot })=(e_i-k_{iz},e_i+k_{iz},k_{i\bot })\nonumber \\= & {} \left( \frac{m_i^2+k_{i\bot }^2}{x_iM_0},x_iM_0,k_{i\bot }\right) . \end{aligned}$$

(5)

It is easy to obtain

$$\begin{aligned} e_i= & {} \frac{x_iM_0}{2}+\frac{m_i^2+k_{i\perp }^2}{2x_iM_0},\nonumber \\ k_{iz}= & {} \frac{x_iM_0}{2}-\frac{m_i^2+k_{i\perp }^2}{2x_iM_0}, \end{aligned}$$

(6)

where $e_i$ denotes the energy of the i-th constituent. The momenta $k_{i\bot }$ and $k_{iz}$ constitute a momentum vector $\vec {k}_i=(k_{i\bot }, k_{iz})$ and correspond to the components in the transverse and z directions, respectively.

Being enlightened by [34] the spin and spatial wave function for $\Lambda _Q$ is written as

(7)

and for $\Sigma _Q$

(8)

where $\Psi ^{SS_z}_0(\tilde{p}_i,\lambda _i)$ represents $\Psi ^{SS_z}(\tilde{p}_1,\tilde{p}_2,\tilde{p}_3,\lambda _1,\lambda _2,\lambda _3)$, $U,\,V$ and $\bar{U}$ are spinors of the quarks, $\varphi (x_i,k_{i\perp })$ denotes $\varphi (x_1,x_2,x_3,k_{1\perp },k_{2\perp },k_{3\perp })$, $p_1$ is the momentum of the heavy quark Q, $\,p_2\,,p_3$ are the momenta of the two light quarks, $\bar{P}=p_1+p_2+p_3$, , and $\lambda _1,\lambda _2, \lambda _3$ are the helicities of the constituents.

With the normalization of the state $|\mathcal {B}_{Q}\rangle$

$$\begin{aligned}&\langle \mathcal {B}_{Q}(P',S',S'_z)|\mathcal {B}_{Q}(P,S,S_z)\rangle \nonumber \\&\quad =2(2\pi )^3P^+ \delta ^3(\tilde{P}'-\tilde{P})\delta _{S'S}\delta _{S'_zS_z}, \end{aligned}$$

(9)

and

$$\begin{aligned}&\int \left( \prod ^3_{i=1}\frac{dx_id^2k_{i\perp }}{2(2\pi )^3}\right) 2(2\pi )^3\delta \left( 1-\sum x_i\right) \delta ^2\nonumber \\&\quad \times \left( \sum k_{i\perp }\right) \varphi ^*(x_i,k_{i\perp })\varphi (x_i,k_{i\perp })=1, \end{aligned}$$

(10)

one can obtain

$$\begin{aligned} A_0= & {} \frac{1}{4\sqrt{P^+M_0^3(m_1+e_1)(m_2+e_2)(m_3+e_3)}},\nonumber \\ A_1= & {} \frac{1}{4\sqrt{3P^+M_0^3(m_1+e_1)(m_2+e_2)(m_3+e_3)}}, \end{aligned}$$

(11)

where $p_i\cdot \bar{P}=e_iM_0\,(i=1,2,3)$ is used.

The spatial wave function is [35, 36]

$$\begin{aligned}&\varphi (x_1,x_2,x_3,k_{1\perp },k_{2\perp },k_{3\perp })=\frac{e_1e_2e_3}{x_1x_2x_3M_0} \varphi (\overrightarrow{k}_1,\beta _1)\nonumber \\&\quad \times \varphi \left( \frac{\overrightarrow{k}_2-\overrightarrow{k}_3}{2},\beta _{23}\right) \end{aligned}$$

(12)

with $\varphi (\overrightarrow{k},\beta )=4(\frac{\pi }{\beta ^2})^{3/4}\mathrm{exp}(\frac{-k_z^2-k^2_\perp }{2\beta ^2})$.

2.2 The form factors of $\Lambda _{b}\rightarrow \Lambda _{c}$ in LFQM

The form factors for the weak transition $\Lambda _{b}\rightarrow \Lambda _{c}$ are defined in the standard way as

$$\begin{aligned}&\langle \Lambda _{c}(P',S',S_z') \mid \bar{c}\gamma _{\mu } (1-\gamma _{5})b\mid \Lambda _{b}(P,S,S_z) \rangle \nonumber \\&\quad = \bar{U}_{\Lambda _{c}}(P',S'_z) \left[ \gamma _{\mu } f^s_{1}(q^{2}) +i\sigma _{\mu \nu } \frac{ q^{\nu }}{M_{\Lambda _{b}}}f^s_{2}(q^{2}) +\frac{q_{\mu }}{M_{\Lambda _{b}}} f^s_{3}(q^{2}) \right] \nonumber \\&\qquad \times U_{\Lambda _{b}}(P,S_z) \nonumber \\&\qquad -\bar{U}_{\Lambda _{c}}(P',S'_z)\left[ \gamma _{\mu } g^s_{1}(q^{2}) +i\sigma _{\mu \nu } \frac{ q^{\nu }}{M_{\Lambda _{b}}}g^s_{2}(q^{2})+ \frac{q_{\mu }}{M_{\Lambda _{b}}}g^s_{3}(q^{2}) \right] \nonumber \\&\qquad \times \gamma _{5} U_{\Lambda _{b}}(P,S_z). \end{aligned}$$

(13)

Since $S=S'=1/2$, we write $\mid \Lambda _{b}(P,S,S_z)\rangle$ and $\mid \Lambda _{c}(P',S',S'_z)\rangle$ as $\mid \Lambda _{b}(P,S_z)\rangle$ and $\mid \Lambda _{c}(P',S'_z)\rangle$ respectively.

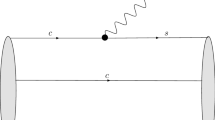
The lowest order Feynman diagram responsible for the $\Lambda _{b}\rightarrow \Lambda _{c}$ weak decay is shown in Fig. 1. Following the approach given in Refs. [8, 10, 35, 36] the transition matrix element can be calculated with the vertex functions of $\mid \Lambda _{b}(P,S_z) \rangle$ and $\mid \Lambda _{c}(P',,S'_z) \rangle$ supposing u and d quarks are spectators,

(14)

where

$$\begin{aligned} m_1=m_b, \quad m'_1=m_c, \quad m_2=m_{u}, \quad m_3=m_{d} \end{aligned}$$

(15)

and Q ($Q'$) represents the heavy quark b (c), $p_1$ ($p'_1$) denotes the four-momentum of the heavy quark b (c), P ($P'$) stands as the four-momentum of $\Lambda _{b}$ ($\Lambda _{c}$). Setting $\tilde{p}_2=\tilde{p}'_2$, we have

$$\begin{aligned} x'=\frac{P^+}{P^{'+}}x, \quad k'_{\perp }=k_{\perp }+x_2q_{\perp }. \end{aligned}$$

(16)

In terms of the approach given in Ref. [35] we extract the form factors defined in Eq. (13) from the Eq. (14)

Fig. 1

The Feynman diagram for $\Lambda _{b}\rightarrow \Lambda _{c}$ and $\Sigma _{b}\rightarrow \Sigma _{c}$ transitions, where $\bullet$ denotes $V-A$ current vertex

(17)

Expanding the traces in above formulas is straightforward, but the expressions are rather tedious, thus we collect he explicit expressions in Appendix A. It is noted that the form factors $f_3(q^2)$ and $g_3(q^2)$ cannot be extracted in terms of the above method for we have imposed the condition $q^+=0$. However, they do not contribute to the semi-leptonic decays $\Lambda _b\rightarrow \Lambda _c l\bar{\nu }_l$ if the masses of electron and neutrino are ignored.

2.3 The form factors of $\Sigma _{b}\rightarrow \Sigma _{c}$ in LFQM

Similarly, the hadronic matrix element for transition $\Sigma _{b}\rightarrow \Sigma _c$ can also be obtained with the vertex functions of $\mid \Sigma _{b}(P,S_z) \rangle$ and $\mid \Sigma _{c}(P',S'_z) \rangle$,

(18)

For the transition some form factors can also be defined as in Eq. (13), while $f^v_i$ and $g^v_i$ replace $f^s_i$ and $g^s_i$ ($i=1,2,3$) in Eq. (13).

The expressions of the form factors are

(19)

The interested readers can refer to appendix A to simplify the form factors before numerically evaluating.

3 Numerical Results

3.1 The $\Lambda _{b}\rightarrow \Lambda _c$ form factors and some decay modes

In order to evaluate these form factors numerically one needs the parameters of the concerned model. Here we employ the masses of quarks presented in Ref. [16] and list them in Table 1. Indeed, we know very little about the parameters $\beta _1$ and $\beta _{23}$ in the wave function of the initial baryon and $\beta _1'$ and $\beta _{23}'$ in that of the final baryon. Generally the reciprocal of $\beta$ is related to the electrical radium of the baryon. Since the strong interaction between q and $q'$ is half of that between $q\bar{q}'$ if it is a Coulomb-like potential one can expect the electrical radium of $qq'$ to be $1/\sqrt{2}$ times that of $q\bar{q}'$ i.e. $\beta _{qq'}\approx \sqrt{2}\beta _{q\bar{q}'}$. In Ref. [37] in terms of the binding energy the authors also obtained the same results, so in our work we use these $\beta$’s values which were obtained in the mesons case [38]. With these parameters we calculate the form factors and make theoretical predictions on the transition rates. We set $\beta _1\approx \sqrt{2}\beta _{b\bar{s}}$, $\beta _1'\approx \sqrt{2}\beta _{c\bar{s}}$ and suppose $\beta _2=\beta _2'\approx \sqrt{2} \beta _{u\bar{d}}$. It is found that the predicted width of the semilepton decay is larger than the data. Then we readjust the parameter $\beta _2$ to reduce the theoretical prediction to be closer to the data and thus we could fix the parameter. At last we obtain $\beta _1=0.851$ GeV, $\beta '_1=0.760$ GeV and $\beta _2=\beta _2'=0.911$ GeV. Here $\beta _2$ and $\beta _2'$ are close to $2.9 \beta _{u\bar{d}}$, which means the distance between u and d quarks is smaller than the normal situation where u and d are evenly distributed in the inner space of the baryon. Indeed, it implies the diquark structure.

Table 1 Quark mass and the parameter $\beta$ (in units of GeV)

Table 2 The $\Lambda _{b}\rightarrow \Lambda _c$ form factors given in the three-parameter form

Fig. 2

Form factor for the decay $\Lambda _{b} \rightarrow \Lambda _{c} l\bar{\nu }_l$ (a) and $\Sigma _{b} \rightarrow \Sigma _{c} l\bar{\nu }_l$ (b)

Table 3 The widths and polarization asymmetries of $\Lambda _b\rightarrow \Lambda _c l\bar{\nu }_l$

It is noted, we derive the form factors in terms of the LFQM in the space-like region, thus applying them to evaluate the transition rates, one needs to extend them to the physical region (time-like). Following the standard scheme, we derive the form factors for the baryonic transitions. The procedure for the derivation was depicted in literature and our previous work in all details, so that we do not keep it in the context, but for readers’ convenience, relevant stuff is retained in the attached appendix. Then, we explicitly list the corresponding parameters which are needed for numerical computations in Table 2 (Fig. 2).

Fig. 3

Differential decay rates $d\Gamma /d\omega$ for the decay $\Lambda _{b} \rightarrow \Lambda _{c}$ (a) and $\Sigma _{b} \rightarrow \Sigma _{c}$ (b)

Table 4 The widths and up-down asymmetries of non-leptonic decays $\Lambda _b\rightarrow \Lambda _c M$

Using the form factors, we evaluate the rates of $\Lambda _{b} \rightarrow \Lambda _{c} l\bar{\nu }_l$. The decay rates are listed in Table 3 where we update the results which were obtained in our earlier paper [8] with the parameters fixed in [38] as inputs. Comparing them with that obtained by other authors in Refs. [4, 6,7,8], one can notice that the differences among all the results are rather small. We plot the differential decay rates $d\Gamma /d\omega$ in Fig. 3a which also is consistent with those given in [4].

From the theoretical aspects, calculating the corresponding quantities for the non-leptonic decays seems to be much more complicated than for the semi-leptonic ones. The theoretical framework adopted in this work is based on the factorization assumption, namely the hadronic transition matrix element is factorized into a product of two independent matrix elements of currents,

$$\begin{aligned}&\langle \Lambda _{c}(P',S_z')M \mid \mathcal {H} \mid \Lambda _{b}(P,S_z) \rangle \nonumber \\&\quad =\frac{G_FV_{bc}V^*_{qq'}}{\sqrt{2}}\langle M \mid \bar{q'} \gamma ^{\mu } (1-\gamma _{5}) q \mid 0\rangle \nonumber \\&\qquad \times \langle \Lambda _{c}(P',S_z') \mid \bar{c} \gamma ^{\mu } (1-\gamma _{5}) b \mid \Lambda _{b}(P,S_z) \rangle , \end{aligned}$$

(20)

Table 5 The $\Sigma _{b}\rightarrow \Sigma _c$ form factors given in the three-parameter form

Table 6 The widths (in unit $10^{10}~\mathrm{s}^{-1}$) and polarization asymmetries of $\Sigma _b\rightarrow \Sigma _c l\bar{\nu }_l$

where the term $\langle M \mid \bar{q'} \gamma ^{\mu } (1-\gamma _{5}) q \mid 0\rangle$ is determined by the decay constant and the transition $\Lambda _{b}\rightarrow \Lambda _{c}$ is calculated in the previous sections. Since the decays $\Lambda _{b}^0\rightarrow \Lambda _{c}+M^-$ is the so-called color-favored transition, the factorization should be a good approximation. The study on these non-leptonic decays can check how close to reality the obtained form factors for the heavy bottomed baryons would be. In Table 4 we present the results of this work and previous papers together. One can notice that they are very close to each other, and it means that the heavy-quark–light-diquark picture is indeed a good approximation.

3.2 $\Sigma _{b}\rightarrow \Sigma _c$ form factors and some decay modes

Now we calculate the form factors for the transition $\Sigma _b\rightarrow \Sigma _c$. Using the values set for $\Lambda _b$ and $\Lambda _c$, we determine the parameters $\beta _1$ and $\beta _1'$. Generally the parameters $\beta _{23}$ and $\beta _{23}'$ would be different from those for $\Lambda _b$ and $\Lambda _c$ because the total spin of the ud subsystem in $\Sigma _{b(c)}$ is 1 but that is 0 in $\Lambda _{b(c)}$. The situation is similar to the spin configurations of a pseudoscalar vs a vector. Even though there are no data available, we boldly use the same parameters gained from $\Lambda _b\rightarrow \Lambda _c$ to make our predictions and the validity or approximation would be tested in the future measurements.

Table 7 The widths (in unit $10^{10}~\mathrm{s}^{-1}$) and up-down asymmetries of non-leptonic decays $\Sigma _b\rightarrow \Sigma _c M$

The parameters of the form factor are listed in Table 5. As discussed in the footnote of Table 5 there should be an additional factor $m_{\Sigma _b}/(m_{\Sigma _b}+m_{\Sigma _c})$ for the $F_0$ of $f_2$ and $g_2$ [10]. Taking into account of this factor the results are close to those given in [10]. The differential decay rates $d\Gamma /d\omega$ are depicted in Fig. 3b whose line-shape is fully consistent with those for $\Omega _b\rightarrow \Omega _c$ in Fig. 8 of Ref. [4]. It is understandable because the decay $\Omega _b\rightarrow \Omega _c$ and $\Sigma _b\rightarrow \Sigma _c$ are similar under the flavor SU(3) symmetry. Since $\Omega _b$ does not decay via strong interaction, the weak decays are dominant. The results of semi-leptonic decay of $\Sigma _b\rightarrow \Sigma _c$ can be found in Table 6. The total width $\Gamma$ and the longitudinal asymmetry $a_L$ are close to our previous result but not the transverse asymmetry $a_T$. The longitudinal polarization asymmetry $P_L$ deviate from our previous result by a certain extent (Table 7). The non-leptonic decays are presented in Table 7.

The interpretation of the difference is not trivial. When one constructs the vertex function, the first principle is to retain the momentum conservation, then there are two schemes to be selected, i.e. whether let the diquark polarization depend on the total momentum of the baryon P or the momentum of the diquark $p_2$. In our earlier paper [40], we discussed the two schemes for constructing the vertex function of $\Sigma _{b(c)}$. Comparing the numerical results of the transition rates of $\Sigma _b\rightarrow \Sigma _c^*$, we found that the values calculated with the two schemes only slightly deviated from each other. Then the conclusion might be that the two schemes are actually equivalent. In our study on the transition [10], we only adopted the scheme where the diquark polarization only depends on momentum $p_2$, but not P. One conjecture is that the momentum dependence may lead to the small deviations of the transverse asymmetry $a_T$ as is shown in this work. The difference, even though is not large, may imply a distinction of the momentum dependence, which needs to be further investigated and we will do it in our following works.

4 Conclusions and discussions

In terms of the extended light front quark model we explore the leptonic and non-leptonic weak decays of $\Lambda _b\rightarrow \Lambda _c$ and $\Sigma _b\rightarrow \Sigma _c$ with the three-quark picture of baryon.

Based on our earlier works for studying hyperon and meson decays in terms of the LFQM, this work has two purposes. The first one is to make a further confirmation of two possible ways of determining the momentum dependence of the diquark polarization during constructing the vertex functions of baryons. In our earlier work [10] , we suggested a possible momentum dependence of the diquark polarization. Namely, we conjectured that the polarization of the diquark should depend on its momentum $p_2$. Later [40], we employed another possible scheme where the diquark polarization depends on the total momentum of the baryon P. All the two schemes respect the principle of momentum conservation. The numerical results on the transition rates of $\Sigma _b\rightarrow \Sigma _c^*$ obtained in the two schemes are very close to each other. In this work, we use neither of the two schemes to evaluate the transition rates of $\Sigma _{b}\rightarrow \Sigma _{c}$ in LFQM, because we treat the two light quarks as free individuals rather than demanding them to reside in a “diquark”. Then we compare the results with that obtained in terms of the diquark pictures. We notice that the rates obtained in the two approaches are very close, but for longitudinal and transverse asymmetry $a_T$ for the semi-leptonic decay of $\Sigma _{b}\rightarrow \Sigma _{c}$ which are more sensitive to the approaches, an obvious deviation appears, i.e the values of $a_T$ are different for the two cases. Therefore, there may exist a more profound physics which leads to the difference. In our coming work we will further study those schemes, namely investigate their validity. Beside a theoretical analysis, the experimental data would compose an acceptable probe-stone. Therefore, we suggest the experimentalists to carry out high accuracy measurements on $a_L$ and $a_T$ of $\Sigma _{b}\rightarrow \Sigma _{c}$ transitions which would a great help.

The second purpose of this work is to test the reasonability and application of the diquark picture which is definitely a good approximation at least at the leading order according to the acute discussions on this topic. Therefore, in this work, we use the three-body picture of baryons, i.e. treat the two spectator light quarks as individual on-mass-shell constituents with definite masses and momenta. Indeed, the two light quarks compose a color-anti-triplet and spin-0 (for $\Lambda _{b(c)}$ or spin-1 (for $\Sigma _{b(c)}$) subsystem. In this picture, we do not priori assume they are loosely bound into a physical composite: diquark. Comparing the numerical results of the decay rates of $\Lambda _b\rightarrow \Lambda _c$ and $\Sigma _b\rightarrow \Sigma _c$ with that obtained in terms of the diquark which is supposed to be a point-like boson with a form factor, we find them to be very close. The consistency implies that the diquark picture indeed is valid, namely, in a heavy baryon ($\Lambda _{b(c)}$, or $\Sigma _{b(c)}$ etc.) two light quarks may be bound into a physical system and can behave as a point-like boson, especially when it serves as a spectator during the transition between two heavy baryons.

Appendices

Appendix A: The form factor

In this appendix we work out the full expressions of these form factors $f^{s}_i\,{(i=1,2)}$ by expanding the corresponding traces.

It is straightforward to calculate the four traces

(A1)

(A2)

(A3)

(A4)

where $\bar{P}^+=P^+$, $\bar{P}^{'+}=P^{'+}$, $\bar{P}^i_{\perp }=P^i_{\perp }$, $P^{'i}_{\perp }=P^{'i}_{\perp }$, $p^{+}_1=x_1P^+$, $p^{'+}_1=x_1P^{'+}$, $p^{i}_{1\perp }=x_1P^i_{\perp }+k^{i}_{1\perp }$, ${p'}_{1\perp }^{i}=x_1P^{'i}_{\perp }+k^{'i}_{1\perp }$, $p_1\cdot \bar{P}=e_1M_0$, ${p'}_1\cdot \bar{P}'={e'}_1{M'}_0$ and $(p_1-x_1\bar{P})\cdot (p'_1-x'_1\bar{P}')=-k_{1\perp }\cdot k'_{1\perp }$ have been used. The four traces are the same as those in Ref. [16]

Then it is also simple to deduce the others

(A5)

where these relations $\bar{P}\cdot \bar{P'}=({{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2)/2$, $p_2\cdot \bar{P}={p'}_2\cdot \bar{P}=e_2M_0$, $p_3\cdot \bar{P}={p'}_3\cdot \bar{P}=e_3M_0$, $p_2\cdot \bar{P'}={p'}_2\cdot \bar{P'}={e'}_2{M'}_0$, $p_3\cdot \bar{P'}={p'}_3\cdot \bar{P'}={e'}_3{M'}_0$ and $p_2\cdot p_3=({M_0}^2 + {m_1}^2 - {m_2}^2 - {m_3}^2 - 2 M_0e_1)/2$ are needed.

With these explicit expressions of the these traces the detailed forms of $f^{s}_i\,{(i=1,2)}$ and $g^{s}_i\,{(i=1,2)}$ can be obtained,

$$\begin{aligned} f^s_1= & {} \int \frac{ d x_2 d^2 k_{2\perp }}{2(2\pi )^3}\frac{ d x_3 d^2 k_{3\perp }}{2(2\pi )^3} \frac{k_{1\perp }\cdot k'_{1\perp }+(x_1M_0+m_1)(x'_1M'_0+m'_1)}{\sqrt{M_0^3(m_1+e_1) (m_2+e_2)(m_3+e_3)(m_1'+e_1') (m_2'+e_2')(m_3'+e_3')}}\nonumber \\&\times \frac{\phi _{\Lambda _{c}}^*(x',k'_{\perp }) \phi _{\Lambda _{b}}(x,k_{\perp })}{16\sqrt{x_1x'_1}}4\left[ {M_0}{M_0'}( {e_2'}{e_3} + {e_2}{e_3'} + {e_3}{m_2} + {e_3'}{m_2} + {e_2}{m_3}+ {e_2'}{m_3} + {m_2}{m_3}) \right. \nonumber \\&+ \frac{{M_0}{M_0'} \left( -2{e_1}{M_0} + {{M_0}}^2 + {{m_1}}^2 - {{m_2}}^2 - {{m_3}}^2 \right) }{2} + \frac{{m_2}{m_3}\left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{2} \nonumber \\&\left. + \frac{\left( 2{e_1}{M_0} - {{M_0}}^2 - {{m_1}}^2 + {{m_2}}^2 + {{m_3}}^2 \right) \left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{4}\right] ,\nonumber \\ \frac{f^s_2}{M_{\Lambda _{b}}}= & {} \frac{1}{q_{\perp }^i}\int \frac{ d x_2 d^2 k_{2\perp }}{2(2\pi )^3}\frac{ d x_3 d^2 k_{3\perp }}{2(2\pi )^3}\frac{(x_1M_0+m_1)k^{'i}_{1\perp }-(x'_1M'_0+m'_1)k^{i}_{1\perp }}{\sqrt{M_0^3(m_1+e_1) (m_2+e_2)(m_3+e_3)(m_1'+e_1') (m_2'+e_2')(m_3'+e_3')}}\nonumber \\&\times \frac{\phi _{\Lambda _{c}}^*(x',k'_{\perp }) \phi _{\Lambda _{b}}(x,k_{\perp })}{16\sqrt{x_1x'_1}} 4\left[ {M_0}{M_0'}( {e_2'}{e_3} + {e_2}{e_3'} + {e_3}{m_2} + {e_3'}{m_2} + {e_2}{m_3}+ {e_2'}{m_3} + {m_2}{m_3}) \right. \nonumber \\&+ \frac{{M_0}{M_0'} \left( -2{e_1}{M_0} + {{M_0}}^2 + {{m_1}}^2 - {{m_2}}^2 - {{m_3}}^2 \right) }{2} + \frac{{m_2}{m_3}\left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{2} \nonumber \\&\left. + \frac{\left( 2{e_1}{M_0} - {{M_0}}^2 - {{m_1}}^2 + {{m_2}}^2 + {{m_3}}^2 \right) \left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{4}\right] , \nonumber \\ g^s_1= & {} \int \frac{ d x_2 d^2 k_{2\perp }}{2(2\pi )^3}\frac{ d x_3 d^2 k_{3\perp }}{2(2\pi )^3}\frac{-k_{1\perp }\cdot k'_{1\perp }+(x_1M_0+m_1)(x'_1M'_0+m'_1)}{\sqrt{M_0^3(m_1+e_1) (m_2+e_2)(m_3+e_3)(m_1'+e_1') (m_2'+e_2')(m_3'+e_3')}}\nonumber \\&\times \frac{\phi _{\Lambda _{c}}^*(x',k'_{\perp }) \phi _{\Lambda _{b}}(x,k_{\perp })}{16\sqrt{x_1x'_1}} 4\left[ {M_0}{M_0'}( {e_2'}{e_3} + {e_2}{e_3'}+ {e_3}{m_2} + {e_3'}{m_2} + {e_2}{m_3}+ {e_2'}{m_3} + {m_2}{m_3}) \right. \nonumber \\&+ \frac{{M_0}{M_0'} \left( -2{e_1}{M_0} + {{M_0}}^2 + {{m_1}}^2 - {{m_2}}^2 - {{m_3}}^2 \right) }{2} + \frac{{m_2}{m_3}\left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{2} \nonumber \\&+\left. \frac{\left( 2{e_1}{M_0} - {{M_0}}^2 - {{m_1}}^2 + {{m_2}}^2 + {{m_3}}^2 \right) \left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{4}\right] ,\nonumber \\ \frac{g^s_2}{M_{\Lambda _{b}}}= & {} \frac{1}{q_{\perp }^i}\int \frac{ d x_2 d^2 k_{2\perp }}{2(2\pi )^3}\frac{ d x_3 d^2 k_{3\perp }}{2(2\pi )^3}\frac{(x_1M_0+m_1)k^{'i}_{1\perp }+(x'_1M'_0+m'_1)k^{i}_{1\perp }}{\sqrt{M_0^3(m_1+e_1) (m_2+e_2)(m_3+e_3)(m_1'+e_1') (m_2'+e_2')(m_3'+e_3')}}\nonumber \\&\times \frac{\phi _{\Lambda _{c}}^*(x',k'_{\perp }) \phi _{\Lambda _{b}}(x,k_{\perp })}{16\sqrt{x_1x'_1}} 4\left[ {M_0}{M_0'}( {e_2'}{e_3} + {e_2}{e_3'}+ {e_3}{m_2} + {e_3'}{m_2} + {e_2}{m_3}+ {e_2'}{m_3} + {m_2}{m_3}) \right. \nonumber \\&+ \frac{{M_0}{M_0'} \left( -2{e_1}{M_0} + {{M_0}}^2 + {{m_1}}^2 - {{m_2}}^2 - {{m_3}}^2 \right) }{2} + \frac{{m_2}{m_3}\left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{2} \nonumber \\&+ \left. \frac{\left( 2{e_1}{M_0} - {{M_0}}^2 - {{m_1}}^2 + {{m_2}}^2 + {{m_3}}^2 \right) \left( {{M_0}}^2 + {{M_0'}}^2 + {{q_\perp }}^2 \right) }{4}\right] . \end{aligned}$$

(A6)

By the same way the traces in the form factors $f^{v}_i\,{(i=1,2)}$ and $g^{v}_i\,{(i=1,2)}$ also can be directly calculated. Since they are very long, we omit them for saving space. Since these form factors $f^{s(v)}_i\,{(i=1,2)}$ and $g^{s(v)}_i\,{(i=1,2)}$ are evaluated in the frame $q^+=0$ i.e. $q^2=-q^2_{\perp }\le 0$ (the space-like region) one needs to extend them into the time-like region. One can employ a three-parameter form [36]

$$\begin{aligned} F(q^2)=\frac{F(0)}{\left( 1-\frac{q^2}{M_{\mathcal {B}_{b}}^2}\right) \left[ 1-a\left( \frac{q^2}{M_{\mathcal {B}_{b}}^2}\right) +b\left( \frac{q^2}{M_{\mathcal {B}_b}^2}\right) ^2\right] },\nonumber \\ \end{aligned}$$

(A7)

where $F(q^2)$ denotes the form factors $f^{s(v)}_i$ and $g^{s(v)}_i$. Using the form factors in the space-like region we may numerically calculate the parameters a,  b and F(0) in the un-physical region, namely fix $F(q^2\le 0)$. As discussed in previous section, these forms are extended into the physical region with $q^2\ge 0$ through Eq. (A7).

Appendix B: Semi-leptonic decays of $\mathcal {B}_b\rightarrow \mathcal {B}_c l\bar{\nu }_l$

The helicity amplitudes are related to the form factors for $\mathcal {B}_b\rightarrow \mathcal {B}_c l\bar{\nu }_l$ through the following expressions [41,42,43]

$$\begin{aligned} H^V_{\frac{1}{2},0}= & {} \frac{\sqrt{Q_-}}{\sqrt{q^2}}\left( \left( M_{b}+M_{c}\right) f_1-\frac{q^2}{M_{b}}f_2\right) ,\nonumber \\ H^V_{\frac{1}{2},1}= & {} \sqrt{2Q_-}\left( -f_1+ \frac{M_{b}+M_{c}}{M_{b}}f_2\right) ,\nonumber \\ H^A_{\frac{1}{2},0}= & {} \frac{\sqrt{Q_+}}{\sqrt{q^2}}\left( \left( M_{b}-M_{c}\right) g_1+\frac{q^2}{M_{b}}g_2\right) ,\nonumber \\ H^A_{\frac{1}{2},1}= & {} \sqrt{2Q_+}\left( -g_1- \frac{M_{b}-M_{c}}{M_{b}}g_2\right) , \end{aligned}$$

(B1)

where $Q_{\pm }=2(P\cdot P'\pm M_{b}M_{c})$ and $M_{b}\, (M_{c})$ represents $M_{\mathcal {B}_b}$ or $M_{\mathcal {B}_c}$. The amplitudes for the negative helicities are obtained in terms of the relation

$$\begin{aligned} H^{V,A}_{-\lambda '-\lambda _W}=\pm H^{V,A}_{\lambda ',\lambda _W}, \end{aligned}$$

(B2)

where the upper (lower) sign corresponds to V(A). The helicity amplitudes are

$$\begin{aligned} H_{\lambda ',\lambda _W}=H^V_{\lambda ',\lambda _W}- H^A_{\lambda ',\lambda _W}. \end{aligned}$$

(B3)

The helicities of the W-boson $\lambda _W$ can be either 0 or 1, which correspond to the longitudinal and transverse polarizations, respectively. The longitudinally (L) and transversely (T) polarized rates are respectively [41,42,43]

$$\begin{aligned} \frac{d\Gamma _L}{d\omega }= & {} \frac{G_F^2|V_{cb}|^2}{(2\pi )^3}~ \frac{q^2~p_c~M_{c}}{12M_{b}}\left[ |H_{\frac{1}{2},0}|^2+|H_{-\frac{1}{2},0}|^2\right] ,\nonumber \\ \frac{d\Gamma _T}{d\omega }= & {} \frac{G_F^2|V_{cb}|^2}{(2\pi )^3}~ \frac{q^2~p_c~M_{c}}{12M_{b}}\left[ |H_{\frac{1}{2},1}|^2+|H_{-\frac{1}{2},-1}|^2\right] ,\nonumber \\ \end{aligned}$$

(B4)

where $p_c$ is the momentum of $\mathcal {B}_c$ in the reset frame of $\mathcal {B}_b$.

The integrated longitudinal and transverse asymmetries defined as

$$\begin{aligned} a_L= & {} \frac{\int _1^{\omega _\mathrm{max}} d\omega ~q^2~ p_c \left[ |H_{\frac{1}{2},0}|^2-|H_{-\frac{1}{2},0}|^2\right] }{\int _1^{\omega _\mathrm{max}} d\omega ~q^2~ p_c \left[ |H_{\frac{1}{2},0}|^2+|H_{-\frac{1}{2},0}|^2\right] }, \nonumber \\ a_T= & {} \frac{\int _1^{\omega _\mathrm{max}} d\omega ~q^2~ p_c \left[ |H_{\frac{1}{2},1}|^2-|H_{-\frac{1}{2},-1}|^2\right] }{\int _1^{\omega _\mathrm{max}} d\omega ~q^2~ p_c \left[ |H_{\frac{1}{2},1}|^2+|H_{-\frac{1}{2},-1}|^2\right] }. \end{aligned}$$

(B5)

The ratio of the longitudinal to transverse decay rates R is defined by

$$\begin{aligned} R=\frac{\Gamma _L}{\Gamma _T}=\frac{\int _1^{\omega _\mathrm{max}}d\omega ~q^2~p_c\left[ |H_{\frac{1}{2},0}|^2+|H_{-\frac{1}{2},0}|^2 \right] }{\int _1^{\omega _\mathrm{max}}d\omega ~q^2~p_c \left[ |H_{\frac{1}{2},1}|^2+|H_{-\frac{1}{2},-1}|^2\right] }, \end{aligned}$$

(B6)

and the longitudinal polarization asymmetry $P_L$ is given as

$$\begin{aligned} P_L= & {} \frac{\int _1^{\omega _\mathrm{max}} d\omega ~q^2~ p_c \left[ |H_{\frac{1}{2},0}|^2-|H_{-\frac{1}{2},0}|^2+ |H_{\frac{1}{2},1}|^2-|H_{-\frac{1}{2},-1}|^2\right] }{\int _1^{\omega _\mathrm{max}} d\omega ~q^2~ p_c \left[ |H_{\frac{1}{2},0}|^2+|H_{-\frac{1}{2},0}|^2+ |H_{\frac{1}{2},1}|^2+|H_{-\frac{1}{2},-1}|^2\right] }.\nonumber \\ \end{aligned}$$

(B7)

Appendix C: $\mathcal {B}_b\rightarrow \mathcal {B}_c M$

In general, the transition amplitude of $\mathcal {B}_b\rightarrow \mathcal {B}_c M$ can be written as

$$\begin{aligned}&\mathcal{M}(\mathcal {B}_b\rightarrow \mathcal {B}_c P)=\bar{u}_{\Lambda _c}(A+B\gamma _5)u_{\Lambda _b}, \nonumber \\&\mathcal{M}(\mathcal {B}_b\rightarrow \mathcal {B}_c V)=\bar{u}_{\Lambda _c}\epsilon ^{*\mu }\nonumber \\&\quad \times \left[ A_1\gamma _{\mu }\gamma _5+ A_2(p_c)_{\mu }\gamma _5+B_1\gamma _{\mu }+ B_2(p_c)_{\mu }\right] u_{\Lambda _b},\nonumber \\ \end{aligned}$$

(C1)

where $\epsilon ^{\mu }$ is the polarization vector of the final vector or axial-vector mesons. Including the effective Wilson coefficient $a_1=c_1+c_2/N_c$, the decay amplitudes in the factorization approximation are [39, 44]

$$\begin{aligned} A= & {} \lambda f_P(M_{b}-M_{c})f_1(M^2), \nonumber \\ B= & {} \lambda f_P(M_{b}+M_{c})g_1(M^2), \nonumber \\ A_1= & {} -\lambda f_VM\left[ g_1(M^2)+g_2(M^2)\frac{M_{b}-M_{c}}{M_{b}}\right] , \nonumber \\ A_2= & {} -2\lambda f_VM\frac{g_2(M^2)}{M_{b}},\nonumber \\ B_1= & {} \lambda f_VM\left[ f_1(M^2)-f_2(M^2)\frac{M_{b}+M_{c}}{M_{b}}\right] , \nonumber \\ B_2= & {} 2\lambda f_VM\frac{f_2(M^2)}{M_{b}}, \end{aligned}$$

(C2)

where $\lambda =\frac{G_F}{\sqrt{2}}V_{cb}V_{q_1q_2}^*a_1$ and M is the meson mass. Replacing P, V by S and A in the above expressions, one can easily obtain similar expressions for scalar and axial-vector mesons.

The decay rates of $\mathcal {B}_b\rightarrow \mathcal {B}_cP(S)$ and up-down asymmetries are [39]

$$\begin{aligned} \Gamma= & {} \frac{p_c}{8\pi }\left[ \frac{(M_{b}+M_{c})^2-M^2}{M_{b}^2}|A|^2+ \frac{(M_{b}-M_{c})^2-M^2}{M_{b}^2}|B|^2\right] , \nonumber \\ \alpha= & {} -\frac{2\kappa \mathrm{Re}(A^*B)}{|A|^2+\kappa ^2|B|^2}, \end{aligned}$$

(C3)

where $p_c$ is the $\mathcal {B}_c$ momentum in the rest frame of $\mathcal {B}_b$ and $\kappa =\frac{p_c}{E_{\mathcal {B}_c}+M_{c}}$. For $\mathcal {B}_b\rightarrow \mathcal {B} V(A)$ decays, the decay rates and up-down asymmetries are

$$\begin{aligned} \Gamma= & {} \frac{p_c (E_{\Lambda _c}+M_{c})}{4\pi M_{b}}\left[ 2\left( |S|^2+|P_2|^2\right) +\frac{E^2}{M^2}\left( |S+D|^2+|P_1|^2\right) \right] , \nonumber \\ \alpha= & {} \frac{4M^2\mathrm{Re}(S^*P_2)+2E^2\mathrm{Re}(S+D)^*P_1}{2M^2\left( |S|^2+|P_2|^2 \right) +E^2\left( |S+D|^2+|P_1|^2 \right) }, \end{aligned}$$

(C4)

where E is energy of the vector (axial vector) meson, and

$$\begin{aligned} S= & {} -A_1, \nonumber \\ P_1= & {} -\frac{p_c}{E}\left( \frac{M_{b}+M_{c}}{E_{\Lambda _c}+M_{c}}B_1+M_bB_2\right) , \nonumber \\ P_2= & {} \frac{p_c}{E_{\Lambda _c}+M_{c}}B_1,\nonumber \\ D= & {} -\frac{p^2_c}{E(E_{\Lambda _c}+M_{c})}(A_1- M_bA_2). \end{aligned}$$

(C5)