1 Introduction

After the pioneering work on the anisotropic relativistic compact star by Bowers and Liang [1], many researchers have investigated the possible origin of anisotropy in compact stars. Ruderman [2] proposed that at high density \(\sim 10^{15}\) g/cc the matter starts interacting relativistically that arises the anisotropy in pressure. It is also suggested that due to the formation of super-fluid neutrons inside neutron stars, pressure anisotropy may also arise [3]. As a results of research by many authors pressure anisotropy can be trigger by types of phase transition [4], pion-condensation [5], slow rotation [6], strong magnetic field [7] etc. Letelier and his co-author [8,9,10] have shown that such anisotropic matters can be considered as the composition of two perfect fluids, or a perfect fluid and a null fluid, or two null fluids.

Many researchers are also interested to investigate the properties of compact stars in higher dimensions. The concepts of extra dimensions were first proposed by Kaluza [11] and Klein [12] independently when they unify the gravity and EM-force. Liddle et al. [13] have analyzed the effect of extra dimensions in the maximum mass of neutron stars (NS). They have assumed an equation of state for non-interacting cold neutrons and found that the maximum mass of NS was reduces by the presence of extra dimensions. Chattopadhyay and Paul [14] have considered the Vaidya–Tikekar spacetime in n-dimensional Einstein’s field equations to analyze the properties of compact stars. Bhar et al. [15] incorporated the conformal Killing equations in n-dimensional Einstein’s field equation and discussed anisotropic compact stars.

Various extended theories of gravity have been used to investigate the physical properties of compact stars. Pani et al. [16] have used general class of alternative theories which includes scalar-tensor theories, a scalar field coupled to quadratic curvature invariant and indirectly f(R) theories as special cases. In their work, they have developed a systematic tool to rule out physical theories that are incompatible with observations. The concept of embedding 4-dimensional spacetime in 5-dimensional hyperspace was used by Castro et al. [17]. Here they have embedded four dimensional spacetime into five dimensional braneworld. It is shown that on choosing equation of state for hadronic, hybrid and quark stars, the maximum mass is controlled by brane tension \(\lambda \) which lies in the range \(3.89\times 10^{36} (\equiv 1.44M_\odot )< \lambda < 10^{38}\) dyne/cm\(^2\). It is important to remind that constructing exact interior solutions representing non-uniform stellar distributions is nearly impossible in the context of the braneworld. This is because the nonlocality and non-closure of the braneworld equations, produced by the projection of the bulk Weyl tensor on the brane, lead to a very complicated system of equations which make the study of non-uniform distributions very hard [18]. It is yet to discover the criteria about what restriction should be imposed on braneworld equations to obtain a closed system [19]. To solve this problem, it is necessary to understand the bulk geometry and how a 4D spacetime cab be embedded. On the other hand, Karmarkar [20] embedded 4-dimensional spacetime into 5-dimensional Euclidean space known as class I. This method implies an equation that links the metric coefficients \(g_{tt}\) and \(g_{rr}\) thereby simplifying to solve the field equations. A similar concept was also used in string theory on embedding branes e.g. in the Randall–Sundrum model [21].

Assuming anisotropic fluid distribution, Mak and Harko [22] derived the condition for lower limit of mass for any anisotropic compact stars which was strongly depends on degree of anisotropy. Dev and Gleiser [23] derived the critical condition for compactness parameter 2M / R for anisotropic relativistic stars and was also found strongly depends on nature and degree of anisotropy. They have also shown that for anisotropic compact stars the red-shift can go arbitrary large. In there second paper, Dev and Gleiser [24] stressed on stability of anisotropic compact stars. Here they have found that, depends on the nature of anisotropy there can exist stable anisotropic star even at \(\Gamma < 4/3\) while its isotropic counterpart isn’t. Herrera et al. [25] obtained an algorithm to generate all spherically symmetric anisotropic fluid distributions from two generators. One of the generators was linked with anisotropy and other with re-shift function. On the other hand, Lake [26] used Newtonian hydrostatic equation for isotropic fluid distribution and generate infinite number of anisotropic solutions simply by assuming density.

Recently, Ivanov [27] derived a condition which is similar to Karmarkar condition, for conformally flat spacetime. However, the solutions resulting from the two theories are completely different. In Karmarkar spacetime there are no physical solutions describing isotropic fluid distributions, however, physical solution exist if electric charge or anisotropy or both are incorporated [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. In this article also we are exploring new physical solutions satisfying field equations under class I category and discuss the solutions to model compact stars.

The present article has been designed as follows: In Sect. 2, we have written the Einstein field equations for static and spherically symmetric matter distribution. The Embedding class I spacetime satisfying the Karmarkar condition has described in Sect. 3. Section 4 contains our new class I solutions along with mass, compactness parameter, surface redshift and gravitational redshift. We have explored the acceptance of our solutions in Sect. 5. The determination of constants by using the matching condition and analysis of all energy conditions have been done in Sects. 6 and 7, respectively. The equilibrium and stability are analyzed in the subsections of Sect. 8: Sect. 8.1 displayed the equilibrium situation and the stability analysis has done in Sect. 8.2. The generating functions for our model have calculated in Sect. 9. Moment of inertia and Mass relationship are analyzed in Sect. 10. Finally, The result and discussions have been done in Sect. 11.

2 Einstein’s field equations

To describe the interior of a static and spherically symmetric fluid sphere we consider the line element in Schwarzschild coordinate system \((t, r, \theta , \phi )\) as:

$$\begin{aligned} ds^2 = e^{\nu (r)}dt^2 - e^{\lambda (r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2) \end{aligned}$$
(1)

where \(e^{\nu (r)}\) and \(e^{\lambda (r)}\) are unknown functions of the radial coordinate r only and called metric potential functions.

Fig. 1
figure 1

Metric potential functions (above) and energy density (below) vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

As we are going to investigate the solutions of Einstein’s field equations for anisotropic compact stars, so we consider the energy momentum tensor for the anisotropic fluid sphere, which is of the following form:

$$\begin{aligned} T_{\alpha \beta } = \{p_r(r)-p_t(r)\}\chi _\alpha \chi _\beta + \{\rho (r)+p_t(r)\}U_\alpha U_\beta -p_t(r) g_{\alpha \beta } \end{aligned}$$
(2)

where \(\rho (r)\), \(p_r(r)\) and \(p_t(r)\) are representing the energy density, radial pressure and transverse pressure of the fluid configuration, respectively. \(\chi ^\alpha \) and \(U^\alpha \) are the unit space-like vector and four velocity, respectively, satisfying \(U^\alpha U_\alpha = -\chi ^\alpha \chi _\alpha = 1,~U^\mu \chi _\mu =0\).

Therefore, the Einstein field equations for the line element (1) and energy momentum tensor (2) are as follows:

$$\begin{aligned} \rho (r)= & {} \frac{1}{8\pi }\left\{ \frac{1 - e^{-\lambda (r)}}{r^2} + \frac{\lambda '(r)e^{-\lambda (r)}}{r}\right\} \end{aligned}$$
(3)
$$\begin{aligned} p_r(r)= & {} \frac{1}{8\pi } \left\{ \frac{\nu '(r) e^{-\lambda (r)}}{r} - \frac{1 - e^{-\lambda (r)}}{r^2}\right\} \end{aligned}$$
(4)
$$\begin{aligned} p_t(r)= & {} \frac{e^{-\lambda (r)}}{32\pi }\bigg \{2\nu ''(r) + \{\nu '(r)\}^2 - \nu '(r)\lambda '(r)\nonumber \\&+ \frac{2\nu '(r)}{r}-\frac{2\lambda '(r)}{r}\bigg \} \end{aligned}$$
(5)

where \(\prime = \frac{d}{dr}\), represents the derivative with respect to the radial coordinate r.

The anisotropic factor is defined as \(\Delta (r) = p_t(r)-p_r(r)\). Therefore, with the help of Eqs. (4) and (5) we can get the general expression of anisotropic factor for static and spherically symmetric fluid configuration in the following form:

$$\begin{aligned} \Delta (r)= & {} \frac{ e^{-\lambda (r)}}{8\pi }\bigg \{{\nu ''(r) \over 2}-{\lambda '(r) \nu '(r) \over 4}+{\{\nu '(r)\}^2 \over 4}\nonumber \\&-{\nu '(r)+\lambda '(r) \over 2r}+{e^\lambda (r)-1 \over r^2}\bigg \}. \end{aligned}$$
(6)

3 The Karmarkar condition

The Karmarkar condition is an important tool to study the stellar fluid spheres because of its special character. In general theory of relativity, it is recognized that an n-dimensional spacetime is called of class p if it is embedded in \((n+p)\)-dimensional Pseudo Euclidean flat space. In the year 1921, Kasner [43] investigated that the 4-dimensional spacetime of spherically symmetric object can always be embedded in 6-dimensional Pseudo Euclidean space and later Gupta and Goyel [44] have shown the same result with respect to another coordinate transformation. In 1924, Eddington [45] found that an n-dimensional spacetime can always be embedded in m-dimensional Pseudo Euclidean space with \(m = n(n+1)/2\) and the required minimum extra dimension to embedded is less than or equal to the number \((m-n)\) or same as \(n(n-1)/2\). Therefore, the 4-dimensional spherically symmetric line element (1) is of embedding class II. In the literature, there are some special class spacetimes such as the Schwarzschild interior and exterior solutions are of class I and class II, respectively, Friedman–Robertson–Lemaitre [46,47,48] spacetime is of class I and the Kerr metric is of class V [49]. In the year 1948, Karmarkar derived a condition [20] in terms of the components of Riemannian curvature tensor as:

$$\begin{aligned} R_{1414}R_{2323} = R_{1212}R_{3434}+R_{1224}R_{1334}. \end{aligned}$$
(7)

This condition is known as the Karmarkar condition. Any 4-dimensional spacetime can be embedded in 5-dimensional flat space i.e. becomes an embedding class I whenever it satisfies the Karmarkar condition. The Karmarkar condition is only the necessary condition to become a class I, Pandey and Sharma [50] provided the sufficient condition as \(R_{2323} \ne 0\).

Fig. 2
figure 2

Radial pressure and transverse pressure vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image
Fig. 3
figure 3

Anisotropic factor (above) and adiabatic index (below) vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

Now, all the non-zero components of Riemannian curvature tensor \(R_{\alpha \beta \gamma \delta }\) for the metric (1) are :

$$\begin{aligned} R_{1212}= & {} \frac{1}{2}\lambda ^\prime (r) r,~~~~~~R_{2424} = \frac{1}{2}\{\nu ^\prime (r) r e^{\nu (r)-\lambda (r)}\}\\ R_{2323}= & {} r^2 \sin ^2\theta (\{-e^{-\lambda (r)}\},~~R_{3434}= \sin ^2\theta R_{2424}, \\ R_{1414}= & {} \frac{e^{\nu (r)}}{4}[2\nu ''(r) + \{\nu '(r)\}^2 - \nu '(r)\lambda '(r)]. \end{aligned}$$

Taking into account all these non-vanishing components of Riemannian curvature tensor, the Karmarkar condition (7) yields the following differential equation:

$$\begin{aligned} 2\nu ''(r) + \{\nu '(r)\}^2 =\frac{e^{\lambda (r)} \nu '(r)\lambda '(r)}{e^{\lambda (r)}-1}. \end{aligned}$$
(8)

After solving the above differential Eq. (8) we get a relationship between two metric potential functions

$$\begin{aligned} e^{\nu (r)}=\left\{ A+B\int \sqrt{e^{\lambda (r)}-1}~dr\right\} ^2 \end{aligned}$$
(9)

where A and B are non-zero unknown integration constants, which shall be determined by applying some boundary conditions at the surface of compact stars. The condition (9) is a peculiar characteristic of the class I spacetime, where two metric potential functions are related to each other and hence researches can easily generate class I models for anisotropic fluid spheres with the help of a suitable form of one of the metric potential functions.

Therefore, the expression of anisotropic factor given in Eq. (6) becomes [51]:

$$\begin{aligned} \Delta (r) = {\nu '(r) \over 32\pi e^{\lambda }}\left\{ {\nu '(r) e^{\nu } \over 2rB^2}-1\right\} \left\{ {2\over r}-{\lambda '(r) \over e^{\lambda }-1}\right\} . \end{aligned}$$
(10)

by using Eqs. (8) and (9).

From Eq. (10) one can see that the pressure anisotropy \(\Delta (r)\) is zero throughout the fluid sphere if either first or second or both the factors on right-hand side of Eq. (10) are zero. The vanishing of first factor on the right side of Eq. (10) yields the Kohlar–Chao solution [52] whereas if the second factor is zero then the corresponding solution will be the Schwarzschild interior solution [53].

Finally, we arrive at a point to find out class I solutions but we have four independent equations (3)–(5) and (9) with five unknowns, namely \(\lambda (r),~\nu (r),~\rho (r),~p_r(r)\) and \(p_t(r)\). Therefore, it is impossible to find the exact solutions, for this purpose we shall consider a new metric potential function to generate our models.

4 New embedding class I solutions

According to earlier information, we consider a completely new metric potential function to obtain the closed form solutions of Einstein’s field equation:

$$\begin{aligned} e^{\lambda (r)}=1+cr^2\left\{ {{\,\mathrm{erf}\,}}[1+ar^2]\right\} ^2 \end{aligned}$$
(11)

where \(c > 0\) (\(\mathrm{km}^{-2}\)), \(a \ne 0 \) (\(\mathrm{km}^{-2}\)) are undetermine constants, to be determine from boundary condition and \({{\,\mathrm{erf}\,}}[x]\) is known as the error function, which is defined as

$$\begin{aligned} {{\,\mathrm{erf}\,}}[x]=\frac{1}{\sqrt{\pi }}\int _{-x}^x e^{-t^2}dt. \end{aligned}$$
(12)
Fig. 4
figure 4

Radial EoS parameter and transverse EoS parameter vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

We get another metric potential function by employing Eq. (11) in Eq. (9) as:

$$\begin{aligned} e^{\nu (r)}= & {} \frac{1}{4a^2\pi }\left[ 2Aa\sqrt{\pi }+B\sqrt{c}\left\{ e^{-h^2}+\sqrt{\pi } h g\right\} \right] ^2 \end{aligned}$$
(13)

where \(g = {{\,\mathrm{erf}\,}}[1 + ar^2], ~ h = 1 + ar^2\). The exact behaviors of these two metric potentials functions \(e^{-\lambda (r)}\) and \(e^{\nu (r)}\) are shown in Fig. 1 (above).

Now, taking into account these two metric potential functions given in Eqs. (11) and (13), we obtain the exact expressions of \(\rho (r)\), \(p_r(r)\), \(p_t(r)\) and \(\Delta (r)\) as:

$$\begin{aligned} \rho (r)= & {} \frac{c g\left[ 3g+r^2\left\{ c~g^2+8ae^{-h^2}\pi ^{-\frac{1}{2}}\right\} \right] }{8\pi \left\{ 1+cr^2 g^2\right\} ^2} \end{aligned}$$
(14)
$$\begin{aligned} p_r(r)= & {} g\left[ 8\pi \left\{ 1+cr^2 g^2\right\} \left\{ S_1+2aA\sqrt{\pi c} e^{h^2}\right\} \right] ^{-1}\nonumber \\&c\left[ 4aB\sqrt{\pi } e^{h^2}-g\left\{ S_1+2aA\sqrt{\pi c}e^{h^2}\right\} \right] \nonumber \\ p_t(r)= & {} c\Big [Bc\sqrt{\pi }g^2\big \{(1+2ar^2)+\sqrt{\pi }e^{h^2}(ar^2-1)\nonumber \\&\times g\big \}+8\sqrt{\pi }(ar)^2\{B-A\sqrt{c}g\}+2aS_2\Big ]\nonumber \\&\left[ 8\pi ^{3 \over 2}\left\{ 1+cr^2g^2\right\} ^2\left\{ S_1+2aA\sqrt{\pi c}~e^{h^2}\right\} \right] ^{-1}\nonumber \\ \Delta (r)= & {} \frac{r^2}{8\pi ^{3 \over 2}}\left\{ c^2 g^3-4ace^{-h^2}\right\} \Big [S_{1}g+2a\nonumber \\&\times \sqrt{\pi }e^{h^2}(A\sqrt{c}g-B)\Big ]\Big [\left\{ 1+cr^2g^2\right\} ^2\nonumber \\&\times \left\{ S_1+2aA\sqrt{\pi c}e^{h^2}\right\} \Big ]^{-1} \end{aligned}$$
(15)

whereas

$$\begin{aligned} S_1= & {} Bc\{1+h \sqrt{\pi }e^{h^2}g\}\nonumber \\ S_2= & {} g\Big [2B\pi e^{h^2}-2Bcr^2 e^{-h^2}-A\sqrt{c}\pi e^{h^2} g\Big ]. \end{aligned}$$
(16)

Therefore, the gradients of energy density \(\rho (r)\) and radial pressure \(p_r(r)\) are obtain as

$$\begin{aligned} \frac{d\rho (r)}{dr}= & {} \frac{cre^{-2h^2}}{4\pi ^2\{1+cr^2 g^2\}^3}\Big [16a^2r^2S_3-c\pi e^{2h^2}\nonumber \\&g^4 S_4-4a\sqrt{\pi }e^{h^2(r)}g(r)S_{5}\Big ] \end{aligned}$$
(17)
$$\begin{aligned} \frac{dp_r(r)}{dr}= & {} \frac{1}{4\pi ^{\frac{3}{2}}S_6}\Big [S_7+8a^2Bc\sqrt{\pi }e^{h^2}g(r)S_8+4ac S_9\nonumber \\&-4\pi aBc^2e^{2h^2}g^4 S_{10}-c^2\sqrt{\pi }e^{h^2}\nonumber \\&\times g^5S_{11}-4\sqrt{\pi } aBce^{h^2}g^3S_{12}\Big ] \end{aligned}$$
(18)
Fig. 5
figure 5

Mass function (above) and compactness parameter (below) vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

whereas,

$$\begin{aligned} S_3= & {} 1-3cr^2g^2,~~~S_{4}=5+cr^2g^2\nonumber \\ S_{5}= & {} 4ar^2h+cr^2g^2\{3+4ar^2h\}-5\nonumber \\ S_6= & {} \{1+cr^2g^2\}^2 \Big \{(Bc\sqrt{\pi }rh e^{h^2}g^2\nonumber \\&+2aAr \sqrt{c\pi }e^{h^2}g+Bcrg^2 \Big \}\nonumber \\ S_7= & {} 2B^2c^3\pi rh e^{2h^2}g^6+B^2c^3rh^2 \pi ^{\frac{3}{2}}\nonumber \\&\times e^{3h^2}g^7+16a^3ABre^{2h^2}\pi \sqrt{c}g\nonumber \\ S_8= & {} Br-2Ar\sqrt{c}g\nonumber \\ S_{9}= & {} g^2\Big [B^2r\left\{ 2a\pi h e^{2h^2}-c\right\} -4aA\pi r\nonumber \\&\times e^{2h^2}\left\{ aA+B (1+2ar^2)\sqrt{c}g\right\} \Big ]\nonumber \\ S_{10}= & {} Br\big \{2+ar^2(4+3ar^2)\big \}-Ar\sqrt{c}\nonumber \\ S_{11}= & {} 7-4a^2A^2\pi re^{2h^2}+B^2r\big \{4a\pi e^{2h^2}(1+2ar^2)-c\big \}\nonumber \\&-\,4aABr\pi h e^{2h^2}\sqrt{c}g\nonumber \\ S_{12}= & {} Br\{2c+a\pi e^{2h^2}+4acr^2\}\nonumber \\&+\,2aAr\pi e^{2h^2}\sqrt{c}g. \end{aligned}$$
(19)

We get the following expressions for the mass function m(r) and compactness parameter u(r), respectively

$$\begin{aligned} m(r)= & {} \int _0^r 4\pi \rho (r^\prime ) (r^\prime )^2 dr = \frac{c r^3 g^2}{2 \left\{ 1+cr^2 g^2\right\} } \end{aligned}$$
(20)
$$\begin{aligned} u(r)= & {} {m(r) \over r} = \frac{c r^2 g^2}{2 \left\{ 1+cr^2 g^2\right\} }. \end{aligned}$$
(21)

Also, the interior redshift \(Z_g(r)\) and surface redshift \(Z_s(r)\) are

$$\begin{aligned} Z_g(r)= & {} e^{-\nu /2}-1 = 2a\sqrt{\pi }\Big [B\sqrt{c}\left\{ e^{-h^2}+\sqrt{\pi } h(r) g\right\} \nonumber \\&+\,2Aa\sqrt{\pi }\Big ]^{-1}-1 \end{aligned}$$
(22)
$$\begin{aligned} Z_s(r)= & {} \sqrt{1-2u(r)}-1=\sqrt{\left\{ 1+cr^2g^2\right\} }-1. \end{aligned}$$
(23)

To explore the behaviors of the mass, compactness parameter, surface and gravitational redshifts we provide the graphical representations of them in Figs. 5 and 7. The mass and compactness parameter are zero at the centres of the fluid spheres, gradually increasing towards the surfaces of the fluid configurations and become maximum at the surfaces (see Fig. 5). The surface redshift and gravitational redshift have the opposite behavior throughout the fluid spheres, shown in Fig. 7. Moreover, at the surfaces (\(r = R\)) \(Z(R) = Z_s(R) = Z_g(R)\), obvious from Fig. 7. The the behavior of interior redshift explain the profile of interior density as well. If a photon comes out from center to surface, it has to travel longer path and much denser region (i.e. core). This leads to more dispersion resulting into loss of energy. Whereas a photon comes out from near the surface will travel shorter path and less denser region and therefore less dispersion and less energy loss. Hence, the interior redshift is maximum at the center and minimum at the surface. However, the surface redshift depends on overall mass and radius or in other word the surface gravity. As mass increases the radius will also increases slightly which will yields more surface gravity and more surface redshift. Thus, the trend of interior and surface redshifts are opposite.

Fig. 6
figure 6

Functions \(\rho (r)-p_r(r)\), \(\rho (r)-p_t(r)\) and \(\rho (r)-p_r(r)-2p_t(r)\) vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

5 The central values and physical analysis

For our model, we get the following results for the density and pressure at the centres of compact stars:

$$\begin{aligned} \rho _c= & {} \frac{3cg^2_{0}}{8\pi }>0, ~~~\forall ~~ c>0 \end{aligned}$$
(24)
$$\begin{aligned} p_{r_{c}} = p_{t_{c}}= & {} \sqrt{c}g_{0}\Big [2a e \sqrt{\pi }(2B-A\sqrt{c}g_{0})\nonumber \\&-Bcg_{0} (1+e \sqrt{\pi }g_{0})\Big ]\Big [8\pi \big \{2aA e \sqrt{\pi }\nonumber \\&+B\sqrt{c}(1+e\sqrt{\pi }g_{0})\big \}\Big ]^{-1} \end{aligned}$$
(25)

where \(g_0 = g(0) = {{\,\mathrm{erf}\,}}[1]\).

The positive behavior of the central pressure (\(p_{r_{c}} = p_{tc} > 0\)) implies

$$\begin{aligned} \frac{A}{B} < \frac{4ae\sqrt{\pi }-cg_0(1+e\sqrt{\pi }g_0)}{\sqrt{c}g_0}. \end{aligned}$$
(26)

Moreover, according to the Zeldovich condition [54] \(p_{r_{c}}/\rho _c \le 1.\) Therefore, from this condition we obtain the following inequality:

$$\begin{aligned} \frac{4ae\sqrt{\pi }-4cg_0(1+e\sqrt{\pi }g_0)}{\sqrt{c}g_0(1+6ae\sqrt{\pi })} \le \frac{A}{B}. \end{aligned}$$
(27)

Therefore, the inequalities (26) and (27) yield a boundary restriction on the constants A and B as:

$$\begin{aligned}&\frac{4ae\sqrt{\pi }-4cg_0(1+e\sqrt{\pi }g_0)}{\sqrt{c}g_0(1+6ae\sqrt{\pi })}\le \frac{A}{B}\nonumber \\&< \frac{4ae\sqrt{\pi }-cg_0(1+e\sqrt{\pi }g_0)}{\sqrt{c}g_0}. \end{aligned}$$
(28)
Fig. 7
figure 7

Surface redshift (above) and gravitational redshift (below) vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

To demonstrate the physically acceptance of our models on anisotropic compact stars we draw the graphs for all the physical parameters, metric potential functions \(e^{-\lambda (r)}\), \(e^{\nu (r)}\), energy density \(\rho (r)\), radial pressure \(p_r(r)\), transverse pressure \(p_t(r)\), anisotropic factor \(\Delta (r)\) and equation of state (EoS) parameters \(\omega _r(r)\),  \(\omega _t(r)\) in Figs. 1, 2, 3 (above) and 4, respectively. Figure 1 (above) shows that \(e^{-\lambda (r)}\) and \(e^{\nu (r)}\) are finite and non-singular everywhere within the fluid spheres and they coincide at the surfaces. The energy density is positive and as usual maximum at the centres and then decreasing towards the the boundaries, clear from Fig. 1 (below). The radial and transverse pressures both are positive and monotonically decreasing from the centre of the stars. Further, \(p_r(r)\) becomes zero at the boundaries of the stellar objects and \(p_t(r)\) is non-vanishing there (see Fig. 2). The anisotropic factor \(\Delta (r)\) is positive and finite within the stars, maximum and zero at the boundaries and centres of the stars, respectively, obvious from Fig. 3 (above). The parameter \(\eta (r) = \frac{p_r(r)}{p_t(r)}\) can analyze the effect of anisotropy in the equilibrium position of fluid configurations in similar way of Newtonian treatment. The profile of \(\eta (r)\) (see Fig. 10 (below)) discloses that the anisotropic force is increasing through out the fluid spheres i.e. behaves like outward force, similar to the result in Fig. 3 (above). Figure 4 indicates the behaviors of EoS parameters \(\omega _r(r)\) and \(\omega _t(r)\) and from the figure one can notice that both the parameters are with in the region \(0< \omega _r(r), \omega _t(r) < 1\) i.e. our solutions are for the real feasible fluid distributions. Therefore, all this significant results confirm that our solutions are physically acceptable.

Fig. 8
figure 8

Forces for the compact stars Vela X-1 (above left), Cen X-3 (above right), EXO 1785-248 (below left), LMC X-4 (below right) vs the radial coordinate r corresponding to numerical values of constants given in Table 2

Full size image

6 The matching condition and determination of constants

We have seen that there are some constants within our solutions, so to determine the values of these involving constants we are going to match our interior solution with the Schwarzschild vacuum solution at the surface of the star \(r = R\). The Schwarzschild vacuum solution is given by the following metric

$$\begin{aligned} ds^2= & {} \left( 1-\frac{2M}{r}\right) dt^2-\left( 1-\frac{2M}{r}\right) ^{-1}dr^2\nonumber \\&-r^2(d\theta ^2+\sin ^2\theta d\phi ^2) \end{aligned}$$
(29)

where M is the total mass of the anisotropic fluid sphere contained within the sphere of radius R.

By matching at the boundary of the compact star \(r = R\) (\(> 2M\) to avoid the singularity) we get:

$$\begin{aligned} e^{\frac{\nu (R)}{2}}= & {} \frac{2Aa\sqrt{\pi }+B\sqrt{c}\left\{ e^{-h^2(R)}+\sqrt{\pi } h^2(R)g(R)\right\} }{2a\sqrt{\pi }}\nonumber \\= & {} \sqrt{ 1-{2M \over R}} \end{aligned}$$
(30)
$$\begin{aligned} e^{\lambda (R)}= & {} 1+cR^2g^2(R)= \left( 1-{2M \over R}\right) ^{-1}. \end{aligned}$$
(31)

Also, the radial pressure \(p_r(r)\) at the boundary \(r = R\) vanishes i.e.

$$\begin{aligned} p_r(R)= & {} 0. \end{aligned}$$
(32)

Using these boundary conditions (30)–(32), we obtain

$$\begin{aligned} c= & {} \frac{2M}{(R-2M)R^2 g^2(R)} \end{aligned}$$
(33)
$$\begin{aligned} A= & {} - \frac{\sqrt{R-2M}}{4\sqrt{R}a}\Big [4a+cg(R)\big \{e^{-h^2(R)}\pi ^{-\frac{1}{2}}\nonumber \\&+h(R)g(R)\big \}\Big ] \end{aligned}$$
(34)
$$\begin{aligned} B= & {} \frac{\sqrt{c(R-2M)}g(R)}{2\sqrt{R}} \end{aligned}$$
(35)

where a is a free parameter to obtain well-behaved solutions in all respects and mass M, radius R will be chosen accordingly different stars.

7 The energy conditions

It is well-known in the literature that the physical mass distributions must satisfy all the energy conditions within its interiors. The energy conditions are: (2) null energy condition (NEC), (2) weak energy condition (WEC) and (3) strong energy condition (SEC), these conditions represent by following inequalities:

$$\begin{aligned} \text {NEC}&:&\rho (r)-p_i(r) \ge 0,\nonumber \\ \text {DEC}&:&\rho (r) \ge |p_i|, \end{aligned}$$
(36)
$$\begin{aligned} \text {WEC}&:&\rho (r) \ge 0,~\rho (r)-p_i(r) \ge 0,\nonumber \\ \text {SEC}&:&\rho (r)-p_r(r)-2p_t(r) \ge 0. \end{aligned}$$
(37)

Here \(i \equiv (r,~t)\), r for radial and t for tranverse components. For the verification of all energy conditions, we plot all the L.H.Ss of above inequalities in Fig. 6. From Fig. 6 it is evident that our solutions satisfy all the energy conditions within the interiors of fluid configurations.

8 The equilibrium and stability analysis

The equilibrium position and stable state are most important situations for the non-collapsing compact object within our Universe. In this section, we are going to check the equilibrium and stability of the fluid distributions represented by our solutions.

8.1 The equilibrium condition

The together effect of gravitational force, Hydrostatic force and Anisotropic force holds any anisotropic stellar object in the equilibrium position. At the equilibrium position, the balancing force equation is known as TOV-equation. The generalized TOV-equation for anisotropic fluid distribution can be written as [55, 56]

$$\begin{aligned} -{M_g(r)\over r^2}\{\rho +p_r\}e^{{\lambda -\nu }\over 2}-{dp_r \over dr}+{2\Delta \over r} = 0 \end{aligned}$$
(38)

where \(M_g(r)\) represents the effective gravitational mass. The Tolman–Whittaker mass formula gives the exact form of the effective gravitational \(M_g(r)\) as:

$$\begin{aligned} M_g(r)= & {} 4\pi \int _0^r \left( T_0^0-T_1^1-T_2^2-T_3^3 \right) r^2e^{\{\nu +\lambda \}/ 2}dr . \end{aligned}$$
(39)

On using the energy–momentum tensor (2) and field equations (3) and (4), the Eq. (39) becomes

$$\begin{aligned} M_g(r) = {1 \over 2} r^2 \nu '(r) e^{\{\nu (r)-\lambda (r)\}/ 2}. \end{aligned}$$
(40)

Therefore, using the value of \(M_g(r)\), Eq. (38) reduces as:

$$\begin{aligned} -\frac{\nu '(r)\{\rho (r)+p_r(r)\}}{2}-{dp_r(r) \over dr}+{2\Delta (r) \over r}=0 . \end{aligned}$$
(41)

Moreover, the Eq. (41) can be written as:

$$\begin{aligned} F_g(r)+F_h(r)+F_a(r)=0 \end{aligned}$$
(42)

where \(F_g(r) = -\frac{1}{2}\nu '(r)\{\rho (r)+p_r(r)\}\), \(F_h(r) = -{dp_r(r) \over dr}\) and \(F_a(r) = {2\Delta (r) \over r}\) are called the gravitational force, hydrostatic force and anisotropic force, respectively.

For our present solutions the three different forces are obtained in the following forms:

$$\begin{aligned} F_g(r)= & {} -\frac{1}{2\pi S_6}\Big [aBc^2r^2g^3\big \{8a^2Ae^{h^2}\sqrt{c\pi }r^3 g\nonumber \\&+Bc \pi r e^{2h^2}g^3(1+3ar^2)+2aS_{13}g\nonumber \\&+Bc\sqrt{\pi }r e^{h^2}g^2(1+2ar^2)\big \}\Big ] \end{aligned}$$
(43)
$$\begin{aligned} F_h(r)= & {} -\frac{1}{4\pi ^{\frac{3}{2}}S_6}\Big [S_7+8a^2Bc\sqrt{\pi }e^{h^2}gS_8+4ac S_9\nonumber \\&-4\pi aBc^2e^{2h^2}g^4S_{10}-c^2\sqrt{\pi }e^{h^2}g^5 S_{11}\nonumber \\&-4\sqrt{\pi } aBce^{h^2}g^3S_{12}\Big ] \end{aligned}$$
(44)
$$\begin{aligned} F_a(r)= & {} 2r\left\{ c^2g^3-4ace^{-h^2}\right\} \Big [S_{1}g+2a\sqrt{\pi }e^{h^2}\nonumber \\&\times (A\sqrt{c}g(r)-B)\Big ]\Big [8\pi ^{3 \over 2}\left\{ 1+cr^2g^2\right\} ^2\nonumber \\&\times \left\{ S_1+2aA\sqrt{\pi c}e^{h^2}\right\} \Big ]^{-1} \end{aligned}$$
(45)

whereas,

$$\begin{aligned} S_{13}= & {} B\pi e^{2h^2} r+2Bcr^3+Ar\pi e^{2h^2}\sqrt{c}g \end{aligned}$$

and \(S_1, S_2\),\(S_6,~S_7,~S_8,~S_9,~S_{10},~S_{11},~S_{12}\) are given in Eqs. (16) and (19), respectively.

The behaviors of these three forces are shown in Fig. 8 and it is ascertained that our solutions representing fluid distributions are in equilibrium positions.

8.2 The stability condition

Here, we are willing to analysis the stability condition for our models with the help of (1) stability factor, (2) Adiabatic index and (3) Harrison–Zeldovich–Novikov criterion.

8.2.1 Causality condition

In General Theory of Relativity, the maximum velocity is the velocity of light, which is equal to 1 in the gravitational unit.

1. Causality condition: The causality condition states that whenever sound passes through the physical fluid distribution then its velocity must be less than the velocity of light, otherwise non-physical stellar configuration. The radial velocity \(v_r(r)\) and transverse velocity \(v_t(r)\) of sound inside the compact star can be determined using the following formulae:

$$\begin{aligned} v_r(r)=\sqrt{{dp_r(r) \over d\rho (r)}}~~~\text {and}~~~v_t(r)=\sqrt{{dp_t(r) \over d\rho (r)}}. \end{aligned}$$
(46)

Therefore, according to causality condition \(0 \le v_r(r), v_t(r) < 1\). Figure 9 reveals that our models satisfy the causality condition i.e. our models represent the physical stellar fluids.

2. Stability condition: In the year 1992, Herrera [57] proposed the cracking method to study the stability of an anisotropic stellar fluid under the radial perturbations. Later, using the concept of cracking Abreu et al. [58] provided the conditions for anisotropic fluid model with respect to the stability factor \(\left[ \{v_t(r)\}^2 - \{v_r(r)\}^2\right] \) as:

  1. (i)

    The condition for potentially stable region is \(-1< \{v_t(r)\}^2 - \{v_r(r)\}^2 < 0\).

  2. (ii)

    The condition for potentially unstable region is \( 0< \{v_t(r)\}^2 - \{v_r(r)\}^2< 1\).

Our solutions satisfy the condition \( -1< \{v_t(r)\}^2 - \{v_r(r)\}^2 < 0\), clear from Fig. 10 (above) and hence our models of anisotropic compact stars are potentially stable.

Fig. 9
figure 9

Radial sound speed and transverse sound speed vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

8.2.2 Adiabatic index

The relativistic adiabatic index plays an important role to analyze the stability of stellar fluid spheres. The relativistic adiabatic index \(\Gamma _r(r)\) is defined as:

$$\begin{aligned} \Gamma _r(r) = {\rho (r)+p_r(r) \over p_r(r)}~{dp_r(r) \over d\rho (r)}. \end{aligned}$$
(47)

For Newtonian limit, any stable configuration will alter its stability by initiating an adiabatic gravitational collapse if \(\Gamma _r(r) \le 4/3\) and catastrophic if \(< 4/3\) [59]. According to Chan et al. [60] this condition changes for relativistic and/or anisotropic fluid which depends on the nature of anisotropy. Figure 3 (below) shows that the adiabatic index \(\Gamma _r(r) > 4/3\) for our solutions with positive anisotropy. More strict condition on adiabatic index for stable region was derived by Moustakidis [61] and found that the critical value of adiabatic index \(\Gamma _{crit}\) depends on \(\xi \)-parameter (amplitude of lagrangian displacement from equilibrium) and compactness parameter \(\beta =M/R\). On assuming particular form of \(\xi \)-parameter he obtained the constraint as

$$\begin{aligned} \Gamma _{crit}={4 \over 3}+{19 \over 42} ~2\beta . \end{aligned}$$
(48)

Any stable configuration should have \(\Gamma \ge \Gamma _{crit}\). For the presented this condition is fulfilled (Fig. 3 below).

Fig. 10
figure 10

Stability factor (above) and \(\eta (r)\) (below) vs the radial coordinate r corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image
Fig. 11
figure 11

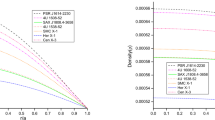
Mass vs the central density \(\rho _c\) corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image

8.2.3 Harrison–Zeldovich–Novikov criterion

The Harrison–Zeldovich–Novikov [54, 62] static stability criterion states that the mass should increase with the increase of central density \(\rho _c\) for the stable state of compact stars, i.e. \(\frac{\partial M(\rho _c)}{\partial \rho _c} > 0\) for the stable state of compact stars. For our solutions, we obtain the mass as a function of the central density as:

$$\begin{aligned} M(\rho _c)= & {} \frac{8 \pi \rho _c R^3 g^2(R)}{16\pi \rho _c R^2 g^2(R)+6g_0^2}\nonumber \\ \text {i.e.}~\frac{\partial M}{\partial \rho _c}= & {} \frac{12 \pi R^3 g_0^2g^2(R)}{\left\{ 8\pi \rho _c R^2 g^2(R)+3g_0^2 \right\} ^2}>0. \end{aligned}$$
(49)

The obtained solutions hold static stability criterion and hence stable, clear from Fig. 11.

9 Generating functions

To obtain all possible anisotropic solutions of Einstein’s field equations, Herrera [6] proposed an algorithm with the help of generating functions as:

$$\begin{aligned} e^{\lambda (r)} =\frac{Z^2(r) e^{\int \left\{ \frac{4}{r^2Z(r)}+2Z(r)\right\} dr }}{r^6\left\{ C-2\int \left[ \frac{Z(r)\{1+\Pi (r)r^2\}}{r^8} e^{\int \left\{ \frac{4}{r^2Z}+2Z\right\} dr}\right] dr \right\} }\nonumber \\ \end{aligned}$$
(50)

where, C is an arbitrary integration constant and the corresponding generating functions are:

$$\begin{aligned} Z(r)= & {} \frac{\nu '(r)}{2}+\frac{1}{r} \end{aligned}$$
(51)
$$\begin{aligned} \Pi (r)= & {} 8\pi \{p_r(r)-p_t(r)\}. \end{aligned}$$
(52)

Now, adopting the class I condition (9), the generating functions in Eqs. (51) and (52) take the following forms:

$$\begin{aligned} Z(r)= & {} \frac{B\sqrt{e^{\lambda (r)}-1}}{A+B\int \sqrt{e^{\lambda (r)}-1}dr}+\frac{1}{r} \end{aligned}$$
(53)
$$\begin{aligned} \Pi (r)= & {} 8\pi \{p_r(r)-p_t(r)\}. \end{aligned}$$
(54)

The generating functions for our present solutions are obtained as:

$$\begin{aligned} Z(r)= & {} \frac{1}{r}+2a Br \sqrt{c\pi }g\Big [2Aa\sqrt{\pi }\nonumber \\&+B\sqrt{c}\left\{ e^{-h^2}+\sqrt{\pi } hg\right\} \Big ]^{-1} \end{aligned}$$
(55)
$$\begin{aligned} \Pi (r)= & {} -8\pi \Delta (r) \end{aligned}$$
(56)

where \(\Delta (r)\) is given in Eq. (15).

Fig. 12
figure 12

M–R diagram and ranges of mass corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image
Fig. 13
figure 13

I–M diagram corresponding to numerical values of constants given in Table 2 for four well-known compact stars

Full size image
Table 1 Masses and radii of the four celestial compact stars with their approximate moment of inertia
Full size table

10 Moment of inertia and mass relationship

Bejger and Haensel [67] adopted a method where a static solution can become rotating by using an approximate expression of moment of inertia I given as

$$\begin{aligned} I = {2 \over 5} \Big [1+{(M/R) \cdot \mathrm{km} \over M_\odot }\Big ] {MR^2}. \end{aligned}$$
(57)

Using the above expression we have plotted the trend of I w.r.t. mass M in Fig. 13. From this graph and using the observed ranges of masses in Table 1 we have predicted the possible approximate moment of inertia (see the last section). It is to be noted that I–M graph is more sensitive to the equation of state as compared to that of M–R graph.

Table 2 Numerical values of constants for the four celestial compact stars
Full size table
Table 3 Estimated values of the central and surface densities, cental pressure, surface redshift at the boundary and twice of compactness parameter with buchdahl limit for four celestial compact stars corresponding to the values of constants given in Table 2
Full size table

11 Result and discussions

In the present article, we have developed few models for anisotropic compact stars in the framework of Karmarkar condition by introducing a completely new metric potential function \(e^{\lambda (r)}.\) To demonstrate the physical acceptance of our proposed models, we have performed varies physical experiments with the help of different physical parameters. For clarity, we have provided the graphical presentations (Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13) for the physical parameters involved in our models by matching our interior solution with the exterior Schwarzschild solution for four well-known compact stars. All the features of our model are following:

  • Metric potentials: The finite and nonsingular metric potential functions are necessary to generate the physical viable models of anisotropic compact stars. In our models, \(e^{\lambda (0)}\) = 1 and \(e^{\nu (0)} = \frac{1}{4a^2\pi }\left[ 2Aa\sqrt{\pi }+B\sqrt{c}\left\{ e^{-1}+\sqrt{\pi } g_0\right\} \right] ^2 =\) positive constant for nonzero a. i.e. the metric potential functions are well-behaved at the centre of the stars. The graphical representations of \(e^{-\lambda (r)}\) and \(e^{\nu (r)}\) indicate that they are finite and regular throughout the radius of stars (see Fig. 1 (above)) and hence they are suitable to generate the models for anisotropic compact stars.

  • Energy density and pressures: The energy density \(\rho (r)\), radial pressure \(p_r(r)\) and transverse pressure \(p_t(r)\) should remain positively finite throughout the interior of fluid spheres. The energy density and radial pressure are maximum at the centre and decreasing in nature towards the surface. Also, the radial pressure should vanish at the surface of fluid sphere. Figures 1 (below) and 2 approve that our obtained energy density and pressures (radial and transverse) are good in behavior as they have satisfied all those conditions. To compare with observational data we have calculated the numerical values of central, surface densities and central pressure for different compact stars given in Table 3. The central and surface densities both are of order \(10^{14}\) and the central pressure is of order \(10^{34}\), which are almost same with observational data.

  • Equation of state parameters: For real matter distribution the equation of state(EoS) parameters \(\omega _r(r) = \frac{p_r(r)}{\rho (r)}\) and \(\omega _t(r) = \frac{p_t(r)}{\rho (r)}\) should lie in \(0<\omega _r(r), \omega _t(r) <1 \) [63]. In our present models, both the EoS parameters are within the region \(0<\omega _r(r), \omega _t(r) <1\) (see Fig. 4), which is another important testimony of our well-behaved models.

  • Anisotropy: The anisotropic factor \(\Delta (r) =\)  \( p_t(r) - p_r(r)\) should vanishes at the stellar centre. If \(\Delta (r) > 0\) then the anisotropic force \(F_a(r) = \frac{2\Delta (r)}{r}\) is outward directed i.e. play as a impulsive force, which can support more compact construction. And if \(\Delta (r) < 0\) then the anisotropic \(F_a(r)\) is inward directed. In our models, \(\Delta (0) = 0\) and positively increasing within the stellar interiors, clear from Fig. 3 (above) and consequently the anisotropic force is repulsive in nature, assist to construct more compact stars. The similar result is seen in the behavior of \(\eta (r)\), it indicates the anisotropy as a outward force.

  • Energy conditions: To illustrate the present models are of physical matter distributions we have plotted the L.H.Ss of all inequalities in Eq. (37) and evidently we can see from Fig. 6 along with Fig. 1 (below) that our solutions satisfied all the energy conditions.

  • Mass function and compactness parameter: The profiles of mass function m(r) and compactness parameter u(r) are shown in Fig. 5 for four compact stars. The m(r) and u(r) tends to zero when r tends to zero and monotonically increasing toward the surfaces. According to Buchdahl[] the mass to radius ration \(\frac{M}{R} < \frac{4}{9}\) or equivalently \(2u_s = 2u(R) < \frac{8}{9}\). We have computed the numerical values \(2u_s\), provided in Table 3 and all these values indicate that our solutions satisfied the Buchdahl limit.

  • Equilibrium: The anisotropic compact stars are in equilibrium under the action of gravitational, hydrostatic and anisotropic forces. The matter distributions represented by our solutions are in equilibrium positions, clear from Fig. 8. Here, hydrostatic and anisotropic forces are repulsive and gravitational force is attractive in nature.

  • Stability: We have analyzed the stability situation with the help of (1) Causality condition, (2) Adiabatic index, (3) Harrison–Zeldovich–Novikov criterion. Figures 9 and 10 (above) indicate that the sound velocities (radial \(v_r(r)\) and transverse \(v_r(r)\)) are positive and less than 1 and the stability factor \(\{v_r(r)\}^2 - \{v_r(t)\}^2\) is negative i.e. our solutions represent physical matter distributions, which are potentially stable. The profiles of adiabatic index (Fig. 3 (below)) and mass in terms of central density (Fig. 11) are another two evidences for stable configuration represented by our solutions.

  • M–RGraph: The profile of mass-surface radius relationship is shown in Fig. 12. It is found that for the ranges of masses given in Table 1 have the same corresponding radii provided on the same table. These means that our solutions yield the ranges of masses and radii very closed to that the observed values. Therefore, the solutions may represent the chosen compact stars.

  • I–MGraph: Since the M–R graph was in good agreement with the observed masses and radii of the chosen stars, we can estimate the corresponding moment of inertia I from the I–M graph (Fig. 13). For Vela X-1, \(I\approx 1.543\times 10^{45}~\mathrm{g\,cm}^2\); Cen X-3, \(I\approx 1.221\times 10^{45}~\mathrm{g~cm}^2\); EXO 1785-248, \(I\approx 0.964\times 10^{45}~\mathrm{g~cm}^2\) and LMC X-4, \(I\approx 0.707 \times 10^{45}~\mathrm{g~cm}^2\).

  • Surface redshift and gravitational redshift: The variations of surface redshift and gravitational redshift are shown in Fig. 7. From that figure, we can see that surface redshift \(Z_s(r) \rightarrow 0\) as \(r \rightarrow 0\) and thereafter monotonically increasing unto the surfaces of stellar spheres. The gravitational redshift \(Z_g(r)\) has opposite behavior, it is maximum at the centres and decreasing toward the surfaces of the fluid configurations. Moreover, \(Z_s(r)\) and \(Z_g(r)\) are coincided at the surfaces \( r = R\), i.e. \(Z(R) = Z_s(R) = Z_g(R)\). Further, we have calculated the numerical values of surface redshift \(Z_s(r)\) at the boundaries of the celestial stars i.e. the maximum values, given in Table 3 and all these maximum values of \(Z_s(r)\) are within the range suggested by Ivanov [68].

Finally, with respect to all obtained significant results, we can conclude that our models are physically acceptable to describe celestial anisotropic compact stars.