Identification of jet-like events using a multiplicity detector

Abstract

We present a method for studying the detection of jets in high energy hadronic collisions using multiplicity detectors at forward rapidity. Such a study enhances the physics scope of multiplicity detectors at forward rapidities in LHC. At LHC energies the jets may be produced with significant cross section at forward rapidities. A multi-resolution wavelet analysis technique can locate the spatial position of jets due to its feature of space-scale locality. The discrete wavelet proves to be very effective in probing physics simultaneously at different locations in phase space and at different scales to identify jet-like events. The key feature this analysis exploits is the difference in particle density in localized regions of the detector due to jet-like and underlying events. We find that this method has a significant sensitivity towards detecting jet position and its size. The jets can be found with the efficiency and purity of the order of 46% with a cut of three times the root mean square of the typical wavelet coefficients distribution in minimum bias events.

1 Introduction

At the center-of-mass (CM) energies of the Large Hadron Collider (LHC), multi-jet events may be produced with measurable cross-section in forward rapidities [1]. Typical 3-jets events arising from $qg \rightarrow qgg$ : $gg \rightarrow ggg$ should appear in the ratio of 0.3:1 as discussed in [2]. The partonic interaction of a low “x” gluon and the high “x” quark will lead to a jet in forward direction, where x is the fraction of momentum carried by the partons. One of the first measurement of inclusive jet production cross section at forward rapidities was performed in $p\bar{p}$ collision at $\sqrt{s} = 1.8\, \hbox {TeV}$ with the D0 detector at the Fermilab Tevatron [1]. The differential cross- section $d^{2}\sigma /(dE_{T} d\eta$) was measured up to $|\eta |$ < 3, where $E_{T}$ is the transverse energy of the jet, $\sigma$ is the cross-section for jet production and $\eta$ is the jet pseudorapidity. The results are found to be in good agreement with next-to-leading order predictions from QCD [3] and indicate a preference for certain parton distribution functions.

In pp collisions, di-jet events will appear with jets lying back-to-back in azimuthal angle. In high energy experiments (e.g. ALICE) these may be easily studied using the central barrel detectors. However one may encounter events where the barrel detectors see two of more than two jets in an event where the topology may suggest a missing jet which may be in other part of the phase space (forward rapidity). If even the direction of such a missing jet can be found, more physical information can be extracted from such an event. The multi-jet cross section is sensitive to the strong coupling constant ($\alpha _{s}$) and parton distribution functions (PDFs) [4, 5]. The 3-jet cross section is directly related to the pQCD matrix element as $\alpha _{s}^{3}$ and hence poses higher sensitivity towards $\alpha _{s}$ than di-jet cross section [6, 7]. The multi-jet azimuthal angular correlation can also be studied and is a useful tool to test the theoretical prediction of multi-jet production processes [8,9,10].

Jets in general produce particles which are confined to a cone and hence the spatial particle density within the jet region is expected to be very different compared to a generic (minimum bias) event in pp collisions.

The aim of this study is to explore if this distinction of localized high particle multiplicity density can be exploited successfully to predict the jet direction or identify jet-like events. This study focusses on present high energy experiments as ALICE at the LHC [12], with possible applications also to STAR (at RHIC) [11]. In the forward region of such experiments there are a set of charged particle detectors and a photon multiplicity detector. We have conducted this study using charged particles in the forward rapidity covering 2.3 < $\eta$ < 3.9.

In this paper, we have used a multi-resolution analysis by discrete wavelet transformation (DWT) which has been successfully used in engineering, mathematics, computer science, astrophysics, multiparticle productions and DCC search [13,14,15,16,17,18,19,20,21]. In our study, we demonstrate that the DWT proves to be very useful in identifying jet-like events in terms of their position and size. There is no information loss due to completeness and orthogonality of the DWT basis. Moreover, the wavelet transformation has advantages over traditional Fourier methods in analyzing physical situations where the signal contains discontinuities and sharp spikes. We have applied the wavelet transformation to the data of the PYTHIA [23, 24] Monte Carlo simulation generated for pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$.

2 Model description

The simulation study is carried out using version 6.425 of the PYTHIA6 [23, 24] event generator. To make results more realistic, the response of the multiplicity detector [25,26,27] is also taken into account. These detectors have typical values of efficiency and purity of 60%. We have generated two sets of data, one for “minimum bias” and other for “jets” in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$. Since we are using charged particles in our study, the magnetic field could have significant effect and thus the study is performed by incorporating field ON condition. The type of B field used in STAR and ALICE experiments is solenoidal one, having a typical magnitude of 0.5 T.

Fig. 1

A typical PYTHIA simulated jet event of jet $E_{T}$ > 20 GeV falling on forward rapidity (2.3 < $\eta$ < 3.9) in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$

Fig. 2

Multiplicity distribution for minimum bias (red marker) and jet events (blue marker) in four particular $\eta -\phi$ bins in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ from MC truth

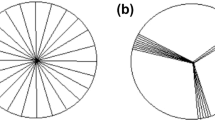
The di-jet events are generated without any initial and final state radiations and at least one of the jets is allowed to fall in the forward rapidities (2.3 < $\eta$ < 3.9). The jet transverse energy ($E_{T}$) is taken as $10< E_{T} < 100$ GeV and transverse momentum ($p_{T}$) transfer of hard scattering is taken as $20< p_{T} < 100$ GeV/c. A typical charged particle distribution in $\eta$ - $\phi$ plane from a jet event is shown in Fig. 1. Figure 2 shows charged particle density distribution for minimum bias (MB) and jet events in $\eta$ coverage, 2.3 $< \eta<$ 3.9 and full azimuthal coverage for four particular $\eta$ - $\phi$ bins in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$. These four bins cover $\eta$ - $\phi$ as 2.3 $< \eta<$ 2.7 & $\pi /2 \le \phi < \pi$ (Bin 1), 2.7 $< \eta<$ 3.1 & $\pi /2 \le \phi < \pi$ (Bin 2), 3.1 $< \eta<$ 3.5 & $\pi /2 \le \phi < \pi$ (Bin 3) and 3.5 $< \eta<$ 3.9 & $\pi /2 \le \phi < \pi$ (Bin 4) where we have allowed the jet to fall on. The multiplicity distribution for jets is fitted with a double Negative Binomial Distribution (NBD) function, while a single NBD function is used for minimum bias events. The double NBD is needed to account for two types of particle production processes, one due to non-jet (soft processes) and other due to jets (hard processes).

Throughout this paper, the generator-level results are named as “MC truth”, while the results after applying the detector response are denoted as “Digits”.

3 A multi-resolution discrete wavelet technique

A discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. The DWT generalizes the standard Fourier analysis. We have performed our study with the idea of multi-resolution analysis by using the well known Haar wavelet. For an input represented by a list of $2^n$ numbers, the Haar wavelet transform may be considered to simply pair up input values, storing the difference and passing the sum. This process is repeated recursively, pairing up the sums to provide the next scale, finally resulting in $2^{n} -1$ differences and one final sum. For the mathematical illustration, we consider a one-dimensional phase-space, described by the dimensionless variable x in the interval [0, 1]. We can divide this phase space in $2^j$ bins of size $\varDelta x$ = $1/2^{j}$, where j is a positive integer $j < j_{max}$, with $j_{max}$ corresponding to the finest resolution that can be attained. Let us consider a function f(x) that represents any observable on this interval such that

$$\begin{aligned} f^{(j)}(x)=\sum _{k=0}^{2^j-1}f_k^j\,\phi _k^j(x) \end{aligned}$$

(1)

where $\phi _k^j(x)$ is given by

$$\begin{aligned} \phi ^j_k(x)=\left\{ \begin{array}{ll} 1 &{} \quad k/2^j\le x < (k+1)/2^j \\ 0 &{} \quad \mathrm{otherwise} \end{array} \right. \,. \end{aligned}$$

(2)

$f_k^j(x)$ is the value of f(x) in the kth bin. The family of bin functions $\phi ^j_k(x)$ can be rewritten as the translations and dilation of a single function $\phi (x)$, called the mother function:

$$\begin{aligned} \phi ^j_k(x)=\phi (2^jx-k)\,, \end{aligned}$$

(3)

where, in the present case, $\phi (x)$ is the top-hat function.

In Eq. 3, the index j denotes the resolution scale and k the position at scale j. In the multi-resolution analysis the sample function f(x) can be find at various scales. For example, to find the structure at lower scale one can replace two adjacent bins 2k and $2k + 1$ by a single bin of size $2\varDelta x = 1/2^{j-1}$ and corresponding bin function is given by

$$\begin{aligned} \phi ^{j-1}_k(x)=\phi ^j_{2k}(x)+\phi ^j_{2k+1}(x)\,, \end{aligned}$$

(4)

In the new bin k, by defining the value $f^{j-1}_k$ of the function as the average of the values in the previous smaller bins:

$$\begin{aligned} f^{j-1}_k=\frac{1}{2}(f^j_{2k}+f^j_{2k+1})\,. \end{aligned}$$

(5)

The resulting sample function at scale $j-1$ is given by:

$$\begin{aligned} f^{(j-1)}(x)=\sum _{k=0}^{2^{j-1}-1}f^{j-1}_k\,\phi ^{j-1}_k(x)\,. \end{aligned}$$

(6)

$f^{j-1}_k$’s are called the mother function coefficients (MFCs) and the Eq. 6 express the mother function representation of the distribution f(x) at scale $j-1$. This procedure can be repeated from the finest resolution scale $j_{max}$ to the lowest one $j=0$.

In the above procedure, another information that can be encoded is the difference $\tilde{f}^{(j-1)}(x)\equiv f^{(j)}(x)-f^{(j-1)}(x)$ and similarly can be represented as:

$$\begin{aligned} \tilde{f}^{(j-1)}(x)=\sum _{k=0}^{2^{j-1}-1}\tilde{f}^{j-1}_k\, \psi ^{j-1}_k(x)\,, \end{aligned}$$

(7)

where the $\psi ^{j-1}_k$’s are called father function coefficients (FFCs) and given by:

$$\begin{aligned} \psi ^{j-1}_k(x)=\phi ^j_{2k}(x)-\phi ^j_{2k+1}(x)\,. \end{aligned}$$

(8)

The FFCs can be obtained by the operation of translations and dilations $\psi ^j_k(x)=\psi (2^jx-k)$.

The FFCs in Eq. 7 are related to MFCs at previous scale j as

$$\begin{aligned} \tilde{f}^{j-1}_k=\frac{1}{2}(f^j_{2k}-f^j_{2k+1})\,. \end{aligned}$$

(9)

The FFCs at a given scale j measure the variation of the sampled distribution f between two adjacent bins.

To identify jet-like events, we have divided ($\eta - \phi$) region in both the physical space and scale space. The Haar basis is easy to visualize but not localized in scale space as the top-hat function is discontinuous. The simplest wavelet which is localized both in space and in scale is often called D4-wavelet [22]. Throughout our analysis we have used D4-wavelet to investigate the scale dependence of multiplicity fluctuations.

In our analysis the input is the multiplicity in different $\eta$ and $\phi$ coverages. We have divided the accessible space in 16 $\eta - \phi$ bins (4 bins in $\eta$ in the range $2.3< \eta < 3.9$ and 4 bins in $\phi$ in the range $0< \phi < 2 \pi$ ) and measure the multiplicity in each bin. So in total we have a input column matrix of $2^{4}$ dimension. The wavelet transformation gives us the bin-to-bin fluctuation, in our case multiplicity fluctuations, in the form of wavelet coefficients (FFCs).

In Minimum Bias case, we expect that the multiplicity distribution over many events would be uniform in all the bins, which will result in no or very less multiplicity fluctuations and hence the wavelet coefficients will approach to a small value. However, in case of jet events, most of the particles in an event will be localized in a single or in at most two bins, which will result in higher fluctuations, with wavelet coefficients attaining higher and higher values. At a level or bin size in $\eta - \phi$, where the values of the fluctuation coefficients are higher gives us an estimate of the size of the jet.

4 Results

Using wavelet transformations, we obtain the father function coefficients and plot these coefficients for minimum bias as well as jet events and try to quantify the results. In Fig. 3 FFC distributions in different scales from MC truth are plotted. From the plots, a clear difference in FFCs distribution for minimum bias and jet events are observed. The distribution is broader for jet events sample as the fluctuations are large in these events. Also the broadening of FFCs distribution is large for scale J $=$ 2. The FFCs at a given scale carry information about the degree of fluctuations at higher scales. Due to completeness and orthogonality of the DWT basis, there is no information loss at any scale. Broader FFC distribution reflects more bin-to-bin multiplicity fluctuations, reflecting a jet-like behaviour. The scale describes the size of the jets on the detector. Figure 4 shows the FFC distributions in different scales from Digits and the similar behaviour is observed as in case of MC truth. In order to quantify the analysis, we introduced a parameter $\xi$, called as strength parameter.

Fig. 3

FFCs distribution for scale J $=$ 1, 2, 3 in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ from MC truth. The jet events have jet $E_{T}$ > 20 GeV

Fig. 4

FFCs distribution for scale J=1, 2, 3 in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ from Digits. The jet events have jet $E_{T}$ > 20 GeV

4.1 Strength parameter

In order to quantify the results and obtaining a cut to select jet like events, we introduce a strength parameter $\xi$. The value of strength parameter ($\xi$) is given by :

$$\begin{aligned} \xi = \frac{\sqrt{\sigma ^{2}_{jet} - \sigma ^{2}_{mb}}}{\sigma _{mb}} \end{aligned}$$

(10)

where $\sigma _{jet}$ and $\sigma _{mb}$ are the widths of the FFCs distributions for jets and MB events, respectively.

The parameter $\xi$ simply determines the deviation from the normal distribution. Figure 5 shows the variation of $\xi$ with scale parameter J. We can see the variation is similar in both MC truth and Digits level, but the values are little lower at Digits level. This suggests the jet-like signal remains after passing through detector response. The maximum value of the strength parameter is for J $=$ 2.

The results shown so far are for an ideal situation with a full jet event sample. Now we consider a more realistic scenario of mixing the MB sample with different percentage of jet events selected randomly and repeat the same analysis. We have studied seven such samples with jet event percentage: $1\%$, $5\%$, $10\%$, $20\%$, $30\%$, $40\%$ and $50\%$. Strength parameters is extracted for samples with different jet events percentage and plotted in Fig. 6. The figure shows that the strength parameter increases with increasing percentage of jet events. However the magnitude of the strength parameter is higher for MC truth than for Digits. In Fig. 7 strength parameter is plotted against the scale J $=$ 1, 2, 3 and the magnitude is higher for J $=$ 2 both for MC truth and Digits.

Fig. 5

Strength ($\xi$) vs. scale parameter (J) in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ from MC truth and Digits

4.2 Model comparison

It is important here to check for any model dependence of present analysis. For this we have carried out the analysis with another event generator, PHOJET [28]. The FFCs distribution for events generated from PHOJET are compared to those from PYTHIA6 [23, 24]. Figure 8 shows the FFCs distribution for both the models for different scales. There is a good agreement between the models.

Fig. 6

Strength ($\xi$) vs. fraction of jet events mixed in MB sample in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ from MC truth and Digits

Fig. 7

Strength ($\xi$) vs. scale parameter with different jet percentage in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ from MC truth and Digits

Fig. 8

FFCs distribution in PYTHIA6 and PHOJET for scale J $=$  1, 2, 3 in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ for MC truth

4.3 Energy dependence

Figure 9 shows the strength parameter dependence on jet transverse energy for scale J $=$ 1, 2, 3 for MC truth and Digits. We have generated four event samples with jet $E_{T}$ ranging from 20–30 GeV, 30–40 GeV, 40–60 GeV and 20–100 GeV. From the figure we can see that the magnitude of $\xi$ is highest for jet $E_{T}$ = 40–60 GeV i.e. for high jet $E_{T}$ case.

Fig. 9

Strength ($\xi$) vs. scale parameter for different jet transverse energies in pp collisions at $\sqrt{s} = 7 \,\hbox {TeV}$ from MC truth and Digits

4.4 Efficiency, purity of selecting jet like events

Efficiency and purity of selecting jet-like events in a multiplicity detector is calculated by applying different rms cuts from normal FFCs distribution on a sample of mixed MB+jet events with $50\%$ jets. The efficiency and purity are defined as:

$$\begin{aligned} Efficiency= & {} \frac{N_{j}}{N_{ja}} \end{aligned}$$

(11)

$$\begin{aligned} Purity= & {} \frac{N_{j}}{N_{jlike}} \end{aligned}$$

(12)

where, $N_{j}$ = No. of jet events identified, $N_{ja}$ = No. of jet events added in the MB sample and $N_{jlike}$ = No. of jet like events. Figures 10 and 11 show the variation of efficiency / purity with the root mean square (RMS) cuts obtained from the FFCs distribution of MB events for MC truth and Digits, respectively. For a cut of 3 times the rms of the FFCs distribution of MB events the efficiency and purity values are about 46$\%$.

Fig. 10

Efficiency, purity vs. rms cut on MB FFCs distribution at $\sqrt{s} = 7 \,\hbox {TeV}$ from MC truth

Fig. 11

Efficiency, purity vs. rms cut on MB FFCs distribution at $\sqrt{s} = 7 \,\hbox {TeV}$ from Digits

5 Summary

We have reported a multi-resolution analysis technique to identify jet-like events in a multiplicity detector at LHC energies. The analysis is carried out using charged particle multiplicities. The observation of jet-like events can be used to tag 3-jet events in ALICE at the LHC. The multi-resolution simulation study shows the good sensitivity towards selecting jet-like events, in the forward multiplicity detector. The value of $\xi$ is 0.22, 0.65 and 1.42 for event samples with 1%, 10% and 50% jet-like events respectively. A $\xi$ value of zero would have indicated no sensitivity of the method towards identification of jet-like events. Such an analysis can be carried out in real data in future with pp collisions at 0.9, 2.76, 7, 8 and 13 TeV data collected by ALICE.