Abstract
The Dyson–Schwinger quark equation is solved for the quark-gluon vertex using the most recent lattice data available in the Landau gauge for the quark, gluon and ghost propagators, the full set of longitudinal tensor structures in the Ball-Chiu vertex, taking into account a recently derived normalisation for a quark-ghost kernel form factors and the gluon contribution for the tree level quark-gluon vertex identified on a recent study of the lattice soft gluon limit. A solution for the inverse problem is computed after the Tikhonov linear regularisation of the integral equation, that implies solving a modified Dyson–Schwinger equation. We get longitudinal form factors that are strongly enhanced at the infrared region, deviate significantly from the tree level results for quark and gluon momentum below 2 GeV and at higher momentum approach their perturbative values. The computed quark-gluon vertex favours kinematical configurations where the quark momentum p and the gluon momentum q are small and parallel. Further, the quark-gluon vertex is dominated by the form factors associated to the tree level vertex \(\gamma _\mu \) and to the operator \(2 \, p_\mu + q_\mu \). The higher rank tensor structures provide small contributions to the vertex.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The interaction of quarks and gluons is described by Quantum Chromodynamics [1,2,3,4], a renormalisable gauge theory associated to the color gauge group SU(3). Of its correlation functions, the quark-gluon vertex has a fundamental role in hadron phenomenology, in the understanding of chiral symmetry breaking mechanism and the realisation of confinement. Despite its relevance for strong interactions, our knowledge of the quark-gluon vertex from first principles calculations is relatively poor. At the perturbative level, only recently a full calculation of the twelve form factors associated to this vertex was published [5] but only for some kinematical configurations, namely the symmetric configuration (equal incoming, outgoing quark and gluon squared momenta), the on-shell configuration (quarks on-shell with vanishing gluon momentum) and what the authors called its asymptotic limit. In particular, the vertex asymptotic limit was used to investigate ansätze that can be found in the literature [6,7,8,9,10,11] with the aim to test their description of the ultraviolet regime.
At the non-perturbative level, the quark-gluon vertex has been studied within continuum approaches to QCD by several authors [11,12,13,14,15,16,17,18,19,20,21,22,23]. Typically, the computation is performed after writing the vertex in terms of other QCD vertices and propagators and taking into account its perturbative tail. Most of the computations include only a fraction of the twelve form factors required to fully describe the quark-gluon vertex. In [17, 22, 23] the authors look for a first principle determination of the vertex by solving the theory at the non-perturbative level, gathering information on the vertex from QCD symmetries and relying on one-loop dressed perturbation theory. The vertex has also been investigated perturbatively within massive QCD, i.e. using the Curci-Ferrari model [18], and all its (perturbative) tensor structures form factors accessed for some kinematical configurations.
Lattice simulations, both for quenched [24,25,26] and full QCD [27], were also used to investigate the quark-gluon vertex. Again, only a limited set of kinematical configurations were accessed and, in particular, its the soft gluon limit, defined by a vanishing gluon momenta, was mostly explored. For full QCD so far only a single form factor, that associated with the tree level tensor structure, was measured on lattice simulation in the soft gluon limit.
One can also find in the literature attempts to combine continuum non-perturbative QCD equations with lattice simulations to study the quark-gluon vertex. Indeed, in [28] a generalised Ball-Chiu vertex was used in the quark gap equation, together with lattice results for the quark, gluon and ghost propagators to investigate the quark-gluon vertex. In [29], the full QCD lattice data for \(\lambda _1\) was studied relying on continuum information about the vertex.
The use of continuum equations with results coming from lattice simulations requires high quality lattice data to feed the continuum equations that should be solved for the vertex. In this approach, the computation of a solution of the continuum equations requires assuming some type of functional dependence for various propagator functions. In recent years, there has been an effort to improve the quality of the lattice data, in the sense of being closer to the continuum and producing simulations with large statistical ensembles, both for propagators and for vertex functions. This approach that combines lattice information and continuum equations relies strongly on the effort to access high precision lattice simulations.
For the practitioner oftentimes it is sufficient to have a good model of the vertex that should incorporate the perturbative tail to describe the ultraviolet regime, some “guessing” for the infrared region and, hopefully, comply with perturbative renormalisation [5,6,7,8, 31]. A popular and quite successful model was set in [32], named the Maris-Tandy model, that assumes a bare quark-gluon vertex and introduces an effective gluon propagator that is strongly enhanced at infrared scales and recovers the one-loop behaviour at higher momentum. This model simplifies considerably the momentum dependence of the combined effective gluon propagator and quark-gluon vertex and assumes that the dominant momentum dependence is associated only with the gluon momentum. Such type of vertex that appears in the Dyson–Schwinger and the Bethe–Salpeter equations can be seen as a reinterpretation of the full vertex tensor structure, after rewriting its main components in a way that formally can be associated with the effective gluon propagator. Although the Maris-Tandy model is quite successful for phenomenology, it is not able to describe the full set of hadronic properties and fails to explain the mass splittings of the \(\rho \) and \(a_1\) parity partners, underestimates weak decay constants of heavy-light mesons and cannot reproduce simultaneously the mass spectrum and decay constants of radially excited vector mesons to point out some known limitations. For a more complete description see, for example, [30, 33,34,35] and references therein. Several authors have tried to improve the Maris-Tandy model either by studying its dependence on the various parameters, see e.g. [34], or by changing its functional dependence at low momenta, see e.g. [36], to achieve either a better description of Nature or good agreement with the results from lattice simulations.
The goal of the present work is to explore further the quark-gluon vertex in the non-perturbative regime from first principles calculations combining continuum methods with results coming from lattice simulations. Our approach follows the spirit of the calculation performed in [28] that solves the quark Dyson–Schwinger equation for the vertex. In [28] the quark-gluon vertex was described as a generalised Ball-Chiu vertex and single unknown form factor, function only of the gluon momentum, was considered. The current work goes beyond this approximation and includes the full set of longitudinal form factors that appear in the Ball-Chiu vertex. In this work we disregard any contribution due to the transverse form factors and consider the Landau gauge quark-gluon vertex, to profit from the recent high quality lattice data for the quark, the gluon and the ghost propagators. Moreover, our computation also incorporate the recent analysis of the full QCD lattice simulation for the quark-gluon vertex in the soft gluon limit that identifies an important contribution, for the infrared vertex, associated with the gluon propagator [29]. As in other studies, we rely on a Slavnov–Taylor identity to write the vertex longitudinal form factors as a function of the quark wave function, the running quark mass, the quark-ghost kernel form factors and the ghost propagator. The normalisation of the quark-ghost kernel form factors \(X_0\) (see below for definitions) derived in [17] for the soft gluon limit is also taken into account when solving the quark gap equation for the vertex. The normalisation of \(X_0\) played an important role in the analysis of the full QCD lattice data analysis for \(\lambda _1\), the form factor associated with the tree level tensor structure \(\gamma _\mu \), performed in [29] that identified an important contribution for \(\lambda _1\) coming from the gluon propagator.
Our solution for the quark-gluon vertex returns a \(X_0\) that deviates only slightly from the normalisation condition referred above. However, the longitudinal form factors describing the quark-gluon vertex are strongly enhanced in the infrared region. The enhancement of the four longitudinal form factors occurs for quark and gluon momentum below 2 GeV and can be traced back to ghost contribution introduced by the Slavnov–Taylor identity and the gluon dependence of the ansatz. At high momentum the form factors seem to approach their perturbative values. The matching with the perturbative tail is not perfect and this result can be understood partially due to the regularisation for the mathematical problem, i.e. the Tikhonov regularisation, and partially to the parametrisation of the vertex. Indeed, by calling the gluon propagator to describe the various form factors, the inversion of the Dyson–Schwinger equations is quite sensitive to the low momentum scales, where the gluon propagator is much larger, and less sensitive to the ultraviolet regime. In order to overcome this problem, we considered a relatively large cutoff in the inversion and in this way add information on the perturbative tail.
The computed quark-gluon vertex is a function of the angle between the quark four momentum p and the gluon four momentum q that, clearly, favours kinematical configurations where p and q of the order of 1 GeV or below. The enhancement occurs preferably at momenta of \(\sim \, \varLambda _{QCD}\). Furthermore, the vertex is enhanced when all momenta entering the vertex (see Fig. 1) tends to be parallel in pairs, solving in this way the compromise that the momenta are restricted to a region around \(\varLambda _{QCD}\). Within our solution for the quark-gluon vertex, the dominant form factors are associated with the tree level vertex \(\gamma _\mu \) and the operator \(2 \, p_\mu + q_\mu \). The higher rank tensor structures give sub-leading contributions to the vertex.
In the current work, the vertex is written using the Ball-Chiu construction. It is known that the Ball-Chiu vertex has kinematical singularities for the Landau gauge [37] that are associated to the transverse form factors (see definitions below). These singularities can be avoided by considering a different tensor basis for the full vertex as described, for example, in [37]. However, the singularities are not associated to the longitudinal form factors and our calculation only takes into account this class of form factors.
The paper is organised as follows. In Sect. 2 we introduce the notation for the propagators, the Dyson–Schwinger equations and the quark-gluon vertex. Moreover, we use a Slavnov–Taylor identity to rewrite the vertex in terms of the quark propagators functions and the quark-ghost kernel. The parametrisation of the quark-ghost kernel is also discussed. In Sect. 3 the scalar and vector components of the DSE in Minkowski space are given, together with the corresponding kernels. In Sect. 4 the DSE are rewritten in Euclidean space, introduce the vertex ansatz and perform a scaling analysis of the integral equations. In Sect. 5 we give the details of the lattice data used in the current work for the various propagators and on the functions that parametrise the lattice data. The kernels for the Euclidean space DSE are discussed in Sect. 6, together with the solutions for the vertex of the gap equation. The quark-gluon vertex form factors are reported in Sect. 7 for several kinematical configurations. Finally, on Sect. 8 we summarise and conclude.
The quark-gluon vertex
2 The quark gap equation and the quark-gluon vertex
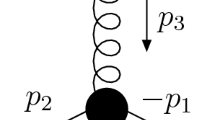
In this section the notation used through out the article is defined. In this first part of this work, the equations discussed are written in Minkowski space with the diagonal metric \(g = ( 1, \, -1, \, -1, \, -1)\). Let us follow the notation of [38] for the quark-gluon vertex represented in Fig. 1 that considers all momenta are incoming and, therefore, verify
The one-particle irreducible Green’s function associated to the vertex reads
where g is the strong coupling constant and \(t^a\) are the color matrices in the fundamental representation.
The quark propagator is diagonal in color and its spin-Lorentz structure is given by
where \(Z(p^2) = 1/A(p^2)\) stands for the quark wave function and \(M(p^2) = B(p^2) / A(p^2)\) is the renormalisation group invariant running quark mass.
The Dyson–Schwinger equation for the quark propagator, also named the quark gap equation, is represented in Fig. 2 and can be written as
where \(Z_2\) is the quark renormalisation constant, \(m^{{\mathrm {bm}}}\) the bare current quark mass and the quark self-energy is given by
where \(Z_1\) is a combination of several renormalisation constants, \(D_{\mu \nu }^{a b}(q)\) is the gluon propagator that, in the Landau gauge, is given by
below both \(D^{ab}_{\mu \nu } (q)\) and \(D (q^2)\) will be referred to as the gluon propagator.
The Dyson–Schwinger equation for the quark. The solid blobs denote dressed propagators and vertices
A key ingredient in gap Eq. (4) is the quark-gluon vertex. Indeed, it is only after knowing \(\varGamma ^a_\mu \) or, equivalently \(\varGamma _\mu \), that \(Z(p^2)\) and \(M(p^2)\) can be computed. The Lorentz structure of the quark-gluon vertex \(\varGamma _\mu \) can be decomposed into longitudinal \(\varGamma ^{(L)}\) and transverse \(\varGamma ^{(T)}\) components relative to the gluon momenta, i.e. one writes
where, by definition,
By choosing a suitable tensor basis in the spinor-Lorentz space, \(\varGamma _\mu \) can be written as a sum of scalar form factors that multiply each of the elements of the basis. The full vertex \(\varGamma _\mu \) requires twelve form factors and for the Ball and Chiu basis [6] it reads
The operators associated to the longitudinal vertex are
while those associated to the transverse part of the vertex read
where \(\sigma _{\mu \nu } = {1\over 2} [\gamma _{\mu },\gamma _{\nu }]\).
2.1 QCD symmetries and the quark-gluon vertex
The global and local symmetries of QCD constrain the full vertex \(\varGamma _\mu \) and connect several of the Green’s functions theory. For example, the global symmetries of QCD require that the form factors \(\lambda _i\) and \(\tau _i\) to be either symmetric or anti-symmetric under exchange of the two first momenta; see, e.g., ref. [38] and references therein. On the other hand, gauge symmetry implies that the Green functions also satisfy the Slavnov–Taylor identities (STI) [39,40,41]. These identities play a major role in our understanding of QCD and, in particular, the longitudinal part of the quark-gluon vertex is constrained by the following identity
where the ghost-dressing function \(F(q^2)\) is related to the ghost two-point correlation function as
and H and \(\overline{H}\) are associated to the quark-ghost kernel. As discussed in [38], these functions can be parametrised in terms of four form factors as
where \(X_i \equiv X_i ( p_1, p_2, p_3 )\) and \( \overline{X}_i \equiv X_i( p_2, p_1, p_3 )\).
The STI given in Eq. (13) can be solved with respect to the vertex [13] to write the longitudinal form factors \(\lambda _i\) in terms of the quark propagator functions \(A(p^2)\), \(B(p^2)\) and the quark-ghost kernel functions \(X_i\) and \(\overline{X}_i\) as
A nice feature of the above solution for the various form factors \(\lambda _i\), that can be checked by direct inspection, is that the symmetry requirements on the \(\lambda _i\) due to charge conjugation are automatically satisfied independently of the functions A, B, \(X_i\) and \(\overline{X}_i\). This is a particularly important point when modelling the vertex.
3 Decomposing the Dyson–Schwinger equation into its scalar and vector components
The Dyson–Schwinger equation for the quark propagator is written in (4), with the quark self-energy being given by (5). This equation can be projected into its scalar and vector components by taking appropriate traces.
The scalar part of the equation is given by the trace of (4) which, after some algebra, reduces to
after insertion of the vertex decomposition (7), taking into account only its longitudinal part, where \(k = p -q\),
\(\lambda _i \equiv \lambda _i (-p , \, p-q, \, q) \) and \(C_F = 4/3\) is the Casimir invariant associated to the SU(3) fundamental representation.
The vector component of (4) is obtained after multiplication by \(/ p\ \) and then taking the trace of the resulting equation to arrive on
The two Eqs. (20) and (22) can be simplified further by modelling the quark-gluon vertex. For example, in [13, 28] the vertex was parametrised using the solution of the Slavnov–Taylor identity (16)–(19) and setting \(X_1 = X_2 = X_3 = 0\). The rationale for such a choice comes from perturbation theory which gives, at tree level, \(X_0 = 1\) and \(X_1 = X_2 = X_3 = 0\). This ansatz, that ignores all form factor associated to the quark-ghost kernel but \(X_0\), assumes that at the non-perturbative level the hierarchy of the form factors follows its relative importance observed in the high momentum regime. Furthermore, in order to compute a solution of the Dyson–Schwinger equations it was introduced a further restriction on \(X_0\), that it depends only on the incoming gluon momenta, i.e. that \(X_0 = X_0 (q^2)\).
In order to solve the Dyson–Schwinger equations for the vertex, it will be assumed that the form factors associated to the quark-ghost kernel, see Eq. (15), factorize as
where \(g_i(p^2_1, p^2_2) = g_i(p^2_2, p^2_1)\) are symmetric functions of its arguments. This type of factorisation is compatible, for example, with the Maris-Tandy quark-gluon description of the quark-gluon vertex [32] and simplifies considerably the analysis of the solutions of the equations to be solved. In [17] it was proved that, to all-orders,
that, for the ansatz (23) implies
A solution that complies with the second relation given in Eq. (24) is to assume that \(X_1 = X_2\) for any kinematical configuration. Note also that by choosing the \(g_i\) to be symmetric functions of the arguments, the form factors \(X_i\) and \(\overline{X}_i\) become identical. If one takes into account these relations into the ansatz for the quark-gluon vertex, then the solutions of the Slavnov–Taylor identities (16)–(19) become
where
and \(k = p - q\). The scalar component of the Dyson–Schwinger equations is now
where the kernels are defined as
Similarly, the vector component of the Dyson–Schwinger equations reduces to
with the kernels given by
4 The Dyson–Schwinger equations in Euclidean space
As already stated, our goal is to solve the Dyson–Schwinger equations for the quark-ghost kernel, said otherwise for the quark-gluon vertex, and this requires the knowledge of the quark, gluon and ghost propagators. For the propagators we will rely on lattice inputs that provide first principles non-perturbative results and also demand that the above expressions should be rewritten in Euclidean space. The Wick rotation to go from Minkowski to Euclidean space is achieved by making use of the following substitutions
on Eqs. (31) and (35). For completeness, we provide now all expressions in Euclidean space.
The scalar component of the Dyson–Schwinger equations reads
while its vector component is given by
The kernels appearing in Eqs. (40) and (41) are
The computation of any solution of the above equations, using lattice inputs for the propagators, requires the use of the renormalised Dyson–Schwinger equations and, therefore, all quantities appearing on these equations should be finite. This requirement constrains the integrand functions \(g_i (p^2,\) \((p-q)^2) \, Y_i (q^2)\) and, in particular, its possible behaviour in the limits where \(q \rightarrow 0\) and \(p \rightarrow + \infty \).
Let us start by investigating the ultraviolet limit of the integrand functions appearing in Eqs. (40) and (41). In the large q limit it follows that
up to logarithmic corrections associated to the various propagators. In this limit, the integrand function appearing on the scalar Eq. (40) read
The requirement of having a finite integral demands that at large q
or that these functions are proportional to a higher negative power of q. The logarithmic corrections, not taken into account in this analysis, are sufficient to avoid the UV logarithmic divergence suggested by the naive power counting. Indeed, these logarithmic corrections introduced by the renormalisation group analysis are, for large momenta, of type \(\left( \log (q^2/ \varLambda ^2) \right) ^\gamma \), with \(\gamma \) standing for the anomalous dimensions. Our large q analysis should take into account the logarithmic corrections coming from the gluon, the ghost and the quark propagators that for \(N_f = 2\) result in \(\gamma = \gamma _{glue} + \gamma _{ghost} + \gamma _{quark} = -137/116\). Then, assuming a large q behaviour as in (51) times the log correction, the integration function at high momenta becomes
resulting in a finite value for the integral. The difference between the naive power counting and taking into account the log corrections is illustrated on Fig. 3, where one can observe the effect due to the log corrections that suppress further the integrand function at high momenta. In what concerns the quark-ghost kernel form factor \(Y_0(q^2)\) at high energies, the power counting analysis is compatible with having a \(Y_0 (q^2) = 1\) at large momenta as required by perturbation theory and by the all-orders result summarised in Eq. (25).
Large p behaviour and logarithmic corrections. The plotted function uses \(\varLambda _{QCD} = 0.3\) GeV
The same analysis for the vector component (41) gives, up to logarithmic corrections,
where \(\{ \cdots \}\) stand for finite expressions involving \(A(p^2)\), \(A(q^2)\), \(B(p^2)\) and \(B(q^2)\). The conditions given in (51) are sufficient to ensure a finite result associate to the UV integration over q for the vector component of the Dyson–Schwinger equations.
The dynamics of QCD generates infrared mass scales for the quark and gluon propagators, see Sects. 5.1 and 5.2, that eliminate possible infinities associated to the low momentum limit in the integral of the quark gap equation and the analysis of the infrared limit does not add any new constraints.
For full QCD, the \(\lambda _1\) form factor was computed in the soft gluon limit, i.e. vanishing gluon momenta, using lattice simulations in [27]. The analysis of the lattice data performed in [29] shows that the lattice data is well described by
where a and b are constants, that in terms of \(Y_1\) and \(Y_3\) translates into
where \(M(p^2) = B(p^2) / A(p^2)\). This result suggests to write
that in the high q limit gives \(X_1 \sim Y_1 (q^2)/q^2\) and regularises the ultraviolet behaviour in agreement with the discussion summarised in (51). Similarly, Eq. (55) also suggests
giving at high q momenta a \(X_3 \sim \tilde{X}_3 (q^2) / q^2\) and, in this way, the ultraviolet problems referred in (51) are solved. Furthermore, for large quark momentum the ansatz (56) and (57) give
implying the vanishing of the kernels (42)–(48) for sufficiently large p.
In short, our ansatz for the quark-gluon vertex used to solve the Dyson–Schwinger equations reads
The quark gap equation should be solved taking into account the constraint (25) that demands
The Landau gauge lattice gluon propagator as given by lattice simulations [46, 47] retuns a \(D(q^2)\) that is strongly enhanced at low momenta. It follows from Eqs. (60) and (61) that within the ansatz considered here, one expects \(X_1\) and \(X_3\) to rise significantly for small \(p^2 + (p-q)^2 = 2 \, p^2 + q^2 - 2 p \cdot q\). On the other hand, at high momenta, the form factors should approach its perturbative value. At tree level in perturbation theory the quark-ghost kernel form factors read \(X_0 = 1\) and \(X_1 = X_3 = 0\), suggesting that \(X_1\) and \(X_3\) give marginal contributions to the full vertex at sufficient high energy. At the qualitative level, the guessed behaviour associated with the ansatz (59)–(61) reproduce the computed quark-ghost kernel form factors computed in [23] using the Dyson–Schwinger equations and one-loop dressed perturbation theory for the quark-ghost kernel. For the inversion of the Dyson–Schwinger equations, i.e. from the numerical point of view, given the strong enhancement of the gluon propagator at low momenta, this can mean a poorer resolution of \(X_1\) and \(X_3\) in the ultraviolet regime.
5 Preparing to solve the Euclidean Dyson–Schwinger equations
The computation of a solution of the Dyson–Schwinger equations requires parameterising either the quark-gluon vertex, if one aims to look at the quark propagator, or the quark propagator functions to extract information on the quark-gluon vertex. In both these cases, a complete description of the gluon and ghost propagators is assumed explicitly.
In the current work, we aim to solve the gap equation for the quark-gluon vertex and, therefore, the knowledge of the various propagators over all range of momenta appearing in the integral equation is required. This is achieved fitting the Landau gauge lattice propagators with model functions that are compatible with the results of 1-loop renormalisation group improved perturbation theory. In this way, it is ensured that the perturbative tails are taken into account properly in the parameterisation of the propagators. The parameterisations considered here are compared to those of [28] in “Appendix B”. As can be seen on Fig. 44, the differences between the two sets of curves are more quantitative than qualitative.
5.1 Landau gauge lattice gluon and ghost propagators
The lattice gluon propagator has been computed in the Landau gauge both for full QCD and for the pure Yang–Mills. The gluon propagator is well known for the pure Yang–Mills theory and it was calculated in [47] for large statistical ensembles and for large physical volumes \(\sim (6.6 \text{ fm })^4\) and \(\sim (8.2 \text{ fm })^4\); see also e.g. [44, 45]. Furthermore, in [47] the authors provide global fits to the lattice data that reproduce the 1-loop renormalisation group summation of the leading logarithmic behaviour. Of the various expressions given there, we will use to solve the integral Dyson–Schwinger equations the following fit to the \((6.6 \text{ fm })^4\) volume result
with the gluon anomalous dimension being \(\gamma = -13/22\), \(Z = 1.36486 \pm 0.00097\), \(M^2_1 = 2.510 \pm 0.030 \text{ GeV }^2\), \(M^2_2 = 0.471 \pm 0.014 \text{ GeV }^2\), \(M^4_3 = 0.3621 \pm 0.0038 \text{ GeV }^4\), \(m^2_0 = 0.216 \pm 0.026 \text{ GeV }^2\) using \(\varLambda _{QCD} = 0.425 \text{ GeV }\) and where \(\omega = 33 \, \alpha _s ( \mu ) / 12 \pi \) with a strong coupling constant \(\alpha _s ( \mu = 3 \text{ GeV } ) = 0.3837\); see [47] for details. This fit to the lattice data has an associated \(\chi ^2/\text {d.o.f.} = 3.15\). The authors provide fits with better values for the \(\chi ^2/\text {d.o.f.}\) However, given that the level of precision achieved on lattice simulations for the quark propagator is considerably smaller than for the gluon propagator, one should not distinguish between the various fitting functions provided in [47]. Our option considers the simplest functional form given in that work.
Pure Yang–Mills gluon (top) and ghost (bottom) lattice dressing functions and the corresponding fit functions used herein. See text for details
The lattice data for the Landau gauge gluon dressing function \(p^2 D (p^2)\), renormalised in the MOM-scheme at the mass scale \(\mu = 3\) GeV and the fit associated to Eq. (63) can be seen on the top part of Fig. 4.
For the ghost propagator we take the data reported in [46] for the \(80^4\) lattice simulation and fit the lattice data to the functional form
getting \(Z = 1.0429~\pm ~0.0054\), \(M^4_1 = 18.2~\pm ~5.7 \text{ GeV }^4\), \(M^2_2 = 33.4~\pm ~6.4 \text{ GeV }^2\), \(M^4_3 = 6.0~\pm ~2.7 \text{ GeV }^4\), \(M^2_4 = 29.5~\pm ~5.7\) GeV\(^2\), \(m^4_1 = 0.237~\pm ~0.049\), \(m^2_0 = 0.09 \pm 0.42 \text{ GeV }^2\) with a \(\chi ^2/\text {d.o.f.} = 0.27\). In the above expression the ghost anomalous dimension reads \(\gamma _{gh} = - 9/44\) with \(\omega \) and \(\varLambda _{QCD}\) taking the same values as in the gluon fitting function (63). The lattice data, renormalised in the MOM-scheme at the mass scale \(\mu = 3\) GeV, and the fitting curve (64) can be seen on the bottom of Fig. 4.
5.2 Lattice quark propagator
For the quark propagator we consider the result of a \(N_f = 2\) full QCD simulation in the Landau gauge [27, 42] for \(\beta = 5.29\), \(\kappa = 0.13632\) and for a \(32^3 \times 64\) lattice. For this particular lattice setup, the corresponding bare quark mass is 8 MeV and the pion mass reads \(M_\pi = 295\) MeV.
Our fittings to the lattice data, see below, take into account that the lattice data is not free of lattice artefacts; see [27] and [42] for details. At high momenta the lattice quark wave function \(Z(p^2)\) is a decreasing function of momenta, a behaviour that is not compatible with perturbation theory that predicts a constant \(Z(p^2)\) in the Landau gauge. As reported in [27, 42], the analysis of the lattice artefacts relying on the H4 method suggests that, indeed, \(Z(p^2)\) is constant at high p. In order to be compatible with perturbation theory, we identify the region of momenta where \(Z(p^2)\) is constant and, for momenta above this plateaux, we replace the lattice estimates of \(Z(p^2)\) by constant values, i.e. the higher value of the quark wave function belonging to the plateaux. The original lattice data and the ultraviolet corrected lattice data can be seen on top of Fig. 5. The UV corrected lattice data is then fitted to the rational function
giving \(Z_0 = 1.11824 \pm 0.00036\), \(M^4_1 = 1.41 \pm 0.18 \text{ GeV }^4\), \(M^2_2 = 6.28 \pm 1.00 \text{ GeV }^2\), \(M^4_3 = 2.11 \pm 0.28 \text{ GeV }^4\), \(M^2_4 = 6.20\) \(\pm 0.98\) \(\hbox {GeV}^2\) for a \(\chi ^2/\text {d.o.f.} = 0.74\). The solid red line on Fig. 5 (top) refers to the fit just described.
Quark wave function (top) and running mass (bottom) lattice functions from full QCD simulations with \(N_f = 2\)
The removal of the lattice artefacts for the running quark mass is more delicate when compared to the evaluation of the quark wave function lattice artefacts [24, 42, 43]. The lattice data published in [27, 42] and reported on Fig. 5 (bottom) was obtained using the so called hybrid corrections to reduce the lattice effects [24] . The hybrid method results in a smoother mass function when compared to the one obtained by applying the multiplicative corrections. The differences on the corrected running mass between the two methods occur for momenta above 1 GeV, with the multiplicative corrected running mass being larger than the corresponding hybrid estimation; see Appendix on [42]. The running mass provided by the two methods, corrected for the lattice artefacts, seems to converge to the same values at large momentum.
The running mass reported on Fig. 5 (bottom) is not smooth enough to be fitted. To model the lattice running mass in a way that reproduces the ultraviolet and the infrared lattice data and is compatible with the perturbative behaviour at high moment, we remove some of the lattice data at intermediate momenta. On Fig. 5 the data in the region with an orange background was not taken into account in the global fit of the running quark mass. The remaining lattice data was fitted to
where \(\gamma _m = 12/29\) is the quark anomalous dimension for \(N_f = 2\) and
The fitted parameters are \(M_q = 349 \pm 10 \text{ MeV } \text{ GeV }^2\), \(m^2_1 = 1.09 \pm 0.43 \text{ GeV }^2\), \(m^2_2 = 0.92 \pm 0.28 \text{ GeV }^2\), \(m^4_3 = 0.42 \pm 0.15 \text{ GeV }^4\), \(m_0 = 10.34 \pm 0.63\) MeV and \(A = -2.98 \pm 0.25\) for a \(\chi ^2/\text {d.o.f.} = 1.97\) after setting \(\lambda = 1 \text{ GeV }^2/\text{ MeV }^2\). The fit function and the full lattice running quark mass data can be seen on Fig. 5 (bottom). Note that in (66) and in (67) p is given in GeV and \(m_q(p^2)\) and \(M(p^2)\) are given in MeV.
The scalar (top) \({\mathscr {N}}^{(0)}_{B} (p,q)\) and vector (bottom) \({\mathscr {N}}^{(0)}_{A} (p,q) / p^2\) kernel components of the Dyson–Schwinger equations. For comparison with the kernels shown in [28], the above kernels do not include the Gauss–Legendre quadrature weights required to perform the integration over the gluon momentum q. This applies also to Figs. 7, 8, 9 and 10
6 Solving the Dyson–Schwinger equations
Let us now discuss the solutions of the Euclidean space Dyson-Schwinger Eqs. (40) and (41) for the quark-ghost kernel, i.e. for the quark-gluon vertex. The momentum integration will be performed as described in “Appendix A”, i.e. by introduction an hard cutoff \(\varLambda \), and with all integrations performed with Gauss–Legendre quadrature. For the angular integration we consider 500 Gauss–Legendre points as in [28]. After angular momentum integration, one is left with the kernels
that can be seen on Figs. 6, 7 and 8, without taking into account the Gauss–Legendre weights associated to the integration over the gluon momentum. The inclusion of the Gauss–Legendre weights associated to the q momentum integration does not change the outcome reported on Figs. 6, 7 and 8 and the main difference being that the associated numerical values are considerably smaller.
The scalar (top) \({\mathscr {N}}^{(1)}_{B} (p,q)\) and vector (bottom) \({\mathscr {N}}^{(1)}_{A} (p,q)/ p^2\) kernel components of the Dyson–Schwinger equations. See also the caption of Fig. 6
The scalar (top) \({\mathscr {N}}^{(3)}_{B} (p,q)\) and vector (bottom) \({\mathscr {N}}^{(3)}_{A} (p,q)/ p^2\) kernel components of the Dyson–Schwinger equations. See also the caption of Fig. 6
The major contributions of the \({\mathscr {N}}^{(0)}_{B}\) and \({\mathscr {N}}^{(0)}_{A}\) kernels occur in a well defined momentum region where \(p \lesssim 1.5\) GeV and \(q \lesssim 1.5\) GeV. Further, for p, \(q \gtrsim 2\) GeV the kernels become marginal. The results for \({\mathscr {N}}^{(0)}_{B}\) and \({\mathscr {N}}^{(0)}_{A}\) reproduce the corresponding behaviour observed in [28]. It follows that the integration over momentum in Eqs. (40) and (41) associated to the kernels \({\mathscr {N}}^{(0)}_{B}\) and \({\mathscr {N}}^{(0)}_{A}\) kernels, that are coupled to \(X_0(q^2)\), is finite.
The function \({\mathscr {N}}^{(1)}_{A} (p, q)\) displays a similar pattern and, again, the integration over the gluon momentum associated with \({\mathscr {N}}^{(1)}_{A}\) is expected to be well behaved. On the other hand the remaining kernels, i.e. \({\mathscr {N}}^{(1)}_{B} (p, q)\), \({\mathscr {N}}^{(3)}_{B} (p, q)\) and \({\mathscr {N}}^{(3)}_{A} (p, q)\), are all increasing functions of q. The requirement of a finite integration over q demands that \(X_1\) and \(X_3\) should approach zero fast enough to compensate the increase with q of these kernel functions; see the discussion of the kernels ultraviolet limit in Sect. 4. The ansatz (59)–(61) adds a multiplicative gluon propagator term that is just enough to regularize the high momentum associated to \({\mathscr {N}}^{(1)}_{B} (p, q)\), \({\mathscr {N}}^{(3)}_{B} (p, q)\) and \({\mathscr {N}}^{(3)}_{A} (p, q)\). Indeed if one takes into account the multiplicative gluon propagator contribution to the kernels, those who are divergent become well behaved. This can be seen on Figs. 9 and 10 where the kernels, now including the multiplicative gluon propagator term, are reported. The new versions of \({\mathscr {N}}^{(1)}_{B} (p, q)\), \({\mathscr {N}}^{(3)}_{B} (p, q)\) and \({\mathscr {N}}^{(3)}_{A} (p, q)\) mimic the pattern observed for \({\mathscr {N}}^{(0)}_{B}\), \({\mathscr {N}}^{(0)}_{A}\) and \({\mathscr {N}}^{(1)}_{A} (p, q)\) and, once more, their main contribution to the integral equations happens for \(p \lesssim 2\) GeV and \(q \lesssim 2\) GeV. The inclusion of the gluon propagator in the kernels makes the integration over q finite.
The Dyson–Schwinger equations are solved using a hard cutoff that is set to \(\varLambda = 20\) GeV. All quantities are renormalised in the MOM scheme, using the same renormalisation scale as in [28], i.e \(\mu = 4.3\) GeV, so that one can compare easily the results of the two works. The renormalized quantites satisfy the identities
The bare quark mass quoted in the lattice simulation for the ensemble used here reads \(m^{bm} = 8\) MeV [27]. In the following we set \(Z_1 = 1\), take the value for \(Z_2\) from the vector component of the gap equation at the cutoff and ”measure“ the bare quark mass using the scalar component of the gap equation at the cutoff momenta. In this way \(m^{b.m.}\) does not coincide with the value quoted in the simulation but, as can be seen below, its value is close to the 8 MeV quoted above.
The results shown on Sects. 6.1, 6.2, 6.3 and 6.4 were computed using the same value for \(\alpha _s( \mu ) = 0.295\) as in [28]. In Sect. 6.5 we allow \(\alpha _s( \mu )\) to deviate from this value and provide a “best value”. From Sect. 6.5 onwards, the results reported use the optimal value for the strong coupling constant.
One-loop dressed perturbation theory
6.1 One-loop dressed perturbation theory for \(X_0(q^2)\)
The four longitudinal quark-gluon form factors were parametrised in terms of the three quark-ghost kernel form factors \(X_0\), \(Y_1\) and \(Y_3\). However, the quark gap equation provides only two independent equations and, therefore, it is not possible to compute all the form factors at once for the full range of momenta.
A first look at the quark-ghost kernel form factors is possible if one computes \(X_0\) within one-loop dressed perturbation theory with a simplified version of a quark-ghost kernel where one sets \(Y_1 = Y_3 = 0\) and, then, solve the gap equation to estimate \(Y_1\) and \(Y_3\). The way the solutions of the Dyson–Schwinger equations for \(Y_1\) and \(Y_3\) are built also illustrates the numerical procedure used to solve the integral equations.
The one-loop dressed approximation to the quark-ghost kernel is represented on Fig. 11 that, in the simplified version of kernel, translates into the following integral equation
with \(H_1 (q^2)\) representing the ghost-gluon vertex. When solving this equation we consider two version of the ghost-gluon vertex, namely its tree level version where \(H_1(q^2) = 1\) and an enhanced dressed vertex as given in [48] where
for \(c = 1.26\), \(a = 0.80\) GeV, \(b = 1.3\) GeV and \(w = 0.65\) GeV. For a recent analysis of the quark-ghost vertex see [49]. Equation (70) was solved after introducing a cutoff \(\varLambda = 100\) GeV, after performing the angular integration using 1000 Gauss–Legendre points and considering 2000 Gauss–Legendre points for the integration over k. The introduction of a Gauss–Legendre quadrature reduces the integral Eq. (70) to a linear system of equations that was solved using the QR decomposition of the matrix appearing in the linear system.
The numerical solutions for \(X_0\) can be seen on Fig. 12 and are, essentially, those reported in [28]. According to one-loop dressed perturbation theory, the deviations of \(X_0 (q^2)\) from its tree level value are, at most, of the order of 15%. We have also looked at the iterative solutions for Eq. (70) but no convergence was observed, therefore, the solutions reported on Fig. 12 are those computed from a single iteration.
Simplified one-loop dressed perturbation theory estimation for \(X_0(q^2)\)
The estimation of \(X_0\) allows to solve the gap equation for \(Y_1\) and \(Y_3\). In order to solve the Dyson–Schwinger equations, after the angular integration, the scalar and vector components of the equations are rewritten in the form of the larger linear system
from now on we will adopt the short name version \(B = {\mathscr {N}} X\) to refer to this linear system of equations. Note that \(Y_1\) has mass dimensions, while \(X_0\) and \(Y_3\) are dimensionless. Note that the kernels in \({\mathscr {N}}\) also have different dimensions and it is only after multiplication that we recover the proper dimensionful equation.
A direct solution of \(B = {\mathscr {N}} X\) results in a meaningless result, with the components of X oscillating over very large values due to the presence of very small eigenvalues of the matrix \({\mathscr {N}}\), that translates the ill defined problem in hands. The linear system can be solved using the Tikhonov regularisation [50] that replaces the original linear system by a minimisation of the functional \(|| B - {\mathscr {N}} X ||^2 + \epsilon ||X||^2\), where \(\epsilon \) is a small parameter to be determined in the inversion. This functional favours solutions that solve approximately the linear system but whose norm is small. For real symmetric matrices, Tikhonov regularisation replaces the original system by its normal form \( {\mathscr {N}}^T B = ( {\mathscr {N}}^T {\mathscr {N}} + \epsilon )X\). Although in our case \({\mathscr {N}}\) is not a symmetric matrix, we will solve the system as given in its normal form.
The determination of the optimal \(\epsilon \) is done by solving \( {\mathscr {N}}^T B = ( {\mathscr {N}}^T {\mathscr {N}} + \epsilon )X\) for various values of \(\epsilon \) and look at how \(|| B - {\mathscr {N}} X ||^2\) and \(||X||^2\) behave as a function of the regularisation parameter \(\epsilon \). The outcome of the inversions for different \(\epsilon \) can be seen on Fig. 13. For smaller values of \(\epsilon \), i.e. when one is closer to the original ill defined problem, the corresponding solution of the linear system results on \(Y_1\) and \(Y_3\) with larger norms. The larger values of the regularisation parameter \(\epsilon \) are associated to solutions of the modified linear system with smaller \(Y_1\) and \(Y_3\) norms. The optimal value of \(\epsilon \) is given by the solution whose residuum, i.e. the difference between the lhs and the rhs of the original equations, is among the smallest values just before the norms of \(Y_1\) and \(Y_3\) start to grow but without changing the residuum. On the above figure we point out three solutions in the region where \(\epsilon \) takes approximately its optimum value.
Our first comment on Fig. 13 being that both the scalar and vector components of the Dyson–Schwinger equations can be resolved with the ansatz considered, i.e. setting \(X_0(p^2)\) to its one-loop dressed perturbative result and getting \(Y_1(p^2)\) and \(Y_3(p^2)\) from solving the modified gap equations, provided we let the norm of \(Y_1\) and \(Y_3\) to be large enough. Of course, for large norms \(Y_1\) and \(Y_3\) are free to vary over a large range of values and the solutions with smaller norms are preferred.
Residuum versus norm for the scalar and vector equation when solving the gap equation for \(X_1\) and \(X_3\) with \(X_0\) as given by one-loop dressed perturbation theory. The left plot refers to the inversion using \(H_1(q^2) = 1\), while the right plot are the results for the inversion using the improved gluon-ghost vertex. Smaller values of the regularising parameter \(\epsilon \) are associated to solutions with larger norms, while larger values of \(\epsilon \) produce \(Y_1\) and \(Y_3\) with smaller norms. Recall that \(Y_1\) has mass dimensions, while \(Y_3\) is dimensionless
From Fig. 13 three typical solutions close to the optimal solution, as defined previously, are identified. For the \(X_0\) perturbative solution using the tree level (TL) ghost-gluon vertex, the characteristics of these solutions are
for \(m^{b.m.} = 6.852\) MeV, \(Z_2 = 1.0016\), where \(\varDelta \text{ Sca } = B - Z_2 m^{b.m.} - K_B X\), \(||Y_2||\) is given in GeV, and \(\varDelta \text{ Vec } = A - Z_2 - K_A X\) with \(||Y_3||\) being dimensionless. For all these solutions \(||X_0 - 1||^2 = 0.24214\). On the other hand, the characteristics of the solutions computed with the enhanced (Enh) ghost-gluon vertex given by Eq. (71) are
have the same \(m^{b.m.}\) and \(Z_2\) as the previous ones and \(||X_0 - 1||^2 = 0.45283\). In both cases, the norms of \(X_0\), \(Y_1\) and \(Y_3\) are the norms of the corresponding part of the vector that appear in the linear system .
The quality of the solutions can be appreciated on Fig. 14 where we show both the l.h.s. of the scalar and vector components of the gap equation, together with the difference between the l.h.s. and the computed r.h.s. using the \(X_0\) from one-loop perturbation theory and \(Y_1\) and \(Y_3\) that solve the modified linear system. The relative error both for the scalar and vector components of the Dyson–Schwinger equations are shown on Fig. 15. On the figures we have defined
\(||\varDelta \text{ Sca }||^2\) and \(||\varDelta \text{ Vec }||^2\) should be understood as the sum of the squares of the components of the linear systems (73) and (74), respectively, over the Gauss–Legendre points. As Fig. 15 shows, the relative error on the DSE equations is below 10% for the scalar equation and below 8% for the vector equation. Surprisingly, despite the larger values of \(||\varDelta \text{ Vec }||^2\) relative to \(||\varDelta \text{ Sca }||^2\), the vector component of the gap equation is better resolved. This is also due to the fact that \(A(p^2)\) spans a narrower range of values relative to \(B(p^2)\). We have tried to rescale the linear system by \(1/A(p^2)\) for the vector equation and by \(1/B(p^2)\) for the scalar equation to try to improve the quality of the solutions, specially at large momentum. However, the numeric solutions of the rescaled linear systems produced \(Y_1\) and \(Y_3\) that don’t seem reasonable and, for example, result in a \(Y_1\) at the cutoff that is far away from zero. Further, for the rescaled systems the \(\varDelta \text{ Sca }\) and \(\varDelta \text{ Vec }\) are larger than the ones obtained without rescaling the linear system. For all these reasons we disregard the rescaled linear system solutions.
Scalar (top) and Vector (bottom) Dyson–Schwinger equations and the differences between its lhs and rhs when using the tree level ghost-gluon vertex (top) and the enhanced gluon-ghost vertex (bottom)
Relative error on the solution of the Scalar (top) and Vector (bottom) Dyson–Schwinger equation when using the tree level ghost-gluon vertex (top) and the enhanced gluon-ghost vertex (bottom)
The quark-ghost kernel form factors \(X_1\) and \(X_3\) computed for the tree level ghost-gluon vertex (top) and the enhanced gluon-ghost vertex (bottom)
The quark-ghost kernel form factors \(Y_1\) and \(Y_3\) computed for the various \(\epsilon \) associated to the solutions I (TL) – III (TL) and I (Enh) – III (Enh) can be seen on Fig 16. For \(Y_1\) the outcome of resolving the integral equations using either the tree level or the enhanced ghost-gluon vertex result on essentially the same function. Further, the various solutions provide essentially the same \(Y_1(p^2)\), with the exception of III (TL) and III (Enh) that return a suppressed form factor relative to the other solutions. For \(Y_3\) the situation is similar, with the form factor associated to the solutions I (TL) and I (Enh) being enhanced at momentum above 2 GeV. Looking at Fig. 15, one can observe that solutions II (TL) and II (Enh) are those with smaller relative errors over the full range of momentum considered. So, from now on we will take these solutions as our best solutions associated to the perturbative \(X_0\) form factor. Note that the scalar equation is solved with a relative error \(\lesssim \) 8% and the vector equation is solved with a relative error \(\lesssim \) 6%.
The quark-ghost kernel form factors \(X_0\), \(X_1\) and \(X_3\) were also computed in [23], see their Fig. 4, combining the quark gap equation with a one-loop dressed perturbation theory for the quark-ghost kernel. The comparison between the results of the two calculations is not straightforward. Indeed, if in our calculation \(X_0\) is assumed to be a function only of the gluon momentum, in [23] the authors take into account its full momentum dependence and evaluate how it changes with the quark momentum, the gluon momentum and the angle between these two momenta. There calculation results on a \(X_0\) that is always close to its tree level value \(X_0 = 1\) and whose values are in the range [1, 1.12]. A qualitative comparison with the here reported form factor, shows that, from the point of view of the dynamical range of values, our \(X_0\) computed using the enhanced ghost-gluon vertex is closer to that reported in [23]. In both cases \(X_0\) is always close to its tree level value and differs from unit by, at most, 10%.
The comparison between the remaining form factors is slightly more involved. Indeed, the \(X_1\), \(X_2\) and \(X_3\) referred in [23] compared with the expressions given in Eqs. (60) and (61) and not directly with the \(Y_1\) and \(Y_3\) reported in Fig. 16. Note that there are signs differences on the definition of the various quark-ghost kernel form factors between [23] and the current work. Due to the presence of the gluon propagator in (60) and (61) one expects some angular dependence of the quark-ghost kernel form factors. Further, due to the parameterisation used for the gluon propagator, the form factors are expected to be enhanced when, simultaneous, the quark and gluon momenta become smaller, i.e. in the infrared limit. This is precisely what is observed for the \(X_1\) and \(X_2\) reported in [23].
Our estimations for \(X_1\) and \(X_2\) for the solutions referred previously and for the particular kinematics \(p = 0\), sometimes called the soft quark limit, can be seen on Fig. 17. The first comment about these form factors is that they seem to be independent of the ghost-gluon vertex and, indeed, the form factors associated to the solution using a tree level ghost-gluon vertex, named (TL) in the figure, are essentially indistinguishable from those computed using the enhanced ghost-gluon vertex, named (Enh) in the figure. The quark-ghost kernels form factors \(X_1\) and \(X_3\) differ from there perturbative values at low momenta, i.e. for \(q \lesssim 1\) GeV for \(X_1\) and for \(q \lesssim 2\) GeV for \(X_3\). According to [23], these two form factors increase (in absolute value) for momenta below \(\sim 1\) GeV, a result that is in good qualitative agreement with our estimations. From their Fig. 4, it is not clear if \(X_3 \ne 0\) extends over a wider range of momenta, when compared to \(X_1\). Our calculation returns a \(X_3\) that differ from zero on larger range of momenta, when compared with \(X_1\). Furthermore, the \(X_1\) and \(X_3\) computed in [23] are monotonic increase functions (absolute values) when the zero momentum limit is approached. The form factors reported on Fig. 17 show a pattern of maxima, with \(X_1\) having a single maximum for \(q \sim 350\) MeV and \(X_3\) showing several maxima (in absolute value) at momenta \(q \sim 250\) MeV, \(\sim 600\) MeV and \(\sim 1\) GeV. Note that the zero crossing for \(X_3\) occur for momenta that are of the same order of magnitude of \(\varLambda _{QCD}\), the gluon mass (or twice \(\varLambda _{QCD}\)) and the usual considered as a non-perturbative mass scale (1 GeV). It is not obvious why the zero crossing of \(X_3\) occur for such mass scales and why the crossing is not seem for \(X_1\). If the form factors reported on Fig. 4 of [23] never cross the zero value, that is not the case of the form factors represented on Fig 17. \(X_1\) shows various zeros that, curiously, seem to disappear for the solution with the smaller norm. On the other hand, \(X_3\) cross zero for \(q \approx 363\) MeV and 835 MeV for solutions II and III. This is a major difference between the two sets of solutions under discussion. Another important difference being the dynamical range of values. Our \(X_1\) is within the range of values [0, 3.5] \(\hbox {GeV}^{-1}\), while the same form factor computed in [23] is within [0, 0.2] \(\hbox {GeV}^{-1}\) which represents a factor of \(\sim 20\) smaller than our estimation. However, the two calculations report a \(|X_3|\) within the range [0, 0.5] \(\hbox {GeV}^{-2}\). Our result overestimates \(X_1\) relative to [23] but returns a \(|X_3|\) within the same dynamical range of values. Another major difference being that the maxima of the form factors does not occur at vanishing momenta as in [23] but at finite and small momenta, \(\sim \varLambda _{QCD}\) for \(X_1\) and \(\sim 2 \, \varLambda _{QCD}\) for the absolute maxima of \(|X_3|\).
The estimations of \(X_0\), \(X_1\) and \(X_3\) suggest that the quark-gluon vertex is dominated, at the infrared by those terms that are associated with \(X_1\). If this is the case, then, given the definitions (26)–(29) one expects that the dominant contributions to the quark-gluon vertex to be associated with the form factors
and since \(Z \sim 1\) and \(B \propto M(p^2)\), one expects the dominant form factor for the quark-gluon vertex to be associated with the tree level operator, i.e. with \(\lambda _1\).
6.2 Solving the Dyson–Schwinger equations
Let us now discuss the simultaneous computation of \(X_0\), \(X_1\) and \(X_3\) from the modified linear system of equations that replace the original Dyson–Schwinger integral equations. The procedure to build the linear system as well as the regularisation of the corresponding linear system of equations follow the steps described in the previous section. First the angular integration is performed using 800 Gauss–Legendre points. Then, for the momentum integration the cutoff \(\varLambda = 20\) GeV is introduced and we consider 200 Gauss–Legendre points to perform the integration over the loop momentum. Further, to determine the solutions of the Dyson–Schwinger equations, now already in the form of a linear system of equations, the scalar component and the vector component of the gap equation are grouped into a large linear system as follows
that again we refer, as a short name, by \(B = {\mathscr {N}} X\). The upper component of the large vector X contains the form factor \(X_0\) defined in all the set of Gauss–Legendre points used in the integration over the loop momenta. The remaining components of the large X vector are the form factors \(Y_1\) and \(Y_3\) defined at the lower first half set of Gauss–Legendre points used in the integration over the momentum. This means that the solution of the linear system (78) returns \(X_0(q^2)\) for \(q \in [ 0 , \, \varLambda ]\) and \(Y_1(q^2)\) and \(Y_3(q^2)\) for \(q \in [ 0 , \, \varLambda / 2]\). For \(Y_1\) and \(Y_3\) and for \(p > \varLambda /2\) the form factors will be assumed to vanish. In order to fulfil the boundary conditions for \(X_0 (q^2)\) we write \(X_0 (q^2) = 1 + \tilde{X}_0(q^2)\) and solve the linear system for \(\tilde{X}_0(q^2)\), rebuilding \(X_0 (q^2)\) at the end. The resulting linear system is then regularised using the Tikhonov regularisation and the corresponding \({\mathscr {N}}^T B = ( {\mathscr {N}}^T {\mathscr {N}} + \epsilon )X\) linear system is solved for various \(\epsilon \). The choice of the optimal regularisation parameter \(\epsilon \) follows the criteria discussed in Sect. 6.1. We have checked that by interchanging the roles of \(X_0\), \(Y_1\) and \(Y_3\) when building the large linear system the solutions are unchanged; more on that below. The differences only occur for those functions calculated only for \(q \in [ 0 , \, \varLambda / 2]\), compared to the version of the linear system were they are computed in the range \(q \in [ 0 , \, \varLambda ]\). In the first case, i.e. for the solutions computed only for \(q \in [ 0 , \, \varLambda / 2]\), there appears a discontinuity at \(q = \varLambda /2\) (recall that the form factors are set to zero for momenta above \(\varLambda /2\)) but for smaller q the form factors of all versions of the linear system are indistinguishable.
Residuum versus norm for the scalar and vector equation when solving the gap equation for \(X_0\), \(Y_1\) and \(Y_3\). The smaller values of the regularising parameter \(\epsilon \) are associated to solutions with larger norms, while larger values of \(\epsilon \) produce form factors with smaller norms. Recall that \(Y_1\) has mass dimensions, while \(X_0\) and \(Y_3\) are dimensionless
On Fig. 18 the residuum squared of the scalar (top) and vector (bottom) components of the gap equation are shown against the norm of various form factors. Smaller values of \(\epsilon \) are associated to solutions with larger norms and appear at the right side of the plots, while larger values of \(\epsilon \) are associated to solutions with smaller norms that show up on the left side of the plots. As shown on the figure, the residuum for both equations has a stronger dependence on \(\epsilon \) and can take quite small values. For the solutions featured in the plot, the smallest residuum squared reaches values of the order of \(10^{-5}\) for the scalar equation and \(10^{-4}\) for its vector component. Similar values for the minimum residuum were also observed for the solutions computed using the perturbative estimation of \(X_0\).
On Fig. 18 we identify four solutions associated to an \(\epsilon \) around its optimal value and whose characteristics are
for \(m^{b.m.} = 6.852\) MeV, \(Z_2 = 1.0016\), where \(\varDelta \text{ Sca }\) and \(||Y_1||\) are given in GeV, while \(\varDelta \text{ Vec }\), \(||X_0||\) and \(||Y_3||\) are dimensionless.
The lhs of the Dyson–Schwinger equations, scalar component on top and vector component at bottom, together with \(\varDelta \text{ Sca }\) and \(\varDelta \text{ Vec }\) (top). The plots on the left are the relative error for the scalar equation (top) and vector equation (bottom)
The relative errors for the solutions I–IV of the regularised linear system are show on Fig. 19. In general the solution for the vector component of the equation is satisfactory, with the scalar component of the equation being more demanding and not all of the solutions I–IV resolve the scalar part of the gap equation with a relative error below 10%. Only solutions III and IV resolve the DSE equations with a relative error below 8%. In particular for these solutions the value of \(||X_0 - 1||\) is of the order of \(10^{-2}\) suggesting that the non-perturbative solution prefers having a \(X_0 \simeq 1\) and, in this sense and for this form factor, are close to the result from perturbation theory discussed in Sect. 6.1. The observed growth of the relative error for \(p \gtrsim 10\) GeV is probably related also to the missing components of \(Y_1\) and \(Y_3\) which are set to zero for this range of momenta.
The form factors \(X_0\), \(Y_1\) and \(Y_3\) associated to the solutions I–IV can be seen on Figs. 20, 21 and 22. On Fig. 20 besides solutions I –IV we also show the perturbative \(X_0(q^2)\) computed using one-loop dressed perturbation theory with the tree level ghost-gluon vertex and its enhanced version. The perturbative solutions and those obtained solving the Dyson–Schwinger equations have rather different structures, with perturbation theory providing larger \(X_0(p^2)\) and predicting a relatively large tail. Indeed, the solutions of the regularised linear system recover their tree level value \(X_0 (p^2) = 1\) from \(p \gtrsim 10\) GeV onwards, while the perturbative solution only reproduces its tree level value at much larger momentum. The momentum scale associated to the absolute maxima of \(X_0(p^2)\) occurs at essentially the same \(p \approx 400\) MeV, while the perturbative results points to a maximum of \(X_0(p^2)\) at momenta slightly above the GeV scale. Qualitatively, the non-perturbative solutions all have the same pattern for this form factor. The exception being Sol. I which clearly overestimates \(|X_0|\) for \(p \gtrsim 1\) GeV. The solutions III and IV resolve the gap equation with the smaller relative errors that is below 8% – see Fig. 19. The non-perturbative solution of the DSE gives a \(X_0(p^2)\) that differs from its tree level value by less than 5%, that are above unit for momenta \(p \lesssim 1\) Gev. At this momenta scale the form factors take values below one, reaching a minimum for p just above 1 GeV, and approaching its tree level value at high momentum from below. The differences between the non-perturbative \(X_0\) and its tree level value for \(p \gtrsim 10\) GeV are rather small.
\(X_0(p^2)\) from inverting the Dyson–Schwinger equations together with its estimation using one-loop dressed perturbation theory by solving exactly Eq. (70)
\(Y_1(p^2)\) from inverting the Dyson–Schwinger equations
Our non-perturbative estimations for \(Y_1(p^2)\) can be viewed on Fig. 21. All the solutions I–IV reproduce the same pattern for this form factor, with a positive maxima around \(p \simeq 400\) MeV and with \(Y_1\) becoming small for \(p \gtrsim 1.5\) GeV. In particular, for the solutions III and IV, \(Y_1(p^2)\) is particularly small (\(\lesssim 0.4\) GeV) for \(p \gtrsim 1.5\) GeV. One should not forget that the quark-ghost form factor appearing in the quark-ghost kernel is not \(Y_1\) but this function times the gluon propagator – see Eq. (60). The same applies to \(Y_3\) as can be seen on Eq. (61). Once more, as the norm of \(Y_1\) decreases, the form factors seems to prefer to take only positive values.
\(X^{(3)}(p^2)\) from inverting the Dyson–Schwinger equations
The form factor \(Y_3(p^2)\) is reported on Fig. 22. It turns out that this function is positive for \(p \lesssim 400\) MeV and for \(p \gtrsim 1\) GeV, takes negative values in between, with a maximum at \(p \simeq 1.5\) GeV, and then slowly approaches its tree level value from above. Given the way the solutions are computed, on Fig. 22 \(Y_3(p^2)\) shows a jump at \(p \simeq 10\) GeV that corresponds to \(p = \varLambda /2\). A similar behaviour can be seen on Fig. 21 for \(Y_1(p^2)\). However, given that for \(p \simeq 10\) GeV one has a \(Y_1(p^2) \simeq 0\), this sudden jump is not so easily observed.
\(X^{(0)}(p^2)\), \(Y_1(p^2)\) and \(Y_3(p^2)\) computed from inverting the Dyson–Schwinger equations (Sol. III) after build the large linear system (78) in all possible ways, i.e. by permuting the role of the form factors in X. See text for details
Finally, on Fig. 23 we provide the various solutions for \(X_0(p^2)\), \(Y_1(p^2)\) and \(Y_3(p^2)\) after permuting the role of the form factors when writing the extended vector X. For the so-called \(X_0 \, X_1 \, X_3\) the extended vector included \(X_0\) over the full set of Gauss–Legendre points with \(Y_1\) and \(Y_3\) being obtained only in the range \(p \in [ 0 \, , \, \varLambda /2]\). For the so-called \(X_1 \, X_0 \, X_3\) the extended vector included \(Y_1\) over the full set of Gauss–Legendre points with \(X_0\) and \(Y_3\) being obtained only in the range \(p \in [ 0 \, , \, \varLambda /2]\). For the so-called \(X_3 \, X_0 \, X_1\) the extended vector included \(Y_3\) over the full set of Gauss–Legendre points with \(X_0\) and \(Y_1\) being obtained only in the range \(p \in [ 0 \, , \, \varLambda /2]\). We call the readers attention to the stability of the solution of the various linear systems. Furthermore, the comparison of Fig. 16 from Sect. 6.1 and Fig. 23 show quite similar \(Y_1\) and \(Y_3\) suggesting, once again, that \(X_0\) almost does not deviates from its tree level value.
Residua versus norm of the form factors from inverting the Dyson–Schwinger equations with \(X_0 = 1\)
6.3 Solving the DSE for \(X_0 = 1\)
The non-perturbative solutions of the Dyson–Schwinger equations discussed on the previous paragraph suggest that \(X_0(p^2) \simeq 1\). Therefore, herein we investigate the results by solving the DSE with \(X_0(p^2) = 1\). The residua of the scalar and vector equations against the norm of the two remaining form factor \(Y_1\) and \(Y_3\) can be seen on Fig. 24. The characteristics of the solutions highlighted in the figure and associated to an \(\epsilon \) close to its optimal value are
for \(m^{b.m.} = 6.852\) MeV, \(Z_2 = 1.0016\), where \(\varDelta \text{ Sca }\) and \(||Y_1||\) are given in GeV, while \(\varDelta \text{ Vec }\), \(||X_0||\) and \(||Y_3||\) are dimensionless. The relative error on the Dyson–Schwinger equations for these solutions can be seen on Fig. 25 which shows that solution I resolves the DSE up to \(p \simeq 10\) GeV with an error that is smaller than 3% for the scalar equation and error of about 1% for the vector equation. However, the form factor \(Y_3\) associated to solution I does not seem to be converged for momenta above 2 GeV. The solution named IV solves the scalar equation with a relative error below 10% and the vector equation with a relative error below 6%.
Relative error for the DSE associated to the highlighted solutions of the Dyson–Schwinger equations for \(X_0 = 1\)
The solutions of the DSE for \(Y_1\) and \(Y_3\) when \(X_0 = 1\)
The form factors \(Y_1(p^2)\) and \(Y_3(p^2)\) associated to the solutions I–IV are reported on Fig. 26 and reproduce the same patterns as the solutions computed in the previous sections.
6.4 Full form factors and comparison of solutions
In Sects. 6.1, 6.2 and 6.3 we have solved the Dyson–Schwinger equations assuming that the quark-ghost kernel form factors are given by Eqs. (59)–(61). So, besides, \(X_0\), the full form factors appearing in H and \(\overline{H}\), see Eq. (15), should be multiplied by the gluon propagator at the proper kinematical configuration. Herein, we aim to compare the various solutions found in previous section and, in this way, provide an estimation of the systematics associated to our ansatz, and also to provide the form of the full functions appearing on H and \(\overline{H}\). Looking at the relative errors on the Dyson–Schwinger equations and at the convergence of the form factors at higher momenta, the comparison will be done using Sol. II computed using the perturbative \(X_0\) and the tree level ghost-gluon vertex, Sol. III computed when the gap equation is solved for the full set of form factors and Sol. IV when the gap equation is solved for \(X_0 = 1\).
The quark-ghost kernel form factor \(X_0(p^2)\)
Let us start with the \(X_0\) that we have assumed to be only a function of the gluon momenta. The perturbative solutions are compared with the solution obtained inverting the Dyson–Schwinger equations for the full set of form factors used in our ansatz can be seen in Fig. 27. This figure repeats partially Fig. 20 providing a clear view of the solutions. All solutions show a \(X_0\) that essentially is close to its tree level value, i.e. \(X_0 = 1\), with the perturbative solutions having the largest deviation from unit.
The quark-ghost kernel form factor \(Y_1(p^2)\)
The form factor \(Y_1(p^2)\) can be seen on Fig. 28 for all the solutions. Note that all solutions reproduce essentially the same function of the gluon momentum, with \(Y_1(p^2)\) being small for \(p\gtrsim 1.5\) GeV and showing a sharp peak at \(p \simeq 400\) MeV. \(Y_1(p^2)\) is positive defined except for a small range of momenta \(p \in [ 0.75 \, , \, 1.4]\) GeV where it takes small negative values.
The form factor \(Y_3(p^2)\) can be seen on Fig. 29 for all the solutions. Surprisingly, \(Y_3(p^2)\) seems to have a relative large tail that appears in all the solutions. Up to momenta \(p \simeq 3\) GeV the solutions reproduce essentially the same function. However for \(p \simeq 3\) GeV the solution associated to \(X_0 = 1\) is enhanced relative to all the others, with the solutions associated to the one-loop perturbative \(X_0\) being slightly enhanced relative to the non-perturbative solution obtained from inverting the gap equation. \(Y_3(p^2)\) shows a maxima at \(p \simeq 200\) MeV, an absolute maxima at \(p \simeq 1.4\) GeV and an absolute minima at \(p \simeq 650\) MeV. This form factor is positive defined at infrared momenta \(p \lesssim 350\) MeV and the high momenta \(p \gtrsim 900\) MeV taking negative values in \(p \in [ 0.35 \, , \, 0.9]\) GeV.
In summary, Figs. 26, 27, 28 and 29 resume the computations of the quark-ghost kernel form factors performed so far.
6.5 Tunning \(\alpha _s\)
The quark-ghost kernel form factor \(Y_3(p^2)\)
The results for the relative errors on the scalar and vector components of the Dyson–Schwinger equation seen on Figs. 15, 19, 25 show a relative error that for \(p \gtrsim 10\) GeV grow with p and take its maximum value \(\sim 10\)% at the cutoff. This can be viewed in many ways and one of them being that our choice for the strong coupling constant is not the best one. In our approach we mix quenched lattice results with dynamical simulations and, in order to be able to solve the gap equation for the quark-ghost kernel, the renormalization constant \(Z_1\), see Eq. (5), is set to identity.Footnote 1 Although the original integral equation is linear on the form factors \(X_0\), \(Y_1\) and \(Y_3\), the regularized system that is solved introduces an extra parameter that needs to be fixed in the way described above and, therefore, changing the strong coupling constant changes the balance between the regularizating parameter \(\epsilon \) and the various form factors, allowing for adjustments on the solutions. Therefore, the relative errors on the integral equations can be adjusted by changing the strong coupling constant.
In this section, we report on the results of solving the regularised linear system of equations that replace the original equations in the way it is described on Sect. 6.2 for \(\alpha _s(\mu ) = 0.20\), 0.22 and 0.25. The properties of the inversions of the regularised system for the various values of the strong coupling constant can be found in Figs. 30, 31 and 32 and should be compared with Fig. 25 of the Sect. 6.2.
Norm versus Residuum (top) and relative error of the solutions of the gap equation for \(\alpha _s(\mu ) = 0.20\). The solutions on the right plot are those marked on the left plot with I being that associated to the most right mark
Norm versus Residuum (top) and relative error of the solutions of the gap equation for \(\alpha _s(\mu ) = 0.22\). The solutions on the right plot are those marked on the left plot with I being that associated to the most right mark
Norm versus Residuum (top) and relative error of the solutions of the gap equation for \(\alpha _s(\mu ) = 0.25\). The solutions on the right plot are those marked on the left plot with I being that associated to the most right mark
As the figures shows, lowering the value of \(\alpha _s( \mu )\) solves the problem of the increase of the relative error observed in Sect. 6.2. Moreover, of the various solutions considered, for \(\alpha _s(\mu ) = 0.22\) one can observe solutions whose relative error is of the order of \(\sim 1\)% for the scalar equation and \(\sim 3\)–4% for the vector components, the solutions named Sol. I and II in Fig. 31. The relative error associated to the remaining solutions given on Figs. 25, 30, 31 and 32 are larger and, therefore, we take \(\alpha _s(\mu ) = 0.22\) as the optimal value for the strong coupling constant within our approach. The corresponding quark-ghost kernel can be seen on Figs. 33, 34 and 35, together with the corresponding solution computed using \(\alpha _s(\mu ) = 0.295\). The solutions for the two values of \(\alpha _s\) are similar, although those associated to the smaller value of \(\alpha _s\) achieve higher values. If at momenta \(p \gtrsim 1\) GeV Sol. I takes absolute values that are higher than those of Sol. II, at lower momenta the difference between the two solutions is marginal.
The quark-ghost kernel form factor \(X_0(p^2)\) computed using \(\alpha _s(\mu ) = 0.22\)
The quark-ghost kernel form factor \(X_1(p^2)\) computed using \(\alpha _s(\mu ) = 0.22\)
The quark-ghost kernel form factor \(X_3(p^2)\) computed using \(\alpha _s(\mu ) = 0.22\)
7 The Quark-Gluon vertex form factors
In the previous section we have computed the quark-ghost kernel form factors \(X_0(q^2)\), \(Y_1(q^2)\), \(Y_3(q^2)\) that, together with the quark, gluon and ghost propagators, define the full form factors as given in Eqs. (59), (60) and (61). Once the full quark-ghost kernel form factors are known, then the longitudinal quark-gluon form factors can be computed using Eqs. (26)–(29), after performing the rotation to the Euclidean space and identifying the \(g_i(p^2_1, p^2_2)\) functions to
For completeness, we write the full expressions for the longitudinal form factors in Euclidean space
Note that by taking into account structures of the quark-ghost kernel other than \(X_0\) the quark-gluon vertex deviates considerably from a Ball-Chiu type and it is now a function both of p, q and of the angle between the quark and gluon momenta. The angular dependence appears associated to the scalar products (pq) and also on the argument of the gluon propagator \(D\left( (p^2 + k^2)/2 \right) \).
Longitudinal quark-gluon form factor for \(\theta = 0\)
For the calculation of \(\lambda _1\)–\(\lambda _4\) we will use Sol. II computed using \(\alpha _s( \mu ) = 0.22\); see Sect. 6.5 for details. We recall the reader that the calculation performed here considers only the longitudinal form factors and that the ansatz for the vertex takes into account the dependence between the angle of the incoming quark momentum and the incoming gluon momentum.
Longitudinal quark-gluon form factor for \(\theta = 2 \pi / 3\)
The overall picture of the various form factors when the angle between the incoming quark momentum p and the incoming gluon momentum q is \(\theta = 0\) can be seen on Fig. 36. On Fig. 37 the \(\lambda _1\) to \(\lambda _4\) are given for a \(\theta = 2 \pi /3\). The form factors \(\lambda _1\) to \(\lambda _4\) are finite for all p and q and approach asymptotically their perturbative values. Further, for our definition of the operators \(L^{(1)}_\mu \) – \(L^{(4)}_\mu \), see Eq. (11) for their definition in Minkowski space, the corresponding form factors are essentially positive defined. The exception being \(\lambda _4\) that takes both positive and negative values and whose maximum absolute value is negative and appears for small p and q. The relative magnitude of the \(\lambda _i\) suggest that the quark-gluon vertex is essentially saturated by \(\lambda _1\) and \(\lambda _3\), with \(\lambda _2\) and \(\lambda _4\) playing a minor role, i.e. the tensor structures of the longitudinal part of the vertex seem to be sub-leading; see also the discussion for the soft quark limit, defined by a vanishing quark momentum, and the symmetric limit below.
Our result differs significantly from the perturbative estimation of the form factors [5], where all the strength appears associated to \(\lambda _1\). For example, for the kinematical configuration defined by \(p^2 = (p-q)^2\) at vanishing p they have \(\lambda _1 \approx 1.1\) and \(\lambda _2 \approx 0.12\) \(\hbox {GeV}^{-2}\) and \(\lambda _3 \approx 0.18\) \(\hbox {GeV}^{-1}\) for a current mass \(m_q = 115\) MeV, a renormalisation scale \(\mu = 2\) GeV and for \(\alpha _s = 0.118\). Of course, one should look to the relative values of the various \(\lambda \)’s and not to their absolute values. For the comparison of the contributions from the various form factors one can use the non-perturbative momentum scale of 1 GeV to build dimensionless quantities. Then, as seen on Figs. 36 and 37 the scales for \(\lambda _1\) and \(\lambda _3\) are similar, while the maximum of \(\lambda _2\) is about 10% relative to the maxima of \(\lambda _1\) and \(\lambda _3\) and the maximum for \(\lambda _4\) is about half of that for \(\lambda _2\).
The comparison of our results with those reported in [17, 22, 23] is difficult to perform but in these works \(\lambda _1\) clearly dominates. On [17] \(\lambda _2\) reaches at most 16% of the maximum value of \(\lambda _1\), while \(\lambda _3\) seems to have the possibility of taking large values. On [22, 23], \(\lambda _2\) and \(\lambda _3\) take, at most, a numerical value that is about 23% of the maxima of \(\lambda _1\), with \(\lambda _4\) being essentially negligible. Our solution shows a vertex dominated by \(\lambda _1\) and \(\lambda _3\) with these form factors reaching numerical values of the same order of magnitude – see also Fig. 42.
As seen on Figs. 36 and 37 the quark-gluon form factors are significantly enhanced for low values of p and q. The momentum region where one observes the enhancement of the \(\lambda _1\) to \(\lambda _4\) happens for \(p \lesssim 1 \) GeV and \(q \lesssim 1\) GeV, with its maximum values showing up for \(p \approx q \approx \varLambda _{QCD}\) – see, also, the discussion below on the angular dependence.
The infrared enhancement of \(\lambda _1\) to \(\lambda _4\) with the gluon momentum is a direct consequence of using the Slavnov–Taylor identity (13) to rewrite the form factor. Indeed, as can be seen on Eqs. (80)–(83), all the form factors have, as a global factor, the ghost dressing function \(F(q^2)\). The ghost dressing function is enhanced, roughly by a factor of three, in the infrared, see Fig. 4, implying the increase of the \(\lambda _i\) as \(q = 0\) is approached.
The infrared enhanced of the form factors with the quark incoming momentum is more subtle. It is linked to our ansatz that relies on the analysis of the soft gluon limit of the Landau gauge lattice data for \(\lambda _1\) performed in [29]. Indeed, this work identified a dependence of \(\lambda _1\) on the gluon propagator that was incorporated in the ansatz, making the quark-ghost kernel form factors \(X_1\) and \(X_3\) proportional to \(D ( (p^2 + (p-q)^2 / 2)\). This term is crucial to have well behaved kernels in the integral equations, i.e. to ensure that the Dyson–Schwinger equations are finite, and it introduces an additional dependence on the angle between the quark and the gluon momenta. The gluon propagator is a decreasing function of its argument and, therefore, for a given q and angle between the quark and gluon momenta, the terms proportional to \(X_1\) and \(X_3\) increase as p decreases. This explains, in part, the observed enhanced of the quark-gluon form factors together with the increase of the ghost dressing function.
\(\lambda _1\) for \(p = 0.5\) GeV (top) and \(p = 1\) GeV (bottom) and various \(\theta \)
\(\lambda _2\) for \(p = 0.5\) GeV (top) and \(p = 1\) GeV (bottom) and various \(\theta \)
\(\lambda _3\) for \(p = 0.5\) GeV (top) and \(p = 1\) GeV (bottom) and various \(\theta \)
\(\lambda _4\) for \(p = 0.5\) GeV (top) and \(p = 1\) GeV (bottom) and various \(\theta \)
The dependence of the quark-gluon form factors in the angle between p and q can be seen on Figs. 38, 39, 40 and 41. These figures also provide a clear picture of the maxima of the various form factors as functions of the gluon momenta. For \(\lambda _1\) and \(\lambda _3\) the maxima are for \(q \approx 300\) MeV, while for \(\lambda _2\) the maximum is at \(q \approx 600\) MeV. \(\lambda _4\) seems to be a more complicated function of p, q and \(\theta \). Indeed, this later form factor shows various maxima of the same order of magnitude for different p, q and \(\theta \) values.
All the form factors appear to be monotonous decreasing functions of the angle between the incoming quark and incoming gluon momenta \(\theta \). If the pattern of the q dependence of \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\) seems to be independent of \(\theta \), \(\lambda _4\) seems to reverse is behaviour relative to the \(q-axis\) for \(\theta \gtrsim \pi /3\). Clearly, the maximum values for all the form factors occurs for \(\theta = 0\), i.e. the quark-gluon vertex favours the kinematical configurations with small values of p and q and also of the angle between the quark and gluon momentum.Footnote 2 It follows that the quark-gluon vertex favours small quark and gluon momenta and parallel four-vectors p and q.
From the point of view of the momentum dependence, our solution for the quark-gluon vertex is closer to that of the Maris-Tandy model [32] than those computed in [17, 22, 23], in the sense that we observe a rather strong enhancement at low momenta. Indeed, compared to these last references, the herein computed form factors are significantly larger. Recall that the Maris-Tandy model considers a single form factor, that would be (effective) equivalent to our \(\lambda _1\), and ignores the dependence of the vertex on the quark momentum. In particular, for this model we also checked that the region where our quark-gluon form factors are enhanced occurs essentially within the same range of momenta as the corresponding effective form factor of the Maris-Tandy model. Note also that the maxima of the form factors computed in the present work occur for momenta where the kernels appearing in the original equations take their maximum values – see Figs. 6, 9 and 10.
The form factors for the soft quark kinematical configuration (top) and for the completely symmetric kinematical configuration (bottom)
It is difficult to measure the relative importance of the contribution of the longitudinal form factors \(\lambda _1\) – \(\lambda _4\) to the quark-gluon vertex. However, an idea of their relative importance can be “measured” looking at particular kinematical configurations. Herein we consider the soft quark limit where the incoming quark momentum vanish and the totally symmetric limit where \(p^2 = q^2 = k^2\) and \(\theta = 2 \pi / 3\). The corresponding form factors multiplied by appropriated powers of momenta to build dimensionless function can be seen on Fig. 42 (computed using the \(\theta = 2 \pi /3\) data). If for the symmetric configuration the dominant form factor seems to be \(\lambda _1\), for the soft quark limit that role is played by \(p ~ \lambda _3\). Note that the maximum of the later is about 1.3 times larger than the maximum of the former. Curiously, the maxima of \(\lambda _1\) and \(p \lambda _3\) occur at exactly the same momentum scale \(p = 310\) MeV. As the figure shows it seems that the quark-gluon vertex is dominated by \(\lambda _1\) and \(\lambda _3\), as observed also when studying the solutions associated with the perturbative \(X_0\) as discussed at the end of Sect. 6.1, with the tensor structures associated to \(\lambda _2\) and \(\lambda _4\) playing a minor role.
The soft gluon limit prediction for \(\lambda _1\). See text for details
Finally, let us consider the soft gluon limit whose \(\lambda _1\) form factor has recently being computed using full QCD lattice simulations [27]. The data was investigated in [29] revealing an important contribution to \(\lambda _1\) linked with the gluon propagator. Our estimation of \(\lambda _1\) in the soft gluon limit can be seen on Fig. 43 – see the full curve in black. This curve was (arbitrarely) normalised to reproduce the lattice data at 1 GeV of the \(\beta = 5.29\) and \(M_\pi = 295\) MeV simulationFootnote 3 Clearly, our ansatz underestimates \(\lambda _1\) in the infrared region. As discussed in [29], in the soft gluon limit
where p is the quark incoming momenta, and in our notation
Our solutions has \(Y_1(0) \approx 0\) GeV and \(Y_3 (0) \approx 0\) and, therefore, it underestimates \(\lambda _1 (p^2)\) in the infrared region. Note that herein \(Y_1\) and \(Y_3\) are assumed to be a function only of the gluon momentum and, due to the integration over the gluon momenta q in the Dyson–Schwinger equations, these form factor are multiplied by \(q^3\) that, possibly, prevent the inversion to resolve correctly \(Y_1(q^2)\) and \(Y_3(q^2)\) in the deep infrared region. If in the calculation of the soft gluon limit one assumes that \(Y_1(0)\) deviates from zero by a small quantity, the agreement with the lattice data is considerably improved both in the infrared and in the ultraviolet. This is represented by the two full curves in colour of Fig. 43 where \(Y_1(0)\) is set to a small value. The colour curves suggest a \(Y_1(0) \sim 0.05\)–0.07 GeV. Further, the agreement in the ultraviolet region can also be improved if \(Y_3(0) \) assumes small and positive values; recall that \(Y_3(q^2)\) approaches zero from the above when \(q^2 \rightarrow 0\) as can be seen on Fig. 35.
8 Summary and conclusions
In this work we investigated the non-perturbative regime of the Landau gauge quark-gluon vertex (QGV), taking into account only its longitudinal components, and relying on lattice results for the quark, gluon and ghost propagators, together with continuum exact relations, namely a Slavnov–Taylor identity and the quark propagator Dyson–Schwinger equation. Furthermore, we incorporate the exact normalisation condition for the quark-ghost kernel form factor \(X_0\) derived in [17]. In addition, we take into account an empirical relation that links the gluon propagator and the soft gluon limit of the form factor \(\lambda _1\) checked against full QCD lattice simulations [29]. The full set of the quark-ghost kernel tensor structures are taken into account to build an ansatz for the longitudinal quark-gluon vertex that is a function of both the incoming quark p and gluon q momenta, and the angle between p and q.
The quark-ghost kernel requires four scalar form factors \(X_0\), \(X_1\), \(X_2\), \(X_3\) [38]. For the construction of the quark-ghost kernel a perfect symmetry between incoming and outgoing quark momentum is assumed, which simplified the description of the QGV in terms of \(X_0\), \(X_1 = X_2\) and \(X_3\). Charge conjugation demands that for the soft gluon limit, defined by \(q = 0\), \(\lambda _4 = 0\) and our construction implements such constraint. Noteworthy to mention that our ansatz goes beyond the Ball-Chiu type of vertex [6] and includes it as a particular case, when \(X_1 = X_3 = 0\) and \(X_0 = 1\).
The Dyson–Schwinger equations are solved for the quark-gluon vertex that are written in terms of the unknown functions \(X_0\), \(X_1\) and \(X_3\). From the point of view of the quark-ghost kernel form factors, these are linear integral equations. The corresponding mathematical problem is ill defined and needs to be regularised in order to obtain a meaningful solution. The original integral equations for the scalar and vector components of the quark gap equation are transformed into a set of linear system using Gauss–Legendre quadratures to perform the integrations and after doing the angular integration. In our approach we rely on the Tikhonov linear regularisation that is equivalent to minimize \(|| B - {\mathscr {N}} X ||^2 + \epsilon ||X||^2\). The solutions are found numerically after writing the regularised linear system in its normal form. The small parameter \(\epsilon \) is set by looking at the balance between the associated error on the Dyson–Schwinger equations, i.e. the difference between the l.h.s and the r.h.s. \(|| B - {\mathscr {N}} X ||^2\), and the norm of the corresponding quark-ghost form factors, i.e. \(||X||^2\), for each solution of the regularised linear system.
The resulting quark-gluon vertex form factors \(\lambda _1\)–\(\lambda _4\) show a strong enhancement in the infrared region and deviate significantly from their tree level results for quark and gluon momenta below \(\sim 2\) GeV. At high momentum the form factors approach their perturbative values. In what concerns the gluon momentum, the observed infrared enhancement for the QGV form factors can be traced back to the multiplicative contribution of the ghost dressing function introduced through the Slavnov–Taylor identity. Recall that the gluon dressing function peaks at \(q = 0\) and, therefore, favours that the incoming and outgoing quark momentum to be parallel. On the other hand, the infrared enhancement associated to the quark momentum is linked to the gluon dependence that was observed on the analysis of the soft gluon limit of the QGV and, clearly, favours small quark momentum \(p \sim 0\) and also p parallel to q; see Eqs. (60), (61) and (80)–(83) and, in particular, the argument appearing on the gluon propagator term. The maxima of the computed form factors are essentially at the maxima of \(X_0\), \(X_1\) and \(X_3\) and they appear for momenta \(p, \, q \sim \varLambda _{QCD}\), which again seems to set the appropriate non-perturbative momentum scale. Recall that the momentum scale comes from the use of lattice data for the propagators. Further, we find that the quark-gluon vertex is dominated by the form factors associated to the tree level vertex \(\gamma _\mu \) and to \(2 \, p_\mu + q_\mu \), with the higher rank tensor structures giving small contributions. Overall, our findings are in qualitative agreement with previous works both with phenomenological approaches, as in the case of the effective vertex introduced in [32], and those based on first principles ab initio continuum methods, see e.g. [23] and references therein.
The high momentum behaviour of the quark-gluon vertex form factors reproduces their perturbative values. However, the matching between the computed form factors and their perturbative tail is not yet implemented. In addition, we verified that for the soft gluon limit, \(\lambda _1\) is not able to reproduce quantitatively the lattice data from full QCD simulations, apart the qualitative momentum behaviour. This can be traced back to the poor resolution of the kernel in the deep infrared region, due to the \(q^3\) factor coming from the momentum integration. As we have verified, a small tuning of \(X_1\) and \(X_3\) at \(q = 0\) is enough to reproduce the soft gluon limit lattice data within the present framework. This two challenging problems, together with inclusion of the transverse part of the vertex, call for an improvement of the approach devised herein and are to be tackled in a future work. Despite of that, we expect that the present results can help understanding the non-perturbative dynamics of quarks and gluons in the infrared region and that can motivate further applications to the study of hadron phenomenology based on quantum field theoretical approaches as those using Bethe–Salpeter and/or Faddeev equations – see e.g. [51] and references therein.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Data on the form factors available on request to the authors.]
Notes
It can also be viewed as been included in the definition of the various form factors.
For example, for \(p = 0.5\) GeV \(\lambda _1\) and \(\lambda _3\) there is an enhancement of a factor of \(\sim 2.7\) and \(\sim 2.0\), respectively, between the maxima values for \(\theta = 0\) relative to \(\theta = \pi \). For \(\lambda _2\) and \(\lambda _4\) this enhancement is \(\sim 3.5\) and \(\sim 3.2\). The corresponding factors for an incoming quark momentum \(p = 1\) GeV are \(\sim 1.5\) for \(\lambda _1\), \(\sim 4.4\) for \(\lambda _2\), \(\sim 2.3\) for \(\lambda _3\) and a suppression by a factor of \(\sim 0.6\) for \(\lambda _4\). Also, for \(\lambda _1\) and \(\lambda _3\) the maxima at \(\theta = \pi /2\) is about half of the maxima at \(\theta = 0\).
The normalisation essentially removes the F(0) that can appear in the expression for \(\lambda _1\); see Eq. (80).
References
W.J. Marciano, H. Pagels, Phys. Rep. 36, 137 (1978). https://doi.org/10.1016/0370-1573(78)90208-9
R. Alkofer, L. von Smekal, Phys. Rep. 353, 281 (2001). https://doi.org/10.1016/S0370-1573(01)00010-2. arxiv:hep-ph/0007355
C.S. Fischer, J. Phys. G 32, R253 (2006). https://doi.org/10.1088/0954-3899/32/8/R02. arxiv:hep-ph/0605173
D. Binosi, J. Papavassiliou, Phys. Rept. 479, 1 (2009). https://doi.org/10.1016/j.physrep.2009.05.001. arxiv:0909.2536 [hep-ph]
R. Bermudez, L. Albino, L.X. Gutiérrez-Guerrero, M.E. Tejeda-Yeomans, A. Bashir, Phys. Rev. D 95(3), 034041 (2017). https://doi.org/10.1103/PhysRevD.95.034041. arxiv:1702.04437 [hep-ph]
J.S. Ball, T.W. Chiu, Phys. Rev. D 22, 2542 (1980). https://doi.org/10.1103/PhysRevD.22.2542
D.C. Curtis, M.R. Pennington, Phys. Rev. D 42, 4165 (1990). https://doi.org/10.1103/PhysRevD.42.4165
A. Bashir, R. Bermudez, L. Chang, C.D. Roberts, Phys. Rev. C 85, 045205 (2012). https://doi.org/10.1103/PhysRevC.85.045205. arxiv:1112.4847 [nucl-th]
S.X. Qin, L. Chang, Y.X. Liu, C.D. Roberts, S.M. Schmidt, Phys. Lett. B 722, 384 (2013). https://doi.org/10.1016/j.physletb.2013.04.034. arxiv:1302.3276 [nucl-th]
M .J. Aslam, A. Bashir, L .X. Gutierrez-Guerrero, Phys. Rev. D 93(7), 076001 (2016). https://doi.org/10.1103/PhysRevD.93.076001. arxiv:1505.02645 [hep-th]
D. Binosi, L. Chang, J. Papavassiliou, S .X. Qin, C .D. Roberts, Phys. Rev. D 95(3), 031501 (2017). https://doi.org/10.1103/PhysRevD.95.031501. arxiv:1609.02568 [nucl-th]
R. Alkofer, C.S. Fischer, F.J. Llanes-Estrada, K. Schwenzer, Annals Phys. 324, 106 (2009). https://doi.org/10.1016/j.aop.2008.07.001. arxiv:0804.3042 [hep-ph]
A.C. Aguilar, J. Papavassiliou, Phys. Rev. D 83, 014013 (2011)
A.C. Aguilar, D. Ibañez, V. Mathieu, J. Papavassiliou, Phys. Rev. D 85, 014018 (2012). https://doi.org/10.1103/PhysRevD.85.014018. arxiv:1110.2633 [hep-ph]
A. Windisch, M. Hopfer, R. Alkofer, Acta Phys. Polon. Supp. 6, 347 (2013). https://doi.org/10.5506/APhysPolBSupp.6.347. arxiv:1210.8428 [hep-ph]
M. Hopfer, R. Alkofer, Acta Phys. Polon. Supp. 6(3), 929 (2013). https://doi.org/10.5506/APhysPolBSupp.6.929. arxiv:1304.4360 [hep-ph]
A .C. Aguilar, D. Binosi, D. Ibañez, J. Papavassiliou, Phys. Rev. D 90(6), 065027 (2014). https://doi.org/10.1103/PhysRevD.90.065027. arxiv:1405.3506 [hep-ph]
M. Peláez, M. Tissier, N. Wschebor, Phys. Rev. D 92(4), 045012 (2015). https://doi.org/10.1103/PhysRevD.92.045012. arxiv:1504.05157 [hep-th]
D. Binosi, L. Chang, J. Papavassiliou, C.D. Roberts, Phys. Lett. B 742, 183 (2015). https://doi.org/10.1016/j.physletb.2015.01.031. arxiv:1412.4782 [nucl-th]
H. Sanchis-Alepuz, R. Williams, Phys. Lett. B 749, 592 (2015). https://doi.org/10.1016/j.physletb.2015.08.067. arxiv:1504.07776 [hep-ph]
R. Williams, C.S. Fischer, W. Heupel, Phys. Rev. D 93(3), 034026 (2016). https://doi.org/10.1103/PhysRevD.93.034026. arxiv:1512.00455 [hep-ph]
A.C. Aguilar, J.C. Cardona, M.N. Ferreira, J. Papavassiliou, Phys. Rev. D 96(1), 014029 (2017). https://doi.org/10.1103/PhysRevD.96.014029. arxiv:1610.06158 [hep-ph]
A.C. Aguilar, J.C. Cardona, M.N. Ferreira, J. Papavassiliou, Phys. Rev. D 98(1), 014002 (2018). https://doi.org/10.1103/PhysRevD.98.014002. arxiv:1804.04229 [hep-ph]
J. Skullerud, D.B. Leinweber, A.G. Williams, Phys. Rev. D 64, 074508 (2001). https://doi.org/10.1103/PhysRevD.64.074508. arxiv:hep-lat/0102013
J.I. Skullerud, P.O. Bowman, A. Kizilersu, D.B. Leinweber, A.G. Williams, JHEP 0304, 047 (2003). https://doi.org/10.1088/1126-6708/2003/04/047. arxiv:hep-ph/0303176
A. Kizilersu, D.B. Leinweber, J.I. Skullerud, A.G. Williams, Eur. Phys. J. C 50, 871 (2007). https://doi.org/10.1140/epjc/s10052-007-0250-6. arxiv:hep-lat/0610078
O. Oliveira, A. Kızılersu, P.J. Silva, J.-I. Skullerud, A. Sternbeck, A.G. Williams, Acta Phys. Polon. Supp. 9, 363 (2016). arxiv:1605.09632
E. Rojas, J.P.B.C. de Melo, B. El-Bennich, O. Oliveira, T. Frederico, JHEP 1310, 193 (2013). https://doi.org/10.1007/JHEP10(2013)193. arxiv:1306.3022 [hep-ph]
O. Oliveira, T. Frederico, W. de Paula, J.P.B.C. de Melo, Eur. Phys. J. C 78(7), 553 (2018). https://doi.org/10.1140/epjc/s10052-018-6037-0. arxiv:1807.00675 [hep-ph]
L. Chang, C.D. Roberts, Phys. Rev. C 85, 052201 (2012). https://doi.org/10.1103/PhysRevC.85.052201. arxiv:1104.4821 [nucl-th]
A. Bashir, M.R. Pennington, Phys. Rev. D 50, 7679 (1994). https://doi.org/10.1103/PhysRevD.50.7679
P. Maris, P.C. Tandy, Phys. Rev. C 60, 055214 (1999). https://doi.org/10.1103/PhysRevC.60.055214. arxiv:nucl-th/9905056
A. Bashir, L. Chang, I.C. Cloet, B. El-Bennich, Y.X. Liu, C.D. Roberts, P.C. Tandy, Commun. Theor. Phys. 58, 79 (2012). https://doi.org/10.1088/0253-6102/58/1/16. arxiv:1201.3366 [nucl-th]
F.F. Mojica, C.E. Vera, E. Rojas, B. El-Bennich, Phys. Rev. D 96(1), 014012 (2017). https://doi.org/10.1103/PhysRevD.96.014012. arxiv:1704.08593 [hep-ph]
F.E. Serna, C. Chen, B. El-Bennich, arxiv:1812.01096 [hep-ph]
S x Qin, L. Chang, Y x Liu, C .D. Roberts, D .J. Wilson, Phys. Rev. C 84, 042202 (2011). https://doi.org/10.1103/PhysRevC.84.042202. arxiv:1108.0603 [nucl-th]
A. Kizilersu, M. Reenders, M.R. Pennington, Phys. Rev. D 52, 1242 (1995). https://doi.org/10.1103/PhysRevD.52.1242. arxiv:hep-ph/9503238
A.I. Davydychev, A. Osland, L. Saks, Phys. Rev. D 63, 014022 (2000)
A.A. Slavnov, Theor. Math. Phys. 10, 99 (1972)
A.A. Slavnov, Teor. Mat. Fiz. 10, 153 (1972)
J.C. Taylor, Nucl. Phys. B 33, 436 (1971)
O. Oliveira, P.J. Silva, J.I. Skullerud, A. Sternbeck, arxiv:1809.02541 [hep-lat]
J.I. Skullerud, A.G. Williams, Phys. Rev. D 63, 054508 (2001). https://doi.org/10.1103/PhysRevD.63.054508. arxiv:hep-lat/0007028
D. Dudal, O. Oliveira, N. Vandersickel, Phys. Rev. D 81, 074505 (2010). arxiv:1002.2374
A. Ayala, A. Bashir, D. Binosi, M. Cristoforetti, J. Rodríguez-Quintero, Phys. Rev. D 86, 074512 (2012). arxiv:1208.0795
A.G. Duarte, O. Oliveira, P.J. Silva, Phys. Rev. D 94, 014502 (2016). arxiv:1605.00594
D. Dudal, O. Oliveira, P.J. Silva, Annals Phys. 397, 351 (2018). https://doi.org/10.1016/j.aop.2018.08.019. arxiv:1803.02281 [hep-lat]
D. Dudal, O. Oliveira, J. Rodriguez-Quintero, Phys. Rev. D 86, 105005 (2012) https://doi.org/10.1103/PhysRevD.86.105005, https://doi.org/10.1103/PhysRevD.86.109902. arxiv:1207.5118 [hep-ph]
A.C. Aguilar, M.N. Ferreira, C.T. Figueiredo, J. Papavassiliou, arxiv:1811.08961 [hep-ph]
A.N. Tikhonov, A.V. Goncharsky, V.V. Stepanov, A.G. Yagola, Numerical Methods for the Solution of Ill Posed Problems (Kluwer Academic Publishers, Norwell, 1995)
G. Eichmann, H. Sanchis-Alepuz, R. Williams, R. Alkofer, C.S. Fischer, Prog. Part. Nucl. Phys. 91, 1 (2016). https://doi.org/10.1016/j.ppnp.2016.07.001. arxiv:1606.09602 [hep-ph]
Acknowledgements
This work was partly supported by the Fundação de Amparo à Pesquisa do Estado de São Paulo [FAPESP Grant No. 17/05660-0], Conselho Nacional de Desenvolvimento Científico e Tecnológico [CNPq Grant 308486/2015-3] and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) of Brazil. This work is a part of the project INCT-FNA Proc. No. 464898/2014-5. O. Oliveira acknowledge support from CAPES process 88887.156738/2017-00 and FAPESP Grant Number 2017/01142-4. JPCBM acknowledges CNPq, contracts 401322/2014-9 and 308025/2015-6. This work was part of the project FAPESP Temático, No. 2017/05660-0.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: 4D spherical coordinates and integration over momentum
Fits to the renormalized propagators at \(\mu = 4.3\) GeV: (top-left) pure Yang–Mills gluon propagator; (top-right) pure-Yang–Mills ghost dressing function; (bottom-left) quark wave function; (bottom-right) running quark mass
In 4D the spherical coordinates are related to the cartesian coordinates as follows
where
The 4D volume element reads
Setting the outgoing quark momenta \(p = (p, \, 0, \, 0 , \, 0 )\) it follows that
and the angular integration in the Dyson–Schwinger equations can be written as
where, in the last identity, we set \( x = \cos \phi _1\). It follows that momentum integration in the Dyson–Schwinger equations reads
where \(\varLambda \) stands for the cutoff introduced to regulate the theory.
Appendix B: comparing propagator fits with previous works
For completeness and in order to allow for a better comparison between the of the current work with those reported in [28], we provide the fits used in both works with the gluon propagator, the ghost propagator and the quark wave function curves renormalised at \(\mu = 4.3\) GeV within the MOM scheme. On Fig. 44 the curves referred to as JHEP are those of [28], while those designated as NEW are the curves mentioned in Sects. 5.1 and 5.2. As the figure shows, there are differences between the two sets of curves, not only at the infrared region but also on the running at high momentum.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Oliveira, O., de Paula, W., Frederico, T. et al. The quark-gluon vertex and the QCD infrared dynamics. Eur. Phys. J. C 79, 116 (2019). https://doi.org/10.1140/epjc/s10052-019-6617-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6617-7