Phenomenology of the inflation-inspired NMSSM at the electroweak scale

Abstract

The concept of Higgs inflation can be elegantly incorporated in the Next-to-Minimal Supersymmetric Standard Model (NMSSM). A linear combination of the two Higgs-doublet fields plays the role of the inflaton which is non-minimally coupled to gravity. This non-minimal coupling appears in the low-energy effective superpotential and changes the phenomenology at the electroweak scale. While the field content of the inflation-inspired model is the same as in the NMSSM, there is another contribution to the $\mu$ term in addition to the vacuum expectation value of the singlet. We explore this extended parameter space and point out scenarios with phenomenological differences compared to the pure NMSSM. A special focus is set on the electroweak vacuum stability and the parameter dependence of the Higgs and neutralino sectors. We highlight regions which yield a SM-like $125\,\hbox {GeV}$ Higgs boson compatible with the experimental observations and are in accordance with the limits from searches for additional Higgs bosons. Finally, we study the impact of the non-minimal coupling to gravity on the Higgs mixing and in turn on the decays of the Higgs bosons in this model.

1 Introduction

In the history of our universe, there has been a period in which the size of the universe exponentially increased. This short period is known as inflationary epoch, and many models have been developed in order to explain the inflation of the early universe. Unfortunately, most of these models of inflation cannot be tested directly in the laboratory; the observation of the universe is the only discriminator to disfavor or support such models. Therefore, testing the phenomenology of a particle physics model of inflation at the electroweak scale with colliders is of interest both from the point of view of particle physics and cosmology.

One possibility to describe inflation is the extension of a particle physics model by additional scalar fields which drive inflation but are removed from the theory afterwards. A more economical approach is the idea of using the Higgs field of the Standard Model (SM) as inflaton [1,2,3]. The simplest version, however, is under tension as it suffers from a fine-tuning and becomes unnatural [4]. A less minimal version of Higgs-portal inflation with an additional complex scalar field can in addition solve further problems of the SM, see Refs. [5, 6]. Also the concept of critical Higgs inflation can raise the range of perturbativity to the Planck scale and solve further problems of the SM, see Refs. [7,8,9]. Other solutions are offered by scale-free extensions of the SM. A natural way of such an implementation can be realized in canonical superconformal supergravity (CSS) models as proposed by Refs. [10, 11] based on earlier work by Ref. [12].

The Higgs inflation in the supergravity framework is triggered by a non-minimal coupling to Einstein gravity. For the supergravity Lagrangian this can be achieved with an additional term $X({\hat{\Phi }})\,R$ of chiral superfields ${\hat{\Phi }}$ and the curvature multiplet R (the supersymmetrized field version of the Ricci scalar which contains the scalar curvature in the Grassmannian coordinate $\theta ^2$), following the notation of Ref. [12]. The Lagrangian then reads

$$\begin{aligned} \mathcal {L}_X= & {} -6 \int {\text {d}}^2\theta \mathcal {E} \left[ R + X({\hat{\Phi }})\,R \right. \nonumber \\&\left. - \frac{1}{4} \left( {\bar{\mathcal {D}}}^2 - 8\,R \right) \hat{\Phi }^\dag \,{\hat{\Phi }} + \mathcal {W}({\hat{\Phi }}) \right] + \text {h.}\,\text {c.} + \ldots , \end{aligned}$$

(1)

where $X({\hat{\Phi }})$ as well as the Superpotential $\mathcal {W}({\hat{\Phi }})$ are holomorphic functions of the (left) chiral superfields ${\hat{\Phi }}$, $\mathcal {E}$ is the vierbein multiplet and $\bar{\mathcal {D}}$ a covariant derivative. The ellipses encode further gauge terms. The only possible choice of such a non-minimal coupling suitable for inflation is given by [12]

$$\begin{aligned} X = \chi \,\hat{H}_u \cdot \hat{H}_d, \end{aligned}$$

(2)

where $\chi$ is a dimensionless coupling and $\hat{H}_{d,u}$ contain the two $SU(2)_{\text {L}}$ Higgs doublets of the Next-to-Minimal Supersymmetric Standard Model (NMSSM).¹ The extension by an additional scalar singlet like in the NMSSM has been shown to be a viable model for inflation, although this version suffers from a tachyonic instability [13]. In order to avoid this instability, a stabilizer term has been introduced in Refs. [11, 13] that is suppressed at low energies. The stabilizer term can be avoided in a model with minimal supergravity couplings where the Kähler potential has a shift symmetry in the doublet fields [14]; however, cosmological phenomenology and observations have meanwhile ruled out this possibility [15].

The simplest implementation of a superconformal model which can accommodate the non-minimal coupling term $\chi \,\hat{H}_u \cdot \hat{H}_d$ is the well-known $\mathbb {Z}_3$-invariant NMSSM augmented by an additional $\mu$ term, which we call $\mu$-extended NMSSM ($\mu$NMSSM) in the following. We neglect all additional $\mathbb {Z}_3$-violating parameters in the superpotential at the tree level (see the discussion below). These terms are not relevant for the physics of inflation: the function X could potentially also contain an $\hat{S}^2$ term, since it has the same structure as $\hat{H}_u\cdot \hat{H}_d$ and is allowed by gauge symmetries. However, inflation driven by this term does not lead to the desired properties as pointed out in Ref. [12]. The other term, which is not present in the NMSSM, is a singlet tadpole proportional to $\hat{S}$ that is not quadratic or bilinear in the chiral superfields and thus would need a dimensionful coupling to supergravity instead of the dimensionless $\chi$.

In this work, we are going to study the low-energy electroweak phenomenology of the model outlined in Refs. [10, 11] and Ref. [13], where previously the focus was put on the description of inflation and the superconformal embedding of the NMSSM into supergravity. We have generated a model file for FeynArts [16, 17], where SARAH [18,19,20,21] has been used to generate the tree-level couplings of the $\mu$NMSSM, and we have implemented the one-loop counterterms. The loop calculations have been carried out with the help of FormCalc [22] and LoopTools [22]. In order to predict the Higgs-boson masses, we have performed a one-loop renormalization of the Higgs sector of the $\mu$NMSSM which is compatible with the renormalization schemes that have been employed in Refs. [23, 24] for the cases of the MSSMand NMSSM, respectively. This allowed us to add the leading MSSM-like two-loop corrections which are implemented in FeynHiggs [25,26,27,28,29,30,31,32] in order to achieve a state-of-the-art prediction for the Higgs masses and mixing. The parameter space is checked for compatibility with the experimental searches for additional Higgs bosons using HiggsBounds version 5.1.0beta [33,34,35,36,37] and with the experimental observation of the SM-like Higgs boson via HiggsSignals version 2.1.0beta [38]. In addition, we check the electroweak vacuum for its stability under quantum tunneling to a non-standard global minimum and for tachyonic Higgs states in the tree-level spectrum. Finally, we investigate some typical scenarios and study their collider phenomenology at the Large Hadron Collider (LHC) and a future electron-positron collider. For this purpose in some analyses we use SusHi [39, 40] for the calculation of neutral Higgs-boson production cross-sections. We emphasize the possibility of light ${\mathcal {CP}}$-even singlets in the spectrum with masses below $100\,\text {GeV}$ that could be of interest in view of slight excesses observed in the existing data of the Large Electron–Positron collider (LEP) [41] and the Compact Muon Solenoid (CMS) [42] which are compatible with bounds from A Toroidal LHC ApparatuS (ATLAS) [43]. For one scenario that differs substantially from the usual NMSSM, we exemplarily discuss the total decay widths and branching ratios of the three lightest Higgs bosons and their dependence on the additional parameters of the $\mu$NMSSM.

The paper is organized as follows: we start with a description of our model and the theoretical framework in Sect. 2 by discussing analytically the phenomenological differences of the Higgs potential in the $\mu$NMSSM compared to the $\mathbb {Z}_3$-invariant NMSSM. We study vacuum stability and the incorporation of higher-order corrections for the Higgs boson masses. Then, we derive the trilinear self-couplings of the Higgs bosons and comment on the remaining sectors of the model which are affected by the additional $\mu$ term. In Sect. 3, we focus on the parameter space of interest and investigate the Higgs-boson masses as well as the stability of the electroweak vacuum numerically and also show the neutralino spectrum. Furthermore, we study the effect of the additional $\mu$ parameter on Higgs-boson production and decays. Lastly, we conclude in Sect. 4. In the Appendix we present the beta functions for the superpotential and some soft-breaking parameters of the general NMSSM (GNMSSM) [44,45,46] including all $\mathbb {Z}_3$-breaking terms.

2 Theoretical framework

In this section we introduce the model under consideration, the $\mu$NMSSM, which differs by an additional $\mu$ term from the scale-invariant NMSSM. We derive the Higgs potential and investigate vacuum stability and the prediction for the Higgs-boson masses of the model. Furthermore, we discuss the trilinear self-couplings of the Higgs bosons and comment on the electroweakinos – i.e. charginos and neutralinos – as well as on the sfermion sector. We constrain our analytical investigations in this section mostly to tree-level relations. Higher-order contributions, e.g. for the Higgs-boson masses, are explained generically and are evaluated numerically in the subsequent phenomenological section.

2.1 Model description

For the Higgs sector of the NMSSM the superpotential is of the form²

$$\begin{aligned} \mathcal {W}_{\text {Higgs}}&= \lambda \,\hat{S}\,\hat{H}_u\cdot \hat{H}_d + \tfrac{1}{3}\,\kappa \,\hat{S}^3. \end{aligned}$$

(3)

where $\hat{H}_u$ and $\hat{H}_d$ are the well-known $SU(2)_{\text {L}}$ doublets of the MSSM, and $\hat{S}$ is the additional $SU(2)_{\text {L}}$ singlet. The $SU(2)_{\text {L}}$-invariant product $\hat{H}_u\cdot \hat{H}_d$ is defined through $\hat{H}_u\cdot \hat{H}_d=\sum _{a,b}\epsilon _{ab}\,\hat{H}_d^a\,\hat{H}_u^b$ with $\epsilon _{21}=1$, $\epsilon _{12}=-1$ and $\epsilon _{aa}=0$ with $a,b \in \{1,2\}$. As outlined in Ref. [11], a Kähler transformation starting from Jordan-frame supergravity introduces a correction in the superpotential, which is of the form

$$\begin{aligned} \mathcal {W}_{\text {Higgs}}&\rightarrow \mathcal {W}_{\text {Higgs}} + \tfrac{3}{2}\,m_{3/2}\,\chi \, \hat{H}_u\cdot \hat{H}_d. \end{aligned}$$

(4)

The parameter $m_{3/2}$ denotes the gravitino mass, and $\chi$ is the coupling of Eq. (2). The scalar Higgs fields are denoted by $H_u$, $H_d$ and S in the following. During electroweak symmetry breaking, they receive the vacuum expectation values (vevs) $v_u$, $v_d$ and $v_s$, respectively. Expanding around the vevs, we decompose the fields as follows:

$$\begin{aligned} H_u&\equiv \begin{pmatrix} h_u^+ \\ h_u \end{pmatrix} = \begin{pmatrix} \eta _u^+ \\ v_u + \tfrac{1}{\sqrt{2}}\left( \sigma _u + i\,\phi _u\right) \end{pmatrix}, \nonumber \\ H_d&\equiv \begin{pmatrix} h_d \\ h_d^- \end{pmatrix} = \begin{pmatrix} v_d + \tfrac{1}{\sqrt{2}}\left( \sigma _d + i\,\phi _d\right) \\ \eta _d^- \end{pmatrix}, \end{aligned}$$

(5a)

$$\begin{aligned} S&\equiv v_s + \tfrac{1}{\sqrt{2}}\left( \sigma _s + i\,\phi _s\right) . \end{aligned}$$

(5b)

The additional bilinear contribution to the superpotential in Eq. (4) generates a term which is analogous to the $\mu$ term of the MSSM, but with

$$\begin{aligned} \mu&=\tfrac{3}{2}\,m_{3/2}\,\chi . \end{aligned}$$

(6)

When the singlet S acquires its vev, an effective $\mu _{\text {eff}}=\lambda \,v_s$ is dynamically generated. Often, the sum $\left( \mu +\mu _{\text {eff}}\right)$ is the phenomenologically more relevant parameter of the model. It takes the form

$$\begin{aligned} \mu + \mu _{\text {eff}}&= \tfrac{3}{2}\,m_{3/2}\,\chi \, + \lambda \,v_s\, \end{aligned}$$

(7)

and corresponds to the MSSM-like higgsino mass term. In the following, we consider both quantities $\mu$ and $\mu _{\text {eff}}$ as independent input parameters, where $\mu$ is linearly dependent on the gravitino mass $m_{3/2}$. In order to be a viable dark-matter candidate, the gravitino mass can range from a few eV to multiple TeV, see e.g. Ref. [47]. The value of $\chi$ is a priori not fixed; for cosmological reasons we adopt

$$\begin{aligned} \chi \simeq 10^5 \; \lambda \end{aligned}$$

(8)

according to Refs. [11, 13]. The additional contribution to the superpotential in the $\mu$NMSSM is thus mainly steered by the gravitino mass, whereas $v_s$ can be traded for $\mu _{\text {eff}}$. If we require a $\mu$ parameter above the electroweak scale, $\mu \gtrsim 1\,\hbox {TeV}$, and in addition a sizable coupling $\lambda \gtrsim 0.1$, the typical gravitino mass turns out to be much below the electroweak scale at $m_{3/2}\gtrsim 10\,\hbox {MeV}$. However, if we allow for very small values of $\lambda \ll 10^{-2}$ and very large values of $\mu \gg 1\,\text {TeV}$, the gravitino mass could as well be above the TeV scale. In the latter case, the phenomenology of the $\mu$NMSSM is not necessarily similar to the MSSM: the singlets only decouple for $\lambda \rightarrow 0$ with $\kappa \propto \lambda$ and therefore $v_s\rightarrow \infty$. If the constraint $\kappa \propto \lambda$ is dropped, interesting effects can occur; e.g. we will discuss a scenario with small $\lambda$ and small $\mu _{\text {eff}}$ in our numerical studies. In contrast to the NMSSM, the higgsino mass can be generated by $\mu$ alone and thus even a vanishing $v_s$ is not in conflict with experimental bounds.

In order to avoid the cosmological gravitino problem [48], where the light gravitino dark matter overcloses the universe [49, 50], one has to control the reheating temperature in order to keep the production rate of the light gravitinos low [51]. This potential problem may affect the model under consideration for gravitino masses in the range from MeV to GeV; it disappears for much heavier gravitinos ($\mathord {\gtrsim }\,10\,\text {TeV}$). In the latter case the inflationary $\mu$ term would dominate over the NMSSM-like $\mu _{\text {eff}}$ and drive the higgsino masses to very high values (unless $\mu _{\text {eff}}$ is tuned such that the sum $(\mu +\mu _{\text {eff}})$ remains small). For gravitino masses $m_{3/2} > 1 \,\text {GeV}$ it affects Big Bang Nucleosynthesis via photo-deconstruction of light elements, see Ref. [48]. As discussed in Ref. [11], in the $\mu$NMSSM there is no strict constraint on the reheating temperature $T_R$. We note that a reheating temperature below $T_R \lesssim 10^8$–$10^9\,\text {GeV}$, as advocated in Ref. [52], avoids the gravitino problem. The rough estimate of $m_{3/2} \sim 10\,\text {MeV}$ even needs $T_R \lesssim 10^5\,\text {GeV}$ in order to not overclose the universe with thermally produced gravitinos after inflation [53,54,55,56]. Interestingly, such low reheating temperatures preserve high-scale global minima after inflation, see Ref. [57], and disfavor the preparation of the universe in a meta-stable state after the end of inflation [58]. In any case, the reheating temperature at the end of inflation is very model dependent and rather concerns the inflationary physics. A study to estimate the reheating temperature $T_R$ is given in Ref. [59]. Therein, a relation is drawn between the decay width of the inflaton and $T_R$. Interestingly, if we naïvely assume that this width at the end of inflation is equal to the SM-like Higgs width $\Gamma _h \approx 4 \times 10^{-3}\,\text {GeV}$, we can estimate a rather low reheating temperature $T_R \sim \sqrt{\Gamma _h M_{\text {Pl}}} \approx 10^7\,\text {GeV}$ with the Planck mass $M_{\text {Pl}}\approx 2.4 \times 10^{18}\,\text {GeV}$. For our studies below we assume that a reheating temperature as low as $T_R\lesssim 10^9\,\text {GeV}$ can be achieved even with large couplings.

Since the bilinear $\mu$ term breaks the $\mathbb {Z}_3$ symmetry, additional parameters are allowed compared to the NMSSM. In the general NMSSM (GNMSSM) – including the bilinear singlet mass parameter $\nu$ and the singlet tadpole coefficient $\xi$ – the Higgs sector of the superpotential is given by

$$\begin{aligned} \mathcal {W}_{\text {Higgs}}&= \lambda \,\hat{S}\,\hat{H}_u\cdot \hat{H}_d + \tfrac{1}{3}\,\kappa \,\hat{S}^3 + \mu \,\hat{H}_u\cdot \hat{H}_d\nonumber \\&\quad +\, \tfrac{1}{2}\,\nu \,\hat{S}^2 + \xi \,\hat{S}. \end{aligned}$$

(9)

However, we assume that the non-minimal coupling of the Higgs doublets to supergravity is the only source of superconformal and thus $\mathbb {Z}_3$ symmetry breaking – as outlined in Section 5 of Ref. [11]. In this case, all other superpotential parameters that are forbidden by $\mathbb {Z}_3$ symmetry remain exactly zero at all scales: the beta functions for the parameters of the superpotential are proportional to the respective parameter itself and thus they cannot be generated radiatively.

Because the $\mathbb {Z}_3$ symmetry is broken (which avoids the typical domain-wall problem of the NMSSM [60]), another symmetry at the high scale is required in order to solve the tadpole problem [61,62,63,64,65,66]: without such a symmetry, Planck-scale corrections could possibly induce large contributions to the tadpole term [67]. The superconformal embedding of the $\mu$NMSSM, where the $\mu$ term is generated from the Kähler potential, serves as this symmetry. As pointed out in Ref. [67], other possibilities consist of discrete or continuous non-gauge symmetries, so-called R symmetries. Imposing discrete $\mathbb {Z}_4$ or $\mathbb {Z}_8$ R symmetries as proposed in Refs. [45, 68, 69] provide a viable solution, since dimensionful linear and bilinear terms are forbidden as long as the symmetry is not broken.³

Furthermore, each parameter in the superpotential induces a corresponding soft-breaking term; additional mass terms are allowed:

$$\begin{aligned} -\mathcal {L}_{\text {soft}}&= \left[ A_\lambda \,\lambda \,S\,H_u\cdot H_d + \tfrac{1}{3}\,A_\kappa \,\kappa \,S^3 + B_\mu \,\mu \,H_u\cdot H_d \right. \nonumber \\&\quad \left. +\, \tfrac{1}{2}\,B_\nu \,\nu \,S^2 + C_\xi \,\xi \,S + \text {h.}\,\text {c.}\right] \nonumber \\&\quad +\, m_{H_d}^2\,|H_d|^2 + m_{H_u}^2\,|H_u|^2 + m_s^2\,|S|^2. \end{aligned}$$

(10)

It should be noted that the beta functions for soft-breaking parameters are not only proportional to themselves, but also receive contributions from the other soft-breaking parameters. Thus, in contrast to the terms in the superpotential, finite contributions may emerge even if a soft-breaking parameter is set to zero at the tree level. The beta functions for the parameters of the superpotential in Eq. (9) and its corresponding soft-breaking parameters in Eq. (10) can be found in Refs. [44, 71, 72]; however, since we employ different conventions we list them in Appendix A.

Contrary to studies in the GNMSSM (see Refs. [44,45,46, 73]), where the MSSM-like $\mu$ term can be easily shifted away and absorbed in a redefinition of the other parameters – especially the tadpole contribution – we cannot do so in the inflation-inspired $\mu$NMSSM. First of all, the $\mu$ term is introduced via the R symmetry-breaking non-minimal coupling to supergravity only. The other parameters in the singlet sector are not supposed to be generated by this breaking. Secondly, by redefining the parameters, we would introduce a tadpole term and shift the effect simply there. Note that the authors of Ref. [45] perform this shift in order to eliminate the linear (i.e. tadpole) term in the superpotential and keep $\mu$, while others (e.g. Ref. [74]) shift the $\mu$ term to zero and keep the tadpole and bilinear terms for the singlet in the superpotential. As discussed above, in the $\mu$NMSSM considered in this paper due to the superconformal symmetry breaking at the Planck scale solely the $\mathbb {Z}_3$-breaking $\mu$ term is present.

2.2 Higgs potential

With the superpotential of Eq. (9) and the soft-breaking Lagrangian of Eq. (10), we derive the following Higgs potential, where we stick to real parameters:

$$\begin{aligned} V&= \left[ m_{H_d}^2 + \left( \mu + \lambda \,S\right) ^2\right] |H_d|^2\nonumber \\&\quad +\, \left[ m_{H_u}^2 + \left( \mu + \lambda \,S\right) ^2\right] |H_u|^2+\, \left( m_{S}^2 + B_\nu \,\nu \right) S^2 \nonumber \\&\quad +\, 2\,C_\xi \,\xi \,S + \tfrac{2}{3}\,\kappa \,A_\kappa \,S^3\nonumber \\&\quad +\, \left[ \xi + \nu \,S + \kappa \,S^2 + \lambda \,H_u\cdot H_d\right] ^2\nonumber \\&\quad +\, 2\left( B_\mu \,\mu + \lambda \,A_\lambda \,S\right) H_u\cdot H_d\nonumber \\&\quad +\, \tfrac{1}{8}\left( g_1^2 + g_2^2\right) \left( |H_d|^2 - |H_u|^2\right) ^2\nonumber \\&\quad +\, \tfrac{1}{2}\,g_2^2\,|H_d^\dagger \,H_u|^2. \end{aligned}$$

(11)

This potential can be expanded in the components of the Higgs fields in Eq. (5). Defining the vectors in field space $\mathcal {S}^{\text {T}} = \left( \sigma _d,\sigma _u,\sigma _s\right)$, $\mathcal {P}^{\text {T}} = \left( \phi _d,\phi _u,\phi _s\right)$ and $\mathcal {C}^{\text {T}} = \left( \phi _d^-,\phi _u^-\right) = \left( \eta _d^+,\eta _u^+\right) ^*$, it reads

$$\begin{aligned} V&= \text {const} - \mathcal {T}_S^{\text {T}}\,\mathcal {S} - \mathcal {T}_P^{\text {T}}\,\mathcal {P}\nonumber \\&\quad +\, \tfrac{1}{2}\,\mathcal {S}^{\text {T}}\,{\mathcal {M}}_S^2\,\mathcal {S}+\, \tfrac{1}{2}\,\mathcal {P}^{\text {T}}\,{\mathcal {M}}_P^2\,\mathcal {P} + \mathcal {C}^{\text {T}}\,{\mathcal {M}}_C^2\,\mathcal {C}^{*}\nonumber \\&\quad +\, \sum \limits _{ijk\,=\,1}^{6} \tfrac{1}{\sqrt{2}}\,\lambda _{ijk}^\prime \left( \mathcal {S},\mathcal {P}\right) _i \left( \mathcal {S},\mathcal {P}\right) _j \left( \mathcal {S},\mathcal {P}\right) _k\nonumber \\&\quad +\, \sum \limits _{i\,=\,1}^{6} \sum _{jk\,=\,1}^{2}\tfrac{1}{\sqrt{2}}\,\tilde{\lambda }_{ijk}^\prime \left( \mathcal {S},\mathcal {P}\right) _i \left( \mathcal {C}\right) _j\left( \mathcal {C}^{*}\right) _k + \cdots , \end{aligned}$$

(12)

where the ${\mathcal {CP}}$-even and ${\mathcal {CP}}$-odd tadpole coefficients $\mathcal {T}_S$ and $\mathcal {T}_P$, the ${\mathcal {CP}}$-even, ${\mathcal {CP}}$-odd and charged squared mass matrices $\mathcal {M}_S^2$, $\mathcal {M}_P^2$ and $\mathcal {M}_C^2$ are given below, and the trilinear couplings $\lambda _{ijk}^\prime$ and $\tilde{\lambda }_{ijk}^\prime$ are specified in Sect. 2.5, though in a basis where the Goldstone mode corresponds to a mass eigenstate and does not mix with the other states at lowest order. The ellipses denote quadrilinear terms which are immaterial for the following.

We substitute the electroweak vevs $v_u$ and $v_d$ by their ratio $\tan \beta = v_u/v_d$ and the sum of their squares $v^2 \equiv v_u^2 + v_d^2 =(174\,\text {GeV})^2$. The symbols $t_\beta$, $c_\beta$ and $s_\beta$ denote $\tan \beta$, $\cos \beta$ and $\sin \beta$, respectively. Furthermore, $g_1$ and $g_2$ are substituted by the W and Z gauge-boson masses,

$$\begin{aligned} m_W^2 = \tfrac{1}{2}\,g_2^2\,v^2, \quad m_Z^2 = \tfrac{1}{2}\left( g_1^2 + g_2^2\right) v^2. \end{aligned}$$

(13)

Using the abbreviations

$$\begin{aligned} a_1&= B_\mu \,\mu + \xi \,\lambda + \mu _{\text {eff}}\left( \nu + \frac{\kappa }{\lambda }\,\mu _{\text {eff}}+ A_\lambda \right) , \end{aligned}$$

(14a)

$$\begin{aligned} a_2&= 2\,v\,\lambda \left( \mu + \mu _{\text {eff}}\right) , \end{aligned}$$

(14b)

$$\begin{aligned} a_3&= v\,\lambda \left( \nu + 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}+ A_\lambda \right) , \end{aligned}$$

(14c)

$$\begin{aligned} a_4&= \frac{1}{\mu _{\text {eff}}}\left[ v^2\,\lambda ^2\,c_\beta \,s_\beta \left( \nu + \frac{\kappa }{\lambda }\,\mu _{\text {eff}}+ A_\lambda \right) \right. \nonumber \\&\quad \left. - v^2\,\lambda ^2\,\mu - \xi \,\lambda \left( \nu + C_\xi \right) \right] , \end{aligned}$$

(14d)

$$\begin{aligned} a_5&= 4\left( \frac{\kappa }{\lambda }\right) ^2\mu _{\text {eff}}^2 +\, \frac{\kappa }{\lambda }\left[ \mu _{\text {eff}}\left( A_\kappa + 3\,\nu \right) - v^2\,\lambda ^2\,c_\beta \,s_\beta \right] , \end{aligned}$$

(14e)

$$\begin{aligned} a_6&= v\,\lambda \left( \nu + 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}- A_\lambda \right) , \end{aligned}$$

(14f)

$$\begin{aligned} a_7&= -6\left( \frac{\kappa }{\lambda }\right) ^2\mu _{\text {eff}}^2 + 2\,\frac{\kappa }{\lambda }\left( \xi \,\lambda - 4\,\nu ^2\right) + B_\nu \,\nu , \end{aligned}$$

(14g)

we can write the explicit expressions for the tadpole coefficients $\mathcal {T}_{S,P}$ as

$$\begin{aligned}&\mathcal {T}_S = \begin{pmatrix} \sqrt{2}\,v\left\{ s_\beta \,a_1 - c_\beta \left[ m_{H_d}^2 + \left( \mu + \mu _{\text {eff}}\right) ^2 + v^2\,\lambda ^2\,s_\beta ^2 + \tfrac{1}{2}\,m_Z^2\,c_{2\beta }\right] \right\} \\ \sqrt{2}\,v\left\{ c_\beta \,a_1 - s_\beta \left[ m_{H_u}^2 + \left( \mu + \mu _{\text {eff}}\right) ^2 + v^2\,\lambda ^2\,c_\beta ^2 - \tfrac{1}{2}\,m_Z^2\,c_{2\beta }\right] \right\} \\ \sqrt{2}\,\frac{\mu _{\text {eff}}}{\lambda }\left[ a_4 - m_S^2 - a_5 - a_7 - v^2\,\lambda ^2 - \left( \nu + 2\,\mu _{\text {eff}}\,\frac{\kappa }{\lambda }\right) ^2\right] \end{pmatrix}, \end{aligned}$$

(15a)

$$\begin{aligned}&\quad \mathcal {T}_P = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \equiv \mathbf {0}. \end{aligned}$$

(15b)

The minimization of the Higgs potential requires all tadpole coefficients in Eq. (15a) to be equal to zero. With the conditions $\mathcal {T}_S=\mathbf {0}$ we choose to eliminate $m_{H_d}^2$, $m_{H_u}^2$ and $m_S^2$ according to

$$\begin{aligned} m_{H_d}^2&= -\left( \mu + \mu _{\text {eff}}\right) ^2 - v^2\,\lambda ^2\,s_\beta ^2 - \tfrac{1}{2}\,m_Z^2\,c_{2\beta } + a_1\,t_\beta , \end{aligned}$$

(16a)

$$\begin{aligned} m_{H_u}^2&= -\left( \mu + \mu _{\text {eff}}\right) ^2 - v^2\,\lambda ^2\,c_\beta ^2 + \tfrac{1}{2}\,m_Z^2\,c_{2\beta } + \frac{a_1}{t_\beta }, \end{aligned}$$

(16b)

$$\begin{aligned} m_S^2&= a_4 - a_5 - a_7 - v^2\,\lambda ^2 - \left( \nu + 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) ^2. \end{aligned}$$

(16c)

Substituting these expressions in the symmetric mass matrices ${\mathcal {M}}_{S,P,C}$ we find

$$\begin{aligned} \mathcal {M}_S^2&= \begin{pmatrix} m_Z^2\,c_\beta ^2 + a_1\,t_\beta &{}\quad \left( 2\,v^2\,\lambda ^2 - m_Z^2\right) c_\beta \,s_\beta - a_1 &{}\quad a_2\,c_\beta - a_3\,s_\beta \\ \cdot &{}\quad m_Z^2\,s_\beta ^2 + a_1/t_\beta &{}\quad a_2\,s_\beta - a_3\,c_\beta \\ \cdot &{}\quad \cdot &{}\quad a_4 + a_5 \end{pmatrix}, \end{aligned}$$

(17a)

$$\begin{aligned} \mathcal {M}_P^2&= \begin{pmatrix} a_1\,t_\beta &{}\quad a_1 &{}\quad -a_6\,s_\beta \\ \cdot &{}\quad a_1/t_\beta &{}\quad -a_6\,c_\beta \\ \cdot &{}\quad \cdot &{}\quad a_4 - 3\,a_5 - 2\,a_7 \end{pmatrix}, \end{aligned}$$

(17b)

$$\begin{aligned} \mathcal {M}_C^2&= \left[ \left( m_W^2 - v^2\,\lambda ^2\right) \,c_\beta \,s_\beta + a_1\right] \begin{pmatrix} t_\beta &{}\quad 1\\ \cdot &{}\quad 1/t_\beta \end{pmatrix}. \end{aligned}$$

(17c)

Diagonalizing Eq. (17c) yields zero for the massless charged Goldstone boson, and the charged Higgs-boson mass $m_{H^\pm }$ at the tree level is given by

$$\begin{aligned} m_{H^\pm }^2&= m_W^2 - v^2\,\lambda ^2 + \frac{a_1}{c_\beta \,s_\beta }, \end{aligned}$$

(18)

which we employ as an input parameter. Inserting Eq. (14a) we can then eliminate $A_\lambda$ via

$$\begin{aligned} A_\lambda&= \frac{c_\beta \,s_\beta }{\mu _{\text {eff}}}\left( m_{H^\pm }^2 - m_W^2 + v^2\,\lambda ^2\right) - \frac{1}{\mu _{\text {eff}}}\left( B_\mu \,\mu + \xi \,\lambda \right) \nonumber \\&\quad - \,\left( \nu + \frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) . \end{aligned}$$

(19)

Substituting $A_\lambda$ in the abbreviations of Eq. (14) yields ($a_2$, $a_5$ and $a_7$ are not changed)

$$\begin{aligned} a_1^\prime&= c_\beta \,s_\beta \left( m_{H^\pm }^2 - m_W^2 + v^2\,\lambda ^2\right) , \end{aligned}$$

(20a)

$$\begin{aligned} a_3^\prime&= v\,\lambda \left[ \frac{\kappa }{\lambda }\,\mu _{\text {eff}}+ \frac{1}{\mu _{\text {eff}}}\left( a_1^\prime - B_\mu \,\mu - \xi \,\lambda \right) \right] , \end{aligned}$$

(20b)

$$\begin{aligned} a_4^\prime&= c_\beta \,s_\beta \left( \frac{v\,\lambda }{\mu _{\text {eff}}}\right) ^2\left( a_1^\prime - B_\mu \,\mu - \xi \,\lambda \right) \nonumber \\&\quad -\, \frac{1}{\mu _{\text {eff}}}\left[ \mu \,v^2\,\lambda ^2 + \xi \,\lambda \left( \nu + C_\xi \right) \right] , \end{aligned}$$

(20c)

$$\begin{aligned} a_6^\prime&= v\,\lambda \left[ 3\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}+ 2\,\nu - \frac{1}{\mu _{\text {eff}}}\left( a_1^\prime - B_\mu \,\mu - \xi \,\lambda \right) \right] \nonumber \\&= -a_3^\prime + 2\,v\,\lambda \left( 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}+ \nu \right) . \end{aligned}$$

(20d)

The tree-level masses of the three neutral ${\mathcal {CP}}$-even Higgs bosons $m_{h_{1,2,3}}^2$ are determined by diagonalizing Eq. (17a). Analogously, diagonalizing Eq. (17b) yields the masses $m_{a_{1,2}}^2$ of the ${\mathcal {CP}}$-odd Higgs bosons at the tree level; the third eigenvalue is equal to zero and belongs to the neutral Goldstone boson.

Higgs doublets :

The mass-matrix elements of the doublet fields in the upper-left $\left( 2\times 2\right)$ block matrices of Eqs. (17a)–(17b) contain the abbreviation $a_1^\prime$. From Eq. (20a) it is apparent that they are determined by SM parameters and $m_{H^\pm }$, $\lambda$ and $t_\beta$ like in the NMSSM. Neglecting the mixing between the doublet and singlet sector, the mass of the light ${\mathcal {CP}}$-even doublet state has an upper bound of $m_Z^2\,c^2_{2\beta }+\lambda ^2\,v^2\,s^2_{2\beta }$. In the limit $m_{H^\pm }\gg m_Z$, the other two doublet fields decouple and obtain a mass close to $m_{H^\pm }$. Smaller values of $m_{H^\pm }$ increase the mixing of both ${\mathcal {CP}}$-even doublet fields. Also $t_\beta$ needs to be close to one for large doublet mixing.

Higgs singlets :

The $\left( 3,3\right)$ elements of $\mathcal {M}_S$ and $\mathcal {M}_P$ in Eqs. (17a) and (17b) set the mass scale of the Higgs singlets. They contain the terms $a_4^\prime$ from Eq. (20c), $a_5$ from Eq. (14e), and $a_7$ from Eq. (14g). All $\mathbb {Z}_3$-violating parameters besides $\mu$ and $B_\mu$ appear in these terms; in our later analysis we set these parameters besides $\mu$ and $B_\mu$ to zero, but for completeness we mention them in the following discussion of this section.

The parameter $A_\kappa$ appears only in the term $a_5$, whereas $B_\nu$ only appears in $a_7$. Thus it is obvious that the diagonal mass-matrix elements for the singlet fields – and therefore their masses – can be controlled by these two quantities, without changing any other matrix element. If all $\mathbb {Z}_3$-violating parameters except $\mu$ and $B_\mu$ were set to zero, we would rediscover the NMSSM-specific feature that $A_\kappa$ is bound from below and above to avoid tachyonic singlet states at the tree level.

The ratio $\kappa /\lambda$ which appears in both terms, $a_5$ and $a_7$, has sizable impact on the mass scale of the singlets. If $\kappa \ll \lambda$ the ${\mathcal {CP}}$-even singlet entry is purely controlled by $a_4^\prime$, which in turn is proportional to $1/\mu _{\text {eff}}$; in the same limit, the ${\mathcal {CP}}$-odd singlet entry is controlled by $a_4^\prime$ and the remainder of $a_7$ which is $B_\nu \,\nu$. Also note that $a_4^\prime$ contains a term which is linear in $\mu$. In the opposite case $\kappa \gtrsim \lambda$, the term $a_5$ is likely to dominate the $\left( 3,3\right)$ matrix element for the ${\mathcal {CP}}$-even singlet due to the suppression of $a_4^\prime$ by $\mu _{\text {eff}}$ if it is of the order of a few $100\,\hbox {GeV}$. The term $a_5$ is proportional to $(\kappa /\lambda )^2\,\mu _{\text {eff}}^2$, such that the ${\mathcal {CP}}$-even singlet exhibits a strong dependence on $\mu _{\text {eff}}$. On the other hand for $\mu \gtrsim \mu _{\text {eff}}$, the term $a_4'$ can balance the large $\kappa$-enhanced contribution in $a_5$; thus, possible upper bounds on $\kappa$ as derived in Ref. [75] might be evaded.

For the case of the ${\mathcal {CP}}$-odd singlet, the terms in $a_5$ and $a_7$ that are quadratic in $\mu _{\text {eff}}$ cancel each other. Then the size of the other parameters (especially $A_\kappa$, $\mu$ and $\mu _{\text {eff}}$) determines which contribution is dominant. For moderate values of $\kappa \approx \lambda \gtrsim 0.1$ together with small $A_\kappa$ the ${\mathcal {CP}}$-odd singlet develops a dependence on $\mu /\mu _{\text {eff}}$, as we will discuss later. Lastly, we note that in the case of $\kappa \gg \lambda$ and $A_\kappa \ne 0\,\text {GeV}$ the ${\mathcal {CP}}$-even and ${\mathcal {CP}}$-odd singlet masses are controlled through $(\kappa /\lambda )^2\,\mu _{\text {eff}}^2$ and $(\kappa /\lambda )\,\mu _{\text {eff}}\,A_\kappa$, respectively. Later, this will allow us to present a rescaling procedure that keeps both singlet masses constant over a large parameter range.

Doublet–singlet mixing :

The masses of the doublet-like and the singlet-like Higgs states can be significantly shifted by mixing between both sectors. The relevant matrix elements are the ones in the third columns of Eqs. (17a) and (17b). They contain the abbreviations $a_2$, $a_3^\prime$ and $a_6^\prime$, see Eqs. (14b), (20b) and (20d), respectively. The mixing vanishes in the limit $\lambda \rightarrow 0$ with constant $\kappa /\lambda$, and it is enhanced for larger values of $\lambda$. For fixed $\lambda$ it is also strongly enhanced in the limit $\mu _{\text {eff}}\rightarrow 0\,\text {GeV}$.

In the ${\mathcal {CP}}$-even sector, two terms contribute to the doublet–singlet mixing: $a_2$ which depends on the sum $(\mu +\mu _{\text {eff}})$, and $a_3^\prime$ which does not directly depend on $\mu$, but only on the soft-breaking term $B_\mu \,\mu$. In the case of large $\mu$ and $\mu _{\text {eff}}$ of the same sign, $a_2$ often dominates the mixing with the lighter doublet, eventually yielding a tachyonic singlet or doublet Higgs; this behavior can be avoided by choosing a proper value for $B_\mu$ (or $\xi$) to cancel the large effect in $a_2$ by $a_3^\prime$. In the case of similar $\mu$ and $\mu _{\text {eff}}$ of opposite signs, $a_3^\prime$ will always dominate the mixing. Again, the mixing strength can be adjusted by setting $B_\mu$ (or $\xi$).

The doublet–singlet mixing in the ${\mathcal {CP}}$-odd sector contains only one term $a_6^\prime$ which is similar to $a_3^\prime$ with opposite sign. Furthermore, the ${\mathcal {CP}}$-odd mixing elements can be modified by non-zero $\xi$ and $\nu$. As indicated above, due to the dependences of $a_3^\prime$ and $a_6^\prime$ on $1/\mu _{\text {eff}}$, a small $\mu _{\text {eff}}\ll 100\,\hbox {GeV}$ yields a strong mixing between singlets and doublets.

We subsequently discuss vacuum structure and vacuum stability bounds in the $\mu$NMSSM around the electroweak scale. We do not discuss tachyonic instabilities during inflation or the stabilization of the inflationary direction, since they are not of relevance for our study (see e.g. Refs. [11, 13]).

2.3 Vacuum structure and vacuum stability bounds

The space of model parameters can be constrained using experimental exclusion limits and theoretical bounds. Those constraints can be applied to rule out certain parts of the parameter space. In this context, constraints from the stability of the electroweak vacuum appear to be very robust and theoretically well motivated. It has already been noticed in the early times of supersymmetry that constraints from the electroweak vacuum stability on the trilinear soft SUSY-breaking parameters can be important [76,77,78,79,80,81,82,83,84]. Recently they have been rediscussed in light of the Higgs discovery [85,86,87,88,89]. These constraints are usually associated with non-vanishing vacuum expectation values of sfermion fields (e.g. staus or stops) and thus known under the phrase “charge- and color-breaking minima”. Such minima can invalidate the electroweak vacuum and therefore lead to unphysical parameter configurations (see below).

However, the existence of charge- and color-breaking minima is only a necessary condition for the destabilization of the electroweak vacuum. Clearly one has to compare the value of the potential at this new minimum with the desired electroweak one, and only if the non-standard vacuum is deeper the corresponding scenario is potentially excluded. In fact, some of the points with a deeper non-standard vacuum may be valid when accepting meta-stable vacua under the condition that the transition time from the local electroweak vacuum to the global true vacuum appears to be longer than the age of the universe [90]. However, the possibility of the existence of meta-stable vacua is of limited practical relevance for our analysis: typically only parameter points in close neighborhood to the stable region are affected by such considerations; well-beyond the boundary region, the false vacua become rather short-lived and thus are strictly excluded. In addition, there are thermal corrections in the early universe which give a sizable and positive contribution to the effective potential as the one-loop corrections are proportional to $m^2(\phi )\,T^2$ for the field-dependent masses $m(\phi )$. For finite temperature, they shift the ground state to the symmetric phase around $\phi = 0\,\text {GeV}$ [91, 92]. We presume, however, that our inflationary scenario preselects a vacuum at field values different from zero and, thanks to the relatively low reheating temperatures in our scenario, gets caught in it, see Ref. [57]. Following the inflationary scenario of Ref. [11], the trajectory in field space lies at $\beta = \pi /4$ with $h_u^2 = h_d^2 = h^2$ and $s = 0\,\text {GeV}$; the presence of the singlet field S is needed for the stabilization of the inflationary trajectory in order to not fall into the tachyonic direction as pointed out by Refs. [11, 13]. Inflation ends at field values $h = \mathcal {O}(0.01)$ in units of the Planck mass. For small $\lambda \sim 10^{-2}$, the D-flat trajectory remains stable after inflation ends according to Ref. [11], and will change to $\beta \ne \pi /4$ and $s \ne 0\,\text {GeV}$ when the SUSY-breaking terms become important. NMSSM-specific effects like the relevance of singlet Higgs bosons and the additional contribution to the $125\,\text {GeV}$ Higgs boson are usually connected to a large value of $\lambda$. This is not necessarily the case in the $\mu$NMSSM, where striking differences also appear for small values of $\mu _{\text {eff}}$. Moreover, we will take it as a working assumption that after inflation ends, even for larger values of $\lambda$ the universe will remain in the state with the inflationary field direction until it settles down in a minimum closest to this direction. If it is the global minimum of the zero-temperature potential, reheating may not be sufficient to overcome the barrier and to select a false (and maybe meta-stable) vacuum. The thermal history of the universe plays then no role for the choice of the vacuum, and in this case the universe would remain in the global minimum. Accordingly, we adopt the prescription to exclude all points with a global minimum that does not coincide with the electroweak vacuum. This means that we do not consider meta-stable electroweak vacua as they are excluded by the selection rule. A similar discussion and argument has been given in Ref. [93], where a selection of the vacuum with the largest expectation values was promoted, irrespective whether or not it is the global minimum of the theory.

We will see that actually in most cases scenarios are excluded because of a tachyonic Higgs mass. Tachyonic masses are related to the fact that the electroweak point – around which the potential is expanded – is not a local minimum in the scalar potential, but rather resembles a saddle point or even local maximum, and the true vacuum lies at a deeper point along this tachyonic direction. Thus, the true vacuum has vevs different from the input values, and the electroweak breaking condition $\mathcal {T}_S = \mathbf {0}$ in Eq. (15a) does not select a minimum.

We briefly sketch how to get constraints on the relevant model parameters in the (neutral) Higgs sector of the $\mu$NMSSM. Similar observations for the NMSSM have been intensively discussed in the literature [94, 95]. Already the presence of an additional Higgs singlet (see e.g. Refs. [96,97,98]) invalidates the well-known results that no charge-breaking Higgs vevs exist at lowest order in the MSSM (see e.g. Refs. [82, 99]) and in two-Higgs-doublet models (see e.g. Refs. [100, 101]). On the other hand, in the NMSSM the inclusion of such charge-breaking minima has rather little impact on the overall vacuum stability and gives no further information, see Ref. [102]. In a similar manner, we neglect non-vanishing squark vevs (see discussion below) and therefore we only have to deal with the following potential:

$$\begin{aligned} V&= \kappa ^2\,s^4 + \tfrac{1}{8}\left( g_1^2 + g_2^2\right) \left( h_u^2 - h_d^2 \right) ^2\nonumber \\&\quad +\, \left( \lambda ^2\,s^2 + 2\,\lambda \,\mu \,s\right) \left( h_u^2 + h_d^2 \right) \nonumber \\&\quad -\, 2\,\lambda \left( \kappa \,s^2 + A_\lambda \,s\right) h_u\,h_d\nonumber \\&\quad +\, \lambda ^2\,h_u^2\,h_d^2 + \tfrac{2}{3}\,\kappa \,A_\kappa \,s^3 + \left( m_{H_u}^2 + \mu ^2\right) h_u^2\nonumber \\&\quad +\, \left( m_{H_d}^2 + \mu ^2\right) h_d^2 + m_S^2\,s^2 - 2\,B_\mu \,\mu \,h_u\,h_d, \end{aligned}$$

(21)

where we just presented the real fields as we do not consider spontaneous ${\mathcal {CP}}$ violation.⁴ Notice also that we do not consider the shifted theory with all fields $\phi \rightarrow \phi - v_\phi$ expanded around the electroweak point, $h_u = v_u, h_d = v_d, s = \mu _{\text {eff}}/\lambda$. In our case for the stability analysis, the potential vanishes at the origin, and the electroweak minimum is one of the minima not located at the origin. It is not necessarily the global minimum. Furthermore, compared to Eq. (11), we neglect all additional $\mathbb {Z}_3$-breaking terms besides the contributions of $\mu$ and $B_\mu \,\mu$ of the $\mu$NMSSM (see the discussion above).

The “desired” electroweak vacuum can be constructed by fulfilling the minimization conditions at the tree level, $\mathcal {T}_S = \mathbf {0}$, with $\mathcal {T}_S$ given by Eq. (15a). The vevs of the doublet fields are taken as fixed input parameters, whereas the value of $\mu _{\text {eff}}$ is treated as variable similar to $\mu$. These equations can be solved for the soft-breaking masses $m_{H_u}^2$, $m_{H_d}^2$ and $m_S^2$ according to Eq. (16).

The masses of the Higgs sector are determined in such a way that the desired vacuum with $\langle h_u \rangle = v_u$, $\langle h_d \rangle = v_d$ and $\langle s \rangle = \mu _{\text {eff}}/ \lambda$ is a viable vacuum of the potential V in Eq. (21). However, one has to ensure that there is no deeper minimum of V. This can only be achieved reasonably-well through a numerical evaluation. For that purpose, we determine the stationary points of the potential V and then compare the corresponding values of V at these points with the desired minimum given by

$$\begin{aligned} V_{\text {min}}^{\text {des}}&= - \frac{1}{8}\left( g_1^2 + g_2^2\right) v^4\,c^2_{2\beta }\nonumber \\&\quad -\, \frac{1}{4}\,\lambda ^2\,v^4\,s^2_{2\beta } - v^2\,\mu _{\text {eff}}^2 \left[ 1 - \frac{\kappa ^2}{\lambda ^2}\,s_{2\beta } \right] \nonumber \\&\quad -\, \frac{\kappa ^2}{\lambda ^4}\,\mu _{\text {eff}}^4 - v^2\,\mu \,\mu _{\text {eff}}- \frac{1}{3} \frac{\kappa \,A_\kappa }{\lambda ^3}\,\mu _{\text {eff}}^3\nonumber \\&\quad +\, \frac{1}{2}\,v^2\,A_\lambda \,\mu _{\text {eff}}\,s_{2\beta } - B_\mu \,\mu \,v^2\,s_{2\beta }. \end{aligned}$$

(22)

From the expression in Eq. (22), one can derive a few general results: (a) for small values of $\lambda$ the desired minimum gets deeper and – as the singlet contribution decouples from the rest of the potential – it becomes more difficult for a non-standard vacuum to appear and to be deeper than the desired minimum; (b) the ($\mu$)NMSSM potential at the desired minimum is usually deeper than in the case of the MSSM⁵ and is mainly driven by $\mu _{\text {eff}}$; (c) the contribution of $A_\lambda$ plays a subdominant role compared to $A_\kappa$ whose impact is strongly influenced by $\mu _{\text {eff}}$ and $\lambda$; (d) parameter points with $V_{\text {min}}^{\text {des}} > 0$ have to be excluded because the trivial minimum at $\langle h_u \rangle = \langle h_d \rangle = \langle s \rangle = 0\,\text {GeV}$ is obviously deeper.

In our analysis, we focus for clarity on constraints from the tree-level potential, considering the appearance of global non-standard minima and, as discussed above, disregarding the possibility of meta-stable false vacua. Employing higher-order (i.e. one-loop) corrections does not necessarily give more accurate predictions of vacuum stability, see Ref. [103]. An approach to include one-loop effects using a certain numerical procedure has been implemented in the public code collection of Vevacious, see Ref. [104], including a tunneling calculation also at finite temperature using CosmoTransitions [105]. The tree-level evaluation is much faster and numerically more stable; moreover, it has been argued that the one-loop effective potential is problematic for tunneling rate calculations [106].

Constraints on the NMSSM parameters There are two main constraints known for the trilinear soft SUSY-breaking parameters $A_\kappa$ and $A_\lambda$. The first constraint relies on the existence of a non-vanishing singlet vev to generate $\mu _{\text {eff}}\ne 0\,\text {GeV}$. This can be easily derived from the Higgs potential with only $s\ne 0\,\text {GeV}$ and is given by the requirement [75]

$$\begin{aligned} A_\kappa ^2 > 9\,m_S^2. \end{aligned}$$

(23)

This lower bound on $A_\kappa$ is inappropriate for the $\mu$NMSSM, as there always exists a non-vanishing higgsino mass term from $\mu = \tfrac{3}{2}\,m_{3/2}\,\chi$. As shown in Sect. 3, this constraint has hardly any impact on our analyses. We simply keep it for illustrative reasons.

The second constraint, on $A_\lambda$, follows from a non-tachyonic charged Higgs mass, since a tachyonic mass ($m^2 < 0\,\text {GeV}^2$ ) means that the potential has negative curvature at this stationary point derived by the minimization conditions. Thus, the true vacuum would have some non-zero vev for a charged Higgs component. Configurations like this are possible in the NMSSM, whereas they do not exist as global or local minima in the MSSM [82]. From the (tree-level) charged Higgs mass in Eq. (18), we get an indirect bound on $A_\lambda$. Taking $m_{H^\pm }$ as input value, we can eliminate $A_\lambda$ as free parameter, see Eq. (19). Hence, we can ensure that $m_{H^\pm }^2$ is always positive. Still, it is worth noticing that by this procedure $A_\lambda$ gets strongly enhanced for small $\mu _{\text {eff}}$ (compared to $m_{H^\pm }$) and thus drives tachyonic neutral Higgs bosons.

Charge and color breaking There exist quite strong constraints in the MSSM from the formation of non-standard minima which break the electric and color charges, known as charge- and color-breaking (CCB) minima. The famous “A-parameter bounds” read traditionally [76, 80, 82, 107]

$$\begin{aligned} A_t^2&< 3\, \left( m_{H_u}^2 + \mu ^2 + m_{{\tilde{Q}}}^2 + m_{{\tilde{t}}}^2 \right) , \end{aligned}$$

(24a)

$$\begin{aligned} A_b^2&< 3\, \left( m_{H_d}^2 + \mu ^2 + m_{{\tilde{Q}}}^2 + m_{{\tilde{b}}}^2 \right) , \end{aligned}$$

(24b)

where $m_{{\tilde{Q}}}^2$ and $m_{{\tilde{t}},{\tilde{b}}}^2$ are the soft SUSY-breaking masses for the superpartners of the left-handed $SU(2)_{\text {L}}$ quark doublet, ${\tilde{Q}}$, and of the right-handed quark singlets, ${\tilde{t}}$ and ${\tilde{b}}$. Several modifications and improvements of Eq. (24) are present in the literature, see e.g. Refs. [82, 84, 90]. These constraints follow from the “D-flat” directions in the scalar potential of the MSSM, i.e. $h_u = {\tilde{t}}_L = {\tilde{t}}_R$ and $h_d = {\tilde{b}}_L = {\tilde{b}}_R$, respectively. Thus the quartic terms associated with squared gauge couplings vanish. In addition, one has to be reminded that Eq. (24) are only necessary conditions for the formation of a non-trivial minimum with non-vanishing squark vevs in that specific direction. In the case of a violation of Eq. (24), one has to check that the generated CCB vacuum is actually deeper than the electroweak minimum. In the MSSM the desired minimum takes on a comparably small numerical value, only depending on $c_{2\beta }$ (and the $B_\mu$ term which can be replaced by the ${\mathcal {CP}}$-odd Higgs mass $M_A$):

$$\begin{aligned} V_{\text {min}}^{{\text {MSSM}}}&= -\tfrac{1}{8}\left( g_1^2 + g_2^2\right) v^4\,c^2_{2\beta } -\tfrac{1}{2}\,M_A^2\,v^2\,s^2_{2\beta } . \end{aligned}$$

(25)

In principle, the A-parameter bounds (24) can be simply transferred to the $\mu$NMSSM, where $\mu$ has to be replaced by $(\mu + \mu _{\text {eff}})$, as they can be transferred to the NMSSM [108]. The net effect is roughly the same in the MSSM, NMSSM and $\mu$NMSSM; if $A_t$ fulfills Eq. (24a), no CCB will appear. Constraints on $\mu _{\text {eff}}$ alone may get weakened, because the desired minimum also gets deeper for larger $\mu _{\text {eff}}$. Moreover, the additional singlet direction stabilizes the potential with respect to CCB minima since the $\mu _{\text {eff}}$ term originates from a quadrilinear scalar coupling, and the vacuum with non-vanishing $\mu _{\text {eff}}$ or $v_s$ is typically deeper than a CCB vacuum. Generically, constraints from the coupling to the wrong Higgs doublet relating down-type sfermion vevs to the up-type Higgs and vice versa, see Refs. [109, 110], are expected to be valid for $(\mu + \mu _{\text {eff}})$ and not weakened if the singlet is fixed at its vev. Similarly, there are bounds on $A_{t,b}$ not related to D-flat directions as discussed in Ref. [111]. These can be reasonably-well determined only numerically. Generically speaking, for the $\mu$NMSSM the risk of generating a CCB vacuum is reduced because (a) the dependence of the desired minimum on $\mu _{\text {eff}}$ drives the electroweak vevs to be more stable, and (b) not as large values of $A_t$ are needed to raise the SM-like Higgs mass because of the additional NMSSM-specific tree-level contribution.

Constraints from CCB minima as given in Eq. (24), are less important in comparison to the MSSM for both, the NMSSM and the $\mu$NMSSM, even if large stop corrections are needed to shift the SM-like Higgs mass (as in the case for small $\lambda$). If the singlet-field direction were neglected and the stop D-flat direction ${\tilde{t}}_R = {\tilde{t}}_L = \tilde{t}$ defined, one could directly apply Eq. (24) for the $\mu$NMSSM, keeping $v_s \ne 0\,\text {GeV}$ and replacing $\mu \rightarrow \mu + \mu _{\text {eff}}$. However, with the singlet as dynamical degree of freedom, the stability of the electroweak vacuum is improved as the only singlet–stop contribution is actually a quadrilinear term $\lambda \,h_d\,s\,{{\tilde{t}}}^2$ and the occurrence of a true vacuum with $\langle h_{u,d} \rangle \ne v_{u,d}$, $\langle s \rangle \ne v_s$ and $\langle {\tilde{t}} \rangle \ne 0\,\text {GeV}$ is disfavored.

Meta-stability and tunneling rates Lastly, we comment on vacuum-to-vacuum transitions in case of a local electroweak vacuum. It is in general of interest to see how long such a meta-stable state could survive compared with the life-time of the universe. We have outlined some arguments why – in view of the inflationary history of the universe – we disregard meta-stable long-lived vacua. We will see in Sect. 3.3 that totally stable points survive in a wide range of the parameter space.

For an estimate of the bounce action of the unstable configuration [112], we define an effectively single-field scalar potential linearly interpolating between the electroweak local minimum and the true vacuum found by the numerical minimization of the scalar potential at different field values and apply an exact solution of the quartic potential given by Ref. [113]. See also Ref. [114] for the application of this method to the $\mu$NMSSM.

2.4 Higher-order corrections to Higgs-boson masses and mixing

It is well-known that perturbative corrections beyond the tree level alter the Higgs masses and mixing significantly in supersymmetric models. For instance, in the MSSM such large corrections are needed to lift the lightest ${\mathcal {CP}}$-even Higgs mass beyond the Z-boson mass. On the other hand, in the NMSSM and similarly the $\mu$NMSSM there are scenarios where an additional tree-level term lowers the tension between the tree-level SM-like Higgs mass and the measured value of the SM-like Higgs boson at $125\,\hbox {GeV}$. Still, since loop corrections to the Higgs spectrum have a large impact, in our phenomenological analysis we take into account contributions of higher order as described in the following.

The masses of the Higgs bosons are obtained from the complex poles of the full propagator matrix. The inverse propagator matrix is a $(6 \times 6)$ matrix that reads

$$\begin{aligned} {\hat{{\varvec{\Delta }}}}^{-1}{\left( k^2\right) }= & {} i \left[ k^2\mathbf {1} - \begin{pmatrix} \mathcal {M}_S^2 &{}\quad 0\\ 0 &{}\quad \mathcal {M}_P^2 \end{pmatrix} \right. \nonumber \\&\quad \left. + \begin{pmatrix} {\hat{{\varvec{\Sigma }}}}_S{\left( k^2\right) } &{}\quad 0\\ 0 &{}\quad {\hat{{\varvec{\Sigma }}}}_P{\left( k^2\right) } \end{pmatrix} \right] . \end{aligned}$$

(26)

Here ${\hat{{\varvec{\Sigma }}}}_S$ and ${\hat{{\varvec{\Sigma }}}}_P$ denote the matrices of the renormalized self-energy corrections to the neutral ${\mathcal {CP}}$-even and ${\mathcal {CP}}$-odd Higgs fields. In the ${\mathcal {CP}}$-conserving limit there are no transition elements between ${\mathcal {CP}}$-even and ${\mathcal {CP}}$-odd degrees of freedom, which is why Eq. (26) is block diagonal.

In principle, contributions from mixing with the longitudinal Z boson have to be considered as well. However, these contributions as well as those from mixing with the Goldstone mode enter the mass predictions only at subleading two-loop level [115, 116]. Since these contributions are numerically small [117] we neglect them in the following and use a $(5\times 5)$ propagator matrix. The $(5\times 5)$ matrices are denoted by the symbols ${\hat{{\varvec{\Delta }}}}_{hh}$ for the propagators and ${\hat{{\varvec{\Sigma }}}}_{hh}$ for the renormalized self-energies in the following. The complex poles of the propagator are given by the values of the squared external momentum $k^2$ for which the determinant of ${\hat{{\varvec{\Delta }}}}_{hh}^{-1}$ vanishes,

$$\begin{aligned} \det {\left[ {\hat{{\varvec{\Delta }}}}^{-1}_{hh}{\left( k^2\right) } \right] _{k^2\;=\;M_{h_i}^2\;+\;i\,\Gamma _{h_i}\,M_{h_i}}}&\overset{!}{=} 0. \end{aligned}$$

(27)

The real part, $M_{h_i}^2$, of each pole yields the loop-corrected mass of the corresponding Higgs boson $h_i$.

In this work, a model file for FeynArts [16, 17] of the GNMSSM at the tree level has been generated with the help of SARAH [18,19,20,21]. In addition, the one-loop counterterms for all vertices and propagators have been implemented, and a renormalization scheme which is consistent with Refs. [23, 24] for the cases of the MSSM and NMSSM has been set up. All $\mathbb {Z}_3$-violating parameters are renormalized in the $\overline{\text {DR}}$ scheme, see Appendix A for a list of the respective beta functions. The numerical input values of all $\overline{\text {DR}}$-renormalized parameters are understood to be given at a renormalization scale which equals the top-quark pole mass. The renormalized self-energies of the Higgs bosons ${\hat{{\varvec{\Sigma }}}}_{hh}$ are evaluated with the help of FormCalc [22] and LoopTools [22] by taking into account the full contributions from the GNMSSM at the one-loop order. For other variations of the NMSSM, similar calculations of Higgs-mass contributions up to the two-loop order have been performed in Refs. [118,119,120,121,122,123,124,125,126]. A comparison of results from public codes using different renormalization schemes can be found in Refs. [127, 128].

As an approximation, we have added the leading two-loop contributions in the MSSM of $\mathcal {O}{\left( \alpha _t\alpha _s\right) }$ [129] and $\mathcal {O}{\left( \alpha _{t}^2\right) }$ [130, 131] at vanishing external momentum to their MSSM-like counterparts in the $\mu$NMSSM (for a discussion of this approximation in the NMSSM see Ref. [124]). They are taken from their current implementation in FeynHiggs [25,26,27,28,29,30,31,32].⁶ We thus have

$$\begin{aligned} {\hat{{\varvec{\Sigma }}}}_{hh}{\left( k^2\right) } \approx \left. {\hat{{\varvec{\Sigma }}}}^{(\text {1L})}_{hh}{\left( k^2\right) } \right| ^{{\text {GNMSSM}}} + \left. {\hat{{\varvec{\Sigma }}}}^{(\text {2L})}_{hh}{\left( k^2\right) } \right| _{k^2=0}^{{{\text {MSSM, leading}}}}. \end{aligned}$$

(28)

We note that the two-loop contributions of $\mathcal {O}{\left( \alpha _b\alpha _s\right) }$ to the MSSM-like Higgs self-energies are not included in our calculation. However, in the definition of the bottom-Yukawa coupling we employ a running $\overline{\text {DR}}$ bottom mass at the scale $m_t$ [116] which enters ${\hat{{\varvec{\Sigma }}}}^{(\text {1L})}_{hh}{\left( k^2\right) }\big |^{{\text {GNMSSM}}}$, and we take into account large $t_\beta$-enhanced contributions to the bottom mass as discussed in Refs. [116, 135,136,137,138,139,140]. We expect that the missing two-loop piece of $\mathcal {O}{\left( \alpha _b\alpha _s\right) }$ is numerically subleading (for a discussion in the MSSM see [141, 142]).

Higher-order propagator-type corrections are not only needed for predicting the Higgs-boson masses, but also for the correct normalization of S-matrix elements involving Higgs bosons as external particles. The wave-function normalization factors incorporating the effects of the mixing between the different Higgs bosons can be written as a non-unitary matrix $Z_{ij}^{{\mathrm{mix}}}$. It is constructed from the Higgs self-energies and their derivatives with respect to $k^2$, evaluated at the various physical poles; for details we refer the reader to Refs. [24, 143,144,145,146]. A recent application in the framework of the NMSSM can be found in Ref. [147]. Here, we follow the setup outlined in Section 2.6 of Ref. [24] and determine the matrix elements of $Z_{ij}^{{\mathrm{mix}}}$ from the eigenvalue equation

$$\begin{aligned}&\left[ \text {diag}{\left( m_{h_1}^2,m_{h_2}^2,m_{h_3}^2,m_{a_1}^2,m_{a_2}^2\right) }\right. \nonumber \\&\qquad \left. -{\hat{{\varvec{\Sigma }}}}_{hh}\big |_{k^2\;=\;M_{h_i}^2\;+\;i\,\Gamma _{h_i}\,M_{h_i}} \right] _{kl} \,Z^{{\mathrm{mix}}}_{il} \nonumber \\&\quad = \left( M_{h_i}^2+i\,\Gamma _{h_i}\,M_{h_i}\right) Z^{{\mathrm{mix}}}_{ik}. \end{aligned}$$

(29)

The normalization of each eigenvector is fixed by

$$\begin{aligned}&\left[ \frac{{\mathrm {d}}{\hat{{\varvec{\Delta }}}}^{-1}_{hh}}{{\mathrm {d}}k^2}\bigg |_{k^2\;=\;M_{h_i}^2\;+\;i\,\Gamma _{h_i}\,M_{h_i}} \right] _{kl}\,Z^{{\mathrm{mix}}}_{ik}\,Z^{{\mathrm{mix}}}_{il}\nonumber \\&\quad = \left[ \mathbf {1} + \frac{{\mathrm {d}}{\hat{{\varvec{\Sigma }}}}_{hh}}{{\mathrm {d}}k^2}\bigg |_{k^2\;=\;M_{h_i}^2\;+\;i\,\Gamma _{h_i}\,M_{h_i}} \right] _{kl} \,Z^{{\mathrm{mix}}}_{ik}\,Z^{{\mathrm{mix}}}_{il} = 1. \end{aligned}$$

(30)

In our numerical analysis we denote the three ${\mathcal {CP}}$-even mass eigenstates $h_i$ as $h^0$, $H^0$ and $s^0$, and the two ${\mathcal {CP}}$-odd mass eigenstates $a_i$ as $A^0$ and $a_s$. These assignments become ambiguous as soon as loop corrections are included. In our analysis we use the largest admixture to a loop-corrected mass state in order to define the assignment. For this purpose we employ the previously discussed loop-corrected mixing matrix $Z^{{\mathrm{mix}}}_{ij}$. In this way $s^0$ denotes the dominantly singlet-like state. The light doublet-like state is named $h^0$ and the heavy doublet-like state is $H^0$. The ${\mathcal {CP}}$-odd Higgs bosons are the predominantly singlet-like state $a_s$ and the doublet-like state $A^0$.

2.5 Trilinear Higgs-boson self-couplings

In order to discuss possible distinctions between the NMSSM and the $\mu$NMSSM, the Higgs-boson self-couplings are particularly relevant. Experimentally these self-couplings can be probed through Higgs pair production or through decays of a heavier Higgs boson to two lighter ones. Through electroweak symmetry breaking there is also a strong correlation with Higgs-boson decays into Higgs bosons and gauge bosons, e.g. $A^0\rightarrow Zh^0$ or $H^0\rightarrow Za_s$. For both, the Higgs mixing between singlets and doublets is essential. We take both types of decays into account when checking against experimental limits from Higgs boson searches, but only exemplify the parameter dependence for the decays involving only Higgs bosons in our numerical analysis below.

The Higgs self-couplings are introduced in Eq. (12). In order to simplify their presentation in the neutral sector we define $\phi _i$ to be the i-th component of $\Phi =\left( \sigma _d,\sigma _u,\sigma _s,A,\phi _s\right)$, where in the ${\mathcal {CP}}$-odd sector the Goldstone boson is in a basis where it does not mix with the other Higgs bosons at lowest order (see discussion in Sect. 2.2).⁷ We denote the couplings as $\lambda _{ijk}$ for the interactions among three Higgs bosons $\phi _i\phi _j\phi _k$ in the basis $\Phi$. For the couplings among the ${\mathcal {CP}}$-even components – expressed in gauge couplings (see Eq. (13) for the relation to the gauge-boson masses) – we obtain at the tree level

$$\begin{aligned} \lambda _{111}&=-\tfrac{3}{2}\left( g_1^2+g_2^2\right) c_{\beta }\,v, \end{aligned}$$

(31a)

$$\begin{aligned} \lambda _{112}&=\tfrac{1}{2}\left( g_1^2+g_2^2-4\,\lambda ^2\right) s_{\beta }\,v, \end{aligned}$$

(31b)

$$\begin{aligned} \lambda _{113}&=-2\,\lambda \left( \mu +\mu _{\text {eff}}\right) , \end{aligned}$$

(31c)

$$\begin{aligned} \lambda _{122}&=\tfrac{1}{2}\left( g_1^2+g_2^2-4\,\lambda ^2\right) c_{\beta }\,v, \end{aligned}$$

(31d)

$$\begin{aligned} \lambda _{123}&=\lambda \left( \nu +A_\lambda + 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) , \end{aligned}$$

(31e)

$$\begin{aligned} \lambda _{133}&= 2\,\lambda \left( \kappa \,s_{\beta }\,v-\lambda \,c_{\beta }\,v\right) , \end{aligned}$$

(31f)

$$\begin{aligned} \lambda _{222}&=-\tfrac{3}{2}\left( g_1^2+g_2^2\right) s_{\beta }\,v, \end{aligned}$$

(31g)

$$\begin{aligned} \lambda _{223}&=-2\,\lambda \left( \mu +\mu _{\text {eff}}\right) , \end{aligned}$$

(31h)

$$\begin{aligned} \lambda _{233}&= 2\,\lambda \left( \kappa \,c_{\beta }\,v-\lambda \,s_{\beta }\,v\right) , \end{aligned}$$

(31i)

$$\begin{aligned} \lambda _{333}&=-2\,\kappa \left( A_\kappa + 3\,\nu \right) - 12\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}. \end{aligned}$$

(31j)

The couplings of ${\mathcal {CP}}$-even components to ${\mathcal {CP}}$-odd components are given by

$$\begin{aligned} \lambda _{144}&=-\tfrac{1}{2}\left( g_1^2+g_2^2\right) c_{\beta }\,v, \end{aligned}$$

(31k)

$$\begin{aligned} \lambda _{244}&=\tfrac{1}{2}\left( g_1^2+g_2^2-4\,\lambda ^2\right) s_{\beta }\,v, \end{aligned}$$

(31l)

$$\begin{aligned} \lambda _{344}&=-2\,\lambda \left( \mu +\mu _{\text {eff}}\right) , \end{aligned}$$

(31m)

$$\begin{aligned} \lambda _{345}&=-\lambda \left( \nu +A_{\lambda }+2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) , \end{aligned}$$

(31n)

$$\begin{aligned} \lambda _{155}&=\tfrac{1}{2}\left( g_1^2+g_2^2-4\,\lambda ^2\right) c_{\beta }\,v, \end{aligned}$$

(31o)

$$\begin{aligned} \lambda _{255}&=-\tfrac{1}{2}\left( g_1^2+g_2^2\right) s_{\beta }\,v, \end{aligned}$$

(31p)

$$\begin{aligned} \lambda _{355}&=-2\,\lambda \left( \mu +\mu _{\text {eff}}\right) . \end{aligned}$$

(31q)

Similarly we can write down the couplings $\tilde{\lambda }_i$ for the interaction $\phi _iH^+H^-$ of the neutral Higgs bosons in the basis $\Phi$ to the physical charged Higgs bosons (the Goldstone bosons are again in a basis where they do not mix) as follows:

$$\begin{aligned} \tilde{\lambda }_1&= \lambda ^2\,s_{\beta }\,s_{2\beta }\,v + \tfrac{1}{2}\left( g_1^2+g_2^2\right) c_{\beta }\,c_{2\beta }\,v - g_2^2\,c_{\beta }\,v, \end{aligned}$$

(32a)

$$\begin{aligned} \tilde{\lambda }_2&= \lambda ^2\,c_{\beta }\,s_{2\beta }\,v - \tfrac{1}{2}\left( g_1^2+g_2^2\right) s_{\beta }\,c_{2\beta }\,v - g_2^2\,s_{\beta }\,v, \end{aligned}$$

(32b)

$$\begin{aligned} \tilde{\lambda }_3&=-\lambda \left[ 2\left( \mu +\mu _{\text {eff}}\right) + \left( \nu + 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}+ A_\lambda \right) s_{2\beta }\right] . \end{aligned}$$

(32c)

The remaining couplings which are not present above are equal to zero. Again $s_x$ and $c_x$ are defined as $s_x=\sin (x)$ and $c_x=\cos (x)$. In most of the cases when $\mu$ or $\mu _{\text {eff}}$ appear, the coupling depends on the sum $\left( \mu +\mu _{\text {eff}}\right)$. For the interactions of the neutral Higgs bosons, only a few couplings carry an (additional) proportionality to $\mu _{\text {eff}}$ itself, see $\lambda _{123}$, $\lambda _{345}$ and $\lambda _{333}$ which all involve the singlet state. This dependence manifests itself for the former two couplings in the Higgs-to-Higgs decays $s^0\rightarrow h^0\,h^0$, $H^0\rightarrow s^0\,h^0$ and $A^0\rightarrow s^0\,a_s$. In the charged Higgs sector, the decay $s^0\rightarrow H^+\,H^-$ has a direct dependence on $\mu _{\text {eff}}$ at the tree level in addition to $(\mu +\mu _{\text {eff}})$ for a dominantly singlet-like state $s^0$, as can be seen in ${\tilde{\lambda }}_3$. For both cases a very pronounced mixing of the singlet states with the Higgs doublets, and an individual dependence on $\mu _{\text {eff}}$ and on the sum $(\mu +\mu _{\text {eff}})$ can also occur in other Higgs-to-Higgs decays. We will emphasize later that Higgs mixing is crucial for the observed dependences on $\mu _{\text {eff}}$ and $\mu$. We consider the decays at the tree level, however, including the external corrections to Higgs-boson masses and mixing as discussed in Sect. 2.4. Though, we emphasize that higher-order contributions to Higgs-boson self-couplings and Higgs-boson decays can be large, see Refs. [147,148,149,150] for corresponding calculations in the NMSSM.

2.6 Neutralino and chargino masses

We write the neutralino and chargino sector in the gauge-eigenstate bases

$$\begin{aligned} \big (\psi ^0\big )^{\text {T}}&=\left( \tilde{B}^0, \tilde{W}_3^0, \tilde{h}_d^0, \tilde{h}_u^0, \tilde{s} \right) , \big (\psi ^+\big )^{\text {T}}=\left( \tilde{W}^+,\tilde{h}_u^+ \right) \nonumber \\&\quad \text {and }\;\; \big (\psi ^-\big )^{\text {T}}= \left( \tilde{W}^-,\tilde{h}_d^- \right) , \end{aligned}$$

(33)

which includes the bino component $\tilde{B}^0$, the neutral and charged wino components $\tilde{W}_3^0$ and $\tilde{W}^\pm$, the neutral and charged higgsino components $\tilde{h}_{u,d}^0$ and $\tilde{h}_{u,d}^\pm$, and the singlino component $\tilde{s}^0$ in the form of Weyl spinors. Their mass terms in the Lagrangian can be written in the form

$$\begin{aligned} -\mathcal {L}_{\chi {\text {-masses}}}&=\tfrac{1}{2}\big (\psi ^0\big )^{\text {T}} {\mathcal {M}}_{\chi }\,\psi ^0 +\tfrac{1}{2}\left[ \big (\psi ^-\big )^{\text {T}}{\mathcal {M}}_{\chi ^\pm }\,\psi ^+\right. \nonumber \\&\quad \left. +\, \big (\psi ^+\big )^{\text {T}}{\mathcal {M}}_{\chi ^\pm }^{\text {T}}\,\psi ^-\right] +\text {h.}\,\text {c.}. \end{aligned}$$

(34)

The symmetric mass matrix of the neutralinos and the mass matrix of the charginos are given by

$$\begin{aligned} {\mathcal {M}}_{\chi }&= \begin{pmatrix} M_1 &{}\quad 0 &{}\quad -m_Z\,s_{\text {w}}\,c_\beta &{}\quad m_Z\,s_{\text {w}}\,s_\beta &{}\quad 0\\ \cdot &{}\quad M_2 &{}\quad m_Z\,c_{\text {w}}\,c_\beta &{}\quad -m_Z\,c_{\text {w}}\,s_\beta &{}\quad 0\\ \cdot &{}\quad \cdot &{}\quad 0 &{}\quad -\left( \mu + \mu _{\text {eff}}\right) &{}\quad -\lambda \,v\,s_\beta \\ \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad 0 &{}\quad -\lambda \,v\,c_\beta \\ \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad 2\,\tfrac{\kappa }{\lambda }\,\mu _{\text {eff}}+ \nu \end{pmatrix}, \end{aligned}$$

(35a)

$$\begin{aligned} {\mathcal {M}}_{\chi ^\pm }&= \begin{pmatrix} M_2 &{}\quad \sqrt{2}\,m_W\,s_\beta \\ \sqrt{2}\,m_W\,c_\beta &{}\quad \mu +\mu _{\text {eff}}\end{pmatrix}. \end{aligned}$$

(35b)

The abbreviations $s_{\text {w}}=g_2/\sqrt{g_1^2+g_2^2}$ and $c_{\text {w}}=g_1/\sqrt{g_1^2+g_2^2}$ denote the sine and cosine of the weak-mixing angle, respectively. We see that the mass scale of the MSSM-like higgsinos is given by the sum $(\mu +\mu _{\text {eff}})$, and the mass scale of the singlino is controlled by $(2\,\kappa /\lambda \,\mu _{\text {eff}}+\nu )$. If only the electroweakinos were taken into account at the tree level, it is apparent that the $\mu$NMSSM would be indistinguishable from the NMSSM, since any shift in masses and mixing induced through $\mu$ could be compensated through shifts in $\mu _{\text {eff}}$. However, such shifts will induce differences in the Higgs sector.

Including the singlino elements (with $\nu =0\,\text {GeV}$ as discussed in Sect. 2.1), an NMSSM-like neutralino spectrum can be generated, where $(\mu + \mu _{\text {eff}})$ serves as the NMSSM-like $\mu _{\text {eff}}$ term and $\kappa$ is rescaled as

$$\begin{aligned} \kappa&\rightarrow \tilde{\kappa }=\kappa \,\frac{\mu +\mu _{\text {eff}}}{\mu _{\text {eff}}} . \end{aligned}$$

(36)

This rescaling on the other hand affects the Higgs spectrum, thus giving a possible handle to distinguish the $\mu$NMSSM from the NMSSM.

For the case where $\kappa$ and $\lambda$ are kept fixed, an interesting behavior can be observed for light higgsinos. For small $(\mu + \mu _{\text {eff}})$ huge cancellations may occur between the two contributions with large $\mu > 0\,\text {GeV}$ and $\mu _{\text {eff}}$ of the same size but opposite sign. As a consequence, the singlino state becomes much heavier compared to the case of the NMSSM (of the order of $\mu _{\text {eff}}$). Such a scenario is displayed in Fig. 1 where the neutralino–chargino spectrum is shown for the cases $\mu \in \{0,200,1000\}$ GeV ($\nu$ is set equal to zero). The left column with $\mu =0\,\text {GeV}$ corresponds to the case of the NMSSM. The masses are obtained by diagonalizing the tree-level mass matrices in Eq. (35). With respect to the $\mathbb {Z}_3$-invariant NMSSM, the most significant alteration is visible in the singlino component (blue): the mass shows an about-linear increase with $\mu$ since the sum $(\mu +\mu _{\text {eff}})$ is kept fixed. Due to the varying mixing, some influence on the masses of the other two neutral higgsino states (orange) can be seen despite a constant higgsino mass parameter $(\mu +\mu _{\text {eff}})$; the impact on the gaugino states (red and purple) remains negligible. The chargino masses (rose) are not influenced by the different choices.

In a scenario as discussed above, with light higgsinos as well as large $\mu$ and $\mu _{\text {eff}}$ of opposite signs, the lightest neutralino is typically not the singlino state as the singlino mass is pushed up, see Fig. 1. The lightest supersymmetric particle (LSP), however, tends to be the gravitino, which is at risk to overclose the universe as dark matter candidate. In this case, the inflationary scenario has to be such that the reheating temperature stays below a certain value and gravitinos are not overproduced in the early universe, see our discussion in Sect. 2.1.

2.7 Sfermion masses

The mass term for each charged sfermion – for which we distinguish the superpartners of the left- and right-handed components by the notation $\tilde{f}_{\text {L}}$ and $\tilde{f}_{\text {R}}$, respectively – takes the following form in the Lagrangian

$$\begin{aligned} -\mathcal {L}_{{\tilde{f}}{\text {-masses}}}=\left( \tilde{f}_{\text {L}}^\dagger , \tilde{f}_{\text {R}}^\dagger \right) {\mathcal {M}}^2_{{\tilde{f}}} \begin{pmatrix}\tilde{f}_{\text {L}}\\ \tilde{f}_{\text {R}}\end{pmatrix}, \end{aligned}$$

(37)

Fig. 1

The masses of the neutralinos and charginos are shown for different values of $\mu$. The effective higgsino mass parameter is fixed at $\mu + \mu _{\text {eff}}= -200\,\text {GeV}$, and the mass parameters for the gauginos are set to $M_1 = 100\,\text {GeV}$ and $M_2 = 300\,\text {GeV}$. The other relevant parameters are given in the legend of the figure. The mostly bino- and wino-like states $\tilde{B}^0$ (purple) and $\tilde{W}^0$ (red) as well as the charginos $\tilde{\chi }^{\pm }$ (rose) have (nearly) constant masses. The masses of the two mostly higgsino-like states $\tilde{H}^0$ (orange) and the mostly singlino-like state $\tilde{S}^0$ (blue) vary visibly

where the squared mass matrix reads

$$\begin{aligned} {\mathcal {M}}^2_{\tilde{f}}&= \begin{pmatrix} m_f^2 + m_{\tilde{f}_{\text {L}}}^2 + m_Z^2\,c_{2\beta } \left( T^{(3)}_f - Q_f\,s_{\text {w}}^2\right) &{}\quad m_f \left[ A_f - \theta _f \left( \mu + \mu _{\text {eff}}\right) \right] \\ m_f \left[ A_f - \theta _f \left( \mu + \mu _{\text {eff}}\right) \right] &{}\quad m_f^2 + m_{\tilde{f}_{\text {R}}}^2 + m_Z^2\,c_{2\beta }\,Q_f\,s_{\text {w}}^2 \end{pmatrix}, \end{aligned}$$

(38a)

$$\begin{aligned} \theta _f&= \left\{ \begin{array}{ll} t_\beta , &{}\quad f\in \{e,\mu ,\tau ,d,s,b\}, \\ \frac{1}{t_\beta }, &{}\quad f\in \{u,c,t\}. \end{array}\right. \end{aligned}$$

(38b)

Therein we denote the fermion mass by $m_f$, the bilinear soft-breaking parameters by $m_{\tilde{f}_{{\text {L,R}}}}$, the trilinear soft-breaking parameter by $A_f$, and the electric and weak charges by $Q_f$ and $T^{(3)}_f$.

In this sector we encounter the sum $(\mu +\mu _{\text {eff}})$ in the off-diagonal elements of the sfermion mass matrices as the only difference compared to the NMSSM or MSSM. If this sum becomes large, $A_f/\theta _f$ needs to be adjusted in order to avoid tachyonic sfermions in particular for the third generation squarks. In that case, bounds from vacuum stability (see e.g. Eq. (24)) can also constrain the viable size of $\left( \mu +\mu _{\text {eff}}\right)$.

3 Phenomenological analysis

In this section we investigate various scenarios of the $\mu$NMSSM with a particular focus on the $\mu$ parameter. We will point out differences between the $\mu$NMSSM and the ordinary $\mathbb {Z}_3$-preserving NMSSM, where the latter corresponds to the limit $\mu = 0\,\text {GeV}$ of the $\mu$NMSSM. At first we qualitatively define the investigated scenarios, before we numerically analyze them.

3.1 Viable parameter space compatible with theoretical and experimental bounds

In the previous sections we have analytically discussed the relevant sectors of the $\mu$NMSSM with respect to effects of the inflation-inspired $\mu$ parameter. Before we provide a phenomenological analysis – including the higher-order effects specified in Sect. 2.4 – we discuss the viability of various parameter regions. As discussed in Sect. 2.1 we focus on scenarios with non-zero $\mu$ and $B_\mu$, but set all other $\mathbb {Z}_3$-violating parameters in the superpotential (9) and soft-breaking Lagrangian (10), i.e. $\xi$, $C_\xi$, $\nu$ and $B_\nu$, equal to zero.

The $\mu$ parameter of the model is positive by construction in the inflation-inspired model, see Eqs. (6) and (8). Furthermore, we only investigate scenarios with $\mu \lesssim 2\,\hbox {TeV}$ to stay in the phenomenologically interesting region for the collider studies. Still, we point out that also much larger scales are viable from the inflationary point of view. As discussed in Sect. 2.1, $\mu \simeq \frac{3}{2} \, m_{3/2} \, 10^5 \, \lambda$ implies that much larger values of $\mu$ are possible depending on $\lambda$ and $m_{3/2}$. However, large values of $\mu$ can cause tachyonic states as discussed in Sect. 2.2.

We characterize the scenarios in the following parameter regions: small values of $\mu \simeq 1\,\text {GeV}$,⁸ large values of $\mu \gtrsim 1\,\text {TeV}$ with $\mu _{\text {eff}}\simeq -\mu$, and values of $\mu$ $\mathord {\gtrsim }\,100\,\text {GeV}$ with moderate or small $|\mu _{\text {eff}}|$ $\mathord {\lesssim }\,100\,\text {GeV}$.

small ${\varvec{\mu \simeq 1}}\,{{\mathbf {GeV}}}$:

in the case of small $\mu$ also the soft-breaking term $B_\mu \,\mu$ becomes small. Since in addition we set all other $\mathbb {Z}_3$-violating parameters to zero, we recover the standard NMSSM in this limit (see the discussion in Fig. 1). Thus, differences between the NMSSM and the $\mu$NMSSM can directly be deduced by comparing scenarios with zero and non-zero $\mu$ parameter.

large ${\varvec{\mu \pmb {\gtrsim } 1}}\,{\mathbf {TeV}}$ with:

${\varvec{\mu _{\text {eff}}\simeq -\mu }}$ as discussed in Sect. 2.6, the higgsino masses depend only on the sum $\left( \mu +\mu _{\text {eff}}\right)$ at the tree level. The same combination contributes to the sfermion mixing in combination with the trilinear soft SUSY-breaking terms. In order to keep these quantities small at a large value of $\mu$, one can assign the same value with opposite sign to $\mu _{\text {eff}}$; note, however, that the region $|\mu +\mu _{\text {eff}}|\lesssim 100\,\text {GeV}$ is experimentally excluded by direct searches for charginos [151, 152]. An immediate consequence of large, opposite sign $\mu _{\text {eff}}$ and $\mu$ is that the singlino and the singlet-like Higgs states receive large masses of the order of $|\mu _{\text {eff}}|$ [see the (5, 5) entry in Eq. (35a) and the (3, 3) elements in Eqs. (17a) and (17b)], which provides a potential distinction from the standard NMSSM. Similar to the increase of the singlino mass, fixing $\left( \mu +\mu _{\text {eff}}\right)$ together with an increase in $\mu$ – and thus an increase in the absolute value of $\mu _{\text {eff}}$ – lifts the masses of the singlet states also in the Higgs sector. In the neutralino sector these contributions can be absorbed by a rescaling of $\kappa$, see Sect. 2.6; however, in the Higgs sector $\mu _{\text {eff}}$ also appears in other combinations, thus leaving traces which can potentially distinguish the $\mu$NMSSM from the NMSSM.

${\varvec{\mu \,\pmb {\mathord {\gtrsim }\,} 100}}\,{\mathbf {GeV}}$ with :

 ${\varvec{\pmb {|}\mu _{\text {eff}}\pmb {|}\,\pmb {\mathord {\lesssim }\,}100}}\,{\mathbf {GeV}}$ if we allow for a large $\mu$ parameter without constraining the sum $\left( \mu +\mu _{\text {eff}}\right)$, the spectra of higgsinos, sfermions and Higgs bosons are changed at the same time. A large sum $\left( \mu +\mu _{\text {eff}}\right)$ causes very large mixing between the singlet and doublet sectors (see discussion in Sect. 2.2), eventually driving one Higgs state tachyonic. In some part of the parameter space this can be avoided by tuning $B_\mu$ accordingly. Another constraint arises from the sfermion sector, most notably the sbottoms and staus: a large $\left( \mu +\mu _{\text {eff}}\right)$ induces large terms in the off-diagonal elements of the sfermion mass matrices (enhanced by $\tan \beta$ for the case of down-type sfermions) which can potentially cause tachyons, also depending on the values of the trilinear soft-breaking parameters $A_f$. As discussed in Sect. 2.3, constraints from charge- and color-breaking minima induced by too large soft-breaking trilinear parameters (see Eq. (24) with $\mu$ promoted to $\left( \mu +\mu _{\text {eff}}\right)$), have a much smaller impact in the $\mu$NMSSM as compared to the MSSM [108].

A special case of this scenario is the possibility of having $\mu$ at the electroweak scale in combination with an almost vanishing $|\mu _{\text {eff}}|\ll \mu$. This implies that $\left( \mu +\mu _{\text {eff}}\right)$ remains at the electroweak scale. In contrast to the standard NMSSM this scenario allows the occurrence of both, $\kappa \gg \lambda$ and a light singlet sector. As discussed in Sect. 2.2, the mixing between singlets and doublets is in this case dominated by terms proportional to $\mu _{\text {eff}}^{-1}$. We will explicitly discuss such a scenario in Sect. 3.5.

Table 1 The input parameters which are fixed throughout our numerical analysis (interpreted as on-shell parameters if not specified otherwise). The gaugino mass parameters are denoted as $M_i$ with $i=1,2,3$. The trilinear soft-breaking terms for the sfermions $A_{f_g}$ carry the generation index $g=1,2,3$. The charged Higgs mass $m_{H^\pm }$ is fixed to the shown value, if not mentioned otherwise

There are more parameters that are relevant for the following phenomenological studies. We keep those fixed which behave similarly as in the MSSM and NMSSM. The choice of our constant input values is given in Table 1. Furthermore, we specify the values of $t_\beta$, $\kappa$, $\lambda$, and $A_\kappa$ directly at the respective places. Besides the analyses where we explicitly study the dependence on $B_\mu$, we use $B_\mu = 0\,\text {GeV}$ as default value.

As our analysis is focused on the impact of the inflation model, we are not going to discuss the influence of the sfermion parameters. If not mentioned otherwise, we use $m_{{\tilde{f}}} \equiv m_{{\tilde{f}}_L} = m_{{\tilde{f}}_R}$ and $A_{f_3} / m_{{\tilde{f}}} = 2$, which maximizes the prediction for the SM-like Higgs-boson mass at $\mu +\mu _{\text {eff}}=0\,\text {GeV}$. The gluino mass parameter $M_3$ is set well above the squark masses of the third generation which is in accordance with the existing LHC bounds. For completeness, we also give the parameters of the SM which are most relevant for our numerical study in Table 1.

The gaugino-mass parameters $M_1$ and $M_2$ do not play a big role in the following analysis, but are necessary input parameters for the mass matrices of the charginos and neutralinos in Eqs. (35). We set $M_2 = 500\,\text {GeV}$ and fix $M_1$ via the usual GUT relation, see Table 1. Our phenomenological analysis is most sensitive to the neutralino and chargino spectrum if a Higgs boson can decay into them. This is in particular the case if the particle spectrum contains light higgsinos, whose masses are controlled through $\left( \mu +\mu _{\text {eff}}\right)$. For a scenario with light higgsinos and a light singlino we will later also discuss the electroweakino phenomenology at a linear collider, see Sect. 3.4.

Fig. 2

The loop-corrected Higgs-boson spectrum and the tree-level neutralino spectrum are shown in the $\mu$NMSSM for scenarios with $\mu \in \{0,200,1000\}\,\text {GeV}$ and $\mu +\mu _{\text {eff}}=-200\,\text {GeV}$ fixed. The parameters are chosen such that the state $h^0$ (black) that is mostly SM-like has a mass around $125\,\text {GeV}$; the gray band shows a $3\,\text {GeV}$ interval around the experimentally measured Higgs mass. Furthermore, the masses of the ${\mathcal {CP}}$-even singlet-like state $s^0$ (blue), the ${\mathcal {CP}}$-odd singlet-like state $a_s$ (purple), and the heavy ${\mathcal {CP}}$-even Higgs doublet and MSSM-like ${\mathcal {CP}}$-odd components $H^0,A^0$ with values close to the input $m_{H^\pm }\sim 800\,\text {GeV}$ (red) are shown, where the assignments are made according to the loop-corrected mixing matrix $Z^{{\mathrm{mix}}}_{ij}$ for the Higgs sector, see Sect. 2.4. For the neutralino sector on the right, yellow lines show the dominantly bino-like state $\tilde{B}^0$, and green lines the wino-like state $\tilde{W}^0$. The singlino $\tilde{S}^0$ is shown in rose and the two (doublet) higgsinos $\tilde{H}^0$ appear in orange. The assignments are determined by the tree-level mixing matrix. The parameter values are given in the plot and in Table 1

As we use $\mu \simeq \frac{3}{2}\,m_{3/2}\,10^5\,\lambda$ and focus on $\mu \lesssim 2\,\text {TeV}$, we are considering scenarios where the gravitino typically is the LSP. We do not specify the mediator mechanism of SUSY breaking; however, we assume that such a light gravitino is always possible. Although the gravitino is the Dark Matter candidate, traditional collider searches for a neutralino LSP do apply in our case: for instance, if the next-to LSP (NLSP) is gaugino-like, it can decay into a photon and the gravitino, where the NLSP lifetime is typically so large that it can escape the detector [153]. We roughly estimate the NLSP phenomenology via the approximate partial decay width of the neutralino NLSP into a photon or Z boson and gravitino $\psi _{3/2}$ according to Refs. [154,155,156]

$$\begin{aligned} \Gamma _{{\tilde{\chi }}^0_1 \rightarrow \gamma \psi _{3/2}}\simeq & {} \frac{\left| N_{11} \, c_{\text {w}} + N_{12} \, s_{\text {w}}\right| ^2}{48\,\pi \,M_{\text {Pl}}^2} \frac{m_{{\tilde{\chi }}_1^0}^5}{m_{3/2}^2}, \nonumber \\ \Gamma _{{\tilde{\chi }}^0_1 \rightarrow Z \psi _{3/2}}\simeq & {} \frac{\left| -N_{11} \, s_{\text {w}} + N_{12} \, c_{\text {w}}\right| ^2}{48\,\pi \,M_{\text {Pl}}^2} \frac{m_{{\tilde{\chi }}_1^0}^5}{m_{3/2}^2}\left( 1-\frac{m_Z^2}{m_{{\tilde{\chi }}_1^0}^2}\right) ^4,\nonumber \\ \end{aligned}$$

(39)

where we expanded in a small gravitino mass $m_{3/2}$ and use $s_{\text {w}}$ and $c_{\text {w}}$ for the sine and cosine of the weak mixing angle, respectively. The neutralino mixing matrix elements $N_{ij}$ follow from the diagonalization of Eq. (35a). As an example for the decay of the NLSP with $m_{{\tilde{\chi }}_1^0} \simeq 100 \, \text {GeV}$ and $m_{3/2} \simeq 10\,\text {MeV}$, we find a lifetime of $\tau \equiv 1/\Gamma = \mathcal {O}(1 \, \mathrm {s})$. Thus, the NLSP decays outside of the detector and is counted as missing energy. Nevertheless, such decays might be of certain interest with respect to future experimental searches for long-lived particles like the MATHUSLA experiment [157]. Note that for a higgsino-like NLSP the decay into a Z boson and the gravitino is obtained by replacing the mixing factor in Eq. (39) by $|{-}N_{13}c_\beta +N_{14}s_\beta |^2$. If kinematically open, also the decay into a (singlet-like) ${\mathcal {CP}}$-even or ${\mathcal {CP}}$-odd Higgs boson and the gravitino can occur (see Ref. [155]), but this decay mode does not change the qualitative features described above.

We have chosen $m_{H^\pm }$ as an input parameter and adjust $A_\lambda$ according to Eq. (19). If not denoted otherwise, we set $m_{H^\pm } = 800\,\text {GeV}$. We use HiggsBounds version 5.1.0beta [33,34,35,36,37] in order to implement the constraints on the parameter space of each of our scenarios resulting from the search limits for additional Higgs bosons. In this context, the exclusion limits from $H,A \rightarrow \tau \tau$ decays are particularly important. For relatively low values of $\tan \beta$ the choice of $m_{H^\pm }=800\,\text {GeV}$ is well compatible with these bounds. The code HiggsBounds determines for each parameter point the most sensitive channel and evaluates whether the parameter point is excluded at the $95\%$ confidence level (C.L.). We use those exclusion bounds as a hard cut in the parameter spaces of our analyses.

We also indicate the regions of the parameter space which provide a Higgs boson that is compatible with the observed state at $125\,\hbox {GeV}$. These regions are obtained with the help of HiggsSignals version 2.1.0beta [38]. The code HiggsSignals evaluates a total $\chi ^2$ value, obtained as a sum of the $\chi ^2$ values for each of the 85 implemented observables. Four more observables are added, which test the compatibility of the predicted Higgs-boson mass with the observed value of $125\,\hbox {GeV}$. This latter test includes a theoretical uncertainty on the predicted Higgs-boson mass of about $3\,\hbox {GeV}$, such that a certain deviation from the four measured mass values (from the two channels with either a $\gamma \gamma$ or a $ZZ^{(*)}$ final state from both experiments ATLAS and CMS) is acceptable. Thus, in total HiggsSignals tests 89 observables.

Since all our two-dimensional figures include a region with a SM-like Higgs boson,⁹ we classify the compatibility with the observed state as follows: we determine the minimal value of $\chi ^2$, denoted by $\chi _m^2$, in the two-dimensional plane and then calculate the deviation $\Delta \chi ^2=\chi ^2-\chi _m^2$ from the minimal value in each parameter point. We allow for a maximal deviation of $\Delta \chi ^2 < 5.99$, which corresponds to the $95\%$ C.L. region in the Gaussian limit. All parameter points that fall in this region $\Delta \chi ^2<5.99$ are considered to successfully describe the observed SM-like Higgs boson.

Lastly, we note that HiggsBounds and HiggsSignals are operated through an effective-coupling input. We will comment on the results of the two codes where appropriate.

For our implementation of the constraints from the electroweak vacuum stability we refer to Sect. 2.3. For informative reasons, we distinguish long-lived vacua from short-lived ones in the numerical analysis. We do not explicitly enforce a perturbativity bound on $\kappa$ and $\lambda$, but discuss this issue below.

3.2 Higgs-boson and neutralino mass spectra

In this section, we point out the differences of the Higgs-boson and neutralino mass spectra in the $\mu$NMSSM with respect to the NMSSM. Similar to the case of the MSSM, the charged and the ${\mathcal {CP}}$-even heavy doublet as well as the MSSM-like ${\mathcal {CP}}$-odd Higgs bosons are (for sufficiently large $m_{H^\pm }\gg M_Z$) quasi-degenerate.

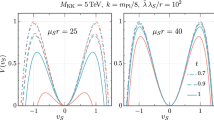
In Fig. 2, we show the masses of the Higgs bosons for vanishing $A_\kappa$ in the left, $A_\kappa = 100\,\text {GeV}$ in the middle frame, and the masses of the neutralinos in the right frame. Each frame contains three different scenarios which are characterized by the three values $\mu \in \{0, 200, 1000\}\,\text {GeV}$ while keeping all other parameters fixed: $\mu + \mu _{\text {eff}}= -200\,\text {GeV}$, $t_\beta =3.5$, $\lambda =0.2$, $\kappa =0.2\,\lambda$, and the other parameters as given in Table 1. The additional $\mu$ term has the biggest influence on the singlet-like states $s^0$ and $a_s$, as well as the singlino-like state $\tilde{S}^0$. In analogy to the discussion in Fig. 1, the reason for this behavior is the fixed sum $\left( \mu +\mu _{\text {eff}}\right)$: an increase in $\mu$ causes a larger negative $\mu _{\text {eff}}$ which primarily drives the singlet-mass terms in the (3, 3) elements of Eqs. (17a) and (17b), and the singlino-mass term in the (5, 5) element of Eq. (35a) to large values. In the investigated parameter region, the mass of the ${\mathcal {CP}}$-odd singlet is also very sensitive to $A_\kappa$: in order to avoid a tachyonic state $a_s$ over a large fraction of the parameter space, it is essential to keep $A_\kappa$ sufficiently large. However, in the left frame a scenario is shown where even a vanishing $A_\kappa$ is possible. It generates a rather light ${\mathcal {CP}}$-odd singlet-like state, whereas a sizable $A_\kappa = 100\,\text {GeV}$ (middle) lifts this mass up. There is thus the potential for a distinction between the NMSSM-limit for $\mu = 0\,\text {GeV}$ and the $\mu$NMSSM with a large $\mu = 1\,\text {TeV}$. Note that in the middle frame for $\mu = 200\,\text {GeV}$, the purple and blue lines are on top of each other.

The masses of the neutralino sector do not depend on $A_\kappa$ at the tree level. Concerning the Higgs sector, only the two cases in Fig. 2 with $\mu =0\,\hbox {GeV}$ and $A_\kappa \in \{0, 100\}\,\text {GeV}$ yield a SM-like Higgs boson that is compatible with the experimental data with $\chi ^2$ values of maximal 77. These two cases are also compatible with searches for additional Higgs bosons probed by HiggsBounds. The two cases with $\mu =1\,\hbox {TeV}$ and $A_\kappa \in \{0, 100\}\,\text {GeV}$ yield minimal $\chi ^2$ values of 82.6 and 84.0, respectively. The larger values of $\chi ^2$ mainly arise because the SM-like Higgs-boson mass is slightly below $122\,\text {GeV}$. The large variation with $\mu$ for the mass prediction of the mostly SM-like Higgs boson is mainly induced by a large mixing with the ${\mathcal {CP}}$-even singlet. The mixing for $\mu =200\,\text {GeV}$ in this scenario becomes very large for both values of $A_\kappa$ such that these cases are outside the parameter region that is compatible with the constraints by HiggsSignals. Note that the apparent preference for $\mu =0\,\text {GeV}$ over $\mu \in \{200, 1000\}\,\text {GeV}$ in this scenario is purely accidental and could be reversed by a slight shift in the input parameters, see the discussion below.

Fig. 3

In a similar manner as in Fig. 2, the spectra of Higgs bosons and neutralinos are shown in the $\mu$NMSSM. The neutralino masses are invariant under changes in $\mu$ by identifying the sum $\left( \mu +\mu _{\text {eff}}\right)$ of the $\mu$NMSSM with the $\mu _{\text {eff}}$ term of the NMSSM, and by rescaling $\kappa$ according to Eq. (36). We set $\kappa =0.8\,\lambda$, and for $\mu =0\,\text {GeV}$ we assign $\mu _{\text {eff}}=-200\,\text {GeV}$. The Higgs mass spectra are slightly affected by the rescaling

As already mentioned in Sect. 2.6, the electroweakino sector alone, at least at the tree level, does not allow one to distinguish the $\mu$NMSSM from the NMSSM: one can keep the neutralino–chargino spectrum at the tree level invariant by identifying the sum $\left( \mu +\mu _{\text {eff}}\right)$ with the $\mu _{\text {eff}}$ term of the NMSSM, and rescaling $\kappa$ according to Eq. (36). However, as pointed out above, the rescaling does have an impact on the Higgs spectrum. We show in Fig. 3 spectra for $\mu \in \{0, 200, 1000\}\,\text {GeV}$ and $A_\kappa \in \{0, 100\}\,\text {GeV}$ with fixed $\mu +\mu _{\text {eff}}=-200\,\text {GeV}$. The neutralino spectrum is shown in only one column in the very right frame. In analogy to Fig. 2, the left and middle frames show the Higgs-boson masses for the two values of $A_\kappa$ where one still can see the effect of a varying $\mu$ term. While contributions to the mass matrices in Eqs. (17) which are proportional to $\left( \mu +\mu _{\text {eff}}\right)$ or $\kappa \,\mu _{\text {eff}}$ are kept constant, other terms ${\propto }\,\mu _{\text {eff}}^{-1},\mu _{\text {eff}}^{-2}$ induce variations. Accordingly, the singlet-like Higgs masses in Fig. 3 are only slightly sensitive to $\mu$, much less than the changes observed in Fig. 2. A rising $\mu$ slightly increases the mass splitting between the singlet-like and the SM-like Higgs state.

Still, while the Higgs masses remain almost constant for not too small $\mu _{\text {eff}}$, the doublet–singlet mixing can be strongly affected by varying $\mu$ and $\mu _{\text {eff}}$ (but keeping their sum constant), in particular if the doublet–singlet mixing almost vanishes at a certain choice of $\mu$ and $\mu _{\text {eff}}$. In general, the mixing between the singlet and doublet states is affected by a large $|\mu _{\text {eff}}|$. However, by rescaling $\kappa$ according to Eq. (36) all contributions linear in $\mu _{\text {eff}}$ are absorbed, while the contributions ${\propto }\,\mu _{\text {eff}}^{-1}$ depend on the values of $t_\beta$, $M_{H^\pm }$ and $B_\mu$, see Eqs. (20a) and (20b).¹⁰ In Sect. 3.5 we will further investigate scenarios with very small $\mu _{\text {eff}}$ and enhanced Higgs-boson mixing.

Fig. 4

Contours for the SM-like Higgs mass (black) and the masses of the two singlet-like states (${\mathcal {CP}}$-even in blue and ${\mathcal {CP}}$-odd in red) in the plane $\kappa /\lambda$ versus $(\mu + \mu _{\text {eff}})$, where $\lambda = 0.6$ and $\mu = 500\,\text {GeV}$ are kept fixed and $\kappa$ and $\mu _{\text {eff}}$ vary. In the left plot $A_\kappa = 0\,\text {GeV}$ is used; in the right one $A_\kappa = 100\,\text {GeV}$. Furthermore, $\tan \beta = 2.5$ is set in both plots. The other relevant parameters are listed in Table 1. The few red and purple points have a short- and long-lived meta-stable electroweak vacuum, respectively, whereas blue points have a stable electroweak vacuum. Rose points are excluded because of tachyonic tree-level masses. The orange points cannot reproduce a non-vanishing $\mu _{\text {eff}}$ at the electroweak vacuum via the constraint of Eq. (23). With the gray vertical band we mark a naïve direct experimental exclusion bound from the chargino mass $m_{\chi ^\pm } > 94\,\text {GeV}$. Green areas are allowed by HiggsBounds and HiggsSignals (indicated as “HBHS” in the legend)

Fig. 5

The same as Fig. 4, except that $A_\kappa = 100\,\text {GeV}$ is used in both plots, and the parameter $\mu$ is set to $\mu = 1000\,\text {GeV}$ (left) and $1500\,\text {GeV}$ (right)

In Fig. 3 only the case $A_\kappa =100\,\hbox {GeV}$ in combination with $\mu =0\,\hbox {GeV}$ is allowed by HiggsBounds and HiggsSignals ($\chi ^2=80.1$), since the other scenarios are either ruled out by the decay of the SM-like Higgs into a pair of light ${\mathcal {CP}}$-odd singlets or by a too large deviation of the SM-like Higgs-boson mass from $125\,\hbox {GeV}$. In addition to our discussion above, we emphasize that in particular the latter exclusion can be easily avoided through a slight adjustment of the input parameters.

3.3 Parameter scan

We have discussed above the dependence of the Higgs masses and of the condition for the stability of the electroweak vacuum on the model parameters. Apart from the fixed parameters in Table 1, we choose seven “free” parameters that we vary in the following regimes for our analyses:

$$\begin{aligned} \mu _{\text {eff}}&\in [ -2, 2 ]\,\text {TeV}, \quad \mu \in [ 0, 2 ]\,\text {TeV}, \nonumber \\ B_\mu&\in [ -3, 3 ]\,\text {TeV}, \nonumber \\ \lambda&\in [ 10^{-4}, 1 ], \quad \kappa \in [ 10^{-4}, 1 ], \nonumber \\ A_\kappa&\in \{0, 100\}\,\text {GeV}, \quad \tan \beta \in [ 1.5, 3.5 ], \end{aligned}$$

(40)

where the largest values of $\lambda$ and $\kappa$ in the specified range of (40) violate the approximate perturbativity bound $\lambda ^2 + \kappa ^2 \lesssim 0.5$.¹¹ For the results presented in the following, this bound is always fulfilled and lies outside the plot ranges. Values of $\tan \beta \gtrsim 4$ push the model into the MSSM-like regime and are of less interest for studying the $\mu$NMSSM effects.

We have performed a scan over the parameter space defined in (40) and identified regions which are compatible with current observations concerning the properties of the SM-like Higgs boson at $125\,\text {GeV}$ and the limits from searches for additional Higgs bosons with HiggsBounds and HiggsSignals as described above. In the following, we present a selection of results from this scan; different regions of vacuum stability are illustrated, and the experimental constraints from Higgs physics are indicated. While we display some typical examples, it should be noted that similar observations hold for other regions in the parameter space as well.

Fig. 6

The same as Fig. 4 but for $\mu = 1000\,\text {GeV}$, $\tan \beta = 3.5$ and $\lambda = 0.3$

Fig. 7

Dependence of mass contours and vacuum stability, see Fig. 4 for an explanation of the color code, on the $\mathbb {Z}_3$-breaking soft SUSY-breaking $B_\mu$ term and $(\mu +\mu _{\text {eff}})$ for $\lambda = 0.5$. On the left-hand side, the value $A_\kappa = 0\,\text {GeV}$ was chosen, while on the right $A_\kappa = 100\,\text {GeV}$

In Figs. 4, 5, 6, 7, we present a selection of parameter regions. Before we discuss them individually, their common features are explained. The colored dots in the background display different states of the electroweak vacuum: we distinguish stable (blue), long-lived meta-stable (purple), short-lived meta-stable (red), and tachyonic (rose). As discussed above, we regard not only tachyonic but also meta-stable regions as excluded in the context of this inflationary scenario, but nevertheless display long- and short-lived meta-stable regions for illustration. Furthermore, we indicate those points that do not fulfill Eq. (23) and thus have no singlet vev (orange), although, as explained in Sect. 2.3, this constraint is not relevant for the $\mu$NMSSM. We overlay mass contours for the SM-like Higgs $h^0$ (black), the ${\mathcal {CP}}$-even singlet-like Higgs $s^0$ (blue), and the ${\mathcal {CP}}$-odd singlet-like Higgs $a_s$ (red). The spectrum is calculated taking into account the full one-loop and the known MSSM-like two-loop contributions as described in Sect. 2.4. The assignment of the labels $h^0$, $s^0$ and $a_s$ to the loop-corrected states is determined by the largest respective contribution in the mixing matrix $Z^{{\mathrm{mix}}}_{ij}$. We emphasize again that the parameters of the stop sector specified in Table 1 for the given scale of SUSY masses maximize the SM-like Higgs mass for $\mu +\mu _{\text {eff}}= 0\,\text {GeV}$; therefore, lower values for the SM-like Higgs mass could easily be obtained by reducing the mixing in the stop sector. Finally, we also indicate a naïve exclusion bound from direct searches for charginos by the gray-shaded band: Ref. [152] reports a lower bound on the chargino mass of $94\,\text {GeV}$ which translates into the requirement that $|\mu +\mu _{\text {eff}}|$ must be above that value in the $\mu$NMSSM. Lastly, all Figs. 4, 5, 6, 7 show the region of parameter points that successfully passed HiggsBounds and HiggsSignals and thus, in particular, yield a SM-like Higgs boson compatible with the observed state at $125\,\text {GeV}$. This region is represented through the larger, light green dots in the background. We refer to Sect. 3.1 for our statistical interpretation of the results obtained from the two codes.

A large part of the parameter region that is consistent with the measured SM-like Higgs mass is also in concordance with an absolutely stable electroweak vacuum. Small intersections between stable regions and regimes with tachyonic Higgs states exist, where there are meta-stable non-standard vacua. The strongest constraints arise from the existence of tachyonic masses for one of the physical Higgs states at the tree level. In the remaining region only a small fraction of points has a global minimum which does not coincide with the electroweak vacuum whereas the majority has a true electroweak vacuum. For the short-lived meta-stable regions, the vacuum lifetime is longer than the age of the universe.

In Fig. 4 we indicate the Higgs-mass contours and the constraints from vacuum stability in the plane of $\left( \mu +\mu _{\text {eff}}\right)$ and $\kappa /\lambda$ with fixed $\mu$ and $\lambda$. Note that for this choice of variables the tree-level doublet sector in Eqs. (17a), (17b) and (20a) remains constant; any structure visible in the prediction of the SM-like Higgs mass is thus induced by mixing with the singlet state, or by loop corrections. The chosen parameter values are indicated in the legends of the figures and in Table 1; in the left plot $A_\kappa =0\,\text {GeV}$ is used, while in the right plot $A_\kappa =100\,\text {GeV}$. The value of $A_\kappa$ has an impact in particular on the mass scale of the ${\mathcal {CP}}$-odd singlet-like Higgs which is much lighter on the left-hand side. In fact, for a light ${\mathcal {CP}}$-odd singlet-like Higgs a parameter region opens up where decays of the SM-like Higgs into a pair of them become kinematically allowed. The ${\mathcal {CP}}$-even singlet-like Higgs is also somewhat lighter for $A_\kappa =0\,\text {GeV}$, while the SM-like Higgs is scarcely affected. The contour lines of the Higgs masses stop when one Higgs becomes tachyonic. The reason why this does not exactly coincide with the border between the blue and pink dotted regions are the loop corrections to the Higgs spectrum while the constraints from vacuum stability were investigated at the tree level. It can be seen that the boundaries at the left of the stable region are parallel to one of the displayed Higgs-mass contours – the corresponding particle becomes tachyonic at this boundary. The boundary to the right of the stable region can be understood when comparing the right plots of Figs. 4 and 5, which differ from each other by the value of $\mu$: in the right plot of Fig. 5 a contour for the SM-like Higgs mass which is parallel to the tachyonic border appears around $\mu +\mu _{\text {eff}}=250\,\text {GeV}$ and $\kappa /\lambda =0.5$. In Fig. 4 such a contour is not visible as this particular parameter region is excluded by a tachyonic SM-like state at the tree level. Note that the NMSSM- and $\mu$NMSSM-specific one-loop contributions to the Higgs spectrum are particularly large in that region (about $60\,\text {GeV}$ additional shift compared to the same scenario in the MSSM-limit with $\lambda \rightarrow 0$ and $\kappa /\lambda$ constant), see also Ref. [124]; a dedicated analysis taking into account two-loop effects beyond the MSSM-limit might be necessary for a robust prediction of the Higgs mass close to the right border of the stable region, see e.g. Ref. [123]. It should be noted that in Fig. 4 the region where the Higgs mass is close to the right border of the stable region is disfavored by the limits from chargino searches at LEP.

As expected, the region allowed by HiggsBounds and HiggsSignals is a subset of the region where the SM-like Higgs has a mass in the vicinity of $125\,\hbox {GeV}$. In the green-marked region, $\Delta \chi ^2$ is at maximum 5.99. The minimal value $\chi _m^2$ from HiggsSignals is 74.6 in both figures. One can see on the left-hand side of Fig. 4 that this region is split into two: in between the two regions the SM-like Higgs can decay into a pair of ${\mathcal {CP}}$-odd singlet-like Higgs bosons $h^0 \rightarrow a_sa_s$ with a branching ratio of up to $90\,\%$; this behavior is not compatible with the observed signal strengths implying a limit on decays of the state at $125\,\text {GeV}$ into non-SM particles. For a very light ${\mathcal {CP}}$-odd singlet, the admixture between the SM-like Higgs and the ${\mathcal {CP}}$-even singlet component is reduced, since the latter becomes heavier in this region. In the scenario under consideration, the decay $h^0 \rightarrow a_sa_s$ is dominated by the coupling among the two singlet states, $\lambda _{355}$ in Eq. (31q), such that a reduced admixture between $h^0$ and $s^0$ also closes the decay $h^0 \rightarrow a_sa_s$. This is why – despite the very light ${\mathcal {CP}}$-odd Higgs $a_s$ – the region at $\mu +\mu _{\text {eff}}\simeq -300\,\hbox {GeV}$ and $\kappa /\lambda \simeq 0.4$ is allowed by the constraints from both HiggsSignals and HiggsBounds.

In Fig. 5 we present scenarios similar to the right-hand side of Fig. 4 with $A_\kappa = 100 \, \text {GeV}$, but with different values of $\mu$ (note the larger scale at the x-axis). Thus, the influence of this parameter that distinguishes the $\mu$NMSSM from the NMSSM can be seen directly. Obviously, the parameter region with a stable vacuum is enlarged: for a given value $(\mu +\mu _{\text {eff}})$ the tachyonic border moves to smaller ratios of $\kappa /\lambda$ as $\mu$ increases. Concerning the Higgs spectrum, the most notable difference is seen for the SM-like Higgs mass: for $\mu = 1\,\text {TeV}$ a turning point at about $\mu +\mu _{\text {eff}}=-800\,\text {GeV}$ is visible, which moves to smaller values of $\kappa /\lambda$ for $\mu = 1.5\,\text {TeV}$. For the larger value of $\mu$ one can see that the possibility emerges for scenarios with the correct SM-like Higgs mass but positive $(\mu +\mu _{\text {eff}})$. Again all tested points which yield a SM-like Higgs boson close to $125\,\hbox {GeV}$ successfully pass the constraints implemented in HiggsBounds and HiggsSignals. The minimal values of $\chi _m^2$ from HiggsSignals are 74.9 and 74.6 on the left-hand and on the right-hand side of Fig. 5, respectively.

Figure 6 shows scenarios with larger $\tan \beta$ and smaller $\lambda$ compared to the previous figures. Like in Fig. 4 we set $A_\kappa =0\,\hbox {GeV}$ on the left, and $A_\kappa =100\,\hbox {GeV}$ on the right-hand side, but $\mu = 1\,\text {TeV}$ is used. We observe again that a larger value of $A_\kappa$ widens the allowed parameter region, because the mass of the ${\mathcal {CP}}$-odd singlet is lifted up, giving rise to a drastic effect in this case. In fact, for $A_\kappa =0\,\hbox {GeV}$ only a rather small area in the plane of $(\mu +\mu _{\text {eff}})$ and $\kappa /\lambda$ is allowed, while the allowed region is very significantly enhanced for $A_\kappa =100\,\hbox {GeV}$. In the plot on the right-hand side one can see a (nearly) closed $125\,\text {GeV}$ contour for the mass of the SM-like Higgs with even larger values in the enclosed area. Adjusting the parameters of the stop sector in order to obtain a smaller contribution to the SM-like Higgs mass can render a SM-like Higgs with a mass of about $125\,\text {GeV}$ in the whole enclosed region. Close to the tachyonic borders we find larger regions with a long-lived meta-stable vacuum (purple) than in Figs. 4 and 5. However, in this part of the plot the prediction for the mass of the SM-like Higgs is below the experimental value. On the right-hand side of Fig. 6 a large region is allowed by the constraints from HiggsBounds and HiggsSignals. Only low values of $|\mu +\mu _{\text {eff}}|<m_h/2$ are excluded by HiggsSignals due to the decay of the SM-like Higgs boson into a pair of higgsinos. However, this region is anyhow not compatible with the LEP bound on light charginos. The minimal values of $\chi _m^2$ from HiggsSignals are 74.7 in both plots.

In Fig. 7 we change the parameter on the y-axis: $B_\mu$ is varied and $\kappa$ is kept fixed. We set $A_\kappa =0\,\text {GeV}$ on the left-hand side, and $A_\kappa =100\,\hbox {GeV}$ on the right-hand side. One can see that non-zero values for $B_\mu$ can have a significant impact on the predicted Higgs masses and might determine whether or not a scenario is excluded. For larger negative values of $B_\mu$, one can see an area where the electroweak vacuum is meta-stable and long-lived, while the area in the lower left corner of the plots indicates that the electroweak vacuum is unstable and short-lived. The effect of a larger $A_\kappa$ mainly lifts the tachyonic boundary at the top so that values of $B_\mu = 1\,\text {TeV}$ are allowed for $A_\kappa = 100\,\text {GeV}$ and leaves the other regions invariant. However, towards the upper limit of $B_\mu$, there is a small short-lived area. As a new feature, we find large regions with a meta-stable vacuum but a SM-like Higgs with a mass of $125\,\text {GeV}$ for both values of $A_\kappa$. Accordingly, scenarios with too large negative values of $B_\mu$ are excluded due to a rapidly decaying vacuum despite providing a SM-like Higgs boson close to the observed mass. The constraints from HiggsBounds and HiggsSignals indicate that a large part of the region with the correct Higgs mass is compatible with the experimental data. For both plots HiggsSignals yields a minimal value of $\chi _m^2 = 74.9$. Only in those scenarios where the decay channel $h^0 \rightarrow a_sa_s$ is kinematically allowed – which happens in the plot for $A_\kappa = 0\,\text {GeV}$ for $\mu + \mu _{\text {eff}}\gtrsim -300\,\text {GeV}$ and $\mu + \mu _{\text {eff}}\lesssim -700\,\text {GeV}$ – the parameter region is incompatible with the data on the detected Higgs boson.

We briefly summarize the observed features and give an outlook for the phenomenological studies in the following. The allowed parameter region is mainly constrained by configurations where one Higgs field is tachyonic at the tree level. It can be seen that the tachyonic boundaries follow the Higgs mass contours in the Figs. 4, 5, 6, 7; in addition, there are effects from $\mu _{\text {eff}}^{-1}$ terms as discussed in Sect. 2.2 which enhance the doublet–singlet mixing and eventually cause tachyons. This feature can be observed towards the right end of the Figs. 4, 5, 6. The experimental limits and constraints confine the allowed regions further around the region where the SM-like Higgs has a mass of about $125\,\text {GeV}$ and exclude parameter regions where for instance the decay of the SM-like Higgs into a pair of light ${\mathcal {CP}}$-odd singlets has a large branching ratio. In this context, the singlet sector has a significant impact on the features discussed in Figs. 4, 5, 6, 7.

In the NMSSM, one usually expects to find the phenomenologically most interesting regions (accommodating a $125\,\text {GeV}$ Higgs) for rather large values of $\lambda \gtrsim 0.1$, since the NMSSM contribution to the SM-like Higgs mass at the tree level is enhanced. In addition, large $\lambda$ enhances the doublet–singlet mixing. However, in the $\mu$NMSSM, there is another way to obtain a large doublet–singlet mixing also for small values of $\lambda$: this is the region of low $\mu _{\text {eff}}$ where terms proportional to $\mu _{\text {eff}}^{-1}$ become large, as discussed in Sect. 3.1. We will investigate this class of scenarios, which are not possible in the NMSSM but generic to the $\mu$NMSSM, in Sect. 3.5 in more detail.

Similar to the NMSSM, the chosen value of $A_\kappa$ has a strong influence on the singlet-like Higgs masses, which is relevant for the tachyonic regions. In a large part of the viable parameter space the relation ${\text {sign}}{(A_\kappa )} = -{\text {sign}}{(\mu _{\text {eff}})}$ applies, where for $A_\kappa = 0\,\text {GeV}$ both signs of $\mu _{\text {eff}}$ are allowed in general. This dependence on the relative signs of $A_\kappa$ and $\mu _{\text {eff}}$ can be derived from the discussion in Sect. 2.2 about the Higgs singlets and especially the functional dependence of $a_5$ in Eq. (14e) versus $a_4'$ in Eq. (20c): large negative values of the sum $(a_4' + a_5)$ drive the ${\mathcal {CP}}$-even singlet tachyonic. In the investigated scenarios above, which have either $A_\kappa = 0\,\text {GeV}$ or $A_\kappa = 100\,\text {GeV}$, the sign of $\mu _{\text {eff}}$ is negative in most of the viable parameter space. Accordingly, there is a preference for negative $(\mu + \mu _{\text {eff}})$. The allowed region with small positive values occurs where the negative value of $\mu _{\text {eff}}$ is overcompensated by the positive value of $\mu$. In Sect. 3.5 we will investigate a scenario where we keep $(\mu + \mu _{\text {eff}})$ fixed at a positive value, while for $A_\kappa$ small negative and small positive values are used for $\mu _{\text {eff}}> 0\,\text {GeV}$ and $\mu _{\text {eff}}< 0\,\text {GeV}$, respectively. There we will also discuss the dependence of the singlet masses on $\mu$ and $\mu _{\text {eff}}$ in more detail.

3.4 Higgs-boson and electroweakino production

In this and the next section we discuss phenomenological features of Higgs-boson mixing and thus consequences on Higgs-boson production and decays due to the $\mu$ parameter of the $\mu$NMSSM. For vanishing $\mu$ the phenomenology of the Higgs bosons equals the one of the NMSSM, for which typical benchmark scenarios can be found in Ref. [159] (see also Ref. [160]). Naturally they differ from MSSM-type benchmark scenarios through singlet states modifying the phenomenology: since the singlet states $s^0$ and $a_s$ neither directly couple to fermions nor to gauge bosons, but only through their admixture with the doublet states, their direct production – both at a hadron collider and a lepton collider – is negligible in many scenarios. However, besides their direct production light singlet states can also be potentially observable via their production in cascade decays of heavier Higgs bosons, as we will discuss in the following.

Table 2 Scenarios that yield a light ${\mathcal {CP}}$-even singlet-like Higgs boson. The Higgs boson at about $125\,\hbox {GeV}$ is SM-like. All other parameters are chosen in accordance to Table 1

In most parts of our numerical study, we make use of the approximation of SM-normalized effective couplings of a Higgs boson to gluons – calculated at leading order – which we insert into HiggsBounds for the evaluation of the Higgs-production cross-sections for the neutral Higgs bosons at the LHC. This treatment should be sufficiently accurate for determining the allowed regions in our scans over the parameter space. In the following, however, we will investigate to what extent the $\mu$NMSSM can accommodate the slight excesses in the data over the background expectation at a mass around 95–$98\,\text {GeV}$ that have been reported recently by CMS [42] in the $\gamma \gamma$ channel¹² and earlier at LEP [41] in the $b\bar{b}$ channel. For this purpose we use more sophisticated predictions for the Higgs-production cross-sections in order to compare with the experimental results. We obtain those predictions from SusHi [39, 40, 161,162,163,164,165,166,167], for which a dedicated version for the NMSSM exists [168]. The predictions include $\hbox {N}^{3}\hbox {LO}$ QCD corrections for the top-quark contribution of the light ${\mathcal {CP}}$-even Higgs bosons, while we have neglected contributions from heavy squarks and gluinos beyond the resummed contributions in the bottom-Yukawa coupling.

In the NMSSM, the observed excesses in the data around 95–$98\,\text {GeV}$ can be interpreted in terms of a singlet-like state $s^0$, see Ref. [74] for a discussion of the LEP result, and Ref. [169] for a discussion of the CMS data. At first sight it seems to be non-trivial to describe both excesses simultaneously, since accommodating the LEP excess would require a rather large rate $s^0\rightarrow b\bar{b}$, which in turn would suppress the channel $s^0\rightarrow \gamma \gamma$ that is employed in the interpretation of the CMS excess. As it was pointed out in Ref. [147] based on a detailed analysis of the Higgs mixing properties, this is nevertheless possible – albeit in a relatively narrow region of the parameter space, which is somewhat enlarged if the possibility of non-vanishing phases giving rise to ${\mathcal {CP}}$-violating effects is taken into account. We investigate in the following to which extent the additional freedom that is present in the $\mu$NMSSM with respect to the possible values of the masses in combination with the mixing properties has an impact regarding a possible interpretation of the observed excesses. In Table 2 we present four scenarios with $s^0$ masses in the range 95–$98\,\hbox {GeV}$ that have a phenomenology addressing the excesses observed both at LEP and CMS. Scenarios 1 and 3 have a small value of $\mu$ and are NMSSM-like (inspired by the scenarios investigated in Ref. [147]), while Scenarios 2 and 4 both have $\mu$ values that significantly differ from zero, and Scenario 4 furthermore has a non-zero value of $B_\mu$. These two $\mu$NMSSM scenarios are intrinsically different from the NMSSM. Similar scenarios could also be obtained by changing the signs of $(\mu +\mu _{\text {eff}})$ and $A_\kappa$ simultaneously.

Table 3 Cross-sections for electroweakinos at an electron–positron collider for Scenario 1 defined in Table 2

Interpreting the LEP excess as the contribution of a singlet-like state $s^0$ in the considered mass range yields a “signal strength” of

$$\begin{aligned} \frac{ \sigma {\left( e^+e^-\rightarrow Zs^0\right) }\cdot \text {BR}{\left( s^0\rightarrow b\bar{b}\right) }}{\sigma ^{{\text {SM}}}{\left( e^+e^-\rightarrow ZH\right) }\cdot \text {BR}^{{\text {SM}}}{\left( H\rightarrow b\bar{b}\right) }}&\simeq 0.2-0.3, \end{aligned}$$

(41)

while a “signal rate” of $\sigma (pp\rightarrow s^0\rightarrow \gamma \gamma )\simeq 0.1\,\hbox {pb}$ would be compatible with the CMS observation. As mentioned above, the cross-section $gg\rightarrow s^0$ in our analysis is obtained from SusHi [161, 162] for the $13\,\hbox {TeV}$ LHC at $\hbox {N}^{3}\hbox {LO}$ QCD. The renormalization- and factorization-scale uncertainties amount to about $\pm 5\%$. Sizable values for the cross-sections $gg\rightarrow s^0$ and $e^+e^-\rightarrow Zs^0$ as well as the branching ratio $\hbox {BR}(s^0\rightarrow b\bar{b})$ arise if the admixture of $s^0$ with the SM-like Higgs boson is sufficiently large. A sizable $\hbox {BR}(s^0\rightarrow \gamma \gamma )$ can occur as a consequence of a significant $H_u$ component of the singlet state $s^0$, whereas a small $H_d$ component suppresses the decay into $b\bar{b}$. In all the listed scenarios the ${\mathcal {CP}}$-odd singlet-like Higgs boson $a_s$ has a mass below $300\,\text {GeV}$. It should be noted that the occurrence of the state $s^0$ at low masses in combination with a very heavy $a_s$ state through a large value of $A_\kappa$ would usually yield a meta-stable (long-lived) vacuum. The listed scenarios involve a certain amount of tuning in the choice of $A_\kappa$ since an increase in $A_\kappa$ by a few GeV yields a tachyonic $s^0$ state. It is well-known from the NMSSM that a too large $A_\kappa$ yields a tachyonic ${\mathcal {CP}}$-even singlet-like Higgs boson $s^0$, see Eq. (37) in Ref. [158] or Eq. (26) in Ref. [170] for lower and upper bounds on $A_\kappa$. Similarly, we have noted a very pronounced dependence of the masses of both states, $s^0$ and $a_s$, on $A_\kappa$ for the $\mu$NMSSM scenarios investigated here.

Of course, a large admixture of $s^0$ with the SM-like Higgs boson in turn has an impact on the SM-like Higgs properties, visible through the increase in $\chi ^2$ returned by HiggsSignals. In fact, from the listed scenarios only Scenario 3 with $\chi ^2=82$ is compatible with the SM-like Higgs boson at the 95% C.L. The other scenarios have $\chi ^2$ values outside of the 95% C.L. region, as they have a slightly larger mixing of the singlet state with the SM-like Higgs boson. The enhanced mixing increases the $s^0$ cross-sections, but on the other hand yields reduced relative couplings to fermions and gauge bosons for the SM-like Higgs boson $h^0$. It is thus apparent that explaining the excesses through a singlet state that only couples to SM particles through its admixture with the SM-like Higgs boson is under a certain tension from the measured SM-like Higgs-boson properties for both the $\mu$NMSSM and the NMSSM, if one requires signal rates that fully saturate the amount of deviation from the SM indicated by the excesses observed by LEP and CMS.

Scenarios with light singlet-like Higgs bosons tend to have a light singlino. For Scenario 1 we provide the light electroweakino spectrum, i.e. the masses of ${\tilde{\chi }}^0_{1,2,3}$ and ${\tilde{\chi }}^\pm _1$, in Table 3. Due to $\mu +\mu _{\text {eff}}=-140\,\hbox {GeV}$ the scenario has light higgsino-like states, whereas the gauginos are close in mass to $M_1=239\,\hbox {GeV}$ and $M_2=500\,\hbox {GeV}$. The higgsino-like states are strongly admixed with the singlino, e.g. the singlino-fraction of ${\tilde{\chi }}^0_2$ is 59%, the singlino-fraction of $\tilde{\chi }^0_3$ is 40%. It is apparent that the three lightest neutralinos and the light chargino are very close to each other in mass. At the LHC, ATLAS and CMS have only recently started to probe such compressed mass spectra by dedicated analyses, see e.g. Refs. [171, 172]. In fact, an electron–positron collider may be required to ultimately probe scenarios of this kind, see for instance Ref. [173] tackling such compressed higgsino-like scenarios at the International Linear Collider (ILC). For Scenario 1 we provide the cross-sections for the two center-of-mass energies $\sqrt{s}=350\,\hbox {GeV}$ and $\sqrt{s}=500\,\hbox {GeV}$, which are considered for Higgs-boson and top-quark precision studies at the ILC [174], in Table 3. Although in this scenario the LSP is the gravitino, the lightest neutralino ${\tilde{\chi }}_1^0$ has a lifetime of a few milliseconds such that it only gives rise to a missing-energy signature. Besides the possibility to tag $e^+e^-\rightarrow {\tilde{\chi }}_1^0{\tilde{\chi }}_1^0$ through initial-state radiation (ISR), the production of one or more heavier neutralinos or charginos results in detectable SM particles. The possibility to polarize the initial state is an important tool to enhance the signal-to-background ratio, and allows one to minimize systematic uncertainties. This capability is mandatory for performing precision measurements. In Table 3 we provide results for three different polarizations: an unpolarized initial state (as reference only), and polarizations of $\pm 80$% and $\mp 30$% for the initial-state electron and positron, respectively. Such polarizations are foreseen in the current baseline design of the ILC. As one can see from Table 3, polarized beams with $\hbox {Pol}(e^+,e^-)=(+30\%,-80\%)$, corresponding to the so-called effective polarization [175] $\hbox {Pol}_{\text {eff}}=89\,\%$, enhance the production cross-sections of ${\tilde{\chi }}^0_1{\tilde{\chi }}^0_2$ and ${\tilde{\chi }}^0_1{\tilde{\chi }}^0_3$ by about a factor 1.5 as well as the one of ${\tilde{\chi }}^+_1{\tilde{\chi }}^-_1$ by about a factor 2. The fact that the production cross-sections of ${\tilde{\chi }}^0_2{\tilde{\chi }}^0_2$ and ${\tilde{\chi }}^0_2{\tilde{\chi }}^0_3$ are significantly smaller than the other quoted cross-sections is due to a cancellation between the higgsino components $\tilde{h}_d^0$ and $\tilde{h}_u^0$.

As discussed above, the electroweakino spectrum of the $\mu$NMSSM is a priori indistinguishable from the NMSSM if one restricts the analysis to information from the electroweakino sector and employs tree-level predictions, see Sect. 3.2. Previous studies of the electroweakino sector, see e.g. Ref. [173] and Refs. [176, 177], discussed the ILC capabilities for distinguishing the MSSM from the NMSSM electroweakino sector. From such studies one can infer that a determination of the parameters of the electroweakino sector with an accuracy at the percent level is possible using the measurements of the light electroweakino masses and the corresponding production cross-sections for different polarizations, see e.g. Refs. [178, 179] and references therein. This holds even if only the lightest electroweakinos are accessible. Based on earlier comprehensive studies where similar rates as in the scenarios of Table 3 were considered, the input parameters of the corresponding sector can be extracted: as an example, the values of $M_1$ and $M_2$ can be determined from the measurement of light gauginos, or the value of $(\mu +\mu _{\text {eff}})$ from the measurement of light higgsinos. In this regard beam polarization plays a crucial role: it allows one to even resolve scenarios where only a few light particles are kinematically accessible. Furthermore, the clean environment at an electron–positron collider allows the application of an ISR method [173] to detect and precisely measure scenarios where the light spectrum is close together in mass, as it is the case for instance for the compressed electroweakino spectrum in Scenario 1 leading to very soft decay characteristics. Complementing the particle spectrum via measuring additional heavier electroweakino masses and parts of the scalar and colored sector at the LHC would allow global fits of the model parameters, so that a model distinction between the $\mu$NMSSM, NMSSM and the MSSM might be feasible.

3.5 Higgs-boson mixing and decays

We now extend our previous discussion on Higgs-boson mixing and consider Higgs-boson decays. In this context we investigate in particular the influence of $\mu$ and $\mu _{\text {eff}}$ on the masses of the two light singlets. For our discussion of the possibilities for distinguishing the $\mu$NMSSM from the NMSSM we assume that the sum $\left( \mu +\mu _{\text {eff}}\right)$ is identified with the $\mu _{\text {eff}}$ term of the NMSSM, and $\kappa$ is rescaled according to Eq. (36). As discussed in Sect. 3.2, the rescaling of $\kappa$ significantly reduces the dependence of all Higgs masses on $\mu$ and $\mu _{\text {eff}}$ over a large region of the parameter space. Light ${\mathcal {CP}}$-even singlets and decays of the SM-like Higgs boson into them were already part of the discussion in Figs. 4, 5, 6, 7, but therein we focused on constraints from vacuum stability and general features in the parameter space. Now we investigate Higgs-boson decays in more detail.

Fig. 8

The behavior of the masses of the three lightest neutral Higgs states in a scenario with $\lambda =1/4$, $\kappa =1/5$, $\tan \beta =4$ and $A_\kappa =7\,\hbox {GeV}$ is shown. In contrast to Figs. 4, 5, 6, 7, the black and blue lines show the mass contours of the lightest and second lightest ${\mathcal {CP}}$-even Higgs mass eigenstate, respectively. The remaining parameters are chosen according to Table 1

For the discussion of the dependence of the masses of the light singlet states on $\mu$ and $\mu _{\text {eff}}$ we choose a scenario based on Table 1 and fix in addition $\lambda =1/4$, $\kappa =1/5$, $\tan \beta =4$, $A_\kappa =7\,\text {GeV}$. We vary $(\mu +\mu _{\text {eff}})$ between $-600$ and $450\,\hbox {GeV}$ and $\mu$ between 1 and $1000\,\hbox {GeV}$. The lower end of the range of $\mu$ values corresponds to the NMSSM-limit, $\mu \rightarrow 0\,\text {GeV}$. The results are depicted in Fig. 8, where we show the masses of the three lightest neutral Higgs bosons as a function of $\mu$ and $(\mu +\mu _{\text {eff}})$. The background colors indicate the constraints from vacuum stability and from the experimental results on the Higgs sector using the same color coding as in Figs. 4, 5, 6, 7. It is apparent that with increasing $\mu$ the range in $(\mu +\mu _{\text {eff}})$ that is allowed by the constraints from vacuum stability is also increasing, which is in accordance to our observations in the previous section. Since the mixing between the light ${\mathcal {CP}}$-even doublet state and the ${\mathcal {CP}}$-even singlet-like state is large in the parts of the displayed parameter plane where the masses of the two lightest ${\mathcal {CP}}$-even states are close to each other, we label the ${\mathcal {CP}}$-even states in Fig. 8 as the mass eigenstates $h_1^0$ and $h_2^0$ rather than as $h^0$ and $s^0$. However, for large values of $\mu$ the two lightest ${\mathcal {CP}}$-even Higgs bosons are sufficiently separated in mass so that the light ${\mathcal {CP}}$-even doublet state $h_1^0$ can be identified with $h^0$ and exhibits only a mild dependence on $\mu$, since such a dependence is only induced through the mixing with the singlet at tree-level. For smaller values $200\,\text {GeV}\lesssim \mu \lesssim 300\,\hbox {GeV}$ the contour lines of $m_{h_1^0}$ become very dense, and the mass of the singlet-like state $h_2^0$ approaches values below $150\,\text {GeV}$, implying a large mixing between the ${\mathcal {CP}}$-even light doublet state and the singlet state. With further decreasing $\mu$ the mass eigenstates $h_1^0$ and $h_2^0$ flip their role, i.e. $h_1^0$ is singlet-like, and $h_2^0$ corresponds to the SM-like doublet state in this region.

We now focus on the region of large $\mu$ where both states can be clearly separated: the region with a SM-like Higgs mass of $m_{h_1^0}\sim 125\,\text {GeV}$ is strongly affected by the values of $\lambda$ and/or $\tan \beta$ through their impact on the NMSSM-like tree-level contribution to the doublet states, see the quantity $a'_1$ in Eq. (20). In addition, it is well-known that this state receives large radiative corrections that depend on the mass splitting in the stop sector, which is proportional to $X_t = A_t - (\mu + \mu _{\text {eff}}) / \tan \beta$. As discussed above, we have chosen $A_t$ in such a way that the contribution is maximized at $\mu + \mu _{\text {eff}}= 0\,\hbox {GeV}$ and thus decreases to both directions. This behavior is visible in Fig. 8 for the contours displaying the mass of $h_1^0$ at values of $\mu \gtrsim 300\,\hbox {GeV}$. The behavior of the singlet-like states is important for the phenomenology: as explained in Sect. 2.2, for a scenario with $\kappa \sim \lambda$ the mass of the ${\mathcal {CP}}$-even singlet $s^0$ is mainly controlled by $a_5$, see Eq. (14e), and therefore proportional to $\mu _{\text {eff}}$. As in our scenario $A_\kappa$ is small, the mass of the ${\mathcal {CP}}$-odd singlet $a_s$ is dominated by $a_4^\prime$, see Eq. (20c), and therefore proportional to $\sqrt{|\mu /\mu _{\text {eff}}|}$. Those mass dependences of the singlet-like $m_{h_2^0} \gtrsim 150\, \text {GeV}$ (blue) and $m_{a_s}$ (red) can be clearly identified in Fig. 8: for $m_{h_2^0}$, the lines are roughly diagonal, and thus the mass contours follow lines with constant $\mu _{\text {eff}}$. For the mass of $a_s$, the dependence on the square root $\sqrt{|\mu /\mu _{\text {eff}}|}$ leads to the shape of the contours. We emphasize that the behavior displayed in Fig. 8 is specific to a small value of $A_\kappa \ll \mu$ or $\mu _{\text {eff}}$ for $\kappa \sim \lambda$.

As above, the parameter range allowed by constraints from HiggsBounds and HiggsSignals is indicated by light-green dots in the background. For values of $\mu \gtrsim 300\,\hbox {GeV}$, the light ${\mathcal {CP}}$-even Higgs $h_1^0$ corresponds to the SM-like state. In this region, the decay $h_1^0$ into higgsinos forbids low values of $|\mu +\mu _{\text {eff}}|$, while the decay $h_1^0\rightarrow a_sa_s$ is kinematically closed. For $\mu \lesssim 500\,\text {GeV}$ the mixing between the ${\mathcal {CP}}$-even doublet state and the singlet state becomes larger which is not compatible with the observation of the properties of the SM-like Higgs. The minimal value of $\chi ^2$ in this figure is $\chi _m^2 = 76.4$ and thus slightly worse than the scenarios studied in Sect. 3.3. There is also a small allowed region with $\Delta \chi ^2<5.99$ at low values of $\mu$, where a SM-like Higgs boson is present. In this region the mass of the singlet state $s^0$ has crossed the mass of the doublet state $h^0$, and the states $h_1^0$ and $h_2^0$ have changed their character as discussed previously. The doublet–singlet mixing in this case yields a positive contribution to the mass of the SM-like state $h_2^0$, lifting the tree-level value towards the experimentally allowed mass window (in the allowed region at low values of $\mu$ the mass of $h_2^0$ is about $126\,\text {GeV}$). In this region the decay $h_2^0\rightarrow a_sa_s$ is kinematically open, but sufficiently suppressed to be in accordance with experimental observations.

We conclude that the additional $\mu$ term of the $\mu$NMSSM lifts up the ${\mathcal {CP}}$-odd Higgs mass and enlarges the allowed parameter space compared to the NMSSM. Still, in particular due to the large admixture of the singlet and doublet states, such a scenario is difficult to distinguish from the standard NMSSM, if not all Higgs states are fully determined. As a consequence of the strong admixture of the Higgs bosons and the influence of their masses on the kinematics, all decay modes show a non-trivial dependence on the coupling structure. The decay rates of the heavy Higgs bosons $H^0$ and $A^0$ into any combination of the three light Higgs bosons remain small throughout the parameter plane, i.e. the branching ratios are below $3\%$. The maximal branching ratios for $A^0\rightarrow h^0 a_s$ and $A^0\rightarrow s^0 a_s$ are reached at large $\mu$ and $|\mu _{\text {eff}}|$, i.e. in the lower right corner of Fig. 8. The two decays show a different dependence on $\mu$ and $\mu _{\text {eff}}$, which is in accordance with our discussion in Sect. 2.5. Whereas $h_2^0\rightarrow a_s a_s$ is kinematically only allowed for very low $\mu$ in this scenario, the decay $h_2^0\rightarrow h_1^0h_1^0$ is – when kinematically open – strongly dependent on $\mu _{\text {eff}}$. We will demonstrate below the dependence of the different decay modes on $\mu$ and $\mu _{\text {eff}}$ in a scenario with essentially fixed Higgs-boson masses.

We now discuss a scenario that is intrinsically different from the NMSSM and shows a peculiar dependence of Higgs mixing and thus Higgs-boson decays on $\mu$ and $\mu _{\text {eff}}$. As indicated in the third item of Sect. 3.1 the $\mu$NMSSM allows large values of $\kappa$ in combination with low values of $\mu _{\text {eff}}$ and $\lambda$ without being constrained by higgsino-like states. In the following we vary $\mu$ from 0 to $240\,\hbox {GeV}$ and fix $\mu +\mu _{\text {eff}}=160\,\hbox {GeV}$ and thus simultaneously reduce $\mu _{\text {eff}}$ from 160 to $-80\,\hbox {GeV}$. We choose a very small value of $\lambda =0.02$ and a value of $\kappa =0.02$, which we rescale as $\kappa \rightarrow \tilde{\kappa }$ according to Eq. (36). The Higgs bosons therefore stay almost constant in mass, such that differences in Higgs-boson decays are solely induced by differences in the mixing among the Higgs bosons and not by kinematics. Note that in the limit $\mu _{\text {eff}}\rightarrow 0\,\text {GeV}$ the rescaled parameter $\tilde{\kappa }$ gets pushed beyond the perturbativity limit. This and the fact that at the tree-level one scalar mass becomes tachyonic are the reasons why the region around $\mu _{\text {eff}}= 0\,\text {GeV}$ is omitted for the lines in Figs. 9, 10, 11. Besides the parameters in Table 1 we set $\tan \beta =4$, $A_\kappa =-{\text {sign}}{(\mu _{\text {eff}}{\,\tilde{\kappa }})}\,1.3\,\hbox {GeV}$, which is like in Fig. 8 small compared to $\mu$ and $|\mu _{\text {eff}}|$, and $B_\mu =0\,\hbox {GeV}$. Note that the rescaling procedure for $\kappa$ according to Eq. (36) turns $\tilde{\kappa }$ negative in this scenario, when $\mu +\mu _{\text {eff}}> 0$ is fixed and $\mu$ takes on values larger than $(\mu +\mu _{\text {eff}})$. This case might be unsuitable for inflation, see Ref. [10]. The opposite case $\mu _{\text {eff}}>0$ and $\mu +\mu _{\text {eff}}<0$ cannot appear in our model, since $\mu$ is always positive. The green-shaded area, which we show in the figures depicting SM-like Higgs properties, indicates the region that is compatible with the constraints from HiggsSignals, where as before we demand $\Delta \chi ^2<5.99$ with a minimum of $\chi _m^2=77.5$. For $\mu _{\text {eff}}\in [-22,22]\,\text {GeV}$ the decay $h^0\rightarrow a_sa_s$ is enhanced such that this region is not compatible with the allowed fraction of non-SM decays of the SM-like Higgs boson. It should be noted that all of the shown area is allowed by the constraints from HiggsBounds. We emphasize that the effects that will be discussed in the following are related to a small value of $\mu _{\text {eff}}$: i.e. in the scenario discussed in Fig. 3, despite the same rescaling procedure for $\kappa$ with respect to $\mu _{\text {eff}}$, the mixing among the Higgs states is much less influenced by the choice of $\mu$, since a large value of $\mu$ results in an even larger negative value of $\mu _{\text {eff}}$.

Fig. 9

The mass spectrum (left) and total decay widths (right) for the three lightest Higgs bosons in a scenario with small $\lambda =0.02$ and fixed $\mu +\mu _{\text {eff}}=160\,\hbox {GeV}$ are shown. The value of $\kappa$ is rescaled as $\kappa \rightarrow \tilde{\kappa }$ according to Eq. (36) with $\kappa = 0.02$. Furthermore, $|A_\kappa |= 1.3\,\text {GeV}$ with the opposite sign of ${(}\mu _{\text {eff}}\,{\tilde{\kappa })}$. The other parameters are given in Table 1. The green area indicates compatibility with the constraints from HiggsSignals

Fig. 10

(left) Branching ratio of $h^0$ into a pair of light ${\mathcal {CP}}$-odd singlets; (right) Branching ratios of $s^0$ into non-SM particles and Higgs bosons; both for the same scenario as in Fig. 9. The green area indicates compatibility with the constraints from HiggsSignals. The branching ratio $\hbox {BR}(s^0\rightarrow {\tilde{\chi }}_i{\tilde{\chi }}_j)$ includes all branching ratios of $s^0$ into pairs of neutralinos and charginos

Fig. 11

Branching ratios of $A^0$ (left) and $H^0$ (right) into pairs of lighter Higgs bosons; both for the same scenario as in Fig. 9. The branching ratios $\hbox {BR}(A^0\rightarrow {\tilde{\chi }}_i{\tilde{\chi }}_j)$ and $\hbox {BR}(H^0\rightarrow {\tilde{\chi }}_i{\tilde{\chi }}_j)$ include all kinematically allowed channels into pairs of neutralinos and charginos

In the standard NMSSM a measurement of the masses of the whole neutralino and neutral Higgs spectrum would fix all free parameters, in particular $\mu _{\text {eff}}$, $\lambda$, $\kappa$ and $A_\kappa$. With these parameters also the Higgs mixing is completely determined (at the tree level). A small value of $\lambda$ in any case implies a small mixing between the singlet and doublet states of the Higgs sector. This is not the case in the $\mu$NMSSM: we show our results in Figs. 9, 10, 11. As explained above, in the considered parameter region the Higgs-boson masses are almost constant, see Fig. 9 on the left-hand side. The two heavy Higgs bosons $H^0$ and $A^0$ both have a mass very close to $800\,\hbox {GeV}$ within a range of $3\,\hbox {GeV}$. The neutralino masses are constant, in detail $m_{{\tilde{\chi }}_i^0}=\{134.7,163.9,252.1,320.0,516.1\}\,\text {GeV}$, where the particle with mass $m_{{\tilde{\chi }}_3^0}=m_{{\tilde{s}}}=320\,\hbox {GeV}$ corresponds to the singlino-like state with a purity of 99.9%. The two lightest neutralinos are higgsino-like states. Though the mixing in the neutralino sector remains constant, the mixing between the light ${\mathcal {CP}}$-even Higgs boson $h^0$ and the singlet component $s^0$ is strongly enhanced for $\mu _{\text {eff}}\rightarrow 0\,\hbox {GeV}$. We depict the total widths for the three lightest Higgs bosons on the right-hand side of Fig. 9. The enhancement of the total width of $h^0$ for $\mu _{\text {eff}}\rightarrow 0\,\hbox {GeV}$ is due to the decay $h^0\rightarrow a_sa_s$. This is also apparent in the left plot of Fig. 10, where the branching ratio for the decay of the SM-like state $h^0$ into a pair of light ${\mathcal {CP}}$-odd singlets is displayed. For $s^0$ both the decays into $h^0h^0$ and $a_sa_s$ are of relevance, whereas other non-standard decay modes – e.g. into a pair of higgsinos – have a small rate, see the right-hand sides of Figs. 9 and 10. Apart from decays into Higgs bosons, $s^0$ decays into massive SM gauge bosons. As mentioned above, all of the shown area in Fig. 10 is allowed by the constraints from HiggsBounds, i.e. both $a_s$ and $s^0$ are compatible with searches for additional Higgs bosons. However, for the state $s^0$ the region around $\mu _{\text {eff}}=\pm 10\,\hbox {GeV}$ is close to the boundary of the region that is excluded by the limits from Higgs searches, see below. As a result, we conclude that in this scenario with small $\mu _{\text {eff}}$ the singlet $s^0$ can again be directly produced at a hadron collider through its admixture with the two ${\mathcal {CP}}$-even doublets, see the discussion in Sect. 3.4. For $\mu =\{150,170\}\,\hbox {GeV}$ the mass of the singlet is $m_{s^0}=\{323.9,324.8\}\,\hbox {GeV}$, and the gluon-fusion production cross-section is $\sigma (gg\rightarrow s^0)=\{270,274\}\,\hbox {fb}$. The production rates through bottom-quark annihilation is negligible. Given the large branching ratios $\hbox {BR}(s^0\rightarrow a_sa_s)\sim 57\%$, $\hbox {BR}(s^0\rightarrow h^0h^0)\sim 19\%$, $\hbox {BR}(s^0\rightarrow W^+W^-)\sim 15\%$ and $\hbox {BR}(s^0\rightarrow ZZ)\sim 7\%$, the most sensitive searches are those with a decay into a pair of SM-like Higgs or gauge bosons. As an example, for $m_X\sim 320\,\hbox {GeV}$ the upper limits $\sigma (pp\rightarrow X\rightarrow h^0h^0)\lesssim 500\,\hbox {fb}$ [180] and $\sigma (pp\rightarrow X\rightarrow ZZ)\lesssim 200\,\hbox {fb}$ [181] are already within a factor 10 of the signal rates that can be obtained at $\mu =\{150,170\}\,\hbox {GeV}$. Lastly, also the decays of the heavy Higgs bosons – whose total decay widths only vary within 10% for the considered scenario – show potentially observable branching ratios into pairs of lighter Higgs bosons in the limit $\mu _{\text {eff}}\rightarrow 0\,\hbox {GeV}$, see Fig. 11. At such low values of $\tan \beta$ both heavy Higgs bosons $H^0$ and $A^0$ are not predominantly decaying into bottom quarks or tau leptons, but decay into a pair of top quarks with a branching ratio of about $30\%$. Thus, decay modes into Higgs bosons could actually serve as discovery modes. However, note that our scenario includes light electroweakinos, into which heavy Higgs bosons tend to decay with large branching fractions. The branching ratios $\hbox {BR}(A^0\rightarrow {\tilde{\chi }}_i{\tilde{\chi }}_j)$ and $\hbox {BR}(H^0\rightarrow {\tilde{\chi }}_i{\tilde{\chi }}_j)$, shown in Fig. 11, both exceed 60% except for small values of $\mu _{\text {eff}}$. Both branching ratios include all kinematically allowed decays into pairs of neutralinos and charginos. This adds to the motivation for dedicated searches for heavy Higgs bosons decaying either into a pair of lighter Higgs bosons or into supersymmetric particles, see also the discussion in Refs. [182, 183].

We conclude that a small value of $\mu _{\text {eff}}$ in the discussed scenario strongly enhances the mixing among the Higgs bosons despite a low value of $\lambda$, which makes both singlet states potentially accessible at colliders. We have demonstrated that the Higgs-boson decays are not only controlled through the self-coupling dependences given in Sect. 2.5 for gauge eigenstates, but are also strongly dependent on the mixing of the Higgs bosons. In the standard NMSSM, light singlet states are usually associated with $\kappa <\lambda$, since the limits from chargino searches at LEP imply $|\mu _{\text {eff}}|\gtrsim 120\,\hbox {GeV}$, and therefore $v_s\gg 120\,\hbox {GeV}$. Accordingly, only small $\kappa \ll \lambda <1$ results in two light singlet states. However, in the $\mu$NMSSM scenario that we have considered $\kappa /\lambda$ and $\mu$ can be large in combination with a small $\mu _{\text {eff}}$. Whereas the ${\mathcal {CP}}$-odd singlet $a_s$ can be as light as a few GeV, the ${\mathcal {CP}}$-even singlet $s^0$ is usually in the ballpark of a few hundred GeV in such scenarios. This scenario is intrinsically different from the behavior of Higgs masses and mixing known in the NMSSM.

We are left with a discussion of vacuum stability in this scenario of large values of $\kappa$ together with small values of $\lambda$ and $\mu _{\text {eff}}$, for which we consider a wider range of parameters, i.e. we allow for different values of $\mu +\mu _{\text {eff}}$. Our results are shown in Fig. 12, where we varied both $\mu$ and $\mu +\mu _{\text {eff}}$ similar to Fig. 8 but for small $\lambda = 0.02$ and initial $\kappa = \lambda$. In contrast to Fig. 8 we rescale $\kappa$ according to Eq. (36) in order to achieve a flat neutralino spectrum. Except at vanishing values of $\mu _{\text {eff}}$, which correspond to a diagonal line from $(\mu ,\mu +\mu _{\text {eff}})=(0,0)\,\text {GeV}$ to $(\mu ,\mu +\mu _{\text {eff}})=(500,500)\,\text {GeV}$, also the Higgs spectrum is almost constant throughout the plane due to the rescaling of $\kappa$. The behaviour discussed in Figs. 9, 10, 11 appears along the horizontal (orange, dashed) line at $\mu +\mu _{\text {eff}}=160\,\text {GeV}$ indicated in Fig. 12. Very similar results to the ones described in Figs. 9, 10, 11 are obtained for smaller or larger values of $\mu +\mu _{\text {eff}}>0\,\text {GeV}$ close to $\mu _{\text {eff}}\approx 0\,\text {GeV}$. Fig. 12 demonstrates that a large fraction of the $(\mu ,\mu +\mu _{\text {eff}})$-plane yields a stable vacuum. The vacuum appears to be unstable, but long-lived, in a valley around the diagonal line of $\mu _{\text {eff}}\approx 0\,\text {GeV}$ discussed above as well as the lower left corner of the plot and along $\mu +\mu _{\text {eff}}\simeq 500\,\text {GeV}$. Along the same line and for small values of $\mu +\mu _{\text {eff}}$ tachyonic states rule out the parameter space. Those two bands, i.e. $\mu _{\text {eff}}\approx 0\,\text {GeV}$ and $\mu +\mu _{\text {eff}}\approx 0\,\text {GeV}$, are also the only regions in parameter space, which do not include a SM-like Higgs boson compatible with experimental measurements, indicated by the green area obtained with HiggsBounds and HiggsSignals. Two more comments are on order: In the upper right triangle of Fig. 12, i.e. $\mu +\mu _{\text {eff}}>0\,\text {GeV}$ and $\mu _{\text {eff}}<0\,\text {GeV}$, $\tilde{\kappa }$ is negative, which might not be compatible with inflation. Moreover we want to point out that a very similar scenario can be found for even smaller $\lambda$, as long as the initial value $\kappa \approx \lambda$ is kept.

Fig. 12

Vacuum stability analysis for a scenario with small value of $\lambda$, but potentially large values of $\tilde{\kappa }$ along the diagonal line of $\mu _{\text {eff}}\approx 0\,\hbox {GeV}$. The masses of the SM-like Higgs boson and the singlet-like ${\mathcal {CP}}$-even and -odd states are indicated in black, blue and red, respectively. The green area is allowed by HiggsBounds and HiggsSignals; with the gray band, the direct exclusion bound on light charginos is shown. Superimposed with orange dashes is the line of constant $\mu +\mu _{\text {eff}}= 160\,\text {GeV}$, along which Figs. 9, 10, 11 are defined

4 Conclusions

We have analyzed the phenomenology at the electroweak scale of an inflation-inspired extension of the Next-to-Minimal Supersymmetric Standard Model (NMSSM). We have put special emphasis on the spectra of additional, non-SM-like Higgs bosons and the branching ratios of their decays. This model has the same field content as the NMSSM, but at early times in the universe the D-flat direction of the Higgs doublet plays the role of the inflaton. Such a model can successfully describe inflation without the need of introducing a dedicated inflaton field. The singlet superfield $\hat{S}$ of the NMSSM is needed to stabilize the inflationary direction at the origin of $\hat{S} = 0$. Inflation occurs due to a non-minimal coupling of the doublet Higgs fields to gravity $\mathord {\sim }\,\chi \,H_u \cdot H_d$, where the proportionality factor involves the gravitino mass $m_{3/2}$ at low energies. Thus, this model is characterized by an MSSM-like $\mu$ term, which is generated from the coupling $\chi$ and involves $m_{3/2}$, in addition to the usual effective $\mu _{\text {eff}}$ term of the NMSSM. The latter arises since the scalar component of the singlet superfield acquires a vacuum expectation value as in the NMSSM. At low energies, i.e. the electroweak scale, this model differs from the NMSSM by the additional $\mu$ term which breaks the accidental $\mathbb {Z}_3$ symmetry of the NMSSM; we denote this model as the $\mu$NMSSM. The higgsino-mass term in the $\mu$NMSSM is composed of the sum $(\mu + \mu _{\text {eff}})$. We have classified and discussed various scenarios regarding the prospects to distinguish the $\mu$NMSSM from the NMSSM, where the latter corresponds to the limit $\mu = 0\,\hbox {GeV}$ of the $\mu$NMSSM. We have derived constraints on the model parameters from theoretical and phenomenological considerations. For that purpose, we have computed the SM-like Higgs mass at the one-loop order in the $\mu$NMSSM and added as approximation at the two-loop level the known two-loop results from the MSSM which are implemented in FeynHiggs. We have probed our scenarios against the rate measurements of the SM-like Higgs boson and the limits from searches for additional Higgs bosons at colliders with the codes HiggsBounds and HiggsSignals. Furthermore, we have checked whether the electroweak ground state of the Higgs potential corresponds to the absolute minimum of the theory, i.e. the true vacuum, or whether the Higgs potential has a deeper non-standard minimum such that the electroweak vacuum eventually decays. In the inflationary scenario considered here, configurations with a meta-stable electroweak vacuum in general do not yield a viable phenomenology. In fact, the most stringent constraints arise from the possible appearance of tachyonic Higgs states at the tree level.

The additional freedom of varying $\mu$ and $B_\mu$ in the $\mu$NMSSM allows one to choose values for the parameters of the NMSSM which would otherwise be excluded. In this extended parameter space, we have focused on relatively small values of $\tan \beta$, since in this case – like in the NMSSM– the light doublet-like Higgs mass squared is increased by a shift ${\propto }\,\lambda ^2\,v^2$; in this way the loop corrections which are required in order to acquire a SM-like Higgs at $125\,\hbox {GeV}$ can be smaller. As expected, in particular the requirement of a SM-like Higgs boson at about $125\,\hbox {GeV}$ yields important constraints on the parameter space. Concerning the constraints from vacuum stability, we find that the region with a phenomenologically viable Higgs spectrum is strongly correlated with the region of a stable electroweak vacuum, where the electroweak ground state corresponds to the true vacuum at the electroweak scale. An exception is the case where the soft SUSY-breaking $B_\mu \,\mu$ term is large. We have demonstrated that large negative values of $B_\mu \,\mu$ destabilize the vacuum.

For most of the numerical analyses in this paper we have fixed the sum $(\mu +\mu _{\text {eff}})$, since $\mu$ enters at the tree level only in this combination in the mass matrices for the charginos and sfermions as well as in the MSSM-like part of the neutralino mass matrix. Accordingly, the particle spectrum of the $\mu$NMSSM in those sectors resembles the one of the NMSSM if the sum $(\mu +\mu _{\text {eff}})$ in the $\mu$NMSSM is identified with the $\mu _{\text {eff}}$ term of the NMSSM. Moreover, we have pointed out the possibility to further reduce the influence of the non-minimal coupling to supergravity $\mathord {\sim }\,\mu$ on the neutralino sector by a rescaling of the parameter $\kappa$. This rescaling compensates the dependence of the singlino component of the neutralino mass matrix on $\mu _{\text {eff}}$, so that the neutralino, chargino and sfermion sectors of the $\mu$NMSSM and the NMSSM become indistinguishable from each other at tree level. We have demonstrated that the dependence of the Higgs masses on $\mu$ is significantly weakened after this transformation, but the individual dependences on $\mu$ and $\mu _{\text {eff}}$ still have a large impact on the Higgs mixing and thus the branching ratios of Higgs decays. The modified value of $\kappa$ resulting from the rescaling can also have an important influence on Higgs phenomenology.

Since with the above parameter settings the neutralino sector of the $\mu$NMSSM is NMSSM-like, we have not performed a detailed numerical analysis of the neutralino sector – besides our discussion of Higgs decays into electroweakinos. In general, the gravitino is found to be the LSP since it is tightly connected to the size of $\mu$. For phenomenological reasons in our scenarios it typically has a mass of $\mathcal {O}(10\,\text {MeV})$. The NLSP, which is either singlino- or bino-like, tends to be sufficiently long-lived such that it only gives rise to missing-energy signatures in collider searches. Accordingly, typical constraints from SUSY searches including missing energy apply without large modifications. The character of the NLSP is influenced by a variation of the corresponding parameters, i.e. $(\mu +\mu _{\text {eff}})$ for the higgsino mass and $M_1$ or $M_2$ for the bino or wino mass, respectively. Our choices for $M_{1,2}$ are rather arbitrary in this context. Their impact could be scrutinized with a dedicated study of the neutralino phenomenology in the $\mu$NMSSM.

In some of our analyses we have kept $\lambda$ large in order to lift up the mass of the SM-like Higgs boson at the tree level through genuine NMSSM effects, and in order to allow for sizable doublet–singlet mixing. However, we emphasize that large mixing between the doublet and singlet fields can also be achieved through small $\lambda$ in combination with nearly vanishing $\mu _{\text {eff}}$. Such a scenario is viable in the $\mu$NMSSM and gives rise to a phenomenology that significantly differs from the NMSSM.

A phenomenologically very interesting set of scenarios includes light singlet states. The direct production of these states at colliders suffers from their nature as gauge singlets: couplings to SM particles only emerge through the admixture with doublet-like Higgs states. Similarly, Higgs-to-Higgs decays involving doublet and singlet fields are strongly correlated with Higgs mixing. We have shown this effect exemplarily for decays of the SM-like Higgs boson into a pair of light ${\mathcal {CP}}$-odd singlets, which depends on the fraction of the ${\mathcal {CP}}$-even singlet component in the SM-like Higgs boson $h^0$. In the $\mu$NMSSM, this mixing is not only controlled through $\lambda$, but also depends sensitively on the values of $\mu$ and $\mu _{\text {eff}}$. We conclude that in order to distinguish the Higgs sectors of the $\mu$NMSSM and the NMSSM, the detection of singlet states in the Higgs spectrum and their couplings to other Higgs bosons and the SM particles will be crucial. We have discussed four scenarios that yield a light ${\mathcal {CP}}$-even singlet-like Higgs around $97\,\hbox {GeV}$, motivated by slight excesses in experimental searches performed with CMS and at LEP. These scenarios are associated with a compressed spectrum of light electroweakinos. We have pointed out that searches at a future electron-positron collider would provide complementary information to the results achievable at the LHC in scenarios of this kind.

Beta functions

The beta functions for the parameters of the Higgs sector in the superpotential of the GNMSSM in Eq. (9) and their corresponding soft SUSY-breaking parameters in Eq. (10) can be found in Refs. [44, 71, 72]; however, since we employ different conventions we list them in the following. At the one-loop order, we define $\beta {\left( x\right) }=16\, \pi ^2\, \frac{{\text {d}}{x}}{{\text {d}}{\ln {\mu _r^2}}}$ as the beta function of parameter x in the $\overline{\text {DR}}$ scheme with the renormalization scale $\mu _r$ of mass dimension one.

The symbols $y_t=m_t/v_u$, $y_b=m_b/v_d$ and $y_\tau =m_\tau /v_d$ denote the top, bottom and tau Yukawa couplings, respectively. The trilinear soft-breaking parameters are denoted as $A_t$ for the stops, $A_b$ for the sbottoms and $A_\tau$ for the staus. Analog contributions from the first and second generation of quarks and squarks are not depicted. The parameters $M_1$ and $M_2$ denote the soft-breaking bino and wino masses.

$$\begin{aligned} \beta {\left( \xi \right) }&= \xi \left( \lambda ^2 + \kappa ^2\right) , \end{aligned}$$

(42a)

$$\begin{aligned} \beta {\left( C_\xi \right) }&= 2\left( \lambda ^2\,A_\lambda + \kappa ^2\,A_\kappa \right) \nonumber \\&\quad +\, 2\,\frac{\lambda \,\mu }{\xi }\left[ m_{H_d}^2 + m_{H_u}^2 + B_\mu \left( \nu + A_\lambda \right) \right] \nonumber \\&\quad +\, \frac{\kappa \,\nu }{\xi }\left[ 2\,m_S^2 + B_\nu \left( \nu + A_\kappa \right) \right] , \end{aligned}$$

(42b)

$$\begin{aligned} \beta {\left( \mu \right) }&= 2\,\mu \left( -g_1^2 - 3\,g_2^2 + 2\,\lambda ^2 + 3\,y_t^2 + 3\,y_b^2 + y_\tau ^2\right) , \end{aligned}$$

(42c)

$$\begin{aligned} \beta {\left( B_\mu \right) }&= g_1^2\,M_1 + 3\,g_2^2\,M_2 + 2\,\lambda ^2\,A_\lambda + 3\,y_t^2\,A_t \nonumber \\&\quad +\, 3\,y_b^2\,A_b + y_\tau ^2\,A_\tau + \frac{\lambda }{\mu }\left( 2\,\lambda \,B_\mu \,\mu + \kappa \,B_\nu \,\nu \right) , \end{aligned}$$

(42d)

$$\begin{aligned} \beta {\left( \nu \right) }&= 2\,\nu \left( \lambda ^2 + \kappa ^2\right) , \end{aligned}$$

(42e)

$$\begin{aligned} \beta {\left( B_\nu \right) }&= 4\left( \lambda ^2\,A_\lambda + \kappa ^2\,A_\kappa \right) + 2\,\frac{\kappa }{\nu }\left( 2\,\lambda \,B_\mu \,\mu + \kappa \,B_\nu \,\nu \right) , \end{aligned}$$

(42f)

$$\begin{aligned} \beta {\left( \lambda \right) }&= \tfrac{1}{2}\,\lambda \,\left( -g_1^2 - 3\,g_2^2 + 4\,\lambda ^2 + 2\,\kappa ^2 \right. \nonumber \\&\quad \left. +\, 3\,y_t^2 + 3\,y_b^2 + y_\tau ^2\right) , \end{aligned}$$

(42g)

$$\begin{aligned} \beta {\left( A_\lambda \right) }&= g_1^2\,M_1 + 3\,g_2^2\,M_2 + 4\,\lambda ^2\,A_\lambda + 2\,\kappa ^2\,A_\kappa \nonumber \\&\quad +\, 3\,y_t^2\,A_t + 3\,y_b^2\,A_b + y_\tau ^2\,A_\tau , \end{aligned}$$

(42h)

$$\begin{aligned} \beta {\left( \kappa \right) }&= 3\,\kappa \left( \lambda ^2 + \kappa ^2\right) , \end{aligned}$$

(42i)

$$\begin{aligned} \beta {\left( A_\kappa \right) }&= 6\left( \lambda ^2\,A_\lambda + \kappa ^2\,A_\kappa \right) . \end{aligned}$$

(42j)

In addition we list the one-loop beta functions for the electroweak vevs¹³ and the soft-breaking Higgs masses:

$$\begin{aligned} \beta {\left( v_d\right) }&= -v_d\left( -\tfrac{1}{2}\,g_1^2 - \tfrac{3}{2}\,g_2^2 + \lambda ^2 + 3\,y_b^2 + y_\tau ^2\right) , \end{aligned}$$

(43a)

$$\begin{aligned} \beta {\left( m_{H_d}^2\right) }&= 2\left( -g_1^2\,M_1^2 - 3\,g_2^2\,M_2^2 + \lambda ^2\,M_\lambda ^2 \right. \nonumber \\&\quad \left. +\, 3\,y_b^2\,M_b^2 + y_\tau ^2\,M_\tau ^2 - \tfrac{1}{2}\,g_1^2\,M_\xi ^2\right) , \end{aligned}$$

(43b)

$$\begin{aligned} \beta {\left( v_u\right) }&= -v_u\left( -\tfrac{1}{2}\,g_1^2 - \tfrac{3}{2}\,g_2^2 + \lambda ^2 + 3\,y_t^2\right) , \end{aligned}$$

(43c)

$$\begin{aligned} \beta {\left( m_{H_u}^2\right) }&= 2\left( -g_1^2\,M_1^2 - 3\,g_2^2\,M_2^2 + \lambda ^2\,M_\lambda ^2 \right. \nonumber \\&\quad \left. +\, 3\,y_t^2\,M_t^2 + \tfrac{1}{2}\,g_1^2\,M_\xi ^2\right) , \end{aligned}$$

(43d)

$$\begin{aligned} \beta {\left( v_s\right) }&= -2\,v_s\left( \lambda ^2 + \kappa ^2\right) , \end{aligned}$$

(43e)

$$\begin{aligned} \beta {\left( m_S^2\right) }&= 4\left( \lambda ^2\,M_\lambda ^2 + \kappa ^2\,M_\kappa ^2\right) , \end{aligned}$$

(43f)

where we use the following abbreviations containing the bilinear soft-breaking parameters $m_{\tilde{Q}}$, $m_{\tilde{t}}$ and $m_{\tilde{b}}$ for the squarks, and $m_{\tilde{L}}$ and $m_{\tilde{\tau }}$ for the sleptons of the third generation (while suppressing the first and second generation; the notation is introduced in Sect. 2.7)

$$\begin{aligned} M_\lambda ^2&= m_{H_d}^2 + m_{H_u}^2 + m_S^2 + A_\lambda ^2, \end{aligned}$$

(44a)

$$\begin{aligned} M_\kappa ^2&= 3\,m_S^2 + A_\kappa ^2, \end{aligned}$$

(44b)

$$\begin{aligned} M_\xi ^2&= m_{H_u}^2 - m_{H_d}^2 + m_{\tilde{Q}}^2 - 2\,m_{\tilde{t}}^2 + m_{\tilde{b}}^2 - m_{\tilde{L}}^2 + m_{\tilde{\tau }}^2, \end{aligned}$$

(44c)

$$\begin{aligned} M_t^2&= m_{H_u}^2 + A_t^2 + m_{\tilde{Q}}^2 + m_{\tilde{t}}^2, \end{aligned}$$

(44d)

$$\begin{aligned} M_b^2&= m_{H_d}^2 + A_b^2 + m_{\tilde{Q}}^2 + m_{\tilde{b}}^2, \end{aligned}$$

(44e)

$$\begin{aligned} M_\tau ^2&= m_{H_d}^2 + A_\tau ^2 + m_{\tilde{L}}^2 + m_{\tilde{\tau }}^2\,. \end{aligned}$$

(44f)