1 Introduction

Since antiparticles were first predicted and observed [1], it has been clear that there exist high degree of matter-antimatter symmetry. This observation is a stark contradiction to the phenomena of everyday and cosmological evidence, particularly the fact that our universe consists of almost entirely matter with little primordial antimatter. The successful of this discovery is verified by the predictions of Big-Bang Nucleosynthesis (BBN) [2], the highly precise measurements of the cosmic microwave background [3, 4] and the absence of intense radiation from matter-antimatter annihilation [5]. The origin of the baryon number asymmetry is an open issue of the modern Cosmology and particle physics. Various baryogenesis scenarios explain how there are more matter than antimatter in this universe [6,7,8,9,10,11,12,13,14,15], which might occur during the matter or the radiation eras. The existence of processes which violate C and CP tells us that there is a fundamental asymmetry between matter and antimatter.Footnote 1 Thus the possibility arises of processes which preferentially produce matter rather than antimatter (although our present theoretical understanding doesn’t allow us to deduce this directly from the observed CP violation). However, even if this is the case, the ratio of particles and antiparticles will be very close to unity providing they are in equilibrium, as will be the case when the universe was very hot. Only as it cools and the equilibrium is removed will the tiny asymmetry in the particle interactions be amplified to an actual asymmetry in number densities. These requirements to produce matter-antimatter asymmetry, namely, (a) non-conservation of baryon number, (b) CP violation and (c) non-equilibrium are known as the Sakharov conditions [16]. In order to connect to dark energy, the authors [17, 18] have studied a class of models of spontaneous baryo(lepto)genesis by introducing a interaction between the dynamical dark energy scalars and the ordinary matter. Recently, Davoudiasl et al. [19] have proposed a mechanism for generating the baryon number asymmetry in thermal equilibrium during the expansion of the Universe by means of a dynamical breaking of CP. The interaction responsible for CP violation is given by a coupling between the derivative of the Ricci scalar R and the baryon current \(J^{\mu }\) of the form

$$\begin{aligned} \frac{1}{M_{*}^2} \int \sqrt{-g} dx^{4} \partial _{\mu }(R) J^{\mu }, \end{aligned}$$
(1)

where \(M_{*}\) is the cutoff scale characterizing the effective theory, g and R being respectively, the metric determinant and the Rurvature scalar. Other scenario to extend this well known theory by using a similar couplaging between the Ricci scalar and the baryonic current has been discussed by many authors. This scenario extends the well known theory that uses a similar coupling between the Ricci scalar and the baryonic current. In [20], f(R) theories of gravity are reviewed in the context of the so called gravitational baryogenesis. Some variant forms of gravitational baryogenesis by using higher order terms containing the partial derivative of the Gauss-Bonnet scalar coupled to the baryonic current are discussed in [21] whereas in [22], the gravitational baryogenesis scenario, generated by an f(T) theory of gravity where T is the torsion scalar are proposed.

The purpose of this paper is to investigate the gravitational baryogenesis mechanism in f(R, T) modified theory of gravity, a theory in which matter and geometry are minimally coupled and well known as generalization of General Theory of Relativity. This Theory was firstly introduced by the authors of [23] and several works with interesting results have been found in [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

The paper is organized as follows: A brief review in f(R, T) gravity is performed in Sect. 2. We investigate the essential features of baryogenesis in f(R, T) gravity by calculating the corresponding baryon to entropy ratio in universe containing a dark energy and the perfect fluid with constant equation of state parameter in Sect. 3. Some conclusions are presented in the last section.

2 Brief review in f(R, T) gravity

Let us consider the total action in modified f(R, T) gravity by

$$\begin{aligned} S = \int \sqrt{-g} dx^{4} \left[ \frac{1}{16\pi G} f(R,T)+\mathcal {L}_m \right] , \end{aligned}$$
(2)

where R, T are the curvature scalar and the trace of the energy-momentum tensor, respectively, G being the gravitation constant.

From the matter Lagrangian density \(\mathcal {L}_m\), we defined the energy-momentum tensor of the matter as

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}\mathcal {L}_m\right) }{\delta g^{\mu \nu }}. \end{aligned}$$
(3)

Varying the action (2) with respect to the metric formalism, the field equations are obtained as

$$\begin{aligned}&f_{R}R_{\mu \nu }-\frac{1}{2} g_{\mu \nu }f(R,T)+ \mathcal {D}_{\mu \nu } f_{R}\nonumber \\&\quad = 8\pi G T_{\mu \nu }- f_{T}(T_{\mu \nu }+\Theta _{\mu \nu })\,, \end{aligned}$$
(4)

where

$$\begin{aligned} \mathcal {D}_{\mu \nu } =\,&g_{\mu \nu }\Box -\nabla _{\mu }\nabla _{\nu }, \end{aligned}$$
(5)
$$\begin{aligned} \Theta _{\mu \nu }\equiv \,&g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }}=-2T_{\mu \nu }+g_{\mu \nu }\mathcal {L}_m\nonumber \\&-2g^{\alpha \beta }\frac{\partial ^2 \mathcal {L}_m}{\partial g^{\mu \nu }\partial g^{\alpha \beta }}. \end{aligned}$$
(6)

We note that \(f_{R}, f_{T}\) are the partial derivatives of f(R, T) with respect to R and T, respectively. The field equations (4) are reduced to Einstein field equations when \(f(R,T) \equiv R\).

Contracting Eq. (4) with the tensor metric components \(g^{\mu \nu }\), one gets the relation between the Ricci scalar R and the trace T of the energy momentum tensor

$$\begin{aligned} f_{R} R-2f(R,T) +3\Box f_{R} =8\pi G T -f_{T}(T+\Theta ). \end{aligned}$$
(7)

Let us now consider the spatially flat FLRW spacetime

$$\begin{aligned} ds^{2}= dt^{2}-a(t)^{2}[dx^{2}+ dy^{2}+dz^{2}], \end{aligned}$$
(8)

where a(t) is the scale factor and the matter content of the universe is a perfect fluid for which the matter Lagrangian density can be taken as \(\mathcal {L}_m = -p \). For this, the Eqs. (4) and (7) become

$$\begin{aligned} 3H^2= & {} \frac{8\pi G+f_T}{f_R}\rho \nonumber \\&+ \frac{1}{f_R}\bigg [ \frac{1}{2}(f-Rf_R)-3\dot{R}Hf_{RR}+ p f_T \bigg ], \end{aligned}$$
(9)
$$\begin{aligned} -2\dot{H}-3H^2= & {} \frac{8\pi G+f_T}{f_R}p \nonumber \\&+ \frac{1}{f_R}\bigg [2H\dot{R}f_{RR}+\ddot{R} f_{RR}+ \dot{R}^{2}f_{RRR}\nonumber \\&- \frac{1}{2}(f-Rf_R)- p f_T \bigg ], \end{aligned}$$
(10)

where the dot denotes the derivative with respect to the cosmic time t and \(H=\frac{\dot{a}}{a}\), the Hubble parameter. In the above equations, \(\rho \) is the matter density, p the matter pressure and the trace \(T= \rho -3p\).

3 f(R, T) baryogenesis

In f(R, T) gravity where we take account a minimal coupling between matter and geometry, we consider a CP-violating interaction term generating by the baryon asymmetry of the universe of the form,

$$\begin{aligned} \frac{1}{M_{*}^2} \int \sqrt{-g} dx^{4} \Big ( \partial _{\mu }(R+T)\Big ) J^{\mu }. \end{aligned}$$
(11)

We define the baryon to entropy ratio as

$$\begin{aligned} \frac{n_B}{s} \simeq -\frac{15 g_b}{4\pi ^2 g_{*}} \bigg [ \frac{1}{M_{*}^2\mathcal {T}} \Big (\dot{R}+\dot{T}\Big ) \bigg ] \arrowvert {\mathcal {T}_D}, \end{aligned}$$
(12)

where \(\mathcal {T}_D\) is the decoupling temperature and \(n_B\), the baryon number. The “dot” denote the derivative with respect the cosmic time. We assume in this paper that a thermal equilibrium exists. For this reason we consider that the universe evolves slowly from an equilibrium state to an equilibrium state with the energy being linked to the temperature \(\mathcal {T}\) as

$$\begin{aligned} \rho = \frac{\pi ^2}{30}g_{*} {\mathcal {T}}^{4}. \end{aligned}$$
(13)

In (13), \(g_{*}\) represents the number of the degrees of freedom of the effectively massless particles and \(\mathcal {T}\), the decoupling temperature .

In the context of GR, if we assume that the matter content of the universe as perfect fluid with constant equation of state parameter \(w=\frac{p}{\rho }\), the Ricci scalar R and the trace \(T= \rho (1-3w) \) of the energy-momentum tensor of matter are related as

$$\begin{aligned} R= -8\pi G (1-3w)\rho . \end{aligned}$$
(14)

If the universe is filled by the radiation, the baryon number to entropy ratio (12) is equal zero in GR. This results is different zero for the other content of the matter. However, a net baryon asymmetry may be generated during the radiation dominated era in f(R, T) theories of gravity. To do, we focus on attention on two particulars f(R, T) models namely \(f(R,T) = R +\alpha T + \beta T^2\) and \(f(R,T) =R+ \mu R^2 + \lambda T\) to describe how we can recover the baryogenesis epoch with these models. We calculate the baryon to entropy ratio for each model by considering a universe filled by the dark energy and perfect fluid with constant equation of state parameter \( w= \frac{p}{\rho }\) and assuming that the scale factor evolve as power-law \(a(t) = B t^{\gamma }\) where B is a constant parameter.

3.1 \(f(R,T) = R +\alpha T + \beta T^2\) cases

For the first case, by using the FRW Eq. (9) and both the expressions of the scale factor and equation of state parameter that we assumed, we find the analytically expression of the energy density as

$$\begin{aligned} \rho = \frac{-\delta t^2 + \sqrt{\delta ^2 t^4 +12 \zeta \gamma ^2 t^2 }}{2 \zeta t^2}, \end{aligned}$$
(15)

where \( \delta = 8\pi G +\frac{\alpha }{2}(3-w)\) and \(\zeta = \beta (\frac{3}{2}-7w-\frac{3w^2}{2})\).

Equaliting this expression with (13), we obtain the decoupling cosmic time \(t_{D}\) expressed in function of the decoupling temperature \({\mathcal {T_D}}\) as

$$\begin{aligned} t_{D}=\frac{30\sqrt{3}\gamma }{\sqrt{30\delta \pi ^2 g_{*} {\mathcal {T_D}}^{4} + \zeta \pi ^4 g_{*} {\mathcal {T_D}}^{8} }}. \end{aligned}$$
(16)

Using Eq. (16), we arrive at a final expression of the baryon-to-entropy ratio for the present f(R, T) particular model

$$\begin{aligned} \frac{n_B}{s}\simeq & {} -\frac{ g_b \sqrt{g_{*} \pi ^2 {\mathcal {T_D}}^{4}\big (30\delta +\zeta \pi ^2 g_{*} {\mathcal {T_D}}^{4} } \big ) }{3600\sqrt{3}\gamma ^2 \pi ^2 g_{*}M_{*}^2\mathcal {T}_D} \nonumber \\&\times \left[ \frac{{15 \gamma ^3 (3w-1)}}{ \sqrt{ \frac{ {\gamma ^4 {\big (15 \delta +\zeta \pi ^2 g_{*} {\mathcal {T_D}}^{4} } \big )}^2 }{ {\pi ^4 {g_{*}^2} {\mathcal {T_D }^{8}} { \big (30 \delta +\zeta \pi ^2 g_{*} {\mathcal {T_D}}^{4} } \big )}^2 } }} \right. \nonumber \\&\left. + 2 \pi ^2 g_{*} {\mathcal {T_D}}^{4} (2\gamma -1) \big (30\delta +\zeta \pi ^2 g_{*} {\mathcal {T_D}}^{4} \big ) \right] . \end{aligned}$$
(17)

In the radiation dominated phase, \( \delta = 8\pi G +\frac{4}{3}\alpha \), \(\zeta =-\beta \). Hence, Eq. (17) reduces to

$$\begin{aligned} \frac{n_B}{s} \simeq - \frac{ g_{b} {\mathcal {T_D}}^{5} (2\gamma -1) \pi \sqrt{g_{*} {\big (30\delta - \beta g_{*}\pi ^2 {\mathcal {T_D}}^{4} \big )}^{3}}}{3600\sqrt{3}\gamma ^2 M_{*}^2 }. \end{aligned}$$
(18)

We can show from Eq. (18) that the resulting baryon to entropy ratio is non-zero in contrast for the GR if \(\gamma \ne \frac{1}{2}\). Within the choice of the free parameters and depending on matter content, we can adjust the baryon to entropy ratio Eq. (18) to satisfy the observational constraints. For illustrating we assume that the cutoff scale \(M_{*}\) takes the value \(M_{*} = 10^{12}\) GeV, also that the critical temperature is equal to \({\mathcal {T_D}} = M_I = \mathbf{2 \times 10^{16}}\) GeV, with \(M_I\) being the upper bound for tensor mode fluctuations constraints on the inflationary scale, \(g_b \simeq \mathcal {O}(1)\) and \(g_{*} \simeq 106\), which is the total number of the effectively massless particle in the Universe [20]. The choice of \({\mathcal {T_D}} = M_I = \mathbf{2 \times 10^{16}} \) GeV is particular interesting because it implies that tensor mode fluctuations should be observed in the next generation of the experiments. For more details, see the references [11, 13,14,15, 20, 21]. In Table 1, we present some values of baryon to entropy ratio \(\frac{n_{B}}{s}\) for \(\gamma =\mathbf{0. 4}\), \(\alpha = 10^{-20}\), \(M_{*} = 10^{12}\) GeV, \({\mathcal {T_D}} = \mathbf{2 \times 10^{16} }\) GeV by using various values of the parameter \(\beta \).

Table 1 Some values of baryon to entropy ratio for \(\gamma =0.4\) and \(\alpha = 10^{-20}\)
Full size table

According to the results of this table, we observe that for \(\beta = \mathbf{-4\times 10^{-9}}\), \(n_{B}/s\) \(\mathbf{= 9.01\times 10^{-11}}\), which is very agreement with observations and practically equal to the observed value (\(n_{B}/s \mathbf{\simeq 9.42\times 10^{-11}}\)) whereas when \(\beta > \mathbf{-4\times 10^{-9}}\), we denote a significantly small values.

In addition, we plot in Fig. 1, the \(\gamma \)- dependence of the baryon to entropy ratio for \(M_{*} = 10^{12}\) GeV, \({\mathcal {T_D}} = \mathbf{2\times 10^{16}}\) GeV. From the curves of the Fig. 1, one can notice that, the intersection of each curve with the curve that displays the observational value (dashed lines) are in good agreement value of baryon to entropy ratio for specific value of \(\gamma \) including 0 and 0.5. Also, we note that each curve goes towards 0 when the parameter \(\gamma \) tends to 0.5 which is compatible with theoretical results.

Fig. 1
figure 1

The baryon to entropy ratio for the model \(f(R,T) = R +\alpha T + \beta T^2\). The graphs are plotted for \(\alpha =10^{-20}\) and for the varying values of \(\beta \), \(\beta = \mathbf{-5\times 10^{-10}}\) (blue), \(\beta =\mathbf{-4\times 10^{-10}}\) (magenta), \(\beta =\mathbf{-3 \times 10^{-10}}\) (green), \(\beta =\mathbf{-2\times 10^{-10}}\) (red), \(\beta = \mathbf{-10^{-10}}\) (orange). The dashed curve represents the observational value

Full size image

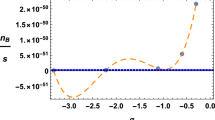
To see how the \(f(R,T) = R +\alpha T + \beta T^2\) models can be constrained in baryogenesis epoch, the Fig. 2 shows the baryon to entropy ratio as function of the free parameter \(\beta \). To do so, we fix the second parameter \(\alpha \) and we consider \(M_{*} = 10^{12}\) GeV and \({\mathcal {T_D}} = \mathbf{2\times 10^{16}}\) GeV.

Fig. 2
figure 2

The baryon to entropy ratio for the model \(f(R,T) = R +\alpha T + \beta T^2\) in function of \(\alpha \). The graphs are plotted for \(\gamma =0.13\) and for the varying values of \(\beta \), \(\beta = \mathbf{-3\times 10^{-10}}\) (blue), \(\beta =\mathbf{-2.5 \times 10^{-10}}\) (magenta), \(\beta =\mathbf{-2 \times 10^{-10}}\) (green), \(\beta =\mathbf{-1.5\times 10^{-10}}\) (red), \(\beta = \mathbf{-10^{-10}}\) (orange) and dashed curve, the observational value

Full size image

3.2 \(f(R,T) = R+ \mu R^2 + \lambda T\) cases

The first FRW Eq. (9) becomes

$$\begin{aligned} 3H^2 (1+2\mu R)= & {} \rho \big ( 8\pi G +\frac{1}{2}\lambda (3-w) \big )\nonumber \\&-\frac{1}{2}\mu R^2 -6\mu \dot{R} H. \end{aligned}$$
(19)

Making use the scale factor that we assumed, we can solve (19) explicitly

$$\begin{aligned} \rho = \frac{ 3 t^2 \gamma ^2-\Gamma }{\Delta t^4}, \end{aligned}$$
(20)

where \(\Gamma = 4\mu \gamma ^2 \big (\gamma ^2-4\gamma +1)\) and \( \Delta = 8\pi G +\frac{1}{2}\lambda (3-w)\).

For the special model considered, one can express the decoupling cosmic time \(t_{D}\) as

$$\begin{aligned} t_{D} = \sqrt{ \frac{45 \gamma ^2 +\sqrt{2025\gamma ^4-30g_{*}\Gamma \Delta \pi ^2 {\mathcal {T_D}}^{4}}}{g_{*} \Delta \pi ^2 {\mathcal {T_D}}^{4}}}, \end{aligned}$$
(21)

where we assumed that \(2025\gamma ^4-30g_{*}\Gamma \Delta \pi ^2 {\mathcal {T_D}}^{4}> 0 \) and \(\Delta > 0\). Then, we reformulate the baryon to entropy ratio (12) as

$$\begin{aligned} \frac{n_B}{s}\simeq & {} - \frac{15 g_b {(g_{*} {\Delta })}^{\frac{3}{2}} {\mathcal {T_D}}^{9} \pi ^3}{ M_{*}^2 {{\Bigg [45\gamma ^2 + {{ \Big ( 2025\gamma ^4-30g_{*} \Gamma \Delta \pi ^2 {\mathcal {T_D}}^{4} }} \Big )}^{\frac{1}{2}} \Bigg ] }^{\frac{5}{2}}} \left[ \Gamma (2-6w) \right. \nonumber \\&\left. + \frac{3\gamma \Big (-2\Delta +\gamma (-1+3w+4 \Delta ) \Big )\Big (45\gamma ^2 + {\big (2025\gamma ^4-30g_{*}\Gamma \Delta \pi ^2 {\mathcal {T_D}}^{4} \big )}^{\frac{1}{2}}\Big )}{g_{*}\Delta \pi ^2 {\mathcal {T_D}}^{4}} \right] . \end{aligned}$$
(22)

In the radiation dominated epoch, \(\Delta = 8\pi G +\frac{4\lambda }{3}\) and the baryon to entropy ratio (22) becomes

$$\begin{aligned} \frac{n_B}{s}\simeq & {} - \frac{90}{M_{*}^2} \gamma g_{b} \pi \Delta ^{\frac{3}{2}} {g_{*}}^{\frac{1}{2}} {\mathcal {T_D}}^{5}(2\gamma -1)\Bigg [45\gamma ^2 \nonumber \\&+ \Big (2025\gamma ^4-30g_{*} \Gamma \Delta \pi ^2 {\mathcal {T_D}}^{4}\Big )^{\frac{1}{2}} \Bigg ] ^{-\frac{3}{2}}. \end{aligned}$$
(23)

We see from this results that the baryon to entropy ratio is non-zero in case where \(\gamma \ne \frac{1}{2}\) for the special f(R, T) model considered. Notice that for \(\gamma = 0.3\) and \(\mu = \lambda = 10^{-5}\), the baryon to entropy ratio \(n_{B}/s = \mathbf{8.28\times 10^{-11}}\), which is a compatible with the observational value. In the same way, we plot in Fig. 3, the evolution of baryon to entropy ratio (23) versus \(\gamma \) for \(M_{*} = 10^{12}\) GeV and \({\mathcal {T_D}} = \mathbf{2\times 10^{16}}\) GeV in comparison with the curve traducing the observational value.

Fig. 3
figure 3

The \(\gamma \)- dependence of baryon to entropy ratio for the model \(f(R,T) = R+ \mu R^2 + \lambda T\) for \(M_{*} = 10^{12}\) GeV, \({\mathcal {T_D}} = \mathbf{2\times 10^{16}}\) GeV. The curves are plotted for \(\lambda = 10^{5}\) and for \(\mu = \mathbf{10^{-5}}\) (blue), \(\mu =\mathbf{2\times 10^{-5}}\) (magenta), \(\mu =\mathbf{3 \times 10^{-5}}\) (green), \(\mu =\mathbf{4 \times 10^{-5}}\) (red), \(\mu = \mathbf{5\times 10^{-10}}\) (orange) and dashed, the observational value

Full size image

Likewise to the first model, we plot in Fig. 4, the numerical results of baryon to entropy ratio of the second model as function of \(\mu \) to see how we can constrain this model in baryogenesis epoch.

Fig. 4
figure 4

The baryon to entropy ratio for the model \(f(R,T) = R +\lambda T + \mu T^2\) in function of \(\mu \). The graphs are plotted for \(\gamma =0.28\) and for the varying values of \(\lambda \), \(\lambda = \mathbf{10^{2}}\) (blue), \(\lambda =\mathbf{1.5 \times 10^{2}}\) (magenta), \(\lambda =\mathbf{2 \times 10^{2}}\) (green), \(\lambda =\mathbf{2.5\times 10^{2}}\) (red), \(\lambda = \mathbf{3 \times 10^{2}}\) (orange) and the dashed curve represents observational value

Full size image

In Figs. 2 and 4, we have noticed that how we can constrain each model to see the observational value of baryon to entropy ratio in the frame of the modified theories of gravity. The different values of the parameters that can constrain these models in baryogenesis era are denoted by the intersection of each curve for specific parameter with the observational curve of baryon to entropy ratio.

4 Conclusion

The paper is devoted to the study of gravitational baryogenesis mechanism in the context of f(R, T) theories. According that the CP-violating interaction that will generate the baryon asymmetry of the Universe and considering that the matter content of the universe as perfect fluid with constant equation of state parameter, we evaluate the baryon to entropy ratio for two particulars f(R, T) models. In contrast with GR, we show for both models that the baryon to entropy ratio is non-zero in radiation dominated epoch if the parameter \(\gamma \ne \frac{1}{2}\) and the baryogenesis epoch can be reproduced in such theory.