Non-Bessel–Gaussianity and flow harmonic fine-splitting

Abstract

Both collision geometry and event-by-event fluctuations are encoded in the experimentally observed flow harmonic distribution $p(v_n)$ and 2k-particle cumulants $c_n\{2k\}$. In the present study, we systematically connect these observables to each other by employing a Gram–Charlier A series. We quantify the deviation of $p(v_n)$ from Bessel–Gaussianity in terms of harmonic fine-splitting of the flow. Subsequently, we show that the corrected Bessel–Gaussian distribution can fit the simulated data better than the Bessel–Gaussian distribution in the more peripheral collisions. Inspired by the Gram–Charlier A series, we introduce a new set of cumulants $q_n\{2k\}$, ones that are more natural to use to study near Bessel–Gaussian distributions. These new cumulants are obtained from $c_n\{2k\}$ where the collision geometry effect is extracted from it. By exploiting $q_2\{2k\}$, we introduce a new set of estimators for averaged ellipticity $\bar{v}_2$, ones which are more accurate compared to $v_2\{2k\}$ for $k>1$. As another application of $q_2\{2k\}$, we show that we are able to restrict the phase space of $v_2\{4\}$, $v_2\{6\}$ and $v_2\{8\}$ by demanding the consistency of $\bar{v}_2$ and $v_2\{2k\}$ with $q_2\{2k\}$ equation. The allowed phase space is a region such that $v_2\{4\}-v_2\{6\}\gtrsim 0$ and $12 v_2\{6\}-11v_2\{8\}-v_2\{4\}\gtrsim 0$, which is compatible with the experimental observations.

1 Introduction

It is a well-established picture that matter produced in a heavy ion experiment shows collective behavior. Based on this picture, the initial energy density manifests itself in the final particle momentum distribution. Accordingly, as the main consequence of this collectivity, the final particle momentum distribution has extensively been studied by different experimental groups in the past years. As a matter of fact, the experimental groups at Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) measure the flow harmonics $v_n$ [1,2,3,4,5,6,7,8], the coefficients of the momentum distribution Fourier expansion in the azimuthal direction [9,10,11]. All these observations can be explained by several models based on the collective picture.

Finding the flow harmonics is not straightforward, because the reaction-plane angle (the angle between the orientation of the impact parameter and a reference frame) is not under control experimentally. Additionally, the Fourier coefficients cannot be found reliably due to the low statistic in a single event. These issues enforce us to use an analysis more sophisticated than a Fourier analysis. There are several methods to find the flow harmonics experimentally, namely the event-plane method [12], multiparticle correlation functions [13, 14] and Lee–Yang zeros [15, 16]. The most recent technique to find the flow harmonics is using the distribution of the flow harmonic $p(v_n)$. This distribution has been obtained experimentally by employing the unfolding technique [17, 18].

It is well known that the initial shape of the energy density depends on the geometry of the collision and the quantum fluctuations at the initial state. As a result, the observed flow harmonics fluctuate event-by-event even if we fix the initial geometry of the collision. In fact, the event-by-event fluctuations are encoded in $p(v_n)$ and experimentally observed flow harmonics as well. It is worthwhile to mention that the observed event-by-event fluctuations are a reflection of the initial state fluctuations entangled with the modifications during different stages of the matter evolution, namely collective expansion and hadronization. For that reason, exploring the exact interpretation of the flow harmonics is crucial to understand the contribution of each stage of the evolution on the fluctuations. Moreover, there has not been found a well-established picture for the initial state of the heavy ion collision so far. The interpretations of the observed quantities contain information about the initial state. This information can shed light upon the heavy ion initial state models too.

According to the theoretical studies, the flow harmonics $v_n\{2k\}$ obtained from 2k-particle correlation functions are different, and their difference is due to non-flow effects [13, 14] and event-by-event fluctuations [19]. We should point out that experimental observations show that $v_2\{2\}$ is considerably larger than $v_2\{4\}$, $v_2\{6\}$ and $v_2\{8\}$. Additionally, all the ratios $v_2\{6\}/v_2\{4\}$, $v_2\{8\}/v_2\{4\}$ and $v_2\{8\}/v_2\{6\}$ are different from unity [20, 21]. Alternatively, the distribution $p(v_n)$ is approximated by a Bessel–Gaussian distribution (corresponding to a Gaussian distribution for $v_n$ fluctuations) as a simple model [10, 22]. Based on this model, the difference between $v_2\{2\}$ and $v_2\{4\}$ is related to the width of the $v_2$ fluctuations. However, this model cannot explain the difference between the other $v_2\{2k\}$.

In the past years, several interesting studies of the non-Gaussian $v_n$ fluctuations have been done [23,24,25,26,27,28]. Specifically, it has been shown in Ref. [27] that the skewness of the $v_2$ fluctuations is related to the difference $v_2\{4\}-v_2\{6\}$. Also, the connection between kurtosis of $v_3$ fluctuations and the ratio $v_3\{4\}/v_3\{2\}$ has been studied in Ref. [28]. It is worth noting that the deviation of $v_n$ fluctuations from a Gaussian distribution immediately leads to the deviation of $p(v_n)$ from a Bessel–Gaussian distribution. In [29], the quantities $v_n\{4\}-v_n\{6\}$ and $v_n\{6\}-v_n\{8\}$ for a generic narrow distribution are computed.

In the present work, we will introduce a systematic method to connect $v_n\{2k\}$ to the distribution $p(v_n)$. In Sect. 2, we have an overview of the known concepts of cumulants, flow harmonic distributions and their relation with the averaged flow harmonics $\bar{v}_n$. Section 3 is dedicated to the Gram–Charlier A series in which we find an approximate flow harmonic distribution in terms of $c_n\{2k\}$. Specifically for the second harmonics, we show that the deviation of $p(v_2)$ from Bessel–Gaussianity is quantified by the fine-splitting $v_2\{2k\}-v_2\{2\ell \}$ where $k,\ell \ge 2$ and $k\ne \ell$. These studies guide us to defining a new set of cumulants $q_n\{2k\}$ where they depend on the event-by-event fluctuations only. In Sect. 4, we use the new cumulants to introduce more accurate estimations for the average ellipticity. As another application of new cumulants, we use $q_2\{2k\}$ to constrain the $v_2\{4\}$, $v_2\{6\}$ and $v_2\{8\}$ phase space in Sect. 5. We show that the phase space is restricted to a domain where $v_2\{4\}-v_2\{6\}\gtrsim 0$¹ and $12 v_2\{6\}-11v_2\{8\}-v_2\{4\}\gtrsim 0$. We present the conclusion in Sect. 6. The supplementary materials can be found in the appendices. We would like to emphasize that in Appendix C, we found a one-dimensional distribution for $p(v_n)$ which is different from that mentioned in Sect. 3. Additionally, an interesting connection between the expansion of $p(v_n)$ in terms of the cumulants $c_n\{2k\}$ and the relatively new concept of multiple orthogonal polynomials in mathematics is presented in Appendix D.

2 Flow harmonic distributions and 2k-particle cumulants

This section is devoted to an overview of already well-known concepts concerning the cumulant and its application to study the collectivity in the heavy ion physics. We present this overview to smoothly move forward to the harmonic distribution of the flow and its deviation from Bessel–Gaussianity.

2.1 Correlation functions vs. distribution

According to the collective picture in the heavy ion experiments, the final particle momentum distribution is a consequence of the initial state after a collective evolution. In order to study this picture quantitatively, the initial anisotropies and flow harmonics are used extensively to quantify the initial energy density and final momentum distribution.

The initial energy (or entropy) density of a single event can be written in terms of the initial anisotropies, namely the ellipticity and triangularity. Specifically, ellipticity and triangularity (shown by $\varepsilon _2$ and $\varepsilon _3$, respectively) are cumulants of the distribution indicating how much it is deviated from a two-dimensional rotationally symmetric Gaussian distribution [30].

The final momentum distribution is studied by its Fourier expansion in the azimuthal direction,

$$\begin{aligned} \frac{1}{N}\frac{\text {d}N}{\text {d}\phi }=\frac{1}{2\pi }\left[ 1+\sum _{n=1}^{\infty } 2 v_n \cos n(\phi -\psi _n)\right] . \end{aligned}$$

(1)

In the above, $v_n$ and $\psi _n$ are unknown parameters, which can be found easily via $\hat{v}_n\equiv v_n \text {e}^{in\psi _n}=\langle \text {e}^{i n \phi } \rangle$. Here, the averaging is obtained by using the distribution $\frac{1}{N}\frac{\text {d}N}{\text {d}\phi }$ in a given event. The parameter $\hat{v}_n$ is called flow harmonic. Instead of a complex form, we occasionally use the flow harmonics in Cartesian coordinates,

$$\begin{aligned} v_{n,x}=v_n\cos n\psi _n,\qquad v_{n,y}=v_n\sin n\psi _n. \end{aligned}$$

(2)

Low multiplicity in a single event, randomness of the reaction plane angle and non-flow effects are the main challenges in extracting the experimental values of the flow harmonics. By defeating these experimental challenges, one would be able to find the distribution $p(v_{n,x},v_{n,y})$ for each centrality class which is a manifestation of the event-by-event fluctuations. In finding $p(v_{n,x},v_{n,y})$, we rotate the system at each single event such that the reaction-plane angle $\varPhi _{\text {RP}}$ is set to be zero. In this case, the averaged ellipticity $\bar{v}_2\equiv \langle v_{2,x} \rangle$ is a manifestation of the geometrical initial ellipticity for events in a given centrality class irrespective of the fluctuations. In general, we are able to define the averaged flow harmonic $\bar{v}_n\equiv \langle v_{n,x} \rangle$ too. In odd harmonics, however, this average would be zero for spherical ion collisions with the same sizes.

A practical way to study a distribution function $p({\mathbf {r}})$ is using two-dimensional cumulants, where ${\mathbf {r}}$ stands for a generic two-dimensional random variable. Consider $G({\mathbf {k}})$ as the characteristic function of the probability distribution $p({\mathbf {r}})$. The characteristic function is, in fact, the Fourier transformed $p({\mathbf {r}})$,

$$\begin{aligned} G({\mathbf {k}})\equiv \langle \text {e}^{i {\mathbf {r}}\cdot {\mathbf {k}}} \rangle = \int \text {d}x\text {d}y\,\text {e}^{i {\mathbf {r}}\cdot {\mathbf {k}}} p({\mathbf {r}}). \end{aligned}$$

(3)

Consequently, we can define the cumulative function as ${\mathcal {C}}({\mathbf {k}})=\log G({\mathbf {k}})$. Two-dimensional cumulants are obtained from

$$\begin{aligned} \begin{aligned} \log \langle \text {e}^{i {\mathbf {r}}\cdot {\mathbf {k}}} \rangle&=\sum _{m,n}\frac{i^{m+n}k_x^m k_y^n {\mathcal {A}}_{mn}}{m! n!}\\&=\sum _{m=0}^{\infty }\sum _{n=-\infty }^{\infty } \frac{i^m k^m \text {e}^{in\varphi _k} \;{\mathcal {C}}_{m,n}}{m!}, \end{aligned} \end{aligned}$$

(4)

where ${\mathcal {A}}_{mn}$ and ${\mathcal {C}}_{m,n}$ are the 2D cumulants in Cartesian and polar coordinates, respectively. The two-dimensional cumulants have already been used to quantify the initial energy density shape by Teaney and Yan in Ref. [30]. However, we use the two-dimensional cumulants to study the harmonic distribution of the flows in the present study². In the second line in the above, we used $k=\sqrt{k_x^2+k_y^2},\,\varphi _k=\text {atan2}(k_x,k_y)$. In Appendix A, we study 2D cumulants in these two coordinates and their relations in more detail.

The random $\varPhi _{\text {RP}}$ rotates the point $(v_{n,x},v_{n,y})$ with a random phase in the range $[0,2\pi )$ at each event. As a result, the distribution $p(v_{n,x},v_{n,y})$ is replaced by $\tilde{p}(v_{n,x},v_{n,y})$, which is a rotationally symmetric distribution.³ We should mention that the distribution $\tilde{p}(v_{n,x},v_{n,y})$ is experimentally accessible. In Ref. [18], the unfolding technique has been used by the ATLAS collaboration to remove the statistical uncertainty (due to the low statistics at each event) and non-flow effects from a distribution of the “observed” flow harmonics $(v_{n,x}^{\text {obs}},v_{n,y}^{\text {obs}})$. In this case, the only unknown parameter in finding an accurate $p(v_{n,x},v_{n,y})$ is the reaction-plane angle. Since there is no information in the azimuthal direction of $\tilde{p}(v_{n,x},v_{n,y})$, we can simply average out this direction to find a one-dimensional distribution,⁴

$$\begin{aligned} p(v_n)=v_n \int _{0}^{2\pi }\text {d}\varphi \, p(v_n \cos \varphi ,v_n \sin \varphi ). \end{aligned}$$

(5)

Note that we can interchangeably use $\tilde{p}(v_{n,x},v_{n,y})$ or $p(v_{n,x}$ $,v_{n,y})$ in the above because obviously the effect of the random reaction-plane angle and the azimuthal averaging are the same.

In polar coordinates, we have $\tilde{p}(v_{n,x},v_{n,y})\equiv \tilde{p}(v_n)$. As a result, the characteristic function of the distribution $\tilde{p}(v_{n,x},v_{n,y})$ in polar coordinates is given by

$$\begin{aligned} \begin{aligned}&\langle \text {e}^{i v_n k\cos (\varphi -\varphi _k)} \rangle _{\text {2D}}\\&\quad =\int _0^{\infty }\int _0^{2\pi } v_n \text {d} v_n\text {d}\varphi \; \tilde{p}(v_n)\;\text {e}^{ i v_n k\cos (\varphi -\varphi _k)}\\&\quad = \int _0^{\infty } \text {d}v_n\,p(v_n) J_0(k v_n)=\langle J_0(k v_n) \rangle _{\text {1D}}, \end{aligned} \end{aligned}$$

(6)

where we used Eq. (5) in the above. Here, $J_0(x)$ is the Bessel function of the first kind. Also, $\langle \cdots \rangle _{\text {2D}}$ means averaging with respect to $\tilde{p}(v_{n,x},v_{n,y})$, while $\langle \cdots \rangle _{\text {1D}}$ specifies the averaging with respect to $p(v_n)$. Equation (6) indicates that we can study the radial distribution $p(v_n)$ instead of $\tilde{p}(v_{n,x},v_{n,y})$ if we use $G(k)=\langle J_0(k v_n) \rangle$ as the characteristic function of $p(v_n)$⁵.

The cumulants of $p(v_n)$ can be found by expanding the cumulative function $\log \langle J_0 (k v_n)\rangle$ in terms of ik. The coefficients of ik in this expansion (up to some convenient constants) are the desired cumulants,

$$\begin{aligned} \log \langle J_0 (k v_n)\rangle = \sum _{m=1}\frac{(ik)^{2m} c_n\{2m\}}{4^m(m!)^2}. \end{aligned}$$

(7)

where $c_n\{2m\}$ are those obtained from 2k-particle correlation functions [13, 14],

$$\begin{aligned} c_n\{2\}= & {} \langle v_n^2 \rangle , \end{aligned}$$

(8a)

$$\begin{aligned} c_n\{4\}= & {} \langle v_n^4 \rangle -2\langle v_n^2 \rangle ^2, \end{aligned}$$

(8b)

$$\begin{aligned} c_n\{6\}= & {} \langle v_n^6 \rangle -9\langle v_n^4 \rangle \langle v_n^2 \rangle +12\langle v_n^2 \rangle ^3, \end{aligned}$$

(8c)

$$\begin{aligned} c_n\{8\}= & {} \langle v_n^8 \rangle -16\langle v_n^6 \rangle \langle v_n^2 \rangle -18\langle v_n^4 \rangle ^2, \\&+144\langle v_n^4 \rangle \langle v_n^2\rangle ^2-144\langle v_n^2 \rangle ^4.\nonumber \end{aligned}$$

(8d)

The cumulants $c_n\{2k\}\propto v_n^{2k}\{2k\}$ (see Eq. (12)) are indicating the characteristics of the distribution $p(v_n)$ while the cumulants ${\mathcal {A}}_{mn}$ (or equivalently ${\mathcal {C}}_{m,n}$) in Eq. (4) are shown the characteristics of $p(v_{n,x},v_{n,y})$. The interconnection between $v_n\{2k\}$ and ${\mathcal {A}}_{mn}$ have been studied previously in the literature. We point out that in order to define $p(v_{n,x},v_{n,y})$, we considered $\varPhi _{\text {RP}}=0$ for all events. In this case, the cumulant ${\mathcal {A}}_{30}=\langle (v_{n,x}$ $-\langle v_{n,x}\rangle )^3 \rangle$ is related to the skewness of $p(v_{n,x},v_{n,y})$. For the case $n=2$, this quantity is found for the first time in Ref. [27], and it is argued that ${\mathcal {A}}_{30}\propto v_2\{4\}-v_2\{6\}$. In other words, ${\mathcal {A}}_{30}$ is related to the fine-splitting between $v_2\{4\}$ and $v_2\{6\}$. In Ref. [28], the kurtosis of $p(v_{3,x},v_{3,y})$ in the radial direction has also been calculated, and it is shown it is proportional to $v_3^4\{4\}$⁶.

One may wonder whether the distribution $p(v_n)$ contains more information than $c_n\{2k\}$ because the odd moments of $p(v_n)$ are absent in the definitions of $c_n\{2k\}$ [29]. However, it is worth mentioning that the moments can be found by expanding the characteristic function G(k) in terms of ik,

$$\begin{aligned} G(k)=\langle J_0 (k v_n)\rangle =1+\frac{\langle v_n^2 \rangle }{4} k^2+\frac{\langle v_n^4 \rangle }{64} k^4+\cdots , \end{aligned}$$

(9)

for the radial distributions like $p(v_n)$. Since the above series is convergent,⁷ we can find the characteristic function G(k) by finding the moments $\langle v_n^{2k} \rangle$. Having the characteristic function in hand, we immediately find $p(v_n)$ by inversing the last line in Eq. (6),⁸

$$\begin{aligned} p(v_n)=v_n \int _0^{\infty }k\, \text {d}k \,J_o(k v_n) G(k). \end{aligned}$$

(10)

It means that by assuming the convergence of the series in Eq. (9) the distribution $p(v_n)$ can be found completely by using only even moments.

Equivalently, we can use the following argument: for the distribution $\tilde{p}(v_{n,x},v_{n,y})$, one simply finds the only non-vanishing moments are $\langle v_{n_x}^{2k} v_{n_y}^{2\ell } \rangle$. It means that in the polar coordinates only $\langle v_n^{2(k+\ell )}\rangle$ are present. Additionally, by finding the two-dimensional cumulants of $\tilde{p}(v_{n,x},v_{n,y})$ in polar coordinates ${\mathcal {C}}_{m,n}$ (Eq. (4)), we find that the only non-zero cumulants are ${\mathcal {C}}_{2k,0}\propto c_n\{2k\}$ (see Appendix A).

As a result, in the presence of random reaction-plane angle, $c_n\{2k\}$’s are all we can learn from the original $p(v_{n,x},v_{n,y})$, whether we use 2k-particle correlation functions or obtain it from the unfolded distribution $p(v_n)$ in principle. However, we should note that the efficiency of the two methods in removing single event statistical uncertainty and non-flow effects could be different, which leads to different results in practice.

Furthermore, the whole information about the fluctuations is not encoded in $p(v_{n,x},v_{n,y})$. In fact, the most general form of the fluctuations are encoded in a distribution as $p(v_{1,x},v_{1,y},v_{2,x},v_{2,y},\ldots )$. It is worth mentioning that the symmetric cumulants, which have been introduced in Ref. [33] and have been measured by the ALICE collaboration [34], are non-vanishing. Additionally, the event-plane correlations (which are related to the moments $\langle \hat{v}_m^q (\hat{v}^*_{n})^{q\,m/n} \rangle$) have been obtained by the ATLAS collaboration [35, 36]. They are non-zero too. These measurements indicate that $p(v_{1,x},v_{1,y},v_{2,x},v_{2,y},\ldots )$ cannot be written as $\prod _n p(v_{n,x},v_{n,y})$. In the present work, however, we do not focus on the joint distribution and leave this topic for studies in the future. Let us point out that moving forward to find a generic form for the moments of the harmonic distribution of the flow was already done in Ref. [37].

2.2 Approximated averaged ellipticity

A question arises now: how much information is encoded in $p(v_n)$ from the original $p(v_{n,x},v_{n,y})$? In order to answer this question, we first focus on $n=3$. Unless there is no net triangularity for spherical ion collisions, the non-zero triangularity at each event comes from the fluctuations. Hence, we have $\bar{v}_3=0$ for such an experiment. In this case, the event-by-event randomness of $\varPhi _{\text {RP}}$ is similar to the rotation of the triangular symmetry plane due to the event-by-event fluctuations. It means that $p(v_{3,x},v_{3,y})$ itself is rotationally symmetric, and the main features of $p(v_{3,x},v_{3,y})$ and $\tilde{p}(v_{3,x},v_{3,y})$ are the same. As a consequence, $p(v_3)$ or equivalently $c_3\{2k\}$ can uniquely reproduce the main features of $p(v_{3,x},v_{3,y})$.

However, it is not the case for $n=2$ due to the non-zero averaged ellipticity $\bar{v}_2$. The distribution $p(v_{2,x},v_{2,y})$ is not rotationally symmetric and reshuffling $(v_{2,x},v_{2,y})$ leads to information loss from the original $p(v_{2,x},v_{2,y})$. Therefore, there is at least some information in $p(v_{2,x},v_{2,y})$ that we cannot obtain from $p(v_2)$ or $c_2\{2k\}$. Nevertheless, it is still possible to find some features of $p(v_{2,x},v_{2,y})$ approximately. For instance, we mentioned earlier in this section that the skewness of this distribution in the $v_{2,x}$ direction is proportional to $v_2\{4\}-v_2\{6\}$.

The other important feature of $p(v_{2,x},v_{2,y})$ is $\bar{v}_2$, for which it is not obvious how to find it from $c_2\{2k\}$. In fact, we are able to approximately find $\bar{v}_2$ in terms of $c_2\{2k\}$ by approximating $p(v_{2,x},v_{2,y})$. The most trivial approximation is a two-dimensional Dirac delta function located at $(\bar{v}_2,0)$,

$$\begin{aligned} p(v_{2,x},v_{2,y})\simeq \delta (v_{2,x}-\bar{v}_2,v_{2,y}). \end{aligned}$$

This corresponds to the case that there are no fluctuations, and the only source for ellipticity is coming from an ideally elliptic initial geometry. Considering Eq. (5), the moments $\langle v_2^{2q} \rangle$ can easily be obtained as follows:

$$\begin{aligned} \langle v_2^{2q} \rangle= & {} \int d v_{2,x} d v_{2,y} (v_{2,x}^2+v_{2,x}^2)^{q} \delta (v_{2,x}-\bar{v}_2,v_{2,y}{\nonumber }\\= & {} \bar{v}_2^{2q}. \end{aligned}$$

(11)

Now by using Eq. (8), we find $c_2\{2\}=\bar{v}_2^2$, $c_2\{4\}=-\bar{v}_2^4$, $c_2\{6\}=4\bar{v}_2^6$, etc. It is common in the literature to show the averaged ellipticity $\bar{v}_2$, which is approximated by $c_2\{2k\}$ as $v_2\{2k\}$. Note that the quantity $v_2\{2k\}$ is defined for the case that the flow harmonic distribution is considered to be a delta function. Furthermore, we can assume the ideal case: that for any harmonics the distribution $p(v_{n,x},v_{n,x})$ has a sharp and clean peak around $\bar{v}_n$. By the assumption mentioned, we have [14]

$$\begin{aligned} \begin{aligned} v_n^2\{2\}&=c_n\{2\},\\ v_n^4\{4\}&=-c_n\{4\},\\ v_n^6\{6\}&=c_n\{6\}/4,\\ v_n^8\{8\}&=-c_n\{8\}/33. \end{aligned} \end{aligned}$$

(12)

Nevertheless, we know that $\bar{v}_n$ can be non-zero for odd n when the collided ions are not spherical or have different sizes.⁹

The delta function approximation for $p(v_{2,x},v_{2,y})$ is not compatible with the experimental observation. In this case, we have

$$\begin{aligned} v_2\{2\}=v_2\{4\}=\cdots =\bar{v}_2, \end{aligned}$$

(13)

by definition, while different $v_2\{2k\}$ have different values based on the experimental observation. Specifically, the difference between $v_2\{2\}$ and other $v_2\{2k\}$ for $k>1$ is considerably large [20, 21].

We can improve the previous approximation by replacing the delta function with a Gaussian distribution. In this case, we model the fluctuations by the width of the Gaussian distribution. Let us assume that $p(v_{2,x},v_{2,y})\simeq {\mathcal {N}}(v_{2,x},v_{2,y})$ where ${\mathcal {N}}(v_{2,x},v_{2,y})$ is a two-dimensional Gaussian distribution located at $(\bar{v}_2,0)$,¹⁰

$$\begin{aligned} {\mathcal {N}}(v_{2,x},v_{2,y})=\frac{1}{2\pi \sigma ^2} \text {e}^{-\frac{(v_{2,x}-\bar{v}_2)^2+v_{2,y}^2}{2\sigma ^2}}. \end{aligned}$$

(14)

Using the above and Eq. (5), one can simply find $p(v_2)=\text {BG}(v_2;\bar{v}_2)$ where $\text {BG}(v_2;\bar{v}_2)$ is the well-known Bessel Gaussian distribution [10, 22],

$$\begin{aligned} \text {BG}(v_2;\bar{v}_2)=\left( \frac{v_2}{\sigma ^2}\right) I_0\left( \frac{v_2 \bar{v}_2}{\sigma ^2}\right) \text {e}^{-\frac{v_2^2+\bar{v}_2^2}{2\sigma ^2}}. \end{aligned}$$

(15)

Here, $I_0(x)$ is the modified Bessel function of the first kind. Now, we are able to find the moments $\langle v_2^{2q} \rangle$ by using this approximated $p(v_2)$. According to the relations in Eq. (8), we find

$$\begin{aligned} \begin{aligned} v_2\{2\}&=\sqrt{\bar{v}_2^2+2\sigma ^2}\\ v_2\{4\}&=v_n\{6\}=v_n\{8\}=\cdots =\bar{v}_2, \end{aligned} \end{aligned}$$

(16)

where we used the notation $v_2\{2k\}$ introduced in Eq. (12). This result explains the large difference between $v_2\{2\}$ and $v_2\{2k\}$ for $k>1$. In fact, the presence of fluctuations is responsible for it. This description for the difference between $v_2\{2\}$ and other flow harmonics was argued first in Ref. [22]. It is found that the splitting between $v_2\{2\}$ and other flow harmonics contains information from the two-dimensional distribution [22].

The above two examples lead to the following remarks:

• In order to relate $\bar{v}_n$ to $c_n\{2k\}$, one needs to estimate the shape of $p(v_n)$ where $\bar{v}_n$ is implemented in this estimation explicitly. We show this estimated distribution by $p(v_n;\bar{v}_n)$.

• One can check the accuracy of the estimated distribution by studying the fine-splitting $v_n\{2k\}-v_n\{2\ell \}$ and comparing it with the experimental data.

We should say that the first remark is very strong and we can estimate $\bar{v}_n$ by a weaker condition. Obviously, if we estimate only one moment or cumulant of $p(v_n)$ as a function of $\bar{v}_n$, in principle, we can estimate $\bar{v}_n$ by comparing the estimated moment or cumulant with the experimental data. But the question is how to introduce such a reasonable estimation practically. In the following sections, we introduce a method to estimate $\bar{v}_n$ from a minimum information of $p(v_n)$. One notes that $\bar{v}_2=v_2\{4\}=\cdots$ is true only if we approximate $p(v_2)$ by a Bessel–Gaussian distribution. In the next section, we find an approximated distribution around Bessel–Gaussianity.

3 Radial-Gram–Charlier distribution and new cumulants

In Sect. 2.2, we argued that the quantity $\bar{v}_n$, which is truly related to the geometric features of the collision, can be obtained by estimating a function for $p(v_{n,x},v_{n,y})$. We observed that the Dirac delta function choice for $p(v_{n,x},v_{n,y})$ leads to $\bar{v}_n=v_n\{2k\}$ for $k>0$, while by assuming the distribution to be a 2D Gaussian located at $(\bar{v}_n,0)$ (the Bessel–Gaussian in one dimension) we find $\bar{v}_n=v_n\{2k\}$ for $k>1$. One notes that in modeling the harmonic distribution of the flow by a delta function or Gaussian distribution, the parameter $\bar{v}_n$ is an unfixed parameter, which is eventually related to the $v_n\{2k\}$. In any case, the experimental observation indicates that the $v_n\{2k\}$ are split; therefore, the above two models are not accurate enough.

Instead of modeling $p(v_{n,x},v_{n,y})$, we will try to model $p(v_n)$ with an unfixed parameter $\bar{v}_n$, namely $p(v_n;\bar{v}_n)$. In this section, we introduce a series for this distribution such that the leading term in this expansion is the Bessel–Gaussian distribution. The expansion coefficients would be a new set of cumulants that specifies the deviation of the distribution from Bessel–Gaussianity. In fact, by using these cumulants, we would be able to model $p(v_n;\bar{v}_n)$ more systematically.

It is well known that a given distribution can be approximated by a Gram–Charlier A series which approximates the distribution in terms of its cumulants (see Appendix B). Here we use this concept to find an approximation for $p(v_n;\bar{v}_n)$ in terms of the cumulants $c_n\{2k\}$. One of the formal methods of finding the Gram–Charlier A series is using orthogonal polynomials. In addition to this well-known method, we will introduce an alternative method, which is more practical for finding the series of a one-dimensional $p(v_n;\bar{v}_n)$ around the Bessel–Gaussian distribution.

3.1 Gram–Charlier A series: 1D distribution with support ${\mathbb {R}}$

Before finding the approximated distribution around the Bessel–Gaussian, let us have practice with the alternative method of finding Gram–Charlier A series by applying it to a one-dimensional distribution p(x) with support $(-\infty ,\infty )$.¹¹ This method will be used in the next section to find the radial-Gram–Charlier distribution for arbitrary harmonics.

The characteristic function for a one-dimensional distribution is $\langle \text {e}^{i k x}\rangle$, and the cumulants $\kappa _n$ of such a distribution are found from $\log \langle \text {e}^{i k x}\rangle =\sum _{n=1} (ik)^n \kappa _n/n!$. The first few cumulants are presented in the following:

$$\begin{aligned} \kappa _1= & {} \langle x \rangle , \end{aligned}$$

(17a)

$$\begin{aligned} \kappa _2= & {} \langle x^2 \rangle -\langle x \rangle ^2,\end{aligned}$$

(17b)

$$\begin{aligned} \kappa _3= & {} \langle x^3 \rangle -3\langle x \rangle \langle x^2 \rangle +2\langle x \rangle ^3,\end{aligned}$$

(17c)

$$\begin{aligned} \kappa _4= & {} \langle x^4 \rangle -4\langle x \rangle \langle x^3 \rangle -3\langle x^2 \rangle ^2,\\&+12 \langle x \rangle ^2\langle x^2 \rangle -6\langle x \rangle ^4,\nonumber \end{aligned}$$

(17d)

where the averages are performed with respect to p(x) in the right-hand side.

Now, consider an approximation for the original distribution where its cumulants are coincident with the original p(x) only for a few first cumulants. We show this approximated distribution by $p_q(x)$ where the cumulants $\kappa _n$ for $1\le n \le q$ are the same as the cumulants of the original p(x).

Assume the following ansatz for this approximated distribution:

$$\begin{aligned} p_q(x)=\frac{1}{\sqrt{2\pi }\sigma }\text {e}^{-\frac{x^2}{2\sigma ^2}}\sum _{i=0}^{q}T_i(x), \end{aligned}$$

(18)

where

$$\begin{aligned} T_i(x)=\sum _{k=0}^{i} a_{i,k} x^k \qquad a_{0,0}=1. \end{aligned}$$

(19)

In the above, $a_{i,k}$ (except $a_{0,0}$) are unknown coefficients. Note that $p_0(x)$ is nothing but a Gaussian distribution located at the origin. One can find the unknown coefficients $a_{i,k}$ by using the equations in (17) together with the normalization condition iteratively. In what follows we show how it works: let us present the moments obtained from $p_q(x)$ as $\langle x^m \rangle _q$. Also, assume that the first moment (which is the first cumulant too) is zero. At the end, we recover the first moment by applying a simple shift. Now for the first iteration ($q=1$) we have $\langle 1 \rangle _{1}=1+a_{1,0}=1$ from the normalization condition and $\langle x \rangle _{1}=\sigma ^2a_{1,1}=\kappa _1=0$ from Eq. (17a). It is a linear two-dimensional system of equations and the solution is $a_{1,0}=a_{1,1}=0$. In the next step ($q=2$), we have three equations [one normalization condition and the two equations (17a) and (17b)]. By considering $\kappa _2=\sigma ^2$, we find $a_{2,0}=a_{2,1}=a_{2,2}=0$. However, the third iteration is non-trivial. The equations are

$$\begin{aligned} \langle 1 \rangle _{3}&=1+a_{3,0}+\sigma ^2a_{3,2}=1,\\ \langle x \rangle _{3}&=\sigma ^2 a_{3,1}+3\sigma ^4 a_{3,3}=\kappa _1=0,\\ \langle x^2 \rangle _{3}&=\sigma ^2+\sigma ^2 a_{3,0}+3\sigma ^4 a_{3,2}=\sigma ^2,\\ \langle x^3 \rangle _{3}&=3\sigma ^4 a_{3,1}+15\sigma ^6 a_{3,3}=\kappa _3.\\ \end{aligned}$$

The above equations can be solved easily, $a_{3,0}=a_{3,2}=0$ and $a_{3,1}=-3\sigma ^2 a_{3,3}=-\kappa _3/(2\sigma ^4)$, which leads to $T_3(x)=\kappa _3/(6\sigma ^3) He_3(x/\sigma )$. Here, $He_n(x)$ is the probabilistic Hermite polynomial defined as $He_n(x)=\text {e}^{x^2/2}(-d/\text {d}x)^n \text {e}^{-x^2/2}$. We are able to continue the iterative calculations to any order and find

$$\begin{aligned} p(x)=\frac{1}{\sqrt{2\pi }\sigma } \text {e}^{-\frac{(x-\kappa _1)^2}{2\sigma ^2}}\sum _{n=0} \frac{h_n}{n!} He_n((x-\kappa _1)/\kappa _2^{1/2}). \end{aligned}$$

(20)

In the above, $h_0=1$ and $h_1=0$ together with

$$\begin{aligned} h_3= & {} \gamma _1,\nonumber \\ h_4= & {} \gamma _2,\nonumber \\ h_5= & {} \gamma _3,\nonumber \\ h_6= & {} \gamma _4+10\gamma _1^2,\nonumber \\&\;\;\vdots \end{aligned}$$

(21)

where $\gamma _n$ are the standardized cumulants defined as

$$\begin{aligned} \gamma _{n-2}=\frac{\kappa _n}{\kappa _2^{n/2}}. \end{aligned}$$

(22)

Note that in Eq. (20), we arbitrarily shifted the distribution to the case that the first moment of p(x) is $\kappa _1$. In addition, we assumed that the width of the Gaussian distribution is exactly equal to $\kappa _2$. Equation (20) is the well-know Gram–Charlier A series for the distribution p(x).

One could consider Eq. (20) as an expansion in terms of Hermite polynomials. Using the fact that $He_n(x)$ are orthogonal with respect to the weight $w(x)=\text {e}^{-x^2/2}$ $/\sqrt{2\pi }$,

$$\begin{aligned} \int _{-\infty }^{\infty } \text {d}x\, w(x) He_m(x)He_n(x) = m! \,\delta _{mn}, \end{aligned}$$

we find the coefficients $h_n$ in Eq. (21) (see Red. [38]). To this end, we change the coordinate as $x\rightarrow (x-\kappa _1)/\sigma$. As a result, we have

$$\begin{aligned} h_n=\int _{-\infty }^{\infty } \text {d}x \; p(x) He_n((x-\kappa _1)/\sigma ). \end{aligned}$$

By using the series form of the Hermite polynomial, we find $h_n$ as a function of p(x) moments. Rewriting moments in terms of cumulants [reverting the equations in (17)], one finds Eq. (20).

3.2 Radial-Gram–Charlier distribution

Using standard methods, we can extend the one-dimensional Gram–Charlier A series (20) to two dimensions (see Appendix B.2),

$$\begin{aligned} p({\mathbf {r}})= & {} {\mathcal {N}}({\mathbf {r}})\sum _{\begin{array}{c} m,n=0 \end{array}}\frac{h_{mn}}{m!n!} He_m\left( \frac{x-\mu _x}{\sigma _x}\right) He_n\left( \frac{y-\mu _y}{\sigma _y}\right) ,\nonumber \\ \end{aligned}$$

(23)

where $h_{mn}$ are written in terms of two-dimensional cumulants ${\mathcal {A}}_{mn}$ [see Eqs. (72)–(74)], and ${\mathcal {N}}({\mathbf {r}})$ is a two-dimensional Gaussian distribution similar to Eq. (14) located at $(\mu _x,\mu _y)$ and $\sigma _x\ne \sigma _y$.

It is worth noting that the concept of a 2D Gram–Charlier A series has been employed in heavy ion physics first in Ref. [30] by Teaney and Yan. They used this series to study the energy density of a single event.¹² However, we use this to study the harmonic distribution of the flow in the present work.

Now let us consider a two-dimensional Gram–Charlier A series for $p(v_{n,x},v_{n,y})$. By this consideration, one can find a corresponding series for $p(v_n)$ by averaging out the azimuthal direction. We should say that the results of this averaging for the second and third harmonics are different. For $n=3$, the distribution $p(v_{3,x},v_{3,y})$ is rotationally symmetric and, as we already remarked in the previous section, the whole information of the distribution is encoded in $c_3\{2k\}$. As a result, we are able to rewrite the 2D cumulants ${\mathcal {A}}_{mn}$ in terms of $c_3\{2k\}$. It has been done in Ref. [28], and an expansion for $p(v_3)$ has been found. On the other hand, for $n=2$ the whole information of $p(v_{2,x},v_{2,y})$ is not in $c_2\{2k\}$. Therefore, we are not able to rewrite all ${\mathcal {A}}_{mn}$ in terms of $c_2\{2k\}$ after averaging out the azimuthal direction of a 2D Gram–Charlier A series.

For completeness, we study the azimuthal averaging of Eq. (23) in the most general case in Appendix C. In this appendix, we show that the distribution in Ref. [28] is reproduced only by assuming ${\mathcal {A}}_{10}={\mathcal {A}}_{01}=0$. Also, we discuss the information we find from the averaged distribution compared to the two-dimensional one. However, the method which we will follow in this section is different from that pointed out in Appendix C. Consequently, the most general series we will find here is not coincident with the distribution obtained in Appendix C.

Before finding a Gram–Charlier A series for arbitrary harmonic, let us find the series for odd harmonics (mentioned in Ref. [28]) by employing orthogonal polynomials. The result will be used to find the series for the most general case later. Since we have $\bar{v}_3=0$ for $n=3$, the Bessel–Gaussian distribution reduces to a radial Gaussian distribution as $(v_3/\sigma ^2) \text {e}^{-v_3^2/(2\sigma ^2)}$. Moreover, the Laguerre polynomials $L_n(x)$ are orthogonal with respect to the weight $w(x)=\text {e}^{-x}$ in the range $[0,\infty )$,

$$\begin{aligned} \int _{0}^{\infty } \text {d}x\,\text {e}^{-x} L_n(x)L_m(x)=\delta _{mn}. \end{aligned}$$

By changing the coordinate as $x=v_3^2/(2\sigma ^2)$, the measure $w(x)\text {d}x$ changes to $(v_3 /\sigma ^2) \text {e}^{-v_3^2/(2\sigma ^2)} dv_3$; the radial Gaussian distribution appears as the weight for orthogonality of $L_n(v_3^2/(2\sigma ^2))$. Hence, we can write a general distribution $p(v_3)$ like

$$\begin{aligned} p(v_3)=\frac{v_3}{\sigma ^2} \text {e}^{-\frac{v_3^2}{2\sigma ^2}}\sum _{n=0}^{\infty } \frac{(-1)^n\ell ^{\text {odd}}_{2n}}{n!} L_n(v_3^2/(2\sigma ^2)), \end{aligned}$$

(24)

where the coefficients $\ell ^{\text {odd}}_{2n}$ can be found by¹³

$$\begin{aligned} \ell ^{\text {odd}}_{2n}=n!(-1)^n\int _{0}^{\infty } dv_3 \; p(v_3) L_n(v_3^2/(2\sigma ^2)). \end{aligned}$$

(25)

Considering the series form of the Laguerre polynomial,

$$\begin{aligned} L_n(x)=\sum _{k=0}^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{(-1)^k}{k!} x^k, \end{aligned}$$

(26)

we immediately find $\ell ^{\text {odd}}_n$ in terms of moments $\langle v_3^{2q} \rangle$. Then one can invert the equations in (8) to write the moments $\langle v_3^{2q} \rangle$ in terms of cumulants $c_3\{2q\}$. If we do so and by choosing $2\sigma ^2=\langle v_3^2 \rangle =c_3\{2\}$,¹⁴ we find $\ell ^{\text {odd}}_0=1$ and $\ell ^{\text {odd}}_2=0$ together with

$$\begin{aligned} \begin{aligned} \ell _4^{\text {odd}}&=\varGamma _2^{\text {odd}},\\ \ell _6^{\text {odd}}&=\varGamma _4^{\text {odd}},\\ \ell _8^{\text {odd}}&=\varGamma _6^{\text {odd}}+18(\varGamma _2^{\text {odd}})^2,\\ \ell _{10}^{\text {odd}}&=\varGamma _8^{\text {odd}}+100(\varGamma _2^{\text {odd}})(\varGamma _4^{\text {odd}}), \end{aligned} \end{aligned}$$

(27)

where in the above we defined the standardized cumulants $\varGamma ^{\text {odd}}_{2k}$ as

$$\begin{aligned} \varGamma _{2k-2}^{\text {odd}}=\frac{c_3\{2k\}}{c_2^k\{2\}}, \end{aligned}$$

(28)

similar to Eq. (22).

The expansion (24) together with Eq. (27) is exactly the series found in Ref. [28] which is true for any odd n. This approximated distribution is called the radial-Gram–Charlier (RGC) distribution in Ref. [28].

It should be noted that it is a series for the case that $\bar{v}_n=0$. In the following, we will try to find a similar series for $p(v_n;\bar{v}_n)$ where $\bar{v}_n$ could be non-vanishing.

In order to find the Gram–Charlier A series for the distribution $p(v_n,;\bar{v}_n)$ in the general case, we come back to the iterative method explained in Sect. 3.1 where we found the distribution (20) by considering the ansatz (18) and iteratively solving the equations in (17).

Here, we assume that $p_q(v_n;\bar{v}_n)$ is an approximation of $p(v_n)$ where only the cumulants $c_n\{2k\}$ with $1\le k\le q$ are the same as the original distribution. Now suppose an ansatz that has the following properties:

• Its leading order corresponds to the Bessel–Gaussian distribution.

• In the limit $\bar{v}_n\rightarrow 0$, the distribution approaches (24).

Using such an ansatz, we calculate the moments $\langle v_n^{2k} \rangle$ with some unknown parameters and find them by solving the equations in (8) iteratively.

We introduce the following form for the ansatz:

$$\begin{aligned} p_q(v_n;\bar{v}_n)=\left( \frac{v_n}{\sigma ^2}\right) \text {e}^{-\frac{v_n^2+\bar{v}_n^2}{2\sigma ^2}}\sum _{i=0}^{q}{\mathcal {Q}}_i(v_n;\bar{v}_n), \end{aligned}$$

(29)

where

$$\begin{aligned} {\mathcal {Q}}_i(v_n;\bar{v}_n)=\sum _{k=0}^{i} a_{i,k} \left( -\frac{v_n}{\bar{v}_n}\right) ^k\,I_k\left( \frac{v_2 \bar{v}_2}{\sigma ^2}\right) . \end{aligned}$$

(30)

One simply finds that by choosing $a_{0,0}=1$ the distribution $p_0(v_n;\bar{v}_n)$ is the Bessel–Gaussian distribution. On the other hand, the function ${\mathcal {Q}}_i(v_n;\bar{v}_n)$ in the limit $\bar{v}_n \rightarrow 0$ reduces to

$$\begin{aligned} \sum _{k=0}^{i} a_{i,k} \frac{(-1)^k}{k!} \left( \frac{v_n}{2\sigma ^2}\right) ^k. \end{aligned}$$

(31)

By comparing the above expansion with Eq. (26), we realize that if we choose $a_{i,k}\propto \left( {\begin{array}{c}i\\ k\end{array}}\right)$, ${\mathcal {Q}}_i(v_n;\bar{v}_n)$ is proportional to $L_n(v_n^2/(2\sigma ^2))$. In order to reproduce Eq. (24), we choose

$$\begin{aligned} a_{i,k} = \ell _{2i} \,\frac{(-1)^i}{i!}\,\left( {\begin{array}{c}i\\ k\end{array}}\right) , \end{aligned}$$

(32)

where $\ell _{2i}$ are unknown coefficients.

Similar to Sect. 3.1, we indicate the moments of $p_q(v_n;\bar{v}_n)$ by $\langle v_n^{2m} \rangle _q$. For the first iteration, we have the normalization condition $\langle 1 \rangle _0=\ell _0=1$. For the second iteration, the normalization condition is trivially satisfied, $\langle 1 \rangle _1=1$, while from Eq. (8a) we have $\langle v_n^2 \rangle _1 = \bar{v}_n^2+2\sigma ^2 (1+\ell _2)=c_n\{2\}$. At this stage, we choose $\ell _2=0$ to have¹⁵

$$\begin{aligned} c_n\{2\}=\bar{v}_n^2+2\sigma ^2. \end{aligned}$$

(33)

For the next iteration, we find that the normalization condition and Eq. (8a) are automatically satisfied, $\langle 1 \rangle _2=1$, $\langle v_n^2 \rangle _2=c_n\{2\}$, while Eq. (8b) leads to a non-trivial equation for $\ell _4$,

$$\begin{aligned} c_n\{6\}=\ell _4(c_n\{2\}-\bar{v}_n^2)^2-\bar{v}_n^4. \end{aligned}$$

(34)

Using the above equation, we immediately find $\ell _4$. In a similar way, we are able to continue this iterative calculation and find $\ell _{2q}$ from the only non-trivial algebraic equation at each step. A summary of the few first results is as follows: $\ell _0=1$ and $\ell _2=0$; moreover,

$$\begin{aligned} \begin{aligned} \ell _4&=\frac{c_n\{4\}+\bar{v}_n^4}{(c_n\{2\}-\bar{v}^2)^2},\\ \ell _6&=\frac{c_n\{6\}+6 c_n\{4\}\bar{v}_n^2+2\bar{v}_n^6}{(c_n\{2\}-\bar{v}^2)^3},\\ \ell _8&=\frac{c_n\{8\}+12 c_n\{6\} \bar{v}_n^2+18 c_n^2\{4\}+42 c_n\{4\} \bar{v}_n^4+9\bar{v}_n^8}{(c_n\{2\}-\bar{v}^2)^4}. \end{aligned} \end{aligned}$$

(35)

One may wonder if, similar to the two previous cases, we are able to write all the coefficients $\ell _{2k}$ in terms of some standardized cumulants. These standardized cumulants should smoothly approach the contents of Eq. (28). In fact, it motivates us to define a new set of cumulants,

$$\begin{aligned} q_n\{2\}= & {} c_n\{2\}-\bar{v}_n^2, \end{aligned}$$

(36a)

$$\begin{aligned} q_n\{4\}= & {} c_n\{4\}+\bar{v}_n^4,\end{aligned}$$

(36b)

$$\begin{aligned} q_n\{6\}= & {} c_n\{6\}+6 c_n\{4\}\bar{v}_n^2+2\bar{v}_n^6,\end{aligned}$$

(36c)

$$\begin{aligned} q_n\{8\}= & {} c_n\{8\}+12 c_n\{6\} \bar{v}_n^2+6c_n\{4\}\bar{v}_n^4-9\bar{v}_n^8,\end{aligned}$$

(36d)

$$\begin{aligned} q_n\{10\}= & {} c_n\{10\}+20(c_n\{8\}-12 c_n^2\{4\})\bar{v}_n^2,\\&+30\, c_n\{6\} \bar{v}_n^4-480\,c_n\{4\} \bar{v}_n^6-156\, \bar{v}_n^{10}.\nonumber \end{aligned}$$

(36e)

Now, we can define the standardized form of this new set of cumulants as follows:

$$\begin{aligned} \varGamma _{2k-2}=\frac{q_n\{2k\}}{q_n^k\{2\}}. \end{aligned}$$

(37)

Using the above definitions, we can rewrite the coefficients $\ell _{2k}$ in the following form:

$$\begin{aligned} \begin{aligned} \ell _4&=\varGamma _2,\\ \ell _6&=\varGamma _4,\\ \ell _8&=\varGamma _6+18\varGamma _2^2,\\ \ell _{10}&=\varGamma _8+100\varGamma _2\varGamma _4, \end{aligned} \end{aligned}$$

(38)

which are in agreement with the equations in (27) in the limit $\bar{v}_n\rightarrow 0$.

Let us to summarize the series in (29) as follows:

$$\begin{aligned} p(v_n;\bar{v}_n)=\frac{v_n}{\sigma ^2} \text {e}^{-\frac{v_n^2+\bar{v}_n^2}{2\sigma ^2}}\sum _{i=0}^{\infty }\frac{(-1)^i\ell _{2i}}{i!} \tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n), \end{aligned}$$

(39)

where $\tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n)$ is similar to ${\mathcal {Q}}_i(v_n;\bar{v}_n)$ in Eq. (30) up to a numerical factor,

$$\begin{aligned} \begin{aligned} \tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n)&=\frac{(-1)^i \ell _{2i}}{i!} {\mathcal {Q}}_i(v_n;\bar{v}_n)\\&=\sum _{k=0}^{i}\left( {\begin{array}{c}i\\ k\end{array}}\right) \left( -\frac{v_n}{\bar{v}_n}\right) ^k\,I_k\left( \frac{v_n \bar{v}_n}{\sigma ^2}\right) . \end{aligned} \end{aligned}$$

(40)

Recall that the two distributions (20) and (24) could be found by using the orthogonality of $He_n(x)$ and $L_n(x)$. We can ask if there is any similar approach to finding Eq. (39). Surprisingly, $\tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n)$ is related to a generalized class of orthogonal polynomials which are called multiple orthogonal polynomials (see Ref. [39]). These generalized versions of the polynomials are orthogonal with respect to more than one weight. Specifically, the polynomials related to $\tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n)$ have been introduced in Ref. [40]. In order to avoid relatively formal mathematical material here, we refer the interested reader to Appendix D where we briefly review the multiple orthogonal polynomials and re-derive Eq. (39) by employing them.

An important point as regards the distribution (39) is the convergence of its summation. For sure, finding the convergence condition of the infinite sum in Eq. (39) is beyond the scope of the present paper. However, if we find that at least a few first terms in Eq. (39) are sufficient to give a reasonable approximation of $p(v_n)$, then there is no concern about the convergence or divergence of this series practically.¹⁶

Fig. 1

Comparing the harmonic distribution of the flow from iEBE-VISHNU (shaded region) and the Gram-Charlier A series different approximations

Fig. 2

Examining the accuracy of the Gram–Charlier A series with the actual distribution obtained from simulation by studying $\chi ^2/\text {NDF}$

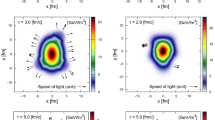
In order to show in how far the distribution (39) is a good approximation, we need to have a sample for $p(v_n)$ where its $\bar{v}_n$ is known. To this end, we generate heavy ion collision events by employing a hydrodynamic based event generator which is called iEBE-VISHNU [41]. The reaction-plane angle is set to zero in this event generator. Thus, we can simply find $p(v_{n,x}v_{n,y})$ and subsequently $\bar{v}_n$. The events are divided into 16 centrality classes between 0 to 80 percent and at each centrality class we generate 14000 events. The initial condition model is set to be MC-Glauber.

Let us recover the notation in Eq. (29) and assume that $p_q(v_n;\bar{v}_n)$ is the distribution (39) where the summation is done up to $i=q$. We first compute the $c_2\{2k\}$ and $\bar{v}_2$ from iEBE-VISHNU output and plug the results in Eq. (39). After that we can compare the original simulated distribution $p(v_n)$ with the estimated $p_q(v_2;\bar{v}_2)$. The results are presented in Fig. 1 for the events in 65–70$\%$, 70–75$\%$ and 75–80$\%$ centrality classes, in which we expect the distribution is deviated from the Bessel–Gaussian. In this figure, the black curve corresponds to the Bessel–Gaussian distribution ($p_0(v_n;\bar{v}_n)$) and the red, green and blue curves correspond to $p_q(v_2;\bar{v}_2)$ with $q=2$, 3 and 4, respectively. Recall that $q=1$ has no contribution because $\ell _2$ vanishes. As can be seen in the figure, the black curve shows that the distribution is deviated from Bessel–Gaussian and the distribution $p_q(v_2;\bar{v}_2)$ with $q\ne 0$ explains the generated data more accurately.

In order to compare the estimated distributions more quantitatively, we plotted $\chi ^2/\text {NDF}$, comparing the estimated distribution $p_q(v_2;\bar{v}_2)$ with iEBE-VISHNU output. We plotted the results in Fig. 2 for $q=0,2,3,4,5,6$ and 7 for the events in the 65–70$\%$, 70–75$\%$ and 75–80$\%$ centrality classes. The value of $\chi ^2/\text {NDF}$ associated with the Bessel–Gaussian distribution is much greater than the others. Therefore, we multiplied its value by 0.878 to increase the readability of the figure.

As Fig. 2 demonstrates, the Bessel–Gaussian distribution has less compatibility with the distribution. In addition, the quantity $\chi ^2/\text {NDF}$ becomes closer to 1 by increasing q.¹⁷ It is relatively close to 1 for higher values of q. One may deduce from the figure that the series converges because $\chi ^2/\text {NDF}$ for $q=6$ and $q=7$ are very close to each other and very close to 1. However, we should say that although it is an strong evidence for the series convergence, there is no guaranty that by adding higher terms the series remain stable. Additionally, we checked the convergence of the series for the case of interest in heavy ion physics. This convergence might not be true for an arbitrary distribution in general. In any case, what we learn from the above arguments is that at least a few first terms in the series (39) gives a good approximation compared to the original harmonic distribution of the flows.

Fig. 3

The cumulants $q_2\{2k\}$ obtained from the iEBE-VISHNU event generator

3.3 New cumulants

Let us come back to the cumulants in Eq. (36) and point out their properties. Considering the new cumulants $q_n\{2k\}$, we note the following remarks:

• Referring to Eq. (13), all the cumulants $q_n\{2k\}$ for $k\ge 1$ are vanishing for the distribution $\delta (v_{n,x}-\bar{v}_n,v_{n,y})$.

• Referring to Eq. (16), the only non-zero $q_n\{2k\}$ for the Bessel–Gaussian distribution is $q_n\{2\}=2\sigma ^2$.

• In the limit $\bar{v}_n\rightarrow 0$, the cumulants $q_n\{2k\}$ approach $c_n\{2k\}$.

The above remarks indicate that $q_n\{2k\}$ contains information originating from the fluctuations only and the explicit effect of the collision geometry $\bar{v}_n$ is extracted from it.¹⁸

It is important to note that although we have found $q_n\{2k\}$ by RGC distribution inspiration, we think it is completely independent of that and there must be a more direct way to find $q_n\{2k\}$ independent of the RGC distribution.

Concerning the difference between $c_n\{2k\}$ and $q_n\{2k\}$ in terms of the Gram–Charlier expansion, we should mention that the cumulants $c_n\{2k\}$ appear as the coefficients of the expansion when we expand the distribution $p(v_n)$ around a radial-Gaussian distribution [see Eq. (24)] while $q_n\{2k\}$ are those that appear in the expansion around the Bessel–Gaussian distribution. Now, if the distribution we study is more Bessel–Gaussian rather than the radial-Gaussian, we need infinitely many $c_n\{2k\}$ cumulants to reproduce the correct distribution. For instance, for the second harmonics all $v_2\{2k\}$ are non-zero and have approximately close values. It is because we are approximating a distribution which is more Bessel–Gaussian rather than radial-Gaussian. On the other hand for the third harmonics, we expect that the underling distribution is more radial-Gaussian, and practically we see a larger difference between $v_3\{2\}$ and $v_3\{4\}$ compared to the second harmonics [8]. Based on the above arguments, we deduce that the $q_n\{2k\}$ are a more natural choice for the case that $\bar{v}_n$ is non-vanishing.

Nevertheless, the cumulants $q_n\{2k\}$ (unlike $c_n\{2k\}$) are not experimentally observable because of the presence of $\bar{v}_n$ in their definition. However, they are useful to systematically estimate the distribution $p(v_n)$ and consequently estimate the parameter $\bar{v}_n$. This will be the topic of the next section.

4 Averaged ellipticity and harmonic fine-splitting of the flow

In this section, we would like to exploit the cumulants $q_n\{2k\}$ to find an estimation for $\bar{v}_n$. Note that if we had prior knowledge about one of the $q_2\{2k\}$ or even any function of them [for instance $g(q_2\{2\},q_2\{4\},\ldots )$], we could find $\bar{v}_n$ exactly by solving the equation $g(q_2\{2\},q_2\{4\},\ldots )$ $=0$ in principle. Because the cumulants $c_n\{2k\}$ are experimentally accessible, one would practically solve the equation $g(\bar{v}_n)=0$. Unfortunately we have no such prior knowledge as regards $q_2\{2k\}$, but we are still able to estimate $\bar{v}_n$ approximately by assuming some properties for $p(v_n)$.

Any given distribution can be quantified by $q_n\{2k\}$. While $p(v_n)$ is approximately Bessel–Gaussian, we can guess that

$$\begin{aligned} q_n\{2\}\gg q_n\{4\} \gg q_n\{6\} \gg q_n\{8\}\gg \cdots \,. \end{aligned}$$

In fact, this is confirmed by the simulation. The cumulants $q_2\{2k\}$ are obtained from the iEBE-VISHNU output and presented in Fig. 3. Therefore, as already remarked, we expect that the few first cumulants $q_n\{2k\}$ are enough to quantify the main features of a distribution near Bessel–Gaussian.

Let us concentrate on $n=2$ from now on. Recall that $q_2\{4\}=q_2\{6\}=\cdots =0$ corresponds to a Bessel–Gaussian distribution. This choice of cumulants is equivalent to a distribution with $v_2\{4\}=v_2\{6\}=\cdots$, which is not compatible with the splitting of $v_2\{2k\}$ observed in the experiment. As we discussed at the beginning of this chapter, we find $\bar{v}_2$ by estimating any function of cumulants $q_2\{2k\}$. Here we use the most simple guess for this function, which is $g(q_2\{2\},q_2\{4\},\ldots )=q_2\{2k\}$. Therefore, the equation $q_2\{2k\}=0$ for each $k \ge 1$ corresponds to a specific estimation for $p(v_2)$.

For $k=1$, we have $q_2\{2\}=0$, which means $\bar{v}_2=v_2\{2\}$. For this special choice, all the $\varGamma _{2k-2}$ in Eq. (37) diverge unless we set all other $q_2\{2k\}$ to zero too. As a result, this choice corresponds to the delta function for $p(v_{2,x},v_{2,y})$.

The first non-trivial choice is $q_2\{4\}=0$. Referring to Eq. (36b), we find

$$\begin{aligned} \bar{v}_2\{4\}=v_2\{4\}, \end{aligned}$$

(41)

where in the above $\bar{v}_2\{4\}$ refers to $\bar{v}_2$, which is estimated from $q_2\{4\}=0$. This is exactly the assumption that has been made in Ref. [27] to find the skewness experimentally. By estimating $\bar{v}_2$, we find the other $q_2\{2k\}$. We present a few first cumulants in the following:

$$\begin{aligned} q_2\{4\}= & {} 0 \end{aligned}$$

(42a)

$$\begin{aligned} q_2\{6\}= & {} -24\, v_2^5\{6\}\,\varDelta _2\{4,6\}+{\mathcal {O}}(\varDelta ^{3/2})\end{aligned}$$

(42b)

$$\begin{aligned} q_2\{8\}= & {} -24\, v_2^7\{8\}\,\left( \varDelta _2\{4,6\}-11\varDelta _2\{6,8\}\right) {\nonumber }\\&+{\mathcal {O}}(\varDelta ^{3/2})\end{aligned}$$

(42c)

$$\begin{aligned} q_2\{10\}= & {} 240\, v_2^9\{10\}\,\left( 3\varDelta _2\{6,8\}-19\varDelta _2\{8,10\}\right) {\nonumber }\\&+{\mathcal {O}}(\varDelta ^{3/2}), \end{aligned}$$

(42d)

where we used the notation

$$\begin{aligned} \varDelta _n\{2k,2\ell \}=v_n\{2k\}-v_n\{2\ell \} \end{aligned}$$

(43)

for the fine-splitting between different $v_n\{2k\}$’s. Furthermore, in Eq. (42) we expanded $q_2\{2k\}$ in terms of fine-splitting $\varDelta _2\{2k,2\ell \}$.

Note that the above $q_2\{2k\}$ are characterizing an estimated distribution $p(v_2;\bar{v}_2\{4\})$. For such an estimated distribution, $q_2\{6\}$ is proportional to the skewness introduced in Ref. [27]. Interestingly, $q_2\{8\}$ is proportional to $\varDelta _2\{4,6\}-11\varDelta _2\{6,8\}$, which has been considered to be zero in Ref. [27]. However, here we see that this combination can be non-zero and its value is related to the cumulant $q_2\{8\}$. In fact, the same quantity can be computed for a generic narrow distribution [29]. In turns out that this quantity can be non-vanishing in the small fluctuation limit.

The equations in (42) indicate that by assuming $q_2\{4\}=0$ all the other cumulants of $p(v_2;\bar{v}_2\{4\})$ are written in terms of the fine-splitting $\varDelta _2\{k,\ell \}$. Therefore, the distribution $p(v_2;\bar{v}_2\{4\})$ satisfies all the fine-splitting structure of $v_2\{2k\}$ by construction.

One can simply check in how far the estimation $\bar{v}_2\{2k\}$ is accurate by using a simulation. We exploit again the iEBE-VISHNU event generator to compare the true value of $\bar{v}_2$ ($\bar{v}_2^{\text {True}}$) with $\bar{v}_2\{4\}=v_2\{4\}$. The result is depicted in Fig. 4 by brown and green curves for $\bar{v}_2^{\text {True}}$ and $\bar{v}_2\{4\}$, respectively. As the figure illustrates, $\bar{v}_2\{4\}$ is not compatible with $\bar{v}_2^{\text {True}}$ for centralities higher than $50\%$ where we expect that a Bessel–Gaussian distribution does not work well. It should be noted that all other $v_2\{2k\}$ for $k>2$ never are close to the true value of $\bar{v}_2$ in higher centralities because all of them are very close to $v_2\{4\}$.

In order to improve the estimation of $\bar{v}_2$, we set $q_2\{6\}=0$ in Eq. (36c). This equation has six roots, where only two of them are real and positive. In addition, as can be seen from Fig. 4, the true value of $\bar{v}_2$ is always smaller than $v_2\{4\}$ ($=\bar{v}_2\{4\}$) in higher centralities. In fact, it is true for all $v_2\{2k\}$ for $k>2$. Based on this observation, we demand the root to be smaller than $v_2\{4\}$. In fact, we have checked that the equation $q_2\{2k\}=0$ for $k=3,4,5$ has only one root which is real, positive and smaller than $v_2\{2k\}$ for $k=2,3,4,5$.

Fig. 4

Using iEBE-VISHNU output, the true value of $\bar{v}_2$ is compared with the estimators $\bar{v}_2\{2k\}$

In Fig. 4, $\bar{v}_2\{6\}$ is plotted by a red curve which is obtained by solving $q_2\{6\}=0$ numerically. As can be seen, it is clorse to the real value of $\bar{v}_2$ rather than $v_2\{4\}$. In fact, we are able to find this root analytically too,

$$\begin{aligned} \bar{v}_2\{6\}=v_2\{6\}-\sqrt{v_2\{6\}\varDelta _2\{4,6\}}+{\mathcal {O}}(\varDelta ), \end{aligned}$$

(44)

which is compatible with the red curve in Fig. 4 with good accuracy. Using the estimator (44), we find the other $q_2\{2k\}$ as follows:

$$\begin{aligned} q_2\{4\}= & {} -4\, v_2^3\{6\}\,\sqrt{v_2\{6\}\varDelta _2\{4,6\}}+{\mathcal {O}}(\varDelta ), \end{aligned}$$

(45a)

$$\begin{aligned} q_2\{6\}= & {} 0,\end{aligned}$$

(45b)

$$\begin{aligned} q_2\{8\}= & {} 264\, v_2^7\{8\}\,\left( \varDelta _2\{6,8\}-\varDelta _2\{4,6\}\right) {\nonumber }\\&+{\mathcal {O}}(\varDelta ^{3/2}),\end{aligned}$$

(45c)

$$\begin{aligned} q_2\{10\}= & {} 240\, v_2^9\{10\}\,\left( 3\varDelta _2\{6,8\}-19 \varDelta _2\{8,10\}\right) {\nonumber }\\&+{\mathcal {O}}(\varDelta ^{3/2}). \end{aligned}$$

(45d)

By comparing Eqs. (42) and (45), we note that $q_2\{2k\}$ (except $q_2\{10\}$) are different because the estimated distributions $p(v_2;\bar{v}_2\{4\})$ and $p(v_2;\bar{v}_2\{6\})$ are different.

We can go further and estimate $\bar{v}_2$ by solving the equation $q_2\{8\}=0$. The result is plotted by a blue curve in Fig. 4. Also, its analytical value can be found as follows:

$$\begin{aligned} \bar{v}_2\{8\}= & {} v_2\{8\}-\frac{1}{\sqrt{10}}\sqrt{v_2\{8\}\left( 11 \varDelta _2\{6,8\}-\varDelta _2\{4,6\}\right) }{\nonumber }\\&+{\mathcal {O}}(\varDelta ). \end{aligned}$$

(46)

As Fig. 4 indicates, comparing $\bar{v}_2\{6\}$, the estimator $\bar{v}_2\{8\}$ is a worse estimation of $\bar{v}_2$ (except between the range $30\%$ to $50\%$ centralities). We might expect that because $q_2\{8\}\ll q_2\{6\}$ (see Fig. 3), the quantity $\bar{v}_2\{8\}$ should be a better approximation than $\bar{v}_2\{6\}$. But this argument is not true. In fact, the cumulants $q_2\{2k\}$ for the true distribution are small, but they are non-zero at any centralities. Let us rewrite Eqs. (36b)–(36d) as follows:

$$\begin{aligned}&\bar{v}_2^4-\delta _4v_2^4\{4\}=0, \end{aligned}$$

(47a)

$$\begin{aligned}&2\bar{v}_2^6-6 v_2^4\{4\}\bar{v}_2^2+4\,\delta _6\,v_2^6\{6\}=0,\end{aligned}$$

(47b)

$$\begin{aligned}&9\bar{v}_2^8+6v_2^4\{4\}\bar{v}_2^4-48 v_2^6\{6\} \bar{v}_2^2+33\,\delta _8\,v_2^8\{8\}=0, \end{aligned}$$

(47c)

where

$$\begin{aligned} \delta _{2k}=1-\frac{q_2\{2k\}}{c_2\{2k\}}. \end{aligned}$$

(48)

The estimator $\bar{v}_2\{2k\}$ ($k=2,3,4$) can be found by solving Eqs. (47)a,b,c) where we set $\delta _{2k}=1$. Alternatively, by employing the actual value of $\delta _{2k}$ from the simulation we find $\bar{v}_2^{\text {True}}$. In fact, the difference between $\bar{v}_2^{\text {True}}$ and $\bar{v}_2\{2k\}$ is a manifestation of the inaccuracy in the setting $\delta _{2k}=1$. In other words, demanding $q_2\{2k\}=0$ is not exactly correct. Looking at the problem from this angle, by referring to Fig. 4, we realize that $\delta _4=1$ is the most inaccurate approximation. Also, $\delta _6=1$ is more accurate than $\delta _8=1$.

Fig. 5

The quantity $\delta _{2k}$ for $k=2,3,4$ and 5 with respect to centrality class

Fig. 6

The averaged flow harmonic estimator $\bar{v}_2\{2k\}$ obtained from the ATLAS experimental data [18]

By using iEBE-VISHNU generated data, we can check the accuracy of the $\delta _{2k}=1$ estimation by comparing different values of $\delta _{2k}$ (for $k=2,3,4,5$) calculated from the simulation. The result is plotted in Fig. 5. This figure confirms the difference between the estimators $\bar{v}_2\{2k\}$ discussed above. The quantity $\delta _{4}$ has the greatest deviation from unity. Also, we see that $\delta _{8}$ deviates from unity for centralities above $55\%$ while $\delta _6$ (and $\delta _{10}$) is closer to 1 up to $65\%$ centrality. Moreover, $\delta _6$ ($\delta _{10}$) is larger than $\delta _8$ for all centralities. This can be considered as a reason for the fact that $\bar{v}_2\{8\}$ is less accurate than $\bar{v}_2\{6\}$ (and $\bar{v}_2\{10\}$).

Furthermore, let us mention that the cumulant $q_2\{6\}$ changes its sign (see Figs. 3 and 5) for the centralities around 60–$65\%$. It means it is exactly equal to 0 at a specific point in this range, and we expect that $\bar{v}_2\{6\}$ becomes exactly equal to $\bar{v}_2^{\text {True}}$ at this point. This can be seen also in Fig. 4 where the red curve ($\bar{v}_2\{6\}$) crosses the brown curve ($\bar{v}_2^{\text {True}}$).

The situation for $q_2\{10\}$ is very similar to $q_2\{6\}$. As a result, it is not surprising that we find the estimator $\bar{v}_2\{10\}$ to be similar to $\bar{v}_2\{6\}$. We have found $\bar{v}_2\{10\}$ by solving $q_2\{10\}=0$ numerically. The result is plotted by a black curve in Fig. 4. As can be seen, the results of $\bar{v}_2\{6\}$ and $\bar{v}_2\{10\}$ are approximately similar.

Now, we are in a position to estimate the $\bar{v}_2$ of the real data by using $\bar{v}_2\{2k\}$. According to the above discussions, we expect that $\bar{v}_2\{6\}$, $\bar{v}_2\{8\}$ and $\bar{v}_2\{10\}$ are closer to the real value of the averaged ellipticity $\bar{v}_2$ compared to $v_2\{4\}$ (or any other $v_2\{2k\}$ for $k>2$). The result is plotted in Fig. 6. In finding the estimated $\bar{v}_2$, we employed $v_2\{2k\}$ reported by the ATLAS collaboration in Ref. [18]. The value of $\bar{v}_2\{4\}$ is exactly equal to $v_2\{4\}$, which is plotted by the green curve in the figure. By plugging experimental values of $v_2\{2k\}$ into Eqs. (36c), (36d) and (36e) and setting them to 0, we have numerically found $\bar{v}_2\{6\}$ (red curve), $\bar{v}_2\{8\}$ (blue curve) and $\bar{v}_2\{10\}$ (black curve), respectively.¹⁹ The errors of $\bar{v}_2\{10\}$ are too large for the present experimental data, and a more precise observation is needed to find a more accurate estimation. Exactly similar to the iEBE-VISHNU simulation, the value of $\bar{v}_2\{8\}$ is between $v_2\{4\}$ and $\bar{v}_2\{6\}$.²⁰ Therefore, we expect the true value of the averaged ellipticity to be close to the value of $\bar{v}_2\{6\}$.²¹

In this section, we introduced a method to estimate $p(v_2,\bar{v}_2)$. By considering the cumulants $c_2\{2k\}$ of the true distribution $p(v_2)$, we estimated $\bar{v}_2$ by assuming that the cumulant $q_2\{2k\}$ of $p(v_2,\bar{v}_2)$ is zero for a specific value of k. These estimations for $q_2\{6\}=0$ and $q_2\{8\}=0$ are presented analytically in Eqs. (44) and (46) and also with red and blue curves in Fig. 4 numerically. We exploited a hydrodynamic simulation to investigate the accuracy of our estimations. We found that $\bar{v}_2\{6\}$ is more accurate than $\bar{v}_2\{8\}$. Finally, we found the experimental values for $\bar{v}_2\{6\}$, $\bar{v}_2\{8\}$ and $\bar{v}_2\{10\}$.

Until now, we considered the cumulants $v_n\{2k\}$ as an input to find an estimation for $\bar{v}_n$. In the next section, we try to restrict the phase space of the allowed region of $v_n\{2k\}$ by using cumulants $q_n\{2k\}$.

5 Constraints on the flow harmonics phase space

Referring to Eqs. (44) and (46), we see that these estimators lead to real values for $\bar{v}_2\{4\}$ and $\bar{v}_2\{6\}$ only if we have $11 \varDelta _2\{6,8\}\ge \varDelta _2\{4,6\}\ge 0$. In this section, we would like to investigate these constraints and their validity range.

We first consider Eq. (47b). The quantities $v_2\{2k\}$ and $\bar{v}_2$ are real valued. Therefore, it is a well-defined and simple question what the allowed values are of $v_2\{4\}$ and $v_2\{6\}$ such that Eq. (47b) has at least one real root. The polynomial in the left-hand side of Eq. (47b) goes to positive infinity for $\bar{v}_2\rightarrow \pm \infty$. As a result, it has at least one real root if the polynomial is negative in at least one of its minima. This condition is satisfied for

$$\begin{aligned} \delta _6^{1/6} v_2\{6\} \le v_2\{4\}. \end{aligned}$$

(49)

Since $\delta _6$ is unknown, there is no bound on $v_2\{4\}$ and $v_2\{6\}$. Although we do not know the exact value of $\delta _6$, we know that $0.9 \lesssim \delta _6^{1/6} \lesssim 1$ based on our simulation (see Fig. 5). In this case, if we take into account $v_2\{6\} \le v_2\{4\}$, we immediately deduce the inequality in Eq. (49). On the other hand, we may observe that $v_2\{6\}$ is slightly greater than $v_2\{4\}$. This observation means that $\delta _6$ is definitely smaller than unity. Here, we show both cases by an approximate inequality as $v_2\{4\}\gtrsim v_2\{6\}$ due to the smallness of $\delta _6^{1/6}$.

Fig. 7

The allowed region of the $v_2\{6\}$–$v_2\{8\}$ phase space for the two fixed values of $v_2\{4\}$ and $\delta _6=\delta _8=1$

Alternatively, it is well known that the initial eccentricity point $(\varepsilon _{2,x},\varepsilon _{2,y})$ is bounded into a unit circle [25], and it leads to a negative skewness for $p(\varepsilon _{2,x},\varepsilon _{2,y})$ in non-central collisions. By considering the hydrodynamic linear response, the skewness in $p(\varepsilon _{2,x},\varepsilon _{2,y})$ is translated into the skewness of $p(v_{2,x},v_{2,y})$ and the condition $v_2\{4\}>v_2\{6\}$ [27]. However, it is possible that the non-linearity of the hydrodynamic response changes the order in the inequality to the case that $v_2\{6\}$ is slightly greater than $v_2\{4\}$. This is compatible with the result which we have found from a more general consideration.

Now, we concentrate on Eq. (47c). Due to the complications in finding the analytical allowed values of $v_2\{2k\}$, we investigate it numerically. First, we consider the case that $\delta _6=\delta _8=1$. In this case, we fix a value for $v_2\{4\}$ and after that randomly generate $v_2\{6\}$ and $v_2\{8\}$ between 0 to 0.15. Putting the above generated and fixed values into Eq. (47c), we find $\bar{v}_2$ numerically. If the equation has at least one real solution, we accept $(v_2\{6\},v_2\{8\})$, otherwise we reject it. The result is presented as scatter plots in Fig. 7. As can be seen from the figure, some region of the $v_2\{2k\}$ phase space is not allowed. The condition $11 \varDelta _2\{6,8\}\ge \varDelta _2\{4,6\}$ (see the square root in (46)) indicates that the border of this allowed region can be identified with $v_2\{8\}=(12v_2\{6\}-v_2\{4\})/11$ up to order $\varDelta _2\{2k,2\ell \}$. This is shown by a red line in Fig. 7. Alternatively, the numerically generated border of the allowed region slightly deviates from the analytical border line. It happens for the region that $v_2\{4\}$ is considerably different from $v_2\{6\}$ and $v_2\{8\}$. The reason is that $\varDelta _2\{2k,2\ell \}$ is not small in this region, and the condition $11 \varDelta _2\{6,8\}\ge \varDelta _2\{4,6\}$ is not accurate anymore.

Let us combine the constraint obtained from Eqs. (47b) and (47c). For a more realistic study, we use the ATLAS data for $v_2\{4\}$ as an input. Instead of using a fixed value for $v_2\{4\}$, we generate it randomly with a Gaussian distribution where it is centered around the central value of $v_2\{4\}$, and we have a width equal to the error of $v_2\{4\}$. The result for 40–$45\%$ centralities is presented in Fig. 8a. For this case, we expect that the Bessel–Gaussian distribution works well. As a result, we assume $\delta _6\simeq \delta _8\simeq 1$ (see Fig. 5). From the ATLAS results [18], we have $v_2\{4\}=0.112\pm 0.002$ in 40–$45\%$ centralities. The black star in the figure shows the experimental value of $(v_2\{6\},v_2\{8\})$ (the ellipse shows the one sigma error without considering the correlations between $v_2\{6\}$ and $v_2\{8\}$). The width of the bands is due to the one sigma error of $v_2\{4\}$. As the figure shows, the experimental result is compatible with the allowed region of $(v_2\{6\},v_2\{8\})$.

For more peripheral collisions, we expect a non-zero value for $\delta _{2k}$. In the 65–$70\%$ centrality class (the most peripheral class of events reported by ATLAS in Ref. [18]), we have $v_2\{4\}\simeq 0.093\pm 0.002$. According to our simulation in this centrality class, we expect the values of $\delta _6$ and $\delta _8$ to be 0.88 and 0.8, respectively. However, here we do not choose fixed values for $\delta _6$ and $\delta _8$. Instead, we generate a random number between 0.8 to 1 and assign the result to both $\delta _6$ and $\delta _8$. The result is presented in Fig. 8b. Referring to this figure, the allowed region is compatible with the experiment similar to the previous case. For non-zero values of $\delta _6$ and $\delta _8$, the allowed region can be identified by $v_2\{6\}=\delta _6^{-1/6} v_2\{4\}$ and $v_2\{8\}=\delta _8^{-1/8}(12v_2\{6\}-v_2\{4\})/11$. These two constraints (similar to Fig. 8a) are presented by two bands in Fig. 8b. In this case, the width of the bands is due to the inaccuracy in $\delta _6$ and $\delta _8$ together with $v_2\{4\}$.

By considering the correlation between $v_2\{6\}$ and $v_2\{8\}$, the experimental one sigma region of the $v_2\{6\}$–$v_2\{8\}$ space would not be a simple domain. Nevertheless, for the present inaccurate case which is depicted in Fig. 8, we are able to restrict the one sigma domain by comparing it with the allowed region showed by the blue dots.

Let us summarize the constraint on the harmonic fine-splitting of the flow as follows:

$$\begin{aligned}&\varDelta _2\{4,6\} \gtrsim 0, \end{aligned}$$

(50a)

$$\begin{aligned}&11 \varDelta _2\{6,8\}-\varDelta _2\{4,6\} \gtrsim 0, \end{aligned}$$

(50b)

which correspond to the region filled by the blue dots in Fig. 8. Note that we used the approximate inequality in Eq. (50b) because of not only ignoring $\delta _8^{1/8}$ but also ignoring terms with order ${\mathcal {O}}(\varDelta ^2)$.

Fig. 8

Combining the constraints $\varDelta _2\{4,6\} \gtrsim 0$ and $11 \varDelta _2\{6,8\}-\varDelta _2\{4,6\} \gtrsim 0$ to find the allowed region of $v_2\{6\}$-$v_2\{8\}$ phase space. In this case, $\delta _6$, $\delta _6$ and $v_2\{4\}$ are not completely fixed. The region is compatible with the ATLAS data reported in Ref. [18]

Let us point out that the inequalities in Eq. (50) can be written as

$$\begin{aligned} \frac{11}{12} \frac{v_2\{8\}}{v_2\{4\}}+\frac{1}{12}\lesssim \frac{v_2\{6\}}{v_2\{4\}} \lesssim 1. \end{aligned}$$

(51)

In Ref. [18], the ratios $v_2\{6\}/v_2\{4\}$ and $v_2\{8\}/v_2\{4\}$ have been calculated experimentally. In Fig. 9, we compare the relations $v_2\{6\}/v_2\{4\}$ with $11v_2\{6\}/12v_2\{4\}+1/12$. As can be seen, the conditions in Eq. (51) are satisfied in all centralities. Furthermore, the inequality in the right-hand side of Eq. (51) is not saturated, while we need a more accurate experimental observation to decide on the saturation of the inequality in the left-hand side.

Fig. 9

Experimental values of ratios $v_2\{6\}/v_2\{4\}$ and $11v_2\{6\}/12v_2\{4\}+1/12$ with respect to the centrality class from the ATLAS data [18]

Finally, we would like to mention that Eq. (36e) does not lead to any constraint on $v_2\{2k\}$ for $0.5 \lesssim \delta _{10} \lesssim 1$. The reason is that $\bar{v}_2=0$ is a minimum of the following relation:

$$\begin{aligned}&156\, \bar{v}_2^{10}-480\,v_2^4\{4\} \bar{v}_2^6-120\, v_2^6\{6\} \bar{v}_2^4\\&\quad +20(12 v_2^8\{4\}+33v_2^8\{8\})\bar{v}_2^2-456\,\delta _{10} v_2^{10}\{10\}, \end{aligned}$$

and its value in the minimum is $-456 \,\delta _{10} v_2^{10}\{10\}$. It means that for $\delta _{10}>0$ the equation always has real roots.

6 Conclusion and outlook

In the present work, we have employed the concept of the Gram–Charlier A series to relate the distribution $p(v_n)$ to $c_n\{2k\}$. We have found an expansion around the Bessel–Gaussian distribution where the coefficients of the expansion have been written in terms of a new set of the cumulants $q_n\{2k\}$. We have shown that the corrected Bessel–Gaussian distribution can fit the actual distribution $p(v_n)$ much better than the Bessel–Gaussian distribution. The new cumulants $q_n\{2k\}$ were written in terms of $c_n\{2k\}$ and the averaged flow harmonic $\bar{v}_n$. Because the only non-vanishing new cumulants are $q_n\{2\}$ for a Bessel–Gaussian distribution, they are a more natural choice to study the distributions near the Bessel–Gaussian case than $c_n\{2k\}$.

By using the cumulants $q_n\{2k\}$, we could systematically introduce different estimations for $p(v_n)$ and consequently relate the averaged ellipticity $\bar{v}_2$ to the flow harmonic fine-splitting $v_2\{2k\}-v_2\{2\ell \}$ for $k,\ell \ge 2$ and $k\ne \ell$. As a specific example for the $\bar{v}_2$ estimator, we have shown that $\bar{v}_2\{6\}\simeq v_2\{6\}-\sqrt{v_2\{6\}(v_2\{4\}-v_2\{6\})}$. We have used the iEBE-VISHNU event generator to compare the true value of the $\bar{v}_2$ to the estimated one; also, we have shown that the estimator $\bar{v}_2\{6\}$ is more accurate than $v_2\{2k\}$ for $k>1$. As another application of new cumulants, we have constrained the phase space of the flow harmonics $v_n\{2k\}$ to the region $v_2\{4\}-v_2\{6\}\gtrsim 0$ and $12 v_2\{6\}-11v_2\{8\}-v_2\{4\}\gtrsim 0$. It is experimentally confirmed that $v_2\{4\}-v_2\{6\}>0$. But we need a more accurate experimental observation for the quantity $12 v_2\{6\}-11v_2\{8\}-v_2\{4\}$.

One should note that we have shown the compatibility of the allowed phase space of $v_2\{2k\}$ with experimental results of (high-multiplicity) Pb–Pb collisions. Recently, the flow harmonics were measured for p–p, p–Pb and low-multiplicity Pb–Pb collisions by ATLAS [42]. In the light of $q_2\{2k\}$ cumulants, it would be interesting to study the similarity and difference between the splitting of $v_2\{2k\}$ in these systems and examine the compatibility of the results with the allowed region comes from $q_2\{2k\}$.

Furthermore, we have only focused on the distribution $p(v_n)$ in the present study. However, based on the observation of symmetric cumulants and event-plane correlations, we expect that a similar systematic study for the distribution $p(v_1,v_2,\ldots )$ can connect this joint distribution to the observations. Such a study would be helpful to relate the initial state event-by-event fluctuations to the observation. This would be a fruitful area for further work.

Appendices

Two-dimensional cumulants in cartesian and polar coordinates

The Cartesian cumulants ${\mathcal {A}}_{mn}$ can be found in terms of the moments $\langle x^{k} y^{\ell } \rangle$ by using the first line of the Eq. (4). A few first cumulants can be found as follows:

$$\begin{aligned} {\mathcal {A}}_{10}= & {} \langle x\rangle , \end{aligned}$$

(52a)

$$\begin{aligned} {\mathcal {A}}_{01}= & {} \langle y\rangle ,\end{aligned}$$

(52b)

$$\begin{aligned} {\mathcal {A}}_{20}= & {} \langle x^2\rangle -\langle x\rangle ^2,\end{aligned}$$

(52c)

$$\begin{aligned} {\mathcal {A}}_{11}= & {} \langle x y\rangle -\langle x\rangle \langle y\rangle ,\end{aligned}$$

(52d)

$$\begin{aligned} {\mathcal {A}}_{02}= & {} \langle y^2\rangle -\langle y\rangle ^2,\end{aligned}$$

(52e)

$$\begin{aligned} {\mathcal {A}}_{30}= & {} \langle x^3\rangle -3\langle x\rangle \langle x^2\rangle +2\langle x\rangle ^3, \end{aligned}$$

(52f)

$$\begin{aligned} {\mathcal {A}}_{21}= & {} \langle x^2 y\rangle -\langle x^2\rangle \langle y \rangle -2 \langle x\rangle \langle x y\rangle +2\langle x\rangle ^2 \langle y\rangle , \end{aligned}$$

(52g)

$$\begin{aligned} {\mathcal {A}}_{12}= & {} \langle x y^2\rangle -\langle x \rangle \langle y^2\rangle -2 \langle x y\rangle \langle y\rangle +2\langle x\rangle \langle y\rangle ^2, \end{aligned}$$

(52h)

$$\begin{aligned} {\mathcal {A}}_{03}= & {} \langle y^3\rangle -3\langle y\rangle \langle y^2\rangle +2\langle y\rangle ^3. \end{aligned}$$

(52i)

Note that for a fixed number $\chi$ we have ${\mathcal {A}}_{mn} \rightarrow \chi ^{m+n} {\mathcal {A}}_{mn}$ by replacing $x\rightarrow \chi x$ and $y\rightarrow \chi y$. We call $m+n$ as the order of ${\mathcal {A}}_{mn}$. Consequently, there are $m+n+1$ number of cumulants with the order $m+n$.

In order to find the cumulants ${\mathcal {C}}_{m,n}$ in polar coordinates $x=r\cos \varphi$ and $y=r\sin \varphi$, we use the second line of Eq. (4). Considering the Jacobi–Anger identity

$$\begin{aligned} \text {e}^{i {\mathbf {r}}\cdot {\mathbf {k}}}=\text {e}^{i r k \cos (\varphi -\varphi _k)}=\sum _{n=-\infty }^{\infty }i^n J_n(kr)\,\text {e}^{in(\varphi -\varphi _k)},\qquad \end{aligned}$$

(53)

we are able to write Eq. (4) as follows:

$$\begin{aligned} \begin{aligned}&\log \left( \sum _{m=0}^{\infty }\sum _{n=-\infty }^{\infty } \frac{(ik)^{2m+n} \text {e}^{-in\varphi _k}}{2^{2m+n}m!(m+n)!}\langle r^{2m+n} \text {e}^{in\varphi }\rangle \right) \\&\quad =\sum _{m=0}^{\infty }\sum _{n=-\infty }^{\infty } \frac{{\mathcal {C}}_{m,n}\; (ik)^m \text {e}^{in\varphi _k}}{m!}, \end{aligned} \end{aligned}$$

(54)

where in the left-hand side we have used the series form of the Bessel function $J_n(kr)$.

In Eq. (54), the combination $(ik)^{2m+n}\text {e}^{-in\varphi _k}$ has appeared in the left-hand side. It means that if we have odd |n|, then the power of ik is odd, and if we have even |n|, then the power of ik is even. Therefore, the only non-vanishing ${\mathcal {C}}_{m,n}$ are those for which both m and |n| are odd or even. The other consequence of the combination $(ik)^{2m+n}\text {e}^{-in\varphi _k}$ is that we have ${\mathcal {C}}_{m,n}=0$ for $|n|>m$. The reason is that in the right-hand side of the Eq. (54), the combination $(ik)^{m'} \text {e}^{i n' \varphi _k}$ has appeared. Therefore, in order to have a non-vanishing ${\mathcal {C}}_{m,n}$ we need to have some terms in the left-hand side such that $2m+n=m'$ and $n=-n'$. It immediately leads to $m=(m'+n')/2\ge 0$ and $m+n=(m'-n')/2\ge 0$. One should note that the $(m+n)!$ in the denominator of Eq. (54) diverges if $m+n<0$. As a result, we deduce that ${\mathcal {C}}_{m',n'}$ can be non-vanishing if $|n'|\le m'$. Strictly speaking, for $m\ge 0$ only the cumulants

$$\begin{aligned} {\mathcal {C}}_{m,-m},\quad {\mathcal {C}}_{m,-m+2},\quad \cdots \quad {\mathcal {C}}_{m,m-2},\quad {\mathcal {C}}_{m,m}, \end{aligned}$$

(55)

are non-zero. Also, note that we have ${\mathcal {C}}_{m,-n}={\mathcal {C}}_{m,n}^*$ because the distribution is a real function.

Based on the above considerations one can find all non-trivial values of ${\mathcal {C}}_{m,n}$ in terms of moments $\langle r^{m} \text {e}^{in\varphi }\rangle$ by using Eq. (54). A few first two-dimensional cumulants in polar coordinates are presented explicitly in the following:

$$\begin{aligned} {\mathcal {C}}_{1,1}= & {} \frac{1}{2}\langle r \text {e}^{-i \varphi }\rangle , \end{aligned}$$

(56a)

$$\begin{aligned} {\mathcal {C}}_{2,0}= & {} \frac{1}{2}\left[ \langle r^2\rangle -\langle r \text {e}^{i\varphi }\rangle \langle r \text {e}^{-i\varphi }\rangle \right] , \end{aligned}$$

(56b)

$$\begin{aligned} {\mathcal {C}}_{2, 2}= & {} \frac{1}{4}\left[ \langle r^2\,\text {e}^{ -2i \varphi }\rangle -\langle r\,\text {e}^{ -i \varphi }\rangle ^2\right] , \end{aligned}$$

(56c)

$$\begin{aligned} {\mathcal {C}}_{3, 1}= & {} \frac{3}{8}\left[ \langle r^3 \text {e}^{-i\varphi }\rangle +2\langle r \text {e}^{i\varphi }\rangle \langle r \text {e}^{ -i\varphi }\rangle ^2\right. {\nonumber }\\&\left. -\langle r \text {e}^{i\varphi }\rangle \langle r^2 \text {e}^{ -2i\varphi }\rangle -2\langle r^2\rangle \langle r \text {e}^{ -i\varphi }\rangle \right] ,\end{aligned}$$

(56d)

$$\begin{aligned} {\mathcal {C}}_{3,3}= & {} \frac{1}{8}\left[ \langle r^3 \,\text {e}^{ -3i \varphi }\rangle -3\langle r \,\text {e}^{ -i \varphi }\rangle \langle r^2 \,\text {e}^{ -2i \varphi }\rangle +2\langle r \,\text {e}^{ -i \varphi }\rangle ^3\right] .\nonumber \\ \end{aligned}$$

(56e)

The first cumulant, ${\mathcal {C}}_{0,0}$, is equal to zero by considering the normalization condition of the probability distribution.

By redefinition

$$\begin{aligned} W_{0,n}={\mathcal {C}}_{n,0},\quad W^c_{n,m}=\mathfrak {R}({\mathcal {C}}_{m,n}), \quad W^s_{n,m}=-\mathfrak {I}({\mathcal {C}}_{m,n}), \end{aligned}$$

we find the cumulants in polar coordinate which has been obtained in Ref. [30]. In Ref. [30], the translational and rotational invariance have been used to eliminate $W^c_{1,1}$, $W^s_{1,1}$ and $W^s_{2,2}$. In our notation, it is equivalent to ${\mathcal {C}}_{1,1}={\mathcal {C}}_{1,-1}=0$ and ${\mathcal {C}}_{2,2}={\mathcal {C}}_{2,-2}$.

One notes that by replacing r with $\chi r$ we have ${\mathcal {C}}_{m,n} \rightarrow \chi ^m \, {\mathcal {C}}_{m,n}$. In other words, the order of ${\mathcal {C}}_{m,n}$ is indicated by m in polar coordinates. Referring to Eq. (55), we find that there are $m+1$ cumulants with order m in polar coordinates. As a result, we are able to find a one-to-one relation between ${\mathcal {C}}_{m, n}$ and ${\mathcal {A}}_{k\ell }$ with the same order by equating the two sides of the equation,

$$\begin{aligned} \begin{aligned}&\sum _{m,n}\frac{{\mathcal {A}}_{mn} (ik)^{m+n}\cos ^m\varphi _k \sin ^n\varphi _k }{m!n!}\\&\quad =\sum _{m=0}^{\infty }\sum _{n=-\infty }^{\infty } \frac{{\mathcal {C}}_{m,n}\; (ik)^m \text {e}^{in\varphi _k}}{m!}. \end{aligned} \end{aligned}$$

(57)

In the left-hand side of the above equality, we rewrite $\sum _{m,n}((ik_x)^m (ik_y)^n {\mathcal {A}}_{mn}/(m!n!))$ in polar coordinates. A few first cumulants in polar coordinates can be written in terms of ${\mathcal {A}}_{mn}$ as follows:

$$\begin{aligned} {\mathcal {C}}_{1,1}= & {} \frac{1}{2}\left[ {\mathcal {A}}_{10}-i{\mathcal {A}}_{01}\right] , \end{aligned}$$

(58a)

$$\begin{aligned} {\mathcal {C}}_{2,0}= & {} \frac{1}{2}\left[ {\mathcal {A}}_{20}+{\mathcal {A}}_{02}\right] ,\end{aligned}$$

(58b)

$$\begin{aligned} {\mathcal {C}}_{2, 2}= & {} \frac{1}{4}\left[ {\mathcal {A}}_{20}-{\mathcal {A}}_{02}-2i{\mathcal {A}}_{11}\right] , \end{aligned}$$

(58c)

$$\begin{aligned} {\mathcal {C}}_{3, 1}= & {} \frac{3}{8}\left[ {\mathcal {A}}_{30}+{\mathcal {A}}_{12}-i({\mathcal {A}}_{03}+{\mathcal {A}}_{21})\right] ,\end{aligned}$$

(58d)

$$\begin{aligned} {\mathcal {C}}_{3,3}= & {} \frac{1}{8}\left[ {\mathcal {A}}_{30}-3{\mathcal {A}}_{12}+i({\mathcal {A}}_{03}-3{\mathcal {A}}_{21})\right] . \end{aligned}$$

(58e)

The cumulants ${\mathcal {C}}_{m,-n}$ can be obtained easily by using the reality condition. One can invert the above equations to find ${\mathcal {A}}_{mn}$ in terms of ${\mathcal {C}}_{m,n}$ too,

$$\begin{aligned} {\mathcal {A}}_{10}= & {} {\mathcal {C}}_{1,1}+{\mathcal {C}}_{1,-1}, \end{aligned}$$

(59a)

$$\begin{aligned} {\mathcal {A}}_{01}= & {} i({\mathcal {C}}_{1,1}-{\mathcal {C}}_{1,-1}),\end{aligned}$$

(59b)

$$\begin{aligned} {\mathcal {A}}_{20}= & {} {\mathcal {C}}_{2,0}+{\mathcal {C}}_{2,2}+{\mathcal {C}}_{2,-2},\end{aligned}$$

(59c)

$$\begin{aligned} {\mathcal {A}}_{11}= & {} i({\mathcal {C}}_{2,2}-{\mathcal {C}}_{2,-2}),\end{aligned}$$

(59d)

$$\begin{aligned} {\mathcal {A}}_{02}= & {} {\mathcal {C}}_{2,0}-{\mathcal {C}}_{2,2}-{\mathcal {C}}_{2,-2},\end{aligned}$$

(59e)

$$\begin{aligned} {\mathcal {A}}_{30}= & {} {\mathcal {C}}_{3,3}+{\mathcal {C}}_{3,1}+{\mathcal {C}}_{3,-1}+{\mathcal {C}}_{3,-3},\end{aligned}$$

(59f)

$$\begin{aligned} {\mathcal {A}}_{21}= & {} \frac{i}{3}\left( 3{\mathcal {C}}_{3,3}+{\mathcal {C}}_{3,1}-{\mathcal {C}}_{3,-1}-3{\mathcal {C}}_{3,-3}\right) ,\end{aligned}$$

(59g)

$$\begin{aligned} {\mathcal {A}}_{12}= & {} -\frac{1}{3}\left( 3{\mathcal {C}}_{3,3}-{\mathcal {C}}_{3,1}-{\mathcal {C}}_{3,-1}+3{\mathcal {C}}_{3,-3}\right) ,\end{aligned}$$

(59h)

$$\begin{aligned} {\mathcal {A}}_{03}= & {} -i\left( {\mathcal {C}}_{3,3}-{\mathcal {C}}_{3,1}+{\mathcal {C}}_{3,-1}-{\mathcal {C}}_{3,-3}\right) . \end{aligned}$$

(59i)

For rotationally symmetric distributions, only the moments $\langle r^{2m} \rangle$ survive in the polar coordinates. In such a case, the only non-zero polar cumulants are ${\mathcal {C}}_{2k,0}$. For instance, all the cumulants in Eq. (58) vanish except ${\mathcal {C}}_{2,0}$ where it is equal to $\langle r^2 \rangle /2$. A few of the first ${\mathcal {C}}_{2k,0}$ are given by

$$\begin{aligned} {\mathcal {C}}_{2,0}= & {} \frac{1}{2}\left[ \langle r^2 \rangle \right] , \end{aligned}$$

(60a)

$$\begin{aligned} {\mathcal {C}}_{4,0}= & {} \frac{3}{8}\left[ \langle r^4 \rangle -2\langle r^2 \rangle ^2\right] , \end{aligned}$$

(60b)

$$\begin{aligned} {\mathcal {C}}_{6,0}= & {} \frac{5}{16}\left[ \langle r^6 \rangle -9\langle r^4 \rangle \langle r^2 \rangle +12\langle r^2 \rangle ^3\right] , \end{aligned}$$

(60c)

$$\begin{aligned} {\mathcal {C}}_{8,0}= & {} \frac{35}{128}\left[ \langle r^8 \rangle -16\langle r^6 \rangle \langle r^2 \rangle -18\langle r^4 \rangle ^2\right. {\nonumber }\\&\left. +144\langle r^4 \rangle \langle r^2\rangle ^2-144\langle r^2 \rangle ^4 \right] . \end{aligned}$$

(60d)

By replacing r with $v_n$ in Eq. (60) and comparing it with Eq. (8), we find that $c_n\{2k\}\propto {\mathcal {C}}_{2k,0}$.

Gram–Charlier A series

1.1 Gram–Charlier A series: one dimension

In Sect. 3.1, we have introduced an iterative method to find the Gram–Charlier A series for a one-dimensional distribution. Also, we briefly explained the standard method of finding the series by using the orthogonal polynomials. Here, we use another standard method of finding the Gram–Charlier A series.

Let us consider the characteristic function of a given distribution p(x) as $G(t)=\int \text {d}x\, \text {e}^{i t x} p(x)$. Then one can find the cumulants of the distribution by using the cumulative function,

$$\begin{aligned} \log G(t)=\sum _{n=1}\kappa _n (i t)^n/n!. \end{aligned}$$

(61)

Now assume that p(x) can be approximated by a known distribution, namely a Gaussian distribution,

$$\begin{aligned} {\mathcal {N}}(x)=\frac{1}{\sqrt{2\pi }\sigma }\text {e}^{-\frac{(x-\mu '_1)^2}{2\sigma ^2}}. \end{aligned}$$

By setting the mean value $\mu '=0$ and the width $\sigma =1$ for simplicity, the generating function of a Gaussian distribution can be simply found to be $G_{{\mathcal {N}}}(t)=\text {e}^{-t^2/2}$. Referring to Eq. (61), we have $G(t)=\text {e}^{\sum _{n=1}\kappa _n (i t)^n/n!}$. Additionally, we consider the fact that the mean value and the variance of the distribution p(x) are $\kappa _1=\mu '=0$ and $\kappa _2=\sigma ^2=1$. It means that we are able to write G(t) for a generic distribution p(x) as follows:

$$\begin{aligned} \begin{aligned} G(t)&=\text {e}^{\sum _{n=3}\kappa _n (i t)^n/n!}\text {e}^{-t^2/2}\\&= \text {e}^{\sum _{n=3}\kappa _n (i t)^n/n!}G_{{\mathcal {N}}}(t). \end{aligned} \end{aligned}$$

(62)

Now, we are able to find p(x) by using an inverse Fourier transformation. By considering the relation $\int \text {d}t (i t)^n \text {e}^{-i t x}$ $\times \text {e}^{-t^2/2}=(-\text {d}/\text {d}x)^n \int \text {d}t \text {e}^{-i t x}\text {e}^{-t^2/2}$, we have

$$\begin{aligned} \begin{aligned} p(x)&=\text {e}^{\sum _{n=3}\kappa _n (-\text {d}/\text {d}x)^n/n!} \left[ \int \text {d}t \text {e}^{-i t x}\text {e}^{-t^2/2}\right] /2\pi \\&=\text {e}^{\sum _{n=3}\kappa _n (-\text {d}/\text {d}x)^n/n!}\left[ \text {e}^{-x^2/2}/\sqrt{2\pi }\right] . \end{aligned} \end{aligned}$$

(63)

By scaling $x\rightarrow x/\sigma$ and shifting $x\rightarrow x-\mu '$, we find²²

$$\begin{aligned} p(x)=\text {e}^{\sum _{n=3}\kappa _n (-\text {d}/\text {d}x)^n/n!}{\mathcal {N}}(x). \end{aligned}$$

(64)

Recall that the probabilistic Hermite polynomial is defined as $He_r(x)=\text {e}^{x^2/2}(-\text {d}/\text {d}x)^r \text {e}^{-x^2/2}$. As a result, one can simply find

$$\begin{aligned} \left( -\frac{d}{\text {d}x}\right) ^n {\mathcal {N}}(x)=\frac{1}{\sigma ^n} He_n((x-\mu ')/\sigma ) {\mathcal {N}}(x). \end{aligned}$$

(65)

It is worth noting that Eq. (64) is exact. We are able to approximate this exact relation by expanding it in terms of number of derivatives. The result of such an expansion is called a Gram–Charlier A series,

$$\begin{aligned} \begin{aligned} p(x)=\frac{1}{\sqrt{2\pi }\sigma }&\text {e}^{-\frac{(x-\kappa _1)^2}{2\sigma ^2}}\sum _{n=1} \frac{h_n}{n!} He_n((x-\kappa _1)/\sigma ), \end{aligned} \end{aligned}$$

where $h_n$ was presented in Eq. (21) ($h_1=1,h_2=0$).

1.2 Gram–Charlier A series: two dimensions

Consider the following two-dimensional Gaussian distribution:

$$\begin{aligned} {\mathcal {N}}({\mathbf {r}})=\frac{1}{2\pi \sigma _x \sigma _y} \text {e}^{-\frac{(x-\mu '_x)^2}{2\sigma _x^2}-\frac{(y-\mu '_y)^2}{2\sigma _y^2}}, \end{aligned}$$

(66)

which is more general than Eq. (14). Referring to Eq. (3), we find the characteristic function of Eq. (66) as follows:

$$\begin{aligned} G_{{\mathcal {N}}}({\mathbf {k}})=\text {e}^{-\frac{1}{2}(k_x \sigma _x+k_y \sigma _y)}. \end{aligned}$$

(67)

Now, assume that the mean values $\langle x \rangle$ and $\langle y \rangle$ ($\langle \cdots \rangle =\int \text {d}x \text {d}y \cdots p({\mathbf {r}})$) are exactly equal to $\mu '_x$ and $\mu '_y$, respectively, and alternatively set $\mu '_x=\mu '_y=0$ by a shift. Then the characteristic function of $p({\mathbf {r}})$ can be written as follows:

$$\begin{aligned} \begin{aligned} G({\mathbf {k}})&=\exp {\sum _{m,n}\frac{(i\,k_x)^m (i\,k_y)^n {\mathcal {A}}_{mn}}{m! n!}}\\&=\left[ \exp {\sum _{m,n}\frac{(i\,k_x)^m (i\,k_y)^n {\mathcal {A}}'_{mn}}{m! n!}}\right] G_{{\mathcal {N}}}({\mathbf {k}}), \end{aligned} \end{aligned}$$

(68)

where in the last line the ${\mathcal {A}}'_{mn}$ are exactly as ${\mathcal {A}}_{mn}$ except

$$\begin{aligned} {\mathcal {A}}'_{20}={\mathcal {A}}_{20}-\sigma _x,\qquad {\mathcal {A}}'_{20}={\mathcal {A}}_{02}-\sigma _y. \end{aligned}$$

(69)

Note that we could choose ${\mathcal {A}}_{20}=\sigma _x$ and ${\mathcal {A}}_{02}=\sigma _y$ similar to what we did in one dimension. But here we do not use this convention for the future purpose.

We can find $p({\mathbf {r}})$ by an inverse Fourier transformation,

$$\begin{aligned} p({\mathbf {r}})=\left[ \exp {\sum _{m,n}\frac{(-1)^{m+n} {\mathcal {A}}'_{mn}}{m! n!}}\left( \frac{d^{m+n}}{\text {d}x^m \text {d}y^n}\right) \right] {\mathcal {N}}({\mathbf {r}}),\qquad \end{aligned}$$

(70)

where for finding the above we replaced $(i k_x)^m(i k_x)^n$ with $(-1)^{m+n}(d^{m+n}/\text {d}x^m dy^n)$ in Eq. (68).

The Gram–Charlier A series can be found by expanding the exponential in Eq. (70) in terms of a number of derivatives. By recovering $\mu '_x$ and $\mu '_y$ by a reverse shift in ${\mathbf {r}}$, we find

$$\begin{aligned} p({\mathbf {r}})={\mathcal {N}}({\mathbf {r}})\sum _{\begin{array}{c} m,n=0 \end{array}}\frac{h_{mn}}{m!n!} He_m\left( \frac{x-\mu _x}{\sigma _x}\right) He_n\left( \frac{y-\mu _y}{\sigma _y}\right) .\nonumber \\ \end{aligned}$$

(71)

In the above, we have used a trivial extension of Eq. (65) to two dimensions. The coefficients $h_{mn}$ for $m+n\le 2$ in Eq. (71) are given as follows (we set ${\mathcal {A}}_{11}=0$ for simplicity):

$$\begin{aligned} \begin{aligned} h_{00}&= 1,\\ h_{10}&=h_{01}=0,\\ h_{20}&=\frac{{\mathcal {A}}_{20}}{\sigma _x^2}-1,\; h_{11}=0,\; h_{02}=\frac{{\mathcal {A}}_{02}}{\sigma _y^2}-1. \end{aligned} \end{aligned}$$

(72)

Additionally, we have

$$\begin{aligned} h_{mn}=\frac{{\mathcal {A}}_{mn}}{\sigma _x^m\sigma _y^n},\qquad 3\le m+n\le 5. \end{aligned}$$

(73)

For $m+n=6$ we have

$$\begin{aligned} \begin{aligned} h_{60}&=\frac{1}{\sigma _x^6}\left[ {\mathcal {A}}_{60}+10{\mathcal {A}}_{30}^2\right] ,\\ h_{51}&=\frac{1}{\sigma _x^5\sigma _y}\left[ {\mathcal {A}}_{51}+10{\mathcal {A}}_{30}{\mathcal {A}}_{21}\right] ,\\ h_{42}&=\frac{1}{\sigma _x^4\sigma _y^2}\left[ {\mathcal {A}}_{42}+4{\mathcal {A}}_{30}{\mathcal {A}}_{12}+6{\mathcal {A}}_{21}^2\right] ,\\ h_{33}&=\frac{1}{\sigma _x^3\sigma _y^3}\left[ {\mathcal {A}}_{33}+{\mathcal {A}}_{30}{\mathcal {A}}_{03}+9{\mathcal {A}}_{12}{\mathcal {A}}_{21}\right] ,\\ h_{24}&=\frac{1}{\sigma _x^2\sigma _y^4}\left[ {\mathcal {A}}_{24}+4{\mathcal {A}}_{03}{\mathcal {A}}_{21}+6{\mathcal {A}}_{12}^2\right] ,\\ h_{15}&=\frac{1}{\sigma _x\sigma _y^5}\left[ {\mathcal {A}}_{15}+10{\mathcal {A}}_{03}{\mathcal {A}}_{12}\right] ,\\ h_{06}&=\frac{1}{\sigma _y^6}\left[ {\mathcal {A}}_{06}+10{\mathcal {A}}_{03}^2\right] .\\ \end{aligned} \end{aligned}$$

(74)

The other $h_{mn}$ can be found accordingly.

1.3 Gram–Charlier A series and energy density expansion

We should mention that the Gram–Charlier A series [Eq. (71)] is exactly what has been used in Ref. [30] to quantify the initial energy density deviation from a rotationally symmetric Gaussian distribution.²³

In Ref. [30], the cumulants of the energy density $\rho ({\mathbf {r}})$ have been expanded in terms of the moments

$$\begin{aligned} \hat{\varepsilon }_{m,n}\equiv \varepsilon _{m,n}\text {e}^{i n\varPhi _{m,n}}=-\frac{\{r^m \text {e}^{in\varphi }\}}{\{r^m\}}, \end{aligned}$$

(75)

where $m,n=0,1,\ldots \;$ and

$$\begin{aligned} \{\cdots \}=\frac{\int \cdots \rho ({\mathbf {r}})\text {d}x\text {d}y}{\int \rho ({\mathbf {r}}) \text {d}x\text {d}y}. \end{aligned}$$

Due to the translational invariance, we can freely choose the origin of the coordinates such that $\{r \text {e}^{\pm i \varphi }\}=0$. Using this and referring to Eq. (56) and Eq. (75), one finds

$$\begin{aligned} \begin{aligned}&{\mathcal {C}}_{2,0}=\frac{1}{2}\{ r^2\}, \\&{\mathcal {C}}_{2, 2}=-\frac{1}{4}\{ r^2\}\varepsilon _{2,2}\text {e}^{-2i\varPhi _{2,2}}, \\&{\mathcal {C}}_{3, 1}=-\frac{3}{8}\{ r^3\}\varepsilon _{3,1}\text {e}^{-3i\varPhi _{3,1}},\\&{\mathcal {C}}_{3,3}=-\frac{1}{8}\{ r^3\}\varepsilon _{3,3}\text {e}^{-3i\varPhi _{3,3}}.\\ \end{aligned} \end{aligned}$$

(76)

It is common in the literature to define the initial anisotropies as $\varepsilon _1\equiv \varepsilon _{3,1},\; \varepsilon _2\equiv \varepsilon _{2,2}$ and $\varepsilon _3\equiv \varepsilon _{3,3}$. According to Eq. (76), the initial anisotropies are itself cumulants. In fact, the parameter $\varepsilon _n$ quantifies the global features of the initial energy density. For instance, $\varepsilon _1$, $\varepsilon _2$ and $\varepsilon _3$ quantify the dipole asymmetry, ellipticity and triangularity of the distribution, respectively. The symmetry planes $\varPhi _1\equiv \varPhi _{3,1},\; \varPhi _2$ $\equiv \varPhi _{2,2}$ and $\varPhi _3\equiv \varPhi _{3,3}$ quantify the orientation of the dipole asymmetry, ellipticity and triangularity with respect to a reference direction.

Furthermore, one can relate two-dimensional cumulants in Cartesian coordinates, ${\mathcal {A}}_{mn}$, to those in polar coordinates, ${\mathcal {C}}_{m,n}$ by using Eq. (59). Using them, we find

$$\begin{aligned} \begin{aligned}&{\mathcal {A}}_{20}=\frac{1}{2}\{r^2\}(1-\varepsilon _2\cos 2\varPhi _2 ),\\&{\mathcal {A}}_{11}=-\frac{1}{2}\{r^2\}\varepsilon _2\sin 2\varPhi _2 , \\&{\mathcal {A}}_{02}=\frac{1}{2}\{r^2\}(1+\varepsilon _2\cos 2\varPhi _2 ), \\&{\mathcal {A}}_{30}=-\frac{1}{4}\{ r^3\}(3\varepsilon _1\cos \varPhi _1+\varepsilon _3\cos 3\varPhi _3), \\&{\mathcal {A}}_{21}=-\frac{1}{4}\{ r^3\}(\varepsilon _1\sin \varPhi _1+\varepsilon _3\sin 3\varPhi _3),\\&{\mathcal {A}}_{12}=-\frac{1}{4}\{ r^3\}(\varepsilon _1\cos \varPhi _1-\varepsilon _3\cos 3\varPhi _3),\\&{\mathcal {A}}_{03}=-\frac{1}{4}\{ r^3\}(3\varepsilon _1\sin \varPhi _1-\varepsilon _3\sin 3\varPhi _3). \end{aligned} \end{aligned}$$

(77)

Now, we use Eq. (71) to find a Gram–Charlier A series for the energy density. The result is the following:

$$\begin{aligned} \begin{aligned} \rho (r,\varphi ) \propto \text {e}^{-\frac{r^2}{\{r^2\}}}\left[ 1+\sum _{n=1}^{3} a_n(r)\varepsilon _n\cos n(\varphi -\varPhi _n)\right] , \end{aligned} \end{aligned}$$

(78)

where

$$\begin{aligned} \begin{aligned} a_1(r)&=-\frac{r\{r^3\}(r^2-2\{r^2\})}{\{r^2\}^3},\\ a_2(r)&=-\frac{r^2}{\{r^2\}},\\ a_3(r)&=-\frac{r^3\{r^3\}}{3\{r^2\}^3}. \end{aligned} \end{aligned}$$

(79)

In the above, we assumed that $\sigma _x^2=\sigma _y^2=\{r^2\}/2$. This result coincides with that presented in Ref. [30]. The cumulants ${\mathcal {C}}_{m,n}$, $m>3$ cannot be written simply in terms of one moment $\varepsilon _{m,n}$, however, it is always possible to find a Gram–Charlier A series, see Eq. (78), to any order beyond triangularity.

A radial distribution from 2D Gram–Charlier A series

The Bessel–Gaussian distribution (15) was obtained by averaging out the azimuthal direction of a two-dimensional Gaussian distribution (14). Alternatively, one can do the same calculation and find a one-dimensional series by averaging out the azimuthal direction of Eq. (71). We should emphasize that this calculation has already been done in Ref. [28] for the case that $p({\mathbf {r}})$ is rotationally symmetric around the origin. However, we will try to find such a radial series for a more general case.

For simplicity, we assume that $\mu '_y\equiv {\mathcal {A}}_{01}=0$ ($\mu '_x\equiv {\mathcal {A}}_{10}$) together with $\sigma \equiv \sigma _x=\sigma _y={\mathcal {A}}_{20}={\mathcal {A}}_{02}$. Also, we consider the fact that ${\mathcal {A}}_{11}=0$. These considerations are compatible with $p(v_{n,x},v_{n,y})$. For such a case, $h_{20}=h_{11}=h_{02}=0$.

By averaging out the azimuthal direction of Eq. (71), we will find a distribution which has the following form:

$$\begin{aligned} \begin{aligned} p(r)&=\left( \frac{r}{\sigma ^2}\right) \text {e}^{-\frac{r^2+\mu '^2_x}{2\sigma ^2}} \left[ I_0\left( \frac{r \mu '_x}{\sigma ^2}\right) \sum _{i=1}P_{1,i}(r)\right. \\&\quad \left. +\left( \frac{r\mu '_x}{2\sigma ^2}\right) I_1\left( \frac{r \mu '_x}{\sigma ^2}\right) \sum _{i=1} P_{2,i}(r)\right] . \end{aligned} \end{aligned}$$

(80)

We can find the polynomials $P_{1,i}(r)$ and $P_{2,i}(r)$ by direct calculations. For $i=1,2$, one simply finds that $P_{1,1}(r)=1$ and $P_{2,1}(r)=P_{1,2}(r)=P_{2,2}(r)=0$. The polynomials for $i=3$ are given by

$$\begin{aligned} \begin{aligned} P_{1,3}(r)&=\frac{\mu '_x}{2\sigma }h_{12}+\frac{\mu '_x}{2\sigma }\left( 1-\frac{\mu '^2_x}{3\sigma ^2}\right) h_{30}\\&\quad +\frac{1}{6}\left[ 3h_{12}-\left( \frac{3\mu '^2_x}{\sigma ^2}+1\right) h_{30}\right] \left( \frac{r^2}{\mu '_x\sigma }\right) ,\\ P_{2,3}(r)&=-\frac{2\sigma }{\mu '_x}\left( 1+\frac{\sigma ^2}{\mu '^2_x}\right) h_{12}\\&\quad +\frac{\mu '_x}{\sigma }\left( 1+\frac{2\sigma ^4}{3\mu '^4_x}\right) h_{30}+\frac{h_{30}}{3}\left( \frac{r^2}{\mu '_x\sigma }\right) . \end{aligned} \end{aligned}$$

(81)

Finding $P_{1,4}(r)$ and $P_{2,4}(r)$ is straightforward, but they are more complicated. For that reason, we decided not to present them considering the limited space. Note that for each $P_{a,i}(r)$ only cumulants ${\mathcal {A}}_{mn}$ (if there are any) with order $m+n=i$ are present²⁴.

In Sect. 2.1, we have argued that the one-dimensional distributions like $p(v_n)$ can be characterized by $c_n\{2k\}$. As a result, we expect to relate ${\mathcal {A}}_{mn}$ to $c_n\{2k\}$ by considering Eq. (80) (replace r with $v_n$ and $\mu '_x$ with $\bar{v}_n$). Considering Eq. (8) and using Eq. (80) up to $i=4$, we find $c_n\{2k\}$ for $k=1,2,3$ as follows:

$$\begin{aligned} c_n\{2\}= & {} \bar{v}_n^2+2\sigma ^2, \end{aligned}$$

(82a)

$$\begin{aligned} c_n\{4\}= & {} -\bar{v}_n^4+4\bar{v}_n\left( {\mathcal {A}}_{12}+{\mathcal {A}}_{30}\right) {\nonumber }\\&+{\mathcal {A}}_{40}+2{\mathcal {A}}_{22}+{\mathcal {A}}_{04}, \end{aligned}$$

(82b)

$$\begin{aligned} c_n\{6\}= & {} 4\bar{v}_n^6-8\bar{v}_n^3(3{\mathcal {A}}_{12}+2{\mathcal {A}}_{30}){\nonumber }\\&+6\bar{v}_n^2({\mathcal {A}}_{40}-{\mathcal {A}}_{04}). \end{aligned}$$

(82c)

The above result is not surprising. In fact, it is a general relation of ${\mathcal {A}}_{mn}$ of the distribution $p(v_{n,x},v_{n,y})$ with $c_n\{2k\}$ of $p(v_n)$. Recall the equality $\langle \text {e}^{i v_n k\cos (\varphi -\varphi _k)} \rangle _{\text {2D}}$ $=\langle J_0(k v_n) \rangle _{\text {1D}}$ in Eq. (6) where the average $\langle \cdots \rangle _{\text {2D}}$ is performed with respect to the distribution $\tilde{p}(v_{n,x},v_{n,y})$. For the case that the average is performed with respect to $p(v_{n,x},v_{n,y})$, this relation should be replaced by

$$\begin{aligned} \frac{1}{2\pi }\int _{0}^{2\pi }\text {d}\varphi _k\,\langle \text {e}^{i v_n k\cos (\varphi -\varphi _k)} \rangle _{\text {2D}}=\langle J_0(k v_n) \rangle _{\text {1D}}. \end{aligned}$$

(83)

Using the above, Eq. (4) and Eq. (7), we find

$$\begin{aligned}&\log \frac{1}{2\pi }\int _{0}^{2\pi }\text {d}\varphi _k\,\exp \sum _{m,n}\frac{{\mathcal {A}}_{mn} (ik)^{m+n} }{m!n!}\left( \cos ^m\varphi _k \sin ^n\varphi _k\right) \\&\quad =\sum _{m=1}\frac{(ik)^{2m} c_n\{2m\}}{4^m(m!)^2}. \end{aligned}$$

By expanding both sides in terms of k and comparing the coefficients, one finds the relation between $c_n\{2k\}$ and ${\mathcal {A}}_{mn}$. The results for $c_n\{2\}$ and $c_n\{4\}$ are as follows:

$$\begin{aligned} c_n\{2\}= & {} {\mathcal {A}}_{01}^2+{\mathcal {A}}_{10}^2+{\mathcal {A}}_{02}+{\mathcal {A}}_{20}, \end{aligned}$$

(84a)

$$\begin{aligned} c_n\{4\}= & {} -{\mathcal {A}}_{01}^4-2 {\mathcal {A}}_{10}^2 {\mathcal {A}}_{01}^2+2 {\mathcal {A}}_{02} {\mathcal {A}}_{01}^2-2 {\mathcal {A}}_{20} {\mathcal {A}}_{01}^2\\&+4 {\mathcal {A}}_{03} {\mathcal {A}}_{01} +8 {\mathcal {A}}_{10} {\mathcal {A}}_{11} {\mathcal {A}}_{01}+4 {\mathcal {A}}_{21} {\mathcal {A}}_{01}\nonumber \\&-{\mathcal {A}}_{10}^4+{\mathcal {A}}_{02}^2-2 {\mathcal {A}}_{02} {\mathcal {A}}_{10}^2+4 {\mathcal {A}}_{11}^2 +{\mathcal {A}}_{20}^2+{\mathcal {A}}_{04} {\nonumber }\\&+4 {\mathcal {A}}_{10} {\mathcal {A}}_{12}+2 {\mathcal {A}}_{10}^2 {\mathcal {A}}_{20}-2 {\mathcal {A}}_{02} {\mathcal {A}}_{20}{\nonumber }\\&+2 {\mathcal {A}}_{22} +4 {\mathcal {A}}_{10} {\mathcal {A}}_{30}+{\mathcal {A}}_{40}.{\nonumber }\end{aligned}$$

(84b)

The relation for $c_n\{6\}$ is more complicated. Note that by setting the simplifications we used in finding Eq. (80), the above relations reduce to Eq. (82a) and Eq. (82b).

In general, $c_n\{2k\}$ is written in terms of a large number of ${\mathcal {A}}_{pq}$; therefore, we are not able to write ${\mathcal {A}}_{pq}$ in terms of cumulants $c_n\{2k\}$. However, it is possible to ignore the cumulants ${\mathcal {A}}_{pq}$ with $p+q\ge 4$ in some cases. For $n=2$, this truncation leads to a reasonable approximation for $c_2\{4\}$ and $c_2\{6\}$, and we are able to find ${\mathcal {A}}_{30}$ in terms of $c_2\{2\}$, $c_2\{4\}$ and $c_2\{6\}$, which has been done in Ref. [27]. In Ref. [28], however, it has been shown that keeping 2D Cartesian cumulants up to fourth order does not lead to a reasonable approximation for $c_2\{8\}$. Therefore, we are not able to simply find the fourth order ${\mathcal {A}}_{mn}$ in terms of $c_2\{2k\}$.

Referring to Eq. (39), we see that the coefficients $\ell _{2i}$ (as a function of $c_n\{2k\}$ and $\bar{v}_n$) appear as an overall factors at each order of approximation. In contrast, the coefficients $h_{mn}$ in Eq. (80) do not appear in the polynomial $P_{a,i}(r)$ as an overall factor. Now, let us compute the limit $\mu '_x\rightarrow 0$. A straightforward calculation shows that

$$\begin{aligned} I_0\left( \frac{r \mu '_x}{\sigma ^2}\right) P_{1,3}(r)+\left( \frac{r\mu '_x}{2\sigma ^2}\right) I_1\left( \frac{r \mu '_x}{\sigma ^2}\right) P_{2,3}(r)\rightarrow 0. \end{aligned}$$

As a result, the bracket in Eq. (80) is equal to 1 up to $i=3$.

However, the bracket for $i=4$ is non-trivial in the limit $\mu '_x\rightarrow 0$,

$$\begin{aligned} \begin{aligned}&I_0\left( \frac{r \mu '_x}{\sigma ^2}\right) P_{1,4}(r)+\left( \frac{r\mu '_x}{2\sigma ^2}\right) I_1\left( \frac{r \mu '_x}{\sigma ^2}\right) P_{2,4}(r)\\&\quad \rightarrow \frac{1}{8} (h_{40}+2h_{22}+h_{04})\left( 1-\frac{r^2}{\sigma ^2}+\frac{r^4}{8\sigma ^4}\right) . \end{aligned} \end{aligned}$$

The last line in the above can be written as

$$\begin{aligned} \frac{1}{8} (h_{40}+2h_{22}+h_{04}) L_2\left( \frac{r^2}{2\sigma ^2}\right) . \end{aligned}$$

(85)

This result is interesting because it shows that the distribution (80) has a simpler form only if we assume $\mu '_x\equiv {\mathcal {A}}_{10}\rightarrow 0$. Let us again consider the harmonic distribution of the flow ($r \rightarrow v_n$ and $\mu '_x \rightarrow \bar{v}_n$). By setting ${\mathcal {A}}_{20}={\mathcal {A}}_{02}=\sigma ^2$ and ${\mathcal {A}}_{10}={\mathcal {A}}_{01}={\mathcal {A}}_{11}=0$, we find from Eq. (84b) that

$$\begin{aligned} c_n\{2\}= & {} 2\sigma ^2,\\ c_n\{4\}= & {} {\mathcal {A}}_{40}+2{\mathcal {A}}_{22}+{\mathcal {A}}_{04}. \end{aligned}$$

Therefore, the explicit form of Eq. (80) up to $i=4$ is given by

$$\begin{aligned} \begin{aligned} p(v_n)=\left( \frac{v_n}{\sigma ^2}\right) \text {e}^{-\frac{v_n^2}{2\sigma ^2}} \left[ 1+\left( \frac{1}{2}\frac{c_n\{4\}}{c_n^2\{2\}}\right) L_2\left( \frac{v_n^2}{2\sigma ^2}\right) \right] , \end{aligned} \end{aligned}$$

(86)

which is compatible with Eq. (24) and with Ref. [28]. We can check that for ${\mathcal {A}}_{11}\ne 0$ the above result is true too.²⁵

It is worth noting that we have not assumed the original distribution to be rotationally symmetric. In fact, the original distribution can have non-zero ${\mathcal {A}}_{30}$ or ${\mathcal {A}}_{12}$ too, but they have not appeared in $c_n\{2k\}$ or the distribution (86). This is due to the fact that their information is lost during the averaging.

One could wonder that, while $h_{12}$ and $h_{30}$ are present in the polynomials $P_{1,3}(v_n)$ and $P_{2,3}(v_n)$ in Eq. (81), it may be possible to find all $h_{mn}$ from Eq. (80) by fitting it to an experimental $p(v_n)$. We should mention that always a combination of $h_{mn}$ appears in the polynomials $P_{a,i}(v_n)$. As a result, if we assume that the series is convergent and we have access to an accurate experimental distribution, we can only find a combination of $h_{mn}$ due to the information loss during the averaging. Specifically, in the simple case of Eq. (86), only ${\mathcal {A}}_{40}+2{\mathcal {A}}_{22}+{\mathcal {A}}_{04}$ can be found by fitting.

In any case, the distribution (80) is different from that mentioned in Eq. (39). These two different series refer to two different truncations. Note that $q_{n}\{2k\}$ can be written in terms of ${\mathcal {A}}_{pq}$ with $p+q\le 2k$. For instance, if we keep ${\mathcal {A}}_{mn}$ up to fourth order, all the cumulants $q_n\{2k\}$ are non-zero. Therefore, in principle, the summation (39) goes to infinity while the summation (80) is truncated up to $i=4$.

RGC distribution from multiple orthogonal polynomials

In Sect. 3, we have discussed how the orthogonality conditions of $He_n(x)$ and $L_n(x)$ can be used to find Eqs. (20) and (24), respectively. However, ordinary orthogonal polynomials cannot be employed for the more general distribution series (39). Recall that in one dimension the polynomials ${\mathcal {P}}_n(x)$ and ${\mathcal {P}}_m(x)$ are orthogonal with respect to the measure $w(x)\text {d}x$ if $\int {\mathcal {P}}_n(x){\mathcal {P}}_m(x) w(x)$ $\text {d}x=\zeta _n\delta _{nm}$. This relation can be equivalently written as $\int x^m$ ${\mathcal {P}}_n(x) w(x) \text {d}x=0$ for $0\le m<n$ [39].

We will show that we can obtain Eq. (39) by employing a generalization of the orthogonal polynomials. These generalized orthogonal polynomials are called multiple orthogonal polynomials (MOPs) [39]. The MOPs are orthogonal with respect to more than one weight. Let us define r different weights $\mathbf {w}(x)=(w_1(x),\ldots ,w_r(x))$ and a multi-index $\mathbf {n}=(n_1,\ldots ,n_r)$ ($n_i\in {\mathbb {N}}_0$). Then the type I multiple orthogonal polynomial is given as ${\varvec{{\mathcal {P}}}}_{\mathbf {n}}=({\mathcal {P}}_{1,\mathbf {n}},\ldots ,{\mathcal {P}}_{r,\mathbf {n}})$ where ${\mathcal {P}}_{j,\mathbf {n}}$ is a polynomial with degree at most $n_j$.²⁶ These polynomials obey the following orthogonality condition:

$$\begin{aligned} \int x^m {\varvec{{\mathcal {P}}}}_{\mathbf {n}}\cdot \mathbf {w}(x)\,\text {d}x=0,\qquad 0\le m < N+r-1, \end{aligned}$$

(87)

where $N=\sum _{i=1}^{r} n_i$, and a dot indicates the inner product. Note that, for $r=1$, the above relation returns to the ordinary orthogonal polynomial.

Here, we restrict ourselves to the weakly complete systems. In this case, the multi-index $\mathbf {n}$ always has the following form [43, 44]:

$$\begin{aligned} (n_1,\ldots ,n_r)=(\underbrace{k+1,\ldots k+1}_{j \text { times}},\underbrace{k,\ldots k}_{r-j \text { times}}),\quad k\in {\mathbb {N}}_0. \end{aligned}$$

(88)

Here $0\le j<r$. In this case, we can define a one-to-one map between a single index i and $\mathbf {n}$ as $i(\mathbf {n})=r k+j+1$. Consequently, we are able to define

$$\begin{aligned} {\mathcal {Y}}_{i(\mathbf {n})}(x)={\varvec{{\mathcal {P}}}}_{\mathbf {n}}\cdot \mathbf {w}(x). \end{aligned}$$

(89)

As a result, Eq. (87) can be written as

$$\begin{aligned} \int \text {d}x \, x^m {\mathcal {Y}}_{i}(x)=0,\qquad 0\le m<i. \end{aligned}$$

(90)

Note that the above relation is not an ordinary orthogonality condition because ${\mathcal {Y}}_i$ is not a single finite degree polynomial times a weight.

An example of the MOPs can be found in Ref. [40] where the polynomials are orthogonal with respect to a weight vector $(w_{\nu ,c}(x),w_{\nu +1,c}(x))$. Here,

$$\begin{aligned} w_{\nu ,c}(x)=x^{\nu /2}I_{\nu }(2\sqrt{x})\text {e}^{-c x} \end{aligned}$$

(91)

is defined for $x>0$, $\nu >-1$ and $c>0$. In this study, we are interested in these specific MOPs because they are related to $\tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n)$ in Eq. (40).

For the present specific case, we have $r=2$. As a result, the index $\mathbf {n}$ has the form (k, k) or $(k+1,k)$ referring to Eq. (88). The explicit form of a few first polynomials ${\varvec{{\mathcal {P}}}}_{\mathbf {n}}$ for $\nu =0$ is given by

$$\begin{aligned} \begin{aligned} {\mathcal {P}}_{1,(0,0)}&=1,\\ {\mathcal {P}}_{2,(0,0)}&=-c,\\ {\mathcal {P}}_{1,(1,1)}&=1+3\left( 1+\frac{2c}{3}\right) c^2 x,\\ {\mathcal {P}}_{2,(1,1)}&=-3c\left( 1+c+\frac{2c^2}{3}\right) -c^3 x, \end{aligned} \end{aligned}$$

(92)

and

$$\begin{aligned} \begin{aligned} {\mathcal {P}}_{1,(1,0)}&=1+c^2 x,\\ {\mathcal {P}}_{2,(1,0)}&=-2\left( 1+\frac{c}{2}\right) c,\\ {\mathcal {P}}_{1,(2,1)}&=1+6 c^2\left( 1+\frac{4c}{3}+c^2\right) x+c^4 x^2,\\ {\mathcal {P}}_{2,(2,1)}&=-4c\left( 1+\frac{3c}{2}+2 c^2+\frac{3c^3}{2}\right) \\&\quad -4c^3(1+c)x. \end{aligned} \end{aligned}$$

(93)

We refer the interested reader to Ref. [40] for the general form of ${\varvec{{\mathcal {P}}}}_{\mathbf {n}}$. In Ref. [40], ${\mathcal {P}}_{1,(n_1,n_2)}$ and ${\mathcal {P}}_{2,(n_1,n_2)}$ have been shown by $A_{n_1,n_2}^{(\nu ,c)}$ and $B_{n_1,n_2}^{(\nu ,c)}$.

The function ${\mathcal {Y}}_i(x)$ in Eq. (89) has the following simple form [40]:

$$\begin{aligned} {\mathcal {Y}}^{\nu ,c}_{i}(x)=\sum _{k=0}^{i} \left( {\begin{array}{c}i\\ k\end{array}}\right) (-c)^k x^{(\nu +k)/2}I_{\nu +k}(2\sqrt{x})\text {e}^{-cx}. \end{aligned}$$

(94)

Now, we can choose

$$\begin{aligned} \nu =0,\qquad c=\frac{2\sigma ^2}{\bar{v}_n^2}, \end{aligned}$$

and change the coordinate

$$\begin{aligned} x=\left( \frac{v_n\bar{v}_n}{2\sigma ^2}\right) ^2. \end{aligned}$$

Referring to Eq. (40), one finds

$$\begin{aligned} {\mathcal {Y}}_i^{0,\frac{2\sigma ^2}{d\bar{v}_n}}\left( \frac{v_n^2\bar{v}_n^2}{4\sigma ^4}\right) =\tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n)\text {e}^{-(v_n^2/2\sigma ^2)}. \end{aligned}$$

(95)

Consequently, the orthogonality condition (90) up to an irrelevant numerical factor can be written as

$$\begin{aligned} \begin{aligned} \int _{0}^{\infty } dv_n\, v_n^{2m}\,\tilde{{\mathcal {Q}}}'_i(v_n;\bar{v}_n)=0,\qquad 0\le m<i, \end{aligned} \end{aligned}$$

(96)

where

$$\begin{aligned} \tilde{{\mathcal {Q}}}'_i(v_n;\bar{v}_n)=\frac{v_n}{\sigma ^2} \text {e}^{-\frac{v_n^2+\bar{v}_n^2}{2\sigma ^2}} \tilde{{\mathcal {Q}}}_i(v_n;\bar{v}_n). \end{aligned}$$

(97)

As a result, we are able to write $p(v_n;\bar{v}_n)$ as a series of $\tilde{{\mathcal {Q}}}'_i(v_n;\bar{v}_n)$,

$$\begin{aligned} p(v_n;\bar{v}_n)=\sum _{i=0}^{\infty }\frac{(-1)^i\ell _{2i}}{i!} \tilde{{\mathcal {Q}}}'_i(v_n;\bar{v}_n), \end{aligned}$$

(98)

with unknown $\ell _{2i}$. Note that Eq. (98) is exactly Eq. (39).

Let us define the following quantity:

$$\begin{aligned} m'_{ri}= \int d v_n\, v_n^{2r} \tilde{{\mathcal {Q}}}'_i(v_n;\bar{v}_n). \end{aligned}$$

(99)

Due to Eq. (96), we find that $m'_{ri}=0$ for $0\le r<i$. As a result, we are able to write the moments of $p(v_n;\bar{v}_n)$ as follows:

$$\begin{aligned} \begin{aligned} \langle v_n^{2r} \rangle&=\int _{0}^{\infty }dv_n v_n^{2r} p(v_n;\bar{v}_n)\\&= \sum _{i=0}^{\infty }\frac{(-1)^i\ell _{2i}}{i!} \int _{0}^{\infty }dv_n\, v_n^{2r} \tilde{{\mathcal {Q}}}'_i(v_n;\bar{v}_n)\\&= \sum _{i=0}^{r}\frac{(-1)^i\ell _{2i}}{i!} m'_{ri}. \end{aligned} \end{aligned}$$

(100)

Using the above relation, we find the following recurrence relation for $\ell _{2r}$:

$$\begin{aligned} \ell _{2r}=(-1)^{r}r!\left[ \frac{\langle v_n^{2r} \rangle -\sum _{i=0}^{r-1}\frac{(-1)^i\ell _{2i}}{i!} m'_{ri}}{m'_{rr}}\right] , \end{aligned}$$

(101)

where $r\ge 0$.

Note that $m'_{ri}$ in Eq. (99) is completely computable, for instance $m'_{0,0}=1$. Consequently, we have $\ell _0=1/m'_{0,0}$ for $r=0$, which leads to $\ell _0=1$. The next iteration is as follows:

$$\begin{aligned} \ell _2= & {} \frac{\ell _0 m'_{1,0}-\langle v_n^2 \rangle }{m'_{1,1}}\\= & {} \frac{\langle v_n^2 \rangle -\bar{v}_n^2-2\sigma ^2}{2\sigma ^2}. \end{aligned}$$

By considering Eq. (8a) and Eq. (33), we find $\ell _2=0$. Similarly, we have

$$\begin{aligned} \ell _4= & {} \frac{\langle v_n^4 \rangle -2 \langle v_n^2 \rangle ^2-\bar{v}_n^2}{(\langle v_n^2 \rangle -\bar{v}_n^2)^2}{\nonumber }\\= & {} \frac{c_n\{4\}+\bar{v}_n^2}{(c_n\{2\}-\bar{v}_n^2)^2}, \end{aligned}$$

(102)

where in the last line we used Eq. (8a) and Eq. (8b). One can continue this procedure to find all the values of $\ell _{2i}$ as mentioned in Eq. (35).