Some hadronic parameters of charmonia in $\varvec{N_{\text {f}}=2}$ lattice QCD

Abstract

The phenomenology of leptonic decays of quarkonia holds many interesting features: for instance, it can establish constraints on scenarios beyond the Standard Model with the Higgs sector enriched by a light CP-odd state. In the following paper, we report on a two-flavor lattice QCD study of the $\eta _c$ and $J/\psi$ decay constants, $f_{\eta _c}=387(3)(3)\, {\mathrm{MeV}}$ and $f_{J/\psi }=399(4)(2)\, {\mathrm{MeV}}$. We also examine some properties of the first radial excitation $\eta _c(2S)$ and $\psi (2S)$.

1 Introduction

The discovery at LHC of the Higgs boson with a mass of 125.09(24) GeV [1] has been a major milestone in the history of Standard Model (SM) tests: the spontaneous breaking of electroweak symmetry generates masses of charged leptons, quarks and weak bosons. A well-known issue with the SM Higgs is that the quartic term in the Higgs Lagrangian induces for the Higgs mass $m_H$ a quadratic divergence with the hard scale of the theory: it is related to the so-called hierarchy problem. Several scenarios beyond the SM are proposed to fix that theoretical caveat. Minimal extensions of the Higgs sector contain two complex scalar isodoublets $\Phi _{1,2}$ which, after the spontaneous breaking of the electroweak symmetry, lead to 2 charged particles $H^\pm$, 2 CP-even particles h (SM-like Higgs) and H, and 1 CP-odd particle A. In that class of scenarios, quarks are coupled to the CP-odd Higgs through a pseudoscalar current. Those extensions of the Higgs sector have interesting phenomenological implications, especially as far as pseudoscalar quarkonia are concerned. For example, their leptonic decay is highly suppressed in the SM because it occurs via quantum loops but it can be reinforced by the new tree-level contribution involving the CP-odd Higgs boson, in particular in the region of parameter space where the new boson is light ($10\, {\mathrm{GeV}} \lesssim m_A \lesssim 100\, {\mathrm{GeV}}$) and where the ratio of vacuum expectation values $\tan \beta$ is small ($\tan \beta <10$) [2, 3]. Any enhanced observation with respect to the SM expectation would be indeed a clear signal of New Physics. Let us finally note that the hadronic inputs, which constrain the CP-odd Higgs coupling to heavy quarks through processes involving quarkonia, are the decay constants $f_{\eta _c}$ and $f_{\eta _b}$.

This paper reports an estimate of hadronic parameters in the charmonia sector using lattice QCD with $N_f=2$ dynamical quarks: namely, the pseudoscalar decay constant $f_{\eta _c}$, because of its phenomenological importance, but also the vector decay constant $f_{J/\psi }$ as well as the ratio of masses $m_{\eta _c(2S)}/m_{\eta _c}$ and $m_{\psi (2S)}/m_{J/\psi }$. The two latter quantities are very well measured by experiments and their estimation has helped us to understand how much our analysis method can address the systematic effects, on quarkonia physics, coming from the lattice ensembles we have considered. We present also our findings for the following ratios of decay constants: $f_{\eta _c(2S)}/f_{\eta _c}$ and $f_{\psi (2S)}/f_{J/\psi }$.

This work is an intermediary step before going to the bottom sector, the final target of our program, because it is more promising for the phenomenology of extended Higgs sectors. An extensive study of the spectoscopy of charmonia has been done in [4, 5] while only two lattice estimates of $f_{\eta _c}$ and $f_{J/\psi }$ are available so far at $\mathrm{N}_\mathrm{f}=2$ [6] and $\mathrm{N}_\mathrm{f}=2+1$ [7, 8].

Table 1 Parameters of the simulations: bare coupling $\beta = 6/g_0^2$, lattice resolution, hopping parameter $\kappa$, lattice spacing a in physical units, pion mass, number of gauge configurations and bare charm quark masses

2 Lattice computation

2.1 Lattice set-up

This study has been performed using a subset of the CLS ensembles. These ensembles were generated with $N_f=2$ nonperturbatively $\mathcal {O}(a)$-improved Wilson-Clover fermions [9, 10] and the plaquette gauge action [11] for gluon fields, by using either the DD-HMC algorithm [12,13,14,15] or the MP-HMC algorithm [16]. We collect in Table 1 our simulation parameters. Two lattice spacings $a_{\beta =5.5}=0.04831(38)$ fm and $a_{\beta =5.3}=0.06531(60)$ fm, resulting from a fit in the chiral sector [17], are considered. We have taken simulations with pion masses in the range $[190\,, 440]~{\mathrm{MeV}}$. The charm quark mass has been tuned after a linear interpolation of $m^2_{D_s}$ in $1/\kappa _c$ at its physical value [18], after the fixing of the strange quark mass [19]. The statistical error on raw data is estimated from the jackknife procedure: two successive measurements are sufficiently separated in trajectories along the Monte-Carlo history to neglect autocorrelation effects. Moreover, statistical errors on quantities extrapolated at the physical point are computed as follows. Inspired by the bootstrap prescription, we perform a large set of $N_{\mathrm{event}}$ fits of vectors of data whose dimension is the number of CLS ensembles used in our analysis (i.e.$\ n=6$) and where each component i of those vectors is filled with an element randomly chosen among the $N_{\mathrm{bins}}(i)$ binned data per ensemble. The variance over the distribution of those $N_{\mathrm{event}}$ fit results, obtained with such “random” inputs, is then an estimator of the final statistical error. Finally, we have computed quark propagators through two-point correlation functions using stochastic sources which are different from zero in a single timeslice that changes randomly for each measurement. We have also applied spin dilution and the one-end trick to reduce the stochastic noise [20, 21]. In our study we have neglected any contribution from disconnected diagrams.

2.1.1 GEVP discussion

The two-point correlation functions under investigation read

$$\begin{aligned} C_{\Gamma \Gamma '}(t)=\frac{1}{V} \sum _{\vec {x},\vec {y}} {\langle }{\,\bigl [\bar{c}\,\Gamma c\bigr ](\vec {y},t)\,\bigl [\bar{c}\,\gamma _0\,\Gamma ' \gamma _0\,c\bigr ](\vec {x},0)\,}{\rangle } \end{aligned}$$

(1)

where V is the spatial volume of the lattice, $\langle \cdots \rangle$ is the expectation value over gauge configurations, and the interpolating fields $\bar{c} \Gamma c$ can be non-local. As a preparatory work, different possibilities were explored to find the best basis of operators, combining levels of Gaussian smearing, interpolating fields with a covariant derivative $\bar{c} \Gamma (\vec {\gamma }\cdot \vec {\nabla }) c$ and operators that are odd under time parity. Solving the Generalized Eigenvalue Problem (GEVP) [22, 23] is a key point in this analysis. Looking at the literature we have noticed that people tried to mix together the operators $\bar{c} \Gamma c$ and $\bar{c} \gamma _0 \Gamma c$ in a unique GEVP system [4, 6]. In our point of view, this approach raises some questions: let us take the example of the interpolating fields $\{P=\bar{c} \gamma _5 c\,;\, A_0=\bar{c} \gamma _0 \gamma _5 c\}$. The asymptotic behaviours of the 2-pt correlation functions defined with these interpolating fields read

$$\begin{aligned} \left\{ \begin{aligned} {\langle }{\,P(t)\,P(0)\,}{\rangle }\,;\,{\langle }{\,A_0(t)\,A_0(0)\,}{\rangle }\quad \xrightarrow {\ t \rightarrow \infty \ }\quad {\mathrm{cosh}}[m_P(T/2-t)]\\ {\langle }{\,P(t)\,A_0(0)\,}{\rangle }\,;\,{\langle }{\,A_0(t)\,P(0)\,}{\rangle }\quad \xrightarrow {\ t \rightarrow \infty \ }\quad {\mathrm{sinh}}[m_P(T/2-t)] \end{aligned} \right. \end{aligned}$$

The matrix of $2\times 2$ correlators of the GEVP is then

$$\begin{aligned}&C(t)=\begin{bmatrix} {\langle }{\,P(t)\,P(0)\,}{\rangle }&{\langle }{\,A_0(t)\,P(0)\,}{\rangle }\\ {\langle }{\,P(t)\,A_0(0)\,}{\rangle }&{\langle }{\,A_0(t)\,A_0(0)\,}{\rangle } \end{bmatrix}\\&\quad {\mathrm{GEVP}}: C(t)\,v_n(t,t_0)\ =\ \lambda _n(t,t_0)\,C(t_0)\,v_n(t,t_0). \end{aligned}$$

In the general case, the spectral decomposition of $C_{ij}(t)$ is

$$\begin{aligned}&C_{ij}(t)=\sum _n Z^i_n Z^{*j}_n [D_{ij}\rho ^{(1)}_n(t) + (1-D_{ij}) \rho ^{(2)}_n(t)]\\&\quad \text {where}\quad D_{ij}=0\ \text {or}\ 1 \end{aligned}$$

and with

$$\begin{aligned}&\rho ^{(1),(2)}(t) \sim e^{-m_Pt}\,{\mathrm{cosh}} [m_P(T/2-t)]\\&\quad \text {or}\quad e^{-m_Pt}\,\mathrm{\sinh }[m_P(T/2-t)] \end{aligned}$$

The dual vector $u_n$ to $Z's$ is defined by

$$\begin{aligned} \sum _j Z^{*j}_m u^j_n = \delta _{mn} \end{aligned}$$

Inserted in the GEVP, it gives

Fig. 1

Effective masses obtained from the $2\times 2$ subsystem (left panel) and the $3 \times 3$ subsystem (right panel) of our toy model, with $T=64$ and $t_0=3$

$$\begin{aligned} \sum _j C_{ij}(t)u^j_n= & {} \sum _{j,m} Z^i_m Z^{*j}_m u^j_n \bigl [D_{ij}\rho ^{(1)}_m(t) + (1-D_{ij}) \rho ^{(2)}_m(t) \bigr ]\\= & {} \sum _m \rho ^{(2)}_m(t) Z^i_m \sum _j Z^{*j}_m u^j_n \\&+ \sum _m \bigl (\rho ^{(1)}_m(t)-\rho ^{(2)}_m(t)\bigr )Z^i_m \sum _j D_{ij} Z^{*j}_m u^j_n\\= & {} \rho ^{(2)}_n(t) Z^i_n + \sum _m \bigl (\rho ^{(1)}_m(t)\\&-\rho ^{(2)}_m(t)\bigr )Z^i_m \sum _j D_{ij} Z^{*j}_m u^j_n \end{aligned}$$

If $D_{ij}$ is independent of i, j, we can write

$$\begin{aligned} C(t)u_n = \rho (t) Z_n\quad \text {and}\quad \lambda _n(t,t_0)=\frac{\rho _n(t)}{\rho _n(t_0)} \end{aligned}$$

However, in the case of mixing T-odd and T-even operators in a single GEVP, the D’s do depend on i and j: the previous formula for $\lambda _n(t,t_0)$ is then not correct. Hence, approximating every correlator by sums of exponentials forward in time, together with the assumption that the $D_{ij}$ are independent of i and j, may face caveats. A toy model with 3 states in the spectrum helps to understand this issue:

The effective energy $E^{\text {eff}}$ obtained by solving the GEVP writes

$$\begin{aligned} aE^{\text {eff}}_{n}=\ln \left( \frac{\lambda _n(t,t_0)}{\lambda _n(t+a,t_0)}\right) \end{aligned}$$

In our numerical application, we have chosen $T=64$, $t_0=3$ and compared $2\times 2$ and $3 \times 3$ subsystems: results can be seen in Fig. 1. Our observation is that until $t=T/4$, neglecting the time-backward contribution in the correlation function has no effect. Based on this study, we can affirm that the method is safe for the ground state and the first excitation. In contrast, one may wonder what would happen with a dense spectrum when the energy of the third or a higher excited state is extracted: in that case there will be a competition between the contamination from higher states, which are not properly isolated by the finite GEVP system, and the omission of the backward in time contribution to the generalised eigenvalue under study, even at times $t < 1$ fm.

2.1.2 Interpolating field basis

Building a basis of operators with

$$\begin{aligned}&\bigl \{\bar{c}\,\Gamma c\ ;\ \bar{c}\, \Gamma (\vec {\gamma } \cdot \vec {\nabla }) c\bigr \} \quad \text {where}\\&\nabla _\mu \psi (x) =\frac{U_\mu (x)\psi (x+a\hat{\mu }) - U^\dag _\mu (x-a\hat{\mu })\psi (x-a\hat{\mu })}{2a} \end{aligned}$$

can have advantages and this was already explored [24, 25]. But there are sometimes bad surprises...a good example being the pseudoscalar-pseudoscalar correlator defined by

$$\begin{aligned} C(t)\ =\ {\langle }{\,\bigl [\bar{c}\,\gamma ^5 (\vec {\gamma }\cdot \vec {\nabla }) c\bigr ](t)\,\bigl [\bar{c}\,\gamma ^5 (\vec {\gamma }\cdot \vec {\nabla }) c\bigr ](0)\,}{\rangle } \end{aligned}$$

whose behaviour will be anticipated using the quark model method.

In the formalism of quark models, the c quark field reads

$$\begin{aligned} c(\vec {p}_c)\ =\ \begin{pmatrix} c_1\\ c_2=\dfrac{\vec {\sigma } \cdot \vec {p}_c}{2m_c}\,c_1 \end{pmatrix} \end{aligned}$$

being developped into a large and a small component. Notice that the c quark field is a spinor of type u while the ${\bar{c}}$ antiquark field is of type v, so at this stage we need to express ${\bar{v}}$ in terms of u. Defining the charge conjugation operator by ${{\mathscr {C}}}=-i\gamma ^0 \gamma ^2$ and using the Dirac representation for the $\gamma$ matrices, we can write

$$\begin{aligned} v = {{\mathscr {C}}}(\bar{u})^T\qquad \Longrightarrow \qquad {\bar{v}} = (u)^T\gamma ^0{{\mathscr {C}}}^\dagger \gamma ^0 \end{aligned}$$

The ${\bar{c}}$ antiquark field is then

$$\begin{aligned} {\bar{c}}(\vec {p}_{{\bar{c}}})\ =\ -i\begin{pmatrix} c^T_1\,{\dfrac{\vec \sigma ^T\cdot \vec p_{{\bar{c}}}}{2m_c}}\,\sigma _2\&\ c^T_1\,\sigma _2 \end{pmatrix} \end{aligned}$$

Assuming the charmonium at rest, we have

$$\begin{aligned} \vec {p}_c=-\vec {p}_{\bar{c}}\qquad \text {and}\qquad (\vec {\sigma }\cdot \vec {p}_{\bar{c}})^T \sigma _2 = \sigma _2 (\vec {\sigma }\cdot \vec {p}_c) \end{aligned}$$

(2)

Then ordinary Pauli matrices algebra leads to

$$\begin{aligned} \bar{c}\,\gamma ^5 (\vec {\gamma }\cdot \vec {\nabla }) c&= \sum \limits _{n=1}^3 -i\begin{pmatrix}c^T_1\,{\dfrac{\vec \sigma ^T\cdot \vec {p}_{\bar{c}}}{2m_c}}\,\sigma _2\&\ c^T_1\,\sigma _2\end{pmatrix}\\&\qquad \begin{pmatrix}-\sigma _n&{}0\\ 0&{}\sigma _n\end{pmatrix} D_n\begin{pmatrix}c_1\\ \dfrac{\vec \sigma \cdot \vec {p}_c}{2m_c}\,c_1 \end{pmatrix}\\&= \sum \limits _{n=1}^3 c_1^T\left[ {{-\dfrac{\vec \sigma ^T\cdot \vec {p}_{\bar{c}}}{2m_c}}\,\sigma _2\,\sigma _n + \sigma _2\,\sigma _n\,{\dfrac{\vec \sigma \cdot \vec {p}_c}{2m_c}}}\right] {p_c}_n\,c_1\\&\qquad \qquad \text {assuming}\ D_n\sim i\,{p_c}_n\\&=\sum \limits _{n=1}^3 c^T_{1}\sigma _2\, \dfrac{-(\vec {\sigma }\cdot \vec {p}_c )\,\sigma _n + \sigma _n\, (\vec {\sigma }\cdot \vec {p}_c)}{2m_c}\,{p_c}_n\,c_1\\&=\ \sum \limits _{n,m=1}^3 c^T_{1}\sigma _2\, \dfrac{\sigma _n\,\sigma _m - \sigma _m\,\sigma _n}{2m_c}\,{p_c}_n\,{p_c}_m\,c_1\\&=\sum \limits _{n,m,\ell =1}^3 i\,c^T_{1}\sigma _2\, \dfrac{\epsilon _{nm\ell }\,\sigma _\ell }{m_c}\,{p_c}_n\,{p_c}_m\,c_1\ =\ 0 \end{aligned}$$

The previous approach is very naive with respect to quantum field theory, in particular the approximation $D_i c_1 \sim p_i c_1$, but as a conclusion one can see that interpolating fields $\bar{c}\,\gamma ^5 (\vec {\gamma }\cdot \vec {\nabla }) c$ potentially give very noisy correlators. And, indeed, we have found a numerical cancellation between the “diagonal” contribution

$$\begin{aligned} A(t)=\sum _i {\langle }{\,\bigl [\bar{c}\,\gamma ^5 \gamma _i \nabla _i\, c\bigr ](t)\,\bigl [\bar{c}\, \gamma ^5 \gamma _i \nabla _i\, c\bigr ](0)\,}{\rangle } \end{aligned}$$

and the “off-diagonal” contribution

$$\begin{aligned} B(t)=\sum _{i\ne j} {\langle }{\,\bigl [\bar{c}\,\gamma ^5 \gamma _i \nabla _i\, c\bigr ](t)\,\bigl [\bar{c}\, \gamma ^5 \gamma _j \nabla _j\, c\bigr ](0)\,}{\rangle } \end{aligned}$$

resulting in a very noisy correlator C(t) which is compatible with zero.

2.1.3 Summary

To summarise, we have considered four Gaussian smearing levels for the quark field c, including no smearing, to build $4\times 4$ matrix of correlators without any covariant derivative nor operator of the $\pi _2$ or $\rho _2$ kind [24], from which we have also extracted the $\mathcal{O}(a)$ improved hadronic quantities we have examined. Solving the GEVP for the pseudoscalar-pseudoscalar and vector-vector matrices of correlators

$$\begin{aligned}&C_{PP}(t)v^P_n(t,t_0)=\lambda ^P_n(t,t_0) v^P_n(t,t_0)C_{PP}(t_0)\nonumber \\&\quad \text {and}\quad C_{VV}(t)v^V_n(t,t_0)=\lambda ^V_n(t,t_0) v^V_n(t,t_0)C_{VV}(t_0) \end{aligned}$$

(3)

we obtain the correlators that will have the largest overlap with the nth excited state as follows:

$$\begin{aligned} \tilde{C}^n_{A_0 P}(t)&= \sum _i C_{A^L_0 P^{(i)}}(t) v^{P,i}_n(t,t_0)\\ \tilde{C}^n_{P P}(t)&= \sum _i C_{P^L P^{(i)}}(t) v^{P,i}_n(t,t_0)\\ \tilde{C}'^n_{P P}(t)&= \sum _{i,j} v^{P,i}_n(t,t_0) C_{P^{(i)} P^{(j)}}(t) v^{P,j}_n(t,t_0)\\ \tilde{C}^n_{V V}(t)&= \frac{1}{3} \sum _{i,k} C_{V^L_k V^{(i)}_k}(t) v^{V,i}_n(t,t_0)\\ \tilde{C}'^n_{VV}(t)&= \frac{1}{3} \sum _{i,j,k} v^{V,i}_1(t,t_0) C_{V^{(i)}_k V^{(j)}_k}(t) v^{V,j}_n(t,t_0)\\ \tilde{C}^n_{TV}(t)&= \frac{1}{3} \sum _{i,k} C_{T^L_{k0} V^{(i)}_k}(t) v^{V,i}_n(t,t_0)\\ \tilde{C}^n_{\delta PP}(t)&= \frac{\tilde{C}^n_{PP}(t+1)-\tilde{C}^n_{PP}(t-1)}{2a}\\ \tilde{C}^n_{\delta TV}(t)&= \frac{\tilde{C}^n_{TV}(t+1) - \tilde{C}^n_{TV}(t-1)}{2a} \end{aligned}$$

and their symmetric counterpart with the exchange of operators at the source and at the sink. The quark bilinears are $P=\bar{c}\gamma _5 c$, $A_0=\bar{c}\gamma _0\gamma _5 c$, $V_k=\bar{c}\gamma _k c$ and $T_{k0}=\bar{c}\gamma _k\gamma _0 c$. Moreover, in those expressions, the label L refers to a local interpolating field while sums over i and j run over the four Gaussian smearing levels.

The projected correlators have the following asymptotic behaviour

$$\begin{aligned}&\tilde{C}'^n_{P P}(t)\xrightarrow [\ t/a \gg 1\ ]{} \frac{\mathcal{Z}'_{{PP}_n}}{am_{P_n}} e^{-m_{P_n} T/2} \cosh [m_{P_n} (T/2 -t)]\\&\tilde{C}^n_{A_0 P}(t)\xrightarrow [\ t/a \gg 1\ ]{} -\frac{\mathcal{Z}_{{AP}_n}}{am_{P_n}}e^{-m_{P_n} T/2} \sinh [m_{P_n} (T/2-t )]\\&\tilde{C}^n_{P P}(t)\xrightarrow [\ t/a \gg 1\ ]{}\frac{\mathcal{Z}_{{PP}_n}}{am_{P_n}} e^{-m_{P_n} T/2} \cosh [m_{P_n} (T/2 -t)]\\&\tilde{C}'^n_{VV}(t)\xrightarrow [\ t/a \gg 1\ ]{} \frac{\mathcal{Z}'_{{VV}_n}}{am_{V_n}} e^{-m_{V_n} T/2} \cosh [m_{V_n} (T/2 -t)]\\&\tilde{C}^n_{VV}(t)\xrightarrow [\ t/a \gg 1\ ]{} \frac{\mathcal{Z}_{{VV}_n}}{am_{V_n}}e^{-m_{V_n} T/2} \cosh [m_{V_n} (T/2-t )]\\&\tilde{C}^n_{T V}(t)\xrightarrow [\ t/a \gg 1\ ]{} \frac{\mathcal{Z}_{{TV}_n}}{am_{V_n}} e^{-m_{V_n} T/2} \sinh [m_{V_n} (T/2 -t)]\\&\tilde{C}^n_{\delta P P}(t)\xrightarrow [\ t/a \gg 1\ ]{} -1/a\, \sinh (am_{P_n}) \frac{\mathcal{Z}_{{PP}_n}}{am_{P_n}} e^{-m_{P_n} T/2}\\&\quad \sinh [m_{P_n} (T/2 -t)]\\&\tilde{C}^n_{\delta T V}(t)\xrightarrow [\ t/a \gg 1\ ]{} -1/a\,\sinh (am_{V_n}) \frac{\mathcal{Z}_{{TV}_n}}{am_{V_n}} e^{-m_{V_n} T/2}\\&\quad \cosh [m_{V_n} (T/2 -t)] \end{aligned}$$

2.1.4 Decay constant extraction

Considering the $\mathcal{O}(a)$ improved operators

$$\begin{aligned}&A^I_0=(1+b_A Z a m_{c}^{AWI})\left( A_0 + a c_A \frac{\partial _0+\partial ^*_0}{2} P\right) \quad \text {and}\nonumber \\&V^I_k=(1+b_V Z a m_{c}^{AWI})\left( V_k + ac_V \frac{\partial _\nu + \partial ^*_\nu }{2}T_{k\nu }\right) \end{aligned}$$

(4)

where the lattice derivatives are defined by

$$\begin{aligned} \partial _\nu F(x)&= \frac{F(x+a\hat{\nu })-F(x)}{a}\qquad \text {as well as}\nonumber \\ \partial ^*_\nu F(x)&=\frac{F(x)-F(x-a\hat{\nu })}{a}, \end{aligned}$$

(5)

the $f_{\eta _c}$ decay constants is extracted in the following way:

$$\begin{aligned} \left\{ \begin{array}{l} {\langle }{0}\,{\vert }\,{A^R_0}\,{\vert }\,{\eta _c(\vec {p}=0)}{\rangle } = -f_{\eta _c} m_{\eta _c}\\ \quad = -Z_A(1 + b_A Z a m^{AWI}_c) m_{\eta _c} f^0_{P_c}(1 + f^1_{P_c}/f^0_{P_c})\\ af^0_{P_c}=\frac{1}{am_{\eta _c}} \frac{\mathcal{Z}_{{AP}_1}}{\sqrt{\mathcal{Z}'_{{PP}_1}}};\quad af^1_{P_c} = \frac{1}{am_{\eta _c}} c_A \sinh (a m_{\eta _c}) \frac{\mathcal{Z}_{{PP}_1}}{\sqrt{\mathcal{Z}'_{{PP}_1}}} \end{array} \right. \end{aligned}$$

(6)

while the $f_{J/\psi }$ decay constant is obtained with:

$$\begin{aligned} \left\{ \begin{array}{l} {\langle }{0}\,{\vert }\,{V^R_i}\,{\vert }\,{J/\psi (\epsilon , \vec {p}=0)}{\rangle } = \epsilon _i f_{J/\psi } m_{J/\psi }\\ \quad = \epsilon _i Z_V(1 + b_V Z a m^{AWI}_c) m_{J/\psi } f^0_{V_c}(1 + f^1_{V_c}/f^0_{V_c})\\ af^0_{V_c}=\frac{1}{am_{J/\psi }} \frac{\mathcal{Z}_{{VV}_1}}{\sqrt{\mathcal{Z}'_{{VV}_1}}};\qquad af^1_{V_c}\\ \qquad = - \frac{1}{am_{J/\psi }}c_V \sinh (a m_{J/\psi }) \frac{\mathcal{Z}_{{TV}_1}}{\sqrt{\mathcal{Z}'_{{VV}_1}}} \end{array} \right. \end{aligned}$$

(7)

Fig. 2

Effective mass of the $\eta _c(2S)$ state extracted from the correlator $\tilde{C}^2_{A_0P}$ computed using either a fixed time $t_{\text {fix}}$ (left plot) or a running time t (right plot) to project $C_{A^L_0P}$ along the ground state generalized eigenvector $v^P_2$

Fig. 3

Effective mass of the $\psi (2S)$ state extracted from the correlator $\tilde{C}^2_{VV}$ computed using either a fixed time $t_{\text {fix}}$ (left plot) or a running time t (right plot) to project $C_{V^LV}$ along the first excited state generalized eigenvector $v^V_2$

The R superscript denotes the renormalized improved operators. The renormalization constants $Z_A$ and $Z_V$ have been non perturbatively measured in [26, 27].¹ We have also used non-perturbative results and perturbative formulae from [28,29,30] for the improvement coefficients $c_A$, $c_V$, $b_A$ and $b_V$, and the matching coefficient Z between the quark mass $m_{c}$ defined through the axial Ward Identity

$$\begin{aligned} m_{c}^{AWI}=\frac{\frac{\partial _0 +\partial ^*_0}{2} C_{A^L_0P^L}(t) +ac_A \partial _0 \partial ^*_0 C_{P^LP^L}(t)}{2C_{P^LP^L}(t)} \end{aligned}$$

and its counterpart defined through the vector Ward Identity

$$\begin{aligned} am_{c}^{VWI}=\frac{1}{2} \left( \frac{1}{\kappa _c} - \frac{1}{\kappa _{cr}}\right) \end{aligned}$$

The decay constants of the considered radial excited states are given by

$$\begin{aligned} \left\{ \begin{array}{l} {\langle }{0}\,{\vert }\,{A^R_0}\,{\vert }\,{\eta _c(2S)(\vec {p}=0)}{\rangle } = -f_{\eta _c(2S)} m_{\eta _c(2S)}\\ \quad = -Z_A(1 + b_A Z a m^{AWI}_c) m_{\eta _c(2S)} f^0_{P'_c}(1 + f^1_{P'_c}/f^0_{P'_c})\\ af^0_{P'_c}=\frac{1}{am_{\eta _c(2S)}} \frac{\mathcal{Z}_{{AP}_2}}{\sqrt{\mathcal{Z}'_{{PP}_2}}};\\ \quad af^1_{P'_c} = \frac{1}{am_{\eta _c(2S)}} c_A \sinh (a m_{\eta _c(2S)}) \frac{\mathcal{Z}_{{PP}_2}}{\sqrt{\mathcal{Z}'_{{PP}_2}}} \end{array} \right. \end{aligned}$$

(8)

and

$$\begin{aligned} \left\{ \begin{array}{l} {\langle }{0}\,{\vert }\,{V^R_i}\,{\vert }\,{\psi (2S)(\epsilon , \vec {p}=0)}{\rangle } = \epsilon _i f_{\psi (2S)} m_{\psi (2S)}\\ \quad = \epsilon _i Z_V(1 + b_V Z a m^{AWI}_c) m_{\psi (2S)} f^0_{V'_c}(1 + f^1_{V'_c}/f^0_{V'_c})\\ af^0_{V'_c}=\frac{1}{am_{\psi (2S)}} \frac{\mathcal{Z}_{{VV}_2}}{\sqrt{\mathcal{Z}'_{{VV}_2}}};\\ \quad af^1_{V'_c} = - \frac{1}{am_{\psi (2S)}}c_V \sinh (a m_{\psi (2S)}) \frac{\mathcal{Z}_{{TV}_2}}{\sqrt{\mathcal{Z}'_{{VV}_2}}} \end{array} \right. \end{aligned}$$

(9)

2.2 Analysis

Let us first consider the mass and the decay constant of the ground states. Since the fluctuations on effective masses obtained from $\tilde{C}^1_{A_0P}$ and $C^1_{VV}$ are large with time, we have decided to use generalized eigenvectors at fixed time $t_{\text {fix}}$, $v^{P(V)}_ 1 (t_{\mathrm{fix}}, t_0)$, in order to perform the corresponding projections. In practice we have chosen $t_{\text {fix}}/a = t_0/a + 1$ but we have checked that the results do not depend on $t_{\text {fix}}$.

For the excited states, the formulae written in Sect. 2.1.3 do apply. Although the fluctuations on effective masses obtained from $\tilde{C}^2_{A_0P}$ and $\tilde{C}^2_{VV}$ are larger than for their ground states counterparts, the correlators $\tilde{C}^2_{A_0P}$ and $\tilde{C}^2_{VV}$ computed with a projection on $v^{P(V)}_2(t_{\mathrm{fix}},t_0)$ show a bigger slope than the same correlators computed with a projection on $v^{P(V)}_2(t,t_0)$. We interpret that observation as a stronger contamination of higher excited states for the $t_\text {fix}$ projection which can spoil the determination of the ${\eta _c(2S)}$ and ${\psi (2S)}$ masses. Since the masses take part in the computation of the decay constants, such a contamination can propagate into the extraction of $f_{\eta _c(2S)}$ and $f_{\psi (2S)}$. Figures 2 and 3 illustrate that point with the correlators $\tilde{C}^2_{A_0P}$ and $\tilde{C}^2_{VV}$ on the ensemble F7.

For the ground states, the time range $[t_{\mathrm{min}},t_{\mathrm{max}}]$ used to fit the projected correlators is set so that the statistical error on the effective mass $\delta m^{\mathrm{stat}}(t_{\mathrm{min}})$ is larger enough than the systematic error $\Delta m^{\mathrm{sys}}(t_{\mathrm{min}})\equiv \exp [-\Delta t_{\mathrm{min}}]$ with $\Delta = E_4 - E_1 \sim 2\,{\mathrm{GeV}}$. That guesstimate is based on our $4\times 4$ GEVP analysis, though we do not want to claim here that we really control the energy-level of the third excited state. Actually our criterion is rather $\delta m^{\mathrm{stat}}(t_{\mathrm{min}})> 4\Delta m^{\mathrm{sys}}(t_{\mathrm{min}})$ to be more conservative. On the other side, $t_{\mathrm{max}}$ is set after a qualitative inspection of the data which count for the plateau determination. Since $\Delta ^{(P)} \sim \Delta ^{(V)}$, fit intervals are identical for pseudoscalar and vector charmonia.

For the first excited states, the time range has been set by looking at effective masses and where the plateaus start and end, including statistical uncertainty. There, we have estimated the systematic error by shifting the fit range to larger times $[t_{\text {min}}, t_{\text {max}}] \rightarrow [t_{\text {min}}+2a,t_{\text {max}}+3a]$.

Finally, we have taken $t_0=3a$ at $\beta =5.3$ and $t_0=5a$ at $\beta =5.5$: the landscape is unchanged by increasing $t_0$. The raw data we have obtained in our analysis is collected in Table 3 of the Appendix. The extrapolation to the physical point of the quantities we have measured uses a linear expression in $m^2_\pi$ with inserted cut-off effects in $a^2$:

$$\begin{aligned} X(a,m_\pi )=X_0 + X_1 m^2_\pi + X_2 (a/a_{\beta =5.3})^2 \end{aligned}$$

(10)

We remind that $\kappa _c$ have been tuned at every $\kappa _{\mathrm{sea}}$ so that $m_{D_s}(\kappa _s,\kappa _c,\kappa _{\mathrm{sea}})=m^{\mathrm{phys}}_{D_s}$ (it was necessary to tune the strange quark mass $\kappa _s$, though it is not a relevant quantity for the study discussed here).

Fig. 4

Effective masses $am_{\eta _c}$ and $am_{\eta _c(2S)}$ (left panel), $am_{J/\psi }$ and $am_{\psi (2S)}$ (right panel) extracted from a $4\times 4$ GEVP for the lattice ensemble F7; we also plot the plateaus obtained in the chosen fit interval

Fig. 5

Extrapolation at the physical point of $m_{\eta _c}$ (left panel) and $m_{J/\psi }$ (right panel) by linear expressions in $m^2_\pi$ and $a^2$

Figure 4 shows the effective masses of the $\eta _c$, $\eta _c(2S)$, $J/\psi$ and $\psi (2S)$ mesons for the set F7 which are obtained by the following expressions

$$\begin{aligned} \left\{ \begin{array}{l} am_{\eta _c}^{\mathrm{eff}}(t)\ =\ {\mathrm{argcosh}} \left( \frac{\lambda ^P_1(t+a,t_0)+\lambda ^P_1(t-a,t_0)}{2\lambda ^P_1(t,t_0)}\right) \\ am_{J/\psi }^{\mathrm{eff}}(t)\ =\ {\mathrm{argcosh}} \left( \frac{\lambda ^V_1(t+a,t_0)+\lambda ^V_1(t-a,t_0)}{2\lambda ^V_1(t,t_0)}\right) \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{l} am_{\eta _c(2S)}^{\mathrm{eff}}(t)\ =\ {\mathrm{argcosh}} \left( \frac{\lambda ^P_2(t+a,t_0)+\lambda ^P_2(t-a,t_0)}{2\lambda ^P_1(t,t_0)}\right) \\ am_{\psi (2S)}^{\mathrm{eff}}(t)\ =\ {\mathrm{argcosh}} \left( \frac{\lambda ^V_2(t+a,t_0)+\lambda ^V_2(t-a,t_0)}{2\lambda ^V_1(t,t_0)}\right) \end{array} \right. \end{aligned}$$

The drawn lines correspond to our plateaus for the fitted masses. One can observe that our plateaus are large for the ground states but they are unfortunately of a much worse quality for the radial excitations. The latter data also show large fluctuations with time, for which we did not find any satisfying explanation yet. If $t_{\mathrm{fix}}$ were used in the correlators projection procedure, the price to pay would be a strong contamination by other states in $\tilde{C}^2_{A_0P}$ and $\tilde{C}^2_{VV}$ other than the ones of interest.

2.2.1 Ground state results

We show in Fig. 5 the extrapolation to the physical point of $m_{\eta _c}$ and $m_{J/\psi }$. The dependence on $m^2_\pi$ and $a^2$ is mild, with cut-off effects almost negligible. However the contribution to the meson masses besides the mass term $2m_c$ is difficult to catch. All in all, there is a variation of $m_{\eta _c}$ and $m_{J/\psi }$ smaller than $100\,\text {MeV}$, i.e. smaller than 3% of the mass, for the different lattice ensembles. This creates a sort of zoom effect on the fluctuations (they are at least 2 orders of magnitude larger than the statistical error) which explains why the quality of the fit seems poor. At the physical point, $m_{\eta _c}$ and $m_{J/\psi }$ are compatible with the experimental values 2.983 GeV and 3.097 GeV:

$$\begin{aligned} m_{\eta _c}=2.982(1)(19)\,{\mathrm{GeV}}\;\,\text {and}\;\, m_{J/\psi }=3.085(2)(20)\, {\mathrm{GeV}} \end{aligned}$$

(11)

where the first error is statistical and the second error accounts for the uncertainty on the lattice spacing. The latter clearly dominates and hides a possible mismatch between our extrapolated results at the physical point and experiment, in particular coming from the mistuning of $\kappa _c$ due to the mistuning of $\kappa _s$.

Fig. 6

Extrapolation at the physical point of $f_{\eta _c}$ (left panel) and $f_{J/\psi }$ (right panel) by linear expressions in $m^2_\pi$ and $a^2$

Table 2 LO and NLO fit parameters and results for $f_{\eta _c}$ and $f_{J/\psi }$, with their respective $\chi ^2$ per degrees of freedom

We display in Fig. 6 the extrapolations at the physical point of $f_{\eta _c}$ and $f_{J/\psi }$. They are mild and cut-off effects on $f_{\eta _c}$ are of the order of 4% at $\beta =5.3$ while they are stronger for $f_{J/\psi }$, about 10%. In addition to the fit formula Eq. (10) we have tried to fit our data with an “NLO” ansatz,

$$\begin{aligned} f_{\eta _c}&=X'_{\eta _c\,0} + X'_{\eta _c\,1} m^2_\pi + X'_{\eta _c\,2} (a/a_{\beta =5.3})^2\nonumber \\&\quad + X'_{\eta _c\,3} m^2_\pi \ln m^2_\pi ,\nonumber \\ f_{J/\psi }&=X'_{J/\psi \,0} + X'_{J/\psi \,1} m^2_\pi + X'_{J/\psi \,2} (a/a_{\beta =5.3})^2\nonumber \\&\quad + X'_{J/\psi \,3} m^2_\pi \ln m^2_\pi . \end{aligned}$$

(12)

We have collected in Table 2 results of the LO and NLO fits, together with fit parameters and $\chi ^2$ per degree of freedom. As $\chi ^2\hbox {(NLO)}$ is worse than $\chi ^2\hbox {(LO)}$ and the fit parameters $X'_1$ and $X'_3$ are compatible with zero, while $X_1$ is different from zero, we have decided to consider the LO result as our prefered one and not include the discrepancy between (LO) and (NLO) in the systematic error on $f_{\eta _c}$ and $f_{J/\psi }$. We do not have enough data points to be really confident in (NLO) fits on quantities whose chiral dependence is small anyway.

We get at the physical point

$$\begin{aligned} f_{\eta _c}=387(3)(3)\, {\mathrm{MeV}}\quad \text {and} \quad f_{J/\psi }=399(4)(2)\, {\mathrm{MeV}}, \end{aligned}$$

(13)

where the systematic error comes from the uncertainty on lattice spacings.

Moreover, one can derive a phenomenological estimate of $f_{J/\psi }$. Indeed, using the expression of the electronic decay width

$$\begin{aligned} \Gamma (J/\psi \rightarrow e^+e^-)=\dfrac{4\pi }{3}\,\dfrac{4}{9}\,\alpha ^2(m^2_c)\dfrac{f^2_{J/\psi }}{m_{J/\psi }} \end{aligned}$$

together with the experimental determination of the $J/\psi$ mass and width, and setting $\alpha _{\mathrm{em}}(m^2_c)={1}/{134}$ [31, 32], one gets

$$\begin{aligned} f^{\text {``exp''}}_{J/\psi }=407(6)\,\text {MeV} \end{aligned}$$

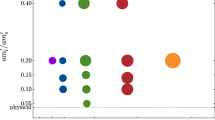
We collect the various lattice QCD results and the phenomenological estimate of $f_{J/\psi }$ in Fig. 7.

Fig. 7

Collection of lattice results of $f_{\eta _c}$ (left panel) and $f_{J/\psi }$ (right panel)

Fig. 8

Extrapolation at the physical point of $m_{\eta _c(2S)}/m_{\eta _c}$ (left panel) and $m_{\psi (2S)}/m_{J/\psi }$ (right panel) by linear expressions in $m^2_\pi$ and $a^2$. Errors include the systematic error obtained by changing the time range to fit $m_{\eta _c(2S)}$ and $m_{\psi (2S)}$ as described in Sect. 2.2

Fig. 9

Extrapolation at the physical point of $f_{\eta _c(2S)}/f_{\eta _c}$ (left panel) and $f_{\psi (2S)}/f_{J/\psi }$ (right panel) by linear expressions in $m^2_\pi$ and $a^2$. Errors include the systematic error obtained by changing the time range to fit $f_{\eta _c(2S)}$ and $f_{\psi (2S)}$ as described in Sect. 2.2

2.2.2 First radial excitation results

The situation is, unfortunately, less favorable with the excited states. Figure 8 shows the extrapolation to the continuum limit of the ratios $m_{\eta _c(2S)}/m_{\eta _c}$ and $m_{\psi (2S)}/m_{J/\psi }$, compared to the experimental values. Since the cut-off effects are small, of the order of 5%, there is no hope to have points in the continuum limit significantly lower than our lattice data. We get

$$\begin{aligned} m_{\eta _c(2S)}/m_{\eta _c}=1.279(6)\ \gg \ (m_{\eta _c(2S)}/m_{\eta _c})^{\mathrm{exp}}=1.220 \end{aligned}$$

and

$$\begin{aligned} m_{\psi (2S)}/m_{J/\psi }=1.263(7)\ \gg \ (m_{\psi (2S)}/m_{J/\psi })^{\mathrm{exp}}=1.190 \end{aligned}$$

In [33], lattice results were much closer to the experiment but the slope in $a^2$ was probably overrestimated from the coarsest lattice point: points at lattice spacings similar to those used in our work are compatible with our data.

The situation is even more confusing for the ratios of decay constants, as shown in Fig. 9

$$\begin{aligned}&f_{\eta _c(2S)}/f_{\eta _c} =0.84(8)<1\quad \text {while}\\&\quad f_{\psi (2S)}/f_{J/\psi } =1,22(9)>1 \end{aligned}$$

We have not found any explanation for such a large spin breaking effect. Projected correlators $\tilde{C}^2$ in the pseudoscalar and the vector sector show the same quality fit with similar fluctuations. We also have performed a global fit of individual correlators $C_{V^{(i)}V^{(j)}}(t)$ by a series of 3 exponential contributions

$$\begin{aligned} C_{V^{(i)}V^{(j)}}(t)= & {} Z^i_1Z^{*j}_1 e^{-m_{V_1} T/2} \cosh [m_{V_1}(T/2-t)]\\&+ Z^i_2Z^{*j}_2 e^{-m_{V_2} T/2} \cosh [m_{V_2}(T/2-t)] \\&+ Z^{ij}_3 e^{-m^{ij}_3 T/2} \cosh [m^{ij}_3(T/2-t)] \end{aligned}$$

where the “effective” remaining mass $m_3$, resumming any contributions but the ground state and the first excited state, can be different for every correlator. Decay constants of $J/\psi$ and $\psi (2S)$ are proportional to $Z^0_1/\sqrt{m_{V_1}}$ and $Z^0_2/\sqrt{m_{V_2}}$ (the local-local vector 2-pt correlator corresponds to $i=j=0$) and we find the hierarchy $Z^0_2/\sqrt{m_{V_2}}\gtrsim Z^0_1/\sqrt{m_{V_1}}$ in our sets of data. There is no hope to get in the continuum limit $f_{\psi (2S)}/f_{J/\psi }<1$ using this procedure either. Neglecting disconnected diagrams could be a source of the problem and including more flavours in the sea might help reduce the spin breaking effects, as it was observed on quantities like $f_{D^*_s}/f_{D_s}$ [35,36,37,38]. Moreover, the width $\Gamma (\psi (2S) \rightarrow e^+e^-)$ is smaller than its ground state counterpart $\Gamma (J/\psi \rightarrow e^+e^-)$, that is 2.34 keV versus 5.56 keV [34]; written in terms of the decay constant $f_{\psi (2S)}$ and the mass $m_{\psi (2S)}$, this is a serious clue that $f_{\psi (2S)}/f_{J/\psi }<1$.² In addition, a lattice study, performed in the framework of NRQCD, gives $f_{\Upsilon '}/f_{\Upsilon }<1$ in the bottomium sector [39].

3 Conclusion

In that paper we have reported a $N_f=2$ lattice QCD study about the physics of quarkonia. The decay constants $f_{\eta _c}$ and $f_{J/\psi }$ are in the same ballpark as the two previous lattice estimations available so far in the literature, with the good news that cut-off effects seem to be limited to 10%. The issues with radial excitations are difficult to circumvent. As a first solution, the basis of operators in the GEVP analysis could be enlarged by including interpolating fields with covariant derivatives or operators of the $\pi _2$ and $\rho _2$ kind. But both of them suffer either from big statistical fluctuations, because of numerical cancellation among various contributions, or from the more serious conceptual problem that, in GEVP, mixing T-even and T-odd operators has no real sense. Second, $m_{\eta _c(2S)}/m_{\eta _c}$ and $m_{\psi (2S)}/m_{J/\psi }$ are not significantly affected by cut-off effects, so that they are 5% larger than the experimental ratios. The information that $f_{\eta _c(2S)}/f_{\eta _c} \sim 0.8$ is interesting, as the decay constants $f_{\eta _c}$ and $f_{\eta _c(2S)}$ are hadronic inputs that govern the transitions $\eta _c \rightarrow l^+ l^-$, $h \rightarrow \eta _c l^+ l^-$, $\eta _c(2S) \rightarrow l^+ l^-$ and $h \rightarrow \eta _c(2S) l^+ l^-$ with a light CP-odd Higgs boson as an intermediate state.³ Unfortunately, our result for $f_{\psi (2S)}/f_{J/\psi }>1$ makes the picture less bright, unless one admits that there are very large spin breaking effects. Further investigation to address this issue is undoubtedly required.

Table 3 Masses and decays constants of $\eta _c$, $\eta _c(2S)$, $J/\psi$ and $\psi (2S)$, in lattice units, extracted on each CLS ensemble used in our analysis

Meanwhile, the next step into the measurement of $f_{\eta _b}$, particularly relevant in models with a light CP-odd Higgs, is underway using step scaling in masses in order to extrapolate the results to the bottom region.

Appendix

We collect in Table 3 the values of $\eta _c$ and $J/\psi$ masses and decay constants extracted at each ensemble of our analysis, as well as the ratios of masses and decay constants $m_{\eta _c(2S)}/m_{\eta _c}$, $m_{\psi (2S)}/m_{J/\psi }$, $f_{\eta _c(2S)}/f_{\eta _c}$ and $f_{\psi (2S)}/f_{J/\psi }$.