1 Introduction

Semileptonic decays of hadrons have been thoroughly studied and have brought much information on the nature of weak interactions and some aspects of QCD [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. The relative good control of the reactions within the Standard Model (SM) has led to new work searching for evidence of new physics beyond the standard model (BSM) [17,18,19].

One of the magnitudes that has captured attention as a source of information of new physics BSM is the polarization of vector mesons in B decays. One intriguing feature was observed in the \(B \rightarrow \phi K^*\) decays, where naively it was expected that the transverse amplitudes would be highly suppressed while the experiment showed equal strength for longitudinal and transverse polarizations [20, 21]. Theoretical papers have followed [22, 23], as well as new experimental measurements on related reactions, like \(B^0_s \rightarrow \phi \phi \) [24], \(B^+ \rightarrow \rho ^0 K^{*+}\) [25], \(B^0_s \rightarrow K^{*0} \bar{K}^{*0} \) [26], which had been addressed in papers dealing with \(B \rightarrow VV\) decays [27, 28], \(B \rightarrow V T\) decays [29], and some particular reactions as the \(B_{(s)} \rightarrow D^{(*)}_{(s)} \bar{D}_s^*\) [30]. More recently the topic has caught up in studies of weak decays into a vector and two leptons as the experiments on \(B \rightarrow K^* l^+ l^-\) [31], \(B \rightarrow K^* l^+ l^-\) [32], \(B^0 \rightarrow K^{*0} \mu ^+ \mu ^-\) [33,34,35], and theoretical works on \(B \rightarrow K^* \nu \bar{\nu }\) [36, 37], \(B \rightarrow K^* l^+ l^-\) [37], \(B \rightarrow K^{*0} l^+ l^-\) [38], \(B \rightarrow K_J^* l^+ l^-\) [39] and \(B \rightarrow K_2^* \mu ^+ \mu ^-\) [40].

In the present work we retake this line of research and study the polarization amplitudes in semileptonic \(\bar{B} \rightarrow V \bar{\nu } l\) decays, applied in particular to the \(\bar{B} \rightarrow D^* \bar{\nu } l\) reaction. We look at the problem from a different perspective to the conventional works where the formalism is based on a parametrization of the decay amplitudes in terms of certain structures involving Wilson coefficients and form factors. A different approach was followed recently in the study of B or D weak decays into two pseudoscalar mesons, one vector and a pseudoscalar and two vectors [41]. Starting from the operators of the Standard Model at the quark level, a mapping is done to the hadronic level and the detailed angular momentum algebra of the different processes is carried out leading to very simple analytical formulas for the amplitudes. By means of that, reactions like \(\bar{B}^0 \rightarrow D^{-}_s D^+, D^{*-}_s D^+, D^{-}_s D^{*+}, D^{*-}_s D^{*+}\), and others, can be related up to a global form factor that cancels in ratios by virtue of heavy quark symmetry. The approach proves very successful in the heavy quark sector and, due to the angular momentum formalism used, the amplitudes are generated explicitly for different third components of the spin of the vectors involved. In view of this, the formalism is ideally suited to study polarizations in these type of decays.

Work along the line of [41] is also done in [42] in the study of the semileptonic \(B, B^*,D, D^*\) decays into \(\bar{\nu } l\) and a pseudoscalar or vector meson. Once again, we can relate different reactions up to a global form factor. If one wished to relate the amplitudes of different spin third components for the same process, the form factor cancels in the ratio and the formalism makes predictions for the Standard Model without any free parameters.

In the present work we extend the formalism and allow a \((\gamma ^\mu - \alpha \gamma ^\mu \gamma _5)\) structure for the weak hadronic vertex which makes it easy to make predictions for different values of \(\alpha \) that could occur in different models BSM (\(\alpha =1\) here for the SM). We evaluate different ratios for the \(B \rightarrow D^* \bar{\nu } l\) reaction. Work on this particular reaction, looking at the helicity amplitudes within the Standard Model, was done in [43]. A recent work on this issue is presented in [44] where the \(B \rightarrow D^* \bar{\nu }_\tau \tau \) is studied separating the longitudinal and transverse polarizations. The same reaction, looking into \(\tau \) and \(D^*\) polarization, is studied in [45]. Helicity amplitudes are also discussed in the related \({\bar{B^*}} \rightarrow P l \bar{\nu }_l\) reactions in the recent paper [46].

The formalism of Ref. [42] produces directly the amplitudes in terms of the third component of the \(D^*\) spin along the \(D^*\) direction. This corresponds to helicity amplitudes of the \(D^*\). The formulas are very easy for these amplitudes and allow to understand analytically the results that one obtains from the final computations. Not only that, but they indicate which combinations one should take that make the results most sensitive to the parameter \(\alpha \) that will differ from unity for models BSM.

We find some observables which are very sensitive to the value of \(\alpha \), which should stimulate experimental work to investigate possible physics BSM.

2 Formalism

We want to study the \(B \rightarrow D^{*} \bar{\nu } l\) decay, which is depicted in Fig. 1 for \(B^- \rightarrow D^{*0} \bar{\nu }_{l} l^- \)

Fig. 1
figure 1

Diagrammatic representation of \(B^- \rightarrow D^{*0} \bar{\nu }_{l} l^-\) at the quark level

Full size image

The Hamiltonian of the weak interaction is given by

$$\begin{aligned} H= \mathcal {C} L^\alpha Q_\alpha \,, \end{aligned}$$
(1)

where the \(\mathcal {C}\) contains the couplings of the weak interaction. The constant \(\mathcal {C}\) plays no role in our study because we are only concerned about ratios of rates. The leptonic current is given by

$$\begin{aligned} L^\alpha =\langle {{\bar{u}}}_l |\gamma ^\alpha (1-\gamma _5)| v_\nu \rangle \,, \end{aligned}$$
(2)

and the quark current by

$$\begin{aligned} Q^\alpha =\langle {{\bar{u}}}_c|\gamma ^\alpha (1-\gamma _5)|u_b\rangle \,. \end{aligned}$$
(3)

In the evaluation of \(B^- \rightarrow D^{*0} \bar{\nu }_{l} l^-\) decay we need

$$\begin{aligned} \overline{\sum } \sum \left| t\right| ^2= & {} \sum _\mathrm{lep~ pol} L^\alpha {L^\beta }^{*} \overline{\sum _\mathrm{quark}}\sum _\mathrm{pol} Q_\alpha Q_\beta ^{*} \nonumber \\\equiv & {} {L}^{\alpha \beta } \overline{\sum }\sum Q_\alpha Q_\beta ^{*} \,, \end{aligned}$$
(4)

where t is the transition amplitude, and for simplicity

$$\begin{aligned} {L}^{\alpha \beta }={\sum _\mathrm{lep~ pol}} L^\alpha {L^\beta }^{*}, \end{aligned}$$
(5)

which can be easily obtained with the result [47]

$$\begin{aligned} {L}^{\alpha \beta } = 2~ \frac{p_\nu ^\alpha p_l^\beta +p_l^\alpha p_\nu ^\beta -p_\nu \cdot p_l g^{\alpha \beta }-i \epsilon ^{\rho \alpha \sigma \beta } p_{\nu \rho } p_{l\sigma }}{m_\nu m_l},\nonumber \\ \end{aligned}$$
(6)

where we adopt the Mandl and Shaw normalization for fermions [48]. In Ref. [42] a study of the meson decays \(J M \rightarrow \bar{\nu }_{l} l J' M'\) was done, where \( J M (J' M')\) are the modulus and third component of the initial (final) meson spin, and the rates for the different \(J, J'\) cases were evaluated. The sum over the M and \(M'\) components of Eq. (4) was done in Ref. [42]. Here we shall keep track of the individual M and \(M'\) contributions.

In evaluating the quark current, we use the ordinary spinors [49]

$$\begin{aligned} u_r= \widetilde{A}\left( \begin{array}{c} \chi _r\\ \widetilde{B} {{\varvec{\sigma }}}\cdot {{\varvec{p}}} \, \chi _r \end{array} \right) \,; \widetilde{A}= \sqrt{\frac{E_p +m}{2\, m}}\,; \widetilde{B}= \frac{1}{E_p +m}\,, \end{aligned}$$
(7)

where \(\chi _r\) are the Pauli bispinors and m, p and \(E_p\) are the mass, momentum and energy of the quark. As in Ref. [47] we take

$$\begin{aligned} \frac{p_b}{m_b}=\frac{p_B}{m_B}\,; \qquad \frac{E_b}{m_b}=\frac{E_B}{m_B}\, , \end{aligned}$$
(8)

where \(m_B\), \(p_B\), and \(E_B\) are the mass, momentum and energy of the B meson, and the same for the c quark related to the \(D^*\) meson. Theses ratios are tied to the velocity of the quarks or B mesons and neglect the internal motion of the quarks inside the meson. We evaluate the matrix elements in the frame where the \({\bar{\nu }} l\) system is at rest, where \({{\varvec{p}}}_B={{\varvec{p}}}_{D^*}={{\varvec{p}}}\), with p given by

$$\begin{aligned} p = \frac{\lambda ^{1/2} (m_{B}^2, M_\mathrm{inv}^{2(\nu l)}, m^2_{D^*})}{2 M_\mathrm{inv}^{(\nu l)}} \, , \end{aligned}$$
(9)

where \(M_\mathrm{inv}^{(\nu l)}\) is the invariant mass of the \(\nu l\) pair. By using Eq. (8) we can write

$$\begin{aligned}&u_r= A\left( \begin{array}{c} \chi _r\\ B {{\varvec{\sigma }}}\cdot {{\varvec{p}}}_B\, \chi _r \end{array} \right) \,; A= \sqrt{\frac{E_B+m_B}{2 m_B}}\,;\nonumber \\&\quad B= \frac{1}{m_B+E_B} \, ~~ \end{aligned}$$
(10)

and \(A',B'\) would be defined for the \(D^*\) meson, simply changing the mass in Eq. (7).

In the present work, we are only interested in the \(B^- \rightarrow D^{*0} \bar{\nu }_{l} l^-\) decay, which means \(J=0,J'=1\) decay.

As in [42] we need to evaluate \({L}^{\alpha \beta } Q_\alpha Q_\beta ^{*}\) which sums over the polarizations of \(\bar{\nu }_{l} l\), but keeping \(M'\) fixed. We have

$$\begin{aligned} \sum \left| t\right| ^2= L^{00} M_0 M^{*}_0 + L^{ij} N_i N_j^{*} \,, \end{aligned}$$
(11)

where

$$\begin{aligned} M_0=-A A^{\prime } (B+B^{\prime }) \, p \, \delta _{M 0} \,\delta _{M^{\prime } 0} \,, \end{aligned}$$
(12)

and \(N_i\), written in spherical coordinates, is

$$\begin{aligned} N_\mu= & {} A A^{\prime } \left\{ 1+BB^{\prime } p^2 \,(-1)^{-M^{\prime }} + \sqrt{2} \right. \nonumber \\&\left. \times (Bp+B^{\prime } p (-1)^{-M^{\prime }} )\,{\mathcal {C}}(1 1 1; M^{\prime },0,M^{\prime }) \right\} \delta _{\mu ,M^{\prime }} \,\delta _{M 0} \,, \nonumber \\ \end{aligned}$$
(13)

with \({\mathcal {C}}(\cdots )\) a Clebsch-Gordan coefficient.

In addition to the p dependence (and hence \(M_\mathrm{inv}^{(\nu l)}\)) of these amplitudes, in [42] there is an extra form factor coming from the matrix element of radial B and \(D^*\) quark wave functions. However, in our approach we normalize the different helicity contributions to the total and the effect of this extra form factor disappears.

The magnitude \(L^{ij} N_i N_j^{*}\) can be written in spherical coordinates as

$$\begin{aligned} \sum _{i,j} L^{ij} N_i N_j^{*} = \sum _{\alpha ,\beta } (-1)^{\alpha } L^{\alpha \beta } N_{-\alpha } N^{*}_{\beta } \, , \end{aligned}$$
(14)

and then, following the steps of the appendix of Ref. [42] we obtain

  1. 1)

    \(M'=0\)

    $$\begin{aligned} \sum |t|^2= & {} \frac{m^2_l}{m_{\nu } m_l} \frac{M_\mathrm{inv}^{2(\nu l)}-m^2_l}{M_\mathrm{inv}^{2(\nu l)}} \big \{A A' (B+B')p \big \}^2 \nonumber \\&+ \frac{2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \big \{A A' (1+B B' p^2) \big \}^2 \, . \nonumber \\ \end{aligned}$$
    (15)
  2. 2)

    \(M'=1\)

    $$\begin{aligned} \sum |t|^2= & {} \frac{2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \nonumber \\&\times \big \{A A' [(1-B B'p^2) +(B p-B' p)]\big \}^2 \, . \nonumber \\ \end{aligned}$$
    (16)
  3. 3)

    \(M'=-1\)

    $$\begin{aligned} \sum |t|^2= & {} \frac{2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \nonumber \\&\times \big \{A A' [(1-B B'p^2) -(B p-B' p)]\big \}^2 \, . \nonumber \\ \end{aligned}$$
    (17)

where \(\widetilde{p}_\nu \), \(\widetilde{E}_\nu \), \(\widetilde{E}_l\) are the momentum of the \(\bar{\nu }\), its energy and the lepton energy in the rest frame of the \(\bar{\nu } l\) system

$$\begin{aligned} \widetilde{p}_\nu= & {} \widetilde{p}_l=\frac{\lambda ^{1/2}(M_\mathrm{inv}^{2(\nu l)}, m^2_\nu ,m^2_l)}{2 M_\mathrm{inv}^{(\nu l)}} \,, \nonumber \\ \widetilde{E}_\nu= & {} \frac{M_\mathrm{inv}^{2(\nu l)}+ m^2_\nu -m^2_l}{2\,M_\mathrm{inv}^{(\nu l)}} \,, \nonumber \\ \widetilde{E}_l= & {} \frac{M_\mathrm{inv}^{2(\nu l)}+ m^2_l-m^2_\nu }{2\,M_\mathrm{inv}^{(\nu l)}} \,. ~~~~ \end{aligned}$$
(18)

\(M'\) in Eqs. (15), (16), and (17) stands for the third component of the \(D^*\) spin in the direction of \(D^*\). Hence these are the helicities of the \(D^*\). Note that in the boost from the B rest frame to the frame where B and \(D^*\) have the same momentum and \(\bar{\nu } l\) are at rest, the direction of \(D^*\) does not change and the helicities are the same. We can see that the sum of these expressions for the three helicities gives the same result as the sum obtained in Ref. [42] using properties of Clebsch-Gordan and Racah coefficients.

3 Results

The differential width is given for \(B \rightarrow D^{*} \bar{\nu } l\) by

$$\begin{aligned} \frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}= \frac{2m_{\nu } 2m_l}{(2\pi )^3} \,\frac{1}{4M^2_B} p'_{D^*} \widetilde{p}_\nu \sum |t|^2 \, , \end{aligned}$$
(19)

where \(p'_{D^*}\) is the \(D^*\) momentum in the B rest frame and \(\widetilde{p}_\nu \) the \(\bar{\nu }\) momentum in the \(\nu l\) rest frame,

$$\begin{aligned} p'_{D^*}=\frac{\lambda ^{1/2}(m^2_B,M_\mathrm{inv}^{2(\nu l)}, m^2_{D^*})}{2 m_B} \, . \end{aligned}$$
(20)

The factor \(m_{\nu } m_l\) in the numerator of Eq. (19) is due to the normalization used in [48] and cancels exactly the same factor appearing in the denominator of Eqs. (15), (16) and (17).

Fig. 2
figure 2

Values of Bp and \(B' p\) as a function of \(M_\mathrm{inv}^{(\nu l)}\) of Eqs. (9), (7)

Full size image

It is interestig to look individually at the distribution of the three third components of the \(D^*\) spin. For this we plot Bp, \(B' p\) as a function of \(M_\mathrm{inv}^{(\nu l)}\) in Fig. 2. We can see that \(B'p\) is always bigger than Bp and that both Bp and \(B' p\) go to unity as \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0\) (for \(m_l=m_\nu =0\)). Moreover, when \(M_\mathrm{inv}^{(\nu l)}\) goes to its maximum, then \(p \rightarrow 0\) and Bp, \(B' p\) go to zero.

Taking into account the behaviour of Bp and \(B' p\) depicted in Fig. 2, we can see that when \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0\) then \(\sum |t|^2 \) goes to \(\frac{2 (A A')^2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) F\), with \(F \rightarrow 4, 0, 0\) for \(M'=0,1,-1\) respectively, with \((A A')^2\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \) going to a constant. Conversely, when \(M_\mathrm{inv}^{(\nu l)} \) goes to its maximum, \(\sum |t|^2 \) goes to the same value \(\frac{2 (A A')^2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \) for \(M'=0,1,-1\) cases.

It is also interesting to see that

$$\begin{aligned}&\overline{\sum }\sum (|t|^2_{M'=-1} -|t|^2_{M'=+1}) = \frac{8}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \, \nonumber \\&\quad \times (A A')^2 (1 - B B' p^2)(B' p-B p) \, . ~~~~~~~ \end{aligned}$$
(21)

This means that the differential width \(d \varGamma /d M_\mathrm{inv}^{(\nu l)}\) for this difference goes as \((1 - B B' p^2)(B' p-B p) \) and the difference of these two distributions goes to zero, both as \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0\) or \(M_\mathrm{inv}^{(\nu l)} \) going to its maximum. We show also these results in Figs. 3 and 4. The total differential width is given by

$$\begin{aligned} R=\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=0} + \frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=-1} +\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=+1} \, .\nonumber \\ \end{aligned}$$
(22)
Fig. 3
figure 3

Total differential width R, and individual contributions of \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=0}\), \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=-1}\), and \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=+1}\)

Full size image

In Fig. 3 we show the individual contribution of each \(M'\) and the total. In Fig. 4 we show the contribution of each \(M'\) and the difference of \(M'=-1\) and \(M'=+1\), divided by the total differential width R. In this latter figure we can see how fast the individual \(M'=-1\) and \(M'=+1\) components go to zero.

In the search for contributions BSM one usually compares some magnitude with experiment and diversions of experiment with respect to the SM predictions are seen as a signal of possible new physics. So far the experimental errors do not make the cases compelling. The present case could offer a good opportunity, since the individual contributions for different \(M'\) vary appreciably when diverting from the Standard Model, as we show in the next section.

Fig. 4
figure 4

The same as Fig. 3 but for different ratios. The lines (a), (b) and (c) show \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=0}\), \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=-1}\), and \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=+1}\) respectively, and line (d) denotes the difference of \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=-1}-\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=+1}\), all divided by the total differential width R of Eq. (22)

Full size image

We also appreciate in Fig. 4 that the ratio of \( \frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=-1}-\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=+1}\) divided by the total differential width goes fast to zero for \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0\) or maximum, while individually each of the contributions goes to \(\frac{1}{3}\) at the maximum of \(M_\mathrm{inv}^{(\nu l)}\). In Fig. 4 we also see a smooth transition from 1 to \(\frac{1}{3}\) for the \(M'=0\) case. The rapid transition to zero of some of the amplitudes discussed and the wide change of values for the (a), (b), (c) and (d) cases in the figure make these magnitudes specially suited to look for extra contribution beyond the SM.

To give a further insight into this issue we stress that the reason for the zero strength at \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0 \) in the case of \(M'=\pm 1\), is tied not to the lepton current, since we always get \((A A')^2\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \), which goes to a constant for \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0\), but to the quark current. Indeed, if we look at Eqs. (12), (13), we can see that both \(\frac{M_0}{AA'}\) and \(\frac{N_\mu }{AA'} (\mu =0)\) are different from zero for \(M'=0\) in the limit of \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0\). However, for \(M'=\pm 1\), \(M_0=0\) and \(N_\mu \) goes to zero in that limit. This said, the models beyond the SM which could provide finite contribution for \(M'=\pm 1\), or a sizeably bigger one, are those that go beyond the \(\gamma ^\mu - \gamma ^\mu \gamma _5\) structure in the quark current, like leptoquarks or right-handed quark currents of the type \(\gamma ^\mu + \gamma ^\mu \gamma _5\) [50,51,52]. We discuss this case below.

4 Consideration of right-handed quark currents

The literature about models BSM is large and this is not the place to discuss it. Yet, we would like to mention more recent papers on models which could be easily tested within the present approach, minimal gauge extensions of the SM [53, 54], leptoquarks [55], scalar leptoquarks [56, 57], vector leptoquarks [58,59,60], Pati-Salam gauge models [61,62,63] and right-handed models [19, 64].

Some models BSM have quark currents that contain the combination \(\gamma ^\mu + \gamma ^\mu \gamma _5\). The models mentioned above could be accommodated with an operator

$$\begin{aligned}&a(\gamma ^\mu -\gamma ^\mu \gamma _5)+b(\gamma ^\mu +\gamma ^\mu \gamma _5) \, \nonumber \\&\quad =(a+b)\left\{ \gamma ^\mu -\frac{a-b}{a+b}\gamma ^\mu \gamma _5 \right\} \,.~~~~ \end{aligned}$$
(23)

We shall call \(\frac{a-b}{a+b}=\alpha \) and study the distributions for different \(M'\) as a function of \(\alpha \). We have thus the operator

$$\begin{aligned} \gamma ^\mu -\alpha \gamma ^\mu \gamma _5 \, . \end{aligned}$$

Using the same formalism of [42] it is easy to see the results as a function of \(\alpha \). We obtain the following results:

$$\begin{aligned} M_0=- A A^{\prime } (B+B^{\prime }) p \delta _{M 0} \,\delta _{M^{\prime } 0} \,\alpha \end{aligned}$$
(24)

and \(N_i\) written in spherical coordinates is

$$\begin{aligned} N_\mu= & {} A A^{\prime }\left\{ \big [1+BB^{\prime } p^2 \,(-1)^{-M^{\prime }}\big ]\alpha + \sqrt{2} \right. \, \nonumber \\&\left. \times [Bp+B^{\prime } p (-1)^{-M^{\prime }} ] \ {\mathcal {C}}(1 1 1; M^{\prime },0,M^{\prime }) \right\} \delta _{\mu ,M^{\prime }} \,\delta _{M 0} \,. \nonumber \\ \end{aligned}$$
(25)

Then, the different helicity contributions are given by

  1. 1)

    \(M'=0\)

    $$\begin{aligned} \sum |t|^2= & {} \frac{m^2_l}{m_{\nu } m_l} \frac{M_\mathrm{inv}^{2(\nu l)}-m^2_l}{M_\mathrm{inv}^{2(\nu l)}} \big \{A A' (B+B')p \big \}^2 \alpha ^2 \nonumber \\ \,&+ \frac{2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \nonumber \\&\times \big \{A A' (1+B B' p^2) \big \}^2 \alpha ^2 \, . \nonumber \\ \end{aligned}$$
    (26)
  2. 2)

    \(M'=1\)

    $$\begin{aligned} \sum |t|^2= & {} \frac{2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \nonumber \\ \,&\times \big \{A A' [(1-B B'p^2)\alpha +(B p-B' p)]\big \}^2 \, . \nonumber \\ \end{aligned}$$
    (27)
  3. 3)

    \(M'=-1\)

    $$\begin{aligned} \sum |t|^2= & {} \frac{2}{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \nonumber \\ \,&\times \big \{A A' [(1-B B'p^2)\alpha -(B p-B' p)]\big \}^2 \, . \nonumber \\ \end{aligned}$$
    (28)

Since \(1 - B B' p^2\) and \(B' p-B p\) go individually to zero for \(M_\mathrm{inv}^{(\nu l)} \rightarrow 0\), then we see that the \(M_\mathrm{inv}^{(\nu l)}\) distributions for \(M'=\pm 1\) still go to zero in that limit. Yet, the individual contributions depend strongly on \(\alpha \).

Fig. 5
figure 5

The same as Fig. 4 but for different \(\alpha \)

Full size image

In Fig. 5 we show the results of \(M'=\pm 1\) and \(M'=0\) for different values of \(\alpha \). We can see that for \(\alpha =0.5\) the contribution of \(M'=+1\) eventually vanishes. However, for \(\alpha =1.5\) it is much bigger and close to the distribution of \(M'=-1\). For \(\alpha =-0.5\) the values for \(M'=+1\) and \(M'=-1\) are exchanged with respect to \(\alpha =0.5\) and the \(M'=+1\) contribution is much bigger than the one of \(M'=-1\). Such cases should be easy to differentiate experimentally.

Fig. 6
figure 6

The difference of \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=-1}-\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=+1}\) of Eq. (29) as a function of \(\alpha \), divided by the total differential width R

Full size image

We also see that now

$$\begin{aligned}&\overline{\sum }\sum (|t|^2_{M'=-1} -|t|^2_{M'=+1}) = \frac{8 \, \alpha }{m_{\nu } m_l} \,\left( \widetilde{E}_\nu \widetilde{E}_l +\frac{1}{3} \widetilde{p}_\nu ^2 \right) \, \nonumber \\&\quad \times (A A')^2 (1 - B B' p^2)(B' p-B p) \, . ~~~~~~~~ \end{aligned}$$
(29)

Then, it is also interesting to see what happens for the ratio \(\frac{1}{R}(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=-1}-\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M'=+1})\). We show these results in Fig. 6. We can see that this magnitude keeps rising up as \(\alpha \) goes from 1.5 to about 0.2. For \(\alpha =0.1\) the shape changes drastically, and as \(\alpha \) goes to zero it changes very fast. This is because for \(\alpha \rightarrow -\alpha \) the magnitude changes sign. We also show the value of the magnitude for \(\alpha =-0.5\), which indeed is symmetric of the one for \(\alpha =0.5\) with respect to the \(M_\mathrm{inv}^{(\nu l)}\) axis. It is clear that magnitudes like this, which can change sign from one model to another, should be very useful in the search of contributions BSM.

5 Connection with the conventional formalism and discussion on heavy quark symmetry

In Ref. [42] one relates the weak amplitudes for the \({B} \rightarrow D \bar{\nu } l, D^* \bar{\nu } l\), \({B}^* \rightarrow D \bar{\nu } l, D^* \bar{\nu } l\). This means that there is only one independent amplitude for all these processes. This is reminiscent of the heavy quark symmetry [65, 66] where all form factors can be cast in terms of only one in the limit of infinite masses of the mesons. In view of this, let us face this issue here to see the heavy quark symmetry implicit in the approach of [42] which we follow here.

The key point in our approach, which allows us to express the quark matrix elements in terms of the meson variables, is Eq. (8). Let is take the first relation \(\frac{p_b}{m_b}=\frac{p_B}{m_B}\). In the B meson at rest there is a distribution of quark momenta due to the internal motion of the quarks, \({{{\varvec{p}}}_{in}}\). If we make a boost to have the B with a velocity of \({\varvec{v}}\), we will have

$$\begin{aligned} {p'}_{bL}=\frac{{p}_{in,L}+vp_{in}^0}{\sqrt{1-v^2}} \,, \qquad p'_{bT}=p_{bT} \,, \, \end{aligned}$$

where we have split \({{\varvec{p_{in}}}}\) into a longitudinal and transverse parts along the direction of \({\varvec{v}}\). We can write now

$$\begin{aligned} \frac{{p}_{bL}}{p_B}= & {} \frac{{p}_{in,L}+vp_{in}^0}{\sqrt{1-v^2}} \div \frac{m_B v}{\sqrt{1-v^2}} =\frac{{p}_{in,L}+vp_{in}^0}{m_B v} \, \\= & {} \frac{p_{in}^0}{m_B}+\frac{{p}_{in,L}}{m_B v}=\frac{m_b}{m_B}+\frac{{p}_{in,L}}{m_B v} \,. \end{aligned}$$

The relative correction factor is

$$\begin{aligned} \frac{{p}_{in,L}}{m_B v}\div \frac{m_b}{m_B} =\frac{{p}_{in,L}}{m_b v} \simeq \frac{{p}_{in,L}}{m_B v} \,, \end{aligned}$$

but since \({p}_{in,L}\) has positive and negative components the correction is of order

$$\begin{aligned} \left( \frac{{p}_{in,L}}{m_B v} \right) ^2 \simeq \frac{1}{3} \frac{{p}^2_{in}}{m_B^2 v^2} \,. \end{aligned}$$
(30)

Let us remark that around \(M_\mathrm{inv}^{(\nu l)}|_\mathrm{min}\), p from Eq. (9) becomes infinite and thus \(v=1\). Hence, the correction terms are of the order of \(\frac{1}{3} \frac{{p}^2_{in}}{m_B^2 v^2}\). With typical values of \(|{\varvec{p}}_{in}|\simeq 300\) MeV, this is a correction of one permil. For the \(D^*\) meson is a correction of less than \(1\%\). We can make v smaller as \(M_\mathrm{inv}^{(\nu l)} \) grows and still keep these numbers very small. Certainly, when we go to the end point, for \(M_\mathrm{inv}^{(\nu l)}/\mathrm{max}\), when both B and \(D^*\) are at rest, the argument would fail since \(v=0\). However, in this case the approximation is equally good since the Bp term is zero and only \(A,A'\) matter and \(E_b=m_b\) at the level of \(\frac{p^2_{in}}{2m^2_B}\) and \(E_B=M_B\), hence \(\widetilde{A}\) in Eq. (7) and A in Eq. (10) are again remarkably close. Incidentally, the transverse components in the boosted frame lead to a correction of

$$\begin{aligned} \frac{{p}_{in,T}}{p_B} =\frac{{p}_{in,T} \sqrt{1-v^2}}{m_B v} \rightarrow \frac{2}{3} \frac{{p}^2_{in}(1-v^2)}{m_B v^2} \,, \end{aligned}$$

and their effect is further negligible. One can repeat the argumentation for the second relation of Eq. (8). This indicates that in the \(\bar{\nu } l\) rest frame, where we evaluate the matrix elements, Eq. (8) is very accurate. However, it is only exact in the strict limit that \(m_B,m_{D^*}\) go to infinite. Hence, it should not be surprising that our method implements automatically the symmetries of heavy quark physics.

In order to test this hypothesis let us first study the \(\bar{B} \rightarrow D \bar{\nu } l\) transition. We have [67, 68]

$$\begin{aligned} \frac{<D, P'|{\mathcal {J}}_\mu (0)|B, P>}{\sqrt{m_B m_D}}= & {} ( v+v')_\mu h_{+}(w)\nonumber \\&+(v-v')_\mu h_{-}(w) \,, \end{aligned}$$
(31)

where \(v=\frac{P}{M_B}\), \(v'=\frac{P'}{M_D}\) and

$$\begin{aligned} w= v v'= \frac{M^2_B+M^2_D-M_\mathrm{inv}^{2(\nu l)}}{2M_B M_D} \,, \end{aligned}$$
(32)

(\(M_D \rightarrow M_{D^*}\) for the \(\bar{B} \rightarrow D^* \bar{\nu } l\) transition). Similarly (using \(\epsilon ^{0123}=1\)) we have [8, 67, 68]

$$\begin{aligned}&\frac{<D^*,\lambda , P'|{\mathcal {J}}_\mu (0)|B, P>}{\sqrt{m_B m_{D^*}}} = i \epsilon _{\mu \nu \alpha \beta } (\epsilon ^{(\lambda )\nu })^* v^\alpha v^{'\beta } h_V \, \nonumber \\&\qquad -(\epsilon ^{(\lambda )*} (w+1) h_{A_1} + (\epsilon ^{(\lambda )*} \cdot v) (v_\mu h_{A_2} + v'_\mu h_{A_3}). \nonumber \\ \end{aligned}$$
(33)

In the heavy quark limit, with the quark masses going to infinite, one finds [8, 67, 68]

$$\begin{aligned}&h_+(w)=h_{A_1}(w)=h_{A_3}(w)=h_{V}(w)=\xi (w) \,, \nonumber \\&h_{-}(w)=h_{A_2}(w)=0, \end{aligned}$$
(34)

with \(\xi (w)\) the Isgur Weise function, and with a certain normalization of \(\mathcal {J}_\mu \), \(\xi (w)\) at the end point, \(M_\mathrm{inv}^{(\nu l)}/\mathrm{max}=M_B-M_{D,D^*} (p=0)\),

$$\begin{aligned} \xi (w=1) =1. \end{aligned}$$
(35)

This condition appears naturally in the quark model since for \(w=1\) the momentum transfer is zero and the wave functions with very large quark masses are also equal. Hence the quark transition form factor is unity.

We take the \(D^*\) polarization vectors consistent with our convention in [42] for the angular momentum states

$$\begin{aligned}&M'=0 \,, \qquad&\epsilon ^{(0)\nu }\equiv \left( \frac{p}{M_{D^*}},0,0,\frac{E_{D^*}}{M_{D^*}} \right) ,\nonumber \\&M'=1 \,, \qquad&\epsilon ^{(+)\nu }\equiv -\frac{1}{\sqrt{2}}\left( 0,1,i,0 \right) , \nonumber \\&M'=-1 \,, \qquad&\epsilon ^{(-)\nu }\equiv \frac{1}{\sqrt{2}}\left( 0,1,-i,0 \right) . \end{aligned}$$
(36)

By using these polarization factors we compare the \({\mathcal {J}}_0\), \({\mathcal {J}}_i\) (\({\mathcal {J}}_{\tilde{\mu }}\) in spherical basis) matrix elements with \(M_0\) and \(N_{\tilde{\mu }}\) of the expressions found in [42].

  1. 1)

    \(J=0,J'=0\) (\(\bar{B} \rightarrow D \bar{\nu } l\) )

    $$\begin{aligned} M_0= & {} A A' (1+B B'P^2) \, \delta _{M 0} \, \delta _{M' 0} \,, \nonumber \\ N_{\tilde{\mu }}= & {} -A A' (B+B') \, p \,\delta _{M0} \,\delta _{M' 0} \, \delta _{\mu 0} \,. \end{aligned}$$
    (37)
  2. 2)

    \(J=0,J'=1\) (\(\bar{B} \rightarrow D^* \bar{\nu } l\))

    \(M_0\) and \(N_{\tilde{\mu }}\) are given by Eqs. (12) and (13).

We find

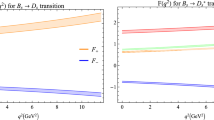
$$\begin{aligned} h_{+}= & {} \frac{\sqrt{m_B m_D}}{m_B+m_D} A A' (B + B'), \nonumber \\ h_{-}= & {} 0, \nonumber \\ h_{A_1}= & {} \frac{1}{w+1} A A'(1-B B' p^2) \frac{1}{\sqrt{m_B m_{D^*}}}, \nonumber \\ h_{V}= & {} \sqrt{m_B m_{D^*}} A A'\frac{(B-B')}{E_{D^*}-E_B}, \nonumber \\ h_{A_2}= & {} 0, \nonumber \\ h_{A_3}= & {} \frac{M^2_{D^*}M_B}{E_B-E_{D^*}} \frac{A A'}{E_{D^*}\sqrt{m_B m_{D^*}}} \, \nonumber \\&\times \left\{ \frac{1}{M_{D^*}}(1-B B' p^2)-(B+B') \right\} . \end{aligned}$$
(38)

Because of our normalization for the spinors from Ref. [48], \(\bar{u}u=1\), [see Eq. (10)], all these functions are normalized to the value \(\frac{1}{2\sqrt{m_B m_{D^*}}}\) at \(w=1~(p=0)\), while with the prescription \(\bar{u}u=2M\) implicit in Eqs. (31), (33), they are normalized to 1. Multiplying our form factors by \(2\sqrt{m_B m_{D^*}}\) we find the form factors normalized to 1 as in Eqs. (31), (33) which allow us to compare with other formalisms. In Fig. 7 we plot all these functions normalized to 1 at \(w=1\). We can see that \(h_{+}\) (calculated with \(m_{D^*}\)), \(h_{A_1}\), \(h_{V}\) and \(h_{A_3}\) are identical, even when we would not expect it from the different expressions in Eq. (38). We can then see that our formalism implements exactly the symmetry of heavy quark physics, and provides an w dependence for these functions.

Fig. 7
figure 7

\(h_{+}\), \(h_{A_1}\), \(h_{V}\) and \(h_{A_3}\) of Eq. (38) as a function of w normalized to 1 at \(w=1\)

Full size image

It is interesting to compare our results with those of [9]. There a quark model calculation is done, and the quark matrix elements are evaluated, including the transition form factor from B to \(D^*\) which we do not evaluate since it cancels in ratios of amplitudes for different \(M'\). This transition form factor, evaluated in the quark model, is close to 1 at \(w=1\), where there is no momentum transfer, and decreases as the momentum transfer increases. This allows us to compare our calculated \(h_{+}\) factor normalized to 1 at \(w=1\) with \(h_{+}\) of Ref. [9]. We see that \(h_{+}\) in [9] is qualitatively similar to ours, although it falls faster with w. The difference with us are of the order of \(15\%\) at the maximum value of w, indicating in any case a soft transition matrix element.

Next, in order to connect with the conventional formalism we follow Refs. [18, 69] and have

$$\begin{aligned}&\frac{<D^*,\lambda , P_{D^*}|{\mathcal {J}}_\mu (0)|B, P_B>}{\sqrt{m_B m_{D^*}}} \nonumber \\&\quad = \frac{2i V(q^2)}{m_B+m_{D^*}} \epsilon _{\mu \nu \alpha \beta } (\epsilon ^{(\lambda )\nu })^* P^{\alpha }_B P^{\beta }_{D^*} \, \nonumber \\&\qquad - 2 m_{D^*} A_0(q^2) \frac{\epsilon ^{(\lambda )*} \cdot q}{q^2} q_\mu \, \nonumber \\&\qquad - ({m_B +m_{D^*}}) A_1(q^2) \left[ \epsilon ^{(\lambda )^*}_\mu -\frac{\epsilon ^{(\lambda )^*} \cdot q}{q^2} q_\mu \right] \, \nonumber \\&\qquad + A_2(q^2) \frac{\epsilon ^{(\lambda )*} \cdot q}{m_B+m_{D^*}} \left[ (P_B+P_{D^*})_\mu -\frac{m^2_B-m^2_{D^*}}{q^2}q_\mu \right] \,, \nonumber \\ \end{aligned}$$
(39)

where \(q_\mu =P_{B\mu }-P_{D^*\mu }\). Once again, comparing this expression with our results for \(\mu =0\), \(\mu =1,2,3\) with \(M'=0,+1,-1\), we obtain the following results:

$$\begin{aligned}&V(q^2)=A A' (B-B') \frac{m_B +m_{D^*}}{2(E_{D^*}-E_B)} \,, \end{aligned}$$
(40)
$$\begin{aligned}&A_0(q^2)=\frac{1}{2}A A' (B+B') \,, \end{aligned}$$
(41)
$$\begin{aligned}&A_1(q^2)= \frac{1}{m_B +m_{D^*}} A A' (1-BB'p^2) \,. \end{aligned}$$
(42)
$$\begin{aligned}&(m_B +m_{D^*})A_1(q^2) \frac{E_{D^*}}{m_{D^*}} -\frac{2p^2(E_B-E_{D^*})}{m_{D^*}(m_B +m_{D^*})} A_2(q^2) \, \nonumber \\&\quad = A A' (1+B B' p^2) \,,~~ \end{aligned}$$
(43)

from where we find

$$\begin{aligned} A_2(q^2)= & {} \frac{-m_{D^*}(m_B +m_{D^*})}{2(E_B-E_{D^*})}A A' \, \nonumber \\&\times \left\{ 2 BB'-\frac{1}{p^2} \left( \frac{E_{D^*}}{m_{D^*}}-1\right) (1- BB'p^2) \right\} .\nonumber \\ \end{aligned}$$
(44)

As in [18] (Eq.(B.5)), we define here \(h_{A_1}(w)\) as

$$\begin{aligned} h_{A_1}(w)=\frac{2}{w+1} \frac{1}{R_{D^*}} A_1(q^2) \,, \end{aligned}$$
(45)

with \(R_{D^*}= \frac{2 \sqrt{m_B m_{D^*}}}{m_B+m_{D^*}}\). Hence \(h_{A_1}(w)\) here is identical to \(h_{A_1}\) of Eq. (38).

In [18, 69] the \(A_i, V\) form factors are parameterized as

$$\begin{aligned} A_0(q^2)= & {} \frac{R_0(w)}{R_{D^*}} h_{A_1}(w) \,,\nonumber \\ A_2(q^2)= & {} \frac{R_2(w)}{R_{D^*}} h_{A_1}(w) \,, \nonumber \\ V(q^2)= & {} \frac{R_1(w)}{R_{D^*}} h_{A_1}(w) \,. \end{aligned}$$
(46)

Our expressions in Eqs. (40), (41), (42), (43), (44) and (45) fulfill these conditions in the strict heavy quark limit with \(R_0(w)=1\), \(R_2(w)=1\), \(R_1(w)=1\), such that \(R_{D^*} A_i\) and \(R_{D^*} V\) are exactly equal to \(h_{A_1}\). This is seen in Fig. 8. Diversions from the strict heavy quark limit of the Standard Model, including higher order corrections in heavy quark effective theory (HQEF) and phenomenological information, are incorporated in this formalism parameterizing \(h_{A_1}(w)\), \(R_0(w)\), \(R_1(w)\), \(R_2(w)\) with the results [18, 69]

$$\begin{aligned}&h_{A_1}(w)=h_{A_1}(1)[1-8\rho ^2 z+(53\rho ^2-15)z^2 \, \nonumber \\&\quad -(231\rho ^2-91)z^3] \,, \nonumber \\&R_1(w)=R_1(1)-0.12(w-1)+0.05(w-1)^2 \,,\nonumber \\&R_2(w)=R_2(1)+0.11(w-1)-0.06(w-1)^2 \,,\nonumber \\&R_0(w)=R_0(1)-0.11(w-1)+0.01(w-1)^2 \,, \end{aligned}$$
(47)

where \(z=\frac{\sqrt{w+1}-\sqrt{2}}{\sqrt{w+1}+\sqrt{2}}\), with

$$\begin{aligned}&R_0(1)=1.14 \pm 0.07 \,,\nonumber \\&R_1(1)=1.401 \pm 0.034 \pm 0.018 \,,\nonumber \\&R_2(1)=0.864 \pm 0.024 \pm 0.008 \,,\nonumber \\&\rho ^2=1.214 \pm 0.034 \pm 0.009 \,,\nonumber \\&h_{A_1}(1)= 0.921 \pm 0.013 \pm 0.020 \,. \end{aligned}$$
(48)
Fig. 8
figure 8

\(R_{D^*}V\), \(R_{D^*} A_0\), \(h_{A_1}\) and \(R_{D^*} A_2\) from Eqs. (40), (41), (44), and (45) as a function of w normalized to 1 at \(w=1\)

Full size image
Fig. 9
figure 9

the same as Fig. 8 but from Eqs. (46), (47) and (48)

Full size image

The results for \(h_{A_1}\) \(R_{D^*}V\), \(R_{D^*} A_0\), \(R_{D^*} A_2\) are shown in Fig. 9. Comparison of Fig. 8 with Fig. 9 shows the difference with our approach, implying the heavy quark limit, with the more accurate results including higher order corrections in HQEF. We can appreciate a bigger slope as a function of w for the improved model (as already seen comparing with Ref. [9]) and also a different normalization at \(w=1\). The differences are not small, since the values of \(R_i (1)\) in Eq. (48) compared with those in the heavy quark limit implicit in our approach where \(R_i=1\), contain deviations from \(14\%\) to \(40\%\). Yet, the claim we make here is that the differences become much smaller when we use our approach to calculate ratios of amplitudes. To see the accuracy of our model to provide ratios, we evaluate again the contribution of \(M'=0,\pm 1\), divided by the sum of the three contributions, for different values of \(\alpha \), with the form factor of the improved model and compare the results with those obtained in Fig. 5. To evaluate those contributions in the improved model we look at the formulas of Eqs. (26), (27), (28), and looking at the expressions of Eqs. (40), (41), (42), (43), (44) and (45) we substitute,

$$\begin{aligned}&AA'(B+B')\,p \rightarrow 2 A_0 p \,,\nonumber \\&AA'(1+B B' p^2) \rightarrow \frac{E_{D^*}(m_B+m_{D^*})}{m_{D^*}} A_1 \nonumber \\&\quad -\frac{2 p^2 (E_B-E_{D^*})}{m_{D^*}(m_B+m_{D^*})} A_2 \,,\nonumber \\&AA'(1 - B B' p^2) \rightarrow (m_B+m_{D^*}) A_1 \,,\nonumber \\&AA'(B -B')\,p \rightarrow \frac{2(E_{D^*}-E_B)}{(m_B+m_{D^*})} V p \,. \end{aligned}$$
(49)

The results are shown in Fig. 10 for different values of \(\alpha \). One can appreciate some differences from Fig. 5, but they are very small. For \(M_\mathrm{inv}^{(\nu l)}\) maximum, which corresponds to \(w=1\) the results are practically identical. The differences are more visible for small \(M_\mathrm{inv}^{(\nu l)}\), a region which is anyway suppressed by phase space in the mass distributions. The fact that the three contributions are equal at \(w=1~(M_\mathrm{inv}^{(\nu l)}/\mathrm{max})\) in both approaches is trivial since only \(A_1\) contributes there and the kinematical factors in \(\sum |t|^2\) are identical for all \(M'\). The fact that close to \(M_\mathrm{inv}^{(\nu l)}/\mathrm{max}\) the behaviour in both cases is so close can also be traced to the fact that for a certain range of p momentum the \(A_1\) term is still largely dominant. Yet, this could be seen as a manifestation of a general behaviour of the helicity amplitudes close to the end point discussed in Ref. [70].

Fig. 10
figure 10

The same as Fig. 5 but from Eqs. (46), (47), (48), and (49)

Full size image

The comparison of these two approaches is useful. Once again, we can see some differences in the distributions of Figs. 5 and 10 for low and intermediate values of \(M_\mathrm{inv}^{(\nu l)}\). Should one see in an experiment some discrepancy with respect to our predictions of Fig. 5 this should not be taken as evidence of physics BSM. Indeed, there are corrections in these distributions in Fig. 10 when one includes higher order corrections in HQEF. The differences with respect to Fig. 10 would be more significant. Yet, the most significant thing is the large sensitivity of the difference of the \(M=-1\) and \(M=1\) contributions to small changes of \(\alpha \), which is shared in both approaches. The other point worth stressing is that since close to the end point our approach and the improved one are practically indistinguishable, the predictions in that region are rather model independent, and, yet, different for different values of \(\alpha \). Differences found in experiment with respect to these predictions for \(\alpha =1\) in that region would clearly manifest some physics beyond the Standard Model.

6 Conclusions

We have taken advantage of a recent reformulation of the weak decay of hadrons, where, instead of parameterizing the amplitudes in terms of particular structures with their corresponding form factors, the weak transition matrix elements at the quark level are mapped into hadronic matrix elements and an elaborate angular momentum algebra is performed that allows one to correlate the decay amplitudes for a wide range of reactions. The formalism allows one to obtain easy analytical formulas for each reaction in terms of the angular momentum components of the hadrons. One global form factor also appears in the approach related to the radial wave functions of the hadrons involved, but since this form factor is common to many reactions and in particular is exactly the same for the different spin components of the hadrons within the same reaction, it cancels in ratios of amplitudes or differential mass distributions.

In the present paper we have taken this formalism and extended it to the case of hadron matrix elements with an operator \(\gamma ^\mu -\alpha \gamma ^\mu \gamma _5\), which can accommodate many models beyond the standard model by changing \(\alpha \). We have applied the formalism to study the \(B \rightarrow D^{*} \bar{\nu } l\) reaction and the amplitudes for different helicities of the \(D^*\) are evaluated. We see that \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}\) depends strongly on the helicity amplitude and also on the \(\alpha \) parameter. In particular the difference \(\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M=-1} -\frac{d \varGamma }{d M_\mathrm{inv}^{(\nu l)}}|_{M=+1} \) is shown to be very sensitive to the \(\alpha \) parameter and changes sign when we go from \(\alpha \) to \(-\alpha \). Such a magnitude, with its strong sensitivity to this parameter, should be an ideal test to investigate models beyond the Standard Model and we encourage its measurement in this and analogous reactions, as well as the theoretical calculations for different models.

We have taken advantage to relate our approach, which implies the heavy quark limit, to the conventional one using explicit polarization vectors, by calculating the form factors \(V(q^2)\), \(A_0(q^2)\), \(A_1(q^2)\), \(A_2(q^2)\) in our approach and comparing them to the parameterization of the improved conventional model which incorporates higher order corrections in HQEF and phenomenological information. The form factors are qualitatively similar but one can observe clear differences. Yet, when one uses them to evaluate ratios of amplitudes, or partial differential mass distributions, the differences are small, and near the end point \(w=1\) the distributions are practically identical.