Abstract
We scrutinize the recently further strengthened hints for new physics in semileptonic B-meson decays, focusing on the ‘clean’ ratios of branching fractions \(R_K\) and \(R_{K^*}\) and examining to which pattern of new effects they point to. We explore in particular the hardly considered, yet fully viable, option of new physics in the right-handed electron sector and demonstrate how a recently proposed framework of leptons in composite Higgs setups naturally solves both the \(R_K\) and \(R_{K^*}\) anomalies via a peculiar structure of new physics effects, predicted by minimality of the model and the scale of neutrino masses. Finally, we also take into account further observables, such as \(\mathcal{B}(B_s \rightarrow \mu ^+\mu ^-)\), \(\varDelta M_{B_s}\), and angular observables in \(B \rightarrow K^{*} \mu ^+ \mu ^-\) decays, to arrive at a comprehensive picture of the model concerning (semileptonic) B decays. We conclude that – since it is in good agreement with the experimental situation in flavor physics and also allows to avoid ultra-light top partners – the model furnishes a very promising scenarios of Higgs compositeness in the light of LHC data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Decays of B mesons offer a promising place to search for new physics (NP), since in the Standard Model (SM) of Particle Physics flavor changing neutral processes are strongly suppressed and thus effects of NP might be sizable in (flavor-changing) B decays. The case is strengthened by the fact that the bottom quark is the heaviest down-type quark and resides in the same weak doublet as the \(t_L\), which due to its large mass is thought to furnish a major link to the completion of the SM at smallest distances.
In fact, several anomalies have been found in \(b \rightarrow s \ell ^+ \ell ^-\) transitions, such as the long-standing anomaly in the angular analysis of the \(B \rightarrow K^* \mu ^+ \mu ^-\) decay [1,2,3,4,5], as well as deficits in the branching fractions \(B \rightarrow K \mu ^+ \mu ^-\) [6] and \(B_s \rightarrow \phi \mu ^+ \mu ^-\) [7]. While these anomalies might be interpreted as a sign of new physics,Footnote 1 some caution is in order because potentially sizable hadronic uncertainties are challenging to control.
A much cleaner probe of NP is given by ratios of branching fractions, like
which tests lepton flavor universality (LFU), and where large hadronic uncertainties basically drop out [17] (see below). Interestingly, this theoretically very clean observable has also been measured at LHCb [18] and exhibits a sizable (\(25 \%\)) depletion with respect to the SM prediction [17, 19] \(\left| R_K^\mathrm{SM}-1 \right| < 1\%\)Footnote 2 in the \(q^2 \equiv (p_{\ell ^-}+p_{\ell ^+})^2 \in [1,6]\,\mathrm{GeV}^2\) bin, i.e.,
This corresponds to a deviation of almost \(3\,\sigma \). This intriguing hint for NP was recently strengthened with the measurement of the ratio
which was found to be low by a similar amount [20]
where again \(| R_{K^*}^{[1.1,6]\,\mathrm{SM}}-1|< 1\%\) and \(| R_{K^*}^{[0.045,1.1]\,\mathrm{SM}}-1| \lesssim 5\%\), resulting in tensions of \(2.5\,\sigma \) and \(2.2\,\sigma ,\) respectively. A naive combination of both results leads to a discrepancy with the SM of about \(4\,\sigma \), employing only observables that are theoretically well under control.Footnote 3
In this article, we will focus on these clean observables, and study first the structure of NP required to explain the found deviations in an effective field theory (EFT) approach. We will in particular stress a solution with sizable effects in the right-handed electron sector, complementary to the common solution which is linked to the left-handed muon sector. We will then show how a recently proposed composite Higgs model, incorporating a non-trivial, yet minimal, implementation of the lepton sector [21, 22] can explain the \(R_K\) and \(R_{K^*}\) anomalies simultaneously, due to the peculiar chirality structure of the involved currents. The setup contains less degrees of freedom than standard realizations and is very predictive, leading in general to a non-negligible violation of LFU, while allowing at the same time for a strong suppression of flavor changing neutral currents (FCNCs).Footnote 4
We will also discuss predictions of the setup for less clean observables in \( b \rightarrow s \ell ^+ \ell ^-\) decays and take into account further flavor constrains on the model. We will in particular focus on the angular analysis of the \(B \rightarrow K^*\mu ^+ \mu ^-\) decay, where pseudo-observables have been defined that also allow to cancel leading hadronic uncertainties [23,24,25,26,27,28,29,30,31], and where results are available from all 3 LHC pp experiments as well as from Belle, which are again pointing to a \(\sim 4\,\sigma \) deviation from the SM. It turns out that non-negligible effects are also predicted in this decay, allowing a significant improvement with respect to the SM, while still addressing the \(R_{K^{(*)}}\) anomalies and meeting the most stringent flavor bounds.
The remainder of this article is organized as follows. In the next section, we will provide an analysis of the NP required to address the anomalies in LFU violating decays in terms of \(D=6\) operators, parametrizing heavy physics beyond the SM in a model-independent way. We will then examine the structure of operators generated by the composite lepton model and present numerical predictions for \(R_{K^*}\), scrutinizing the correlation with \(R_K\) as well as \(B_s - {\bar{B}}_s\) mixing and taking into account constraints from \(B_s \rightarrow \mu ^+\mu ^-\). Finally, we will give our predictions for the angular observable \(P_5^\prime \), confronting them with the experimental results, before ending with our conclusions.
2 Pattern of the \(R_K, R_{K^*}\) anomalies
Employing the framework of effective field theory, a clear picture of the required structure of heavy NP to explain the \(R_{K^{(*)}}\) anomalies can be obtained. The relevant operators \(\mathcal{O}_i\), contributing to semi-leptonic \(B_s\) decays to leading approximation, are contained in the effective Hamiltonian [32, 33]
and read
and \({\mathcal{O}^\ell _{7,9,10}}^{\prime }\) equivalently with \(P_L \leftrightarrow P_R\), where \(P_{L,R} \equiv (1\mp \gamma _5)/2\).Footnote 5 In fact, as the relevant energy scale is much below \(m_W\), also the SM contributions are best expressed in terms of contributions to the operators (6), \(C=C^\mathrm{SM}+C^\mathrm{NP}\) , where (at \(\mu =4.8\) GeV) [38]
respecting LFU, i.e., \(C_i^{e\,\mathrm{SM}}=C_i^{\mu \,\mathrm{SM}}=C_i^{\tau \,\mathrm{SM}}\), and \({\mathcal{O}^\ell _{7,9,10}}^{\prime \,\mathrm{SM}}=0\).
The operators above are written in terms of leptonic vector (\({\mathcal{O}_9^\ell }^{(\prime )}\)) and axial-vector (\({\mathcal{O}_{10}^\ell }^{(\prime )}\)) currents, which is convenient to add higher oder corrections including SM gauge bosons (the photon couples vectorial). NP, on the other hand, is conveniently parametrized in the chiral basis, writing the Hamiltonian (5) as
with
since often NP models treat a certain chirality in a special way and one can take advantage of the accidental hierarchy of SM contributions
to directly see the importance of NP effects via their interference with the SM contributions (see [39, 40]). The coefficients of the two bases are related in a simple way via \(C_9^\ell =(C_{ bs_{L} \ell _{R}}+C_{ bs_{L} \ell _{L}})/2\), \(C_{10}^\ell =(C_{ bs_{L} \ell _{R}}-C_{ bs_{L} \ell _{L}})/2\), and similarly for the primed operators with \({ bs}_{L} \rightarrow { bs}_{R}\). In this basis, we arrive atFootnote 6
Given that we are considering corrections to \(R_K\) of (up to) \(\sim 30\%\), the corresponding NP contributions to the Wilson coefficients will also be of this order, if they interfere with the leading SM contribution \(C_{ bs_{L} \ell _{L}}^\mathrm{SM}\) (barring significant cancellations). In consequence, it makes sense to expand \(R_K\) to leading order in the NP coefficients \(C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}\), to allow for a transparent theoretical interpretation, which we will do below. We keep however terms containing right handed lepton currents up to quadratic order, going beyond the chiral linear approximation [40], since they do not interfere with the leading (left-handed) SM contribution (for vanishing lepton masses). Thus, on the one hand, potentially larger effects are required to explain the anomalies (as happens in the explicit model under consideration), and generically, due to the suppressed interference, quadratic terms become important. Note however that (as long as \(C_{ bs_{X} \ell _{R}}^{\mathrm{NP}} < C_{ bs_{L} \ell _{L}}^\mathrm{SM}\)) higher terms are still suppressed.Footnote 7 Neglecting also the strongly suppressed interference with \(C_{ bs_{L} \ell _{R}}^\mathrm{SM}\), we arrive at
For generic \(30\%\) corrections to \(R_K\), this formula is exact up to \(\lesssim 10\%\) corrections, which are smaller than the experimental uncertainty.Footnote 8 In particular, it captures the leading effects of all NP Wilson coefficients considered.
We directly observe that \(R_K<1\) can be realized in two ways. It could origin from a destructive (constructive) interference of the combined left-handed muon (electron) contributions with the leading SM piece or, more generally, a negative sign in the difference of muon and electron contributions \(C_{ bs_{L+R} (\mu -e)_{L}}^{\mathrm{NP}} \equiv C_{ bs_{L} \mu _{L}}^{\mathrm{NP}}+C_{ bs_{R} \mu _{L}}^{\mathrm{NP}}-C_{ bs_{L} e_{L}}^{\mathrm{NP}}-C_{ bs_{R} e_{L}}^{\mathrm{NP}}\). On the other hand, it could stem from couplings to right-handed lepton currents. In that case, as discussed, the quadratic NP contribution dominates in general. From (14) it then follows directly that \(R_K<1\) requires the effect to come from the electron sector. Of course, a combination is possible, such that right-handed muon currents are allowed, however, while for the case of electron currents, any operator alone could accommodate \(R_K<1\), for the muon case, right handed contributions alone are not feasible, no matter what is the quark chirality.
More valuable information on the physical origin of the possible B-physics anomalies can be obtained by considering in addition the ratio \(R_{K^*}\), which tests different combinations of Wilson coefficients, to which we will turn now. The theoretical prediction in this case reads (\(p\approx 0.86\))Footnote 9
Expanding again in \(C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}\), keeping quadratic terms only in \(C_{ bs_{X} \ell _{R}}^{\mathrm{NP}}\) and neglecting the strongly suppressed interference with \(C_{ bs_{L} \ell _{R}}^\mathrm{SM}\), we obtain
From this expression it is evident that \(R_{K^*}\) probes right-handed quark currents since in their absence it becomes equivalent to \(R_K\) to leading approximation. A similar conclusion holds in the absence of left-handed lepton currents, unless both left- and right-handed quark currents appear in LFU violating NP contributions.
The findings above are visualized in Fig. 1, where we show the correlations between \(R_K\) and \(R_{K^*}\), employing Eqs. (13) and (18). The colored lines correspond to the effects of the various NP Wilson coefficients. We consider all the coefficients entering these expressions, including combinations, such as to allow simultaneously for NP in the muon and electron sectors and in different chirality combinations. The most important dependencies of \(R_K\) and \(R_{K^*}\) are on the difference of purely left-handed contributions involving muons and electrons \(C_{ bs_{L} (\mu -e)_{L}}^{\mathrm{NP}} \equiv C_{ bs_{L} \mu _{L}}^{\mathrm{NP}} - C_{ bs_{L} e_{L}}^{\mathrm{NP}}\), on the corresponding quantity involving right-handed quark currents \(C_{ bs_{R} (\mu -e)_{L}}^{\mathrm{NP}} \equiv C_{ bs_{R} \mu _{L}}^{\mathrm{NP}} - C_{ bs_{R} e_{L}}^{\mathrm{NP}}\), where the direction of positive values is indicated by an arrow, and on the four coefficients involving right handed lepton currents, entering at quadratic order in NP. Note that for the latter case, a simultaneous presence of left- and right-handed quark currents is necessary, in order to break the degeneracy \(R_K=R_{K^*}\), while in case only one coefficient is turned on, the effect of either of them is indistinguishable in the \(R_K\) vs. \(R_{K^*}\) plane. We thus consider the distinct individual contributions \(C_{ bs_{X} \mu _{R}}^{\mathrm{NP}}\) and \(C_{ bs_{X} e_{R}}^{\mathrm{NP}}\) (being equal for \(X=L,R\)) as well as the simultaneous presence of left- and right-handed quark currents via \(C_{ bs_{L} \ell _{R}}^{\mathrm{NP}}=C_{ bs_{R} \ell _{R}}^{\mathrm{NP}}\equiv C_{ bs_{(L=R)} \ell _{R}}^{\mathrm{NP}}\), to capture the most relevant different scenarios. The effect of further combining different contributions to \(R_K\) and \(R_{K^*}\) can be easily inferred by considering the analytic Eqs. (13) and (18) in addition to the figure. The size of the coefficients corresponding to a certain point in the plane is visualized via the shape of the lines – solid lines correspond to \(0< |C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}| < 1\), dashed lines to \(1< |C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}| < 2.5\), while dotted lines feature \(2.5< |C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}| < 5\). Since the interference of NP effects in the right-handed lepton sector with SM contributions is suppressed, generically larger coefficients are required here in order to obtain sizable effects.
From the plot it becomes clear that the LHCb results, visualized by the black uncertainty bars, uniquely single out either a left-handed-left-handed NP effect, where \(C_{ bs_{L} \mu _{L}}^{\mathrm{NP}} (C_{ bs_{L} e_{L}}^{\mathrm{NP}})\) needs to feature a negative (positive) sign, or an effect in the right-handed electron sector via \(C_{ bs_{X} e_{R}}^{\mathrm{NP}}\), as the preferred solution to the \(R_K^{(*)}\) anomalies.Footnote 10 This is a very interesting finding with respect to the model considered in the remainder of the paper. In fact, while a number of models accommodate the former option of dominating left-handed effects (including leptonic vector currents), see [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73] for \(Z^\prime \) realizations, the latter solution hardly exists in the form of explicit models in the literature, however just emerges in the composite model presented in Sect. 3.
Predictions for \(R_K\) vs. \(R_{K^*}\) in dependence on the values of the NP Wilson coefficients entering Eqs. (13) and (18), where solid, dashed, and dotted lines correspond to \(0< |C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}| < 1\), \(1< |C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}| < 2.5\), and \(2.5< |C_{ bs_{X} \ell _{Y}}^{\mathrm{NP}}| < 5\), respectively. The \(1\,\sigma \) allowed range from LHCb is depicted by the black uncertainty bars. Both anomalies can be addressed simultaneously via \(\mathcal{O}_{ bs_{X} e_{R}}\) or via \(\mathcal{O}_{ bs_{L} (\mu -e)_{L}}\). In the lower panel, the exact predictions are added as faint colored lines. See text for details
We finally stress again that for the predictions of the model discussed in the next section, we employ full results including higher order corrections and the (small) effects of \(C_7^\mathrm{SM}\), performing a quadratic fit in the NP Wilson coefficients to the NLO results.Footnote 11 We also display, in the right panel of Fig. 1, the results employing these full expressions, visualized via faint colored lines. Note that now, in the case of right-left contributions, the prediction does not just depend on the difference of muon and electron contributions any more and varying \(C_{ bs_{R} \mu _{L}}^{\mathrm{NP}}\) and \(C_{ bs_{R} e_{L}}^{\mathrm{NP}}\) independently leads to a (very modest) spread of the predictions in the \(R_K\) vs. \(R_{K^*}\) plane, depicted by the blue shaded region. Generally, the approximate results describe the relevant physics quite accurately.
In summary, consistently explaining the \(R_K\) and \(R_{K^*}\) anomalies requires both quark FCNCs involving the b quark and LFU violation in the \(\mu \) vs. e system (with effects either in left-handed currents in both sectors, or with a non-negligible right-handed electron contribution). The model that we will discuss now naturally leads to both effects, via exchange of composite vector resonance, whose couplings are not aligned with the SM couplings and the biggest contributions are actually expected in quark transitions involving the third generation and LFU violation involving light SM leptons. Since larger corrections are predicted for electrons, the setup matches nicely with the fact that this sector is less constrained, and, as we will see, sizable effects are in fact possible without problems with, e.g., \(B_s \rightarrow \ell ^+ \ell ^-\) decays.
3 Predictions in composite framework and further observables
Composite Higgs models offer a priori a compelling framework to explain the neutral flavor anomalies. The presence of a rich spectrum of bound states at the TeV scale, including heavy vector resonances (of \(Z^{\prime }\) type) with sizable couplings to some of the SM fermions, make these scenarios natural candidates to address the tension between data and SM predictions. Moreover, and contrary to most of the solutions to these anomalies that one can find in the literature, they also offer an interplay with electroweak symmetry breaking (EWSB) and some rationale to solve the hierarchy problem. If one considers that fermion masses are generated via the mechanism of partial compositeness, a sizable violation of lepton flavor universality, like suggested by \(R_K\) and \(R_{K^{*}}\), necessarily requires the charged leptons to feature a sizable degree of compositeness in their left-handed (LH) and/or right-handed (RH) chirality, \(\epsilon _{\ell _R}\), \(\epsilon _{\ell _L}\). Since charged lepton masses scale in general as \( \sim g_{*} v\epsilon _{\ell _L} \epsilon _{\ell R}\), where \(g_{*}\) is the characteristic coupling within the strong sector, both chiralities can not be composite at the same time. Therefore, these models will either predict effects in \(\mathcal {O}_{bs_{L,R} \ell _L}\) or in \(\mathcal {O}_{bs_{L,R}\ell _R}\) scaling like \(\sim g_{*}^2/m_{*}^2 V_{ts}\epsilon _{b_X}^2 \epsilon _{\ell _Y}^2\), where X and Y denote the possible chiralities involved in the quark- and lepton-sector, respectively, and \(m_{*}\) is the typical mass scale of the first vector resonances.
The model under consideration falls into the second category and was presented in detail in [21, 22]. One of its most interesting features is that charged leptons partially substitute the role of the top quark as a trigger of EWSB, and a link between violation of lepton flavor universality and the absence of top partners at the LHC is established. Indeed, if the composite operators interacting with the RH charged leptons transform in sufficiently large irreducible representations of the global group within the strong sector, the leading charged lepton contribution to the Higgs quartic coupling will appear at order \(\sim |\epsilon _{\ell _R}|^2\) instead of the usual \(\sim |\epsilon _{\ell _R}|^4\). Since the leading top contribution can be expected to appear at order \(|\epsilon _{t_L}|^4\), the contribution arising from the lepton sector can be comparable to the top one, even with a smaller degree of compositeness. Moreover, if all the three lepton generations are partially composite, the lepton contribution will be enhanced by a factor \(N_\mathrm{gen}\sim 3\), compensating the color factor \(N_c = 3\) present in the top case and allowing to lift the problematic top partners via destructive interference between the two sectors in the Higgs potential.Footnote 12 One of the important findings of [21, 22] is that the very same representations making this possible also provide the required quantum numbers for a minimal implementation of a type-III seesaw mechanism for neutrino masses, which can in fact motivate RH charged-lepton compositeness, as we will see now.Footnote 13 If one follows this very minimal avenue, considering each generation of RH leptons to interact with a single composite operator, all RH charged leptons in fact inherit the degree of compositeness of their RH neutrino counterparts, and the latter is required to be sizable to allow for large enough neutrino masses (see [21, 22, 77,78,79,80] for more details in both type-I and type-III seesaw models). Then, the different scaling of the neutrino and charged lepton mass matrices requires \(0\ll \epsilon _{\tau _R}\ll \epsilon _{\mu _R} \ll \epsilon _{e_R}\), in order to have simultaneously hierarchical charged lepton masses and a non-hierarchical neutrino mass matrix [21]. An immediate consequence of the above chirality structure is that mostly the operators \(\mathcal{O}_{ bs_{X} e_{R}}\) will be generated (as well as subdominantly \(\mathcal{O}_{ bs_{X} \mu _{R}}\)). Moreover, possible modifications of Z couplings which are extremely constrained by electroweak precision data are avoided due to custodial symmetry, contrary to what happens for the case of composite LH leptons, where it is not possible to protect the coupling to both fields in the SM doublet at the same time.
To be concrete, we are considering a strongly interacting sector featuring the Higgs as a pseudo Nambu–Goldstone boson (pNGB) arising from the symmetry breaking \(SO(5)\rightarrow SO(4)\), known as the Minimal Composite Higgs model (MCHM) [81, 82]. The quark fields are embedded in \(\mathbf{5}^u_L,\mathbf{1}^u_R,\mathbf{5}^d_L,\mathbf{1}^d_R\) representations of SO(5), while all lepton fields are embedded in only two representations, \(\mathbf{5}_L^\ell , \mathbf{14}_R^\ell \), per generation. As mentioned before, we can explain the tiny neutrino masses via a type-III seesaw mechanism, since the symmetric representation \(\mathbf{14}_R^\ell \cong \mathbf {(1,1) + (2,2) + (3,3)}\) of \(SO(5) \cong SU(2)_L \times SU(2)_R\) can host both an electrically charged \(SU(2)_L\) singlet lepton (\(\ell _R\)) and a heavy fermionic seesaw triplet of \(SU(2)_L\). This unification of right handed leptons comes along with a more minimal quark representation than in known models, because the enhanced leptonic contribution to the Higgs potential, originating from the symmetric SO(5) representation, allows for a viable electroweak symmetry breaking with all right handed SM-quarks inert under SO(5) and the left-handed ones in the fundamental (see [21, 22] for details). Thus, the model features less degrees of freedom than standard incarnations, such as the MCHM\(_5\).
One of the main challenges of all these scenarios featuring composite leptons is the generation of dangerous FCNCs through the exchange of the very same vector resonances producing the violation of LFU. Since, in general, they will also contribute to extremely well measured lepton flavor violating processes like \(\mu \rightarrow e\gamma \), \(\tau \rightarrow \mu \gamma \), \(\mu \rightarrow eee\), and \(\mu -e\) conversion, they typically require the addition of some non-trivial flavor symmetry. In the model at hand, it turns out that the reduced number of composite operators mixing with the light leptons naturally allows for a very strong flavor protection along the lines of minimal flavor violation, since a single spurion allows to break the flavor symmetry [21]. Regarding the quark sector, in the model at hand the left handed current \({\bar{s}}_L \gamma ^\mu b_L\) (i.e., \(X=L\)) will in general dominate, with the compositeness of \(b_L\) following from the large top mass, but also non-negligible contributions from right-handed quarks are possible.
Let us conclude this discussion by stressing that if the effect of the model would be mostly due to the muon instead of the electron, neither the \(R_{K^*}\) nor the \(R_K\) anomaly could be addressed. Once the effect originates from a right-handed lepton current, it is required that the electron channel dominates in order to resolve the anomalies, see Fig. 1. On the other hand, contrary to the case of NP mostly in the muon current, in this case both chiralities for the quark current are fine. Thus, the very peculiar pattern of effects in our composite lepton scenario fits very well with experimental observation, predicting
Before presenting our final numerical results for these observables, we show in Fig. 2 the pattern of Wilson coefficients generated in the composite Higgs model. Here, and in the following, the points shown correspond to a scan over the parameter space of a 5D gauge-Higgs-unification description of the composite Higgs framework detailed above. Brane and bulk masses have been generated randomly (see [21] for more details), requiring the correct SM spectrum to emerge at low energies, while the pNGB decay constant has been chosen as \(f=1.2\) TeV, such as to solve the hierarchy problem while being in agreement with electroweak precision data. The large density of points in the lower right quadrant confirms numerically the expectation lined out before of \(\mathcal {O}_{bs_{L} \ell _R}\) dominating in general, while in some regions of parameter space also \(\mathcal {O}_{bs_{R} \ell _R}\) can be significant, all leading to the pattern (20).
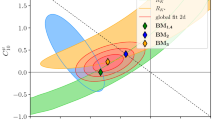
After this general discussion, we present our predictions in the \(R_{K^*}\) vs. \(R_K\) plane in the left panel of Fig. 3. One can clearly observe the sought pattern of \(R_K \sim R_{K^*} <1\), emerging as discussed in detail above. It is worth mentioning that points with SM-like values of \(R_K\) and \(R_{K^{*}}\) correspond to points of the scan with small FCNCs in the quark sector, since violation of LFU is always present in the model. This can be seen in particular in Fig. 2, since the points never reach the \((y=0)-\)axis. As explained above, this is due to the fact that different values of \(\epsilon _{\ell _R}\), \(0\ll \epsilon _{\tau _R}\ll \epsilon _{\mu _R} \ll \epsilon _{e_R}\), are always needed in order to reproduce the spectrum in the lepton sector. Given that the masses of the vector resonances mediating these processes are fixed by f to be relatively high, and that one needs to overcome the absence of interference with the SM contribution, agreement with the experimental values of \(R_K\) and \(R_{K^{*}}\) requires points with rather sizable FCNCs, which can be obtained in the considered parameter space.
Since along with \(\mathcal {O}_{bs_{X} e_R}\) also, subleadingly, \(\mathcal {O}_{bs_{X} \mu _R}\) is generated, all the points need to face constraints from the rather well-measured branching ratio \(\mathcal{B}(B_s \rightarrow \mu ^+\mu ^-)\), which, in the chiral basis, is given by [83]Footnote 14
where [84,85,86] (see also [36])
Note that in general the muonic final states are more stringently constrained experimentally, leaving more room for effects in the electron channel, which does not constrain the model at hand at all. The former, on the other hand, has a (mild) impact on the setup. In general, avoiding effects in \(B_s \rightarrow \ell ^+ \ell ^-\), requires either a leptonic or a quark vector-current - in fact the decay tests products of axial-vector currents. In consequence, the negative \(C_{ bs_{L} \mu _{L}}^{\mathrm{NP}}\) solution to the \(R_{K^{(*)}}\) anomalies could be accompanied by a \(C_{ bs_{R} \mu _{L}}^{\mathrm{NP}}\) contribution, to cancel effects in \(B_s \rightarrow \ell ^+ \ell ^-\), which would however go in the wrong direction with respect to \(R_{K^*}\). The second option is an addition of \(C_{ bs_{L} \mu _{R}}^{\mathrm{NP}}\), which is less problematic since suppressed by the smaller interference with the SM, and corresponds to the \(C_9\) solution of the \(b \rightarrow s \ell ^+ \ell ^-\) anomalies. Note that to go into the direction of the very modest (negative) deviation from the SM prediction in \(B_s\rightarrow \mu ^+ \mu ^-\), for a fixed chirality for one fermion current, the other should feature the larger effect in the opposite chirality (for positive Wilson coefficients), i.e., \(C_{ bs_{X} \mu _{Y}}^{\mathrm{NP}}-C_{ bs_{X} \mu _{X}}^{\mathrm{NP}}>0\) or \(C_{ bs_{Y} \mu _{X}}^{\mathrm{NP}}-C_{ bs_{X} \mu _{X}}^{\mathrm{NP}}>0\), \((X,Y)\in \{(L,R),(R,L)\}\) (see Eq. (21)). This means in particular that an effect stemming solely from a negative \(C_{ bs_{L} \mu _{L}}^{\mathrm{NP}}\) goes in principle in a favorable direction.
For the composite Higgs model considered, effects are coming from non-vanishing \(C_{ bs_{L-R} \mu _{R}}^{\mathrm{NP}}, \) but are modest in general, as can be seen from Fig. 4 where we show the ratio \(\mathcal{B}(B_s \rightarrow \mu ^+ \mu ^-)/\mathcal{B}(B_s \rightarrow \mu ^+ \mu ^-)_\mathrm{SM}\), together with the experimental \(1\,\sigma \) range, the latter depicted by the red dashed lines. Most of the points lie within the corresponding range (while basically all meet the \(2\,\sigma \) constraints). The impact of the \(1\,\sigma \) bound on the composite solution to the \(R_{K^{(*)}}\) anomalies is visualized in the right panel of Fig. 3, where we reject the parameter-space points that do not meet this constraint. As can be seen, the effect is very modest.
We now move to study the correlation with \(B_s - {\bar{B}}_s\) mixing, focusing on the mass difference between the heavy and light mass eigenstate \(\varDelta M_{B_s} \equiv M_H^s - M_L^s\) (see e.g. [87]). The relevant additional operators, entering \(B_s - {\bar{B}}_s\) mixing, are contained in the \(\varDelta B=2\) Lagrangian [46]
where
and are generated predominantly via the exchange of gluon resonances in the composite Higgs framework. Note that we neglect again scalar (and tensor) operators, not present for the model at hand to good approximation. Our general prediction, obtained via a fit to the numerical results [46] at the scale \(\mu =2\,\)TeV, reads
where \(\varDelta M_{B_s}^\mathrm{SM}=1.313\times 10^{-11}\,\)GeV.
In Fig. 5 we provide again the results in the \(R_{K^*}\) vs. \(R_K\) plane, where now the color code depicts the size of the corrections to the SM value of \(\varDelta M_{B_s}\), with light (dark) blue corresponding to modest (sizable) modifications. We find that there is a considerable amount of points with (20–30) % effects in \(R_{K^{(*)}}\) and deviations in \(\varDelta M_{B_s}\) at the \(\lesssim 20\%\) level, which is in the ballpark of the uncertainty in the SM prediction. In consequence, values \(R_K \sim R_{K^*} \sim \) (0.7–0.8) are possible, while constraints from \(B_s - {\bar{B}}_s\) mixing are met. One should note that, quite generally, the size of quark FCNCs required to obtain large deviations in \(R_K\) and \(R_{K^{*}}\) leads to large modifications in \(\varDelta M_{B_s}\). However, small deviations in \(\varDelta M_{B_s}\) can be achieved via a cancellation between LH and RH quark currents, so the presence of both \(C_{ bs_{L} \ell _{X}}^{\mathrm{NP}}\) and \(C_{ bs_{R} \ell _{X}}^{\mathrm{NP}}\) is somewhat preferred, moving away from the \(R_K = R_{K^*}\) line (see Fig. 1). This, which may seem like a trivial fact, makes a large difference when compared to the rest of \(Z^{\prime }\) explanations of these anomalies. The reason is that, only for the case studied here of NP mostly in RH electrons, one can have an effect in both \(\bar{b}_R \gamma ^{\mu } s_R\) and \(\bar{b}_L \gamma ^{\mu } s_L\) and still get agreement with both \(R_K\) and \(R_{K^{*}}\) (as discussed in the previous section). This means in particular that, if the prediction for \(\varDelta M_{B_s}\) quoted by [88] is taken at face value, accepting some accidental cancellations, the scenario considered here would provide the only allowed \(Z^{\prime }\) model accommodating both anomalies.Footnote 15
Finally, another interesting set of observables in the field of semi-leptonic B decays are the angular dependencies of the \(B \rightarrow K^*\mu ^+ \mu ^-\) decay rate. Of particular interest is the coefficient \(P_5^\prime \), which belongs to a class of observables constructed such as to cancel hadronic uncertainties [23,24,25,26,27,28,29,30,31], which shows an interesting deviation with respect to the SM prediction, see e.g., [8, 16]. Our results for \(P_5^\prime \) in the \(q^2\in [4.3,8.68]\,\mathrm{GeV}^2\) bin are given in Fig. 6, where we plot the correlation between \(P_5^\prime \) and \(R_K\), visualizing again the size of the corrections to \(\varDelta M_{B_s}\) as different shades of blue. The SM prediction \({P_5^\prime }_{[4.3,8.68]}\approx -\ 0.8\) and the experimentally preferred value \({P_5^\prime }_{[4.3,8.68]}\approx - \ 0.2\) [8, 16] are given as red and green dashed lines, respectively. From this final plot it is evident that the proposed composite model can address the \(R_{K}\) and \(R_{K^{*}}\) anomalies, being in agreement with \(B_s - {\bar{B}}_s\) mixing and \(\mathcal{B}(B_s \rightarrow \ell ^+ \ell ^-)\), while also the fit to the \(P_5^\prime \) results can be improved (via the light-blue points approaching \({P_5^\prime }_{[4.3,8.68]}\approx -\ 0.2\) and featuring \(R_K \sim \) (0.7–0.8)). It thus furnishes an interesting setup both with respect to the gauge hierarchy problem – avoiding light top partners – and concerning the current pattern of experimental results in flavor physics.
Before concluding, let us mention further ways to test the proposed composite Higgs scenario. First, finding non-vanishing coefficients of four-lepton operators at future lepton colliders (in particular of type \(({\bar{e}}_R \gamma ^\mu e_R) ({\bar{e}}_R \gamma _\mu e_R)\) [21, 80]) could be interpreted as a hint for lepton compositeness. Moreover, along the line of ‘conventional’ light top partners, the model at hand contains leptonic resonances \(\ell ^\prime \) somewhat below the typical resonance scale, \(m_{\ell ^\prime } < m_{Z^\prime }\) [22], which could be searched for directly. Finally, due to the very fact that these particles can be lighter than the \(Z^\prime \), new decay channels such as \(Z^\prime \rightarrow \ell ^\prime \ell \) open up, which have been investigated in [90], and would be a smoking gun for the setup.
4 Conclusions
We have scrutinized hints for lepton flavor universality violation in B-meson decays, focusing first on the general properties of the anomalies in an EFT approach. Here, we emphasized a simultaneous solution to the \(R_K\) and \(R_{K^*}\) anomalies via effects in right-handed lepton currents, not worked out before. We stressed that this solution requires the dominant contribution originating from electron (and not muon) currents and presented a composite Higgs scenario, where this pattern emerges in a natural way. In fact, the model provides one of the very few scenarios, that features all ingredients to consistently resolve the anomalies, without being actually constructed for that purpose: it predicts LFU violation and sizable FCNCs involving the third quark generation, features a strong protection from FCNCs in the lepton sector, and allows for the absence of ultra-light top partners at the LHC. We also discussed the impact of operators addressing the \(R_{K^{(*)}}\) measurements on other flavor observables, such as \(\mathcal{B}(B_s \rightarrow \ell ^+\ell ^-)\), \(\varDelta M_{B_s}\), and \(P_5^\prime \). For the explicit model at hand, we found that all constraints are met, while it is possible to simultaneously resolve the (more controversial) \(P_5^\prime \) anomaly.
Notes
This is valid above the muon threshold, \(q^2 \sim 4 m_\mu ^2\).
Note that in the case of \(R_K\) this holds also in the presence of NP, while for \(R_{K^*}\) it holds within the SM, still allowing for a clean test of the latter.
Beyond that, in these models the leptonic contribution to the Higgs mass is parametrically enhanced relative to the quark contribution by (inverse) powers of SO(5) breaking spurions, such that a light Higgs does not necessarily lead to light top partners, resolving tensions with LHC searches.
The scalar and pseudo-scalar operators \({\mathcal{O}^\ell _{S,P}}^{(\prime )}\) are already considerably constrained from \(B_s \rightarrow \mu ^+ \mu ^-\) and play no important role in the following discussions [34, 35] (for the electron channel, sizable effects are still possible in principle [36], however the operators play no role for our analysis of Sect. 3). This is also true for tensor operators, which can not be generated from operators invariant under the SM gauge group to leading order [37].
The individual branching fractions are given by [13, 17, 39, 41]

where

\(m_{A\pm B}^2 \equiv m_A^2\pm m_B^2\), and we neglected lepton masses, CP violation, and higher order corrections (which are however included in our numerical analysis, employing CP averaged quantities). Here, \(f_+\) and \(f_T\) are the QCD form factors (see [42, 43]) and \(h_K(q^2)\) parametrizes non-factorizable contributions from the weak hamiltonian [13]. Neglecting the strongly suppressed \(C_7^{(\prime )}\) contributions (which could only become relevant approaching the photon pole at \(q^2 = 0\) and are in any case constrained to be pretty SM like [44]) and the non-factorizable \(h_K(q^2)\), the QCD form factor \(f_+(q^2)\) drops out in the ratio \(R_K\) (13).
If quadratic terms in \(C_{ bs_{X} \ell _{R}}\) are kept, a \(\sim 30\%\) effect in \(R_K\) is per se in agreement with a convergence of the expansion in NP contributions, no matter from which operator it is induced (see also [45]).
If the fourth order in \(C_{ bs_{X} \ell _{R}}\) is included, which corresponds to adding

it holds even at the \(\mathcal{O}(1\%)\) level, which becomes negligible compared to other uncertainties. Still, for the numerical results presented in Sect. 3, we will use the exact expressions, including in addition higher order QCD corrections [46] as well as the effect of \(C_7^\mathrm{SM}\).
Neglecting terms suppressed by \(m_\ell ^2/q^2\), NLO, and non-factorizable corrections (as well as CP violation), the individual branching fractions can be expressed in terms of six transversity amplitudes \(A_{0,\perp ,\parallel }^{L,R}\) as [47] (see also [39, 41, 48, 49])

where the form factors \(\xi _{\perp ,\parallel }\) are given, e.g., in Appendix E of [47]. We directly dropped electromagnetic dipole contributions, becoming important only for \(q^2 \rightarrow 0\), which would appear in the three square brackets above as \(2 m_b m_B/q^2 \{C_7+C_7^\prime ,\,C_7-C_7^\prime ,\,q^2/m_B^2 (C_7-C_7^\prime )\}\). Defining the integrated form factors
$$\begin{aligned}&g_{\perp ,\parallel ,0}^{[q_\mathrm{min}^2,q_\mathrm{max}^2]}= \int _{q_\mathrm{min}^2}^{q_\mathrm{max}^2} dq^2 ([m_{B-K^*}^2]^2-2m_{B+K^*}^2q^2 +q^4)^{\frac{1}{2}}\\&\quad \times \frac{2(q^3 - m_B^2 q)^2}{m_B^2}\ \left\{ |\xi _\perp |^2,\,|\xi _\perp |^2,\, {\frac{(m_B^2-q^2)^2}{8q^2 m_{K^*}^2}}|\xi _\parallel |^2 \right\} , \end{aligned}$$we can write \(R_{K^*}\) as two combinations of Wilson coefficients, weighted by the polarization fraction \(p \equiv \frac{g_0+g_\parallel }{g_0+g_\parallel +g_\perp }\), where \(p \approx 0.86\) to good approximation for the \(q^2\) range considered here (with some per cent deviation for the low \(q^2\) bin) [39, 47].
It becomes also evident that a negative NP contribution to \(C_9^\mu =(C_{ bs_{L} \mu _{R}}+C_{ bs_{L} \mu _{L}})/2\), as advocated as a solution to the \(B \rightarrow K^*\mu ^+ \mu ^-\) anomaly (see, e.g., [8, 16]), allows for a good fit of the \(R_K^{(*)}\) anomalies, basically because (for moderate values of the coefficients) the effect of \(C_{ bs_{L} \mu _{L}}^{\mathrm{NP}}\) dominates via the SM interference. A positive \(C_9^e\), on the other hand, also allows for a straightforward solution.
We used the code Flavio (v0.21.1) [46] for the numerical prediction.
See also [74] for a (different) composite explanation of LFU violation.
Here, we neglect scalar and pseudoscalar operators, not generated in the model at hand to good approximation.
Note that solutions to the \(R_K\) anomaly are also subject to competitive constraints from searches for tails in the high \(p_T\) di-lepton spectrum [89]. However, due to the suppressed couplings to light quarks, our setup avoids these bounds. Moreover, di-lepton searches will be less effective, since one typically expects the neutral vector mediators to decay via a lepton partner, leading to different decay topologies [90], see also below.
References
R. Aaij et al., Phys. Rev. Lett. 111, 191801 (2013). https://doi.org/10.1103/PhysRevLett.111.191801
R. Aaij et al., JHEP 02, 104 (2016). https://doi.org/10.1007/JHEP02(2016)104
S. Wehle et al., Phys. Rev. Lett. 118(11), 111801 (2017). https://doi.org/10.1103/PhysRevLett.118.111801
CMS Collaboration, Measurement of the \(P_1\) and \(P_5^{\prime }\) angular parameters of the decay \(\rm B\mathit{^0 \rightarrow \rm K}^{*0} \mu ^+ \mu ^-\) in proton-proton collisions at \(\sqrt{s}=8~\rm TeV\). CMS-PAS-BPH-15-008 (2017)
ATLAS Collaboration, Angular analysis of \(B^0_d \rightarrow K^{*}\mu ^+\mu ^-\) decays in \(pp\) collisions at \(\sqrt{s}= 8\) TeV with the ATLAS detector. ATLAS-CONF-2017-023 (2017)
R. Aaij et al., JHEP 06, 133 (2014). https://doi.org/10.1007/JHEP06(2014)133
R. Aaij et al., JHEP 09, 179 (2015). https://doi.org/10.1007/JHEP09(2015)179
S. Descotes-Genon, J. Matias, J. Virto, Phys. Rev. D 88, 074002 (2013). https://doi.org/10.1103/PhysRevD.88.074002
W. Altmannshofer, D.M. Straub, Eur. Phys. J. C 73, 2646 (2013). https://doi.org/10.1140/epjc/s10052-013-2646-9
F. Beaujean, C. Bobeth, D. van Dyk, Eur. Phys. J. C 74, 2897 (2014). https://doi.org/10.1140/epjc/s10052-014-2897-0 [Erratum: Eur. Phys. J. C 74, 3179 (2014). https://doi.org/10.1140/epjc/s10052-014-3179-6]
T. Hurth, F. Mahmoudi, JHEP 04, 097 (2014). https://doi.org/10.1007/JHEP04(2014)097
R. Gauld, F. Goertz, U. Haisch, Phys. Rev. D 89, 015005 (2014). https://doi.org/10.1103/PhysRevD.89.015005
W. Altmannshofer, D.M. Straub, Eur. Phys. J. C 75(8), 382 (2015). https://doi.org/10.1140/epjc/s10052-015-3602-7
S. Descotes-Genon, L. Hofer, J. Matias, J. Virto, JHEP 06, 092 (2016). https://doi.org/10.1007/JHEP06(2016)092
T. Hurth, F. Mahmoudi, S. Neshatpour, Nucl. Phys. B 909, 737 (2016). https://doi.org/10.1016/j.nuclphysb.2016.05.022
W. Altmannshofer, C. Niehoff, P. Stangl, D.M. Straub, Eur. Phys. J. C 77(6), 377 (2017). https://doi.org/10.1140/epjc/s10052-017-4952-0
G. Hiller, F. Kruger, Phys. Rev. D 69, 074020 (2004). https://doi.org/10.1103/PhysRevD.69.074020
R. Aaij et al., Phys. Rev. Lett. 113, 151601 (2014). https://doi.org/10.1103/PhysRevLett.113.151601
M. Bordone, G. Isidori, A. Pattori, Eur. Phys. J. C 76(8), 440 (2016). https://doi.org/10.1140/epjc/s10052-016-4274-7
R. Aaij et al., JHEP 08, 055 (2017). https://doi.org/10.1007/JHEP08(2017)055
A. Carmona, F. Goertz, Phys. Rev. Lett. 116(25), 251801 (2016). https://doi.org/10.1103/PhysRevLett.116.251801
A. Carmona, F. Goertz, JHEP 05, 002 (2015). https://doi.org/10.1007/JHEP05(2015)002
J. Matias, F. Mescia, M. Ramon, J. Virto, JHEP 04, 104 (2012). https://doi.org/10.1007/JHEP04(2012)104
S. Jäger, J. Martin Camalich, JHEP 05, 043 (2013). https://doi.org/10.1007/JHEP05(2013)043
S. Descotes-Genon, T. Hurth, J. Matias, J. Virto, JHEP 05, 137 (2013). https://doi.org/10.1007/JHEP05(2013)137
J. Lyon, R. Zwicky, Resonances gone topsy turvy—the charm of QCD or new physics in \(b \rightarrow s \ell ^+ \ell ^-\)? Report no. EDINBURGH-14-10, CP3-ORIGINS-2014-021-DNRF90, DIAS-2014-21 (2014). arXiv:1406.0566
S. Descotes-Genon, L. Hofer, J. Matias, J. Virto, JHEP 12, 125 (2014). https://doi.org/10.1007/JHEP12(2014)125
S. Jäger, J. Martin Camalich, Phys. Rev. D 93(1), 014028 (2016). https://doi.org/10.1103/PhysRevD.93.014028
M. Ciuchini, M. Fedele, E. Franco, S. Mishima, A. Paul, L. Silvestrini, M. Valli, JHEP 06, 116 (2016). https://doi.org/10.1007/JHEP06(2016)116
B. Capdevila, S. Descotes-Genon, L. Hofer, J. Matias, JHEP 04, 016 (2017). https://doi.org/10.1007/JHEP04(2017)016
V.G. Chobanova, T. Hurth, F. Mahmoudi, D. Martinez Santos, S. Neshatpour, JHEP 07, 025 (2017). https://doi.org/10.1007/JHEP07(2017)025
B. Grinstein, M.J. Savage, M.B. Wise, Nucl. Phys. B 319, 271 (1989). https://doi.org/10.1016/0550-3213(89)90078-3
G. Buchalla, A.J. Buras, M.E. Lautenbacher, Rev. Mod. Phys. 68, 1125 (1996). https://doi.org/10.1103/RevModPhys.68.1125
G. Hiller, M. Schmaltz, Phys. Rev. D 90, 054014 (2014). https://doi.org/10.1103/PhysRevD.90.054014
F. Beaujean, C. Bobeth, S. Jahn, Eur. Phys. J. C 75(9), 456 (2015). https://doi.org/10.1140/epjc/s10052-015-3676-2
R. Fleischer, R. Jaarsma, G. Tetlalmatzi-Xolocotzi, JHEP 05, 156 (2017). https://doi.org/10.1007/JHEP05(2017)156
R. Alonso, B. Grinstein, J. Martin Camalich, Phys. Rev. Lett. 113, 241802 (2014). https://doi.org/10.1103/PhysRevLett.113.241802
B. Capdevila, S. Descotes-Genon, L. Hofer, J. Matias, J. Virto, PoS LHCP2016, 073 (2016)
G. Hiller, M. Schmaltz, JHEP 02, 055 (2015). https://doi.org/10.1007/JHEP02(2015)055
G. D’Amico, M. Nardecchia, P. Panci, F. Sannino, A. Strumia, R. Torre, A. Urbano, JHEP 09, 010 (2017). https://doi.org/10.1007/JHEP09(2017)010
A. Ali, P. Ball, L.T. Handoko, G. Hiller, Phys. Rev. D 61, 074024 (2000). https://doi.org/10.1103/PhysRevD.61.074024
C. Bouchard, G.P. Lepage, C. Monahan, H. Na, J. Shigemitsu, Phys. Rev. D 88(5), 054509 (2013). https://doi.org/10.1103/PhysRevD.88.079901 [Erratum: Phys. Rev. D 88(7), 079901 (2013). https://doi.org/10.1103/PhysRevD.88.054509]
A.J. Buras, J. Girrbach-Noe, C. Niehoff, D.M. Straub, JHEP 02, 184 (2015). https://doi.org/10.1007/JHEP02(2015)184
A. Paul, D.M. Straub, JHEP 04, 027 (2017). https://doi.org/10.1007/JHEP04(2017)027
R. Contino, A. Falkowski, F. Goertz, C. Grojean, F. Riva, JHEP 07, 144 (2016). https://doi.org/10.1007/JHEP07(2016)144
D. Straub, P. Stangl, C. Niehoff, E. Gurler, W. Zeren, J. Kumar, S. Reicher, F. Beaujean, flav-io/flavio v0.21.1 (2017). https://doi.org/10.5281/zenodo.569011
C. Bobeth, G. Hiller, G. Piranishvili, JHEP 07, 106 (2008). https://doi.org/10.1088/1126-6708/2008/07/106
C. Hambrock, G. Hiller, S. Schacht, R. Zwicky, Phys. Rev. D 89(7), 074014 (2014). https://doi.org/10.1103/PhysRevD.89.074014
A. Bharucha, D.M. Straub, R. Zwicky, JHEP 08, 098 (2016). https://doi.org/10.1007/JHEP08(2016)098
A. Crivellin, G. D’Ambrosio, J. Heeck, Phys. Rev. Lett. 114, 151801 (2015). https://doi.org/10.1103/PhysRevLett.114.151801
A. Crivellin, G. D’Ambrosio, J. Heeck, Phys. Rev. D 91(7), 075006 (2015). https://doi.org/10.1103/PhysRevD.91.075006
C. Niehoff, P. Stangl, D.M. Straub, Phys. Lett. B 747, 182 (2015). https://doi.org/10.1016/j.physletb.2015.05.063
D. Aristizabal Sierra, F. Staub, A. Vicente, Phys. Rev. D 92(1), 015001 (2015). https://doi.org/10.1103/PhysRevD.92.015001
A. Celis, J. Fuentes-Martin, M. Jung, H. Serodio, Phys. Rev. D 92(1), 015007 (2015). https://doi.org/10.1103/PhysRevD.92.015007
A. Greljo, G. Isidori, D. Marzocca, JHEP 07, 142 (2015). https://doi.org/10.1007/JHEP07(2015)142
A. Falkowski, M. Nardecchia, R. Ziegler, JHEP 11, 173 (2015). https://doi.org/10.1007/JHEP11(2015)173
B. Allanach, F.S. Queiroz, A. Strumia, S. Sun, Phys. Rev. D 93(5), 055045 (2016). https://doi.org/10.1103/PhysRevD.93.055045 [Erratum: Phys. Rev. D 95(11), 119902 (2017). https://doi.org/10.1103/PhysRevD.95.119902]
C.W. Chiang, X.G. He, G. Valencia, Phys. Rev. D 93(7), 074003 (2016). https://doi.org/10.1103/PhysRevD.93.074003
S.M. Boucenna, A. Celis, J. Fuentes-Martin, A. Vicente, J. Virto, Phys. Lett. B 760, 214 (2016). https://doi.org/10.1016/j.physletb.2016.06.067
E. Megias, G. Panico, O. Pujolas, M. Quiros, JHEP 09, 118 (2016). https://doi.org/10.1007/JHEP09(2016)118
W. Altmannshofer, S. Gori, S. Profumo, F.S. Queiroz, JHEP 12, 106 (2016). https://doi.org/10.1007/JHEP12(2016)106
A. Crivellin, J. Fuentes-Martin, A. Greljo, G. Isidori, Phys. Lett. B 766, 77 (2017). https://doi.org/10.1016/j.physletb.2016.12.057
I. Garcia Garcia, JHEP 03, 040 (2017). https://doi.org/10.1007/JHEP03(2017)040
D. Bhatia, S. Chakraborty, A. Dighe, JHEP 03, 117 (2017). https://doi.org/10.1007/JHEP03(2017)117
C. Bonilla, T. Modak, R. Srivastava, J.W.R. Valle, \(U(1)_{B_3-3L_\mu }\) gauge symmetry as a simple description of \(b\rightarrow s\) anomalies. Phys. Rev. D 98(9), 095002 (2018). https://doi.org/10.1103/PhysRevD.98.095002
R. Alonso, P. Cox, C. Han, T.T. Yanagida, Phys. Lett. B 774, 643 (2017). https://doi.org/10.1016/j.physletb.2017.10.027
J. Ellis, M. Fairbairn, P. Tunney, Anomaly-free models for flavour anomalies. Eur. Phys. J. C 78(3), 238 (2018). https://doi.org/10.1140/epjc/s10052-018-5725-0. arXiv:1705.03447
Y. Tang, Y.-L. Wu, Flavor non-universal gauge interactions and anomalies in B-meson decays. Chin. Phys. C 42(3), 033104 (2018). https://doi.org/10.1088/1674-1137/42/3/033104. arXiv:1705.05643
C.-W. Chiang, X.-G. He, J. Tandean, X.-B. Yuan, \(R_{K^{(*)}}\) and related \(b\rightarrow s\ell \bar{\ell }\) anomalies in minimal flavor violation framework with \(Z^{\prime }\) boson. Phys. Rev. D96(11), 115022. https://doi.org/10.1103/PhysRevD.96.115022. arXiv:1706.02696
S.F. King, JHEP 08, 019 (2017). https://doi.org/10.1007/JHEP08(2017)019
D. Buttazzo, A. Greljo, G. Isidori, D. Marzocca, JHEP 11, 044 (2017). https://doi.org/10.1007/JHEP11(2017)044
E. Megias, M. Quiros, L. Salas, Phys. Rev. D 96(7), 075030 (2017). https://doi.org/10.1103/PhysRevD.96.075030
J.M. Cline, J. Martin Camalich, Phys. Rev. D 96(5), 055036 (2017). https://doi.org/10.1103/PhysRevD.96.055036
J.M. Cline, Phys. Rev. D 97(1), 015013 (2018). https://doi.org/10.1103/PhysRevD.97.015013
G. Ballesteros, A. Carmona, M. Chala, Eur. Phys. J. C 77(7), 468 (2017). https://doi.org/10.1140/epjc/s10052-017-5040-1
M. Chala, JHEP 01, 122 (2013). https://doi.org/10.1007/JHEP01(2013)122
M. Carena, A.D. Medina, N.R. Shah, C.E.M. Wagner, Phys. Rev. D 79, 096010 (2009). https://doi.org/10.1103/PhysRevD.79.096010
F. del Aguila, A. Carmona, J. Santiago, JHEP 08, 127 (2010). https://doi.org/10.1007/JHEP08(2010)127
C. Hagedorn, M. Serone, JHEP 02, 077 (2012). https://doi.org/10.1007/JHEP02(2012)077
A. Carmona, F. Goertz, Nucl. Part. Phys. Proc. 285–286, 93 (2017). https://doi.org/10.1016/j.nuclphysbps.2017.03.017
R. Contino, Y. Nomura, A. Pomarol, Nucl. Phys. B 671, 148 (2003). https://doi.org/10.1016/j.nuclphysb.2003.08.027
K. Agashe, R. Contino, A. Pomarol, Nucl. Phys. B 719, 165 (2005). https://doi.org/10.1016/j.nuclphysb.2005.04.035
K. De Bruyn, R. Fleischer, R. Knegjens, P. Koppenburg, M. Merk, A. Pellegrino, N. Tuning, Phys. Rev. Lett. 109, 041801 (2012). https://doi.org/10.1103/PhysRevLett.109.041801
C. Bobeth, M. Gorbahn, T. Hermann, M. Misiak, E. Stamou, M. Steinhauser, Phys. Rev. Lett. 112, 101801 (2014). https://doi.org/10.1103/PhysRevLett.112.101801
R. Aaij et al., Phys. Rev. Lett. 118(19), 191801 (2017). https://doi.org/10.1103/PhysRevLett.118.191801
T. Aaltonen et al., Phys. Rev. Lett. 102, 201801 (2009). https://doi.org/10.1103/PhysRevLett.102.201801
A.J. Buras, in Probing the standard model of particle interactions. Proceedings, Summer School in Theoretical Physics, NATO Advanced Study Institute, 68th Session, Les Houches, France, July 28–September 5, 1997. Pt. 1, 2 (1998), pp. 281–539
L. Di Luzio, M. Kirk, A. Lenz, Phys. Rev. D 97, 095035 (2018). https://doi.org/10.1103/PhysRevD.97.095035
A. Greljo, D. Marzocca, Eur. Phys. J. C 77(8), 548 (2017). https://doi.org/10.1140/epjc/s10052-017-5119-8
M. Chala, M. Spannowsky, Phys. Rev. D 98(3), 035010 (2018). https://doi.org/10.1103/PhysRevD.98.035010
Acknowledgements
We are grateful to Marco Nardecchia, David Straub and Jorge Martin Camalich, for useful comments and discussions. FG thanks the CERN Theory Department, where part of this work was performed, for its hospitality. The research of AC was supported by a Marie Skłodowska-Curie Individual Fellowship of the European Community’s Horizon 2020 Framework Programme for Research and Innovation under contract number 659239 (NP4theLHC14) and by the Cluster of Excellence Precision Physics, Fundamental Interactions and Structure of Matter (PRISMA—EXC 1098) and Grant 05H12UME of the German Federal Ministry for Education and Research (BMBF).
Author information
Authors and Affiliations
Corresponding author
Additional information
CERN-TH-2017-257, MITP/17-095.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Carmona, A., Goertz, F. Recent \(\varvec{B}\) physics anomalies: a first hint for compositeness?. Eur. Phys. J. C 78, 979 (2018). https://doi.org/10.1140/epjc/s10052-018-6437-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6437-1