Multi-component dark matter: the vector and fermion case

Abstract

Multi-component dark matter scenarios constitute natural extensions of standard single-component setups and offer attractive new dynamics that could be adopted to solve various puzzles of dark matter. In this work we present and illustrate properties of a minimal UV-complete vector-fermion dark matter model where two or three dark sector particles are stable. The model we consider is an extension of the Standard Model (SM) by spontaneously broken extra $U(1)_X$ gauge symmetry and a Dirac fermion. All terms in the Lagrangian which are consistent with the assumed symmetry are present, so the model is renormalizable and consistent. To generate mass for the dark-vector $X_\mu$ the Higgs mechanism with a complex singlet S is employed in the dark sector. Dark matter candidates are the massive vector boson $X_\mu$ and two Majorana fermions $\psi _\pm$. All the dark sector fields are singlets under the SM gauge group. The set of three coupled Boltzmann equations has been solved numerically and discussed. We have performed scans over the parameter space of the model implementing the total relic abundance and direct detection constraints. The dynamics of the vector-fermion dark matter model is very rich and various interesting phenomena appear, in particular, when the standard annihilations of a given dark matter are suppressed then the semi-annihilations, conversions and decays within the dark sector are crucial for the evolution of relic abundance and its present value. Possibility of enhanced self-interaction has been also discussed.

1 Introduction

The experimental data from the WMAP [1] and more recently the Planck [2] collaborations provided an independent and indisputable confirmation for the presence of dark matter (DM) in the Universe. Nevertheless, in spite of a huge theoretical and experimental effort, its nature is still unknown. Till now only gravitational interactions of DM have been detected in a series of independent observations like the flatness of rotation curves of spiral galaxies [3], gravitational lensing [4], and collision of galaxy clusters with its pronounced illustration known as the Bullet cluster [5]. All attempts to detect DM non-gravitational interactions with ordinary matter have failed so far implying more and more stringent limits on DM-nucleon cross-section, see e.g. LUX [6] and XENON-1T [7] results. The most popular models of DM are based on the assumption that it is composed of weakly interacting massive particles (WIMPs). Unfortunately, it turns out that the WIMP scenarios suffer from various difficulties when confronted with observations on small cosmological scales. For instance, the “too-big-to-fail” [8, 9] and the “cusp-core” [10,11,12,13] problems are widely discussed in the literature. In particular, the DM densities inferred in the central regions of DM dominated galaxies are usually smaller than expected from WIMP simulations [14, 15]. It turns out that an appealing solution to those problems is to assume that dark matter self-interacts strongly [16]. The assumption of self-interacting dark matter (SIDM) implies that central (largest) DM density could be reduced. Usually, self-interacting DM scenarios require the presence of light DM and also light DM mediators.

Dark matter could also be searched for through indirect detection experiments, which assume that in regions of large DM density, its pairs are likely to annihilate. Then secondary particles released in this process, e.g. gamma rays, neutrinos, electrons, positrons, protons, and anti-protons, could be observed on Earth, which could reveal some properties of DM. Independent analysis of the Fermi-LAT data [17] by various groups have shown an excess of gamma ray in the energy range $1{-}3\;\hbox {GeV}$ that can be interpreted as a result of DM annihilation in the Galactic Center. Besides the 1–3 GeV excess gamma rays, there exists an observation of unidentified $3.55\;\hbox {keV}$ X-ray line found by [18] and [19]. As shown by several groups, this unknown X-ray line can also be explained by DM annihilation. To explain the indirect signals relatively large DM mass is needed, e.g. $\sim 50\;\hbox {GeV}$ in [20].

Since very different DM masses are needed to solve the small-scale problems (through self-interaction) and to interpret the potential indirect signals, therefore in order to accommodate both observations, a multi-component DM seems to be a natural option. Various multi-component DM models have been proposed and studied in the literature, for instance, multi-scalar DM [21,22,23,24,25,26,27,28,29,30,31,32,33], multi-fermion DM [34,35,36,37,38,39,40,41,42], multi-vector DM  [43, 44], scalar-fermion DM [45,46,47,48,49,50,51,52,53,54], scalar-vector DM [55,56,57], vector-fermion DM [58, 59], and various other generic multi-component DM [60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77] scenarios. Models of multi-component DM were also considered and adopted in astrophysical simulations, e.g. by [78,79,80,81]. Needless to say, the dynamics of multi-component DM is much richer than that of a simple WIMP, and therefore attractive to study by itself, even without any phenomenological direct application. In particular multi-component DM models allow to have, besides the standard annihilations and co-annihilations; conversion, semi-annihilation, and decay processes which make the dark sector (thermal) dynamics much more involved and interesting. Note that most of the models mentioned above, discuss the implications of one or two of these multi-component DM properties.

In this work, we propose a minimal UV complete vector-fermion DM model that predicts two or three stable dark states. Our model involves an extension of the SM by an Abelian dark gauge symmetry $U(1)_X$. The model is minimal in a sense that it contains only three new fields in the dark sector; a dark gauge boson $X_\mu$, a Dirac fermion $\chi$, and a complex scalar S, which serves as a Higgs field in the hidden sector. They are singlets under the SM gauge group but they are all charged under the dark $U(1)_X$ gauge symmetry and therefore they interact with each other. The complex scalar S acquires a vacuum expectation value (vev) and gives mass to the dark gauge boson $X_\mu$ by the dark sector Higgs mechanism. It also contributes to the mass of the Dirac fermion $\chi$ through the Yukawa coupling. Moreover, the presence of the Dirac mass for the fermion introduces a mixing of its chiral components. After diagonalization of the mass matrix, the Dirac fermion splits into two Majorana fermions $\psi _\pm$ with mass eigenvalues $m_\pm$. As a result, after the dark sector symmetry breaking we have three potentially stable interacting particles: a dark vector and two Majorana fermions. Their stability is ensured by a residual $Z_2\!\times \!Z_2^\prime$ discrete symmetry, which also dictates the possible form of dark sector interactions. The communication with the visible (SM) sector proceeds only via the Higgs portal $\kappa |H^2||S^2|$.

Our minimal vector-fermion dark matter model has many attractive features. First of all, the very fact that in the multi-component DM literature, the vector-fermion dark matter possibility has not been studied in detail¹ speaks for itself and therefore the goal of this work is to provide an extensive analysis of the minimal vector-fermion scenario. Some of the interesting features of the model are: (1) the presence of a second scalar helps to achieve the stability of the SM Higgs potential even at the tree level, see e.g. [82,83,84], (2), a possibility of enhancing vector component self interactions, see e.g. [85], (3) a very small/large mass splitting among the dark sector states (vector and Majorana fermions) are possible without large tuning of the parameters, (4) our model is a gauged version of the model considered by Weinberg [86] for different purposes, and (5) more importantly the minimality of the model; since there is only one parameter, the dark gauge coupling coupling $g_{\textsc {x}}$, which controls the dynamics in the dark sector, including the conversion, semi-annihilation and decay processes. In this work, we are going to illustrate the relevance of conversions, semi-annihilations, and decays in the vector-fermion DM model.

The paper is organized as follows. In Sect. 2 the vector-fermion (2-3 component) model of DM is presented. Solutions of three coupled Boltzmann equations are discussed in Sect. 3 focusing on conversion, semi-annihilation, and decay processes. There we show results of a detailed scan over the parameter space of the model satisfying the observed total relic density and direct detection constraints. In Sect. 4 we focus on the region with large self-interaction cross-section. Section 5 contains summary and conclusions. Moreover, we supplement our work with an “Appendix A”, collecting details of the derivation of Boltzmann equations, and an “Appendix B”, describing the method adopted to obtain constraints for a multi-component DM model by direct detection experiments.

2 Vector-fermion multi-component dark matter model

In this section, we explore the possibility of having a multi-component dark matter model with a vector boson and a Dirac fermion (charged under a dark sector gauge symmetry) which may serve as dark matter candidates. As mentioned in the Introduction, we consider a minimal extension of the SM by an additional $U(1)_X$ gauge symmetry of the dark sector with a complex scalar field S and a Dirac fermion $\chi$, both charged under the dark-sector gauge group. We employ the Higgs mechanism in the dark sector such that the vev of the complex scalar S generates a mass for the $U(1)_X$ gauge field $X_\mu$. The dark-segment fields have the following quantum numbers under the gauge group $SU(3)_c\!\times \!SU(2)_L\!\times \!U(1)_Y\!\times \! U(1)_X$,

$$\begin{aligned} S&=({\mathbf {1}},{\mathbf {1}},0,1),\quad \chi =\left( {\mathbf {1}},{\mathbf {1}},0,\tfrac{1}{2}\right) . \end{aligned}$$

(1)

We assume that none of the SM fields is charged under the dark gauge symmetry $U(1)_X$.

We can write down the Lagrangian for our simplest vector-fermion MCDM model as

$$\begin{aligned} {\mathcal {L}}&={\mathcal {L}}_{\mathrm{SM}}+{\mathcal {L}}_{\mathrm{DS}}+{\mathcal {L}}_{\mathrm{portal}}, \end{aligned}$$

(2)

where ${\mathcal {L}}_{\mathrm{SM}}$ is the SM Lagrangian, ${\mathcal {L}}_{\mathrm{DS}}$ is the dark-sector Lagrangian,

(3)

and ${\mathcal {L}}_{\mathrm{portal}}$ is the Lagrangian for the Higgs portal interactions between the SM and the dark sector,

$$\begin{aligned} {\mathcal {L}}_{\mathrm{portal}}&=-\kappa |S|^2|H|^2. \end{aligned}$$

(4)

Note that the portal coupling is the only communication between the SM and the dark sector. Above, in Eq. (3) $X_{\mu \nu }\equiv \partial _\mu X_\nu -\partial _\nu X_\mu$ is the field strength tensor for the $X_\mu$ field and ${{\mathcal {D}}}_\mu$ is the covariant derivative defined as

$$\begin{aligned} {{\mathcal {D}}}_\mu =\partial _\mu +i\,g_{\textsc {x}}\,q_{\textsc {x}}\, X_\mu , \end{aligned}$$

(5)

where $g_{\textsc {x}}$ is the coupling constant corresponding to the gauge group $U(1)_X$, whereas $q_{\textsc {x}}$ are the $U(1)_X$ charges 1 and $\tfrac{1}{2}$ for S and $\chi$ (as defined in 1), respectively. Moreover, in Eq. (3) $m_D$ is the Dirac mass, $y_{\textsc {x}}$ is the dark Yukawa coupling and ${{\mathcal {C}}}\!\equiv \! -i \gamma _2\gamma _0$ is the charge-conjugation operator, where $\gamma _0,\gamma _2$ are the gamma matrices. It is important to note that the dark sector is invariant with respect to the charge conjugation symmetry ${{\mathcal {C}}}$ under which the dark fields transform as follows:

$$\begin{aligned} X_\mu \xrightarrow {{{\mathcal {C}}}} -X_\mu ,\quad S \xrightarrow {{{\mathcal {C}}}} S^*, \quad \chi \xrightarrow {{{\mathcal {C}}}} \chi ^c\equiv -i\gamma _2 \chi ^*. \end{aligned}$$

(6)

The symmetry forbids a kinetic mixing between the weak hypercharge $U(1)_Y$ and the dark $U(1)_X$, so that $X_\mu$ can not decay into SM particles.

It is useful to collect the full scalar potential of our model,

$$\begin{aligned} \begin{aligned} V(H,S)=&-\mu _H^2 |H|^2-\mu _S^2 |S|^2 \\&+\lambda _H |H|^4+\lambda _S |S|^4+\kappa |H|^2 |S|^2. \end{aligned} \end{aligned}$$

(7)

Tree-level positivity/stability of the above scalar potential requires the following conditions to be satisfied:

$$\begin{aligned} \lambda _H>0,\quad \lambda _S>0, \quad \kappa >-2\sqrt{\lambda _H\lambda _S}. \end{aligned}$$

(8)

It is straightforward to find the minimization conditions for the scalar potential (7) as

$$\begin{aligned} \begin{aligned} \big (2\lambda _H v^2-2\mu _H^2+\kappa v_{\textsc {x}}^2\big )v&=0, \\ \big (2\lambda _S v_{\textsc {x}}^2-2\mu _S^2+\kappa v^2\big )v_{\textsc {x}}&=0, \end{aligned} \end{aligned}$$

(9)

where $\langle H^\intercal \rangle \equiv (0,v/\sqrt{2})$ and $\langle S\rangle \equiv v_{\textsc {x}}/\sqrt{2}$ are the vevs of the respective fields.² In order to have both vevs non-zero (v provides masses to the SM gauge bosons and the dark-sector scalar vev $v_{\textsc {x}}$ generates mass for the dark vector) we require $\kappa ^2>4\lambda _H\lambda _S$ and the values of vevs are:

$$\begin{aligned} v^2=\frac{4\lambda _S\mu _H^2-2\kappa \mu _S^2}{4\lambda _H\lambda _S-\kappa ^2}, \quad v_{\textsc {x}}^2=\frac{4\lambda _H\mu _S^2-2\kappa \mu _H^2}{4\lambda _H\lambda _S-\kappa ^2}. \end{aligned}$$

(10)

We expand the Higgs doublet and the singlet around their vevs as:

$$\begin{aligned} H=\frac{1}{\sqrt{2}}\begin{pmatrix} \sqrt{2} \pi ^+\\ v+h+i\pi ^0\end{pmatrix}, \quad S=\frac{1}{\sqrt{2}}\big (v_{\textsc {x}}+\phi +i\sigma \big ), \end{aligned}$$

(11)

where $\pi ^{0,\pm }$ and $\sigma$ are the would-be Goldstone modes that disappear in the unitary gauge. Hence, only the scalars h and $\phi$ correspond to the physical states. The mass squared matrix for the scalar fluctuations $(h,\phi )$ is given by,

$$\begin{aligned} {{\mathcal {M}}}^2=\begin{pmatrix} 2\lambda _H v^2&{} \kappa v v_{\textsc {x}}\\ \kappa v v_{\textsc {x}}&{} 2\lambda _S v_{\textsc {x}}^2\end{pmatrix}. \end{aligned}$$

(12)

The above mass squared matrix ${{\mathcal {M}}}^2$ can be diagonalized by the orthogonal rotational matrix ${{\mathcal {R}}}$, such that,

$$\begin{aligned} {{\mathcal {M}}}^2_{\text {diag}}\equiv & {} {{\mathcal {R}}}^{-1}{{\mathcal {M}}}^2{{\mathcal {R}}}=\begin{pmatrix} m_{h_1}^2 &{}0\\ 0&{}m_{h_2}^2\end{pmatrix}, \nonumber \\ \text {where}\quad {{\mathcal {R}}}= & {} \begin{pmatrix}\cos \!\alpha &{} -\sin \!\alpha \\ \sin \!\alpha &{}\cos \!\alpha \end{pmatrix}, \end{aligned}$$

(13)

and $(h_{1},h_{2})$ are the two physical mass-eigenstate Higgs bosons with masses $(m_{h_{1}}^2,m_{h_2}^2)$, defined in terms of $(h,\phi )$ as

$$\begin{aligned} \begin{pmatrix} h_1 \\ h_2\end{pmatrix} ={{\mathcal {R}}}^{-1}\begin{pmatrix} h\\ \phi \end{pmatrix}. \end{aligned}$$

(14)

The mixing angle $\alpha$ could be expressed in terms of mass matrix elements as follows:

$$\begin{aligned} \tan (2\alpha )=\frac{\kappa v v_{\textsc {x}}}{ v^2\lambda _H- v_{\textsc {x}}^2\lambda _S}\,. \end{aligned}$$

(15)

We will later adopt $\sin \!\alpha$ as an independent input parameter while scanning over model parameters. The masses for the two eigenstates $h_1$ and $h_2$ are

$$\begin{aligned} m_{h_1}^2&=v^2 \lambda _H + v_{\textsc {x}}^2 \lambda _S + (v^2\lambda _H- v_{\textsc {x}}^2\lambda _S)/\!\cos (2\alpha ), \end{aligned}$$

(16)

$$\begin{aligned} m_{h_2}^2&=v^2 \lambda _H + v_{\textsc {x}}^2 \lambda _S - (v^2\lambda _H- v_{\textsc {x}}^2\lambda _S)/\!\cos (2\alpha )\,. \end{aligned}$$

(17)

In this analysis we will treat the two Higgs masses as independent parameters. It is always assumed that $h_1$ is the observed state with $m_{h_1}\!=\!125\;\hbox {GeV}$. The other mass eigenstate could be either lighter or heavier than $h_1$. After the spontaneous symmetry breaking (SSB) the SM fermions acquire mass from the SM Higgs doublet, whereas the dark sector fermion $\chi$ receives mass from the dark-scalar S through the Yukawa interaction term and from the Dirac mass term. After the SSB the dark fermionic sector Lagrangian can be rewritten as,

$$\begin{aligned} {{\mathcal {L}}}_{\textsc {df}}&=\frac{i}{2}\big ({\bar{\chi }} \gamma ^\mu \partial _\mu \chi +\bar{\chi ^c} \gamma ^\mu \partial _\mu \chi ^c\big )-\frac{m_D}{2}\big ({\bar{\chi }}\chi +\bar{\chi ^c} \chi ^c\big )\nonumber \\&\quad -\frac{y_{\textsc {x}}v_{\textsc {x}}}{2}\big (\bar{\chi ^c }\chi +{\bar{\chi }}\chi ^c \big ) -\frac{g_{\textsc {x}}}{4} \big ({\bar{\chi }} \gamma ^\mu \chi -\bar{\chi ^c} \gamma ^\mu \chi ^c\big ) X_\mu \nonumber \\&\quad -\frac{y_{\textsc {x}}}{2}\big (\bar{\chi ^c} \chi +{{\bar{\chi }}}\chi ^c \big )\phi . \end{aligned}$$

(18)

In the above Lagrangian the field $\chi$ and its charge-conjugate $\chi ^c$ mix through the Yukawa interactions. One can easily diagonalize the above Lagrangian in terms of the following Majorana mass-eigenstates $\psi _\pm$ ($=\psi _\pm ^c$)

$$\begin{aligned} \psi _{\!+}\equiv \frac{1}{\sqrt{2}}\big (\chi +\chi ^c\big ), \quad \psi _{\!-}\equiv \frac{1}{i\sqrt{2}}\big (\chi -\chi ^c\big ), \end{aligned}$$

(19)

with mass eigenvalues,

$$\begin{aligned} m_\pm =m_D\pm y v_{\textsc {x}}. \end{aligned}$$

(20)

In the new basis we can rewrite the above dark fermionic Lagrangian as,

$$\begin{aligned} {{\mathcal {L}}}_{\textsc {df}}&=\frac{i}{2}\big ({\bar{\psi }}_{\!+} \gamma ^\mu \partial _\mu \psi _{\!+} +{\bar{\psi }}_{\!-} \gamma ^\mu \partial _\mu \psi _{\!-}\big )-\frac{1}{2}m_+{\bar{\psi }}_{\!+}\psi _{\!+}\nonumber \\&\quad -\frac{1}{2} m_-{\bar{\psi }}_{\!-} \psi _{\!-}-\frac{i}{4}g_{\textsc {x}}\big ({\bar{\psi }}_{\!+} \gamma ^\mu \psi _{\!-} - {\bar{\psi }}_{\!-} \gamma ^\mu \psi _{\!+}\big ) X_\mu \nonumber \\&\quad -\frac{y_{\textsc {x}}}{2}\big ({\bar{\psi }}_{\!+}\psi _{\!+} -{\bar{\psi }}_{\!-} \psi _{\!-} \big )\phi . \end{aligned}$$

(21)

The mass splitting between $\psi _+$ and $\psi _-$ is controlled by the Yukawa coupling and $v_{\textsc {x}}$:

$$\begin{aligned} \varDelta m\equiv m_+-m_- =2 y_{\textsc {x}}v_{\textsc {x}}. \end{aligned}$$

(22)

Hereafter, we will assume $y_{\textsc {x}}\!>\! 0$ and since $v_{\textsc {x}}$ could be chosen positive therefore we have $m_+\!>\!m_-$.

Note that the above Lagrangian is invariant with respect to a discrete symmetry $Z_2\!\times \!Z_2^\prime$, under which the SM fields are even whereas the dark sector fields transform non-trivially, as given in Table 1. It is easy to see that the above $Z_2$ is a direct consequence of the charge conjugation symmetry (6). It is worth to notice that since $v_{\textsc {x}}$ is real (without compromising any generality) therefore the charge conjugation remains unbroken so that $X_\mu$ cannot decay into SM particles, see also [59]. On the other hand $Z_2^\prime$ is implied by the $U(1)_X$ gauge symmetry. Note that the $Z_2^{\prime \prime }$ is responsible for the stability of $\psi _-$ since it is lighter than $\psi _+$. It is interesting to notice that our model has also a discrete $Z_4$ symmetry³ under which the three dark matter components are charged. The $Z_4$ charges are:

$$\begin{aligned} \Phi \rightarrow e^{i\pi n_{\Phi }} \Phi , \quad {\mathrm{where}}\quad \Phi =(X_\mu ,\psi _\pm ,\phi ), \end{aligned}$$

(23)

with $n_\Phi =(1,\pm \tfrac{1}{2},0)$, whereas all the SM particles are neutral under this symmetry. However, for our analysis the $Z_2\!\times \!Z_2^\prime$ (along with $Z_2^{\prime \prime }$) completely specifies all the relevant properties of $Z_4$, therefore hereafter we only consider $Z_2\!\times \!Z_2^\prime$.

Table 1 Discrete symmetries of the vector-fermion DM model

Fig. 1

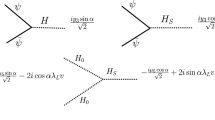
The most relevant Feynman rules for vector-fermion dark matter sector (X is the dark vector and $\psi _\pm$ are the dark fermions) and its mixing with the SM, where V represents the SM gauge bosons (Z, W), f denotes the SM fermions, and ${{\mathcal {R}}}$ is the rotation matrix, defined in Eq. (13), where the two scalars $h_1,h_2$ mix with mixing angle $\alpha$

As it can be seen from the above fermionic Lagrangian there is only one interaction term between all three components of the dark segment (the vector boson $X_\mu$ and the two Majorana fermions $\psi _\pm$):

$$\begin{aligned} -\frac{i}{4}g_{\textsc {x}}\big ({\bar{\psi }}_{\!+} \gamma ^\mu \psi _{\!-} - {\bar{\psi }}_{\!-} \gamma ^\mu \psi _{\!+}\big ) X_\mu \,. \end{aligned}$$

(24)

In Fig. 1, we collect all the relevant vertices that desckineticribe interactions of the dark segment of the theory.

As depicted in Fig. 2, depending on the masses of dark particles, there are three cases⁴ in which two or all three particles could be stable and serve as dark matter:

• The first case is when $m_+ \!>\! m_-+m_X$, the Majorana fermion $\psi _{\!+}$ will decay into a stable vector $X_\mu$ and a stable Majorana fermion $\psi _{\!-}$. This is a 2CDM case, the white area (left) in Fig. 2.

• The second case is when $m_X\!>\! m_++m_-$, the vector $X_\mu$ will decay into two stable Majorana fermions $\psi _\pm$. This is a 2CDM case, the white area (right) in Fig. 2.

• The third case is when $m_+ \!+\!m_-\!>\!m_X\!>\!m_+\!-\!m_-$, so that none of the three particle will decay and hence all are stable. This is a 3CDM case, shown as gray region in Fig. 2. Note that the boundaries (right/left) of the gray region correspond to the case when $m_X=m_+\pm m_-$.

2.1 Input parameters

Here we outline the strategy adopted to investigate the vector-fermion dark matter (VFDM) model. First of all, we would like to count the free parameters in the model and the number of constraints. There are five parameters in the scalar potential (7), namely, mass parameters $\mu _H,\,\mu _S$, quartic couplings $\lambda _H,\lambda _S$ and the portal coupling $\kappa$. Additionally, there are three parameters in the dark gauge and fermionic part, i.e. the dark gauge coupling $g_{\textsc {x}}$, the fermion Dirac mass $m_D$, and the Yukawa coupling $y_{\textsc {x}}$, see Eq. (3). In total there are eight parameters of the model, however there are two constraints from the SM Higgs vev v and the Higgs mass $m_{h_1}$, hence leaving six parameters free. We adopt the following set as an independent input parameters:

$$\begin{aligned} m_{h_2},\,m_X,\, m_+,\, m_-,\, \sin \!\alpha ,\, g_{\textsc {x}}. \end{aligned}$$

(25)

Note that the mixing angle $\sin \!\alpha$ is constrained by the SM-like Higgs couplings with the gauge bosons. We employed $|\sin \!\alpha |\!\le \!0.33$, the current LHC $2\sigma$ bound [87].

Fig. 2

Schematic diagram for the 2- and 3-component vector-fermion dark matter scenarios. We consider $m_+$ to have a fixed value and the gray region represent parameter space where the all three dark sector particles ($X_\mu ,\psi _+,\psi _-$) are stable, whereas the white regions represent the 2-component scenarios where $\psi _+$ and $X_\mu$ are unstable, respectively

Remaining parameters could be expressed in terms of the input set as follows (note the potential mass parameters $\mu _H,\,\mu _S$ are already traded for $v,\, v_{\textsc {x}}$, see Eq. 10):

$$\begin{aligned} v_{\textsc {x}}&=\frac{m_X}{g_{\textsc {x}}}, \quad \kappa =\frac{(m_{h_1}^2 -m_{h_2}^2) \sin (2 \alpha )}{2vv_{\textsc {x}}}, \end{aligned}$$

(26)

$$\begin{aligned} \lambda _H&=\frac{m_{h_1}^2\cos ^2\alpha +m_{h_2}^2\sin ^2\alpha }{2 v^2},&\end{aligned}$$

(27)

$$\begin{aligned} \lambda _S&=\frac{m_{h_1}^2\sin ^2\alpha +m_{h_2}^2\cos ^2\alpha }{2 v_{\textsc {x}}^2},&\end{aligned}$$

(28)

$$\begin{aligned} y_{\textsc {x}}&=\frac{(m_+-m_-)}{2 v_{\textsc {x}}}, \quad m_D=\frac{(m_++m_-)}{2}\,. \end{aligned}$$

(29)

Note that the Yukawa coupling $y_{\textsc {x}}\!=\!\varDelta m/(2 v_{\textsc {x}})\! =\! \varDelta m/(2m_X)\! \times \!g_{\textsc {x}}$, therefore for fixed $m_X$ the Yukawa coupling $y_{\textsc {x}}$ is proportional to $g_{\textsc {x}}$. In other words, for fixed $m_X$, the vev $v_{\textsc {x}}$ must vary if $g_{\textsc {x}}$ is being changed, implying a variation of $y_{\textsc {x}}$. This remark is important hereafter, e.g. for fixed $\varDelta m$ and $m_X$ one has to adjust $g_{\textsc {x}}$ in order to satisfy constraints from direct detection experiments even in the case when DM is dominated by $\psi _\pm$.

3 Vector-fermion dark matter phenomenology

In this section we present coupled Boltzmann equations for the evolution of number density of dark matter particles ($X_\mu ,\psi _+,\psi _-$) in VFDM model. Figures 3, 4 and 5 contain Feynman diagrams relevant for collision terms for the annihilation, semi-annihilation and conversion processes, respectively. It is assumed that dark matter components scatter against SM particles frequently enough so that their temperatures are the same as that of the thermal bath.

Fig. 3

The vector dark matter $X_\mu$ and Majorana fermion dark matter $\psi _\pm$ annihilation diagrams. Above V and $({\bar{f}})f$ denote the SM vector bosons ($W^\pm$ and Z) and the SM (anti)fermions (quarks and leptons)

Fig. 4

Semi-annihilation diagrams for the dark particles $X, \psi _\pm$. In these processes two of the dark sector particles annihilate to a dark sector particle and a SM particle in the thermal bath

Fig. 5

Dark matter conversion processes involving X and $\psi _\pm$. These processes are important to keep thermal equilibrium within the dark sector

The Boltzmann equations for the DM components ($X_\mu , \psi _+,\psi _-$), can written as:

$$\begin{aligned} \frac{dn_{X}}{dt}&= -3H n_{X}-\left\langle \sigma ^{XX\phi \phi ^\prime }_{v_{\text {M}\varnothing \text {l}}} \right\rangle \left( n_{X}^2-{\bar{n}}_{X}^2\right) \nonumber \\&\quad -\left\langle \sigma ^{X\psi _{\!+}\psi _{\!-} h_i}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{X}n_{\psi _{\!+}}-{\bar{n}}_{X} {\bar{n}}_{\psi _{\!+}}\frac{ n_{\psi _{\!-}}}{{\bar{n}}_{\psi _{\!-}}}\right) \nonumber \\&\quad -\left\langle \sigma ^{X\psi _{\!-}\psi _{\!+} h_i}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{X}n_{\psi _{\!-}}-{\bar{n}}_{X} {\bar{n}}_{\psi _{\!-}}\frac{ n_{\psi _{\!+}}}{{\bar{n}}_{\psi _{\!+}}}\right) \nonumber \\ {}&\quad -\left\langle \sigma ^{Xh_i\psi _{\!+}\psi _{\!-} }_{v_{\text {M}\varnothing \text {l}}}\right\rangle {\bar{n}}_{h_i}\left( n_{X}-{\bar{n}}_{X} \frac{ n_{\psi _{\!+}}n_{\psi _{\!-}}}{{\bar{n}}_{\psi _{\!+}}{\bar{n}}_{\psi _{\!-}}}\right) \nonumber \\&\quad -\left\langle \sigma ^{XX\psi _+\psi _+}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{X}^2- {\bar{n}}_{X}^2\frac{n_{\psi _+}^2}{{\bar{n}}_{\psi _+}^2}\right) \nonumber \\&\quad -\left\langle \sigma ^{XX\psi _-\psi _-}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{X}^2- {\bar{n}}_{X}^2\frac{n_{\psi _-}^2}{{\bar{n}}_{\psi _-}^2}\right) \nonumber \\&\quad +\varGamma _{\psi _{\!+}\rightarrow X\psi _{\!-}}\left( n_{\psi _{\!+}}-{\bar{n}}_{\psi _{\!+}}\frac{n_{X}}{{\bar{n}}_{X}}\frac{n_{\psi _{\!-}}}{{\bar{n}}_{\psi _{\!-}}}\right) , \end{aligned}$$

(30)

$$\begin{aligned} \frac{dn_{\psi _-}}{dt}&= -3H n_{\psi _-}-\left\langle \sigma ^{\psi _-\psi _-\phi \phi ^\prime }_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{\psi _-}^2-{\bar{n}}_{\psi _-}^2\right) \nonumber \\&-\left\langle \sigma ^{\psi _-\psi _+ X h_i}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{\psi _-}n_{\psi _+}-{\bar{n}}_{\psi _-} {\bar{n}}_{\psi _+}\frac{ n_{X}}{{\bar{n}}_{X}}\right) \nonumber \\&\quad -\left\langle \sigma ^{X\psi _{\!-}\psi _{\!+} h_i}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{X}n_{\psi _{\!-}}-{\bar{n}}_{X} {\bar{n}}_{\psi _{\!-}}\frac{ n_{\psi _{\!+}}}{{\bar{n}}_{\psi _{\!+}}}\right) \nonumber \\&\quad -\left\langle \sigma ^{\psi _- h_iX\psi _+}_{v_{\text {M}\varnothing \text {l}}}\right\rangle {\bar{n}}_{h_i} \left( n_{\psi _-}- {\bar{n}}_{\psi _-}\frac{n_{\psi _+}}{{\bar{n}}_{\psi _+}}\frac{ n_{X}}{{\bar{n}}_{X}}\right) \nonumber \\&\quad -\left\langle \sigma ^{\psi _-\psi _-XX}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{\psi _-}^2-{\bar{n}}_{\psi _-}^2 \frac{n_{X}^2}{{\bar{n}}_{X}^2}\right) \nonumber \\&\quad - \left\langle \sigma ^{\psi _-\psi _-\psi _+\psi _+}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{\psi _-}^2- {\bar{n}}_{\psi _-}^2\frac{n_{\psi _+}^2}{{\bar{n}}_{\psi _+}^2}\right) \nonumber \\&\quad +\varGamma _{\psi _+\rightarrow X\psi _-} \left( n_{\psi _+}- {\bar{n}}_{\psi _+}\frac{n_{\psi _-}}{{\bar{n}}_{\psi _-}}\frac{ n_{X}}{{\bar{n}}_{X}}\right) , \end{aligned}$$

(31)

$$\begin{aligned} \frac{dn_{\psi _+}}{dt}&= -3H n_{\psi _+}-\left\langle \sigma ^{\psi _+\psi _+\phi \phi ^\prime }_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{\psi _+}^2-{\bar{n}}_{\psi _+}^2\right) \nonumber \\&\quad -\left\langle \sigma ^{\psi _+\psi _- X h_i}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{\psi _+}n_{\psi _-}-{\bar{n}}_{\psi _+} {\bar{n}}_{\psi _-}\frac{ n_{X}}{{\bar{n}}_{X}}\right) \nonumber \\&\quad -\left\langle \sigma ^{X\psi _{\!+}\psi _{\!-} h_i}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{X}n_{\psi _{\!+}}-{\bar{n}}_{X} {\bar{n}}_{\psi _{\!+}}\frac{ n_{\psi _{\!-}}}{{\bar{n}}_{\psi _{\!-}}}\right) \nonumber \\&\quad -\left\langle \sigma ^{\psi _+ h_iX\psi _-}_{v_{\text {M}\varnothing \text {l}}}\right\rangle {\bar{n}}_{h_i} \left( n_{\psi _+}- {\bar{n}}_{\psi _+}\frac{n_{\psi _-}}{{\bar{n}}_{\psi _-}}\frac{ n_{X}}{{\bar{n}}_{X}}\right) \nonumber \\&\quad -\left\langle \sigma ^{\psi _+\psi _+XX}_{v_{\text {M}\varnothing \text {l}}}\right\rangle \left( n_{\psi _+}^2-{\bar{n}}_{\psi _+}^2 \frac{n_{X}^2}{{\bar{n}}_{X}^2}\right) \nonumber \\&\quad - \langle \sigma ^{\psi _+\psi _+\psi _-\psi _-}_{v_{\text {M}\varnothing \text {l}}}\rangle \left( n_{\psi _+}^2- {\bar{n}}_{\psi _+}^2\frac{n_{\psi _-}^2}{{\bar{n}}_{\psi _-}^2}\right) \nonumber \\&\quad -\varGamma _{\psi _+\rightarrow X\psi _-} \left( n_{\psi _+}- {\bar{n}}_{\psi _+}\frac{n_{\psi _-}}{{\bar{n}}_{\psi _-}}\frac{ n_{X}}{{\bar{n}}_{X}}\right) , \end{aligned}$$

(32)

where $\langle \sigma ^{ijkl}_{v_{\text {M}\varnothing \text {l}}}\rangle \equiv \langle \sigma ^{ijkl}{v_{\text {M}\varnothing \text {l}}}\rangle$ is the thermally averaged cross-section for the process $ij\rightarrow kl$ as defined in Eq. (A.17). Above $h_i=h_1,h_2$ and $\phi \phi ^\prime$ denote all the allowed SM particles including $h_1,h_2$. In the above Boltzmann equations (30)–(32), the first term $3H n_{i}$ is the usual term in an expanding universe with Hubble parameter H. The second term in Eqs. (30)–(32) is the standard annihilation term for each dark particle corresponding to Feynman diagrams Fig. 3, whereas, the third, fourth and fifth terms are capturing the effects of semi-annihilations shown in Feynman diagrams Fig. 4, and the sixth and seventh terms are conversion processes within the dark sector shown in Fig. 5. Note the last term in these Boltzmann equations is for the case considered in Sec. 3.1.1 when $\psi _+$ is unstable and it decays to stable particles $X_\mu$ and $\psi _-$. However, for the case discussed in Sec. 3.1.2 where $X_\mu$ is unstable and it decays to stable particles $\psi _+$ and $\psi _-$, we replace $\psi _+\leftrightarrow X$ and change signs of the last terms in Eqs. (30)–(32). Moreover, for the case studied in Sec. 3.1.3 when all three dark particles $X_{\mu },\psi _\pm$ are stable then the last terms in the above Boltzmann equations are zero. The details of the derivation of above collision terms are presented in “Appendix A”.

After solving the Boltzmann equations we calculate the present relic density of the dark species as,

$$\begin{aligned} \varOmega _i h^2=\frac{h^2 s_0}{\rho _{\text {cr}}}m_iY_i=2.742\times 10^{8}\left( \frac{m_i}{\text {GeV}}\right) Y_i, \end{aligned}$$

(33)

where $s_0$ is the total entropy density today, $\rho _{\text {cr}}$ is the critical density, $m_i$ is the mass of the dark particle and $Y_i$ is the yield of the dark particle today. Total dark matter relic density is a sum of the individual relics, i.e.

$$\begin{aligned} \varOmega _{\text {tot}} h^2=\sum _i \varOmega _i h^2. \end{aligned}$$

(34)

The total relic density $\varOmega _{\mathrm{tot}} h^2$ is compared to the observed dark matter relic density $\varOmega _{\text {obs}} h^2\!=\!0.1197 \pm 0.0022$ by the PLANCK satellite [2].

The simple form of the derived Boltzmann equations relies on the assumption of kinetic equilibrium between visible and hidden sectors which is maintained by frequent scatterings of dark matter species on relativistic SM states. Effects of kinetic decoupling are negligible in the calculation of relic densities only if its temperature $T_{kd}$ is smaller or comparable to the chemical decoupling temperature, $T_{cd}$, at which DM annihilation is no longer effective. $T_{kd}$ can be estimated by comparing the scattering rates $\varGamma _s(T)$ for the processes $DM SM\rightarrow DM SM$ with the Hubble rate H(T) [88].

$$\begin{aligned} \varGamma _s(T)=n_r \langle \sigma _s v \rangle \frac{T}{m_{DM}}, \end{aligned}$$

(35)

where $n_r$ is the equilibrium density of relativistic states in the thermal bath, $\langle \sigma _s v \rangle$ is the thermally averaged scattering cross-section and $T/m_{DM}$ describes momentum transfer at each collision. $m_{DM}$ is the mass of the dominant DM component, so either $m_X$ or $m_\pm$. Considering scatterings of $\psi _\pm$ and X on SM quarks and leptons we find using the expansion of the scattering amplitudes [89] that

$$\begin{aligned} T_{kd}\simeq \frac{1.8\times 10^{-8}\;{\mathrm{GeV}}^{-3/2}}{g_{\textsc {x}}\sin \alpha } \frac{\xi \sqrt{m_X} m^2_{h_1} m^2_{h_2}}{|m^2_{h_1}-m^2_{h_2}|}, \end{aligned}$$

(36)

where $\xi =1$ if scattering of X dominates and $\xi =2\sqrt{m_X m_\pm }/(m_+-m_-)$ for the $\psi _\pm$ domination. Choosing typical values that are used in further discussions $g_{\textsc {x}}\sim \sin \alpha \sim 0.1$ and $m_{DM} \sim {{\mathcal {O}}}(100)\;\hbox {GeV}$, we obtain $T_{kd}\lesssim 0.5$ GeV which is well below the temperature of the chemical decoupling in this case ($T_{cd}\simeq m_{DM}/20$). It becomes comparable to $T_{cd}$ only for degenerate Higgs masses, but we checked that for the parameters we adopt always $T_{kd}<T_{cd}$.

Even without solving the above coupled set of Boltzmann equations (30)–(32) some generic observations could be made:

• Conversions are present even in the absence of the dark sector self-interactions, an existence of a mediator is the only requirement. On the other hand, the existence of semi-annihilations and decays of dark particle depend on the presence a vertex with three dark states, which have different transformation rules under the dark symmetry (such that a singlet could be formed), in our model such an interaction is in Eq. (24).

• When, for a given dark matter species, a standard annihilation channel is suppressed then its abundance might be very sensitive to the presence of other ingredients of the dark segment. In this case semi-annihilation plays a major role, e.g. if $\psi _-\psi _- \rightarrow h_ih_i$ (or any SM states) is suppressed then $\psi _-$ can still disappear, for instance, through $\psi _- \psi _+ \rightarrow X_\mu h_i$ followed by unsuppressed annihilation of pairs of $X_\mu$, see also [45]. In other words, $X_\mu$ can work as a catalyzer that enables disappearance of $\psi _-$. In this case, it is possible that the presence of other ($\psi _+$ and/or $X_\mu$) dark components might be crucial for the determination of the asymptotic abundance of the major DM element. Also, decays within the dark sector may play a relevant role in the determination of the final abundance.

• Standard WIMPs decouple from thermal equilibrium at $m/T \!\sim \!20\!-\!25$, which implies that the heavy states decouple earlier (large T). However, in the multi-component scenario, it might be possible that the decoupling of a heavier dark component is delayed so that it happens later than that of a lighter one. The effect is again a consequence of interactions with remaining dark matter states.

In particular, as a proof of principle, below we consider two interesting possibilities in our specific vector-fermion DM scenario:

• (A) ${y_{\textsc {x}}\ll 1 (m_+\simeq m_-)}$: Small $y_{\textsc {x}}$ implies suppressed $\psi _\pm \psi _\pm$ annihilation, so $\psi _\pm$ dominates the dark matter abundance. Since the annihilation is slow therefore $Y_{\psi _\pm }$ is controlled by semi-annihilation which is sensitive to $g_{\textsc {x}}$ and to the presence of other dark components. In order to have semi-annihilation controlled exclusively by $g_{\textsc {x}}$ one should assume $m_++m_- > m_X+m_{h_2}$.

• (B) ${y_{\textsc {x}}\gg 1 (m_+\gg m_-)}$: In this case, one expects fast $\psi _\pm \psi _\pm$ annihilation and so that $X_\mu$ may dominate the dark matter abundance. If in addition $\sin \!\alpha \ll 1$ then XX annihilation would be suppressed so that $Y_X$ shall be controlled by semi-annihilation and conversion processes which are sensitive to the gauge coupling $g_{\textsc {x}}$ and Yukawa coupling $y_{\textsc {x}}$. In both cases, $X_\mu$ would be effectively replaced by $\psi _\pm$, which then would disappear through enhanced standard annihilation.

It is worth to emphasize the importance of the gauge coupling $g_{\textsc {x}}$ between all the dark components $X_\mu$, $\psi _+$ and $\psi _-$. This is the most relevant coupling which determines interesting aspects of dynamics of dark matter density evolution. If the gauge coupling $g_{\textsc {x}}$ was very small then the model would reduce to a simple sum of two non-interacting components ($\psi _+,\psi _-$), i.e. a rather uninteresting scenario. Note that $g_{\textsc {x}}$ is a consequence of the presence of the $(-,-)$ state and, as illustrated by our vector-fermion model, existence of this state is quite natural. Note that if the $(-,-)$ state would have been absent then only two fermion dark components ($\psi _+,\psi _-$) would have been allowed by the stabilizing symmetries. However, in this case, only annihilation and conversion processes – without semi-annihilations and decays – would have been allowed. Again not a very appealing scenario.

3.1 Multi-component cases

In the following sections we consider various interesting setups with two or three dark particles. Matrix elements squared needed for collision terms in the Boltzmann equations (30)–(32) are computed by employing the CalcHEP [90], whereas for thermal averaging and solutions of the Boltzmann equations, we adopt our dedicated C++ code.⁵

3.1.1 2CDM: a vector and a Majorana fermion as dark matter

In this section we show results for the scenario with $m_+>m_-+m_X$, so that $\psi _+$ is unstable and can decay into lighter Majorana fermion $\psi _-$ and the vector boson $X_\mu$. Fig. 6 shows results of a scan over $\sin \!\alpha , g_{\textsc {x}}, m_X$ for fixed $m_{h_2}, m_-$ and $\varDelta m=(m_X+10)\;\hbox {GeV}$. All the points satisfy the correct relic density (for the total abundance) observed by PLANCK at $5\sigma$ and the recent direct detection experimental bound from LUX2016 at $2\sigma$. Note that, since the Yukawa coupling to dark fermions is proportional to $\varDelta m/v_X \!=\! (\varDelta m/m_X) g_X$ therefore for fixed $\varDelta m$ and $m_X$ the annihilation cross-sections for the both $\psi _-$ and X are proportional to $(g_X \sin 2\alpha )^2$ therefore, if the remaining parameters are fixed, the requirement of correct DM abundance determines $g_X \sin 2\alpha$. Then the mass of the DM component decides which component contributes more to the $\varOmega _{DM}$.The left panels are for close $h_1$ and $h_2$ masses, $m_{h_2}=120$ and $m_{h_2}=130\;\hbox {GeV}$ which allows for cancellation between $h_1$ and $h_2$ contributions to the direct detection cross-section on nuclei and therefore for consistency with LUX2016 data even for coupling constants that are not so small ($g_{\textsc {x}}\!=\!0.3-1.0$ with majority of points located above $g_{\textsc {x}}\!\sim \! 0.3$). Note that also $\sin \alpha$ does not need to be particularly small due to efficient cancellation between $h_1$ and $h_2$ contributions to the direct detection.

Fig. 6

Upper panels: The plots show results of scans over the parameter space of a 2CDM case, where $X_\mu$ and $\psi _-$ are stable. All the points satisfy the correct relic density observed by PLANCK at $5\sigma$ and the recent direct detection experimental bound from LUX2016 at $2\sigma$. Lower panels: The plots show results of scans over the parameter space of a 1CDM (assuming the fermions $\psi _\pm$ are decoupled from the dark sector and hence $X_\mu$ is the only dark matter particle) and 2CDM (where $X_\mu$ and $\psi _-$ are stable) cases, respectively. In the 2CDM case, all the points are taken from the corresponding upper panel plots. Note that for the 1CDM case, in most of the parameter space, the single dark matter $X_\mu$ is under-abundant, whereas in the 2CDM the presence of second component $\psi _-$ provides the remaining relic density. The point denoted by the black star $\star$ located in the upper-left panel at $m_X=245$ GeV corresponds to the same parameters as those adopted in the middle panel of Fig. 7

The right panels correspond to parameter points such that around $m_X\!=\!200\;\hbox {GeV}$ there is a resonant enhancement of XX annihilation through the $h_2$ s-channel exchange. Of course, there is also a non-resonant contribution from $\psi _-\psi _-$ annihilation. In the case of $h_2$ resonance, in order to satisfy the relic abundance constraint, the relevant coupling constants must be small, i.e. $g_X \sin \alpha \ll 1$, it turns out that for the region of $\sin \alpha$ considered here the gauge coupling constants must be in the range $g_{\textsc {x}}\!\sim \!0.03-0.13$.

Lower panels in Fig. 6 show the abundances of both components separately, $\varOmega _{X}^{\textsc {2cdm}}$ and $\varOmega _{-}^{\textsc {2cdm}}$, for our model and corresponding $\varOmega _X^{\textsc {1cdm}}$ calculated in a 1-component VDM assuming the Majorana fermions are decoupled (which is achieved by $m_D\rightarrow \infty$). The abundance and direct detection cross-section in the VDM model were calculated for the same parameters as those adopted in the 2-component model, just truncated to $m_{h_2}, m_X, \sin \!\alpha , g_{\textsc {x}}$. It is worth to focus at X masses between 110 and $200\;\hbox {GeV}$ in the lower-left panel, where for each given $m_X$ there is a clear shift upwards of the X abundance in the 2CDM scenario (filled triangles are above empty boxes). This is a nice illustration how the presence of the other components of the dark sector may influence the abundance of X. Similarly, in the lower-right plot, an analogous shift is observed for $m_X \lesssim 200\;\hbox {GeV}$, this shift is enhanced by small $\sin \!\alpha$, e.g. for $\sin \!\alpha \sim 0.1$ the X abundance receives an extra factor $\sim 10^2$. Usually, the presence of other constituents of the dark sector implies both an upward shift of $\varOmega _X$, when compared to the 1CDM, and provides a necessary extra contribution by $\varOmega _-^{\textsc {2cdm}}$ in order to satisfy the abundance constraint.

Fig. 7

Solutions of the Boltzmann equations for three sample points from the 2CDM case where $X_\mu$ and $\psi _-$ are stable are shown in the upper panels. These plots show the evolution of the dark matter particle yield $Y_i(x) \equiv n_i/s$ ($n_i$ is the number density, s is the total entropy density and x is defined as $x \equiv m_X/T$) for different species $i=\psi _+,\psi _-$ and $X_\mu$. The colored curves are obtained by making use of a dedicated C++ code to solve the corresponding Boltzmann equations, whereas the gray points are the corresponding results from the micrOMEGAs code. The left, middle and right plots are for the values of parameter $g_{\textsc {x}}=0.02,0.2$ and 1, respectively. The values of other model parameters are shown in the legends of plots and the relic density of two dark matter particles $\varOmega _{X,-} \; h^2$ is also given in each plot. The tables contain first two non-vanishing coefficients of thermally-averaged cross-sections (pb) expanded in powers of $x^{-1}$, given by $\langle \sigma ^{ijkl}v_{\text {M}\varnothing \text {l}}\rangle \! =\! a_Nx^{-N} + a_{N+1}x^{-(N+1)} + \cdots$, and the decay width $\langle \varGamma _{\psi _+\rightarrow X\psi _-}\rangle$ (GeV)

In the plots of Fig. 7, and similar figures in the following sections, we show dark matter yields $Y_i(x) \!\equiv \! n_i/s$ (s is the total entropy density and x is defined as $x \!\equiv \! m_X/T$) for different species $i=\psi _+,\psi _-$ and $X_\mu$. Note that we plot bare values of yields, with no extra normalization adopted. Moreover, the tables in Fig. 7 and similar figures in the following section contain first two non-vanishing coefficients of thermally-averaged cross-sections (pb) expanded in powers of $x^{-1}$, given by $\langle \sigma ^{ijkl}v_{\text {M}\varnothing \text {l}}\rangle \! =\! a_Nx^{-N} + a_{N+1}x^{-(N+1)} + \cdots$, and the decay width $\langle \varGamma _{\psi _+\rightarrow X\psi _-}\rangle$ (GeV). The plots in Fig. 7 illustrate solutions of the Boltzmann equations for three selected sample points. The middle panel shows solutions for parameters that reproduce correct total DM abundance and also satisfy the direct detection LUX limits, so the corresponding point is also present in the scan results shown in the upper-left panel of Fig. 6 as a black star $\star$. In order to illustrate the relevance of the $g_{\textsc {x}}$ coupling, the left, middle and right plots are obtained for $g_{\textsc {x}}=0.02, 0.2$ and 1, respectively, while other parameters remain unchanged. It is clear that the dependence of the abundance for the major DM component ($\psi _-$) on $g_{\textsc {x}}$ is very strong. The gray dots and boxes show results obtained using the micrOMEGAs code for 2CDM [91]. As it is seen in the plots they agree very well with the solid lines which correspond to solutions obtained from our dedicated C++ code that solves the set of three Boltzmann equations (30)–(32). In order to identify the most important processes for a given parameter set, in the tables below the panels in Fig. 7 we collect the first two non-vanishing coefficients in the expansion of thermally averaged cross-sections in powers of $x^{-1}$.

Let’s look closer at the middle table of Fig. 7. The cross-sections shown there correspond to the point in the parameter space marked by $\star$ which is located in the upper left panel of Fig. 6 at $m_X = 245$ GeV. As seen from the middle upper panel of Fig. 7 the abundance is dominated by $\psi _-$, and X is a sub-leading component abundance of which is by nearly two orders of magnitude smaller than for $\psi _-$, while the abundance of $\psi _+$ is absolutely negligible. Note that both $\psi _-$ and X decouple from equilibrium roughly at the same temperature, this is the first signal that there must be some correlation between annihilation mechanisms responsible for their disappearance. Since the abundance of $\psi _+$ could be neglected the only relevant processes are $XX \rightarrow \text {SM}$, $\psi _-\psi _- \rightarrow \text {SM}$ and $XX \rightarrow \psi _-\psi _-$. Note that the ratio of cross-sections for the first and the second process is $\sim 1.8$ while their abundances differ by almost two orders of magnitude, therefore the process for additional depletion of X abundance must be $XX \rightarrow \psi _-\psi _-$. This illustrates how sub-leading components may influence the abundance of a dominant component.

3.1.2 2CDM: two Majorana fermions as dark matter

In this section we show results for the scenario with $m_X>m_-+m_+$, so $X_\mu$ is unstable and can decay into the Majorana fermions $\psi _-$ and $\psi _+$.

Fig. 8

The plots show results of scans over the parameter space of a 2CDM case, for which $\psi _+$ and $\psi _-$ are stable. All the points satisfy the correct relic density observed by PLANCK at $5\sigma$ and the recent direct detection experimental bound from LUX2016 at $2\sigma$. The point denoted by the star $\star$ located in the right panel at $m_-=199.25$ GeV corresponds to the same parameters as those adopted in the middle panel of Fig. 9

Figure 8 shows results of a scan over $\sin \!\alpha , \,g_{\textsc {x}},\, m_-$ for fixed $m_{h_2}, m_X$ and $\varDelta m= 100\;\hbox {GeV}$ (left panel) or $50\;\hbox {GeV}$ (right panel). All the points satisfy the correct relic density (for the total abundance) observed by PLANCK at $5\sigma$ and the recent direct detection experimental bound from LUX2016 at $2\sigma$. In this case the $\psi _-$ turns out to be the dominant DM component in most of the parameter space. The second Higgs boson mass was chosen to be $m_{h_2}=120, 125, 130\;\hbox {GeV}$ and $390, 400, 410\;\hbox {GeV}$ in the left and right panels, respectively. Therefore the left panel allows for partial cancellation between an exchange of $h_1$ and $h_2$ both for $\psi _\pm$ annihilation diagrams and also for $\psi _\pm$-nuclei scattering process to avoid the direct detection limits even if couplings are not small. Since $50\;\hbox {GeV}\le m_- \le 200\;\hbox {GeV}$ therefore one can observe both a resonance behavior at $m_-\!\sim \!m_{h_1}/2 \!\sim \! m_{h_2}/2$ in $\psi _\pm \psi _\pm$ annihilation trough s-channel $h_{1,2}$ exchange and also a threshold effect at $m_-\sim m_{h_1} \sim m_{h_2}$ for annihilation into $h_ih_j$ final state. The vertical structure observed in Fig. 8 around $m_-\sim 60\;\hbox {GeV}$ corresponds to a domination of $\psi _\pm \psi _\pm \rightarrow h_i^*\rightarrow VV,\bar{f} f$. As it is seen from the plot large values of $g_{\textsc {x}}$ are needed, this is a consequence of partial cancellation between $h_1$ and $h_2$ exchange. On the other hand, the independence on $g_{\textsc {x}}$ could be understood as a result of resonance enhancement around $m_-\! \sim \! m_{h_1}/2\! \sim \! m_{h_2}/2$: even a tiny change of $m_-$ can compensate large variation of $g_{\textsc {x}}$. The other triple-branch structure that starts around $m_- \sim 120\;\hbox {GeV}$ corresponds to a threshold for the process $\psi _\pm \psi _\pm \rightarrow h_i h_j$. Its initial steepness represents the opening of the $h_i h_j$ final state that must be compensated by suppression of $g_{\textsc {x}}$ in order to generate correct dark matter abundance.

The right panel of Fig. 8 with its three distinct branches corresponds to a vicinity of the resonance at $m_-\!\sim \! m_{h_2}/2 \!=\! (390, 400, 410)/2\;\hbox {GeV}$. In this case $g_{\textsc {x}}$ must be small to compensate the resonance enhancement, therefore direct detection limits are easily satisfied.

In Fig. 9, we illustrate solutions of the Boltzmann equations for three sample points in the parameter space. The middle panel corresponds to the correct abundance and is in agreement with the LUX upper limits on the DM-nucleon cross-section, which is also present in the scan results shown in the right panel of Fig. 8 as a black star $\star$. As in the previous case of stable $X_\mu$ and $\psi _-$, here we also observe relevance of semi-annihilation and conversion processes and strong $g_{\textsc {x}}$ dependence. One can see a discrepancy with micrOMEGAs results, which are substantial especially in the left panel. The reason for that is the influence of unstable component $X_\mu$, which can be properly described only with a set of 3 coupled Boltzmann equations, whereas in micrOMEGAs one has to assume it is in chemical equilibrium with one of the stable components.

Fig. 9

Solutions of the Boltzmann equations for three sample points from the 2CDM case where $\psi _-$ and $\psi _+$ are stable are shown in the upper panels. The left, middle and right plots are for the values of parameter $g_{\textsc {x}}=0.1,0.5$ and 5, respectively. The values of other parameters are shown in the legends of plots and other details are same as in Fig. 7. The tables contain first two non-vanishing coefficients of thermally-averaged cross-sections (pb) expanded in powers of $x^{-1}$, given by $\langle \sigma ^{ijkl}v_{\text {M}\varnothing \text {l}}\rangle \! =\! a_Nx^{-N} + a_{N+1}x^{-(N+1)} + \cdots$, and the decay width $\langle \varGamma _{X \rightarrow \psi _+\psi _-}\rangle$ (GeV)

3.1.3 3CDM: a vector and two Majorana fermions as dark matter

In this section we show results for the scenario with $m_+ +m_->m_X>m_+-m_-$, so all the three dark components are stable. Figure 10 contains results of a scan performed adopting our dedicated code⁶ that solves the set of the three Boltzmann equations (30)–(32).

Fig. 10

These plots show results of scan over the parameter space of a 3CDM case, where $X_\mu$ and $\psi _\pm$ are stable. In this scan we fix three different values of $m_X$, $m_{h_2}$ and $\varDelta m$ and vary $m_-$ and $g_x$ as shown in the plots. The left and right plots represent the same data set however points markers are changed from $m_X$ (left) to $m_{h2}$ (right), whereas the color represent the values of dark Yukawa coupling $y_{\textsc {x}}$. All the points shown satisfy the correct relic density observed by PLANCK at $5\sigma$ and the recent direct detection experimental bound from LUX2016 at $2\sigma$. The point denoted by the black star $\star$ in the these plots at $m_-=246.4$ GeV corresponds to the same parameters as those adopted in the middle panel of Fig. 11

Fig. 11

Solutions of the Boltzmann equations for three sample points from the 3CDM case where all three dark states ($X,\psi _\pm$) are stable are shown in the upper panels. The left, middle and right plots are for the values of parameter $g_{\textsc {x}}=0.1,0.745$ and 2, respectively. The values of other parameters (same in all the panels) are shown in the legends of plots. The tables contain first two non-vanishing coefficients of thermally-averaged cross-sections (pb) expanded in powers of $x^{-1}$, given by $\langle \sigma ^{ijkl}v_{\text {M}\varnothing \text {l}}\rangle \! =\! a_Nx^{-N} + a_{N+1}x^{-(N+1)} + \cdots$. Note that for these points the dark fermion Yukawa coupling is very small, i.e. $y\ll 1$, as a result the direct annihilation processes for $\psi _\pm$ are inefficient, therefore the main annihilation processes are through the semi-annihilations and conversions to X which further annihilate to SM

All the points presented in Fig. 10 satisfy the correct relic density (for the total abundance) observed by PLANCK at $5\sigma$ and the direct detection experimental bound from LUX2016 at $2\sigma$. The scan is performed over $m_-, \; g_x$ with fixed values of $\sin \!\alpha \!=\!(0.05,0.1,0.2)$, $m_X\!=\!(200,150,100) \;\hbox {GeV}$ and $m_{h_2}\!=\!(200,120,50) \;\hbox {GeV}$. Note that the left and right panels of Fig. 10 are for the same data-set but for different filling style, in the left and right panel the filling corresponds to $m_X$ and $m_{h_2}$, respectively. Here we have tested sensitivity to $\varDelta m\equiv m_+-m_-$ focusing on small $\varDelta m\!=\!(0.1, 1, 10)$ GeV. As it is seen from the Fig. 10, for $m_-\sim m_+\gtrsim 200$ GeV relatively small $U(1)_X$ coupling is required, $g_{\textsc {x}}=0.5-1$, in order to suppress too fast $\psi _\pm \psi _\pm$ s-channel annihilation. Note that $y_{\textsc {x}}\!=\! \varDelta m\, g_{\textsc {x}}/(2m_X)$ therefore this annihilation is already quite strongly suppressed by the small Yukawa coupling $y_{\textsc {x}}$. An important final state is $t{\bar{t}}$, so if $m_-\sim m_+ \lesssim m_t$ this annihilation channel closes so that even large $g_{\textsc {x}}$ is allowed/necessary, as observed in the figure.

Figure 11 shows solutions of the Boltzmann equations for three sample points in the parameter space of 3CDM. The middle panel represents the point marked as a black star $\star$ in the scan results of Fig. 10 that satisfies relic abundance and LUX2016 constraints. As in the previous cases for 2CDM, here we also observe relevance of semi-annihilation and conversion processes and strong $g_{\textsc {x}}$ dependence on the yields of dark matter components.

Table 2 Sets of parameters implying limiting VDM and FDM cases with proper $\varOmega _{DM}$. Relic densities of $X_\mu$ and $\psi _-$ are provided, density of $\psi _+$ is negligible. All the masses are in GeV

3.2 Limiting cases

In this section we are going to discuss special regions in the parameter space of the model that result in simpler, models of DM.

3.2.1 The vector dark matter (VDM) model

If mass splitting between $\psi _+$ and $\psi _-$ is small comparing to $m_X$, then, for fixed $g_X$, the Yukawa coupling $y_X$ is suppressed as $y_X=\varDelta m/(2 v_x)=(\varDelta m/m_X)(g_X/2)$. Therefore, in this limit, since Yukawa couplings become irrelevant, the model might be reduced to the 1-component VDM model (see e.g. [83, 85] where the same notation as here has been adopted). Note however that even though fermionic DM decouple from the SM, nevertheless it is still present and may influence cosmological dynamics and contribute to the observed amount of DM. In order to enable efficient $\psi _\pm$ annihilation it is sufficient to assume that $2 m_D > m_X+m_i$ and/or $m_X > m_i$ ($m_D\equiv (m_++m_-)/2$) so that at present only $X_\mu$ contributes to the observed DM abundance and could be successfully fitted by tuning $g_X$. Samples of parameter sets that imply proper $\varOmega _{DM}$ and fit in the VDM limit are shown in Table. 2. In Ref. [85] the VDM has been analyzed focusing on the possibility of enhancing self-interaction, and some regions of the parameters space where elastic XX scattering is amplified and all other constraints are satisfied have been found.

3.2.2 The fermion dark matter (FDM) model

Another interesting limit of our model is a renormalizable model of fermionic DM, see e.g. [92,93,94,95]. Those models usually employ an extra singlet real scalar field that couples to the SM Higgs doublet via the Higgs portal and to a singlet dark Dirac fermion as well. In the fermionic DM limit of our model, we recover a model of a Majorana singlet DM that couples to a complex scalar S. Since our model is invariant under local $U(1)_X$ therefore in the limit of small gauge coupling, $g_X \ll 1$, and substantial mass-splitting between $\psi _+$ and $\psi _-$ (so for enhanced Yukawa coupling, $y_X$), effectively we obtain a renormalizable model symmetric under a global $U(1)_X$ of a single Majorana dark fermion $\psi _-$ interacting with S. The scalar S controls communication between dark sector and the SM. Examples of parameter sets that imply proper $\varOmega _{DM}$ and fit in the FDM limit are shown in Table 2. The model is slightly more restrictive than those considered earlier in [92,93,94,95] since our DM is a Majorana fermion and the scalar potential is more restricted, as being invariant under the global $U(1)_X$, however predictions of those models are similar, see [94]. In order to obtain fermionic (Majorana) DM model one should reduce $g_X$ in order to decouple $X_\mu$, keeping in mind that certain minimal interaction strength is necessary for $X_\mu$ to maintain kinetic equilibrium. Note that in order to reduce the model to a single fermionic DM model, we have to remove somehow $\psi _+$ and $X_\mu$. The easiest way to get rid of $\psi _+$ is to assume that it is the heaviest dark state, so that it will have a chance to decay quickly. If the following mass ordering, $m_+> m_X > m_-$ is fulfilled, then indeed the dominant DM component is the Majorana fermion $\psi _-$, while other dark components disappear. The model contains, of course, two scalar Higgs bosons that mix in the standard manner and play a role of mediators between the dark sector and the SM. Self-interaction in the FDM model has been discussed in [96]. It turns out that for the self-interactions to be sufficiently strong, the scalar mediator, $h_2$, has to be very light what implies well-known problems [97] in the early Universe if $h_2$ is present during the era of BBN.

3.2.3 The fermion dark matter (FDM) model with a stable vector mediator

Another interesting limit of our model has been considered very recently in [98]. If, in our model, $\varDelta m \rightarrow 0$ then the Yukawa coupling $y_X$ vanishes and masses of Majorana fermions $\psi _+$ and $\psi _-$ become degenerate. Then our model reduces to the model considered in [98], which is just a model of a Dirac fermion as a DM and a stable vector mediator. Their [98] mediator corresponds to our vector component of DM, $X_\mu$, while the dark Dirac fermion is an analog of our degenerate Majorana dark fermions $\psi _+$ and $\psi _-$. The authors of [98] show that the model can indeed predict enhanced DM self-interaction while satisfying all existing experimental constraints if mass of the stable vector mediator is of the order of $1\;\hbox {MeV}$. This has been also confirmed in the appropriate ($\varDelta m \rightarrow 0$, $m_X \sim {{\mathcal {O}}}(1) \;\hbox {MeV}$) region of the parameter space of our model. In this case the DM abundance is dominated by mass-degenerate $\psi _\pm$, even though formally it is a 3-component case (3CDM) if $\varDelta m < m_X$.

3.3 Distinguishing limiting cases

As it has been discussed in the previous section the model discussed here simplifies in various regions of the parameter space where it reduces to a single-component dark matter mode i.e. FDM or VDM. In remaining parts of the parameter space it describes a genuine 2 or 3 component dark matter. In this context it is natural to rise the question how could one disentangle those three possibilities. Some attempts to address this sort of question have already been made in the literature, see e.g. [99, 100], where the authors considered a possibility to disentangle spin, 0, 1/2 or 1 dark matter at $e^+e^-$ future colliders. The VDM model they considered was the same as the limiting version of our model discussed in Sect. 3.2.1, however their FDM was slightly different than ours from Sect. 3.2.2. Of course, they did not discuss multi-component scenario. An exhaustive discussion, that takes into account all existing experimental constraints within a single model that allows for 2 or 3 DM components is still missing. Such an analyzes lies beyond the scope of this paper however it shall be investigated in the near future [101]. Nevertheless few comments are here in order.

• Direct detection

  Contributions to DM-nucleon scattering consists of the sum of standard $\sigma _{X-N}$ and $\sigma _{\psi _\pm -N}$ cross-sections that are not sensitive to the presence of all the 2-3 DM components, rather this is a sum of contributions that exist in 1-component models. There exists however a more interesting inelastic scattering process which is sensitive to the multi-component nature of the model considered here, i.e. $\psi _+ N\rightarrow \psi _- X N$, note that all the dark particle are involved, so that this process might provide a signature of the multi-component scenario or perhaps some useful correlation with other observables. This process could be enhanced (and therefore efficiently constrained) for small $m_X$ which on the other hand helps to enhance $\psi _\pm$ self-interaction.

• Indirect detection

  Similarly indirect detection experiments, besides standard $XX\rightarrow SM$ and $\psi _\pm \psi _\pm \rightarrow SM$ contributions receive also more interesting one $\psi _+\psi _-\rightarrow X h_i$ followed by $h_i$ decays.

• Colliders

  $e^+e^-$ colliders provide a clean environment that might be used to test the multi-DM scenario considered here. Namely one can investigate the process $e^+e^-\rightarrow Z^* \rightarrow h_i Z \rightarrow \chi _D\chi _D Z$ with $\chi _D=X$ or $\psi _\pm$. Energy-distribution of Z might be adopted to gain some information on the invisible objects being produced. Initial estimation indicates that in some regions of the parameter space, for sufficiently large luminosity one should be able to disentangle 1- and 2-3 component scenarios.

4 Self-interacting DM

It is well known that the cosmological small-scale structure problems, such as the ’cusp vs. core’ and the ’too-big-to-fail’ problems could be ameliorated if DM self-interaction was sufficiently strong at the dwarf galaxy scale [14, 16, 102,103,104,105,106,107], the required value of the cross-section is

$$\begin{aligned} 0.1\,\frac{{{\mathrm{cm}}^2}}{\mathrm{g}}< \frac{\sigma _T}{m_{DM}} < 10\, \frac{{{\mathrm{cm}}^2}}{\mathrm{g}}, \end{aligned}$$

(37)

where $\sigma _T\equiv \int d\varOmega (1-\cos \theta ) d\sigma /d\varOmega$ is the so-called momentum transfer cross section between DM particles. However, DM self-scattering cross-section as large as $\sigma _T/m_{DM} \simeq 10~{{\mathrm{cm}}^2/g}$ turns out to be disallowed by observations at the cluster scale with the typical constraint $\sigma _T/m_{DM} < 1~{{\mathrm{cm}}^2/g}$ [5, 108,109,110,111]. Therefore in the following we will try to find a region in the parameter space where $0.1~{{\mathrm{cm}}^2}/{\mathrm{g}}<\sigma _T/m_{DM}<1~{{\mathrm{cm}}^2}/{\mathrm{g}}$. ss A possible strategy that may generate large DM self-interaction is to introduce a mediator which is much lighter than the DM particles. In the VFDM model, there are two options, the mediator could be either $h_2$ or DM component $X_\mu$. As shown in [85] the choice of light $h_2$ implies number of severe constraints therefore here we will focus on the case of light vector DM component, which may serve as a mediator in elastic $\psi _+\psi _-$ scattering. The main contribution to the amplitude for $\psi _+\psi _- \rightarrow \psi _+\psi _-$ comes from the t-channel $X_\mu$-exchange. The transfer cross-section for the two Majorana eigenstates interacting with a vector mediator was discussed in [112]. In case of the small mass splitting $m_+-m_- \ll m_D$, we can use the result obtained in a Born approximation for the Dirac fermion [113]

$$\begin{aligned} \sigma _T\equiv & {} \int d\varOmega (1-\cos \theta ) \frac{d\sigma }{d\varOmega }= \frac{g_{\textsc {x}}^4}{16\pi m_-^2 v^4}\left( \frac{m_+}{m_-}-\frac{1}{2}\right) \nonumber \\&\times \left[ \log \left( 1+\frac{m^2_- v^2}{m_X^2}\right) -\frac{m^2_- v^2}{m_X^2+m^2_- v^2}\right] \end{aligned}$$

(38)

The above perturbative result is valid if $g_X^2 m_-/m_X \lesssim 16\pi$ and $(m_+-m_-)\ll m_D$. The substantial enhancement could be achieved for light $X_\mu$ with its mass e.g. $m_X \sim {{\mathcal {O}}}(1 \;\hbox {MeV})$. In addition in case of small mass splitting the contribution from t-channel $h_2$ exchange is suppressed. For $m_- \gg m_X$ also the s-channel $X_\mu$ exchange could be neglected. Here we consider the scenario with three stable components, therefore $m_X > m_+-m_-$.

In the region of parameters considered here abundance of $\psi _\pm$ and $X_\mu$ might be comparable, however for instance domination of $\psi _\pm$ could also be reached by facilitating XX annihilation by assuming $m_2 < m_X$, then appropriate $g_X$ might be adjusted to tune the proper total DM abundance. Note that the Yukawa coupling $y_X$ remains small so that the potential relevance of $h_2$ mediation is therefore limited. If $(m_+-m_-)\ll m_D$ then both indirect detection of $\psi _\pm \psi _\pm$ annihilating at present time and the cross-section for $\psi _\pm$-nucleon scattering would be sufficiently suppressed. The mixing angle is as usually assumed to be small, $\sin \theta \ll 1$, what provides additional suppression of both direct and indirect detection. Concluding, it seems that there exists the region of parameter space consistent with the data and providing substantial self-interaction of DM components and large ratio of masses ($m_D \gg m_X$) for DM components. This illustration of possibility for enhanced self-interaction in our model is located in a region of parameter space, which is similar to the limit considered in Sect. 3.2.3, i.e. for fermionic Dirac DM and stable vector mediator discussed very recently in [98].

Fig. 12

Contours of self-interaction cross-section $\sigma _T/m_{D}$ at dwarf galaxies scale ($v=10$ km/s) in the ($m_{D}, m_X$) plane. For each point the value of $g_X$ was fitted using relic density constraint

In the Fig. 12, we show results of detailed scans focused on that region. The relic abundance was calculated using micrOMEGAs code [91] by placing $\psi _+$ and $\psi _-$ in one dark sector and X in another. Here we assume that both fermions are kept in equilibrium with each other by the efficient exchange processes $\psi _\pm X \leftrightarrow \psi _\pm h_2$. The scan was made over masses in the range $m_X\in [1,15]$ MeV, $m_D\in [1,10]$ GeV for fixed values of $m_{h_2}\in \{1,2,5\}$ MeV and $\sin \alpha \in \{10^{-5},10^{-6},10^{-7}\}$. Parameter $g_x$ was fitted imposing the condition that density of fermions satisfies relic abundance constraint whereas contribution of X is negligible. The latter is achieved by the effective annihilation $XX\rightarrow h_2h_2$ if $h_2$ is lighter than X. We choose the mass splitting $m_+-m_- = 10^{-5}$ GeV. In this way we can ensure that both states are present with nearly the same relic abundance. Moreover as it leads to the suppression of the Yukawa coupling, therefore we can avoid the indirect detection bounds. Another strong constraint comes from the limit on the invisible Higgs decay $h_1\rightarrow h_2 h_2$. It results in the bound $\sin \alpha \le 10^{-5}$, which on the other hand suppresses the DM-nucleon scattering cross-section to the range which is in agreement with direct detection experiments.

Similar scenario was discussed in the case of Dirac fermion in [98]. Since here we focus on the small mass splitting therefore our model effectively also contains a Dirac dark fermion and a stable vector as in [98]. Therefore, our results for $\sigma _T/m_D$ shown in Fig. 12 indeed agree with those obtained in [98]. Note however, this accordance takes place only in this particular region of the parameter space, while in general the models are quite different, for instance, by the presence of Yukawa interactions that are allowed in our model due to specific assignments of dark charges. More comprehensive analysis of our model will be presented elsewhere.

5 Summary and conclusions

Multi-component dark matter scenarios are natural extensions of a simple WIMP dark matter. They predict more than one stable component in a dark sector and therefore they constitute a much richer dynamical structure. In this work we have presented a minimal UV-complete vector-fermion DM model with two or three stable particles. Its dynamical properties were discussed. Our vector-fermion DM model involves a dark sector with a $U(1)_X$ gauge symmetry. The dark matter contents are the dark gauge boson $X_\mu$, a Dirac fermion $\chi$, and a complex scalar S, all are charged under the dark $U(1)_X$ gauge symmetry and are neutral under the SM gauge symmetry. Moreover, all the SM particles are neutral under the dark $U(1)_X$ gauge symmetry. The dark sector communicates with the visible sector (SM) through the Higgs portal $\kappa |H|^2|S|^2$. To generate the dark gauge boson $X_\mu$ mass we have employed the Higgs mechanism in the dark sector.

After the dark sector spontaneous symmetry breaking and mass diagonalization, our vector-fermion DM scenario comprises a dark vector $X_\mu$ and two dark Majorana fermions $\psi _\pm$. Out of eight free parameters of the model, the SM Higgs vev $v\!=\!246\;\hbox {GeV}$ and the SM-like Higgs mass $m_{h_1}\!=\!125\;\hbox {GeV}$ are fixed which leaves us with six independent parameters. We have chosen the physical basis where the six independent parameters are four masses $m_X,m_\pm , m_{h_2}$, the mixing angle $\sin \!\alpha$, and the dark gauge coupling $g_{\textsc {x}}$. To guarantee perturbativity we assumed $g_{\textsc {x}}\!\le \!4\pi$. We have employed $\sin \!\alpha \le 0.33$, which is consistent with the $2\sigma$ constraint from current measurements of the SM-like Higgs boson couplings to the SM gauge bosons at the LHC. Our VFDM model has an exact charge conjugation symmetry and the dark gauge symmetry which result in an accidental discrete $Z_2\!\times \!Z_2^\prime$ symmetry. The charge assignments under this $Z_2\!\times \!Z_2^\prime$ symmetry are: $X_\mu (-,-),\psi _{+}(-,+), \psi _{-}(+,-)$ and $h_{1,2}(+,+)$ (also all SM gauge bosons and fermions are even under both discrete symmetries). The dynamics of the dark sector is mainly controlled by the gauge coupling $g_{\textsc {x}}$ which couples the three dark fields, i.e. $X_\mu {\bar{\psi }}_{+}\gamma ^\mu \psi _{-}$.

In this work, we have analyzed the dynamics of the dark sector in the thermal freeze-out paradigm by solving the three coupled Boltzmann equations for the dark sector species ($X_\mu ,\psi _+,\psi _-$). The vector-fermion DM dynamics turns out to be different in many ways than the standard single component WIMP dark matter scenarios. In our model, depending on the masses of the dark sector particle $m_X, m_{+}, m_{-}$ there are the following three distinct cases where either two or all three dark sector particles are stable.

• (i) ${m_+>m_X+m_-}$: A two-component dark matter case where the stable particles are the vector $X_\mu$ and the Majorana fermion $\psi _-$, see Sect. 3.1.1. In this case we have performed scans over $m_X, g_{\textsc {x}}$ for different values of $m_\pm ,m_{h_2}$ and $\sin \!\alpha$ to search for regions in the parameter space where the dark matter total relic density and current direct detection constraints are satisfied. Importance of the presence of other dark sector states and their interactions, in particular, the semi-annihilations and conversions has been manifested. Moreover, we have compared the two-component vector-fermion case with the single-component vector dark matter and highlighted the presence of second component, the latter one is especially useful to compensate the under-abundance of the single-component vector dark matter.

• (ii) ${m_X>m_++m_-}$: A two-component dark matter case where the stable particles are the two Majorana fermions $\psi _+$ and $\psi _-$, see Sect. 3.1.2. In this case we have performed scans over $m_-,g_{\textsc {x}}$ for different choices of $m_X,\varDelta m,m_{h_2}$ and $\sin \!\alpha$ which satisfy the correct total relic abundance and direct detection bounds. As in the previous case, we have highlighted the importance of the presence of more than one stable states in the dark sector and their interactions. In particular, we have illustrated effects of semi-annihilations in Fig. 9, which are primarily controlled by the single coupling $g_{\textsc {x}}$.

• (iii) ${m_++m_->m_X>m_+-m_-}$: A three-component dark matter scenario where all three dark sector particles $(X_\mu ,\psi _+,\psi _-)$ are stable, see Sect. 3.1.3. As in the two-component DM cases we have performed scan over $m_-, g_{\textsc {x}}$ for different choices of $m_X,\varDelta m,m_{h_2}$ and $\sin \!\alpha$. To demonstrate the importance of three stable dark matter particles, we have illustrated in Fig. 11 the case with two Majorana fermions nearly degenerate in mass, i.e. $y\ll 1$, hence their standard annihilations are suppressed, due to small Yukawa couplings, and the semi-annihilations are most important for their annihilations.

Note that all the points presented in our scans satisfy the total relic density $\varOmega _{\mathrm{tot}}h^2$ at $5\sigma$ as observed by PLANCK and also the $2\sigma$ direct detection bound from LUX2016. Moreover, to understand the dark matter dynamics we have shown the evolution of the yields of dark matter components for each of the above cases for selected benchmark points, supplemented by tables containing all cross-sections for processes involved in collision terms. Also we compared our results for two-component cases with those obtained from the micrOMEGAs code [91] and satisfactory agreement has been found, see Figs. 7 and 9.

We have also discussed limiting cases of the model that are realized in appropriate regions of the parameter space. One of them corresponds to a model with Dirac fermion DM and stable vector mediator, this is an interesting scenario. A possibility of self-interacting DM has also been addressed and the region of parameter space where $\sigma _T/m_{DM}$ can be substantially enhanced has been found.

To summarize, the absence of any direct, indirect or collider signatures of dark matter suggests a direction that leads beyond the single component WIMP-like dark matter. In particular, multi-component dark matter scenarios offer very rich dynamical structures which could solve current dark matter puzzles. In this work, we have presented a minimal renormalizable vector-fermion dark matter model where the presence of gauge symmetry and charge conjugation in the hidden sector implies the existence of two or three stable (vector and/or Majorana fermions) dark matter particles. The dynamics of the dark sector in our model is primarily controlled by a single parameter, the dark gauge coupling $g_{\textsc {x}}$ through the interaction $\big ({\bar{\psi }}_{\!+} \gamma ^\mu \psi _{\!-} - {\bar{\psi }}_{\!-} \gamma ^\mu \psi _{\!+}\big ) X_\mu$ which connects all dark sector states $X_\mu$, $\psi _+$ and $\psi _-$. Such an interaction allows semi-annihilation and decay processes within the dark sector. We have explored the parameter space of our two/three-component VFDM scenarios requiring the correct total relic density and compliance with the current direct detection bounds.

Appendices

Appendix A: Boltzmann equations for multi-component dark matter

We review here the derivation of the Boltzmann equation for the evolution of number density for the multi-component dark matter in the homogeneous and isotropic universe. Let us consider a generic dark sector which allows interactions with the visible sector and the dark sector, i.e., annihilations (co-annihilations), semi annihilations, conversions, and decays. We can write the Boltzmann equation for $\chi _i$ particle as

$$\begin{aligned} \frac{dn_i}{dt}+3H n_i= {{\mathcal {C}}}_i+{{\mathcal {D}}}_i, \end{aligned}$$

(A.1)

where H is the Hubble expansion parameter, whereas, ${{\mathcal {C}}}_i$ and ${{\mathcal {D}}}_i$ are collision and decay terms for the $\chi _i$ particle with the visible sector and the dark sector. In general, the collision term ${{\mathcal {C}}}_i$ may involve $2\rightarrow 2$, $3\rightarrow 2$ and similar scattering processes, however, in order to keep the discussion simple, we focus only on $2\rightarrow 2$ processes. We assume that all the dark components have the same temperature as the thermal bath. Similarly, the decay term ${{\mathcal {D}}}_i$ may involve more than 2-body decays however we limit our-self to 2-body decays, the generalization is straightforward. For $2\rightarrow 2$ scattering processes and the 2-body decay processes, we can write down the collision and the decay terms as follows,

$$\begin{aligned} {{\mathcal {C}}}_i =\sum _{j,k,l} {{\mathcal {C}}}_{ij\rightarrow kl}, \quad {{\mathcal {D}}}_i =\sum _{j,k} {{\mathcal {D}}}_{i\rightarrow jk}, \end{aligned}$$

(A.2)

where the summation is over all possible interactions of $\chi _i$ with the visible sector as well as dark-sector particles. The collision ${{\mathcal {C}}}_{ij\rightarrow kl}$ and the decay ${{\mathcal {D}}}_{i\rightarrow jk}$ terms read:

$$\begin{aligned} {{\mathcal {C}}}_{ij\rightarrow kl}&=-\!\int \! d\varPi _id\varPi _jd\varPi _kd\varPi _l (2\pi )^4\delta ^4(p_i+p_j-p_k-p_l) \nonumber \\&\quad \times \Big [|{{\mathcal {M}}}_{ij\rightarrow kl}|^2f_i f_j(1\pm f_k)(1\pm f_l)\nonumber \\&\quad -|{{\mathcal {M}}}_{kl\rightarrow ij}|^2 f_k f_l(1\pm f_i)(1\pm f_j)\Big ], \end{aligned}$$

(A.3)

$$\begin{aligned} {{\mathcal {D}}}_{i\rightarrow jk}&=-\!\int \! d\varPi _id\varPi _jd\varPi _k (2\pi )^4\delta ^4(p_i-p_j-p_k) \nonumber \\&\quad \times \Big [|{{\mathcal {M}}}_{i\rightarrow jk}|^2f_i(1\pm f_j)(1\pm f_k)\nonumber \\&\quad -|{{\mathcal {M}}}_{jk\rightarrow i}|^2f_j f_k(1\pm f_i)\Big ], \end{aligned}$$

(A.4)

where the phase space integrand is,

$$\begin{aligned} d\varPi _i=\frac{d^3p_i}{(2\pi )^3 2E_i}, \end{aligned}$$

(A.5)

with $|{{\mathcal {M}}}_{ij\rightarrow jk}|^2$ and $|{{\mathcal {M}}}_{i\rightarrow jk}|^2$ being the matrix element squared summed over initial and final spins for the reaction $ij \rightarrow kl$ and $i\rightarrow jk$, respectively. Above the factors of the form $(1\pm f_i)$ are due to the spin statistics, the plus sign for bosons and the minus sign for fermions. Here $f_i$ denotes the distribution function of a given kind of particles, connected with the number density as follows:

$$\begin{aligned} n_i=g_i\int \frac{d^3p}{(2\pi )^3}f_i(E,T), \end{aligned}$$

(A.6)

with $g_i$ being the number of spin degrees of freedom.

Hereafter it is assumed that appropriate symmetry factors for initial [114] and final⁷ states are included in $|{{\mathcal {M}}}|^2$.

We adopt the following assumptions:

• Time reversal (T) invariance holds, so the amplitudes satisfy, ${{\mathcal {M}}}_{ij\rightarrow kl}={{\mathcal {M}}}_{kl\rightarrow ij}$ and ${{\mathcal {M}}}_{i\rightarrow jk}={{\mathcal {M}}}_{jk\rightarrow i}$ ,

• $m \gg T$, $(m_i-\mu _i)/T \gg 1$ (where m is the mass of dark matter species, T is temperature, and $\mu _i$ is the chemical potential), so that the Bose-Einstein (for bosons) and the Fermi-Dirac (for fermions) distribution functions could be approximated by the Maxwell-Boltzmann distribution functions,

• In the absence of quantum degeneracies (which is assumed since the particles form a very dilute gas), in (A.3-A.4) the blocking and stimulated emission factors can be neglected, so $1 \pm f_i\simeq 1$ will be adopted,

• The initial chemical potentials are negligible,

• Standard Model particles are in thermal equilibrium with the thermal bath,

• Scattering processes with the thermal bath enforce kinetic equilibrium (also after decoupling and out of chemical equilibrium), so that phase-space distribution functions for particles involved in the collision satisfy [115]

  $$\begin{aligned} f_i(E,T)=\frac{n_i(T)}{{\bar{n}}_i(T)}\times {\bar{f}}_i(E,T), \end{aligned}$$

  (A.7)

  where ${\bar{f}}_i(E)$ is the thermal Maxwell-Boltzmann equilibrium distribution function for zero chemical potential and

  $$\begin{aligned}&f_i(E,T)=e^{(-E+\mu _i)/T}=e^{\mu _i/T}{\bar{f}}_i(E,T), \end{aligned}$$

  (A.8)
  $$\begin{aligned}&n_i(T) = g_i e^{\mu _i/T} \int \frac{d^3p_i}{(2\pi )^3}{\bar{f}}_i(E)=e^{\mu _i/T} {\bar{n}}_i(T). \end{aligned}$$

  (A.9)

With the above assumptions we can rewrite the above collision term as,

$$\begin{aligned} {{\mathcal {C}}}_{ij\rightarrow kl}&= -\int \!d\varPi _id\varPi _jd\varPi _kd\varPi _l (2\pi )^4\delta ^4(p_i\!+\!p_j\!-\!p_k\!-\!p_l) \nonumber \\&\quad \times \big \vert {{\mathcal {M}}}_{ij\rightarrow kl}\big \vert ^2\left[ \frac{n_i n_j}{{\bar{n}}_i{\bar{n}}_j}{\bar{f}}_i {\bar{f}}_j-\frac{n_k n_l}{{\bar{n}}_k{\bar{n}}_l} {\bar{f}}_k {\bar{f}}_l\right] . \end{aligned}$$

(A.10)

The thermal equilibrium distributions satisfy the following relation due to the conservation of energy,

$$\begin{aligned} {\bar{f}}_i {\bar{f}}_j=e^{-(E_i+E_j)/T}=e^{-(E_k+E_l)/T}={\bar{f}}_k{\bar{f}}_l. \end{aligned}$$

(A.11)

After performing the integration over the outgoing momenta, the collision term can be written as,

$$\begin{aligned} {{\mathcal {C}}}_{ij\rightarrow kl}&=-\left\langle \sigma ^{ijkl}v_{\text {M}\varnothing \text {l}}\right\rangle \left[ n_i n_j-{n_k n_l}\frac{{\bar{n}}_i{\bar{n}}_j}{{\bar{n}}_k{\bar{n}}_l}\right] . \end{aligned}$$

(A.12)

where $v_{\text {M}\varnothing \text {l}}$ is the Møller velocity

$$\begin{aligned} v_{\text {M}\varnothing \text {l}}=\frac{\sqrt{(p_i\cdot p_j)^2-m_i^2m_j^2}}{E_iE_j}, \end{aligned}$$

(A.13)

and the total cross-section summed over initial and final spins

$$\begin{aligned} \sigma ^{ijkl}(p_i,p_j)&=\frac{1}{4E_iE_j v_{\text {M}\varnothing \text {l}} }\int d\varPi _kd\varPi _l \nonumber \\&\quad \times (2\pi )^4\delta ^4(p_i+p_j-p_k-p_l) |{{\mathcal {M}}}_{ij\rightarrow kl}|^2. \end{aligned}$$

(A.14)

The thermally averaged cross section is defined as,

$$\begin{aligned} \left\langle \sigma ^{ijkl}v_{\text {M}\varnothing \text {l}}\right\rangle&\equiv \frac{1}{{\bar{n}}_i{\bar{n}}_j} \nonumber \\&\quad \times \int \frac{d^3p_i}{(2\pi )^3} \frac{d^3p_j}{(2\pi )^3} \sigma ^{ijkl} (p_i,p_j) v_{\text {M}\varnothing \text {l}}{\bar{f}}_i{\bar{f}}_j,\nonumber \\ \end{aligned}$$

(A.15)

where the equilibrium number density ${\bar{n}}_i$ is defined as,

$$\begin{aligned} {\bar{n}}_i\equiv g_i\int \frac{d^3p_i}{(2\pi )^3}{\bar{f}}_i(\mathbf{p}). \end{aligned}$$

(A.16)

After integrations over the momenta and changing variables we can rewrite the above equations as

$$\begin{aligned} \left\langle \sigma ^{ijkl}v_{\text {M}\varnothing \text {l}}\right\rangle (x_i)&= \frac{m_i}{8\pi ^4 x_i \bar{n}_i\bar{n}_j}\nonumber \\&\quad \times \!\!\int _{(m_i+m_j)^2}^\infty ds\sqrt{s} K_1\left( \frac{x_i\sqrt{s}}{m_i}\right) p_{ij}^2(s) g_{i} g_{j} {{\bar{\sigma }}}_{ij\rightarrow kl}(s), \end{aligned}$$

(A.17)

$$\begin{aligned} \bar{n}_i(x_i)&=\frac{g_{i}}{2\pi ^2 } \frac{m^3_{i} }{x_i} K_2\left( x_i\right) , \quad \text {and} \quad x_i\equiv m_i/T, \end{aligned}$$

(A.18)

where ${{\bar{\sigma }}}_{ij\rightarrow kl}(s)$ is the total cross-section averaged over initial and summed over final spins ($=\sigma ^{ijkl}/(g_ig_j)$) while $K_{1,2}$ are the Bessel functions of second kind and $p_{ij}^2$ is a square of the incoming particle momenta in the center of mass frame,

$$\begin{aligned} p_{ij}^2(s)=\frac{\big [s-(m_i+m_j)^2\big ]\big [s-(m_i-m_j)^2\big ]}{4s}~, \end{aligned}$$

(A.19)

which is related to the Møller velocity (A.13) by

$$\begin{aligned} p_{ij}=\frac{E_iE_j}{\sqrt{s}}v_{\text {M}\varnothing \text {l}}~. \end{aligned}$$

(A.20)

Following similar steps as above for calculating the ${{\mathcal {C}}}_{ijkl}$ function (A.3), one can calculate the ${{\mathcal {D}}}_{i\rightarrow jk}$ function (A.4). Assuming T invariant amplitudes for the decaying process, ${{\mathcal {M}}}_{i\rightarrow jk}={{\mathcal {M}}}_{jk\rightarrow i}$ and using the fact that thermal equilibrium distributions satisfy the following relation,

$$\begin{aligned} {\bar{f}}_i =e^{-E_i/T}=e^{-(E_j+E_k)/T}={\bar{f}}_j{\bar{f}}_k, \end{aligned}$$

(A.21)

we can rewrite the decay contribution as,

$$\begin{aligned} {{\mathcal {D}}}_{i\rightarrow jk}&=-\int d\varPi _id\varPi _jd\varPi _k (2\pi )^4\delta ^4(p_i-p_j-p_k) \nonumber \\&\quad \times |{{\mathcal {M}}}_{i\rightarrow jk}|^2 \frac{{\bar{f}}_i}{{\bar{n}}_i} \left[ n_i - {\bar{n}}_i\frac{n_j n_k}{{\bar{n}}_j{\bar{n}}_k} \right] . \end{aligned}$$

(A.22)

The decay width is defined as usually

$$\begin{aligned} \varGamma _{i\rightarrow jk}=\frac{1}{2 m_i} \int d\varPi _j d\varPi _k (2\pi )^4 \delta ^4(p_i-p_j-p_k) |{{\mathcal {M}}}_{i\rightarrow jk}|^2 \end{aligned}$$

(A.23)

where $|{{\mathcal {M}}}_{i\rightarrow jk}|^2$ is a matrix element squared summed over initial and final spins. After performing the integration over the outgoing momenta,

$$\begin{aligned} {{\mathcal {D}}}_{i\rightarrow jk}&=-\langle \varGamma _{i\rightarrow jk}\rangle \left[ n_i-{\bar{n}}_i\frac{n_j n_k}{{\bar{n}}_j{\bar{n}}_k}\right] . \end{aligned}$$

(A.24)

where thermally averaged decay rate $\langle \varGamma _{i\rightarrow jk}\rangle$ is defined as,

$$\begin{aligned} \langle \varGamma _{i\rightarrow jk}\rangle \equiv \frac{1}{{\bar{n}}_i}\int \frac{d^3p_i}{(2\pi )^3} \frac{m_i}{E_i}\varGamma _{i\rightarrow jk} {\bar{f}}_i = \frac{K_1(x_i)}{K_2(x_i)}{\bar{\varGamma }}_{i\rightarrow jk}, \end{aligned}$$

(A.25)

where $K_{1,2}$ are the Bessel functions and ${\bar{\varGamma }}_{i\rightarrow jk}$ is the width averaged over the initial and summed over final spins, i.e. ${\bar{\varGamma }}_{i\rightarrow jk}\equiv \varGamma _{i\rightarrow jk}/g_i$.

Appendix B: Direct detection of multi-component dark matter

In the MCDM scenario, the standard direct detection bounds given by experimental groups in terms of DM-nucleon scattering cross-section and DM mass cannot be imposed, unless one of the components is responsible for nearly all recoil events [57, 62, 116]. Furthermore, the combined differential event rate in multi-component case may have a distinctive shape, which allows to discriminate it from single-component scenario [117]. In a general case, one has to confront the theoretical predictions with the results of experiments to put a constraint on the parameter space of the model. In our analysis, we follow [118]. The differential recoil event rate for a given DM component i can be written as [119]

$$\begin{aligned} \frac{dR_i}{dE_R}=\frac{\sigma _{i N}\rho _i}{2 m_i \mu ^2_{iN}} F^2(E_R)\,\eta _i (E_R), \end{aligned}$$

(B.26)

where $\rho _i = \varOmega _i/\varOmega _{\mathrm{tot}}\times 0.3 {\mathrm{GeV}}/\mathrm{cm}^3$ is the local density of that DM component, $\sigma _{i N}$ is its nucleus scattering cross-section, $\mu _{iN}$ is the reduced mass of DM-nucleus system, F is the nuclear form factor, which we take as the conventional Helmi form and the function $\eta _i$ is a mean inverse speed of the DM particles in the local earth frame

$$\begin{aligned} \eta (E_R)=\int _{|v|>v_{\mathrm{min}}}\!\! d^3{\mathbf {v}}\,\frac{f({\mathbf {v}})}{v}. \end{aligned}$$

(B.27)

For the velocity distribution $f_G(v)$ in our Galaxy we use a truncated Maxwell-Boltzmann distribution with $v_{\mathrm{esc}}=550\;\mathrm{km}/\mathrm{s}$.

$$\begin{aligned} f_G ({\mathbf {v}})= \frac{1}{N_{\mathrm{esc}}(\pi v^2_0)^{3/2}}\,e^{-{\mathbf {v}}^2/v^2_0}\,\theta (v_{\mathrm{esc}}-v), \end{aligned}$$

(B.28)

where $v_0 = 220 \;\mathrm{km}/\mathrm{s}$ is the mean DM velocity relative to galaxy and $N_{\mathrm{esc}}$ is the normalization factor. The distribution of DM as observed from the Earth takes into account its velocity ${\mathbf {v}}_{\mathrm{e}}$ relative to the galactic halo rest frame

$$\begin{aligned} f({\mathbf {v}}) = f_G({\mathbf {v}}+{\mathbf {v}}_{\mathrm{e}}). \end{aligned}$$

(B.29)

The total $dR/dE_R$ differential recoil event rate is obtained by summing the rates for all DM components.

Various DM direct detection experiments measure different kinds of detection signals, eg. prompt scintillation signal S1, ionization charge signal S2, the electron equivalent energy or energy released in photons. To put a constraints on a region of DM parameter space, one has to compute the expected experimental signal from the recoil event rate $dR/dE_R$ of multi-component DM obtained above. We focus on the predictions for the S1 signal measured by LUX experiment [6]. Following [118] we count the number of events N in the signal range $S1\in [S1_a,S2_b]$ as described in [120]

$$\begin{aligned} N_{[S1_a,S1_b]}&= Ex \int _{S1_a}^{S2_b} dS1 \left[ \sum _{n=1}^\infty \epsilon (S1)\mathrm{Gauss}(S1|n,\sigma ) \nonumber \right. \nonumber \\&\quad \left. \times \!\int _0^\infty dE_R \mathrm{Poiss}(n|\nu (E_R))\epsilon _{S2}(E_R)\frac{dR}{dE_R}\right) , \end{aligned}$$

(B.30)

where additional S2 efficiency $\epsilon _{S2}(E_R) \!=\! \theta (E_R - 3\mathrm{keV})$ is cutting the recoil energies from below and $\nu (E_R)\!=\!g_1 L_y E_R$ is the averaged expected number of photoelectrons from a given recoil event, which is calculated based on LUX gain factor $g_1 = 0.0985$ and photon yield $L_y$ adopted from the middle plot of Fig. 1. in [121]. The Poisson distribution gives the probability of obtaining n photoelectrons, which in the detector produce signal S1 normally distributed around n with $\sigma \! =\! \sqrt{n(\sigma ^2_{\mathrm{PMT}}+g_1)}$, where $\sigma _{\mathrm{PMT}}$ is the single-photon resolution [122]. We include also the detector efficiency for events passing analysis selection criteria $\epsilon (S1)$, taken as a black curve from Fig. 2 in [6], and calculate the expected signal taking into account the total exposure $Ex = 4.47\times 10^4$ $\mathrm{kg}\times \mathrm{days}$.

We assume that all candidate events observed by LUX agree with the background-only model, using $S1_a=1$ and $S1_b=50$ we constraint the number of events in the range $N_{[1,50]}<3.09$ at $95\%$ C.L. (2$\sigma$) based on the Poisson statistics.