Diffractive scattering on the deuteron projectile in the NLO: triple interaction of reggeized gluons

Abstract

High-mass diffractive production of protons on the deuteron target is studied in the next-to-leading order (NLO) of the perturbative QCD in the BFKL approach. The non-trivial part of the NLO contributions coming from the triple interactions of the exchanged reggeons is considered. Analytic formulas are presented and shown to be infrared free and so are ready for practical calculation.

1 Introduction

In perturbative QCD, collisions on heavy nuclear targets have long been the object of extensive study. In the BFKL approach the structure function of DIS on a heavy nuclear target is given by a sum of fan diagrams in which BFKL pomerons propagate and split by the triple pomeron vertex. This sum satisfies the well-known Balitski–Kovchegov equation derived earlier in different approaches [1, 2]. The corresponding inclusive cross-sections for gluon production were derived in [3, 4]. The description of nucleus–nucleus collisions has met with less success. For collision of two heavy nuclei in the framework of the color glass condensate and JIMWLK approaches, numerical Monte Carlo methods were applied [5,6,7,8,9,10,11,12]. Analytical approaches, however, have only given modest approximate results [13,14,15]. The methods developed so far refer to the collision with heavy nuclei and rely basically on the semi-classical approximation valid in the limit of a very small coupling constant where the amplitudes behave as $1/g^2$. To move to nuclei with a smaller number of nucleons one needs to develop an approach which explicitly uses the composition of the nucleus as a composite of a few nucleons which interact with the projectile in the manner specific to the Regge kinematics. This approach is clearly provided by the framework of the exchange of reggeized gluons which combine into colorless pomerons or higher BKP states [20, 21] (the BFKL framework). To understand the problem one of the authors (M.A.B.) turned to the simplest case of nucleus–nucleus interaction, namely the deuteron–deuteron collisions [16, 17]. It was found that in this case the diagrams which give the leading contribution are different from the heavy nucleus case and include non-planar diagrams subdominant in $1/N_c$ where $N_c$ is the number of colors. In [18] this technique was applied to the diffractive proton production off the deuteron and it was found that the contribution from the diagrams involving both nucleons in the deuteron is dominant with respect to simple triple pomeron diagrams connected to only one deuteron component. In the reggeized gluon language, interaction between two pairs of reggeized gluon dominates over such an interaction with only one initial pair.

Higher orders provided by additional BFKL interactions give new terms which at large rapidities have the same order and lead to the appearance of fully developed BFKL pomerons and BKP states formed within the deuteron. However, there also appear true second order terms, which correspond either to a second order BFKL interaction or to new elements in the interaction involving not two pairs of reggeized gluons (reggeons) but three pairs of them. Such a NLO interaction was studied in the odderon problem [19], where the corresponding expressions were derived and, most importantly, the absence of an infrared divergence was demonstrated. Thus, this NLO interaction became ready for numerical analysis.

In this paper we study the NLO interactions involving three pairs of reggeons for the diffractive production of the protons off the deuteron, the process studied in LO in [18]. This problem is much more difficult than a similar odderon one due to the smaller symmetry and the appearance of certain new diagrams which are absent for the odderon just by absence of symmetry. These extra diagrams prevent one from using the technique of [19] based on the expression, found earlier in [22], for two-gluon emission, which substantially simplified calculation for the odderon. Unfortunately we are bound to use a novel technique and perform rather cumbersome calculations. We shall discover that these extra diagrams individually contain an infrared divergency of a very unpleasant character. Our main result is to demonstrate that after summation of all numerous contributions this infrared divergency is canceled and as for the odderon in [19] the final expressions are ready for numerical study.

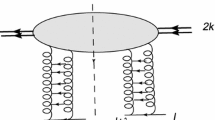
The NLO contributions to the diffractive production of protons off the deuteron with interaction of three pairs of reggeons involve three types of diagrams, shown in Fig. 1. The bulk of the contribution comes from the diagram in Fig. 1a, in which the intermediate gluon is produced by the process R+R$\rightarrow$R+R+G where R stands for the reggeon and G for the gluon. In Fig. 1b we show another contribution to the cross-section with two gluons in the intermediate state. Finally, Fig. 1c shows one more possible diagram for this process in which the intermediate gluon arises from two processes R+R$\rightarrow$R+G. However, in fact the latter contribution is canceled between the direct and conjugated diagrams and does not need to be considered.

Fig. 1

NLO diagrams with interaction of three pairs of reggeons

To conclude this introduction we recall the basic formulas connecting the diagrams with the cross-section itself. We work in the center-of-mass system of the colliding proton and one of the nucleons of the deuteron. The inclusive cross-section of the diffractive proton production $d(2k)+p(l)\rightarrow p(l')+X$ is given by

$$\begin{aligned} I(l')\equiv \frac{(2\pi )^32l'_-\mathrm{d}\sigma }{\mathrm{d}l'_-\mathrm{d}^2l'_\perp }= \frac{1}{s}\mathrm{Im}\mathcal{A}, \end{aligned}$$

(1)

where the amplitude $\mathcal{A}$ corresponds to Fig. 1. Let the final proton momentum be $l'=l+\lambda$. The missing mass is then $M^2=-4k_+\lambda _-$. In terms of the overall and pomeron rapidities Y and y we have $M^2=M_0^2\exp (Y-y)$ where $M_0\sim 1$ GeV. Putting $t=|\lambda _\perp |^2$ we rewrite the diffractive cross-section as

$$\begin{aligned} J(y,t)\equiv \frac{\mathrm{d}\sigma }{\mathrm{d}y\mathrm{d}t}=\frac{M^2}{32\pi ^2s^2}\mathrm{Im}\,\mathcal {A}. \end{aligned}$$

(2)

Separating the deuteron lines we standardly find (see [23])

$$\begin{aligned} \mathcal{A}=\int \mathrm{d}z F(z)|\psi _d(r_\perp =0,z)|^2, \end{aligned}$$

(3)

where

$$\begin{aligned} F(z)=\frac{1}{k_+}\int \frac{\mathrm{d}\kappa _+}{2\pi }H(\kappa _+)\mathrm{e}^{izm\kappa _+/k_+}, \end{aligned}$$

(4)

H is the high-energy part of $\mathcal{A}$ and $\kappa _+$ is the $+$-component of the momentum $\kappa$ transferred to one of the nucleons in the deuteron with $\kappa _-=\kappa _\perp =0$. For comparison, in the same process with a heavy nucleus projectile, the contribution from the collision with two nucleons is given by (1) with

$$\begin{aligned} \mathcal{A}=\frac{1}{4}A(A-1)\int \mathrm{d}^2b\mathrm{d}z_1\mathrm{d}z_2 F(z_1-z_2)\rho (\mathbf{b},z_1)\rho (\mathbf{b},z_2), \end{aligned}$$

(5)

where $\rho (\mathbf{b},z_1)$ is the nuclear density normalized to unity.

The Glauber approximation corresponds to the contribution which follows when F(z) does not depend on z. Then the square of the deuteron wave function converts into the average $\langle 1/2\pi r^2 \rangle$, and in (5) we find integration over the impact parameter $\mathbf{b}$ of the square of the profile function $T(\mathbf{b})$. In standard cases the high-energy part contains $\delta (\kappa _+)$:

$$\begin{aligned} H(\kappa _+)=2\pi \delta (\kappa _+)D,\quad \text {so that } F=\frac{1}{k_+}D. \end{aligned}$$

(6)

Then for the deuteron

$$\begin{aligned} \mathcal{A}=\frac{D}{k_+}\langle 1/2\pi r^2\rangle _d \end{aligned}$$

(7)

and for a large nucleus

$$\begin{aligned} \mathcal{A}=\frac{1}{4}A(A-1)\frac{D}{k_+}\int \mathrm{d}^2bT^2(\mathbf b). \end{aligned}$$

(8)

The paper is organized as follows. In the next section we discuss the main part of the contribution to the high-energy amplitude H corresponding to the transition R+R$\rightarrow$R+R+G for the production of the intermediate gluon realized by vertex $\Gamma _{\mathrm{RR}\rightarrow \mathrm{RRG}}$. Next we discuss the two-gluon intermediate state corresponding to Fig. 1b. In the last section we draw some conclusions. Some long and cumbersome calculations are transferred to the three appendices.

2 Contribution from the RR$\rightarrow$RRG vertex

The diagram which describes the NLO corrections due to RR$\rightarrow$RRG vertex $\Gamma _{\mathrm{RR}\rightarrow \mathrm{RRG}}$ is shown in Fig. 1a in the introduction. It should be supplemented by a similar diagram with interchanged nucleons in the deuterons and conjugated contributions. The interchange of the nucleons does not change the amplitude. This is due to the symmetry of the vertex with respect to permutations of both the two incoming reggeons and the outgoing reggeons. So it is sufficient to study the diagram in Fig. 1a and double its contribution. The vertex $\Gamma _{RR\rightarrow RRG}$ itself does not depend on impact factors and does not feel evolution. So finding its contribution can be simplified by suppressing the evolution and taking some simple impact factors for the pomerons. We take simple quarks for the four scattering centers assuming that their interaction is due to colorless exchange.

The total number of transferred momenta is seven: $q_1$, $q_2$, $q_3$, $r_1$, $r_2$, $r_3$, and $q_4=r_4$. The momentum of the real gluon p is $p=q_1+q_2-r_1-r_2$. We choose as independent momenta $q_1$, $r_1$ and p. Then we have

$$\begin{aligned} q_2= & {} p+\lambda -q_1,\ \ q_3=q_1-p-\kappa -\lambda ,\ \ q_4=r_4=\kappa -q_1,\\ r_2= & {} \lambda -r_1,\ \ r_3=q_1-\kappa -\lambda . \end{aligned}$$

So we have six longitudinal integrations. There are five conditions arising from mass-shell conditions for real intermediate particles and sums of direct and crossed diagrams for the rest, which give

$$\begin{aligned} (2\pi )^5\delta (q_{1-})\delta (q_{2-})\delta (r_{1+})\delta (r_{4+}) \delta (p^2), \end{aligned}$$

multiplied by $4s^2$. The integrations over $q_{1+}$, $q_{1-}$ and $r_{1+}$ are done with the help of $\delta$-functions, which puts $q_{1+}=\kappa _+$, $q_{1-}=r_{1+}=0$. Of the three integrations over $p_{\pm }$ and $r_{1-}$ the $\delta$ functions

$$\begin{aligned} (2\pi )^2\delta (p^2)\delta (p_-+\lambda _-) \end{aligned}$$

allow one to integrate over $p_{\pm }$ and we are finally left with only one longitudinal integration over $r_{1-}$ with $p_-=-\lambda _-$.

Apart from the four pomerons the diagram of Fig. 1a involves the Lipatov vertex on the left $f^{b_3a_3c}L(-p,r_3)$ where $a_3$, $b_3$ and c are the color indices of the two reggeons 3 (incoming and out going) and of the real gluon. It does not depend on longitudinal variables and enters only the transversal integral. On the right we meet the RR$\rightarrow$RRP vertex of the structure

$$\begin{aligned}&\Gamma ^{a_2a_1c}(q_2,q_1|r_2,r_1)\\&\quad =f^{a_2a_1c} \left( \Gamma (q_2,q_1|r_2,r_1)-\Gamma (q_1,q_2|r_2,r_1) \right) . \end{aligned}$$

It does depend on the longitudinal variables and is symmetric in $r_1,r_2$ and antisymmetric in $q_1,q_2$.

Doing summation over colors we obtain the imaginary part $H_1$ coming from Fig. 1a as

$$\begin{aligned} {\mathrm{Im}}\, H_1= & {} g^4\frac{2s^2}{ p_-}\int \frac{\mathrm{d}r_{1-}}{2\pi }\int \mathrm{d}\tau _\perp \nonumber \\&\times \,P_{Y-y}(q_{1\perp },q_{4\perp })P_{Y-y}(q_{2\perp }, q_{3\perp })L(r_3-q_3,r_3)\nonumber \\&\times \,{\mathrm{Im}}\,\left( \Gamma _(q_2,q_1|r_2,r_1)-\Gamma (q_1,q_2|r_2,r_1) \right) P_{y}(r_{1\perp },r_{2\perp })\nonumber \\&\times \,P_{y}(r_{3\perp },r_{4\perp }), \end{aligned}$$

(9)

where $\tau _\perp$ is the transverse phase volume; y is defined as before via $M^2$. We include in each pomeron a factor $N_cg^2$. Then in the final factor just $g^4$ appears. Note that $2s^2/p_-=8s^2k_+/M^2$.

In (9) we have used the fact that the momentum part of $\Gamma$ is antisymmetric under $q_{1+}\leftrightarrow q_{2+}$, since the color factor is antisymmetric under this exchange. In the vertex $\Gamma$ we have to take longitudinal variables in accordance with our results for the q,

$$\begin{aligned} q_{1+}= & {} \kappa _+,\ \ q_{1-}=0,\ \ q_{2+}=p_+-\kappa _+,\ \ q_{2-}=0,\ \\ r_{1+}= & {} 0,\ \ r_{2+}=0, r_{2-}=\lambda _{-}-r_{1-},\ \ p_-=-\lambda _-,\ \ p^2=0, \end{aligned}$$

and the transverse momenta inside the pomerons are constrained by

$$\begin{aligned}&q_{1\perp }+q_{4\perp }=q_{2\perp }+q_{3\perp }=0,\ \ r_{1\perp }+r_{2\perp }=-r_{3\perp }-r_{4\perp }\nonumber \\&=\lambda _{\perp }=l'_\perp . \end{aligned}$$

(10)

The interchange of the two projectiles in the deuteron plus complex conjugate contribution multiply (9) by factor 4.

Note that in contrast to the more or less trivial cases of the scattering off a composite the obtained expression does not contain $\delta (\kappa _+)$, which could lift the integration in (4) and bring the resulting cross-section into the Glauber form. In our case $\kappa _+$ appears in the cross-section via the longitudinal momentum $q_{1+}=\kappa _+$. Therefore in (9) after doing the integration over $r_{1-}$ one has to perform an integration over $q_{1+}$ with the weight dictated by (4). As we shall see, this integration goes over a finite interval of rapidities of the order $\delta$ due to the condition that all intermediate gluons should lie at finite rapidity distances from the real intermediate gluon. After integration over $q_{1+}$ one finds first terms proportional to $\delta$, which should be dropped, since hopefully they are to be canceled by other terms of the same order, namely terms with pairwise interaction between reggeons, with extra BFKL interactions or with this interaction in the second order. The remaining terms are well convergent and do not depend on $\delta$ nor on the exponential in (4), since the exponent is small. These terms lead to F(z) independent of z and thus to the same Glauber expression, Eq. (7), for the amplitude with

$$\begin{aligned} F=\frac{1}{k_+}\int \frac{\mathrm{d}q_{1+}}{2\pi }\mathrm{Im}\,H. \end{aligned}$$

(11)

As mentioned, the left Lipatov vertex in the diagram in Fig.1a is on-shell and does not depend on $r_{1-}$ nor on $q_{1+}$ So we have to longitudinally integrate only the vertex RR$\rightarrow$RRP. Therefore combining the coefficients in (9) and (2) our final result for the cross-section from the vertex $\Gamma$ has the form

$$\begin{aligned} \frac{\mathrm{d}\sigma _{\Gamma }}{\mathrm{d}y\mathrm{d}t}= & {} \langle 1/2\pi r^2 \rangle _d\frac{g^4N_c^4}{\pi ^2} \int \mathrm{d}\tau _\perp \mathcal{M}P_{Y-y}(q_{1\perp },q_{4\perp }) \nonumber \\&\times P_{Y-y}(q_{2\perp },q_{3\perp }) P_{y}(r_{1\perp },r_{2\perp })P_{y}(r_{3\perp },r_{4\perp }), \end{aligned}$$

(12)

where

$$\begin{aligned} \mathcal{M}= & {} L(r_3-q_3,r_3)\mathrm{Im}\,\int \frac{\mathrm{d}\kappa _+\mathrm{d}r_{1-}}{4\pi ^2}\nonumber \\&\times \,\left( \Gamma (q_2,q_1|r_2,r_1)-\Gamma (q_1,q_2|r_2,r_1) \right) . \end{aligned}$$

(13)

The total vertex $\Gamma$ is a sum of 5 pieces $\Gamma =\sum _{i=1}^5 \Gamma _i$. The diagrams with vertices $\Gamma _i$ are shown in Fig. 2.

Fig. 2

Diagrams containing vertex parts $\Gamma _i$, $i=1,\ldots ,5$. $\Gamma _{1,2,5}$ correspond to A, B and D. $\Gamma _{3,4}$ correspond to C

The actual longitudinal integrations in $\Gamma _i$, $i=1,\ldots ,5$ are long and tedious. They are described in Appendices 1, 2 and 3. To avoid proliferation of notations we denote the resulting integrated $\Gamma$ with the same letter $\Gamma$. Collecting our results derived in the appendices, we find for different pieces the following expressions:

$$\begin{aligned} \Gamma _1=\frac{i}{8\pi }{\hat{T}}_0\frac{1}{2(\mathbf{p}+\mathbf{r}_2)^2} \ln \frac{(\mathbf{q}_1-\mathbf{r}_1)^2\mathbf{p}^2}{(\mathbf{p}+\mathbf{r}_2)^4}+(\text {Sym}), \end{aligned}$$

where ${\hat{T}}_0$ is given by (59). We have

$$\begin{aligned} \Gamma _2=-\frac{i}{4\pi }{\hat{T}}_1\frac{1}{2\mathbf{p}^2} \ln \frac{(\mathbf{q}_1-\mathbf{r}_1)^2\mathbf{p}^2}{(\mathbf{p}-\mathbf{q}_2)^4}+ (\text {Sym}), \end{aligned}$$

where ${\hat{T}}_1$ is given by (63). We have

$$\begin{aligned} \Gamma _3=\frac{i}{4\pi }V_0\frac{1}{2(\mathbf{q}_1-\mathbf{r}_1)^2}\ln \frac{(\mathbf{q}_1-\mathbf{r}_1)^2}{\mathbf{p}^2}+(\text {Sym}). \end{aligned}$$

where $V_0$ is given by (65).

$$\begin{aligned} \Gamma _4=-\frac{i}{8\pi }V_1\frac{1}{2\mathbf{p}^2}\ln \frac{(\mathbf{q}_1-\mathbf{r}_1)^2}{\mathbf{p}^2} +(\text {Sym}), \end{aligned}$$

where $V_1$ is given by (70). Here $+(\text {Sym})$ means addition of

$$\begin{aligned} -\left( q_1\leftrightarrow q_2 \right) + \left( r_1\leftrightarrow r_2 \right) - \left( q_1\leftrightarrow q_2, r_1\leftrightarrow r_2 \right) . \end{aligned}$$

The most complicated part comes from $\Gamma _5=\Gamma ^A+\Gamma ^B$. We find

$$\begin{aligned} \Gamma ^A= & {} \frac{i}{8\pi }\left\{ I^A_0 \left[ T_2 \left( 2\frac{(\mathbf{p},\mathbf{q}_2-\mathbf{r}_2)^2}{\mathbf{p}^4}-\frac{(\mathbf{q}_2-\mathbf{r}_2)^2}{\mathbf{p}^2}\right) \right. \right. \\&+T_1\frac{(\mathbf{p},\mathbf{q}_2-\mathbf{r}_2)}{\mathbf{p}^2}+T_0 +T_{-1}\frac{(\mathbf{p},\mathbf{q}_2-\mathbf{r}_2)}{(\mathbf{q}_2-\mathbf{r}_2)^2}\\&\left. +\frac{U_0}{p_+}\frac{(\mathbf{p},\mathbf{q}_1-\mathbf{r}_1)}{(\mathbf{q}_1-\mathbf{r}_1)^2} -\frac{V_0}{p_+}\frac{(\mathbf{q}_1-\mathbf{r}_1,\mathbf{q}_2-\mathbf{r}_2)}{(\mathbf{q}_1-\mathbf{r}_1)^2(\mathbf{q}_2-\mathbf{r}_2)^2} \right] \\&-\frac{1}{2(\mathbf{q}_1-\mathbf{r}_1)^2}\ln \frac{(\mathbf{q}_2-\mathbf{r}_2)^2}{\mathbf{p}^2} \\&\left. \left( \frac{U_0}{p_+} -\frac{1}{(\mathbf{q}_2-\mathbf{r}_2)^2}\, \frac{V_0}{p_+}\right) \right\} - \left( q_1\leftrightarrow q_2 \right) , \end{aligned}$$

where

$$\begin{aligned} I_0^A=\frac{\pi -\phi _2}{\sqrt{\mathbf{p}^2(\mathbf{q}_2-\mathbf{r}_2)^2-(\mathbf{p},\mathbf{q}_2-\mathbf{r}_2)^2}}, \end{aligned}$$

$\phi _2$ is the angle between $\mathbf{p}$ and $\mathbf{q}_2-\mathbf{r}_2$, $0\le \phi \le \pi$ and the coefficients $T_n$, $U_0$ and $V_0$ are given by (74). We have

$$\begin{aligned} \Gamma ^B= & {} -\frac{i}{8\pi }\left\{ I^B_0\left[ {\tilde{T}}_2\left( 2 \frac{(\mathbf{p},\mathbf{q}_1-\mathbf{r}_1)^2}{\mathbf{p}^4}-\frac{(\mathbf{q}_1-\mathbf{r}_1)^2}{\mathbf{p}^2}\right) \right. \right. \\&+ {\tilde{T}}_1\frac{(\mathbf{p},\mathbf{q}_1-\mathbf{r}_1)}{\mathbf{p}^2}+{\tilde{T}}_0 +{\tilde{T}}_{-1}\frac{(\mathbf{p},\mathbf{q}_1-\mathbf{r}_1)}{(\mathbf{q}_1-\mathbf{r}_1)^2}\\&\left. +\frac{{\tilde{U}}_0}{p_+}\frac{(\mathbf{p},\mathbf{q}_2-\mathbf{r}_2)}{(\mathbf{q}_2-\mathbf{r}_2)^2} -\frac{{\tilde{V}}_0}{p_+}\frac{(\mathbf{q}_1-\mathbf{r}_1,\mathbf{q}_2-\mathbf{r}_2)}{(\mathbf{q}_1-\mathbf{r}_1)^2(\mathbf{q}_2-\mathbf{r}_2)^2} \right] \\&\left. +\frac{1}{2(\mathbf{q}_2-\mathbf{r}_2)^2}\ln \frac{(\mathbf{q}_1-\mathbf{r}_1)^2}{\mathbf{p}^2} \left( \frac{{\tilde{U}}_0}{p_+}-\frac{1}{(\mathbf{q}_1-\mathbf{r}_1)^2}\, \frac{{\tilde{V}}_0}{p_+} \right) \right\} \\&-\left( q_1\leftrightarrow q_2 \right) , \end{aligned}$$

where

$$\begin{aligned} I_0^B=\frac{\phi _1}{\sqrt{\mathbf{p}^2(\mathbf{q}_1-\mathbf{r}_1)^2-(\mathbf{p},\mathbf{q}_1-\mathbf{r}_1)^2}}, \end{aligned}$$

$\phi _1$ is the angle between $\mathbf{p}$ and $\mathbf{q}_1-\mathbf{r}_1$, $0\le \phi \le \pi$ and the coefficients ${\tilde{T}}_n$, ${\tilde{U}}_0$ and ${\tilde{V}}_0$ are given by (76).

The separate terms in $\Gamma _3$, $\Gamma _4$ and $\Gamma _5$ contain non-integrable divergence at $\mathbf{q}_1\rightarrow \mathbf{r}_1,\mathbf{r}_2$ and $\mathbf{q}_2\rightarrow \mathbf{r}_1,\mathbf{r}_2$. However, in Sect. 7.6 it is demonstrated that these singularities cancel in the sum of all $\Gamma _i$, $i=3,4,5$.

In (13) the integrated $\Gamma$ is to be multiplied by the Lipatov vertex,

$$\begin{aligned} L(r_3-q_3,r_3)=-2\left( (q_2e)_\perp -(pe)_\perp \frac{q_2^2}{p_\perp ^2} \right) . \end{aligned}$$

The integrated $\Gamma$ contains products $(ae)_\perp$ with different a. A summation over polarization leads to the transformation

$$\begin{aligned} L(r_3-q_3,r_3)(ae)\rightarrow 2\left( (q_2a)_\perp -(pa)_\perp \frac{q_2^2}{p_\perp ^2} \right) . \end{aligned}$$

So in the end one obtains $\mathcal{M}$ as a well-defined function of the transverse momenta, ready for practical evaluations.

3 Two intermediate gluons

To begin we find that of the two additional contributions shown in Fig. 1b, c only the first with two intermediate gluons gives non-zero contribution. Indeed the contribution to the unitarian term from the diagram in Fig. 1c cancels between the amplitude and its conjugated term. In this diagram on the right-hand side (rhs) from the cut we find a purely imaginary contribution due to the single incoming reggeon $q_1$. On the left-hand side (lhs) we have a similar purely imaginary quantity plus an extra gluon $q_4=r_4$, which gives $+i$. So the total contribution to the unitarian term is imaginary and will be canceled by the conjugated one.

So we are left only with the contribution from the two-gluon intermediate states, Fig. 1b. This diagram is quite similar to the diagram in Fig. 2d but with a different cut. This makes its calculation somewhat different.

3.1 Longitudinal integration

The cut separates the diagram into two parts: lhs and rhs. For the lhs we find

$$\begin{aligned} {\mathrm{lhs}}= & {} \frac{1}{p^2+i0}\left[ 2(k_1e_2)(Le_1)-2(k_2e_1(Le_2) \right. \nonumber \\&\left. +(e_1e_2)(L(k_2-k_1)) \right] , \end{aligned}$$

(14)

where we denoted $L=L(-p,r_3)$ and $e_1=e(k_1)$ and $e_2=e(k_2)$ are the 4-dimensional polarization vectors with $e_+=0$. For the rhs we have

$$\begin{aligned} {\mathrm{rhs}}= & {} 16\pi ^2\delta (k_1^2)\delta (k_2^2) \left( (q_1e_1)_\perp -(k_1e_1)\frac{q_1^2}{k_{1\perp }^2}\right) \nonumber \\&\times \,\left( (q_2e_2)_\perp -(k_2e_2)\frac{q_2^2}{k_{2\perp }^2}\right) . \end{aligned}$$

(15)

Integrations over $q_{1+}$ and $q_{2_+}$ are done using the two $\delta$ functions. As a result we get factor the $1/(4r_{1-}r_{2-})$, and $q_{1,2+}$ can be expressed as

$$\begin{aligned} q_{1+}=\frac{k_{1\perp }^2}{2r_{1-}},\quad q_{2+}=\frac{k_{2\perp }^2}{2r_{2-}}. \end{aligned}$$

(16)

The final longitudinal integration is over $r_{1-}$ with $r_{2-}=\lambda _--r_{1-}$. In the denominator appears

$$\begin{aligned} D= & {} r_{1-}r_{2-}p^2=r_{1-}r_{2-}\left[ -2\lambda _-\left( \frac{k_{1\perp }^2}{2r_{1-}}+ \frac{k_{2\perp }^2}{2r_{2-}} \right) +p_\perp ^2 \right] \nonumber \\= & {} -\lambda _-\left( k_{1\perp }^2r_{2-}+k_{2\perp }^2r_{1-} \right) +r_{1-}r_{2-}p_\perp ^2. \end{aligned}$$

(17)

Putting $r_{1-}=x\lambda _-$ and so $r_{2-}=(1-x)\lambda _-$ we rewrite

$$\begin{aligned} D&=-\lambda _-^2 \left( (1-x)k_{1\perp }^2+xk_{2\perp }^2-x(1-x)p_\perp ^2 \right) \nonumber \\&=-\lambda _-^2(k_{1\perp }-xp_\perp )^2. \end{aligned}$$

(18)

So we see that the contribution from diagram Fig. 1b contains the same denominator as the contribution from $\Gamma _5$ (see the appendix). However, as we discuss in Sect. 7.3 the collinear singularity from $D=0$ is spurious, since the numerator vanishes.

The rhs does not depend on $r_{1-}$. The lhs contains factors depending on $r_{1-}$. Making explicit the x-dependence we have in the lhs

$$\begin{aligned} (k_1e_2)= & {} (k_1e_2)_\perp -(k_2e_2)_\perp \frac{1-x}{x}\frac{k_{1\perp }^2}{k_{2\perp }^2},\\ (k_2e_1)= & {} (k_2e_1)_\perp -(k_1e_1)_\perp \frac{x}{1-x}\frac{k_{2\perp }^2}{k_{1\perp }^2},\\ (Le_1)= & {} (b_1,e_1)_\perp -(k_1e_1)_\perp \left( \frac{x}{1-x} \frac{k_{2\perp }^2}{k_{1\perp }^2}-2x\frac{q_3^2}{k_{1\perp }^2} \right) ,\\ (Le_2)= & {} (b_2,e_2)_\perp -(k_2e_2)_\perp \left( \frac{1-x}{x} \frac{k_{1\perp }^2}{k_{2\perp }^2}-2x\frac{q_3^2}{k_{2\perp }^2}\right) , \end{aligned}$$

$$\begin{aligned} (L,k_2-k_1)= & {} -k_{1\perp }^2r_3^2\frac{1-x}{(1-x)k_{1\perp }^2+xk_{2\perp }^2}-\frac{1}{2}k_{1\perp }^2\frac{1-x}{x}\nonumber \\&+\,\frac{1}{2}k_{2\perp }^2\frac{x}{1-x}+xq_2^2+(k_1,q_3+r_3)_\perp .\nonumber \\ \end{aligned}$$

(19)

Naturally this expression changes sign if $k_{1\perp }\leftrightarrow k_{2\perp }$ and $x\leftrightarrow 1-x$. The form (19) is convenient for the study of the limit $k_{1\perp }\rightarrow 0$. Here $b_1=q_3+r_3-k_1$, $b_2=q_3+r_3-k_2$. So the lhs contains singular factors 1 / x and $1/(1-x)$ and grows linearly with x at large x. The singularities at $x=0$ and $x=1$ are to be integrated in the principal value sense. At large x the integrand reduces to 1 / x and the integral over the whole axis converges.

The longitudinal integral over $r_{1-}$ takes the form

$$\begin{aligned} J=-\int \frac{\mathrm{d}x}{8\pi \lambda _-}\frac{X_1-X_2+X_3}{(k_{1\perp }-xp_\perp )^2}. \end{aligned}$$

(20)

We define transverse vectors

$$\begin{aligned} l_1=q_1-k_1\frac{q_1^2}{k_{1\perp }^2},\ \ l_2=q_2-k_2\frac{q_2^2}{k_{2\perp }^2},\ \ l_{1\pm }=l_{2\pm }=0. \end{aligned}$$

Then after summation over polarizations we get

$$\begin{aligned} X_1= & {} 8\left( l_2, k_1-k_2\frac{1-x}{x}\frac{k_{1\perp }^2}{k_{2\perp }^2} \right) _\perp \nonumber \\&\times \,\left[ l_1,b_1-k_1\frac{x}{1-x}\frac{k_{2\perp }^2}{k_{1\perp }^2}\left( 1-2(1-x) \frac{q_3^2}{k_{2\perp }^2} \right) \right] _\perp , \nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} X_2= & {} 8\left( l_1, k_2-k_1\frac{x}{1-x}\frac{k_{2\perp }^2}{k_{1\perp }^2} \right) _\perp \nonumber \\&\times \,\left[ l_2,b_2-k_2\frac{1-x}{x}\frac{k_{1\perp }^2}{k_{2\perp }^2} \left( 1-2x\frac{q_3^2}{k_{1\perp }^2} \right) \right] _\perp , \end{aligned}$$

(22)

$$\begin{aligned} X_3= & {} (L,k_2-k_1)(l_1l_2), \end{aligned}$$

(23)

where $(L,k_2-k_1)$ is given by (19). Doing the products in (21) and (22) we rewrite them in terms of transverse products

$$\begin{aligned} \frac{1}{8}X_1= & {} (k_1l_2)(b_1l_1)-(k_2l_2)(b_1l_1)\frac{1-x}{x} \frac{k_{1\perp }^2}{k_{2\perp }^2}\nonumber \\&-\,(k_1l_2)(k_1l_1)\frac{x}{1-x}\frac{k_{2\perp }^2}{k_{1\perp }^2} \left( 1-2(1-x)\frac{q_3^2}{k_{2\perp }^2} \right) \nonumber \\&+\,(k_2l_2)(k_1l_1) \left( 1-2(1-x)\frac{q_3^2}{k_{2\perp }^2} \right) , \end{aligned}$$

(24)

$$\begin{aligned} \frac{1}{8}X_2= & {} (k_2l_1)(b_2l_2)-(k_1l_1)(b_2l_2) \frac{x}{1-x}\frac{k_{2\perp }^2}{k_{1\perp }^2}\nonumber \\&-\,(k_2l_1)(k_2l_2)\frac{1-x}{x}\frac{k_{1\perp }^2}{k_{2\perp }^2} \left( 1-2x\frac{q_3^2}{k_{1\perp }^2} \right) \nonumber \\&+\,(k_2l_2)(k_1l_1) \left( 1-2x\frac{q_3^2}{k_{1\perp }^2} \right) . \end{aligned}$$

(25)

The integrals over x are all standard. With $(k_{1\perp }-xp_\perp )^2\equiv d$ we have

$$\begin{aligned}&I=\int \frac{\mathrm{d}x}{d}=\frac{\pi }{\sqrt{k_1^2p^2-(k_1p)^2}} =\frac{\pi }{\sqrt{k_2^2p^2-(k_2p)^2}},\\&\int \frac{\mathrm{d}x}{xd}=\frac{(k_1p)}{k_{1\perp }^2}I,\ \ \int \frac{\mathrm{d}x}{(1-x)d}=\frac{(k_2p)}{k_{2\perp }^2}I,\\&\int \frac{x\mathrm{d}x}{d}=\frac{k_1p}{p^2}I,\ \ \int \frac{(1-x)\mathrm{d}x}{d}=\frac{k_2p}{p^2}I,\\&\int \frac{x\mathrm{d}x}{(1-x)d}=\frac{(k_1k_2)}{k_{2\perp }^2}I,\ \ \int \frac{(1-x)\mathrm{d}x}{xd}=\frac{(k_1k_2)}{k_{1\perp }^2}I, \end{aligned}$$

and finally

$$\begin{aligned} I_1=\int \frac{\mathrm{d}x}{d}\frac{(1-x)k_{1\perp }^2-xk_{2\perp }^2}{(1-x)k_{1\perp }^2+xk_{2\perp }^2}= \frac{k_1^2-k_2^2}{p^2}I \end{aligned}$$

(antisymmetric under $k_1\leftrightarrow k_2$). In these and the following formulas all vectors are 2-dimensional Euclidean.

Using them we finally find for the integrated quantities

$$\begin{aligned} Z_1= & {} \int \frac{dx}{d} X_1=8I\left\{ (k_1l_2)(b_1l_1)-(k_2l_2)(b_1l_1) \frac{(k_1k_2)}{k_{2\perp }^2}\right. \nonumber \\&-\,(k_1l_2)(k_1l_1)\frac{(k_1k_2)}{k_{1\perp }^2}+2(k_1l_2)(k_1l_1) \frac{(k_1p)}{k_{1\perp }^2}\,\frac{q_3^2}{p^2}\nonumber \\&\left. +\,(k_2l_2)(k_1l_1)-2(k_2l_2)(k_1l_1)\frac{(k_2p)}{k_{2\perp }^2}\, \frac{q_3^2}{p^2} \right\} , \end{aligned}$$

(26)

$$\begin{aligned} Z_2= & {} \int \frac{dx}{d} X_2=Z_1(k_1\leftrightarrow k_2) \end{aligned}$$

(27)

and

$$\begin{aligned} Z_3= & {} \int \frac{dx}{d} X_3=I(l_1l_2)\left\{ (k_2^2-k_1^2) \left( 1-\frac{r_3^2}{p^2} \right) \right. \nonumber \\&\left. +k_2^2-k_1^2 +(q_3+r_3,k_2-k_1) \phantom {\left( 1-\frac{r_3^2}{p^2} \right) }\right\} . \end{aligned}$$

(28)

3.2 The cross-section

Apart from the factor $Z_1-Z_2+Z_3$ the contribution to the high-energy part will include color, longitudinal and transverse factors, which can be readily read from the diagram.

The final longitudinal factor comes from $-1/\lambda _-$ in D and factors $2k_+$ from each projectile quark and $2l_-$ from each target one, which gives the total $-16k_+^2l_-^2/\lambda _-$. The color factor $(1/2)N_c^4$ is the same as in Fig. 2d.

$$\begin{aligned} f^{a_2a_1c}f^{ce_2e_1}f^{e_1b_1a_1}f^{e_1b_1a_2}=\frac{1}{2}N_c^4. \end{aligned}$$

The transverse factor T is obtained after transverse integration of the sum $Z_1-Z_2+Z_3$ with the pomerons coupled to the projectiles and targets

$$\begin{aligned} T(y,t)&=\int \mathrm{d}\tau _\perp (Z_1-Z_2+Z_3)P_{Y-y}(q_1)P_{Y-y}(q_2)\nonumber \\&\quad \times \, P_y(q_1,q_1-\lambda )P_y(q_1,\lambda -q_1), \end{aligned}$$

(29)

where $t=-\lambda _\perp ^2$. As before we include in each pomeron the factor $N_cg^2$. Then the final extra factor will be just $g^4$.

Note that $Z_i$, $i=1,2,3$, contain singular terms. They first come from the function $I(k_1,k_2)$, which is singular when $k_{1\perp }$ is parallel to $p_\perp$ (collinear singularity) and when one of the 2-dimensional vectors $k_1,k_2$ or p goes to zero. The first singularity goes, since the coefficient vanishes as the 4-vectors get to lie in the same direction. The second singularity is integrable by itself but it may be accompanied by explicit singularities in the Z which have the structure $(kp)_\perp /k^2$ where k is any of the 2-dimensional vectors $k_{1\perp },\ \ k_{2\perp }$ or $p_\perp$. This combined singularity is canceled after averaging over angles and all the rest singularities turn out to be integrable.

To see this we present expressions for $Z_i$ in the limit $k_{1\perp }\rightarrow 0$. From (26) we find directly

$$\begin{aligned} Z_1(k_{1\perp }\rightarrow 0)&=-8q_1^2I\left[ (pl_2)\left( 1-\frac{2q_2^2+(pk_1)_\perp }{p_\perp ^2} \right) \right. \nonumber \\&\quad \left. +\,(kl_2)_\perp \left( \frac{(pk_1)_\perp }{k_{1\perp }^2}+1-2\frac{(pk_1)_\perp q_2^2}{p_\perp ^4} \right) \right] . \end{aligned}$$

(30)

For $Z_2$ we find after making the change $k_{1\perp }\leftrightarrow k_{2\perp }$

$$\begin{aligned} Z_2(k_{1\perp }\rightarrow 0)=-8Iq_1^2(pl_2)_\perp \frac{(pk_1)_\perp }{k_{1\perp }^2} \left( 1-\frac{(pk_1)_\perp }{p_\perp ^2} \right) . \end{aligned}$$

(31)

Finally,

$$\begin{aligned} Z_3(k_{1\perp }\rightarrow 0)=\frac{(pk_1)_\perp }{k_{1\perp }^2}q_1^2\left( (pk_1)_\perp \frac{r_3^2-q_2^2}{p_\perp ^2}-(r_3-q_2,k_1)_\perp \right) . \end{aligned}$$

(32)

Inspecting these expressions we see that in the limit $k_{1\perp }\rightarrow 0$, apart from the integral I, $Z_1$ and $Z_3$ remain finite and $Z_2$ has a singularity proportional to $(pk_1)_\perp /k_{1\perp }^2$. The latter singularity is, as mentioned, liquidated after integration over the angle between $k_{1\perp }$ and $p_\perp$. So in the end the only remaining singularity is in I and it is integrable.

Dividing by 2 to have the imaginary part, we finally find for the diagram

$$\begin{aligned} \mathrm{Im}\,H=-g^4\frac{s^2}{4\lambda _-}T(y,t). \end{aligned}$$

(33)

The contribution to the cross-section will be given by

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}y\mathrm{d}t} =\frac{1}{8}\alpha _s^2T(y,t)\langle 1/2\pi r^2 \rangle _d. \end{aligned}$$

(34)

The total contribution will be given by twice the sum of the contributions given by the diagram in Fig. 2b and the diagram with interchange of the gluons, $1\leftrightarrow 2$. We take into account that the color factor and terms $Z_i$, $i=1,2,3$, change sign under this interchange. So the net result will be symmetrization of the pomeron part. Thus we find the cross-section to be

$$\begin{aligned} \frac{\mathrm{d}\sigma _{2\mathrm{gluon}}}{\mathrm{d}y\mathrm{d}t} =\frac{1}{4}\alpha _s^2T^{\mathrm{tot}}(y,t)\langle 1/2\pi r^2 \rangle _d, \end{aligned}$$

(35)

where

$$\begin{aligned} T^{\mathrm{tot}}(y,t)= & {} \int \frac{\mathrm{d}^2q_1\mathrm{d}^2q_2\mathrm{d}^2r_1}{(2\pi )^6}(Z_1-Z_2+Z_3)\nonumber \\&\times \, \left( P_{Y-y}(q_1)P_{Y-y}(q_2)P_y(q_1,q_1-\lambda )\right. \nonumber \\&\left. \times \,P_y(q_1,\lambda -q_1) +(q_1\leftrightarrow q_2) \right) . \end{aligned}$$

(36)

4 Conclusions

We considered the high-mass diffraction on the deuteron in the perturbative QCD reggeon (BFKL-Barters) framework. It has already been shown in [18] that interaction with both components in the deuteron leads to a cross-section which may dominate over the naive triple-pomeron contribution. In this paper we study the NLO contributions due to the novel structure appearing in the next order and describing the triple interactions between the exchanged reggeons. The corresponding cross-sections are presented in Eqs. (12) and (35). The important result found in relation to these cross-sections is the demonstration that they are free from infrared divergencies and therefore are fit for the practical evaluation.

As to these practical calculations we have to stress that the found NLO corrections are not the only ones. Another contribution comes from the second order BFKL interaction in the diagrams considered in [18]. Unfortunately one cannot use for them the results found in the study of similar correction to the BFKL equation neither in the vacuum nor octet channels, since the color structure is different in our case. Thus the study of this particular correction requires a new derivation, which, as is well known, is quite long and complicated. Because of this we postpone it to the future separate publication.

Finally, we have to note that before attempting to perform practical calculations in the NLO one should try to find corrections to the LO due to appearance of the BKP states in the course of evolution. Their behavior at large energies is well known and is subdominant with respect to BFKL pomeron. So one may hope that their influence is also subdominant. However, to make some concrete estimates one should be able to present their wave functions in some possibly approximate form admitting practical use. This point is also to be studied later.

Appendices

Appendix 1. Integration over $r_{1-}$

1.1 General rules

Variable $r_{1-}$ enters one or two Feynman denominators and also may appear in the numerators. One can find (numerically) that at fixed p the on-mass shell vertex multiplied by the polarization vector $\epsilon$ with $\epsilon _+=0$ goes as $1/r_{1-}^2$ as $r_{1-}\rightarrow \infty$ [24]. This allows one to perform the integration over $r_{1-}$ by closing the contour in the complex plane and taking residues at poles.

In reality the integrand is a sum of terms $\Gamma _i$ with $i=1,\ldots ,5,$ which individually do not go to zero at $r_{1-}\rightarrow \infty$ and contain Feynman poles as well as poles at $r_{1-}=0$ or $r_{2-}=0$. Since we know that the sum of these terms goes to zero at large $r_{1-}$ fast enough, we can forget about the behavior of individual contributions at $r_{1-}\rightarrow \infty$ and just take the residues in, say, the lower half-plane. However, it is important that in all diagrams the residues are to be taken in the same (lower) half-plane. Using these rules we can do integrations in the terms $\Gamma _i$ with $i=1,\ldots ,5$ separately. Explicit expressions for the vertex RR$\rightarrow$RRP can be taken from our paper [24].

1.2 Figure 2a

On mass shell, multiplied by the polarization vector $\epsilon$ the corresponding amplitude $\Gamma _{1}$ is given by

$$\begin{aligned} \Gamma _{1}=-C_1\frac{1}{t^2k_1^2}X_1,\ \ X_1=-b{\bar{B}}-c\bar{C}+e{\bar{E}}. \end{aligned}$$

(37)

Here the denominators are $t^2k_1^2=(-2p_+r_{1-}+t_\perp ^2+i0)(-2q_{1+}r_{1-}+k_{1\perp }^2+i0)$. The color coefficient is $C_1=-(1/2)N_cf^{a_2a_1c}$ The coefficients b, c and e are

$$\begin{aligned} b= & {} 2p_+\left( (q_1\epsilon )_\perp -(p\epsilon )_\perp \frac{q_{1+}}{p_+}\right) - 2q_{1+}(r_2\epsilon )_\perp ,\\ c= & {} 2p_+\left( (q_2\epsilon )_\perp -(p\epsilon )_\perp \frac{q_{2+}}{p_+} \right) - 2q_{2+}(r_2\epsilon )_\perp ,\\ e= & {} -2(p+r_2,\epsilon )_\perp =-2(t\epsilon )_\perp . \end{aligned}$$

They do not depend on $r_{1-}$ nor on $r_{2-}$ We finally have

$$\begin{aligned} {\bar{B}}= & {} -4r_{1-},\ \ \bar{C}=-4r_{1-}+2\frac{r_1^2}{q_{1+}},\\ {\bar{E}}= & {} -2r_{1-}(2q_{1+}+q_{2+})+q_1^2+q_2^2-k_1^2+r_1^2\\&+\,(a_1,t+q_2)_\perp +2r_1^2\frac{q_{2+}}{q_{1+}}-\frac{r_1^2q_2^2}{q_{1+}r_{1-}}, \end{aligned}$$

where $a_1=q_1+r_1$. From this we find

$$\begin{aligned} X_1= & {} -4(q_2\epsilon )_{\perp }p_+\frac{r_1^2}{q_{1+}}-\,2(t\epsilon )_\perp \\&\times \, \left( r_1^2+q_1^2+q_2^2-k_1^2+(a_1,t+q_2)_\perp \right) \\&+\,4r_{1-}p_+(t+2r_1,\epsilon )_\perp +4r_{1-}q_{1+}(t\epsilon )_\perp \\&+\,2(t\epsilon )_\perp \frac{q_2^2r_1^2}{q_{1+}r_{1-}}. \end{aligned}$$

We separate the term with a pole at $r_{1-}=0$ presenting

$$\begin{aligned} X_1={\tilde{X}}_1+\frac{1}{r_{1-}}Y_1,\ \ Y_1=2(te)_\perp \frac{r_1^2q_2^2}{q_{1+}}, \end{aligned}$$

where $Y_1$ does not depend on $r_{1-}$.

After integration we get

$$\begin{aligned} \Gamma _{1}=-C_1 \left( I_{A_1}^{(1)}X_1^{(1)}+I_{A_1}^{(2)}Y_1 \right) . \end{aligned}$$

Here $X_1^{(1)}=X_1(r_{1-}=k_{1\perp }^2/2q_{1+})$ and the integrals are

$$\begin{aligned} I_{A_1}^{(1)}&=\int \frac{\mathrm{d}r_{1-}}{2\pi }\frac{1}{(t^2+i0)(k_1^2+i0)}\nonumber \\&=-\frac{i}{2}\theta (-q_{1+})\frac{1}{p_+k_{1\perp }^2-q_{1+}t_\perp ^2} \end{aligned}$$

(38)

and $I_{A_1}^{(2)}$ is the contribution of the residue at $r_{1-}=0$ in the lower half-plane of the part with $Y_1$

$$\begin{aligned} I_{A_1}^{(2)}=-\frac{i}{2}\frac{1}{k_{1\perp }^2 t_\perp ^2}. \end{aligned}$$

1.3 Figure 2b

On mass shell, multiplied by the polarization vector $\epsilon$, the corresponding amplitude $\Gamma _{2}$ is given by

$$\begin{aligned} \Gamma _2=-C_2\frac{1}{{\bar{t}}^2k_1^2}X_2,\ \ X_2={\bar{a}} A+ {\bar{b}} B+{\bar{c}} C+{\bar{e}} E. \end{aligned}$$

(39)

Here the color factor is $C_2=N_c f^{a_2a_1c}$ and the denominators are

$$\begin{aligned} {\bar{t}}^2k_1^2=(2q_{1+}p_-+{\bar{t}}_\perp ^2)(-2q_{1+}r_{1-}+k_{1\perp }^2+i0). \end{aligned}$$

The coefficients ${\bar{a}},\ldots ,{\bar{e}}$ are

$$\begin{aligned} {\bar{a}}= & {} (p\epsilon )_\perp \frac{{\bar{t}}^2}{p_+}\ \ \mathrm{where}\ \ {\bar{t}}^2=2q_{1+}p_-+{\bar{t}}_\perp ^2,\\ {\bar{b}}= & {} 2p_-(r_1\epsilon )_\perp +2r_{1-}\left( (q_2\epsilon )_\perp - (p\epsilon )_\perp \frac{q_{2+}}{p_+} \right) \\&+\,2(p\epsilon )_\perp \left( r_{1-}-r_{1-}\frac{q_2^2}{p_\perp ^2}+\frac{(pr_1)_\perp }{p_+} \right) ,\\ {\bar{c}}= & {} 2p_-(r_2\epsilon )_\perp +2r_{2-}\left( (q_2\epsilon )_\perp - (p\epsilon )_\perp \frac{q_{2+}}{p_+} \right) \\&+\,2(p\epsilon )_\perp \left( r_{2-}-r_{2-}\frac{q_2^2}{p_\perp ^2}+\frac{(pr_2)_\perp }{p_+} \right) ,\\ {\bar{e}}= & {} 2(q_2\epsilon )_\perp +2(p\epsilon )_\perp \left( 1-\frac{q_{2+}}{p_+}- \frac{q_2^2}{p_\perp ^2} \right) . \end{aligned}$$

Furthermore

$$\begin{aligned} A= & {} 3q_{1+}-\frac{q_1^2}{r_{1-}},\ \ B=4q_{1+},\ \ C=4q_{1+}-2\frac{q_1^2}{r_{1-}},\\ E= & {} -2q_{1+}(2r_{1-}+r_{2-})+r_2^2+r_1^2-k_1^2+q_1^2+2q_1^2\frac{r_{2-}}{r_{1-}}\nonumber \\&-\,(a_1,{\bar{t}}-r_2)_\perp -\frac{q_1^2r_2^2}{r_{1-}q_{1+}}. \end{aligned}$$

Again we find some terms with poles at $r_{1-}=0$ and can present

$$\begin{aligned} X_2=\tilde{X_2}+\frac{Y_2}{r_{1-}},\ \ Y_2=-q_1^2\left( {\bar{a}}+2{\bar{c}}_1+{\bar{e}} \frac{r_2^2}{q_{1+}}+ 2\bar{e}p_- \right) \end{aligned}$$

with ${\bar{c}}_1={\bar{c}}(r_{2-}=-p_-)$.

We get the result

$$\begin{aligned} \Gamma _{2}=-C_2\left( X_2^{(1)}\frac{p_+}{-q_{1+}p_\perp ^2+p_+{\bar{t}}_\perp ^2}I_{A_2}^{(1)} +Y_2I_{A_2}^{(2)}\frac{1}{2q_{1+}p_-+{\bar{t}}_\perp ^2} \right) , \end{aligned}$$

where $X_2^{(1)}=X_2(r_{1-}=k_{1\perp }^2/2q_{1+})$ and the integrals are

$$\begin{aligned} I_{A_2}^{(1)}= & {} \int \frac{\mathrm{d}r_{1-}}{2\pi }\frac{1}{k_1^2+i0}= \int \frac{\mathrm{d}r_{1-}}{2\pi } \frac{1}{-2q_{1+}r_{1-}+k_{1\perp }^2+i0}\\= & {} \frac{i}{2}\theta (-q_{1+})\frac{1}{q_{1+}} \end{aligned}$$

and

$$\begin{aligned} I_{A_2}^{(2)}=-\frac{i}{2}\frac{1}{k_{1\perp }^2}. \end{aligned}$$

1.4 Figure 2c

This diagram generates two terms with different color factors. The corresponding amplitudes $\Gamma _{3}$ and $\Gamma _{4\epsilon }$ are given by

$$\begin{aligned} \Gamma _{3,4\epsilon }=C_{3,4}\frac{1}{k_1^2}X_{3,4}, \end{aligned}$$

(40)

where $C_3=-C_2$ and $C_4=C_1$ and the denominator is $k_1^2=-2q_{1+}r_{1-}+k_{1\perp }^2+i0$.

We have

$$\begin{aligned} X_3= & {} -(a_1\epsilon )_\perp +2\frac{(p\epsilon )_\perp }{p_+} \left( \frac{q_1^2}{r_{1-}}-q_{1+} \right) \\&-\, 2\frac{(p\epsilon )_\perp q_2^2}{p_\perp ^2r_{2-}} \left( \frac{r_1^2}{q_{1+}} -r_{1-} \right) \end{aligned}$$

and

$$\begin{aligned} X_4= & {} -(a_1\epsilon )_\perp -\frac{(p\epsilon )_\perp }{p_+} \left( \frac{q_1^2}{r_{1-}}-q_{1+} \right) \\&+\,\frac{(p\epsilon )_\perp q_2^2}{p_+r_{1-}r_{2-}} \left( \frac{r_1^2}{q_{1+}} -r_{1-} \right) . \end{aligned}$$

Here $a_i=q_i+r_i$, $i=1,2$.

As before we separate terms with poles at $r_{1-}=0$ and $r_{2-}=0$,

$$\begin{aligned} X_{3,4}={\tilde{X}}_{3,4}+\frac{Y^{(1)}_{3,4}}{r_{1-}} +\frac{Y^{(2)}_{3,4}}{r_{2-}}, \end{aligned}$$

(41)

where

$$\begin{aligned} Y^{(1)}_3= & {} 2(p\epsilon )_\perp \frac{q_1^2}{p_+},\ \ Y^{(2)}_3=-2(p\epsilon )_\perp \frac{q_2^2}{p_\perp ^2} \left( \frac{r_1^2}{q_{1+}}-\frac{p_\perp ^2}{2p_+} \right) ,\\ Y^{(1)}_4= & {} (p\epsilon )_\perp \left( -\frac{q_1^2}{p_+} +2\frac{q_2^2r_1^2}{p_\perp ^2q_{1+}} \right) ,\ \ Y^{(2)}_4\\= & {} (p\epsilon )_\perp \left( -\frac{q_2^2}{p_+}+2\frac{q_2^2r_1^2}{p_\perp ^2q_{1+}} \right) . \end{aligned}$$

The longitudinal integrals are the same for both parts and the same as for $\Gamma _2$. From the pole at $r_{1-}=k_{1\perp }^2/2q_{1+}$ we get

$$\begin{aligned} \Gamma _{3,4}^{(1)}=C_{3,4}X_{3,4}^{(1)}I_{A_2}^{(1)}, \end{aligned}$$

(42)

where $X_{3,4}^{(1)}=X_{3,4}(r_{1-}=k_{1\perp }^2/2q_{1+})$. From the poles at $r_{1-}=0$ at $r_{2-}=0$ we get the second contribution

$$\begin{aligned} \Gamma _{3,4}^{(2)}=C_{3,4}Y^{(1)}_{3,4}I_{A_2}^{(2)} -C_{3,4}Y^{(2)}_{3,4}I_{A_2}^{(2)}. \end{aligned}$$

(43)

1.5 Figure 2d

On mass shell and convoluted with the polarization vector, the corresponding amplitude $\Gamma _{5}$ is given by

$$\begin{aligned} \Gamma _{5}= & {} C_5\frac{1}{k_1^2k_2^2}X_5,\ \ X_5=2(k_2L_1)L_{2}- 2(k_1L_2)L_{1}\nonumber \\&+(L_1L_2)(k_1-k_2)_\epsilon . \end{aligned}$$

(44)

Here $k_{1,2}=q_{1,2}-r_{1,2}$, $C_5=C_1+C_2$, The denominators are

$$\begin{aligned} k_2^2k_1^2=(-2q_{2+}r_{2-}+k_{2\perp }^2+i0)(-2q_{1+}r_{1-}+k_{1\perp }^2+i0). \end{aligned}$$

The Lipatov vertices convoluted with polarization vectors are

$$\begin{aligned} L_1= & {} (a_1 e)_\perp -\frac{(pe)_\perp }{p_+}\left( \frac{q_1^2}{r_{1-}}-q_{1+}\right) ,\\ L_2= & {} (a_2 e)_\perp -\frac{(pe)_\perp }{p_+} \left( \frac{q_2^2}{r_{2-}}-q_{2+}\right) . \end{aligned}$$

Also we have

$$\begin{aligned} (k_1-k_2)_\epsilon =(k_1-k_2,\epsilon )_\perp -\frac{(p\epsilon )_\perp }{p_+}(q_{1+}-q_{2+}). \end{aligned}$$

One finds

$$\begin{aligned} (k_2L_1)= & {} (pL_1)=-p_+r_{1-}-p_-q_{1+}+(pa_1)_\perp \nonumber \\&+\,r_1^2\frac{p_+}{q_{1+}}+ q_1^2\frac{p_-}{r_{1-}}, \end{aligned}$$

(45)

$$\begin{aligned} (k_1L_2)=(pL_2)= & {} -p_+r_{2-}-p_-q_{2+}+(pa_2)_\perp \nonumber \\&+\,r_2^2\frac{p_+}{q_{2+}}+ q_2^2\frac{p_-}{r_{2-}} \end{aligned}$$

(46)

and finally

$$\begin{aligned} (L_1L_2)= & {} (a_1a_2)_\perp +q_{1+}r_{2-}+q_{2+}r_{1-}-r_1^2\frac{q_{2+}}{q_{1+}}\\&-\,r_2^2\frac{q_{1+}}{q_{2+}}-q_1^2 \frac{r_{2-}}{r_{1-}}-q_2^2\frac{r_{1-}}{r_{2-}} +\frac{q_1^2r_2^2}{r_{1-}q_{2+}} +\frac{q_2^2r_1^2}{r_{2-}q_{1+}}. \end{aligned}$$

Separating the poles at $r_{1-}=0$ and $r_{2-}=0$ we present as before

$$\begin{aligned} X_5={\tilde{X}}_5+\frac{Y_5{(1)}}{r_{1-}}+\frac{Y_5{(2)}}{r_{2-}}. \end{aligned}$$

Here $Y_5^{(1)}$ is a sum of three terms,

$$\begin{aligned} Y_5^{(1)}&= 2p_-q_1^2 \left[ (a_2 e)_\perp +(pe)_\perp \frac{q_{2+}}{p_+} \right] \nonumber \\&\quad +\,2q_1^2\frac{(pe)_\perp }{p_+} \left[ p_+p_--p_-q_{2+}+(pa_2)_\perp +r_2^2\frac{p_+}{q_{2+}} \right] \nonumber \\&\quad +\,q_1^2 \left[ (k_1-k_2+p,e)_\perp -2(pe)_\perp \frac{q_{1+}}{p_+} \right] \left[ p_-+\frac{r_2^2}{q_{2+}} \right] \end{aligned}$$

(47)

and

$$\begin{aligned} Y_5^{(2)}&= -2\frac{(pe)_\perp }{p_+}q_2^2 \left[ p_+p_--p_-q_{1+}+(pa_1)_\perp +r_1^2\frac{p_+}{q_{1+}} \right] \nonumber \\&\quad -\,2p_-q_2^2\left[ (a_1e)_\perp +(pe)_\perp \frac{q_{1+}}{p_+} \right] \nonumber \\&\quad +\,q_2^2\left[ (k_1-k_2-p,e)_\perp +2(pe)_\perp \frac{q_{2+}}{p_+} \right] \left[ p_-+\frac{r_1^2}{q_{1+}} \right] . \end{aligned}$$

(48)

A new longitudinal integral appears:

$$\begin{aligned} I_5= \int \frac{\mathrm{d}r_{1-}}{2\pi }\frac{1}{(2q_{2+}(r_{1-}-\lambda _-)+k_{2\perp }^2+i0) (-2q_{1+}r_{1-}+k_{1\perp }^2+i0)}, \end{aligned}$$

(49)

where $k_1=q_1-r_1$, $k_2=q_2-r_2$, and we also have contributions from residues at $r_{1-}=0$ and $r_{2-}=0$.

In $I_5$ according to our rules we have to take residues in the lower half-plane. This opens two possibilities. If both $q_{1+}$ and $q_{2+}$ are positive, then only the pole at $r_{2-}=k_{2\perp }^2/2q_{2+}$ lies in the lower half-plane. If $q_{2+}>0$ and $q_{1+}<0$ then also the second pole at $r_{1-}=k_{1\perp }^2/2q_{1+}$ lies in the lower half-plane. So we find two contributions $I_5=I_5^A+I_5^B$, where

$$\begin{aligned} I_5^A=\frac{-i}{2}\theta (q_{2+})\frac{1}{q_{1+}k_{2\perp }^2+q_{2+}k_{1\perp }^2+2p_-q_{1+}q_{2+}} \end{aligned}$$

(50)

with $r_{2-}=k_{2\perp }^2/2q_{2+}$ and

$$\begin{aligned} I_5^B=-\theta (-q_{1+})I_5^{(1)} \end{aligned}$$

(51)

with $r_{1-}=k_{1\perp }^2/2q_{1+}$.

Taking into account contributions from the poles at $r_{1-}=0$ and at $r_{2-}=0$ we find the total contribution from Fig. 2d,

where $X_5^A=X_5(r_{2-}=k_{2\perp }^2/2q_{2+})$ and $X_5^B=X_5(r_{1-}=k_{1\perp }^2/2q_{1+})$.

Appendix 2. Integration over $\kappa _+$. Light-cone poles

To find the final expression for the diffractive cross-section we have to study the eventual integration over $\kappa _+=q_{1+}$, that is, over $q_{1+}$ or $q_{2+}$ with weight $\exp (iu)$, $u=zm\kappa _+/k_+$. This integration leads to the function F(z) according to (4). We separate it into two parts: the terms which follow from the poles at $r_{1-}=0$ or $r_{2-}=0$ studied in this section and those which follow from the Feynman poles to be studied in the next section.

The characteristic of contributions from light-cone poles is that they do not restrict in any way the region of integration in $\kappa _+$, which can vary from $-\infty$ to $+\infty$.

We shall study contributions with $q_{1+}=\kappa _+$, so we can use the formulas of the previous subsection and integrate over $q_{1+}$. We call the parts of the amplitudes coming from light-cone poles $\Gamma _i^{(2)}$, with $i=1,\ldots ,5$.

In our amplitudes listed in the preceding section there appear the following integrals over $q_{1+}$, which follow from the residues at $r_{1-}=0$ or $r_{2-}=0$. In $\Gamma _1$ we have

$$\begin{aligned} I_1=\int _{-\infty }^{\infty }\frac{\mathrm{d}q_{1+}\mathrm{e}^{iu}}{q_{1+}}. \end{aligned}$$

In $\Gamma _2$ we find three integrals

$$\begin{aligned} I_2^{(n)}=\int _{-\infty }^{\infty }\frac{q_{1+}^n \mathrm{d}q_{1+}\mathrm{e}^{iu}}{2q_{1+}p_-+{\bar{t}}_\perp ^2},\ \ n=1,0,-1. \end{aligned}$$

In $\Gamma _3$ we have

$$\begin{aligned} I_3=\int _{-\infty }^{\infty } dq_{1+} e^{iu}. \end{aligned}$$

In $\Gamma _4$ there appear two integrals, $I_3$ and $I_1$. Finally, in $\Gamma _5$ we find two integrals,

$$\begin{aligned} I_5^{(n)}=\int _{-\infty }^{\infty }\frac{q_{1+}^n \mathrm{d}q_{1+}\mathrm{e}^{iu}}{2q_{1+}p_-+p_\perp ^2-k_{2\perp }^2},\quad n=1,0. \end{aligned}$$

We only need the real parts of these integrals, since they appear with purely imaginary coefficients after taking the residue.

In fact they are reduced to just the two integrals $I_1$ and $I_3$. The integrals $I_2^{(n)}$ with $n=1,0$ can be rewritten as

$$\begin{aligned} I_2^{(1,0)}= & {} \frac{1}{2p_-}\int _{-\infty }^{\infty } \frac{q_{1+}^{1,0} \mathrm{d}q_{1+}\mathrm{e}^{iu}}{q_{1+}+a_2} =\frac{1}{2p_-}\mathrm{e}^{-iw_2}\\&\times \,\int _{-\infty }^{\infty } \frac{(q_{1+}-a_2)^{1,0} \mathrm{d}q_{1+}\mathrm{e}^{iu}}{q_{1+}}, \end{aligned}$$

where

$$\begin{aligned} a_2=\frac{{\bar{t}}_\perp ^2}{2p_-}, w_2=\frac{2mz{\bar{t}}_\perp ^2}{M^2}\ll 1. \end{aligned}$$

If we neglect $w_2$ in the exponent the two integrals reduce to $I_3$ and $I_1$.

The integrals $I_5^{(1,0)}$ are obtained from $I_2^{(1,0)}$ after the substitution ${\bar{t}}_\perp ^2\rightarrow p_\perp ^2-k_{2\perp }^2$.

Finally, the integral $I_2^{(-1)}$ can be presented as a difference

$$\begin{aligned} I_2^{(-1)} =\frac{1}{2p_-a_2}I_1-\frac{1}{a_2}I_2^{(0)}. \end{aligned}$$

Now the two basic integrals are

$$\begin{aligned} I_3=2\pi \delta \left( \frac{mz}{k_+} \right) \propto \delta (z), \end{aligned}$$

which does not contribute to the Glauber approximation, and

$$\begin{aligned} I_1=i\int _{-\infty }^\infty \frac{\mathrm{d}q_{1+}}{q_{1+}} \sin \left( q_{1+}\frac{mz}{k_+} \right) =i\pi \,\mathrm{sign}(z), \end{aligned}$$

which is pure imaginary and odd in z. So it will give zero in the amplitude.

Thus, light-cone poles do not contribute to the diffractive amplitude.

Appendix 3. Integration over $\kappa _+$: Feynman poles

1.1 Integration regions and problems

Integration over $q_{1+}$ should be done taking into account limitations coming from the requirement that the rapidity $y_1$ of the intermediate gluon with momentum $k_1$ or $k_2$ cannot be very different from y. Otherwise the diagram with the RR$\rightarrow$RRP vertex transforms into the one with R$\rightarrow$RP vertex with an extra interaction between the reggeons with momenta $q_1$ and $q_2$. So

$$\begin{aligned} y-\delta<y_1<y+\delta , \end{aligned}$$

(52)

where one may choose $\delta \gg 1$, but much smaller than $\ln (s/s_0)$. Our integrals go over negative values of $q_{1+}$ or positive values of $q_{2+}$. Putting in the first case $|q_{1+}|=p_+x$ we get the condition

$$\begin{aligned} x_1<x< x_2,\ \ x_{1(2)}=\mathrm{e}^{-(+)\delta }x_0,\ \ x_0=\frac{|k_{1\perp }|}{|p_\perp |}. \end{aligned}$$

(53)

In the second case we put $q_{2+}=p_+x$ and the integration limits in x are the same with $|k_{1,\perp }|\rightarrow |k_{2\perp }|$.

Actually the integrand in the integration over x contains an exponential factor

$$\begin{aligned} \mathrm{e}^{-iu}, \ \ u=x\xi ,\ \ \xi =-2mz\frac{p_\perp ^2}{M^2}. \end{aligned}$$

(54)

Note that our study is only valid when $M^2\rightarrow \infty$, so that $\xi$ is small.

At fixed $\delta$ our integrals are naturally dependent on $\delta$. One expects that this dependence is canceled by other contributions of the same order, which involve extra BFKL interactions between reggeons and correction to the BFKL interaction. Such contributions, also cut at rapidity $\delta$ from the fixed rapidity of the intermediate real gluon, hopefully contain terms proportional to the cut integration region in rapidity, that is, to $\delta$. Thus in our calculations terms proportional to $\delta$ actually should be dropped, since they are to be canceled by similar terms coming from other contributions. This can only be true if the divergence of our integrals at both $x\rightarrow 0$ and $x\rightarrow \infty$ is logarithmic.

At first sight this poses the first problem in our study. Inspecting our expressions for $\Gamma _i$, $i=1,\ldots ,5$ one discovers that after integration over $r_{1-}$ $\Gamma _{2,3,4}$ contain terms which do not vanish at $x\rightarrow \infty$. The sum of them tend to the limit at $x\rightarrow \infty$

$$\begin{aligned} \Gamma \simeq \frac{i}{2}(pe)_\perp \frac{1}{p_+}\left( 1-2\frac{q_1^2}{k_1^2} \right) (-C_2-2C_3+C_4), \end{aligned}$$

where the color factors correspond to the contribution of diagrams 2,3 and 4. In the sum $-C_2-2C_3+C_4=1/2$, so that the limiting value is different from zero. This generates linear divergence at large x in the limit $M^2\rightarrow \infty$. The corresponding integral is

$$\begin{aligned} J_1=\int _{x_1}^{x_2} \mathrm{d}x\mathrm{e}^{-iu}\simeq \int _{x_1}^{x_2} \mathrm{d}x =x_2-x_1 \ . \end{aligned}$$

(55)

We shall see that after symmetrizing over participating reggeons this linear divergence is canceled. So after integration over $q_{1+}$ and dropping terms proportional to $\delta$ one finds the cross-section (12).

However, this is not the end of the story. In the result of integration over $q_{1+}$ one finds various terms which are singular at $k_{1\perp }^2=0$ or $k_{2\perp }^2=0$ and so exhibit infrared divergence. Also we find a collinear divergence in the contribution from $\Gamma _5$. As we shall demonstrate, the latter cancels because of the properties of $X_5$. Terms singular at say $k_{1\perp }^2=0$ coming from $\Gamma _{3,4,5}$ behave as badly as $1/|k_{1\perp }|^3$ or $\ln |k_{1\perp }|/|k_{1\perp }|^2$. However, in the sum of all contributions all such singular terms cancel and the remaining expression is free from the infrared divergence.

There are also terms which behave as $1/p_\perp ^2$ as $p_\perp ^2\rightarrow 0$, which may also lead to a divergence. However, in our case the value of $p_\perp ^2$ is limited from below by the condition that the Regge kinematics should be valid for the lower pomerons. Fixing their minimal energy square $s_1$ as $s_1>s_0$ we find the condition $|p_\perp ^2|>M^2s_0/2s$. So if the terms which behave like $1/p_\perp ^2$ remain in the total contribution, they do not lead to an infrared divergence but rather to the behavior $\ln (s/M^2)$ instead. No other dangerous singularities are found in the terms generated by the vertex RR$\rightarrow$RRP.

In our calculations we choose $\delta \gg 1$ and drop all terms proportional to $\delta$.

1.2 $\Gamma _1$

We recall that after taking the residue at $r_{1-}=k_{1\perp }^2/(2q_{1+})$,

$$\begin{aligned} \Gamma _1=i\frac{1}{2}C_1\theta (-q_{1+})\frac{1}{-q_{1+}t_\perp ^2+p_+k_{1\perp }^2}X_1^{(1)}. \end{aligned}$$

We find

$$\begin{aligned} X_1^{(1)}= T_0+\frac{p_+}{q_{1+}}T_{-1}, \end{aligned}$$

where $T_{0,-1}$ do not depend on $q_{1+}$, and explicitly we have

$$\begin{aligned} T_0= & {} -2(te)_\perp \left( r_1^2+q_1^2+q_2^2+(a_1,t+q_2)_\perp \right) \\&+\,2k_{1\perp }^2(te)_\perp +4(te)_\perp \frac{q_2^2r_1^2}{k_{1\perp }^2} \end{aligned}$$

and

$$\begin{aligned} T_{-1}=-4(q_2e)_\perp r_1^2+2k_{1\perp }^2(t+2r_1,e)_\perp . \end{aligned}$$

Note that $T_0$ contains a term with a pole at $k_{1\perp }^2=0$. $T_{-1}$ does not contain this pole. Integration goes over the negative $q_{1+}$. Putting $q_{1+}=-p_+x$ we find

$$\begin{aligned} \Gamma _1=-i\frac{1}{4\pi }C_1 \left( I_0^{(1)}T_0-I_{-1}^{(1)}T_{-1} \right) , \end{aligned}$$

(56)

where

$$\begin{aligned} I_0^{(1)}= \int _{x_1}^{x_2}\frac{\mathrm{d}x\mathrm{e}^{-iu}}{x t_\perp ^2+k_{1\perp }^2},\ \ I_{-1}^{(1)} =\int _{x_1}^{x_2}\frac{\mathrm{d}x\mathrm{e}^{-iu}}{x(x t_\perp ^2+k_{1\perp }^2)} \end{aligned}$$

and u is given by (54).

At $x_1=0$ the integral $I_0^{(1)}$ has a weak logarithmic singularity at $k_{1\perp }^2=0$. So it is integrable and does not present difficulties itself. But $T_0$ contains a pole term in $k_{1\perp }^2$. So the first term in (56) is in fact singular. The second term does not exist at $x_1=0$ and is also singular at $k_{1\perp }^2=0$. We write

$$\begin{aligned} I_{-1}^{(1)}=\frac{1}{k_{1\perp }^2}J_0-\frac{t_\perp ^2}{k_{1\perp }^2}I_{0}^{(1)}, \end{aligned}$$

where $J_0$ is given by

$$\begin{aligned} J_0=\int _{x_1}^{x_2}\frac{\mathrm{d}x}{x} \cos (u)=\int _{\xi x_1}^{\xi x_2}\frac{du}{u}\cos u = \mathrm{ci}\,(\xi x_2) - \mathrm{ci}\,(\xi x_1). \end{aligned}$$

(57)

Here we have left only the real part, which is of interest. As a result

$$\begin{aligned} \Gamma _1=-i\frac{1}{4\pi }C_1 \left( I_{0}^{(1)}{\hat{T}}_0-J_0{\hat{T}}_{-1} \right) , \end{aligned}$$

(58)

where the new functions are

$$\begin{aligned} {\hat{T}}_0= & {} -2(te)_\perp \left( r_1^2+q_1^2+q_2^2-k_{1\perp }^2-t_\perp ^2 +(a_1,t+q_2)_\perp \right) \nonumber \\&+\,4t_\perp ^2(r_1e)_\perp +4\frac{r_1^2}{k_{1\perp }^2}\left( q_2^2(te)_\perp -t_\perp ^2(q_2e)_\perp \right) \end{aligned}$$

(59)

and

$$\begin{aligned} {\hat{T}}_{-1}=\frac{1}{k_{1\perp }^2}T_{-1}=2(t+2r_1,e)_\perp -4(q_2e)_\perp \frac{r_1^2}{k_{1\perp }^2}. \end{aligned}$$

(60)

Note that at $k_{1\perp }=0$ we have $t_\perp =q_{2\perp }$. Therefore at $k_{1\perp }^2=0$ the pole in ${\hat{T}}_0$ is weakened to $1/|k_\perp |$. This means that the first term in (58) is integrable. Singularities are separated in the second term which contains both the singularities at $x_1=0$ and combined singularities at $x_1=0$ and $k_{1\perp }^2=0$. Both of them are proportional to $\delta$ and have to be discarded.

1.3 $\Gamma _2$

After taking the residue at $r_{1-}=k_{1\perp }^2/(2q_{1+})$

$$\begin{aligned} \Gamma _2=-i\frac{1}{2}C_2\theta (-q_{1+})\frac{1}{-q_{1+}p_\perp ^2+p_+{\bar{t}}_\perp ^2}\frac{p_+}{q_{1+}}X_2^{(1)}. \end{aligned}$$

One finds

$$\begin{aligned} X_2^{(1)}=\frac{q_{1+}^2}{p_+^2}T_2+\frac{q_{1+}}{p_+}T_1+T_0, \end{aligned}$$

where the $T_i$ do not depend on $q_{1+}$ and are given by

$$\begin{aligned} T_2= & {} -(pe)_\perp p_\perp ^2\left( 1-2\frac{q_1^2}{k_{1\perp }^2} \right) ,\\ T_1= & {} {\bar{t}}_\perp ^2(pe)_\perp \left( 3-2\frac{q_1^2}{k_{1\perp }^2} \right) \\&-\,4\left( p_\perp ^2(r_1+r_2-p,e)_\perp +q_2^2(pe)_\perp -2(pe)_\perp (p,r_1+r_2)_\perp \right) \\&+\,4\frac{q_1^2}{k_{1\perp }^2} \left( p_\perp ^2(r_2-q_2,e)_\perp +(q_2^2+k_{1\perp }^2-2(pr_2)_\perp )(pe)_\perp \right) \\&+\,2E_0(pe)_\perp +2(q_2^2(pe)-p_\perp ^2(q_2e)_\perp ) \left( 1-2\frac{q_1^2}{k_{1\perp }^2} \right) ,\\ T_0= & {} 2 \left( q_2e)_\perp -(pe)_\perp \frac{q_2^2}{p_\perp ^2} \right) (E_0+2q_1^2). \end{aligned}$$

Here

$$\begin{aligned} E_0= & {} E(q_{1+}=0)=r_1^2+r_2^2-q_1^2-k_{1\perp }^2\nonumber \\&-(q_1+r_1,{\bar{t}}-r_2)_\perp -2\frac{q_1^2r_2^2}{k_{1\perp }^2}. \end{aligned}$$

(61)

In $T_1$ the four lines correspond to contributions from ${\bar{a}}A$, $({\bar{b}}+{\bar{c}})B$, ${\bar{c}}(C-B)$ and ${\bar{e}}E$, respectively. All of them contain poles in $k_{1\perp }^2=0$.

Integration over $q_{1+}$ gives

$$\begin{aligned} \Gamma _2=-i\frac{1}{4\pi }C_2 \left( -I_1^{(2)}T_2+I_0^{(2)}T_1-I_{-1}^{(2)}T_0 \right) , \end{aligned}$$

where

$$\begin{aligned} I_n^{(2)} =\int _{x_1}^{x_2}\frac{\mathrm{d}x x^n\mathrm{e}^{-iu}}{xp_\perp ^2+{\bar{t}}_\perp ^2}. \end{aligned}$$

In contrast to $\Gamma _1$ these integrals are have a finite limit at $k_{1\perp }^2=0$, although $I^{(2)}_{-1}$ is singular at $x_1=0$. To separate the singularities we present

$$\begin{aligned} I_1^ {(2)}=\frac{1}{p_\perp ^2}J_1-\frac{{\bar{t}}_\perp ^2}{p_\perp ^2}I_0^{(2)}, \ \ I_{-1}^{(2)}=\frac{1}{{\bar{t}}_\perp ^2}J_0-\frac{p_\perp ^2}{{\bar{t}}_\perp ^2}I_0^{(2)}, \end{aligned}$$

where $J_1$ is given by (55), to finally obtain

$$\begin{aligned} \Gamma _2=-i\frac{1}{4\pi }C_2 \left( -\frac{1}{p_\perp ^2}J_1T_2 -\frac{1}{{\bar{t}}_\perp ^2}J_0T_0 +I_0^{(2)}{\hat{T}}_1 \right) , \end{aligned}$$

(62)

with a new function

$$\begin{aligned} {\hat{T}}_1=T_1+\frac{{\bar{t}}_\perp ^2}{p_\perp ^2}T_2+\frac{p_\perp ^2}{{\bar{t}}_\perp ^2}T_0. \end{aligned}$$

(63)

Remarkably in $\hat{T_1}$, which is a sum of functions each having a pole at $k_{1\perp }^2=0$, the leading singularity at $k_{1\perp }^2=0$ cancels. Indeed the terms proportional to $q_1^2/k_{1\perp }^2$ in (63) are (modulo $q_1^2/k_{1\perp }^2$): from $T_2$

$$\begin{aligned} 2p_\perp ^2(pe)_\perp , \end{aligned}$$

from $T_1$

$$\begin{aligned}&-2{\bar{t}}_\perp ^2(pe)_\perp +4\left( p_\perp ^2(r_2-q_2,e)_\perp + (q_2^2-2(pr_2)_\perp )(pe)_\perp \right) \nonumber \\&\quad -4(q_2^2(pe)_\perp -p_{\perp }^2(q_2e)_\perp )-4r_2^2(pe)_\perp , \end{aligned}$$

from $T_0$

$$\begin{aligned} -4r_2^2\left( (q_2e)_\perp -(pe)_\perp \frac{q_2^2}{p_\perp ^2} \right) . \end{aligned}$$

At $k_{1\perp }^2=0$ we have ${\bar{t}}_{\perp }=-r_{2\perp }$ and $r_{2\perp }-q_{2\perp }=-p_\perp$. The term $p_\perp ^2T_2/ {\bar{t}}_\perp ^2$ cancels the first term in $T_1$. The second term in $T_1$ becomes

$$\begin{aligned} 4(pe)_\perp \left( q_2^2-p_\perp ^2-2(pr_2)_\perp \right) =4(pe)_\perp r_2^2 \end{aligned}$$

and cancels the last term in $T_1$. Finally, with ${\bar{t}}_\perp ^2=r_2^2$ the term $p_\perp ^2T_0/{\bar{t}}_\perp ^2$ becomes

$$\begin{aligned} 4p_\perp ^2\left( (qe)_\perp -(pe)_\perp \frac{q_2^2}{p_\perp ^2} \right) \end{aligned}$$

and cancels the remaining third term in $T_1$. So the factor multiplying $q_1^2/k_{1\perp }^2$ in (63) vanishes at $k_{1\perp }^2=0$. Numerical studies show that in fact at $k_{1\perp }\rightarrow 0$ this term behaves as $|k_{1\perp }|$. This means that the last term in (62) is integrable and so regular. The contributions singular at $x_1\rightarrow 0$, $k_{1\perp }^2\rightarrow 0$ or simultaneously in these two limits are contained in the first two terms. As we shall see the term with $J_1$ will be eventually canceled. The second term is proportional to $\delta$ and should be dropped according to our approach. So the meaningful part of $\Gamma _2$ is contained in the third term in (62).

1.4 $\Gamma _3$

After taking the residue at $r_{1-}=k_{1\perp }^2/(2q_{1+})$ we have

$$\begin{aligned} \Gamma _3=iC_3\frac{1}{2q_{1+}}\theta (-q_{1+})X_3. \end{aligned}$$

Note that at $r_{1-}=k_{1\perp }^2/(2q_{1+})$ we have

$$\begin{aligned} r_{2-}=\frac{q_{1+}p_\perp ^2-p_+k_{1\perp }^2}{2p_+q_{1+}},\ \ \frac{1}{r_{2-}}=\frac{2q_{1+}p_+}{d},\ \ d=q_{1+}p_\perp ^2-p_+k_{1\perp }^2. \end{aligned}$$

We find

$$\begin{aligned} X_3=\frac{q_{1+}}{p_+}T_1+T_0+\frac{p_+}{d}V_0, \end{aligned}$$

(64)

where

$$\begin{aligned} T_1= & {} -2(pe)_\perp \left( 1-2\frac{q_1^2}{k_{1\perp }^2} \right) ,\nonumber \\ T_0= & {} -(a_1e)_\perp ,\nonumber \\ V_0= & {} 2(pe)_\perp (k_{1\perp }^2-2r_1^2)\frac{q_2^2}{p_\perp ^2}. \end{aligned}$$

(65)

Integration over $q_{1+}=-xp_+$ gives

$$\begin{aligned} \Gamma _3=i\frac{1}{4\pi }C_3 \left( T_1J_1-T_0J_0+I_{-1}^{(3)}V_0 \right) . \end{aligned}$$

(66)

Here $J_1$ and $J_0$ are the old integrals which do not depend on any variables, and $I_{-1}^{(3)}$ is new:

$$\begin{aligned} I_{-1}^{(3)}= \int _{x_1}^{x_2}\frac{\mathrm{d}x\mathrm{e}^{-iu}}{x(xp_\perp ^2+k_{1\perp }^2)}= \frac{1}{k_{1\perp }^2}J_0-\frac{p_\perp ^2}{k_{1\perp }^2}I_0^{(3)}, \end{aligned}$$

where

$$\begin{aligned} I_0^{(3)}=\int _{x_1}^{x_2}\frac{\mathrm{d}x\mathrm{e}^{-iu}}{xp_\perp ^2+k_{1\perp }^2}. \end{aligned}$$

So we finally have

$$\begin{aligned} \Gamma _3=i\frac{1}{4\pi }C_3\left[ T_1J_1+J_0 \left( -T_0 +\frac{1}{k_{1\perp }^2}V_0 \right) - I_0^{(3)}\frac{p_\perp ^2}{k_{1\perp }^2}V_0 \right] . \end{aligned}$$

(67)

The integral $I_0^{(3)}$ converges at $x_1=0$ and has a weak (logarithmic) singularity at $k_{1\perp }^2=0$. It is integrable over $k_{1\perp }$ by itself but $V_0$ contains a pole term in $k_{1\perp }^2$. So dropping the term with $J_1$, apart from the trivial singular term with $J_0$ we get a strongly singular term

$$\begin{aligned} \Gamma _3^{\mathrm{sing}}=iC_2\frac{1}{\pi }(pe)_\perp \frac{q_2^2r_1^2}{k_{1\perp }^2}I^{(3)}_0, \end{aligned}$$

(68)

which is not integrable in $k_{1\perp }$.

1.5 $\Gamma _4$

After taking the residue at $r_{1-}=k_{1\perp }^2/(2q_{1+})$ we have

$$\begin{aligned} \Gamma _4=iC_4\frac{1}{2q_{1+}}\theta (-q_{1+})X_4^{(1)}, \end{aligned}$$

where $X_4^{(1)}=X_4(r_{1-}=k_{1\perp }^2/(2q_{1+}))$.

So we find

$$\begin{aligned} X_4^{(1)}=\frac{q_{1+}}{p_+}T_1+T_0+\frac{q_{1+}}{d}V_1, \end{aligned}$$

(69)

where

$$\begin{aligned} T_1= & {} (pe)_\perp \left( 1-2\frac{q_1^2}{k_{1\perp }^2} \right) ,\nonumber \\ T_0= & {} -(a_1e)_\perp ,\nonumber \\ V_1= & {} -2(pe)_\perp (k_{1\perp }^2-2r_1^2)\frac{q_2^2}{k_{1\perp }^2}. \end{aligned}$$

(70)

Integration over $q_{1+}=-xp_+$ gives

$$\begin{aligned} \Gamma _4=i\frac{1}{4\pi }C_4 \left( J_1T_1-J_0T_0-I^{(3)}_0V_1 \right) . \end{aligned}$$

(71)

Dropping the term with $J_1$ we find a trivial term with $J_0$ and a highly singular term similar to that in $\Gamma _3$

$$\begin{aligned} \Gamma _4^{\mathrm{sing}}=-\frac{i}{\pi }C_4(pe)_\perp \frac{q_2^2r_1^2}{k_{1\perp }^2}I_0^{(3)}. \end{aligned}$$

(72)

It differs from a similar term in $\Gamma _3$ only by the sign. However, since $C_3/C_4=2$ these terms do not cancel in the sum.

1.6 $\Gamma _5^{(A,B)}$

1. Case A $r_{2-}=k_{2\perp }^2/2q_{2+}$ ($q_{2+}>0$).

We express $q_{1+}=p_+-q_{2+}$. We then have

$$\begin{aligned} r_{1-}=\frac{p_\perp ^2}{2p_+}-\frac{k_{2\perp }^2}{2q_{2+}},\ \ \frac{1}{r_{1-}}=\frac{2p_+q_{2+}}{q_{2+}p_\perp ^2-p_+k_{2\perp }^2}\equiv \frac{2p_+q_{2+}}{d_2}. \end{aligned}$$

The common denominator is

$$\begin{aligned} D=p_+k_{2\perp }^2+q_{2+}(k_{1\perp }^2-k_{2\perp }^2-p_\perp ^2)-2p_-q_{2+}^2. \end{aligned}$$

Putting $q_{2+}=xp_+$ we rewrite it as $D=p_+R_2$ with $R_2=(k_{2\perp }-xp_\perp )^2$.

As before we present

$$\begin{aligned} X_5^{(A)}=x^2T_2+xT_1+T_0+T_{-1}\frac{1}{x}+U_0\frac{1}{q_{1+}} +V_0\frac{1}{d_2}, \end{aligned}$$

(73)

where

$$\begin{aligned} T_2= & {} p_\perp ^2\alpha _2(pe)_\perp ,\\ T_1= & {} -p_\perp ^2(a_2e)_\perp -p_\perp ^2\alpha _2(a_1+p,e)_\perp +\frac{1}{2} p_\perp ^2\alpha _2(\kappa _2e)_\perp \\&+\,2(pe)_\perp \left( \alpha _2(pa_2)_\perp +(pa_2)_\perp -c_2 \right) ,\\ T_0= & {} 2(a_2e)_\perp \left( (pa_1)_\perp -q_1^2 \right) -\alpha _2b_{12} (pe)_\perp \\&-2(a_1+p,e)_\perp (pa_2)_\perp +\,4(pe)_\perp (pa_2)_\perp \frac{q_1^2}{p_\perp ^2}\\&+c_2(\kappa _2e)_\perp +2\alpha _2r_1^2(pe)_\perp +2b_{22}(pe)_\perp \frac{q_1^2}{p_\perp ^2},\\ T_{-1}= & {} k_{2\perp }^2(a_2e)_\perp -2b_{22}(q_1e)_\perp ,\\ U_0= & {} p_+r_1^2 \left( 2(a_2e)_\perp -\alpha _2(\kappa _2e)_\perp \right) , \end{aligned}$$

$$\begin{aligned} V_0&=-2p_+k_{2\perp }^2q_1^2(a_2e)_\perp +p_+b_{22}q_1^2(\kappa _2e)_\perp +2p_+b_{22}q_1^2(pe)_\perp \nonumber \\&\times \,\left( 1+\frac{k_{2\perp }^2}{p_\perp ^2} \right) +4p_+q_1^2(pa_2)_\perp (pe)_\perp \frac{k_{2\perp }^2}{p_\perp ^2}. \end{aligned}$$

(74)

In these formulas

$$\begin{aligned} \alpha _2=1-2\frac{q_2^2}{k_{2\perp }^2},\ \ b_{ij} =2r_i^2-k_{j\perp }^2,\ \ \kappa _2=k_1-k_2-p, \end{aligned}$$

and

$$\begin{aligned} c_2=(a_1a_2)_\perp +r_1^2+r_2^2+q_2^2-k_{2\perp }^2-2\frac{q_2^2r_1^2}{k_{2\perp }^2}. \end{aligned}$$

2. Case B $r_{1-}=k_{1\perp }^2/2q_{1+}$ ($q_{1+}<0$).

We express $q_{2+}=p_+-q_{1+}$. We then have

$$\begin{aligned} r_{2-}=\frac{p_\perp ^2}{2p_+}-\frac{k_{1\perp }^2}{2q_{1+}},\ \frac{1}{r_{2-}}=\frac{2p_+q_{1+}}{q_{1+}p_\perp ^2-p_+k_{1\perp }^2}\equiv \frac{2p_+q_{1+}}{d_1}. \end{aligned}$$

The denominator is

$$\begin{aligned} D=p_+k_{1\perp }^2+q_{1+}(k_{2\perp }^2-k_{1\perp }^2-p_\perp ^2)-2p_-q_{1+}^2. \end{aligned}$$

Putting $q_{1+}=xp_+$ with $x<0$ we rewrite the denominator as $D=p_+R_1$ with $R_1=(k_{1\perp }-xp_\perp )^2$.

Writing again

$$\begin{aligned} X_5^{(B)}=x^2{\tilde{T}}_2+x{\tilde{T}}_1+{\tilde{T}}_0 +{\tilde{T}}_{-1}\frac{1}{x}+{\tilde{U}}_0\frac{1}{q_{2+}}+ {\tilde{V}}_0\frac{1}{d_1} \end{aligned}$$

(75)

we find

$$\begin{aligned} {\tilde{T}}_2= & {} -p_\perp ^2\alpha _1(pe)_\perp ,\nonumber \\ {\tilde{T}}_1= & {} -2(pe)_\perp \left( (pa_1)_\perp +\alpha _1(pa_2)_\perp +(a_1a_2)_\perp \right. \nonumber \\&\left. -\,k_{1\perp }^2+r_1^2+q_1^2 -\alpha _1r_2^2 \right) \nonumber \\&+\,\alpha _1p_\perp ^2(a_2+p,e)_\perp +p_\perp ^2(a_1e)_\perp +\frac{1}{2}\alpha _1(\kappa _1e)_\perp ,\nonumber \\ {\tilde{T}}_0= & {} (pe)_\perp \left( \alpha _1b_{21}+2b_{11}\frac{q_2^2}{p_{\perp }^2} -4(pa_1)\frac{q_2^2}{p_\perp ^2} \right) \nonumber \\&+2(a_2+p,e)_\perp (pa_1)_\perp +2(a_1e)_\perp (pa_2)_\perp +2q_1^2(a_1e)_\perp \nonumber \\&+(\kappa _1e)_\perp (a_1a_2)_\perp ,\nonumber \\ {\tilde{T}}_{-1}= & {} 2b_{11}(q_2,e)_\perp -k_{1\perp }^2(a_1e)_\perp ,\nonumber \\ {\tilde{U}}_0= & {} -p_+r_2^2 \left( \alpha _1(\kappa _1e)_\perp +2(a_1e)_\perp \right) ,\nonumber \\ {\tilde{V}}_0= & {} 2p_+q_2^2k_{1\perp }^2(a_1e)_\perp +p_+b_{11}q_2^2 \left( (\kappa _1e)_\perp -2(pe)_\perp \right) \nonumber \\&-\,2p_+q_2^2(pe)_\perp \frac{k_{1\perp }^2}{p_\perp ^2} \left( b_{11}+2(pa_1)_\perp \right) . \end{aligned}$$

(76)

In these formulas

$$\begin{aligned} \alpha _1=1-2\frac{q_1^2}{k_{1\perp }^2},\ \ b_{ij}=2r_i^2 -k_{j\perp }^2,\ \ \kappa _1=k_1-k_2+p. \end{aligned}$$

We pass to the final integration of $\Gamma _5$ over $q_{1+}$ or $q_{2+}$.

Integration of $X_5^A$.

We have to integrate over the transferred “+”-momentum $\kappa _+$, which is equivalent to integration over $q_{1+}$ or $q_{2+}$. In case A it is convenient to integrate over $q_{2+}=xp_+$ with $x>0$. Before integration

$$\begin{aligned} \Gamma _5^A=C_5X_5^{(A)}F_5^A, \end{aligned}$$

where

$$\begin{aligned} F_5^A=-\frac{i}{2}\theta (q_{2+})\frac{1}{q_{1+}k_{2\perp }^2+q_{2+}k_{1\perp }^2+2p_-q_{1+}q_{2+}}. \end{aligned}$$

The denominator can be written in Euclidean metric as

$$\begin{aligned}&q_{1+}k_{2\perp }^2+q_{2+}k_{1\perp }^2+2p_-q_{1+}q_{2+}=-p_+D_2,\\&D_2=(\mathbf{k}_2-x\mathbf{p})^2. \end{aligned}$$

Presenting $X_5^{(A)}$ according to Eq. (73) we shall have the integrated $\Gamma _5^A$ as

$$\begin{aligned} \Gamma _5^A=\frac{i}{4\pi }C_5 \left( \sum _{n=-1}^2T_{n}I^A_n +\frac{U_0}{p_+}K_1^A-\frac{V_0}{p_+}K^A_2 \right) , \end{aligned}$$

(77)

where

$$\begin{aligned} I^A_n= & {} \int _{x_1}^{x_2}\frac{x^n \mathrm{d}x}{(k_2-xp)^2},\\ K_1^A= & {} \int _{x_1}^{x_2}\frac{\mathrm{d}x}{(1-x)(k_2-xp)^2},\\ K_2^A= & {} \int _{x_1}^{x_2}\frac{ \mathrm{d}x}{(xp^2-k_2^2)(k_2-xp)^2}, \end{aligned}$$

and all vectors are to be taken in Euclidean 2-dimensional metric (E2DM) with $k_2^2,p^2\ge 0$. All integrals are well convergent at small x, so that we can safely put $x_1=0$. At large x the $I^A_n$ with $n=1,2$ diverge and we have to separate the diverging terms. All integrals are standard and apart from these divergent terms they are expressed via the integral

$$\begin{aligned} I^A_0=\int _{x_1}^{x_2}\frac{ \mathrm{d}x}{(k_2-xp)^2}=\frac{\pi -\phi _2}{\sqrt{p^2k_2^2-(pk_2)^2}}, \end{aligned}$$

(78)

where $\phi _2$ is the angle between $\mathbf{k}_2$ and $\mathbf{p}$, $0<\phi _2<\pi$. All the remaining integrals are given as follows:

$$\begin{aligned} I^A_1= & {} \frac{1}{p^2}\delta +\frac{(pk_2)}{p^2}I^A_0,\\ I^A_2= & {} \frac{1}{p^2}J_1+2\frac{(pk_2)}{p^2}I^A_1-\frac{k_2^2}{p^2}I^A_0,\\ I^A_{-1}= & {} \frac{1}{k_2^2}\delta +\frac{(pk_2)}{k_2^2}I^A_0,\\ K^A_1= & {} -\frac{1}{2k_1^2}\ln \frac{k_2^2}{p^2}+\frac{(pk_1)}{k_1^2}I^A_0,\\ K_2^A= & {} -\frac{1}{2k_1^2k_2^2}\ln \frac{k_2^2}{p^2} +\frac{(k_1k_2)}{k_1^2k_2^2}I^A_0. \end{aligned}$$

Here $\mathbf{k}_1=\mathbf{p}-\mathbf{k}_2$. The integral $J_1$ is given by (55).

The basic integral $I^A_0$ contains both a collinear singularity at $\phi _2=0$ and a comparatively weak (integrable) singularity at $k_2\rightarrow 0$ where it behaves as $1/k_2$. Note that the denominator in $I^A_0$ is symmetric in $k_1$ and $k_2$;

$$\begin{aligned} k_1^2p^2-(pk_1)^2=k_2^2p^2-(pk_2)^2 =k_1^2k_2^2-(k_1k_2)^2, \end{aligned}$$

(79)

so that $I^A_0$ also contains a similar singularity at $k_1\rightarrow 0$

The collinear singularity is in fact absent, since the whole $X^A$ vanishes when $k_1$ and $k_2$ are directed along p. Indeed recall that $k_{2+}=q_{2+}=xp_+$ and $k_{2-}=-r_{2-}$ Then $r_{2-}=k_{2\perp }^2/2q_{2+}$ implies that $k_2^2=0$, that is, the gluon $k_2$ lies on its mass-shell. The collinear singularity occurs at $k_\perp =xp_\perp$ from which we find $k_{2\perp }/k_+=p_\perp /p_+$. Taking its square we have

$$\begin{aligned} \frac{k_{2\perp }^2}{k_{2+}^2}=\frac{p_\perp ^2}{p_+^2}\ \ \mathrm{or}\ \ \frac{k_{2-}}{k_{2+}}=\frac{p_-}{p_+}. \end{aligned}$$

The last equation means $k_{2-}=xp_-$, so that the 4-vector $k_2=xp$. Since $p=k_1+k_2$, we have $k_1=(1-x)p$ and both $k_1$ and $k_2$ are parallel to p. But for such $k_1$ and $k_2$ $X_5=0$, since (in the 4-dimensional Lorentz metric)

$$\begin{aligned}&(L_1k_2)=x(L_1p)=\frac{x}{1-x}(L_1k_1)=0, \\&\quad (L_2,k_1)=\frac{1-x}{x}(L_2k_2)=0, \end{aligned}$$

and

$$\begin{aligned} (k_1-k_2,e)=(1-2x)(pe)=0. \end{aligned}$$

Dropping the divergent term with $J_1$ for the reasons discussed earlier we present the integrated $\Gamma ^A$ as a sum of two terms, one of which is proportional to $\ln k_2^2$ and the other proportional to $I^A_0$:

$$\begin{aligned} \Gamma ^A= & {} \frac{i}{4\pi }C_5\left\{ -\frac{1}{2p_+k_1^2} \left( U_0-\frac{1}{k_2^2}V_0 \right) \ln \frac{k_2^2}{p^2}\right. \nonumber \\&+\,I^A_0\left( \Big (2\frac{(pk_2)^2}{p^4}-\frac{k_2^2}{p^2}\Big )T_2 +\frac{(pk_2)}{k_2^2}T_{-1}\right. \nonumber \\&\left. \left. +\,\frac{(pk_1)}{p_+k_1^2}U_0-\frac{(k_1k_2)}{p_+k_1^2k_2^2}V_0 \right) \right\} . \end{aligned}$$

(80)

Our aim is to analyze possible non-integrable divergencies of this expression in the limit $k_2\rightarrow 0$. The power-like singularities come both from singularities in integrals $I^A_n$, $K_1^A$ and $K_2^A$ and from the coefficients $T_n$, $U_0$ and $V_0$. Obviously the term with $T_2$ is non-singular due to the factor $(pk_2)^2$. Also non-singular terms in $T_1$, $T_0$ and $U_0$ do not lead to non-integrable singularity as $k_2\rightarrow 0$. So dangerous terms include terms of the order $1/k_2^2$ in $T_1$, $T_0$ and terms non-vanishing as $k_2\rightarrow 0$ in $T_{-1}$, $U_0$ and $V_0$.

We start from $T_1$. Terms of order $1/k_2^2$ come from coefficient $\alpha _2=1-2q_2^2/k_{2\perp }^2$. Collecting them we find in the limit $k_2\rightarrow 0$ (in E2DM)

$$\begin{aligned} T_1=-4\frac{q_2^2}{k_2^2}\left( q_{1}^2(pe)-p^2(q_1e)\right) . \end{aligned}$$

Next we find that terms proportional to $1/k_2^2$ are in fact absent in $T_0$ and $U_0$. We are left with $T_{-1}$ and $V_0$. In the limit $k_2\rightarrow 0$ (also in E2DM)

$$\begin{aligned} T_{-1}=-4r_2^2(q_1e),\ \ V_0=-4p_+r_2^2q_1^2(pe). \end{aligned}$$

The singular terms from $T_1$, $T_{-1}$ and $V_0$ give in the sum

$$\begin{aligned}&4\frac{(pk_2)q_2^2}{k_2^2}\left( p^2(q_1e)-q_1^2(pe) \right) \\&\quad +\,4\frac{r_2^2(pk_2)}{k_2^2}\left( q_1^2(pe)-p^2(q_1e)\right) . \end{aligned}$$

At $k_2=0$ we have $q_2=r_2$ so that all power-like singularities cancel.

So the only dangerous terms at $k_2\rightarrow 0$ are the logarithmic ones. They come only from the contribution proportional to $V_0$ and lead to the singular term (in Lorentz metric)

$$\begin{aligned} \Gamma ^A_{k_2\rightarrow 0}=\frac{i}{\pi }C_5\frac{q_1^2r_2^2(pe)_\perp }{2p_\perp ^2}\, \frac{1}{k_{2\perp }^2}\ln \frac{k_{2\perp }^2}{p_\perp ^2}. \end{aligned}$$

(81)

To finish with case A we consider the behavior at $k_1\rightarrow 0$. Obviously in this case only terms with $U_0$ and $V_0$ may lead to non-integrable singularities. So we have to calculate values of $U_0$ and $V_0$ at $k_1\rightarrow 0$ and so $k_2\rightarrow p$. Elementary calculations give in E2DM

$$\begin{aligned} U_0=4p_+r_1^2\left( (q_2e)-\frac{q_2^2}{p^2}(pe)\right) ,\quad V_0=p^2U_0. \end{aligned}$$

As a result the singular terms proportional to $(pk_1)/k_1^2$ cancel, so that $\Gamma ^A$ is integrable at $k_1=0$. Its only singularity is at $k_2\rightarrow 0$ and is given by (81).

Integration of $X_5^B$

Case B is considered quite similarly. Now we integrate over $q_{1+}=xp_+$ with $x<0$. Before integration

$$\begin{aligned} \Gamma _5^B=C_5X_5^{(B)}F_5^B, \end{aligned}$$

where

$$\begin{aligned} F_5^B=\frac{i}{\theta }(-q_{1+})\frac{1}{q_{1+}k_{2\perp }^2+q_{2+}k_{1\perp }^2+2p_-q_{1+}q_{2+}}. \end{aligned}$$

The denominator can be written in Euclidean metric as

$$\begin{aligned}&q_{1+}k_{2\perp }^2+q_{2+}k_{1\perp }^2+2p_-q_{1+}q_{2+}=-p_+D_1,\\&\quad D_1=(\mathbf{k}_1-x\mathbf{p})^2. \end{aligned}$$

Writing $X_5^{(B)}$ according to Eq. (75) we shall get the integrated $\Gamma _5^B$,

$$\begin{aligned} \Gamma _5^B=-\frac{i}{4\pi }C_5\left( \sum _{n=-1}^2{\tilde{T}}_{n}I^B_n +\frac{{\tilde{U}}_0}{p_+}K_1^B-\frac{{\tilde{V}}_0}{p_+}K_2^B \right) , \end{aligned}$$

(82)

where tildes mean case B. The integrals are

$$\begin{aligned} I^B_n= & {} \int _{-x_2}^{-x_1}\frac{x^n \mathrm{d}x}{(k_1-xp)^2},\\ K_1= & {} \int _{-x_2}^{-x_1}\frac{\mathrm{d}x}{(1-x)(k_1-xp)^2},\\ K_2= & {} \int _{-x_2}^{-x_1}\frac{ \mathrm{d}x}{(xp^2-k_1^2)(k_1-xp)^2} \end{aligned}$$

and all vectors are taken in E2DM. All integrals are well convergent at small $x_i\rightarrow 0$ so that we van safely put $x_1=0$. At large |x| $I^B_n$ with $n=1,2$ diverge and we have to separate the diverging terms. All integrals are expressed via the integral

$$\begin{aligned} I^B_0=\int _{-x_2}^{-x_1}\frac{ \mathrm{d}x}{(k_1-xp)^2}=\frac{\phi _1}{\sqrt{p^2k_1^2-(pk_1)^2}}, \end{aligned}$$

(83)

where $\phi _1$ is the angle between $\mathbf{k}_1$ and $\mathbf{p}$, $0<\phi _1<\pi$. All the remaining integrals are given as follows:

$$\begin{aligned} I^B_1= & {} -\frac{1}{p^2}\delta +\frac{(pk_1)}{p^2}I^B_0,\\ I^B_2= & {} \frac{1}{p^2}J_1+2\frac{(pk_1)}{p^2}I^B_1-\frac{k_1^2}{p^2}I^B_0,\\ I^B_{-1}= & {} -\frac{1}{k_1^2}\delta +\frac{(pk_1)}{k_1^2}I^B_0,\\ K^B_1= & {} \frac{1}{2k_2^2}\ln \frac{k_1^2}{p^2}+\frac{(pk_2)}{k_2^2}I^B_0,\\ K_2^B= & {} \frac{1}{2k_1^2k_2^2}\ln \frac{k_1^2}{p^2}+\frac{(k_1k_2)}{k_1^2k_2^2}I^B_0.\\ \end{aligned}$$

The denominator in $I^B_0$ is the same as in $I^A_0$ (see (18)), the difference between them is in the numerator. As in case A the basic integral $I^B_0$ contains both a collinear singularity at $\phi _1=\pi$ and comparatively weak (integrable) singularities at $k_1\rightarrow 0$ and $k_2\rightarrow 0$ where it behaves as $1/k_1$ or $1/k_2$. As mentioned, the collinear singularity is in fact absent, since the whole $X^B$ vanishes when $k_1$ and $k_2$ are parallel to p. Dropping the divergent term with $J_1$ for the reasons discussed earlier we present the integrated $\Gamma ^B$ as a sum of two terms, one of which is proportional to $\ln k_1^2$ and the other proportional to $I^B_0$:

$$\begin{aligned} \Gamma ^B= & {} -\frac{i}{4\pi }C_5\left\{ \frac{1}{2p_+k_2^2} \Big (\tilde{U}_0-\frac{1}{k_1^2}\tilde{V}_0\Big )\ln \frac{k_1^2}{p^2}\right. \nonumber \\&+\,I^B_0\left[ \Big (2\frac{(pk_1)^2}{p^4}-\frac{k_1^2}{p^2}\Big )\tilde{T}_2+\frac{(pk_1)}{p^2}{\tilde{T}}_1+{\tilde{T}}_0\right. \nonumber \\&\left. \left. +\,\frac{(pk_1)}{k_1^2}{\tilde{T}}_{-1} +\frac{(pk_2)}{p_+k_2^2}{\tilde{U}}_0-\frac{(k_1k_2)}{p_+k_1^2k_2^2}{\tilde{V}}_0\right) \right\} . \end{aligned}$$

(84)

We first analyze possible non-integrable singularities as $k_1\rightarrow 0$. The power-like singularities come again from singularities of the integrals $I^B_n$, $K_1^B$ and $K_2^B$ and from the coefficients ${\tilde{T}}_n$, ${\tilde{U}}_0$ and $\tilde{K}_0$. As in case A, the term with ${\tilde{T}}_2$ is non-singular due to the factor $(pk_1)^2$. Also non-singular terms in ${\tilde{T}}_1$, ${\tilde{T}}_0$ and ${\tilde{U}}_0$ do not lead to a non-integrable singularity as $k_1\rightarrow 0$. So as in case A, dangerous terms include terms of the order $1/k_1^2$ in ${\tilde{T}}_1$, ${\tilde{T}}_0$ and terms non-vanishing as $k_1\rightarrow 0$ in ${\tilde{T}}_{-1}$, ${\tilde{U}}_0$ and ${\tilde{V}}_0$

We start from ${\tilde{T}}_1$. Terms of order $1/k_1^2$ come from the coefficient $\alpha _1=1-2q_1^2/k_{1\perp }^2$. Collecting them we find in the limit $k_1\rightarrow 0$ (in E2DM)

$$\begin{aligned} {\tilde{T}}_1=4\frac{q_1^2}{k_1^2}\left( q_{2}^2(pe)-p^2(q_2e) \right) . \end{aligned}$$

Next we find that terms proportional to $1/k_1^2$ are in fact absent in ${\tilde{T}}_0$ and ${\tilde{U}}_0$. We are left with ${\tilde{T}}_{-1}$ and ${\tilde{V}}_0$. In the limit $k_1\rightarrow 0$ in E2DM

$$\begin{aligned} {\tilde{T}}_{-1}=4r_1^2(q_2e),\ \ {\tilde{V}}_0=4p_+r_1^2q_2^2(pe). \end{aligned}$$

The singular terms from ${\tilde{T}}_1$, ${\tilde{T}}_{-1}$ and ${\tilde{V}}_0$ give in the sum

$$\begin{aligned}&-4\frac{(pk_1)q_1^2}{k_1^2}\left( p^2(q_2e)-q_2^2(pe) \right) \nonumber \\&\quad -4\frac{r_1^2(pk_1)}{k_1^2}\left( q_2^2(pe)-p^2(q_2e)\right) . \end{aligned}$$

At $k_1=0$ we have $q_1=r_1$ so that all power-like singularities cancel.

So the only dangerous terms at $k_1\rightarrow 0$ are the logarithmic ones. They come only from the contribution proportional to ${\tilde{V}}_0$ and lead to the singular term (in Lorentz metric)

$$\begin{aligned} \Gamma ^B_{k_1\rightarrow 0}=-\frac{i}{\pi }C_5\frac{q_2^2r_1^2(pe)_\perp }{2p_\perp ^2}\, \frac{1}{k_{1\perp }^2}\ln \frac{k_{1\perp }^2}{p_\perp ^2}. \end{aligned}$$

(85)

Finally, we consider the behavior at $k_2\rightarrow 0$. In this case only terms with ${\tilde{U}}_0$ and ${\tilde{V}}_0$ may lead to non-integrable singularities. So we have to calculate the values of ${\tilde{U}}_0$ and ${\tilde{V}}_0$ at $k_2\rightarrow 0$ and so $k_1\rightarrow p$. Calculations give in E2DM

$$\begin{aligned} {\tilde{U}}_0=-4p_+r_2^2\left( (q_1e)-\frac{q_1^2}{p^2}(pe)\right) ,\ \ {\tilde{V}}_0=p^2{\tilde{U}}_0 . \end{aligned}$$

So the singular terms proportional to $(pk_2)/k_2^2$ cancel, and $\Gamma ^B$ turns out to be integrable at $k_2=0$. Its only singularity is at $k_1\rightarrow 0$ and is given by (85).

1.7 Final singularities

We first consider the dangerous non-integrable logarithmic singularity at $k_1\rightarrow 0$, which comes from $\Gamma _3$, $\Gamma _4$ and $\Gamma ^B$. As we have found from $\Gamma _3$ and $\Gamma _4$ in the sum, the singular term is

$$\begin{aligned} \Gamma ^{\mathrm{sing}}_{3+4}=\frac{i}{\pi }(C_3-C_4)(pe)_\perp \frac{q_{2\perp }^2r_{1\perp }^2}{k_{1\perp }^2}\int _{x_1}^{x_2} \frac{\mathrm{d}x}{xp_\perp ^2+k_{1\perp }^2}. \end{aligned}$$

Passing to E2DM we rewrite this as

$$\begin{aligned} \Gamma ^{\mathrm{sing}}_{3+4}=-\frac{i}{\pi }(C_3-C_4)(pe)\frac{q_{2}^2r_{1}^2}{k_1^2}\int _{x_1}^{x_2}\frac{\mathrm{d}x}{xp^2+k_1^2}. \end{aligned}$$

The integral gives

$$\begin{aligned} \int _{x_1}^{x_2}\frac{\mathrm{d}x}{xp^2+k^2}=\frac{1}{p^2} \ln \frac{x_2p^2+k_1^2}{x_1p^2+k_1^2}. \end{aligned}$$

At this point we recall that $x_1=(k_1/p)\mathrm{e}^{-\delta }$ and $x_2=(k_1/p)\mathrm{e}^\delta$ with $\delta \gg 1$. Then we find

$$\begin{aligned} \int _{x_1}^{x_2}\frac{\mathrm{d}x}{xp^2+k^2}=\frac{1}{p^2}\ln \frac{pk\mathrm{e}^\delta }{k_1^2}=-\frac{1}{2p^2}\ln \frac{k_1^2}{p^2} \end{aligned}$$

and the singular term from $\Gamma _{3+4}$ becomes

$$\begin{aligned} \Gamma ^{\mathrm{sing}}_{3+4}=\frac{i}{\pi }(C_3-C_4)(pe) \frac{q_{2}^2r_{1}^2}{2p^2k_1^2} \left( \ln \frac{k_1^2}{p^2}-2\delta \right) . \end{aligned}$$

(86)

Now we pass to the singular contribution from $\Gamma ^B$ given by (85). It was obtained by taking $x_1=0$. However, it does not change if one takes $x_1=(k_1/p)\mathrm{e}^{-\delta }$ instead (unlike $I^{(3)}_0$, due to convergence at high $x_2$). The logarithm in (85) comes in fact from

$$\begin{aligned} \ln \frac{(k_1^2+x_1p^2)^2}{(\mathbf{k}_1+x_1\mathbf{p})^2}-(x_1\rightarrow x_2)= \ln \frac{(k_1^2+k_1p\mathrm{e}^{-\delta })^2}{(\mathbf{k}_1+(k_1/p)\mathbf{p}\mathrm{e}^{-\delta })^2}-(\delta \rightarrow -\delta ). \end{aligned}$$

In the limit $\delta \gg 1$ this goes into $\ln (k_1^2/p^2)$, which is the same if we took $x_1=0$ and $x_2\rightarrow \infty$ from the start.

In E2DM (85) reads

$$\begin{aligned} \Gamma ^{\mathrm{sing}}_B=\frac{i}{\pi }C_5\frac{q_2^2r_1^2(pe)}{2p^2k_1^2}\ln \frac{k_{1\perp }^2}{p_\perp ^2}. \end{aligned}$$

(87)

Dropping the term with $\delta$ in(86) and summing with (87)we find the final logarithmic singularity

$$\begin{aligned} \Gamma ^{\mathrm{sing}}_{3+4+B}=\frac{i}{\pi }(C_3-C_4+C_5)(pe) \frac{q_2^2r_1^2}{2p^2k_1^2}\ln \frac{k_1^2}{p^2}. \end{aligned}$$

(88)

Recalling that $C_3=-1$, $C_4=-1/2$ and $C_5=1/2$ we find that this singularity is canceled.

Thus the only singular term in the whole integrated $\Gamma$ are those proportional either to $J_1$ or to $\delta$. Hopefully the latter can safely be discarded due to cancelations with similar terms from the diagrams with pairwise interregional interaction. Terms with $J_1$ actually go after symmetrization, as will be demonstrated below.

1.8 Terms with $J_1$

These terms are present in linear diverging expressions in $\Gamma _i$. $i=2,\ldots ,5$ The corresponding contributions from $\Gamma _{2,3,4}$ are

$$\begin{aligned} \Gamma _2= & {} \frac{1}{4\pi }C_2J_1\frac{1}{p_\perp ^2}T_2^{(2)},\ \ T_2^{(2)}=-(pe)_\perp p_\perp ^2\alpha _1,\\ \Gamma _3= & {} \frac{1}{4\pi }C_3J_1T_1^{(3)},\ \ T_1^{(3)}=-2(pe)_\perp \alpha _1,\\ \Gamma _4= & {} \frac{1}{4\pi }C_4J_1T_1^{(3)},\ \ T_1^{(3)}=(pe)_\perp \alpha _1, \end{aligned}$$

where $\alpha _1=1-2q_1^2/k_{1\perp }^2$. In the sum we get

$$\begin{aligned} \Gamma _{2+3+4}= & {} \frac{1}{4\pi }\alpha _1(pe)_\perp J_1(-C_2-2C_3+C_4)\nonumber \\= & {} \frac{1}{8\pi }\alpha _1(pe)_\perp J_1. \end{aligned}$$

(89)

We have to add to this contribution the three others obtained by interchanges $(q_1\leftrightarrow q_2)$ and $(r_1\leftrightarrow r_2)$. At these exchanges both longitudinal and transversal momentum components are to be exchanged. The exchange $q_1 \leftrightarrow q_2$ does not change the momentum part since one has to integrate both over $q_{1,2+}$ and $q_{1,2\perp }$. However, this exchange gives a minus sign due to a change of the color factor. The exchange $r_1\leftrightarrow r_2$ does not change the color factor but we have to take residues in the lower half-plane of $r_{1-}$. This means the upper half-plane of the variable $r_{2-}$. Therefore simultaneously with changing $r_{1\perp }\leftrightarrow r_{2\perp }$ after taking the residue one should change $-i\theta (-q_{1+})\leftrightarrow i\theta (q_{2+})$, which is equivalent to taking $x\rightarrow -x$ in our formulas plus the overall minus sign. In practice this means that in terms with $J_1$ we have to take the minus sign. Denoting the result of adding the interchanged contribution as Sym we get

$$\begin{aligned} {\mathrm{Sym}}\,\Gamma _{2+3+4}= & {} -\frac{i}{8\pi }J_1(pe)_\perp \,\left( \frac{q_1^2}{(q_1-r_1)_\perp ^2}-\frac{q_2^2}{(q_2-r_1)_\perp ^2}\right. \nonumber \\&\left. -\frac{q_1^2}{(q_1-r_2)_\perp }+\frac{q_2^2}{(q_2-r_1)^2} \right) . \end{aligned}$$

(90)

This expression should be integrated with the pomeron symmetric in $r_{1\perp }$ and $r_{2\perp }$. Then the result of integration vanishes. So in the end no terms proportional to $J_1$ come from $\Gamma _{2+3+4}$. This means that the sum of these vertices has no linear divergency after symmetrization.

From $\Gamma _5$ we have two contributions:

$$\begin{aligned} \Gamma ^A= & {} \frac{i}{4\pi }C_5J_1\frac{1}{|p_\perp ^2|}T_2,\ \ T_2=-|p_\perp ^2|\alpha _2(pe)_\perp ,\\ \Gamma ^B= & {} -\frac{i}{4\pi }C_5J_1\frac{1}{|p_\perp ^2|}{\tilde{T}}_2,\ \ {\tilde{T}}_2=|p_\perp ^2|\alpha _1(pe)_\perp . \end{aligned}$$

In the sum we find

$$\begin{aligned} \Gamma _5=\frac{i}{2\pi }C_5J_1(pe)_\perp \left( \frac{q_2^2}{k_{2\perp }^2}+\frac{q_1^2}{k_{1\perp }^2}-1 \right) . \end{aligned}$$

(91)

Symmetrization can be done either by changing $q_1\leftrightarrow q_2$ or changing $r_1\leftrightarrow r_2$. In both cases we have the sign minus. So

$$\begin{aligned} {\mathrm{Sym}}\,\Gamma ^5= & {} \frac{i}{2\pi }C_5J_1(pe)_\perp \left( \frac{q_2^2}{(q_2-r_2)_\perp ^2}+\frac{q_1^2}{(q_1-r_1)_\perp ^2} \right. \nonumber \\&\left. -\frac{q_2^2}{(q_2-r_1)_\perp ^2}-\frac{q_1^2}{(q_1-r_2)_\perp ^2} \right) . \end{aligned}$$

(92)

This expression is antisymmetric in $r_{1\perp }$ and $r_{2\perp }$ and so vanishes after integration with the pomeron.

Thus the whole contribution from the vertex $\Gamma$ does not contain terms proportional to $J_1$ and so it does not contain a linear divergence.