1 Introduction

The UV completion of general relativity (GR) such that GR is recovered in the IR limit has led to the development of Horava-Lifshitz gravity [1, 2]. The concept of different Lifshitz scaling of space and time has been used to analyze type IIA string theory [3], type IIB string theory [4], AdS/CFT correspondence [5,6,7,8], dilaton black branes [9, 10], and dilaton black holes [11, 12]. But this is not the only way of achieving this. There is another alternative theory where the UV completion of GR is obtained by making the metric depend on the energy of the test particle. This theory is termed as Gravity’s Rainbow [13] in literature. Although there are conceptual differences it is believed that gravity’s rainbow is related to the Horava-Lifshitz gravity [14]. This is due to the fact that both gravity’s rainbow and Horava-Lifshitz gravity are based on the modification of the usual energy–momentum dispersion relation in the UV limit. This modification is carried out keeping in mind that it should reduce to the usual energy–momentum dispersion relation in the IR limit. We know that in relativity, the form of the energy–momentum relation is governed by the Lorentz symmetry. So it is not strange that gravity’s rainbow will disrespect such a symmetry in the UV limit. In this connection it must be noted that in spite of being one of the most important symmetries in nature, there are various different quantum gravity approaches in literature which indicates that Lorentz symmetry might only be valid at low energy scales, and quite obviously it will breakdown in the high energy UV limit [15,16,17,18,19]. Specific models where this breakdown is expected to occur are discrete spacetime [20], string field theory [21], spacetime foam [22], the spin-network in loop quantum gravity (LQG) [23], non-commutative geometry [24], etc. Now such a deformation of the standard energy–momentum dispersion relation in the UV limit of the theory will imply the existence of a maximum energy scale. Based on the existence of such a maximum energy scale the idea of doubly special relativity (DSR) [25] has been conceived. Gravity’s rainbow is simply a generalization of DSR applied to curved spacetime [26]. As stated earlier the geometry of the spacetime in gravity’s rainbow depend on the energy of the test particles. So it is clear that due to such dependence each test particle of different energy will feel a different geometry of spacetime, thus undergoing motions differently. Thus the geometry of spacetime in gravity’s rainbow is represented by a family of energy dependent metrics forming a rainbow of metrics. This justifies the name. The interesting conceptual background of the theory have generated a lot of research interest in recent times [27,28,29,30,31,32,33,34,35,36]. In this theory the modification in the energy–momentum dispersion relation is introduced by energy dependent rainbow functions, \(\mathcal {F}(E)\) and \(\mathcal {G}(E)\), such that

$$\begin{aligned} E^2\mathcal {F}^2(E)-p^2\mathcal {G}^2(E)=m^2. \end{aligned}$$
(1.1)

It may be noted that here \(E = E_{s}/E_P\), where \(E_{s}\) is the maximum energy that a probe in that system can take, and \(E_p\) is the Planck energy. By definition \(E_s\) cannot exceed \(E_p\). The rainbow functions are chosen in such a way so that they produce the usual energy–momentum relation of GR in the low energy IR limit of the theory [37,38,39,40,41,42,43,44,45], and so they are required to satisfy

$$\begin{aligned} \lim \limits _{E_s/E_P\rightarrow 0} \mathcal {F}(E)=1,\qquad \lim \limits _{E_s/E_P\rightarrow 0} \mathcal {G}(E)=1. \end{aligned}$$
(1.2)

The metric in gravity’s rainbow is written as

$$\begin{aligned} g^{\mu \nu }(E)=\eta ^{ab}e^\mu _a(E) e^\nu _b(E). \end{aligned}$$
(1.3)

In 1961, Brans and Dicke [46] developed an idea which is considered as a relativistic theory of gravitation parallel to GR. The theory is known as the Brans–Dicke (BD) theory of gravitation. In GR the right hand side of the field equations consists of the stress energy tensor which is the source of the gravitational field. But in case of BD theory the manner in which the mass–energy pressure acts is completely different from the way in which it acts in case of GR. In GR it is the geometric curvature of space-time that completely controls the motion of bodies in a gravitational field, but in case of BD theory, due to the use of a contrasting mechanism, this dependence on geometry is considerably reduced. These are the basic attributes that differentiate BD theory from the traditional theories of GR. Hence the theory demands a lot of research. Being a scalar-tensor theory of gravitation the most important feature of BD theory is that it consists of an additional scalar field \(\phi \) which is absent in GR. The presence of the scalar field has a strong consequence, making the effective gravitational constant a function of space coordinates. There is a dimensionless BD coupling constant \(\omega \) which can be tuned as per choice so as make the theory consistent with observational evidences. This is a unique feature of the theory and it is quite obvious that due to this provision the theory will admit more solutions compared to GR thus enhancing its universality. Just like GR, BD theory also predicts gravitational deflection of light and the perihelia precession of planets that orbit the Sun. But these phenomena totally depend on the value of the BD parameter \(\omega \) which means that it is possible to constrain the possible values of \(\omega \) from observations of our solar system and other gravitational systems. It is thought that GR can be obtained from the BD theory in the limit \(\omega \rightarrow \infty \) [47].

Here we will be probing the Vaidya space-time [48] in the energy dependent deformations of BD gravity [49, 50]. In Ref. [50], time dependent Vaidya spacetime was studied in the background of BD gravity theory. In Ref. [51], Rudra et al studied the rainbow deformations of Vaidya spacetime in the background of Galileon gravity theory and obtained interesting results. Galileon gravity is a form of scalar tensor theory of gravity, where there is a self-interacting term of the form \(\nabla {\phi }^{2}~ ^{\fbox {}}~\phi \), so that GR is recovered at high densities. It contains a scalar field \(\phi \) and a potential \(V(\phi )\) in its action. Since BD gravity also has a similar set-up we are motivated to probe the energy dependent modifications of the time dependent Vaidya space-time in its background. This will be done via a gravitational collapse mechanism. Nonetheless, we will also study the thermodynamical properties of the system. It may be noted that the gravitational collapse under different set-ups has been studied previously using gravity’s rainbow [51,52,53,54]. The deformation of the thermodynamics of black holes (BH) due to gravity’s rainbow has also been studied [55,56,57]. The BH thermodynamics will get modified by the rainbow functions. This is due to the fact that, the energy E which defines the rainbow functions is basically the energy of a quantum particle near the event horizon of the BH, emitted in the Hawking radiation. Now we can obtain a bound on energy \(E \ge 1/\Delta x \), using the uncertainty principle \(\Delta p \ge 1/\Delta x \). Furthermore, the uncertainty in position of a particle near the event horizon can be taken to be equal to the radius of the event horizon radius

$$\begin{aligned} E\ge 1/{\Delta x} \approx 1/{r_+}. \end{aligned}$$
(1.4)

This energy bound modifies the temperature of the BH, and this modified temperature of the BH can be used to calculate the corrected entropy of the BH in gravity’s rainbow. The energy of a quantum particle near the event horizon is considered as the energy of the test particle. This is the energy which is used in defining the rainbow functions that modify the energy momentum relations. The metric when deformed by these rainbow functions, quite naturally deforms the BH thermodynamics. This deformation in the thermodynamics of a BH predicts the possibility of a BH remnant. Remnants of BH can have important implications in the detection of mini BHs at the Large Hadron Collider (LHC) [58]. This energy which is used in constructing rainbow functions is dynamical in nature depending on the radial coordinate [14]. Although the explicit dependence of this energy on the radial coordinate is unimportant for us, yet it is important to note that the rainbow functions are dynamical in nature, and hence cannot be gauged away by rescaling the metric.

Over the years gravitational collapse [59] of stars has been a problem of great curiosity both in classical GR as well as modified gravity theories. The reason being that we can get at least two types of singularities from such a phenomenon. A singularity covered by an event horizon is a BH whereas an uncovered singularity is popularly known as a naked singularity (NS). Now to determine the exact initial conditions which lead to the formation of BH or NS is a challenging astrophysical problem. To be more precise, the quest of a physical initial condition leading to the formation of a NS [60,61,62] is a really interesting problem given the validity of cosmic censorship hypothesis (CCH) laid down by Penrose [63] which states that the end result of a collapsing scenario is bound to be a singularity covered by an event horizon, i.e. a BH. Moreover the NS being local or global (weak and strong form of CCH) and the strength of the singularity are also important issues worthy of studying. Here we will study the chosen geometry focussing ourselves on this problem.

The paper is organized as follows. In Sect. 2, the field equations for the rainbow deformed Brans–Dicke gravity are generated. In Sect. 3, the solution of the given system is found. Section 4 is devoted to the study of gravitational collapse in the system considered. In Sect. 5, we focus ourselves on the thermodynamical aspects of the system. Finally the paper ends with some concluding remarks in Sect. 6.

2 Brans–Dicke gravity’s rainbow

The self-interacting BD theory [46] is described by the following action (choosing \(8\pi G=c=1\))

$$\begin{aligned} S=\int d^{4} x \sqrt{-g}\left[ \phi R- \frac{\omega (\phi )}{\phi } {\phi }^{,\alpha } {\phi ,}_{\alpha }-V(\phi )+ \mathcal{L}_{m}\right] \end{aligned}$$
(2.1)

where \(V(\phi )\) is the self-interacting potential for the BD scalar field \(\phi \) and the constant \(\omega \) is the BD parameter.

The Vaidya metric deformed by gravity’s rainbow in the background of BD theory can be given by

$$\begin{aligned} ds^{2}= & {} -\frac{1}{\mathcal {F}^{2}(E)}\left( 1-\frac{m(t,r)}{r} \right) dt^2\nonumber \\&+\frac{2}{\mathcal {F}(E)\mathcal {G}(E)}dtdr\nonumber \\&+\frac{1}{\mathcal {G}^{2}(E)}r^2 d\Omega _{2}^2\nonumber \\= & {} f(t,r)dt^2 +\frac{2}{\mathcal {F}(E)\mathcal {G}(E)}dtdr\nonumber \\&+\frac{1}{\mathcal {G}^{2}(E)}r^2 d\Omega _{2}^2, \end{aligned}$$
(2.2)

where \(\mathcal {F}(E)\) and \(\mathcal {G}(E)\) are the rainbow functions.

From the Lagrangian density given by Eq. (2.1) we obtain the field equations [46]

$$\begin{aligned} G_{\mu \nu }= & {} \frac{\omega (\phi )}{{\phi }^{2}}\left[ \phi _{ , \mu } \phi _{, \nu } - \frac{1}{2}g_{\mu \nu } \phi _{, \alpha } \phi ^{ , \alpha } \right] \nonumber \\&+\frac{1}{\phi }\left[ \phi _{, \mu ; \nu } -g_{\mu \nu }~ \Box \phi \right] -\frac{V(\phi )}{2 \phi } g_{\mu \nu }+\frac{1}{\phi }T_{\mu \nu } \end{aligned}$$
(2.3)

and

$$\begin{aligned} \Box \phi =\frac{1}{3+2\omega }T-\frac{1}{3+2\omega }\left[ 2V(\phi )-\phi \frac{dV(\phi )}{d\phi }\right] \end{aligned}$$
(2.4)

where \(T=T_{\mu \nu }g^{\mu \nu }\).

Now we consider two types of fluids namely, Vaidya null radiation and a perfect fluid having the form of the energy momentum tensor

$$\begin{aligned} T_{\mu \nu }=T_{\mu \nu }^{(n)}+T_{\mu \nu }^{(m)} \end{aligned}$$
(2.5)

with

$$\begin{aligned} T_{\mu \nu }^{(n)}=\sigma l_{\mu }l_{\nu } \end{aligned}$$
(2.6)

and

$$\begin{aligned} T_{\mu \nu }^{(m)}=(\rho +p)(l_{\mu }\eta _{\nu }+l_{\nu }\eta _{\mu })+pg_{\mu \nu } \end{aligned}$$
(2.7)

where \(\rho \) and p are the energy density and pressure for the perfect fluid and \(\sigma \) is the energy density corresponding to Vaidya null radiation. Here \(T_{\mu \nu }^{(n)}\) and \(T_{\mu \nu }^{(m)}\) are respectively the contributions from vaidya null radiation and perfect fluid. In the co-moving co-ordinates (\(t,r,\theta _{1},\theta _{2},\ldots ,\theta _{n}\)), the two eigen vectors of energy–momentum tensor namely \(l_{\mu }\) and \(\eta _{\mu }\) are linearly independent future pointing null vectors having components

$$\begin{aligned} l_{\mu }= & {} (1,0,0,\ldots ,0) \quad and \quad \eta _{\mu }\nonumber \\= & {} \left( \frac{1}{2}\left( 1-\frac{m}{r^{n-1}}\right) ,-1,0,\ldots ,0 \right) \end{aligned}$$
(2.8)

and they satisfy the relations

$$\begin{aligned} l_{\lambda }l^{\lambda }=\eta _{\lambda }\eta ^{\lambda }=0,~ l_{\lambda }\eta ^{\lambda }=-1 \end{aligned}$$
(2.9)

Imposing the rainbow deformations in the linearly independent future pointing null vectors \(l_{\mu }\) and \(\eta _{\mu }\) we get,

$$\begin{aligned}&l_{\mu }=\left( \frac{1}{\mathcal {F}(E)},0,0,0\right) \quad {\text {and}} \nonumber \\&\eta _{\mu }=\left( \frac{1}{2\mathcal {F}(E)}\left( 1-\frac{m(t,r)}{r}\right) ,-\frac{1}{\mathcal {G}(E)},0,0 \right) \end{aligned}$$
(2.10)

satisfying the following conditions

$$\begin{aligned} l_{\mu }l^{\mu }=\eta _{\mu }\eta ^{\mu }=0 \quad {\text {and}} \quad l_{\mu }\eta ^{\mu }=-1. \end{aligned}$$
(2.11)

Therefore, the non-vanishing components of the total energy-momentum tensor will be as follows

$$\begin{aligned} T_{00}= & {} \frac{\sigma }{\mathcal {F}^{2}(E)}+\frac{\rho }{\mathcal {F}^{2}(E)}\left( 1-\frac{m(t,r)}{r}\right) , ~~~T_{01}=-\frac{\rho }{\mathcal {F}(E)\mathcal {G}(E)}, \nonumber \\ T_{22}= & {} \frac{pr^2}{\mathcal {G}^2(E)}, ~~~T_{33}=\frac{pr^2 sin^2\theta }{\mathcal {G}^2(E)} \end{aligned}$$
(2.12)

The (00)-component of the field equation is given as

$$\begin{aligned}&\frac{\mathcal {G}(E)\left[ \mathcal {G}(E)\left( r-m\right) m'+\mathcal {F}(E)r\dot{m}\right] }{\mathcal {F}^{2}(E)r^{3}}\nonumber \\&\quad = \frac{\omega }{\phi ^{2}}\left[ \dot{\phi }^{2}+\frac{1}{2\mathcal {F}^{2}(E)}\left( 1-\frac{m}{r}\right) ^{2}\phi '^{2} \mathcal {G}^{2}(E)\right] +\frac{\ddot{\phi }}{\phi }\nonumber \\&\qquad -\phi \left[ \frac{\mathcal {G}(E)m}{2\mathcal {F}(E)r^{2}}-\frac{\mathcal {G}(E)m'}{2\mathcal {F}(E)r}\right] \nonumber \\&\qquad - \phi '\left[ \frac{\mathcal {G}^{2}(E)m}{2\mathcal {F}^{2}(E)r^{2}}-\frac{\mathcal {G}^{2}(E)m^{2}}{2\mathcal {F}^{2}(E)r^{3}}\right. \nonumber \\&\qquad \left. -\frac{\mathcal {G}^{2}(E)m'}{2\mathcal {F}^{2}(E)r}+\frac{\mathcal {G}^{2}(E)m m'}{2\mathcal {F}^{2}(E)r^{2}}+\frac{\mathcal {G}(E)\dot{m}}{2\mathcal {F}(E)r}\right] \nonumber \\&\qquad +\frac{1}{\mathcal {F}^{2}(E)\phi }\left( 1-\frac{m}{r}\right) \Box \phi +\frac{1}{\mathcal {F}^{2}(E)} \left( 1-\frac{m}{r}\right) \frac{V(\phi )}{2\phi }\nonumber \\&\qquad +\frac{1}{\mathcal {F}^{2}(E)\phi }\left[ \sigma + \rho \left( 1-\frac{m}{r}\right) \right] \end{aligned}$$
(2.13)

The (11)-component of the field equation is

$$\begin{aligned} \frac{\omega }{\phi ^{2}}\phi '^{2}+\frac{\phi ''}{\phi }=0 \end{aligned}$$
(2.14)

The (10) and (01)-components are

$$\begin{aligned}&-\frac{\mathcal {G}(E)m'}{\mathcal {F}(E)r^{2}}=\frac{\omega }{\phi ^{2}}\left[ \dot{\phi }' -\frac{1}{2\mathcal {F}(E)\mathcal {G}(E)}\left\{ \phi '^{2}\left( 1-\frac{m}{r}\right) \mathcal {G}^{2}(E)\right\} \right] \nonumber \\&\quad +\frac{1}{\phi }\left[ \dot{\phi }'+\left( \frac{\mathcal {G}(E)m}{2\mathcal {F}(E)r^{2}} -\frac{\mathcal {G}(E)m'}{2\mathcal {F}(E)r}\right) \phi '\right. \nonumber \\&\quad \left. -\frac{1}{\mathcal {F}(E)\mathcal {G}(E)}\Box \phi \right] -\frac{V(\phi )}{2\phi \mathcal {F}(E)\mathcal {G}(E)} -\frac{\rho }{\phi \mathcal {F}(E)\mathcal {G}(E)} \end{aligned}$$
(2.15)

Finally the (22) and (33)-components are given by

$$\begin{aligned} \frac{1}{2}rm''= & {} \frac{\omega r^{2}}{2\phi ^{2}}\left( 1-\frac{m}{r}\right) \phi '^{2}\nonumber \\&-\frac{1}{\phi }\left[ \frac{\mathcal {F}(E)r}{\mathcal {G}(E)} \dot{\phi }+\left( r-m\right) \phi '-\frac{r^{2}}{\mathcal {G}^{2}(E)}\Box \phi \right] \nonumber \\&+\frac{V(\phi )r^{2}}{2\phi \mathcal {G}^{2}(E)}-\frac{pr^{2}}{\mathcal {G}^{2}(E)\phi } \end{aligned}$$
(2.16)

where \(\Box \phi \) is given by,

$$\begin{aligned} \Box \phi= & {} \mathcal {F}(E)\mathcal {G}(E)\dot{\phi }'+\frac{\mathcal {G}^{2}(E)}{2r}\left( 1-m'\right) \phi '\nonumber \\&+ \frac{\mathcal {F}(E)\mathcal {G}(E)}{2r}\dot{\phi }+\left( 1-\frac{m}{r}\right) \mathcal {G}^{2}(E)\phi '' \end{aligned}$$
(2.17)

Here dot and dash represent derivatives with respect to t and r respectively.

3 The solution

In this section we will find the solutions of the field equations given in the previous section. From Eq. (2.14) we get,

$$\begin{aligned} \phi (r,t)=\left[ r+r\omega -f_{1}(t)\right] ^{\frac{1}{1+\omega }}f_{2}(t) \end{aligned}$$
(3.1)

where \(f_{1}(t)\) and \(f_{2}(t)\) are arbitrary functions of time. We assume that the matter field follows the barotropic equation of state given by,

$$\begin{aligned} p=k\rho \end{aligned}$$
(3.2)

where k is a constant. Using the Eqs. (2.15), (2.16), (2.17), (3.1) and (3.2) we get the following differential equation for the graviton mass m,

$$\begin{aligned}&\left[ \frac{\mathcal {G}(E)}{2kr\mathcal {F}(E)}\right] m''+\left[ \frac{\mathcal {G}(E)}{2k\mathcal {F}(E)r}\frac{\phi '}{\phi }+\frac{\mathcal {G}(E)}{\mathcal {F}(E)r^{2}}\right] m'\nonumber \\&\quad +\left[ \frac{\left( k+1\right) \omega \mathcal {G}(E)}{2k\mathcal {F}(E)r}\left( \frac{\phi '}{\phi }\right) ^{2}+\frac{\mathcal {G}(E)\left( k-2\right) }{2k\mathcal {F}(E)r^{2}}\frac{\phi '}{\phi }\right. \nonumber \\&\quad \left. +\frac{\mathcal {G}(E)\left( k+1\right) }{kr\mathcal {F}(E)}\frac{\phi ''}{\phi }\right] m+ \left[ \left( \frac{\omega }{\phi }-\frac{1}{k}\right) \frac{\dot{\phi }'}{\phi }\right. \nonumber \\&\quad \left. - \frac{\mathcal {G}(E)}{\mathcal {F}(E)}\frac{\left( k+1\right) }{k}\frac{\phi ''}{\phi }- \frac{\omega \left( k+1\right) \mathcal {G}(E)}{2\mathcal {F}(E)k}\left( \frac{\phi '}{\phi }\right) ^{2}\right. \nonumber \\&\quad \left. +\frac{\mathcal {G}(E)\left( 1-k\right) }{2k\mathcal {F}(E)r}\frac{\phi '}{\phi }+\left( \frac{1-k}{2kr}\right) \frac{\dot{\phi }}{\phi }+\frac{2-k\phi }{2k\mathcal {F}(E)\mathcal {G}(E)}\frac{V(\phi )}{\phi ^{2}}\right] =0\nonumber \\ \end{aligned}$$
(3.3)

Unfortunately due to high complexity, a general solution for the above differential equation cannot be obtained by the known mathematical methods. So we seek solutions for special cases. We see that if we consider \(\phi (r,t)\) in a form where the variable r and t can be separated, we can put the equation in the Cauchy–Euler form from where we can get a solution. So to facilitate further computations we consider \(f_{1}(t)=0\) in Eq. (3.1). So the expression for \(\phi \) takes the form

$$\begin{aligned} \phi (r,t)=\left( r+r\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t) \end{aligned}$$
(3.4)

Obviously it must be admitted that this assumption produces a particular class of solution of the collapsing system and not the general solution. But this class of solution is of interest to us as far as the mathematical integrity of the problem is concerned. Now using Eq. (3.4) in Eq. (3.3) we get the following differential equation,

$$\begin{aligned}&r^{2}m''+\left[ \frac{1}{1+\omega }+2k\right] rm'+\left[ \frac{k-3\omega -2}{\left( 1+\omega \right) ^{2}}\right] m\nonumber \\&\quad = \left[ \frac{k-2\omega -1}{\left( 1+\omega \right) ^{2}}\right] r-\frac{2k\mathcal {F}(E)}{\mathcal {G}(E)}\frac{\dot{f_{2}(t)}}{f_{2}(t)}\nonumber \\&\qquad \times \left[ \frac{1}{1+\omega }\left\{ \frac{\omega }{\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)}-\frac{1}{k}\right\} +\frac{1-k}{2k}\right] r^{2}\nonumber \\&\qquad -\left[ \frac{2-k\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)V(\phi )}{\mathcal {G}^{2}(E)\left( 1+\omega \right) ^{\frac{2}{1+\omega }}\left( f_{2}(t)\right) ^{2}}\right] r^{3} \end{aligned}$$
(3.5)

We solve the above equation and get the following solution for m,

$$\begin{aligned} m(t,r)= & {} f_{3}(t)r^{\omega _{1}}+f_{4}(t)r^{\omega _{2}}\nonumber \\&+\frac{\left( k-2\omega -1\right) r}{\left( 1+\omega \right) ^{2} \left( 1-\omega _{1}\right) \left( 1-\omega _{2}\right) }\nonumber \\&-\frac{2k\mathcal {F}(E)}{\mathcal {G}(E)}\frac{\dot{f_{2}(t)}}{f_{2}(t)}\frac{r^{2}}{\left( 2-\omega _{1}\right) \left( 2-\omega _{2}\right) }\nonumber \\&\times \left\{ \frac{1}{1+\omega }\left( \frac{\omega }{\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)} -\frac{1}{k}\right) +\frac{1-k}{2k}\right\} \nonumber \\&-\frac{2-k\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)V(\phi )}{\mathcal {G}(E)^{2}\left( 1+\omega \right) ^{\frac{2}{1+\omega }}\left\{ f_{2}(t)\right\} ^{2}}\frac{r^{3}}{\left( 3-\omega _{1}\right) \left( 3-\omega _{2}\right) }\nonumber \\ \end{aligned}$$
(3.6)

where \(\omega _{1}\) and \(\omega _{2}\) are given by,

$$\begin{aligned} \omega _{1},\omega _{2}= & {} \frac{1}{2\left( 1+\omega \right) }\left[ \left\{ -2k+\left( 1-2k\right) \omega \right\} \right. \nonumber \\&\left. \pm \sqrt{\left\{ 2k+\omega \left( 2k-1\right) \right\} ^{2}-4\left( k-3\omega -2\right) }\right] \end{aligned}$$
(3.7)

From the above relation it is seen that the admissible range of the barotropic parameter k is given by

$$\begin{aligned}&k\in \left( -\infty ~, \frac{1+\omega +\omega ^{2}-\sqrt{-7-26\omega -30\omega ^{2}-12\omega ^{3}}}{2\left( 1+2\omega +\omega ^{2}\right) }\right] \nonumber \\&\quad \bigcup \left[ \frac{1+\omega +\omega ^{2}+\sqrt{-7-26\omega -30\omega ^{2}-12\omega ^{3}}}{2\left( 1+2\omega +\omega ^{2}\right) }, \infty \right) \nonumber \\ \end{aligned}$$
(3.8)

Using Eq. (3.6) in Eq. (2.2) we get the rainbow deformed Vaidya metric in BD gravity as follows,

$$\begin{aligned} ds^{2}= & {} -\frac{1}{\mathcal {F}^{2}(E)}\left( 1-f_{3}(t)r^{\omega _{1}-1}-f_{4}(t)r^{\omega _{2}-1}\right. \nonumber \\&-\frac{\left( k-2\omega -1\right) }{\left( 1+\omega \right) ^{2} \left( 1-\omega _{1}\right) \left( 1-\omega _{2}\right) }\nonumber \\&\left. +\frac{2k\mathcal {F}(E)}{\mathcal {G}(E)}\frac{\dot{f_{2}(t)}}{f_{2}(t)}\frac{r}{\left( 2-\omega _{1}\right) \left( 2-\omega _{2}\right) }\right. \nonumber \\&\times \left\{ \frac{1}{1+\omega }\left( \frac{\omega }{\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)} -\frac{1}{k}\right) +\frac{1-k}{2k}\right\} \nonumber \\&\left. +\left\{ \frac{2-k\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)V(\phi )}{\mathcal {G}(E)^{2} \left( 1+\omega \right) ^{\frac{2}{1+\omega }}\left\{ f_{2}(t)\right\} ^{2}}\right\} \frac{r^{2}}{\left( 3-\omega _{1}\right) \left( 3-\omega _{2}\right) } \right) dt^2\nonumber \\&+\frac{2}{\mathcal {F}(E)\mathcal {G}(E)}dtdr+\frac{1}{\mathcal {G}^{2}(E)}r^2 d\Omega _{2}^2 \end{aligned}$$
(3.9)

4 Gravitational collapse

In this section, we use the concept of radial null geodesics to explore the existence of NS in generalized Vaidya space-time. We first need to check whether it is possible to have outgoing radial null geodesics that were terminated in the past at the central singularity \(r=0\). The type of the singularity (NS or BH) can be determined by the existence of radial null geodesics emerging from the singularity. The singularity is said to be locally naked if there exist such geodesics and is said to be BH if geodesics do not exist. The catastrophic gravitational collapse causes two possible types of singularities which could be NS or a BH. Although CCH states that, a gravitational collapse always results in a BH, yet there is no rigorous proof for that. We have already seen that inhomogeneous dust cloud may result in a NS through a collapse [64]. Fluids with different equations of state other than dust also give rise to considerable results [65]. So the validity of the hypothesis is quite questionable. At least keeping the above literature in view the censorship hypothesis needs to get generalized [66].

We assume that R(t,  r) is the physical radius at time t of the shell labelled by r. At the starting epoch \(t=0\) we should have \(R(0,~r)=r\). In the inhomogeneous case, different shells could become singular at different times. Now if there are future directed radial null geodesics emanating out of the singularity, with a well defined tangent at the singularity \(\frac{dR}{dr}\) must tend to a finite limit in the limit of approach to the singularity in the past along these trajectories. When reaching the points \((t_0, ~r)=(t_{0}, ~0)\), the singularity \(R(t_0,0)=0\) occurs which corresponds to the physical situation where matter shells are crushed to zero radius. This type of singularity (\(r=0\)) is called a central singularity. The singularity is a NS if there exists future directed non-space like curves in the space time with their past end points rooted in the singularity. Now if the outgoing null geodesics are traced back so as they terminate in the past at the central singularity (\(r=0\) at \(t=t_0\)) where \(R(t_0, 0)=0\), then along these geodesics we should have \(R\rightarrow 0\) as \(r\rightarrow 0\) [67].

The equation for outgoing radial null geodesics can be obtained from Eq. (2.2) by putting \(ds^{2}=0\) and \(d\Omega _{2}^{2}=0\) as

$$\begin{aligned} \frac{dt}{dr}=\frac{2\mathcal {F}(E)}{\mathcal {G}(E)\left( 1-\frac{m(t,r)}{r}\right) }. \end{aligned}$$
(4.1)

From the above expression it is quite clear that at \(r=0,~t=0\) there is a singularity of the above differential equation. Suppose we consider a parameter \(X=\frac{t}{r}\). Using this parameter we can study the limiting behavior of the function X as we approach the singularity at \(r=0,~t=0\) along the radial null geodesic. If we denote the limiting value by \(X_{0}\) then using L’Hospital’s rule we have

$$\begin{aligned} \begin{array}{c} X_{0}\\ \\ {} \end{array} \begin{array}{c} =lim~~ X \\ t\rightarrow 0\\ r\rightarrow 0 \end{array} \begin{array}{c} =lim~~ \frac{t}{r} \\ t\rightarrow 0\\ r\rightarrow 0 \end{array} \begin{array}{c} =lim~~ \frac{dt}{dr} \\ t\rightarrow 0\\ r\rightarrow 0 \end{array} \begin{array}{c} =lim~~ \frac{2\mathcal {F}(E)}{\mathcal {G}(E)\left( 1-\frac{m(t,r)}{r}\right) } \\ t\rightarrow 0\quad \\ r\rightarrow 0\quad {} \end{array} \end{aligned}$$
(4.2)

Using Eqs. (3.6) and (4.2), we have

$$\begin{aligned} \frac{2}{X_{0}}&= \begin{array}{l} \lim \\ t\rightarrow 0\\ r\rightarrow 0 \end{array} \frac{\mathcal {G}(E)}{\mathcal {F}(E)}\left[ 1-f_{3}(t)r^{\omega _{1}-1}-f_{4}(t)r^{\omega _{2}-1}\right. \nonumber \\&-\frac{\left( k-2\omega -1\right) }{\left( 1+\omega \right) ^{2}\left( 1-\omega _{1}\right) \left( 1-\omega _{2}\right) }\nonumber \\&\left. +\frac{2k\mathcal {F}(E)}{\mathcal {G}(E)}\frac{r}{\left( 2-\omega _{1}\right) \left( 2-\omega _{2}\right) }\right. \nonumber \\&\left. \times \frac{\dot{f_{2}(t)}}{f_{2}(t)}\left\{ \frac{1}{1+\omega }\left( \frac{\omega }{\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)} -\frac{1}{k}\right) +\frac{1-k}{2k}\right\} \right. \nonumber \\&\left. +\left\{ \frac{2-k\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)V(\phi )}{\mathcal {G}(E)^{2} \left( 1+\omega \right) ^{\frac{2}{1+\omega }}\left\{ f_{2}(t)\right\} ^{2}}\right\} \frac{r^{2}}{\left( 3-\omega _{1}\right) \left( 3-\omega _{2}\right) }\right] \nonumber \\ \end{aligned}$$
(4.3)

Here we will take the potential \(V(\phi )\) in the power law form, i.e., \(V(\phi )=V_{0}\phi ^{n}\), n and \(V_{0}\) being a real number. Now choosing \(f_{2}(t)=\gamma t\),  \(f_{3}(t)=\alpha t^{1-\omega _{1}}\),  \(f_{4}(t)=\beta t^{1-\omega _{2}}\)  and  \(n=-1\) we obtain an algebraic equation for \(X_{0}\) as

$$\begin{aligned}&\alpha X_{0}^{3-\omega _{1}}+\beta X_{0}^{3-\omega _{2}}+\frac{\left( k-2\omega -1\right) }{\left( 1+\omega \right) ^{2}\left( 1-\omega _{1}\right) \left( 1-\omega _{2}\right) }X_{0}^{2}\nonumber \\&\quad +\left[ \frac{\mathcal {F}(E)}{\mathcal {G}(E)} \left\{ 2-\frac{\omega -k\left( 1+\omega \right) -1}{\mathcal {G}(E)\left( 2-\omega _{1}\right) \left( 2-\omega _{2}\right) \left( 1+\omega \right) }\right\} -1\right] X_{0}\nonumber \\&\quad -\frac{\left( 2-kV_{0}\right) }{\mathcal {G}^{2}(E)\left( 1+\omega \right) ^{\frac{2}{1+\omega }}\gamma ^{2} \left( 3-\omega _{1}\right) \left( 3-\omega _{2}\right) }=0 \end{aligned}$$
(4.4)

where \(\alpha \), \(\beta \) and \(\gamma \) are arbitrary constants. It must be mentioned over here that the choices of \(f_{2}(t)\), \(f_{3}(t)\) and \(f_{4}(t)\) are somewhat self-similar in nature. The choices have been made depending on the definition of \(X_{0}\) in Eq. (4.2) such that the ratio t / r can be formed. Non self similar assumptions can also be made, but that will result in either removal of terms or creation of mathematically undefined terms. As a result of this a lot of information about the system will be lost which is undesirable.

Fig. 1
figure 1

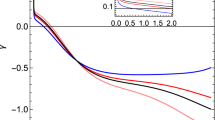
Show the variation of slope \(X_0\) of outgoing radial null geodesic at \(r = 0\) in Penrose diagram as a function of the equation of state parameter k for different values of \(\alpha \) and \(\beta \) respectively in Brans–Dicke gravity’s rainbow. In Fig. 1 the other parameters are fixed at \(\beta =0.2\), \(\gamma =5\), \(V_{0}=0.1\), \(\omega =-0.5\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\). In Fig. 2 the other parameters are taken as \(\alpha =0.1\), \(\gamma =5\), \(V_{0}=0.1\), \(\omega =-0.5\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\)

Full size image
Fig. 2
figure 2

Show the variation of slope \(X_0\) of outgoing radial null geodesic at \(r = 0\) in Penrose diagram as a function of the equation of state parameter k for different values of \(\gamma \) and \(V_{0}\) respectively in Brans–Dicke gravity’s rainbow. In Fig. 3 the other parameters are fixed at \(\alpha =0.1, \beta =0.2\), \(V_{0}=0.1\), \(\omega =-0.5\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\). In Fig. 4 the other parameters are taken as \(\alpha =0.1, \beta =0.2\), \(\gamma =5\), \(\omega =-0.5\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\)

Full size image

Now if we get only non-positive solution of the equation we can assure the formation of a BH. Getting a real positive root indicates a chance to get a NS. Since the obtained equation is a highly complicated one, it is extremely difficult to find out an analytic solution of \(X_{0}\) in terms of the variables involved. So our idea is to find out different numerical solutions of \(X_{0}\), by assigning particular numerical values to the associated parameters, i.e., \(\alpha \), \(\beta \), \(\gamma \), \(V_{0}\), k and \(\omega \).

4.1 Numerical analysis

Since there are many parameters to deal with, we have generated plots for the function \(X_{0}\) by varying a particular parameter and fixing others. This helps in understanding the dependencies effectively. Since the evolution of universe and its different phases are characterized by the value of the equation of state k, in Figs. 1, 2 and 3, we have obtained the profiles for the variable \(X_{0}\) with respect to the barotropic EoS parameter k. Motivated from Refs. [68, 69], we have used the following rainbow functions,

$$\begin{aligned} \mathcal {F}(E)=1, \quad \mathcal {G}(E)=\sqrt{1-\eta \left( \frac{E_{1}}{E_{p}}\right) } \end{aligned}$$
(4.5)

In the above expressions, \(E_{p}\) is the planck energy given by \(E_{p}=1/\sqrt{G}=1.221 \times 10^{19}\) GeV, where G is the gravitational constant and \(E_{1}=1.42 \times 10^{-13}\) [68, 69]. In Ref. [69], the value of \(\eta \) has been roughly computed as \(\eta \approx 1\), following which we have used \(\eta =1\) in our study.

From all the five plots we see that the trajectories for \(X_{0}\) appear in the positive level, thus ruling out the possibility of formation of BH as an end state of collapse. This is a counter-example of Cosmic censorship hypothesis. In Fig. 1, \(k-X_{0}\) plots have been obtained for different values of parameter \(\alpha \). We see that with the increase in the value of \(\alpha \), the trajectories push towards the k-axis, thus exhibiting a reduced tendency of formation of NS. We get a similar scenario when \(\beta \) and \(\gamma \) is varied in Figs. 1 and 2 respectively. In Fig. 2, \(k-X_{0}\) trajectories are obtained for different values of the field potential parameter \(V_{0}\). Here we see a reversed result. With the increase in the value of \(V_{0}\) the \(X_{0}\) profiles tend towards higher positive range, thus decreasing the tendency of BH formation. Finally in Fig. 3, we obtained plots for variable values of BD parameter \(\omega \). Here an increase in the value of the \(\omega \) parameter decreases the tendency of NS formation mimicking the first three cases. We know that in the limit \(\omega \rightarrow \infty \), GR is recovered from the BD gravity. So here we can see that in the limit when the theory tends towards GR, the tendency of formation of BH increase. This shows that there is a greater tendency of the cosmic censorship hypothesis to be true in case of GR. But as the gravity is modified, with greater deviations the hypothesis loses its significance and we get counter-examples as in the present work. As this is our prime motivation, we have worked with small values of \(\omega \) so that we can study the scenarios with greater deviations from GR.

4.2 Strength of singularity

The strength of singularity is defined as the measure of its destructive capacity. The prime concern is that whether extension of space-time is possible through the singularity or not under any situation. Following Tipler [70] a curvature singularity is said to be strong if any object hitting it is crushed to zero volume. In [70] the condition for a strong singularity is given by,

$$\begin{aligned} \begin{array}{c} S=lim~~ \tau ^{2}\psi \\ \tau \rightarrow 0\\ \end{array} \begin{array}{c} =lim~~ \tau ^{2}R_{\mu \nu }K^{\mu }K^{\nu }>0 \\ \tau \rightarrow 0\\ \end{array} \end{aligned}$$
(4.6)

where \(R_{\mu \nu }\) is the Ricci tensor, \(\psi \) is a scalar given by \(\psi =R_{\mu \nu }K^{\mu }K^{\nu }\), where \(K^{\mu }=\frac{dx^{\mu }}{d\tau }\) is the tangent to the non spacelike geodesics at the singularity and \(\tau \) is the affine parameter. In the paper [71] Mkenyeleye et al have shown that,

$$\begin{aligned} \begin{array}{c} S=lim~~ \tau ^{2}\psi \\ \tau \rightarrow 0\\ \end{array} \begin{array}{c} =\frac{1}{4}X_{0}^{2}\left( 2\dot{m_{0}}\right) \\ ~\\ \end{array} \end{aligned}$$
(4.7)

where

$$\begin{aligned} \begin{array}{c} m_{0}=lim~~ m(t,r) \\ t\rightarrow 0\\ r\rightarrow 0 \end{array} \end{aligned}$$
(4.8)

and

$$\begin{aligned} \begin{array}{c} \dot{m_{0}}=lim~~ \frac{\partial }{\partial ~t}\left( m(t,r)\right) \\ t\rightarrow 0\\ r\rightarrow 0 \end{array} \end{aligned}$$
(4.9)

Using Eq. (3.6) in the above relation (4.7) we get

$$\begin{aligned}&\begin{array}{c} S=lim~~ \tau ^{2}\psi \\ \tau \rightarrow 0\\ \end{array}\nonumber \\&\quad =\frac{1}{2}X_{0}^{2}\bigg [\alpha \left( 1-\omega _{1}\right) X_{0}^{-\omega _{1}}+\beta \left( 1-\omega _{2}\right) X_{0}^{-\omega _{2}}\nonumber \\&\qquad +\frac{2k\mathcal {F}(E)}{\mathcal {G}(E)\left( 2-\omega _{1}\right) \left( 2-\omega _{2}\right) }\left\{ \frac{2\omega }{\gamma \left( 1+\omega \right) ^{\frac{2+\omega }{1+\omega }}}\right. \nonumber \\&\qquad \left. +\frac{1-k}{2k}-\frac{1}{k\left( 1+\omega \right) }\bigg \}\frac{1}{X_{0}^{2}}\right] \end{aligned}$$
(4.10)

In the paper [71] it has also been shown that the relation between \(X_{0}\) and the limiting values of mass is given by,

$$\begin{aligned} X_{0}=\frac{2}{1-2m_{0}'-2\dot{m_{0}}X_{0}} \end{aligned}$$
(4.11)

where

$$\begin{aligned} \begin{array}{c} m_{0}'=lim~~ \frac{\partial }{\partial ~r}\left( m(t,r)\right) \\ t\rightarrow 0\\ r\rightarrow 0 \end{array} \end{aligned}$$
(4.12)

and \(\dot{m_{0}}\) is given by the Eq. (4.9). Using Eqs. (3.6), (4.9) and (4.12) in Eq. (4.11) we get an equation for \(X_{0}\) which can be solved to check the existence of positive roots. The existence of such a positive root signifies that the singularity is naked. Using these positive values of \(X_{0}\) in the Eq. (4.10) we get the conditions for which \(S=lim~~ \tau ^{2}\psi >0\), which gives the conditions under which we get a strong naked singularity.

5 Thermodynamics

In this section, we would like to focus on the thermodynamical aspects of Vaidya spacetime in BD gravity’s rainbow. To investigate the effect of such a spacetime on the thermalization process, here we consider the the thermalization temperature by the following relation [72],

$$\begin{aligned} T=\frac{1}{4\pi }\frac{d}{dr}f(t,r)|_{r=r_{h}}, \end{aligned}$$
(5.1)

where \(r_{h}\) is the event horizon obtained from the relation \(f(t,r)=0\), i.e,

$$\begin{aligned}&-\frac{1}{\mathcal {F}^{2}(E)}\Bigg (1-f_{3}(t)r^{\omega _{1}-1}-f_{4}(t)r^{\omega _{2}-1}\nonumber \\&\quad -\frac{\left( k-2\omega -1\right) }{\left( 1+\omega \right) ^{2} \left( 1-\omega _{1}\right) \left( 1-\omega _{2}\right) }\nonumber \\&\quad \left. +\frac{2k\mathcal {F}(E)}{\mathcal {G}(E)}\frac{\dot{f_{2}(t)}}{f_{2}(t)}\frac{r}{\left( 2-\omega _{1}\right) \left( 2-\omega _{2}\right) }\right. \nonumber \\&\quad \times \left\{ \frac{1}{1+\omega }\left( \frac{\omega }{\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)} -\frac{1}{k}\right) +\frac{1-k}{2k}\right\} \nonumber \\&\quad \left. +\left\{ \frac{2-k\left( 1+\omega \right) ^{\frac{1}{1+\omega }}f_{2}(t)V(\phi )}{\mathcal {G}(E)^{2} \left( 1+\omega \right) ^{\frac{2}{1+\omega }}\left\{ f_{2}(t)\right\} ^{2}}\right\} \frac{r^{2}}{\left( 3-\omega _{1}\right) \left( 3-\omega _{2}\right) } \right) =0.\nonumber \\ \end{aligned}$$
(5.2)

The real positive root of the above equation describes the radius of the event horizon. Figure 4 presents the typical behavior of f(t, r) in terms of r for different values of the parameter k. Here we have used the values of the other parameters such as \(E_{1}, E_{P}, n, F, V_{0}, f_{2}(t), f_{3}(t), f_{4}(t)\) as described in Sect. 4. Figure 4a shows the horizon structure of the Vaidya spacetime in BD gravity’s rainbow and in Fig. 4b we have shown the zoomed range of outer horizon obtained from Fig. 4a.These two figures yield \(r_{h}\approx 1\) for the selected value of the parameters. In [73] a time dependent geometry in massive theory of gravity has been analyzed and thermodynamical aspect of such geometry has been studied.

Thermalization temperature given by Eq. (5.1), due to the Vaidya spacetime in BD gravity’s rainbow, takes the form

$$\begin{aligned} T= & {} \frac{1}{4\pi \mathcal {F}(E)}\Bigg [r^{-2+\omega _{1}}f_{3}(t)(\omega _{1}-1)\nonumber \\&+\frac{1}{\mathcal {G}(E)f_{2}(t)^{2}}\Bigg (-2(1+\omega )^{\frac{-2}{(1+\omega )}}\Bigg ( \frac{2r}{(\omega _{1}-3)(\omega _{2}-3)}\nonumber \\&\left. +\frac{k\dot{f_{2}(t)}\omega (1+\omega )^{-1+\frac{1}{1+\omega }}}{(\omega _{1}-2)(\omega _{2}-2)}\right) \nonumber \\&+f_{2}(t)\left( \frac{k(2+n+2\omega )V_{0}r^{n+1}f_{2}(t)^{n}(1+\omega )^{\frac{n-2-\omega }{1+\omega }}}{(\omega _{1}-3)(\omega _{2}-3)}\right. \nonumber \\&\left. +\frac{\dot{f_{2}(t)}(1+k+(k-1)\omega )}{(1+\omega )(\omega _{1}-2)(\omega _{2}-2)}\right) +f_{4}(t)(\omega _{2}-1)r^{-2+\omega _{2}}\Bigg )\Bigg ].\nonumber \\ \end{aligned}$$
(5.3)
Fig. 3
figure 3

Show the variation of Slope \(X_0\) of outgoing radial null geodesic at \(r = 0\) in Penrose diagram as a function of the equation of state parameter k for different values of the Brans–Dicke parameter \(\omega \) in Brans–Dicke gravity’s rainbow. In figure, the other parameters are fixed at \(\alpha =0.1, \beta =5\), \(\gamma =1\), \(V_{0}=0.1\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\)

Full size image
Fig. 4
figure 4

Show the variation of the metric function f(t, r) against r for different values of the equation of state parameter k in Brans–Dicke gravity’s rainbow. In a the other parameters are fixed at \(\alpha =0.1, \beta =0.2\), \(t=2\), \(n=-1\), \(\omega =-0.5\) \(\gamma =5\), \(V_{0}=0.1\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\). b Represents the zoomed range of the outer horizon obtained in a

Full size image
Fig. 5
figure 5

a–d Show the variation of the thermalization temperature T, Total energy U, Helmholtz free energy \(F_{1}\) and specific heat in constant volume C against r respectively for different values of equation of state parameter k in Brans–Dicke gravity’s rainbow. The other parameters are fixed at \(\alpha =0.1, \beta =0.2\), \(t=2\), \(n=-1\), \(\omega =-0.5\) \(\gamma =5\), \(V_{0}=0.1\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\)

Full size image
Fig. 6
figure 6

a–d Show the variation of the thermalization temperature T, Helmholtz free energy \(F_{1}\), total energy U and specific heat in constant volume C against the Brans–Dicke parameter \(\omega \) respectively for different values of the equation of state parameter k in Brans–Dicke gravity’s rainbow. The other parameters are fixed at \(r_{h}\approx 1\), \(\alpha =0.1, \beta =0.2\), \(t=10^{-1}\), \(n=-1\), \(\gamma =5\), \(V_{0}=0.1\), \(\eta =1\), \(E_{1}=1.42 \times 10^{-13}\), \(E_{p}=1.221 \times 10^{19}\)

Full size image

Setting the BD parameter \(\omega =-0.5\) and all the other parameters as chosen earlier, we have plotted the thermalization temperature T against r for four different value of k. It is observed that for \(k=-1/3\), \(k=1/3\) and \(k=2\) at first the temperature is increasing function of r. The maximum temperature will occur in the region \((r_{h}-0.5,r_{h}+0.5)\) (\(r_{h}\approx 1\)) and the temperature is decreasing for the radius \(r>r_{h}\). For \(k=-3\), the temperature is increasing function of r. In Fig. 6a, T is plotted against the BD parameter \(\omega \) for \(r_{h}\approx 1\). It is observed that for the case of \(\omega <0\), T increases as \(\omega \) increases and for \(\omega >0\), T decreases as \(\omega \) increases. The entropy is given by

$$\begin{aligned} S=\pi ^{2} r_{h}^{2}, \end{aligned}$$
(5.4)

where we take \(\pi G=1\). Consequently the total energy can be obtained from the relation

$$\begin{aligned} U=\int T dS. \end{aligned}$$
(5.5)

Using Eqs. (5.3) and (5.4), Eq. (5.5) yields the expression of total energy as follows

$$\begin{aligned} U= & {} \frac{\pi }{12\mathcal {F}(E)}\Bigg [\frac{6r^{\omega _{1}}(\omega _{1}-1)}{\omega _{1}}-\frac{r^{3}(1+\omega )^{-\frac{1}{1+\omega }}}{\mathcal {G}}(E)f_{2}(t)^{2}\nonumber \\&(\omega _{1}-3)(\omega _{2}-3)\Bigg (-\frac{6kV_{0}f_{2}(t)^{n+1}(2+n+2\omega )r^{n}(1+\omega )^{\frac{n}{1+\omega }}}{(3+n+3\omega )}\nonumber \\&-\frac{3(\omega _{1}-3)(\omega _{2}-3)(-2k\omega +(1+\omega )^{\frac{1}{1+\omega }}(1+k-(1-k)\omega f_{2}(t)))}{r(1+\omega )(\omega _{1}-2)(\omega _{2}-2)}\nonumber \\&\dot{f_{2}(t)}+8(1+\omega )^{-\frac{1}{1+\omega }}\Bigg )+\frac{6f_{4}(t)(\omega _{2}-1)r^{\omega _{2}}}{\omega _{2}}\Bigg ]. \end{aligned}$$
(5.6)

Figures 5b and 6b display the typical behavior of U against r and \(\omega \) respectively for four different values of k. Here we find that for \(\omega >0\), the internal energy decreases as \(\omega \) increases.

Another important thermodynamical quantity is the Helmholtz free energy, which reads

$$\begin{aligned} F_{1}=U-TS. \end{aligned}$$
(5.7)

Exploiting Eqs. (5.3), (5.4) and (5.6), Eq. (5.7) yields

$$\begin{aligned} F_{1}= & {} \frac{\pi }{12\mathcal {F}(E)}\Bigg [-\frac{3}{\omega _{2}}(\omega _{2}-1)(\omega _{2}-2)r^{\omega _{2}}f_{4}(t)\nonumber \\&-\frac{1}{\mathcal {G}(E)(\omega _{1}-3)(\omega _{2}-3)}\Bigg (-\frac{4}{f_{2}(t)^{2}}r^{3}(1+\omega )^\frac{-2}{1+\omega }\nonumber \\&+3kV_{0}f_{2}(t)^{n-1}r^{n+3}(1+\omega )^{-1+\frac{(n-1)}{1+\omega }}\frac{(1+n+\omega )(2+n+2\omega )}{(3+n+3\omega )}\Bigg )\nonumber \\&-3r^{\omega _{1}}f_{3}(t) (\omega _{1}-2)\Bigg (1-\frac{1}{\omega _{1}}\Bigg )\Bigg ]. \end{aligned}$$
(5.8)

Figures 5c and 6c represent the typical behavior of \(F_{1}\) in terms of r and BD parameter \(\omega \) respectively considering different era of the evolution of the universe. Finally we have considered the specific heat in constant volume

$$\begin{aligned} C=\left( \frac{dU}{dT}\right) _{V}. \end{aligned}$$
(5.9)

The above expression yields

$$\begin{aligned} C= & {} 2\pi ^{2}(1+\omega )^{2}f_{2}(t)^{2}(\omega _{1}-3)(\omega _{2}-3)\nonumber \\&\mathcal {G}(E)\Bigg [r^{\omega _{1}-1}f_{3}(t)(\omega _{1}-1)+r^{\omega _{2}-1}f_{4}(t)(\omega _{2}-1)\nonumber \\&-\frac{r}{\mathcal {G}(E)f_{2}(t)^{2}}\Big (2(1+\omega )^\frac{-2}{1+\omega } \Bigg (\frac{3r}{(\omega _{1}-3)(\omega _{2}-3)}\nonumber \\&+\frac{k\omega \dot{f_{2}}(t)(1+\omega )^{-1+\frac{1}{1+\omega }}}{(\omega _{1}-2)(\omega _{2}-2)}\Bigg )\nonumber \\&-f_{2}(t)\Bigg (\frac{(1+k+(k-1)\omega )\dot{f_{2}}(t)}{(1+\omega )(\omega _{1}-2)(\omega _{2}-2)}\nonumber \\&+\frac{k V_{0}r^{n+1}(2(1+\omega )+n)(1+\omega )^{-1+\frac{n-1}{1+\omega }}}{(\omega _{1}-3)(\omega _{2}-3)}\Bigg )\Bigg )\Bigg ]\nonumber \\&\Bigg [k V_{0}(1+\omega +n)(2(1+\omega )+n)f_{2}(t)^{n+1}r^{n}(1+\omega )^{\frac{n-1}{1+\omega }}\nonumber \\&-4(1+\omega )^{\frac{2\omega }{1+\omega }}+\mathcal {G}(E)f_{2}(t)^{2}(\omega _{1}-3)(\omega _{2}-3)(1+\omega )^{2}\nonumber \\&\left( f_{3}(t)(\omega _{1}-2)(\omega _{1}-1) r^{\omega _{1}-3}\right. \nonumber \\&\left. +f_{4}(t)(\omega _{2}-2)(\omega _{2}-1)r^{\omega _{2}-3}\right) \Bigg ]^{-1} \end{aligned}$$
(5.10)

In Figs. 5d and 6d, we can observe the variation of specific heat against the radius r and BD parameter \(\omega \) respectively. It is observed that the specific heat is taking positive and negative values like any other thermodynamical system. These thermal fluctuations lead to some instability in the system with possible phase transition. Such instabilities get corrected due to the presence of thermal fluctuations. A lot of studies have been done in this direction [74,75,76,77,78,79]. Also from Fig. 6d we can conclude that specific heat is an increasing function of the BD parameter \(\omega \) in the region \(\omega >0\) for almost all chosen values of k .

6 Conclusions and discussions

In this note we have studied an energy dependent modification of a time dependent geometry in the background of Brans–Dicke gravity theory. The time dependent Vaidya metric representing a realistic star was modified by rainbow functions in Brans–Dicke gravity. The necessary field equations were formed and a solution was found. We studied a gravitational collapse phenomenon under such conditions to characterize the system. The concept of the existence of outgoing radial null geodesics was used to explore the nature of the gravitational singularity formed due to the collapse. The existence of such outgoing geodesics from the central singularity confirms the singularity to be a naked one. The absence of such geodesics would indicate that the singularity is a black hole. In our analysis we have considered the effects of both the graviton mass as well as the rainbow deformations for the given time dependent system. We have performed numerical simulations and checked the nature of singularity by setting different initial conditions. In all such cases we performed our analysis in the late universe \((k<-1/3)\), i.e. a universe driven by dark energy. In our study we have seen that under various scenarios the singularity formed is a naked one. This is a significant counter-example of the cosmic censorship hypothesis. We have also checked the strength of singularity and obtained the conditions under which the singularity can be called a strong singularity.

Lastly we have studied the thermodynamical behavior of this system considering some important thermodynamical quantities. It is observed that BD parameter \(\omega \) affect those thermodynamic quantities. For the case of \(\omega <0\), thermalization temperature T increases as \(\omega \) increases and for \(\omega >0\), T decreases as \(\omega \) increases. The internal energy and specific heat have also been studied and it is found that for \(\omega >0\), the internal energy decreases as \(\omega \) increases. For some special values of k we have seen some instability with possible phase transition.