Abstract
We obtain classical string solutions on \(\mathbb {R}^t \times \hbox {S}^2\) by applying the dressing method on string solutions with elliptic Pohlmeyer counterparts. This is realized through the use of the simplest possible dressing factor, which possesses just a pair of poles lying on the unit circle. The latter is equivalent to the action of a single Bäcklund transformation on the corresponding sine-Gordon solutions. The obtained dressed elliptic strings present an interesting bifurcation of their qualitative characteristics at a specific value of a modulus of the seed solutions. Finally, an interesting generic feature of the dressed strings, which originates from the form of the simplest dressing factor and not from the specific seed solution, is the fact that they can be considered as drawn by an epicycle of constant radius whose center is running on the seed solution. The radius of the epicycle is directly related to the location of the poles of the dressing factor.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The holographic duality AdS/CFT [1,2,3] constitutes a broad framework, which connects gravitational theories in spaces with AdS asymptotics to conformal field theories defined on their respective boundary. As a weak/strong duality, it links the strongly (weakly) coupled regime of any one of the two theories to the weakly (strongly) coupled regime of its dual counterpart. The holographic duality has found many applications on both sides of it, such as in the study of strongly coupled CFTs (hydrodynamics, condensed matter systems and so on), and in the study of strongly coupled gravitational dynamics.
Classical string solutions have shed light to many aspects of the holographic duality. Such solutions correspond to the planar limit, where the rank of the gauge group of the boundary theory is infinite keeping the t’Hooft coupling finite but large enough in order to neglect the backreaction of the string to the background geometry. Thus, they probe non-perturbative effects of a large N boundary CFT. A wide class of such solutions propagating on the sphere, on AdS space or on their tensor product has been found in the literature. Such solutions include the GKP string [4], the BMN particle [5], the giant magnons [6, 7], the single spikes [8] as well as a wider class of spiky string solutions [9,10,11,12,13], which includes the former as special limits [14]. (See also [15], for a review of the subject.)
The symmetric space non-linear sigma models (NLSMs) that describe strings propagating in the corresponding symmetric space, are well known to be reducible to integrable systems of the same family as the sine-Gordon equation and multi-component generalizations of the latter [16,17,18,19]. This procedure, the so called Pohlmeyer reduction [20, 21], is non-trivial, since the transformation connecting the original NLSM fields to the field variables of the reduced theory is non-local. Despite this fact, it has been shown that the reduced system can also be derived from a local Lagrangian being a gauged WZW model with an integrable potential [22,23,24,25].
The integrable systems of the family of the sine-Gordon equation possess Bäcklund transformations, which connect solutions in pairs. Given a seed solution, these transformations generate a new non-trivial one. Iterative application of the Bäcklund transformations leads to infinite towers of solutions. The archetypical example is the sine-Gordon equation, where using the vacuum as seed solution, one can construct the one-kink solutions and then a whole class of multi-kink/breather solutions [26]. The analogue of this procedure in the NLSM is the so called “dressing method” [27, 28]. This method has been applied in the literature to produce string solutions on dS space [29], on the sphere [30, 31] and on AdS space [32, 33] that correspond to one- or multi-kink solutions of the Pohlmeyer reduced system.
Although the Pohlmeyer reduction is a straightforward procedure, in other words it is trivial to find the solution of the Pohlmeyer reduced system, given a solution of the NLSM, the inverse is highly non-trivial for two reasons: firstly due to the fact that Pohlmeyer reduction involves a non-local transformation and secondly due to the fact that Pohlmeyer reduction is a many-to-one mapping; there are many NLSM solutions with the same Pohlmeyer counterpart. For this reason, the accumulated knowledge about the integrable sine-Gordon systems is ineffective in the NLSM case. Nevertheless, recently, a method for the inversion of Pohlmeyer reduction was developed [34, 35], which can be applied in the case of elliptic solutions of the reduced system. This method implements a connection between solutions of the NLSM and the eigenfunctions of the \(n=1\) Lamé problem in order to construct the NLSM solutions with elliptic Pohlmeyer counterparts. In the case of strings propagating on \(\mathbb {R}^t\times \hbox {S}^2\) [14], it turns out that these are the spiky strings and their various limits.
In this work, we use classical elliptic string solutions as seed for the construction of higher genus string solutions on \(\mathbb {R}^t\times \hbox {S}^2\), via the dressing method. This is made possible due to the simple and universal description of the elliptic solutions achieved in our previous work [14] via the inversion of Pohlmeyer reduction. We carry out this study in both the NLSM and the Pohlmeyer reduced theory, namely the sine-Gordon equation, in order to understand the correspondence between the dressing method and the Bäcklund transformations of the latter more deeply.
Although more general higher genus solutions of both the NLSM and the sine-Gordon equation can be expressed in terms of Riemann’s hyperelliptic theta function [36,37,38], it is difficult to study their properties in this form. Unlike this approach, the solutions presented in this work are genus two solutions, which are expressed in terms of simple trigonometric and elliptic functions, and, thus, their properties can be studied analytically. This study is the first application of the dressing method on a non-trivial background, whose Pohlmeyer counterpart is neither the vacuum nor a kink solution, i.e. a solution connected to the vacuum via Bäcklund transformations [30, 31]. The development of this kind of solutions can also be very useful in systems whose Pohlmeyer reduced theory does not possess a vacuum solution; the cosh-Gordon equation is such an example [35].
The structure of the paper is as follows: In Sect. 2 we review the construction of the elliptic string solutions on \(\mathbb {R}^t\times \hbox {S}^2\) presented in [14], as well as their Pohlmeyer counterparts. In Sect. 3, we review the dressing method and in Sect. 4, we apply it to obtain the dressed elliptic string solutions. In Sect. 5, we study the relation between the dressing method and the Bäcklund transformations of the sine-Gordon equation and we obtain the Pohlmeyer counterparts of the dressed elliptic string solutions presented in Sect. 4. In Sect. 6 we discuss our results and possible future extensions. Finally, there is an appendix containing some interesting limits of the sine-Gordon solutions and some more technical details on the dressing method.
2 Review of elliptic string solutions on \(\mathbb {R}^t \times \hbox {S}^2\)
The non-linear sigma models describing strings propagating in symmetric spaces are reducible to integrable systems similar to the sine-Gordon equation, a procedure widely known as Pohlmeyer reduction. A typical example is that of strings propagating on \(\mathbb {R}^t \times \hbox {S}^2\) (\(\mathbb {R}^t\) stands for time), which are reducible to the sine-Gordon equation itself. An important ingredient of the Pohlmeyer reduction is the embedding of the symmetric target space in a higher dimensional flat space, in this case the four-dimensional Minkowski space. In this language, the string action is written as
where \(X \in \mathbb {R}^{(1,3)}\) and \(\xi _\pm \equiv ( \xi ^1 \pm \xi ^0 ) / 2\). The inner product of two four-vectors A and B with respect to the Minkowski metric, \(g = {\mathrm {diag}}\{ -1 ,1 ,1 ,1 \}\), is denoted as \(A \cdot B\), while \(\mathbf {X}\) stands for the three-vector composed by the three spatial components of X. The usual treatment of this system takes advantage of the \(X^0\) equation of motion, \(\partial _+\partial _- X^0 = 0\), to select a gauge (the static gauge), where the \(X^0\) coordinate is proportional to the time-like worldsheet coordinate, namely \(X^0 \sim \xi ^0\). However, for our purposes, it is more suitable to select a more general gauge, which we will call the linear gauge, where it holds that
Trivially, the linear and static gauges are connected via a boost in the worldsheet coordinates. In the linear gauge, one may perform Pohlmeyer reduction as usual, to show that the reduced system is the sine-Gordon equation
where \(\mu ^2 := - {m_+} {m_-} / {R^2}\) and the Pohlmeyer field \(\varphi \) is defined as
The sine-Gordon equation has solutions which can be expressed in terms of elliptic functions and depend solely on either the time-like or the space-like worldsheet coordinate [14]. These read
which implies
for translationally invariant solutions and
for the static ones. As Eqs. (2.6) and (2.7) indicate, these elliptic solutions are identified by the value of the integration constant E, which may take any real value \(E > -\mu ^2\). In analogy to the simple pendulum, the elliptic solutions have different qualitative behaviour depending on whether the integration constant is smaller or larger than \(\mu ^2\); we will call the former as “oscillatory” solutions or trains of kink and anti-kink pairs and the latter as “rotating” solutions or trains of kinks.
In general, there is no systematic method to invert the Pohlmeyer reduction, as it was explained in the introduction. However, in the specific case of the elliptic solutions of the sine-Gordon equation, a systematic method to build the corresponding NLSM solutions has been developed [14]. This method was initially applied in the case of strings propagating in \(\hbox {AdS}_3\) and \(\hbox {dS}_3\) [34] and subsequently for the construction of minimal surfaces in \(\hbox {H}^3\) [35]. Given the specific solutions of the Pohlmeyer reduced system, the NLSM equations of motion can be solved via separation of variables, leading to pairs of effective Schrödinger problems, each pair containing one flat potential and one \(n=1\) Lamé potential. Using properties of the latter, it is possible to find appropriate solutions of the equations of motion that additionally satisfy the geometric and Virasoro constraints, effectively inverting the Pohlmeyer reduction for the class of elliptic solutions of the reduced system. The corresponding string solutions read
where the index 0/1 denotes whether the Pohlmeyer counterpart of the solution is a translationally invariant or static solution of the sine-Gordon equation and the function \(\varPhi \) is defined as
The function \(\varPhi \) is quasi-periodic, obeying
The moduli of the Weierstrass elliptic function in the above expressions are given by
the parameters \(\ell \) and \(\wp \left( a \right) \) are given by
and \(x_1\) is one of the roots of the cubic polynomial associated with the Weierstrass elliptic function, namely \(x_1 = {E}/{3}\). The other two roots are \(x_{2/3} = - {E}/{6} \pm {m^2}/{2}\).
The parameter a is a free parameter of the construction and can be selected anywhere in the imaginary axis. All solutions that correspond to the same parameter E have the same Pohlmeyer counterpart, independently of the value of the parameter a and form a Bonnet family of worldsheets. The sign of a is connected to the sign of \(\ell \) via
The solutions (2.9) form four classes of solutions, determined by whether the Pohlmeyer counterpart is oscillatory or rotating as well as static or translationally invariant. They are the known spiky/helical strings [11] and they have many interesting limits, such as the the GKP strings (static, \(a=\omega _2\)) [4], the BMN particle (translationally invariant, \(E=-\mu ^2\)) [5], the giant magnons (static, \(E=\mu ^2\)) [6] or the single spike (translationally invariant, \(E=\mu ^2\)) [8], which can be easily studied in this formulation.
In general, the elliptic string solutions in spherical coordinates can be written in the form
where
The string solutions with static Pohlmeyer counterparts can be conceived as rigidly rotating string configurations. The ones with oscillatory counterparts are smooth, whereas the ones with rotating counterparts contain spikes, which move with the speed of light. Similarly, the string solutions with translationally invariant counterparts can be understood as wave propagating solutions and they are always spiky.
In order to form a closed string of finite size, the parameter a has to be selected, so that the string obeys appropriate periodic conditions. It turns out that the necessary condition is
where \(n_{0/1}\) is an integer when the solution has a rotating counterpart and an even integer when it has an oscillatory counterpart. More information is provided in [14].
3 Review of the dressing method
The theories emerging after the Pohlmeyer reduction of the non-linear sigma models describing the propagation of classical strings in symmetric spaces possess Bäcklund transformations, which connect pairs of solutions. These transformations are a manifestation of the model’s integrability. The dressing method [21, 27,28,29, 39,40,41] is the direct analogue of the Bäcklund transformations in the NLSM. In the literature, it has been used in order to generate non-trivial solutions [29,30,31,32,33], whose seed solution corresponds to the vacuum of the reduced theory. In this section, we review a few elements of the theory of NLSMs on symmetric spaces, the dressing method in general, and the case of spheres \(\hbox {S}^n\) in particular. This is by no means a complete review of the subject. It is rather a quick introduction to some concepts used in this paper. In the next section, we apply the dressing method on an elliptic seed string solution on \(\hbox {S}^2\) in order to generate new non-trivial string solutions. In the following, without loss of generality, we take the radius of the target space sphere equal to one.
3.1 The non-linear sigma model
The action of the non linear sigma model is
where f takes values in the Lie group F and it is a function of the worldsheet coordinates \(\xi ^\pm \). Varying this action with respect to f yields the equation of motion
We introduce the currents \(J_\pm := \partial _\pm ff^{-1}\), which allow the expression of the equation of motion (3.2) as
By construction, the currents \(J_\pm \) obey the relation
Introducing a complex parameter \(\lambda \), the Eqs. (3.3) and (3.4) can be packed to one, namely,
In this form, Eqs. (3.3) and (3.4) can be recovered as the residues of (3.5) at \(\lambda = \pm 1\).
We introduce the following auxiliary system of first order differential equations
Equation (3.5) is just the compatibility condition for this system.
The NLSM action (3.1) is invariant under the transformations
Thus, it possesses a global \(F_L\times F_R\) symmetry. The associated left and right conserved currents are
respectively. Notice that the left current was already defined earlier, where we suppressed the superscript L for notational simplicity. In the following, we will continue to do so for the left currents and we will only write the superscript R for the right currents if necessary. The corresponding conserved charges are
3.2 The dressing method
Let \(F=\mathrm {SL}(n,\mathbb C)\) and suppose that we already know a solution f – the seed solution – of the equation of motion (3.5). The dressing transformation allows us to construct a new solution \(f'\) from the seed solution f. In principle, we can solve the auxiliary system (3.6) with the condition \(\varPsi (0)=f\) and find \(\varPsi (\lambda )\). The dressing transformation involves constructing a new solution \(\varPsi '(\lambda )\) of the auxiliary system (3.6) of the form
The \(n\times n\) matrix \(\chi (\lambda )\) is called the dressing factor. It can be shown [27] that the general form of \(\chi \) is
It turns out that at the level of the \(F=\mathrm {SL}(n,\mathbb C)\) NLSM, the poles can be selected at arbitrary positions on the complex plane and we are left with the problem of specifying the appropriate residues. There are two conditions that the residues must satisfy, which are adequate for their specification. The first one is the demand that \(\chi (\lambda )\chi (\lambda )^{-1} = I\). Taking the residues of this equation at the positions of the poles \(\lambda _i\) and \(\mu _i\) provides a set of algebraic equations for \(Q_i\) and \(R_i\). Notice that one has to be careful when a pole of \(\chi (\lambda )\) coincides with a pole of \(\chi (\lambda )^{-1}\), since in this case the product \(\chi (\lambda )\chi (\lambda )^{-1} \) will have a second order pole, which has to be considered separately.
The solution \(\varPsi ' ( \lambda )\) of the auxiliary system gives rise to a new solution \(f' = \varPsi ' ( 0 )\) of the NLSM. It follows that \(f'\) and \(\varPsi ' ( \lambda )\) must satisfy Eq. (3.6), namely,
Using (3.10) this reduces to
Taking the residues of the previous equations at the positions of the poles \(\lambda _i\) and \(\mu _j\), yields two more relations for the unknown matrices \(Q_i\) and \(R_i\), which are first order differential equations for the latter. These, combined with the set of algebraic equations derived from the residues of the equation \(\chi (\lambda )\chi (\lambda )^{-1} = I\), are sufficient for the specification of the residues \(Q_i\) and \(R_i\). More details are provided in appendix A and in [27].
We now turn to the effect of the dressing transformation on the sigma model charge. The latter gets altered by
We notice that the left hand side of (3.13) is independent of \(\lambda \). In the limit \(|\lambda |\rightarrow \infty \) (3.13) reduces to
Using (3.15) we arrive at the equation
which relates the charges of the seed and dressed solutions.
3.3 Involutions
As it has already been mentioned, the previous results refer to the \(\mathrm {SL}(n,\mathbb C)\) NLSM. For our purposes f must take values in some symmetric space F / G, where F, G are Lie groups and \(G\subset F\). This can be achieved by constraining appropriately the field f to take values in the coset F / G with the help of an involution. An involution is a bijective mapping \(\sigma : \,F\rightarrow F\) with the properties
and
where \(f_1,f_2\in F\). Furthermore, we demand that the involution \(\sigma \) obeys
On the Lie algebra side, the mapping \(\sigma \) is just a linear operator acting on the vector space \(\mathbf {f}\), having the property \(\sigma ^2=1\). Since \(\sigma ^2=1\), \(\sigma \) has eigenvalues \(\pm 1\) and thus the vector space \(\mathbf {f}\) can be decomposed as follows
where \(\mathbf {g}\) and \(\mathbf {p}\) are the \(+1\) and \(-1\) eigenspaces respectively. Trivially it holds that
where \(\mathbf {g}\) is by definition the Lie algebra corresponding to the subgroup G and \(\mathbf {p}\) is its orthogonal complement. Thus, the involution \(\sigma \) naturally splits the group F to the subgroup G and the coset F / G.
We consider now the following coset valued field
It can be easily shown that it is indeed invariant under the coset equivalence relation \(f\sim fg\). Acting on \(\mathscr {F}\) with \(\sigma \) gives the following relation
This is the constraint we need to impose on the fields f of the NLSM (3.1) in order to restrict them inside the coset F / G. In the following, we assume that the sigma model field is appropriately constrained into the coset F / G and we denote it again as f. The NLSM action with target space the coset F / G is not invariant under the full \(F_L\times F_R\) symmetry group, but only under transformations of the type
This implies that the conserved charges \(\mathscr {Q}_L,\mathscr {Q}_R\) are not independent anymore. They are related by
In general, when we want to study the NLSM with a symmetric target space F / G, we start with the model on the group \(\mathrm {SL}(n,\mathbb C)\). Using one or possibly more involutions denoted by \(\sigma _+\), we restrict to the subgroup \(F\subset \mathrm {SL}(n,\mathbb C)\) and then via another involution \(\sigma _-\) we further restrict the target space to be \(F/G\subset F\). In this work we are interested in the spheres \(S^n=\mathrm {SO}(n+1)/\mathrm {SO}(n)\). For this purpose, we need three involutions [28].
Firstly, we demand invariance (\(\sigma _+(f) = f\)), under the involution
Obviously, this involution restricts the target space to be \(\mathrm {SU}(n+1)\subset \mathrm {SL}(n+1,\mathbb C)\). The auxiliary system equations (3.6) and invariance of the group element f under this involution imply that \(\varPsi (\lambda )\) obeys
We require that the new solution \(f'\), found after the application of the dressing method, also belongs in \(\mathrm {SU}(n+1)\). This means that the condition (3.27) should be obeyed by \(\varPsi '(\lambda )\), which in turn implies that \(\chi (\lambda )= (\chi (\bar{\lambda })^\dagger )^{-1}\). Applying the above to the dressing factor, as given by Eq. (3.11), implies that the poles and the residues obey
simplifying the dressing factor \(\chi \). The simplest case to consider is a dressing factor with only one pole. In this case, if the initial solution f was the vacuum solution, the dressed one \(f'\) turns out to be the one soliton solution. By adding more poles to the dressing factor one would get the N-soliton solution in general.
The second involution needed is the following
Demanding that \(\sigma _-(f)=f^{-1}\), – see equation (3.23) – restricts the target space to be \(\mathrm {SU}(n+1)/\mathrm {U}(n)\). Then, the auxiliary system (3.6) implies that when f obeys \(\sigma _-(f)=f^{-1}\), \(\varPsi (\lambda )\) obeys
Applying the above on \(\varPsi '(\lambda )\), results in the following relation for the dressing factor: \(\chi (\lambda ^{-1})=f'\theta \chi (\lambda )\theta ^{-1}f^{-1}\). This in turn implies that poles in the dressing factor come in pairs \(\{\lambda , \lambda ^{-1}\}\). Thus, the simplest case to consider is that of a dressing factor with two poles \(\lambda _1\) and \(\lambda _2 = 1 / \lambda _1\). In this case, the corresponding residues must satisfy
Finally, we demand invariance of f under the involution
This is just the reality condition to be imposed on the solution, so that it belongs to the coset \(\mathrm {SO}(n+1)/\mathrm {SO}(n)\). The auxiliary system (3.6) implies that \(\varPsi ( \lambda )\) must obey
Demanding the above for \(\varPsi ' ( \lambda )\) leads to the fact that the poles in the dressing factor must come in pairs \(\{\lambda , \bar{\lambda }\}\). Had we imposed this involution to the \(\mathrm {SU}(N)\) model, we would have concluded that the simplest possible dressing factor would have two poles \(\lambda _1\) and \(\lambda _2 = \bar{\lambda }_1\) with the corresponding residues obeying
Notice that imposing the reality involution together with the unitarity involution adds an extra complexity to finding the appropriate dressing factor. The latter involution enforces the poles of \(\chi ( \lambda )\) to come in pairs of numbers being complex conjugate to each other. The former involution enforces the poles of \(\chi ( \lambda ) ^{-1}\) to be the complex conjugates of the poles of \(\chi ( \lambda )\). Thus, when studying \(\mathrm {SO}(N)\) models or coset subspaces of the latter, the dressing factor \(\chi ( \lambda )\) necessarily has poles that coincide with the poles of its inverse \(\chi ( \lambda ) ^{-1}\), complicating the specification of the residues \(Q_i\) as we discussed above. In the simplest case of two poles, it obviously holds that \(\mu _1 = \bar{\lambda }_1 = \lambda _2\) and \(\mu _2 = \bar{\lambda }_2 = \lambda _1\).
In the case of interest, we have to impose the constraints originating from the coset involution \(\sigma _-\) and the reality involution. This implies that naively, the dressing factor in the case of the \(\mathrm {SO}(n+1)/\mathrm {SO}(n)\) NLSM comes with quadruplets of poles \(\{\lambda _1, \lambda _2 = \bar{\lambda }, \lambda _3 = \lambda ^{-1}, \lambda _4 = \bar{\lambda }^{-1}\}\). The corresponding residues obey \(Q_2 = \bar{Q}_1\), \(Q_3 = - \lambda _2^2 f' \theta Q_1 \theta f\) and \(Q_4 = \bar{Q}_3\). However, the simplest possible dressing factor does not have four poles, but only two. When \(|\lambda _1| = 1\), it holds that \(\bar{\lambda }= \lambda ^{-1}\) and the quadruplet reduces to a doublet of poles. This is the case that we will consider from now on. In this case, the dressing factor assumes the form
where
and the vector p is any constant complex vector obeying \({p^T}p = 0\) and \(\bar{p} = \theta p\). More details are provided in the appendix A and in [27, 42].
3.4 The mapping from unit vectors to orthogonal matrices
We map any vector X on the unit sphere \(\hbox {S}^n\) to an element f of the \(\mathrm {SO}(n+1)/\mathrm {SO}(n)\) coset, via [28]
where \(X_0\) is a given constant vector with unit norm. This trivially transforms the NLSM action (3.1) to the string action (2.1). In the following, we denote
and in our \(\hbox {S}^2\) applications, we will select
unless otherwise specified. For any unit vector X, it is true that
implying that \({\theta ^2} = I\). Additionally, since in a trivial manner \( ( {I - 2X{X^T}} )^T = {I - 2X{X^T}} \), the Eq. (3.40) implies that \({f^T} = {f^{ - 1}}\), i.e. f is an orthogonal matrix. Furthermore, it holds that \(\det ( {I - 2X{X^T}} ) = - 1\), implying that \(\det f = 1\), and, thus, \(f \in \text {SO}(n+1)\). Finally, it is easy to show that the matrix f obeys \(\sigma _- ( f ) := \theta f \theta ^{-1} = f^{-1}\), which implies that f is an element of \(\text {SO}(n+1) / \text {SO}(n)\).
Let \(\alpha \) be the angle between the unit vectors \(X_0\) and X. Then, the special orthogonal matrix f represents a rotation in the plane defined by \(X_0\) and X by an angle equal to \(2\alpha \). The matrix f has one real eigenvector, namely \(\chi _0 = X_0 \times X\), with eigenvalue equal to one and two complex eigenvectors, \(\chi _\pm = - e^{\pm i \alpha } X_0 + X\), which are complex conjugate to each other and obey \(\chi _\pm ^T \chi _\pm = 0\), with eigenvalues equal to \(e^{\pm 2 i \alpha }\), respectively.
3.5 Pohlmeyer reduction and virasoro constraints
As it was described in [19] the sigma model on a symmetric space admits a Pohlmeyer reduction, which amounts to exploiting the conformal symmetry of the NLSM at the classical level in order to set the components of the energy momentum tensor to be constant, i.e.
It was shown in [25] that at algebraic level the Pohlmeyer reduction is equivalent to imposing the condition,
where \(\varLambda _\pm \) are constant elements in a maximal abelian subspace of \(\mathbf {p}\) and \(\xi _\pm \in F\). The degree of freedom left after the reduction is \(\gamma = \xi _-^{-1}\xi _+\). In order to see how this is equivalent to (3.41), we will use the parametrization (3.37) for the coset element f. The components of the energy momentum tensor of the NLSM are
From (3.8), (3.42) and (3.37), it follows that
If we make the identification \({\mathrm {Tr}}\varLambda _\pm ^2=-8m_\pm ^2\), Eq. (3.44) will become (3.41). This indicates the equivalence between (3.42) and (3.41). More details on this can be found in [25].
In order to see if the dressing transformation is compatible with Pohlmeyer reduction, we go back to (3.13), divide by \((1\pm \lambda )\) and find the residues at \(\lambda =\pm 1\). This gives the following relations
Using Eq. (3.42) yields
Therefore, if we set
Eq. (3.46) will take the form of the Pohlmeyer constraint (3.42). This shows that the dressing procedure respects the constraint (3.42) or equivalently (3.41). The element \(\varXi \) will be chosen so that the degree of freedom of the reduced system \(\tilde{\gamma }=\tilde{\xi }_-^{-1}\tilde{\xi }_+\) is an element of the subgroup G.
Interpreting \(X^i\) as the coordinates of a string moving on a sphere, it can be shown that the NLSM charge is related to the angular momentum of the string. Using (3.44) and (3.9) we find that
Therefore, the sigma model charge is proportional to the string angular momentum.
4 Dressed elliptic string solutions
In this section, we apply the dressing method that we reviewed in Sect. 3, to the elliptic string solutions of Sect. 2, using the simplest possible dressing factor, in order to construct new classical string solutions propagating on \(\mathbb {R}^t \times \hbox {S}^2\).
The non-trivial seed solution (2.9) of Sect. 2 renders the straightforward application of the dressing method very difficult. This is due to the corresponding auxiliary system, which is a complicated system of coupled partial differential equations with non-constant coefficients. In order to avoid these difficulties, we implement an intuitive detour, by expressing the seed solution as a worldsheet dependent rotation matrix, acting on a constant vector, which coincides with the rotation axis of the seed solution, i.e. the z-axis. Furthermore, the parametrization of the coset \(\mathrm {SO}(3)/\mathrm {SO}(2)\) is carried out, so that this constant vector corresponds to its identity element via the mapping (3.37). In this way, we manage to express one of the two PDEs of the auxiliary system in a form where one of the two worldsheet coordinates does not appear explicitly, making the solution of the system possible. Simultaneously, all components of the auxiliary field equations acquire a given parity under the inversion \(\lambda \rightarrow 1 / \lambda \), facilitating the application of the coset involution. Finally, the expression of the seed solution as a rotation matrix acting on a constant vector simplifies the translation of the dressed solution from the form of a coset element to a unit vector.
4.1 The auxiliary system for an elliptic seed solution
In order to implement the dressing method, we have to solve the auxiliary system (3.6). This reads
where f is a given seed solution of the NLSM and \(\varPsi ( \lambda )\) must obey the condition \(\varPsi \left( 0 \right) = f\). As seed solutions, we are going to use the \(\mathrm {SO}(3)/\mathrm {SO}(2)\) coset elements f corresponding to the elliptic string solutions (2.9) through the mapping (3.37). These solutions depend in a trivial manner on either the time-like or space-like worldsheet coordinate. It follows that it is technically advantageous to express the auxiliary system (4.1) as a system of differential equations with independent variables the time-like and space-like coordinates \(\xi ^0\) and \(\xi ^1\), instead of the left- and right-moving coordinates \(\xi ^\pm \). Following these lines, the auxiliary system assumes the form
where \(i=0,1\) and
It turns out to be convenient to express the initial solution X as an orthogonal matrix \(U ( \xi ^0 , \xi ^1 )\) acting on another unit vector \(\hat{X}\), as
It has to be noted that \(\hat{X}\) is not a solution of the NLSM. In terms of the vector \(\hat{X}\), the seed solution f reads
where
Obviously \(\hat{f} \in \text {SO}(3)\). It is also convenient to define \(\hat{\varPsi } ( \lambda )\) as
Then, the equations of the auxiliary system (4.2), expressed in terms of hatted quantities, assume the form
One can always select the orthogonal matrix U so that \(\hat{X} = {X_0}\). For this specific selection, \(\hat{f} = I\) and the equations of the auxiliary system get simplified to the form
Furthermore, the condition \(\varPsi \left( 0 \right) = f\) translates to the condition \(\hat{\varPsi } \left( 0 \right) = U^T\).
Without loss of generality, we perform the analysis in the case of seed solutions with static Pohlmeyer counterparts. The latter read
where
Notice that \(F_1\) and \(F_2\) obey \(F_1^2( {{\xi ^1}} ) + F_2^2( {{\xi ^1}} ) = 1\). Moreover, \(F_1\), \(F_2\) and \(\varphi \) satisfy
where
In terms of the functions \(F_1\), \(F_2\) and \(\varphi \), the Virasoro constraints are expressed as
Similarly, the equations of motion imply
Equation (4.11) implies that the seed elliptic string solution can be expressed as \(X = U{X_0}\), where
and the matrices \(U_1\) and \(U_2\) are given by
The equations of the auxiliary system require the calculation of the quantities
It is a matter of simple algebra to show that
where \(T_i\) are the \(\mathrm {SO}(3)\) generators, namely,
Adopting the notation
the Eqs. (4.28), (4.29) and (4.30) imply that
Notice that none of the coefficients \(k_i^j\) depends on the time-like coordinate \(\xi ^0\).
Similarly, we adopt the notation
Observing that
the equations of the auxiliary system (4.10) imply that
where \(\lambda = e^z\). The above imply that the coefficients \(\kappa _i^j\) obey the properties
or in a shorthand notation
where
It is a matter of algebra to show that \(\kappa _0^T{\kappa _0}\) equals
Using the Virasoro constraints (4.20) and (4.21), we can express \(\varDelta \) in terms of the quantities E and \(m_\pm \),
Thus, the quantity \(\varDelta \) is a constant. Moreover, it can be easily shown that \(\varDelta ( {1/\lambda } ) = \varDelta (\lambda )\). The quantity \(\varDelta \) could be considered as the generalization of the parameter \(\ell ^2\) of the elliptic seed solution after a “boost” in the worldsheet coordinates with complex rapidity z / 2.
4.2 The solution of the auxiliary system
Since all coefficients in the equations of the auxiliary system (4.36) are functions of \(\xi ^1\) only, we may proceed to solve those that involve the derivatives of \(\hat{\varPsi }\) with respect to \(\xi ^0\) as ordinary differential equations, upgrading the undetermined constants to undetermined functions of \(\xi ^1\). These equations are a set of three identical linear first order systems, one for each column of \(\hat{\varPsi }\), \(\hat{\varPsi }_i\), \(i=1,2,3\). This linear system has the solution
where
The vectors \(v_0\) and \(v_\pm \) have been selected so that \(v_0^T {v_0} = 1\), whereas \(v_\pm ^T{ v_\pm } = 0\). Furthermore, the vectors \(v_\pm \) obey the relations \(\left( \frac{ v_+ + v_-}{2} \right) ^T \left( \frac{ v_+ + v_-}{2} \right) = \left( \frac{ v_+ - v_-}{2i} \right) ^T \left( \frac{ v_+ - v_-}{2i} \right) = 1\).
Using the definitions (4.33)–(4.35), as well as the equations of motion (4.22)–(4.24), it is a matter of algebra to show that
Then, the definitions (4.38) and (4.39) imply that
or in a shorthand notation
The vectors \(v_0\) and \(v_\pm \) can be written in terms of \({{ \kappa }_0}\) as
The vectors
form a basis, which obeys \(e_i^T {e_j} = \delta _{ij}\) and \(e_i \times e_j = \varepsilon _{ijk}e_k\). Notice that as \(\lambda \rightarrow 0\),
and furthermore
Using the fact that \(\kappa _0^T {\kappa _0}\) is constant, one can show that
implying that
where
It is a matter of algebra to show that
where
and
The quantity \(\tilde{a}\) has the property \(\tilde{a} ( 1 / \lambda ) = \tilde{a} ( \lambda )\).
Substituting the above to the spatial derivative equation of the auxiliary system, we get
implying that
where the function \(\varPhi \) is the same quasi-periodic function that appears in the construction of the elliptic strings and it is defined in Eq. (2.10). Then,
or equivalently
where \({C_i^1} = {c_i^+}+{c_i^-}\), \({C_i^2} = i ({c_i^+} - {c_i^ -} )\) and \({C_i^3} = {c_i^0}\). The vectors \({E_j}\) are defined as
and they obey \(E_i^T {E_j} = \delta _{ij}\) and \(E_i \times {E_j} = - \varepsilon _{ijk}E_k\). Notice that as \(\lambda \rightarrow 0\),
and thus,
Therefore,
Additionally, the properties (4.60) imply
Finally, notice that the basis vectors \(E_i\) have the property
Defining the matrices E and C as the matrices comprised by the three columns being the vectors \(E_j\) and \(C_j\) respectively, the solution can be written in the form
Following the discussion of Sect. 3.3, the solution of the auxiliary system should obey the following constraints
In terms of the matrix \({\hat{\varPsi } }\), they are written as
The reality condition (4.88) implies that the matrix C obeys the constraint
The orthogonality condition (4.87) implies that the matrix C is also orthogonal
The coset condition (4.89) implies that
since the matrix E obeys \(E ( 1 / \lambda ) =\theta E ( \lambda ) \theta \), which is a direct consequence of equation (4.81).
Finally, the solution should satisfy the condition
Since the matrix E obeys
it follows that the coefficients matrix should obey
Thus, it is simple to satisfy all the conditions (4.90)–(4.92) and (4.95), selecting
implying that the solution of the auxiliary system that obeys all the appropriate involutions and the initial condition, is
4.3 The dressed solution in the case of two poles
As analysed in Sect. 3, the simplest possible dressing factor has two poles lying on the unit circle at positions complex conjugate to each other. In this case, the dressed solution is
where \(\chi \left( \lambda \right) \) is given by Eqs. (3.35) and (3.36). The constant vector p obeys \({p^T}p = 0\), \(\bar{p} = \theta p\) and thus, it may be parametrized in terms of two real numbers \(\rho \) and \(\omega \) as
We also define
In order to visualize and understand the behaviour of the dressed solution, we would like to find the unit vector \(X'\) that corresponds to the coset element \(f'\) through the mapping (3.37). For this purpose we define
Then
where
in a similar manner to the definitions we used to solve the auxiliary system. Then,
or
where
The vectors \(X_\pm \) obey the property \(X_\pm ^T (X_\pm ) = 0\), they are complex conjugate to each other and they are eigenvectors of \(\hat{f} '\) since
We recall that in Sect. 3.4 it was shown that the orthogonal matrix \(f = ( I - 2{X_0}X_0^T ) ( {I - 2X{X^T}} )\) has three eigenvectors, the vector \(\chi _0 = X_0 \times X\) with eigenvalue equal to one, and the vectors \(\chi _\pm = { - {e^{\pm i\theta _1 }}{X_0} + X} \) with eigenvalues \(e^{\pm 2 i a}\), where a is the angle between \(X_0\) and X. It follows that the vectors \(X_\pm \) are proportional to the eigenvectors \(\hat{\chi }_\pm ' = { - {e^{\pm i\theta _1 }}{X_0} + \hat{X} '} \). Furthermore, the vector \(\hat{X} '\) forms an angle \(\theta _1\) with \(X_0\). The proportionality constant can be fixed so that their inner product matches that of \(\hat{\chi }_\pm ' \), which equals \(2 \sin ^2 \theta _1\). Thus,
and finally,
Thus, the dressed string solution is
where \(\hat{X} '\) is given by (4.109).
It is easy to show that the vector \(X_1\) is a unit vector, which is perpendicular to \(X_0\), due to the fact that \(X_- = \theta X_+\). Thus, the Eq. (4.109) implies that the arc connecting the endpoints of the vectors \(X_0\) and \(\hat{X} '\) is equal to \(\theta _1\). Since the seed solution is given by \(X = U \hat{X} = U X_0\) and the dressed solution is given by \(X' = U \hat{X}'\), this property is transferred to the points of the seed and dressed solutions that correspond to the same worldsheet parameters \(\xi ^{0/1}\). In other words, the dressed string solution can be visualized as being drawn by a point in the circumference of an epicycle of arc radius \(\theta _1\), which moves so that its center lies on the seed string solution.
This statement provides a nice geometric visualization of the action of the dressing on the shape of the string. It is a general property that follows from the Eq. (4.109), which is the outcome of the form of the dressing factor in the case it has only two poles (3.35), as well as the mapping (3.37) between unit vectors and elements of the coset \(\mathrm {SO}(3)/\mathrm {SO}(2)\). It follows that the epicycle picture is not a specific property of the dressed elliptic solutions; it is rather a generic property that holds whenever the simplest dressing factor is adopted. This interesting property of the dressing method deserves further investigation in the case of strings propagating on other symmetric spaces or in the case of a more complicated dressing factor. A further implication of the above is the fact that at the limit \(\theta _1 \rightarrow 0\) the dressed solution tends to the seed, whereas as \(\theta _1 \rightarrow \pi \) the dressed solution tends to the reflection of the seed with respect to the origin of the enhanced space.
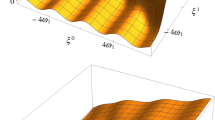
In Fig. 1, four representative dressed elliptic string solutions are depicted. In these plots, the dressed string solutions are depicted with a thick black line, whereas the seed solutions are depicted with a thin one. In the top row, the seed solution has a translationally invariant elliptic Pohlmeyer counterpart, whereas in the bottom row it has a static one. On the left column the seed solution has an oscillating counterpart with \(E=\mu ^2 / 10\) and a selected so that \(n=10\), whereas on the right column the seed solution has a rotating counterpart with \(E=6\mu ^2 /5\) and a selected so that \(n=7\). In all cases the pair of poles of the dressing factor lies at \(\lambda = e^{\pm i\frac{\pi }{12}}\). Large spheres are points of the dressed solution, whereas small spheres are points of the seed solution. Spheres with the same color correspond to the same worldsheet coordinates \(\xi _0\) and \(\xi _1\) and they are connected via an epicycle plotted with the same color, too.
Our analysis focused on the case of seed solutions that are elliptic string solutions with static Pohlmeyer counterparts. It is trivial to show that had we used elliptic strings with translationally invariant counterparts as seed solutions, we would have resulted in dressed string solutions that can be acquired from the ones presented here after the trivial operation \({\xi ^0} \leftrightarrow {\xi ^1}\).
5 The sine-Gordon equation counterparts
The elliptic string solutions presented in Sect. 2 can be naturally classified with respect to their Pohlmeyer counterparts. Furthermore, in [14] it was also shown that many of the properties of these solutions are connected to the properties of their corresponding sine-Gordon counterparts. For example, the number of spikes equals the topological number in the sine-Gordon theory. For these reasons, we proceed to specify in this section the sine-Gordon equation counterparts of the dressed elliptic string solutions, which are obtained in Sect. 4.
5.1 Bäcklund transformations
The sine-Gordon equation (2.3) possesses the well-known Bäcklund transformations
connecting pairs of solutions. As described in the introduction, they can be used for the construction of new solutions from a seed one. Their merit is the fact that this is achieved via solving a pair of first order differential equations, instead of the original second order one. The usual application of these transformations is the construction of the kink solutions, using the vacuum \(\varphi = 0\) as seed.
A nice property of the Bäcklund transformations is the fact that their iterative use does not require further solving of differential equations. Multi-kink solutions can be acquired from the single-kink ones algebraically, using the Bianchi permutability theorem. If \(\varphi _1\) is related to the seed \(\varphi \) through a Bäcklund transformation with parameter \(a_1\) and \(\varphi _2\) is related to the same seed \(\varphi \) through a Bäcklund transformation with parameter \(a_2\), then a new solution \(\varphi _{12}\) that is connected to \(\varphi _1\) through a Bäcklund transformation with parameter \(a_2\) (or equivalently to \(\varphi _2\) through a Bäcklund transformation with parameter \(a_1\)) will be given by
5.2 Virasoro constraints
A basic ingredient of the Pohlmeyer reduction is the fact that the energy momentum tensor can be set constant, with obvious consequences for the form of the Virasoro constraints. In the following, as a first step towards the specification of the Pohlmeyer counterparts of the dressed solutions discovered in Sect. 4, we show explicitly that they obey the Virasoro constraints as expected by the analysis in Sect. 3.5.
We have shown that the dressed solution is written as
The vectors \(X_0\) and \(X_1\) are unit vectors, orthogonal to each other, thus the vectors \(\left\{ X_0 , X_1 , X_0 \times X_1 \right\} \) form an orthonormal basis.
From the definition (4.106) of the vector \(X_+\), we have
and we have already shown that \({\partial _{0/1}}{E_i} = {{\kappa }_{0/1}} \times {E_i} \). Therefore,
In a similar manner, \({X_ - } = \theta {X_ + }\), and, thus,
The third element of the vector \(X_1\) vanishes, as it is perpendicular to \(X_0\). Thus, the third element of its derivative also vanishes. Since \(X_1\) is a constant norm vector, its derivatives are perpendicular to itself. The above imply that the derivatives of \(X_1\) are perpendicular to both \(X_0\) and \(X_1\), thus parallel to \(X_0 \times X_1\),
The formulae (5.6) and (5.7) that provide the derivatives of \(X_\pm \), can be used to calculate the coefficients \(c_{0/1}\). It is a matter of algebra to show that
Recalling the definitions (4.38) and (4.39) of the \(\kappa _i\) in terms of the real vectors \(k_i\), it is obvious that
where \(\bar{i} = 0\) when \(i = 1\) and vice versa. The vectors \(X_\pm \) obey the relation \(\sqrt{2{X_ +^T } {X_ - }} = - i{X_0^T} \left( {{X_ + } - {X_ - }} \right) \), which is a direct consequence of the properties of the vector p. This property, combined with the Eqs. (5.10) and (5.11), allow us to write Eq. (5.9) as,
implying
Equation (5.4) implies that
A direct consequence of the above is
We remind the reader that we have defined the vectors \(k_i\) so that \({U^T} ( {{\partial _j}U} ) = k_j^i{T_i}\), implying \({U^T}\left( {{\partial _i}U} \right) \hat{X}' = {{k}_i} \times \hat{X}'\). Taking advantage of this and the form of the derivatives of the vector \(X_1\) (5.8), we find
Putting everything together, it is now a matter of simple algebra to show that
implying that the dressed solution satisfies the Virasoro constraints as long as the undressed solution does so.
5.3 Dressing vs Bäcklund transformation
Let us now study the connection of the Pohlmeyer field corresponding to the dressed solution to that of the seed. In exactly the same way that we derived (5.17) and (5.18), we find
Taking advantage of the fact that \(k_0^2 = k_0^3k_1^1 - k_1^3k_0^1 = 0\), we may write the derivatives of the 1 and 2 components of the vectors \(k_0\) and \(k_1\) (4.49) and (4.50) as
We remind the reader that \({\partial _1} k_{0/1} = 0\). The above imply that the perpendicular to \(X_0\) part of the the derivatives of \(k_0\) and \(k_1\) can be written as
Defining
these relations can be written in a shorthand notation as
We recall that the vectors \(X_0\), \(X_1\) and \(X_0 \times X_1\) form an orthonormal basis. We may project the above relations in the directions of the last two vectors of this basis to yield
In the following we adopt the notation
In this notation, appropriately combining the Eqs. (5.8) and (5.13) yields
The above equations and (5.25) imply that
The Virasoro constraints (5.17) and (5.18) directly imply that
In a similar manner, Eq. (5.19) and the definition of the Pohlmeyer field (2.4) imply that
It is a direct consequence of (5.35), (5.36) and (5.37) that
up to an overall sign which corresponds to the freedom of reflection of the Pohlmeyer field. The Eqs. (5.35)–(5.39) imply that
Substituting the above in (5.33) and (5.34) yields
which are the usual Bäcklund transformations (5.1) and (5.2) with parameter
It follows that the dressed string solutions obtained in Sect. 4 have Pohlmeyer counterparts that are connected to the elliptic solutions of the sine-Gordon equation presented in Sect. 2 via a single Bäcklund transformation with parameter determined by the position of the poles of the dressing factor.
5.4 Bäcklund transformation of elliptic solutions
The last step towards obtaining the Pohlmeyer counterparts of the dressed elliptic string solutions of Sect. 4 is the application of a Bäcklund transformation to the elliptic solutions of the sine-Gordon equation (2.5). Such solutions have been studied in the past [43,44,45,46] in a different context and language.
In general, a much wider class of solutions of the sine-Gordon equation can be expressed in terms of hyperelliptic functions [36, 37]. Such solutions can be classified in terms of the genus of the relevant torus. The elliptic solutions that we have studied in Sect. 2 are the simple case of genus-one solutions. Pairs of solutions connected via a Bäcklund transformation are characterized by genuses whose difference equals one. This extra hole in the relevant torus is a degenerate one meaning that one of the corresponding periods is infinite. Therefore, the solutions that we are going to construct applying a Bäcklund transformation to elliptic solutions are degenerate cases of genus two solutions of the sine-Gordon equation. In a different approach one may find other genus two solutions via separation of variables [47, 48].
The technical advantage of using an elliptic solution as seed is the fact that they depend solely on either the space-like or time-like worldsheet coordinate. Writing down the Bäcklund transformations (5.1) and (5.2) in terms of the coordinates \(\xi ^0\) and \(\xi ^1\) yields
Without loss of generality, we start our analysis considering that \(\varphi \) is a translationally invariant elliptic solution of the sine-Gordon equation as given by Eq. (2.6). Equation (2.5) directly implies that
The sign of the quantities \({\cos }\frac{\varphi }{2}\), \({\sin }\frac{\varphi }{2}\) and \({{\partial _0} \varphi }\) depends on whether \(\varphi \) is an oscillating or rotating solution. Although these signs are not going to play a crucial role in the following, Eq. (2.6) implies
for oscillating solutions, and
for the rotating ones with increasing \(\varphi \).
The Eq. (5.46) contains only the derivative of \(\tilde{\varphi }\) with respect to \(\xi ^1\) and simultaneously all other functions that appear depend solely on \(\xi ^0\). Therefore, it can be solved as an ordinary differential equation, substituting the undetermined constant of integration with an undetermined unknown function of \(\xi ^0\). The latter equation assumes the form
where
One should be careful in the inversion of (5.53) and (5.54), so that \(\hat{\varphi }\) is continuous and smooth and A has the correct sign. Defining the inverse tangent function so that its codomain is \(\left( - \pi / 2 , \pi / 2 \right) \), an appropriate selection for \(\hat{\varphi }\) and A is
where \(k \in \mathbb {Z}\) and we defined the sign \(s_c\) as
For a translationally invariant oscillating seed solution given by (2.6) it holds that \(\left\lfloor {\frac{\varphi }{{2\pi }} + \frac{1}{2}} \right\rfloor = 0\), whereas for a rotating one \(\left\lfloor {\frac{\varphi }{{2\pi }} + \frac{1}{2}} \right\rfloor = \left\lfloor {\frac{{{\xi ^0}}}{{2{\omega _1}}} + \frac{1}{2}} \right\rfloor \).
Notice also that the monotonicity of \(\hat{\varphi }\) is the same as that of the seed solution \(\varphi \) when \(\left| a \right| > 1\) and opposite when \(\left| a \right| < 1\). We define
The quantity \({A^2} - {B^2} \equiv D^2\), which is going to play an important role in the following, is actually a constant, namely,
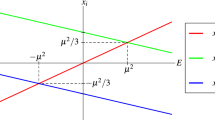
For a given value of E, the constant \(D^2\) may assume any value larger or equal to \(D_{\min }^2 = ( \mu ^2 - E ) / 2\). The latter assumes any given value larger than the minimum one, for exactly four distinct values of the Bäcklund transformation parameter a; let a be one of them, then the other three are \(-a\) and \(\pm 1/a\). Therefore, there is exactly one value of the Bäcklund parameter a corresponding to a given value of \(D^2\) in each of the segments \( ( - \infty , -1 ]\), \( [ - 1 , 0 )\), (0, 1] and \( [ 1 , \infty )\). There is an exception to this rule; there are only two distinct values of a, corresponding to the minimum value of \(D^2 = D_{\min }^2\), namely \(a = \pm 1 \).
It is clear that in the case of oscillating solutions, since \(E < \mu ^2\), the quantity \({D^2}\) is always positive. On the contrary, in the case of rotating solutions the sign of this quantity depends on the value of a. Therefore, for cases where \({D^2}\) can become negative, we are able to select the sign of \(A \pm B\), choosing the direction of rotation of the solution \(\varphi \). In the following, we will assume that rotating solutions are characterized by increasing \(\varphi \), and, thus, for these solutions B is always negative. We define
Substituting
the Eq. (5.52) assumes the form
whose solution is
Therefore, \({\tilde{\varphi } }\) assumes the form
Returning to the Bäcklund transformation (5.45) that we have not used so far, we may write it as
since \(\varphi \) does not depend on \(\xi ^1\). It is a matter of trivial algebra to write it in the form
which is significantly simplified with the use of Eqs. (5.53) and (5.54) to
Equation (5.55) and the equation of motion imply that \({\partial _0}B = {{{\mu ^2}}}\sin \varphi / 2\). Moreover, Eq. (5.56) implies that \({\partial _0} {\hat{\varphi }} = - {{{\mu ^2}\left( {{a^2} - {a^{ - 2}}} \right) B}}/({{2{A^2}}})\), while equation (5.57) implies that \({\partial _0}A = {{{\mu ^2}B}}\sin \varphi / ( {{2A}} )\). Finally, the function g satisfies \( {\partial _0}g = {D} ( {1 - {g^2}} )f' ( {{\xi ^0}} ) / 2 \). Performing the substitution (5.62) and putting everything together, we arrive at
The denominator in the above relation is always positive. Therefore, the sign of \(f'\left( {{\xi ^0}} \right) \), and, thus, the monotonicity of \(f\left( {{\xi ^0}} \right) \), is determined by the sign of the numerator. The function f is increasing when \(\left| a \right| > 1\) and decreasing when \(\left| a \right| < 1\).
We define \(\tilde{a}\) so that
and demand that it lies within the cell of the Weierstrass elliptic function, whose vertices are the four complex numbers \(\pm \omega _1 \pm \omega _2\). Then, the Weierstrass differential equation \({\wp '}^2 = 4 \wp ^4 -g_2 \wp -g_3\) and the Eq. (5.70) imply that \(\wp {'^2} ( {\tilde{a}} ) = {{{\mu ^4}}}{D^2}{ ( {{a^2} - {a^{ - 2}}} )^2} / 4 \), which specifies \(\tilde{a}\) up to an overall sign. We select the \(\tilde{a}\) such that
or in other words, so that the real part of \(\tilde{a}\) has always opposite sign than \(s_d\).
Equation (5.70) implies that \(\wp ( {\tilde{a}} )\) is larger than at least two of the three roots. When \(D^2 > 0\), it is also larger than the largest root, implying that \(\tilde{a}\) lies in the real axis, in the interval \(\left( 0 , \omega _1 \right) \), when \(\left| a \right| < 1\), and in the interval \(\left( -\omega _1 , 0 \right) \), when \(\left| a \right| > 1\). When \(D^2 < 0\), \(\wp ( {\tilde{a}} )\) lies between the two larger roots and therefore \(\tilde{a}\) lies in the linear segment with endpoints \(\omega _1 \) and \(\omega _3 \equiv \omega _1 + \omega _2\), when \(\left| a \right| > 1\), and \(- \omega _1 \) and \(- \omega _3 \), when \(\left| a \right| < 1\). In the special limiting case \(a = \pm 1\), the derivative of the function f vanishes, and, thus, \(\wp ' ( {\tilde{a}} )\) vanishes too. At this limit, \(\wp ( {\tilde{a}} )\) assumes the value of the root \(x_2\), implying that \(\tilde{a}\) is equal to \(\pm \omega _1\) for oscillating backgrounds and \(\pm \omega _3\) for the rotating ones. In the latter case, there is yet another a for which \(\tilde{a}\) assumes the value \(\pm \omega _1\), and, thus, once again \(\wp ' ( {\tilde{a}} )\) vanishes. This is the specific choice \(a = \pm ( {E \pm \sqrt{E - {\mu ^2}} } )/\mu \), which sets \(D = 0\). These are depicted in Fig. 2.
Using the above definitions, it can be shown that
implying
where the function \(\varPhi \) is the same quasi-periodic function that appears in the expressions of the elliptic strings and it is defined in (2.10). Putting everything together
Equations (5.72) and (5.73) imply that when \(D^2 < 0\), the function \(\varPhi ( {{\xi ^0};\tilde{a}} )\) is real, whereas when \(D^2 > 0\), the function \(\varPhi ( {{\xi ^0};\tilde{a}} )\) is purely imaginary. Therefore, in all cases the solution \(\tilde{\varphi }\) is real. It can be written in a manifestly real form as,
Equation (5.75) reveals that there is a bifurcation of the qualitative characteristics of the dressed elliptic solutions of the sine-Gordon equation that occurs at \(E=\mu ^2\). As we have commented above, in the case of an oscillatory seed solution \(D^2\) is always positive, whereas in the case of rotating seeds, there is a range of Bäcklund parameters that sets it negative. Equation (5.75) implies that the solutions with \(D^2>0\) look like a localized kink at the region \(D{\xi ^1} + i \varPhi ( {{\xi ^0};\tilde{a}} ) = 0\). Far from this region, they assume a form that is completely determined by the seed solution and it has the same periodicity properties as the latter. Thus, solutions with \(D^2\) are localized disturbances on the elliptic background. On the contrary, solutions with \(D^2<0\) do not have this property. They do not describe any kind of localized kink and they do not have the same periodicity properties as the seed solution in any region.
The same procedure can be repeated for a static elliptic seed solution. As expected by the symmetries of the sine-Gordon equation, the acquired solution reads
which can be acquired by Eq. (5.74) interchanging the two coordinates and adding an overall angle \(\pi \).
To sum up, the dressed elliptic string solution (4.110) has a sine-Grodon counterpart that is given by the Eq. (5.76), where the Bäcklund parameter is given by the Eq. (5.44).
The parameters appearing in the dressed string solutions and the solutions of the sine-Gordon equation presented in this section are also connected. The function \(\varDelta ( \lambda )\), when \(\lambda = e^{i\theta _1}\), which is the case of interest, is real and assumes the value \(\varDelta = - ( \mu ^2 ( a^2 + a^{-2} ) - 2 E ) / 4\), where a is given by (5.44). This is exactly equal to the opposite of the parameter \(D^2\) defined in (5.60) that appears in the dressed elliptic sine-Gordon solutions. This is in line with the form of the dressed string solution; whenever \(D^2\) is positive and thus \(\varDelta \) is negative, the trigonometric functions that appear in the dressed string solution will actually be hyperbolic functions when expressed in a manifestly real form, a fact expected for solutions with a kink counterpart.
Similarly, when \(\lambda = e^{i\theta _1}\), the function \(\tilde{a} \left( \lambda \right) \) appearing in the dressed elliptic string solutions, assumes a given value so that \(\wp ( \tilde{a} ) = - E / 6 + \mu ^2 ( a^2 + a^{-2} ) / 4\), and, furthermore, \(\wp ' ( \tilde{a} ) = - i \sqrt{\varDelta } \mu ^2 ( a^2 - a^{-2} ) / 2\). Comparing to the defining properties (5.70) and (5.71) of the parameter \(\tilde{a}\) of the corresponding sine-Gordon solutions, the two parameters coincide, as long as one defines \(\sqrt{\varDelta } = i \sqrt{-\varDelta }\), whenever \(\varDelta < 0\).
6 Discussion
The construction of dressed elliptic strings propagating on \(\mathbb {R}^t \times \hbox {S}^2\) was presented. These solutions correspond to genus two solutions of the sine-Gordon equation with one of the two holes of the relevant torus being degenerate. Arbitrary genus solutions of both the sine-Gordon and the non-linear sigma model equations are known in an abstract form [36,37,38]. Our approach adds to the relevant literature, because the solutions are expressed in terms of simple trigonometric/hyperbolic and elliptic functions, whose properties and qualitative behaviour are much easier to study and understand. Alternatively, specific non-degenerate genus two solutions can be constructed via a completely different approach [49]; the Pohlmeyer counterparts of the latter are genus-two solutions of the sine-Gordon equation [47] that can be constructed via separation of variables after the application of the Lamb ansatz.
The dressing of the elliptic string solutions is presented in both the non-linear sigma model and the Pohlmeyer reduced theory. In the first case it corresponds to the application of the simplest possible dressing factor, whereas in the second case to a single Bäcklund transformation. Especially the latter calculation is an original non-trivial application of the dressing method, since the seed solution [9, 11, 14] is neither a solution whose Pohlmeyer counterpart is the vacuum, nor connected to this via a finite number of Bäcklund transformations, as in most cases presented in the literature [29,30,31,32,33]. The similarities between the two pictures, even at technical level, reveal the deep connection between the dressing method and the Bäcklund transformations [28].
Independently of the choice of the seed solution, in the special case where the dressing factor has the minimal number of poles, namely two poles lying on the unit circle, the effect of the dressing transformation on the seed solution acquires a nice geometrical picture. The dressed string is drawn by an epicycle of given radius, whose center runs over the seed solution. This picture adds to the conceptual understanding of the action of the dressing transformation on a given solution. It would be interesting to find the equivalent geometrical picture in other systems, such as strings propagating on AdS or dS spaces [9, 10, 34] or minimal surfaces in hyperbolic spaces [35], as well as in the case of more general dressing factors.
In this work, the general solution to the auxiliary system for an elliptic seed solution (4.97) is obtained. Although we apply the simplest dressing factor, more complicated ones can be used in a straightforward way, without the need of solving again any differential equations. These would correspond to performing multiple Bäcklund transformations to the seed solution of the sine-Gordon equation. The above fact is connected to the existence of the addition theorem (5.3), which allows the performance of multiple Bäcklund transformations algebraically.
The study of dressed solutions emerging from a dressing factor with four poles presents a certain interest, as an extension of our results. In the standard analysis, where the seed is the vacuum, such solutions correspond to the non-trivial scattering of two kinks or even bound states of the latter, the so called breathers. However, since in our case the seed solution already contains a train of kinks (or kink-antikinks) such phenomena appear in the dressed solutions we have studied, without the need of a second Bäcklund transformation. The non-trivial interaction of the kink induced by the dressing with the kinks forming the background can be studied in the solutions with \(D^2>0\), whereas a qualitatively different picture is expected whenever \(D^2<0\). The study of more complicated dressed solutions however, will contain the extra feature of the non-trivial interaction of the two kinks that are both induced by the dressing in the presence of the non-trivial background.
Further investigation on the physical properties of the dressed elliptic strings is also very interesting. An interesting feature of the elliptic string solutions is the fact that they have several singular points, which are spikes. These can be kinematically understood, as points of the string that travel at the speed of light [4] due to initial conditions. As they cannot change velocity, no matter what the forces are which are exerted on them, they continue to exist indefinitely, as long as they do not interact with each other. In the already studied spiky string solutions [9,10,11,12,13], which are elliptic, the spikes rotate around the sphere with the same angular velocity, and thus, they never interact. Interacting spikes emerge in higher genus solutions. The simplest possible examples of this kind, which allow the study of spike interactions, are those obtained in this work.
The elliptic strings, are also characterized by a constant angular opening between consecutive spikes. The latter is holographically mapped to a quasi-momentum in the spin chain of the boundary theory. The dressed elliptic strings are not characterized by a single period, and, thus, their dispersion relations will depend on more than one quasi-momenta. Thus, these solutions may provide a tool for a further non-trivial check of the connection between the string dispersion relation and the anomalous dimensions of gauge theory operators in the strong coupling limit.
References
J.M. Maldacena, The large \(N\) limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 38, 1113 (1999) [Adv. Theor. Math. Phys. 2, 231 (1998)]. arXiv:hep-th/9711200
S.S. Gubser, I.R. Klebanov, A.M. Polyakov, Gauge theory correlators rom noncritical string theory. Phys. Lett. B 428, 105 (1998). arXiv:hep-th/9802109
E. Witten, Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 2, 253 (1998). arXiv:hep-th/9802150
S.S. Gubser, I.R. Klebanov, A.M. Polyakov, A semiclassical limit of the gauge/string correspondence. Nucl. Phys. B 636, 99 (2002). arXiv:hep-th/0204051
D.E. Berenstein, J.M. Maldacena, H.S. Nastase, Strings in flat space and pp waves from \(N=4\) super Yang–Mills. JHEP 0204, 013 (2002). arXiv:hep-th/0202021
D.M. Hofman, J.M. Maldacena, Giant magnons. J. Phys. A 39, 13095 (2006). arXiv:hep-th/0604135
H.Y. Chen, N. Dorey, K. Okamura, Dyonic giant magnons. JHEP 0609, 024 (2006). arXiv:hep-th/0605155
R. Ishizeki, M. Kruczenski, Single spike solutions for strings on \(\text{ S }^2\) and \(\text{ S }^3\). Phys. Rev. D 76, 126006 (2007). arXiv:0705.2429 [hep-th]
A.E. Mosaffa, B. Safarzadeh, Dual spikes: new spiky string solutions. JHEP 0708, 017 (2007). arXiv:0705.3131 [hep-th]
M. Kruczenski, Spiky strings and single trace operators in gauge theories. JHEP 0508, 014 (2005). arXiv:hep-th/0410226
K. Okamura, R. Suzuki, A perspective on classical strings from complex sine-Gordon solitons. Phys. Rev. D 75, 046001 (2007). arXiv:hep-th/0609026
B.H. Lee, C. Park, Unbounded multi magnon and spike. J. Korean Phys. Soc. 57, 30 (2010). arXiv:0812.2727 [hep-th]
M. Kruczenski, J. Russo, A.A. Tseytlin, Spiky strings and giant magnons on \(\text{ S }^5\). JHEP 0610, 002 (2006). arXiv:hep-th/0607044
D. Katsinis, I. Mitsoulas, G. Pastras, Elliptic string solutions on \(\mathbb{R} \times \text{ S }^2\) and their Pohlmeyer reduction. arXiv:1805.09301 [hep-th]
A .A. Tseytlin, Review of AdS/CFT Integrability, chapter II.1: classical \(\text{ AdS }_5 \times \text{ S }^5\) string solutions. Lett. Math. Phys. 99, 103 (2012). arXiv:1012.3986 [hep-th]
B.M. Barbashov, V.V. Nesterenko, Relativistic string model in a space-time of a constant curvature. Commun. Math. Phys. 78, 499 (1981)
H.J. De Vega, N.G. Sanchez, Exact integrability of strings in D-dimensional de Sitter space-time. Phys. Rev. D 47, 3394 (1993)
A.L. Larsen, N.G. Sanchez, Sinh-Gordon, cosh-Gordon and Liouville equations for strings and multistrings in constant curvature space-times. Phys. Rev. D 54, 2801 (1996). arXiv:hep-th/9603049
M. Grigoriev, A.A. Tseytlin, Pohlmeyer reduction of \(\text{ AdS }_5 \times \text{ S }^5\) superstring sigma model. Nucl. Phys. B 800, 450 (2008). arXiv:0711.0155 [hep-th]
K. Pohlmeyer, Integrable Hamiltonian systems and interactions through quadratic constraints. Commun. Math. Phys. 46, 207 (1976)
V.E. Zakharov, A.V. Mikhailov, relativistically invariant two-dimensional models in field theory integrable by the inverse problem technique. Sov. Phys. JETP 47, 1017 (1978) [Zh. Eksp. Teor. Fiz. 74, 1953 (1978)]
I. Bakas, Conservation laws and geometry of perturbed coset models. Int. J. Mod. Phys. A 9, 3443 (1994). arXiv:hep-th/9310122
I. Bakas, Q.H. Park, H.J. Shin, Lagrangian formulation of symmetric space sine-Gordon models. Phys. Lett. B 372, 45 (1996). arXiv:hep-th/9512030
C.R. Fernandez-Pousa, M.V. Gallas, T.J. Hollowood, J.L. Miramontes, The symmetric space and homogeneous sine-Gordon theories. Nucl. Phys. B 484, 609 (1997). arXiv:hep-th/9606032
J.L. Miramontes, Pohlmeyer reduction revisited. JHEP 0810, 087 (2008). arXiv:0808.3365 [hep-th]
L.D. Faddeev, L.A. Takhtajan, V.E. Zakharov, Complete description of solutions of the sine-Gordon equation. Dokl. Akad. Nauk Ser. Fiz. 219, 1334 (1974) [Sov. Phys. Dokl. 19, 824 (1975)]
J.P. Harnad, Y.Saint Aubin, S. Shnider, Backlund transformations for nonlinear \(\sigma \) models with values in Riemannian symmetric spaces. Commun. Math. Phys. 92, 329 (1984)
T.J. Hollowood, J.L. Miramontes, Magnons, their solitonic avatars and the Pohlmeyer reduction. JHEP 0904, 060 (2009). arXiv:0902.2405 [hep-th]
F. Combes, H.J. de Vega, A.V. Mikhailov, N.G. Sanchez, Multistring solutions by soliton methods in de Sitter space-time. Phys. Rev. D 50, 2754 (1994). arXiv:hep-th/9310073
M. Spradlin, A. Volovich, Dressing the giant magnon. JHEP 0610, 012 (2006). arXiv:hep-th/0607009
C. Kalousios, M. Spradlin, A. Volovich, Dressing the giant magnon II. JHEP 0703, 020 (2007). arXiv:hep-th/0611033
A. Jevicki, C. Kalousios, M. Spradlin, A. Volovich, Dressing the giant gluon. JHEP 0712, 047 (2007). arXiv:0708.0818 [hep-th]
A. Jevicki, K. Jin, C. Kalousios, A. Volovich, Generating AdS string solutions. JHEP 0803, 032 (2008). arXiv:0712.1193 [hep-th]
I. Bakas, G. Pastras, On elliptic string solutions in \(\text{ AdS }_{3}\) and \(\text{ dS }_{3}\). JHEP 1607, 070 (2016). arXiv:1605.03920 [hep-th]
G. Pastras, Static elliptic minimal surfaces in \(\text{ AdS }_4\). Eur. Phys. J. C 77(11), 797 (2017). arXiv:1612.03631 [hep-th]
V.P. Kotlarov, Finite-gap solutions of the sine-Gordon equation. arXiv:1401.4410 [nlin.SI]
V.A. Kozel, A.P. Kotlyarov, Almost periodic solutions of the sine-Gordon equation. Dokl. Akad. Nauk Ukrain. SSR Ser. 10, 878–881 (1976)
N. Dorey, B. Vicedo, On the dynamics of finite-gap solutions in classical string theory. JHEP 0607, 014 (2006). arXiv:hep-th/0601194
V.E. Zakharov, A.V. Mikhailov, On the integrability of classical spinor models in two-dimensional space-time. Commun. Math. Phys. 74, 21 (1980)
J.P. Harnad, Y.Saint Aubin, S. Shnider, Superposition of solutions to Bäcklund transformations for the SU(\(n\)) principal \(\sigma \) model. J. Math. Phys. 25, 368 (1984)
J.P. Antoine, B. Piette, Classical non-linear sigma models on Grassmann manifolds of compact or non-compact type. J. Math. Phys. 28, 2753 (1987)
Y.Saint Aubin, Backlund transformations and soliton type solutions for \(\sigma \) models with values in real Grassmannian spaces. Lett. Math. Phys. 6, 441 (1982)
M. Jaworski, J. Zagrodzinski, Quasiperiodic solutions of the sine-Gordon equation. Phys. Lett. A 92, 427 (1982)
J. Zagrodzinski, Dispersion equations and a comparison of different quasiperiodic solutions of the sine-Gordon equation. J. Phys. A 15, 3109 (1982)
J. Zagrodzinski, Solitons and wavetrains: unified approach. J. Phys. A 17, 3315 (1984)
M. Jaworski, Kink-phonon interaction in the sine-Gordon system. Phys. Lett. A 125, 115 (1987)
G.L. Lamb, Analytical descriptions of ultrashort optical pulse propagation in a resonant medium. Rev. Mod. Phys. 43, 99 (1971)
A.D. Osborne, A.E.G. Stuart, Separable solutions of the two-dimensional sine-Gordon equation. Phys. Lett. A 67, 328 (1978)
T. Klose, T. McLoughlin, Interacting finite-size magnons. J. Phys. A 41, 285401 (2008). arXiv:0803.2324 [hep-th]
Acknowledgements
The research of G.P. is funded by the “Post-doctoral researchers support” action of the operational programme “human resources development, education and long life learning, 2014–2020”, with priority axes 6, 8 and 9, implemented by the Greek State Scholarship Foundation and co-funded by the European Social Fund-ESF and National Resources of Greece. The authors would like to thank M. Axenides, E. Floratos, G. Georgiou and G. Linardopoulos for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Some further details on the dressing method
1.1 A.1: The general solution for the residues
In this appendix, we review the basic results of [27, 28] considering the specification of the residues appearing in the expression for the dressing factor and hence the specification of the dressed non-linear sigma model solution.
We consider the general form for the dressing factor as given by Eq. (3.11). Let us first consider the case of poles obeying \(\lambda _i\ne \mu _j\) for any i, j. Since \(\chi (\lambda )\chi (\lambda )^{-1} = I\), it holds that
Taking the residues of the above expression at \(\lambda _i\) and \(\mu _j\) yields the following relations for the yet unspecified matrices \(Q_i\) and \(R_i\),
If the pole \(\lambda _k\) coincides with the pole \(\mu _l\), then the product \(\chi (\lambda )\chi (\lambda )^{-1}\) will have a second order pole whose coefficient should vanish separately. In this case, vanishing of the residues at \(\lambda = \lambda _k = \mu _l\) implies
Furthermore, \(\varPsi ' ( \lambda ) = \chi ( \lambda ) \varPsi ( \lambda )\) must satisfy the equations of the auxiliary system (3.13). Substituting the expressions (3.11) into the latter and taking the residues at the positions of the poles yields
Equations (A.2)–(A.5) suffice to determine the matrices \(Q_i\) and \(R_i\) [27]. They equal
where
The matrix \(\gamma \) is the inverse of the matrix \(\varGamma \) with elements given by
The vectors \(f_i\), \(h_j\) are arbitrary constant complex vectors, which obey \(f_i^\dag {h_j} = 0\) when \(\lambda _i = \mu _j\) and C is an arbitrary constant matrix.
1.2 A.2: The constraints in the case of two poles
Our case of interest includes only a pair of poles, lying in the unit circle and being complex conjugate to each other. As we discussed in Sect. 3.3, the unitarity involution enforces the poles of \(\chi (\lambda )^{-1}\) to lie in positions complex conjugate to those of the poles of \(\chi (\lambda )\). Thus \(\mu _1 = \bar{\lambda }_1 = \lambda _2\) and \(\mu _2 = \bar{\lambda }_2 = \lambda _1\). It can be shown that there is a particular solution for the residues, where the elements of the matrix \(\varGamma \) connecting coinciding poles of \(\chi (\lambda )\) and \(\chi (\lambda )^{-1}\) are vanishing [27, 42], namely \(\varGamma _{12} = \varGamma _{21} = 0\). Therefore, for this particular solution, the matrix \(\varGamma \) is diagonal and its inverse is obviously \(\gamma = {\mathrm {diag}}\left\{ 1 / \varGamma _{11} , 1 / \varGamma _{22} \right\} \). Furthermore, it holds that \(f_1^\dag {h_2} = f_2^\dag {h_1} = 0\).
The unitarity involution implies that the residues of the dressing factor obey \(R_i = Q_i^\dag \). It follows that \(f_1 = h_1\) and \(f_2 = h_2\). The reality involution implies that \(Q_2 = \bar{Q}_1\). Then, it follows that \(f_2 = \bar{f}_1\). The above are sufficient to conclude that the dressing factor is of the form given by Eqs. (3.35) and (3.36), where \(p \equiv f_1\). Then, the coset involution implies \(Q_2 = - \lambda _2^2 f' \theta Q_1 \theta f\). This in turn implies that \(f_2 = \theta f_1\) or else the complex vector p should obey \(\bar{p} = \theta p\). Finally, the constraint \(f_1^\dag {h_2} = f_2^\dag {h_1} = 0\) enforces the vector p to possess the property \(p^T p = 0\). This concludes the derivation of this particular solution for the dressing factor in the case of two poles, complex conjugate to each other, that are lying on the unit circle, which is used throughout Sect. 4.3.
B: Double root limits of the dressed SG solutions
The dressed solutions of the sine-Gordon equation (5.74) reduce to simpler expressions in the special case of a double root of the corresponding Weierstrass elliptic function. This is physically expected, since in these limits, the seed solution is either the vacuum or the one-kink solution, implying that the corresponding dressed solution should coincide to the one-kink or two-kink solution, respectively.
In the following, without loss of generality, we assume \(a>1\). The first case to consider is the limit \(E \rightarrow - \mu ^2\). In this limit, the translationally invariant seed solution tends to the vacuum \(\varphi = 0\), and, thus, our expressions should degenerate to the well-known expressions of single kinks of the sine-Gordon equation. Indeed, the two smaller roots coincide, therefore the imaginary period of the Weierstrass elliptic function diverges, whereas the real period acquires the specific value
The parameter D acquires the value
Finally, it is a matter of simple algebra to show that the solution (5.74) acquires the usual expression
In the case of static seeds, in the limit \(E \rightarrow - \mu ^2\), the seed solution tends to the unstable vacuum \(\varphi = \pi \) and the dressed solutions tend to solutions evolving from one unstable vacuum to another.
Another interesting case is the limit \(E \rightarrow \mu ^2\). In the case of a static seed solution, this is a single static kink. Therefore, we should expect that our solutions should degenerate to the usual two-kink solutions of the sine-Gordon equation, in the frame where one of the two is stationary. In this case, the two larger roots coincide, and, thus, the real period of the Weierstrass elliptic function diverges. The seed solution is written as
or
The parameter D assumes the value
and the parameter \(\tilde{a}\) equals
Finally, the solution (5.76) degenerates to the form
which is indeed the form of the two-kink solution in the frame that one of those is stationary. It corresponds to the outcome of the addition formula (5.3) with \(\varphi = 0\), \(a_1 = - \ 1\) and \(a_2 = a\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Katsinis, D., Mitsoulas, I. & Pastras, G. Dressed elliptic string solutions on \(\mathbb {R}\times \hbox {S}^2\). Eur. Phys. J. C 78, 668 (2018). https://doi.org/10.1140/epjc/s10052-018-6129-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6129-x