Is it possible to measure new general relativistic third-body effects on the orbit of Mercury with BepiColombo?

Abstract

Recently, Will calculated an additional contribution to the Mercury’s precession of the longitude of perihelion $\varpi$ of the order of ${\dot{\varpi }}_\text {W}\simeq 0.22~\text {milliarcseconds per century}$ ($\text {mas cty}^{-1}$). It is partly a direct consequence of certain 1pN third-body accelerations entering the planetary equations of motion, and partly an indirect, mixed effect due to the simultaneous interplay of the standard 1pN pointlike acceleration of the primary with the Newtonian N-body acceleration, to the quadrupole order, in the analytical calculation of the secular perihelion precession with the Gauss equations. We critically discuss the actual measurability of the mixed effects with respect to direct ones. The current uncertainties in either the magnitude of the Sun’s angular momentum $S_\odot$ and the orientation of its spin axis ${\varvec{\hat{S}}}_\odot$ impact the precessions ${\dot{\varpi }}_{J_2^\odot },~{\dot{\varpi }}_\text {LT}$ induced by the Sun’s quadrupole mass moment and angular momentum via the Lense–Thirring effect to a level which makes almost impossible to measure ${\dot{\varpi }}_\text {W}$, even in the hypothesis that it comes entirely from the aforementioned 1pN third-body accelerations. On the other hand, from the point of view of the Lense–Thirring effect itself, the mismodeled quadrupolar precession $\delta {\dot{\varpi }}_{J_2^\odot }$ due to the uncertainties in ${\varvec{\hat{S}}}_\odot$ corresponds to a bias of $\simeq 9\%$ of the relativistic one. The resulting simulated mismodeled range and range-rate times series of BepiColombo are at about the per cent level of the nominal gravitomagnetic ones.

1 Introduction

Recently, Will [18] calculated a new general relativistic contribution

$$\begin{aligned} {\dot{\varpi }}_\text {W} \simeq 0.22~\text {mas cty}^{-1} \end{aligned}$$

(1)

to the secular precession of the longitude of the perihelion $\varpi$ of Mercury arising from the other planets of our solar system up to Saturn. A similar scenario, but with the perturbing body moving in an inner orbit with respect to the test particle, was treated in Yamada and Asada [19]. The precession of Eq. (1) is, partly, a direct consequence of some post-Newtonian accelerations of order $\mathcal {O}\left( c^{-2}\right)$ (1 pN) induced by a distant, pointlike body X; see¹ $\left[ \varvec{a}\right] _\text {Cross}$ in Eq. (4) of Will [18]. On the other hand, a mixed, indirect contribution, allegedly of the same order of magnitude of the direct ones, comes also from the interplay between the standard Newtonian third-body² acceleration, which, to the quadrupole order, is

$$\begin{aligned} {\varvec{A}}_\text {X} = -{\mu _\text {X}r\over r_\text {X}}\left[ \varvec{\hat{r}}-3\left( \varvec{\hat{r}}\varvec{\cdot }{\varvec{\hat{r}}}_\text {X}\right) {\varvec{\hat{r}}}_\text {X}\right] , \end{aligned}$$

(2)

and the usual 1pN pointlike acceleration due to only the primary’s mass

$$\begin{aligned} {\varvec{A}}^M_\text {1pN} = {\mu \over c^2 r^2}\left[ \left( {4\mu \over r} - v^2\right) \varvec{\hat{r}} + 4\left( \varvec{v}\varvec{\cdot }\varvec{\hat{r}}\right) \varvec{v} \right] \end{aligned}$$

(3)

in the perturbative calculation by means of the Gauss equations inasmuch the same way as in the case of the Newtonian acceleration due to the quadrupole mass moment of the primary and Eq. (3) [9, 17]. In particular, the largest contribution

$$\begin{aligned} {\dot{\varpi }}_\text {W max}\simeq 0.16~\text {mas cty}^{-1} \end{aligned}$$

(4)

to the new precession of Eq. (1) is due to the direct and mixed effects which do not depend on the velocity ${\varvec{v}}_\text {X}$ of the distant perturber. Will [18] did not display the direct and indirect contributions to Eq. (4) separately, so that it is not possible to establish the weights of both the effects. Actually, it may have its importance in view of the fact that, as explained below, the mixed effects may be unobservable. The direct acceleration in Eq. (4) of Will [18] which contains ${\varvec{v}}_\text {X}$ gives rise to a de Sitter-like precession which is about 0.4 times smaller than Eq. (4) [18]. In Appendix B, we offer our contribution by analytically working out the direct precessions induced by all the accelerations entering $\left[ \varvec{a}\right] _\text {Cross}$ in Eq. (4) of Will [18] without making any simplifying assumptions concerning the orbital configuration of both the perturbed test particle and the distant pointlike perturber X. For Mercury, we find a total pN third-body perihelion precession induced by the planets from Venus to Saturn which amounts to $0.15~\text {mas cty}^{-1}$, which disagrees with Eq. (1). In particular, the total direct precession due to the first two accelerations entering Eq. (4) of Will [18] amounts to $0.087~\text {mas cty}^{-1}$ instead of³ Eq. (4).

In view of the fact that the largest 1pN contribution to the Mercury’s perihelion precession of

$$\begin{aligned} {\dot{\varpi }}_\text {1pN}= & {} \left( {1 + 2 \gamma - \beta \over 3}\right) {3n_\mathrm{b}\mu \over c^2 p} \nonumber \\= & {} \left( {1 + 2 \gamma - \beta \over 3}\right) 42.98~\text {arsec cty}^{-1} \end{aligned}$$

(5)

is rescaled in terms of the PPN parameters $\beta ,~\gamma$, which are equal to 1 in general relativity, Will [18] argues that, since the forthcoming BepiColombo mission is expected to improve out knowledge of $\beta ,~\gamma$ to the $10^{-6}$ level [6, 14], then it would be likely possible to measure Eq. (1). Indeed, the resulting theoretical mismodeling in Eq. (5) would be as little as

$$\begin{aligned} \delta {\dot{\varpi }}_\text {GR} \simeq 0.03~\text {mas cty}^{-1}. \end{aligned}$$

(6)

More specifically, Will [18] in the Abstract writes: “At a few parts in $10^{-6}$ of the leading general relativistic precession of 42.98 arcseconds per century, these effects are likely to be detectable by the BepiColombo mission”. Furthermore, Will [18] at pag. 191101-4 writes: “If BebiColombo can reach a part per million accuracy in measuring the perihelion advance, [...] it will measure, for the first time, relativistic effects on Mercury’s orbit arising from the planets that surround it.” Conversely, if one is interested in determining the Sun’s quadrupole mass moment and angular momentum through their precessions, Eq. (1) would act as a systematic bias on them. Will [18] at pag. 191101-4 writes about his new effects: “[...] their existence and cross-correlations may play a role [...] in measurements of the contributions to Mercury’s perihelion advance arising from the solar quadrupole moment and frame dragging that will be carried out using data from BepiColombo”.

In this Communication, we will show that measuring Eq. (1), or our smaller result in Appendix B, is unlikely, mainly because of the uncertainties in the magnitude of the Sun’s angular momentum entering the gravitomagnetic apsidal rate of change and in the spatial orientation of the Sun’s spin axis affecting especially the precession induced by the solar quadrupole mass moment. As a byproduct, our results will be useful in assessing the impact of the latter source of systematic uncertainty on the possible measurement of the Lense–Thirring effect itself with BepiColombo. Finally, our exact calculation of the direct precessions have a general validity, and can be fruitfully applied in several astronomical and astrophysical scenarios like, e.g., exoplanets or the stellar system orbiting the supermassive black hole in the Galactic Center characterized by arbitrary eccentricities and inclinations.

2 Our analysis

As a general remark, we note that the indirect, mixed effects, which arise from the simultaneous interplay of at least two accelerations $\text {A, B}$ in the calculation of the averaged precessions of the Keplerian orbital elements with the Gauss equations [9, 17], are likely undetectable in practical data reductions. Indeed, as far as our case is concerned in which A is, say, Eq. (3) and B is Eq. (2), data analysts of virtually all groups scattered around the world routinely model the Newtonian N-body interactions and the 1PN pointlike acceleration due to the primary to the best of our current knowledge of the parameters entering them which, of course, is necessarily imperfect. Thus, the actual output of data reductions like residuals of, say, ranges, range-rates, etc. would not show the indirect, mixed effects in full. They could only contain negligible signatures, if any, due to the mismodeling in the planetary masses and in the PPN parameters $\beta ,\gamma$ in terms of which the 1PN point particle acceleration is expressed. Instead, at least in principle, the observables’ residuals should fully display the direct effects (unless they have been somewhat removed in the estimation of, say, the initial state vectors) induced by some new accelerations, like those of $[\varvec{a}]_\text {Cross}$ in Eq. (4) of Will [18] which, perhaps, may still not be included in the dynamical models fit to the observations by some groups. Otherwise, one should not model both Eqs. (2) and (3) at all, and subtract their theoretically computed signals from the resulting huge residuals. It does not seem certainly viable. Even from the point of view of a covariance analysis, while it would be possible, in principle, to explicitly solve for and estimate dedicated scaling parameter(s) accounting for every single acceleration entering the equations of motion, this could not be done for the indirect, mixed effects. In the following analysis, we will treat Eq. (1) as if it were a potentially measurable effect, irrespectively of its origin.

In addition to the well known 1PN pointlike precession of Eq. (5) due to solely the primary’s mass, there are other two further effects affecting the perihelion of Mercury which should be regarded as serious sources of potential systematic uncertainties: they are due to the first even zonal harmonic $J_2^\odot$ of the multipolar expansion of the Sun’s Newtonian gravitational potential, and the general relativistic gravitomagnetic field of the Sun induced by its angular momentum ${\varvec{S}}_\odot$. Their precessions depend not only on the size of $J_2^\odot ,~S_\odot$, but also on the orientation of the Sun’s spin axis ${\varvec{\hat{S}}}_\odot$ in space which must enter the error budget as well. Their exact expressions, valid in any coordinate system and for arbitrary orbital configurations, are [7]

$$\begin{aligned} {\dot{\varpi }}_{J_2}&= -{3n_\mathrm{b}R^2 J_2\over 4p^2}\left\{ 2\left[ -1 + \left( \varvec{\hat{S}}\varvec{\cdot }\varvec{\hat{\mathrm {m}}}\right) \left( \varvec{\hat{S}}\varvec{\cdot }\varvec{\hat{\mathrm {n}}}\right) \left( 1-\cot I\right) \right] \right. \nonumber \\&\quad \left. +3\left[ \left( \varvec{\hat{S}}\varvec{\cdot }\varvec{\hat{\mathrm {m}}}\right) ^2 + \left( \varvec{\hat{S}}\varvec{\cdot }\varvec{\hat{\mathrm {l}}}\right) ^2\right] \right\} , \end{aligned}$$

(7)

$$\begin{aligned} {\dot{\varpi }}_\text {LT}&= -{2GS\over c^2 a^3\left( 1-e^2\right) ^{3/2}}\varvec{\hat{S}}\varvec{\cdot }\left[ 2~\varvec{\hat{\mathrm {n}}} + \left( \cot I-\csc I\right) \varvec{\hat{\mathrm {m}}}\right] . \end{aligned}$$

(8)

The Sun’s quadrupole mass moment and angular momentum are currently known to the level of accuracy listed in Table 1 along with the nominal values of the precessions of Eqs. (7), (8). It can be noted that, if, on the one hand, it could be hoped that the expected determinations of $J_2^\odot$ by BepiColombo to the $\simeq 10^{-10}$ level [1, 6, 14] may be accurate enough to make Eq. (1) at least larger than the mismodelled $J_2^\odot$-induced precession, on the other hand, a lingering $\simeq 6\%$ uncertainty in $S_\odot$ would imply an a priori theoretical uncertainty in the Lense–Thirring precession of Eq. (8) as large as $0.13~\text {mas cty}$ corresponding to $\simeq 58\%$ of Eq. (1) and $\simeq 86\%$ of our result in Table 2.

Table 1 Relevant Sun’s physical parameters along with the most recent uncertainties for some of them appeared in the literature, and nominal quadrupolar and Lense–Thirring perihelion precessions for Mercury. As far as $S_\odot$is concerned, the values quoted for its size and uncertainty were obtained by calculating the mean and the standard deviation of the figures quoted in Table 1 of Iorio [8]

Table 2 Doubly averaged 1pN third-body perihelion precessions of Mercury, in mas cty$^{-1}$, induced by Venus, Earth, Mars, Jupiter, Saturn via Eqs. (B1)–(B7). The resulting total precession amounts to $0.15~\text {mas cty}^{-1}$; in particular, Eqs. (B1)–(B4) yield a combined overall precession of $0.087~\text {mas cty}^{-1}$, contrary to $0.16~\text {mas cty}^{-1}$ claimed by Will [18]. The discrepancy seems to be due to the indirect, mixed effects

As announced before, also the current uncertainties in the Carrington elements parameterizing ${\varvec{\hat{S}}}_\odot$ play a crucial role in view of the resulting mismodeling in Eq. (7). Indeed, a standard Root-Sum-Square (RSS) calculation of the error in ${\dot{\varpi }}_{J_2^\odot }$ due to the uncertainties in $i_\odot ,~\Omega _\odot$, treated as two independent variables, yields

$$\begin{aligned} \delta {\dot{\varpi }}_{J_2^\odot }< & {} \sqrt{\left( {\partial {{\dot{\varpi }}_{J_2}}\over \partial {\Omega _\odot }}\right) ^2\upsigma ^2_{\Omega _\odot } + \left( {\partial {{\dot{\varpi }}_{J_2}}\over \partial {i_\odot }}\right) ^2\upsigma ^2_{i_\odot }}\nonumber \\= & {} 0.18~\text {mas cty}^{-1} \end{aligned}$$

(9)

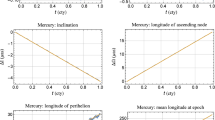
Furthermore, Figs. 1, and 2 straightforwardly depict Eq. (7) as function of $J_2^\odot ,~i_\odot ,~\Omega _\odot$ as independent variables allowed to vary within their ranges of assumed uncertainties [2, 6]. Their full range of variation is about twice Eq. (9). Instead, as shown by

$$\begin{aligned} \delta {\dot{\varpi }}_\text {LT}< & {} \sqrt{\left( {\partial {{\dot{\varpi }}_\text {LT}}\over \partial {\Omega _\odot }}\right) ^2\upsigma ^2_{\Omega _\odot } + \left( {\partial {{\dot{\varpi }}_\text {LT}}\over \partial {i_\odot }}\right) ^2\upsigma ^2_{i_\odot }}\nonumber \\= & {} 3\times 10^{-4}~\text {mas cty}^{-1} \end{aligned}$$

(10)

the Lense–Thirring precession is not significantly impacted by the uncertainty in the Sun’s spin axis orientation. From the point of view of a possible measurement of the Lense–Thirring effect, Eq. (9) corresponds to a $9\%$ uncertainty in the gravitomagnetic precession. Figure 3 shows the impact of the uncertainties in the Carrington elements on the direct BepiColombo observables, i.e. range and range-rate. It can be noticed that the resulting mismodeled signatures amount to $\simeq 1-1.5\%$ of the nominal Lense–Thirring ones. Schettino et al. [13], with dedicated covariance analyses performed with simulated data of BepiColombo, detailed the practical difficulty of satisfactorily separating $J_2^\odot$ from $S_\odot$, and the impact of $S_\odot$ itself in estimating of $J_2^\odot$ in various scenarios.

Fig. 1

Plot of ${\dot{\varpi }}_{J_2^\odot }\left( \Delta \mathrm {\Omega }_\odot ,~\Delta i_\odot \right)$, with the Sun’s spin axis $\varvec{\hat{S}}_\odot$ parameterized in terms of the Carrington elements $\mathrm {\Omega }_\odot ,~i_\odot$, as a function of $\Delta \mathrm {\Omega }_\odot ,~\Delta i_\odot$ allowed to vary within ${\mp } 1^{\circ },~{\mp } 0.002^{\circ }$ [2], respectively. As a model of the $J_2^\odot$-induced precession of Mercury, Eq. (7) was used along with $J_2^\odot = 2.295\times 10^{-7}$ [16], and $\Omega _\odot = 73.5^{\circ },~i_\odot = 7.155^{\circ }$ [2]. The full range of variation amounts to about $\Delta {\dot{\varpi }}_{J_2^\odot }\simeq 0.35~\text {mas cty}^{-1}$. Cfr. with Fig. 2. It is just twice the error calculated in Eq. (9)

Fig. 2

Family of parametric plots of ${\dot{\varpi }}_{J_2^\odot }\left( \Delta J_2^\odot ;~\Delta \mathrm {\Omega }_\odot ,~\Delta i_\odot \right)$, with the Sun’s spin axis $\varvec{\hat{S}}_\odot$ expressed in terms of the Carrington elements $\mathrm {\Omega }_\odot ,~i_\odot$, as a function of $\Delta J_2^\odot$ allowed to vary within ${\mp } 5.5\times 10^{-10}$ [6]. As a model of the $J_2^\odot$-induced precession of Mercury, Eq. (7) was used along with the reference values $J_2^\odot = 2.295\times 10^{-7}$ [16], and $\Omega _\odot = 73.5^{\circ },~i_\odot = 7.155^{\circ }$ [2]. Each curve corresponds to given values of $\Delta \mathrm {\Omega }_\odot ,~\Delta i_\odot$ within ${\mp } 1^{\circ },~{\mp } 0.002^{\circ }$ [2], respectively. For fixed values of $\Delta J_2^\odot$, the full range of variation amounts to about $\Delta {\dot{\varpi }}_{J_2^\odot }\simeq 0.35~\text {mas cty}^{-1}$, in agreement with Fig. 1. It is just twice the error calculated in Eq. (9)

3 Conclusions

The overall post-Newtonian third-body precession of the longitude of the perihelion of Mercury recently calculated by Will [18] amounts to ${\dot{\varpi }}_\text {W} \simeq 0.22~\text {mas cty}^{-1}$; according to Will [18], it should be measurable by the forthcoming BepiColombo mission. If, on the one hand, a determination of $J_2^\odot$ at the $\simeq 5\times 10^{-10}$ level, expected from BepiColombo, may reduce the mismodeling in the quadrupolar perihelion precession of Mercury down to $\delta {\dot{\varpi }}_{J_2^\odot }\simeq 35\%~{\dot{\varpi }}_\text {W} \simeq 4\%~{\dot{\varpi }}_\text {LT}$, on the other hand, the uncertainties in ${\varvec{\hat{S}}}_\odot$ would yield $\delta {\dot{\varpi }}_{J_2^\odot }\simeq 81\%~{\dot{\varpi }}_\text {W} = 9\%~{\dot{\varpi }}_\text {LT}$. Furthermore, the current $\simeq 6\%$ uncertainty in $S_\odot$ would cause a further bias as large as $\delta {\dot{\varpi }}_\text {LT}\simeq 58\%~{\dot{\varpi }}_\text {W}$. It seems that the indirect contributions to ${\dot{\varpi }}_\text {W}$ arising from the mixing of the Newtonian N-body term with the 1pN pointlike acceleration of the Sun in the perturbative analytical calculation, which may not be measurable, amounts to about $0.07~\text {mas cty}^{-1}$. Indeed, our calculation returns $0.15~\text {mas cty}^{-1}$ for the total direct post-Newtonian perihelion precession of Mercury induced by the other planets from Venus to Saturn, making, thus, even more pessimistic the perspective of measuring it. The simulated Earth–Mercury range and range-rate time series due to the imperfect knowledge of ${\varvec{\hat{S}}}_\odot$ are about at a per cent level of the nominal Lense–Thirring signatures. Finally, we not that our exact calculation for such kind of general relativistic precessions are valid for any orbital configuration of both the test particle and the third body. Thus, they can be applied also to other astronomical and astrophysical natural laboratories characterized by large eccentricities and inclinations like, e.g., several exoplanetary systems and the stars orbiting the supermassive black hole in Sgr $\hbox {A}^{*}$ in which the coplanarity condition is not fulfilled.

Fig. 3

Upper row (blue): mismodelled Earth–Mercury range (in m) and range-rate ($\hbox {cm s}^{-1}$) $J_2^\odot$-induced perturbations due to the uncertainties $\upsigma _{\Omega _\odot },~\upsigma _{i_\odot }$ in the Carrington elements $\Omega _\odot ,~i_\odot$ of the Sun’s spin axis ${\varvec{\hat{S}}}_\odot$ as in Beck and Giles [2] during the expected extended mission of BepiColombo from 2026 March 14 to 2028 May 1. Lower row (red): nominal Earth–Mercury range and range-rate perturbations due to the Sun’s angular momentum $S_\odot$ through the Lense–Thirring effect during the same temporal interval. A coordinate system with the mean ecliptic at the epoch J2000.0 as fundamental reference $\left\{ x,~y\right\}$ plane was assumed. The initial values of the Earth and Mercury osculating orbital elements were retrieved from the Web-Interface HORIZONS maintained by the JPL, NASA. For the nominal values of the Sun’s physical parameters used, see Table 1

Appendices

A Notations and definitions

Here, basic notations and definitions used in the text are presented [2,3,4, 10, 15]

G : :

Newtonian constant of gravitation

c : :

Speed of light in vacuum

$m_\text {X}:$ :

Mass of the distant pointlike perturber X

$\mu _\text {X}\doteq Gm_\text {X}:$ :

Gravitational parameter of the distant pointlike perturber X

$r_\text {X}:$ :

Distance of the distant pointlike perturber X from the primary

${\varvec{\hat{r}}}_\text {X}:$ :

Unit vector of the position vector of the distant pointlike perturber X

${\varvec{v}}_\text {X}:$ :

Velocity vector of the distant pointlike perturber X

M : :

Mass of the primary

$\mu \doteq GM:$ :

Gravitational parameter of the primary

R : :

Equatorial radius of the primary

$J_2:$ :

Dimensionless quadrupole mass moment of the primary

S : :

Magnitude of the angular momentum of the primary

$\varvec{\hat{S}}:$ :

Unit vector of the spin axis of the primary

$\mathrm {\Omega }_\odot :$ :

Longitude of the ascending node of the Sun’s equatorial plane with respect to the Vernal Equinox along the Ecliptic. One of the Carrington elements

$i_\odot :$ :

Inclination of the Sun’s equatorial plane to the plane of the Ecliptic. One of the Carrington elements

${\varvec{\hat{S}}}_\odot = \left\{ \sin i_\odot \sin \mathrm {\Omega }_\odot ,~-\sin i_\odot \cos \mathrm {\Omega }_\odot ,~ \cos i_\odot \right\} :$ :

Sun’s spin axis unit vector in terms of the Carrington elements

r : :

Distance of the test particle from the primary

$\varvec{\hat{r}}:$ :

Unit vector of the position vector of the test particle

$\varvec{v}:$ :

Velocity vector of the test particle

a : :

Semimajor axis

$n_\mathrm{b}\doteq \sqrt{\mu a^{-3}}:$ :

Keplerian mean motion

e : :

Eccentricity

$p\doteq a(1-e^2):$ :

Semilatus rectum

I : :

Inclination of the orbital plane to the reference $\left\{ x,~y\right\}$ plane adopted

${\varOmega }:$ :

Longitude of the ascending node

$\varvec{\hat{\mathrm {l}}}\doteq \left\{ \cos {\varOmega },~\sin {\varOmega },~0\right\} :$ :

Unit vector directed along the line of the nodes toward the ascending node

$\varvec{\hat{\mathrm {m}}}\doteq \left\{ -\cos I\sin {\varOmega },~\cos I\cos {\varOmega },~\sin I\right\} :$ :

Unit vector directed transversely to the line of the nodes in the orbital plane

$\varvec{\hat{\mathrm {n}}}\doteq \left\{ \sin I\sin {\varOmega },~-\sin I\cos {\varOmega },~ \cos I\right\} :$ :

Unit vector of the orbital angular momentum

$\omega :$ :

Argument of pericenter

$\varpi \doteq {\varOmega } + \omega :$ :

Longitude of pericenter

B Exact calculation of the direct perihelion precession

The first line of Eq. (4) of Will [18] returns the following 1pN acceleration of order $\mathcal {O}\left( G^2\right)$

$$\begin{aligned} {\varvec{A}}_{G^2} = {2\mu \mu _\text {X}\over c^2 r_\text {X}^3}\left[ \varvec{\hat{r}} - 6 \left( \varvec{\hat{r}} \varvec{\cdot }{\varvec{\hat{r}}}_\text {X} \right) {\varvec{\hat{r}}}_\text {X} + 3\left( \varvec{\hat{r}} \varvec{\cdot }{\varvec{\hat{r}}}_\text {X} \right) ^2 \varvec{\hat{r}} \right] . \end{aligned}$$

(B1)

We were successful in obtaining an exact expression for the doubly-averaged perihelion precession induced by Eq. (B1) without any a-priori simplifying assumption on the orbital geometries of both the perturbed test particle and the distant pointlike perturber. Nonetheless, it is far too cumbersome to be explicitly displayed here; thus, we show it only to the zeroth order in the eccentricity e. It reads

$$\begin{aligned} \frac{{{\text {d}}}{\varpi }}{{{\text {d}}}{t}} =&-{\mu _\text {X}\sqrt{\mu a}\over 16 c^2 a^3_\text {X}\left( 1 - e^2_\text {X}\right) ^{3/2}}\left\{ 1 + 48 \left( -1 + \cos I\right) \right. \nonumber \\&\left. \times \cos I \left( \cos ^2 I_\text {X} -\cos ^2\Delta \Omega \sin ^2 I_\text {X}\right) \right. \nonumber \\&\left. + 3 \left( 2 \cos 2 \Delta \Omega \sin ^2 I + \cos 2 I \Big (1 + \cos 2 I_\text {X} \right. \right. \nonumber \\&\left. \left. \left. \times \left( 3 + \cos 2 \Delta \Omega - 9 \cos 2\omega \right) \right. \right. \right. \nonumber \\&+ \left. \left. \left. 6 \cos 2 \Delta \Omega \cos 2\omega \sin ^2 I_\text {X}\right) + \cos 2 I_\text {X} \right. \right. \nonumber \\&\left. \left. \times \left( 9 \cos 2\omega + 2 \sin ^2\Delta \Omega \right) \right. \right. \nonumber \\&+ \left. \left. 2 \left( 3\cos 2\omega \left( \sin ^2 I + 3 \cos 2 \Delta \Omega \sin ^2 I_\text {X}\right) \right. \right. \right. \nonumber \\&\left. \left. \left. + 4 \left( 3 \left( \sin I \sin 2 I_\text {X}\sin \Delta \Omega -\right. \right. \right. \right. \right. \nonumber \\&+ \left. \left. \left. \left. \left. \cos I \sin ^2 I_\text {X} \sin 2\Delta \Omega \right) \sin 2\omega + \cos \Delta \Omega \sin 2 I_\text {X}\nonumber \right. \right. \right. \right. \\&\times \left. \left. \left. \left. \left( -2 \sin I + 3 \sin 2 I \sin ^2\omega + \tan \left( {I\over 2}\right) \right) \right) \right) \right) \right\} \nonumber \\&+ \mathcal {O}\left( e^2\right) . \end{aligned}$$

(B2)

If the hypothesis of circularity and coplanarity with the test particle is assumed for the orbit of X [18], the exact precession yields a shift per orbit

$$\begin{aligned} \Delta \varpi = -{2\uppi \mu _\text {X}a^2 \sqrt{1-e^2}\over c^2a^3_\text {X}}. \end{aligned}$$

(B3)

The second line of Eq. (4) of Will [18] yields the following 1pN acceleration of order $\mathcal {O}\left( G\right)$

$$\begin{aligned} {\varvec{A}}_{G}= & {} {\mu _\text {X} r\over c^2 r^3_\text {X}}\Big \{ 4\varvec{v}\left[ \left( \varvec{v}\varvec{\cdot }\varvec{\hat{r}} \right) - 3\left( \varvec{\hat{r}}\varvec{\cdot }{\varvec{\hat{r}}}_\text {X} \right) \left( \varvec{v}\varvec{\cdot }{\varvec{\hat{r}}}_\text {X} \right) \right] \nonumber \\&- \left. v^2\left[ \varvec{\hat{r}} -3\left( \varvec{\hat{r}}\varvec{\cdot }{\varvec{\hat{r}}}_\text {X}\right) {\varvec{\hat{r}}}_\text {X} \right] \right\} . \end{aligned}$$

(B4)

We were able to calculate its exact, doubly averaged perihelion precession without a priori simplifying assumptions on $e,~I,~\Omega ,~\omega ,~e_\text {X},~I_\text {X},~\Omega _\text {X},~\omega _\text {X}$. Unfortunately, it is particularly cumbersome, and cannot be explicitly displayed here. An important feature of it is that, for arbitrary orbital configurations, the precession due to Eq. (B4) is not defined for $e\rightarrow 0$ since it contains terms of order $\mathcal {O}\left( e^{-k}\right) ,~k=2,~4$. By expanding it in powers of e, we have

$$\begin{aligned} \frac{{{\text {d}}}{\varpi }}{{{\text {d}}}{t}}&= {9\sqrt{\mu a}\mu _\text {X}\left( 1 - 2e^2\right) \over 4c^2 e^4 a_\text {X}^3\left( 1 - e_\text {X}^2\right) ^{3/2}}\left\{ \cos 2\omega \left[ (1 + 3 \cos 2I_\text {X}) \sin ^2 I \right. \right. \nonumber \\&\quad +\left. \left. \left( 3 + \cos 2I\right) \sin ^2 I_\text {X}\cos 2\Delta \Omega - 2 \sin 2I \sin 2I_\text {X}\cos \Delta \Omega \right] \right. \nonumber \\&\quad +\left. 4\sin 2\omega \left( -\cos I \sin ^2 I_\text {X} \sin 2\Delta \Omega + \sin I \sin 2I_\text {X} \sin \Delta \Omega \right) \right\} \nonumber \\&\quad +\mathcal {O}\left( e^0\right) . \end{aligned}$$

(B5)

By assuming $e_\text {X}=0,~I = I_\text {X},~\Omega = \Omega _\text {X}$ [18], the resulting full shift per revolution of the test particle turns out to be

$$\begin{aligned} \Delta \varpi = -{7\uppi \mu _\text {X}a^2 \sqrt{1-e^2}\over 2c^2a^3_\text {X}}. \end{aligned}$$

(B6)

In the case of Mercury, the discrepancy between the full precession and the coplanarity-based approximated one, from which Eq. (B6) was derived, amounts to $\simeq -0.03~\text {mas cty}^{-1}$ for X=Venus.

The third line of Eq. (4) of Will [18] provides us with the following 1pN “gravitomagnetic” acceleration of order $\mathcal {O}\left( G\right)$ due to the velocity ${\varvec{v}}_\text {X}$ of the third body

$$\begin{aligned} {\varvec{A}}_{v_\text {X}} = -{\mu _\text {X}\over c^2 r_\text {X}^2}\left[ 4\varvec{v}\varvec{\times }\left( {\varvec{\hat{r}}}_\text {X}\varvec{\times }{\varvec{v}}_\text {X} \right) - 3\left( {\varvec{\hat{r}}}_\text {X} \varvec{\cdot }{\varvec{v}}_\text {X} \right) \varvec{v}\right] . \end{aligned}$$

(B7)

Its exact, doubly averaged perihelion precession turns out to be

$$\begin{aligned} \frac{{{\text {d}}}{\varpi }}{{{\text {d}}}{t}} = {2\mu _\text {X}n_\mathrm{b}^\text {X}\over c^2 a_\text {X}\left( 1-e^2_\text {X}\right) }\left[ \cos I_\text {X} + \sin I_\text {X}\tan \left( {I\over 2}\right) \cos \Delta \Omega \right] .\nonumber \\ \end{aligned}$$

(B8)

For $\Delta \Omega =0,~I=I_\text {X},~e_\text {X}=0$, Eq. (B8) agrees with the precession which can be inferred from the fourth term of Eq. (1) of Will [18] by taking the ratio of it to the orbital period $P_\mathrm{b}$ of the perturbed test particle. The numerical discrepancy between Eq. (B8) and the approximated expression by Will is negligible; indeed, in the case of Mercury perturbed by Venus, they differ by just $2\times 10^{-5}~\text {mas cty}^{-1}$ yielding both ${\dot{\varpi }} = 0.014~\text {mas cty}^{-1}$. The total contribution of all planets from Venus to Saturn to the Mercury’s precession of Eq. (B8) amounts to ${\dot{\varpi }} = 0.06~\text {mas cty}^{-1}$.

See Table 2 for a detailed overview of the contributions of the planets from Venus to Saturn to the Mercury’s direct 1pN third-body perihelion precession. It can be noted that, while the total “gravitomagnetic” effect arising from the third line of Eq. (4) of Will [18] agrees with the results by Will [18] himself, our total precession due to the first two lines of Eq. (4) of Will [18] is about half than that claimed by Will [18]. Such a discrepancy seems to be attributable to the indirect, mixed effects.