Magnetic dipole moments of the negative parity $J^{PC}=2^{--}$ mesons in QCD

Abstract

Magnetic dipole moments of the negative parity light and heavy tensor mesons are calculated within the light cone QCD sum rules method. The results are compared with the positive parity counterparts of the corresponding tensor mesons. The results of the analysis show that the magnetic dipole moments of the negative parity light mesons are smaller compared to those of the positive parity mesons. Contrary to the light meson case, magnetic dipole moments of the negative parity heavy mesons are larger than the ones for the positive parity mesons.

1 Introduction

The study of the spectroscopy of particles plays a critical role in understanding the dynamics of quantum chromodynamics (QCD), both at large and short distances. According to the conventional quark model, the particles are characterized by the $J^{PC}$ quantum numbers $P=(-1)^{L+1}$ and $C=(-1)^{L+S}$, where L and S are the orbital angular momentum and the total spin, respectively. The spectroscopy of the particles with the quantum numbers $J^{PC}=0^{\pm +}$, $1^{\pm -}$, $1^{++}$ are widely investigated elsewhere in the literature. The mass and residues of light tensor mesons are studied firstly in [1] in the framework of the QCD sum rules method. Later similar studies are extended for the strange tensor mesons in [2]. The masses and decay constants of the ground states of the heavy $\chi _{Q_2}$ tensor mesons are investigated within the same framework in [3]. The relevant quantities in understanding the internal structure of the mesons and baryons are their electromagnetic form factors and multipole moments, such as the dipole moments. The dipole moments for the heavy and light tensor mesons with the quantum number $J^P=2^+$ are investigated in the framework of the light cone QCD sum rules in [4] and [5], respectively. The negative parity tensor mesons have received less attention. The first attempt has recently been made to calculate the mass and decay constants of the negative parity $\bar{q}q$, $\bar{q}s$, $\bar{s}s$, $\bar{q}c$, $\bar{s}c$, $\bar{q}b$, $\bar{s}b$, and $\bar{c}b$ tensor mesons within the QCD sum rules method in [6].

In the present work, we calculate the magnetic dipole moments of these negative parity tensor mesons in the framework of the light cone QCD sum rules method (for more about the light cone QCD sum rules approach, see [7] and [8]).

The paper is organized as follows. Section 2 is devoted to the derivation of the light cone QCD sum rules for the magnetic dipole moment of the negative parity mesons $\bar{q}q$, $\bar{q}s$, $\bar{s}s$, $\bar{q}c$, $\bar{s}c$, $\bar{q}b$ and $\bar{s}b$. In Sect. 3, numerical analysis of the obtained sum rules for the dipole moments of the $2^{--}$ tensor mesons is performed. This section also contains the discussions and a brief summary of the present study.

2 Theoretical framework

In this section we derive the light-cone sum rules for the magnetic dipole moments of the negative parity tensor mesons. For this goal, we consider the 3-point correlation function,

$$\begin{aligned} \Pi _{\mu \nu \rho \alpha \beta } (p,q)= & {} - \int d^4x \int d^4y e^{i(px+qy)} \nonumber \\&\left\langle 0 \left| {\mathcal T} \Big \{ j_{\mu \nu } (x) j_\rho ^{el}(y) \bar{j}_{\alpha \beta }(0) \Big \} \right| 0 \right\rangle , \end{aligned}$$

(1)

where $j_{\mu \nu }$ is the interpolating current for the tensor meson with $J^{PC}=2^{--}$,

$$\begin{aligned} j_{\mu \nu } = {i\over 2} \left[ \bar{q}_1(x) \gamma _\mu \gamma _5 {\mathop {\mathcal D}\limits ^{\leftrightarrow }}_\nu q_2(x) + \bar{q}_2 (x) \gamma _\nu \gamma _5 {\mathop {\mathcal D}\limits ^{\leftrightarrow }}_\mu q_1(x) \right] .\nonumber \\ \end{aligned}$$

(2)

The electromagnetic current $j_\rho ^{el}$ in Eq. (1) is defined as,

$$\begin{aligned} j_\rho ^{el} = e_{q_1} \bar{q}_1 \gamma _\rho q_1 + e_{q_2} \bar{q}_2 \gamma _\rho q_2, \end{aligned}$$

where $e_{q_i}$ is the electric charge of the corresponding quark. The momenta p and q are carried by the currents $j_{\mu \nu }$ and $j_\rho ^{el}$, respectively.

The covariant derivative ${\mathop {\mathcal D}\limits ^{\leftrightarrow }}$ is defined as

$$\begin{aligned} {\mathop {\mathcal D}\limits ^{\leftrightarrow }}_\mu (x) = {1\over 2} \Big [ {\mathop {\mathcal D}\limits ^{\rightarrow }}_\mu (x) - {\mathop {\mathcal D}\limits ^{\leftarrow }}_\mu (x) \Big ] , \end{aligned}$$

(3)

where

$$\begin{aligned} {\mathop {\mathcal D}\limits ^{\rightarrow }}_\mu (x)= & {} {\mathop {\partial }\limits ^{\rightarrow }}_\mu (x) - i {g\over 2} \lambda ^a A_\mu ^a (x) , \\ {\mathop {\mathcal D}\limits ^{\leftarrow }}_\mu (x)= & {} {\mathop {\partial }\limits ^{\leftarrow }}_\mu (x) + i {g\over 2} \lambda ^a A_\mu ^a (x). \end{aligned}$$

Here $A_\mu ^a (x)$ is the gluon field, satisfying the Fock–Schwinger gauge condition $x^\mu A_\mu ^a (x)=0$, which we have used in the present work, and $\lambda ^a$ are the Gell-Mann matrices.

The correlation function can be rewritten in terms of the external background electromagnetic field. For this goal, it is necessary to introduce plane wave background electromagnetic field,

$$\begin{aligned} F_{\mu \nu } = i (q_\mu \varepsilon _\nu -q_\nu \varepsilon _\mu ) e^{iqx}, \end{aligned}$$

where $\varepsilon _\mu$ and $q_\mu$ are the polarization and four-momentum vectors of this field, respectively. The radiated photon can be absorbed into the background field. This allows us to rewrite the correlation function as,

$$\begin{aligned} \varepsilon ^\rho \, \Pi _{\mu \nu \rho \alpha \beta } = i \int d^4x e^{ipx} \left\langle 0 \left| T \Big \{ j_{\mu \nu } (x) \bar{j}_{\alpha \beta } (0) \right| 0 \right\rangle _F, \end{aligned}$$

(4)

where the subindex F means that the vacuum expectation value is calculated in the background electromagnetic field.

Note that the correlation function given in Eq. (1) can be obtained from Eq. (4) by expanding it in powers of $F_{\mu \nu }$ and taking only the terms linear in $F_{\mu \nu }$ (more technical details about the external background field method can be found in [9, 10]). The main advantage of using the background field method is that it separates the hard and soft contributions in a gauge invariant way. Hence, the main object of our discussion is the correlation function given in Eq. (4). Here a cautionary note is in order. Since the current $J_{\mu \nu }$ contains derivatives, we first replace $\bar{J}_{\alpha \beta }(0)$ in Eq. (4) with $\bar{J}_{\alpha \beta }(y)$, and after carrying out the derivative with respect to y we set the variable y to zero.

To obtain the sum rules for the magnetic dipole moment the tensor mesons, one should insert the spin-2 mesons into the correlation function. Separating the contribution of the ground state tensor mesons we obtain,

$$\begin{aligned} \varepsilon ^\rho \Pi _{\mu \nu \rho \alpha \beta }= & {} i {\left\langle 0 \left| j_{\mu \nu } \right| T(p,\epsilon ) \right\rangle \over p^2-m_T^2} \left\langle T(p,\epsilon ) \left| \right. T(p\right. \nonumber \\&\left. +\,q,\epsilon ) \right\rangle _F {\left\langle T(p+q,\epsilon ) \left| \bar{j}_{\alpha \beta } \right| 0 \right\rangle \over (p+q)^2-m_T^2}+ \cdots , \end{aligned}$$

(5)

where dots mean contributions of the higher states of spin-2 mesons. The matrix element $\left\langle 0 \left| j_{\mu \nu } \right| T(p,\epsilon ) \right\rangle$ is defined as,

$$\begin{aligned} \left\langle 0 \left| j_{\mu \nu } \right| T(p,\epsilon ) \right\rangle = g_T m_T^3 \epsilon _{\mu \nu } , \end{aligned}$$

(6)

where $g_T$ is the decay constant, and $\epsilon _{\mu \nu }$ is the polarization matrix of the tensor meson.

In the presence of the background electromagnetic field, the transition matrix element $\left\langle T(p\epsilon ) \vert T(p+q,\epsilon ) \right\rangle _F$ is parametrized as follows:

$$\begin{aligned}&\left\langle T(p,\epsilon ) \vert T(p+q,\epsilon ) \right\rangle _F = \epsilon _{\alpha ^\prime \beta ^\prime }^*(p) \Bigg \{ 2 (\varepsilon p) \Bigg [ g^{\alpha ^\prime \rho } g^{\beta ^\prime \sigma } F_1(q^2)\nonumber \\&\quad -\, g^{\beta ^\prime \sigma } {q^{\alpha ^\prime } q^\rho \over 2 m_T^2} F_3(q^2) + {q^{\alpha ^\prime } q^\rho \over 2 m_T^2}\, {q^{\beta ^\prime } q^\sigma \over 2 m_T^2} F_5(q^2) \Bigg ] \nonumber \\&\quad +\,(\varepsilon ^{\sigma } q^{\beta ^\prime } - \varepsilon ^{\beta ^\prime } q^\sigma ) \Bigg [ g^{\alpha ^\prime \rho } F_2(q^2) - {q^{\alpha ^\prime } q^\rho \over 2 m_T^2} F_4(q^2) \Bigg ] \Bigg \}\nonumber \\&\quad \epsilon _{\rho \sigma } (p+q), \end{aligned}$$

(7)

where $F_i(q^2)$ are the form factors.

In the analysis of the experimental data, it is more convenient to use the form factors of a definite multipole in a given reference frame. Relations between these two sets of form factors for the arbitrary integer, and half-integer spin are derived in [11], and the relations for the real photon case are:

$$\begin{aligned} F_1(0)= & {} G_{E_0}(0) , \nonumber \\ F_2(0)= & {} G_{M_1}(0) , \nonumber \\ F_3(0)= & {} - 2 G_{E_0}(0) + G_{E_2}(0) + G_{M_1}(0) , \nonumber \\ F_4(0)= & {} - G_{M_1}(0) + G_{M_3}(0) , \nonumber \\ F_5(0)= & {} G_{E_0}(0) - [ G_{E_2}(0) + G_{M_1}(0) ]\nonumber \\&+\, G_{E_4}(0) + G_{M_3}(0) , \end{aligned}$$

(8)

where $G_{E_\ell }(0)$ and $G_{M_\ell }(0)$ are the electric and magnetic multipoles. Substituting these form factors in Eq. (7) we get,

$$\begin{aligned}&\left\langle T(p,\epsilon )\left| T(p+q,\epsilon ^\prime ) \right. \right\rangle _F = \epsilon _{\alpha ^\prime \beta ^\prime }^*(p) \Bigg \{ 2 (\varepsilon p) \Bigg [ g^{\alpha ^\prime \rho } g^{\beta ^\prime \sigma } G_{E_0}\nonumber \\&\quad -\, {q^{\alpha ^\prime } q^\rho \over 2 m_T^2} g^{\beta ^\prime \sigma } (-2 G_{E_0} + G_{E_2} + G_{M_1} ) \nonumber \\&\quad +\, {q^{\alpha ^\prime } q^\rho \over 2 m_T^2} {q^{\beta ^\prime } q^\sigma \over 2 m_T^2} ( G_{E_0} - G_{E_2} - G_{M_1} + G_{E_4} + G_{M_3} ) \Bigg ] \nonumber \\&\quad +\,(\varepsilon ^{\sigma } q^{\beta ^\prime } - \varepsilon ^{\beta ^\prime } q^\sigma ) \Bigg [ g^{\alpha ^\prime \rho } G_{M_1} - {q^{\alpha ^\prime } q^\rho \over 2 m_T^2} ( - G_{M_1}\nonumber \\&\quad +\,G_{M_3} ) \Bigg ] \Bigg \} \epsilon _{\rho \sigma } (p+q). \end{aligned}$$

(9)

In order to obtain the correlation function from the physical side, we substitute Eqs. (6) and (9) into Eq. (5), and perform summation over the spins of the tensor particles by using,

$$\begin{aligned} \epsilon _{\mu \nu } (p) \epsilon _{\alpha \beta }^*(p)= & {} {1\over 2} {\mathcal P}_{\mu \alpha } {\mathcal P}_{\nu \beta }+ {1\over 2} {\mathcal P}_{\mu \beta } {\mathcal P}_{\nu \alpha }- {1\over 3} {\mathcal P}_{\mu \nu } {\mathcal P}_{\alpha \beta } ,\nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned} {\mathcal P}_{\mu \nu } = -g_{\mu \nu } + {p_\mu p_\nu \over m_T^2},~ \end{aligned}$$

we obtain,

$$\begin{aligned}&\Pi _{\mu \nu \rho \alpha \beta } (p,q) \, \varepsilon ^\rho = {m_{T}^6 g_{T}^2 \over (p^2-m_{T}^2) [(p+q)^2-m_{T}^2]}\nonumber \\&\quad \times \Big \{ {1\over 2} {\mathcal P}_{\mu \alpha ^\prime }(p) {\mathcal P}_{\nu \beta ^\prime }(p) + {1\over 2} {\mathcal P}_{\mu \beta ^\prime }(p) {\mathcal P}_{\nu \alpha ^\prime }(p) \nonumber \\&\quad -\,{1\over 3} {\mathcal P}_{\mu \nu }(p) {\mathcal P}_{\alpha ^\prime \beta ^\prime }(p) \Big \} \times \Bigg \{2 (\varepsilon p) \Bigg [ g^{\alpha ^\prime \rho } g^{\beta ^\prime \sigma } G_{E_0}(0)\nonumber \\&\quad -\, g^{\beta ^\prime \sigma } {q^{\alpha ^\prime } q^\rho \over 2 m_{T}^2} \Big ( - 2 G_{E_0}(0)+G_{E_2}(0) \nonumber \\&\quad +\,G_{M_1}(0)\Big ) + {q^{\alpha ^\prime } q^\rho \over 2 m_{T}^2}\, {q^{\beta ^\prime } q^\sigma \over 2 m_{T}^2} \Big (G_{E_0}(0)\nonumber \\&\quad -\, [G_{E_2}(0) + G_{M_2}(0)] + G_{E_4}(0) + G_{M_3}(0)\Big ) \Bigg ]\nonumber \\&\quad +\,\Big (\varepsilon ^\sigma q^{\beta ^\prime } - \varepsilon ^{\beta ^\prime } q^\sigma \Big ) \Bigg [ g^{\alpha ^\prime \rho } G_{M_1}(0)\nonumber \\&\quad -\, {q^{\alpha ^\prime } q^\rho \over 2 m_{T}^2} \Big ( - G_{M_1}(0) + G_{M_2}(0)\Big ) \Bigg ] \Bigg \} \nonumber \\&\quad \times \Big \{ {1\over 2} {\mathcal P}_{\rho \alpha }(p+q) {\mathcal P}_{\sigma \beta }(p+q) \nonumber \\&\quad + {1\over 2} {\mathcal P}_{\rho \beta }(p+q) {\mathcal P}_{\alpha \sigma }(p+q) -\, {1\over 3} {\mathcal P}_{\rho \sigma }(p) {\mathcal P}_{\alpha \beta }(p+q) \Big \}.\nonumber \\ \end{aligned}$$

(11)

One can easily see that the expression of the correlation function contains many independent structures and any one of these structures can be used in the analysis of the multipole moments of the tensor mesons. In this work, we restrict ourselves to calculate the magnetic dipole form factor only and for this aim, we choose the structure,

$$\begin{aligned} \left[ (\varepsilon _{\beta } q_\nu - \varepsilon _{\nu } q_\beta ) g_{\mu \alpha } + (\varepsilon _{\beta } q_\mu - \varepsilon _{\mu } q_\beta ) g_{\nu \alpha }\right] , \end{aligned}$$

whose coefficient is,

$$\begin{aligned} \Pi= & {} {m_T^6 g_T^2 \over (p^2-m_T^2) [(p+q)^2 - m_T^2]} \nonumber \\&\Bigg \{ {1\over 4} G_{M_1} + \text{ other } \text{ structures } \Bigg \} + \cdots . \end{aligned}$$

(12)

The choice of this structure is dictated by the fact that it contains contributions coming solely from spin-2 states, and does not include any contribution from the contact terms (see [12]).

Before calculating the operator product expansion (OPE) from the QCD side few words about the QCD factorization of the correlation function are in order. It should be noted here that at the operator level, formulation of the QCD factorization for the hadronic form factors is discussed in [13]. We are planning to discuss the factorization procedure of the correlator function (4) at tree and ${\mathcal O}(\alpha _s)$ level elsewhere in future.

Using OPE, we calculate the correlation from the QCD side in deep Euclidean region where $p^2 \rightarrow -\infty$ and $(p+q)^2 \rightarrow -\infty$. After contracting all quark fields we obtain,

$$\begin{aligned}&\Pi _{\mu \nu \rho \alpha \beta } (p,q) \, \varepsilon ^\rho = {-i \over 16} \int e^{ip\cdot x} d^4x \left\langle 0 \left| \Big \{ S_{q_1} (y\right. \right. \nonumber \\&\quad -\,x) \gamma _\mu \gamma _5 \Big [ {\mathop {\partial }\limits ^{\rightarrow }}_\nu (x) {\mathop {\partial }\limits ^{\rightarrow }}_\beta (y) - {\mathop {\partial }\limits ^{\rightarrow }}_\nu (x) {\mathop {\partial }\limits ^{\leftarrow }}_\beta (y) \nonumber \\&\quad -\, {\mathop {\partial }\limits ^{\leftarrow }}_\nu (x) {\mathop {\partial }\limits ^{\rightarrow }}_\beta (y) + {\mathop {\partial }\limits ^{\leftarrow }}_\nu (x) {\mathop {\partial }\limits ^{\leftarrow }}_\beta (y) \Big ] S_{q_2} (x\nonumber \\&\quad \left. \left. -y) \gamma _\alpha \gamma _5 \Big \}\right| 0 \right\rangle _F+ \{ \beta \leftrightarrow \alpha \} + \{ \nu \leftrightarrow \mu \} \nonumber \\&\quad +\,\{ \beta \leftrightarrow \alpha ,~ \nu \leftrightarrow \mu \} . \end{aligned}$$

(13)

As has been noted, we set $y=0$ after performing the derivatives with respect to y. It follows from Eq. (13) that in the calculation of the correlation function the quark propagators are needed. The expression of the light quark propagator is given as,

$$\begin{aligned}&S_q(x-y) = S^{free} (x-y) - {\langle \bar{q} q \rangle \over 12} \Bigg [1 -i {m_q \over 4} (\not \!{x}-\not \!{y}) \Bigg ]\nonumber \\&\quad -\, {(x-y)^2 \over 192} m_0^2 \langle \bar{q} q \rangle \Bigg [1 -i {m_q \over 6} (\not \!{x}-\not \!{y}) \Bigg ] \nonumber \\&\quad -\, i g_s \int _0^1 du \Bigg \{ {\not \!x - \not \!{y} \over 16 \pi ^2 (x-y)^2} G_{\mu \nu }(u(x-y)) \sigma ^{\mu \nu }\nonumber \\&\quad -\, u (x^\mu -y^\mu ) G_{\mu \nu }(u(x-y)) \gamma ^\nu \nonumber \\&\quad \times {i \over 4 \pi ^2 (x-y)^2} - i {m_q \over 32 \pi ^2} G_{\mu \nu }(u(x-y)) \sigma ^{\mu \nu }\nonumber \\&\quad \Bigg [ \ln \left( -{(x-y)^2 \Lambda ^2 \over u} + 2 \gamma _E \right) \Bigg ] \Bigg \}, \end{aligned}$$

(14)

where

$$\begin{aligned} S_q^{free} (x-y) = {i (\not \!x-\not \!y) \over 2 \pi ^2 (x-y)^4} - {m_q \over 4 \pi ^2 (x-y)^2} , \end{aligned}$$

is the free quark propagator. In the expression of light quark propagator given above, $\Lambda$ is some cut off parameter separating low momentum nonperturbative regime from the high momentum perturbative region, whose value should be of the order of a few 100 MeV. For definiteness, in the present work we choose $\Lambda =0.5~\mathrm{{GeV}}$ (see for example [14]). It should be remembered that the light cone expansion of the light quark propagator is obtained in [15], which gets contributions from nonlocal three $\bar{q}G q$, and four-particle $\bar{q}q\bar{q}q$, $\bar{q}G^2 q$ operators, where $G_{\mu \nu }$ is the gluon strength tensor. Expansion in conformal spin proves that the contributions coming from four-particle operators are small and can be neglected [16].

The expression of the complete heavy quark propagator in the coordinate space is given as,

$$\begin{aligned}&S_Q(x-y) = S_Q^{free} - {g_s \over 16 \pi ^2} \int _0^1 du G_{\mu \nu }(u(x-y))\nonumber \\&\quad \times \Bigg ( i \Big [\sigma ^{\mu \nu } (\not \!{x}-\not \!{y}) + (\not \!{x}-\not \!{y}) \sigma ^{\mu \nu }\Big ] \nonumber \\&\quad \times {K_1 (m_Q\sqrt{-(x-y)^2})\over \sqrt{-(x-y)^2}} + 2 \sigma ^{\mu \nu } K_0(m_Q\sqrt{-(x-y)^2})\Bigg )\Bigg \}\nonumber \\&\quad +\cdots , \end{aligned}$$

(15)

respectively, where $K_i(m_Q\sqrt{-x^2})$ are the modified Bessel functions. The free part of the heavy quark propagator has the following form:

$$\begin{aligned}&S_Q^{free}(x-y) = {m_Q^2 \over 4 \pi ^2} \Bigg \{ {K_1(m_Q\sqrt{-(x-y)^2}) \over \sqrt{-(x-y)^2}} \\&\quad +\,i {(\not \!{x}-\not \!{y}) \over -(x-y)^2} K_2(m_Q\sqrt{-(x-y)^2}) \Bigg \} . \end{aligned}$$

The correlation function given in Eq. (13) gets contributions from following parts: (a) Perturbative contribution, (b) “Mixed contribution”, (c) Long distance contribution. The perturbative contribution is obtained by replacing one of the quark propagators by,

$$\begin{aligned} S(x-y) = \int d^4z \, S^{free}(x-z) \not \!\!{A} (z) S^{free}(z-y) , \end{aligned}$$

(16)

and the other propagator is replaced by the free quark propagator . The “mixed contribution” is calculated by replacing one of the quark propagators by (16) and the other quark propagator is taken as the full propagator given in Eqs. (14) or (15). The long distance contribution is obtained from Eq. (13) by replacing the light quark propagator that emits a photon (if we have two light quark propagators, only one of them should be replaced) by

$$\begin{aligned} S_{\mu \nu }^{ab}(x-y) \rightarrow -{1\over 4} \bar{q}^a (x) \Gamma _\rho q^b (y) \left( \Gamma _\rho \right) _{\mu \nu }, \end{aligned}$$

(17)

where $\Gamma _\rho =\left\{ 1,\gamma _5,\gamma _\mu ,i\gamma _5\gamma _\mu , \sigma _{\mu \nu }/\sqrt{2}\right\}$. Moreover, matrix elements of the nonlocal operators, such as $\bar{q}(x) \Gamma q(y)$, $\bar{q}(x) F_{\mu \nu }\Gamma q(y)$, and $\bar{q}(x) G_{\mu \nu } \Gamma q(y)$ appear between vacuum and photon states, when a photon interacts with the light quark fields at large distance. Parametrization of these matrix elements in terms of the photon distribution amplitudes (DAs) is given in [10],

$$\begin{aligned}&\langle \gamma (q) \vert \bar{q}(x) \sigma _{\mu \nu } q(0) \vert 0 \rangle = -i e_q \langle \bar{q} q \rangle (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu )\\&\quad \int _0^1 du e^{i \bar{u} qx} \left( \chi \varphi _\gamma (u) + \frac{x^2}{16} \mathbb {A} (u) \right) \\&-\frac{i}{2(qx)} e_q \langle \bar{q} q \rangle \left[ x_\nu \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{qx}\right) - x_\mu \left( \varepsilon _\nu \right. \right. \\&\left. \left. \quad - q_\nu \frac{\varepsilon x}{q x}\right) \right] \int _0^1 du e^{i \bar{u} q x} h_\gamma (u) \\&\quad \langle \gamma (q) \vert \bar{q}(x) \gamma _\mu q(0) \vert 0 \rangle = e_q f_{3 \gamma } \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x} \right) \\&\quad \int _0^1 du e^{i \bar{u} q x} \psi ^v(u) \\&\quad \langle \gamma (q) \vert \bar{q}(x) \gamma _\mu \gamma _5 q(0) \vert 0 \rangle = - \frac{1}{4} e_q f_{3 \gamma } \epsilon _{\mu \nu \alpha \beta } \varepsilon ^\nu q^\alpha x^\beta \\&\quad \int _0^1 du e^{i \bar{u} q x} \psi ^a(u) \\&\qquad \langle \gamma (q) | \bar{q}(x) g_s G_{\mu \nu } (v x) q(0) \vert 0 \rangle \\&\quad = -i e_q \langle \bar{q} q \rangle \left( \varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu \right) \int {\mathcal D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} {\mathcal S}(\alpha _i) \\&\qquad \langle \gamma (q) | \bar{q}(x) g_s \tilde{G}_{\mu \nu } i \gamma _5 (v x) q(0) \vert 0 \rangle \\&\quad = -i e_q \langle \bar{q} q \rangle \left( \varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu \right) \int {\mathcal D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \tilde{\mathcal S}(\alpha _i) \\&\qquad \langle \gamma (q) \vert \bar{q}(x) g_s \tilde{G}_{\mu \nu }(v x) \gamma _\alpha \gamma _5 q(0) \vert 0 \rangle \\&\quad = e_q f_{3 \gamma } q_\alpha (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int {\mathcal D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} {\mathcal A}(\alpha _i)\\&\qquad \langle \gamma (q) \vert \bar{q}(x) g_s G_{\mu \nu }(v x) i \gamma _\alpha q(0) \vert 0 \rangle \\&\quad = e_q f_{3 \gamma } q_\alpha (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int {\mathcal D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} {\mathcal V}(\alpha _i) \\&\langle \gamma (q) \vert \bar{q}(x) \sigma _{\alpha \beta } g_s G_{\mu \nu }(v x) q(0) \vert 0 \rangle = e_q \langle \bar{q} q \rangle \\&\quad \left\{ \left[ \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x}\right) \left( g_{\alpha \nu } - \frac{1}{qx} (q_\alpha x_\nu + q_\nu x_\alpha )\right) \right. \right. q_\beta \end{aligned}$$

$$\begin{aligned}&\quad -\, \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x}\right) \left( g_{\beta \nu } - \frac{1}{qx} (q_\beta x_\nu + q_\nu x_\beta )\right) q_\alpha \\&\quad -\, \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q x}\right) \left( g_{\alpha \mu } - \frac{1}{qx} (q_\alpha x_\mu + q_\mu x_\alpha )\right) q_\beta \\&\quad +\,\left. \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q.x}\right) \left( g_{\beta \mu } - \frac{1}{qx} (q_\beta x_\mu + q_\mu x_\beta )\right) q_\alpha \right] \\&\quad \int {\mathcal D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} {\mathcal T}_1(\alpha _i) \\&\quad + \left[ \left( \varepsilon _\alpha - q_\alpha \frac{\varepsilon x}{qx}\right) \left( g_{\mu \beta } - \frac{1}{qx}(q_\mu x_\beta + q_\beta x_\mu )\right) \right. q_\nu \\&- \left( \varepsilon _\alpha - q_\alpha \frac{\varepsilon x}{qx}\right) \left( g_{\nu \beta } - \frac{1}{qx}(q_\nu x_\beta + q_\beta x_\nu )\right) q_\mu \\&\quad -\, \left( \varepsilon _\beta - q_\beta \frac{\varepsilon x}{qx}\right) \left( g_{\mu \alpha } - \frac{1}{qx}(q_\mu x_\alpha + q_\alpha x_\mu )\right) q_\nu \\&\quad +\,\left. \left( \varepsilon _\beta - q_\beta \frac{\varepsilon x}{qx}\right) \left( g_{\nu \alpha } - \frac{1}{qx}(q_\nu x_\alpha + q_\alpha x_\nu ) \right) q_\mu \right] \\&\quad \int {\mathcal D} \alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} {\mathcal T}_2(\alpha _i) \\&\quad + \frac{1}{qx} (q_\mu x_\nu - q_\nu x_\mu ) (\varepsilon _\alpha q_\beta - \varepsilon _\beta q_\alpha ) \\&\quad \int {\mathcal D} \alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} {\mathcal T}_3(\alpha _i) \\&\quad + \left. \frac{1}{qx} (q_\alpha x_\beta - q_\beta x_\alpha ) (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu )\right. \\&\left. \int {\mathcal D} \alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} {\mathcal T}_4(\alpha _i) \right\} \\&\quad \langle \gamma (q) \vert \bar{q}(x) e_q F_{\mu \nu } (vx) q(0) \vert 0 \rangle = -i e_q \langle \bar{q} q \rangle \left( \varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu \right) \\&\quad \int {\mathcal D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} {\mathcal S}^\gamma (\alpha _i)\\&\quad \langle \gamma (q) \vert \bar{q}(x) \sigma _{\alpha \beta } F_{\mu \nu } (vx) q(0) \vert 0 \rangle = e_q \langle \bar{q} q \rangle {1\over qx} (q_\alpha x_\beta \\&\quad -\, q_\beta x_\alpha ) \left( \varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu \right) \\&\quad \times \int {\mathcal D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} {\mathcal T}_4^\gamma (\alpha _i), \end{aligned}$$

where $\varphi _\gamma (u)$ is the leading twist–2, $\psi ^v(u)$, $\psi ^a(u)$, ${\mathcal A}$ and ${\mathcal V}$ are the twist–3, and $h_\gamma (u)$, $\mathbb {A}$, ${\mathcal S}$, $\widetilde{\mathcal S}$, ${\mathcal S}^\gamma$, ${\mathcal T}_i$ ($i=1,~2,~3,~4$), ${\mathcal T}_4^\gamma$ are the twist–4 photon DAs, $\chi$ is the magnetic susceptibility, and the measure ${\mathcal D} \alpha _i$ is defined as

$$\begin{aligned} \int {\mathcal D} \alpha _i = \int _0^1 d \alpha _{\bar{q}} \int _0^1 d \alpha _q \int _0^1 d \alpha _g \delta (1-\alpha _{\bar{q}}-\alpha _q-\alpha _g) . \end{aligned}$$

Equating the coefficients of the Lorentz structure $\left[ (\varepsilon _{\beta } q_\nu - \varepsilon _{\nu } q_\beta ) g_{\mu \alpha } + (\varepsilon _{\beta } q_\mu - \varepsilon _{\mu } q_\beta ) g_{\nu \alpha }\right]$ from both representations of the correlation function, the sum rules for the magnetic moments of the negative parity tensor mesons are obtained. To suppress the contributions of the higher states and continuum, double Borel transformation with respect to the variables $-p^2$ and $-(p+q)^2$ is performed. After this transformation, finally, for the magnetic moments of the negative parity tensor mesons we get the following sum rules:

• Light tensor mesons

$$\begin{aligned}&{m_T^6 g_T^2 \over 4} e^{-m_{T}^2/M^2} G_{M_1}(q^2=0) = {1\over 24} M^2 E_0(x)\nonumber \\&\quad \Big [ e_{q_1} m_{q_2} \langle \bar{q}_1 q_1 \rangle \Big ( \mathbb {A}(u_0) + 4 u_0 j_1(h_\gamma ) - 2 \widetilde{j}_1(h_\gamma ) \Big ) \nonumber \\&\quad -\, e_{q_2} m_{q_1} \langle \bar{q}_2 q_2 \rangle \Big ( \mathbb {A}(\bar{u}_0) + 2 j_2(h_\gamma ) + \widetilde{j}_2(h_\gamma ) \Big ) \Big ] \nonumber \\&\quad -\, {1\over 48 \pi ^2} M^4 E_1(x) (3-4 u_0) (e_{q_1} - e_{q_2}) m_{q_1} m_{q_2} \nonumber \\&\quad -\, {1\over 48} f_{3\gamma } M^4 E_1(x) \Big [e_{q_2} \Big ( 8 j_2(\psi _v) - \psi _a(\bar{u}_0) \nonumber \\&\quad + \,4 \psi _v(\bar{u}_0) +\psi _a^\prime (\bar{u}_0) \Big ) \nonumber \\&\quad - \,e_{q_1} \Big (8 j_1(\psi _v) - \psi _a(u_0) + 2 u_0 (4 \psi _v(u_0) -\psi _a^\prime (u_0))\Big )\Big ] \nonumber \\&\quad -\, {1\over 240 \pi ^2} M^6 E_2(x) (5 - 18 u_0) (e_{q_1} - e_{q_2}) \nonumber \\&\quad -\, {1\over 72} m_0^2 [e_{q_2} \langle \bar{q}_1 q_1 \rangle (m_{q_1} - 3 m_{q_2}) \nonumber \\&\quad +\, e_{q_1} \langle \bar{q}_2 q_2 \rangle (3 m_{q_1} - m_{q_2})] . \end{aligned}$$

(18)

• Heavy tensor mesons

$$\begin{aligned}&{m_{T}^6 g_{T}^2 \over 4} e^{-m_{T}^2/M^2} G_{M_1}(q^2=0) \nonumber \\&\quad \!= {1 \over 1152 \pi ^2} \Big [e_q \langle g_s^2 G^2 \rangle M^2 \left( 2 m_Q^2 {\mathcal I}_2 - m_Q^4 {\mathcal I}_3\right) \Big ]\nonumber \\&\qquad -\, {e^{-m_Q^2/M^2}\over 3456 m_Q \pi ^2} M^2 \Big \{9 m_Q \left( e_q \langle g_s^2 G^2 \rangle - 96 e_Q m_Q \pi ^2 \langle \bar{q} q \rangle \right) \nonumber \\&\qquad -\, 4 e_q \pi ^2 \Big [18 m_Q^2 \langle \bar{q} q \rangle \left( \mathbb {A} (u_0) + 2 \widetilde{j}_1(h_\gamma ) + 4 \widetilde{j}_2(h_\gamma )\right) \nonumber \\&\qquad +\, \langle g_s^2 G^2 \rangle \langle \bar{q} q \rangle \chi \varphi _\gamma (u_0) - 36 f_{3\gamma } m_Q^3 \psi ^a (u_0)\Big ]\Big \} \nonumber \\&\qquad +\,{1\over 32 \pi ^2} e_Q m_Q^4 M^4 \left( {\mathcal I}_2 - m_Q^2 {\mathcal I}_3\right) \nonumber \\&\qquad +\,{e^{-m_Q^2/M^2}\over 96} e_q M^4 \Big \{8 f_{3\gamma } \widetilde{j}_1(\psi ^v) - 8 m_Q \langle \bar{q} q \rangle \chi \varphi _\gamma (u_0) \nonumber \\&\qquad -\, f_{3\gamma } \Big [6 \psi ^a (u_0) - 4 \psi ^v(u_0) + \psi ^{a\prime }(u_0)\Big ]\Big \} \nonumber \\&\qquad + {e^{-m_Q^2/M^2}\over 16 \pi ^2} e_q M^6 \nonumber \\&\qquad +\,{1\over 32\pi ^2} m_Q^2 M^6 \Big [2 e_Q {\mathcal I}_2 - 3 e_Q m_Q^2 {\mathcal I}_3 - 4 e_Q m_Q^4 {\mathcal I}_4 \nonumber \\&\qquad -\, 2 e_q m_Q^4 {\mathcal I}_4 - 2 (e_Q - e_q) m_Q^6 {\mathcal I}_5 \Big ] \end{aligned}$$

$$\begin{aligned}&\qquad -\, {e^{-m_Q^2/M^2}\over 6912 M^2} m_Q \Big \{432 e_Q m_0^2 m_Q^2 \langle \bar{q} q \rangle \nonumber \\&\qquad -\, e_q \langle g_s^2 G^2 \rangle \Big [4 \langle \bar{q} q \rangle \mathbb {A} (u_0) - 4 (5 - 4 u_0) \langle \bar{q} q \rangle \widetilde{j}_1(h_\gamma ) \nonumber \\&\qquad -\, 40 \langle \bar{q} q \rangle \widetilde{j}_2(h_\gamma ) + m_Q \Big (8 m_Q \langle \bar{q} q \rangle \chi \varphi _\gamma (u_0)\nonumber \\&\qquad -\, f_{3\gamma } (8 \widetilde{j}_1(\psi ^v) - 6 \psi ^a (u_0) - 4 \psi ^v(u_0) - \psi ^{a\prime }(u_0))\Big )\Big ]\Big \} \nonumber \\&\qquad -\, {e^{-m_Q^2/M^2}\over 3456 M^4} e_q \langle g_s^2 G^2 \rangle m_Q^3 \Big [\langle \bar{q} q \rangle \Big (\mathbb {A} (u_0) + 2 \widetilde{j}_1(h_\gamma ) \nonumber \\&\qquad +\,4 \widetilde{j}_2(h_\gamma )\Big ) - 2 f_{3\gamma } m_Q \psi ^a (u_0) \Big ] \nonumber \\&\qquad -\, {e^{-m_Q^2/M^2}\over 3456 M^6} e_q \langle g_s^2 G^2 \rangle m_Q^5 \langle \bar{q} q \rangle \mathbb {A} (u_0) - {e^{-m_Q^2/M^2}\over 3456 m_Q \pi ^2} e_q \nonumber \\&\qquad \times \Big \{4 (\langle g_s^2 G^2 \rangle - 18 m_Q^4) \pi ^2 \langle \bar{q} q \rangle \mathbb {A} (u_0) \nonumber \\&\qquad +\,\langle g_s^2 G^2 \rangle \Big [3 m_Q^3 + \pi ^2 \Big (4 (2 + u_0) \langle \bar{q} q \rangle \widetilde{j}_1(h_\gamma ) \nonumber \\&\qquad +\,16 \langle \bar{q} q \rangle \widetilde{j}_2(h_\gamma ) - m_Q \{12 m_Q \langle \bar{q} q \rangle \chi \varphi _\gamma (u_0) \nonumber \\&\qquad -\, f_{3\gamma } [12 \widetilde{j}_1(\psi ^v) + 2 \psi ^a (u_0) \nonumber \\&\qquad +\,(2 - u_0) (4 \psi ^v(u_0) - \psi ^{a\prime }(u_0))]\}\Big )\Big ] \Big \} , \end{aligned}$$

(19)

where

$$\begin{aligned} u_0={M_1^2 \over M_1^2 +M_2^2} ,\quad M^2={M_1^2 M_2^2 \over M_1^2 +M_2^2} . \end{aligned}$$

The functions $j_n(f(u))$, and $\widetilde{j}_1(f(u))~(n=1,2)$ are defined as:

$$\begin{aligned} j_1(f(u^\prime ))= & {} \int _{u_0}^1 du^\prime f(u^\prime ) , \\ \widetilde{j}_1(f(u^\prime ))= & {} \int _{u_0}^1 du^\prime (u^\prime - u_0) f(u^\prime ) , \\ j_2(f(u^\prime ))= & {} \int _{0}^{\bar{u}_0} du^\prime f(u^\prime ) , \\ \widetilde{j}_2(f(u^\prime ))= & {} \int _{0}^{\bar{u}_0} du^\prime (u^\prime - \bar{u}_0) f(u^\prime ) ,\\ E_n(x)= & {} 1 - e^{-x} \sum _{k=0}^{n} {x^k\over k!} = {1\over n!} \int _0^x dx^\prime x^{\prime n} e^{-x^\prime } ,\\ {\mathcal I}_n= & {} \int _{m_Q^2}^{s_0} ds\, {e^{-s/M^2} \over s^n} , \end{aligned}$$

with $x=s_0/M^2$, $s_0$ being the continuum threshold, and the Borel parameter $M^2$ is defined as,

$$\begin{aligned} M^2 = {M_1^2 M_2^2 \over M_1^2 + M_2^2}~\text{ and },~u_0={M_1^2\over M_1^2 + M_2^2} . \end{aligned}$$

Since we have the same heavy tensor mesons in the initial and final states, we can set $M_1^2=M_2^2=2 M^2$, as the result of which we have,

$$\begin{aligned} u_0={M_1^2 \over (M_1^2+M_2^2)}={1\over 2} . \end{aligned}$$

3 Numerical analysis

In this section, we perform the numerical analysis of the sum rules for the magnetic dipole moments of the negative parity tensor mesons derived in the previous section. The input parameters used in the numerical analysis are, $\langle \bar{u} u \rangle (\mu =1~\mathrm{{GeV}}) = \langle \bar{d} d \rangle (\mu =1~\mathrm{{GeV}}) = -(1.65 \,\pm \, 0.15)\times 10^{-2}~\mathrm{{GeV}}^3$, $\langle \bar{s} s \rangle \vert _{\mu =1~\mathrm{{GeV}}} = (0.8 \pm 0.2) \langle \bar{u} u \rangle (\mu =1~\mathrm{{GeV}})$, $m_0^2=(0.8\pm 0.2)~\mathrm{{GeV}}^2$ [17] which are obtained from the mass sum rule analysis for the light baryons [18, 19] and B meson [20]. Furthermore, we have used the $\overline{MS}$ values of the heavy quarks masses whose values are $\bar{m}_b(\bar{m}_b)=(4.16\pm 0.03)~\mathrm{{GeV}}$ and $\bar{m}_c(\bar{m}_c)=(1.28\pm 0.03)~\mathrm{{GeV}}$ [21, 22]. The magnetic susceptibility $\chi$ of quarks is calculated in the framework of the QCD sum rules in [23,24,25]. In further numerical analysis we have used $\chi (1~\mathrm{{GeV}}) = -(2.85 \pm 0.5)~\mathrm{{GeV}}^{-2}$ [23]. As we have already noted, the masses of the negative parity tensor mesons are calculated in [6], which we have used in the present work. By using the results of [6] for the mass sum rules, we further have calculated the decay constants of $J=2^-$ mesons which are needed in the numerical analysis.

The key input parameters in the present numerical analysis are the DAs. Below we display only the expressions of the DAs that enter to the sum rules for the magnetic dipole moments.

$$\begin{aligned} \varphi _\gamma (u)= & {} 6 u \bar{u} \Big [ 1 + \varphi _2(\mu ) C_2^{\frac{3}{2}}(u - \bar{u}) \Big ] , \nonumber \\ \psi ^v(u)= & {} 3 [3 (2 u - 1)^2 -1 ]+\frac{3}{64} (15 w^V_\gamma - 5 w^A_\gamma ) \nonumber \\&[3 - 30 (2 u - 1)^2 + 35 (2 u -1)^4] , \nonumber \\ \psi ^a(u)= & {} [1- (2 u -1)^2] [ 5 (2 u -1)^2 -1 ]\nonumber \\&\frac{5}{2} \Bigg (1 + \frac{9}{16} w^V_\gamma - \frac{3}{16} w^A_\gamma \Bigg ) , \nonumber \\ {\mathcal A}(\alpha _i)= & {} 360 \alpha _q \alpha _{\bar{q}} \alpha _g^2 \Bigg [ 1 + w^A_\gamma \frac{1}{2} (7 \alpha _g - 3)\Bigg ] , \nonumber \\ {\mathcal V}(\alpha _i)= & {} 540 w^V_\gamma (\alpha _q - \alpha _{\bar{q}}) \alpha _q \alpha _{\bar{q}} \alpha _g^2 , \nonumber \\ h_\gamma (u)= & {} - 10 (1 + 2 \kappa ^+ ) C_2^{\frac{1}{2}}(u - \bar{u}) , \nonumber \\ \mathbb {A}(u)= & {} 40 u^2 \bar{u}^2 (3 \kappa - \kappa ^+ +1 ) + 8 (\zeta _2^+ - 3 \zeta _2)\nonumber \\&\quad [u \bar{u} (2 + 13 u \bar{u}) + 2 u^3 (10 -15 u + 6 u^2) \ln (u) \nonumber \\&+\, 2 \bar{u}^3 (10 - 15 \bar{u} + 6 \bar{u}^2) \ln (\bar{u}) ]. \end{aligned}$$

(20)

The values of the constant parameters in the DAs are given as: $\varphi _2(1~\mathrm{{GeV}}) = 0$, $w^V_\gamma = 3.8 \pm 1.8$, $w^A_\gamma = -2.1 \pm 1.0$, $\kappa = 0.2$, $\kappa ^+ = 0$, $\zeta _1 = 0.4$, $\zeta _2 = 0.3$, $\zeta _1^+ = 0$ and $\zeta _2^+ = 0$ [10].

The sum rules for the magnetic dipole moments of the negative parity $J^{PC}=2^{--}$ tensor mesons which are obtained in the previous section contain two more arbitrary parameters, in addition to the input parameters summarized above: Borel mass parameter $M^2$ and the continuum threshold $s_0$. In the analysis of the sum rules, the working regions of these two parameters should be determined, such that the magnetic dipole moments exhibit weak dependence on these parameters. The working region of $M^2$ should satisfy the following requirements: The upper limit of $M^2$ is determined from the condition that the higher states contributions constitute maximum 40% of the perturbative ones. The lower bound of $M^2$ is obtained by requiring that the OPE should be convergent, i.e., the higher twist contributions should be less than the leading twist contributions. From these conditions, we have obtained the working domains of $M^2$ of the $J^{PC}=2^{--}$ tensor mesons, which are listed in Table 1.

The working regions of the continuum threshold $s_0$ for the $J^{PC}=2^{--}$ tensor mesons are determined from the analysis of the two–point correlation function in [6], which we have used in our numerical calculations. The values of the continuum threshold $s_0$ of the corresponding tensor mesons are also listed in Table 1.

Table 1 The working regions of the Borel parameter $M^2$, and the corresponding values of the continuum threshold $s_0$ for the $J^{PC}=2^{--}$ tensor mesons (these values are taken from [6])

Fig. 1

Dependence of the magnetic dipole moment of the negative parity $K_2^+$ tensor meson, on Borel mass square $M^2$, at several fixed values of the continuum threshold, in units of Nuclear Magneton $\mu _N$

Fig. 2

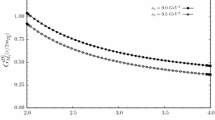
The same as Fig. 1, but for the negative parity ${\mathcal D}_2^0$ tensor meson

Using the values of the input parameters and the working regions of $M^2$ and $s_0$, the values of the magnetic dipole moments can be determined. As n example, in Figs. 1 and 2 we present the dependence of the magnetic dipole moments of $K_2^+$ and ${\mathcal D}_2^0$ mesons on $M^2$ at several fixed values of $s_0$, respectively. It follows from these figures that the magnetic dipole moments show a weak dependence on $M^2$ in its working region. Similar analysis for the other $J^{PC}=2^{--}$ tensor mesons are carried out whose results are presented in Table 2.

Table 2 The values of the magnetic dipole moments of the negative and positive parity tensor mesons in units of the nuclear magneton $\mu _N$

For completeness, we also give the values of the magnetic dipole moments for the positive parity tensor mesons in the same table. From the comparison of the results we deduce that:

• In the case of light tensor mesons, the magnetic dipole moments of the negative parity mesons are 2–5 times smaller compared to that for the positive parity mesons.

• For the heavy tensor mesons, however, the situation is to the contrary namely, the magnetic moments of the negative parity tensor mesons are larger compared to the ones for the positive parity mesons.

These results can be explained by the fact that, the terms proportional to the quark mass appearing in the expressions of the sum rules for the magnetic moment of the popsitive and negative parity mesons, have opposite sign. Therefore, the contributions coming from the heavy quark mass terms are constructive (destructive) for the negative (positive) parity tensor mesons. Additionally, this difference can be attributed to the differences in masses and residues of the tensor mesons of both parities.

Finally, we shall briefly discuss how one can measure the magnetic dipole moment in experiments. One of the methods for determination of the multipole moments of particles is based on the soft photon emission of the hadrons [26], since the photon carries information about the higher multipole moments of the emitted particle. The matrix element for the radiative process can be written in terms of the photon energy $E_\gamma$ as follows:

$$\begin{aligned} M \sim {A\over E_\gamma } + B (E_\gamma )^0 + C E_\gamma + \cdots \end{aligned}$$

The contribution coming from the magnetic dipole moment is described by the term $(E_\gamma )^0$. Therefore, by measuring the widths of the radiative decays, one can determine the magnetic dipole moment of the tensor mesons under consideration.

In summary, the magnetic dipole moments of the light and heavy $J^{PC}=2^{--}$ tensor mesons are calculated in the framework of the light cone QCD sum rules method. Comparison of the predictions for the magnetic dipole moments of the negative and positive parity mesons is also presented. It is observed that the results for the magnetic dipole moments of the negative parity light mesons are smaller compared to the ones for the corresponding positive parity tensor mesons, while the situation is to the contrary for the heavy tensor mesons.