1 Introduction

Spherically symmetric solutions in gravity are fundamental tools in order to describe the structure and physical properties of compact stars. There is a large number of interior exact spherically symmetric solutions of Einstein’s theory of gravitation (for reviews see [1, 2]). But, very few of them satisfy the necessary physical and continuity conditions for a compact fluid. Some of them were given by Mak and Harko [3,4,5] for an isotropic neutral spherically symmetric matter distribution.

A charged compact star may be more stable [6] and prevent the gravitationally collapse [7, 8], therefore it is interesting to consider the case with charge. The charged solutions of Einstein–Maxwell field equations which describe a strange quark star were found by Mak and Harko [9] considering a symmetry of conformal motions with MIT bag model.

Since the Einstein’s theory of gravity has significant observational problems at large cosmological scales [10,11,12,13,14,15,16,17], one need to search new theories of gravitation which are acceptable even at these scales. Some compact star solutions in such modified theories as the hybrid metric-Palatini gravity [18] and Eddington-inspired Born–Infeld (EIBI) gravity [19], were studied numerically.

One can consider that a charged astrophysical object can described by the minimal coupling between the gravitational and electromagnetic fields known as Einstein–Maxwell theory. However, the above problems of Einstein’s gravity at large scales can also lead to investigate the \(Y(R)F^2\) type modification of Einstein–Maxwell theory [20,21,22,23,24,25,26,27,28,29,30]. Such non-minimal modifications can also be found in [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42] to obtain more information on the interaction between electromagnetic and gravitational fields and all other energy forms. The non-minimal couplings also can arise in such compact objects as black holes, quark stars and neutron stars which have very high density gravitational and electromagnetic fields [42]. If the extreme situations are disappeared, that is far from the compact stars the model turns out to be the Einstein–Maxwell case.

Here we consider the non-minimal \(Y(R)F^2\) type modification to the Einstein–Maxwell theory and generalize the exact solutions for radiation fluid case \(k=1\) in [42] to the cases with \(k\ne 1\), inspired by the study [9]. We obtain the inner region solutions and construct the corresponding model which turns to the Einstein–Maxwell theory in the outer region. We note that the inner solutions recover the solution obtained by Misner and Zapolsky [43] for charge-less case and \(b=0\). We find the surface gravitational redshift, matter mass, total mass and charge in terms of boundary radius and the parameters k and \(\alpha \) via the continuity and boundary conditions.

We organize the paper as follows: In Sect. 2, we give the non-minimal \(Y(R)F^2\) gravity model and field equations in order to describe a compact fluid. In Sect. 3, we obtain exact static, spherically symmetric solutions of the model under the conformal symmetry and the corresponding Y(R) function. In Sect. 4, we determine the total mass, charge and gravitational redshift of the star in terms of boundary radius and the parameters of the model k and \(\alpha \). We summarize the results in the last section.

2 The model for a compact star

Compact stars have very intense energy density, pressure and gravitational fields. They also can have very high electric fields in order to balance the huge gravitational pulling [6,7,8, 44,45,46,47,48,49]. Even if they collapse, very high electric fields necessary to explain the formation of electrically charged black holes [50, 51]. Moreover they can have very strong magnetic fields [52]. Therefore the new non-minimal interactions between these electromagnetic and gravitational fields with \(Y(R)F^2\) type can arise under the extreme situations. Thus we consider the following non-minimal model for compact stars, which involves the Lagrangian of the electromagnetic source \(A\wedge J\) and the matter part \(L_{mat}\) in the action [42]

(1)

Here \(e^a\) is the orthonormal co-frame 1-form, \( {\omega ^a}_b\) is the Levi-Civita connection 1-form obtaining by the relation \(T^a = de^a + \omega ^{a}_{\;\;b} \wedge e^b=0\), F is the electromagnetic tensor 2-form which is derived from the electromagnetic potential A via the exterior derivative, that is \( F=dA\); \(\lambda _a\) is the Lagrange multiplier which gives torsion-less space-times, \(T^a=0\); R is the Ricci scalar and J is the electromagnetic current density in the star.

The co-frame variation of the action (1) is given by the following gravitational field equation after eliminating the connection variation,

$$\begin{aligned} - \frac{1}{2 \kappa ^2} R_{bc} \wedge *e^{abc}= & {} Y (\iota ^a F \wedge *F - F \wedge \iota ^a *F)\nonumber \\&+\, Y_R F_{mn} F^{mn}*R^a\nonumber \\&+\, D [ \iota _b\;d(Y_R F_{mn} F^{mn} )]\wedge *e^{ab}\nonumber \\&+\,(\rho +p)u^a*u + p*e^a, \end{aligned}$$
(2)

where we have used the velocity 1-form \(u=u_a e^a \) for time-like inertial observer and \( \frac{dY}{dR} = Y_R \). Furthermore we have considered the matter energy momentum tensor has the energy density \(\rho \) and the pressure p as diagonal elements for the isotropic matter in the star. It is worth to note that the total energy–momentum tensor which is right hand side of the gravitational field Eq. (2) satisfies the conservation relation [42]. The electromagnetic potential variation of the action gives the following modified Maxwell field equation

$$\begin{aligned} d(*Y F)=J. \end{aligned}$$
(3)

We have also the identity \( dF = d(dA)= 0 \). We will find solutions to the field equations (2) and (3) under the condition

$$\begin{aligned} Y_R F_{mn} F^{mn} = - \frac{ k}{ \kappa ^2} \end{aligned}$$
(4)

which eliminates the instabilities of the higher order derivatives in the theory. Here we note that the constant kFootnote 1 determines the strength of the non-minimal coupling between gravitational and electromagnetic fields. The case with \(k=0\) leads to \(Y(R)= constant \) and this case corresponds to minimal Einstein–Maxwell theory which can be considered as the exterior vacuum Reissner–Nordström solution with \(R=0\). The additional features of the constraint (4) can be found in [42]. On the other hand, the trace of the non-minimally coupled gravitational field equation (2) gives

$$\begin{aligned} \frac{1-k}{\kappa ^2} R*1 = (\rho - 3p)*1. \end{aligned}$$
(5)

Since the case with \(k= 1\) or \(\rho = 3p \) is investigated as the radiation fluid stars in [42], we concentrate on the case with \(k\ne 1\) or \(\rho \ne 3p\) in this study.

3 Spherically symmetric solutions under conformal symmetry

We take the following static, spherically symmetric metric and Maxwell 2-form with the electric component E which has only radial dependence

$$\begin{aligned}&ds^2 = -f^2(r)dt^2 + g^2(r)dr^2 + r^2d\theta ^2 +r^2\sin ^2\theta d \phi ^2,\end{aligned}$$
(6)
$$\begin{aligned}&F = E(r) e^1\wedge e^0. \end{aligned}$$
(7)

Then the charge in the star can be obtained from the integral of the current density 3-form J over the volume V with radius r using the Maxwell equation (3)

$$\begin{aligned} q(r) = \frac{1}{4\pi }\int _V J =\frac{1}{4\pi } \int _{V} d*YF = YEr^2. \end{aligned}$$
(8)

The Ricci scalar for the metric (6) is calculated as

$$\begin{aligned} R = \frac{2}{g^2} \left( \frac{f' g' }{fg} - \frac{f''}{f} + \frac{2g'}{gr} - \frac{2f'}{fr} + \frac{g^2 -1 }{r^2} \right) . \end{aligned}$$
(9)

For \(k\ne 1 \) or \(\rho \ne 3p \) the gravitational field equation (2) gives

$$\begin{aligned}&\frac{1}{\kappa ^2 g^2}\left( \frac{2g'}{rg} + \frac{g^2-1}{r^2}\right) + \frac{k}{\kappa ^2 g^2}\left( \frac{f''}{f} -\frac{f'g'}{fg} + \frac{2f'}{rf} \right) \nonumber \\&\quad =YE^2 + \rho , \end{aligned}$$
(10)
$$\begin{aligned}&\frac{1}{\kappa ^2 g^2}\left( - \frac{2f'}{rf} + \frac{g^2-1}{r^2}\right) +\frac{k}{\kappa ^2 g^2}\left( \frac{f''}{f} -\frac{f'g'}{fg} - \frac{2g'}{rg}\right) \nonumber \\&\quad =YE^2 - p, \end{aligned}$$
(11)
$$\begin{aligned}&\frac{1}{ \kappa ^2 g^2}\left( \frac{f''}{f} - \frac{f'g'}{fg} +\frac{f'}{rf} -\frac{g'}{rg}\right) \nonumber \\&\qquad +\, \frac{k}{ \kappa ^2 g^2}\left( \frac{g'}{rg} - \frac{f'}{rf} + \frac{g^2 -1 }{r^2}\right) =Y E^2 + p, \end{aligned}$$
(12)

under the condition (4)

$$\begin{aligned} \frac{dY}{dR} = \frac{k}{ 2\kappa ^2 E^2}. \end{aligned}$$
(13)

The conservation of the total energy–momentum tensor for the gravitational field equation (2) requires that

$$\begin{aligned} p' + (p+\rho ) \frac{f'}{f} - 2(YE)'E - \frac{4YE^2}{r}=0. \end{aligned}$$
(14)

Assuming the metric (6) has the conformal symmetry \( L_\xi g_{ab} = \phi (r) g_{ab} \) which describe the interior gravitational field of stars [9, 53,54,55], the metric functions \(f^2(r) \) and \(g^2(r)\) were found in [53] as

$$\begin{aligned} f^2(r)=a^2 r^2,\quad g^2(r) = \frac{\phi ^2_0}{\phi ^2}= \frac{1}{X}. \end{aligned}$$
(15)

Here \(\phi (r)\) is an arbitrary function of r, \( L_\xi \) is Lie derivative of the metric tensor along the vector field \(\xi \), X is a new function, \( \phi _0 \) and a are arbitrary constants. Then we obtain the following differential equation system from (10)–(14) under the symmetry,

$$\begin{aligned}&k\left( \frac{X'}{2\kappa ^2 r} + \frac{2X }{\kappa ^2 r^2}\right) -\frac{X'}{\kappa ^2 r} + \frac{ 1-X }{\kappa ^2 r^2} = YE^2 + \rho , \end{aligned}$$
(16)
$$\begin{aligned}&\frac{3k X'}{2 \kappa ^2 r} + \frac{1- 3 X}{\kappa ^2 r^2} = Y E^2 -p,\end{aligned}$$
(17)
$$\begin{aligned}&k\left( -\frac{X'}{2\kappa ^2 r } + \frac{1-2X}{\kappa ^2 r^2}\right) + \frac{X'}{\kappa ^2r } + \frac{X}{\kappa ^2 r^2} = YE^2 +p, \end{aligned}$$
(18)
$$\begin{aligned}&p' + \frac{p}{r} +\frac{\rho }{r} - 2(YE)'E - \frac{4YE^2}{r} =0. \end{aligned}$$
(19)

with the condition (13). Since we aim to extend the solution given in [42] to compact stars without introducing an equation of state, we take the following metric function with the real numbers \(\alpha > 2\) and \(b\ne 0\) inspired by [9],

$$\begin{aligned} g^2(r) = \frac{1}{X} = \frac{3}{ 1 + br^\alpha }. \end{aligned}$$
(20)

We see that the metric function is regular at center of coordinate \(r=0\) and leads to the following regular Ricci scalar

$$\begin{aligned} R= - b(\alpha +2) r^{\alpha -2}. \end{aligned}$$
(21)

Then we found the following class of solutions to the system of equation (16)–(20)

$$\begin{aligned}&E^2(r) = \frac{(1+k) ( br^\alpha (\alpha -2) +1)^{\frac{k(4\alpha +6) +\alpha }{(1+k) \alpha }} }{6\kappa ^2 r^2}, \end{aligned}$$
(22)
$$\begin{aligned}&p(r) = \frac{1+ k}{6\kappa ^2 r^2} - \frac{br^\alpha ( 2\alpha k -\alpha +2k -4 )}{6\kappa ^2 r^2}, \end{aligned}$$
(23)
$$\begin{aligned}&\rho (r) = \frac{1+ k}{2\kappa ^2 r^2} + \frac{br^\alpha ( 2k-\alpha )}{2\kappa ^2 r^2}, \end{aligned}$$
(24)
$$\begin{aligned}&Y(r) = C\left[ 1 + b(\alpha -2)r^\alpha \right] ^{-\frac{3(\alpha +2)k}{(1+k)\alpha }}. \end{aligned}$$
(25)

where C is an integration constant. We see that the solutions are dependent on the parameter k introduced by (13) together with the parameter \(\alpha \) in the metric function (20). The charge of the star (8) inside a spherical volume with radius r can be calculated by the charge-radius equality

$$\begin{aligned} q^2(r) = \frac{ (1+k)r^2 \left[ 1+b(\alpha -2)r^\alpha \right] ^{-\frac{2\alpha k- \alpha + 6 k }{(1+k)\alpha } }}{6\kappa ^2}. \end{aligned}$$
(26)

It can be seen that the charge is regular at \(r=0\) for \(\alpha >2\). By solving r in terms of R as the inverse function r(R) from (21), we re-express the non-minimal coupling function (25) as

$$\begin{aligned} Y(R)= C \left[ 1 + b(\alpha -2) \left( \frac{-R}{\alpha b +2b} \right) ^{\frac{\alpha }{\alpha -2}} \right] ^{-\frac{3(\alpha +2)k}{(1+k)\alpha }}. \end{aligned}$$
(27)
Fig. 1
figure 1

Variation of the pressure (a) and energy density (b) as a function of the radial distance r inside the star with the boundary radius \(r_b=10~\hbox {km}\) and the parameter \(\alpha =3\)

Full size image

We can consider that the exterior vacuum region is described by Reissner–Nordström metric with \(R=0\). Then the nonminimal function becomes \(Y(R) = C\) and our model involves the Einstein–Maxwell theory as a minimal case at the exterior region with \(C=1\). Thus we have the more general Lagrangian of the non-minimal theory which describe the compact stars for \(\alpha >2\)

$$\begin{aligned} L= & {} \frac{1}{2\kappa ^2} R*1 - \left[ 1+ b(\alpha -2) ( \frac{-R}{\alpha b +2b} )^{\frac{\alpha }{\alpha -2} } \right] ^{-\frac{3(\alpha +2)k}{(1+k)\alpha }}\nonumber \\&\times \, F\wedge *F + 2A\wedge J + L_{mat} + \lambda _a\wedge T^a. \end{aligned}$$
(28)

The field equations of the Lagrangian (28) accept the solutions with the electric field (22), pressure (23), energy density (24), electric charge (26) and the following metric tensor in the star

$$\begin{aligned} ds^2 _{in}= - a^2r^2dt^2 + \frac{3}{1+br^\alpha } dr^2 + r^2 d\Omega ^2. \end{aligned}$$
(29)

We will determine the power \(\alpha \) and k in the model from observational data and the constant b from the matching and continuity conditions (33). In the absence of the electromagnetic source and matter, the Lagrangian of the non-minimally coupled theory (28) can reduce to the Einstein–Maxwell Lagrangian with \(Y(R)=1\) at the exterior of the star as a vacuum case, and field equations of the minimal theory accept the well known Reissner–Nordström metric

$$\begin{aligned} ds^2_{out}= & {} -\left( 1-\frac{2M}{r} + \frac{\kappa ^2Q^2}{r^2}\right) dt^2\nonumber \\&+\left( 1-\frac{2M}{r} + \frac{\kappa ^2Q^2}{r^2}\right) ^{-1}dr^2 + r^2d\Omega ^2 \end{aligned}$$
(30)

with the exterior electric field \( E(r) = \frac{Q}{ r^2}\), where Q is total electric charge of the star.

4 Continuity conditions

The continuity of the interior (29) and exterior Reissner–Nordström metric at the boundary of the charged star \(r=r_b\) leads to

$$\begin{aligned}&a^2 = \frac{\kappa ^2 Q^2 - 2Mr_b + r_b^2 }{r_b^4},\end{aligned}$$
(31)
$$\begin{aligned}&b =\frac{ 2r_b^2 - 6Mr_b + 3\kappa ^2Q^2 }{r_b^{2+\alpha }}. \end{aligned}$$
(32)

At the boundary of the star the pressure (23) should be zero

$$\begin{aligned} p(r_b)= & {} \frac{1+ k}{6\kappa ^2 r_b^2} - \frac{br_b^\alpha ( 2\alpha k -\alpha +2k -4 )}{6\kappa ^2 r_b^2} = 0, \end{aligned}$$
(33)

the condition determines the constant b in the non-minimal theory (28) as

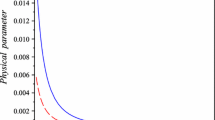
$$\begin{aligned} b = \frac{1+k}{(2\alpha k- \alpha +2k -4 )r_b^\alpha }. \end{aligned}$$
(34)

Using this constant, variation of the pressure and energy density as a function of the radial distance r inside the star is given in Fig. 1. The interior of the star is considered as the specific fluid which has very high gravitational fields, electromagnetic fields and matter. Then the electromagnetic fields obey the modified Maxwell field equation \(d*YF =J \) in matter. The integral of the modified Maxwell equation (3) gives the charge in volume with radius r in the star, \(q(r) = YEr^2 \) (26). On the other hand, the Ricci scalar is zero at the exterior of the star and then, using (27), we can take the non-minimal function as \(Y=1\) and obtain the Maxwell field equation \(d*F=0\) which leads to the total charge \(Q= E r^2\) at the exterior region. Here the displacement field YE inside of the star turns out to be the electric field E outside. Setting by \(r=r_b\) in Eq. (26) the total charge of the star \(Q=q(r_b)\) is found as

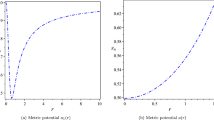
$$\begin{aligned} Q^2 = \frac{ (1+k)r_b^2 \left[ 1+ \frac{(1+k)(\alpha -2)}{(2\alpha k- \alpha +2k -4 )} \right] ^{-\frac{2\alpha k- \alpha + 6 k }{(1+k)\alpha } }}{6\kappa ^2}. \end{aligned}$$
(35)

Then the outside electric field is given by \(E=Q/r^2\). The total charge-boundary radius ratio obtained from (35) is plotted by Fig. 2a dependent on the parameter \(\alpha \) for some different k values.

Fig. 2
figure 2

Variation of the dimensionless quantities which are related with the total electric charge Q and the matter mass \(M_m\) as a function of the dimensionless parameter \(\alpha \) for some different k values

Full size image

The matter mass of the star \(M_m\) can be found from the integral of the energy density \(\rho \)

$$\begin{aligned} M_m= & {} \frac{\kappa ^2}{2} \int _0^{r_b} \rho r^2 dr\nonumber \\= & {} \frac{r_b (1+k) ((k-\frac{1}{2})\alpha ^2 + (2k-3)\alpha + 2k -2 )}{2(2\alpha k -\alpha +2k -4)(\alpha +1)}.\nonumber \\ \end{aligned}$$
(36)

The figure of the matter mass \(M_m\) is shown in Fig. 2b for increasing \(\alpha \) and some different k values. We see that the total charge and matter mass of the star increase with the increasing k values.

When we compare the constant b given by the Eqs. (34) and (32), we find the following mass-charge relation for the model

$$\begin{aligned} \frac{M}{r_b}= \frac{4\alpha k -2\alpha +3k-9}{6(2\alpha k -\alpha + 2k -4 )} + \frac{\kappa ^2 Q^2}{2r_b^2}. \end{aligned}$$
(37)

By substituting the total charge (35) in (37), the total mass-radius ratio \(M/r_b\) can be found in terms of the parameters \(\alpha \) and k of the model

$$\begin{aligned} \frac{M}{r_b}= & {} \frac{4\alpha k -2\alpha +3k-9}{6(2\alpha k -\alpha + 2k -4 )}\nonumber \\&+\, \frac{1+k}{12} \left[ 1+ \frac{(1+k)(\alpha -2)}{2\alpha k -\alpha +2k -4}\right] ^{-\frac{\alpha (2k-1) +6k}{(1+k)\alpha }}. \end{aligned}$$
(38)

The gravitational redshift z at the boundary is obtained from

$$\begin{aligned} z= & {} \left( 1-\frac{2M}{r_b} + \frac{\kappa ^2 Q^2}{r_b^2}\right) ^{- \frac{1}{2}} -1\nonumber \\= & {} \sqrt{\frac{3(2\alpha k -\alpha +2 k -4)}{2\alpha k -\alpha +3k -3} } -1. \end{aligned}$$
(39)

By taking the limit \(\alpha ,k \rightarrow \infty \), the maximum redshift is found as \(z = \sqrt{3} -1 \approx 0.732\) same with \(k=1\) in [42]. The upper redshift bound is smaller than the Buchdahl bound \(z = 2\) and the bound given in [56].

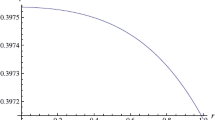
The mass-radius relation and the gravitational redshift-radius relation are shown in Fig. 3a, b, respectively, depending on the parameter \(\alpha \) for some k values. We see that as the k value increases, the mass and redshift increases.

Fig. 3
figure 3

Variation of the dimensionless quantity which is related with the gravitational mass M and the gravitational surface redshift z as a function of the dimensionless parameter \(\alpha \) for some different k values

Full size image

To obtain an interval for the parameter k we consider the energy density condition inside the star

$$\begin{aligned} \rho (r) = \frac{1+ k}{2 \kappa ^2 r^2} -\frac{b(\alpha -2k)r^{(\alpha -2)} }{2 \kappa ^2 } \ge 0. \end{aligned}$$
(40)

At the center of the star the condition

$$\begin{aligned} \lim \limits _{r\rightarrow 0} \rho (r) = \frac{1+k}{2\kappa ^2 r^2} \ge 0 \end{aligned}$$
(41)

gives \(k\ge -1 \). On the other hand, at the boundary \(r=r_b\) the condition (40) turns out to be

$$\begin{aligned} 1 \ge \frac{(\alpha -2k)}{2\alpha k -\alpha +2 k -4}. \end{aligned}$$
(42)

The solution of the inequality (42) is

$$\begin{aligned} k \ge 1\quad or\quad -1< k \le \frac{\alpha +4}{2\alpha +2}. \end{aligned}$$
(43)

Then we can choose \(k\ge 1\) without loss of generality. The derivative of the pressure p(r) according to the energy density \(\rho (r)\) is calculated as

$$\begin{aligned} \frac{dp}{d\rho } = \frac{(2\alpha k - \alpha +2k -4 ) (\alpha r^\alpha +2 r_b^\alpha -2 r^\alpha )}{ 6(2\alpha k - \alpha +2k -4)r_b^\alpha + 3(\alpha -2k)(\alpha -2)r^\alpha }.\nonumber \\ \end{aligned}$$
(44)

The phase speed of the sound waves in the star is defined by \( (\frac{dp}{d\rho } )^{1/2} \) and the speed satisfies the causality condition \( (\frac{dp}{d\rho } )^{1/2} <1 \) for \(k\ge 1\) and \(\alpha >2 \) values (see Fig. 6a for some values), where the speed of light \( \mathtt {c} =1\). Thus each possible values of the parameters \(k>1\) and \(\alpha >2\) in the modified model give a mass, charge-radius ratio and redshift z.

4.1 The simple model with \(\alpha =3\)

We consider the simple case setting by \(\alpha = 3\) in the non-minimally coupled model (28)

$$\begin{aligned} L= & {} \frac{1}{2\kappa ^2} R*1 - \left[ 1 - \frac{R^3}{(\alpha +2)^3 b^2} \right] ^{-\frac{ 5 k}{(1+k) }}F\wedge *F \nonumber \\&+\, 2A\wedge J + L_{mat} + \lambda _a\wedge T^a. \end{aligned}$$
(45)

Here we note that the non-minimal coupling function Y(R) can be expanded as the binomial series in power of \(R^3\) for \(\left| \frac{R^3}{(\alpha +2)^3 b^2}\right| < 1\).

$$\begin{aligned} Y(R)= & {} \left[ 1 - \frac{R^3}{(\alpha +2)^3 b^2} \right] ^{-\frac{ 5 k}{1+k }} = 1 + \frac{5k}{1+k} \frac{R^3}{(\alpha +2)^3 b^2}\nonumber \\&+\,\mathcal {O}(R^6) \end{aligned}$$
(46)

The non-minimal model (45) accept the interior metric as a solution

$$\begin{aligned} ds^2 = - a^2r^2dt^2 + \frac{3}{1+br^3} dr^2 + r^2(d\theta ^2 +sin^2\theta d\phi ^2 )\nonumber \\ \end{aligned}$$
(47)

together with the following electric field, pressure, energy density and electric charge from (22)–(26) inside of the star

$$\begin{aligned} E^2(r)= & {} \frac{(1+k) ( br^3 +1)^{\frac{1+6k}{1+k}} }{6\kappa ^2 r^2} , \end{aligned}$$
(48)
$$\begin{aligned} p(r)= & {} \frac{1+ k}{6\kappa ^2 r^2} + \frac{br ( 8 k -7 )}{6\kappa ^2}, \end{aligned}$$
(49)
$$\begin{aligned} \rho (r)= & {} \frac{1+ k}{2\kappa ^2 r^2} + \frac{br ( 2k-3 )}{2\kappa ^2 }, \end{aligned}$$
(50)
$$\begin{aligned} q^2(r)= & {} \frac{ (1+k)r^2 \left[ 1+br^3 \right] ^{-\frac{4 k-1 }{(k+1)} }}{6\kappa ^2}. \end{aligned}$$
(51)
Fig. 4
figure 4

The dimensionless quantities which are related with the matter mass (a) and total electric charge (b) versus the dimensionless parameter k for \(\alpha = 3\)

Full size image
Fig. 5
figure 5

The dimensionless quantity which is related with the gravitational mass (a) and the gravitational surface redshift (b) versus the dimensionless parameter k for \(\alpha = 3\)

Full size image
Fig. 6
figure 6

Variation of the phase speed \(v=\frac{dp}{d\rho } \) as a function of radial distance r using the boundary radius \(r_b=10~\hbox {km}\) and some k values for \(\alpha =3 \) (a) and \(\alpha =5 \) (b)

Full size image

Then under the boundary and matching conditions the total charge, mass and gravitational redshift can be expressed by the followings

$$\begin{aligned}&Q^2 = \frac{ (1+k)r_b^2 \left[ 1+ \frac{(1+k) }{(8 k- 7 )} \right] ^{-\frac{4 k-1 }{(1+k)} }}{6\kappa ^2},\end{aligned}$$
(52)
$$\begin{aligned}&\frac{M}{r_b}= \frac{15k-15}{6(8 k -7)} + \frac{1+k}{12} \left[ 1+ \frac{(1+k)}{8 k -7}\right] ^{-\frac{4 k-1 }{(1+k)} },\end{aligned}$$
(53)
$$\begin{aligned}&z= \sqrt{\frac{3(8k-7)}{9k -6 } } - 1. \end{aligned}$$
(54)

from (35)–(39). We note that the redshift has the upper bound \(z\approx 0.633 \) for \(\alpha =3\), which is smaller than the general redshift bound of the model which is \(\sqrt{3} -1 \approx 0.732\). As the simple model with \(\alpha =3 \), we depict the related physical quantities in Figs. 4, 5 and 6. We give the corresponding k values by taking the observed mass-radius ratios of some known stars and calculate the other quantities in Table 1. Here we note that each star have its own k value and the each k value can be determined by the observational mass and radius of the star.

Table 1 The dimensionless parameter k, the charge-radius ratio \(\frac{\kappa ^2Q^2}{r_b^2} \) and the surface redshift z obtained by using the observational mass M and the radius \(r_b\) for some neutron stars
Full size table

In order to obtain an approximate equation of state of the matter inside the star from Eqs. (49) and (50), we fit the parametric \(p-\rho \) curve with the equation

$$\begin{aligned} \kappa ^2 p=\frac{\kappa ^2c^2\rho }{3} - \frac{k-1}{6}B_0 \end{aligned}$$
(55)

where we have used \(B_0= 1~\hbox {km}^{-2}\) as a dimension-full constant. We note that if \(k=1\) we obtain the radiation fluid case \(p=c^2\rho /3\) [42]. The curve fitting is shown in Fig. 7. It is interesting to see that the fitting equation of state corresponds to the MIT bag model [61, 62] which is given by \(p=\frac{ c^2 \rho }{3} - \frac{4 c^2B }{3} \). In this model the bag constant B is related to the parameter k as \(B= \frac{k-1}{8} \frac{\mathrm{km}^{-2}}{c^2\kappa ^2} \). If we set \(k=1.015 \), we find \( B = 1.88 \times 10^{-13} \frac{\mathrm{cm}^{-2}}{c^2\kappa ^2} = 10^{14}~\mathrm{g}/\mathrm{cm}^3 \), where we have used \(\kappa ^2 = \frac{8 \pi G}{c^4} = 2.1 \times 10^{-48} \frac{\mathrm{s}^2}{\mathrm{g}~\mathrm{cm}}\) and \( c= 2.99 \times 10^{10} \frac{\mathrm{cm}}{\mathrm{s}}\). Then \(B < 10^{14}~\mathrm{g}/\mathrm{cm}^3\) for \(1< k< 1.015 \) and \(B > 10^{14}~\mathrm{g}/\mathrm{cm}^3\) for \(k> 1.015\). Additionally, we see that the parameter k takes values approximately in the interval \(1<k<1.2\) from the Table 1 for realistic compact stars. In the case \(\alpha =3\), the non-minimal Einstein–Maxwell model with \(k=1.015\) gives the gravitational mass \(M=0.65 M_{\odot } \) using the radius \(r_b =9.46~\hbox {km}\). We see that this mass is less than the mass obtained for conformal symmetric charged stellar models in the minimal Einstein–Maxwell theory [9]. We note that the both models have the conformal symmetry and very similar interior metric solutions. Although this modified Einstein–Maxwell model has free parameters which can be set to be consistent with various compact star observations, the model in [9] determines a unique charged configuration of quark matter in terms of the Bag constant. Alternatively, the mass in our model increases to \(2.09M_\odot \) for \(\alpha =4\), and \(2.64M_\odot \) for \(\alpha =5\). That is, we can confine k as \(k=1.015\) which gives the Bag constant and consider \(\alpha \) is a free parameter, in order to describe compact stars.

Fig. 7
figure 7

The pressure versus energy density inside the star for \(r_b=10~\hbox {km},\) and \(\alpha =3 \). The solid curves in (a) and (b) represent the relation between p and \(\rho \) from (49) and (50) and the dotted curves represent the equation of state \(p=\frac{\rho }{3} - \frac{k-1}{6} \) by obtained from curve fitting

Full size image

5 Conclusion

We have extended the solutions of the previous the non-minimally coupled \(Y(R)F^2\) theory [42] to the case with \(\rho \ne 3p\) under the symmetry of conformal motions. In the case without any assumption of the equation of state, we have acquired one more parameter k in the solutions and the corresponding model. The pressure and energy density in the solutions are decreasing function with r in the interior of the star.

By matching the interior solution with the exterior Reissner–Nordström solution and applying the zero pressure condition at the boundary radius of star \(r=r_b\), we determine some physical properties of the star such as the ratio of the total mass and charge to boundary radius \(r_b\) and gravitational redshift depending on the parameters k and \(\alpha \).

We note that the total mass and charge increase with increasing k values and we have not reach an upper bound for k in the extended non-minimal model. But the increasing k values give an upper bound for the gravitational redshift, \(z \approx 0.732\), which is smaller than the more general restriction found in [56] for compact charged objects. It is interesting to note that each \(\alpha \) and k value in this model (28) determines a different non-minimally coupled theory and each theory with the different parameters gives different mass-radius, charge-radius ratios and gravitational redshift configuration. We calculated k values and the corresponding other quantities of the compact stars with the simple case \(\alpha =3\) via the some observed mass-radius values in Table 1. In this case, we also obtained the approximate equation of state (55) by fitting the \(p-\rho \) curve of the model. By comparing the fitting equation of state with the MIT bag model for \(\alpha =3\), we found the gravitational mass \(M=0.65 M_\odot \) which is smaller than the mass obtained for conformal symmetric quark stars [9] in the Einstein–Maxwell theory. However the mass in our model increases as \(\alpha \) increases. The non-minimally coupled model has the arbitrary parameters \(\alpha \) and k which can be set in order to be consistent with compact star observations. Even for \(\alpha =3\), each k value can describe a charged compact star.