Realistic simplified gaugino-higgsino models in the MSSM

Abstract

We present simplified MSSM models for light neutralinos and charginos with realistic mass spectra and realistic gaugino-higgsino mixing, that can be used in experimental searches at the LHC. The formerly used naive approach of defining mass spectra and mixing matrix elements manually and independently of each other does not yield genuine MSSM benchmarks. We suggest the use of less simplified, but realistic MSSM models, whose mass spectra and mixing matrix elements are the result of a proper matrix diagonalisation. We propose a novel strategy targeting the design of such benchmark scenarios, accounting for user-defined constraints in terms of masses and particle mixing. We apply it to the higgsino case and implement a scan in the four relevant underlying parameters $\{\mu , \tan \beta , M_{1}, M_{2}\}$ for a given set of light neutralino and chargino masses. We define a measure for the quality of the obtained benchmarks, that also includes criteria to assess the higgsino content of the resulting charginos and neutralinos. We finally discuss the distribution of the resulting models in the MSSM parameter space as well as their implications for supersymmetric dark matter phenomenology.

1 Introduction

Supersymmetry (SUSY) is one of the most popular theories beyond the Standard Model (SM) of particle physics. Extending the Poincaré algebra by relating the fermionic and bosonic degrees of freedom of the theory, supersymmetry provides a solution to many of the shortcomings and limitations of the Standard Model. In particular, supersymmetric theories solve the infamous hierarchy problem plaguing the Standard Model, feature gauge coupling unification at high energy and generally include a natural explanation for the presence of dark matter in the universe. Consequently, supersymmetry searches constitute a significant part of the LHC physics program.

Up to now, no evidence for supersymmetry has been found. Limits on the masses of the supersymmetric partners of the Standard Model particles are consequently pushed to higher and higher energy scales. Most of these results have, however, been derived either in the framework of the minimal supersymmetric realisation, known as the Minimal Supersymmetric Standard Model (MSSM) [1, 2], or within MSSM-inspired simplified models for new physics [3,4,5,6].

Simplified models are effective Lagrangian descriptions minimally extending the Standard Model in terms of new particles and interactions. They have been designed as useful tools for the characterisation of new phenomena, allowing for the reinterpretation of the results in a straightforward manner thanks to a reduced set of degrees of freedom. In the context of MSSM-inspired simplified models, the experimental attention was initially mainly focused on the analysis of signatures that could originate from the strong production of squarks and gluinos, the corresponding cross sections being expected to be larger by virtue of the properties of the strong interaction. LHC null results have implied that severe constraints are now imposed on the masses of these strongly interacting superpartners. In particular, the analysis of about 36 fb$^{-1}$ of LHC collision data at a centre-of-mass energy of 13 TeV pushes the lower bounds on these masses far into the multi-TeV regime [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Processes involving the production of a pair of electroweak superpartners (neutralinos, charginos and sleptons) have also been considered for some time. The electroweak nature of these processes yields, however, smaller production rates and subsequently softer bounds on the corresponding masses [23,24,25,26]. Neutralinos, charginos and sleptons of a few hundreds of GeV are indeed still allowed by current data.

We focus in this work on simplified models describing electroweak gauginos and higgsinos and their dynamics. Recent searches of both ATLAS and CMS are in general interpreted within the framework of two sets of simplified models. In the first case, the Standard Model is extended by a set of mass-degenerate pure wino states, and the lightest superpartner is a pure bino state. The winos are then assumed to decay either into a system made of a bino and a weak gauge or Higgs boson, regardless of the fact that these decays are strictly speaking not allowed by supersymmetric gauge invariance, or into a bino and jets or leptons via intermediate off-shell sfermions. When the gaugino-higgsino mixing is not negligible and the mass splitting between the lightest states is sufficiently large, the decays to weak gauge and Higgs bosons become allowed and provide opportunities to obtain bounds on the MSSM parameter space. The strength of the constraints then depends on the mixing and the mass splitting [27]. On the other hand, heavier higgsino-like electroweakinos decay dominantly into lightest neutralinos and weak gauge bosons, thanks to their mixing with the gauginos, but only if the channels are kinematically accessible. In compressed mass scenarios, the corresponding experimental searches rely on the detection of the soft decay products of the gauge bosons, e.g. low transverse-momentum opposite-charge leptons of the same flavour (electrons or muons) [28, 29]. The second set of models under consideration is inspired by gauge-mediated supersymmetry breaking scenarios [30,31,32,33,34,35,36], in which the lightest superpartner is the gravitino. This simplified model additionally contains two neutral and one charged higgsino state, which are quasi mass-degenerate. They hence decay into a gravitino and a neutral gauge or Higgs boson, together with possibly accompanying undetected soft objects.

In all of the above approaches to MSSM-inspired simplified models for the gaugino-higgsino sector, one naively ignores all interrelationships between the masses of the neutralinos and the charginos and the features of the associated mixing matrices through their respective dependence on the free parameters in the MSSM Lagrangian. Starting from the MSSM, the neutralinos and charginos that are not of interest are decoupled by imposing the corresponding mixing matrix elements to be vanishing and their masses to be very large. On the other hand, the masses of the relevant neutralinos and charginos are fixed by hand to the desired values, independently of the corresponding elements in the mixing matrices that are set to 0, 1, or $\pm 1/\sqrt{2}$ (in the higgsino case). This approach is justified by the assumption that the MSSM has sufficiently many free parameters to reproduce such a pattern closely enough, which is particularly true when one considers the extra freedoms originating from the loop corrections.

In certain configurations, e.g. when the lightest states are nearly degenerate pure higgsinos and the gauginos are decoupled, this simple method works quite well. However, when one targets next-to-minimal simplified models where a mass splitting between the second-lightest state and its neighbours is introduced, some amount of mixing between the different gaugino and higgsino fields must be included in order to maintain viability with respect to the initial MSSM motivation. This concerns in particular identities guaranteed by gauge invariance and/or supersymmetry that could be violated when one tweaks by hand masses and mixing matrix elements, like in the above-mentioned wino set of simplified models. Such non-minimal setups are already probed by both LHC collaborations in their searches for supersymmetry [28, 29]. It is therefore important to interpret the results in meaningful benchmark scenarios where supersymmetry and gauge symmetries are preserved, allowing in this way only for theoretically-relevant interpretations.

In this work, we present simplified MSSM models for light neutralinos and charginos with realistic mass spectra and realistic gaugino-higgsino mixing, that can be used, e.g., in experimental searches at the LHC. Starting from the MSSM without additional CP-violation, we design our simplified model by decoupling all coloured superpartners as well as the sleptons and the sneutrinos. The gaugino-higgsino sector is thus described, at tree-level, by four parameters that are the bino and wino mass parameters $M_1$ and $M_2$, the supersymmetric higgs(ino) off-diagonal mass parameter $\mu$, and the ratio of the vacuum expectation values of the neutral components of the two Higgs doublets $\tan \beta$. We then define a strategy to efficiently scan this four-dimensional parameter space for given sets of light neutralino and chargino masses, that also allows to maximise the gaugino or higgsino content, couplings to certain sparticles etc. This procedure therefore allows to find approximate solutions for simplified MSSM models that have a realistic and properly defined gaugino-higgsino sector in contrast to many of the overly simplified models studied so far.

The remainder of this paper is organised as follows. We first review in Sect. 2 the MSSM chargino-neutralino sector, discuss its analytic symmetries, and study the spectra and decompositions of the physical states after numerical diagonalisation of the neutralino and chargino mass matrices. In Sect. 3, we describe our strategy to scan the four-dimensional MSSM parameter space, define a quality measure for the goodness of our fit to the desired simplified model, and indicate how our scan strategy can be generalised. In Sect. 4, we present a case study for higgsino-like light neutralinos and charginos, analyse their representation in the MSSM parameter space, and investigate the implications for the Higgs-stop sector as well as the phenomenology of supersymmetric dark matter. Our conclusions are given in Sect. 5.

2 Theoretical definitions

The simplified model that we investigate in this work takes the gaugino-higgsino sector from the MSSM in all its complexity, as it is defined by supersymmetry and gauge invariance. In other words, we compute all elements of the neutralino and chargino mixing matrices and the physical mass spectrum through a proper diagonalisation of the relevant mass matrices at tree level. In our procedure, the mass spectrum of the neutralinos and charginos is thus not treated independently from their couplings, as it has been done previously in (overly) simplified models. By decoupling other supersymmetric particles, the model does, however, still not become overly complex, and this partly justifies that we neglect higher-order effects. The latter are nevertheless not so relevant for our purpose, the idea being to design models closely enough reproducible in the MSSM.

2.1 MSSM chargino-neutralino sector

In the MSSM and at tree-level, the gaugino-higgsino (or equivalently neutralino-chargino) sector is defined by four parameters

$$\begin{aligned} \{\mu ,\tan \beta , M_{1}, M_{2}\}, \end{aligned}$$

(1)

that are the off-diagonal Higgs(ino) mass parameter, the ratio of the vacuum expectation values of the neutral components of the two doublets of Higgs fields and the two soft supersymmetry-breaking electroweak gaugino mass parameters, respectively.

The $\mu$ parameter originates from the MSSM superpotential (${\mathcal {W}}_{\text {MSSM}}$). It reads, when we assume that the superpotential contains only R-parity conserving terms,

$$\begin{aligned} {\mathcal {W}}_{\text {MSSM}}&= \ \mu H_{1} \cdot H_{2} - y^{e}_{ij} H_{1}\cdot L_{i}E_{j}\nonumber \\&\quad -\, y^{d}_{ij} H_{1}\cdot Q_{i}D_{j} - y^{u}_{ij} Q_{i} \cdot H_{2}U_{j}, \end{aligned}$$

(2)

where $H_1$ and $H_2$ denote the two weak doublets of Higgs superfields. Q, L, and U, D and E are the two weak doublets and three weak singlets of quark and lepton superfields, respectively. Expanding the superpotential ${\mathcal {W}}_{\text {MSSM}}$ in terms of the component fields of the various superfields, it includes in particular an off-diagonal mass term proportional to $\mu$ for the two higgsino fields $\widetilde{H}_1$ and $\widetilde{H}_2$. The second parameter in Eq. (1) is defined as the ratio of the vacuum expectation values of the scalar components $h_1$ and $h_2$ of the two Higgs superfields

$$\begin{aligned} \tan \beta = \frac{v_{2}}{v_{1}} \end{aligned}$$

(3)

with

$$\begin{aligned} \left\langle h_{1} \right\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} v_{1} \\ 0 \end{pmatrix} \qquad \mathrm{and}\qquad \left\langle h_{2} \right\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 0 \\ v_{2} \end{pmatrix}, \end{aligned}$$

(4)

the non-vanishing values of $v_1$ and $v_2$ giving rise to the spontaneous breaking of the electroweak symmetry, $SU(2)_{\text {L}}\times U(1)_{\text {Y}}\rightarrow U(1)_{\text {EM}}$. Since supersymmetry has not yet been observed, it must be a broken symmetry. As usual, we remain agnostic of which mechanism is invoked to break supersymmetry, and thus explicitly include in the MSSM Lagrangian soft supersymmetry-breaking interaction terms that leave the gauge symmetries intact and that do not introduce any new quadratic divergences at the loop-level. Among the allowed supersymmetry breaking terms, the bino ($\widetilde{B}$) and wino ($\widetilde{W}$) mass terms are the only ones relevant for our work,

$$\begin{aligned} \mathcal {L}^{\text {MSSM}}_{\text {soft}} = - \frac{1}{2}\left( M_{1} \widetilde{B} \widetilde{B} + M_{2} \widetilde{W}_{i} \widetilde{W}^{i} + \text {h.c.}\right) + \cdots . \end{aligned}$$

(5)

The chargino mass eigenvalues are obtained by diagonalising the chargino mass matrix X that can be extracted from Eqs. (2) and (5). This matrix is given, in the $(i \widetilde{W}^-, \widetilde{H}^-_1)$ and $(i \widetilde{W}^+, \widetilde{H}^+_2)$ basis, by

$$\begin{aligned} \mathbf {X} = \begin{pmatrix} M_{2}&{}\sqrt{2} M_Ws_\beta \\ \sqrt{2} M_Wc_\beta &{} \mu \end{pmatrix}, \end{aligned}$$

(6)

where $M_W$ stands for the mass of the W-boson and where we have introduced the $c_\beta$ and $s_\beta$ notations for the cosine and sine of the $\beta$ angle, respectively. This matrix can be diagonalised by means of two unitary rotation matrices $\mathcal{U}$ and $\mathcal{V}$,

$$\begin{aligned} \mathrm{diag} (M_{\tilde{\chi }^\pm _1}, M_{\tilde{\chi }^\pm _2}) = {\mathcal {U}}^{*} \mathbf {X} {\mathcal {V}}^{-1}, \end{aligned}$$

(7)

where $M_{\tilde{\chi }^\pm _1} < M_{\tilde{\chi }^\pm _2}$ are the masses of the two chargino states. The $\mathcal{U}$ and $\mathcal{V}$ mixing matrices respectively relate the negatively-charged and positively-charged gaugino-higgsino basis to the physical chargino mass basis $(\chi ^\pm _1, \chi ^\pm _2)$,

$$\begin{aligned} \begin{pmatrix} \chi ^-_1 \\ \chi ^-_2 \end{pmatrix} = \mathcal{U} \begin{pmatrix} i \widetilde{W}^- \\ \widetilde{H}^-_d \end{pmatrix} \quad \text {and}\quad \begin{pmatrix} \chi ^+_1 \\ \chi ^+_2 \end{pmatrix} = \mathcal{V} \begin{pmatrix} i \widetilde{W}^+ \\ \widetilde{H}^+_u \end{pmatrix}. \end{aligned}$$

(8)

Similarly, in the neutral sector the neutralino mass matrix can be computed from Eqs. (2) and (5). This matrix can be written, in the $(i\widetilde{B}, i \widetilde{W}^3, \widetilde{H}_1^0, \widetilde{H}_2^0)$ basis, as

$$\begin{aligned} \mathbf {Y} = \begin{pmatrix} M_1 &{} 0 &{} -M_W t_W c_\beta &{} M_W t_W s_\beta \\ 0 &{} M_2 &{} M_W c_\beta &{} -M_W s_\beta \\ - M_W t_W c_\beta &{} M_W c_\beta &{} 0 &{} -\mu \\ M_W t_W s_\beta &{} -M_W s_\beta &{} -\mu &{} 0 \end{pmatrix}, \end{aligned}$$

(9)

where $t_W \equiv \tan \theta _W$ stands for the tangent of the electroweak mixing angle. This symmetric matrix can be diagonalised by means of a single unitary matrix $\mathcal{N}$,

$$\begin{aligned} \mathcal{N}^* \mathbf{Y} \mathcal{N}^{-1} = \mathrm{diag}\, (M_{\tilde{\chi }^0_1}, M_{\tilde{\chi }^0_2}, M_{\tilde{\chi }^0_3}, M_{\tilde{\chi }^0_4}), \end{aligned}$$

(10)

where $M_{\tilde{\chi }^0_1}< M_{\tilde{\chi }^0_2}< M_{\tilde{\chi }^0_3} < M_{\tilde{\chi }^0_4}$ stand for the masses of the four neutralino states $\chi _i^0$ with $i=1$, 2, 3 and 4. The mixing matrix $\mathcal{N}$ allows one to relate the four physical neutralino mass eigenstates to the neutral higgsino and gaugino interaction eigenstates,

$$\begin{aligned} \begin{pmatrix} \chi ^0_1 \\ \chi ^0_2 \\ \chi ^0_3 \\ \chi ^0_4 \end{pmatrix} = \mathcal{N} \begin{pmatrix} i \widetilde{B} \\ i \widetilde{W}^3 \\ \widetilde{H}_d^0 \\ \widetilde{H}_u^0 \end{pmatrix}. \end{aligned}$$

(11)

Non-trivial analytic inversions of the gaugino mass matrices have been proposed in the past. Besides the knowledge of three gaugino masses, typically those of one or two charginos and of two or one heavier neutralinos, they require the choice of a value for $\tan \beta$ as well as additional information and/or numerical consistency checks to resolve sign ambiguities [37].

2.2 Symmetry transformations

For a better understanding of the structure of the parameter space of our simplified model, we discuss in this subsection two linear transformations of the mixing matrices that affect the electroweakino couplings, but leave their mass spectrum unchanged. These symmetries hence allow us to deduce multiple benchmark scenarios fitting equally well a preselected mass configuration and chargino and neutralino decomposition in terms of gaugino and higgsino eigenstates.

We restrict our study to the case where the $\mu$, $M_{1}$ and $M_{2}$ parameters are real in order not to introduce additional sources of CP-violation in the theory. However, we keep the sign of these three mass parameters free, so that they can therefore be either positive or negative. The mass eigenvalues of the chargino mass matrix X only depend on the relative sign between the $\mu$ and $M_{2}$ parameters. This means that the simultaneous flip of the signs of the $M_2$ and $\mu$ parameters,

$$\begin{aligned} M_2 \rightarrow M_{2}^{\prime } = -M_{2} \quad \text {and}\quad \mu \rightarrow \mu ^{\prime } = -\mu , \end{aligned}$$

(12)

leaves both chargino masses invariant. The chargino mixing matrices are, however, impacted and transform as

$$\begin{aligned} \mathcal{U} \rightarrow {\mathcal {U}}^{\prime } = -{\mathcal {U}} \sigma _{3} \quad \text {and}\quad \mathcal{V} \rightarrow {\mathcal {V}}^{\prime } = {\mathcal {V}} \sigma _{3}, \end{aligned}$$

(13)

where $\sigma _3$ is the third Pauli matrix. In general, these two sign flips also lead to effects on the neutralino mass spectrum, unless one extends the transformation of Eq. (12) as

$$\begin{aligned} \begin{aligned} M_1 \rightarrow M_{1}^{\prime }&= -M_{1}, \\ M_2 \rightarrow M_{2}^{\prime }&= -M_{2}, \\ \mu \rightarrow \mu ^{\prime }&= -\mu . \end{aligned} \end{aligned}$$

(14)

The neutralino masses are thus left invariant by the transformation of Eq. (14), that modifies the neutralino mixing matrix $\mathcal{N}$ as

$$\begin{aligned} \mathcal{N} \rightarrow \mathcal {N}^{\prime } = i \mathcal {N} \begin{pmatrix} \phantom {-}1 &{} \phantom {-}0 &{} \phantom {-}0 &{} \phantom {-}0\\ \phantom {-}0 &{} \phantom {-}1 &{} \phantom {-}0 &{} \phantom {-}0\\ \phantom {-}0 &{} \phantom {-}0 &{} - 1 &{} \phantom {-}0\\ \phantom {-}0 &{} \phantom {-}0 &{} \phantom {-}0 &{} - 1\\ \end{pmatrix}. \end{aligned}$$

(15)

On different grounds, the inversion of $\tan \beta$,

$$\begin{aligned} \tan \beta \rightarrow [\tan \beta ]^{\prime } = \frac{1}{\tan \beta }, \end{aligned}$$

(16)

also leaves the chargino and neutralino mass spectrum invariant. The mixing matrices ${\mathcal {U}}$ and ${\mathcal {V}}$ are, however, interchanged, as are the decompositions of the Weyl fields $\chi ^{+}_{i}$ and $\chi ^{-}_{i}$ in terms of their gaugino and higgsino content,

$$\begin{aligned} \mathcal{U} \rightarrow {\mathcal {U}}^{\prime } = {\mathcal {V}} \begin{pmatrix} 0 &{} 1\\ 1 &{} 0\end{pmatrix} \quad \text {and}\quad \mathcal{V} \rightarrow {\mathcal {V}}^{\prime } = {\mathcal {U}} \begin{pmatrix} 0 &{} 1\\ 1 &{} 0\end{pmatrix}. \end{aligned}$$

(17)

The total gaugino-higgsino content of the Dirac chargino spinors is, however, unaffected. As mentioned above, the transformation of Eq. (16) also leaves the neutralino mass eigenvalues invariant. The neutralino mixing matrix $\mathcal{N}$ is in contrast modified. The inversion of $\tan \beta$ physically interchanges the roles of $\widetilde{H}^{0}_{1}$ and $\widetilde{H}^{0}_{2}$, so that the decomposition of the neutralinos in terms of the two higgsino states is swapped with an extra sign flip,

$$\begin{aligned} \mathcal{N} \rightarrow \mathcal {N}^{\prime } = \mathcal {N} \begin{pmatrix} \phantom {-}1 &{} \phantom {-}0 &{} \phantom {-}0 &{} \phantom {-}0\\ \phantom {-}0 &{} \phantom {-}1 &{} \phantom {-}0 &{} \phantom {-}0\\ \phantom {-}0 &{} \phantom {-}0 &{} \phantom {-}0 &{} - 1\\ \phantom {-}0 &{} \phantom {-}0 &{} - 1 &{} \phantom {-}0\\ \end{pmatrix}. \end{aligned}$$

(18)

Fig. 1

Variation of the neutralino and chargino mass spectra for scenarios featuring $\mu > 0$, as a function of $|\mu |$ (upper left), $\tan \beta$ (upper right), $\delta M_{2}/|\mu |$ (lower left) and $\delta M_{1} / M_{2}$ (lower right) when all other parameters are fixed to their reference value given in Eq. (20). The colour-coding (with increased line width for better visibility) indicates the bino (purple), wino (blue) and higgsino (red) content of the different particles

2.3 Mass spectra and gaugino-higgsino content

As stated at the beginning of this section, the parameter space describing the MSSM gaugino-higgsino sector is four-dimensional and specified by the parameters $\mu$, $\tan \beta$, $M_{1}$ and $M_2$. For convenience, we trade the gaugino mass parameters $M_1$ and $M_2$ for the relative mass differences $\delta M_{2}/|\mu |$ and $\delta M_{1} / M_{2}$ defined by

$$\begin{aligned} M_{2} = |\mu |\ \left(1+{\delta M_{2}\over |\mu |}\right) \quad \mathrm{and} \quad M_{1} = M_{2}\,\left(1+{\delta M_{1}\over M_{2}}\right). \end{aligned}$$

(19)

The resulting mass spectrum and neutralino and chargino decompositions are related to these parameters in a complex and non-trivial manner, which makes it difficult to get a global understanding of the response of the spectrum to a variation in these parameters. Therefore, we explore the parameter space in a systematic way by first defining a default scenario

$$\begin{aligned} |\mu | = 2 M_{W},\quad \tan \beta =2 \vee \frac{1}{2},\quad {\delta M_{2}\over |\mu |} = 0\quad \mathrm{and}\quad {\delta M_{1} \over M_{2}} = 0,\nonumber \\ \end{aligned}$$

(20)

and then varying one of these parameters at a time.

Fig. 2

Same as Fig. 1 for $\mu < 0$

The results are shown in Figs. 1 and 2 for scenarios featuring a positive and a negative $\mu$ parameter, respectively. In these figures, we provide a global overview on how a variation of one of the model input parameters affects the mass spectra and the neutralino and chargino decompositions in terms of the gaugino and higgsino states. Starting from the reference scenario of Eq. (20), we vary either the $\mu$ parameter (upper left panels of the figures), $\tan \beta$ (upper right panels of the figures), the ratio $\delta M_{2}/|\mu |$ (lower left panels of the figures) or the ratio $\delta M_{1} / M_2$ (lower right panels of the figures). Although opposite choices for the sign of $\mu$ correspond to different regions in the parameter space, they can potentially lead to similar mass spectra (cf. the discussion in Sect. 2.2). In the upper, middle and lower parts of each subfigure, we show the respective dependence of the bino (only for neutralinos), wino and higgsino content of each electroweakino state on the considered model parameter. Trivially, we retrieve the fact that the chargino sector does not depend on the bino mass parameter $M_1$, and thus also not on $\delta M_{1} / M_{2}$.

The mixing pattern of the gaugino and higgsino states is driven by the off-diagonal elements in the mass matrices of Eqs. (6) and (9), which are all roughly proportional to the W-boson mass. Therefore, maximally mixed states arise only when either $|\mu |$, $M_1$, $M_2$, $|\pm \mu -M_{1}|$, $|\pm \mu -M_{2}|$ or $|M_{1}-M_{2}|$ is of $\mathcal {O}(M_W)$ or smaller. Conversely, nearly pure gaugino and higgsino states in the chargino sector occur for $|\mu |\gtrsim M_{W}$ and $|\mu -M_{2}|\gtrsim M_W$, while pure states in the neutralino sector additionally require also $|-\mu -M_{2}|\gtrsim M_W$ and $|\pm \mu -M_{1}|\gtrsim M_W$.

The diagonalisation of the chargino and neutralino mass matrices can possibly yield negative mass eigenvalues. In this case, they are made positive by absorbing the sign into the mixing matrices that get imaginary, which thus affects the couplings. The original sign of the mass can be deduced by examining the variation of the curves in Figs. 1 and 2. A change of sign can be traced back to a curve hitting zero and exhibiting a discontinuous local derivative. This configuration occurs when any of the $\mu$, $M_{1}$ and $M_{2}$ mass parameters is of $\mathcal {O}\left(M_{W}\right)$. Outside this range, two of the neutralinos always feature a dominant higgsino content, and their masses have opposite signs. The sign of the masses of the other two neutralinos is driven by the sign of the $M_{1}$ or $M_{2}$ parameters, depending on the dominant bino or wino nature of the neutralinos under consideration, provided the mixing is small. Moreover, one observes that the neutralino mass lines can only cross if the masses have opposite signs. Otherwise, one gets an avoided crossing where the neutralino content is exchanged.

The results presented in the upper left panels of Figs. 1 and 2 confirm that when $|\mu |$, and subsequently also $M_{1}$ and $M_{2}$, exceeds the W-boson mass scale, the overall magnitude of the electroweakino masses is solely set by $|\mu |$ and increases uniformly with it. In the special case corresponding to $\delta M_{2}/|\mu |=\delta M_{1}/M_{2}=0$, the mass differences as well as the elecroweakino decompositions moreover become independent of $|\mu |$. In contrast, variations of $\delta M_{2} / |\mu |$ and $\delta M_{1} / M_{2}$ influence the electroweakino mass differences, as shown in the lower panels of Figs. 1 and 2. These parameters are thus those that will allow us to determine MSSM benchmark points defined by an overall mass scale and a given mass splitting between the superpartners. In particular, one can obtain a spectrum where the lighter (heavier) states are nearly pure higgsinos when $\delta M_{2}/|\mu | \gg 0$ ($\delta M_{2}/|\mu | \ll 0$). Different values of $\tan \beta$ or $\delta M_{1}/M_{2}$ then raise or lower the value at which the turnover occurs. Similarly, varying both $\delta M_2/|\mu |$ and $\delta M_{1} / M_{2}$ allows one to obtain scenarios featuring nearly pure bino or wino states as the heaviest or lightest states. Finally, as illustrated on the upper right panels of the figures, we observe that the $\tan \beta$-dependence of the spectrum exhibits a peak or a dip at $\tan \beta =1$ with an amplitude that is typically smaller than about $M_W/2$. Except this feature, the effect of $\tan \beta$ on the spectrum is small, which therefore allows us to use this parameter for small adjustments once all other parameters have been chosen. When $\tan \beta \ll 1$ or $\tan \beta \gg 1$, the dependence on $\tan \beta$ moreover vanishes.

The sign of the $\mu$ parameter has little influence on the mass spectrum upon variations of $|\mu |$, $\delta M_{2}/|\mu |$ or $\delta M_{1} / M_{2}$. Negative $\mu$ values only induce a more compressed spectrum compared to the case of a positive $\mu$ parameter. In the chargino sector, the opposite signs of $\mu$ and $M_{2}$ in this case lead to an unavoided crossing of the mass eigenvalues at $\tan \beta \sim 1$, as well as to an opposite behavior when increasing or decreasing $\tan \beta$ with respect to 1. For $\mu < 0$, gaugino-higgsino mixings and eletroweakino mass splittings indeed increase with $\tan \beta$ variations, whilst they decrease for $\mu > 0$. In addition, mixed bino/wino-states are rare and can only be obtained by fine-tuning the parameters due to the non-existence of any direct bino/wino coupling in the Lagrangian. Moreover, wino states mix more easily with higgsino states than bino states as the hypercharge and weak couplings satisfy $g_{Y} < g_{2}$, or equivalently as $\sin \theta _{W}<\cos \theta _{W}$.

3 Scan strategy

In this section, we first select a strategy to explore the parameter space of the MSSM gaugino/higgsino sector in an efficient way. We then define criteria for acceptable benchmark points that fit best a pre-defined mass spectrum of light neutralinos and charginos and discuss how additional requirements, such as a large higgsino content of these sparticles, can also be included. Finally, we briefly reflect on possible generalisations of these strategies.

3.1 Parameter space exploration

The observations made in the previous section allow for the identification of general characteristics of the gaugino-higgsino parameter space that are useful for building realistic benchmark scenarios. Following most of the experimental studies at the LHC, we focus on configurations with only two light neutralinos ($\chi ^{0}_{1}$, $\chi ^{0}_{2}$) and a light chargino ($\chi ^{\pm }_{1}$). For illustrative purposes, we take the desired chargino mass $M_{\chi ^\pm _1}$ as an input and ask for an equidistant mass splitting $\varDelta M_{21}$ of the two neutralinos,

$$\begin{aligned} M_{\chi ^0_1} = M_{\chi ^\pm _1} - \frac{\varDelta M_{21}}{2} \quad \text {and}\quad M_{\chi ^0_2} = M_{\chi ^\pm _1} + \frac{\varDelta M_{21}}{2}. \end{aligned}$$

(21)

The scan procedure described in the following can, however, easily be generalised to other setups.

In principle, we scan over all four parameters $\mu$, $\tan \beta$, $M_{1}$ and $M_{2}$, but we immediately reduce this parameter space on the basis of the transformations that leave the neutralino-chargino mass spectrum invariant. Regions of the parameter space that are not explored are then derived by transforming the mixing matrices as described in Sect. 2.2. As a consequence, we only scan over the regions $\tan \beta \in [1;100]$ and $M_{2}>0$. In contrast, the sign of the higgsino mass parameter $\mu$ can strongly affect the structure of the theory and the experimental signatures, so that we consider both $\mu < 0$ and $\mu > 0$. As upper bounds on the absolute values of the mass parameters, we impose 5 TeV, which we only raise when we see that our results cluster near them. Values of $M_2<0$ and $\tan \beta <1$ are obtained with sign flips and a $\tan \beta$ inversion, as explained in Sect. 2.2. The three dimensionful parameters $\mu$, $M_1$ and $M_2$ are finally further constrained by the requirements on the desired gaugino/higgsino decomposition.

As an illustration of the above strategy, we search for benchmark scenarios featuring a spectrum where the lightest states are all higgsino-like. The range of $\mu$ can then be restricted by observing (cf. Sect. 2.3) that the masses of neutralinos and charginos with a dominant higgsino contribution lie in the range $|\mu | \pm \mathcal {O}\left(M_{W}\right)$. The scan ranges are thus given by

$$\begin{aligned} \begin{aligned} |\mu |&\in \Big [ \min (M_{\chi ^\pm _1}) - \mathcal {O}(M_W), \ \max (M_{\chi ^\pm _1})+\mathcal {O}(M_W) \Big ],\\ |M_{1}|&\in \Big [ \min (M_{\chi ^\pm _1})-\mathcal {O}(M_W),\ 5~\mathrm{TeV}\Big ]\ ,\\ M_2&\in \Big [ \min (M_{\chi ^\pm _1})-\mathcal {O}(M_W),\ 5~\mathrm{TeV}\Big ],\\ \tan \beta&\in \left[ 1, 100 \right], \end{aligned} \end{aligned}$$

(22)

with

$$\begin{aligned} \text {sign}\left(\mu \right) \in \{-,+\} \quad \text {and}\quad \text {sign}\left(M_{1}\right) \in \{-,+\}, \end{aligned}$$

(23)

and where $\min (M_{\chi ^\pm _1})$ and $\max (M_{\chi ^\pm _1})$ represent the minimal and maximal desired values for the light chargino mass.

It is easy to see that an equidistant scan in these parameters is not very efficient. For instance, variations at large values of $\tan \beta$ only weakly affect the spectrum and the gaugino/higgsino decompositions, since these depend on $\sin \beta$ and $\cos \beta$ rather than $\tan \beta$. Also, a scan over multiple orders of magnitude for the gaugino mass parameters does not efficiently cover masses in the lower ranges where $|M_{1}|,|M_{2}|\sim |\mu |$, where the masses of the higgsino-like neutralinos and charginos are affected the most. We therefore reparameterise the prior distributions in $M_1$, $M_2$ and $\tan \beta$ as

$$\begin{aligned} \begin{aligned} M_1&= \pm M \left(1 - \frac{\epsilon }{2} \right),\\ M_2&= M \left(1 + \frac{\epsilon }{2} \right), \\ \tan \beta&= \tan \beta _{\min } \exp \bigg [x_\beta \ln \frac{\tan \beta _{\max }}{\tan \beta _{\min }}\bigg ] \end{aligned} \end{aligned}$$

(24)

with

$$\begin{aligned} \begin{aligned} M&= M_{\min } \exp \bigg [ x_M\ln \frac{M_{\max }}{M_{\min }}\bigg ],\\ x_{M}&\in \left[0,1\right], \\ \epsilon&\in \left[-2,2\right], \\ x_{\beta }&\in \left[0,1\right]. \end{aligned} \end{aligned}$$

(25)

In the expressions of Eqs. (24) and (25), the minimum and maximum values of $\tan \beta$ and M are dictated by the scan range, with $M_{\min }$ and $M_{\max }$ referring both to $M_1$ and $M_2$. The scan time can be further reduced with an iterative procedure, where at each iteration the parameter range in $|\mu |$, $x_{M}$, $\epsilon$, and $x_{\beta }$ is halved keeping the currently best parameters central. The total parameter space volume then shrinks each time by a factor of $(1/2)^4=1/16$ with an additional factor of 1/2 from the sign determination of $M_{1}$ in the first iteration.

3.2 Benchmark selection

The quality of our fit of the desired mass spectrum is parameterised by the relative differences between the input masses and their fit values compared to the corresponding grid spacings $\varDelta M_{\chi ^{\pm }_{1}}$ and $\varDelta (\varDelta M_{21})$,

$$\begin{aligned} \begin{aligned} d_{1} =&\ \frac{1}{\varDelta M_{\chi ^{\pm }_{1}}} \bigg [M_{\chi ^\pm _1}-M_{\chi ^\pm _1}^\mathrm{fit}\bigg ] =: \frac{\delta M_{\chi ^{\pm }_{1}}}{\varDelta M_{\chi ^{\pm }_{1}}}\ , \\ d_{2} =&\ \frac{2}{\varDelta (\varDelta M_{21})} \bigg [\frac{\varDelta M_{21}}{2}- \left(M_{\chi ^0_2}^\mathrm{fit}-M_{\chi ^\pm _1}^\mathrm{fit}\right)\bigg ]=: \frac{\delta (\varDelta M_{21})}{\varDelta (\varDelta M_{21})}\ , \\ d_{3} =&\ \frac{2}{\varDelta (\varDelta M_{21})} \bigg [\frac{\varDelta M_{21}}{2}- \left(M_{\chi ^\pm _1}^\mathrm{fit}-M_{\chi ^0_1}^\mathrm{fit}\right)\bigg ]=: \frac{\delta ' (\varDelta M_{21})}{\varDelta (\varDelta M_{21})}\ . \end{aligned} \end{aligned}$$

(26)

A perfect fit then has $d_{1}=d_{2}=d_{3}=0$, while the penalty score of a configuration with respect to its nearest neighbour grid point is given by

$$\begin{aligned} \text {score} = \sqrt{\frac{d^{2}_{1}+d^{2}_{2}+d^{2}_{3}}{3}} \end{aligned}$$

(27)

with $\sqrt{1/3}\sim 0.58$ for a nearest neighbour grid point with a single outlier. We consider a configuration acceptable if

$$\begin{aligned} \mathrm{score}<0.1, \end{aligned}$$

(28)

which represents a reasonable compromise between scan time and accuracy:

$$\begin{aligned}&\delta M_{\chi ^{\pm }_{1}}< 0.1 \sqrt{3} \varDelta M_{\chi ^{\pm }_{1}} = 0.17 \varDelta M_{\chi ^{\pm }_{1}}, \nonumber \\&\frac{\delta ^{(')} (\varDelta M_{21})}{2} < 0.1 \sqrt{3} \varDelta (\varDelta M_{21}) = 0.17 \varDelta (\varDelta M_{21}). \end{aligned}$$

(29)

While this procedure allows us to find an approximately correct chargino and neutralino mass spectrum, it still does not maximise their average higgsino (or gaugino) content. This type of additional condition can be included by reweighting the score with

$$\begin{aligned} \text {score}_{\text {new}} \ \frac{\tilde{f}_{\text {old}}}{\widetilde{f}_{\text {new}}} < \text {score}_{\text {old}}, \end{aligned}$$

(30)

which balances accuracy of mass spectrum and decomposition for scores that are neither too small nor too large. In the case study of Sect. 4, $\tilde{f}$ represents the average higgsino content of the light neutralinos $\chi ^0_1$, $\chi ^{0}_{2}$ and the light $\chi ^{\pm }_{1}$ particles.

Table 1 Targeted mass ranges, splittings and spacings for light higgsino-like neutralinos and charginos

3.3 Generalisation

The specific setup described above can be generalised by modifying the desired mass spectrum of Eq. (21) to non-equidistant mass differences with the according adjustments in the conditions of Eq. (26). A qualitatively very distinct modification is the requirement of one-sided mass limits. Second, the maximisation of the higgsino content through the function $\tilde{f}$ and/or the reweighting condition in Eq. (30) can be replaced. A specific example would be the maximisation of couplings to specific particles. In practice, a trial scan often helps in defining more precisely acceptable configurations and conditions that do not overly constrain the interesting regions of parameter space. Scan ranges can often be guessed by using the observations made in Sect. 2.3. Reparameterisations as the one in Eq. (24) are moreover useful when scanning over multiple orders of magnitude in one or several parameters and can be optimised by studying the posterior distributions in the input parameters.

Fig. 3

Scores and average higgsino contents of $\chi ^{0}_{1}$, $\chi ^{0}_{2}$ and $\chi ^{\pm }_{1}$ for the models found in our MSSM fits of light chargino mass $M_{\chi ^\pm _1}$ and neutralino mass splitting $\varDelta M_{21}$. The dashed lines indicate that the latter are always smaller than $\mathcal {O} \left(M_{W}\right)$ (remember that $M_W=M_Zc_W$)

4 Case study: Higgsino-like neutralinos and charginos

In this section, we present a case study of a specific simplified MSSM model with a realistic neutralino-chargino sector, whose general properties were discussed in Sect. 2. We then apply and test the parameter scan method presented in Sect. 3 and examine the properties of the underlying benchmark points. Our case study has higgsino-like light neutralinos and charginos with equidistant mass splitting and includes both signs of the higgsino mass parameter $\mu$.

4.1 Definition of the simplified model

As it is usually done in simplified models, we decouple the sparticles that are not of direct relevance to our study, i.e. squarks, gluinos, and non-SM Higgs particles, by setting their masses to a sufficiently high value, here 1.5 TeV. Their phenomenological impact at the LHC is then negligible due to limited kinematical phase space, suppressed virtual propagators, and parton distribution functions that vanish at large parton momentum fractions. Decoupling sparticles with unrealistically high mass values can result in numerical instabilities in the employed Monte Carlo generators, e.g. from missing cancellations in higher-order corrections, and should be avoided.

The targeted light neutralino and chargino mass spectra are defined by a set of central light chargino masses $M_{\chi ^{\pm }_{1}}$ and correlated light neutralino masses that are split in an equidistant way by $\varDelta M_{21}$ (cf. Eq. (21)). Their ranges are constrained empirically through negative experimental searches for neutralinos or charginos, whose masses must exceed the mass of the $Z^{0}$-boson, and theoretically (cf. Sect. 2.3) to mass splittings of the two higgsino-like neutralinos that do not exceed $\mathcal {O}(M_{W})$. We therefore aim to fit the $\mathcal {O}(10^4)$ mass spectra in the ranges shown in Table 1 by scanning the parameter space as described in Sect. 3. The lower limit on the chargino mass is inspired by the combined LEP limit of 92.4 GeV in the higgsino region for any lightest neutralino mass. This limit rises to 103.5 GeV for mass splittings larger than 5 GeV [38, 39].

4.2 Quality of the scan

The quality of our MSSM fits of these predefined desired scenarios can be evaluated in Fig. 3, where we show the distribution of scores defined in Eq. (27) for $\mu > 0$ (upper left) and $\mu <0$ (upper right) as well as the average higgsino contents of $\chi ^{0}_{1}$, $\chi ^{0}_{2}$ and $\chi ^{\pm }_{1}$ (lower left and right, respectively). The size of the deviations between the targeted and fitted physical masses can be deduced from the scores using Eq. (29).

The score distributions in Fig. 3 indicate that in our specific case study, the mass splittings between light higgsinos should not exceed $M_W$ for $\mu > 0$ and $M_Z \cdot \sqrt{s_{W} c_{W}}$ for $\mu < 0$. Large neutralino mass splittings $\varDelta M_{21}$ mostly entail higgsino contents of less than 70% and as low as $\sim 50\%$ for the largest values of $\varDelta M_{21}$. This result is nearly independent of the physical chargino mass $M_{\chi ^{\pm }_{1}}$.

In Fig. 4, we therefore show the higgsino content as a function of $\varDelta M_{21}$ only for both $\mu >0$ (blue crosses) and $\mu <0$ (red diamonds). We find that it falls off quadratically for mass splittings below roughly 25 GeV. For positive values of $\mu$, the fall-off then becomes linear beyond this value.

4.3 MSSM scenarios

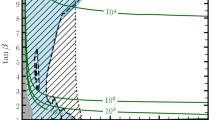
In Fig. 5, we display the fitted MSSM parameters $|\mu |$ (a, b), $\tan \beta$ (c, d), $M_{1}$ (e, f) and $M_{2}$ (g, h) for $\mu > 0$ and $\mu < 0$, respectively. Due to the limited sensitivity of the fit, the last three are shown logarithmically. In the following discussion of these figures, we focus on general trends, exceptional behaviour, and the amount of fine-tuning that is necessary to reproduce the desired mass spectrum and higgsino content. Statistically, fine-tuned models are unlikely to be realised in nature and are often taken as a hint for new, so far poorly understood symmetries in physics.

Fig. 4

Higgsino content as a function of $\varDelta M_{21}$ for our fit scenarios with $\mu > 0$ (blue crosses) and $\mu < 0$ (red diamonds). In both cases it falls quadratically for $\varDelta M_{21} < 25 \ \text {GeV}$. For $\mu >0$, the fall-off is linear beyond this value

Fig. 5

Fitted MSSM parameters $|\mu |$ (a, b), $\tan \beta$ (c, d), $M_{1}$ (e, f) and $M_{2}$ (g, h) for $\mu > 0$ and $\mu < 0$, respectively. Due to the limited sensitivity of the fit, the last three are shown logarithmically. Chargino masses below 92.4 GeV are excluded by LEP in the higgsino region for any lightest neutralino mass. This limit rises to 103.5 GeV for mass splittings larger than 5 GeV[38, 39]

The $\mu$-parameter distributions found for $\mu < 0$ and $\mu > 0$ are shown in Fig. 5a, b, respectively. They confirm our hypothesis that $|\mu |$ is mostly fixed by the chargino mass $M_{\chi ^{\pm }_{1}}$. The additional dependence on $\varDelta M_{21}$ is characterised by

$$\begin{aligned} |\mu | = M_{\chi ^{\pm }_{1}} + \frac{\varDelta M_{21}}{2}+\epsilon _{\mu } M_{W}, \end{aligned}$$

(31)

where $\epsilon _{\mu }$ parameterises the deviations from these linear dependencies that are at most of $\mathcal{O}(M_W)$. For 95% of the models, $\epsilon _{\mu }$ lies within $\left[-0.09, 0.08\right]$ for $\mu > 0$ and $\left[-0.17,0.0\right]$ for $\mu < 0$ with the largest deviations found in the region $\mu < 0$, $\varDelta M_{21} \gtrsim 20 \ \text {GeV}$ and $M_{\chi ^{\pm }_{1}} \lesssim 170 \ \text {GeV}$. The two leading terms in Eq. (31) are thus accurate about $10-20$ GeV.

Fig. 6

Upper figures: logarithmic representation of the fine-tuning level of simplified light higgsino models in terms of the relative acceptable ranges of the underlying MSSM parameters for $\mu >0$ (a) and $\mu <0$ (b). Large negative numbers therefore indicate large fine-tuning. Lower figures: number of boundary violations of the initial parameter ranges for $\mu >0$ (c) and $\mu <0$ (d). Chargino masses below 92.4 GeV are excluded by LEP in the higgsino region for any lightest neutralino mass. This limit rises to 103.5 GeV for mass splittings larger than 5 GeV [38, 39]

The $\tan \beta$-parameter distributions found for $\mu < 0$ and $\mu > 0$ are shown in Fig. 5c, d, respectively. A general, though weak trend is that one obtains smaller $\tan \beta$ for larger $\varDelta M_{21}$ for $\mu > 0$, but larger $\tan \beta$ for larger $\varDelta M_{21}$ for $\mu <0$. This corresponds to the opposite dependencies on $\tan \beta$ observed in the upper right parts of Figs. 1 and 2 in Sect. 2. The weak dependence of the spectrum for large values of $\tan \beta$ has been discussed before. As we can observe now, it appears in particular for $\mu <0$ or $\mu >0$ and small $\varDelta M_{21}$, while the allowed range of $\tan \beta$ becomes more limited for $\mu >0$ and large neutralino mass splittings.

In Fig. 5e–h, the distributions of the gaugino mass parameters $M_{1}$ and $M_{2}$ are shown for both $\mu > 0$ and $\mu < 0$. The distributions of both parameters vary by almost two orders of magnitude and roughly inversely to the neutralino mass splitting $\varDelta M_{12}$. We parameterise the fitted gaugino mass parameters $M_1$ and $M_2$ by

$$\begin{aligned} M_{1,2} = M_{\chi ^{\pm }_{1}} - \frac{\varDelta M_{21}}{2} + \epsilon _{M_{1,2}}\frac{M_{W}^{2}}{\varDelta M_{21}}. \end{aligned}$$

(32)

This expression does not reproduce the correlation of $\varDelta M_{21}$ and $\tan \beta$ discussed above and is thus less accurate than our parameterisation of $|\mu |$ in Eq. (31). In particular, the parameters $\epsilon _{M_{1,2}}$, that parameterise deviations from the two leading terms, lie in the large ranges $\epsilon _{M_{1,2}}\in [0.18,0.82],[1.26,2.42]$ for $\mu >0$ and $\epsilon _{M_{1,2}}\in [0.10,3.05],[0.82,1.43]$ for $\mu < 0$ and for 95% of the models. This is due to the known fact that pure higgsinos, often associated with $M_{1,2}\gg \mu$, have small mass splittings, so that the requested spectrum is not very sensitive to the exact values of the gaugino masses. The region of $|\mu |\simeq M_1$, but $M_2\gg |\mu |$, known as the “well-tempered bino/higgsino” region to identify the resulting light gaugino states as mixed binos and higgsinos, allows for the approximate analytic diagonalization of the reduced three-dimensional neutralino mass matrix [40]. We already observed this increased mixing in Fig. 4, where the higgsino content fell linearly for sizeable mass splittings $\varDelta M_{21}$.

Models that reproduce similar physical masses or mixings, but originate from very different, sometimes isolated fundamental parameters, signal the presence of fine-tuning. We quantify this fine-tuning by multiplying for each benchmark the variations of the fundamental parameters $|\mu |$, $M_1$, $M_2$ and $\tan \beta$ leading to acceptable scores (below 0.1) and then dividing by the corresponding total ranges as defined in Eq. (22). The result is shown in Fig. 6a, b for positive and negative values of $\mu$, respectively. Due to the logarithmic representation, large negative numbers correspond to large fine-tuning. It occurs more often for large mass splittings and/or positive values of $\mu$ confirming that conversely pure higgsino scenarios usually have small mass splittings and are then less sensitive to specific choices e.g. of $M_1$, $M_2$ or $\tan \beta$. Furthermore, in some cases acceptable models also lie outside the parameter ranges given in Eq. (22). The number of such initial boundary violations is displayed in Fig. 6c, d, again for $\mu >0$ and $\mu <0$, respectively. As one can see, acceptable models in larger regions of the parameter space exist often for (nearly) mass degenerate light neutralinos, where large $M_{1,2}$ allow for compressed higgsino mass spectra, and in the case $\mu <0$, where $\tan \beta$ can be very large.

4.4 The Higgs-stop sector

The large MSSM parameter space allows one (at least at tree-level) to decouple squarks, gluinos and sleptons without any impact on the gaugino-higgsino sector. Care is, however, required for the decoupling of the higgs-stop sector due to the large impact of stop radiative corrections on the mass of the observed SM-like Higgs boson, that has to match the measured value of 125 GeV. In the absence of stop mixing, the squared CP-even and CP-odd neutral Higgs boson masses are related to the top quark mass $m_t$ and the stop mass $m_{\tilde{t}}$ through [41]

$$\begin{aligned} m^{2}_{h^{0}} + m^{2}_{H^{0}} = m^{2}_{A^{0}}+M^{2}_{Z}+\frac{3G_{F}m^{4}_{t}}{\sqrt{2}\pi ^{2} s^{2}_{\beta }} \ln \frac{m^{2}_{\tilde{t}}}{m^{2}_{t}}, \end{aligned}$$

(33)

where $G_F$ is the Fermi constant. This entails

$$\begin{aligned} m^{2}_{\tilde{t}} \simeq m^{2}_{t} \exp \left(\frac{\sqrt{2}\pi ^{2} s^{2}_{\beta }}{3G_{F}m^{4}_{t}}\left(m^{2}_{h^{0}}-M^{2}_{Z}\right)\right) \end{aligned}$$

(34)

for $m_{H^0}\simeq m_{A^0}$ or $m_{\tilde{t}} \in [ 885 \text { GeV}, 1330 \text { GeV}]$, as long as $\tan \beta >2$. The full additional parameter space for the Higgs-stop sector includes the squared off-diagonal Higgs mass parameter $m_{12}^2$, the soft SUSY-breaking mass parameters $m^{2}_{\tilde{Q}_{3}}$ and $m^{2}_{{\tilde{t}}_R}$, and the trilinear coupling $A_{t}$, all taken to be real to avoid new sources of CP-violation. A scan over this additional parameter space for a given MSSM higgsino model with fixed $\mu$ and $\tan \beta$ and full stop mixing leads to a successful decoupling of the heavy Higgs bosons. The corresponding regions in the CP-odd neutral Higgs mass and the physical stop masses are

$$\begin{aligned} \begin{aligned} m_{A^0}&\in [992,4386]~\mathrm{GeV}~(\mu>0), \\ m_{{\tilde{t}}_1}&\in [752,1481]~\mathrm{GeV}~(\mu>0),\\ m_{{\tilde{t}}_2}&\in [1607,2487]~\mathrm{GeV}~(\mu >0),\\ \end{aligned} \end{aligned}$$

(35)

and

$$\begin{aligned} \begin{aligned} m_{A^0}&\in [1063,3925]~\mathrm{GeV}~(\mu<0),\\ m_{{\tilde{t}}_1}&\in [809,1212]~\mathrm{GeV}~(\mu<0),\\ m_{{\tilde{t}}_2}&\in [1840,2413]~\mathrm{GeV}~(\mu <0).\\ \end{aligned} \end{aligned}$$

(36)

for positive and negative values of $\mu$, respectively. As is well known, a light SM-like Higgs boson of mass 125 GeV requires in general a light stop with a mass below or around 1 TeV and a large stop mass splitting of at least 1 TeV.

Fig. 7

Upper figures: logarithmic ratio of predicted and observed relic abundance of light higgsino dark matter for $\mu >0$ (a) and $\mu <0$ (b). Lower figures: ratios of predicted cross sections and Xenon1T exclusion limits for the direct detection of higgsino dark matter for $\mu >0$ (c) and $\mu <0$ (d)

4.5 Implications on dark matter

An important motivation for supersymmetry is its prediction of a classic WIMP (weakly interacting massive particle) dark matter candidate, the lightest neutralino. The relic abundance of dark matter in the universe has been determined very precisely by the Planck collaboration to be $\varOmega _{\chi }^\mathrm{Pl}h^{2} = 0.1199 \pm 0.0027$ [42]. We therefore compare the relic density $\varOmega _{\chi }^\mathrm{MO}$ predicted for light higgsino MSSM models by the public code micrOMEGAs [43] to the observed one in Fig. 7a, b for $\mu >0$ and $\mu <0$. The main observation here is the appearance of the $\chi _{1}^{0} \chi ^{0}_{1}\rightarrow W^{+}W^{-}$ threshold. When this process is kinematically allowed, the annihilation cross section of $\chi _{1}^{0}$ increases, and therefore the dark matter relic abundance decreases. Close to (above) this threshold, the cross section is sufficiently small to explain (at least partially) the measured dark matter relic abundance. In Fig. 7c, d we show the ratios of predicted direct detection cross sections over the Xenon1T exclusion limits [44]. In the higgsino mass range of $M_Z$ to 400 GeV studied here, the cross sections predicted by micrOMEGAs decrease with the mass splitting from $10^{-6}$ to $10^{-11}$ pb. Since the Xenon1T experiment has recently reached a sensitivity of $\sigma _\chi ^\mathrm{Xe1T}\sim 10^{-10}$ pb for WIMP masses of about 100 GeV, only cross sections below the black line and very small mass splittings are still allowed. However, since searches at the LHC and in direct detection experiments depend on different sets of assumptions, both are complementary, and they should both be taken into account. In the dark matter context, the potential LHC constraints on the considered models include both results from direct searches for supersymmetry and for dark matter in general, like when using monojet probes that are expected to be golden handles on compressed electroweakino spectra [45]. Models with light gravitinos imply, of course, a very different dark matter phenomenology.

5 Conclusion

Simplified SUSY models have become a popular tool for model-independent searches at the LHC. Recently, the LHC experiments ATLAS and CMS have also applied this approach to light neutralinos and charginos with predefined physical mass spectra and pure gaugino or higgsino content. We have emphasised in this paper that these models can violate physical principles such as supersymmetry, gauge invariance, or the consistent combination of production cross sections and decay branching ratios and that they must therefore be embedded in full MSSM models, whose relevant four-dimensional parameter space is spanned by $\mu$, $\tan \beta$, $M_1$ and $M_2$.

Exploiting the symmetries of the neutralino and chargino mass matrices, we diagonalised them and discussed the leading and sub-leading dependencies of the resulting physical mass spectra and decompositions on these parameters. We then devised an efficient scan strategy for the full parameter space given a desired physical mass spectrum and introduced a measure for the quality of our full MSSM reproduction of this spectrum, that could also include criteria such as a maximal gaugino or higgsino component or couplings to specific sparticles. As a case study, we investigated the MSSM realisations of light higgsinos, finding an upper bound on the possible mass splitting among the lightest neutralinos of $\mathcal{O}(M_W)$ and a lower bound on the higgsino content of about 70%. We saw that large mass splittings required a more substantial level of fine-tuning, whereas for small mass splittings even larger regions of parameter space than those scanned by us led to viable scenarios. As expected, squarks, gluinos, and sleptons could be decoupled to 1.5 TeV, as could the heavier Higgs bosons without spoiling the reproduction of a SM-like light Higgs boson of mass 125 GeV. The latter required, however, a light stop of mass below or around 1 TeV with its heavier partner split by at least 1 TeV. The observed dark matter relic density could be reproduced close to the threshold of neutralino annihilation into pairs of W-bosons, whereas for higher masses the higgsinos can only represent a fraction of the observed dark matter. The corresponding direct detection cross sections are within reach of current experiments such as Xenon1T.

While we have indicated how our strategy can be generalised to other scenarios such as those with non-equidistant mass splitting of the light neutralinos and chargino or those with specific couplings of gauginos, higgsinos and other sparticles, specific studies of these other scenarios are beyond the scope of the present work and should be performed with a detailed application in mind.