1 Introduction

Determining the origin of the wide range of values spanned by the quark masses, and more generally, the structure of the lepton and quark mass spectrum, is one of the central problems of High Energy Physics. We have considered a previous search associated to this question. It was motivated by the suspicion about that the large degeneration of the non-interacting massless QCD vacuum (the state which is employed for the construction of the standard Feynman rules of Perturbative QCD) in combination with the strong forces carried by the QCD fields, could be able to generate a large dimensional transmutation effect. This fact, in turns, could then imply the generation of quark and gluon condensates and masses. The investigation of quark and gluon condensation effects had been widely considered in the literature [1,2,3,4,5,6,7,8]. A close connected line of activity relates with investigating of the Nambu–Jona-Lasinio (NJL) model for QCD, which also had furnished helpful information about quark physics, although the NJL terms are assumed as being of phenomenological nature, due to their non renormalizability [9,10,11,12,13,14]. Our previous works on the theme appeared in references [15,16,17,18,19,20,21,22,23,24]. Assumed that the idea in them is correct, the following picture could arise. A sort of Top condensate model might be the effective action for massless QCD. In it, a Top quark condensate, arising within the same inner context of the Standard Model (SM), could play the role of the Higgs field. Thus, the SM could be “closed” by generating all the masses within its proper context. We imagine this effect might occurs as follows: In a first step, the six quarks could get their masses thanks to a flavour symmetry breaking determined by the quark and gluon condensates. Afterwards, the electron, muon and tau leptons, would receive their intermediate masses thanks to radiative corrections mediated by the mid strength electromagnetic interactions with quarks. Finally, the only weak interacting character of the three neutrinos with all the particles, could determine their even smaller mass values.

Its is clear, that such a picture will need to satisfy the very strong experimental constraints imposed by the large experimental evidence about the validity of the SM model, which had came from the Large Hadron Collider (LHC). However, before hand we have no enough appealing reasons to discard the indications at hand about the possibility for the idea to be correct. Let us resume briefly those indications. In Ref. [16], with the use of a BC squeezed state like vacuum state (formed with nearly zero momenta gluons and ghost particles) modified Feynman rules for massless QCD were derived. The case of gluon condensation in the absence of quark pair condensation was initially considered. Then, a proper selection of the parameters allowed to derive an addition to the gluon free propagator: a Dirac’s Delta function centered at zero momenta multiplied by the metric tensor. Such a term were before discussed by Munczek and Nemirovsky in [2]. Before, in reference [15] it was simply proposed this modification and used to argue that it predicts a non vanishing value of the gluon condensate in the first corrections. The physical state and zero ghost number conditions were also imposed to fix the parameters of the squeezed vacuum. Then, the results obtained for gluons motivated the idea of also considering the quarks as massless and to search for the possibility to generate their masses dynamically, thanks to the condensation of quark pairs. For this purpose the Bardeen–Cooper–Schrieffer (BCS) like initial state was generalized in reference [17] to include the quark pair condensates in massless QCD. In this case, in a similar way as for gluons, the quark propagators simply were modified again by the addition of a term being the product of a Dirac’s Delta function at zero momentum and the spinor identity matrix. Next, in Refs. [17, 18] the main conclusion obtained from this starting approach followed from a simple discussion of the Dyson equation for quarks. It was considered by taking the quark self-energy in its lowest order in the power expansion in the condensate parameters. The coefficient of the zero momentum Delta function was fixed to reproduce the estimate of the gluonic Lagrangian mean value, following from the sum rules approaches. After that, the solution of the Dyson equation was able to predict the “constituent”values of 1/3 of the nucleon mass for the light quarks. The initial approach was also further studied in [19, 20] order to define a regularization scheme for eliminating the singularities which could appear in the Feynman diagram expansion due to the Delta functions at zero momentum entering in the modified propagators. However, due to the unusual characteristics of the approach, we decided in reference [21, 22] to also investigate the possibility of re-expressing the condensation effects in the modified propagators as equivalent vertices in the Lagrangian.

The result of Refs. [21, 22] were the central steps in leading to the model to be presented here. It was obtained that the condensate effects introduced in massless QCD by employing a squeezed state as modified vacuum, were equivalent to the addition of a new four legs vertex term in the Lagrangian, including two gluon and two quark lines. But, the vertex was a non local one including a zero momentum delta function. The obtained vertex term structure was not a fully gauge invariant one, but this drawback can be understood as due to the simple non gauge invariant form employed for the squeezed free vacuum state. However, the resulting curious structure directly led to the idea of constructing a local and gauge invariant form of the theory: It became clear that it is possible to include a similar kind of two gluon and two quark vertices, presumably incorporating the gluon and quark condensates, but in a gauge invariant and local form. This modification was presented in reference [23], where, it was also possible to argue that the new terms added to the action do not break the power counting renormalizability of massless QCD. This observation, then led to a surprising conclusion, also exposed in reference [23], about that the Nambu–Jona-Lasinio four fermion vertices also turn out to become renormalizable counterterms of the considered Lagrangian. The resulting theory included an additional set of six fermion fields showing a negative metric. However, the modified quark propagator also showed a rapidly decaying momentum dependence thanks to its Lee–Wick structure [25] which suggests that the negative metric states could result to be non propagating thanks to the radiative corrections [26]. The mentioned properties opened the opportunity that the proposed model can show the mass generation properties which the NJL models exhibit.

In the present work we start properly defining the model proposal and its consequences. That is, to begin we will concretely define the local and gauge invariant form of QCD Lagrangian being power counting renormalizable. The action will simply be the massless QCD one, plus six additional terms, one for each flavour, of similar vertices formed by products of two quark and two covariant derivatives. The Lagrangian will also include new NJL type of four quark vertices, which are not usually allowed by the power counting renormalizability. Further the free gluon and quark propagators will be determined by evidencing the modified Lee–Wick structure of the quark propagators quadratically decaying at large momenta. Then, the formula for the divergence indices of the Feynman diagrams will be derived, allowing to evidence the possibility of adding the NJL terms in a power counting renormalizable form. The issue of the might be surprising lacking in the literature of the identified possibility of incorporating NJL terms in the QCD action in a renormalizable form, is also explained. Next, the renormalized form of the action will be written and the expressions and diagrams for all the usual and counterterm vertices defined. The renormalized diagram expansion is then employed to evaluate the one loop divergences of the gluon selfenergy. The divergence of the polarization tensor, as imposed by the gauge invariance, resulted to be transversal. The calculation of the rest of the large number of primitive divergences will be presented elsewhere. After properly defining the Feynman expansion including all the required counterterms, we plan to study the one loop unitarity of the model by checking if the propagating quark modes show positive metric. In this sense, it can be remarked that the BRST quantization of the model can help to implement unitarity because the physical subspace of states, which is annihilated by the BRST charge, usually is of positive metric. Then, the negative metric quark states could be excluded from the set of physical states. However, the analysis of this question will be considered after properly define the renormalized perturbative expansion. In that stage, also the evaluation of the effective potential for investigating the presence of a flavour symmetry breaking will be considered.

Section 2 presents the Lagrangian structure of the model and writes its associated propagators and vertices to discuss the power counting renormalizability. Next, in Sect. 3 the index of divergence is derived and the primitive divergences are identified. Section 4 presents in detail the renormalized Feynman expansion. The resulting perturbative expansion is employed in Sect. 5 for evaluating the one loop divergences of the gluon selfenergy. The results are summarized in the last section.

2 The QCD Lagrangian including NJL terms

The action of the model in the extended D dimensional Minkowsky space is written in the local and gauge invariant form

$$\begin{aligned} S =&\int dx^{D}\text { }\left( \,-\frac{1}{4}F_{\mu \nu }^{a}(x)F^{a\mu \nu }(x)\right. \nonumber \\&-\frac{1}{2\alpha }\partial _{\mu }A^{a\mu }(x)\partial _{\nu }A^{a\nu }(x)+\partial _{\mu }\chi ^{*a}(x)D^{ab\mu }\chi ^{b}(x)\nonumber \\&+\sigma \sum _{q}\overline{\Psi }_{q}^{i}(x)\text { }i\gamma ^{\mu }D_{\mu } ^{ij}\Psi _{q}^{j}(x)\nonumber \\&-\sum _{q}\varkappa _{q}\,\overline{\Psi }_{q}^{j}\text { }(x)\overleftarrow{D}^{ji\mu }\text { }D_{\mu }^{ik}\Psi _{q}^{k} (x)\, \end{aligned}$$
(1)
$$\begin{aligned}&+\sum _{f}\sum _{q_{1},q_{2},q_{_{3}},q_{_{4}}}\lambda _{f}\text { } ^{(f)}\Lambda _{(j_{2},r_{2},q_{_{2}})(j_{4},r_{4},q_{4})}^{(j_{1},r_{1} ,q_{1})(j_{3,},r_{3},q_{3})}\nonumber \\&\quad \left. \times \overline{\Psi }_{q_{_{1}}}^{j_{1},r_{1} }(x)\overline{\Psi }_{q_{_{2}}}^{j_{2},r_{2}}(x)\Psi _{q_{_{3}}}^{j_{3},r_{3} }(x)\Psi _{q_{4}}^{j_{4},r_{4}}\text { }(x)\right) , \end{aligned}$$
(2)

where \(i,k,j,...=1,2,3\) are color indices and the spinor ones are hidden to simplify notation, the \(q=1,...,6\) indices indicate the flavour of the quarks. It should be underlined that the main different elements in this action with respect to the massless QCD, are the presence of the two last terms and the possible change in the sign of the Dirac Lagrangian implied by the values considered for the constant \(\sigma =\pm \,1\). Note the appearance of six new couplings \(\varkappa _{q}\), one for each quark (flavour) index q. The last term is the added Nambu–Jona-Lasinio like four quarks action. The coefficients \(^{(f)}\Lambda _{(j_{2},r_{2},q_{_{2}})(j_{4},r_{4},q_{4} )}^{(j_{1},r_{1},q_{1})(j_{3,},r_{3},q_{3})} \) are assumed to be such that the corresponding action term in the above Lagrangian remains invariant under an arbitrary symmetry transformation of the quark fields (color or Lorentz ones) for each particular of the let say F values of the index \(\ f=1,2,...,F\) . For bookkeeping purposes, the conventions for the various quantities are defined as follows

$$\begin{aligned} F_{\mu \nu }^{a}&=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}-g\text { }f^{abc}A_{\mu }^{b}A_{\nu }^{c}, \end{aligned}$$
(3)
$$\begin{aligned} \Psi _{q}^{k}(x)&\equiv \left( \begin{array} [c]{c} \Psi _{q}^{k,1}(x)\\ \Psi _{q}^{k,2}(x)\\ \Psi _{q}^{k,3}(x)\\ \Psi _{q}^{k,4}(x) \end{array} \right) , \end{aligned}$$
(4)
$$\begin{aligned} \Psi _{q}^{\dag k}(x)&\equiv (\Psi _{q}^{k}(x))^{T*}\nonumber \\&=\left( \begin{array} [c]{cccc} (\Psi _{q}^{k,1}(x))^{*}&(\Psi _{q}^{k,2}(x))^{*}&(\Psi _{q} ^{k,3}(x))^{*}&(\Psi _{q}^{k,4}(x))^{*} \end{array} \right) , \end{aligned}$$
(5)

where, as mentioned before, q \(=1,...,6\) indicates the flavour index. The expressions for the Dirac conjugate spinors and covariant derivatives are

$$\begin{aligned} \overline{\Psi }_{q}^{j}\text { }(x)&=\Psi _{q}^{\dag k}(x)\gamma ^{0},\text { } \end{aligned}$$
(6)
$$\begin{aligned} D_{\mu }^{ij}&=\partial _{\mu }\delta ^{ij}-i\text { }g\text { }A_{\mu }^{a} T_{a}^{ij},\ \overleftarrow{D}_{\mu }^{ij}=-\overleftarrow{\partial }_{\mu }\delta ^{ij}-i\text { }g\text { }A_{\mu }^{a}T_{a}^{ij}, \end{aligned}$$
(7)
$$\begin{aligned} D_{\mu }^{ab}&=\partial _{\mu }\delta ^{ab}-g\text { }f^{abc}\text { }A_{\mu } ^{c}, \end{aligned}$$
(8)

in which the Dirac’s matrices, SU(3) generators and the metric tensor are defined in this section in the conventions of reference [27], as

$$\begin{aligned} \{\gamma ^{\mu },\gamma ^{\nu }\}&=2g^{\mu \nu },\ \ \ \ [T_{a},T_{b}]=i\text { }f^{abc}T_{c}.\text { }\gamma ^{0}=\beta ,\nonumber \\ \gamma ^{j}&=\beta \text { } \alpha ^{j},\text { }j=1,2,3,\nonumber \\ g^{\mu \nu }&\equiv \left( \begin{array} [c]{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} -1 &{} 0 &{} 0\\ 0 &{} 0 &{} -1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) ,\text { }\beta =\left( \begin{array} [c]{cc} I &{} 0\\ 0 &{} -I \end{array} \right) ,\nonumber \\ \alpha ^{j}&\equiv \left( \begin{array} [c]{cc} 0 &{} \sigma ^{j}\\ \sigma ^{j} &{} 0 \end{array} \right) ,\text { }j=1,2,3,\nonumber \\ \sigma ^{1}&=\left( \begin{array} [c]{cc} 0 &{} 1\\ 1 &{} 0 \end{array} \right) ,\text { }\sigma ^{2}=\left( \begin{array} [c]{cc} 0 &{} -i\\ i &{} 0 \end{array} \right) ,\nonumber \\ \sigma ^{3}&=\left( \begin{array} [c]{cc} 1 &{} 0\\ 0 &{} -1 \end{array} \right) ,\text { }I=\left( \begin{array} [c]{cc} 1 &{} 0\\ 0 &{} 1 \end{array} \right) . \end{aligned}$$
(9)

Other definitions and relations for the coordinates are

$$\begin{aligned} x\equiv x^{\mu }=(x^{0},\overrightarrow{x})=(x^{0},x^{1},x^{2},x^{3}),\text { }x_{\mu }=g_{\mu \nu }x^{\nu },\text { }x^{0}=t. \end{aligned}$$
(10)

The notations to be employed in this work are chosen to coincide with the ones used in the text in reference [27]. This criterium was adopted in order to become able of employing the large set of evaluations, definitions and auxiliary formulae presented in that reference for QCD. As underlined before, a basic new element in the proposed action are the six vertices of the form

$$\begin{aligned} -\sum _{q}\varkappa _{q}\,\overline{\Psi }_{q}^{j}(x)\gamma _{\mu } \overleftarrow{D}^{ji\mu }\gamma _{\nu }D^{ik\nu }\Psi _{q}^{k}(x), \end{aligned}$$
(11)

where the six coefficients \(\varkappa _{q}\) will be called “condensate parameters”, since they enter in similar ‘positions’ to the parameters appearing in the “motivating ”non local vertex derived in the previous work [22]. The \(\varkappa _{q}\) are now six new dimensional constants of the theory. A new element with respect to the massless QCD in the proposed action is allowing a change in the sign of the Dirac Lagrangian. The interest of this change was discussed in reference [24]. If the modification in the sign is allowed, it will lead to free quark propagators which are expressed as usual positive metric Dirac propagator of massive fermions plus a negative metric massless propagators. The usual sign assignment determines that the massive propagator shows negative metric. Since experiments seem to indicate that the massive quarks in QCD should be physically relevant within the model, the negative sign of the Dirac action was adopted. However, it can be remarked that in reference [24] it was also argued that such a change in the sign can be introduced in the same physical action by a change of field and coordinates transformation. Thus, since the same action is associated to the quantization procedure, the fixed negative signs can be associated to a quantization of the same physical system but using alternative transformed field variables and coordinates.

2.1 The free propagators

The Lagrangian associated to the action in (1) can be decomposed in the quadratic in the fields approximation \(\mathcal {L}_{0}\) and the one determining the interaction vertices \(\mathcal {L}_{i}\) to write

$$\begin{aligned} S&=\int dx^{D}\mathcal {L=}\text { }S_{0}+S_{i}\nonumber \\&=\int dx^{D}\mathcal {L}_{0}+\int dx^{D}\mathcal {L}_{i}. \end{aligned}$$
(12)

After finding the inverse of the kernels defining the free form of the action

$$\begin{aligned} S_{0} =&\int dx^{D}\left( \frac{1}{2}A^{a\mu }\left( g_{\mu \nu }\partial ^{2}-\left( 1-\frac{1}{\alpha }\right) \partial _{\mu }\partial _{\nu }\right) A^{a\nu }+\right. \nonumber \\&\left. -\chi ^{*a}\partial ^{2}\chi ^{a}+\sum _{q}\overline{\Psi }_{q}^{i} (\sigma \text { }i\text { }\gamma ^{\mu }\partial _{\mu }+x_{f}\text { }\partial ^{2})\Psi _{q}^{i}\text { }\right) , \end{aligned}$$
(13)

it follows that the gluon quark and ghost propagators can be evaluated in the form

$$\begin{aligned} D_{\mu \nu }^{ab}(p)&=\frac{\delta ^{ab}d_{\mu \nu }(p)}{p^{2}+i\epsilon } =\frac{\delta ^{ab}\left( g_{\mu \nu }-(1-\alpha )\frac{p_{\mu }p_{\nu }}{p^{2}}\right) }{p^{2}+i\epsilon }, \end{aligned}$$
(14)
$$\begin{aligned} S_{q}^{ij}(p)&=\frac{\sigma \text { }\delta ^{ij}}{\sigma \text { }\varkappa _{q}\text { }p^{2}-\gamma _{\nu }p^{\nu }}\nonumber \\&=\sigma \text { }\delta ^{ij}\left( \frac{1}{\gamma _{\nu }p^{\nu }-\frac{1}{\sigma \varkappa _{q}}}-\frac{1}{\gamma _{\nu }p^{\nu }}\right) ,\text { } q=1,2,...,6, \end{aligned}$$
(15)
$$\begin{aligned} D^{ab}(p)&=-\frac{\delta ^{ab}}{p^{2}+i\epsilon }=-\frac{\delta ^{ab}}{p^{2}+i\epsilon }. \end{aligned}$$
(16)

The difference between these Green functions and the ones related with massless QCD is present only in the quark propagators which each of them appears expressed as a difference between the usual massive Dirac propagator and another one, also usual but massless. Note that in dependence of the sign \(\sigma \) of the Dirac action, the massive component shows a normal positive or negative metric. As noted before, the negative sign of \(\sigma \) fix the massive term as showing positive metric. The gluon and ghost free propagators are the usual ones, and their notation coincides with the one in reference [27]. The most curious property of these free propagators is that all of them behave as \(\frac{1}{p2}\) at large momenta. Therefore, since the maximal number of fields plus derivative factors in any of the Lagrangian terms is four, interestingly, the model appear to be power counting renormalizable. The masses of each of the massive quarks become just proportional to the inverse of its corresponding condensate parameter (couplings) \(\varkappa _{q},\) \(\ q=1,...,6\). As it was mentioned, the massive propagator has the appropriate sign corresponding to positive norm states when \(\sigma =-\,1\). On another hand, the massless component has the sign related with negative norm states. It can be remarked that within QCD, assumed to describe Nature, it is currently interpreted that nor gluons or quarks show asymptotic states. Thus, the negative metric of the massless free states seem not be a direct drawback of the model. However, the fact that in very high energy processes, a description based in massive quarks in short living asymptotic states, seems to describe the experiences, suggests that an approach in which the massive quarks have positive norms and massless do not appear (thanks to radiative corrections) would be convenient. Then, the negative value of \(\sigma \) was allowed to be considered in the model.

Fig. 1
figure 1

The new types of vertices. The three legs ones, at difference with the usual thee legs vertices in usual QCD, does not contains linear terms in the gamma matrices. The two-gluon-two-quark four legs vertices are the local counterparts of the non local vertices representing quark condensate effects obtained in references [21, 22]. The four quark legs vertices are the ones generated by the NJL four quark interactions. There is a maximal number F of such vertices being invariant under the symmetries of QCD

Full size image

2.2 The vertices

The modified action (1) determines new vertices in addition to the usual in massless QCD. The new types of vertices appearing are illustrated in Fig. 1. There are a total of \(16+F\) different vertices: \(v_{i} ,i=1,...16\,+F\). The \(\ v_{1}\) to \(v_{4}\) will indicate the usual ones in massless QCD, the three gluon legs, four gluon legs and the ghost-gluon and quark-gluon interaction vertices, respectively. The additional \(v_{5}\) \(-v_{10}\) vertices are associated to the new six kinds of three legs quark gluon interaction. Further, the \(v_{11}-v_{16}\) additional new vertices correspond to the special new 4 legs vertices in which two gluon and two quarks interact. It should be recalled that precisely these the new added vertices were motivating the interest in the model under consideration. Finally, the last new vertices \(v_{17}-v_{16+F}\) are associated with the now allowed F of the NJL type of terms included in the Lagrangian, where F is the number of introduced \(\Lambda \) interaction terms defining the four fermion actions which remain invariant under the symmetries of QCD. The interaction Lagrangian terms corresponding to these mentioned vertices have the forms

$$\begin{aligned} \mathcal {L}_{i} =\,&\frac{g}{2}f^{abc}\left( \partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}\right) A^{b\mu }A^{c\nu }\nonumber \\&-\frac{g^{2}}{4}f^{abe}f^{cde}A_{\mu } ^{a}A_{\nu }^{b}A^{c\mu }A^{d\nu }\nonumber \\&-g\text { }f^{abc}(\partial ^{\mu }\chi ^{a*})\chi ^{b}A_{\mu }^{c} +\sum _{q=1,...,6}\sigma g\overline{\Psi }_{q}^{i}\gamma ^{\mu }T_{a}^{ij}\Psi _{q}^{j}A_{\mu }^{a}\nonumber \\&-i\sum _{q=1,...,6}\varkappa _{q}\text { }g\text { }\left( \overline{\Psi } _{q}^{i}\partial ^{\mu }(T_{a}^{ij}\Psi _{q}^{j}A_{\mu }^{a})+\overline{\Psi } _{q}^{i}A_{\mu }^{a}\partial ^{\mu }(T_{a}^{ij}\Psi _{q}^{j})\right) \nonumber \\&+\sum _{q=1,...,6}\text { }\varkappa _{q}\text { }g^{2}\text { }\overline{\Psi }_{q}^{i}A^{c\mu }T_{c}^{ij}T_{b}^{jk}A_{\mu }^{b}\Psi _{q}^{k}\nonumber \\&+ \sum _{f}\sum _{q_{1},q_{2},q_{_{3}},q_{_{4}}}\lambda _{f}\text { } ^{(f)}\Lambda _{(j_{2},r_{2},q_{_{2}})(j_{4},r_{4},q_{4})}^{(j_{1},r_{1} ,q_{1})(j_{3,},r_{3},q_{3})}\nonumber \\&\times \overline{\Psi }_{q_{_{1}}}^{j_{1},r_{1} }(x)\overline{\Psi }_{q_{_{2}}}^{j_{2},r_{2}}(x)\Psi _{q_{_{3}}}^{j_{3},r_{3} }(x)\Psi _{q_{4}}^{j_{4},r_{4}}\text { }(x). \end{aligned}$$
(17)

3 The divergence index of the model

Let us consider an arbitrary connected Feynman diagram of the proposed model including \(n_{B}=n_{g}+n_{gh}\) boson internal lines, in which the entering \(n_{gh}\) ghost lines are considered as boson ones as well as the number of gluon lines \(n_{g}.\) The external boson lines are equally constituted as the sum of the gluon and ghost ones as \(N_{B}=N_{g}+N_{gh}.\) Similarly,the number of internal fermion lines of any type of quark will be denoted as \(n_{F}\) and the corresponding external ones as \(N_{F}\)  [27]. For each kind i of the considered vertices of the model, let us define the number of boson lines connected to it as \(b_{i}\), and the number of fermion lines also attached to it as \(f_{i}.\) Define also the total number of vertices of kind i appearing in the diagram as \(n_{i}\) and the number of spatial derivatives entering in the definition of the vertex \(\delta _{i}\) . Therefore, the total number of derivatives which appear in the diagram \(\delta \) can be written as

$$\begin{aligned} \delta =\sum _{i=1,...,N_{V}}n_{i}\delta _{i}\text { }. \end{aligned}$$
(18)

But, the total number of free propagator ends associated to the internal boson lines, plus a half of the propagator ends related to external lines boson lines should coincide with the total number of boson lines arriving to all the vertices. Also, the same property is valid for fermion propagators. Thus, the following relations for any connected (or disconnected) diagram are valid

$$\begin{aligned} 2n_{B}+N_{B}&=\sum _{i=1,...,N_{V}}n_{i}b_{i}, \end{aligned}$$
(19)
$$\begin{aligned} 2n_{F}+N_{F}&=\sum _{i=1,...,N_{V}}n_{i}f_{i}. \end{aligned}$$
(20)

They allow to express the total numbers of boson and fermion lines in terms of the number of external ones and the parameters defining the vertices as follows

$$\begin{aligned} n_{B}&=\frac{1}{2}\left( \sum _{i=1,...,N_{V}}n_{i}b_{i}-N_{B}\right) , \end{aligned}$$
(21)
$$\begin{aligned} n_{F}&=\frac{1}{2}\left( \sum _{i=1,...,N_{V}}n_{i}f_{i}-N_{F}\right) . \end{aligned}$$
(22)

Let us define for later use, the number of vertices of the interaction of one gluon with two quarks as defined by the Dirac Lagrangian as \(n_{i}\) for \(i=4\), that is as \(n_{4}\) \(\equiv \) \(n_{gqq}\). Considering that the number of independent D dimensional momentum integrations of the diagram is equal to the number of propagators minus the number of independent momentum conservation laws associated to all the vertices, and remembering that this number is given by the number of vertices minus one for connected diagrams, it follows for the number of closed loops l in those connected diagrams (the number of independent momentum integrations) the expression

$$\begin{aligned} l=\frac{1}{2}\sum _{i=1,...,N_{V}}n_{i}(b_{i}+f_{i}-2)-\frac{1}{2}(N_{B} +N_{F})+1. \end{aligned}$$
(23)

Now is possible to define the superficial degree of divergence index of the diagrams in the model by counting the momenta dependence as

$$\begin{aligned} d_{G}=D\text { }l+\left( \delta -\frac{N_{FP}}{2}\right) -2n_{B}-2n_{F}, \end{aligned}$$
(24)

where D l is the number of independent momentum integrations in the diagram, \(\delta \) is the number of momenta entering in all the definitions of the appearing vertices, \(2n_{B}\) is the number of momenta defining the decreasing asymptotic behavior of the product of all bosonic propagators (gluon and ghost ones). Here is important to note that for ghosts, the number of the momenta appearing in the vertices are not determining an equal number of divergent momenta factors. This is because, in the number \(N_{FP}\) of ghost-gluon vertices associated to the external ghost lines, only half of them determines a momentum really diverging when all the independent integration momenta go to infinity. Therefore the number of divergent momenta determined by the vertices is reduced to \(\delta -\frac{N_{FP}}{2}\)  [27]. The essential difference of the formula for the degree of divergence (24) with the one related to QCD is the term \(2n_{F}\). This term, which supports the superficial convergence of the diagrams, precisely doubles the one associated to QCD. This represents a drastic change in the behavior of the divergences in the proposed model with respect to QCD or to simple NJL models. After substituting the expression for the entering quantities \(d_{G}\) can be rewritten as follows

$$\begin{aligned} d_{G} =&\frac{1}{2}\sum _{i=1,...,N_{V}}n_{i}\left( \frac{D-2}{2} (b_{i}+f_{i}+\delta _{i}-D\right) \nonumber \\&-\frac{(D-2)}{2}N_{B}-\frac{(D-2)}{2}N_{F}+D-\frac{N_{FP}}{2} . \end{aligned}$$
(25)

But, at \(D=4\) for all the diagram in the model, it is valid \(b_{i} +f_{i}+\delta _{i}=4-\delta _{i,4_{}}.\) Thus, in this case the degree of divergence can be written as

$$\begin{aligned} d_{G}=4-N_{G}-\frac{3}{2}N_{FP}-N_{F}-n_{gqq}. \end{aligned}$$
(26)

This result indicates that all the connected diagrams are superficially convergent when the number of external lines is larger than 4. Therefore, the model is power counting renormalizable in spite of including four fermion interaction terms. Such a conclusion is surprising and thus the possibility of completely construct the theory and investigate its predictions for the quark masses must be carefully examined. Consider now the set of numbers \((N_{G},N_{FP},N_{F},n_{gqq})\) formed by the numbers of external gluon, ghost and quark lines and also including in the fourth component the number of usual gluon quark interaction Dirac vertices \(n_{gqq} \). Employing the above formula a finite set of superficially divergent Feynman diagrams can be determined for the perturbative expansion. At this point it should be underlined that precisely the new action terms including two-gluons-two-quarks vertices, allowed the decreasing behavior of the quark propagator at large momenta. This fact, permitted that most of the Lagrangian terms defining the NJL models also became allowed to be included in the Lagrangian without affecting the power counting renormalizability. Henceforth, the mass generation properties embodied in usually non-renormalizable NJL phenomenological theories, seem that can dynamically work now in the considered context.

The sum of fourth order terms in the quark fields should be a general expression being invariant under the symmetries of QCD, which became able to allow the cancelation of the divergences appearing in each order of the perturbative expansion. In the normal NJL theory, the usual Dirac propagator, with its “one over the momentum modulus” behavior at large momenta, makes the model non-renormalizable. It may be also noted that the power counting rules for the model are similar to the ones working in the simpler \(\lambda \phi ^{4}\) scalar field theory with the usual scalar field propagator \(\frac{1}{p^{2}}\) . This can be explicitly implemented in the Lagrangian, simply by absorbing the six dimensional constants \(\varkappa _{q}\) in a redefinition of the quark fields. This change makes the couplings associated to the NJL terms to becomes dimensionless constants. One important remark following from the previous discussion can be added. Let us assume that a renormalization procedure of pure massless QCD is reconsidered. Then, the new added kind of vertices \(\overline{\text { }\Psi }\) \((x)\overleftarrow{D}\) \(D\Psi (x)\), could be reasonably identified as possible counterterms for this purpose, since they do not destroy power counting renormalizability. This circumstance leads to the idea about that the proposed model could result to be physically equivalent to the quantized massless QCD.

3.1 A remark on the power counting renormalizability

In this subsection we will shortly remark about an important issue: to give a reasonable explanation for the lack of noticing during decades of the proposed kind of Lagrangians incorporating the NJL terms in a power counting renormalizable form. In particular it can be underlined that the addition of dimension higher than four of the fields Lagrangian terms, which were incorporated in the submitted work, are allowed due to a subtle point that seemingly remained unnoticed in the literature. This happening could had been determined by a special circumstance which is hidden in the analysis commonly done to estimate the renormalizability of theories. Specifically, it can noticed that one type of the terms which were added to the QCD Lagrangian in (1) were the “two-quarks-two-covariant-derivatives” ones, which show a higher than the allowed dimension of the fields in the usual rules for renormalizability (See reference [28]). However, it should stressed that each of these terms is not an homogenous monomial as a polynomial in the fields. In fact, they are the sum of a quadratic term in the fields, plus two other contributions which are of order three and four. Therefore, the absence in the literature of the consideration of such kind of terms (as being compatible with the renormalizability) can be naturally determined by the fact that such terms, in addition to two proper vertices (being monomials of order higher than two in the fields), also contain an order two in the fields contribution: the one having two quark fields and a D’Alembertian acting on one of them. This Lagrangian term enforces through quantization, that the quark propagators will have a Lee–Wick structure, which shows a one over squared momentum behavior at large momenta. But, the common rules of power counting renormalizability are radically determined in form by the momentum behavior of the free propagators. In QCD the behavior of the Dirac propagator is “1/p”. However, the Lee–Wick type of propagator (which is rigorously fixed by the quantization of the model as noted before) exhibits a “\(1/p^2\)” dependence. Therefore, the contribution to the divergence index formula in the proposed model radically deviates from the assumption in the usual analysis of power counting renormalizability. Indeed, the usual discussion considers vertices which are homogeneous monomials in the fields showing higher than two fields. The vertices being associated to such terms do no change in any way the free propagators of the theory. Then, the usual restrictions on their dimensionality properly work. Therefore, it can be estimated that the above argue can justify the lack of interest in such terms for long periods. However, the strong phenomenological value of the usually considered non renormalizable NJL terms determines the relevance of examining possibilities of incorporating them in the QCD action in a renormalizable form.

4 The renormalized Feynman expansion

In this section we will develop the renormalized Feynman expansion of the model. For this purpose the fields \(A_{\mu }^{a},\chi ^{*},\chi \), \(\overline{\psi }_{q}\) and \(\psi _{q},q=1,2,...,6,\) in the bare action (1) will be substituted in terms of the renormalized fields through the multiplicative mappings

$$\begin{aligned} A_{\mu }^{a}&\rightarrow Z_{3}^{\frac{1}{2}}A_{\mu }^{a},\text { } \end{aligned}$$
(27)
$$\begin{aligned} \chi ^{*}&\rightarrow \widetilde{Z}_{3}^{\frac{1}{2}}\chi ^{*},\quad \chi \rightarrow \widetilde{Z}_{3}^{\frac{1}{2}}\chi \text { }, \end{aligned}$$
(28)
$$\begin{aligned} \overline{\psi }_{q}&\rightarrow Z_{q,2}^{\frac{1}{2}}\text { }\overline{\psi }_{q}\text { },\quad \quad \psi _{q}\rightarrow Z_{q,2}^{\frac{1}{2} }\text { }\psi _{q},\quad \quad q=1,...,6, \end{aligned}$$
(29)

and the bare coupling parameters of the action g,  \(\alpha \) and \(\varkappa _{q}\) \((q=1,...,6),\) will be expressed in terms of their renormalized couplings as follows

$$\begin{aligned} g-&>Z_{g}\text { }g, \end{aligned}$$
(30)
$$\begin{aligned} \alpha -&>Z_{3}\alpha , \end{aligned}$$
(31)
$$\begin{aligned} \varkappa _{q}-&>Z_{\varkappa _{q}}\text { }\varkappa _{q},\quad \quad q=1,...,6, \end{aligned}$$
(32)
$$\begin{aligned} \lambda _{f}-&>Z_{f}\text { }\lambda _{f}\quad \quad f=1,...,F. \end{aligned}$$
(33)

With this substitutions done in the original action (1), it can be transformed in the sum of three terms as follows

$$\begin{aligned} S&= \text { }S_{0}+S_{i}+S_{c}\nonumber \\&=\int dx^{D}\mathcal {(L}_{0}+\mathcal {L}_{i}+\mathcal {L}_{c}). \end{aligned}$$
(34)

The quadratic in the fields term \(S_{0}\), is the sum of the also quadratic terms of the bare action, but in this case expressed in terms of the renormalized fields and couplings

$$\begin{aligned} S_{0}&=\sum _{n=1}^{n=3}S_{0}^{(n)}=\sum _{n=1}^{n=3}\int dx^{D} \mathcal {L}_{0}^{(n)}, \end{aligned}$$
(35)
$$\begin{aligned} S_{0}^{(1)}&=\int dx^{D}\frac{1}{2}A^{a\mu }(x)\delta ^{ab}\left( g_{\mu \nu }\partial ^{2}-\left( 1-\frac{1}{\alpha }\right) \partial _{\mu }\partial _{\nu }\right) A^{b\nu }(x), \end{aligned}$$
(36)
$$\begin{aligned} S_{0}^{(2)}&=\int dx^{D}(\partial ^{\mu }\chi ^{a*}(x))\partial _{\mu } \chi ^{a}(x), \end{aligned}$$
(37)
$$\begin{aligned} S_{0}^{(3)}&=\sum _{q}\int dx^{D}\overline{\Psi }_{q}^{i}(x)\left( \sigma \text { }i\gamma ^{\mu }\partial _{\mu }+\varkappa _{q}\partial ^{2}\right) \Psi _{q}^{j}(x). \end{aligned}$$
(38)

The second term \(S_{i}\) in (34) is the sum of all Lagrangian terms of the more than second order in the fields of the bare action, but in which the fields are also substituted in terms of their renormalized values, and the bare couplings are also substituted by the renormalized versions. Its expression is

$$\begin{aligned} S_{i} =&\sum _{n=1}^{n=7}S_{i}^{(n)}=\sum _{n=1}^{n=7}\int dx^{D} \mathcal {L}_{i}^{(n)}, \end{aligned}$$
(39)
$$\begin{aligned} S_{i}^{(1)} =&\int dx^{D}\frac{g}{2}f^{abc}(\partial _{\mu }A_{\nu } -\partial _{\nu }A_{\mu })A^{b\mu }A^{c\nu }, \end{aligned}$$
(40)
$$\begin{aligned} S_{i}^{(2)} =&-\int dx^{D}\frac{g^{2}}{4}f^{abe}f^{cde}A_{\mu }^{a}A_{\nu }^{b}A^{c\mu }A^{d\nu }, \end{aligned}$$
(41)
$$\begin{aligned} S_{i}^{(3)} =&-\int dx^{D}gf^{abc}(\partial ^{\mu }\chi ^{a*})\chi ^{b} A_{\mu }^{c}, \end{aligned}$$
(42)
$$\begin{aligned} S_{i}^{(4)} =&-\sum _{q=1,...,6}\int dx^{D}\sigma g\overline{\Psi }_{q} ^{i}\gamma ^{\mu }T_{a}^{ij}\Psi _{q}^{j}A_{\mu }^{a}, \end{aligned}$$
(43)
$$\begin{aligned} S_{i}^{(5)} =&-i\sum _{q=1,...,6}\int dx^{D}\varkappa _{q}g\nonumber \\&\times \left( \overline{\Psi }_{q}^{i}\partial ^{\mu }(T_{a}^{ij}\Psi _{q}^{j}A_{\mu } ^{a})+\overline{\Psi }_{q}^{i}A_{\mu }^{a}\partial ^{\mu }(T_{a}^{ij}\Psi _{q} ^{j})\right) , \end{aligned}$$
(44)
$$\begin{aligned} S_{i}^{(6)} =&\sum _{q=1,...,6}\int dx^{D}\text { }\varkappa _{f}\text { } g^{2}\overline{\Psi }_{q}^{i}A^{c\mu }T_{c}^{ij}T_{b}^{jk}A_{\mu }^{b}\Psi _{q}^{k}, \end{aligned}$$
(45)
$$\begin{aligned} S_{i}^{(7)} =&\sum _{f}\sum _{q_{1},q_{2},q_{_{3}},q_{_{4}}}\lambda _{f}\text { }^{(f)}\Lambda _{(j_{2},r_{2},q_{_{2}})(j_{4},r_{4},q_{4})}^{(j_{1},r_{1} ,q_{1})(j_{3,},r_{3},q_{3})}\nonumber \\&\times \int dx^{D}\text { }\overline{\Psi }_{q_{_{1}}}^{j_{1},r_{1}}(x)\Psi _{q_{_{2}}}^{j_{2},r_{2}}(x)\overline{\Psi }_{q_{_{3}}}^{j_{3},r_{3}} (x)\Psi _{q_{4}}^{j_{4},r_{4}}\text { }(x). \end{aligned}$$
(46)

Finally, the third term \(S_{c}\) is the difference between the renormalized action and the bare action expressed in terms of the renormalized fields and couplings. It can be written in the form

$$\begin{aligned} S_{c}&=\sum _{n=1}^{n=11}S_{c}^{(n)}=\sum _{n=1}^{n=11}\int dx^{D} \mathcal {L}_{c}^{(n)}, \end{aligned}$$
(47)
$$\begin{aligned} S_{c}^{(1)}&=(Z_{3}-1)\int dx^{D}\frac{1}{2}A^{a\mu }\delta ^{ab}(g_{\mu \nu }\partial ^{2}-\partial _{\mu }\partial _{\nu })A^{b\nu }, \end{aligned}$$
(48)
$$\begin{aligned} S_{c}^{(2)}&=(\widetilde{Z}_{3}-1)\int dx^{D}(\partial ^{\mu }\chi ^{a*})\partial _{\mu }\chi ^{a}, \end{aligned}$$
(49)
$$\begin{aligned} S_{c}^{(3)}&=\sigma \sum _{q}(Z_{2}^{q}-1)\int dx^{D}\overline{\Psi }_{q} ^{i}(x)\text { }i\gamma ^{\mu }\partial _{\mu }\Psi _{q}^{i}(x), \end{aligned}$$
(50)
$$\begin{aligned} S_{c}^{(4)}&=(Z_{1}-1)\int dx^{D}\text { }\frac{g}{2}\text { } f^{abc}(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu })A^{b\mu }A^{c\nu }, \end{aligned}$$
(51)
$$\begin{aligned} S_{c}^{(5)}&=-(Z_{4}-1)\int dx^{D}\text { }\frac{g^{2}}{4}\text { } f^{abe}f^{cde}A_{\mu }^{a}A_{\nu }^{b}A^{c\mu }A^{d\nu }, \end{aligned}$$
(52)
$$\begin{aligned} S_{c}^{(6)}&=-(\widetilde{Z}_{1}-1)\int dx^{D}g\text { }f^{abc} (\partial ^{\mu }\chi ^{a*})\chi ^{b}A_{\mu }^{c}, \end{aligned}$$
(53)
$$\begin{aligned} S_{c}^{(7)}&=-\sum _{q=1,...,6}(Z_{1F}^{q}-1)\int dx^{D}\sigma g\text { }\overline{\Psi }_{q}^{i}\gamma ^{\mu }T_{a}^{ij}\Psi _{q}^{j}A_{\mu }^{a},\end{aligned}$$
(54)
$$\begin{aligned} S_{c}^{(8)}&=\sum _{q=1,...,6}(Z_{\varkappa _{q}}^{1}-1)\int dx^{D}\text { }\varkappa _{q}\text { }\overline{\Psi }_{q}^{i}\partial ^{2}\Psi _{q}^{j},\end{aligned}$$
(55)
$$\begin{aligned} S_{c}^{(9)}&=-i\sum _{q=1,...,6}(Z_{\varkappa _{q}}^{2}-1)\int dx^{D}\text { }\varkappa _{q}g\nonumber \\&\quad \left( \overline{\Psi }_{q}^{i}\partial ^{\mu } (T_{a}^{ij}\Psi _{q}^{j}A_{\mu }^{a})+\overline{\Psi }_{q}^{i}A_{\mu }^{a} \partial ^{\mu }(T_{a}^{ij}\Psi _{q}^{j})\right) ,\end{aligned}$$
(56)
$$\begin{aligned} S_{c}^{(10)}&=\sum _{q=1,...,6}(Z_{\varkappa _{q}}^{3}-1)\int dx^{D}\text { }\varkappa _{f}\text { }g^{2}\overline{\Psi }_{q}^{i}A^{c\mu }T_{c}^{ij}T_{b} ^{jk}A_{\mu }^{b}\Psi _{q}^{k},\end{aligned}$$
(57)
$$\begin{aligned} S_{c}^{(11)}&=\sum _{f}\sum _{q_{1},q_{2},q_{_{3}},q_{_{4}}}(Z_{\lambda }(Z_{2,q_{1}}Z_{2,q_{2}}Z_{2,q_{3}}Z_{2,q_{4}})^{^{\frac{1}{2}}}-1)\nonumber \\&\quad \times \lambda _{f}\text { }^{(f)}\Lambda _{(j_{2},r_{2},q_{_{2}})(j_{4},r_{4},q_{4})} ^{(j_{1},r_{1},q_{1})(j_{3,},r_{3},q_{3})}\nonumber \\&\quad \times \int dx^{D}\text { }\overline{\Psi }_{q_{_{1}}}^{j_{1},r_{1}}(x)\Psi _{q_{_{2}}}^{j_{2},r_{2}}(x)\overline{\Psi }_{q_{_{3}}}^{j_{3},r_{3}} (x)\Psi _{q_{4}}^{j_{4},r_{4}}\text { }(x), \end{aligned}$$
(58)

in which the following definitions of the appearing new parameters had been considered

$$\begin{aligned} Z_{1}&=Z_{g}Z_{3}^{\frac{3}{2}},\end{aligned}$$
(59)
$$\begin{aligned} \widetilde{Z}_{1}&=Z_{g}\widetilde{Z}_{3}Z_{3}^{\frac{1}{2}},\end{aligned}$$
(60)
$$\begin{aligned} Z_{4}&=Z_{g}^{2}Z_{3}^{2},\end{aligned}$$
(61)
$$\begin{aligned} Z_{1F}^{q}&=Z_{g}Z_{2}^{q}Z_{3}^{\frac{1}{2}},\quad q=1,...,6,\end{aligned}$$
(62)
$$\begin{aligned} Z_{\varkappa _{q}}^{1}&=Z_{\varkappa _{q}}Z_{q,2},\quad q=1,...,6, \end{aligned}$$
(63)
$$\begin{aligned} Z_{\varkappa _{q}}^{2}&=Z_{\varkappa _{q}}Z_{q,2}Z_{3}^{\frac{1}{2}} Z_{g},\quad q=1,...,6, \end{aligned}$$
(64)
$$\begin{aligned} Z_{\varkappa _{q}}^{3}&=Z_{\varkappa _{q}}Z_{q,2}Z_{3}Z_{g}^{2},\quad q=1,...,6. \end{aligned}$$
(65)

4.1 The generating functional for the Feynman diagrams

Henceforth, considering the above definitions for the action of the model and introducing the auxiliary external sources for the fields, the explicit form of the generating functional of the perturbative expansion can be written in the form

$$\begin{aligned}&Z[j,\eta ,\overline{\eta },\xi ,\xi ^{*}] =\frac{1}{\mathcal {N}}\int D[A,\overline{\Psi }_{q},\Psi _{q},{{\chi }}^{*} ,{{\chi }}]\nonumber \\&\qquad \times \exp [i\text {}[S[A,\Psi _{q},\overline{\Psi }_{q},{{\chi }}^{*},{{\chi }}]\nonumber \\&\qquad +\int dx^{D}({{j(x)A(x)+\xi }}^{*} {{(x)\chi (x)+\chi }}^{*}{{(x)\xi (x)} }\nonumber \\&\qquad + \sum _{q=1,...,6}(\overline{{\eta }}_{q}(x)\Psi _{q}(x)+\overline{\Psi }_{q}(x)\eta _{q}(x)))]\nonumber \\&\quad =\frac{1}{\mathcal {N}}\exp \left[ i\text { }\left( S\left[ \frac{\delta }{i\text { }\delta j}{,\frac{\delta }{-i\text { }\delta \eta _{q}},}\frac{\delta }{i\text { }\delta \overline{\eta }_{q}},{\frac{\delta }{-i\text { }\delta \xi }},\frac{\delta }{i\text { }\delta \xi _{q}^{*}}\right] \right. \right. \nonumber \\&\qquad \left. \left. -{S}_{0}{\left[ \frac{\delta }{i\text { }\delta j},\frac{\delta }{-i\text { }\delta \eta _{q}} ,\frac{\delta }{i\text { }\delta \overline{\eta }_{q}},\frac{\delta }{-i\text { }\delta \xi },\frac{\delta }{i\text { }\delta \xi _{q}^{*}}\right] }\right) \right] \nonumber \\&\qquad \times \,Z^{(0)}[j,\eta ,\overline{\eta } ,\xi ,\xi ^{*}]. \end{aligned}$$
(66)

where \(\mathcal {N}\) is chosen for assuring that Z vanish when all the sources are equal to zero. In the above expression \(Z^{(0)}\) is the free partition function, which is the product of eight separate factors for gluons, ghosts and for each type of quark, in the form

$$\begin{aligned}&Z^{(0)}[j,\eta ,\overline{\eta },\xi ,\xi ^{*}] =Z_{G}^{(0)}[j]\times Z_{GH}^{(0)}[\xi ,\xi ^{*}]\times {\displaystyle \prod \limits _{q=1,...,6}} Z_{q}^{(0)}[\eta _{q},\overline{\eta }_{q}].\nonumber \\&\quad =\int D[A,\overline{\Psi }_{q},\Psi _{q},{{\chi }}^{*},{{\chi }}]\exp [i\text {} (S_{0}[A,\Psi _{q},\overline{\Psi }_{q},{{\chi }}^{*},{{\chi } }]\nonumber \\&\qquad +\int dx^{D}\left( j(x)A(x)+{{\xi } }^{*}{{(x)\chi (x)+\chi }}^{*}{{(x)\xi (x)}}\right. \nonumber \\&\qquad \left. \left. + \sum _{q=1,...,6}\left( \overline{{\eta }}_{q}(x)\Psi _{q}(x)+\overline{\Psi }_{q}(x)\eta _{q}(x)\right) \right) \right] ,\nonumber \\&\quad =\int D[A]\exp \left[ i\left( \int dx^{D}\frac{1}{2}A^{a\mu } (x)\delta ^{ab}(g_{\mu \nu }\partial ^{2}\right. \right. \nonumber \\&\qquad -\left. \left( 1-\frac{1}{\alpha }\right) \partial _{\mu }\partial _{\nu }\right) A^{b\nu }(x)\nonumber \\&\qquad \left. \left. + \int dx^{D}\text { }{{j}}_{\mu }(x){{A}}^{\mu }(x)\right) \right] \nonumber \\&\qquad \times \int D[{{\chi }}^{*},{{\chi }}]\exp \left[ i\left( \int dx^{D}(\partial ^{\mu }\chi ^{a*}(x))\partial _{\mu }\chi ^{a}(x)\right. \right. \nonumber \\&\qquad \left. \left. +\int dx^{D}\text { }\left( { \xi }^{a*}{ (x)\chi }^{a}{ (x)+\chi }^{a*}{ (x)\xi }^{a}{ (x)}\right) \right) \right] \nonumber \\&\qquad \times {\displaystyle \prod \limits _{q}} \int D[\overline{\Psi }_{q},\Psi _{q}]\exp \left[ i\text { }\left( \int dx^{D}\overline{\Psi }_{q}^{i}(x)\left( \sigma \text { }i\gamma ^{\mu } \partial _{\mu }+\varkappa _{q}\partial ^{2}\right) \Psi _{q}^{j}(x). \right. \right. \nonumber \\&\qquad \left. \left. \times \int dx^{D}\left( \overline{{\eta }}_{q}(x)\Psi _{q} (x)+\overline{\Psi }_{q}(x)\eta _{q}(x)\right) \right) \right] . \end{aligned}$$
(67)

The expressions for the gluon, ghost and quark free partition functions follow in the forms

$$\begin{aligned} Z_{G}^{(0)}[j]&=\exp \left( \frac{i}{2}\int dx^{D}dy^{D}\text { }j^{a\mu }(x)D_{\mu \nu }^{ab}(x-y)j^{b\nu }(x)\right) , \end{aligned}$$
(68)
$$\begin{aligned} D_{\mu \nu }^{ab}(x.y)&=\delta ^{ab}\int \frac{dk^{D}}{(2\pi )^{D}}\frac{\exp (-ik(x-y))}{k^{2}+i\epsilon }(g_{\mu \nu }-(1-\alpha )k_{\mu }k_{\nu }), \end{aligned}$$
(69)
$$\begin{aligned} Z_{GH}^{(0)}[\xi ,\xi ^{*}]&=\exp \left( \frac{i}{2}\int dx^{D} dy^{D}\text { }\xi ^{*a}(x)D^{ab}(x-y)\xi ^{b}(x)\right) , \end{aligned}$$
(70)
$$\begin{aligned} D^{ab}(x.y)&=-\,\delta ^{ab}\int \frac{dk^{D}}{(2\pi )^{D}}\frac{\exp (-ik(x-y))}{k^{2}+i\epsilon }, \end{aligned}$$
(71)
$$\begin{aligned} Z_{q}^{(0)}[\eta _{q},\overline{\eta }_{q}]&=\exp \left( i\int dx^{D} dy^{D}\text { }\overline{\eta }_{q}^{r_{1}}(x)S_{q}^{r_{1}r_{2}}(x-y)\eta _{q}^{r_{2}}(x)\right) ,\nonumber \\&\quad q=1,...,6, \end{aligned}$$
(72)
$$\begin{aligned} S_{q}^{r_{1}r_{2}}(x-y)&=\int \frac{dk^{D}}{(2\pi )^{D}}\frac{-\sigma }{\gamma _{\mu }k^{\mu }-\sigma \varkappa _{q}k^{2}}\exp (-ik(x-y)). \end{aligned}$$
(73)
Fig. 2
figure 2

The gluon, ghost and quark propagators for the renormalized fields

Full size image

4.2 The Feynman diagram expansion

The just defined generating functional leads to the Feynman rules which are presented in detail in Appendix A. The free propagators for the gluon, ghost and quark fields, in these rules and their corresponding diagrams are shown in Fig. 2. The essential difference with QCD propagators is in the form of the six quark ones, which now decrease at large momenta in a quadratic form. The Feynman rules for the seven vertices of cubic and quartic order in the fields coming from the bare action, after expressed in terms of the renormalized fields and couplings are depicted in the Fig. 4 of the Appendix A. The three first vertices \(V_{1}\) to \(V_{3}\) are identical to the ones in QCD, and the fourth one \(V_{4}\) only includes as a modification the allowed change \(\sigma \) in the sign of the Dirac action. The vertices \(V_{5}\) and \(V_{6}\) are the ones coming from the new local, gauge invariant and renormalizable terms added to action for each flavour value. The diagrams and their corresponding analytic expressions for the counterterm vertices are presented in the Fig. 5 of the Appendix A. The standard expressions V and W for the vertices of QCD and the function \(d_{\mu \nu }(k)\) defining the gluon propagator appearing in the above graphics for propagators, vertices and counterterms have the explicit forms [27]

$$\begin{aligned}&\displaystyle V_{\mu _{1}\mu _{2}\mu _{3}}^{a_{1}a_{2}a_{3}}(k_{1},k_{2},k_{3}) = \text { }f^{a_{1}a_{2}a_{3}}((k_{1}-k_{2})_{\mu _{3}}g_{\mu _{1}\mu _{2} })\nonumber \\&\displaystyle \qquad +(k_{2}-k_{3})_{\mu _{1}}g_{\mu _{2}\mu _{3}})+(k_{3}-k_{1})_{\mu _{2}} g_{\mu _{1}\mu _{3}}), \end{aligned}$$
(74)
$$\begin{aligned}&\displaystyle W_{\mu _{1}\mu _{2}\mu _{3}\mu _{4}}^{a_{1}a_{2}a_{3}a_{4}} =(f^{13,24} -f^{14,32})g_{\mu _{1}\mu _{2}}g_{\mu _{3}\mu _{4}}\nonumber \\&\displaystyle \qquad +(f^{12,34}-f^{14,23} )g_{\mu _{1}\mu _{3}}g_{\mu _{2}\mu _{4}}\nonumber \\&\displaystyle \qquad + (f^{13,42}-f^{12,34})g_{\mu _{1}\mu _{4}}g_{\mu _{3}\mu _{2}}, \end{aligned}$$
(75)
$$\begin{aligned}&\displaystyle f^{\text { }ij,kl} =f^{\text { }a_{i}a_{j}a}f^{\text { }a_{k}a_{l}a}, \end{aligned}$$
(76)
$$\begin{aligned}&\displaystyle d_{\mu \nu }(k) =\left( g_{\mu \nu }-(1-\alpha )\frac{k_{\mu }k_{\nu }}{k^{2}}\right) . \end{aligned}$$
(77)
Fig. 3
figure 3

The diagrams with two gluon legs: \((2,0,0,2),2\times (2,0,0,1),2\times (2,0,0,0)\), contributing to the primite divergences. Only diagrams not already present in gluodynamics are shown

Full size image

5 Primitively divergent graphs and their divergence

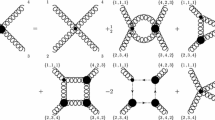
Let us consider in this section the primitively divergent graphs of the model. We will evaluate those ones corresponding to two external gluon legs. That is, being associated to the sets of four numbers \((N_{G},N_{FP},N_{F} ,n_{gqq})\) taking the specific values \((2,0,0,2), 2\times (2,0,0,1)\) and \(2\times (2,0,0,0)\). Note that there are sets of four numbers corresponding to two graphs. This is the meaning of the factors “2” of the sets (2, 0, 0, 1) and (2, 0, 0, 0). They are depicted in the Fig. 3 below. The divergences of the rest of primitively divergent graphs, due to their large number will be considered in a separate work. After evaluated the whole set of divergent counterterms in the one loop approximation, in addition to the ones present in pure gluodynamics (See [27]), this information will allow to study the renormalization group properties of the model in the one loop approximation. However, the evaluation will started in this work by calculating the one loop divergence associated to the gluon self-energy diagrams shown in Fig. 3 . After writing the analytical expressions by using the Feynman rules the set of five terms can be written in the form

$$\begin{aligned} \Pi _{\mu \nu }^{(1)}(k)&=\left( -\frac{\delta ^{ab}g^{2}}{2i}\right) \sum _{q}\int \frac{dp}{(2\pi )^{D}}T_{r}^{D}\nonumber \\&\quad \times [\gamma _{\mu }S_{m_{q}}(k+p)\gamma _{\nu }S_{m_{q}}(p) +\gamma _{\mu }S_{0}(k+p)\gamma _{\nu }S_{0}(p)\nonumber \\&\quad -\gamma _{\mu }S_{m_{q} }(k+p)\gamma _{\nu }S_{0}(p)-\gamma _{\mu }S_{0}(k+p)\gamma _{\nu }S_{m_{q}}(p)], \end{aligned}$$
(78)
$$\begin{aligned} \Pi _{\mu \nu }^{(2)}(k)&=\left( -\frac{\delta ^{ab}g^{2}}{2i}\right) \sum _{q} \sigma \varkappa _{q}\int \frac{dp}{(2\pi )^{D}}T_{r}^{D}\nonumber \\&\quad \times [S_{m_{q}}(k+p)\gamma _{\nu }S_{m_{q}}(p)+S_{0}(k+p)\gamma _{\nu }S_{0}(p)\nonumber \\&\quad -S_{m_{q}}(k+p)\gamma _{\nu }S_{0}(p)\nonumber \\&\quad -S_{0}(k+p)\gamma _{\nu }S_{m_{q}}(p)](2p_{\mu }+k_{\mu }),\ \end{aligned}$$
(79)
$$\begin{aligned} \Pi _{\mu \nu }^{(3)}(k)&=\left( -\frac{\delta ^{ab}g^{2}}{2i}\right) \sum _{q} \sigma \varkappa _{q}\int \frac{dp}{(2\pi )^{D}}T_{r}^{D}\nonumber \\&\quad \times [S_{m_{q}}(k+p)\gamma _{\mu }S_{m_{q}}(p)+S_{0}(k+p)\gamma _{\mu }S_{0}(p)\nonumber \\&\quad -S_{_{m}} (k+p)\gamma _{\mu }S_{0}(p)\nonumber \\&\quad -S_{0}(k+p)\gamma _{\mu }S_{_{m}}(p)](2p_{\nu }+k_{\nu }), \end{aligned}$$
(80)
$$\begin{aligned} \Pi _{\mu \nu }^{(4)}(k)&=\left( -\frac{\delta ^{ab}g^{2}}{2i}\right) \sum _{q} (\sigma \varkappa _{q})^{2}\int \frac{dp}{(2\pi )^{D}}T_{r}^{D}\nonumber \\&\quad \times [S_{m_{q} }(k+p)S_{m_{q}}(p)+S_{0}(k+p)S_{0}(p)\nonumber \\&\quad -S_{m_{q} }(k+p)S_{0}(p)-S_{0}(k+p)S_{m_{q}}(p)]\nonumber \\&\quad (2p_{\mu }+k_{\mu })(2p_{\nu }+k_{\nu }),\ \end{aligned}$$
(81)
$$\begin{aligned} \Pi _{\mu \nu }^{(5)}(k)&=\left( -\frac{\delta ^{ab}g^{2}}{2i}\right) \sum _{q} (\sigma \varkappa _{q})^{2}\int \frac{dp}{(2\pi )^{D}}T_{r}^{D}[S_{_{m}} (p)-S_{0}(p)], \end{aligned}$$
(82)

where \(m_{q}=\frac{\sigma }{\varkappa _{q}},q=1,...,6\), are the quark masses and the \(S_{m_{q}}(p)\) and \(S_{0}(p)\) are Dirac free propagators

$$\begin{aligned} S_{m_{p}}(p)&=\frac{1}{m_{p}-p_{\alpha }\gamma ^{\alpha }}, \end{aligned}$$
(83)
$$\begin{aligned} S_{0}(p)&=\frac{1}{-p_{\alpha }\gamma ^{\alpha }}. \end{aligned}$$
(84)

The above quantities can be evaluated from the general integrals

$$\begin{aligned} I_{\mu \nu }^{(1)}(k,m_{1},m_{2})&=\int \frac{dp}{(2\pi )^{D}}T_{r}^{D} [\gamma _{\mu }S_{m_{1}}(k+p)\gamma _{\nu }S_{m_{2}}(p)]\nonumber \\&=\int \frac{dp}{(2\pi )^{D}}4\frac{\left( m_{1}m_{2}-(p+k).kg_{\mu \nu }+2p_{\mu \nu }+p_{\mu }k_{\nu }+k_{\mu }p_{\nu }\right) }{(m_{1}^{2}-(p+k)^{2})(m_{2}^{2}-(p)^{2})}, \end{aligned}$$
(85)
$$\begin{aligned} I_{\mu \nu }^{(2)}(k,m_{1},m_{2})&=-\int \frac{dp}{(2\pi )^{D}}T_{r} ^{D}[S_{m_{1}}(k+p)\gamma _{\nu }S_{m_{2}}(p)](2p_{\mu }+k_{\mu })\nonumber \\&=-\int \frac{dp}{(2\pi )^{D}}4\frac{(m_{2}k_{\mu }k_{\nu }+2(m_{1} +m_{2}).p_{\mu }p_{\nu }+(m_{1}+m_{2})p_{\nu }k_{\mu }+2m_{2}p_{\mu }k_{\nu } )}{(m_{1}^{2}-(p+k)^{2})(m_{2}^{2}-(p)^{2})},\end{aligned}$$
(86)
$$\begin{aligned} I_{\mu \nu }^{(3)}(k,m_{1},m_{2})&=-\int \frac{dp}{(2\pi )^{D}}T_{r} ^{D}[S_{m_{1}}(k+p)\gamma _{\mu }S_{m_{2}}(p)](2p_{\nu }+k_{\nu })\nonumber \\&=-\int \frac{dp}{(2\pi )^{D}}4\frac{(m_{2}k_{\mu }k_{\nu }+2(m_{1} +m_{2}).p_{\mu }p_{\nu }+(m_{1}+m_{2})p_{\mu }k_{\nu }+2m_{2}p_{\nu }k_{\mu } )}{(m_{1}^{2}-(p+k)^{2})(m_{2}^{2}-(p)^{2})},\end{aligned}$$
(87)
$$\begin{aligned} I_{\mu \nu }^{(4)}(k,m_{1},m_{2})&=\int \frac{dp}{(2\pi )^{D}}T_{r} ^{D}[S_{m_{1}}(k+p)S_{m_{2}}(p)](2p_{\mu }+k_{\mu })(2p_{\nu }+k_{\nu })\nonumber \\&=\int \frac{dp}{(2\pi )^{D}}4\frac{(m_{1}m_{2}+p^{2}+p.k)(2p_{\mu }+k_{\mu })(2p_{\nu }+k_{\nu })}{(m_{1}^{2}-(p+k)^{2})(m_{2}^{2}-(p)^{2})}, \end{aligned}$$
(88)
$$\begin{aligned} I_{\mu \nu }^{(5)}(k,m)&=\int \frac{dp}{(2\pi )^{D}}T_{r}^{D}[S_{_{m}} (p)-S_{0}(p)]\nonumber \\&=\sigma \text { }m\int \frac{dp}{(2\pi )^{D}}4\frac{1}{(p^{2}-m^{2})}, \end{aligned}$$
(89)

which are functions of two general values of the masses \(m_{1}\) and \(m_{2}\) . Only their values at the mass pairs \((m_{1},m_{2})=(m_{q}\),\(m_{q}),(m_{q} \),0), (0,\(m_{q}),(0\),0) are needed. The appearing momentum integrals can be transformed by using the Feynman trick

$$\begin{aligned}&\frac{1}{(m_{1}^{2}-(p+k)^{2})(m_{2}^{2}-(p)^{2})}\nonumber \\&\quad =\int _{0}^{1}dx\frac{1}{\left[ (p+x\text { }k)^{2}-R_{m_{1}m_{2}}^{2}(x)\right] ^{2}}, \end{aligned}$$
(90)
$$\begin{aligned}&R_{m_{1}m_{2}}^{2}(x) \nonumber \\&\quad =k^{2}x(x-1)+m_{2}^{2}(1-x)+m_{1}^{2}-i\epsilon . \end{aligned}$$
(91)

After substituting the above representation for the denominators in the defined four integrals I , making the integration variable shift \(p\rightarrow p+x\) k and using the momentum integrals [29]

$$\begin{aligned}&\int \frac{dp}{(2\pi )^{D}}\frac{1}{[p^{2}-R_{m_{1}m_{2}}^{2}(x)^{2}]^{2}}\nonumber \\&\quad =\frac{i}{(16\pi ^{2})^{\frac{D}{4}}}\frac{\Gamma (2-\frac{D}{2})}{\Gamma (2)}(R_{m_{1}m_{2}}^{2}(x))^{\frac{D}{2}-2}, \end{aligned}$$
(92)
$$\begin{aligned}&\int \frac{dp}{(2\pi )^{D}}\frac{p_{\mu }p_{\nu }}{[p^{2}-R_{m_{1}m_{2}} ^{2}(x)]^{2}}\nonumber \\&\quad =\frac{iR_{m_{1}m_{2}}^{2}(x)}{(16\pi ^{2})^{\frac{D}{4}} }\frac{\Gamma (2-\frac{D}{2})}{D\Gamma (2)}R_{m_{1}m_{2}}^{2}(x)^{\frac{D}{2} -2}, \end{aligned}$$
(93)
$$\begin{aligned}&\int \frac{dp}{(2\pi )^{D}}\frac{p^{2}p_{\mu }p_{\nu }}{[p^{2}-R_{m_{1}m_{2}} ^{2}(x)]^{2}}\nonumber \\&\quad =\frac{1}{D}g_{\mu \nu }\int \frac{dp}{(2\pi )^{D}}\frac{(p^{2})^{2}}{[p^{2}-R_{m_{1}m_{2}}^{2}(x)^{2}]^{2}}\nonumber \\&\quad =g_{\mu \nu }\frac{i(D+2)R_{m_{1}m_{2}}^{2}(x)}{(D-2)(16\pi ^{2})^{\frac{D}{4}}}\frac{\Gamma (2-\frac{D}{2})}{\Gamma (2)}R_{m_{1}m_{2}}^{2}(x)^{\frac{D}{2}-2}, \end{aligned}$$
(94)

the I integrals can be rewritten as

$$\begin{aligned}&I_{\mu \nu }^{(1)}(k,m_{1},m_{2}) =\frac{i\text { }\Gamma (2-\frac{D}{2} )}{(16\pi ^{2})^{\frac{D}{4}}\Gamma (2)}\nonumber \\&\quad \times \int _{0}^{1}dx\text { }(R_{m_{1}m_{2} }^{2}(x))^{\frac{D}{2}-2}\text { }4[-R_{m_{1}m_{2}}^{2}(x)g_{\mu \nu }\nonumber \\&\quad +m_{1}m_{2}+x(1-x)k^{2})+2x(x-1)k_{\mu }k_{\nu }], \end{aligned}$$
(95)
$$\begin{aligned}&I_{\mu \nu }^{(2)}(k,m_{1},m_{2}) =\frac{i\text { }\Gamma (2-\frac{D}{2} )}{(16\pi ^{2})^{\frac{D}{4}}\Gamma (2)}\nonumber \\&\quad \times \int _{0}^{1}dx\text { }(R_{m_{1}m_{2} }^{2}(x))^{\frac{D}{2}-2}\text { }4[g_{\mu \nu }\frac{2}{D-2} (m_{1}+m_{2})\nonumber \\&\quad \times (-x(x-1)k^{2}+m_{2}^{2}(1-x)+m_{1}^{2}x-i\epsilon )\nonumber \\&+k_{\mu }k_{\nu }\ (m_{2}(1-3x)-m_{1}x+2(m_{1}+m_{2})\ x^{2}], \end{aligned}$$
(96)
$$\begin{aligned}&I_{\mu \nu }^{(3)}(k,m_{1},m_{2}) =\frac{i\text { }\Gamma (2-\frac{D}{2} )}{(16\pi ^{2})^{\frac{D}{4}}\Gamma (2)}\nonumber \\&\quad \int _{0}^{1}dx\text { }(R_{m_{1}m_{2} }^{2}(x))^{\frac{D}{2}-2}\text { }4[g_{\mu \nu }\frac{2}{D-2} (m_{1}+m_{2})\nonumber \\&\quad \times (-x(x-1)k^{2}+m_{2}^{2}(1-x)+m_{1}^{2}x-i\epsilon )\nonumber \\&\quad +k_{\mu }k_{\nu }\ (m_{2}(1-3x)-m_{1}x+2(m_{1}+m_{2})\ x^{2}], \end{aligned}$$
(97)
$$\begin{aligned}&I_{\mu \nu }^{(4)}(k,m_{1},m_{2}) =\frac{i\text { }\Gamma (2-\frac{D}{2} )}{(16\pi ^{2})^{\frac{D}{4}}\Gamma (2)}\nonumber \\&\quad \times \int _{0}^{1}dx\text { }(R_{m_{1}m_{2} }^{2}(x))^{\frac{D}{2}-2}\text { }4[g_{\mu \nu }(\frac{4(D-2)}{D(D-2)}\text { }(R^{2}(x))^{2}\nonumber \\&\quad +4\frac{(m_{1}m_{2}+x(x-1)k^{2})}{D-2}R_{m_{1}m_{2}}^{2}(x))\ \nonumber \\&\quad +k_{\mu }k_{\nu }(1-2x)^{2}(\frac{(D+4)}{(D-2)}R_{m_{1}m_{2}}^{2}(x)+x(x-1)k^{2}+m_{1}m_{2}) ],\end{aligned}$$
(98)
$$\begin{aligned}&I_{\mu \nu }^{(5)}(k,m) =-\sigma \frac{i}{(16\pi ^{2})^{\frac{D}{4}}} m^{\frac{D}{2}-1}\frac{\Gamma (2-\frac{D}{2})}{(1-\frac{D}{2})\Gamma (2)}. \end{aligned}$$
(99)

The obtained expressions show their divergence determined by the \(D\rightarrow 4\) limit of the factor

$$\begin{aligned} \frac{\Gamma (2-\frac{D}{2})}{1-\frac{D}{2}}=-\frac{2}{\epsilon } -1+\gamma +O(\epsilon ^{1}), \end{aligned}$$
(100)

with the definition \(D=4-\epsilon .\) Thus, the divergent part of the self-energy contributions under consideration can be expressed as:

$$\begin{aligned} \Pi _{\mu \nu }^{(1{\text {div}})}(k) =\,&P\left[ \sum _{q}\left( -\frac{\delta ^{ab} g^{2}}{2i}\right) (I_{\mu \nu }^{(1)}(k,m_{q},m_{q})\right. \nonumber \\&\left. +\,I_{\mu \nu }^{(1)}(k,m_{q} ,0)-I_{\mu \nu }^{(1)}(k,0,m_{q})-I_{\mu \nu }^{(1)} (k,0,0))\right] \nonumber \\ =\,&\frac{1}{16\pi ^{2}}\frac{2}{\epsilon }\left( \frac{\delta ^{ab}g^{2}}{2}\right) \sum _{q}4\times (-m_{q}^{2})\text { }g_{\mu \nu }, \end{aligned}$$
(101)
$$\begin{aligned} \Pi _{\mu \nu }^{(2{\text {div}})}(k) =&-P\left[ \sum _{q}\left( -\frac{\delta ^{ab}g^{2}}{2}\right) \sigma \varkappa _{q}(I_{\mu \nu }^{(2)}(k,m_{q},m_{q})\right. \nonumber \\&\left. +I_{\mu \nu }^{(2)}(k,m_{q},0)-I_{\mu \nu }^{(2)}(k,0,m_{q})-I_{\mu \nu }^{(2)} (k,0,0))\right] \nonumber \\ =&\frac{1}{16\pi ^{2}}\frac{2}{\epsilon }\frac{\delta ^{ab}g^{2}}{2}\sum _{q}4\times (-m_{q}^{2})\text { }g_{\mu \nu }, \end{aligned}$$
(102)
$$\begin{aligned} \Pi _{\mu \nu }^{(3{\text {div}})}(k) =&-P\left[ \sum _{q}\left( -\frac{\delta ^{ab}g^{2}}{2i}\right) \sigma \varkappa _{q}(I_{\mu \nu }^{(3)}(k,m_{q},m_{q})\right. \nonumber \\&\left. +\,I_{\mu \nu }^{(3)}(k,m_{q},0)-I_{\mu \nu }^{(3)}(k,0,m_{q})-I_{\mu \nu }^{(3)} (k,0,0))\right] \nonumber \\ =&\frac{1}{16\pi ^{2}}\frac{2}{\epsilon }\frac{\delta ^{ab}g^{2}}{2}\sum _{q}4\times (-m_{q}^{2})\text { }g_{\mu \nu }, \end{aligned}$$
(103)
$$\begin{aligned} \Pi _{\mu \nu }^{(4{\text {div}})}(k) =&P\left[ \sum _{q}\left( -\frac{\delta ^{ab} g^{2}}{2i}\right) (\sigma \varkappa _{q})^{2}(I_{\mu \nu }^{(4)}(k,m_{q},m_{q})\right. \nonumber \\&+I_{\mu \nu }^{(4)}(k,m_{q},0)-I_{\mu \nu }^{(4)}(k,0,m_{q})-I_{\mu \nu }^{(4)} (k,0,0))\nonumber \\ =&\frac{1}{16\pi ^{2}}\frac{2}{\epsilon }\frac{\delta ^{ab}g^{2}}{2}\sum _{q}(\sigma \varkappa _{q})^{2}(12\times (+m_{q}^{2})\text { }g_{\mu \nu }\nonumber \\&-\frac{1}{3}m_{q}^{2}(k^{2}g_{\mu \nu }-k_{\mu }k_{\nu })),\end{aligned}$$
(104)
$$\begin{aligned} \Pi _{\mu \nu }^{(5{\text {div}})}(k)&=\frac{1}{16\pi ^{2}}\frac{2}{\epsilon }\frac{\delta ^{ab}g^{2}}{2}\sum _{q}4\times (\sigma \varkappa _{q})^{2}m_{q}^{2}\text { }, \end{aligned}$$
(105)

in which P[Q(x)] indicates the pole part in x of a quantity Q(x).

Thus, the summation of all the divergent contributions leads to

$$\begin{aligned} \sum _{n=1,...,4}\Pi _{\mu \nu }^{(n{\text {div}})}(k)&=-\frac{1}{16\pi ^{2}}\frac{2}{\epsilon }\frac{\delta ^{ab}g^{2}}{6}(k^{2}g_{\mu \nu } -k_{\mu }k_{\nu })\sum _{q}(\sigma \varkappa _{q})^{2}m_{q}^{2}\nonumber \\&=-\frac{1}{8\pi ^{2}}\delta ^{ab}g^{2}(k^{2}g_{\mu \nu }-k_{\mu }k_{\nu } )\frac{1}{\epsilon }. \end{aligned}$$
(106)

This result shows that the sum of all primitively divergent diagrams, excluding the tadpole term, becomes transverse in the momentum, as gauge invariance requires. It also arise as being independent of the new six new parameters \(\ \varkappa _{q},\) \(q=1,...,6.\). Thus, in this case the one loop divergence can be eliminated by the counterterms only dependent of the strong coupling g. The same study should be done for the various other primitively divergent diagrams. This task will be considered as a direct extension of the present work.

6 Summary

A proposal of a massless QCD including NJL action terms in a local and renormalizable form is started to be investigated in detail. The new terms included in the action determine masses for all the six quarks which are given by the reciprocal of the new six flavour condensate couplings linked with each quark type. Here, after defining the divergence indices of the theory and identifying the primitive divergences, the renormalized Feynman expansion is presented. The expansion is employed in this work to evaluate the quadratic in the gauge coupling and all orders in the flavour couplings the divergence of the gluon polarization operator. After the complete evaluation of all the various primitive divergences arising, the results will allow to further consider the one loop renormalization of the model in coming works. The extension of the study also will be devoted to investigate the possibility to generate a quark mass hierarchy as a dynamic flavour symmetry breaking in the context of the model. In this process, it might be suspected that after the divergences are removed, the contributions to the vacuum energy associated to diagrams showing two different kinds of fermion lines, might tend to rise the energy with respect to the diagrams exhibiting equal values of the quark masses, making them more energetic that the ones in which a single quark mass parameter gets a finite value. It is interesting to remark that the occurrence of this flavour symmetry breaking, may be allowed by the fact that included two-gluon-two-quark vertices directly break chiral invariance. The framework seems appropriate to dynamically realize the so called Democratic Symmetry Breaking properties of the mass hierarchy remarked by H. Fritzsch [30].

Let us shortly comment about a relevant issue if at the end the proposed model is assumed to describe nature. It is connected with the question about how the discussion might be able in describing the known and experimentally verified chiral symmetry breaking effects in standard QCD. At the present stage of the study, we estimate that the observed phenomenology about the chiral breaking could appear in the analysis as linked, in first place, with the explicit chiral breaking determined by the newly added two-gluon-two quark terms. In this connection, it can be recalled that such terms were appearing in reference [23] as closely linked with quark and gluon condensate effects, which naturally imply chiral breaking effects. Further, in the to be evaluated (after ending the construction of the renormalized perturbative expansion) vacuum energy as a function of the new six couplings, the small experimental values of the light quark masses u, d, and s could be expected to be predicted if (as suspected) a hierarchical quark mass spectrum results from an also occurring flavour symmetry breaking effect. That is, we expect that a picture in which, by example, the pi meson emerge as a light Goldstone boson after the chiral breaking has the chance of appearing in the proposed model. The checking of the validity of these expectations is one of the main motivations for the extension of the present work.

It can be also imagined that the appearance of six different couplings in the theory, could be reduced to only one by employing the Zimmermann’s reduction of the couplings approach [31]. This possibility also suggests a way for linking the model with the SM assuming that the single coupling could be expected to play the role of the Higgs field. This property is also suggested by the known results which show that the Top condensate models can be re-formulated in a way being closer to the SM [32] thanks in good part to the gauge invariance, which is explicit in the present model. It can be concluded that the discussion supports the starting idea of the study about that massless QCD could generate an intense dimensional transmutation effect. Its feasibility will be investigated in the extension of this work. In ending, it could be helpful to remark that in the gluodynamic limit of the results of reference [23] (which motivated the discussion in this paper) the appearance of Gaussian means over color fields suggested the possibility of a first principles derivation of the linear confining effects predicted by the stochastic vacuum models of QCD [33].