Entangled de Sitter from stringy axionic Bell pair I: an analysis using Bunch–Davies vacuum

Abstract

In this work, we study the quantum entanglement and compute entanglement entropy in de Sitter space for a bipartite quantum field theory driven by an axion originating from Type IIB string compactification on a Calabi–Yau three fold ($\mathbf{CY^3}$) and in the presence of an $\mathbf{NS5}$ brane. For this computation, we consider a spherical surface $\mathbf{S}^2$, which divides the spatial slice of de Sitter ($\mathbf{dS_4}$) into exterior and interior sub-regions. We also consider the initial choice of vacuum to be Bunch–Davies state. First we derive the solution of the wave function of the axion in a hyperbolic open chart by constructing a suitable basis for Bunch–Davies vacuum state using Bogoliubov transformation. We then derive the expression for density matrix by tracing over the exterior region. This allows us to compute the entanglement entropy and Rényi entropy in $3+1$ dimension. Furthermore, we quantify the UV-finite contribution of the entanglement entropy which contain the physics of long range quantum correlations of our expanding universe. Finally, our analysis complements the necessary condition for generating non-vanishing entanglement entropy in primordial cosmology due to the axion.

1 Introduction

The information encoded in entanglement entropy is very powerful to distinguish quantum states with long range correlation as appearing in the context of condensed matter physics [1,2,3]. It plays a significant role in the field of quantum information [4,5,6,7,8] and cosmology [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. It is also useful in quantum field theory to identify the specific nature of the long range quantum correlations that we generally get using the standard vacuum states like the Chernikov–Tagirov, Bunch–Davies, Hartle–Hawking or the most general $\alpha$ vacuum [26,27,28]. Till date quantum entanglement has been one of the most mysterious and at the same time fascinating features of foundational aspects of quantum mechanics. This is because it is believed that performing a local measurement may instantaneously affect the outcome of the measurement beyond the physical light cone under consideration. This is interpreted as the violation of causality and commonly known as the Einstein–Podolsky–Rosen (EPR) paradox [29]. However, it is important to note that neither quantum information gets transferred in such a physical measurement, nor does it change the causality constraints. Nevertheless, quantum entanglement may have applications to explain the origin of various physical phenomena [30,31,32]. The prime example is the well-known Schwinger effect in de Sitter [33, 34] space describing pair production of particles in the presence of a uniform electric field [19]. In this specific context, the pair production occurs spontaneously with a certain finite coordinate separation in field space. Such physical states of the particle pairs are required to be correlated quantum mechanically.

Fig. 1

Schematic diagram for the computation algorithm of entanglement entropy in de Sitter space due to axion

In the present work we consider an axion field theory obtained from compactification of Type IIB string theory on a Calabi–Yau three fold ($\mathbf{CY}^3$) but in the presence of an NS5 brane. So that the model consist of effective potential which breaks the shift symmetry associated with the axion field in a controlled manner. This model has been analysed as a candidate for driving inflation [35,36,37] as well as a quintessence model for the late time acceleration of our universe [38]. Furthermore, in a recent analysis it was shown that this model captures the interesting phenomenon of violation of Bell’s inequality in primordial cosmology [16,17,18] by formation of EPR pair. In the present analysis we will strengthen the formation of EPR pair by demonstrating that the entanglement entropy of the axionic EPR pair is non-zero, which confirms the existence of superhorizon long range correlation in primordial cosmology. This connection also will be helpful in the future to provide an algorithm to contrast various models of inflation [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74]. Additionally, we compute $\hbox {R}\acute{e}$nyi entropy in $3+1$ D de Sitter space and its connection with quantum entanglement in presence of the axionic model.

In Fig. 1, we have schematically shown the logic involved in computing the entanglement entropy in de Sitter space. The plan of the rest of the paper is as follows. In Sect. 2 we briefly review the strategy for computing the entanglement entropy in de Sitter space. In Sect. 3 we follow the above strategy for the afore mentioned stringy axionic model. In Sect. 4 we present our conclusion and future prospects. Finally, in the appendix we give the detailed derivation of the entanglement entropy and Rényi entropy in the present context.

Fig. 2

Schematic diagram for the geometrical construction of the bipartite system. First we consider $\mathbf{S^2}$ with radius $R\gg R_{\mathbf{dS}}=H^{-1}$, which at late global time $\tau _{\mathrm{global}}$ can mapped to half of a $\mathbf{S^3}$ with boundary $\mathbf{S^2}$ at the equator. For simplicity we can also use hyperbolic slices where the interior of the $\mathbf{S^3}$ mimics the role of the “left” (L) slices. Corresponding Penrose diagrams are drawn for completeness [15]

2 Computational strategy: brief review

Here we briefly review the method to derive the entanglement entropy in $3+1$ dimensional de Sitter space following Ref. [15] and the references therein. We consider a closed surface $\Sigma$ in a hypersurface where time is frozen. Consequently, the space-like hypersurface is divided into an interior and exterior region which are identified as RI (which is L in open chart) and RII (which is R in open chart) region in the representative schematic diagram shown in Fig. 2. If we represent the total Hilbert space of the system under consideration by $\mathcal{H}$, then in the present context one can use the approximate bipartite decomposition [75] given by¹ $\mathcal{H}=\mathcal{H}_{\mathbf{INT}}\otimes \mathcal{H}_{\mathbf{EXT}}.$ This implies that $\mathcal{H}$ can be written as a direct product of two Hilbert spaces $\mathcal{H}_{\mathbf{INT}}$ and $\mathcal{H}_{\mathbf{EXT}}$, which is consistent with the requirement of local QFT. In this context, the building blocks of $\mathcal{H}_{\mathbf{INT}}$ and $\mathcal{H}_{\mathbf{EXT}}$ are the localised modes in the RI and RII region respectively. This allows us to construct the density matrix for the internal RI region by tracing over all degrees of freedom in the external RII region and is given by

$$\begin{aligned} \rho =\mathbf{Tr}_{\mathbf{R}}|\mathbf{BD}\rangle \langle \mathbf{BD}|. \end{aligned}$$

(2.1)

Here the vacuum state $|\mathbf{BD}\rangle$ is the Bunch–Davies vacuum. Using the well-known Von Neumann entropy formula, the entanglement entropy in de Sitter space can be expressed in terms of the density matrix as

$$\begin{aligned} S=-\mathbf{Tr}[\rho \ln \rho ], \end{aligned}$$

(2.2)

which quantifies how much a given quantum state is quantum mechanically entangled. In this paper we compute this expression explicitly and establish its relationship with Bell’s inequality violation in cosmology [16,17,18].

Here we consider $\Sigma$ to be a closed surface $\mathbf{S}^2$ which has radius $R_{\mathbf{S}^2}$ with the restriction, $R_{\mathbf{S}^2}\gg R_{\mathbf{dS}}=H^{-1}$, where H is the Hubble parameter and $R_{\mathbf{dS}}$ is the de Sitter radius. This surface $\mathbf{S}^2$ separates the spatial slice into the interior (L) and exterior (R) region which is shown in Fig. 2. The reduced density matrix, which is a key ingredient for computing entanglement entropy, is obtained by tracing over the exterior (R) region. Also it is important to note that the total entanglement entropy can be expressed as a sum of UV divergent and UV finite contribution as

$$\begin{aligned} S=S_{\mathbf{UV}\text {-}{} \mathbf{divergent}}+S_{\mathbf{UV}\text {-}{} \mathbf{finite}}. \end{aligned}$$

(2.3)

When the $\mathbf{S}^2$ is taken at the boundary of $3+1$ D de Sitter space then $\mathbf{SO(1,3)}$ symmetry² plays significant role to define the entanglement entropy for a given principal quantum number. We note that entanglement entropy in de Sitter space is completely different from that of the dynamical gravity [76,77,78,79,80,81,82,83,84,85], which we are not considering.

In $3+1$ dimensions, the UV-divergent contribution is appearing due to the local quantum field theoretic effects and it takes the following simplified form [15, 19, 30, 31]:

$$\begin{aligned} S_{\mathbf{UV}\text {-}{} \mathbf{divergent}}= & {} \mathbf{c_1}\frac{\mathcal{A}_{\mathbf{ENT}}}{\epsilon ^2_{\mathbf{UV}}}+[\mathbf{c_2}+(\mathbf{c_3}m^2+\mathbf{c_4}H^2)\mathcal{A}_{\mathbf{ENT}}]\nonumber \\&\times \ln \left( \epsilon _{\mathbf{UV}}H\right) , \end{aligned}$$

(2.4)

where $\epsilon _{\mathbf{UV}}$ is the short distance lattice UV cut-off of the bipartite local quantum field theory under consideration, $\mathcal{A}_{\mathbf{ENT}}$ represents the proper area of the entangling region and $\mathbf{c_i}\forall i=1,2,3,4$ are the numerical coefficients which carries different physical significance in the present computation. For example, in Eq. (2.4), the first term represent area dependent contribution to the UV divergent part of the entropy, which originates from entanglement between particles in the vicinity of the entangling surface under consideration. Furthermore, taking flat space limit, where the Hubble parameter $H\rightarrow 0$, the UV-divergent part of the entropy of the bipartite local quantum field theoretic system for scalar field (axion) can be expressed as:³

$$\begin{aligned} \lim _{H\rightarrow 0}S_{\mathbf{UV}\text {-}{} \mathbf{divergent}}= & {} \mathbf{c_1}\frac{\mathcal{A}_{\mathbf{ENT}}}{\epsilon ^2_{\mathbf{UV}}}+\left[ \mathbf{c_2}+\mathbf{c_3}m^2\mathcal{A}_{\mathbf{ENT}}\right] \nonumber \\&\times \ln \left( \epsilon ^2_{\mathbf{UV}}e^{1-e}\right) . \end{aligned}$$

(2.7)

In this context the coefficients $\mathbf{c_2}$ and $\mathbf{c_3}$ contribute in the flat limit result of the entropy of the system under consideration. Also it is important to note that the coefficients $\mathbf{c_2}$ and $\mathbf{c_3}$ are short distance lattice UV cut-off independent and therefore universal in nature. On the other hand, the last term in Eq. (2.4), explicitly incorporates the effect of bulk extrinsic and intrinsic curvature contribution in de Sitter background.

In our computation of the entanglement entropy in de Sitter space we only restrict our discussion within the UV-finite contributions which contain the physics of long range correlations of the quantum mechanical state. The most important fact is that the total entanglement entropy in de Sitter space is invariant under $\mathbf{SO(1,4)}$ isometry group and consequently both UV-divergent and UV-finite contributions remain invariant under the same group. However, for the computation we only use the connected subgroup of $\mathbf{SO(1,4)}$, which is $\mathbf{SO(1,3)}$ in this context. For more details see Ref. [15]. Additionally, in the present context in the subhorizon scale, where $kc_S \eta \gg -1$,⁴ plays crucial role as the long range entanglement is valid within this scale. In the superhorizon scale, where $kc_S \eta \ll -1$ or more precisely at late time scale i.e. at the limit case $\eta \rightarrow 0$, long range contributions in the de Sitter entanglement entropy freezes. However, in this limit some additional contribution appears which only contributes to short distance scale and the associated entanglement can be expressed in a local form in (quasi) de Sitter space. Consequently, at late time scale, $\eta \rightarrow 0$ of the UV-finite contributions in the entanglement entropy can be written as [15, 19]:

$$\begin{aligned} S_{\mathbf{UV}\text {-}{} \mathbf{finite}}= & {} \mathbf{c}_{\mathbf{5}}\mathcal{A}_{\mathbf{ENT}}H^2-\frac{\mathbf{c}_{\mathbf{6}}}{2}\ln \left( \mathcal{A}_{\mathbf{ENT}}H^2\right) \nonumber \\&+\,{\mathbf{finite~contributions}}. \end{aligned}$$

(2.8)

Here the UV-finite part gets contributions from two different sources. First part being proportional to the area of entangling surface of $\mathbf{S}^2$ and the proportionality factor is dependent on an overall coefficient and Hubble parameter H. Second part is proportional to the logarithm of the product of area of $\mathbf{S}^2$ and Hubble parameter H and the proportionality factor is identified to be the interesting part of the entanglement entropy which we compute explicitly from the prescribed setup.

Additionally it is important to note the overall characteristic coefficient as appearing in the first term in UV-finite contribution is not completely independent. Once we know the coefficient of the logarithmic term, one can determine the other coefficient in terms of this contribution.

Furthermore, taking the flat space limit, $H\rightarrow 0$, the UV-finite contributions to the entanglement entropy can be expressed as:⁵

$$\begin{aligned} \lim _{H\rightarrow 0}S_{\mathbf{UV}\text {-}{} \mathbf{finite}}= & {} -\frac{3\mathbf{c}_\mathbf{6}}{2}\ln \left( \mathcal{A}_{\mathbf{ENT}}\right) +\mathbf{c}_{\mathbf{6}}\mathcal{H}_{\epsilon _{\mathbf{UV}}}\nonumber \\&+\,\mathbf{finite~contributions}. \end{aligned}$$

(2.12)

Furthermore, we introduce a new parameter $\mathcal{A}_{\mathbf{C}}$ representing the entangling area in comoving coordinates, which is defined as, $\mathcal{A}_{\mathbf{C}}=\mathcal{A}_{\mathbf{ENT}}H^2\eta ^2.$ In terms of newly introduced parameter the UV-finite part of the entanglement entropy can be written as

$$\begin{aligned} S_{\mathbf{UV-finite}}= & {} \mathbf{c_5}\frac{\mathcal{A}_{\mathbf{C}}}{\eta ^2}+\mathbf{c_6}\ln \eta -\frac{\mathbf{c}_{\mathbf{6}}}{2}\ln \left( \mathcal{A}_{\mathbf{C}}\right) \nonumber \\&+\,\mathbf{finite}\,\mathbf{contributions}, \end{aligned}$$

(2.13)

where the coefficient of the logarithmic contribution, ${\mathbf{c}_{\mathbf{6}}}$, characterises the long range correlations. In our computation our prime objective is to compute the expression for ${\mathbf{c}_{\mathbf{6}}}$ in de Sitter space. On general ground, ${\mathbf{c}_{\mathbf{6}}}$ can be expressed as a sum of two possible contributions of the extrinsic curvature of the entangling surface ($\Sigma \equiv \mathbf{S^2}$) in comoving coordinate system as [86]:

$$\begin{aligned} {\mathbf{c}_{\mathbf{6}}}= & {} \left[ \mathbf{g_1}\int _{\Sigma \equiv \mathbf{S^2}}K_{AB}K_{AB}+\mathbf{g_2}\int _{\Sigma \equiv \mathbf{S^2}}\left( K_{AA}\right) ^2\right] \equiv S_{\mathbf{intr}},\nonumber \\ \end{aligned}$$

(2.14)

where $\mathbf{g_1}$ and $\mathbf{g_2}$ are two undetermined coefficients and $K_{AB}$ is the extrinsic curvature of entangling surface. Here we note that the coefficient ${\mathbf{c}_{\mathbf{6}}}$ is identified as the interesting part of the UV-finite contribution to the entanglement entropy, as represented by $S_{\mathbf{intr}}$, which we compute in this paper.

In the next section,we compute the entanglement entropy for axionic Bell pairs using the results of this section.

3 Entanglement for axionic Bell pair

3.1 Geometrical construction and underlying symmetries

Let us first discuss the underlying symmetries of the present setup in de Sitter space. For this purpose, let us consider, a surface $\mathbf{S}^2$ defined by the relation, $\sum ^{3}_{i=1}x^2_{i}=R^2_{\mathbf{S}^2},$ where $R_{\mathbf{S}^2}$ is the radius of the spherical surface $\mathbf{S}^2$ and $x_{i}\forall i=1,2,3$ are the flat coordinates. To consider a spherical surface sufficiently large compared to the size of the horizon one need to consider here $R_{\mathbf{S}^2}\gg \eta$, where $\eta$ is the conformal time defined as, $\eta =\int \mathrm{d}t/a(t).$ Here a(t) is the scale factor which is appearing in the spatially flat $k=0$ FLRW metric in $3+1$ dimensions, written in the conformally flat form

$$\begin{aligned} \mathrm{d}s^2= & {} \left( -\,\mathrm{d}t^2+a^2(t)\sum ^{3}_{i=1} \mathrm{d}x^2_{i}\right) =a^2(\eta )\left( -\,\mathrm{d}\eta ^2+\sum ^{3}_{i=1}\mathrm{d}x^2_{i}\right) .\nonumber \\ \end{aligned}$$

(3.1)

We note that for $R_{\mathbf{S}^2}\gg \eta$ one can suppress the conformal time coordinate and we achieve this by fixing the value of $R_{\mathbf{S}^2}$ in the $\eta \rightarrow 0$ limit. This surface in this context is invariant by an $\mathbf{SO(1,3)}$ subgroup, which is the $\mathbf{SO(1,4)}$ quasi-de Sitter isometry group in left region. Technically this is commonly known as left invariant in which we perform our rest of the computation presented in this paper. Also for our purpose we use de Sitter global coordinate system in which the equal time slices are three sphere $\mathbf{S}^3$. In this context the entangling surface is two sphere $\mathbf{S}^2$, which is the equator of three sphere $\mathbf{S}^3$. Furthermore, using quasi-de Sitter isometry group as $\eta =0$ one can consider a map which transform $\mathbf{S}^2$ to the equator of three sphere $\mathbf{S}^3$ on the boundary of $3+1$ D quasi-de Sitter space. However, this gives rise to divergent contributions, which can be regularised by transforming back to the $\mathbf{S}^2$ to a surface at global time $\tau _\mathrm{global}$.

In the present situation we also use hyperbolic slices which are geometrically characterised by the equation, $\sum ^{5}_{j=1}Y^2_{j}= H^{-2},$ where for Euclidean signature we can write down the following parametric equations:

$$\begin{aligned} Y_{j}= & {} H^{-1}\times \left\{ \begin{array}{ll} \cos \tau _{\mathrm{E}}~\sin \rho _{\mathrm{E}}~\hat{\mathbf{n}}_{j}&{}\quad \mathbf for j=1,2,3\\ \sin \tau _{\mathrm{E}} &{}\quad \mathbf for j=4\\ \cos \tau _{\mathrm{E}}~\cos \rho _{\mathrm{E}} &{} \quad \mathbf for j=5. \end{array} \right. \end{aligned}$$

(3.2)

Here $\hat{\mathbf{n}}_{j}\forall j=1,2,3$ are the jth component of the unit vector defined in $\mathbf{R}^{3}$.

In this hyperbolic slices the metric with Euclidean signature can be expressed as

$$\begin{aligned} \mathrm{d}s^2_{\mathrm{E}}=H^{-2}\left[ \mathrm{d}\tau ^2_{\mathrm{E}} +\cos ^2\tau _{\mathrm{E}}\left( \mathrm{d}\rho ^2_{\mathrm{E}}+\sin ^2\rho _{\mathrm{E}}~\mathrm{d}\Omega ^2_{\mathbf{2}}\right) \right] , \end{aligned}$$

(3.3)

where $\mathrm{d}\Omega ^2_{\mathbf{2}}$ is defined in the two sphere $\mathbf{S}^2$. Furthermore, we perform the following analytic continuation in the fifth coordinate:

$$\begin{aligned} Y_{5}=H^{-1}\cos \tau _{\mathrm{E}}~\cos \rho _{\mathrm{E}}\rightarrow X_{0}=iY_{5}=iH^{-1}\cos \tau _{\mathrm{E}}~\cos \rho _{\mathrm{E}}\nonumber \\ \end{aligned}$$

(3.4)

and redefine the rest of the coordinates as, $X_{k}=Y_{k}~\forall k=1,2,3,4.$ Consequently, in the Lorentzian signature one can write the following geometrical equation:

$$\begin{aligned} \sum ^{4}_{l=0}X^2_{l}=\left( -X^2_0+\sum ^{4}_{k=1}X^2_k\right) =H^{-2}. \end{aligned}$$

(3.5)

On the other hand, in the Lorentzian signature one can consider three different regions, which are characterised as

$$\begin{aligned}&{} \mathbf{R}:\left\{ \begin{array}{ll} \tau _{\mathrm{E}}=\frac{\pi }{2}-it_{\mathbf{R}} &{} \quad \mathbf for t_{\mathbf{R}}\ge 0\\ \rho _{\mathrm{E}}=-ir_{\mathbf{R}} &{} \quad \mathbf for r_{\mathbf{R}}\ge 0.\end{array}\right. \end{aligned}$$

(3.6)

$$\begin{aligned}&{} \mathbf{C}:\left\{ \begin{array}{ll} \tau _{\mathrm{E}}=t_{\mathbf{C}}&{}\quad \mathbf for -\frac{\pi }{2}\le t_{\mathbf{C}}\le \frac{\pi }{2}\\ \rho _{\mathrm{E}}=\frac{\pi }{2}-ir_{\mathbf{C}} &{}\quad \mathbf for -\infty<r_{\mathbf{c}}< \infty .\end{array} \right. \end{aligned}$$

(3.7)

$$\begin{aligned}&{} \mathbf{L}:\left\{ \begin{array}{ll} \tau _{\mathrm{E}}=-\frac{\pi }{2}+it_{\mathbf{L}}&{} \quad \mathbf for t_{\mathbf{L}}\ge 0\\ \rho _{\mathrm{E}}=-ir_{\mathbf{L}} &{}\quad \mathbf for r_{\mathbf{L }}\ge 0. \end{array} \right. \end{aligned}$$

(3.8)

Furthermore, in hyperbolic slices the metric with Lorentzian signature can be expressed for the three regions as

$$\begin{aligned}&{} \mathbf{R}:\left\{ \begin{array}{ll} \mathrm{d}s^2_{\mathbf{R}}=H^{-2}\left[ -\mathrm{d}t^2_{\mathbf{R}}+\sinh ^2t_{\mathbf{R}}\,\left( \mathrm{d}r^2_{\mathbf{R}}+\sinh ^2r_{\mathbf{R}}~\mathrm{d}\Omega ^2_{\mathbf{2}}\right) \right] , \end{array} \right. \end{aligned}$$

(3.9)

$$\begin{aligned}&{} \mathbf{C}:\left\{ \begin{array}{ll} \mathrm{d}s^2_{\mathbf{C}}=H^{-2}\left[ \mathrm{d}t^2_{\mathbf{C}}+ \cos ^2t_{\mathbf{C}}\left( -\mathrm{d}r^2_{\mathbf{C}}+\cosh ^2r_{\mathbf{C}}~\mathrm{d}\Omega ^2_{\mathbf{2}}\right) \right] , \end{array} \right. \end{aligned}$$

(3.10)

$$\begin{aligned}&{} \mathbf{L}:\left\{ \begin{array}{ll} \mathrm{d}s^2_{\mathbf{L}}=H^{-2}\left[ -\mathrm{d}t^2_{\mathbf{L}}+ \sinh ^2t_{\mathbf{L}}\left( \mathrm{d}r^2_{\mathbf{L}}+ \sinh ^2r_{\mathbf{L}}~\mathrm{d}\Omega ^2_{\mathbf{2}}\right) \right] . \end{array} \right. \nonumber \\ \end{aligned}$$

(3.11)

In Fig. 2 is a schematic diagram for the geometrical construction and underlying symmetries of the bipartite system.

3.2 Wave function of the axion in an open chart

In this section our prime objective is to compute the expression for the entanglement entropy in de Sitter space driven by an axion field. This axion field originates from the R-R sector of Type IIB string theory compactified on a Calabi–Yau three fold ($\mathbf{CY^3}$) in the presence of an $\mathbf{NS~5}$ brane. For details of the compactification and the resulting effective action, in $3+1$ dimensions, for the axion field, see Refs. [35,36,37,38, 87]. Using this effective action we discuss that such stringy axions can be treated as necessary ingredient to study quantum entanglement in the context of primordial cosmology.⁶

Let us start with the aforementioned effective action for axion field:

$$\begin{aligned} S_{\mathrm{axion}}=\int \mathrm{d}^{4}x \sqrt{-g}\left[ -\frac{1}{2}(\partial \phi )^2 +V(\phi )\right] , \end{aligned}$$

(3.12)

where $\phi$ is the axion field and the corresponding effective potential can be expressed as

$$\begin{aligned} V(\phi )=\mu ^3\phi +\Lambda ^4_{G}\cos \left( \frac{\phi }{f_{a}}\right) = \mu ^3\left[ \phi +bf_{a}\cos \left( \frac{\phi }{f_{a}}\right) \right] ,\nonumber \\ \end{aligned}$$

(3.13)

where $\mu ^3$ is the mass scale, $f_a$ is the axion decay constant and we have defined a new parameter b as, $b= \Lambda ^4_{G}/\mu ^3 f_{a}$. In this case scale $\Lambda _{G}$ is given by $\Lambda _{G}=\sqrt{m_{SUSY} L^3/ \sqrt{\alpha ^{\prime }}g_{s}}~e^{-cS_{\mathrm{inst}}},$ where $S_{\mathrm{inst}}$ is the instanton action, $c\sim \mathcal{O}(1)$ is a constant factor, $m_{SUSY}$ is the supersymmetry breaking scale, $\alpha ^{\prime }$ is the Regge slope parameter, $g_s$ is the string coupling constant and $L^6$ is the volume factor in string units. Using this action we compute the wave function of the axion in open chart. In Fig. 3 we have shown the schematic behaviour of the axion potential. For the computation of the wave function here we consider the following two possibilities:

Fig. 3

Schematic behaviour of the axion effective potential obtained from String Theory

• 1. Case I:

  In the first approximation of the computation we restrict ourself up to the linear term of the effective potential:

  $$\begin{aligned} V(\phi )\approx & {} \mu ^3\phi . \end{aligned}$$

  (3.14)

  Here the linear term of the effective potential can be treated as a source term in the equation of motion where the axion has no mass.

• 2. Case II:

  On the other hand, in the small field limit $\phi \ll f_a$, where analytic solution of the equation of motion is possible, one can approximate the non-perturbative contribution as, $\cos \left( \frac{\phi }{f_{a}}\right) \approx 1-\frac{1}{2}\left( \frac{\phi }{f_{a}}\right) ^2$. Consequently in small field limit $\phi \ll f_a$ one can approximate the total effective potential for axion as

  $$\begin{aligned} V(\phi )\approx & {} \Lambda ^4_{C}+\mu ^3\phi - \frac{\Lambda ^4_{C}}{2}\left( \frac{\phi }{f_{a}}\right) ^2\nonumber \\= & {} \mu ^3\left[ bf_{a}+\phi \right] -\frac{m^2_{\mathrm{axion}}}{2}\phi ^2. \end{aligned}$$

  (3.15)

  Here we define the effective mass of the axion as

  $$\begin{aligned} m^2_{\mathrm{axion}}= & {} \frac{\mu ^3 b}{f_{a}}=\frac{\Lambda ^4_{G}}{f^2_{a}}, \end{aligned}$$

  (3.16)

  where the axion decay constant in general follows a time dependent profile and for our purpose we use the choice $f_a=\sqrt{100-\frac{80}{1+\left( \ln \frac{\eta }{\eta _c}\right) ^2}}~H$, which was used in Refs. [16,17,18] to demonstrate Bell’s inequality violation in primordial cosmology. It is important to mention here that the one point function from axionic fluctuation in primordial cosmology is exactly proportional to the parameter $m_{\mathrm{axion}}/f_a$ and such contributions are appearing in Case II, which we further use for the computation of the entanglement entropy to prove the existence of EPR Bell pairs in cosmology.

Furthermore, using Eq. (3.12) one can write down the following equation of motion for the axion for the above-mentioned two cases:

$$\begin{aligned}&{\underline{\mathbf{For~Case~I{:}}}}\quad \Box \phi =\mu ^3, \end{aligned}$$

(3.17)

$$\begin{aligned}&{\underline{\mathbf{For~Case~II{:}}}}\quad \left( \Box +m^2_{\mathrm{axion}}\right) \phi =\mu ^3=\frac{m^2_{\mathrm{axion}}f_a}{b},\nonumber \\ \end{aligned}$$

(3.18)

where $\Box$ is the $3+1$ D D’Alembertian operator which can be expressed in open chart as [90]:

$$\begin{aligned} \Box= & {} \left[ \frac{1}{a^3(t)}\partial _{t}\left( a^3(t)\partial _{t}\right) -\frac{1}{H^2a^2(t)}\hat{\mathbf{L}}^2_{{\mathbf{H}}^{\mathbf{3}}}\right] . \end{aligned}$$

(3.19)

Also the exact time dependence in the scale factor a(t) for an open chart of the de Sitter background is given by

$$\begin{aligned} a(t)= & {} \frac{1}{H}\sinh t. \end{aligned}$$

(3.20)

Additionally, the Laplacian operator $\hat{\mathbf{L}}^2_{\mathbf{H}^{\mathbf{3}}}$ in hyperbolic slice $\mathbf{H^3}$ can be written as [90]:

(3.21)

which satisfies the following eigenvalue equation:

$$\begin{aligned} \hat{\mathbf{L}}^2_{\mathbf{H}^{\mathbf{3}}}\mathcal{Y}_{plm}(r,\theta ,\Phi )= & {} -(1+p^2)\mathrm{\mathcal Y}_{plm}(r,\theta ,\Phi ). \end{aligned}$$

(3.22)

Here $\mathcal{Y}_{plm}(r,\theta ,\Phi )$ are the eigenfunctions of $\hat{\mathbf{L}}^2_{\mathbf{H}^{\mathbf{3}}}$, which can be written using method of separation of variable here one can decompose $\mathcal{Y}_{plm}(r,\theta ,\Phi )$ into a radial and angular part as

$$\begin{aligned} \mathcal{Y}_{plm}(r,\theta ,\Phi )= & {} \frac{\Gamma \left( ip+l+1\right) }{\Gamma \left( ip+1\right) }~\frac{p}{\sqrt{\sinh r}}~\mathcal{P}^{-\left( l+\frac{1}{2}\right) }_{\left( ip-\frac{1}{2}\right) }\nonumber \\&\times \left( \cosh r\right) Y_{lm}(\theta ,\Phi ), \end{aligned}$$

(3.23)

where $Y_{lm}(\theta ,\Phi )$ is the spherical harmonic function and $\mathcal{P}^{-\left( l+\frac{1}{2}\right) }_{\left( ip-\frac{1}{2}\right) }\left( \cosh r\right)$ represents associated Legendre polynomial.

The full solution of the equations of motions for the $\mathbf{Case~I}$ and $\mathbf{Case~II}$ can be expressed in the following forms:

$$\begin{aligned} \phi (t,r,\theta ,\Phi )= & {} \sum _{\Lambda }\left[ a_{\Lambda }\mathcal{U}_{\Lambda }(t,r,\theta ,\Phi )+a^{\dagger }_{\Lambda }\mathcal{U}^{*}_{\Lambda }(t,r,\theta ,\Phi )\right] ,\nonumber \\ \end{aligned}$$

(3.24)

where $\mathcal{U}_{\Lambda }(t,r,\theta ,\Phi )$ forms a complete basis of mode function labelled by index $\Lambda$ which is fixed by the three quantum numbers p, l and m and an index $\sigma =\pm$ for $\mathbf{R}$ and $\mathbf{L}$ hyperboloid in the present context.

It is important to note that equation of motions for the $\mathbf{Case~I}$ and $\mathbf{Case~II}$ are inhomogeneous differential equations with constant source and for this the total solutions of these equations can be expressed as

$$\begin{aligned} \mathcal{U}_{\Lambda }(t,r,\theta ,\Phi )= & {} \mathcal{U}_{\sigma plm}(t,r,\theta ,\Phi )\nonumber \\= & {} \frac{1}{a(t)}\chi _{p,\sigma }(t)\mathcal{Y}_{plm}(r,\theta ,\Phi )\nonumber \\= & {} \frac{H}{\sinh t}\chi _{p,\sigma }(t)\mathcal{Y}_{plm}(r,\theta ,\Phi ), \end{aligned}$$

(3.25)

where the time dependent part of the wave function $\chi _{p,\sigma }(t)$ forms a complete set of positive frequency function which can be written as a sum of complementary part ($\chi ^{(c)}_{p,\sigma }(t)$) and particular integral part ($\chi ^{(p)}_{p,\sigma }(t)$):

$$\begin{aligned} \chi _{p,\sigma }(t)= & {} \chi ^{(c)}_{p,\sigma }(t)+\chi ^{(p)}_{p,\sigma }(t). \end{aligned}$$

(3.26)

Here our prime objective is to explicitly compute both of the contributions and use them further in the computation of entanglement entropy.

Furthermore, one can write down the following equation of motion for the complementary part of the time dependent contribution in the total solution:

$$\begin{aligned} \mathcal{D}_{t}\chi ^{(c)}_{p,\sigma }(t)= & {} 0, \end{aligned}$$

(3.27)

where $\mathcal{D}_{t}$ is the differential operator in the present context, which can be expressed for the above-mentioned two cases as:

$$\begin{aligned} \mathcal{D}_{t}= & {} \left\{ \begin{array}{ll} \left[ \partial ^2_t +3\coth t~ \partial _t+\frac{(1+p^2)}{\sinh ^2t}\right] ~~~~~~~~~~~~~~~~~ &{} {{\mathbf{for~Case~I}}}\,\\ \left[ \partial ^2_t +3\coth t~ \partial _t+\frac{(1+p^2)}{\sinh ^2t}+\frac{m^2_{\mathrm{axion}}}{H^2}\right] &{} {{\mathbf{for~Case~II}}}. \end{array} \right. \nonumber \\ \end{aligned}$$

(3.28)

The final solution for the complementary time dependent part for Case I and Case II are given by

$$\begin{aligned}&{\underline{\mathbf{Case~I:}}}\nonumber \\&\quad \chi ^{(c)}_{p,\sigma }(t)=\left\{ \begin{array}{ll} \frac{1}{2\sinh \pi p}\left[ \frac{\left( e^{\pi p}+\sigma \right) }{\Gamma (2+ip)}\mathcal{P}^{ip}_{1}(\cosh t_{\mathbf{R}})-\frac{\left( e^{-\pi p}+\sigma \right) }{\Gamma (2-ip)}\mathcal{P}^{-ip}_{1}(\cosh t_{\mathbf{R}})\right] &{}\quad {{\mathbf{for~R}}}\\ \frac{\sigma }{2\sinh \pi p}\left[ \frac{\left( e^{\pi p}+\sigma \right) }{\Gamma (2+ip)}\mathcal{P}^{ip}_{1}(\cosh t_{\mathbf{L}})-\frac{\left( e^{-\pi p}+\sigma \right) }{\Gamma (2-ip)}\mathcal{P}^{-ip}_{1}(\cosh t_{\mathbf{L}})\right] &{}\quad {{\mathbf{for~L}}}. \end{array} \right. \end{aligned}$$

(3.29)

$$\begin{aligned}&{\underline{\mathbf{Case~II:}}}\nonumber \\&\chi ^{(c)}_{p,\sigma }(t)=\left\{ \begin{array}{ll} \frac{1}{2\sinh \pi p}\left[ \frac{\left( e^{\pi p}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}+ip\right) }\mathcal{P}^{ip}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{R}})-\frac{\left( e^{-\pi p}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}-ip\right) }\mathcal{P}^{-ip}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{R}})\right] &{} \quad {{\mathbf{for~R}}}\\ \frac{\sigma }{2\sinh \pi p}\left[ \frac{\left( e^{\pi p}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}+ip\right) }\mathcal{P}^{ip}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{L}})-\frac{\left( e^{-\pi p}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}-ip\right) }\mathcal{P}^{-ip}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{L}})\right] &{} \quad {{\mathbf{for~L}}}, \end{array} \right. \end{aligned}$$

(3.30)

where in Case II we introduce a parameter $\nu$, which is defined for axion as

$$\begin{aligned} \nu= & {} \sqrt{\frac{9}{4}-\frac{m^2_{\mathrm{axion}}}{H^2}}=\sqrt{\frac{9}{4}-\frac{\mu ^3 b}{f_a H^2}}=\sqrt{\frac{9}{4}-\frac{\Lambda ^4_G}{f^2_a H^2}}.\nonumber \\ \end{aligned}$$

(3.31)

From the above solutions obtained for Case I and Case II we observe the following characteristic features:

• In the above solutions $\sigma$ can take two values i.e. $\sigma =\pm 1$. For each values of $\sigma$ one can write down the final results in two regions – $\mathbf{R}$ and $\mathbf{L}$ regions of the hyperboloid ($\mathbf{H^3}$).

• In the result for Case II, in the limit $m_{\mathrm{axion}}\ll H$ the parameter $\nu$ is given by $\nu =3/2$. For this value of $\nu$, the solutions for Case I and Case II coincide. For this reason one can treat Case I as a special situation of Case II.

• Similarly in the limit $m_{\mathrm{axion}}=\sqrt{2}H$ we have $\nu =1/2$. This is an important class of solution where axion is conformally coupled. Using this class of solution one can get back the flat space limit result of the entanglement entropy as the metric for de Sitter space is conformally flat.

• In the case where $m_{\mathrm{axion}}<\sqrt{2}H$ parameter $\nu$ lies within the range $1/2<\nu <3/2$ and this is also an important class of solution which is commonly known as the solution in the low mass region.

• Furthermore, in the limit $m_{\mathrm{axion}}=H$ parameter $\nu$ is given by $\nu =5/2$ and this is a restrictive class of solution where axion mass is exactly equal to the Hubble friction.

• For $m_{\mathrm{axion}}\gg H$, we have $\nu =i\sqrt{\frac{m^2_{\mathrm{axion}}}{H^2} -\frac{9}{4}}\approx im_{\mathrm{axion}}/H$. This is an important class of solution in the present context corresponding to high mass. Note that, for $\sqrt{2}H<m_{\mathrm{axion}}<3H/2$, the parameter $\nu$ is lying within the window, $0<\nu <1/2$.

• For $\mathbf{R}$ and $\mathbf{L}$ hyperboloid regions, the solutions have singularities at, $\nu \equiv \nu _{1}=-\frac{1}{2}- ip$ and $\nu \equiv \nu _{2}=-\frac{1}{2} +ip$. This implies that to get non-singular solution the magnitude of the axion mass must satisfy the constraint $\left| \frac{m_{\mathrm{axion}}}{H}\right| \ne \sqrt{(p^2+4)(p^2+1)}$.

• Additionally it is important to note that the final solution for the complementary time dependent part is symmetric under the exchange of the sign of the quantum number p i.e. $\chi ^{(c)}_{p,\sigma }(t)=\chi ^{(c)}_{-p,\sigma }(t)$.

• In this context the overall normalisation constant of the time dependent complementary part of the solution is fixed by the following Klein–Gordon inner product [90]: $\left( \left( \chi ^{(c)}_{p,\sigma }(t),\chi ^{(c)}_{p,\sigma ^{\prime }}(t)\right) \right) =\mathcal{N}_{p\sigma }\delta _{\sigma \sigma ^{\prime }}$, where $\mathcal{N}_{p\sigma }$ is the overall normalisation constant, which is given by

  $$\begin{aligned} \mathcal{N}_{p\sigma }= & {} \left\{ \begin{array}{ll} \frac{4}{\pi }\frac{\left[ \cosh \pi p+\sigma \right] }{|\Gamma \left( 2+ip\right) |^2}~~~~~~~~~~~~~~~~~ &{} {{\mathbf{for ~Case ~I}}}\\ \frac{4}{\pi }\frac{\left[ \cosh \pi p-\sigma \cos \left( \nu -\frac{1}{2}\right) \right] }{|\Gamma \left( \nu +\frac{1}{2}+ip\right) |^2}~~~~~~~~~~~~~~~~~ &{} {{\mathbf{for ~Case ~II}}}.~\end{array} \right. \nonumber \\ \end{aligned}$$

  (3.32)

Furthermore, one can write down the following equation of motion for the particular integral part of the time dependent contribution in the total solution:

$$\begin{aligned} \mathcal{D}_{t}\chi ^{(p)}_{p,\sigma }(t)= & {} \mathcal{J}, \end{aligned}$$

(3.33)

where $\mathcal{D}_{t}$ is the differential operator as given in Eq. (3.28) and $\mathcal{J}=\mu ^3$. For Case II depending on the time dependence of the axion effective mass as well as the time dependent axion decay constant, source function might be time dependent or constant. But for general consideration we assume that the source function is time dependent.

The final solution for the time dependent “particular integral” part is given by

$$\begin{aligned} \chi ^{(p)}_{p,\sigma }(t)=\int \mathrm{d}t^{\prime }~G_{\sigma }(t,t^{\prime })~\mathcal{J}(t^{\prime }), \end{aligned}$$

(3.34)

where $G_{\sigma }(t,t^{\prime })$ is the Green’s function for axion field, given by

$$\begin{aligned} G_{\sigma }(t,t^{\prime })= & {} \sinh ^2 t\sum ^{\infty }_{n=0}\frac{1}{\left( p^2-p^2_{n}\right) }\chi ^{(c)}_{p_{n},\sigma }(t)\chi ^{(c)}_{p_{n},\sigma }(t^{\prime }).\nonumber \\ \end{aligned}$$

(3.35)

Here, $\chi ^{(c)}_{p_{n},\sigma }(t)$ represents the solution for the complementary part with a slight modification due to the replacement of p by $p_{n}~\forall ~n=0,\ldots , \infty$ and is represented by

$$\begin{aligned}&{\underline{\mathbf{Case~I:}}}\nonumber \\&\quad \chi ^{(c)}_{p_{n},\sigma }(t)=\left\{ \begin{array}{ll} \frac{1}{2\sinh \pi p_{n}}\left[ \frac{\left( e^{\pi p_{n}}+\sigma \right) }{\Gamma (2+ip_{n})}\mathcal{P}^{ip_{n}}_{1}(\cosh t_{\mathbf{R}})-\frac{\left( e^{-\pi p_{n}}+\sigma \right) }{\Gamma (2-ip_{n})}\mathcal{P}^{-ip_{n}}_{1}(\cosh t_{\mathbf{R}})\right] ~~~~~~~~ &{} {{\mathbf{for ~R}}}\\ \frac{\sigma }{2\sinh \pi p_{n}}\left[ \frac{\left( e^{\pi p_{n}}+\sigma \right) }{\Gamma (2+ip_{n})}\mathcal{P}^{ip_{n}}_{1}(\cosh t_{\mathbf{L}})-\frac{\left( e^{-\pi p_{n}}+\sigma \right) }{\Gamma (2-ip_{n})}\mathcal{P}^{-ip_{n}}_{1}(\cosh t_{\mathbf{L}})\right] &{} {{\mathbf{for ~L}}}.~~~~~ \end{array} \right. \end{aligned}$$

(3.36)

$$\begin{aligned}&{\underline{\mathbf{Case~II:}}}\nonumber \\&\chi ^{(c)}_{p_{n},\sigma }(t)=\left\{ \begin{array}{ll} \frac{1}{2\sinh \pi p_{n}}\left[ \frac{\left( e^{\pi p_{n}}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}+ip_{n}\right) }\mathcal{P}^{ip_{n}}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{R}})-\frac{\left( e^{-\pi p_{n}}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}-ip_{n}\right) }\mathcal{P}^{-ip_{n}}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{R}})\right] ~~ &{} {{\mathbf{for ~R}}}\\ \frac{\sigma }{2\sinh \pi p_{n}}\left[ \frac{\left( e^{\pi p_{n}}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}+ip_{n}\right) }\mathcal{P}^{ip_{n}}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{L}})-\frac{\left( e^{-\pi p_{n}}-i\sigma ~e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}-ip_{n}\right) }\mathcal{P}^{-ip}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{\mathbf{L}})\right] &{} {{\mathbf{for ~L}}}. \end{array} \right. \end{aligned}$$

(3.37)

Furthermore, using the results obtained for the total solution of the EOM given in Eq. (3.24) we expand the field in terms of creation and annihilation operators in Bunch–Davies vacuum, which is given by

(3.38)

where the Bunch–Davies vacuum state is defined as

$$\begin{aligned}&a_{\sigma p l m}|\mathbf{BD}\rangle =0\quad \forall \sigma =(+1,-1);\nonumber \\&\quad p=0,\ldots ,\infty ;l=0,\ldots ,p-1,m=-\,l,\ldots ,+\,l.\nonumber \\ \end{aligned}$$

(3.39)

In this context, the Bunch–Davies mode function $\mathcal{U}_{\sigma plm}(r,t,\theta ,\phi )$ can be expressed as

$$\begin{aligned} \mathcal{U}_{\sigma plm}(r,t,\theta ,\Phi )= & {} \frac{H}{\sinh t}\chi _{p,\sigma }(t)\mathcal{Y}_{plm}(r,\theta ,\Phi ). \end{aligned}$$

(3.40)

After substituting Eq. (3.40) in Eq. (3.38) we get the following expression for the wave function:

$$\begin{aligned} \phi (r,t,\theta ,\Phi )= & {} \frac{H}{\sinh t}\int ^{\infty }_{0} \mathrm{d}p \sum ^{p-1}_{l=0}\sum ^{+l}_{m=-l}\nonumber \\&\times \,\sum _{\sigma =\pm 1}\left[ a_{\sigma plm}\chi _{p,\sigma }(t)+a^{\dagger }_{\sigma plm}\chi ^{*}_{p,\sigma }(t)\right] \nonumber \\&\times \,\mathcal{Y}_{plm}(r,\theta ,\Phi ). \end{aligned}$$

(3.41)

Below we use the following sets of shorthand notations to denote various associated Legendre polynomials as appearing for the solutions of the wave functions:

$$\begin{aligned}&{\underline{\mathbf{Complementary~solution}}{:}}\nonumber \\&\quad \mathcal{P}^{q}=\left\{ \begin{array}{ll} \mathcal{P}^{ip}_{1}(\cosh t_{q})&{}\quad {{\mathbf{for~Case~I}}}\\ \mathcal{P}^{ip}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{q}) &{}\quad {{\mathbf{for~Case~II}}}. \end{array}\right. \end{aligned}$$

(3.42)

$$\begin{aligned}&{\underline{\mathbf{Particular~solution}}{:}}\nonumber \\&\quad \mathcal{P}^{{q},n}=\left\{ \begin{array}{ll} \mathcal{P}^{ip_n}_{1}(\cosh t_{q})&{}\quad {{\mathbf{for~Case~I}}}\\ \mathcal{P}^{ip_n}_{\left( \nu -\frac{1}{2}\right) }(\cosh t_{q}) &{}\quad {{\mathbf{for~Case~II}}}, \end{array} \right. \end{aligned}$$

(3.43)

where the index $q=\mathbf{R},\mathbf{L}$ for the right and left handed hyperbolic region in the open chart.

Thus, the total time dependent part of the solution can be simplified to the following form:

(3.44)

where we use the following redefined symbol:

$$\begin{aligned} \bar{\mathcal{P}}^{q,n}=\sinh ^2t~ \mathcal{P}^{q,n}\int \mathrm{d}t^{\prime }~\chi ^{(c)}_{p_n,\sigma ,q}(t^{\prime })~\mathcal{J}(t^{\prime }). \end{aligned}$$

(3.45)

Here $p_n\forall n=0,\ldots ,\infty$, $\sigma =\pm 1$ and $q=\mathbf{R},\mathbf{L}$. Also the normalisation constant $\mathcal{N}_{p}$ for the complementary part is defined as, $\mathcal{N}_{p}=2\sinh \pi p ~\sqrt{\mathcal{N}_{p\sigma }}$, where $\mathcal{N}_{p\sigma }$ is defined in Eq. (3.32). For the particular part if we replace p by $p_n$ then the normalisation constant $\mathcal{N}_{p_n}$ can be defined as, $\mathcal{N}_{p_n}=2\sinh \pi p_n ~\sqrt{\mathcal{N}_{p_n\sigma }}$.

In Eq. (3.44), expansion coefficient functions for the complementary solution ($\alpha ^{\sigma }_{q}$, $\beta ^{\sigma }_{q}$) for $q=\mathbf{R},\mathbf{L}$ are defined as

$$\begin{aligned} \alpha ^{\sigma }_{\mathbf{R}}= & {} \frac{1}{\sigma }\alpha ^{\sigma }_{\mathbf{L}}= \left\{ \begin{array}{ll} \frac{\left( \sigma +e^{\pi p}\right) }{\Gamma \left( 2+ip\right) }&{}\quad {{\mathbf{for~Case~I}}}\\ \frac{\left( e^{\pi p}-i\sigma e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}+ip\right) }&{} \quad {{\mathbf{for~Case~II}}}. \end{array} \right. \end{aligned}$$

(3.46)

$$\begin{aligned} \beta ^{\sigma }_{\mathbf{R}}= & {} \frac{1}{\sigma }\beta ^{\sigma }_{\mathbf{L}}=\left\{ \begin{array}{ll} -\frac{\left( \sigma +e^{-\pi p}\right) }{\Gamma \left( 2-ip\right) }&{} \quad {{\mathbf{for~Case~I}}}\\ -\frac{\left( e^{-\pi p}-i\sigma e^{-i\pi \nu }\right) }{\Gamma \left( \nu +\frac{1}{2}-ip\right) }&{} \quad {{\mathbf{for~Case~II}}}. \end{array} \right. \end{aligned}$$

(3.47)

Expansion coefficients for particular solution ($\bar{\alpha }^{\sigma }_{q}$, $\bar{\beta }^{\sigma }_{q}$) can be obtained by replacing p by $p_n$ in Eqs. (3.46) and (3.47). Before going to the further details, let us first analyse Eq. (3.44):

• The full solution is valid for $p\ne p_{n}\forall n=0,\ldots ,\infty$, which is the necessary condition to solve the inhomogeneous differential equation using Green’s function technique.

• If the source is absent, then the solution for the complementary part is perfectly consistent with Ref. [15].

Furthermore, using Eq. (3.44) we write the following matrix equation in a compact form:

(3.48)

where for the complementary part of the solution we define the following matrices:

$$\begin{aligned}&\mathcal{M}^{I}_{J}=\left( \begin{array}{ccc} \alpha ^{\sigma }_{q} &{}\quad \beta ^{\sigma }_{q} \\ \beta ^{\sigma ^{*}}_{q} &{}\quad \alpha ^{\sigma ^{*}}_{q} \end{array}\right) , \quad \chi ^{I}=\left( \begin{array}{ccc} \chi _{\sigma }(t) \\ \chi ^{*}_{\sigma }(t), \end{array}\right) ,\nonumber \\&\quad \mathcal{P}^{J}=\left( \begin{array}{ccc} \mathcal{P}^{q} \\ \mathcal{P}^{{q^*}},\\ \end{array}\right) . \end{aligned}$$

(3.49)

Similarly for the particular solution we also define the following matrices:

$$\begin{aligned} \left( \mathcal{M}_{(n)}\right) ^{I}_{J}= & {} \left( \begin{array}{ccc} \bar{\alpha }^{\sigma }_{q,n} &{}~~~ \bar{\beta }^{\sigma }_{q,n} \\ \bar{\beta }^{\sigma ^{*}}_{q,n} &{}~~~ \bar{\alpha }^{\sigma ^{*}}_{q,n} \end{array}\right) ,~~~~~~ \mathcal{P}^{J}_{(n)}=\left( \begin{array}{ccc} \mathcal{P}^{q,n} \\ \mathcal{P}^{{q^*},n}\\ \end{array}\right) ,\nonumber \\ \end{aligned}$$

(3.50)

where $\sigma =\pm 1$, $q=\mathbf{R},\mathbf{L}$ and $I,J=1,2,3,4$.

On the other hand the redefined normalisation constant for the particular part of the solution $\mathcal{N}_{p,(n)}$ can be expressed as, $\mathcal{N}_{p,(n)}=2\sinh \pi p_n ~\sqrt{\mathcal{N}_{p_n\sigma }} ~\left( p^2-p^2_n\right)$. Furthermore, using Eq. (3.48) the Bunch–Davies mode function can be written as

(3.51)

where $a_{I}=(a_{\sigma }, a^{\dagger }_{\sigma })$ represents a set of creation and annihilation operator.

On the other hand we define

$$\begin{aligned} b_{J}= & {} a^{(c)}_{I}\mathcal{M}^{I}_{J},~~~ b_{J(n)} = a^{(p)}_{I(n)}\left( {\mathcal{M}_{(n)}}\right) ^{I}_{J}, \end{aligned}$$

(3.52)

where $a^{(c)}_{I}=(a^{(c)}_{\sigma }, a^{(c)\dagger }_{\sigma })$ and $a^{(p)}_{I(n)}=(a^{(p)}_{\sigma ,n}, a^{(p)\dagger }_{\sigma ,n})$ are the set of creation and annihilation operators which act on the complementary and particular part, respectively. Thus, the operator contribution for the total solution is:

$$\begin{aligned} a_{I}= & {} \left[ a^{(c)}_{I}+\sum ^{\infty }_{n=0}a^{(p)}_{I(n)}\right] , \end{aligned}$$

(3.53)

where by inverting Eq. (3.52) we have expressed:

$$\begin{aligned} a^{(c)}_{I}= & {} b_{J}\left( \mathcal{M}^{-1}\right) ^{I}_{J},~~~ a^{(p)}_{I(n)} = b_{J(n)}\left( \mathcal{M}^{-1}_{(n)}\right) ^{I}_{J}. \end{aligned}$$

(3.54)

We define the following inverse matrices:

$$\begin{aligned}&\left( \mathcal{M}^{-1}\right) ^{I}_{J}=\left( \begin{array}{ccc} \gamma _{\sigma q} &{}\quad \delta _{\sigma q} \\ \delta ^{*}_{\sigma q}&{}\quad \gamma ^{*}_{\sigma q} \end{array}\right) ,\nonumber \\&\quad \left( \mathcal{M}^{-1}_{(n)}\right) ^{I}_{J} =\left( \begin{array}{ccc} \bar{\gamma }_{\sigma q,n} &{}\quad \bar{\delta }_{\sigma q,n} \\ \bar{\delta }^{*}_{\sigma q,n} &{}\quad \bar{\gamma }^{*}_{\sigma q,n} \end{array}\right) , \end{aligned}$$

(3.55)

where $\sigma =\pm 1$, $q=\mathbf{R},\mathbf{L}$ and $I,J=1,2,3,4$. The entries of these inverse matrices are given by

$$\begin{aligned}&\gamma _{j\sigma }= \left\{ \begin{array}{ll} \frac{\Gamma \left( 2+ip\right) ~e^{\pi p}}{4\sinh \pi p}\left( \begin{array}{ccc} \frac{1}{e^{\pi p}+1} &{}\quad \frac{1}{e^{\pi p}-1} \\ \frac{1}{e^{\pi p}+1} &{}\quad -\frac{1}{e^{\pi p}-1} \end{array}\right) &{}\quad {{\mathbf{for~Case~I}}}\\ \frac{\Gamma \left( \nu +\frac{1}{2}+ip\right) ~e^{\pi p+i\pi \left( \nu +\frac{1}{2}\right) }}{4\sinh \pi p}\left( \begin{array}{ccc} \frac{1}{e^{\pi p+i\pi \left( \nu +\frac{1}{2}\right) }+1} &{}\quad \frac{1}{e^{\pi p+i\pi \left( \nu +\frac{1}{2}\right) }-1} \\ \frac{1}{e^{\pi p+i\pi \left( \nu +\frac{1}{2}\right) }+1} &{}\quad -\frac{1}{e^{\pi p+i\pi \left( \nu +\frac{1}{2}\right) }-1} \end{array}\right)&\quad {{\mathbf{for~Case~II}}}. \end{array} \right. \end{aligned}$$

(3.56)

$$\begin{aligned}&\delta ^{*}_{j\sigma }=\left\{ \begin{array}{ll} \frac{\Gamma \left( 2-ip\right) }{4\sinh \pi p}\left( \begin{array}{ccc} \frac{1}{e^{\pi p}+1} &{}\quad -\frac{1}{e^{\pi p}-1} \\ \frac{1}{e^{\pi p}+1} &{}\quad \frac{1}{e^{\pi p}-1} \end{array}\right) &{}\quad {{\mathbf{for~Case~I}}}\\ \frac{\Gamma \left( \nu +\frac{1}{2}-ip\right) ~e^{i\pi \left( \nu +\frac{1}{2}\right) }}{4\sinh \pi p}\left( \begin{array}{ccc} \frac{1}{e^{\pi p}+e^{i\pi \left( \nu +\frac{1}{2}\right) }} &{}\quad -\frac{1}{e^{\pi p}-e^{i\pi \left( \nu +\frac{1}{2}\right) }} \\ \frac{1}{e^{\pi p}+e^{i\pi \left( \nu +\frac{1}{2}\right) }} &{}\quad \frac{1}{e^{\pi p}-e^{\pi p+i\pi \left( \nu +\frac{1}{2}\right) }} \end{array}\right)&{{\mathbf{for~Case~II}}}. \end{array} \right. \end{aligned}$$

(3.57)

Similarly $\bar{\gamma }_{j\sigma ,n}$ and $\bar{\delta }^{*}_{j\sigma ,n}$ can be obtained by replacing p by $p_n$ in Eqs. (3.56) and (3.57). Furthermore, we introduce a set of rules which are useful to differentiate the operations of these operators in the complementary and particular solution. These rules are:

• Rule I:

  The operator corresponding to the complementary solution is insensitive to the particular solution i.e. $a^{(c)}_{I}\left[ \sum ^{\infty }_{n=0}\frac{1}{\mathcal{N}_{p,(n)}}\left( \mathcal{M}_{(n)}\right) ^{I}_{J}\mathcal{P}^{J}_{(n)}\right] = 0.$

• Rule II:

  The operator corresponding to the particular solution is insensitive to the complementary solution i.e. $a^{(p)}_{I(n)}\left[ \frac{1}{\mathcal{N}_p}\mathcal{M}^{I}_{J}\mathcal{P}^{J}\right] =0.$

For simplification we quantify the components of $a_{I} =(a_{\sigma },a^{\dagger }_{\sigma })$ for $\sigma =\pm 1$ as

$$\begin{aligned} a_{\sigma }= & {} \sum _{q=\mathbf{R},\mathbf{L}}\left\{ \left[ \gamma _{q\sigma }b_{q}+\delta ^{*}_{q\sigma }b^{\dagger }_{q}\right] \right. \nonumber \\&\left. +\sum ^{\infty }_{n=0}\left[ \bar{\gamma }_{q\sigma ,n}\bar{b}_{q,n}+\bar{\delta }^{*}_{q\sigma ,n}\bar{b}^{\dagger }_{q,n}\right] \right\} , \end{aligned}$$

(3.58)

$$\begin{aligned} a^{\dagger }_{\sigma }= & {} \sum _{q=\mathbf{R},\mathbf{L}}\left\{ \left[ \gamma ^{*}_{q\sigma }b^{\dagger }_{q}+\delta _{q\sigma }b_{q}\right] \right. \nonumber \\&\left. +\sum ^{\infty }_{n=0}\left[ \bar{\gamma }^{*}_{q\sigma ,n}\bar{b}^{\dagger }_{q,n}+\bar{\delta }_{q\sigma ,n}\bar{b}_{q,n}\right] \right\} . \end{aligned}$$

(3.59)

Furthermore, the Bunch–Davies vacuum state can be expressed in terms of the direct product of $\mathbf{R}$ and $\mathbf{L}$ vacua by using Bogoliubov transformation as

$$\begin{aligned} |\mathbf{BD}\rangle =e^{\hat{\mathcal{O}}}~(|\mathbf{R}\rangle \otimes |\mathbf{L}\rangle ). \end{aligned}$$

(3.60)

Here we assume that the Hilbert space corresponding to the Bunch–Davies vacuum state $\mathcal{H}_{\mathbf{BD}}$ can be decomposed into two separable portions as, $\mathcal{H}_{\mathbf{BD}}:=\mathcal{H}_{\mathbf{R}}\otimes \mathcal{H}_{\mathbf{L}}$, where $\mathcal{H}_{\mathbf{R}}$ and $\mathcal{H}_{\mathbf{L}}$ are the Hilbert space corresponding to $\mathbf{R}$ and $\mathbf{L}$ vacuum state. In the present context operator $\hat{\mathcal{O}}$ is given by

$$\begin{aligned} \hat{\mathcal{O}}= & {} \frac{1}{2}\sum _{i,j=\mathbf{R},\mathbf{L}}m_{ij}~b^{\dagger }_{i}~b^{\dagger }_{j}+\frac{1}{2}\sum _{i,j=\mathbf{R},\mathbf{L}}\sum ^{\infty }_{n=0}\bar{m}_{ij,n}~ \bar{b}^{\dagger }_{i,n}~\bar{b}^{\dagger }_{j,n},\nonumber \\ \end{aligned}$$

(3.61)

where the coefficients $m_{ij}$ and $\bar{m}_{ij,n}$ will be determined later. In Eq. (3.60) we will keep only linear terms in the exponential for simplicity.

Note that $\mathbf{R}$ and $\mathbf{L}$ vacuum states can be expressed as

$$\begin{aligned} |\mathbf{R}\rangle =|\mathbf{R}\rangle _{(c)}+|\mathbf{R}\rangle _{(p)},\quad |\mathbf{L}\rangle = |\mathbf{L}\rangle _{(c)}+|\mathbf{L}\rangle _{(p)}, \end{aligned}$$

(3.62)

with (c) and (p) representing the complementary and particular part, respectively. Furthermore, in principle one can express the particular part as

$$\begin{aligned} |\mathbf{R}\rangle _{(p)}= & {} \sum ^{\infty }_{n=0}|\mathbf{R}\rangle _{(p),n},~~~ |\mathbf{L}\rangle _{(p)}=\sum ^{\infty }_{n=0}|\mathbf{L}\rangle _{(p),n}. \end{aligned}$$

(3.63)

Also the annihilation operator satisfy

$$\begin{aligned} b_{q}|{q}\rangle _{(c)}= & {} 0\quad \forall ~q=(\mathbf{R},\mathbf{L}), \end{aligned}$$

(3.64)

$$\begin{aligned} \bar{b}_{q,n}|{q}\rangle _{(p)}= & {} 0\quad \forall ~q=(\mathbf{R},\mathbf{L}),~n=0,\ldots ,\infty , \end{aligned}$$

(3.65)

as well as the following commutation relations:

$$\begin{aligned}&\left[ b_i,b^{\dagger }_j\right] =\delta _{ij},\quad \left[ b_i,b_j\right] =0= \left[ b^{\dagger }_i,b^{\dagger }_j\right] .\end{aligned}$$

(3.66)

$$\begin{aligned}&\left[ \bar{b}_{i,n},\bar{b}^{\dagger }_{j,m}\right] = \delta _{ij}{\delta }_{nm},\quad \left[ \bar{b}_{i,n},\bar{b}_{j,m}\right] = 0= \left[ \bar{b}^{\dagger }_{i,m},\bar{b}^{\dagger }_{j,m}\right] .\nonumber \\ \end{aligned}$$

(3.67)

Furthermore, one can write the annihilation of Bunch–Davies vacuum in terms of the annihilations of $\mathbf{R}$ and $\mathbf{L}$ vacua as

$$\begin{aligned} a_{\sigma }|\mathbf{BD}\rangle =\sum _{q=\mathbf{R},\mathbf{L}}\sum ^{4}_{s=1}\mathcal{A}^{(q)}_{s}=0, \end{aligned}$$

(3.68)

where neglecting contribution from the higher powers of creation operators, $\mathcal{A}^{(q)}_{s}\forall s=1,2,3,4$ are defined as

$$\begin{aligned} \sum _{q=\mathbf{R},\mathbf{L}}\mathcal{A}^{(q)}_{1}= & {} \sum _{q=\mathbf{R},\mathbf{L}}\gamma _{q\sigma }b_q~e^{\hat{\mathcal{O}}}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) \nonumber \\\approx & {} \sum _{i,j=\mathbf{R},\mathbf{L}}m_{ij}\gamma _{j\sigma }b^{\dagger }_{i}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) ,~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

(3.69)

$$\begin{aligned} \sum _{q=\mathbf{R},\mathbf{L}}\mathcal{A}^{(q)}_{2}= & {} \sum _{q=\mathbf{R},\mathbf{L}}\delta ^{*}_{q\sigma }b^{\dagger }_q~e^{\hat{\mathcal{O}}}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) \nonumber \\\approx & {} \sum _{q=\mathbf{R},\mathbf{L}}\delta ^{*}_{q\sigma }b^{\dagger }_q\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

(3.70)

$$\begin{aligned} \sum _{q=\mathbf{R},\mathbf{L}}\mathcal{A}^{(q)}_{3}= & {} \sum _{q=\mathbf{R},\mathbf{L}}\sum ^{\infty }_{n=0}\bar{\gamma }_{q\sigma ,n}\bar{b}_{q,n}~e^{\hat{\mathcal{O}}}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) \nonumber \\\approx & {} \sum _{i,j=\mathbf{R},\mathbf{L}}\sum ^{\infty }_{n=0}\bar{m}_{ij,n}\bar{\gamma }_{j\sigma ,n}b^{\dagger }_{i,n}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) ,~~~~~~~~~~~ \end{aligned}$$

(3.71)

$$\begin{aligned} \sum _{q=\mathbf{R},\mathbf{L}}\mathcal{A}^{(q)}_{4}= & {} \sum _{q=\mathbf{R},\mathbf{L}}\sum ^{\infty }_{n=0}\bar{\delta }^{*}_{q\sigma ,n}\bar{b}^{\dagger }_{q,n}~e^{\hat{\mathcal{O}}}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) \nonumber \\\approx & {} \sum _{q=\mathbf{R},\mathbf{L}}\sum ^{\infty }_{n=0}\bar{\delta }^{*}_{q\sigma ,n}\bar{b}^{\dagger }_{q,n}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) .~~~~~~~~~~~~ \end{aligned}$$

(3.72)

This implies that the following condition holds:

$$\begin{aligned}&\left[ \left( m_{ij}\gamma _{j\sigma }+\delta ^{*}_{i\sigma }\right) b^{\dagger }_{i}+\sum ^{\infty }_{n=0}\left( \bar{m}_{ij,n} \bar{\gamma }_{j\sigma ,n}+\bar{\delta }^{*}_{i\sigma ,n}\right) \bar{b}^{\dagger }_{i,n}\right] \nonumber \\&\quad \times \left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) = 0. \end{aligned}$$

(3.73)

Thus, the complementary part and particular part vanish independently as the solutions are independent of each other. Consequently, we get the following constraints:

$$\begin{aligned}&\left( m_{ij}\gamma _{j\sigma }+\delta ^{*}_{i\sigma }\right) =0, \end{aligned}$$

(3.74)

$$\begin{aligned}&\left( \bar{m}_{ij,n}\bar{\gamma }_{j\sigma ,n}+\bar{\delta }^{*}_{i\sigma ,n}\right) = 0\quad \forall n. \end{aligned}$$

(3.75)

Furthermore, using Eqs. (3.74) and (3.75), the mass matrices corresponding to the complementary part and particular part can be expressed as

$$\begin{aligned}&m_{ij}= -\delta ^{*}_{i\sigma }\left( \gamma ^{-1}\right) _{\sigma j}\equiv \left( \begin{array}{ccc} m_{\mathbf{RR}} &{}\quad m_{\mathbf{RL}} \\ m_{\mathbf{LR}} &{}\quad m_{\mathbf{LL}} \end{array}\right) ,\nonumber \\&\bar{m}_{ij,n}=-\bar{\delta }^{*}_{i\sigma ,n} \left( \bar{\gamma }^{-1}\right) _{\sigma j,n}\equiv \left( \begin{array}{ccc} \bar{m}_{\mathbf{RR},n} &{}\quad \bar{m}_{\mathbf{RL},n} \\ \bar{m}_{\mathbf{LR},n} &{}\quad \bar{m}_{\mathbf{LL},n} \end{array}\right) .\nonumber \\ \end{aligned}$$

(3.76)

Next substituting the right hand side of the above-mentioned equations explicitly the entries of the mass matrices can be expressed for $i,j=\mathbf{R},\mathbf{L}$ as

$$\begin{aligned} m_{ij}= \left\{ \begin{array}{ll} \frac{\Gamma \left( 2-ip\right) }{\Gamma \left( 2+ip\right) }\frac{2i}{e^{2\pi p}-1}\left( \begin{array}{ccc} 0 &{}\quad i\sinh p\pi \\ i\sinh p\pi &{}\quad 0 \end{array}\right) \approx e^{i\theta }\frac{~e^{-p\pi }}{\sinh \pi p}\left( \begin{array}{ccc} 0 &{}\quad i\sinh p\pi \\ i\sinh p\pi &{}\quad 0 \end{array}\right) &{}\quad {{\mathbf{Case~I}}}\\ -\frac{\Gamma \left( \nu +\frac{1}{2}-ip\right) }{\Gamma \left( \nu +\frac{1}{2}+ip\right) }\frac{2~e^{i\pi \nu }}{e^{2\pi p}+e^{2i\pi \nu }}\left( \begin{array}{ccc} \cos \pi \nu &{}\quad i\sinh p\pi \\ i\sinh p\pi &{}\quad \cos \pi \nu \end{array}\right) \approx e^{i\theta }\frac{\sqrt{2}~e^{-p\pi }}{\sqrt{\cosh 2\pi p+\cosh 2\pi \nu }}\left( \begin{array}{ccc} \cos \pi \nu &{}\quad i\sinh p\pi \\ i\sinh p\pi &{}\quad \cos \pi \nu \end{array}\right)&\quad {{\mathbf{Case~II}}}. \end{array}\right. \end{aligned}$$

(3.77)

Entries of the matrix $\bar{m}_{ij,n}$ can similarly written by replacing p by $p_n$ in Eq. (3.77).

Fig. 4

Behaviour of the eigenvalues ($\lambda _{\pm }$) in de Sitter space for ‘$+$’ branch of solution. This figure clearly shows that we cover both large and small axion mass limit situations

Before further discussion here we point out few important features:

• For Case I we observe that for the complementary and particular part of the solution

  $$\begin{aligned} m_{\mathbf{RR}}= & {} 0=m_{\mathbf{LL}},\quad \bar{m}_{\mathbf{RR},n}= 0=\bar{m}_{\mathbf{LL},n}. \end{aligned}$$

  (3.78)

  But for Case II we find that

  $$\begin{aligned}&m_{\mathbf{RR}}=m_{\mathbf{LL}}=e^{i\theta }\frac{\sqrt{2}~e^{-p\pi }\cos \pi \nu }{\sqrt{\cosh 2\pi p+\cosh 2\pi \nu }},\nonumber \\&\bar{m}_{\mathbf{RR},n}=\bar{m}_{\mathbf{LL},n}=e^{i\theta }\frac{\sqrt{2}~e^{-p_n\pi }\cos \pi \nu }{\sqrt{\cosh 2\pi p_n+\cosh 2\pi \nu }},\nonumber \\ \end{aligned}$$

  (3.79)

  which is non-vanishing for $0<\nu <3/2$ and $\nu >3/2$. A special case appear for $\nu =3/2$, where the result vanishes and one can get back the result of Case I. Another important observation is that simultaneously it is not possible to fix $p=0,\nu =3/2$ for complementary solution and $p_n=0,\nu =3/2$ for particular solution, as both of them give divergent contribution in the diagonal component of the mass matrix.

• For Case I we see that for the complementary and particular part of the solution

  $$\begin{aligned}&m_{\mathbf{RL}}=m_{\mathbf{LR}}=e^{i\left( \theta +\frac{\pi }{2}\right) }~e^{-p\pi },\nonumber \\&\bar{m}_{\mathbf{RL},n}=\bar{m}_{\mathbf{LR},n}=e^{i\left( \theta +\frac{\pi }{2}\right) }~e^{-p_n\pi }. \end{aligned}$$

  (3.80)

  But for Case II we find that

  $$\begin{aligned}&m_{\mathbf{RL}}=m_{\mathbf{LR}}=\frac{e^{i\left( \theta +\frac{\pi }{2}\right) }\sqrt{2}~e^{-p\pi }\sinh p\pi }{\sqrt{\cosh 2\pi p+\cos 2\pi \nu }},\nonumber \\&\bar{m}_{\mathbf{RL},n}=\bar{m}_{\mathbf{LR},n}=\frac{e^{i\left( \theta +\frac{\pi }{2}\right) }\sqrt{2}~e^{-p_n\pi }\sinh p_n\pi }{\sqrt{\cosh 2\pi p_n+\cos 2\pi \nu }}.\nonumber \\ \end{aligned}$$

  (3.81)

  Here also, Case II coincides with Case I for $\nu =3/2$. Additionally, the non-vanishing off-diagonal components for both cases indicate the signature of quantum entanglement, which finally gives rise to a non-vanishing entanglement entropy. In what follows, we will explore this possibility in detail.

• Creation operators of b oscillators can be redefined by absorbing the overall phase contribution $e^{i\theta }$.

• The eigenvalues for the complementary part and particular part of the solution are given by

  $$\begin{aligned} \lambda _{\pm }= & {} \frac{1}{2}\left[ (m_{\mathbf{LL}}+m_{\mathbf{RR}})\right. \nonumber \\&\left. \pm \sqrt{(m_{\mathbf{LL}}-m_{\mathbf{RR}})^2+4m_{\mathbf{RL}}m_{\mathbf{LR}}}\right] , \end{aligned}$$

  (3.82)
  $$\begin{aligned} \lambda _{\pm ,n}= & {} \frac{1}{2}\left[ (\bar{m}_{\mathbf{LL},n}+\bar{m}_{\mathbf{RR},n})\right. \nonumber \\&\left. \pm \sqrt{(\bar{m}_{\mathbf{LL}}-\bar{m}_{\mathbf{RR},n})^2+4\bar{m}_{\mathbf{RL},n}\bar{m}_{\mathbf{LR},n}}\right] .\nonumber \\ \end{aligned}$$

  (3.83)

  Their explicit expressions are

  $$\begin{aligned}&{\underline{\mathbf{Case~I:}}}\nonumber \\&\lambda _{\pm }=\pm m_{\mathbf{RL}}=\pm ~ e^{i\left( \theta +\frac{\pi }{2}\right) }~e^{-p\pi }, \end{aligned}$$

  (3.84)
  $$\begin{aligned}&\lambda _{\pm ,n}=\pm \bar{m}_{\mathbf{RL},n}=\pm ~e^{i\left( \theta +\frac{\pi }{2}\right) }~e^{-p_n\pi }, \end{aligned}$$

  (3.85)

  ${\underline{\mathbf{Case~II:}}}$

  $$\begin{aligned} \lambda _{\pm }= & {} m_{\mathbf{RR}}\pm m_\mathbf{RL}\nonumber \\= & {} e^{i\theta }\frac{\sqrt{2}~e^{-p\pi }\left( \cos \pi \nu \pm i\sinh p\pi \right) }{\sqrt{\cosh 2\pi p+\cos 2\pi \nu }}, \end{aligned}$$

  (3.86)
  $$\begin{aligned} \lambda _{\pm ,n}= & {} \bar{m}_{\mathbf{RR},n}\pm \bar{m}_{\mathbf{RL},n}\nonumber \\= & {} e^{i\theta }\frac{\sqrt{2}~e^{-p_n\pi }\left( \cos \pi \nu \pm i\sinh p_n\pi \right) }{\sqrt{\cosh 2\pi p_n+\cos 2\pi \nu }}. \end{aligned}$$

  (3.87)

  However, this is not a physical basis as it is extremely complicated to trace over the $\mathbf{R}$ and $\mathbf{L}$ contributions when the Bunch–Davies vacuum state is represented using Eqs. (3.60) and (3.61). In Fig. 4a, b, we have shown the behaviour of the eigenvalue ($\lambda _{\pm }$) vs. the momentum p for fixed values of the mass parameter $|\nu |$ in the small and large axion mass limits. Here we cover the mass parameter range $0<|\nu |<3/2$ for both cases. In Fig. 4a for the small mass limit range for large values of the momentum p the two branches of solution for $|\nu |=0$ and $|\nu |=1/2,3/2$ coincides with each other and in the small values of the momentum p the two branches of solution can be separately visualised. Exactly opposite situation appears when we consider the large mass limit in Fig. 4b. Furthermore, in Fig. 4c, d, we have explicitly shown the behaviour of the eigenvalue ($\lambda _{\pm }$) vs. mass parameter $|\nu |$ for the fixed values of the momentum p in the small and large mass limits. For fixed value of p ($p=1$ and $p=2$) in the large mass limit, we initially get decaying behaviour and then after $|\nu |=3/2$ they saturate. On the other hand, for same values of p, in the large mass limit, we get oscillating behaviour. Combined effects for large and small mass limits are plotted in Fig. 4e, where we have explicitly shown that for $\nu ^2 <0$ (for $p=1$ and $p=2$) we get a distinguishable behaviour of the mass eigen values. Once $\nu ^2\rightarrow 0$ magnitude of the eigenvalues increase and, finally, when $\nu ^2>0$, both of the plots show apeariodic oscillations.

To find a suitable basis where we can trace over all contributions from $\mathbf{R}$ and $\mathbf{L}$ region we need to perform another Bogoliubov transformation incorporating new sets of operators, which are given by

$$\begin{aligned}&c_{\mathbf{R}}=u~b_{\mathbf{R}}+v~b^{\dagger }_{\mathbf{R}},\quad c_{\mathbf{L}}= \bar{u}~b_{\mathbf{L}}+\bar{v}~b^{\dagger }_{\mathbf{L}}. \end{aligned}$$

(3.88)

$$\begin{aligned}&C_{\mathbf{R},n}=U_n~b_{\mathbf{R},n}+V_n~b^{\dagger }_{\mathbf{R},n},\quad C_{\mathbf{L},n}= \bar{U}_n~b_{\mathbf{L},n}+\bar{V}_n~b^{\dagger }_{\mathbf{L},n},\nonumber \\ \end{aligned}$$

(3.89)

with the following constraints:

$$\begin{aligned}&|u|^2-|v|^2= 1,\quad |\bar{u}|^2-|\bar{v}|^2= 1. \end{aligned}$$

(3.90)

$$\begin{aligned}&|U_n|^2-|V_n|^2= 1,\quad |\bar{U}_n|^2-|\bar{V}_n|^2= 1. \end{aligned}$$

(3.91)

Using the above set of operators one can write the Bunch–Davies vacuum state in terms of a new Bogoliubov transformed basis represented by the $\mathbf{R}^{\prime }$ and $\mathbf{L}^{\prime }$ vacuum state as

$$\begin{aligned} |\mathbf{BD}\rangle= & {} e^{\hat{\mathcal{O}}}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) =\frac{1}{\mathcal{N}_{p}}e^{\hat{\mathcal{Q}}}\left( |\mathbf{R}^{\prime }\rangle \otimes |\mathbf{L}^{\prime }\rangle \right) , \end{aligned}$$

(3.92)

where we have introduced a new operator $\hat{\mathcal{Q}}$, defined in the basis as

$$\begin{aligned} \hat{\mathcal{Q}}= & {} \gamma _{p}~c^{\dagger }_{\mathbf{R}}~c^{\dagger }_{\mathbf{L}}+\sum ^{\infty }_{n=0}\Gamma _{p,n}~C^{\dagger }_{\mathbf{R},n}~C^{\dagger }_{\mathbf{L},n}, \end{aligned}$$

(3.93)

where $\gamma _{p}$ and $\Gamma _{p,n}$ are defined as the coefficients of the complementary and particular part of the operator, which play significant role to construct the density matrix as well as the entanglement entropy. In this context the exponential of the operator $e^{\hat{\mathcal{Q}}}$ is approximated by

$$\begin{aligned} e^{\hat{\mathcal{Q}}}= & {} \sum ^{\infty }_{k=0}\frac{1}{k!}\hat{\mathcal{Q}}^{k}=\left[ \mathrm{I}+\hat{\mathcal{Q}}+\frac{1}{2}\hat{\mathcal{Q}}^2+\cdots \right] \approx \left[ \mathrm{I}+\hat{\mathcal{Q}}\right] .\nonumber \\ \end{aligned}$$

(3.94)

The overall normalisation factor $\mathcal{N}_{p}$ is defined as

$$\begin{aligned} \mathcal{N}_{p}= & {} \left| e^{\hat{\mathcal{Q}}}\left( |\mathbf{R}^{\prime }\rangle \otimes |\mathbf{L}^{\prime }\rangle \right) \right| \nonumber \\\approx & {} \left[ 1-\left( |\gamma _p|^2+ \sum ^{\infty }_{n=0}|\Gamma _{p,n}|^2\right) \right] ^{-1/2}. \end{aligned}$$

(3.95)

Here due to the second Bogoliubov transformation the direct product of the $\mathbf{R}$ and $\mathbf{L}$ vacuum state is connected with the direct product of the new $\mathbf{R}^{\prime }$ and $\mathbf{L}^{\prime }$ vacuum state as

$$\begin{aligned} \left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) \rightarrow \left( |\mathbf{R}^{\prime }\rangle \otimes |\mathbf{L}^{\prime }\rangle \right) =\mathcal{N}_p~e^{-\hat{\mathcal{Q}}}~e^{\hat{\mathcal{O}}}\left( |\mathbf{R}\rangle \otimes |\mathbf{L}\rangle \right) .\nonumber \\ \end{aligned}$$

(3.96)

Before going to further details let us first mention the following useful commutation relations of the creation and annihilation operators of the $\mathbf{R}^{\prime }$ and $\mathbf{L}^{\prime }$ vacua:

$$\begin{aligned}&\left[ c_i,c^{\dagger }_j\right] =\delta _{ij},\quad \left[ c_i,c_j\right] =0= \left[ c^{\dagger }_i,c^{\dagger }_j\right] .\end{aligned}$$

(3.97)

$$\begin{aligned}&\left[ C_{i,n},C^{\dagger }_{j,m}\right] =\delta _{ij}{\delta }_{nm},\quad \left[ C_{i,n},C_{j,m}\right] =0= \left[ C^{\dagger }_{i,m},C^{\dagger }_{j,m}\right] .\nonumber \\ \end{aligned}$$

(3.98)

In this context, the operations of creation and annihilation operators defined on the Bunch–Davies vacuum state are

$$\begin{aligned}&c_{\mathbf{R}}|\mathbf{BD}\rangle =\gamma _{p}~c^{\dagger }_{\mathbf{L}}|\mathbf{BD}\rangle ,\quad c_{\mathbf{L}}|\mathbf{BD}\rangle =\gamma _{p}~c^{\dagger }_{\mathbf{R}}|\mathbf{BD}\rangle , \end{aligned}$$

(3.99)

$$\begin{aligned}&C_{\mathbf{R},n}|\mathbf{BD}\rangle =\Gamma _{p,n}~C^{\dagger }_{\mathbf{L},n}|\mathbf{BD}\rangle ,\quad C_{\mathbf{L},n}|\mathbf{BD}\rangle =\Gamma _{p,n}~C^{\dagger }_{\mathbf{R},n}|\mathbf{BD}\rangle .\nonumber \\ \end{aligned}$$

(3.100)

Furthermore, one can express the annihilation operators after second Bogoliubov transformation in terms of the annihilation operator obtained after first Bogoliubov transformation as

$$\begin{aligned} c_{J}= b_{I}\mathcal{G}^{I}_{J},\quad C_{J(n)}=\bar{b}_{J(n)}\left( \mathcal{G}_{(n)}\right) ^{I}_{J}. \end{aligned}$$

(3.101)

Here the matrices $\mathcal{G}^{I}_{J}$ and $\left( \mathcal{G}_{(n)}\right) ^{I}_{J}$ are defined as

$$\begin{aligned} \mathcal{G}^{I}_{J}=\left( \begin{array}{ccc} U_q &{}\quad V^{*}_q \\ V_q &{}\quad U^{*}_q \end{array}\right) ,\quad \left( \mathcal{G}_{(n)}\right) ^{I}_{J}=\left( \begin{array}{ccc} \bar{U}_{ q,n} &{}\quad \bar{V}^{*}_{\sigma q,n} \\ \bar{V}_{ q,n} &{}\quad \bar{U}^{*}_{ q,n} \end{array}\right) ,\nonumber \\ \end{aligned}$$

(3.102)

where the entries of the matrices are given by

$$\begin{aligned}&U_q\equiv \mathbf{diag}\left( u,\bar{u}\right) ,\quad V_q \equiv \mathbf{diag} \left( v,\bar{v}\right) ,\nonumber \\&\quad \bar{U}_{q,n}\equiv \mathbf{diag}\left( U_n,\bar{U}_n\right) ,\quad \bar{V}_{q,n} \equiv \mathbf{diag}\left( V_n,\bar{V}_n\right) .\nonumber \\ \end{aligned}$$

(3.103)

Furthermore, using Eqs. (3.88) and (3.89), in Eqs. (3.99) and (3.100), we get the following sets of homogeneous equations for the two cases:

$$\begin{aligned}&{\underline{\mathbf{For~Case{-}I:}}} \nonumber \\&v-\gamma _{p} m_{\mathbf{RL}}\bar{v}^{*}= 0,\quad \bar{v}-\gamma _{p} m_{\mathbf{RL}}v^{*}= 0, \end{aligned}$$

(3.104)

$$\begin{aligned}&m_{\mathbf{RL}}u-\gamma _{p} \bar{u}^{*}= 0,\quad m_{\mathbf{RL}}\bar{u}-\gamma _{p} u^{*}= 0,\end{aligned}$$

(3.105)

$$\begin{aligned}&V_n-\Gamma _{p,n} \bar{m}_{\mathbf{RL},n}\bar{V}^{*}_n=0,\quad \bar{V}_n-\Gamma _{p,n} \bar{m}_{\mathbf{RL},n}V^{*}_n= 0, \end{aligned}$$

(3.106)

$$\begin{aligned}&\bar{m}_{\mathbf{RL},n}U_n-\Gamma _{p,n} \bar{U}^{*}_n = 0,\quad \bar{m}_{\mathbf{RL},n}\bar{U}_n-\Gamma _{p,n} U^{*}_n= 0, \end{aligned}$$

(3.107)

$$\begin{aligned}&{\underline{\mathbf{For~Case{-}II:}}}\nonumber \\&m_{\mathbf{RR}}u+v-\gamma _{p} m_{\mathbf{RL}}\bar{v}^{*}= 0,\nonumber \\&m_{\mathbf{RR}}\bar{u}+\bar{v}-\gamma _{p} m_{\mathbf{RL}}v^{*}= 0, \end{aligned}$$

(3.108)

$$\begin{aligned}&m_{\mathbf{RL}}u-\gamma _{p} \bar{u}^{*}-\gamma _{p}m_{\mathbf{RR}} \bar{v}^{*}= 0,\nonumber \\&m_{\mathbf{RL}}\bar{u}-\gamma _{p} u^{*}-\gamma _{p}m_{\mathbf{RR}}v^{*}= 0, \end{aligned}$$

(3.109)

$$\begin{aligned}&\bar{m}_{\mathbf{RR},n}U_n+V_n-\Gamma _{p,n} \bar{m}_{\mathbf{RL},n}\bar{V}^{*}_n= 0,\nonumber \\&\bar{m}_{\mathbf{RR},n}\bar{U}_n+\bar{V}_n-\Gamma _{p,n} \bar{m}_{\mathbf{RL},n}V^{*}_n= 0, \end{aligned}$$

(3.110)

$$\begin{aligned}&\bar{m}_{\mathbf{RL},n}U_n-\Gamma _{p,n} \bar{U}^{*}_n-\Gamma _{p,n} \bar{m}_{\mathbf{RR},n}\bar{V}^{*}_n= 0,\nonumber \\&\bar{m}_{\mathbf{RL},n}\bar{U}_n-\Gamma _{p,n} U^{*}_n-\Gamma _{p,n} \bar{m}_{\mathbf{RR},n}V^{*}_n= 0. \end{aligned}$$

(3.111)

From these equations it is important to note that:

• 1. For the complementary part in Case I considering the diagonal and off-diagonal terms we get:⁷

  $$\begin{aligned} m_{\mathbf{RR}}= & {} m_{\mathbf{LL}}=m^{*}_{\mathbf{RR}}=0, \end{aligned}$$

  (3.112)
  $$\begin{aligned} m_{\mathbf{RL}}= & {} m_{\mathbf{LR}}=-m^{*}_\mathbf{RL}=e^{i\frac{\pi }{2}}~e^{-p\pi }. \end{aligned}$$

  (3.113)

  Similarly for Case II for the diagonal and off-diagonal terms we get

  $$\begin{aligned} m_{\mathbf{RR}}= & {} m_{\mathbf{LL}}=m^{*}_{\mathbf{RR}}=\frac{\sqrt{2}~e^{-p\pi }\cos \pi \nu }{\sqrt{\cosh 2\pi p+\cos 2\pi \nu }}, \end{aligned}$$

  (3.114)
  $$\begin{aligned} m_{\mathbf{RL}}= & {} m_{\mathbf{LR}}=-m^{*}_{\mathbf{RL}}=e^{i\frac{\pi }{2}}\frac{\sqrt{2}~e^{-p\pi }\sinh p\pi }{\sqrt{\cosh 2\pi p+\cos 2\pi \nu }}.\nonumber \\ \end{aligned}$$

  (3.115)

• 2. For the particular solution part in Case I considering the diagonal and off-diagonal terms we get

  $$\begin{aligned} \bar{m}_{\mathbf{RR},n}= & {} \bar{m}_{\mathbf{LL},n}=\bar{m}^{*}_{\mathbf{RR},n}=0, \end{aligned}$$

  (3.116)
  $$\begin{aligned} \bar{m}_{\mathbf{RL},n}= & {} \bar{m}_{\mathbf{LR},n}=-\bar{m}^{*}_{\mathbf{RL},n}=e^{i\frac{\pi }{2}}~e^{-p_n\pi }. \end{aligned}$$

  (3.117)

  Similarly for Case II for the diagonal and off-diagonal terms we get

  $$\begin{aligned} \bar{m}_{\mathbf{RR},n}= & {} \bar{m}_{\mathbf{LL},n}=\bar{m}^{*}_{\mathbf{RR},n}=\frac{\sqrt{2}~e^{-p_n\pi }\cos \pi \nu }{\sqrt{\cosh 2\pi p_n+\cos 2\pi \nu }}, \end{aligned}$$

  (3.118)
  $$\begin{aligned} \bar{m}_{\mathbf{RL},n}= & {} \bar{m}_{\mathbf{LR},n}=-\bar{m}^{*}_{\mathbf{RL},n}=e^{i\frac{\pi }{2}}\frac{\sqrt{2}~e^{-p_n\pi }\sinh p_n\pi }{\sqrt{\cosh 2\pi p_n+\cos 2\pi \nu }}.\nonumber \\ \end{aligned}$$

  (3.119)

• 3. In Case II, if we consider $\gamma _p$ and $\Gamma _{p,n}$ are purely imaginary i.e. $\gamma ^{*}_{p}=-\gamma _{p}$,    $\Gamma ^{*}_{p,n}=-\Gamma _{p,n}$, and if we set, $v^{*}=\bar{v},~~ u^{*}=\bar{u},~~ V^{*}_n=\bar{V}_n,~~ U^{*}_n=\bar{U}_n$. Consequently four sets of equation reduces to two sets of homogeneous equations for the two cases the normalisation $|u|^2-|v|^2=1$ and $|U_n|^2-|V_n|^2=1$ are explicitly imposed for the complementary and particular part of the solution.

Finally, the non-trivial solutions obtained from these system of equations for the two cases can be expressed as

$$\begin{aligned}&{\underline{\mathbf{For~Case{-}I:}}} \nonumber \\&\gamma _{p}=m_{\mathbf{RL}},\quad \frac{1}{m_{\mathbf{RL}}}. \end{aligned}$$

(3.120)

$$\begin{aligned}&\Gamma _{p,n} =\bar{m}_{\mathbf{RL,n}},\quad \frac{1}{\bar{m}_{\mathbf{RL},n}}. \end{aligned}$$

(3.121)

$$\begin{aligned}&{\underline{\mathbf{For~Case{-}II:}}}\nonumber \\&\gamma _{p}=\frac{1}{2m_{\mathbf{RL}}} \left[ \left( 1+m^2_{\mathbf{RL}}-m^2_{\mathbf{RR}}\right) \right. \nonumber \\&\left. \quad \pm \sqrt{\left( 1+m^2_{\mathbf{RL}}-m^2_{\mathbf{RR}}\right) ^2-4m^2_{\mathbf{RL}}}\right] . \end{aligned}$$

(3.122)

$$\begin{aligned}&\Gamma _{p,n}=\frac{1}{2\bar{m}_{\mathbf{RL},n}}\left[ \left( 1+\bar{m}^2_{\mathbf{RL},n}-\bar{m}^2_{\mathbf{RR},n}\right) \right. \nonumber \\&\left. \quad \pm \sqrt{\left( 1+\bar{m}^2_{\mathbf{RL},n}-\bar{m}^2_{\mathbf{RR},n}\right) ^2-4\bar{m}^2_{\mathbf{RL},n}}\right] . \end{aligned}$$

(3.123)

Fig. 5

Behaviour of $|\gamma _{p}|$ in de Sitter space for ‘$+$’ branch of solution. This figure clearly shows that we cover both large and small mass limit situations

Furthermore, substituting the entries of the mass matrices one can further simplify the result as

$$\begin{aligned}&{\underline{\mathbf{For~Case{-}I:}}}\nonumber \\&\gamma _{p}= \pm i ~e^{\mp p\pi }. \end{aligned}$$

(3.124)

$$\begin{aligned}&\Gamma _{p,n}=\pm i ~e^{\mp p_n\pi }. \end{aligned}$$

(3.125)

${\underline{\mathbf{For~Case{-}II:}}}$

$$\begin{aligned}&\gamma _{p}=i\frac{\sqrt{2}}{\sqrt{\cosh 2\pi p +\cos 2\pi \nu }\pm \sqrt{\cosh 2\pi p +\cos 2\pi \nu +2}}.\end{aligned}$$

(3.126)

$$\begin{aligned}&\Gamma _{p,n} =i\frac{\sqrt{2}}{\sqrt{\cosh 2\pi p_n +\cos 2\pi \nu }\pm \sqrt{\cosh 2\pi p_n +\cos 2\pi \nu +2}}.\nonumber \\ \end{aligned}$$

(3.127)

In Fig. 5a, b, we have explicitly shown the behaviour of $|\gamma _{p}|$ vs. the momentum p for the fixed values of the mass parameter $|\nu |$ in the small and large mass limits. Here we cover the mass parameter range $0<|\nu |<3/2$ for both of the cases. In Fig. 5a, b, for the small mass limit range for large values of the momentum p the two branches of solution for $|\nu |=0$ and $|\nu |=1/2,3/2$ coincide with each other and in the small values of the momentum p the two branches of solution can be separately visualised. Furthermore, in Fig. 5c, d, we have shown the behaviour of $|\gamma _{p}|$ vs. mass parameter $|\nu |$ for the fixed values of the momentum p in the small and large mass limits. For fixed value of p at $p=1$ and $p=2$ in the large mass limit situation, we initially get decaying behaviour and then after $|\nu |=3/2$ both of the results obtained for $p=1$ and $p=2$ saturates. On the other hand, for same values of p in the large mass limit, we get oscillating behaviour. Combined effects for large and small mass limits are plotted in Fig. 5e, where we have explicitly shown that for $\nu ^2 <0$ for $p=1$ and $p=2$ we get distinguishable behaviour of the mass eigen values. Once $\nu ^2\rightarrow 0$ magnitude of the eigenvalues increase and, finally, when $\nu ^2>0$ both of the plots show apeariodic behaviour.

3.3 Construction of density matrix

In this subsection our prime objective is construct the density matrix using the Bunch–Davies vacuum state which is expressed in terms of newly obtained sets of annihilation and creation operators in the Bogoliubov transformed frame. Most importantly, we already know that the full Bunch–Davies vacuum state can be expressed as a product of the vacuum state for each oscillator in the Bogoliubov transformed frame. Here each oscillators are labelled by the quantum numbers p, l and m. After tracing over the right part of the Hilbert space we get the following expression for the density matrix for the left part of the Hilbert space:

$$\begin{aligned} (\rho _{\mathbf{L}})_{p,l,m}= & {} \mathbf{\mathrm Tr}_{\mathbf{R}}|\mathbf{BD}\rangle \langle \mathbf{BD}|, \end{aligned}$$

(3.128)

where the Bunch–Davies vacuum state takes the form:

(3.129)

The above two equations lead to the density matrix for the left part of the Hilbert space as

$$\begin{aligned} (\rho _{\mathbf{L}})_{p,l,m}= & {} \left( 1-|\gamma _{p}|^2\right) \sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\nonumber \\&+f^{2}_{p}\sum ^{\infty }_{n=0}\sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r}|n,r;p,l,m\rangle \langle n,r;p,l,m|,\nonumber \\ \end{aligned}$$

(3.130)

where $\gamma _{p}$ and $\Gamma _{p,n}$ are defined in the earlier section and have defined the source normalisation factor ${ f}_{p}$ as

$$\begin{aligned} { f}_{p}= & {} \left( \sum ^{\infty }_{n=0}\frac{1}{1-|\Gamma _{p,n}|^2}\right) ^{-1}. \end{aligned}$$

(3.131)

In Eq. (3.130), the states $|k;p,l,m\rangle$ and $|n,r;p,l,m\rangle$ are defined in terms of the quantum state in left Hilbert space as

$$\begin{aligned}&|k;p,l,m\rangle = \frac{1}{\sqrt{n!}}(c^{\dagger }_{\mathbf{L}})^{k}|\mathbf{L}^{\prime }\rangle ,\nonumber \\&|n,r;p,l,m\rangle = \frac{1}{\sqrt{r!}}(C^{\dagger }_{\mathbf{L},n})^{r}|\mathbf{L}^{\prime }\rangle . \end{aligned}$$

(3.132)

Here we note the following crucial points:

• 1. The density matrix is diagonal for a given set of the $\mathbf{SO(1,3)}$ quantum numbers p, l, m. This leads to the total density matrix to take the form

  $$\begin{aligned} \rho _{\mathbf{L}}= & {} \left( 1-|\gamma _{p}|^2\right) \mathbf{diag}\left( 1,|\gamma _{p}|^2,|\gamma _{p}|^{4},|\gamma _{p}|^{6}\cdots \right) \nonumber \\&+f^{2}_{p}\sum ^{\infty }_{n=0}\mathbf{diag}\left( 1,|\Gamma _{p,n}|^2,|\Gamma _{p,n}|^{4},|\Gamma _{p,n}|^{6}\cdots \right) .\nonumber \\ \end{aligned}$$

  (3.133)

• 2. To find a suitable normalisation of the total density matrix, we use the following two results:

  $$\begin{aligned}&\sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}=\lim _{k\rightarrow \infty }\frac{1-|\gamma _{p}|^{2k}}{1-|\gamma _{p}|^2}\quad \underrightarrow{|\gamma _{p}|<1}\quad \frac{1}{1-|\gamma _{p}|^2}, \end{aligned}$$

  (3.134)
  $$\begin{aligned}&\sum ^{\infty }_{n=0}\sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r} =\sum ^{\infty }_{n=0}\lim _{r\rightarrow \infty }\frac{1-|\Gamma _{p,n}|^{2r}}{1-|\Gamma _{p,n}|^2}\nonumber \\&\quad \underrightarrow{|\Gamma _{p,n}|<1 \forall n}\quad \sum ^{\infty }_{n=0}\frac{1}{1-|\Gamma _{p,n}|^2}=f^{-1}_{p}. \end{aligned}$$

  (3.135)

  Consequently using these results we get

  $$\begin{aligned}&{} \mathbf{Tr}\left[ \left( 1-|\gamma _{p}|^2\right) \mathbf{diag}\left( 1,|\gamma _{p}|^2,|\gamma _{p}|^{4},|\gamma _{p}|^{6}\cdots \right) \right] \nonumber \\&\quad =\left( 1-|\gamma _{p}|^2\right) \sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}=1,\end{aligned}$$

  (3.136)
  $$\begin{aligned}&{} \mathbf{Tr}\left[ f^2_p\sum ^{\infty }_{n=0}\mathbf{diag}\left( 1,|\Gamma _{p,n}|^2,|\Gamma _{p,n}|^{4}, |\Gamma _{p,n}|^{6}\cdots \right) \right] \nonumber \\&\quad =f^2_p\sum ^{\infty }_{n=0}\sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r}=f_p. \end{aligned}$$

  (3.137)

  This implies that the normalisation condition of this total density matrix is fixed by the expression, $\mathbf{Tr}\rho _{\mathbf{L}} = 1+f_p$. This is consistent with Ref. [15] where $f_p=0$. But to maintain always $\mathbf{Tr}\rho _{\mathbf{L}}= 1$ the total density matrix can be redefined by changing the normalisation constant as:

  $$\begin{aligned} \begin{array}{lll} (\rho _{\mathbf{L}})_{p,l,m}=\underbrace{\frac{\left( 1-|\gamma _{p}|^2\right) }{1+f_p}\sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|}_{\mathbf{Complementary~part}}+\underbrace{\frac{f^{2}_{p}}{1+f_p}\sum ^{\infty }_{n=0}\sum ^{\infty }_{r=0}| \Gamma _{p,n}|^{2r}|n,r;p,l,m\rangle \langle n,r;p,l,m|}_{\mathbf{Particular~part}}.\end{array} \end{aligned}$$

  (3.138)

  One may choose some other appropriate convention for normalisation factors such that it maintains always $\mathbf{Tr}\rho _{\mathbf{L}}= 1$ even in the presence of the source.⁸

• 3. For each set of values of the $\mathbf{SO(1,3)}$ quantum numbers p, l, m, the density matrix yields $(\rho _{\mathbf{L}})_{p,l,m}$ and so the total density matrix can be expressed as a product of all such possible contributions,

  $$\begin{aligned} \rho _{\mathbf{L}}= \prod ^{\infty }_{p=0} \prod ^{p-1}_{l=0} \prod ^{+l}_{m=-l}(\rho _{\mathbf{L}})_{p,l,m}. \end{aligned}$$

  (3.140)

  This also indicates that in such a situation entanglement is absent among all states which carries non-identical $\mathbf{SO(1,3)}$ quantum numbers p, l, m.

• 4. Finally, the total density matrix can be written in terms of entanglement modular Hamiltonian of the axionic Bell pair as, $\rho _{\mathbf{L}}=e^{-\beta \mathcal{H}_{\mathbf{ENT}}},$ where at finite temperature $T_{\mathbf{dS}}$ of de Sitter space the parameter $\beta$ is defined as, $\beta =2\pi /T_{\mathbf{dS}}.$ This also implies that at finite temperature the modular Hamiltonian can be expressed as⁹

  

  (3.142)

  If we assume that the dynamical Hamiltonian in de Sitter space is represented by entangled Hamiltonian then for a given principal quantum number p the Hamiltonian for axionic Bell pairs can be expressed as

  $$\begin{aligned} \mathcal{H}_{p}= & {} \left[ E_{p}c^{\dagger }_p c_{p}+\sum ^{\infty }_{n=0}\mathcal{E}_{p,n}C^{\dagger }_{p,n}C_{p,n}\right] . \end{aligned}$$

  (3.143)

  Acting this Hamiltonian on the Bunch–Davies vacuum state we find

  $$\begin{aligned}&\mathcal{H}_{p}|\mathbf{BD}\rangle \approx \left[ 1-\left( |\gamma _p|^2+\sum ^{\infty }_{n=0}|\Gamma _{p,n}|^2\right) \right] ^{1/2}\nonumber \\&\qquad \times \left[ E_{p}c^{\dagger }_p c_{p} +\sum ^{\infty }_{n=0}\mathcal{E}_{p,n}C^{\dagger }_{p,n}C_{p,n}\right] \nonumber \\&\qquad \times \exp \left[ \gamma _{p}~c^{\dagger }_{\mathbf{R}}~c^{\dagger }_{\mathbf{L}}+\sum ^{\infty }_{m=0}\Gamma _{p,m}~C^{\dagger }_{\mathbf{R},m}~C^{\dagger }_{\mathbf{L},m}\right] \left( |\mathbf{R}^{\prime }\rangle \otimes |\mathbf{L}^{\prime }\rangle \right) \nonumber \\&\quad =E_{\mathbf{T},p}|\mathbf{BD}\rangle , \end{aligned}$$

  (3.144)

  where the total energy spectrum of this system can be written as

  $$\begin{aligned} E_{\mathbf{T},p}= & {} E_p+\sum ^{\infty }_{n=0}\mathcal{E}_{p,n}, \end{aligned}$$

  (3.145)

  where the energy spectrum corresponding to the complementary and particular part of the wave function are given by

  $$\begin{aligned} E_p= & {} -\frac{1}{2\pi }\ln (|\gamma _p|^2),\quad \mathcal{E}_{p,n} = -\frac{1}{2\pi }\ln \left( B_{p,n}\right) .\nonumber \\ \end{aligned}$$

  (3.146)

  One can also recast the total energy spectrum of this system as

  $$\begin{aligned} E_{\mathbf{T},p}= & {} -\frac{1}{2\pi }\ln \left( |\gamma _p|^2 O_p\right) , \end{aligned}$$

  (3.147)

  where $O_{p}$ is defined as

  $$\begin{aligned} O_{p}= & {} \prod ^{\infty }_{n=0}B_{p,n}\quad \mathrm{with}\ B_{p,n}=\frac{1}{1-|\Gamma _{p,n}|^2}. \end{aligned}$$

  (3.148)

  Here in the absence of the source term $B_{p,n}=1\forall n$ and consequently $\ln O_p =0$. Note that for a conformally coupled axion ($\nu =1/2$) and for a minimally coupled axion ($\nu =3/2$) the $\mathbf{SO(1,3)}$ principal quantum number p dependent spectrum can be expressed as

  $$\begin{aligned} E_p = \pm p,\quad \mathcal{E}_{p,n} = -\frac{1}{2\pi }\ln \left( \frac{1}{1-e^{\mp 2p_n \pi }}\right) . \end{aligned}$$

  (3.149)

  In this case, the total energy spectrum is given by

  $$\begin{aligned} E_{\mathbf{T},p}= & {} -\frac{1}{2\pi }\ln \left( \prod ^{\infty }_{n=0}\frac{e^{\mp 2p\pi }}{1-e^{\mp 2p_n \pi }}\right) \nonumber \\= & {} \pm p-\frac{1}{2\pi }\ln \left( \prod ^{\infty }_{n=0}\frac{1}{1-e^{\mp 2p_n \pi }}\right) . \end{aligned}$$

  (3.150)

  This implies that for a conformally coupled axion ($\nu =1/2$) and for a minimally coupled axion ($\nu =3/2$) the entangled Hamiltonian $(\mathcal{H}_{\mathbf{ENT}})$ and the Hamiltonian for axion ${(\mathcal{H}_p})_{\mathbf{R \times H^3}}$ are equivalent in the absence of the linear source term in the effective action. On the other hand, if we consider any arbitrary mass parameter $\nu$ in that case the $\mathbf{SO(1,3)}$ principal quantum number p dependent spectrum can be expressed as

  $$\begin{aligned} E_p =-\frac{1}{2\pi }\ln \frac{2}{\left[ \sqrt{\cosh 2\pi p +\cos 2\pi \nu }\pm \sqrt{\cosh 2\pi p +\cos 2\pi \nu +2}\right] ^2},\nonumber \\ \end{aligned}$$

  (3.151)
  $$\begin{aligned}&\mathcal{E}_{p,n} = -\frac{1}{2\pi }\ln \left( \frac{1}{1-\frac{2}{\left[ \sqrt{\cosh 2\pi p_n +\cos 2\pi \nu }\pm \sqrt{\cosh 2\pi p_n +\cos 2\pi \nu +2}\right] ^2}}\right) .\nonumber \\ \end{aligned}$$

  (3.152)

  In this case, the total energy spectrum is given by

  $$\begin{aligned}&E_{\mathbf{T},p}=-\frac{1}{2\pi }\ln 2+\frac{1}{\pi }\ln \left[ \sqrt{\cosh 2\pi p +\cos 2\pi \nu }\right. \nonumber \\&\quad \left. \pm \,\sqrt{\cosh 2\pi p +\cos 2\pi \nu +2}\right] \nonumber \\&\quad -\frac{1}{2\pi }\ln \left( \prod ^{\infty }_{n=0}\frac{1}{1-\frac{2}{\left[ \sqrt{\cosh 2\pi p_n +\cos 2\pi \nu }\pm \sqrt{\cosh 2\pi p_n +\cos 2\pi \nu +2}\right] ^2}}\right) .\nonumber \\ \end{aligned}$$

  (3.153)

  This implies that for with arbitrary parameter $\nu$ the entangled Hamiltonian $(\mathcal{H}_\mathbf{ENT})$ and the Hamiltonian for axion ${(\mathcal{H}_p})_{\mathbf{R \times H^3}}$ are significantly differ as well in the absence of the linear source term in the effective action.

  In Fig. 6a, b we have shown the behaviour of the total energy spectrum for axion with respect to the $\mathbf{SO(1,3)}$ quantum number p for a fixed value of the mass parameter $\nu$ without source contribution and with source contribution respectively. From both plots it is clearly observed that for minimally coupled axion ($\nu =3/2$) (green) the energy spectrum is linear. Also in this case with source the slope and intercept will change. Also it is important to mention that for a conformally coupled axion ($\nu =1/2$) the situation is exactly similar and the behaviour overlaps with the result obtained for minimally coupled axion ($\nu =3/2$). Furthermore, if we increase the value of the mass parameter to $\nu =5$ (blue) then it shows a small deviation for very small values of p. Next if we go the large mass range, where $\nu ^2<0$ the energy spectrum shows significant deviation from the linearity for the large values of p. For example, we have considered $\nu =3i/2$ (orange) and $\nu =5i$ (red) for our analysis. From both plots it is clear that for $\nu =5i$ (red) deviation from linearity is more faster than the behaviour obtained for $\nu =3i/2$ (orange).

  In Fig. 6c, d we have shown the behaviour of the total energy spectrum for axion with respect mass parameter $\nu ^2$ for a fixed value of the $\mathbf{SO(1,3)}$ quantum number p without source contribution and with source contribution respectively. From both plots it is clearly observed that in the presence of the source the behaviour of the energy spectrum significantly changes compared to the result obtained without source.

Fig. 6

Behaviour of energy spectrum for axion in de Sitter space for ‘$+$’ branch of solution of $|\gamma _p|$ and $|\Gamma _{p,n}|$

3.4 Computation of the entanglement entropy

In this subsection we derive the expression for the entanglement entropy in de Sitter space. In general the entanglement entropy can be written in terms of density matrix using Von Neumann measure as

$$\begin{aligned} S(p,\nu )= & {} -\mathrm{\mathbf Tr }\left[ \rho _{\mathbf{L}}(p)\ln \rho _{\mathbf{L}}(p)\right] , \end{aligned}$$

(3.154)

where the parameter $\nu$ is defined earlier. For Case I and Case II the expression for the entanglement entropy in terms of the complementary and particular part of the obtained solution for a given $\mathbf{SO(1,3)}$ principal quantum number p can be expressed as¹⁰:

(3.156)

Then the quantifying formula for the entanglement entropy in de Sitter space in the presence of the axion can be expressed as a sum over all possible quantum states which carries $\mathbf{SO(1,3)}$ principal quantum number p. Technically, this sum can be written in terms of an integral as

$$\begin{aligned} \sum _{\mathbf{States}}\sum ^{\infty }_{p=0}\rightarrow V_{\mathbf{H}^{\mathbf{3}}} \int ^{\infty }_{p=0}~\mathrm{d}p. \end{aligned}$$

(3.157)

Consequently, the final expression for the entanglement entropy in $3+1$ D de Sitter space is given by the following expression:

$$\begin{aligned} S(\nu )= & {} \sum _{\mathbf{States}}\sum ^{\infty }_{p=0}S(p,\nu )\rightarrow V_{\mathbf{H}^{\mathbf{3}}} \int ^{\infty }_{p=0}~\mathrm{d}p~\mathcal{D}_{3}(p)~S(p,\nu ),\nonumber \\ \end{aligned}$$

(3.158)

where $\mathcal{D}_3(p)$ characterises the density of quantum states corresponding to the radial functions on $\mathbf{H^3}$, $\mathcal{D}_3(p)=\frac{p^2}{2\pi ^2}.$ The volume of the hyperboloid $\mathbf{H^3}$ is denoted by the overall factor $V_{\mathbf{H}^{\mathbf{3}}}$. This volume is infinite and can be regularise with a large radial cut-off $r= L_c$ in the hyperboloid $\mathbf{H^3}$. Technically, here regularisation in volume stands for embedding surface of entanglement from zero to finite conformal time. After performing the regularisation the volume of the hyperboloid $\mathbf{H^3}$ for $r\le L_c$ can be written as¹¹

$$\begin{aligned} V_{\mathbf{H}^{\mathbf{3}}}= & {} V_{\mathbf{S}^{\mathbf{2}}}\int ^{L_c}_{r=0}\mathrm{d}r~\sinh ^2r\nonumber \\= & {} \pi \left[ \sinh 2L_c -2L_c\right] \nonumber \\&\quad \underrightarrow{\mathbf{large}~L_c~\mathbf{limit}}\quad \frac{\pi }{2}\left[ e^{2L_c}-4L_c\right] , \end{aligned}$$

(3.159)

where we use the fact that the volume of $\mathbf{S^2}$ is given by $V_{\mathbf{S}^{\mathbf{2}}}=4\pi$. Here one can interpret each of the term obtained in the regularised volume as:

• Here the entangling area $\mathbf{A_{ENT}}$ is given by

  $$\begin{aligned} \mathbf{A_{ENT}}\sim & {} \pi \sinh 2L_c\quad \underrightarrow{\mathbf{large}~\hbox {L}_{\mathrm{c}}~\mathbf{limit}}\quad \frac{\pi }{2}~e^{2L_c}. \end{aligned}$$

  (3.160)

• Consequently the second term is interpreted as logarithm of the entangling area $\mathbf{A_{ENT}}$, which is precisely the following factor:

  $$\begin{aligned} \ln {\mathbf{A}_{ENT}}\sim & {} \ln (\pi \sinh 2L_c)\quad \underrightarrow{\mathbf{large}~\hbox {L}_{\mathrm{c}}~\mathbf{limit}}\quad 2L_c\nonumber \\&+\ln \left( \frac{\pi }{2}\right) . \end{aligned}$$

  (3.161)

Finally, the volume of the hyperboloid $\mathbf{H^3}$ for $r\le L_c$ can be written in terms of the entangling area $\mathbf{A_{ENT}}$ as

$$\begin{aligned}&V_{\mathbf{H}^{\mathbf{3}}}\sim \left[ {\mathbf{A}_{\mathbf{ENT}}} -\pi \sinh ^{-1}\left( \frac{\mathbf{A_{ENT}}}{\pi }\right) \right] \nonumber \\&\quad \underrightarrow{\mathbf{large}~\hbox {L}_{\mathrm{c}}~\mathbf{limit}}\quad \left[ {\mathbf{A}_{\mathbf{ENT}}} -\pi \ln \mathbf{A_{ENT}}+\pi \ln \left( \frac{\pi }{2}\right) \right] . \nonumber \\ \end{aligned}$$

(3.162)

In this context the cut-off regulator $L_c$ is large and in this limit this is identified with the conformal time as, $L_c\sim -\ln \eta$. We also define the regularised volume of the hyperboloid $\mathbf{H^3}$ as, $V^\mathbf{REG}_{\mathbf{H}^{\mathbf{3}}}=\frac{V_{\mathbf{S}^{\mathbf{3}}}}{2}=2\pi .$ Thus the volume of the hyperboloid $\mathbf{H^3}$ for $r\le L_c$ can be recast in terms of conformal time for the large $L_c$ limit as

$$\begin{aligned} V_{\mathbf{H}^{\mathbf{3}}}\sim & {} V^\mathbf{REG}_{\mathbf{H}^{\mathbf{3}}}\left[ \frac{1}{4\eta ^2} +\ln \eta \right] . \end{aligned}$$

(3.163)

Finally, summing over all possible principal quantum numbers p of $\mathbf{SO(1,3)}$ we get from Eq. (3.158) the following expression for the entanglement entropy in de Sitter space:

$$\begin{aligned} S(\nu )= & {} {\mathbf{c}_{\mathbf{6}}}\left[ \frac{1}{4\eta ^2} +\ln \eta \right] , \end{aligned}$$

(3.164)

where ${\mathbf{c}_{\mathbf{6}}}$ is defined as

$$\begin{aligned} {\mathbf{c}_{\mathbf{6}}}\equiv S_{\mathbf{intr}}= \frac{1}{\pi }\int ^{\infty }_{p=0}~\mathrm{d}p~p^2~S(p,\nu ), \end{aligned}$$

(3.165)

which represents the long range quantum entanglement in the presence of axion.

Furthermore, substituting the expression for the entanglement entropy $S(p,\nu )$ computed in the presence of the axionic Bell pair and integrating over all possible $\mathbf{SO(1,3)}$ principal quantum numbers, lying within the window $0<p<\infty$, we get the following expression for the coefficient ${\mathbf{c}_{\mathbf{6}}}$:

(3.166)

where the integrals $\mathcal{I}_1$ and $\mathcal{I}_2$ can be written in $3+1$ dimensional space time as

$$\begin{aligned} \mathcal{I}_1= & {} -\frac{1}{\pi }\int ^{\infty }_{p=0}~\mathrm{d}p~p^2~\left[ \ln \left( 1-|\gamma _{p}|^2\right) \right. \nonumber \\&\left. +\frac{|\gamma _{p}|^2}{\left( 1-|\gamma _{p}|^2\right) } \ln \left( |\gamma _{p}|^2\right) \right] , \end{aligned}$$

(3.167)

$$\begin{aligned} \mathcal{I}_2= & {} -\frac{1}{\pi }\int ^{\infty }_{p=0}~\mathrm{d}p~p^2. \end{aligned}$$

(3.168)

Here it is important to mention that:

• For both Case I and Case II the integral $\mathcal{I}_2$ diverges in $3+1$ D within $0<p<\infty$. To make it finite we need to regularise this by introducing a cut-off $\Lambda _{\mathbf{C}}$ in $x=2\pi p$ as

  $$\begin{aligned} \mathcal{I}_2= & {} -\frac{1}{8\pi ^4}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2\nonumber \\= & {} -\frac{\Lambda ^3_{\mathbf{C}}}{24\pi ^4}. \end{aligned}$$

  (3.169)

• For Case I we have two possible solution for $\gamma _{p}$. For $\gamma _p=e^{-\pi p}$ the integral $\mathcal{I}_1$ is always finite for Case I. But for the other solution of $\gamma _p=e^{\pi p}$ the integral $\mathcal{I}_1$ is divergent. To make the consistency throughout the analysis we put a cut-off $\Lambda _{\mathbf{C}}$ on the integral $\mathcal{I}_1$ obtained from both of the solutions of $\gamma _p$. Here we explicitly show that in the final expression for $\mathcal{I}_{1}$ after taking the limit $\Lambda _{\mathbf{C}}\rightarrow \infty$ final result is finite for $\gamma _p=e^{-\pi p}$ and diverges for $\gamma _p=e^{\pi p}$. Here we introduce a change in variable by using $x=2\pi p$ and introducing the cut-off $\Lambda _{\mathbf{C}}$ for $\gamma _p=e^{-x/2}$ we get

  

  (3.170)

  where $\text {Li}_n(x)\forall n=2,3,4$ is the polylogarithm function of n th kind, which is defined as $\text {Li}_n(x)=\sum ^{\infty }_{k=1}\frac{x^k}{k^n}.$ After taking $\Lambda _{\mathbf{C}}\rightarrow \infty$ for $\gamma _p=e^{-x/2}$ we get $\lim _{\Lambda _{\mathbf{C}}\rightarrow \infty }\mathcal{I}_{1}=\frac{1}{90}.$ Furthermore, taking the source free limit in which $f_p\rightarrow 0$ we get

  $$\begin{aligned} \lim _{\Lambda _{\mathbf{C}}\rightarrow \infty , f_p\rightarrow 0}\mathbf{c_6}\equiv S_{\mathbf{intr}}=\frac{1}{90}, \end{aligned}$$

  (3.171)

  which is perfectly consistent with the results obtained from $\nu =1/2$ and $\nu =3/2$ cases without source in Ref. [15]. This also implies that in the absence of the source with $\Lambda _{\mathbf{C}}\rightarrow \infty$ for this specific branch of solution the final result of the interesting part of the entanglement entropy is not very sensitive to the cut-off of $\mathbf{SO(1,3)}$ principal quantum number p.

  On the other hand, for $\gamma _p=e^{x/2}$ in $3+1$ D introducing the cut-off $\Lambda _{\mathbf{C}}$ in the rescaled principal quantum number x we get

  $$\begin{aligned} \mathcal{I}_1= & {} -\frac{1}{8\pi ^4}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2~\left[ \ln \left( 1-e^{x}\right) +\frac{x~e^{x}}{\left( 1-e^{x}\right) }\right] \nonumber \\= & {} -\frac{1}{8\pi ^4}\left[ -\Lambda ^3_{\mathbf{C}} \ln \left( 1-e^{\Lambda _{\mathbf{C}}}\right) -4 \Lambda ^2_{\mathbf{C}} \text {Li}_2\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\left. +\,8 \Lambda _{\mathbf{C}} \text {Li}_3\left( e^{\Lambda _{\mathbf{C}}}\right) -8 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}}}\right) +\frac{4 \pi ^4}{45}\right] , \end{aligned}$$

  (3.172)

  in which after taking the source free limit in which $f_p\rightarrow 0$ we get

  

  (3.173)

  which is perfectly consistent with the results obtained from $\nu =1/2$ and $\nu =3/2$ cases without source for this branch of solution for $\gamma _p$. In this context, this implies that in absence of the source with $\Lambda _{\mathbf{C}}\rightarrow \mathrm{Large}$ for this specific branch of solution the final result of the interesting part of the entanglement entropy is highly sensitive to the cut-off of $\mathbf{SO(1,3)}$ principal quantum number p.

• For Case II we are dealing with the situation where due to arbitrary $\nu$ dependence the expressions for the solutions of the $\gamma _p$ are very complicated, which are given by

  $$\begin{aligned} \gamma _{p}=\frac{i\sqrt{2}}{\left[ \sqrt{\cosh 2\pi p +\cos 2\pi \nu }\pm \sqrt{\cosh 2\pi p +\cos 2\pi \nu +2}\right] }.\nonumber \\ \end{aligned}$$

  (3.174)

  Let us first analyse the representative integral $\mathcal{I}_{1}$ using both of the solutions obtained for arbitrary $\nu$. Following the previous logical argument here we also put a cut-off $\Lambda _{\mathbf{C}}$ to perform the integral on the rescaled $\mathbf{SO(1,3)}$ quantum number $x=2\pi p$ and after performing the integral we will check the behaviour of both of the results. First of all we start with the following integral with ± signature, as given by

  

  (3.175)

  where $G_{\pm }(x,\nu )$ is defined as

  $$\begin{aligned}&G_{\pm }(x,\nu )\nonumber \\&\quad =\frac{1}{\left[ \sqrt{\cosh x +\cos 2\pi \nu }\pm \sqrt{\cosh x +\cos 2\pi \nu +2}\right] ^{2}}.\nonumber \\ \end{aligned}$$

  (3.176)

  However, it is not possible to solve this integral analytically using the exact mathematical structure. Small mass limit situations are studied in the $\nu =1/2$ and in the $\nu =3/2$ cases, is appearing in Case I. Here we consider large mass limit situation which is specifically important to study the physical imprints from Case II. In this large mass limit situation we divide the total window of the $\mathbf{SO(1,3)}$ principal quantum number p into two sub-regions, as given by $0<p<|\nu |$ and $|\nu |<p<\Lambda _{\mathbf{C}}$ and in these consecutive regions of interest the two solutions for $\gamma _p$ can be approximated by

  $$\begin{aligned} |\gamma _p|= & {} \left\{ \begin{array}{ll} e^{-\pi |\nu |}&{}\quad {{\mathbf{for }}}~ 0<p<|\nu |\\ e^{-\pi p} &{}\quad {\mathbf{for }}~ |\nu |<p<\Lambda _{\mathbf{C}}/2\pi , \end{array} \right. \end{aligned}$$

  (3.177)

  and

  $$\begin{aligned} |\gamma _p|= & {} \left\{ \begin{array}{ll} e^{\pi |\nu |}&{}\quad {\mathbf{for }}~0<p<|\nu |\\ e^{\pi p} &{}\quad {\mathbf{for }}~|\nu |<p<\Lambda _{\mathbf{C}}/2\pi . \end{array} \right. \end{aligned}$$

  (3.178)

  Consequently, for this large mass limit situation the regularised specified integral $\mathcal{I}_1$ for the first solution for $|\gamma _p|$ can be written as

  $$\begin{aligned} \mathcal{I}_1= & {} \left\{ \begin{array}{ll} -\frac{A(\nu )}{8\pi ^4}\left[ \ln \left( 1-e^{-2\pi \nu }\right) -\frac{2\pi \nu ~e^{-2\pi \nu }}{\left( 1-e^{-2\pi \nu }\right) }\right] &{}\quad {{\mathbf{for }}}~0<x<2\pi |\nu | \\ -\frac{B(\nu ,\Lambda _{\mathbf{C}})}{8\pi ^4} &{}\quad {{\mathbf{for }}}~2\pi |\nu |<x<\Lambda _{\mathbf{C}}, \end{array} \right. \nonumber \\ \end{aligned}$$

  (3.179)

  and for the second solution for $|\gamma _p|$ it can be written as

  $$\begin{aligned} \mathcal{I}_1= & {} \left\{ \begin{array}{ll} -\frac{A(\nu )}{8\pi ^4}\left[ \ln \left( 1-e^{2\pi \nu }\right) +\frac{2\pi \nu ~e^{2\pi \nu }}{\left( 1-e^{2\pi \nu }\right) }\right] &{}\quad {{\mathbf{for }}}~0<x<2\pi |\nu |\\ -\frac{C(\nu ,\Lambda _{\mathbf{C}})}{8\pi ^4} &{}\quad {{\mathbf{for }}}~2\pi |\nu |<x<\Lambda _{\mathbf{C}}. \end{array} \right. \nonumber \\ \end{aligned}$$

  (3.180)

  Here $A(\nu )$, $B(\nu ,\Lambda _{\mathbf{C}})$ and $C(\nu ,\Lambda _{\mathbf{C}})$ are defined as

  $$\begin{aligned}&A(\nu )=\int ^{2\pi \nu }_{x=0}~\mathrm{d}x~x^2=\frac{8\pi ^3}{3}\nu ^3, \end{aligned}$$

  (3.181)
  $$\begin{aligned}&B(\nu ,\Lambda _{\mathbf{C}})=\int ^{\Lambda _{\mathbf{C}}}_{x=2\pi \nu }~\mathrm{d}x~x^2~\left[ \ln \left( 1-e^{-x}\right) -\frac{x~e^{-x}}{\left( 1-e^{-x}\right) }\right] \nonumber \\&\quad =\frac{1}{3} \left[ {\Lambda ^4_{\mathbf{C}}}-4 {\Lambda ^3_{\mathbf{C}}} \ln \left( 1-e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. +\,{\Lambda ^3_{\mathbf{C}}} \ln (\sinh {\Lambda _{\mathbf{C}}}-\cosh {\Lambda _{\mathbf{C}}}+1) -12 {\Lambda ^2_{\mathbf{C}}}\text {Li}_2\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\left. \qquad +\,24 {\Lambda _{\mathbf{C}}} \text {Li}_3\left( e^{\Lambda _{\mathbf{C}}}\right) -24 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. -\,16\pi ^4\nu ^4 +32\pi ^3 \nu ^3 \ln \left( 1-e^{2\pi \nu }\right) +24 \text {Li}_4\left( e^{2\pi \nu }\right) \right. \nonumber \\&\qquad \left. -\,8\pi ^3\nu ^3 \ln (\sinh (2\pi \nu )-\cosh (2\pi \nu )+1)\right. \nonumber \\&\qquad \left. +\,48 \pi ^2\nu ^2 \text {Li}_2\left( e^{2\pi \nu }\right) -48 \pi \nu \text {Li}_3\left( e^{2\pi \nu }\right) \right] , \end{aligned}$$

  (3.182)
  $$\begin{aligned}&C(\nu ,\Lambda _{\mathbf{C}})=\int ^{\Lambda _{\mathbf{C}}}_{x=2\pi \nu }~\mathrm{d}x~x^2~\left[ \ln \left( 1-e^{x}\right) +\frac{x~e^{x}}{\left( 1-e^{x}\right) }\right] \nonumber \\&\quad =\left[ -{\Lambda ^3_{\mathbf{C}}} \ln \left( 1-e^{\Lambda _{\mathbf{C}}}\right) -4 {\Lambda ^2_{\mathbf{C}}} \text {Li}_2\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\left. \qquad +\,8 {\Lambda _{\mathbf{C}}} \text {Li}_3\left( e^{\Lambda _{\mathbf{C}}}\right) -8 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}}}\right) +8\pi ^3\nu ^3 \ln \left( 1-e^{2\pi \nu }\right) \right. \nonumber \\&\qquad \left. +\,16\pi ^2\nu ^2 \text {Li}_2\left( e^{2\pi \nu }\right) -16\pi \nu \text {Li}_3\left( e^{2\pi \nu }\right) \right. \nonumber \\&\qquad \left. +\,8 \text {Li}_4\left( e^{2\pi \nu }\right) \right] . \end{aligned}$$

  (3.183)

  Furthermore, to check the dependency of the cut-off and mass parameter $\nu$ in the final results obtained for both of the solutions of $|\gamma _p|$ obtained for the large mass limit situation for the range $0<x<2\pi |\nu |$ we take the limit $|\nu |\gg 1$, which gives the following results for the first solution for $|\gamma _p|$:

  $$\begin{aligned} \lim _{|\nu |\gg 1}\mathcal{I}_1\approx & {} \frac{2\nu ^4}{3}e^{-2\pi \nu }\left[ 1+\mathcal{O}\left( \nu ^{-1}\right) \right] . \end{aligned}$$

  (3.184)

  Consequently in the absence of the source in the large mass limit the interesting part of the entanglement entropy can be written as

  $$\begin{aligned} \lim _{|\nu |\gg 1, f_p\rightarrow 0}{\mathbf{c}_{\mathbf{6}}}\equiv S_{\mathbf{intr}}\approx \frac{2\nu ^4}{3}e^{-2\pi \nu }\left[ 1+\mathcal{O}\left( \nu ^{-1}\right) \right] .\nonumber \\ \end{aligned}$$

  (3.185)

  For the second solution of $|\gamma _p|$, we can write

  $$\begin{aligned} \lim _{|\nu |\gg 1}\mathcal{I}_1= & {} -\frac{\nu ^3}{3\pi }\left[ \ln \left( 1-e^{2\pi \nu }\right) +\frac{2\pi \nu ~e^{2\pi \nu }}{\left( 1-e^{2\pi \nu }\right) }\right] ,\nonumber \\ \end{aligned}$$

  (3.186)

  and in the absence of the source in the large mass limit the interesting part of the entanglement entropy can be written as

  $$\begin{aligned}&\lim _{|\nu |\gg 1, f_p\rightarrow 0}{\mathbf{c}_{\mathbf{6}}}\equiv S_{\mathbf{intr}}\nonumber \\&\quad =-\frac{\nu ^3}{3\pi }\left[ \ln \left( 1-e^{2\pi \nu }\right) +\frac{2\pi \nu ~e^{2\pi \nu }}{\left( 1-e^{2\pi \nu }\right) }\right] . \end{aligned}$$

  (3.187)

  Both of the results obtained for the large $|\nu |$ limit situation in absence of the source are consistent with the results obtained Ref. [15].

Fig. 7

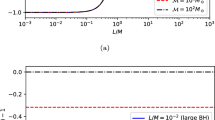
Normalised entanglement entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ vs. mass parameter $\nu ^2$ in $3+1$ D de Sitter space in the absence of the axionic source ($f_p=0$) and in the presence of the axionic source ($f_p=10^{-7}$) for ‘$+$’ branch of solution of $|\gamma _p|$ and $|\Gamma _{p,n}|$. Here we set $\Lambda _{\mathbf{C}}=10{,}000$. In both cases we have normalised the entanglement entropy with the result obtained from $\nu =1/2$, which is the conformal limit result

In Fig. 7a, b, we have explicitly shown the behaviour of entanglement entropy in $3+1$ D de Sitter space in the absence ($f_p=0$) and in the presence ($f_p=10^{-7}$) of the axionic source with respect to the mass parameter $\nu ^2$ where we consider both small and large mass limit situation. In both cases we have normalised the entanglement entropy with the result obtained from $\nu =1/2$, which is the conformal limit result. In Fig. 7a, it is clearly observed that in the absence of the axionic source in the large mass limit range where $\nu ^2<0$, the normalised entanglement entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ saturates to zero asymptotically for large values of $\nu ^2$ on the negative axis. In the large mass limit range actually the interesting part of the entanglement entropy for axion EPR Bell pair can be expressed in terms of its mass for the solution $\gamma _p=e^{-\pi |m_{\mathrm{axion}}/H|}$ as

(3.188)

which implies less entanglement for the large mass limit situation. Furthermore, if we increase the value of $\nu ^2$ and move towards the $\nu ^2>0$ region then the normalised entanglement entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ will increase to its maximum value $\left( S_{\mathrm{intr}}/S_{\nu =1/2}\right) _{\mathrm{max}}=1$ at $\nu =1/2$. Furthermore, between $3/2<\nu <5/2$ normalised entanglement entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ shows one oscillation and reaches its maximum value $\left( S_{\mathrm{intr}}/S_{\nu =1/2}\right) _{\mathrm{max}}=1$ again. Similar situation occurs within the interval $5/2<\nu <7/2$ and the same oscillating feature will repeat itself. But all such oscillations are apeariodic in nature and for large positive values of the $\nu ^2$ the period of oscillation increases. Similarly in Fig. 7b, it is clearly depicted that in the presence of the axionic source in the large mass limit range where $\nu ^2<0$, the normalised entanglement entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ saturates to zero asymptotically for large values of $\nu ^2$ on the negative axis to a large value, say $\left( S_{\mathrm{intr}}/S_{\nu =1/2}\right) _{\mathrm{sat}}\sim 0.99975$, which is appearing in the representative figure. This is obviously higher than the result obtained from without source. On the other hand, in presence of the axionic source if we increase the value of $\nu ^2$ and move towards the $\nu ^2>0$ region then the normalised entanglement entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ will increase to its maximum value $\left( S_{\mathrm{intr}}/S_{\nu =1/2}\right) _{\mathrm{max}}=1$ at $\nu =1/2$, which is exactly similar to the result obtained without axionic source. However, if we compare the two results then we see that in the absence of the axionic source the rate of increase in the normalised value of the entanglement entropy is much higher compared to the result when axionic source is present. This feature clearly indicates that the normalised entanglement entropy for all values of the mass parameter $\nu ^2$ is significantly higher in the presence of the axionic source compared to the result obtained for without source. Furthermore, in between $3/2<\nu <5/2$ normalised entanglement entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ in the presence of the axionic source shows one oscillation and reaches its maximum value $\left( S_{\mathrm{intr}}/S_{\nu =1/2}\right) _{\mathrm{max}}=1$ again very fast compared to the result obtained for without source. In presence of the source, similar situation occurs in the subsequent intervals and the oscillating feature will repeat itself with increasing apeariodic nature for large positive values of the mass parameter $\nu ^2$. But in the presence of the source position of the minima in consecutive oscillations significantly increase compared to the case of without source. Additionally, it is important to note that for $\nu =1/2$ (dashed line), $\nu =3/2$ (green dashed line) and $\nu =7/2$ (purple dashed line) we get the same peak heights (maximum) of the oscillations and we get maximum normalised entanglement entropy at $\left( S_{\mathrm{intr}}/S_{\nu =1/2}\right) _{\mathrm{max}}=1$.

On the other hand, for the solution $\gamma _p=e^{\pi |m_{\mathrm{axion}}/H|}$ the entanglement entropy for axion Bell pair in the large mass limit range is very large:

(3.189)

which implies very large entanglement for the large mass limit situation in a non-trivial way. However, in this paper further we have not analysed this case in detail due to its complicated structure.

3.5 Computation of the Rényi entropy

In this section we further use the expression for the density matrix to compute the Rényi entropy, which is defined by the following expression:¹²

$$\begin{aligned} S_{q}(p,\nu )= & {} \frac{1}{1-q}\ln ~\mathrm{\mathbf Tr}~\left[ \rho _{\mathbf{L}}(p)\right] ^q\quad \mathrm{with}\ q>0. \end{aligned}$$

(3.190)

From this definition of the Rényi entropy one can point out the following characteristics:

• Here by taking the limit $q\rightarrow 1$ one can produce the entanglement entropy for a given $\mathbf{SO(1,3)}$ principal quantum number p and mass parameter $\nu$ i.e. $\lim _{q\rightarrow 1}S_{q}(p,\nu )= S(p,\nu ).$ Here $S_{q}(p,\nu )$ characterise the Rényi entropy corresponding to single $\mathbf{SO(1,3)}$ principal quantum number p and mass parameter $\nu$. However, here it is important to note that this statement is only true in the absence of any source. In presence of a source one can generally write the following expression:

  $$\begin{aligned} \lim _{q\rightarrow 1}S_{q}(p,\nu )= & {} S(p,\nu )+\Delta S(p,\nu ,f_p), \end{aligned}$$

  (3.191)

  where $\Delta S(p,\nu ,f_p)$ is the additional contribution which is appearing due to axion and vanishes in the limit, $\lim _{f_p\rightarrow 0}\Delta S(p,\nu ,f_p)=0.$

• Furthermore, by taking the limit $q\rightarrow 0$ in the definition of the Rényi entropy one can produce the Hartley entropy for a given $\mathbf{SO(1,3)}$ principal quantum number p and mass parameter $\nu$ i.e. $\lim _{q\rightarrow 0}S_{q}(p,\nu )= S_{\mathbf{H}}(p,\nu ).$ This is actually a measure of the dimension of the density matrix and can be written as, $S_{\mathbf{H}}(p,\nu )=\ln \left( \mathbf{dim}~ [\mathcal{H}_\mathbf{occupied}]\right) ,$ where $\mathcal{H}_{\mathbf{occupied}}$ represents the image of the density matrix.

• In the limit $q\rightarrow \infty$ Rényi entropy produces the largest eigenvalue of density matrix for a given $\mathbf{SO(1,3)}$ principal quantum number p and mass parameter $\nu$ given by

  $$\begin{aligned} \lim _{q\rightarrow \infty }S_{q}(p,\nu )= & {} \lambda _{p,\nu }+\Delta \lambda _{p,\nu ,f_p}=-\ln \left( [\rho _{\mathbf{L}}]_\mathbf{max}\right) ,\nonumber \\ \end{aligned}$$

  (3.192)

  where $[\rho _{\mathbf{L}}]_{\mathbf{max}}$ represents the largest eigenvalue of density matrix. Also $\Delta \lambda _{p,\nu ,f_p}$ is the additional contribution arising from the source term and vanishes in the limit, $\lim _{f_p\rightarrow 0}\Delta \lambda _{p,\nu ,f_p}=0.$

• In absence of the axionic source, the quantifying formula for the Rényi entropy for a specified $\mathbf{SO(1,3)}$ principal quantum number p and mass parameter $\nu$ can be expressed as

  $$\begin{aligned} S_{q}(p,\nu )= & {} \frac{q}{1-q}\ln \left( 1-|\gamma _p|^2\right) \nonumber \\&-\frac{1}{1-q}\ln \left( 1-|\gamma _p|^{2q}\right) . \end{aligned}$$

  (3.193)

  Furthermore, the specific information as regards the long range quantum correlation in $3+1$ dimension is obtained by integrating over the $\mathbf{SO(1,3)}$ quantum number p and a regularised volume integral over hyperboloid, as given by

  $$\begin{aligned} S_{q,\mathbf{intr}}= & {} \frac{1}{\pi }\int ^{\infty }_{p=0}\mathrm{d}p~p^2~S_{q}(p,\nu ), \end{aligned}$$

  (3.194)

  which satisfy the constraint $\lim _{q\rightarrow 1}S_{q,\mathbf{intr}}=S_{\mathbf{intr}}\equiv \mathbf{c_{6}}.$ But since our prime objective of this paper is to see the imprints of stringy axion, we have to compute the modified expression for the Rényi entropy for a given $\mathbf{SO(1,3)}$ principal quantum number p and mass parameter $\nu$. In the next subsection we explicitly compute this result, in the presence of the source.

The general expression for the Rényi entropy is written in Eq. (3.190), where parameter $\nu$ is defined earlier. For the Case I and Case II the expression for the Rényi entropy in terms of the complementary and particular part of the obtained solution for a given $\mathbf{SO(1,3)}$ principal quantum number p can be expressed as

$$\begin{aligned} S_{q}(p,\nu )= & {} \left[ \frac{q}{1-q}\ln \left( 1-|\gamma _{p}|^2\right) -\frac{1}{1-q}\ln \left( 1-|\gamma _{p}|^{2q}\right) \right] \nonumber \\&-\frac{q}{1-q}\ln \left( 1+f_p\right) \nonumber \\&+\frac{1}{1-q}\ln \left[ 1+\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-|\gamma _{p}|^2\right) ^{-k}}{\left( 1-|\gamma _{p}|^{-2k}\right) } \right] .\nonumber \\ \end{aligned}$$

(3.195)

Now to study the properties of the derived result we check the following physical limit situations:

• First of all we take the $q\rightarrow 1$ limit for which we get the following simplified expression:

  $$\begin{aligned}&\lim _{q\rightarrow 1}S_{q}(p,\nu )=-\ln \left( 1-|\gamma _p|^2\right) \nonumber \\&\quad -\frac{|\gamma _p|^2}{\left( 1-|\gamma _p|^2\right) }\ln |\gamma _p|^2-\ln \left( 1+f_p\right) \nonumber \\&\quad +\ln \left( 1-f_p\frac{|\gamma _p|^2}{\left( 1-|\gamma _p|^2\right) ^2}\right) . \end{aligned}$$

  (3.196)

  Furthermore, we take the difference between the results obtained from Eqs. (3.156) and (3.196), which we define as

  $$\begin{aligned}&\Delta S(p,\nu ,f_p)=S(p,\nu )-\lim _{q\rightarrow 1}S_{q}(p,\nu )\nonumber \\&\quad =-\frac{f_p}{1+f_p}\left[ \frac{q}{1-q}\ln \left( 1-|\gamma _{p}|^2\right) -\frac{1}{1-q}\ln \left( 1-|\gamma _{p}|^{2q}\right) \right] \nonumber \\&\qquad +f_p\ln \left( 1+f_p\right) -\ln \left( 1-f_p\frac{|\gamma _p|^2}{\left( 1-|\gamma _p|^2\right) ^2}\right) , \end{aligned}$$

  (3.197)

  which shows that in the presence of the source, the entanglement entropy and Rényi entropy in the limit $q\rightarrow 1$ is not same. Now if we further take the limit $f_p\rightarrow 0$ then we get $\lim _{f_p\rightarrow 0}\Delta S(p,\nu ,f_p)=0,$, which is consistent with the result known for free theory.

• Next we take the $q\rightarrow 0$ limit for which we get $\lim _{q\rightarrow 0}S_{q}(p,\nu )=\ln \left[ \sum ^{\infty }_{n=1}1\right] \rightarrow \infty .$ This directly implies that the dimension of the image of the density matrix is given by for the present computation as, $\mathbf{dim}~ [\mathcal{H}_{\mathbf{occupied}}]\rightarrow \infty ,$ which is perfectly consistent with the fact that the density matrix in the present computation is infinite dimensional.

• Finally, we take the $q\rightarrow \infty$ limit for which we get the following simplified expression:

  $$\begin{aligned} \lim _{q\rightarrow \infty }S_{q}(p,\nu )\approx & {} -\ln \left( 1-|\gamma _{p}|^2\right) +\ln \left( 1+f_p\right) .\nonumber \\ \end{aligned}$$

  (3.198)

  This directly implies that the largest eigenvalue of density matrix given by for the present computation as, $[\rho _{\mathbf{L}}]_\mathbf{max}= \left( 1-|\gamma _{p}|^2\right) \frac{1}{1+f_p},$ which is perfectly consistent with the fact that the density matrix in the present computation is infinite dimensional. Now if we further take the limit $f_p\rightarrow 0$ then we get $\lim _{f_p\rightarrow 0}\Delta \lambda _{p,\nu ,f_p}=0,$ which is consistent with the result known for free theory in the absence of the axion source contribution.

Then the final expression for the interesting part of the Rényi entropy in $3+1$ D de Sitter space can be expressed as:

$$\begin{aligned} S_{q,\mathbf intr}= \frac{1}{\pi }\int ^{\infty }_{p=0}~\mathrm{d}p~p^2~S_{q}(p,\nu ), \end{aligned}$$

(3.199)

which represents the long range entanglement of the quantum state under consideration for the limit $q\rightarrow 1$.

Furthermore, substituting the explicit expression for the entanglement entropy $S(p,\nu )$ computed in the presence of the axion and integrating over all possible $\mathbf{SO(1,3)}$ principal quantum number, lying within the window $0<p<\infty$, we get the following expression:

(3.200)

where the integrals $\mathcal{J}_{1,q}$, $\mathcal{J}_{2,q}$ and $\mathcal{J}_{3,q}$ are defined as

$$\begin{aligned} \mathcal{J}_{1,q}= & {} \frac{1}{\pi }\int ^{\infty }_{p=0}~\mathrm{d}p~p^2~\left[ \frac{q}{1-q}\ln \left( 1-|\gamma _{p}|^2\right) \right. \nonumber \\&\left. -\frac{1}{1-q}\ln \left( 1-|\gamma _{p}|^{2q}\right) \right] , \end{aligned}$$

(3.201)

$$\begin{aligned} \mathcal{J}_{2,q}= & {} -\frac{1}{\pi }\frac{q}{1-q}\int ^{\infty }_{p=0}~\mathrm{d}p~p^2, \end{aligned}$$

(3.202)

$$\begin{aligned} \mathcal{J}_{3,q}= & {} \frac{1}{\pi }\frac{1}{1-q}\int ^{\infty }_{p=0}~\mathrm{d}p~p^2\nonumber \\&\times \ln \left[ 1+\sum ^{q}_{k=1}{}^{q}\mathbf{C}_{k} f_p^{k }\frac{\left( 1-|\gamma _{p}|^2\right) ^{-k}}{\left( 1-|\gamma _{p}|^{-2k}\right) }\right] . \end{aligned}$$

(3.203)

Here it is important to note that:

• For both Case I and Case II the integral $\mathcal{J}_{2,q}$ diverges in $3+1$ D. To make it finite we need to regularise this by introducing a change in variable by using $x=2\pi p$ and introducing a cut-off $\Lambda _{\mathbf{C}}$ in the rescaled principal quantum number x as given by

  $$\begin{aligned} \mathcal{J}_{2,q}= & {} -\frac{1}{8\pi ^4}\frac{q}{1-q}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2\nonumber \\= & {} -\frac{\Lambda ^3_{\mathbf{C}}}{24\pi ^4}\frac{q}{1-q}. \end{aligned}$$

  (3.204)

• For Case I we have two possible solution for $\gamma _{p}$. For $\gamma _p=e^{-\pi p}$ the integrals $\mathcal{J}_{1,q}$ and $\mathcal{J}_{3,q}$ are always finite for Case I. But for the other solution of $\gamma _p=e^{\pi p}$ the integrals $\mathcal{J}_{1,q}$ and $\mathcal{J}_{3,q}$ are divergent. To have consistency throughout the analysis we put a cut-off $\Lambda _{\mathbf{C}}$ on the integrals $\mathcal{J}_{1,q}$ and $\mathcal{J}_{3,q}$ obtained from the two solutions of $\gamma _p$. Here after introducing the cut-off $\Lambda _{\mathbf{C}}$ in $x=2\pi p$ for $\gamma _p=e^{-x/2}$ we get

  $$\begin{aligned}&\mathcal{J}_{1,q}=\frac{1}{8\pi ^4}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2~~\left[ \frac{q}{1-q}\ln \left( 1-e^{-x}\right) \right. \nonumber \\&\left. \qquad \qquad -\frac{1}{1-q}\ln \left( 1-e^{-xq}\right) \right] \nonumber \\&\quad =\frac{1}{8\pi ^4}\frac{1}{45 (q-1) q^3}\left[ -15 \Lambda _{\mathbf{C}}^3 q^4 \ln \left( -e^{-\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. +\,15 \Lambda _{\mathbf{C}}^3 q^3 \ln \left( -e^{-\Lambda _{\mathbf{C}} q}\right) +45 \Lambda _{\mathbf{C}}^2 q^4 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. -\,45 \Lambda _{\mathbf{C}}^2 q^2 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}} q}\right) -90 \Lambda _{\mathbf{C}} q^4 \text {Li}_3\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\left. \qquad +90 q^4 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. +90 \Lambda _{\mathbf{C}} q \text {Li}_3\left( e^{\Lambda _{\mathbf{C}} q}\right) -90 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}} q}\right) \right. \nonumber \\&\left. \qquad -\,\pi ^4 q^4+\pi ^4\right] ,\end{aligned}$$

  (3.205)
  $$\begin{aligned}&\mathcal{J}_{3,q} = \frac{1}{8\pi ^4}\frac{1}{1-q}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2~~\ln \left[ 1\right. \nonumber \\&\quad \qquad \left. +\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-e^{-x}\right) ^{-k}}{\left( 1-e^{xk}\right) }\right] . \end{aligned}$$

  (3.206)

  Taking $\mathbf{\Lambda }_{\mathbf{C}}\rightarrow \infty$ for $\gamma _p=e^{-x/2}$ we get

  $$\begin{aligned} \lim _{\mathbf{\Lambda }_{\mathbf{C}}\rightarrow \infty }\mathcal{J}_{1,q}= & {} \frac{ (q+1) \left( q^2+1\right) }{360 q^3}, \end{aligned}$$

  (3.207)

  and further taking $q\rightarrow 1$, we get $\lim _{\mathbf{\Lambda }_{\mathbf{C}}\rightarrow \infty ,q\rightarrow 1}\mathcal{J}_{1,q}=\frac{1}{90}.$ Exact analytical form of the integral $\mathcal{J}_{3,q}$ for any q is not computable. But in the limit case $f_p\rightarrow 0$ we get $\lim _{\Lambda _{\mathbf{C}}\rightarrow \infty ,q\rightarrow 1,f_p\rightarrow 0}\mathcal{J}_{3,q}=0.$ This implies that in the source free limit where $f_p\rightarrow 0$ we get:

  $$\begin{aligned} \lim _{\Lambda _{\mathbf{C}}\rightarrow \infty , f_p\rightarrow 0,q\rightarrow 1}S_{q,\mathbf intr}= \frac{1}{90}=S_\mathbf{intr}, \end{aligned}$$

  (3.208)

  which is consistent with the results obtained from $\nu =1/2$ and $\nu =3/2$ cases without source in $3+1$ D.

  On the other hand, for $\gamma _p=e^{x/2}$ in $3+1$ D introducing the cut-off $\Lambda _{\mathbf{C}}$ in the rescaled principal quantum number x we get

  $$\begin{aligned} \mathcal{J}_{1,q}= & {} \frac{1}{8\pi ^4}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2~~\left[ \frac{q}{1-q}\ln \left( 1-e^{x}\right) \right. \nonumber \\&\left. -\frac{1}{1-q}\ln \left( 1-e^{xq}\right) \right] \nonumber \\= & {} \frac{1}{8\pi ^4}\frac{1}{45 (q-1) q^3}\left[ 45 \Lambda _{\mathbf{C}}^2 q^4 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\left. -45 \Lambda _{\mathbf{C}}^2 q^2 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}} q}\right) \right. \nonumber \\&\left. -90 \Lambda _{\mathbf{C}} q^4 \text {Li}_3\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\left. +90 q^4 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}}}\right) +90 \Lambda _{\mathbf{C}} q \text {Li}_3\left( e^{\Lambda _{\mathbf{C}} q}\right) \right. \nonumber \\&\left. -90 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}} q}\right) -\pi ^4 q^4+\pi ^4\right] , \end{aligned}$$

  (3.209)
  $$\begin{aligned} \mathcal{J}_{3,q}= & {} \frac{1}{8\pi ^4}\frac{1}{1-q}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2~~\ln \left[ 1\right. \nonumber \\&\left. +\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-e^{x}\right) ^{-k}}{\left( 1-e^{-xk}\right) }\right] . \end{aligned}$$

  (3.210)

  After taking $q\rightarrow 1$ we get

  

  (3.211)

  The exact analytical form of the integral $\mathcal{J}_{3,q}$ for any q is not computable. But in the limit case $f_p\rightarrow 0$ we get $\lim _{\Lambda _{\mathbf{C}}\rightarrow \mathrm{Large},q\rightarrow 1,f_p\rightarrow 0}\mathcal{J}_{3,q}=0.$ This implies that in the source free limit in which $f_p\rightarrow 0$ we get

  

  (3.212)

  which is perfectly consistent with the results obtained from $\nu =1/2$ and $\nu =3/2$ cases without source for this branch of solution for $\gamma _p$ in $3+1$ D.

• For Case II following a similar procedure we get

  $$\begin{aligned} \mathcal{J}_{1,q}= & {} \frac{1}{8\pi ^4}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2~~\left[ \frac{q}{1-q}\ln \left( 1-2G_{\pm }(x,\nu )\right) \right. \nonumber \\&\left. -\frac{1}{1-q}\ln \left( 1-(2G_{\pm }(x,\nu )\right) ^q)\right] , \end{aligned}$$

  (3.213)
  $$\begin{aligned} \mathcal{J}_{3,q}= & {} \frac{1}{8\pi ^4}\frac{1}{1-q}\int ^{\Lambda _{\mathbf{C}}}_{x=0}~\mathrm{d}x~x^2\nonumber \\&\times \ln \left[ 1+\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-2G_{\pm }(x,\nu )\right) ^{-k}}{\left( 1-(2G_{\pm }(x,\nu ))^{-k}\right) }\right] ,\nonumber \\ \end{aligned}$$

  (3.214)

  where $G_{\pm }(x,\nu )$ is defined earlier. Here we consider large mass limit situation which is specifically important to study the physical imprints from Case II as mentioned earlier. In this large mass limit situation we divide the total window of the $\mathbf{SO(1,3)}$ principal quantum number p into two sub-regions, as given by $0<p<|\nu |$ and $|\nu |<p<\Lambda _{\mathbf{C}}$:

  Consequently, for this large mass limit situation the regularised specified integral $\mathcal{J}_{1,q}$ and $\mathcal{J}_{3,q}$ for the first solution for $|\gamma _p|$ in $3+1$ D can be written as

  $$\begin{aligned}&\mathcal{J}_{1,q} =\left\{ \begin{array}{ll} \frac{A(\nu )}{8\pi ^4}\left[ \frac{q}{1-q}\ln \left( 1-e^{-2\pi \nu }\right) -\frac{1}{1-q}\ln \left( 1-e^{-2\pi \nu q}\right) \right] ~~~~~~ &{} {{\mathbf{for }}}~0<x<2\pi |\nu |\\ \frac{D(\nu ,\Lambda _{\mathbf{C}},q)}{8\pi ^4} &{} {{\mathbf{for }}} \quad 2\pi |\nu |<x<\Lambda _{\mathbf{C}}. \end{array}\right. \end{aligned}$$

  (3.215)
  $$\begin{aligned}&\mathcal{J}_{3,q} =\left\{ \begin{array}{ll} \frac{A(\nu )}{8\pi ^4}\frac{1}{1-q}~\ln \left[ 1+\sum ^{q}_{k=1}{}^{q}\mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-e^{-2\pi \nu }\right) ^{-k}}{\left( 1-e^{2\pi \nu k}\right) }\right] ~~ &{} {{\mathbf{for }}}\, 0<x<2\pi |\nu |\\ \frac{1}{8\pi ^4}\frac{1}{1-q}\int ^{\Lambda _{\mathbf{C}}}_{x=2\pi \nu }~\mathrm{d}x~x^2~~\ln \left[ 1+\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} f_p^{k }\frac{\left( 1-e^{-x}\right) ^{-k}}{\left( 1-e^{xk}\right) }\right] &{} {{\mathbf{for }}} \quad \,2\pi |\nu |<x<\Lambda _{\mathbf{C}},~~~ \end{array} \right. \end{aligned}$$

  (3.216)

  and for the second solution for $|\gamma _p|$ can be written as

  $$\begin{aligned} \mathcal{J}_{1,q}= & {} \left\{ \begin{array}{ll} \frac{A(\nu )}{8\pi ^4}\left[ \frac{q}{1-q}\ln \left( 1-e^{2\pi \nu }\right) -\frac{1}{1-q}\ln \left( 1-e^{2\pi \nu q}\right) \right] &{}\quad {{\mathbf{for }}}\, 0<x<2\pi |\nu |\\ \frac{E(\nu ,\Lambda _{\mathbf{C}},q)}{8\pi ^4} &{}\quad {{\mathbf{for }}} \,2\pi |\nu |<x<\Lambda _{\mathbf{C}}. \end{array} \right. \end{aligned}$$

  (3.217)
  $$\begin{aligned} \mathcal{J}_{3,q}= & {} \left\{ \begin{array}{ll} \frac{A(\nu )}{8\pi ^4}\frac{1}{1-q}~\ln \left[ 1+\sum ^{q}_{k=1}{}^{q}\mathbf{C}_{k} f_p^{k }\frac{\left( 1-e^{2\pi \nu }\right) ^{-k}}{\left( 1-e^{-2\pi \nu k}\right) }\right] &{}\quad {{\mathbf{for }}}\, 0<x<2\pi |\nu |\\ \frac{1}{8\pi ^4}\frac{1}{1-q}\int ^{\Lambda _{\mathbf{C}}}_{x=2\pi \nu }~\mathrm{d}x~x^2~~\ln \left[ 1+\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-e^{x}\right) ^{-k}}{\left( 1-e^{-xk}\right) }\right] &{} \quad {{\mathbf{for }}} \,2\pi |\nu |<x<\Lambda _{\mathbf{C}}. \end{array} \right. \end{aligned}$$

  (3.218)

  Here $A(\nu )$ is defined earlier and $D(\nu ,\Lambda _{\mathbf{C}})$ and $E(\nu ,\Lambda _{\mathbf{C}})$ are defined as

  $$\begin{aligned}&D(\nu ,\Lambda _{\mathbf{C}},q)=\int ^{\Lambda _{\mathbf{C}}}_{x=2\pi \nu }~\mathrm{d}x~x^2~\left[ \frac{q}{1-q}\ln \left( 1-e^{-x}\right) \right. \nonumber \\&\qquad \left. -\,\frac{1}{1-q}\ln \left( 1-e^{-xq}\right) \right] \nonumber \\&\quad =\frac{1}{3 (q-1) q^3}\left[ 8\pi ^3\nu ^3 q^4 \ln \left( -e^{-2\pi \nu }\right) \right. \nonumber \\&\qquad \left. -\,8\pi ^3\nu ^3 q^3 \ln \left( -e^{-2\pi \nu q}\right) -12\pi ^2 \nu ^2 q^4 \text {Li}_2\left( e^{2\pi \nu }\right) \right. \nonumber \\&\qquad \left. +\,12\pi ^2 \nu ^2 q^2 \text {Li}_2\left( e^{2\pi \nu q}\right) \right. \nonumber \\&\left. \qquad +\,12 \pi \nu q^4 \text {Li}_3\left( e^{2\pi \nu }\right) -6 q^4 \text {Li}_4\left( e^{2\pi \nu }\right) \right. \nonumber \\&\qquad \left. -\, 12\pi \nu q \text {Li}_3\left( e^{2\pi \nu q}\right) \right. \nonumber \\&\qquad \left. +\,6 \text {Li}_4\left( e^{2\pi \nu q}\right) -\Lambda _{\mathbf{C}}^3 q^4 \ln \left( -e^{-\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. +\,\Lambda _{\mathbf{C}}^3 q^3 \ln \left( -e^{-\Lambda _{\mathbf{C}} q}\right) \right. \nonumber \\&\qquad \left. +\,3 \Lambda _{\mathbf{C}}^2 q^4 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}}}\right) -3 \Lambda _{\mathbf{C}}^2 q^2 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}} q}\right) \right. \nonumber \\&\qquad \left. -\,6 \Lambda _{\mathbf{C}} q^4 \text {Li}_3\left( e^{\Lambda _{\mathbf{C}}}\right) +6 q^4 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. +\,6 \Lambda _{\mathbf{C}} q \text {Li}_3\left( e^{\Lambda _{\mathbf{C}} q}\right) -6 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}} q}\right) \right] , \end{aligned}$$

  (3.219)
  $$\begin{aligned}&E(\nu ,\Lambda _{\mathbf{C}},q)=\int ^{\Lambda _{\mathbf{C}}}_{x=2\pi \nu }~\mathrm{d}x~x^2~\left[ \frac{q}{1-q}\ln \left( 1-e^{x}\right) \right. \nonumber \\&\qquad \left. -\,\frac{1}{1-q}\ln \left( 1-e^{xq}\right) \right] \nonumber \\&\quad =\frac{1}{(q-1) q^3}\left[ -4\pi ^2\nu ^2 q^4 \text {Li}_2\left( e^{2\pi \nu }\right) \right. \nonumber \\&\qquad \left. +\,4\pi ^2\nu ^2 q^2 \text {Li}_2\left( e^{2\pi \nu q}\right) +4\pi \nu q^4 \text {Li}_3\left( e^{2\pi \nu }\right) \right. \nonumber \\&\qquad \left. -\,2 q^4 \text {Li}_4\left( e^{2\pi \nu }\right) -4\pi \nu q \text {Li}_3\left( e^{2\pi \nu q}\right) +2 \text {Li}_4\left( e^{2\pi \nu q}\right) \right. \nonumber \\&\qquad \left. +\,\Lambda _{\mathbf{C}}^2 q^4 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}}}\right) -\Lambda _{\mathbf{C}}^2 q^2 \text {Li}_2\left( e^{\Lambda _{\mathbf{C}} q}\right) -2 \Lambda _{\mathbf{C}} q^4 \text {Li}_3\left( e^{\Lambda _{\mathbf{C}}}\right) \right. \nonumber \\&\qquad \left. +\,2 q^4 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}}}\right) +2 \Lambda _{\mathbf{C}} q \text {Li}_3\left( e^{\Lambda _{\mathbf{C}} q}\right) -2 \text {Li}_4\left( e^{\Lambda _{\mathbf{C}} q}\right) \right] .\nonumber \\ \end{aligned}$$

  (3.220)

  Furthermore, to check the dependency of the cut-off and mass parameter $\nu$ in the final results obtained for both of the solutions of $|\gamma _p|$ obtained for the large mass limit situation for the range $0<x<2\pi |\nu |$ we take the limit $\Lambda _{\mathbf{C}}\rightarrow \infty$ and $q\rightarrow 1$, which gives the following results for the first solution for $|\gamma _p|$ in $3+1$ D:

  $$\begin{aligned}&\lim _{\Lambda _{\mathbf{C}}\rightarrow \infty ,q\rightarrow 1}\mathcal{J}_{1,q}\nonumber \\&\quad = \frac{\nu ^3}{3}\left( \frac{2 \nu }{e^{2 \pi \nu }-1}-\frac{\ln \left( 1-e^{-2 \pi \nu }\right) }{\pi }\right) . \end{aligned}$$

  (3.221)

  Furthermore, taking the $|\nu |\gg 1$ limit case we, finally, get

  $$\begin{aligned}&\lim _{\Lambda _{\mathbf{C}}\rightarrow \infty ,q\rightarrow 1,|\nu |\gg 1}\mathcal{J}_{1,q}\nonumber \\&\quad \approx \frac{2\nu ^4}{3}e^{-2\pi \nu }\left[ 1+\mathcal{O}\left( \nu ^{-1}\right) \right] . \end{aligned}$$

  (3.222)

  On the other hand if we take the source limit $f_p\rightarrow 0$ then for the integral $\mathcal{J}_{3,q}$ we get $\lim _{\Lambda _{\mathbf{C}}\rightarrow \infty ,q\rightarrow 1,|\nu |\gg 1,f_p\rightarrow 0}\mathcal{J}_{3,q} = 0.$ Consequently in the absence of the source in the large mass limit with $q\rightarrow 1$ the interesting part of the Rényi entropy can be written as

  $$\begin{aligned}&\lim _{\Lambda _{\mathbf{C}}\rightarrow \infty ,q\rightarrow 1,|\nu |\gg 1, f_p\rightarrow 0}S_{q,\mathbf intr}\nonumber \\&\quad \approx \frac{2\nu ^4}{3}e^{-2\pi \nu }\left[ 1+\mathcal{O}\left( \nu ^{-1}\right) \right] =S_{\mathbf{intr}}. \end{aligned}$$

  (3.223)

  For the second solution for $|\gamma _p|$ taking the $|\nu |\gg 1$ limit case we get

  $$\begin{aligned}&\lim _{\Lambda _{\mathbf{C}}\rightarrow \mathrm{Large},q\rightarrow 1,|\nu |\gg 1}\mathcal{J}_{1,q}\nonumber \\&\quad = \frac{\nu ^3}{3}\left( \frac{2 \nu e^{2 \pi \nu }}{e^{2 \pi \nu }-1}-\frac{\ln \left( 1-e^{2 \pi \nu }\right) }{\pi }\right) , \end{aligned}$$

  (3.224)

  and $\lim _{\Lambda _{\mathbf{C}}\rightarrow \infty ,q\rightarrow 1,|\nu |\gg 1,f_p\rightarrow 0}\mathcal{J}_{3,q} = 0.$ Consequently, in the absence of the source in the large mass limit the interesting part of the Rényi entropy can be written as

  $$\begin{aligned}&\lim _{\Lambda _{\mathbf{C}}\rightarrow \mathrm{Large},q\rightarrow 1,|\nu |\gg 1, f_p\rightarrow 0}S_{q,\mathbf intr}\nonumber \\&\quad =\frac{\nu ^3}{3}\left( \frac{2 \nu e^{2 \pi \nu }}{e^{2 \pi \nu }-1}-\frac{\ln \left( 1-e^{2 \pi \nu }\right) }{\pi }\right) =S_\mathbf{intr}.\nonumber \\ \end{aligned}$$

  (3.225)

  Both of the results obtained for large $\nu$ limit situation in absence of the source are consistent with the results obtained in this paper.

Fig. 8

Normalised Rényi entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ vs. mass parameter $\nu ^2$ in $3+1$ D de Sitter space in the absence of the axionic source ($f_p=0$) and in the presence of axionic source ($f_p=10^{-7}$) for $q=0.1$ (black), $q=0.3$ (purple), $q=0.5$ (green), $q=0.7$ (blue), $q=0.9$ (red) with $`+'$ branch of solution of $|\gamma _p|$ and $|\Gamma _{p,n}|$. Here we set $\Lambda _{\mathbf{C}}=10{,}000$. In both the cases we have normalised the entanglement entropy with the result obtained from $\nu =1/2$, which is the conformal limit result. a Normalised Rényi entropy vs. $\nu ^2$ in $3+1$ D de Sitter space without axionic source ($f_p=0$). b Normalised Rényi entropy vs. $\nu ^2$ in $3+1$ D de Sitter space with axionic source ($f_p=10^{-7}$)

Fig. 9

Normalised Rényi entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ vs. mass parameter $\nu ^2$ in $3+1$ D de Sitter space in the absence of the axionic source ($f_p=0$) and in the presence of the axionic source ($f_p=10^{-7}$) for $q=0.1$ (black), $q=0.3$ (purple), $q=0.5$ (green), $q=0.7$ (blue), $q=0.9$ (red) with ‘$+$’ branch of solution of $|\gamma _p|$ and $|\Gamma _{p,n}|$. Here we set $\Lambda _{\mathbf{C}}=300$. In both cases we have normalised the entanglement entropy with the result obtained from $\nu =1/2$, which is the conformal limit result

In Fig. 8a, b, we have explicitly shown the behaviour of Rényi entropy in $3+1$ D de Sitter space in the absence ($f_p=0$) and presence ($f_p=10^{-7}$) of the axionic source with respect to the mass parameter $\nu ^2$ where we consider both small and large mass limit situation with cut-off of rescaled principal quantum number fixed at the value $\Lambda _{\mathbf{C}}=10000$. In both cases we have normalised the entanglement entropy with the result obtained from $\nu =1/2$, which is the conformal limit result. In Fig. 8a, it is clearly observed that in the absence of axionic source in the large mass limit range where $\nu ^2<0$, the normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ saturates to zero suddenly through a jump at $\nu =0$ with $q=0.5$ (green), $q=0.7$ (blue), $q=0.9$ (red) for large values of $\nu ^2$ on the negative axis. But for $q=0.1$ (black) and $q=0.7$ (purple) $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ saturates to zero very slowly for the very large mass limit range with $\nu ^2<0$. On the other hand, if we increase the value of $\nu ^2$ and move towards the $\nu ^2>0$ region then the normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ will increase to its maximum value $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{max}}=1$ at $\nu =1/2$ for all values of q, where $q>0$. Furthermore, in between $3/2<\nu <5/2$ normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ shows one oscillation and reaches its maximum value $\left( S_{\mathrm{intr}}/S_{\nu =1/2}\right) _{\mathrm{max}}=1$ again exactly at $\nu =3/2$ for all values of q, where $q>0$. Here it is important to note that, as the value of q increases, the position (height) of the minima of the oscillation decrease and exactly reaches the result with normalised entanglement entropy once we go to the $q\rightarrow 1$ limit situation. Here for $q=0.9$ (red) we have represented this feature explicitly. Similar situation occurs within the interval $5/2<\nu <7/2$ and the same oscillating feature will repeat itself for all values of q, where $q>0$. But all such oscillations are apeariodic in nature and for large positive values of the mass parameter $\nu ^2$ the period of oscillation increases for all values of q, where $q>0$. Also in Fig. 8a, for $\nu =1/2$ (black dashed line), $\nu =3/2$ (orange dashed line) and $\nu =7/2$ (magenta dashed line) we get the same maxima of the oscillations at $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{max}}=1$. In Fig. 8b, it is clearly depicted that in the presence of axionic source in the large mass limit range where $\nu ^2<0$, the normalised Rényi entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ saturates to unity for $q=0.9$ (red) or other value for $q=0.5$ (green) and $q=0.7$ (blue) through a jump at $\nu =0$ for large values of $\nu ^2$ on the negative axis. Except from the jump at $\nu =0$ in normalised Rényi entropy for $q=0.9$ (red) it replicates the limit situation $q\rightarrow 1$ as required to produce normalised entanglement entropy. Such little deviation appears due to the presence of the axionic source term which is explicitly derived earlier. Most importantly for a given value of q with $q>0$ the height of the maxima of oscillation gives the maximum value of the normalised Rényi entropy and its magnitude increases with decreasing value of q, which follows the restriction $q>0$. On the other hand, in the presence of the axionic source if we increase the value of $\nu ^2$ and move towards the $\nu ^2>0$ region then the normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ will decrease to its minimum value $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{min}}=1$ at $\nu =1/2$, which is the maximum value of normalised Rényi entropy without axionic source. Furthermore, in between $3/2<\nu <5/2$ the normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ in the presence of the axionic source shows one oscillation and reaches its minimum value $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{max}}=1$ at $\nu =3/2$. In the presence of the source contribution the minimum value of the normalised Rényi entropy is appearing in the subsequent intervals and the oscillating feature will repeat itself with increasingly aperiodic nature for large positive values of the mass parameter $\nu ^2$. But in the presence of the source the position of the minima in consecutive oscillations significantly increase compared to the result that is obtained without source. Additionally, it is important to note that in Fig. 8b, for $\nu =1/2$ (black dashed line), $\nu =3/2$ (orange dashed line) and $\nu =7/2$ (magenta dashed line) we get the same minimum of the oscillations at $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{min}}=1$.

Fig. 10

Normalised Rényi entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ vs. mass parameter $\nu ^2$ in $3+1$ D de Sitter space in the absence of the axionic source ($f_p=0$) and in the presence of the axionic source ($f_p=10^{-7}$) for $q\rightarrow \infty$ with ‘$+$’ branch of solution of $|\gamma _p|$ and $|\Gamma _{p,n}|$, which signifies largest eigenvalue of density matrix. Here we set $\Lambda _{\mathbf{C}}=10{,}000$. In both cases we have normalised the entanglement entropy with the result obtained from $\nu =1/2$, which is the conformal limit result

Furthermore, in Fig. 9a, b, we have explicitly shown the behaviour of the Rényi entropy in $3+1$ D de Sitter space in absence ($f_p=0$) and presence ($f_p=10^{-7}$) of the axionic source with respect to the mass parameter $\nu ^2$ where we consider both small and large mass limit situation with different cut-off of rescaled principal quantum number fixed at the small value $\Lambda _{\mathbf{C}}=300$. In both cases we have normalised the entanglement entropy with the result obtained from $\nu =1/2$, which is the conformal limit result. In Fig. 9a, it is clearly observed that, in the absence of the axionic source in the large mass limit range where $\nu ^2<0$, the normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ saturates to different values depending on the different values of the parameter q as given by $q=0.1$ (black), $q=0.3$ (purple), $q=0.5$ (green), $q=0.7$ (blue), $q=0.9$ (red) with large values of $\nu ^2$ on the negative axis. On the other hand, if we increase the value of $\nu ^2$ and move towards the $\nu ^2>0$ region then we get the exactly similar features to those appearing for Fig. 8a. In Fig. 9b, it is clearly depicted that in the presence of the axionic source in the large mass limit range where $\nu ^2<0$, the normalised Rényi entropy $S_{\mathrm{intr}}/S_{\nu =1/2}$ saturates at different values for different values of the parameter q for large values of $\nu ^2$ on the negative axis. Most importantly for a given value of q with $q>0$ the height of the maxima of oscillation increases with increasing value of q with $\Lambda _{\mathbf{C}}=300$. On the other hand, in presence of the axionic source if we increase the value of $\nu ^2$ and move towards the $\nu ^2>0$ region then the normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ will increase to its maximum value $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{max}}=1$ at $\nu =1/2$, which is also the maximum value of normalised Rényi entropy without axionic source with $\Lambda _{\mathbf{C}}=300$. Furthermore, in between $3/2<\nu <5/2$ normalised Rényi entropy $S_{q,\mathrm{intr}}/S_{q,\nu =1/2}$ in the presence of the axionic source shows one oscillation and reaches its maximum value $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{max}}=1$ at $\nu =3/2$. Additionally, it is important to note that in Fig. 9b, for $\nu =1/2$ (black dashed line), $\nu =3/2$ (orange dashed line) and $\nu =7/2$ (magenta dashed line) we get the same maximum of the oscillations at $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{max}}=1$.

Next, in Fig. 10a, b, we have explicitly shown the behaviour of the normalised Rényi entropy in $3+1$ D de Sitter space in the absence ($f_p=0$) and the presence ($f_p=10^{-7}$) of the axionic source with respect to the mass parameter $\nu ^2$ where we consider both small and large mass limit situation along with the limit case $q\rightarrow \infty$, which produces the largest eigenvalue of the density matrix. Here it is important to note that the feature obtained for the $q\rightarrow \infty$ case looks similar to the result obtained for normalised entanglement entropy in de Sitter space in $3+1$ D. However, the differences are appearing in the height of the minimum of the oscillations obtained from the $\nu ^2>0$ region. It also establishes that the results obtained for $q\rightarrow \infty$ and $q\rightarrow 1$ are not same. Here also in Fig. 10a, b, for $\nu =1/2$ (black dashed line), $\nu =3/2$ (orange dashed line) and $\nu =7/2$ (magenta dashed line) we get the same maxima of the oscillations at $\left( S_{q,\mathrm{intr}}/S_{q,\nu =1/2}\right) _{\mathrm{max}}=1$.

4 Conclusion

To summarise, in the present article, we have addressed the following points:

• Firstly we have started our discussion with the computational strategy for quantifying the expression for the entanglement entropy in de Sitter space for a bipartite quantum field theory of the axion with a linear contribution in the effective potential as appearing from string theory using a specific compactification technique. Here we consider two subclass of models for axion, in Case I only linear field contribution is appearing and for Case II additionally a quadratic field combination is appearing in the effective potential for axion in $\phi <f_a$ regime.

• Furthermore, we have discussed about the basic setup for computing all possible UV-divergent and UV-finite contribution of the entanglement entropy in $3+1$ dimension. We have also discussed the importance of UV-finite contribution compared to the UV-divergent part to quantify the interesting part of the entanglement entropy.

• Next, we have discussed the geometrical construction and underlying symmetries of the system under consideration in $3+1$ D de Sitter space. Also we have discussed the string theory origin of the axion effective potential and its role in the present context.

• Furthermore, we have derived the expression for the wave function of the axion which is the solution of the field equation in a hyperbolic slice, commonly known as open chart. We have explicitly shown that the total solution can be written as a sum of a complementary solution and a particular solution, which is a completely new solution in the presence of the axion source term in the equation of motion.

• Next using the Bunch–Davies initial condition for the choice of the vacuum state we have written the total solution of the wave function in terms of creation and annihilation operators. Using this fact we construct a suitable basis by applying a Bogoliubov transformation for the Bunch–Davies vacuum state using which we construct the expression for the density matrix by tracing over the exterior region of the prescribed axionic quantum field theory in de Sitter space.

• Furthermore, using the expression for the density matrix and also using the Von Neumann measure of entropy we have derived the new formula for the entanglement entropy in $3+1$ dimensional de Sitter space in the presence of the axion source and we have also checked the consistency of our result by comparing with the result obtained in Ref. [15], which was derived for a free massive scalar field without linear contribution in the effective potential. Here it is important to note that the large mass limit range we have provided the exact analytical expression for the entanglement entropy. But to analyse the correctness of our derived result and to compare with Ref. [15] we have further used numerical techniques to study the behaviour of the entanglement entropy with mass parameter $\nu ^2$ for Case I and Case II.

• Similarly we have computed the modified expression for the Rényi entropy in the presence of the axion source in $3+1$ dimensional de Sitter space using which after taking $q\rightarrow 1$ we have found that in the presence of the axion linear contribution it is not possible to get the exact analytical formula for the entanglement entropy using Von Neumann entropy measure. Once we switch off the contribution from the linear term of the axion in the effective potential we can get back the exact formula for the entanglement entropy as appearing in Ref. [15] by taking the $q\rightarrow 1$ limit. Our analysis also clearly implies that the definition of the Rényi entropy is not universal for any arbitrary structures of the effective potential. Only for a free theory where no such linear contribution appears, the definition is universal. Here the large mass limit range we have provided the exact analytical expression for the Rényi entropy. But to analyse the correctness of our result and to compare with Ref. [15] we have further used numerical techniques to study the behaviour of the entanglement entropy with mass parameter $\nu ^2$ for Case I and Case II. Additionally, by using numerical techniques and taking $q\rightarrow \infty$ we have studied the behaviour of largest eigenvalue of the density matrix with respect to the mass parameter $\nu ^2$ for both cases in the presence of the axion source.

• In this context it is important to mention here that the appearance of non-vanishing entanglement entropy in de Sitter space in $3+1$ D directly verifies the correctness of the existence of the one point function in primordial cosmology due to axionic pair. Moreover, it is one of the important facts of cosmological evolution of our universe and temperature fluctuations of the Cosmic Microwave Background (CMB) originating from quantum fluctuations during the initial inflationary era as it acts as a theoretical tool using which one might be able to lift the degeneracy amongst the cosmological predictions of various models.

The future prospects of our work are appended below:

• In our analysis we choose Bunch–Davies vacuum state to specify the solution of wave function. Also it is used to determine rest of the quantities related to quantum entanglement. In future one can generalise this study of quantum entanglement in de Sitter space in the presence of the axion using $\alpha$ vacua [91].

• Using this prescribed methodology one can further derive the expression for two point and any other higher n point correlation function in superhorizon, subhorizon and horizon crossing scale to study the cosmological consequences of quantum fluctuation using the Bunch–Davies vacuum and the $\alpha$ vacua.

• The conditions for violation of Bells inequality in the context of primordial cosmology are fixed by the further study of the quantum state in detail. In this connection computation of quantum discord, entanglement negativity and other possible strong measures in the presence of the axion will also play an important role. We have not addressed all these issues in this paper.

Appendices

Appendix

1.1 A Derivation of the entanglement entropy

For Case I and Case II the expressions for the entanglement entropy can be expressed as a sum over four contributions, which can be expressed as

$$\begin{aligned} S(p,\nu )= & {} \sum ^{4}_{m=1}\Delta _{m}(p,\nu ), \end{aligned}$$

(A.1)

where the four explicit contributions in terms of the functions $\Delta _{m}(p,\nu )\forall m=1,2,3,4$ as appearing in the entanglement entropy is given by

$$\begin{aligned}&\Delta _{1}(p,\nu )=-\mathbf{\mathrm Tr}\left[ \frac{\left( 1-|\gamma _{p}|^2\right) }{1+f_p}\sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right. \nonumber \\&\quad \times \left. \ln \left( \frac{\left( 1-|\gamma _{p}|^2\right) }{1+f_p}\sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right) \right] \nonumber \\&\quad =-\ln \left( 1-|\gamma _{p}|^2\right) -\frac{|\gamma _{p}|^2}{\left( 1-|\gamma _{p}|^2\right) }\ln \left( |\gamma _{p}|^2\right) \nonumber \\&\qquad +f_p\ln \left( 1+f_p\right) , \end{aligned}$$

(A.2)

$$\begin{aligned}&\Delta _{2}(p,\nu )=-\mathbf{\mathrm Tr}\left[ \frac{f^2_p}{1+f_p}\sum ^{\infty }_{n=0}\right. \nonumber \\&\quad \sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r}|n,r;p,l,m\rangle \langle n,r;p,l,m|\nonumber \\&\qquad \left. \times \ln \left( \frac{\left( 1-|\gamma _{p}|^2\right) }{1+f_p}\sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right) \right] \nonumber \\&\quad =-\frac{f_p}{1+f_p}\left[ \ln \left( 1-|\gamma _{p}|^2\right) +\frac{|\gamma _{p}|^2}{\left( 1-|\gamma _{p}|^2\right) }\ln \left( |\gamma _{p}|^2\right) \right] , \end{aligned}$$

(A.3)

$$\begin{aligned}&\Delta _{3}(p,\nu )=-\mathbf{\mathrm Tr}\left[ \frac{\left( 1-|\gamma _{p}|^2\right) }{1+f_p}\sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right. \nonumber \\&\qquad \left. \times \ln \left( 1+\left( 1-|\gamma _{p}|^2\right) ^{-1}f^2_p \right. \right. \nonumber \\&\qquad \left. \left. \times \left( \sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right) ^{-1}\right. \right. \nonumber \\&\qquad \left. \left. \times \left( \sum ^{\infty }_{n=0}\sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r}|n,r;p,l,m\rangle \langle n,r;p,l,m|\right) \right) \right] \nonumber \\&\quad =-\frac{1}{1+f_p}\ln \left( 1+f_p \right) , \end{aligned}$$

(A.4)

$$\begin{aligned}&\Delta _{4}(p,\nu )=-\mathbf{\mathrm Tr}\left[ \frac{f^2_p}{1+f_p}\sum ^{\infty }_{n=0}\right. \nonumber \\&\qquad \left. \times \sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r}|n,r;p,l,m\rangle \langle n,r;p,l,m|\right. \nonumber \\&\qquad \left. \times \ln \left( 1+\left( 1-|\gamma _{p}|^2\right) ^{-1}f^2_p \right. \right. \nonumber \\&\qquad \left. \left. \times \left( \sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right) ^{-1}\right. \right. \nonumber \\&\qquad \left. \left. \times \left( \sum ^{\infty }_{n=0}\sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r}|n,r;p,l,m\rangle \langle n,r;p,l,m|\right) \right) \right] \nonumber \\&\quad =-\frac{f_p}{1+f_p} \ln \left( 1+f_p\right) . \end{aligned}$$

(A.5)

Consequently the expression for the entanglement entropy in terms of the complementary and particular part of the obtained solution can be expressed as

(A.6)

B Derivation of the Rényi entropy

For Case I and Case II the expressions for the Rényi entropy can be expressed as a sum over four contributions, which can be expressed as

$$\begin{aligned} S_{q}(p,\nu )= & {} \sum ^{3}_{m=1}V_{m,q}(p,\nu ), \end{aligned}$$

(B.1)

where the four explicit contributions in terms of the functions $V_{m,q}(p,\nu )\forall m=1,2,3$ as appearing in the entanglement entropy is given by

$$\begin{aligned}&V_{1,q}(p,\nu )\nonumber \\&\quad =\frac{1}{1-q}\ln \left[ \mathbf{\mathrm Tr}\left\{ \left( \frac{\left( 1-|\gamma _{p}|^2\right) }{1+f_p}\right) ^q\right. \right. \nonumber \\&\ \ \quad \left. \left. \times \left( \sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right) ^q\right\} \right] \nonumber \\&\quad =\left[ \frac{q}{1-q}\ln \left( 1-|\gamma _{p}|^2\right) \right. \nonumber \\&\ \ \left. \quad -\frac{1}{1-q}\ln \left( 1-|\gamma _{p}|^{2q}\right) \right] -\frac{q}{1-q}\ln \left( 1+f_p\right) , \end{aligned}$$

(B.2)

$$\begin{aligned}&V_{2,q}(p,\nu )=\frac{1}{1-q}\ln \left[ 1\right. \nonumber \\&\quad \left. +\sum ^{q}_{k=1}{}^{q}C_{k}{} \mathbf{Tr}\left\{ \frac{(f_p)^{2k}}{(1+f_p)^k}\right. \right. \nonumber \\&\quad \left. \left. \times \left( \sum ^{\infty }_{n=0}\sum ^{\infty }_{r=0}|\Gamma _{p,n}|^{2r}|n,r;p,l,m\rangle \langle n,r;p,l,m|\right) ^{k}\right\} \right. \nonumber \\&\quad \ \times \left. \mathbf{Tr}\left\{ \left( \frac{\left( 1-|\gamma _{p}|^2\right) }{1+f_p}\right) ^{-k}\left( \sum ^{\infty }_{k=0}|\gamma _{p}|^{2k}|k;p,l,m\rangle \langle k;p,l,m|\right) ^{-k}\right\} \right] \nonumber \\&\quad =\frac{1}{1-q}\ln \left[ 1+\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-|\gamma _{p}|^2\right) ^{-k}}{\left( 1-|\gamma _{p}|^{-2k}\right) }\right] . \end{aligned}$$

(B.3)

Consequently the expression for the entanglement entropy in terms of the complementary and particular part of the obtained solution can be expressed as

$$\begin{aligned} S_{q}(p,\nu )= & {} \left[ \frac{q}{1-q}\ln \left( 1-|\gamma _{p}|^2\right) \right. \nonumber \\&\left. - \frac{1}{1-q}\ln \left( 1-|\gamma _{p}|^{2q}\right) \right] -\frac{q}{1-q}\ln \left( 1+f_p\right) \nonumber \\&+\frac{1}{1-q}\ln \left[ 1+\sum ^{q}_{k=1}{}^{q}{} \mathbf{C}_{k} (f_p)^{k }\frac{\left( 1-|\gamma _{p}|^2\right) ^{-k}}{\left( 1-|\gamma _{p} |^{-2k}\right) }\right] .\nonumber \\ \end{aligned}$$

(B.4)