1 Introduction

The observational data indicates that the present universe is expanding as well as accelerating [1, 2]. Many theoretical models have been proposed to interpret this recent acceleration either by modifying the right hand side of the Einstein’s gravity equation with specific forms of the energy momentum tensor \(T_{\mu \nu }\), which can cause a negative pressure, or by modifying the left hand side, i.e. the geometry of the space time. In the first approach, one need an exotic cosmic component, dubbed “dark energy”, with equation of state satisfying, \(\omega <-\frac{1}{3}\). The most successful model of the universe, which explains the recent acceleration of the universe, is the standard \(\varLambda \)CDM model. This model incorporates the cosmological constant \( \varLambda \), characterised by the equation of state \( \omega _{\varLambda }=- 1,\) as the dark energy. Even though this model fits substantially well with the observational data, it is faced with some drawbacks, mainly the coincidence problem and the cosmological constant problem. The model is unable to explain the observed coincidence between the densities of non-relativistic matter and cosmological constant of the current universe, known as the coincidence problem. The cosmological constant problem is regarding the large discrepancy between the theoretically predicted value of the cosmological constant and its observed value. The value of the cosmological constant predicted from field theoretical estimation is about \(10^{121}\) times larger than the observed value. To alleviate these problems, time varying dark energy models have been considered. For the various models of dynamical dark energy, one may refer the review [3] and the references therein. There are two main classes of dark energy models, the quintessence models [4, 5], with equation of state \(\omega >- 1,\) and phantom dark energy models with \( \omega <- 1. \) Compared to the quintessence form, phantom dark energy leads to unusual cosmological scenarios, like big-rip [6] where the universe may undergo super-exponential expansion, which effectively rip away the structures in the long run of the expansion of the universe.

There are attempts to explain the recent acceleration without invoking the exotic dark energy component. It was shown by several authors that a bulk viscous dark matter can cause an accelerated expansion of the universe. The effect of bulk viscosity was primarily analysed in the context of acceleration in the early universe, the inflationary epoch [7]. In recent times, the effect of bulk viscous matter in causing the late acceleration was analysed by many [8,9,10,11,12,13,14]. In a recent review, Brevik et al. [15] have shown important implications and capabilities of viscosity in describing inflationary era and late time acceleration of the universe; see also Ref. [16].

The detailed mechanism for the origin of bulk viscosity in the universe is still not correctly understood. From the theoretical point of view, the bulk viscosity can originate due to the deviation from the local thermodynamic equilibrium. It manifest as an effective pressure to bring back the system to its thermal equilibrium, which was broken when the cosmological fluid expands (or contracts) too fast. The bulk viscosity pressure thus generated, ceases as soon as the fluid reaches the equilibrium condition.

There exist two main formalism to account for the bulk viscosity in cosmological theories, the non-causal theory where the dissipative perturbations propagate with infinite speed, and the causal theory, where the perturbations are propagating with finite speed. The non-causal formalism was developed by Eckart [17] and many used it in cosmology due to its easiness in analysing the evolutionary behaviour of the cosmological parameters. Later Landau and Lifshitz [18] gives an equivalent formalism. The causal formalism was developed mainly by Israel, Stewart and Hiscock [19,20,21,22,23].

In Eckart theory only the first order deviation from the equilibrium is considered, which effectively leads to the superluminal velocities of the dissipative signals, hence the theory is non-causal [19]. Moreover, the resulting equilibrium states are unstable. However, it illustrates a linear relationship between the bulk viscous pressure and the rate of expansion [24] of the universe. This facilitates the easy analytical method for the parameters in the context of expanding universe.

Based on the Eckart formalism, Brevik and Gorbunova [25] have shown that the viscosity associated with matter, proportional to the expansion rate, can drive the universe into a phantom epoch. Fabris et al. [8] have considered a model with viscous coefficient proportional to \(\rho ^{\nu }\) (where \(\rho \) is the density and \(\nu \) is a constant) and have shown that, for \(\nu =-\left( \alpha +\frac{1}{2}\right) ,\) (\(\alpha \) is defined by the Chaplygin gas equation for pressre \(p=-A/\rho ^{\alpha }\)) the model predicts a late acceleration similar to the generalised Chaplygin gas model of dark energy. They have also concluded that, even though the model is similar to the Chaplygin gas model at the background level, it does not show any oscillations in the power spectrum that plaugues the generalised Chaplygin gas model. This can be considered as a positive indication of bulk viscous models. Later Avelino et al. [26] have studied the bulk viscous matter model using the Eckart formalism, where the bulk viscosity were taken to be proportional to both the velocity and the acceleration of the universe. They have shown that the model can in general predict the late acceleration of the universe. These authors also addressed the asymptotic behaviour of this model and argued that the models are not stable asymptotically. Later in a more general analysis on bulk viscous matter dominated model of the universe based on the Eckart formalism by Athira and Mathew [13], they have proved that the model has considerably good background evolution and is asymptotically stable if the bulk viscous coefficient is a constant. All these analyses were based on the non-causal theory of viscosity. But for physically sound conclusions, one must use the causal theory of bulk viscosity.

As mentioned earlier the causal theory of viscosity was proposed by Israel and Stewart [21, 22], taking into account the higher order deviations from the equilibrium, especially the second order deviations, which results in the proper causal connection in the theory. Unlike Eckart theory, the equilibria arising are stable [27]. Moreover, the Eckart theory can be obtained from it as a first order approximation. In certain studies, a truncated version of this theory has been used, where they omit some divergence terms in the expression for the evolution of the bulk viscous pressure, which contains terms corresponding to second order deviations [23, 28] from equilibrium.

Initial work where the full causal theory has been used in the context of the inflation occurring during the early period of the evolution of the universe. Maartens and Mendez [29] studied the early inflation caused by bulk viscous cosmic fluid using the full causal theory and found that the resulting solutions are thermodynamically consistent. Another interesting study of the cosmology of flat FLRW bulk viscous universe is in Ref. [30], where the authors find exact solutions corresponds to the early inflationary phase of the universe with a bulk viscous coefficient proportional to the Hubble parameter. In a later work by the same authors using full causal theory, a new class of exact solutions were found by reducing the evolutionary equations of the universe to Abel-type first order differential equations [31]. Zimdahl [32] combined the equivalence between cosmological particle creation and effective viscous fluid pressure using the Israel–Stewart model, finding that there exists an inherent self-limitation to the effective bulk viscous pressure due to the adiabatic particle production. One obtained solutions which indicates a transition from the inflationary phase to later non-inflationary epoch. Zakari and Jou [33] also studied the viscous driven inflationary epoch using the causal theory. Cooley et al. [34] analysed the entropy production in a viscous universe using Israel–Stewart theory. Our concern here is the use of causal viscous formalism in analysing the late accelerating epoch of the universe. We would say that such studies are comparatively less in number in the literature.

After the discovery of the late acceleration of the universe, the full causal theory of viscosity have been used to analyse the late stage of the universe having viscous cosmic components. Cataldo et al. [35] have analysed the possibility of late acceleration, using Israel–Stewart formalism of bulk viscosity. In this work, the authors have used an ansatz for the Hubble parameter (inspired from the non-causal theory), and they have shown that the universe might have undergone a transition to the phantom behaviour leading to big-rip singularity. Piattella et al. [36] have considered a bulk viscous universe using a full causal theory with the aim of unifying dark matter and dark energy. They have found numerical solutions to the gravitational potential using an ansatz for the viscous pressure depends on the density of the viscous fluid and compared it with the standard \(\varLambda \)CDM model. Their conclusion is that, in gross comparison with the standard \(\varLambda \)CDM model, the viscous model with the full causal theory leads to some disfavoured features compared to the truncated version of the model. So by and large in solving the viscous model using the causal theory, it seems that many have used some ansatz either for the Hubble parameter or for the viscous pressure. In the present study, we investigate the evolution of a bulk viscous matter dominated universe using the Israel–Stewart theory of bulk viscosity. We are trying to get the cosmic history by obtaining analytical solutions of the Friedmann equations.

The paper is organised as follows: in Sect. 2 the Hubble parameter for the bulk viscous matter dominated universe is obtained, the behaviour of the scale factor is analysed and the age of the universe is calculated. The evolution of cosmological parameters such as the deceleration parameter, the equation of state parameter, the matter density evolution and the curvature scalar have been discussed in Sect. 3. In Sect. 4, the validity of the local and generalised second law of thermodynamics has been investigated. Sections 5 and 6 deal with the statefinder analysis and estimation of the model parameters, respectively. The conclusions of this study are given in Sect. 7.

2 FLRW universe dominated with bulk viscous matter

A spatially flat, homogeneous and isotropic universe is described by the Friedmann–Lemaitre–Robertson–Walker (FLRW) metric,

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+a(t)^{2}(\mathrm{d}r^{2}+r^{2}\mathrm{d}\theta ^{2}+r^{2}\sin ^{2}\theta \mathrm{d}\phi ^{2}), \end{aligned}$$
(1)

where \((r,\theta ,\phi )\) are the co-moving coordinates, t is the cosmic time and a(t) is a scale factor of the universe. The Friedmann equations describing the evolution of the flat universe, dominated by bulk viscous matter, are

$$\begin{aligned}&H^{2}=\frac{\rho _{m}}{3} \end{aligned}$$
(2)
$$\begin{aligned}&2\frac{\ddot{a}}{a}+\left( \frac{\dot{a}}{a}\right) ^{2}=-P_\mathrm{eff} \end{aligned}$$
(3)

where \(H=\frac{\dot{a}}{a}\) is the Hubble parameter, \( \rho _{m} \) is the matter density, \( P_\mathrm{eff} \) is the effective pressure. An overdot represents the derivative with respect to cosmic time t and we have taken \(c= 8\pi G=1.\) The conservation equation for the viscous fluid is

$$\begin{aligned} \dot{\rho }_{m}+3H(\rho _{m}+P_\mathrm{eff})=0. \end{aligned}$$
(4)

In these equations \(P_\mathrm{eff}\) is given by

$$\begin{aligned} P_\mathrm{eff}=p+\varPi , \end{aligned}$$
(5)

where p is the normal pressure, given by \( p=(\gamma - 1)\rho \), \( \gamma \) is the barotropic index and \( \varPi \) is the bulk viscous pressure. The radiation component is avoided and it is a rational simplification as long as we are concerned with the late time evolution of the universe. The bulk viscous pressure in Eckart’s theory is of the form \(\varPi =-3H\xi \), where \( \xi \) is the term representing the bulk viscosity of the fluid and as a transport coefficient it can be a function of the Hubble parameter of the universe. For sufficiently large \(\xi \), it is possible that the negative pressure term can dominate and an accelerating cosmology can arise.

According to Israel–Stewart causal theory, the effective pressure satisfies the condition

$$\begin{aligned} \tau \dot{\varPi }+\varPi =-3\xi H-\frac{1}{2}\tau \varPi \left( 3H+\frac{\dot{\tau }}{\tau }-\frac{\dot{\xi }}{\xi }- \frac{\dot{T}}{T}\right) , \end{aligned}$$
(6)

where \(\tau \), \( \xi \) and T are the relaxation time, bulk viscosity and temperature, respectively, and they are functions of the density of the fluid in general, defined by the following equations [37]:

$$\begin{aligned} \tau= & {} \alpha \rho ^{s-1}, \end{aligned}$$
(7)
$$\begin{aligned} \xi= & {} \alpha \rho ^{s} ,\end{aligned}$$
(8)
$$\begin{aligned} T= & {} \beta \rho ^{r}, \end{aligned}$$
(9)

where \(\alpha \), \(\beta \) and s are constant parameters satisfying the conditions, \( \alpha \ge 0 \) and \( \beta \ge 0 \) and \( r=\frac{\gamma -1}{\gamma } \). For relaxation time \(\tau =0\), the differential equation for \(\varPi \) reduces to the simple Eckart equation for the viscous pressure. Avoiding the second term on the right hand side of the equation will result in the so-called truncated equation.

The Friedmann equation (2) can be combined with Eqs. (4) and (5) to express the bulk viscous pressure \(\varPi \) as

$$\begin{aligned} \varPi =- [2\dot{H}+3H^2+(\gamma -1)\rho ], \end{aligned}$$
(10)

and the time derivative is

$$\begin{aligned} \dot{\varPi }=- [2\ddot{H}+6H\dot{H}+(\gamma -1)\dot{\rho } ]. \end{aligned}$$
(11)

Then the evolution of the bulk viscosity as given by Eq. (6) can be expressed as

$$\begin{aligned}&\ddot{H} + \frac{3}{2} [1+(1-\gamma ) ]H\dot{H} \nonumber \\&\quad +3^{1-s}\alpha ^{-1}H^{2-2s}\dot{H}-(1+r)H^{-1}\dot{H^{2}}\nonumber \\&\quad +\frac{9}{4}(\gamma -2)H^{3}+\frac{1}{2}3^{2-s}\alpha ^{-1}\gamma H^{4-2s}=0, \end{aligned}$$
(12)

where we have used the density dependence of \(\tau ,\) \( \xi \) and T as given previously. We are considering non-relativistic matter for which \( \gamma =1 \) and we also took \( s=\frac{1}{2} \) [38], implying that the bulk viscosity is directly proportional to the Hubble parameter. The above equation then takes the form

$$\begin{aligned} \ddot{H}+b_1H\dot{H}-H^{-1}\dot{H^{2}}+b_2H^{3}=0, \end{aligned}$$
(13)

where \( b_1 \) and \(b_2\) are taken as

$$\begin{aligned} b_1=3\left( 1+\frac{1}{\sqrt{3}\alpha } \right) , \quad b_2=\frac{9}{4}\left( \frac{2}{\sqrt{3}\alpha }-1 \right) . \end{aligned}$$
(14)

For calculational purposes we change the variable from cosmic time t to \( x = \ln a \); then the above differential equation becomes

$$\begin{aligned} \frac{\mathrm{d}^2 H}{\mathrm{d} x^2}+b_1\frac{\mathrm{d} H}{\mathrm{d} x}+b_2H=0. \end{aligned}$$
(15)

On solving this we obtained the evolution of the Hubble parameter:

$$\begin{aligned} H=H_0 (C_1 a^{-m_1}+C_2a^{-m_2}), \end{aligned}$$
(16)

where \( H_0\) is the present Hubble parameter,

$$\begin{aligned} C_1= & {} \frac{1+\sqrt{1+6\alpha ^{2}}-\sqrt{3}\alpha \tilde{\varPi _0}}{2\sqrt{1+6\alpha ^{2}}},\end{aligned}$$
(17)
$$\begin{aligned} C_2= & {} \frac{-1+\sqrt{1+6\alpha ^{2}}+\sqrt{3}\alpha \tilde{\varPi _0}}{2\sqrt{1+6\alpha ^{2}}}, \end{aligned}$$
(18)
$$\begin{aligned} m_1= & {} \frac{\sqrt{3}}{2\alpha } (\sqrt{3} \alpha +1-\sqrt{1+6\alpha ^{2}} ), \end{aligned}$$
(19)

and

$$\begin{aligned} m_2=\frac{\sqrt{3}}{2\alpha } (\sqrt{3}\alpha +1+\sqrt{1+6\alpha ^{2}}). \end{aligned}$$
(20)

In Eqs. (17) and (18), \( \tilde{\varPi _0}=\frac{\varPi }{3H_{0}^{2}} \) is the dimensionless bulk viscous pressure parameter and constants \(C_1\) and \(C_2\) together satisfies, \( C_1 + C_2=1.\) However, we could obtain the behaviour of Hubble parameter by numerical methods. For this purpose, we evaluated the parameters, \(\alpha , \tilde{\varPi _0}\) and the present Hubble parameter \(H_0\) in the present model using the cosmological data on supernovae (see Sect. 6). In Fig. 1, the evolution of the Hubble parameter with scale factor corresponding to the best estimated values of model parameters is shown. The limit of zero viscosity in the non-relativistic matter implies \(\alpha \rightarrow 0,\) equivalently the viscous pressure \(\varPi \rightarrow 0,\) and the Hubble parameter will reduces to, \( H \sim a^{-{3}/{2}}\), which corresponds to the ordinary (non-viscous) matter dominated phase. Equation (16) also shows that the Hubble parameter will become infinite as \(a \rightarrow 0\). Hence the density will also become infinite at the origin, which suggests the presence of the big bang at the origin.

Fig. 1
figure 1

The evolution Hubble parameter H with scale factor a for the best estimated values of the model parameters

Full size image

2.1 Behaviour of the scale factor

The Hubble parameter given in Eq. (16) can be integrated, resulting in

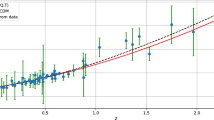
$$\begin{aligned}&a^{m_1}{_2F_1}\left[ 1,\frac{m_1}{m_1-m_2}, \quad 1+\frac{m_1}{m_1-m_2}\frac{a^{m_1-m_2} C_2}{C_1}\right] \nonumber \\&\quad =C_1 m_1 H_0(t-t_0)\nonumber \\&\qquad +{_2F_1}\left[ 1,\frac{m_1}{m_1-m_2},1+\frac{m_1}{m_1-m_2},-\frac{C_2}{C_1}\right] , \end{aligned}$$
(21)

where \({_2F_1}[\ldots ]\) is the hyper-geometric function with respective arguments. It is to be noted that the hyper-geometric function on the left hand side itself depends on the scale factor. This equation can be used to assess the evolution of the scale factor. The nature of the evolution of a(t) is not explicitly evident from the above equation due to the appearance of hyper-geometric functions in the equation. The behaviour of the scale factor with \( H_{0}(t-t_0) \) for the best estimated values of parameters is shown in Fig. 21.

Fig. 2
figure 2

The evolution of the scale factor a with \(H_0(t-t_0)\) for the best estimated values of the model parameters

Full size image

The scale factor is approximately linear at sufficiently early time, which corresponds to the decelerated epoch, and it evolves exponentially with time in the extreme future epoch, corresponding to the de Sitter phase. This asymptotic behaviour indicates the transition from the early decelerated phase to a later accelerated expansion of the universe. The figure also shows that as \(t \rightarrow 0\), the scale factor \(a \rightarrow 0,\) indicating the presence of the big bang at the origin, hence the age of the universe is properly defined. On comparing with the corresponding model using the Eckart formalism [13] (in which the viscosity is taken to be proportional to both the velocity and the acceleration of the universe) the evolution of the scale factor in the present model is almost similar.

The transition redshift \(z_T,\) corresponding to the switch-over from deceleration to acceleration, can be obtained as follows. From the Hubble parameter in Eq. (16), the derivative of \( \dot{a} \) with respect to a can be written as

$$\begin{aligned} \frac{\mathrm{d}\dot{a}}{\mathrm{d}a}=H_{0} [C_{1}(1-m_{1})a^{-m_1}+C_2(1-m_{2})a^{-m_2} ]. \end{aligned}$$
(22)

Equating this to zero, we can get the transition scale factor \( a_{T} \):

$$\begin{aligned} a_{T}=\left[ -\dfrac{C_{2}(1-m_{2})}{C_{1}(1-m_{1})}\right] ^{\frac{1}{m_{2}-m_{1}}}, \end{aligned}$$
(23)

then the transition redshift \( z_{T} \) can be written

$$\begin{aligned} z_{T}=\left[ -\dfrac{C_{2}(1-m_{2})}{C_{1}(1-m_{1})}\right] ^{-\frac{1}{m_{2}-m_{1}}}-1. \end{aligned}$$
(24)

For the best estimated values of the parameters, the transition redshift is \( z_{T}\sim 0.52^{+0.010}_{-0.016} \). This is within the WMAP range \(z_T=(0.45-0.73)\) [39]. In Ref. [13], the authors have estimated the transition redshift for a bulk viscous universe using the Eckart formalism to be around 0.49. In the present study using the causal formalism, we have considered only the velocity dependence for the bulk viscous coefficient and the transition is found to have occurred slightly earlier.

Fig. 3
figure 3

The age of the universe in Gyr with \(H_0\) in km s\(^{-1}\) Mpc\(^{-1}\). The point marked in the plot corresponds to the age 9.72 Gyr, obtained in the model for the best estimated values of the parameters

Full size image

2.2 The age of the universe

The age of the universe can be determined from the scale factor, Eq. (2). On equating the scale factor to zero for \(t=t_B,\) the big-bang time, the age \(t_0 - t_B\) of the universe can be obtained. The age for different values of \(H_0\) is shown in Fig. 3, where we have used the best estimate of the model parameters. An estimation using the scale factor equation will lead to a simple equation for the age:

$$\begin{aligned} t_0-t_B=0.6985 H_0^{-1}. \end{aligned}$$
(25)

The age of the universe corresponds to the best estimates of \( \alpha \), \( \tilde{\varPi _{0}} \) and \( H_0 \) and is found to be around 9.72 Gyr. This is considerably less than the standard value of the age, 13.74 Gyr, deduced from CMB anisotropy data [40], and \(12.9 \pm 2.9\) Gyr, from the oldest globular clusters [41]. Also the age from the present model is less than the age in the corresponding model using the Eckart non-causal formalism, around 10.9 Gyr [13].

3 Evolution of other cosmological parameters

3.1 The behaviour of deceleration parameter

The deceleration parameter gives a measure of the rate at which the expansion of the universe is taking place. If the deceleration parameter is positive, then the universe is in decelerating phase and vice versa. The deceleration parameter, q,  can be expressed as

$$\begin{aligned} q= -\frac{\ddot{a}a}{\dot{a}^{2}}=-\frac{\ddot{a}}{a}\frac{1}{H^{2}} =- 1-\frac{\dot{H}}{H^{2}}. \end{aligned}$$
(26)

On substituting the Hubble parameter and its derivative, the deceleration parameter becomes

$$\begin{aligned} q(a)=- 1 + \frac{C_{1} m_{1}a^{-m_{1}}+C_{2} m_{2}a^{-m_{2}}}{C_1 a^{-m_1}+C_2a^{-m_2}}. \end{aligned}$$
(27)

Using the best estimates of the model parameter, the coefficients take the values \(m_1=0.31\) and \(m_2=5.29.\) Hence as \(a \rightarrow \infty \) the term \(a^{-m_2}\) decreases faster than the term \(a^{-m_1},\) hence the \(a^{-m_2}\) term can be neglected, consequently the deceleration parameter in this limit becomes \(q \rightarrow - 1+m_1.\) On the other hand, as \(a \rightarrow 0\), the term \(a^{-m_1}\) becomes negligibly small, and as a result the deceleration parameter becomes \(q \rightarrow -1 + m_2.\)

Fig. 4
figure 4

The evolution of the deceleration parameter q with respect to the redshift z for the best estimated values of the model parameters

Full size image

The deceleration parameter of the current epoch, corresponding to \( z=0 \), is

$$\begin{aligned} q_{0}=- 1+C_1{m_1}+C_2{m_2}=\frac{1}{2} (1+3 \tilde{\varPi _0} ). \end{aligned}$$
(28)

For the best estimated values of \( \alpha \) and \( \tilde{\varPi _0},\) the present value of the deceleration parameter is found to be \( q_0\sim - 0.59^{+ \ 0.015}_{- 0.016},\) which is quite close to the WMAP value, \(q_0=- 0.60\) [39]. By using Eckart theory and taking the velocity and acceleration dependence for the bulk viscous coefficient, we have \(q_0 \sim - 0.64\) [13]. The evolution of q is shown in Fig. 4. From the figure it is seen that the deceleration parameter will be stabilised around \(-0.7\) in the far future of the evolution of the universe and this is in confirmation with the previously obtained limit \(q=-1+m_1 \sim - 0.7.\) So even though the present model is predicting a never-ending accelerating phase, the universe is not reaching the exact de Sitter phase and this is in marked deviation from the corresponding models using the Eckart formalism [13], in which the model evolves asymptotically to the de Sitter phase. The evolution of the parameter q shows that the model is within the quintessence class. In the earlier epoch, the value of q is positive and considerably large, around \(q \sim 4,\) and it is in confirmation with the previously obtained asymptotic limit \(q=- 1+m_2.\) In the corresponding model with the Eckart formalism, the deceleration parameter was found to be around \(q \sim 2\) in the remote past of the universe [13]. So the viscous matter behaves as a hard stiff fluid in the earlier epoch and evolves to a negative pressure fluid in the later phase. In this sense, the present model seems to be similar, except for the fact that in the Eckart formalism the model will ultimately evolve to de Sitter phase, while in the causal formalism the fluid is comparatively stiffer in the earlier phase but not ending with an exact de Sitter phase ultimately.

Fig. 5
figure 5

The evolution of equation of state parameter \(\omega \) with redshift z for the best estimated value of model parameters

Full size image

3.2 Evolution of equation of state parameter

The equation of state parameter \( \omega \) has a significant effect on the future expansion profile of the universe. The universe enters the accelerating epoch when \( \omega <-\frac{1}{3} \). The equation of state can be obtained from the Hubble parameter using the relation

$$\begin{aligned} \omega =-1-\frac{1}{3}\frac{\mathrm{d} \ln h^{2}}{\mathrm{d}x}, \end{aligned}$$
(29)

where \( h=\frac{H}{H_{0}} \) and \( x=\ln a \). Substituting the expression for the Hubble parameter, the equation of state parameter is found to be

$$\begin{aligned} \omega =-1+\frac{2(C_1m_1 a^{-m_1}+C_2m_2a^{-m_2})}{3\left( {C_1 a^{-m_1}+C_2a^{-m_2}}\right) }. \end{aligned}$$
(30)

Since as per the best estimates of the model parameters, \(m_2>m_1,\) in the limiting condition \(a \rightarrow \infty ,\) the equation of state parameter is \(\omega \rightarrow -1+\frac{2}{3}m_1 \sim -0.79,\) which corresponds to its quintessence nature. At \(a \rightarrow 0,\) it becomes \(\omega \rightarrow -1+\frac{2}{3}m_2 \sim 2.5\) and this corresponds to stiff fluid characteristics. So the viscous matter, being of a stiff fluid nature in the past, evolves to the characteristic of a fluid capable of providing negative pressure as the universe expands. In the Eckart formalism approach, the bulk viscous matter behaves as a stiff fluid with an equation of state equal to \(+ \) 1 in the past and it becomes \(- \) 1 corresponding to the de Sitter phase. The present value of the equation of state parameter is

$$\begin{aligned} \omega _{0}=-1+\frac{2(C_{1}m_{1}+C_{2}m_{2})}{3}, \end{aligned}$$
(31)

and with the best estimated values of the model parameters, it comes to be around \(\omega _0 \sim -0.73^{+0.01}_{-0.01}\) and slightly higher than the value obtained by the combined analysis of WMAP + BAO + \(H_{0}\) + SN data, around \(-\, 0.93\) [42, 43]. The evolution of the equation of state parameter with redshift for best estimated values of the model parameters is shown in Fig. 5. At this juncture one should note the work by Brevik et al. [44] analysing the possibility of a little rip in which the equation of state approaches \(- \) 1 asymptotically from below. In their work they have used a very special equation of state, \(p=-\rho -f(\rho )-\xi (H),\) where \(f(\rho )\) is a chosen function of the density of bulk viscous matter and \(\xi (H)\) is the bulk viscous pressure, depending on the Hubble parameter. They have shown the possibility of a little rip with some assumed form for \(f(\rho ).\) On the other hand we have not used any such pre-assumed form for the equation of state. There are also some results telling us that the bulk viscous matter can lead to phantom nature in the early period of the universe [29,30,31]. In the present analysis using the causal viscous formalism due to Israel and Stewart, we get the result that the bulk viscous matter will behave like a strong stiff fluid in the early period and it shows the behaviour of the quintessence dark energy in the later universe, such that the equation of state is stabilised at around \(\omega \sim - 0.79\) in the far future of the evolution of the universe.

3.3 Evolution of the matter density

The matter density parameter is defined by

$$\begin{aligned} \varOmega _{m}=\frac{\rho _{m}}{\rho _{crit}}, \end{aligned}$$
(32)

where \( \rho _{crit}=3H_{0}^{2} \) is the critical density. Using Eqs. (2) and (16) we get

$$\begin{aligned} \varOmega _{m}(a)=(C_{1}a^{-m_{1}}+C_{2}a^{-m_{2}})^{2}. \end{aligned}$$
(33)

From the above equation the present matter density parameter, \( \varOmega _{m_{0}}\), can be obtained by taking the scale factor \( a=1 \). We get

$$\begin{aligned} \varOmega _{m_{0}}=(C_1+C_2)^{2}=1, \end{aligned}$$
(34)

since in the present model only matter is the major component. For zero bulk viscosity and bulk viscous pressure, the parameter takes the value \( C_{1}=1 \), \( C_{2}=0 \) and \( m_{1}\sim \frac{3}{2} \), respectively, \( \varOmega _{m}(a)\sim a^{-3} \), for the usual matter dominated universe. From Eq. (33), it is seen that as \(a \rightarrow \infty \) the density will go to \(\varOmega _m \rightarrow a^{-2m_1}\), while as \(a \rightarrow 0\) it behaves as \(\varOmega _m \rightarrow a^{-2m_2}.\)

Fig. 6
figure 6

The variation of the matter density parameter \(\varOmega _{m}\) with scale factor a corresponding to the extracted values of the model parameters

Full size image

The evolution of matter density parameter with scale factor for the best estimated values of \( \alpha \) and \( \tilde{\varPi _{0}}\) is shown in Fig. 6. The figure shows that, as the scale factor \( a\rightarrow 0 \), the matter density increases rapidly and approaches an infinitely large value. This implies the big bang at the beginning of the universe. The decreasing nature of density in the future depicts the absence of the big rip. In the overall way the evolution of density parameter in the present model is similar to that using the Eckart formalism [13].

3.4 Evolution of curvature scalar

The evolution of the curvature scalar of the universe enables one to confirm the occurrence of an initial singularity in the model. The curvature scalar R, for a flat universe, is defined as [45]

$$\begin{aligned} R=-6 (\dot{H}+2H^2 ). \end{aligned}$$
(35)

Using the Hubble parameter, the evolution equation of the curvature scalar can be obtained:

$$\begin{aligned} R(a)&=6 H_0^2 a^{-2 (m_1+m_2 )} (a^{m_2} C_1+a^{m_1} C_2 ) \nonumber \\&\quad \times [a^{m_2} C_1(m_1-2) +a^{m_1} C_2 (m_2-2) ]. \end{aligned}$$
(36)

The above equation shows that the curvature scalar \( R\rightarrow \infty \) when \( a \rightarrow 0, \) implying an initial singularity corresponding to the big bang. The behaviour of the curvature scalar with scale factor for the best estimated values of model parameters is shown in Fig. 7. This evolution of the curvature scalar suggests the presence of a big bang at the origin of the universe.

Fig. 7
figure 7

The variation of curvature scalar R against scale factor a for the best estimated values of parameters

Full size image

4 Entropy and second law of thermodynamics

In the FLRW universe the bulk viscosity causes the production of local entropy. The law of production of local entropy on the FLRW space-time is expressed as [46],

$$\begin{aligned} T\nabla _{\nu }S^{\nu }=\xi (\nabla _{\nu }u^{\nu })^2=9H^{2}\xi , \end{aligned}$$
(37)

where T is the temperature and \( \nabla _{\nu }S^{\nu } \) is the rate of generation of entropy in a volume unit. The condition for the validity of the second law of thermodynamics then becomes

$$\begin{aligned} T\nabla _{\nu }S^{\nu }\ge 0. \end{aligned}$$
(38)

This in turn implies that the bulk viscosity must satisfy \( \xi \ge 0\). From Eq. (8), the bulk viscosity for \(s=1/2\) is

$$\begin{aligned} \xi =\alpha \rho ^{{1}/{2}}. \end{aligned}$$
(39)

Substituting Eqs. (2) and (16) in the above equation, we get

$$\begin{aligned} \xi (a)=\sqrt{3} \alpha H_0(C_1 a^{-m_1}+C_2a^{-m_2}). \end{aligned}$$
(40)
Fig. 8
figure 8

The evolution of the bulk viscosity coefficient \(\xi \) with redshift z for the best estimated values of parameters

Full size image

For the best estimates of the model parameters \( m_2>m_1, \) the bulk viscosity has the following behaviour. As \( a \rightarrow 0, \) the bulk viscosity satisfies \( \xi \sim \sqrt{3} \alpha H_0 C_2 a^{-m_{2}}. \) Since the magnitude of \(m_2\) is large, \( \xi \) has a large positive value in the early phase. At \( a \rightarrow \infty \), it evolves to \( \xi \sim \sqrt{3} \alpha H_0 C_1 a^{-m_{1}}. \) Here the value \( \xi \) will be small in the future as the value \(m_1\) is small and will be positive. Corresponding to the present epoch with \( a_0=1, \) the bulk viscosity becomes \( \xi =\sqrt{3}\alpha H_{0}.\) All these together implies that the viscosity \(\xi >0\) always. This in turn implies that the condition given in Eq. (38) always is satisfied, hence the second law of thermodynamics is satisfied throughout the evolution of the universe. The evolution of \( \xi \) with respect to the redshift z, for the best estimated values of parameters is shown in Fig. 8. Therefore the rate of entropy production is always positive. Here also the present model shows remarkable difference from the Eckart formalism model. In analysing the model in the Eckart formalism [13], it was found that the local second law of thermodynamics is violated during an early phase of the universe. Contrary to this, there is no violation of the local second law in the present causal model. In this sense the causal model is to be favoured over the one based on the Eckart formalism. Another distinct behaviour observed in the present model is that the bulk viscosity decreases with time. However, in the Eckart formalism, the bulk viscosity coefficient is increasing from a negative value region to a positive region [13].

The entropy production from the horizon can also be accounted, which leads to the generalised second law (GSL), which states that the sum of the total entropy of the fluid components of the universe and that of the horizon must always increase with time [47, 48]. This can be expressed as

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}(S_{m}+S_{h})\ge 0, \end{aligned}$$
(41)

where \( S_{m} \) and \( S_{h} \) represent the entropy of matter and that of the horizon, respectively. The apparent horizon radius \( r_{A} \), for a spatially flat FLRW universe, is given as [49]

$$\begin{aligned} r_{A}=\frac{1}{H}. \end{aligned}$$
(42)

Using Eqs. (2), (4) and (5) the time derivative of \( r_{A} \) is obtained:

$$\begin{aligned} \dot{r_{A}}=\frac{r_{A}^{2}}{2}(\varPi +\rho _{m}). \end{aligned}$$
(43)

The entropy of the apparent horizon is proportional to the area of the Hubble horizon and is defined as [50]

$$\begin{aligned} S_{h}=2\pi A=8\pi ^{2} r_{A}^{2}, \end{aligned}$$
(44)

where \( A=4\pi r_{A}^{2} \) is the area of the Hubble horizon. The time evolution of the entropy of the horizon is

$$\begin{aligned} \dot{S_{h}}=16\pi ^{2}r_{A}\dot{r_{A}}. \end{aligned}$$
(45)

For the temperature of the apparent horizon we use the relation [51]

$$\begin{aligned} T_{h}=\frac{1}{2\pi r_{A}}\left( 1-\frac{\dot{r_{A}}}{2 H r_{A}}\right) . \end{aligned}$$
(46)

Using Eqs. (42), (43), (45) and (46), we can write

$$\begin{aligned} T_{h}\dot{S_{h}}=4\pi r_{A}^{2}(\varPi +\rho _{m})\left( 1-\frac{\dot{r_{A}}}{2}\right) . \end{aligned}$$
(47)

To determine the change in entropy of the matter component, we can apply the Gibbs relation,

$$\begin{aligned} T_{m}\mathrm{d}S_{m}=\mathrm{d}E+P_\mathrm{eff}\mathrm{d}V, \end{aligned}$$
(48)

where \( T_{m} \) is the temperature of the bulk viscous matter, \( E=\rho _{m}V, \) the total energy of the bulk viscous matter and \( V=\frac{4}{3}\pi r_{A}^{3} \) is the volume enclosed by the Hubble horizon. Using Eq. (5), the Gibbs equation becomes

$$\begin{aligned} T_{m}\mathrm{d}S_{m}=V\mathrm{d}\rho _{m}+(\varPi +\rho _{m})\mathrm{d}V. \end{aligned}$$
(49)

In thermal equilibrium, the temperatures of the viscous matter and that of the horizon are equal, \( T_{m}=T_{h} \). The Gibbs equation (49) can be re-written as

$$\begin{aligned} T_{h}\dot{S_{m}}=4\pi r_{A}^{2}(\varPi +\rho _{m})(\dot{r_{A}}-1). \end{aligned}$$
(50)

The time variation of the total entropy can be obtained by adding Eqs. (47) and (50),

$$\begin{aligned} T_{h}(\dot{S_{h}}+\dot{S_{m}})=\frac{A}{4}r_{A}^{2}(\varPi +\rho _{m})^{2}. \end{aligned}$$
(51)

Since the radius and the area of the apparent horizon are always positive, from Eq. (51) it is evident that \( \dot{S_{h}}+\dot{S_{m}}\ge 0 \), for a given temperature. Hence the GSL is satisfied. Therefore, in the model in the Eckart formalism [13] and in the present model, the generalised second law of thermodynamics is satisfied.

5 Statefinder diagnostic

In [52] Sahni et al. have published a geometric diagnostic technique for contrasting various models of dark energy. For all models predicting the Hubble parameter, scale factor, deceleration parameter etc., to distinguish between the models, it is better to use quantities involving higher derivatives of H or the scale factor. The statefinder parameter pair \(\lbrace r,s \rbrace \) introduced by them depends on the third order derivative of the scale factor. A characteristic property of the statefinder parameter pair is that \( \lbrace {r,s}\rbrace =\lbrace {1,0}\rbrace ,\) is a fixed point for the \( \varLambda \)CDM model. Evolutionary trajectories of these parameters and their difference from the fixed \(\varLambda \)CDM point distinguishes the models from each other and also from the standard \( \varLambda \)CDM model. The statefinder parameters are defined as

$$\begin{aligned} r= & {} \frac{\dddot{a}}{aH^{3}}=\frac{1}{2h}\frac{\mathrm{d}^{2}h^{2}}{\mathrm{d}x^{2}} +\frac{3}{2h^{2}}\frac{\mathrm{d}h^{2}}{\mathrm{d}x}+1, \end{aligned}$$
(52)
$$\begin{aligned} s= & {} \frac{r-1}{3\left( q-\frac{1}{2}\right) }=-\left( \frac{\frac{1}{2h}\frac{\mathrm{d}^{2}h^{2}}{\mathrm{d}x^{2}}+\frac{3}{2h^{2}}\frac{\mathrm{d}h^{2}}{\mathrm{d}x}}{\frac{3}{2h^{2}}\frac{\mathrm{d}h^{2}}{\mathrm{d}x} +\frac{9}{2}}\right) . \end{aligned}$$
(53)

For the present bulk viscous matter dominated model, these parameters take the form

$$\begin{aligned} r= & {} \frac{r_1+r_2+a^{m} C_1 C_2 \left( m-2\right) \left( m-1\right) }{\left( a^{m_2} C_1+a^{m_1} C_2\right) ^2}, \end{aligned}$$
(54)
$$\begin{aligned} s= & {} \frac{2 [s_1 m_1+s_2 m_2+a^{m} C_1 C_2 (m-3)m ]}{{3 [s_1+s_2+2 a^{m} C_1 C_2 (m-3) ]}}, \end{aligned}$$
(55)

here

$$\begin{aligned} r_1= & {} {a^{2 m_2} C_1^2 \left( m_1-1\right) \left( 2 m_1-1\right) }, \\ r_2= & {} a^{2 m_1} C_2^2 \left( m_2-1\right) \left( 2 m_2-1\right) ,\\ s_1= & {} a^{2m_2} C_1^2 \left( 2 m_1-3\right) , \\ s_2= & {} a^{2m_1} C_2^2 \left( 2 m_2-3\right) , \end{aligned}$$

and \(m=m_1+m_2.\)

Fig. 9
figure 9

The evolutionary trajectory of the bulk viscous model of the universe in the r–s plane for the best estimated values of the model parameters

Full size image

The evolution of the statefinder parameters in the r–s plane is shown in Fig. 9. The plot exhibits that the trajectory begins from the second quadrant of the r–s plane, \( r>0 \) and \( s<0 \), and enters into the first quadrant, \(\lbrace r,s\rbrace >0\). For the present universe, the statefinder parameter takes the form

$$\begin{aligned} r_0= & {} \frac{6 \sqrt{3} \tilde{\varPi _0}+\alpha (22+9 \tilde{\varPi _0} (2+\tilde{\varPi _0} ) )}{4 \alpha }, \end{aligned}$$
(56)
$$\begin{aligned} s_0= & {} 1+\frac{1}{\sqrt{3} \alpha }+\frac{1}{\tilde{\varPi _0}}+\frac{\tilde{\varPi _0}}{2}. \end{aligned}$$
(57)

Hence the present values of the statefinder pair is \(\lbrace r_0,s_0\rbrace =\lbrace 0.582, 0.128\rbrace \) for the best estimated model parameters. This indicates that the present bulk viscous model is distinguishably different from the \( \varLambda \)CDM model. From Fig. 9 we can also infer that the bulk viscous model resembles the \(\varLambda \)CDM model during an early evolutionary phase of the universe and in the present time the model is moving away from \(\varLambda \)CDM model. In the first quadrant the trajectory is lying in the region \( r<1 \) and \( s>0 \); this represents the quintessence nature. This is a marked deviation from the corresponding model using the Eckart formalism in which the model approaches the \(\varLambda \)CDM model in the future [13] in the r–s plane.

6 The model parameter estimation using supernovae data

In this section we describe the evaluation of the model parameters by constraining it with the observational data on type Ia supernovae. We have used the “Union” SNe Ia data set [53], consisting of 307 type Ia supernovae from 13 independent data sets. Our aim here is to extract the best fit for the parameters \( \alpha \), \( \tilde{\varPi }_{0} \) and the present value Hubble parameter \( H_{0}. \) We obtained the parameter values by applying the \( \chi ^{2} \) minimisation method.

The luminosity distance \( d_{L} \) in a flat universe is

$$\begin{aligned} d_{L}(z,\alpha ,\tilde{\varPi _{0}},H_{0})=c(1+z)\int _{0}^{z} \frac{\mathrm{d}z'}{H(z',\alpha ,\tilde{\varPi _{0}},H_{0})}. \end{aligned}$$
(58)

The difference between apparent and absolute magnitudes of supernovae depends on the distance. The equation that relates the theoretical distance moduli \( \mu _\mathrm{th} \), the apparent magnitude m, the absolute magnitude M and \( d_{L} \) is given by

$$\begin{aligned} \mu _\mathrm{th}(z,\alpha ,\tilde{\varPi _{0}},H_{0})= & {} m-M\nonumber \\= & {} 5\log _{10}\left[ \frac{d_{L}(z,\alpha ,\tilde{\varPi _{0}},H_{0})}{\mathrm{Mpc}}\right] +25.\nonumber \\ \end{aligned}$$
(59)
Table 1 A comparison of best estimated values of bulk viscous model parameters with the standard \(\varLambda \)CDM model
Full size table

The observational distance modulus \( \mu '_{i} \), obtained from SNe Ia data set is compared with \( \mu _\mathrm{th} \) calculated using Eq. (59) corresponding to different values of the redshifts. The \( \chi ^2 \) function can be written as

$$\begin{aligned} \chi ^{2}(\alpha ,\tilde{\varPi _{0}},H_{0})= \sum _{i=1}^n \frac{\left[ \mu _\mathrm{th}(z,\alpha ,\tilde{\varPi _{0}},H_{0}) -\mu '_{i}\right] ^2}{\sigma _{i}^2}, \end{aligned}$$
(60)

where n is the total number of data points and \( \sigma _{i}^2 \) is the variance of the ith measurement. The best estimated values of the parameters \( \alpha ,\tilde{\varPi _{0}}\) and \(H_{0} \) have been obtained by \( \chi ^{2} \) minimization. For comparison, the parameter values for the \( \varLambda \)CDM model have also been extracted using the same data. The best estimated parameter values is shown in Table 1. The \( \chi ^{2}_\mathrm{min} \) function per degree of freedom is defined by \( \chi ^{2}_\mathrm{d.o.f.} =\frac{\chi ^{2}_\mathrm{min}}{n-n'}\), \( n' \) is the number of parameters in the model. Here \( n=307 \) and \( n'=3 \). The present value of the Hubble parameter obtained from the bulk viscous model is comparable with that of the \( \varLambda \)CDM model.

The confidence interval plane for the model parameters \( \alpha \) and \(\tilde{\varPi _{0}} \) is shown in Fig. 10. The contours corresponds to 68.3, 95.4, 99.73 and \(99.99\%\) probabilities as one moves from inside. The probabilistic correction to the parameters value corresponding to 68.3% probability are shown in Table 1. It is these values which have been used to generate the evolutionary status of various cosmological parameters present in the previous sections.

Fig. 10
figure 10

The confidence intervals for the model parameters \(\alpha \) and \(\tilde{\varPi _0}\) correspond to 68.3,  95.4,  99.73,  and \(99.99\%\) probabilities. The best estimated values of the model parameters are indicated by a point

Full size image

7 Conclusions

In the present work, the evolution of flat FLRW bulk viscous non-relativistic matter dominated universe has been investigated. We have used relativistic second order full causal theory for the evolution of the bulk viscous pressure as given by Eq. (6). The bulk viscous coefficient is taken as \(\xi =\alpha \rho ^{1/2},\) this means it is effectively depending on the expansion velocity of the universe. We solved the Friedmann equations analytically to obtain the Hubble parameter as given by Eq. (16). In the limit of zero viscosity, the present model reduces to the non-viscous matter dominated universe satisfying \( H \sim a^{-\frac{3}{2}}.\)

We have also obtained the scale factor of the expansion. The asymptotic behaviour of the scale factor indicates the transition from an early decelerated to a late accelerated epoch, and its evolution as shown in Fig. 21 indicates the presence of a big bang at the origin of the universe. Hence the age of the universe is defined and is determined using the best estimated values of the parameters, and it is around 9.72 Gyr. This is considerably less than the age obtained from the CMB anisotropic data and from the data of the oldest globular clusters.

The evolution of the deceleration parameter q is obtained as shown in Fig. 4. From this the transition redshift was obtained, \(z_{T}\sim 0.52^{+0.010}_{-0.016}.\) The present value of the deceleration parameter is obtained: \( q_0\sim -0.59^{+0.015}_{-0.016}\), and it is in the range obtained by WMAP data analysis. As \( a \rightarrow \infty \), q stabilises around the value \( -\ 0.7. \) So, unlike in the Eckart formalism approach, where the bulk viscous universe ultimately goes over to a de Sitter phase, the present model is lying well within the range of quintessence behaviour asymptotically. In its overall evolution, the deceleration parameter begins with \( q \sim 4 \) in the remote past and stabilises around \(- 0.7\) in the far future of the universe.

The evolution of the equation of state parameter, \(\omega \), is obtained as in Eq. (30) and the variation of it with redshift is shown in Fig. 5. The present value of the equation of state parameter is found to be \(\omega _0 \sim - 0.73^{+ \ 0.01}_{- 0.01}.\) Hence the present universe is accelerating and acceleration has begun in the recent past. The value of \(\omega _0\) obtained in this model is slightly higher than that obtained from WMAP + BAO + \(H_{0}\) + SN data. The future evolution of \(\omega \) indicates a never-ending acceleration phase but not approaching the de Sitter phase. This is a marked deviation from the corresponding model using the Eckart formalism, in which the expansion ultimately ends up with a de Sitter epoch. From the evolution of \(\omega \) it was found that the equation of state starts with \( + 2.5 \) in the remote past and evolves to \(- 0.79\) in the future stages. This indicates that the bulk viscous matter shows a stiff fluid characteristic in the earlier epoch and then evolves to the quintessence nature in the later stages.

The matter density parameter \( \varOmega _m, \) obtained in the present model, is given in Eq. (33) and its evolution with respect to the scale factor is shown in Fig. 6. The evolution of the matter density as \(a \rightarrow 0\) indicates the presence of the big bang at the origin of the universe. The decrease in density along with the expansion of the universe suggests the absence of a big rip in the future. For zero bulk viscosity the density reduces to \(\varOmega \sim a^{-3},\) corresponding to the ordinary matter dominated era. In the overall way the behaviour of \(\varOmega _m\) in the present model is similar to that obtained using the Eckart formalism [13].

The evolution of the curvature scalar R is given in Eq. (36) and is plotted with scale factor in Fig. 7. When \(a \rightarrow 0, \) \(R \rightarrow \infty \), implying the presence of the big bang at the origin of the universe.

The evolution of the bulk viscosity in the present model shows that it starts with a large positive value in the early phase of the evolution and evolves to smaller values during the later evolutionary phase of the universe. Throughout the evolution it satisfies the condition \(\xi \ge 0\). Therefore, the entropy production is always positive and, hence, the local second law of thermodynamics is satisfied in the present model. Here also the present model differs from the model using Eckart theory [13]. In a model using the Eckart formalism, the coefficient of the bulk viscosity increases from negative to positive values as the universe expands, hence the local second law is violated in the early epoch. The generalised second law is valid in the present model like in the non-causal Eckart model of the bulk viscous universe.

In order to contrast the present model from the standard dark energy models the statefinder geometric diagnostic has been carried out. The evolution of the model in the r–s plane is shown in Fig. 5. The present value of the statefinder parameter pair is obtained: \(\lbrace r_0,s_0\rbrace =\lbrace 0.582,0.128\rbrace .\) This suggests that the present model is distinct from the standard \(\varLambda \)CDM model. The present bulk viscous model resembles the \(\varLambda \)CDM model in an early phase of the evolution. The evolution of the trajectory on the r–s plane is lying in the region \(r<1\) and \(s>0\), this indicates the quintessence nature of bulk viscous matter in the later stages of the expanding universe. In contrast, in the model using the Eckart formalism, the model will approach the \(\varLambda \)CDM model in the future and this is a marked difference from the causal approach.