1 Introduction

Over the last two decades models with extra spatial dimensions [1,2,3,4,5,6,7,8,9,10,11,12,13] have been increasingly playing a central role in physics beyond the standard models of particles [14] and cosmology [15,16,17]. Such higher dimensional scenarios occur naturally in string theory. Depending on different possible compactification schemes for the extra dimensions, a large number of models have been constructed. In all these models, our visible universe is identified as one of the 3-branes embedded within a higher dimensional spacetime and is described through a low energy effective theory on the brane carrying the signatures of extra dimensions [18,19,20].

Among various extra dimensional models proposed over the last several years, the warped extra dimensional model pioneered by Randall and Sundrum (RS) [6] earned special attention since it resolves the gauge hierarchy problem without introducing any intermediate scale (between Planck and TeV) in the theory. Subsequently different variants of the warped geometry model and the issue of modulus (also known as radion) stabilization were extensively studied in [21,22,23,24,25,26,27,28,29,30,31]. A generic feature of many of these models is that the bulk spacetime is endowed with high curvature scale \(\sim \) four dimensional Planck scale.

It is well known that the Einstein–Hilbert action can be generalized by adding higher order curvature terms which naturally arise from the diffeomorphism property of the action. Such terms also have their origin in string theory from quantum corrections. In this context F(R) [32,33,34,35,36,37,38], Gauss–Bonnet (GB) [39,40,41] or more generally Lanczos–Lovelock gravity are some of the candidates in higher curvature gravitational theory.

In general the higher curvature terms are suppressed with respect to the Einstein–Hilbert term by the Planck scale. Hence in the low curvature regime, their contributions are negligible. However, higher curvature terms become extremely relevant at the regime of large curvature. Thus, for a bulk geometry where the curvature is of the order of the Planck scale, the higher curvature terms should play a crucial role. Motivated by this idea, in the present work, we consider a generalized warped geometry model by replacing the Einstein–Hilbert bulk gravity action with a higher curvature F(R) gravitational theory [36, 37, 42,43,44,45,46,47]. In such a scenario, several models have been studied to explore their phenomenological implications. Some of these are formulated by placing the standard model fields inside the bulk. For these models the localization property of a bulk fermion field on the brane [48,49,50,51,52,53,54,55] has been a subject of great interest to explore the chiral nature of massless fermions and also the hierarchical masses of fermions among different generations [54]. In this context, it is observed that the overlap of the bulk fermion wave function on our visible brane plays a crucial role in determining the effective radion–fermion coupling, which in turn determines the phenomenology of the radion with brane matter fields.

In view of the above, it is worthwhile to address the role of higher curvature terms as regards fermion localization. We aim to address this in the present work.

Our paper is organized as follows: the mapping between higher curvature and scalar degrees of freedom is discussed in Sect. II. The description of warped geometry in the F(R) model and its solutions are described in Sect. III and Sect. IV. Section V addresses the localization property of the bulk fermion field in the backdrop of the higher curvature scenario and its consequences. The paper ends with some concluding remarks.

2 Transformation of a F(R) theory to scalar–tensor theory

In this section, we briefly describe how a higher curvature F(R) gravity model in a five dimensional scenario can be recast in terms of Einstein gravity with a scalar field. The F(R) action is expressed as

$$\begin{aligned} S=(1/2\kappa ^2)\int \mathrm{d}^4x \mathrm{d}y \sqrt{G} F(R) \end{aligned}$$
(1)

where \(x^{\mu } = (x^0, x^1, x^2, x^3)\) are the usual four dimensional coordinates and y is the extra dimensional spatial linear coordinate. R is the five dimensional Ricci curvature and G is the determinant of the metric. Moreover, \(\frac{1}{2\kappa ^2}\) is taken as \(2M^3\) where M is the five dimensional Planck scale. Introducing an auxiliary field \(A(x,\phi )\), the above action (1) can equivalently be written as

$$\begin{aligned} S=(1/2\kappa ^2)\int \mathrm{d}^4x \mathrm{d}y \sqrt{G} [F'(A)(R-A) + F(A)]. \end{aligned}$$
(2)

By the variation of the auxiliary field \(A(x,\phi )\), one easily obtains \(A=R\). Plugging back this solution \(A=R\) into the action (2), the initial action (1) can be reproduced. At this stage, let us perform a conformal transformation of the metric:

$$\begin{aligned} G_{MN}(x,\phi ) \rightarrow \tilde{G}_{MN} = \exp {(\sigma (x,\phi )}G_{MN}(x,\phi ); \end{aligned}$$

M, N run form 0 to 5. \(\sigma (x,\phi )\) is the conformal factor, related to the auxiliary field by \(\sigma = (2/3)\ln F'(A)\). Using this relation between \(\sigma (x,\phi )\) and \(A(x,\phi )\), one ends up with the following scalar–tensor action:

$$\begin{aligned} S= & {} (1/2\kappa ^2)\int \mathrm{d}^4x \mathrm{d}y \sqrt{\tilde{G}} \left[ \tilde{R} + 3\tilde{G}^{MN}\partial _M\sigma \partial _N\sigma \right. \\&\left. -\,\left( \frac{A}{F'(A)^{2/3}} - \frac{F(A)}{F'(A)^{5/3}}\right) \right] \end{aligned}$$

where \(\tilde{R}\) is the Ricci scalar formed by \(\tilde{G}_{MN}\). \(\sigma (x,\phi )\) is the scalar field emerging from the higher curvature degrees of freedom. Clearly the kinetic part of \(\sigma (x,\phi )\) is non-canonical. In order to make the scalar field canonical, we transform \(\sigma \) \(\rightarrow \) \(\Phi (x,\phi ) = \sqrt{3}\frac{\sigma (x,\phi )}{\kappa }\). In terms of \(\Phi (x,\phi )\), the above action takes the following form:

$$\begin{aligned} S=\int \mathrm{d}^4x \mathrm{d}y \sqrt{\tilde{G}} \left[ \frac{\tilde{R}}{2\kappa ^2} + \frac{1}{2}\tilde{G}^{MN}\partial _M\Phi \partial _N\Phi - V(\Phi ) \right] \end{aligned}$$

where \(V(\Phi ) = \frac{1}{2\kappa ^2}[\frac{A}{F'(A)^{2/3}} - \frac{F(A)}{F'(A)^{5/3}}]\) is the scalar field potential, which depends on the form of F(R). Thus the action of F(R) gravity in five dimensions can be transformed into the action of a scalar–tensor theory by a conformal transformation of the metric.

3 Warped spacetime in F(R) model and corresponding scalar–tensor theory

In the present paper, we consider a five dimensional AdS spacetime with two 3-brane scenario in the F(R) model. The form of F(R) is taken as \(F(R) = R + \alpha R^2\) where \(\alpha \) is a constant with the square of the inverse mass dimension. Considering \(\phi \) as the extra dimensional angular coordinate, two branes are located at \(\phi = 0\) (hidden brane) and at \(\phi = \pi \) (visible brane), respectively, while the latter one is identified with the visible universe. Moreover, the spacetime is \(S^1/Z_2\) orbifolded along the coordinate \(\phi \). The action for this model is

$$\begin{aligned} S = \int \mathrm{d}^4x \mathrm{d}y \sqrt{G} \left[ \frac{1}{2\kappa ^2}(R + \alpha R^2) + \Lambda + V_h\delta (\phi ) + V_v\delta (\phi -\pi ) \right] \nonumber \\ \end{aligned}$$
(3)

where \(\Lambda (< 0)\) is the bulk cosmological constant and \(V_h\), \(V_v\) are the brane tensions on the hidden and the visible brane, respectively.

This higher curvature-like F(R) model (in Eq. (3)) can be transformed into a scalar–tensor theory by using the technique discussed in the previous section. Performing a conformal transformation of the metric,

$$\begin{aligned} G_{MN}(x,\phi ) \rightarrow \tilde{G}_{MN} = \exp {\left( \frac{1}{\sqrt{3}}\kappa \Phi (x,\phi )\right) }G_{MN}(x,\phi ), \end{aligned}$$
(4)

the above action (in Eq. (3)) can be expressed as a scalar–tensor theory with the action given by

$$\begin{aligned} S= & {} \int \mathrm{d}^4x \mathrm{d}y \sqrt{\tilde{G}} \left[ \frac{\tilde{R}}{2\kappa ^2} + \frac{1}{2}\tilde{G}^{MN}\partial _M\Phi \partial _N\Phi - V(\Phi ) + \Lambda \right. \nonumber \\&+\,\exp {\left( -\frac{5}{2\sqrt{3}}\kappa \Phi \right) } V_h\delta (\phi )\nonumber \\&\left. +\,\exp {\left( -\frac{5}{2\sqrt{3}}\kappa \Phi \right) } V_v\delta (\phi -\pi ) \right] \end{aligned}$$
(5)

where the quantities in tilde are reserved for scalar–tensor (ST) theory. \(\tilde{R}\) is the Ricci curvature formed by the transformed metric \(\tilde{G}_{MN}\). \(\Phi (x,\phi )\) is the scalar field corresponding to the higher curvature degrees of freedom and \(V(\Phi )\) is the scalar potential, which for this specific choice form of F(R) has the form

$$\begin{aligned} V(\Phi )= & {} \frac{1}{8\kappa ^2\alpha } \exp {\left( -\frac{5}{2\sqrt{3}}\kappa \Phi \right) } \left[ \exp {\left( \frac{3}{2\sqrt{3}}\kappa \Phi \right) } - 1 \right] ^2\nonumber \\&-\Lambda \left[ \exp { \left( -\frac{5}{2\sqrt{3}}\kappa \Phi \right) }-1 \right] . \end{aligned}$$
(6)

One can check that the above potential (in Eq. (6)) is stable for the parametric regime \(\alpha > 0\). The stable value (\(\langle \Phi \rangle \)) and the mass squared (\(m_{\Phi }^2\)) of the scalar field (\(\Phi \)) are given by the two equations

$$\begin{aligned} \exp {\left( \frac{3}{2\sqrt{3}}\kappa \langle \Phi \rangle \right) } = \left[ \sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2 \right] \end{aligned}$$
(7)

and

$$\begin{aligned} m_{\Phi }^2 = \frac{1}{8\alpha } \left[ \sqrt{9 - 40\kappa ^2\alpha \Lambda } \right] \left[ \sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2 \right] ^{-\frac{2}{3}}. \end{aligned}$$
(8)

Furthermore, the minimum value of the potential i.e. \(V(\langle \Phi \rangle )\) is non-zero and serves as a cosmological constant. Thus the effective cosmological constant in scalar–tensor theory is \(\Lambda _{\mathrm{eff}} = \Lambda - V(\langle \Phi \rangle )\) where \(V(\langle \Phi \rangle )\) is

$$\begin{aligned} V(\langle \Phi \rangle )= & {} \Lambda + \left[ \sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2 \right] ^{-\frac{5}{3}}\nonumber \\&\times \left[ \quad -\Lambda + (1/8\kappa ^2\alpha )\left[ \sqrt{9 - 40\kappa ^2\alpha \Lambda }-3 \right] ^2 \right] .\nonumber \\ \end{aligned}$$
(9)

The above form of \(V(\langle \Phi \rangle )\) with \(\Lambda < 0\) clearly indicates that \(\Lambda _{\mathrm{eff}}\) is also negative.

4 Solutions in scalar–tensor and in the corresponding F(R) theory

Considering \(\xi \) as the fluctuation of the scalar field over its vev, the final form of action for the scalar–tensor theory in the bulk can be written as

$$\begin{aligned} S= & {} \int \mathrm{d}^4x \mathrm{d}y \sqrt{\tilde{G}} \left[ \frac{\tilde{R}}{2\kappa ^2} + \frac{1}{2}\tilde{G}^{MN}\partial _M\xi \partial _N\xi \right. \nonumber \\&\left. - (1/2)m_{\Phi }^2\xi ^2 + \Lambda _{\mathrm{eff}} \right] \end{aligned}$$
(10)

where the terms up to quadratic order in \(\xi \) are retained for \(\kappa \xi < 1\). A detailed justification of neglecting the higher order terms as well as their possible effects will be discussed in the end part of this section.

Taking a negligible backreaction of the scalar field (\(\xi \)) on the background spacetime, the solution of the metric \(\tilde{G}_{MN}\) is exactly the same as in the RS model, i.e.

$$\begin{aligned} \mathrm{d}\tilde{s}^2 = e^{- 2 k|y|} \eta _{\mu \nu } \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } - \mathrm{d}y^2 \end{aligned}$$
(11)

where \(k = \sqrt{\frac{-\Lambda _{\mathrm{eff}}}{24M^3}}\). With this metric, the scalar field equation of motion in the bulk is

$$\begin{aligned} -\partial _y[\exp {(-4ky)}\partial _y\xi ] + m_{\Phi }^2\exp {(-4ky)}\xi (y) = 0 \end{aligned}$$
(12)

where the scalar field \(\xi \) is taken as a function of the extra dimensional coordinate only. Considering a non-zero value of \(\xi \) on branes, Eq. (12) has the general solution,

$$\begin{aligned} \xi (y) = e^{2ky} \left[ Ae^{\nu ky} + Be^{-\nu ky} \right] \end{aligned}$$
(13)

with \(\nu = \sqrt{4 + m_{\Phi }^2/k^2}\). Moreover, A and B are obtained from the boundary conditions, \(\xi (0)=v_h\) and \(\xi (\pi r_c)=v_v\), as follows:

$$\begin{aligned} A = v_v e^{-(2+\nu )kr_c\pi } - v_h e^{-2\nu kr_c\pi } \end{aligned}$$
(14)

and

$$\begin{aligned} B = v_h (1 + e^{-2\nu kr_c\pi }) - v_v e^{-(2+\nu )kr_c\pi }. \end{aligned}$$
(15)

It may be observed that the scalar field degrees of freedom are related to the curvature by

$$\begin{aligned} \xi (y) = \frac{2}{\sqrt{3}\kappa }\ln [1 + 2\alpha R] - \langle \Phi \rangle . \end{aligned}$$
(16)

Recall that \(\langle \Phi \rangle =\frac{2}{\sqrt{3}\kappa } \ln [\sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2]\).

From the above expression, we can relate the boundary values of the scalar field (i.e. \(\xi (0)=v_h\) and \(\xi (\pi r_c)=v_v\)) with the Ricci scalar ,

$$\begin{aligned} v_h = \frac{2}{\sqrt{3}\kappa } \ln \left[ \frac{1 + 2\alpha R(0)}{\sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2} \right] \end{aligned}$$
(17)

and

$$\begin{aligned} v_v = \frac{2}{\sqrt{3}\kappa } \ln \left[ \frac{1 + 2\alpha R(\pi r_c)}{\sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2} \right] \end{aligned}$$
(18)

where R(0) and \(R(\pi )\) are the values of the curvature on the Planck and TeV branes, respectively. Later on, we shall derive the expression of the bulk scalar curvature which in this scenario becomes dependent on the bulk coordinate y. Thus the parameters that are used in the scalar–tensor theory are actually related to the parameters of the original F(R) theory.

It deserves to be mentioned that the solutions obtained in Eqs. (11) and (13) are based on the conditions that the bulk scalar potential is retained up to a quadratic term (see Eq. (10)) and the backreaction of the bulk scalar field is neglected on the five dimensional spacetime. Both these conditions follow from the assumption that \(\kappa v_h< 1\). Relaxation of this assumption is crucial to check the status of higher order self interaction terms in the bulk scalar potential. Here we find the solutions of the field equations when \(V(\Phi )\) is retained up to a cubic term in \(\Phi \). In this scenario, the five dimensional action in ST theory turns out to be

$$\begin{aligned} S= & {} \int \mathrm{d}^4x \mathrm{d}y \sqrt{\tilde{G}} \left[ \frac{\tilde{R}}{2\kappa ^2}+ \frac{1}{2}\tilde{G}^{MN}\partial _M\xi \partial _N\xi \right. \nonumber \\&\left. - (1/2)m_{\Phi }^2\xi ^2 + \frac{g}{3}\xi ^3 + \Lambda _{\mathrm{eff}} \right] \nonumber \\ \end{aligned}$$
(19)

where g is the self cubic coupling of \(\Phi (\phi )\); it can easily be determined from the form of \(V(\Phi )\) presented in Eq. (6):

$$\begin{aligned} g = -\frac{\sqrt{3}\kappa }{16\alpha }\frac{[2\sqrt{9 - 40\kappa ^2\alpha \Lambda } + 3]}{[\sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2]^{\frac{2}{3}}}. \end{aligned}$$
(20)

Considering the metric ansatz

$$\begin{aligned} \mathrm{d}\tilde{s}^2 = e^{- 2 A(\phi )} \eta _{\mu \nu } \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } - \mathrm{d}y^2, \end{aligned}$$
(21)

the gravitational and the scalar field equations of motion take the following form:

$$\begin{aligned}&4 A'^2(y) - A''(y) = -(2\kappa ^2/3)(\frac{1}{2}m_{\Phi }^2\xi ^2 - \frac{g}{3}\xi ^3) , \end{aligned}$$
(22)
$$\begin{aligned}&A'^2(y)= \frac{\kappa ^2}{12}\xi '^2 - (\kappa ^2/6)(\frac{1}{2}m_{\Phi }^2\xi ^2 - \frac{g}{3}\xi ^3) , \end{aligned}$$
(23)
$$\begin{aligned}&\xi ''(y) = 4A'\xi ' + m_{\Phi }^2\xi (\phi ) - g\xi ^2(\phi ). \end{aligned}$$
(24)

To determine the solutions of the above differential equations, we apply the iterative method by considering the form of the metric determined in Eq. (11) as the zeroth order solution. In the leading order correction of \(\kappa v_h\), \(\xi (\phi )\) and \(A(\phi )\) turn out to be

$$\begin{aligned} \xi (y)= & {} \left[ Ae^{(2+\nu )ky} + Be^{(2-\nu )ky} \right] \ \nonumber \\&-\, \frac{\kappa v_h}{16\sqrt{3}\alpha k^2} \frac{[2\sqrt{9 - 40\kappa ^2\alpha \Lambda } + 3]}{[\sqrt{9 - 40\kappa ^2\alpha \Lambda } - 2]^{\frac{2}{3}}}\nonumber \\&\times \, \left[ \quad \frac{\exp { \left[ 2(2+\nu )ky-4\nu kr_c\pi \right] }}{m_{\Phi }^2r_c^2 + 8kr_c(2+\nu )-4(2+\nu )^2}\right. \nonumber \\&+\,\left. \frac{2v_v}{v_h}\frac{\exp {\left[ 4ky-(2+\nu )kr_c\pi \right] }}{m_{\Phi }^2r_c^2 + 16kr_c- 16} \right] \end{aligned}$$
(25)

and

$$\begin{aligned} A(y)= & {} ky + \frac{\kappa ^2v_h^2}{12}\left[ e^{-4\nu kr_c\pi } e^{-2(2+\nu )ky}\right. \nonumber \\&\left. +\, e^{2(2-\nu )ky} \left( 1+\frac{v_v}{v_h}e^{-(2+\nu )kr_c\pi } \right) \right] . \end{aligned}$$
(26)

Thus due to the inclusion of the bulk scalar field backreaction, the warp factor gets modified and the correction term is proportional to \(\kappa ^2v_h^2\), which is indeed small for \(\kappa v_h< 1\).

However, from the solutions of scalar–tensor theory, one can extract the solution in the F(R) model by an inverse conformal transformation as indicated earlier (see Eq. (4)):

$$\begin{aligned} \mathrm{d}s^2= & {} \exp {\left[ -\frac{\kappa }{\sqrt{3}}(\langle \Phi \rangle +\xi (y)) \right] }\nonumber \\&\times \,\left[ e^{- 2 A(y)} \eta _{\mu \nu } \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } - \mathrm{d}y^2 \right] \end{aligned}$$
(27)

where \(\mathrm{d}s^2\) is the line element in the F(R) model and \(\xi (y)\) and A(y) are given in Eqs. (25) and (26), respectively.

At this point, we need to verify whether the above solution of \(G_{MN}\) (in Eq. (27)) satisfies the field equations of the original F(R) theory. The five dimensional gravitational field equation for F(R) theory is given by

$$\begin{aligned}&\frac{1}{2}G_{MN}F(R) - R_{MN}F'(R) - G_{MN}\Box F'(R)\nonumber \\&\qquad +\,\nabla _{M}\nabla _{N}F'(R) = -\frac{1}{2}\Lambda G_{MN}. \end{aligned}$$
(28)

In the present context, we take the form of F(R) as \(F(R) = R + \alpha R^2\) and thus the above field equation is simplified to the form

$$\begin{aligned} \frac{1}{2}G_{MN}R - R_{MN} + \frac{\alpha }{2}G_{MN}R^2- & {} 2\alpha RR_{MN}\nonumber \\ - \,2\alpha G_{MN}\Box R + 2\alpha \nabla _{M}\nabla _{N}R= & {} -\frac{1}{2}\Lambda G_{MN}. \end{aligned}$$
(29)

It may be shown that the solution of \(G_{MN}\) in Eq. (27) satisfies the above field equation to the leading order of \(\kappa v_h\). It may be recalled that the equivalence of the chosen F(R) model was transformed to the potential of the scalar–tensor model in the leading order of \(\kappa v_h\). Thus it guarantees the validity of the solution of the spacetime metric (i.e. \(G_{MN}\)) in the original F(R) theory.

Using the metric solution given in Eq. (27), one calculates the five dimensional Ricci scalar as follows:

$$\begin{aligned} R(y)= & {} -20k^2 - \frac{20}{\sqrt{3}}e^{[-\frac{\sqrt{3}}{2}\kappa cr_cy k^2]}k^2\kappa c\nonumber \\&-\, 5e^{[-2\frac{\sqrt{3}}{2}\kappa cr_cy k^2]}k^2\kappa ^2 c^2 \end{aligned}$$
(30)

where c is an integration constant. The presence of higher curvature gravity admits a general class of warped spacetime solutions where the bulk curvature depends on the extra dimensional coordinate, which is in contrast to the original RS situation where the bulk curvature is constant. Therefore, the present construction may lead to a new phenomenological scenario in the context of braneworld physics which includes the effects of higher curvature terms present in the gravitational action. We now show how the higher curvature terms affect the localization of fermion field within the five dimensional spacetime.

5 Fermion localization in F(R) theory

Consider a bulk massive fermion field propagating in a background spacetime characterized by the action in Eq. (3). The lagrangian for the Dirac fermions is given by

$$\begin{aligned} \mathcal {L}_{\mathrm{Dirac}} = \sqrt{-G} \left[ \bar{\Psi }i\Gamma ^{a}D_{a}\Psi - m_5\bar{\Psi }\Psi \right] . \end{aligned}$$
(31)

Using the metric solution in the F(R) model presented in Eq. (27), the above lagrangian can be written as

$$\begin{aligned} \mathcal {L}_{Dirac} = e^{-4A(y)} e^{-\frac{5\kappa }{2\sqrt{3}} \left( \langle \Phi \rangle +\xi (y) \right) } \left[ \bar{\Psi }i\Gamma ^{a}D_{a}\Psi - m_5\bar{\Psi }\Psi \right] \end{aligned}$$

where \(a=(x^{\mu },y)\) are the bulk coordinates, \(\Psi =\Psi (x^{\mu },y)\) is the bulk fermion field and \(m_5\) is its mass. \(\Gamma ^{a} = \left( e^{A(y)}e^{\frac{\kappa }{2\sqrt{3}} \left( \langle \Phi \rangle +\xi (y) \right) }\gamma ^{\mu }, -i\gamma ^{5}e^{\frac{\kappa }{2\sqrt{3}} \left( \langle \Phi \rangle +\xi (y) \right) } \right) \) denotes the five dimensional gamma matrices where \(\gamma ^{\mu }\) and \(\gamma ^{5}\) represent 4D gamma matrices in the chiral representation. The curved gamma matrices obey the Clifford algebra, i.e. \([{\Gamma ^{a},\Gamma ^{b}] = 2G^{ab}}\). The covariant derivative \(D_{a}\) can be calculated by using the metric in Eq. (27) and is given by

$$\begin{aligned}&D_{\mu } = \partial _{\mu } + \frac{i}{2}\gamma _{\mu }\gamma ^{5}e^{\frac{\kappa }{2\sqrt{3}} \left( \langle \Phi \rangle +\xi (y) \right) } \left( A'(y)+\frac{\kappa }{2\sqrt{3}}\xi '(y) \right) ,\\&D_{5} = e^{\frac{\kappa }{2\sqrt{3}} \left( \langle \Phi \rangle +\xi (y) \right) }\partial _{y}. \end{aligned}$$

Using this set-up, the Dirac lagrangian \(\mathcal {L}_{Dirac}\) turns out to be

$$\begin{aligned} \mathcal {L}_{\mathrm{Dirac}}= & {} e^{-4A(y)}e^{-\frac{5\kappa }{2\sqrt{3}} \left( \langle \Phi \rangle +\xi (y) \right) } \bar{\Psi } \left[ ie^{A(y)}\right. \nonumber \\&\times \,\, e^{\frac{\kappa }{2\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) }\gamma ^{\mu }\partial _{\mu } + \gamma ^{5} \left[ e^{\frac{\kappa }{2\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) }\right. \nonumber \\&\times \left. \left. \left( \partial _{y}-2A'(y)-\frac{\kappa }{\sqrt{3}}\xi '(y) \right) \right] - m_5 \right] \Psi . \end{aligned}$$
(32)

We decompose the five dimensional spinor via a Kaluza–Klein (KK) mode expansion as \(\Psi (x^{\mu },y) = \sum \chi ^n(x^{\mu })\zeta ^n(y)\), where the superscript n denotes the nth KK mode. \(\chi ^n(x^{\mu })\) is the projection of \(\Psi (x^{\mu },y)\) on the 3-brane and \(\zeta ^n(y)\) is the extra dimensional component of 5D spinor. Left (\(\chi _L\)) and right (\(\chi _R\)) states are constructed by \(\chi ^n_{L,R} = \frac{1}{2}(1 \mp \gamma ^{5})\chi ^n\). Thus the KK mode expansion can be written in the following way:

$$\begin{aligned} \Psi (x^{\mu },y) = \sum [\chi _L^{n}(x^{\mu })\zeta _L^{n}(y) + \chi _R^{n}(x^{\mu })\zeta _R^{n}(y)]. \end{aligned}$$
(33)

Substituting the KK mode expansion of \(\Psi (x^{\mu },y)\) in the Dirac field lagrangian given in Eq. (32), we obtain the following equations of motion for \(\zeta _{L,R}(y)\):

$$\begin{aligned}&e\quad ^{-A(y)}e^{-\frac{2\kappa }{\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) } \left[ \pm e^{\frac{\kappa }{2\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) }\left( \partial _{y}-2A'(y)\right. \right. \nonumber \\&\quad +\left. \left. \frac{\kappa }{\sqrt{3}}\xi '(y) \right) + m_5 \right] \zeta ^n_{R,L}(y) = -m_n\zeta ^n_{L,R}(y) \end{aligned}$$
(34)

where \(m_{n}\) is the mass of the nth KK mode. The 4D fermions obey the canonical equation of motion \(i\gamma ^{\mu }\partial _{\mu }\chi ^n_{L,R} = m_{n}\chi ^n_{L,R}\). Moreover, Eq. (34) is obtained provided the following normalization conditions hold:

$$\begin{aligned}&\int _{0}^{\pi } \mathrm{d}y e^{-3A(y)}e^{-\frac{2\kappa }{\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) }\zeta _{L,R}^{m}\zeta _{L,R}^{n} = \delta _{m,n} ,\end{aligned}$$
(35)
$$\begin{aligned}&\int _{0}^{\pi } \mathrm{d}y e^{-3A(y)}e^{-\frac{2\kappa }{\sqrt{3}} \left( \langle \Phi \rangle +\xi (y) \right) }\zeta _{L}^{m}\zeta _{R}^{n} = 0. \end{aligned}$$
(36)

In the next two subsections, we discuss the localization scenario for massless and massive KK modes, respectively.

5.1 Massless KK mode

For a massless mode, the equation of motion of \(\zeta _{L,R}\) takes the following form:

$$\begin{aligned}&\left[ \pm e^{\frac{\kappa }{2\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) }\left( \partial _{y}-2A'(y) - \frac{\kappa }{\sqrt{3}}\xi '(y) \right) \right. \nonumber \\&\quad \left. + m_5 \right] \zeta ^n_{R,L}(y) = 0 \end{aligned}$$
(37)

where A(y) and \(\xi (y)\) are given in Eqs. (26) and (25), respectively. Using these forms of A(y) and \(\xi (y)\), we determine the solutions of \(\zeta _{L,R}(y)\) as follows:

$$\begin{aligned} \zeta _{L,R}(y)= & {} \sqrt{\frac{k}{e^{\bigg (\frac{p}{k}+\frac{q}{2k}\bigg )}\bigg [e^{2k\pi r_c}-1} \bigg ]} e^{2ky}\nonumber \\&\times \exp { \bigg [\frac{p}{2k}e^{(2+\nu )ky} - \frac{q}{4k}e^{-2(2+\nu )ky}\bigg ]} \end{aligned}$$
(38)

for \(m_5 = 0\); and

$$\begin{aligned} \zeta _{L,R}(y)= & {} \sqrt{\frac{k \pm m_5}{e^{(\frac{p}{k}+\frac{q}{2k})}\bigg [e^{(2k\pm m_5)\pi r_c}-1} \bigg ]} e^{(2k \pm m_5)y}\nonumber \\&\times \exp \quad {\bigg [\frac{p}{2k}e^{(2+\nu )ky} - \frac{q}{4k}e^{-2(2+\nu )ky}} \bigg ] \end{aligned}$$
(39)

for \(m_5 \ne 0\).

p and q obey the following expressions:

$$\begin{aligned} p= & {} \frac{2}{\sqrt{3}}k\kappa \left[ v_v e^{-(2+\nu )kr_c\pi }\right. \nonumber \\&\left. +\,e^{-4kr_c\pi }\frac{\kappa v_h k^{3/2}}{2\sqrt{3}} \frac{[2\sqrt{9 - 40\kappa ^2\alpha \Lambda } + 3]}{\sqrt{9 - 40\kappa ^2\alpha \Lambda }} \right] , \end{aligned}$$
(40)
$$\begin{aligned} q = \frac{2}{3} k\kappa ^2 v_h^2 e^{-8k\pi r_c}, \end{aligned}$$
(41)

where we use the explicit form of \(m_{\Phi }^2\) (see Eq. (8)). Moreover, the overall normalization constants in Eqs. (38) and (39) are determined by using the normalization condition presented earlier in Eq. (35). It may be noticed that left and right chiral modes have the same solution when \(m_5=0\), but the degeneracy between the two chiral modes is lifted in the presence of a non-zero bulk fermionic mass term.

It is worthwhile to study how the localization scenario depends on the higher curvature parameter (\(\alpha \)) as well as on the bulk mass parameter (\(m_5\)).

5.1.1 Effect of higher curvature parameter

From Eq. (38) and using the expressions of p and q, we obtain Fig. 1 between \(\zeta _{L,R}\) and y for various values of the higher curvature parameter \(\alpha \). We focus into the region near the TeV brane (see Fig. 1) to depict the localization properties of the left and right chiral modes.

Fig. 1
figure 1

\(\zeta _{L,R}(=\zeta _{L,R}(F(R))\) in the diagram) vs. y for \(M=1\), \(\Lambda =-1\) and \(m_5=0\)

Full size image

Figure 1 clearly demonstrates that, for \(m_5=0\), the two chiral modes get more and more localized on the TeV brane as the value of the parameter \(\alpha \) increases. On the other hand, for small values of \(\alpha \), the fermions are clearly localized deep inside the bulk spacetime. Thus without any bulk mass term, the fermions can be localized at different regions inside the bulk by adjusting the value of the higher curvature parameter.

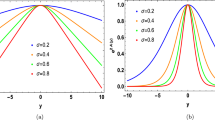
From Eq. (39), we obtain the plots (Figs. 2 and 3) of the left and right chiral massless modes for various values of the parameter \(\alpha \) in the presence of a non-zero bulk fermionic mass.

Fig. 2
figure 2

\(\zeta _{L}(=\zeta _{L}(F(R))\) in the diagram) vs. y for \(M=1\), \(\Lambda =-1\) and \(m_5=0.5\)

Full size image
Fig. 3
figure 3

\(\zeta _{R}(=\zeta _{R}(F(R))\) in the diagram) vs. y for \(M=1\), \(\Lambda =-1\) and \(m_5=0.5\)

Full size image

Figures 2 and 3 reveal that, again, as the higher curvature parameter \(\alpha \) increases, the peak of both the left and the right massless chiral wave functions shift towards the visible brane. Thus \(\alpha >0\) indicates more localization in comparison to the RS situation. It may be mentioned that the condition \(\alpha >0\) is in agreement with various astrophysical constraints for \(F(R)=R+\alpha R^2\) as well as with the braneworld stability requirement (see [27]).

Moreover, using the solution of \(\zeta _{L,R}(y)\) (in Eq. (39)), we obtain the effective coupling [56] between radion and zeroth order fermionic KK mode as follows:

$$\begin{aligned} \lambda _L= & {} \sqrt{\frac{k}{24M^3}} e^{A(\pi r_c)} \bigg (\frac{e^{(k+2m_5)\pi r_c}}{e^{(k+2m_5)\pi r_c} -1} \bigg )\nonumber \\&\times \bigg [\exp {\bigg [\frac{p}{2k}e^{(2+\nu )kr_c\pi } - \frac{q}{4k}e^{-2(2+\nu )kr_c\pi }} \bigg ] \bigg ]^2 \end{aligned}$$
(42)

for the left handed chiral mode and

$$\begin{aligned} \lambda _R= & {} \sqrt{\frac{k}{24M^3}} e^{A(\pi r_c)} \left( \frac{e^{(k-2m_5)\pi r_c}}{e^{(k-2m_5)\pi r_c} -1} \right) \nonumber \\&\times \bigg [\exp {\bigg [\frac{p}{2k}e^{(2+\nu )kr_c\pi } - \frac{q}{4k}e^{-2(2+\nu )kr_c\pi }} \bigg ] \bigg ]^2 \end{aligned}$$
(43)

for the right handed mode.

With the form of p and q given in Eqs. (40) and (41), it is evident that the effective radion–fermion coupling increases (for both left and right chiral mode) with the higher curvature parameter \(\alpha \). It is expected because the peak of both the left and the right chiral wave functions get shifted towards the visible brane as \(\alpha \) increases.

To explore the radion phenomenology, we observe that for the mass of the radion field in the presence of higher order curvature term (\(F(R)=R+\alpha R^2\)) [27]

$$\begin{aligned} m_{rad}^2&= \frac{20}{\sqrt{3}}\frac{\alpha k^4}{M^6} \epsilon ^2 e^{-2kr_c\pi } v_h^2v_v^2\nonumber \\&\quad \left[ 1 + \frac{40}{\sqrt{3}}\alpha k^2\kappa v_h \right] \left[ \frac{v_h}{v_v} - 1 \right] ^2. \end{aligned}$$
(44)

It is evident that \(m_{rad}\) increases with the increasing value of \(\alpha \) and becomes zero as \(\alpha \) tends to zero. It is expected because without any higher curvature term, the gravitational action contains only an Einstein–Hilbert term and thus the mass of the radion becomes zero (see [22]).

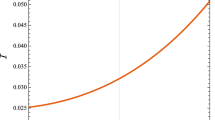
As the ratio \(\frac{\lambda _{L,R}}{m_{rad}}\) determines the fermion to radion scattering amplitude, we plot this in the Fig. 4 with respect to the parameter \(\alpha \).

Fig. 4
figure 4

\(\frac{\lambda _{L,R}}{m_{rad}}\) vs. \(\alpha \) in F(R) theory for \(M=1\), \(\Lambda =-1\) and \(m_5=0\)

Full size image

It is evident from Fig. 4 that the contribution of the radion in the scattering amplitude of fermions decreases as the value of the higher curvature parameter \(\alpha \) increases. Thus the presence of a higher curvature term reduces the signature in such scattering processes.

5.2 Massive KK mode

In this section, we study the localization of higher Kaluza–Klein modes. For massive KK modes, the equation of motion for the fermionic wave function is given by

$$\begin{aligned}&e ^{-A(y)}e^{-\frac{2\kappa }{\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) } \left[ \pm e^{\frac{\kappa }{2\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) } \left( \partial _{y}-2A'(y)\right. \right. \nonumber \\&\quad \times -\left. \left. \frac{\kappa }{\sqrt{3}}\xi '(y) \right) + m_5 \right] \zeta ^n_{R,L}(y) = -m_n\zeta ^n_{L,R}(y); \end{aligned}$$
(45)

\(m_n\) is the mass of the nth KK mode. Using the rescaling

$$\begin{aligned} \omega ^{(n)}_{L,R} = e^{\frac{5}{2}A(y)} e^{\frac{5\kappa }{4\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) }\zeta ^{(n)}_{L,R} \end{aligned}$$
(46)

we find that the two helicity states, \(\zeta _L\) and \(\zeta _R\) satisfy the same equation of motion, given by

$$\begin{aligned}&\frac{\partial ^2\omega ^{(n)}}{\partial y^2}\quad + e^{-\frac{\kappa }{\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) }\left[ e^{\frac{\kappa }{\sqrt{3}}\left( \langle \Phi \rangle +\xi (y) \right) } \left( -\frac{1}{4}A'^2 \right. \right. \nonumber \\&\qquad -\left. \left. \frac{\kappa ^2}{48}\xi '^2 -\frac{\kappa }{4\sqrt{3}}A'\xi ' + m_{n}^2e^{2A(y)}\right) + m_5^2 \right] \omega _{L,R} = 0.\nonumber \\ \end{aligned}$$
(47)

Using the forms of A(y) and \(\xi (y)\), we obtain the solution of Eq. (47) given by the hypergeometric function as follows:

$$\begin{aligned}&\zeta \quad ^{(n)}_{L,R}(y) = \sqrt{k} \exp {\left[ -\frac{p}{8k}e^{(2+\nu )ky} \right] }\nonumber \\&\quad \times \exp \quad {\left[ -\frac{1}{8k}\sqrt{q^2e^{4(2+\nu )ky}+k^2+4m_{n}^2e^{2ky}+4m_5^2} \right] }\nonumber \\&\quad \times \mathrm{Hypergeometric}U\left[ \frac{5}{8}+ \frac{qe^{2(2+\nu )ky}}{8k}\right. \nonumber \\&\quad + \frac{\sqrt{q^2e^{4(2+\nu )ky}+k^2+4m_{n}^2e^{2ky}+4m_5^2}}{8k},\nonumber \\&\quad 1\left. + \frac{\sqrt{q^2e^{4(2+\nu )ky}+k^2+4m_{n}^2e^{2ky}+4m_5^2}}{4k},\frac{p}{4k}e^{(2+\nu )ky} \right] . \nonumber \\ \end{aligned}$$
(48)

The mass spectrum can be obtained from the requirement that the wave function is well behaved on the brane. Demanding the continuity of \(\xi _{L,R}\) at \(y=0\) and at \(y=\pi r_c\), the KK mass term can be obtained as follows:

$$\begin{aligned} m_n^2= & {} e^{-2A(\pi r_c)} e^{-\frac{\kappa }{\sqrt{3}}\left( \langle \Phi \rangle +\xi (\pi r_c) \right) } \left[ k^2(n^2 + 2n + 1) + m_5^2 \right] \nonumber \\ \end{aligned}$$
(49)

where \(n=1,2,3,\ldots \). The above expression of the mass spectrum is in agreement with [55].

Now from the requirement of resolving the gauge hierarchy problem, the warp factor at TeV brane acquires the value \(= 36\), which produces a large suppression in the right hand side of Eq. (49) through the exponential factor. Since \(k, m_5\sim M\), the mass of KK modes (\(n=1,2,3,\ldots \)) turn out to be at the TeV scale.

Using the solution of \(\zeta ^n_{L,R}(y)\) (in Eq. (48)), we determine the coupling between massive KK fermion modes and the radion field:

$$\begin{aligned}&\lambda \quad ^{(n)} = \sqrt{\frac{k}{24M^3}}e^{A(\pi r_c)} e^{\frac{\kappa }{2\sqrt{3}}\left( \langle \Phi \rangle +\xi (\pi r_c) \right) }\nonumber \\&\quad \times \exp {\left[ -\frac{p}{4k}e^{(2+\nu )k\pi r_c} \right] }\nonumber \\&\quad \times \exp {\left[ -\frac{1}{4k}\sqrt{q^2e^{4(2+\nu )k\pi r_c}+k^2+4m_{n}^2e^{2k\pi r_c}+4m_5^2} \right] }\nonumber \\&\quad \times \left[ \mathrm{Hypergeometric}U\left[ \frac{5}{8}+\frac{qe^{2(2+\nu )k\pi r_c}}{8k} \right. \right. \nonumber \\&\quad + \frac{\sqrt{q^2e^{4(2+\nu )k\pi r_c}+k^2+4m_{n}^2e^{2k\pi r_c}+4m_5^2}}{8k},\nonumber \\&\quad 1\left. \left. + \frac{\sqrt{q^2e^{4(2+\nu )k\pi r_c}+k^2+4m_{n}^2e^{2k\pi r_c}+4m_5^2}}{4k},\right. \right. \nonumber \\&\quad \left. \left. \frac{p}{4k}e^{(2+\nu )k\pi r_c}\right] \right] ^2 \nonumber \\ \end{aligned}$$
(50)

where \(\lambda ^{(n)}\) is the coupling between the nth KK fermion mode and the radion field, and p, q are given in Eqs. (40), (41) respectively. With increasing \(\alpha \), the third argument of the hypergeometric function increases in the above expression and as a result \(\lambda ^{(n)}\) decreases.

Equation (48) indicates the relation between \(\zeta _{L,R}\) and y for various values of l from which one can find the dependence of the localization for the massive KK fermion modes on the backreaction parameter. From this result, the behavior of the first KK mode (\(n=1\)) is described in Fig. 5.

Fig. 5
figure 5

\(\zeta ^{(1)}_{L,R}(=\zeta ^{(1)}_{L,R}(F(R))\) in the diagram) vs. y for \(M=1\), \(\Lambda =-1\) and \(m_5=0.5\)

Full size image

Figure 5 clearly depicts that the wave function for the first massive KK mode gets more and more localized near the Planck brane with increasing value of the higher curvature parameter. Consequently, the coupling parameter decreases near the visible brane as \(\alpha \) increases. This may explain the invisibility of massive KK mode fermions in the search for the signature of warped extra dimensions in collider physics.

Moreover, it can also be shown (from Eq. (48)) that, as the order of KK mode increases from \(n=1\), the localization of fermions becomes sharper near Planck brane.

It may be mentioned that the bulk fermion mass term (\(m_5\)) also affects the localization of the fermion field. Using the solution of \(\zeta _{L,R}(y)\) presented in Eq. (39), it can be shown that, for a fixed value of the backreaction parameter, the left chiral mode of the zeroth KK fermion has higher peak values on the TeV brane as the bulk fermion mass increases, whereas the right chiral mode shows the reverse nature, which is in agreement with [50, 55].

6 Fermion localization in the corresponding scalar–tensor (ST) theory

Till now we have described the fermion localization in the original F(R) gravity model. To bring out the equivalence in the ST theory, we need to transform the original Dirac lagrangian (shown in Eq. (31)) into a scalar–tensor version of the model and a conformal transformation of \(G_{MN}\) (as mentioned in Eq. (4)) fulfills the purpose. With such a conformal transformation, \(L_{Dirac}\) takes the following form:

$$\begin{aligned} L_{Dirac} = \sqrt{\tilde{G}} [e^{-\frac{2}{\sqrt{3}}\kappa \Phi } \bar{\Psi }i\tilde{\Gamma }^{a}\tilde{D}_{a}\Psi - m_5e^{-\frac{5}{\sqrt{3}}\kappa \Phi } \bar{\Psi }\Psi ]. \end{aligned}$$
(51)

Recall that \(\tilde{G}_{MN}\) (the quantities in tilde are reserved for ST theory) is the spacetime metric in ST theory and given by (see Eq. (21))

$$\begin{aligned} \mathrm{d}\tilde{s}^2 = e^{- 2 A(\phi )} \eta _{\mu \nu } \mathrm{d}x^{\mu } \mathrm{d}x^{\nu } - \mathrm{d}y^2 \end{aligned}$$

where A(y) is obtained in Eq. (26). \(\tilde{\Gamma }^{a} = (e^{A(y)}\tilde{\gamma }^{\mu }, -i\tilde{\gamma }^{5})\) is for the five dimensional gamma matrices where \(\tilde{\gamma }^{\mu }\) and \(\tilde{\gamma }^{5}\) represent 4D gamma matrices in ST theory. By using the form of \(\tilde{G}_{MN}\), the covariant derivative \(D_{a}\) can be calculated and is given by

$$\begin{aligned}&\tilde{D}_{\mu } = \partial _{\mu } - \frac{1}{2}\tilde{\Gamma }_{\mu }\tilde{\Gamma }^{5}A'(y)e^{-A(y)},\\&\tilde{D}_{5} = \partial _{y}. \end{aligned}$$

Further from Eq. (51), it is evident that \(\Psi (x^{\mu },y)\) is not canonical and thus the canonical Dirac field (\(\tilde{\Psi }\)) in ST theory is defined by

$$\begin{aligned} \tilde{\Psi }(x^{\mu },y) = e^{-\frac{1}{\sqrt{3}}\kappa \Phi } \Psi (x^{\mu ,y}). \end{aligned}$$

In terms of such a canonical field, the Dirac lagrangian turns out to be

$$\begin{aligned} L_{\mathrm{Dirac}}= & {} \sqrt{\tilde{G}} \left[ \bar{\tilde{\Psi }}i\tilde{\Gamma }^{a}\tilde{D}_{a}\tilde{\Psi } - m_5e^{-\frac{2}{\sqrt{3}}\kappa \Phi } \bar{\tilde{\Psi }}\tilde{\Psi }\right. \nonumber \\&\left. +\frac{1}{\sqrt{3}}\kappa \Phi '(y)\left( \bar{\tilde{\Psi }}\tilde{\gamma }^5\tilde{\Psi } \right) \right] .\end{aligned}$$
(52)

As before, we consider \(\xi (y)\) as the fluctuation of the scalar field (\(\Phi (y)\)) over its vev (\(\langle \Phi \rangle \)) i.e. \(\Phi (y) = \langle \Phi \rangle + \xi (y)\). Therefore \(L_{Dirac}\) can be expressed as

$$\begin{aligned} L_{D\mathrm{irac}}= & {} \sqrt{\tilde{G}} \left[ \bar{\tilde{\Psi }}i\tilde{\Gamma }^{a}\tilde{D}_{a}\tilde{\Psi } - m_5e^{-\frac{2}{\sqrt{3}}\kappa \langle \Phi \rangle } \bar{\tilde{\Psi }}\tilde{\Psi }\right. \nonumber \\&+\frac{1}{2\sqrt{3}}\kappa m_5 \bar{\tilde{\Psi }}\tilde{\Psi } \xi (y) - \frac{1}{24}\kappa ^2 m_5 \bar{\tilde{\Psi }}\tilde{\Psi } \xi (y)^2\nonumber \\&+\left. \frac{1}{\sqrt{3}}\kappa \xi '(y)\left( \bar{\tilde{\Psi }}\tilde{\gamma }^5\tilde{\Psi } \right) \right] \end{aligned}$$
(53)

where the higher order terms of \(\kappa \xi \) are neglected due to the consideration of \(\kappa \xi < 1\). It may be noted that the effective mass of the bulk fermion field in ST theory gets suppressed by a factor of \(e^{-\frac{\kappa }{2\sqrt{3}}\langle \Phi \rangle }\) in comparison to that of F(R) theory i.e. \(\tilde{m_5} = m_5e^{-\frac{\kappa }{2\sqrt{3}}\langle \Phi \rangle }\), where \(\tilde{m_5}\) symbolizes the bulk mass in ST theory. Moreover, the last three terms in the expression of Eq. (53) denote the coupling between the scalar field (\(\xi (y)\), generated from higher curvature degrees of freedom) and the fermion field. Clearly such couplings carry the signature of higher curvature effects.

With the explicit forms of \(\tilde{D}_{\mu }\) and \(\tilde{D}_5\), \(L_{Dirac}\) is finally written as

$$\begin{aligned} L_{Dirac}= & {} e^{-4A(y)} \bar{\tilde{\Psi }}\left[ ie^{A(y)}\tilde{\gamma }^{\mu }\partial _{\mu }\right. \nonumber \\&+ \tilde{\gamma }^{5}\left( \partial _{y}-2A'(y)+\frac{\kappa }{\sqrt{3}}\xi '(y) \right) \nonumber \\&-\left. m_5 \left( e^{-\frac{\kappa }{2\sqrt{3}}\langle \Phi \rangle } - \frac{\kappa }{2\sqrt{3}}\xi (y) + \frac{\kappa ^2}{24}\xi ^2(y) \right) \right] \Psi .\nonumber \\ \end{aligned}$$
(54)

At this stage, the five dimensional spinor \(\tilde{\Psi }(x^{\mu },y)\) is decomposed via the KK mode expansion as follows:

$$\begin{aligned} \tilde{\Psi }(x^{\mu },y) = \sum [\tilde{\chi }_L^{n}(x^{\mu })\tilde{\zeta }_L^{n}(y) + \tilde{\chi }_R^{n}(x^{\mu })\tilde{\zeta }_R^{n}(y)]. \end{aligned}$$
(55)

n denotes the nth KK mode and the subscripts L, R indicate the left, right chiral (or helicity) states, respectively. The above KK mode expansion along with the Dirac field lagrangian given in Eq. (54) leads to the following equation of motion for \(\tilde{\zeta }^{(n)}_{L,R}(y)\):

$$\begin{aligned}&e^{-A(y)}\quad \left[ \quad \pm \left( \partial _{y} - 2A'(y) + \frac{\kappa }{\sqrt{3}}\xi '(y) \right) \right. \nonumber \\&\qquad \left. +m_5 \left( e^{-\frac{\kappa }{2\sqrt{3}}\langle \Phi \rangle } - \frac{\kappa }{2\sqrt{3}}\xi (y) + \frac{\kappa ^2}{24}\xi ^2(y) \right) \right] \tilde{\zeta }^n_{R,L}(y)\nonumber \\&\quad =-\tilde{m}_n\tilde{\zeta }^n_{L,R}(y) \end{aligned}$$
(56)

where \(\tilde{m}_{n}\) is the mass of the nth KK mode in ST theory. The 4D fermions obey the canonical equation of motion \(i\tilde{\gamma }^{\mu }\partial _{\mu }\tilde{\chi }^n_{L,R} = \tilde{m}_{n}\tilde{\chi }^n_{L,R}\). Moreover, Eq. (56) is obtained provided the following normalization conditions hold:

$$\begin{aligned}&\int _{0}^{\pi } \mathrm{d}y e^{-3A(y)}\tilde{\zeta }_{L,R}^{m}\tilde{\zeta }_{L,R}^{n} = \delta _{m,n} , \end{aligned}$$
(57)
$$\begin{aligned}&\int _{0}^{\pi } \mathrm{d}y e^{-3A(y)}\tilde{\zeta }_{L}^{m}\tilde{\zeta }_{R}^{n} = 0. \end{aligned}$$
(58)

In the next two subsections, we discuss the localization scenario for massless and massive KK modes (for ST theory), respectively.

6.1 Massless KK mode

For the massless mode, the equation of motion of \(\tilde{\zeta }_{L,R}\) takes the following form:

$$\begin{aligned}&e^{-A(y)}\quad \left[ \quad \pm \left( \partial _{y} - 2A'(y) + \frac{\kappa }{\sqrt{3}}\xi '(y) \right) \right. \nonumber \\&\left. \quad +m_5 \left( e^{-\frac{\kappa }{2\sqrt{3}}\langle \Phi \rangle } - \frac{\kappa }{2\sqrt{3}}\xi (y) + \frac{\kappa ^2}{24}\xi ^2(y) \right) \right] \tilde{\zeta }^n_{R,L}(y) = 0.\nonumber \\ \end{aligned}$$
(59)

Using the explicit solution of \(\xi (y)\) and A(y) (see Eqs. (25) and (26)), we obtain the solution of Eq. (59) as follows:

$$\begin{aligned} \tilde{\zeta }_{L,R}(y)= & {} \sqrt{\frac{k}{\bigg [e^{2k\pi r_c}-1 \bigg ]}} e^{2ky}\nonumber \\&\times \exp { \bigg [\frac{p}{2k}e^{(2+\nu )ky} - \frac{q}{4k}e^{-2(2+\nu )ky}} \bigg ] \end{aligned}$$
(60)

for \(m_5 = 0\) and

$$\begin{aligned} \tilde{\zeta }_{L,R}(y)= & {} \sqrt{\frac{k \pm \tilde{m}_5}{e^{(\frac{p}{k}+\frac{q}{2k})}\bigg [\bigg (1\mp \frac{\kappa v_h}{2\sqrt{3}} m_5 e^{(2+\nu )k\pi r_c} \bigg )e^{(2k\pm m_5)\pi r_c}-1 \bigg ]}}\nonumber \\&\times \exp \quad \bigg [(2k \pm \tilde{m}_5)y \mp \frac{\kappa v_h}{2\sqrt{3}}m_5 e^{(2+\nu )ky} \nonumber \\&\pm \frac{\kappa ^2 v_h^2}{24}m_5 e^{2(2+\nu )ky} \bigg ]\exp {\bigg [\frac{p}{2k}e^{(2+\nu )ky} - \frac{q}{4k}e^{-2(2+\nu )ky}} \bigg ] \nonumber \\ \end{aligned}$$
(61)

for \(m_5 \ne 0\).

p and q are given in Eqs. (40) and (41), respectively. Moreover, the overall normalization constants in Eqs. (60) and (61) are determined by using the normalization condition presented earlier in Eq. (57).

From Eq. (60), we obtain Fig. 6 for the relation between \(\tilde{\zeta }_{L,R}\) and y for various values of \(\alpha \).

The constant y hypersurfaces at \(y=0\) and \(y=36\) represent the Planck and TeV branes, respectively. We focus on the region near the TeV brane (see Fig. 6) to depict the localization properties of the left and right modes.

Fig. 6
figure 6

\(\tilde{\zeta }_{L,R}(=\zeta _{L,R}(ST)\) in the diagram) vs. y for \(M = 1\), \(\Lambda = -1\) and \(m_5=0\)

Full size image

Figure 6 clearly reveals that, similar to F(R) theory, the massless left and right chiral modes (for \(m_5 = 0\)) get more localized on the TeV brane as the value of \(\alpha \) increases.

From Eq. (61), we obtain the plots of left and right chiral modes for various \(\alpha \) in the presence of non-zero bulk fermionic mass.

Figures 7 and 8 reveal that, as the value of \(\alpha \) increases, the peaks of both the left and the right chiral wave functions get shifted towards the visible brane.

Moreover, using the solution of \(\tilde{\zeta }_{L,R}(y)\) (in Eq. (61)), we obtain the effective coupling [56] between the radion and the zeroth order fermionic KK mode (in ST theory) as follows:

$$\begin{aligned} \tilde{\lambda }_L&=\sqrt{\frac{k}{24M^3}} e^{A(\pi r_c)} \bigg [\exp { \bigg [\frac{p}{2k}e^{(2+\nu )kr_c\pi } - \frac{q}{4k}e^{-2(2+\nu )kr_c\pi }} \bigg ] \bigg ]^2\nonumber \\&\frac{\exp {\bigg [(k + 2\tilde{m}_5)\pi r_c - \frac{\kappa v_h}{\sqrt{3}}m_5 e^{(2+\nu )k\pi r_c} + \frac{\kappa ^2 v_h^2}{12}m_5 e^{2(2+\nu )k\pi r_c} \bigg ]}}{\bigg [ \bigg (1 - \frac{\kappa v_h}{2\sqrt{3}} m_5 e^{(2+\nu )k\pi r_c} \bigg )e^{(k + 2\tilde{m}_5)\pi r_c}-1 \bigg ]}\nonumber \\ \end{aligned}$$
(62)

for the left handed chiral mode and

$$\begin{aligned} \tilde{\lambda }_R&=\sqrt{\frac{k}{24M^3}} e^{A(\pi r_c)} \bigg [\exp { \bigg [\frac{p}{2k}e^{(2+\nu )kr_c\pi } - \frac{q}{4k}e^{-2(2+\nu )kr_c\pi }} \bigg ]\bigg ]^2\nonumber \\&\frac{\exp {\bigg [(k - 2\tilde{m}_5)\pi r_c + \frac{\kappa v_h}{\sqrt{3}}m_5 e^{(2+\nu )k\pi r_c} + \frac{\kappa ^2 v_h^2}{12}m_5 e^{2(2+\nu )k\pi r_c} \bigg ]}}{\bigg [\bigg (1 + \frac{\kappa v_h}{2\sqrt{3}} m_5 e^{(2+\nu )k\pi r_c} \bigg )e^{(k - 2\tilde{m}_5)\pi r_c}-1 \bigg ]}\nonumber \\ \end{aligned}$$
(63)

for the right handed mode.

Fig. 7
figure 7

\(\tilde{\zeta }_{L}(=\zeta _{L}(ST)\) in the diagram) vs. y for \(M = 1\), \(\Lambda = -1\) and \(m_5=0.5k\)

Full size image
Fig. 8
figure 8

\(\tilde{\zeta }_{R}(=\zeta _{R}(ST)\) in the diagram) vs. y for \(M = 1\), \(\Lambda = -1\) and \(m_5=0.5k\)

Full size image

Comparing the above two expressions with Eqs. (42) and (43), it is clear that the coupling between radion and zeroth KK fermionic mode is different from that of F(R) theory and the difference is indeed small for \(\kappa v_h < 1\). However, the effective radion–fermion coupling in ST theory increases (for both the left and the right chiral modes) with the parameter \(\alpha \), which is in agreement with the corresponding F(R) theory.

6.2 Massive KK mode

For massive KK modes, the equation of motion for the fermionic wave function is given by

$$\begin{aligned}&e^{-A(y)} \left[ \pm \left( \partial _{y} - 2A'(y) + \frac{\kappa }{\sqrt{3}}\xi '(y) \right) \right. \nonumber \\&\qquad \left. +m_5 \left( e^{-\frac{\kappa }{2\sqrt{3}}\langle \Phi \rangle } - \frac{\kappa }{2\sqrt{3}}\xi (y) + \frac{\kappa ^2}{24}\xi ^2(y) \right) \right] \tilde{\zeta }^n_{R,L}(y)\nonumber \\&\quad =-\tilde{m}_n\tilde{\zeta }^n_{L,R}(y). \end{aligned}$$
(64)

Recall that \(\tilde{m}_n\) is the mass of the nth KK mode in ST theory. With the help of the rescaling wave function \(\tilde{\omega }_{L,R} = e^{\frac{5}{2}A(y)}\tilde{\zeta }_{L,R}\), we obtain the solution of \(\tilde{\zeta }^{(n)}_{L,R}\) as follows:

$$\begin{aligned} \tilde{\zeta }\quad ^{(n)}_{L,R}(y)= & {} \sqrt{k} \exp {\left[ -\frac{p}{8k}e^{(2+\nu )ky} \right] }*\exp {\left[ -\frac{1}{8k}\sqrt{q^2e^{4(2+\nu )ky}+k^2+4\tilde{m}_{n}^2e^{2ky}+4\tilde{m}_5^2+\frac{\kappa ^2 v_h^2}{3}m_5^2e^{2(2+\nu )ky}} \right] }\nonumber \\&\times \left( HypergeometricU\left[ \frac{5}{8} + \frac{qe^{2(2+\nu )ky}}{8k}\right. \right. +\frac{\sqrt{q^2e^{4(2+\nu )ky}+k^2+4\tilde{m}_{n}^2e^{2ky}+4\tilde{m}_5^2+\frac{\kappa ^2 v_h^2}{3}m_5^2e^{2(2+\nu )ky}}}{8k},\nonumber \\&1+ \frac{\sqrt{q^2e^{4(2+\nu )ky}+k^2+4\tilde{m}_{n}^2e^{2ky}+4\tilde{m}_5^2+\frac{\kappa ^2 v_h^2}{3}m_5^2e^{2(2+\nu )ky}}}{4k}, \left. \left. p*\frac{e^{(2+\nu )ky}}{4k} \right] \right) \end{aligned}$$
(65)
Fig. 9
figure 9

\(\tilde{\zeta }^{(1)}_{L,R}(=\zeta ^{(1)}_{L,R}(ST)\) in the diagram) vs. y for \(M = 1\), \(\Lambda = -1\) and \(\frac{m_5}{k}=0.5\)

Full size image

where we use the explicit form of warp factor (A(y)) and scalar field (\(\xi (y)\)). However, from the continuity of \(\tilde{\zeta }^{(n)}_{L,R}\) at \(y=0\) and at \(y=\pi r_c\), the KK mass spectrum in ST theory is obtained and given by

$$\begin{aligned} m_n^2 = e^{-2A(\pi r_c)} \left[ k^2(n^2 + 2n + 1) + m_5^2 e^{-\frac{\kappa }{\sqrt{3}}\langle \Phi \rangle }\right] \end{aligned}$$
(66)

where \(n=1,2,3, \cdots \). The expression of the KK mass tower is different in comparison to that of F(R) theory. However, the difference is again small for \(\kappa v_h < 1\).

Using the solution of \(\tilde{\zeta }^n_{L,R}(y)\) (in Eq. (65)), we determine the coupling between massive KK fermion modes and the radion field, given by

$$\begin{aligned} \tilde{\lambda } ^{(n)}= & {} \sqrt{\frac{k}{24M^3}}e^{A(\pi r_c)} \exp {\left[ -\frac{p}{4k}e^{(2+\nu )k\pi r_c} \right] } \exp {\left[ -\frac{1}{4k}\sqrt{q^2e^{4(2+\nu )k\pi r_c}+k^2+4\tilde{m}_{n}^2e^{2k\pi r_c}+4\tilde{m}_5^2 +\frac{\kappa ^2 v_h^2}{3}m_5^2e^{2(2+\nu )k\pi r_c}}\right] }\nonumber \\&\left[ \mathrm{Hypergeometric}U\left[ \frac{5}{8} + \frac{qe^{2(2+\nu )k\pi r_c}}{8k}\right. \right. +\frac{\sqrt{q^2e^{4(2+\nu )k\pi r_c}+k^2+4\tilde{m}_{n}^2e^{2k\pi r_c}+4\tilde{m}_5^2 +\frac{\kappa ^2 v_h^2}{3}m_5^2e^{2(2+\nu )k\pi r_c}}}{8k},\nonumber \\&1+ \frac{\sqrt{q^2e^{4(2+\nu )k\pi r_c}+k^2+4\tilde{m}_{n}^2e^{2k\pi r_c}+4\tilde{m}_5^2+\frac{\kappa ^2 v_h^2}{3}m_5^2e^{2(2+\nu )k\pi r_c}}}{4k},\left. \left. p*\frac{e^{(2+\nu )k\pi r_c}}{4k} \right] \right] ^2 \end{aligned}$$
(67)

where \(\tilde{\lambda }^{(n)}\) is the coupling between the nth KK fermion mode and the radion field in ST theory. Similar to F(R) theory, \(\tilde{\lambda }^{(n)}\) decreases as \(\alpha \) increases.

Further from Eq. (65), one can find the dependence of the localization for massive KK fermion modes on the parameter \(\alpha \). From this, the behavior of the first KK mode (\(n=1\)) is described in Fig. 9.

Figure 9 depicts that the wave function for the first massive KK mode (in ST theory) gets more and more localized near the Planck brane with increasing value of \(\alpha \). As a result, the coupling parameter decreases near the visible brane as the value of \(\alpha \) increases.

At this stage, it deserves mentioning that, although the solution of fermionic wave function and the expression of radion–fermion coupling become different (however, the differences are indeed small for \(\kappa v_h < 1\)) in F(R) and its corresponding ST theory, the localization properties for both the massless and the massive KK fermionic modes remain identical in the two theories.

7 Conclusion

We consider a five dimensional AdS compactified warped geometry model with two 3-branes embedded within the spacetime. Due to large curvature (\(\sim \) Planck scale), the bulk spacetime is governed by higher curvature F(R) gravity. In the scenario of non-constant curvature, we study in full generality how the higher curvature terms affect the localization of a bulk fermion field within the entire spacetime where F(R) contains the next higher order curvature term to Einstein gravity, i.e. \(F(R)=R+\alpha R^2\). Moreover, we have also explored the localization property of the bulk fermion field in the conformally transformed scalar–tensor version of the model. Our findings are as follows.

  1. 1.

    In F(R) theory:

    • For massless KK mode:

      In the absence of bulk fermion mass, the left and right chiral modes can be localized at different regions in the spacetime by adjusting the value of the higher curvature parameter \(\alpha \). However, the localization of both the chiral modes becomes sharper near the TeV brane as the value of \(\alpha \) increases.

      For non-zero bulk fermion mass, the left and the right modes get more and more localized as the higher curvature parameter becomes larger. Correspondingly the overlap of the fermion wave function with the visible brane increases with \(\alpha \), which is depicted in Figs. 2 and 3.

      The effective coupling between the radion and the zeroth order fermionic KK mode is obtained (in Eqs. (42) and (43)). It is found that the radion–fermion coupling (for both the left and the right chiral modes) increases with increasing value of the higher curvature parameter. This is a direct consequence of the fact that the peaks of the left and right chiral modes shift towards the visible brane as the parameter \(\alpha \) increases. To explore the radion phenomenology, the mass of the radion field is also determined in Eq. (44). It is found that the contribution of the radion in scattering amplitude of fermions decreases as the value of the parameter \(\alpha \) increases, which is depicted in Fig. 4. Thus the presence of higher curvature term reduces the possibility of radion detection in such a scattering processes.

      Another important point to note is that, for a fixed form of F(R), the left chiral mode has higher peak values on the TeV brane as the bulk fermion mass increases, whereas the localization of the right chiral mode shows an opposite behavior. This is in agreement with [50, 55].

    • For massive KK mode:

      The requirement of solving the gauge hierarchy problem confines the mass of the higher KK modes at the TeV scale. Moreover, the mass squared gap (\(\Delta m_n^2 =m_{n+1}^2-m_n^2\)) depends linearly on n, which is also evident from the mass spectrum in Eq. (49).

      The couplings between the radion and the massive KK fermionic mode are determined (in Eq. (50)) in the presence of higher order curvature term (i.e. \(F(R)=R+\alpha R^2\)). It is found that the coupling parameter decreases with the increasing higher curvature parameter.

      From the perspective of the localization scenario, the wave function of the massive KK modes are localized near the Planck brane, which increases with the order of the KK mode. As a result, the couplings of the massive KK fermionic modes with the visible brane matter fields become extremely weak and therefore drastically reduce the possibility of finding the signatures of such massive fermion KK modes in TeV scale experiments.

  2. 2.

    In scalar–tensor theory:

    Finally we investigate the localization property of the bulk fermion field in the scalar–tensor version of the theory. We observe that though the solution of the fermionic wave function as well as the expression of radion–fermion coupling differs slightly from that in the corresponding F(R) model, the localization properties for both the massless and the massive KK fermionic modes remain identical in the two theories.