1 Introduction

Lattice gauge theory at very high temperatures and/or baryon densities predicts an interesting window onto the properties of Quantum Chromodynamics (QCD) in the guise of a new phase, Quark–gluon Plasma (QGP), which pervaded the early universe, and may be present in the core of neutron stars. To realize this predicted phase, current experimental program of ultra-relativistic heavy ion collisions (URHIC) have been designed at different colliders with different center of mass energies, viz. Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory (BNL) at \(\sqrt{s}\)= 200 GeV per nucleon in Au + Au collisions and Large Hadron Collider (LHC) at European Organization for Nuclear Research (CERN) at \(\sqrt{s}\)= 2.76 TeV per nucleon in Pb + Pb collisions. Recent analysis suggests that the events of URHIC should be analyzed by incorporating the effect of the magnetic field because an intensely strong magnetic field, perpendicular to the reaction plane, is expected to be produced at very early stages of collisions when the event is off-central [1,2,3,4,5]. Depending on the centrality, the strength of the magnetic field may reach between \(m_{\pi }^2\) (\(\simeq 10^{18}\) Gauss) at RHIC [6] to 10 \(m_{\pi }^2\) at LHC [7]. At extreme cases it may reach values of 50 \(m_{\pi }^2\). A very strong magnetic field (\(\sim 10^{23}\) Gauss) was also produced in the early universe during the electroweak phase transition due to the gradients in Higgs field [8]. Ultimately such a strong magnetic field might significantly affect the production of particles and alter their dynamics at very early stage of the collisions. Since a magnetic field induces an anisotropy to the momentum of the affected particles, we might expect it to affect the anisotropic flow of the particles.

Naive classical estimates predict that the magnetic field may be very strong; typically up to \(t_{B} \simeq 0.2\) fm [9]. However, the realistic calculations on the charge transport properties of the plasma (namely, conductivity) may suggest that the magnetic field may remain substantial for significantly longer time [10]. Simultaneously heavy quark and antiquarks pairs also develop into physical resonances over a formation time \(t_\mathrm{form}\sim 1/E_\mathrm{bind}\) related to the binding energy of the state, e.g. the charm–anti-charm (\( c \bar{c}\)) pairs form resonances at \(t_{c \bar{c}} \sim 0.3 \) fm. Thus it becomes reasonable to assume that charmonium production may get significantly influenced by the strong magnetic field. The same argument applies to the bottomonium production. A large number of studies on the in-medium properties of \(Q \bar{Q}\) bound states has been carried out using the phenomenological potential models [11,12,13], where the effects of the medium are encoded in a temperature dependent potential with non-perturbative inputs from the lattice simulations. However, lattice calculations of free energies and other quantities [14] obtained from the correlation functions of Polyakov loop are often taken as input for the potential. Although these quantities have been thought to be related to the color-singlet and color-octet heavy quark potentials at finite temperature, a precise answer is still missing. Recently quarkonia at finite temperature has been studied by taking advantage of the hierarchies between the non-relativistic scales associated with quarkonia and the thermal energy scales characterizing the system through the effective field theories, viz. NRQCD, pNRQCD etc. [15]. The in-medium modifications of the quarkonium states can be studied from the first principle of QCD by the spectral functions [16] but the reconstruction of the spectral function from the lattice meson correlators turns out to be very difficult. Recently in a new theoretical development, the heavy quark potential have also been synthesized in the strong coupling regime through a novel idea of gauge-gravity duality  [17,18,19].

Recently the properties of quarkonia states in a hot medium were explored in perturbative thermal QCD framework by correcting both the perturbative and non-perturbative terms of the \(Q \bar{Q}\) potential through the dielectric function in the real-time formalism [20, 21] in both isotropic as well as anisotropic hot QCD medium, where the anisotropy in the momentum space arose at the very early stages of the collisions due to the different expansion rate in the longitudinal and transverse direction [22]. As mentioned earlier, magnetic field is also produced at the early stages of the collisions, thus it becomes worthwhile to examine the effects of the magnetic field on the properties of quarkonia bound states, which is the central theme of our present work. Quantum mechanically both the quarkonium and the heavy meson spectra have been analyzed through the solution of the non-relativistic Schrödinger equation with both harmonic oscillator and Cornell potential with an additional spin–spin interaction term [23, 24]. Moreover, lattice studies have also recently explored the possible anisotropies emerging in the static quark–anti-quark potentials both at \(T = 0\) and \(T \ne 0\) through the Wilson loop expectation value and Polyakov loop correlator, respectively, in the presence of a magnetic background with respect to the direction of the magnetic field [25, 26].

Here we have tried to investigate the effect of strong and homogeneous magnetic field on the properties of quarkonia states. We have first calculated the gluon self-energy at finite temperature in a strong magnetic background and then obtain the heavy quark potential by taking the static limit of the effective gluon propagator to see the effects of the magnetic field alone on the quarkonium states even in a thermal medium. This is due to the fact that the magnetic field is assumed to be much stronger than the temperature as well as the mass of the quarks in a quark loop of the gluon self-energy (\(eB \gg T^2\) and \(eB \gg m^2\)), known as the “Strong Magnetic Field Approximation (SMFA)”. As a consequence the Debye mass obtained from the static limit of the gluon self-energy becomes almost independent of the temperature, hence the potential even in the thermal medium depends mainly on the magnetic field because the medium dependence in the potential enters through the Debye mass. Moreover, another condition for the non-relativistic potential approach for heavy quarkonia to be valid is that the mass of the heavy quark (either charm or bottom quark) should be larger than the dominant scale available in the problem (\(m_Q>>\sqrt{eB}\)) (dimensionally) because \(\sqrt{eB}\) is the most dominant scale available in the strongly magnetized thermal medium. Thus the above-mentioned two conditions constrain the lower and upper limit of the magnetic fields, respectively, for which our work is valid. As a by-product of this constraint, the magnetic field expected to be produced at RHIC may not satisfy the condition of SMFA. So our work which is valid only in SMFA will be suitable for describing the LHC events where the magnetic fields expected to be produced are well within the limit of the validity of our work.

Our work is arranged in the following way: in Sect. 2.1 we will discuss the quark propagator at finite temperature within SMFA. In Sect. 2.1.2 we will calculate the gluon self-energy at finite temperature in the presence of a strong magnetic field. In Sect. 2.2 we will compute the screening mass in SMFA by taking the static limit of the gluon self-energy. In Sect. 3, we will obtain the potential from the inverse Fourier transform of the effective propagator in the static limit and explore how the properties of quarkonia could be affected by the presence of a strong magnetic field. Finally we will conclude in Sect. 4.

2 One-loop gluon self-energy and the screening mass in SMFA

The gluon self-energy can be affected by the magnetic field in two ways: first, the quark propagator gets affected due to the Landau quantization of the energy levels (known as Landau levels) in the presence of the magnetic field. Second, the strong coupling runs with both the magnetic field and the temperature. However, in SMFA, it runs exclusively with the magnetic field as we have discussed in the introduction.

Schwinger was the first to obtain the fermionic propagator in coordinate space by the proper-time formalism [27]; then Tsai has obtained the same in momentum space and used it to calculate the vacuum polarization in magnetic field [28]. The vacuum polarization tensor has also been obtained in a gauge invariant manner in both the strong and the weak magnetic field limit [29,30,31]. We shall now extend these calculations to QCD to calculate the gluon self-energy, which will in turn helps to study the properties of quarkonia quantum field theoretically in the presence of a strong magnetic field.

2.1 Fermionic propagator in the presence of the magnetic field

2.1.1 Vacuum in a static and homogeneous magnetic field

For the sake of simplicity, we assume the magnetic field to be constant and homogeneous. We also assume the magnetic field to be along the z-direction and of magnitude B. Such a magnetic field can be obtained from a vector potential \(A_\mu = (0,0,Bx,0)\). The choice of vector potential is not unique as the same magnetic field can also be obtained from a symmetric potential given by \(A_\mu = (0,\frac{-By}{2},\frac{Bx}{2},0)\). Using the proper-time method formulated by Schwinger, the fermion propagator in such a magnetic field can be written in the coordinate space as [27]

$$\begin{aligned} S(x,x^\prime ) = \phi (x,x^\prime )\int \frac{\mathrm{d}^4 p}{(2\pi ) ^4}\mathrm{e}^{ip(x-x^\prime )}S(p), \end{aligned}$$
(1)

where the phase factor, \(\phi (x,x^\prime )\) is given by

$$\begin{aligned} \phi (x,x^\prime ) = \mathrm{e}^{ie\int _x^{x^\prime }A(\xi )d\xi }, \end{aligned}$$
(2)

which becomes unity for a closed fermion loop with two fermion lines, i.e., \(\phi (x,x^\prime )=1\) [32].

However, the same propagator was first calculated by [28, 32] in the momentum space as

$$\begin{aligned} iS(p)= & {} \int _0^\infty \frac{1}{eB}\frac{\mathrm{d}s}{\cos (s)} \mathrm{e}^{-is\left[ m^2-p_{\Vert }^2+\frac{\tan (s)}{s} p_\bot ^2\right] }\nonumber \\&\left[ \left\{ \cos (s) +\gamma _{1}\gamma _{2} \sin (s)\right\} (m+\gamma \cdot p_{\Vert }) -\frac{\gamma \cdot p_{\bot }}{\cos (s)}\right] .\nonumber \\ \end{aligned}$$
(3)

The propagator (3) in the momentum space can also be expressed in a more convenient way using the associated Laguerre polynomials (\(L_n\)),

$$\begin{aligned} iS(p)=\sum _n\frac{-id_n(\alpha )D+d^\prime _n(\alpha ) \bar{D}}{p_L^2+2neB} +i\frac{\gamma \cdot p_\bot }{p_\bot ^2}~, \end{aligned}$$
(4)

where the following quantities are defined as [32]

$$\begin{aligned}&D=(m+\gamma \cdot p_\Vert )+\gamma \cdot p_\bot \frac{m^2-p_\Vert ^2}{p_\Vert ^2},\\&\bar{D}=\gamma _{1}\gamma _{2}(m+\gamma \cdot p_\Vert ),\\&d_n(\alpha )=(-1)^n e^{-\alpha }C_n(2\alpha ),\\&C_n(2\alpha )=L_{n}(2\alpha )-L_{n-1}(2\alpha ),\\&d^{'}_{n}(\alpha )=\frac{\partial d_n}{\partial \alpha },\\&p_L^2=m^2-p_\Vert ^2,\\&\alpha =\frac{{p_\bot }^2}{eB},\\&p_{\Vert }^2=p_{0}^2-p_{z}^2, \\&p_{\bot }^2=p_{x}^2+p_{y}^2. \end{aligned}$$

The order of the Laguerre polynomial also corresponds to the number of energy eigenvalues in a magnetic field, known as Landau levels. In SMFA, the particles occupy the lowest Landau level (LLL) (\(n=0\)) only, thus, in SMFA, the fermion propagator in Eq. (4) reduces to the following form:

$$\begin{aligned} iS_0(p)=\frac{(1+\gamma ^{0}\gamma ^{3}\gamma ^{5}) (\gamma ^{0}p_{0}-\gamma ^{3}p_{z}+m)}{p_{\parallel }^2-m^2+i\epsilon } \mathrm{e}^{-\frac{p_{\perp }^2}{\mid qB\mid }}, \end{aligned}$$
(5)

where m and q are the mass and electric charge of the fermion, respectively.

2.1.2 Heat bath in a strong homogeneous magnetic field

In thermal medium, the system possesses additional thermal scales, viz. T, gT etc., which are well separated in the weak coupling regime (\(T>gT>\cdot \cdot \)), in addition to the quark masses. So at finite temperature, strong magnetic field approximation implies that both conditions \(eB>>T^2\) and \(eB>>m^2\) are to be satisfied. To switch on the temperature in the vacuum propagator (5) in the real-time formalism, the matrix propagator is diagonalized by the matric U as

$$\begin{aligned} S_{ab}(p)=U_{ac} (p) {\begin{pmatrix} S_0(p) &{} 0\\ 0 &{}-S_0^*(p) \end{pmatrix}}_{cd} U_{db}(p), \end{aligned}$$
(6)

where the matrix U(p) is given by

$$\begin{aligned} U(p)= \begin{pmatrix} \tilde{N}_2 &{} -\tilde{N}_1 \mathrm{e}^{-\beta \mu /2}\\ \tilde{N}_1 \mathrm{e}^{-\beta \mu /2}&{} \tilde{N}_2 \end{pmatrix}, \end{aligned}$$
(7)

with

$$\begin{aligned} \tilde{N_1}(p_0)= & {} \sqrt{n^{+}_p}~\theta (p_0)+ \sqrt{n^{-}_p}~\theta (-p_0),\end{aligned}$$
(8)
$$\begin{aligned} \tilde{N_2}(p_0)= & {} \sqrt{1-n^{+}_p}~\theta (p_0)+ \sqrt{1-n^{-}_{p}}~\theta (-p_0),\end{aligned}$$
(9)
$$\begin{aligned} n^{\pm }_p (p_0)= & {} \frac{1}{e^{\beta (p_0\mp \mu )+1}}, \end{aligned}$$
(10)

where \(\beta \) is the inverse of the temperature and \(\mu \) is the chemical potential. In the present work we are working for baryonless medium (\(\mu =0\)), i.e. \(n^{+}_p = n^{-}_p = n_p\). Plugging Eq. (7) in Eq. (6), we get the fermion propagator:

$$\begin{aligned} S(p) = \begin{pmatrix} S_0(p)\tilde{N}_2^{2}+S_0^{*}(p)\tilde{N}_1^{2}&{} -S_0(p)\tilde{N_1}\tilde{N_2}+S_0^{*}(p)\tilde{N_1}\tilde{N_2} \\ S_0(p)\tilde{N_1}\tilde{N_2}-S_0^{*}(p)\tilde{N_1}\tilde{N_2}&{} - S_0(p)\tilde{N}_1^{2}-S_0^{*}(p)\tilde{N}_2^{2} \end{pmatrix}.\nonumber \\ \end{aligned}$$
(11)

For calculating the gluon self-energy in an equilibrium medium, we need only the 11-component of the matrix propagator expressed in Eq. (11),

$$\begin{aligned} S_{11}(p)= & {} S_0(p)\tilde{N}_2^2+S_0^{*}(p) \tilde{N}_1^2 ~, \end{aligned}$$
(12)
$$\begin{aligned} iS_{11}(p)= & {} \Bigg [\frac{1}{{p_{\parallel }^2-m^2+ i\epsilon }}+2\pi in_{p}\delta (p_{\parallel }^2-m^2)\Bigg ]\nonumber \\&\times (1+\gamma ^{0}\gamma ^{3}\gamma ^{5})(\gamma ^{0}p_{0}-\gamma ^{3} p_{z}+m) e^{\frac{-p_{\perp }^2}{\mid qB \mid }}, \end{aligned}$$
(13)

where the distribution function is given by

$$\begin{aligned} n_p(p_0) = \frac{1}{\mathrm{e}^{\beta \mid p_0\mid } + 1}. \end{aligned}$$

The above description for fermionic propagator can easily be generalized to quarks of fth flavor with which we are going to calculate the gluon self-energy.

2.2 Gluon self-energy in a hot QCD medium in the presence of a strong magnetic field

As mentioned earlier, since we are working within SMFA, we may consider the strong coupling to run with the magnetic field only. For this purpose we closely follow the running coupling in [33], where the coupling runs with the momentum parallel and perpendicular to the magnetic field separately. In our case of the magnetic field (\(\mathbf {B}= B\hat{z}\)), we will use the coupling dependent on the longitudinal component only because the energy of Landau levels for quarks in SMFA depend only on the longitudinal component of momentum. In fact, the coupling dependent on the transverse momentum does not depend on the magnetic field at all. So in our calculation, the relevant coupling is given by [33]

$$\begin{aligned} \alpha _{s}^\Vert (k_3)=\frac{1}{{\alpha _s^0(\mu _0)}^{-1}+\frac{11N_c}{12\pi } \ln \left( \frac{k^2_3+M^2_B}{\mu _0^2}\right) +\frac{1}{3\pi }\sum _f \frac{|q_f B|}{\sigma }}, \end{aligned}$$
(14)

where

$$\begin{aligned} \alpha _s^0(\mu _0) = \frac{12\pi }{11N_c\ln \left( \frac{(\mu _0^2+M^2_B)}{\Lambda _V^2}\right) }. \end{aligned}$$
(15)

In the above Eq. (14), \(M_B\) is taken \(\sim ~1\) GeV as an infrared mass and the string tension, \(\sigma =0.18 \mathrm{{GeV}}^2\).

For system in equilibrium, we need only the “11”-component of the gluon self-energy matrix calculated in the real-time formalism, which is given by

$$\begin{aligned} {\Pi ^{\mu \nu }}(k)= & {} \frac{ig^2}{2} \sum _f \int \frac{d^{4}p}{(2\pi )^4}tr[\gamma ^{\mu }S_{11}(p)\gamma ^{\nu }S_{11}(q)]\nonumber \\= & {} \frac{ig^2}{2} \sum _f \int \frac{d^{4}p}{(2\pi )^4}tr [(\gamma ^{\mu }(1+\gamma ^{0}\gamma ^{3}\gamma ^{5}) (\gamma ^{0}p_{0}\nonumber \\&-\gamma ^{3}p_{z}+m_f)\nonumber \\&\times \gamma ^{\nu }(1+\gamma ^{0}\gamma ^{3}\gamma ^{5}) (\gamma ^{0}q_{0}-\gamma ^{3}q_{z}+m_f)]\nonumber \\&\times \left\{ \frac{1}{p_{\parallel }^2-m_f^2+i\epsilon } +2\pi i n_{p}\delta (p_{\parallel }^2-m_f^2)\right\} \nonumber \\&\times \left\{ \frac{1}{q_{\parallel }^2-m_f^2+i\epsilon }\right. \nonumber \\&\left. +\,2\pi i n_{q}\delta (q_{\parallel }^2-m_f^2)\right\} \mathrm{e}^{\frac{{-p_{\perp }}^2}{|q_f|B}}\mathrm{e}^{\frac{{-q_{\perp }}^2}{|q_f|B}}, \end{aligned}$$
(16)

where the factor 1/2 arises due to trace in color-space and the trace due to \(\gamma \) matrices is given by

$$\begin{aligned} L^{\mu \nu }=8\left[ p_{\parallel }^{\mu }q_{\parallel } ^{\nu }+p_{\parallel }^{\nu }q_{\parallel }^{\mu } -g_{\parallel }^{\mu \nu }((p.q)_{\parallel }-m_f^2) \right] . \end{aligned}$$
(17)

Separating the momentum integration into longitudinal (\(\parallel \)) and transverse (\(\perp \)) components with respect to the magnetic field, the gluon self-energy can be factorized into \(\parallel \) and \(\perp \) components of momentum integration

$$\begin{aligned} \Pi ^{\mu \nu }(k)=\sum _f \Pi _{\parallel }^{\mu \nu }(k_{\parallel })A_f(k_{\perp })~, \end{aligned}$$
(18)

where the transverse component is given by

$$\begin{aligned} A_f(k_{\perp })= & {} \int \mathrm{d}p_{x} \mathrm{d}p_{y} \mathrm{e}^{\frac{{-p_{\perp }}^2}{|q_{f}|B}}\mathrm{e}^{\frac{{-q_{\perp }}^2}{|q_{f}|B}}\nonumber \\= & {} \frac{\pi |q_{f}|B}{2}\mathrm{e}^{-\frac{k_{\perp }^2}{2|q_{f}|B}}. \end{aligned}$$
(19)

It may be noted that in LLL approximation, the dependence of self-energy on the magnetic field is fully encapsulated in the transverse component whereas the longitudinal part carries no dependence on the magnetic field. We will now calculate the longitudinal component of the self-energy by decomposing Eq. (16) into vacuum and thermal parts:

$$\begin{aligned} \Pi ^{\mu \nu }_{\parallel }=(\Pi ^{\mu \nu }_{\parallel })_{V}+ (\Pi ^{\mu \nu }_{\parallel })_{n}+(\Pi ^{\mu \nu }_{\parallel })_{n^2}, \end{aligned}$$
(20)

where \((\Pi ^{\mu \nu }_{\parallel })_{V}\) is the vacuum part, \((\Pi ^{\mu \nu }_{\parallel })_{n}\) and \((\Pi ^{\mu \nu }_{\parallel })_{n^2}\) are the thermal contributions due to single and double distribution functions, respectively. They are explicitly given by

$$\begin{aligned} (\Pi ^{\mu \nu }_{\parallel })_{V}= & {} \frac{ig^2}{2(2\pi )^4} \int \mathrm{d}p_0 \mathrm{d}p_z L^{\mu \nu }\nonumber \\&\times \left\{ \frac{1}{(q_{\parallel }^2-m_f^2+i\epsilon )}\frac{1}{(p_{\parallel }^2-m_f^2+i\epsilon )}\right\} , \end{aligned}$$
(21)
$$\begin{aligned} (\Pi ^{\mu \nu }_{\parallel })_{n}= & {} \frac{ig^2(2\pi i)}{2(2\pi )^4}\int \mathrm{d}p_0 \mathrm{d}p_z L^{\mu \nu }\nonumber \\&\times \left\{ \frac{n_{p}\delta (p_{\parallel }^2-m_f^2)}{(q_{\parallel }^2 -m_f^2+i\epsilon )} +\frac{n_{q}\delta (q_{\parallel }^2-m_f^2)}{(p_{\parallel }^2-m_f^2+i\epsilon )}\right\} , \end{aligned}$$
(22)
$$\begin{aligned} (\Pi ^{\mu \nu }_{\parallel })_{n^2}= & {} \frac{ig^2}{2(2\pi )^4} \int dp_0 dp_z L^{\mu \nu }\nonumber \\&\times \lbrace (-4\pi ^2)n_{p}n_{q}\delta (p_{\parallel }^2-m_f^2) \delta (q_{\parallel }^2-m_f^2)\rbrace ~. \end{aligned}$$
(23)

We will now calculate the vacuum term for the gluon self-energy.

2.2.1 Vacuum contribution (\(T=0\), \(eB \ne 0\))

The vacuum term in the strong magnetic field can be calculated easily as it is similar to the calculation of self-energy in vacuum without magnetic field except the fact that the dimension of the momentum integration is now reduced from 4 to 2. This dimensional reduction in fact removes the divergences usually encountered in 4-dimension, thus we do not need any regularization any more. Using the identity

$$\begin{aligned} \frac{1}{x \mp i\epsilon }={{\varvec{P}}} \left( \frac{1}{x}\right) \pm i \pi \delta (x), \end{aligned}$$
(24)

the real part of the vacuum term in the gluon self-energy has been calculated as

$$\begin{aligned} \mathfrak {R}{\Pi ^{\mu \nu }(k) \mid }_V=\left( g_{\parallel }^{\mu \nu } -\frac{k_{\parallel }^{\mu }k_{\parallel }^{\nu }}{k_{\parallel }^2} \right) \Pi (k^2), \end{aligned}$$
(25)

where the form factor, \(\Pi (k^2)\) is given by

$$\begin{aligned} \Pi (k^2)= & {} \frac{g^2}{4\pi ^2}\sum _{f}\mid q_{f}B \mid \mathrm{e}^{-\frac{k_{\perp }^2}{2|q_{f}|B}}\nonumber \\&\times \left[ \frac{2m_{f}^2}{k_{\parallel }^2} \left( 1-\frac{4m_{f}^2}{k_{\parallel }^2}\right) ^{-1/2} \left\{ \ln \frac{1-{\Big (1-\frac{4m_{f}^2}{k_{\parallel }^2}\Big )}^{1/2}}{1+{\Big (1+\frac{4m_{f}^2}{k_{\parallel }^2} \Big )}^{1/2}} + i\pi \right\} -1\right] .\nonumber \\ \end{aligned}$$
(26)

Therefore the 00-component (\(\mu =\nu =0\)) of the real part of the vacuum term of the gluon self-energy (using the metric \(g^{\mu \nu }_{\parallel }=\mathrm{diag}(1,0,0,-1)\) is given by

$$\begin{aligned} \mathfrak {R}{\Pi ^{00}(k)\mid }_{V}=-\frac{k_{z}^2}{k_{\parallel }^2} ~\Pi (k^2). \end{aligned}$$

In the limit of massless quarks \((m_{f}=0)\), the gluon self-energy due to vacuum term in the static limit (\(k_0=0\), \(\mathbf {k} \rightarrow 0\)) is given by the scale available for the magnetic field only in SMFA

$$\begin{aligned} \mathfrak {R}{\Pi ^{00} (k_0=0,\mathbf {k}\rightarrow 0)\mid }_V =\frac{g^2}{4\pi ^2}\sum _{f}\mid q_{f}B \mid . \end{aligned}$$
(27)

For the physical quark masses \((m_{f}\ne 0\)), the vacuum term in the static limit (\(k_0=0\), \(\mathbf {k} \rightarrow 0\)) vanishes

$$\begin{aligned} \mathfrak {R}{\Pi ^{00} (k_0=0,\mathbf {k}\rightarrow 0)\mid }_V=0. \end{aligned}$$
(28)

2.2.2 Medium contribution

The (thermal) medium contribution to the gluon self-energy contains two terms: the first one (22) involves single distribution function and the second one (23) involves the product of two distribution functions. We will first consider the medium contribution due to the single distribution function only. Using the property of Dirac delta function, the gluon self-energy in Eq. (22) is reduced to

$$\begin{aligned} (\Pi ^{\mu \nu }_{\parallel })_{n}= & {} -\frac{g^2}{2(2\pi )^3} \int \mathrm{d}p_0 \mathrm{d}p_z L^{\mu \nu }\nonumber \\&\times \Bigg [ \frac{n_{p}(p_0)\Big \{\delta (p_{0}-\omega _{p}) +\delta (p_{0}+\omega _{p})\Big \}}{(q_{0}^2-q_{z}^2-m_f^2 +i\epsilon )(2\omega _{p})}\nonumber \\&+\,\frac{n_{q}(q_0)\Big \{\delta (q_{0}-\omega _{q}) +\delta (q_{0}+\omega _{q})\Big \}}{(p_{0}^2-p_{z}^2-m_f^2 +i\epsilon )(2\omega _{q})}\Bigg ]. \end{aligned}$$
(29)

Taking \(\mu =\nu =0\), the real part of the 00-component of \((\Pi ^{\mu \nu }_{\parallel })_{n}\) becomes

$$\begin{aligned} \mathfrak {R}{\Pi ^{00}_\parallel (k_0,k_z)\mid }_n= & {} -\frac{g^2}{2(2\pi )^3}\int \mathrm{d}p_0 \mathrm{d}p_z L^{00}\nonumber \\&\times \Bigg [ \frac{n_{p}(p_0)\Big \{\delta (p_{0}-\omega _{p}) +\delta (p_{0}+\omega _{p})\Big \}}{(q_{0}^2-\omega _q^2) (2\omega _{p})}\nonumber \\&+\,\frac{n_{q}(q_0)\Big \{\delta (q_{0}-\omega _{q}) +\delta (q_{0}+\omega _{q})\Big \}}{(p_{0}^2-\omega _p^2) (2\omega _{q})}\Bigg ],\nonumber \\ \end{aligned}$$
(30)

where the 00 component of \(L^{\mu \nu }\) is

$$\begin{aligned} L^{00}=8[p_{0}q_{0}+p_{z}q_{z}+m_f^{2}], \end{aligned}$$
(31)

and the other notations are

$$\begin{aligned} \omega _p= & {} \sqrt{p_z^2+m_f^2},\\ \omega _q= & {} \sqrt{(p_z-k_z)^2+m_f^2}. \end{aligned}$$

After performing the \(p_{0}\) integration we get from Eq. (30)

$$\begin{aligned} \mathfrak {R}{\Pi ^{00}_\parallel (k_0,k_z)\mid }_n= & {} -\frac{g^2}{4(2\pi )^3}\int dp_z\Bigg [\frac{L^{00}_{1}~n_p^{+}}{\omega _p[(\omega _p-k_0)^2-\omega _q^2]}\nonumber \\&+\frac{L^{00}_{2}~n_p^{-}}{\omega _p[(\omega _p+k_0)^2-\omega _q^2]}\nonumber \\&+\frac{L^{00}_{3}~n_q^{+}}{\omega _q[(\omega _q+k_0)^2-\omega _p^2]}\nonumber \\&+\frac{L^{00}_{4}~n_q^{-}}{\omega _q[(\omega _q-k_0)^2-\omega _p^2]} \Bigg ] , \end{aligned}$$
(32)

where we have defined

$$\begin{aligned} L^{00}_{1}= & {} L^{00}(p_0=\omega _p)= 8(2\omega _p^2-\omega _{p}k_0-p_{z}k_{z}),\\ L^{00}_{2}= & {} L^{00}(p_0=-\omega _p)= 8(2\omega _p^2+\omega _{p}k_0-p_{z}k_{z}),\\ L^{00}_{3}= & {} L^{00}(p_0=\omega _q+k_0)\\= & {} 8(2\omega _p^2+\omega _{q}k_0-3p_{z}k_{z}+k_{z}^2),\\ L^{00}_{4}= & {} L^{00}(p_0=-\omega _q+k_0)\\= & {} 8(2\omega _p^2-\omega _{q}k_0-3p_{z}k_{z}+k_{z}^2), \end{aligned}$$

and

$$\begin{aligned} n_p^{+}= & {} n_p(p_0=\omega _p),\\ n_p^{-}= & {} n_p(p_0=-\omega _p),\\ n_q^{+}= & {} n_q(p_0=\omega _q+k_0),\\ n_q^{-}= & {} n_q(p_0=-\omega _q+k_0). \end{aligned}$$

In the limit of massless quarks (\(m_{f}=0\)), the gluon self-energy in Eq. (32) gets simplified into

$$\begin{aligned} \mathfrak {R}{\Pi ^{00}_\parallel (k_0,k_z)\mid }_n= & {} \frac{8g^2}{2(2\pi )^3} \Bigg [\frac{k_z^2}{k_0^2-k_z^2}-\frac{k_{z}T}{k_0^2-k_z^2}\ln (2)\nonumber \\&+\frac{k_{z}T}{k_0^2-k_z^2}\ln (1+e^{-\frac{k_z}{T}})\Bigg ]. \end{aligned}$$
(33)

Using Eq. (18) and multiplying the transverse component, \(A(k_\perp )\) from Eq. (19), the contribution to the real part of the self-energy from the component having single distribution function becomes

$$\begin{aligned} \mathfrak {R}{\Pi ^{00} (k_0,k_x,k_y,k_z)\mid }_n= & {} \frac{g^2}{4\pi ^2}\sum _{f} |q_{f}|B \mathrm{e}^{-\frac{(k_{x}^2+k_{y}^2)}{2|q_f|B}}\nonumber \\&\times \Bigg [\frac{k_z^2}{k_0^2-k_z^2}-\frac{k_{z}T}{k_0^2-k_z^2}\ln (2)\nonumber \\&+\frac{k_{z}T}{k_0^2-k_z^2}\ln (1+\mathrm{e}^{-\frac{k_z}{T}})\Bigg ], \end{aligned}$$
(34)

which, in the static limit (\(k_0=0\), \(\mathbf {k} \rightarrow 0\)) becomes

$$\begin{aligned} \mathfrak {R}{\Pi ^{00}(k_0=0,\mathbf {k}\rightarrow 0) \mid }_n= & {} -\frac{g^2}{4\pi ^2}\sum _{f} |q_{f}|B\nonumber \\&+\frac{g^2}{8\pi ^2}\sum _{f} |q_{f}|B. \end{aligned}$$
(35)

However, for the physical quark masses \((m_{f}\ne 0\)), the self-energy in Eq. (30) reduces to, by putting \(k_0=0\)

$$\begin{aligned} \mathfrak {R}{\Pi ^{00}_\parallel (k_0=0,k_z) \mid }_n=-\frac{g^2}{2(2\pi )^3}\int \mathrm{d}p_z I_{n}, \end{aligned}$$
(36)

where the integrand, \(I_n\), is given by

$$\begin{aligned} I_{n}= & {} \frac{8p_{z}n_p}{\omega _{p}k_{z}} -\frac{8(p_{z}-k_{z})n_q}{\omega _{q}k_{z}}+\frac{16m_{f}^2n_p}{\omega _{p}k_{z}(2p_{z}-k_{z})}\nonumber \\&-\frac{16m_{f}^2n_q}{\omega _{q}k_{z}(2p_{z}-k_{z})}, \end{aligned}$$
(37)

and the distribution functions are given by

$$\begin{aligned} n_{p}=\frac{1}{e^{\beta |\omega _{p}|}+1}, \quad n_{q}=\frac{1}{e^{\beta |\omega _{q}|}+1}. \end{aligned}$$

Furthermore, taking the \(k_z \rightarrow 0\) limit, the integrand, \(I_{n}\), is simplified into

$$\begin{aligned} I_{n}=-\frac{8}{T}n_{p}(1-n_{p}). \end{aligned}$$

Thus for the physical quark masses \((m_{f}\ne 0\)), the contribution to the gluon self-energy having a single distribution function in the static limit reduces to

$$\begin{aligned}&\mathfrak {R}{\Pi ^{00} (k_0=0,\mathbf {k}\rightarrow 0) \mid }_n\nonumber \\&\quad = \frac{g^2}{4\pi ^{2}T}\sum _{f}|q_{f}B|\int _{0}^{\infty }\mathrm{d}p_{z} \frac{\mathrm{e}^{\beta \omega _{p}}}{(1+\mathrm{e}^{\beta \omega _{p}})^2}. \end{aligned}$$
(38)
Fig. 1
figure 1

Left panel: Separation is seen only between low and high T at high eB. Right panel: High eB can distinguish massless and massive fermions (quarks)

Full size image

Finally the medium contribution to the gluon self-energy involving the product of two distribution functions given in Eq. (23) does not contribute to the real part of the gluon self-energy, i.e.

$$\begin{aligned} \mathfrak {R}{\Pi ^{00} (k_0=0,\mathbf {k}\rightarrow 0)\mid }_{n^2}=0. \end{aligned}$$
(39)

We have thus so far evaluated the vacuum as well as medium contribution to one-loop gluon self-energy; therefore we add them up to obtain the real part of the one-loop gluon self-energy in the static limit for massless quarks,

$$\begin{aligned} \mathfrak {R}\Pi ^{00}(k_0=0,\mathbf {k}\rightarrow 0)= \frac{g^2}{8\pi ^2}\sum _{f} |q_{f}|B , \end{aligned}$$
(40)

and for the physical quark masses (\(m_f \ne 0\))

$$\begin{aligned}&\mathfrak {R}\Pi ^{00}(k_0=0,\mathbf {k}\rightarrow 0)\nonumber \\&\quad =\frac{g^2}{4\pi ^{2}T} \sum _{f}|q_{f}B|\int _{0}^{\infty } \mathrm{d}p_{z}\frac{\mathrm{e}^{\beta \omega _{p}}}{(1+\mathrm{e}^{\beta \omega _{p}})^2}. \end{aligned}$$
(41)

2.3 Debye screening mass in the strong magnetic field

The Debye screening manifests itself in the collective oscillation of the medium via the dispersion relation and is obtained by the static limit of the longitudinal part (00 component) of the gluon self-energy, i.e.

$$\begin{aligned} m_{D}^2=\mathfrak {R}\Pi ^{00} (k_0=0,\mathbf {k}\rightarrow 0). \end{aligned}$$
(42)

Therefore, Eq. (40) gives the very simple form for the square of the Debye mass for massless quarks, which is already derived in [34, 35]

$$\begin{aligned} m_{D}^2=\frac{g^2}{8\pi ^2}\sum _{f}|q_{f}|B. \end{aligned}$$
(43)

It shows that \(m_D^2\) depends strongly on the magnetic field and is independent of the temperature, thus the collective behavior of the medium gets strongly affected by the presence of a strong magnetic field. However, for physical quark masses, the Debye mass is given by Eq. (41),

$$\begin{aligned} m_{D}^2=m_{D}^2(m_f=0) \times \frac{2}{T}\int _{0}^{\infty } \mathrm{d}p_{z}\frac{\mathrm{e}^{\beta \omega _{p}}}{(1+\mathrm{e}^{\beta \omega _{p}})^2}, \end{aligned}$$
(44)

which depends on both magnetic field and temperature. However, \(m_D^2\) depends strongly on the magnetic field and the dependence on the temperature is very weak and the screening mass becomes temperature-independent beyond a certain temperature.

Now, for the SMFA to be valid, we have to be careful in choosing the range of the temperature and magnetic field. For example, for temperatures up to 300 MeV, the starting value of eB has to be much higher than \(0.09~\mathrm{{GeV}}^2\). Here we have taken the starting magnetic field to be \(eB=10~m_\pi ^2\sim 0.2~\mathrm{GeV}^2\). However, for the upper bound on the magnetic field, the constraint comes from the heavy quark mass (\(m_Q \gg \sqrt{eB}\)) as discussed in the introduction. So, we have taken the highest magnetic field for charmonium states to be \(eB=25~m_\pi ^2\), which gives us \(\sqrt{eB}\sim 0.7~\mathrm{GeV}\). Thus, to see the variation of the Debye masses with the strong magnetic field, we have numerically calculated \(m_D^2\) as a function of eB (in units of \(m_\pi ^2\)) for the temperature range T = 200–300 MeV in Fig. 1a and noticed that \(m_D^2\) is almost linearly increasing with eB for smaller temperature. For higher temperatures, \(m_D^2\) deviates slightly from the linearly increasing trend.

As we understood earlier in SMFA, the strongly magnetized thermal medium with massless quarks possesses only one scale related to the magnetic field (eB) so by the dimensional arguments the square of the Debye mass is linear in eB whereas for the medium with physical quark masses, even in SMFA there is a weak competition between the dominant scale, eB and much weaker scales, mass (m) and temperature (T) (rather their ratio, m / T) in the form of Boltzmann damping factor (\(\exp (-m/T)\)) as in Eq. (44). This is seen in Fig. 1b, where a comparison of Debye masses with and without incorporating the quarks masses is made.

Fig. 2
figure 2

The effect of the temperature is only pronounced at low temperature and high magnetic field

Full size image

To see the temperature dependence of the Debye mass explicitly we have plotted \(m_D\) with the temperature directly with increasing values of \(eB= 10 m_\pi ^2\), \(15 m_\pi ^2\) and \(25 m_\pi ^2\) in Fig. 2. We can see how weakly the screening mass depends on temperature. It increases very slightly with temperature and beyond a point, the screening mass is practically a constant with magnetic field. The effect of the temperature is slightly more pronounced for high magnetic field and low temperature.

Very recently the effects of a magnetic background on color-screening phenomena in QGP were also explored through the estimation of both the magnetic and the electric screening masses by measuring the Polyakov loop correlators on the lattice for various temperatures [36]. It is found that the magnetic field induces an increase of both the magnetic and the electric screening masses and, to some extent, also the appearance of an anisotropy in Polyakov loop correlators. Both screening masses are found to increase linearly with the magnetic field and the influence of the magnetic field on the two masses is enhanced at lower temperatures and is asymptotically diminished in the higher temperature. Thus our aforesaid results on the Debye mass qualitatively agree with their findings for the electric screening mass, which is of interest to us for the screening of the heavy quark potential. However, their lattice estimates for the electric screening masses are approximately larger by an order of magnitude than our results. This large difference may be attributed to nonperturbative effects, which is beyond the scope of this work.

3 Heavy quark potential in a hot QCD medium

The derivation of potential between a heavy quark Q and its anti-quark (\(\bar{Q}\)) either from EFT (pNRQCD) or from first principle QCD may not be plausible because the hierarchy of the non-relativistic scales and thermal scales assumed in the weak coupling EFT calculations may not be satisfied and the data available is not of sufficient quality in the present lattice correlator studies, respectively; one may use the potential model to circumvent the problem.

Since the mass of the heavy quark (\(m_Q\)) is very large, so the requirements \(m_Q \gg \sqrt{eB} \gg \Lambda _{QCD}\) and \(T \ll m_Q\) are satisfied for the description of the interactions between a pair of heavy quark and anti-quark at finite temperature in the presence of the magnetic field in terms of quantum mechanical potential. Thus we can obtain the medium modification to the vacuum potential by correcting both its short- and long-distance part with a dielectric function \(\epsilon (\mathbf k )\) as

$$\begin{aligned} V(r,T)=\int \frac{d^3\mathbf k }{(2\pi )^{3/2}} ({\mathrm{e}^{i\mathbf k .\mathbf r }-1})\frac{V(\mathbf k )}{\epsilon (\mathbf k )}, \end{aligned}$$
(45)

where we have subtracted a r-independent term (to renormalize the heavy quark free energy) which is the perturbative free energy of quarkonium at infinite separation. The dielectric function is related to the 00-component of effective gluon propagator in the static limit as

$$\begin{aligned} \frac{1}{\epsilon (\mathbf k )}=\displaystyle {\lim _{k_0 = 0}}\mathbf{k }^{2}D_{11}^{00}(k_{0},\mathbf k ), \end{aligned}$$
(46)

and \(V(\mathbf k )\) is the Fourier transform (FT) of the Cornell potential. To obtain the FT of the potential, we regulate both terms with the same screening scale. However, different scales for the Coulomb and linear pieces were also employed in [37] to include non-perturbative effects in the free energy beyond the deconfinement temperature through a dimension-two gluon condensate.

Fig. 3
figure 3

Effect of the magnetic field on potential

Full size image

At present, we regulate both terms by multiplying with an exponential damping factor, switched off after the FT is evaluated. This has been implemented by assuming r as a distribution (\(r \rightarrow \) \(r \exp (-\gamma r))\). The FT of the linear part, \(\sigma r\exp {(-\gamma r)}\), is

$$\begin{aligned} -\frac{i}{\mathbf{k \sqrt{2\pi }}}\left( \frac{2}{(\gamma -i \mathbf k )^3} -\frac{2}{(\gamma +i\mathbf k )^3} \right) . \end{aligned}$$
(47)

After putting \(\gamma =0\), we obtain the FT of the linear term \(\sigma r\):

$$\begin{aligned} \tilde{(\sigma r)}=-\frac{4\sigma }{\mathbf{k ^4\sqrt{2\pi }}}. \end{aligned}$$
(48)

The FT of the Coulomb piece is straightforward and is given by

$$\begin{aligned} V_C(\mathbf k )=-\sqrt{(2/\pi )} \frac{\alpha _s}{\mathbf{k ^2}}, \end{aligned}$$
(49)

thus the FT of the full Cornell potential becomes

$$\begin{aligned} {V}(\mathbf k )=-\sqrt{(2/\pi )} \frac{\alpha _s}{\mathbf{k ^2}}-\frac{4\sigma }{\sqrt{2 \pi } \mathbf k ^4}. \end{aligned}$$
(50)

The 00-component of effective gluon propagator in the static limit has been obtained with the help of the 00-component of one-loop gluon self-energy. We have already calculated the 00-component of one-loop gluon self-energy in the presence of a strong magnetic field at finite temperature in Eq. (41), hence the 00-component of the effective gluon propagator in the static limit is given by

$$\begin{aligned} D_{11}^{00}(0,\mathbf k )=\frac{1}{\mathbf{k ^2+m_{D}^2}}. \end{aligned}$$
(51)

Therefore the real part of the static potential can be obtained by substituting the dielectric permittivity \(\epsilon (\mathbf k )\) from Eq. (46) and the Fourier transformation from Eq. (50) into the definition of the potential (45),

$$\begin{aligned} V(r;T,B) =V_C(r;T,B)+ V_S(r;T,B), \end{aligned}$$
(52)

where the Coulombic and string term of the potential (with the dimensionless quantity \(\hat{r}=rm_{D}\)) are given by

$$\begin{aligned} V_{C}(r;T,B)= & {} -\alpha _s m_{D}\Big (\frac{\mathrm{e}^{-\hat{r}}}{\hat{r}}+1\Big ), \end{aligned}$$
(53)
$$\begin{aligned} V_{S}(r;T,B)= & {} \frac{2\sigma }{m_{D}}\Big [\frac{(\mathrm{e}^{-\hat{r}}-1)}{\hat{r}}+1\Big ], \end{aligned}$$
(54)

respectively. It is thus evident that the medium dependence in the potential enters through the Debye mass, which in turn depends on both temperature and magnetic field for physical quark masses and depends only on the magnetic field for massless quarks. This gives a characteristic dependence of the potential on both temperature and magnetic field. The r-independent terms in the potential ensure that V(r, T) reduces to the Cornell potential in the \(T \rightarrow 0 \) limit [38]. However, such terms could also arise naturally from the basic computations of the real-time static potential in hot QCD [39] and from the real and imaginary time correlators in a thermal QCD medium [40]. These terms in the potential are needed in computing the masses of the quarkonium states and to compare the results with the lattice studies. It is equally important while comparing our effective potential with the free energy in lattice studies.

Fig. 4
figure 4

The effect of string term on potential is depending on the magnetic field

Full size image

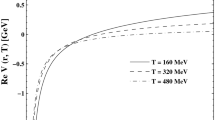
Since we are exploring the effect of medium on the potential between Q and \(\bar{Q}\) in the strong magnetic field approximation so we probe it by varying the strength of the magnetic field (eB) from \(10~m_\pi ^2\) to \(25~m_\pi ^2\) (in Fig. 3a) at a temperature T=150 MeV. It is found that as the strength of the magnetic field increases the potential becomes stronger. To see the competition between the magnetic field and temperature, we have plotted the potential in Fig. 3b in a hotter medium (T = 300 MeV). As we have seen earlier in Fig. 1a that the (square) Debye screening mass increases very little with temperature, here also the potential changes little as compared to Fig. 3a. This small dependence on temperature stems from SMFA as we have observed in the Debye screening mass.

Usually potential model studies are limited to the medium modification of the perturbative part of the potential only where it is assumed that the string tension vanishes abruptly at the deconfinement point. Since the phase transition in QCD for physical quark masses is found to be a crossover [41], the string tension may not vanish at the deconfinement temperature. This issue, usually overlooked in the literature where only a screened Coulomb potential was assumed above \(T_c\) and the linear term was neglected, is certainly worth an investigation. To see the effect of the linear term on the potential, in addition to the Coulomb term, we have plotted the potential (in Fig. 4a) with (\(\sigma \ne 0\)) and without string term (\(\sigma =0\)) in a magnetic field \(eB=10~m_\pi ^2\). As we know already in vacuum (\(T=0\)), the inclusion of the linear term makes the potential for the short-distance interaction less attractive and for the long-distance interaction the linear term makes the potential more repulsive, compared to the Coulomb term alone. However, the medium modification causes the linear term to be attractive and overall the medium modifications to both the Coulomb and the string term make the potential more attractive (seen in Fig. 4a) as compared to the vacuum potential.

To see the effect of the scale (Debye mass) at which the screening takes place on both the linear and the Coulombic term we have plotted the potential at a larger magnetic field, \(eB=25~m_\pi ^2\) in Fig. 4b, where we found that the increase of the scale (screening mass) makes the linear term less attractive, compared to the lower scale (eB). To understand the observations in Fig. 4, we have probed the range of interactions, viz. short-range (\(r=0.2\) fm), intermediate (\(r=0.5\) fm) and long-range (\(r=1\) fm) interactions of \(Q \bar{Q}\) potential as a function of the magnetic field (eB) in Fig. 5 and found that only the long-range interaction (\(r=1\) fm) has been affected noticeably. Our overall observation is that as the strength of the magnetic field increases the long-range QCD force becomes more and more short range, thus implying that the magnetic field facilitates early dissolution of \(Q \bar{Q}\) states.

Fig. 5
figure 5

Effect of the magnetic field on short- and long-range behavior of the potential

Full size image

It is important to mention here that we have not observed any anisotropy in our potential with respect to the direction of magnetic field, which is expected as a common sense because the magnetic field breaks the translational invariance of space. In our perturbative framework too, at the starting point the quark propagator in the strong magnetic field approximation gets factorized into functions involving the parallel and perpendicular components with respect to the direction of the magnetic field (\(\mathbf {B}=B\hat{z}\)) and so obviously the gluon self-energy is decoupled into parallel and perpendicular components. But on thermalizing the quark propagator and gluon self-energy at finite temperature in the strong magnetic field through the distribution function, there is no room to introduce the momentum anisotropy in the distribution function because the quarks’ dispersion relation is restricted to the LLL only (\(E_0(p_z)=\sqrt{p_z^2+m_f^2}\)), i.e. only the longitudinal component of the momentum is present; hence no anisotropy arises between transverse and longitudinal components. One of us had recently derived an anisotropic heavy quark potential [20, 21] in perturbative thermal QCD, where the anisotropy in the potential in the coordinate space had arisen from the manifested momentum anisotropy with respect to the direction of anisotropy in the distribution function.

However, recently a novel magnetic field-induced anisotropic behavior was first observed in the heavy quark potential in the longitudinal–traverse plane with respect to the direction of \(\mathbf {B}\) [25]. Later the set-up was extended to measure Polyakov loop correlators on the lattice to extract the potential for both zero and finite temperature in place of earlier Wilson loop expectation values used at zero temperature, for different orientations with respect to \(\mathbf {B}\) [26]. The reason of the anisotropy is the averaging of both the Wilson loop expectation value and the Polyakov loop correlators being different for different orientations with respect to the magnetic field.

3.1 Dissociation of heavy quarkonia in magnetic field

In this section, we shall discuss the dissociation of charmonium and bottomonium states due to an external strong magnetic field in a hot QCD medium. The concept of dissociation temperature becomes irrelevant here because the scale at which the collective oscillations develop depends only on the magnetic field – albeit we are considering a hot QCD medium because in the strong magnetic field approximation (\(eB \gg T^2\)), the scale at which the collective oscillation sets in is associated with the magnetic field only because eB is the most dominant scale in the strong magnetic field limit (if the partons are assumed massless), not the thermally generated scales. This in turn makes the potential depend only on the magnetic field through the dependence of the Debye mass on the magnetic field. Thus, it makes sense here to discuss the dissociation of quarkonium states due to the magnetic field only as far as SMFA is valid.

As we know that, in the presence of a medium, the potential between a heavy quark (Q) and its anti-quark (\(\bar{Q}\)) will be screened, if the screening is strong enough, the potential becomes too weak to form the resonance. Thus we can argue that the quarkonium states will be dissolved in a medium if the Debye screening radius, \(r_D\) (=\(\frac{1}{m_D}\)) in a given medium is smaller than the bound state radius of a particular resonance state; then the medium inhibits the formation of the particular resonance and Q and \(\bar{Q}\) will be dissolved into the medium. Since the screening mass in the strong magnetic field increases with the magnetic field, the (critical) magnetic field at which the \(Q \bar{Q}\) potential becomes too feeble to hold \(Q \bar{Q}\) together becomes smaller for the excited states. We can thus estimate the lower limit of the critical magnetic field for various charmonium and bottomonium states by the criterion: \(\sqrt{\langle {r^i}^2 \rangle }= {r_D} (B_d^i)\), i.e., for a magnetic field larger than \({B_d}^i\), the ith quarkonium states cease to exist. For example, \(J/\psi \) will be dissociated at \(eB=14 m_\pi ^2\) and its excited state, \(\psi ^\prime \) is dissociated at smaller magnetic field, at \(eB= m_\pi ^2\), whereas \(\Upsilon \) will be dissociated at \(eB=130 m_\pi ^2\) and \(\Upsilon ^\prime \) is dissociated at the smaller magnetic field of \(eB= 13 m_\pi ^2\).

To understand the in-medium properties of the quarkonium states quantitatively, one need to solve the Schrödinger equation with the medium-modified potential, V(r; B, T). There are some numerical methods to solve the Schrödinger equation either in partial differential form (time-dependent) or eigen value form (time-independent) by the finite difference time domain method (FDTD) or matrix method, respectively. In the latter method, the stationary Schrödinger equation can be solved in a matrix form through a discrete basis, instead of the continuous real-space position basis spanned by the states \(|\overrightarrow{x}\rangle \). Here the confining potential V is subdivided into N discrete wells with potentials \(V_{1},V_{2},...,V_{N+2}\) such that, for the ith boundary potential, \(V=V_{i}\) for \(x_{i-1}< x < x_{i}; ~i=2, 3,...,(N+1)\). Therefore for the existence of a bound state, there must be an exponentially decaying wave function in the region \(x > x_{N+1}\) as \(x \rightarrow \infty \) and it has the form

$$\begin{aligned} \Psi _{N+2}(x)= & {} P_{{}_E} \exp [-\gamma _{{}_{N+2}}(x-x_{N+1})]\nonumber \\&+ Q_{{}_E} \exp [\gamma _{{}_{N+2}}(x-x_{N+1})] , \end{aligned}$$
(55)

where \(P_{{}_E}= \frac{1}{2}(A_{N+2}- B_{N+2})\), \(Q_{{}_E}= \frac{1}{2}(A_{N+2}+ B_{N+2}) \) and, \( \gamma _{{}_{N+2}} = \sqrt{2 \mu (V_{N+2}-E)}\). The eigenvalues can be obtained by identifying the zeros of \(Q_{E} \). Using this method, we have found that \(J/\psi \) and \(\Upsilon \) are dissociated at \(eB=5 m_\pi ^2\) and \(eB=50 m_\pi ^2\), respectively.

Though the dissociation magnetic fields, obtained from the two methods, apparently look different, it is easy to see that qualitatively they are similar. Using both methods, we found that the dissociation magnetic field for \(\Upsilon \) is roughly an order of magnitude greater than the dissociation magnetic field for \(J/\psi \). Even though their absolute value, obtained from the two different methods, differ, they lie in the same ball park, which is \(\sim \) 10\(m_\pi ^2\) for \(J/\psi \) and \(\sim \) 100\(m_\pi ^2\) for \(\Upsilon \).

4 Conclusions

In this article, we have explored the effects of strong and homogeneous magnetic fields on the properties of quarkonium states. For that purpose we have derived the potential between a heavy quark and its anti-quark by the medium corrections to both Coulomb and linear term of \(Q\bar{Q}\) potential at \(T=0\), unlike the medium correction to the Coulomb term alone. Although the medium considered is thermal, due to the strong magnetic field approximation, all other scales present in the thermal medium become irrelevant: the scale related to the magnetic field dominates. This is exactly what happens in the collective oscillation of the medium in the form of the Debye mass. In fact, the Debye mass becomes completely independent of the temperature for massless quarks and depends very weakly on temperature for massive quarks. However, beyond a certain temperature, the dependence is so weak that it is almost insignificant. As a result the heavy quark potential mainly depends on the magnetic field with a very feeble dependence on the temperature. This is expected as the effect of the medium on the potential enters through the Debye mass. In particular the long-distance part of the potential gets significantly affected, whereas the short-distance part is mildly affected.

We have then studied the dissociation of quarkonium states in a medium. Since the potential in SMFA depends mainly only on the magnetic field, we have discussed the dissociation of quarkonium states due to the magnetic field only. We have estimated the critical value of the magnetic field beyond which the resonance does not form by two methods. The first one gives a lower limit of the critical magnetic field for both charmonium and bottomonium states at which the Debye screening radius becomes smaller than the bound state radius of a particular resonance state. The other one comes from the consideration of the binding energies of a specific state obtained from the energy eigenvalues of the Schrödinger equation. In brief, \(J/\psi \) is dissociated at \(eB \sim 10 m_\pi ^2\) and \(\Upsilon \) is dissociated at \(eB \sim 100 m_\pi ^2\).