On the compatibility of the IceCube results with a universal neutrino spectrum

Abstract

There is mounting evidence that the IceCube findings cannot be described simply invoking a single power-law spectrum for cosmic neutrinos. We discuss which the minimal modifications are of the spectrum that are required by the existing observations and we obtain a universal cosmic neutrino spectrum, i.e. valid for all neutrino flavors. Our approach to such task can be outlined in three points: (1) we rely on the throughgoing muon analysis above 200 TeV and on the high-energy starting events (HESE) analysis below this energy, requiring the continuity of the spectrum; (2) we assume that cosmic neutrinos are subject to three-flavor neutrino oscillations in vacuum; (3) we make no assumption on the astrophysical mechanism of production, except for no $\nu _\tau$ $(\overline{\nu }_\tau )$ component at the source. We test our model using the information provided by HESE shower-like events and by the lack of double pulses and resonant events. We find that a two-component power-law spectrum is compatible with all observations. The model agrees with the standard picture of pion decay as a source of neutrinos, and indicates a slight preference for a $p\gamma$ mechanism of production. We discuss the tension between the HESE and the “throughgoing muons” datasets around few tens TeV, focussing on the angular distributions of the spectra. The expected number of smoking-gun signatures of $\nu _\tau$-induced events (referred to as double pulses) is quantified: in the baseline model we predict 0.65 double pulse events in 5.7 years. Uncertainties in the predictions are quantified.

1 Introduction

IceCube has observed a new component of the neutrino spectrum, that exceeds the atmospheric neutrino flux above few hundreds TeV [1, 2]. This new component extends, at least, up to few PeV and it has an intensity close to the Waxman–Bahcall upper bound [3].

This is one of the most exciting recent results in neutrino physics, even though we do not know which are the sources of these neutrinos. The energy spectrum displays non-trivial and even unexpected features, such that the aim of the present work is to investigate what is the consequence of a global interpretation of the IceCube findings.

We base our analysis on a minimal set of hypotheses, namely:

• 1. the spectrum is continuous and regular, which is not only a simple mathematical requirement but also a reasonable assumption, as the existence of major discontinuities would require some specific motivation, which we do not have currently;

• 2. the cosmic neutrinos are subject to three-flavor neutrino oscillations, as recently proved by terrestrial experiments and observations;

• 3. the new population of cosmic neutrinos derives from some unspecified astrophysical mechanisms of production, where $\nu _e$ ($\bar{\nu }_e$) and $\nu _\mu$ ($\bar{\nu }_\mu$) are created at the source.

Moreover, we consider the most recent datasets obtained by IceCube, discussing the relevant backgrounds.

These hypotheses restrict significantly the overall shape of the spectrum. The hard power-law spectrum, which describes the induced muons up to a few PeV, can be extended to low energy either by assuming a piecewise functional form or by adding a softer power-law component, but there is no tangible difference, as the resulting flux is quite constrained. This has direct implications for the physics of muon neutrinos events – HESE tracks or throughgoing events. Neutrino oscillations allow us to derive the electron and tau neutrino spectra. Possible deviation from the standard pion decay scenario are analyzed. We show that there is a hint of a slight excess of electron neutrinos and antineutrinos, but this is not significant. Several tests of the ensuing physical picture are discussed, including tau neutrino events (which are detectable), Glashow resonance events, examining their relation with the specific dataset or range of the neutrino spectrum. We examine the dependence of the predictions upon the specific dataset and upon the energy range of the universal spectrum.

2 Neutrino oscillations

In this section we update the description of cosmic neutrino oscillations proposed in [4]. This consists in the use of three “natural” parameters to describe the probabilities of oscillations of cosmic neutrinos. After a brief review of [4], we discuss our updating procedure, which is based on the latest results on the oscillation parameters [5].

2.1 The parameters $P_0$, $P_1$, $P_2$

The average survival/oscillation probabilities in vacuum are given by

$$\begin{aligned} P_{\ell \ell '}=\sum _{i=1}^n \left| U_{\ell i}^2\right| \left| U_{\ell ' i}^2\right| \quad \ell ,\ell ' = e,\mu ,\tau \end{aligned}$$

(1)

where $\ell (\ell ')$ denotes the neutrino flavor and U is the standard mixing matrix.

The approach of Palladino and Vissani in [4] to compute the average survival/oscillation probabilities, of cosmic neutrinos in vacuum, is based on two simple considerations:

• the matrix P, containing the probabilities of oscillation $P_{\ell \ell '}$ is symmetric under the exchange of the flavor indices $\ell \leftrightarrow \ell '$;

• the elements of the mixing matrix must obey the condition $\sum _\ell P_{\ell \ell '}=1$.

For these reasons, the number of independent parameter is $n(n-1)/2$, where n is the number of neutrinos. For $n=3$ we have just 3 independent parameters. Calling them $P_0,P_1$ and $P_2$, we can write, as shown in [4], the probabilities as the following matrix:

$$\begin{aligned} P=\left( \frac{{1}}{3}\right) _{3x 3}+ \begin{pmatrix} 2P_0 &{}-P_0+P_1 &{} -P_0-P_1 \\ &{} P_0/2-P_1+P_2 &{} P_0/2-P_2 \\ &{} &{} P_0/2+P_1+P_2 \\ \end{pmatrix}. \end{aligned}$$

(2)

The expressions of these parameters in terms of the conventional oscillation parameters (three mixing angles and one CP violating phase) are

$$\begin{aligned} P_0&=\frac{1}{2} \left[ (1-\epsilon )^2 \left( 1-\frac{\sin ^2 (2\theta _{12})}{2}\right) +\epsilon ^2 -\frac{1}{3} \right] ,\end{aligned}$$

(3)

$$\begin{aligned} P_1&=\frac{1-\epsilon }{2}\left( \gamma \cos 2\theta _{12}+\beta \frac{1-3\epsilon }{2} \right) ,\end{aligned}$$

(4)

$$\begin{aligned} P_2&=\frac{1}{2}\left[ \gamma ^2 + \frac{3}{4}\beta ^2 (1-\epsilon )^2 \right] , \end{aligned}$$

(5)

where

$$\begin{aligned} \epsilon&= \sin ^2\theta _{13} \quad \alpha = \sin \theta _{13}\cos \delta \sin 2\theta _{12}\sin 2\theta _{23},\\ \beta&= \cos 2\theta _{23} \quad \gamma = \alpha - \frac{\beta }{2}\cos 2\theta _{12}(1+\epsilon ). \end{aligned}$$

2.2 The oscillation probabilities of cosmic neutrinos

The values of the conventional oscillation parameters are given in [5]; in Table 1 we report their best fit values and the 68% confidence level interval, denoting by NH the normal hierarchy/ordering and with IH the inverted hierarchy/ordering.

Table 1 The best fit values and 68% intervals of the oscillation parameters [5]

Fig. 1

Distribution of $P_0, \ P_1, \ P_2$ for normal hierarchy (blue) and for inverted hierarchy (red)

The distributions of the oscillation parameters are sampled according to likelihood functions reported in figure 1 of [5]. This approach is necessary because the parameters $\sin ^2\theta _{23}$ and $\delta /\pi$ are not Gaussian distributed. On the contrary, for $\sin ^2\theta _{12}$ and $\sin ^2\theta _{13}$ it is sufficient to use Gaussian distributions, with mean the central value and with standard deviation the average of the errors quoted in the table above. Performing Monte Carlo extractions according to such procedure, we obtain the distributions for $P_0$, $P_1$ and $P_2$ shown in Fig. 1; their modes and 68% CL intervals are reported in Table 2.

From the table it is clear that

$$\begin{aligned} P_0> P_1 > P_2; \end{aligned}$$

(6)

$P_0$ is the largest parameter and also the one with the smallest uncertainty. From the plot we see that the parameter $P_2$ satisfies the condition $P_2>0$ consistently with Eq. (5). The asymmetric errors quoted in the table are such that the integral of the normalized distribution $\mathcal L_P$ of a generic parameter P obeys the conditions:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \int _{{P_\text {M}}-\varDelta P_-}^{{P_\text {M}}+\varDelta P_+} \mathcal {L}_P (t) \ \mathrm{d}t = 0.68 ,\\ \mathcal {L}_P ({P_\text {M}}-\varDelta P_{-}) = \mathcal {L}_P ({P_\text {M}}+\varDelta P_{+}), \end{array} \right. \end{aligned}$$

(7)

where $P_\text {M}$ is the mode and $\varDelta P_+$, $\varDelta P_-$ are the asymmetric errors.

For our analyses, we decided to assume normal hierarchy, as it is favored with respect to the inverted one at the level of 1.9–2.1$\sigma$ [5]. Using inverted hierarchy would result in survival/oscillation probabilities compatible within $1\sigma$ with those obtained using direct hierarchy. The choice of hierarchy impacts the results much less than the choice of the mechanism of neutrino production. In fact, the current uncertainty budget in the predictions is dominated by the fact that the mechanism of cosmic neutrino production is unknown and by the experimental uncertainties, rather than by neutrino oscillations.

3 The IceCube dataset

In this section we present two recent datasets provided by the IceCube collaboration after 6 years of data taking: the throughgoing muon dataset and the high-energy starting events (HESE) dataset.

Table 2 The modes and 68% intervals that we obtained for the natural parameters

Notation: from now on we denote by $\phi _\ell$ the flux of $\nu _\ell$ and of $\bar{\nu }_\ell$. Whenever we are only interested in the flux of neutrinos (or antineutrinos), we denote it by $\phi _{\nu _\ell }$ (or $\phi _{\bar{\nu }_\ell }$). When the subscript is not present $(\phi )$, the all-flavor flux is considered.

3.1 Throughgoing muons

The IceCube collaboration has acquired data from 2009 to 2015, collecting a sample of charged current events due to upgoing muon neutrinos; due to the position of IceCube, the field of view, for this class of events, is restricted to the northern hemisphere [6]. The highest-energy sample (with reconstructed energy above $\sim$ 200 TeV) corresponds to 29 events of this type; a purely atmospheric origin of them is excluded at more than 5$\sigma$ of significance. The most energetic event corresponds to a reconstructed muon energy equal to 4.5 PeV.

The corresponding cosmic muon flavor (neutrino and antineutrino) flux has been obtained with a power-law fit to the data:

$$\begin{aligned} \frac{\mathrm{d}\phi _\mu ^{\mathrm{data}}}{\mathrm{d}E}=F_\mu \times \frac{10^{-18} }{{\mathrm{GeV} \, {\mathrm{cm}}^{2} \,\hbox {s sr }}} \left( \frac{E}{100 \, \mathrm{TeV}} \right) ^{-\alpha }. \end{aligned}$$

(8)

The parameters are $F_\mu =0.90^{+0.30}_{-0.27}$ and $\alpha =2.13 \pm 0.13$. This analysis is sensitive mostly to muon neutrinos and antineutrinos plus a little contribution from the $\tau$-leptons that decay into muons.¹

No correlation with known $\gamma$-ray sources has been found by analyzing the arrival directions of these 29 events [6, 7].

3.2 High-energy starting events

The most recent data concern 2078 days (5.7 years) of detection. This dataset includes 82 HESE [8]: they have been classified in 22 tracks and 58 showers (two of them are not classified being coincident events). These events are characterized by a deposited energy larger than 30 TeV, and the most energetic HESE has deposited an energy of 2 PeV into the detector.

The flux attributed to astrophysical neutrinos is described, in first approximation, by an isotropic distribution and a power-law spectrum. The per-flavor flux is

$$\begin{aligned} \frac{\mathrm{d}\phi _\ell ^{\mathrm{data}}}{\mathrm{d}E}= F \times \frac{10^{-18}}{\mathrm{GeV}\,\hbox {cm}^{2}\,\hbox { s sr }}\, \left( \frac{E}{100 \,{\mathrm{TeV}}} \right) ^{-\alpha } \end{aligned}$$

(9)

with $F_\ell =2.5 \pm 0.8$ and $\alpha =2.92^{+0.33}_{-0.29}$ [8]. In IceCube analyses it is usually assumed that $F_e = F_\mu = F_\tau$.

Although the bulk of HESE coming from the southern sky suggests a power-law spectrum with spectral index $\alpha \approx 2.9$, the subset of highest energy (above 200 TeV) HESE is in agreement with a much harder spectrum and, more precisely, follows the same distribution suggested by the throughgoing muons: see figure 6 of [9] and figure 5 of [6], and discussions therein. In other words, the flux of the highest-energy HESE observed from the southern sky is compatible with the same hard spectrum $\alpha \approx 2$ as suggested by throughgoing muons.

4 Atmospheric background of HESE

Before continuing the discussion, it is important to recall what are the backgrounds for high-energy neutrinos. A precise knowledge of the different background sources is relevant for the correct identification of the astrophysical signal, which we perform in Sect. 5.

When cosmic rays collide with the terrestrial atmosphere, lots of mesons are produced: from pion decay (and from kaon decay, in smaller amounts) muons and neutrinos are produced, constituting the main source of background for high-energy neutrino detection. We call these two sources of background as atmospheric muons and conventional neutrino background.

Another contribution to the background is given by the decay of heavy, charmed mesons: the neutrinos which come from these decays are called “prompt neutrinos”.

4.1 Atmospheric muons

Atmospheric muons, mainly generated by pion decay, have an energy spectrum $\propto E^{-3.7}$. This is due to the fact that, with increasing energy, the probability that pions interact before decaying grows linearly with E. Since muons come from pion decay, their spectrum is steeper than the $E^{-2.7}$ spectrum of primary cosmic rays. This is an unavoidable source of background for the HESE analysis; on the other hand, it does not affect the throughgoing muon analysis, since atmospheric muons are absorbed crossing the Earth. It has been estimated by the IceCube collaboration that the number of atmospheric muons, contributing to HESE background after 5.7 years of exposure, is

$$\begin{aligned} b_\mu = 25.2 \pm 7.3. \end{aligned}$$

(10)

According to table 4 of [1], 90% of them ($23.0 \pm 7.3$) are identified as track-like events and 10% ($2.2 \pm 0.7$) as shower-like events. This is due to the fact that a certain misidentification of tracks is possible from an experimental point of view.

4.2 Prompt neutrinos

Prompt neutrinos are produced in the decay of heavy mesons, which contain the charm quark (charmed mesons). These particles are highly unstable and decay before interacting, following the same $E^{-2.7}$ spectrum of primary cosmic rays.

To date, the contribution of prompt neutrinos to the IceCube dataset has not been identified yet, although it is expected to exist: see e.g. [10,11,12]. An upper limit has been set by the IceCube collaboration [1], while Palladino et al. [13] have calculated that their contribution to HESE is smaller than 3.5 events, in 4 years of exposure, at 90% confidence level (CL). Scaling such estimate with the present exposure, we find that the contribution of prompt neutrinos is expected to be smaller than 5 HESE, at 90% CL.

Since at the time of the writing the best fit value of prompt neutrino events is 0, the probability density function (PDF) of prompt neutrinos can be reasonably approximated by an exponential function:

$$\begin{aligned} \mathcal {L}_{p}(b_p)= \frac{1}{b_p^0} \exp \left( -\frac{b_p}{b_p^0} \right) \end{aligned}$$

(11)

with $b_p^0=2.17$. Using this likelihood function for prompt neutrinos, we find that their contribution to HESE background is equal to 2.5 events at 68% CL and 5 events at 90% CL.

Table 3 Summary of the backgrounds expected in HESE analysis after 5.7 years of exposure

According to table 4 of [1] about 20% of prompt neutrinos produce track-like events, whereas about 80% of them produce shower-like events.

4.3 Conventional background

Neutrinos produced in the decay of pions (and kaons, in smaller amounts) constitute the so called conventional background. These neutrinos have an $E^{-3.7}$ energy spectrum, for the same reason discussed in the case of atmospheric muons.

From the three year dataset (see table 4 of [1]) we expect $6.6 \times 5.7/2.7 \simeq 14$ events due to conventional neutrino background, with an uncertainty of about four events, with a slightly larger upper range.

However, a more precise value can be derived using results reported at the ICRC conference [8]. In fact, it is quoted that the total background due to conventional and prompt neutrinos is:

$$\begin{aligned} b_{\pi k}+b_p= 15.6^{+11.4}_{-3.9}. \end{aligned}$$

(12)

The best fit value of prompt neutrinos is zero events [8]. We conclude that the best fit value of the conventional background is of 15.6 events; then we can estimate the uncertainty by the Poisson error $\sqrt{15.6}=3.9$ events, which agrees with the lower range of uncertainty cited in [8] and, once again, is consistent with the above estimate.

The estimation of the upper bound of the prompt component used in [8] and included in the upper range of uncertainty cited in [8], is based on older data [1]. The value of the upper bound can reconstructed as follows: using again the value reported in table 4 of [1] the expected number of prompt neutrinos is 9 at 90% CL and it is 0 at the best fit. The corresponding 68% CL bound is 4.5 events, using an exponential likelihood function that reproduces the 90% CL bound, just as was done in the previous subsection. This number converts in the expectation that we need, simply scaling the prediction with the exposure as follows:

$$\begin{aligned} b_{p}= \frac{5.7}{2.7} \times 4.5 = 9.5 \ \ \ \hbox {at}~ 68\%~ \hbox {CL}, \end{aligned}$$

which, evidently, is much more conservative than the value that we discussed in the previous section (and that we will adopt in the following). Assuming that the total uncertainty is obtained summing in quadrature the uncertainty on conventional and prompt backgrounds, we find the uncertainty (higher range) on the conventional background in the following manner:

$$\begin{aligned} \varDelta ^+b_{\pi k}=\sqrt{\varDelta (b_{\pi k}+b_p)^2 - \varDelta b_p^2} = 6.3. \end{aligned}$$

In conclusion, we estimate that the contribution of the conventional background to the expected number of HESE, after 5.7 years of exposure, is equal to

$$\begin{aligned} b_{\pi k}=15.6^{+6.3}_{-3.9}. \end{aligned}$$

(13)

The ratio between the positive and the negative uncertainties is 1.6, whereas in the three years dataset (table 4 of [1]) it is equal to 1.4. This result is consistent, within about 10%, with the estimation obtained simply using table 4 of [1].

According to table 4 of [1], 70% of them ($10.9^{+5.8}_{-3.6}$) contribute to track-like events, whereas 30% of them ($4.7^{+2.5}_{-1.5}$) contribute to shower-like events. The uncertainties on the expected number of showers and tracks reproduce the total uncertainty when summed in quadrature.

4.4 Summary of backgrounds

We summarize the backgrounds relevant to the HESE analysis in Table 3.

The expected number of background tracks in the HESE dataset is equal to $34.3^{+12.3}_{-8.7}$, as reported in Table 3. This number is larger than the observed 22 tracks. Moreover, we expect that also $\sim 20\%$ of cosmic neutrinos produce tracks in the HESE dataset, according to table 4 of [1]. On the other hand, as discussed in [14], the misidentification of some tracks, which could be identified as showers, could play an important role for this kind of analysis. In conclusion, since the track-like subset is supposedly dominated by the atmospheric background rather than by the signal, it is quite hard to extract useful information on $\phi _\mu$ from HESE, and this is the reason why we do not use this subset of data in our analysis.

On the contrary, we include the tracks contained into the throughgoing muons dataset, since they are affected by the atmospheric background at the level of 30%, as estimated in [7]. Moreover, we repeat that this kind of analysis is free from atmospheric muons, since they are absorbed into the Earth.

As a final remark, let us consider that the atmospheric background affects shower-like events, in the HESE dataset, at the level of 15%. Indeed the expected number of showers, due to atmospheric background, is

$$\begin{aligned} b_s= 6.9^{+3.3}_{-1.7} \end{aligned}$$

(14)

combining the number of shower events expected from atmospheric muons given in Eq. (10), the most recent 68% CL limit on the prompt background given in Eq. (11), the conventional background given in Eq. (13). We denote by $\mathcal {L}_s(b_s)$ the distribution function of this background. This number has been obtained using a Monte Carlo simulation and combining the showers expected from atmospheric muons, conventional neutrinos and prompt neutrinos.

It is reasonable, therefore, to consider throughgoing muons and shower-like HESE in our analysis, due to their small atmospheric background. On the other hand, it is cautious to neglect track-like HESE in the rest of the analysis, due to the huge atmospheric background, which does not allow one to extract useful information on the astrophysical signal.

5 The neutrino spectrum

In Sect. 5.1 we define the “universal” spectrum, starting from the muon neutrino spectrum. This kind of spectrum reconciles all the recent IceCube measurements. In Sect. 5.2 we evaluate the spectrum of tau neutrinos, showing that neutrino oscillations are sufficient to strongly constrain it. In Sect. 5.3 we evaluate the spectrum of electron neutrinos and electron antineutrinos. In this case we analyze $\nu _e$ and $\bar{\nu }_e$ separately, since they produce different signals in the detector and, as a consequence, they are distinguishable.

5.1 The shape of muon neutrino spectrum

Combining all the information provided by the IceCube collaboration with their different analyses, it is evident that the assumption of a single power-law model is not the best choice to explain the present data. In Refs. [9, 13, 15,16,17,18,19,20,21] this aspect has been emphasized, invoking the presence of at least two populations of high-energy neutrinos with different energy spectra.

In this paper we test the compatibility of a two-component power-law spectrum with the observations (HESE showers, double pulses, resonant events) and with the standard production mechanisms of high-energy neutrinos, expected to occur in astrophysical environments.

Fig. 2

The two-component power-law benchmark spectrum (2PL) as defined by Eqs. (16), (18), and (19), compared with the throughgoing muons flux (green band) and a flux with the slope suggested by HESE below 200 TeV (blue band) – compare with Eq. (15)

Above 200 TeV we can rely on the throughgoing muon analysis (green band in Fig. 2), while below 200 TeV we rely on the HESE analysis (blue band in Fig. 2), for the reasons discussed in the previous section. In order to proceed, we define the broken power-law flux in the following manner:

$$\begin{aligned} \frac{\mathrm{d}\phi _{br}}{\mathrm{d}E}=\frac{N_\mu ^{br} \ 10^{-18}}{\mathrm{GeV}\, \hbox { cm}^2 \, \hbox {s sr}} \left\{ \begin{array}{cc} E_{200}^{-2.13} \ \text{ for } \ E\ge 200 \text{ TeV } \\ E_{200}^{-2.92} \ \text{ for } \ E<200 \text{ TeV } \\ \end{array} \right. \end{aligned}$$

(15)

where $E_{200}=E/\mathrm 200 \ TeV$ and the normalization at 200 TeV is $N_\mu ^{br}=0.206$ (in units of Eq. (15)); this value corresponds to the normalization of the throughgoing muons flux at 200 TeV, using the best fit values. The choice of the break at 200 TeV represents:

• the minimal modification that reconciles the throughgoing muon and the HESE dataset;

• the least arbitrary, since the energy threshold of the throughgoing muon analysis is about 200 TeV.

Now, we define our “benchmark” two-component power-law flux $\phi _\mu$ for the muon neutrino plus antineutrino spectrum as follows:

$$\begin{aligned} \frac{\mathrm{d}\phi _\mu }{\mathrm{d}E}=\frac{N_\mu }{2} \frac{10^{-18}}{\mathrm{GeV }\, \hbox {cm}^2 \, \hbox {s sr}} \left( E_{100}^{-\alpha }+E_{100}^{-\beta } \right) \end{aligned}$$

(16)

where $E_{100} = E/{100}\,\hbox {TeV}$. Thanks to the prefactor $N_\mu /2$, the normalization $N_\mu$ denotes directly the normalization of the two-component power-law flux at 100 TeV. The choice of the normalization at 100 TeV reproduces, reasonably well, the behavior of the broken power-law flux. The value can be slightly different but we have verified that choosing 150 TeV or 200 TeV the analyses proposed in the next sections are not affected appreciably.

In order to determine the parameters $N_\mu$, $\alpha$, $\beta$ of Eq. (16), we define a “distance” between this benchmark flux and the broken power-law flux $\phi _{br}$, i.e. the flux suggested by the data. The distance between the two functions is defined as follows:

$$\begin{aligned} \mathrm{d}(N_\mu ,\alpha ,\beta )= \int _{{30}\,\mathrm{TeV}}^{{10}\,{\mathrm{PeV}}} \frac{\left| \phi _\mu (E,N_\mu ,\alpha ,\beta ) -\phi _{br}(E) \right| }{\phi _{br}(E)} \ \mathrm{d} \log E. \end{aligned}$$

(17)

Such a distance is minimized by the following set of values:

$$\begin{aligned} N_\mu = 1.5, \ \ \ \alpha =2.08, \ \ \ \beta =3.5. \end{aligned}$$

(18)

Since the normalization of the throughgoing muon flux is known with an uncertainty of about $30\%$, we take it into account considering that

$$\begin{aligned} N_\mu = 1.5 \pm 0.5. \end{aligned}$$

(19)

The two descriptions of the fluxes are presented in Fig. 2.

Let us recall that assuming three-flavor neutrino oscillations and the same mechanism of production for all cosmic neutrinos, we expect that the shape of neutrino spectra is the same for all flavors, and only their normalization is expected to be different. For this reason, we refer to such an assumption with the terminology of ‘universal spectrum of neutrinos’.

In Fig. 2 we see that the sum of the two-component power-law fluxes (pink band), with spectral indices $\alpha =2.08$ and $\beta =3.50$, reproduces well the $\sim E^{-2.92}$ behavior at low energy and the $\sim E^{-2.13}$ behavior at high energy, within the uncertainties on the spectral index and on the normalization.

It is important to remark that we assume the shape of the spectrum suggested by the low-energy HESE data, but we do not yet use the normalization suggested by the same data. In fact, HESE data refer to an all-flavor analysis, but the flavor partition of the neutrinos is dictated by the mechanism of production, which to date is unknown. Therefore, we include the information on HESE in the analysis by adopting the following procedure:

• we start from the measured flux of throughgoing muons;

• we extrapolate this flux at low energy with the shape suggested by the HESE data;

• we adopt the smooth spectrum of Eq. (16)—in this manner we determine the “universal” cosmic neutrinos spectrum;

• we use the universal spectrum, neutrino oscillations and experimental constraints to predict the flux $\phi _\tau$ and $\phi _e$.

The last step of this procedure concerns the following two sections. In other words, we are going to test whether for some production mechanisms the assumption of a universal spectrum agrees with HESE.

5.2 The flux of $\nu _\tau$

The most plausible mechanism of high-energy neutrino production is the pion decay scenario, which yields $\phi _e \simeq \phi _\tau \simeq \phi _\mu$ at Earth.

Despite the popularity of this hypothesis, in the following we choose to adopt an unbiased position, i.e. we assume that the mechanism of production is unknown. Therefore, we perform a test on the flavor composition to verify what is the astrophysical scenario that is in better agreement with the observations.

To begin with, let us discuss the general constraints that come from theoretical and experimental considerations.

5.2.1 Constraints from neutrino oscillations

The assumption of this subsection is just the following.

The only expectation we have on the production mechanism of neutrinos is that almost no $\nu _\tau$ are produced at the source. This applies to any reasonable astrophysical scenario. Therefore, the flavor composition at the source, defined as $\xi _\ell ^0=\phi _\ell ^0/\phi ^0$ (where $\phi ^0$ denotes the all-flavor neutrino flux at the source), is given by

$$\begin{aligned} (\xi _e^0:\xi _\mu ^0:\xi _\tau ^0)=(x:1-x:0), \quad x \in [0,1]. \end{aligned}$$

(20)

We do not distinguish between neutrinos and antineutrinos for the moment; we just consider the total flux for each flavor $\ell$. Using this notation we have:

• $x=1$ denotes the neutron decay scenario;

• $x=1/3$ denotes the pion decay scenario;

• $x=0$ denotes the damped muon scenario, in which muons, produced by pion decay, interact before decaying. Therefore only $\nu _\mu$ (or $\bar{\nu }_\mu$ or both) are produced.

Since in Sect. 5.1 we have defined the two-component power-law spectrum of muon neutrinos, it is interesting to compute the ratio between the flux $\phi _\tau$ and the flux $\phi _\mu$ after neutrino oscillations. The ratio is given by the following expression:

$$\begin{aligned} R_{\tau \mu }=\frac{P_{e\tau } x + P_{\mu \tau } (1-x) }{P_{e\mu } x + P_{\mu \mu } (1-x)}, \end{aligned}$$

(21)

which using the natural parametrization becomes

$$\begin{aligned} R_{\tau \mu }=\frac{2+3P_0 (1-3x)-6P_1 x-6P_2(1-x)}{2+3P_0(1-3x)-6P_1(1-2x)+6P_2(1-x)}. \end{aligned}$$

(22)

Since $P_1,P_2$ are small, this ratio is equal to

$$\begin{aligned} {R_{\tau \mu } \simeq 1 + \mathcal {O}(P_1) + \mathcal {O}(P_2)} \end{aligned}$$

(23)

for every mechanism of production.

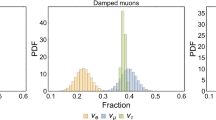
Randomly sampling x in [0, 1] according to a uniform distribution, so as to consider also mixed mechanisms of production, we obtain the distribution of $R_{\tau \mu }$ represented in Fig. 3 by orange bars. The ratio between the flux of $\nu _\tau$ and the flux of $\nu _\mu$ is, in good approximation, a Gaussian function. The best fit value and the 68% CL interval are

$$\begin{aligned} R_{\tau \mu } = 1.08 \pm 0.05. \end{aligned}$$

(24)

Therefore, the amount of cosmic $\nu _\tau$ is the same as $\nu _\mu$, to a very good approximation. This result takes into account also the uncertainties on neutrino oscillations.

Combining Eq. (24) with the normalization of $\phi _\mu$ (see Eq. (19)), we find

$$\begin{aligned} N_\tau ^{\mathrm{th}}=1.62 \pm 0.51. \end{aligned}$$

(25)

Let us notice that neutrino oscillations are sufficient to firmly constrain the flux of tau neutrinos and antineutrinos, whenever the flux $\phi _\mu$ is measured.

In the next subsection we analyze whether it is possible to improve the knowledge of $\phi _\tau$, using informations provided by the observations.

5.2.2 Constraints from observations: double pulses

As we have seen in the previous subsection, tau neutrino production at the source is neglected in most plausible neutrino production scenario, but, thanks to neutrino oscillations, we expect the $\nu _\tau (\overline{\nu }_\tau )$ flux to be approximately equal to the flux of $\nu _\mu (\overline{\nu }_\mu )$, regardless of the mechanism of production of high-energy neutrinos (see Eq. (24)).

Unfortunately, it is quite hard to measure the flux of $\nu _\tau$ directly because, until some hundreds of TeV, tau neutrinos do not produce a peculiar signature in neutrino telescopes. With increasing energy the possibility to tag a $\nu _\tau$ increases, since the first vertex of interaction, in which the $\tau$ is created, and the second vertex of interaction, in which the $\tau$ decays, become distinguishable. This process has been proposed by the IceCube collaboration in [22] and it is called “double pulse”.

In [23] Palladino et al. derived accurate parametrizations of various effective areas relevant for the analysis. The effective area of the double pulse is given by

$$\begin{aligned} A^{\text {2P}}_\tau = \bar{A}_{\text {2P}} \left( \frac{E_\nu }{1\,\text { PeV}} \right) ^{\beta } \ \exp \left( -\frac{E_\text {min}}{E_{\nu }} \right) \end{aligned}$$

(26)

with

$$\begin{aligned} \left\{ \begin{array}{l}\bar{A}_\text {2P}={2.33}\,\hbox {m}^{2},\\ \beta =0.455\\ E_\text {min}={0.5}\,\hbox {PeV.}\end{array} \right. \end{aligned}$$

This analytical parametrization reproduces well the effective area of double pulses provided by the IceCube collaboration in [22].

Using our benchmark flux reported in Eq. (16), the expected number of double pulse events can be estimated to be

$$\begin{aligned} {\mathcal {R}_{\mathrm{2P}}}= 4 \pi \text{ T } \int _0^\infty \frac{\mathrm{d}\phi _\tau }{\mathrm{d}E} \ A^{\text {2P}}_\tau \ \mathrm{d}E \end{aligned}$$

(27)

where T is the exposure time. Considering 5.7 years of exposure the expected number of events is

$$\begin{aligned} {\mathcal {R}_{\mathrm{2P}}}(N_\tau )= 0.44 \times N_\tau . \end{aligned}$$

(28)

Up to now no double pulse events have been observed by the IceCube collaboration; it is then possible to associate a likelihood to the normalization $N_\tau$, given by the lack of observations. Using Poissonian statistics, the probability to observe zero events is given by

$$\begin{aligned} \mathcal {L}_{\tau }^\mathrm{obs} \propto \exp \left[ -{\mathcal {R}_{\mathrm{2P}}}(N_\tau )\right] . \end{aligned}$$

(29)

5.2.3 Theory and observations

Combining theoretical expectations, due to neutrino oscillations, with the most recent measurements of the flux of $\nu _\mu$ and with the absence of double pulse events, it is possible to put a strong constraint on the expected flux of $\nu _\tau$ with cosmic origin.

The likelihood of $\phi _\tau$, apart from a normalization factor, is

$$\begin{aligned} \mathcal {L}_\tau (N_\tau )&\propto N_\tau \int _0^\infty \frac{\mathrm{d}N_\mu }{N_\mu ^2}\,\big [\text{ PDF }_{\tau \mu }\left( {N_\tau }/{N_\mu } \right) \nonumber \\&\quad \times \,\displaystyle \mathcal {L}_\tau ^\mathrm{obs}(N_\tau ) \times \mathcal {L}_\mu (N_\mu ) \big ] \end{aligned}$$

(30)

where the meaning of the three functions under the sign of integral is as follows:

• (1)  $\text{ PDF }_{\tau \mu }$ is the distribution of $R_{\tau \mu }=N_\tau /N_\mu$, which is displayed in Fig. 3,

• (2)  $\mathcal {L}_\tau ^\mathrm{obs}$ is the likelihood for the normalization coefficient $N_\tau$ given in Eq. (29), and

• (3)  the likelihood for the normalization coefficient $N_\mu$, namely $\mathcal L_\mu (N_\mu )$, is a Gaussian function with mean value equal to 1.5 and standard deviation equal to 0.5, consistently with Eq. (19). Finally, note the Jacobian factor

  $$\begin{aligned} \text{ PDF }_{\tau \mu }(y) \mathrm{d}y = \text{ PDF }_{\tau \mu }(N_\tau /N_\mu ) N_\tau \, \mathrm{d} N_\mu /N_\mu ^2 \end{aligned}$$

  in Eq. (30). The resulting function $\mathcal {L}_\tau (N_\tau )$ is, in good approximation, a Gaussian function, with

  $$\begin{aligned} N_\tau =1.48 \pm 0.54. \end{aligned}$$

  (31)

  This result is more precise but very similar to the one of Eq. (25). This implies that

  because of neutrino oscillations, the flux of tau neutrinos is constrained by the observed flux of muon neutrinos.

  It is important to remark that the above results do not depend upon the mechanism of production, since we take into account a generic mechanism in the computation of the function $R_{\tau \mu }$.

5.3 The flux of $\nu _e$ and $\bar{\nu }_e$

As already done for tau neutrinos, we can consider theoretical and experimental constraints for the flux of $\nu _e$ and $\bar{\nu }_e$ separately. Let us remark that the flux of $\bar{\nu }_e$ is constrained by the non-observation of resonant events, which we discuss in Sect. 5.3.2.

Fig. 3

The distributions of $R_{\tau \mu }$ (yellow) and of $R_{e \mu }$ (red) obtained from all neutrino production mechanisms (uniformly weighted) which neglect tau (anti-)neutrinos at the source

5.3.1 Constraints from neutrino oscillations

We follow the same procedure adopted in Sect. 5.2.1 also for electron neutrinos and antineutrinos. In this case the ratio between $\phi _e$ and $\phi _\mu$ is given by

$$\begin{aligned} R_{e \mu }=\frac{P_{ee} x + P_{e\mu } (1-x) }{P_{e\mu } x + P_{\mu \mu } (1-x)}. \end{aligned}$$

(32)

Using the natural parametrization it becomes equal to

$$\begin{aligned} R_{e \mu }=\frac{2-6P_0 (1-3x) + 6 P_1(1-x)}{2+3P_0(1-3x)-6P_1(1-2x)+6P_2(1-x)}. \end{aligned}$$

(33)

Also in this case we consider a generic mechanism of production, performing a uniform extraction of x between 0 and 1. The resulting distribution of $R_{e \mu }$ is non-Gaussian, as can be noticed from Fig. 3 (red bars). The mode and the 68% CL interval are given by

$$\begin{aligned} R_{e \mu } = 0.81^{+0.85}_{-0.10}. \end{aligned}$$

(34)

Combining the last result with Eq. (19) we find

$$\begin{aligned} N_e^{\mathrm{th}}=1.46^{+1.18}_{-0.62}. \end{aligned}$$

(35)

The uncertainty on $N_e^{\mathrm{th}}$ is quite large; therefore neutrino oscillations alone are not sufficient to constrain accurately $\phi _e$. This is due to the fact that, unlike the ratio $R_{\tau \mu }$, the ratio $R_{e\mu }$ strongly depends upon the mechanism of production.

In order to constrain $\phi _e$ we can rely on the existing data:

• 1. the showers observed in HESE dataset;

• 2. the lack of resonant events.

Let us emphasize that only at this point, i.e. when we consider these two experimental ingredients, we can obtain indications on the mechanism of cosmic neutrino production.

5.3.2 Flux of $\bar{\nu }_e$: Glashow resonance

The process

$$\begin{aligned} \bar{\nu }_e + e^- \rightarrow W^- \end{aligned}$$

(36)

is called “Glashow resonance” [24] and happens for electron antineutrinos with an energy of as 6.32 PeV (resonance). Assuming that the flux of neutrinos has no energy cut-off below 6.32 PeV, the resonant events, produced in the interaction of $\bar{\nu }_e$ with the electrons in the ice, must be observed. In Refs. [4, 23, 25,26,27] the possibility to discriminate the production mechanisms of high-energy neutrinos using the resonant events has been investigated, since different production mechanisms produce a different amount of $\bar{\nu }_e$.

The Glashow resonance cross section is given by

$$\begin{aligned} \sigma _{\text{ G }}^\text {hadr} (E)= & {} \frac{G_{\text{ F }}^2 \ (\hbar c)^2 \ M_{\text{ W }}^2}{3\pi }\frac{E\times \overline{\text {BR}}}{E}_{\text{ G }}\left[ \left( \frac{E}{E_{\text{ G }}}-1\right) ^2\right. \\&\left. +\left( \frac{\varGamma _{\text{ W }}}{m_{\text{ G }}} \right) ^2\right] \end{aligned}$$

where $G_{\text{ F }}$ is the Fermi constant, $M_{\text{ W }} \simeq {80.4} \ \text{ GeV }$ is the mass of the $W^-$ boson, $\varGamma _{\text{ W }}={2.1} \ \text{ GeV }$ is its FWHM, and $E_{\text{ G }}=M_{\text{ W }}^2/2 M_e \simeq {6.32}\,\hbox {PeV}$ is the energy at which the cross section is largest. The coefficient $\overline{\text {BR}} \simeq 20/3$ denotes the ratio between the branching ratio of the hadronic channel and the branching ratio of $W^- \rightarrow \bar{\nu }_\mu + \mu ^-$. Here we consider the hadronic channels only, which produce a distinguishable signal in the detector (for a discussion of the leptonic ones see [23]).

The expected number of events can be computed using the following general formula:

$$\begin{aligned} {\mathcal {R}_\ell }= 4\pi \text {T} \int _0^\infty \frac{\mathrm{d}\phi _\ell }{\mathrm{d}E} \ A_\ell \ \mathrm{d}E \end{aligned}$$

(37)

where $A_\ell$ is the effective area for each flavor, T is the exposure time (fixed to 5.7 years) and the flux is given by Eq. (16). For the specific case of resonant events we use the flux of $\bar{\nu }_e$. A useful and original approximation of the hadronic Glashow resonance effective area is obtained using the Dirac $\delta$ function, as follows:

$$\begin{aligned} A_{\bar{\nu }_e}^{\text {G}}(E)= 1.15 \times 10^6 \times \delta \left( \frac{E}{{1}\,\hbox {TeV}}-6320 \right) \text {m}^2. \end{aligned}$$

(38)

Using the benchmark flux defined in Eq. (16), the expected number of resonant events, after 5.7 years of exposure, is equal to

$$\begin{aligned} {\mathcal {R}_{\mathrm{G}}}(N_e, \epsilon )= 2.3 \ N_e \times \epsilon \end{aligned}$$

(39)

where the parameter that quantifies the asymmetry between electron neutrinos and antineutrinos is simply

$$\begin{aligned} \epsilon = \frac{\phi _{\bar{\nu }_e}}{\phi _{\bar{\nu }_e}+\phi _{\nu _e}}, \ \ \ \ \ 0\le \epsilon \le 1. \end{aligned}$$

(40)

The quantity $\epsilon$ is related to the mechanism of production and provides complementary information with respect to the parameter x (see Eq. (20)). Let us summarize:

• $\epsilon =1$ derives from neutron decay scenario, because only $\bar{\nu }_e$ are produced in this mechanism;

• $\epsilon \simeq 1/2$ comes from the proton–proton interaction, in which an about equal amount of $\nu _e$ and $\bar{\nu }_e$ is produced;

• $\epsilon \simeq 1/4$ comes from the ideal $p\gamma$ mechanism ($\delta$ approximation, i.e. only the $\varDelta ^+$ resonance is produced)—in more realistic scenarios, analyzed in [27, 28], $\epsilon$ is larger that 1/4, due to the production of $\pi ^-$;

• $\epsilon =0$ is obtained in extreme scenarios, in which there are no antineutrinos at the source at all. This happens when only $\pi ^+$ are produced and only the first decay ($\pi ^+ \rightarrow \mu ^+ + \nu _\mu$) is allowed. For example, it could happen in an ideal $p\gamma$ mechanism, in which muons interact before decaying (damped muons scenario).

Since no resonant events have been detected by IceCube up to now [8], it is possible to associate a prior distribution to the normalization of the $\bar{\nu }_e$ flux, i.e. to $N_e \times \epsilon$, related to the non-observation of resonant events. Using Poissonian statistics the likelihood is given by

$$\begin{aligned} \mathcal {L}_{\bar{\nu }_e}(N_e , \epsilon ) \propto \exp \left[ -{\mathcal {R}_{\mathrm{G}}}(N_e, \epsilon )\right] \end{aligned}$$

(41)

with the condition $\epsilon \in [0,1]$.

Finally, just as for double pulse events, we remark that the assumption on the low-energy part of the spectrum does not affect the result, since only very high-energy neutrinos contribute to the resonant events; the broken power law or the two-component power law are equivalent for the purpose of estimating the number of Glashow resonance events.

5.3.3 The flux of $\nu _e$ + $\bar{\nu }_e$: HESE and theory

The strongest constraint on the normalization of the $\phi _e$ flux comes from the number of showers observed with contained events (HESE). In fact, the $\phi _\mu$ flux gives a small contribution to the showers, whereas the flux of $\phi _\tau$ is fixed (within the uncertainty) by the theoretical and experimental constraints analyzed in Sect. 5.2. This means that the degrees of freedom needed to reproduce the observed number of showers are $N_e$ and $\epsilon$.²

We use the effective areas of HESE, reported in [2] and on the IceCube website, to evaluate the expected number of events for each neutrino flavor. We compute these expectations using equation (37).

Using the benchmark flux given in Eq. (16), the expected numbers of showers for each neutrino flavor are given by

$$\begin{aligned} {\mathcal {R}_e} = N_e [k_{\nu _e} (1-\epsilon ) + k_{\bar{\nu }_e} \epsilon ] ,\\ {\mathcal {R}_\mu } = N_\mu k_\mu , \\ {\mathcal {R}_\tau } = N_\tau k_\tau , \end{aligned}$$

where the coefficients $k_\ell$ are equal to

$$\begin{aligned} k_{\nu _e}=14.7; \ \ k_{\bar{\nu }_e}= 17.8; \ \ k_\mu =1.3; \ \ k_\tau = 9.3. \end{aligned}$$

(42)

The coefficient $k_\mu$ takes into account the small, but not negligible contribution to the expected number of showers, given by $\nu _\mu$, which interact via neutral current interactions. This has been derived considering that about 20% of $\nu _\mu$ produces shower-like events, as discussed in [29]. For ${\mathcal {R}_e}$ we need to distinguish between the contribution of $\nu _e$ and $\bar{\nu }_e$, since only $\bar{\nu }_e$ can produce resonant events. Let us notice that

$$\begin{aligned} k_{\bar{\nu }_e} - k_{\nu _e} > 2.3, \ \text {see Eq.}~ (39) \end{aligned}$$

(43)

because in the effective areas also the leptonic channels are included, which give showers below 6.32 PeV, which are not distinguishable from those produced by deep inelastic scattering [23].

Using the previous coefficients $k_\ell$, we define the likelihood $\mathcal {L}_{\mathrm{HESE}}$ as follows, taking into account that the observed number of showers is ${\mathcal {R}_s}=58$:

$$\begin{aligned} \displaystyle \mathcal {L}_{\mathrm{HESE}} (N_e, \epsilon )\propto & {} [b_s+N_\mu (k_\mu + k_\tau )+{\mathcal {R}_e}(N_e,\epsilon )]^{{\mathcal {R}_s}} \nonumber \\&\displaystyle \times \, \exp [-(b_s+N_\mu (k_\mu +k_\tau )+{\mathcal {R}_e}(N_e,\epsilon )],\nonumber \\ \end{aligned}$$

(44)

which is the key ingredient to evaluate the coefficients $N_e$ and $\epsilon$.

Including the prior distribution $\text{ PDF }_{e\mu }$ shown in Fig. 3, $\mathcal {L}_{\bar{\nu }_e}$ in Eq. (41), $\mathcal {L}_\mu$ in Eq. (19), $\mathcal {L}_s$ in Eq. (14), we compute the complete likelihood function of $N_e$ and $\epsilon$ as follows:

$$\begin{aligned} \mathcal {L}_e (N_e, \epsilon )= & {} {N_e} \int _0^\infty {\frac{\mathrm{d}N_\mu }{N_\mu ^2}} \int _0^\infty \mathrm{d}b_s\ \mathcal {L}_{\mathrm{HESE}}(N_e,\epsilon ) \nonumber \\&\times \text{ PDF }_{e\mu }\left( \frac{N_e}{N_\mu } \right) \ \mathcal {L}_{\bar{\nu }_e}(N_e,\epsilon ) \ \mathcal {L}_\mu (N_\mu ) \ \mathcal {L}_s(b_s).\nonumber \\ \end{aligned}$$

(45)

In the previous expression we are using $N_\mu \simeq N_\tau$ (see Eq. (24)), in order to simplify the calculation.

Fig. 4

The likelihood of $N_e$ as a function of the normalization of $\phi _e$ and of $\epsilon$, the fraction of electron antineutrinos

The results are illustrated in Fig. 4. The regions are defined using the Gaussian 2-dimensional approximation:

$$\begin{aligned} (1-\text{ CL }_1) \times \mathcal {L}_e^\mathrm{max} \le \mathcal {L}_e \le (1-\text{ CL }_2) \times \mathcal {L}_e^\mathrm{max}. \end{aligned}$$

(46)

Marginalizing the 2-dimensional likelihood we obtain, separately, an estimate for $N_e$ and $\epsilon$:

$$\begin{aligned} \begin{array}{l} {N_e = 2.01^{+0.49}_{-0.43}} , \\ \epsilon < 0.54 \hbox { at}~90\%~\hbox {CL}. \end{array} \end{aligned}$$

(47)

We have checked that the choice between the spectrum given in Eq. (16) and the spectrum given in Eq. (15) affects the previous analysis by no more than 5%.

The same consideration applies considering a different normalization point (within a factor 2) in the flux defined in Eq. (16). This demonstrates the robustness of the analyses proposed in this paper.

In Table 4 we summarize the results obtained in this section. With these results on the normalization factors of the neutrino fluxes $N_\ell$ ($\ell =e,\mu ,\tau$) and on $\epsilon$, we have concluded the definition of our model for a universal spectrum of the cosmic neutrinos given in Eq. (16).

Table 4 Summary of the normalizations of the high-energy neutrino flux at Earth defined in Eq. (16), divided per flavor. The parameter $\epsilon$ given in Eq. (40) is the fraction of electron antineutrinos with respect to the $\phi _e$ flux

We have also tested our procedure considering a single power-law model with $\alpha =2.92$ and $N_\mu =2.5 \pm 0.8$, as suggested by the most recent IceCube analysis of HESE data alone [8]. In this case we obtain $N_e=3.1 \pm 0.5$ and $N_\mu \simeq N_\tau$. There are no preferences for $\epsilon$ in this scenario, since with an $E^{-2.92}$ spectrum the resonant events are strongly suppressed.

Before passing to discuss the predictions, it is useful to see again Fig. 4 keeping in mind Table 4. It can be noticed that $N_e\simeq N_\tau \simeq N_\mu$ (expected from $\pi$ production) is contained into the 1$\sigma$ region; moreover, a small value for $\epsilon$ is preferable.

6 Predictions and critical aspects of the model

Having introduced and described our model, we can assess the expectations. We will discuss in the following three specific instances: (1) we examine in Sect. 6.1 the flavor composition of the universal spectrum defined above and compare it with some important cases; (2) we discuss in Sect. 6.2 the expected number of double pulse and Glashow resonance events, examining the uncertainties and showing their relevance; (3) we consider in Sect. 6.3 the angular distribution of the events and emphasize the critical importance of testing it for the low-energy part of the spectrum, possibly, using new detectors in the northern hemisphere.

6.1 Flavor composition at Earth

First of all, we discuss what flavor composition of the universal spectrum we obtain from our model and compare it with the theoretical expectations from some specific models for cosmic neutrino production.

Theory Using the natural parametrization described in the first section it is trivial to compute the flavor composition expected from a theoretical standpoint for different mechanisms of production. For a generic mechanism, with initial flavor composition

$$\begin{aligned} (\xi _e^0:\xi _\mu ^0:\xi _\tau ^0 )= (x:1-x:0) \end{aligned}$$

(48)

the fraction $\xi _e$ of $\nu _e$ + $\bar{\nu }_e$ after neutrino oscillations is equal to

$$\begin{aligned} \xi _e(x)=x \left( \frac{1}{3}+2 P_0 \right) +(1-x) \left( \frac{1}{3}-P_0+P_1 \right) \end{aligned}$$

(49)

where $x=1$ denotes the neutron decay scenario, $x=1/3$ the pion decay scenario and $x=0$ the damped muon scenario, as already discussed in Sect. 5.2.1. This flavor ratio is useful because it allows a clear discrimination of the different theoretical predictions, due to the fact that $P_{e\mu }\simeq P_{e\tau } \approx P_{ee}/2$, i.e. $\nu _e$ is the neutrino that mixes the least with other neutrinos.

Observations Using the fluxes reported in Table 4, we compute the flavor composition. The normalization of the total flux (a pure number; see Eq. (16)) is given by

$$\begin{aligned} N_{\text {tot}}= N_e+ N_\mu + N_\tau = {5.01 \pm 0.84} \end{aligned}$$

(50)

where the uncertainty is obtained summing in quadrature the uncertainties on the different normalizations. The observed flavor ratio of $\nu _e+\bar{\nu }_e$ is thus equal to

$$\begin{aligned} {\xi _e^{\mathrm{obs}}} = \frac{N_e}{N_e+N_\mu +N_\tau }={0.40 \pm 0.11} \end{aligned}$$

(51)

where the uncertainty is, as usual, given by

$$\begin{aligned} \varDelta \xi _e^{\mathrm{obs}}=\sqrt{\left( \frac{\varDelta N_e}{N_e} \right) ^2 + \left( \frac{\varDelta N_{\text {tot}}}{N_{\text {tot}}} \right) ^2}. \end{aligned}$$

(52)

The three histograms represent the predictions due to oscillations, while the gray vertical band covers the 68% range given in Eq. (51).

Using the single power-law spectrum suggested by IceCube in [8] we find that $\xi _e^{\mathrm{obs}}=0.38 \pm 0.08$. This proves that the flavor analysis is very stable and it slightly depends on the spectral assumption. On the other hand, the spectral assumption is crucial for the very high-energy events, i.e. double pulse and resonant events.

Fig. 5

Comparison between the theoretical flavor ratio expected from different mechanisms of production (colored histograms) and the observed one (shaded area)

Comparison The comparison between theoretical expectations (Eq. (49)) and the observed flavor ratio (Eq. (51)) is shown in Fig. 5. This indicates compatibility with the pion decay scenario, which is also the most plausible mechanism of production from a theoretical point of view. The neutron decay scenario is excluded at about 1.4$\sigma$, but a stronger constraint is given by the fact that $\epsilon =1$ (i.e. the neutron decay scenario) is excluded at least at 3$\sigma$ (see Fig. 4). On the other hand, the damped muon scenario is still compatible with the expectations within 1.3$\sigma$.

Taking simultaneously into account the flavor ratio $\xi _e$ and the preference for small $\epsilon$, we conclude that, under the hypothesis that no energy cut-off is present below $\sim 7{-}8\,\mathrm{PeV}$, there is an hint for $p\gamma$ as mechanism of production. In this scenario high-energy neutrinos are likely to be produced in the decay of $\pi ^+$ and, in smaller amount, in the decay of $\pi ^-$. As a consequence, the flux of $\nu _e$ is larger than the flux of $\bar{\nu }_e$.

6.2 Observable high-energy events of new type

Only the high-energy part of the spectrum is relevant for the computation of double pulse events and Glashow resonance events: these events are related to the $\propto E^{-2.1}$ part of the spectrum. There is thus no difference in expectations when we use the spectrum suggested by throughgoing muons, or the broken power-law spectrum of Eq. (15), or the two-component power-law spectrum of Eq. (16). Let us proceed to evaluate the expectations assuming $T=5.7$ years of exposure.

Double pulse events In Sect. 5.2 we have seen that $\phi _\tau \simeq \phi _\mu$, due to neutrino oscillations. We remark that it is always true for a generic production mechanism, not only for the pion decay scenario.

This result gives rise to an important theoretical prediction. Combining Eqs. (31) and (28) (or similarly Eqs. (25) and (28)), we find that the expected number of double pulse events after $T=5.7$ years of exposure is

$$\begin{aligned} {\mathcal {R}_{\mathrm{2P}}^{\mathrm{th}}=0.65\pm 0.24} \end{aligned}$$

(53)

if we assume the absence of an energy cut-off. As a test of our calculations, we note that the IceCube collaboration used a $E^{-2}$ spectrum to evaluate the number of double pulse events [22]; considering this fact, our results are in excellent agreement with [22] and also with [23].

Fig. 6

Cumulative distribution function (CDF) of double pulse events as a function of the energy. The CDF is obtained from the integrand of Eq. (27), namely by the product of the double pulse effective area and the tau neutrino flux, corresponding to the throughgoing muons flux (blue line) and to the two-components power law (orange line) model

The cumulative distribution function (CDF) of the double pulse signal, shown as a function of the maximum neutrino energy in Fig. 6, leads to three important conclusions:

• 1. only neutrinos above 0.1–0.2 PeV contribute to the double pulse event signal. In other words, the assumption on the low-energy part of the neutrino spectrum does not affect significantly the number of expected events;

• 2. a hypothetical cut-off in the neutrino spectrum beyond the measured energies would reduce the possibility to observe a double pulse event. More specifically, an energy cut-off at 2, 5 and 10 PeV would reduce the number cited in Eq. (53) by 45, 30 and 15%, respectively;

• 3. in any case, half of the expected double pulse events are produced by neutrinos with an initial energy of 2 PeV, that is, once again, those neutrinos that have been already observed by IceCube. As a consequence, tau neutrinos must be observed in the future: it is only a matter of exposure.

The last consideration is very remarkable, because the observation of tau neutrinos would be the definitive proof that cosmic neutrinos have been detected.

Glashow resonance events Let us use the best fit value of $N_e$, reported in Eq. (47), with the expected number of resonant events given by Eq. (39) and assuming pion decay as mechanism of production (as suggested by the result of Sect. 6.1).

The number of events depends upon $\epsilon$. Assuming $\epsilon =1/2$, namely for pp production, this is

$$\begin{aligned} {\mathcal {R}_{\mathrm{G}}^{\mathrm{(pp)}}=2.28\pm 0.52}, \end{aligned}$$

(54)

while in the case $\epsilon =1/4$, which is the idealized case of $p\gamma$ production (or minimum value expected), this is

$$\begin{aligned} {\mathcal {R}_{\mathrm{G}}^{\mathrm{p}\upgamma }=1.14\pm 0.26}. \end{aligned}$$

(55)

These considerations show that, if the baseline model is correct and, in particular, the spectrum does not have a cut-off for energies much smaller than 6.32 PeV, Glashow resonance events should be seen in the future years. Note that the preference for small values for $\epsilon$, visible from Fig. 4 and the relevant discussion, derives just from the non-observation of resonant events in the current IceCube dataset.The presence of an energy cut-off much smaller than 6.32 PeV diminishes or inhibits the possibility to separate the contribution of $\nu _e$ and $\bar{\nu }_e$ and, as a consequence, to extract useful information on the parameter $\epsilon$. (On the contrary, the constraint on $N_e$ can be calculated also when a cut-off is present, and we have checked that its impact is negligible with respect to the result obtained in this paper.)

We mention in passing speculative scenarios for the production of the neutrinos, with major deviations from the previous standard cases: considering the value $\epsilon =1$ for the neutron decay and $\epsilon =0$ for the damped muon scenario with only $\pi ^+$ at the source, the expected number of resonant events would become 4.2 and 0, respectively.

6.3 The angular distribution of the flux

The flux of high-energy neutrinos detected by IceCube with HESE [8] is better seen from the southern sky and appears to be isotropic; if this were the case, it should be present also in the northern sky. The observations consist mostly of shower events, but if neutrinos are of cosmic origin, also muon neutrinos should be present due to conventional neutrino oscillations. Summarizing, the current framework of interpretation of HESE requires that, in the energy region above 30 TeV, the one that has been investigated in [8], there are also muon neutrinos and antineutrinos, coming from the northern sky, with an energy distribution $\sim E^{-2.9}$ and with similar intensity as the other flavors.

We would like to discuss why it is not credible that this flux extends to TeV energies, elaborating an argument first proposed in [13].

The key remark is that the IceCube collaboration has performed a search for prompt neutrinos just in this low-energy region. This search was based on the reliable expectation that the prompt neutrinos are distributed with a power law $\sim E^{-2.7}$; the corresponding signature events are track events (contained and throughgoing muons), due to muon neutrinos and antineutrinos. The analysis did not reveal any significant excess over the background due to pion and kaon decay. In this manner, a strong upper limit on the normalization of prompt neutrino flux has been derived. The 90% CL upper bound, namely the maximum flux compatible with this analysis, is given, e.g., in [13]: see Eqs. 8 and 9 there. In the search conducted by IceCube, the muon neutrinos and antineutrinos were supposed to be produced in the atmosphere; however, the result of the search applies also to other, new and speculative, components.

Problems arise when one extrapolates the obtained upper bound to higher energies, or conversely, one extends the HESE power-law distribution to low energy. In fact, assuming the upper bound discussed above, we expect only 3.5 HESE events from the whole sky, see Table 1 in [13], which is one order of magnitude smaller than the number of observed HESE. See Sect. 5 of [13] for a thorough discussion, with the only proviso that the slope of the neutrino flux, consistent with the new HESE dataset, is now $\alpha \approx 2.9$, while in [13] it was $\alpha \approx 2.4\div 2.7$; the new softer flux, prolonged to low energies, would be in stronger disagreement with the upper bound on prompt neutrinos mentioned above.

The above conclusion can be regarded as a critical aspect of our model; for this reason, it is important to proceed with a detailed examination and objective evaluation of the assumptions and of the extrapolations that are behind it. Keeping in mind that the aim is the assessment, and remaining aware that, at present, it is not yet possible to reach a definitive judgment, we deem it important to ask the questions of the hypothesis of isotropy; the extrapolation of the spectrum; and the assumption as regards the background. Let us examine these possibilities, considering three different (but non-exclusive) scenarios:

• 1. The flux that explains HESE events is not isotropic but comes mostly or only from the southern hemisphere. A similar possibility has been already discussed in [9, 13]. The multi-component model proposed in [13], which predicts a Galactic contribution between 10 and 20%, is still compatible with the most recent experimental constraints concerning the Galactic flux, provided by ANTARES [30] and IceCube [31].³

• 2. There is another very drastic change of slope between 1 and 30 TeV in the cosmic neutrinos, although it is quite hard to imagine a physical motivation that could produce this effect.

• 3. There is a larger contamination in the southern sky from conventional atmospheric background than currently assumed, which could be related to an efficiency of the veto smaller than expected. This is a kind of speculative scenario that would be in agreement also with the $E^{-3.5}$ component of our two-component power-law model, since the conventional atmospheric background (both muons and neutrinos) follows an $E^{-3.7}$ spectrum.

Concerning the last point, one should note that conventional neutrinos, prompt neutrinos and penetrating muons (see Sect. 3), are relevant for the HESE analysis, whereas mostly prompt neutrinos (discussed in Sect. 4.2) are relevant for the throughgoing muon analysis above 200 TeV. Thus the backgrounds are different, and muons, in particular, are seen only from the southern hemisphere.

7 Summary and conclusions

The findings of IceCube indicate the importance of going beyond a description of the new events based on the single power-law model, that has been used in the past to analyze the flavor composition [4, 29, 32,33,34,35]. The first analysis of the neutrino spectrum using two components has been performed in [36] but it uses only HESE. In the analysis proposed here, we combine theoretical models (mechanisms of production, neutrino oscillations) with experimental informations regarding the shape of the spectrum in different energy regions, the absence of double pulses, the absence of resonant events and the observed number of showers in HESE dataset.

Furthermore, we have evaluated the natural parameters of cosmic neutrino oscillations [4], using the most recent oscillation results [5], and used these results in the analysis.

We have estimated the flux of each neutrino flavor, based on theoretical and experimental constraints, assuming:

• neutrino oscillations and considering the most general mechanism of production;

• a two-component power-law spectrum that is in agreement with throughgoing muons at high energy and with the shape suggested by HESE at low energy;

• the number of shower-like events observed in HESE dataset;

• the absence of double pulses and resonant events in current IceCube dataset.

We have obtained that such neutrino spectrum is in good agreement with all IceCube measurements. Moreover, we have estimated the normalizations, flavor by flavor.

Let us remark that the three-flavor neutrino oscillation paradigm strongly constrains the flux of tau neutrinos, which must be very similar to the flux of muon neutrinos for every plausible mechanism of production. From this constraint an important prediction follows; the expected number of double pulse events is about 0.7 after 6 years of exposure. Therefore, tau neutrinos must be observed with the increase of exposure.

We obtained a preference for the pion decay as mechanism of production of high-energy neutrinos. In addition, we notice a preference for small values for the ratio $\phi _{\overline{\nu }_e}/\phi _e$, which could be an indication towards $p\gamma$ as a mechanism of production, unless the neutrinos spectra have no energy cut-off below the Glashow resonance energy. As regards the other mechanisms of production:

• the neutron decay scenario is disfavored at 1.4$\sigma$ by the flavor composition and at 3$\sigma$ by the lack of resonant events;

• the damped muon scenario, on the contrary, is still marginally compatible with the data, being disfavored at 1.3$\sigma$ using the flavor composition.

We found that, with 6 years of exposure, 2.4 resonant events are expected in the pp scenario of neutrino production; in the case of the $p\gamma$ scenario the expected number of events can reach, with the same exposure, a minimum value of 1.2. Let us remark that in realistic $p\gamma$ interaction also $\pi ^-$ are produced, therefore the true prediction for the rate resonant events is between 0.2 and 0.4 per year.

Finally, we have remarked that it is not easy to reconcile the absence of new track events from the northern sky at $\sim$ TeV with the presence of HESE showers above 30 TeV, without invoking a non-trivial dependence of the low-energy spectrum upon the angle—i.e., some major deviation from the hypothesis of isotropy. With the present data it is not possible to solve this issue.

The contribution of the neutrino telescopes, placed in the northern hemisphere, is fundamental to clarify the situation. Particularly, the incoming KM3NeT has a crucial role, since it is comparable to IceCube in terms of dimension and it is complementary in terms of position. In fact, KM3NeT will observe the southern hemisphere using throughgoing muons and the northern hemisphere using contained events. Also GVD [37], still under construction, can give a contribution to improve the knowledge in the field of high-energy neutrino astronomy.

We would like to conclude stressing that the kind of analysis proposed in this paper, easy and fast to implement, is also very promising for the future.