Fate of an accretion disc around a black hole when both the viscosity and dark energy is in effect

Abstract

This paper deals with the viscous accretion flow of a modified Chaplygin gas towards a black hole as the central gravitating object. A modified Chaplygin gas is a particular type of dark energy model which mimics of radiation era to phantom era depending on the different values of its parameters. We compare the dark energy accretion with the flow of adiabatic gas. An accretion disc flowing around a black hole is an example of a transonic flow. To construct the model, we consider three components of the Navier–Stokes equation, the equation of continuity and the modified Chaplygin gas equation of state. As a transonic flow passes through the sonic point, the velocity gradient being apparently singular there, it gives rise to two flow branches: one in-falling, the accretion and the other outgoing, the wind. We show that the wind curve is stronger and the wind speed reaches that of light at a finite distance from the black hole when dark energy is considered. Besides, if we increase the viscosity, the accretion disc is shortened in radius. These two processes acting together make the system deviate much from the adiabatic accretion case. It shows a weakening process for the accretion procedure by the work of the viscous system influencing both the angular momentum transport and the repulsive force of the modified Chaplygin gas.

1 Introduction

Accretion means enriching. Astrophysical accretion, either in a protoplanetary disc or around a massive central engine, means fall of mass towards a gravitating center. The present article discusses the flow of diffused material towards a particular type of compact object, namely a black hole (BH). Though first a theoretical prediction, BHs are nowadays almost proved to be present in X-ray binaries, center of galaxies, especially in active galactic nucleis (AGNs) or in several sources of gravitational waves [1]. However, most of the evidence is indirect, i.e., the critical behaviour of in-falling matter towards a steep gravitational well brings leads to information. Due to the conservation of angular momentum, the in-falling flow towards a BH forms a disc like structure. In the disc, the accreting fluid simultaneously obeys $\frac{\partial }{\partial r}\left( \Omega R^2 \right) >0$ and $\frac{\partial \Omega }{\partial R}<0$, where $\Omega$ is the local angular velocity for Keplerian motion (i.e., $\Omega ^2 R=\frac{GM}{R^2}$, which implies $\Omega = \left( \frac{GM}{R^3}\right) ^\frac{1}{2}$), and R is the radial distance from the center. Physically which means that angular momentum increases and angular velocity decreases outwards. This gives birth of the outward angular momentum transport. The outward force due to angular momentum is of order $\frac{1}{R^3}$ and the inward gravitational pull is of order $\frac{1}{R^2}$, so when going towards a compact object, there is a region where gravitational pull is defeated by the outward force of angular momentum and forms a layer which is called the CENtrifugal force driven BOundary Layer (CENBOL). For a Keplerian orbit, the centrifugal force is balanced by the gravitational force but once the system turns to be a transonic one, the in-falling matter will be piled up at the CENBOL and may create shock waves. Shock wave formation from CENBOL is allowed for a large region of parametric space. We can shrink the parameter space by adding viscosity. But viscosity is such a property as to increase the temperature and again the temperature causes the increment in viscosity. So understanding viscosity in a direct way creates a loop.

The initial models of accretion with formation of a disc around BH were due to Prendergust [2], Gorbatsky [3] and Shakura [4]. The scenario, however, was modified after Shakura and Sunyaev’s work [5] as they unified all the concepts already discussed and proposed a mechanism of angular momentum transport. The efficiency of this mechanism can be parametrised by

$$\begin{aligned} \alpha _{ss}=\frac{v_\mathrm{t}}{c_\mathrm{s}} + \frac{H^2}{4\pi \rho c_\mathrm{s}^2}, \end{aligned}$$

(1)

where $\frac{\rho c_\mathrm{s}^2}{2}=\epsilon _r + \frac{3}{2} \rho \frac{k_\mathrm{B} T}{m_\mathrm{p}}$ is thermal energy density of matter, $\epsilon _r$ is energy density of the radiation, $c_\mathrm{s}$ and $v_\mathrm{t}$ are the speed of sound inside the fluid and turbulent velocity, respectively. $k_\mathrm{B}$, T, $m_\mathrm{p}$, $\rho$ and H are Boltzmann constant, temperature, mass of proton, density and disk height, respectively. $\alpha _{ss}$ became popularly known as the Shakura–Sunyaev parameter (SSP). This idea worked quite well in several areas, where the value of the SSP, $\alpha _{ss}$, lies between 0.1 to 0.4. Yet it was unable to predict some global changes of disc structure, e.g., irregularities in the observed Fe, K$\alpha$ spectrum of active galactic nuclei. We are to replace the shear velocity $- \omega _{r \phi }$ by the value $\alpha _{ss} \rho c_\mathrm{s}^2$.

Studies of accretion procedures with SSP changed the whole way of thinking. A study of viscous accretion phenomena around rotating gravitational objects with hard surfaces, i.e., mostly around objects like neutron stars and strange objects, has been made in [6]. Viscosity due to turbulence, governed by magneto-rotational instability, especially when the temperature $T \ge 10^5 K$, was studied in [7]. One has shown that the values of $v_\mathrm{t}$ and $\alpha _{ss}$ increase quite rapidly as the disk becomes thinner and thinner. The same trend of using $\alpha _{ss}$ as the representative of viscosity can be found in various articles [8,9,10]. There is even another interesting fact. There exists a theoretical lower bound of the ratio of the shear viscosity to entropy density (according to string theory and gauge/gravity duality), mathematically stating that $\frac{\eta }{S} \scriptstyle \gtrsim \frac{\mu \hbar }{4 \pi k_\mathrm{B}}$, where $\hbar$ is the reduced Planck constant and $\mu \le 1$. Now, say, for water this ratio is much higher than the prescribed lower limit. We find some contributions in the literature where the author of [11] has tried to reach the lower limit considering the accretion process towards a BH to be the background. In this work the shear viscosity part is represented with the help of $\alpha _{ss}$ and it simplified the challenge a lot.

After giving a brief review of the local astrophysical phenomena like accretion we will shift our focus towards the great changes in cosmological studies from the late-1990s onward. To justify the late time cosmic acceleration detected by the Ia supernova observations [12], one is required to modify either the ‘gravity part’ or the ‘matter/stress energy part’ of the Einstein field equation. The latter initiated the idea of modelling dark energy (DE) which is a kind of exotic fluid, homogeneously filling the universe. This exerts a negative pressure and violates the strong energy condition ($\rho +3 p > 0$) and weak energy condition ($\rho + p > 0$) as the universe keeps on expanding. The best fit DE model ever proposed up to the present is the cosmological constant $\Lambda =-1$ [13]. Except this, there are different proposed candidates of DE. Since 2004, different authors have studied the properties of DE accretion towards a BH. The first ever attempt among them was done by [14] where the authors have made calculations like in Michel’s paper [15] in addition to the Einstein field equation derived for the FLRW metric and have shown that the mass of the BH can be reduced by the accretion of phantom energy. Once the expanding universe crosses the phantom barrier and the weak energy condition is violated ($\rho + p < 0$), their predictions as regards the causes of such mass reduction occurrences were the accretion of the particles of phantom scalar field. They have compared this with the negatively energised particle creation in the Hawking radiation process. However, they have ignored the back reactions of phantom matter on the BH metric. If the background matter density is low, this ignorance does not make any change. But once the density is comparable to the BH density  $\frac{M}{R^3} \sim \frac{M}{M^3} \sim \frac{1}{M^2}$, the metric of the BH should be modified significantly. This matter has been studied by [16] and one has also shown that the horizon will shrink, but the singularity never will become naked. Finite and infinite cosmic time, whenever it may be, the energy density of a cosmological BH will turn zero. These articles are quite sensitive to find the fate of the BH at the future cosmological singularity coined the ‘Big Rip’ [17]. Both of these authors have predicted that even a long time before the big rip to occur, the BHs will get evaporated away. Now the cyclic universe is another scenario where the cosmos fluctuates but the BHs are to radially increase only. Analysis of [18] indicates that although through phantom energy accretion BHs do not disappear before the cyclic universal cosmological turn around, they do not cause problems. A recent study [19] says the process of phantom acceleration is not as general as suggested by [14]; rather the distribution of the scalar field remaining outside the BH would be an interesting area for investigation. In the literature we may find many other papers where DE accretion on a compact object is studied [20,21,22].

Now we will look at the galactic rotational curve where the missing mass problem is solved by introducing the idea of some exotic matter, called dark matter (DM), which is silently present in the galaxy’s outer layers and responsible for the higher angular momentum observed there. The DM density profile at the core areas of the galaxies is critical to indirect searches but remains poorly constrained. In objects such as M87, the DM profile may be significantly enhanced on subspace scales by the central super massive BHs [23]. Currently we can find some papers where the presence of DM, particularly even close to the core of the milky way, has been studied [24]. A well-accepted theory of galaxy formation must account for the large amount of non-DM, which apparently provides $\ge 80\%$ of the virial mass in clusters like Coma and which may constitute massive halos around large galaxies. It has been known for over a decade that tiny gas rich dwarfs favour central DM cores over cusps [25, 26]. Silk and Bloman [27,28,29] pointed out that the $cos-B$ satellite observations of the cosmic flux of $\gamma$-rays can place severe constraints on the density of the DM near the center of the galaxies. Although the precise form of the constraint depends upon which kinds of interacting particles are considered (say photinos, higgsinos, shentrinos [26] and neutrinos [30,31,32] with mass m in the GeV range [33]). It appears that the data are sensitive to $\gamma$-ray signal from a lump of weakly interacting DM with density of order $10^{-22}$ gm/cc over a region of size 100–200 pc from the galactic center. The typical DM density is in a range of order $10^{-24}$ gm/cc. However, the DM density at the center of the galaxy is expected to be much enhanced due to the gravitational attraction of the central component of the galaxy. The central component having mass of order $0.7\times 10^{10}$ $M_{\odot }$, where $M_{\odot }$ is the mass of the sun, then the DM density may reach $4 \times 10^{-21}$ gm/cc.

Several works have been done towards unification of DE and DM. Based on the modelling of the speed of sound as a function of the parameter of EoS [34], via superfluid Chaplygin gas modelling [35], consideration of the dynamics of a generalised Born–Infeld theory [36] and many other contributions in the literature may be found where the unification or interaction of DM and DE is studied. Very particularly a modified Chaplygin gas (MCG) is found to be the type of DE representative which efficiently fits when the unification or interactions is to be achieved. MCG is a DE model which suits well enough for different data. For different values of parameters it shows radiation to phantom phenomena. The EoS is given by [37,38,39]

$$\begin{aligned} p=\alpha \rho -\frac{\beta }{\rho ^n} \end{aligned}$$

(2)

where $\alpha$, $\beta$ and n are constants. This is why for DE accretion towards a BH, the MCG is one of the best models to be considered. Previously, Biswas et al. [40] have studied the accretion of MCG on BH and found that the wind is dominating rather than the accretion and they have commented that the BH accretion disc may get fainter by this process and will ultimately weaken the BH feeding-up process. In another work [41] one depicted the change in flow density through accretion and wind branch. This work even pointed towards the formation of a CENBOL.

Many authors have tried to constrain the MCG parameter with the various observational data available. We will recall particularly two among them. The first one [42] used type Ia supernovae and the BAO dataset to predict the best fit parameter values. The values are:

Parameter	Best fit values for constitution + CMB + BAO	Best fit values for Union2 + CMB + BAO
$\alpha$	$0.061 \pm 0.079$	$0.110 \pm 0.097$
n	$0.053 \pm 0.089$	$0.089 \pm 0.099$

However, another article [43] the authors used Union2, SNIa, OHD, CBF, BAO and CMB data to constrain the MCG model and the best fit parameter values with $1 \sigma$ and $2\sigma$ confidence level are:

Parameter	Best fit values
$\alpha$	$0.00189^{+0.00583+0.00660}_{-0.00756-0.00915}$
n	$0.1079^{+0.3397+0.4678}_{-0.2539-0.0.2911}$

In the present work we wish to incorporate the viscosity. With the MCG EoS, the viscous accretion towards a BH will be studied. We will roughly take $\alpha$ to be very small $\sim 0.05$ and n to be nearly equal to 0.1. Along with this we will compare the whole system with the adiabatic fluid case where we will take the EoS to be $P=K \rho ^{\Gamma }$, where the value of $\Gamma$ will be in general taken as 1.6.

In the next section we will construct the mathematics of the model, i.e., the construction of a first order ODE along with initial values. In the next section, we will solve the system numerically and will analyse the case thoroughly. In the penultimate section, we shall incorporate a variety of astrophysical data and results derived from them to give some physical estimates of the parameters used by us. A brief summary and conclusion will be given in the final section.

2 Mathematical construction of the model

Bondi formulated spherical accretion and wind for a non-rotating star in the Newtonian approach [44]. Here we assume a steady and axisymmetric disc. In Ref. [40] the authors described accretion and wind flow for an inviscid fluid around a compact object, in a pseudo-Newtonian approach. We here try to study the accretion and the wind flow with viscous fluid parametrised by the parameter $\alpha _{ss}$. The general disc outflow equations are mainly based on the well-known Navier–Stokes equation, treating the system as fluid flow;

$$\begin{aligned} \frac{\partial \vec {V}}{\partial t} +\left( \vec {V}.\vec {\bigtriangledown }\right) \vec {V}=\vec {F}-\frac{1}{\rho } \vec {\bigtriangledown }p + \gamma \bigtriangledown ^2 \vec {V}, \end{aligned}$$

(3)

where $\vec {V}$ is the velocity vector, t is the classical time, $\vec {\bigtriangledown }$ is the classical divergence operator, p is the pressure of the fluid, $\vec {F}$ is the force vector, $\rho$ is the density of the fluid, $\gamma$ is the kinematic viscosity and $\bigtriangledown ^2$ is the classical Laplacian operator. General relativistic equations are highly non-linear and very difficult. To simplify we assume the system is in steady state, $\frac{\partial \vec {V}}{\partial t}=0$, but to keep the force factor equivalent to the general relativistic one we will replace it by a pseudo-Newtonian force and for the corresponding components we get the following.

• (a) Radial momentum balance equation:

  $$\begin{aligned} u\frac{\mathrm{d}u}{\mathrm{d}x} + \frac{1}{\rho } \frac{\mathrm{d}p}{\mathrm{d}x}-\frac{\lambda ^2}{x^3}+F_\mathrm{g}\left( x\right) =0, \end{aligned}$$

  (4)

  where all the variables are expressed in dimensionless units $u=u_r=\frac{v}{c}$, $x=\frac{r}{r_\mathrm{g}}$, $r_\mathrm{g}=\frac{GM}{c^2}$, $\lambda$= s where M and c are the mass of the BH and speed of light, respectively. r, v and $\lambda$ are radial co-ordinate and radial velocity and angular momentum of the disc, p and $\rho$ are the dimensionless isotropic pressure and density;

  $$\begin{aligned} F_\mathrm{g}\left( x\right) = \frac{\left( x^2-2j\sqrt{x}+ j^2\right) ^2}{x^3\lbrace \sqrt{x} \left( x-2\right) +j\rbrace ^2} \end{aligned}$$

  (5)

  is the gravitational force corresponding to the pseudo-Newtonian potential [45], where j is the dimensionless specific angular momentum for the rotating BH.

• (b) Azimuthal momentum balance equation:

  $$\begin{aligned} u \frac{\mathrm{d}\lambda }{\mathrm{d}x} = \frac{1}{x \Sigma } \frac{\mathrm{d}}{\mathrm{d}x} \left[ x^2 \alpha _\mathrm{s} \left( p+\rho u^2\right) h\left( x\right) \right] , \end{aligned}$$

  (6)

  where $\Sigma$ is the vertically integrated density given by

  $$\begin{aligned} \Sigma = I_\mathrm{c} \rho _\mathrm{e} h\left( x\right) , \end{aligned}$$

  (7)

  when $I_\mathrm{c}$ is a constant (related to the equation of state of the fluid) equal one [40], $\rho _\mathrm{e}$ is the density at the equatorial plane, $h\left( x\right)$ is the half thickness of the disc. Assuming the vertical equilibrium from the vertical component of Eq. (3) we get the expression for h(x):

  $$\begin{aligned} h\left( x\right) = c_\mathrm{s} \sqrt{\frac{x}{F_\mathrm{g}}}. \end{aligned}$$

  (8)

• (c) The vertically integrated mass conservation relation, i.e., the equation of continuity for disc accretion:

  $$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x} \left( x u \Sigma \right) = 0. \end{aligned}$$

  (9)

  Differentiating Eq. (2) with respect to $\rho$ we have

  $$\begin{aligned} c_\mathrm{s}^2 = \frac{\partial p}{\partial \rho } = \alpha + \frac{\beta n}{\rho ^{n+1}}. \end{aligned}$$

  (10)

Thus we get from Eqs. (9) and (10)

$$\begin{aligned} \frac{1}{\rho } \frac{\mathrm{d}p}{\mathrm{d}x}= & {} - \frac{2 c_\mathrm{s}^3}{\left( n+1\right) \left( c_\mathrm{s}^2 - \alpha \right) } \frac{\mathrm{d} c_\mathrm{s}}{\mathrm{d}x}\nonumber \\= & {} -\frac{1}{n+1} \frac{\mathrm{d}}{\mathrm{d}x} \left( c_\mathrm{s}^2 \right) - \frac{\alpha }{n+1} \frac{\mathrm{d}}{\mathrm{d}x} \left\{ ln \left( c_\mathrm{s}^2 -\alpha \right) \right\} .\nonumber \\ \end{aligned}$$

(11)

Now integrating Eq. (9) we get the mass conservation equation

$$\begin{aligned} {\dot{M}} = \Theta \rho c_\mathrm{s} \frac{x^\frac{3}{2}}{F_\mathrm{g}^\frac{1}{2}} u, \end{aligned}$$

(12)

where $\Theta$ is a geometrical constant. Replacing the value of $\rho$ from Eq. (10) in (12) and differentiating the whole term we get a differential equation for $c_\mathrm{s}$,

$$\begin{aligned} \frac{\mathrm{d} c_\mathrm{s}}{\mathrm{d}x}= & {} \left( \frac{3}{2x} -\frac{1}{2F_\mathrm{g}} \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x} + \frac{1}{u} \frac{\mathrm{d}u}{\mathrm{d}x} \right) \nonumber \\&\times \left\{ \frac{\left( n+1 \right) c_\mathrm{s} \left( c_\mathrm{s}^2 -\alpha \right) }{\left( 1-n \right) c_\mathrm{s}^2 + \alpha \left( n+1 \right) } \right\} , \end{aligned}$$

(13)

and from Eqs. (6) and (2) we get

$$\begin{aligned} \frac{\mathrm{d} \lambda }{\mathrm{d}x}= & {} \frac{x \alpha _s}{u} \left[ \frac{1}{2} \left( \frac{5}{x} - \frac{1}{F_\mathrm{g}} \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x} \right) \left\{ \frac{\left( n+1 \right) \alpha - c_\mathrm{s}^2}{n} + u^2 \right\} \right. \nonumber \\&\left. + 2 u \frac{\mathrm{d}u}{\mathrm{d}x} + \left\{ \left( \frac{\left( n+1 \right) \alpha - c_\mathrm{s}^2}{n} + u^2 \right) \frac{1}{c_\mathrm{s}}\right. \right. \nonumber \\&\left. \left. - \left( c_\mathrm{s}^2 +u^2 \right) \left( \frac{1}{n+1} \frac{2 c_\mathrm{s}}{c_\mathrm{s}^2 - \alpha } \right) \right\} \frac{\mathrm{d}c_\mathrm{s}}{\mathrm{d}x} \right] . \end{aligned}$$

(14)

Thus we get all the needed values to replace $\frac{1}{\rho } \frac{\mathrm{d}p}{\mathrm{d}x}$ in Eq. (4); hence we obtain

$$\begin{aligned} \frac{\mathrm{d}u}{\mathrm{d}x} = \frac{\frac{\lambda ^2}{x^3}- F_\mathrm{g}\left( x \right) + \left( \frac{3}{x} - \frac{1}{F_\mathrm{g}} \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x} \right) \frac{ c_\mathrm{s}^4}{\lbrace \left( 1-n \right) c_\mathrm{s}^2 + \alpha \left( n+1 \right) \rbrace }}{u - \frac{2 c_\mathrm{s}^4}{u \lbrace \left( 1-n \right) c_\mathrm{s}^2 + \alpha \left( n+1 \right) \rbrace }}. \end{aligned}$$

(15)

As unlike a neutron star, the BH does not posses any hard surface (rather there is an event horizon), the flow towards a BH is necessarily transonic. Far from the BH the accretion speed must be very low and close to the horizon this should be equal to the speed of light. So it is clear that somewhere in between the fluid flow velocity must be equal to the speed of sound inside it. This point is called the sonic point. We can observe that the denominator of (15) will be zero at a particular value of u and $c_\mathrm{s}$. Therefore for the sake of the stability of the disc the numerator also has to be zero. This point of the disc is called the critical point. Now applying the L’Hospital rule in Eq. (15) at the critical point (say $x =x_\mathrm{c}$) we get a quadratic equation of $\frac{\mathrm{d}u}{\mathrm{d}x}$ in the form

$$\begin{aligned} A \left( {\frac{\mathrm{d}u}{\mathrm{d}x}}\right) _{x=x_\mathrm{c}}^2 + B \left( \frac{\mathrm{d}u}{\mathrm{d}x} \right) _{x=x_\mathrm{c}} + C =0. \end{aligned}$$

(16)

Here

$$\begin{aligned} A= & {} 1 + \frac{1}{c_{\mathrm{sc}}^2} - \frac{4 \left( n+1 \right) \left( c_\mathrm{{sc}}^2 -\alpha \right) }{{\left\{ \left( 1-n \right) c_\mathrm{{sc}}^2 +\alpha \left( n+1 \right) \right\} }^2},\\ B= & {} \frac{4 \lambda u}{x_\mathrm{c}^3} + \frac{2 u_\mathrm{c} c_\mathrm{{sc}} \left( 1-n \right) }{ \left\{ \left( 1-n \right) c_\mathrm{{sc}}^2 +\alpha \left( n+1 \right) \right\} } \\&- \frac{2 u_\mathrm{c} \left( n+1 \right) \left( c_\mathrm{{sc}}^2 -\alpha \right) }{{\left\{ \left( 1-n \right) c_\mathrm{{sc}}^2 +\alpha \left( n+1 \right) \right\} }^2} \\&\times \left( \frac{3}{x_\mathrm{c}} - \frac{1}{F_\mathrm{g}} \left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x}\right) _{x=x_\mathrm{c}} \right) \\&+\left[ \left( c_\mathrm{{sc}}^2 +u_\mathrm{c}^2 \right) \left( \frac{1}{n+1} \frac{2 c_\mathrm{{sc}}}{c_\mathrm{{sc}}^2 - \alpha } \right) \right. \\&-\left( \frac{3}{x_\mathrm{c}} - \frac{1}{F_\mathrm{g}} \left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x}\right) _{x=x_\mathrm{c}} \right) \\&\times \frac{4 u_\mathrm{c} }{c_\mathrm{{sc}}{\left\{ \left( 1-n \right) c_\mathrm{{sc}}^2 +\alpha \left( n+1 \right) \right\} }}\\&\left. - \left( \frac{\left( n+1 \right) \alpha - c_\mathrm{{sc}}^2}{n} + u^2 \right) \frac{1}{c_\mathrm{{sc}}} \right] \\&\times \left\{ \frac{ u_\mathrm{c} \left( n+1 \right) \left( c_\mathrm{{sc}}^2 -\alpha \right) }{2c_\mathrm{{sc}}^3} \right\} , \end{aligned}$$

and $C= D+ E+ F$. The values of D, E and F are

$$\begin{aligned} D= & {} \left[ \left( c_\mathrm{{sc}}^2 +u_\mathrm{c}^2 \right) \left( \frac{1}{n+1} \frac{2 c_\mathrm{{sc}}}{c_\mathrm{{sc}}^2 - \alpha } \right) \right. \\&\left. -\left( \frac{3}{x_\mathrm{c}} - \frac{1}{F_\mathrm{g}} \left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x}\right) _{x=x_\mathrm{c}} \right) \right. \\&\times \frac{4 u_\mathrm{c} }{c_\mathrm{{sc}}{\left\{ \left( 1-n \right) c_\mathrm{{sc}}^2 +\alpha \left( n+1 \right) \right\} }} \\&\left. - \left( \frac{\left( n+1 \right) \alpha - c_\mathrm{{sc}}^2}{n} + u^2 \right) \frac{1}{c_\mathrm{{sc}}} \right] \\&\times \left( \frac{3}{2x_\mathrm{c}} -\frac{1}{2F_\mathrm{g}} \left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x} \right) _{x=x_\mathrm{c}} \right) \\&\times \left\{ \frac{\left( n+1 \right) c_\mathrm{{sc}} \left( c_\mathrm{{sc}}^2 -\alpha \right) }{\left( 1-n \right) c_\mathrm{{sc}}^2 + \alpha \left( n+1 \right) } \right\} ,\\ E= & {} \left( \frac{3}{x_\mathrm{c}} - \frac{1}{F_\mathrm{g}} \left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x}\right) _{x=x_\mathrm{c}} \right) \frac{u_\mathrm{c} c_\mathrm{{sc}} \left( 1-n \right) }{{\left\{ \left( 1-n \right) c_\mathrm{{sc}}^2 +\alpha \left( n+1 \right) \right\} }} \\&+\left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x}\right) _{x=x_\mathrm{c}}+ \left\{ \frac{1}{F_\mathrm{g}^2} \left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x} \right) ^2_{x=x_\mathrm{c}} \right. \\&\left. - \frac{1}{F_\mathrm{g}} \left( \frac{\mathrm{d}^2 F_\mathrm{g}}{\mathrm{d}x^2}\right) _{x=x_\mathrm{c}} - \frac{3}{x_\mathrm{c}^2}\right\} \frac{u_\mathrm{c}^2}{2},\\ F= & {} \frac{\lambda \alpha _{ss}}{x_\mathrm{c}^2 u_\mathrm{c}} \left( \frac{1}{F_\mathrm{g}} \left( \frac{\mathrm{d}F_\mathrm{g}}{\mathrm{d}x}\right) _{x=x_\mathrm{c}} - \frac{5}{x_\mathrm{c}} \right) \\&\times \left\{ \frac{\left( n+1 \right) \alpha - c_\mathrm{{sc}}^2}{n} + u_\mathrm{c}^2 \right\} . \end{aligned}$$

While we are working with a particular type of EoS we supply n and $\alpha$, i.e., by the vanishing denominator, $D\left( u_\mathrm{c}, c_\mathrm{{sc}}, n, \alpha \right) =0$ will be reduced to an equation $D\left( u_\mathrm{c}, c_\mathrm{{sc}}\right) =0$, which tells us the relation between $u_\mathrm{c}$ and $c_\mathrm{{sc}}$; on the other hand by a vanishing numerator, i.e., $N\left( \lambda _\mathrm{c}, x_\mathrm{c}, j, c_\mathrm{{sc}}, n, \alpha \right) =0$, it will be reduced to $N\left( \lambda _\mathrm{c}, x_\mathrm{c}, c_\mathrm{{sc}}\right) =0$ once we provide the information as regards the accreting fluid and the rotation of the BH. We will choose where the sonic point will be formed and adjust the value of angular momentum at the critical point, which ultimately forms an algebraic equation of $c_\mathrm{{sc}}$, $N \left( c_\mathrm{{sc}}=0 \right)$. Thus we can easily solve $c_\mathrm{{sc}}$ and hence calculate the value of $u_\mathrm{c}$. These will be used as the initial values to solve (16). As we proceed towards the BH from the critical point we can have two solutions due to the quadratic nature of (16). The same will happen if we recede far from the BH. From these new four points (13), (14), (15) we can build the whole of the solution sets. In the next section we will plot the solutions and analyse them physically.

3 Numerical solutions and their physical interpretations

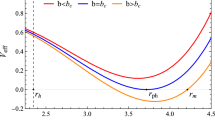
We will plot the numerically derived solutions in this section. Figure 1a, b are the plots of log(u) vs. log(x) for adiabatic flow and MCG flow, respectively. The solid line is for accretion and the dotted line is showing the behaviour of the wind. The set of Figs. 1a to 3b is drawn for a nonrotating BH and the viscosity is increased gradually.

Fig. 1

a, b are plots of log(u) vs. log(x) for non-viscous accretion disc flow around a non-rotating BH for adiabatic and MCG, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

Fig. 2

a, b are plots of log(u) vs. log(x) for viscous ($\alpha _{ss}=10^{-4}$) accretion disc flow around a non-rotating BH for adiabatic and MCG, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

A popular explanation of angular momentum transportation entails that whenever a particle is falling into a BH the momentum lost by it is gained by a farthest point particle, which starts just to rotate, i.e., enters in the disc. We think every layers’ rotation is a cause of the rotation of just the adjacent next layer to it. If we go outwards the angular momentum increases but the angular velocity decreases. This causes the increment of the radial inward velocity towards the central engine. When a particle starts up at a distance of $10^3$ Schwarzschild radii, the inward radial velocity is low. This increases gradually and at some point, close to the central gravitating object, the flow velocity meets the speed of sound inside the fluid, i.e., it reaches the sonic point. Now how far from the BH the sonic point will be formed is manually chosen for this figure. If we get close to the BH, the density $\rho$ is high and the speed of sound is also high. This shows that $\frac{\rho c_\mathrm{s}^2}{2}$, i.e., the energy of the accreting fluid should be high. To set the sonic point close to the BH means we are giving it a high amount of energy. For if we set the sonic point far away, the less energy is given to it. After crossing the sonic point speed, as BH accretion is a transonic process, the radial inward speed steeply increases and close to the BH event horizon it is almost equal to the speed of light. In the accretion branch at the farthest point, where the radial velocity is almost zero, we can find that the specific angular momentum is nearly equal to the Keplerian angular momentum there. So once we cross the radial distance and go further the centrifugal force created will defeat the inward attraction. We will analyse the wind branch which is less close to the BH, which is obviously due to the strong gravitational force there. This strong inward force will not allowed anything to get out. As we increase our radial distance from the BH, this wind speed increases and it reaches a local maximum at a distance $x_{\mathrm{max}}^{\mathrm{wind}} > x_\mathrm{c}$, the sonic point distance. If $x > x_{\mathrm{max}}^{\mathrm{wind}}$ the graph of the velocity gradually decreases and the rate of it is low. This shows even far from a BH we can feel the outward throwing force.

This scenario changed a lot when we change the type of the EoS and use the equation of MCG. First, for the radial velocity to get started, the fluid has to come closer to the BH. DE is something which exerts negative pressure and tries not to be bound in some predicted volume – it tries to expand. So to bind it in an astrophysical phenomenon like an accretion disc, we need to go close to the BH to feel a larger force of attraction. Once it starts to accrete its inward radial speed increases and becomes almost equal to the speed of light near the BH. So the inner region properties of the accretion branch for DE are more or less matching with that of the adiabatic flow. The huge difference we can follow in the wind branch. Wind speed, unlike for the accretion branch, in spite of being almost constant after a distance, becomes almost equal to the speed of light at a finite distance. This says the matter is thrown apart from the BH accretion disc with a speed equal to light there. This again supports the nature of the DE which would be exerting negative pressure enhancing the outwards motion. Up to this point we have rebuilt and enriched the result found by Ref. [40].

Fig. 3

a, b are plots of log(u) vs log(x) for viscous ($\alpha _{ss}=10^{-2}$) accretion disc flow around a non-rotating BH for adiabatic and MCG, respectively. Accretion and wind curves are depicted by solid and dotted lines respectively

Fig. 4

a, b are plots of log(u) vs. log(x) for non-viscous accretion disc flow around a rotating BH (with specific angular velocity $j=0.5$) for the adiabatic and MCG cases, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

Next we have added viscosity to the system. The parameter $\alpha _{ss}$ will regulate the value of the viscosity throughout. First we take the very low $\alpha _{ss}=10^{-4}$. We have plotted the viscous accretion cases in the Fig. 2a, b. The first change we can see in the plot of log(u) vs. log(x) in Fig. 2a where the fluid is adiabatic and $j=0$. We see the accretion disc last up to several hundreds of Schwarzschild radii only. Why is this shortening? We can explain this in two ways. Firstly, from the outward angular momentum transportation idea we can say that as the momentum is transported layer after layer outwards, due to the viscosity some more part of it is transported than the inviscid one and soon it becomes Keplerian. To revise the angular momentum more radial velocity is lost and closer than the inviscid case we find the edge of the disc. Secondly, the matter which is coming from outwards whenever it tries to get in the accretion process it is opposed by the opposite viscous force/ frictional force between two outer layer coming from the viscosity. This incidence forces the accretion particle to come closer to the region to get the accretion phenomenon started. The accretion of MCG is showing the same pattern in Fig. 1b. The difference is only that the radius of the accretion disc is more reduced than the adiabatic one.

We plot log(u) vs. log(x) for $\alpha _{ss}=10^{-2}$ in Fig. 3a, b. We see the accretion disc length getting shortened. This happens only due to the high rate of outward transportation of angular momentum and after that $\frac{\lambda }{\lambda _k}$ exceeds unity. This means that beyond the distance the disc is super-Keplerian. For the wind branch of the MCG we see as we increase the viscosity the inner part of the wind branches are able to get close to the BH. On the other hand, adiabatic flow, as we go far from the BH, decreases rapidly. But for the MCG case, even if we go far, we can see a mild amount of accretion continuing.

The next set of curves are drawn for the specific angular velocity $j=0.5$. Figure 4a, b is for the inviscid cases for the adiabatic and MCG cases, respectively. An increment in rotation of the BH decreases the gravitating inward force. This is because the pseudo-Newtonian force is a decreasing function of j. This attracts the particle less. So angular momentum is transported more vigorously outward and sooner it reaches the point where $\frac{\lambda }{\lambda _k}$ becomes unity. This is why we see the accretion to stop closer than in the non-rotating case. We plot the $\alpha _{ss}=10^{-4}$ and $10^{-2}$ cases for a BH with rotation $j=0.5$ in Figs. 5a and 6a (adiabatic) and Figs. 5b and 6b (MCG), respectively. Overall trends follow the trend of the figures drawn in Figs. 1a to 3b.

Table 1 Model parameter for the Palomar–Green data, with corresponding mass and accretion rate range of $10^7< M < 10^{8.5} M_{\odot }$ and $0.02< {\dot{M}}< 0.70$ ($M_{\odot }$ yr) [47]

Fig. 5

a, b are plots of log(u) vs. log(x) for viscous ($\alpha _{ss}=10^{-4}$) accretion disc flow around a rotating BH (with specific angular velocity $j=0.5$) for adiabatic and MCG, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

Fig. 6

a, b are plots of log(u) vs. log(x) for a viscous ($\alpha _{ss}=10^{-2}$) accretion disc flow around a rotating BH (with specific angular velocity $j=0.5$) for adiabatic and MCG, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

We plot Figs. 7a, 8 and 9b for $j=0.9$. Keeping the general trends the same we see that the accretion disc length is reduced as we increase the rotation parameter j. As a whole we can conclude that viscosity shortens the physical length of the accretion disc the same is done by the DE accretion. again if the rotation parameter of the BH is high the disc length reduces more.

Fig. 7

a, b are plots of log(u) vs. log(x) for non-viscous accretion disc flow around a rotating BH (with specific angular velocity $j=0.9$) for adiabatic and MCG, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

Fig. 8

a, b are plots of log(u) vs. log(x) for viscous ($\alpha _{ss}=10^{-4}$) accretion disc flow around a rotating BH (with specific angular velocity $j=0.9$) for adiabatic and MCG cases, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

Fig. 9

a, b are plots of log(u) vs. log(x) for viscous ($\alpha _{ss}=10^{-2}$) accretion disc flow around a rotating BH (with specific angular velocity $j=0.9$) for adiabatic and MCG cases, respectively. Accretion and wind curves are depicted by solid and dotted lines, respectively

4 Observational evidence and results from different simulation models

The estimation of $\alpha _{ss}$ in a BH accretion disc was studied in [46] for the fast time where the mass of the central engine was taken to be $10^7 M_{\odot }$–$10^9 M_{\odot }$ and the sub-Eddington accretion rates such that $\frac{L}{L_{\mathrm{EDD}}}= 1$–0.01 were considered (Table 1).

The viscosity parameter $\alpha _{ss}$ in AGN accretion discs is required to be greater than 0.001 for most cases but it may be smaller than 0.1. For different dynamic power spectrum emitted from different X-ray sources, like ESO $243-49$ HLX-I, Holmberg IX $X-1$, M81 $X-6$ and NGC5408 $X-1$. We can find the accretion power to be decreased with time. During 500 days of observations, the signal for first 112 days was strong, becoming weaker during the latter period. The quasi-periodic signal near 112 days has significantly decreased after 800 days and evolved into a quasi-periodicity of 190 days [48]. We can speculate that the latter period accretion is dominated by DE accretion (Table 2).

To support the viscosity parameter’s value we will take the choice of $\alpha _{ss}=0.02$ as a reference value w, motivated by observations of AGNs. Siemiginowska and Czerny (1989) interpreted the quasar variability as the local thermal timescale at a radius corresponding to the observed wavelength in the accretion disk, and they determined the value of 0.1 for a small sample of quasars. The same method, when applied for larger sample objects (the Palomar–Green quasar sample) gave the constraints $0.01<\alpha _{ss}<0.03$ for sources with luminosities $0.01 L_{\mathrm{EDD}}<L<L_{\mathrm{EDD}}$ [47]. For blazars, the values in the range $0.104<\alpha _{ss}<0.337$ were formed from their intra day variability (Xie et al. [49]). Kelly et al. have given the value of the viscosity parameter $\alpha _{ss}=10^{-3}$ estimated at a distance of $100 R_{\mathrm{schw}}$. Kozlowski [50] sampled an accretion disc to be of temperature 20,000K, and the corresponding viscosity parameter is 0.044 for the BH mass $8.0 X 10^8 M_{\odot }$ and 0.015 for 8.0 X $10^4 M_{\odot }$. Next we will tabulate different values of $\alpha _{ss}$ for known micro quasars: GRS $1915+165$ and IGR $17091-324$ [51,52,53].

Table 2 Determination of $\alpha _{ss}$ values based on the known IGR and GRS mass values [51,52,53] and mass-$\alpha _{ss}$ relation presented in the table. *Mass-$\alpha _{ss}$ factor $\left( \frac{M}{M_{\odot }} \left( \frac{\alpha _{ss}}{0.02} \right) ^{-1.88}\right)$, **IGR mass estimation from [51] and [52]. ***IGR mass estimation from [53]

We can clearly observe from the tables that the values of the different viscosity parameters we have used are completely supported by astrophysical data. Thus, we can say that our model may be valid. Besides we will like to mention again Ref. [54] where the presence of the dark matter or, more broadly, exotic matters can be found near the central regions of a galaxy. Now as the accretion rates are very prominent there, we can take our results to be a better modelling of dark energy accretion with a viscous nature towards a black hole.

5 Brief summary and conclusion

This paper deals with MCG accretion on BHs. We have studied the viscous and non-viscous flows of both adiabatic and MCG. The central engine has been treated to be both non-rotating and rotating. We have incorporated the viscosity via the introduction of SSP. Mainly we have solved the three components of the Navier–Stokes equation along with the equation of continuity and the equation of state numerically. We make the transonic flow continuous throughout the radial distance traversed from very far region to very close to a BH. We have taken two branches – accretion and wind, which will coincide at the sonic point. The accretion branch shows the radial inward velocity of accreting matter towards the BH. The wind on the other hand shows the velocity with which the fluid goes far from the central engine. For adiabatic flow we see the radial inward velocity increases as we go towards the BH and the wind decreases towards the BH. For the MCG case, the wind increases as we go far from the BH and it becomes equal to the speed of light at a finite distance. This says MCG throws out material from the accretion disc and weakens that. When we include rotation for the central engine, i.e., a BH, we see that for adiabatic cases the behaviour of the viscous accretion flow is the same as the non-rotating case until some distance, then it suddenly falls. For MCG accretion with viscosity, while the central BH is rotating, both accretion and wind flow reaches the maximum earlier, which means the length of the disc is shortened. So we can say the specific angular velocity of the central engine helps MCG to weaken the disc. We have also seen how the specific angular momentum of the disc flow affects accretion and wind. The behaviour of accretion and wind flow is on average the same when we increase the specific angular momentum up to a limit, but for extremely high values the accretion discs no longer exist for both the adiabatic and the MCG cases.

The accretion process feeds up the BH and thus the mass increases. If MCG is throwing the accreting material out of the disc, it weakens the BH indirectly as we increase the viscosity, outward angular momentum transport is more efficient along with the negatively pressure creating fluid, MCG. So viscosity catalyses the effect of the MCG. This supports previous work with DE accretion showing that in the future towards the Big-Rip it will weaken the BH so much that the BH may not exist at that point.