1 The set up and motivation

The standard model of inflation is driven by a scalar inflaton (quanta of the inflationary field) field can be traced back to early efforts to solve the basic problems of the Big-Bang cosmology, namely horizon, flatness and monopole [1, 2] problems. The nominal inflationary paradigm contains two mainly different segments: the slow-roll and the (p)reheating regimes. In the slow-roll phase the kinetic part of energy (which has the canonical form here) of the scalar field is negligible with respect to the potential part of energy \(V(\phi )\), which implies a nearly de Sitter expansion of the universe. However, after the slow-roll epoch the kinetic energy becomes comparable to the potential energy and thus the inflaton field oscillates around the minimum at the (p)reheating phase and progressively the universe is filled by radiation [3, 4]. In order to achieve inflation one can use tachyon scalar fields for which the kinetic term does not follow the canonical form (k-inflation [5]). It has been found that tachyon fields which are associated with unstable D-branes [6] may be responsible for the cosmic acceleration phase in early times [5, 7, 8]. Notice that the tachyon potential has the following two properties: the maximum of the potential occurs when \(\phi \rightarrow 0\), while the corresponding minimum takes place when \(\phi \rightarrow \infty \). For tachyonic models of inflation with ground state at \(\phi \rightarrow \infty \), the inflaton rolls toward its ground state without oscillating about it and the reheating mechanism does not work [9]. For a quasi-power-law time dependence, which will be considered in the present work, there is a weak scale factor dependence of the tachyon energy density. Therefore in the post-inflation era the tachyon density would always dominate radiation unless there is a mechanism by which tachyons decay into radiation. Our tachyon model in the present work is an unphysical toy model but there is a solution for the reheating problem in the context of warm inflation [10,11,12,13,14,15,16,17], which, however, is beyond the scope of the present work. From the dynamical viewpoint one may present the equation of motion of tachyon field using a special Lagrangian [18], which is non-minimally coupled to gravity:

$$\begin{aligned} L=\sqrt{-g}\left[ \frac{R}{16\pi G}-V(\phi )\sqrt{1-g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi }\right] \;. \end{aligned}$$
(1)

Considering a spatially flat Friedmann–Lemaitre–Robertson–Walker (FLRW) (hereafter FLRW) universe the stress-energy tensor components are represented by

$$\begin{aligned} T^{\mu }_{\nu }=\frac{\partial L}{\partial (\partial _{\mu }\phi )}\partial _{\nu }\phi -g^{\mu }_{\nu }L=\mathrm{diag}(-\rho _{\phi },p_{\phi },p_{\phi },p_{\phi }) \end{aligned}$$
(2)

equation where \(\rho _{\phi }\) and \(p_{\phi }\) are the energy density and pressure of the tachyon field. Combining the above set of equations one can find

$$\begin{aligned} \rho _{\phi }=\frac{V(\phi )}{\sqrt{1-\dot{\phi }^2}} \end{aligned}$$
(3)

and

$$\begin{aligned} P_{\phi }=-V(\phi )\sqrt{1-\dot{\phi }^2} \end{aligned}$$
(4)

where \(\phi \) is the tachyon scalar field in units of the inverse Planck mass \(M_{\mathrm{pl}}^{-1}\), and \(V(\phi )\) is the potential associated with the tachyon scalar field. In the past few years, there was a debate among particle physicists and cosmologists regarding those phenomenological models which can be produced in extra dimensions. For example, the reduction of a higher-dimensional gravitational scale, down to the TeV-scale, could be presented by an extra dimensional scenario [19,20,21]. In these scenarios, the gravity field propagates in the bulk, while standard models of particles are confined to the lower-dimensional brane. In this framework, the extra dimension induces additional terms in the first Friedmann equation [22,23,24]. Especially, if we consider a quadratic term in the energy density then we can extract an accelerated expansion of the early universe [25,26,27,28,29]. We will study the tachyon inflation model in the framework of the Randall–Sundrum II braneworld [30], which contains a single, positive tension brane and a non-compact extra dimension. We note that this is not the only scenario where these characteristics are present. For example DBI Galileon inflation [31,32,33,34] has these properties in its \(T_3\) brane and a cosmological inflation analysis of this model agrees at \(1\sigma \) confidence level with the Planck data [35]. Following the lines of Ref. [36], we attempt to study the main properties of the tachyon inflation in which the scale factor evolves as \(a(t)\propto \exp (A[\ln t]^{\lambda })\), where \(\lambda >1\) and \(A>0\) (“logamediate inflation”). For the \(\lambda =1\) case cosmic expansion evolves as ordinary power-law inflation \(a\propto t^p\) where \(p=A\) [37, 38]. More details regarding the cosmic expansion in various inflationary solutions can be found in the papers by Barrow [37, 38]. In these papers there is no comment about the behavior around the \(\lambda =0\) case of the logamediate solution. In the current work, we investigate the possibility of using the logamediate solution in the case of tachyon inflation on the brane.

Specifically, the structure of the article is as follows: In Sect. 2 we briefly discuss the main properties of tachyon inflation, while in Sect. 3 we provide the perturbation parameters. In Sect. 4 we study the performance of our predictions against the Planck 2015 data. Finally, the main conclusions are presented in Sect. 6.

2 Tachyon inflation

In this section we consider a FLRW universe with tachyon component in the inflation era; the basic cosmological equations in the context of the Randall–Sundrum II (RSII) brane [30] are

$$\begin{aligned}&H^2=\frac{1}{3}\rho _{\phi }\left( 1+\frac{\rho _{\phi }}{2\tau }\right) , \end{aligned}$$
(5)
$$\begin{aligned}&{\dot{\rho }}_{\phi }+3H(\rho _{\phi }+p_{\phi })=0, \end{aligned}$$
(6)

and

$$\begin{aligned} \dot{H}=-\frac{1}{2M_p^2}(\rho _{\phi }+P_{\phi })\left( 1+\frac{\rho _{\phi }}{\tau }\right) \end{aligned}$$
(7)

where \(H=\frac{\dot{a}}{a}\) and a are the Hubble parameter and the scale factor, respectively, a dot means the derivative with respect to the cosmic time. The parameter \(\tau \) in Eq. (5) represents the brane tension [22,23,24]. The value of this term is constrained to be \(\tau >(1MeV)^4\) by considering the nucleosynthesis epoch [26]. Another, stronger limitation for the value of \(\tau \) is found by the usual tests of the deviation from Newton’s law \(\tau \ge (10 Tev)^{4} \) [39]. The model is described in natural units, \(8\pi G=\frac{h}{2\pi }=c=1\). Using Eqs. (3)–(7), we can derive the background evolution motion of a tachyon scalar field coupled by the scale factor in the high energy limit \(\rho _{\phi }\gg \tau \). We have

$$\begin{aligned}&3H^2=\frac{V^2(\phi )}{2\tau \sqrt{1-\dot{\phi }^2}}\nonumber \\&\frac{\ddot{\phi }}{1-\dot{\phi }^2}+3H\dot{\phi }+\frac{1}{V}\frac{\mathrm{d} V}{\mathrm{d}\phi }= 0 , \nonumber \\&\dot{H}=-\frac{\rho ^2\dot{\phi }^2}{2M_p^2\tau }. \end{aligned}$$
(8)

In Ref. [38], a complete analysis around the slow-roll parameters was made for canonical scalar fields which leads to slow-roll condition \(3H\dot{\phi }\simeq -\frac{\mathrm{d}V(\phi )}{\mathrm{d}\phi }\). We will consider our model in the slow-roll limit of tachyonic scalar fields, \(\dot{\phi }\ll 1\), \(\ddot{\phi }\ll 3H\dot{\phi }\), which leads to \(3HV\dot{\phi }\simeq -\frac{\mathrm{d}V(\phi )}{\mathrm{d}\phi }\) [40]. In the slow-roll regime of tachyon fields, from Eqs. (8) \(\dot{\phi }\) can be presented in terms of the Hubble parameter and its derivative:

$$\begin{aligned} \dot{\phi }=\sqrt{-\frac{\dot{H}}{3H^2}}, \end{aligned}$$
(9)

and this will be used. Using Eqs. (7) and (8) we can find a real velocity field \(\dot{\phi }\) by Eq. (9). Now we consider the logamediate inflation model in which its scale factor behaves as [37, 38]

$$\begin{aligned} a(t)=a_0\exp (A[\ln t]^{\lambda })\;, \end{aligned}$$
(10)

and one can present the compact solution of Eq. (9) thus:

$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}t}\simeq \sqrt{\frac{1}{A\lambda (\ln t)^{\lambda -1}}}\Rightarrow \phi -\phi _0=\frac{1}{\sqrt{A\lambda }}\int (\ln t)^{\frac{1-\lambda }{2}}\mathrm{d}t,\nonumber \\ \end{aligned}$$
(11)

which leads to

$$\begin{aligned}&\phi =\phi _0+\frac{g(t)}{K}\nonumber \\&g(t)=\gamma \left( \frac{3-\lambda }{2},-\ln t\right) \end{aligned}$$
(12)

where \(K=\sqrt{3\lambda A}\) and \(\gamma (a,x)\) is the incomplete gamma function [41, 42], where a is an integer constant and x is a variable, for example in our case \((a,x)=(\frac{3-\lambda }{2},-\ln t)\). The dimensionless slow-roll parameters of the model can be introduced by the standard definition in terms of the scalar field,

$$\begin{aligned} \varepsilon= & {} -\frac{\dot{H}}{H^2}=\frac{[\ln (g^{-1}[K(\phi -\phi _0)])]^{1-\lambda }}{\lambda A}\nonumber \\ \eta= & {} \frac{1}{2H}\left[ -\frac{\ddot{V}}{\dot{V}}+\frac{\dot{H}}{H} +\frac{\dot{V}}{V}\right] =\varepsilon \left[ -1+\frac{1}{g^{-1}[K(\phi -\phi _0)]}\right] ,\nonumber \\ \end{aligned}$$
(13)

where \(g^{-1}(t)\) is the inverse of the function g(t). In the above relations we have used the approximation \(\ln t\gg \lambda -1\), which may be used at the early time. The number of e-foldings can be represented for the model by

$$\begin{aligned} N= & {} \int _{t_1}^{t} H\mathrm{d}t'=\int _{\phi _1}^{\phi }\frac{H}{\dot{\phi '}}\mathrm{d}\phi '\nonumber \\ N= & {} (\ln [g^{-1}(K[\phi -\phi _0])])^{\lambda }-(\lambda A)^{\frac{\lambda }{1-\lambda }} \end{aligned}$$
(14)

where \(\phi _1\) is introduced at the beginning of the inflation when \(\varepsilon =1\). Using Eq. (14) we can find the tachyon scalar field in terms of the variable of the number of e-folds N,

$$\begin{aligned} \phi =\phi _0+g\left[ \exp \left( [N+(\lambda A)^{\frac{\lambda }{1-\lambda }}]^{\frac{1}{\lambda }}\right) \right] , \end{aligned}$$
(15)

which will be used. The potential of the tachyon field may be represented by using Eq. (8)

$$\begin{aligned} V(\phi )=6\tau (\lambda A)^2\frac{(\ln g^{-1}[K(\phi -\phi _0)])^{2(\lambda -1)}}{(g^{-1}[K(\phi -\phi _0)])^2}. \end{aligned}$$
(16)

3 Perturbation

Although assuming a spatially flat, isotropic and homogeneous FRW universe may be useful and reasonable, there are observed deviations from isotropy and homogeneity in our universe. These deviations motivate us to use perturbation theory in cosmology. In the context of general relativity and gravitation, the inhomogeneity grows with time, so it was very small in the past time. Therefore first order or linear perturbation theory can be used for scalar field models at the inflation epoch. Considering Einstein’s equation, the inflaton field in the FRW universe connects to the metric components of this universe, so the perturbed inflaton field must be studied in the perturbed FRW geometry. The most general linear perturbation of spatially flat FRW metric is presented by

$$\begin{aligned} \mathrm{d}s^2= & {} -(1+2C)\mathrm{d}t^2+2a(t)D_{,i}\mathrm{d}x^i \mathrm{d}t\nonumber \\&+\, a^2(t)[(1-2\psi )\delta _{ij}+2E_{,ij}+2h_{ij}]\mathrm{d}x^{i}\mathrm{d}x^{j}, \end{aligned}$$
(17)

which includes scalar perturbations \(C, D, \psi , E\) and traceless-transverse tensor perturbations \(h_{ij}\). The power-spectrum of the curvature perturbation \(P_R\) that is derived from the correlation of first order scalar field perturbation in the vacuum state can be constrained by observational data. For tachyon fields, this parameter at the first level is represented by [36, 43]

$$\begin{aligned} \mathcal {P}_R= \left( \frac{H^2}{2\pi \dot{\phi }}\right) ^2\frac{1}{V(1-\dot{\phi }^2)^{\frac{3}{2}}}. \end{aligned}$$
(18)

This parameter is essential for our perturbed analysis, which is presented in Ref. [43]. In the slow-roll and high energy limit, using Eq. (8), we may simplify the above relation to

$$\begin{aligned} \mathcal {P}_{R}= & {} \frac{1}{4\pi ^2 V}\left( \frac{V^2}{2\tau V'}\right) ^2\nonumber \\\simeq & {} \frac{3(A\lambda )^6}{4\pi ^2\sqrt{6\tau }}\exp \left( -\left( \frac{N}{A}\right) ^{\frac{1}{\lambda }}\right) \left( \frac{N}{A}\right) ^{\frac{4(\lambda -1)}{\lambda }} \end{aligned}$$
(19)

where \(V'=\frac{\mathrm{d}V}{\mathrm{d}\phi }\). Two other important perturbation parameters are the spectral index \(n_s=1+\frac{\mathrm{d}\ln P_R}{\mathrm{d}\ln k}\) and its running \(n_{\mathrm{run}}=\frac{\mathrm{d} n_s}{\mathrm{d}\ln k}\). From Eq. (18), in the slow-roll limit, these parameters are represented by

$$\begin{aligned} n_s= & {} 1+2\varepsilon \left[ -2+\frac{1}{g^{-1}(K[\phi -\phi _0])}\right] \simeq 1+\frac{4(1-\lambda )}{\lambda }\frac{1}{N} , \nonumber \\ n_{\mathrm{run}}= & {} \frac{4(\lambda -1)}{(\lambda A)^2}(\ln g^{-1}[K(\phi -\phi _0)])^{1-2\lambda }. \end{aligned}$$
(20)

These parameters also may be constrained by observational data. Up to now, we have considered scalar perturbation parameters. During the inflation era, there are two independent components of gravitational waves, \(h_{+}, h_{\times }\), or tensor perturbations of the metric with the same equation of motion. The amplitude of the tensor perturbation is given by

$$\begin{aligned} \mathcal {P}_{g}=8\left( \frac{H}{2\pi }\right) ^2\left( \frac{3}{\tau ^2}\right) ^{\frac{1}{4}} H^{\frac{1}{2}}=\frac{2}{\pi ^2}\left( \frac{3}{6^5\tau ^7}\right) ^{\frac{1}{4}}V^{\frac{5}{2}}, \end{aligned}$$
(21)

as been presented in Ref. [44]. The tensor-to-scalar ratio is another important parameter,

$$\begin{aligned} r= & {} \frac{\mathcal {P}_g}{\mathcal {P}_R}=\left( \frac{2\pi ^8 4^3}{3^4\tau ^7}\right) ^{\frac{1}{4}}\frac{(2\tau V')^4}{V^{\frac{9}{2}}}\nonumber \\\simeq & {} \frac{197}{K}\left( \frac{N}{A}\right) ^{\frac{\lambda -1}{2\lambda }} \exp \left( -\frac{3}{2}\left( \frac{N}{A}\right) ^{\frac{1}{\lambda }}\right) \nonumber \\= & {} \frac{197}{K}\left( \frac{4(\lambda -1)}{a\lambda }\frac{1}{1-n_s}\right) ^{\frac{\lambda -1}{2\lambda }}\exp \left( -\frac{3}{2}\left( \frac{4(\lambda -1)}{A\lambda (1-n_s)}\right) ^{\frac{1}{\lambda }}\right) .\nonumber \\ \end{aligned}$$
(22)

The r–\(n_s,\) trajectory for inflation models can be compared to the Planck observational data.

4 Comparison with observation

The analysis of Planck data sets has been done in Ref. [45]. The results of this analysis indicate that the single scalar field models of inflation in the slow-roll limit have a limited spectral index, and a very low spectral running and tensor-to-scalar ratio. We have

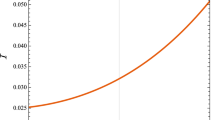
$$\begin{aligned} n_s= & {} 0.968\pm 0.006 ,\nonumber \\ r= & {} \frac{\mathcal {P}_g}{\mathcal {P}_R}< 0.11,\nonumber \\ n_{\mathrm{run}}= & {} \frac{\mathrm{d}n_s}{\mathrm{d}\ln k}=-0.003\pm 0.007. \end{aligned}$$
(23)

The upper bound set on the tensor-to-scalar ratio function and running of the tensor-to-scalar ratio has been obtained by using the results of the Planck team and joint analysis of BICEP2/Keck Array/Planck [46]. In the present section we will try to test the performance of tachyon inflation against the results of observation (23). In Fig. 1 we render the confidence contours in the \((n_s,r)\) plane. The values of the pair \((\lambda ,A)\) are fixed for each trajectory. The curves are related to the pairs \((\lambda ,A)\) as \((29.4\times 10^{-12})\), \((39 \times 10^{-15})\), \((19.3\times 10^{-6})\) and \((49.5\times 10^{-4})\) from top to bottom. The main difference between our braneworld model and ordinary scalar field models [36, 37] is that there is no transition from \(n_s<1\) to \(n_s>1\) for all values of \(\lambda \). For the big values of \(\lambda \) with special combinations of \((\lambda , A)\) there are curves which behave as the Harrison–Zel’dovich spectrum i.e. \(n_s=1\).

Fig. 1
figure 1

\(1\sigma \) and \(2\sigma \) confidence regions borrowed from Planck [47], r–\(n_s\) trajectories of the present model. The solid red, dashed yellow, dotted blue and dot-ashed green lines correspond to the combinations \((29.4\times 10^{-12})\), \((39 \times 10^{-15})\), \((19.3\times 10^{-6})\) and \((49.5\times 10^{-4})\) of \((\lambda , A)\). There is no transition from \(n_s<1\) to \(n_s>1\)

Full size image

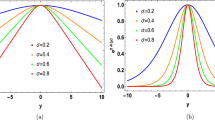
In Fig. 2, the dot-dashed green line and dashed blue line are related to the pairs \((29.12 \times 10^{-3}),(3 \times 10^{-12})\) respectively. In this figure for the large value of \(\lambda =69\) and small value of \(A=10^{-50}\), the trajectory located out of the \(95\%\) confidence means that large values of \(\lambda \) are not compatible with the Planck data.

Fig. 2
figure 2

\(1\sigma \) and \(2\sigma \) confidence regions borrowed from Planck [47], r–\(n_s\) trajectories of the present model. The dot-dashed green, dashed blue and solid red lines related to pairs \((29.12\times 10^{-3}), (3 \times 10^{-12})\) and \((69 \times 10^{-50})\). The trajectory located out of \(95\%\) confidence for the large value of \(\lambda \)

Full size image

In Figs. 1 and 2 the curves of our model compared with 68 and \(95\%\) confidence regions from Planck 2015 result [45] at \(k_{*}=0.05~\mathrm{Mpc}^{-1}\).

Fig. 3
figure 3

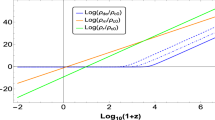
\(n_s\)–\(n_{\mathrm{run}}\) diagram. The area corresponds to Planck data and \(n_s\)–\(n_{\mathrm{run}}\) trajectories relate to our model. The dashed yellow, dotted blue, solid red, and dot-dashed green lines correspond to the combinations \((19.6\times 10^{-9})\), \((29.4\times 10^{-3})\), \((39.2\times 10^{-20})\), \((49.3\times 10^{-9})\)

Full size image

In Fig. 3, we plotted \(n_{\mathrm{run}}\)–\(n_{s}\) trajectories for some pairs \((\lambda , A)\) which have been used in the previous figures. There is no running in the scalar spectral index for the combination \((19.6\times 10^{-9})\).

5 Comparison with other models

Below we will compare the current predictions with those of viable potentials from the literature. This can help us to understand the variants of the tachyon–brane inflationary model from the observationally viable inflationary scenarios.

  • The Starobinsky or \(R^{2}\) inflation model [48]: in the Starobinsky inflation model the asymptotic behavior of the effective potential is presented as \(V(\phi )\propto [1-2\mathrm {e} ^{-B\phi /M_{\mathrm{pl}}}+\mathcal {O}(\mathrm {e}^{-2B\phi /M_{\mathrm{pl}}})]\), which provides us with the following predictions in the slow-roll limit [49, 50]: \(r\approx 8/B^{2}N^{2}\) and, \(n_{s}\approx 1-2/N\) where \(B^{2}=2/3\). Therefore, if we select \(N=50\) then we obtain \((n_{s},r)\approx (0.96,0.0048)\). For \(N=60\) we find \((n_{s},r)\approx (0.967,0.0033)\). It has been found that the Planck data [45] favors the Starobinsky inflation. Obviously, our results (see Figs. 1 and 2) are consistent with those of \(R^{2}\) inflation.

  • The chaotic model of inflation [51]: in this inflationary model the potential is given by \(V(\phi ) \propto \phi ^{k}\). The basic slow-roll parameters for this potential are represented as \(\epsilon =k/4N\), \(\eta =(k-1)/2N\), which leads to \(n_{s}=1-(k+2)/2N\) and \(r=4k/N\). It has been found that monomial potentials with \(k\ge 2\) are not in agreement with the Planck data [45]. Using \(k=2\) and \(N=50\) we present \(n_{s}\simeq 0.96\) and \(r\simeq 0.16\). For \(N=60\) we find \(n_{s}\simeq 0.967\) and \(r\simeq 0.133\). It is interesting to note that this model also corresponds to the results of intermediate inflation [52,53,54,55] with a Hubble rate during inflation which is given by \(H\propto t^{k/(4-k)}\) with \(n_{s}=1-(k+2)r/8k\) and the \(k=-2\) case gives \(n_{s}=1\) exactly to the first order.

  • Hyperbolic model of inflation [56]: in hyperbolic inflation the potential is represented by \(V(\phi ) \propto \mathrm {sinh}^{b}(\phi /f_{1})\). Initially, this potential was proposed in the context of the late time acceleration phase or dark energy [57]. Recently, the properties of this scalar field potential have been investigated back in the inflationary epoch [56]. The slow-roll parameters are written as

    $$\begin{aligned}&\varepsilon =\frac{b^{2}M_{\mathrm{pl}}^{2}}{2f_{1}^{2}}\mathrm {coth}^{2}(\phi /f_1), \\&\eta =\frac{bM_{\mathrm{pl}}^{2}}{f_{1}^{2}}\left[ (b-1)\mathrm {coth}^{2}(\phi /f_1)+1\right] , \end{aligned}$$

    and

    $$\begin{aligned} \phi =f_1\;\mathrm {cosh}^{-1}\left[ e^{NbM_{\mathrm{pl}}^{2}/f^{2}}\mathrm {cosh} (\phi _{\mathrm{end}}/f_1)\right] , \end{aligned}$$

    where \(\phi _{\mathrm{end}}\simeq \frac{f}{2}\mathrm {ln}\left( \frac{\theta +1}{\theta -1}\right) \). Comparing this model to the observational data, it is found that \(n_{s}\simeq 0.968\), \(r\simeq 0.075\), \(1<b \le 1.5\) and \(f_1\ge 11.7M_{\mathrm{pl}}\) [56].

  • Other models of inflation: The origin of brane [58, 59] which is motivated by the physics of extra dimensions and, on the other hand, the exponential [60, 61] inflationary models are motivated by the physics of extra dimensions. It has been found in our study that these models are in agreement with the Planck data, although the Starobinsky inflation is the winner from the comparison [45].

6 Conclusions

In this work we investigated the tachyon inflation on the brane in the context of a spatially flat Friedmann–Robertson–Walker universe. We adopted a specific form of scale factor from Barrow [37] solutions, namely the logamediate scale factor. Within this context, we estimated analytically the slow-roll parameters potential of the model and compared the predictions with those of other famous inflationary models in the literature. Confronting the model with the latest observational data, we found that the tachyon inflationary model on the brane is consistent with the results presented in Planck 2015 within \(1\sigma \) uncertainties for a special class of parameters \((\lambda ,A)\).