1 Introduction

In the framework of electromagnetic field interactions in a dielectric medium, both at the classical level and at the quantum one, a very rich phenomenology appears, involving several phenomena, from the standard dispersion law to Hawking-like pair creation. We have developed in our previous studies an analysis of the Hopfield model, which has be made relativistically covariant, and suitably extended in order to keep into account in a semi-phenomenological way the possibility that e.g. the dielectric susceptibility (and/or the resonance frequency) depends on spacetime variables, with the aim of simulating the standard Kerr effect in a nonlinear dielectric [1, 2]. Quantization has been taken into account in [1, 3]. The analysis with scalar models has been developed in [2, 4], with the aim of gain knowledge of the basic physics at hand without all tricky technicalities which are associated with gauge invariance. A further step towards a more complete analysis is contained in [5], where a full four dimensional electromagnetic field in a nonlinear dielectric medium and the analogue Hawking effect have been investigated.

As a further contribution to our investigation of the Hopfield model, we extend our analysis by considering a dielectric medium which does not fill all the space as in our previous work. We propose a \(1+1\) dimensional toy-model which consists of an half-line filling dielectric medium, with the aim to set up a simplified situation where technicalities related to gauge invariance and, as a consequence, physics of constrained systems are avoided, and still interesting features appear. In particular, we simulate the electromagnetic field and the polarization field by means of two coupled scalar fields which are indicated as \(\phi , \psi \) respectively, in a model which is inherited by the Hopfield model. The interface between the vacuum region and the dielectric one is represented by \(z=0\), and the dielectric medium fills the region \(z\ge 0\). The electromagnetic field \(\phi \) is involved with both the vacuum region and the dielectric one, whereas the polarization \(\psi \) is different from zero only in the dielectric region. By analyzing the particle spectrum of the model we find that, in order to obtain a physically meaningful behavior, one has to introduce boundary conditions depending on the particle spectrum one is dealing with. Indeed, for the electromagnetic field one finds that smooth solutions with continuous \(\phi ,\partial _z \phi \) at the interface \(z=0\) does not correspond to a complete scattering basis, due to the presence of a spectral gap (i.e. a gap in the particle spectrum) associated with the presence of the dielectric medium. Note that, for simplicity, we are purposefully dealing with a transparent dielectric medium (absorption would require further efforts at the quantum level). For particles in the spectral gap, we have to impose Dirichlet boundary conditions at the interface, meaning a complete reflection for the associated electromagnetic modes. This is the first interesting achievement of our analysis.

We also introduce a nonlinear contribution in the polarization field \(\psi \), with the aim of mimicking a third order nonlinearity in a nonlinear dielectric medium. We obtain exact solutions, which correspond to propagating solitons, and study their energy propagation both in a global sense (spatial integrals) and in a local one (Poynting vectors). This is the second achievement of our analysis.

It is worth mentioning that there exists a huge literature concerning electromagnetic field in the presence of a dielectric medium filling an half-space, mainly in a framework where phenomenological refractive index appears. We limit ourselves to quoting a classical textbook [6], for classical scattering of light, and the seminal study [7], concerning the effects of spatial dispersion. See also [8] on energy propagation. As to quantization of the \(1+1\) dimensional system, we refer to [9, 10], where a phenomenological approach to the electromagnetic field in inhomogeneous and dispersive media is assumed.

2 The half-line filling model

We will consider a \(1+1\) dimensional problem, where a straight line, parametrized by the coordinate z, is filled by a dielectric medium for \(z\ge 0\). The dielectric is described by a field \(\psi \), and interacts with a “scalar” electromagnetic field \(\phi \). The system is described by the action

$$\begin{aligned} S[\phi ,\psi ]= & {} \int _{\mathbb R} \mathrm{d}t \left[ \int _{\mathbb R} \frac{1}{2} \partial _\mu \phi \partial ^\mu \phi \ \mathrm{d}z \right. \nonumber \\&\left. +\int _{z\ge 0} \left[ \frac{1}{2} \dot{\psi }^2- \frac{\omega _0^2}{2} \psi ^2-g\phi \dot{\psi }\right] \mathrm{d}z \right] , \end{aligned}$$
(2.1)

where the dot indicates time derivative.

We require for \(\psi \) to be smooth in \(z\ge 0\), to vanish elsewhere, but we do not add continuity conditions in \(z=0\). For \(\phi \) there is the requirement of smoothness in \(z\ge 0\), and in \(z<0\), and to be of class \(C^1(\mathbb R)\). Our aim is to show that such boundary conditions are not sufficient in order to get a “good problem”.

The equations of motion are thus

$$\begin{aligned}&\Box \phi =0, \quad \psi =0, \quad \text{ for } \quad z<0, \end{aligned}$$
(2.2)
$$\begin{aligned}&\Box \phi +g\dot{\psi }=0, \quad \ddot{\psi }+\omega _0^2 \psi -g\dot{\phi }=0,\quad \text{ for } \quad z\ge 0, \end{aligned}$$
(2.3)

with the condition

$$\begin{aligned} \phi (0^+)=\phi (0^-), \quad \ \phi '(0^+)=\phi ' (0^-), \end{aligned}$$
(2.4)

where the prime indicates the spatial derivative.

We further require for the energy to be finite, which is equivalent to the condition

$$\begin{aligned} \int _{\mathbb R} [\dot{\phi }^2+\phi ^{\prime 2}+\dot{\psi }^2+\omega _0^2\psi ^2]\mathrm{d}z<\infty . \end{aligned}$$
(2.5)

Physically, any initial condition compatible with (2.5) should be possible.

Fig. 1
figure 1

The Sellmeier dispersion relation in the lab. The shaded region evidences the gap

Full size image

2.1 General solution and plane wave bases

We can take the Fourier transform of the fields in order to get the general solution. If we define \(\phi =\phi _<+\phi _\ge \), where

$$\begin{aligned}&\phi _<(t,z)=\phi (t,z)\chi _{(-\infty ,0)}(z),\end{aligned}$$
(2.6)
$$\begin{aligned}&\phi _\ge (t,z)=\phi (t,z)\chi _{[0,\infty )}(z), \end{aligned}$$
(2.7)

and \(\chi \) is the characteristic function, and similar for \(\psi \), then we get

$$\begin{aligned} \phi _<(t,z)&=\int _{\mathbb R} \frac{\mathrm{d}k}{4\pi \omega (k)} \left[ c(k) e^{-i\omega (k)t\,{+}\,ikz}+c(k)^* e^{i\omega (k)t-ikz} \right] ,\end{aligned}$$
(2.8)
$$\begin{aligned} \phi _\ge (t,z)&=\sum _{a=\pm }\int _{\mathbb R} \frac{\mathrm{d}k}{4\pi \omega _a(k)n(\omega _a(k))}\nonumber \\&\qquad \times \left[ b_a(k) e^{-i\omega _a(k)t+ikz}+b_a(k)^* e^{i\omega _a(k)t-ikz} \right] ,\end{aligned}$$
(2.9)
$$\begin{aligned} \psi _<(t,z)&=0, \end{aligned}$$
(2.10)
$$\begin{aligned} \psi _\ge (t,z)&=\sum _{a=\pm }\int _{\mathbb R} \frac{\mathrm{d}k}{4\pi \omega _a(k)n(\omega _a(k))} \frac{\omega ^2_a(k)-k^2}{ig\omega _a(k)}\nonumber \\&\qquad \times \left[ b_a(k) e^{-i\omega _a(k)t+ikz}-b_a(k)^* e^{i\omega _a(k)t-ikz} \right] , \end{aligned}$$
(2.11)

where

$$\begin{aligned}&\omega (k)=|k|,\end{aligned}$$
(2.12)
$$\begin{aligned}&\omega _\pm (k)=\frac{1}{2} \sqrt{g^2+(\omega _0+|k|)^2}\pm \frac{1}{2} \sqrt{g^2+(\omega _0-|k|)^2},\end{aligned}$$
(2.13)
$$\begin{aligned}&n(\omega )=1+\frac{g^2\omega _0^2}{(\omega _0^2-\omega ^2)^2}. \end{aligned}$$
(2.14)

In particular, \(\omega _\pm \) are the positive branches corresponding to the dispersion relation

$$\begin{aligned} k_0^2=k^2+\frac{g^2k_0^2}{k_0^2-\omega _0^2}, \end{aligned}$$
(2.15)

where \(k_0\) is the time component of the two-momentum.

The coefficients \(c, b_\pm \) are related by imposing the boundary conditions for \(\phi \) on \(z=0\). Equivalently, we can look for a basis of plane wave solutions, say, a scattering basis. After some tedious algebra we get the positive frequency “basis” \((\phi _k,\psi _k)^t\) defined by

$$\begin{aligned}&e^{i|k|t}\phi _k(t,z)\nonumber \\&\quad =\left[ \theta (k) \left( e^{ikz}+\frac{k-q}{k+q}e^{-ikz} \right) \right. \nonumber \\&\qquad \left. +\,\theta (-k) \frac{2q}{k+q} e^{ikz}\right] \chi _{(-\infty ,0)}(z)\nonumber \\&\qquad +\,\left[ \theta (k) \frac{2k}{k+q} e^{iqz} +\theta (-k)\left( e^{iqz}+\frac{q-k}{k+q}e^{-iqz} \right) \right] \nonumber \\&\qquad \times \, \chi _{[0,\infty )}(z),\end{aligned}$$
(2.16)
$$\begin{aligned}&e^{i|k|t}\psi _k(t,z)=\frac{k^2-q^2}{ig|k|}\left[ \theta (k) \frac{2k}{k+q} e^{iqz}\right. \nonumber \\&\qquad \qquad \qquad \qquad \left. +\,\theta (-k)\left( e^{iqz}+\frac{q-k}{k+q}e^{-iqz} \right) \right] \chi _{[0,\infty )}(z), \end{aligned}$$
(2.17)

where

$$\begin{aligned} q=q(k)=k\sqrt{\frac{k^2-g^2-\omega _0^2}{k^2-\omega _0^2}} \end{aligned}$$
(2.18)

is such that \(\omega (k)=\omega _a(q(k))\).

Notice that q(k), and then the scattering basis, is defined only for \(|k|<\omega _0\) or \(|k|>\sqrt{\omega _0^2+g^2}\equiv \bar{\omega }\). This leads to the problem being ill defined, which we will now investigate.

3 The spectral boundary conditions

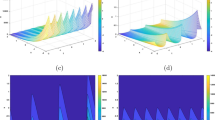
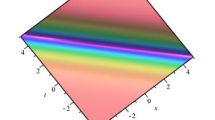
In order to understand the ill definiteness of the problem let us first discuss the simple origin of the trouble. The point is that the modes with \(\omega _0\le |k|\le \bar{\omega }\) correspond to the gap in the dispersion relations in the medium (see the Fig. 1).

Thus, for such modes the relation \(\omega (k)=\omega _a(q(k))\) cannot be satisfied. For these, \(b_a=0\) and the Neuman condition on \(z=0\) implies that \(c(k)=0\) for the modes in the gap. From the physical point of view this means that modes with k-vector in the gap cannot propagate in \(z<0\), which sounds absurd! As to say that a \(\phi \)-laser with frequency centered, say, at \(\omega =(\omega _0+\bar{\omega })/2\) cannot work because somewhere far away (no matter how much) is present a dielectric with a gap in the spectrum.

From the mathematical point of view, this corresponds to incompleteness of the scattering basis, because it does not allow for describing all possible finite energy initial states, since initial states living in vacuum with modes in the gap are complementary to the scattering basis, as we will now argue.

3.1 Incompleteness of the scattering basis

In some sense we can say that the scattering basis is complete in the right side, inside the matter. Indeed, if we define \(k_\pm =\omega _\pm (p) p/|p|\), for \(z>0\) we can write

$$\begin{aligned} e^{ipz} \theta (z)=\,&\theta (z)\theta (-p) \beta (p) \left( \frac{p+k_+}{p-k_+} \phi _{k_+}(0,z) - \frac{p+k_-}{p-k_-} \phi _{k_-}(0,z) \right) \nonumber \\&+\,\theta (z)\theta (p)\beta (p)\nonumber \\&\times \,\left( \frac{2p}{p-k_+}\phi _{k_+}(0,z) -\frac{2p}{p-k_-}\phi _{k_-}(0,z) \right. \nonumber \\&\left. +\,\phi _{-k_+}(0,z)-\phi _{-k_-}(0,z) \right) \nonumber \\ =:\,&\theta (z) \bar{\phi }_p(z), \end{aligned}$$
(3.1)

where

$$\begin{aligned} \beta (p)=\left( \frac{p+k_+}{p-k_+}-\frac{p+k_-}{p-k_-} \right) ^{-1}. \end{aligned}$$
(3.2)

This way, the generators \(e^{ipz}\) are realized for \(z>0\). Notice that for \(z<0\)

$$\begin{aligned} \bar{\phi }_p(z)=\beta (p) \left( \frac{2p}{p-k_+} e^{ik_+z}+\frac{2p}{p-k_-} e^{ik_-z}\right) . \end{aligned}$$
(3.3)

In a similar way we can reproduce the combination reproducing \(e^{-ipz}\) in \(z>0\). This does not provide an equivalent set of functions since there remain further possible combination, which are

$$\begin{aligned}&\frac{p}{k_+} \phi _{k_+}-\phi _{k_-}-\phi _{-k_-}-\phi _{-k_+}=2\theta (-z)\nonumber \\&\quad \times \,\left( \frac{p}{k_+} \sin (k_+z) -i\cos (k_-z) \right) ,\end{aligned}$$
(3.4)
$$\begin{aligned}&\phi _{k_+} -\frac{p}{k_-} \phi _{k_-}+\phi _{-k_-}+\phi _{-k_+}=2\theta (-z)\nonumber \\&\quad \times \,\left( \cos (k_+z) -i\frac{p}{k_-} \sin (k_-z) \right) , \end{aligned}$$
(3.5)

which do not provide a complete set of solutions since exactly the modes with vector k in the gap are absent. We have looked at the field \(\phi \) only, since for \(\psi \) we can add arbitrary k modes with frequency \(\omega _0\) so that there are no problems of completeness.

Thus we see that in order to have a complete set of solutions we should add those modes which vanish in \(z>0\) and have the spectral parameter k in the gap \(\omega _0\le |k| \le \bar{\omega }\).

The completion of the basis is obtained by adding the gap modes

$$\begin{aligned} \phi _{g,k}(z)=c(k) \sin (kz) \theta (-z). \end{aligned}$$
(3.6)

Now we can construct the projection operators in order to specify the spectral boundary conditions.

3.2 Inner product, Hamiltonian and boundary conditions

Let us define

$$\begin{aligned}&\chi _>=\chi _{[0,\infty )}(z),\nonumber \\&\chi _<=\chi _{(-\infty ,0)}(z). \end{aligned}$$
(3.7)

We also define the symplectic matrix

$$\begin{aligned} \Omega :=\left[ \begin{array}{cc} 0_{2\times 2} &{} -i {I}_{2\times 2} \\ i {I}_{2\times 2} &{} 0_{2\times 2} \end{array} \right] , \end{aligned}$$
(3.8)

the multicomponent field

$$\begin{aligned} \Psi :=\left( \begin{array}{c} \phi \\ \psi \\ \pi _\phi \\ \pi _\psi \end{array} \right) , \end{aligned}$$
(3.9)

and also the inner product

$$\begin{aligned} <\Psi _1,\Psi _2> \,=(\Psi _1,\Omega \Psi _2), \end{aligned}$$
(3.10)

where (., .) stands for the standard product in \(L^2\). Then we obtain

$$\begin{aligned}&<\Psi _1,\Psi _2> \,=-\frac{i}{2} \int \mathrm{d}z \nonumber \\&\times \,\left[ \phi _1^*\overleftrightarrow {\partial }_0 \phi _2+(\psi _1^*\overleftrightarrow {\partial }_0 \psi _2+ g (\psi _1^*\phi _2 - \phi ^*_1 \psi _2) )\chi _>\right] .\nonumber \\ \end{aligned}$$
(3.11)

In order to better understand the problem of completeness and of the boundary conditions, we introduce the Hamiltonian operator H such that the equations of motion are written in a Hamiltonian form:

$$\begin{aligned} \partial _0 \left( \begin{array}{c} \phi \\ \psi \\ \pi _\phi \chi _>\\ \pi _\psi \chi _>\end{array} \right) = \left( \begin{array}{c} \pi _\phi \\ (\pi _\psi +g \phi )\chi _>\\ \partial _z^2\phi -g \pi _\psi \chi _>-g^2 \phi \chi _>\\ -\omega _0^2 \psi \chi _>\end{array} \right) \Longleftrightarrow \partial _0 \Psi = H \psi , \end{aligned}$$
(3.12)

where

$$\begin{aligned} H:= \left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0\\ g \chi _>&{} 0 &{} 0 &{}\chi _>\\ \partial _z^2 -g^2 \chi _>&{} 0 &{} 0 &{}-g \chi _>\\ 0 &{} -\omega _0^2 \chi _>&{} 0 &{} 0 \end{array} \right] . \end{aligned}$$
(3.13)

It is not difficult to show that the operator

$$\begin{aligned} \hat{H} := i H \end{aligned}$$
(3.14)

is formally selfadjoint with respect to the inner product \(<.,.>\) defined above. In order to verify this, we must integrate by part the derivative contributions appearing in the operator \(\hat{H}\). So doing, we discover that in \(z=0\) some boundary terms appear, which are a priori possible hindrances to the hermiticity of the operator itself. These boundary terms are of the form

$$\begin{aligned} \phi (0^+) \partial _z \phi (0^+)-\phi (0^-) \partial _z \phi (0^-); \end{aligned}$$
(3.15)

we can get rid of them in three ways: (a) we can impose the continuity of the field and of its derivative at \(z=0\), as in the case of a standard problem of scattering in the presence of a step-like potential barrier; (b) we can impose Dirichlet boundary conditions at \(z=0\); (c) we can apply Neumann boundary conditions at \(z=0\). We point out that our function space, endowed with the aforementioned inner product, is a Krein space (negative norm states, which amount to antiparticles in a quantum field theory framework, appear). Selfadjointness means in this case that

$$\begin{aligned} H_c :=(\Omega \hat{H} \Omega )^\dagger \end{aligned}$$
(3.16)

coincides with \(\hat{H}\). We note that the spectrum of the Hamiltonian operator coincides with the one-particle frequencies \(\omega ,\omega _\alpha \) which were discussed in the previous section. Note also that such frequencies are conserved, as separation of variables easily shows.

In order to judge about the selfadjointness problem, we could proceed as follows: let us consider eigenstates \(\Psi = \exp (-i \omega t) f(z)\), with the spatial part f(z) smooth with compact support. This requirement is such that boundary terms immediately disappear, as in the case (a) above, but there remains a problem. Indeed, such a choice of functional space implies that the fields and their partial derivatives with respect to z are continuous in \(z=0\), and this requirement eliminates the boundary terms. Still, there is an unsatisfactory property from a physical point of view, i.e. the electric field would vanish for all the frequencies belonging to the mass gap, which is not a physically acceptable property for what was discussed previously. Then we must provide a further specification for the physical domain of \(\hat{H}\). If we require that Dirichlet boundary conditions are satisfied at \(z=0\) for all the frequencies in the mass gap of our dispersion law, then we obtain a satisfactory behavior for our operator.

As it is a selfadjoint operator, its eigenfunctions are orthogonal for \(\omega \not = \omega '\). We can define a projector \(P_{gap}\) which is such that the boundary conditions become

$$\begin{aligned} B \phi := P_{gap} \phi |_{z=0}=0. \end{aligned}$$
(3.17)

With these boundary conditions one takes into account properly the fact that, in the mass gap, \(z=0\) becomes a sort of infinite barrier which expels the field from inside the dielectric medium because the Sellmeier relation displays a mass-gap region in the spectrum. This unusual feature is due to the transparency of the medium, which simplifies greatly the quantum version of the model but does not allow one to obtain a completely satisfactory model. Notice that continuity of the field and of its z-derivative is not a boundary condition, but takes into account the finiteness of the barrier for all frequencies outside the mass gap (the electric field can live both inside and outside). Our analysis for the Hopfield model is in agreement with the short discussion appearing in [7] and concerning the exciton behavior in the case of absence of spatial dispersion (see Sect. 2 therein).

It is also remarkable that a spectral boundary condition of the type

$$\begin{aligned} B_s \phi := P_{gap} \phi |_{z=0}\oplus \partial _z (1-P_{gap}) \phi |_{z=0}=0, \end{aligned}$$
(3.18)

would produce unphysical results, as it would imply no transmission in the scattering basis for the field \(\phi \).

4 Solitonic solution

In this section, we introduce a nonlinear term in the polarization field \(\psi \) and look for solitonic solutions of the field equations. We recall that solitons in Kerr dielectric media are usually derived in the framework of the so-called nonlinear Schroedinger equation (NLS). See e.g. [11] for NLS, and [12] for solitonic solutions in fiber optics. See also [13] for further discussion.

We look for a static solution in the dielectric, in the comoving frame; we rewrite the Hamiltonian action (2.1) in a covariant form, and add a self interaction \(\psi ^4\) term simulating the Kerr effect, i.e. generating a dielectric perturbation moving with substantially constant velocity in the bulk dielectric medium:

$$\begin{aligned}&S[\phi ,\psi ] = \int _{\mathbb R} \mathrm{d}t \Biggl \{ \int _{\mathbb R} \frac{1}{2} \partial _\mu \phi \partial ^\mu \phi \, \mathrm{d}z \nonumber \\&+ \int _{z\ge 0} \biggl [ \frac{1}{2} (v^\mu \partial _\mu \psi )^2 - \frac{{\omega _0}^2}{2} \psi ^2 - g \phi v^\mu \partial _\mu \psi - \frac{\lambda }{4!} \psi ^4 \, \mathrm{d}z \biggr ] \Biggr \} .\nonumber \\ \end{aligned}$$
(4.1)

Note that (2.1) is obtained by means of \(v^\mu =(1,0)\) and \(\lambda =0\).

We set \(v=\gamma V\) for the velocity of the dielectric perturbation on the z-axis, and imposing the staticity \(\phi (t,z) \equiv \phi (z)\), \(\psi (t,z) \equiv \psi (z)\), we obtain

$$\begin{aligned} \psi (z)&= \frac{a}{\cosh (bz)} , \end{aligned}$$
(4.2)
$$\begin{aligned} \phi (z)&= \frac{2agv}{b} \arctan \biggl [ \tanh \biggl (\frac{b}{2}z\biggr ) \biggr ] , \end{aligned}$$
(4.3)

where

$$\begin{aligned} a&:= \sqrt{ \frac{12}{\lambda } (g^2v^2 - \omega _0^2) } , \end{aligned}$$
(4.4)
$$\begin{aligned} b&:= \frac{1}{v} \sqrt{g^2v^2 - \omega _0^2 } . \end{aligned}$$
(4.5)

Note that the static solution exists if and only if \(b>0\), so \(v>\omega _0/g\).

All of this is true in the comoving frame; in order to obtain solutions in the lab frame, we boost our functions by \(z \rightarrow \gamma (z-Vt)\), so

$$\begin{aligned} \psi (t,z)&= \frac{a}{\cosh (b\gamma (z-Vt))} , \end{aligned}$$
(4.6)
$$\begin{aligned} \phi (t,z)&= \frac{2agv}{b} \arctan \biggl [ \tanh \biggl (\frac{b}{2}\gamma (z-Vt)\biggr ) \biggr ] . \end{aligned}$$
(4.7)

This is our solution in the dielectric (\(z>0\)). It is useful to provide also for \(z>0\)

$$\begin{aligned} \phi ' (t,z) = agv \gamma \frac{1}{\cosh (b \gamma (z-Vt))}. \end{aligned}$$
(4.8)

Now, we want to glue this solution with that in the vacuum; since the dielectric is moving, the field in vacuum is time-dependent, so the general solution to \(\square \phi = 0\) is

$$\begin{aligned} \phi (t,z) = \alpha (z-t) + \beta (z+t) , \end{aligned}$$
(4.9)

while \(\psi =0\) in \(z<0\).

We have to impose the gluing conditions at \(z=0\) for every time t: we want the continuity of the field \(\phi \) and of its normal derivative \(\partial _n\phi \) (which is equivalent, in the lab frame, to \(\partial _z\phi \)).

We obtain

$$\begin{aligned} \alpha '(z-t)&= \frac{a\gamma gv(1+V)}{2\cosh (b\gamma V(z-t))} , \end{aligned}$$
(4.10)
$$\begin{aligned} \beta '(z+t)&= \frac{a\gamma gv(1-V)}{2\cosh (b\gamma V(z+t))} . \end{aligned}$$
(4.11)

We can interpret our solution in this way: we have a progressive wave \(\alpha (z-t)\) that hits upon the dielectric. After the collision, we will have a reflected wave \(\beta (z+t)\) and a transmitted wave (4.7), plus the polarization field (4.6).

In order to confirm our physical interpretation, we are going to calculate the total energy of the system.

4.1 Solitonic energy

The Hamiltonian of the theory (in lab frame) is

$$\begin{aligned} \mathcal {H} = \frac{1}{2} \bigl (\dot{\phi }^2 + {\phi '}^2 + \dot{\psi }^2 + \omega _0^2 \psi ^2\bigr ) + \frac{\lambda }{4!} \psi ^4 ; \end{aligned}$$
(4.12)

we split our calculus in vacuum and dielectric parts: we start with the vacuum part.

In vacuum, the Hamiltonian is reduced to (\(\psi =0\))

$$\begin{aligned} \mathcal {H}_V= & {} \frac{1}{2} \bigl (\dot{\phi }^2 + {\phi '}^2\bigr ) = \frac{a^2\gamma ^2g^2v^2}{4}\nonumber \\&\times \,\biggl [ \frac{(1+V)^2}{\cosh ^2(b\gamma V(z-t))} + \frac{(1-V)^2}{\cosh ^2(b\gamma V(z+t))} \biggr ] ;\nonumber \\ \end{aligned}$$
(4.13)

therefore, the total energy in \(z<0\) is

$$\begin{aligned} E_V = \int _{-\infty }^0 \mathrm{d}z \, \mathcal {H}_V = \frac{a^2\gamma g^2v^2}{2bV} \bigl [ (1+V^2) - 2V \tanh (b\gamma Vt) \bigr ] . \end{aligned}$$
(4.14)

We note immediately that \(E_V\) is strictly positive, and that is a decreasing function of t, as we expected.

The Hamiltonian in the dielectric is equivalent to (4.12), and explicitly

$$\begin{aligned} \mathcal {H}_D = \frac{a^2\gamma ^2g^2v^2}{\cosh ^2(b\gamma (z-Vt))} ; \end{aligned}$$
(4.15)

the energy in the dielectric is

$$\begin{aligned} E_D = \int _0^{+\infty } \mathrm{d}z \, \mathcal {H}_D = \frac{a^2\gamma g^2v^2}{b} \bigl [ 1 + \tanh (b\gamma Vt) \bigr ] . \end{aligned}$$
(4.16)

\(E_D\) is an increasing function, and it is positive too.

This calculus confirms our physical picture: we have an energy flux from \(z\rightarrow -\infty \) to \(z\rightarrow +\infty \), because energy in vacuum decreases in time, while the dielectric is progressively filled and its energy increases.

It is worthwhile noting that energy in vacuum does not converge to zero, because there exists a reflected wave \(\beta (z+t)\). At \(t\rightarrow +\infty \), both \(E_V\) and \(E_D\) become constant, and this situation corresponds to a “fulfilled” system.

Now, we obtain the total amount of energy: since action (4.1) is invariant under temporal translation, total energy is a Noether charge, so we expect that it is time-independent. Indeed

$$\begin{aligned} E_{tot} = E_V + E_D = \frac{a^2\gamma g^2v^2}{2bV} (1+V)^2 ; \end{aligned}$$
(4.17)

as expected it is time-independent, and \(E_{tot} > 0\).

It is interesting to observe that our solitonic solution fulfills four properties which are associated as ‘definitory properties’ to solitons in [14]: (1) finite total energy; (2) finite, non-singular and localized energy density, where localization means that at any time t the region where \(\mathcal {H}\ge \delta \), for any \(\delta \in (0,\max _z \mathcal {H})\), is bounded; (3) the solitonic solution is non-singular; (4) the solitonic solution is non-dissipative (in the sense that \(\max _z \mathcal {H}\) does not vanishes as \(t\rightarrow \infty \)). There is also a fifth (and last) property, i.e. classical stability in the sense of Lyapunov, which is shown to be implemented in the following section.

4.2 Transmission and reflection coefficients

The naive expectation for the process at hand is the following: one would expect that the scattering of the solitonic wave starts from the left, \(z\ll 0\), at very early times, \(t\rightarrow -\infty \), with a progressive wave moving towards the interface \(z=0\), and that at very far times in the future, \(t\rightarrow +\infty \), one gets two separate packets, the first counter-propagating in the vacuum region \(z\ll 0\) (reflected wave) and the second one progressing in the dielectric medium \(z\gg 0\) with velocity V (transmitted wave). We show that this is the case, and we provide the reflection and the transmission coefficients.

Usually, one could approach the problem by using the component \(J_z\) of the current density. In the present case, this is not possible because there is no charge displacement in the medium and then \(J_z=0\). We can then approach the problem by recalling that the canonical stress-energy tensor can be calculated, and in particular the component \(T_{0z}\) represents the flux of energy through a surface orthogonal to the z-direction. To be more specific, we calculate \(T_{0z}\) for the only field which propagates in our system: the ‘electromagnetic field’ \(\phi \).Footnote 1 We get

$$\begin{aligned} T^{\mu \nu }=\frac{\partial L}{\partial \partial _\mu \phi } \partial ^{\nu } \phi -\eta ^{\mu \nu } L, \end{aligned}$$
(4.18)

and, in particular, we are interested in

$$\begin{aligned} T^{0z}=(\partial ^0 \phi )(\partial ^z \phi ) =:S^z, \end{aligned}$$
(4.19)

where \(S^z\) is the equivalent of the Poynting vector for the electromagnetic field. Then we get

$$\begin{aligned} S_z=-\dot{\phi } \phi '. \end{aligned}$$
(4.20)

Let us consider the vacuum region \(z<0\):

$$\begin{aligned} S_z = (\alpha ')^2-(\beta ')^2. \end{aligned}$$
(4.21)

In the dielectric region \(z\ge 0\) we obtain

$$\begin{aligned} S_z= V (\phi _D')^2, \end{aligned}$$
(4.22)

where we indicate with \(\phi _D\) the field \(\phi \) in the dielectric region. Let us consider the field at \(t\ll 0\) and for \(z \ll 0\). In order to get a field which is appreciably different from zero, we should impose \(t \sim z\), in such a way to obtain the peak value for \(\alpha '\), whereas \(\beta ' \sim 0\) and \(\phi _D'= 0\). In such a situation, we have

$$\begin{aligned} \alpha ' (z-t) \sim \frac{a \gamma g v (1+V)}{2}. \end{aligned}$$
(4.23)

This situation represents the initial pulse which moves towards \(z=0\) from the left. It is also useful to note that for \(t\ll 0\) and \(z>0\) one has \(\phi _D' (z+V |t|)\sim 0\).

Let us now consider \(t\gg 0\), i.e. the final state. In the region \(z\ll 0\), we get a field appreciably different from zero only for \(t \sim -z\), i.e. we get a reflected packet with

$$\begin{aligned} \beta ' (z+t) \sim \frac{a \gamma g v (1-V)}{2}. \end{aligned}$$
(4.24)

In the dielectric region, we obtain a non-vanishing contribution only for \(t\sim z/V\), which correspond to the peak of the transmitted packet. Summarizing, we have the Poynting vector for the initial packet, for the reflected one and for the transmitted one, respectively:

$$\begin{aligned} S_z (t\ll 0,z\ll 0, z\sim t)\simeq & {} (\alpha ')^2 = \frac{a^2 \gamma ^2 g^2 v^2 (1+V)^2}{4},\nonumber \\ \end{aligned}$$
(4.25)
$$\begin{aligned} S_z (t\gg 0,z\ll 0, z\sim -t)\simeq & {} (\beta ')^2 = \frac{a^2 \gamma ^2 g^2 v^2 (1-V)^2}{4},\nonumber \\ \end{aligned}$$
(4.26)
$$\begin{aligned} S_z (t\gg 0,z\gg 0, z\sim V t)\simeq & {} V(\phi _D')^2. \end{aligned}$$
(4.27)

We can then obtain the reflection and the transmission coefficients:

$$\begin{aligned} R:= & {} \frac{S_z (t\gg 0,z\ll 0, z\sim -t) }{S_z (t\ll 0,z\ll 0, z\sim t)}=\left( \frac{1-V}{1+V} \right) ^2,\end{aligned}$$
(4.28)
$$\begin{aligned} T:= & {} \frac{S_z (t\gg 0,z\gg 0, z\sim V t) }{S_z (t\ll 0,z\ll 0, z\sim t)}= \frac{4 V}{(1+V)^2}. \end{aligned}$$
(4.29)

They satisfy

$$\begin{aligned} R+T=1. \end{aligned}$$
(4.30)

It is interesting to point out that the Poynting vector \(S_z\) is continuous at the surface \(z=0\), as would be expected for the Poynting vector in the full electromagnetic case:

$$\begin{aligned} (\alpha ')^2 (t) - (\beta ')^2 (t)= V (\phi _D')^2 (t). \end{aligned}$$
(4.31)

Indeed, one obtains

$$\begin{aligned} \frac{a^2 \gamma ^2 g^2 v^2 (1+V)^2}{4 \cosh ^2 (b \gamma V t)}- \frac{a^2 \gamma ^2 g^2 v^2 (1-V)^2}{4 \cosh ^2 (b \gamma V t)}= \frac{a^2 \gamma ^2 g^2 v^2 V}{\cosh ^2 (b \gamma V t)}. \end{aligned}$$
(4.32)

5 Stability

Stability of solitons is a nontrivial problem, addressing which one has to face in dimension greater than two with a strong no-go theorem due to Hobart and Derrick. A subtle distinction between absolute stability and stability in the sense of Lyapunov has to be taken into account, as discussed e.g. in [15, 16]. We consider for simplicity the case of an infinite dielectric, but extensions to our previous framework are possible (see below). In our analysis, we follow the ideas contained in [16], and we are able to infer the stability of our soliton solution.

The starting point consists in writing the Hamiltonian operator as a function of the field momenta and the fields themselves:

$$\begin{aligned} H=H(\pi _\phi ,\pi _\psi ,\phi ,\psi ). \end{aligned}$$
(5.1)

Then one has to consider an expansion of H up to the second order in the field and momenta variations \(\delta \pi _\phi , \delta \pi _\psi ,\delta \phi , \delta \psi \) around the soliton solution, taking into account that the first order contribution vanishes (as the soliton solution is ‘on shell’, i.e. satisfies the Hamiltonian equations of motion). By defining

$$\begin{aligned} \delta P= & {} \left( \begin{array}{c} \delta \pi _\phi \\ \delta \pi _\psi \\ \end{array} \right) ,\end{aligned}$$
(5.2)
$$\begin{aligned} \delta Q= & {} \left( \begin{array}{c} \delta \phi \\ \delta \psi \\ \end{array} \right) , \end{aligned}$$
(5.3)

and indicating by \(\delta P^t,\delta Q^t\) the transposed vectors, we get

$$\begin{aligned} H(\pi _\phi ,\pi _\psi ,\phi ,\psi )= & {} H_0+ \frac{1}{2} \delta P^t\ T\ \delta P\nonumber \\&+\, \frac{1}{2} \delta Q^t\ V\ \delta Q + \delta P\ G\ \delta Q+\cdots ,\nonumber \\ \end{aligned}$$
(5.4)

where \(H_0\) is the zeroth-order contribution associated with the solitonic solutions, and where higher order contributions are neglected. For simplicity, we work in the lab frame. Explicitly, we get

$$\begin{aligned} T= \left[ \begin{array}{cc} 1 &{} 0\\ 0 &{} 1\\ \end{array} \right] , \end{aligned}$$
(5.5)
$$\begin{aligned} G= \left[ \begin{array}{cc} 0 &{} 0\\ g &{} 0\\ \end{array} \right] , \end{aligned}$$
(5.6)

and

$$\begin{aligned} V= \left[ \begin{array}{cc} -\partial _z^2 +g^2&{} 0\\ 0 &{} \omega _0^2+\frac{\lambda }{2} \psi _0^2\\ \end{array} \right] , \end{aligned}$$
(5.7)

where \(\psi _0\) corresponds to the solitonic solution. Then one finds a second order operator,

$$\begin{aligned} K= \left[ \begin{array}{cc} T &{} G\\ G^t &{} V\\ \end{array} \right] , \end{aligned}$$
(5.8)

where \(G^t\) stays for the transposed matrix. It can be noted that, having \(G\not =0\), in our model appear gyroscopic-like contributions, which require that stability in the Lyapunov sense is shifted from the requirement of minimality of the energy functional, to more general conditions [16]. According to the analysis in [16], by introducing the symplectic matrix (3.8), a stationary solution

$$\begin{aligned} e^{-i \omega t} X(z) \end{aligned}$$
(5.9)

where X(z) is the suitable vector function depending only on z, is stable in the sense of Lyapunov if the equation

$$\begin{aligned} \det (K-\omega \Omega ) =0 \end{aligned}$$
(5.10)

admits only real solutions \(\omega \in {\mathbf {R}}\). Note that the symplectic eigenvector X satisfies

$$\begin{aligned} K X = \omega \Omega X. \end{aligned}$$
(5.11)

In the present case, by using with some ingenuity the rule

$$\begin{aligned} \det A = \det A_{11} \det (A_{22} -A_{21} A_{11}^{-1} A_{12}), \end{aligned}$$
(5.12)

which holds for a block square matrix A with equal square blocks \(A_{11},A_{12},A_{21},A_{22}\),

$$\begin{aligned} A= \left[ \begin{array}{cc} A_{11} &{} A_{12}\\ A_{21} &{} A_{22}\\ \end{array} \right] , \end{aligned}$$
(5.13)

one obtains

$$\begin{aligned} \det (K-\omega \Omega ) = \det \left[ \begin{array}{cc} -\partial _z^2 -\omega ^2 &{} -i\omega g\\ i\omega g &{} \omega _0^2 -\omega ^2+\frac{\lambda }{2} \psi _0^2 \\ \end{array} \right] =0. \end{aligned}$$
(5.14)

We can observe that momentarily neglecting the contribution associated with \(\psi _0\), one in essence obtains the dispersion relation in the dielectric medium, as is easy to realize by means of a Fourier analysis of the above operator. We know that \(\omega \) is real when \(\omega ^2\) is outside the forbidden interval \((\omega _0^2,\omega _0^2+g^2)\), which corresponds to the well-known mass gap in the Sellmeier dispersion relation delimiting the reality of the refractive index in optics. We have also to keep into account that the \(\psi _0\) contribution, for positive \(\lambda \), is a positive and bounded operator which represents a small perturbation with respect to the (unbounded) operator \(\omega _0^2 -\omega ^2\). Such a perturbation is substantially not able to perturb in any sensible way the reality of \(\omega \), in the sense that if we define

$$\begin{aligned} s^2 :=\omega _0^2 +\frac{\lambda }{2} \sup (\psi _0^2), \end{aligned}$$
(5.15)

then stability in the above sense is ensured as far as

$$\begin{aligned} \omega ^2< & {} \omega _0^2,\end{aligned}$$
(5.16)
$$\begin{aligned} \omega ^2> & {} s^2+g^2, \end{aligned}$$
(5.17)

which correspond to the stability conditions for the case at hand.

In the case of semi-infinite dielectric medium, one finds that the Hamiltonian H is split into two expressions, one for the vacuum region and the other for the dielectric region. As a consequence, the operator K above is split into two expressions too:

$$\begin{aligned} K = \left[ \begin{array}{c} K_< \quad \quad z<0,\\ K_> \quad \quad z\ge 0, \end{array} \right. \end{aligned}$$
(5.18)

where \(K_>\) is formally the same as in the infinite dielectric medium discussed above, and \(K_<\) is a free field contribution associated only with \(\pi _\phi ,\phi \) (as the polarization field contribution vanishes). The latter contribution does not affect the stability properties discussed above.

6 Conclusions

In the framework of a \(1+1\) dimensional toy-model which consists of an half-line filling dielectric medium, simulating the electromagnetic field and the polarization field by means of two coupled scalar fields \(\phi \), \(\psi \), respectively, in a Hopfield-like model, we have achieved substantially two relevant results. The first one is that boundary conditions associated with the spectrum of quasi-particles (polaritons) are necessary in order to match with meaningful physics. Indeed, in order to avoid an unphysical behavior in the case of the ‘mass gap’, one is forced to impose reflection at \(z=0\) for the electromagnetic field \(\phi _\omega \) when \(\omega \) falls in the mass gap. This is a somewhat unexpected condition, which can be related to the requirement of transparency of the dielectric medium. The second result is that, in a nonlinear model, solitonic solutions exist, whose behavior has been studied. All relevant properties of solitons are shown to be fulfilled. Indeed, we have considered the energy behavior both in a global sense, by studying how the energy changes with time in the different parts of our setting, and in a local sense, by means of the analysis, based on \(T_{0z}\), which represents the flux of energy through a surface orthogonal to the z-direction. We have also studied stability in the Lyapunov sense of the solitonic solutions.