1 Introduction

The left–right symmetric model (LRSM) [1,2,3,4,5] remains one of the best motivated high-energy completions of the Standard Model of Particle Physics (SM). It ties together the Majorana nature of neutrinos, their tiny masses in comparison to the electroweak (EW) scale \(v_\mathrm{EW}\), and the chiral structure of EW interactions, seemingly disparate phenomena, to the simultaneous breakdown of \((B-L)\) conservation and left–right parity invariance at a scale \(v_R\gg v_\mathrm{EW}\). Predicting a plethora of observations, the model is readily testable at current and near-future experiments; see [6,7,8,9,10,11] and the references therein.

At the Large Hadron Collider (LHC), searches [12, 13] for \(W_R\) gauge bosons and heavy Majorana neutrinos N, if kinematically accessible, focus on the well-studied, lepton number-violating \((\varDelta L = \pm 2)\) Drell–Yan process [14],

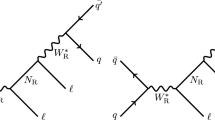
$$\begin{aligned} p p \rightarrow W_R^\pm \rightarrow N \ell ^\pm _1 \rightarrow \ell ^\pm _1 \ell ^\pm _2 +nj. \end{aligned}$$
(1)

As seen in Fig. 1a, Eq. (1) proceeds for \(m_N<M_{W_R}\) first through the on-shell production of \(W_R\), then by its decay to N. Recent investigations [16,17,18,19,20], however, have shown that one can obtain a considerable increase in sensitivity to the LRSM at colliders by relaxing the requisite charged lepton and jet multiplicities stipulated by Ref. [14] for Eq. (1) and similarly for the related single-top channel [21]. This is particularly true for \(M_{W_R}\gg m_N,~v_\mathrm{EW}\), which occurs naturally when \(v_R \gtrsim \mathscr {O}(10)\) TeV with neutrino triplet Yukawas \(y^{\varDelta _R} \lesssim \mathscr {O}(10^{-2})\). Incidentally, such scenarios are also favored by searches for flavor-changing neutral Higgs (FCNH) transitions [22,23,24,25] and neutron EDMs [26, 27]. Along these lines, we reevaluate the necessity of \(W_R\) being kinematically accessible to test LR symmetry at hadron colliders.

In the limit that \(M_{W_R}\) is of the order or above the total collider energy \(\sqrt{s}\) but \(m_N\ll \sqrt{s}\), Eq. (1) can still proceed if mediated instead by a far off-shell \(W_R\). This is akin to the SM Fermi contact interaction. For \(m_N\lesssim \mathscr {O}(1)\mathrm{~TeV}\), 8 TeV searches [12, 13] for Eq. (1) are insensitive to this configuration due to the search premise itself: resonant \(W_R\) production implies that momenta of final-state particles scale with \(M_{W_R}\), justifying the use of TeV-scale selection cuts in [12, 13]. The choices of the cuts are motivated by limits from dijet searches that indicate \(M_{W_R}\gtrsim 2.5\mathrm{~TeV}\) [28, 29]. Non-resonant \(W_R\) mediation, however, implies that the partonic scale is naturally \(\sqrt{\hat{s}}\sim m_N\lesssim \mathscr {O}(1)\mathrm{~TeV}\), and therefore it is unlikely to lead to final states satisfying the kinematical criteria. For \(m_N\gtrsim \mathscr {O}(1)\) TeV, present methods are sufficient [30].

Fig. 1
figure 1

Born diagrams for heavy Majorana N production and decay via a \(W_R\), b \(W_\mathrm{SM}\) currents. Drawn using JaxoDraw [15]

Full size image

Interestingly, while the underlying dynamics differ, for the \((M_{W_R},m_N)\) range in consideration, the mass scale and topology of Eq. (1) are identical to the heavy Majorana neutrino direct production (DP) process

$$\begin{aligned} p p \rightarrow W_\mathrm{SM}^{\pm *} \rightarrow \ell ^\pm _1 N \rightarrow \ell ^\pm _1 \ell ^\pm _2 +nj. \end{aligned}$$
(2)

As shown in Fig. 1b, this process, which may also be labeled as prompt production, transpires through off-shell SM W bosons and occurs at the scale \(m_N\) for \(m_N> M_{W_\mathrm{SM}}\) [31,32,33,34,35]. Subsequently, hadron collider searches for Eq. (2) can be interpreted as searches for Eq. (1) in the \(M_{W_R}\gtrsim \sqrt{s}\) limit. Moreover, despite its off-shell nature, the \(W_R\) chiral couplings to quark and leptons remain encoded in azimuthal and polar distributions of the \(\ell ^\pm \ell ^\pm nj\) system [36]. Thus, in principle, the dynamics of Eq. (1) can still be determined, even in mixed \(W_R^{(*)}\)–\(W_\mathrm{SM}^{(*)}\) scenarios as considered in [36,37,38]. It follows that this holds too for \(ee/pp\rightarrow Z_R^{(*)}\rightarrow NN\)

In the LRSM, heavy N production can in principle also proceed through Eq. (2) and its neutral current equivalent via neutrino mixing. However, such mixing between left-handed flavor states \(\ell \) and heavy mass eigenstate N, which scales as \(V_{\ell N} \sim \sqrt{m_\nu / m_N}\), is necessarily small for the choice of \(m_N\) in discussion and observed \(m_\nu \). Subsequently, we neglect the contribution of Eq. (2) in the LRSM throughout this study. For further discussions, see, e.g., Refs. [37, 39, 40].

In this context, we reinterpret \(\sqrt{s}=8\) TeV LHC limits on heavy Majorana neutrino DP cross sections [41, 42] for the LRSM. For \(m_N = \) 200–500 GeV and right–left coupling ratio \(\kappa _R = g_R/g_L\), we find \((M_{W_R} / \kappa _R) < \) 1.1–1.8 TeV are excluded at 95% CLs. While weak, the limits are competitive with searches for resonant \(M_{W_R}-N\) production [13, 30]; however, for such low mass scales, the validity of this approach requires \(\kappa _R\gg 1\). Projected sensitivities [43] to DP at the high-luminosity LHC and a hypothetical 100 TeV Very Large Hadron Collider (VLHC) are recast into projections for the LRSM. At 14 (100) TeV and with \(\mathscr {L}=1~(10)~\text {ab}^{-1}\), one can probe \((M_{W_R} / \kappa _R) < \) 7.9–8.9 (14–40) TeV for \(m_N = \) 100–700 (1200) GeV. We also translate sensitivity to \((M_{W_R} / \kappa _R)\) for coefficients of gauge invariant dimension-six operators in an effective field theory with right-handed neutrinos (NEFT) [44].

This study continues in the following order: in Sect. 2, the components of LRSM and NEFT relevant for this work are reviewed. We describe our methodology for reinterpreting (V)LHC limits in Sect. 3, and report results in Sect. 4. We summarize and conclude in Sect. 5.

2 Theoretical framework

We now briefly summarize the main relations of the minimal LRSM and NEFT relevant to this analysis.

2.1 Minimal left–right symmetric model

In the notation of [36], the \(W_R\) quark chiral currents are

$$\begin{aligned} \mathscr {L}_{W_R-q-q'} = \frac{-\kappa _R^q g_L}{\sqrt{2}}\sum _{i,j=u,\dots }\overline{u}_i V_{ij}^{R} W_{R \mu }^+ \gamma ^\mu P_R d_j + \text {H.c.} \end{aligned}$$

Here, up-(down-)type quarks with flavor i(j) are represented by \(u_i (d_j)\); \(P_{R(L)} = \frac{1}{2}(1\pm \gamma ^5)\) is the right-hand (RH) [left-hand (LH)] chiral projection operator; \(V_{ij}^\mathrm{R}\) denotes the RH analog of the Cabbibo–Kobayashi–Masakawa (CKM) matrix \(V_{ij}^\mathrm{L}\); and \(\kappa _{R}^{q}\in \mathbb {R}\) is an overall normalization for the \(W_R\) interaction strength with respect to the SM weak coupling \(g_L=\sqrt{4\pi \alpha _\mathrm{EM}}/\sin \theta _W\). Despite nature maximally violating parity at low energies, \(V_{ij}^\mathrm{R}\) retains its resemblance to \(V_{ij}^\mathrm{L}\), with \(\vert V_{ij}^\mathrm{R} \vert = \vert V_{ij}^\mathrm{L}\vert \) for generalized charge conjugation and \(\vert V_{ij}^\mathrm{R} \vert \approx \vert V_{ij}^\mathrm{L}\vert + \mathscr {O}(m_b/m_t)\) for generalized parity [26, 27, 45,46,47]. Throughout this study, we assume five massless quarks and, for simplicity, take \(\vert V^L_{ij}\vert ,~\vert V^R_{ij}\vert \) to be diagonal with unit entries.

For leptonic coupling to \(W_R\), we consider first the decomposition of neutrino chiral states i, j into mass states \(m,m'\): Assuming \(i (m) =1,\dots ,3\), LH (light) states and \(j (m')=1,\dots ,n\), RH (heavy) states, we can relate the chiral neutrino states and mass eigenstates by the rotation

$$\begin{aligned} \begin{pmatrix} \nu _{Li} \\ N_{Rj}^c \end{pmatrix} = \begin{pmatrix} U_{3\times 3} &{} V_{3\times n} \\ X_{n\times 3} &{} Y_{n\times n} \end{pmatrix} \begin{pmatrix} \nu _{m} \\ N_{m'}^c \end{pmatrix}. \end{aligned}$$
(3)

Without the loss of generality, we take the rotation of the charged leptons into the mass basis as the identity. The \(U_{3 \times 3}\) component of Eq. (3) is then recognized as the observed light neutrino mixing matrix. In analogy to \(U_{\ell m}\), the entry \(Y_{\ell m'} (X_{\ell m})\) quantifies the mixing between the heavy (light) mass state \(N_{m'} (\nu _{m})\) and the RH chiral state with corresponding flavor \(\ell \). Hence, the mixing entries scale as \(\vert Y_{\ell m'}\vert ^2 \sim \mathscr {O}(1)\) and \(\vert X_{\ell m}\vert ^2 \sim 1 - \vert Y_{\ell m'}\vert ^2 \sim \mathscr {O}(m_{\nu _m}/m_{N_{m'}})\) [14]. Explicitly, the RH flavor state \(N_{\ell }\) in the mass basis is then [35, 36]

$$\begin{aligned} N_{\ell } = \sum _{m=1}^{3} X_{\ell m}\nu _{m}^c + \sum _{m'=1}^{n}Y_{\ell m'} N_{m'}. \end{aligned}$$
(4)

With this, the \(W_R\) chiral currents for leptons are [35, 36]

$$\begin{aligned} \mathscr {L}_{W_R-\ell -\nu /N}= & {} \frac{-\kappa _R^\ell g_L}{\sqrt{2}} \sum _{\ell =e}^{\tau } \overline{N_{\ell }} W_{R \mu }^+ \gamma ^\mu P_R \ell ^-+\text {H.c.} \\= & {} \frac{-\kappa _R^\ell g_L}{\sqrt{2}} \sum _{\ell =e}^{\tau } \left[ \sum _{m=1}^3 \overline{\nu ^{c}_m} X_{\ell m}^\dagger + \sum _{m'=1}^3 \overline{N_{m'}} Y_{\ell m'}^\dagger \right] \\&\times W_{R \mu }^+ \gamma ^\mu P_R \ell ^- +\text {H.c.} \end{aligned}$$

As for quarks, \(\kappa _R^\ell \in \mathbb {R}\) normalizes the \(W_R\) coupling to leptons. Throughout this analysis, we adopt the conventional benchmark scenario and consider only the lightest heavy neutrino mass state \(N_{m'=1}\), which we denote N.

2.2 Effective field theory with heavy neutrinos

Heavy neutrino effective field theory (NEFT) [44, 48, 49] is a powerful extension of the SM EFT [50, 51] that allows for a consistent and agnostic parameterization of new, high-scale, weakly coupled physics when N mass scales comparable to \(v_\mathrm{EW}\). As TeV-scale L violation implies [52, 53] the existence of a particle spectrum beyond the canonical Type I seesaw [54,55,56,57], it is natural to consider DP sensitivities in terms of NEFT operators.

After extending the SM by three \(N_R\), the most general renormalizable theory that can be constructed from SM symmetries is the Type I seesaw Lagrangian,

$$\begin{aligned} \mathscr {L}_\mathrm{Type~I} = \mathscr {L}_\mathrm{SM} + \mathscr {L}_{N~\text {Kin.+Mass}} + \mathscr {L}_{N~\text {Yukawa}}. \end{aligned}$$
(5)

Respectively, the three terms are the SM Lagrangian, the kinetic and Majorana mass terms for \(N_R\), and the Yukawa couplings responsible for Dirac neutrino masses. From this, the NEFT Lagrangian can be built by further extending \(\mathscr {L}_\mathrm{Type~I}\) before EW symmetry breaking (EWSB) by all SU(3) \(\otimes \) SU\((2)_L\) \(\otimes \) U\((1)_Y\)-invariant, irrelevant (mass dimension \(d>4\)) operators containing Type I seesaw fields:

$$\begin{aligned} \mathscr {L}_\mathrm{NEFT}= & {} \mathscr {L}_\mathrm{Type~I} + \sum _{d=5}\sum _{i} \frac{\alpha _i}{\Lambda ^{(d-4)}}\mathscr {O}_{i}^{(d)}. \end{aligned}$$
(6)

Here, \(\alpha _i<\mathscr {O}(4\pi )\) are dimensionless coupling coefficients, \(\Lambda \gg \sqrt{\hat{s}}\) is the mass scale of the underlying theory, and \(\mathscr {O}_{i}^{(d)}\) are gauge invariant permutations of Type I field operators. The list of \(\mathscr {O}_{i}^{(d)}\) are known explicitly for \(d=5\) [48], 6 [44], and 7 [49], and can be built for larger d following [58, 59].

At \(d=6\), the four-fermion \(\mathscr {O}_i^{(6)}\) giving rise to the same parametric dependence on \(m_N\) in the partonic cross section \(\hat{\sigma }\) as both DP and the LRSM for \(M_{W_R}\gg \sqrt{\hat{s}}\) are

$$\begin{aligned} \mathscr {O}_V^{(6)}= & {} (\overline{d}\gamma ^\mu P_R u ) (\overline{e}\gamma _\mu P_R N_R ) \quad \text {and}\quad \nonumber \\ \mathscr {O}_{S3}^{(6)}= & {} (\overline{Q}\gamma ^\mu P_R N_R)\varepsilon (\overline{L}\gamma _\mu P_R d). \end{aligned}$$
(7)

In Eq. (7), \(\varepsilon \) is the totally antisymmetric tensor. After EWSB and decomposing \(N_R\) according to Eq. (4), but neglecting \(\mathscr {O}(X_{\ell m})\) terms, the operators become

$$\begin{aligned} \mathscr {O}_V^{(6)}= & {} \sum _{m'=1} (\overline{d}\gamma ^\mu P_R u) (\overline{\ell }\gamma _\mu P_R~Y_{\ell m'}~N_{m'} ) \quad \text {and}\quad \nonumber \\ \mathscr {O}_{S3}^{(6)}= & {} \sum _{m'=1} (\overline{Q}\gamma ^\mu P_R ~Y_{\ell m'} N_{m'} ) (\overline{\ell }\gamma _\mu P_R d). \end{aligned}$$
(8)

As in the LRSM case, we consider only the \(N_{m'=1}\) state with mixing as given in Eqs. (40), (41).

3 Mimicking direction production with left–right symmetry

In this section we describe our procedure for extracting bounds on LRSM and NEFT quantities from observed and expected (V)LHC limits on heavy Majorana neutrino DP rates. Our computational setup is summarized in Sect. (3.1). We start by constructing the observable \(\varepsilon (M_{W_R})\), which we will ultimately constrain.

The Born-level, partonic heavy N production cross section via (on- or off-shell) \(W_R\) currents,

$$\begin{aligned} q_1\overline{q_2} \rightarrow W_R^{\pm (*)} \rightarrow N ~\ell ^\pm _1, \end{aligned}$$
(9)

with arbitrary lepton mixing is given generically by [36]

$$\begin{aligned} \frac{\mathrm{d}\hat{\sigma }^\mathrm{LRSM}}{\mathrm{d}\varOmega _\ell } = \frac{3\hat{\sigma }^\mathrm{LRSM}_\mathrm{Tot.}}{2^3\pi (2+r_N)} [(1-\cos \theta _\ell )^2 + r_N\sin ^2\theta _\ell ] \end{aligned}$$
(10)

where \(r_N\equiv m_N^2/\hat{s}\) and the total cross section is

$$\begin{aligned} \hat{\sigma }^\mathrm{LRSM}_\mathrm{Tot.}= & {} \frac{\kappa _R^{q2}\kappa _R^{\ell 2} g_L^4}{2^7~3N_c~\pi } \frac{\vert Y_{\ell N}\vert ^2~\hat{s}(1-r_N)^2(2+r_N)}{[(\hat{s}-M_{W_R}^2)^2 + (M_{W_R}\Gamma _{W_R})^2]} \end{aligned}$$
(11)
$$\begin{aligned}\approx & {} \frac{\kappa _R^{q2}\kappa _R^{\ell 2} g_L^4 }{2^7~3N_c~\pi }\vert Y_{\ell N}\vert ^2 \frac{\hat{s}}{M_{W_R}^4}(1-r_N)^2(2+r_N). \end{aligned}$$
(12)

In the last line we take the \(M_{W_R}\gg \sqrt{\hat{s}}\) limit. For DP, the analogous partonic cross section is

$$\begin{aligned} \frac{\mathrm{d}\hat{\sigma }^\mathrm{DP}}{\mathrm{d}\varOmega _\ell } = \frac{3\hat{\sigma }^\mathrm{DP}_\mathrm{Tot.}}{2^3\pi (2+r_N)} [(1-\cos \theta _\ell )^2 + r_N\sin ^2\theta _\ell ] \end{aligned}$$
(13)

where the total partonic rate for \(\sqrt{\hat{s}}\gg M_{W_\mathrm{SM}}\) is, similarly,

$$\begin{aligned} \hat{\sigma }^\mathrm{DP}_\mathrm{Tot.}= & {} \frac{g_L^4}{2^7~3N_c~\pi } \frac{\vert V_{\ell N}\vert ^2~\hat{s}(1-r_N)^2(2+r_N)}{\left[ (\hat{s}-M_{W_R}^2)^2 + (M_{W}\varGamma _{W})^2\right] } ~ \end{aligned}$$
(14)
$$\begin{aligned}\approx & {} \frac{g_L^4 \vert V_{\ell N}\vert ^2}{2^7~3N_c~\pi } \frac{1}{\hat{s}}(1-r_N)^2(2+r_N) . \end{aligned}$$
(15)

Comparing the differential and integrated expressions one sees crucially that the angular and \(m_N\) dependence in the two processes are the same. This follows from the maximally parity violating \(V\pm A\) structures of the \(W_\mathrm{SM}/W_R\) couplings. Naïvely, one expects the orthogonal chiral couplings to invert the leptons’ polarizations with respect to the mediator. However, as the mediators’ polarizations are also relatively flipped with respect to the initial-state quarks, the outgoing lepton polarization with respect to initial-state quarks, i.e., \(\cos \theta _\ell \), is the same. Hence, universality of \(W_R\) chiral couplings to quarks and leptons in the LRSM can be tested without resonantly producing it. The precise handedness of the couplings can be inferred from azimuthal and polar distributions of the \(\ell ^\pm \ell ^\pm j j\) final state [36] as well as single-top channel [60]. As DP searches do not (and should not) rely on forward–backward cuts, which are sensitive to parity asymmetries, their reinterpretation in terms of the LRSM for non-resonant \(W_R\) is justified.

Branching rates of N to a final state A can be expressed in terms of the calculable \(N\rightarrow A\) partial widths,

$$\begin{aligned} {\mathrm{BR}\left( N\rightarrow A\right) } \equiv \frac{\varGamma \left( N\rightarrow A\right) }{\sum _i ~\varGamma \left( N\rightarrow A_i\right) }. \end{aligned}$$
(16)

For \(M_{W_R}\gg m_N\), the \(M_{W_R}\) dependence in Eq. (16) cancels. Hence, the Born-level, partonic same-sign lepton cross section in the LRSM,

$$\begin{aligned} q_1\overline{q_2} \rightarrow W_R^{\pm *} \rightarrow N ~\ell ^\pm _1 \rightarrow \ell ^\pm _1 ~\ell ^\pm _2 ~X, \end{aligned}$$
(17)

under the narrow width approximation for N is

$$\begin{aligned}&\hat{\sigma }(q_1\overline{q_2} \rightarrow N ~\ell ^\pm _1 \rightarrow \ell ^\pm _1 ~\ell ^\pm _2 ~X) \nonumber \\&\quad \approx \hat{\sigma }^\mathrm{LRSM}_\mathrm{Tot.} ~\times ~ {\mathrm{BR}\left( N \rightarrow \ell ^\pm _2 ~X\right) } \end{aligned}$$
(18)
$$\begin{aligned}&\equiv \varepsilon ^{\ell _1\ell _2}(M_{W_R}) ~\times ~ \tilde{\hat{\sigma }}. \end{aligned}$$
(19)

In the last line we collect LRSM parameters into the single, dimensionful (TeV\(^{-4}\)) coefficient

$$\begin{aligned} \varepsilon ^{\ell _1\ell _2}(M_{W_R}) = \frac{\kappa _R^{q 2}\kappa _R^{\ell 2}}{M_{W_R}^4}\vert Y_{\ell _1 N}\vert ^2 ~ \text {BR}(N \rightarrow ~\ell ^\pm _2 ~q'_1\overline{q'_2}). \end{aligned}$$
(20)

The “reduced” partonic cross section \(\tilde{\hat{\sigma }}\) contains all kinematical and \(m_N\) dependence that must be convolved with parton distribution functions (PDFs) to build the hadronic cross section. For the \(e^\pm \mu ^\pm \) mixed-flavor state, a summation over \( \varepsilon ^{e\mu }\) and \(\varepsilon ^{\mu e}\) is implied.

Inclusive, hadronic level cross sections are obtained from the Collinear Factorization Theorem,

$$\begin{aligned}&\sigma (pp \rightarrow A+X) = f \otimes f \otimes \hat{\sigma }\end{aligned}$$
(21)
$$\begin{aligned}&\quad = \frac{1}{\delta _{ij}+1} \sum _{i,j=u,g,\dots }\int ^1_{\tau _0} \mathrm{d}\xi _1 \int ^1_{\tau _0/\xi _1} \mathrm{d}\xi _2 \nonumber \\&\qquad \times [f_{i/p}(\xi _1,\mu _f)f_{j/p}(\xi _2,\mu _f) + (1\leftrightarrow 2)]\hat{\sigma }(ij\rightarrow A).\nonumber \\ \end{aligned}$$
(22)

It expresses the production rate of A (and arbitrary beam remnant X) in pp collisions as the convolution \((\otimes )\) of the \(ij\rightarrow A\) partonic process rate and the process-independent PDFs \(f_{k/p}(\xi ,\mu _f)\), which for parton species k with longitudinal momentum \(p_z = \xi E_p\) resums collinear splittings up to the scale \(\mu _f\). The kinematic threshold \(\tau _0\) is the scale below which the process is kinematically forbidden. For heavy N production, \(\tau _0 = m_N^2 / s\). In terms of \(\varepsilon (M_{W_R})\), the hadronic equivalent of Eq. (19) is

$$\begin{aligned} \sigma (p ~p \rightarrow N ~\ell ^\pm _1 \rightarrow \ell ^\pm _1 ~\ell ^\pm _2 + X) = \varepsilon (M_{W_R}) \times \tilde{\sigma }. \end{aligned}$$
(23)

Here, \(\tilde{\sigma }\) is the “reduced” hadronic cross section and is related to \(\tilde{\hat{\sigma }}\) by the convolutions \(\tilde{\sigma } = f \otimes f \otimes \tilde{\hat{\sigma }}\). As the next-to-leading order (NLO) in QCD corrections for arbitrary DY processes largely factorize from the hard scattering process [61, 62], Eq. (23) holds at NLO:

$$\begin{aligned} \sigma ^\mathrm{NLO}(p ~p \rightarrow N ~\ell ^\pm _1 \rightarrow \ell ^\pm _1 ~\ell ^\pm _2 + X) = \varepsilon (M_{W_R}) \times \tilde{\sigma ^\mathrm{NLO}}.\nonumber \\ \end{aligned}$$
(24)

Premising that reported LHC limits on the DP cross section can be applied to the LRSM for kinematically inaccessible \(W_R\), Eq. (24) shows how to translate the upper bound on the rate into an upper bound on \(\varepsilon (M_{W_R})\).

For the NEFT operators in Eq. (7), the corresponding partonic scattering rates are given by [44]

$$\begin{aligned}&\hat{\sigma }_{S3}(u\overline{d}\rightarrow N\ell ^\pm _1 \rightarrow \ell ^\pm _1\ell ^\pm _2 X) = \frac{\alpha _{S3}^2 \vert Y_N\ell _1\vert ^2}{2^7~3N_c \pi } \frac{\hat{s}}{\Lambda ^4} \nonumber \\&\quad \times (1-r_N)^2(2+r_N) \times \text {BR} (N \rightarrow \ell _2 X), \qquad \end{aligned}$$
(25)
$$\begin{aligned}&\hat{\sigma }_V(u\overline{d}\rightarrow N\ell ^\pm _1 \rightarrow \ell ^\pm _1\ell ^\pm _2 X) = \frac{4\alpha _V^2}{\alpha _{S3}^2}\hat{\sigma }_{S3}. \end{aligned}$$
(26)

Comparing with Eqs. (10)–(13), one finds the mapping

$$\begin{aligned}&\mathscr {O}_{S3}^{(6)} : \varepsilon ^{\ell _1\ell _2}(M_{W_R}) = \frac{\alpha _{S3}^2}{\Lambda ^4}\vert Y_N\ell _1\vert ^2 \text {BR} (N\rightarrow \ell _2 X), \end{aligned}$$
(27)
$$\begin{aligned}&\mathscr {O}_V^{(6)} : \varepsilon ^{\ell _1\ell _2}(M_{W_R}) = \frac{4\alpha _V^2}{\Lambda ^4}\vert Y_N\ell _1\vert ^2 \text {BR} (N\rightarrow \ell _2 X). \end{aligned}$$
(28)

This allows the further interpretation of \(\varepsilon (M_{W_R})\).

3.1 Computational setup

Practically speaking, the NLO-accurate reduced cross section is determined using the FeynRules-based [63,64,65] NLO-accurate Effective Left-Right Symmetric Model file of [20] and MadGraph5_amc@NLO [66]. The process

$$\begin{aligned} p p \rightarrow W_R^{\pm *} \rightarrow N \mu ^\pm ~+X \end{aligned}$$
(29)

is calculated at NLO accuracy assuming test inputs:

$$\begin{aligned}&\{M_\mathrm{Test}\} : M_{W_R}= {200}\mathrm{~TeV}, \quad \kappa _R^{\ell ,q}=1,\nonumber \\&\vert Y_{\mu N} \vert = 1, \quad {\mathrm{BR}\left( N\rightarrow \mu X\right) }=1. \end{aligned}$$
(30)

For the choice of EW inputs, PDFs, etc., we follow Ref. [20]. Denoting the \(\varepsilon (M_{W_R})\) corresponding to the Eq. (30) as \(\varepsilon (M_\mathrm{Test})\), \(\tilde{\sigma }^\mathrm{NLO}\) is obtained from the relationship

$$\begin{aligned} \tilde{\sigma }^\mathrm{NLO} = \frac{\sigma ^\mathrm{NLO}(p ~p \rightarrow N ~\mu ^\pm + X; \{M_\mathrm{Test}\})}{\varepsilon (M_\mathrm{Test})}. \end{aligned}$$
(31)
Fig. 2
figure 2

a As a function of \(m_N\), observed 8 TeV LHC upper bound on \(\varepsilon ^{\mu \mu }(M_{W_R})\) (dash-dot), expected 14 TeV sensitivity with \(\mathscr {L}=100\mathrm{~fb^{-1}}\) (solid-triangle) and \(1\mathrm{~ab^{-1}}\) (dash-dot-diamond), and expected 100 TeV VLHC sensitivity with \(10\mathrm{~ab^{-1}}\) (dot-star). b Same as a but with \(e^\pm \mu ^\pm \) (dash-dot) and \(e^\pm e^\pm \) (solid-triangle) at 8 TeV and \(e\mu \) (dot-star) at 100 TeV. c, d Same as a, b, respectively, but for lower bounds on \((M_{W_R}/\kappa _R)\). All limits are obtained at 95% CL\(_s\)

Full size image

4 Results and discussion

We now report the observed sensitivity to the LRSM from DP searches in the \(\mu \mu /ee/e\mu \) channels by the CMS experiment at \(\sqrt{s}=8\) TeV with \(\mathscr {L}=19.7\mathrm{~fb^{-1}}\) [41, 42]. We also report expected sensitivities based on 14 TeV projections with \(\mathscr {L}=100\mathrm{~fb^{-1}}\) and \(1\mathrm{~ab^{-1}}\) [43], as well as at 100 TeV with \(\mathscr {L}=10\mathrm{~ab^{-1}}\) [43]. In all cases, 95% confidence level (CL) limits are obtained/reproduced via the CL\(_s\) method [67,68,69], using the information available in [41,42,43], and assuming Poisson distributions for signal and background processes. After obtaining the expected (observed) DP cross section limits \(\sigma ^{\mathrm{95\% CL}_s}_\mathrm{Exp.~(Obs.)}\), LRSM constraints are determined from the “reduced” cross section \(\tilde{\sigma }\), as defined in Eq. (31), with the relation

$$\begin{aligned} \varepsilon ^{\ell _1\ell _2}_\mathrm{Exp.~(Obs.)}(M_{W_R}) = \frac{\sigma ^{\mathrm{95\% CL}_s}_\mathrm{Exp.~(Obs.)}}{\tilde{\sigma }^\mathrm{NLO}}. \end{aligned}$$
(32)

In Fig. 2 we plot as a function of \(m_N\) the 8 TeV CMS upper bounds on \(\varepsilon (M_{W_R})\) for the (a) \(\mu \mu \) (dash-dot) as well as (b) \(e\mu \) (dash-dot) and ee (upside-down triangle) channels. One finds comparable limits for all modes, with

$$\begin{aligned}&\mu ^\pm \mu ^\pm : \varepsilon ^{\ell \ell }(M_{W_R}) \lesssim {0.05}\mathrm{~TeV}^{-4}, \end{aligned}$$
(33)
$$\begin{aligned}&e^\pm \mu ^\pm ,~e^\pm e^\pm : \varepsilon ^{\ell \ell }(M_{W_R}) \lesssim {0.1}\mathrm{~TeV}^{-4}. \end{aligned}$$
(34)

For \(m_N\lesssim 150\mathrm{~GeV}\), \(W_\mathrm{SM}\) production greatly diminishes sensitivity. A weaker limit for e-based channels is due to the larger fake and charge misidentification rates for electrons than for muons, particularly from top quarks. These features are seen consistently in projections.

In Fig. 2a, the expected sensitivity to \(\varepsilon ^{\mu \mu }(M_{W_R})\) at 14 TeV with \(\mathscr {L}=100\mathrm{~fb^{-1}}\) (solid-triangle) and \(1\mathrm{~ab^{-1}}\) (dash-dot-diamond) are shown. We find that, for \(m_N= \)100–700 GeV, one can potentially exclude:

$$\begin{aligned}&\mathscr {L}^{14\mathrm{~TeV}}_{100\mathrm{~fb^{-1}}} : \varepsilon ^{\mu \mu }(M_{W_R}) \lesssim {5\times 10^{-4}\mathrm{~TeV}^{-4}}, \end{aligned}$$
(35)
$$\begin{aligned}&\mathscr {L}^{14\mathrm{~TeV}}_{1\mathrm{~ab^{-1}}} : \varepsilon ^{\mu \mu }(M_{W_R}) \lesssim {9\times 10^{-5}\mathrm{~TeV}^{-4}}. \end{aligned}$$
(36)

At a future 100 TeV VLHC, the large increase in parton density coupled with proposed integrated luminosity goals of 10–20\(\mathrm{~ab^{-1}}\) [70] implies a considerable jump in sensitivity to \(\varepsilon (M_{W_R})\) for EW-scale N. For \(m_N=\)100–1200 GeV, the \(\mu \mu \) (dot-star) in Fig. 2a) and \(e\mu \) (dot-star) in Fig. 2b) final state can probe with \(10\mathrm{~ab^{-1}}\):

$$\begin{aligned}&\varepsilon ^{\mu \mu }(M_{W_R}) \lesssim {2\times 10^{-7}\text {-}1\times 10^{-6}\mathrm{~TeV}^{-4}}, \end{aligned}$$
(37)
$$\begin{aligned}&\varepsilon ^{e\mu }(M_{W_R}) \lesssim {2\times 10^{-7}\mathrm{-}7\times 10^{-6}\mathrm{~TeV}^{-4}}. \end{aligned}$$
(38)

Derived limits on \(\varepsilon (M_{W_R})\) hold for rather generic LR scenarios. Under the strong (but typical) assumptions of a minimal LRSM setting, we can rewrite constraints as lower bounds on the ratio of \(M_{W_R}\) and \(\kappa _R^{q,\ell }\). Specifically, assuming gauge coupling universality, one has

$$\begin{aligned} \kappa _R\equiv \kappa _R^{q} = \kappa _R^{\ell }. \end{aligned}$$
(39)

For single flavor final states, we take the aligned lepton mixing limit Eq. (40), whereas for the mixed flavor channel, we take the maximally mixed limit Eq. (41), i.e.,

$$\begin{aligned}&\vert Y_{\ell N}\vert \approx 1 \quad \text {and}\quad \text {BR}(N\rightarrow \ell ^\pm X) \approx 1, \text {or} \end{aligned}$$
(40)
$$\begin{aligned}&\vert Y_{e N}\vert \approx \vert Y_{\mu N}\vert \approx 1/\sqrt{2} \quad \text {and} \nonumber \\&\text {BR} (N \rightarrow e^\pm X) \approx \text {BR} (N\rightarrow \mu ^\pm X) \approx 1/2. \end{aligned}$$
(41)

While N can decay with equal likelihood to \(\ell _i^+\) and \(\ell _i^-\), the same-sign charge stipulation reduces the effective branching by 1 / 2. With this, we invert \(\varepsilon (M_{W_R})\), giving

$$\begin{aligned} \frac{M_{W_R}}{\kappa _R} = \frac{1}{\root 4 \of {\eta \times \varepsilon ^{\ell _1\ell _2}(M_{W_R})}}, \quad \eta = \left\{ \begin{matrix} 2, &{} \ell _1 = \ell _2 \\ 4, &{} \ell _1 \ne \ell _2 \end{matrix}\right. , \end{aligned}$$
(42)

where \(\eta \) accounts for charge and flavor multiplicities.

In Fig. 2c, d, respectively, we show the lower bounds on \((M_{W_R}/\kappa _R)\) for the same configurations as (a) and (b). For all channels, the observed 8 TeV limits span:

$$\begin{aligned}&m_N=100\mathrm{-}200\mathrm{~GeV}: \left( \frac{M_{W_R}}{\kappa _R}\right) \gtrsim {0.7-1.8}\mathrm{~TeV}, \\&m_N=200\mathrm{-}700\mathrm{~GeV}: \left( \frac{M_{W_R}}{\kappa _R}\right) \gtrsim {1.1-1.8}\mathrm{~TeV}. \end{aligned}$$

At \(\sqrt{s}=14\) TeV with \(\mathscr {L}=100\mathrm{~fb^{-1}}\) and \(1\mathrm{~ab^{-1}}\), the \(\mu \mu \) final state can exclude for \(m_N= \)100–700 GeV:

$$\begin{aligned}&\mathscr {L}^{14\mathrm{~TeV}}_{100\mathrm{~fb^{-1}}} : \left( \frac{M_{W_R}}{\kappa _R}\right) \lesssim {5.2\mathrm{-}5.8}\mathrm{~TeV}, \end{aligned}$$
(43)
$$\begin{aligned}&\mathscr {L}^{14\mathrm{~TeV}}_{1\mathrm{~ab^{-1}}} : \left( \frac{M_{W_R}}{\kappa _R}\right) \lesssim {7.8\mathrm{-}8.9}\mathrm{~TeV}. \quad \end{aligned}$$
(44)

Comparable sensitivity in the ee and \(e\mu \) channels is expected. At 100 TeV with \(10\mathrm{~ab^{-1}}\), the \(\mu \mu \) and \(e\mu \) channels for \(m_N=\)100–1200 GeV are sensitive to

$$\begin{aligned}&\mu ^\pm \mu ^\pm : \left( \frac{M_{W_R}}{\kappa _R}\right) \lesssim {25\mathrm{-}40}\mathrm{~TeV}, \end{aligned}$$
(45)
$$\begin{aligned}&e^\pm \mu ^\pm : \left( \frac{M_{W_R}}{\kappa _R}\right) \lesssim {14\mathrm{-}33}\mathrm{~TeV}. \end{aligned}$$
(46)

We note that the sharp cutoffs at \(m_N=500,~700,\) and 1200 GeV for the several scenarios in Fig. 3a are due to the limited number of mass hypotheses considered in [41,42,43]. A dedicated analysis would show sensitivity to larger \(m_N\).

Fig. 3
figure 3

a Observed and expected 95% CL\(_s\) sensitivities to the \((M_{W_R},m_N)\) parameter space \((\kappa _R=1)\) for various collider configurations via direct and indirect searches in the \(\mu ^\pm \mu ^\pm \) final state. b Observed and expected 95% CL\(_s\) sensitivities to the NEFT dimension-six operators \(\mathscr {O}^{(6)}_V\) and \(\mathscr {O}^{(6)}_{S3}\) in the \(\mu ^\pm \mu ^\pm \) channel for the collider configurations in Fig. 2a

Full size image
Table 1 Observed [41, 42] and expected [43] 95% CL\(_s\) sensitivities to \(\varepsilon (M_{W_R})\) and \((M_{W_R}/\kappa _R)\) in the LRSM as well as \(\Lambda /\root 4 \of {\alpha _V^2 \text {BR}}\) in NEFT assuming various pp collider energies \((\sqrt{s})\) and integrated luminosity caches \((\mathscr {L})\)
Full size table

To compare with searches for resonant \(W_R\)–N production, we plot in Fig. 3a the region of the \((M_{W_R},m_N)\) parameter space excluded by the ATLAS experiment at 8 TeV with \(20.3\mathrm{~fb^{-1}}\) in the \(\mu \mu \) channel [13], along with our corresponding sensitivities for \(\kappa _R=1\). For \(m_N\approx \)100–500 GeV, we find that the reinterpretation of CMS’s DP limits are actually within 1.5\({\times }\) of present \(M_{W_R}\) limits from resonant \(W_R-N\) and dijet (not shown) searches [12, 13, 28, 29]. However, for such low mass scales, the validity of this approach requires \(\kappa _R\gg 1\). With 100\(\mathrm{~fb^{-1}}\) at 14 TeV, projected sensitivities are competitive with the \(\mathscr {O}(5)\) TeV reach from resonant searches using the full HL-LHC dataset [16, 19, 36]. With 1\(\mathrm{~ab^{-1}}\) at 14 TeV, and more so with 10\(\mathrm{~ab^{-1}}\) at 100 TeV, the DP channel can probe super heavy \(v_R\) scales favored by low-energy probes [23,24,25,26,27]. These findings suggest searches for heavy Majorana neutrinos via off-shell \(W_R\) may be of some usefulness at current and future collider experiments.

For completeness, upper limits on \(\varepsilon ^{\mu \mu }(M_{W_R})\) are recast in terms of the NEFT operators in Eq. (8). Using Eqs. (27), (28), the lower bounds on \((\Lambda /\sqrt{\alpha _{V,S3}})\) are

$$\begin{aligned} \frac{\Lambda }{\root 4 \of {\alpha _V^2 {\mathrm{BR}\left( N\rightarrow \mu X\right) }}}> & {} \root 4 \of {\frac{4 \vert Y_{\mu N}\vert ^2}{\varepsilon ^{\mu \mu }_\mathrm{Exp~(Obs)}(M_{W_R})}}, \end{aligned}$$
(47)
$$\begin{aligned} \frac{\Lambda }{\root 4 \of {\alpha _{S3}^2 {\mathrm{BR}\left( N\rightarrow \mu X\right) }}}> & {} \root 4 \of {\frac{\vert Y_{\mu N}\vert ^2}{\varepsilon ^{\mu \mu }_\mathrm{Exp~(Obs)}(M_{W_R})}}. \end{aligned}$$
(48)

As a function of \(m_N\), the observed and expected sensitivities to \(\mathscr {O}_V\) for the several configurations in Fig. 2a and mixing choice in Eq. (40) are shown in Fig. 3b. Over the respective ranges of \(m_N\), they span approximately

$$\begin{aligned}&\mathscr {L}^{8\mathrm{~TeV}}_{19.7\mathrm{~fb^{-1}}} : \frac{\Lambda }{\root 4 \of {\alpha _V^2 {\mathrm{BR}\left( N\rightarrow \mu X\right) }}} > {2.1\mathrm{-}3.0}\mathrm{~TeV}, \end{aligned}$$
(49)
$$\begin{aligned}&\mathscr {L}^{14\mathrm{~TeV}}_{100\mathrm{~fb^{-1}}} : \frac{\Lambda }{\root 4 \of {\alpha _V^2 {\mathrm{BR}\left( N\rightarrow \mu X\right) }}} > {8.7\mathrm{-}9.7}\mathrm{~TeV}, \end{aligned}$$
(50)
$$\begin{aligned}&\mathscr {L}^{14\mathrm{~TeV}}_{1\mathrm{~ab^{-1}}} : \frac{\Lambda }{\root 4 \of {\alpha _V^2 {\mathrm{BR}\left( N\rightarrow \mu X\right) }}} > {13\mathrm{-}15}\mathrm{~TeV}, \end{aligned}$$
(51)
$$\begin{aligned}&\mathscr {L}^{100\mathrm{~TeV}}_{10\mathrm{~ab^{-1}}} : \frac{\Lambda }{\root 4 \of {\alpha _V^2 {\mathrm{BR}\left( N\rightarrow \mu X\right) }}} > {42\mathrm{-}68}\mathrm{~TeV}. \end{aligned}$$
(52)

We summarize our reported findings in Table 1.

5 Summary and conclusion

While the LRSM naturally addresses shortcomings of the SM, it is not guaranteed its entire particle spectrum lies within the kinematic reach of the LHC or a future 100 TeV VLHC. Indeed, low-energy probes favor the LR breaking scale to be above the LHC’s threshold [22,23,24,25,26,27].

In this context, we argue that when LRSM gauge bosons are too heavy to be produced resonantly, on-shell production of sub-TeV Majorana neutrinos via the process \(pp\rightarrow W_R^* \rightarrow N\ell ^\pm \rightarrow \ell ^\pm \ell ^\pm + nj\) is still possible when mediated by far off-shell \(W_R\). In this regime, the process’ mass scale and topology are identical to the direct production (DP) process \(pp\rightarrow W_\mathrm{SM}^{*} \rightarrow N\ell ^\pm \rightarrow \ell ^\pm \ell ^\pm + nj\). Subsequently, searches for DP of heavy Majorana neutrinos can be translated into searches for LR symmetry.

We have recast current [12, 13] and projected [36, 43] sensitivities to the DP process at pp colliders into observed and expected sensitivities for the LRSM, in the heavy \(M_{W_R}\) limit. We find the following:

  1. 1.

    At the 8 TeV LHC, for \(m_N=\)100–500 GeV and right–left coupling ratio \(\kappa _R = g_R/g_L\), searches have excluded at 95% CL\(_s\) \((M_{W_R}/\kappa _R)< \)0.7–1.8 TeV. For \(m_N\gtrsim 200\) GeV, this is within 1.5\({\times }\) of searches for resonant \(W_R\) and \(W_R\)–N production.

  2. 2.

    At 14 TeV with \(100\mathrm{~fb^{-1}}~(1\mathrm{~ab^{-1}})\), one can exclude at 95% CL\(_s\) \({(M_{W_R}/\kappa _R) < }\)5.2–5.8 (7.8–8.9) TeV for \(m_N=\)100–700 GeV, well beyond the \(\mathscr {O}(5)\) TeV anticipated reach of resonant \(W_R\) searches.

  3. 3.

    At 100 TeV with \(10\mathrm{~ab^{-1}}\), one can probe \((M_{W_R}/\kappa _R) < \)14–40 TeV at 95% CL\(_s\) for \(m_N=\)100–1200 GeV, thereby greatly complementing low-energy probes of \(\mathscr {O}(10)\) TeV \(v_R\).

  4. 4.

    In terms of an Effective Field Theory featuring heavy neutrinos, we find limits on mass/coupling scales for gauge invariant, dimension-six operators comparable to the aforementioned limits in the LRSM.