The possible $B\pi$ molecular state and its radiative decay

Abstract

Recently, several exotic bosons have been confirmed as multi-quark states. However, there are violent disputes about their inner structures, namely if they are molecular states or tetraquarks, or even mixtures of the two structures. It would be interesting to search experimentally for non-strange four-quark states with open charm or bottom which are lighter than $\Lambda _c$ or $\Lambda _b$. Reasonable arguments indicate that they are good candidates of pure molecular states $D\pi$ or $B\pi$ because pions are the lightest boson. Both $B\pi$ and $D\pi$ bound states do not decay via the strong interaction. The $B\pi$ molecule may decay into $B^*$ by radiating a photon, whereas the $D\pi$ molecule can only decay via weak interaction. In this paper we explore the mass spectra of the $B\pi$ molecular states by solving the corresponding instantaneous B–S equation. Then the rate of radiative decay $|\frac{3}{2},\frac{1}{2}\rangle \rightarrow B^*\gamma$ is calculated and our numerical results indicate that the processes can be measured by the future experiment. We also briefly discuss the $D\pi$ case. Due to the constraint of the final state phase space it can only decay via weak interaction.

1 Introduction

Many charmonium-like or bottomonium-like resonances X, Y and Z bosons, such as X(3872) [1], X(3940) [2], Y(3940) [3], Z(4430) [4] Y(4260) [5, 6], $Z_c$(4020) [7], $Z_c$(3900) [8, 9], $Z_b(10{,}610)$ and $Z_b(10{,}650)$ [10] have been experimentally observed. The data show that there is no room in the regular representations of $O(3)\otimes SU_f(3)\otimes SU_s(2)$ to accommodate these newly observed resonances. Especially as some of them are charged it is suggested that these exotic bosons are in multi-quark states. Since their masses are close to that of charmonia or bottomonia those states should have hidden charm or bottom components. Whereas a newly observed exotic state X(5568) [11] measured at the $B_s^0 \pi ^\pm$ invariant mass spectrum is believed to possess four differently flavored quarks (antiquarks). If the resonance is eventually confirmed it must be a four-quark state with open bottom [12,13,14,15]. However the LHCb detector [16] did not find X(5568) with 3 $fb^{-1}$ pp collision data at $s=\sqrt{7}$ and $\sqrt{8}$ TeV.

Even though so many exotic resonances are confirmed as multi-quark bosons, there is an acute dispute about their inner structure. By contrast to the regular quark–antiquark structure, the system containing two quarks and two anti-quarks may have different combination patterns: it may reside in a molecular state, a tetra-quark or a mixing of the two structures [17,18,19,20,21,22,23,24,25,26,27,28]. An intuitive opinion suggests that a narrow-width (i.e. several tens of MeV) exotic particle might be in a molecular state, whereas a wide-width (i.e. several 100 MeV) should be a tetraquark. However definitely, this naive consideration cannot be a criterion for judging the exotic structure by merely its width. At most it provides a hint to help confirming the inner structure. As a matter of fact, so far no exotic state has ever been firmly determined as a molecular state. Actually, if an exotic boson is confirmed to be in a molecular state, a careful study would be very helpful to understand the dynamics which result in the different inner structures. Because we lack available data at present, let us theoretically construct such states which should be ideal molecular systems. We would assume that bound states of $B\pi$ and $D\pi$ should be ideal molecular systems.

The authors of Ref. [28] argued that the newly observed X(5568) contains constituents of $su\bar{b}\bar{d}$; it has an additional valence quark different from $\Xi _b$ with usb contents. It has a mass of 5619.5 MeV, it is lighter than the mass of $\Xi _b$, so that X(5568) seems not to be a $su\bar{b}\bar{d}$ tetraquark, if it indeed exists. The other researches [29,30,31] support the idea that such a tetraquark with constituents of $su\bar{b}\bar{d}$ should be heavier than $\Xi _b$.

Following this argument we would be tempted to suppose that if a non-strange four-quark state with open bottom or charm exists and is lighter than $\Lambda _b$ or $\Lambda _c$, the only possible choice is that they are pure molecular states of $B\pi$ or $D\pi$. The reason is that a pion is the lightest boson. It especially is lighter than a valence quark. Even though the reason why pions are so light is still not fully understood, the fact that they are lighter than valence quarks is surely confirmed. More concretely, since the mass of $\pi$ is lighter than any constituent quark, the molecular state of $B\pi$ or $D\pi$ generally should be lighter than the tetraquark state with the same quark-structure and as well as the corresponding baryons such as $\Lambda _b$ or $\Lambda _c$. We are going to search experimentally for exotic four-quark states which are lighter than $\Lambda _b$ or $\Lambda _c$ because there is a strong evidence that they are hadronic molecules. If the bound state of $B\pi$ ($D\pi$) is experimentally confirmed we will have all reason to believe that other molecular states indeed exist in nature. That is why the exploration of $B\pi$ and $D\pi$ bound states is crucially important.

Obviously, the molecules $B\pi$ or $D\pi$ do not decay via strong interactions; therefore, one expects to observe them only in radiative and/or weak processes. It would definitely make detection more difficult but it is not impossible. Indeed the bound state $B\pi$ may decay into $B^*\gamma$ with a larger rate than weak decay modes. Thus we will more focus on the $B\pi$ bound state and its radiative decay in this paper.

In the quantum field theory at the lowest order two particles interact with each other by exchanging certain particles. For our case the molecular state consists of two color-singlet mesons; we can derive the effective hamiltonian which corresponds to exchanging scalar (such as $\sigma$) or vector (such as $\rho$) mesons between B and $\pi$ (or D and $\pi$).

In Ref. [32] the authors employed the Bethe–Salpeter equation to study the $K\bar{K}$ or BK molecular state and their decays. In this work we follow their approach to study the molecular state of $B\pi$. Here we only are concerned with the ground states, i.e. the orbital angular momentum between the two constituent mesons, which is zero ($l=0)$ so the $J^{P}$ of the molecular state is $0^+$. Since the isospins of B and $\pi$ are 1 / 2 and 1, the isospin state of $B\pi$ can reside in either 3/2 or 1/2 states. Different isospin states have different effective vertices for the strong-interaction which determines if the bound states can be formed as a physical object. We will first solve the B–S equation to explore the possibility of forming the bound state and obtain the corresponding B–S wave function. With the wave function we will estimate its radiative decay rate in the same framework.

After this introduction we will present the B–S equations for the $0^+$ molecular state and derive the formula for its radiative decay rate. Then in Sect. 3 we will present our numerical results. We will explicitly display all input parameters. Section 4 is devoted to a brief summary. As we indicated above, we concentrate in this work on the $B\pi$ molecular states. In the last section we will briefly discuss the $D\pi$ case.

Fig. 1

The bound states of $B\pi$ formed by exchanging light vector mesons (a) and $B^*$ (b)

2 The bound states of $B\pi$ and their radiative decay in the Bethe–Salpeter framework

2.1 The molecular state of $B\pi$

Since the isospins of B and $\pi$ are 1/2 and 1 the possible bound states of $B\pi$ should be in two isospin assignments i.e. $|I,I_3\rangle$ are $|\frac{1}{2},\pm \frac{1}{2}\rangle$ $|\frac{3}{2},\pm \frac{1}{2}\rangle$ and $|\frac{3}{2},\pm \frac{3}{2}\rangle$. Let us work on the isospin states

$$\begin{aligned} \left| \frac{1}{2},\frac{1}{2}\right\rangle =\sqrt{\frac{2}{3}}|B^0\pi ^+\rangle -\sqrt{\frac{1}{3}}|B^+\pi ^0\rangle , \end{aligned}$$

$$\begin{aligned} \left| \frac{3}{2},\frac{1}{2} \right\rangle =\sqrt{\frac{1}{3}}|B^0\pi ^+\rangle +\sqrt{\frac{2}{3}}|B^+\pi ^0\rangle . \end{aligned}$$

and

$$\begin{aligned} \left| \frac{3}{2},\frac{3}{2}\right\rangle =|B^+\pi ^+\rangle . \end{aligned}$$

While the states $|\frac{1}{2},-\frac{1}{2}\rangle$, $|\frac{3}{2},-\frac{1}{2}\rangle$ and $|\frac{3}{2},-\frac{3}{2}\rangle$ are just the charge conjugate states of $|\frac{1}{2},\frac{1}{2}\rangle$, $|\frac{3}{2},\frac{1}{2}\rangle$ and $|\frac{3}{2},\frac{1}{2}\rangle$, therefore their properties are the same.

2.2 The Bethe–Salpeter (B–S) equation for $0^+$ molecular state

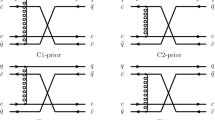
Two mesons may form a bound state by exchanging appropriate mesons. The scenario is depicted in Fig. 1. The relative and total momenta of the bound state in the equations are defined as

$$\begin{aligned}&p = \eta _2p_1 - \eta _1p_2,\quad p' = \eta _2p'_1 - \eta _1p'_2,\nonumber \\&P = p_1 + p_2 = p'_1 + p'_2 , \end{aligned}$$

(1)

where p and $p'$ are the relative momenta before and after the effective vertices, $p_1$ ($p'_1$) and $p_2$ ($p'_2$) are the momenta of the constituents before and after the effective vertices, P is the total momentum of the bound state, $\eta _i = m_i/(m_1+m_2)$ and $m_i\, (i=1,2)$ is the mass of the i-th constituent meson.

The corresponding B–S equation was deduced in Refs. [32, 33] as

$$\begin{aligned}&{E^2-(E_1+E_2)^2\over (E_1+E_2)/E_1E_2} \widetilde{\chi }_{{}_\mathcal {P}}^{}(\mathbf{p}) ={i\over 2}\int {\mathrm{d}^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} }K(\mathbf{p},\mathbf{p}')\widetilde{\chi }_{{}_\mathcal {P}}^{}(\mathbf{p}')\nonumber \\&F(\mathbf p-\mathbf p')^2 , \end{aligned}$$

(2)

where E is the total energy of the bound state, $E_i = \sqrt{\mathbf{p}^2 + m_i^2}$ and $\widetilde{\chi }_{{}_\mathcal {P}}^{}(\mathbf{p})$ is the B–S wave function in the three-momentum space. Therefore, the key point is to determine the kernel function $K(\mathbf{p},\mathbf{p}')$.

Since the constituent mesons are not point particles, a form factor at each effective vertex should be introduced to reflect the finite-size effects of these hadrons. The form factor is assumed to be in the form:

$$\begin{aligned} F(\mathbf{k}) = {2\Lambda ^2 - M_\mathrm{V}^2 \over 2\Lambda ^2 + \mathbf{k}^2},\quad \mathbf{k} = \mathbf{p}-\mathbf{p}' , \end{aligned}$$

(3)

where $\Lambda$ is a cutoff parameter and usually fixed by fitting data. For exchanging a light vector ($\rho$ or $\omega$) between the mesons as shown in Fig. 1a, the kernel is [32]

$$\begin{aligned} K(\mathbf{p},\mathbf{p}')= & {} i C_{I,I_3}\,{g_{_{BBV}}g_{_{ V\pi \pi }}'}\,\nonumber \\&\times \, {(\mathbf{p}+\mathbf{p}')^2 + 4\eta _1\eta _2 E^2 + (\mathbf{p}^2-\mathbf{p}'{}^2)^2/M_\mathrm{V}^2 \over (\mathbf{p}-\mathbf{p}')^2 + M_\mathrm{V}^2}.\nonumber \\ \end{aligned}$$

(4)

The Feynman diagram for exchanging $\sigma (f_0(500))$ is the same as in Fig. 1a, the kernel is

$$\begin{aligned} K(\mathbf{p},\mathbf{p}') = i C_{I,I_3}\,4m_Bm_\sigma {g_{_{BB\sigma }}g_{_{\sigma \pi \pi }}}\, {1 \over (\mathbf{p}-\mathbf{p}')^2 + M_\mathrm{\sigma }^2} . \end{aligned}$$

(5)

While for exchanging $B^*$ the kernel (shown in Fig. 1b) is

$$\begin{aligned}&K(\mathbf{p},\mathbf{p}') \nonumber \\&\quad = -i C_{I,I_3}\,{g_{_{B^*BB}}g_{_{B^*\pi \pi }}}\,\nonumber \\&\qquad \times \, {(\mathbf{p}-\mathbf{p}')^2 + E^2 + [\eta _1E^2-(\mathbf{p}^2-{} \mathbf{p}'{}^2)] [\eta _1E^2+(\mathbf{p}^2-{} \mathbf{p}'{}^2)]/M_{ B^*}^2 \over (\mathbf{p}+v\mathbf{p}')^2 + M_{ B^*}^2-(\eta _1-\eta _2)^2E^2}.\nonumber \\ \end{aligned}$$

(6)

Since the function $\widetilde{\chi }(\mathbf {p})$ only depends on the norm of the three-momentum we first may integrate over the azimuthal angle in Eq. (2),

$$\begin{aligned} \frac{i}{2}\int {\mathrm{d}^3\mathbf {p}'\over (2\pi )^3}\, {\overline{} K}(\mathbf{p},\mathbf{p}')F(\mathbf p-\mathbf p')^2, \end{aligned}$$

to obtain a new form $U(|\mathbf {p}|,|\mathbf {p}'|)$ corresponding to Eq. (4) which can be found in Ref. [32]. Then the B–S equation turns into a simplified one-dimensional integral equation

$$\begin{aligned} \widetilde{\chi }(\mathbf{|p|}) ={(E_1+E_2)/E_1E_2\over E^2-(E_1+E_2)^2 }\int {\mathrm{d} \mathbf {|p}'|}\, {\overline{} U}(\mathbf{|p|},\mathbf{|p}'|)\widetilde{\chi }(\mathbf{|p}'|).\nonumber \\ \end{aligned}$$

(7)

In terms of the approach given in Refs. [32, 33] the isospin factor can be obtained. For the $B^0\pi ^+$ molecule, the corresponding isospin factor $C_{I.I_3}$ appearing in Eqs. (4) and (5) takes different values as $C_{\frac{1}{2},\frac{1}{2}}$ are $1-\sqrt{2}$ , 1, 1 and $2-\sqrt{2}$ whereas $C_{\frac{3}{2},\frac{1}{2}}$ are $1+2\sqrt{2}$, 1, 1 and $2+2\sqrt{2}$ corresponding to respectively exchanging $\rho$, $\omega$, $\sigma$ and $B^*$. Whereas for the $B^+\pi ^0$ molecule, the isospin factor changes as $C_{\frac{1}{2},\frac{1}{2}}$ being $1-2\sqrt{2}$, 1, 1 and $-2\sqrt{2}$; $C_{\frac{3}{2},\frac{1}{2}}$ are $1+\sqrt{2}$, 1, 1 and $2+\sqrt{2}$, instead. Since the values of $C_I$ are different for $B^0\pi ^+$ and $B^+\pi ^0$ we will solve their B–S equations, respectively. For the $B^+\pi ^+$ system the isospin factor $C_{\frac{3}{2},\frac{3}{2}}$ would take the values 1, 1, 2, and 1, corresponding to exchanging three different vector mesons, $\rho$, $\omega$ and $B^*$, and $\sigma$.

In order to employ the wave function one first needs to normalize it. The normalization condition is

$$\begin{aligned}&-\frac{1}{\pi ^2}\int \frac{\mathrm{d}^3\mathbf {p}}{(2\pi )^3} [\widetilde{\chi }_{{}_\mathcal {P}}^{}(\mathbf{|p|})]^2R\nonumber \\&-\frac{1}{4\pi ^2}\int \frac{\mathrm{d}^3\mathbf {p}\mathrm{d}^3\mathbf {p'}}{(2\pi )^6}\widetilde{\chi }_{{}_\mathcal {P}}^{}(\mathbf{|p|})\widetilde{\chi }_{{}_\mathcal {P}}^{}(\mathbf{|p|}')\nonumber \\&\quad [F(\mathbf {p}-\mathbf {p'})]^2\frac{\partial K(\mathbf {p},\mathbf {p'})}{\partial E}=1. \end{aligned}$$

(8)

The detailed derivation can be found in Ref. [32], where also the expression of R is present.

Fig. 2

The radiative decay of the bound state

2.3 Estimating the decay rate of $B\pi$ molecule to $B^*+\gamma$

It is crucial to ask how we can identify the molecular four-quark system when B and $\pi$ constitute a bound state, i.e. a hadronic molecule. To confirm the inner structure one needs to measure its spectrum via its production and decay patterns. B and $\pi$ constitute a ground state hadronic molecule, which cannot decay via strong interaction. Actually, the overwhelming decay portals of these bound states are induced by the weak interaction, where the rates are small. Because of the complex background experimental detections are rather difficult, especially for the hadron colliders. Fortunately some molecular states can decay by radiating a photon. Obviously such a process is easier to be observed and results as well in a $B\pi$ molecule.

The Feynman diagrams for radiative decays of the $B\pi$ molecule are shown in Fig. 2. Figure 2a corresponds to exchanging $\rho$, $\omega$ or $\pi$, while Fig. 2b is for exchanging B or $B^*$. Following Refs. [32, 33, 35] the transition matrix elements by exchanging $\rho (\omega )$, $\pi$, B and $B^*$ are

$$\begin{aligned} M_{\rho (\omega )}= & {} i\frac{\sqrt{2E}g_{BB^*\rho }g_{\rho \pi \gamma }}{m_{B^*}}C'_{I,I_3}\int \frac{\mathrm{d}^4p}{(2\pi )^4}q_c{p_1'}_a{\epsilon _1}_b\varepsilon ^{abc\mu }\nonumber \\&\times \, ({p_2}-q)_\sigma {p_2'}_\alpha {\epsilon _2}_\beta \varepsilon ^{\alpha \beta \nu \sigma }\frac{g_{\mu \nu }-q_\mu q_\nu /M_\rho ^2}{M^2_\rho -q^2}\nonumber \\&F(|\mathbf {q}|)^2\chi (p), \end{aligned}$$

(9)

$$\begin{aligned} M_{\pi }= & {} i\sqrt{2E}g_{BB^*\pi }g_{\pi \pi \gamma }C'_{I,I_3}\int \frac{\mathrm{d}^4p}{(2\pi )^4} 4q_bq_\beta {\epsilon _1}_b{\epsilon _2}_\beta \nonumber \\&\times \, \frac{g_{\mu \nu }-q_\mu q_\nu /M_\pi ^2}{M^2_\pi -q^2}F(|\mathbf {q}|)^2\chi (p),\end{aligned}$$

(10)

$$\begin{aligned} M_{B^*}= & {} -i\frac{\sqrt{2E}g_{BB^*\gamma }g_{B^*B^*\pi }}{m_{B^*}}C'_{I,I_3}\int \frac{\mathrm{d}^4p}{(2\pi )^4} {p_2'}_a\nonumber \\&\times \, (p_1+q)_c{\epsilon _2}_\beta \varepsilon ^{a\beta \mu c}{p_2}_\sigma ({p_1'}+q)_\alpha {\epsilon _1}_b \nonumber \\&\times \, \varepsilon ^{\alpha b\nu \sigma }\frac{g_{\mu \nu }-q_\mu q_\nu /M_B^{*2}}{M^2_{B^*}-q^2}F(|\mathbf {q}|)^2\chi (p) ,\end{aligned}$$

(11)

$$\begin{aligned} M_{B}= & {} i\sqrt{2E}g_{BB\gamma }g_{B^*B\pi }C'_{I,I_3}\int \frac{\mathrm{d}^4p}{(2\pi )^4} 4q_bq_\beta {\epsilon _1}_b{\epsilon _2}_\beta \nonumber \\&\times \, \frac{g_{\mu \nu }-q_\mu q_\nu /M_B^2}{M^2_B-q^2}F(|\mathbf {q}|)^2\chi (p), \end{aligned}$$

(12)

where $\epsilon _1$ and $\epsilon _2$ are the polarizations of $B^*$ and photon respectively. For $B^0\pi ^+$ the isospin factor $C_{\frac{3}{2},\frac{1}{2}}$ takes a value $\frac{2}{\sqrt{3}},\;0,\;\frac{2}{\sqrt{3}},\;\frac{1}{\sqrt{3}},\;\frac{1}{\sqrt{3}}$ corresponding to exchanging $\rho$, $\omega$, $\pi$, B and $B^*$, whereas for $B^+\pi ^0$ the isospin factors $C_{\frac{3}{2},\frac{1}{2}}$ are, respectively, $\sqrt{\frac{2}{3}},\sqrt{\frac{2}{3}},\; \sqrt{\frac{2}{3}},\;2\sqrt{\frac{2}{3}},\; 2\sqrt{\frac{2}{3}}$. To simplify our calculation we set $p_0=0$ in the kinetic part of the integrand in Eq. (9), for example, in Eq. (10), $p_0=0$ applies merely to $q_c{p_1'}_a{\epsilon _1}_b\varepsilon ^{abc\mu }({p_2}-q)_\sigma {p_2'}_\alpha {\epsilon _2}_\beta \varepsilon ^{\alpha \beta \nu \sigma }\frac{g_{\mu \nu }-q_\mu q_\nu /M_V^2}{M_V-q^2}$, then the integrand turns into

$$\begin{aligned} M_\rho= & {} i\sqrt{2E}g_1g_2C'_{I,I_3}\int \frac{\mathrm{d}^3p}{(2\pi )^3}q_c{p_1'}_a{\epsilon _1}_b\varepsilon ^{abc\mu }\nonumber \\&\times \, ({p_2}-q)_\sigma {p_2'}_\alpha {\epsilon _2}_\beta \varepsilon ^{\alpha \beta \nu \sigma }\frac{g_{\mu \nu }-q_\mu q_\nu /M_\rho ^2}{M^2_\rho -q^2}\nonumber \\&\times \,F(|\mathbf {q}|)^2\tilde{\chi }(\mathbf {p}), \end{aligned}$$

(13)

where the definition $\widetilde{\chi }_{_P}(\mathbf{p})= \int \mathrm{d}p^0 \, \chi _{_P}(p) \,$ is used. In the new expression the argument of $\widetilde{\chi }_{_P}(\mathbf{p})$ is a three-momentum $\mathbf{p}$ instead of the four momentum p. It is noted that this simplification is similar to the instantaneous approximation for solving the B–S equation, which is usually adopted.

Generally we can define two form factors for the transition

$$\begin{aligned} M=F_1\epsilon _1\cdot \epsilon _2+F_2\epsilon _1\cdot P\epsilon _2\cdot P, \end{aligned}$$

(14)

and $F_1$ and $F_2$ can be extracted from Eq. (13) and calculated numerically.

3 Numerical results

To solve the B–S equation and numerically calculate the radiative decay rate some input parameters are needed. The mass of B, $B^*$, $\rho$, $\omega$, $\pi$ are taken from the databook [34].

We also need to determine the relevant coupling constants appearing at the effective vertices. By calculating the transition $\rho \rightarrow \pi \pi$ and comparing the result with the data [34] one can fix the coupling $g_{\rho \pi \pi }=5.97$. Similarly we fix $g_{\omega \pi \pi }=0.175$, $g_{\rho \pi \gamma }=0.417$ GeV$^{-1}$, $g_{\omega \pi \gamma }=1.215$ GeV$^{-1}$. However for determining the coupling constants involving $B^{(*)}$ mesons there are no available data, so we fix $g_{D^*D\pi }=8.05$ and $g_{D^*D\gamma }=0.706$ GeV$^{-1}$ by using relations $g_{B^*B^*\pi }=g_{B^*B\pi }=g_{D^*D\pi }$ and $g_{B^*B^*\gamma }=g_{B^*B\gamma }=g_{D^*D\gamma }$ which are reasonable within the heavy quark limit. $g_{BB\rho }=g_{B^*B\rho }=3$ is taken from Ref. [35]. The $g_{{BB\sigma }}=0.76$ was fixed in Ref. [36]. If one sets $m_\sigma =500$ MeV and $\Gamma _\sigma =550$ MeV, $g_{\sigma \pi \pi }=4.09$ is obtained. $\Lambda$ is the cutoff parameter which will be used while searching for a solution of the B–S equation. In Ref. [37] the value of $\Lambda$ is suggested to be 0.88–1.1 Gev. In this work letting $\Lambda$ span in the range from 0.8 to 1.2 GeV, we solve the B–S equation.

Table 1 The $\Lambda$ for different bound energies of $B\pi (I=\frac{3}{2}, I_{z}=\frac{1}{2}$)

Fig. 3

The B–S wave function of the molecular state of $B^0\pi ^+$ ($\Delta E=40$ MeV)

Table 2 The $\Lambda$ for different bound energies of $B^+\pi ^+(I=\frac{3}{2}, I_{z}=\frac{3}{2}$)

Table 3 The form factors and decay widths for different binding energies of $B^0\pi ^+(I=\frac{3}{2}, I_{z}=\frac{1}{2}$)

We now solve the B–S equation. $\mathbf |p|(|p'|)$ takes n discrete values which are arranged in order from small to large. The gap between two adjacent values is $\Delta \mathbf p$, then $\chi (\mathbf{|p|})$ can constitute a column matrix and the coefficients on the right side of Eq. (7) make an $n\times n$ matrix M. Our strategy is as follows. The binding energy is $\Delta E=m_1+m_2-E$, thus we write up the determinant of $M(\Delta E,\Lambda )-I$ (I is a unit matrix) where $M(\Delta E,\Lambda )$ is a matrix function of the binding energy $\Delta E$ and parameter $\Lambda$. Then setting equation $|M(\Delta E,\Lambda )-I|=0$ which is equivalent to the secular equation in regular quantum mechanics, by varying $\Delta E$ we obtain a series of solutions for $\Lambda$. We will check whether the obtained values of $\Lambda$ fall within the range of 0.8–1.2 GeV which is priori set. If the answer is yes we can conclude that the bound state exists. With the $\Delta E$ and $\Lambda$ obtained, the B–S wave function is achieved.

When we try to solve the B–S equation for the $B\pi$ system in isospin $|\frac{1}{2},\frac{1}{2}\rangle$ state, we find that by setting different binding energies one cannot achieve a value of $\Lambda$ which falls within the supposed range 0.8–1.2 GeV. Therefore we can determine that a $B\pi$ bound state of isospin (1 / 2, 1 / 2) does not exist in Nature. By contrary, the isospin $|\frac{3}{2},\frac{1}{2}\rangle$ $B\pi$ bound state does exist. According to the aforementioned $C_{I,I_3}$ values one can understand that the interaction between B and $\pi$ in $|\frac{1}{2},\frac{1}{2}\rangle$ system is not strong enough to bind the constituents but it is sufficiently large for $|\frac{3}{2},\frac{1}{2}\rangle$. In Table 1 we present the $\Lambda$ values for the bound state of $B\pi$ state $|\frac{3}{2},\frac{1}{2}\rangle$. The normalized wave function is depicted in Fig. 3. For the bound state $B^+\pi ^+$ besides the strong interaction the electromagnetic interaction also applies; however, on comparing the electromagnetic coupling $e^2$ with the effective strong coupling $g_1g_2$, one can safely ignore the contribution of the electromagnetic interaction after all (Table 2).

Even though $|\frac{3}{2},\frac{1}{2}\rangle$ bound states do not decay via strong interaction, they decay into other hadrons by emitting a photon, i.e a radiate decay. The form factors $F_1$ and $F_2$ in the transition $M\rightarrow B^*\pi$ are calculated numerically. The theoretically estimated decay rates are present in Table 3 for different binding energies.

4 Conclusion and discussions

In this work we study the bound state of $B\pi$ which seems to be identified as a pure molecular state. Meanwhile, as long as it is experimentally observed, we can firmly determine the existence of hadronic molecules. Combining future experimental data with the results provided in this work, we can gain valuable information as regards the structures of the four-quark exotic states and, moreover, the applicable dynamics.

We suggest that by solving the B–S equation with appropriate effective interaction between two constituent hadrons one can determine whether the four-quark system can be bound as a molecular state. Since the constituents are hadrons the effective interactions can be derived in terms of field theory. Since the isospins of B and $\pi$ are 1/2 and 1 respectively the bound state can be $|\frac{1}{2},\frac{1}{2}\rangle$, $|\frac{3}{2},\frac{1}{2}\rangle$ and $|\frac{3}{2},\frac{3}{2}\rangle$. Priori setting a reasonable range for the parameter $\Lambda$ within 0.8–1.2 GeV according to the suggestions given in literature, one can numerically solve the B–S equation to gain the binding energies and wave functions of the systems with quantum number $|\frac{3}{2},\frac{1}{2}\rangle$ and $|\frac{3}{2},\frac{3}{2}\rangle$. Our numerical results show that there is not a solution for the bound state with quantum number $|\frac{1}{2},\frac{1}{2}\rangle$.

In Refs. [38, 39] the authors explored the coupled-channel scattering of $B_s\pi$ $-B\bar{K}$ in the framework of unitary chiral perturbation Theory and found that X(5568) could not be a molecular state. However, it does not completely forbid $B_s\pi$ even $B\pi$ to form molecular states with certain quantum numbers because it is believed that the chiral perturbation theory is more suitable to predict existence of bound states near the thresholds. In fact the authors of Ref. [40] indeed found a broad resonance above the threshold in the coupled-channel analysis of $D\pi$. It might imply that the existence of a bound state or resonance is absolutely forbidden.

Since the parameter cannot be determined very precisely our prediction of the mass spectrum of the bound state is also not very accurate as the errors come with uncertainties of theoretical input. As solving the B–S equation of the system for different binding energies, the corresponding parameter $\Lambda$ and B–S wave function are obtained. With the wave function we can estimate the radiative decay rate of $B\pi \big (|\frac{3}{2},\frac{1}{2}\rangle \big )\rightarrow B^*\gamma$. It is found that the partial width can vary in a certain range with different input values of $\Lambda$. We hope the future measurement will tell us the measured values of the binding energy and the partial width of the radiative decay. The data would check our calculation and help to fix the relevant parameters. Definitely smart experimentalists will do good jobs if they would measure them in the near future in order to determine whether the bound states exist.

Even though in this work we only deal with the $B\pi$ molecular states the same approach can easily be applied to study the $D\pi$ molecular states. The only difference is that the evaluated $D\pi$ mass is smaller than $D^*$, so that $D\pi$ molecule cannot decay via electromagnetic interaction due to the constraint of the final state phase space, thus it only has weak decay portals. Definitely, since the rates of weak decays are obviously small, measurements on such $D\pi$ molecular states become even more difficult; however, they are not impossible.

If the result of our experimental measurements is positive we would have confidence as regards the existence of molecular states and learn more about their inner structures.

Appendix A: The effective interactions

[33, 37, 41,42,43,44]

$$\begin{aligned} \mathcal {L}_{BB\rho }= & {} ig_{BB\rho }[\bar{B}^0\partial _\mu B^+\rho ^{-\mu }-\partial _\mu \bar{B}^0 B^+\rho ^{-\mu } \nonumber \\&+\, \bar{B}^0\partial _\mu B^0\rho ^{0\mu }-\partial _\mu B^- B^+\rho ^{0\mu }+h.c.], \end{aligned}$$

(15)

$$\begin{aligned} \mathcal {L}_{BB\omega }= & {} ig_{BB\omega }[\bar{B}^0\partial _\mu B^0\omega ^{\mu }-\partial _\mu B^- B^+\omega ^{\mu }+h.c. ], \end{aligned}$$

(16)

$$\begin{aligned} \mathcal {L}_{\rho \pi \pi }= & {} ig_{\rho \pi \pi }[\partial _\mu \pi ^+ \pi ^-\rho ^{0\mu }+\partial _\mu \pi ^0 \pi ^+\rho ^{-\mu } \nonumber \\&-\,\partial _\mu \pi ^+\pi ^0\rho ^{-\mu } +h.c.], \end{aligned}$$

(17)

$$\begin{aligned} \mathcal {L}_{B^*B\pi }= & {} ig_{B^*B\pi }[\partial _\mu \pi ^+B^{0*}B^-\pi ^+B^{0*}\partial _\mu B^-\partial _\mu \pi ^+B^{0}B^{-*}\nonumber \\&+\,\pi ^+\partial _\mu B^{0} B^{-*}+h.c.],\end{aligned}$$

(18)

$$\begin{aligned}&i\frac{g_{B^*B\pi }}{\sqrt{2}}[\pi ^0\partial _\mu B^0\bar{B}^{0*}-\partial _\mu \pi ^0B^0\bar{B}^{0*}\nonumber \\&\quad +\,\partial _\mu \pi ^0 B^+B^{-*}-\pi ^0\partial _\mu B^+ B^{-*}+h.c.] ,\end{aligned}$$

(19)

$$\begin{aligned} \mathcal {L}_{B^*B\gamma }= & {} ig_{B^*B\gamma }e\varepsilon ^{\mu \nu \alpha \beta }\partial _\mu A_\nu (B^*_\alpha \partial _\beta B^\dagger \nonumber \\&-\,\partial _\beta B^*_\alpha B^\dagger +h.c.) , \end{aligned}$$

(20)

$$\begin{aligned} \mathcal {L}_{\rho \pi \gamma }= & {} ig_{\rho \pi \gamma }e\varepsilon ^{\mu \nu \alpha \beta }\partial _\mu A_\nu (\rho ^0_\alpha \partial _\beta \pi ^0\nonumber \\&-\,\partial _\beta \rho ^0_\alpha \pi ^0+\rho ^+_\alpha \partial _\beta \pi ^-\partial _\beta \rho ^+_\alpha \pi ^-+h.c.), \end{aligned}$$

(21)

$$\begin{aligned} \mathcal {L}_{BB\gamma }= & {} e A_\mu (\partial _\mu B B^\dagger - B \partial _\mu B^\dagger ), \end{aligned}$$

(22)

$$\begin{aligned} \mathcal {L}_{B^*B^*\pi }= & {} - \frac{g_{B^*B^*\pi }}{m_{B^*}}\varepsilon ^{\mu \nu \alpha \beta }\partial _{\mu }B^*_{\nu }{ B^*}^\dagger _{\alpha } \partial _\beta {\pi }, \end{aligned}$$

(23)

$$\begin{aligned} \mathcal {L}_{B^*B\rho }= & {} - \frac{g_{B^*B\rho }}{m_{B^*}}\varepsilon ^{\mu \nu \alpha \beta } (B\partial _{\mu }\rho _{\nu }\partial _{\alpha }{B_\beta ^{*\dagger }}+\partial _{\mu }{B}_\nu \partial _{\alpha }\rho _{\beta }B^\dagger ),\nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} \mathcal {L}_{BB\sigma }= & {} -2m_Bg_{BB\sigma }\sigma B B^\dagger , \end{aligned}$$

(25)

$$\begin{aligned} \mathcal {L}_{\sigma \pi \pi }= & {} -2m_\sigma g_{\sigma \pi \pi }\sigma \pi \pi ^\dagger . \end{aligned}$$

(26)