1 Introduction

In the past few years, the scientific interest in the study of gravitational effects on quantum-mechanical systems has been renewed and many systems has been studied [1,2,3,4,5,6,7,8,9,10,11,12]. For example, in [3] it was shown that the energy spectrum associated with one-electron atoms in an arbitrary curved spacetime is different from the one obtained in the usual flat Minkowski spacetime. The energy levels are shifted by the gravitational field and the effects of the curvature appear as perturbations in the relativistic fine structure. In [12] neutrinos have been studied in this context, and in [13], the effects of magnetic fields on the metric have been considered.

Another kind of system that may be investigated with this purpose are the cosmic strings. Cosmic strings are very interesting systems, that are supposed to be formed during a symmetry breaking phase transition in the early universe [14,15,16,17,18,19,20] and may be considered as topological defects in the spacetime structure. The spacetime around them is locally flat, but this is not a global property. The presence of such kind of topological defects can also influence the behavior of a quantum-mechanical system, as in [8], where the Dirac equation has been solved in the presence of a Coulomb and a scalar potentials in the cosmic string spacetime and it was shown that its presence destroys the degeneracy of all the energy levels. In [21], solutions of the Klein–Gordon equation in Gödel-type spaces with an embedded cosmic string are considered, and it was shown that the presence of topological defects in the spacetime breaks the degeneracy of energy levels in the cases of Som–Raychaudhuri, spherical and hyperbolic Gödel solutions.

Noninertial effects of rotating frames on physical systems is another kind of aspect that have been studied in much work in the literature, as for example in [22, 23]. For instance, the Mashhoon effect is the coupling of the spin of the particles with the angular velocity of the rotating frames and it arises from the influence of these noninertial frames when interference effects are considered [24]. In [25], the Landau quantization for neutral particles with a permanent magnetic dipole moment has been studied, and it has been shown that the noninertial effects modify the cyclotron frequency. The molecular Aharonov–Carmi effect has been considered for \(C_{60}\) molecules in [26], and the energy shift of the valence electrons due to molecular rotation has been calculated.

On the other hand, the study of scalar potentials in quantum mechanics is very important in order to establish basic proprieties of several systems of interest. The absence of Klein’s paradox for scalar potentials is an important feature of this approach. In this way, if a potential is vectorlike, the possibility of a tunneling solution arises, but this situation does not occur when the confining potential is a scalar [27].

In addition, the scalar potential can simulate effective masses, as is well known from nuclear or solid state physics, and the effect of the spatial dependence of these effective masses has been found in many physical systems. Recently, the study of some of these systems has attracted the attention from many authors [28,29,30,31,32,33,34,35,36]. Applications have been found in fields such as the electronic properties of the semiconductors [37], \(^{3}\)He clusters [38], quantum liquids [39], semiconductor heterostructures [40] and others. One side of this research is concerned with the development of methods and techniques for studying how do these mass variations affect the dynamics of quantum systems.

Solutions of non-relativistic wave equations with spatial dependence of the effective mass have been obtained for many systems. The Schrödinger equation with a smooth mass and a step potential has been solved by Dekar et al. [41], where the behavior of the transmission coefficient have been compared to an abrupt step potential. Besides, the supersymmetric quantum-mechanical formalism to the Schrödinger equation has been extended to describe particles characterized by position-dependent effective masses [42]. Exact solutions of a spatially dependent mass Dirac equation via Laplace transformation method [43] have been also obtained explicitly. This method is an integral transform and recently have been used to solve the Schrödinger equation in non-relativistic problems.

In the present paper, we will study spin-0 bosons in a cosmic string spacetime by considering the Klein–Gordon equation in the presence of a Coulomb-like scalar potential \(s\left( r\right) =\eta /r\), where \(r=\sqrt{ x^{2}+y^{2}}\) is the radial coordinate and \(\eta \) a constant. In addition, a rotating frame in the cosmic string spacetime will be considered, and we will show that noninertial effects restrict the physical region of the spacetime where the particle can be placed, and furthermore the energy levels are shifted by the noninertial effects on the particle. This interesting feature is an indicator of a deeper phenomenon: the coupling between the angular quantum number and the angular velocity of the rotating frame. In the following, we show that the presence of a Coulomb-like scalar potential can form bound states for the Klein–Gordon equation in this spacetime.

The paper is organized as follows: in Sect. 2, we will describe the cosmic string spacetime and the transformation from spacetime coordinates to rotating coordinates. In Sect. 3, we will present a equation for spin-0 bosons in a cosmic string spacetime for the potential \(V\left( r\right) =\eta /r\) and in Sect. 4, we will obtain the numerical computation of the Klein–Gordon by a root-finding procedure. Finally, Sect. 5 presents our conclusions. In this work, we use natural units, \(\hbar =c=G=1\).

2 The cosmic string spacetime

The metric of a cosmic string is a solution of Einstein’s equations and it describes a spacetime determined by an infinitely long straight string with nonvanishing thickness. The string spacetime is assumed to be static and cylindrically symmetric, and then the metric representing this system is given by [2, 18]

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{\prime 2}+\mathrm{d}r^{\prime 2}+\alpha ^{2}r^{\prime 2}\mathrm{d}\phi ^{\prime 2}+\mathrm{d}z^{\prime 2}, \end{aligned}$$
(1)

where \(\alpha =1-4G\mu \) and \(\mu \) is the mass density of the string. In this metric, the azimuthal angle range is \(\phi ^{\prime }\in [0,2\pi )\), while the r coordinate range is \(r \in [0,\infty )\). The parameter \(\alpha \) may assume values in which \(\alpha \le 1\) or \(\alpha >1\), and, in this case, it corresponds to a spacetime with negative curvature. Moreover, \(\alpha \) represents the deficit angle of the conical spacetime and \(\alpha =1\) corresponds to a flat spacetime. In this work, we are interested in studying the case \(0<\alpha <1\). The generalization of this formulation for a noninertial reference frame may be made by considering the coordinate transformation

$$\begin{aligned} t^{\prime }=t,\quad r^{\prime }=r, \quad \phi ^{\prime }=\phi +\omega t, \quad z^{\prime }=z, \end{aligned}$$
(2)

where \(\omega \) is angular velocity of the rotating frame. Inserting this transformation into Eq. (1) we obtain the line element

$$\begin{aligned} \mathrm{d}s^{2}&=-\mathrm{d}t^{2}+\mathrm{d}r^{2}+\alpha ^{2}r^{2}\left( \mathrm{d}\phi +\omega \mathrm{d}t\right) ^{2}+\mathrm{d}z^{2} \nonumber \\&=-\left( 1-\alpha ^{2}r^{2}\omega ^{2}\right) \mathrm{d}t^{2}+2\alpha ^{2}r^{2}\omega \mathrm{d}t\mathrm{d}\phi \nonumber \\&\quad +\mathrm{d}r^{2}+\alpha ^{2}r^{2}\mathrm{d}\phi ^{2}+\mathrm{d}z^{2}, \end{aligned}$$
(3)

which may be associated with the covariant metric tensor

$$\begin{aligned} g_{\mu \eta }=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -( 1-\alpha ^{2}r^{2}\omega ^{2}) &{} 0 &{} 0 &{} \alpha ^{2}r^{2}\omega \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ \alpha ^{2}r^{2}\omega &{} 0 &{} 0 &{} \alpha ^{2}r^{2} \end{array} \right) , \end{aligned}$$

which is a non-diagonal metric tensor where the effects of the topology and the rotation of the reference frame are taken into account. An interesting feature of Eq. (3) is the condition

$$\begin{aligned} 0<r<1/\alpha \omega . \end{aligned}$$
(4)

This condition is related to the fact that for \(r> 1/\alpha \omega \) the velocity of the particle is greater than the velocity of the light, for this reason, it is convenient to restrict r to the range \((0,1/\alpha \omega )\). Thus, the wave function of the quantum particle must vanish at \( r=1/\alpha \omega \) and this system presents two different classes of solutions that depend on the value of the product \(\alpha \omega \). The first case is obtained by adopting the limit \(\alpha \omega \ll 1\) (\( 1/\alpha \omega \rightarrow \infty \)), and as a second case, we have considered an arbitrary relation \(\alpha \omega .\)

3 Klein–Gordon equation in the cosmic string spacetime

In flat Minkowski spacetime, the spin-0 particles are represented by the usual Klein–Gordon equation. In this section we will present a equation for these particles in a curved spacetime. In order to determine this equation one may replace the ordinary derivatives by covariant derivatives in the equation and the result is

$$\begin{aligned} -\frac{1}{\sqrt{-g}}\partial _{\mu } ( g^{\mu \nu }\sqrt{-g}\partial _{\nu }\psi ) +m^{2}\psi =0, \end{aligned}$$
(5)

which is the Klein–Gordon equation in a curved spacetime [44], where m is the particle mass and g is the determinant of the metric tensor. An arbitrary scalar potential may be taken into account by making a modification in the mass term as \(m\rightarrow m+V\left( r\right) \). Substituting the mass term into (5) we obtain the following differential equation:

$$\begin{aligned} -\frac{1}{\sqrt{-g}}\partial _{\mu } ( g^{\mu \nu }\sqrt{-g}\partial _{\nu }\psi ) +\left( m+V\right) ^{2}\psi =0. \end{aligned}$$
(6)

Solutions of Eq. (6) are, in general, very difficult to find and the known ones are limited to a small set of potentials and spacetimes. In the following, we will obtain two classes of solutions of the Klein–Gordon equation in a cosmic string space for Coulomb-like scalar potentials as an example. By considering the line element (3), we obtain

$$\begin{aligned}&\left[ -\partial _{t}^{2}+\partial _{r}^{2}+\frac{1}{r}\partial _{r}+\partial _{z}^{2}+2\omega \partial _{t}\partial _{\phi }\right. \nonumber \\&\quad \left. +\left( \frac{1}{\alpha ^{2}r^{2}}-\omega ^{2}\right) \partial _{\phi }^{2}-\left( m+V\right) ^{2}\right] \psi =0, \end{aligned}$$
(7)

which is the Klein–Gordon equation in the cosmic string spacetime. Equation (7) is independent of t, z and \(\phi \), so it is reasonable to write the solution as

$$\begin{aligned} \psi ( t,r,z,\phi ) =\mathrm{e}^{-i\varepsilon t}\mathrm{e}^{il\phi }\mathrm{e}^{ip_{z}z}R\left( r\right) , \end{aligned}$$
(8)

where \(l=0,\pm 1,\pm 2,\pm 3\), \(\varepsilon \) can be interpreted as the energy of the particle and \(p_{z}\) is the momentum in the z direction. Substituting (8) into Eq. (7), we obtain the radial differential equation

$$\begin{aligned}&\bigg [ \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}-\frac{l^{2}}{\alpha ^{2}r^{2}} -\left( m+V\right) ^{2} \nonumber \\&\quad + ( \varepsilon +\omega l) ^{2}-p_{z}^{2}\bigg ] R\left( r\right) =0. \end{aligned}$$
(9)

From Eq. (9), we can see that the term \(\omega l\) works as a time-like vector potential, i.e., the noninertial effect of rotating frames in the Klein–Gordon equation is equivalent to a time-like vector potential.

It is possible to define a four-current \(J_{\mu }\) in terms of our preceding results. Equation (6) can be expressed as

$$\begin{aligned} -\nabla ^{\nu }\nabla _{\nu }\psi +\left( m+V\right) ^{2}\psi =0, \end{aligned}$$
(10)

where \(\nabla _{\nu }\) is the covariant derivative.

The conservation law for \(J_{\mu }\) follows from the procedure of multiplying (10) and its complex conjugate by \(\psi \) from the left and by \(\psi ^{*}\) from the right, respectively. The sum of those resulting equations leads to

$$\begin{aligned} \nabla ^{\nu }J_{\nu }=0, \end{aligned}$$
(11)

where

$$\begin{aligned} J_{\nu }=\frac{i}{2m} ( \psi ^{*}\nabla _{\nu }\psi -\psi \nabla _{\nu }\psi ^{*}) . \end{aligned}$$
(12)

Hence, we can identify \(J^{0}\) as a charge density and, thus, we have particles with charge \(+e\) and particles with charge \(-e\) in accordance with the existence of particles and antiparticles in the theory. From (8) and (12), we can see that the charge density (covariant component) is given by

$$\begin{aligned} J_{0}=\frac{\varepsilon }{m}\left| \psi \right| ^{2}. \end{aligned}$$
(13)

3.1 Potential \(V\left( r\right) =\eta /r\)

We want to solve the radial equation for a scalar potential of the type \( V\left( r\right) =\eta /r\), where \(\eta \) is a constant. So, substituting this potential into Eq. (9) we obtain the following expression:

$$\begin{aligned} \left[ \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}-\frac{\beta ^{2}}{r^{2}}- \frac{2\gamma }{r}-\delta ^{2}\right] R\left( r\right) =0, \end{aligned}$$
(14)

where

$$\begin{aligned} \delta ^{2}=m^{2}+p_{z}^{2}- ( \varepsilon +\omega l) ^{2},\quad \beta ^{2}=l^{2}/\alpha ^{2}+\eta ^{2},\quad \gamma =m\eta . \end{aligned}$$
(15)

In order to investigate the solutions of Eq. (14), we will consider a transformation of the radial coordinate

$$\begin{aligned} \rho =2\delta r, \end{aligned}$$
(16)

and as a result, the equation will take the form

$$\begin{aligned} \left[ \frac{\mathrm{d}^{2}}{\mathrm{d}\rho ^{2}}+\frac{1}{\rho }\frac{\mathrm{d}R}{\mathrm{d}\rho }-\frac{\beta ^{2}}{\rho ^{2}}-\frac{\gamma }{\delta \rho }-\frac{1}{4}\right] R ( \rho ) =0. \end{aligned}$$
(17)

Normalizable eigenfunctions may be obtained if we propose the solution

$$\begin{aligned} R ( \rho ) =\rho ^{\beta }e^{-\frac{\rho }{2}}F ( \rho ) , \end{aligned}$$
(18)

and substituting (18) into Eq. (17) and remembering that the parameter \(\beta \) is constant, we obtain the differential equation associated with the radial solution

$$\begin{aligned} \rho \frac{\mathrm{d}^{2}F}{\mathrm{d}\rho ^{2}}+ ( 2\beta +1-\rho ) \frac{\mathrm{d}F}{\mathrm{d}\rho }-\left( \beta +\frac{\gamma }{\delta }+\frac{1}{2}\right) F=0. \end{aligned}$$
(19)

This is the confluent hypergeometric equation, which is a second order linear homogeneous differential equation. The general solution of Eq. (19) is given by

$$\begin{aligned} F=AM ( a,b;\rho ) +B\rho ^{1-b}M ( a-b+1,2-b;\rho ) \end{aligned}$$
(20)

where

$$\begin{aligned} b= & {} 2\beta +1, \\ a= & {} \beta +\frac{\gamma }{\delta }+\frac{1}{2}, \end{aligned}$$

with arbitrary constants A and B. Here, the confluent hypergeometric function \(M ( a,b;\rho ) \) is denoted by

$$\begin{aligned} M ( a,b;\rho ) =_{1}F_{1} ( a,b;\rho ) . \end{aligned}$$
(21)

We can see that the second term in (20) has a singular point at \(\rho =0\), so we set \(B=0\).

3.2 Limit \(\alpha \omega \ll 1\) \((1/\alpha \omega \rightarrow \infty )\)

Considering now the limit \(\alpha \omega \ll 1\), which is the slow rotation regime, the boundary condition implies that the expression

$$\begin{aligned} _{1}F_{1}\left( \beta +\frac{\gamma }{\delta }+\frac{1}{2},2\beta +1;\frac{ 2\delta }{\alpha \omega }\rightarrow \infty \right) \end{aligned}$$
(22)

must be finite. Due to the asymptotic behavior of solution, it is necessary that the hypergeometric function be a polynomial function of degree N, which means that the parameter \(\beta +\frac{\gamma }{\delta }+\frac{1}{2}\) should be a negative integer. This condition implies that

$$\begin{aligned} \beta +\frac{\gamma }{\delta }+\frac{1}{2}=-N, \quad N=0,1,2,\ldots , \end{aligned}$$
(23)

and combining this equation and Eq. (15) we finally obtain the energy spectrum

$$\begin{aligned} \varepsilon _{\pm }=-\omega \left| l\right| \pm \sqrt{p_{z}^{2}+m^{2} \left[ 1-\frac{\eta ^{2}}{\left( N+\frac{1}{2}+\sqrt{l^{2}/\alpha ^{2}+\eta ^{2}}\right) ^{2}}\right] .} \end{aligned}$$
(24)
Fig. 1
figure 1

The plots of radial coordinate R as a function of variable \(\rho \) displayed for three different values of N with the parameters \(\alpha =0.8\), \(\omega =0.1\), \(\eta =-0.5\) and \(l=0\)

Full size image
Fig. 2
figure 2

The plots of \(\left| \psi \right| ^{2}\) as functions of \(\rho \) displayed for three different values of N with the parameters \(\alpha =0.8\), \(\omega =0.1\), \(\eta =-0.5\) and \(l=0\)

Full size image

This is the energy spectrum for both particle (\(\varepsilon _{+}\)) and antiparticle (\(\varepsilon _{-}\)).We can see that the energy spectrum associated with the Klein–Gordon equation in cosmic string space for the Coulomb-like scalar potential depends on \(\alpha \), the deficit angle of the conical spacetime. For \(l=0\) and \(\omega =0\) the discrete set of energies are symmetrical about \(\varepsilon =0\). In this way, the presence of noninertial effects of rotating frames in spacetime breaks the symmetry of energy levels about \(\varepsilon =0\).

Fig. 3
figure 3

The plots of particle energy spectrum \(\varepsilon \) as the function of variables N and l for \(\alpha =0.9\), \(\omega =0.01\), \(\eta =5\), and \(m=1000\)

Full size image

As said before, the parameter \(\omega \) is the angular velocity of the rotating frame, so we can observe that the energy levels are shifted by noninertial effects on the particle.

Fig. 4
figure 4

The plots of negative energy spectrum \(\varepsilon \) as the function of variables N and l for \(\alpha =0.9\), \(\omega =0.01\), \(\eta =0.5\), and \(m=1000\)

Full size image

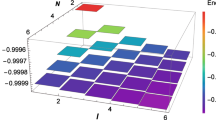
As may be seen in Fig. 1, the radial solution \(R ( \rho ) \) decreases with the coordinate \(\rho \) and becomes negligible far away from the cosmic string as \(\rho \rightarrow \infty \). In Fig. 2, we illustrate the plots of \(\left| \psi \right| ^{2}\) as a function of variable \(\rho \) for three different values of N. The plots of the energy spectrum \( \varepsilon \) as functions of the variables N and l are shown in Figs. 3 and 4.

Fig. 5
figure 5

Plot of \(\ \left| \psi \right| ^{2}\) in polar coordinates where \(\rho =\sqrt{x^{2}+y^{2}}\), x is the horizontal axis and y is the vertical axis for \(N=3\), \(m=100\), \(\alpha =0.5\), \(\omega =0.1\), and \(\eta =-0.4\)

Full size image

The behavior of \(\ \left| \psi \right| ^{2}\) for \(N=3\), \(m=100\), and \(\alpha =0.5\) in polar coordinates, is plotted in Fig. 5, where we can see that the scalar bosons tend to be better localized at the white region.

4 Arbitrary \(\omega \alpha \)

Now if we do not impose the condition \(\alpha \omega \ll 1\) for the scalar particle equation, as pointed out before, due to noninertial effects, the physical condition implies that the eigenfunction vanishes at \(r\rightarrow 1/\alpha \omega \), which means

$$\begin{aligned} _{1}F_{1}\left( \beta +\frac{\gamma }{\delta }+\frac{1}{2},2\beta +1;\frac{ 2\delta }{\alpha \omega }\right) =0. \end{aligned}$$
(25)

The quantization condition in (25) has no closed form solutions in terms of simple functions, and then it must be solved by numerical methods. In this work, we proceed to obtain the numerical computation of \(\bar{N}\) by a root-finding procedure. By solving this quantization condition, one obtains

$$\begin{aligned} \beta +\frac{\gamma }{\delta }+\frac{1}{2}=\bar{N}, \end{aligned}$$
(26)

where \(\bar{N}\) now is an undetermined number. The values of the \(\beta ,\gamma \) and \(\delta \) given by (15) yields the possible energy levels

$$\begin{aligned} \varepsilon _{\pm }=-\omega \left| l\right| \pm \sqrt{p_{z}^{2}+m^{2} \left[ 1-\frac{\eta ^{2}}{\left( -\bar{N}+\frac{1}{2}+\sqrt{l^{2}/\alpha ^{2}+\eta ^{2}}\right) ^{2}}\right] .} \end{aligned}$$
(27)

Similar to the case where \(\alpha \omega \ll 1\), we can see that the discrete set of energies for both particle (\(\varepsilon _{+}\)) and antiparticle (\(\varepsilon _{-}\)) is composed of two contributions: the first term is associated to the Coulomb-like potential embedded in a cosmic string background and the second term is associated to the noninertial effect of rotating frames, which in turn is a Sagnac-type effect [45, 46]. From (24) and (27), we can see that energy spectrum is inversely proportional to \(\alpha \) for a \(\eta \) fixed. If \(\eta \) increases (decreases) for a \(\alpha \) fixed, the energy spectrum decreases (increases). The first numerical values of \(\bar{N}\) and their respective energies are listed in Tables 1 and 2.

Table 1 The first values of \(\bar{N}\) that satisfy the quantization condition for \(\omega =0.2\)
Full size table
Table 2 The first values of \(\bar{N}\) that satisfy the quantization condition for \(\omega =0.25\)
Full size table

The first values of \(\bar{N}\) that satisfy the quantization condition for arbitrary \(\alpha \omega \) are consistent with the results for the limit \( \alpha \omega \ll 1\). The explanation for this result is found in the asymptotic behavior of the confluent hypergeometric function \( _{1}F_{1} ( A,B;\rho ) \). If \(\rho \rightarrow \infty ,\) the asymptotic behavior of function is given by

$$\begin{aligned} _{1}F_{1} ( A,B;\rho ) \simeq \frac{\Gamma \left( B\right) }{ \Gamma \left( B-A\right) }\mathrm{e}^{-i\pi A}\rho ^{-A}+\frac{\Gamma \left( B\right) }{\Gamma \left( A\right) }\mathrm{e}^{\rho }\rho ^{A-B}, \end{aligned}$$

we can see that the presence of \(\mathrm{e}^{\rho }\) in the second term spoils the normalizability of \(R ( \rho ) \), but if \(A=-N\) (non-negative integer) this behavior can be remedied and the normalizability of \(R ( \rho ) \) is obtained. The numerical computation of \(\bar{N}\) in Table 1 suggests that \(\bar{N}\) tends to a non-negative integer as the product \( \alpha \omega \) is small, i.e., \(1/\alpha \omega \rightarrow \infty \).

5 Conclusions

In this paper we have determined the Klein–Gordon equation in the presence of a Coulomb-like scalar potential in a curved spacetime. From these results a compact expression for the energy spectrum associated with the Klein–Gordon equation in a cosmic string space has been provided.

We have shown that the noninertial effects restrict the physical region of the spacetime where the particle can be observed and shift its energy levels. This feature is an indicator of the coupling between the angular quantum number and the angular velocity of the rotating frame.

We also have shown that the presence of a Coulomb-like scalar potential allows the formation of bound states and the energy spectrum associated with this equation in a cosmic string space depends on the deficit angle of the conical spacetime.

Due to noninertial effects, the system presents two different classes of solutions that depend on the value of the product \(\alpha \omega \). The first case is obtained by adopting the limit \(\alpha \omega \ll 1\), which means a not so fast rotation, and as a second case, we consider an arbitrary relation \( \alpha \omega .\) For both classes of solutions, we have found the energy spectrum and the eigenfunctions.

We have shown that the discrete set of energies is composed of two contributions. The first term is associated to the Coulomb potential embedded in a cosmic string background and the second one is associated to the noninertial effect of rotating frames.

With these results it is possible to have an idea about the general aspects of the behavior of spin-0 particles inside a cosmic string space where a scalar potential exists. Potential physical applications of the results of this paper include the theory of defects in solids involving condensed matter physics. The idea is to explore the well-known analogy between cosmic strings and disclinations in solids [47] with the metric which describes a disclination corresponding to the spatial part of the line element of the cosmic string.