Non-zero $\theta _{13}$ and leptonic CP phase with $A_4$ symmetry

Abstract

We consider a model based on $A_4$ symmetry to explain the phenomenon of neutrino mixing. The spontaneous symmetry breaking of $A_4$ symmetry leads to a co-bimaximal mixing matrix at leading order. We consider the effect of higher order corrections in neutrino sector and find that the mixing angles thus obtained, come well within the $3\sigma$ ranges of their experimental values. We study the implications of this formalism on the other phenomenological observables, such as CP violating phase, Jarlskog invariant and the effective Majorana mass $|M_{ee}|$. We also obtain the branching ratio of the lepton flavour violating decay $\mu \rightarrow e \gamma$ in the context of this model and find that it can be less than its present experimental upper bound.

1 Introduction

Neutrinos are the least interacting entities among the standard model particles and exist in three flavours (electron neutrino, muon neutrino and tau neutrino). They change their flavour as they propagate and this phenomenon is known as neutrino oscillation which occurs since the flavour eigenstates of neutrinos are mixture of mass eigenstates. The mixing is described by PMNS matrix [1, 2], which can be parameterized in terms of three mixing angles and three CP violating phases as

$$\begin{aligned}&V_\mathrm{PMNS} = U_\mathrm{PMNS}.P_\nu \nonumber \\&\quad = \left( \begin{array}{ccc} c^{}_{12} c^{}_{13} &{} s^{}_{12} c^{}_{13} &{} s^{}_{13} e^{-i\delta } \\ -s^{}_{12} c^{}_{23} - c^{}_{12} s^{}_{13} s^{}_{23} e^{i\delta } &{} c^{}_{12} c^{}_{23} - s^{}_{12} s^{}_{13} s^{}_{23} e^{i\delta } &{} c^{}_{13} s^{}_{23} \\ s^{}_{12} s^{}_{23} - c^{}_{12} s^{}_{13} c^{}_{23} e^{i\delta } &{} -c^{}_{12} s^{}_{23} - s^{}_{12} s^{}_{13} c^{}_{23} e^{i\delta } &{} c^{}_{13} c^{}_{23} \end{array} \right) P^{}_\nu ,\nonumber \\ \end{aligned}$$

(1)

where $c_{ij}=\cos \theta _{ij}$ and $s_{ij}=\sin \theta _{ij}$, $\theta _{12}$, $\theta _{23}$ and $\theta _{13}$ are the three mixing angles, $\delta _\mathrm{CP}$ is the Dirac phase and the other two Majorana phases come in $P_{\nu }$

$$\begin{aligned} P_{\nu }=\mathrm{diag}(e^{i\rho },e^{i\sigma },1). \end{aligned}$$

Neutrino oscillation experiments gained a lot of interest as a probe to neutrino mixing and mass spectrum since the oscillation probability depends on mixing angles, Dirac CP phase and the mass square differences ($\Delta m^2_{21}$ and $\Delta m^2_{23}$). Results from earlier experiments indicated that $\theta _{13}$ is very small, can be zero and the lepton mixing is very close to TBM (tri-bimaximal mixing) see also [3,4,5,6,7,8,9,10,11,12], which predicts $\sin \theta _{13}=0$, $\sin ^2\theta _{23}={1}/{2}$ and $\tan ^2\theta _{12}={1}/{2}$. This made it possible to explain the neutrino mixing as TBM type, with small deviation due to perturbation in the charged-lepton or neutrino sector. There are many models which explain TBM mixing pattern on the basis of $A_4$ symmetry [13] with a certain set of Higgs scalars and vacuum alignments. Recent experimental observations of moderately large $\theta _{13}$ [14, 15], made neutrino mixing a little far from TBM type, but close to co-bimaximal mixing which predicts non-zero $\theta _{13}$ ($\theta _{13}\ne 0$, $\theta _{23}={\pi }/{4}$, $\delta _\mathrm{CP}=\pm {\pi }/{2}$) [16]. Supersymmetric models based on $A_4$ family symmetry, combined with the generalized CP symmetry [17], can also predict trimaximal (TM) lepton mixing, (in which either only the first column or only the second column of the lepton mixing matrix is assumed to take the TBM form), together with either zero CP violation or $\delta _\mathrm{CP} = \pm \pi /2$. Also models based on $S_4$ family symmetry and generalized CP symmetry [18] predict trimaximal lepton mixing and the Dirac CP is predicted to be either conserved or maximally broken. In Ref. [19], a minimal extension of the simplest $A_4$ model has been considered, which not only can induce non-zero $\theta _{13}$ value, consistent with the recent observations, but also can correlate the CP violation in neutrino oscillation with the octant of the atmospheric mixing angle $\theta _{23}$. In this paper, we would like to consider a model based on $A_4$ symmetry which gives co-bimaximal mixing in neutrino sector at leading order. To accommodate deviations in mixing angles to make them compatible with the experimental results, we include a perturbation in neutrino sector due to higher order corrections, which can be represented as five-dimensional operators. The best-fit values and $3\sigma$ ranges of neutrino oscillation parameters taken from Ref. [20] are given in Table 1.

The paper is organized as follows. The details of our model is presented in Sect. 2. In Sects. 3 and 4, we discuss the vacuum alignment and lepton flavour violating muon decay $\mu \rightarrow e \gamma$ in the context of the model. In Sect. 5, we describe the higher order corrections in neutrino sector and we conclude our discussion in Sect. 6.

Table 1 The best-fit values and the $3\sigma$ ranges of the neutrino oscillation parameters from Ref. [20]

2 The model

The model is based on $A_4$ group [21], which is the group of even permutation of four objects and is the smallest non-Abelian discrete group with triplet irreducible representation. It has four irreducible representations: 1, $1^{\prime }$, $1^{\prime \prime }$ and 3, with the multiplication rule

$$\begin{aligned} 3 \times 3=1+1^{\prime }+1^{\prime \prime }+3+3. \end{aligned}$$

(2)

As we know, $A_4$ allows the charged-lepton mass matrix to be diagonalized by the Cabibbo–Wolfenstein matrix [22]

$$\begin{aligned} U_{\omega }=\frac{1}{\sqrt{3}}\left( \begin{array}{ccc} 1&{}1&{}1\\ 1&{}\omega &{}\omega ^2\\ 1&{}\omega ^2&{}\omega \end{array} \right) , \end{aligned}$$

(3)

where $\omega =e^{2 \pi i/3}=-1/2+i \sqrt{3}/2$.

In this work, our discussion is limited to the leptonic sector. The particle content of the model includes, in addition to standard model fermions (i.e., the lepton doublets $l_{iL}$ and charged lepton singlets $l_{iR}$), three right-handed neutrinos ($\nu _{iR}$), four Higgs doublets ($\phi _i$, $\phi _0$) and three Higgs singlets ($\chi _i$). They belong to four irreducible representations of $A_4$ as given in Table 2.

Table 2 Particle content of the model along with their quantum numbers

Here $A_4$ symmetry is accompanied by an additional $U(1)_X$ symmetry as discussed in Ref. [13], which prevents the existence of Yukawa interactions of the form $\bar{l}_{iL}\nu _{iR}\tilde{\phi _i}$ and $\bar{l}_{iL} l_{iR}\phi _0$ as $l_{iL}$, $l_{iR}$, $\tilde{\phi }_0$ have quantum number $X=1$, and all other fields have $X=0$. The phenomenologically disallowed Nambu-Goldstone boson does not arise in this case as $U(1)_X$ symmetry does not break spontaneously but explicitly. Thus, the Yukawa Lagrangian for the leptonic sector is given as [23]

$$\begin{aligned} \mathcal {L}= & {} -\left\{ \left[ \lambda _1 \left( \bar{l}_{iL}\phi _i\right) l_{1R}\right] + \left[ \lambda _2\left( \bar{l}_{iL}\phi _i\right) ^{\prime \prime }l_{2R}\right] + \left[ \lambda _3\left( \bar{l}_{iL}\phi _i\right) ^{\prime }l_{3R}\right] \right\} \nonumber \\&-\left\{ \lambda _0 \left[ \left( \bar{l}_{iL} \nu _{iR} \right) \tilde{\phi }_0\right] +\frac{1}{2}\left[ M\left( \bar{\nu }_{iR}\hat{\nu }_{iR}\right) \right] +\lambda _{\chi }\left[ \left( \bar{\nu }_{iR}\hat{\nu }_{iR}\right) _3\chi _i\right] \right\} \nonumber \\&+\,\mathrm{h.c.}, \end{aligned}$$

(4)

where $\hat{\nu }_{iR}$ are antiparticles of $\nu _{iR}$ and $(\bar{l}_{iL}\phi _i)^{\prime }$, $(\bar{l}_{iL}\phi _i)^{\prime \prime }$ and $\left( \bar{\nu }_{iR}\hat{\nu }_{iR}\right) _3$ are $1^{\prime }$, $1^{\prime \prime }$ and triplet representations of $A_4$ respectively. As the scalars $\phi _i$, $\phi _0$ and $\chi _i$ get vacuum expectation values $v_i$, $v_0$ and $\omega _i$ respectively, the above Lagrangian becomes

$$\begin{aligned} \mathcal {L}=-\bar{l}_{L}M_ll_R-\bar{\nu }_LM_D\nu _R-\frac{1}{2}\bar{\nu }_R M_R \hat{\nu }_R+\mathrm{h.c}, \end{aligned}$$

(5)

where $M_l$, $M_D$ and $M_R$ are charged-lepton, Dirac neutrino and right-handed neutrino mass matrices and have the forms

$$\begin{aligned} M_l=\left( \begin{array}{ccc} \lambda _1 v_1&{}\lambda _2 v_1 &{}\lambda _3 v_1 \\ \lambda _1 v_2 &{}\lambda _2v_2\omega ^2 &{}\lambda _3v_2\omega \\ \lambda _1v_3 &{}\lambda _2v_3\omega &{}\lambda _3v_3\omega ^2 \end{array} \right) , \end{aligned}$$

(6)

Fig. 1

Variation of $\sin ^2 \theta _{13}$ with $\theta$ (left panel) and the correlation plots between $\sin ^2 \theta _{12}$ and $\sin ^2 \theta _{13}$ (right panel). The black dashed line in the left panel denotes the central value of $\sin ^2 \theta _{13}$ and the red dot-dashed lines represent the corresponding $3\sigma$ values

$$\begin{aligned} M_D=\lambda _0v_0I, \end{aligned}$$

(7)

where I is the identity matrix, and

$$\begin{aligned} M_R=\left( \begin{array}{ccc} M&{}\lambda _{\chi }\omega _3&{}\lambda _{\chi }\omega _2\\ \lambda _{\chi }\omega _3&{}M&{}\lambda _{\chi }\omega _1\\ \lambda _{\chi }\omega _2&{}\lambda _{\chi }\omega _1&{}M \end{array} \right) . \end{aligned}$$

(8)

For the vacuum alignment $v_i=v$, the charged lepton sector can be diagonalized by the transformation:

$$\begin{aligned} U_{\omega }\cdot M_l \cdot I= \left( \begin{array}{ccc} \sqrt{3}v\lambda _1&{}0&{}0 \\ 0&{}\sqrt{3}v\lambda _2&{}0 \\ 0&{}0&{}\sqrt{3}v\lambda _3 \end{array} \right) , \end{aligned}$$

(9)

where $U_\omega$ is the Cabibbo–Wolfenstein matrix given in Eq. (3). The light neutrino mass is given by the type-I seesaw formula

$$\begin{aligned} M_{\nu }=-M_D^{T}\cdot M_R^{-1} \cdot M_D. \end{aligned}$$

(10)

Since $M_D$ is proportional to an identity matrix, the neutrino mixing matrix will be the one which diagonalizes the right-handed neutrino mass matrix $M_R$. The Majorana mass matrix $M_R$ can be parameterized as

$$\begin{aligned} M_R= \left( \begin{array}{ccc} A&{}C&{}D\\ C&{}A&{}B\\ D&{}B&{}A \end{array} \right) , \end{aligned}$$

(11)

in a basis where charged-lepton mass matrix is not diagonal. However, in the charged lepton mass diagonal basis $M_R^d=U_{\omega }^{\dagger } \cdot M_R \cdot U_{\omega }^*$ and can be diagonalized by tri-bimaximal (TBM) mixing matrix for $D=C=0$, which we don’t need as it gives vanishing $\theta _{13}$. Even if these conditions are not satisfied some of the off-diagonal elements of $M_R$ become zero in TBM basis and one can go to the TBM basis through the transformation

$$\begin{aligned} M_R^{\prime }= & {} U_T^{\dagger }\cdot M_R \cdot U_T^*\nonumber \\ {}= & {} \left( \begin{array}{ccc} A+B&{}\frac{1}{\sqrt{2}}(D+C)&{}0\\ \frac{1}{\sqrt{2}}(D+C)&{}A&{}\frac{i}{\sqrt{2}}(D-C)\\ 0&{}\frac{i}{\sqrt{2}}(D-C)&{}B-A \end{array} \right) , \end{aligned}$$

(12)

where

$$\begin{aligned} U_T=\left( \begin{array}{ccc} 0&{} 1&{}0\\ \frac{1}{\sqrt{2}}&{}0&{}\frac{i}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&{}0&{}\frac{-i}{\sqrt{2}} \end{array} \right) . \end{aligned}$$

(13)

With the condition $D=-C$, $M_R^{\prime }$ becomes

$$\begin{aligned} \left( \begin{array}{ccc} A+B&{}0&{}0\\ 0&{}A&{}i\sqrt{2}D\\ 0&{}i\sqrt{2}D&{}B-A \end{array} \right) , \end{aligned}$$

(14)

which can be diagonalized by $U_R$, having the form

$$\begin{aligned} U_R=\left( \begin{array}{ccc} 1&{}0&{}0\\ 0&{}c&{}is\\ 0&{}is&{}c \end{array} \right) , \end{aligned}$$

(15)

where s and c stand for $\sin \theta$ and $\cos \theta$ respectively and satisfy the relation

$$\begin{aligned} \frac{cs}{c^2-s^2}=\frac{\sqrt{2}D}{B}= \frac{\sqrt{2}\omega _2}{\omega _1}. \end{aligned}$$

(16)

It should be noted that, this ratio should be real, since $\omega _{1,2}$ are VEV of real scalar fields $\chi _i$. The condition $C=-D$ can be realized with the vacuum alignment $\langle \chi _i \rangle =(\omega _1,\omega _2,-\omega _2)$ [24]. Thus, the lepton mixing matrix becomes

$$\begin{aligned} U=U_{\omega }\cdot U_T \cdot U_R, \end{aligned}$$

(17)

which basically known as co-bimaximal mixing matrix and predicts the mixing angles and CP violating Dirac phase as $\theta _{13} \ne 0$, $\theta _{23}={\pi }/{4}$ and $\delta _\mathrm{CP} =\pm {\pi }/{2}$. Also, the mixing angles $\theta _{12}$ and $\theta _{13}$ are not independent and one can express $\sin ^2\theta _{12}$ in terms of $\sin ^2\theta _{13}$ as

$$\begin{aligned} \sin ^2\theta _{12}=\frac{1-3\sin ^2 \theta _{13}}{3(1-\sin ^2\theta _{13})},\quad \mathrm{with} \ \sin \theta _{13} = \frac{s}{\sqrt{3}}. \end{aligned}$$

(18)

To illustrate these results, we show in Fig. 1 the variation of $\sin ^2 \theta _{13}$ with $\theta$ (left panel) and the correlation plot between $\sin ^2 \theta _{13}$ and $\sin ^2 \theta _{12}$ (right panel). From the figure it can be seen that the observed values of solar ($\theta _{12}$) and reactor ($\theta _{13}$) mixing angles can be accommodated in this model.

3 Vacuum alignment

The complete scalar potential is given by

$$\begin{aligned} V=V(\phi _i)+ V(\chi _i)+V(\phi _0)+V(\phi _i \chi _i)+V(\phi _i \phi _0) \end{aligned}$$

(19)

with

$$\begin{aligned} V(\phi _i)= & {} \mu _{\phi _i}^2\sum _j \phi _j^{\dagger }\phi _j +\frac{\lambda _1^{\phi _i}}{2}\left( \sum _j \phi _j^{\dagger }\phi _j\right) ^2 \\&+\lambda _2^{\phi _i} (\phi _1^{\dagger }\phi _1 + \omega \phi _2^{\dagger }\phi _2 + \omega ^2\phi _3^{\dagger }\phi _3 ) (\phi _1^{\dagger }\phi _1 \\&+ \omega ^2 \phi _2^{\dagger }\phi _2 + \omega \phi _3^{\dagger }\phi _3 ) + \lambda _3^{\phi _i} [ (\phi _2^{\dagger }\phi _3) (\phi _3^{\dagger }\phi _2)\\&+ (\phi _3^{\dagger }\phi _1) (\phi _1^{\dagger }\phi _3)+( \phi _1^{\dagger }\phi _2) ( \phi _2^{\dagger }\phi _1)]\\&+ \left\{ \frac{\lambda _4^{\phi _i}}{2}\left[ \left( \phi _2^{\dagger }\phi _3 \right) ^2 + \left( \phi _3^{\dagger }\phi _1 \right) ^2+\left( \phi _1^{\dagger }\phi _2 \right) ^2\right] +\mathrm{h.c.} \right\} ,\\ V(\chi _i)= & {} \mu _{\chi _i}^2\sum _j \chi _j\chi _j +\delta ^{\chi _i}\chi _1\chi _2\chi _3 +\lambda _1^{\chi _i}\left( \sum _j \chi _j \chi _j\right) ^2\\&+ \lambda _2^{\chi _i} (\chi _1\chi _1 + \omega \chi _2\chi _2 + \omega ^2\chi _3\chi _3 ) (\chi _1\chi _1 + \omega ^2 \chi _2\chi _2 \\&+ \omega \chi _3\chi _3 )+ \lambda _3^{\chi _i} [(\chi _2\chi _3 )^2 + (\chi _3\chi _1 )^2 + (\chi _1\chi _2)^2], \\ V(\phi _0)= & {} \mu _{\phi _0}^2\phi _0^{\dagger }\phi _0 + \lambda _1^{\phi _0}\left( \phi _0^{\dagger }\phi _0\right) ^2, \end{aligned}$$

$$\begin{aligned} V(\phi _i\chi _i)= & {} \delta ^{\phi _i\chi _i}(\phi _2^{\dagger }\phi _3\chi _1 + \phi _3^{\dagger }\phi _1\chi _2 +\phi _1^{\dagger }\phi _2\chi _3 ) \nonumber \\&+ \lambda _1^{\phi _i\chi _i}\sum _{j,k}\phi _j^{\dagger }\phi _j\chi _k\chi _k+ \lambda _2^{\phi _i\chi _i} (\phi _1^{\dagger }\phi _1 + \omega \phi _2^{\dagger }\phi _2 \nonumber \\&+ \omega ^2 \phi _3^{\dagger }\phi _3 ) (\chi _1\chi _1 + \omega ^2 \chi _2\chi _2 + \omega \chi _3\chi _3 ) \nonumber \\&+ \lambda _3^{\phi _i\chi _i} (\phi _2^{\dagger }\phi _3\chi _2\chi _3 +\phi _3^{\dagger }\phi _1\chi _3\chi _1+\phi _1^{\dagger }\phi _2\chi _1\chi _2)\nonumber \\&+\mathrm{h.c.}, \end{aligned}$$

(20)

$$\begin{aligned} V(\phi _i\phi _0)= & {} \lambda _1^{\phi _i\phi _0}\left( \sum _j\phi _j^{\dagger }\phi _j \right) \phi _0^{\dagger }\phi _0 +\lambda _2^{\phi _i\phi _0}\left( \sum _j \phi _j^{\dagger }\phi _0~ \phi _0^{\dagger }\phi _j\right) \nonumber \\&+[\lambda _3^{\phi _i\phi _0} (\phi _1^{\dagger }\phi _0 \phi _2^{\dagger }\phi _3 + \phi _2^{\dagger }\phi _0\phi _3^{\dagger }\phi _1 +\phi _3^{\dagger }\phi _0\phi _1^{\dagger }\phi _2 ) \nonumber \\&+ \lambda _4^{\phi _i\phi _0} (\phi _1^{\dagger }\phi _0\phi _3^{\dagger }\phi _2 + \phi _2^{\dagger }\phi _0\phi _1^{\dagger }\phi _3 +\phi _3^{\dagger }\phi _0\phi _2^{\dagger }\phi _1 )\nonumber \\&+ \mathrm{h.c.}], \end{aligned}$$

(21)

$$\begin{aligned} V(\chi _i\phi _0)= & {} \lambda ^{\phi _0\chi _i}\left( \sum _j\chi _j\chi _j\right) \phi _0^{\dagger }\phi _0. \end{aligned}$$

(22)

The last term in Eq. (21) breaks $U(1)_X$ symmetry explicitly and removes Goldstone boson which occurs due to the spontaneous breaking of $U(1)_X$ symmetry. In this model, we have the vacuum alignment $\langle \phi _0\rangle = u$, $\langle \phi _i\rangle =\left( v,v,v\right)$, and $\langle \chi _i\rangle =\left( w_1,w_2,-w_2\right)$ which is a possible minimum of scalar potential for $V(\phi _i\chi _i)=0$. A vanishing $V(\phi _i\chi _i)$ can be achieved in the limit $\chi _i$ decouples from rest of the field as mentioned in Ref. [13]. The decoupling of $\chi _i$ requires $\lambda _{\chi }\rightarrow 0$, $\lambda ^{\phi _0\chi _i}\rightarrow 0$. To generate an acceptable neutrino mass spectrum $\lambda _{\chi }$ has to be nonzero but can be small. A small but nonzero $\lambda _{\chi }$ will generate a sufficiently small $V(\phi _i\chi _i)$ which will be too small to alter vacuum alignment considerably. In this limit the minimization condition on u is given by

$$\begin{aligned}&\mu _{\phi _0}^2u+2\lambda _1^{\phi _0}(u^*u)u+\lambda _1^{\phi _i\phi _0} (\mid v_1\mid ^2+\mid v_2 \mid ^2+\mid v_3\mid ^2)u \\&\quad + \lambda _2^{\phi _i\phi _0}\left( \sum _{j,k}v_j^*v_k\right) u\\&\quad +{\lambda _3^{\phi _i\phi _0}}^* [v_1 v_2 v_3^* + v_2 v_3 v_1^*+v_3 v_1 v_2^*] \\&\quad + {\lambda _4^{\phi _i\phi _0}}^* [v_1 v_3 v_2^* + v_2 v_1 v_3^*+v_3 v_2 v_1^*]=0 \end{aligned}$$

The above equation has a solution

$$\begin{aligned} u=\frac{{\lambda _3^{\phi _i\phi _0}}^*[v_1 v_2 v_3^* + v_2 v_3 v_1^*+v_3 v_1 v_2^*]+ {\lambda _4^{\phi _i\phi _0}}^*[v_1 v_3 v_2^* + v_2 v_1 v_3^*+v_3 v_2 v_1^*]}{\mu _{\phi _0}^2+(\lambda _1^{\phi _i\phi _0} + \lambda _2^{\phi _i\phi _0})(\sum _{j}|v_j|^2)} \end{aligned}$$

(23)

for $| u|^2\ll | v_i|^2$.

• (a) Thus, for this case, i.e., for $| u|^2\ll | v_i|^2$ minimization conditions on $v_i$ are given as

  $$\begin{aligned} \frac{\partial V}{\partial v_i^*}= & {} \mu _{\phi _i}^2v_i+\lambda _1^{\phi _i}v_i\sum _j| v_j|^2+\lambda _2^{\phi _i}v_i\left( 2| v_i|^2-\sum _{j\ne i}| v_j|^2 \right) \nonumber \\&+\lambda _3^{\phi _i}v_i\left( \sum _{j\ne i} |v_j|^2\right) + \lambda _4^{\phi _i}v_i^*\sum _{j\ne i}v_j^2=0. \end{aligned}$$

  (24)

  Considering $\lambda _4^{\phi _i}$ as real, one can get the solution

  $$\begin{aligned} v_i=v=\sqrt{\frac{-\mu _{\phi _i}^2}{3\lambda _1^{\phi _i}+2\left( \lambda _3^{\phi _i}+\lambda _4^{\phi _i}\right) }}, \end{aligned}$$

  (25)

  which is allowed.

• (b) Minimization conditions on $w_i$ is given by

  $$\begin{aligned} \frac{\partial V}{\partial w_1}= & {} 2\left[ \mu _{\chi _i}^2 + {\lambda _2^{\chi _i}}^{\prime }\left( w_2^2+w_3^2\right) \right] w_1 +\delta ^{\chi _i}w_2w_3\nonumber \\&+\,4{\lambda _1^{\chi _i}}^{\prime }w_1^3=0,\end{aligned}$$

  (26)
  $$\begin{aligned} \frac{\partial V}{\partial w_2}= & {} 2\left[ \mu _{\chi _i}^2 + {\lambda _2^{\chi _i}}^{\prime }\left( w_1^2+w_3^2\right) \right] w_2 +\delta ^{\chi _i}w_1w_3\nonumber \\&+\,4{\lambda _1^{\chi _i}}^{\prime }w_2^3=0,\end{aligned}$$

  (27)
  $$\begin{aligned} \frac{\partial V}{\partial w_3}= & {} 2\left[ \mu _{\chi _i}^2 + {\lambda _2^{\chi _i}}^{\prime }\left( w_2^2+w_1^2\right) \right] w_3 +\delta ^{\chi _i}w_2w_1\nonumber \\&+\,4{\lambda _1^{\chi _i}}^{\prime }w_3^3=0, \end{aligned}$$

  (28)

  one of the solutions of above set of equations is $w_1\ne 0$, $w_3=-w_2\ne 0$, which is the vacuum alignment condition for $\langle \chi _i\rangle$.

4 Effect of additional higgs doublets on lepton flavour violating decay $\mu \rightarrow e\gamma$

Since $\mid u\mid ^2\ll v^2$ one can neglect the mixing between $\phi _i$ and $\phi _0$ and the mass-squared matrices in the $\mathrm{Re}[\phi _i^0]$, $\mathrm{Im}[\phi _i^0]$, and $\phi _i^{\pm }$ bases have the same form [25].

$$\begin{aligned} M^2=\left( \begin{array}{c c c} a &{} b &{} b\\ b &{} a &{} b \\ b &{} b &{} a \end{array} \right) , \end{aligned}$$

(29)

where $a=2 (\lambda _1^{\phi _i}+2\lambda _2^{\phi _i})v^2$, $-4\lambda _4^{\phi _i}v^2$, $-2(\lambda _3^{\phi _i}+\lambda _4^{\phi _i})v^2$, and $b=2 (\lambda _1^{\phi _i}-\lambda _2^{\phi _i}+ \lambda _3^{\phi _i}+\lambda _4^{\phi _i})v^2$, $2\lambda _4^{\phi _i}v^2$, $(\lambda _3^{\phi _i}+\lambda _4^{\phi _i})v^2$ for $\mathrm{Re}[\phi _i^0]$, $\mathrm{Im}[\phi _i^0]$, and $\phi _i^{\pm }$ respectively. Hence, there are three linear combinations of $\phi _i$s, $\phi =\frac{1}{\sqrt{3}}\left( \phi _1+\phi _2+\phi _3\right)$, $\phi ^{\prime }=\frac{1}{\sqrt{3}}\left( \phi _1+\omega \phi _2+\omega ^2\phi _3\right)$, and $\phi ^{\prime \prime }=\frac{1}{\sqrt{3}}\left( \phi _1+\omega ^2\phi _2+\omega \phi _3\right)$ with vacuum expectation values $\sqrt{3}v$, 0, and 0 respectively. The Higgs doublet $\phi$ with mass-squared eigenvalues $(3\lambda _1^{\phi _i}+2\lambda _3^{\phi _i}+2\lambda _4^{\phi _i})v^2$, 0, 0 for $\mathrm{Re}[\phi ^0]$, $\mathrm{Im}[\phi ^0]$ and $\phi ^{\pm }$ can be identified as standard model Higgs doublet which gives masses to charged leptons. One can see this by expressing Yukawa interactions of $\phi _i$s with leptons in charged lepton mass diagonal basis

$$\begin{aligned} \mathcal {L}= & {} \left( \frac{m_e}{\sqrt{3}v}\overline{\left( \nu _e,e\right) }_Le_R+ \frac{m_{\mu }}{\sqrt{3}v}\overline{(\nu _{\mu },\mu )}_L\mu _R+ \frac{m_{\tau }}{\sqrt{3}v}\overline{\left( \nu _{\tau },\tau \right) }_L\tau _R\right) \phi \nonumber \\&+ \left( \frac{m_e}{\sqrt{3}v}\overline{(\nu _{\mu },\mu )}_Le_R+ \frac{m_{\mu }}{\sqrt{3}v}\overline{\left( \nu _{\tau },\tau \right) }_L\mu _R+ \frac{m_{\tau }}{\sqrt{3}v}\overline{\left( \nu _{e},e\right) }_L\tau _R\right) \phi ^{\prime } \nonumber \\&+ \left( \frac{m_e}{\sqrt{3}v}\overline{\left( \nu _{\tau },\tau \right) }_Le_R+ \frac{m_{\mu }}{\sqrt{3}v}\overline{\left( \nu _{e},e\right) }_L\mu _R+ \frac{m_{\tau }}{\sqrt{3}v}\overline{(\nu _{\mu },\mu )}_L\tau _R\right) \phi ^{\prime \prime }\nonumber \\ \end{aligned}$$

(30)

The Higgs doublets $\phi ^{\prime }$ and $\phi ^{\prime \prime }$ contributes to flavour violating decays such as $\mu \rightarrow e\gamma$. The prominent contribution comes from $\phi ^{\prime }$ and the branching ratio is given by [25],

$$\begin{aligned} \mathrm{Br} (\mu \rightarrow e\gamma )=\frac{9}{32\pi ^2}m_{\tau }^4 \left( \frac{M_R^2-M_I^2}{M_R^2M_I^2}\right) ^2 \left( \frac{v_0^2}{3v^2}\right) ^2 \end{aligned}$$

(31)

where $M_R^2=2(3\lambda _2^{\phi _i}-\lambda _3^{\phi _i}-\lambda _4^{\phi _i})v^2$, $M_I^2=-6\lambda _4^{\phi _i}v^2$ are mass-squared eigenvalues of $\frac{1}{\sqrt{3}} (\mathrm{Re}[\phi _1]+\omega \mathrm{Re}[\phi _2]+\omega ^2 \mathrm{Re}[\phi _3])$ and $\frac{1}{\sqrt{3}}(\mathrm{Im}[\phi _1]+\omega \mathrm{Im}[\phi _2]+\omega ^2 \mathrm{Im}[\phi _3])$ respectively and $v_0^2= (1/2\sqrt{2}G_F )$. The predicted branching ratio will be below the experimental upper limit $\mathrm{Br} (\mu \rightarrow e\gamma )<4.2\times 10^{-13}$ [26] for

$$\begin{aligned} \left( \frac{M_R^2-M_I^2}{M_R^2M_I^2}\right) ^{\frac{1}{2}}< 1.56\times 10^{-3}~ \mathrm{GeV}^{-1}. \end{aligned}$$

(32)

5 Perturbation in neutrino sector

In this section, we will consider the perturbations to mass matrices due to higher order corrections. Prominent corrections come from five-dimensional operator $\lambda _{ij}\bar{\nu }_{iR}\hat{\nu }_{jR}\chi _i\chi _j$ which modifies right-handed neutrino mass matrix. Charged lepton and Dirac neutrino masses also receive corrections from $\lambda _{jk}^{\prime }\bar{l}_{il}\phi _il_{jR}\chi _i$ and $\lambda _{jk}^{\prime }\bar{l}_{il}\tilde{\phi _0} \nu _{jR}\chi _i$ respectively, and here we are neglecting those corrections since they allow the mixing of $\chi _i$ with other fields.

All elements of Majorana mass matrix $M_R$ receive corrections which is proportional to $\omega _1^2+\omega _2^2$ for diagonal elements and $\omega _1\omega _2$ for off diagonal elements. Since $0.04<(\omega _2/\omega _1)<0.22$, obtained from Eq. (16), using the allowed value of $s= \sqrt{3}\sin \theta _{13}$, we neglect corrections to off- diagonal elements.

$$\begin{aligned}&\delta M_R\simeq \left( \begin{array}{c c c} \lambda _{11}\omega _1^2 &{} 0 &{} 0 \\ 0 &{}\lambda _{22}\omega _1^2 &{}0 \\ 0 &{}0&{} \lambda _{33}\omega _1^2 \end{array} \right) . \end{aligned}$$

(33)

These corrections will modify the light neutrino mass matrix and the inverse of modified light neutrino mass matrix in TBM basis can be parameterized as

$$\begin{aligned} M_{\nu }^{-1}= & {} \left( \begin{array}{c c c} B+A&{}0&{}0\\ 0 &{} A &{}i\sqrt{2}D \\ 0 &{}i\sqrt{2}D &{}B-A \end{array} \right) \nonumber \\&+\, \left( \begin{array}{c c c} \frac{1}{2}\left( \lambda _{22}+\lambda _{33}\right) &{}0&{}\frac{i}{2}\left( \lambda _{33}-\lambda _{22}\right) \\ 0 &{} \lambda _{11} &{}0 \\ \frac{i}{2}\left( \lambda _{33}-\lambda _{22}\right) &{}0&{}\frac{-1}{2}\left( \lambda _{33}+\lambda _{22}\right) \end{array} \right) \omega _1^2. \end{aligned}$$

(34)

Hence, in the charged lepton diagonal basis light neutrino mass matrix can be diagonalized by

$$\begin{aligned} U=U_{\omega }\cdot U_T \cdot U_R \cdot U_{13}, \end{aligned}$$

(35)

where

$$\begin{aligned} U_{13}=\left( \begin{array}{c c c} c^{\prime } &{} 0&{} s^{\prime }e^{-i\phi }\\ 0 &{} 1 &{} 0\\ -s^{\prime }e^{i\phi } &{}0 &{} c^{\prime } \end{array} \right) . \end{aligned}$$

(36)

with $s^{\prime }=\sin \theta ^{\prime }$ and $c^{\prime }=\cos \theta ^{\prime }$.

Fig. 2

Allowed parameter space in $\theta ^\prime -\theta$ (left panel), $\theta -\phi$ (right panel) and $\theta ^\prime - \phi$ planes compatible with the observed data

To obtain mixing angles we compare lepton mixing matrix U (35) with PMNS matrix (1), i.e.,

$$\begin{aligned} U=U_\mathrm{PMNS}. \end{aligned}$$

(37)

The mixing angles $\sin ^2\theta _{12}$, $\sin ^2\theta _{23}$ and $\sin ^2\theta _{13}$ are related to the elements of U as

$$\begin{aligned}&\sin ^2\theta _{12}=\frac{|U_{12}|^2}{1-|U_{13}|^2},\quad \sin ^2\theta _{23}=\frac{|U_{23}|^2}{1-|U_{13}|^2},\nonumber \\&\sin ^2\theta _{13}=|U_{13}|^2, \end{aligned}$$

(38)

where $U_{ij}$ is the $ij\mathrm{th}$ element of the lepton mixing matrix U. Now using Eqs. (3), (13), (35) and (38), we obtain

$$\begin{aligned}&\sin ^2\theta _{13}=\frac{1}{3}[ 2s^{\prime ^2}- 2\sqrt{2} sc^{\prime }s^{\prime }\sin \phi +s^{2}c^{\prime 2}],\end{aligned}$$

(39)

$$\begin{aligned}&\sin ^2\theta _{12}=\frac{1-s^{2}}{3- ( 2s^{\prime 2}- 2\sqrt{2} sc^{\prime }s^{\prime }\sin \phi +s^{^2}c^{\prime 2})}, \end{aligned}$$

(40)

$$\begin{aligned}&\sin ^2\theta _{23}=\frac{1}{2}+\frac{\sqrt{3}cc^{\prime }s^{\prime }\cos \phi }{3-( 2s^{\prime ^2}- 2\sqrt{2} sc^{\prime }s^{\prime }\sin \phi +s^{2}c^{\prime 2})}, \end{aligned}$$

(41)

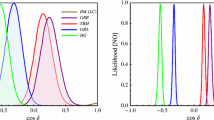
Another important parameter is $J_\mathrm{CP}$, the Jarlskog invariant, which is a measure of CP violation, is found to have the value in this model as

$$\begin{aligned} J_\mathrm{CP}= & {} \mathrm{Im} [U_{11}U_{22}U_{21}^*U_{12}^*] \nonumber \\= & {} \frac{c}{6\sqrt{3}} [\sqrt{2}s{c^{\prime }}^2- (1+c^2)c^{\prime }s^{\prime }\sin \phi -\sqrt{2}s{s^{\prime }}^2]. \end{aligned}$$

(42)

In standard parametrization, the value of $J_\mathrm{CP}$ is

$$\begin{aligned} J_\mathrm{CP}=\frac{1}{8}\sin 2\theta _{12}\sin 2\theta _{23}\sin 2\theta _{13}\cos \theta _{13}\sin \delta _\mathrm{CP}. \end{aligned}$$

(43)

Comparing Eqs. (42) and (43), we obtain

$$\begin{aligned}&\sin \delta _\mathrm{CP}=\frac{\sqrt{2} s(c^{\prime 2}-s^{\prime 2})-c^{\prime }s^{\prime } (1+c^2)\sin \phi }{\sqrt{X^\prime (2-X^\prime +s^2)\left( 1-\frac{Y^{\prime 2}}{(3-X^\prime )^2} \right) }}, \end{aligned}$$

(44)

where

$$\begin{aligned}&X^\prime =\left[ 2s^{\prime 2}- 2\sqrt{2} sc^{\prime }s^{\prime }\sin \phi +s^{2}c^{\prime 2} \right] ,\nonumber \\&Y^\prime =2\sqrt{3}cc^{\prime }s^{\prime }\cos \phi . \end{aligned}$$

(45)

To show that the model predicts the mixing angles compatible with the observed data,we obtain the allowed parameter space compatible with the $3 \sigma$ range of the observed data by varying the parameters s between $[-1,1]$, $s^{\prime }$ between $[-0.1,0.1]$ and $\phi$ between $[-\pi ,\pi ]$, we show the allowed parameter space in various planes in Fig. 2. Using these allowed values of different parameters, we show the correlation plots between $\sin ^2 \theta _{13}$ and $\sin ^2 \theta _{23}$ (left panel), $\sin ^2 \theta _{13}$ and $\sin ^2 \theta _{12}$ (right panel) and between $\sin ^2 \theta _{13}$ and $\delta _\mathrm{CP}/J_{CP}$ (bottom panel) in Fig. 3. From these plots it can be seen that by including higher order correction to right handed neutrino mass matrix, it is possible to accommodate the observed data.

Fig. 3

Correlation plots between $\sin ^2 \theta _{13}$ and $\sin ^2 \theta _{23}$ (left panel), and $\sin ^2 \theta _{13}$ and $\sin ^2 \theta _{12}$ (right panel) and between $\sin ^2 \theta _{13}$ and $\delta _\mathrm{CP}/J_{CP}$ (bottom panel) including the corrections

In this model, light neutrinos acquire Majorana masses through Type-I seesaw which indicates neutrinos are of Majorana type. Majorana nature of neutrinos predicts the existence of neutrino-less double beta decay ($0\nu \beta \beta$), which is a process where two neutrons inside a nucleus convert into two protons without emitting neutrinos, i.e., $(A,Z)\rightarrow (A,Z+2)+2e$. Several experiments like KamLAND-Ze [27], EXO [28] and GERDA [29] are searching for the neutrino-less double beta decay. These experiments put upper bound on $|M_{ee}|$, the (1, 1) element of neutrino mass matrix, since the half-life of $0\nu \beta \beta$ decay is proportional to $|M_{ee}|^2$. The expression for $|M_{ee}|$ in the flavor basis is

$$\begin{aligned} |M_{ee}|=| U_{11}^2 m_1+U_{12}^2 m_2+ U_{13}^2 m_3|, \end{aligned}$$

(46)

where $m_1$, $m_2$, and $m_3$ are light neutrino masses and $U_{1j}$’s are elements of first row of the lepton mixing matrix U, which are given as

$$\begin{aligned} U_{11}= & {} \frac{2}{\sqrt{6}}c^{\prime }-\frac{i}{\sqrt{3}}ss^{\prime }e^{i\phi }, \nonumber \\ U_{12}= & {} \frac{1}{\sqrt{3}}c, \nonumber \\ U_{13}= & {} \frac{2}{\sqrt{6}}s^{\prime }e^{-i\phi }+\frac{i}{\sqrt{3}}sc^{\prime }\; . \end{aligned}$$

(47)

The lowest upper bound on $|M_{ee}|$ is 0.22 eV came from GERDA phase-I data. Here we study the variation of $|M_{ee}|$ with the lightest neutrino mass $m_1~(m_3)$, in the case of normal (inverted) hierarchy as shown in Fig. 4. In our calculation we have used the relations

$$\begin{aligned} m_2= & {} \sqrt{m_1^2+\Delta m_{21}^2},\nonumber \\ m_3= & {} \sqrt{m_1^2+\Delta m_{31}^2}, \end{aligned}$$

(48)

for normal hierarchy and

$$\begin{aligned} m_1= & {} \sqrt{m_3^2+\Delta m_{13}^2}, \nonumber \\ m_2= & {} \sqrt{m_3^2+\Delta m_{13}^2+\Delta m_{21}^2}, \end{aligned}$$

(49)

for inverted hierarchy, and obtained upper limit on $m_1$ ($m_3$) as 0.071 (0.065) eV taking into account the cosmological upper bound on $\Sigma _im_i$ as 0.23 eV [30]. Another observable is the kinetic electron neutrino mass in beta decay ($m_e$), which is probed in direct search for neutrino masses, can be expressed as

$$\begin{aligned} m_{e}=\sqrt{ |U_{11}|^2 m_1^2 +|U_{12}|^2 m_2^2+ |U_{13}|^2 m_3^2}. \end{aligned}$$

(50)

In the right panel of Fig. 4, we show the variation of $m_e$ with the lightest neutrino mass $m_1$ ($m_3$) for normal hierarchy (inverted hierarchy) case, and the upper limit on $m_e$ is found to be 0.07 (0.08) eV.

Fig. 4

Variation of $|M_{ee}|$ with the lightest neutrino mass $m_1$ $(m_3)$ (left panel) and $m_e$ vs. $m_1$ $(m_3)$ in the right panel for the normal mass hierarchy (inverted mass hierarchy) case

6 Conclusions

We consider a model based on $A_4$ symmetry, which gives co-bimaximal form ($\theta _{23}={\pi }/{4}$, $\delta _\mathrm{CP}=\pm {\pi }/{2}$ and $\theta _{13}\ne 0$) for the leading order neutrino mixing matrix. There are four Higgs doublets $\phi _0$, and $\phi _i$, for $i=1,2,3$ in this model. One of the three linear combinations ($\phi$) of $\phi _i$ behaves exactly as standard model Higgs doublet while neutral component of the other two ($\phi ^{\prime }$, $\phi ^{\prime \prime }$) contribute to the lepton flavour violating decays such as $\mu \rightarrow e \gamma$. We have considered higher order corrections in neutrino sector coming from five-dimensional operators after spontaneous breaking of $A_4$ symmetry. The mixing angles, thus obtained are found to be within the $3\sigma$ ranges of their experimental values. The CP violating phase $\delta _\mathrm{CP}$ is found to be around the region $\pm \pi /2$, and the upper limit on the Jarlskog invariant is $\mathcal{O}(10^{-2})$. We also studied the variation of the effective neutrino mass $|M_{ee}|$ with the lightest neutrino mass $m_1$ ($m_3$) in the case of normal (inverted) hierarchy and found its value to be lower than the experimental upper limit for all allowed values of $m_1$ ($m_3$).