Introduction to the physics of the total cross section at LHC

Abstract

This review describes the development of the physics of hadronic cross sections up to recent LHC results and cosmic ray experiments. We present here a comprehensive review – written with a historical perspective – about total cross sections from medium to the highest energies explored experimentally and studied through a variety of methods and theoretical models for over 60 years. We begin by recalling the analytic properties of the elastic amplitude and the theorems about the asymptotic behavior of the total cross section. A discussion of how proton–proton cross sections are extracted from cosmic rays at higher than accelerator energies and help the study of these asymptotic limits, is presented. This is followed by a description of the advent of particle colliders, through which high energies and unmatched experimental precisions have been attained. Thus the measured hadronic elastic and total cross sections have become crucial instruments to probe the so called soft part of QCD physics, where quarks and gluons are confined, and have led to test and refine Regge behavior and a number of diffractive models. As the c.m. energy increases, the total cross section also probes the transition into hard scattering describable with perturbative QCD, the so-called mini-jet region. Further tests are provided by cross section measurements of $\gamma p$, $\gamma ^* p$ and $\gamma ^* \gamma ^*$ for models based on vector meson dominance, scaling limits of virtual photons at high $Q^2$ and the BFKL formalism. Models interpolating from virtual to real photons are also tested.

It seems to us to be a necessary task to explore bit-by-bit the rigorous consequences of analyticity, unitarity and crossing. Who knows if someday one will not be able to reassemble the pieces of the puzzle. – A. Martin and F. Cheung, based on 1967 A.M. Lectures at Brandeis Summer School and Lectures at SUNY and Stony Brook (Martin and Cheung in Analyticity properties and bounds of the scattering amplitudes. Gordon and Breach Science, New York, 1970).

1 Introduction

This review aims at illustrating the development of studies of total hadronic cross sections in a historical perspective, primarily for hadrons and photons at high energies.

The optical theorem relates a total cross section linearly to the absorptive part of a forward elastic amplitude. Moreover, at very high energies, as the imaginary part of the forward amplitude dominates the real part, the elastic differential cross section in the forward direction becomes proportional to the square of the total cross section. Thus, discussions of total cross sections become entwined with that of elastic cross sections. Hence, in this review considerable attention is also paid both to experimental and theoretical aspects of the elastic cross sections.

As this rather lengthy review discusses many subjects, we provide below a quick overview to help the reader choose sections of the review that may be of particular interest. Serving mostly as a guide through the large amount of material we shall deal with, no references are included in this general introduction, but they are of course available in the individual sections, at the beginning of which we provide a description of contents and a brief guide to the subsections.

In Sect. 2, kinematics and partial wave expansions are obtained for the elastic amplitude and general principles, such as unitarity, are employed to derive the optical theorem. An introduction to the asymptotic behavior is provided via the Regge formalism, the Pomeranchuk theorem and finite energy sum rules. Through analyticity, Martin–Froissart rigorous upper bounds are established for the total cross sections. For charged particles, the EM (Coulomb) amplitude is mostly real (and large near the forward direction) and hence measurements of the needed real part of the “strong” forward amplitude (and measurement of the ratio of the real to the imaginary part of the forward scattering amplitude, the so-called $\rho (s)$ parameter) often involve Coulomb interference and soft radiation. We discuss it in some detail and supplement it with a proposal to employ soft radiation as a tool to measure total cross sections.

In Sect. 3, we discuss how cosmic radiation is employed as a non-accelerator method to measure total cross sections and provide valuable information at energies substantially larger than those of earth bound accelerators such as the Large Hadron Collider (LHC). Along with some history of the subject beginning with Heisenberg, a description of the Glauber formalism for nuclei is presented for the extraction of pp cross sections from data and corresponding uncertainties in the models are discussed. We follow the historical path which led to the advances in experimental techniques and theoretical methods that continue to provide a unique window towards fundamental physics and astrophysics, at energies otherwise unreachable through accelerators in the foreseeable future. Recent theoretical results about the power-law spectra in the cosmic ray energy distribution both for fermions (electrons/positrons) and bosons (helium and other nuclei) are briefly discussed and shown to agree with high precision data from AMS, Auger and other Collaborations.

Section 4 deals with pre-LHC measurements of $\sigma _{\mathrm{total}}$, the total $pp$ and ${\bar{p}}p$ cross section, such as those made at the CERN Intersecting Storage Rings (ISR), the CERN $S\bar{p}pS$ and the FermiLab Tevatron. These pioneering experiments verified the rise with energy of $\sigma _{\mathrm{total}}$ – suspected from experiments with cosmic rays – and of the slope parameter B(s), which defines the behaviour of the elastic differential cross section in the forward region, as well as discovered considerable variations in the $\rho$ parameter. The black-disk limit and how close we may be to it are also discussed herein.

In Sect. 5, we provide theoretical scenarios and phenomenology of the elastic amplitude and hadronic cross sections, that span over 80 years, beginning with the original Molière theory of multiple scattering, followed by Heisenberg’s considerations about the energy behavior of $\sigma _{\mathrm{total}}$, and culminating in various QCD-inspired models. Eikonal and Regge models are discussed along with hadronic matter distribution. We recall the development in QED of the need for soft-photon re-summation to avoid the infra-red (IR) catastrophe, and the semi-classical, but Lorentz covariant, methods for soft radiation subsequently developed. As a corollary, a Regge trajectory for the photon is obtained. These methods are extended to discuss soft QCD radiation and the divergent nature of strong coupling constant for small transverse momenta $\alpha _s(k_t)$. Asymptotic behavior of scattering amplitudes in QCD, the Balitsky, Fadin, Kuraev and Lipatov (BFKL) equation and spontaneously broken gauge theories are discussed along with the Reggeisation of the gauge particles therein. Next, eikonal mini-jet models for $\sigma _{\mathrm{total}}$ and their phenomenology are developed. A brief description of the AdS/CFT correspondence for $\sigma _{\mathrm{total}}$ is presented. Also, some details of the phenomenology of $\sigma _{\mathrm{total}}$ by the COMPETE and COMPASS Collaborations are provided.

Details of the energy and momentum-transfer dependence, the slope, the dip, the real and the imaginary parts of the elastic (and diffractive) amplitude are discussed in Sect. 6. Early models and their updates such as Durham, Tel Aviv, mini-jet and multi-pomeron models, are presented as required by more refined data. A concise summary of the model results is also provided

Photon processes are discussed in Sect. 7 beginning with kinematics of interest for real versus virtual photons and the relevant parton model variables. Sakurai’s vector meson dominance, Gribov’s model and photo-production at HERA are taken up next, along with $\gamma \gamma$ and $\gamma \gamma ^*$ processes at LEP and factorisation. The transition from real to virtual photon processes is discussed and models such as Haidt’s are presented. The results of the Tel Aviv and mini-jet models with soft-gluon resummation are discussed. The Balitsky–Kovchegov (BK) equation and its various applications such as geometrical scaling are considered and directions beyond into Pomeron loops, explored.

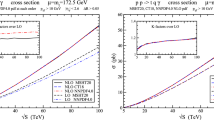
Section 8 discusses the layout of the LHC experimental areas as had been planned before its start. Expectations were to produce total cross section data with $5\%$ accuracy after a 3 year run. It is gratifying to note that forward physics data with $3\%$ accuracy have already been achieved. The highest energy physics results are shown for the total, elastic and inelastic pp cross sections at presently reached LHC energies, $\sqrt{s} = 7,\ 8$ and 13 TeV, obtained by the TOTEM, ATLAS and CMS groups. Predictions at $\sqrt{s} = 14\ \mathrm{TeV}$ are indicated.

2 The theoretical framework from unitarity and analyticity

This chapter is devoted to a review of the basic formalism pertaining to elastic scattering and to the well-established theorems on total, elastic and inelastic cross sections. Here analyticity and unitarity play a crucial role for the scattering of hadrons, protons and mesons, such as pions and kaons, while scattering of their QCD constituents and their contribution to total cross section dynamics will be introduced when dealing with QCD models.

For this material, there exist both books and reviews, nonetheless we reproduce most of the relevant material to introduce, in a modern language, the necessary notation and put together all the theorems which are important for our present understanding of hadronic physics or for optimal fitting of the existing data. One case at hand is whether the limitations imposed by the Froissart bound are satisfied and another case is the application to very high energy data fitting by Finite Energy Sum Rules (FESR), derived from analyticity and crossing.

We shall discuss the early formalism of the partial wave expansion of the elastic scattering amplitude, needed to understand the Martin–Froissart theorem, and relate it to the Regge pole expansion which played a major role in phenomenological description of inclusive and total cross sections in the 1960s and 1970s. To accommodate such a description and the rise of $\sigma _{\mathrm{total}}$, the Pomeron trajectory corresponding to the exchange of a state with the quantum numbers of the vacuum was introduced. Thus, a picture of $\sigma _{\mathrm{total}}$, with a Regge and a Pomeron exchange, unrelated to the underlying parton dynamics of scattering, was one of the first and still very successful descriptions. Finally, from the partial wave expansion for the amplitude, and through the optical theorem, we shall introduce the eikonal representation of the total cross section. This representation is at present the major formalism, into which QCD models for the energy behaviour of $\sigma _{\mathrm{total}}$ are embedded.

This section is divided into subsection headings as indicated in the following:

• General principles behind relativistic scattering amplitudes in Sect. 2.1

• Kinematics and analyticity of elastic amplitudes in Sect. 2.2

• Probability conservation and unitarity in Sect. 2.3

• The optical theorem and total cross section in Sect. 2.4

• Partial wave expansion of elastic amplitudes in Sect. 2.5

• Regge expansion and asymptotic behaviour of amplitudes in Sect. 2.6

• Finite energy sum rules and duality for the elastic amplitudes in Sect. 2.7

• Various derivations of the Martin–Froissart bound in Sect. 2.8

• The Pomeranchuk theorem in Sect. 2.9

• Determination of $\rho$ through Coulomb interference in Sect. 2.10 with considerations about Coulomb interference and soft radiation in Sects. 2.10.1 and 2.10.2.

2.1 General principles

Strong interactions are presently understood in terms of interactions between quarks and gluons. Quantum chromodynamics (QCD) can give remarkably accurate results within perturbation theory, when dealing with very high energy collisions and their final products in the large momentum-transfer processes. However, the bulk of collisions among high energy particles involves low-momentum partons which escape the perturbative treatment. For this purpose, we have to resort to some general principles – valid beyond perturbation theory – to establish the necessary formalism and derive some general theorems. Later we shall develop some tools to include QCD phenomena in this general picture.

These general principles were established in the late 1950s and consist of unitarity, analyticity and crossing symmetry. Each of them is related to basic axioms:

• unitarity to the conservation of probability in scattering processes;

• analyticity to causality and

• crossing symmetry to the relativistic nature of the interaction.

These basic principles are also at the foundations of relativistic Quantum Field Theory (QFT) [2].

We shall describe in detail how one obtains the so-called Froissart bound, which imposes limits to the asymptotic behavior of the total cross section in two particle scattering. This limit was obtained first by Froissart [3] and successively reformulated by Martin [4] and Lukaszuk [5]. The importance of this limit cannot be underestimated, as most efforts to describe theoretically the total cross section behaviour or most fits to present data must contemplate the asymptotic satisfaction of the Froissart bound. For this reason we shall describe how this limit is obtained in several different derivations, pointing out in all cases the common hypothesis, which is always the presence of a finite mass in final state scattering.

The basic quantity to study in particle physics is the probability that a certain set of particles in a given initial state $|i\rangle$ undergo a collision and scatter into a final state $|f\rangle$.

To this effect, the process is described by the quantity

$$\begin{aligned} S_{fi}=\langle f|S|i\rangle \end{aligned}$$

(2.1)

where S is called the S-matrix (S for scattering) and $S_{fi}$ are the matrix elements. Since the scattering must also include the possibility that nothing occurs, the S-matrix is written in terms of the T-matrix, namely

$$\begin{aligned} S_{fi}= \delta _{fi}+i (2\pi )^4\delta ^4(P_f-P_i)T_{fi} \end{aligned}$$

(2.2)

where the four-dimensional $\delta$-function imposes energy–momentum conservation on all particle momenta $p_j$, and, with obvious notation, $P_{i,f}=\sum _{\mathrm{all}}p_{i,f}$. The relevant matrix elements define the scattering and are functions of the momenta of the scattering particles, in particular of the various invariants which can be constructed with the momenta. Let us then turn to the kinematics before going further into the dynamics.

2.2 Kinematics of elastic scattering

Let us consider the two body process

$$\begin{aligned} a(p_1)+b(p_2) \rightarrow c(p_3)+d(p_4). \end{aligned}$$

(2.3)

Usually, two different set-ups are most frequently encountered: center of mass collisions, as in most if not all present day accelerator experiments at high energies and fixed target collisions, as is the case for cosmic ray proton-air collisions or low-energy photo-production experiments. It is usual to call Laboratory frame where fixed target collisions take place. However, there is another frequently encountered possibility, namely the kinematic configuration of two collinear particles of different momentum. This situation is found in electron– and photon–proton collisions at HERA and generally speaking is typical of parton–parton collisions. We shall present in the following the kinematics of all these three different possibilities.

In the c.m. frame of particles a and b, we write

$$\begin{aligned}&p_1^\mu =(E_a,0,0,p),\end{aligned}$$

(2.4)

$$\begin{aligned}&p_2^\mu =(E_b,0,0,-p),\end{aligned}$$

(2.5)

$$\begin{aligned}&p_3^\mu =(E_c,q\sin \theta ,0,q\cos \theta ),\end{aligned}$$

(2.6)

$$\begin{aligned}&p_4^\mu =(E_d,-q\sin \theta ,0,-q\cos \theta ), \end{aligned}$$

(2.7)

which can be described by two independent variables, to be chosen among three relativistic invariants, the so called Mandelstam variables, i.e.

$$\begin{aligned}&s=(p_1+p_2)^2=(p_3+p_4)^2 ,\end{aligned}$$

(2.8)

$$\begin{aligned}&t=(p_1-p_3)^2 =(p_2-p_4)^2,\end{aligned}$$

(2.9)

$$\begin{aligned}&u=(p_1-p_4)^2=(p_2-p_3)^2. \end{aligned}$$

(2.10)

For general processes, we have

$$\begin{aligned} s+t+u=m_a^2+ m_b^2+m_c^2+m_d^2=h \end{aligned}$$

(2.11)

and thus for elastic scattering, namely

$$\begin{aligned} a+b\rightarrow a+b \end{aligned}$$

(2.12)

we have $p\equiv q$ with

$$\begin{aligned} p^2= & {} \frac{s^2+(m^2_a-m^2_b)^2 -2s(m^2_a+m^2_b)}{4s},\end{aligned}$$

(2.13)

$$\begin{aligned}= & {} \frac{[s-(m_a+m_b)^2][s-(m_a-m_b)^2]}{4s}, \end{aligned}$$

(2.14)

and

$$\begin{aligned}&s= m_a^2+m_b^2+2p^2+2\sqrt{m_b^2+p^2}\sqrt{m_b^2+p^2},\end{aligned}$$

(2.15)

$$\begin{aligned}&t=-2p^2[1-\cos \theta ] \end{aligned}$$

(2.16)

where $\theta$ is the scattering angle in the c.m. frame.

For collisions not taking place in the center of mass, the kinematics reads differently. While $pp$ and ${\bar{p}}p$ scattering in present day accelerators take place through center of mass collisions, this was not true for early experiments, where typically a proton or antiproton was directed to a fixed hydrogen target, and it is also not true for meson proton scattering, such as $\pi p$, Kp or $\gamma p$, where pions, kaons or photons are directed to a fixed hydrogen target. In such cases, for the kinematics in the laboratory frame we get

$$\begin{aligned} s=m_a^2+m_b^2+2m_aE_b \end{aligned}$$

(2.17)

so that

$$\begin{aligned}&s_{pp}=2m_p^2+2m_pE_{lab},\end{aligned}$$

(2.18)

$$\begin{aligned}&s_{\pi p}=m_p^2+m_\pi ^2+2m_pE_\pi ,\end{aligned}$$

(2.19)

$$\begin{aligned}&s_{\gamma p}=m_p^2+2m_pE_\gamma . \end{aligned}$$

(2.20)

In all the above cases, the proton is at rest in the laboratory. A different case is the one encountered at HERA, where the two beams, photons and protons, collide with different momenta. For real photons of momentum q colliding with a proton of energy $E_p$, one has

$$\begin{aligned} q=\frac{s-m^2}{2m^2} E_p \left( 1-\sqrt{1-\frac{m^2}{E^2_p}}\right) . \end{aligned}$$

(2.21)

The kinematics is still different for virtual photon scattering and will be described in Sect. 7.

Because of energy–momentum conservation and of the condition imposed by Eq. (2.11), physical processes can take place only for those values of the variables s, t and u which lie in the so called physical region. Such a region is defined as [2]

$$\begin{aligned} stu\ge as+bt+cu \end{aligned}$$

(2.22)

where

$$\begin{aligned}&ah=(m_1^2m_2^2-m_3^2m_4^2)(m_1^2+m_2^2-m_3^2-m_4^2),\end{aligned}$$

(2.23)

$$\begin{aligned}&bh=(m_1^2m_3^2-m_2^2m_4^2)(m_1^2+m_3^2-m_2^2-m_4^2),\end{aligned}$$

(2.24)

$$\begin{aligned}&ch=(m_1^2m_4^2-m_2^2m_3^2)(m_1^2+m_4^2-m_2^2-m_3^2). \end{aligned}$$

(2.25)

For the equal-mass case, this reduces to the condition $stu\ge 0$ and the allowed regions are shown in the dashed areas of Fig. 1.

Fig. 1

Physical region for equal-mass elastic scattering

2.3 Unitarity and the scattering amplitude

The measurement of the total cross section is based on two complementary methods: counting the number of collisions and, measuring the very forward scattering probability. The second method is based on a fundamental physical property i.e., the conservation of probability, which is embedded in the unitarity property of the S-matrix, namely

$$\begin{aligned} SS^\dagger =\mathbf{1}. \end{aligned}$$

(2.26)

In terms of the matrix elements, we have

$$\begin{aligned} (SS^\dagger )_{fi}=\sum _n S_{fn} S_{ni}^*=\delta _{fi} \end{aligned}$$

(2.27)

where n runs on all possible intermediate states. This condition ensures the normalisation and orthogonality of states in the reaction. In particular, for the $i=f$ case, Eq. (2.27) ensures that the sum over all allowed transitions from a given state $|i\rangle$ to any possible final state, is one, namely

$$\begin{aligned} \sum _n |S_{ni}|^2=1. \end{aligned}$$

(2.28)

Equation (2.28) is the statement of conservation of probability in the scattering.

We can now proceed to derive the optical theorem, by using Eqs. (2.27) and (2.2) to obtain

$$\begin{aligned} T_{fi}-T^*_{if}=(2\pi )^{4} i\sum _n\delta ^4(P_f-P_n)T_{fn}T^*_{in}. \end{aligned}$$

(2.29)

Because the left-hand side of this equation is linear in T, while the right-hand side is quadratic, if the T-matrix can be expanded in a small parameter (say a coupling constant), then unitarity ensures that the T-matrix elements are hermitian. In the general case, one uses Eq. (2.29) to obtain the optical theorem, namely

$$\begin{aligned} 2 \hbox {Im} T_{ii}=(2\pi )^4\sum _n\delta ^4(P_i-P_n)|T_{{in}}|^2 \end{aligned}$$

(2.30)

where the amplitude $T_{ii}$ indicates elastic scattering in the forward direction and where the right-hand side, a part from a normalisation factor, gives the total cross section for scattering from an initial state $|i\rangle$ into any possible final state, as shown in the following subsection. The reader is warned that different authors use different normalisations for the elastic scattering amplitudes and hence due care must be taken in using various unitarity expressions.

2.4 The optical theorem and the total cross section

We follow here the definitions and normalisations as in [6]. Let us start with the general definition of total cross section, by first introducing the probability that a given two particle initial state $|i\rangle$ scatters into all possible final states $|f\rangle$, namely

$$\begin{aligned} \sum _f P_{fi}=\sum _{f\alpha }\int \left[ \prod _{n=1}^{N_f} \frac{\mathrm{d}^3p_n}{(2\pi )^32E_n}(S^\dagger _{if}S_{fi})\right] \end{aligned}$$

(2.31)

where the sun runs over all final states and all possible quantum numbers $\alpha$ of all possible final states. Next we use the S-matrix definition in terms of the T-matrix

$$\begin{aligned} \sum _f P_{fi}= & {} \sum _{f\alpha }\int \prod _{n=1}^{N_f} \frac{\mathrm{d}^3p_n}{(2\pi )^32E_n} \nonumber \\&\times |T_{fi}|^2 (2\pi )^4\delta ^4(P_f-P_i) (2\pi )^4\delta ^4(P_f-P_i)\nonumber \\ \end{aligned}$$

(2.32)

and define the probability of the scattering per unit volume and unit time, by using the conventional way to interpret $(2\pi )^4\delta ^4(P_f-P_i)$ as the four-dimensional scattering volume VT. Using the language of the laboratory frame, where the initial state consists of a target particle (T) and a projectile (P), a further step is taken by considering the scattering per target particle, dividing by the target particle density $2E_{T}$, and obtaining the cross section by further dividing this probability by the flux of incoming particles, $2E_{P}v_{P, lab}$. We then have

$$\begin{aligned}&\sigma _{\mathrm{tot}} \nonumber \\&\quad \equiv \sum _{f\alpha } \frac{(\mathrm{Probability} \ \mathrm{per}\ \mathrm{target} \ \mathrm{particle}\ \mathrm{per} \ \mathrm{unit} \ \mathrm{time})}{\mathrm{flux} \ \mathrm{of} \ \mathrm{incoming}\ \mathrm{particles}} \nonumber \\&\quad =\sum _{f\alpha } \frac{(\mathrm{Prob.}\ \mathrm{per}\ \mathrm{target}\ \mathrm{particle}\ \mathrm{per}\ \mathrm{unit}\ \mathrm{time})}{2E_{P} v_{P,lab}}\nonumber \\&\quad =\frac{(2\pi )^4}{4E_{T}E_{P}v_{P,lab}}\sum _{f\alpha }\int \prod _{n=1}^{N_f} \frac{\mathrm{d}^3p_n}{(2\pi )^32E_n} |T_{fi}|^2\delta ^4(P_f-P_i) . \nonumber \\ \end{aligned}$$

(2.33)

The next step is to use Eq. (2.30) to relate the total cross section to the imaginary part of the forward scattering amplitude so as to obtain, in the cm frame,

$$\begin{aligned} \sigma _{\mathrm{total}}=\frac{\mathrm{Im} T_{ii}}{2k\sqrt{s}} \end{aligned}$$

(2.34)

where k is the center of mass momentum of the incoming particles and $\sqrt{s}$ the c.m. energy. We then see that the total cross section can be measured in two different ways, either through the total count of all the final states hitting the detector or through the imaginary part of the forward elastic amplitude. In the next section, we will establish some definitions and properties of the elastic scattering amplitude.

2.5 The elastic scattering amplitude and its partial wave expansion

For two equal-mass particle scattering in the c.m. system, the Mandelstam invariants s, t, u take a particularly simple form and the physical region for the s-channel is defined as

$$\begin{aligned}&q^2_s=\frac{s-4m^2}{4}>0,\quad \cos \theta _s=1+\frac{t}{2q^2_s}<1; \end{aligned}$$

(2.35)

$$\begin{aligned}&\hbox {or } s>4m^2,\quad t\le 0,\quad u \le 0. \end{aligned}$$

(2.36)

Let then the elastic scattering amplitude $A(s,\cos \theta _s)$ be expanded in a series of Legendre polynomials

$$\begin{aligned} A^{F}(s,\cos \theta _s) =\frac{\sqrt{s}}{\pi q_s}\sum _{l=0}^\infty (2l+1)P_l(\cos \theta _s)a_l^F(s), \end{aligned}$$

(2.37)

where the subscript F refers to the normalisation used by Froissart. Martin’s normalisation differs by a factor $\pi$, namely

$$\begin{aligned} A^{M}(s,\cos \theta _s) =\frac{\sqrt{s}}{ q_s}\sum _{l=0}^\infty (2l+1)P_l(\cos \theta _s)a_l^M(s). \end{aligned}$$

(2.38)

For simplicity, we shall now use $\theta _s\equiv \theta$. Using elastic unitarity, it is rather simple to obtain some limits on the partial wave amplitudes $a_l$.

2.6 Asymptotic behaviour and Regge theory

We present here a brief description of the Regge expansion which has been very useful in molding our ideas about the behavior of elastic and total cross sections as a function of energy. The Regge picture forms the backbone of high energy phenomenology of cross sections. To illustrate its central theme, let us consider the partial wave expansion of an elastic scattering between two equal mass spinless particles of mass m

$$\begin{aligned} A(s,\cos \theta _s) = \sum _{l=0}^\infty (2l+1)P_l(z_s)a(l,s), \end{aligned}$$

(2.39)

where the partial wave amplitude $a(l,s) = (\frac{\sqrt{s}}{\pi q_s}) a_l^F(s)$ and $z_s = \cos \theta _s$. This expansion, for physical s-channel scattering ($s > 4 m^2$) certainly converges for $|z_s|\le 1$. The Regge expansion consists in obtaining a representation valid for large $z_s$ through a continuation from integral values of l to continuous (complex) values of l via the Sommerfeld–Watson (W–S) transformation. In non-relativistic potential scattering, Regge was able to prove that, for a superposition of Yukawa potentials, the amplitude a(l, s) is an analytic function of l and its only singularities are poles [the famous Regge poles, $l = \alpha (s)$)] and that bound states and resonances are simply related to them. The situation in the relativistic case is less clear and technically more involved [7, 8]. For integral values of l, Eq. (2.39) can be inverted to give

$$\begin{aligned} a(l,s) = \frac{1}{2} \int _{-1}^{1} A(s,z) P_l(z). \end{aligned}$$

(2.40)

While the above equation permits an analytic continuation of the function a(l, s) to complex values of l, it is not suitable for completing the W–S transformation due to the bad asymptotic behavior of P(l, z) for complex l [7]. Hence, a technical nicety, the Froissart–Gribov projection, is required. Assume that A(s, z) is polynomially bounded so that a fixed s-dispersion relation (with N subtractions) can be written down in the variable z:

$$\begin{aligned} A(s,z)= & {} \sum _{n = 0}^{N - 1} \gamma _n z^n +\frac{z^N}{\pi } \int _{z_r}^\infty \frac{\mathrm{d}z^{\prime } D_t(s,z^{\prime })}{z^{'N}(z^{\prime }-z)} \nonumber \\&+\,\frac{z^N}{\pi }\int _{-z_l}^{-\infty } \frac{\mathrm{d}z^{\prime } D_u(s,z^{\prime })}{z^{'N}(z^{\prime }-z)}, \end{aligned}$$

(2.41)

where $D_t$ and $D_u$ are the t and u channel discontinuities of the amplitude. Substituting the above in Eq. (2.40), we find that

$$\begin{aligned} a(l,s)= & {} \frac{1}{\pi }\left[ \int _{z_r}^{\infty }\mathrm{d}x D_t(s,x) Q_l(x)\right. \nonumber \\&\left. +\int _{-z_l}^{-\infty }\mathrm{d}x D_u(s,x) Q_l(x)\right] , \end{aligned}$$

(2.42)

obtained upon using the identity

$$\begin{aligned} Q_l(x) = \frac{1}{2} \int _{-1}^{1}(\mathrm{d}x) \frac{P_l(z)}{z - x}. \end{aligned}$$

(2.43)

Since for positive integral values of l, $Q_l(-z) = (-1)^{l +1} Q_l(z)$, we may rewrite Eq. (2.42) as

$$\begin{aligned} a(l,s) = \frac{1}{\pi }\int _{z_o}^{\infty }\mathrm{d}x [D_t(s,x)+(-1)^l D_u(s,x)] Q_l(x),\nonumber \\ \end{aligned}$$

(2.44)

where $z_o$ is the smaller of $z_l$ and $z_r$. To avoid obtaining dangerous factors such as $\mathrm{e}^{i\pi l}$ for complex l when we analytically continue Eq. (2.44), it is useful to define the “signatured” Froissart–Gribov amplitudes $a^{\pm }(l,s)$

$$\begin{aligned} a^{\pm }(l,s) = \frac{1}{\pi }\int _{z_o}^{\infty }\mathrm{d}x [D_t(s,x) \pm D_u(s,x)] Q_l(x), \end{aligned}$$

(2.45)

which can be continued for all $\mathfrak {R}e\ l > N$, since in this region, the above integrals converge. The positive signature amplitude $a^+(l,s) = a(l,s)$ for even l and the negative signature $a^-(l,s) = a(l,s)$ for odd l. Thus, the W–S transformation is to be performed on the signatured total amplitudes

$$\begin{aligned} A^{\pm }(s,z) = \sum _{l = 0}^{l = \infty } (2l + 1) a^{\pm }(l,s) P_l(z), \end{aligned}$$

(2.46)

separately. The physical amplitude is then given by the combination

$$\begin{aligned} A(s,z)= & {} \frac{1}{2}[ A^+(s,z) + A^+(s,-z) \nonumber \\&+\, A^-(s,z) - A^-(s,-z)]. \end{aligned}$$

(2.47)

For each of the amplitudes in Eq. (2.46), one first replaces the sum by a contour C which encircles all the integers in the sum

$$\begin{aligned} A^{\pm }(s,z) = \frac{i}{2} \int _{C} \frac{(2l + 1) a^{\pm }(l,s) P_l(-z)}{\sin \pi l}, \end{aligned}$$

(2.48)

since the function $\sin \pi l$ has poles at all the integers with residue $(-1)^l/\pi$ and use has been made of the property that for integers $P_l(-z) = (-1)^l P_l(z)$. The next step is to open the contour as in Fig. 2 and one finds a large semi-circle in the positive quadrant, a background integral running vertically at $\mathfrak {R}e\ l = -1/2$ and the contributions from any singularities in $a^{\pm }(l,s)$. We expect Regge poles and perhaps Regge cuts. Ignoring the cuts for the moment, we may write

$$\begin{aligned} A^{\pm }(s,z) = \frac{i}{2}\int _{C^{\prime }} \frac{(2l + 1) a^{\pm }(l,s) P_l(-z)}{\sin \pi l}\ \nonumber \\ - \sum _j \frac{\pi \beta _j^{\pm } (2\alpha _j^{\pm } + 1)P_{\alpha _j^{\pm }} (-z)}{\sin \pi \alpha _j^{\pm }}, \end{aligned}$$

(2.49)

Fig. 2

Graphical representation of the Sommerfeld–Watson transformation contour in the angular momentum plane

where the sum includes all poles with $\mathfrak {R}e\ \alpha _j(s) > -1/2$ and the corresponding $\beta _j^{\pm }(s)$ denote their residue. For large z (which is synonymous with large t for fixed s), $P_\alpha (z) \rightarrow \ z^\alpha$ and thus, in this limit $A^{\pm }(s,z)$ would be controlled by the Regge pole to the farthest right (called the leading Regge pole). Hence, one arrives at the Regge asymptotic behavior result that

$$\begin{aligned} A^{\pm }(s,t) \rightarrow \ \chi ^{\pm }(s) t^{\alpha _{\pm }(s)}, \end{aligned}$$

(2.50)

in the limit $t \rightarrow \ \infty$ for fixed s. Of course, had we made the Regge expansion in the t channel, we would have obtained the result

$$\begin{aligned} A^{\pm }(s,t) \rightarrow \ \chi ^{\pm }(t) s^{\alpha _{\pm }(t)}, \end{aligned}$$

(2.51)

in the limit $s \rightarrow \ \infty$ for t fixed. Putting in the proper phases, we obtain for the pole contribution to the amplitude (which dominates the background integral for all Regge poles with $\mathfrak {R}e\ \alpha (t) > -1/2$) to be of the form

$$\begin{aligned} A(s,t) \rightarrow \ -\gamma ^+(t)\frac{\mathrm{e}^{-i\pi \alpha ^+(t)} + 1}{\sin \pi \alpha ^+(t)}\left( \frac{s}{s_0}\right) ^{\alpha ^+(t)}\ \nonumber \\ -\gamma ^-(t)\frac{\mathrm{e}^{-i\pi \alpha ^-(t)} - 1}{\sin \pi \alpha ^-(t)}\left( \frac{s}{s_0}\right) ^{\alpha ^-(t)}. \end{aligned}$$

(2.52)

Using the form – valid for large s (i.e. ignoring masses) –

$$\begin{aligned} \sigma _{\mathrm{tot}}(s) = \left( \frac{16 \pi }{s}\right) \mathfrak {I}m\ A(s,0), \end{aligned}$$

(2.53)

we have

$$\begin{aligned} \sigma _{\mathrm{tot}}(s)\rightarrow & {} \frac{16 \pi }{s_0}\left[ \gamma ^+(0)\left( \frac{s}{s_0}\right) ^{\alpha ^+(0) - 1} \right. \nonumber \\&\left. +\, \gamma ^-(0)\left( \frac{s}{s_0}\right) ^{\alpha ^-(0) - 1}\right] . \end{aligned}$$

(2.54)

If $\alpha ^+(0) = 1$, then the total cross section would go to a constant value. This is the celebrated Pomeron pole. It has the added virtue that the ratio of the real part to the imaginary part of the forward elastic amplitude would be strictly zero, i.e.

$$\begin{aligned} \frac{\mathfrak {R}e\ A(s,0)}{\mathfrak {I}m\ A(s, 0)}|_{\alpha ^+(0) = 1}\rightarrow 0, \end{aligned}$$

(2.55)

exhibiting the limiting feature of diffraction scattering. Hence, the early excitement about the Pomeron.

By contrast, were $\alpha ^-(0) = 1$, not only would the relative roles of the real and the imaginary parts be reversed but there would be a genuine spin 1 massless physical particle pole (analogous to the photon) in the elastic amplitude. Since in the hadronic spectrum we have no massless particles – of any spin – we would conclude that $\gamma ^-(0) =0$ if $\alpha ^-(0) = 1$. Hence, there would be no contribution to the total cross section from an $\alpha ^-(0) = 1$ Regge pole (since it would have a vanishing residue). However, the real part may be finite then.

Experimental data clearly indicate that (i) all total cross sections increase at high energies and that (ii) the “rho” parameter

$$\begin{aligned} \rho (s,o)| = \frac{\mathfrak {R}e\ A(s,0)}{\mathfrak {I}m\ A(s, 0)} \ll 1. \end{aligned}$$

(2.56)

The question then arises as to how to implement these facts phenomenologically in a Regge picture. Some theoretical progress has been made regarding the imaginary part in QCD. In the BFKL Pomeron [9] model, one finds that the Pomeron intercept is slightly greater than 1, i.e., $\alpha ^+(0) = 1 + \epsilon$, where $\epsilon = (4 \alpha _s N_c/\pi ) \ln 2$, where $\alpha _s$ is the QCD coupling constant and $N_c$ is the number of colours (3 for QCD). Thus, $\sigma _{\mathrm{tot}} \approx \ (s/s_0)^\epsilon$ would rise with energy. While for small enough $\epsilon$, this may work for some energy band, it would eventually be in conflict with the Froissart bound discussed at length in the subsequent sections. The Froissart upper bound only permits a maximum increase $\sigma _{\mathrm{tot}} \le \ \sigma _P\ \ln ^2(s/s_0)$.

Powers of logarithms can arise due to the confluence of two (or more) pole singularities. For example, if in the angular momentum plane, there occurs a double pole at $l = \alpha (t)$, its contribution to the W–S integral would be through a derivative (in l evaluated at $l = \alpha$) [10]. Asymptotically then, if a simple pole gave $A(s,t)\approx (s/s_0)^\alpha$, a double pole would give $A(s,t)\approx (s/s_0)^\alpha \ln (s/s_0)$. To saturate the Froissart bound, we need two derivatives in $\alpha$ i.e., a third order pole, with of course $\alpha (0) =1$. On the other hand, the more general case, i.e., generation of a fractal power such as

$$\begin{aligned} \mathfrak {I}m A(s,t) \rightarrow (s/s_0) [\ln (s/s_0)]^{1/p}\ (\hbox {with } 1/2<p<1)\nonumber \\ \end{aligned}$$

(2.57)

(as found in a phenomenologically successful model for total cross section to be discussed later in Sect. 5.9.7 of this review) would require a confluence of an indefinite number of pole trajectories all converging at $\alpha (0) = 1$. We remark here in passing that, near a threshold, due to unitarity, a confluence of an infinite number of trajectories (the “threshold poles”) does occur and it has been well studied [10]. It is an open problem to deduce what happens in the vacuum channel of QCD with (almost massless) quarks and gluons. This problem is particularly difficult in QCD because it can only be answered satisfactorily after unitarity is imposed – a daunting task indeed.

The spectrum of mesonic masses leads one to conclude that there are four almost-degenerate Regge trajectories with intercepts close to 1 / 2 [8]. Hence, in a total cross section for the scattering of particle a with b, these terms provide the next to the leading contribution (about half a unit lower than the Pomeron) of the form $\sigma (ab)_{\mathrm{Regge}}(s) = \sum _{i=1}^4 \sigma _i(ab) (s/s_0)^{(\alpha _{i} -1)}$ with the sum running over the $\rho$, $\omega$, f and $A_2$ Regge trajectories. This nomenclature recalls the lowest spin resonance associated with a given Regge trajectory. As discussed in the FESR and duality section, the approximate degeneracy $\alpha _i \approx \ 1/2$ is deduced from the absence of resonances in “exotic” channels.

Thus, a phenomenological parametrisation based on the Regge picture for the high energy total cross section of particles a and b may be formulated as [11]

$$\begin{aligned} \sigma _{\mathrm{tot}}(ab)= & {} \sigma _P(ab)[\ln (s/s_0)]^{1/p} + \sigma _o(ab)\ \nonumber \\&+ \sum _i \sigma _i(ab)(s/s_0)^{(\alpha _{i} -1)}, \end{aligned}$$

(2.58)

where the constants $\sigma _P(ab)$, $\sigma _o(ab)$, and $\sigma _i(ab)$ are the respective coefficients of the “Pomeron”, an overall constant and the various Regge terms for the scattering process a on b. The constant p obeys the condition ($1/2\le p \le 1$) and $\alpha _i \approx 0.5$.

Regarding the asymptotic behavior of the $\rho$ parameter, defined in Eq. (2.56), let us use the generic fractal amplitude as given in Eq. (2.57)

$$\begin{aligned} A_{\mathrm{fractal}}(s,0) = A_0 \left( \frac{s \mathrm{e}^{-i\pi /2}}{s_0}\right) \left[ \ln \frac{s \mathrm{e}^{-i\pi /2}}{s_0}\right] ^{1/p}, \end{aligned}$$

(2.59)

where $A_0$ is a real constant and we have employed the phase rule $s\rightarrow s \mathrm{e}^{-i\pi /2}$ for crossing-even amplitudes [12]. This would give for the asymptotic form for $\rho$

$$\begin{aligned} \rho _{\mathrm{fractal}}(s,0)\rightarrow \ \frac{ \pi }{2 p\ \ln (s/s_0)}. \end{aligned}$$

(2.60)

This generalises for arbitrary p a rigorous result [13], valid for an amplitude saturating the Froissart bound (here achieved for $p = 1/2$).

While it may be difficult to distinguish between a total cross section increasing as ($[\ln (s/s_0)]^2$) or [$\ln (s/s_0)$] [or some power in-between for $1/2<p<1$], it may be easier to use experimental measurements of $\rho$ and employ Eq. (2.60) to decipher the value of p, since $\rho$ depends on (1 / p) linearly. In any event, one has two consistency conditions provided by Eqs. (2.58) and (2.60) for the parameter p.

In the next section, we discuss an important off-shoot from the Regge expansion which goes under the names of finite energy sum rules and duality.

2.7 Constraints from FESR and duality for the total cross sections

Analyticity in the complex (energy) plane for a function (say a form factor or an elastic scattering amplitude) quite generally implies that its values in the “low” and “high” parts of the complex plane must be intricately related. This obvious fact has been used successfully to relate integrals over the low-energy parts of amplitudes to those over their asymptotic high energy (Regge) parts.

To illustrate what is involved, consider the simplest but physically quite important example of the charge form factor F(s) of the proton normalised as $F(0) = 1$. Under the usual hypothesis that for space-like values $s = - Q^2 < 0$, the function is real and that it has a right-hand cut beginning at the physical charged particle-antiparticle thresholds, $s_o = 4m_\pi ^2, s_1 = 4m_K^2, s_2 = 4m_p^2,\ldots ,$ we may write a dispersion relation

$$\begin{aligned} F(s) = 1 + \frac{s}{\pi } \int _{s_o}^\infty \frac{\mathrm{d}s^{\prime } \mathfrak {I}m F(s^{\prime })}{s^{\prime } (s^{\prime } - s - i\epsilon )}. \end{aligned}$$

(2.61)

Let us use the extra (experimental) information that, for large (space-like) $Q^2 \rightarrow \infty$, $F(Q^2)\rightarrow 0$. Then Eq. (2.61) gives us a sum rule

$$\begin{aligned} \frac{1}{\pi } \int _{s_o}^\infty \frac{\mathrm{d}s \mathfrak {I}m F(s)}{s} = 1, \end{aligned}$$

(2.62)

which provides a relationship between the integrals over the low and high energy parts of (the imaginary parts) of the form factor. Since also, the neutron charge form factor goes to zero for large $Q^2$, we would obtain an expression analogous to Eq. (2.62) also for the neutron except that the right-hand side would be zero. In vector meson dominance (VMD) models, the couplings of the $\rho$, $\omega$ and the $\phi$ to the nucleons get constrained accordingly.

Actually experimental data regarding form factors are much more stringent: it appears that the fall off of the proton form factor is of the “dipole” type. For purposes of illustration, let us assume that $Q^2 F(Q^2) \rightarrow 0$ as $Q^2 \rightarrow \infty$. Then we can derive a “superconvergence” relation

$$\begin{aligned} \int _{s_o}^\infty (\mathrm{d}s) \mathfrak {I}m F(s) = 0. \end{aligned}$$

(2.63)

Equation (2.63) tells us that $\mathfrak {I}m F(s)$ must change sign at least once. To meet this exigency then, a generalised vector meson (GVMD) model with other vector mesons $\rho ^{\prime }, \omega ^{\prime }, \phi ^{\prime }$ etc. with their couplings (of reversed signs) to the nucleons have to be introduced. It is not our purpose here to advocate GVMD models but to illustrate very simply that dispersion relations with some knowledge – be it experimental or theoretical – about the behaviour of an amplitude at some value, allows us to put constraints at other values.¹

Let us now turn to a specific case that of the elastic meson-baryon amplitudes, with an eye towards their later applications to photon–nucleon total cross sections. For fixed t, in order to exploit the crossing symmetry between the s and the u channels, one defines the variable [8]

$$\begin{aligned} \nu = \frac{s - u}{4m} = \omega + \frac{t}{4m}, \end{aligned}$$

(2.64)

so that $\omega$ denotes the energy of the meson in the rest frame of the baryon and m denotes the mass of the baryon. For a crossing-odd scattering amplitude [8] $T(\nu ,t) = T^*(-\nu ,t)$, we may write a fixed-t dispersion relation

$$\begin{aligned} T(\nu , t) =(\hbox {possible poles})+\frac{2\nu }{\pi } \int _o^\infty (\mathrm{d}\nu ^{\prime }) \frac{\mathfrak {I}m T (\nu ^{\prime },t)}{(\nu ^{'2} - \nu ^2)}.\nonumber \\ \end{aligned}$$

(2.65)

Let us assume generic asymptotic Regge terms of the form

$$\begin{aligned} T_{\mathrm{Regge}}(\nu , t) = \sum _i \beta _i(t) \left[ \frac{\pm 1 - \mathrm{e}^{-i\pi \alpha _i(t)}}{\varGamma (\alpha _i(t)+1) \sin \pi \alpha _i(t)}\right] \nu ^{\alpha _i(t)}. \nonumber \\ \end{aligned}$$

(2.66)

Using arguments previously given, if all the $\alpha (t) < -1$, we would obtain a superconvergence relation

$$\begin{aligned} \int _o^\infty (\mathrm{d}\nu ) \mathfrak {I}m T(\nu , t) = 0. \end{aligned}$$

(2.67)

Instead, we can subtract the contributions from all $\alpha _i(t) > -1$ to obtain a superconvergence relation of the form

$$\begin{aligned} \int _o^\infty (\mathrm{d}\nu ) \left[ \mathfrak {I}m T(\nu , t) - \sum _{\alpha _i(t)>-1} \frac{\beta _i(t)}{\varGamma (\alpha _i(t)+1)} \nu ^{\alpha _i(t)}\right] = 0.\!\!\!\nonumber \\ \end{aligned}$$

(2.68)

Since asymptotically – by construction – the integrand in Eq. (2.68) goes to zero, we may replace the upper limit of the integration to be $\nu = N$ and include the left over Regge terms with $\alpha < -1$, and find

$$\begin{aligned}&\int _o^N (\mathrm{d}\nu ) \left[ \mathfrak {I}m T(\nu , t) - \sum _{\alpha _i(t)>-1} \frac{\beta _i(t)}{\varGamma (\alpha _i(t)+1)} \nu ^{ \alpha _i(t)}\right] \nonumber \\&\qquad + \sum _{\alpha _j<-1}\frac{\beta _j(t)}{\varGamma (\alpha _j(t) +1)}\int _N^\infty (\mathrm{d}\nu ) \nu ^{\alpha _j(t)} = 0. \end{aligned}$$

(2.69)

Doing the integral, we have the finite energy sum rule (FESR)

$$\begin{aligned} \mathcal{S}_o = \frac{1}{N} \int _o^N (\mathrm{d}\nu ) \mathfrak {I}m T(\nu , t) = \sum _{\mathrm{all}\ \alpha } \frac{\beta N^\alpha }{\varGamma (\alpha (t) +2)}. \end{aligned}$$

(2.70)

Also, higher moment sum rules may be written. For even integer n, we have

$$\begin{aligned} \mathcal{S}_n= & {} \frac{1}{N^{n+1}} \int _o^N (\mathrm{d}\nu )\nu ^n \mathfrak {I}m T(\nu , t)\ \nonumber \\= & {} \sum _{\mathrm{all}\ \alpha } \frac{\beta N^\alpha }{(\alpha (t) + n +1)\varGamma ( \alpha (t) +1)}. \end{aligned}$$

(2.71)

FESR can also be constructed for crossing even amplitudes and we shall return to them later.

As emphasised in [8], the relative importance of successive terms in a FESR is the same as in the usual Regge expansion: if a secondary pole is unimportant at a high energy above $\nu = N$ then this term would be unimportant to exactly the same instant in the sum rule. For $\pi N$ elastic scattering in the t-channel iso-spin $I_t = 1$, FESR have been exploited with much success to obtain information as regards the $\rho$ and the $\rho ^{\prime }$ trajectories [14]. Different variants of the idea have been used; see for example [15].

In FESR, the scattering amplitude is multiplied by an integral power of the laboratory energy. This was generalised to continuous moment sum rules (CMSR) [16]. In contrast to FESR, in CMSR, the multiplicative energy factor is non-integral. However, CMSR turn out to be simply a superposition of FESR, if the real part of the amplitude is calculated using dispersion relations [17]. For a review of the applications of these ideas to specific processes; see [18].

An interesting fall out from FESR was the concept of duality [19] which in its final form may be phrased as follows. Consider a generic amplitude A(s, t) and decompose its imaginary part (in the s-channel) in terms of the s-channel resonances and a smooth background. Then the assertion is that “direct” (s) channel resonances are “dual” to the crossed (t) channel Regge trajectories and the Pomeron term(s) is(are) dual to the background. Explicitly, it means that in Eq. (2.71) the integral over the left-hand side would contain contributions from s (and u) channel (baryonic) resonances whereas the right-hand side would contain contributions from mesonic Regge trajectories.

Let us give a practical example of FESR for total cross section. Suppose experimental data are available for a certain total cross section $\sigma _{\mathrm{tot}}$ within a given energy range. Optical theorem then allows us to convert this into a knowledge about the imaginary part of the forward elastic amplitude in the same energy range. Integrals of this amplitude over the available energy range must match a similar integral for a model describing the same asymptotic amplitude (ergo the asymptotic total cross section). Thus, unknown parameters in the model, usually Regge residues and intercepts, can be fixed.

For the phenomenology of high energy pp and $p\bar{p}$ total cross sections of interest at the Tevatron and LHC, one forms combinations of the sum and difference of the two cross sections, thus focusing attention on crossing-even $A_+(\nu )$ and crossing-odd $A_-(\nu )$ forward amplitudes. For the odd amplitude $A_-(\nu )$, the procedure described above is applicable. For the even amplitude $A_+(\nu )$, one constructs an odd amplitude $\nu A_+(\nu )$, to which the above arguments again apply. We shall discuss how it works in practice when we discuss models for total cross sections.

2.8 The Froissart–Martin bound

We shall now derive the Froissart bound following three slightly different methods, the original one by Froissart [3], the one by Martin in [1, 4], and Gribov’s derivation in [20]. These different derivations expose the different assumptions underlying them.

2.8.1 Froissart’s derivation of the asymptotic behaviour of the scattering amplitude

In [3], the bound on the total cross section is given an intuitive explanation. It must be noted (in hindsight) that this intuitive explanation relies upon the existence of confinement. Indeed, the whole description applies not to parton scatterings but to hadronic scattering. Let us go through Froissart’s intuitive explanation. Let the two particles (hadrons) see each other at large distances through a Yukawa-type potential, namely $g\mathrm{e}^{-\kappa r}/r$, where $\kappa$ is some momentum cut-off. Let a be the impact parameter, then the total interaction seen by a particle for large a is proportional to $g\mathrm{e}^{-\kappa a}$. When $g\mathrm{e}^{-\kappa a}$ is very small, there will be practically no interaction, while, when $g\mathrm{e}^{-\kappa a}$ is close to 1, there will be maximal probability for the interaction. For such values of a, $\kappa a=\ln |g|$ one then can write for the cross section $\sigma \simeq ( \pi /\kappa ^2) \ln ^2|g|$. If g is a function of energy and we assume that it can grow with energy at most like a power of s, then one immediately obtains that the large energy behaviour of the total cross section is bound by $\ln ^2 s$. What $\kappa$ is remains undefined for the time being, except that it has dimensions of a mass.

Following this heuristic argument, Froissart’s paper proceeds to the actual derivation of the bound. The derivation is based on the validity of the Mandelstam representation and the optical theorem. From the validity of the Mandelstam representation for the scattering amplitude and the convergence of the partial wave expansion, he derives an upper limit on each partial wave, which depends on the value $\mathbf{L}$ of angular momentum, after which the partial wave amplitudes become negligible. All the $a_l$ are then put equal to their maximum value $a_l=1$ and, then, in the forward direction, one has

$$\begin{aligned} \sum _0^\infty (2l+1) a_l=L^2+ \hbox {negligible terms}\le L^2. \end{aligned}$$

(2.72)

The value of L is determined as being such that for $l\le L$

$$\begin{aligned} |a_l| \le \frac{q_sB(s)}{\sqrt{s}(L-N)} \left\{ \frac{1}{x_0+ (x_0-1)^{1/2}} \right\} ^{L-N}=1 \end{aligned}$$

(2.73)

where $N-1$ is the minimum number of subtractions needed for the validity of the Mandelstam fixed-s dispersion relations and B(s) behaves at most like a polynomial in s, q being the c.m.momentum. Equation (2.73) leads to

$$\begin{aligned} L\simeq (q_s/\kappa ) \ln (B(s)), \end{aligned}$$

(2.74)

and from this through the optical theorem to the bound

$$\begin{aligned} \sigma _{\mathrm{total}}\le \ln ^2s. \end{aligned}$$

(2.75)

2.8.2 André Martin’s derivation

Martin’s derivation does not require the existence of the Mandelstam representation and is thus more general. Also, it provides an estimate of the constant pre factor to the maximum square of the logarithmic growth. We shall write $s =4k^2$ ignoring all particle masses except when necessary and use his normalisation of the elastic amplitude.

$$\begin{aligned} \sigma _{\mathrm{TOT}}(s)= & {} \left( \frac{16\pi }{s}\right) \sum _{l=0}^\infty (2l+1) \hbox {Im}\, f_l(s)\nonumber \\= & {} \left( \frac{16\pi }{s}\right) A_s(s,0), \end{aligned}$$

(2.76)

wherein

$$\begin{aligned}&f_l(s) = \frac{\eta _l(s)\mathrm{e}^{2i\delta _l(s)} - 1}{2i};\nonumber \\&\quad \hbox {Im}\, f_l(s) = \left( \frac{1}{2}\right) [1 - \eta _l(s) \cos (2 \delta _l(s))]; \end{aligned}$$

(2.77)

$0<\eta _l(s)<1$ is the inelasticity and $\delta _l(s)$ is the real part of the phase shift and

$$\begin{aligned} A_s(s,x) = \sum _{l=0}^\infty (2l+1) \hbox {Im}\, f_l(s) P_l(x);\quad x = \left( 1 + \frac{2t}{s}\right) ,\nonumber \\ \end{aligned}$$

(2.78)

denotes the s-channel absorptive part of the elastic amplitude. This partial wave series should converge upto $t > 4m^2_\pi$.

For the Froissart bound, Martin uses the majorisation scheme

(2.79)

(2.80)

(2.81)

Let us make a few remarks:

• (i) The first statement, Eq. (2.79), assumes that even for large s, the partial wave amplitude is elastic and a maximum i.e., $\eta _l(s)=1$ and $\delta _l(s)=\pi /2$. This is a gross overestimate since we expect that at large s, $\eta _l(s)\rightarrow 0$, so realistically we should take 1 / 2 and not 1 for low l. This then would get the heuristic result Martin obtains towards the end of a recent paper [21] improving the total cross section bound by a factor 2.

• (ii) Let us also note that Eq. (2.79) assumes that the partial wave amplitudes have a sharp cutoff, i.e., its value is exactly 1 for all l up to $L_T$, then brusquely it drops to $\epsilon$ for $l = L_T +1$ and then identically to 0 for all higher l. Clearly, this is a very unphysical assumption for a partial wave amplitude and cannot be true in any theory which enjoys analyticity in the variable l.

• (iii) The more reasonable behavior for large l, through the convergence of the partial expansion in the Lehmann ellipse leads to $\hbox {Im}\, f_l(s)\rightarrow \mathrm{e}^{[-l/(s/s_o)]}$ times a very smooth function of l and s. [Eq. (3.4) et sec in Martin’s book [1]]. This is also the $p\ge (1/2)$ discussed in [11] in the context of our BN (Bloch and Nordsieck) inspired model discussed later in Sect. 5.9.4, and is the minimum realistic dropoff. However, in obtaining the upper bound, Martin assumes it is identically zero beyond a certain l which is certainly true but again unrealistic.

Now to a derivation of the upper bound. Clearly from Eqs. (2.78) and (2.79), we have

$$\begin{aligned} A_s(s,x) > \sum _0^{L_T}(2l+1)P_l(x) = P_{L_T +1}^{\prime }(x) + P_{L_T}^{\prime }(x).\nonumber \\ \end{aligned}$$

(2.82)

To prove the last identity in Eq. (2.82), use the recursion identity $(2l+1)P_l(x) = P_{l+1}^{\prime }(x)- P_{l-1}^{\prime }(x)$ and then write the sum to be performed in the opposite order (beginning from the end)

$$\begin{aligned} \sum _0^{L_T}(2l+1)P_l(x)= & {} \left[ P_{L_T +1}^{\prime }(x)- P_{L_T -1}^{\prime }(x)\right] \nonumber \\&+ \left[ P_{L_T}^{\prime }(x) - P_{L_T -2}^{\prime }(x)\right] \nonumber \\&+ \left[ P_{L_T -1}^{\prime }(x) - P_{L_T -3}^{\prime }(x)\right] +\cdots \nonumber \\ \end{aligned}$$

(2.83)

All terms cancel, leaving only two terms

$$\begin{aligned} \sum _0^{L_T}(2l+1)P_l(x) = P_{L_T +1}^{\prime }(x)+ P_{L_T}^{\prime }(x).\quad \hbox {Q.E.D.} \end{aligned}$$

(2.84)

For large $L_T$, using Eqs. (2.78) and (2.84), we have

$$\begin{aligned} A_s(s,x) > 2P_{L_T}^{\prime }(x). \end{aligned}$$

(2.85)

Use the Laplace integral for the Legendre function to bound the right-hand side:

$$\begin{aligned} P_l(x) = \frac{1}{\pi }\int _0^\pi (\mathrm{d}\chi )\left[ x + \sqrt{x^2-1} \cos \chi \right] ^l, \end{aligned}$$

(2.86)

so that we can write for the derivative in a useful form

$$\begin{aligned} P_l'(x)= & {} \frac{l x}{\pi (x^2 -1)} \int _0^\pi (\mathrm{d}\chi )\left[ x + \sqrt{x^2-1} \cos \chi \right] ^{l-1} \nonumber \\&\times \left[ x -\frac{1}{x} + \sqrt{x^2 -1} \cos \chi \right] . \end{aligned}$$

(2.87)

Since $x>1$, we can bound the above

$$\begin{aligned} P_l^{\prime }(x) > \frac{l x}{\pi (x^2 -1)}\int _0^\pi (\mathrm{d}\chi )\left[ x + \sqrt{x^2-1} \cos \chi \right] ^l.\nonumber \\ \end{aligned}$$

(2.88)

Using the mean value theorem, we can impose the bound

$$\begin{aligned} P_l^{\prime }(x) > \frac{l x \phi _o}{\pi (x^2 -1)}\left[ x + \sqrt{x^2-1} \cos \phi _o\right] ^l, \end{aligned}$$

(2.89)

for any $0<\phi _o<\pi$. Since $x\rightarrow 1$ and $(x^2-1)\rightarrow (4t/s)$,

$$\begin{aligned} 2 P_{L_T}^{\prime }(x) > (\hbox {Constant})L_T \left( \frac{s}{4t}\right) \left[ x + \sqrt{x^2-1} \cos \phi _o\right] ^{L_T}\nonumber \\ \end{aligned}$$

(2.90)

and hence using Eq. (2.85), we have

$$\begin{aligned}&\left[ (\hbox {Constant})\left( \frac{t}{s}\right) A_s(s,t)\right]>L_T \left[ x + \sqrt{x^2-1} \cos \phi _o\right] ^{L_T}\!\!\!\!\nonumber \\&\quad > \left[ 1 +\sqrt{x^2-1} \cos \phi _o\right] ^{L_T}. \end{aligned}$$

(2.91)

Taking logarithms of both sides we have

$$\begin{aligned}&\ln \left[ (\hbox {Constant})\left( \frac{t}{s}\right) A_s(s,t)\right] \nonumber \\&\quad >L_T \ln \left[ 1 + \sqrt{x^2-1} \cos \phi _o\right] \rightarrow L_T \sqrt{4t/s}\ \cos \phi _o . \nonumber \\ \end{aligned}$$

(2.92)

We need only two subtractions in $A_s(s,t)$ and so $A_s(s,t)< (s/s_o)^2/\ln (s/s_o)$. Using it in the above, we arrive finally at the maximum value allowed for $L_T$

$$\begin{aligned} L_T < \sqrt{(s/4t)}\ \left[ \frac{\ln (s/s_o)}{\cos \phi _o}\right] . \end{aligned}$$

(2.93)

Now the Froissart bound for the total cross section follows from

$$\begin{aligned} \sigma _{\mathrm{TOT}} < \frac{16 \pi }{s}L_T^2 = \frac{4\pi [\ln (s/s_o)]^2}{t \cos ^2\phi _o}. \end{aligned}$$

(2.94)

Letting $t = 4 m_\pi ^2$ and $\phi _o = \pi$, we have the Froissart–Martin result

$$\begin{aligned} \sigma _{\mathrm{TOT}} < \left[ \frac{\pi }{m_\pi ^2}\right] [\ln (s/s_o)]^2. \end{aligned}$$

(2.95)

All of this can be duplicated in the eikonal scheme and of course much more simply as shown below.

2.8.3 Eikonal picture derivation

In the limit of large s and fixed $t<0$, the eikonal picture emerges under the hypothesis of identifying the impact parameter b formally as $(l + 1/2)\rightarrow b\sqrt{s}/2$, so that

$$\begin{aligned} P_l\left( 1 + \frac{2t}{s}\right) \rightarrow I_o(b\sqrt{t}), \end{aligned}$$

(2.96)

where $I_o$ is the Bessel function of the “imaginary argument”. With this identification, Eq. (2.78) reads

$$\begin{aligned} A_s(s,x) = \left( \frac{s}{2}\right) \int _0^\infty (bdb)\ \hbox {Im}\,F(b,s) I_o(b\sqrt{t}), \end{aligned}$$

(2.97)

where the “b-wave amplitude” reads

$$\begin{aligned} F(b,s)= \frac{\eta (b,s)\mathrm{e}^{2i\delta (b,s)} - 1}{2i}. \end{aligned}$$

(2.98)

We may now impose a similar majorisation scheme as before

$$\begin{aligned}&\hbox {Im}\, F(b,s)= 1\quad \hbox {for}\ b\le b_T; \qquad \hbox {and}\nonumber \\&\qquad \hbox {Im}\, F(b,s)= 0\quad \hbox {for}\ b> b_T, \end{aligned}$$

(2.99)

whence

$$\begin{aligned} A_s(s,t) > \left( \frac{s}{2}\right) \int _0^{b_T}(b db)I_o(b\sqrt{t}). \end{aligned}$$

(2.100)

The last integral can be done. Changing variables $Y_T=b_T \sqrt{t}$, we have

$$\begin{aligned} \left[ \frac{2t}{s} A_s(s,t)\right] > \int _0^{Y_T}(y \mathrm{d}y)I_o(y) = Y_T I_1(Y_T). \end{aligned}$$

(2.101)

For large $Y_T$,

$$\begin{aligned} I_1(Y_T)\rightarrow \ \frac{\mathrm{e}^{Y_T}}{\sqrt{2\pi Y_T}}, \end{aligned}$$

(2.102)

so that, for large $Y_T$

$$\begin{aligned} \left[ \frac{2t}{s} A_s(s,t)\right]> \frac{\sqrt{Y_T}\mathrm{e}^{Y_T}}{\sqrt{2\pi }} > \mathrm{e}^{Y_T}, \end{aligned}$$

(2.103)

upon which by taking the logarithms of both sides, and remembering that $A_s(s,t)<\ (s/s_o)^2/\ln (s/s_o)$, we obtain from

$$\begin{aligned} \left[ \frac{2t}{s} A_s(s,t)\right]> \frac{\sqrt{Y_T}\mathrm{e}^{Y_T}}{\sqrt{2\pi }} > \mathrm{e}^{Y_T}, \end{aligned}$$

(2.104)

that

$$\begin{aligned} Y_T < \ln (s/s_1), \end{aligned}$$

(2.105)

and thus that

$$\begin{aligned} \sigma _{\mathrm{TOT}} < \left( \frac{s}{2}\right) \int _0^{b_T} (b\mathrm{d}b) = \left[ \frac{\pi }{m_\pi ^2}\right] [\ln (s/s_1)]^2, \end{aligned}$$

(2.106)

upon imposing $t=4m_\pi ^2$.

2.8.4 Gribov’s derivation

What follows is almost verbatim from Sec. (1.4) of [20]. To show that asymptotically

$$\begin{aligned} \hbox {Im}\, A(s,t)|_{t=0}\le \hbox {const} \cdot s \log ^2 {{s}\over {s_0}}\quad s\rightarrow \infty , \end{aligned}$$

(2.107)

Gribov proceeds as follows. His notation differs slightly from the one in the previous section. Defining

$$\begin{aligned} A(s,t)=\sum _{l=0}^\infty (2l+1)f_l(s)P_l(z), \end{aligned}$$

(2.108)

with the partial wave amplitudes defined as

$$\begin{aligned} f_l(s)=8 \pi i [1-\eta _l\mathrm{e}^{2i\delta _l(s)}]. \end{aligned}$$

(2.109)

[With respect to Martin, the difference is a factor of $16 \pi$.]

Using the fact that the singularity of $\hbox {Im}_s A(s,t)$ closest to the physical region of the s-channel is situated at $t=4\mu ^2$, one tries to estimate $f_l(s)$ at large s. At large l, the partial wave amplitude must fall exponentially in order to ensure convergence for $t>0$. This is a consequence of

$$\begin{aligned}&P_l(\cosh \alpha ) \simeq {{\mathrm{e}^{l\alpha }}\over { \sqrt{2\pi l \sinh \alpha } }};\quad \mathrm{for}\ l\rightarrow \infty \nonumber \\&\cosh \alpha =1+{{2t}\over {s}}. \end{aligned}$$

(2.110)

To ensure convergence for $t<4\mu ^2$, the partial wave amplitudes must then decrease as

$$\begin{aligned} f_l \approx \mathrm{e}^{-l\alpha _0},\quad \cosh \alpha _0=1+{{8\mu ^2}\over {s}}. \end{aligned}$$

(2.111)

Now, in the limit $s\gg t$, $\cosh \alpha \approx 1+ \alpha ^2/2$, hence $\alpha _0={{\sqrt{4\mu ^2}}\over {k_s}}$ and one can write

$$\begin{aligned} f_l(s )\approx c(s,l) \mathrm{e}^{-{{l}\over {k_s}} \sqrt{4\mu ^2}},\quad l\rightarrow \infty ,\quad s\rightarrow \infty \end{aligned}$$

(2.112)

where $k_s=\sqrt{s-4\mu ^2}/2$. The function c(s, l) may be a slowly varying (non-exponential) function of l.

To establish the Froissart bound, Gribov now assumes that the scattering amplitude grows no faster than a power of s, in the vicinity of the $t=4\mu ^2$ pole in the t-channel. This condition is analogous to the one about subtraction in Martin’s derivation, just before Eq. (2.93). If $A(s,t)<(s/s_0)^N$, one can then see that this also valid for $\hbox {Im}\, c(s,l)$. Let us see how.

$$\begin{aligned} \left( {{s}\over {s_0}}\right) ^N> & {} \hbox {Im} (A(s,t) \nonumber \\= & {} \sum _{l=0}^\infty (2l+1) \hbox {Im}\, f_l(s) P_l\left( 1+{{t}\over {2k_s^2}}\right) . \end{aligned}$$

(2.113)

Since all the $\hbox {Im}\, f_l(s)$ are positive due to the unitarity condition as well as the $P_l$ for $t>0$, it must also be true for each term on the sum, namely

$$\begin{aligned} \left( {{s}\over {s_0}}\right) ^N>\hbox {Im}\, c(l,s) \left( 2 \pi l {{\sqrt{t}} \over {k_s}}\right) ^{-1/2}\mathrm{e}^{{{l}\over {k_s}}(\sqrt{t}-\sqrt{4\mu ^2})}\nonumber \\ \end{aligned}$$

(2.114)

and for $t<4\mu ^2$ it will also be

$$\begin{aligned} \hbox {Im} \, c(l,s) < \left( {{s}\over {s_0}}\right) ^N \end{aligned}$$

(2.115)

and finally we have

$$\begin{aligned} \hbox {Im}\, f_l(s)\le \left( {{s}\over {s_0}}\right) ^N \mathrm{e}^{-{{2\mu }\over {k_s}} l }. \end{aligned}$$

(2.116)

With the bound on $\hbox {Im}\, f_l(s)$, we can now derive the bound on the imaginary part of the forward scattering amplitude and hence on the total cross section.

$$\begin{aligned}&\hbox {Im}\, A(s,t=0)=\sum _{l=0}^{\infty } (2l+1)\hbox {Im}\, f_l(s),\end{aligned}$$

(2.117)

$$\begin{aligned}&\quad \le 8\pi \sum _{l=0}^{L} (2l+1) + \sum _{l=L}^{\infty } (2l+1)\hbox {Im}\, f_l(s) \end{aligned}$$

(2.118)

where one has divided the sum into a term where the partial waves are large and for which the partial waves take the maximum value allowed by unitarity, and one which contains all the higher partial waves. To estimate the value of L after which the partial waves are small, consider that they will become less than 1 when

$$\begin{aligned} \left( {{s}\over {s_0}}\right) ^N \mathrm{e}^{-{{2\mu }\over {k_s}} L }\le 1\quad \hbox {or}\quad L \le {{k_s}\over {2\mu }} \log {{s}\over {s_0}}. \end{aligned}$$

(2.119)

Now using

$$\begin{aligned} \sum _{l=0}^{L} (2l+1)=L^2 \end{aligned}$$

(2.120)

we immediately obtain

$$\begin{aligned} \hbox {Im}\, A(s,t=0) \propto L^2 \propto s\log ^2 {{s}\over {s_0}}. \end{aligned}$$

(2.121)

The question arises as to how large are the neglected terms. We can estimate them by using $f_{L+n}\sim f_L \mathrm{e}^{-{{2\mu }\over {k_s}}n}$ and then sum the second series as

$$\begin{aligned} \sum _{n=0}^{\infty } 2(L+n)\mathrm{e}^{-{{2\mu }\over {k_s}}n}\sim L{{k_s}\over {\mu }} +{{k_s^2}\over {2\mu ^2}}\ll L^2. \end{aligned}$$

(2.122)

These terms are at most of order $L^2/\log (s/s_0)$ and are subdominant.

Now, using the optical theorem, $\hbox {Im}\,A(s,0)=s \sigma {tot}(s)$ one obtains the bound

$$\begin{aligned} \sigma _{\mathrm{tot}}(s)\le \sigma _0 \log ^2{{s}\over {s_0}}. \end{aligned}$$

(2.123)

Thus this demonstration uses

• position of the t-channel singularity closest to the s-channel physical region, at $t=4\mu ^2$

• convergence of the partial wave series for $t>0$ (and at most up to the singularity)

• large l-behaviour of the Legendre polynomials for $z>1$

• that the amplitude does not grow with s faster than a fixed power

• unitarity condition to ensure that $\hbox {Im}\, f_l(s)$ is positive.

2.9 The Pomeranchuk theorem

Here again we follow Gribov. The Pomeranchuk theorem [22] says that, if total hadronic cross sections go to a constant at very high energy, then asymptotically particle-particle or particle-antiparticle total cross sections should be equal. It was derived using the property of crossing symmetry of the elastic scattering amplitude.

We know, since the early 1970s, that total cross section grow with energy [23], and therefore the Pomeranchuk theorem could be considered obsolete. However, there are two reasons to discuss it, one of them being that our understanding of high energy particle collisions if dominated by gluon–gluon scattering in QCD framework, would give the same result as the Pomeranchuk theorem, as discussed later in this section. On the other hand, since the total cross section is not a constant at high energy, there is space for the existence of the so-called Odderon, whose exchange may be relevant at very high energies. We shall discuss more about this point in later sections.

The Pomeranchuk theorem is derived very simply. First of all, let us move from the discrete representation of the scattering amplitude in angular momentum l to the impact-parameter space. To do this, one notices that, for the total cross section not to decrease at very high energy, one needs contributions from higher and higher partial waves. At high energy, and in the forward direction, the main contribution to the total cross section comes from higher partial waves. For large l then we can use the asymptotic expression for the Legendre polynomials,

$$\begin{aligned} P_l(\cos \theta )\approx J_0\left( (2l)\frac{\theta }{2}\right) \ \ l\gg 1 \ \ \theta \approx 0. \end{aligned}$$

(2.124)

We can then substitute the sum over the partial waves with an integral and introduce the impact-parameter variable $l k_s=b$. Then the partial wave expansion becomes

$$\begin{aligned} A(s,t)\approx k^2_s\int \mathrm{d}^2b f(b,s)J_0(b\sqrt{-t}). \end{aligned}$$

(2.125)

To obtain a constant total cross section, assume the integral to be dominated by values of the impact parameter whose distribution is independent of the energy: in such a case, the s and t dependences can be factorised. One puts $f(b,s)\approx a(s) B(b)$, to obtain

$$\begin{aligned} A(s,t)\approx s a(s) F(t). \end{aligned}$$

(2.126)

Assuming the further possibility that a(s) has no residual s-dependence, from the optical theorem there follows the constant high energy behaviour of the total cross section. To summarise, constant total cross sections can be seen to arise if one can factorise the s and t dependence in the scattering amplitude, and if the dominant partial wave amplitudes also become constant at very high energy. Both assumptions are not necessarily satisfied. These two assumptions, however, allow demonstration of the Pomeranchuk theorem, when we use crossing symmetry to relate two processes, in which one particle in the initial state is substituted with an antiparticle from the final state. This amounts to relating the analyticity properties in the s-channel to those in the u-channel. The argument goes as follows.

Fig. 3

Physical region for equal-mass elastic scattering

Let us consider the two processes

$$\begin{aligned}&a+b \rightarrow c+d,\end{aligned}$$

(2.127)

$$\begin{aligned}&a+{\bar{d}}\rightarrow c+{\bar{b}} \end{aligned}$$

(2.128)

and let A(s, t) be the amplitude which describes the first of the above processes. The s-channel physical region for process $a+b\rightarrow c+d$ is shown in Fig. 3, i.e. with the usual right-hand cut starting at $s=4\mu ^2$ and the left-hand cut starting at $s=0$. It is convenient to assume that the amplitude for $a+b\rightarrow c+d$ corresponds to the value above the right-hand cut, namely, to be given by $\lim _{\epsilon \rightarrow 0} A(s+i\epsilon ,t)$, whereas the crossed process $a+{\bar{d}}\rightarrow c+{\bar{b}}$ corresponds to exchange $s=(p_a+p_b)^2 =(p_c+p_d)^2$ with $u=(p_a-p_d)^2=(p_c-p_b)^2$. For the crossed process, the physical region corresponds to $\lim _{\epsilon \rightarrow 0}A(u+i\epsilon ,t)=\lim _{\epsilon \rightarrow 0}A(-s+i\epsilon -t -4\mu ^2,t)=\lim _{\epsilon \rightarrow 0}A(-(s-i\epsilon )-t -4 \mu ^2,t)$, and therefore the physical region for this process, in the s-channel is obtained by approaching the real axis, on the left-hand side, from below, as indicated in Fig. 3. Because the amplitude A(s, t) is real for $0<s<4\mu ^2, t<0$, its value at the edge of the cuts complex conjugates, namely

$$\begin{aligned} A(s-i\epsilon ,t<0)=A^*(s+i\epsilon ,t<0), \end{aligned}$$

(2.129)

but the amplitude at the left-hand side is for process $a+{\bar{d}}\rightarrow c+{\bar{b}}$, whereas the one at the right-hand side is the amplitude for $a+b\rightarrow c+d$ and one then can write

$$\begin{aligned} A_{a+{\bar{d}}\rightarrow c+{\bar{b}}}(s)\rightarrow [A_{a+b\rightarrow c+d}(s)]^*\quad \hbox {for } s\approx -u. \end{aligned}$$

(2.130)

Now apply the above result to the elastic amplitude for $a+b\rightarrow a+b$ and consider the imaginary part of the forward amplitude. If the s-dependence is of the simple type which leads to constant total cross section, namely $A(s,t)\simeq sF(t)$ at large s, then optical theorem gives

$$\begin{aligned} \sigma (a+b) \approx \sigma (a+{\bar{b}})\quad \hbox {asymptotically}. \end{aligned}$$

(2.131)

For more complicated s and t-dependences in the amplitude, i.e. those that do not imply constant total cross sections, Eq. (2.131) can still be obtained in some simple cases such as $A(s,t)\simeq s \ln {s}^{\beta } F(t)$. However, the derivation then needs the additional hypothesis that the real part of the amplitude does not exceed asymptotically the imaginary part, a hypothesis de facto supported by experimental data.

2.10 Determination of the $\rho$ parameter through Coulomb interference and soft radiation

Here we discuss how near the forward direction, the real part of the hadronic amplitudes is determined through its interference with the Coulomb amplitude. We highlight some of the subtleties associated with the procedure. Also, a proposal is presented for obtaining information as regards the behavior of the purely nuclear amplitude through the measurement of the soft radiation spectrum in a quiet event, i.e., unaccompanied by any other visible particle.

2.10.1 Coulomb interference

At high energies, the $\rho$-parameter, which denotes the ratio of the real to the imaginary part of the forward (complex) nuclear scattering amplitude A(s, 0)

$$\begin{aligned} \rho (s) = \frac{\mathfrak {R}e A(s, 0)}{\mathfrak {I}m A(s, 0)}, \end{aligned}$$

(2.132)

is rather small (about $0.12\div 0.14$). Since, the total (nuclear) cross section depends only on $\mathfrak {I}m A(s, 0)$ and through the optical theorem, the elastic differential cross section in the forward direction depends on $\rho$ quadratically

$$\begin{aligned} \left( \frac{\mathrm{d}\sigma _{\mathrm{el}}}{\mathrm{d}t}\right) (t = 0) = \left( \frac{\sigma _{\mathrm{tot}}^2}{16\pi }\right) [1 + \rho ^2], \end{aligned}$$

(2.133)

it is difficult to measure $\rho$ accurately and in any event such a measurement would not determine the sign of the real part of the nuclear amplitude.

Fortunately, when we augment the nuclear with the Coulomb amplitude (due to one-photon exchange, in the lowest order), the interference between the Coulomb and the real part of the nuclear amplitude (for small t) allows us to determine both the sign and the value of $\rho$. The Rutherford singularity (${\propto } \alpha /t$) renders the Coulomb amplitude sufficiently large to become competitive with the nuclear term, for small t. On the other hand, away from very small angles, the Coulomb term dies out and one can safely revert to the purely nuclear amplitude. However, to obtain numerically accurate information as regards $\rho$, some care is required to obtain the correct Coulomb phase for the nuclear problem.

To see what is involved, let us consider first Coulomb scattering in non-relativistic potential scattering. The classical Rutherford amplitude (or, the Born approximation, quantum-mechanically), with a Coulomb 1 / r potential, for the scattering of two charges ($Z_1 e$) and ($Z_2 e$), is given by

$$\begin{aligned} f_C(k, \vartheta ) = \frac{2 Z_1 Z_2 \mu \alpha }{t}, \end{aligned}$$

(2.134)

where $\mu$ denotes the reduced mass, $t= - 4 k^2 \sin ^2 \vartheta /2$ and $\alpha \approx \ 1/137$ is the fine structure constant. But the exact (quantum-mechanical) Coulomb scattering amplitude has an oscillating phase $\mathrm{e}^{i\phi _S}$ multiplying the above. This phase is given by [24]

$$\begin{aligned} \phi _S = \left( \frac{Z_1 Z_2 \alpha c}{v}\right) \ \ln (\sin ^2\vartheta /2), \end{aligned}$$

(2.135)

where v denotes the relative velocity and the presence of $\alpha$ reminds us of the quantum nature of this phase The physical reason for this phase is that the Coulomb potential is infinite range and however far, a charged particle is never quite free and hence is never quite a plane wave. For pp or $p\bar{p}$ scattering, in the relativistic limit ($v\rightarrow \ c$) and for small angles, Eq. (2.135) reduces to

$$\begin{aligned} \phi _S \approx \ (\mp 2\alpha )\ \ln \left( \frac{2}{\vartheta }\right) . \end{aligned}$$

(2.136)

Equation (2.136) is exactly the small-angle limit of the relativistic Coulomb phase obtained by Solov’ev [25]. On the other hand, this result was in conflict with an earlier potential theory calculation by Bethe [26] employing a finite range (R) nuclear potential in conjunction with the Coulomb potential. According to Bethe, the effective Coulomb phase reads

$$\begin{aligned} \phi _B \approx \ (\pm 2\alpha ) \ln (k R \vartheta ). \end{aligned}$$

(2.137)

This discrepancy was clarified by West and Yennie [27]. These authors computed the effective Coulomb phase through the absorptive part of the interference between the nuclear and the Coulomb amplitude. They found – again in the small angle, high energy limit –

$$\begin{aligned} \phi _{WY} = (\mp \alpha )\left[ 2 \ln \left( \frac{2}{\vartheta }\right) + \int _{-s}^0 \frac{\mathrm{d}t^{\prime }}{|t^{\prime } - t|}\left\{ 1 - \frac{A(s,t')}{A(s,t)}\right\} \right] .\nonumber \\ \end{aligned}$$

(2.138)

If one ignores the t dependence of the nuclear amplitude, the integral term above is zero and one obtains Solov’ev’s result. On the other hand, a result similar to that of Bethe is reproduced, if one assumes the customary fall-off $\mathrm{e}^{B t/2}$ for the nuclear vertex and a dipole form factor for the EM vertex. Explicitly, if we choose

$$\begin{aligned} \frac{A(s,t{'})}{A(s,t)} = \mathrm{e}^{B(t^{\prime } - t)/2} \bigg (\frac{1 - t/\varLambda ^2}{1 - t^{\prime } /\varLambda ^2}\bigg )^2, \end{aligned}$$

(2.139)

we find

$$\begin{aligned} \phi _{WY} \approx \ (\pm \alpha )\left[ \gamma + \ln (B|t|/2) + \ln \left( 1 + \frac{8}{B \varLambda ^2}\right) \right] ,\nonumber \\ \end{aligned}$$

(2.140)

where $\gamma \approx 0.5772$ is the Euler–Mascheroni constant. This expression for the effective Coulomb phase agrees with Block [51], upto terms proportional to ($|t|/\varLambda ^2$), which are quite small near the forward direction. Hence, Eq. (2.140) is sufficiently accurate for determining $\rho$ through interference at LHC energies and beyond.

Block has defined a practically useful parameter $t_o$ for which the interference term is a maximum: $t_o= [8\pi \alpha /\sigma _{\mathrm{tot}}]$. For the maximum LHC energy of $14~\hbox {TeV}$, $t_o\approx 7\times 10^{-4}~\hbox {GeV}^2$. Putting it all together, the Coulomb corrected, differential cross section for $pp$ or ${\bar{p}}p$ reads [51]

$$\begin{aligned} \left[ \frac{\mathrm{d}\sigma }{\mathrm{d}|t|}\right] _{o}= & {} \left( \frac{\sigma _{\mathrm{tot}}^2}{16\pi }\right) \left[ G^4(t)\left( \frac{t_o}{t}\right) ^2\mp \, 2\frac{t_o}{|t|} (\rho \pm \phi _{WY})\right. \nonumber \\&\times \left. G^2(t) \mathrm{e}^{-B|t|/2}+\, (1 + \rho ^2) \mathrm{e}^{-B|t|} \right] , \end{aligned}$$

(2.141)

where for the magnetic form factor, one may employ $G(t)= [\frac{1}{1 - t/\varLambda ^2}]^2$, with $\varLambda ^2\approx 0.71~\hbox {GeV}^2$.

One other aspect of the EM radiative corrections needs to be investigated. So far, we have not considered real soft-photon emissions in the scattering process. As is well known, contributions due to an infinite number of soft photons can be summed via the Bloch–Nordsieck theorem. If $(\mathrm{d}\sigma /\mathrm{d}t)_o$ denotes the differential cross section without the emitted soft-photons, the inclusion of soft radiation introduces a parameter which is the external energy resolution $\varDelta E$. A compact expression for the corrected cross section can be written as follows [28]:

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t} = \left( \frac{\varDelta E}{E}\right) ^{\hat{\beta }} \left( \frac{\mathrm{d}\sigma }{\mathrm{d}t}\right) _o, \end{aligned}$$

(2.142)

where the radiative factor $\hat{\beta }$ combines the various combinations of the momenta of the charged emitting particles in our equal-mass elastic case

$$\begin{aligned} \hat{\beta } = \left( \frac{2\alpha }{\pi }\right) [I_{12} + I_{13} - I_{14} - 2], \end{aligned}$$

(2.143)

where

$$\begin{aligned} I_{ij} = 2 (p_i\cdot p_j)\int _0^1 \frac{\mathrm{d}y}{[m^2 + 2(p_i\cdot p_j - m^2) y(1-y)]}.\nonumber \\ \end{aligned}$$

(2.144)

In the high energy limit, $I_{12}(s)\rightarrow \ 2 \ln (s/m^2)$ and $I_{14}(s)\rightarrow 2\ln (|u|/m^2)$, so that the sum $I_{12} - I_{14}\rightarrow 0$ vanishes, leaving us with $I_{13}(t)$. For small-angle scattering of interest here, we have the correction from real photon emission of the form

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t} = \left( \frac{\varDelta E}{E}\right) ^{\beta (t)} \left( \frac{\mathrm{d}\sigma }{\mathrm{d}t}\right) _o, \end{aligned}$$

(2.145)

where

$$\begin{aligned} \beta (t) \approx \left( \frac{4\alpha }{\pi }\right) \left( \frac{-t}{3m^2}\right) ;\quad (-t\ll m^2), \end{aligned}$$

(2.146)

which is rather small and vanishes as $t = 0$. The physical reason is that the amount of radiation is small for low velocities. For the CM elastic amplitude, the energy loss $\varDelta E$ due to real soft bremsstrahlung is estimated by the lack of collinearity in the outgoing particles. Thus, $(\varDelta E/E)\approx \varDelta \vartheta$. Even for $\varDelta \vartheta \sim \ 10^{-4}$, the real radiative correction is extremely small and thus can be ignored.

2.10.2 Soft photon radiation as a possible tool for measurements of the total cross section

Through the above expressions, we may compute the differential probability for a single soft photon produced in association with the near forward elastic process. That is, the differential cross section for the process $p(p_1)+p(p_2)\rightarrow p(p_1^{\prime })+p(p_2^{\prime })+ \gamma (k)$, for small $|t|\ll m^2$ and small k is given by

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}k \mathrm{d}t} \approx \left( \frac{4 \alpha }{\pi k}\right) \left( \frac{-t}{3 m^2}\right) \left( \frac{\mathrm{d}\sigma }{\mathrm{d}t}\right) _o, \end{aligned}$$

(2.147)

where m denotes the nucleon mass.

To obtain a leading order of magnitude estimate, let us insert only the nuclear amplitude in Eq. (2.147) and integrate over all t:

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}k} \approx \left( \frac{4 \alpha }{3 m^2}\right) \left( \frac{1}{k}\right) \left[ \frac{\sigma _{\mathrm{tot}}}{4 \pi B}\right] ^2. \end{aligned}$$

(2.148)

Putting in nominal values for the LHC, $\sigma _{\mathrm{tot}}\approx 100~\hbox {mb}$ and for the diffractive width $B\approx 20~\hbox {GeV}^{-2}$, we estimate

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}k} \approx \left( \frac{1}{k}\right) (4.35 \times 10^{-3}~\hbox {mb}). \end{aligned}$$

(2.149)

This would lead us to a comfortable soft photon-production rate [associated with elastic scattering]

$$\begin{aligned} {\dot{\mathcal{N}}} \approx (435~\hbox {Hz})\ \ln \left( \frac{k_{\max }}{k_{\min }}\right) \left( \frac{\mathcal{L}}{10^{32}/\hbox {cm}^2/\hbox {s}}\right) , \end{aligned}$$

(2.150)

where $\mathcal{L}$ is the machine luminosity. Thus, observation of only soft photons accompanied by no other visible particles (an otherwise quiet event) would be very useful in determining some crucial nuclear high amplitude parameters. Transcending the specific model estimates, what the soft radiation spectrum really measures is the mean value of $\langle -t\rangle$ associated with the elastic cross section $\sigma _{\mathrm{el}}$.

A simple variant of the procedure outlined above of obtaining information as regards the background process through the spectrum of a single photon in an otherwise quiet event was utilized earlier at LEP. One way adopted to measure the number of neutrinos into which the $Z^o$ could decay consisted in measuring the rate for the process

$$\begin{aligned} \mathrm{e}^- + \mathrm{e}^+ \rightarrow \gamma (k) + \hbox {nothing visible}. \end{aligned}$$

(2.151)

Thus, measuring the initial state photon radiation, allowed one to deduce the correct branching ratio of $Z^o$ into all neutrino–antineutrino pairs, which obviously escaped experimental detection. On the other hand, at LHC, if indeed a single soft photon spectrum in a quiet event – up to some very small angle – can be measured, one can be reasonably be sure that two protons (to conserve baryon number) must have been produced which escape within the very small angular cone on either side of the beam. Relaxing the angular aperture might allow one to learn something about single diffraction cross section as well. We shall not pursue this interesting topic here any further.

3 Non-accelerator experiments

In this section, we discuss the measurement of proton–proton scattering as performed through cosmic ray experiments, the results and their interpretation.

Until the advent of particle accelerators in the mid-1950s, information as regards high-energy elementary particle scattering, and hence its dynamics, was obtained through the observation of cosmic ray showers, which resulted from the interaction of primary particles (those arriving from the interstellar space and beyond) with the earth’s atmosphere. The energy distribution of the primary particles was measured through the depth and extent of particle showers observed after the interaction, following a technique we shall describe in more detail later in this section.

Through these observations, it was possible to extract proton–proton total cross sections. To this day, the extraction of proton–proton total cross sections from cosmic ray measurements reaches center of mass energies usually higher than contemporary accelerator data. As we shall see however, this extraction procedure is still affected to a large extent upon modelling.

The energy spectrum of cosmic ray particles is shown in Fig. 4 from the 2014 Review of Particle Physics (PDG) [29], where an up-to-date review of the subject can be found.

Fig. 4

The energy distribution of the cosmic ray flux, multiplied by $E^{2.6}$, from [29] and 2015 update

We shall follow the historical development of the methods proposed to extract pp cross sections from p-air scattering data and present results thus obtained. This section is structured as follows:

• Heisenberg’s observations about the effective cross section for scattering in the Yukawa theory, interesting because they involve still currently debated questions such as the simultaneous occurrence of multiple scattering processes and the range of applicability of perturbation theory, are presented in Sect. 3.1,

• Glauber’s model for high energy particle scattering, which is the basis of present methods for the extraction of proton–proton scattering from p-air cross sections, is outlined in Sect. 3.2,

• in Sect. 3.3 developments in the extraction of pp scattering from cosmic ray data from early 1970s, after the appearance of the ISR data, up to phenomenological analyses following 1980s accelerator results in the TeV energy range, are delineated further as follows:

  • early models are in Sect. 3.3.1

  • more precise extractions after data from the CERN Super proton–antiproton Synchrotron ($S\bar{p}pS$) in Sect. 3.3.2,

  • appearance of mini-jet descriptions are presented in Sect. 3.3.3,

  • uncertainties in the extraction of the p-air data are presented in Sects. 3.3.4, 3.3.5, 3.3.6, with updated analysis of pp data extraction by Bloch, Halzen and Stanev in Sect. 3.3.7,

• further clarifications about extraction of p-air cross section from cosmic rays in Sect. 3.4,

• a discussion of critical indices for cosmic ray radiation is presented in Sect. 3.5,

• cosmic ray results after the new pp total cross section measurements at LHC, from the AUGER and Telescope Array Collaborations can be found in Sect. 3.6, with associated uncertainties due to diffraction discussed in Sect. 3.6.1,

• eikonal models as tools for extraction of $pp$ data are discussed in Sect. 3.7, with results from a two-channel model in Sect. 3.7.1 and a recent one-channel analysis briefly presented in Sect. 3.7.2.

3.1 Heisenberg and cosmic radiation

In a collection of papers prepared by Heisenberg in 1943 to commemorate A. Sommerfeld’s 75th birthday, and later translated in 1946 [30] there appear two important issues. The first concerns the observed power-law flux of cosmic ray particles as they appear on Earth along with hypotheses regarding the flux of primary cosmic radiation. We shall return to this problem in Sect. 3.5.1. The second is a description of the Theory of explosion-like showers, interesting for the strict analogy established by Heisenberg between mesons and light quanta.

This collection of papers has an interesting history of its own. As stated in the foreword by T. H. Johnson, the American editor and translator of the book from German to English, the volume was published in Berlin in 1943 in commemoration of the 75th birthday of Arnold Sommerfeld. The articles present a general view of the state-of-the-art of cosmic ray research. However, and here lies the historical interest of this note, on the very day which the book was intended to commemorate, and before many copies had been distributed, bombs fell on Berlin destroying the plates and the entire stock of printed volumes. To make the material available to American physicists, S. Goudsmith loaned his copy of the German book and T. H. Johnson translated it. Also interesting are some of the comments by Heisenberg in the foreword to the German edition. After mentioning that investigations on cosmic radiation had been sharply curtailed by the misfortunes of the times, Heisenberg recalls that the papers come from symposia held in Berlin during 1941 and 1942, and that the American literature on the subject had been available only up to the summer of 1941, so that the present collection could be considered to give a unified representative picture of the knowledge of cosmic radiation at about the end of the year 1941. The book is dedicated to Arnold Sommerfeld, the teacher of atomic physics in Germany, as Heisenberg says.

In a brief note, page 124, Heisenberg is interested in estimating the effective cross section for scattering in the Yukawa theory, to be applied to cosmic ray showers. He objects to what was, at the time, the current interpretation of the Yukawa theory as a perturbative one and discusses the presence of multiple simultaneous processes when the energy of the colliding particles is above a certain value. Thus, above this value, the assumption that perturbation theory converges reasonably, i.e. that the probability for the simultaneous emission of many particles be small, is not valid. According to Heisenberg, there are two reasons for the occurrence of multiple processes, namely the close relationship of the Yukawa particle (the $\pi$ meson) with light quanta, and the peculiarity of the meson-nucleon interaction. Unlike QED, whose convergence depends only on the dimensionless constant $\alpha$, Yukawa’s theory depends on a constant with the dimensions of a length (of order $10^{-13}~\hbox {cm}$) and thus perturbation theory will diverge as soon as the wavelength of the particle concerned is smaller than this length. Thus in high energy scattering processes, with very short wavelength of the colliding particles, there occur the possibility of multiple particle processes.

As for the close analogy between light quanta and meson emission, the similarity lies in the fact that in the collision of two high energy hadrons, several mesons can be created in a way similar to when an infinite number of light quanta is emitted in charged particle collisions. One can describe soft photon emission in a semi-classical way as taking place because in the sudden deflection of an electron, the electromagnetic field surrounding the charged particle becomes detached from the particle and moves away like a relatively small wave packet. This process can be described by a delta function in space-time, whose Fourier transform is constant. Interpreting this spectrum as the expected spectrum of the radiation, one can calculate the mean number $\mathrm{d}n(E)$ of light quanta emitted in a given energy interval $\mathrm{d}E$ and thus

$$\begin{aligned} \mathrm{d}n(E)\approx \frac{\mathrm{d}E}{E}, \end{aligned}$$

(3.1)

which is the usual infinite number of emitted soft ($E\rightarrow 0$) photons. In complete analogy, the sudden change in direction of a nucleon will result in multiple meson emission, as the difference of the associated Yukawa fields becomes detached and, as Heisenberg puts it, “wanders off into space”. However there is of course a difference, namely that the pions are massive and therefore the total number of emitted pions will be finite and increase with the logarithm of the collision energy. This effect thus gives in principle the possibility of an increasing multiplicity accompanying the high energy collision, but, according to Heisenberg, it is not enough to explain the experiments. Thus a second element is introduced. There are non-linear terms in the Yukawa theory which distort the spectrum and give rise to a sufficiently large emission to explain experiments. This part, however, is described only in qualitative terms, at least not in this reference. As we shall see later more developed models lead to a cross section that saturates the Froissart bound.

3.2 The Glauber model for high energy collisions

We shall now discuss Glauber’s theory of high energy scattering [31]. It derives in part from Moliere’s theory of multiple scattering [32], whose simpler derivation was obtained by Bethe [33] in 1955 and which we shall outline in Sect. 5. Prior to that, Rossi and Greisen had discussed cosmic ray theory [34] and many of the concepts they used were later elaborated in the theory of high energy scattering.

Glauber starts by recalling the complexity of high energy collisions, that comes from the large number of final states which open up as the energy increases, but comments on the fact that at high energy it is possible to use a number of approximations to deal with this complexity. The inspiration for the treatment of such collisions comes from the diffraction properties of optics, and this gives the model its name, i.e. optical model. The major difference of course lies in the fact that in optics the obstacles, namely the target of the colliding system, is fixed and macroscopic, whereas in nuclei, and of course also in nucleons, the scattering is constituted of moving microscopic particles. Thus a quantum mechanical treatment needs to be developed. The model originally deals with elastic scattering alone, treating inelastic scattering as if the particles not scattered elastically had been absorbed by the nucleus. This is the origin of the term absorption still used for inelastic scattering. Glauber explicitly mentions that this work can be considered as an extension and generalisation of the Moliére method of multiple scattering [32]. Notice, however, a basic difference between Glauber’s treatment and Moliére, namely that Glauber deals with amplitudes, while Moliére with probabilities. We shall comment on this in Sect. 5.

The scattering amplitude $f(\theta )$ is related to the differential cross section in the solid angle $\mathrm{d}\varOmega$ as

$$\begin{aligned} \mathrm{d}\sigma =\frac{\mathrm{Flux}\ \mathrm{through}\ \mathrm{d}\varOmega }{\mathrm{Incident}\ \mathrm{flux}} \mathrm{d}\varOmega =|f(\theta )|^2\mathrm{d}\varOmega \end{aligned}$$

(3.2)

and is related to the potential $V({\mathbf {r}})$ through the integral equation

$$\begin{aligned} f({\mathbf {k}},{\mathbf {k}'})\equiv f(\theta )=-\frac{m}{2\pi \hbar ^2}\int (\mathrm{d}^3{\mathbf {r}}) V({\mathbf {r}}) \mathrm{e}^{-i{\mathbf {k}'}\cdot {\mathbf {r}}} \psi _{\mathbf {k}}({\mathbf {r}}).\nonumber \\ \end{aligned}$$

(3.3)

To obtain this expression, a boundary condition has been applied, namely that the potential $V({\mathbf {r}})$ is different from zero only in a limited region so that as $r \rightarrow \infty$ the wave function takes the asymptotic form

$$\begin{aligned} \psi _{\mathbf {k}}({\mathbf {r}}) \sim \mathrm{e}^{i{\mathbf {k}}\cdot {\mathbf {r}}} + f(\theta ) \frac{\mathrm{e}^{i kr}}{r}. \end{aligned}$$

(3.4)

Glauber then proceeds to establish some general properties and starts by looking for the consequences of particle conservation. For a real potential, he obtains

$$\begin{aligned}&\frac{1}{2i} \{ f( {\mathbf {k}},{\mathbf {k}'})-f^*( {\mathbf {k}'},{\mathbf {k}}) \}\nonumber \\&\quad = \frac{k}{4\pi } \int f({\mathbf {k}_r},{\mathbf {k}'})f^*({\mathbf {k}}_r,{\mathbf {k}}) \mathrm{d}\varOmega _r, \end{aligned}$$

(3.5)

which assumes a particularly simple form for the case ${\mathbf {k}}'={\mathbf {k}}$,

$$\begin{aligned} \mathfrak {I}m f( {\mathbf {k}},{\mathbf {k}})=\frac{k}{4\pi } \int |f({\mathbf {k}}_r,{\mathbf {k}}) |^2\mathrm{d}\varOmega _r=\frac{k}{4 \pi }\sigma _{\mathrm{scatt}} \end{aligned}$$

(3.6)

where $\sigma _{\mathrm{scatt}}$ is the total scattering cross section. The above relation is also formulated as the optical theorem. For the case ${\mathbf {k}}\ne {\mathbf {k}'}$, Eq. (3.5) corresponds to the condition that the operator, which yields the final state, is unitary, namely to the so called unitarity condition.

If the final states, as we know to be the case in high energy scattering, will include also inelastic processes, then the potential to be considered in such case is a complex potential. For a complex potential Eq. (3.5) becomes

$$\begin{aligned}&\frac{1}{2i} \{ f( {\mathbf {k}'},{\mathbf {k}})-f^*( {\mathbf {k}},{\mathbf {k}'}) \} \nonumber \\&\quad = \frac{k}{4\pi } \int f({\mathbf {k}_r},{\mathbf {k}'})f^*({\mathbf {k}}_r,{\mathbf {k}}) \mathrm{d}\varOmega _r\nonumber \\&\qquad - \frac{m}{2\pi \hbar ^2}\int (\mathfrak {I}m V(\mathbf{r})) \psi ^*_{\mathbf {k}'} \psi _{\mathbf {k}} (\mathrm{d}^3{\mathbf {r}}). \end{aligned}$$

(3.7)

Again for the case ${\mathbf {k}}= {\mathbf {k}'}$ one can write the generalised optical theorem, namely

$$\begin{aligned} \mathfrak {I}m f({\mathbf {k}},{\mathbf {k}})=\frac{k}{4 \pi }(\sigma _{\mathrm{scatt}}+\sigma _{abs})=\frac{k}{4 \pi }\sigma _{\mathrm{tot}} \end{aligned}$$

(3.8)

where the absorption cross section $\sigma _{abs}$ has been introduced to account for particles which have “disappeared”. In the optical language, these particles have been absorbed by the scattering material, while in high energy language this cross section corresponds to the inelastic cross section, namely to the creation of a final state different from the initial one.

The three cross sections defined above, $\sigma _{\mathrm{scatt}},\sigma _{abs},\sigma _{\mathrm{tot}}$, can also be expressed using the partial wave expansion for the scattering amplitude. Writing

$$\begin{aligned} f(\theta )=\frac{1}{2ik}\sum _i(2l+1)(C_l-1)P_l(z), \end{aligned}$$

(3.9)

one obtains

$$\begin{aligned}&\sigma _{\mathrm{scatt}}= \int |f(\theta )|^2 \mathrm{d}\varOmega =\frac{\pi }{k^2}\sum _i (2l+1)|C_l-1|^2\nonumber \\&\sigma _{\mathrm{tot}}= \frac{2\pi }{k^2}\sum _i (2l+1)[1-\mathfrak {R}e C_l]\nonumber \\&\sigma _{abs}= \sigma _{\mathrm{tot}} -\sigma _{\mathrm{scatt}}=\frac{\pi }{k^2}\sum _i(2l+1)[1-|C_l|^2]. \end{aligned}$$

(3.10)

The expression for the scattering amplitude for an axially symmetric potential is obtained by Glauber, under certain approximations, as

$$\begin{aligned} f({\mathbf {k}}',{\mathbf {k}})=\frac{k}{2\pi i}\int \mathrm{e}^{i ({\mathbf {k}}-{\mathbf {k}}')\cdot {\mathbf {b}}}\{\mathrm{e}^{i\chi ({\mathbf {b}})}-1 \}\mathrm{d}^2{\mathbf {b}}\end{aligned}$$

(3.11)

where

$$\begin{aligned} \chi ({\mathbf {b}})=-\frac{1}{\hbar v}\int _{-\infty }^{+\infty }V({\mathbf {b}}+{\hat{k}}z)\mathrm{d}z. \end{aligned}$$

(3.12)

He notes that an important test of the self consistency of this approximation is furnished by the unitarity theorem, and he proceeds to show that, in the absence of absorption, i.e. for $\chi$ purely real, one has

$$\begin{aligned} \sigma _{\mathrm{scatt}}= & {} \int \mathrm{d}\varOmega _{k'}|f({\mathbf {k}},{\mathbf {k}}')|^2=\sigma _{\mathrm{tot}}\nonumber \\= & {} \frac{4\pi }{k}\mathfrak {I}m f({\mathbf {k}},{\mathbf {k}}), \end{aligned}$$

(3.13)

since for $\chi$ purely real

$$\begin{aligned} \sigma _{\mathrm{scatt}}= & {} \int |\mathrm{e}^{i\chi ({\mathbf {b}})}-1 |^2\mathrm{d}^2{\mathbf {b}}\nonumber \\= & {} 2\int (1-\mathfrak {R}e\ \mathrm{e}^{i \chi ({\mathbf {b}})})\mathrm{d}^2{\mathbf {b}}\nonumber \\= & {} \sigma _{\mathrm{tot}}. \end{aligned}$$

(3.14)

If there is absorption, namely $\chi$ is complex, then the conservation of probability implies for the inelastic cross section to be obtained from the difference $\sigma _{\mathrm{tot}}-\sigma _{\mathrm{scatt}}$, and one has

$$\begin{aligned} \sigma _{abs}=\int (1-|\mathrm{e}^{i\chi ({\mathbf {b}})}|^2)\mathrm{d}^2{\mathbf {b}}. \end{aligned}$$

(3.15)

In what follows in Glauber’s paper, various examples are discussed and solved, whenever possible. These are:

• an absorptive potential (negative imaginary) confined to a sphere of radius a and in such case the sphere can be considered to be opaque in the optical sense

• a square potential well

• a Gaussian potential

• the Coulomb potential

• a screened Coulomb potential

In nuclear applications, the incident particle is subject both to nuclear forces and to the Coulomb field, and superposition of the phase-shift functions for $\chi (b)$ for the nuclear and Coulomb interactions is suggested. Thus the nuclear phase-shift function needs to be added to the Coulomb one, given by

$$\begin{aligned} \chi _c(b)=2\frac{Z\mathrm{e}^2}{\hslash v}\ln \frac{b}{2a}+\frac{Z\mathrm{e}^2}{\hslash v}\frac{b^2}{2a^2}+\mathcal{O}\left( \frac{b^4}{a^4}\right) , \end{aligned}$$

(3.16)

which represents an expansion in the ratio between the impact-parameter distance b and the range a for which the potential is non-zero. According to Glauber, this procedure will take proper account of the two types of effects and of the interference between the two types of scattering.

3.2.1 Scattering with bound particles

In the first part of his lectures on high energy collision theory, Glauber discusses scattering of one-on-one particle. To study actual scattering experiments of particles on nuclei, one needs to take into account that particles are usually in a bound state and thus transitions from one state to another, bound or free, can take place. The generalisation is done first treating the one-dimensional problem and then going to the three-dimensional one. The basic expression for the scattering amplitude in such cases takes the form

$$\begin{aligned}&F_{if}({\mathbf {k}}',{\mathbf {k}})\nonumber \\&\quad =\frac{k}{2\pi i} \int \mathrm{e}^{i({\mathbf {k}}-{\mathbf {k}}')\cdot {\mathbf {b}}}\int u^*_f({\mathbf {q}})[ \mathrm{e}^{i\chi ({\mathbf {b}}-{\mathbf {s}})}-1] u_i({\mathbf {q}})\mathrm{d}{\mathbf {q}}\ \mathrm{d}{\mathbf {b}}\nonumber \\ \end{aligned}$$

(3.17)

where ${\mathbf {s}}$ corresponds to the impact-parameter coordinate relative to the individual state of the target as shown in Fig. 5.

Fig. 5

View of the Glauber model geometry in the transverse plane relative to the z axis of scattering direction

The initial states $u_i$ have been defined from the wave function expression

$$\begin{aligned} \varPsi (x,t)=\mathrm{e}^{i(kx-\omega t)}\phi (x,t)u_i. \end{aligned}$$

(3.18)

The phase-shift function is now generalised from the previous expression so as to include the impact parameter of the target particles, and is thus given as

$$\begin{aligned} \chi ({\mathbf {b}}-{\mathbf {s}})=-\frac{1}{\hslash \ v}\int _{-\infty }^{+\infty }V({\mathbf {b}}-{\mathbf {s}}+{\hat{k}}z) \mathrm{d}z. \end{aligned}$$

(3.19)

3.2.2 The Glauber model for high energy scattering of protons by nuclei

In [35], the previously developed theory for multiple scattering is applied to describe the results of an experiment by Bellettini et al. [36] for the scattering of $20~\hbox {GeV}/c$ protons on different nuclei. The starting formula is the one for proton-nucleon collision in the diffraction approximation (small angle), with spin effect neglected, i.e.

$$\begin{aligned} f({\mathbf {k}}-{\mathbf {k}}')=\frac{ik}{2\pi }\int (\mathrm{d}^2{\mathbf {b}}) \mathrm{e}^{i({\mathbf {k}}-{\mathbf {k}}') \cdot {\mathbf {b}}} \varGamma ({\mathbf {b}}) \end{aligned}$$

(3.20)

with

$$\begin{aligned} \varGamma (b)=\frac{1}{2\pi i k}\int \mathrm{d}^2{\mathbf {q}}\mathrm{e}^{-i{\mathbf {b}}\cdot {\mathbf {q}}}f({\mathbf {q}}). \end{aligned}$$

(3.21)

When $\varGamma ({\mathbf {b}})$ only depends on the scattering angle, one can perform the integration over the azimuthal angle, i.e.

$$\begin{aligned} f({\mathbf {k}}-{\mathbf {k}}')=ik\int b\mathrm{d}b J_0(|{\mathbf {k}}-{\mathbf {k}}'|b)\varGamma (b). \end{aligned}$$

(3.22)

The proton–proton scattering amplitude at high energies and small angle is taken to be

$$\begin{aligned} f({\mathbf {q}})=f(0)\mathrm{e}^{-\frac{1}{2}\beta ^2q^2} \end{aligned}$$

(3.23)

where $f(0)=(i+\rho )k\sigma _{\mathrm{total}}/4\pi$. The values used by Glauber and Matthiae in [35] are $\rho =-0.22$, $\beta ^2=10(\hbox {GeV}/c^2)^{-2}$ and $\sigma _{\mathrm{total}}=39.0~\hbox {mb}$. What is needed to compare with data (also later in the case of cosmic ray data) are the elastic and the inelastic proton–nucleon cross section. After a number of simplifying approximations, the nuclear elastic scattering amplitude is defined by means of a suitable nuclear phase-shift function $\chi _N(b)$ as

$$\begin{aligned} F_N(\varDelta )=ik\int b\mathrm{d}b J_0(\varDelta b)[1-\mathrm{e}^{i\chi _N(b)}]. \end{aligned}$$

(3.24)

For large atomic number A, the function $\chi _N(b)$ can take a simple form [31]

$$\begin{aligned} i\chi _N(b)=-\frac{1}{2\pi k}\int \mathrm{e}^{-i{\mathbf {q}}\cdot {\mathbf {b}}} f(q)S(q)\mathrm{d}^2{\mathbf {q}}\end{aligned}$$

(3.25)

where f(q) is the proton–proton scattering amplitude and S(q) is the nuclear form factor, i.e. the Fourier transform of the nuclear density. The overall density of the nucleon in this case is taken as the sum of the single particle densities. Through Eq. (3.24), one can then use the optical theorem to calculate the total cross section. A further approximation could be made if the nuclear radius is large compared to the range of the nuclear forces. In such a case, the form factor is peaked near zero and Eq. (3.24) is approximated as

$$\begin{aligned} F_N(\varDelta )=ik\int b\mathrm{d}b J_0(\varDelta b)[1-\mathrm{e}^{(2\pi i/k)f(0)T(b) }] \end{aligned}$$

(3.26)

with the thickness function $T(b)=\int \mathrm{d}z \rho ({\mathbf {b}}+{\hat{k}}z)$. At the time when their paper was written, Eq. (3.26) was referred usually as the optical nuclear model. However, according to Glauber and Matthiae, it is not a very good approximation, since the size of the nuclei of interest in this study were not much bigger that the range of the nuclear forces. Thus different approximations were looked for.

The quantity of interest here is the total inelastic cross section. This will be obtained as the difference between the rate for all possible final states and the elastic differential cross section. For large $\varDelta$ values, and for the large nuclear radius approximation, the following expression is proposed

$$\begin{aligned}&\sum _{f\ne i}|F_{fi}(\varDelta )|^2 = \left( \frac{k}{2\pi }\right) ^2 \int (\mathrm{d}^2{\mathbf {b}}) (\mathrm{d}^2{\mathbf {B}}) \mathrm{e}^{i{\mathbf {\varDelta }}\cdot {\mathbf {b}}-\sigma _{\mathrm{total}}T(B)}\nonumber \\&\qquad \times \left\{ \exp \left[ \frac{T(B)}{k^2}\int \mathrm{e}^{-i{\mathbf {q}}\cdot {\mathbf {b}}}|f(q)|^2\mathrm{d}^2 {\mathbf {q}}\right] -1\right\} . \end{aligned}$$

(3.27)

Since actually the large radius approximation does not quite hold for light nuclei, one needs to use a non-approximate expression. Different models for the nuclear density functions and the nuclear forces are discussed and the results plotted and compared with the data due to Bellettini et al.

The situation is easier for small $\varDelta$, namely for small scattering angles, $\varDelta \ll R^{-1}$ where R is the nuclear radius. When $\varDelta$ becomes small, and the nuclear radius is large compared to the interaction range, for large A one can use

$$\begin{aligned}&\sum _{f\ne i} |F_{fi}(\varDelta )|^2=|f(\varDelta )|^2\nonumber \\&\quad \times \left\{ N_1- \frac{1}{A}\left| \int \mathrm{e}^{i{\mathbf {\varDelta }}\cdot {\mathbf {b}}+i\chi _N(\mathbf {b})} T({\mathbf {b}})(\mathrm{d}^2{{\mathbf {b}}})\right| ^2 \right\} , \end{aligned}$$

(3.28)

where $N_1$ refers to the number of free nucleons.

This model can be used then to extract information as regards $pp$ total cross section from cosmic ray experiments, given the correlation between the proton-nuclei cross section and $\sigma _{\mathrm{total}}$. However, apart from modelling the nuclear density, which by itself may introduce some degree of theoretical uncertainty, there is another problem connected with the extraction of data from the cosmic ray shower, namely how to extract the energy of the initial hadron or proton from the actual measurement of the shower. To this we turn in the next sections.

3.3 Cosmic rays: measurements and extraction of pp data

Cosmic rays have traditionally afforded information as regards particle scattering at very high energies. Indeed, the rise of the total cross section, hinted at by the earliest experiments at the CERN Intersecting Storage Rings (ISR), could be seen clearly in cosmic ray experiments as shown in [37, 38]. In [37], Yodh et al. stress the inconclusiveness of data concerning the energy behavior of the total cross section. Since the rise, if at all, would be logarithmic, it is pointed out that one needs to go to much higher energies, such as those reached by cosmic ray experiments, where even logarithmic variations can be appreciable. Figure 6 from [37] shows results from cosmic ray experiments compared with ISR earliest results [39]. Subsequent ISR measurement of $\sigma ^{pp}_{\mathrm{tot}}$ then confirmed the early rise and the cosmic ray observations.

Fig. 6

Figure 2 from [37], in which measurements for the inelastic p-air cross section from cosmic ray experiments are compared with various theoretical models and values extracted from then available ISR results [39] for $\sigma _{\mathrm{total}}^{pp}$. Reprinted with permission from [37], ©1972 by the American Physical Society

In order to relate pp total cross sections to p-air measurements, Yodh et al. followed Glauber multiple scattering theory [35] using a method previously discussed in [40]. A value for $\sigma _{\mathrm{tot}}^{pp}$ could be obtained essentially through the following basic ideas:

• what can be measured in cosmic-rays is the inelastic p-air cross section,

• once a model for the p-nucleus elastic amplitude is advanced, the inelastic p-nucleus cross section follows from $\sigma _{\mathrm{inel}}=\sigma _{\mathrm{total}}- \sigma _{\mathrm{elastic}}$,

• the pp cross section corresponds to the mean free path for interaction of a proton in a nucleus and can be input to an effective inelastic cross section for protons in air.

Different theoretical models for pp cross section were then inserted in the calculation and compared with cosmic ray data as well as an early ISR measurement [39]. The results were given as a set of different curves, of which the one fitting cosmic rays data followed a behaviour saturating the Froissart bound. With the latter parametrisation, the curve at $\ E_{lab}= 10^5~\hbox {GeV}$ gives a most reasonable value of

$$\begin{aligned} \sigma _{\mathrm{tot}}^{pp}=60~\hbox {mb}\quad \hbox {at}\ E_{lab}= 10^5~\hbox {GeV} \end{aligned}$$

(3.29)

corresponding to a c.m. energy $\sqrt{s}=450~\hbox {GeV}$. We notice that the above value is very close to what subsequent fits to $\sigma _{\mathrm{tot}}^{pp}$ (up to the LHC energies) have given [41].

In the following, after briefly recalling the status of the problem in the early 1970s [42], we shall summarise subsequent developments following [43], for the connection between p-air and $pp$. Then we shall see how Durand and Pi [44] applied their mini-jet model [45] to cosmic rays. We shall examine the discussion by Engel et al. [46], followed by Block et al. [47, 48]. Subsequently we update these with a discussion from a review [49], including later results by Block [50, 51] along with work by Lipari and Lusignoli (LL) [52].

3.3.1 Cosmic ray experiments and the extraction of energy dependence of $\sigma _{\mathrm{total}}^{pp}$ up to 10 TeV after the ISR data

The question of model dependence of the relation between pp total cross section and p-air inelastic cross section was discussed by Gaisser, Noble and Yodh in 1974 [53, 54]. The starting point was of course the ISR confirmation of the rise of the total pp cross section, suggested from cosmic ray experiments [37]. The question being posed in the physics community was basically whether a behavior already saturating the Froissart bound was in action or one was observing a transient behavior due to some sort of threshold, or to the rising importance of parton–parton scattering [55].

An answer to this question was considered impossible to obtain from the then available accelerator data alone, so the question of reliability of cosmic rays estimates of $\sigma _{\mathrm{total}}^{pp}$ naturally arose. The conclusion of this paper is that not only the extraction of $\sigma _{p\text {-}\mathrm{air}}$ from air showers is by itself affected by rather large uncertainties, but there is also a large model dependence in the extraction of the pp cross section from the observation of unaccompanied hadrons in the atmosphere. More investigation of the modelling for both crucial steps was needed.

Before proceeding, we mention the work by Cline, Halzen and Luthe [55] who interpreted the rising cross sections as receiving a contribution from the scattering of the constituent of the protons, the so-called partons, quarks and gluons. Parton-parton scattering would give rise to jets of particles in the final state. An early estimate of a jet cross section contribution, given as

$$\begin{aligned} \sigma _{\mathrm{tot}}=\int _{p_T=(2\div 3)\hbox {GeV}/c}^{p_T=\sqrt{s}/2} \frac{\mathrm{d}\sigma }{\mathrm{d}p_T} \mathrm{d}(\hbox {phase space}) \end{aligned}$$

(3.30)

was obtained in this paper for jets with final transverse momentum $p_T > (2\div 3)~\hbox {GeV}/c$ and is shown in Fig. 7. by the shaded area. Adding such an estimated contribution to a constant or diffractive term, strongly suggested the (jet) phenomenon could to be responsible for the observed rise. It must be noticed that hadron jets had not been observed at ISR. Indeed, to get a sizeable contribution from such a simple model, sufficient to fully explain the cosmic ray excess at high energy, softer jets, contributing from a smaller $p_T \simeq 1~\hbox {GeV}$, are needed: and such small $p_T$ jets would be very hard to observe.

Fig. 7

This early attempt to estimate jet contributions to the rising total cross section shows cosmic ray extracted pp total cross section as well as ISR results. Reprinted with permission from [55], ©1973 by the American Physical Society

What appears here for the first time is the idea of small transverse momentum cluster of particles, which can be ascribed to elementary processes which start appearing in sizeable amounts, what will be later called mini-jets. It will be necessary to reach a much higher cm energy, to actually see particle jets and mini-jets at the CERN $S{\bar{p}}pS$, a proton–antiproton accelerator which would explore energies as high as $\sqrt{s}=540~\hbox {GeV}$.

However, in 1974, accelerator data could give information on the total hadronic cross section only up to $\sqrt{s}\lesssim 60~\hbox {GeV}$ and new accelerators reaching higher energies, such as near and around the TeV region, were very much in the future. Thus the question of whether it could be possible to extract the total $pp$ cross section at c.m. energies around $10 ~\hbox {TeV}$ and choose among different theoretical models for $\sigma ^{pp}_{\mathrm{tot}}$ was of great interest and was further examined in [42]. The state-of-the-art for total cross section studies (circa 1974) is shown in Fig. 8, where added lines and arrow indicate results in the range of LHC energies, as expected, for instance, in [41, 56].

Fig. 8

State-of-the-art of total cross section models in 1974 from [42] and comparison with expected results at LHC13. Reprinted with permission from [42], ©1974 American Physical Society

As already known, the cascade development through which one measures p-air cross section is sensitive only to production processes, and the quantity measured is an inelastic cross section. Then one could write the simplest possible model, which would ascribe the breaking up of the stricken nucleus both to elastic and inelastic scattering from the nucleon–nucleon scattering, using Glauber’s formalism, as

$$\begin{aligned} \sigma _{\mathrm{inel}}^{p\text {-}\mathrm{air}}\equiv \sigma _{abs}=\int \mathrm{d}^2{\mathbf {b}}\left[ 1-\mathrm{e}^{-\sigma _{\mathrm{total}}T({\mathbf {b}})}\right] \end{aligned}$$

(3.31)

where $\sigma _{\mathrm{total}}$ indicates the total nucleon–nucleon (proton–proton) cross section. $T({\mathbf {b}})$ indicates the profile function of the stricken nucleus of atomic number A. Two limits of Eq. (3.31) can be taken as

$$\begin{aligned}&\sigma _{abs}\simeq A \sigma _{\mathrm{total}}\quad \sigma _{\mathrm{total}}\,\, \hbox {small},\end{aligned}$$

(3.32)

$$\begin{aligned}&\sigma _{abs}\simeq \pi R^2_A \simeq C A^{2/3}\quad \sigma _{\mathrm{total}}\,\, \hbox {large} \end{aligned}$$

(3.33)

where $R_A$ is the nuclear radius.

Such a simple model is unable to provide enough information on $\sigma _{\mathrm{total}}$ at high energy, where $\sigma _{\mathrm{total}}^{pp}$ can become large, and a more precise expression seemed required. Within the Glauber model, convoluting the nucleon profile function with the nuclear density function $\rho ({\mathbf {r}})$, the following expression was proposed:

$$\begin{aligned} \sigma _{abs}=\int \mathrm{d}^2{\mathbf {b}}[1-{\large |}1-\varGamma _A({\mathbf {b}}){\large |}^2] \end{aligned}$$

(3.34)

where

$$\begin{aligned} \varGamma _A({\mathbf {b}}) =1-\left[ 1-\int \mathrm{d}^2{\mathbf {b}}' \mathrm{d}z \varGamma _N({\mathbf {b}}-{\mathbf {b}}')\rho (z,{\mathbf {b}}')\right] ^A,\nonumber \\ \end{aligned}$$

(3.35)

$\varGamma _N({\mathbf {b}})$ is the nucleon profile function. There exist various models for the nuclear density, as already mentioned, depending on the nucleus being light, heavy or in between. Often, as in [42], the gaussian form is used. Next, one needs a nucleon profile function and the frequently used expression is again a gaussian distribution, namely

$$\begin{aligned} \varGamma _N({\mathbf {b}})=\sigma _{\mathrm{total}}\frac{\mathrm{e}^{-b^2/2B}}{4\pi B}. \end{aligned}$$

(3.36)

This expression is based on the description of the elastic differential cross section in the small $-t$-region, namely:

$$\begin{aligned} \frac{\mathrm{d} \sigma _{\mathrm{elastic}}}{\mathrm{d}t}=\left| \int \mathrm{d}^2 {\mathbf {b}}\varGamma _N({\mathbf {b}})\right| ^2= \left[ \frac{\mathrm{d} \sigma _{\mathrm{elastic}}}{\mathrm{d}t}\right] _o\ \mathrm{e}^{Bt} \end{aligned}$$

(3.37)

where B is defined in the usual way,

$$\begin{aligned} B(s)=\left[ \frac{\mathrm{d}}{\mathrm{d}t} \left( \ln \frac{\mathrm{d}\sigma _{\mathrm{elastic}}}{\mathrm{d}t}\right) \right] \Bigg |_{t=0}. \end{aligned}$$

(3.38)

It became clear, however, that there were other uncertainties to take into account, in particular those related to processes which could not easily be classified as elastic or inelastic, but, rather, were quasi-elastic.

3.3.2 Prescriptions for more precise extraction of $\sigma _{\mathrm{tot}}^{pp}$ after the advent of the CERN $S{p\bar{p}}S$ data

The need to extract from cosmic ray experiments more precise information as regards the proton–proton cross section led to scrutinize better the original use of the definition of inelastic cross section for nucleon–nucleus collision. Following the discussion by Gaisser, Sukhatme and Yodh in [43], the inelastic p-air expression for the cross section should include various processes which are neither totally elastic nor inelastic. Such are

• $\sigma _{\mathrm{quasi}\text {-}\mathrm{el}}$: quasi-elastic excitations of the air-nucleus,

• $\sigma ^*$: processes where there are diffractive excitations of one of the nucleons in the stricken nucleus,

• $\varDelta \sigma$: multiple collisions with excited nucleon intermediate states

However, the cascade shower which is measured in cosmic rays is not sensitive to these processes. Thus, the p-air inelastic cross section which is being extracted from the cosmic ray cascade is not

$$\begin{aligned} \sigma _{\mathrm{inel}}^{p\text {-}\mathrm{air}}=\sigma _{\mathrm{total}}^{p\text {-}\mathrm{air}}-\sigma _{\mathrm{elastic}}^{p\text {-}\mathrm{air}}, \end{aligned}$$

(3.39)

but rather

$$\begin{aligned} \sigma _{\mathrm{inel}}^{p\text {-}\mathrm{air}}= & {} \sigma _{\mathrm{total}}^{p\text {-}\mathrm{air}}-\sigma _{\mathrm{elastic}}^{p\text {-}\mathrm{air}} \nonumber \\- & {} \sigma _{\mathrm{quasi}\text {-}\mathrm{el}}-\sigma ^*-\varDelta \sigma . \end{aligned}$$

(3.40)

Hence, in order to be able to extract information as regards $pp$ cross sections from p-air, one needs to have a model for various nuclear excitation processes and for the diffractive part of the nucleon–nucleon cross section which contributes to $\varDelta \sigma$. These various processes can be taken into account through the Glauber technique. Equation (3.40) requires [43] knowledge of the following quantities:

• $\sigma _{\mathrm{total}}^{pp}$

• $B^{pp}(t=0)$, the forward elastic slope parameter

• $\sigma _{\mathrm{SD}}^{pp}$, $\sigma _{DD}^{pp}$, the total single and double diffractive $pp$ cross sections

• $\frac{\mathrm{d}^2\sigma }{\mathrm{d}t \mathrm{d}M_X^2}$ the shape of the diffractive cross section for $p\ p \rightarrow p+X$ near $t_{\min } \approx - [m^2 (M^2 - m^2)^2]/2 s^2$

• the nuclear density

In [43] use is made of unitarity to either exclude some of the then current models or to restrict the various contributions entering Eq. (3.40). In particular, when inclusion of diffractive processes are taken into account, the Pumplin limit [57], to be discussed in Sect. 6, has to be included:

$$\begin{aligned} \sigma _{\mathrm{elastic}}+\sigma _{\mathrm{diffractive}}\le \frac{1}{2}\sigma _{\mathrm{total}}. \end{aligned}$$

(3.41)

The total, elastic and quasi-elastic p-air cross sections can be calculated in a straightforward manner using the model parameters for $\sigma _{\mathrm{total}}^{pp}$, $\sigma _{\mathrm{elastic}}^{pp}$, $B^{pp}$ and $\rho$, as for instance in [12]. In brief, after having determined the values of $\sigma _{\mathrm{total}}$ as a function of $\sqrt{s}$ as well as that of B(s), the scheme of the calculation is to start with the elastic $pp$ scattering amplitude at small angle,

$$\begin{aligned} f({\mathbf {q}})=\frac{k\sigma _{\mathrm{total}}}{4\pi }(\rho +i)\mathrm{e}^{-Bq^2/2}, \end{aligned}$$

(3.42)

which is now fully determined and insert it into the nucleon–nucleon profile function

$$\begin{aligned} \varGamma _j({\mathbf {b}})=1-\mathrm{e}^{i\chi _j}=\frac{1}{2\pi k}\int \mathrm{d}^2 {\mathbf {q}}\mathrm{e}^{-i{\mathbf {q}}\cdot {\mathbf {b}}}f({\mathbf {q}}), \end{aligned}$$

(3.43)

which assumes that each nucleon has a static profile, thus automatically identical to a given function, the same for all. This nucleon–nucleon profile function is put into the profile factor for the nucleus

$$\begin{aligned} \varGamma =1-\mathrm{e}^{i\chi }=1-\mathrm{e}^{i\sum _{j=1,A}\chi _j} \end{aligned}$$

(3.44)

and then this is put into the nucleon–nucleus scattering amplitude, together with the nuclear density of nucleons in the nucleus $\rho ({\mathbf {r}})$. The nuclear amplitude is thus written as

$$\begin{aligned}&F({\mathbf {q}})=\frac{ik}{2\pi }\theta (q^2)\int \mathrm{d}^2{\mathbf {b}}\mathrm{e}^{i{\mathbf {q}}\cdot {\mathbf {b}}} \nonumber \\&\quad \times \int \cdots \int \cdots \varGamma ({\mathbf {b}}, {\mathbf {s}}_1,\ldots ,{\mathbf {s}}_A)\prod _{i=1}^A \rho ({\mathbf {r}}_i)\mathrm{d}^3{\mathbf {r}}_i \end{aligned}$$

(3.45)

with $\varGamma ({\mathbf {b}}, {\mathbf {s}}_1,\ldots ,{\mathbf {s}}_A)$ being the profile function for the nucleus, $\mathbf {s}$ being the component of $\mathbf {r}$ in the $\mathbf {b}$ plane. One now uses the basic Glauber hypothesis that the overall phase shift $\chi$ of a nucleon on a nucleus is the sum of the phase-shifts of individual nucleon–nucleon phase-shifts, and the following is now the proposed nucleon–nucleus amplitude:

$$\begin{aligned}&F({\mathbf {q}})=\frac{ik}{2\pi }\theta (q^2) \int \mathrm{d}^2{\mathbf {b}}\mathrm{e}^{i{\mathbf {q}}\cdot {\mathbf {b}}}\nonumber \\&\quad \times \left[ 1-\left[ 1-\int \mathrm{d}^ 3\mathbf {r} \rho (r) \varGamma _j({\mathbf {b}}-{\mathbf {s}})\right] ^A\right] \end{aligned}$$

(3.46)

where $\varGamma _j$ is the nucleon–nucleon profile function. One can now see how, by using various models for the nuclear density, and various models for nucleon–nucleon scattering, one can estimate $\sigma _{\mathrm{elastic}}^{p\text {-}\mathrm{air}}$, $\sigma _{\mathrm{total}}^{p\text {-}\mathrm{air}}$ through the optical theorem, i.e.

$$\begin{aligned}&\sigma _{\mathrm{total}}^{p\text {-}\mathrm{air}}=\frac{4\pi }{k}\mathfrak {I}mF(0),\end{aligned}$$

(3.47)

$$\begin{aligned}&\sigma _{\mathrm{elastic}}^{p\text {-}\mathrm{air}}=\int \mathrm{d}\varOmega _k {\large |}F({\mathbf {q}}){\large |^2}. \end{aligned}$$

(3.48)

Before proceeding, let us notice that the Block and Cahn model [12] fits B(s) and $\sigma _{\mathrm{total}}$ from available data in a large energy range and the result is a curve where B(s) and $\sigma _{\mathrm{total}}$ can be plotted against each other. The effect is that the larger values of $\sigma _{\mathrm{total}}^{pp}$ correspond to larger values of B(s), as one can see from the straight line in Fig. 9 from [47].

Fig. 9

Relations between the total $pp$ cross section $\sigma _{\mathrm{total}}$, the slope parameter B(s) and $\sigma ^{p\text {-}\mathrm{air}}$ from Block, Halzen and Stanev [47]. Reprinted with permission from [47], ©1999 by the American Physical Society

The above takes care of the first two terms in Eq. (3.40), and we now turn to the last three terms. While different models were used for the nuclear density function in evaluating the proton-nucleus amplitude, for the calculation of the other three terms, whose details are in the appendix of [43], only a gaussian density distribution is used. The calculation of $\sigma _{\mathrm{quasi}\text {-}\mathrm{el}}$ is obtained from [35] by integrating the expression for quasi-elastic scattering and making an expansion, i.e.

$$\begin{aligned} \sigma _{\mathrm{quasi}\text {-}\mathrm{el}} =\pi R^2\sum _{n=1}^{\infty }\frac{\epsilon ^n}{n} \end{aligned}$$

(3.49)

with

$$\begin{aligned}&R^2=\frac{2}{3}\langle a^2\rangle ,\end{aligned}$$

(3.50)

$$\begin{aligned}&\epsilon =\frac{1+\rho ^2}{16\pi }\frac{\sigma _{\mathrm{total}}}{B} \end{aligned}$$

(3.51)

a being the rms nuclear radius. Given an input for the nuclear radius, in this model, the quasi-elastic term is again obtained from the $pp$ parameters. Next one needs to estimate $\sigma ^*$, which represents the correction for diffraction dissociation of the nuclear target. This is estimated, in Gaisser’s model, from

$$\begin{aligned} \sigma ^*=\frac{\sigma _{\mathrm{SD}}^{pp}}{\sigma _{\mathrm{inel}}^{pp}}\left( \frac{2\pi }{3}\langle r^2\rangle \right) \end{aligned}$$

(3.52)

where the last term in round bracket represents the cross section for absorptive p-nucleus interaction involving only one nucleon. One can use unitarity to put bounds on the ratio $\frac{\sigma _{\mathrm{SD}}^{pp}}{\sigma _{\mathrm{inel}}^{pp}}$ and from the Block and Cahn model, one obtains for $\sigma ^*$ a range of values between 28 and 15 mb as the energy changes from $\sqrt{s}=20~\hbox {GeV}$ to $10~\hbox {TeV}$.

As stated in [43], the last term, $\varDelta \sigma$, is a correction to Glauber’s model, to include cases when one nucleon is excited in one encounter and then returns to the ground state through a subsequent encounter. This correction is evaluated to be of the order of $10~\hbox {mb}$. For its estimate, the differential cross section for diffractive excitation of the nucleon to a mass M is modelled to be

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}M^2 \mathrm{d}t}=A(M) \mathrm{e}^{B(M^2)t}. \end{aligned}$$

(3.53)

Once the five steps of the calculation have been performed in terms of the given input from B(s) and $\sigma _{\mathrm{total}}$ for various energies, one can now try to extract the proton–proton cross section from the measured p-air cross section.

The procedure consists of two steps. First, one finds curves of fixed value of $\sigma _{p\text {-}\mathrm{air}}$ in the $(B(s),\sigma _{\mathrm{total}}^{pp})$-plane, namely one finds the corresponding points in the $(B,\sigma _{\mathrm{total}})$ plane which show that particular p-air cross section. This procedure gives curves such as the ones shown in Fig. 9 from a later paper by Block, Halzen and Stanev (BHS) [47] to which we shall return next. To obtain then $\sigma _{\mathrm{total}}$ at a given energy from this procedure depends on the model for pp scattering. In a given model let one draw the line which corresponds to predicted values for B(s) at a given energy. The same model will also give a value for $\sigma _{\mathrm{total}}(s)$ and thus a line can be drawn to join these various points in the $(B(s),\sigma _{\mathrm{total}}(s))$ plane. This line will meet the constant $\sigma _{\mathrm{inel}}^{p\text {-}\mathrm{air}}$ at some points. Now if the experiment says that a proton of energy $\sqrt{s}\simeq 30~\hbox {TeV}$ has produced $\sigma _{p\text {-}\mathrm{air}}=450~\hbox {mb}$, say, all we need to do is to look at which set of $\{B,\sigma _{\mathrm{total}}\}$ values the model crosses the constant contour. It is possible that the model cannot give such a high value for the p-air cross section for the B and $\sigma _{\mathrm{total}}^{pp}$ values input by the model. This was for instance the case for one model by Goulianos [58], in which diffraction dominated the cross section, or a model by Block and Cahn, in which both $\sigma _{\mathrm{total}}^ {pp}$ and B(s) were not asymptotically growing. In such cases, seen clearly in (Fig. 6 of) [43], these values can never give a cross section for p-air as the one observed. Thus, the cosmic ray observation allows one to exclude these models, at least within the validity of the given construction based on the Glauber model and on a correct estimate of the cosmic ray composition. But other models can give values which would be as high as the observed cross section: in such cases, when the line crosses (say a value $450~\hbox {mb}$) of the p-air curve, one has correspondence between the experimental point for $\sigma _{p\text {-}\mathrm{air}}$ and the value of $\sigma _{\mathrm{total}}^{pp}$ in that particular model. One can also prepare a different plot, which shows which value of $\sigma _{p\text {-}\mathrm{air}}$ one can get for a given $\sigma _{\mathrm{total}}^{pp}$ for different values of the slope parameter. Depending on how different models obtain/parametrise B vs. $\sigma _{\mathrm{total}}$, one can then extract the relevant information.

Conclusions about the validity of a given model, from plots such as the one in Fig. 9, depends also on the uncertainties about the measured values for $\sigma ^{p\text {-}\mathrm{air}}$. In particular, as emphasised in [43], fluctuations in individual hadronic interactions and on the chemical composition of the primary particles in the observed showers influence the final result.

3.3.3 The Durand and Pi mini-jet model for p-air interactions

So far, we have discussed approaches which use the Glauber method to extract information as regards $\sigma _{\mathrm{total}}^{pp}$ from cosmic ray measurements at very high energy. As we have seen, in some cases, such approach yielded information not only on the energy dependence but also about the model validity at such very high energies. This was for instance the case of a diffractive dominance model [58] or one of two models by Block and Cahn [12]. We now discuss a rather different approach.

The approach followed by Durand and Pi [44] employs their QCD-driven model [59] to predict $\sigma _{abs}(p\text {-}\hbox {Air})$.² This model, which is described in detail in Sect. 5 for the case of pp scattering, uses an eikonal formalism with QCD mini-jets as input for the energy dependence and an impact-parameter distribution (of quarks and gluons in a proton) modelled after the proton e.m. form factor. In this paper the model is extended to scattering of protons on nuclei of nucleon number A, by basically treating the process as the scattering of quarks and gluons from the incoming protons against quarks and gluons in the nucleus. We shall now follow their description to see how the model is applied to p-air or more generally to $p-A$.

The authors start with the proton-nucleus profile function which enters the (proton-nucleus) scattering amplitude f(t) for the given process (t being the momentum transfer), i.e.

$$\begin{aligned} f(t)=i\pi \int b\mathrm{d}b J_0(b \sqrt{-t})\varGamma (b). \end{aligned}$$

(3.54)

Instead of the usual parametrisation given as

$$\begin{aligned}&\varGamma (b)=\frac{\sigma _{\mathrm{total}}}{4\pi } \mathrm{e}^{-b^2/2B},\end{aligned}$$

(3.55)

$$\begin{aligned}&B=\left[ \frac{\mathrm{d}}{\mathrm{d}t} \left( \ln \frac{\mathrm{d}\sigma }{\mathrm{d}t} \right) \right] _{t=0}, \end{aligned}$$

(3.56)

Equation (3.54) is written in terms of an eikonal function whose high energy behavior will entirely be based on the mini-jet model, namely

$$\begin{aligned}&f(t)=i\pi \int b\mathrm{d}b J_0(b\sqrt{-t})[1-\mathrm{e}^{-{\tilde{\chi }}_{pA}}],\end{aligned}$$

(3.57)

$$\begin{aligned}&{\tilde{\chi }}_{pA}=\frac{1}{2} (\sigma _0+ \sigma _{\mathrm{QCD}}){\tilde{A}}(b) \end{aligned}$$

(3.58)

in close connection with the similar treatment for pp. In this, as in other similar models, the eikonal function is assumed to have a negligible real part. Corrections for this can be included. The absorption cross section is then given as

$$\begin{aligned} \sigma _{abs}(pA)=2 \pi \int b \mathrm{d}b [1- \mathrm{e}^{-2 {\tilde{\chi }}_{pA}(b,s)}]. \end{aligned}$$

(3.59)

We now sketch the procedure followed by Durand and Pi and postpone a discussion of how this production cross section differs from the total inelastic cross section. For an eikonal mini-jet model such as the one discussed here one needs to start with the following input:

• 1. how partons of given energy, momentum and position ${\mathbf {b}}$ are distributed in the nucleus

• 2. an elementary cross section for parton–parton scattering $\mathrm{d}{\hat{\sigma }}/\mathrm{d}{\hat{t}} ({\hat{s}},{\hat{t}})$

• 3. density of nucleons in the nucleus.

Consider the $p-A$ scattering process as built from the uncorrelated scattering of an incoming proton with an average target nucleon a, which carries a fraction 1 / A of the nucleus momentum. Quarks and gluons in the incoming proton then scatter against quarks and gluons in the average nucleon a inside the nucleus. This model assumes that, at high energy, the parton distribution in the nucleus A is given by the parton distributions in the nucleon a convoluted with the distribution of nucleons in the nucleus A. We are now dealing with a proton-nucleus scattering and, as in the original mini-jet model for pp scattering, the impact-parameter dependence is factored out from the energy and transverse momentum dependence. Let $\rho _a({\mathbf {b}})$ be the average impact-parameter distribution of partons in nucleon a, and $f_{i,a}(x,|{\hat{t}}|)$ the usual nucleon Parton Density Function (PDFs), where x is the fractional longitudinal momentum carried by the parton, $\hat{t}$ the parton–parton momentum-transfer in the scattering. Next, parton distributions inside the nucleus are proposed for a model of A uncorrelated nucleons. In the model, parton distributions inside a nucleus, $f_{i,A}(x,|{\hat{t}}|,b)$, are obtained as a convolution of the distribution of partons in the nucleon $f_{i,a}(x,|{\hat{t}}|) \rho _a({\mathbf {b}})$ with the distribution of nucleons in the nucleus, $\rho _A({\mathbf {r}})$, namely

$$\begin{aligned} f_{i,A}(x,|{\hat{t}}|,b)= & {} \frac{1}{A}\sum _{a=1}^{A}\int \mathrm{d}^2 {\mathbf {r}}_\perp \mathrm{d}z f_{i,a}(x,|{\hat{t}}|) \nonumber \\&\times \rho _a(|{\mathbf {b}}-{\mathbf {r}}_\perp |)\rho _A({\mathbf {r}}_\perp ,z) \end{aligned}$$

(3.60)

with $\rho _A({\mathbf {r}}_\perp ,z)$ being the nuclear density function, subject to the normalisation condition

$$\begin{aligned} \int \mathrm{d}^2{\mathbf {r}}_\perp \mathrm{d}z \rho _A({\mathbf {r}}_\perp ,z)=A. \end{aligned}$$

(3.61)

Nuclear binding and small differences between protons and neutrons are neglected and one arrives at the following simplified expression:

$$\begin{aligned}&f_{i,A}(x,|{\hat{t}}|,b)\nonumber \\&\quad =f_{i,A}(x,|{\hat{t}}|)\int \mathrm{d}^2{\mathbf {r}}_\perp \mathrm{d}z \rho _a(|{\mathbf {b}}-{\mathbf {r}}_\perp |)\rho _A({\mathbf {r}}_\perp ,z). \end{aligned}$$

(3.62)

Folding the above with the elementary parton cross sections and integrating in the sub-process variables, leads to very simple result that the QCD contribution, also called mini-jets, to the eikonal is the same as the one calculable for pp scattering, and the difference between the hadronic and the nuclear eikonal function only lies in the impact-parameter distribution, namely the eikonal function for pA scattering is written as

$$\begin{aligned} \chi ^{\mathrm{QCD}}_{pA}(b,s)=\frac{1}{2}{\tilde{A}}(b)\sigma _{\mathrm{QCD}} \end{aligned}$$

(3.63)

where $\sigma _{\mathrm{QCD}}$ is the mini-jet cross section which will be used to describe (fit) $\sigma _{\mathrm{total}}^{pp}$ and ${\tilde{A}}(b)$ is a convolution of the nuclear density with the parton density $A({\mathbf {b}})$ in the proton, i.e.

$$\begin{aligned} {\tilde{A}}(b)=\int \mathrm{d}^2{\mathbf {r}}_\perp \mathrm{d}z \rho _A({\mathbf {r}}_\perp ,z)A(|{\mathbf {b}}-{\mathbf {r}}_{\perp }|). \end{aligned}$$

(3.64)

The next step in the calculation is to deal with the non-QCD part, what can be defined as the soft scattering contribution, ${\tilde{\sigma }}_{\mathrm{soft}}$. One may ask if this quantity is the same as in $pp$ scattering. The model indicates that the same $\sigma _{\mathrm{QCD}}$ gives the high energy contribution (and hence the rise with energy) to both nucleon and nuclear proton scattering. But there is no reason to expect the soft part to be the same. Indeed the phenomenology indicates a smaller ${\tilde{\sigma }}_{\mathrm{soft}}$ in fits to the data. The point of view here is that it should be smaller, because soft processes (in mini-jet language -see later- final partons with $p_t < p_{t \min }$) may not be sensitive to such processes as much as the pp cross section. Whatever the reason, the end result is that a good fit yields ${\tilde{\sigma }}_{\mathrm{soft}}=31.2 ~\hbox {mb}$, instead of the value $\sigma _{\mathrm{soft}}^{pp} = 49.2 ~\hbox {mb}$ used to describe $pp$ scattering.

Folding the impact-parameter distribution of partons of their model with different nuclear distributions according to the nuclear composition of air, gives the result for p-air, and obtains the expression for the absorption cross section for protons in air

$$\begin{aligned}&\sigma _{abs}(pA)=\int \mathrm{d}^2{\mathbf {b}}(1-\mathrm{e}^{-2{\tilde{\chi }}_{pA}(b,s)}),\end{aligned}$$

(3.65)

$$\begin{aligned}&{\tilde{\chi }}_{pA}(b,s)=\frac{1}{2}({\tilde{\sigma }}_0+\sigma _{\mathrm{QCD}}){\tilde{A}}(b). \end{aligned}$$

(3.66)

We show their result in Fig. 10 for two different nuclear density models, and ${\hat{\sigma }}_0=31.2~\hbox {mb}$ fitted to low energy nuclear data, a value 30% lower than what enters the fit to free pp scattering. The fit to AKENO and Fly’s Eye are quite acceptable. However, the inverse procedure, that of trying to extract from the cosmic ray data a value for $\sigma _{\mathrm{total}}^{pp}$ poses some problems. The Fly’s eye value of $\sigma _{abs}(p\text {-Air})=540\pm 50~\hbox {mb}$ is seen to correspond to a $\sigma _{\mathrm{total}}^{pp}=106 \pm 20 ~\hbox {mb}$ at the cms energy of 30 TeV, a decidedly low value, especially after the latest TOTEM results at LHC.

Fig. 10

The absorption cross section for p-air as calculated in the QCD model by Durand and Pi in [44] compared with cosmic ray data. Reprinted with permission from [44], ©1988 by the American Physical Society

3.3.4 More about uncertainties in extracting $\sigma ^{pp}_{\mathrm{tot}}$ from cosmic ray data, after the Tevatron

While cosmic ray measurements can shed light on the behaviour of $\sigma _{\mathrm{tot}}^{pp}$ at very high energies, the hope to exclude or confirm a given model for pp scattering is clouded by large uncertainties.

An updated analysis of such uncertainties was done in 1998 by Engel et al. [46], and a summary of their analysis is presented in the following. The starting point is the calculation of the absorption cross section with the Glauber model [35]. First, Engel et al. [46] discuss the relation between nucleon–nucleon and nucleon–nucleus cross sections. This discussion is based on the procedure used to extract $\sigma _{\mathrm{tot}}^{pp}$ from $\sigma ^{p\text {-}\mathrm{air}}$, following Gaisser et al. in [43], where the definition of a production cross section is adopted, namely

$$\begin{aligned} \sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}=\sigma _{p\text {-}\mathrm{air}}^{\mathrm{tot}} -\sigma _{p\text {-}\mathrm{air}}^{\mathrm{el}} -\sigma _{p\text {-}\mathrm{air}}^{\mathrm{q}\text {-}\mathrm{el}} \end{aligned}$$

(3.67)

with $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{q}\text {-}\mathrm{el}}$ the quasi-elastic p-air cross section where no particle production takes place, but there are inelastic contributions as intermediate states while the nucleon interacts with the nucleus. In this procedure a crucial role is played by the B-parameter, and the relation between $\sigma _{\mathrm{total}}$ and $\sigma _{\mathrm{elastic}}$ in elementary hadronic cross sections. After this, a discussion of how air shower experiments infer the p-air cross section is presented and the relevant uncertainties summarised.

In this model, the basic sources of uncertainties arise from modelling of:

• 1. $\sigma ^{p\text {-}\mathrm{air}}$, the interaction cross section between hadrons and the atmosphere, vs. $\sigma ^{pp}$, the proton–proton cross sections (total and elastic)

• 2. $\sigma ^{pp}$ the hadron–hadron cross section

• 3. the shower development and the primary cosmic ray composition and the relation with $\lambda _{p\text {-}\mathrm{air}}$, the interaction length of hadrons in the atmosphere.

In the model, the profile function of the stricken nucleus is obtained through a combination of the following inputs: (i) the elastic differential cross section in the forward region, (ii) $\sigma _{\mathrm{total}}$ and (iii) B(s), the slope parameter at $t=0$, defined as in Eq. (3.56). The connection between B(s) and the elementary hadron–hadron cross sections, $\sigma _{\mathrm{elastic}}$ and $\sigma _{\mathrm{total}}$ is, as before, obtained from the optical theorem and the gaussian approximation for the forward region, namely

$$\begin{aligned} \sigma ^{\mathrm{el}}_{AB}=(1+\rho ^2)\frac{(\sigma ^{\mathrm{tot}}_{AB})^2}{16 \pi B(s)}. \end{aligned}$$

(3.68)

While Eq. (3.68) is a good approximation to the data, the high energy behavior of $\sigma ^{\mathrm{tot}}_{AB}$ and B(s) depends on the model used. In [46], one of two models discussed is the standard Donnachie and Landshoff (DL) fit [60], i.e.

$$\begin{aligned} \sigma ^{\mathrm{tot}}_{AB}=X_{AB}s^{\epsilon }+Y_{AB}s^{-\eta } \end{aligned}$$

(3.69)

with $\epsilon \simeq 0.08$ and $\eta \simeq 0.45$. The Regge–Pomeron interpretation of the expression for the slope parameter would lead to

$$\begin{aligned} B(s)=B_0+2\alpha ' (0)\ln \left( \frac{s}{s_0}\right) . \end{aligned}$$

(3.70)

We shall see later, in Sect. 5, that a linear extrapolation in ($\ln s$) up to present LHC results can be challenged [61] and that the high energy behavior of B(s) is still an open problem.

In general, once fits to the elastic and total cross sections have been obtained in a given model, the by now familiar plot of B vs $\sigma _{\mathrm{total}}$ is used with curves of constant p-air cross section drawn in it. Intersection of the model lines with a given curve allows one to extract pp cross section in a given model at the given cosmic ray energy. One such plot, from [46] is reproduced in Fig. 11. This plot gives rise to large uncertainties: for instance the same low p-air cross section can be obtained with a small B-value and a range of $\sigma _{\mathrm{total}}^{pp}$ values, and so on. Given a certain model and its fit to elastic and inelastic data, and then its input into p-air cross section, three observations are worth repeating:

Fig. 11

Contour plot of constant p-air cross section in the B(s) vs $\sigma _{\mathrm{total}}^{pp}$ plane from [46]. Solid symbols are experimental accelerator points, dashed line is the DL model, dotted line a geometrical model. Dashed area excluded by the unitarity constraint, the five curves are the region within one or two standard deviations from the central Fly’s Eye experiment, $\sigma ^ {prod}_{p\text {-}\mathrm{air}}=540 \pm 50\ ( mb)$ measurement. The open point is the expectation of the DL model at 30 TeV cm energy. Reprinted with permission from [46], ©1998 by the American Physical Society

• model for the pp interactions usually show that at high energy the larger B(s) the larger is $\sigma _{\mathrm{total}}$

• along a line of constant $\sigma ^{p\text {-}\mathrm{air}}$, larger B(s) values correspond to smaller $\sigma _{\mathrm{total}}$

• extrapolations of the slope parameter to higher energy depends on the model and it may lead to large uncertainties in $\sigma ^{p\text {-}\mathrm{air}}$.

Two models are shown in Fig. 11, the Donnachie and Landshoff (DL) models [60] and a geometrical scaling model. Geometrical scaling was a useful approach to the behavior of the elastic differential cross section up to ISR energies. The hypothesis of geometrical scaling is that the entire energy dependence of the cross section comes from a single source, a radius R(s), thus implying automatically the black-disk limit $\mathcal{R}_{\mathrm{el}}=\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}=1/2$. Geometrical scaling, however, is not observed by experiments at $S{\bar{p}}pS$ energies and beyond. We shall return to this point in the section about models and elastic scattering.The dashed area indicates the region excluded by unitarity, as discussed in Sect. 3.6.

3.3.5 Extracting information from cosmic ray showers

The uncertainties encountered in determining values for $\sigma _{\mathrm{total}}$ from $\sigma ^{p\text {-}\mathrm{air}}$ are only one of the problems encountered in trying to find the asymptotic behavior of proton–proton scattering. More uncertainties lie with the air shower technique which is used to extract $\sigma ^{p\text {-}\mathrm{air}}$. Such uncertainties are summarised in a parameter, sometimes called a, more often k, which relates the interaction length of protons in air, i.e.

$$\begin{aligned} \lambda _{p\text {-}\mathrm{air}}=14.5 \frac{m_p}{\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}} \end{aligned}$$

(3.71)

where 14.5 is the mean atomic mass of air, to the attenuation length $\varLambda$ defined as

$$\begin{aligned} \varLambda =a \lambda _{p\text {-}\mathrm{air}}. \end{aligned}$$

(3.72)

The attenuation length $\varLambda$ is a measure of the initial proton energy, and is obtained from the air showers generated by the interaction of the primary cosmic ray with the atmosphere. This uncertainty entering data extraction is the rate of energy dissipation by the primary proton. The p-air cross section is thus affected by uncertainty related to the parameter a.

But uncertainty also comes from the composition of the most penetrating cosmic rays, and this is also related to the question of the origin of cosmic rays. Engel et al. [46] discuss how different Monte Carlo programs simulate air shower development using the same $\varLambda =70\pm 6~\hbox {g}/\hbox {cm}^2$ and extract different values for $\sigma ^{p\text {-}\mathrm{air}}$ according to the chosen parameter set.

3.3.6 Air shower modelling

The energy of the particle starting the shower and the interaction length of the proton in air are obtained from the depth and extension of the electromagnetic shower they initiated. The most important processes of interest for air shower modelling are electron and muon bremsstrahlung and pair production. The electromagnetic shower, which develops as an electron or a photon starts losing energy because of EM processes such as bremsstrahlung and pair production, can be divided into three phases:

• the shower grows as long as all the particles have energy larger than the typical ionisation energy $\epsilon _0$ which corresponds to an electron energy too small for pair production, and such as to typically induce ionisation in the nuclei

• the shower maximum, which has an extension determined by the fluctuations around the point where all the particles have energy just about $\epsilon _0$

• the shower tail where particles lose energy only by ionisation or by absorption, or decay.

To determine the quantity $X_{\max }$ one can use a simple model due to Heitler and summarised in [49].

These processes are characterized by a typical quantity, the radiation length $X_0$, which represents the mean distance after which the high-energy electron has lost 1 / e of its initial energy. Namely, $X_0$ is the constant which defines the energy loss of the electron as it traverses a distance X,

$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}x}=-\frac{E}{X_0}. \end{aligned}$$

(3.73)

Then, in a simplified model in which only bremsstrahlung and pair production are responsible for energy losses, the air shower can be modeled, as follows. At each step the electron, or photon can split into two branches, each of which will then split into two other branches as long as the energy of each branch is ${>}\epsilon _0$. At a depth X, the number of branchings is roughly $n=X/X_0$ and after n branchings, the total number of particles will be $2^n$. The maximum depth of the shower will be reached when the initial energy $E_0$ is equally distributed among the maximum number of secondaries, each one of which has energy just above the ionisation limit $\epsilon _0$, Thus, $E_0=N_{\max }\epsilon _0$, $N_{\max }=2^{n_{\max }}=2^{X_{\max }/X_0}=E_0/\epsilon _0$. This leads to

$$\begin{aligned} X_{\max }=X_0 \left[ \frac{\ln \frac{E_0}{\epsilon _0}}{\ln 2}\right] . \end{aligned}$$

(3.74)

The matter is further complicated by the fact that not all groups employ the $X_{\max }$ method.

The attenuation length $\varLambda$ is obtained from the tail of the function describing the $X_{\max }$ distribution.

3.3.7 Block, Halzen and Stanev: models vs. measured attenuation length

Shortly after Ref.  [46], the uncertainties arising through the a parameter values used by different experiments, were again discussed [47, 48] in light of the QCD-inspired model for $\sigma _{\mathrm{tot}}^{pp}$ in [62], referred to as BHM model. This model incorporates analyticity and unitarity, in a context in which QCD shapes the parameterisation of the terms which contribute to the rise of the cross section. We shall discuss it later in more detail.

Anticipating more recent debates, we notice that the cosmic ray experiments can give information on the interaction p-air, and hence on pp, but the extraction of data depends not only on the rate at which the primary particle dissipates energy in the atmosphere, but on cosmic ray composition. In this work, Block, Halzen and Stanev choose to ignore the possibility that the most penetrating particles may not be protons, and focus instead on the consistency of the values extracted by cosmic ray experiments with those extracted by the Glauber method implemented with their model for pp scattering.

They rename the parameter a as k, and use the slightly different nomenclature

$$\begin{aligned}&\varLambda _m=k\lambda _{p\text {-}\mathrm{air}}=k \frac{14.5m_p}{\sigma _{\mathrm{inel}}^{p\text {-}\mathrm{air}}} ,\end{aligned}$$

(3.75)

$$\begin{aligned}&\sigma _{p\text {-}\mathrm{air}}^{\mathrm{inel}}=\sigma _{p\text {-}\mathrm{air}} -\sigma _{p\text {-}\mathrm{air}}^{\mathrm{el}} -\sigma _{p\text {-}\mathrm{air}}^{\mathrm{q}\text {-}\mathrm{el}} , \end{aligned}$$

(3.76)

where the subscript m in Eq. (3.75) stands for measured, k measuring the rate at which the primary proton dissipates energy into the electromagnetic shower as observed by the experiment, and $\sigma _{p\text {-}\mathrm{air}}$ is the total p-air cross section. Once more, here are the steps as described in this paper:

• 1. experiments obtain $\sigma _{\mathrm{inel}}^{p\text {-}\mathrm{air}}$ from Eq. (3.75) at a given energy of the most penetrating primary particle, measuring $\varLambda _m$ and estimating a value for k,

• 2. model builders use Eq. (3.76), with Glauber’s theory and a nuclear density model as described in [43], and draw constant contours of fixed $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{inel}}$ in the B(s) and $\sigma _{\mathrm{tot}}^{pp}$ plane,

• 3. the QCD-inspired model by [62] establishes the correspondence between B(s) and $\sigma _{\mathrm{tot}}^{pp}$: (i) at any given energy, extrapolated values for $\sigma _{\mathrm{tot}}^{pp}$ and B(s) can be determined through a fit of the model parameters of all the pp and ${\bar{p}}p$ accelerator data. Thus a plot such as the one in Fig. 11, where the dashed line is for the DL model, is now constructed for the BHM model,

• 4. the intersection of a given curve for p-air, which corresponds to the measured $\sigma _{\mathrm{inel}}^{p\text {-}\mathrm{air}}$ for primary proton energy, with the B(s) vs. $\sigma _{\mathrm{tot}}^{pp}$ line determines the $\sigma _{\mathrm{tot}}^{pp}$ value at that energy.

Figure 12, shows the one-to-one correspondence established between $\sigma _{\mathrm{tot}}^{pp}$ and $\sigma ^{\mathrm{inel}}_{\mathrm{pair}}$ via the constant contours in the ($B,\sigma _{\mathrm{tot}}^{pp}$) plane, according to the BHM model.

Fig. 12

Plot of the predicted pp cross section vs. for any given value of a measured $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{inel}}$, using the constant contour procedure, from Fig. 3 of [47]. Reprinted with permission from [47], ©1999 by the American Physical Society

It appears that in such a procedure, one has to first trust two models, (i) the Glauber model along with the relation between B(s) and $\sigma _{\mathrm{tot}}^{pp}$, and (ii) the model which extrapolates B(s) and $\sigma _{\mathrm{tot}}^{pp}$ at ultrahigh energies, but then one has also to trust the correctness of the extraction procedure of $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{inel}}$ from the air showers.

In [47] a contradiction is seen to arise between the predictions for pp in the model as obtained from accelerator data and cosmic ray extracted values.

In their conclusion, the authors point a finger to the parameter k, as already noted before [46]. Different experiments use different values for k, obtained from different analyses of shower simulation. The authors thus proceeded to do a $\chi ^2$ fit to the cosmic ray data and extract a value for k, and obtain $k=1.33\pm 0.04\pm 0.0026$, which falls in between values used by different Monte Carlo simulations.

Shortly there after, in a subsequent paper [48], to reduce the dependence on the determination of the parameter k, a simultaneous fit to both accelerator data and cosmic ray data was done by the same authors and a reconciliation between pp cross section between accelerator data and cosmic ray data was obtained when a value $k=1.349\pm 0.045\pm 0.028$ was used. The resulting agreement is shown in Fig. 13 from [48]. This analysis now gives a value $\sigma ^{\mathrm{total}}_{pp}(\sqrt{s}=14~\hbox {TeV})=107.9\pm 1.2~\hbox {mb}$ and the predictions from the model are now in agreement with extracted cosmic ray pp data.

Fig. 13

pp scattering total cross section predictions compared to rescaled Cosmic ray data from [48], as described in the text. Reprinted with permission from [48], ©2000 by the American Physical Society

Other questions arise if one were to challenge the assumed primary composition or Eq. (3.76), as we shall see through a summary of a review paper by Anchordoqui et al. [49], to which we now turn.

3.4 The extraction of p-air cross section from cosmic rays

A good review of the experimental techniques used to measure cosmic ray showers and extracting information from them can be found in [49] and lectures covering many aspects of cosmic ray physics can be found in [63].

This 2004 review focuses on cosmic ray phenomenology from the top of the atmosphere to the earth surface. For primary cosmic ray energies above $10^5~\hbox {GeV}$, the flux is so low that direct detection of the primary particles above the upper atmosphere is practically impossible. In that range, however, the primary particle has enough energy to penetrate deeply in the atmosphere and generate Extensive Air Showers (EAS), namely a measurable cascade of detectable products. Various techniques are used to detect the cascade products, and different types of detectors are employed.

In addition to various ways to extract from air showers information about primary composition of the incoming cosmic rays and energy of the primaries thus selected, one tries to extract $\sigma _{\mathrm{total}}^{pp}$from $\sigma ^{p\text {-}\mathrm{air}}$. There are various Monte Carlo simulation programs which do this, the ones mentioned in this review being SiBYLL [64], QGSJET [65] and DPMJET [66]. DPMJET simulates hadronic interactions up to the very high cosmic energies of interest using the Dual Parton Model [67]. The other two are both based on the eikonal approximation and mini-jet cross sections, but differ in how they introduce the impact-parameter distribution of partons in the hadrons. According to this review, in SYBILL the b-distribution is the Fourier transform of the proton e.m. form factor, whereas in QGSJET it is taken to be a Gaussian, i.e.

$$\begin{aligned}&A(s,\mathbf {b})= \mathrm{e}^{-b^2/R^2(s)},\end{aligned}$$

(3.77)

$$\begin{aligned}&R^2(s)\simeq 4R^2_0+4\alpha '_{\mathrm{eff}}\ln ^2 \frac{s}{s_0}. \end{aligned}$$

(3.78)

In this way, they can easily obtain the diffraction peak in agreement with the experimentally observed increase with energy. DPMJET has its name from the Dual Parton Model and is based on soft and hard Pomeron exchanges.

Fig. 14

The above is Fig. 5 from [49] and shows the energy dependence of the $pp$ inelastic cross section compared with different models for the impact-parameter distribution inside the protons. This figure is courtesy of L. Anchordoqui. Reprinted from [49], ©(2004) Elsevier

We can see now how various models for proton–proton scattering influence the information as regards the behaviour of the total $pp$ cross section at the highest energy available. In Fig. 14, values for $\sigma _{\mathrm{inel}}$ from cosmic ray data from AGASA and Fly’s Eye are plotted against the two model entries from SYBILL and QGSJET for the inelastic $pp$ cross section. At low energy, data come from CERN ISR and the cross sections are normalised to these values. The experimental errors indicated in this figure are mostly due to a limited understanding of the interaction of protons with nuclei and also nuclei with nuclei at such very high energies, as we shall try to show in the following. An even greater uncertainty seems to come from the modelling of the $pp$ cross section itself, as indicated by the two different bands. This uncertainty is actually not as large as it appears in this figure, since data at $\sqrt{s}\approx (60\div 1800)~\hbox {GeV}$ severely limit the high energy behaviour, as one can see from the section on models and fits.

Let us now turn to describe how one extracts the data for $pp$ cross section from p-nucleus, basically p-air data, always following [49]. In order to simulate cosmic ray showers, current event generators will need first of all to extrapolate the $pp$ cross section to very high energy (but this is by now provided by the many models and fits described in the next section) but also to make a model for the impact-parameter distribution of nucleons in nuclei. Indeed, all the event generators or models included in the event generators, use the Glauber formalism, with the nucleon density folded into that of the nucleus.

In Ref.  [49], the distinction between a production and an inelastic p-air cross section as related to the total vs. the inelastic pp cross section is clearly emphasised. We anticipate here that the definition of $\sigma ^{pp}_{\mathrm{inelastic}}$ is model dependent. Following Ref. [68], two expressions are discussed:

$$\begin{aligned} {\tilde{\sigma }}_{\mathrm{inel}}\approx \int \mathrm{d}^2{\mathbf {b}}\{1-\exp [-\sigma _{\mathrm{total}}T_A({\mathbf {b}})]\},\end{aligned}$$

(3.79)

$$\begin{aligned} {\tilde{\sigma }}_{\mathrm{prod}}\approx \int \mathrm{d}^2{\mathbf {b}}\{1-\exp [-\sigma _{\mathrm{inel}}T_A({\mathbf {b}})]\} \end{aligned}$$

(3.80)

where $T_A({\mathbf {b}})$ gives the impact-parameter distribution of the hadronic matter in the target (air for instance) folded with that of the projectile particle. $\sigma _{\mathrm{total}}$ and $\sigma _{\mathrm{inel}}$ are the relevant quantities for $pp$ scattering or hadron–hadron scattering. Here ${\tilde{\sigma }}_{\mathrm{inel}}$ uses the usual eikonal format, with as input the total $pp$ cross section. The physical description amounts to consider all the possible ways in which the proton can interact with another proton, $\sigma _{\mathrm{total}}$ and this will then be input to the formal expression for the inelastic p-air cross section. Then the result, compared with p-air data should allow one to extract the $pp$ data. The second equation starts with the $pp$ inelastic cross section and thus corresponds to breaking up single protons in the nucleus. What will it give for p-air? Clearly it is a scattering process in which at least one proton has broken up, generating a new particle. According to Anchordoqui et al., ${\tilde{\sigma }}_{\mathrm{prod}}$ gives the cross section for processes in which at least one new particle is generated. For this to happen, one must exclude elastic $pp$ processes, and this is why the input in this case is the inelastic $pp$ cross section. This latter quantity, ${\tilde{\sigma }}_{\mathrm{prod}}$, is the one which enters the cascade, since this is what will start the cascade.

Notice that, in the cascade, $\pi$–p is also playing a role and this cross section needs to be entered in the simulations as well. The $\pi -p$ cross section is smaller than the one for $pp$, but only by perhaps a factor 2 / 3. The relevant parameters in modelling these processes are two, the mean free path, $\lambda = 1/(n{\tilde{\sigma }}_{\mathrm{prod}})$ and the inelasticity $K=1-E_{\mathrm{lead}}/E_{\mathrm{proj}}$, where n is the density of nucleons in the atmospheric target and $E_{\mathrm{lead}}$ and $E_{\mathrm{proj}}$ are energy of the most energetic hadron with a long life time in the shower and the energy of the projectile particle, respectively.

3.4.1 Extraction of $\sigma _{\mathrm{tot}}^{pp}$ in Block and Halzen model

The extraction of $\sigma _{\mathrm{tot}}^{pp}$ from cosmic ray data has been considered once again in [51]. Block summarises his description of the connection between p-air and $pp$ data and examines different methods by which data are extracted and analyzed. In addition, a different model for $\sigma _{\mathrm{tot}}^{pp}$ is used. The discussion covers now two different methods by which one can obtain $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}$ from the $X_{\max }$ distribution.

In the first of the methods examined, which is the one used by Fly’s Eye, AGASA, Yakutsk and EASTOP, the measured quantity is of course $\varLambda _m$, which implies that, in order to extract first of all a value for $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}$ one needs the value of the parameter k. The range of values used by different experiments for the parameter k is given in the paper and it lies within ($1.15\div 1.6$) from EASTOP to Fly’s Eye experiment. The smallest value is the one used by EASTOP, which is also the most recent and corresponds to more modern shower modelling,

A second method is the one used by the HiRes group, which, according to Block, has developed a quasi-model-free method of measuring $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}$. Basically, the shower development is simulated by randomly generating an exponential distribution for the first interaction point in the shower. By fitting the distribution thus obtained, one can obtain $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}= 460\pm 14\pm 39\pm 11~\hbox {mb}$ at $\sqrt{s}=77~\hbox {TeV}$.

The analysis in this paper differs from the one in [48] in two respects, one concerning the model used for $\sigma _{\mathrm{tot}}^{pp}$, and the other the treatment of different cosmic ray experiments. The extraction of $\sigma ^{\mathrm{prod}}_{p\text {-}\mathrm{air}}$ from the model used for pp description does not use all the results from the QCD-inspired model. A hybrid combination enter into the ($B(s),\ \sigma _{\mathrm{tot}}^{pp}$) plane, namely: (i) $\sigma _{\mathrm{tot}}^{pp}$ is obtained from an analytic amplitude expression, which saturates the Froissart bound [69], i.e. $\sigma _{\mathrm{tot}}^{pp}\simeq \ln ^2 s$ at asymptotic energies, with parameters fitted to both pp and ${\bar{p}}p$ accelerator data, (ii) B(s) is obtained via a fit to data from the QCD-inspired model [50]. Values for $\sigma _{\mathrm{tot}}^{pp}$ at LHC remain unchanged, but changes appear in the thus determined value for the parameter k.

3.4.2 The inelastic cross section and model uncertainties, including diffraction

A short review by D’Enterria et al. [70] deals with various hadronic quantities entering cosmic rays analyses, such as multiplicity distributions and energy flow. In addition, extracting an inelastic cross section from total and elastic scattering requires, in most models, a theoretical description of diffraction, single and double, low and high mass.

In Regge-based models, diffraction uses a multichannel formalism along the line of previous analyses by Miettinen and Thomas [71], also discussed by Pumplin [72, 73], and based on the Good and Walker decomposition of diffractive scattering [74]. Within a Reggeon Field Theory (RFT) framework, a QCD based description of diffraction has been applied to cosmic rays by Ostapchenko [75] and in the simulation program QGSJET [65]. The formalism uses a multichannel decomposition, and the physics contents include description of non-perturbative effects, such as gluon saturation, and semi-hard interactions. We shall see in the section dedicated to the elastic differential cross section how other authors have introduced diffraction within Regge field theory, in particular Khoze, Martin and Ryskin and Gotsman, Levin and Maor, also using a Good and Walker (GW) formalism with a Regge model for the high mass diffraction, through triple Pomeron interactions.

Another approach is found in the work by Lipari and Lusignoli (LL) [52], who have combined the mini-jet approach with the GW description of diffractive states. The approach by LL is based on the mini-jet description, which the authors consider most useful to implement in simulation programs, and on a continuous distribution of diffractive states, all contributing to the total diffraction cross section. Their work on diffraction is described in the part of our review dedicated to the elastic cross section.

Later, in Sect. 3.6.1, we shall discuss again this point, following a recent analysis by Engel and Ulrich [76].

3.5 Modelling the cosmic ray flux and energy distribution of particles

Of course, a fundamental problem – still unsolved – concerns the origin of the primary cosmic ray flux, specially at high energies, of interest for this review. Related issues concern the composition and the energy distribution of the cosmic ray constituents. As some progress has been made in this regard, in the following we shall briefly review it.

3.5.1 Power-law flux and critical indices of cosmic radiation

As stated at the beginning of this chapter, starting with Heisenberg, many physicists, including Landau [77] and Fermi [78], devoted much time and effort to understanding the observed isotropy and a stable power-law energy spectrum of the cosmic radiation flux. Presently, it is known experimentally that [79] the energy distribution law of cosmic ray nuclei in the energy range $5~\mathrm{GeV}< E < 100~\mathrm{TeV}$ obtained via the differential flux per unit time per unit area per steradian per unit energy obeys

$$\begin{aligned} \left[ \frac{\mathrm{d}^4 N}{\mathrm{d}t \mathrm{d}A \mathrm{d}\varOmega \mathrm{d}E}\right] \approx \frac{(1.8\ {\mathrm{nucleons}})}{\mathrm{sec}\ {\mathrm{cm}}^{2}\ \mathrm{sr}\ \mathrm{GeV}}\left( \frac{1~\mathrm{GeV}}{E}\right) ^\alpha \end{aligned}$$

(3.81)

wherein the experimental critical index $\alpha \approx 2.7$. At the “knee” of the distribution, i.e. at energy $E\sim 1\ \mathrm{PeV}$, there is a shift in the critical index to the value $\alpha \approx 3.1.$

In a recent series of papers [80,81,82,83] the hypothesis has been made that cosmic rays are emitted from the surfaces of astronomical objects (such as neutron stars) by a process of evaporation from an internal nuclear liquid to a dilute external gas which constitutes the vacuum. On this basis, an inverse power in the energy distribution with a power-law exponent of 2.701178 has been obtained in excellent agreement with the experimental value of 2.7.

The heat of nuclear matter evaporation via the entropy allows for the computation of the exponent. The evaporation model employed is based on the entropy considerations of Landau and Fermi that have been applied to the liquid drop model of evaporation in a heavy nucleus excited by a collision. This model provides a new means of obtaining power-law distributions for cosmic ray energy distributions and, remarkably, an actual value for the exponent which is in agreement with experiment and explains the otherwise puzzling smoothness of the cosmic ray energy distribution over a wide range of energies without discontinuities due to contributions from different sources required by current models. The argument runs as follows.

3.5.2 Evaporation of fluid particles

The heat capacity c per nucleon of a Landau-Fermi liquid drop at a non-relativistic low temperature T is given by

$$\begin{aligned} c = \frac{\mathrm{d}E}{\mathrm{d}T}= T \frac{\mathrm{d}s}{\mathrm{d}T} = \gamma T\quad \mathrm{as}\ T \rightarrow 0. \end{aligned}$$

(3.82)

Equation (3.82) implies an excitation energy $E = (\gamma /2)T^2$ and an entropy $\varDelta s = \gamma \ T$ so that

$$\begin{aligned} \varDelta s(E) = \sqrt{(2 \gamma E)} = k_\mathrm{B} \sqrt{\frac{E}{E_o}}. \end{aligned}$$

(3.83)

Consider the evaporation of nucleons from such a droplet excited say by an external collision. Given the entropy per nucleon $\varDelta s$ in the excited state, the heat of evaporation $q_{\mathrm{vaporisation}} = T (\varDelta s)$, determines the energy distribution of vaporized nucleons through the activation probability

$$\begin{aligned} P(E) = \mathrm{e}^{- \varDelta s(E)/k_\mathrm{B}} = \mathrm{e}^{-\sqrt{E/E_o}}, \end{aligned}$$

(3.84)

using Eq. (3.83). We now turn to relativistic cosmic ray particle production through evaporation.

3.5.3 Cosmic ray particle production

The sources of cosmic rays here are the evaporating stellar winds from gravitationally collapsing stellar (such as neutron star) surfaces considered as a big nuclear droplet facing a very dilute gas, i.e. the vacuum. Neutron stars differ from being simply very large nuclei in that most of their binding is gravitational rather than nuclear, but the droplet model of large nuclei should still offer a good description of nuclear matter near the surface where it can evaporate.

The quantum hadronic dynamical models of nuclear liquids have been a central theoretical feature of nuclear matter [84]. It is basically a collective Boson theory with condensed spin zero bosons (alpha nuclei) and spin one bosons (deuteron nuclei) embedded about equally in the bulk liquid. In the very high energy limit, the critical exponent $\alpha$ occurring in Eq. (3.81) in this model are computed as follows [80,81,82].

3.5.4 The critical exponent for classical and quantum particles

The density of states per unit energy per unit volume for ultra-relativistic particles is proportional to the square of the energy. The mean energy per particle in an ideal gas of particles obeying classical or quantum statistics can be succinctly described using, for classical (Boltzmann) statistics $\eta = 0$ whereas for quantum statistics, $\eta = 1$ for bosons and $\eta = -1$ for fermions, as:

$$\begin{aligned}&E_\eta = \frac{\int _o^\infty \left[ \frac{\epsilon ^3 \mathrm{d}\epsilon }{\mathrm{e}^{\epsilon /k_\mathrm{B} T} - \eta }\right] }{\int _o^\infty \left[ \frac{\epsilon ^2 \mathrm{d}\epsilon }{\mathrm{e}^{\epsilon /k_\mathrm{B} T} - \eta }\right] } = \alpha _\eta k_\mathrm{B} T\nonumber \\&\eta = 0; \Longrightarrow \ \alpha _{\mathrm{Boltzmann}} = 3;\nonumber \\&\eta = 1; \Longrightarrow \ \alpha _{\mathrm{bosons}} = \frac{3 \zeta (4)}{\zeta (3)} \approx 2.701178;\nonumber \\&\eta = -1; \Longrightarrow \ \alpha _{\mathrm{fermions}} = \frac{7 \alpha _1}{6} \approx 3.151374, \end{aligned}$$

(3.85)

where

$$\begin{aligned} \zeta (s) = \sum _{n=o}^\infty \frac{1}{n^s}, \end{aligned}$$

(3.86)

is the Riemann zeta function.

To establish $\alpha$ as a power-law exponent when the energy $E = \alpha (k_\mathrm{B} T)$, one computes (i) the entropy as

$$\begin{aligned} E = \alpha k_\mathrm{B} T = \alpha k_\mathrm{B} \frac{\mathrm{d}E}{\mathrm{d}S};\ \Longrightarrow \ S = k_\mathrm{B} \alpha \ \ln \left( \frac{E}{E_o}\right) \end{aligned}$$

(3.87)

and (ii) employs the heat of vaporisation to compute the evaporation energy spectrum

$$\begin{aligned} \mathrm{e}^{-S/k_\mathrm{B}} = \left( \frac{E_o}{E}\right) ^\alpha \end{aligned}$$

(3.88)

as in Eq. (3.81). A more detailed interacting quantum field theoretical calculation of ${\alpha }$ power-law exponents involves the construction of single particle spectral functions in the context of thermal quantum field theory. While they have here been computed the critical indices for the free Fermi and free Bose field theories, the results are already in quite satisfactory agreement with experimental cosmic ray power-law exponents.

In a recent paper, the AMS Collaboration [85] has reported detailed and extensive data concerning the distribution in energy of electron and positron cosmic rays. A central result of the experimental work resides in the energy regime $30~\hbox {GeV}< E < 1$ TeV, wherein the power-law exponent of the energy distribution is measured to be $\alpha _{\mathrm{experiment}} = 3.17$. In virtue of the Fermi statistics obeyed by electrons and positrons, the theoretical value was predicted as $\alpha _{\mathrm{theory}} = 3.151374$ in very good agreement with the AMS data.

The reason for this remarkable agreement would appear to be due to a Feynman parton structure for the high energy asymptotic tails of the single particle spectral functions. In this case that structure would be described by free non-interacting particles thanks to asymptotic freedom in QCD. Following Feynman’s physical reasoning and employing dispersion relations in a finite temperature many body quantum field theory context, in principle, it is possible to compute rather small corrections to the renormalised energy dependent power-law exponent $\alpha (E)$ for interacting theories. For further details about a phase transition and the behaviour around the “knee” etc. an interested reader may consult [83] and references therein.

3.6 Cosmic ray results after start of the LHC

Since 2011, accelerator data for $\sigma ^{pp}_{\mathrm{tot}}$ at LHC c.m. energy of $\sqrt{s}\ge 7$ TeV have provided new accurate information on the high energy behavior of the total $pp$ cross section. The question of whether one is now reaching a region of saturation of the Froissart bound was posed again. At around the same time, a new generation of cosmic ray experiments, which probes ultra-high cosmic ray energies, started to provide data. In 2012 the measurement of $\sigma _{p\text {-}\mathrm{air}}$ was released by the AUGER Collaboration [86] for an equivalent cm. energy $\sqrt{s}_{pp}=57\pm 0.3 \ (\hbox {stat.}) \pm 6 \ (\hbox {sys.})$ TeV. The result depends on the simulation program, in particular models of hadronic interactions, as described in [86, 87], and the model used for extracting the proton-air production cross section. The spread of results is shown in Fig. 15 from [86].

Fig. 15

Figure 2 of [86], showing the AUGER Collaboration result for $\sigma ^{\mathrm{prod}}_{p\text {-}\mathrm{air}}$ in comparison with other cosmic ray results, with references as indicated in the figure. Various dotted or dashed curves indicate different models used to extract the data through different simulation programs as indicated. Reprinted from [86], ©2012 by the American Physical Society

One important difference between AUGER result and previous results lies in the assumed primary composition: all the measurements in the highest energy group, HiRes, Fly’s Eye, Yakutsk and Akeno, assume pure proton composition, whereas AUGER opts for a 25% helium component.

Further uncertainties lie in how diffraction is taken into account in the calculation. In [88], one can find a recent discussion of the tension between LHC results on single and double diffraction as reported by TOTEM, ATLAS and CMS Collaborations, and their impact on the cosmic ray results.

Averaging the result between the different hadronic models leads to

$$\begin{aligned} \sigma ^{\mathrm{prod}}_{p\text {-}\mathrm{air}}=[505 \pm 22 (\hbox {stat})^{+28}_{-36}(\hbox {sys})]~\hbox {mb} \end{aligned}$$

(3.89)

Fig. 16

Figure 3 of [86], showing the AUGER Collaboration result for $\sigma ^{\mathrm{prod}}_{p\text {-}\mathrm{air}}$ in the $\{B(s),\sigma ^{\mathrm{inel}}_{pp}(s) \}$ plane. The unitarity limit is indicated, as is the uncertainty due to modelling of the pp cross section. Reprinted from [86], ©(2012) by the American Physical Society

at a center of mass energy of $(57\pm 6)$ TeV. The correlation between the parameters of the Glauber model which converts p-air to pp, B(s) and $\sigma _{\mathrm{inel}}$(proton–proton), is shown in Fig. 16, which includes a comparison with accelerator data, at their respective energies. The hatched area in the figure corresponds to the unitarity limit imposed by the relation between the total, the inelastic and the elastic cross section, derived as follows:

$$\begin{aligned} B \ge \left[ \frac{\sigma _{\mathrm{in}}}{4 \pi }\right] . \end{aligned}$$

(3.90)

The above inequality may more usefully written in terms of their commonly used units as [86]

$$\begin{aligned} B \hbox {GeV}^2 \ge \left[ \frac{\sigma _{\mathrm{in}}}{\mathrm{mb}}\right] \left[ \frac{\mathrm{mb}\, \mathrm{GeV}^2}{4 \pi }\right] \gtrsim \left[ \frac{1}{5}\right] \left( \frac{\sigma _{\mathrm{in}}}{\mathrm{mb}}\right) . \end{aligned}$$

(3.91)

[A heuristic derivation of Eq. (3.91) proceeds as follows. Assume that there exists an effective B so that the elastic differential cross section can be approximated as

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t} \approx \ \frac{\sigma _{\mathrm{tot}}^2}{16 \pi } \mathrm{e}^{Bt}, \end{aligned}$$

(3.92)

so that

$$\begin{aligned} \sigma _{\mathrm{el}} = \frac{\sigma _{\mathrm{tot}}^2}{16 B \pi }. \end{aligned}$$

(3.93)

Since $\sigma _{\mathrm{el}} = \sigma _{\mathrm{tot}} - \sigma _{\mathrm{in}}$, Eq. (3.93) may be written as

$$\begin{aligned} B = \frac{\sigma _{\mathrm{tot}}^2}{16 \pi (\sigma _{\mathrm{tot}} - \sigma _{\mathrm{in}})}. \end{aligned}$$

(3.94)

Let $x = \sigma _{\mathrm{in}}/\sigma _{\mathrm{tot}}$, so that Eq. (3.94) reads

$$\begin{aligned} \frac{4 \pi B}{\sigma _{\mathrm{in}}} = \frac{1}{4 x(1 -x)} \ge 1, \end{aligned}$$

(3.95)

from which Eq. (3.91) follows.]

The inequality Eq. (3.91) is mildly stringent. For example, at LHC [7 TeV], the left side is ${\sim } 20$ whereas the right side is ${\sim } 15$. Incidentally, the lower limit is reached only in the black-disk limit when $\sigma _{\mathrm{in}} = \sigma _{\mathrm{el}} = \sigma _{\mathrm{tot}}/2$. This provides yet another evidence that we are still nowhere near the black-disk limit. But this would be discussed in much more detail in our section on the elastic cross section.

Finally, the extraction of the pp total and inelastic cross sections for $\sqrt{s_{pp}} \simeq 57$ TeV, leads to the quoted results for pp scattering:

$$\begin{aligned} \sigma ^{\mathrm{inel}}_{pp}= & {} [ 92\pm 7 (\hbox {stat})^{+9}_{-11}\hbox {sys})\pm 7 (\hbox {Glauber})]~\hbox {mb} ,\end{aligned}$$

(3.96)

$$\begin{aligned} \sigma ^{\mathrm{tot}}_{pp}= & {} [ 133 \pm 13(\hbox {stat}) ^{+17}_{-20}(\hbox {sys})\pm 16 (\hbox {Glauber})]~\hbox {mb}.\nonumber \\ \end{aligned}$$

(3.97)

There is a strong warning in the paper, that the error from the application of the Glauber model may actually be larger than what is quoted here. It is also noted that this error is smaller for the inelastic cross section, and this can be accounted for by the inelastic cross section being less dependent on the B(s) parameter than the total. We shall return later to the question of how to estimate the needed inelastic cross section for cosmic rays. We notice that, very recently, the AUGER Collaboration has released results [89] estimated in the two energy intervals in $\log (E_{Lab}/\hbox {eV})$ from 17.8 to 18 and from 18 to 18.5. The corresponding values for $\sigma ^{p\text {-}\mathrm{air}}$ are within the errors of the 2012 measurements, the central values lying in a curve lower than the one drawn across the central 2012 reported value. These results are shown in the right-hand plot of Fig. 18, in the context of a mini-jet model whose results are discussed in Sect. 3.7.2.

In the next subsection we shall summarise the method used by the AUGER Collaboration to extract the proposed values for $\sigma ^{\mathrm{tot}}_{pp}$ in [86].

3.6.1 A recent analysis of Glauber theory with inelastic scattering

The details of the actual inputs used in the various Montecarlo simulations used by the AUGER Collaboration to extract $\sigma ^{\mathrm{prod}}_{p\text {-}\mathrm{air}}$ and thence pp total and inelastic cross sections can be found in an internal report by Engel and Ulrich [76]. Here we shall summarise the salient aspects of this analysis that includes inelastic screening through a two channel Good-Walker approach in the Glauber theory.

Considering just two states: $|p\rangle$ and $|p^*\rangle$, where the first is the proton and $p^*$ is an effective state standing for all inelastic states. A coupling parameter $\lambda$ is introduced so that the 1-channel elastic amplitude $\varGamma _{pp}$ becomes a $2 \times 2$ matrix:

$$\begin{aligned}&|p\rangle = \left( \begin{matrix} 1\\ 0\\ \end{matrix} \right) ;\quad |p^*\rangle = \left( \begin{matrix} 0\\ 1\\ \end{matrix} \right) \nonumber \\&\quad \Longrightarrow \ \tilde{\varGamma }_{pp} = \left( \begin{matrix} 1 &{} \lambda \\ \lambda &{} 1 \\ \end{matrix} \right) \varGamma _{pp}. \end{aligned}$$

(3.98)

The elastic impact-parameter amplitude for a hadron h on a nucleus with A nucleons becomes

$$\begin{aligned}&\varGamma _{hA}(\mathbf{b}; \mathbf{s}_1,\ldots , \mathbf{s}_A) \nonumber \\&\quad = \langle p| \tilde{\varGamma }_{hA}(\mathbf{b}; \mathbf{s}_1,\ldots , \mathbf{s}_A)|p\rangle \nonumber \\&\quad = 1 - \langle p| \prod _{j=1}^A [ 1 - \tilde{\varGamma }_{hN}(\mathbf{b} - \mathbf{s}_j) ]|p\rangle . \end{aligned}$$

(3.99)

After diagonalisation, it reads

$$\begin{aligned}&\varGamma _{hA}(\mathbf{b}; \mathbf{s}_1,\ldots , \mathbf{s}_A) \nonumber \\&\quad =1 - \frac{1}{2}\langle p| \prod _{j=1}^A [ 1 -(1 + \lambda )\tilde{\varGamma }_{hN} (\mathbf{b} - \mathbf{s}_j) ]|p\rangle \nonumber \\&\qquad -\, \frac{1}{2}\langle p| \prod _{j=1}^A [ 1 -(1 - \lambda )\tilde{\varGamma }_{hN}(\mathbf{b} - \mathbf{s}_j)]|p\rangle . \end{aligned}$$

(3.100)

For the Gaussian profile functions, an analytic closed form expression for $\varGamma _{hA}(\mathbf{b}; \mathbf{s}_1,\ldots , \mathbf{s}_A)$ is obtained and, through it, analytic but somewhat long expressions for total, elastic and quasi-elastic cross sections for proton-nucleus are obtained and can be found in [76].

The parameter $\lambda ^2(s)$ is related to the ratio of $\sigma _{\mathrm{SD}}(s)$ to $\sigma _{\mathrm{elastic}}(s)$ and hence to available accelerator data on single diffractive dissociation (SD) and elastic pp-scattering. It can be parametrised and extrapolated to higher energies as needed. Thus, accelerator data can in principle determine (modulo extrapolation) $\lambda ^2(s)$. In practice, empirical functions such as the following are employed

$$\begin{aligned}&\sigma _{\mathrm{SD}}(s) = \left[ \frac{s\ \log [10^3~\mathrm{GeV}^{-2} s]}{4s + 400~\mathrm{GeV}^2}\right] (\hbox {mb});\nonumber \\&\quad \mathrm{valid\ for}\ \zeta _{\max } = \frac{M^2_{D,\max }}{s} < 0.05. \end{aligned}$$

(3.101)

Here $M_{D,\max }$ is the maximum invariant mass of the diffractive system expected to be coherently produced by a nucleon. Typical values $\zeta _{\max } = (0.05 \div 0.15)$ are considered to describe SD. The choice of $\zeta _{\max }$ controls the scale of $\sigma _{\mathrm{SD}}$ and thus $\lambda$. At very high energies $\lambda ^2$ should decrease since we expect $\sigma _{\mathrm{SD}} \sim \ln (s)$ and $\sigma _{\mathrm{elastic}} \sim \ln ^2(s)$. These authors find that, for the AUGER measurement at $\sqrt{s} = 57~\hbox {TeV}$, $\lambda (\sqrt{s} = 57~\hbox {TeV}) = (0.35 \div 0.65)$. This is then folded into the errors associated with the various cross section estimates.

The conversion of the proton-air to proton–proton cross section proceeds along the lines discussed earlier, i.e., plots of B vs. $\sigma _{\mathrm{inel}}$ are used with constant values of p-air production cross sections drawn and the intersection giving the pp inelastic cross section at that energy. With $\lambda = 0.5$, these authors deduce that at $\sqrt{s} = 57$ TeV:

$$\begin{aligned}&\sigma _{pp}^{\mathrm{inel}} = [92\pm 7(\hbox {stat})^{+9}_{-11}(\hbox {sys}) \pm 1(\hbox {slope})\pm 3(\lambda )]~\hbox {mb}\nonumber \\&\sigma _{pp}^{\mathrm{tot}} = [133\pm 13(\hbox {stat})^{+17}_{-20} (\hbox {sys}) \pm 13(\hbox {slope}) \pm 6(\lambda )]~\hbox {mb},\nonumber \\ \end{aligned}$$

(3.102)

also shown in Eqs. (3.96) and (3.97).

3.6.2 The Telescope-Array measurement at 95 TeV c.m. energy

In 2015, the Telescope Array (TA) Collaboration has presented a measurement of the p-air cross section at the never attained before c.m. energy of $\sqrt{s}=95$ TeV. The method used is that of K-factor, in which the attenuation length, and hence the p-air cross section, is proportional to the slope of the tail of the $X_{\max }$ distribution. As seen before, the factor K depends on the model used for the shower evolution. In [90], averaging over different models, a value $K=1.2$ is obtained, with an uncertainty (model dependence) of ${\sim } 3\%$. Including a systematic error from the uncertainty on the primary cosmic ray composition, the procedure therein described leads to a value

$$\begin{aligned} \sigma _{p\text {-}\mathrm{air}}^{\mathrm{inel}}=(567\pm 70.5[\hbox {Stat}]^{+29}_{-25}[\hbox {Sys}])~\hbox {mb} \end{aligned}$$

(3.103)

at an energy of $10^{18.68}~\hbox {eV}$. The proton-air cross section from this measurement appears to lie higher than the more recent AUGER values, but it is consistent with the observed trend within all the errors. Some of the difference could be ascribed to assuming a different primary composition, a question still not fully resolved. Results from a higher statistical sample are expected shortly.

The TA Collaboration has also presented a value for the total pp cross section, following the procedures from [43, 46], which we have described in Sects. 3.3.2 and 3.3.4. Using Glauber theory and the BHS QCD-inspired fit [47], they propose:

$$\begin{aligned} \sigma ^{\mathrm{tot}}_{pp}=170^{+48}_{-44}[\hbox {Stat}.]^{+19}_{-17}[\hbox {Sys}] ~\hbox {mb}. \end{aligned}$$

(3.104)

While consistent within the errors with the trend shown by the lower energy measurement by the AUGER Collaboration, the above value for the pp total cross section is thus higher than the value extracted by AUGER. In this respect we should notice that the methods used by the two collaborations to pass from p-air to proton–proton are not the same. In the next subsection, we present another model about how to extract pp cross section from that of p-air.

3.7 Eikonal models for inelastic p-air scattering

As we have seen, in order to extract information as regards the basic pp scattering, cosmic ray measurements require models to link the inelastic p-air cross section to the total and elastic ones. Glauber theory provides such a connection, through an eikonal formalism in impact-parameter space. However, one-channel eikonals provide an incomplete picture at high energy, as has been noticed since a long time. As we shall see in more detail in the sections dedicated to the total and the elastic cross section, a single channel eikonal model with an approximately real profile function is unable to clearly discriminate between elastic and inelastic processes. As a result, various techniques have been developed: we have described in the preceding a two channel model as that due to Engel and Ulrich, and recalled the analytical model with QCD-inspired input by Bloch and Halzen. The present uncertainties and difficulties with these extractions lead to large errors and hence, in part, to the inability to fully exploit the very high energy data provided by the cosmic ray experiments.

In the following we shall briefly outline the results from a multichannel model by Gotsman, Levin and Maor and then show corresponding results that can be obtained in a single-channel eikonal model with QCD mini-jets and compare them with present data.

3.7.1 A multichannel model inclusive of diffraction and triple Pomeron coupling

An example of a QCD model used to extract p-air cross section can be found in [91]. This is a multi-channel model, to which we shall return in the section dedicated to elastic scattering. It includes diffraction contributions and triple-Pomeron exchanges. The final formula for the inelastic p-air cross section is given as

$$\begin{aligned}&\sigma _{\mathrm{in}}(p+A;Y)\nonumber \\&\quad =\int \mathrm{d}^2{\mathbf {b}}\left[ 1- \exp \left( -\left\{ \sigma ^{pp}_{\mathrm{tot}}\frac{S_A(b)}{1+\tilde{g}G_{3\mathcal{P}}G_{enh}(Y)S_A(b)} \right. \right. \right. \nonumber \\&\qquad -\left. \left. \left. \,(\sigma ^{pp}_{\mathrm{el}}+\sigma ^{pp}_{\mathrm{diff}})\frac{S_A(b)}{(1+\tilde{g}G_{3\mathcal{P}}G_{enh}(Y)S_A(b))^2} \right\} \right) \right] \nonumber \\ \end{aligned}$$

(3.105)

with $S_A(b)$ the nuclear density, $G_{3\mathcal{P}}$ the triple Pomeron coupling, $G_{enh}(Y)$ the Green’s function of the Pomeron exchange, $\tilde{g}$ includes the parameters of the GW diffraction couplings, which are used to determine $\sigma _{\mathrm{tot}}, \sigma _{\mathrm{el}},\ \sigma _{\mathrm{diff}}$.

A comparison between data and results from this model is shown in Fig. 17 from [91]. From Eq. (3.105) and the figure, one can notice the following:

• both recent AUGER and Telescope Array data (within their large errors) can be described by the model. Shown are two curves: for $G_{3\mathcal{{P}}}=0$ or $G_{3\mathcal{{P}}}=0.03$;

• the impact-parameter (b-)dependence, over which the eikonal is integrated, includes only the nuclear shape. In the exponent, it can be factored out of the QCD part. Namely, there is convolution of the nuclear distribution with the inner nucleon structure;

• the case $G_{3\mathcal{P}}=0$, reduces Eq. (3.105) to

  $$\begin{aligned}&\sigma _{\mathrm{in}}(p+A;Y)\\&\quad =\int \mathrm{d}^2{\mathbf {b}}[1-\exp (-S_A(b)\{\sigma ^{pp}_{\mathrm{tot}} -(\sigma ^{pp}_{\mathrm{el}}+\sigma ^{pp}_{\mathrm{diff}})\})]; \end{aligned}$$

• the curve where also $\sigma ^{pp}_{\mathrm{diff}}=0$ lies higher than the data.

Thus, the authors conclude that a small triple Pomeron coupling and $\sigma ^{pp}_{\mathrm{diff}}\ne 0$ can give a good description of data, when a two channel GW formalism is employed to describe total and elastic pp cross sections.

Fig. 17

The inelastic p-air cross section from the two channel model of Gotsman, Maor and Levin, compared with cosmic ray data, from [91]. Reprinted with permission from [91], ©(2013) by the American Physical Society

An interested reader may also consult some related work in [88] that is based on QCD and the Regge picture.

3.7.2 A single-channel model with QCD mini-jets

In a recent work [92], a single channel eikonal formalism has been proposed for a somewhat different reconstruction of the quantity $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}$ measured in cosmic rays, from the underlying pp dynamics.

The starting point of this approach is the realisation that in single-channel mini-jet models, $\sigma _{\mathrm{elastic}}$ includes both purely elastic and correlated-inelastic processes [41, 56].

The model we present here exploits this observation and has the virtue of eliminating the complicated and model dependent untangling of the elastic and diffractive parts to deduce the needed inelastic non-diffractive contribution, called here $\sigma ^{pp}_{\mathrm{inel}\text {-}\mathrm{uncorr}}$, that serves as an input in the Glauber reconstruction of $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}$. The argument runs as follows.

As Eq. (3.40) makes evident, cosmic rays measure and probe the part of the scattering process that is shorn of its elastic and quasi-elastic parts. We may thus identify the needed remainder to be the “inelastic-uncorrelated” part of the cross section. If such is indeed the case, then $\sigma _{\mathrm{inel}}$ computed through a single channel mini-jet eikonal formalism based on an exponentiation of the basic parton–parton scattering would indeed correspond to the inelastic-uncorrelated cross section for pp scattering, as we have discussed in [41]. This last point will also be discussed in more detail in Sect. 5.

Fig. 18

p-air production cross section as deduced from the mini-jet model of [93, 94] and its comparison with experimental cosmic ray data. At left we show the model predictions using MSTW parton densities [95] and different nuclear density models, at right using both MSTW and GRV densities [96], and including recent AUGER data [89] as well as those at $\sqrt{s}=95~\hbox {GeV}$ from the Telescope Array Detector [90]. Reprinted with permission from [92], ©2015 Springer

Under the above hypothesis, the steps relating pp dynamics to the cosmic data in a one channel formalism become rather simple and can be outlined as follows:

• 1. Neglecting the real part of the scattering amplitude at $t=0$, the same eikonal $\chi _I(s,b)$ can be used to describe both $\sigma _{\mathrm{tot}}^{pp}(s)$ and $\sigma _{\mathrm{inel}\text {-}\mathrm{uncorr}}(s)$:

  $$\begin{aligned}&\sigma _{\mathrm{tot}}^{pp}= 4 \pi \int (b\mathrm{d}b) [1-\mathrm{e}^{-\chi _I(b,s)}],\end{aligned}$$

  (3.106)
  $$\begin{aligned}&\sigma _{\mathrm{inel}\text {-}\mathrm{uncorr}}^{pp}= 2\pi \int (b\mathrm{d}b) [1-\mathrm{e}^{-2\chi _I(b,s)}] . \end{aligned}$$

  (3.107)

  In the mini-jet model of [93, 94],

  $$\begin{aligned} 2\chi _I(b,s)\equiv n^{pp}(b,s)=n^{pp}_{\mathrm{soft}} + A(b,s)\sigma ^{\mathrm{QCD}}_{\mathrm{jet}}(p_{t\min },s)\!\!\!\nonumber \\ \end{aligned}$$

  (3.108)

  where the impact-parameter function A(b, s) describes the impact-parameter space parton distributions in the proton, obtained through soft-gluon resummation, and $\sigma ^{\mathrm{QCD}}_{\mathrm{jet}}(p_{t\min },s)$ is calculated through elementary parton–parton scattering and library used parton density functions (PDFs), as already discussed in the context of the Durand and Pi model in Sect. 3.3.3;

• 2. Next, the usual Glauber impact-parameter expression is used for the cosmic ray production cross section:

  $$\begin{aligned} \sigma _{\mathrm{prod}}^{p\text {-}\mathrm{air}}(E_{lab})= 2 \pi \int (b\mathrm{d}b)[1-\mathrm{e}^{-n^{p\text {-}\mathrm{air}} (b,s)}] \end{aligned}$$

  (3.109)

  with

  $$\begin{aligned} n^{p\text {-}\mathrm{air}}(b,s)=T_N(b)\sigma _{\mathrm{inel}\text {-}\mathrm{uncorr}}^{pp}(s) \end{aligned}$$

  (3.110)

  where $\sigma _{\mathrm{inel}\text {-}\mathrm{uncorr}}^{pp}(s)$ in Eq. (3.110) is obtained from Eqs. (3.106) and (3.107), with the same QCD term, but a different parametrisation of the low energy part, as also discussed in the Durand and Pi model. $T_N({\mathbf {b}})$ is the nuclear density, for which the standard gaussian choice is made:

  $$\begin{aligned} T_{N}(b) = \frac{A}{\pi R_{N}^{2}}{\text {e}}^{-b^{2}/ R_{N}^{2}}, \end{aligned}$$

  (3.111)

  properly normalised to

  $$\begin{aligned} \int \mathrm{d}^{2} \mathbf b T_{N}(b) = A. \end{aligned}$$

  (3.112)

  The parameters used in the profile (3.111), namely the average mass number of an “air” nucleus, A, and the nuclear radius, $R_{N}$, are again standard:

  $$\begin{aligned} A = 14.5 ,\quad R_{N} = (1.1~\hbox {fermi}) A^{1/3}. \end{aligned}$$

  (3.113)

The authors of [92] have used the above in an eikonal model for the elastic amplitude based on gluon resummation (with a singular $\alpha _s$), which we label BN from the Bloch and Nordsieck classical theorem on the infrared catastrophe in QED. The BN model and the choice of $\chi (b,s)$ are discussed in the elastic cross section part of this review.

We show here only the final model results and their comparison with experimental data in Fig. 18. In this figure, the left hand panel shows a comparison of data with the results from two different nuclear density models, the gaussian distribution and a Wood–Saxon type potential, as in [97], as well as with different low energy contributions. The right-hand panel shows a comparison of p-air data, including the most recent AUGER and Telescope Array results just discussed, with two different parton densities used in the BN model, as indicated. The band highlights the uncertainty due to the low-x behavior of these two PDFs parametrisations.

We notice that in this model, the impact-parameter distribution of partons is not folded in with the nuclear density distribution, rather it is factored out, just as in the model described in Sect. 3.7.1. This assumption may not be valid at low energies. In the above mini-jet model this uncertainty is buried in the low energy contribution $n^{p\text {-}\mathrm{air}}_{\mathrm{soft}}$, but it is likely to be correct in the very high energies region now being accessed. Thus the model differs from the usual Glauber applications.

The AUGER data at $\sqrt{s} \approx 57~\hbox {TeV}$ are very well reproduced by this model. It is reasonable to conclude that a single channel eikonal model that describes well $\sigma _{\mathrm{tot}}^{pp}$ indeed generates a correct uncorrelated-inelastic pp-cross section. The latter in turn provides the proper input to generate $\sigma _{p\text {-}\mathrm{air}}^{\mathrm{prod}}$ as observed in cosmic rays. Work is still in progress to understand the implications of the above description on the construction of multi-channel models.

3.8 Conclusions

In this section, we have presented an overview of how, over the past 60 years, cosmic ray experiments have provided much needed information (albeit with large errors). They have helped guide the theorists towards more realistic particle physics models and make better predictions for their asymptotic behaviour. However, many uncertainties still affect the extraction of the more fundamental $pp$ cross section from the cosmic ray experiments, some of them related to the Glauber formalism and the modelling of quasi-elastic contributions, and others pertaining to diffraction in $pp$ scattering and its relation to p-air processes. Other uncertainties depend on understanding the actual composition of cosmic rays and the relation between the measured high-energy power-law distributions of cosmic electron/positron, proton and nuclei and the origin of high energy cosmic rays.

4 The measurement of $\sigma _{\mathrm{total}}$ before the LHC: description of experiments and their results

In this chapter, we give a brief account of crucial hadronic cross section experiments at particle accelerators, beginning in the 1950s up to the Tevatron, including how the measurements were done at each machine. Relevant experimental data with figures, plots and tables shall be shown. Whenever it appears useful, there would be a discussion of the error estimates and the difference between results from different experimental groups.

The focus of these experiments has been to determine the following four basic physical quantities:

• (i) total cross section $\sigma _{\mathrm{total}}$;

• (ii) elastic cross section $\sigma _{\mathrm{elastic}}$;

• (iii) slope of the forward elastic amplitude B;

• (iv) $\rho$-parameter, that is the ratio of the real to the imaginary part of the forward elastic amplitude.

Before the advent of particle accelerators in the 1950s, cosmic ray experiments were the only source for measurements of total proton cross sections. The situation changed with the first measurements at particle accelerators, which took place at fixed target machines; see for instance [98]. These measurements were followed in the 1960s by extensive ones, again at fixed target machines, at the CERN ProtoSynchrotron [99], at Brookhaven National Laboratory [100] and in Serpukhov [101]. These earlier measurements showed decreasing total cross sections, more so in the case of ${\bar{p}}p$, only slightly in the case of proton–proton. These results were in agreement with the picture of scattering as dominated at small momentum transfer by exchange of Regge trajectories (leading to a decrease) and multi peripheral production, resulting in the exchange of the Pomeron trajectory, with the quantum numbers of the vacuum, and intercept $\alpha _P(0)=1$. Things changed dramatically when the CERN Intersecting Storage Ring (ISR) started operating in 1971. We show the scheme of operation of the ISR in Fig. 19 from [102]. Cross sections were seen to rise. Since then, accelerator measurements for the total cross section for $pp$ as well as for ${\bar{p}}p$ have been performed only at colliders and the cross section has continued to increase, with the latest measurement released at c.m. energies of $\sqrt{s}=7$ and $8 ~\hbox {TeV}$ at the Large Hadron Collider (LHC7 and LHC8) by the TOTEM experiment [103], with predictions and measurement in general agreement with latest cosmic ray experiments [86].

Fig. 19

A schematic view of the ISR set up from [102]. Reprinted from [102], ©(1979) with permission by Elsevier

The spirit of this section is to show how many different experiments took place from early 1970s until the end of the century, and established beyond doubt the rising behavior of the total cross section while the center of mass increased by almost a factor 100 from the first ISR experiment, at 23 GeV c.m., to the 1800 GeV at the Tevatron.

This section is structured as follows:

• the description of measurements through fixed target experiments is given in Sect. 4.1,

• the measurements at the CERN Intersecting Storage Rings (ISR) are discussed in Sect. 4.2, including a discussion of measurement of the $\rho$ parameter with description of the various methods to measure the total cross section in Sect. 4.2.2 and ISR final results in Sect. 4.2.3,

• experiments confirming the rise of the total cross section at the CERN $Sp\bar{p}S$ are presented in Sect. 4.3, with results from UA1 in Sect. 4.3.1, which includes a comment on the energy dependence of the slope parameter, UA4 and UA4/UA2 results are in Sect. 4.3.2, UA5 and the ramping run in Sect. 4.3.3,

• measurements at the FermiLab TeVatron are described in Sect. 4.4 with results from E710, CDF and E811 in Sect. 4.4.1 and an overview of the Black Disk model, for a long time a very useful and commonly held model in Sect. 4.4.2,

• further discussion of the $\rho$ parameter is in Sect. 4.4.3.

4.1 Fixed target experiments

Proton-nuclei cross sections by Bellettini et al. [104] were among the first experiments to measure the expected diffraction pattern from the optical model, for elastic scattering of protons on nuclei. In this experiment, the momenta of the proton before and after the scattering were measured, the recoil of the nucleus was not measured at all. The experimental technique was the same as the one used for the measurement of proton–proton scattering [99].

A system of quadrupoles and bending magnets transported a well collimated (almost monochromatic) beam of protons of average momentum $19~\hbox {GeV}/c$ from the CERN ProtoSynchrotron to the experimental area. The incident proton beam was defined by scintillation counters $C_{1,2,3}$ while the scattered protons were detected by another set of counters, $C_{4,5}$, placed after the target. An anti-coincidence counter, placed directly in the path of the beam, was used to reduce the background trigger rate from unscattered particles. The position of the incident and scattered protons were measured by sonic spark chambers, $S_{1,2,3,4,5}$. It is clear from the above description why such experiments received their name: the transmission method.

A description of the transmission method can be found in [105], where the measurement of pion–proton total cross section between 2 and 7 $\hbox {GeV}/c$ laboratory momentum is described. The total cross sections for $pp$ and ${\bar{p}}p$ were measured [100] along with that for $\pi \ p$ and $K\ p$ on both hydrogen and deuterium targets. In this set of experiments total cross sections were measured between 6 and 22 GeV/c at intervals of 2 GeV/c and the method utilized was that of a conventional good-geometry transmission experiment with scintillation counters subtending various solid angles at targets of liquid H2 and D2. The results showed a variation of the cross section with momentum, namely a small but significant decrease in $\sigma _T(pp)$ [and $\sigma _T(pn)$] in the momentum region above 12 GeV/c was found.

The measurement of total cross section in these transmission experiments was done essentially by following the initial and final particle paths through a series of (scintillation) counters placed at subsequent intervals and covering different solid angle portions. For each set of counters, at a given solid angle, a transmission factor was defined to take into consideration signals from the various detecting components and the total cross section at a given momentum transfer value (t) was computed from the expression

$$\begin{aligned} \sigma (t)=(1/N)\ln (T_E/T_F) \end{aligned}$$

(4.1)

where N was the number of nuclei per $\hbox {cm}^{2}$ in the target, $T_E$ and $T_F$ the transmission factors for an empty or a full target, respectively. Subsequently partial differential cross sections measured at different t-values were fitted either by a polynomial or preferably by an exponential and extrapolated to zero.

In Figs. 20 and 21, we show schematic views of the transmission set up for the measurement of the total cross section from [100, 105].

Fig. 20

A schematic view of the transmission type experiment from [105]. Reprinted from [105], ©(1966) by the American Physical Society

Fig. 21

A schematic view of the transmission type experiment from [100]. Reprinted with permission from [100], ©(1965) by the American Physical Society

4.2 The ISR measurement and the rise of the total cross section

At ISR, in order to measure physical cross sections, completely different methods had to be employed. At least three such methods were used, two of them depending on the so-called luminosity of the accelerator, one independent. Luminosity is the key parameter for cross section measurements at intersecting storage rings and is defined as the proportionality factor between the number of interactions taking place at each beam crossing, R, and the particle cross section $\sigma$ to be measured, i.e. $R=L \sigma$. The concept of luminosity had been introduced in the mid-1950s, when storage rings had started being discussed in the community. The name itself is probably due to Bruno Touschek, who used it when proposing the construction of the first electron–positron colliding beam accelerator, AdA, in 1960 [106] and the process $\mathrm{e}^+\mathrm{e}^-\rightarrow \gamma \gamma$ was suggested as the monitor process for other final states.

At the CERN Intersecting Storage Rings (ISR), $\sigma _{\mathrm{total}}$ and/or $\sigma _{\mathrm{elastic}}$ were measured by a number of different experiments, with different methods, in different t-regions. A list of all these experiments up to the end of 1978, can be found in the extensive review of physics at the ISR by Giacomelli and Jacob [102]. We reproduce information as regards some of them in Table 1. While early measurements of the elastic scattering at $\sqrt{s}=30$ and $45~\hbox {GeV}$ were not conclusive, a combination of various methods allowed one to definitely establish the rise of the $\sigma _{\mathrm{total}}$, as clearly shown in Fig. 22 from [23], where the rise appears beyond doubt.

Table 1 Experiments measuring the total and the elastic cross section at ISR as of 1977. For complete references see [102], where C and R refer to Completed and Running experiments, respectively

Fig. 22

From Amaldi et al. measurement [23], one can clearly see the rise of the total cross section. Reprinted from [23], ©(1973) with permission from Elsevier

Unlike fixed target experiments which used the transmission method to measure the total cross section, storage ring experiments such as those performed at the ISR, needed either a measurement of the total rate, and hence an accurate estimate of the luminosity, or a measurement of the differential elastic cross section and its extrapolation to the optical point, namely $t=0$. Such measurements are described in [108] where first results from the operation of the ISR at beam momenta of $11.8~\hbox {GeV}$ and $15.4~\hbox {GeV}$ are reported along with values for $\sigma _{\mathrm{total}},\rho$ and $\sigma _{\mathrm{elastic}}$. These are shown here in Table 2.

Table 2 Results of early measurements at ISR from [108]

4.2.1 ISR measurements for the total cross section and the elastic scattering amplitude

A luminosity dependent measurement of the total cross section which uses the optical point method, relies on the luminosity and on extrapolation of the elastic rate down to $t=0$. Through the optical theorem, one sees that the total (nuclear) cross section depends only on $\mathfrak {I}m A(s, 0)$ and the elastic differential cross section in the forward direction can be written as

$$\begin{aligned} \left( \frac{\mathrm{d}\sigma _{\mathrm{el}}}{\mathrm{d}t}\right) (t = 0) = \left( \frac{\sigma _{\mathrm{tot}}^2}{16\pi }\right) [1 + \rho ^2], \end{aligned}$$

(4.2)

with only a quadratic dependence on the ratio of the real to the imaginary part of the forward (complex) nuclear scattering amplitude A(s, 0),

$$\begin{aligned} \rho (s) = \frac{\mathfrak {R}e A(s, 0)}{\mathfrak {I}m A(s, 0)}. \end{aligned}$$

(4.3)

However, a method relying only on Eq. (4.2) does not allow a precise determination of the nuclear amplitude, since at high energies, from ISR onwards, the $\rho$-parameter is rather small (${\sim } 0.1$). It is then difficult to measure $\rho$ accurately and in any event such a measurement would not determine the sign of the real part of the nuclear amplitude.

Fortunately, when we augment the nuclear with the Coulomb amplitude (due to one-photon exchange, in the lowest order), the interference between the Coulomb and the real part of the nuclear amplitude (for small t) allows us to determine both the sign and the value of $\rho$.

At ISR, experiments using this method fitted the observed elastic scattering rate to the expression

$$\begin{aligned} R(t)\propto \frac{\mathrm{d}\sigma }{\mathrm{d}t}=\pi |f_c+f_N|^2 \end{aligned}$$

(4.4)

where $f_c$ is the Coulomb scattering amplitude and $f_N$ the nuclear scattering amplitude. The two amplitudes are both complex, with a relative phase to be determined theoretically. The expression for the Coulomb amplitude is then written as

$$\begin{aligned} f_C=-2\alpha \frac{G^2(t)}{|t|}\mathrm{e}^{i\alpha \phi } \end{aligned}$$

(4.5)

where the minus sign holds for proton–proton scattering, with opposite sign for ${\bar{p}}p$ scattering, $\alpha$ is of course the fine structure constant and G(t) is the proton electromagnetic form factor. This expression corresponds to “spinless” scattering, a good approximation at high energies. A more complete discussion inclusive of magnetic terms can be found in [50], part of which was presented in Sect. 2. Here we follow the abbreviated discussion in [108]. The expression used for the proton electromagnetic form factor was the usual dipole expression

$$\begin{aligned} G(t)=\left[ \frac{1}{1 - t/\varLambda ^2}\right] ^2, \end{aligned}$$

(4.6)

with $\varLambda ^2\approx \ 0.71~\hbox {GeV}^2$. To complete the parametrisation of the Coulomb amplitude, one needs to specify the phase, which was taken to be

$$\begin{aligned}&\alpha \phi =\alpha [\ln (t_0/|t|) -C] \nonumber \\&t_0=0.08~\hbox {GeV}^2,\quad C=\hbox {Euler's constant}=0.577. \end{aligned}$$

(4.7)

For the nuclear, or hadronic amplitude, use was made of the optical theorem, namely

$$\begin{aligned} f_N=\frac{\sigma _{\mathrm{total}}}{4\pi }(\rho +i)\mathrm{e}^{Bt/2} \end{aligned}$$

(4.8)

and of a parametrisation of the very small t behaviour described by a falling exponential, with B the so-called slope parameter, in fact a function of s. One immediately sees that the rate of elastic events involves all the quantities we are interested in, namely

$$\begin{aligned} R(t)= & {} K \left[ \left( \frac{2\alpha }{t}\right) ^2 G^4(t)- ( \rho +\alpha \phi ) \frac{\alpha }{\pi } \sigma _{\mathrm{total}}\frac{G^2(t)}{|t|} \mathrm{e}^{Bt/2}\right. \nonumber \\&\left. +\left( \frac{\sigma _{\mathrm{total}}}{4\pi }\right) ^2(1+\rho ^2)\mathrm{e}^{Bt}\right] , \end{aligned}$$

(4.9)

where K is a proportionality constant and the sign in front of $\alpha$ holds to $pp$ scattering and is reversed for ${\bar{p}}p$.

Recently, there has been a study of the amplitudes for pp and $p\bar{p}$ elastic scattering in the Coulomb-Nuclear Interference region based on derivative dispersion relations [117]. Work on this subject was done early on by Bourrely et al. [118] and more recently also in collaboration with Khuri [119]. An interested reader may consult these references.

4.2.2 The four methods used at ISR

Here we present a short discussion of the four methods used at ISR to measure the total cross section.

The Pisa–Stony Brook method (R801) to measure the total cross section at ISR was based on measuring the luminosity $\mathcal{L}$ and the inclusive interaction rate $R_{\mathrm{el}}+ R_{\mathrm{inel}}$, through the definition

$$\begin{aligned} R(\hbox {number of events}/\hbox {second})=\mathcal{L} (\hbox {cm}^{-2}~\hbox {sec}^{-1}) \sigma _{\mathrm{total}}(\hbox {cm}^2).\!\!\!\!\nonumber \\ \end{aligned}$$

(4.10)

This method had the advantage of making a totally model independent measurement.

Two different approaches were adopted by the CERN-Rome group. They measured the differential elastic cross section at small angles, but not in the Coulomb region, and then extrapolated it to the optical limit, i.e. $t=0$. The measurement was based on the parametrisation of the hadronic part of the cross section given by Eq. (4.2), which assumed a constant (in t) exponential t-dependence of the scattering amplitude, and a parameter $\rho$ constant in the range of t of interest. Elastic events at smaller and smaller scattering angles were measured through the so-called Roman pots, which were detectors inserted in containers called the Roman pots and which could penetrate the beam pipe and get very close to the beam.

Fig. 23

The measurement of the total cross section by the R801, Pisa–Stony Brook, experiment. This figure is courtesy of G. Bellettini, also published in [113]. Reprinted from [113] ©(1973) with permission from Elsevier

The CERN-Rome group also applied a third complementary method, the one described in the previous subsection, which measured the rate in the region where the Coulomb and nuclear amplitudes interfere. At ISR this happens in a region $0.001<|t|<0.01~\hbox {GeV}^2$. From Eq. (4.9) one can fit $\mathrm{d}\sigma /\mathrm{d}t$ in terms of $\sigma _{\mathrm{total}}, \rho , \mathcal{L}$ and the slope parameter B.

A fourth method was adopted by a combined Pisa–Stony Brook (PBS) and CERN-Rome Collaboration. By combining the measurement of the total interaction rate $R_{\mathrm{tot}}$, i.e. the PBS approach, Eq. (4.10), with the Cern-Rome method, Eq. (4.2), based on the optical theorem, one obtains a luminosity independent measurement, i.e.

$$\begin{aligned} \sigma _{\mathrm{total}}=\frac{16\pi (\mathrm{d}N/\mathrm{d}t)_{t=0}}{N_{\mathrm{tot}}(1+\rho ^2)} \end{aligned}$$

(4.11)

where $(dN/\mathrm{d}t)_{t=0}$ is the elastic rate measured at $t=0$ and $N_{\mathrm{tot}}$ is the total rate. This was a combined Pisa–Stony Brook and CERN-Rome measurement.

For a description of the luminosity measurements at ISR, we refer the reader to [102].

These measurements indicated a rising total cross section. The result was surprising, given the then accepted constant cross section emerging from the simple Pomeron pole model with an intercept $\alpha _P(0)\ =\ 1$. The measurement was repeated several times against possible systematic errors. We show in Fig. 23 from [113], the published results for the total cross section as a function of s, the squared center of mass energy. The Pisa–Stony Brook experiment also produced a beautiful pictorial description of single diffraction [120], but because of the difficulty in separating the non-diffractive background, these results were not published.

Fig. 24

Proton–proton differential elastic scattering cross section $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$ in the very small |t| region, at ISR operating energy $\sqrt{s}=52.8~\hbox {GeV}$ from [121]. Shown are the Coulomb region, the interference and the beginning of the nuclear region. Reprinted from [121] ©(1985) with permission by Elsevier

4.2.3 A final analysis of ISR results

A final analysis from the group from Northwestern, comprehensive of both $pp$ and ${\bar{p}}p$ scattering in the full range of ISR energies is given in [121]. This analysis was published after the CERN $S{\bar{p}}pS$ had already been operational for a couple of years and the rise of the total cross section had been confirmed. We shall now summarise this paper.

In the following we use the notation of [121], where the slope parameter B is indicated by b. The method used for measuring $\sigma _{\mathrm{total}}$, $\rho$ and b, is luminosity dependent and is based on measuring the differential elastic rate and then making a simultaneous fit of the elastic differential cross section in and around the Coulomb region, typically $0.5 \times 10^{-3}<|t|<50\times 10^{-3}~\hbox {GeV}^2$. For $\alpha \phi \ll 1$, from the Rutherford scattering formula and the optical theorem, the usual expression is used to parametrise elastic scattering in this region, i.e.

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}|t|}= & {} 4 \pi \alpha ^2 G^4(t)/|t|^2 \mp \sigma _{\mathrm{total}}\alpha (\rho \pm \alpha \phi )G^2(t)\mathrm{e}^{-b|t|/2}/|t| \nonumber \\&+\,(1+\rho ^2)\sigma _{\mathrm{total}}^2 \mathrm{e}^{-b|t|}/16\pi . \end{aligned}$$

(4.12)

For this method, a precise determination of the luminosity is crucial. Notice the known expression for Coulomb scattering allows a calibration of the |t| scale. We show in Fig. 24, one of the many plots presented by this collaboration, for $pp$, at $\sqrt{s}=52.8~\hbox {GeV}$. This figure clearly shows the transition between the Coulomb region $-t \lesssim 0.005~\hbox {GeV}^2$ and the nuclear region, $-t > 0.01~\hbox {GeV}^2$ through the interference region. Similar distributions are presented in the paper for the full range of ISR energies, $\sqrt{s}=23.5$–$62.3~\hbox {GeV}$ for $pp$ and $\sqrt{s}=30.4$–$62.3~\hbox {GeV}$ for ${\bar{p}}p$. The measured differential cross sections as a function of |t| are presented and a simultaneous fit of Eq. (4.12) allows one to extract the values we reproduce in Table 3.

Table 3 Resulting values for $\sigma _{\mathrm{total}}$, $\rho$ and b at ISR from [122]

4.2.4 Measurements of $\rho$ and the slope parameter

The CERN-Rome experiment had measured the ratio of the real to the imaginary part of the forward elastic scattering amplitude. The trend with energy of the $\rho$ parameter was confirmed by other experiments as well and found in good agreement with a dispersion relation calculation by Amaldi. These results are shown in Fig. 25 from [122].

Fig. 25

The ratio $\rho$ from $\sqrt{s}=5~\hbox {GeV}$ up to the highest ISR energy, from a compilation in [122]. Reprinted from [122] ©(1983) with permission by Elsevier

We mention here the question of the |t| dependence of the slope at ISR. In [111], the distributions of the differential rates for $pp$ elastic scattering are presented nominally for 4 different ISR energies, $\sqrt{s}=21.5$, 30.8, 44.9 and $53~\hbox {GeV}$.³ All three sets of data points exhibit a break for $|t|\sim 0.1~\hbox {GeV}^2$. For all the energies under consideration, the measurement of the slope in the smaller |t| interval, was found to be larger than the one at larger |t|. At 53 GeV, the two slopes would be $b(0.050<|t|<0.112~\hbox {GeV}^2)=12.40~\hbox {GeV}^{-2}$ and $b(0.168<|t|<0.308~\hbox {GeV}^2)=10.80~\hbox {GeV}^{-2}$. The steepening of the slope at small |t| values increases the forward scattering cross section above the value extrapolated from larger |t| by about 20%.

We now turn to a 1982 paper by a group CERN–Naples together with some members of the Pisa–Stony Brook Collaboration [123]. Measurements were done for ${\bar{p}}p$ and for $pp$ at the ISR energy $\sqrt{s}=52.8~\hbox {GeV}$ for the quantities $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$, $\sigma _{\mathrm{elastic}}$ and, using the optical theorem $\sigma _{\mathrm{total}}$. The measurement of the elastic cross section was obtained by measuring the elastic rate while simultaneously measuring the luminosity of the colliding beams. The differential cross section – in the small-|t| region – was then parametrised as usual, i.e.

$$\begin{aligned} \mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t=A\exp (bt). \end{aligned}$$

(4.13)

A fit to the data yielded $\sigma _{\mathrm{elastic}}$ and b. Elastic scattering was studied in the t range $0.01{-}1.0~\hbox {GeV}^2$ using different parts of the detector. The fitting took account of the Coulomb corrections, through Eq. (4.12).

In Table 1 of this paper, the results for $0.01<|t|<0.05~\hbox {GeV}^2$ are displayed and the following final values for the slope are given

$$\begin{aligned} b(p\bar{p})= & {} 13.92\pm 0.37\pm 0.22\nonumber \\&b(pp)=13.09\pm 0.37\pm 0.21 \end{aligned}$$

(4.14)

where errors quoted are statistical only, and include error on luminosity and uncertainty on determination of the |t| interval (see [123] for details). When reporting the results for the slope at larger |t| intervals, i.e. $0.09{-}1.0~\hbox {GeV}^2$ for $pp$ and ${\bar{p}}p$, the slope was found to be smaller, $10.34\pm 0.19\pm 0.06~\hbox {GeV}^{-2}$ and $10.68\pm 0.20 \pm 0.06~\hbox {GeV}^{-2}$, respectively, in agreement with [111]. Results for the slope in the smaller interval were in agreement not only with [111] but also with [124] whose measurement covers the interval $|t|=1.0\times 10^{-3}$ to $31 \times 10^{-3}~\hbox {GeV}^2$. The larger |t| interval is not discussed in [124]. Results for the slope in the larger |t| interval are summarised in Table 4.

Table 4 Values of the slope parameter at $\sqrt{s}=52.8~\hbox {GeV}$ in different t intervals, as shown

Notice that this experiment also gives explicit values for $\sigma _{\mathrm{total}}$, the ratio $\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}$, and the ratio $\sigma _{\mathrm{total}}/b$, all of which will be discussed in the context of models.

We now look at Amaldi’s later work in [125, 126]. Reference [125] contains a complete review of all the data collected at ISR for the usual slope, total, elastic cross section and real part of the amplitude in the forward direction, while [126] discusses in detail the optical picture and its connection to the Pomeron exchange description.

Before going to illustrate accelerator measurements at higher energies, we note a recent review of ISR results by Amaldi [127], where the history of the discovery of the rise of the total cross section at the ISR is described.

4.3 Measurements at the $Sp\bar{p}S$

In the early 1980s, an hitherto unimagined energy value in the CM was reached at the CERN $Sp\bar{p}S$, i.e., $\sqrt{s}=540~\hbox {GeV}$. At the $Sp\bar{p}S$, the luminosity [128] due to $N_p$ protons and $N_{\bar{p}}$ antiprotons crossing at zero angle with effective area A is $\mathcal{L}=fN_p N_{\bar{p}}/A$ where f is the frequency of revolution of the bunches. The effective area is given by $A=wh$ where the effective width (w) and height (h) of the crossing bunches are

$$\begin{aligned} w=\int \mathrm{d}x N_p (x)N_{\bar{p}}(x)\quad h=\int \mathrm{d}y N_p(y) N_{\bar{p}}(y) \end{aligned}$$

(4.15)

where $N_p(x)$ is the normalised proton density profile along the transverse horizontal axis at the crossing point. At the time of the UA1 early measurement a systematic error of 8% on the integrated luminosity measurement was reported due to various uncertainties in the factors entering the luminosity formula.

At $S{\bar{p}}pS$ the total cross section was measured by experiments UA1 and UA4, later on followed by a combined collaboration UA2/UA4 and by a ramping run measurement by UA5.

4.3.1 Early total cross section measurements: UA1 and UA4

UA1 experiment made a measurement of the elastic scattering cross section [128], with forward detectors covering angles down to $5~\hbox {mrad}$, measuring the elastic differential cross section for $0.04<-t<0.45~\hbox {GeV}^2$. The data collected by UA1 were fitted by the usual exponential form $\mathrm{d}N_{\mathrm{el}}/\mathrm{d}t\propto \mathrm{e}^{Bt}$. A measurement of the integrated luminosity allowed the extraction of values $B=13.7\pm 0.2 \pm 0.2~\hbox {GeV}^{-2}$ for $|t|=0.21$–$0.45~\hbox {GeV}^2$ and $B= 17.1 \pm 0.1~\hbox {GeV}^2$ for $|t|=0.04$–$0.18~\hbox {GeV}^2$. The values $\sigma _{\mathrm{tot}}=67.6\pm 5.9 \pm 2.7~\hbox {mb}$ and $\sigma _{\mathrm{el}}/\sigma _{\mathrm{total}}=0.209\pm 0.18\pm 0.08$ were thus obtained. The UA4 experiment had also made an earlier measurement of $\sigma _{\mathrm{total}}$ [129] and we show both measurements in Fig. 26 from [128]. The two curves shown in this figure correspond to two different fits by Block and Cahn [130], where a simultaneous analysis of $\sigma _{\mathrm{total}}$ and $\rho$, from $s=25~\hbox {GeV}^2$ to the ISR data is performed. The two fits follow from the expression for the even amplitude at $t=0$ [131], i.e.

$$\begin{aligned} \mathcal{M}_+=-is\left[ A+\frac{B(\ln {s/s_0}-i\pi /2)^2}{1+a(\ln {s/s0} -i\pi /2)^2}\right] +C. \end{aligned}$$

(4.16)

Let the parameter a take a small value. Then at intermediate-to-high energies such as that at the $Sp\bar{p}S$, one obtains a linear (fit2, lower, dashes) $\ln {s}$ dependence, while obtaining a constant behaviour for the total cross section at really high energies. The other curve (fit 1, upper, full) follows from an expression for the amplitude which saturates the Froissart bound, namely is quadratic in $\ln {s}$ [130]. Fit 2, with a very small value for the parameter a, i.e. $a=0.005\pm 0.0031$, gives a slightly better fit, as the authors themselves point out. The problem with this fit is that, at extremely high energies, the total cross section would go to a constant, a behaviour still not yet observed even at very high cosmic ray energies.

Fig. 26

This figure from [128] shows the total cross section as measured by UA1 at the CERN $S{\bar{p}}pS$  compared with the UA4 early measurement [129]. The two curves correspond to different fits by Block and Cahn. For details see [128], from which this figure is extracted. Reprinted from [128] ©(1983) with permission by Elsevier

In [132], the behaviour of the slope parameter B was fitted with the asymptotic form $\ln ^2s$, that is with the same curvature as the total cross section. Such form follows from the standard parametrisation of the forward scattering amplitude as in Eq. (4.8). The rationale behind this choice of behavior is that if $B \sim (\ln s)$ and $\sigma _{\mathrm{tot}} \sim (\ln s)^2$, asymptotically there is a problem with unitarity, i.e., $\sigma _{\mathrm{el}} > \sigma _{\mathrm{tot}}$. But, if $\sigma _{\mathrm{total}}$ saturates the Froissart bound, i.e., $\sigma _{\mathrm{total}}\sim \ln ^2{s}$, and we require that the slope parameter B rises as $\sigma _{\mathrm{total}}$, then there is a problem with the simple Regge–Pomeron picture, because we would expect

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}\propto \left( \frac{s}{s_0}\right) ^{2[\alpha _{\mathrm{Pom}} (t)-1]}=\mathrm{e}^{-2\alpha ' \ln (s)|t|} \end{aligned}$$

(4.17)

namely the slope parameter to be proportional to $\ln s$. [This argument holds even with three Pomeron trajectories, intersecting at 1, and conspiring to produce a total cross section to increase as $(\ln s)^2$]. Where, in such picture, a $\ln ^2{s}$ for the slope parameter B would come from is not clear. On the other hand, using the Block and Cahn simple analytic expression, only a constant or a $\ln ^2{s}$ behaviour results.

This debate is still of interest, as we discuss in the following sections of this review.

4.3.2 UA4 and UA2

UA4 was the experiment dedicated to the measurement of the total and elastic cross section, and of the parameter $\rho$. UA4 measured the total cross section with the luminosity independent method by comparing the forward differential cross section with the total elastic and inelastic rate [129, 133]. In [129] the value $\sigma _{\mathrm{total}}=66~\hbox {mb}$ with a 10% statistical error was reported. Subsequently, using the same method and through a comparison with a luminosity dependent measurement, the final value of $\sigma _{\mathrm{total}}=61.9 \pm 1.5~\hbox {mb}$ was given [133]. The difference with previous measurements was attributed to a 1.1% overestimate of the beam momentum above the nominal energy $E=270~\hbox {GeV}$ and thus to an overestimate of 2.2% on the total cross section. The inelastic rate at intermediate angles was measured by a set of dedicated telescopes, while the total inelastic rate in the central pseudorapidity region was measured by the UA2 detector. UA4 was able to measure very small scattering angles, as small as ${\sim } 1~\hbox {mrad}$, down to values $0.002<|t|<1.5~\hbox {GeV}^2$. This was accomplished through the use of the Roman Pot technique, already employed at the ISR. The result confirmed the shrinking of the diffraction peak, with a value of the slope, B, defined, as customary, from the parametrisation $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t=\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t(t=0)\exp (Bt)$. We show in Fig. 27 a plot of the total cross section from [133], where the UA4 result is compared with earlier measurements at ISR and fixed target machines.

Fig. 27

The result of the UA4 experiment for the measurement of the total cross sectionat the CERN $Sp\bar{p}S$ from [133]. Reprinted from [133] ©(1984) with permission by Elsevier

The ratio $\rho$ was also measured and found to be surprisingly large, namely $\rho =0.24 \pm 0.4$. As the authors themselves note in a subsequent paper [134], this measurement was affected by poor beam optics and limited statistics. It was then repeated by a combined UA4/UA2 collaboration under very clean conditions with higher precision and better control of systematic errors, and found to be

$$\begin{aligned} \rho =0.135\pm 0.15, \end{aligned}$$

(4.18)

which supersedes previous measurements and was in agreement with the original theoretical expectations.

Fig. 28

The total cross section for $pp$ and ${\bar{p}}p$ from [135], including the measurement by the UA5 Collaboration, compared with models and data, as explained in the text. Reprinted from [135], ©(1986) by Springer

4.3.3 The ramping run and UA5 measurement

The UA5 experiment measured the total $p\bar{p}$ cross section at $\sqrt{s}=200$ and $900~\hbox {GeV}$ [135]. Data were normalised at ${900}~\hbox {GeV}$ from an extrapolation by Amos el al. [121] and the result, $\sigma _{\mathrm{total}}^{900}=65.3\,{\pm }\, 0.7\,{\pm }\,1.5 ~\hbox {mb}$, was found to be consistent with previous measurements. We show in Fig. 28 the result of UA5 measurement compared with the UA4 measurement [133], with the extrapolation from [121], the expectations from Donnachie and Landshoff Regge–Pomeron exchange model [136], as well as a description by Martin and Bourrely [131, 137], with explicit analytic and crossing symmetric form of the even signature amplitude at $t=0$ as in Eq. (4.16).

4.4 Reaching the TeV region

Starting from 1985, an even higher center of mass energy for proton–antiproton scattering was reached in FermiLab near Chicago through the TeVatron accelerator. At the Tevatron, the total cross section was measured by three experiments: E710 [138, 139], Collider Detector Facility (CDF) [140] and E811 [141].

4.4.1 Measurements at the TeVatron

Experiment E710 at the Tevatron was the first to measure the total interaction rate and the forward elastic cross section [142]. In the detector for elastic events, two Roman pots were placed one above and one below the beam, with drift chambers and trigger scintillators. The inelastic rate was measured at large and intermediate angles through ring shaped scintillators and tracking drift chambers, respectively. The first measurement by E710 was based on the optical theorem, i.e.

$$\begin{aligned} \frac{\mathrm{d}N_{\mathrm{elastic}}}{\mathrm{d}t}\Bigg |_{t=0}=L \frac{\mathrm{d}\sigma }{\mathrm{d}t}\Bigg |_{t=0}=L \frac{\sigma _{\mathrm{total}}^2}{16 \pi }(1+\rho ^2) \end{aligned}$$

(4.19)

and extrapolation to zero of the usual exponential behavior of the elastic rate measured in the interval $0.025<|t|<0.08~\hbox {GeV}^2$, i.e.

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}=\frac{\mathrm{d}\sigma }{\mathrm{d}t}\Bigg |_{t=0} \mathrm{e}^{Bt}. \end{aligned}$$

(4.20)

Coulomb effects were included in the analysis, although small in the range used for the extrapolation. A second measurement [139] used the luminosity independent method, described in the previous subsection, and the total cross section was obtained from

$$\begin{aligned} \sigma _{\mathrm{total}}=\frac{16 \pi }{1+\rho ^2}\frac{1}{N_{\mathrm{elastic}}+N_{\mathrm{inelastic}}} \frac{\mathrm{d}N_{\mathrm{elastic}}}{\mathrm{d}t}|_{t=0}. \end{aligned}$$

(4.21)

CDF at the FermiLab Tevatron Collider repeated the $\sigma _{\mathrm{total}}$ measurement at $\sqrt{s}=546~\hbox {GeV}$ and extended it to $\sqrt{s}=1.8~\hbox {TeV}$ using the luminosity independent method [140]. The measurement of the primary particle scattered in the forward direction was possible only on the antiproton side. CDF used the Roman Pot detector technique. Inside the pots, two scintillation counters were used for triggering, with a drift chamber backed by silicon detectors measuring the particle trajectory at 5 points. In Fig. 29 we show the layout of the detector assembly, which also shows the bellows technique employed to move the silicon detectors in and out of the beam. Elastic events were distinguished by left-right collinearity, while silicon detectors behind the chambers allowed one to reach off-line higher angular resolution.

Fig. 29

Schematic view of the CDF Roman Pots operation at the FNAL Tevatron from [143]. Reprinted with permission from [143], ©(1993) by the American Physical Society

Fig. 30

Comparison with lower energy data of results for the total cross section from the two experiments which first measured the total cross section at the Tevatron, E710 and CDF, from [140]. Reprinted with permission from [140] ©(1993) by the American Physical Society

The total cross section was obtained from a measurement of the forward elastic and inelastic interaction rate. The rate of inelastic events for scattering at intermediate angles was measured through two telescopes. On the antiproton side, quasi-elastic antiprotons were detected allowing the measurement of single diffraction with the result

$$\begin{aligned} \sigma _{\mathrm{SD}}(x>0.85)=7.89\pm 0.33~\hbox {mb} \end{aligned}$$

(4.22)

to be compared with the previous UA4 result of $\sigma _{\mathrm{SD}}(x>0.85)=10.4\pm 0.8~\hbox {mb}$, indicating the difficulty in controlling systematic errors in diffractive event measurements. The measurement of the small-angle elastic cross section was reported in [143].

The result for the total cross section measured by CDF differs by more than 3 standard deviations from the E710 result, as one can see in Fig. 30. This figure shows a comparison between these two results from [140]. CDF also measured the total cross section at $\sqrt{s}=546~\hbox {GeV}$ and the result with $\sigma _{\mathrm{total}}=61.26 \pm 0.93$, obtained assuming $\rho =0.15$, was consistent with the UA4 result, assuming the same value for $\rho$.

Because of the discrepancy by more than 3 standard deviations between the CDF and the E710 measurements, E811 analyzed the very small-angle data, $0.0045<|t|<0.036~\hbox {GeV}^2$, using the luminosity independent method in order to measure $\sigma _{\mathrm{total}}$ [141] and the $\rho$-parameter [144] and obtained a result consistent with the one from E710. We show a compilation of all the TeVatron results for $\sigma _{\mathrm{total}}$ in Fig. 31.

Fig. 31

Results for the total cross section at the TeVatron, in a compilation by E811, from [141]. Reprinted from [141] ©(1998) with permission by Elsevier

The final numbers for $\sigma _{\mathrm{tot}}(p\bar{p})$ measured at the Tevatron by the three different experiments, CDF, E710 and E811 are a follows:

$$\begin{aligned}&\sigma _{\mathrm{total}}^{\mathrm{CDF}}=80.03\pm 2.24~\hbox {mb}, \\&\sigma _{\mathrm{total}}^{\mathrm{E}710}=72.8\pm 1.63~\hbox {mb}, \\&\sigma _{\mathrm{total}}^{\mathrm{E}811}=71.42\pm 2.41~\hbox {mb}. \end{aligned}$$

Notice that at $\sqrt{s}=1.8 ~\hbox {TeV}$, the CDF result

$$\begin{aligned} \frac{\sigma _{\mathrm{elastic}}}{\sigma _{\mathrm{total}}}=0.246\pm 0.004 \end{aligned}$$

(4.23)

agrees with the E710 value $0.23 \pm 0.012$ [140].

4.4.2 A comment on the black disk model

Fits to the total cross section from measurements prior to ISR and up to the latest Tevatron data accomodate a $\ln ^2{s}$ rise. It should however be mentioned that in models such as in Refs. [11, 93] for instance, the rise can be $(\ln {s})^{1/p}$ where $1/2<1/p<1$.

The $\ln ^2{s}$ behaviour would reflect a geometrical picture such as that arising from of a black disk with all partial waves to be zero beyond a maximum impact-parameter value $b<R$, i.e. angular momentum values $bk=l<L_{\max }=kR$. As discussed in more detail in Sect. 6, the black disk picture gives

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}\sim \pi R^2 \frac{J_1^2(Rq)}{|t|} \end{aligned}$$

(4.24)

with $\sqrt{-t}\ =\ q\ =\ k\theta$ and $J_1$ the Bessel function of order 1. At small values of Rq, $J_1$ can be approximated by an exponential with slope defined by the interaction radius and one can write

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}\approx \frac{\pi R^4}{4} \mathrm{e}^{R^2t/4}. \end{aligned}$$

(4.25)

Integrating the above equation, one obtains the elastic and the total cross sections in the black-disk limit, i.e.

$$\begin{aligned} \sigma _{\mathrm{elastic}}=\pi R^2,\quad \sigma _{\mathrm{total}}=2\pi R^2,\quad \frac{\sigma _{\mathrm{elastic}}}{\sigma _{\mathrm{total}}}=\frac{1}{2}. \end{aligned}$$

(4.26)

As we shall see in later sections, even considering latest LHC and cosmic ray results at $57~\hbox {TeV}$, such behaviour is not observed yet for the ratio of the two cross sections. Indeed what one has so far, before the LHC measurements described in the next sections, is shown in Table 5.

Table 5 Total and elastic cross section from ISR to the Tevatron

4.4.3 The $\rho$ parameter at the Tevatron

In previous subsections we have described the measurement of various quantities related to $\sigma _{\mathrm{total}}$, among them the $\rho$-parameter, the ratio of the real to the imaginary part of the forward scattering amplitude. The behaviour of the $\rho$ parameter with energy has been discussed in many papers. In most of the literature concerning models for the total cross section, $\rho$ is considered to be small and often taken to be $\approx 0$ so as to simplify many analytical calculation, as in most mini-jet models for instance. The sudden change of perspective arose in the 1980s, when the experiment UA4 at the CERN $Sp\bar{p}S$ reported a measurement well above previous theoretical estimates. These results, however, were soon superseded by a more precise measurement, in agreement with theoretical expectations. At the Tevatron, in the range $0.001\le |t|\le 0.14 \ (\hbox {GeV}/c)^2$, a three-parameter least square fit, gave [145],

$$\begin{aligned}&\rho =0.140\pm 0.069,\end{aligned}$$

(4.27)

$$\begin{aligned}&B=16.99\pm 0.047 \ (\hbox {GeV}/c)^2,\end{aligned}$$

(4.28)

$$\begin{aligned}&\sigma _{\mathrm{total}}=72.8\pm 3.1 ~\hbox {mb}. \end{aligned}$$

(4.29)

These values are consistent within the quoted errors with the earlier E710 values [138, 139, 142] and supersede them.

In Fig. 32, we show a compilation from [146]. The full line represents the result from the QCD-inspired model by Block and other collaborators, which will be discussed in the section dedicated to models.

Fig. 32

The $\rho$ parameter as a function of the CM energy and its comparison with the prediction from [146]. Reprinted with permission from [146], ©(1999) by the American Physical Society

4.5 Conclusions

The period of experimentation discussed above led to an enormous change in the view that physicists had held until then, due to the observed rise in the total cross section, changes in the value of $\rho$ and the beginning of tension in the dependence of the slope parameter with energy. These results would lead to radically different formalisms and models for higher energy experiments during the following three decades. This is a subject matter which we shall discuss at length in the coming sections of this review.

5 Theoretical scenarios and phenomenological applications

In this section an overview of the state-of-the-art of theoretical and phenomenological aspects of total cross sections is presented.

We show in Fig. 33 a compilation of total cross section data, from accelerators and cosmic ray experiments, with photon cross sections normalised at low energy together with proton data [147]. The dashed and full curves overimposed to the data are obtained from a mini-jet model with soft-gluon $k_t$ resummation [93, 94, 148], which we call BN model, and which will described later in Sect. 5.9.4.

Fig. 33

Total cross section data for pp and $p{\bar{p}}$ scattering together with normalised $\gamma p$ and $\gamma \gamma \$ data. Curves describe predictions from a mini-jet model with soft gluon resummation, and has been updated from the corresponding one in [147] courtesy of A. Grau, with MSTW08 curve courtesy of D. Fagundes

One is often asked what one can learn from total cross section measurements. Although the total cross section is proportional to the imaginary part of the elastic scattering amplitude in the forward region, and thus it can shed only a limited light on the dynamics of scattering, the interest in such a quantity – since more than 60 years – indicates that it can give information on fundamental questions of particle physics.

Indeed, the total cross section is the golden observable as far as QCD confinement dynamics is concerned: its behavior is dominated by the large distance behavior of the interaction, and thus by QCD confinement dynamics. This dominance of large distance behavior implies very low-momentum exchanges, characterized, at high energy, by gluons with $k_t\rightarrow 0$. These very soft quanta need to be resummed, not unlike what happens in QED, and the problem of the high energy behavior of total cross sections appears related to the one of radiative corrections to parton–parton scattering. Resummation for such effects, and hence integration over the infrared region, being mandatory, a knowledge or a model for the behavior of emitted gluons in this domain is needed for any parameter free description. In our opinion, models which do not access the infrared region, for instance introducing an infrared cut-off, may provide good phenomenological descriptions and some understanding of the dynamics, but so far fail to shed light on the essential problem.

The still unsolved problem of confinement is presently the reason why there is no model allowing to calculate the total cross section from first principles from low energies to high energies. In the context of the total cross section, we shall define as low energy the region after the resonances have died out, $\sqrt{s}\approx (5\div 10)$ GeV for protons, and as high energy the region where $(10\div 20)$ GeV $\le \sqrt{s}\lesssim (10\div 20)$ TeV. We shall refer to higher energies, accessible through cosmic rays, as the very high energy region.

The above distinction between low and high energy is not purely phenomenological. As the c.m. energy rises, partons inside the scattering hadrons can undergo hard or semi-hard collisions. Such collisions, by definition, are describable with perturbative QCD (pQCD). In this regime, partons of momentum $p=xP_h$ are extracted from a hadron of momentum $P_h$ with a 1 / x spectrum and scatter into final state partons of transverse moment $p_t$, with a strength calculable through the asymptotic freedom expression for the strong coupling constant, given to lowest order as

$$\begin{aligned} \alpha _{AF}(Q^2)= \frac{1}{b_o \ln {Q^2/\varLambda ^2_{\mathrm{QCD}}} }; \end{aligned}$$

(5.1)

Eq. (5.1) is valid for $Q^2\gg \varLambda _{\mathrm{QCD}}^2$, basically for $Q^2\sim p_t^2 \gtrsim 1~{\hbox {GeV}}^2$. At the same time, as the c.m. energy rises, parton emission for given momentum p probes decreasing values of x, and, due to the 1 / x spectrum, leading to an increase of the cross section, as $x\ll 1$. Combining the spectrum behavior with Eq. (5.1), and calling high energy the region where pQCD starts taking over, we see that the transition to the perturbative region will occur when

$$\begin{aligned} 1/x\ge \sqrt{s}/2\,p_{t\min }\gg 1\quad \hbox {and}\quad p_{t\min }\simeq 1~\mathrm{GeV}. \end{aligned}$$

(5.2)

For $x\simeq (0.1\div 0.2)$ the turning point where pQCD starts playing a substantial role can be seen to occur when

$$\begin{aligned}&\sqrt{s} \gtrsim (2 / x)~\mathrm{GeV},\end{aligned}$$

(5.3)

$$\begin{aligned}&\sqrt{s}\sim (10\div 20)~\mathrm{GeV}. \end{aligned}$$

(5.4)

Indeed, data indicate that, after the resonances die out, the ${\bar{p}}p$ cross section keeps on decreasing until reaching a cm energy between 10 and 20 GeV. It is here that the cross section undergoes a relatively fast rise, easily described by a power law, which levels off as the energy keeps on increasing. In the case of $pp$, the initial decrease is very mild and the rise may start earlier. Notice that for pion cross sections, the onset of the high energy region may be considered to start earlier, as one can see from a compilation of $\pi \pi$ and $\pi p$ total cross sections, shown in Fig. 34 from [149]. In this figure, the overlaid curves correspond to the same model as in Fig. 33, discussed later.

Fig. 34

Proton and pion total cross sections, as indicated, from [149]. Reprinted from [149], ©(2010) with permission from Elsevier

As for the high energy behaviour of all total cross sections, there are two main features which need to be properly addressed in any description of data in the TeV region: (i) how to include the mechanism which drives the rise on the one side and (ii) what dynamics transforms the early, almost sudden, power law-like rise into the smoother observed behaviour, consistent with the Froissart bound, $\sigma _{\mathrm{total}}\lesssim \log ^2s$. A cartoon description of this transformation appears in Fig. 35. There is a general understanding that the rise is produced by an increasing number of low-momentum parton–parton collisions, and a similar general understanding that an effect called “saturation”, brings about a balance and the Froissart-like behaviour. However, models differ in their detailed description. In our model, such a saturation is a consequence of the scheme we propose for infrared gluon $k_t$-resummation.

Fig. 35

The softening of the total cross section from early rise to logarithmic type behavior, consistent with the Froissart bound

The large number of models available can be divided in various groups as follows:

• geometrical models

• eikonal models

• Gauge boson trajectories: the photon and the gluon

• Reggeon field theory

• QCD mini-jets

• AdS/CFT approaches

• fits with Froissart bound asymptotic constraint.

We shall dedicate some space to each of these different approaches, with, however, particular attention to the QCD models and to efforts on resummation, resulting in what is phenomenologically described as the Pomeron Trajectory. To put this in perspective, we present an extended summary of the problem of infrared radiative corrections in QED, including the question of the photon trajectory, and then a brief overview of the Balitsky, Fadin, Kuraev and Lipatov (BFKL) approach to hadron scattering.

Not all readers are expected to be familiar with all the theoretical backgrounds, and it is clearly impossible to render justice to a field which has been active at least for 70 years, with new data appearing both from accelerator and cosmic ray experiments. The literature on the subject is very large and still increasing and the problem presents yet unsolved aspects. Because many books and reviews are available on specific models, our choice in this review has been to follow a historical path and highlight some of less treated aspects in models. The following aspects will be examined:

• Molière’s theory in Sect. 5.1,

• Heisenberg model in Sect. 5.2,

• on the Froissart bound in Sect. 5.3,

• the impact picture: Cheng and Wu (also with Walker) and Bourelly, Soffer and Wu in Sect. 5.4,

• Donnachie and Landshoff Regge–Pomeron description in Sect. 5.5,

• hadronic matter distribution in Sect. 5.6,

• role of resummation in QED in Sect. 5.7,

  • a digression on the Rutherford singularity in Sect. 5.7.1

  • Bloch Nordsieck theorem in Sect. 5.7.2,

  • Touschek and Thirring about covariant formalism of Bloch and Nordsieck theorem in Sect. 5.7.3,

  • Schwinger’s exponentiation in Sect. 5.7.4,

  • Double logarithms in QED: the Sudakov form factor in Sect. 5.7.5,

  • Early 60s and exponentiation in Sect. 5.7.6,

  • Semi-classical approach to resummation in QED in Sect. 5.7.7,

  • Reggeisation of the photon in Sect. 5.7.8,

• role of resummation in QCD in Sect. 5.8,

  • BFKL approach in Sect. 5.8.1,

  • The Odderon in Sect. 5.8.2,

  • Odderon in QCD in Sect. 5.8.3,

  • Gribov, Levin and Ryskin in Sect. 5.8.4,

  • BFKL inspired models in Sect. 5.8.5

• mini-jet models in Sect. 5.9,

  • Non-unitary models and the rise of $\sigma _{\mathrm{total}}$ in Sect. 5.9.1,

  • QCD-inspired eikonal models in Sect. 5.9.2,

  • Mini-jets and infrared $k_t$ resummation in Sect. 5.9.4 through Sect. 5.9.7,

• AdS/CFT models in Sect. 5.10,

• phenomenological fits in Sect. 5.11,

• the asymptotic behavior of total cross section models in theories with extra dimensions in Sect. 5.12

Further discussion of related items can be found in the coming Sect. 7, where one will also find a presentation of the non-linear Balitsky–Kovchegov (BK) equation.

5.1 Molière theory of multiple scattering

Most models for the total cross section are based on the optical theorem, and many of them use models for the differential elastic cross section. In this subsection we wish to recall the general features of one such model, Moliére’s theory of multiple scattering [32], developed for the scattering of electrons on atoms, summarised, and compared to other pre-existent models, by Bethe [33].

Moliére’s theory of multiple scattering is valid for small angle scattering, i.e. $\sin \theta \approx \theta$, and is based on the transport equation for $f(\theta ,t)$, with $f(\theta ,t)\mathrm{d}\theta$ the number of electrons scattered within an angle $\mathrm{d}\theta$ after passing through a slab of atoms of thickness t, and an ansatz for the probability of small-angle single scattering. The starting point is

$$\begin{aligned} \frac{\partial f(\theta ,t)}{\partial t}= & {} -Nf(\theta ,t) \int \sigma (\chi )\chi \mathrm{d}\chi \nonumber \\&+\,N\int f(\theta ',t)\sigma ({\chi }) \mathrm{d}{\mathbf {\chi }} \end{aligned}$$

(5.5)

where N is the number of scattering atoms per unit volume, $\sigma (\chi )\chi \mathrm{d}\chi$ is the electron–atom cross section into the angular interval $\mathrm{d}\chi$ after traversing a thickness t. In Eq. (5.5) the first term corresponds to electrons which were scattered away from the studied position, namely probability of being originally at angle $\theta$ times the number scattered away in any direction, while the second is the probability of electrons scattered into the observed position from any process, and ${\mathbf {\theta }}'= {\mathbf {\theta }} -{\mathbf {\chi }}$, $\mathrm{d}{\mathbf {\chi }}=\chi \mathrm{d}\chi \mathrm{d}\phi /2\pi$. Taking the Fourier transform of $f(\theta ,t)$

$$\begin{aligned} f(\theta ,t)=\int _0^\infty \eta \mathrm{d}\eta J_0(\eta \theta )g(\eta ,t) \end{aligned}$$

(5.6)

one can use Eq. (5.5) obtaining, in the notation of Moliére,

$$\begin{aligned} g(\eta ,t)=\mathrm{e}^{\varOmega (\eta ,t)-\varOmega _0(t)} \end{aligned}$$

(5.7)

where

$$\begin{aligned} \varOmega (\eta ,t)=N t \int _0^\infty \sigma (\chi )\chi \mathrm{d}\chi J_0(\eta \chi ) \end{aligned}$$

(5.8)

with $\varOmega _0(t)\equiv \varOmega (\eta =0,t)$ having the physical meaning of the total number of collisions. Notice that Eq. (5.7) uses the fact that $g(\eta ,0)=1$, which follows from the fact that the incident beam is exactly in the direction $\theta =0$, i.e. $f(\theta ,0)=\delta ({\mathbf {\theta }})$. One can then solve for $f(\theta ,t)$ obtaining

$$\begin{aligned} f(\theta ,t)= & {} \int _0^\infty \eta \mathrm{d}\eta J_0(\eta \theta ) \nonumber \\&\times \exp \left[ -Nt\int _0^\infty \sigma (\chi )\chi \mathrm{d}\chi \{1- J_0(\eta \chi )\} \right] .\nonumber \\ \end{aligned}$$

(5.9)

Bethe points out that this equation is exact provided the scattering angle is small. He then proceeds to describe the approximations used by Moliére to evaluate the integral and, in the remaining sections, to compare these results with others.

Moliére’s theory of multiple scattering analyzes and proposes models for the scattering probability and it is an early example of resummation of small-angle scattering.

5.2 The Heisenberg model

An early estimate of the total hadronic cross section was obtained by Heisenberg in 1952⁴ [150],

$$\begin{aligned} \sigma _{\mathrm{total}}\approx \frac{\pi }{m^2_\pi }\ln ^2\frac{\sqrt{s}}{\langle E_0\rangle } \end{aligned}$$

(5.10)

where $\langle E_0\rangle$ is the average energy per emitted pion. We will describe the argument behind Eq. (5.10) following the very clear presentation by Kang and Nastase [151], who then use it to derive similar results in AdS/CFT.

The description of scattering is the by now familiar picture of two hadrons colliding and interacting through their surrounding cloud of pions. Due to Lorentz contraction at high energy, we are dealing with two thin pancakes, and the scattering degrees of freedom are in the transverse plane, where the impact parameter b describes the scattering, as in Fig. 36 from [151]. In such a picture, the total cross section is written as

$$\begin{aligned} \sigma _{\mathrm{total}}= \pi b_{\max }^2 \end{aligned}$$

(5.11)

where $b_{\max }$ is the largest impact-parameter value which still allows pion emission, so that the expression at the r.h.s. of Eq. (5.11) can also be considered the maximum value which the total cross section can take, as the energy increases.

Fig. 36

Description of the scattering in impact-parameter space from [151], leading to Heisenberg total cross section formulation, and to the AdS/CFT derivation, as discussed later. ©2005 Elsevier. Open access under CC BY License

The challenge is then to find $b_{\max }$ and its energy dependence. Let $\mathcal{E}$ be the energy emitted in the scattering at impact parameter b, and $\langle E_0\rangle$ the average pion energy for scattering at a c.m energy $\sqrt{s}$. One can then write

$$\begin{aligned} \mathcal{E}=\alpha \ \sqrt{s} \ge n \langle E_0\rangle \end{aligned}$$

(5.12)

where n is the number of pions emitted with $\alpha$ a proportionality constant which reflects the overlap of the wave functions of the pions surrounding the colliding hadrons. As the transverse distance between the two hadrons increases, the pion wave function can be expected to decrease as an exponential, and, at the maximum distance for the scattering to still take place, one can write

$$\begin{aligned} \alpha =\mathrm{e}^{-b_{\max }m_\pi }, \end{aligned}$$

(5.13)

since $m_\pi$ is the size of the pion cloud. One then obtains Eq. (5.10). This equation, however, does not provide much information, unless one can determine how the average pion energy depends on the c.m. energy. To obtain this energy dependence, for instance whether the total cross section is a constant or increasing with the square of the logarithm of the c.m. energy or any other behavior, one needs a model to calculate $\langle E_0\rangle$. Notice that if $\langle E_0\rangle$ is proportional to $\sqrt{s}$, then the total cross section would go to a constant, whereas the rise with a logarithmic power is only ensured by a constant average pion energy. We shall now see, from [151], which was the procedure followed by Heisenberg.

One starts with calculating the differential energy radiated away during the collision for the case of a free massive scalar pion of energy $E_0$,

$$\begin{aligned} \frac{\mathrm{d}\mathcal{E}}{\mathrm{d}E_0}=A=\hbox {constant}, \end{aligned}$$

(5.14)

which is found to be a constant up to a maximum energy $E_{0,\max }=\gamma m_\pi$ with $\gamma \approx \sqrt{s}/ M_H$, $M_H$ being the hadron mass.

Apparently a similar argument was also pictured by Sommerfeld in his theory of the production of X-rays (according to Touschek [152]). If the collision takes place in a time interval much shorter than the one characterizing the emission, then the process can be described by a $\delta$-function in time, whose Fourier transform is a constant. This would lead to a constant spectrum for the energy emitted in the process, namely Eq. (5.14).

The number of emitted pions per unit energy radiated is then obtained:

$$\begin{aligned} \frac{\mathrm{d}n}{\mathrm{d}E_0}=\frac{A}{E_0}. \end{aligned}$$

(5.15)

Now, to get the energy $\mathcal{E}$ and the number n of emitted mesons, we integrate Eqs. (5.14) and (5.15) between $m_\pi$ (we need to emit at least one pion) and $E_{0,\max }$. With the maximum energy, which can be emitted, given by $E_{0,\max }\approx \sqrt{s}\ m_\pi /M_H$, one gets

$$\begin{aligned} \mathcal{E}=\int _{m_\pi }^{E_{0,\max }} \mathrm{d}\mathcal{E} \approx A (\sqrt{s}\ m_\pi /M_H -m_\pi ) \end{aligned}$$

(5.16)

and

$$\begin{aligned} n=\int \mathrm{d}n =A \int \frac{\mathrm{d}E_0}{E_0}=A \ln \frac{E_{0,\max }}{m_\pi }, \end{aligned}$$

(5.17)

which immediately gives the average energy $\langle E_0\rangle$ from

$$\begin{aligned} \langle E_0\rangle =\frac{\mathcal {E}}{n}= \frac{(\sqrt{s} \ m_\pi /M_H -m_\pi )}{\ln \frac{E_{0,\max }}{m_\pi } }. \end{aligned}$$

(5.18)

This indicates that the average energy $\langle E_0\rangle$ increases with the c.m. energy $\sqrt{s}$, apart from logarithmic terms. For such a case, then the total cross section would go to a constant. The above result follows, according to [151], from the equation of motion for a free pion. But the pion is not free at high energy and the equation of motion, $[\Box -m^2_\pi ]\phi =0$ is not valid. At this point Heisenberg took the Dirac–Born–Infeld-like action for the scalar pion

$$\begin{aligned} S=l^{-4} \int \mathrm{d}^4 x \sqrt{1+l^4[(\partial _\mu \phi )^2+m^2\phi ^2 ]} \end{aligned}$$

(5.19)

with a length scale l and obtained

$$\begin{aligned} \frac{\mathrm{d}\mathcal{E}}{\mathrm{d}E_0}=\frac{A}{E_0} \rightarrow \frac{\mathrm{d}n}{\mathrm{d}E_0} =\frac{A}{E_0^2}. \end{aligned}$$

(5.20)

Now, using Eq. (5.20), one repeats the above steps, namely

$$\begin{aligned} \mathcal{E}=\int _{m_\pi }^{\sqrt{s}\ m_\pi /M_H} \mathrm{d}\mathcal{E}=A \ln \frac{E_{0,\max }}{m_\pi } \end{aligned}$$

(5.21)

and

$$\begin{aligned} n= \int \mathrm{d}n = A \int \frac{\mathrm{d}E_0}{E_0^2} \approx \frac{A}{m_\pi } \left( 1- \frac{M_H}{\sqrt{s}}\right) . \end{aligned}$$

(5.22)

At this point, one can calculate the average energy

$$\begin{aligned} \langle E_0\rangle \equiv \frac{\mathcal {E}}{n}= m_\pi \frac{\ln \frac{E_{0,\max }}{m_\pi } }{[1-\frac{m_\pi }{E_{0,\max }}]}=m_\pi \frac{\ln \gamma }{1-1/\gamma }\approx m_\pi \ln \gamma \nonumber \\ \end{aligned}$$

(5.23)

with $\gamma \approx \sqrt{s}/M_H$. With this energy distribution for the pion field, the average energy $E_0\propto m_\pi$ grows only logarithmically. This then immediately leads to a maximal behavior consistent with the Froissart limit.

Kang and Nastase comment further on this result. They write that the minimum energy emitted could be mistakenly understood to be $m_\pi$, but it is instead the pion energy, which for a free pion would grow linearly with $\sqrt{s}$. On the other hand one needs an action with higher power of the derivatives, such as the Dirac–Born–Infeld action, to obtain a constant value for $\langle E_0\rangle$ proportional to the pion mass. In their subsequent treatment in terms of AdS/CFT, the model by Kang et al. is applied to the case of pure gauge theories and the authors will talk interchangeably of pions and lightest glueballs.

One can unify the two derivations from the previous part, by using

$$\begin{aligned} \frac{\mathrm{d}\mathcal{E}}{\mathrm{d}E_0}=A\left( \frac{\mu }{E_0}\right) ^{p} \end{aligned}$$

(5.24)

and hence

$$\begin{aligned} \frac{\mathrm{d}n}{\mathrm{d}E_0}=A\frac{1}{E_0}\left( \frac{\mu }{E_0}\right) ^{p}, \end{aligned}$$

(5.25)

which would give the two previous cases in the limit $p=0$, i.e. constant cross section and average pion energy increasing with c.m. energy, or $p=1$ with constant average pion energy and cross sections limited by $\ln ^2\sqrt{s}$. For dimensional reasons, we must introduce the pion mass already in Eq. (5.24).

Then both the above results can be written in a single expression, with $0<p<1$. We write for simplicity $m_\pi =\mu$ and then $E_{0,\max }\approx \gamma \mu$. Integrating Eqs. (5.24) and (5.25), we get

$$\begin{aligned} \mathcal{E}= & {} \frac{A\mu }{1-p} (\gamma ^{1-p}-1),\end{aligned}$$

(5.26)

$$\begin{aligned}&\xrightarrow [p \rightarrow 1] \ A\mu \ln \gamma ,\end{aligned}$$

(5.27)

$$\begin{aligned}&\xrightarrow [p\rightarrow 0] \ A\mu \gamma \end{aligned}$$

(5.28)

and

$$\begin{aligned} n=\frac{A}{p}\left[ 1-\left( \frac{1}{\gamma }\right) ^{p}\right]&\xrightarrow [p\rightarrow 1]\ A\left[ 1-\frac{1}{\gamma }\right] ,\end{aligned}$$

(5.29)

$$\begin{aligned}&\xrightarrow [p\rightarrow 0]\ A\gamma \ln {\gamma } \end{aligned}$$

(5.30)

so that

$$\begin{aligned} \langle E_0\rangle =\frac{\mu p}{1-p}\frac{\gamma ^{1-p}-1}{1-\gamma ^{-p}} \end{aligned}$$

(5.31)

and as a result we have the two limits

$$\begin{aligned} \langle E_0\rangle&\xrightarrow [p\rightarrow 1] \ \mu \frac{\ln \gamma }{1- \frac{1}{\gamma }},\end{aligned}$$

(5.32)

$$\begin{aligned}&\xrightarrow [p\rightarrow 0] \ \mu \frac{\gamma }{\ln \gamma } \end{aligned}$$

(5.33)

as it should be.

5.3 A general observation about the various ways to obtain the Froissart bound

Heisenberg’s argument is geometrical to begin with, but dynamics enters in defining the average pion energy. The geometrical argument is also the one used by Froissart [3], and in all the other derivations of the bound, including Martin’s [4] and Gribov’s [20], as seen in Sect. 2. These derivations are all obtained with

• optical theorem, $\sigma _{\mathrm{total}}\propto \mathfrak {I}mA(s,t=0)$

• partial wave expansion truncated at $L_{\max }$ so that

  $$\begin{aligned} \mathfrak {I}mA(s,t=0)\le \sum _0^{L_{\max }}(2l+1)=L^2_{\max }. \end{aligned}$$

  (5.34)

In other words the derivations are related to the partial waves falling off at high energy for a finite $L_{\max }$ which, in impact-parameter space, then becomes proportional to a $b_{\max }$. The connection between $L_{\max }$, alias $b_{\max }$, and the energy comes from the high l-behaviour of the Legendre functions, and the energy dependence enters because the scattering amplitudes are said to grow at most like a polynomial in s. The difference between Heisenberg’s argument and the S-matrix derivations seems to be that for the latter case the energy dependence comes from the hypothesis on the amplitudes taken to grow with energy, whereas for Heisenberg, to obtain the limit one needs an average pion energy to be a constant and total energy emitted proportional to the c.m. energy.

Let us repeat here the heuristic argument given by Froissart, at the beginning of his paper, to obtain his result. It must be noted that this intuitive explanation relies upon the existence of confinement. Indeed, the whole description applies not to parton scattering but to hadron scattering.

Let the two hadrons see each other at large distances through a Yukawa-type potential, namely $g\mathrm{e}^{-\kappa r}/r$, where $\kappa$ is some momentum cut-off. Let a be the impact parameter, then the total interaction seen by a particle for large a is proportional to $g\mathrm{e}^{-\kappa a}$. When $g\mathrm{e}^{-\kappa a}$ is very small, there will be practically no interaction, while, when $g\mathrm{e}^{-\kappa a}$ is close to 1, there will be maximal probability for the interaction. For such values of a, $\kappa a=\ln |g|$ one can then write for the cross section $\sigma \simeq ( \pi /\kappa ^2) \ln ^2|g|$. If g is a function of energy and we assume that it can grow with energy at most like a power of s, then one immediately obtains that the large energy behaviour of the total cross section is bound by $\ln ^2 s$. What $\kappa$ is, remains undefined for the time being, except that it has dimensions of a mass.

Since Heisenberg’s early result, many attempts have been made to reproduce it with modern field theory techniques. Leaving aside for the moment, the Regge–Pomeron language, one can summarise this result and related attempts, including those of Froissart and Martin, as follows:

• confinement is input to the derivation as one considers pions as a cloud around the interacting hadrons, represented by a fall-off of the cross section at large impact-parameter values. In [150] a value $b_{\max }$ is defined and related to the energy emitted. In Froissart’s heuristic explanation of his derivation, the potential is of the Yukawa type, with the coefficient of the term in the exponential in r, proportional to a constant $\kappa$, which will later turn out to be the pion mass (similar to the coefficient in Heisenberg’s exponential)

• with such an exponential behaviour, $\sigma _{\mathrm{tot}}$, by definition proportional to $b_{\max }^2$, will be proportional to

  • inverse of the scale, which is $m_\pi$

  • a logarithm of a function of the energy scales of the collision, $f(\sqrt{s},m_\pi ,m_H)$

• the average emitted pion energy is what determines the function $f(\sqrt{s},m_\pi ,m_H)$, through the relation $\langle E_0\rangle =\sqrt{s} \mathrm{e}^{-b_{\max }m_\pi }$

• for a free pion field $f(\sqrt{s},m_\pi ,m_H) = \frac{\gamma }{\ln \gamma }$, while for the more realistic case of not free pions, Heisenberg obtains $f(\sqrt{s},m_\pi ,m_H)= \ln \gamma$ with $\gamma \approx \sqrt{s}/M_H.$

To obtain the logarithmic dependence in the cross section, it is then necessary to understand the behaviour of the function $f(\sqrt{s},m_\pi ,m_H)$. In Froissart, the elastic amplitude is assumed proportional to a finite power of the energy and this brings in the energy term in the logarithm.

Finally, let us notice a recent paper by Azimov [153], where the fundamentals of the Froissart bound are revisited and the possibility of a different asymptotic behaviour of the total cross section is proposed.

5.4 The impact picture

The impact picture for particle scattering is still at the basis of many of the proposed descriptions for the total cross section. It is often obtained as a direct consequence of an optical model for scattering, with direct connection to the optical theorem.

5.4.1 Cheng and Wu description of high energy scattering, including work with Walker

In 1970 Cheng and Wu [154] (CW) described the general qualitative features of the impact picture for high energy scattering.

The final picture had arisen through a long series of papers, the first of which studied the high energy limit of elastic two body scattering amplitudes in (massive) quantum electrodynamics [155]. In this paper, a systematic study, at high energy, of all two body elastic scattering amplitudes was performed and the concept of “impact factor” was introduced for electrons, positrons, nuclei (all point-like) and the (massive) photon. “After 16 months and 2000 pages of calculations”, as the authors say, it was found that the matrix element for the elastic scattering process $a+b\rightarrow a+b$, for small values of the momentum transfer $\mathbf{r}_1\simeq \ 0$, can be stated in the form [155]

(5.35)

This expression introduces the impact factor . In Eq. (5.35) the amplitude is cast as an integral over an internal variable, which obtains from higher order diagrams, with $r_2$ and $r_3$ being averages over initial and final particle momenta. The results obtained in this paper, which relies on a non-zero photon mass $\lambda$ to avoid infrared divergences, contradicts, according to the authors, previous results on Regge-poles and the droplet model for diffractive scattering, both of which rely on potential model results.

In [154] the impact picture and the eikonal approximation, which will later lead to their numerical prediction for high energy scattering (with Walker), are presented and, in [156], the limiting behaviour of cross sections at infinite energy is stated in the following major predictions for two body scattering:

• 1. the ratio of the real to the imaginary part of the elastic amplitude

  $$\begin{aligned} \frac{\mathfrak {R}eM(s,0)}{\mathfrak {I}m M(s,0)}=\frac{\pi }{ \ln |{\mathcal {S}}| }+\mathcal{O} ( \ln |\mathcal{S}| )^{-2} \end{aligned}$$

  (5.36)

  where ${\mathcal S}$ is obtained asymptotically as

  $$\begin{aligned}&{\mathcal S}=\left\{ -\frac{(-s)^a}{[\ln (-s)]^2} +\frac{(-u)^a}{[\ln (-u)]^2}\right\} ^{1/a}\nonumber \\&\quad \rightarrow \frac{s/s_0}{[\ln (s/s_0)^{2/a}} \end{aligned}$$

  (5.37)

  for $-t\simeq 0$. This expression shows that ${\mathcal S}$ increases at least like a power of s, with a a positive constant;

• 2. the asymptotic behaviour of the total cross section is given as

  $$\begin{aligned} \sigma _{\mathrm{total}}=2\pi ^2 R^2+\mathcal{O}(\ln |\mathcal{S}|) \end{aligned}$$

  (5.38)

  with $R=R_0\ln |\mathcal{S}|$, and $R_0$ is a constant.

• 3. for the elastic cross section, the impact picture, extended to $t\ne 0$ leads to a prediction on the position of the first dip, namely to geometrical scaling, a result previously obtained in [13] on very general grounds, i.e.

  $$\begin{aligned} -t_{\mathrm{dip}} \sigma _{\mathrm{total}}=2\pi ^3 \beta _1^2+ {\mathcal O}(\ln |{\mathcal S}|)^{-1}) \end{aligned}$$

  (5.39)

  with $\beta _1$ corresponding to the position of the first zero of the $J_1(\pi \beta )$;

• 4. the ratio of elastic to the total cross section goes to a constant, namely

  $$\begin{aligned} \frac{\sigma _{\mathrm{elastic}}}{\sigma _{\mathrm{total}}}=\frac{1}{2}. \end{aligned}$$

  (5.40)

The authors note that, with the exception of the result in Eq. (5.36), all the above is model independent and believed to be firm, whereas the first one could only be valid in QED. We shall return to this point in a later section.

In 1973 Cheng, Walker and Wu proposed a quantitative model, based on such picture, to the study of total cross sections [157], and, later, also applied it to study the ratio of the elastic to the total cross section [158].

The impact picture presented by Cheng, Walker and Wu (CCW) represents the collision, as seen by each individual particle, as that of two thin pancakes, Lorentz contracted along the direction of motion. The pancakes are seen as being made of

• 1. a black core, where essentially total absorption takes place, with a logarithmically expanding radius $R(s)\simeq R_0\ln s$, which owes its existence to the production of relatively low energy particles in the center-of-mass system

• 2. a grey or partially absorptive fringe, roughly independent of the energy.

One of the immediate predictions of this picture is that the ratio of the total to the elastic cross section becomes 1/2 at very high energy. As we discuss later in this review in the context of diffraction, this is a problem with the one channel eikonal representation.

Lifting notation and everything else from [157], for an elastic channel j, the amplitude at high energy is written as

$$\begin{aligned} M_j(s,\varDelta )=\frac{is}{2\pi }\int \mathrm{d}\mathbf {x}_\perp \exp (-i{\mathbf {\varDelta }}\cdot {\mathbf {x}}_\perp )D_j(s,{\mathbf {x}}_\perp ) \end{aligned}$$

(5.41)

where ${\mathbf {\varDelta }}$ is the momentum transfer and $D_j$ is written as

$$\begin{aligned} D_j(s,{\mathbf {x}}_\perp )= & {} 1-\exp ( -f_j (E\mathrm{e}^{i\pi /2})^c )\nonumber \\&\times \exp (-\lambda ( x_\perp ^2+x_{jo}^2 )^{1/2}) \end{aligned}$$

(5.42)

with E the laboratory energy of the projectile (incident particle). While c and $\lambda$ are universal constants, $f_j$ and $x_{jo}$ are parameters, which, however, are the same for particles and antiparticles. The factor $\mathrm{e}^{-i\pi /2}$ is present to allow for crossing symmetry in the amplitudes. The normalisation of the amplitude is such that the differential cross section is given by

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}=|M_j(s,{\mathbf {\varDelta }})|^2 \end{aligned}$$

(5.43)

where $t=- \varDelta ^2$. The optical theorem then leads to the expression for the total cross section

$$\begin{aligned} \sigma _{\mathrm{total}}(j)=A_js^{-1/2} +\frac{4.893}{s}\mathfrak {I}m M_j(s,0). \end{aligned}$$

(5.44)

In the above equation, the authors added a term, defined as a background term, and the factor 4.893 is a conversion factor to mb. The asymptotic energy scale is now controlled by the power c in Eq. (5.42). When the paper [157] was written, the parameter was fixed through the fit to hadronic data, including results from ISR experiments. The value of the parameter was given as $c=0.082925$.

In a subsequent paper [158], the model is further defined. The amplitude is written as the sum of 3 terms, namely a vector and a tensor exchange, and the Pomeron contribution. The authors write

$$\begin{aligned}&\sigma _{\mathrm{total}}(pp/p{\bar{p}})\nonumber \\&\quad = 4.893\left[ \frac{\mathfrak {I}m A_p(s,0)}{s}+ s^{-1/2} ( {\bar{\gamma }}_f\mp {\bar{\gamma }}_\omega )\right] ~\hbox {mb} \end{aligned}$$

(5.45)

where the subscripts f and $\omega$ refer to the tensor and vector exchange. The Pomeron contribution appears through the eikonal formulation, i.e.

$$\begin{aligned} A_p(s,t)=\frac{is}{2\pi }\int \mathrm{d}x_\perp \mathrm{e}^{ -i{\mathbf {\varDelta }}\cdot {\mathbf {x}}_\perp } D(s, x_\perp ) \end{aligned}$$

(5.46)

with

$$\begin{aligned} D(s, x_\perp )=1-\exp [-S(s)F(x_\perp ^2) ]. \end{aligned}$$

(5.47)

With this, CWW obtain the fit to the elastic scattering parameter, presently called the slope parameter, further discussed in Sect. 6, B(s), which is seen to rise slowly with energy. It is also seen that the ratio of the elastic to the total cross section should rise by 7% at ISR.

5.4.2 The impact-parameter description by Soffer, Bourrely and Wu

A particularly clear description of how the impact picture developed after CW work can be found in a short review paper by Soffer [159] in [160]. It is recalled that QED was the only known relativistic quantum field theory in the late 1960s and that CW introduced the small photon mass in order to avoid what Soffer calls unnecessary complications. It is recalled that the summation of all diagrams for Compton scattering leads [156] to the asymptotic expression of Eq. (5.37).

In the model built by Soffer with Bourrely and Wu (BSW), the scattering amplitude for proton scattering is written as

$$\begin{aligned} a(s,t)=a^N(s,t)\pm sa^c(t) \end{aligned}$$

(5.48)

where the signs refer to ${\bar{p}}p$ and $pp$  respectively, the hadronic amplitude is given by $a^N(s,t)$ and the factor s has been factorised out of the Coulomb amplitude $a^c(t)$.

The hadronic amplitude is obtained from the impact picture [161] as

$$\begin{aligned} a^N(s,t)=is \int _0^\infty b \mathrm{d}b J_0(b\sqrt{-t})(1-\mathrm{e}^{-\varOmega (s,b)}). \end{aligned}$$

(5.49)

The eikonal function $\varOmega (s,b)$ is split into two terms, reflecting different dynamical inputs, namely

$$\begin{aligned} \varOmega (s,b)=R_0(s,b)+{\hat{S}}(s,b) \end{aligned}$$

(5.50)

where $R_0(s,b)$ includes the Regge contribution important in the low-energy region and is different for $pp$ and ${\bar{p}}p$, whereas the second term ${\hat{S}}(s,b)$ is the same for both processes and gives the rising contribution to the total cross section. In this paper, a factorised expression is chosen so that

$$\begin{aligned} {\hat{S}}(s,b)=S_0(s) F(b^2) \end{aligned}$$

(5.51)

with the energy dependence given as in the CW model, namely

$$\begin{aligned} S_0(s)= \frac{s^c}{\ln ^{c'}{s/s_0}}+\frac{u^c}{\ln ^{c'}{u/u_0}}. \end{aligned}$$

(5.52)

The impact-parameter dependence, and hence the t-dependence, is inspired by the proton electromagnetic form factor, namely it is the Fourier transform of

$$\begin{aligned} {\tilde{F}(t)}=f[ G(t)]^2\left[ \frac{a^2+t}{a^2-t}\right] \end{aligned}$$

(5.53)

where G(t) is given by a parameterisation inspired by the proton electromagnetic form factor, i.e.

$$\begin{aligned} G(t)=[ (1-t/m_1^2)(1-t/m_2^2) ]^{-1}. \end{aligned}$$

(5.54)

This model had six parameters, which were fixed from existing data. As in most models, the appearance of LHC data required some adjustment of the parameters. In Fig. 37 we show some current predictions from this model, up to very high energy cosmic rays [162].

Fig. 37

Total cross section predictions at LHC and beyond, from Soffer’s contribution to Diffraction 2012 [162]. Reprinted from [162], ©(2013) with permission by AIP Publishing LLC

The elastic differential cross section is defined as

$$\begin{aligned} \frac{\pi }{s^2}|a(s,t)|^2 \end{aligned}$$

(5.55)

and the total cross section at $\sqrt{s}=40~\mathrm{TeV}$ is predicted to reach a value of $121.2~\hbox {mb}$ [163].

Fig. 38

Donnachie and Landshoff universal description of proton, meson and photon total cross sections with Regge and Pomeron pole exchange. The figures are courtesy of the authors, reprinted from [60], ©(1992) with permission by Elsevier

5.5 The universal Regge and Pomeron pole description by Donnachie and Landshoff

In Sect. 2, we have seen that the analyticity properties of the elastic scattering amplitude in the complex angular momentum plane, make it possible to see that the amplitudes for large t and small s exhibit a power-law behaviour. Using crossing, one then obtains the usual large s and small t behaviour to describe elastic scattering and different low energy processes.

The very successful parametrisation of all total cross sections provided in 1992 by Donnachie and Landshoff (DL) [60]

$$\begin{aligned} \sigma ^{\mathrm{TOT}}=Ys^{-\eta }+Xs^\epsilon \end{aligned}$$

(5.56)

was inspired by Regge and Pomeron exchange, and proposed as a universal expression valid for all hadronic total cross sections. In Eq. (5.56) the first term is identified as arising from $\rho , \omega , f, a$ ($J=1,2$) exchanges, the second from Pomeron exchange, a vacuum trajectory, which, before the observation of the rise of $\sigma _{\mathrm{total}}$ had been given a constant intercept $\alpha _P(0)=0$. Requiring the same values for $X, \epsilon$ and $\eta$, the DL fit to $pp$ and ${\bar{p}}p$ data gave

$$\begin{aligned} \epsilon =0.0808\quad \eta =0.4525. \end{aligned}$$

(5.57)

What is remarkable about this expression is that the same value of $\epsilon$ and $\eta$ appeared to fit all available cross section data, within the existing experimental errors, namely $\pi ^{\pm } p$, $K^{\pm } p$, $\gamma p$, ${\bar{p}} n$, pn.The interpretation of this expression for what concerns the first term is that it correspond to a simple Regge pole with intercept $\alpha (0)=1-\eta$. Clearly, if one uses only one such decreasing term for different sets of data, $\eta$ is understood as being the intercept of an effective trajectory, which actually takes into account different Regge term contributions as well as possible contributions from non-Regge terms, including the exchange of more than one Pomeron. As for the Pomeron, this is considered as an entity whose distribution and density function were actually measured at HERA, and to which we shall return in the section dedicated to photon processes, Sect. 7. The fact that the power is the same for different processes finds its justification in that the Pomeron has the quantum numbers of the vacuum. Thus, for crossing symmetric processes such as $pp$ and ${\bar{p}}p$ not only the power is the same, but also the coefficient X. This is borne out by the fit to various processes, which we reproduce in Fig. 38.

In the introduction to this section, we have mentioned the interpretation of the rise in terms of QCD processes like mini-jets, which will also be discussed later in more detail. We mention here that in [164] this possibility was considered unlikely because, when the contribution from vector and tensor meson exchange to the total cross section is subtracted off, the rise appears to be present already at $\sqrt{s}\le 5~\mathrm{GeV}$ and, in some cases, even earlier [165]. In the 1992 paper [60], this statement is softened, although it is still said that the form $Xs^\epsilon$ is unaffected by the onset at higher energies of new production processes, such as charm or mini-jets. A word of caution is, however, added, namely that at the Tevatron one can expect a large number of mini-jets.

The question of the rise is also discussed with respect to the impact picture by Cheng, Walker and Wu [157, 158]. DL considered unhelpful to adopt a geometrical approach and to talk of hadrons becoming bigger and blacker as the energy increases. We note that an early rise with the same power as the one found by DL is also to be found in the CWW [157].

On the other hand, if the rise is due to mini-jets, at high energy the rise should only depend on the gluon densities, and thus be flavour independent. However, as in the case of $\gamma p$ and $\gamma \gamma$, there may be other ingredients, quark densities, internal structure such as hadronic matter distribution etc. which change the way the cross sections rise. Indeed, as we shall show in the section dedicated to $\gamma p$ processes, mini-jet models do not expect the rise to be the same for photons as for protons until such very high asymptotic energies are reached where only gluons play a role.

The advantage of the DL formulation is that it provides a simple and useful parametrisation of total cross sections, without the need to introduce the question of the inner structure of protons. The disadvantages are that it does not connect directly to QCD and it violates the limiting behavior imposed by the Froissart bound.

5.6 Hadronic matter distribution

A crucial role in many of the models for the total cross section is played by the distribution of matter in the colliding hadrons in the plane perpendicular to the initial direction of motion. Practically the only model which does not use an impact-parameter description is the simple version of the Regge–Pomeron model by Donnachie and Landshoff [60] or phenomenological fits based on analyticity and other general properties, discussed later in this section. However, any dynamical description of hadron scattering uses information as regards the breaking up of the proton, which is what is described by the total cross section.

Models in current usage fall into one of the following major categories:

• matter distributions obtained from the Fourier transform of colliding hadron form factors (FF),

• parameterisations inspired by form-factor (FF) models, such as the BSW [161], or QCD-inspired model by Block and various collaborators [166, 167],

• QCD dipole models, based on the BFKL equation in transverse momentum space [168, 169],

• Fourier transform of transverse momentum distribution of QCD radiation emitted during the collision, using $k_t$ Soft Gluon Resummation (SGR), extended to the infrared region, as in the so-called BN model, described later in this section [93, 94, 148].

The basic function of these models for the matter distribution in impact-parameter space, is to provide a cut-off in space which describes the fact that hadrons have a finite size, namely that quarks and gluons are confined into hadrons. From this point of view, models which reflect this finite size, such as the dipole model for the proton factor, can be a good description, but the problem in this case lies in the energy dependence.

Form factors in fact are a phenomenological description of the inner structure and need to be placed in a QCD context for a model independent understanding. Also, the problem with form-factor models, is that in some cases, such as the case of photon total cross sections, the form factor is not known. One can always use a dipole (for protons) or monopole (for pions) functional form, but then one may have to change phenomenologically the scale parameter. On the other hand, QCD-inspired matter distributions, which are based on parton structure, can be useful only if they are able to access the Infrared Region (IR), since the needed impact-parameter description has to describes very large b-values. Thus we require a model for ultra-soft, infrared, soft-gluon emissions. One such model was proposed in [148] and its application to total cross section will be described in Sect. 5.9.4. In order to approach models based on resummation, we shall dedicate the next subsections to a discussion of resummation in gauge theories, QED first, and then QCD.

5.7 Role of resummation in QED

We shall here first present a review of resummation in QED, including the Sudakov form factor.

In this subsection, we shall provide the reader with a history of resummation beginning with the pioneering work on the infrared catastrophe by Bloch and Nordsieck and its importance for subsequent development both in QED and QCD. The non-covariant formulation by Bloch and Nordsieck was substituted by a covariant one by Touschek and Thirring in 1951. Previously, in 1949 Schwinger had anticipated the need for resummation in perturbative QED. In the 1950s and the 1960s, there were further refinements by Touschek, Brown and Feynman, Lomon and Yennie Frautschi and Suura. A different path to resummation was initiated by Sudakov which later played a pivotal role in QCD resummation. For QCD, resummations of soft-gluon transverse momentum were developed by Dokshitzer Dyakonov and Troian, Parisi and Petronzio, Collins and Soper, Curci Greco and Srivastava, Pancheri and Srivastava. In a subsection to follow, we shall illustrate the highly influential work by Balitsky, Fadin, Kuraev and Lipatov, based on the evolution equation formalism. Finally, their connection with total cross section computations will be established.

The importance of large distance scattering in models for the total cross section leads naturally to consider the importance of very small momentum interactions, namely the InfraRed (IR) momentum region is dual to the large distance region. When particle momenta are very small, resummation of all processes involving small momenta is necessary. In QED this has been the subject of interest for almost a 100 years, in QCD for more than 40. In the following we shall present a mini-review of the problem of resummation in QED, followed by a discussion of the QCD case. The latter is of course still not solved, a possible ansatz to describe the IR region and the connection of resummation with the asymptotic behaviour of the total cross section will be presented later, in the context of the eikonal mini-jet models.

All total cross sections reflect the effective area defined by the (average) perpendicular distance between the two incident particles and hence are controlled by scattering at large distances. Long distances correspond to their dual i.e., small (transverse) momenta. Thus, the importance for a theoretical understanding – in any model for high energy total cross section – of scatterings at very small momenta. Unbroken gauge theories, abelian[QED] or not [QCD], are plagued by two types of singularities both originating from the masslessness of the gauge boson. The exchange of a massless gauge boson in any elastic scattering between (generalised) charges gives rise to the Rutherford singularity as the momentum transfer goes to zero. Thus, a total cross section becomes infinite simply because of the infinite range of the potential. There is a further, infra-red (IR) singularity which arises since any charged particle can emit and absorb gauge particles of vanishing momenta leading to all vertices and amplitudes be divergent in this limit [The IR catastrophe]. Hence, the need for individual IR singularities (in perturbation theory) to be summed and a discussion of the various ways to accomplish this resummation is the purpose of this section. But before embarking on it, let us pause to discuss briefly the Rutherford singularity.

5.7.1 The Rutherford singularity

In QED, the elastic scattering amplitude between say two electrons in the forward direction is indeed infinite. However, consider the scattering of a (moderately) high energy electron from a neutral atom considered as a collection of Z electrons and a (point-like) nucleus with charge (Ze). At momentum transfers sufficiently large compared to the binding energy of the electrons, it would not be misleading to compute the elastic (eA) amplitude in the Born approximation – using the impulse approximation – as an incoherent sum of the incident electron scattering from the individual charges of the atom [an atomic “parton” model]. But this computation would hardly suffice for a reasonable estimate of the total cross section since optical theorem relates the total cross section to the [imaginary part] of the elastic amplitude at zero momentum transfer which in this approximation would diverge by virtue of the Rutherford divergence. However, as the momentum transfer goes to zero, the incident electron sees the total charge of the atom which is zero and thus there should be no divergence. The answer to this problem is of course well known: the coherence between the electrons, which is neglected in the impulse approximation, is the culprit and cannot be neglected. If t is the momentum transfer, the cross section contains a factor ($[Z - F(t)]^2$), where F(t) denotes the form factor of an electron in the atom

$$\begin{aligned} \left( \frac{\mathrm{d}\sigma }{\mathrm{d}\varOmega }\right) = \left( \frac{2 m \alpha }{t}\right) ^2 [Z - F(t)]^2. \end{aligned}$$

(5.58)

Since $F(0)=Z$, there is no Rutherford singularity and the cross section is indeed finite as it should. In fact, a measurement of the forward differential cross section has been traditionally used to determine the charge radius (or the size) of the atom.

We are recalling these well known facts from atomic scattering for two reasons. One is to remind ourselves that elastic scatterings at low-momentum transfers depend crucially on the coherence size of the system and hence they cannot be neglected even at high energies. The second reason is that, for QCD, these facts take on a shade more relevant. Individual elastic scattering amplitudes for all coloured particles possess the Rutherford singularity which, however, must disappear for hadronic scattering amplitudes since hadrons are color singlets [“neutral atoms”]. By analogy from the atomic case, the final amplitudes must reflect their coherence size i.e., the distribution of color charges within the hadron.

But this is hardly the end of the story for QCD. It is widely believed (often called IR slavery) that quarks and glue in QCD are confined through the IR divergences and that the strong coupling constant $\alpha _s(t)$ becomes very large at small momenta t. There are indications for it already in the divergence of the one-loop asymptotic freedom (AF) formula for $\alpha _s(t)$. Hence, a natural paradigm for QCD emerges: If the divergence of the (effective) coupling constant at small t is responsible for confinement, the nature and the intensity of its divergence must set the size of a hadron. But then, the same must also enter into determining the size of the high energy total cross sections. We shall return to these issues later when we discuss models for total cross sections.

After this brief interlude, let us now discuss the underlying issues beneath the IR divergences in QED and QCD.

5.7.2 Infra-red catastrophe and the Bloch–Nordsieck cure

The Infra-Red (IR) catastrophe was clearly brought to the fore by Bloch and Nordsieck through their two classic papers of 1937 [170, 171]. Bloch and Nordsieck observed that previous analyses of radiative corrections to scattering processes were defective in that they predicted a divergent low frequency correction to the transition probabilities. This was evident from the soft photon emission spectrum in the scattering of an electron from a Coulomb field (as described by Mott and Sommerfeld [172] and by Bethe and Heitler [173]): as the emitted photon frequency $\omega \rightarrow \ 0$, the spectrum takes the form $\mathrm{d}\omega /\omega$.

The two authors had noticed that, while the ultraviolet [UV] difficulties were already present in the classical theory, the IR divergence had no classical counterpart. They anticipated that only the probability for the simultaneous emission of infinitely many quanta can be finite and that the probability for the emission of any finite number of them must vanish.

To cure this “infrared catastrophe” phenomenon, a semi-classical description was proposed. They noticed that, for emitted photons of frequencies larger than a certain $\omega _0$, the probability for emitting each additional photon is proportional to ${{\mathrm{e}^2}\over {{\hbar }c}} \log {E/{\hbar }\omega _0}$, which becomes large as $\omega _0 \rightarrow 0$. Thus, the actual expansion is not ${{\mathrm{e}^2}\over {{\hbar }c}}$, which would be small, but a larger number, driven by the logarithm. This led them to analyze the scattering process in terms of what came to be called Bloch–Nordsieck states, namely states with one electron plus the electromagnetic field, and to substitute the expansion in ${{\mathrm{e}^2}\over { {\hbar }c}}$ with a more adequate one. The important result they obtained, in a non-covariant formalism, was that, albeit the probability of emission of any finite number of quanta is zero, when summing on all possible numbers of emitted quanta, the total transition probability was finite. This was so because, by summing on all possible frequencies and numbers of photons, one obtained the result which one would have obtained by neglecting entirely the interaction with the electromagnetic field. Since they could show that the probability for emission of any finite number of quanta was zero, whereas the total transition probability was finite and the total radiated energy was finite, then they anticipated that the mean total number of quanta had to be infinite. Thus the idea that any scattering process is always accompanied by an infinite number of soft photons was introduced and proved to be true (later, also in a covariant formalism).

In the Bloch and Nordsieck paper we see the emergence of the concept of finite total energy, with exponentiation of the single photon spectrum which is logarithmically divergent. They obtain that the probability per unit time for a transition in which $n_{s\lambda }$ light quanta are emitted always includes a factor proportional to

$$\begin{aligned} \exp \{ -\alpha \lim _{\omega _0\rightarrow 0} \int _{\omega _0}^{\omega _1} {{d\omega }\over {\omega }} \int \mathrm{d}\varOmega _k \times \varDelta \end{aligned}$$

(5.59)

where

$$\begin{aligned} \varDelta = \left[ \left( {{{\varvec{\mu }}}\over {1-\mu _s}} -{{{\varvec{\nu }}}\over {1-\nu _s}} \right) ^2- \left( {{\mu _s}\over {1-\mu _s}} -{{\nu _s}\over {1-\nu _s}} \right) ^2 \right] \nonumber \\ \end{aligned}$$

(5.60)

where ${\varvec{\mu }}$ and ${\varvec{\nu }}$ are the momenta of the incoming and outgoing electron, $\mu _s$ and $\nu _s$ the projection of $\varvec{\mu }$ and $\varvec{\nu }$ along the momentum $\mathbf k$ of the emitted photon. Because of the exponentiation of a divergent term, the transition probability for a finite number of emitted photons is always zero. On the other hand, when summation is done over all possible photon numbers and configurations, the result is finite. Clearly there was still something missing because the fact that one must emit an infinite number of photons is obtained by exponentiating an infinite divergent term, and there is no hint of how to really cure the IR divergence. In addition the language used is still non-covariant.

Before going to the covariant formulation, we notice that the argument relies on the transition probability being proportional to

$$\begin{aligned} \varPi _{s\lambda } \mathrm{e}^{- {\bar{n}}_{s\lambda }} {{ {\bar{n}}_{s\lambda }^{n_{s\lambda }} } \over { n_{s\lambda }! }} \end{aligned}$$

(5.61)

namely to a product of Poisson distributions, each of them describing the independent emission of $n_{s\lambda }$ soft photons, and upon neglecting the recoil effects.

5.7.3 Covariant formalism by Touschek and Thirring

Touschek and Thirring reformulated the Bloch and Nordsieck problem in a covariant formalism [174]. They proved that $|\chi _0^\dagger \chi _0^\prime |^2$, the probability for a transition from a state $\chi _0$ with no photons to a state with an average number ${\bar{n}}$ of photons, $\chi '_0$, was given by $\mathrm{e}^{-{\bar{n}}}$, which goes to zero as ${\bar{n}}$ goes to infinity, namely that the probability of emission of any finite number of quanta was zero.

Let us consider the Touschek and Thiring derivation. They point out the importance of the Bloch and Nordsieck solution and that, although the results they obtain are not new and have been discussed by several authors, their solution being the only one which admits an accurate solution justifies a general reformulation of the problem. As already noted in [170] the simplification which enables one to find an accurate solution rests on the neglect of the recoil of the source particles.

Touschek and Thirring set out to determine the probability for the production of a certain number n of quanta in a 4-momentum interval $\varDelta$. They obtain that the probability amplitude for the creation of n particles in a state r is given by

$$\begin{aligned} (F^r_n\chi _0)= & {} {{1}\over {(2\pi )^{3n}}}\times {{1}\over {\sqrt{n!}}} \int _{\varDelta }\mathrm{d}k_1\cdots \int _\varDelta \mathrm{d}k_n \varPi _i\delta (k^2_i-\mu ^2)\\&\times \, u^{r*}_n(k_1,\ldots ,k_n) (\chi _0' (\phi (k_1)+\delta \phi (k1))\\&\cdots (\phi (k_n)+\delta \phi (k_n))\chi _0) \end{aligned}$$

where use has been made of a complete set of orthogonal functions $u^r_n$ which satisfy the completeness relation. $\chi _0$ is the eigenvector describing an incoming state with no quanta at all in the interval $\varDelta$, while $\chi _0'$ is the corresponding one for the final state. For the probability to have n photons in the final state they obtain

$$\begin{aligned} \sum _r |F^r_n\chi _0|^2={{1}\over {n!}} {\bar{n}}^n |\chi _0' \chi _0|^2 \end{aligned}$$

(5.62)

with

$$\begin{aligned} {\bar{n}}={{1}\over {(2\pi )^3 }} \int _\varDelta \mathrm{d}k \delta (k^2-\mu ^2)|\delta \phi (k)|^2 \end{aligned}$$

(5.63)

and, by imposing that the total probability to be 1, they obtain the Bloch and Nordsieck result

$$\begin{aligned} |\chi _0'\chi _0|^2=\mathrm{e}^{-{\bar{n}}}. \end{aligned}$$

(5.64)

For the derivation, it is necessary that the motion of the source particles be not affected by the emission of soft quanta, namely that the wave operator describing the source field be a c-number. Then $\phi ^{\mathrm{out}}$ differs by $\phi ^{\mathrm{in}}$ only by a multiple of the unit matrix and, transforming to k-space, it may be written as

$$\begin{aligned} \phi ^{\mathrm{out}}(x)={{1}\over {(2\pi )^3}}\int \mathrm{d}k \delta (k^2-\mu ^2) [\phi ^{\mathrm{in}}(k)+\delta \phi (k)] \mathrm{e}^{ikx}\nonumber \\ \end{aligned}$$

(5.65)

where $\delta \phi (k)=-\rho (k)\epsilon (k)$, with $\rho (k)$ the Fourier transform of the source density describing the source particles. In their paper TT first derive their results for a source scalar field, then they generalise it to a vector source function $j_\mu (x)$ for a point-like electron, i.e.

$$\begin{aligned} j_\mu (x)=e\int p_\mu (\tau ) \delta (x-\tau p(\tau )) \mathrm{d}\tau \end{aligned}$$

(5.66)

where $p_\mu (\tau )=p_\mu$ for $\tau$ less than 0 and $p_\mu (\tau )=p'_\mu$ for $\tau$ larger than 0. Notice that the sudden change in momentum imposes the restriction that in order to apply the results to a real scattering process, the photon frequencies should always be much smaller than $1/\tau$, where $\tau$ is the effective time of collision. Otherwise the approximation (of a sudden change in momentum) will break down. One then obtains

$$\begin{aligned} j_\mu (k)= \frac{i e}{(2\pi )^{3/2}}\left( {{p_\mu }\over {(pk)}}-{{p'_\mu }\over {(p'k)}}\right) \end{aligned}$$

(5.67)

and the average number of quanta ${\bar{n}}$ now becomes

$$\begin{aligned} {\bar{n}}={{\mathrm{e}^2}\over {(2\pi )^3}}\int _\varDelta \mathrm{d}k \delta (k^2-\mu ^2)\left[ {{(p\epsilon )}\over {(pk)}}-{{(p'\epsilon )}\over {(p'k)}}\right] ^2 \end{aligned}$$

(5.68)

where $\epsilon$ is a polarisation vector. Notice that the photon mass $\mu$ remains different from zero, so as to ensure convergence of all the integrals. However, this is not necessary when higher order QED processes are taken into account, as was shown by explicit Quantum Electrodynamics calculations, starting with Schwinger’s work [175].

5.7.4 Schwinger’s ansatz on the exponentiation of the infrared factor and the appearance of double logarithms

The solution found by Bloch and Nordsieck, and later brought into covariant form by Touschek and Thirring, did not really solve the problem of electron scattering in an external field and of how to deal with finite energy losses. This problem was discussed and solved in QED, where the logarithmic divergence attributable to the IR catastrophe from emission of real light quanta of zero energy was compensated through the emission and absorption of virtual quanta. This cancellation took place in the cross section, and not between amplitudes. In a short paper in 1949 and, shortly after, in the third of his classic QED papers, Julian Schwinger [175] examined the radiative corrections to (essentially elastic) scattering of an electron by a Coulomb field, computing second order corrections to the first order amplitude and then cancelling the divergence in the cross section between these terms and the cross section for real photon emission. The result, expressed as a fractional decrease $\delta$ in the differential cross section for scattering through an angle $\theta$ in the presence of an energy resolution $\varDelta E$ of the scattered electron, is of order $\alpha$ and given by

$$\begin{aligned} \delta ={{2\alpha }\over {\pi }}\log \left( {{E}\over {\varDelta E}}\right) \times F(E,m,\theta ) \end{aligned}$$

(5.69)

where $F(E,m,\theta )$ in the extreme relativistic limit is just $\log (2E/m)$. Notice here the first appearance of a double logarithm, which will play a crucial role in resummation and exponentiation of radiative corrections.

Schwinger notices that $\delta$ diverges logarithmically in the limit $\varDelta E\rightarrow 0$ and points out that this difficulty stems from the neglect of processes with more than one low frequency quantum. Well aware of the Bloch and Nordsieck result, he notices that it never happens that a scattering event is unaccompanied by the emission of quanta and proposes to replace the radiative correction factor $1-\delta$ with $\mathrm{e}^{-\delta }$, with further terms in the series expansion of $\mathrm{e}^{-\delta }$ expressing the effects of higher order processes involving multiple emission of soft photons.

In 1949 however, such refinements, namely the exponentiation of the radiative correction factor, were still far from being needed, given the available energies for scattering processes as Schwinger points out, estimating the actual correction to then available experiments, to be about $10\%$. Almost 20 years had to pass before the exponentiation became an urgent matter for extraction of results from collider experiments, such those at SPEAR, ADONE, ACO, VEPP-2M, where the double logarithm term $\alpha \log (E/\varDelta E) \log (2E/m)$ would climb to $20 \div 30\%$ and beyond [176].

IR radiative corrections were also considered by Brown and Feynman [177] some time after Schwinger, and the concept of an external parameter ($\varDelta E$) which sets the scale of the IR correction was confirmed.

It is not clear whether Touschek and Thirring were aware of the Schwinger results when they formulated the covariant version of the Bloch Nordsieck method. They do not cite his results, and their interest is primarily on obtaining a covariant formulation of the Bloch and Nordsieck method. Quite possibly, at the time they were not interested in the practical applications of the problem, which is instead the focus of Schwinger’s calculation.

5.7.5 The Sudakov form factor

The problem of the double logarithms in perturbation theory was investigated by Sudakov [178] who studied the existence of double logarithms for vertex functions and established their exponentiation.

Consider the vertex function in QED [$e(p)\rightarrow \ e(q)\ +\ \gamma (l)$] with all three particles off shell in the kinematic limit $l^2\gg p^2,q^2\gg m^2$. Here the relevant double logarithmic parameter is computed to be ($2\alpha \ln (l^2/p^2) \ln (l^2/q^2)$) and considerations to all orders show that it exponentiates. Thus, the primitive vertex $\gamma ^\mu$ in the stated limit gets replaced by

$$\begin{aligned} \gamma ^\mu \mathrm{e}^{- [2\alpha \ln (l^2/p^2) \ln (l^2/q^2)]}. \end{aligned}$$

(5.70)

These double logarithms imply that as $q^2$ becomes very large, the vertex goes to zero, a rather satisfactory result. From a practical point of view, it was shown by Abrikosov et al. [179] that the competing process where a large number of soft real photons are emitted has a far greater probability and thus it far overwhelms the Sudakov probability.

Incidentally, the double logarithms are completely symmetric in the variables ($p^2, q^2, l^2$). Thus, if an electron say $p^2\gg q^2,l^2$, a similar result to Eq. (5.70) holds. The Sudakov limit when extended to QCD does become relevant. For example, in the light-quark parton model of QCD, one can therefore justify the fact that very far off mass shell quarks are suppressed through the Sudakov “form factor”.

5.7.6 Status of the field in the early 1960s

In the 1950s, with Feynman diagram technique available to the theoretical physics community, many higher order QED calculations came to be part of standard theoretical physics handbooks.

Many important contributions to the radiative correction problem appeared in the 1950s and early 1960s [177, 180, 181], with a major step in the calculation of IR radiative corrections done in 1961 by Yennie , Frautschi and Suura (YFS) [182]. In their classic paper, they went though the cancellation of the IR divergence at each order in perturbation theory in the cross section and obtained the final compact expression for the probability of energy loss. Their result is apparently disconnected from the Bloch and Nordsieck result. In their paper, they compute higher and higher order photon emission in leading order in the low photon momentum, showing that the leading terms always come from emission from external legs in a scattering diagram. In parallel, order by order, they extract the IR divergent term from the virtual diagrams, making the terms finite through the use of a minimum photon energy. They show that the result is just as valid using a minimum photon mass, and finally eliminating the minimum energy, they show the final result to be finite.

5.7.7 A semi-classical approach to radiative corrections

A semiclassical approach to resummation in QED can be found in [152], where the Bloch and Nordsieck approach is adopted and an important point made that the picture of an experimentalist as counting single photons as they emerge from a high energy scattering among charged particles is unrealistic. It is noted that perturbation theory is unable to deal with the flood of soft photons which accompany any charged particle reaction. Then the question of how light quanta are distributed in momentum is discussed. As discussed above, Bloch and Nordsieck had shown that, by neglecting the recoil of the emitting electron, the distribution of any finite number of quanta would follow a Poisson type distribution, namely

$$\begin{aligned} P(\{n,{\bar{n}}\})={{1}\over {n!}}{\bar{n}}^n \mathrm{e}^{-{\bar{n}}} \end{aligned}$$

(5.71)

and Touschek and Thirring had recast ${\bar{n}}$ in a covariant form. In [152] the constraint of energy–momentum conservation is added to this distribution. This is a major improvement, which has sometimes been neglected in subsequent applications of the method to strong interaction processes.

Let us repeat the argument through which Touschek obtained the final four-momentum probability distribution describing an energy–momentum loss $K_\mu$. The final expression is the same as the one proposed earlier by YFS, but the derivation is very different and its physical content more transparent. Touschek also discusses the different energy scales which will become very important later, when dealing with resonant states, and in particular with $J/\varPsi$ production. The derivation is semi-classical and at the end it will be clear that the quanta considered are both real and virtual photons. The underlying reason for this can be understood from a consideration by Brown and Feynman [177] in their computation of radiative corrections to Compton scattering. Brown and Feynman note that it is difficult to distinguish between real and virtual quanta of extremely low energy since, by the uncertainty principle, a measurement made during a finite time interval will introduce an uncertainty in the energy of the quantum which may enable a virtual quantum to manifest as a real one.

In [152] the probability of having a total four-momentum loss $K_\mu$ in a charged particle scattering process, is obtained by considering all the possible ways in which $n_k$ photons of momentum $k_\mu$ can give rise to a given total energy loss $K_\mu$ and then summing on all the values of $k_\mu$. That is, we can get a total final 4-momentum $K_\mu$ pertaining to the total loss, through emission of $n_{k_1}$ photons of momentum $k_1$, $n_{k_2}$ photons of momentum $k_2$ and so on. Since the photons are all emitted independently (the effect of their emission on the source particle being neglected), each one of these distributions is a Poisson distribution, and the probability of a 4-momentum loss in the interval $\mathrm{d}^4 K$ is written as

$$\begin{aligned} \mathrm{d}^4P(K)=\sum _{n_k}\varPi _{k}P(\{n_k,{\bar{n}}_k\}) \delta ^4\left( K-\sum _{k} k n_k\right) \mathrm{d}^4K\nonumber \\ \end{aligned}$$

(5.72)

where the Block and Nordsieck result of independent emission is introduced through the Poisson distribution and four momentum conservation is ensured through the four-dimensional $\delta$ function, which selects the distributions $\left\{ n_k,{\bar{n}_k} \right\}$ with the right energy–momentum loss $K_\mu$. The final expression is

$$\begin{aligned} \mathrm{d}^4 P(K)={{\mathrm{d}^4K}\over {(2\pi )^4}}\int \mathrm{d}^4x \ \exp [-h(x)+iK\cdot x] \end{aligned}$$

(5.73)

with

$$\begin{aligned} h(x)=\int \mathrm{d}^3 {\bar{n}}_k (1-\exp [-ik\cdot x]), \end{aligned}$$

(5.74)

which is the same as the expression obtained by YFS through order by order cancellation of the IR divergence in the cross section. In this derivation, which is semiclassical, no mention or no distinction is made between virtual and real photons as stated above, but it is clear that the contribution of real photons corresponds to the term which is multiplied by the exponential $\mathrm{e}^{-ik\cdot x}$, since this retains the memory that the total energy–momentum emission is constrained. Thus, single real photons of momentum (k) are all correlated through the Fourier transform variable x. The next step was to perform realistic calculations of the radiative correction factors, using an apparently difficult expression. The first objective was to obtain the correction factor for the energy, by integrating Eq. (5.73) over the 3-momentum variable. Through a very elegant argument based on analyticity, Touschek obtained the probability for a total energy loss $\omega$ as

$$\begin{aligned} \mathrm{d}P(\omega )=N \beta (E) {{\mathrm{d}\omega }\over {\omega }} \left( {{\omega }\over {E}}\right) ^{\beta (E)} \end{aligned}$$

(5.75)

where N is a normalisation factor [180, 181]. In the high energy limit,

$$\begin{aligned} \beta (E)={{4\alpha }\over {\pi }}\left( \log {{2E}\over {m_e}} -{{1}\over {2}}\right) . \end{aligned}$$

(5.76)

Integrating the four-dimensional distribution over the energy and longitudinal momentum variables, one obtains a transverse momentum distribution of the total emitted radiation [183], namely

$$\begin{aligned} {{\mathrm{d}^2P({\mathbf {K}}_\perp )}\over {\mathrm{d}^2{\mathbf {K}}_\perp }}= & {} \int \mathrm{d}\omega \ \mathrm{d}K_z {{\mathrm{d}^4 P(K)}\over {\mathrm{d}^4K}}\end{aligned}$$

(5.77)

$$\begin{aligned}= & {} {{1}\over {(2\pi )^2}}\int \mathrm{d}^2{\mathbf {b}}\ \mathrm{e}^{ i{\mathbf {b}}\cdot {\mathbf {K}}_\perp - \int \mathrm{d}^3 {\bar{n}}(k) [ 1-\mathrm{e}^{-i{\mathbf {b}} \cdot {\mathbf {k}}_\perp ] }}\end{aligned}$$

(5.78)

$$\begin{aligned}= & {} {{1}\over {(2\pi )^2}}\int \mathrm{d}^2{\mathbf {b}}\ \mathrm{e}^{ i{\mathbf {b}}\cdot {\mathbf {K}}_\perp -h(\mathbf{b})}. \end{aligned}$$

(5.79)

This expression, unlike the energy distribution, does not admit a closed form expression. In an Abelian gauge theory with an energy independent (as in the case of QED), but not small coupling constant, the corresponding $\beta$ factor becomes large. A useful approximation for the function $\mathrm{d}^2P({\mathbf {K}}_\perp )$ was obtained as [183]

$$\begin{aligned} \mathrm{d}^2{\tilde{P}}({\mathbf {K}}_\perp )= & {} \frac{\beta (2\pi )^{-1}}{\varGamma (1+\beta /2)} \frac{\mathrm{d}^2{\mathbf {K}}_{\perp }}{2E^2A} \left( \frac{K_\perp }{2E\sqrt{A}}\right) ^{\beta /2-1}\mathcal{K}_{1-\beta /2}\nonumber \\&\times \left( \frac{K_\perp }{E\sqrt{A}}\right) \end{aligned}$$

(5.80)

where this approximate expression is normalised to 1, as is the original distribution, and it also admits the same average square transverse momentum, given by

$$\begin{aligned} \langle K_\perp ^2\rangle =2\beta E^2 A \end{aligned}$$

(5.81)

with E the maximum energy allowed for single gluon emission. $\beta$ is in general obtained from

$$\begin{aligned} \beta =\int \mathrm{d}^4 n \theta (n_0)n_0\delta (n_0-1)j_\mu (n)j^{*\mu }(n) \delta (n^2) \end{aligned}$$

(5.82)

with

$$\begin{aligned} j_\mu (n)=\frac{ie}{ (2\pi )^{3/2} } \sum \epsilon _i \frac{p_{i\mu }}{p_i\cdot n}. \end{aligned}$$

(5.83)

The sum runs on all the emitting particles of momenta $p_{i\mu }$, and with $\epsilon _i=\pm$ depending on whether the particle is positively or negatively charged, entering or leaving the scattering area.

5.7.8 Reggeisation of the photon

In the previous subsection, we have discussed photon resummation. Here we turn to the question of Reggeisation in QED and, in the next subsection, in QCD. Both play an important role in models for the total cross section. In fact, while the Froissart bound regulates the asymptotic behavior of total cross sections, asymptotic Regge behavior of the scattering amplitudes and the optical theorem allow direct calculation of the total cross section. Thus, the question of Reggeisation in QED and later in QCD became the center of attention in the 1960s and 1970s.

The question in the early ’70s was whether the photon reggeises and soon after the discovery of QCD, whether the gluon reggeises. Related questions in QED and QCD were regarding the vacuum channel leading singularity which we shall call the Pomeron. Reggeisation of gauge bosons, in Abelian and non-Abelian gauge theories, has played an important role in models for the total cross section. These fundamental questions of compelling relevance for the theories as well as for high energy phenomenology were vigorously pursued by several groups and in Sect. 5.8.1 we shall discuss the BFKL approach, starting with Lipatov and Fadin and Kuraev, then by Lipatov and Balitsky, on the gluon Regge trajectory [184,185,186]. These analyses can be followed more easily if a discussion of the photon Regge trajectory is first introduced. To this we now turn.

Reggeisation of elementary particles such as the photon or the electron was amply discussed in the 1960s. In QED, the infrared divergence and its cancellation bore many complications and the conclusion was that the electron reggeised, not so for the photon. The electron in fact had been shown to reggeise by Gell-Mann et al. in a massive photon (Abelian) QED up to the fourth order [187] and by Cheng and Wu to the sixth order. Such a theory possesses a conserved current but due to the mass of the photon, there are no IR divergences. Radiative corrections turned the elementary electron inserted into the Lagrangian into a moving Regge trajectory passing through $j = 1/2$ at the mass m of the electron. Such a miracle did not occur for the massive photon; it did not turn into a Regge pole. Moreover, in the vacuum channel, in the leading logarithmic approximation (LLA), no “Pomeron” trajectory but a fixed square root branch point at the angular momentum $j = 1 + (11 \pi /32) \alpha ^2$ was found [156].

The question remained open as to what happens in massless QED. The reggeisation of a massless photon poses a problem in that all charged particle scattering amplitudes have IR divergences which are cancelled in the cross sections. Through a summation of IR radiative corrections (not needed in the massive abelian theory) and imposition of di-triple Regge behavior, it was found by Pancheri [188] that a photon trajectory does emerge.

In other words, a reggeised behaviour of QED cross sections can be obtained from the well known factorisation and exponentiation of infra-red corrections and, from this, a trajectory for the photon, as was shown in [188]. We shall describe it here.

In this approach, just as later in the approach to the gluon trajectory of Lipatov et al., reggeisation arises through the exponentiation of single soft photon emission accompanying the scattering. Since in QED any reaction is necessarily an inclusive one because of soft photon radiation, the process to examine is

$$\begin{aligned} e(p_1)+e(p_2)\rightarrow e(p_3)+e(p_4) + X \end{aligned}$$

(5.84)

where X stays for any undetermined number of soft photons, hence for which $M_X^2\ll s$, where $s=(p_1+p_2)^2$. One can now compare the cross section for process (5.84) with the one corresponding to the di-triple Regge limit in hadronic physics [189]. Defining the 5 independent invariants of process Eq. (5.84) as

$$\begin{aligned}&s_1=(p_1+p_2-p_3)^2,\quad s_2=(p_1+p_2-p_4)^2,\end{aligned}$$

(5.85)

$$\begin{aligned}&t_1=(p_2-p_4)^2,\quad t_2=(p_1-p_3)^2,\end{aligned}$$

(5.86)

$$\begin{aligned}&M^2_X=(p_1+p_2-p_3-p_4)^2, \end{aligned}$$

(5.87)

the limit $t_1\simeq t_2=t$ with t fixed, and $M^2_X\ll s,s_1,s_2$, we are within one of the kinematic limits of interest for the inclusive di-triple Regge limit. For $-t\ll s, M^2_X\ll s\simeq s_1\simeq s_2$, the cross section of interest becomes

$$\begin{aligned} \frac{\mathrm{d}^2\sigma }{\mathrm{d}t \mathrm{d}(M^2_X/s)}\rightarrow \left( \frac{M^2_X}{s} \right) ^{1-2\alpha _\gamma (t)} F(t). \end{aligned}$$

(5.88)

We have seen that for X corresponding to a four-vector $K^2\ll s$ soft photon resummation applied to Eq. (5.84) at leading order leads to

$$\begin{aligned} \frac{\mathrm{d}^5\sigma }{\mathrm{d}t\mathrm{d}^4 K}=\left( \int \mathrm{d}^4 x \mathrm{e}^{iK\cdot x -h(x)} \right) \frac{\mathrm{d}\sigma _0}{\mathrm{d}t} \end{aligned}$$

(5.89)

where $\mathrm{d}\sigma _0/\mathrm{d}t$ corresponds to the Born cross section for $\mathrm{e}^+\mathrm{e}^-\rightarrow \mathrm{e}^+\mathrm{e}^-$ and the resummed soft photon spectrum is obtained from the regularised soft photon spectrum

$$\begin{aligned} h(x)=\int \mathrm{d}^3{\bar{n}(k) }[1-\mathrm{e}^{-ik \cdot x}]. \end{aligned}$$

(5.90)

One can rewrite the single photon spectrum as

$$\begin{aligned} \mathrm{d}^3{\bar{n}(k) }=\beta (s,t,u)\frac{\mathrm{d}^3k}{2k}f(\varOmega _k) \end{aligned}$$

(5.91)

where the function $f(\varOmega _k)$ is normalised to 1 and gives the angular distribution of the emitted soft photon. With such a definition, the dependence from the momenta of emitting particles is specified by $\beta (s,t,u)$, which is a relativistic invariant function of the Mandelstam variables. This compact expression is useful when overall integration over the soft photon momenta is performed. From

$$\begin{aligned} \frac{\mathrm{d}P(\omega )}{\mathrm{d}\omega }=\int \mathrm{d}^3{\mathbf {K}} \frac{\mathrm{d}^4 P}{\mathrm{d}^4K}=\int \frac{\mathrm{d}t}{2\pi } \mathrm{e}^{i\omega t -h(t)} \end{aligned}$$

(5.92)

and

$$\begin{aligned} h(t)=\beta (s,t,u)\int \frac{\mathrm{d}k}{k}[1-\mathrm{e}^{-ikt}] \end{aligned}$$

(5.93)

the overall energy dependence from soft photon emission is now

$$\begin{aligned} \frac{\mathrm{d}P(\omega )}{\mathrm{d}\omega }=\mathcal{N}\beta (s,t,u)\frac{\mathrm{d}\omega }{\omega } \left( \frac{\omega }{E}\right) ^{\beta (s,t,u)} \end{aligned}$$

(5.94)

where E is a typical scale of the process, and $\mathcal {N}$ a normalisation factor, i.e.

$$\begin{aligned} \mathcal{N}=\frac{\gamma ^{-\beta (s,t,u)}}{\varGamma (1+\beta (s,t,u))} \end{aligned}$$

(5.95)

$\gamma$ being the Euler constant. To leading order, E is the upper limit of integration of the soft photon spectrum, and can be taken to be proportional to the emitter energy. This choice of the scale makes it easier to modify Eq. (5.94) when higher order corrections are considered [152].

We can now inspect the function $\beta (s,t,u)$ which will lead us to a phenomenological definition of the photon trajectory through Eqs. (5.94) and (5.88). For process (5.84), one has

$$\begin{aligned} \beta (s,t,u)=-\frac{\mathrm{e}^2}{2(2\pi )^3}\int \mathrm{d}^2 {\hat{n}}\sum _{i,j=1}^4 \frac{p_{i\mu } \epsilon _i}{p_i\cdot n}\frac{p_j^\mu \epsilon _j}{p_j\cdot n} \end{aligned}$$

(5.96)

with the four-vector $n^2=0$, $\epsilon _i=\pm 1$, for an electron or a positron in the initial state, or positron and electron in the final and the integration is over the angular distribution $\mathrm{d}^2 {\hat{n}}$. Performing this integration leads to the following expressions

$$\begin{aligned}&\beta (s,t,u)=\frac{2 \alpha }{\pi }\{ I_{12}+I_{13} -I_{14}-2\},\end{aligned}$$

(5.97)

$$\begin{aligned}&I_{ij}=2(p_i\cdot p_j)\int _0^1 \frac{\mathrm{d}y}{m^2+2y(1-y)[(p_i\cdot p_j)-m^2]}.\nonumber \\ \end{aligned}$$

(5.98)

The soft photon approximation is the elastic approximation of Eq. (5.84) and one can now take the Regge limit $s\gg -t, -u$ and $s\gg m^2$, i.e.

$$\begin{aligned} I_{12}-I_{14}\rightarrow 0\quad t\ll s, \ s\rightarrow \infty \end{aligned}$$

(5.99)

obtaining, in this limit,

$$\begin{aligned}&\beta ({s,t,u})\rightarrow \beta (t)\nonumber \\&\quad =\frac{2\alpha }{\pi }\left[ (2m^2-t)\int \frac{\mathrm{d}y}{m^2-ty(1-y)}-2 \right] . \end{aligned}$$

(5.100)

We notice that this function has the correct limit $\beta (t)\rightarrow 0$ for $t=0$, since this is the exact elastic limit and it corresponds to no radiation at all at $t = 0$.

The next step is to integrate Eq. (5.94) up to a maximally observable $\varDelta E$ using as a scale the c.m. energy of the process (5.84), i.e. $s=4E^2$. Then one obtains

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t} = \left( \frac{\varDelta E}{\sqrt{s}}\right) ^{ \beta (t)} \left( \frac{\mathrm{d}\sigma _0}{\mathrm{d}t}\right) . \end{aligned}$$

(5.101)

We can now establish a correspondence between the correction rising from soft photon emission and the di-triple Regge limit of Eq.  (5.88). This can be done by integrating the spectrum of the inclusive mass $M^2_X$ up to the maximally allowed value, which we can call $\varDelta E$ in the case of no momentum resolution. We then immediately get

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}t}=\int \mathrm{d}{M^2_X/s}\frac{\mathrm{d}^2\sigma }{\mathrm{d}t \mathrm{d}(M^2_X/s)},\end{aligned}$$

(5.102)

$$\begin{aligned}&\quad \rightarrow \left( \frac{M^2_X}{s}\right) ^{2(1- \alpha _{\gamma }(t))}=\left( \frac{\varDelta E}{\sqrt{s}}\right) ^{4(1-\alpha _\gamma (t))} \end{aligned}$$

(5.103)

and hence are led to the correspondence

$$\begin{aligned} \alpha _\gamma (t)=1-\frac{\beta (t)}{4} \end{aligned}$$

(5.104)

and to [188]

$$\begin{aligned}&\alpha _\gamma (t)\nonumber \\&\quad =1-\frac{\alpha }{\pi }\left( \frac{2m^2_e-t}{\sqrt{-t} \sqrt{4m^2_e-t}}\log \frac{\sqrt{4m^2_e-t}+\sqrt{-t}}{\sqrt{4m^2_e-t} -\sqrt{-t}}-1\right) .\nonumber \\ \end{aligned}$$

(5.105)

Notice that to establish the above correspondence one had to assume Eq. (5.88), which obtains from the di-triple Regge limit with a vacuum trajectory $\alpha _V(0)=1$, i.e. the cross section for two reggeised photons into any final state

$$\begin{aligned} R_\gamma +R_\gamma \rightarrow X \end{aligned}$$

(5.106)

is controlled at large energy by a trajectory $\alpha _{\mathrm{vacuum}} (0)=1$. This assumption seems reasonable [for estimates about the photon trajectory computed to order $\alpha$] since the perturbative result for the vacuum trajectory is a branch cut, but whose deviation from unity begins at order $\alpha ^2$.

To summarise: the proposed photon trajectory [188]

$$\begin{aligned} \alpha _\gamma (t)=1-\frac{\alpha }{2\pi }\left[ (2m_\mathrm{e}^2-t)\int _o^1\frac{\mathrm{d}y}{m^2_e-ty(1-y)}-2\right] \nonumber \\ \end{aligned}$$

(5.107)

is an expression obtained in the large s, small t limit, from resummation of all soft photons emitted in the scattering $\mathrm{e}^+\mathrm{e}^-\rightarrow \mathrm{e}^+\mathrm{e}^-$. In these expressions, $m_e$ is the mass of the fermion which emits the soft photons and the expression exhibits a threshold behaviour with a square root singularity (Notice that being fermions, the threshold behaviour is different from the one required for a pion loop, for instance). The above expression may also be expressed as a dispersion integral

$$\begin{aligned}&\alpha _\gamma (t)=1-\frac{\alpha }{\pi }\left[ (2m_\mathrm{e}^2-t)\phantom {\int }\right. \end{aligned}$$

(5.108)

$$\begin{aligned}&\qquad \times \left. \int _{4m_\mathrm{e}^2}^\infty \frac{\mathrm{d}t^{\prime }}{(t^{\prime } - t - i\epsilon )\sqrt{(t^{\prime }(t^{\prime } - 4m_\mathrm{e}^2))}} - 1\right] \nonumber \\&\quad = 1 + \left( \frac{\alpha }{\pi }\right) t \int _{4m_\mathrm{e}^2}^\infty \frac{\mathrm{d}t^{\prime } (t^{\prime } - 2m_\mathrm{e}^2)}{t^{\prime }(t^{\prime } - t - i\epsilon )\sqrt{(t^{\prime }(t^{\prime } - 4m_\mathrm{e}^2))}}\nonumber \\ . \end{aligned}$$

(5.109)

From Eq. (5.108), we may directly compute the imaginary part of the photon trajectory, which is positive definite:

$$\begin{aligned} \mathfrak {I}m\ \alpha _\gamma (t)= \vartheta (t - 4 m_\mathrm{e}^2) \alpha \frac{(t - 2m_\mathrm{e}^2)}{\sqrt{(t(t - 4m_\mathrm{e}^2))}}, \end{aligned}$$

(5.110)

and which has the asymptotic limit

$$\begin{aligned} \mathfrak {I}m\ \alpha _\gamma (t) \rightarrow \ \alpha ,\quad \mathrm{for}\ t \gg 4 m_\mathrm{e}^2, \end{aligned}$$

(5.111)

exactly the same result found by Lipatov for the iso-spin one vector boson trajectory in non-Abelian SU(2) model with a doublet Higgs field [184]. We shall discuss it in the next subsection.

We see that the trajectory goes to 1 as $t\rightarrow 0$, in addition to having the threshold singularity corresponding to the fermion loop. The actual $t\rightarrow 0$ and $|t|\rightarrow \infty$ limits are also easily taken and lead to

$$\begin{aligned} \alpha _\gamma (t)\rightarrow & {} 1-\left( \frac{\alpha }{3\pi }\right) \frac{-t}{m^2_e}\quad |t|\ll m^2_e,\end{aligned}$$

(5.112)

$$\begin{aligned} \alpha _\gamma (t)\rightarrow & {} 1-\frac{\alpha }{\pi } \log \frac{-t}{4m^2_e}\quad |t|\gg 4m^2_e \end{aligned}$$

(5.113)

namely one recovers the linearity of the trajectory at small |t| and the asymptotic logarithmic limit at large t.

5.7.9 Comments on the reggeisation of the photon

In the literature, one finds the statement that in QED the photon does not reggeise [see, for example Gell-Mann et al. [187]], apparently in conflict with the Regge trajectory for the photon $\alpha _\gamma (t)$ found and discussed in the previous section. Hence, an explanation for the seeming discrepancy is mandatory.

The question of Reggeisation in field theory was begun by Gell-Mann et al. in the 1960s and continued in subsequent literature [190,191,192]. Precisely to avoid IR divergences due to the zero mass of the photon, they and most others, considered massive fermion QED with a conserved vector current but with a massive photon (vector boson). Then perturbation theory was used to show that up to the sixth order the fermion reggeises whereas the vector boson (photon) did not.

On the other hand, massless QED requires a resummation making it non-perturbative and under the hypotheses stated in the previous section, the photon does reggeise. Moreover, it was found in [193] that all gauge vector bosons – including the photon – reggeise in a grand unified theory [GUT] based on a semi-simple group with a single coupling constant. However, it is difficult to assign significance to the result obtained in [193] in view of the lack of any phenomenological confirmation of GUT.

The problem of reggeisation of the gauge bosons in the electro-weak $SU(2)\times U(1)$ theory has been discussed in the leading log approximation by Bartels et al. in [194]. Through a set of bootstrap equations they find that the W boson does reggeise whereas the $Z^o$ and the photon do not.

5.8 High energy behaviour of QCD scattering amplitudes in the Regge limit

In the preceding section, we have described in some detail the question of gauge boson trajectories because in Regge theory, the high energy behavior of the scattering amplitude is given by the exchange of Regge trajectories. We have shown there how an effective Regge-like behaviour can be obtained in QED, from soft photon resummation in charged particle reactions. In QCD, the role of soft photons is taken on by soft gluons, but, as we know, with enormous differences: not only a running coupling constant, but also an unknown (very likely a singular) behavior in the infrared. On the other hand, QCD resummation is fundamental to the cross sections, since, at high energy, the behavior of the total cross section is dominated by large distance effects, which correspond to very small momenta, and this immediately leads to the question of resummation of such quanta with very small momenta.

While at low energy Reggeons (such as the $\rho$ trajectory) dominate the hadronic scattering amplitude, at high energy the leading effect is obtained through a Pomeron exchange, in correspondence with a leading vacuum singularity in an even charge conjugation channel, $C=+1$. Thus theoretically, it was natural to identify the Pomeron as emerging from the exchange of two gluons (accompanied by soft-gluon resummation) which does not change the quantum numbers of the process. Phenomenologically, the one-to-one correspondence between the asymptotic total cross section and the Pomeron trajectory, made the Pomeron go from a fixed pole ($\alpha _P= 1$) at low energies, to a moving pole with intercept larger than one, to justify the rising cross section observed at the ISR. As for the $C=-1$ possible partner of the Pomeron, it is called an Odderon, but it is an object so far only seen clearly in theoretical papers, as recently quibbed in [195]. The Odderon is also a QCD effect, and its trajectory so far seems to correspond to a constant $\alpha _O=1$. We shall briefly discuss the Odderon in Sects. 5.8.2 and 5.8.3.

Clearly, for phenomenological applications, the dynamics of scattering among quarks and gluons needs to be understood, from high-$p_t$ jets to that of the infrared gluon emission. In particular, for scattering in the soft region, the zero momentum region needs to be incorporated adequately. Since the latter, and most important aspect of the problem, has not yet been completely solved, we can only try to give here some specific examples of how one approaches the problem of the total cross section in QCD, starting with the preliminary building blocks such as the Balitsky–Fadin–Kuraev–Lipatov (BFKL) equation in Sect. 5.8.1, followed by the Gribov, Levin and Ryskin (GLR) treatment in Sect. 5.8.4 and then the Balitsky, Kovchegov, Peschanski equation in Sect. 7.3. A specific model that realises many of these QCD notions, the Durham-St. Petersburg model, will be presented in Sect. 5.8.5 and then rediscussed in more detail in Sect. 6. Recently an extensive description of QCD as applied to the high energy scattering amplitudes in the Regge limit has appeared [196], with both a theoretical and experimental up-to-date outlook. The field is very vast and cannot be covered in depth in this review. In the following, we shall attempt to outline some of the most important physics chapters in the story hoping that our summary would provide a starting point to a worker interested in the field.

5.8.1 Non abelian gauge theory with Higgs symmetry breakdown and the BFKL integral equation

With the advent of SU(2) Yang Mills (YM) theory containing a triplet of vector gauge bosons which acquire a mass through an iso-doublet Higgs field, investigations turned into answering the reggeisation questions for the massive gauge bosons and the Pomeron in the vacuum channel of the theory. Such a theory is renormalisable and endows the gauge vector bosons a mass M through the spontaneous symmetry breakdown mechanism.

In a series of papers, Lipatov et al. [184], Fadin, Kuraev and Lipatov [197, 198]; Balitsky and Lipatov [199,200,201], did fundamental work in this field which goes under the generic name of the BFKL formalism.

Lipatov et al. found that the gauge vector boson reggeises, i.e., the elementary iso-vector gauge particle of angular momentum $j = 1$ at mass $t = M^2$ turns into a Regge trajectory. Their expression may be written as a dispersion integral

$$\begin{aligned} \alpha _V(t)= & {} 1 + \frac{\alpha _{YM}}{\pi } (t - M^2)\nonumber \\&\times \int _{4M^2}^\infty \frac{\mathrm{d}t^{\prime }}{(t^{\prime } - t - i\epsilon )\sqrt{(t^{\prime }(t^{\prime } - 4M^2))}}, \end{aligned}$$

(5.114)

where $\alpha _{YM} = g^2/(4\pi )$ and g is the gauge coupling constant. The above expression verifies explicitly that the gauge vector boson trajectory goes to 1 at $t = M^2$.

It is instructive to note the remarkable similarity between the expression Eq. (5.108) for $\alpha _\gamma (t)$ found in QED with the gauge vector boson trajectory given in Eq. (5.114). $\alpha _\gamma$ goes to 1 at the physical mass $t = 0$ of the QED gauge boson (the photon), just as the non-Abelian gauge boson trajectory $\alpha _V$ goes to 1 at its physical mass $t = M^2$. Furthermore, the absorptive part of $\alpha _V(t)$ reads

$$\begin{aligned} \mathfrak {I}m\ \alpha _V(t)= \vartheta (t - 4 M^2) \alpha _{YM} \frac{(t - M^2)}{\sqrt{(t(t - 4M^2))}}, \end{aligned}$$

(5.115)

and it differs from its corresponding expression Eq. (5.110) for $\mathfrak {I}m\ \alpha _\gamma (t)$ in the replacement $(\alpha , m_e)\ \rightarrow \ (\alpha _{YM}, M)$ and in the numerator ($t - 2m_\mathrm{e}^2$) to ($t - M^2$). Asymptotically, as stated earlier, the difference vanishes. For large |t|, both imaginary parts go to their respective $\alpha$ or $\alpha _{YM}$.

The situation regarding the vacuum channel or the nature of the Pomeron in this YM theory is still rather obscure. In Lipatov’s original paper, it is stated that if only two particle singularities in the t channel were included, a bare Pomeron trajectory did emerge which may be transcribed in the form

$$\begin{aligned} \alpha _P^{(o)}(t)= & {} 1 + \frac{\alpha _{YM}}{\pi } (2t - 5M^2/2) \nonumber \\&\times \int _{4M^2}^\infty \frac{\mathrm{d}t^{\prime }}{(t^{\prime } - t - i\epsilon )\sqrt{(t^{\prime }(t^{\prime } - 4M^2))}}. \end{aligned}$$

(5.116)

But going further and including three particle thresholds in the t channel, led Lipatov to conclude that there is a branch cut in the angular momentum plane in the vacuum channel due to the exchange of two reggeised vector bosons. This was confirmed in a later paper by Fadin, Kuraev and Lipatov. They obtained the result that the leading j-plane singularity in the vacuum channel is a branch point at $j =\ 1 + \alpha _{YM} [8 \ln (2)/\pi ]$ which for an SU(N) theory would read

$$\begin{aligned} \alpha _{\mathrm{Pom}}^{YM} = 1 + \alpha _{YM} \left[ \frac{4 N \ln (2)}{\pi }\right] . \end{aligned}$$

(5.117)

Hence, they conclude that in the main LLA, the total cross sections in a non-abelian gauge theory, would violate the Froissart bound. The reason for this violation is that s channel unitarity is not satisfied in the LLA (which assumes $\alpha _{YM}\ \ln (s/M^2) \sim \ 1$) and presumably a proper computation of the vacuum exchange in the t channel would require excursions beyond LLA which must also include contributions of order $\alpha _{YM}\ \ln (s/M^2) \gg 1$.

At this juncture, s channel elastic unitarity may be imposed via the eikonal expansion as proposed by Cheng and Wu. Such eikonal procedures in various forms have been followed over the years by various groups as discussed in various parts of our review.

Development of ideas and results from QED and non-abelian SU(2) with a Higgs mechanism to the theory of interest namely QCD [unbroken $SU(3)_{\mathrm{colour}}$] runs into a host of well known difficulties. At the level of quarks and glue, one can address the question of the reggeisation of the gluon trajectory. Unlike the YM theory with spontaneous symmetry breakdown which endows the gauge boson with a mass M as discussed in the last subsection, gluon remains massless. The difficulty is seen immediately as $M \rightarrow 0$ in the vector boson trajectory Eq. (5.114), which diverges at the lower limit. The reason for this divergence is clear in that all gauge boson thresholds condense at $t = 0$ as the gauge boson mass vanishes. [Such is not the case for QED due to the absence of non-linear couplings of a photon to itself].

On the other hand, in the large t limit, we see from Eq. (5.115) that, for SU(N) YM, $\mathfrak {I}m\ \alpha _V (t) \rightarrow (\frac{N}{2}) \alpha _{YM}$. Hence, we expect that

$$\begin{aligned} \mathfrak {I}m\ \alpha _{\mathrm{gluon}}(t) \rightarrow \ \left( \frac{3}{2}\right) \alpha _s\quad \mathrm{as}\ t \rightarrow \infty , \end{aligned}$$

(5.118)

[at least for constant $\alpha _s$]. This expectation agrees with explicit computations by Lipatov, Balitsky and Fadin in LLA which reads

$$\begin{aligned}&\alpha _{\mathrm{gluon}}(t) -1 = \left[ \left( \frac{3 t}{2\pi ^2}\right) \alpha _s\right] \int \frac{(\mathrm{d}^2k)}{k^2 [(q - k)^2]}\nonumber \\&\quad \approx \ - \left( \frac{3}{2\pi }\right) \alpha _s \ln (-t/\lambda ^2) . \end{aligned}$$

(5.119)

The scale $\lambda$ corresponds to the lower integration cut-off, introduced to avoid the IR region where perturbative QCD cannot be applied.

It is useful to note the similarities and differences betweens BFKL and the approach to the photon trajectory obtained through resummation in QED, as described in Sect. 5.7.8. In that approach, and its extension to QCD leading to what we call the BN (for Bloch Nordsieck) model for the total cross section (see Sect. 5.9.4), the IR divergence is cancelled at the level of the observable cross sections and the asymptotic behavior is obtained directly from the cross section. On the other hand, the BFKL result is obtained in terms of matrix elements, which are calculated in different orders in the coupling constant through dispersion relations and unitarity.

In our approach [188] for the photon trajectory, we obtain both a linear term in t for small t values as well as a logarithmic behavior for large t. For large t, the correspondence between the two trajectories $\alpha _\gamma (t)$ as given by Eq. (5.113) and $\alpha _{\mathrm{gluon}}(t)$ as given by Eq. (5.119) [written for $SU(N_c)$] is immediate:

$$\begin{aligned} -\frac{\alpha }{\pi } \ln \left( \frac{-t}{4m^2}\right) \mapsto -\frac{\alpha _s N_c }{2\pi }\ln \left( \frac{-t}{\lambda ^2}\right) , \end{aligned}$$

(5.120)

from which the substitution $\alpha \rightarrow (N_c/2)\alpha _s$ maps one into another. The small t-behaviour is much more complicate, because of the unknown infrared behaviour of the strong coupling constant. In Sect. 5.9.4 we shall describe a model for the coupling constant, which allows one to apply resummation in the infrared region, and its application to total cross section studies.

For high energy hadronic (or, photonic) amplitudes, we are primarily interested in the nature of the Pomeron emerging from QCD. The physical underlying picture is that a Pomeron is a bound state of two Reggeised gluons. For this purpose the BFKL approach may be summarised as follows. In LLA, colour singlet hadronic/photonic amplitudes are related to their angular momentum amplitudes through a Mellin transform

$$\begin{aligned}&A(s, t= - q^2) = is \int _{\sigma -i\infty }^{\sigma +i\infty } \left[ \frac{\mathrm{d}\omega }{2\pi i}\right] s^\sigma f_\sigma (q^2)\nonumber \\&f_\sigma (q^2) = \int (\mathrm{d}^2k)(\mathrm{d}^2k^{\prime }) \mathbf{\varPhi }^{(1)}(k,q) \mathbf{\varPhi }^{(2)}(k^{\prime },q) f_\sigma (k,k^{\prime }; q),\nonumber \\ \end{aligned}$$

(5.121)

where $k,k^{\prime }$ denote the transverse momenta of the exchanged gluons and the function $f_\sigma (k, k^{\prime }; q)$ can be interpreted as the t channel partial wave amplitude for gluon–gluon scattering with all gluons off mass shell, with squared masses: $- k^2$, $-k'^2$, $-(q-k)^2$, $-(q - k^{\prime })^2$. The gluon propagators are included in the function $f_\sigma (k, k^{\prime }; q)$. The $\mathbf{\varPhi }^{1,2}$ functions describe the internal structure of the colliding particles 1 and 2. Gauge invariance is then imposed so that

$$\begin{aligned} \varPhi ^{1,2}(k, q)|_{k=0} = 0 = \varPhi ^{1,2}(k, q)|_{k=q}. \end{aligned}$$

(5.122)

This property is crucial for using a gluon mass $\mu$ in its propagator (as in the SSB YM theory of the last subsection) because for colour singlet states there is no IR divergence and the limit $\mu \rightarrow 0$ exists. There is no such IR safety for colour non-singlet amplitudes.

Armed with the above, for high energy analysis of colour singlet amplitudes, one may imagine to freely employ all the results of the SSB YM of the last subsection extended to the $SU(N=3)$ case. But such is not the case basically because of asymptotic freedom, i.e., $\alpha _{YM}$ must be replaced by $\alpha _s(q^2)$, which for large $q^2$ goes to zero logarithmically

$$\begin{aligned} \alpha _s(q^2) \rightarrow \ \frac{4 \pi }{(11 N- 3n_f) \ln (q^2/\varLambda ^2)};\quad \mathrm{for}\ q^2\gg \varLambda ^2\nonumber \\ \end{aligned}$$

(5.123)

with $n_f$ the number of flavours. On the other hand, for $q^2 \le \ \varLambda ^2$, $\alpha _s$ begins to diverge and hence perturbative QCD becomes inapplicable. However, one may derive some useful results in the symptomatic freedom (AF) limit. As $\ln (q^2/\varLambda ^2)\gg 1$, an infinite set of poles condense to $j \rightarrow 1$, whose behaviour may be approximately described through a moving cut

$$\begin{aligned} \alpha _{\mathrm{Pom}}(q^2)|_{\ln (q^2/\varLambda ^2)\gg 1} \rightarrow 1 + \left[ \frac{4N \ln (2)}{\pi }\right] \alpha _s(q^2). \end{aligned}$$

(5.124)

The fixed Pomeron branch cut at $\alpha _{\mathrm{Pom}}^{YM} = 1 + [\frac{4N \ln (2)}{\pi }] \alpha _{YM}$ found in Eq. (5.117) is “made to move” as $\alpha _s(q^2)$ for large $q^2$.

In various phenomenological models [186, 202, 203] on the other hand, the Pomeron trajectory is taken to asymptote to $-\infty$ as $q^2 \rightarrow \infty$

$$\begin{aligned} \alpha _P(q^2) = \alpha (0) - \alpha _1 \ln (1 + \alpha _2 q^2), \end{aligned}$$

(5.125)

thus the forward slope of the Pomeron – not directly coupled to $\alpha (0)$ – is given by

$$\begin{aligned} \alpha _P^{\prime }(0) = \alpha _1 \alpha _2. \end{aligned}$$

(5.126)

5.8.2 The Odderon

In the following, we shall first give a brief introduction to the Odderon. The Odderon was first introduced on phenomenological grounds in the early 1970s by Lukaszuk and Nicolescu [204] as a $C=-1$ exchange term in the amplitude, and further discussed in [205]. Since then, there has been no experimental confirmation of its existence, although no confirmation of its non-existence has arrived either. One reason for this sort of limbo in which the Odderon lives is that this is not a dominant effect and since fitting of the data requires a number of terms and concurrent parameters, it is often possible to mimic its presence by adding some terms.

Consider the crossing-odd amplitudes in pp and $p\bar{p}$ scatterings defined as

$$\begin{aligned} F_{-} = \frac{1}{2} [F_{pp} - F_{p\bar{p}}]. \end{aligned}$$

(5.127)

Basically, there are three types of Odderons classified according to their increasing order in energy asymptotic behaviour [50]:

• Order zero Odderons $F_{\mathrm{odd}}^{(0)}$ are real and hence only change the real parts of the elastic amplitudes

• Order one Odderons $F_{\mathrm{odd}}^{(1)}$ change the cross section (between a pp and $p\bar{p}$) by a constant amount

• Order two Odderons $F_{\mathrm{odd}}^{(2)}$ [also called maximally singular] lead to a cross section difference increasing as $\ln (s/s_o)$ as well as real parts that are not equal asymptotically.

Given that the high energy elastic amplitudes are predominantly imaginary, the zero order Odderons are hard to look for. For obvious reasons, the hunt has been to look for order two or maximally odd amplitudes. We shall discuss in various places the results of such searches.

Another quantity which could shed light on the presence of the Odderon, is the parameter $\rho (s)$, the ratio of the real to the imaginary part of the scattering amplitude for hadrons in the forward direction. Possibly, the rather precise measurements of this parameter at LHC could allow one to draw some conclusions about its presence. From this point of view, we notice that the somewhat low, preliminary value for the parameter $\rho$ at LHC8 could be invoked to be a signal of the Odderon. Also diffractive production of pseudo-scalar and tensor mesons in ep scattering are suggested to be a good place were effects from the Odderon could be detected.

An extensive review of the status of the Odderon appeared in 2003 by Ewerz [206]. The Odderon could be responsible for the difference between the elastic differential cross sections for $pp,\ p {\bar{p}}$, past the forward peak. According to Ewerz [207] for instance, hadronic exchanges occurring only through mesonic reggeons are not sufficient to explain the cancellation of the dip in ${\bar{p}}p$. In this respect however, one can see that the dip may be slowly reappearing in $\ p {\bar{p}}$, as some analysis of the data show. One can in fact observe that $p {\bar{p}}$ data for the elastic differential cross section from ISR to the TeVatron indicate that the observed change in curvature becomes more and more pronounced as the energy increases. Whatever the Odderon does, it would seem that as the energy increases, it may disappear.

A discussion of the “missing Odderon” can be found in Donnachie, Dosch and Nachtmann [208] where once more the evidence for the phenomenological Odderon is discussed and found lacking.

A proposal was made to detect the Odderon at RHIC and LHC by Avila, Gauron and Nicolescu [209]. The model by Avila, Campos, Menon and Montanha which incorporates both the Froissart limiting behavior as well as Pomeron and Regge exchanges [210] is described later in the elastic scattering chapter.

5.8.3 Odderons in QCD

In the Regge language, an Odderon is defined [211] as a singularity at the angular momentum $J = 1$ at $t = 0$ in the crossing-odd amplitude. Hence, the obvious question arose as to whether an Odderon could be associated with three-gluon exchanges in QCD [212,213,214] and a definite affirmative answer in pQCD was obtained in [215].

Presently, apart from the phenomenological interest, there has been a strong QCD attention paid to NLO corrections to the Odderon trajectory [216] and on the properties of the Odderon in strong coupling regime [217].

In [195], a model for soft high-energy scattering, which includes a tensor Pomeron and vector Odderon has appeared with detailed description of Feynman-type rules for effective propagators and vertices.

5.8.4 Gribov–Levin–Ryskin (GLR) model

In 1984 Gribov, Levin and Ryskin [218] wrote a paper meant to establish the theoretical basis of a QCD approach to parton scattering, in which the focus was on semi-hard scattering. In the first section they defined semi-hard scattering. The framework is that of deep inelastic scattering as in Fig. 39. The focus on DIS has resulted in introducing an external scale $q^2$ which rendered the extrapolation to real photons and, for a while, application to purely hadronic processes difficult.

Fig. 39

Deep inelastic scattering representative figure from [218]. Reprinted from [218], ©(1984) with permission by Elsevier

GLR argument starting point is that, as the fractional energy of the scattering partons, x, decreases, the increase of the number of partons can be so high as to give a cross section as large, or even larger, as the actual hadronic cross section. But this cannot continue indefinitely. When the density of partons becomes very large, the partons within a given hadron cannot be any more considered to be independent and they instead start to interact with each other. GLR define the probability $W(x,q^2)$ that partons interact with each other in a hadron as

$$\begin{aligned} W(x,q^2)=\frac{\alpha _s(q^2)}{q^2 R^2_h}F(x,q^2) \end{aligned}$$

(5.128)

where $F(x,q^2)$ is the parton density function, i.e. gives the number of partons which interact with the probing virtual photon, and $R_h$ the hadron radius. In Eq. (5.128), the ratio $\frac{\alpha _s(q^2)}{q^2}$ is the parton–parton cross section and $\varDelta b^2_\perp =R^2_h/F(x,q^2)$ is the average perpendicular distance between partons, measured through the area where they are and the number density. This is a semi-classical description. When the parton–parton cross section is smaller than the average distance, $W<1$ and for $W \ll 1$ rescattering will not occur, when it is larger, i.e. $W\lesssim 1$ rescattering will occur. $W= 1$ is called the unitarity limit. This function allows then to distinguish three regions in the x-variable, depending on whether pQCD applies (or does not apply) for the calculation of the parton density function $F(x,q^2)$. Thus, while there is a whole region where nothing can be obtained, for $W\le \alpha _s$ the authors have been able to obtain interesting results.

It is worth noting that their picture [Fig. 1.9 of their paper] is at the basis of the subsequent work by this group. Consider then the function $F(x,q^2)$ rewritten as

$$\begin{aligned} F(x,q^2)=W(x,q^2) \frac{q^2 R^2_h}{\alpha _s(q^2)}, \end{aligned}$$

(5.129)

which is plotted as a function of x in Fig. 40. The curve denotes the region $W(x,q^2)\le 1$. The subsequent behaviour is controlled by the ratio $W/\alpha _s$, both numbers being less than 1.

One distinguishes 3 regions, with regions B and region C separated at a value $x_b(q^2)$, where $F(x,q^2)=q^2 R^2_h$. For $x<x_b$, $q^2 R^2_h<F\le \frac{q^2 R^2_h}{\alpha _s(q^2)}$. In region C, $W/\alpha _s>1$. Here the interactions are very strong and near the unitarity limit, and the authors have not be able to take them into account. Region A, is where $W\ll \alpha _s$, region where pQCD applies, it correspond to large $x\sim 1$ and parton interactions are negligible. In region B, $W/\alpha \lesssim 1$ and, for W not too large, the authors say that with the Reggeon-type diagram technique developed in subsequent chapters they are able to take into account interactions in this region. However, if Wis largish, $W \sim 1$, they have not been able to sum all the essential diagrams and only can give qualitative considerations. We show the three regions in Fig. 40. A is the region where perturbative QCD can be applied, B is the result of this paper, C is not to be obtained yet.

Fig. 40

x-dependence of the structure function from [218]. Reprinted from [218], ©(1984) with permission by Elsevier

There is a useful, again semi-quantitative, argument to determine the value $x_b(q^2)$, which we reproduce in the following. The conditions are

$$\begin{aligned}&F\sim q^2 \quad \hbox {and hence}\quad \ln F \sim \ln q^2,\end{aligned}$$

(5.130)

$$\begin{aligned}&\frac{\partial F}{\partial x} \sim \frac{\alpha _s}{x}F \end{aligned}$$

(5.131)

the second equation indicating that the origin of the partons as the number of partons increase is due to bremsstrahlung (hence the bremsstrahlung spectrum). Using the running $\alpha _s$ expression one obtains

$$\begin{aligned} \frac{\partial \ln F}{\partial \ln x}\sim \frac{1}{\ln F}, \end{aligned}$$

(5.132)

from which

$$\begin{aligned} \ln \frac{1}{x_b(q^2)}\sim \ln ^2 q^2. \end{aligned}$$

(5.133)

After determining this value, the paper goes on to discuss the inclusive jet spectrum, the authors introduce the quantity $k_0$ which corresponds to the limiting value $x_b(k_0^2)$, i.e. $2k_0/\sqrt{s}=x_b(k_0^2)$ and, using Eq. (5.133), with $q^2=k_0^2$, they obtain

$$\begin{aligned}&\ln \frac{1}{x_b(k_0^2)}\sim \ln ^2 (x_b^2),\end{aligned}$$

(5.134)

$$\begin{aligned}&k_0\sim \mathrm{e}^{c\sqrt{\ln s}}. \end{aligned}$$

(5.135)

The last equation obtains by neglecting a $\ln k_0$ term relative to $\ln ^2k_0$ in Eq. (5.133).

As a consequence of the behaviour thus obtained for the increase in the number of partons below $x_b(q^2)$, the authors find that semi-hard processes have a large cross section and contribute substantially to the average multiplicity as well. In particular, since the average multiplicity is proportional to the phase space factor $k_0^2$, one obtains also

$$\begin{aligned} {\bar{n}}\sim \mathrm{e}^{2c \sqrt{\ln {s}}}. \end{aligned}$$

(5.136)

The parameter c is determined in subsequent chapters.

The important result of this paper is that semi-hard processes become responsible for large part of the cross section, because of the behaviour with energy described through the above equations. Just as the average multiplicity increases, the average transverse momentum is also proportional to $k_0$ and thus

$$\begin{aligned} \langle q_t\rangle \sim k_0\propto \varLambda \mathrm{e}^{c \sqrt{\ln s}}. \end{aligned}$$

(5.137)

Therefore at very high energy many jets with comparatively large transverse momenta are produced.

The above qualitative description of the region of small x is then further developed in chapter 2 of the paper. The authors promise to show how to apply the Leading Logarithm Approximation (LLA) to the small x region and to deal with the screening effects due to the parton–parton interactions. Their aim in the second chapter is to calculate the structure function $F(x,q^2)$ when both $\ln q^2/q_0^2$ and $\ln 1/x$ are large. Two problems are encountered: the necessity to develop LLA in two large logarithms and how to deal with unitarity i.e. the increase of the structure function at very small x.

Notice that in the subsection dealing with unitarisation in the Double Logarithm Approximation (DLA), a crucial role is played by the quantity

$$\begin{aligned} \xi - \xi _0 =b\int _{q^2_0}^{q^2} \frac{\mathrm{d}k^2}{k^2} \frac{\alpha _s}{4\pi } \end{aligned}$$

(5.138)

with $b=11N-3N_f$. In their Sect. 3.2, the structure of the theory is developed. One of the conclusions is that it is necessary to take into account not just corrections of the type $\alpha _s \ln (1/x)\ln (q^2)$ but also $\alpha _s \ln (1/x)$ and $\alpha _s \ln (q^2)$, that multi ladder “fan” diagrams in the t-channel are crucial for unitarisation. It is asserted that all other corrections are negligible, at least, up to the normalisation of the structure functions. The asymptotic limit of resumming diagrams which grow as $(\alpha _s \ln (q^2))^n$ and those which grow as $(\alpha _s \ln (1/x))^n$, i.e. the asymptotic behaviour in the DLA, gives

$$\begin{aligned} F\propto \exp \left\{ \sqrt{2(\xi -\xi _0)}y\right\} . \end{aligned}$$

(5.139)

where $y=8N/b\ln 1/x$.

In Sect. 4, a discussion of the Reggeon Diagram Technique (RTD) in QCD is given. In this version of RTD, the primary object is an LLA ladder, which can also be conventionally called a Pomeron. The vertices of interaction between ladders are also calculated in perturbative QCD. In Fig. 41 we reproduce Fig. 3.1 of the GLR paper, where the Pomeron and the vertices are schematically indicated.

Fig. 41

The QCD Pomeron from [218] and the triple pomeron vertices. Reprinted from [218], ©(1984) with permission by Elsevier

Before proceeding, one should notice two important differences with respect to an approach based on mini-jets and soft gluon resummation, such as the one we shall describe in Sect. 5.9.4:

• 1. When dealing with parton–parton probability of interaction or even single jet production as in Eq. (5.3) of their paper, i.e.

  $$\begin{aligned} \frac{E \mathrm{d}\sigma ^{\mathrm{jet}}}{\mathrm{d}^3p}\sim \frac{\mathrm{d}{\hat{\sigma }}}{\mathrm{d}p_t^2} F(x_1,p_t^2)F(x_2,p_t^2)\sim \frac{\alpha _s}{p_t^4} F_1 F_2\nonumber \\ \end{aligned}$$

  (5.140)

  the expression for jet-production is linear in $\alpha _s$, not quadratic; this corresponds to a view in which soft or semi-hard partons are all treated on equal footing, whereas mini-jet models distinguish between hard parton–parton collisions from soft-gluon emission, which is separately resummed.

• 2. The other consideration is an observation at the beginning of Sect. 4.3 of their paper about infrared divergence. The authors acknowledge that the quarks being coloured, the quark–quark amplitude is divergent, but the divergences are absent when discussing the scattering of colourless objects, such as hadrons. The rationale being that the divergences cancel if one takes into account the interactions with the spectator quarks which, together with the interacting quarks constitute the hadron.

Section 5 of the GLR paper is dedicated to large $p_t$ processes. It is in this section, that the gluon Regge trajectory is called in to play an important role in the correlations between two large $p_t$ gluon jets. In this case, the double inclusive cross section in the region

$$\begin{aligned} 1\ll \varDelta \eta \ll \frac{1}{N\alpha _s(p_t^2)} \end{aligned}$$

(5.141)

is given by

$$\begin{aligned}&\frac{ E_cE_d \mathrm{d}\sigma ^{2\text {-}\mathrm{jet}} }{\mathrm{d}^3p_c\mathrm{d}^3p_d}\nonumber \\&\quad = \frac{36}{(16 \pi ^2)^2 p_c^2 p_d^2} \int \frac{\mathrm{d}^2k_1 \mathrm{d}^2k_2 }{\pi ^4} \alpha _s^2(p_t^2)\phi (x_1, k_1^2) \phi (x_2, k_2^2)\nonumber \\&\qquad \times \, \delta ^2(\mathbf{k}_{1t} + \mathbf{k}_{2t} - \mathbf{p}_{ct} - \mathbf{p}_{dt}) \left( \frac{{\tilde{s}}}{4p_{ct}p_{dt}}\right) ^{2{\bar{\alpha }}_G(q_t^2)} T_G^4,\nonumber \\ \end{aligned}$$

(5.142)

with the gluon trajectory given as

$$\begin{aligned} \alpha _G(q_t^2)\simeq \frac{3\alpha _s(q_t^2)}{2\pi }\ln \frac{q_t^2}{\mu ^2}, \end{aligned}$$

(5.143)

and $\mu$ an infrared cut-off introduced because the trajectory is infrared divergent [197, 198]. Of course the infrared divergent part of the reggeisation is cancelled by the emission of real soft gluons. After this is taken into account, it is given as

$$\begin{aligned} {\tilde{\alpha }}_G(p_t^2)=\frac{3\alpha _s(p_t^2)}{2\pi }\ln \frac{p_t^2}{\max \{p_{\varSigma ^2},k_0^2 \}}+\mathcal{O}(\alpha _s), \end{aligned}$$

(5.144)

with $p_{\varSigma }=p_{ct}-p_{\mathrm{d}t}$. Thus

$$\begin{aligned} \frac{ E_cE_d \mathrm{d}\sigma ^{2\text {-}\mathrm{jet}} }{ \mathrm{d}^3p_c\mathrm{d}^3p_d }\propto \left( \frac{{\tilde{s}}}{4p_{ct}p_{\mathrm{d}t}} \right) ^{2{\bar{\alpha }}_G(q_t^2)} T_G^4. \end{aligned}$$

(5.145)

Finally a form factor $T_G$ is defined as follows:

$$\begin{aligned} T_G(p_t^2,(\varDelta p)^2) \simeq \exp \left[ - \frac{3\alpha _s(p_t^2)}{4\pi }\ln ^2\frac{q_t^2}{(\varDelta p)^2}\right] , \end{aligned}$$

(5.146)

which incorporates the probability that the global momentum of the emitted (bremsstrahlung) gluons which accompany the emission of a hard gluon of momentum $p_t$ is smaller than a $\varDelta p\ll p_t$.

Electron–positron processes and the properties of produced jets and correlations are both examined in the remaining part of Sect. 5, and mostly in Sect. 6. After this section, the authors turn to a discussion of the phenomenology of semihard processes from the perturbative QCD viewpoint.

5.8.5 KMR model with BFKL Pomeron

We shall now examine a specific model in which the theoretical input from the BFKL Pomeron is included into a phenomenological application. Models of this type have been developed by various groups, such as the Durham–St. Petersburg group of Khoze, Martin and Ryskin (KMR), the Telaviv group of Gotsman, Levin and Maor (GLM), Ostapchenko et al., among others, and they will also be discussed in Sect. 6. Here we shall describe the model by Khoze et al. [219, 220] which has been applied to both the elastic and the total cross section for quite some time. A description of the KMR model for the total cross section and its extension to elastic scattering can be found in [221]. In this paper, the discussion is focussed on how to take into account the single and double diffractive components of the scattering and the following features are discussed

• an estimate for the diffractive components in a two channel model and comparison with the Pumplin bound [57]

• the t-dependence of the slope parameter B(t), at different energies and how this dependence is related to the relative importance of pion loops in the calculation of the Pomeron trajectory

• survival probabilities of rapidity gaps.

A simplified version of the model can be found in Appendix A of [221]. From the expression for the total cross section in impact-parameter space

$$\begin{aligned}&\sigma _{\mathrm{total}}=2\int \mathrm{d}^2{\mathbf {b}}_t A_{\mathrm{el}}(b_t),\end{aligned}$$

(5.147)

$$\begin{aligned}&\sigma _{\mathrm{elastic}}=\int \mathrm{d}^2 {\mathbf {b}}_t |A_{\mathrm{el}}(b_t)|^2 \end{aligned}$$

(5.148)

it is clear that $A_{\mathrm{el}}$ is purely imaginary in the model. A two-channel eikonal is considered, elastic $p\rightarrow p$ and $p\rightarrow N^*\rightarrow p$, see Eq. (33) of their Appendix A, which will be discussed in more detail in the section of this review on the elastic cross section. In the case of a single channel they write

$$\begin{aligned} \mathfrak {I}m A_{\mathrm{el}}=\left[ 1-\mathrm{e}^{-\varOmega (b_t)/2}\right] . \end{aligned}$$

(5.149)

With an effective (for illustration) Pomeron trajectory written as $\alpha _P(t)=\alpha _P(0)+\alpha '_P t=1+\varDelta +\alpha '_P t$ and vertex with exponential t-dependence $\beta _p \exp (B_0 t)$, the opacity is written as

$$\begin{aligned} \varOmega (b,s)=\frac{ \beta _P ^2 (s/s_0)^{\alpha _P(0)-1} }{4\pi B_P} \mathrm{e}^{-b_t^2/4B_P}. \end{aligned}$$

(5.150)

This result is obtained starting with the usual Regge–Pomeron expression, i.e.

$$\begin{aligned}&\mathfrak {I}mA_{\mathrm{el}}(s,t)=\beta _P^2(t)\left( \frac{s}{s_0}\right) ^{ \alpha _P(t)-1},\end{aligned}$$

(5.151)

$$\begin{aligned}&\quad =\beta _P^2(t)\left( \frac{s}{s_0}\right) ^{\alpha _P(0)-1} \mathrm{e}^{\alpha '_P\ t\ \log \frac{s}{s_0}}. \end{aligned}$$

(5.152)

The amplitude in b-space is then obtained as the Fourier transform of Eq. (5.152) with $t=-q^2$

$$\begin{aligned} \mathcal{F}[A(s,t)]= & {} \frac{1}{(2\pi )^2}\int \mathrm{d}^2{\mathbf {q}}\mathrm{e}^{i{\mathbf {b}}\cdot {\mathbf {q}}} A(s,t),\end{aligned}$$

(5.153)

$$\begin{aligned}= & {} \left( \frac{s}{s_0}\right) ^{\varDelta } \mathrm{e}^{(B_0 /2+\alpha '_P\ \log \frac{s}{s_0}) b^2)/4} \end{aligned}$$

(5.154)

and then eikonalised, obtaining

$$\begin{aligned}&\sigma _{\mathrm{total}}=4\pi \mathfrak {I}m A(s,0)=2\int \mathrm{d}^2{\mathbf {b}}[ 1-\mathrm{e}^{ -\varOmega (b,s)/2)} ],\nonumber \\\end{aligned}$$

(5.155)

$$\begin{aligned}&\varOmega (b,s)=\frac{ \beta _P ^2 (s/s_0)^{\alpha _P(0)-1} }{4\pi B_P} \mathrm{e}^{-b^2/4B_P},\end{aligned}$$

(5.156)

$$\begin{aligned}&B_P=\frac{1}{2}B_0+\alpha '_P \log (s/s_0). \end{aligned}$$

(5.157)

In two more recent papers [222, 223] the crucial question of the transition from soft to hard is examined again. We shall first summarise their picture of the transition from [223] and then, in the next section, dedicated to the elastic differential cross section, describe their latest results. The (QCD) Pomeron is here associated with the BFKL singularity. It is noted that, although the BFKL equation should be written for gluons away from the infrared region, after resummation and stabilisation, the intercept of the BFKL Pomeron depends only weakly on the scale for reasonably small scales. We reproduce in Fig. 42 their description of the connection between the intercept of the BFKL Pomeron and the value for $\alpha _s$. The figure shows how the intercept $\varDelta$ goes to a smooth almost constant behaviour as $\alpha _s$ increases.

Fig. 42

Evolution of the Pomeron intercept from [223]. Reprinted with permission from [223], ©(2012) INFN Frascati Physics Series

Basically, the Pomeron picture by these authors is summarised as follows [224]. In the soft domain, Reggeon field theory with a phenomenologically soft Pomeron dominates. In the hard domain, perturbative QCD and a partonic approach must be used. In pQCD, the Pomeron is associated with the so called BFKL vacuum singularity. In the perturbative domain, there is thus a single hard Pomeron exchanged, with $\alpha _P^{\mathrm{bare}}=1.3 + \alpha '_{\mathrm{bare}} t$ with $\alpha '_{\mathrm{bare}}\lesssim 0.05~\mathrm{GeV}^{-2}$. In mini-jet language, which we shall describe in the next subsection, this corresponds to having the mini-jet cross section rising as ${\simeq } s^{0.3}$. The slope is associated to the size of the Pomeron, i.e. $\alpha '_P\propto 1/\langle k_t^2\rangle$. Thus the bare Pomeron is associated to the hard scale, of the order of a few GeV. In a mini-jet model this hard Pomeron is obtained from parton–parton scattering folded in with the densities and summed over all parton momenta. This is their perturbative description. But then transition from hard to soft takes place, as one moves to smaller $k_t$ values. In KMR approach, this is due to multipomeron effects, while in $k_t$-resummation language (see next subsection), this comes about because of resummation of soft $k_t$-effects, which lower the scale determining $\langle k_t^2\rangle$ from the hard scale, to the soft one. As a result, in the case of the BFKL Pomeron, the slope increases by a factor ${\sim } 5$, while at the same time the intercept decreases and one has an effective linear trajectory, $\alpha _P^{\mathrm{eff}}\simeq 1.08 +0.25 t$. A behaviour such as this, a transition from soft to hard, from a bare to an effective trajectory for the Pomeron, was also found by these authors to be present in virtual photo production of vector mesons at HERA.

After this general overview of the model, let us see how KMR apply it to elastic scattering. The basic building blocks of this model are the following parameters:

• the bare Pomeron intercept $\varDelta =\alpha _P(0)-1, s$-dependent

• the bare Pomeron slope $\alpha '\simeq 0$

• a parameter d, which controls the BFKL diffusion in $k_t$

• the strength $\lambda$ of the triple-Pomeron vertex

• the relative weight of the diffractive states $\gamma$, determined by low-mass diffractive dissociation

• the absolute value N of the initial gluon density.

KMR have discussed this model in comparison with the recent TOTEM data and the values obtained by this program for the total, elastic and diffrative cross section are given, in this paper, in Tables 6 and 7 for two different models, the original KMR [225] and the 3-channel eikonal [222].

Table 6 Values for various total cross section components, in the original KMR model [225], prior to the LHC data

Table 7 Values for various total cross section components in t the KMR 3-channel eikonal from [222], inclusive of LHC TOTEM data at $\sqrt{s}=7\ \mathrm{TeV}$

5.9 Mini-jet models

When ISR confirmed the rise of the total cross section already hinted at by cosmic ray experiments, an interpretation was soon put forward that the rise was due to the appearance of partonic interactions [55]. This early estimate of jet production contribution to the rise of the total cross section and a comparison with existing cosmic ray and accelerator data can be seen from Fig. 7 in Sect. 3.3.1. In this figure, one could see the appearance of the first parton model for the rise of the total cross section and its comparison with data, with the shaded area to represent an estimate of the parton contribution. Subsequently, models in which the hard component in the rise could be calculated from pQCD or could be inspired by pQCD have been put forward, as shall be discussed below.

5.9.1 Non-unitary mini-jet model by Gaisser and Halzen

When data at the CERN $S{\bar{p}}pS$ gave further evidence of the rise of the total cross section, the idea was subsequently elaborated by Gaisser and Halzen [226], who made a model in which the rising part of the total cross section was obtained from the QCD two jet cross section, calculated using QCD parton–parton cross sections, folded in with parton densities. In this calculation,

$$\begin{aligned} \sigma _{\mathrm{total}}= \sigma _0+\sigma _{\mathrm{jet}}(p_{T \min }) \end{aligned}$$

(5.158)

with

$$\begin{aligned} \sigma _{\mathrm{jet}}(p_{T\min })=\int _{4p_{T\min }^2/s} \frac{\mathrm{d}\sigma }{\mathrm{d}x_1}\mathrm{d}x_1 \end{aligned}$$

(5.159)

and

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}x_1}=\frac{\pi }{18 p_{T\min }^2}\nonumber \\&\quad \times \int \mathrm{d}x_2 F(x_1,Q^2)F(x_2,Q^2)\alpha _s^2(Q^2)H(x_1,x_2,4xp_{T \min }^2)\nonumber \\ \end{aligned}$$

(5.160)

Table 8 Table of predicted values for $\sigma _{\mathrm{total}}$ by Gaisser and Halzen [226]

Fig. 43

The first model for the total cross section which used QCD calculated jet cross sections to describe the rise, is shown, from [226]. Reprinted with permission from [226], Fig.(1), ©(1985) by the American Physical Society

with $H(x_1,x_2,4xp_{T \min }^2)$ obtained from the cross sections for parton–parton scattering, integrated over all scattering angles and parton density functions $F(x_i,Q^2)$. In the above equation, there appear the by-now familiar parameter $p_{T\min }$, which regularises the parton–parton cross section, otherwise divergent as $1/p_{T\min }^2$ for small momenta of the outgoing partons. Since these jet cross sections rise very rapidly with energy, the parameter $p_{T\min }$ was taken to be energy dependent. In Table 8, we reproduce the values of $p_{T\min }$ needed to describe existing total cross section data from low energy to high energy values. With $\sigma _0=38 ~\hbox {mb}$, Fig. 43 shows the corresponding plot, up to cosmic ray energies. This model had no flexibility to satisfy unitarity. It was just a simple parametrisation, but it already had the merit of including soft-hard partonic interactions. The importance of such semihard processes had been highlighted in [218], also discussed in [227,228,229,230].

5.9.2 Eikonalisation of mini-jet models

A subsequent step which would avoid an energy dependent value of the parameter $p_{T \min }$, was the introduction of multiple scattering, as had been pointed by Durand [231]. This possibility was realised by Durand and Pi in [45] who proposed to use the mini-jet cross section as input to the total cross section through the eikonal representation. Their proposed expression enforced the idea that QCD processes at high energy drive the rise of the total cross sections, while at the same time satisfying unitarity. The price to pay, as always the case when using the eikonal representation, was the introduction of the impact-parameter distribution for the scattering partons. In this, as in most other models, the impact-parameter distribution at high energy was taken to be different from the one at low energy. At low energy, the distribution was considered to be dominated mostly by quark scattering, and, accordingly, taken to be a convolution of the proton electromagnetic form factors, while for the gluons, it was a convolution of a proton-like and a pion-like form factor. In the following, we shall reproduce the expressions they use and the values of the parameters which give the fits shown in Fig. 44.

Fig. 44

Description of the total cross section in the eikonal mini-jet model by Durand and Pi from Ref.  [45]. Reprinted with permission from [45], Fig.(1), ©(1989) by the American Physical Society

The $pp$ and ${\bar{p}}p$ elastic scattering amplitudes were written as

$$\begin{aligned} f_{pp,{\bar{p}}p}=i \int b \mathrm{d}b J_0(b\sqrt{t}) [1-\mathrm{e}^{-\chi _{pp, {\bar{p}}p}(b,s)}] \end{aligned}$$

(5.161)

with

$$\begin{aligned} \chi = \chi ^R+i \chi ^I. \end{aligned}$$

(5.162)

We use here the notation of Ref. [45], noting that the definition of $\chi$ has a $-i$ with respect to the more usual definition, for instance the one in the model described in Sect. 5.9.6. The normalisation is such that

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}=\pi |f(s,t)|^2 \end{aligned}$$

(5.163)

and then, using the optical theorem, one has the usual expressions

$$\begin{aligned} \sigma _{\mathrm{total}}= & {} 4\pi \mathfrak {I}m f(s,0=)\nonumber \\= & {} 4\pi \int _0^\infty b \mathrm{d}b [1-\cos \chi ^I(b,s)\mathrm{e}^{-\chi ^R(b,s)}],\end{aligned}$$

(5.164)

$$\begin{aligned} \sigma _{\mathrm{elastic}}= & {} 2\pi \int _0^\infty b \mathrm{d}b |1-\mathrm{e}^{-\chi (b,s)}|^2\nonumber \\= & {} 2\pi \int _0^\infty b \mathrm{d}b \big [ 1-2\cos \chi ^I(b,s)\mathrm{e}^{-\chi ^R(b,s)}\nonumber \\&+\,\mathrm{e}^{-2\chi ^R(b,s)} \big ],\end{aligned}$$

(5.165)

$$\begin{aligned} \sigma _{\mathrm{inel}}= & {} 2\pi \int _0^\infty b \mathrm{d}b [1-\mathrm{e}^{-2\chi ^R(b,s)}]. \end{aligned}$$

(5.166)

The authors had emphasised that the term $\mathrm{e}^{-2\chi _R}$ can be interpreted semi-classically as the probability that no collision takes place in which particles are produced. The function $\chi ^R$ is calculated using parton–parton scattering, impact parameter distributions as mentioned, and, through this function, the remaining component $\chi ^I$ is obtained from a dispersion relation. This allowed them to obtain both the real and the imaginary part of the amplitude and through these, the $\rho$ parameter.The QCD contribution was calculated from mini-jet cross sections and was input to the two, even and odd, eikonals in which the $pp$ and ${\bar{p}}p$ eikonal functions are split. Namely, they write

$$\begin{aligned} \chi _{{\bar{p}}p}=\chi _++\chi _-,\quad \chi _{pp}=\chi _+-\chi _-. \end{aligned}$$

(5.167)

The QCD-like contribution is input to the even eikonal. At very high energy, if no Odderon is present, the two cross sections for $pp$ and ${\bar{p}}p$ are equal and one can hope to be able to calculate this part of the eikonal using perturbative QCD. Actually, even at high energy, there will be a residual contribution from processes which dominate at low energy, and thus the eikonal is split into a soft and a hard part, namely

$$\begin{aligned}&\chi (b,s)=\chi _{\mathrm{soft}}(b,s)+\chi _{\mathrm{QCD}}(b,s),\end{aligned}$$

(5.168)

$$\begin{aligned}&\chi ^I_{\mathrm{QCD}}(b,s)=-\frac{2s}{\pi }{} \mathbf{P }\int _0^\infty \mathrm{d}s'\frac{ \chi ^R(b,s')}{(s'^2-s^2)},\end{aligned}$$

(5.169)

$$\begin{aligned}&\chi ^R_{\mathrm{QCD}}(b,s)=\mathfrak {R}e\ \chi _{\mathrm{QCD}}= \frac{1}{2}\sum _{ij}\frac{1}{1+\delta _{ij}} \times \int \mathrm{d}^2b' \mathrm{d}x_1\mathrm{d}x_2 \nonumber \\&\qquad \times \int _{Q^2_{\min }} \mathrm{d}|{\hat{t} }| \frac{\mathrm{d}{\hat{\sigma }}_{ij}}{\mathrm{d}|{\hat{t} }|}f_i(x_1,|{\hat{t} }|,|{\mathbf {b}}-{\mathbf {b}'}|)f_j(x_2,|{\hat{t} }|,|{\mathbf {b}'}|)\nonumber \\ . \end{aligned}$$

(5.170)

One then assumes an approximate factorisation between impact space and energy distribution, namely the probability functions to find a parton of type i with fractional momentum x at a distance ${\mathbf {b}}$ from the initial proton direction, are factorised as

$$\begin{aligned} f_j(x,{\hat{t} },|{\mathbf {b}}|) \approx f_j(x,{\hat{t} })\rho ({\mathbf {b}}) \end{aligned}$$

(5.171)

where $\rho (b)$ is a function describing matter distribution inside the colliding hadrons. One then can write

$$\begin{aligned} \chi ^R_{\mathrm{QCD}}(b,s)=\frac{1}{2} A(b) \sigma ^R_{\mathrm{QCD}} \end{aligned}$$

(5.172)

with

$$\begin{aligned} A(b)=\int \mathrm{d}^2 b' \rho (b')\rho (|{\mathbf {b} }-\mathbf {b'}|) \end{aligned}$$

(5.173)

and $\int \mathrm{d}^2b A(b)=1$.

For the impact-parameter distribution, for the soft part the following expressions were used:

$$\begin{aligned} A_{\pm }(b)= \frac{\nu _{\pm }^2}{12\pi }\frac{1}{8}(\nu _{\pm }b)^3\mathcal{K}_3(\nu _{\pm }b) \end{aligned}$$

(5.174)

with $\mathcal{K}_3(\nu b)$ the special Bessel function of the third kind which comes from the convolution of the dipole-type expression of the proton e.m form factor. These functions will enter the even and odd soft eikonals. For the hard part, on the other hand, one takes into account that gluons are distributed differently from the valence quarks and the expression which is used is the convolution of gluon form factors given by

$$\begin{aligned} G(k_\perp ^2)=(1+k_\perp ^2/\nu _+^2)^{-2}(1+k_\perp ^2/\mu ^2)^{-1}. \end{aligned}$$

(5.175)

To complete the picture, the authors set the soft eikonals as

$$\begin{aligned}&2\chi _{+,\mathrm{soft}}=A_+(b)\sigma _{\mathrm{soft}}=A_+(b)\left[ \sigma _0+\frac{a}{s^\alpha }\mathrm{e}^{i\alpha \pi /2}\right] ,\end{aligned}$$

(5.176)

$$\begin{aligned}&2\chi _{-,\mathrm{soft}}=A_-(b)\frac{R}{\sqrt{s}}\mathrm{e}^{-i\pi /4} \end{aligned}$$

(5.177)

with $\sigma _0=\sigma _0^R+ i\sigma _0^I; a,\alpha$ adjustable parameters.

The model, a part from the QCD inputs, namely densities and $Q^2_{\min }$, has now 8 parameters, $\sigma _0=\sigma _0^R+ i\sigma _0^I, a,\alpha$ and R for the cross section type terms and $\nu _\pm ,\mu$ for the impact-parameter distributions. The parameters are then fixed so as to obtain a good fit to the total cross sections, elastic and total, to the elastic differential cross section and to the $\rho$ and slope parameters, given by

$$\begin{aligned}&\rho ={\mathfrak {R}}e f(s,0)/{\mathfrak {I}} m f(s,0),\end{aligned}$$

(5.178)

$$\begin{aligned}&B(s)=\frac{\mathrm{d}}{\mathrm{d}t}\left[ \ln \frac{\mathrm{d}\sigma _{\mathrm{elastic}}}{\mathrm{d}t} \right] |_{t=0}. \end{aligned}$$

(5.179)

Within this framework, one obtains the description of the total cross section shown in Fig. 44 and good descriptions of the elastic cross sections and their energy dependence up to $S{\bar{p}}pS$ data. Notice that the slope parameter B(s) is thus fully determined.

We have dedicated a rather long and detailed exposition to this model since many other models follow a similar outline and models similar to this one have been used (and still are) in MonteCarlo simulations such as PYTHIA [232]. Many of the features of the Durand and Pi model are also present in the QCD inspired model which will be described in the next section.

Durand and Pi in [45] made an effort to obtain a description of the $\rho$ parameter which could accomodate the UA4 measurement [233], namely $\rho =0.24\pm 0.04$ and the parameter values for the overall description were influenced by this choice. To explain such a large value, it turned out to be quite difficult, in most case it was related to a possible anomalous rise of the total cross section. The measurement of the $\rho$ parameter at the Tevatron by E-710 [145] and E811 Collaboration [144], however, did not confirm such a high value for $\rho$, which had in any event already been measured again by UA4,s obtaining a lower value, in line with theoretical expectations. That the $\rho$ parameter could not be this high was pointed out in 1990 by Block et al. [234] who discussed the theoretical implications of such measurements, using a previously developed model [166]. We now turn to this model.

5.9.3 QCD-inspired models, Aspen model

Applications of the mini-jet idea to the description of the total and elastic cross sections were developed around the 1990s by many groups, for instance in [235, 236]. We shall illustrate here the one developed by Block with Fletcher, Halzen, Margolis and Valin [234], where the contribution of semi-hard interactions was fully parametrised, separately indicating quark and gluon contributions. This model is also sometimes labelled as the Aspen model⁵ and is at the basis of subsequent developments, where it was applied to photon processes [146] and to the extraction of the proton–proton cross section from cosmic ray experiments [48].

In this model, a QCD-inspired eikonal parametrisation of the data is used. For the total cross section, a result similar to simple $\ln ^2 [s]$ analytic considerations [12] is obtained. One starts with

$$\begin{aligned}&\sigma _{\mathrm{total}}=4 \pi \mathfrak {I}m f_N,\end{aligned}$$

(5.180)

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}t}=\pi |f_N|^2 ,\end{aligned}$$

(5.181)

$$\begin{aligned}&f_N=i\int b\mathrm{d}b J_0(b\sqrt{-t})[1-\mathrm{e}^{-P(b,s)/2}] ,\end{aligned}$$

(5.182)

$$\begin{aligned}&P(b,s)=P_{gg}(b,s)+P_{qg}(b,s)+P_{qq}(b,s),\end{aligned}$$

(5.183)

$$\begin{aligned}&P_{ij}(b,s)=W_{ij}(b,\mu _{ij})\sigma _{ij}(s). \end{aligned}$$

(5.184)

In the above equations, the probability function P(b, s) is seen to be parametrised in terms of three QCD-like terms, corresponding respectively to gluon–gluon, quark-gluon and quark–quark interactions. The impact distribution functions for proton–proton scattering are obtained from the convolution of the two proton-like form factors, and for $i=j$

$$\begin{aligned} W_{ii}(b,\mu _{ii})=\frac{\mu ^2_{ii}}{96 \pi }(\mu _{ii}b)^3 \mathcal{K}_{3}(\mu _{ii}b). \end{aligned}$$

(5.185)

For the gluon–gluon terms, which become more important at high energy and which drive the rise of the cross section, they write

$$\begin{aligned} P_{gg}(b,s)\simeq W_{gg}(b)s^{J-1} \end{aligned}$$

(5.186)

where J gives the large s behaviour of the gluon–gluon cross section integrated over the gluon PDF’s in the proton. For the probabilities involving quarks, and which are important at low energy, the parametrisation is inspired by the x-behaviour of the parton densities and they are written as

$$\begin{aligned}&P_{qq}=W(\mu _{qq}b)\left[ a+b\frac{m_0}{\sqrt{s}}\right] ,\end{aligned}$$

(5.187)

$$\begin{aligned}&P_{qg}=W\left( \sqrt{\mu _{qq}\mu _{gg}} b \right) \left[ a'+b'\ln \frac{m_0}{\sqrt{s}}\right] . \end{aligned}$$

(5.188)

The difference at low energy between $pp$ and ${\bar{p}}p$ cross sections is obtained by first ensuring the correct analyticity properties through the substitution $s\rightarrow s^{-i\pi /2}$ and then introducing an ad hoc odd-crossing amplitude as

$$\begin{aligned} P_{\mathrm{odd}}=W(\mu _{\mathrm{odd}}b)a'' \frac{m_0}{\sqrt{s}}\mathrm{e}^{-i\pi /4}. \end{aligned}$$

(5.189)

The overall set of parameters can be found in the caption of Figure 1 from [234]. We reproduce this figure for the total cross section in Fig. 45. This model has 11 parameters.

Fig. 45

Description of the total cross section in the QCD inspired model by Block et al., from [234]. Reprinted from [234], Fig.(1), ©(1990) by the American Physical Society

Finally, notice an important feature of this model, i.e. how the Froissart-type large energy limit is obtained through the mini-jet contribution in combination with the impact parameter dependence. The authors search for the critical value of the parameter b for which $P_{gg}\le 1$ and, using the large energy behaviour of the mini-jet cross sections, namely $s^{J-1}$, they find

$$\begin{aligned} b_c=\frac{J-1}{\mu _{gg}}\ln \frac{s}{s_0} + \mathcal{O}\left( \ln \ln \frac{s}{s_0}\right) . \end{aligned}$$

(5.190)

Thus, the energy dependence of the QCD cross sections transforms the $s^{j-1}$ behaviour at lower energy into the black-disk cross section at high energy, i.e. into

$$\begin{aligned} \sigma _{\mathrm{total}}=2\pi \left[ \frac{J-1}{\mu _{gg}}\right] ^2 \ln ^2 \frac{s}{s_0}. \end{aligned}$$

(5.191)

5.9.4 Resummation and mini-jets

A model which incorporates many features of QCD is the one developed in [93], following [148] and completed in a number of subsequent papers, in particular in [94]. The model embodies the idea that resummation down into the infrared region is a crucial component of total cross section asymptotics and provides a phenomenological structure linking the infrared behaviour of QCD to the asymptotic limit of the total cross section.

The model is labeled following the idea that exponentiation of the spectrum of soft emitted quanta when $k\rightarrow 0$, first proposed by Bloch and Nordsieck (BN) for QED [170], must be extended to the soft gluons for the QCD processes and that it must be carried through into the infrared region.

Thus, the model is developed along two basic ideas, that the rise of the total cross section is driven by hard processes, called mini-jets [227, 229] and that the softening of the rise into the smooth behaviour consistent with the Froissart bound arises because of soft-gluon emission, resummed and extended down into the zero momentum region of the spectrum of the emitted quanta [11]. To investigate this region, use is made of the ansatz about the infrared behaviour of the effective quark-gluon coupling first introduced in [237] for the intrinsic transverse momentum of Drell–Yan pairs, and later implemented to describe the impact-parameter distribution of partons in high energy collisions [148], as we have described previously.

The basic structure of this model exhibits some of the same features advocated by the work of GLR, KMR or GLM, described in other parts of this review, describing implementation of BFKL dynamics, namely soft exchanges (the soft Pomeron) and perturbative QCD (hard Pomeron) for medium energy partons, but the hadronic amplitude at $t=0$ of this model is built through a probabilistic structure, with the soft resummation contribution built as a term factored from the hard parton–parton scattering, not unlike what one does in QED when applying infrared radiative corrections.

5.9.5 Hadronic matter distribution and QCD soft $k_t$ distribution

Because of its obvious relevance to total cross section estimates through the transverse interaction size of hadrons, we shall start by investigating the transverse momentum distribution of soft quanta in QCD.

The expressions for transverse momentum distribution discussed in the context of QED in Sect. 5.7.7 cannot be extended simply to QCD, since the coupling constant is momentum dependent. When taken into account, the transverse momentum distribution due to soft-gluon emissions became extremely interesting. This was first realised by Dokshitzer et al. [238], who generalised to QCD the Sudakov form-factor expression, originally obtained in QED [178] and discussed above. The application of resummation techniques to the $K_\perp$-distribution of $\mu$ pairs of mass Q produced in hadron–hadron collisions was shortly after studied in [239]. In this paper, it was argued that the “soft limit of QCD could be treated in full analogy with that of QED with the minor [Author’s note: not so minor!] technical change of $\alpha$ into $\alpha (k_\perp )$”.

Today the problem of transverse momentum distributions in QCD is still not completely solved. The reason lies in the lack of our certain knowledge about the momentum dependence of the strong coupling constant $\alpha _s(k_\perp )$ when the gluon momentum goes to zero, as is the case for the soft gluons needed in resummation. Actually, what one needs to know is the integral of $\alpha _s(k_t)$ over the infrared region. The IR limit of $\alpha _s$ enters only when the gluon momenta are close to zero, i.e. only in the resummation process, which implies exponentiation of an integral over gluon’s momenta with a momentum-dependent $\alpha _s$. Because the coupling constant in QCD grows as the momenta become smaller, a Bloch and Nordsieck type resummation of the zero momentum modes of the soft quanta emitted by coloured quarks becomes mandatory. In this case, the applicability of the above methods requires a knowledge of (or, an ansatz for) the strong coupling constant in the IR region.

Following the semiclassical derivation of Eq. (5.77), the exponent describing the b-dependence for QCD now reads

$$\begin{aligned} h( b,E) = \frac{16}{3}\int ^E {{ \alpha _s(k_t^2) }\over {\pi }}{{\mathrm{d} k_t}\over {k_t}}\ln {{2E}\over {k_t}}[1-J_0(k_tb)]. \end{aligned}$$

(5.192)

Its use is complicated by the asymptotic running of the coupling constant on the one hand and our ignorance of the IR behaviour of the theory, on the other.

To overcome the difficulty arising from the infrared region, the function h(b, E), which describes the relative transverse momentum distribution induced by soft-gluon emission from a pair of, initially collinear, colliding partons at LO, is split into

$$\begin{aligned} h(b,E) = c_0(\mu ,b,E)+ \varDelta h(b,E), \end{aligned}$$

(5.193)

where

$$\begin{aligned} \varDelta h(b,E) = \frac{16}{3} \int _\mu ^E {\alpha _s(k_t^2)\over {\pi }}[1- J_o(bk_t)] {{\mathrm{d}k_t}\over {k_t}} \ln { {{2E}\over {k_t}}}.\nonumber \\ \end{aligned}$$

(5.194)

The integral in $\varDelta h(b,E)$ now extends down to a scale $\mu \ne 0$, for $\mu > \varLambda _{\mathrm{QCD}}$ and one can use the asymptotic freedom expression for $\alpha _s(k_t^2)$. Furthermore, having excluded the zero momentum region from the integration, $J_o(bk_t)$ is assumed to oscillate to zero and neglected. The integral of Eq. (5.194) is now independent of b and can be performed, giving

$$\begin{aligned} \varDelta h(b,E)= & {} \frac{32}{33-2N_f} \left\{ \ln \left( {\frac{{2E}}{\varLambda }} \right) \left[ \ln \left( {\ln \left( {\frac{E}{\varLambda }}\right) }\right) \right. \right. \nonumber \\&\left. \left. \displaystyle - \ln \left( {\ln \left( {\frac{\mu }{\varLambda }} \right) }\right) \right] - \ln \left( {\frac{E}{\mu }}\right) \right\} . \end{aligned}$$

(5.195)

$\varLambda$ being the scale in the one-loop expression for $\alpha _s$. In the range $1/E< b < 1/\varLambda$ an effective $h_{\mathrm{eff}}(b,E)$ is obtained by setting $\mu = 1/b$ [239]. This choice of the scale introduces a cut-off in impact-parameter space which is stronger than any power, since the radiation function, for $N_f=4$, is now

$$\begin{aligned} \mathrm{e}^{-h_{\mathrm{eff}}(b,E)} = \left[ {{ \ln (1/b^2\varLambda ^2) }\over { \ln (E^2/\varLambda ^2) }} \right] ^{(16/25)\ln (E^2/\varLambda ^2)}, \end{aligned}$$

(5.196)

which is Equation (3.6) of Ref. [239]. The remaining b dependent term, namely $\exp [-c_0(\mu ,b,E)]$, is dropped, a reasonable approximation if one assumes that there is no physical singularity in the range of integration $0\le k_t \le 1/b$. This contribution, however, reappears as an energy independent smearing function which reproduces phenomenologically the effects of an intrinsic transverse momentum of partons. For most applications, this may be a good approximation. However, when the integration in impact-parameter space extends to very large-b values, as is the case for the calculation of total cross sections, the infrared region may be important and the possibility of a physical singularity for $\alpha _s$ in the infrared region becomes relevant [11]. It is this possibility, which we exploit in studying scattering in the very large impact parameter region, $b\rightarrow \infty$.

Our choice for the infrared behaviour of $\alpha _s(Q^2)$ used in obtaining a quantitative description of the distribution in Eq. (5.194), is a generalisation of the Richardson potential for quarkonium bound states [240], which we have proposed and developed in a number of related applications [241, 242]. Assume a confining potential (in momentum space) given by the one gluon exchange term

$$\begin{aligned} {\tilde{V}}(Q) = K \left( {{\alpha _s(Q^2)}\over {Q^2}}\right) , \end{aligned}$$

(5.197)

where K is a constant calculable from the asymptotic form of $\alpha _s(Q^2)$. Let us choose for $Q^2\ll \varLambda ^2$ the simple form

$$\begin{aligned} \alpha _s(Q^2) = {\frac{B}{(Q^2/\varLambda ^2)^{p}}}, \end{aligned}$$

(5.198)

(with B a constant), so that ${\tilde{V}}(Q)$ for small Q goes as

$$\begin{aligned} {\tilde{V}}(Q) \rightarrow Q^{-2(1 +p)}. \end{aligned}$$

(5.199)

For the potential, in coordinate space,

$$\begin{aligned} V(r)=\int {{\mathrm{d}^3Q}\over {(2\pi )^3}} \mathrm{e}^{i \mathbf{Q.r}} {\tilde{V}}(Q), \end{aligned}$$

(5.200)

Eq. (5.199) implies

$$\begin{aligned} V(r) \rightarrow (1/r)^3 \cdot r^{(2 + 2p)} \sim C\ r^{(2p - 1)}, \end{aligned}$$

(5.201)

for large r (C is another constant). A simple check is that, for p equal to zero, the usual Coulomb potential is regained. Notice that for a potential rising with r, one needs $p > 1/2$. Thus, for $1/2< p< 1$, this corresponds to a confining potential rising less than linearly with the interquark distance r, while a value of $p=1$ coincides with the infrared limit of the Richardson’s potential and is also found in a number of applications to potential estimates of quarkonium properties [243].

Then, again following Richardson’s argument [240], we connect our IR limit for $\alpha _s(Q^2)$ to the asymptotic freedom region using the phenomenological expression:

$$\begin{aligned} \alpha _s(k_t^2)=\frac{1}{b_0}{{p}\over {\ln [1+p({{k_t^2} \over {\varLambda ^2}})^{p}]}} \end{aligned}$$

(5.202)

with $1/b_0={{12 \pi }\over {(33-2N_f)}}$. The expression of Eq.  (5.202) coincides with the usual one-loop formula for values of $k_t\gg \varLambda$, while going to a singular limit for small $k_t$, and generalises Richardson’s ansatz to values of $p<1$. The range $p < 1$ has an important advantage, i.e., it allows the integration in Eq. (5.194) to converge for all values of $k_t=|k_\perp |$. Some considerations for the case $p\simeq b_0$ can be found in [244].

Using Eq. (5.202), one can study the behaviour of h(b, E) for very large-b values which enter the total cross section calculation and recover the perturbative calculation as well. The behaviour of h(b, E) in various regions in b-space was discussed in [93], both for a singular and a frozen $\alpha _s$, namely one whose IR limit is a constant. There we saw that, for the singular $\alpha _s$ case, the following is a good analytical approximation in the very large-b region:

$$\begin{aligned}&b>{{1}\over {N_p\varLambda }}>{{1}\over {M}},\end{aligned}$$

(5.203)

$$\begin{aligned}&h(b,M,\varLambda ) ={{2c_F}\over {\pi }} \left[ {\bar{b}}{{b^2\varLambda ^{2p}} \over {2}}\int _0^{{1}\over {b}}{{\mathrm{d}k}\over {k^{2p-1}}} \ln {{2M}\over {k}}\right] \nonumber \\&\qquad +{{2c_F}\over {\pi }}\left[ 2 {\bar{b}} \varLambda ^{2p}\int _{{1} \over {b}}^{N_p\varLambda } {{\mathrm{d}k}\over {k^{2p+1}}} \ln {{M}\over {k}}+{\bar{b}} \int _{N_p\varLambda }^M {{\mathrm{d}k}\over {k}} {{\ln {{M}\over {k}}}\over {\ln {{k}\over {\varLambda }}}}\right] \!\!\! \nonumber \\&\quad ={{2c_F}\over {\pi }} \left[ {{{\bar{b}}}\over {8(1-p)}}(b^2 \varLambda ^2)^p \left[ 2\ln (2Mb)+{{1}\over {1-p}}\right] \right. \nonumber \\&\qquad +{{\bar{b}}\over {2p}}(b^2\varLambda ^2)^p\left[ 2\ln (Mb)-{{1}\over {p}} \right] \nonumber \\&\qquad +{{\bar{b}}\over {2pN_p^{2p}}}\left[ -2\ln {{M}\over {\varLambda N_p}}+{{1} \over {p}} \right] \nonumber \\&\qquad +\left. {\bar{b}} \ln {{M}\over {\varLambda }}\left[ \ln {{\ln {{M}\over {\varLambda }}}\over {\ln {N_p}}}-1+{{\ln {N_p}} \over {\ln {{M}\over {\varLambda }}}} \right] \right] \end{aligned}$$

(5.204)

where $N_p=(1/p)^{1/2p}$, $c_F=4/3$ for emission from quark legs and ${\bar{b}}=12 \pi /(33-2N_f)$. The upper limit of integration here is called M, to indicate the maximum allowed transverse momentum, to be determined, in our approach, by the kinematics of single gluon emission as in [245]. The above expression exhibits the sharp cut-off at large b values which we shall exploit to study the very large energy behaviour of our model.

The possibility that $\alpha _s$ becomes constant in the infrared can also be considered. We found that such possibility does not contribute anything new with respect to the already known results. In fact, using the expression [239, 246, 247]

$$\begin{aligned} \alpha _s(k_t^2)={{12 \pi }\over {33-2N_f}} {{1}\over {\ln [a^2+ k_t^2/\varLambda ^2]}} \end{aligned}$$

(5.205)

with $a>1$, in the same large b-limit as in Eq. (5.203), we have [93]

$$\begin{aligned}&b>{{1}\over {a\varLambda }}>{{1}\over {M}} ,\end{aligned}$$

(5.206)

$$\begin{aligned}&h(b,M,\varLambda )=(\hbox {constant}) \ln (2Mb) + \hbox {double logs} \end{aligned}$$

(5.207)

namely no sharp cut-off in the impact parameter b, as expected. More precisely, we have the following approximate expression:

$$\begin{aligned} h(b,M,\varLambda )= & {} {{2c_F}\over {\pi }} \left\{ {{ {\bar{\alpha }_s} }\over { 8}} [1+2\ln (2Mb)] \right. \nonumber \\&+\,2{\bar{\alpha }_s} \left[ \ln (Mb)\ln (a{\varLambda }b) - {{1}\over {2}} \ln ^2{(a \varLambda b)} \right] \nonumber \\&\left. +\,{\bar{b}} \left[ \ln {{M}\over {\varLambda }}\ln {{\ln {{M}\over {\varLambda }}} \over {\ln a }}-\ln {{M}\over {a\varLambda }} \right] \right\} \end{aligned}$$

(5.208)

with ${\bar{\alpha }_s}=12\pi /(33-2N_f) \ln (a^2)$. These approximations are reasonably accurate, as one can see from [93], where both the approximate and the exact expressions for $h(b,M,\varLambda )$ have been plotted for the singular as well as for the frozen $\alpha _s$ case. Notice that, in the following sections, we drop for simplicity the explicit appearance of the $\varLambda$ in the argument of $h(b,M,\varLambda )$.

The above expressions derived for the overall soft-gluon emission in a collision, are input for the QCD description of the total cross section [148]. In this description, the impact factor is defined as in

$$\begin{aligned}&\sigma _{\mathrm{total}}=2\int \mathrm{d}^2{\mathbf {b}}[1-\mathrm{e}^{-(\varOmega _{\mathrm{soft}}(s,b) +\varOmega _{\mathrm{hard}}(b,s))/2}],\end{aligned}$$

(5.209)

$$\begin{aligned}&\varOmega _{\mathrm{hard}}(b,s)=A_{BN}(b,s)\sigma _{\mathrm{jet}}(s),\end{aligned}$$

(5.210)

$$\begin{aligned}&A_{BN}=N \int \mathrm{d}^2 {\mathbf {K}}\mathrm{e}^{i{\mathbf {b}}\cdot {\mathbf {K}}} \mathrm{d}^2 P(K), \end{aligned}$$

(5.211)

N being a normalisation factor such that $\int \mathrm{d}^2{\mathbf {b}}A_{BN}=1$ and the subscript BN indicates that this impact factor is obtained through soft-gluon resummation. The detailed application of such model and the phenomenological results are described in the subsection to follow.

5.9.6 Bloch and Nordsieck inspired model for the total cross section

As discussed above, in the BN model soft gluons of momentum $k_t$ are resummed up to a maximum value $q_{\max }$, and partons, mostly gluons at high energy, of momentum $p_t$. Thus, there are three regions for the emitted parton transverse momentum and hence three scales:

• (i) $p_t>p_{t\min }$, with $p_{t\min }\simeq 1~\mathrm{GeV}$, one can apply perturbative QCD (pQCD) and calculate the mini-jet contribution to the scattering process,

• (ii) $\varLambda<k_t<q_{\max }\simeq (10$–$20)\% p_{t\min }$, where $k_t$ indicates the transverse momentum of a single soft gluon which corresponds to initial state soft radiation from partons with $p_t>p_{t\min }$, and for which one needs to do resummation, and $\varLambda \simeq 100\ \hbox {MeV}\simeq m_\pi$,

• (iii) $0<k_t<\varLambda$ for infrared momentum gluons, which require resummation but also an ansatz about the strong coupling in this region.

In the pQCD region, parton–parton scattering and standard Leading Order (LO) parton densities are used to calculate an average mini-jet cross section as

$$\begin{aligned}&\sigma _{\mathrm{mini}\text {-}\mathrm{jets}}\equiv \sigma ^{AB}_\mathrm{jet} (s) = \int _{p_{t\min }}^{\sqrt{s/2}} \mathrm{d} p_t \int _{4 p_t^2/s}^1 \mathrm{d} x_1 \int _{4 p_t^2/(x_1 s)}^1 \mathrm{d} x_2 \nonumber \\&\quad \times \sum _{i,j,k,l} f_{i|A}(x_1,p_t^2) f_{j|B}(x_2,p_t^2)~~ \frac{ \mathrm{d} \hat{\sigma }_{ij}^{ kl}(\hat{s})}{\mathrm{d} p_t}. \end{aligned}$$

(5.212)

Here A and B denote particles ($\gamma , \ p, \dots$), $i, \ j, \ k, \ l$ are parton types and $x_1,x_2$ the fractions of the parent particle momentum carried by the parton. $\hat{s} = x_1 x_2 s$ and $\hat{ \sigma }$ are hard parton scattering cross sections.

Equation (5.212) is a LO parton–parton cross section averaged over the given parton densities, through the phenomenologically determined parton density functions $f_{i|A}(x,p^2)$, DGLAP evoluted at the scale $p_t$ of the mini-jet produced in the scattering. As is well known, however, for a fixed $p_{t\min }$ value, and as $p_{t\min }/\sqrt{s} \rightarrow 0$, gluon–gluon processes become more and more important and, since the LO densities of gluons are phenomenologically determined to increase as $x^{1+\epsilon }$, the mini-jet integrated cross section will increase as $s^\epsilon$, with $\epsilon \sim (0.3\div 0.4)$ depending on the densities. This rise of the parton–parton cross sections, averaged over the parton densities, has its counterpart in the hard Pomeron of BFKL models, where a behaviour $s^\varDelta$ corresponding to hard Pomeron with very small slope is seen to describe the rise of the profile function, before saturation starts changing the hard behaviour into a softer one. Multiplying $\sigma _{\mathrm{hard}}$ with the average probability for two colliding partons to see each other (and interact) at a distance ${\mathbf {b}}$ would give the average number of collisions at impact parameter ${\mathbf {b}}$ when two protons collide. This number can become very large as the energy increases and so proper eikonalisation and unitarisation is introduced, just as in the QCD mini-jet models we have described earlier.

Implementation of unitarity through the eikonal formulation reduces the rise from this hard term, but unless one has a cut-off in the impact-parameter distribution, the rise will not be adequately quenched.

We now let the mini-jet model morphe into an eikonal mini-jet model for $\sigma _{\mathrm{total}}$, i.e.

$$\begin{aligned} \sigma _{\mathrm{total}}=2 \int \mathrm{d}^2 {\mathbf {b}} [1-\cos \mathfrak {R}e\chi (b,s)\ \mathrm{e}^{-\mathfrak {I}m\chi (b,s)}] \end{aligned}$$

(5.213)

where the s-dependence of the imaginary part of the eikonal function $\chi (b,s)$ is driven by the mini-jet cross section and, in first approximation, the eikonal will be taken to be purely imaginary. Since the total cross section is dominated by large impact parameter values, and, at high energy, $\rho (s,t=0)\sim 0.1$, this is reasonable approximation at high energy and in the calculation of the total cross section.

The name mini-jets was first introduced by M. Jacob and R. Horgan to describe the flood of small transverse momentum jet-like events expected to dominate at the $S{\bar{p}}pS$ collider [248, 249]. The importance of mini-jets concerning the rise of the total cross section was doubted however, as discussed for instance by Jacob and Landshoff in [250]. In particular they think impossible for mini-jets to contribute to the total cross section at $\sqrt{s}\simeq 5~\mathrm{GeV}$. This may be true, or, at least we do not know how to incorporate pQCD at such low hadronic c.m. energies, however our phenomenology indicates that the mini-jet contribution start being noticeable around $\sqrt{s}\gtrsim 10~\mathrm{GeV}$. It also appears that when performing a parametrisation of the low energy contribution, the hard part plays a role to ameliorate the overall description, from low to hard energies. Examples of these two different procedures can be found in our application of the BN model to pion scattering [149] and to studies of inelastic cross section at LHC7 [41]. In addition, from a microscopic point of view, mini-jets are the only pQCD phenomenon to which one can ascribe the drive of the rise of the total cross section. Their contribution can be seen as the microscopic description of the hard Pomeron advocated by Reggeon field models.

Fig. 46

LO Partonic picture of mini-jet role in hadron–hadron scattering and representative mini-jet calculation from [251]

We now turn to the question of the impact-parameter distribution in eikonal mini-jet models. As discussed at length in [93], the standard use of hadronic form factors together with standard library Parton Density Functions (PDF) in the mini-jet cross sections does not allow one to reproduce both the initial fast rise of the cross section as well as well as moderating the rise.

The difficulty to use the EM form factors with standard LO pQCD techniques has been one of the problems plaguing the eikonal mini-jet approach. We thus introduced soft-gluon resummation to solve this problem. However, as discussed previously, resummation outside the infrared region and in asymptotic freedom region, even at higher orders or beyond the LLA, can hardly touch the basic question: how to introduce a cut-off in impact-parameter space or, otherwise stated, how to link the asymptotic behavior of the cross section with confinement?

We shall now discuss the model in detail, but we anticipate its outline in graphic form here. We show in Figs. 46, 47, 48 and 49 our cartoon representation of the building of the total cross section. All these figures are reprinted with permission from [251], with ©(2007) by Acta Physica Polonica B. We have discussed in Sect. 5.9.5 our suggestion for the impact parameter distribution. The underlying physics is that this distribution is probed in the scattering when partons start a Brownian-like motion inside the protons, each successive change of direction generated by emission of soft gluons. Thus, a matter distribution A(b, s) can be obtained as the normalised Fourier transform of the expression for soft-gluon resummation in transverse momentum space. Through it, the average number of hard collisions is calculated to be

$$\begin{aligned} \langle n(b,s)\rangle= & {} A_{\mathrm{hard}}^{BN}(b,q_{\max })\sigma _{\mathrm{mini}\text {-}\mathrm{jets}}(s,p_{t\min }) \nonumber \\= & {} \frac{ \mathrm{e}^{-h(b,s)} }{\int \mathrm{d}^2{\mathbf {b}}\mathrm{e}^{ -h(b,s) } } \sigma _{\mathrm{mini}\text {-}\mathrm{jet}}(s,p_{t\min }) \end{aligned}$$

(5.214)

where we have introduced the notation BN to induce that this function is calculated using soft-gluon $k_t$ resummation, and the upper limit of integration $q_{\max }$ carries energy dependence from the scattering partons. We have followed the early work by Chiappetta and Greco about resummation effects in the Drell–Yan process, where this upper limit is defined by the kinematics of single gluon emission [252]. Namely for a process such as

$$\begin{aligned} q(x_1)+q(x_2)\rightarrow X(Q^2) + g(k_t) \end{aligned}$$

(5.215)

with the subenergy of the initial (collinear) parton pair defined as ${\hat{s}}=\sqrt{sx_1x_2}$. In the no-recoil approximation, $Q^2$ is the squared invariant mass of the outgoing parton pair X, with parton transverse momentum $p_t>p_{t\min }$. Kinematics then leads to

$$\begin{aligned} q_{\max }({\hat{s}},y,Q^2)=\frac{\sqrt{{\hat{s}}}}{2} \left( 1-\frac{Q^2}{{\hat{s}}}\right) \frac{1}{\sqrt{1+z\sinh ^2 y}} \end{aligned}$$

(5.216)

and y is the rapidity of the outgoing partons [252]. In our simplified model for the total cross section, we have approximated $q_{\max }({\hat{s}},y,Q^2)$ with its maximum value at $y=0$ and averaged its expression over the parton densities, namely

$$\begin{aligned}&q_{\max }\equiv \langle q_{\max }(s)\rangle ={{\sqrt{s}} \over {2}} \nonumber \\&\quad \times {{ \sum _{i,j}\int {{\mathrm{d}x_1}\over { x_1}} f_{i/a}(x_1)\int {{\mathrm{d}x_2}\over {x_2}}f_{j/b}(x_2)\sqrt{x_1x_2} \int _{z_{\min }}^1 \mathrm{d}z (1 - z)} \over {\sum _{i,j}\int {\mathrm{d}x_1\over x_1} f_{i/a}(x_1)\int {{\mathrm{d}x_2}\over {x_2}}f_{j/b}(x_2) \int _{z_{\min }}^1 (\mathrm{d}z)}}.\!\!\nonumber \\ \end{aligned}$$

(5.217)

Furthermore, as discussed in [41], we have made the ansatz that the LO contribution to the resummation effect comes from emission from valence quarks. Emission from gluons is certainly to be included, and will be dealt with in further work on the model. For a discussion of this point see also [56].

Following the interpretation by Durand and Pi, as discussed before, and in the spirit of Moliére theory of multiple scattering, we now obtain the pQCD contribution to the imaginary part of the scattering amplitude at $t=0$ and hence the total cross section through the identification $\chi (b,s)=\langle n(b,s)\rangle /2$, i.e.

$$\begin{aligned} \sigma _{\mathrm{total}}=2\int \mathrm{d}^2{\mathbf {b}}[1-\mathrm{e}^{-\langle n(b,s)\rangle /2}]. \end{aligned}$$

(5.218)

The perturbative calculation we have outlined does not suffice to account for all the process which contribute to the total cross section. Other partonic processes with momentum $p_t< p_{t\min }$ enter, and, at low energy constitute the dominant contribution. By definition, $p_{t\min }$ separates parton–parton scattering with a pQCD description, from everything else. Thus one needs to parametrise the low-energy part, and in our model we propose a simple approximate factorisation of the average number of collisions as

$$\begin{aligned} \langle n(b,s)\rangle= & {} \langle n(b,s)\rangle _{p_t <{p_{ t\min }}}+\langle n(b,s)\rangle _{p_t>{p_{ t\min }}}\nonumber \\= & {} \langle n(b,s)\rangle _{\mathrm{soft}}+\langle n(b,s)\rangle _{\mathrm{hard}}. \end{aligned}$$

(5.219)

We have proposed two different low energy parametrisations:

• $\langle n\rangle _{\mathrm{soft}}^{BN}=A^{BN}_{\mathrm{soft}}\sigma _0 [1+\frac{2\epsilon }{\sqrt{s}}]$ with $\epsilon =0,1$ according to the process being $pp$ or ${\bar{p}}p$.

• $\langle n\rangle _{\mathrm{soft}}=\hbox {(Form Factors convolution) (polynomial in } 1/\sqrt{s})$

As discussed in Ref. [94], the first of these two low energy parametrisations has the same expression for A(b, s) as in the hard pQCD calculation, except that the value of $q_{\max }$ is chosen ad hoc to reproduce the low-energy data. The second parametrisation is self explaining, and we have started using it when describing $\pi$-p and $\pi \pi$ scattering [149]. Then the elastic and the inelastic total cross sections follow from the usual formulae. Numerically, the sequence of the calculation is as follows:

• 1. choose LO densities (PDFs) for the partons involved in the process to study, such as $\pi , \gamma , \hbox {protons}, \hbox {antiprotons}$ and thus calculate the mini-jet cross section

• 2. for the given $p_{t\min }$ and chosen LO densities calculate the average value for $q_{\max }$, the maximum energy carried by a single soft gluon, through the kinematic expression given before in Eq. (5.216)

• 3. choose a value for the singularity parameter p in the soft-gluon integral and, with the $q_{\max }$ value just obtained, calculate $A_{\mathrm{hard}}^{BN}(b,s)$

• 4. parametrise the low-energy data to obtain $\langle n(b,s)\rangle _{\mathrm{soft}}$

• 5. eikonalise and integrate

Different choices of the PDFs call for different values of the parameters p and $p_{t\min }$. The sequence of calculations and some typical results for different Parton Densities can be found in [251] and are shown in the right-hand panels of Figs. 46, 47, 48 and 49. This approach led to the band of predictions shown in Fig. 50 from [253]. In particular we notice that the upper curve of our predicted band nicely accommodates the TOTEM result, as we have already shown in Fig. 33, reproduced at the beginning of this section.

Fig. 47

Global soft $K_t$ emission breaks the collinearity of partons. At right the maximum momentum. $q_{\max }$, allowed for a single gluon, averaged over different PDFs for valence quarks, [251]. Lower curve parametrises effects at $\sqrt{s}<10~\mathrm{GeV}$

Fig. 48

Representative soft-gluon radiation from initial quarks in LO picture of hadron–hadron scattering. At right, the impact-parameter distribution associated to each parton–parton scattering process, for different average $q_{\max }$ values, at LHC, from [251]. Dotted curve is convolution of proton e.m. form factors

Fig. 49

Representative multiple processes, resulting in eikonalisation of mini-jet basic process corrected for soft-gluon emission. At right, the eikonalised total cross section from different PDFs, as from above input, from [251]. This and all the above three figures are reprinted from [251] ©(2007) with permission by APPB

Fig. 50

Comparison of the BN model, described in the text, with data and other model predictions. Reprinted from [253], ©(2007) with permission by Elsevier

The above is a rather general parametrisation of the total cross section (of hadrons and photons) which we have developed over the past two decades. The central ingredients are pQCD, i.e. mini-jets, and soft resummation in the infrared with a singular but integrable effective couling constants for gluons and quarks, and where unitarisation is achieved through the impact parameter distribution. Not all the details could be specified here, but most can be found in [93, 94].

5.9.7 Soft gluon $k_t$-resummation and the Froissart bound

The physics embodied in the phenomenology described in the previous subsection is that soft-gluon resummation in the infrared region provides a cut-off in impact-parameter space, which leads to a smooth logarithmic behavior. In our model such behavior depends on the ansatz about limit of the effective quark-gluon coupling constant when $k_t\rightarrow 0$. To see this, we start with taking the very large s-limit in Eq. (5.218).

At extremely large energy values, we neglect the low-energy part, and have

$$\begin{aligned} \sigma _{\mathrm{total}}\rightarrow 2\int \mathrm{d}^2{\mathbf {b}}[1-\mathrm{e}^{-n(b,s)_{\mathrm{hard}}(b,s)/2}]. \end{aligned}$$

(5.220)

With the QCD jet cross section driving the rise due to the increase with energy of the number of partonic collisions in Eq. (5.220), let us recall the energy behaviour of the mini-jet cross sections. In the $\sqrt{s}\gg p_{t\min }$ limit, the major contribution to the mini-jet cross sections comes from collisions of gluons carrying small momentum fractions $x_{1,2}\ll 1$, a region where the relevant PDFs behave approximately as powers of the momentum fraction $x^{-J}$ with $J \sim 1.3$ [254]. This leads to the asymptotic high-energy expression for $\sigma _{\mathrm{jet}}$

$$\begin{aligned} \sigma _{\mathrm{jet}} \propto \frac{1}{{p_{t\min }^2 }}\left[ {\frac{s}{{4p_{t\min }^2 }}} \right] ^{J - 1} \end{aligned}$$

(5.221)

where the dominant term is a power of s. Fits to the mini-jet cross sections, obtained with different PDF sets [255], confirm the value $\varepsilon \equiv J-1\sim 0.3$. To match such energy behaviour as in Eq. (5.221) with the gentle rise of the total pp and $p {\bar{p}}$ cross sections at very high energy, we inspect the impact parameter distribution we have put forward using resummation of soft gluons in the infrared region. Let us consider the integral for the function $h(b,q_{\max })$, which is performed up to a value $q_{\max }$, corresponding to the maximum transverse momentum allowed by kinematics of single gluon emission [252]. In principle, this parameter and the overlap function should be calculated for each partonic sub-process, but in the partial factorisation of Eq. (5.214) we use the average value of $q_{\max }$ obtained by considering all the sub-processes that can happen for a given energy of the main hadronic process, as seen before. The energy parameter $q_{\max }$ is of the order of magnitude of $p_{t\min }$. For present low$-x$ behaviour of the PDFs, in the high energy limit, $q_{\max }$ is a slowly varying function of s, starting as $\ln {s}$, with a limiting behaviour which depends on the densities [251]. From Eqs. (5.203) and (5.221) one can estimate the very large s-limit

$$\begin{aligned} n_{\mathrm{hard}} (b,s)= & {} A_{BN}(b,s)\sigma _{\mathrm{jet}}(s,p_{t\min }) \nonumber \\&\sim A_0(s) \mathrm{e}^{-h(b,q_{\max })}{\sigma _1}\left( {{s}\over {s_0}}\right) ^\varepsilon \end{aligned}$$

(5.222)

and, from this, using the very large b-limit,

$$\begin{aligned} n_{\mathrm{hard}} (b,s)\sim A_0(s) \sigma _1 \mathrm{e}^{-(b{\bar{\varLambda }})^{2p}} \left( {{s}\over {s_0}}\right) ^\varepsilon \end{aligned}$$

(5.223)

with $A_0(s)\propto \varLambda ^2$ and with a logarithmic dependence on $q_{\max }$, i.e. a very slowly varying function of s. The large b-limit taken above follows from Eq.  (5.203). We also have

$$\begin{aligned} {\bar{\varLambda }}\equiv & {} {\bar{\varLambda }(b,s)}\nonumber \\= & {} \varLambda \left\{ {{c_F{\bar{b}}}\over {4\pi (1-p)}}\left[ \ln (2q_{\max }(s)b) +{{1}\over {1-p}}\right] \right\} ^{1/2p}.\nonumber \\ \end{aligned}$$

(5.224)

It is now straightforward to see how the two crucial parameters of our model, namely the power $\varepsilon$ with which the mini-jet cross section increases with energy and the parameter p associated to the infrared behaviour of the effective quark-gluon QCD coupling constant, conjure to obtain a rise of the total cross section obeying the limitation imposed by the Froissart bound, namely, asymptotically, $\sigma _{\mathrm{total}}\lesssim (\ln s)^2$. Call $\sigma _T(s)$ the asymptotic form of the total cross section,

$$\begin{aligned} \sigma _T (s) \approx 2\pi \int _0^\infty {\mathrm{d}b^2 } [1 - \mathrm{e}^{ - n_{\mathrm{hard}} (b,s)/2} ] \end{aligned}$$

(5.225)

and insert the asymptotic expression for $\sigma _{\mathrm{jet}}$ at high energies, which grows as a power of s, and the large b-behaviour of $A_{BN}(b,s)$, obtained through soft gluon resummation, and which decreases in b-space at least like an exponential ($1<2p<2$). In such large-b, large-s limit, one has

$$\begin{aligned} n_{\mathrm{hard}} = 2C(s)\mathrm{e}^{ - (b{\bar{\varLambda }})^{2p} } \end{aligned}$$

(5.226)

where $2C(s) = A_0(s) \sigma _1 (s/s_0 )^\varepsilon$. The resulting expression for $\sigma _T$ is

$$\begin{aligned} \sigma _T (s) \approx 2\pi \int _0^\infty {\mathrm{d}b^2 } \left[ 1 - \mathrm{e}^{ - C(s)\mathrm{e}^{ - (b{\bar{\varLambda }})^{2p} } } \right] . \end{aligned}$$

(5.227)

With the variable transformation $u=({\bar{\varLambda }} b)^{2p}$, and neglecting the logarithmic b-dependence in ${\bar{\varLambda }}$ by putting $b=1/\varLambda$, Eq. (5.227) becomes

$$\begin{aligned} \sigma _T (s) \approx {{2\pi }\over {p}}{{1}\over {{\bar{\varLambda }}^2}} \int _0^\infty \mathrm{d}u u^{1/p -1} [1-\mathrm{e}^{ -C(s) \mathrm{e}^{-u} } ]. \end{aligned}$$

(5.228)

Since, as $s\rightarrow \infty$, C(s) grows indefinitely as a power law, the quantity between square brackets $I(u,s)=1-\mathrm{e}^{-C(s)\mathrm{e}^{-u}}$ has the limits $I(u,s)\rightarrow 1$ at $u=0$ and $I(u,s)\rightarrow 0$ as $u=\infty$. Calling $u_0$ the value at which $I(u_0,s)=1/2$ we then put $I(u,s)\approx 1$ and integrate only up to $u_0$. Thus

$$\begin{aligned} {\bar{\varLambda }}^2\sigma _{T}(s)\approx \left( \frac{2\pi }{p}\right) \int _0^{u_0} \mathrm{d}u u^{\frac{1-p}{p}} =2\pi u_0^{1/p} \end{aligned}$$

(5.229)

and since, by construction,

$$\begin{aligned} u_0=\ln \left[ \frac{C(s)}{\ln 2}\right] \approx \varepsilon \ln s \end{aligned}$$

(5.230)

we finally obtain

$$\begin{aligned} \sigma _{T}\approx \frac{2\pi }{{\bar{\varLambda }}^2} \left[ \varepsilon \ln \frac{s}{s_0}\right] ^{1/p} \end{aligned}$$

(5.231)

to leading terms in $\ln s$. We therefore derive the asymptotic energy dependence

$$\begin{aligned} \sigma _T \rightarrow [\varepsilon \ln (s)]^{(1/p)} \end{aligned}$$

(5.232)

apart from a possible very slow s-dependence from ${\bar{\varLambda }}^2$. The same result is also obtained using the saddle point method.

This indicates that the Froissart bound is saturated if $p=1/2$, but also that we have the two following asymptotic limits

$$\begin{aligned}&\sigma _{\mathrm{total}} \rightarrow ( \ln s)^2\quad p \rightarrow 1/2,\end{aligned}$$

(5.233)

$$\begin{aligned}&\sigma _{\mathrm{total}} \rightarrow \ln s\quad p \rightarrow 1 \end{aligned}$$

(5.234)

depending on our approximate singular expression for the strong coupling in the infrared. We notice that the limits $1/2<p<1$ are a consequence of our infrared description. Namely, from the requirement for the soft-gluon integral to be finite ($p<1$) it follows that the cross section should grow at least like a logarithm, while the limitation $p \ge 1/2$ is to ensure the confinement of the partons. Confinement of partons is essential in creating a “mass gap” leading to massive hadrons. Once we have massive hadrons, we have a Lehmann ellipse for hadrons [11]. We recall that the existence of a Lehmann ellipse is essential for obtaining the Martin–Froissart bound for total cross sections. Through our model, we have delineated the two limits: up to a linear confining potential ($p\rightarrow 1$) or down to a barely confining one ($p\rightarrow 1/2$).

Fig. 51

The one-channel predictions from the one-channel QCD mini-jet with soft-gluon resummation model and pp total cross section (BN model) are compared with accelerator data at LHC, from TOTEM [103, 256] and ATLAS measurements [257]. The BN-model results are compared with one-channel model from Khoze et al. [258]. The red dot-dashed curve corresponds to fits to the total cross section by Block and Halzen [259], the dot-dashed blue line represents the fit by Fagundes–Menon–Silva [260]. The figure is from [56]. Reprinted with permission from [56], Fig. (3), ©(2015) by the American Physical Society

Before closing this subsection and the description of the BN model, in Fig. 51, from [56], we show how LHC data up to $\sqrt{s}=8\ \mathrm{TeV}$ can be described by this and other currently used models for the total cross section.

As can be seen from Fig. 50 from [253] it has been the practice to reproduce total cross section data for both pp and ${\bar{p}} p$, up to the TeVatron results. However, the large differences among the Tevatron measurements did not allow a precise description at higher energies, such as those explored at LHC. Once the LHC data have been released, and as it has been the case for all models for the total cross section, we have updated our analysis. To this aim, we have used only pp accelerator data, ISR and the recent LHC measurements, namely ${\bar{p}} p$ points are shown, but have not been used for the phenomenological fit, nor the Cosmic ray extracted values for pp. A more recent set of LO densities, MSTW [95] has been included in the set of predictions for the BN model. The values of p and $p_{t\min }$ which better reproduce the LHC result are obtained by varying $p_{t\min } \simeq 1\div 1.5~\mathrm{GeV}$ and $1/2\lesssim p \lesssim 0.8$. The result, for the total pp cross sections, is shown in Fig. 51.

The BN results, now stabilised at $\sqrt{s}=7$ and $8~\hbox {TeV}$ by tuning the parameters to TOTEM data, show marked differences in the high cosmic ray region. The difference is ascribable to the different low-x behaviour of the PDFs used in the mini-jet calculation, GRV and MSTW, as discussed in [56]. In addition, and as we shall briefly discuss at the end of Sect. 8, as of 2016 there is some tension between measurements by the two experiments presently providing values for the total cross section, TOTEM and ATLAS.

5.10 AdS/CFT correspondence and the total cross section

A short, but compact discussion of the Froissart bound in the context of the string/gauge duality can be found in [261]. In [261], the Pomeron is defined as the leading contribution at large $N_c$ to the vacuum exchange at large s and fixed t. It is stated that in both strong coupling and pQCD, the Pomeron contribution grows as $s^{1+\epsilon }$ with $\epsilon >0$, so that, in order not to violate the Froissart bound, higher order corrections need to be taken into account.

For the scattering of particles 1 and 2 into particles 3 and 4, the standard eikonal representation for the amplitude in the case of large ’t Hooft coupling is then generalised to the expression [262]

$$\begin{aligned} A(s,t)= & {} -2is\int \mathrm{d}z \mathrm{d}z' P_{13}(z) P_{24}(z') \nonumber \\&\times \int \mathrm{d}^2b \mathrm{e}^{iq_\perp \cdot b}[\mathrm{e}^{i\chi (s,b,z,z')}-1] \end{aligned}$$

(5.235)

where the wave function $P_{ij}(z)$ refers to the left moving particles, 1 into 3, and right moving particles, 2 into 4. The variables z and $z'$ correspond to the convolution over moving direction in $AdS_3$ and they are normalised so that, when confinement is implemented, $\int P_{ij}\mathrm{d}z=\delta _{ij}$.

In this description, one obtains the total cross section through the standard geometrical picture $\sigma _{\mathrm{total}}\approx b^2_{\max }$ and the problem is, as usual, that of finding $b_{\max }$.

In this picture, the quantity

$$\begin{aligned} \sigma _{\mathrm{total}}(s,z,z')=2\mathfrak {R}e \int \mathrm{d}^2b[1-\mathrm{e}^{i\chi (s,b,z,z')}] \end{aligned}$$

(5.236)

is the bulk cross section and the physical cross section is obtained after convolution with the wave functions.

The picture in the bulk is split into two regions, respectively called diffractive and black disk, as follows:

• diffractive: in this region $\mathfrak {I}m \chi < \mathfrak {R}e \chi$, and it is $\mathfrak {R}e \chi \approx 1$ which sets the limit for contributions to the scattering, with $b_{\max }=b_{\mathrm{diff}}$.

• black disk: in this region $\mathfrak {I}m \chi > \mathfrak {R}e \chi$, the interaction is dominated by the weak coupling Pomeron and the maximum $b_{\mathrm{black}}$ at which scattering still takes place corresponds to where absorption is of order 1, namely $\mathfrak {I}m \chi \approx 1$.

For the example of an even-signature Regge exchange in four dimensions, according to [261], one can write

$$\begin{aligned}&b_{\mathrm{black}}\sim \lambda ^{-1/4} m_0^{-1}\ln (\beta s/s_0),\end{aligned}$$

(5.237)

$$\begin{aligned}&b_{\mathrm{diff}}\sim m_0^{-1}\ln (\beta s/s_0) \end{aligned}$$

(5.238)

where in the fixed ’t Hooft coupling $\lambda =g^2_{YM}N_c$, and $m_0$ is the scale for the trajectory exchanged with

$$\begin{aligned} \alpha _{t}=2+\alpha '\left( \frac{t}{m_0^2} -1\right) . \end{aligned}$$

(5.239)

With $\alpha ' \sim \lambda ^{-1/2}\ll 1$, one obtains $b_{\mathrm{diff}}\gg b_{\mathrm{black}}$. Thus, a unique result of the strong coupling regime is that the eikonal is predominantly real.

Scattering in the conformal limit, leads to a $\sigma _{\mathrm{total}}\sim s^{1/3}$ in the strong coupling regime. But with confinement the situation is different and the spectrum has a mass gap which then leads to a logarithmic growth. Tan [261] writes

$$\begin{aligned} b_{\mathrm{diff}} \simeq \frac{1}{m_0}\ln (N^2 s/m_0^2). \end{aligned}$$

(5.240)

A full discussion of all these regions and the resulting expressions can be found in [262].

5.11 Phenomenological fits to the total cross section

We shall now describe two different phenomenological fits used to describe pp and ${\bar{p}} p$ total cross section, published by the Particle Data Group, one before and the other after the start of LHC.

5.11.1 Cudell and COMPETE Collaboration

For the two reactions $pp$ and ${\bar{p}}p$ of interest here, we show in Fig. 52 the data compilation from fig. 40.11 of the 2009 Particle Data Group (PDG) [263]. For this and other updates of mini-reviews and figures, we refer the reader to the PDG site. We shall start by summarising Ref. [265] where an overview of the COMPETE program is given. In this paper, the authors describe their data base policy and give a number of web access information, which allow one to download and run fitting programs.

Fig. 52

The total proton cross sections, as compiled before the start of the LHC and hence before of the TOTEM and ATLAS measurements, by the COMPAS Collaboration for the 2009 RPP [263] with model input from [264] ( COMPETE Collaboration). Figure downloaded from http://pdg.lbl.gov/2009/figures/figures.html

The region to be focussed on is the Coulomb-nuclear interference region, and to do this one needs to use, for all the experiments, the following common set of theoretical inputs:

• common parametrisation of electromagnetic form factors, where there is a problem with the usual VMD term, since a fit to the $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$ alone gives a better $\chi ^2/\hbox {d.o.f}$ than the fit to the combined data set of $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$ and $G_E/G_M$,

• common procedure to analyze data in the Coulomb interference region,

• common set of strong interaction elastic scattering parameters,

• common study of Regge trajectories: already there is a problem here since the slope of the meson trajectories is different depending on the flavour content, although not so much for the baryons.

The problem with the above program, of course, is that the Regge description may be only a (albeit good) approximation and while it may eliminate the systematic differences, it will still have a model dependence. But more about this later.

The COMPETE Collaboration had been cleaning and gathering all total cross section data [264] then available at the PDG site [263]. Data have been fitted with the expression

$$\begin{aligned}&\sigma _{{\bar{a}}b}=Z^{ab}+B\ln ^2 \left( \frac{s}{s_0}\right) +Y_1^{ab}\left( \frac{s_1}{s}\right) ^{\eta _1} +Y_2^{ab}\left( \frac{s_1}{s}\right) ^{\eta _2} |,\nonumber \\ \end{aligned}$$

(5.241)

$$\begin{aligned}&\sigma _{ ab}=Z^{ab}+B\ln ^2 \left( \frac{s}{s_0}\right) +Y_1^{ab}\left( \frac{s_1}{s}\right) ^{ \eta _1}-Y_2^{ab}\left( \frac{s_1}{s}\right) ^{\eta _2} \nonumber \\ \end{aligned}$$

(5.242)

where $Z^{ab}, B, Y_i^{ab}$ are in millibarn, $s,\ s_0,\ s_1$ are in $\mathrm{GeV}^2$. The scale $s_1$ is fixed to be $1/\mathrm{GeV}^2$, whereas $\sqrt{s_0}\approx 5~\mathrm{GeV}$. The physical interpretation of this fit is that the power-law terms reproduce the Regge behaviour from the imaginary part of the forward scattering amplitude, with two Regge poles if $\eta _1\ne \eta _2$, whereas the constant term and the $\ln ^2[s]$ term reflect the so-called Pomeron exchange. For a summary of the numerical values of the various parameters, we refer the reader to the PDG review.

The first two terms in Eqs. (5.241) and (5.242) reflect the bulk of semi-perturbative QCD processes which start dominating the total cross sections as soon as the c.m. energy of the hadronic process goes above $\sqrt{s}\approx (10\div 20)~\mathrm{GeV}$. There are various ways to refer to these terms. In our QCD model [93, 94] the term which brings in the rise is the one which comes from gluon–gluon scattering tempered by soft gluon emission from the initial state, as we have described in Sect. 5.9.4. The constant term is more complicated to understand. It is probably due to quark scattering, well past the Regge region. Notice that in the simple Donnachie and Landshoff successful original parametrisation [60], there is no constant term in the cross section. The cross sections only apparently go to a constant, which is where the minimum of the cross section lies, just after the Regge descent and just before the cross section picks up for the asymptotic rise. Indeed, whereas the Regge terms can be put in correspondence with resonances in the s-channel, the constant term is harder to interpret, except as the old Pomeron which was supposed to give constant total cross sections.

Let us now review a comprehensive discussion of fits to pre-LHC total cross sections data [266]. Cudell notes the difficulty to make precise predictions at LHC because of a number of problems with present data on the total cross section:

• No data are available between the ISR energy, $\sqrt{s} \approx (60\div 70)~\mathrm{GeV}$ and the $S{\bar{p}}pS$ at $\sqrt{s} \approx (500\div 600)~\mathrm{GeV}$

• at Tevatron energies, $\sqrt{s} \approx 1800~\mathrm{GeV}$, there is a $2\sigma$ discrepancy between the value calculated by two TeVatron collaborations, E710 and CDF

• the t dependence of the differential elastic cross section as $t \rightarrow 0$ may not be a simple exponential $\exp (Bt)$ where B assumed constant in t thus affecting the measurement of the total cross section.

To the above one should add that total $pp$ cross sections at cosmic ray energies have very large errors, mostly due to the theoretical uncertainty in the procedures adopted to extract $pp$ total cross section from p-air cross section, as discussed. Predictions from the COMPETE Collaboration from [266] are shown in Fig. 53.

Fig. 53

The range of values predicted for the total proton–proton cross section by the COMPETE Collaboration as shown in [266]. Figure is courtesy of J-R Cudell. Reprinted from [266], in CERN Proceedings CERN-PROCEEDINGS-2010-002

Many of the problems discussed by Cudell can be related to the type of unitarisation scheme. A new analytic unitarisation scheme was proposed in [267], but the actual problem is the difficulty of doing a good fit to both elastic and total cross section data.

In [264], it is pointed out that there are problems with the $\rho$ parameter data, where $\rho \equiv \rho (s)=\mathfrak {R}e A(s,t=0)/\mathfrak {I}m A(s,t=0)$. Hence, it is said, that the first and safest strategy is to obtain constraints from the reproduction of $\sigma _{\mathrm{total}}$ only. However, the final result is obtained by fitting the total cross section and $\rho$.

In [264] the fits to lower energy total cross sections are parametrised with

$$\begin{aligned} \sigma ^{a\mp b}=\frac{1}{s}( (R^{+ab}(s)\pm R^{-ab}(s)+P^{ab}(s)+H^{ab}(s) )\nonumber \\ \end{aligned}$$

(5.243)

with

$$\begin{aligned}&R^{+ab}(s)=Y_1^{ab}\cdot (s/s_1)^{\alpha _1},\quad \hbox {with } s_1=1~\mathrm{GeV}^2\nonumber \\&R^{-ab}(s)=Y_2^{ab}\cdot (s/s_1)^{\alpha _2 } \end{aligned}$$

(5.244)

wherein

$$\begin{aligned} P^{ab}(s)= sC^{ab} \end{aligned}$$

(5.245)

describes a simple Pomeron pole at $J=1$ and $H^{ab}(s)$ is the rising term, which can be

• a supplementary simple pole with larger than one intercept

• a double pole at $J=1$, namely $L_{ab}=s(B_{ab}\ln (s/s_1)+A_{ab})$

• a triple pole at $J=1$, namely $L_{ab}=s(B_{ab}\ln ^2(s/s_1)+A_{ab})$

Thus, their parametrisation for $\sigma _{\mathrm{total}}$ is a sum of various $I_n$ terms, with the parametrisation for $\rho$ given below.

For the $\rho$ parameter, in the appendix, the authors list the following parametrisation:

$$\begin{aligned}&R^+_{\mathrm{pole}}=-I^+_{\mathrm{pole}} \cot [\pi /2 \alpha _+],\end{aligned}$$

(5.246)

$$\begin{aligned}&R^-_{\mathrm{pole}}=-I^-_{\mathrm{pole}} \tan [\pi /2 \alpha _-],\end{aligned}$$

(5.247)

$$\begin{aligned}&R_L=\frac{\pi }{2} s C_L,\end{aligned}$$

(5.248)

$$\begin{aligned}&R_{L2}=\pi s \ln (s/s_0)C_{L2} \end{aligned}$$

(5.249)

where

$$\begin{aligned}&I^+_{\mathrm{pole}}=C^+(s/s_1)^{\alpha ^+},\end{aligned}$$

(5.250)

$$\begin{aligned}&I^-_{\mathrm{pole}}=\mp C^-(s/s_1)^{\alpha ^-},\end{aligned}$$

(5.251)

$$\begin{aligned}&I_L=C_Ls \ln (s/s_1),\end{aligned}$$

(5.252)

$$\begin{aligned}&I_{L2}=C_{L2} \ln ^2 (s_0). \end{aligned}$$

(5.253)

At the end of all this, the result favoured now and found in 2008 PDG [263], is the one given by Eqs. (5.241) and (5.242).

The paper [264] also contains a rather long discussion as regards the sign in front of the logarithmic terms, which might hint at the result we had originally found in our Pramana paper [268].

Apart from fits to the total cross section, Cudell and Selyugin in [269] also address the question of the measurement itself, which, as described previously in this review, is based on two methods, the optical point and the luminosity based one. The optical point type measurement, also called the non-luminosity measurement, is based on the extrapolation of the elastic differential cross section to the value $t=0$. The extrapolation has been usually done assuming an exponential behaviour $\exp [{B(s)t}]$ for the differential elastic cross section near the $t=0$ point. However it is well known that the exponent is not strictly linear in t. In this paper [269] the authors examine the possibility that at the LHC expectations based on simple Regge pole models are modified and that the usual expectation of $\sigma _{\mathrm{total}}\approx 90\div 125 ~\hbox {mb}$ be superseded by the higher values predicted from a number of unitarisation schemes, such as hard Pomeron, which would give cross sections around $150~\hbox {mb}$ or U-matrix unitarisation which can give cross sections as high as 230 mb. The impact of such different expectations is discussed, together with the possibility that $\rho$ has a strong t-dependence. In this paper this t-dependence of the $\rho$ parameter is considered to be a possible reason for the difference in the measurement of $\sigma _{\mathrm{total}}$ at the Tevatron.

Closing this example of a recent fit, we recall the latest results from the TOTEM Collaboration, namely $\sigma _{\mathrm{tot}}^{pp}(8~\hbox {TeV})=(101.7\pm 2.9)~\hbox {mb}$ [103] and the preliminary result $\rho (8 ~\hbox {TeV})=0.104\pm 0.027(\hbox {stat})\pm 0.01{\hbox {syst}}$ presented at the 2014 Rencontre de physique de La Thuile. As of 2016, both TOTEM and ATLAS Collaboration have released data at $\sqrt{s}=8$ TeV, as we briefly discuss in Sect. 8.

5.11.2 COMPAS group (IHEP, Protvino)

The COMPAS group has presented (in a version of PDG 2012 [270], updated in the first half of 2013) a phenomenological fit to all total hadronic cross sections and the ratio of the real-to-imaginary parts of the forward elastic scattering hadronic amplitudes. New data on total pp collision cross sections from CERN-LHC-TOTEM and new data from cosmic rays experiment have been added. They note -in agreement with we what we also find and as we have discussed elsewhere in the present review – that, the models giving the best fit of accelerator data also reproduce the experimental cosmic ray nucleon–nucleon data extracted from nucleon-air data with no need of any extra phenomenological corrections to the data.

COMPAS uses four terms in the total hadronic cross section for hadron $a^{\pm }$ on hadron b:

$$\begin{aligned} \sigma _{\mathrm{tot}}(a^{\pm } b)= & {} H \left[ \ln \left( \frac{s}{s^{ab}_M}\right) \right] ^2 + P^{ab}\nonumber \\&+\, R^{ab}_1\left( \frac{s}{s^{ab}_M}\right) ^{-\eta _1} \pm R^{ab}_2\left( \frac{s}{s^{ab}_M}\right) ^{-\eta _2}. \end{aligned}$$

(5.254)

The adjustable parameters are defined as follows:

• $H = \pi /M^2$ (in mb) is named after Heisenberg.

• the scaling parameter $s^{ab}_M = (m_a + m_b + M)^2$.

• A factorisable set $P^{ab}$ (in mb) stands for a constant Pomeron.

• Two factorisable sets $R^{ab}_i$ (in mb), (for $i=1,2$) stand for the two leading Regge–Gribov trajectories.

• The data for purely hadronic reactions used were $\bar{p}$, p, $\pi ^{\pm }$ and $K^{\pm }$ on p, n, d; $\varSigma ^-$ on p.

• Also used, were fits to $\gamma p$, $\gamma d$ and $\gamma \gamma$.

The above parameterisations were used for simultaneous fits to the listed reactions with 35 adjustable parameters. To trace the variation of the range of applicability of simultaneous fit results, several fits were produced with lower energy $\sqrt{s} \ge 5, \ge 6, \ge 7,\ldots \mathrm{GeV}$ cutoffs, until the uniformity of the fit across different collisions became acceptable with good statistical value. Downloadable figures are available on the PDG site. Figure 54 reproduces their results for various total cross sections.

Fig. 54

Total cross sections, as compiled by the Compas Collaboration for PDG [270]. Reprinted with permission from [270], Fig.(46.9), ©(2012) by the American Physical Society

5.12 Asymptotic total cross sections in theories with extra dimensions

The search for asymptotia has been driving many models, with the question asked as to whether present measurements of the total cross section have reached a stable situation, where one cannot expect new phenomena to be detected in the energy behavior of $\sigma _{\mathrm{tot}}$. In this subsection, this question will be addressed by focusing on behavior reflecting extra dimensions.

The rate at which cross sections grow with energy is sensitive to the presence of extra dimensions in a rather model-independent fashion. In [271], one can find a review of how rates would be expected to grow if there are more spatial dimensions than 3 which appear at some energy scale, making connections with black hole physics and string theory. The salient point – as discussed for example in [272] – is that the generalisation of the Froissart–Martin bound for space-time dimensions $D > 4$ leads generically to a power-law growth rather than the maximum square of logarithm growth with energy allowed in $D = 4$.

5.12.1 Asymptotic relation between cross section and entropy

A clear physical argument for estimating the total cross section at a high energy $s = E^2$ was given by Eden, a long time ago [273]. It runs as follows:

(i) If the elastic scattering amplitude at high energy is dominated by the exchange of the lightest particle of mass $\mu$, then the probability of the exchange at a space-like distance r between the particles, reads

$$\begin{aligned} P(r, E) = \mathrm{e}^{-2 \mu r + S(E)}, \end{aligned}$$

(5.255)

where the entropy S(E) (in units of the Boltzmann constant $k_\mathrm{B}$) determines the density of final states.

(ii) The probability becomes of order unity at a distance $R(E) = S(E)/(2\mu )$

(iii) The total cross section is then given by

$$\begin{aligned} \sigma _{\mathrm{tot}}(E) = 2\pi R(E)^2 = \frac{\pi }{2\mu ^2} S(E)^2. \end{aligned}$$

(5.256)

The asymptotic total cross section at large E is thereby determined by the entropy S(E).

A typical entropy estimate may be made via the following reasoning: The equipartition theorem for a gas of ultra-relativistic particles implies a mean particle energy ($\bar{\epsilon }$) varying linearly with temperature $\bar{\epsilon } = 3 k_\mathrm{B} T$. A Boltzmann gas of such particles has a constant heat capacity. A system with a constant heat capacity $C_\infty$ obeys

$$\begin{aligned} E = C_\infty T = C_\infty \frac{\mathrm{d}E}{\mathrm{d}S};\ \Rightarrow \mathrm{d}S = C_\infty \left( \frac{\mathrm{d}E}{E}\right) , \end{aligned}$$

(5.257)

leading to the following important logarithmic relationship between entropy and energy

$$\begin{aligned} S(E) = C_\infty \ln \left( \frac{E}{E_o}\right) . \end{aligned}$$

(5.258)

Hence, the total cross section for a constant heat-capacity system saturates the Froissart–Martin bound:

$$\begin{aligned} \sigma _{\mathrm{tot}}(E) = \left( \frac{\pi }{2}\right) \left( \frac{C_\infty }{\mu }\right) ^2 \ln ^2\left( \frac{E}{E_o}\right) . \end{aligned}$$

(5.259)

In a more general thermodynamically stable situation, the entropy S(E) is determined parametrically by the heat capacity as a function of temperature [271]:

$$\begin{aligned} S(T) = \int _o^T C(T') \frac{\mathrm{d}T'}{T'}. \end{aligned}$$

(5.260)

The saturation Eqs. (5.257) and (5.259) will then hold true only in the high energy and high temperature limit of a stable heat capacity $C(T \rightarrow \infty ) = C_\infty$.

To compute the total high energy cross section for models with extra dimensions, the central theoretical problem is to understand the entropy implicit in such models. Below we list the entropies and total cross sections for a Hagedorn string and for $n = (D-4)$ extra compact dimensions.

5.12.2 Entropies for higher dimensions and string theory

A Hagedorn string entropy grows linearly with energy in the asymptotic limit [274, 275]

$$\begin{aligned} S(E) \rightarrow \frac{E}{T_H}, \end{aligned}$$

(5.261)

where $T_H$ is the Hagedorn temperature. The Hagedorn entropy for bosonic and fermionic strings have a similar linear growth with energy but with different coefficients. Thus, for such theories the total cross section is expected to grow as $\sigma _{\mathrm{tot}}(s) \sim s$.

On the other hand, above the threshold for the observation of $n = (D - 4)$ extra compact dimensions, the total cross section would grow as [271]

$$\begin{aligned} \sigma _{\mathrm{tot}}(s) \sim \left[ \frac{s}{s_o}\right] ^{(n + 2)/2}. \end{aligned}$$

(5.262)

Thus, once even if one such threshold is crossed (that is for $n = 1$ or $D = 5$), $\sigma _{\mathrm{total}}(s) \rightarrow (s/s_o)^{3/2}$. It is fair to conclude from the recent LHC total cross section data that no such extra dimension thresholds have opened up until $\sqrt{s} = 8~\hbox {TeV}$, and notwithstanding large errors with the AUGER cosmic ray data, not even until $\sqrt{s} = 57~\hbox {TeV}$. Such a result is in consonance with the fact that no evidence for beyond the standard model physics such as that due to extra dimensions has been found in any data from LHC for $\sqrt{s} \le 8~\hbox {TeV}$.

The arguments presented in [271] have been accepted in [276] with an aim to extend it and the latter authors suggest that higher dimensions might be ruled out to arbitrarily high energies via the same arguments.

5.13 Concluding remarks

In this section, we have attempted to give an overview of the existing models for the total cross section, highlighting the chronological order of its long history. The total cross section, as the imaginary part of the forward scattering amplitude describes the very large distance behavior of the interaction, but understanding of the underlying strong interaction dynamics can only be completed by studying the amplitude for $-t\ne 0$. This, we shall approach in the next section dedicated to the elastic cross section.

6 The elastic cross section

We shall now summarise the state of the art of the differential elastic cross section, discuss some representative models and present their predictions. We shall try to put in perspective the phenomenological work developed over more than 50 years, up to the latest measurements made at the LHC running at $\sqrt{s}=7\ \mathrm{TeV}$ (LHC7) and $8\ \mathrm{TeV}$ (LHC8) [103, 257, 277, 278].

In Fig. 55 we reproduce the first plot of the elastic differential cross section measurement by the TOTEM Collaboration at LHC [277]. It was the first time since almost 40 years that the distinctive dip in the $pp$ differential cross section had been seen again, shifting to the left by a factor 3, as the energy increased more than a hundred times.

Fig. 55

The first TOTEM measurement of the differential elastic cross section from [277]. Published by IOP under CC BY license

As clearly shown in Fig. 56, elastic scattering is characterized by the following quantities: the optical point, i.e. imaginary and real parts of the scattering amplitude at $t=0$; the precipitous decrease at small t, related to the slope $B(s,t=0)$; the change in slope and occurrence of the dip where the imaginary part of the amplitude becomes smaller than the real part; the |t| behaviour after the dip and connections with perturbative QCD. It is worth noting that at ISR no dip is observed in ${\bar{p}}p$, but only a change in slope, whereas the dip is quite pronounced in $pp$, both at lower and higher energies.

Fig. 56

ISR and Tevatron elastic differential cross sections from talk by K.Eggert, at Hadron Collider Physics Symposium, November 2011, Paris, France. Reproduced with permission

Table 9 TOTEM results, with $\sigma _{\mathrm{inel}}=\sigma _{\mathrm{total}}- \sigma _{\mathrm{elastic}}$, for 7 TeV [256] and for 8 TeV [103, 282], luminosity independent measurements

The TOTEM experiment has measured $\sigma _{\mathrm{total}}$, $\sigma _{\mathrm{inel}}$, $\sigma _{\mathrm{elastic}}$, $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$ at LHC energies $\sqrt{s}=7,\ 8\ \mathrm{TeV}$ and, from these, has given values for the slope parameter B(s, t), at different $-t$-values, the position of the dip and provided a functional form for the behaviour of $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$ after the dip [256, 279, 280]. From these data, one can extract the ratio $\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}$ and check whether the asymptotic black-disk limit has been reached. At the time of this writing, data for the total and elastic cross sections at $\sqrt{s}= 8\ \mathrm{TeV}$ have been published from both the TOTEM [103] and ATLAS [278] Collaborations, with new data appearing from the TOTEM Collaboration for the differential cross section [281]. In Table 9 we present the available results from TOTEM for some of these quantities. In addition, most recent data at $\sqrt{s}=8\ \mathrm{TeV}$ (LHC8), have shown that a pure exponential behavior for the slope in the region $0.027<-t<0.2~\mathrm{GeV}^2$ can be excluded [281] with significance greater than 7 standard deviations.

An exhaustive discussion of all the quantities defining the elastic differential cross section can be found in [12]. Although the review of Ref. [12] pre-dates both the Tevatron and LHC measurements, most of its content and some of its conclusions are still very much valid. In the following we shall describe these different quantities, and the asymptotic theorems which govern their energy dependence. Tables and figures for each of them, $\sigma _{\mathrm{total}}$, B(s, t), $\rho (s,t)$, $t_{\mathrm{dip}}$ are available at the Particle Data Group (PDG) site, here we shall reproduce them as encountered in describing models.

We shall define the following measures of asymptotia: the total cross section itself $\sigma _{\mathrm{total}}$, satisfaction of asymptotic sum rules for the elastic scattering amplitude, the forward slope B(s), the ratio $\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}$. Then we shall examine representative models for elastic scattering, starting from the simplest possible case, the black and gray disk model.

Models for the elastic and total cross sections, are based on two major approaches: the Pomeron–Regge road and the unitarity–Glauber formalism. The Pomeron–Regge theory expresses the differential elastic scattering amplitude in terms of power laws $s^{\alpha (t)}$, and it has provided more than 50 years of good phenomenology for both elastic and diffractive scattering. However, this raises problems with unitarity and the Froissart bound. As well known, the elastic scattering amplitude cannot be just described through a simple pole, since then the high energy behavior of the total cross section would violate the Froissart bound; on the other hand, the diffraction peak is well represented by a Pomeron pole. Thus the problem is that at $t=0$, the elastic differential cross section is proportional to $\sigma _{\mathrm{total}}^2$ (modulo a small contribution from the real part), hence for $t\sim 0$, the cross section at the optical point can increase at most as the fourth power of logarithm, while, at the same time, the differential elastic cross section, as soon as $t\ne 0$ does indeed exhibit the exponential behavior characteristic of the Pomeron pole contribution.

The Glauber-type description is unitary and it can easily embed the Froissart bound, as we have discussed, for instance, in the context of the QCD-inspired model of Block et al. or our BN mini-jet model, both of them discussed in Sect. 5. However, a one channel eikonal, for both elastic and inelastic scattering, fails in its capacity to describe separately the three components of the scattering, elastic, inelastic and (single and double) diffractive, as measured up to present energies. This is immediately obvious if one considers the expression for the inelastic total cross section obtained in the one channel eikonal:

$$\begin{aligned}&F(s,t)=i\int \mathrm{d}^2 {\mathbf {b}}\mathrm{e}^{i{\mathbf {q}}\cdot {\mathbf {b}}} [1-\mathrm{e}^{i\chi (b,s)}],\end{aligned}$$

(6.1)

$$\begin{aligned}&\sigma _{\mathrm{total}}=2\int \mathrm{d}^2 {\mathbf {b}}[1-\cos \mathfrak {R}e\chi (b,s) \mathrm{e}^{-\mathfrak {I}m\chi (b,s)}],\end{aligned}$$

(6.2)

$$\begin{aligned}&\sigma _{\mathrm{elastic}}=\int \mathrm{d}^2 {\mathbf {b}}|[1-\mathrm{e}^{i\chi (b,s)}]|^2,\end{aligned}$$

(6.3)

$$\begin{aligned}&\sigma _{\mathrm{inel}}=\sigma _{\mathrm{total}}-\sigma _{\mathrm{elastic}}=\int \mathrm{d}^2 {\mathbf {b}}[1-\mathrm{e}^{-2\mathfrak {I}m\chi (b,s)}] \end{aligned}$$

(6.4)

where $t=-q^2$. It must be noted that Eq. (6.4) can be obtained by summing all possible inelastic collisions independently distributed in ${\mathbf {b}}$-space. Assuming in fact that for every impact-parameter value the number of possible collisions n(b, s) is Poisson distributed around a mean number of collisions $\bar{n} (b,s)$, i.e.

$$\begin{aligned} P(\{n, \bar{n}(b,s)\})= \frac{\mathrm{e}^{- \bar{n}(b,s)}}{n!} \bar{n}(b,s)^{n} \end{aligned}$$

(6.5)

it immediately follows that a sum on all possible collisions together with integration on all values of the impact parameter, leads to

$$\begin{aligned} \sigma _{\mathrm{independent} \ \mathrm{collisions}}=\int \mathrm{d}^2 {\mathbf {b}}[1-\mathrm{e}^{- \bar{n}(b,s)}]. \end{aligned}$$

(6.6)

Comparing Eqs. (6.4) and (6.6), shows that one can obtain $\mathfrak {I}m\chi (b,s)$ from $\bar{n}(b,s)$, but also that Eq. (6.4) for the inelastic cross section only includes independent collisions. Since diffractive processes, single, double, central, do exhibit correlations, these processes need to be discussed with a formalism beyond the one-channel eikonal.

Thus the question arises in eikonal models as to how to include correlated-inelastic processes, which are identified through particular final state configurations. Among the models which embed some of these properties, are those due to Khoze, Martin and Ryskin (KMR), Gotsman, Levin and Maor (GLM), Ostapchenko, Lipari and Lusignoli, to be seen later in this section.

The way we choose to present this part of the review is to start with general definitions and properties of quantities defining the scattering and some comparison with data from LHC at $\sqrt{s}=7\ \mathrm{TeV}$ (LHC7). Then models for the elastic differential cross section from the optical point to past the dip will be presented, both in their historical development and in their contribution to describe TOTEM data. We shall conclude this section on elastic scattering with a short review of models specifically addressing diffraction and a discussion of the inelastic part of the total cross section.

Each of the items above is discussed as follows:

• general features of the elastic cross section are discussed in Sect. 6.1 with

  • the slope parameter in Sect. 6.1.1,

  • the real part of the scattering amplitude in Sects. 6.1.2 and 6.1.3,

  • sum rules for real and imaginary parts of the scattering amplitude at b=0, in Sect. 6.1.4,

  • asymptotia and the ratio $\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}$ in Sect. 6.1.5,

  • the dip structure and geometrical scaling in Sects. 6.1.6 and 6.1.7,

• early models in impact-parameter space and their updates are to be found in Sect. 6.2 with

  • the Glauber picture applied to $pp$ scattering in Sects. 6.2.1 and 6.2.2,

  • the black disk picture in Sect. 6.2.3,

• models with Regge and Pomeron exchanges are presented in Sect. 6.3 with

  • an early model by Phillips and Barger (PB) and its updates in Sect. 6.3.1,

  • a model by Donnachie and Landshoff in Sect. 6.3.2

  • a model in which the slope parameter increases with energy at the same rate as the total cross section in Sect. 6.3.3,

• models including an Odderon exchange can be found in Sect. 6.4,

• eikonal models are discussed in Sect. 6.5

• selected models including diffraction are to be found in Sect. 6.6 with a comment on single-channel mini-jet models with soft-gluon radiation in Sect. 6.6.7,

• a parametrisation of diffraction to obtain the total, elastic and inelastic cross section from one-channel eikonal models is presented in Sect. 6.7.

6.1 General features of the elastic cross section

As stated earlier, elastic scattering is characterized by the following quantities:

• the optical point, i.e. the imaginary and real parts of the amplitude at $t=0$,

• the precipitous decrease at small t, related to the forward slope $B(s,t=0)$,

• the change in slope and occurrence of the dip where the imaginary part of the amplitude becomes smaller than the real part,

• the |t| behaviour after the dip and connections with perturbative QCD.

In the following we shall describe these different quantities, and the asymptotic theorems which govern their energy dependence.

6.1.1 About the slope parameter

An earlier rather complete discussion of this issue can be found in [12]. Here we discuss its definition and show the present experimental status.

Although most models do not attribute a single exponential behaviour, and hence a single value for the slope, to the small-t behaviour of the elastic differential cross section, experimentalists usually describe the diffraction peak with a single slope and a single term, i.e.

$$\begin{aligned} \mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t(t\simeq 0)=(\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t)_{t=0}\ \mathrm{e}^{B(s)t}. \end{aligned}$$

(6.7)

This expression leads to the approximate result

$$\begin{aligned} B(s)\simeq \frac{1}{16 \pi } \frac{\sigma _{\mathrm{total}}^2 (1+ \rho ^2)}{\sigma _{\mathrm{elastic}}}. \end{aligned}$$

(6.8)

Fig. 57

The energy dependence of the slope parameter, Eq. (6.7), from ISR to LHC7. Data are from [263] for lower energies, from [283] for LHC7. We also include the TOTEM result at $\sqrt{s}=8\ \mathrm{TeV}$ from [281], for the case of a single exponential fit in the $0.027~\mathrm{GeV}^2<-t<0.2~\mathrm{GeV}^2$ region

We plot in Fig. 57, the values for B(s), reported by experiments from ISR to LHC7, using Eq. (6.7) definition. For the TOTEM experiment, the value for B(s) at LHC7 corresponds to the measurement in the interval $0.02<|t|<0.33~\mathrm{GeV}^{-2}$ [283]. There are general considerations which relate the asymptotic behaviour of B(s) to that of the total cross section, in particular one can derive the asymptotic relation, so called MacDowell and Martin bound [284], discussed recently in [285], given as

$$\begin{aligned} B(s)\ge \frac{ \sigma _{\mathrm{total}}}{18 \pi } \frac{\sigma _{\mathrm{total}}}{\sigma _{\mathrm{elastic}}}. \end{aligned}$$

(6.9)

Since the ratio $\sigma _{\mathrm{total}}/\sigma _{\mathrm{elastic}}\ge 1$, the above relation implies that the rise with energy of B(s) will at some point catch up with that of the total cross section. We mention here in passing that at LHC7, the right-hand side of the above inequality is approximately $18~\mathrm{GeV}^{-2}$ and the measured slope on the left-hand side is about $20~\mathrm{GeV}^{-2}$. Hence, the inequality is close to saturation.

To reiterate, if and when the total cross section will have reached an energy such as to saturate the Froissart bound, then one should expect B(s) to grow with energy as $(\ln s)^2$. Fig. 57 indicates that up to the Tevatron measurements, data could to be consistent with a $\log s$ type behaviour. After the LHC7 TOTEM data appeared, the possibility of a stronger rise was examined in [61]. However, the LHC8 result (red dot in Fig. 57) sheds doubts on the single exponential slope analyses, and it would need to be rediscussed when higher LHC data, at 13 and 14 TeV, will be available.

One way to describe the variation in t as one moves away from $t\simeq 0$ has been to introduce the curvature parameter C(s) and parametrise the diffraction peak as

$$\begin{aligned} \mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t=(\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t)_{t=0}\ \mathrm{e}^{B(s)t +C(s)t^2}. \end{aligned}$$

(6.10)

Such a parametrisation needs a change in sign for C(s) as t moves away from the very forward direction. Higher powers, such as a cubic term $t^3$ are also discussed in the recent 2015 TOTEM analysis for the slope [281]. More generally, away from $t\simeq 0$, the slope parameter is a function of both t and s, defined as

$$\begin{aligned} B_{\mathrm{eff}}(s,t)=\frac{\mathrm{d}}{\mathrm{d}t}\log \mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t. \end{aligned}$$

(6.11)

Since models differ in their parametrisation of the forward peak, depending on the extension in t, if the dip region has to be included, Eq. (6.11) is to be used. One can distinguish the following basic modellings for the forward peak

• impact parameter models

• one or more Pomeron pole exchanges

• di-pole and tri-pole exchanges

• Pomeron exchanges unitarised via eikonal representation

• soft-gluon resummation and exponential damping (work in progress).

We see in the following the results from some of these models.

6.1.2 The real part of the elastic scattering amplitude, at $t=0$, and the energy dependence of the $\rho (s)$ parameter

The elastic scattering amplitude has both a real and an imaginary part. At $t=0$, the imaginary part is proportional to the total cross section, but there is no such simple way to obtain the real part, although arguments, based on asymptotic theorems, have been used to extract an asymptotic value for $\rho (s)=\mathfrak {R}e F(s,t=0)/\mathfrak {I}m F(s,t=0) \rightarrow \pi /\ln s$ as $s \rightarrow \infty$.

In the next paragraph we shall describe how one can construct asymptotically a real part for values of $t\ne 0$. In this paragraph, we show an analysis of various high energy data, by Alkin, Cudell and Martynov [286], aimed at determining the parameter $\rho (s)=\mathfrak {R}e F(s,t=0)/\mathfrak {I}m F(s,t=0)$ through integral dispersion relations. The authors use various Pomeron and Odderon models, employing simple Pomeron or double and triple poles. Recall that these three different cases correspond to an asymptotic behaviour for the total cross section given by a power law, a logarithmic rise, or a $(\log s )^2$, while the Odderon term is always rising less than the Pomeron. Reference [286] contains a rather clear description of the phenomenology implied by these different models. We show in Fig. 58 from [286] a compilation of data for the $\rho$ parameter for pp scattering, compared with four different models.

Fig. 58

Data for the $\rho$ parameter for pp scattering compared with different models as indicated in Fig. (10) of [286] ©(2011) by Springer. Reproduced with permission of Springer. Figure is courtesy of J-R Cudell

If one uses the LHC7 TOTEM result to gauge which model gives the best value for $\rho$, then the result of this analysis seems to select the simple Pomeron model, since this is the model which gives a total cross section closest to the TOTEM measurement, i.e. $\sigma _{\mathrm{total}}(7~\hbox {TeV})= (94.9 \div 96.4)\ \mathrm{mb}$ vs. $\sigma _{\mathrm{total}}^{\mathrm{TOTEM}}=98.3 \pm 0.2^{\mathrm{stat}}\pm 2.8^{\mathrm{syst}}~\hbox {mb}$. In such case, $\rho (7~\hbox {TeV})= (0.138 \div 0.186)$. The triple-pole Pomeron model also gives an acceptable total cross section, with $\sigma _{\mathrm{total}}(7~\hbox {TeV})= (94.1 \div 95.1)~\hbox {mb}$, corresponding to $\rho (7~\hbox {TeV})= (0.130 \div 0.142)$. We note here that the determination of the total cross section initially released, used the predictions from [287] with $\rho (7~\hbox {TeV})= 0.138^{+0.01}_{-0.08}$, while the most recent TOTEM analysis, as of this writing, [281], uses a value $\rho (8 ~\hbox {TeV})=0.140\pm 0.007$, using the COMPETE Collaboration favoured value [287].

Using the model by Block et al. [146], we reproduce data and predictions for $\rho$ for both $pp$ and ${\bar{p}}p$ in Fig. 32. Just as in the previous figure, this figure shows that, at high energy, $\rho$ has been measured to be positive, swinging from the negative values at energies below the ISR, to values $\rho \sim 0.12$ at the Tevatron.

Following [288], the behavior of $\rho (s)$ can be seen to arise rather naturally from present phenomenological analyses of the total cross section alone. Consider the asymptotic terms of a frequently used parametrisation for the even amplitude at $t=0$,

$$\begin{aligned} \mathfrak {I}m F_+(s,0)= & {} \frac{1}{4\pi }\left[ H_1\left( \ln \frac{s}{s_0}\right) ^2 \right. \nonumber \\&+\left. H_2 \ln \frac{s}{s_0}+\left( \frac{\pi ^2}{4}H_1+H_3\right) \right] ,\end{aligned}$$

(6.12)

$$\begin{aligned} \mathfrak {R}e F_+(s,0= & {} \frac{1}{4}\left[ H_1\ln \frac{s}{s_0}+\frac{1}{2}H_2 \right] . \end{aligned}$$

(6.13)

While the coefficient $H_1$ is obviously positive, as it is related to the asymptotic behavior of the obviously positive total cross section, the sign of $H_2$ is a priori undefined. Fits to $\sigma _{\mathrm{tot}}^{pp}$ give $H_2\le 0$, even when the $\rho$ parameter is not part of the fits. This immediately shows that $\rho (s)$ can go through zero, as it does for $10~\mathrm{GeV}\lesssim \sqrt{s}\lesssim 30~\mathrm{GeV}$. Asymptotically then one has

$$\begin{aligned} \rho _+(s)= & {} \frac{ \pi \left[ H_1 \ln \frac{s}{s_0}+\frac{1}{2} H_2 \right] }{ \left[ H_1(\ln \frac{s}{s_0})^2 +H_2 \ln \frac{s}{s_0}+\left( \frac{\pi ^2}{4}H_1+H_3\right) \right] },\end{aligned}$$

(6.14)

$$\begin{aligned}= & {} \frac{\pi }{(\ln \frac{s}{s_0})}[1+\text {non-leading in } \ln s/s_0]. \end{aligned}$$

(6.15)

Thus, we see that analyticity coupled with the assumption of Froissart limit saturation predicts that, at sufficiently high energy, $\rho \sim \pi /\log {s}$. While $\rho$ rises at low energy, data from the $Sp{\bar{p}}S$ and the Tevatron region are non-committal and consistent with a constant ${\sim } 0.12$. In our proposed Eikonal Mini-jet with soft-gluon resummation, the imaginary part of the forward scattering amplitude is proportional to $[\log {s}]^{1/p}$, with $1/2<p<1$. Through the substitution $s\rightarrow s\mathrm{e}^{-i\pi /2}$, the expression for the scattering amplitude is made analytic and one can see that $\rho \sim \pi /2p \log {s}$.

The behavior of $\rho$ as the energy swung through the ISR region, and $\sigma _{\mathrm{tot}}^{pp}$ began rising, became an object of intense scrutiny in the early 1970s and led to the first suggestion of the existence of the Odderon, [discussed later] in Sect. 6.4.1. In [204], the observed rise of the total cross section at ISR was the occasion to propose that both the imaginary and the real parts of the amplitude could behave asymptotically as $(\ln s/s_0)^2$ and fits to both $\sigma _{\mathrm{tot}}^{pp}$ and $\rho (s)$ in the then available energy range were seen to be compatible with $\rho (s)$ passing through a zero in the ISR region. We shall mention later, in Sect. 6.4.1 how this proposal was then applied to study charge exchange reactions and then morphed in an added term named the Odderon. One notices the obvious fact that $\rho (s)$ changes sign in the energy region where the total cross section changes curvature. The change in curvature is attributed in mini-jet models to the fact that perturbative QCD processes become observable, which is also the region where an edge-like behavior has been noticed by Block et al. in the scattering amplitude [289].

6.1.3 The asymptotic behaviour of the real part of the scattering amplitude at $t\ne 0$

We shall discuss here how one can construct an asymptotic $\mathcal{R}eF(s,t)$ given the imaginary part $\mathcal{I}mF(s,t)$. A discussion of some of the issues presented here can be found in a 1997 paper by Andre’ Martin [290].

The construction of the elastic scattering amplitude at asymptotic energies uses a number of asymptotic theorems. The imaginary part at $t=0$ is anchored to the optical theorem and its asymptotic value is bound by the Froissart theorem. The real part at $t=0$ is asymptotically obtained through the Khuri–Kinoshita theorem [13]. At $t\ne 0$, models for the imaginary part also allow one to obtain an asymptotic value for the real part. This is discussed in an early paper by Martin [291]. According to Martin, if the total cross section behaves asymptotically as $\log ^2 s$, then the real part of the even amplitude $F_+(s,t)$, again asymptotically, behaves as

$$\begin{aligned} \mathfrak {R}e F_+(s,t)\simeq \rho (s) \frac{\mathrm{d}}{\mathrm{d}t} [t \mathfrak {I}m F_+(s,t)] \end{aligned}$$

(6.16)

where, as usual, $\rho (s)=\mathfrak {R}eF_+(s,0)/\mathfrak {I}m F_+(s,0)$. The result of Eq. (6.16) is obviously consistent with the expression for the differential cross section at $t=0$, namely one has

$$\begin{aligned}&\left( \frac{\mathrm{d}\sigma }{\mathrm{d}t}\right) _{t=0}\sim (\hbox {constant})\nonumber \\&\qquad \times \left\{ (\mathfrak {I}m F(s,0))^2+\left( \frac{\mathrm{d}}{\mathrm{d}t} t\mathfrak {I}mF(s,t)\right) _{t=0}^2 \right\} ,\end{aligned}$$

(6.17)

$$\begin{aligned}&\quad =(\hbox {constant}) (\mathfrak {I}m F(s,0))^2[1+\rho (s)^2]. \end{aligned}$$

(6.18)

It is also interesting to note that the asymptotic expression given by Martin, automatically satisfies one of the two asymptotic sum rules for the elastic amplitude in impact-parameter space, which will be discussed later, in Sect. 6.1.4.

Equation (6.16) was derived by Martin in the asymptotic regime $\sigma _{\mathrm{total}}\sim \log ^2s$, but it is actually more general and holds also for $\sigma _{\mathrm{total}}\sim (\log s)^{1/p}$ with $1/2<p<1$. Let us start with the case $p=1/2$. Defining the even amplitude

$$\begin{aligned}&F_+(s,t)=F_+(s,0) f(t),\end{aligned}$$

(6.19)

$$\begin{aligned}&f(0)=1, \end{aligned}$$

(6.20)

and assuming the asymptotic behaviour

$$\begin{aligned} F_+(s,0)\sim i\beta (\log s/s_0)^2, \end{aligned}$$

(6.21)

the real part is built using the amplitude properties of analyticity and crossing symmetry. Using the additional property of geometrical scaling obeyed by the asymptotic amplitude [288], the argument then runs as follows:

• introducing the scaling variable $\tau =t \log ^2 s$, geometrical scaling [288] says that

  $$\begin{aligned} f(s,t)\equiv f(s,\tau )=f(t (\log s/s_0)^2) \end{aligned}$$

  (6.22)

• for small values of t, the even amplitude must be crossing symmetric, i.e. symmetric under the exchange $s\rightarrow s\mathrm{e}^{-i\pi /2}$, and the Froissart limit and the geometric scaling variable turn into

  $$\begin{aligned}&F_+(s,0)\rightarrow i\beta (\log s/s_0-i\pi /2)^2,\end{aligned}$$

  (6.23)
  $$\begin{aligned}&\quad \simeq i\beta (\log s/s_0)^2 +\beta \pi \log s/s_0 \nonumber \\&\tau \rightarrow t (\log s/s_0-i\pi /2)^2\simeq t (\log s/s_0)^2-i\pi t \log s/s_0 \nonumber \\&\quad \rightarrow \tau \left( 1-\frac{i\pi }{\log s/s_0}\right) ,\end{aligned}$$

  (6.24)
  $$\begin{aligned}&f\left( \tau -i\pi \frac{\tau }{\log s/s_0}\right) \simeq f(\tau ) -i\pi \frac{\tau }{\log s/s_0} \frac{\mathrm{d}f}{\mathrm{d}\tau } \nonumber \\&\quad \simeq f(\tau ) -i\pi \frac{t}{\log s/s_0} \frac{\mathrm{d}f}{\mathrm{d}t}, \end{aligned}$$

  (6.25)

  so that

  $$\begin{aligned}&F_+(s,t)=F_+(s,0) f(\tau ) \nonumber \\&\quad \simeq [i\beta (\log s/s_0)^2 +\beta \pi \log s/s_0]\nonumber \\&\qquad \times \left[ f(\tau ) -i\pi \frac{t}{\log s/s_0} \frac{\mathrm{d}f}{\mathrm{d}t}\right] \nonumber \\&\quad \simeq i \left[ \beta (\log s/s_0)^2 f(\tau )-\beta \pi ^2\frac{t\mathrm{d}f}{\mathrm{d}t}\right] \nonumber \\&\qquad +\,f(\tau )\beta \pi \log s/s_0+\beta \log s/s_0 \pi t \frac{\mathrm{d}f}{\mathrm{d}t}\nonumber \\&\quad \simeq i \beta (\log s/s_0)^2 f(\tau ) + \beta \pi \log s/s_0 \left[ f(\tau )+\tau \frac{\mathrm{d} f(\tau )}{\mathrm{d}\tau }\right] \nonumber \\&\quad \simeq i\beta (\log s/s_0)^2 f(\tau ) +\frac{\pi }{\log s/s_0}\beta ( \log s/s_0)^2\frac{\mathrm{d}( t f(t))}{\mathrm{d}t}.\nonumber \\ \end{aligned}$$

  (6.26)

  Since asymptotically, the Khuri–Kinoshita theorem says that

  $$\begin{aligned} \rho (s)\simeq \frac{\pi }{\log s/s_0}, \end{aligned}$$

  (6.27)

  we thus see that if

  $$\begin{aligned} \mathfrak {I}m F_+(s,t)\simeq \beta (\log s/s_0)^2 f(t), \end{aligned}$$

  (6.28)

  then

  $$\begin{aligned} \mathfrak {R}e F_+(s,t)\simeq \rho (s)\frac{\mathrm{d}}{\mathrm{d}t } ( t \mathfrak {I}m F_+(s,t)). \end{aligned}$$

The demonstration leading to Eq. (6.16) holds even if the total cross section does not saturate the Froissart bound, namely we can also start with

$$\begin{aligned} \mathfrak {I}m F_+(s,0)\simeq \beta (\log s/s_0)^{1/p} \end{aligned}$$

(6.29)

with $1/2\le p \le 1$ and still obtain Eq. (6.16), with

$$\begin{aligned} \rho (s)\simeq \frac{\pi }{2p \log s/s_0}. \end{aligned}$$

(6.30)

The limits on p are obtained here from the phenomenological requirement that the total cross section is asymptotically rising at least like a logarithm, i.e. the case $p=1$, and that it satisfies the Froissart bound, corresponding to $p=1/2$. We have seen, when discussing our mini-jet model in Sect. 5.9.7, how to relate these requirements to a phenomenological description of confinement in the infrared region.

For $p\ne 1$, we shall now sketch the demonstration, which runs very close to the one just given for $p=1/2$.

Let the asymptotic behaviour of the even amplitude at $t=0$ be such that $F_+(s,0)\sim \beta (\log s/s_0)^{1/p}$. Then

$$\begin{aligned}&F_+(s,0)\sim i\beta (\log s/s_0 -i\pi /2)^{1/p},\end{aligned}$$

(6.31)

$$\begin{aligned}&\quad \simeq i\beta (\log s/s_0)^{1p}\left[ 1-\frac{i \pi }{2p \log s/s_0}\right] . \end{aligned}$$

(6.32)

Now the scaling variable $\tau \sim t F_+(s,0)=t (\log s/s_0)^{1/p}$, and the scaling in the variable $\tau$ gives

$$\begin{aligned} f(\tau )\rightarrow f(\tau -\frac{i\pi \tau }{2p \log s/s_0})\simeq f(\tau ) -\frac{i\pi \tau }{2p\log s/s_0}\left( \frac{\mathrm{d} f}{\mathrm{d}\tau }\right) \!\!\!\!\!\nonumber \\ \end{aligned}$$

(6.33)

and

$$\begin{aligned} F_+(s,t)\simeq F_+(s,0) f(\tau ). \end{aligned}$$

(6.34)

Following steps similar to the $p = 1/2$ case and using $\rho (s)$ given by Eq. (6.30) gives the same result as before, i.e.

$$\begin{aligned} \mathfrak {R}eF_+(s,t)\simeq \rho (s)\frac{\mathrm{d}}{\mathrm{d}t}(t \mathfrak {I}m F_+(s,t)). \end{aligned}$$

(6.35)

This expression can be used to obtain a real part in eikonal models with a purely real eikonal function. One would obtain, for the full amplitude at $t=-q^2$,

$$\begin{aligned} A(s,q)= & {} i \int b\mathrm{d}b (1-\mathrm{e}^{-\chi (b,s)})J_0(bq)\nonumber \\&+ \int b\mathrm{d}b (1-\mathrm{e}^{-\chi (b,s)})\nonumber \\&\times \left[ J_0(bq)\rho (s))-\rho (s)\frac{qb}{2} J_1(qb)\right] , \end{aligned}$$

(6.36)

which leads to

$$\begin{aligned} \mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t= \pi \left\{ I_0^2+\rho ^2\left[ I_0-\frac{\sqrt{-t}}{2}I_1\right] ^2\right\} \end{aligned}$$

(6.37)

with

$$\begin{aligned}&I_0=\int b\mathrm{d}b (1-\mathrm{e}^{-\chi (b,s)})J_0(qb),\end{aligned}$$

(6.38)

$$\begin{aligned}&I_1=\int b^2 \mathrm{d}b (1-\mathrm{e}^{-\chi (b,s)})J_1(qb). \end{aligned}$$

(6.39)

Before leaving this discussion of the real part of the scattering amplitude, we notice that the above is valid for the dominant high energy part of the amplitude. Real terms can be present at non leading order in the amplitude, such as the one proposed by Donnachie and Landshoff, arising from a three gluon exchange [292], and described later in this section.

6.1.4 Asymptotic sum rules for the elastic scattering amplitude at impact parameter $b=0$

Here we shall derive two asymptotic sum rules which are integrals over momentum transfer for the real and the imaginary parts of the elastic amplitude [293, 294].

At high energies, ignoring all particle masses, let the complex elastic amplitude F(s, t) be normalised so that

$$\begin{aligned} \sigma _{\mathrm{tot}}(s) = 4 \pi \mathfrak {I}m F(s, 0);\quad \frac{\mathrm{d}\sigma }{\mathrm{d}t} = \pi |F(s, t|^2. \end{aligned}$$

(6.40)

With this normalisation, the elastic amplitude in terms of the complex phase shift $\delta (s, b)$ reads

$$\begin{aligned} F(s, t) = i \int (b\mathrm{d}b) J_o(b\sqrt{-t}) [1 - \mathrm{e}^{2i\delta _R(s,b)} \mathrm{e}^{-2 \delta _I(s, b)}],\nonumber \\ \end{aligned}$$

(6.41)

and its inverse

$$\begin{aligned}{}[1 - \mathrm{e}^{2i\delta _R(s,b)} \mathrm{e}^{-2 \delta _I(s, b)}] = -i \frac{1}{2} \int _{-\infty }^0 \mathrm{d}t J_o(b \sqrt{-t}) F(s, t).\nonumber \\ \end{aligned}$$

(6.42)

Rewriting Eq. (6.42) as

$$\begin{aligned}&1 - [\cos (2\delta _R(s,b))+i \sin (2\delta _R(s,b))] \mathrm{e}^{-2 \delta _I(s, b)}] \nonumber \\&\quad =-i \frac{1}{2} \int _{-\infty }^0 \mathrm{d}t J_o(b \sqrt{-t}) [\mathfrak {R}e F(s, t)+i \mathfrak {I}m F(s,t)],\nonumber \\ \end{aligned}$$

(6.43)

we have

$$\begin{aligned}&1 - \cos (2\delta _R(s,b))\mathrm{e}^{-2 \delta _I(s, b)}\nonumber \\&\quad =\frac{1}{2} \int _{-\infty }^0 \mathrm{d}t J_o(b \sqrt{-t}) \mathfrak {I}m F(s,t)],\end{aligned}$$

(6.44)

$$\begin{aligned}&\sin (2\delta _R(s,b)) \mathrm{e}^{-2 \delta _I(s, b)}\nonumber \\&\quad = \frac{1}{2} \int _{-\infty }^0 \mathrm{d}t J_o(b \sqrt{-t}) \mathfrak {R}e F(s, t). \end{aligned}$$

(6.45)

Consider the hypothesis of total absorption. This is a stronger hypothesis than the one which leads to the Froissart–Martin bound, namely that there must exist a finite angular momentum value, below which all partial waves must be absorbed. Under the stronger hypothesis that in the ultra high energy limit, namely in the central region ($b = 0$) a complete absorption occurs, and in the black-disk limit of $\delta _I(s,0)\rightarrow \infty$, we have the following two asymptotic sum rules

$$\begin{aligned}&S_I = \frac{1}{2} \int _{-\infty }^o \mathrm{d}t\ \mathfrak {I}m F(s, t)\ \rightarrow \ 1\quad \mathrm{as}\ s\rightarrow \infty ,\end{aligned}$$

(6.46)

$$\begin{aligned}&S_R= \frac{1}{2} \int _{-\infty }^o \mathrm{d}t\ \mathfrak {R}e F(s, t)\ \rightarrow \ 0\quad \mathrm{as}\ s\rightarrow \infty . \end{aligned}$$

(6.47)

Satisfaction of these sum rules is a good measure to gauge whether asymptotia and saturation of the Froissart–Martin (FM) bound have been reached. Notice that the FM bound is obtained under a weaker hypothesis than complete absorption and one has $S_I \rightarrow 2$ and $S_R \rightarrow 0$. Our phenomenological analysis of TOTEM, presented in Sect. 6.3.1, leads to (6.46) reducing the FM bound by a factor 2. According to the phenomenology presented in [295], at TOTEM(7TeV), $S_I \approx \ 0.94$ and $S_R\approx \ 0.05$ bolstering our faith in the sum rules.

If $\mathfrak {R}e F(s,t)$ is constructed through the Martin recipe Eq. (6.30), then the second sum rule Eq. (6.47) is automatically satisfied.

6.1.5 Elastic vs. total cross section: the ratio and the unitarity limit

The ratio of the elastic to the total cross section plays an important role in all discussions of asymptotic behaviour. We shall start our analysis by recalling some general characteristics of this ratio from considerations about total absorption.

Let us write the expression for the total and the elastic cross sections in terms of real and imaginary parts of the complex phase shift $\delta (s)$ i.e.

$$\begin{aligned}&f_{\mathrm{el}}(q)=i\int \mathrm{d}^2{\mathbf {b}}\mathrm{e}^{i{\mathbf {q}}\cdot {\mathbf {b}}}[1-\mathrm{e}^{2i \delta (b,s)}],\end{aligned}$$

(6.48)

$$\begin{aligned}&\quad =2\pi i \int b \mathrm{d}b J_0(qb)[1-\mathrm{e}^{2 i \delta _R(s)-2 \delta _I}] ,\end{aligned}$$

(6.49)

$$\begin{aligned}&\sigma _T=2 \mathfrak {R}e \int \mathrm{d}^2{\mathbf {b}}[1-\mathrm{e}^{2 i \delta _R-2 \delta _I}] ,\end{aligned}$$

(6.50)

$$\begin{aligned}&\sigma _{\mathrm{el}}=\int \mathrm{d}^2{\mathbf {b}}|1-\mathrm{e}^{2 i \delta _R-2\delta _I}|^2. \end{aligned}$$

(6.51)

Then we examine two limiting cases

• elastic scattering only, $\delta _I=0$, i.e.

  $$\begin{aligned}&\sigma _T^{(1)}=2\int \mathrm{d}^2{\mathbf {b}}[1-\cos 2 \delta _R],\end{aligned}$$

  (6.52)
  $$\begin{aligned}&\sigma _{\mathrm{el}}^{ (1) }=\int \mathrm{d}^2 {\mathbf {b}}|1-\mathrm{e}^{i 2 \delta _R}|^2=2\int \mathrm{d}^2{\mathbf {b}}[1-\cos 2\delta _R].\nonumber \\ \end{aligned}$$

  (6.53)

Thus $\sigma _{\mathrm{el}}\equiv \sigma _T$, and all the scattering is purely elastic.

• a different limit, $\delta _R=0$, i.e.

$$\begin{aligned}&\sigma _T^{(2)}=2\int \mathrm{d}^2{\mathbf {b}}[1 -\mathrm{e}^{-2 \delta _I}],\end{aligned}$$

(6.54)

$$\begin{aligned}&\sigma _{\mathrm{el}}^{(2)}= \int \mathrm{d}^2 {\mathbf {b}}(1-\mathrm{e}^{ -2 \delta _I})^2,\end{aligned}$$

(6.55)

$$\begin{aligned}&\sigma _T^{(2)}-2\sigma _{\mathrm{el}}^{(2)}=2\int \mathrm{d}^2{\mathbf {b}}\mathrm{e}^{-2 \delta _I}[1-\mathrm{e}^{-2 \delta _I}]\ge 0, \end{aligned}$$

(6.56)

i.e. $\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}$ $\le 1/2$ for $\delta _I>0$.

Other important limits are examined in detail in the Block and Cahn 1984 review [12], and we reproduce here parts of their discussion of the black- and grey-disk limit.

Using Block and Cahn convention, with $t=-q^2$, in the c.m. given by $t=-2k^2(1-cos\theta ^*)$, one has

$$\begin{aligned}&f_{cm}(t)=\frac{k}{\pi }\int \mathrm{d}^2{\mathbf {b}}\mathrm{e}^{i{\mathbf {q}}\cdot {\mathbf {b}}}a(b,s)\end{aligned}$$

(6.57)

$$\begin{aligned}&a(b,s)=\frac{1}{4\pi k}\int \mathrm{d}^2\mathbf {q} \mathrm{e}^{-i{\mathbf {q}}\cdot {\mathbf {b}}}f_{cm}(q),\end{aligned}$$

(6.58)

$$\begin{aligned}&\sigma _{\mathrm{total}}=\frac{4 \pi }{k}\mathfrak {I}mf_{cm}(t=0),\end{aligned}$$

(6.59)

$$\begin{aligned}&\frac{\mathrm{d}\sigma _{\mathrm{el}}}{\mathrm{d}t}=\frac{\pi }{k^2}\frac{\mathrm{d}\sigma _{\mathrm{el}}}{\mathrm{d}\varOmega ^*} =\frac{\pi }{k^2}|f_{cm}(t)|^2. \end{aligned}$$

(6.60)

Writing the amplitude a(b, s) as

$$\begin{aligned} a(b,s)=\frac{i}{2}[1-\mathrm{e}^{2i\chi (b,s)}] \end{aligned}$$

(6.61)

one then has

$$\begin{aligned}&\sigma _{\mathrm{elastic}}=4 \int \mathrm{d}^2{\mathbf {b}}\ |a(b,s)|^2,\end{aligned}$$

(6.62)

$$\begin{aligned}&\sigma _{\mathrm{total}}=4\int \mathrm{d}^2{\mathbf {b}}\mathfrak {I}m\ a(b,s). \end{aligned}$$

(6.63)

The black- and grey-disk model case corresponds to a scattering amplitude zero outside a finite region in impact-parameter space, i.e.

$$\begin{aligned} a(b,s)=\frac{iA}{2} \theta (R(s)-b) \end{aligned}$$

(6.64)

where the radius R(s) of the disk is in general energy dependent. In this very simple model

$$\begin{aligned}&\sigma _{\mathrm{total}}=2A\pi R^2(s),\end{aligned}$$

(6.65)

$$\begin{aligned}&\sigma _{\mathrm{elastic}}=\pi A^2 R^2(s). \end{aligned}$$

(6.66)

In the optical analogy, also extensively described in [125], total absorption corresponds to $A=1$, i.e. $\chi _R=0$ and $\chi _I=\infty$, and $\sigma _{\mathrm{total}}=2\sigma _{\mathrm{elastic}}$. Purely elastic scattering is $A=2$. Defining the ratio

$$\begin{aligned} \mathcal{R}_{\mathrm{el}}=\frac{\sigma _{\mathrm{el}}}{\sigma _{\mathrm{total}}}=\frac{A}{2} \end{aligned}$$

(6.67)

there are the following cases: (i) $A=2$, all the scattering is elastic, a possibility close to the model by Troshin and Tyurin, characterized by large elastic component, recently rediscussed in [296], (ii) $A=1$, total absorption, the scattering is equally divided between elastic and inelastic scattering, iii) $A\le 1$, the total inelastic scattering contribution, which includes also diffraction, is larger than the elastic. It is common practice to refer to the cases $A=1$ and $A<1$ as the black and the gray disk model, respectively [12].

Fig. 59

The ratio of the elastic to the total cross section, using accelerator data, including TOTEM [277, 283] and a compilation which uses the Block and Halzen estimate for the total cross section at $\sqrt{s}=57\ \mathrm{TeV}$ and extraction of the inelastic total cross section from Auger Collaboration data [297,298,299]. The green dot represents the asymptotic estimate by Block and Halzen. Reprinted from [295], ©(2012), with permission from Elsevier

The black disk model is rather simple, but it is of present interest to investigate whether at LHC, the black-disk limit has been reached [259]. Using both the TOTEM data at LHC7 and the cosmic ray data from the Auger Collaboration for the inelastic cross section [297,298,299], it is possible to estimate how close one is to the asymptotic black disk limit. We show this in Fig. 59, where the ratio $\mathcal{R}_{\mathrm{el}}$ is obtained from accelerator data (black triangles) [263], including TOTEM’s [277, 283], and the value extracted from Auger. The ratio at 57 TeV is obtained by using Block and Halzen (BH) estimate for the total cross section [259] $\sigma ^\mathrm{BH}_\mathrm{total}(57~\hbox {TeV})=(134.8\pm 1.5)$ mb, which is based on the analytic amplitude method of Ref.  [300]. We then obtained $\sigma _\mathrm{elastic}(57~\hbox {TeV})=\sigma ^{BH}_\mathrm{total}-\sigma ^\mathrm{Auger}_\mathrm{inelastic}=(44.8\pm 11.6) ~\hbox {mb}$. We also show the asymptotic result (green dot) from Ref.  [259]. For a recent published reference see [86]. From this compilation and a similar one in [301],⁶ the $\mathcal{R}_{\mathrm{el}}=1/2$ limit does not appear to have been reached yet, not even at the highest energy of 57 TeV. One may wonder whether it can in fact be reached. There are good reasons to expect that a more realistic limit is

$$\begin{aligned} \mathcal{R}_{\mathrm{el}}=\frac{\sigma _{\mathrm{elastic}}+\sigma _{\mathrm{diffractive}}}{\sigma _{\mathrm{total}}}\le \frac{1}{2} \end{aligned}$$

(6.68)

where $\sigma _{\mathrm{diffractive}}$ include single and double diffraction. This is the limit advocated by Jon Pumplin [72, 73, 302]. In the subsection dedicated to diffraction we shall describe Pumplin’s model for diffraction and see how the limit of Eq. (6.68) arises.

6.1.6 The differential cross section and the dip structure

A very interesting characteristic of the data released by the TOTEM experiment [277] is the return of the dip, namely the observation of a very distinctive dip at $|t|=0.53~\mathrm{GeV}^2$, signalling that the dip, observed at the ISR only in pp scattering, and not seen or measured in ${\bar{p}}p$, is now reappearing, in pp. The dip position has moved from ISR energies, where $-t _{\mathrm{dip}}\sim 1.3~\mathrm{GeV}^2$ to $-t_{\mathrm{dip}}=0.53~\mathrm{GeV}^2$ at LHC7. Further shrinkage is expected, but the question of how to predict its energy behavior is model dependent, as we show in Fig. 60, where the position of the dip, as measured at various energies, is compared to a linear logarithmic fit [303] and expectations from geometrical models [304]. The uncertainty is related to the difficulty with most models to describe the entire region from the optical point to past the dip, from ISR to LHC energies. Some models which had described this structure at ISR, failed to accurately predict its position and depth at LHC, others describe very well the behavior for small and/or large |t|, but not the entire region, as we shall see.

Fig. 60

The position of the dip as the energy increases, extracted from geometrical models [304] and a linear logarithmic fit. The figure is courtesy of D. Fagundes, following Fig. (6) from [303], ©(2013) by the American Physical Society

In Fig. 60 the dashed and dotted lines (blue) are obtained through models for the amplitude in which Geometrical Scaling is partly embedded [304]. Clearly so long as $\mathcal{R}_{\mathrm{el}} \ne 1/2$, two energy scales are present in pp scattering, one from the elastic and the other from the total cross section. In Sect. 6.1.7 we shall discuss this point in more detail.

6.1.7 Geometrical scaling

The idea of geometric scaling is originally due to Dias de Deus and it has been extensively studied in the literature [303,304,305,306,307,308] both for elastic and inelastic amplitudes, for particle multiplicities, etc. For a recent review; see [309].

We shall here limit ourselves only to its application to elastic amplitudes and the position of the dip as a function of the energy that is of timely relevance for the LHC data on elastic pp data between $\sqrt{s} = (7\div 14)\ \mathrm{TeV}$.

As shown in Fig. 59, the black-disk limit is not reached even until $\sqrt{s} = 57\ \mathrm{TeV}$ and the geometrical scaling dip structure, being anchored upon it, is hence violated. However, we show in the following that a mean geometrical scaling based on the two scales works quite well for the position of the dip versus energy.

Fig. 61

Data up to LHC7 for energy dependence of the dip $-t_{\mathrm{dip}}(s)$ from geometric scaling [left panel] and from mean geometric scaling [right panel]. Green and red crosses are predictions at LHC8 and LHC14 from the empirical model of [303]. Reprinted from [310] with kind permission from Società Itaiana di Fisica

The elastic amplitude F(s, t) has a real and an imaginary part. In the forward direction $t = 0$, the imaginary part is anchored on the total cross section

$$\begin{aligned} \mathfrak {I}m F(s, 0) = \frac{\sigma _{\mathrm{tot}}(s)}{4 \pi }, \end{aligned}$$

(6.69)

and thus is positive-definite and obeys the Froissart–Martin bound. To a certain extent so is real part in the forward direction. It has an upper bound via the Khuri–Kinoshita theorem

$$\begin{aligned} \rho (s,0) = \frac{\mathfrak {R}e F(s,0)}{\mathfrak {I}m F(s,0)} \rightarrow \ \frac{\pi }{\ln (s/s_o)}, \end{aligned}$$

(6.70)

provided the Froissart bound is saturated. By contrast, we have no such general results for $t \ne 0$. As discussed in Sect. 6.1.4 we have two sum rules we expect to be satisfied asymptotically

$$\begin{aligned}&S_I = \frac{1}{2} \int _{-\infty }^o \mathrm{d}t\ \mathfrak {I}m F(s, t)\ \rightarrow \ 1\quad \mathrm{as}\ s\rightarrow \infty ,\end{aligned}$$

(6.71)

$$\begin{aligned}&S_R= \frac{1}{2} \int _{-\infty }^o \mathrm{d}t\ \mathfrak {R}e F(s, t)\ \rightarrow \ 0\quad \mathrm{as}\ s\rightarrow \infty . \end{aligned}$$

(6.72)

Geometrical scaling as applied to the imaginary part of the elastic amplitude -for example- may be stated as follows: that at high energies

$$\begin{aligned}&\mathfrak {I}m F(s, t) \rightarrow \ [\mathfrak {I}m F(s, 0)] \phi (\tau );\ \mathrm{where}\ \tau = (- t) \sigma _{\mathrm{tot}}(s)\nonumber \\&\quad \mathrm{with}\ \phi (\tau = 0) = 1. \end{aligned}$$

(6.73)

For $\mathfrak {R}e F(s, t)$, Martin uses analyticity and a saturation of the Froissart–Martin and the Khuri–Kinoshita limit, to obtain the form

$$\begin{aligned} \mathfrak {R}e F(s, t) = \rho (s, 0) \frac{\mathrm{d}}{\mathrm{d}t} [t \mathfrak {I}m F(s, t)]. \end{aligned}$$

(6.74)

It is easy to see that the sum rule for the real part Eq. (6.72) is identically satisfied, i.e., $S_R = 0$, if Eq. (6.74) is obeyed.

On the other hand,

$$\begin{aligned} \int _o^\infty (\mathrm{d}\tau ) \phi (\tau ) = (8 \pi ) S_I \rightarrow \ (8 \pi )\quad \mathrm{as}\ s\rightarrow \ \infty . \end{aligned}$$

(6.75)

Now let us focus on the movement of the dip in the elastic cross section as a function of s. Geometric scaling would imply that

$$\begin{aligned} t_{\mathrm{dip}}(s) \sigma _{\mathrm{tot}}(s)\ \rightarrow \ \mathrm{a\ constant\ as}\ s\rightarrow \infty . \end{aligned}$$

(6.76)

Writing the high-energy cross sections assuming a simple diffraction pattern, we have (for $-t = q^2$)

$$\begin{aligned}&\sigma _{\mathrm{tot}}(s) = 2 \pi b_T^2;\quad \sigma _{\mathrm{el}}(s) = \pi b_\mathrm{e}^2\nonumber \\&\frac{\mathrm{d}\sigma }{\mathrm{d}t} = \left[ \frac{\sigma _{\mathrm{tot}}^2(s)}{16 \pi }\right] \left[ \frac{2 J_1(qR)}{qR}\right] ^2, \end{aligned}$$

(6.77)

so that the optical point is correct. In the black-disk limit,

$$\begin{aligned} b_T = b_e = R;\quad \mathcal {R}_{\mathrm{el}}^{BD} = \frac{\sigma _{\mathrm{el}}}{\sigma _{\mathrm{tot}}}\rightarrow \ 1/2. \end{aligned}$$

(6.78)

For the black disk, the dip occurs at the first zero when $q_{\mathrm{dip}}^{BD}b_T \approx \ 3.83$. Defining the geometric scaling variable $\tau _{GS} = q^2 \sigma _{\mathrm{tot}}$ and as shown in the left panel of Fig. 61, it does not work. On the other hand, we can define a mean geometric scaling with $b_T \ne b_e$ where the radius R in Eq. (6.77) is taken as the geometric mean and the mean geometric scaling variable $\tau _{GS}^{\mathrm{mean}}$ reads

$$\begin{aligned} R = \sqrt{b_T b_e};\quad \tau _{GS}^{\mathrm{mean}} = q^2 \sqrt{\sigma _{\mathrm{el}} \sigma _{\mathrm{tot}}}. \end{aligned}$$

(6.79)

The dip is now given by

$$\begin{aligned} -t_{\mathrm{dip}}(s) = q^2_{\mathrm{dip}}(s) \approx \ \left[ \frac{(3.83)^2 \pi \sqrt{2}}{\sqrt{\mathcal {R}_{\mathrm{el}}(s)} \sigma _{\mathrm{tot}}(s)}\right] . \end{aligned}$$

(6.80)

On the right-hand panel of Fig. 61, we show a comparison of our mean geometrical scaling prediction with experimental data. The agreement is quite good. We mention in passing that this is yet another example that the black-disk limit is quite far from being reached even up to $57\ \mathrm{TeV}$.

On the other hand, we notice a recent work by Block and collaborators [289], which we shall see in Sect. 6.8, where the Black Disk limit is used to make predictions at very, extremely, large energies.

6.2 Early models in impact-parameter space

Let us now examine various models and fits. Empirical fits abound in total and elastic cross section description. They are helpful in developing models, as a guide toward understanding data. To be most useful, of course, empirical fits should follow constraints imposed by general theorems on analyticity, crossing symmetry and unitarity, all of which (or, more realistically as much as possible) should then be satisfied by the models one builds.

Fig. 62

Comparison between the Chou and Yang model from [311] and existing data for the differential cross section. The two figures correspond to different approximations, left panel, and to a comparison between the form-factor expression and their model for $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$, right panel. Reprinted Figs. (1,2 ) with permission from [311]. ©(1968) by the American Physical Society

Between 1967 and 1968, Chou and Yang [311] and Durand and Lipes [312] presented a framework for calculation of the elastic scattering amplitude between elementary particles based on the impact picture and on physical ideas very similar to those in the Glauber model. The presence of kinks in the elastic differential cross section was discussed. We shall start with Chou and Yang and then discuss the results by Durand and Lipes.

6.2.1 The Chou and Yang model

The Chou and Yang model was first discussed in 1967 and fully written in 1968.To discuss particle scattering, rather than that of nucleons on nuclei, Chou and Yang had to put target and projectile on equal footing, and comply with existing phenomenology. They started in [311], with the partial wave expansion of the scattering amplitude (as we have described in the first section). From

(6.81)

the high energy limit was obtained by transforming the sum into an integral, through the substitution $P_l(\cos \theta )\rightarrow J_0(b\sqrt{-t})$ and the definition . This led to the eikonal expression for the scattering amplitude

$$\begin{aligned} a(t)=\frac{1}{2\pi } \int (1-S)\mathrm{e}^{i{\mathbf {q}}\cdot {\mathbf {b}}} \mathrm{d}^2{\mathbf {b}}\end{aligned}$$

(6.82)

with $t =-q^2$.

The crucial assumption of the Chou and Yang model was that the attenuation of the probability amplitude for two hadrons to go through each other was governed by the local opaqueness of each hadron. In this model, the transmission coefficient S is only a function of the impact parameter b, and Chou and Yang proposed to calculate the transmission coefficient S(b) through the Fourier transform of the form factors of the colliding particles. Subsequently the authors proceeded to show that their proposal for particle scattering was the same as the Glauber proposal for nucleon–nucleus scattering, with the two dimensional Fourier transform of the form factors playing the role of the nuclear density of the Glauber model. In formulating this connection between the two models, a limit of infinitely many nucleons was postulated, namely the nucleus was seen as a droplet of very finely granulated nuclear medium, in the spirit of the droplet model formulated previously by Byers and Wu [313].

The quantity $\langle s\rangle =-\log S(\mathbf {b})$ is called the opacity, with the name deriving from the following physical interpretation: if an incoming wave hits a slab of material of thickness g, the slab partly absorbs and partly transmits the wave and the transmission coefficient through the slab would be

$$\begin{aligned} S=\mathrm{e}^{-\alpha g}. \end{aligned}$$

(6.83)

Thus $\log S(b)$ would be proportional to the thickness of the slab and can be considered as the opaqueness of the slab to the wave. For particle scattering, the thickness of the slab represents how much hadronic matter is encountered by the incoming wave, when the wave passes through the hadron at impact parameter $\mathbf {b}$. Thus S is a function of the impact parameter $\mathbf {b}$, which is then integrated over all possible values. S(b) was considered to be asymptotically energy independent, and so would then be $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$. This was consistent with the fact that, at the time, data suggested that all cross section would reach an asymptotic limit, independent of energy. It should in fact be noted that the Chou and Yang model, was formulated before 1970, i.e., before ISR experiments definitely proved that the total cross section was rising.

To compare with experimental data for $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$, two different phenomenological expressions were considered, a single exponential in t, i.e. a gaussian in $\mathbf {b}$-space, and a sum of two exponentials. The resulting fits to the data available at the time, are shown in Fig. 62, where they are labeled with A and B, respectively. A further comparison with data is done by using the form-factor expression instead of the ansatz on exponential t behaviour of the amplitude, a comparison which we show in the right-hand plot in Fig. 62.

As a conclusion, the major points of this model can be summarised as being the following:

• 1. the transmission coefficient $S(\mathbf {b})$ can be obtained from the convolution of the form factors of the scattering particles,

• 2. this model, with the amplitude expressed through the transmission coefficient S includes the limit of a model previously proposed with Wu [314], in which the scattering differential elastic cross section $\mathrm{d}\sigma /\mathrm{d}t$ was proportional to the fourth power of the proton form factor,

• 3. correction terms are important, namely one needs to use the full $(1- S)$

• 4. one can expect the appearance of a distinctive diffraction pattern in the squared momentum transfer in the elastic differential cross section, with dips and bumps.

6.2.2 The diffractive model of Durand and Lipes

A diffractive picture in impact-parameter space, in a close correspondence to the Chou and Yang model, was formulated by Durand and Lipes in 1968 [312].

In [312], it is shown that the elastic scattering diffractive amplitude should exhibit two diffraction minima, which can be filled by the real part of pp scattering amplitude and that at large momentum transfer the amplitude is proportional to the product of the form factors of the scattering particles. The model uses the impact parameter picture and the paper follows along the lines of Wu and Yang [314] and Byers and Yang [313].

The suggestion that the pp scattering cross section at large momentum transfer be proportional to the fourth power of the proton form factor, suggested by Wu and Yang [314], was prompted by the observations of the rapid decrease of the cross section away from $t=0$. Namely, such a decrease could be seen as the breaking up of the proton extended structure as the momentum transfer was becoming large. For small momentum transfer values, on the other hand, the coherent droplet model by Byers and Yang [313] supplied inspiration.

The basic physical assumptions underlying the diffraction model by Durand and Lipes were: (i) elastic scattering at high energy results from the absorption of the incoming wave into the many inelastic channels which are opening up at high energy as the extended proton structure (where partons are confined) breaks up, (ii) at high energy, the absorption depends on the amount of relative interpenetration of the two scattering protons, namely on the distance between the scattering centers, in impact-parameter space. With these assumptions and the form-factor expression for the matter distribution in two hadrons, Durand and Lipes wrote the scattering amplitude in the (now) familiar form

$$\begin{aligned}&f(s,t)=i \int b \mathrm{d}b J_0(b\sqrt{-t})[1-S(b)],\end{aligned}$$

(6.84)

$$\begin{aligned}&S(b)=\mathrm{e}^{-k\rho (b)},\end{aligned}$$

(6.85)

$$\begin{aligned}&G_A(t) G_B(t)=\int _0^\infty b \mathrm{d}b \rho (b)J_0(b\sqrt{-t}) \end{aligned}$$

(6.86)

where the density of matter inside the scattering region is obtained as the convolution of the form factors of the two particles A and B in the initial state.

The absorption coefficient $\kappa$ was understood to be a function of the initial energy. Using the dipole expression for the proton electromagnetic form factor, they obtained

$$\begin{aligned} S(b)=\mathrm{e}^{-\frac{1}{8}A (\nu b)^3 K_3(\nu b)} \end{aligned}$$

(6.87)

Fig. 63

In this figure from [312] comparison is made with existing data and the diffraction model by Durand and Lipes. The two curves labelled, respectively, a and b refer to fits made with a purely real or an imaginary absorption coefficient. Reprinted with permission from [312], Fig.(1), ©(1968) by the American Physical Society

with A proportional to the absorption coefficient $\kappa$. Predictions including both a real and imaginary parts for A were given, fitting the real part of A through the total cross section. The results of such a model, with value of the parameter $\nu ^2=1~\mathrm{GeV}^2$, are shown in Fig. 63 from [312]. The comparison with data in the very forward region shows a very good agreement with the model. Notice the prediction of two dips which are filled partially through a complex absorption coefficient with a non-zero imaginary part. Some of the observations made by these authors, still of interest, are:

• asymptotically, this diffraction model should describe high energy scattering at fixed momentum transfer, although the asymptotic limit described by the model can also be ascribed in a different language to asymptotic contributions from the Pomeron trajectory (called Pomeranchuk Regge trajectory in this paper) and its cuts, with other contributions, which will disappear at increasing energy, describable by other Regge exchanges,

• two diffraction minima appear in the diffraction model.

6.2.3 The black disk model

One of the most popular representations of the proton as it emerges from high energy scattering, is that of the proton as a black disk. This definition of a black or gray disk is related to the picture of scattering as one of total or partial absorption. To show its making, and before entering into a description of models including diffraction, we shall present here the discussion of some simple elastic scattering models from Sect. 4 of the Block and Cahn review [12]. For definitiveness, these models were illustrated by fixing the parameters so as to reproduce the total cross section and the value of the B-parameter at ISR, respectively $\sigma _{\mathrm{tot}}=43~\hbox {mb}$ and $B=13\ (\mathrm{GeV}/c)^{-2}$.

With a(b, s) the scattering amplitude in impact space and related quantities as in Eqs. (6.57), (6.58), (6.59), and (6.60) the following models are considered,

• an amplitude which is purely imaginary with a constant value $a=iA/2$ inside a radius R, corresponding to a purely black disk for $A=1$, so that near the forward direction one has

  $$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}=\pi A^2 R^4 \left[ \frac{J_1(qR)}{qR}\right] ^2. \end{aligned}$$

  (6.88)

  In this model, the real part can be added as shown in Eq. (6.30), i.e. one has

  $$\begin{aligned}&\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t|_{\mathrm{Black}\, \mathrm{disk}}\nonumber \\&\quad =\pi R(s)^4A^2\left\{ \left[ \frac{J_1(Rq)}{Rq}\right] ^2+\frac{\rho ^2}{4}J_0(Rq)^2 \right\} . \end{aligned}$$

  (6.89)

  Variations of this model include an s-dependent radius, as in the model obtained by Ball and Zachariasen [315] in solving the multiperipheral equation for diffractive elastic scattering, with $R=R_0\log s, A=\kappa [\log (s/s_0)]^{-1}$, and giving a total cross section increasing as $\log s$, and an elastic cross section which is constant,

• a parabolic shape, i.e. $a=iA[1-(b/R)^2]$ inside a radius A, and zero outside,

• a gaussian shape in impact-parameter space,

  $$\begin{aligned} a=1/2A \exp [-(b/R)^2], \end{aligned}$$

  (6.90)

  which leads to $\sigma _{\mathrm{tot}}=2\pi AR^2, \sigma _{\mathrm{el}}=\pi A^2 R^2/2$

• Chou and Yang [311, 316] model, or the Durand and Lipes model [312].

As in both Chou and Yang and Durand and Lipes model, the matter distribution inside the hadrons is described through their electromagnetic form factor, i.e. through the convolution of the Fourier transform of the dipole expression. Writing

$$\begin{aligned}&a(b,s)=\frac{\mathrm{e}^{2i\delta -1}}{2i}\equiv \frac{1}{2}(1-\mathrm{e}^{-\varOmega (b)}),\end{aligned}$$

(6.91)

$$\begin{aligned}&\varOmega (b)=A\frac{1}{8}(\varLambda b)^3K_3(\varLambda b) \end{aligned}$$

(6.92)

and fitting the results to reproduce the total cross section at ISR, it is found that $\varLambda ^2 \sim 0.71 (\mathrm{GeV}/c)^2$. In Fig. 64, we show the profiles of the amplitudes in b-space at left, and the differential cross sections resulting from the different shapes at right, as obtained in [12].

Fig. 64

Shown are examples of profile functions, $\mathfrak {I}m\ a(b,s)$ (at left), and the resulting elastic differential cross section (at right): dot-dashed curve, grey disk; dotted curve, parabolic form; solid curve, Gaussian shape; dashed curve, Chou-Yang model. Reprinted with permission from [12], Figs.(7,8), ©(1985) by the American Physical Society

These figures bring to focus the basic difference between models with a Gaussian matter distribution and the others: the Gaussian shape leads to an exponential decrease in $-t$, with no wiggles or dips and bumps, whereas all the other distributions, grey disk, parabolic shape, or Chou and Yang model, exhibit a diffraction pattern with minima and maxima. Such difference among models persists till today.

Table 10 From [317], parameters obtained from a fit to pp data in the interval $(0.15<|t|<5.0)~\mathrm{GeV}^2$ for the model given in Eq. (6.93)

6.3 Exponentials and parametrisations through Regge and Pomeron exchanges

The models in impact-parameter space summarised so far underline the optical nature of scattering, without specific dynamical inputs, except for the hadron form factors. On the other hand, data on elastic scattering from ISR appeared to conform to a picture in which the elastic scattering amplitude obtains from Regge–Pomeron exchange. We shall examine some of such models. An additional group of models embeds Regge–Pomeron exchanges into the eikonal representation, thus ensuring satisfaction of unitarity, in addition to analyticity of the input Born scattering amplitude. Some of these models include QCD and diffractive contributions, as we shall discuss in a separate subsection.

6.3.1 The model independent analysis by Phillips and Barger (1973)

In 1973, Barger and Phillips (PB) proposed what they called a model independent analysis of $pp$ scattering [317].

They propose two slightly different parameterisations, using a phase and two exponentials to describe the different slope of the cross section as a function of momentum transfer in the range $-t= (0.15\div 5.0)\ \mathrm{GeV}^2$. The first, and more model independent parametrisation, is given as

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}t}=|{\tilde{A}}(s,t)+{\tilde{C}}(s,t)\mathrm{e}^{i\phi (s)}|^2,\end{aligned}$$

(6.93)

$$\begin{aligned}&{\tilde{A}}(s,t)=i\sqrt{A}\mathrm{e}^{\frac{1}{2}B(s)t },\end{aligned}$$

(6.94)

$$\begin{aligned}&{\tilde{C}}(s,t)=i\sqrt{C}\mathrm{e}^{\frac{1}{2}Dt } . \end{aligned}$$

(6.95)

Data from $p_{lab}=12\ \mathrm{GeV}$ to $p_{lab}=1496~\mathrm{GeV}$ ($\sqrt{s}\approx (5\div 53)\ \mathrm{GeV}$) were fitted with this expression. The first exponential is seen to have normal Regge shrinking, namely

$$\begin{aligned} B=B_0+2\alpha ' \log s\quad \alpha '\approx 0.3\ \mathrm{GeV}^{-2}, \end{aligned}$$

(6.96)

while the second exponential term is almost constant. The values of the parameters at each energy value are given in Table 10. Notice that, with this parametrisation, the phase $\phi$ is fitted to be always larger than $\pi /2$, so that the interference term is always negative and, in the energy range examined here, the fitted phase is energy dependent.

To understand better the role played by the energy dependence, the authors proposed a second parametrisation, clearly inspired by Regge phenomenology, i.e.

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}= & {} |{i\sqrt{A}\mathrm{e}^{(\frac{1}{2}B+\alpha '\log s -i\alpha '\pi /2)t}}\nonumber \\&+\left( \frac{\sqrt{C_0}}{s}-i\sqrt{C_\infty }\right) \mathrm{e}^{\frac{1}{2}Dt}|^2 \end{aligned}$$

(6.97)

with an explicit energy dependence and the following parameter values, valid for all the energies: $\sqrt{A}=6.88, B=5.38, \alpha '=0.306, \sqrt{C_0}=10.3, \sqrt{C_\infty }=0.035, D=1.78$, in the units of Table 10.The results are presented in the two panels of Fig. 65 and the figure shows that the quality of the two fits is good and about the same for both models.

Fig. 65

Model independent fits by Phillips and Barger [317]: parameters are energy dependent at left, constant at right. Reprinted from [317], ©(1973) with permission by Elsevier

The PB parametrisation applied to the preliminary TOTEM data at LHC7 gave the results discussed in [295]. This parametrisation, however, misses the optical point by some 5–10%, but the description of the region $0.2<|t|<2.5~\mathrm{GeV}^2$ is quite satisfactory. We shall return to the question of the very small $-t$ behavior later.

In [317], it is also suggested that the “second exponential” can be identified with a term proportional to $p_T^{-14}$, valid, according to the authors, for all available pp data for $s>15~\mathrm{GeV}^2$. Following this suggestion, and mindful of the fact that the form-factor dependence of the amplitude would contribute as $(-t)^{-8}$, we have tried a slight modification of the Barger and Phillips model, which consists in substituting the second term in Eq. (6.93) with a term proportional to the 4th power of the proton form factor, namely to write

$$\begin{aligned}&\mathcal{A}(s,t)=i\left[ \sqrt{A(s)}\mathrm{e}^{Bt/2}+\frac{\sqrt{C(s)}}{(-t+t_0)^4} \mathrm{e}^{i\phi }\right] ,\end{aligned}$$

(6.98)

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}t}=\left| \sqrt{A(s)}\mathrm{e}^{Bt/2}+\frac{\sqrt{C(s)}}{(-t+t_0)^4} \mathrm{e}^{i\phi }\right| ^2, \end{aligned}$$

(6.99)

which leads to

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}=A\mathrm{e}^{Bt}+\frac{C}{(-t+t_0)^8} +2\cos {\phi }\frac{\sqrt{A}\sqrt{C}\mathrm{e}^{Bt/2}}{(-t+t_0)^4}.\nonumber \\ \end{aligned}$$

(6.100)

When applied to LHC7 data, this parameterisation would comprehend both the proposal by Donnachie [318, 319] (further discussed at the end of this section), who advocates a power-law decrease of the type $t^{-8}$, as well as the fit proposed by the TOTEM Collaboration, $t^{-n}$, with $n=7.8\pm 0.3_{stat}\pm {0.1}_{syst}$ [277].

A discussion of how these two models, two exponentials and a phase or one exponential, a form factor and a phase, would be realised at LHC, reading data from [277], can be found in [295].

That the behaviour past the dip at LHC is consistent with an exponential was also noticed in [296].

One can see, however, that the expression

$$\begin{aligned} \sigma _{\mathrm{total}}=4 \sqrt{\pi } [\sqrt{A}+\sqrt{C} \cos \phi ] \end{aligned}$$

(6.101)

gives a value for $\sigma _{\mathrm{total}}$ below the data at all energies, including at LHC7, where the fitted value misses TOTEM datum by some 5%, but particularly so at low energy and that the t-dependence of $B_{\mathrm{eff}}$ for $t\sim 0$, while reasonably well described at LHC, is less so at lower energy values. These two points are connected, since we have already noticed that at very small |t| values at ISR the slope seems to increase. An interpretation of this effect is given in the Durham model [221], with pion loops contributing to the effective Pomeron trajectories at very small t-values [320] and shall be discussed together with diffraction.

To overcome this problem and still provide a useful tool, we have proposed an empirical modification of the original BP model amplitude [303], i.e.

$$\begin{aligned} \mathcal {A}(s,t)=i[G(s,t)\sqrt{A(s)}\mathrm{e}^{B(s)t/2}+\mathrm{e}^{i\phi (s)} \sqrt{C(s)}\mathrm{e}^{D(s)t/2}]\nonumber \\ \end{aligned}$$

(6.102)

and

$$\begin{aligned} G(s,t)=F^2_P(t)=1/(1-t/t_0)^4. \end{aligned}$$

(6.103)

With free parameters in Eqs. (6.102) and (6.103), the resulting analysis of elastic pp data at LHC7 is shown in Fig. 66. This figure includes a comparison with a parametrisation of the tail of the distribution given by the TOTEM Collaboration (dotted line). Such a parametrisation, $(-t)^{-8}$, was suggested in [292], and recently proposed again in [319], where it is shown to describe large $-t$ data from ISR to LHC8, and both for pp and ${\bar{p}}p$, as we shall discuss shortly.

Fig. 66

Fits to the LHC7 data sets with model of Eqs. (6.102) and (6.103) (labeled FFBP in the frame), with $t_0$ a free parameter. Data sets and parameter values can be found in [303]. Inset LHC7 data near the optical point are shown in comparison with the present model, which includes the proton form-factor modification. Reprinted Fig. (2) from [303], ©(2013) by the American Physical Society

Before leaving this model, we remark that the dip present both at lower and higher energies in pp is only a faint appearance in ${\bar{p}}p$. The simple expression for the amplitude with two exponentials and a phase may still be a valid phenomenological tool also for ${\bar{p}}p$, but one cannot draw any conclusion about the energy dependence of the parameters from this channel; as one gets close to the dip, and the first term dies out to zero, non-leading terms, present in ${\bar{p}}p$ and not in pp fill the dip and probably need to be added to the original model, namely one has, as pointed out in many models, a situation such as

$$\begin{aligned} A_{p{\bar{p}}}=A_{pp}+\mathcal{R}(s,t) \end{aligned}$$

(6.104)

where $\mathcal R$ depends on the Regge trajectories exchanged in the t-channel, including a possible Odderon, as we shall see later.

Concerning the coefficient B(s), we notice that in the two exponential model just described, this coefficient is related to the slope as defined in Eq. (6.11) through the relation

$$\begin{aligned} B_\mathrm{eff}(s,t)= & {} \frac{1}{\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t} \times \left[ AB\mathrm{e}^{Bt}+CD\mathrm{e}^{Dt}\right. \nonumber \\&+ \left. \sqrt{A}\sqrt{C}(B+D)\mathrm{e}^{(B+D)t/2} \cos \phi \right] . \end{aligned}$$

(6.105)

The PB model can be seen as an attempt to describe the elastic differential cross section without appealing to unitarity. It was defined as model independent analysis, but it could also be understood as a modelling of elastic scattering through Regge and Pomeron exchanges. Since then many fits to data have appeared with a few Pomerons or many Reggeons and Pomerons. We shall next look at recent contributions, along these lines, by Donnachie and Landshoff.

6.3.2 Soft and hard Pomeron exchanges in Donnachie and Landshoff model

In [318, 319] the authors stress that the data from the TOTEM experiment do confirm the results of Regge theory, which is in many ways a major success of high energy physics. At high energy, however, such success depends on interpreting a power law as the ultimate solution, and at the end, as we shall see, resulting in using models to describe the details of the data. Indeed if one believes that the Froissart bound is actually reflecting the existence of confinement, power laws, which contradict the Froissart bound, must at a certain point give up to the true asymptotic behaviour.

In Ref. [318] a hard Pomeron had been invoked to describe LHC7 data, but in the more recent contribution of Ref.  [319], this is not considered necessary. Instead, a double Pomeron exchange is seen to provide a better fit, as they show. Of particular interest here is the fact that in both their modelling of the data, it is triple gluon exchange, ggg term, which describes the decrease of the elastic differential cross section past the dip in the tail region. This is a purely real contribution, which behaves as $\simeq (-t)^{-8}$ and could be energy independent.

In [318] three different types of data are analyzed:

• pp elastic scattering at the ISR, $\sqrt{s}=30.54~\mathrm{GeV}$

• HERA data for the proton structure function $F_2(x,Q^2)$ at small x, used to determine the hard and soft pomeron powers

• the TOTEM pp data for both the elastic differential distribution as well as the total cross section.

The expression used to fit the LHC data is

$$\begin{aligned}&A_{DL}(s,t)=\sum _{i=0,3}Y_i\mathrm{e}^{-\frac{1}{2}i\pi \alpha _i(t)}(2\nu \alpha '_i)^{\alpha _i(t)}\\&2\nu =\frac{1}{2}(s-u),\quad Y_i=-X_i\ (i=0,1,2),\quad Y_3=iX_3 \end{aligned}$$

with $X_0,X_1,X_2,X_3$ real and positive. The four Regge trajectories are parametrised as

$$\begin{aligned} \alpha _i(t)=1+\epsilon _i+\alpha '_i t \end{aligned}$$

(6.106)

with $\epsilon _i$ treated as free parameters and

• $\alpha _0(t)$ is the hard Pomeron, with $\alpha '_0=0.1~\mathrm{GeV}^{-2}$, which, they find, works well

• $\alpha _1(t)$ is the well known soft Pomeron, with $\alpha '_1=0.25~\mathrm{GeV}^{-2}$,

• $\alpha _2(t)$ is the degenerate $f_2,a_2$ trajectory, with $\alpha '_2=0.8~\mathrm{GeV}^{-2}$

• $\alpha _3(t)$ corresponds to $\omega , \rho$ trajectory, with $\alpha '_3=0.92~\mathrm{GeV}^{-2}.$

The normalisation of the amplitude is

$$\begin{aligned} \sigma ^{\mathrm{TOTAL}}=s^{-1}\mathfrak {I}m A_{DL}(s,t). \end{aligned}$$

(6.107)

The parameters $\epsilon _i$ are related to the proton structure function. Thus a simultaneous fit to the HERA data and to LHC7 gives the figures shown in Figs. 67 and 68, where the differential elastic cross section is computed without and with a hard Pomeron, respectively.

Fig. 67

The elastic differential cross section at LHC7, without inclusion of a hard Pomeron [318]. Figure is courtesy of the authors

Fig. 68

The elastic differential cross section at LHC7, with inclusion of a hard Pomeron, from [318]. Figure is courtesy of the authors

The difference between the two figures is due to the fact that, since the total cross section cannot come out right without a hard pomeron, a hard Pomeron is added to obtain the total cross section as given by TOTEM. This gives the parameters for the hard pomeron as $\alpha '_0=0.1~\mathrm{GeV}^{-2}$ and $\epsilon _0=0.362$.

At large t, the authors add a real term to the amplitude of the type $C st^{-4}$ which they understand as due to triple gluon exchange [292, 321]. In order to make it finite at $t=0$ a possible expression is proposed as

$$\begin{aligned} \frac{C s}{(t_o - t)^4}. \end{aligned}$$

(6.108)

It is pointed out in this paper that in order to correctly model the dip, both the real and the imaginary parts must become very small at the same value of t.

In the more recent contribution [319], where no hard Pomeron is invoked, the amplitude is given as three single Pomeron exchange terms, one double exchange and a triple gluon term. We show a representative fit of the LHC7 data from this paper in Fig. 69.

Fig. 69

The elastic differential cross section at LHC7 from [319], revisited as described in the text. Figure is courtesy of the authors, reprinted from [319], ©(2013) with permission from Elsevier

Each one of the three single-exchange terms is related to a trajectory $\alpha _i(t)$, with

$$\begin{aligned} A(s,t)= & {} F(t) \left[ - \frac{ X_P }{2\nu } \mathrm{e}^{-\frac{1}{2}i\pi \alpha _{P}(t)} (2\nu \alpha ^\prime _P)^{\alpha _P(t)} \right. \nonumber \\&-\frac{ X_+ }{2\nu } \mathrm{e}^{-\frac{1}{2}i\pi \alpha _+(t)} (2\nu \alpha ^\prime _P)^{\alpha _+P(t)} \nonumber \\&\left. \mp \frac{ X_- }{2\nu } \mathrm{e}^{-\frac{1}{2}i\pi \alpha _-(t)} (2\nu \alpha ^\prime _-)^{\alpha _-(t)} \right] \end{aligned}$$

(6.109)

for the pp/${\bar{p}}p$ amplitude, respectively, $\nu =(s-u)/2m$, and F(t) is a form factor. The three trajectories are parametrised as

$$\begin{aligned} \alpha _i(t)=1+\epsilon _i +\alpha _i^\prime t. \end{aligned}$$

(6.110)

To these single-exchange terms, a double Pomeron exchange, PP term, is then added. It corresponds to a trajectory

$$\begin{aligned} \alpha _{PP}(t)=1+2 \epsilon _P+\frac{1}{2}\alpha ^\prime (t) \end{aligned}$$

(6.111)

but the corresponding amplitude term is not just a power $s^{\alpha _{PP}(t)}$, and additional logarithmic terms appear at the denominator.

The tail of the distribution is given by triple gluon exchange [292], and is such that at large |t| one has

$$\begin{aligned} g(t)=C\frac{t_0^3}{t^4}. \end{aligned}$$

(6.112)

A joining with the other parts of the amplitude is obtained by trial and error, as the authors say, and is parametrised with

$$\begin{aligned} \frac{C}{t_0}\mathrm{e}^{2(1-t^2/t_ 0^2)}. \end{aligned}$$

(6.113)

The small |t| in the Coulomb region is included as

$$\begin{aligned} \mp \frac{\alpha _{EM}}{t}. \end{aligned}$$

(6.114)

The description of data from ISR to LHC for pp is very good, less so the description of ${\bar{p}}p$ data, but this is common to many present fits. The values for the 12 parameters which give the best fit to total and elastic data are given in the paper, with in particular $\epsilon _P=0.110$.

6.3.3 The model by Schegelsky and Ryskin

In [61], the emphasis is on the small-t behaviour and a concern that the elastic slope may not be just a simple linear power in $\log s$. The authors start with the usual Regge and Pomeron parametrisation for the elastic scattering amplitude, namely

$$\begin{aligned} T_{ab}=F_a(t)F_b(t)C_P s^{\alpha _P(t)}+F_R(t)s^{\alpha _R(t)} \end{aligned}$$

(6.115)

where the first term corresponds to the Pomeron, the second to a Reggeon and would be negligible at high energy. The differential elastic cross section at high energy thus takes the form

$$\begin{aligned} \frac{\mathrm{d}\sigma _{ab}}{\mathrm{d}t}=\frac{\sigma _0^2}{16\pi }F_a^2(t)F_b^2(t)\left( \frac{s}{s_0}\right) ^{2\epsilon +2\alpha '_P t} \end{aligned}$$

(6.116)

where the slope of the Pomeron trajectory accounts for the growth of the interaction radius caused by a long chain of intermediate (relatively low-energy) interactions. Agreement with data, with an elastic slope given by

$$\begin{aligned} B_{\mathrm{el}}=B_0+2\alpha ^{' eff}_P \log \frac{s}{s_0} \end{aligned}$$

(6.117)

is obtained by assuming a Gaussian type behaviour for the form factors $F_a^2(t)F_b^2(t)=\exp (B_0t)$. The second term in Eq. (6.117) is supposed to be universal, and the value obtained by examining fixed target experiments, i.e. up to $\sqrt{s}=24~\mathrm{GeV}$, is given as $\alpha '=0.14~\mathrm{GeV}^{-2}$. On the other hand, the original analysis by Donnachie and Landshoff [136] at $\sqrt{s}=52.8~\mathrm{GeV}$ would lead to $\alpha '=0.25\ \mathrm{GeV}^{-2}$.

This discrepancy points to the fact that the energy dependence of the elastic slope may be more complicated than a simple logarithm. The first idea is that as the energy increases, multiple interactions take place. In Regge-language, these multiple interactions are described by multiple Pomeron diagrams.

One important point is that in impact parameter representation, as the energy increases towards the black-disk limit, the imaginary part of the elastic scattering amplitude $\rightarrow 1$. However, while asymptotically going to the black-disk limit, at the periphery the amplitude is still growing. This leads, according to the authors, to an effective growth of the slope. The reason is that the continuing increase of the amplitude at the periphery of the impact parameter space implies an increasing radius. In this way the authors understand the discrepancy between their result for $\alpha '_P$ relative to Donnachie and Landshoff. They also provide another way to understand this behaviour, namely the interplay between one and two Pomeron exchanges, which have different signs, so that as the two Pomeron effect increases, the amplitude drops more rapidly.

Assuming an s-dependence different from the simple logarithm of Eq. (6.117), may explain why $\alpha _P^{'\mathrm{eff}} \ne \alpha '_P$. The authors propose

$$\begin{aligned} B_{\mathrm{el}}=B_0+b_1 \log \frac{s}{s_0} + b_2 \log ^2\frac{s}{s_0}, \end{aligned}$$

(6.118)

so that, if one rewrites Eq. (6.118) as

$$\begin{aligned} B_{\mathrm{el}}=B_0+\alpha _P^{'\mathrm{eff}} (s) \log \frac{s}{s_0}\equiv B_0+ b_1 \log \frac{s}{s_0} + b_2 \log ^2\frac{s}{s_0},\nonumber \\ \end{aligned}$$

(6.119)

one would obtain $\alpha _P^{'\mathrm{eff}} (s)=b_1+b_2\log s/s_0$. To determine the coefficients, the authors plot the results from a series of experiments, as we show in the left panel of Fig. 70. For $s_0=1~\mathrm{GeV}^2$, the coefficient $b_1$ is consistent with zero, while, for $b_2$, the authors obtain $b_2=0.037\pm 0.006~\mathrm{GeV}^{-2}$. Since $b_1$ is consistent with zero, the authors propose to drop this term altogether and refit the data with only a $(\log s/s_0)^2$ term. This fit gives $b_2=(0.02860\pm 0.00050)\ \mathrm{GeV}^{-2}$.

Fig. 70

From [61]: at left, the effective slope for the elastic differential cross section from a set of experiments, compared with the proposed effective parametrisation of Eq. (6.118). At right the energy dependence of $2\alpha _P^{'\mathrm{eff}}$. Reprinted with permission from [61], Figs. (1,2), ©(2012) by the American Physical Society

Their result is then discussed in light of the fits done by Block and Halzen in [259] and the possible saturation of the Froissart bound. Unlike Block and Halzen, the authors here do not think that the black-disk limit is yet reached, and believe the proton to be still relatively transparent, so that $\sigma _{\mathrm{total}}=2 \pi R^2$, with $B_{\mathrm{el}}=R^2/4$, is not yet at its geometric value. One word of caution is, however, put forward by these authors, namely that the non-linear logarithmic rise of the elastic slope is basically determined by the recent TOTEM measurement of $B(7 \ \mathrm{TeV})\sim 20\ \mathrm{GeV}^2$. Up to and including the TeVatron measurement, a linear logarithmic energy rise for $B_{\mathrm{el}}$ is in fact actually still compatible, as one can see from Fig. 70.

6.4 Analyses with Pomeron, Odderon and Regge exchanges

The dip structure has been connected to C-odd exchanges in the t-channel, phenomenologically referred to as the Odderon. The existence of such a state is predicted by QCD and has been advocated in particular by Nicolescu, also in collaboration with other authors [211, 322].

As we have mentioned in Sect. 5, the QCD treatment of the Odderon began in 1980 [212, 214]. It was examined extensively by Bartels and others in non-abelian gauge and color glass condensate theories. Present QCD studies of the Odderon trajectory focus on NLO contributions [216] and properties in the strong coupling limit [217]. Still, the major question to face is whether and how to detect its presence in LHC experiments and this takes us to the many phenomenological analyses which include Reggeons, Pomerons and Odderons.

6.4.1 Phenomenological analyses with and without the Odderon contribution

To discuss the proposal to detect the Odderon at RHIC and LHC by Avila, Gauron and Nicolescu (AGN2006) [209], we start with the model by Avila, Campos, Menon and Montanha (ACMM2006) which incorporates both the Froissart limiting behavior as well as Pomeron and Regge exchanges [210].

In [210], the elastic amplitude is normalised so that

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{dq^2}=\frac{1}{16\pi s^2}|\mathfrak {R}e F(s,q^2)+i \mathfrak {I}mF(s,q^2)|^2,\end{aligned}$$

(6.120)

$$\begin{aligned}&\sigma _{\mathrm{tot}}(s)=\frac{\mathfrak {I}m F(s,0)}{s}. \end{aligned}$$

(6.121)

Although, unlike the total cross section, both the real and the imaginary parts of the scattering amplitude enter the elastic differential cross section, in the small t-region, $|t|<0.2~\mathrm{GeV}^2$, the scattering amplitude can be expected to be still mostly imaginary. The steep decrease in this region can be empirically parametrised in terms of an exponential, i.e. one writes

$$\begin{aligned} \mathfrak {I}mF(s,q^2)\approx \alpha (s) \mathrm{e}^{-\beta (s)q^2}. \end{aligned}$$

(6.122)

Experimental data suggest that their energy dependence can be parametrised in terms of polynomials in $\log s$. The difference between pp and ${\bar{p}}p$ is then introduced as

$$\begin{aligned} \frac{\mathfrak {I}m F_{pp}(s,q^2)}{s}= & {} \sum _{i=1}^{n}\alpha _i (s) \mathrm{e}^{-\sum _{i=1}^n \beta _i(s)q^2}\nonumber \\ \frac{\mathfrak {I}m F_{p{\bar{p}}}(s,q^2)}{s}= & {} \sum _{i=1}^{n}{\bar{\alpha }}_i (s) \mathrm{e}^{-\sum _{i=1}^n {\bar{\beta }}_i(s)q^2}\nonumber \\ \alpha _i(s)= & {} A_i+B_i\log s+C_i\log ^2 (s)\nonumber \\ {\bar{\alpha }}_i(s)= & {} {\bar{A}}_i+{\bar{B}}_i\log s+{\bar{C}}_i\log ^2 (s)\nonumber \\ \beta _i(s)= & {} D_i+E_i\log s\nonumber \\ {\bar{\beta }}_i(s)= & {} {\bar{D}}_i+{\bar{E}}_i\log s. \end{aligned}$$

(6.123)

The above parametrisation implies $10n -1$ parameters, having imposed the constraint

$$\begin{aligned} \sum _{i=1}^n(C_i -{\bar{C}}_1)=0, \end{aligned}$$

(6.124)

which is valid when the Froissart bound is reached and can be considered a generalised form of the Pomeranchuk theorem [210].

Concerning the real part of the amplitude, the authors make use of the first order derivative dispersion relations for the even/odd amplitudes, defined as

$$\begin{aligned} F_{pp}(s,q^2)= & {} F_+(s,q^2)+F_-(s,q^2),\end{aligned}$$

(6.125)

$$\begin{aligned} F_{{\bar{p}}p}(s,q^2)= & {} F_+(s,q^2)-F_-(s,q^2), \end{aligned}$$

(6.126)

which lead to

$$\begin{aligned}&\frac{\mathfrak {R}e F_+(s,q^2)}{s}=\frac{K}{s}+\frac{\pi }{2}\frac{\mathrm{d}}{\mathrm{d}\log s}\frac{\mathfrak {I}m F_+(s,q^2)}{s},\end{aligned}$$

(6.127)

$$\begin{aligned}&\frac{\mathfrak {R}e F_-(s,q^2)}{s}=\frac{\pi }{2}\left( 1+\frac{\mathrm{d}}{\mathrm{d}\log s}\frac{\mathfrak {I}m F_-(s,q^2)}{s}\right) . \end{aligned}$$

(6.128)

The validity of the above expressions only extends to a region $0<q^2< q_{\max }^2$ and depends on the value chosen for $q_{\max }$. In the subsequent fit to the experimental data, different values of $q_{\max }$ are considered, leading to different parameter sets.

The above parametrisation, applied to the vast set of lower energy data up to the Tevatron, gives the result shown in Fig. 71. We see that, for the energy $\sqrt{s}=14\ \mathrm{TeV}$, the parametrisation does not show existence of a dip.

Fig. 71

Predictions for the elastic differential cross section by Avila et al. [210] at LHC and the Tevatron for pp and ${\bar{p}}p$. Reprinted with permission from [210] ©(2006) Springer

The above approach has been discussed because its no dip at LHC result in contrast with the TOTEM measurement, can falsify some of the assumptions, or lead to the need to introduce the Odderon, as done in a subsequent work with Nicolescu, as we discuss next.

Avila, Gauron and Nicolescu (AGN2006) [209] examine the data in light of the possible existence of the Odderon, a QCD effect corresponding to a singularity in the complex J-plane at $J=1$ at $t=0$ in the amplitude $F_-$, which is odd under crossing. The Odderon is considered a non-leading QCD effect, which can only be detected in the elastic differential cross section. In this analysis, its contribution is parametrised according to the properties of a number of Regge, Pomeron and Odderon trajectory exchanges, in the context of total cross sections saturating the Froissart bound. With such parametrisation, at LHC energies a dip is expected both for pp and ${\bar{p}}p$ scattering, something which cannot be proved experimentally at LHC. In [209] the suggestion is advanced to try to check the presence of the dip at RHIC, namely at $\sqrt{s}=500~\mathrm{GeV}$.

The AGN2006 analysis describes the ISR data at $\sqrt{s}=52.8~\mathrm{GeV}$ where both pp and ${\bar{p}}p$ elastic differential cross sections were measured. At this energy, while pp shows a dip, ${\bar{p}}p$ does not, and the model with the Odderon describes these features well. At $\sqrt{s}=200\ \mathrm{GeV}$ and $500\ \mathrm{GeV}$, where only $p{\bar{p}}$ scattering was present, the dip has morphed in a break in the slope, with not much difference between the two processes, with the ${\bar{p}}p$ curve remaining slightly higher. At $900\ \mathrm{GeV}$, the break is predicted to be more pronounced and at the Tevatron energies there is the hint of a dip developing, with ${\bar{p}}p$ points remaining higher. Until recently, experimental data at the Tevatron did not go beyond $|t|\simeq 0.6\ \mathrm{GeV}^2$. Presently published data from the D0 Collaboration [323], plotted in Fig. 72, indicate a pronounced break in the slope (as at $S\bar{p}pS$ ), possibly even a dip. This would correspond to the fact that the terms from Regge exchange are becoming increasingly negligible.

Fig. 72

Data for the elastic differential cross section for ${\bar{p}}p$ scattering from the three experiments at the Tevatron, compared with UA4 data, from [323]. Reprinted with permission from [323], Fig. (12), ©(2012) by the American Physical Society

Fig. 73

Predictions for the elastic differential cross section by Avila et al. [209] at LHC for pp and ${\bar{p}}p$ for the case with the odderon. Reprinted with permission from [209], ©(2006) Springer

There are no predictions for LHC7, but at $\sqrt{s}=14\ \mathrm{TeV}$ the dip is now predicted both for pp and ${\bar{p}}p$ as shown in Fig. 73. At LHC running at $\sqrt{s}=14 \ \mathrm{TeV}$ (LHC14) the position of the dip is expected at $|t|\sim 0.35~\mathrm{GeV}^2$, to be compared with the position at the ISR at $|t|\simeq 1.3\ \mathrm{GeV}^2$ and the position at LHC7 reported by TOTEM at $|t|\sim 0.53\ \mathrm{GeV}^2$.

We will discuss now in detail the parametrisation in [209]. The starting point is the maximal asymptotic behaviour of the total cross sections, consistent with data, i.e.

$$\begin{aligned} \sigma _{\mathrm{tot}}\propto & {} \log ^2 s,\end{aligned}$$

(6.129)

$$\begin{aligned} \varDelta \sigma (s)\equiv & {} \sigma _{\mathrm{tot}}^{{\bar{p}}p}-\sigma _{\mathrm{tot}}^{pp}\propto \log s,\quad \hbox {as }s\rightarrow \infty . \end{aligned}$$

(6.130)

According to [209], the choice of a maximal behaviour of the total cross section is not necessarily implying that the imaginary part of $F_-(s,0)$ is also maximal, i.e. that $F_-(s,0)\sim \log s$, but, the authors argue, it is the natural choice that strong interactions be as strong as possible. With this assumption, a parametrisation for the two, even and odd crossing, amplitudes is prepared and then determined by comparison with the data.

These authors start with a general form for the hadronic amplitudes compatible with Eq. (6.130). Their strategy is to consider both the existence and the non-existence of the Odderon, parametrising all the existing data (832 points when the paper was written) for both processes pp and ${\bar{p}}p$ for the quantities $\sigma _{\mathrm{tot}}(s), \ \rho (s)$ and $\mathrm{d}\sigma _{\mathrm{el}}(s,t)/\mathrm{d}t$. After choosing the best description for the existing data, the model is applied to predict future data and to recommend experiments which might measure the difference between the two amplitudes $F_+(s,t)$ and $F_-(s,t)$. The expressions for these even and odd amplitudes are written as sum of Pomeron and Reggeon contributions, following general theorems given in [288, 324, 325], namely

$$\begin{aligned} F_+(s,t)= & {} F_+^H(s,t)+F_+^P(s,t)\nonumber \\&+F_+^{PP}(s,t)+F_+^R(s,t)+F_+^{RP}(s,t)\nonumber \\ F_-(s,t)= & {} F_-^{MO}(s,t)+F_-^O(s,t)\nonumber \\&+ F_-^{OP}(s,t)+F_-^R(s,t)+F_-^{RP}(s,t) \end{aligned}$$

(6.131)

where the superscript H correspond to a polynomial in $\log {\bar{s}}$, with

$$\begin{aligned} {\bar{s}}=\left( \frac{s}{s_0}\right) \mathrm{e}^{-\frac{1}{2}i\pi } \end{aligned}$$

(6.132)

maximally increasing as $\log ^2(s)$ with exponential $t-$ dependence, P is the contribution from the Pomeron Regge pole, PP the Pomeron–Pomeron Regge cut, R corresponds to the secondary Regge trajectories, RP the reggeon-Pomeron cut. For the odd under crossing amplitude, MO represents the maximal Odderon contribution, also increasing as $\log ^2 s$, O is a minimal Odderon Regge pole contribution with $\alpha (0)=1$, OP is a minimal Odderon-Pomeron cut, R a secondary Regge trajectory associated with the particles $\rho (770)$ and $\omega (782)$, RP a reggeon-Pomeron Regge cut.

Fig. 74

The fit for the differential cross sections for pp and ${\bar{p}}p$ at left, and, at right, the predicted oscillation in the difference of the cross sections. Both figures are from Avila, Gauron and Nicolescu [209]. Reprinted with permission from [209] ©(2006) Springer

In [209] the no Odderon case is obtained by choosing parameters such that all the three amplitudes with contributions from the Odderon are zero, i.e. $F_-^{MO}(s,t)=F_-^O(s,t)=F_-^OP(s,t)=0$. Because of the contribution from the Regge and the Reggeon-Pomeron cut, with

$$\begin{aligned}&\frac{1}{s}F_-^R(s,t)=-C^-_R\gamma _R^-(t)\mathrm{e}^{\beta _-^R t}\nonumber \\&\quad \times \left[ i+\tan \left( \frac{\pi }{2} \alpha _-^R(t) \right) \right] \left( \frac{s}{s_0}\right) ^{ \alpha ^-_R(t)-1} \nonumber \\&\frac{1}{s}F_-^{RP}(s,t)= \left( \frac{t}{t_0}\right) ^2C^-_{RP}\mathrm{e}^{\beta _-^{RP} t} \left[ \sin \left( \frac{\pi }{2} \alpha _-^{RP}(t) \right) \right. \nonumber \\&\quad \left. +i \cos \left( \frac{\pi }{2} \alpha _-^{RP}(t) \right) \right] \times \frac{(\frac{s}{s_0})^{\alpha ^-_{RP}(t)-1}}{\log [(s/s_0)\exp (-i\frac{\pi }{2})]} \end{aligned}$$

(6.133)

the amplitude $F_-$ is not zero, but it fails to give a good description of the ISR data at $\sqrt{s} = 52.8\ \mathrm{GeV}$. The results can be summarised with the fact that, starting with the ISR data, the case without Odderon does not reproduce the data at $\sqrt{s}=52.8\ \mathrm{GeV}$ as well as it can do with the Odderon. According to the authors this is due to the fact that the t-dependence of these two remaining terms is constrained by the parameters of the Regge and Pomeron trajectories, which are non-leading and fail to interfere with the even amplitude $F_+$ in the correct way.

Turning to the other case, namely the Odderon being present, the model can count on 12 more parameters, which add to the 23 parameters determining the $F_+$ amplitude.

Numerically, it is now possible to do a good fit to ISR data which show the clear difference between $pp$ and ${\bar{p}}p$, with and without the dip. At LHC 14 TeV, the dip is fully in place, but, unlike intermediate energies, it would be present in both processes, and the difference between the two cross sections is small. The predicted dip is at $|t|\sim 0.4\ \mathrm{GeV}^2$ and the cross section after the dip rises to ${\sim } 10^{-1}\ \mathrm{mb/ GeV}^2$.

A pattern of oscillations is observed to develop in the difference $\varDelta (\frac{\mathrm{d}\sigma }{\mathrm{d}t}(s,t))$ for pp and ${\bar{p}}p$. with two minima, one around $|t|=0.1\ \mathrm{GeV}^2$ and the other around $|t|=1.1\ \mathrm{GeV}^2$. In Fig. 74 we show the fit to the differential cross section at ISR and the predicted difference.

In a subsequent paper [326] the model is extended to higher values of $0<|t|<16\ \mathrm{GeV}^2$. They define as the standard data set the data set proposed by Cudell, Lengyel and Martynov [327]. To generalise the results beyond the range $|t|=2.6~\mathrm{GeV}^2$ new terms are added to the parametrisation originally proposed, namely

• 1. $N_{\pm }$ which behave like $t^{-4}$ and growing like $\log s$. The motivation for $N_-$ was advanced to include the Odderon 3-gluon exchange, with elementary gluons.

• 2. a term $Z_{-}$ which has a role as “cross-over term” for very small $t\sim 0.16\ \mathrm{GeV}^2$

• 3. two linear functions of the type $1+A_{MO/O}t$ multiplying the maximal Odderon and the Odderon pole term, and which are necessary to describe the smallness of the Odderon forward coupling at present energies.

With these many parameters the fit is now very good and the model predicts a dip at 14 TeV around $|t|\sim 0.5\ \mathrm{GeV}^2$ and a shoulder around $|t| \sim 0.8~\mathrm{GeV}^2$. They note that at LHC energies the exponential behaviour of $\mathrm{d}\sigma /\mathrm{d}t$ is no longer valid.

A different set of parametrisation has been considered in [328,329,330] that includes Coulomb interference region as well as large t values, in terms of about 10 parameters.

6.4.2 Jenkovszky’s Pomeron/Odderon dipole model

We now discuss the contribution by Jenkovszky with different collaborators from [331, 332] and references therein. The model described in [332] extends the Donnachie and Landshoff model, to include the dip-bump structure of the differential elastic cross section, non-linear Regge trajectories, a possible Odderon, i.e. C-odd asymptotic Regge exchange. The extension should also be such as to be compatible with s and t-channel unitarity. The authors recall that the first attempt to reproduce the dip-bump structure was done through the Chou and Yang model [316], whose major drawback is that it does not contain any explicit energy dependence. As mentioned, at the beginning of this section, the Chou and Yang model describes an impact parameter distribution obtained from the proton electromagnetic form factor. In the Chou and Yang model, just as in the eikonal models in general, the dip-bump structure is obtained because of the zeroes of the imaginary part of the amplitude, induced by the Fourier transform from b-space. In [332], the pattern of the parametrisation proposed by Barger and Phillips in 1973 [317], already discussed, is followed. The amplitude is normalised so that

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}=\frac{\pi }{s^2}|A(s,t)|^2\quad \hbox {and}\quad \sigma _{\mathrm{total}}=\frac{4\pi }{s}\mathfrak {I}m A(s,t=0)\nonumber \\ \end{aligned}$$

(6.134)

with constants to be determined from the fits, and the amplitudes written such as embodying the Regge–Pomeron description, itself reflecting the collective processes participating to high energy scattering.

The model in [332] is based on four contributions to the scattering amplitudes for pp and ${\bar{p}}p$, and the amplitudes are written as a sum of Regge pole amplitudes, namely

$$\begin{aligned} A^{{\bar{p}}p}_{pp}=A_P(s,t)+A_f(s,t)\pm [A_O(s,t)+ A_\omega (s,t)]\nonumber \\ \end{aligned}$$

(6.135)

where P, O stand for the Pomeron and Odderon contribution respectively C-even and C-odd with intercept $\alpha (0)>1$, f and $\omega$, again C-even and C-odd and $\alpha (0)<1$. The Pomeron and the Odderon are treated on the same footing, their parameters to be determined by the fit to the data. For Pomeron and Odderon, a dipole expression is chosen, with a non-linear trajectory, i.e.

$$\begin{aligned}&A_P(s,t)=i\frac{a_P}{b_P}\frac{s}{s_0}[r_1^2(s)\mathrm{e}^{r_1^2[\alpha _P-1]} -\varepsilon _Pr_2^2(s)\mathrm{e}^{r_2^2[\alpha _P-1]}],\nonumber \\ \end{aligned}$$

(6.136)

$$\begin{aligned}&A_O(s,t)=\frac{a_O}{b_O}\frac{s}{s_0}r_O^2(s)\mathrm{e}^{r_O^2[\alpha _O-1]} \end{aligned}$$

(6.137)

with $r_1^2=b_P+\log (s/s_0)-i\pi /2, \ r_2^2= \log (s/s_0)-i\pi /2, \ r_O^2=b_O+\log (s/s_0)-i\pi /2$. For the Pomeron trajectory, both non linear and linear cases are considered, while the Odderon is taken to lie on a linear trajectory, similar to the reggeon trajectories for f and $\omega$. The adjustable parameters are the trajectory slopes and intercepts, the constants $a_{P/O}$ and $b_{P/O}$ and $\varepsilon$, which quantify the presence of absorption.

The fits to the usual set of observables, differential elastic cross section, total cross section and $\rho$ parameter, lead the authors to conclude that the Odderon contribution is necessary in order to correctly describe the dip-bump structure from ISR to the Tevatron. It should be noticed that in this model there are no wiggles beyond the first dip, since this model does not use the eikonal form for the amplitude, but directly parametrises it in the (s, t) plane. For LHC, we reproduce their predictions in Fig. 75. More particularly, the conclusions from this model in [332] are the following:

• 1. A single shallow dip is expected at LHC followed by a smooth behaviour

• 2. The Odderon, described as a dipole, with a positive intercept and almost flat behaviour in t is indispensable to describe the dip-bump region

• 3. the diffractive minimum in $pp$ at LHC7 is expected at $|t|=0.65\ \mathrm{GeV}^2$, receding to $0.6\ \mathrm{GeV}^2$ at LHC14

• 4. the contribution from the non-leading Regge trajectories can be neglected in the LHC region.

Recently, the possibility to extract the Odderon and the pomeron contribution from $pp$ and ${\bar{p}}p$ data has been revisited in [333]. After early results from LHC8 have been published, the model has been applied [334] to include a threshold singularity in the Pomeron trajectory, required by t-channel unitarity and related to the pion pole to account for the non-linear slope at very small $-t$-values, as reported by the TOTEM Collaboration [281]. The possibility that the amplitude reflects a square root singularity was suggested long time ago [320, 335], and is also present in the work by Khoze, Martin and Ryskin, discussed in Sect. 6.6.3.

Fig. 75

Prediction from the model by Jenkovszky et al. [332] for the elastic differential cross section at LHC, with linear Pomeron and Odderon trajectories. The band indicates uncertainties in the fit procedure. Republished with permission of L. Jenkovszky, from [332], ©(2011) World Scientific; permission conveyed through Copyright Clearance Center, Inc

6.5 Eikonal models driven by Pomeron exchanges, parton dynamics and QCD-inspired inputs

Eikonal models allow one to satisfy unitarity and comply with the asymptotic requirements of the Froissart bound. Models using this formulation differ depending on the particular dynamical input determining the eikonal function. We shall briefly illustrate some results from models which include partonic descriptions of the proton, such as the Islam model, the so-called Aspen model, and resummation of many Pomeron-like exchanges. We also include in this subsection the eikonal-based model by Bourrely, Soffer and TT Wu. In a separate subsection we shall illustrate QCD models which specifically include diffractive processes and derive their input from QCD evolution equations, notably the BFKL approach.

6.5.1 Quarks and gluons in the Islam model

A model based on the eikonal representation but reflecting the internal structure of hadrons is given by the Islam model [336,337,338].

In Islam’s original model for elastic scattering, the scattering is described as a two component process: the first giving rise to diffractive scattering where the two pion clouds surrounding the scattering nucleons interact with each other, whereas the second hard scattering process, dominating at large scattering angle, takes place via vector meson exchange, while the pion clouds independently interact.

In a more recent paper [337] the model evolves into three components, a soft cloud, a hard exchange at low c.m. energy and a hard component at high energy, identified with the BFKL Pomeron. Let us see how this picture is realised, also based on Luddy’s presentation at Blois 2009 [339]. This model is lately referred to as Condensate enclosed Chiral-bag Model, and can be seen pictorially from a drawing of this presentation, Fig. 76.

Fig. 76

Pictorial representation of the Condensate enclosed Chiral-bag model from Luddy’s presentation at Blois 2009. Reprinted from [339], in CERN-PROCEEDINGS-2010-002, ©(2010) CERN. Figure is courtesy of the authors

In this version of the model [337], a qq hard scattering term brings in four new parameters, namely the relative strengths between the $\omega$ exchange term and the hard qq term, the hard pomeron intercept $\alpha _{BFKL}=1+\omega$, the black disk radius $r_0$ and the mass $m_0$ which determines the size of the quark bag. In total this model has 17 parameters which can be fixed giving a quite satisfactory description of the total and differential cross section, at various c.m. energies and of the $\rho$ parameters.

In [339, 340], as in the previous papers, the proton is described through three basic elements: an external cloud of $q {\bar{q}}$ pairs (sea quarks), an inner shell of baryonic charge and a central quark-bag containing the valence quarks. The external cloud and the inner shell have an obvious connection to QCD phenomenology, a pion cloud or some gluon condensate and the valence quarks, while one nucleon probes the baryonic charge of the other via $\omega$-exchange. Thus the picture is:

• 1. At very small values of the momentum transfer, the scattering is diffractive and we see the interaction of one cloud of one nucleon interacting with the cloud of the other nucleon.

• 2. Then the $\omega$-exchange starts dominating.

• 3. At even higher values, it is quark–quark scattering which takes over, i.e. pQCD.

The diffractive contribution

$$\begin{aligned} T_D(s,t)=ipW\int b \mathrm{d}b \ J_0(bq)\varGamma _D(s,b) \end{aligned}$$

(6.138)

is built phenomenologically with a diffraction profile function given as

$$\begin{aligned}&\varGamma _D(s,b)\equiv 1-\mathrm{e}^{i\chi (s,b)} \\&\quad = g(s)\left[ \frac{1}{1+\mathrm{e}^{(b-R(s))/a(s)}}+\frac{1}{1+\mathrm{e}^{-(b-R(s)) /a(s)}}-1\right] . \end{aligned}$$

The above profile function renders the asymptotic behaviour of the total cross section through the function $R(s)=R_0+R_1(\log s -\frac{i\pi }{2})$, $a(s)=a_0+a_1(\log s-\frac{i\pi }{2})$with g(s) an even crossing energy dependent coupling constant. Through the assumed energy dependence of the radius R(s), the function $\varGamma _D(s,b)$ gives rise to an asymptotic energy dependence which saturates the Froissart bound. It is thus possible to obtain the following results, with corresponding asymptotic theorems at the side

$$\begin{aligned} \sigma _{\mathrm{tot}}(s)\sim & {} (a_0+a_1\log s)^2 \ \text {Froissart}{-}\text {Martin bound}\nonumber \\ \rho (s)\simeq & {} \frac{\pi a_1}{a_0+a_1\log s}\text { derivative dispersion relations}\nonumber \\ T_D(s,t)\sim & {} i s \log ^2 s f(|t|\log ^2s) \hbox { AKM scaling}\nonumber \\ T_D^{pp}(s,t)= & {} T_D^{p{\bar{p}}p}(s,t) \hbox { crossing even property} \end{aligned}$$

(6.139)

where AKM stands for Auberson, Kinoshita and Martin scaling [288]. The contribution from $\omega$-exchange is written as

$$\begin{aligned} T_\omega (s,t)=\pm i{\hat{\gamma }} \mathrm{e}^{i{\hat{\chi }}(s,b)}s \frac{F^2(t)}{m^2_\omega -t} \end{aligned}$$

(6.140)

where the first factor represents the absorptive effect from soft hadronic interactions in $\omega$ exchange, and the ± refers to ${\bar{p}}p$ and $pp$ scattering. The squared form factor in the amplitude indicates that one is probing two baryonic charge distributions. Finally the last term, which dominates at larger |t| values, is due to valence quark scattering, with the quarks interacting via reggeised gluon ladders, described through the BFKL Pomeron. This initially single valence quark scattering is then unitarised. We show these predictions in Fig. 77, where the different contributions are indicated separately. A recent fit to data, inclusive of predictions for LHC14, is shown in Fig. 78 from [338]. In 2015, the model took a significant step forward, with incorporation of polarisation of the outer quark–antiquark cloud region of the proton by the enclosed baryonic charge as described in [341].

Fig. 77

The differential elastic cross section from Islam model [340] at $\sqrt{s}=14\ \mathrm{TeV}$. Reprinted from Fig. (2) of [340], in DESY-PROC-2007-02, ©(2007) DESY. Figure is courtesy of the authors

Fig. 78

A 2013 study of the differential elastic cross section in Islam and Luddy model. Reprinted from [338]. Figure is courtesy of the authors

6.5.2 The eikonal model by Bourrely, Soffer and Wu

Another model of interest is due to Bourrely, Soffer and Wu (BSW). In [163], the total as well as the differential cross sections are discussed. Recent results and a comparison with LHC data can be found in [342, 343]. We show in Fig. 79 their pre-LHC predictions at various energies for the elastic differential cross section.

Fig. 79

The elastic differential cross section at various cms energies from BSW model [163] ©(2002) by Springer. Reprinted with permission from Springer

This model follows in the steps of the very early work by Cheng and Wu. A particularly clear description of how the impact picture developed after the work by Cheng and Wu (CW) can be found in a short review paper by Soffer [159] and also in [160]. It is recalled that QED was the only known relativistic quantum field theory in the late ’60s and that CW introduced a small photon mass $\lambda$ in order to avoid what Soffer calls unnecessary complications. After a brief introduction to the CW results, Soffer [159] describes the model developed together with Bourrely and Wu, starting with the elastic amplitude for proton scattering namely

$$\begin{aligned} a(s,t)=a^N(s,t)\pm sa^c(t) \end{aligned}$$

(6.141)

where the ± signs refer to ${\bar{p}}p$ and $pp$  respectively. The hadronic amplitude is given by $a^N(s,t)$ and the factor s has been factorised out of the Coulomb amplitude $a^c(t)$. For the latter, one has

$$\begin{aligned} a^c(t)=2\alpha \frac{G^2(t)}{|t|}\mathrm{e}^{\mp i \alpha \phi (t)} \end{aligned}$$

(6.142)

where $\alpha$ is the fine structure constant, $\phi (t)$ is the phase introduced by West and Yennie [27] as

$$\begin{aligned} \phi (t)=\log \left[ \frac{t_0}{t}\right] -\gamma \end{aligned}$$

(6.143)

$\gamma$ being the Euler constant and $t_0=0.08\ \mathrm{GeV}^2$. G(t) is the proton electromagnetic form factor, and the model chosen by Soffer in [159] is

$$\begin{aligned} G(t)=[ (t-m_1^2)(t-m_2^2) ]^{-1}. \end{aligned}$$

(6.144)

The usual quantities are defined accordingly as

$$\begin{aligned} \sigma _{\mathrm{tot}}= & {} \frac{4\pi }{s}\mathfrak {I}m a(s,t=0) \nonumber \\ \frac{\mathrm{d}\sigma (s,t)}{\mathrm{d}t}= & {} \frac{\pi }{s^2}|a(s,t)|^2 \nonumber \\ B(s,t)= & {} \frac{\mathrm{d}}{\mathrm{d}t}\log \left( \frac{\mathrm{d}\sigma }{\mathrm{d}t}\right) \end{aligned}$$

(6.145)

and the hadronic amplitude is obtained from the impact picture [161] as

$$\begin{aligned} a^N(s,t)=is \int _0^\infty b \mathrm{d}b J_0(b\sqrt{-t})(1-\mathrm{e}^{-\varOmega (s,b)}). \end{aligned}$$

(6.146)

The eikonal function $\varOmega (s,b)$ is split into two terms, reflecting different dynamical inputs, namely

$$\begin{aligned} \varOmega (s,b)=R_0(s,b)+{\hat{S}}(s,b) \end{aligned}$$

(6.147)

where $R_0(s,b)$ includes the Regge contribution important in the low-energy region and is different for $pp$ and ${\bar{p}}p$, whereas the second term ${\hat{S}}(s,b)$ is the same for both processes and gives the rising contribution to the total cross section. This term is factorised into energy dependence and impact parameter dependence as

$$\begin{aligned} {\hat{S}}(s,b)=S_0(s) F(b^2) \end{aligned}$$

(6.148)

with the energy dependence given as in the CW model. Thus the model exhibits a Pomeron energy dependence given by a complex crossing symmetric expression

$$\begin{aligned} S_0(s)= \frac{s^c}{(\log \ s/s_0)^{c'}} + \frac{u^c}{ (\log u/u_0)^{c'}} \end{aligned}$$

(6.149)

where u is the third Mandelstam variable. At high energy and small momentum transfer, the real and imaginary parts of the amplitude can be obtained through the substitution $\log u=\log s -i\pi$. As for the essential impact parameter dependence, and hence the t-dependence, this is parametrised through an expression similar to the proton electromagnetic form factor, namely the Fourier transform $\mathcal{F}(t)$ of $F(b^2)$ is

$$\begin{aligned} \mathcal{F}(t)=f [ G(t)]^2\left[ \frac{a^2+t}{a^2-t}\right] . \end{aligned}$$

(6.150)

This model had six parameters, of which two, c and $c'$, related to the energy dependence, and the other four, $a,m_1,m_2,$ and f describing the impact parameter dependence.

Including the LHC7 data, the values obtained for the six parameters are given in Table 11, from Soffer’s contribution to Diffraction 2012 [342]. The recent discussion of the model in [342] gives the description shown in Figs. 80 and 81, respectively for the scattering amplitude and the differential cross section. Figure 81 shows that the tail of the distribution after the dip reflects the usual oscillations characteristic of eikonal models.

Table 11 Parameter values for the BSW model from Diffraction 2012 [342]

Fig. 80

Absolute values of real and imaginary parts of the elastic differential cross section at 7 TeV from [342, 343]. Reprinted with permission from [342], Fig. (2), ©(2013) by AIP Publishing LLC

Fig. 81

Comparison between TOTEM data [344] and BSW model description of the elastic differential cross section at 7 TeV from [342, 343], calculated with 68% CL. Reprinted with permission from [342], ©(2013) by AIP Publishing LLC

We note that the ${\mathbf {b}}$-dependence, hence the t-dependence, is obtained through the form factor $F({\mathbf {b}}^2)$, which is not the nucleon factor nor a convolution of two nucleon form factors, as it would be in the eikonal mini-jet models or the Glauber models. This form factor is independent of the overall energy.

6.5.3 Many Pomeron structures in eikonal models

We discuss here four papers by Desgrolard, Giffon, Martynov, Petrov, Predazzi and Prokudin, who have worked together in different combinations. These authors have been involved in a precision analysis of resonances and the forward region, as in Desgrolard, Giffon, Martynov and Predazzi [345], but they also deal with the elastic differential cross section [346]. In Petrov and Prokudin [347] the three Pomeron model is introduced. Then the model is again discussed in [348] and the Coulomb interference problem is picked up by the same authors, this time with Predazzi in [349] and before in [348].

The main point of this approach is the need to go beyond one or two Pomeron pole description of the elastic differential cross section, and allow for many Pomerons. Let us begin with Desgrolard, Giffon, Martynov and Predazzi [346], which contains in its introduction a good description of the state-of-the-art in the year 2000, at the time LEP was closed and construction for LHC started.

This model is based on eikonalisation of the input Born amplitude. Namely, the scattering amplitude will be given through the eikonal function $\chi (s,b)$, and one has the usual set of equations

$$\begin{aligned} \sigma _{\mathrm{total}}= & {} \frac{4 \pi }{s}\mathfrak {I}m A(s,t=0),\end{aligned}$$

(6.151)

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}= & {} \frac{\pi }{s^2}|A(s,t)||^2 ,\end{aligned}$$

(6.152)

$$\begin{aligned} \rho= & {} \frac{\mathfrak {R}e A(s,t=0)}{\mathfrak {I}m A(s,t=0)}. \end{aligned}$$

(6.153)

The eikonalised amplitude in (s, t) space can be written through the Fourier–Bessel transform

$$\begin{aligned} A^{{\bar{p}}p}_{pp}=\frac{1}{2s} \int H^{{\bar{p}}p}_{pp}(s,b) J_0(b\sqrt{-t}) b\mathrm{d}b \end{aligned}$$

(6.154)

of the function $H^{{\bar{p}}p}_{pp}$ which is to be defined in terms of an amplitude $h^{{\bar{p}}p}_{pp}$, which is the Fourier transform of the Born amplitude in (s, t) space,

$$\begin{aligned} h^{{\bar{p}}p}_{pp}(s,b)=2s \int a^{{\bar{p}}p}_{pp} (s,-q^2)J_0(bq) q\mathrm{d}q. \end{aligned}$$

(6.155)

The next problem is the nature of the resummation procedure which takes one from the Born amplitude to the full amplitude. The Born input for the crossing-even and crossing-odd amplitudes

$$\begin{aligned} a_{pp}^{{\bar{p}}p}(s,t)= a_+(s,t)\pm a_-(s,t) \end{aligned}$$

(6.156)

will be determined by the available data on the total cross section, the differential elastic cross section and the ratio $\rho (s,t=0)$. The even part is parametrised through the contribution of a Pomeron and an f-reggeon, while the odd part is an Odderon and an $\omega$-Reggeon, i.e.

$$\begin{aligned}&a_+(s,t)=a_P(s,t)+a_f(s,t) ,\end{aligned}$$

(6.157)

$$\begin{aligned}&a_-(s,t)=a_O(s,t)+a_\omega (s,t). \end{aligned}$$

(6.158)

For the Reggeon, the standard form is used, namely

$$\begin{aligned}&a_R(s,t)=a_R{\tilde{s}}^{\alpha _R(t)}\mathrm{e}^{b_R t},\end{aligned}$$

(6.159)

$$\begin{aligned}&\alpha _R(t)=\alpha _R(0)+\alpha _R't \end{aligned}$$

(6.160)

where R stands for the f- or $\omega$-trajectories. For the Pomeron, the authors investigate two possibilities, a monopole (M) or a dipole (D), respectively

$$\begin{aligned} a_P^M(s,t)= & {} a_P{\tilde{s}}^{\alpha _P(t)} \mathrm{e}^{b_P(\alpha _P(t)},\end{aligned}$$

(6.161)

$$\begin{aligned} a_P^D(s,t)= & {} a_P{\tilde{s}}^{\alpha _P(t)} [\mathrm{e}^{b_P(\alpha _P(t)-1)} ( b_P+\log {\tilde{s}})\nonumber \\&+\,d_P\log {\tilde{s}}]. \end{aligned}$$

(6.162)

As for the Odderon, the chosen form is

$$\begin{aligned} a_O(s,t)=(1-\mathrm{e}^{\gamma t})a_O^{(M/D)}(s,t) \end{aligned}$$

(6.163)

with M or D standing for a monopole or a dipole. It should be noticed that in this paper, the authors state that, for the ratio $\rho ( s,t=0)$ to be fitted by the data, it is necessary that the Odderon contribution vanishes at $t=0$.The trajectories are all taken to be linear in t, i.e.

$$\begin{aligned} \alpha _i(t)=\alpha _i(0)+\alpha '_i t\equiv 1+\delta _i +\alpha '_i t. \end{aligned}$$

(6.164)

There is a relationship between eikonalisation and unitarisation [350,351,352], which gives the following constraints

$$\begin{aligned} \delta _P \ge \delta _0,\quad \alpha '_P\ge \alpha '_0. \end{aligned}$$

(6.165)

Most fits give $\delta _O<0$.

Once the Born amplitude is stated, the authors discuss different eikonalisation procedures, one called Ordinary Eikonalisation (OE) in which one puts

$$\begin{aligned} H^{{\bar{p}}p}_{pp,OE}(s,b)=\frac{1}{2i}\left( \sum _1^\infty \frac{[2ih^{{\bar{p}}p}_{pp}(s,b)]^n}{n!}\right) \end{aligned}$$

(6.166)

and the other is the Quasi-Eikonal (QE) with

$$\begin{aligned} H^{{\bar{p}}p}_{pp,QE}(s,b)=\frac{1}{2i}\left( \sum _1^\infty \lambda ^{n-1}\frac{[2ih^{{\bar{p}}p}_{pp}(s,b)]^n}{n!}\right) . \end{aligned}$$

(6.167)

The explicit analytical form is

$$\begin{aligned} H^{{\bar{p}}p}_{pp,QE}(s,b)=\frac{1}{2i\lambda }(\exp [i \lambda \chi ^{{\bar{p}}p}_{pp}]-1). \end{aligned}$$

(6.168)

When $\lambda =1$, one obtains the OE. Still another form of eikonalisation corresponds to the case when the weight $\lambda$ is different for different terms. In the QE case, the various terms in the sum have the same weight, but one can consider the possibility that the terms have different weights, and this case is called the Generalised Eikonal (GE). The case with three $\lambda$’s is discussed in detail, and fits are given. One observation here is the development of structures in the amplitude as a function of t. Apart from the dip, there are oscillations, which are a consequence of the properties of the Bessel function from the Fourier transform. It is possible that some special feature of the eikonal may eliminate these oscillations, but in this model they are still present.

The authors discuss fits within the OE and the QE. They have more freedom to do a best fit with the GE with 2 or 3 parameters, and different cases for fixed or variable parameters for secondary reggeons are examined. The predictions of this model are shown in Fig. 82 from [346]. They emphasise three points:

• (i) The presence of the Odderon contribution is necessary in order to describe the differential cross section in the dip region and at large t, the Odderon intercept consistently turns out to be negative from the fits.

• (ii) The real part of the even amplitude has a zero at small |t|-values, which moves toward 0 as the energy increases, being at $|t|=0.23~\mathrm{GeV}^2$ at $\sqrt{s}=14\ \mathrm{TeV}$. There are also other secondary zeroes.

• (iii) The eikonalised Odderon contributes to reproduce “perfectly” the large |t|-region.

Fig. 82

The elastic differential cross section for pp from Desgrolard, Giffon, Martynov and Predazzi [346]. Reprinted with permission of Springer from [346], ©(2000) Springer

We now proceed to Petrov and Prokudin [347], entitled “The first three Pomerons”. This paper contains a short but useful introduction to various models, and well summarises the state-of-the-art at the time. They observe that the large number of different models describing the scattering both at $t=0$ and for small t-values hints to the fact that the most general way to deal with the problem is to introduce an arbitrary number of Pomerons. In [347] a first step is attempted to formulate an eikonal structure with many Pomerons. They begin with a three Pomeron structure, since, according to the authors, one and two Pomeron structures are inadequate.

Writing the unitarity condition as

$$\begin{aligned} \mathfrak {I}m T(s,{\mathbf {b}})=|T(s,{\mathbf {b}})|^2 + \eta (s,{\mathbf {b}}) \end{aligned}$$

(6.169)

where $T(s,{\mathbf {b}})$ is the scattering amplitude in the impact parameter representation, $\eta (s,{\mathbf {b}})$ the contribution of inelastic channels, the scattering amplitude in terms of an eikonal function $\delta (s,{\mathbf {b}})$ as

$$\begin{aligned} T(s,{\mathbf {b}}) =\frac{\mathrm{e}^{2i\delta (s,{\mathbf {b}})}-1}{2i} \end{aligned}$$

(6.170)

with $\mathfrak {I}m \delta (s,{\mathbf {b}})\ge 0$ for $s> s_{\mathrm{inel}}$. If the eikonal function has only simple poles in the complex J-plane, and the poles are parametrised as linearly rising Regge trajectories, modulo the signature factor, the contribution to the eikonal in t is written as

$$\begin{aligned}&\hat{\delta }(s,t)=\frac{c}{s_0}\left( \frac{s}{s_0}\right) ^{\alpha (0)} \mathrm{e}^{t \rho ^2/4}\nonumber \\&\rho ^2=4 \alpha '(0)\log \frac{s}{s_0} +r^2 \end{aligned}$$

(6.171)

in ${\mathbf {b}}$-space one then obtains

$$\begin{aligned} \delta (s,b)=\frac{c}{s_0}\left( \frac{s}{s_0}\right) ^{\alpha _(0)-1} \frac{\mathrm{e}^{-b^2/ \rho ^2}}{4\pi \rho ^2}. \end{aligned}$$

(6.172)

Three Pomerons are then introduced describing both pp and ${\bar{p}}p$, as follows:

$$\begin{aligned} \delta ^{{\bar{p}}p}_{pp}(s,b)= & {} \delta ^+_{P_1}(s,b)+\delta ^+_{P_2} (s,b)+\delta ^+_{P_3}(sb) \nonumber \\&\mp \delta ^-_{O}(s,b)+\delta ^+_{f}(s,b)\mp \delta ^-_\omega (s,b) \end{aligned}$$

(6.173)

where $P_i$ are the Pomeron contributions, the ± sign refers to even/odd trajectories, O referring to Odderon, f and $\omega$ even and odd trajectories. To restore analyticity and crossing symmetry, one substitutes s with

$$\begin{aligned} {\tilde{s}}=\frac{s}{s_0}\mathrm{e}^{-i\frac{\pi }{2}} \end{aligned}$$

(6.174)

and obtains the appropriate signature factors for the various terms contributing to the eikonal as

$$\begin{aligned}&\delta ^+(s,b)=i\frac{c}{s_0}\left( \frac{\tilde{s}}{s_0}\right) ^{\alpha _(0)-1} \frac{\mathrm{e}^{-b^2/ \rho ^2}}{4\pi \rho ^2},\end{aligned}$$

(6.175)

$$\begin{aligned}&\delta ^-(s,b)=\frac{c}{s_0}\left( \frac{\tilde{s}}{s_0}\right) ^{\alpha _(0)-1} \frac{\mathrm{e}^{-b^2/ \rho ^2}}{4\pi \rho ^2},\end{aligned}$$

(6.176)

$$\begin{aligned}&\rho ^2=4 \alpha '(0)\log {\tilde{s}}+r^2. \end{aligned}$$

(6.177)

The trajectories are dealt with in the linear approximation, with a fit to the meson spectrum determining the parameters of the secondary Regge trajectories, f and $\omega$. The parameters defining the 3 Pomerons and the Odderon contribution (a total of 20) are obtained by a fit to the total cross sections, the $\rho$ parameter and the elastic differential cross section, the latter in the range $0.01\le |t| \le 14\ \mathrm{GeV}^2$. Data for the total elastic cross section are not included in the fit, but are a result of the model. This is not surprising given the fact that by fitting the total and the differential cross section, one fixes both the normalisation (optical point) and the slope. The fits require that the three Pomerons and the Odderon as well have intercept at $t=0$ larger than 1, which also implies that eventually there will be a violation of the Froissart bound, the slope of the Odderon being very close to zero.The exercise is repeated with only two Pomerons, but the result is not very good: in this case, unlike the three pomeron case, the Odderon trajectory is fitted to have intercept less than 1.

This paper also contains a good discussion of the connection of the model to string theory models, and to the predictions for BFKL.

Concerning predictions in the small t region, the model indicates a dip at LHC around $0.5\ \mathrm{GeV}^2$ and a wiggle around $-t \lesssim 3\ \mathrm{GeV}^2$. We show in Fig. 83 the predictions for the elastic differential cross section at RHIC and at LHC.

Fig. 83

The elastic differential cross section for pp from [347]. Reprinted with permission, ©(2002) by Springer

6.5.4 The Aspen model

This model [146] is a QCD-inspired version, applied to both proton and photon processes, of a description of the total and elastic differential cross section based on a large amount of previous work. In the 1984 review, Block and Cahn [12] describe in great detail the constraints arising from unitarity, analyticity and crossing symmetry, introducing their own proposal for low and high energy parametrisation. In the 2006 review, the phenomenological description is updated and an extensive presentation of the subsequent work is given [50]. Thus, in the following the term Aspen model refers explicitly to the description in Appendix A of [50]. A description of this model has already been presented in Sect. 5.9.3, here we recall its main points. The Aspen model uses the eikonal representation in order to ensure unitarity. It embeds in addition the constraints of analyticity, and crossing symmetry. The model includes both a crossing odd and a crossing even eikonal, i.e.

$$\begin{aligned} \chi ^{{\bar{p}}p/pp}= & {} \chi ^{\mathrm{even}}\pm \chi ^{\mathrm{odd}},\end{aligned}$$

(6.178)

$$\begin{aligned} \chi ^{\mathrm{even}}= & {} \chi _{gg}(s,b)+\chi _{qg}(s,b)+\chi _{qq}(s,b) ,\end{aligned}$$

(6.179)

$$\begin{aligned}= & {} i\sum _{ij} [\sigma _{ij}(s)W(b;\mu _{ij})] \end{aligned}$$

(6.180)

with $ij=gg,qg,gg$, $\mu _{qg}=\sqrt{\mu _{qq} \mu _{gg}}$ and

$$\begin{aligned}&W(b;\mu _{ij})=\frac{\mu ^2_{ij}}{96 \pi }(\mu _{ij}b)^3K_3(\mu _{ij}b),\end{aligned}$$

(6.181)

$$\begin{aligned}&\varSigma _{gg}=\frac{9\pi \alpha _s^2}{m_0^2} \end{aligned}$$

(6.182)

and

$$\begin{aligned} \chi ^{\mathrm{odd}}=-\sigma _{\mathrm{odd}}W(b;\mu _{\mathrm{odd}})=-C_{\mathrm{odd}}\varSigma _{gg} \frac{m_0}{\sqrt{s}}W(b;\mu _{\mathrm{odd}})\nonumber \\ \end{aligned}$$

(6.183)

with $W(b;\mu _{\mathrm{odd}})$ having the same functional form as the other b-distributions, $W(b;\mu _{ij})$. All the b-distributions are normalised to 1 and are obtained as the Fourier transform of a dipole. As for the cross sections $\sigma _{ij}(s)$, their QCD inspired parametrisation leads to the following large s-behaviour:

$$\begin{aligned} \sigma _{gg}\sim \log ^2 s,\quad \sigma _{qg}\sim \log s,\quad \sigma _{qq}\sim \hbox {constant}. \end{aligned}$$

(6.184)

For large s-values, the even contribution is made analytic through the substitution

$$\begin{aligned} s\rightarrow s\mathrm{e}^{-i\pi /2}. \end{aligned}$$

(6.185)

The two constants $C_{\mathrm{odd}}$ and $\mu _{\mathrm{odd}}$ are fitted to the data. At high energies, the odd eikonal vanishes like $1/\sqrt{s}$, since this is the term which accounts for the difference between pp and ${\bar{p}}p$ interactions, and at high energies such a difference should vanish. We show in Fig. 84 predictions for LHC14TeV and comparison of the model with the Tevatron data [142, 145]. We note that the predicted curve for LHC has a dip for $-t\simeq 0.5\ \mathrm{GeV}^2$ and second (slight) dip (more like a wiggle) around $1.8~\mathrm{GeV}^2$. Presently, data up to $-t=2.5\ \mathrm{GeV}^2$ at LHC7 show no other structure but the dip at $-t=0.53\ \mathrm{GeV}^2$.

Fig. 84

The elastic differential cross section in the Aspen model from Block’s Report [50]. The full line represents expectations at LHC at $\sqrt{s}= 14\ \mathrm{TeV}$, the dashed line are predictions at the Tevatron collider in comparison with the E710 experiment [142, 145]. Reprinted from [50], ©(2006), with permission by Elsevier

The Aspen model has been the inspiration for the Dynamical Gluon Mass model [353] in which an energy dependent mass $m_0(s)$ for the gluon is introduced to regulate the low-$p_t$ divergence in the mini-jet like eikonal functions. Recently, the group from Campinas has been concerned with the slope and the total and elastic cross sections [285, 301]. The ratio $\mathcal{R}_{\mathrm{el}}=\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}$ is discussed as it can give information as regards different models and their asymptotic behavior. The question whether B(s) is growing linearly with $\log s$ as expected in Regge-Pomeron descriptions, or whether it would grow as $\log ^2 s$ [61] is addressed. This would be relevant in cosmic ray physics, where the ratio $\sigma _{\mathrm{total}}/B$ for proton–proton scattering defines the nucleon–nucleon impact parameter amplitude (profile function), and measurements of the p-air cross section are thus related to this ratio.

Fig. 85

Data for inelastic scattering in different kinematic regions, with model expectations (blue dot) from Block and Halzen (BH) [259] and from the soft $k_t$-resummation model [41]. Figure is courtesy of Olga Shekhovtsova

6.6 Models including the diffractive contribution to the scattering amplitude

Diffractive processes contribute to the total cross section. They are inelastic processes with spatial correlations to the incoming particles, and their experimental definition depends on the type of experiments as well as on the cuts imposed on the final state. Theoretically the description of diffraction is rendered difficult because no exact theorems exist about its energy dependence. We show in Fig. 85 a compilation of data for the inelastic cross section, from lower to very high energies, including some results from LHC experiments in different rapidity regions, and, in some cases, including extrapolations into the diffractive region. The spread of results at LHC7 reflects different experimental cuts and different extrapolations into the low-mass region. The blue band gives the results from the soft $k_t$-resummation model, described in [41]. The blue circle at 14 TeV gives the Block and Halzen (BH) prediction [259].

Discussion of diffraction as distinct from both inelastic and elastic processes has a long history. Models for diffraction are present in the literature since early observations of final state particles appearing in configurations clearly correlated along the incoming projectile. As we shall discuss in the following, some of these models use a quantum mechanics formalism, inspired by Good and Walker decomposition of diffractive scattering [74], while the QCD approaches, such as those by the Durham [221] and Tel Aviv [354] group, use, in addition, a triple Regge formalism, to account for high mass as distinct from low-mass diffraction. Recently a contribution by Gustafson to clarify the connection between some of these approaches has appeared [355].

In the following we shall summarise some representative works concerned with the description of diffraction. We shall describe in some detail the contributions by Pumplin and Miettinen, started with some early work [57, 356] and then followed by Pumplin with Miettinen [357] and by Miettinen and Thomas [71]. A clear description of this approach can be found in [72]. We shall also summarise the application of some of these ideas to mini-jet models by Lipari and Lusignoli [52]. The Regge–Pomeron analysis of diffraction performed by two groups, Durham (KMR) and Tel Aviv (GLM), will follow. A digression to the string theory Pomeron description by the Brown University group [262] will be included, as it is central to the Tel Aviv model. Many phenomenological analyses exist in the literature, for a recent analysis up to Tevatron data, a good summary can be found in the work by Dino Goulianos [358].

6.6.1 The Pumplin limit for diffractive processes

We now discuss the generalisation of the break-up of the total cross section into elastic, diffractive [356, 357] and inelastic components and how to obtain the so-called Pumplin limit [57], i.e.,

$$\begin{aligned} \mathcal{R}_{\mathrm{el}+\mathrm{diff}}(s) = \left[ \frac{\sigma _{el+diff} (s)}{\sigma _{\mathrm{tot}}(s)} \right] \le \frac{1}{2} \end{aligned}$$

(6.186)

to be used instead of the black-disk limit

$$\begin{aligned} \mathcal{R}_{\mathrm{el}}(s) = \left[ \frac{\sigma _{\mathrm{el}}(s)}{\sigma _{\mathrm{tot}}(s)} \right] \le \frac{1}{2}. \end{aligned}$$

(6.187)

Let the “b-wave” unitary S(s, b) matrix be decomposed as

$$\begin{aligned} S^\dagger S = (1 -2i T^\dagger )(1 +2iT) =1;\quad \mathfrak {I}m T = T^\dagger T. \end{aligned}$$

(6.188)

If we define twice the imaginary part of the elastic amplitude by ${\tilde{M}}(s, b) =\ 2 \mathfrak {I}m T_{ii}(s, b)$, Eq. (6.188) leads to the relation

$$\begin{aligned} 2 {\tilde{M}}(s, b) - {\tilde{M}}^2 = 4 \sum _{n\ne 1} |T_{ni}|^2 \equiv \ G_{\mathrm{in}}(s, b), \end{aligned}$$

(6.189)

valid for large s if we neglect the small real part of the elastic amplitude.

The inelastic scattering sum in $G_{\mathrm{in}}$ due to multi-particle production may be written as

$$\begin{aligned} G_{\mathrm{in}}(s, b) = \sum _n \frac{\mathrm{d}^2\sigma ^{(n)}}{\mathrm{d}^2\mathbf{b}}. \end{aligned}$$

(6.190)

If one assumes a statistically independent production of particles, one is led to the Poisson distribution

$$\begin{aligned} \frac{\mathrm{d}^2\sigma ^{(n)}}{\mathrm{d}^2\mathbf{b}} = \left( \frac{Q(s,b)^n}{n!}\right) \mathrm{e}^{-Q(s,b)}. \end{aligned}$$

(6.191)

Then Eq. (6.189) leads to the well known eikonal form for the imaginary part of the elastic amplitude

$$\begin{aligned} \tilde{M}(s, b) = 1 - \mathrm{e}^{-(Q/2)} \equiv \ 1 - \mathrm{e}^{-\varOmega (s,b)}, \end{aligned}$$

(6.192)

with $2 \varOmega (s,b) = Q(s,b) = \langle n(s,b)\rangle$ denoting the mean number of collisions occurring at a given s and b.

It is well to note that Eq. (6.189) has two solutions for ${\tilde{M}}$:

$$\begin{aligned} \tilde{M}(s, b) = 1 \pm \mathrm{e}^{-(Q/2)} \equiv \ 1 \pm \mathrm{e}^{-\varOmega (s,b)}. \end{aligned}$$

(6.193)

The solution chosen in Eq. (6.192) is the smaller one which corresponds to ${\tilde{M}} \rightarrow \ 0$ as the mean number of collisions goes to zero. Hence,

$$\begin{aligned} 0 \le \ \tilde{M}(s, b) \le \ 1. \end{aligned}$$

(6.194)

We note in passing that this choice reduces the Martin–Froissart bound by a factor of 2. It also leads to one of our asymptotic sum rules [293, 294]

$$\begin{aligned} \tilde{M}(s, b = 0) \rightarrow \ 1\quad \mathrm{as}\ s\rightarrow \infty . \end{aligned}$$

(6.195)

Using a phenomenological model such as the Phillips and Barger (PB) model of Ref. [295] for the elastic amplitude, one can see that experimental data at $7\ \mathrm{TeV}$ by the TOTEM group at the LHC support Eq. (6.195). The value is $0.95 \pm 0.01$ [295] at $7\ \mathrm{TeV}$ corresponding to $G_{\mathrm{in}}(s,b=0)\rightarrow 1$. The other mathematically allowed possibility $G_{\mathrm{in}}(s,b=0)\rightarrow 0$ as $s\rightarrow \infty$ that leads to ${\tilde{M}}(s,0)\rightarrow 2$ is ruled out by data at present LHC energies.

The result of Eq. (6.193), however, is incomplete. As discussed at the beginning of this section, if the eikonal function $\varOmega (s,b)$ is constructed through a randomly distributed Poisson sum of incoherent scatterings, then the elastic ratio $\mathcal{R}_{\mathrm{el}}(s)$ turns out to be larger than its experimental value at LHC, which is still ${\simeq } 1/4$, hence quite far from the black disk limit of Eq. (6.187). The reason behind this generic fact is that there is a non-negligible fraction of the inelastic cross section, called diffractive which is not truly random but which maintains quite a bit of coherence with the scattered particles.

One type of contribution to single diffractive events occurs when one of the two scattering particles ends up in a state with the same internal quantum numbers with a close by mass but perhaps with a spin-flip (e.g., $p \rightarrow \ p^*$) [72], while simultaneous break-up of both scattering particles into diffractive states as defined above contributes to double diffraction. Even at high energies, such as at LHC7 for example, the contribution of the summed diffractive cross section to the total is $(10\div 15)\%$ and hence it needs to be properly understood and formulated [302, 357]. References to other work on this subject can be found in [52, 72]. The analysis below follows these references in outline. Other references can be found in the Durham and Tel Aviv analyses, which include contributions coming from high-mass diffraction.

The underlying essential physics of diffraction can be incorporated by supposing that the incident particles are in a superposition of “diffractive eigenstates” defined as

$$\begin{aligned} | A\rangle = \sum _k C_k(A) | \psi _k\rangle , \end{aligned}$$

(6.196)

with $P_k(A) = \sum _k |C_k(A)|^2$ giving the probability of finding the diffractive eigenstate k in A and $\sum _k P_k(A) = 1$. The interaction with the other particle produces a mixture of diffractive and non-diffractive states

$$\begin{aligned} T| A\rangle = \sum _k C_k(A) T_k | \varPsi _k\rangle + \mathrm{non\ diffractive\ states}. \end{aligned}$$

(6.197)

Hence with the breakup of only one particle A of the initial state, the elastic amplitude becomes

$$\begin{aligned} \langle A | T | A\rangle = \sum _k | C_k(A)|^2 T_k = \sum _k P_k(A) T_k \equiv \langle T\rangle ,\nonumber \\ \end{aligned}$$

(6.198)

where the average $\langle .\rangle$ denotes an average over the diffractive state probabilities. As before neglecting the real part of the diffractive amplitudes, we would have the following expressions:

$$\begin{aligned}&\mathcal{A}:\ S_T(s,b) \equiv \ \frac{\mathrm{d}^2\sigma _{\mathrm{tot}}}{\mathrm{d}^2\mathbf{b}} = 4 \mathfrak {I}m \langle A|T|A\rangle \nonumber \\&\quad = 2 \sum _k P_k(A) {\tilde{M}}(s,b) = 2 \langle {\tilde{M}}(s,b)\rangle \nonumber \\ \end{aligned}$$

(6.199)

and

$$\begin{aligned}&\mathcal{B }:\ S_{\mathrm{el}}(s,b) \equiv \ \frac{\mathrm{d}^2\sigma _{\mathrm{el}}}{\mathrm{d}^2\mathbf{b}} = 4 |\langle A|T|A\rangle |^2 \nonumber \\&\quad = 4 |\sum _k P_k(A) T_k|^2 = |\langle {\tilde{M}}(s,b)\rangle |^2. \end{aligned}$$

(6.200)

The sum of the elastic and diffractive differential cross section (in b-space) reads

$$\begin{aligned} \mathcal{C}:\ \frac{\mathrm{d}^2\sigma _{\mathrm{el}+\mathrm{diff}}}{\mathrm{d}^2\mathbf{b}}= & {} 4 \sum _k | \langle \varPsi _k|T|A\rangle |^2 \nonumber \\= & {} \langle {\tilde{M}}(s,b)^2\rangle . \end{aligned}$$

(6.201)

The basic result for the diffractive part of the differential cross section in impact-parameter space is obtained through Eqs. (6.200) and (6.201)

$$\begin{aligned} \mathcal{D}:\ S_{\mathrm{diff}} \equiv \ \frac{\mathrm{d}^2\sigma _{\mathrm{diff}}}{\mathrm{d}^2\mathbf{b}} = \langle {\tilde{M}}(s,b)^2\rangle - \langle {\tilde{M}}(s,b)\rangle ^2. \end{aligned}$$

(6.202)

In words, $S_{\mathrm{diff}}$ is given by the dispersion $\langle (\varDelta {\tilde{M}})^2\rangle$ in the absorption probabilities and hence it would vanish identically were all components of the initial state absorbed equally. If averages are taken over both incident particles, $\mathrm{d}\sigma _{\mathrm{diff}}$ would include both single and double diffraction dissociation.

Now let us see how to obtain the Pumplin upper bound on $S_{\mathrm{diff}}$. Since, by virtue of Eq. (6.194), the absorption probabilities $0 \le {\tilde{M}}_k \le 1$, and ${\tilde{M}}^2_k \le {\tilde{M}}_k$, we have also that

$$\begin{aligned}&\langle {\tilde{M}}(s,b)\rangle = \sum _k P_k M_k \le \ 1;\nonumber \\&\quad \mathrm{and}\quad \langle {\tilde{M}}^2(s,b)\rangle \le \langle {\tilde{M}}(s,b)\rangle . \end{aligned}$$

(6.203)

This leads to the Pumplin inequality

$$\begin{aligned} S_{\mathrm{diff}}(s,b) \le \left[ \frac{1}{2} S_T(s,b) - S_{\mathrm{el}}(s,b)\right] . \end{aligned}$$

(6.204)

and the integrated version of Eq. (6.204) leads to Eq. (6.186) for the ratio of the elastic + diffractive cross section to the total cross section. For pp scattering at ISR, $\sigma _{\mathrm{diff}}\approx (8.5\ \pm 1.5) ~\hbox {mb}$ which is over a half of the limit ${\approx } 14 ~\hbox {mb}$, predicted by the above Eq. (6.204). Presently, even at the highest energies, the limiting value of 1 / 2, as given by $\mathcal{R}_{\mathrm{el}+\mathrm{diff}}(s)$ in Eq. (6.186) is closer to the experimental results than the black-disk limit (1 / 2) for $\mathcal{R}_{\mathrm{el}}(s)$ in Eq. (6.187), as we have seen from Fig. 59.

Pumplin [72] further observed that while s-channel helicity conservation is a good approximation for the elastic amplitude such is not the case for diffraction dissociation.

To proceed, one needs to formulate a model for the probability distribution for diffraction dissociation at high energies, which must respect several requirements:

• (i) for diffraction dissociation into a continuous mass spectrum, an analytic dependence on mass;

• (ii) the constraints that all ${\tilde{M}}(s,b)< 1$;

• (iii) ${\tilde{M}}(s,b) \rightarrow 1$ as $b\rightarrow 0$ (asymptotic constraint);

• (iv) ${\tilde{M}}(s,b) \rightarrow 0$ as $b \rightarrow \infty$ (asymptotic constraint).

As discussed next, a simple probability distribution meeting these requirements, which is amenable to an analytic treatment, is given by [71, 72]

$$\begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}z} = \frac{z^{\lambda - 1}}{\varGamma (\lambda )} \mathrm{e}^{-z} \end{aligned}$$

(6.205)

with $0\le z\le \infty$ and the dispersion $\langle (\varDelta z)^2\rangle =\langle z\rangle = \lambda$.

6.6.2 Specific models with a continuous distribution

In 1979 Miettinen and Thomas [71] discussed how to modify the Glauber eikonal formalism to include diffraction within a picture in which quarks and gluons are – with different spatial distributions – the constituents of a nucleon or a hadron. Since earlier analyses, in particular Good and Walker [74], it had been known that if the different components of a composite system have different distributions (absorption strengths), then inelastic states are excited and the elastic formula for the amplitude needs to be modified. The aim in [71] was to show that, taking into account fluctuations in the wave function, one can find the matter distribution. This is analogous to the distinction between a “charge distribution” extracted from pp elastic scattering and the proton charge distribution obtained through the proton electromagnetic form factor, extracted from ep scattering.

Their first step is to substitute the expression for the elastic amplitude between two hadrons A and B scattering at a distance b

$$\begin{aligned} T_{\mathrm{el}}^{AB}=1-\mathrm{e}^{-\langle \varOmega (b)\rangle _{AB}} \end{aligned}$$

(6.206)

with a different amplitude, corresponding to the different possible configurations i and j in which the two hadrons find each other at the point of collisions,, i.e.

$$\begin{aligned} t^{ij}(b)=1-\mathrm{e}^{-\varOmega _{ij}(b)}. \end{aligned}$$

(6.207)

Calling $p_i$ the probability that the hadron is in a given configuration i, the complete amplitude is obtained by averaging over all the possible configurations

$$\begin{aligned} t_{\mathrm{el}}^{AB}(b)=\sum _{ij}p_i^A p_j^B t_{ij}^{AB}=1-\langle \mathrm{e}^{-\varOmega (b) }\rangle _{AB}. \end{aligned}$$

(6.208)

The connection between the simple eikonal of Eq. (6.205) and this description can be seen by writing Eq. (6.208) as

$$\begin{aligned} t_{\mathrm{el}}^{AB}(b)=1-\mathrm{e}^{-\langle \varOmega (b)\rangle _{AB}}H_{AB}(b) \end{aligned}$$

(6.209)

with the corrections to the simple eikonal embedded into the moments $\mu _k^{AB}(b)$ of the eikonal spectrum, i.e.

$$\begin{aligned}&H_{AB}=\sum _{k=0}\frac{(-1)^k}{k!}\mu _k^{AB}(b),\end{aligned}$$

(6.210)

$$\begin{aligned}&\mu _k^{AB}(b)=\langle ( \varOmega (b)-\langle \varOmega (b)_{AB}\rangle )^k \rangle _{AB}. \end{aligned}$$

(6.211)

The connection to matter distribution in b-space enters the eikonal function $\langle \varOmega (b,s)\rangle _{AB}$ from the overlap of the average matter densities of the incident particles, i.e. the s-dependence is factorised into a constant $K_{AB}$ and

$$\begin{aligned} \langle \varOmega (b,s)\rangle =K_{AB}\int \mathrm{d}^2{\mathbf {b}}' \rho ({\mathbf {b}}') \rho ({\mathbf {b}}-{\mathbf {b}}'). \end{aligned}$$

(6.212)

To exemplify this model, Eq. (6.208) is written as

$$\begin{aligned} t_{\mathrm{el}}^{AB}(b)=\int _0^\infty \mathrm{d}\varOmega P_{AB}(\varOmega ,b)(1-\mathrm{e}^{-\varOmega }) \end{aligned}$$

(6.213)

with the function $P_{AB}(\varOmega ,b)$ defined by the probabilities $p_i^A,\ p_j^B$. Now, the model becomes easy to solve under the hypothesis that the b-dependence of $P_{AB}(b)$ is only a function of the scaling variable $z=\varOmega (b,s)/\langle \varOmega (b,s)\rangle$. A simple function in the variable z is considered, namely

$$\begin{aligned} P_{AB}(z)=N z^a \mathrm{e}^{-\lambda z}, \end{aligned}$$

(6.214)

which obeys the constraints

$$\begin{aligned} \int \mathrm{d}z P_{AB}(z)=1;\quad \int z \mathrm{d}z P_{AB}=1, \end{aligned}$$

(6.215)

as required by normalisation and the first moment condition. One has

$$\begin{aligned} N=\lambda ^\lambda /\varGamma (\lambda );\quad \mathrm{and}\quad a= (\lambda -1). \end{aligned}$$

(6.216)

The integration is then done immediately, and the differential cross sections in ${\mathbf {b}}$-space now become

$$\begin{aligned}&\frac{1}{2} S_T(s,b) = \langle {\tilde{M}}(s,b)\rangle = \int \mathrm{d}P(z) [1 - \mathrm{e}^{-z \varOmega (s,b)/\lambda }]\nonumber \\&\qquad \qquad = 1 - [1 + \varOmega (s,b)/\lambda ]^{- \lambda };\end{aligned}$$

(6.217)

$$\begin{aligned}&S_{\mathrm{el}}(s,b) = 1 - 2[1 + \varOmega (s,b)/\lambda ]^{- \lambda } + [1 + \varOmega (s,b)/\lambda ]^{- 2\lambda };\nonumber \\ \end{aligned}$$

(6.218)

and

$$\begin{aligned} S_{\mathrm{diff}}(s,b) = [1 + 2\varOmega (s,b)/\lambda ]^{-\lambda } - [1 + \varOmega (s,b)/\lambda ]^{-2\lambda }.\nonumber \\ \end{aligned}$$

(6.219)

A few observations about this model are in order:

• (i) As $\lambda \rightarrow \infty$, the earlier eikonal limits are reached since $S_{\mathrm{diff}} \rightarrow 0$.

• (ii) For $\lambda = 1$, Eq. (6.217) reduces to a “Fermi” distribution

  $$\begin{aligned} \frac{1}{2} S_T(s,b) = \langle {\tilde{M}}(s,b)\rangle \rightarrow \ \frac{1}{\varOmega (s,b)^{-1} + 1};\quad [\lambda = 1].\nonumber \\ \end{aligned}$$

  (6.220)

Further extensions of this model can be found in the work by Lipari and Lusignoli [52], who use the mini-jet formalism to study the contributions to the inelastic cross section from different hadronic configurations participating to the scattering. The authors start with a careful discussion of the relation between $\sigma _{\mathrm{jet}}$, the cross section for producing a mini-jet pair, and $\sigma _{\mathrm{inel}}$, the total inelastic cross section. Many authors have had difficulty in understanding why $\sigma _{\mathrm{jet}}$ can be larger than $\sigma _{\mathrm{inel}}$: this is simply a reflection of the fact that the inelastic cross section measures the probability of inelastic interactions between hadrons, whereas $\sigma _{\mathrm{jet}}$ measures the probability of parton–parton collisions, so that, since $\sigma _{\mathrm{inel}}$ includes at least one parton–parton collision, the ratio $\sigma _{\mathrm{jet}}/\sigma _{\mathrm{inel}}$ in fact describes the average number of mini-jet pairs produced in one inelastic collision and this can be quite large.

The authors next consider the average number of collisions $\langle n_{\mathrm{jet}}(b,s,p_\perp ^{\min })\rangle$, taking place at impact parameter ${\mathbf {b}}$,

$$\begin{aligned}&\langle n_{\mathrm{jet}}(b,s,p_\perp ^{\min })\rangle = \int \mathrm{d}^2b_1\int \mathrm{d}^2b_2 P_{\mathrm{int}}({\mathbf {b}}-{\mathbf {b}}_1+{\mathbf {b}}_2)\nonumber \\&\quad \times \int \mathrm{d}p_\perp \int \mathrm{d}x_1\mathrm{d}x_2\sum _{j,k,j',k'}F_j^{h_1}(x_1,b_1,\mu ^2) F_j^{h_2}(x_2,b_2,\mu ^2) \nonumber \\&\quad \times \frac{\mathrm{d}{\hat{\sigma }}_{jk\rightarrow j'k'}}{\mathrm{d}p_\perp } \end{aligned}$$

(6.221)

obtained from the relevant x and b-space distributions for each colliding parton, j going into a hadron h, $F_j^{h}(x,b,\mu ^2)$, where $\mu$ is a hard scale defining the applicability of the mini-jet perturbative description. Since partons have a spatial distribution, this number depends on the probability $P_{\mathrm{int}}({\mathbf {b}})$ that two partons, separated by a distance ${\mathbf {b}}$, interact with each other, a standard practice in mini-jet models.

Defining parton configurations in the colliding hadrons as ${\mathbb C}_1$ and ${\mathbb C}_2$, the average number of mini-jet collisions is obtained by summing over all possible configurations, i.e.

$$\begin{aligned}&\int \mathrm{d}{\mathbb C}_1 \int \mathrm{d}{\mathbb C}_2 P_{h_1} ({\mathbb C}_1)P_{h_2}({\mathbb C}_2) n_{\mathrm{jet}}(b,{\mathbb C}_1,{\mathbb C}_2)\nonumber \\&\quad =\langle n_{\mathrm{jet}}(b,s)\rangle .\nonumber \\ \end{aligned}$$

(6.222)

Upon assumption of the factorisation hypothesis

$$\begin{aligned} n_{\mathrm{jet}}(b,{\mathbb C}_1,{\mathbb C}_2)=\langle n_{\mathrm{jet}}(b,s)\rangle \alpha ({\mathbb C}_1,{\mathbb C}_2) \end{aligned}$$

(6.223)

with $\alpha ({\mathbb C}_1,{\mathbb C}_2)$ a constant, real parameter independent of energy, the final result will be obtained by integrating over all values of the parameter $\alpha$, i.e. over all possible configurations, with a distribution given by a probability function $P(\alpha )$ which must satisfy the two conditions

$$\begin{aligned}&\int \mathrm{d}\alpha \ P(\alpha )=1 ,\end{aligned}$$

(6.224)

$$\begin{aligned}&\int \mathrm{d}\alpha \ \alpha \ P(\alpha )=1 \end{aligned}$$

(6.225)

where the second condition follows from Eq. (6.222). In this generalised Good and Walker structure the proposed final expression for the elastic amplitude is

$$\begin{aligned} F_{\mathrm{el}}(q,s)=\int \frac{\mathrm{d}^2b}{2\pi } \mathrm{e}^{i{\mathbf {q}}\cdot {\mathbf {b}}}\int \mathrm{d}\alpha \ p(\alpha ) \left[ 1-\mathrm{e}^{-\frac{\langle n(b,s)\rangle \alpha }{2}} \right] \nonumber \\ \end{aligned}$$

(6.226)

with the simple eikonal case corresponding to $p(\alpha )\rightarrow \delta (\alpha -1)$. One can see that in such case the elastic cross section includes both elastic and diffractive processes, so that in the simple eikonal case the inelastic diffraction contribution vanishes. The cross sections in momentum space can now be explicitly written as

$$\begin{aligned} \frac{\mathrm{d}\sigma _{\mathrm{el}}}{\mathrm{d}t}= & {} \pi \left[ \int \mathrm{d}b\ b\ J_0(b\sqrt{-t})\int \mathrm{d} \alpha \ p(\alpha )\right. \end{aligned}$$

(6.227)

$$\begin{aligned}&\times \left( 1-\exp \left[ -\frac{\langle n(b,s)\rangle \alpha }{2}\right] \right) ^2. \end{aligned}$$

(6.228)

The differential cross section inclusive of elastic and diffraction processes is calculated to be

$$\begin{aligned}&\frac{\mathrm{d}\sigma _{\mathrm{diff}+\mathrm{el}}}{\mathrm{d}t}=\pi \int \mathrm{d}\alpha \ p(\alpha ) \left[ \int \mathrm{d}b\ b\ J_0(b\sqrt{-t}) \right. \nonumber \\&\quad \times \left. \left( 1-\exp \left[ -\frac{\langle n(b,s)\rangle \alpha }{2}\right. \right) \right] ^2. \end{aligned}$$

(6.229)

An explicit model is built, with the probability function $p(\alpha )$ such as to satisfy the two conditions given by Eqs. (6.224) and (6.225), and chosen to be

$$\begin{aligned} p(\alpha )=\frac{1}{w\varGamma (\frac{1}{w})}\left( \frac{\alpha }{w} \right) ^{\frac{1}{w}-1}\exp \left[ -\frac{\alpha }{w}\right] \end{aligned}$$

(6.230)

as in [71]. The model depends upon the parameter $w=\langle \alpha ^2\rangle -1$. Upon performing the integrations in $\alpha$, one now has

$$\begin{aligned} \frac{\mathrm{d}^2\sigma _{\mathrm{diff}}}{\mathrm{d}^2b}= & {} (1+\langle n(b,s)\rangle w)^{-1/w}\end{aligned}$$

(6.231)

$$\begin{aligned}&-\left( 1+\frac{\langle n(b,s)\rangle w}{2} \right) ^{-2/w},\end{aligned}$$

(6.232)

$$\begin{aligned} \frac{\mathrm{d}^2\sigma _{\mathrm{total}}}{\mathrm{d}^2b}= & {} 2-2 \left( 1+\frac{\langle n(b,s)\rangle w}{2} \right) ^{ -1/w},\end{aligned}$$

(6.233)

$$\begin{aligned} \frac{\mathrm{d}^2\sigma _{\mathrm{elastic}}}{\mathrm{d}^2b}= & {} \left( 1-\left( 1+\frac{\langle n(b,s)\rangle w}{2} \right) ^{-1/w} \right) ^2. \end{aligned}$$

(6.234)

The authors apply a parametrisation of the mini-jet model to evaluate and predict the diffraction cross section as a function of energy. Using the approximation

$$\begin{aligned} \frac{\sigma _{TD}}{\sigma _{\mathrm{el}}} \equiv \frac{\sigma _{BD}}{\sigma _{\mathrm{el}}} \simeq \frac{\sigma _{DD}}{\sigma _{TD}}\equiv \frac{\sigma _{DD}}{\sigma _{BD}} \end{aligned}$$

(6.235)

where T / B refers to Target or Beam Diffraction (D) and DD stands for double diffraction, one obtains

$$\begin{aligned} \sigma _{\mathrm{diff}}=\sigma _{\mathrm{SD}}+\sigma _{DD}\simeq \sigma _{\mathrm{SD}}\left( 1+\frac{\sigma _{\mathrm{SD}}}{4\sigma _{\mathrm{el}}}\right) . \end{aligned}$$

(6.236)

The last term in Eq. (6.236) includes an extra factor of 2 at the denominator, which corrects Eq. (85) of Ref. [52].⁷ The results, for two different choices of the model mini-jet parametrisations, are shown in Fig. 86 in comparison with experimental data, then available, for single diffraction.

Fig. 86

Inelastic diffraction cross section evaluated in an eikonal mini-jet model within a generalised Good and Walker mechanism, and different mini-jet cross section parametrisations. The experimental results correspond to single diffraction only. Reprinted figure with permission from [52], ©(2009) by the American Physical Society

6.6.3 The Durham model by Khoze, Martin and Ryskin

The Durham model by Valery Khoze, Alan Martin and Misha Ryskin (KMR) offers a unified description of both soft and semi-hard interactions. This model, developed and continuously refined over many years, also with other collaborators, presents a QCD based Pomeron and parton phenomenology.

Recent papers by the Durham group [222, 223, 225, 359] describe data on multiparticle production and present differential cross section analyses. The most recent version of the model uses a two- and three-channel eikonal formalism and multipomeron exchange diagrams, incorporating both unitarity and Regge behaviour. In [359], the authors compared their original predictions, for the total cross section and diffractive quantities, with TOTEM results. Adjustments of their earlier parameters appears in [223].

The essential ingredients in their model can be summarised as follows:

• Input Pomeron trajectory for soft and hard processes

• Eikonalisation of the amplitudes

• Inclusion of diffractive processes

• Pion-loop corrections to the Pomeron trajectory and small |t| slope of the elastic differential cross section.

We shall briefly describe each of the first three items and then present their most recent phenomenology for the elastic differential cross section. The inclusion of pion-loop corrections will be treated separately in Sect. 6.6.4.

• KMR1: Pomeron trajectory

This approach uses Reggeon Field Theory with a phenomenological soft Pomeron, while for hard interactions a QCD partonic approach is employed [224]. In the hard domain, where perturbative QCD and the standard partonic approach can be used, their Pomeron is associated with the BFKL singularity. In this perturbative domain, there is a single hard Pomeron exchanged with

$$\begin{aligned}&\alpha _P^{\mathrm{bare}}(t) = (1 + \varDelta ) + t \alpha ^{'\mathrm{bare}};\quad \varDelta = 0.3;\nonumber \\&\quad \alpha ^{'\mathrm{bare}}\lesssim 0.05\ \mathrm{GeV}^{-2}. \end{aligned}$$

(6.237)

It is noted that, although the BFKL equation should be written for gluons away from the infrared region, after resummation and stabilisation, the intercept of the BFKL Pomeron depends only weakly on the scale for reasonably small scales. We reproduce in Fig. 42 their description of the connection between the intercept of the BFKL Pomeron and the value for $\alpha _s$. The figure shows how the intercept $\varDelta$ goes to a smooth almost constant behaviour as $\alpha _s$ increases.

It is useful to note here that in mini-jet pictures, the value of $\varDelta =\ 0.3$ corresponds with the mini-jet cross section growing as ${\simeq } s^{0.3}$. Thus, the bare KMR Pomeron plays a role similar to that of parton–parton scattering folded in with parton densities and summed over all parton momenta in the mini-jet model. Also, the bare slope is interpreted by KMR to be associated with the size of the Pomeron: $\alpha '^{\mathrm{bare}}\sim \ 0.05\ \mathrm{GeV}^{-2} \propto \ 1/\langle k_t^2\rangle$. It is related to a hard scale, of the order of a few GeV, which can find its counterpart in $p_{t\min }$ of the mini-jet models. However, a precise correspondence still needs to be worked out.

On the other hand, the transition from the hard to the soft domain in KMR requires multi-pomeron exchanges through re-summation of soft $k_t$-processes, thus lowering the scale of $\langle k_t^2\rangle$ from the earlier hard to a soft scale. As a result, the BFKL Pomeron (i) bare intercept decreases and at the same time (ii) the slope increases by a factor ${\sim } 5$ from its bare value. Hence, one has an effective linear Pomeron trajectory such as the one given by the Donnachie and Landshoff parametrisation, i.e.

$$\begin{aligned} \alpha _P^{\mathrm{eff}}(t) \simeq \ 1.08 + 0.25 t. \end{aligned}$$

(6.238)

KMR found empirical evidence for the above trajectory also in virtual photo-production of vector mesons at HERA.

Once again, we may find a correspondence of the change in the effective slope with the mini-jet model parameter $p_{t\min }\sim 1.1\ \mathrm{GeV}$ through the observation that $(p_{t\min }/\varLambda )^2\sim 5$ with $\varLambda \sim 500~\hbox {MeV}$.

Fig. 87

Graphical description of mechanism of semi-hard interactions in pp collisions from [360]. Reprinted with permission from [360], ©(2011) by IOP

We add here some further details regarding the “BFKL multi-Pomeron” approach. In the Durham model, the semi-hard particle production due to a single BFKL Pomeron is shown in the left plot of Fig. 87 from [360]. In this figure, Y is the rapidity interval. In (a), the $k_t$ of the partons are not ordered. The multiplicity of partons grows as $x^{-\varDelta }$ with $\varDelta \equiv \alpha _P(0)-1$, and partons drift to lower $k_t$ values because of the running of the strong coupling constant. Notice the imposition of a cut-off $k_0$, below which the cascade is forbidden to develop. In the central figure, (b), the structure of standard DGLAP-based MonteCarlo cascade is strongly ordered in $k_t$: there is a driving process, in the central rapidity region, with the highest parton momentum and then, from the initial parton a cascade ordered from larger to smaller momenta. In this description, because of the singularity of the hard parton–parton cross section ${\sim } 1/k_t^4$, an energy dependent cut-off $k_{\min }$, called an infrared cut-off, needs to be introduced, as can be seen in PYTHIA 8.1 [361]. This cut-off is applied to the hard matrix elements, not to the parton cascade, which is stopped when $k_t=k_0$. This cut-off depends on the chosen PDF set. The multiple interaction possibility is included through eikonalisation, both for the DGLAP and BFKL description. Finally, the third figure, (c), includes absorption of low $k_t$ partons. An effective “infrared” cut-off’, $k_{sat}(x)$ limits the low-$k_t$ partons. This parameter which depends on x, hence on the energy, is dynamically generated by the enhanced multi-Pomeron diagrams. Notice that the variable conjugate to impact parameter b is the momentum transfer exchanged through the Pomeron ladder, while the variable $k_t$ is the transverse momentum of the intermediate parton.

We observe that this description follows from the classic GLR paper [218], where all gluons, those involved in hard scattering as well as the soft ones from radiation before the scattering, are considered on the same footing and described through evolution equations. This differs from an approach such as the soft-$k_t$ resummation model (BN mini-jet model), where soft gluons are treated as a separate factorised term from the hard mini-jet cross section and resummed through a semi-classical procedure a’ la Bloch and Nordsieck (thus the name BN) [170].

• KMR2: Eikonalisation of the scattering amplitude

A simplified description of the model can be found in Appendix A of [221]. Starting with the usual expressions for the total and elastic cross section in impact-parameter space

$$\begin{aligned} \sigma _{\mathrm{total}}=2\int \mathrm{d}^2{\mathbf {b}}_t A_{\mathrm{el}}(b_t),\end{aligned}$$

(6.239)

$$\begin{aligned} \sigma _{\mathrm{elastic}}=\int \mathrm{d}^2 {\mathbf {b}}_t |A_{\mathrm{el}}(b_t)|^2 \end{aligned}$$

(6.240)

the scattering amplitude $A_{\mathrm{el}}$ is approximated as to be completely imaginary,. i.e. there is no real part.

With an effective (for illustration) Pomeron trajectory written as $\alpha _P(t)=\alpha _P(0)+\alpha '_P t=1+\varDelta +\alpha '_P t$ and vertex with exponential t-dependence $\beta _p \exp (B_0 t)$, the starting point is

$$\begin{aligned} \mathfrak {I}mA_{\mathrm{el}}(s,t)= & {} \beta _P^2(t)\left( \frac{s}{s_0}\right) ^{ \alpha _P(t)-1} ,\end{aligned}$$

(6.241)

$$\begin{aligned}= & {} \beta _P^2(t)\left( \frac{s}{s_0}\right) ^{\alpha _P(0)-1} \mathrm{e}^{\alpha '_P\ t\ \log \frac{s}{s_0}} . \end{aligned}$$

(6.242)

Writing the amplitude in b-space as the Fourier transform of Eq. (6.242) with $t=-q^2$

$$\begin{aligned} \mathcal{F}[A(s,t)]= & {} \frac{1}{(2\pi )^2}\int \mathrm{d}^2{\mathbf {q}}\mathrm{e}^{i{\mathbf {b}}\cdot {\mathbf {q}}} A(s,t),\end{aligned}$$

(6.243)

$$\begin{aligned}= & {} \left( \frac{s}{s_0}\right) ^{\varDelta } \mathrm{e}^{(B_0 /2+\alpha '_P\ \log \frac{s}{s_0}) b^2)/4}, \end{aligned}$$

(6.244)

this will be the input for the successive eikonalisation procedure. In the case of a single channel the amplitude is written in terms of the opacity function $\varOmega (b)$, i.e.

$$\begin{aligned} \mathfrak {I}m A_{\mathrm{el}}=[1-\mathrm{e}^{-\varOmega (b)/2}] \end{aligned}$$

(6.245)

and then eikonalising it, one obtains

$$\begin{aligned} \sigma _{\mathrm{total}}=4\pi \mathfrak {I}m A(s,0)=2\int \mathrm{d}^2{\mathbf {b}}[ 1-\mathrm{e}^{ -\varOmega (b,s)/2)} ] \end{aligned}$$

(6.246)

with the opacity

$$\begin{aligned}&\varOmega (b,s)=\frac{ \beta _P ^2 (s/s_0)^{\alpha _P(0)-1} }{4\pi B_P} \mathrm{e}^{-b^2/4B_P},\end{aligned}$$

(6.247)

$$\begin{aligned}&B_P=\frac{1}{2}B_0+\alpha '_P \log (s/s_0). \end{aligned}$$

(6.248)

A Good and Walker model to include low-mass diffractive dissociation is then developed as we shall now describe.

• KMR3: Inclusion of diffractive processes

The KMR approach to diffraction has evolved through the years, as more precise and higher energy data allowed further understanding. We summarise here some of the main ingredients of this model, whose most recent application to LHC data can be found in [224]. The authors begin with s-channel unitarity,

$$\begin{aligned} 2\mathfrak {I}mT_{\mathrm{el}}(s,b)=|T_{\mathrm{el}}(s,b)|^2+G_{\mathrm{inel}}(s,b), \end{aligned}$$

(6.249)

which, for $\varOmega$ real, is satisfied by

$$\begin{aligned} T_{\mathrm{el}}(s,b)= i(1-\mathrm{e}^{-\varOmega /2}). \end{aligned}$$

(6.250)

One then writes the total elastic and inelastic cross sections in impact-parameter space as

$$\begin{aligned} \frac{\mathrm{d}^2\sigma _{\mathrm{inel}}}{\mathrm{d}^2b}=\frac{\mathrm{d}^2\sigma _{\mathrm{total}}}{\mathrm{d}^2b}-\frac{\mathrm{d}^2\sigma _{\mathrm{elastic}}}{\mathrm{d}^2b}=2 \mathfrak {I}mT_{\mathrm{el}}-|T_{\mathrm{el}}|^2, \end{aligned}$$

(6.251)

which coincides with $1-\mathrm{e}^{-\mathfrak {I}m\varOmega }$ and brings the interpretation of $\mathrm{e}^{-\varOmega }$ as the probability for inelastic interactions. One notices that this interpretation is valid also in case of a non-negligible real part of $\varOmega$.

Diffraction is defined as elastic scattering and low-mass proton dissociation, to distinguish it from high-mass dissociation, the two types of processes being graphically described in Fig. 88 from [362]. Apparently the multi-Pomeron vertex controls both the saturation scale and high-mass dissociation. The elastic differential cross section is written as

$$\begin{aligned} \frac{\mathrm{d}\sigma _{\mathrm{el}}}{\mathrm{d}t}=\frac{1}{4\pi }\left| \int \mathrm{d}^2 {\mathbf {b}}\mathrm{e}^{i{\mathbf {q}}_t\cdot {\mathbf {b}}} \sum _{i,k} |a_i |^2 |a_k|^2 (1-\mathrm{e}^{-\varOmega _{ik}(b)/2}) \right| ^2.\nonumber \\ \end{aligned}$$

(6.252)

Fig. 88

Graphical description of low-mass proton dissociation (a) and high-mass dissociation (b) through triple Pomeron and multi-Pomeron corrections, from [362]. Reprinted with permission from [362], ©(2010) by Springer

In [363] a three-channel formalism is used to describe the diffractive final states. Here we shall describe their two-channel formalism. In [221], the GW formalism is applied to the states $pp,\ pN^*,\ N^*N^*$, and the relative processes are introduced through a parameter $\gamma$ which describes the effective coupling of the proton to the excited state $N^*$, which will then decay into the observed low-mass diffractive products. This is done by modifying the one channel description into a two channel one, i.e. by the substitution

$$\begin{aligned}&\beta _p\rightarrow \begin{pmatrix} \beta (p\rightarrow p)&{}\beta (p\rightarrow N^*) \\ \beta (N^*\rightarrow p) &{} \beta (N^*\rightarrow N^*) \end{pmatrix},\end{aligned}$$

(6.253)

$$\begin{aligned}&\quad \simeq \beta (p\rightarrow p) \begin{pmatrix} 1&{}\gamma \\ \gamma &{} 1 \end{pmatrix}. \end{aligned}$$

(6.254)

The expression for the elastic amplitude thus modified to take into account the other channels, is now

$$\begin{aligned}&\mathfrak {I}mA_{\mathrm{el}}(b_t)=1-\frac{1}{4}\mathrm{e}^{-(1+\gamma )^2\varOmega (b_t)/2} \nonumber \\&\quad -\frac{1}{2}\mathrm{e}^{-(1-\gamma ^2)\varOmega (b_t)/2}-\frac{1}{4}\mathrm{e}^{-(1- \gamma )^2\varOmega (b_t)/2}],\end{aligned}$$

(6.255)

$$\begin{aligned}&\mathfrak {I}mA(pp\rightarrow N^*p)(b_t)\nonumber \\&\quad =\frac{1}{4}[\mathrm{e}^{-(1-\gamma )^2\varOmega (b_t)/2}-\mathrm{e}^{-(1+\gamma )^2\varOmega (b_t)/2}] ,\end{aligned}$$

(6.256)

$$\begin{aligned}&\mathfrak {I}mA(pp\rightarrow N^*N^*)(b_t)= \frac{1}{4}[-\mathrm{e}^{-(1-\gamma )^2\varOmega (b_t)/2}\nonumber \\&\quad +2\mathrm{e}^{-(1-\gamma ^2)\varOmega (b_t)/2}-\mathrm{e}^{-(1+\gamma )^2\varOmega (b_t)/2}]. \end{aligned}$$

(6.257)

In this model the opacity function is real and the amplitude acquires a real part through

$$\begin{aligned} \frac{\mathfrak {R}eA}{\mathfrak {I}mA}=\tan \left( \frac{\pi \lambda }{2}\right) \end{aligned}$$

(6.258)

where

$$\begin{aligned} \lambda =\frac{\partial \log (\hbox {Im}\, A)}{\partial \log s}. \end{aligned}$$

(6.259)

The elastic proton-Pomeron vertex is parametrised as

$$\begin{aligned} V{p\rightarrow P}=\frac{\beta _p}{(1-t/a_1)(1-t/a-2 )} \end{aligned}$$

(6.260)

with $\beta ^2_p$ to be obtained from pp total cross section.

• KMR high-mass diffractive dissociation

The previously described decomposition of elastic scattering into GW type states cannot be applied to other types of inelastic processes where the final state has a continuous mass distribution, and does not have the same quantum numbers as the initial proton. As we shall also see in the case of the Tel Aviv model, triple-Pomeron exchanges are invoked for this type of events, with the cross sections written as [221]

$$\begin{aligned}&\frac{M^2 \mathrm{d}\sigma _{\mathrm{SD}}}{\mathrm{d}t \mathrm{d}M^2}=\frac{1}{16\pi ^2} g_{3P}(t) \beta (0) \beta ^2(t) \nonumber \\&\quad \left( \frac{s}{M^2} \right) ^{2\alpha (t)-2} \left( \frac{M^2}{s_0}\right) ^{\alpha (0)-1},\end{aligned}$$

(6.261)

$$\begin{aligned}&\frac{M^2 \mathrm{d}\sigma _{DD}}{\mathrm{d}t \mathrm{d}y_1 \mathrm{d}y_2}=\frac{1}{16\pi ^3}g_{3P}^2(t) \beta ^2(0) \nonumber \\&\quad \times \exp [( 1+\alpha _{\mathbb P}(0)-2\alpha _{\mathbb P}(t) )\varDelta y]\left( \frac{M^2}{s_0}\right) ^{\alpha (0)-1} \end{aligned}$$

(6.262)

Table 12 Values for various total cross section components, in two different models: at left, in the original KMR model, prior to the LHC data [225], at right in the KMR 3-channel eikonal from [222], inclusive of LHC TOTEM data at $\sqrt{s}=7\ \mathrm{TeV}$

where $\beta (t)$ is the coupling of the Pomeron to the proton and $g_{3P}(t)$ is the triple Pomeron vertex, obtained from a fit to low-energy ISR data in [363]. M and y are the diffractive mass and the rapidity regions for double diffractive dissociation. To avoid these contributions to grow too rapidly and violate unitarity, saturation and screening must be imposed and survival probability factors are introduced, as described for instance in [221].

• KMR5 Recent phenomenology

After the general overview of the model, let us see how KMR apply it to elastic scattering at LHC. The basic building blocks of this model are now the three-channel eikonal formalism and multipomeron exchange diagrams, incorporating both unitarity and Regge behaviour. These physical requirements are parametrised through the following procedure:

• the s-dependent bare Pomeron intercept $\varDelta =\alpha _P(0)-1$

• the bare Pomeron slope $\alpha '\simeq 0$

• a parameter d, which controls the BFKL diffusion in $k_t$

• the strength of the triple-Pomeron vertex

• the relative weight of the diffractive states $\gamma _i$, determined by low-mass diffractive dissociation

• the absolute value N of the initial gluon density.

In [359], the authors compare their original predictions, for the total cross section and diffractive quantities, with the TOTEM results, and, as stated earlier, they find the need to do new adjustments of the parameters, acknowledging 7 lessons, among which (i) the fact that Totem result, $\sigma _{\mathrm{inel}}=\sigma _{\mathrm{total}}-\sigma _{\mathrm{el}}=73.5 ~\hbox {mb}$, is higher than the others, CMS and ATLAS extrapolated -KMR believe it is due to low mass diffraction being higher than expected- and that (ii) the ratio $\sigma _{\mathrm{el}}/\sigma _{\mathrm{total}}\simeq 1/4$ according to TOTEM and it cannot grow further. It is also acknowledged that to describe both the forward peak and the dip in $\mathrm{d}\sigma _{\mathrm{el}}/\mathrm{d}t$ the Durham model would need to introduce more parameters.

Adjustment of the parameters leads to new results, which we present in Table 12 from [223]. In this table, some KMR results for total cross sections both prior to and including recent LHC data are shown. This adjustment does ameliorate the situation, bringing their prediction quite close to most recent TOTEM result (at this writing) of $\sigma _{\mathrm{total}}=98.58\pm 2.23~\hbox {mb}$ [344].

Finally, recent descriptions of the elastic differential cross section in the small |t| range in this model is shown in Fig. 89 from [258], where a good description of how the various choices of formalism and parameters lead to the final results.

Fig. 89

The elastic differential cross section for pp or $p{\bar{p}}$ using a two channel eikonal model, which includes the pion loop contribution to the pomeron trajectory, from [258]. Reprinted with permission from [258], ©(2014) by IOP

6.6.4 Very small t behaviour

As already seen when discussing early measurements at ISR, various experiments reported an increase in the effective slope as $-t$ approached zero. Such an effect is also seen when comparing LHC7 data with a phenomenological application such as the PB model revisited in [295, 303]. In this application, the two exponential model with a constant phase describes very well the region $0.2<|t|<2.5~\mathrm{GeV}^2$, but misses the optical point by some $10\%$, signalling that the slope has a more complicated t-dependence than that given by two exponentials. In general, attempts to describe the elastic differential cross section near the optical point as well as the region past the dip encounter difficulty in describing the very small t behavior. Presently, for LHC, a complete description is still lacking. From the theoretical point of view, it can be argued that this region should have contributions from the nearby thresholds in the unphysical region. The presence of this behavior at very small t was advocated long time ago by Anselm and Gribov [320] as well as by Cohen-Tannoudji, Ilyin and Jenkovszky [335] and has been discussed by the Durham [221] and the Cosenza group [203]. In the following, we shall describe two attempts to include such effects, the one in the Durham model, and then a model proposed by Pumplin.

In the KMR model [221], the Pomeron trajectory of Eq. (6.237) is modified so as to include a very small |t| effect. It is then called a two component Pomeron, consisting of three terms: the first two correspond to the usual linear trajectory describing the large scale, small impact-parameter space $b_t$, while the third term corresponds to pion-loop insertions and contributes a correction to the small t-behaviour of the local slope. Such improvement over the linear Pomeron trajectory consists in introducing the pion-loop corrections as prescribed by Anselm and Gribov [320]. The underlying physical idea is that pions being the lightest hadrons and the massless pion limit expected to be neither divergent nor negligible may provide observable corrections to the high energy slope of the elastic differential cross section in the low-momentum transfer limit. The expression proposed in [221] for the modified Pomeron trajectory is

$$\begin{aligned} \alpha _\mathbb {P}(t)=\alpha (0)+\alpha ' t -\frac{\beta ^2_\pi m^2_\pi }{32\pi ^3}h(\tau );\quad \left[ \tau = \frac{4 m_\pi ^2}{|t|}\right] , \end{aligned}$$

(6.263)

where

$$\begin{aligned} h(\tau )= & {} \frac{4}{\tau }F^2_\pi (t)[2\tau - (1+\tau )^{3/2}\log \left( \frac{\sqrt{1+\tau }+1}{\sqrt{1+\tau }-1}\right) \nonumber \\&+\,\log \frac{m^2}{m^2_\pi }] \end{aligned}$$

(6.264)

with $m = 1\ \mathrm{GeV}$ a semi-hard scale. The coefficient $\beta ^2_\pi$ specifies the Pomeron residue to the $\pi \pi$ total cross section and

$$\begin{aligned} F_\pi (t)=\frac{1}{1-t/a_2}. \end{aligned}$$

(6.265)

The above modification should then explain the very small-t dependence of the effective slope of the differential elastic cross section in the KMR model.

Reflecting the same type of singularity in low-t elastic scattering, a model was constructed by Pumplin for the elastic amplitude in impact-parameter space [73] which has the virtue that its Bessel transform, i.e., the elastic amplitude as a function of the momentum transfer $t=-q^2$, has branch points at the “right thresholds”: $t=\mu ^2; (2\mu )^2; (3\mu )^2,\ldots$. Or, it can be modeled as the two-gluon exchanges with a threshold at $t=4m_0^2$, where $m_0$ is the effective gluon mass.

Defining the elastic amplitude as

$$\begin{aligned} \sigma _{\mathrm{total}}(s) = 4 \pi \mathfrak {I}m F(s, t=0), \end{aligned}$$

(6.266)

with

$$\begin{aligned} F(s, t) = i \int _o^\infty b \mathrm{d}b J_o(qb) \tilde{F}(s, b) \end{aligned}$$

(6.267)

and

$$\begin{aligned} \tilde{F}(s, b) = 1 - \mathrm{e}^{-\varOmega (s,b)} \end{aligned}$$

(6.268)

in the limit of a purely imaginary amplitude, which is a good approximation at large s and small t, Pumplin models the b-dependence of the real $\varOmega$, as follows

$$\begin{aligned} \varOmega _o(s, b) = \eta (s) \mathrm{e}^{\mu [b_o(s) - \sqrt{(b^2 + b_o(s)^2)} ]}. \end{aligned}$$

(6.269)

Using the decomposition

$$\begin{aligned} \frac{\mathrm{e}^{- [k \sqrt{q^2 + \mu ^2}]}}{\sqrt{q^2 + \mu ^2}} = \int _o^\infty b\mathrm{d}b J_o(qb) \frac{\mathrm{e}^{- [\mu \sqrt{k^2 + b^2}]}}{\sqrt{k^2 + b^2}}, \end{aligned}$$

(6.270)

it is possible to invert Eq. (6.267) as a convergent power series given by

$$\begin{aligned} F_o(s, t) = ib_o(s)^2 \eta (s) \sum _{n=1} \frac{(-\eta )^{n-1}}{n!} \left[ \frac{y_o(1+y)}{y^3}\right] \mathrm{e}^{y_o-y},\nonumber \\ \end{aligned}$$

(6.271)

where $y_o =\ n\mu b_o(s)$ and $y =\ \sqrt{y_o^2 - t b_o^2(s)}$.

The series expansion for the elastic amplitude obtained in Eq. (6.271) converges rapidly and hence was proposed as quite useful for numerical computations. Also, the resulting slopes and curvature as a function of the momentum transfer are quite smooth. Remaining always in the small t range, the model provides clear insights into the intricacies involved in obtaining accurate estimates of the slopes and curvatures as a function of t. Let B(0) and $C(0) = B^{\prime }(0)/2$ be the forward slope and the forward curvature, respectively. Below we quote their numerical values at $\sqrt{s} = 19.4\$and $\ 546\ \mathrm{GeV}$ obtained in this model.

$$\begin{aligned} \sqrt{s} = 19.4 \mathrm{GeV}:B(0) = 12.44 \mathrm{GeV}^{-2}; C(0) = 7.72 \mathrm{GeV}^{-4}\nonumber \\ \sqrt{s} = 546 \mathrm{GeV}:B(0) = 16.82 \mathrm{GeV}^{-2}; C(0) = 13.65 \mathrm{GeV}^{-4}.\nonumber \\ \end{aligned}$$

(6.272)

However, the sizeable forward curvature cautions against accepting forward slopes obtained through single exponential fits. Another important point is that the curvature decreases strongly as a function of t and changes sign at larger values of t [73, 295].

6.6.5 Elastic diffraction in AdS/CFT

A strong emphasis on the embodiment of $N=4$ Super Yang Mills (SYM) physics [364] is part of the work by the Tel Aviv group, Gotsman, Levin and Maor (GLM). Because of this as well as of the intrinsic interest of the results, we now briefly discuss the approach to this problem in the context of the string/gauge theory developed in a series of papers by the Brown University group [262, 365, 366]. In these papers string/gauge duality has been employed to obtain interesting results for the Pomeron and the physics of elastic amplitudes for small t.

A brief summary of results can be found in [367]. We cannot give here a detailed description of the elegant formalism developed in [262, 365, 366], but present below results regarding the Pomeron intercept and a modified eikonal expression derived from $AdS_5$. In their string/gauge theory, a scalar kernel $\mathcal{K}(s,t,z,z')$ as a function of the four-dimensional invariants (s, t) and two bulk coordinates ($z, z'$) from the fifth dimension, describes the Green’s function for the Pomeron. At $t =0$ its imaginary part reads

$$\begin{aligned} \mathfrak {I}m \mathcal{K}(s,t =0,z,z') \approx \ \frac{s^{j_o}}{\sqrt{\pi \mathcal{D} \ln (s)}} \mathrm{e}^{\ln ^2(z/z')/\mathcal{D} \ln (s)},\nonumber \\ \end{aligned}$$

(6.273)

where the Pomeron intercept $j_o$ and $\mathcal{D}$ are given by

$$\begin{aligned} j_o = 2 - 2/\sqrt{\lambda };\ \ \mathcal{D} = 2/\sqrt{\lambda }, \end{aligned}$$

(6.274)

with $\lambda$ denoting the (large) ’t Hooft coupling constant. Three-loop universal anomalous dimension of the Wilson operators in N=4 SUSY Yang–Mills model were first obtained in [368].

The expression for the imaginary part of the Pomeron propagator in Eq. (6.273) is similar to its corresponding form (in the weak limit) with its BFKL expression

$$\begin{aligned} \mathfrak {I}m \mathcal{K}(s,t =0,p_\perp ,p_\perp ') \approx \ \frac{s^{j_o}}{\sqrt{\pi \mathcal{D} \ln (s)}} \mathrm{e}^{\ln ^2(p_\perp /p_\perp ')/\mathcal{D} \ln (s)},\nonumber \\ \end{aligned}$$

(6.275)

where $j_o = 1 + \alpha N (\frac{4 \ln (2)}{\pi }), \alpha = g_{YM}^2/4\pi$ is the SU(N) coupling constant for N colours and $\mathcal{D} = (14 \zeta (3)/\pi ) \alpha N$. The above allows one to identify the correspondence between diffusion in the gluon mass virtuality given by $\ln (p_\perp ^2)$ in Eq. (6.275) with diffusion in the radial coordinate $\ln (z^2)$ in the dual $AdS_5$ given by Eq. (6.273).

A reduction from $AdS_5$ to the needed $AdS_3$ propagator is then made. The latter depends on the $AdS_3$ chordal distance

$$\begin{aligned} v = \frac{(x_\perp - x_\perp ')^2 + (z - z')^2}{2 z z'} \end{aligned}$$

(6.276)

and a dimension $\varDelta _+(j) - 1$ obtained for the physical spin j operators occurring in BFKL/DGLAP:

$$\begin{aligned} \varDelta _+(j) = 2 + \sqrt{4 + 2\sqrt{\lambda } (j - 2)} = 2 + \sqrt{2\sqrt{\lambda }(j - j_o)},\nonumber \\ \end{aligned}$$

(6.277)

where Eq. (6.274) has been used to obtain the last part of the above equation. Rewriting Eq. (6.277) as

$$\begin{aligned} j(\varDelta ) = 2 + \frac{(\varDelta -2)^2}{2\sqrt{\lambda }} = j(4 - \varDelta ), \end{aligned}$$

(6.278)

one sees the symmetry $\varDelta \Leftrightarrow (4 - \varDelta )$. Hence, the function $\varDelta _+$ interpolates correctly (i) the value $j = j_o$ at $\varDelta = 2$ giving the BFKL exponent as well as (ii) $j = 2$ at $\varDelta = 4$ corresponding to the energy–momentum tensor, the first DGLAP operator. A schematic representation of the relationship between j and$\varDelta$ is shown in Fig. 90. In the eikonal limit – for its domain of validity see [365] – the amplitude for scattering $1+2\rightarrow 3+4$ is written as

$$\begin{aligned} -2is \int (\mathrm{d}^2b)(dzdz') P_{13}(z) P_{24}(z') \mathrm{e}^{ib_\perp \cdot q_\perp } [\mathrm{e}^{i\chi } -1],\nonumber \\ \end{aligned}$$

(6.279)

where $P_{13}(z), P_{24}(z')$ are wave functions in the bulk coordinates and for Pomeron exchange, the generalised eikonal $\chi$ which is a function of ($s,b,z,z'$) is given in terms of the Pomeron kernel by

$$\begin{aligned} \chi (s, b, z, z') = \frac{g_o^2 R^4}{2 (zz')^2 s} \mathcal{K} (s,b,z,z'). \end{aligned}$$

(6.280)

In the limit where Pomeron exchange dominates, for $s\rightarrow \infty$ and $\lambda$ fixed, the eikonal reads

$$\begin{aligned} \chi \sim \frac{\mathrm{e}^{i\pi (1 -j_o/2)} (zz's)^{j_o -1}}{\sqrt{v(2 + v)}}. \end{aligned}$$

(6.281)

Fig. 90

Schematic curve from [262] showing spin j versus dimension $\varDelta$ as given in Eq. (6.278) both for $\lambda \ll 1$ and $\lambda \gg 1$. All curves pass through the points $j =2; \varDelta = 0$ and $j = 2, \varDelta = 4$ where the anomalous dimension vanishes. The dashed lines show $\lambda =0$ DGLAP branch (slope 1); BFKL branch (slope 0) and inverted DGLAP branch (slope $-1$). Reprinted from [262], ©(2007) by Springer

We may pause here to note the similarity and differences between this approach [for $j_o >1$ and moderate values of $z,z'$] and the mini-jet model for total hadronic cross sections. Also in the mini-jet model, the eikonal is proportional to $s^\epsilon$ with $\epsilon \sim 0.3$, a power of the total energy. However, in the mini-jet model, there is an exponential suppression for large b which softens the power-law growth in energy of the eikonal to powers in logarithms of energy of the elastic amplitude. Equation (6.281) by contrast shows that the eikonal decreases only as a power of v (or b) for large v.

6.6.6 Gotsman, Levin and Maor: the Tel Aviv model

Recent descriptions of the model, which embody both Reggeon field theory and features from $N=4$ SYM gauge theory, can be found in [354] and in [369] where the diffractive peak at LHC and a summary of experimental and various model results are presented. High energy predictions for the mass distribution for both low- and high-mass diffraction can be found in [370].

For what concerns the elastic differential cross section, from the optical point to past the dip, this model, similarly to KMR, describes the diffraction peak region where non-perturbative effects are dominant, and is not yet extended to the dip region.

To describe elastic scattering and include the different components of diffraction, single (SD), double (DD), and central (CD), low-mass and high-mass diffraction, GLM introduce both a Good and Walker (GW) formalism with GW diffractive states, as well as non-GW processes.

In previous papers, whose reference can be found in [371], GLM had obtained a good description of the total and the elastic differential cross section in the small $-t$ region, with a given choice of the parameters defining the model. However, TOTEM data, in particular the rather high total cross section value, were seen to require some changes in the parametrisation [354]. Only one parameter seems however to be in need of a change, namely the Pomeron intercept $\varDelta _\mathbb {P}$. Other parameters need not to be changed, at least for a good description of high energy data, namely $\sqrt{s}\gtrsim 500\ \mathrm{GeV}$, where the present interest lies for this model. Before giving some more details on this model, we note the following input elements:

• both GW states and non-GW states contribute to diffraction

• GW states contribute to both low- and high-mass diffraction, non-GW states only to high-mass diffraction

• the amplitude in the eikonal is purely imaginary (the model is basically applied to the low t-region)

• dipole form factors inspired by the proton form factors give the factorisable impact parameter dependence in the eikonal functions

• the s-dependence of the amplitudes comes from a single Pomeron with $\alpha '_\mathbb {P}=0$ and intercept $\varDelta _\mathbb {P}=0.23$

• multi-Pomeron interactions described by enhanced and semi enhanced diagrams contribute to both GW and non-GW states.

From the above one notices once more that the s-dependence of this model is the same as in mini-jet models, with a term $s^\epsilon$, which is not associated with any explicit t-dependence.

To take into account the whole spectrum of diffraction, GLM starts with a simple Good and Walker model with two eigenwave functions $\psi _1$ and $\psi _2$. Upon diagonalisation of the interaction matrix, the wave functions of the two observed states, a hadron and a diffractive state, the latter with mass small compared to the energy of the process, respectively $\psi _h$ and $\psi _D$, are written as

$$\begin{aligned} \psi _h=\alpha \psi _1+\beta \psi _2,\quad \psi _D=-\beta \psi _1+\alpha \psi _2 \end{aligned}$$

(6.282)

with $\alpha ^2+\beta ^2=1.$ One then constructs the scattering amplitude $A_{i,k}(s,b)$ in impact-parameter space ${\mathbf {b}}$, with $i=h,D$ by solving the unitarity condition

$$\begin{aligned} 2\mathfrak {I}m A_{i,k}(s,b)=|A_{i,k}(s,b)|^2+G_{i,k}(s,b) \end{aligned}$$

(6.283)

i.e.

$$\begin{aligned} A_{i,k}(s,b)=i (1-\mathrm{e}^{-\varOmega _{i,k}(s,b)/2}) . \end{aligned}$$

(6.284)

The eikonal function $\varOmega _{i,k}$ is the imaginary part of the scattering amplitude for a single Pomeron exchange, i.e.

$$\begin{aligned} \varOmega _{i,k}=g_i(b)g_k(b)P(s)=g_i(b)g_k(b)s^\varDelta \end{aligned}$$

(6.285)

where the Pomeron-proton vertex $g_i(b)=g_i S_i(b)$ and $S_i(b)$ is the Fourier transform of the proton-like form factor, a dipole with a scale $m_i$. The zero value for the Pomeron slope, i.e. $\alpha '=0$ in GLM is understood to be in agreement with the results from $N=4$ SY as described previously, and is crucial as it allows for resummation of all pomeron interactions One sees that the impact space dependence in each eikonal $\varOmega _{i,k}$ depends on four parameters, the scales $m_i$ and $m_k$ in the form factors and the proportionality factors $g_i,\ g_k$. The amplitude in Eq. (6.284) gives the multipomeron exchange contribution to the elastic and GW diffractive states.

The contribution of GW states is obtained using the formulae

$$\begin{aligned}&a_{\mathrm{el}}(b)=i(\alpha ^4 A_{1,1}+2\alpha ^2\beta ^2A_{1,2}+ \beta ^4A_{2,2}),\end{aligned}$$

(6.286)

$$\begin{aligned}&a_{sd}^{GW}=i \{\alpha \beta \{ -\alpha ^2A_{1,1}+( \alpha ^2-\beta ^2)A_{1,2}+\beta ^2 A_{2,2}\},\nonumber \\\end{aligned}$$

(6.287)

$$\begin{aligned}&a_{dd}^{GW}=i \alpha ^2\beta ^2 \{A_{1,1}-2A_{1,2}+ A_{2,2}\} \end{aligned}$$

(6.288)

with the corresponding cross sections

$$\begin{aligned}&\sigma _{\mathrm{tot}}=2\int \mathrm{d}^2{\mathbf {b}}\ a_{\mathrm{el}}(s,b),\end{aligned}$$

(6.289)

$$\begin{aligned}&\sigma _{i}=\int \mathrm{d}^2{\mathbf {b}}\ |a_{i}(s,b)|^2\quad i=el,sd,dd. \end{aligned}$$

(6.290)

To these contributions, one needs to add non-GW terms, which are produced by Pomeron interactions, in this model only considering triple Pomeron interactions. These contributions involve the triple Pomeron coupling $G_{3\mathbb {P}}$. For single diffraction into a mass M, with $Y=\log (M^2/s)$ the authors obtain

$$\begin{aligned} A^{sd}_{i;k,l}= & {} \int \mathrm{d}^2 {\mathbf {b}}\ 2 \varDelta \left( \frac{G_{3 {\mathbb P}}}{\gamma } \frac{1}{\gamma ^2}\right) ,\end{aligned}$$

(6.291)

$$\begin{aligned}&\times g_i({\mathbf {b}}-{\mathbf {b}'},m_i) g_l({\mathbf {b}'},m_l) g_k({\mathbf {b}'},m_k),\end{aligned}$$

(6.292)

$$\begin{aligned}&\times Q(g_i,m_i,{\mathbf {b}}-{\mathbf {b}'},Y_m),\end{aligned}$$

(6.293)

$$\begin{aligned}&\times Q(g_k,m_k,{\mathbf {b}'},Y-Y_m),\end{aligned}$$

(6.294)

$$\begin{aligned}&\times Q(g_l,m_l,{\mathbf {b}'},Y-Y_m) \end{aligned}$$

(6.295)

where $G_{3 {\mathbb P}}$ is the triple Pomeron vertex proportional to $\alpha _s^2$ and

$$\begin{aligned}&Q(g,m,{\mathbf {b}},Y)=\frac{G_{\mathbb P}(Y)}{1+G_{3 {\mathbb P}}/\gamma ) g G_ {\mathbb P}(Y)S(b,m)},\end{aligned}$$

(6.296)

$$\begin{aligned}&G_{\mathbb P}(Y)=1-\exp \left[ \frac{1}{T(Y)}\right] \frac{1}{T(Y)} \varGamma \left( 0,\frac{1}{T(Y)}\right) ,\end{aligned}$$

(6.297)

$$\begin{aligned}&T(Y)=\gamma \mathrm{e}^{ \varDelta _{\mathbb P}Y},\end{aligned}$$

(6.298)

$$\begin{aligned}&\gamma ^2=\int \frac{\mathrm{d}^2k_t}{4\pi ^2} G^2_{3 {\mathbb P}}. \end{aligned}$$

(6.299)

Similarly, one can obtain the amplitudes ${\tilde{A}}^{dd}_{i,k}$ for double diffraction in terms of the functions Q written above, details can be found in [354]. The final result is that the integrated cross section for single diffraction is the sum of two terms, the GW and non-GW, likewise for double diffraction. To obtain the integrated cross sections however, a further step is required, i.e. the amplitudes $A^{sd}_{i;j,k}$ and $A^{dd}_{j,k}$ are multiplied by the survival probability factors $\mathrm{e}^{-\varOmega _{j,k}}$.

The model cannot be solved from first principles, and needs phenomenological inputs such as the Pomeron intercept, the interaction vertices between the Pomeron with the two GW states, the low-energy amplitude of dipole-target interactions and one constant, for the GW states, $\beta$.

The connection with $N=4\ SYM$ is considered in [364] where the model is discussed in light of satisfaction of two ingredients: (i) the need to deal with a large coupling constant, and (ii) the requirement to match with high energy QCD. Thus, the Pomeron intercept can be large, but the slope of the Pomeron trajectory is very small. These results, already introduced in the previous papers, match with the fact that, in the strong coupling limit, $N=4\ SYM$ theory has a soft Pomeron, i.e. the reggeised graviton with a large intercept, $\alpha _{\mathbb P}=2-2/\sqrt{\lambda }$ with $\lambda =4\pi N_c\alpha _s^{YM}$, $\alpha _s^{YM}$, the QCD coupling constant. The other important ingredient of the GLM model is the natural matching with perturbative QCD, where the only vertex that contributes is the Pomeron vertex: this is also understood in $N=4$ SYM since the Pomerons (gravitons) interact by means of the triple Pomeron vertex, which infact is small, at least $\propto 2/\sqrt{\lambda }$. Another matching result between GLM and $N=4\ SYM$ is that at large $\lambda$, only processes from diffraction dissociation contribute to the scattering amplitude. In GLM model, diffraction indeed plays also a large role, as discussed before.

The main ideas of this model can be summarised as follows:

• a double face Pomeron, with

  • 1. a large intercept, $\alpha _{\mathbb P}(0)-1$, a direct consequence of $\varDelta =1-2/\sqrt{\lambda }$ when $\lambda$ becomes large

  • 2. a short distance behavior, indicated by a small slope $\alpha '_\mathbb { P} \simeq 0$, as a QCD matching prescription

• Good Walker mechanism and triple Pomeron vertex

To the above, one needs to add an important crucial component of GLM description of diffraction, i.e. the survival probabilities for large rapidity gaps. From the eikonal formulation, the survival probabilities are obtained from the quantities

$$\begin{aligned} P_{ik}^S=\exp [-\varOmega _{ik}(s,b)], \end{aligned}$$

(6.300)

which represent the probability that the initial state $|i,k>$ does not break up after the scattering.

After the publication of the TOTEM actual data for the differential cross section and confirmation of earlier results for total elastic and inelastic, GLM were able to consolidate their parameters, and present definite expectations for this model [354]. The detailed results for all the quantities of interest appear in the paper. These include $\sigma _{\mathrm{tot}}, \sigma _{\mathrm{el}}$ and $\sigma _{\mathrm{inel}}$ at $\sqrt{s}=1.8,\ 7, 8, 57\ \mathrm{TeV}$ in addition to $\sigma _{sd}, \ \sigma _{dd}$, for which the separate values obtained for the GW and non-GW contributions are also listed.

We reproduce in Fig. 91 the fit to data in the small t-range for different energies up to LHC14. Since the model is only to be applied at vary small $-t$ values, as one approaches the dip the model starts not to reproduce well the data.

Fig. 91

Description of low-t elastic scattering in GLM from [354]. Reprinted from [354], ©(2012) with permission by Elsevier

Because of the importance of diffraction in this model, a warning is pronounced about the black-disk limit in [371]. The model results indicate a very slow approach of the elastic amplitude to saturation of this limit, in good qualitative agreement with what we have noted elsewhere in this review, namely that the AUGER results for the inelastic cross section indicates $\sigma _{\mathrm{el}}(57~\mathrm{GeV})\ne 0.5 \sigma _{\mathrm{total}}$. To summarise, it is observed that present Reggeon models all introduce at least two different mechanisms for diffraction. In GLM, these two mechanisms are: (i) the GW production of diffractive states with unspecified finite mass, independent of energy, and (ii) diffraction due to Pomeron interactions, with a dependence on the Pomeron parameter $\varDelta _{\mathbb P}$. In other models, there are distinctions between low-mass and high-mass diffraction, and central diffraction. A discussion of this point can be found at the end of Ref. [354].

We note that a model along very similar lines to GLM (and KMR) has also been developed by Ostapchenko [75]. This model is compared with GLM and other similar models for diffraction in [369]. Reference [369] presents a good recent comparative discussion of diffraction amplitudes up to LHC7 energies.

6.6.7 A comment about soft gluons and diffraction

Before ending this brief review of selected contributions present in the literature, we shall comment on the possible interpretation of diffraction in terms of soft-gluon emission. In the BN model of [93, 94], the contribution to diffraction is not present. What drives the increase of the cross section is the result of parton–parton scattering (mini-jets) dressed with soft gluon emission from the initial valence quarks. Eikonalisation then re-sums multiple interactions, each one of them coming with its own cloud of soft gluons. The present version of this model does not explicitly include soft-gluon emission from the spectator quarks. However, diffraction along the initial state protons in such a view should include both emission from the quarks participating to the scattering, but also from the so-called spectator quarks. When the proton is hit by the other hadron, quarks also undergo intra-beam scattering. Such emission is along the colliding particles. This is in agreement with the original view of diffraction a’ la Good and Walker where the target and/or the projectile dissociates into a state with no change of quantum numbers: the only gluon emission process which, by definition, does not change the proton quantum numbers is resummed soft-gluon emission. This is the dynamical picture which should be addressed. If nothing else but diffraction a’ la Good and Walker is present, then this emission could be accompanied by a factor inhibiting parton–parton scattering, namely a survival probability factor.

6.7 One-channel mini-jet model for total, elastic and inelastic cross sections

As just discussed in Sect. 6.6.7, our BN mini-jet model has not yet dealt with diffraction, being so far a one-channel eikonal model. However, this model can provide interesting insight in the distinction between correlated and uncorrelated inelastic processes, and what in included in $\sigma _{\mathrm{elastic}}$ in one-channel eikonal models.

Here we shall discuss the mini-jet contribution to total, elastic and inelastic cross sections, using a one-channel eikonal formulation as described in greater detail in [56]. To construct the total cross section, mini-jets are embedded into the eikonal formulation. Starting with

$$\begin{aligned} \sigma _{\mathrm{total}}=2 \int \mathrm{d}^2 {\mathbf {b}} [1-\mathfrak {R}e( \mathrm{e}^{i\chi (b,s)})] \end{aligned}$$

(6.301)

and neglecting the real part in the eikonal at very high energy, the above expression further simplifies into

$$\begin{aligned} \sigma _{\mathrm{total}} =2 \int \mathrm{d}^2 {\mathbf {b}} [1-\mathrm{e}^{-\chi _I(b,s)}] \end{aligned}$$

(6.302)

where $\chi _I(b,s)=\mathfrak {I}m\chi (b,s)$. Notice that $\mathfrak {R}e\chi (b,s)\simeq 0$ is a reasonable approximation for the scattering amplitude in ${\mathbf {b}}$-space at $t=0$, where very large values of the impact parameter dominate and phenomenologically the ratio of the real to the imaginary part of the forward scattering amplitude $\rho (s) \ll 1$. By properly choosing a function $\chi _I(b,s)$, all total hadronic cross sections, pp, $p{\bar{p}}$, $\pi p$, etc., can be described up to currently available data [149]. In the vast majority of models, new data have often required an adjustment of the parameters which give $\chi _I(b,s)$.

In previous publications, we had proposed a band whose upper border gave a good prediction for LHC results. By updating the model and anchoring the parameter set to LHC results, one can now proceed to refine our predictions for higher energies, LHC13 and beyond to the cosmic rays region.

The eikonal function of the mini-jet model of [93, 94] is given by

$$\begin{aligned} 2\chi _I(b,s)= & {} n_{\mathrm{soft}}^{pp}(b,s)+n_{\mathrm{jet}}^{pp}(b,s)\nonumber \\= & {} A_{FF}(b)\sigma _{\mathrm{soft}}^{pp}(s)+A_{BN}^{pp}(p,PDF;b,s)\nonumber \\&\times \sigma _{\mathrm{jet}}(PDF,p_{t\min };s). \end{aligned}$$

(6.303)

The first term includes collision with $p_t \le p_{t\min }\sim (1\div 1.5 )\ \mathrm{GeV}$, the second is obtained from the mini-jet cross section. The term $n_{\mathrm{soft}}^{pp}(b,s)$ is not predicted by our model so far and we parametrise it here with $\sigma _{\mathrm{soft}}^{pp}(s)$, obtained with a constant and one or more decreasing terms, and $A_{FF}$, the impact-parameter distribution in the non-perturbative term, obtained through a convolution of two proton form factors.

As expected, the second term in Eq. (6.303) is numerically negligible at energies $\sqrt{s}\lesssim 10~\mathrm{GeV}$. The perturbative, mini-jet, part discussed previously is defined with $p_t^{\mathrm{parton}}\ge p_{t\min }$ and is determined through a set of perturbative parameters for the jet cross section, namely a choice of PDFs and the appropriate $p_{t\min }$. Since soft-gluon resummation includes all order terms in soft-gluon emission, our model uses LO, library distributed, PDFs.

The results of the LHC updated analysis of the one-channel BN model have been presented in Fig. 51, where, as mentioned before, the ${\bar{p}} p$ points are shown, but have not been used for the phenomenological fit, and values for pp extracted from cosmic ray experiments have not been used either. In this figure both “old” densities such as GRV [96] and “newer” ones such as MSTW [95] have been included and compared with other models [259] and one-channel model predictions such as in [258, 260]. Table 13 contains the points corresponding to our model results for both GRV and MSTW densities.⁸ Results for MRST densities can be found in [92], together with details of different parameter sets used for the different PDFs.

We notice that our model is able to describe very well all the total cross section accelerator data, and gives good agreement with cosmic ray data. The AUGER point falls within the two different parametrisations we are using, full line for MSTW and dashes for GRV. By construction, both parameterisations remain very close up to LHC7 and LHC8 energies, and start diverging as the energy increases, as a consequence of the uncertainty on the very low-x behavior of the densities.

Table 13 Total cross section values in mb, from the mini-jet model with two different PDFs sets

To summarise in the model we have proposed, past ISR energies, mini-jets appear as hard gluon–gluon collisions accompanied by soft gluon emission $k_t$-resummed down into the infrared region. In this language, we have a dressed hard scattering process, with the mini-jet cross section giving the same energy behavior as the hard Pomeron, and soft-gluon resummation providing the dressing, in which the hard interaction is embedded. The eikonal formulation then transforms this dressed hard gluon interaction into a unitary ladder. The main difference with other mini-jet models such for instance in [372], is the taming mechanism ascribed to soft-gluon resummation in the infrared region.

We now turn to discuss the inelastic cross section. The inelastic total cross section is defined by subtraction from the total and the elastic cross sections. However, experimentally, it is usually defined only in specific phase space regions, and eventually extrapolated via MC simulation programs, which also include parameters and choice of models in the diffractive region. One exception is TOTEM which covers a large rapidity range.

Here, we shall focus on one, theoretically well defined, part of the inelastic cross section, what we define as uncorrelated, which is appropriately described in the mini-jet context and through the one-channel mode. In the following we shall see how.

Since our study [41] on the inelastic cross section at LHC, soon followed by the first experimental results [373], data related to measurements in different kinematic regions have appeared. Extensive and detailed measurements have been obtained for the inelastic proton–proton cross section by CMS [374], ATLAS [373], TOTEM [256, 279], ALICE [375] and LHCb [376] Collaborations. These measurements cover different regions, central and mid-rapidity, large rapidity, high- and low-mass diffractive states. Extensive QCD modelling, including mini-jets [88, 97, 377, 378], goes in describing the different regions.

Fig. 92

In these plots, the bands correspond to uncertainties related to the very low-x behavior of the PDFs used in the calculation of the total and inelastic cross sections. At left, data for the inelastic cross section are compared with GRV and MSTW densities in the eikonalised QCD mini-jet with the soft-gluon resummation model, called the BN model in the text and discussed therein. The inelastic-uncorrelated cross section is compared with inelastic processes for $M^2_X/s > 5 \times 10^{-6}$ as measured by ATLAS [373], CMS [374] and ALICE [375]. We also show comparison with Bloch and Halzen (BH) results [379]. In the right panel, results for our BN-model are shown for pp total cross section together with the inelastic-uncorrelated part of the inelastic cross section, obtained from the one-channel mini-jet model. Accelerator data at LHC include TOTEM [103, 256] and ATLAS measurements [257]. Panels are Fig. (4) and Fig. (5) reprinted from [56] ©(2015) by the American Physical Society

Here, we concentrate on the implication of any given one-channel eikonal model. Thus, we repeat the argument about the relation between the Poisson distribution of independent collisions and diffractive processes given in [41], where we stressed that the inelastic cross section in a one-channel eikonal model coincides with the sum of independently (Poisson) distributed collisions in b-space. Namely, with

$$\begin{aligned} \sigma _{\mathrm{total}}=\sigma _{\mathrm{elastic}}+\sigma _{\mathrm{inel}}, \end{aligned}$$

(6.304)

then, in a one-channel (one-ch) mode,

$$\begin{aligned} \sigma _{\mathrm{inel}}^{\mathrm{one}\text {-}\mathrm{ch}}\equiv \sigma _{\mathrm{tot}}-\sigma _{\mathrm{elastic}}^{\mathrm{one}\text {-}\mathrm{ch}}=\int \mathrm{d}^2 {{\mathbf {b}}} [1-\mathrm{e}^{-2 \chi _I(b,s)}]. \end{aligned}$$

(6.305)

But since

$$\begin{aligned} \sum _1^{\infty } \frac{({\bar{n}})^n \mathrm{e}^{-{\bar{n}}(b,s)}}{n!}=1-\mathrm{e}^{-{\bar{n}}(b,s)} \end{aligned}$$

(6.306)

one can identify the integrand at the right-hand side of Eq. (6.305) with a sum of totally independent collisions, with $2 \chi _I(b,s)={\bar{n}}(b,s)$. We suggest that this means that in so doing one excludes diffraction and other quasi-elastic processes from the integration in Eq. (6.305). Hence, the simple splitting of the total cross section as in Eq. (6.304) needs to be better qualified when a one-channel eikonal is used. In such a case, the “elastic” cross section

$$\begin{aligned} \sigma _{\mathrm{elastic}}^{\mathrm{one}\text {-}\mathrm{ch}}= \int \mathrm{d}^2 {\mathbf {b}} |1-\mathrm{e}^{-\chi _I(b,s)}|^2 \end{aligned}$$

(6.307)

must be including part of the inelastic contribution, i.e.

$$\begin{aligned}&\sigma _{\mathrm{elastic}}^{\mathrm{one}\text {-}\mathrm{ch}}=\sigma _{\mathrm{elastic}}\nonumber \\&\quad +\,\hbox {diffractive or otherwise correlated processes} \end{aligned}$$

(6.308)

and $\sigma _{\mathrm{inel}}^{\mathrm{one}\text {-}\mathrm{ch}}$ is only the non-diffractive part. Within this approach, we can compare Eq. (6.305) with data.

This comparison is shown in the left-hand panel of Fig. 92, from [56] where inelastic cross section data up to AUGER energies [86] are plotted. The blue band corresponds to the expectations from Eq. (6.305) where the same eikonal function $\chi _I(b,s)$ which gives the total cross section as seen in the right-hand plot of Fig. 92 is used. Having anchored the eikonal $\chi _I(b,s)$ to the LHC total cross section, the band indicates the spread of predictions due to the different asymptotic low-x behavior of the employed densities, as the energy increases beyond LHC8. The top curve corresponds to MSTW, the lower one to GRV.

Fig. 93

At left, we show the elastic pp cross section from the one-channel model given by the top curve, with choice of MSTW PDF as in the upper curve of the right-hand plot of Fig. 92. The green curve corresponds to the empirical parametrisation of all differential elastic pp data [303] up to $\sqrt{s}=7$ TeV. Comparison is done with both pp and $p{\bar{p}}$ data. The right-hand panel shows diffraction data from E710 [381], UA5 [382, 383], UA4 [384], ISR [385], CDF [386], CMS [387], TOTEM [256] and ALICE [375] compared with the parametrisation given by Eq. (6.309) mentioned in the text. Reprinted Fig. (6) with permission from [56] ©(2015) by the American Physical Society

The comparison with experimental data is very interesting. While the present LHC inelastic cross section data span a range of values corresponding to different kinematic regions, Eq. (6.305) identifies the region where uncorrelated events described by mini-jet collisions, parton–parton collision with $p_t>p_{t\min }$, play the main role. From the comparison with data, we can identify it with the region $\xi = M^2_X/s \ge 5\times 10^{-6}$ where three LHC experiments, ATLAS [373], CMS [374] and ALICE [375], agree to a common value within a small error. This measurement is in the high-mass region (for instance, at LHC7 the lower bound gives $M_{X}=15.7~\mathrm{GeV}$). LHCb results correspond to a lower cross section, but they do not cover the same region of phase space.

The above results are summarised in Fig. 92 where the bands correspond to different PDFs used in the calculation of mini-jets and to their different extrapolation to very low-x at the cosmic ray energies.

The dashed yellow band is the one-channel inelastic cross section that only includes Poisson-distributed independent scatterings. That is, once the parameters of the eikonal $\chi _I(b,s)$ are chosen to give an optimal reproduction of the total cross section, the computed inelastic cross section immediately gives the uncorrelated part of the total inelastic cross section. The importance of this fact for cosmic ray deduced pp cross sections has been noticed in [92] and discussed in Sect. 3.7.2.

6.7.1 A phenomenological proposal for isolating the diffractive component

The total cross section, which our BN model successfully describes, includes different components, but only one of them is well defined experimentally as well as theoretically, that is the elastic cross section. It is well known that one-channel eikonal models fail to simultaneously describe the total and the elastic cross section through the entire available CM energy range, with the same parameter set. In the last sub-section, we have delineated this shortcoming through the observation [56] that once mini-jets become operative past the soft edge identified by Block et al. in [380], the computed elastic cross section includes correlated inelastic collisions and the computed inelastic lacks the same (i.e., its correlated inelastic part). We now discuss this matter in detail so as to make these statements quantitative. We shall do so through the one-channel mini-jet model with a suitable parametrisation of diffractive data.

In one-channel eikonal models, with the inelastic part given by Eq. (6.305), the elastic part of the total cross section is given by Eq. (6.307). Notice that whereas Eq. (6.305) is exact, in Eq. (6.307) the real part of the eikonal function has been neglected, as in Eq. (6.301).

Equation (6.307) reproduces with a good approximation the elastic cross section data up to the onset of mini-jets, deviating significantly from the data already at energies around 100 GeV. In particular, at the Tevatron, Eq. (6.307) gives an elastic cross section roughly 30% higher than the data. This is shown in the left-hand plot of Fig. 93, where the one-channel result from Eq. (6.307) is plotted together with elastic scattering data and an empirical parametrisation of all elastic differential cross section pp data from ISR to LHC7 [303].

The analysis of [303] is based on the Phillips and Barger model for the elastic differential cross section [317], described in Sect. 6.3.1, implemented by a form factor term to fully reproduce the optical point, and hence the total cross section, as well as the forward slope. Through suitable predictions for the high energy behavior of the parameters, the parameterisation of [303] provides a model independent prediction both for elastic and total cross sections at very high energies, and hence can be used as a good test of different models in the high energy region beyond present accelerator data.

Fig. 94

The total elastic cross section obtained by subtracting Single Diffractive contributions, indicated as $\sigma _{\mathrm{diff}}$, from the one-channel model result. The resulting curve is compared with pp and $p {\bar{p}}$ data and the empirical parametrisation of [303] which is seen to fall within the two model predictions. Reprinted left-hand plot of Fig. (7) with permission from [56], ©(2015) by the American Physical Society

The left-hand plot of Fig. 93 from [56] shows that at low energies, before the onset of mini-jets, one-channel models may be used to describe both elastic and total cross sections. However, past ISR energies the threshold of perturbative QCD, reflected in the appearance of the soft edge, is crossed, and one-channel models fail. One-channel models are also unable to reproduce the behaviour of the differential elastic cross section, and multichannel models with added parameters are then needed to describe diffraction. The difficulty with proper descriptions of diffraction is that at different energies, different parts of the phase space are accessed by different experimental set-ups, as we show in the right-hand plot of Fig. 93.

For the argument to follow, we consider an estimate of $\sigma _{\mathrm{Diff}}$ given by Eq. (36) of [76], which provides a good interpolation of Single Diffractive (SD) data, from ISR to the LHC results from ALICE, CMS and TOTEM, as we show in Fig. 93. i.e.

$$\begin{aligned} \sigma _{\mathrm{Diff}}(s) = \left[ \frac{(0.5~\mathrm{mb})\ s}{s + (10\ \mathrm{GeV})^2}\right] \log \left( \frac{10^3 s}{\mathrm{GeV}^2}\right) . \end{aligned}$$

(6.309)

We have adopted this parameterisation for the full diffractive component at high energy. This is an approximation, justified at very high energy by the TOTEM result for Double Diffraction(DD) [388], namely $\sigma _{DD}\simeq 0.1~\hbox {mb}$, although this result was obtained in a narrow range of pseudo-rapidity and more data are needed to conclude that DD does not play a significant role at LHC energies. At lower energy the definitions vary, as we show in this figure.

We shall now show how the one-channel mini-jet model presented here can be used to predict the full inelastic cross section at higher energies.

We start with the elastic cross section, and we consider now the difference

$$\begin{aligned} \sigma _{\mathrm{elastic}}^{\mathrm{one}\text {-}\mathrm{ch}}=\sigma _{\mathrm{tot}}-\sigma _{\mathrm{inel}}^{\mathrm{one}\text {-}\mathrm{ch}}, \end{aligned}$$

(6.310)

which includes diffractive (stated otherwise, correlated inelastic) contribution, as also discussed in general terms in [68], among others. If

$$\begin{aligned} \sigma _{\mathrm{inel}}=\sigma _{\mathrm{inel}}^{\mathrm{one}\text {-}\mathrm{ch}}+\sigma _{\mathrm{Diff}}, \end{aligned}$$

(6.311)

then we should be able to obtain the measured elastic cross section from

$$\begin{aligned} \sigma _{\mathrm{elastic}}=\sigma _{\mathrm{elastic}}^{\mathrm{one}\text {-}\mathrm{ch}}-\sigma _{\mathrm{Diff}}. \end{aligned}$$

(6.312)

We compare the procedure outlined through Eqs. (6.309) and (6.312) with experimental data and with the empirical parametrisation for the elastic cross section data of [303]. This is shown in Fig. 94 from [56]. We see that such a procedure gives a good description of the elastic cross section at high energy, basically past the CERN $Sp{\bar{p}}S$.

Fig. 95

The inelastic cross section: at high energies, adding diffraction brings the one-channel result in agreement to data. Reprinted right-hand plot of Fig. (7) with permission from [56], ©(2015) by the American Physical Society

Likewise, from Eq. (6.311), we can see that by adding the diffractive part, parametrised as in Eq. (6.309), to the prediction from the one-channel model, it is possible to obtain a good description of the high energy behavior of the inelastic cross section. This is shown in Fig. 95. It must be noticed that this procedure shows agreement with data only past ISR energies (in fact from $Sp{\bar{p}}S$ onwards) and that a model describing both the low and the high energy will have to go beyond the one-channel exercise described here. In Table 14, we show the predictions from this model for the inelastic cross section at LHC13, $\sqrt{s}=13\ \mathrm{TeV}$.⁹

Table 14 Mini-jet model predictions for the inelastic cross section at $\sqrt{s}=13\ \mathrm{TeV}$. Predictions of $\sigma _{\mathrm{inel}}$ in the full phase-space were obtained by adding $\sigma _{\mathrm{diff}} (13\ {\mathrm{TeV}})= 12.9$ mb to $\sigma _{\mathrm{inel}}^{\mathrm{uncorr}}\equiv \sigma _{\mathrm{inel}}^{\mathrm{one}\text {-}\mathrm{ch}}$

Fig. 96

Left panel A compilation of various models for the elastic differential cross section at LHC14, prepared in 2007, before the LHC started, from [340]. Right panel A compilation of model predictions for the elastic differential cross section at $\sqrt{s}=7$ TeV and first comparison with TOTEM data, from K. Eggert’s talk at Hadron Collider Physics Symposium, November 2011, Paris, France. Reproduced with permission of the authors

The result of this subsection confirms the interpretation that at high energies, past the beginning of the rise and the onset of mini-jets, the one-channel inelastic cross section is devoid of most of the diffractive contribution. We have shown that the onset and rise of the mini-jet cross section provide the dynamical mechanism behind the appearance of a soft-edge [380], i.e., a threshold in the total cross section around $\sqrt{s}\simeq (10\div 20)\ \mathrm{GeV}$. Thus, our model for the total pp cross section that utilizes mini-jets with soft-gluon re-summation has a built-in soft-edge. It has been updated with recent PDFs for LHC at $\sqrt{s} = 7, 8\ \mathrm{TeV}$ and predictions made for higher energy LHC data and cosmic rays.

We have also discussed in detail the reasons behind failures to obtain correct values for the elastic cross sections from a one-channel eikonal that obtains the total cross section correctly. It has been shown, through the use of phenomenological descriptions of diffractive (otherwise said, correlated inelastic) cross sections, that one-channel elastic cross section is indeed a sum of the true elastic plus correlated inelastic cross sections. An application of this fact to cosmic ray data analysis for the extraction of pp uncorrelated-inelastic cross sections shall be presented elsewhere.

6.8 Conclusions

As we have seen, the description of the fundamental dynamics of hadronic scattering is still proceeding along different lines, a Regge–Pomeron interpretation, a microscopic description of the scattering, or analytical constraints and asymptotic theorems. These different ways are not incompatible, and may ultimately come together. We conclude this section with two comments, one on the differential elastic cross section, and one on the integrated total cross sections.

6.8.1 The differential elastic cross section before and soon after the LHC started

A comparison of the state-of-the-art of theoretical predictions before and soon after the LHC started operating, can be glimpsed from Fig. 96. In the left panel, we show a compilation of different model predictions at $\sqrt{s}=14\ \mathrm{TeV}$ from [340], done in 2007, and at right we see how predictions at $\sqrt{s}=7\ \mathrm{TeV}$ compared with actual LHC data, as shown from K. Eggert’s talk at Hadron Collider Physics Symposium, November 2011, Paris, France. As new results from LHC appeared at $\sqrt{s}=7~\hbox {TeV}$ the parameters of some models had to be updated, and agreement with the new data was easily obtained. This, however, is not a satisfactory situation, since the parameters should remain stable or at least have a predictable energy dependence leading to further understanding of the dynamics. It is to be hoped that with the new results from LHC which will appear at $\sqrt{s}=13$ and $14\ \mathrm{TeV}$ such understanding may become closer.

6.8.2 A fit to the future imposing Froissart limit and the black disk picture

As a commentary to this and previous sections, we present in Fig. 97 a recent analysis by Block, Durand, Ha and Halzen [389], in which the high energy behavior of all three cross sections, $\sigma _{\mathrm{total}}, \sigma _{\mathrm{inel}},\sigma _{\mathrm{elastic}}$ has been constrained by the Froissart limit, $\sigma _{\mathrm{total}}\sim [\ln s]^2$, and the black disk behavior, $\sigma _{\mathrm{elastic}}/\sigma _{\mathrm{total}}\rightarrow 1/2, \ 8 \pi B/\sigma _{\mathrm{total}}\rightarrow 1$.

Fig. 97

Total pp and $p{\bar{p}}$ cross sections from Fig. 1 of [389], where the curve is a fit to the data, with high energy constraints from the Froissart bound and the black disk limit. Reprinted with permission from [389], Fig.(1), ©(2015) by the American Physical Society

7 Photon processes

Measurements of the total hadronic cross section are made with different projectiles and targets involving altogether different techniques. The list includes:

• heavy ion collisions, most recently LHC experiments for pA scattering,

• collisions between primary particles in cosmic rays with the nuclei of the atmosphere, which have been discussed in the section on cosmic ray measurements, Sect. 3,

• photon processes, which include real and virtual photon scattering on nucleons or nuclei, both in motion, as in HERA, or with fixed target, or photons against photons as in electron–positron collisions.

As of 2015, LHC plans to measure $\gamma p$ and $\gamma \gamma$ collisions but no results are yet available for what concerns total cross sections. LHC can also study $\pi p$ and $\pi \pi$ cross section, as we describe in the next section.

This section will draw from the extensive set of measurements at HERA, performed by the two experiments ZEUS [390] and H1 [391], which have measured the total cross section $\sigma ^{\gamma p}_{\mathrm{tot}}$ at $\sqrt{s}_{\gamma p}\equiv W =209$ and $200\ \mathrm{\mathrm{GeV}}$, respectively. Recently, the ZEUS Collaboration has presented measurements of the energy variation of the cross section in the range $194\ \mathrm{GeV} \le W \le 296\ \mathrm{GeV}$ [392]. Total cross sections at HERA have been measured also with virtual photons, in a wide range of the virtual photon squared momentum $Q^2$, including the transition from $\gamma ^* p$ to $\gamma p$ with the ZEUS Beam Pipe Calorimeter [393,394,395]. The HERA measurements include vector meson production and are of interest for QCD studies, adding an important kinematic variable to the cross section modelling.

We shall review some representative models for photon initiated processes and discuss the transition from virtual to real photons. We touch upon an extensive theoretical literature on the subject through Sakurai’s VMD model; the Gribov picture; Haidt’s phenomenology; applications of the Balitsky–Kovchegov (BK) equation in its various formulations; saturation and geometric scaling; the mini-jet models and factorisation schemes. Various items of interest can be found in the next subsections as follows:

• kinematics is defined in Sect. 7.1,

• Vector Meson Dominance Model proposals are presented in Sect. 7.2,

• the BK evolution equations are introduced in Sect. 7.3,

• the transition from virtual to real photons and analyses by Haidt et al. can be found in Sect. 7.4,

• specific models for $\gamma p$ scattering are in Sect. 7.5,

• vector meson production from real and virtual photon scattering is discussed in Sects. 7.6 and 7.7,

• the total $\gamma ^* p$ cross section can be found in Sect. 7.8,

• data and some models for real and virtual photon-photon scattering are presented in Sects. 7.9 and 7.10.

7.1 Data and kinematics for $e p \rightarrow e X$

The standard process to be studied,

$$\begin{aligned} e + p\rightarrow e' + X, \end{aligned}$$

(7.1)

is shown in Fig. 98.

Fig. 98

Electron/positron–proton scattering

For this process one defines the following kinematic variables:

$$\begin{aligned}&q=p-p',\end{aligned}$$

(7.2)

$$\begin{aligned}&Q^2=-q^2 ,\end{aligned}$$

(7.3)

$$\begin{aligned}&W^2=(q+P)^2 ,\end{aligned}$$

(7.4)

$$\begin{aligned}&y=\frac{P\cdot q}{P\cdot p} ,\end{aligned}$$

(7.5)

$$\begin{aligned}&t=(P-P')^2 ,\end{aligned}$$

(7.6)

$$\begin{aligned}&s = (p + P)^2 = \left( \frac{Q^2}{xy}\right) + M^2 - m_\mathrm{e}^2 \end{aligned}$$

(7.7)

where $q,p,p',P,P'$ are four-momenta. These measurements probe a vast kinematic region for the scattering of photons, which can be generally divided as:

• Photoproduction (PHP) with real photons, with $q^2 \approx 0$

• Deep Inelastic Scattering (DIS) with virtual photons $Q^2=-q^2 \approx (10\div 10^5)\ \mathrm{GeV}^2/c^2$

• The transition region of quasi-real photons, $Q^2 \sim m^2_\rho$

Both the PHP and the DIS have been studied extensively and are reasonably well described by various theoretical models. The third region has received less attention, but its kinematic range provides valuable $\gamma p$ measurements in a continuous range of values for $\sigma _{\mathrm{tot}}^{\gamma p}$ in the HERA energy region [393]. We shall discuss these measurements in a separate subsection.

The hadronic cross section for photons on protons is obtained from electron or positron scattering on protons. The protons can be at rest, as in the early measurements, or in motion as in the measurements taken with HERA at DESY. The leptons in the incoming beam were electrons in the early measurements, positrons at HERA. From 1992 until 2007, at HERA, the lepton energy was $E_e=27.6\ \mathrm{GeV}$ and the proton energy ranged from $E_p=460\ \mathrm{GeV}$ to $E_p=920~\mathrm{GeV}$

In Table 15, we reproduce the data on $\sigma _{\mathrm{tot}}^{\gamma p}$ from HERA. Notice that the earlier experiments [396, 397] spanned through a $\gamma p$ c.m. energy range, and what is reproduced in the table is the average value as given in HEPDATA Reaction Database: http://www.slac.stanford.edu/cgi-hepdata/.

Also, ZEUS indicates that, because of various improvements, their latest value [390] for $\sigma _{\mathrm{tot}}^{\gamma p}$ supersedes the first ones [397, 398]. All these measurements correspond to a photon 4-momentum squared $Q^2< (0.01\div 0.02)\ \mathrm{GeV}^2$.

Table 15 Results of measurements of $\sigma _{\mathrm{tot}}^{\gamma p}$ at HERA

In Table 16, we also reproduce total cross section measurements by the ZEUS experiment as a function of the $\gamma p$ invariant mass W and virtual photon polarisation, EPS in the table, obtained using an extrapolation of General Vector Meson Dominance (GVMD) and the assumption $\sigma _L = 0$, from [399], where details of the extrapolation can be found.

Table 16 $\gamma + p \rightarrow X$

7.1.1 Kinematics for photoproduction

Let us now set the kinematics and the relevant definitions for photoproduction processes, i.e. when $Q^2\approx 0$. The $\gamma p$ cross section is extracted from the process shown in Fig. 98. In the forward direction, the kinematic variables are related to the measurable quantities, energy and lepton scattering angle in the laboratory frame, through

$$\begin{aligned} Q^2=2E_eE'_e(1-\cos \theta _e)\approx E_eE_e'\theta _\mathrm{e}^2,\end{aligned}$$

(7.8)

$$\begin{aligned} y=1-\frac{E_e'}{2E_e}(1+\cos \theta _e)\approx 1-\frac{E_e'}{E_e}. \end{aligned}$$

(7.9)

The relation between ep and $\gamma p$ cross sections can then be expressed through

$$\begin{aligned}&\frac{\mathrm{d}\sigma ^{ep}(y)}{\mathrm{d}y}=\sigma _{\mathrm{tot}}^{\gamma p} \nonumber \\&\qquad \times \frac{\alpha }{\pi }\left[ \frac{1+(1-y)^2}{y}\ln \frac{Q^2_{\max }}{Q^2_{\min }}-2\frac{1-y}{y}\left( 1-\frac{Q^2_{\min }}{Q^2_{\max }}\right) \right] \nonumber \\&\quad =\sigma _{\mathrm{tot}}^{\gamma p}\times \mathbf{\mathcal F} \end{aligned}$$

(7.10)

where $Q^2_{\min }=\frac{m^2_ey^2}{1-y}$. The $\gamma p$ cross section can be extracted after integrating the above expression in the variable y with the integration limits

$$\begin{aligned} y_{\min /\max }=1-\frac{E'_{e\ \max /\min }}{E_e}. \end{aligned}$$

(7.11)

Equation (7.11) defines the flux $\mathcal{F}$ whose determination depends upon the experimental resolution on the incoming and outgoing positrons $\varDelta E_e$ and $\varDelta E'_e$.

7.1.2 Parton model variables

The quantities measured in $e-p$ scattering can be related to the parton model underlying the scattering process. By proper choice of the scattering frame and in the very large momentum limit, the variables relating the parton model description to the process shown in Fig. 99 in Deep Inelastic Scattering can be related to measurable quantities [400].

Fig. 99

Kinematic variables for parton scattering through ep collisions

Following here Ref. [393], with

• x the fraction of proton momentum carried by the struck quark

• y the relative energy transfer from the electron to the proton in the proton rest frame

• W the c.m. energy of the photon and proton system

one has

$$\begin{aligned} y=\frac{Q^2}{sx}, \quad \ W^2=m^2_p+Q^2\left( \frac{1}{x}-1\right) . \end{aligned}$$

(7.12)

If we neglect the proton mass, $W^2 \approx \ s y(1 -x)$. For small $Q^2$ being discussed here, $x\ll 1$, and we have $W^2 \approx \ s y$.

Various kinematic regions of interest can now be discussed. For total cross section measurements in photoproduction $\sigma ^{ep}$ one has

$$\begin{aligned}&0.4<y<0.6\quad \hbox {ZEUS}\quad \hbox {Experiment},\end{aligned}$$

(7.13)

$$\begin{aligned}&0.3<y<0.7\quad \hbox {H}1\quad \hbox {Experiment} \end{aligned}$$

(7.14)

and $Q^2_{\min }\sim 10^{-8}\ \mathrm{GeV}^2$.

In terms of the longitudinal and transversely polarized photon cross section, and neglecting terms of order $m^2_p/s$, the electron–proton cross section is given by

$$\begin{aligned} \frac{\mathrm{d}^2\sigma _{ep}}{\mathrm{d}y\mathrm{d}Q^2}= & {} \frac{\alpha }{2\pi }\frac{1 - x}{Q^2} \left[ \left( \frac{1+(1-y)^2}{y}-\frac{2(1-y)}{y} \frac{Q^2_{\min }}{Q^2}\right) \sigma _T\right. \nonumber \\&\left. + \frac{2(1-y)}{y}\sigma _L \right] \nonumber \\= & {} \left( \frac{x}{y}\right) \frac{\mathrm{d}^2\sigma _{ep}}{\mathrm{d}x\mathrm{d}Q^2}, \end{aligned}$$

(7.15)

where

$$\begin{aligned} Q^2_{\min }\approx m^2_e\frac{y^2}{1-y}. \end{aligned}$$

(7.16)

In DIS, where $Q^2>0$, in the region of interest in the variable y, the $Q^2_{\min }$ can be neglected and the expression for the DIS cross section , in the parton variable x, becomes

$$\begin{aligned} \frac{\mathrm{d}^2\sigma _{ep}}{\mathrm{d}x\mathrm{d}Q^2}= & {} \frac{\alpha }{2\pi } \frac{1-x}{xQ^2} (1+(1-y)^2)\nonumber \\&\left( \sigma _T+ \frac{2(1-y)}{1+(1-y)^2}\sigma _L\right) . \end{aligned}$$

(7.17)

The longitudinal and transverse cross sections are related to the structure functions $F_{2}$ as

$$\begin{aligned} F_2=\frac{Q^2}{4\pi ^2\alpha }(1-x)(\sigma _T+\sigma _L) \end{aligned}$$

(7.18)

and $F_2$ is seen to represent the sum over quark and antiquark densities in the proton.

Now one can relate the total cross section for scattering of a virtual photon on a proton to this sum, i.e.

$$\begin{aligned} \sigma ^{\mathrm{tot}}_{\gamma *p}(x,W)\approx \frac{4\pi ^2 \alpha }{Q^2}F_2(x,Q^2), \end{aligned}$$

(7.19)

and since x is proportional to the cm energy in the photon-proton system, one can thus obtain the total cross section for a range of energies.

On the other hand, in photo-production, $\sigma _L\ll \sigma _T$ and one obtains for the total photo-production cross section

$$\begin{aligned}&\frac{\mathrm{d}\sigma _{ep}}{\mathrm{d}y}=\frac{\alpha }{2\pi }\frac{1+(1-y)^2}{y} \nonumber \\&\quad \times \left[ \ln \left( \frac{Q^2_{\max }}{Q^2_{\min }}\right) -\frac{2(1-y)}{1+(1-y)^2}\left( 1-\frac{Q^2_{\min }}{Q^2_{\max }}\right) \right] \sigma _{\mathrm{tot}}^{\gamma p}(W_{\gamma p}).\nonumber \\ \end{aligned}$$

(7.20)

In this review we are basically interested in models for total cross section. Before discussing the models currently used, since most models do use Vector Meson Dominance in some fashion, it is useful to recall how it was first proposed.

7.2 Photons and vector meson dominance

Gribov, in his description of the interaction of quanta with nuclei, which will be summarised in Sect. 7.2.2, refers to the idea proposed by Bell [401] that, at high energy, Vector Meson Dominance could result in the amplitude for $\pi -nucleus$ to be proportional to surface terms rather than to volume terms.

The idea arose when Bell recalls Adler’s study of neutrino scattering on nuclei,

$$\begin{aligned} \nu +\alpha \rightarrow l+\alpha ^* \end{aligned}$$

(7.21)

where $\alpha ^*$ is a group of strongly interacting particles. Adler noticed that, using Partially Conserved Axial Current (PCAC) and Conserved Vector Current (CVC), incident virtual pions can actually describe the interactions of neutrinos on nuclei by obtaining for the cross section of process (7.21)

$$\begin{aligned} \frac{\partial ^2\sigma }{\partial q^2 \partial W^2}\propto \sigma (W,-q^2) \end{aligned}$$

(7.22)

where $q^2$ is the momentum transfer between the incoming neutrino and the outgoing lepton l and W is the mass of the hadronic system $\alpha ^*$, and $\sigma (W,m^2_\pi )$ would be the total cross section for the reaction $\pi \alpha \rightarrow \alpha ^*$. This result was something of a paradox, because neutrino’s should be sensitive to the entire nucleus, in his language the nucleus should be transparent to the neutrino, and not just to the surface, which is what happens to pions. Following this line of reasoning, Stodolsky [402] produced what at the time appeared as a similar paradox for photo-reactions, by using the $\rho$ -photon analogy. The discussion as to how the cross section for photon-nucleus is not proportional to the atomic number A, but is more similar to surface effects, is interesting and we shall reproduce here the main ingredients of Stodolsky’s argument.

The usual result that the cross section for $\gamma -A$ should be proportional to A, follows from the optical theorem. Taking only the first scattering of the photon, order $\alpha$, the scattered waves are summed up for all the nucleons and then from $\mathfrak {I}m F_{\mathrm{nucleus}}=A\mathfrak {I}m f_{\mathrm{nucleon}}$, the optical theorem gives $\sigma _{\gamma A}=A \sigma _{\gamma \text {-}\mathrm{nucleon}}$. But things are complicated by the fact that quasi-elastic channels may only apparently contribute to the elastic amplitude, and they really should be included as multiple scattering processes. For instance, in $\pi d$ scattering, such quasi-elastic processes are $\pi ^-+p\rightarrow \pi ^0+n$ followed by $\pi ^0+n\rightarrow \pi ^-p$. This process should be considered at the same level as $\pi ^-+p\rightarrow \pi ^-+p$ followed by a second scattering $\pi ^-+n\rightarrow \pi ^-+n$. Thus Stodolsky is led to consider that the photon and the $\rho$-meson have the same quantum numbers and that one can consider $\rho$ -production as a quasi-elastic process, in such a way that the photon will fluctuate into a $\rho$-meson with amplitude proportional to e, and then reconvert into a photon, and this process will give a contribution of order $\mathrm{e}^2$ to the cross section. We are repeating this here since it shows once more that when dealing with complex systems, a straightforward application of the optical theorem may not work.

7.2.1 Sakurai’s VMD

In 1969 Sakurai [403] proposed the Vector Meson Dominance (VMD) for high energy electron–proton inelastic scattering. Following the conjecture [402, 404] that the total photo-absorption hadronic cross section could be calculated from diffractive production of $\rho , \omega$ and $\phi$ mesons, Sakurai went on to show that, when both longitudinal and transversely polarized photon contributions are included in the calculation of the total ep cross section, then the VMD model and experimental results are fully compatible.

In this paper, the following kinematics is defined: $q=({\mathbf {q}}, \nu )$ is as usual the momentum transfer between electrons, $\sqrt{s}$ the missing hadronic mass. Also notice that he uses a metric such that $q^2>0$ corresponds to space-like photons. The inelastic differential ep-cross section is written in terms of the transverse and longitudinal cross section’s $\sigma _T$ and $\sigma _L$ as

$$\begin{aligned}&\frac{\mathrm{d}^2\sigma }{\mathrm{d}q^2}=\frac{E'}{E} \frac{4\pi \alpha ^2}{q^4} \left[ W_2(q^2,\nu ) \cos ^2\frac{\theta }{2} + 2 W_1(q^2,\nu )\sin ^2\frac{\theta }{2} \right] ,\nonumber \\ \end{aligned}$$

(7.23)

$$\begin{aligned}&W_2=\frac{K}{4\pi ^2\alpha } \frac{q^2}{q^2+\nu ^2} (\sigma _T+\sigma _S),\quad W_1= \frac{K}{4\pi ^2\alpha }\sigma _T,\end{aligned}$$

(7.24)

$$\begin{aligned}&K=\nu - \frac{q^2}{2m_p}=\frac{s-m^2_p}{2m_p}. \end{aligned}$$

(7.25)

$\sigma _T$ and $\sigma _S$ are obtained from the transverse and longitudinal components of the electromagnetic current. The VMD hypothesis then relates the electromagnetic matrix element $\langle A| j_\mu |p\rangle$ between a given final hadronic state $|A\rangle$ to the vector meson dominated one as

$$\begin{aligned} \langle A| j_\mu |p\rangle =\frac{m^2_\rho }{f_{\rho }} \frac{1}{q^2+m^2_\rho } \langle A| j_\mu ^{\rho }|p\rangle \end{aligned}$$

(7.26)

where $j_\mu ^{\rho }$ stands for the source density of the neutral $\rho$-meson field and Eq. (7.26) defines the coupling between the photon and the $\rho$-meson. The transverse and longitudinal cross sections are then given by

$$\begin{aligned}&\sigma _T=\left( \frac{e}{f_\rho }\right) ^2 F^2(q^2) \sigma _{\rho p}^\perp (K),\end{aligned}$$

(7.27)

$$\begin{aligned}&\sigma _S=\left( \frac{e}{f_\rho }\right) ^2 F^2(q^2) \frac{q^2}{m^2_{\rho }} \left( \frac{K}{\nu }\right) ^2\xi (K) \sigma _{\rho p}^\perp (K) \end{aligned}$$

(7.28)

with

$$\begin{aligned}&F^2(q^2)=\left( \frac{m^2_\rho }{q^2+m^2_\rho }\right) ^2,\end{aligned}$$

(7.29)

$$\begin{aligned}&\xi =\frac{\sigma _{\rho p}^\parallel }{\sigma _{\rho p}^\perp }. \end{aligned}$$

(7.30)

Accordingly Sakurai obtains for the structure function $W_2$

$$\begin{aligned} \nu W_2 (q^2,\nu )= \frac{m^2_\rho }{4\pi ^2\alpha }\frac{K}{\nu } \frac{1}{1+m^2_\rho /q^2} \mathcal{F} \end{aligned}$$

(7.31)

with

$$\begin{aligned} \mathcal{F}= \left[ \frac{1}{1+m^2_\rho /q^2}\right] ^2 \xi (K)\left( \frac{K}{\nu }\right) ^2+ \frac{m^2_\rho }{q^2}\sigma _{\gamma p}(K). \end{aligned}$$

(7.32)

$\nu W_2 (q^2,\nu )$ is then shown to become a universal function of $\nu /q^2$ in the Bjorken limit $q^2\rightarrow \infty$ and fixed $q^2/\nu$ [400].

Adding the other vector mesons is easily done by considering their isospin properties so that the overall contribution can be written by the simple substitution

$$\begin{aligned} \frac{1}{f_\rho }\rightarrow \frac{1}{f_\rho }\left[ 1+\frac{1}{\sqrt{2}}+ \frac{1}{3}\right] \end{aligned}$$

(7.33)

where one can make the approximation $m^2_\rho \approx m^2_\omega \approx m^2_\phi$. Sakurai derives from VMD, a relationship between the Bjorken scaling function $F_2(x)$ and asymptotic $\sigma _{\gamma p}$

$$\begin{aligned} F_2(x) \rightarrow \left[ \frac{\xi (\infty ) m_\rho ^2}{4 \pi ^2 \alpha }\right] (1 - x)^2 \sigma _{\gamma p}(\infty ). \end{aligned}$$

(7.34)

7.2.2 Gribov’s model

We shall now summarise the model in which Gribov first described the interactions of photons with matter. In [405], Gribov advances the idea that the character of the interaction of photons with nuclei and the development of surface effects [$A^{2/3}$-dependence] at high energies have no connections with $\rho$-mesons or $\pi$-mesons, but are solely determined by distances which are significant in those interactions. In the above paper, Gribov is referring to the idea proposed by Bell [401] about Vector Meson Dominance which was discussed in Sect. 7.2.

In fact, the expression proposed by Gribov for the cross section of photons on nuclei, which includes only hadronic processes, is

$$\begin{aligned} \sigma _{\gamma }=2\pi R^2 (1-Z_3) \end{aligned}$$

(7.35)

where R is the nuclear radius, and $Z_3$ is the charge renormalisation constant due to hadrons, which can be written in terms of the cross section for electron–positron annihilation into hadrons,

$$\begin{aligned} 1-Z_3=\frac{\mathrm{e}^2}{\pi } \int \rho (x^2)\frac{\mathrm{d}x^2}{x^2}. \end{aligned}$$

(7.36)

Gribov’s explanation of Eq. (7.35) is that $2\pi R^2$ is the geometrical cross section for the interaction of hadrons with nuclei and the other factor is related to the length of time that the photons spend in the hadron state. To estimate this time, one first needs to establish the region of validity of Eq. (7.35). This is obtained by first considering a photon of momentum P in the Laboratory frame, and write the relevant longitudinal scale as $\delta =P/\mu ^2$, where $\mu$ is some characteristic mass. Now, let l be the mean free path length of a hadron in the nucleus, the condition of applicability is that $\delta ^2\gg Rl$. If one takes the characteristic mass to be that of the $\rho$-meson and the path length as defined by the interaction, with $l \sim 1/ m_{\pi }$, then Gribov claims that surface effects will start appearing at energies exceeding $10\ \mathrm{GeV}$, which would correspond to a few GeV.

His picture of what happens is as follows: first the photon virtually decays into hadrons (we would now say partons), and then the hadrons start interacting with the nucleons in the nucleus. What matters here is the length of this fluctuation into hadrons, which he takes to last for a time $\delta$. He considers the two possibilities, $\delta \le l$ and of course $\delta \ge l$. Consider the first case and let $\sigma _{\gamma }$ be proportional to:

• 1. the probability of the photon to hit the nucleus $\sim \pi R^2$

• 2. the probability that fluctuations take place inside the nucleus $\propto \frac{\alpha R}{\delta }$

• 3. the probability that the hadrons forming will have time to complete an interaction with a nucleon in the nucleus, $\propto \delta /l.$

Hence $\sigma _{\gamma } \sim \pi R^2 \times \frac{\alpha R}{\delta } \times \delta / l\sim \alpha \pi R^3 / l \propto A^* \sigma _{\gamma N}$. But actually as the energy of the photon increases, the duration of the fluctuation will also increase and the probability of interaction will increase with energy. When the time length of the fluctuation into hadrons exceeds the interaction length, the relevant probability is one and, one gets $\sigma _{\gamma } \sim \pi R^2 \times \frac{\alpha R}{\delta }$ and will decrease as the energy increases. A further effect is due to Bell’s [401] observation about the probability that the interaction takes place outside the nucleus is $\propto l/\delta$ so that one gets $\sigma _{\gamma }\sim \alpha \pi R^3 l/\delta ^2$. When $\delta$ becomes much larger than the interaction length, as the energy increases further, the photon will fluctuate into a hadron outside the nucleus and the hadron which are thus formed will interact with a cross section $\pi R^2$. The argument is not full proof, and it appears more as an a posteriori justification, but the gist of the matter seems to be that the cross section is actually proportional to the nuclear surface and not to the volume. According to Gribov, it is also easy to understand the presence of the factor $1-Z_3$. To understand it, he then looks at the forward scattering amplitude, visualized in a figure like Fig. 100, which we reproduce from [406].

Fig. 100

Cartoon of the forward scattering amplitude from [406]

In the figure, F is the amplitude for scattering of a beam of hadrons on a nucleus of radius R, with momentum transfer q. But in the forward direction, Fig. 101, it is the diagram defining charge renormalisation.

Fig. 101

Charge renormalisation, from [406]

For the interaction of electrons with nuclei depicted by Gribov as in Fig. 102, one has a similar picture, except that instead of $1-Z_3$ the cross section will be determined by the polarisation operator from Fig. 102.

Fig. 102

Interaction of electrons with nuclei from [406]

7.3 QCD evolution equations for photon processes, BK equation

We now turn to the QCD description of photon processes in terms of evolution equations, addressing the transition from the linear BFKL rate equation to the non-linear Balitsky–Kovchegov (BK) equation [407, 408] and what saturation means. The underlying phase transition is also exhibited. We shall then return to models, including the transition from ($\gamma ^{*} p$) to real photon ($\gamma p$) processes and models for (“geometrical”) scaling in the small $Q^2$ region.

7.3.1 Introduction

The BFKL “rate” equation for the density of gluons is linear and is expected to break down as the density becomes large [e.g., as in $\gamma ^*p$ at low x or in hadron-nucleus scattering]. A more appropriate equation valid for large densities is provided by the BK equation [407, 408] that is non-linear and incorporates saturation i.e., a maximum steady-state value for the density. Similar problems occur in a variety of fields of physics, chemistry, biology, logistics, etc. In the following, we shall illustrate the problem and its resolution for the important practical case of the photon number for lasers.

7.3.2 Dynamics behind some simple non-linear rate equations for photons

Here we shall discuss a simple non-linear rate equation and dynamical reasons behind leading to it. The linear rate equation, where the rate is proportional to the number itself, of course leads to an exponential growth or exponential decay as

$$\begin{aligned} \frac{\mathrm{d}I(t)}{\mathrm{d}t} = +\nu I(t);\quad I(t) = I(0) \mathrm{e}^{\nu t}, \end{aligned}$$

(7.37)

depending upon the sign of $\nu$. But in all practical systems, some non-linearity is bound to be present, giving rise to non-exponential behavior in time.

The best studied (and very practical) example is that of the laser. If the rate equation for the mean photon number were linear (as above in Eq. (7.37)), the number of laser photons would increase exponentially. Of course, that cannot be, otherwise we would need an infinite source of energy, hence there must be some dynamical mechanism to saturate the number. The solution to this problem for lasers was first given by Lamb. The famous Lamb equation for the light intensity I(t) may be written as [409]

$$\begin{aligned} \frac{\mathrm{d}I(t)}{\mathrm{d}t} = +\nu [ a - I(t)] I(t). \end{aligned}$$

(7.38)

The second term on the right-hand side of Eq. (7.38) arises dynamically through the creation and annihilation of two-photons at a time, just as the first term is related to the creation and annihilation of single photons. The parameter a is called the pump parameter and its sign is crucial in determining the steady-state value of I. We note here parenthetically that the analog of Eq. (7.38) written in an entirely different context of population and called the logistics equation was first written down by Verhulst [410, 411].

If $a\le 0$, the steady-state value of I [determined by the vanishing of the left side of Eq. (7.38)], is $I_{SS}\rightarrow 0$. Physically, for negative pump parameter, there is no laser activity. On the other hand, for $a>0$, $I_{SS} \rightarrow a$ and hence the laser intensity increases linearly with a.

The innocent looking Eq. (7.38) has buried in it a (second order) phase transition wherein a acts as the order parameter. This is easily seen by considering $I_{SS}$ as a function of a. $I_{SS}$ is continuous at $a=0$ but its derivative is not.

A simple model for a plethora of physical processes such as the mean photon number, intensity, mass growth, magnetisation etc. is provided by analogues of Eq. (7.38) where the parameters $\nu$ and a have different physical significance and their signs play a crucial role in determining the fate of that physical system.

A partial understanding of the genesis of the quadratic term on the right in Eq. (7.38) can be obtained through a consideration of the frequency of a photon mode in a cavity. The frequency of a mode in a cavity is inversely proportional to the length of the cavity L. Thus, if the geometry of the cavity fluctuates via the length scale L, then the frequency of the photon oscillator will be modulated. Because of such a modulation, the cell cavity will emit or absorb two (or more) photons at a time, thus leading to the above rate equation if one truncates to two photons.

Similar rate equations must exist for any system [depending upon its size for example] where growth may be rapid but the growth must cease eventually resulting in a limiting value [such as the maximum size]. In the following section, we shall discuss the relevant case of the gluon density in QCD where the non-linear direct coupling $gg\rightarrow g$ (absent in QED) automatically provides such a non-linear term.

But before going on to discuss the case of QCD, let us consider the special case $a = 0$ in Eq. (7.38) for the number N(t) of photons.

$$\begin{aligned} \frac{\mathrm{d} N(t)}{\mathrm{d}t} = -\nu N^2(t);\quad N(t) = \frac{N(0)}{(1 + \nu t)}. \end{aligned}$$

(7.39)

The above decay pattern ${\sim } (1/t)$ for large t is called a hyperbolic decay law and it has been observed in certain cases of bio-luminescence. In fact, there are many simple physical systems which display hyperbolic decay laws. Typical examples are those which involve the excitation of pairs in the medium, which then recombine to emit light. This naturally gives decay laws which one would expect classically to obey $dN/\mathrm{d}t=-\nu N^2$. Note that this is a purely classical result and does not require coherent effects between the excited states, which would also be expected to give the same decay law.

The important point to remember is that exponential or hyperbolic behavior cannot be theoretically correct for the whole phase space even though they may provide good approximations in restricted regions of phase space. Such is the case in QCD both in hadronic as well as in deep inelastic scatterings.

7.3.3 Non-linear BK equations in QCD

Let us consider the Balitsky approach [407] to the scattering of a virtual photon $\gamma ^*(q)$ on a hadron of momentum p as summarised by E. de Oliveira [412]. For the limit of $x_B = [Q^2/2(q.p)]$ small where $Q^2$ gives a hard scale and $s\gg Q^2$, a dipole picture emerges naturally in the limit of infinite colour $N_c \rightarrow \infty$ when planar diagrams become dominant. The photon does not directly interact with the target hadron but only through an “onium” made up of a quark of a given colour accompanied by an anti-quark of opposite colour to preserve the colour singlet nature of the photon. The onium must then exchange two gluons with the hadron to preserve the colour singlet nature of the target hadron.

Thus, the photon does not interact directly with the target hadron but through a “gas” of non-interacting dipoles. Single dipole scattering with the target hadron leads to BFKL evolution equation and multiple dipole scatterings to the BK equations. To proceed with the dynamics, Balitsky [413] invokes the general notion that a fast particle in a high energy scattering moves along its classical trajectory and the quantum effect consists in the acquisition of an eikonal phase along its prescribed (classical) path. In QCD, for a fast parton (quark or glue), the eikonal phase is given by the Wilson line that is link-ordered along the straight line collinear to the 4-velocity $n^\mu$ of the parton. The Wilson line operator may be written as

$$\begin{aligned} U^\eta (x_\perp ) = {\mathcal P} \exp \left\{ ig \int _{-\infty }^\infty \mathrm{d}u \ n_\mu A^\mu (u n + x_\perp ), \right\} \end{aligned}$$

(7.40)

where $A^\mu (x)$ is the gluon field of the target, $x_\perp$ is the transverse position of the target. In high energy scattering within QCD, Wilson line operators form convenient effective degrees of freedom as partons with different rapidities ($\eta$) “feel” each other through matrix elements of these operators. In the colour dipole model of the photon then the propagation of a quark–antiquark pair takes place through the propagation of the colour dipole via the two Wilson lines ordered collinear to the quark’s velocity. Thus the structure function of the hadron becomes proportional to a matrix element of the colour dipole operator which is given by

$$\begin{aligned} {\tilde{U}}^\eta (x_\perp ; y_\perp ) = 1 - \frac{1}{N_c} Tr\{ {\tilde{U}}^\eta (x_\perp ) {\tilde{U}}^\eta (y_\perp ) \}, \end{aligned}$$

(7.41)

taken between the states of the target hadron. The gluon density is then given approximately by

$$\begin{aligned} x_B G(x_B; \mu ^2 = Q^2) \approx \langle p| {\tilde{U}}^\eta (x_\perp ; 0)|p\rangle |_{x_\perp ^2 = 1/Q^2}. \end{aligned}$$

(7.42)

The energy dependence of the structure function is thus reduced to the dependence of the colour dipoles on the slope of the Wilson lines as determined by the rapidity $\eta$. A whole hierarchy found by Balitsky emerges as given by equations of the type [valid in LLA for $\alpha _s\ll 1$ and $\alpha _s (\ln x_B) \sim 1$]:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\eta } \langle T_{xy}\rangle= & {} \frac{{\bar{\alpha }}_s}{2\pi } \int (\mathrm{d}^2z) {\mathcal M}(x,y;z)\nonumber \\&\times [ \langle T_{xz}\rangle + \langle T_{yz}\rangle - \langle T_{xy}\rangle - \langle T_{xz} T_{yz}\rangle ];\nonumber \\ {\bar{\alpha }}_s= & {} \frac{\alpha _s N_c}{\pi }. \end{aligned}$$

(7.43)

Once the mean-field approximation (i.e., the factorisation) $\langle T_{xz} T_{yz}\rangle = \langle T_{xz}\rangle \langle T_{yz}\rangle$ is made, the above becomes a non-linear, but closed, set of BK evolution equations. In particular, for the Wilson line operators it becomes

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\eta } \langle {\tilde{U}}^\eta _{xy}\rangle= & {} \frac{{\bar{\alpha }}_s}{2\pi } \int (\mathrm{d}^2z) \frac{(x - y)^2}{(x -z)^2 (y-z)^2}\nonumber \\&\times [ \langle {\tilde{U}}^\eta _{xz}\rangle + \langle {\tilde{U}}^\eta _{yz}\rangle - \langle {\tilde{U}}^\eta _{xy}\rangle - \langle {\tilde{U}}^\eta _{xz}\rangle \langle {\tilde{U}}^\eta _{yz}\rangle ].\nonumber \\ \end{aligned}$$

(7.44)

The last (non-linear) term on the right-hand side of the BK equation for color dipoles is due to multiple scattering. This Balitsky–Kovchegov evolution equation is usually written for the dipole hadron cross section in impact-parameter space as

$$\begin{aligned}&\sigma _{\mathrm{dipole}}(x_{01}; Y) = 2 \int (\mathrm{d}^2b_{01}) {\mathcal N}(b_{01};x_{01}; Y)\nonumber \\&x_{01} = (x_0 - x_1);\quad b_{01} = \frac{x_0 + x_1}{2}, \end{aligned}$$

(7.45)

where ${\mathcal N}(b_{01};x_{01}; Y)$ is the quark–antiquark propagator through the hadron, related to the forward scattering amplitude of the dipole with the hadron. The BK equation in “coordinate” space reads

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}Y} {\mathcal N}(b_{01};x_{01}; Y) = \frac{{\bar{\alpha }}_s}{2\pi } \int (\mathrm{d}^2x_2) \frac{x^2_{01}}{x^2_{02} x^2_{12}}\nonumber \\&\quad \times \left[ {\mathcal N}(b_{01} +\frac{x_{12}}{2} ;x_{02}; Y) + {\mathcal N}\left( b_{01} +\frac{x_{02}}{2};x_{01}; Y\right) \right. \nonumber \\&\quad -{\mathcal N}(b_{01};x_{01}; Y) \ - {\mathcal N}\left( b_{01} +\frac{x_{12}}{2};x_{02}; Y\right) \nonumber \\&\quad \times \left. {\mathcal N}(b_{01} +\frac{x_{02}}{2};x_{12}; Y) \right] . \end{aligned}$$

(7.46)

The “time” here is the rapidity $Y \approx \ 1/x_B$ and the equation has four other variables [two from $x_{01}$ and two from $b_{01}$]. The BK equation resums all powers of ($\alpha _s Y$). If the last quadratic term is dropped, then it reduces to the linear BFKL equation

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}Y} {\mathcal N}(b_{01};x_{01}; Y) = \frac{{\bar{\alpha }}_s}{2\pi } \int (\mathrm{d}^2x_2) \frac{x^2_{01}}{x^2_{02} x^2_{12}}\nonumber \\&\quad \times \left[ {\mathcal N}\left( b_{01} +\frac{x_{12}}{2} ;x_{02}; Y\right) + {\mathcal N}\left( b_{01} +\frac{x_{02}}{2};x_{01}; Y\right) \right. \nonumber \\&\quad \left. - {\mathcal N}(b_{01};x_{01}; Y)\right] . \end{aligned}$$

(7.47)

Given the complexity of Eq. (7.46), it is useful to consider special cases to obtain some familiarity with it.

7.3.4 Space-independent BK equation in ($0+1$) dimensions

If one assumes that ${\mathcal N}(b_{01};x_{01}; Y)$ is spatially independent (i.e., independent both of the impact parameter $b_{01}$ and the dipole “size” $x_{01}$), then the BK equation reduces to the previously discussed logistics equation [see Sect. 7.3.2]:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}Y} {\mathcal N}(Y) = \omega [ {\mathcal N}(Y) - {\mathcal N}^2(Y)];\quad \omega > 0. \end{aligned}$$

(7.48)

As discussed previously, it has two steady-state solutions (or fixed points): an unstable solution ${\mathcal N} = 0$ and the other the stable solution ${\mathcal N} = 1$. It should also be clear that the linearized BFKL blow up for large Y has been softened to a maximum value of 1, i.e., a saturation for small $x_B$, independent of the initial condition.

7.3.5 Impact-parameter independent BK equation in ($1+1$) dim

If we drop only the impact parameter dependence but keep the dipole size, we have ${\mathcal N}(b;x; Y) \rightarrow \ {\mathcal N}(r; Y)$ and the BK equation in ($1+1$) dimension reads

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}Y} {\mathcal N}(|x_{01}|; Y) = \frac{{\bar{\alpha }}_s}{2\pi } \int (\mathrm{d}^2x_2) \frac{x^2_{01}}{x^2_{02} x^2_{12}}\nonumber \\&\quad \times [ {\mathcal N}(|x_{02}|; Y) + {\mathcal N}(|x_{12}|; Y) - {\mathcal N}(|x_{01}|; Y)\nonumber \\&\quad - {\mathcal N}(|x_{02}|; Y) {\mathcal N}(|x_{12}|; Y) ]. \end{aligned}$$

(7.49)

Physically, of course, b-independence implies an infinite homogeneous hadronic surface but where the scattering kernel does depend upon the size of the dipole. Numerical computations verify general trends already seen in ($0+1$) dimensions [412]:

• saturation occurs [in contrast to BFKL blowup] for large Y;

• saturation for large Y is independent of the initial condition [that is, independent of the dipole size];

• for small Y, ${\mathcal N}(r;Y)$ is smaller for smaller dipole size;

• for small r, non-linear corrections are by and large negligible;

• for large r, non-linear corrections are important and ${\mathcal N}(r;Y)\approx \ 1$

• saturation scale $Q_s(Y)$:

  $$\begin{aligned} r< \frac{1}{Q_s(Y)};\quad {\mathcal N} \ll 1;\nonumber \\ \ r> \frac{1}{Q_s(Y)};\quad {\mathcal N} \approx \ 1. \end{aligned}$$

  (7.50)

7.3.6 Geometrical scaling in DIS

The approach to saturation is also discussed in a paper by Stasto, Golec-Biernat and Kwiecinski through a discussion of a geometric scaling [414] in the low-x region, observed at HERA for Deep Inelastic Scattering, $\gamma ^* p$ scattering. But the result claimed here is not the same as the usual geometric scaling observed or expected in hadron–hadron scattering. In the purely hadronic case geometric scaling refers to the fact that the scattering amplitude in impact-parameter space G(s, b) is only a function of the ratio $\beta =b^2/R^2(s)$, where R(s) is the interaction radius. To avoid confusion, one should notice that the interaction radius R(s) in the hadronic case increases with energy, whereas the one in DIS decreases with energy, or with $x\rightarrow 0$.

Such a behavior is understood to represent a unitarity bound, which reflects the fact that the growth with x (as $x \rightarrow 0$) of the structure functions is tamed by saturation effects. This is also a version of the Black Disk model.

More precisely, the HERA data on the total $\gamma ^* p$ scattering cross section, suggest a geometrical scaling of the following form [414]

$$\begin{aligned} \sigma ^{\gamma *p}(Q, Y) = \sigma ^{\gamma *p}(\tau );\quad \tau = \frac{Q^2}{Q^2_s(Y)}. \end{aligned}$$

(7.51)

This translates for the scattering amplitude into

$$\begin{aligned} {\mathcal N}(r;Y) \rightarrow \ {\mathcal N}(rQ_s(Y));\quad \mathrm{for\ large\ } Y. \end{aligned}$$

(7.52)

Using the form $Q_s(Y) = Q_o \mathrm{e}^{{\bar{\alpha }}_s \lambda Y}$, the scaling form given in Eq. (7.52) reduces to

$$\begin{aligned} {\mathcal N}(r;Y) \rightarrow \ {\mathcal N}(Q_o\mathrm{e}^{(\ln r + {\bar{\alpha }}_s \lambda Y)}). \end{aligned}$$

(7.53)

Equation (7.53) has been interpreted as a traveling wave with Y as time, (${\bar{\alpha }}_s \lambda$) as the speed $v_s$ of the wave and ($\ln r$) as the spatial coordinate. Such a wave picture emerges rather naturally through a momentum space description as shown next.

In [415], a detailed analysis of “extended” geometrical scaling has been made and its (not at all obvious) connection with the BK equation investigated. These authors conclude through a numerical analysis of the BK equation in momentum space that the BK results are qualitatively different from that of the phenomenological dipole models. In particular, they find that geometrical scaling around the saturation point is only obtained for asymptotic rapidities.

7.3.7 Momentum space BK equation

Let us consider the momentum space amplitude defined through the Fourier transform [416,417,418]

$$\begin{aligned} {\bar{\mathcal N}}(k;Y) = \int \left( \frac{\mathrm{d}^2r}{2\pi r^2}\right) \mathrm{e}^{i \mathbf{k}\cdot \mathbf{r}} {\mathcal N}(r;Y) . \end{aligned}$$

(7.54)

Then the BK equation in momentum space reads

$$\begin{aligned} \frac{\mathrm{d}{\bar{\mathcal N}}(k;Y)}{\mathrm{d}Y} = {\bar{\alpha }}_s \int \left( \frac{\mathrm{d}k^{\prime }}{k^{\prime }}\right) {\mathcal K}(k,k^{\prime }) {\bar{\mathcal N}}(k^{\prime };Y) - {\bar{\alpha }}_s {\bar{\mathcal N}}^2(k;Y).\!\!\!\!\!\nonumber \\ \end{aligned}$$

(7.55)

In [419], it is shown that in the saddle point approximation, the BK equation can be mapped into the FKPP equation [420, 421] of the form

$$\begin{aligned} \partial _t u(\zeta ,t) = \partial _\zeta ^2 u(\zeta ,t) + u(\zeta ,t) - u^2(\zeta ,t), \end{aligned}$$

(7.56)

with the dictionary above: t is time, and $\zeta$ is the coordinate. The crucial point is that FKPP equation does have traveling wave solutions of the form ($\zeta - v t$), in agreement with the geometrical scaling solutions given in Eq. (7.53) with $t = Y$, $\zeta = \ln (r)$ and $v = {\bar{\alpha }}_s \lambda$. This correspondence does provide a window of comfort in the phase space for geometrical scaling.

So far, we have considered a fixed $\alpha _s$. For a discussion of the results of BK evolution as one changes to running $\alpha _s$, we refer the reader to some recent analyses in [422, 423].

7.3.8 Dense hadronic systems

For dense hadronic systems, new phenomena in QCD occur and some have been investigated in detail for heavy ions. For large A nuclei scatterings at high energies, colour glass condensates and colour transparency have been found through an effective field theory constructed from QCD. It will take us far outside the realm of this review but we refer the interested reader to excellent expositions by McLerran [424, 425], Venugopalan [426] and Mueller [427].

7.3.9 Beyond BK, fluctuations, Pomeron loops

That the BK equation does not include fluctuations in the gluon (dipole) number has been particularly emphasised by Bartels et al. [428]. Thus, if the Pomeron is considered as a manifestation of the propagation and exchange of two-gluon singlets, then what is missing in BK becomes the lack of a Pomeron hierarchy as shown in Fig. 103.

Fig. 103

Pomeron-loop graphs absent in BK, from [412]

Work in the past two decades have shown that a Langevin equation can be formulated to include three Pomeron vertices and we just quote some results. It is claimed [429] that a BK equation with white noise of the following form – called the stochastic FKPP or sFKPP – can mimic the Pomeron hierarchy.

$$\begin{aligned} \partial _t u(\zeta ,t)= & {} \partial _\zeta ^2 u(\zeta ,t) + u(\zeta ,t) - u^2(\zeta ,t)\nonumber \\&+\,\nu (\zeta ,t)\sqrt{\left( \frac{2}{N_c}\right) u(\zeta ,t) (u(\zeta ,t) - 1)}, \end{aligned}$$

(7.57)

where white noise $\nu (\zeta ,t)$ is defined as

$$\begin{aligned} \langle \nu (\zeta ,t)\rangle = 0;\quad \langle \nu (\zeta ,t) \nu (\zeta ^{\prime } ,t^{\prime })\rangle = \delta (\zeta - \zeta ^{\prime }) \delta (t - t^{\prime }).\nonumber \\ \end{aligned}$$

(7.58)

Strong fluctuations are also discussed in [430]. For further theoretical work on this subject we refer the reader to the literature.

7.4 Transition from $\sigma (\gamma ^*p)$ to real $\sigma (\gamma p)$: models and phenomenology for low-x physics

After the great successes of Bjorken scaling and the verification of its perturbative QCD calculable violations in deep inelastic total cross section $\sigma (\gamma ^*p)$ for large $Q^2$, came the arduous task of understanding the physics for small $Q^2$ photon masses and eventually to bridging the gap to its continuation to real $\sigma (\gamma p)$ process as $Q^2\rightarrow 0$. Excellent quality data exist in this kinematic region by the H1 and Zeus groups from HERA demanding a theoretical and phenomenological explanation.

Explicitly, the object is to formulate the usual proton EM structure function $F_2(W; Q^2)$ defined as in Eq. (7.19) so that it interpolates smoothly to the real photon cross section $\sigma ^{\gamma p}(W^2)$. It should be mentioned that real photon, $\sigma ^{\gamma p}(W^2)$, cross sections are obtained through the HERA data in $Q^2 = (0.01\div 0.02) \mathrm{GeV}^2$ region. While such a region lies beyond the realm of perturbative QCD, it does offer the possibility of extension as well as a challenge to hadronic total cross section models for its description.

7.4.1 Phenomenological analyses by Haidt et al.

Data from HERA on the structure function $F_2(x, Q^2)$ at small (and medium) values of x have been analyzed in set of papers by D. Haidt [431,432,433] and compared with theoretical expectations. In [431], it was shown that the observed rise at small $x = (Q^2/2 q\cdot p)$ is consistent with a doubly logarithmic increase: a logarithmic increase in 1 / x along with a logarithmic growth also with $Q^2$, i.e.

$$\begin{aligned} F_2(x, Q^2) = a + b \left[ \ln \left( \frac{x_o}{x}\right) \right] \left[ \ln \left( \frac{Q^2}{Q_o^2}\right) \right] , \end{aligned}$$

(7.59)

where $a, b, x_o, Q_o^2$ are constants, and the above expression is valid in the perturbative phase space region at $x < 0.001$. A stronger increase, which may be incompatible with unitarity when extrapolated to asymptotically small values of x, could not be inferred from the data then available.

A few years later, in [432, 433], the HERA data for small values of the Bjorken variable $x = (Q^2/2 q\cdot p) \le 0.01$, were described phenomenologically through the expression

$$\begin{aligned}&F_2(x; Q^2) = m \left[ \ln \left( \frac{x_o}{x}\right) \right] \ln \left( 1 + \frac{Q^2}{Q_o^2}\right) ,\end{aligned}$$

(7.60)

$$\begin{aligned}&m\approx \ 0.4;\quad x_o\approx \ 0.04;\quad Q_o^2\approx \ 0.5 \mathrm{GeV}^2. \end{aligned}$$

(7.61)

The extension from $\ln (Q^2/Q_o^2)$ to $\ln (1+Q^2/Q^2_o)$ allows one to describe both the perturbative and the nonperturbative regime as long as x is below 0.001. This implies for $F_2$ a behaviour proportional to $Q^2$ for $Q^2 < Q_o^2$ and a logarithmic behaviour above.The strategy adopted by Haidt for a smooth continuation of $\sigma ^{\gamma ^*p}(W^2; Q^2)$ to very small values of $Q^2$ consisted in defining a variable $q = \ln (1 + Q^2/Q_o^2)$ and rewriting Eq. (7.60) as

$$\begin{aligned} \sigma ^{\gamma ^*p}(W^2; Q^2) = \left( \frac{4 \pi ^2}{Q_o^2}\right) \left[ \frac{q}{(Q^2/Q_o^2)}\right] \left[ \frac{F_2(W, Q^2)}{q}\right] .\nonumber \\ \end{aligned}$$

(7.62)

A virtue of q is that it interpolates smoothly from small $Q^2$ to $\ln \ Q^2$ ( for large $Q^2$): since $q \rightarrow Q^2/Q_o^2$ as $Q^2 \rightarrow 0$, a transition from $\sigma ^{\gamma ^*p}(W^2; Q^2)$ to $\sigma ^{\gamma p}$ becomes amenable. In the region $x < 0.01$, $W^2\sim Q^2/x$ and thus a behavior of $F_2/q \sim [\ln (1/x)]$ implies $F_2/q \sim [\ln (W^2)]$. The q dependence of the HERA data were then analyzed through a linear form in $\ln (W^2)$:

$$\begin{aligned} \frac{F_2(W^2; q)}{q} = u_o(q) + u_1(q) \ln (W^2/W_o^2). \end{aligned}$$

(7.63)

An almost constant value for the slope $u_1(q) \approx \ 0.4$ was found for large values of q. Inclusion of real $\gamma p$ data at $W = 200\ \mathrm{GeV}$ showed that the transition from the $\gamma ^* p$ data available until the lowest value of $Q^2 = 0.05\ \mathrm{GeV}^2$, to real photons in $\gamma p$ seemed to work well.

As Haidt pointed out, for smaller values of q – outside the measured region – Eq. (7.62) needs to be revised since ($F_2/q$) is a function of x alone whereas $\sigma ^{\gamma p}$ is a function of $W^2$ alone. The suggested replacement to reach real Compton scattering – so that the $Q^2 \rightarrow 0$ limit is reached smoothly – is

$$\begin{aligned} \left( \frac{x_o}{x}\right) \rightarrow \ \left[ \frac{x_o}{x} \left( \frac{Q^2}{Q^2 + Q_w^2}\right) \right] , \end{aligned}$$

(7.64)

where for consistency $0 \le Q_w^2 \le Q_o^2$. Satisfactory agreement with the HERA data were found for $Q_w^2 = 0.05\ \mathrm{GeV}^2$.

An attentive reader would note that Haidt’s variable $q = \ln (1 + Q^2/Q_o^2)$ that becomes linear in $Q^2$ for small $Q^2$, has a parallel in Richardson’s proposal of replacing the asymptotic freedom formula for the QCD coupling constant $\alpha _{AF}(Q^2)$ to $\alpha _R(Q^2)$ so as to obtain a linearly confining potential [434]:

$$\begin{aligned}&\alpha _R(Q^2) = \frac{1}{b\ \ln [1 + Q^2/\varLambda ^2]};\end{aligned}$$

(7.65)

$$\begin{aligned}&\alpha _{R}(Q^2)\rightarrow \left[ \frac{\varLambda ^2}{b\ Q^2}\right] \quad \mathrm{for}\ Q^2\rightarrow 0;\end{aligned}$$

(7.66)

$$\begin{aligned}&\alpha _{R}(Q^2)\rightarrow \ \alpha _{AF}(Q^2) = \frac{1}{b\ \ln [Q^2/\varLambda ^2]} \quad \mathrm{for}\ Q^2\rightarrow \infty .\nonumber \\ \end{aligned}$$

(7.67)

Further discussion and details about singular, confining $\alpha _s(Q^2)$ can be found in Sect. 5 of the present review.

7.4.2 Dipole model and geometrical scaling

As described in Sect. 7.3.6, the phenomenon of saturation and a geometrical scaling for low-x $\gamma ^* p$ processes have been obtained from the QCD dipole model. Here we present its essential formulation and phenomenology.

In this model, the scattering takes place in two steps. First, a virtual (transverse T or longitudinal L) photon of four-momentum Q splits into a $q\bar{q}$ dipole of transverse size $\mathbf{r}$ that is described through a probability distribution $|\varPsi (r, z, Q^2)|^2$, where z is the fraction of longitudinal momentum of a quark of mass $m_f$. Then a subsequent scattering of the produced dipole occurs with the proton that is modeled through a dipole-proton cross section $\tilde{\sigma }(r, x)$. Explicitly,

$$\begin{aligned} \sigma _{T, L}(x; Q^2) = \int (\mathrm{d}^2\mathbf{r}) \int _o^1 (\mathrm{d}z) |\varPsi _{T, L}(r, z; Q^2)|^2 \tilde{\sigma }(x; \mathbf{r}).\nonumber \\ \end{aligned}$$

(7.68)

The splitting wave functions for the photon $\varPsi$ for a quark of flavour f and charge $e_f$ are given by

$$\begin{aligned} |\varPsi _{T}|^2= & {} \left[ \frac{3 \alpha }{2 \pi ^2}\right] \sum _f e_f^2 \{ [z^2 + (1 -z)^2] (\bar{Q}_f K_1(\bar{Q}_f r))^2\nonumber \\&+\, (m_f K_o(\bar{Q}_f r))^2 \}\nonumber \\ |\varPsi _{L}|^2= & {} \left[ \frac{3 \alpha }{2 \pi ^2}\right] \sum _f e_f^2 [2 z(1 - z)\bar{Q}_f K_o(\bar{Q}_f r)]^2, \end{aligned}$$

(7.69)

where $K_{0,1}$ are Macdonald functions and

$$\begin{aligned} \bar{Q}^2_f = z (1 - z) Q^2 + m_f^2. \end{aligned}$$

(7.70)

It is important to note that the above incorporates the change in the dynamics as $Q^2$ varies from large to very small values in two ways. Kinematically, as $Q^2$ goes to zero, the effective quark masses $m_f$ begin to set the scale for the process. The important ranges of integration in Eq. (7.68) changes with the size of the dipoles in two essential ways. The K-functions decrease exponentially for large r dipoles whereas for small size dipoles they provide (inverse) power-law dependence. Also, the dipole cross sections are assumed to “saturate” as follows.

$$\begin{aligned} \tilde{\sigma }(r, x) = \sigma _o g(\hat{r});\quad \hat{r} = \left[ \frac{r}{R_o(x)}\right] , \end{aligned}$$

(7.71)

where $\sigma _o$ is taken as a constant (phenomenologically $\sigma _o \sim 23~\mu \hbox {b}$) and the function g saturates to 1 as $\hat{r} \rightarrow \infty$:

$$\begin{aligned} g(\hat{r}) = [ 1 - \mathrm{e}^{-(\hat{r}^2/4)}]. \end{aligned}$$

(7.72)

The above tames the small x blow up present in the structure functions in DGLAP and BFKL, as required by unitarity.

Geometrical scaling resides in Eq. (7.71) through the fact that $\sigma (\hat{r})$ depends on the dimensionless variable $\hat{r}$ and thus the saturation radius $R_o(x)$ controls the energy behaviour of the cross section. Hence, in the region of small but non-vanishing x, after integration Eq. (7.68) depends only on one dimensionless variable $\tau$:

$$\begin{aligned} \sigma ^{\gamma ^* p}(x, Q^2) = \sigma _o\ h(\tau );\quad \tau = Q^2 R_o^2(x). \end{aligned}$$

(7.73)

Qualitatively, the results – modulo logarithmic corrections – may be summarised as follows.

$$\begin{aligned}&\sigma ^{\gamma ^* p}(x, Q^2) \rightarrow \ \sigma _o\quad \mathrm{for}\ \tau \rightarrow 0\nonumber \\&\sigma ^{\gamma ^* p}(x, Q^2) \rightarrow \left[ \frac{\sigma _o}{\tau }\right] \quad \mathrm{for}\ \tau \gg 1. \end{aligned}$$

(7.74)

A phenomenological form for the saturation radius

$$\begin{aligned}&R_o(x) = \left( \frac{1}{Q_o}\right) \left( \frac{x}{x_o}\right) ^{\lambda /2};\nonumber \\&Q_o = 1~\mathrm{GeV};\quad x_o = 3 \times \ 10^{-4};\quad \lambda = 0.29, \end{aligned}$$

(7.75)

seems to work quite well and exhibits scaling for $x < 10^{-2}$ [414, 435] as shown in the Fig. 104 from [414].

Fig. 104

$\sigma ^{\gamma ^*p}(\tau )$ vs. $\tau$, the scaling variable from [414]. Reprinted with permission, Fig.(1) from [414], ©(2001) by the American Physical Society

For a smooth limit to $Q^2 \rightarrow 0$, the Bjorken variable is shifted to

$$\begin{aligned} x \rightarrow \ \tilde{x} = x \left[ 1 + \frac{4 m_f^2}{Q^2}\right] , \end{aligned}$$

(7.76)

and the parameter

$$\begin{aligned} \zeta = \left( \frac{x}{x_o}\right) ^\lambda \left( \frac{Q^2}{Q_o^2}\right) \end{aligned}$$

(7.77)

is defined that delineates the “soft-x” regime ($\zeta < 1$) from the “hard-x” regime where $\zeta > 1$. A useful interpolation formula that approximately covers both regions has also been given [435] as

$$\begin{aligned} \sigma ^{\gamma ^* p}(x, Q^2) = \sigma _o\ \left\{ \ln \left( 1 + \frac{1}{\zeta }\right) + \frac{1}{\zeta } \ln (1 + \zeta )\right\} . \end{aligned}$$

(7.78)

As previously discussed in the definition of the parameter q in Eq. (7.62) proposed by Haidt, a factor 1 has been added to the argument of the logarithms for a smooth limit $Q^2 \rightarrow 0$. The above expressions reproduce the change in the slope of the high $W^2$ cross section data as $Q^2$ is varied.

7.5 Models for $\gamma p$ cross section

The approaches to the phenomenological or theoretical description of photon-proton total cross sections can be roughly divided into some general categories:

• factorisation models, including the universal Pomeron exchange model by Donnachie and Landshoff description, which extends very simply from $pp$ scattering to photon processes and can then be extended, again very simply, to photon-photon processes

• the Reggeon-calculus approach which follows Gribov’s picture of the interaction, including the Dual Parton model descriptions

• QCD mini-jet models with photon structure functions

• QCD-inspired parametrisations.

We shall start with Donnachie and Landshoff model, which we have already described in the previous sections.

Fig. 105

The energy behavior of the photo production cross section by the ZEUS Collaboration as shown in Fig. (5) from [392]. Reprinted with permission from the ZEUS Collaboration from [392]. OPEN ACCESS

In 1992, Donnachie and Landshoff [60] proposed a universal form for all total cross sections, based on Regge pole behaviour. Their expression, based on a simple and economical parametrisation of the total cross section behaviour, describes the high energy behavior of all total cross section with a universal power law. The universality of the slope is not always observed, as we have discussed in [147]. However the DL expression, with slightly different slopes, offers a good description in the energy range presently reached by accelerators, and is still an object of investigation, both theoretically and experimentally.

We show in Fig. 105 the results from an analysis by the ZEUS Collaboration from HERA. The focus of this analysis is the slope of $\sigma _{\mathrm{tot}}^{\gamma p}$ [392] as a function of the cm energy W, in the energy range spanned by HERA. Parametrising $\sigma _{\mathrm{tot}}^{\gamma p}$ with $W^{2\epsilon }$ gives $\epsilon =0.111\pm 0.009(\hbox {stat})\pm 0.036(\hbox {sys})$.

It must be stressed that while a power-law behavior is a good parametrisation of the energy dependence in the HERA region, this is clearly not sustainable at higher energies, as dictated by the Froissart bound. The behavior to be expected at the high end of cosmic ray energies cannot be gauged from this analysis.

7.5.1 The Tel Aviv group

The work [436, 437] by the Tel Aviv group of Gostman, Levin and Maor (GLM) presents a unified description of DIS total cross section and photo-production. This work follows Gribov’s idea that the scattering of photons on hadrons can be visualized in, the by now standard, two stages, i.e.

• 1. the virtual photon fluctuates into a $q{\bar{q}}$ pair (hadron in Gribov’s language)

• 2. the $q {\bar{q}}$ interacts with the hadronic matter

In this model one calculates the total cross section for a generic $Q^2$, and the final expression is written with a contribution from the transverse (T) cross section as well as one for the longitudinal (L) part. For large $Q^2$, an expression for contribution from fluctuations of the photon into a heavy quark pair is also given.

Following Gribov, the starting expression for the cross section, for a photon of mass $Q^2$ scattering off a proton, is written through a dispersion relation in the initial and final hadronic masses as

$$\begin{aligned} \sigma _{\mathrm{tot}}^{\gamma * p}= \frac{\alpha }{3 \pi } \int \frac{\varGamma (M^2)\mathrm{d}M^2}{M^2+Q^2} \sigma (M^2,M'^2,s) \frac{\varGamma (M'^2)\mathrm{d}M'^2}{M'^2+Q^2}\nonumber \\ \end{aligned}$$

(7.79)

with

$$\begin{aligned} \varGamma ^2(M^2)=R(M^2)=\frac{\sigma (\mathrm{e}^+\mathrm{e}^-\rightarrow \mathrm{hadrons})}{\sigma (\mathrm{e}^+\mathrm{e}^-\rightarrow \mu ^+\mu ^-)}. \end{aligned}$$

(7.80)

For large masses $\varGamma (M^2)\times \varGamma (M'^2)\rightarrow R(M^2)=2$. To describe the hadronic cross section $\sigma (M^2,M'^2)$, the scattering is first divided according to an energy scale, $M_0$, which separates the hard scattering regime where pQCD can be used and the soft region. In the soft region, a second scale is needed, because of the difference between gluon and quark sizes. To be more specific, in the soft region, i.e. for $M,M'<M_0$ the following expression is used:

$$\begin{aligned} \sigma (M^2,M'^2)= & {} \sigma _N^{\mathrm{soft}}(M^2,s)M^2 \delta (M^2-M'^2) \nonumber \\= & {} [\sigma _{qN}+\sigma _{\bar{q} N}]M^2\delta (M^2-M'^2) \end{aligned}$$

(7.81)

and for $M,M'<M_0$, Gribov’s formula is simplified to read

$$\begin{aligned} \sigma (\gamma ^*N)=\frac{\alpha }{3 \pi }\int \frac{R(M^2)M^2\mathrm{d}M^2}{(Q^2+M^2)^2} \sigma _N(M^2,s). \end{aligned}$$

(7.82)

For the soft regime, a Donnachie-Landshoff type expression is used so as to arrive at

$$\begin{aligned} \sigma _T^{\mathrm{soft}}= & {} \frac{\alpha }{3 \pi }\int _{4m^2_\pi }^{M^2_0} \frac{R(M^2)M^2\mathrm{d}M^2}{(Q^2+M^2)^2}\nonumber \\&\times \left\{ A(\frac{s}{M^2})^{\alpha _P-1}+ B\left( \frac{s}{M^2}\right) ^{\alpha _R-1}\right\} \end{aligned}$$

(7.83)

with A and B obtained so as to make the result agree with those from $\rho$-proton interactions. In [436], the constants A and B were obtained from DL type fits to $\pi ^{\pm }p$. Since the cross section thus calculated seems to be higher than the data, some corrections are introduced. The calculation for the hard part is done using published PDF’s for the gluon distributions inside the proton, and is given by

$$\begin{aligned}&\sigma _T^{\mathrm{hard}}= \frac{2\pi \alpha }{3} \int _{M_0^2}^{\infty } \frac{R(M^2)\mathrm{d}M^2}{Q^2+M^2}\nonumber \\&\quad \times \int _0^\infty \frac{ d{\tilde{M}}^2 }{ {\tilde{M}}^4 } \alpha _s\left( \frac{ {\tilde{M}}^2 }{4 }\right) xG\left( x,\frac{ {\tilde{M}}^2}{4}\right) \mathcal{I}(M^2,{\tilde{M}}^2,Q^2)\nonumber \\ \end{aligned}$$

(7.84)

with

$$\begin{aligned}&\mathcal{I}(M^2,{\tilde{M}}^2,Q^2) \nonumber \\&\quad =\frac{M^2-Q^2}{M^2+Q^2} + \frac{ Q^2+{\tilde{M}}^2-M^2 }{ \sqrt{ (Q^2+M^2+{\tilde{M}}^2)^2-4M^2{\tilde{M}}^2 } }.\nonumber \\ \end{aligned}$$

(7.85)

Notice the lower cutoff for the integration in $M^2$.

Equations (7.83) and (7.85) need to be implemented by the contribution of heavy quark pairs. This is obtained from Eq. (7.84) by the substitutions

$$\begin{aligned} 4M^2{\tilde{M}}^2\rightarrow 4(M^2-4m_Q^2){\tilde{M}}^2,\quad R(Q^2)\rightarrow R^{QQ}(M^2).\nonumber \\ \end{aligned}$$

(7.86)

In both the above equations, $x=x(M^2)=(Q^2+M^2)/W^2$, where W is the energy in the photon–nucleon center of mass system. No soft contribution is of course present for the heavy quark term.

An expression similar to the above is also used to describe a longitudinal component to add to the transverse one. For the soft contribution, the authors note that a priori it should be straightforward to replace the factor $M^2$ with $Q^2$, except they find that, in so doing, the contribution from the soft part overestimates the experimental data and needs to be reduced. The strategy adopted is to reduce the value of the parameter $M_0$. For the hard component, the additional degrees of freedom result in an expression proportional to $Q^2$ (hence going to zero for real photons). For details, see [437]. The overall expression is thus

$$\begin{aligned} \sigma (\gamma ^*p)=\sigma _T^{\mathrm{soft}}+\sigma _T^{\mathrm{hard}}+ \sigma _{T,QQ}^{\mathrm{hard}}+\sigma _L^{\mathrm{soft}}+\sigma _L^{\mathrm{hard}}. \end{aligned}$$

(7.87)

The resulting fit for the $\gamma p$ cross section is shown in Fig. 106.

Fig. 106

From [437]. Data in the low-energy range come from fixed target experiments, while cross section values for $W^2>10^4\ \mathrm{GeV}^2$ are from [399]. Reprinted with permission from [437] ©(1999) by Springer

Concerning the pQCD part of this calculation, there are a few points to notice:

• at low energy, the soft part does use some type of vector meson dominance, being parametrised following $\pi ^{\pm }p$, but it needs some adjustments,

• the overall result depends on the gluon densities used for the calculation of the hard part, with MRST [438] densities for the gluon giving a better description than GRV, both GRV94 [439] or GRV98 [96],

• a difficulty in the calculation is related to the low values of $M^2$ integration, where the strategy adopted has been to use

  $$\begin{aligned} xG(x,l^2<\mu ^2)=\frac{l^2}{\mu ^2}xG(x,\mu ^2) \end{aligned}$$

  (7.88)

  and for $Q^2<\mu ^2$ to keep fixed the strong coupling constant.

In our own QCD calculation of the mini-jet cross section, the gluon densities have also been extended to very low x values of the gluon fractional momenta, as discussed in Sect. 5.9.4, and the lower cutoff is given by a phenomenologically determined value $p_{\min }\simeq 1\ \mathrm{GeV}$.

7.5.2 Eikonal mini-jet models for $\gamma p$ scattering

We shall now describe how the eikonal mini-jet model was extended to photon processes [440,441,442], and subsequently modified by Block et al. [146] in the QCD inspired model of [166].

In the GLMN approach [437], the pQCD contribution to the total cross section was calculated using gluon–gluon scattering for the probability of finding a gluon in a proton. For the probability of finding a gluon in a photon, the calculation did not use parton densities, but wave functions and various integrations. A different line of approach to the partonic content of the photon had instead been developed by Drees and Godbole [443] who argued that the hadronic content of the photon consists of quarks and gluons, in a way analogous to the partonic content of the proton or the pion. Thus, one could measure and define photon structure functions, which would submit to DGLAP evolution just like the hadrons. Such photon densities could be inserted into a QCD calculation as in the proton–proton case. This idea would then allow the calculation of jet cross sections and that, for production of mini-jets, namely jets with $p_t\ge \approx 1\ \mathrm{GeV}$. To cure the resulting too large number of mini-jets, a saturation mechanism was invoked in [444], where the VMD model was suggested to be used within the eikonal formalism, in complete analogy with proton–proton scattering, as discussed in the previous section.

A formulation of the calculation of the total $\gamma p$ cross section was proposed by Fletcher et al. [441], following the eikonal mini-jet model for hadronic cross sections developed earlier by Durand et al. [45, 59] and extended to photon processes [440]. The issues involved, at the time, in correctly extending the model to photon-hadron scattering included how to incorporate the photon-hadron coupling into the eikonalisation procedure, use of appropriate photon structure functions, and gluon shadowing at small x.

In the mini-jet approach, one distinguishes the following steps:

• the photon interacts with other hadrons “as a hadron”, namely as an ensemble of quarks and gluons, with a probability $P_{\mathrm{had}}$ which is proportional to $\alpha _{\mathrm{QED}}$,

• once the photon has fluctuated into such a hadronic state, one can apply hadronic models for calculation of total or inelastic cross sections, such as eikonal models with QCD mini-jets to drive the rise,

• the mini-jet cross section will be calculated using parton–parton cross sections and photon densities, following standard parametrisations such as GRV [96], GRS [445], CJKL [446], or using QCD-inspired parametrisations, or gluon mass models, etc.

The proposed expression is

$$\begin{aligned} \sigma _{\mathrm{inel}}^{\gamma p}= P_{\mathrm{had}}\int \mathrm{d}^2{\mathbf {b}}[1-\mathrm{e}^{-n(b,s)}] \end{aligned}$$

(7.89)

where

$$\begin{aligned} n(b,s)=n_0(b,s)+A(b) \frac{\sigma _{\mathrm{parton}}}{P_{\mathrm{had}}}. \end{aligned}$$

(7.90)

In Eq. (7.90), the first term represents the non-perturbative contribution to the average number of collisions, the second is the one which should be calculated perturbatively and which gives the high energy rise of the cross section, through the low-x gluons present in the hadronic content of the photon. $n_0(b,s)$ is of order of magnitude of a similar term present in hadronic interactions, and its estimate depends on the low-energy modelling of the photons in the hadronic state. The second term has to be calculated using the standard parton–parton cross sections folded in with the photon PDFs. In many models [147] the soft term $n_0(b,s)$ is obtained using the Additive Parton Model (ADM) together with VMD, by putting

$$\begin{aligned} n_0(b,s)=A_{VMD}\frac{2}{3}\sigma ^{nn}_{\mathrm{soft}}(s) \end{aligned}$$

(7.91)

where $\sigma ^{pp}_{\mathrm{soft}}(s)$ would be the same soft cross section entering the eikonal mini-jet model for proton–proton and/or proton–antiproton scattering. We shall return to this point later.

The eikonal formulation for this model requires an expression for the impact-parameter distribution in the photon. In [441] VMD and the form-factor hypothesis are used, and the result is that $A_{VMD}$ is obtained as the Fourier transform of the convolution of two form factors, the proton form factor and the “photon” form factor. The latter is taken to be the pion form factor, following again a model in which the number of quarks controls the b-distribution during the collision. For protons, the dipole expression is used, for the pion the monopole expression, so that

$$\begin{aligned}&A_{VMD}(b)=\frac{\nu ^2}{2 \pi }\frac{\mu ^2}{\mu ^2-\nu ^2} \nonumber \\&\qquad \times \left[ \frac{\mu ^2}{\mu ^2-\nu ^2} [ K_0(\nu b)-K_0(\mu b)]-\frac{\mu b}{2 }K_1(\mu b) \right] .\nonumber \\ \end{aligned}$$

(7.92)

In most applications of this model, the same expression for A(b) is used for both the mini-jet term and the soft part. However in general, there is no reason to assume that the parton distribution in b-space is the same at very high energy and at low energy. In fact, in the model to be described next, the so called Aspen model [146], this not so.

Before proceeding, let us examine the quantity $P_{\mathrm{had}}$ which plays a basic role in all the extensions of hadronic models to photon total cross sections.

If the photon, in its interactions with matter, is to be considered just like a hadron, then any model for hadron–hadron scattering should be considered extensible to photon-hadron scattering. The factor $P_{\mathrm{had}}$ represents the probability for a photon to interact like a hadron and was introduced to apply vector meson dominance ideas to the eikonalisation procedure. In principle, $P_{\mathrm{had}}$ may very well have an energy dependence. A possible definition follows the general VMD statement that the wave function of the photon in its interaction with hadrons can be expressed as [447]

$$\begin{aligned} |\gamma \rangle =Z_3|\gamma _{B}\rangle + \sum _{V=\rho ,\omega ,\phi } \frac{e}{f_V}|V\rangle +\frac{e}{f_{q{\bar{q}}}}|q {\bar{q}}\rangle \end{aligned}$$

(7.93)

where the first term corresponds to the bare photon, i.e. in its purely electromagnetic interactions, while the second considers the non-perturbative component, pictured through VMD, and the last gives the contribution to the pQCD behaviour at high energy from quarks and gluons.

Given the general theoretical uncertainty in total cross section models, a phenomenological strategy is to ignore this energy dependence and use a VMD model for $P_{\mathrm{had}}$, or even to use it as a free parameter determined by the normalisation of the total $\sigma _{\mathrm{tot}}^{\gamma p}$ cross section at low energy.

The Aspen model for photons [146] to be described next, is a generalisation of the Block et al. [166] model for protons with some differences. The Block model is based on a QCD-inspired parametrisation and uses the eikonal formalism, which guarantees unitarity, namely one starts with

$$\begin{aligned} \sigma _{\mathrm{total}}=2\int \mathrm{d}^2{\mathbf {b}}[1-\mathrm{e}^{\chi _I(b,s)}\cos (\chi _R(b,s))]. \end{aligned}$$

(7.94)

In the proton case, $\chi (b,s)$ is a complex function, whose even component $\chi ^{\mathrm{even}}$ receives contributions from parton–parton interaction through the three separate terms

$$\begin{aligned} \chi ^{\mathrm{even}}= & {} \chi _{qq}(b,s)+\chi _{qg}(b,s)+\chi _{gg}(b,s)\nonumber \\= & {} i\big [ \sigma _{qq}(s)W(b;\mu _{qq})+ \sigma _{qg}(s)W( b; \sqrt{\mu _{qq}\mu _{gg}}t )\nonumber \\&+\,\sigma _{gg}(s)W(b;\mu _{gg})\big ]. \end{aligned}$$

(7.95)

The extension to $\gamma p$ is done as in [441] through

$$\begin{aligned} \sigma _{\mathrm{tot}}^{\gamma p}(s)= P_{\mathrm{had}}\int \mathrm{d}^2{\mathbf {b}}\left[ 1-\mathrm{e}^{ -\chi _I^{\gamma p}(b,s)}\cos \chi _R^{\gamma p}(b,s)\right] .\nonumber \\ \end{aligned}$$

(7.96)

In this model the value $P_{\mathrm{had}}=1/240$ is used. This value is obtained by fitting the low-energy data and is very close to the expected VMD value. For the cross sections, $\sigma _{ij}(s)$, and the impact-parameter distribution functions for photons, to be used in Eq. (7.96), the following substitutions are made in Eq. (7.95):

$$\begin{aligned} \sigma _{ij}^{pp}\rightarrow \sigma _{ij}^{\gamma p}=\frac{2}{3}\sigma _{ij}^{pp},\end{aligned}$$

(7.97)

$$\begin{aligned} \mu _i^{pp}\rightarrow \mu _{i}^{\gamma p}=\sqrt{\frac{3}{2}}\mu _i^{pp} \end{aligned}$$

(7.98)

where the two substitutions are done in the spirit of the Additive Quark Model. We can anticipate that the same model will be applied also to $\gamma \gamma$ processes with

$$\begin{aligned} \sigma _{ij}^{\gamma \gamma }=\frac{4}{9}\sigma _{ij}^{pp},\end{aligned}$$

(7.99)

$$\begin{aligned} \mu _{i}^{\gamma \gamma }=\frac{3}{2}\mu _i^{pp}. \end{aligned}$$

(7.100)

The predicted total cross section in this model is shown in Fig. 107.

Fig. 107

The total cross section $\sigma _{\mathrm{tot}}^{\gamma p}$ in mb vs. $\sqrt{s}$ in GeV, from [146]. This is Fig. (7) from [146], reprinted with permission, ©(1999) by the American Physical Society

Following the QCD-inspired model outlined above, Luna and collaborators [448] have also extended their dynamical gluon model to photon-proton scattering.

More recently, Block has proposed an analytical amplitude model and has applied it to both photon and neutrino scattering on protons [449].

7.5.3 The BN model: eikonal mini-jet model with soft-gluon resummation

In this section we describe our extension of the Eikonal mini-jet model with $k_t$-resummation in the infrared region, labeled BN model, as it is inspired by the Bloch and Nordsieck (BN) description of the Infrared catastrophe [170]. As described in the previous section, our aim with this model is to introduce, together with the mini-jet cross section, a saturation effect which arises from soft-gluon emission, down into the infrared region, as discussed in the section about the total cross section.

The model is so far relatively simple, with a limited number of parameters, and thus it can, to a certain extent, be considered almost a model for testing confinement through a singular quark-gluon coupling below the perturbative QCD expression.

We start with the simplified expression from [441], namely

$$\begin{aligned} \sigma ^{\gamma p}_{\mathrm{tot}} = 2 P_{\mathrm{had}}\int \mathrm{d}^2 {\mathbf {b}}[1-\mathrm{e}^{-n^{\gamma p}(b,s)/2}] \end{aligned}$$

(7.101)

with

$$\begin{aligned} n^{\gamma p}(b,s)= & {} n_{\mathrm{soft}}^{\gamma p}(b,s) +n^{\gamma p}_{\mathrm{hard}}(b,s)\nonumber \\= & {} n_{\mathrm{soft}}^{\gamma p}(b,s) + A(b,s) \sigma _{\mathrm{jet}}^{\gamma p}(s)/P_{\mathrm{had}} \end{aligned}$$

(7.102)

with $n_{\mathrm{hard}}$ including all outgoing parton processes with $p_t>p_{t\min }$. We differ from other mini-jet models in approximating the eikonal with just the imaginary part [146], in using a different impact parameter distribution for the soft and the hard part [441], but mostly in our expression and origin of the impact parameter distribution for photons. In Eq. (7.102) the impact parameter dependence has been factored out, averaging over densities in a manner similar to what was done for the case of the proton in [148]. Because the jet cross sections are calculated using actual photon densities, which themselves give the probability of finding a given quark or gluon in a photon, $P_{\mathrm{had}}$ needs to be canceled out in $n_{\mathrm{hard}}$. We choose its value, by normalizing the eikonalised cross section to the data in the low energy region, and we use $P_{\mathrm{had}}=1/240 \approx P_{VMD}$. For the average number of hard collisions, we use mini-jets and soft gluon resummation with $n_{\mathrm{hard}}$ given by:

$$\begin{aligned} n_{\mathrm{hard}}(b,s)={{ A^{AB}_{BN}(b,s) \sigma _{\mathrm{jet}} } \over {P_{\mathrm{had}} }} \end{aligned}$$

(7.103)

with the impact distribution function obtained exactly as in the proton–proton case, namely

$$\begin{aligned} A^{AB}_{BN}(b,s)= & {} \mathcal{N} \int \mathrm{d}^2 \mathbf{K}_{\perp } {{\mathrm{d}^2P(\mathbf{K}_\perp )}\over {\mathrm{d}^2 \mathbf{K}_\perp }} \mathrm{e}^{-i\mathbf{K}_\perp \cdot \mathbf{b}} \nonumber \\= & {} {{\mathrm{e}^{-h( b,q_{\max })}}\over {\int \mathrm{d}^2\mathbf{b} \mathrm{e}^{-h(b,q_{\max })} }}\nonumber \\\equiv & {} A^{AB}_{BN}(b,q_{\max }(s)),\ \ \ \end{aligned}$$

(7.104)

except for the fact that $q_{\max }$ the upper limit of integration in the function $h( b,q_{\max })$ is to be calculated using proton and photon densities. $h( b,q_{\max })$ describes the exponentiated, infrared safe, number of single soft gluons of all allowed momenta and is given by

$$\begin{aligned} h( b,q_{\max }(s))= & {} \frac{16}{3}\int _0^{q_{\max }(s) } {{\mathrm{d}k_t}\over {k_t}} {{ \alpha _s(k_t^2) }\over {\pi }} \nonumber \\&\times \left( \log {{2q_{\max }(s)}\over {k_t}}\right) \left[ 1-J_0(k_tb) \right] . \end{aligned}$$

(7.105)

We show typical values taken by $q_{\max }$ for different sets of quark densities in Fig. 108. In our model, the expression for A(b, s) for the hard term in hadron–hadron or hadron-photon scattering remains the same, unlike models that use form factors for instance, where the photon needs to be modeled as a meson and then parametrised.

Fig. 108

The maximum single gluon momentum allowed for soft gluon integration, $q_{\max }$ in GeV, vs. $\sqrt{s}$ in GeV for $\gamma p$ scattering, from [147]. Reprinted with permission from [147], ©(2008) by Springer

Fig. 109

The total cross section $\sigma _{\mathrm{tot}}^{\gamma p}$ in mb vs. $\sqrt{s}$ in GeV, from [147]. Reprinted from [147], ©(2008) by Springer

We show the result of our model in Fig. 109 from [147]. In this figure, the high energy parameter set of this description, consisting of the LO PDFs and $p_{t\min }$ value used for the mini-jet cross section calculation, together with the saturation (singularity) parameter p, were limited to GRV densities for the protons, while two sets of photon PDFs were used. A comparison was made with predictions from some available models, such as indicated in the figure and discussed in [147].

Fig. 110

The total cross section $\sigma _{\mathrm{tot}}^{\gamma p}$ in mb vs. $\sqrt{s}$ in GeV, from [450]. This is Fig.(2) from [450], ©(2015) by the American Physical Society

An updated description of $\gamma p$, is shown in Fig. 110. In this figure, we compare the BN-model results obtained with MRST and GRV densities for the proton, GRS for the photon, with the recent analysis by Block et al. [449]. The band in Fig. 110 correspond to GRV or MRST densities for the proton. The difference with the previous analysis is not large, it depends, as mentioned by now many times, on the small-x behavior of the densities used. From a comparison with accelerator data, we can say only that both curves can be used for cosmic ray extrapolations.

7.6 $\sigma _{\mathrm{total}}(\gamma p)$, and exclusive vector meson production $\sigma (\gamma p \rightarrow V p)$

In addition to the total $\gamma p$ and $\gamma ^* p$ cross section (which will be discussed in some detail in the next subsection) HERA has provided interesting data on vector meson exclusive production.

Fig. 111

Total and exclusive vector meson photoproduction data, from [451]. Reprinted with permission from [451]. OPEN ACCESS

A compendium of total and exclusive vector meson photo-production data are shown as a function of W in Fig. 111 from Levy’s review of HERA experimental results [451]. Recently, this figure appears in updated versions, as in [452, 453] and is of interest for proposals for future electron–positron colliders [452]. There is only one variable here, the c.m. energy W,  and the fits are made as a power law $\sigma (W) \sim W^\delta$. The parameter $\delta$ rises from 0.16 for the $\sigma _{\mathrm{total}}(\gamma p)$, with the mass of the produced vector meson to about 1.2 for $\sigma (\gamma p \rightarrow \varUpsilon (1S) p)$. In Regge language, hadron–hadron total cross section at a CM energy $W = \sqrt{s}$ should grow as $W^{2\epsilon }$, where $\epsilon = (\alpha _P(0) -1)$ and $\alpha _P(0)$ is the intercept of the Pomeron at momentum transfer $t =0$. For photo-production, the value for $\epsilon$ follows the original Donnachie–Landshoff power-law analysis, discussed at length earlier, [60], i.e. $\epsilon =0.0808$. In [454], the value $\epsilon \approx 0.096$ was shown to reproduce well pp scattering, while the ZEUS data for $\gamma p$ can be fitted with $\epsilon =0.111$ in the HERA energy range, as seen in Fig. 105. Thus, $\delta = 2\epsilon \sim 0.192$, not too far from either the HERA value of $\delta \sim \ 0.16$ for $\sigma _{\mathrm{total}}(\gamma p)$ or the ZEUS analysis. At the same time, these differences point to the fact that power-law fits, albeit very useful for phenomenological analyses, are often dependent on the energy range and the type of scattering process.

Fig. 112

The cross section for electroproduction of $\rho$-meson, as measured by the ZEUS Collaboration in Fig. (13) from [455], as a function of the c.m. energy W, and for different $Q^2$ values. Reprinted with permission of the ZEUS Collaboration from [455] ©(2007) ZEUS Collaboration

While $\delta = 2\epsilon$ for $\sigma _{\mathrm{total}}(\gamma p)$, data show that also the photo-production of light-mass vector mesons ($\rho ^o, \omega , \phi$) are consistent with a soft process. In Levy’s review of the data, it is stated that here too there is a large configuration for the photon to fluctuate into a $q\bar{q}$ pair. On the other hand, as the mass of the vector meson increases the system is led from the soft to the hard regime: the heavy quarks squeeze the photon into a smaller configuration leading to color screening and the partonic structure of the proton is resolved. In the hard exclusive regime, the cross section should be proportional to the square of the gluon density and hence there should be a strong dependence on W. This is clearly manifested by the HERA data, as discussed and summarised in [451].

7.7 Electro-production of vector mesons, $\gamma ^*p\rightarrow Vp$

Virtuality of photons adds another variable $Q^2$ to W that is lacking in purely hadronic cross sections. HERA data show interesting results that can be found in [455,456,457]. Here we shall attempt a summary.

7.7.1 Electro-production of $\rho ^o$ meson

In Fig. (13) of [455], reproduced here as Fig. 112, $\sigma (\gamma ^* p \rightarrow \rho ^o p)$ is shown as a function of W for different values of $Q^2$. The data are fitted to a power law $\delta$, which rises from $(0.1\div 0.2$) for low $Q^2$, as expected for soft processes, to about 0.6 for large $Q^2$, consistent with twice the logarithmic derivative of the gluon density, again as expected of a hard process.

7.7.2 Electro-production of heavier vector mesons and $\gamma ^* p \rightarrow \gamma p$

While the general trend of an increase in the cross section with $Q^2$ is similar for $\phi$, $J/ \psi$ and for deeply virtual Compton scattering $\gamma ^* p \rightarrow \gamma p$, there is obviously an uncertainty in how to insert the mass M of the produced vector meson. Quite often, the variable $Q^2 + M^2$ in place of $Q^2$ has been used. In Fig. (8) of Levy, reproduced here in Fig. 113, a plot of $\delta$ versus $Q^2+M^2$ is shown. There is an approximate universality showing an increase in $\delta$ as the scale increases. $\delta$ is found to be small at low scale, consistent with the intercept of a soft Pomeron whereas at larger scales it becomes close to that expected from the square of the gluon density.

Fig. 113

The $Q^2$ dependence of the energy slope for $\gamma ^*p\rightarrow Vp$ cross section, including heavy vector mesons electroproduction and Deeply Virtual Compton Scattering results, from [451] and references therein. Reprinted with permission from [451], ©(2009) by Science Wise Publ

Further studies to determine the best scale to use for vector meson electro-production, led to study the ratio $r_V=\sigma (\gamma ^*p\rightarrow VP)/\sigma _{\mathrm{tot}}(\gamma ^* p)$ as a function of W. This ratio can be parametrised following Regge arguments, in terms of a Pomeron exchange and of the slope of the differential cross section $\mathrm{d}\sigma _V/\mathrm{d}t$ as

$$\begin{aligned} r_V\sim W^{\lambda }/b. \end{aligned}$$

(7.106)

More details about the scale dependence of the parameter $\lambda$ and its connections to the $\delta$ parameter can be found in [456]. Notice that this analysis depends on the energy behavior of $\sigma _{\mathrm{tot}}(\gamma *p)$ to which we turn in the next subsection.

7.8 Total $\gamma ^*p$ cross section

At HERA, extensive measurements in the available phase space have brought a detailed description of the c.m. energy dependence of the total $\gamma ^* p$ cross section, in a range of values of $Q^2$. These measurements highlight the transition from real photon scattering to Deep Inelastic Scattering (DIS) region, i.e. $0\le Q^2\lesssim 10000\ \mathrm{GeV}^2$. A comprehensive description, up to $Q^2=2000\ \mathrm{GeV}^2$, can be seen in Fig. 114 from [458]. The high energy data have been obtained at HERA, lower energies from a number of different experiments, and for which we refer the reader to the cited papers. One can draw a few conclusions from this figure:

Fig. 114

The virtual photon-proton total scattering cross section for different $Q^2$ values of the virtual photon as a function of the squared c.m. energy $W^2$, from [458]. Reprinted with permission

• for real and quasi-real photons, the low energy behavior of $\sigma ({\gamma ^*p})$ exhibits the well known initial decrease with energy, followed by an apparent minimum and then a very mild rise. Thus, the cross section would follow a standard Donnachie–Landshoff parametrisation,

• as $Q^2$ increases beyond $20\ \mathrm{GeV}^2$, the minimum disappears and the cross section is everywhere increasing with energy albeit with different slopes, and the increase with $W^2$ is steeper for larger $Q^2$ values,

• the change in curvature before the high energy rise, moves to higher $W^2$ values as $Q^2$ increases.

In the figure, two different parametrisations are shown, one described by a continuous line, and labeled as ALLM97, which we summarise here, while for the second one, MRSR1, we refer the reader to Refs. [458, 459]. The ALLM [460] parametrisation (of which ALLM97 represents an update) describes the proton structure function following the usual split into a Regge and a Pomeron type term, i.e.

$$\begin{aligned} F_2(x,Q^2)=\frac{Q^2}{Q^2+m_0^2}\large ( F_2^\mathcal{P}(x,Q^2)+F_2^\mathcal{R}(x,Q^2) \large )\nonumber \\ \end{aligned}$$

(7.107)

with $F_2^\mathcal{{P},\mathcal {R}}(x,Q^2)$ a function of a slowly varying variable defined as

$$\begin{aligned} t=\ln \left( \frac{\ln \frac{Q^2+Q_0^2}{\varLambda ^2}}{\ln \frac{Q_0^2}{\varLambda ^2}} \right) . \end{aligned}$$

(7.108)

Fig. 115

H1 and ZEUS data for real and virtual photon scattering from [462]. This is Fig. (11) from [462], ©(2010) by IOP, reprinted with permission

The $F_2$ data were then conveyed to $\sigma _{\mathrm{tot}}(\gamma ^*p)$ using

$$\begin{aligned} \sigma _{\mathrm{tot}}(\gamma ^*p)=\frac{4 \pi ^2 \alpha }{Q^2(1-x)} \frac{Q^2+4M^2x^2}{Q^2} F_2(W^2,Q^2) \end{aligned}$$

(7.109)

where M here is the proton mass. The ALLM $F_2$ is based on 23 parameters, which were updated from pre-Hera data to the nice description shown in Fig. 114.

The $\gamma ^*p$ HERA data have also been studied in terms of Vector Meson Dominance or Color Dipole Picture, as shown and discussed in [461].

Fig. 116

Data for $\gamma \gamma$ total cross section from [464] and bibliographic references therein. Reprinted with permission, ©(2012) INFN Frascati Physics Series

A more recent analysis of HERA data from [462] is shown in Fig. 115, with the virtual photon cross section

$$\begin{aligned} \sigma ^{\mathrm{tot}}_{\gamma ^*p}=\frac{4\pi ^2 \alpha }{Q^2(1-x)}F_2(x,Q^2), \end{aligned}$$

(7.110)

valid for $4 m_p^2 x^2\ll Q^2$, fitted with $F_2(x,Q^2)$ from HERA parametrised according to a power law, i.e.

$$\begin{aligned} \log _{10}F_2(x,Q^2)= & {} c_1+c_2\cdot \log _{10}(x)\nonumber \\&+\,c_3 \cdot \log _{10}(x) \cdot \log _{10}(Q^2/Q_0^2)\nonumber \\&+\,c_4\cdot \log _{10}(x) \cdot ( \log _{10}(Q^2/Q_0^2))^2.\nonumber \\ \end{aligned}$$

(7.111)

Before moving to briefly discuss two photon processes, we point out that the energy range for photo- and electroproduction at HERA is limited to values still far from the asymptotic regime, where purely hadronic cross sections are expected to exhibit a logarithmic behavior. Thus, the question of a power law vs. a logarithmic behaviour is still open, where photon processes are involved.

7.9 $\gamma \gamma$ scattering

Photon–photon scattering was measured in electron–positron collisions from the very beginning of storage ring colliders [463]. As the available beam energy increased, data for $\gamma \gamma \rightarrow hadrons$ became available. A compilation of data for the cross section into hadrons is shown in Fig. 116 from [464], starting from $\sqrt{s_{\gamma \gamma }} = 1.4~\mathrm{GeV}$ at SPEAR up to LEP measurements, reaching $\sqrt{s}=189\ \mathrm{GeV}$. The figure indicates that the trend of the data as a function of the two photon c.m. energy is consistent with a hadronic process, namely it starts with the usual initial decrease followed by a rise. Such behavior is easily obtained in factorisation models.

Indeed there are various models which describe photon-hadron scattering through various forms of factorisation, which would then allow one to obtain $\sigma _{\mathrm{tot}}^{\gamma \gamma }$, through the simple statement

$$\begin{aligned} \sigma _{\mathrm{tot}}^{\gamma \gamma }=\frac{(\sigma _{\mathrm{tot}}^{\gamma p})^2}{\sigma _{\mathrm{tot}}^{pn}} \end{aligned}$$

(7.112)

where $\sigma _{\mathrm{tot}}^{pn}$ indicates some combination of pp and ${\bar{p}}p$ total cross sections. This is the case of the model by Soffer and collaborators [465], which follows from their description of $\gamma p$ total cross section effects in [466].

The Bourelly, Soffer and Wu ansatz [466] is that $\gamma p$ total cross section can be obtained from $\pi p$ as

$$\begin{aligned} \sigma _{\mathrm{tot}}(\gamma p)=\frac{1}{3} \alpha \left( \sigma _{\mathrm{tot}}(\pi ^+p) + \sigma _{\mathrm{tot}}(\pi ^-p) \right) . \end{aligned}$$

(7.113)

For $\sigma _{\mathrm{tot}}(\pi ^{\pm }p)$ the authors use an early impact picture prediction where a simple power-law dependence $s^{0.08}$ was first given. From this simple model, one could obtain $\sigma _{\mathrm{tot}}^{\gamma \gamma }$ and compare it with data for $\gamma \gamma$ extracted from LEP. Through Eq. (7.112) and their earlier fit to proton–proton, the authors [465] obtain the results shown in Fig. 117.

Fig. 117

Description, and comparison with data, of the $\gamma \gamma$ total cross section in the model by Bourrely, Soffer and Wu, Fig. 1 of [465]. Predictions are also shown, and compared with then existing data, for $pp$/${\bar{p}}p$ and $\gamma p$. Reprinted with permission from [465] ©(1999) by World Scientific

While straightforward factorisation models can give a general good description of data up to LEP most recent measurements, the limited energy range and the large errors affecting the extrapolation to full phase-space both at lower and at the highest energies, do not provide enough information to distinguish between standard power-law energy dependence, such as Regge–Pomeron exchanges, mini-jets, or QCD-driven exchanges. Such distinction, as is also the case for $\gamma p$, is left to future colliders or perhaps to LHC. A 2003 compilation of a selection of models is shown in Fig. 118 from [467], where the bibliographic references can be found. Details of models can be found in [468]. A general fit to the LEP data alone, i.e.

$$\begin{aligned} \sigma _{\gamma \gamma }=A s^\epsilon _{\gamma \gamma }+Bs^{-\eta }_{\gamma \gamma } \end{aligned}$$

(7.114)

was done in [467] and is shown in Fig. 119.

Fig. 118

Data and models for $\gamma \gamma \rightarrow \hbox {hadrons}$ from [467]. Reprinted from [467] ©(2003) by Springer

Fig. 119

Data and power-law type fits to LEP data for $\gamma \gamma$ total cross section from [467]. In fit 1, all the parameters of Eq. (7.114) are free, in fit 2, $\epsilon =0.093$, in fit 3 a second Pomeron type term is added to Eq. (7.114) with $\epsilon _1=0.418$. Reprinted from [467] ©(2003) with permission by SISSA

7.10 $\gamma ^* \gamma ^* \rightarrow hadrons$

At LEP, through the measurements of $\mathrm{e}^- \mathrm{e}^+ \rightarrow \mathrm{e}^- \mathrm{e}^+ + hadrons$, $\sigma (\gamma ^* \gamma ^* \rightarrow hadrons)$ have been measured by the L3 [469] and OPAL Collaborations [470]. The kinematics of such processes is shown in Fig. 120, (fig. (1) from OPAL). Measurements for the above process for one untagged electron were made by the ALEPH Collaboration [471], who extracted the so-called photon structure functions $F_{2,L}^\gamma$. In this case one photon is almost real, and the process is studied as a function of a single $Q^2$ value, extracted from the tagged electron.

Fig. 120

Kinematics of $\mathrm{e}^+\mathrm{e}^-\rightarrow \gamma ^* \gamma ^* \mathrm{e}^+\mathrm{e}^-$, as from Fig. (1) of [470], OPAL Collaboration. Reprinted with permission ©(2001) by SPRINGER

For the determination of $\gamma ^*\gamma ^*$ cross section, both scattered $\mathrm{e}^-$ and $\mathrm{e}^+$ have to be tagged at sufficiently large polar angles $\theta _i$, to be observed in the detector. The kinematical variables for the process are as follows.

• the $\mathrm{e}^-\mathrm{e}^+$ CM energy squared is $s_{\mathrm{e}^-\mathrm{e}^+} = (p_1 + p_2)^2$

• the virtualities of the scattered photons are given by $Q_i^2 = (p_i - p_i^{\prime })^2$;

• the usual variables of deep inelastic scattering are defined as

  $$\begin{aligned} y_1 = \left( \frac{q_1\cdot q_2}{p_1\cdot q_2}\right) ;\quad y_2 = \left( \frac{q_1\cdot q_2}{p_2\cdot q_1}\right) ;\nonumber \\ x_1 = \left( \frac{Q_1^2}{2 q_1\cdot q_2}\right) ;\quad x_2 = \left( \frac{Q_2^2}{2 q_1\cdot q_2}\right) ; \end{aligned}$$

  (7.115)

• the hadronic invariant mass squared is $W^2 = (q_1 + q_2)^2$;

• the Bjorken variables $x_i$ are related to $Q_i^2$ and $W^2$ as

  $$\begin{aligned} x_i = \frac{Q_i^2}{[Q_1^2 + Q_2^2 + W^2]}. \end{aligned}$$

  (7.116)

Fig. 121

The above Figs. 8a and 8b from [470]) of the OPAL Collaboration show the cross section for $\gamma ^*\gamma ^*\rightarrow \hbox {hadrons}$ for an average value of the photon’s squared momentum $\langle Q^2\rangle =17.9~\mathrm{GeV}^2$. Reprinted with permission from [470] ©(2001) by Springer

For comparison with models, an additional variable which incorporates the $W^2$ and $Q_i^2$ dependence, is defined, i.e.

$$\begin{aligned} {\bar{Y}}=\ln \left( \frac{W^2}{\sqrt{Q_1^2 Q_2^2}}\right) . \end{aligned}$$

(7.117)

Of course, given three helicities for each virtual photon with different $Q_i^2$, there are a plethora of physical quantities (six in number) that can be measured (4 cross sections $\sigma _{TT}; \sigma _{TL}; \sigma _{LT}; \sigma _{LL}$) and two interference terms ($\tau _{TT}; \tau _{TL}$), where T, L stand for transverse or longitudinal. Detailed expressions for these quantities and discussions can be found in two Phys. Rep. [472, 473].

Here, we shall just comment upon salient aspects of the two determinations at LEP of the total $\sigma (\gamma ^* \gamma ^* \rightarrow hadrons)$, the “cleanest” quantity that can be measured and compared to models. Both OPAL and L3 data were taken at $\sqrt{s_{e\bar{e}}} = (189\div 209)\ \mathrm{GeV}$, with similar hadronic mass $W > 5\ \mathrm{GeV}$ and mean $\langle Q^2\rangle \sim 18\ \mathrm{GeV}^2$ ranges. Figure 121 shows the OPAL extracted $\sigma ^{\gamma ^*\gamma ^*}$ as a function of the virtual photon c.m. energy W, compared with predictions from PHOJET (solid lines) and a Quark Parton Model (QPM) (green dotted lines). The Dual Parton Model (DPM) [67] is beneath the PHOJET [474, 475] event generator (PHOJET1.10) used to simulate double-tagged events and obtain the total luminosity $L_{TT}$, through which the two LEP measurements construct $\sigma (\gamma ^* \gamma ^* \rightarrow \hbox {hadrons})$. DPM contains both hard and soft processes. Hard processes are incorporated via LO QCD, and soft processes are included through a phenomenological analysis of $\gamma p$, $pp, p\bar{p}$ data assuming Regge factorisation.

The comparison with QCD models can be seen from the analysis by the L3 Collaboration, which we show in Fig. 122 from [469]. This figure shows that lowest order BFKL predictions for $\sigma (\gamma ^* \gamma ^* \rightarrow \hbox {hadrons})$ were rather large by a factor of about 20 or more. Subsequent phenomenological results from Next-to-Leading Order (NLO) have reduced this discrepancy by an order of magnitude. It appears that with theoretical improvements suggested in [476,477,478,479,480], the BFKL formalism can be reconciled with the two LEP measurements. However, no definite assessment can be given at present, short of higher energy data becoming available, as also discussed in [481], where further contributions from secondary Reggeon exchanges in QCD have been considered. An interested reader can find further description in the previous references.

Fig. 122

The above (Fig. 6 from [469]) shows the cross section measured by the L3 Collaboration for $\gamma ^*\gamma ^*\rightarrow \hbox {hadrons}$ as a function of the variable Y, for two different $\sqrt{s_{ee}}$ values, with corresponding average photon squared momentum, as indicated in the original figure caption. Reprinted from [469], ©(1999) with permission by Elsevier

7.11 Conclusions

Models for photon scattering probe yet another aspect of the total hadronic cross section, but the absence of data at very high energy, for instance $\sqrt{s}\ge 200~\mathrm{GeV}$ into the TeV region, does not allow for precise tests of model predictions at high energies, such as those probed for instance in cosmic ray experiments. The transition from real to virtual photons and from photons to hadrons are still rather model dependent. Planned future measurements, perhaps at LHC, or at future ep or $\mathrm{e}^+\mathrm{e}^-$ colliders, would shed further light on these transitions in the future.

8 LHC program for near forward physics

In this section, we describe the total and small angle cross section measurements that were programmed to be done at LHC.

Fig. 123

Schematic description of location of major experimental sites around the LHC ring, ATLAS is at IP1 and CMS at IP5

Our presentation of the measurements at LHC follows the extensive documentation prepared before the start of LHC [482,483,484,485,486,487]. Since then the LHC has started functioning and a wealth of results has appeared and updates of the LHC program are planned. An early comprehensive update about various planned experiments can be found in the proceedings of the Blois Workshop, held at CERN in June 2009 [488], as well as in presentations at DIFF2010 at Trento Workshop, ECT*. A recent review of measurements by TOTEM and ATLAS experiment can be found in [489]. For updates as of September 2016, an extensive set of presentations was done at the ECT* 2016 Workshop entitled Forward physics WG: diffraction and heavy ions, with slides available at: https://indico.cern.ch/event/568781/timetable/#al.

The experiment dedicated from the outset to measure the total cross section is the TOTEM experiment [482], but other measurements relevant to physics in the forward region have been and will continue to be performed by all the LHC experiments: ALICE [483], ATLAS [484], CMS [485], LHC-b [486] and LHCf [487]. In addition, these experiments have been providing data about the inelastic cross section, a component of $\sigma _{\mathrm{total}}$ crucial for a full understanding of the dynamics entering both $pp$ and cosmic ray data. Recent results concerning the inelastic total cross section at the present LHC energy of $\sqrt{s}= 13$ TeV, can be found in [490] for CMS and in [491] for ATLAS.

Various experiments study particle flows and diffractive physics through a number of detectors placed at various distances along the beam directions, with different physics goals. We show in Fig. 123 a schematic drawing of the positions of the main experiments around the LHC ring at various Interaction Points (IPs).

Fig. 124

Forward tracking at LHC through calorimeters placed at a distance of $({\sim } 10\div 20)~\hbox {m}$ from the interaction Point (IP)

At LHC the phase space range extends to 11 units in rapidity, since in the variable $y_{\max }=\ln \frac{\sqrt{s}}{m}\approx 9.6$. In the variable pseudo-rapidity, $\eta = - \ln \tan \frac{\theta }{2}$, where $\theta$ is the scattering angle of the detected particles, the coverage goes up to 12 or 13 units. The main CMS and ATLAS calorimeters measure energy deposited in the rapidity range $|\eta |< 5$, with particle detection and identification to be performed by the electromagnetic and hadronic calorimeters for $0<|\eta |<3$, and the hadronic forward (HF for CMS and FCal for ATLAS) calorimeters for $3<|\eta |<5.2$. In this region, data can also be collected by ALICE and LHC-B. For forward physics at LHC-B, see D’Enterria [492]. The forward calorimeters, however, cover only part of the forward region. With most of the energy deposited in the region $8<|\eta |<9$, other calorimeters are needed and placed near the beam. In this region, there is the LHCf experiment measuring particle flows, and the Zero Degree Calorimeters (ZDC) measuring neutral particles, while the extreme rapidity region, beyond $|\eta |=9$ will be covered by Roman Pots (RP), with TOTEM in CMS and ALFA in ATLAS.

Let us now look in more detail at particle detection in the forward region and to the system of detectors covering the rapidity region $|\eta |\simeq 3\div 7$. Up to a distance from the Interaction point (IP) of $(10\div 20)\ m$, as we show schematically in Fig. 124 the strategy is to surround the beam pipe with tracking calorimeters, as follows:

• ATLAS with MBTS, Minimum Bias Trigger Scintillator, at 3.6 m from the interaction point, a Hadronic Forward (FCal) calorimeter covering the region $3.1<|\eta |<4.9$ and LUCID, Luminosity Cerenkov Integrating Detector, a luminosity monitor at 17 m;

• CMS with the Hadronic Forward (HF) calorimeter placed at 11.2 m from the interaction point, covering the rapidity region $|\eta |<5.2$ (inner part for the region $4.5<|\eta |<5.0$), followed by CASTOR, Centauro And STrange Objects Research, which detects energy flows and is a Cerenkov calorimeter surrounding the beam pipe $(15\div 16.5)\ m$ from the interaction point, covering the range $5.2<|\eta |<6.6$ and dedicated to the observation of cascade developments;

• TOTEM with the two tracking detectors $T_1$ and $T_2$ which cover the region ($3.1\le |\eta |\le 6.5$).

Fig. 125

Schematic view of forward physics detectors in CMS, with T1 and T2 from the TOTEM experiment

Fig. 126

Interplay between forward detectors between CMS ZDC and TOTEM Roman Pots. Shown are distances in metres

These detectors are placed in such a way that it is easy to miss particles scattered in the very forward direction and they are implemented by dedicated set ups like Zero Degree Calorimeters and Roman Pots (RP). The Zero Degree calorimeters are placed at 140 meters from the interaction point and cover the rapidity range $|\eta |\ge 8.3$. The ZDC’s are for the detection of neutral particles such as neutrons, photons and $\pi ^0$ and are especially designed for heavy ions and diffractive physics. At a distance of 240 m from the IP3, there is ALFA, Absolute Luminosity For ATLAS, with Roman Pots, to be placed at an angle from the beam pipe of $3~\upmu \hbox {rad}$. In IP5, in the CMS region, after T1, T2, CASTOR and ZDC, there is TOTEM with the Roman Pots. At even longer distances, the High Precision Spectrometers at 420 m [493] dedicated to forward Higgs studies [494, 495].

8.1 The CMS region and cross section measurements

In Fig. 125 we show a schematic view of the layout of various forward physics detectors in and around CMS. A similar layout is found also in the ATLAS region.

We also show a pictorial view of the full set up of forward physics detectors in the CMS region in Fig. 126.

In the following we shall describe in more detail the forward physics and experimental layout of interest for total cross section and other forward physics measurements. We shall focus on TOTEM and ZDC, the two experiments and detectors in the CMS region where very forward scattering angles can be measured and total cross sections extracted.

8.1.1 TOTEM

As stated earlier, TOTEM is the experiment dedicated to the measurement of the total cross section [482]. It is based on the luminosity independent method, which uses both the measurement of the elastic scattering rate at the optical point, $t=0$, or as close as possible to it, as well as a measurement of the entire elastic and inelastic events rate through the two equations

$$\begin{aligned} \mathcal{L}\sigma _{\mathrm{total}}^2= & {} \frac{16\pi }{1+\rho ^2}\frac{\mathrm{d}N_{\mathrm{el}}}{\mathrm{d}|t|}|_{t=0},\end{aligned}$$

(8.1)

$$\begin{aligned} \mathcal{L} \sigma _{\mathrm{total}}= & {} N_{\mathrm{el}}+N_{\mathrm{inel}}, \end{aligned}$$

(8.2)

which lead to

$$\begin{aligned} \sigma _{\mathrm{total}}=\frac{16\pi }{1+\rho ^2} \frac{\mathrm{d}N_{\mathrm{el}}/\mathrm{d}|t|\ |_{t=0}}{N_{\mathrm{el}}+N_{\mathrm{inel}}}. \end{aligned}$$

(8.3)

The measurement of the elastic and inelastic rate is to be done through two detectors, named T1 and T2, placed symmetrically with respect to the CMS experiments. T1 and T2 are trackers embedded into the forward region of the CMS calorimeter, within a distance of 10.5 and $14~\hbox {m}$ from IP5 interaction point of the LHC. These detectors provide the reconstruction of charged tracks and cover a rapidity interval $3.1 \le |\eta |\le 6.5$, with T1 covering the interval $3.1<|\eta |<4.7$ and T2 the interval $5.3<|\eta |<6.5$.

While the measurement of the inelastic rate $N_{\mathrm{inel}}$ does not require special machine conditions, measurements in the very forward region do. The measurement of the differential elastic cross section near the optical point is done through the detection of very forward protons, with a technique known as Roman Pots (RPs) and used for the first time at the ISR [23]. The RPs are placed on the beam pipe of the outgoing beam at distances between 147 and $220~\hbox {m}$ from IP5 and host silicon detectors to be moved very close to the beam, inside the vacuum chamber of the accelerator.

The measurement at the optical point requires special LHC optics, in order to reach the lowest possible value for the momentum transfer t. For this one needs the beam divergence to be small compared with the scattering angle. We show in Fig. 127 a schematic description of the relation between beam size and beam divergence, where $\sigma _x$ and $\sigma _{\theta }$ are functions of the beam emittance $\epsilon$ and the beam divergence, i.e.

$$\begin{aligned} \sigma _x=\sqrt{\epsilon \beta _x^*},\end{aligned}$$

(8.4)

$$\begin{aligned} \sigma _{\theta }=\sqrt{\frac{\epsilon }{\beta _x^*}}. \end{aligned}$$

(8.5)

Physically, $\beta ^*$ is that distance from the focal point where the beam is twice as wide as at the focal point. The beam is “squeezed” or narrower if $\beta ^*$ is low, whereas the beam is “wide” and straight for large $\beta ^*$.

Fig. 127

A cartoon depicting the meaning of the quantity $\beta ^*$ and the relationship between beam size and beam divergence

Thus, the beam divergence ${\sim } 1/\sqrt{\beta ^*}$ is measured by the parameter $\beta ^*$, which needs to be as large as possible. This requires a special value for the parameter $\beta ^*=1540~\hbox {m}$. Since such a large value needs a special injection scheme, in the early stages of LHC operation (circa 2010), a less demanding option was planned with $\beta ^*=90~\hbox {m}$. At that time, the TOTEM Collaboration expected to be able to provide a measurement of the total cross section with a 5% error within the next 3 years, with values of the differential elastic cross section down to values of $|t|> 10^{-2}~\hbox {GeV}^2$. This measurement was to be based on the early optics conditions, $\beta ^*=90~\hbox {m}$ and a luminosity of $10^{29}\div 10^{30}~\hbox {cm}^{-2}~\hbox {s}^{-1}$. Under these conditions, TOTEM Collaboration estimated that about $65\%$ of forward protons would be detected. Later with $\beta ^*=1540~\hbox {m}$, one will be able to reach $|t|> 10^{-3}~\hbox {GeV}^2$ and, with about 90% of the diffractive protons seen in the detector, with an aim to obtain a measurement at the level of $1\%$.

As for the value of $\rho ={\mathfrak {I}m f(t=0)}/{\mathfrak {R}e f(t=0)}$, which we have discussed in earlier sections, it was taken to be $\rho =0.14$ following various predictions. This was considered adequate, since only the squared value for $\rho$ enters in the equation. From the analysis of the COMPETE Collaboration [287], we show a compilation of data and best fits as indicated in Fig. 128.

Fig. 128

Fits by the COMPETE Collaboration [287] show the wide range of expected results at LHC, due to the tension between data from various experiments at the Tevatron (and at $S\bar{p}pS$ as well). The figure is from [496], with total cross section data compared with various options for the high energy dependence. Figure is reproduced from [496], courtesy from J. Kaspar, TOTEM Collaboration

8.1.2 ZDC

Tuning at zero angle on neutrons, and detecting them with the zero degree calorimeter [497] at CMS, in addition to a number of diffractive physics measurements, there has also been the hope to measure $\pi ^+ p$ and $\pi ^+ \pi ^+$ total cross sections in an energy range inaccessible so far, namely in and around 1 TeV [498]. Information on diverse initial state particles and their relative rise with energy of $\sigma _{\mathrm{total}}$ is crucial for understanding the mechanisms behind the rise of the total cross section, whether or not there is a universal rise, and connections to perturbative QCD. Presently, data for $\pi p$ total cross section are only available in an energy range up to $25~\hbox {GeV}$ [263]. The situation for $\pi \pi$ is even less favourable. The mechanism proposed to measure these cross sections in the high energy range is shown in Figs. 129 and 130, namely through detection of neutrons in the very forward direction and production of pions through the charge exchange reaction.

Fig. 129

The charge exchange mechanisms proposed in [498] to measure the total $\pi p$ cross sectionat LHC

Fig. 130

The charge exchange mechanisms proposed in [498] to measure the total $\pi \pi$ cross sectionat LHC

As proof of the feasibility of such experiments, Petrov et al. [498] have extracted data for $\pi ^+ p$ cross section up to $50\div 70~\hbox {GeV}$ using neutron and photon spectra at previous experiments. The results are shown in Fig. 131 from [498], where extracted data points are compared with existing data from the Particle Data Group compilation (PDG) [263]. Also shown are two parametrisations, with full line by Donnachie and Landshoff [60] and dashes to indicate the fit by COMPETE also from [263].

Fig. 131

$\pi ^+p$ total cross section from [498], with both direct and extracted data points extracted with two parametrisations [60] (solid) and [263] (dashes). Reprinted with permission from [498] ©(2009) by Springer

We also show in Fig. 132 a comparison in this energy range between our model [149] and data, and fits from [498] as seen in Fig. 131, as well as comparison with fits by Block and Halzen [69]. The interest of such a measurement can be seen by going to very high energies, where the models differ substantially, as induced in Fig. 133. In the compilation shown in Figs. 132 and 133 (which differ in the energy range) we have plotted, together with the existing data, four predictions for $\pi ^+ p$ total cross section as follows:

Fig. 132

$\pi ^+p$ total cross section data with both direct and extracted data points from [498], compared with parametrisations from DL [60], COMPETE [263] (full), BH [69] and from our model, as indicated. Figure is reprinted from [149], ©(2010) with permission by Elsevier

Fig. 133

Predictions for $\pi ^{+} p$ total cross section in the LHC energy range from different models, as described in the text, and comparison with data on $\pi ^+ p$ total cross section. DL (dots) is from [60], BH (dashes) from [69], PDG COMPETE (full) [263] and PRS (stars) indicates extracted data from [498]. Figure is reprinted from [149], ©(2010) with permission by Elsevier

• a Regge–Pomeron fit from Donnachie and Landshoff [60]

  $$\begin{aligned} \sigma _{\pi ^+p}(\hbox {mb})=13.63 s^{0.0808}+27.56s^{-0.4525} \end{aligned}$$

  (8.6)

• the fit from the COMPETE Collaboration [263] given as

  $$\begin{aligned} \sigma _{\pi ^+p}= & {} Z^{\pi p}+B\ln ^2 \left( \frac{s}{s_0}\right) +Y_1^{\pi ^{+}p} \left( \frac{s_1}{s}\right) ^{\eta _1}\nonumber \\&-Y_2^{\pi {^+}p}\left( \frac{s_1}{s}\right) ^{\eta _2} \end{aligned}$$

  (8.7)

• a fit by Halzen and Block [69] of similar functional expression as the one from PDG, with an additional $\ln {s}$ term, i.e.

  $$\begin{aligned} \sigma ^{ab}= & {} c_0+c_1\ln {(\nu /m_\pi )}+c_2\ln ^2{(\nu /m_\pi )}\nonumber \\&+ \beta (\nu /m_\pi )^{\eta _1}+\delta (\nu /m_\pi )^{\eta _2} \end{aligned}$$

  (8.8)

  with numerical coefficients given by $c_0=20.11~{\hbox {mb}}$, $c_1 = -0.921~{\hbox {mb}}$, $c_2 = 0.1767~{\hbox {mb}}$, $\beta =54.4~{\hbox {mb}}$, $\delta = -4.51~{\hbox {mb}}$, $\eta _1 = -0.5$, $\eta _2 = -0.34$

• the eikonal mini-jet model with initial state soft-gluon $k_t$ resummation described in previous section, with GRV density functions for pion and proton and other parameters close to the values used for $\sigma _{\mathrm{tot}}^{pp}$, namely $p_{t\min }=(1.15\div 1.3)~\hbox {GeV}$, $p=0.75$ and $\varLambda =100~\hbox {MeV}$ in the soft resummation integral; in this model the low-energy data have been independently parametrised with the expression

  $$\begin{aligned} \sigma _{\pi ^+p} = A_0 + A_1\left[ \frac{1~\mathrm{GeV}}{E}\right] ^{\alpha _1} - A_2\left[ \frac{1~\mathrm{GeV}}{E}\right] ^{\alpha _2} \end{aligned}$$

  (8.9)

  with parameters $A_0 = 31.49~\hbox {mb}$, $A_1 = 58.56~\hbox {mb}$, $A_2 = 40.52~\hbox {mb}$, $\alpha _1 = 0.498$, $\alpha _2 = 0.297$.

8.2 The ATLAS region and forward physics

8.2.1 LHCf

LHCf is the smallest of the LHC experiments and is a detector placed at the ATLAS interaction point, with an independent acquisition system, very easy to correlate with ATLAS. The experimental set-up covers a very forward kinematics, $\eta > 8.4$, with angle from beam axis $\theta <450~\upmu \hbox {rad}$, with detection of very forward $\gamma 's$. Because of radiation problems, LHCf can, however, take data only at low machine luminosity and needs to be taken out in high luminosity running conditions.

The LHCf [499] experiment will measure the properties of neutral particles produced in the very forward region and compare them with expectations from the MonteCarlo simulation programs used in Cosmic Ray Physics. The experiment will use these forward particles from the collision to simulate cosmic rays of similar energies in laboratory conditions with particle energies at LHC, at $\sqrt{s}=14~\hbox {TeV}$, corresponding to laboratory energies of $10^{17}~\hbox {eV}$. The aim of this experiment is to clarify some phenomenological problems encountered in extracting physics from cosmic rays, among them a precise determination of the energy, nature and origin of the particles which initiated the Extensive Air Showers observed in cosmic ray experiments. By observing the energy deposition of controlled particles, like neutrons, $\pi ^0$’s and $\gamma$’s, and comparing their properties with the two most used MonteCarlo simulation programs, SYBILL [64, 500] and QGSJET [501], one can hope to resolve some outstanding questions in high energy cosmic ray physics [502, 503]. In cosmic ray physics, presently of great interest is to study the cosmic ray spectra in and around the GZK [504, 505] cut-off, expected to take place at $E_{lab}\approx 10^{19.5} \ eV$. Quite a long time ago, Greisen, Zatsepin and Kuzmin (GZK) predicted that at such energies the flux of cosmic rays could become too small to be observed. This effect corresponds to a reduction in the flux of primary cosmic ray protons once they reach an energy high enough to interact with the photons from the Cosmic Microwave Background (CMB) and produce the $\varDelta (1232)$-resonance, through $p+\gamma ^{CMB}\rightarrow \varDelta \rightarrow \pi p$. Were the cut-off not to be observed, the possibility of exotic sources could not be ruled out. While earlier measurements in the GZK cut-off region had not seen the cut-off, recently the observation of the cut-off has been reported by two experiments, Auger [506] and HiRes [507]. They both observe a decrease of the flux and a change in slope. Some contradictions still exist, as one can see from Fig. 134 from [508]. This figure shows that, even though both HiRES and Auger report the expected GZK flux reduction, there is still a difference in normalisation between their data.

Fig. 134

Results from measurement of the Ultra High Energy Cosmic Ray flux in the region of the GZK cut-off, from [508]. Reprinted from [508], ©(2010) with permission by Elsevier

8.2.2 ATLAS forward detectors

The positioning of ATLAS forward detectors is shown in Fig. 135, where ALFA indicates the detectors for Absolute Luminosity measurement, ZDC is the Zero Degree Calorimeter for ATLAS, LUCID is the LUminosity Cerenkov Integrating Detector. Not shown is MBTS, the minimum Bias Trigger Scintillator, closest to the IP.

Fig. 135

The positioning of ATLAS detectors for forward physics

One distinguishes the coverage of pseudo-rapidity in central and forward detectors regions. For ATLAS, in the central region, $|\eta |$ coverage is up to 2.5 for the inner tracker, 3.2 for the electromagnetic calorimeters, 4.9 for the hadronic calorimeters, and 2.7 for the muon spectrometer. The forward detectors cover rapidity intervals up to $|\eta |< 13.5$ as follows:

• MBTS $2.1< |\eta |<3.8$, is the Minimum bias trigger dedicated to diffractive physics measurements

• LUCID covering $5.6< |\eta |<5.9$, is the luminosity monitor, designed to measure luminosity up to $10^{33}~\hbox {cm}^{-2}~\hbox {s}^{-1}$, with a $3\div 5\%$ precision, is sensitive to charged particles pointing to the primary pp collision, and is needed to provide the minimum bias trigger at high values of pseudorapidity,

• ZDC a Zero Degree Detector, $|\eta |>8.3$, will measure production of neutral particles, $n,\gamma , \pi ^0$, in the forward direction and study both heavy ions and pp collisions,

• ALFA $10.6< |\eta |<13.5$ will measure the absolute luminosity and hadronic physics forward parameters.

The main method designed to measure the luminosity in ATLAS uses Roman Pots to make a reference measurement at low luminosity. This measurement will then be used to calibrate a monitor when luminosity is too high for use of the RPs. LUCID, the Beam Condition Monitor (BCM) and MBTS are the three detector systems for luminosity monitoring.

The very forward region in ATLAS is covered by Roman Pots (RP) which measure elastic pp scattering at the very small angles needed to extrapolate the differential elastic cross section to $t=0$, the optical point for total cross section measurements. As mentioned, this measurement requires special beam optics (high $\beta ^*$) and low luminosity, $L=10^{27}~\hbox {cm}^{-2}~\hbox {s}^{-1}$.

8.2.3 Roman POTS and the ALFA detector

The technique by which one measures the very forward scattering events to extract the differential elastic cross section in the very small t-region and thus the total cross section through the optical method, makes use of the so called Roman Pots. Roman Pots do not really look like pots from ancient Rome, where containers were of round “amphora-like” shape,¹⁰ and thus quite different from the cylindrical shape of the actual RPs. They get their name having been used by the Rome-Cern group at the ISR in the early 1970s and by their function. The actual detectors are cylindrical containers which are connected to the vacuum chamber of the accelerator through bellows. While the beam intensity is building up during injection, the RPs are retracted and do not enter the vacuum chamber. After the beams have stabilised and the collider has reached stable conditions, then the bellows are compressed and the detectors are pushed forward up to a distance of $1~\hbox {mm}$ from the beam. We show in Fig. 136 a schematic view of how the detectors will be placed near the beam so as to detect protons scattered at $|t|\approx 6.5 \times 10^{-4}~\hbox {GeV}^2$.

Fig. 136

A schematic view of the operation of RPs before and during data taking

For such small values of t one has the following relation between scattering angle and beam parameters:

$$\begin{aligned} |t_{\min }|=\frac{p^2}{\gamma }n_d^2\frac{\epsilon _N}{\beta ^*} \end{aligned}$$

(8.10)

where $n_d$ is the distance from the beam in units of beam size, $\epsilon _N$ is the normalised emittance. ALFA will be used to get an absolute measure of the luminosity by detecting protons in the Coulomb region with a sought for precision of 3%, an important improvement above the precision obtainable using machine parameters, which is not expected to be better than 20%. Such high precision is needed for precise determination of Higgs parameters and branching ratios.

The absolute measurement of the luminosity $\mathcal{L}$ is extracted from the differential event rate. Up to $|t|\approx 1~\hbox {GeV}^2$, the differential rate for elastic scattering, to first order in $\alpha$, can be written as

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}=\mathcal{L}\large \left[ \frac{4\pi \alpha ^2}{|t|^2}+\frac{\alpha \rho \sigma _{\mathrm{total}}\mathrm{e}^{-Bt^2/2}}{|t|}+\frac{\sigma _{\mathrm{total}}^2 (1+\rho ^2)\mathrm{e}^{-B|t|}}{16 \pi } \large \right] .\nonumber \\ \end{aligned}$$

(8.11)

By measuring this rate in the Coulomb region, i.e. below $|t|<10^{-3}$ $\mathrm{Ge}\mathrm{V}^2$, and after radiative corrections (see Sect. 4) the absolute luminosity can be extracted. In Fig. 137, we show a cartoon representation of the three regions, Coulomb, interference and purely hadronic, which can give information on various hadronic physics quantities of interest.

Fig. 137

A cartoon sketching the differential elastic cross section as a function of the momentum transfer |t|, showing how different t regions will give information on elastic and total scattering parameters. After presentation by A. Pilkington at Trento Workshop on Diffractive Physics, 4–8 January 2010, ECT*, Italy. Please notice that this figure is purely indicative and it is not in scale

8.3 Updates about LHC forward physics programs

In addition to what already mentioned at the beginning of this section, the interested reader can find descriptions of updates for LHC forward physics presented by various groups, such as a Workshop on High Energy Scattering at Zero Degree held in March 2013 at Nagoya University in Japan. The slides of all the talks at Nagoya as well as presentations at Marseille and Paris in France; at Trento and Reggio Calabria in Italy; CERN, Switzerland; Barcelona, Spain; and at Eilat, Israel, and more, can all be found at: totem.web.cern.ch/Totem/conferences/conf_tab2013.html, et sim. for 2014, 2015, 2016. By comparing these reports with what we have presented here, and which follow the plan as of 2008, one can see the great progress of these years and expect with confidence that future measurements will further reduce errors and clarify many issues.

Indeed considerable progress has been made in the beam optics and proper functioning of various detectors so much so that now we have rather precise data on total, elastic and inelastic cross sections, elastic differential cross sections and various diffractive results in different regions of phase space. Many of these results have been used and discussed throughout this review. For example, using dedicated beam optics and the Roman Pots, at $\sqrt{s} = 8~\hbox {TeV}$, TOTEM at the end of 2012 gives the following values [103]:

$$\begin{aligned} \sigma _{\mathrm{tot}}(8~\hbox {TeV}) = (101.7 \pm 2.9)~\hbox {mb};\nonumber \\ \sigma _{\mathrm{el}}(8~\hbox {TeV}) = (27.1 \pm 1.4)~\hbox {mb};\nonumber \\ \sigma _{\mathrm{in}}(8~\hbox {TeV}) = (74.7 \pm 1.7)~\hbox {mb}. \end{aligned}$$

(8.12)

Thus, the total cross section has been measured with less than $3\%$ error better than the estimated error, after a 3 year run, of $5\%$. An overview of all the measurements of total, inelastic, elastic and diffractive cross sections inclusive of data up to 2016 is presented in Fig. 138.

Fig. 138

A compilation of LHC data on the total, inelastic, elastic and diffractive cross sections, as of September 2016. Superimposed curves correspond to the BN model described in Sect. 6.7 for the total and non-diffractive inelastic cross section, and in Sect. 6.3.1 for the elastic cross section, as in the updated version from [303]. A band has been drawn to drive the eye for the Single and Double Diffraction data. This figure is courtesy of D. Fagundes, A. Grau and Olga Shekhovtsova

9 Conclusions

Huge progress has been made over the past several decades, both experimentally and theoretically, on the subject of high energy total and differential cross sections. In this review we have attempted to outline these developments from early accelerator measurements in the 1950s with fixed target experiments up to proton–proton scattering at the CERN Large Hadron Collider, and beyond, where cosmic ray interactions reach energies as high as 100 TeV in the proton–proton center of mass.

In proton–proton scattering, two milestones stand out, the first of them concerning the energy dependence of the total cross section. The increase with energy of the total cross section is now fully confirmed, and ascribable to the appearance of parton–parton scattering, although questions regarding asymptotia and whether the Froissart bound is saturated, are still under debate. The second milestone is the LHC confirmation of the dip in the differential proton–proton elastic cross section, which had not been observed since the CERN Intersecting Storage Ring experiments in the early 1970s. Experiments at the CERN $S\bar{p}pS$ and at the Tevatron in FermiLab have given hints that the presence of the dip in proton–antiproton scattering may be revealed as higher and higher energies are reached, but confirmation of the dip in this channel needs higher energy experiments which are not presently planned. During the same decades, a large set of measurements were performed at HERA in DESY, using both real and virtual photons on nucleons and nuclei to obtain total and production cross sections for $\gamma p$, $\gamma ^* p$, and through $\mathrm{e}^+\mathrm{e}^-$ machine at LEP for $\gamma \gamma *$ and $\gamma ^* \gamma ^*$ final states. These results are mostly complementary to those from purely hadronic machines and have led to remarkable theoretical developments such as Bjorken scaling, the parton model and various dynamical evolution equations.

From the theoretical point of view, our review spans from Heisenberg’s model to the rich descriptions which have been developed in more than 60 years in terms of QCD, Reggeon field theory, mini-jets, among others. The amount of material on the subject is so huge, that some selection was indispensable. Hence, we are aware that we could not always acknowledge or survey all the work done during the past 50–60 years in a quest of understanding the dynamics underlying the hadronic cross sections.

We have gathered and presented the material which we could relate to and understand. Hence, we apologise to those scientists whose work we may not have recognised adequately. Many excellent reviews on the subject have been written during the past decades that are complementary to our largely historical perspective.

All together, we hope that our work may shed light on the fascination that the subject has held for so many scientists for so many years and that shall continue to fascinate in the future through further results from LHC and cosmic ray experiments.

10 Note about reproduction of other authors’ figures

As indicated in the figure captions, many figures in this review have been extracted from articles published in journals or posted on the web site inSPIRE.

Permission from the publisher was obtained for all the figures, as indicated in the figure captions. We thank all the authors, whose figures we have reproduced. We thank many colleagues who provided us with the original files for the figures extracted from their papers. For figures coming from articles with a large number of authors, we secured permission from the spokesman of the collaboration. In all cases we thank our colleagues from these collaborations for their permission to reproduce these figures.