1 Introduction

The possibility that standard energy-momentum dispersion relations are modified near the Planck scale is one of the scenarios in quantum gravity phenomenology [1, 2]. Such a modified dispersion relation (MDR) was also advocated by the study of nonlinear deformed or doubly special relativity (DSR) [3, 4] in which the Planck length as well as the speed of light is an observer invariant quantity. In particular, Magueijo and Smolin [5, 6] have extended the DSR to general relativity by proposing that the spacetime background felt by a test particle would depend on its energy \(\omega \). Such an energy of the test particle deforms the background geometry and consequently the MDR as

$$\begin{aligned} \omega ^2 f(\omega /\omega _p)^2-p^2 g(\omega /\omega _p)^2=m^2, \end{aligned}$$
(1.1)

where p, m, \(\omega _p\) are the momentum, the mass of the test particle, and the Planck energy, respectively. Thus, quanta of different energies see different background geometry, which is referred to as a rainbow gravity. Since then many efforts have been made devoted to the rainbow gravity related to the gravity and other stimulated work at the Planck scale [7–26].

In connection with black hole thermodynamics in the rainbow gravity, there have also been much work with the following rainbow functions [1, 2, 27–35]:

$$\begin{aligned} f(\omega /\omega _p)=1, \quad g(\omega /\omega _p)=\sqrt{1-\eta \left( {\omega }/{\omega _p}\right) ^n}, \end{aligned}$$
(1.2)

which belong to the most interesting MDRs related to quantum gravity phenomenology among several other types [5, 15, 22, 36–52]. Here, n is a positive integer, \(\eta \) a constant of order unity, and these functions satisfy with \(\lim _{\omega \rightarrow 0} f(\omega /\omega _p) = 1\) and \(\lim _{\omega \rightarrow 0} g(\omega /\omega _p) = 1\) at low energies. In particular, Li et al. [44] have obtained the Schwarzschild–AdS black hole solution in the framework of rainbow gravity with different rainbow functions from Eq. (1.2), and investigated thermodynamic stability without the analysis of phase transition. Recently, Gim and Kim (GK) [53] have shown that the Schwarzschild black hole in the rainbow gravity in an isothermal cavity has an additional Hawking–Page phase transition near the event horizon apart from the standard one, which is of relevance to the existence of a locally small black hole.

On the other hand, an approach of the higher dimensional flat embedding is used to study a local temperature for a freely falling observer outside black holes [54, 55]. And very recently, we have shown that a local temperature seen by a freely falling observer depends only on \(g(\omega /\omega _p)\) [56] so that the choice of \(f(\omega /\omega _p)=1\) makes not only the time-like Killing vector in the rainbow Schwarzschild black hole as usual, but also it makes the local thermodynamic energy independent of the test particle’s energy.

In this paper, we would extend GK’s work of the Schwarzschild black hole in the rainbow gravity to the Schwarzschild–AdS spacetime. In order to study efficiently, we shall describe thermodynamics by using an event horizon \(r_+\) as a variable instead of the mass M as in GK’s work, since in the Schwarzschild–AdS black hole it is difficult to solve for the event horizon as a function of the mass. In Sect. 2, black hole temperature for the Schwarzschild–AdS black hole in the rainbow gravity will be calculated from the definition of the standard surface gravity. Then, making use of the MDR and the Heisenberg uncertainty principle, the energy dependence of a test particle in black hole temperature will be properly rephrased. And the entropy will be derived from the first law of thermodynamics. In Sect. 3, we will study local thermodynamic quantities including temperature, energy and heat capacity in an isothermal cavity with their various limits for each other’s comparison. Furthermore, in order to clearly reconfirm thermodynamic stability, we also analyze constant temperature slices of the Schwarzschild(–AdS) black hole in the rainbow gravity. In Sect. 4, we will study phase transition between various black hole states and the hot flat space through investigating free energies of the Schwarzschild–AdS black hole in the rainbow gravity. Finally, conclusion and discussion will be given in Sect. 5.

2 Temperature and entropy of Schwarzschild–AdS black hole in rainbow gravity

Let us consider the modified Schwarzschild–AdS black hole in rainbow gravity described as [44]

$$\begin{aligned} \mathrm{d}s^2= & {} -\frac{N^2}{f^2(\omega /\omega _p)}\mathrm{d}t^2\nonumber \\&+\frac{1}{g^2(\omega /\omega _p) N^2}\mathrm{d}r^2+\frac{r^2}{g^2(\omega /\omega _p)} \mathrm{d}\Omega ^2, \end{aligned}$$
(2.1)

where

$$\begin{aligned} N^2 = 1-\frac{2G_0M}{r} + \frac{r^2}{l^2_0}. \end{aligned}$$
(2.2)

This is a spherically symmetric solution to the modified field equation in rainbow gravity of

$$\begin{aligned}&G_{\mu \nu }(\omega /\omega _p)+\Lambda (\omega /\omega _p)g_{\mu \nu }(\omega /\omega _p)\nonumber \\&\quad =8\pi G(\omega /\omega _p) T_{\mu \nu }(\omega /\omega _p) \end{aligned}$$
(2.3)

in the absence of matter. Here, \(G_{\mu \nu }(T_{\mu \nu })\) is the Einstein (energy-momentum) tensor, \(G(\omega /\omega _p)(\Lambda (\omega /\omega _p))\) is an energy-dependent Newton (cosmological) constant, and \(G_0(\Lambda _0=-3/l^2_0)\) is the physical Newton (cosmological) constant at the low-energy limit of \(\omega /\omega _p\rightarrow 0\). Here, the energy \(\omega \)-dependent constants are related with the physical ones as

$$\begin{aligned} G(\omega /\omega _p)= & {} \frac{G_0}{g(\omega /\omega _p)},\nonumber \\ \Lambda (\omega /\omega _p)= & {} -\frac{3}{l^2(\omega /\omega _p)}=g^2(\omega /\omega _p)\Lambda _0. \end{aligned}$$
(2.4)

Note that the solution reduces to the usual Schwarzschild–AdS vacuum solution

$$\begin{aligned} \mathrm{d}s^2=-N^2\mathrm{d}t^2+\frac{1}{N^2}\mathrm{d}r^2+r^2 \mathrm{d}\Omega ^2 \end{aligned}$$
(2.5)

in the low-energy limit of \(\omega /\omega _p\rightarrow 0\). The mass defined by \(N^2=0\) is given by

$$\begin{aligned} M(r_+)=\frac{r_+}{2G_0}\left( 1+\frac{r^2_+}{l_0^2}\right) \end{aligned}$$
(2.6)

with the event horizon \(r_+\).

Then the modified Hawking temperature \(T_\mathrm{H}\) is obtained,

$$\begin{aligned} T_\mathrm{H}= \frac{\kappa _\mathrm{H}}{2\pi } = \frac{g(\omega /\omega _p)}{f(\omega /\omega _p)}T^0_\mathrm{H}, \end{aligned}$$
(2.7)

from the surface gravity \(\kappa _H\) at the event horizon as follows:

$$\begin{aligned} \kappa _\mathrm{H}=-\frac{1}{2}\lim _{r\rightarrow r_+}\sqrt{\frac{-g^{11}}{g^{00}}}\frac{(g^{11})'}{g^{00}}. \end{aligned}$$
(2.8)

Here, the standard Hawking temperature \(T^0_\mathrm{H}\) of the Schwarzschild–AdS black hole is given by

$$\begin{aligned} T^0_\mathrm{H} = \frac{1}{4\pi }\left( \frac{1}{r_+}+\frac{3r_+}{l_0^2}\right) . \end{aligned}$$
(2.9)

Making use of the explicit rainbow functions (1.2), the black hole temperature can be written as

$$\begin{aligned} T_\mathrm{H} =\sqrt{1-\eta (\omega /\omega _p)^n}T^0_\mathrm{H} \end{aligned}$$
(2.10)

so that the temperature depends on the energy \(\omega \) of a probe.

Fig. 1
figure 1

The modified Hawking temperatures of the Schwarzschild–AdS black hole in the rainbow gravity for \(\eta =1\) (solid line) and for the upper bound of \(\eta =49/6\) (thick line) with \(l_0=7\), \(G_0=1\), and the standard Hawking temperature (dashed line) with \(l_0=7\)

Full size image

Now, in order to eliminate the \(\omega \) dependence of the probe in the modified Hawking temperature (2.10), one can use the Heisenberg uncertainty principle (HUP) as in Ref. [53]. In the vicinity of the black hole surface, an intrinsic position uncertainty \(\Delta x\) of the probe of order of the event horizon \(r_+\) leads to a momentum uncertainty of order of p [57] as

$$\begin{aligned} p= \Delta p \sim \frac{1}{r_+}. \end{aligned}$$
(2.11)

Plugging the momentum uncertainty into the MDR (1.1), one can determine the energy \(\omega \). We explicitly show this by choosing \(n=2\) in the rainbow functions (1.2) without loss of generality. Then the energy for the massless particle can be solved as

$$\begin{aligned} \omega = \frac{\omega _p}{\sqrt{\eta +{r^2_+}\omega _p^2 }}. \end{aligned}$$
(2.12)

Therefore, one can rewrite the black hole temperature (2.10) as

$$\begin{aligned} T_\mathrm{H}=\frac{r_+}{\sqrt{{r^2_+}+\eta G_0}}T^0_\mathrm{H}, \end{aligned}$$
(2.13)

with \(\omega _p^2=1/G_0\). When \(\eta =0\), it is just the standard Hawking temperature of the Schwarzschild–AdS black hole. Note that as \(r_+\rightarrow 0\), it becomes finite as \(T_H=1/(4\pi \sqrt{\eta G_0})\). This result implies that the standard divergent Hawking temperature of the Schwarzschild–AdS black hole could be regularized in the rainbow gravity as like in the Schwarzschild case [53]. In Fig. 1, we have plotted the modified and the standard Hawking temperatures showing that the former is finite at \(r_+=0\) due to the rainbow gravity effect while the latter blows up.

It seems appropriate to comment that the modified Hawking temperature has its minimum

$$\begin{aligned} T^m_\mathrm{H}=\frac{\sqrt{3}}{2\pi l_0}\sqrt{1-\frac{3\eta G_0}{l^2_0}} \end{aligned}$$
(2.14)

at \(r_+=\frac{l_0}{\sqrt{3}}\sqrt{1-\frac{6\eta G_0}{l_0^2}}\). Moreover, the upper bound for the parameter \(\eta <l_0^2/6 G_0\) is required for \(r_+\) being real. In Fig. 1, the thick line is for \(\eta =l^2_0/6G_0\) where \(r_+\) is zero and the curve has its minimum.

Next, from the first law of black hole thermodynamics, one can obtain the entropy:

$$\begin{aligned} S=\int \frac{\mathrm{d}M}{T_H}=\frac{\pi r_+}{G_0}\sqrt{r^2_+ + \eta G_0} + \pi \eta \sinh ^{-1}\left( \frac{r_+}{\eta G_0}\right) . \end{aligned}$$
(2.15)

Here, we have chosen the integration constant to be satisfied with \(S\rightarrow 0\) as \(r_+\rightarrow 0\). This is the exactly same form with the entropy of the Schwarzschild black hole in the rainbow gravity [53], but explicitly different in \(r_+\). This is nothing new since we know that the standard Schwarzschild black hole and the Schwarzschild–AdS black hole also have the same form of entropy of \(S=\pi r^2_+\), but different in \(r_+\). Moreover, in the standard Schwarzschild–AdS limit of \(\eta =0\), the entropy (2.15) becomes one-fourth of the area of the event horizon \(S=A/4G_0\). Note that the next leading order is logarithmic as \(S \approx A/4G_0+\frac{1}{2}\pi \eta \ln (A/4)\), which is reminiscent of the quantum correction to the entropy [58–62]. From these, one can see that the rainbow metric contributes to the quantum corrected metric.

At this stage, it is appropriate to comment on the choice of \(n=2\) in the rainbow functions (1.2), which makes us analytically solve the MDR (1.1) and eventually gives the logarithmic correction to the entropy. If not, it would be difficult to solve the MDR first, and then have another forms of correction without the logarithmic term to the entropy [32].

3 Schwarzschild–AdS black hole thermodynamics in rainbow gravity

Now, let us study Schwarzschild–AdS black hole thermodynamics in rainbow gravity. In order for the study to be focused and feasible, we take the rainbow functions (1.2) with \(n=2\).

We would like to consider a local observer who is at rest at the radius r, which we mean to introduce a spherical cavity enclosing the Schwarzschild–AdS black hole. Then the local temperature \(T_\mathrm{{loc}}\) seen by the local observer can be obtained:

$$\begin{aligned} T_\mathrm{{loc}} =\frac{T_H}{\sqrt{-g_{00}}} = \frac{\frac{1}{4\pi }\left( \frac{1}{r_+}+\frac{3r_+}{l_0^2}\right) \sqrt{\frac{r^2_+}{r^2_+ + \eta G_0}}}{\sqrt{1-\frac{r_+}{r}\left( 1+ \frac{r^2_+}{l^2_0}\right) +\frac{r^2}{l_0^2}}} \end{aligned}$$
(3.1)

by implementing the redshift factor of the metric [63].

Before proceeding further, let us briefly look into the limits of the modified Hawking temperature (2.13) and local temperature (3.1) of the Schwarzschild–AdS black hole in the rainbow gravity enclosed in a cavity. First, by turning off the rainbow gravity, in the Schwarzschild–AdS limit of \(\eta \rightarrow 0\), the standard Hawking and local temperatures will be

$$\begin{aligned} T^\mathrm{SAdS}_\mathrm{H}= & {} \frac{1}{4\pi }\left( \frac{1}{r_+}+\frac{3r_+}{l_0^2}\right) ,\end{aligned}$$
(3.2)
$$\begin{aligned} T^\mathrm{SAdS}_\mathrm{loc}= & {} \frac{\frac{1}{4\pi }\left( \frac{1}{r_+}+\frac{3r_+}{l_0^2}\right) }{\sqrt{1-\frac{r_+}{r}\left( 1+ \frac{r^2_+}{l^2_0}\right) +\frac{r^2}{l_0^2}}}, \end{aligned}$$
(3.3)

and in the Schwarzschild limit of \(l^2_0\rightarrow \infty \) as well as \(\eta \rightarrow 0\), those become

$$\begin{aligned} T^\mathrm{Sch}_\mathrm{H}= & {} \frac{1}{4\pi r_+}, \end{aligned}$$
(3.4)
$$\begin{aligned} T^\mathrm{Sch}_\mathrm{loc}= & {} \frac{1}{4\pi r_+\sqrt{1-\frac{r_+}{r}}}. \end{aligned}$$
(3.5)
Fig. 2
figure 2

Temperatures for a the Schwarzschild black hole, b the Schwarzschild black hole enclosed in a cavity, c the Schwarzschild–AdS black hole, and d the Schwarzschild–AdS black hole enclosed in a cavity

Full size image
Fig. 3
figure 3

Specific heats for a the Schwarzschild black hole, b the Schwarzschild black hole enclosed in a cavity, c the Schwarzschild–AdS black hole, and d the Schwarzschild–AdS black hole enclosed in a cavity

Full size image
Fig. 4
figure 4

Constant temperature slices of the Schwarzschild black hole confined within a cavity

Full size image

For the sake of a detailed discussion, their corresponding specific heats can also be written down as

$$\begin{aligned}&C^\mathrm{SAdS}=-\frac{2\pi r^2_+}{G_0}\left( \frac{l^2_0+3r^2_+}{l^2_0-3r^2_+}\right) ,\end{aligned}$$
(3.6)
$$\begin{aligned}&C^\mathrm{SAdS}_\mathrm{loc}\nonumber \\&\quad =\frac{4\pi r^2_+(r-r_+)(l^2_0+r^2+rr_++r^2_+)(l^2_0+3r^2_+)}{G_0\left[ r_+(3l^4_0+2l^2_0r^2_++3r^4_+)-2r(l^2_0+r^2)(l^2_0-3r^2_+)\right] }\nonumber \\ \end{aligned}$$
(3.7)

for the Schwarzschild–AdS black hole, and

$$\begin{aligned} C^\mathrm{Sch}= & {} -\frac{2\pi r^2_+}{G_0},\end{aligned}$$
(3.8)
$$\begin{aligned} C^\mathrm{Sch}_\mathrm{loc}= & {} -\frac{4\pi r^2_+}{G_0}\left( \frac{r-r_+}{2r-3r_+}\right) \end{aligned}$$
(3.9)

for the Schwarzschild black hole. Here, the subscript ‘loc’ indicates that the specific heat is obtained from a black hole enclosed in a cavity.

Figure 2a shows the standard Hawking temperature (3.4) of the Schwarzschild black hole which becomes zero as \(r_+\) goes to infinity, while it diverges as \(r_+\) goes to zero. If it is enclosed in a cavity, the local temperature at the cavity (3.5) goes up to infinity. This cavity makes the black hole thermodynamically well defined. Then this thermodynamic stability can easily be seen if one examines the specific heat of T(dS / dT) as in Fig. 3. In Fig. 3a, one sees the negative specific heat as given in Eq. (3.8), which indicates that the Schwarzschild black hole is unstable. On the other hand, as seen in Fig. 3b, the Schwarzschild black hole in the cavity has an asymptote at \(r_+=2r/3\), which is obtained from the condition of \(\mathrm{d}T_\mathrm{loc}/\mathrm{d}r_+=0\), and if \(r_+\) is larger than 2r / 3, the black hole is stable. More precisely, if \(r_+ T_\mathrm{loc}\ge \sqrt{3}/4\pi \), there are two possible solutions in which the larger one is stable while the smaller one is unstable as shown in Figs. 2b and 3b. The equality occurs if the temperature is the minimum at \(r_+=2r/3\). Below the minimum temperature there is no black hole solution. These can be reconfirmed by analyzing constant temperature slices [64] of the Schwarzschild black hole confined in a cavity in Fig. 4a, b, which are obtained by solving Eq. (3.5) in terms of \(r_+\) at a constant temperature. In the diagram, one can easily see that thermodynamic stability is in between \(2r/3<r_+<r\). The turning points of the curves satisfying with \(r_+ T_\mathrm{loc}=\sqrt{3}/4\pi \) remain on the line \(r_+=2r/3\). Two solutions of the Schwarzschild black hole in the cavity are possible to the right of this point, one above the line and one below it. They would meet if a given temperature equals the minimum temperature. For a higher cavity temperature, the constant temperature curve shifts to the left, and for a lower cavity temperature it shifts to the right.

Compared with the standard Schwarzschild black hole, which is asymptotically flat, the temperatures and specific heats of the Schwarzschild–AdS black hole, which is not asymptotic flat, are depicted in Figs. 2 and 3c, d. When compared the Hawking temperature in Fig. 2c with the local temperature in Fig. 2b, one can see that they show the same behavior with each other except that in the case of Fig. 2c the cavity seems to be located at infinity. Thus, the asymptotically AdS geometry naturally plays the role of a cavity. The real positive solutions of the Schwarzschild–AdS black hole can be obtained when \(r_+T_\mathrm{H}\ge 1/2\pi \), where the equality takes place if the temperature is the minimum at \(r_+=l_0/\sqrt{3}\) (\(\eta =0\) case). The larger solution is locally stable and has a positive specific heat, while the smaller solution is unstable and has a negative specific heat as in Figs. 2, 3c.

If the Schwarzschild–AdS black hole is enclosed in a cavity, the local temperature (3.3) and specific heat (3.7) are depicted as in Figs. 2, 3d. As \(r_+\) approaches the radius r of the cavity, the local temperature goes up to infinity, and the specific heat to zero. This is also the case for the Schwarzschild black hole enclosed in the cavity, which can be seen through the factor of \(C\sim (r-r_+)\) in Eqs. (3.7) and (3.9), while the specific heat of the standard Schwarzschild–AdS black hole diverges as in Fig. 3c.

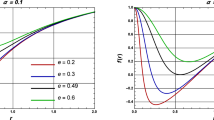
Now, let us go back to the local temperature (3.1), which is seen by the observer at r, is depicted in Fig. 5 where the local temperature of the Schwarzschild–AdS black hole in the rainbow gravity enclosed in a cavity was also drawn for the purpose of comparison, which is divergent as \(r_+\rightarrow 0\).

Fig. 5
figure 5

Local temperature of the Schwarzschild–AdS black hole in the \(\eta =1\) rainbow gravity enclosed in a cavity (solid line) and the standard local temperature of the Schwarzschild–AdS black hole (dotted line) with \(r=10\), \(l_0=7\). Here, \(T_m\) is globally minimum, \(T_M\) is locally maximum, and \(T_0\) is the temperature at \(r_+=0\)

Full size image
Fig. 6
figure 6

Heat capacity of the Schwarzschild–AdS black hole in the \(\eta =1\) rainbow gravity enclosed in the cavity with \(r=10\), \(l_0=7\), \(G_0=1\), where \(r_U\) is the upper bound of the event horizon \(r_+\)

Full size image

Figure 5 is also different from Fig. 1 in that this is the local temperature seen by a local observer at r but not the modified Hawking temperature seen by an observer at the asymptotic infinity. One can see in the figure that for a fixed r the local temperature is divergent as \(r_+\) approaches r, which is the same as the local temperature of the Schwarzschild–AdS black hole. We also observe that there exist a global minimum temperature \(T_m\) at \(r=r_m\), and a local maximum temperature \(T_M\) at \(r=r_M\). Moreover, the temperature remains finite as \(r_+\rightarrow 0\) with \(T_0=1/(4\pi \sqrt{\eta G_0(1+r^2/l^2_0)})\). Thus, as a result of the introduction of the rainbow gravity, one can observe both the existence of the local maximum temperature near the origin and the finiteness of the local temperature at the origin, which were first shown in Ref. [53]. However, we also note that these were originally absent in the modified Hawking temperature (2.13) as in Fig. 1.

Next, making use of the entropy (2.15) and the local temperature (3.1), the thermodynamic first law yields the energy \(E_\mathrm{{tot}}\) as

$$\begin{aligned} E_\mathrm{{tot}}= & {} \int ^{r_+}_{0} T_\mathrm{{loc}} \mathrm{d}S \nonumber \\= & {} \frac{r}{G_0}\left( \sqrt{1+\frac{r^2}{l_0^2}} -\sqrt{\left( 1-\frac{r_+}{r}\right) +\frac{1}{ l_0^2} \left( r^2-\frac{r^3_+}{r}\right) }\right) .\nonumber \\ \end{aligned}$$
(3.10)
Fig. 7
figure 7

Constant temperature slice of the Schwarzschild–AdS black hole in the rainbow gravity confined within a cavity. Here, we choose \(T=0.04564\) as an external cavity temperature where there exist three black hole states

Full size image

To investigate thermodynamic stability of the Schwarzschild–AdS black hole in the rainbow gravity, we calculate the heat capacity as

$$\begin{aligned}&C =\frac{\partial E_\mathrm{{tot}}}{\partial T_\mathrm{{loc}}} \nonumber \\&= \frac{4\pi r^2_+(r-r_+)\left( l_0^2+r^2+rr_++r^2_+\right) \left( l_0^2+3r^2_+\right) \left( 1+\eta \frac{G_0}{r^2_+}\right) ^\frac{3}{2}}{G_0H(r_+,r,\eta ,G_0)}\nonumber \\ \end{aligned}$$
(3.11)

with

$$\begin{aligned}&H(r_+,r,\eta ,G_0)= r_+\left( 3l^4_0+2l^2_0r^2_++3r^4_+\right) \nonumber \\&\quad -2r\left( l^2_0+r^2\right) \left( l^2_0-3r^2_+\right) \nonumber \\&\quad - \eta G_0\left[ 3\left( r^3_+- 4 r^3\right) +6l_0^2\left( r_+-2r\right) -\frac{l_0^4}{r_+}\right] . \end{aligned}$$
(3.12)

When \(\eta \rightarrow 0\), it becomes the specific heat (3.7) for the standard Schwarzschild–AdS black hole in the cavity, and when taking the radius r of the cavity to infinity, it becomes the specific heat (3.6) for the Schwarzschild–AdS black hole. Moreover, when \(l_0\rightarrow \infty \) as well as \(\eta \rightarrow 0\), it reduces to the specific heat (3.9) for the Schwarzschild black hole in the cavity, and with the radius of the cavity as \(r\rightarrow \infty \), it becomes the specific heat (3.8) for the standard Schwarzschild black hole. In Fig. 6 the specific heat is plotted as a function of \(r_+\) and it shows three qualitatively different regions, two stable and one unstable states of the black hole. Specifically, when \(r_+>r_m\), the specific heat is positive so that the black hole is stable, which we will call the large stable black hole (LSB), when \(r_M<r_+<r_m\), it is negative, so the black hole unstable, the intermediate unstable black hole (IUB), and when \(0<r_+<r_M\), it is again positive, and we call it as the small stable black hole (SSB). Note that the SSB appears in the very vicinity of the vanishing event horizon.

In Fig. 7, it shows constant temperature slices of the Schwarzschild–AdS black hole in the rainbow gravity confined in the cavity. Compared with Fig. 4, one can reconfirm that there is also a fine structure near the vanishing event horizon due to the appearance of the local maximum temperature as well as the finiteness of the temperature at the origin, which is enlarged separately in the right-hand side of the diagram. From this figure, we see that the thermodynamic states of the Schwarzschild–AdS black hole in the rainbow gravity confined in the cavity are divided into three regions; region I with positive specific heat which corresponds to the LSB, region II with negative specific heat to the IUB, and region III again with positive specific heat to the SSB, respectively.

4 Free energy and phase transition

Now, let us study the thermodynamic phase transition [65–67]. The on-shell free energy of the Schwarzschild–AdS black hole in the rainbow gravity enclosed in a cavity is obtained by the use of the local temperature \(T_\mathrm{loc}\) in Eq. (3.1) and the thermodynamic energy \(E_\mathrm{tot}\) in Eq. (3.10), explicitly as

$$\begin{aligned} F_\mathrm{{on}}= & {} E_\mathrm{tot}-T_\mathrm{loc}S \nonumber \\= & {} \frac{r}{G_0}\left( \sqrt{1+\frac{r^2}{l^2_0}} -\sqrt{\left( 1-\frac{r_+}{r}\right) +\frac{1}{ l_0^2}\left( r^2-\frac{r^3_+}{r}\right) }\right) \nonumber \\&-\frac{r_+\left( 1+\frac{3r^2_+}{l^2_0}\right) }{4G_0\sqrt{\left( 1-\frac{r_+}{r}\right) +\frac{1}{l_0^2}\left( r^2-\frac{r^3_+}{r}\right) }}\nonumber \\&\times \, \left( 1+\frac{\eta G_0\sinh ^{-1}\left( \frac{r_+}{\eta G_0}\right) }{r^2_+\sqrt{1+\frac{\eta G_0}{r^2_+}}}\right) , \end{aligned}$$
(4.1)

where S is the entropy in Eq. (2.15). When \(\eta =0\), it becomes the on-shell free energy of the Schwarzschild–AdS black hole enclosed in a cavity. Furthermore, when \(l_0\rightarrow \infty \), it recovers the on-shell free energy of the Schwarzschild black hole enclosed in a cavity. In order to understand the phase transition, we also need to introduce off-shell free energy, which is composed of a set of saddle points of the on-shell free energies as

$$\begin{aligned} F_\mathrm{{off}}= E_\mathrm{tot}-T S. \end{aligned}$$
(4.2)

Here, \(E_\mathrm{tot}\) and S are the same as before, while T is an external temperature of heat reservoir to control the phase transition.

Fig. 8
figure 8

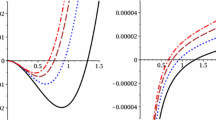
On-shell (solid line) and off-shell (dashed line) free energies \(F(r_+)\) of the Schwarzschild–AdS black hole in the \(\eta =1\) rainbow gravity enclosed in the cavity with \(r=10\), \(l_0=7\), \(G=1\), where \(T_m\) is global minimum, \(T_M\) local maximum temperature, \(T_0\) at \(r_+=0\), and \(T^{(1)}_c\), \(T^{(2)}_c\) phase transition temperatures

Full size image
Fig. 9
figure 9

On-shell free energy F(T) in terms of T with \(r=10\), \(l_0=7\), \(G_0=1\), \(\eta =1\). The circle is magnified to show fine detail which structure comes from the rainbow gravity

Full size image

In Fig. 8, we have plotted both the on-shell \(F_\mathrm{on}(r_+)\) and the off-shell \(F_\mathrm{off}(r_+)\) free energies as a function of \(r_+\). This picture is helpful when one considers thermodynamic stability. On the other hand, in Fig. 9, we have drawn the on-shell free energy as a function of the temperature T, which helps us to understand phase as temperature changes. Some regions including near the vanishing event horizon are magnified to show fine details in Figs. 8 and 9.

First of all, the situation is mainly divided by two as shown in Fig. 8b, c, respectively. First, in Fig. 8c, which describes the well-known Hawking–Page phase transition, when \(T<T_m\), there are no black holes but a pure thermal radiation phase which has zero free energy. When \(T=T_m\), the free energy exhibits an inflexion point in Fig. 8c at \(r_+=r_m\) where the specific heat is ill-defined, but a single unstable black hole is formed which eventually decays into a pure thermal radiation. As the temperature goes up in between \(T_m<T<T^{(1)}_c\), there are two black holes that can be in equilibrium with a thermal radiation, the small black hole is formed at a local maximum of the off-shell free energy, while the large black hole is formed at a local minimum. However, the small black hole, which corresponds to the IUB with the negative specific heat, is locally unstable and so decays either into a thermal radiation or to the large black hole. On the other hand, the large black hole corresponding to the LSB with positive free energy is not globally stable; it is locally stable in between \(T_m<T<T^{(1)}_c\) though, so by the black hole evaporation it would reduce its free energy. In brief, the two small and large black hole states in this temperature range are less probable than a pure thermal radiation. When the temperature becomes \(T^{(1)}_c\), the large black hole is at local minimum with zero free energy, while the small black hole keeps in locally unstable. When the temperature is in the region of \(T^{(1)}_c<T<T_0\), there are still two black holes that the large black hole is now in globally stable, which has both positive heat capacity and negative free energy, but the small black hole has negative heat capacity and positive free energy so that it is unstable to decay the globally stable large black hole state. In short, below the phase transition temperature of \(T^{(1)}_c\), it is more probably a thermal radiation, while above \(T^{(1)}_c\) it is more probably a large black hole so that there exists a Hawking–Page phase transition between them.

Second, in Fig. 8b, which shows off-shell free energies near the vanishing event horizon, one observes a new mixed phase transition of the Schwarzschild–AdS black hole in the rainbow gravity enclosed in a cavity. Note that compared with the previous case, the phenomenon occurs in relatively extremely tiny range of temperature between \(T_0<T^{(2)}_c<T_M\) where three black hole states exist. One of them is the SSB and the others are the same as before, the IUB and LSB. When \(T_0<T<T^{(2)}_c\), the IUB, of which the free energy is at local maximum with positive value and negative specific heat, is unstable so it decays either into a thermal radiation or to the SSB/LSB. When the temperature is \(T^{(2)}_c\), the IUB has zero free energy. When the temperature is in between \(T^{(2)}_c<T<T_M\), all the three black holes are in stable states. When \(T=T_M\), two stable black holes remains. However, regardless how stable the SSB is, it is the LSB with much lower free energy so that the SSB eventually decays into the LSB. Finally, when \(T>T_M\), only the LSB exists.

5 Discussion

In this paper, we have studied local thermodynamics including its phase transition of the Schwarzschild–AdS black hole in the rainbow gravity enclosed in a cavity subject to the MDR. The black hole temperature in the rainbow gravity depends on the energy \(\omega \) of a probe provided by the rainbow functions (1.2), and making use of the HUP and deploying the MDR, we have derived the modified Hawking temperature which is finite at \(r_+=0\). It implies that the divergent standard Hawking temperature of the Schwarzschild–AdS black hole is regularized in the rainbow gravity. Moreover, the parameter \(\eta \) is found to have the upper limit given by the Newton and the cosmological constants where \(r_+\) is zero and the modified Hawking temperature has its minimum value, in contrast to the case of the Schwarzschild black hole in the rainbow gravity having no upper bound [53].

We have summarized in Fig. 2 the temperatures and specific heats of the Schwarzschild(–AdS) black hole with/without a cavity which are obtained from taking the limits of the Schwarzschild–AdS black hole in the rainbow gravity enclosed in a cavity. As a result, from Figs. 2b, c and 3b, c, we have observed again the well-known facts that the Schwarzschild–AdS black hole has a similar thermodynamic behavior to the Schwarzschild black hole in a cavity; for a given temperature of \(T>T_m\), there are two black holes, the larger one is stable and the small one is unstable, needless to say, including the Hawking–Page phase transition from a hot flat space to a black hole at the critical temperature, \(T^{(1)}_c\) for our case.

However, for the Schwarzschild–AdS black hole in the rainbow gravity, due to deformation of temperature near the vanishing event horizon, the modified local Hawking temperature is quite different from the standard Hawking temperature of the Schwarzschild–AdS black hole in a cavity as shown in Fig. 5 where the former is finite even at \(r=r_+\) while the latter is divergent. As a result, it is shown that there exists an additional stable tiny black hole together with the small black hole above \(T_0\). Moreover, it is also shown that there exists an additional critical temperature \(T^{(2)}_c\) at which the locally stable tiny black hole tunnels into the large stable black hole with the finite transition probability seen from Figs. 8 and 9 of the on-shell and off-shell free energies.

Finally, it is appropriate to comment that in the presence of the cosmological constant the HUP in Eq. (2.11), which is used to eliminate the energy dependence of the probe in the modified Hawking temperature, is corrected by the extended uncertainty relation [68, 69]. Therefore, as a further investigation, it will be interesting to analyze the thermodynamic quantities and phase transition in the rainbow gravity by using the generalized uncertainty principle [70–74].