Polarized and unpolarized lepton pair forward–backward asymmetries in $\overline{B}\rightarrow \overline{K}_{0}^{*}(1430) \ell ^+\ell ^-$ and $\overline{B}\rightarrow \overline{K} \ell ^+\ell ^-$ decays in two-Higgs-doublet model

Abstract

In this paper we shall focus on the effects of concrete models such as the SM and 2HDM of type III on the polarized and unpolarized forward–backward asymmetries of $\overline{B}\rightarrow \overline{K}_0^{*}(1430) \ell ^+\ell ^-$ and $\overline{B}\rightarrow \overline{K} \ell ^+\ell ^-$ decays. The obtained results of these decay modes are compared to each other. Also, we obtain the minimum required number of events for detecting each asymmetry and compare it with the number of produced $B\bar{B}$ pairs at the LHC or supposed to be produced at the Super-LHC. At the end, we conclude that the study of these asymmetries for $\overline{B}\rightarrow \overline{K}_0^*(1430) \ell ^+\ell ^-$ and $\overline{B}\rightarrow \overline{K} \ell ^+\ell ^-$ processes are very effective tools for establishing new physics in the future B-physics experiments.

1 Introduction

The flavor-changing neutral current (FCNC) processes induced by $b\rightarrow s \ell ^+ \ell ^-(\ell =e,\mu ,\tau )$ transitions provide an important good testing ground for the Standard Model (SM) at loop level, since they are forbidden in the SM at tree level [1, 2]. Therefore these decays are very sensitive to the physics beyond the SM via the influence of new particles in the loops.

Although the branching ratios of FCNC decays are small in the SM, interesting results are yielded in developing experiments. The inclusive $b\rightarrow X_s \ell ^+ \ell ^-$ decay is observed by the BaBaR [3] and Belle [4] collaborations. These collaborations also measured exclusive modes $B\rightarrow K \ell ^+\ell ^-$ [5–8] and $B\rightarrow K^* \ell ^+\ell ^-$ [8]. These experimental results have high agreement with theoretical predictions [9–17].

There exists another group of rare decays induced by $b\rightarrow s$ transition, such as $B\rightarrow K_2^*(1430) \ell ^+\ell ^-$ and $B\rightarrow K_0^*(1430) \ell ^+\ell ^-$ in which the B-meson decays into a tensor or scalar meson, respectively. These decays are thoroughly investigated in the SM in [18, 19] and the related transition form factors are formulated within the framework of light front quark model [19–21] and QCD sum rules method [22, 23], respectively. Lately these rare decays have been the matter of various physical discussions in the frame work of some new physics models, such as models including universal extra dimension [24], supersymmetry particles [25], and the fourth-generation fermions [26]. Generally, by studying the physical observables of these decay modes there would be a chance for testing SM or probing possible NP models. These physical quantities are for example the branching ratio, the forward–backward asymmetry, the lepton polarization asymmetry, the isospin asymmetry, etc.

The SM of electroweak interactions has been strictly tested over the past 20 years and shows an excellent compatibility with all collider data. The dynamics of electroweak symmetry breaking, however, is not exactly known. While the simplest possibility is the minimal Higgs mechanism, which suggests a single scalar SU(2) doublet, many extensions of the SM predict a large Higgs sector containing more scalars [27, 28].

Two conditions which tightly constrain the extensions of the SM Higgs sector are (1) the value of the parameter $\rho \equiv M_W^2 / M_Z^2 \cos ^2\theta _W \simeq 1$ where $M_W$ ($M_Z$) is the $W^{\pm }$ (Z) boson mass and $\theta _W$ is the Weinberg mixing angle, (2) the absence of large flavor-changing neutral currents. The first condition is spontaneously fulfilled by Higgs sectors that consist only SU(2) doublets (with the possibly additional singlets). The simplest model that contains a charged Higgs boson is a two-Higgs-doublet model (2HDM). The second condition is satisfied in the models in which the masses of fermions are produced through couplings to only one of the Higgs doublets; this is known as natural flavor conservation and forbids the tree-level flavor-changing neutral Higgs interaction phenomena.

Imposing natural flavor conservation by considering an ad hoc discrete symmetry [29], there would be two different ways to couple the SM fermions to two Higgs doublets. The 2HDM of types I and II have been extensively studied in the literature [29–32]. Without considering discrete symmetry a more general form of 2HDM, namely, type III allows for the presence of FCNC at tree level. Consistent with the low energy constraints, the FCNC’s involving the first two generations are highly suppressed, and those involving the third generation are not as severely suppressed as the first two generations. Also, in such a model there exist rich induced CP-violating sources from a single CP phase of vacuum that is absent in the SM, type I and type II. In order to consider the flavor-conserving limit of the type III, we suppose two Yukawa matrices for each fermion type to be diagonal in the same fermion mixing basis [33, 34]. All three structures of 2HDM generally contain two scalars $h^0$, $H^0$, one pseudo-scalar $A^0$ and one charged $H^\pm$ Higgs bosons.

The aim of the present paper is to perform a comprehensive study regarding the polarized and unpolarized forward–backward asymmetries of $\overline{B}\rightarrow \overline{K}_0^{*}(1430) \ell ^+\ell ^-$ and $\overline{B}\rightarrow \overline{K} \ell ^+\ell ^-$ decays in the SM and 2HDM of type III (2HDM-III). We also study the sensitivity of the results to the scalar property or the pseudo-scalar property of the produced mesons.

The paper is organized as follows. In Sect. 2, we describe the content of the general 2HDM and write down the Yukawa Lagrangian for type III. In Sect. 3, we define a general effective Hamiltonian of dimension-six operators of $b\rightarrow s\ell ^+\ell ^-$ transitions, parameterize the hadronic $\overline{B}\rightarrow \overline{K}$ and $\overline{B}\rightarrow \overline{K}_0^{*}$ matrix elements, and derive the general expressions for the polarized and unpolarized lepton forward–backward asymmetries. In Sect. 4, the sensitivity of these polarizations and the corresponding averages to the 2HDM-III parameters are numerically analyzed.

2 The general two-Higgs-doublet model

In a general two-Higgs-doublet model, the two doublets can both couple to the up-type and down-type quarks. Without missing any thing, we use a basis such that the first doublet produces the masses of all the gauge-bosons and fermions [33]:

$$\begin{aligned} \langle \phi _1 \rangle = \left( \begin{array}{c} 0 \\ \frac{v}{\sqrt{2}} \end{array} \right) ,\quad \langle \phi _2 \rangle = 0 \end{aligned}$$

(1)

where v is due to the W mass by $M_W={g\over 2}v$. Based on this, the first doublet $\phi _1$ is the same as the SM doublet, whereas all the new Higgs fields originate from the second doublet $\phi _2$. They are written as

$$\begin{aligned} \phi _1=\frac{1}{\sqrt{2}} \left( \begin{array}{c} \sqrt{2} G^+ \\ v + \chi _1^0 + i G^0 \end{array} \right) ,\quad \phi _2=\frac{1}{\sqrt{2}} \left( \begin{array}{c} \sqrt{2} H^+ \\ \chi _2^0 + i A^0 \end{array} \right) ,\nonumber \\ \end{aligned}$$

(2)

where $G^0$ and $G^\pm$ are the Goldstone bosons that would be absorbed in the Higgs mechanism to provide the longitudinal components of the weak gauge bosons. The $H^\pm$ are the physical charged-Higgs bosons and $A^0$ is the physical CP-odd neutral Higgs boson. The $\chi _1^0$ and $\chi _2^0$ are not physical mass eigenstates but are written as linear combinations of the CP-even neutral Higgs bosons:

$$\begin{aligned} \chi _1^0= & {} H^0 \cos \alpha - h^0 \sin \alpha \end{aligned}$$

(3)

$$\begin{aligned} \chi _2^0= & {} H^0\sin \alpha + h^0 \cos \alpha , \end{aligned}$$

(4)

where $\alpha$ is the mixing angle. Using this basis, the couplings of $\chi _2^0 ZZ$ and $\chi _2^0 W^+ W^-$ have disappeared. We can write the Yukawa Lagrangian for type III as

$$\begin{aligned} -\mathcal{L}_Y= & {} \eta _{ij}^U \overline{Q_{iL}} \tilde{\phi _1} U_{jR} + \eta _{ij}^D \overline{Q_{iL}} \phi _1 D_{jR} + \xi _{ij}^U \overline{Q_{iL}} \tilde{\phi _2} U_{jR}\nonumber \\&+\, \xi _{ij}^D \overline{Q_{iL}} \phi _2 D_{jR}+\hbox {h.c.}, \end{aligned}$$

(5)

where i, j are generation indices, $\tilde{\phi }_{1,2} = i\sigma _2 \phi _{1,2}$, $\eta _{ij}^{U,D}$, and $\xi _{ij}^{U,D}$ are, in general, nondiagonal coupling matrices, and $Q_{iL}$ is the left-handed fermion doublet and $U_{jR}$ and $D_{jR}$ are the right-handed singlets [29]. Note that these $Q_{iL}$, $U_{jR}$, and $D_{jR}$ are weak eigenstates, which can be rotated to the mass eigenstates. As we have mentioned above, $\phi _1$ provides all the fermion masses and, therefore, $\frac{v}{\sqrt{2}}\eta ^{U,D}$ will become the up- and down-type quark-mass matrices after a bi-unitary transformation. Applying the transformation the Yukawa Lagrangian becomes

$$\begin{aligned}&\mathcal{L}_Y= -\overline{U} M_U U - \overline{D} M_D D - \frac{g}{2M_W} (H^0\cos \alpha - h^0 \sin \alpha )\nonumber \\&\quad \times \,(\overline{U} M_U U + \overline{D} M_D D) \nonumber \\&\quad +\, \frac{ig}{2 M_W} G^0 (\overline{U} M_U \gamma ^5 U - \overline{D} M_D \gamma ^5 D )\nonumber \\&\quad +\, \frac{g}{\sqrt{2}M_W} G^- \overline{D} V^\dagger _\mathrm{CKM} \biggr [ M_U \frac{1}{2}(1+\gamma ^5) - M_D \frac{1}{2}(1-\gamma ^5) \biggr ] U \nonumber \\&\quad -\, \frac{g}{\sqrt{2}M_W} G^+ \overline{U} V_\mathrm{CKM} \biggr [ M_D \frac{1}{2}(1+\gamma ^5) - M_U \frac{1}{2}(1-\gamma ^5) \biggr ]D \nonumber \\&\quad -\, \frac{H^0 \sin \alpha + h^0\cos \alpha }{\sqrt{2}} \Biggr [ \overline{U} \biggr ( {\hat{\xi }}^U \frac{1}{2}(1+\gamma ^5) + {\hat{\xi }}^{U\dagger } \frac{1}{2}(1-\gamma ^5) \biggr ) U \nonumber \\&\quad +\,\overline{D} \biggr ( {\hat{\xi }}^D \frac{1}{2}(1+\gamma ^5) + {\hat{\xi }}^{D\dagger } \frac{1}{2}(1-\gamma ^5) \biggr ) D \Biggr ] \nonumber \\&\quad +\, \frac{i A^0}{\sqrt{2}} \Biggr [ \overline{U} \biggr ( {\hat{\xi }}^U \frac{1}{2}(1+\gamma ^5) -{\hat{\xi }}^{U\dagger } \frac{1}{2}(1-\gamma ^5) \biggr ) U\nonumber \\&\quad -\,\overline{D} \biggr ( {\hat{\xi }}^D \frac{1}{2}(1+\gamma ^5) - {\hat{\xi }}^{D\dagger } \frac{1}{2}(1-\gamma ^5) \biggr ) D \Biggr ] \nonumber \\&\quad -\, H^+ \overline{U} \biggr [ V_\mathrm{CKM} {\hat{\xi }}^D \frac{1}{2}(1+\gamma ^5) - {\hat{\xi }}^{U\dagger } V_\mathrm{CKM} \frac{1}{2}(1-\gamma ^5) \biggr ] D\nonumber \\&\quad -\, H^- \overline{D} \biggr [ {\hat{\xi }}^{D\dagger } V^\dagger _\mathrm{CKM} \frac{1}{2}(1-\gamma ^5) - V^\dagger _\mathrm{CKM} {\hat{\xi }}^U \frac{1}{2}(1+\gamma ^5) \biggr ] U, \end{aligned}$$

(6)

where U is a symbol for the mass eigenstates of u, c, t quarks and D is a symbol for the mass eigenstates of d, s, b quarks. The diagonal mass matrices are defined by $M_{U,D}=\hbox {diag}(m_{u,d}, m_{c,s}, m_{t,b})= {v\over \sqrt{2}} (\mathcal{L}_{U,D})^{\dagger } \eta ^{U,D} (\mathcal{R}_{U,D})$, $\hat{\xi }^{U,D} = (\mathcal{L}_{U,D})^{\dagger } \xi ^{U,D} (\mathcal{R}_{U,D})$. The Cabibbo–Kobayashi–Maskawa matrix [35] is given by $V_\mathrm{CKM}=(\mathcal{L}_U)^\dagger (\mathcal{L}_D)$.

The matrices $\hat{\xi }^{U,D}$ contain the FCNC couplings. These matrices are given as [36, 37]

$$\begin{aligned} \hat{\xi }^{U,D}_{ij} = \lambda _{ij} \frac{g\sqrt{m_i m_j}}{\sqrt{2}M_W}, \end{aligned}$$

(7)

by which the quark-mass hierarchy is ensured, while the FCNC for the first two generations are suppressed by the small quark masses is allowed for the third generation.

3 Analytic formulas

3.1 The effective Hamiltonian for $\overline{B} \rightarrow \overline{K} \ell ^{+}\ell ^{-}$ and $\overline{B} \rightarrow \overline{K}_0^*(1430) \ell ^{+}\ell ^{-}$ transitions in SM and 2HDM

The exclusive decays $\overline{B} \rightarrow \overline{K} \ell ^{+}\ell ^{-}$ and $\overline{B} \rightarrow \overline{K}_0^*(1430) \ell ^{+}\ell ^{-}$ are described at quark level by $b\rightarrow s \ell ^{+}\ell ^{-}$ transition. The effective Hamiltonian that is used to describe the $b\rightarrow s \ell ^{+}\ell ^{-}$ transition in 2HDM models is

$$\begin{aligned}&\mathcal{H}_{eff}(b\rightarrow s \ell ^{+}\ell ^{-})\nonumber \\&\quad =-\frac{4 G_F}{\sqrt{2}} V_{tb} V^*_{ts} \left\{ \!\sum _{i=1}^{10} C_i( \mu ) O_i( \mu ) \!+\! \sum _{i=1}^{10} C_{Q_i}( \mu ) Q_i( \mu ) \!\right\} \!,\nonumber \\ \end{aligned}$$

(8)

where the first part is related to the effective Hamiltonian in the SM such that the respective Wilson coefficients get extra terms due to the presence of charged Higgs bosons. The second part which includes new operators is extracted from contributing the massive neutral Higgs bosons to this decay. All operators as well as the related Wilson coefficients are given in [30–32, 34, 38]. Using the above effective Hamiltonian, the amplitude of $b \rightarrow s \ell ^+ \ell ^-$ can be given as

$$\begin{aligned} \mathcal{M}= & {} \langle s \ell ^+ \ell ^- |\mathcal{H}_\mathrm{eff}|b\rangle \nonumber \\= & {} -\frac{G_F \alpha }{2\sqrt{2} \pi } V_{tb} V^*_{ts} \Bigg \{\tilde{C}_{9}^{\mathrm{eff}} \bar{s} \gamma _\mu (1- \gamma _5) b \, \bar{\ell }\gamma ^\mu \ell \nonumber \\&+\, \tilde{C}_{10} \bar{s} \gamma _\mu (1- \gamma _5) b \, \bar{\ell }\gamma ^\mu \gamma _5 \ell \nonumber \\&-\, 2C_7^{\mathrm{eff}}\frac{m_b}{q^2}\bar{s} i \sigma _{\mu \nu }q^\nu (1+\gamma _5) b\,\bar{\ell }\gamma ^\mu \ell \nonumber \\&-\, 2C_7^{\mathrm{eff}}\frac{m_s}{q^2}\bar{s} i \sigma _{\mu \nu }q^\nu (1-\gamma _5) b \, \bar{\ell }\gamma ^\mu \ell \nonumber \\&+\,C_{Q_1} \bar{s} (1 + \gamma _5) b \,\bar{\ell }\ell + C_{Q_2} \bar{s} (1+\gamma _5) b \, \bar{\ell }\gamma _5 \ell \Bigg \}, \end{aligned}$$

(9)

where $q^2$ is the dilepton invariant mass. The evolution of the Wilson coefficients $C_7^{\mathrm{eff}},~\tilde{C}_{9}^{\mathrm{eff}}$, $\tilde{C}_{10}$ from the higher scale $\mu =m_W$ to the lower scale $\mu =m_b$ is described by the renormalization group equation. These coefficients at the scale $\mu =m_b$ are calculated in [38]. The operators $O_i (i=1,\ldots ,10)$ do not mix with $Q_1$ and $Q_2$ and there is no mixing between $Q_1$ and $Q_2$. For this reason the evolutions of the coefficients $C_{Q_1}$ and $C_{Q_2}$ are controlled by the anomalous dimensions of $Q_1$ and $Q_2$, respectively [31, 32]:

$$\begin{aligned} C_{Q_i} (m_b) = \eta ^{-\gamma _Q / \beta _0} C_{Q_i} (m_W),\quad i=1,2, \end{aligned}$$

(10)

where $\gamma _Q = -4$ is the anomalous dimension of the operator $\bar{s}_L b_R$.

The coefficients $C_i (m_W)$ ($i=7,9$, and 10) and $C_{Q_1}(m_W)$ and $C_{Q_2}(m_W)$ are given by

$$\begin{aligned} C_7(m_W)= & {} C_7^{SM}(m_W)+ C_7^{2HDM}(m_W)\nonumber \\= & {} C_7^{SM}(m_W) + \left| \lambda _{tt} \right| ^2 \Bigg ( \frac{y(7-5 y - 8 y^2)}{72 (y-1)^3}\nonumber \\&+\, \frac{y^2 ( 3 y - 2)}{12 (y-1)^4} \, \ln y \Bigg ) +\, \lambda _{tt} \lambda _{bb} \nonumber \\&\times \Bigg ( \frac{y(3-5 y)}{12 (y-1)^2} + \frac{y (3 y - 2)}{6 (y-1)^3} \, \ln y \Bigg )~, \end{aligned}$$

(11)

$$\begin{aligned} C_9(m_W)= & {} C_9^{SM}(m_W)+ C_9^{2HDM}(m_W)\nonumber \\= & {} C_9^{SM}(m_W)+\left| \lambda _{tt} \right| ^2 \Bigg [ \frac{1 - 4 sin^2 \theta _W}{sin^2 \theta _W} \, \frac{x y}{8}\nonumber \\&\times \Bigg ( \frac{1}{y-1} - \frac{1}{(y-1)^2} \, \ln y \Bigg )\nonumber \\&-\, y \Bigg ( \frac{47 y^2 - 79 y + 38}{108 (y-1)^3}\nonumber \\&-\frac{3 y^3 - 6 y^3 + 4}{18 (y-1)^4} \, \ln y \Bigg ) \Bigg ]~, \end{aligned}$$

(12)

$$\begin{aligned} C_{10}(m_W)= & {} C_{10}^{SM}(m_W)+ C_{10}^{2HDM}(m_W)\nonumber \\= & {} C_{10}^{SM}(m_W)+ \left| \lambda _{tt} \right| ^2 \frac{1}{sin^2 \theta _W} \,\frac{x y}{8}\nonumber \\&\times \Bigg ( - \frac{1}{y-1} + \frac{1}{(y-1)^2} \, \ln y \Bigg )~, \end{aligned}$$

(13)

$$\begin{aligned} C_{Q_1} ( m_W )= & {} \frac{m_b m_\ell }{m_{h^0}^2} \frac{1}{\left| \lambda _{tt} \right| ^2} \frac{1}{sin^2 \theta _W} \frac{x}{4} \nonumber \\&\times \Bigg \{ \left( sin^2 \alpha + h\, cos^2 \alpha \right) f_1 (x,y)\nonumber \\&+ \left[ \frac{m_{h^0}^2}{m_W^2} + \left( sin^2 \alpha + h\, cos^2\alpha \right) (1-z) \right] f_2(x,y)\nonumber \\&+\, \frac{sin^2 2 \alpha }{2 m_{H^\pm }^2} \left[ m_{h^0}^2 - \frac{(m_{h^0}^2 + m_{H^0}^2)^2}{2 m_{H^0}^2} \right] f_3 (y) \Bigg \}, \nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned} C_{Q_2} (m_W)= & {} -\frac{m_b m_\ell }{m_{A^0}^2} \frac{1}{\left| \lambda _{tt} \right| ^2} \nonumber \\&\times \left\{ f_1(x,y) + \left[ 1+ \frac{m_{H^\pm }^2 - m_{A^0}^2}{m_W^2} \right] f_2(x,y) \right\} ,\nonumber \\ \end{aligned}$$

(15)

where

$$\begin{aligned}&x=\frac{m_t^2}{m_W^2},\quad y=\frac{m_t^2}{m_{H^\pm }^2}, \quad z=\frac{x}{y},\quad h=\frac{m_{h^0}^2}{m_{H^0}^2}, \end{aligned}$$

(16)

$$\begin{aligned}&B(x)=-\frac{x}{4 (x-1)} + \frac{x}{4 (x-1)^2} \, \ln x, \end{aligned}$$

(17)

$$\begin{aligned}&C(x)=\frac{x}{4} \left( \frac{x-6}{2 (x-1)} + \frac{3 x +2 }{2 (x-1)^2} \ln x \right) ,\end{aligned}$$

(18)

$$\begin{aligned}&f_1 (x,y)=\frac{x\, \ln x}{x-1} - \frac{y\, \ln y}{y-1}, \end{aligned}$$

(19)

$$\begin{aligned}&f_2(x,y)=\frac{x\, \ln y}{(z-x)(x-1)} + \frac{\ln z}{(z-1)(x-1)},\end{aligned}$$

(20)

$$\begin{aligned}&f_3(y)=\frac{1 -y + y\, \ln y}{(y-1)^2}. \end{aligned}$$

(21)

It should be noted that the coefficient $\tilde{C}_9^{\mathrm{eff}}(\mu )$ can be decomposed into the following three parts:

$$\begin{aligned} \tilde{C}_9^{\mathrm{eff}}(\mu )=\tilde{C}_9(\mu )+Y_{SD}(\hat{m}_c, \hat{s})+Y_{LD}(\hat{m}_c, \hat{s})~, \end{aligned}$$

(22)

where the parameters $\hat{m}_c$ and $\hat{s}$ are defined as $\hat{m}_c=m_c/m_b$, $\hat{s}=q^2/m_b^{2}$. $Y_{SD}(\hat{m}_c, \hat{s})$ describes the short-distance contributions from four-quark operators far away from the $c\bar{c}$ resonance regions, which can be calculated reliably in the perturbative theory. The function $Y_{SD}(\hat{m}_c, \hat{s})$ is given by

$$\begin{aligned} Y_{SD}= & {} g(\hat{m}_c, \hat{s}) (3 C_1 + C_2 + 3 C_3 + C_4 + 3 C_5 + C_6) \nonumber \\&-\, \frac{1}{2} g(1, \hat{s}) (4 C_3 + 4 C_4 + 3 C_5 + C_6) \nonumber \\&-\, \frac{1}{2} g(0, \hat{s}) (C_3 \!+\! 3 C_4) \!+\! \frac{2}{9} (3 C_3 \!+\! C_4 \!+\! 3 C_5 \!+\! C_6),\nonumber \\ \end{aligned}$$

(23)

where the explicit expressions for the g functions can be found in [30, 38]. The long-distance contributions $Y_{LD}(\hat{m}_c, \hat{s})$ from the four-quark operators near the $c\bar{c}$ resonance cannot be calculated from first principles of QCD and are usually parameterized in the form of a phenomenological Breit–Wigner formula making use of the vacuum saturation approximation and quark–hadron duality. The function $Y_{LD}(\hat{m}_c, \hat{s})$ is given by [25, 39]

$$\begin{aligned} Y_\mathrm{LD} = {3\pi \over \alpha ^2} C^{(0)} \sum _{V_i=\psi , \psi ', \ldots } k_i \, {\mathcal{B} (V_i \rightarrow \ell ^+ \ell ^-) m_{V_i}\Gamma _{V_i} \over m_{V_i}^2- q^2-im_{V_i}\Gamma _{V_i}}, \end{aligned}$$

(24)

where $\alpha$ is the fine structure constant and $C^{(0)}=(3 C_1 + C_2 + 3 C_3 + C_4 + 3 C_5 + C_6)$. The phenomenological parameters $k_i$ for the $\overline{B} \rightarrow \overline{K} \ell ^+ \ell ^-$ decay can be fixed from ${\mathcal{B}} (\overline{B} \rightarrow J/\psi \overline{K} \rightarrow \overline{K} \ell ^+ \ell ^-) = {\mathcal{B}} (\overline{B} \rightarrow J/\psi \overline{K}) {\mathcal{B}} (J/\psi \rightarrow \ell ^+ \ell ^-)$. For the lowest resonances $\psi$ and $\psi ^{\prime }$ we will use $k_1=2.70$ and $k_2=3.51$, respectively [40]. Also, for the $\overline{B} \rightarrow \overline{K}_0^*(1430) \ell ^+ \ell ^-$ decay such parameters can be determined by ${\mathcal{B}} (\overline{B} \rightarrow J/\psi \overline{K}_0^*(1430) \rightarrow \overline{K}_0^*(1430) \ell ^+ \ell ^-) = {\mathcal{B}} (\overline{B} \rightarrow J/\psi \overline{K}_0^*(1430)) {\mathcal{B}} (J/\psi \rightarrow \ell ^+ \ell ^-)$. However, since the branching ratio of $\overline{B} \rightarrow J/\psi \overline{K}_0^*(1430)$ decay has not been measured yet, we assume that the values of $k_i$ are of the order of one. Therefore, we use $k_1=1$ and $k_2=1$ in the following numerical calculations [25].

3.2 Form factors for $\overline{B} \rightarrow \overline{K} \ell ^{+}\ell ^{-}$ transition

The exclusive $\overline{B} \rightarrow \overline{K} \ell ^{+}\ell ^{-}$ decay is described in terms of the matrix elements of the quark operators in Eq. (9) over the meson states, which can be parameterized in terms of the form factors. The matrix elements needed for the calculation of $\overline{B} \rightarrow \overline{K} \ell ^{+}\ell ^{-}$ decay are

$$\begin{aligned}&\left<\overline{K}(p_{K}) \left| \bar{s}\gamma _\mu (1 \pm \gamma _5) b \right| \overline{B}(p_B) \right>\nonumber \\&\quad = \big [f_+ (q^2) {(p_B + p_{K})}_\mu + f_-(q^2) q_\mu \big ], \nonumber \\&\quad = f_+ (q^2) \left[ {(p_B + p_{K})}_\mu -{(m_B^2-m_K^2)\over {q^2}}q_\mu \right] \nonumber \\&\qquad +\, {(m_B^2-m_K^2)\over {q^2}} f_0(q^2) q_\mu ,\end{aligned}$$

(25)

$$\begin{aligned}&\left<\overline{K}(p_{K}) \left| \bar{s}i \sigma _{\mu \nu } q^\nu (1 \pm \gamma _5) b \right| \overline{B}(p_B) \right>\nonumber \\&\quad = {- f_T (q^2) \over m_B + m_{K}} \big [ {(p_B + p_{K})}_\mu q^2 - (m_B^2 - m_{K}^2 ) q_\mu \big ], \end{aligned}$$

(26)

where $q = p_B-p_{K}$ is the momentum transfer. In deriving Eq. (25) we have used the relationship

$$\begin{aligned} f_-(q^2)={(m_B^2-m_K^2)\over {q^2}} \big [f_0(q^2)-f_+(q^2)\big ]. \end{aligned}$$

(27)

Now, multiplying both sides of Eq. (25) with $q^\mu$ and using the equation of motion, the expression in terms of the form factors for $\left<\overline{K} \left| \bar{s} (1 \pm \gamma _5 ) b \right| \overline{B} \right>$ is calculated as

$$\begin{aligned}&\left<\overline{K}(p_{K}) \left| \bar{s} (1 \pm \gamma _5) b \right| \overline{B}(p_B) \right>=\left<\overline{K}(p_{K}) \left| \bar{s} b \right| \overline{B}(p_B) \right>\nonumber \\&\quad =\frac{1}{m_{b}-m_{s}}[f_+ (q^2) (p_B x+ p_{K}).q +f_-(q^2) q^{2}], \nonumber \\&\quad =\frac{f_0 (q^2)}{m_{b}-m_{s}}(m_B^2-m_K^2) \end{aligned}$$

(28)

$$\begin{aligned}&\left<\overline{K}(p_{K}) \left| \bar{s} \gamma _5 b \right| \overline{B}(p_B) \right>=0. \end{aligned}$$

(29)

For the form factors we have used the light cone QCD sum rules results [41] in which the $q^2$ dependence of the semileptonic form factors, $f_0$ and $f_+$, is given by

$$\begin{aligned} F(q^2)=\,{F(0)\over 1-a_F(q^2/m_{B}^2)+b_F(q^2/m_{B}^2)^2}, \end{aligned}$$

(30)

where the values of the parameters F(0), $a_F$, and $b_F$ for the $\overline{B} \rightarrow \overline{K} \ell ^{+}\ell ^{-}$ decay are listed in Table 1. Also, the $q^2$ dependence of the penguin form factor, $f_T$, is obtained by

$$\begin{aligned} { f_T (q^2) \over m_B + m_{K}}=\frac{1}{m_b} \left[ \left( 1+{{m_b^2-q^2}\over {q^2}}\right) f_+-{{m_b^2-q^2}\over {q^2}}f_0\right] .\nonumber \\ \end{aligned}$$

(31)

Table 1 Form factors for $\overline{B} \rightarrow \overline{K}$ transition obtained in the LCQSR calculation are fitted to the 3-parameter form

3.3 Form factors for $\overline{B} \rightarrow \overline{K}_0^*(1430) \ell ^{+}\ell ^{-}$ transition

Like the exclusive $\overline{B} \rightarrow \overline{K} \ell ^{+}\ell ^{-}$ decay, the matrix elements needed for the calculation of $\overline{B} \rightarrow \overline{K}_0^*(1430) \ell ^{+}\ell ^{-}$ decay are

$$\begin{aligned}&\left<\overline{K}_0^*(1430)(p_{K_0^*}) \left| \bar{s}\gamma _\mu (1 \pm \gamma _5) b \right| \overline{B}(p_B) \right>\nonumber \\&\quad = \pm \big [f_+ (q^2) {(p_B + p_{K_0^*})}_\mu + f_-(q^2) q_\mu \big ], \end{aligned}$$

(32)

$$\begin{aligned}&\left<\overline{K}_0^*(1430)(p_{K_0^*}) \left| \bar{s}i \sigma _{\mu \nu } q^\nu (1 \pm \gamma _5) b \right| \overline{B}(p_B) \right>\nonumber \\&\quad ={\pm f_T (q^2) \over m_B + m_{K_0^*}} \big [ {(p_B + p_{K_0^*})}_\mu q^2 - (m_B^2 - m_{K_0^*}^2 ) q_\mu \big ],\nonumber \\ \end{aligned}$$

(33)

$$\begin{aligned}&\left<\overline{K}_0^*(1430)(p_{K_0^*}) \left| \bar{s} (1 \pm \gamma _5) b \right| \overline{B}(p_B) \right>\nonumber \\&\quad =\pm \left<\overline{K}_0^*(1430)(p_{K_0^*}) \left| \bar{s} \gamma _5 b \right| \overline{B}(p_B) \right>\nonumber \\&\quad = \mp \frac{1}{m_{b}+m_{s}}[f_+ (q^2) (p_B + p_{K_0^*}).q + f_-(q^2) q^{2}]\nonumber \\&\quad = \mp \frac{f_0 (q^2)}{m_{b}+m_{s}}(m_B^2-m_{K_0^*}^2) , \end{aligned}$$

(34)

$$\begin{aligned}&\left<\overline{K}_0^*(1430)(p_{K_0^*}) \left| \bar{s} b \right| \overline{B}(p_B) \right>= 0, \end{aligned}$$

(35)

where $q =p_B -p_{K_0^*}$ and the function $f_0(q^2)$ has been extracted from the Eq. (27). For the form factors we have used the results of three-point QCD sum rules method [42] in which the $q^2$ dependence of all form factors is given by

$$\begin{aligned} F(q^2)=\,{F(0)\over 1-a_F(q^2/m_{B}^2)+b_F(q^2/m_{B}^2)^2}, \end{aligned}$$

(36)

where the values of the parameters F(0), $a_F$, and $b_F$ for the $\overline{B} \rightarrow \overline{K}_0^*(1430) \ell ^{+}\ell ^{-}$ decay are exhibited in Table 2.

Table 2 Form factors for $\overline{B} \rightarrow \overline{K}_0^*(1430)$ transition obtained within three-point QCD sum rules are fitted to the 3-parameter form

3.4 The differential decay rates and forward–backward asymmetries of $\overline{B} \rightarrow \overline{K}_0^{*}(1430) \ell ^{+}\ell ^{-}$

Making use of Eq. (9) and the definitions of the form factors, the matrix element of the $\overline{B} \rightarrow \overline{K}_0^{*}(1430) \ell ^{+}\ell ^{-}$ decay can be written as follows:

$$\begin{aligned} \mathcal{M}= & {} \frac{G_F \alpha _\mathrm{em}}{4\sqrt{2}\pi } V_{ts}^* V_{tb} m_B \nonumber \\&\times \,\{ [\mathcal{A}(p_B\!+\!p_{{K}_0^{*}})_{\mu }\!+\!\mathcal{B}q_{\mu }] \bar{\ell }\gamma ^\mu \ell \!+\! [\mathcal{C}(p_B\!+\!p_{{K}_0^{*}})_{\mu } \nonumber \\&+\,\mathcal{D}q_{\mu }]\bar{\ell }\gamma ^\mu \gamma _5 \ell +[\mathcal{Q}]\bar{\ell }\ell +[\mathcal{N}]\bar{\ell }\gamma _5 \ell \}, \end{aligned}$$

(37)

where the auxiliary functions $\mathcal{A}, \ldots , \mathcal{Q}$ are listed in the following:

$$\begin{aligned} \mathcal{A}= & {} -2\tilde{C}_{9}^{\mathrm{eff}}f_{+}(q^2)-4(m_b+m_s){C}_{7}^{\mathrm{eff}}{{f_T(q^2) }\over {m_B+m_{{K}_0^{*}}}}, \end{aligned}$$

(38)

$$\begin{aligned} \mathcal{B}= & {} -2\tilde{C}_{9}^{\mathrm{eff}}f_{-}(q^2)+4(m_b+m_s) \nonumber \\&\times \,{C}_{7}^{\mathrm{eff}}{{f_T(q^2) }\over {(m_B+m_{{K}_0^{*}}})q^2}(m_B^2-m_{{K}_0^{*}}^2),\end{aligned}$$

(39)

$$\begin{aligned} \mathcal{C}= & {} -2\tilde{C}_{10}f_{+}(q^2),\end{aligned}$$

(40)

$$\begin{aligned} \mathcal{D}= & {} -2\tilde{C}_{10}f_{-}(q^2),\end{aligned}$$

(41)

$$\begin{aligned} \mathcal{Q}= & {} -2C_{Q_{1}}f_{0}(q^2){(m_B^2-m_{{K}_0^{*}}^2)\over {m_b+m_s}},\end{aligned}$$

(42)

$$\begin{aligned} \mathcal{N}= & {} -2C_{Q_{2}}f_{0}(q^2){(m_B^2-m_{{K}_0^{*}}^2)\over {m_b+m_s}}, \end{aligned}$$

(43)

with $q = p_B - p_{{K}_0^{*}} = p_{\ell ^+} + p_{\ell ^-}$.

The unpolarized differential decay rate for the $\overline{B}\rightarrow \overline{K}_0^{*}(1430)\ell ^+\ell ^-$ decay in the rest frame of the B meson is given by

$$\begin{aligned} \frac{\mathrm{d} \Gamma (\overline{B}\rightarrow {{K}_0^{*}}\ell ^+\ell ^-)}{\mathrm{d} \hat{s}} = -\frac{G_F^2 \alpha _\mathrm{em}^2 m_B}{2^{14}\pi ^5} \left| V_{tb}V_{ts}^*\right| ^2 v\sqrt{\lambda }\Delta ,\nonumber \\ \end{aligned}$$

(44)

with

$$\begin{aligned} \Delta= & {} 16 m_{\ell } m_{B}^2 (1-\hat{r}_{{{K}_0^{*}}})\text{ Re }[\mathcal{C}\mathcal{N^*}]+4\hat{s}m_B^2 v^2|\mathcal{Q}|^2 \nonumber \\&+\,16 \hat{s}m_{\ell }^2 m_B^2 |\mathcal{D}|^2+32 m_{\ell }^2 m_B^2 (1-\hat{r}_{{{K}_0^{*}}}) \text{ Re }[\mathcal{C}\mathcal{D^*}]\nonumber \\&+\,16\hat{s}m_{\ell } m_B^2\text{ Re }[\mathcal{D}\mathcal{N^*}] +2 \hat{s}m_B^2 |\mathcal{N}|^2\nonumber \\&+\,\frac{4}{3} m_B^4 \lambda (3-v^2)|\mathcal{A}|^2\nonumber \\&+\,\frac{4}{3}m_B^4 |\mathcal{C}|^2\{2\lambda -(1-v^2)(2\lambda -3 (1-\hat{r}_{{{K}_0^{*}}})^2)\},\nonumber \\ \end{aligned}$$

(45)

where $v=\sqrt{1-4{m}_\ell ^2/q^2}$, $\hat{s}=q^2/m_B^2$, $\hat{r}_{{K}_0^{*}}=m_{{K}_0^{*}}^2/m_B^2$, and $\lambda = 1 + \hat{r}_{{K}_0^{*}}^2 + \hat{s}^2 - 2\hat{s}- 2\hat{r}_{{K}_0^{*}} (1+\hat{s})$.

Table 3 List of the values for the masses of the Higgs particles

Fig. 1

Un polarized asymmetry $\mathcal{A}_{FB}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\mu ^{+}\mu ^{-}$ decay for the Higgs mass sets 1, 2, 3. For each mass set the left sub-figure shows the general allowed region, varying the theoretical and experimental input parameters; the right up (down) sub-figures represent the upper (lower) limit of the corresponding asymmetry

Fig. 2

Unpolarized asymmetry $\mathcal{A}_{FB}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K} \,\mu ^{+}\mu ^{-}$ decay for the Higgs mass sets 1, 2, 3

Fig. 3

Polarized asymmetry $\mathcal{A}_{FB}^{LN}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\mu ^{+}\mu ^{-}$ decay for the Higgs mass sets 1, 2, 3. For each mass set the left sub-figure shows the general allowed region, varying the theoretical and experimental input parameters; the right up (down) sub-figures represent the upper (lower) limit of the corresponding asymmetry

Fig. 4

Polarized asymmetry $\mathcal{A}_{FB}^{LN}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K} \,\mu ^{+}\mu ^{-}$ decay for the Higgs mass sets 1, 2, 3

Fig. 5

Polarized asymmetry $\mathcal{A}_{FB}^{NT}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\mu ^{+}\mu ^{-}$ decay for the Higgs mass sets 1, 2, 3. For each mass set the left sub-figure shows the general allowed region, varying the theoretical and experimental input parameters; the right up (down) sub-figures represent the upper (lower) limit of the corresponding asymmetry

Fig. 6

Polarized asymmetry $\mathcal{A}_{FB}^{NT}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K} \,\mu ^{+}\mu ^{-}$ decay for the Higgs mass sets 1, 2, 3

Fig. 7

Unpolarized asymmetry $\mathcal{A}_{FB}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\tau ^{+}\tau ^{-}$ decay for the Higgs mass sets 1, 2, 3. For each mass set the left sub-figure shows the general allowed region, varying the theoretical and experimental input parameters; the right up (down) sub-figures represent the upper (lower) limit of the corresponding asymmetry

Fig. 8

Unpolarized asymmetry $\mathcal{A}_{FB}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K} \,\tau ^{+}\tau ^{-}$ decay for the Higgs mass sets 1, 2, 3

Fig. 9

Polarized asymmetry $\mathcal{A}_{FB}^{LN}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\tau ^{+}\tau ^{-}$ decay for the Higgs mass sets 1, 2, 3. For each mass set the left sub-figure shows the general allowed region, varying theoretical and experimental input parameters; the right up (down) sub-figures represent the upper (lower) limit of the corresponding asymmetry

Fig. 10

Polarized asymmetry $\mathcal{A}_{FB}^{LN}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K} \,\tau ^{+}\tau ^{-}$ decay for the Higgs mass sets 1, 2, 3

Fig. 11

Polarized asymmetry $\mathcal{A}_{FB}^{NT}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\tau ^{+}\tau ^{-}$ decay for the Higgs mass sets 1, 2, 3. For each mass set the left sub-figure shows the general allowed region, varying the theoretical and experimental input parameters; the right up (down) sub-figures represent the upper (lower) limit of the corresponding asymmetry

Fig. 12

Polarized asymmetry $\mathcal{A}_{FB}^{LN}(q^2)$ in the SM and three tested scenarios of 2HDM-III (A, B, C) for $\overline{B}\rightarrow \overline{K} \,\tau ^{+}\tau ^{-}$ decay for the Higgs mass sets 1, 2, 3

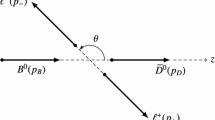
The unpolarized and normalized differential forward–backward asymmetry of the $\overline{B}\rightarrow \overline{K}_0^{*}(1430\ell ^+\ell ^-$ decay in the center of mass frame of leptons is defined by

$$\begin{aligned} \mathcal{A}_{FB} = \frac{\displaystyle \int _{0}^{1} \frac{\mathrm{d}^2\Gamma }{\mathrm{d}\hat{s} \mathrm{d}z}\mathrm{d}z - \int _{-1}^{0} \frac{\mathrm{d}^2\Gamma }{\mathrm{d}\hat{s} \mathrm{d}z}\mathrm{d}z}{\displaystyle \int _{0}^{1} \frac{\mathrm{d}^2\Gamma }{\mathrm{d}\hat{s} \mathrm{d}z} \mathrm{d}z+ \int _{-1}^{0} \frac{\mathrm{d}^2\Gamma }{\mathrm{d}\hat{s} \mathrm{d}z}\mathrm{d}z}, \end{aligned}$$

(46)

where $z=\cos \theta$ and $\theta$ is the angle between three momenta of the B meson and the negatively charged lepton ($\ell ^-$) in the CM (center of mass) frame of leptons.

Using the above-mentioned definition, the result can be written as follows:

$$\begin{aligned} \mathcal{A}_{FB}(\hat{s})=\frac{8 m_B^2 m_{\ell }v \sqrt{\lambda } }{\Delta } \text{ Re }[\mathcal{AQ^*}]. \end{aligned}$$

(47)

Having obtained the unpolarized and normalized differential forward–backward asymmetry, let us now consider the normalized differential forward–backward asymmetries associated with the polarized leptons. For this purpose, we first define the following orthogonal unit vectors $s_i^{\pm \mu }$ in the rest frame of $\ell ^\pm$, where $i=L,N$ or T are the abbreviations of the longitudinal, normal and transversal spin projections, respectively:

$$\begin{aligned} s^{-\mu }_L= & {} \left( 0,{\vec {e}}_L^{\,-}\right) = \left( 0,\frac{{\vec {p}}_{\ell ^-}}{\left| {\vec {p}}_{\ell ^-} \right| }\right) , \end{aligned}$$

(48)

$$\begin{aligned} s^{-\mu }_N= & {} \left( 0,{\vec {e}}_N^{\,-}\right) = \left( 0,\frac{{\vec {p}}_{{{K}_0^{*}}}\times {\vec {p}}_{\ell ^-}}{\left| {\vec {p}}_{{{K}_0^{*}}}\times {\vec {p}}_{\ell ^-} \right| }\right) , \end{aligned}$$

(49)

$$\begin{aligned} s^{-\mu }_T= & {} \left( 0,{\vec {e}}_T^{\,-}\right) = \left( 0,{\vec {e}}_N^{\,-} \times {\vec {e}}_L^{\,-} \right) , \end{aligned}$$

(50)

$$\begin{aligned} s^{+\mu }_L= & {} \left( 0,{\vec {e}}_L^{\,+}\right) = \left( 0,\frac{{\vec {p}}_{\ell ^+}}{\left| {\vec {p}}_{\ell ^+} \right| }\right) , \end{aligned}$$

(51)

$$\begin{aligned} s^{+\mu }_N= & {} \left( 0,{\vec {e}}_N^{\,+}\right) = \left( 0,\frac{{\vec {p}}_{{{K}_0^{*}}}\times {\vec {p}}_{\ell ^+}}{\left| {\vec {p}}_{{{K}_0^{*}}}\times {\vec {p}}_{\ell ^+} \right| }\right) , \end{aligned}$$

(52)

$$\begin{aligned} s^{+\mu }_T= & {} \left( 0,{\vec {e}}_T^{\,+}\right) = \left( 0,{\vec {e}}_N^{\,+} \times {\vec {e}}_L^{\,+}\right) , \end{aligned}$$

(53)

where ${\vec {p}}_{\ell ^{\mp }}$ and ${\vec {p}}_{K_0^{*}}$ are in the CM frame of $\ell ^- \,\ell ^+$ system, respectively. A Lorentz transformation is used to boost the components of the lepton polarization to the CM frame of the lepton pair,

$$\begin{aligned} \left( s^{\mp \mu }_L \right) _{CM}= & {} \left( \frac{\left| {\vec {p}}_{\ell ^{\mp }}\right| }{m_\ell }, \frac{E_{\ell } {\vec {p}}_{\ell ^\mp }}{m_\ell \left| {\vec {p}}_{\ell ^{\mp }} \right| }\right) ,\end{aligned}$$

(54)

$$\begin{aligned} \left( s^{\mp \mu }_N \right) _{CM}= & {} \left( s^{\mp \mu }_N \right) _{RF},\end{aligned}$$

(55)

$$\begin{aligned} \left( s^{\mp \mu }_T \right) _{CM}= & {} \left( s^{\mp \mu }_T \right) _{RF}, \end{aligned}$$

(56)

where RF refers to the rest frame of the corresponding lepton as well as ${\vec {p}}_{\ell ^+} = - {\vec {p}}_{\ell ^-}$ and $m_\ell$ is the mass of leptons and $E_\ell$ is the energy of leptons in the CM frame, respectively.

The polarized and normalized differential forward–backward asymmetry can be defined as

$$\begin{aligned}&\mathcal{A}_{FB}^{ij}(\hat{s}) = \Bigg (\frac{\mathrm{d}\Gamma (\hat{s})}{\mathrm{d}\hat{s}} \Bigg )^{-1} \Bigg \{ \int _0^1 \mathrm{d}z - \int _{-1}^0 \mathrm{d}z \Bigg \} \nonumber \\&\qquad \times \Bigg \{ \Bigg [ \frac{\mathrm{d}^2\Gamma (\hat{s},{\vec {s}}^{\,-} = {\vec {i}},{\vec {s}}^{\,+} = \vec {j})}{\mathrm{d}\hat{s} \mathrm{d}z}\nonumber \\&\qquad -\, \frac{\mathrm{d}^2\Gamma (\hat{s},{\vec {s}}^{\,-} = {\vec {i}},{\vec {s}}^{\,+} = -\vec {j})}{\mathrm{d}\hat{s} \mathrm{d}z} \Bigg ] \nonumber \\&\qquad -\, \Bigg [ \frac{\mathrm{d}^2\Gamma (\hat{s},{\vec {s}}^{\,-} = -{\vec {i}},{\vec {s}}^{\,+} = \vec {j})}{\mathrm{d}\hat{s} \mathrm{d}z}\nonumber \\&\qquad -\,\frac{\mathrm{d}^2\Gamma (\hat{s},{\vec {s}}^{\,-} = -{\vec {i}},{\vec {s}}^{\,+} = -\vec {j})}{\mathrm{d}\hat{s} \mathrm{d}z} \Bigg ] \Bigg \}\nonumber \\&\quad = \mathcal{A}_{FB}({\vec {s}}^{\,-}={\vec {i}},{\vec {s}}^{\,+}=\vec {j}) - \mathcal{A}_{FB}({\vec {s}}^{\,-}={\vec {i}},{\vec {s}}^{\,+}=-\vec {j})\nonumber \\&\qquad -\,\mathcal{A}_{FB}({\vec {s}}^{\,-}=-{\vec {i}},{\vec {s}}^{\,+}=\vec {j}) \nonumber \\&\qquad +\,\mathcal{A}_{FB}({\vec {s}}^{\,-}=-{\vec {i}},{\vec {s}}^{\,+}=-\vec {j}), \end{aligned}$$

(57)

where $\frac{\mathrm{d}\Gamma (\hat{s})}{\mathrm{d}\hat{s}}$ is calculated in the CM frame. Using these definitions for the double polarized FB asymmetries, the following explicit forms for $\mathcal{A}_{FB}^{ij}$’s are obtained:

$$\begin{aligned} \mathcal{A}_{FB}^{LL}= & {} -\mathcal{A}_{FB}^{NN}=-\mathcal{A}_{FB}^{TT}=\mathcal{A}_{FB},\end{aligned}$$

(58)

$$\begin{aligned} \mathcal{A}_{FB}^{LN}= & {} \frac{-16v {\lambda m_{\ell }m_B^3} }{3\sqrt{\hat{s}}\Delta }\text{ Im }[\mathcal{A}\mathcal{C}^*],\end{aligned}$$

(59)

$$\begin{aligned} \mathcal{A}_{FB}^{NL}= & {} \mathcal{A}_{FB}^{LN}, \end{aligned}$$

(60)

$$\begin{aligned} \mathcal{A}_{FB}^{LT}= & {} \frac{-16 {\lambda m_{\ell }m_B^3} }{3\sqrt{\hat{s}}\Delta }|\mathcal{A}|^2,\end{aligned}$$

(61)

$$\begin{aligned} \mathcal{A}_{FB}^{TL}= & {} \mathcal{A}_{FB}^{LT}, \end{aligned}$$

(62)

$$\begin{aligned} \mathcal{A}_{FB}^{NT}= & {} \frac{ 8 m_B^2 m_{\ell }\sqrt{\lambda } }{\Delta }\text{ Im }\left[ -2{{m}_\ell \over {\hat{s}}}(\mathcal{A}\mathcal{C}^*)(1-\hat{r}_{{{K}_0^{*}}})\right. \nonumber \\&\left. -\,(\mathcal{A}\mathcal{N}^*)+2{m}_\ell (\mathcal{D}\mathcal{A}^*) \right] ,\end{aligned}$$

(63)

$$\begin{aligned} \mathcal{A}_{FB}^{TN}= & {} -\mathcal{{ A}}_{FB}^{NT}. \end{aligned}$$

(64)

3.5 The differential decay rates and forward–backward asymmetries of $\overline{B} \rightarrow \overline{K}\ell ^{+}\ell ^{-}$

Imposing $m_s=0$ in the whole afore-mentioned expressions for $\overline{B} \rightarrow \overline{K}_0^{*}(1430)\ell ^{+}\ell ^{-}$ we could obtain similar expressions for $\overline{B} \rightarrow \overline{K}\ell ^{+}\ell ^{-}$ decay, such that all the above equations remain unchanged except the definitions of the auxiliary functions (Eqs. (38)–(43)). One can see from the matrix elements of the above-said decays that, in order to obtain the auxiliary functions of the latter decay, we should perform the following substitutions:

$$\begin{aligned} f_+^{K_0^{*}}\rightarrow -f_+^{K}, \quad f_-^{K_0^{*}}\rightarrow -f_-^{K},\quad f_T^{K_0^{*}}\rightarrow -f_T^{K}. \end{aligned}$$

(65)

4 Numerical results and discussion

In this section we shall focus on the concrete models such as the SM and 2HDM of type III. We study the effects of such models on the polarized and unpolarized forward–backward asymmetries and their averages for $\overline{B}\rightarrow \overline{K}_0^{*}(1430) \ell ^+\ell ^-$ and $\overline{B}\rightarrow \overline{K} \ell ^+\ell ^-$ decays. At the end, we compare the results of different decay modes to each other. The corresponding averages [43] are defined by the following equation:

$$\begin{aligned} \langle \mathcal{A}_{FB}^{ij} \rangle = \frac{\displaystyle \int _{4 \hat{m}_\ell ^2}^{(1-\sqrt{\hat{r}_{M}})^2} \mathcal{A}_{FB}^{ij} \frac{\mathrm{d}\mathcal{B}}{\mathrm{d} \hat{s}} \mathrm{d} \hat{s}}{\displaystyle \int _{4 \hat{m}_\ell ^2}^{(1-\sqrt{\hat{r}_{M}})^2} \frac{\mathrm{d}\mathcal{B}}{\mathrm{d} \hat{s}} \mathrm{d}\hat{s}}, \end{aligned}$$

(66)

where the subscript M refers to the $\overline{K}_{0}^*(1430)$ and $\overline{K}$ mesons. The full kinematical interval of the dilepton invariant mass $q^2$ is $4 m_\ell ^2 \le q^2 \le (m_B - m_M)^2$ for which the long-distance contributions (the charmonium resonances) can give substantial effects by considering the two low lying resonances $J/\psi$ and $\psi ^\prime$, in the interval of $8~\hbox {GeV}^2\le q^2 \le 14~\hbox {GeV}^2$. Because of the hadronic uncertainties, first we introduce the kinematical region of $q^2$ for the muon [25]:

$$\begin{aligned}&\text{ I }\quad 4 m_\ell ^2 \le q^2 \le (m_{J/\psi } - 0.02~\hbox {GeV})^2,\nonumber \\&\text{ II }\quad (m_{J/\psi } + 0.02~\hbox {GeV})^2 \le q^2 \le (m_{\psi ^\prime } - 0.02~\hbox {GeV})^2, \nonumber \\ \\&\text{ III }\quad (m_{\psi ^\prime } + 0.02~\hbox {GeV})^2 \le q^2 \le (m_B-m_M)^2,\nonumber \end{aligned}$$

(67)

and for the tau:

$$\begin{aligned}&\text{ I }\quad 4 m_\ell ^2 \le q^2 \le (m_{\psi '} - 0.02~\hbox {GeV})^2,\nonumber \\&\text{ II }\quad (m_{\psi '} + 0.02~\hbox {GeV})^2 \le q^2 \le (m_B-m_M)^2. \end{aligned}$$

(68)

In order to skip the strong overlap of two resonances for $\mu$ channel, we use the kinematical region of $q^2$:

$$\begin{aligned}&\text{ I }\quad 4 m_\ell ^2 \le q^2 \le (m_{J/\psi } - 0.02~\hbox {GeV})^2,\nonumber \\&\text{ III }\quad (m_{\psi ^\prime } + 0.02~\hbox {GeV})^2 \le q^2 \le (m_B-m_M)^2. \end{aligned}$$

(69)

In 2HDM of type III, apart from the masses of Higgs bosons, two vertex parameters, $\lambda _{tt}$ and $\lambda _{bb}$, are appeared in the calculations of the related Feynman diagrams [30–34]. Since these coefficients can be complex, we can rewrite our expression:

$$\begin{aligned} \lambda _{tt}\lambda _{bb} = |\lambda _{tt}\lambda _{bb}|\,e^{i\theta }, \end{aligned}$$

(70)

in which the range of variations for $|\lambda _{tt}|$, $|\lambda _{bb}|$, and the phase angle $\theta$ are given by the experimental limits of the electric dipole moments of neutron (NEDM), $B^0$–$\bar{B}^0$ mixing, $\rho \,_0$ ($\rho \,_0 \equiv M_W^2 /\rho M_Z^2$) [33], $R_b$, and $\mathcal{B}(b \rightarrow s \gamma )$ [29, 33, 44, 45]. The experimental bounds on NEDM and $Br(b \rightarrow s \gamma )$ as well as $M_{H^+}$ which are obtained at $\mathrm {LEP II}$ constrain $\lambda _{tt}\lambda _{bb}$ to be closely equal to 1 and the phase angle $\theta$ to be between $60^{\circ }{-}90^{\circ }$. Another restriction which comes from the experimental value of $x_d$ parameter, corresponding to the $B^0$–$\bar{B}^0$ mixing, controls $|\lambda _{tt}|$ to be less than 0.3. Also, the experimental value of the parameter $R_b$ which is defined as $R_b\equiv \frac{\Gamma (Z\rightarrow b\bar{b})}{\Gamma (Z\rightarrow \mathrm {hadrons})}$ affects the magnitude of $|\lambda _{bb}|$ in such a way this coefficient could be around 50. Using these constraints and taking $\theta = \pi /2$, we consider the following three typical parameter cases throughout the numerical analysis [33]:

$$\begin{aligned} \hbox {Case A}:\quad |\lambda _{tt}|= & {} 0.03; \quad |\lambda _{bb}|= 100,\end{aligned}$$

(71)

$$\begin{aligned} \hbox {Case B}:\quad |\lambda _{tt}|= & {} 0.15;\quad |\lambda _{bb}|= 50,\end{aligned}$$

(72)

$$\begin{aligned} \hbox {Case C}:\quad |\lambda _{tt}|= & {} 0.3; \quad |\lambda _{bb}|= 30. \end{aligned}$$

(73)

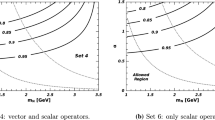
The other main input parameters are the form factors which are listed in Tables 1 and 2. In addition, in this study we have applied four sets of masses of Higgs bosons which are displayed in Table 3 [33].

We investigate $\mathcal{A}_{FB}^{ij}(q^2)$’s and their averages in the SM and 2HDM-III in a set of Figs. 1 2, 3, 4, 5, 6, 7, 8, 9 10, 11 and 12 and Tables 5, 6, 7, 8, 9, 10, 11 and 12, respectively. In these figures and tables the theoretical and experimental uncertainties for $\overline{B}\rightarrow \overline{K}_0^{*}(1430) \ell ^+\ell ^-$ and $\overline{B}\rightarrow \overline{K} \ell ^+\ell ^-$ decays have been taken into account. It should be mentioned that the theoretical uncertainties are extracted from the hadronic uncertainties related to the form factors and the mass of quarks (see Table 4). The experimental uncertainties also originate from the mass of hadrons ($m_B$, $m_{{K}_0^{*}}$, $m_{K}$, $m_{J/\psi }$, $m_{\psi '}$) and the mass of leptons ($m_{\mu }$, $m_{\tau }$) as well as the decay width of ${J/\psi }$, ${\psi '}$ ($\Gamma _{J/\psi }, \Gamma _{\psi '}$) and the branching ratio of ${J/\psi }$, ${\psi '}$ ($\mathcal{B}( J/\psi \rightarrow \ell ^+\ell ^-), \mathcal{B}(\psi '\rightarrow \ell ^+\ell ^-)$) (see Table 4).

Table 4 List of the values for the masses of hadrons and quarks as well as the required decay widthes and branching ratios [49]

Table 5 The ${ \langle \mathcal{A}_{\mathrm{FB}}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\mu ^{+}\mu ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\mu ^{+}\mu ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

Table 6 ${\langle \mathcal{A}_{\mathrm{FB}}^{\mathrm{LN}}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\mu ^{+}\mu ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\mu ^{+}\mu ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

Table 7 ${\langle \mathcal{A}_{\mathrm{FB}}^{\mathrm{NT}}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\mu ^{+}\mu ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\mu ^{+}\mu ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

Table 8 $\mathrm { \langle \mathcal{A}_{FB}^{LT}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\mu ^{+}\mu ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\mu ^{+}\mu ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

Table 9 ${\langle \mathcal{A}_{\mathrm{FB}}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\tau ^{+}\tau ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\tau ^{+}\tau ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

Table 10 ${\langle \mathcal{A}_{\mathrm{FB}}^{\mathrm{LN}}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\tau ^{+}\tau ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\tau ^{+}\tau ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

Table 11 ${\langle \mathcal{A}_{\mathrm{FB}}^{\mathrm{NT}}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\tau ^{+}\tau ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\tau ^{+}\tau ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

Table 12 ${\langle \mathcal{A}_{\mathrm{FB}}^{\mathrm{LT}}\rangle }$ asymmetry for $\overline{B}\rightarrow \overline{K}_0^*(1430) \,\tau ^{+}\tau ^{-}$ and $\overline{B}\rightarrow \overline{K} \,\tau ^{+}\tau ^{-}$ decays in the SM and 2HDM. The errors shown are due to the theoretical and experimental uncertainties. The first errors are related to the theoretical uncertainties and the second ones are due to the experimental uncertainties

At this stage, let us see briefly whether the lepton polarization asymmetries are testable or not. Experimentally, for measuring an asymmetry $\left<\mathcal{A}_{ij}\right>$ of the decay with branching ratio $\mathcal {B}$ at $n\sigma$ level, the required number of events (i.e., the number of $B\bar{B}$) is given by the formula [43]

$$\begin{aligned} N = \frac{n^2}{\mathcal{B} s_1 s_2 \langle \mathcal{A}_{ij} \rangle ^2}, \end{aligned}$$

(74)

where $s_1$ and $s_2$ are the efficiencies of the leptons. The values of the efficiencies of the $\tau$-leptons differ from $50~\%$ to $90~\%$ for their various decay modes [46] and the error in $\tau$-lepton polarization is approximately (10 –$15)~\%$ [47, 48]. So, the error in measurements of the $\tau$-lepton asymmetries is estimated to be about (20 –$30)~\%$, and the error in obtaining the number of events is about $50~\%$.

Based on the above expression for N, in order to detect the polarized and unpolarized forward backward asymmetries in the $\mu$ and $\tau$ channels at $3\sigma$ level, the lowest limit of required number of events are given by (the efficiency of the $\tau$-lepton is considered to be 0.5)

• for $\overline{B} \rightarrow \overline{K}_0^{*}(1430) \mu ^+ \mu ^-$ decay

  $$\begin{aligned} N \sim \left\{ \begin{array}{llll} 10^{12 } &{}\quad (\text{ for } \left<\mathcal{A}_{FB} \right>, \left<\mathcal{A}_{FB}^{LL} \right>, \left<\mathcal{A}_{FB}^{TT} \right>, \left<\mathcal{A}_{FB}^{NN} \right>),\\ 10^{11} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LN} \right>, \left<A_{FB}^{NL} \right>),\\ 10^{9} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LT} \right>~, \left<\mathcal{A}_{FB}^{TL} \right>),\\ 10^{12} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{NT} \right>, \left<\mathcal{A}_{FB}^{TN} \right>),\\ \end{array} \right. \nonumber \end{aligned}$$

• for $\overline{B} \rightarrow \overline{K} \mu ^+ \mu ^-$ decay

  $$\begin{aligned} N \sim \left\{ \begin{array}{ll} 10^{12 } &{}\quad (\text{ for } \left<\mathcal{A}_{FB} \right>, \left<\mathcal{A}_{FB}^{LL} \right>, \left<\mathcal{A}_{FB}^{TT} \right>, \left<\mathcal{A}_{FB}^{NN} \right>),\\ 10^{12} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LN} \right>, \left<\mathcal{A}_{FB}^{NL} \right>),\\ 10^{10} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LT} \right>, \left<\mathcal{A}_{FB}^{TL} \right>),\\ 10^{13} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{NT} \right>, \left<\mathcal{A}_{FB}^{TN} \right>),\\ \end{array} \right. \end{aligned}$$

• for $\overline{B} \rightarrow \overline{K}_0^{*}(1430) \tau ^+ \tau ^-$ decay

  $$\begin{aligned} N \sim \left\{ \begin{array}{ll} 10^{12 } &{}\quad (\text{ for } \left<\mathcal{A}_{FB} \right>, \left<\mathcal{A}_{FB}^{LL} \right>, \left<\mathcal{A}_{FB}^{TT} \right>, \left<\mathcal{A}_{FB}^{NN} \right>),\\ 10^{14} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LN} \right>, \left<\mathcal{A}_{FB}^{NL} \right>),\\ 10^{11} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LT} \right>, \left<\mathcal{A}_{FB}^{TL} \right>),\\ 10^{12} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{NT} \right>, \left<\mathcal{A}_{FB}^{TN} \right>), \end{array} \right. \nonumber \end{aligned}$$

• for $\overline{B} \rightarrow \overline{K} \tau ^+ \tau ^-$ decay

  $$\begin{aligned} N \sim \left\{ \begin{array}{ll} 10^{9 } &{}\quad (\text{ for } \left<\mathcal{A}_{FB} \right>, \left<\mathcal{A}_{FB}^{LL} \right>, \left<\mathcal{A}_{FB}^{TT} \right>, \left<\mathcal{A}_{FB}^{NN} \right>),\\ 10^{11} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LN} \right>, \left<\mathcal{A}_{FB}^{NL} \right>),\\ 10^{9} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{LT} \right>, \left<\mathcal{A}_{FB}^{TL} \right>),\\ 10^{10} &{}\quad (\text{ for } \left<\mathcal{A}_{FB}^{NT} \right>, \left<\mathcal{A}_{FB}^{TN} \right>). \end{array} \right. \nonumber \end{aligned}$$

Now that the minimum required number of events for measuring each asymmetry has been obtained we can compare them to the number produced at the LHC experiments, containing ATLAS, CMS, and LHCb, (${\sim } 10^{12}$ per year) or expected to be produced at the Super-LHC experiments (supposed to be ${\sim } 10^{13}$ per year) to find which asymmetry is testable at the LHC or SLHC.

• Analysis of $\mathcal{A}_{FB}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ and $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$ decays: One can see from Fig. 1, however, the predictions of $\mathcal{A}_{FB}$, in a consideration of the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, for $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ in cases B and C for all mass sets are next to that of the SM which is zero, such coincidence is not generally seen in case A. In this case within the interval $m_{\psi ^\prime }^2<q^2<(m_B-m_{{K}_0^{*}})^2$ a larger discrepancy between predictions of the SM and 2HDM is observed compared with those predictions in the range $4 m_{\mu }^2<q^2< m_{\psi ^\prime }^2$. Also it is understood from these plots that whenever the mass of $H^{\pm }$ increases or the mass of $H^{0}$ decreases this asymmetry shows more sensitivity to the existence of new Higgs bosons in such a manner that the largest deviation from the SM prediction happens for the mass set 3 of the afore-mentioned case and range. In contrast, the magnitudes of averages, in a consideration of the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, in Table 5 could not provide any signs for the presence of new Higgs bosons. It is also explicit from Fig. 2 and Table 5 that we can draw the same conclusions regarding $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$ decay as those of $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ decay.

• Analysis of $\mathcal{A}_{FB}^{LN}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ and $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$ decays: One can observe from Fig. 3 that the predictions of the mass sets 1 (2) and 3 (4) seem to be indistinguishable and the deviation from the SM value in mass sets 2 (4) is larger than that of mass sets 1 (3). Therefore, while this asymmetry is insensitive to the variation of mass of $H^0$, it is susceptible to the change of mass of $H^{\pm }$, here the reduction of mass of such boson. Also, the relevant plots show that this quantity is quite sensitive to the variation of the parameters $\lambda _{tt}$ and $\lambda _{bb}$. For example, by enhancing the magnitude of $|\lambda _{tt}\lambda _{bb}|$ the deviation from the SM value is increased. It can be seen from Fig. 3 and the corresponding table, Table 6, of average values that the largest discrepancy between the SM and 2HDM -III predictions arises in the case C of mass sets 2 and 4. Also, it is found from Table 6 that, in a consideration of the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, none of 2HDM-III expectations overlap with that of the SM. One can observe from Fig. 4 that we can draw similar conclusions concerning $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$ decay to those of $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ decay, except that the two-Higgs-doublet scenario can flip the sign of $\mathcal{A}_{FB}^{LN}$ compared to the SM expectation in the latter decay in cases B and C of all mass sets. Besides, it is understood from Table 6 that, in a consideration of the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, the SM prediction is not located in the range of predictions of cases B and C but in the range of that of case A. Also, one can see from that table that the averages of this asymmetry for $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$ decay are less sensitive to 2HDM-III parameters as compared to those of $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ decay.

• Analysis of $\mathcal{A}_{FB}^{NT}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ and $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$: decays: One can note from Fig. 5 that, whereas the predictions of 2HDM in the domain $4 m_{c}^2<q^2< (m_B-m_{{K}_0^{*}})^2$ for all mass sets and cases conform with that of the SM, such conformity does not happen in the range $4 m_{\mu }^2<q^2< 4m_c^2$. In this range, all discussions regarding $\mathcal{A}_{FB}^{NT}$ are the same as those of $\mathcal{A}_{FB}^{LN}$. It is also understood from Table 7 that, in a consideration of the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, the behavior of averages are similar to those of $\mathcal{A}_{FB}^{LN}$. In addition, one can understand from Fig. 6 that we have the same behaviors for $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$ as those for $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$. Also, one can see from Table 7, considering the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, the averages of this asymmetry for $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$ decay are less sensitive to 2HDM-III parameters as compared to those of $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ decay. Moreover, none of the 2HDM-III averages agree with that of the SM for both decay modes.

• Analysis of $\mathcal{A}_{FB}^{LT}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^{*} \mu ^+ \mu ^-$ and $\overline{B}\rightarrow \overline{K} \mu ^+ \mu ^-$: decays: For each of the decays a high overlap in the corresponding plots is seen, making them indistinguishable, so we do not present them in this paper. Also, one can see from Table 8 that there is a high overlap among different averages for each decay mode

• Analysis of $\mathcal{A}_{FB}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^{*} \tau ^+ \tau ^-$ and $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decays: A comparison between Figs. 7 and 1 as well as Figs. 8 and 2 makes up the same conclusions for this asymmetry as for the mu channel. However, one can conclude from Tables 5 and 9 that the sensitivity of $\left<\mathcal{A}_{FB} \right>$ to the 2HDM-III parameters in $\tau$ channel is the same as for the corresponding figure and is larger than that asymmetry in the $\mu$ channel. Also, one can see from Table 5 that, considering the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, the averages of this asymmetry for $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decay are more sensitive to the 2HDM-III parameters as compared to those of $\overline{B}\rightarrow \overline{K}_0^{*} \tau ^+ \tau ^-$ decay.

• Analysis of $\mathcal{A}_{FB}^{LN}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^* \tau ^+ \tau ^-$ and $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decays: One can find from Figs. 9 and 10 and Table 10 that this asymmetry behavior is similar to the one of the mu channel. Also, one can see from Table 10 that, considering the theoretical and experimental uncertainties on the SM and 2HDM-III predictions, the averages of this asymmetry for $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decay are more sensitive to the 2HDM-III parameters as compared to those of $\overline{B}\rightarrow \overline{K}_0^{*} \tau ^+ \tau ^-$ decay. Moreover, while all 2HDM-III averages overlap with that of the SM in the $\overline{B}\rightarrow \overline{K}_0^* \tau ^+ \tau ^-$ decay to some extent, none of them overlap with the SM prediction in $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decay at all.

• Analysis of $\mathcal{A}_{FB}^{NT}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^* \tau ^+ \tau ^-$ and $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decays: One can observe from Figs. 11 and 12 that there are the same analyses among this asymmetry of mentioned decays and that of their $\mu$ channels. Also, it is found from the Table 11 that in consideration of theoretical and experimental uncertainties on the SM and 2HDM-III predictions, the averages of this asymmetry for $\overline{B}\rightarrow \overline{K}_0^{*} \tau ^+ \tau ^-$ decay are as sensitive to 2HDM-III parameters as those for $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decay. Moreover, while all 2HDM-III averages overlap with that of the SM in $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$ decay to some extent, only the case A of averages overlap with the SM prediction in $\overline{B}\rightarrow \overline{K}_0^{*} \tau ^+ \tau ^-$ decay.

• Analysis of $\mathcal{A}_{FB}^{LT}$ asymmetries for $\overline{B}\rightarrow \overline{K}_0^{*} \tau ^+ \tau ^-$ and $\overline{B}\rightarrow \overline{K} \tau ^+ \tau ^-$: decays: For each of the decays a high overlap in the corresponding plots is seen, making them indistinguishable, so we do not present them in this paper. Also, one can see from Table 12 that there is a high overlap among different averages for each decay mode.