1 Introduction

Neural networks have been applied to a wide variety of problems in high-energy physics [1, 2], from event classification [3, 4] to object reconstruction [5, 6] and triggering [7, 8]. Typically, however, these networks are applied to solve a specific isolated problem, even when this problem is part of a set of closely related problems. An illustrative example is the signal-background classification problem for a particle with a range of possible masses. The classification tasks at different masses are related, but distinct. Current approaches require the training of a set of isolated networks [9, 10], each of which are ignorant of the larger context and lack the ability to smoothly interpolate, or the use of a single signal sample in training [11, 12], sacrificing performance at other values.

In this paper, we describe the application of the ideas in Ref. [13] to a new neural network strategy, a parameterized neural network in which a single network tackles the full set of related tasks. This is done by simply extending the list of input features to include not only the traditional set of event-level features but also one or more parameters that describe the larger scope of the problem such as a new particle’s mass. The approach can be applied to any classification algorithm; however, neural networks provide a smooth interpolation, while tree-based methods may not.

A single parameterized network can replace a set of individual networks trained for specific cases, as well as smoothly interpolate to cases where it has not been trained. In the case of a search for a hypothetical new particle, this greatly simplifies the task – by requiring only one network – as well as making the results more powerful – by allowing them to be interpolated between specific values. In addition, they may outperform isolated networks by generalizing from the full parameter-dependent dataset.

In the following, we describe the network structure needed to apply a single parameterized network to a set of smoothly related problems and demonstrate the application for theoretical model parameters (such as new particle masses) in a set of examples of increasing complexity.

2 Network structure and training

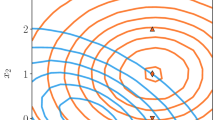
A typical network takes as input a vector of features, \(\bar{x}\), where the features are based on event-level quantities. After training, the resulting network is then a function of these features, \(f(\bar{x})\). In the case that the task at hand is part of a larger context, described by one or more parameters, \(\bar{\theta }\). It is straightforward to construct a network that uses both sets of inputs, \(\bar{x}\) and \(\bar{\theta }\), and operates as a function of both: \(f(\bar{x},\bar{\theta })\). For a given set of inputs \(\bar{x}_0\), a traditional network evaluates to a real number \(f(\bar{x}_0)\). A parameterized network, however, provides a result that is parameterized in terms of \(\bar{\theta }\): \(f(\bar{x}_0,\bar{\theta })\), yielding different output values for different choices of the parameters \(\bar{\theta }\); see Fig. 1.

Training data for the parameterized network has the form \((\bar{x}, \bar{\theta }, y)_i\), where y is a label for the target class. The addition of \(\bar{\theta }\) introduces additional considerations in the training procedure. While traditionally the training only requires the conditional distribution of \(\bar{x}\) given \(\bar{\theta }\) (which is predicted by the theory and detector simulation), now the training data has some implicit prior distribution over \(\bar{\theta }\) as well (which is arbitrary). When the network is used in practice it will be to predict y conditional on both \(\bar{x}\) and \(\bar{\theta }\), so the distribution of \(\bar{\theta }\) used for training is only relevant in how it affects the quality of the resulting parameterized network – it does not imply that the resulting inference is Bayesian. In the studies presented below, we simply use equal sized samples for a few discrete values of \(\bar{\theta }\). Another issue is that some or all of the components of \(\bar{\theta }\) may not be meaningful for a particular target class. For instance, the mass of a new particle is not meaningful for the background training examples. In what follows, we randomly assign values to those components of \(\bar{\theta }\) according to the same distribution used for the signal class. In the examples studied below, the networks have enough generalization capacity and the training sets are large enough that the resulting parameterized classifier performs well without any tuning of the training procedure. However, the robustness of the resulting parameterized classifier to the implicit distribution of \(\bar{\theta }\) in the training sample will in general depend on the generalization capacity of the classifier, the number of training examples, the physics encoded in the distributions \(p(\bar{x} | \bar{\theta }, y)\), and how much those distributions change with \(\bar{\theta }\).

Fig. 1
figure 1

Left, individual networks with input features \((x_1,x_2)\), each trained with examples with a single value of some parameter \(\theta =\theta _a,\theta _b\). The individual networks are purely functions of the input features. Performance for intermediate values of \(\theta \) is not optimal nor does it necessarily vary smoothly between the networks. Right, a single network trained with input features \((x_1,x_2)\) as well as an input parameter \(\theta \); such a network is trained with examples at several values of the parameter \(\theta \)

Full size image

3 Toy example

As a demonstration for a simple toy problem, we construct a parameterized network which has a single input feature x and a single parameter \(\theta \). The network, with one hidden layer of three nodes and sigmoid activation functions, is trained using labeled examples where examples with label 0 are drawn from a uniform background and examples with label 1 are drawn from a Gaussian with mean \(\theta \) and width \(\sigma =0.25\). Training samples are generated with \(\theta =-2,-1,0,1,2\); see Fig. 2a.

As shown in Fig. 2, this network generalizes the solution and provides reasonable output even for values of the parameter where it was given no examples. Note that the response function has the same shape for these values (\(\theta =-1.5,-0.5,0.5,1.5\)) as for values where training data was provided, indicating that the network has successfully parameterized the solution. The signal-background classification accuracy is as good for values where training data exist as it is for values where training data does not.

Fig. 2
figure 2

Top training samples in which the signal is drawn from a Gaussian and the background is uniform. Bottom, neural network response as a function of the value of the input feature x, for various choices of the input parameter \(\theta \); note that the single parameterized network has seen no training examples for \(\theta =-1.5,-0.5,0.5,1.5\)

Full size image

4 1D physical example

A natural physical case is the application to the search for new particle of unknown mass. As an example, we consider the search for a new particle X which decays to \(t\bar{t}\). We treat the most powerful decay mode, in which \(t\bar{t}\rightarrow W^+bW^-\bar{b}\rightarrow qq'b\ell \nu \bar{b}\). The dominant background is standard model \(t\bar{t}\) production, which is identical in final state but distinct in kinematics due to the lack of an intermediate resonance. Figure 3 shows diagrams for both the signal and background processes.

Fig. 3
figure 3

Feynman diagrams showing the production and decay of the hypothetical particle \(X\rightarrow t\bar{t}\), as well as the dominant standard model background process of top quark pair production. In both cases, the \(t\bar{t}\) pair decay to a single charged lepton (\(\ell \)), a neutrino (\(\nu \)) and several quarks (q, b)

Full size image

We first explore the performance in a one-dimensional case. The single event-level feature of the network is \(m_{WWbb}\), the reconstructed resonance mass, calculated using techniques described in Ref. [14]. Specifically, we assume resolved top quarks in each case, for simplicity. Events are simulated at the parton level with madgraph5 [15], using pythia [16] for showering and hadronization and delphes [17] with the ATLAS-style configuration for detector simulation. Figure 4a shows the distribution of reconstructed masses for the background process as well as several values of \(m_X\), the mass of the hypothetical X particle. Clearly the nature of the discrimination problem is distinct at each mass, though similar across masses.

In a typical application of neural networks, one might consider various options:

  • Train a single neural network at one intermediate value of the mass and use it for all other mass values as was done in Refs. [11, 12]. This approach gives the best performance at the mass used in the training sample, but performance degrades at other masses.

  • Train a single neural network using an unlabeled mixture of signal samples and use it for all other mass values. This approach may reduce the loss in performance away from the single mass value used in the previous approach, but it also degrades the performance near that mass point, as the signal is smeared.

  • Train a set of neural networks for a set of mass values as done in Refs. [9, 10]. This approach gives the best signal-background classification performance at each of the trained mass values. However, performance degrades for mass values away from the ones used in training. Most importantly, this approach leads to discontinuities in selection efficiencies across masses, and interpolation of the observed limits is not possible, as the degradation of the performance away from the training points is not defined.

In contrast, we train a single neural network with an additional parameter, the true mass, as an input feature. For a learning task with n event-level features and m parameters, one can trivially reconcieve this as a learning task with \(n+m\) features. Evaluating the network requires supplying the set of event-level features as well as the desired values of the parameters.

Fig. 4
figure 4

Top distributions of neural network input \(m_{WWbb}\) for the background and two signal cases. Bottom, ROC curves for individual fixed networks as well as the parameterized network evaluated at the true mass, but trained only at other masses

Full size image

We note that Ref. [18] previously applied a similar idea with the same goal of improving the interpolation among model parameters. However, in that study the application of BDTs led to a marked decrease in sensitivity at each point compared to isolated algorithms at specific values, and no demonstration was made of the ability to interpolate complex problems in high-dimensional spaces.

Our parameterized neural networks are implemented using the multi-layer perceptron in PyLearn2 [19], with outputs treated with a regressor method and logistic activation function. Input and output data are subject to preprocessing via a scikit-learn [20] pipeline (i.e. transformation to inputs/outputs with a minimum and maximum of zero and one, respectively). Each neural network is trained with 1 hidden layer of three nodes and using Nesterov’s method for stochastic gradient descent [21]. Learning rates were initiated at 0.01, learning momentum was set to 0.9, and minibatch size is set to treat each point individually (i.e. minibatch size of 1). The training samples have approximately 100k examples per mass point.

The critical test is the signal-background classification performance. To measure the ability of the network to perform well at interpolated values of the parameter – values at which it has seen no training data – we compare the performance of a single fixed network trained at a specific value of \(m_{X}^0\) to a parameterized network trained at the other available values other than \(m_{X}^0\). For example, Fig. 4 compares a single network trained at \(m_{X}^0=750\) GeV to a parameterized network trained with data at \(m_{X}=500,1000,1250,1500\) GeV. The parameterized network’s input parameter is set to the true value of the mass \(m_X^0\), and it is applied to data generated at that mass; recall that it saw no examples at this value of \(m_X^0\) in training. Its performance matches or nearly matches that of the single network trained at that value, validating the ability of the single parameterized network to interpolate between mass values without any appreciable loss of statistical performance. Clearly, however, such arguments cannot be applied to extrapolation beyond the boundaries of the training examples. Moreover, we recommend similar hold-out tests be performed to check the quality of the parameterized network on a case-by-case basis.

Here we focus on the performance of the parameterized classifier itself. In order to perform a statistical test at an intermediate value of \(m_{X}\) one will also need to know the distribution of the neural network output at that parameter point, i.e. \(p(f(x, m_X) | m_X)\). The issue of parametrized calibration is discussed in more detail in Ref. [13]. Of course, this issue also applies to the case of a fixed network. In both cases, a straightforward, but computationally expensive strategy is to generate signal samples for each value of \(m_{X}\) that will be tested. An approximate, but more computationally efficient strategy is to use an interpolation algorithm to construct the parametrized distribution [22–24]. This is common practice when parameterizing the distributions with respect to nuisance parameters that describe systematic uncertainties. We advocate using hold-out to test the quality of the parametrized calibration in these situations as well.

Fig. 5
figure 5

Distributions of some of the low-level event features for the decay of \(X\rightarrow t\bar{t}\) with two choices of \(m_X\) as well as the dominant background process

Full size image

5 High-dimensional physical example

The preceding examples serve to demonstrate the concept in one-dimensional cases where the variation of the output on both the parameters and features can be easily visualized. In this section, we demonstrate that the parameterization of the problem and the interpolation power that it provides can be achieved also in high-dimensional cases.

We consider the same hypothetical signal and background process as above, but now expand the set of features to include both low-level kinematic features which correspond to the result of reconstruction algorithms, and high-level features, which benefit from the application of physics domain knowledge. The low-level features are the four-vectors of the reconstructed events, namely:

  • the leading lepton momenta,

  • the momenta of the four leading jets,

  • the b-tagging information for each jet

  • the missing transverse momentum magnitude and angle

  • the number of jets

for a total of 22 low-level features; see Fig. 5. The high-level features combine the low-level information to form approximate values of the invariant masses of the intermediate objects. These are:

  • the mass (\(m_{\ell \nu }\)) of the \(W\rightarrow \ell \nu \),

  • the mass (\(m_{jj}\)) of the \(W\rightarrow qq'\),

  • the mass (\(m_{jjj}\)) of the \(t\rightarrow Wb\rightarrow bqq'\),

  • the mass (\(m_{j\ell \nu }\)) of the \(t\rightarrow Wb\rightarrow \ell \nu b\),

  • the mass (\(m_{WWbb}\)) of the hypothetical \(X\rightarrow t\bar{t}\),

for a total of five high-level features; see Fig. 6.

Fig. 6
figure 6

Distributions of high-level event features for the decay of \(X\rightarrow t\bar{t}\) with two choices of \(m_X\) as well as the dominant background process; see text for definitions

Full size image

The parameterized deep neural network models were trained on GPUs using the Blocks framework [25–27]. Seven million examples were used for training and one million were used for testing, with 50 % background and 50 % signal. The architectures contain five hidden layers of 500 hidden rectified linear units with a logistic output unit. Parameters were initialized from a Gaussian distribution with mean zero and width 0.1, and updated using stochastic gradient descent with mini-batches of size 100 and 0.5 momentum. The learning rate was initialized to 0.1 and decayed by a factor of 0.89 every epoch. Training was stopped after 200 epochs.

The high dimensionality of this problem makes it difficult to visually explore the dependence of the neural network output on the parameter \(m_{X}\). However, we can test the performance in signal-background classification tasks. We use three types of networks. A single parameterized network is trained using 7M training samples with masses \(m_X=500,750,1000, 1250, 1500\) GeV and tested in a sample generated with \(m_X=1000\) GeV; the performance is compared to a single fixed network trained with samples at \(m_X=1000\) (with 7M training examples). In each case, we use approximately the same number of training and testing examples per mass point. Figure 7 shows that the parameterized network matches the performance of the fixed network. A more stringent follow-up test removes the \(m_X=1000\) sample from the training set of the parameterized network, so that this network is required to interpolate its solution. The performance is unchanged, demonstrating that the parameterized network is capable of generalizing the solution even in a high-dimensional example.

Fig. 7
figure 7

Comparison of the signal-to-background discrimination for four classes of networks for a testing sample with \(m_X=1000\) GeV. A parameterized network trained on a set of masses (\(m_X=500,750,1000,1250, 1500\)) is compared to a single network trained at \(m_X=1000\) GeV. The performance is equivalent. A second parameterized network is trained only with samples at \(m_x=500,750,1250, 1500\), forcing it to interpolate the solution at \(m_X =1000\) GeV. Lastly, a single non-parameterized network trained with all the mass points shows a reduced performance. The results are indistinguishable for cases where the networks use only low-level features (shown) or low-level as well as high-level features (not shown, but identical)

Full size image
Fig. 8
figure 8

Comparison of the performance in the signal-background discrimination for the parameterized network, which learns the entire problem as a function of mass, and a single network trained only at \(m_X=1000\) GeV. As expected, the AUC score (integral of the curves in Fig. 7) decreases for the single network as the mass deviates from the value in the training sample. The parameterized network shows improvement over this performance; the trend of improving AUC versus mass reflects the increasing separation between the signal and background samples with mass, see Figs. 5 and 6. For comparison, also shown in the performance a single network trained with an unlabeled mixture of signal samples at all masses

Full size image

Conversely, Fig. 8 compares the performance of the parameterized network to a single network trained at \(m_X=1000\) GeV when applied across the mass range of interest, which is a common application case. This demonstrates the loss of performance incurred by some traditional approaches and recovered in this approach. Similarly, we see that a single network trained an unlabeled mixture of signal samples from all masses has reduced performance at each mass value tested.

In previous work, we have shown that deep networks such as these do not require the addition of high-level features [28, 29] but are capable of learning the necessary functions directly from the low-level four-vectors. Here we extend that by repeating the study above without the use of the high-level features; see Fig. 7. Using only the low-level features, the parameterized deep network achieves essentially indistinguishable performance for this particular problem and training sets of this size.

6 Discussion

We have presented a novel structure for neural networks that allows for a simplified and more powerful solution to a common use case in high-energy physics and demonstrated improved performance in a set of examples with increasing dimensionality for the input feature space. While these example use a single parameter \(\theta \), the technique is easily applied to higher dimensional parameter spaces.

Parameterized networks can also provide optimized performance as a function of nuisance parameters that describe systematic uncertainties, where typical networks are optimal only for a single specific value used during training. This allows statistical procedures that make use of profile likelihood ratio tests [30] to select the network corresponding to the profiled values of the nuisance parameters [13].

Datasets used in this paper containing millions of simulated collisions can be found in the UCI Machine Learning Repository [31] at http://archive.ics.uci.edu/ml/datasets/HEPMASS.