1 Introduction

The traversable Lorentzian wormholes, hypothetical narrow ‘bridges’ or ‘tunnels’ connecting two regions of the same universe or two separate universes, have become a subject of considerable interest in the last couple of years following the pioneering work by Morris and Thorne [2]. Such wormholes, which act as a kind of ‘shortcut’ in spacetime, are an offspring of the Einstein field equations [2, 3] in the hierarchy of the black holes and white holes. The most striking property of such a wormhole is the existence of an inevitable amount of exotic matter around the throat. The existence of this static configuration requires a violation of the null energy condition (NEC) [4–10]. This implies that the matter supporting the wormholes is exotic. As the violation of the energy condition is particularly a problematic issue, Visser et al. [6] have shown that wormhole spacetimes can be constructed with arbitrarily small violation of the averaged null energy condition. It is noted that most of the wormhole solutions have been devoted to the study of static configurations that must satisfy some specific properties in order to be traversable. However, one can study wormhole configurations such as dynamical wormholes [11, 12], wormholes with a cosmological constant \(\Lambda \) [13, 14], rotating wormholes [15, 16] etc. to obtain a panoramic representation of different physical aspects of the wormhole structures.

Scientists have been trying to describe the wormhole structure in two ways: either modifying the Einstein theory or the matter distribution part. In this paper, however, we shall study the wormhole solution in the context of Finsler [17] geometry, which is one of the alternatives of the general relativity. This involves the Riemann geometry as a special case where the four-velocity vector is treated as independent variable. As a historical anecdote we note that Cartan [18] initiated the self-consistent Finsler geometry model in 1935. Thereafter, the Einstein–Finsler equations for the Cartan d-connection were introduced in 1950 [19]. As a consequence, various models of the Finsler geometry in certain applications of physics were studied [20–22]. Though in some of the cases, the Finsler pseudo-Riemannian configurations were considered, investigators were unable to obtain any exact solution. In the beginning of 1996, Vacuru [23, 24] constructed relativistic models of the Finsler gravity in a self-consistent manner. He derived the Finsler gravity and locally anisotropic spinors in the low energy limits of superstring/supergravity theories with N-connection structure, the velocity type coordinates being treated as extra-dimensional ones. Vacaru et al. [25–27] explained the so-called anholonomic frame deformation method (AFDM) by using Finsler geometry methods, which allows one to construct generic off-diagonal exact solutions in various modified gravity theories.

In this direction, a numerous class of exact solutions for the Finsler modifications of black hole, black ellipsoid/torus/brane and string configurations, and locally anisotropic cosmological solutions have been developed for the so-called canonical d-connection and Cartan d-connections. Therefore, it is seen that in recent years the Finsler geometry has drawn much attention due to its potentiality to explain various issues that cannot be explained by Einsteinian gravity. It has been argued that cosmic acceleration can be explained in the context of the Finsler geometry without invoking any dark matter [28] or dark energy [29]. Very recently Chang et al. [30] have studied the kinematics and causal structure in the Finsler spacetime and the study reveals the superluminal phenomena of neutrinos. Pfeifer and Wohlfarth [31] have obtained an action for the Finsler gravity by including the description of matter fields which are coupled to the Finsler spacetime from first principles. An exact vacuum solution for the Finsler spacetime has been found by Li and Chang [32]. They showed that the Finslerian covariant derivative is conserved for the geometrical part of the gravitational field equation.

Inspired by our previous work [1] on compact stars in the context of Finslerian spacetime geometry, we obtain exact wormhole solutions in this paper. We assume some definite forms of wormhole structures and try to find matter distributions that reproduce them. We thus consider specific shape functions and impose restricted choices of redshift functions for the solutions. We study the sensitivity of our solutions with respect to the parameters defining the shape functions. Besides, we also consider a specific energy density and dark energy equation of state, \(p_r=\omega \rho \). The sensitivities of our results for \(\omega < -1\) have also been studied. We find interesting results.

The paper is organized as follows: in Sect. 2 we discuss the basic equations based on the formalism of the Finslerian geometry. Section 3 provides several models of the wormhole. We have also analyzed the models in Sect. 3. The paper ends with a short discussion in Sect. 4.

2 Basic equations based on the Formalism of Finsler geometry

To search wormhole structure one needs to introduce the metric. Let us consider the Finsler structure to be of the form [32]

$$\begin{aligned} F^2=B(r)y^ty^t-A(r)y^ry^r-r^2\bar{F}^2(\theta ,\varphi ,y^\theta ,y^\varphi ). \end{aligned}$$
(1)

In this study, we consider \(\bar{F^2}\) in the following form:

$$\begin{aligned} \bar{F^2}=y^\theta y^\theta +f(\theta ,\phi )y^\phi y^\phi .\end{aligned}$$
(2)

Thus

$$\begin{aligned}&\bar{g}_{ij}=\mathrm{diag}(1,f(\theta ,\phi ))\quad \mathrm{and}\\&\quad \bar{g}^{ij}=\mathrm{diag}(1,\frac{1}{f(\theta ,\phi )})\quad [i,j= \theta , \phi ]. \end{aligned}$$

It is easy to calculate the geodesic spray coefficients \( [G^\mu = \frac{1}{4} g^{\mu \nu } (\frac{\partial ^2 F^2}{\partial x^\lambda \partial y^\nu } y^\lambda - \frac{\partial F^2}{\partial x^\nu })] \) from \(\bar{F^2}\) as

$$\begin{aligned} \bar{G}^\theta =-\frac{1}{4}\frac{\partial f}{\partial \theta }y^{\phi }y^{\phi }, \end{aligned}$$
$$\begin{aligned} \bar{G}^\phi =\frac{1}{4f}\left( 2\frac{\partial f}{\partial \theta }y^\phi y^\theta +\frac{\partial f}{\partial \phi }y^\phi y^\phi \right) . \end{aligned}$$

These yield the Ricci scalar \(\big (Ric\equiv R^\mu _\mu =\frac{1}{F^2}\left( 2\frac{\partial G^\mu }{\partial x^\mu }-y^\lambda \frac{\partial ^2G^\mu }{\partial x^\lambda \partial y^\mu }+2G^\lambda \frac{\partial ^2G^\mu }{\partial y^\lambda \partial y^\mu }-\frac{\partial G^\mu }{\partial y^\lambda }\frac{\partial G^\lambda }{\partial y^\mu }\right) \big )\); in Finsler geometry

$$\begin{aligned}&\bar{F}^2\bar{Ric}=y^\phi y^\phi \left[ \phantom {\left. - \frac{1}{4f} \left( \frac{\partial f}{\partial \theta }\right) ^2+\frac{1}{4f}\frac{\partial f}{\partial \phi }\frac{1}{f}\frac{\partial f}{\partial \phi }+\frac{\partial f}{\partial \theta }\frac{1}{2f}\frac{\partial f}{\partial \theta }-\frac{1}{4f^2}\left( \frac{\partial f}{\partial \phi }\right) ^2\right] }-\frac{1}{2}\frac{\partial ^2 f}{\partial \theta ^2} +\frac{1}{2f}\frac{\partial ^2 f}{\partial \phi ^2} -\frac{1}{2}\frac{\partial }{\partial \phi }\left( \frac{1}{f} \frac{\partial f}{\partial \phi }\right) -\frac{1}{2f^2}\left( \frac{\partial f}{\partial \phi }\right) ^2 \right. \nonumber \\&\quad \left. - \frac{1}{4f} \left( \frac{\partial f}{\partial \theta }\right) ^2 +\frac{1}{4f}\frac{\partial f}{\partial \phi }\frac{1}{f}\frac{\partial f}{\partial \phi }+\frac{\partial f}{\partial \theta }\frac{1}{2f}\frac{\partial f}{\partial \theta }-\frac{1}{4f^2}\left( \frac{\partial f}{\partial \phi }\right) ^2\right] \nonumber \\&\quad +y^\theta y^\theta \left[ -\frac{1}{2}\frac{\partial }{\partial \theta }\left( \frac{1}{f} \frac{\partial f}{\partial \theta }\right) -\frac{1}{4f^2}\left( \frac{\partial f}{\partial \theta }\right) ^2\right] \nonumber \\&\quad + y^\phi y^\theta \left[ \frac{1}{f}\frac{\partial ^2f}{\partial \theta \partial \phi }\!-\!\frac{1}{f^{2}}\left( \frac{\partial f}{\partial \theta }\right) \left( \frac{\partial f}{\partial \phi }\right) \!-\!\frac{1}{2}\frac{\partial }{\partial \theta }\left( \frac{1}{f} \frac{\partial f}{\partial \phi }\right) \!-\!\frac{1}{2}\frac{\partial }{\partial \phi }\left( \frac{1}{f} \frac{\partial f}{\partial \theta }\right) \right] .\nonumber \\ \end{aligned}$$
(3)

Note that the coefficient of \(y^\phi y^\theta =0\) iff f is independent of \(\phi \), i.e.

$$\begin{aligned} f(\theta , \phi ) =f(\theta ), \end{aligned}$$
(4)

where the coefficients of \(y^\theta y^\theta \) and \(y^\phi y^\phi \) are non-zero.

Now, using Eq. (4) in Eq. (3), we get

$$\begin{aligned} \bar{F}^2\bar{Ric}=\left[ -\frac{1}{2f}\frac{\partial ^2 f}{\partial \theta ^2} +\frac{1}{4f^2}\left( \frac{\partial f}{\partial \theta }\right) ^2\right] (y^\theta y^\theta +f y^\phi y^\phi ). \end{aligned}$$

Thus we obtain \(\bar{Ric}\):

$$\begin{aligned} \bar{Ric}= -\frac{1}{2f}\frac{\partial ^2 f}{\partial \theta ^2} +\frac{1}{4f^2}\left( \frac{\partial f}{\partial \theta }\right) ^2, \end{aligned}$$
(5)

which may be a constant or a function of \(\theta \).

For constant value, say \(\lambda \), one can get the Finsler structure \(\bar{F^2}\) as expressed in Eq. (2) in the following categories:

$$\begin{aligned} \bar{F}^2= & {} y^\theta y^\theta + A \sin ^2(\sqrt{\lambda } \theta )y^\phi y^\phi ,\quad (\mathrm{for}~ \lambda > 0);\nonumber \\= & {} y^\theta y^\theta + A \theta ^2 y^\phi y^\phi ,\quad (\mathrm{for}~ \lambda = 0);\nonumber \\= & {} y^\theta y^\theta + A \sinh ^2(\sqrt{-\lambda } \theta )y^\phi y^\phi ,\quad (\mathrm{for}~ \lambda < 0). \end{aligned}$$
(6)

Without any loss of generality one can take A as unity.

Now, the Finsler structure given in Eq. (1) assumes the following form:

$$\begin{aligned} {F}^2= & {} B(r) y^ty^t - A(r) y^ry^r -r^2 y^\theta y^\theta \\&-\, r^2\sin ^2 \theta y^\phi y^\phi + r^2\sin ^2 \theta y^\phi y^\phi -r^2\sin ^2(\sqrt{\lambda } \theta )y^\phi y^\phi . \end{aligned}$$

That is,

$$\begin{aligned} {F}^2 = \alpha ^2 + r^2 \chi (\theta )y^\phi y^\phi , \end{aligned}$$
(7)

where \(\chi (\theta ) = \sin ^2 \theta - \sin ^2(\sqrt{\lambda } \theta )\) and \(\alpha \) is a Riemannian metric.

Hence

$$\begin{aligned} {F} = \alpha \sqrt{ 1 + \frac{r^2 \chi (\theta )y^\phi y^\phi }{\alpha ^2}}. \end{aligned}$$

For the choice \(b_\phi = r\sqrt{ \chi (\theta )} \), we get

$$\begin{aligned} F = \alpha \phi (s), ~~\phi (s) = \sqrt{1+s^2}, \end{aligned}$$
(8)

where

$$\begin{aligned} s =\frac{(b_\phi y^\phi )}{\alpha } = \frac{\beta }{\alpha }, \end{aligned}$$
$$\begin{aligned} b_\mu = ( 0,0,0,b_\phi ),~ ~ b_\phi y^\phi = b_\mu y^\mu = \beta , ~ (\beta ~{\text { is~a ~one~ form}} ). \end{aligned}$$

This indicates that F is the metric of \((\alpha ,~\beta )\)-Finsler space.

Isometric transformations of the Finsler structure [32] yield the Killing equation \(K_V(F) =0\) in the Finsler space as follows:

$$\begin{aligned} \left( \phi (s)-s\frac{\partial \phi (s)}{\partial s}\right) K_V(\alpha ) + \frac{\partial \phi (s)}{\partial s }K_V\beta ) =0, \end{aligned}$$
(9)

where

$$\begin{aligned} K_V(\alpha ) = \frac{1}{2 \alpha }\left( V_{\mu \mid \nu } +V_{\nu \mid \mu } \right) y^\mu y^\nu , \end{aligned}$$
$$\begin{aligned} K_V(\beta ) = \left( V^\mu \frac{\partial b_\nu }{\partial x^\mu } +b_{ \mu }\frac{\partial V^\mu }{\partial x^\nu } \right) y^\nu . \end{aligned}$$

Here “\(\mid \)” indicates the covariant derivative with respect to the Riemannian metric \(\alpha \).

In the present consideration we have

$$\begin{aligned} K_V(\alpha )+ sK_V(\beta )=0 ~~\mathrm{or}~~ \alpha K_V(\alpha )+ \beta K_V(\beta )=0. \end{aligned}$$

This yields

$$\begin{aligned} K_V(\alpha )= 0 \quad \mathrm{and} \quad K_V(\beta )=0, \end{aligned}$$
(10)

or

$$\begin{aligned} V_{\mu \mid \nu } +V_{\nu \mid \mu } =0 \end{aligned}$$
(11)

and

$$\begin{aligned} V^\mu \frac{\partial b_\nu }{\partial x^\mu } +b_{ \mu }\frac{\partial V^\mu }{\partial x^\nu } =0. \end{aligned}$$
(12)

Interestingly, we note that the second Killing equation constrains the first one (Killing equation of the Riemannian space). Hence, it is responsible for breaking the isometric symmetry of the Riemannian space.

Actually, the present Finsler space (for the case \(\bar{F^2}\) as quadric in \( y^\theta ~ \& ~y^\phi \)) can be determined from a Riemannian manifold \(( M, g_{\mu \nu }(x))\) as we have

$$\begin{aligned} F(x,y) =\sqrt{g_{\mu \nu }(x)y^\mu y^\nu }. \end{aligned}$$

It is to be noted that this is a semi-definite Finsler space. As a result, we can use the covariant derivative of the Riemannian space. The Bianchi identities coincide with those of the Riemannian space (being the covariant conservation of Einstein tensor). The present Finsler space reduces to the Riemannian space and consequently the gravitational field equations can be obtained. Again, following Li et al. [33], we can find the gravitational field equations alternatively. They have also proved the covariantly conserved properties of the tensor \(G^\mu _\nu \) in respect of the covariant derivative in Finsler spacetime with the Chern–Rund connection.

It is also to be noted that the gravitational field equation in the Finsler space is controlled to the base manifold of the Finsler space [32], and the fiber coordinates \(y^i\) are set to be the velocities of the cosmic components (velocities in the energy momentum tensor). It is also shown by Li et al. [32] that the gravitational field equation could be derived from the approximation of the work done by Pfeifer et al. [31]. The gravitational dynamics for the Finsler spacetime in terms of an action integral on the unit tangent bundle has been studied by Pfeifer et al. [31]. Again the gravitational field equation in the Finsler space is insensitive to the connection because the \(G_\nu ^\mu \) are obtained from the Ricci scalar, which is, in fact, insensitive to the connections and depends only on the Finsler structure.

Thus the gravitational field equation in the Finsler space could be derived from the Einstein field equation in the Riemannian spacetime with the metric (1) in which the metric \(\bar{g}_{ij}\) is given by

$$\begin{aligned} \bar{g}_{ij} = \mathrm{diag}~(1,~ \sin ^2 \sqrt{\lambda } \theta ). \end{aligned}$$

That is,

$$\begin{aligned} g_{\mu \nu }= \mathrm{diag}~(B,~-A,~ -r^2,~ -r^2\sin ^2 \sqrt{\lambda } \theta ). \end{aligned}$$

Here the new parameter \(\lambda \) plays a significant role in the resulting field equations in Finsler space and consequently affects the Finsler geometric consideration of the wormhole problem.

The Finsler structure (1) yields geodesic spray coefficients:

$$\begin{aligned} G^t=\frac{B'}{2B}y^ty^r, \end{aligned}$$
(13)
$$\begin{aligned} G^r=\frac{A'}{4A}y^ry^r+\frac{B'}{4A}y^ty^t-\frac{r}{2A}\bar{F^2}, \end{aligned}$$
(14)
$$\begin{aligned} G^\theta =\frac{1}{r}y^\theta y^r+\bar{G^\theta }, \end{aligned}$$
(15)
$$\begin{aligned} G^\phi =\frac{1}{r}y^\phi y^r+\bar{G^\phi }. \end{aligned}$$
(16)

Here the prime indicates the derivative with respect to r, and the \(\bar{G}^i\) are calculated from \(\bar{F}^2\). Following Akbar-Zadeh [36], one can calculate the Ricci tensor in the Finsler geometry from Ric as

$$\begin{aligned} Ric_{\mu \nu }=\frac{\partial ^2(\frac{1}{2}F^2Ric)}{\partial y^\mu \partial y^\nu }. \end{aligned}$$
(17)

Also one can define the scalar curvature in Finsler as \(S=g^{\mu \nu }Ric_{\mu \nu }\) and, as a consequence, the modified Einstein tensor in Finsler spacetime can be obtained as

$$\begin{aligned} G_{\mu \nu }\equiv Ric_{\mu \nu }-\frac{1}{2}g_{\mu \nu }S. \end{aligned}$$
(18)

Considering \(\bar{F}\) as a dimensional Finsler spacetime with constant flag curvature \(\lambda \), one can find the Einstein tensors in the Finsler geometry as

$$\begin{aligned} G^t_t=\frac{A'}{rA^2}-\frac{1}{r^2A}+\frac{\lambda }{r^2}, \end{aligned}$$
(19)
$$\begin{aligned} G^r_r=-\frac{B'}{rAB}-\frac{1}{r^2A}+\frac{\lambda }{r^2}, \end{aligned}$$
(20)
$$\begin{aligned} G^\theta _\theta =G^\phi _\phi =-\frac{B''}{2AB}-\frac{B'}{2rAB}+\frac{A'}{2rA^2}+\frac{B'}{4AB}\left( \frac{A'}{A}+\frac{B'}{B}\right) . \end{aligned}$$
(21)

As the matter distribution for constructing a wormhole is still a challenging issue to the physicists, we therefore assume the general anisotropic energy-momentum tensor [35] in the form

$$\begin{aligned} T_\nu ^\mu =(\rho + p_r)u^{\mu }u_{\nu } + p_r g^{\mu }_{\nu }+ (p_r -p_t )\eta ^{\mu }\eta _{\nu }, \end{aligned}$$
(22)

where \(u^{\mu }u_{\mu } = - \eta ^{\mu }\eta _{\mu } = 1\), \(p_t\), and \(p_r\) are the transverse and radial pressures, respectively.

Using the above Finsler structure (1) and the energy-stress tensor (22), one can write the gravitational field equations in the Finsler geometry \((G^\mu _\nu =8\pi _FGT^\mu _\nu )\) as

$$\begin{aligned} 8\pi _F G \rho =\frac{A'}{rA^2}-\frac{1}{r^2A}+\frac{\lambda }{r^2}, \end{aligned}$$
(23)
$$\begin{aligned} -8\pi _F Gp_r=-\frac{B'}{rAB}-\frac{1}{r^2A}+\frac{\lambda }{r^2}, \end{aligned}$$
(24)
$$\begin{aligned} -8\pi _F Gp_t=-\frac{B''}{2AB}-\frac{B'}{2rAB}+\frac{A'}{2rA^2}+\frac{B'}{4AB}\left( \frac{A'}{A}+\frac{B'}{B}\right) . \end{aligned}$$
(25)

Note that the Ric from which the field equations are derived is not dependent on the connections, i.e. it is insensitive to the connections. Secondly, the field equations can be derived from a Lagrangian approach. One can notice also that \(\lambda \), which is the beta part of the Finsler space fundamental function, appearing in the field equations, gives the Finslerian contribution. It is important to take into account the Cartan connection approach, which is the most conventional for studying the gravitational field equations in the framework of general relativity and gravitation. The meaning is given in the fact of the metrical connection (\(g_{kl:m}\)) preserving the angle of two vectors moving along the geodesics and the norm [37]. It is a basic point in the derivation of the gravitational Einstein’s equations. The application of the Cartan d-connection presents a difficulty to the solutions of the gravitational field. We avoid this approach in this study, however, such an approach is possible.

To search for the wormhole solution we follow the convention given by Morris and Thorne [2] and hence write the above equations in terms of the redshift function (f(r)) and shape function (b(r)) by substituting \(B(r) = e^{2f(r)}\) and \(A(r) = \frac{1}{1-\frac{b(r)}{r}}\). Thus for the field equations (23)–(25) we have the following relationships:

$$\begin{aligned} b' +\lambda -1 = 8\pi _F r^2G\rho , \end{aligned}$$
(26)
$$\begin{aligned} \left( 1-\frac{b}{r}\right) \left( \frac{2f'}{r}+\frac{1}{r^2}\right) -\frac{\lambda }{r^2} = 8\pi _F G p_r, \end{aligned}$$
(27)
$$\begin{aligned}&\left\{ 1-\frac{b}{r}\right\} \left\{ f''+\frac{f'}{r}+{f'}^2\right\} -\left\{ \frac{b'}{r}-\frac{b}{r^2}\right\} \left\{ \frac{f'}{2}+\frac{1}{2r}\right\} \nonumber \\&\quad = 8\pi _F Gp_t. \end{aligned}$$
(28)

3 Some models for wormholes

Einstein’s general theory of relativity relates the matter distribution with the geometry of the spacetime produced by the matter contain under consideration. Thus if we know the geometry of the spacetime, then we can find the corresponding matter distribution and vice versa. Also it has the interesting feature that if one knows partly the geometry of the spacetime and some components of energy stress tensor, then one can determine the total structure of the spacetime as well as the matter distribution through the field equations. Therefore, in the following, we shall discuss several models of the wormholes under different conditions.

3.1 Specific shape function and redshift function

In this subsection we assume some definite form of the wormhole structures and try to find the matter distributions that produce it.

Case 1   For a particular shape function, \( b(r)=r_0(\frac{r}{r_0})^n \), where \(r_0\) is the throat radius and n is an arbitrary constant, however, for satisfying the flare-out, one has to take n as less than unity [34]. Now, we shall consider two cases with different redshift functions: (1) \( f(r)= constant \), and (2) \( f(r)=\frac{r_0}{r}\). These two choices are justified as the redshift function f(r) must be finite for all values of r to avoid an event horizon.

Subcase (1a)   \(f(r)= constant\)

Using the above field equations (26)–(28), we get the following stress-energy components:

$$\begin{aligned} \rho = \frac{n(\frac{r}{r_0})^{(n-1)}+(\lambda -1)}{8\pi _Fr^2G}, \end{aligned}$$
(29)
$$\begin{aligned} p_r = \frac{-(\frac{r}{r_0})^{(n-1)}-(\lambda -1)}{8\pi _Fr^2G}, \end{aligned}$$
(30)
$$\begin{aligned} p_t = -\frac{(n-1)(\frac{r_0}{r})^{(n-1)}}{16\pi _Fr^2G}, \end{aligned}$$
(31)
$$\begin{aligned} \rho +p_r = \frac{(n-1)(\frac{r_0}{r})^{(n-1)}}{8\pi _Fr^2G}. \end{aligned}$$
(32)

Subcase (1b)   \(f(r)=\frac{r_0}{r}\)

Similarly, here we find the following stress-energy components:

$$\begin{aligned} \rho = \frac{n(\frac{r}{r_0})^{(n-1)}+(\lambda -1) }{8\pi _Fr^2G}, \end{aligned}$$
(33)
$$\begin{aligned} p_r =\frac{2(\frac{r}{r_0})^{(n-2)}-(\frac{r}{r_0})^{(n-1)}-\frac{2r_0}{r}+1-\lambda }{8\pi _Fr^2G}, \end{aligned}$$
(34)
$$\begin{aligned} p_t= \frac{-\frac{n-1}{2}(\frac{r}{r_0})^{(n-1)}+\frac{r_0}{r} +(\frac{r_0}{r})^2-(\frac{r}{r_0})^{(n-3)}+\frac{n-3}{2}(\frac{r}{r_0})^{(n-2)}}{8\pi _Fr^2G}, \end{aligned}$$
(35)
$$\begin{aligned} \rho +p_r =\frac{2(\frac{r}{r_0})^{(n-2)}+(n-1)(\frac{r}{r_0})^{(n-1)}-\frac{2r_0}{r}}{8\pi _Fr^2G}. \end{aligned}$$
(36)

Case 2   We choose the shape function, \( b(r)=r_0+\rho _0r_0^3 \ln (\frac{r_0}{r})\), where \(r_0\) is the throat radius and \(\rho _0\) is an arbitrary constant. However, for satisfying the flare-out condition, one has to take \(\rho _0\) as less than unity. We shall consider as above two cases with different redshift functions:

Subcase (2a)   \( f(r)= constant\)

We find the unknown parameters

$$\begin{aligned} \rho =\frac{(\lambda -1)r-\rho _0r_0^3}{8\pi _Fr^3G}, \end{aligned}$$
(37)
$$\begin{aligned} p_r=\frac{(1-\lambda )r-\left[ r_0+\rho _0r_0^3\mathrm{ln}(\frac{r_0}{r})\right] }{8\pi _Fr^3G}, \end{aligned}$$
(38)
$$\begin{aligned} p_t=\frac{r_0+\rho _0r_0^3\left[ 1+\mathrm{ln}(\frac{r_0}{r})\right] }{16\pi _Fr^3G}, \end{aligned}$$
(39)
$$\begin{aligned} \rho +p_r=-\frac{r_0+\rho _0r_0^3\left[ 1+\mathrm{ln}(\frac{r_0}{r})\right] }{8\pi _Fr^3G}. \end{aligned}$$
(40)

Subcase (2b)   \(f(r)=\frac{r_0}{r}\)

We obtain the unknown parameters as follows:

$$\begin{aligned} \rho =\frac{(\lambda -1)r-\rho _0r_0^3}{8\pi _Fr^3G}, \end{aligned}$$
(41)
$$\begin{aligned} p_r=\frac{r(1-\lambda )-3r_0+\frac{2r_0^2}{r}+\rho _0r_0^3\mathrm{ln}(\frac{r_0}{r})\left( \frac{2r_0}{r}-1\right) }{8\pi _Fr^3G}, \end{aligned}$$
(42)
$$\begin{aligned} p_t=\frac{\frac{3r_0}{2}-\frac{r_0^3}{r^2}-\frac{r_0^2}{2r}+\rho _0 r_0^3\left[ \frac{1}{2}-\frac{r_0}{2r}+\mathrm{ln}(\frac{r_0}{r})\left( \frac{1}{2}-\frac{3r_0}{2r}-\frac{r_0^2}{r^2}\right) \right] }{8\pi _Fr^3G}, \end{aligned}$$
(43)
$$\begin{aligned} \rho +p_r =\frac{-3r_0+\frac{2r_0^2}{r}+\rho _0r_0^3\left[ \mathrm{ln}(\frac{r_0}{r})\left( \frac{2r_0}{r}-1\right) -1\right] }{8\pi _Fr^3G}. \end{aligned}$$
(44)

Case 3   For the shape function, \( b(r)=r_0+\gamma r_0(1-\frac{r_0}{r})\), where \(r_0\) is the throat radius and \(\gamma \) is an arbitrary constant, however, for satisfying the flare-out condition, one has to take \(\gamma \) as less than unity. We shall consider here also two cases with different redshift functions:

Subcase (3a)   \(f(r) = constant\)

We obtain the unknown parameters

$$\begin{aligned} \rho = \frac{(\lambda -1)r+\gamma \frac{r_0^2}{r}}{8\pi _Fr^3G}, \end{aligned}$$
(45)
$$\begin{aligned} p_r=\frac{(1-\lambda )r-r_0(1+\gamma )+\gamma \frac{r_0^2}{r}}{8\pi _Fr^3G}, \end{aligned}$$
(46)
$$\begin{aligned} p_t=\frac{-2\gamma \frac{r_0^2}{r}+r_0(1+\gamma )}{16\pi _Fr^3G}, \end{aligned}$$
(47)
$$\begin{aligned} \rho +p_r=\frac{2\gamma \frac{r_0^2}{r}-r_0(1+\gamma )}{8\pi _Fr^3G}. \end{aligned}$$
(48)

Subcase (3b)   \(f(r)=\frac{r_0}{r}\)

We obtain the unknown parameters

$$\begin{aligned} \rho = \frac{(\lambda -1)r+\gamma \frac{r_0^2}{r}}{8\pi _Fr^3G}, \end{aligned}$$
(49)
$$\begin{aligned} p_r=\frac{r(1-\lambda )-3r_0+\frac{2r_0^2}{r}+\gamma r_0(1-\frac{r_0}{r})(\frac{2r_0}{r}-1)}{8\pi _Fr^3G}, \end{aligned}$$
(50)
$$\begin{aligned} p_t=\frac{\frac{3r_0}{2}-\frac{r_0^3}{r^2}-\frac{r_0^2}{2r}+\frac{\gamma r_0^2}{r}\left[ \frac{r_0}{2r}-\frac{1}{2}\right] +\gamma r_0\left[ 1-\frac{r_0}{r}\right] \left[ \frac{1}{2}-\frac{3r_0}{2r}-\frac{r_0^2}{r^2}\right] }{8\pi _Fr^3G}, \end{aligned}$$
(51)
$$\begin{aligned} \rho +p_r=\frac{\gamma \frac{r_0^2}{r}-3r_0+\frac{2r_0^2}{r}+\gamma r_0(1-\frac{r_0}{r})(\frac{2r_0}{r}-1)}{8\pi _Fr^3G}. \end{aligned}$$
(52)

3.2 Specific energy density and redshift function

Case 4   For the specific energy density, \(\rho = \rho _0(\frac{r_0}{r})^\alpha \), where \(r_0\), \(\rho _0\), and \(\alpha \) are arbitrary constants, we shall consider two cases with different redshift functions:

Subcase (4a)   \(f(r) = constant\)

Using the above choices of the energy density and the redshift function, we obtain the shape function b(r) from the field Eq. (26) as

$$\begin{aligned} b=c_1-\left[ (\lambda -1)+\frac{8\pi _F r^2G\rho _0}{\alpha -3}\left( \frac{r_0}{r}\right) ^\alpha \right] r, \end{aligned}$$
(53)

where \(c_1 \) is an integration constant.

The radial and transverse pressures are obtained:

$$\begin{aligned} 8\pi _F r^2Gp_r=\frac{8\pi _F r^2G\rho _0}{\alpha -3}\left( \frac{r_0}{r}\right) ^\alpha -\frac{c_1}{r}, \end{aligned}$$
(54)
$$\begin{aligned} 16\pi _F r^2Gp_t=\left[ \frac{c_1}{r}-\left( \frac{\alpha -2}{\alpha -3} \right) 8\pi _F r^2G\rho _0\left( \frac{r_0}{r}\right) ^\alpha \right] , \end{aligned}$$
(55)
$$\begin{aligned} 8\pi _F r^2G(\rho +p_r)=\left( \frac{\alpha -2}{\alpha -3}\right) 8\pi _F r^2G\rho _0\left( \frac{r_0}{r}\right) ^\alpha -\frac{c_1}{r}. \end{aligned}$$
(56)

Subcase (4b)   \( f(r)=\frac{r_0}{r}\)

We obtain the unknown parameters

$$\begin{aligned} b=c_1-\left[ (\lambda -1)+\frac{8\pi _F r^2G\rho _0}{\alpha -3}\left( \frac{r_0}{r}\right) ^\alpha \right] r, \end{aligned}$$
(57)
$$\begin{aligned} 8\pi _F r^2Gp_r= & {} \left[ \frac{8\pi _F r^2G\rho _0}{\alpha -3}\left( \frac{r_0}{r}\right) ^\alpha -\frac{c_1}{r}\right] \left[ 1-\frac{2r_0}{r}\right] \nonumber \\&-2\lambda \frac{r_0}{r}, \end{aligned}$$
(58)
$$\begin{aligned} 8\pi _F r^2Gp_t=\left[ \frac{8\pi _F r^2G\rho _0}{\alpha -3}\left( \frac{r_0}{r}\right) ^\alpha -\frac{c_1}{r}\right] \left[ \left( \frac{r_0}{r}\right) ^2+\frac{r_0}{r}\right] , \end{aligned}$$
(59)
$$\begin{aligned}+ & {} \lambda \left[ \left( \frac{r_0}{r}\right) ^2+\frac{r_0}{r}\right] -\left[ \frac{\alpha -2}{\alpha -3}8 \pi _F r^2 G \rho _0 \left( \frac{r_0}{r}\right) ^\alpha - \frac{c_1}{r} \right] \nonumber \\&\times \left[ \frac{1}{2}-\frac{r_0}{2r}\right] , \end{aligned}$$
(60)
$$\begin{aligned}&8\pi _F r^2G(\rho +p_r)=\left[ \frac{8\pi _F r^2G \rho _0}{\alpha -3}\left( \frac{r_0}{r}\right) ^\alpha -\frac{c_1}{r}\right] \nonumber \\&\quad \times \left[ 1-\frac{2r_0}{r}\right] -2 \lambda \frac{r_0}{r} + 8\pi r^2G\rho _0\left( \frac{r_0}{r}\right) ^\alpha . \end{aligned}$$
(61)

Note that b(r) has the same form as the case \(f = constant\). Therefore, we have the same plots for b(r), \(b(r) - r\), and \(b'(r)\) when \(f = constant \).

Case 5   For the dark energy equation of state, \(p_r=\omega \rho ;~\omega <-1\), we shall consider as above two cases with different redshift functions:

Subcase (5a)   \(f(r)= \) constant

Using the above choices of energy density and redshift function, we obtain the following parameters:

$$\begin{aligned} b=(1-\lambda )r+r_0\left( \frac{r_0}{r}\right) ^{(\frac{1}{\omega })}, \end{aligned}$$
(62)
$$\begin{aligned} 8\pi _F r^2G \rho =-\frac{1}{\omega }\left( \frac{r_0}{r}\right) ^{(\frac{1}{\omega }+1)}, \end{aligned}$$
(63)
$$\begin{aligned} 8\pi _F r^2Gp_r=-\left( \frac{r_0}{r}\right) ^{(\frac{1}{\omega }+1)}, \end{aligned}$$
(64)
$$\begin{aligned} 8\pi _Fr^2Gp_t=\frac{1}{2}\left( \frac{1}{\omega }+1\right) \left( \frac{r_0}{r}\right) ^{(\frac{1}{\omega }+1)}, \end{aligned}$$
(65)

where \(r_0 ^{(\frac{1}{\omega }+1)}\) is an integration constant.

Subcase (5b)   \(f(r)=\frac{r_0}{r}\)

We obtain the unknown parameters as follows:

(66)
$$\begin{aligned} 8\pi _Fr^2G\omega \rho =(1-\lambda )+\left( \frac{2br_0}{r^2}-\frac{2r_0}{r}\right) -\frac{b}{r}, \end{aligned}$$
(67)
$$\begin{aligned} 8\pi _Fr^2Gp_r=(1-\lambda )+\left( \frac{2br_0}{r^2}-\frac{2r_0}{r}\right) -\frac{b}{r}, \end{aligned}$$
(68)
$$\begin{aligned}&8\pi _Fr^2Gp_t=\left[ 1-\frac{b}{r}\right] \left[ \frac{r^2_0}{r^2}+\frac{r_0}{r}\right] -\Bigg [(1-\lambda )\left( 1+\frac{1}{\omega }\right) \nonumber \\&\quad +\frac{1}{\omega }\left\{ \frac{2br_0}{r^2}- \frac{2r_0}{r}\right\} -\left( 1+\frac{1}{\omega }\right) \frac{b}{r} \Bigg ] \left[ \frac{1}{2}-\frac{r_0}{2r}\right] , \end{aligned}$$
(69)

where \(c_3 \) is an integration constant.

Fig. 1
figure 1

Plot showing \(\rho +p_r <0\) for case 1. Here \(n=0.0\), 0.2, 0.5, and 0.8 represented by solid, dotted, dashed and chain curves, respectively. Thick curves represent \(f(r)=r_0/r \) and thin curves represent \(f(r) = \) constant. We have assumed \(r_0=2\) for the throat of the wormhole

Full size image
Fig. 2
figure 2

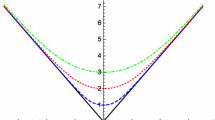
Plot showing \(\rho +p_r <0\) for case 2. Here \(\rho _0 = 0.0\), 0.2, 0.5, and 0.8 are represented by solid, dotted, dashed, and chain curves, respectively. Thick curves represent \(f(r)=r_0/r \) and thin curves represent \(f(r) = \)constant. We have assumed \(r_0=2\) for the throat of the wormhole

Full size image
Fig. 3
figure 3

Plot showing \(\rho +p_r <0\) for case 3. Here \(\gamma =0.0\), 0.2, 0.5, and 0.8 are represented by solid, dotted, dashed and chain curves, respectively. Thick curves represent \(f(r)=r_0/r \) and thin curves represent \(f(r) = \) constant. We have assumed \(r_0=2\) for the throat of the wormhole

Full size image
Fig. 4
figure 4

Plot showing \(\rho +p_r <0\) for Case 4. Here, \( \rho _0 = 0.001\), 0.01, 0.05, 0.10, and 0.15 are represented by black, orange, green, indigo, and red colors, respectively. \(\alpha \) is taken to be 0.0, 1.0, and 2.0 are represented by solid, dashed, and chain curves, respectively. Thick curves represent \(f(r)=r_0/r \) and thin curves represent \(f(r)=constant\). We have assumed \(r_0=2\) and \(c_1=1\)

Full size image
Fig. 5
figure 5

Plots (upper, middle, and lower panels, respectively) showing the behavior of the shape function, radii of the throat where \(b-r\) cuts the r axis, and the nature of the derivative of the shape function for Case 4. Here, \(\rho _0 = 0.001\), 0.01, 0.05, 0.10, and 0.15 are represented by black, orange, green, indigo, and red colors, respectively. \(\alpha \) is taken to be 0.0, 0.5, 1.0, 1.5, and 2.0, represented by solid, dotted, dashed, dot-dashed, and chain curves, respectively. Thick curves represent \(f(r)=r_0/r \) and thin curves represent \(f(r) = \) constant. We have assumed \(r_0=2\) and \(c_1=1\)

Full size image
Fig. 6
figure 6

Plots showing the behavior of the shape function, radii of the throat where \(b-r\) cuts the r axis, and the nature of the derivative of the shape function for Case 5a. Here, \(\lambda = 0.2\), 0.4, and 0.6 are represented by black, orange, and green colors. Solid, dotted, dashed, dot-dashed, and chain curves represent \(\omega =-3.0\), \(-2.5\), \(-2.0\), \(-1.5\), \(-1.1\), respectively. We have assumed \(r_0=2\) for the throat of the wormhole

Full size image
Fig. 7
figure 7

Plots showing the behavior of the shape function, the radii of the throat where \(b-r\) cuts the r axis, and the nature of the derivative of the shape function for Case 5b. Here \(\lambda = 0.2\), 0.4, and 0.6 are represented by black, orange, and green colors. Solid, dotted, dashed, dot-dashed, and chain curves represent \(\omega =-3.0\), \(-2.5\), \(-2.0\), \(-1.5\), \(-1.1\), respectively. We have assumed \(r_0=2\) and \(c_3=3\)

Full size image

4 Discussion and Conclusion

A recent literature survey exhibits that the Finsler geometry has attracted much attention due to its potential to explain various issues, specially cosmic acceleration, which can be explained without invoking dark matter [28] or dark energy [29]. In the context of GR, the violation of NEC (often called exotic matter) is a basic ingredient of static traversable wormholes, although the violation of the energy conditions is quite acceptable as regards certain features of quantum fields, among which the Casimir effect and Hawking evaporation are mentionable. The present work may be looked upon as possible solutions to construct theoretically traversable wormholes in the context of Finsler geometry. In this context, we derived the Einstein gravitational field equations in the Riemannian spacetime with a matter distribution anisotropic in nature. We find out our solution in the conventional way like the Morris–Thorne wormhole solution. We focus our attention mainly on discussing the violation of the null energy condition (NEC) and the constraint on the wormhole geometry, respectively.

In the present work we obtain exact solutions by imposing restricted choices of the redshift function, the shape function, and/or specifying an equations of state. Some of the important features of the present investigation can be formulated as follows:

  1. 1.

    In the first three cases we consider the various choices for the form function, namely, \( b(r)=r_0(\frac{r}{r_0})^n \), \( b(r)=r_0+\rho _0 r_0^3 \ln (\frac{r_0}{r})\), and \(b(r)=r_0+\gamma r_0(1-\frac{r_0}{r})\), and we have analyzed the solution by considering that the redshift function can either be constant or have the functional relation of the radial coordinate.

  2. 2.

    In the next two cases we have found the shape functions for the specific form of energy density, namely, \(\rho = \rho _0(\frac{r_0}{r})^\alpha \) and the dark energy equation of state, \(p_r=\omega \rho ;~\omega <-1\).

After finding all the metric potentials f(r), b(r), and the stress-energy components \(\rho \), \(p_r\), and \(p_t\), we examine whether the results indeed give wormhole structures. It is essentially required that to get a wormhole, the following properties must be satisfied:

  1. 1.

    The redshift function, f(r), should remain finite everywhere to prevent an event horizon.

  2. 2.

    The shape function, b(r), should obey the following flare-out conditions at the throat \(r = r_0\): \(b(r_0) = r_0\) and \(b^\prime (r_0) < 1\), \(r_0\) being the throat radius.

  3. 3.

    Another condition that is needed to satisfy is \(b(r)/r < 1\) for \(r >r_0\).

  4. 4.

    The NEC must be violated for a traversable wormhole, i.e. \(p_r +\rho < 0 \).

The first three conditions are for the geometry of the spacetime and last one is for the matter distribution that produces this spacetime.

We have, however, verified whether our models satisfy all the criteria to represent wormhole structure as follows:

In models 1–3, we have assumed that the spacetime produces wormholes and tried to search for the matter distributions which produce these features. We have found the components of the energy-momentum tensors and Figs. 1, 2, 3, 4 indicate that the matter distributions violate the NEC. Note that violation of NEC is one of the important criteria to hold a wormhole open. Thus the first three models are physically valid. On the other hand, in models 4 and 5, we have found the shape functions for the specific form of energy density and dark energy equation of state. For model 4, one can note that the shape function b(r) assumes the same form for constant or specific redshift function. In Fig. 5, we have vividly depicted different characteristics of the shape function. We observe that the existence of the throat depends on the choices of the parameters. The radius of the throat exists where \(b(r) - r\) cuts the r axis. Also this figure indicates that the flare-out condition is satisfied at the throat i.e. \(b'(r_0)<1\). Thus in model 4, the above four conditions are satisfied for development of wormholes structure.

We have also analyzed, in model 5, different characteristics of the shape functions for different redshift functions in Figs. 6 and 7. These figures satisfy all the geometric criteria of the wormhole structure. In this case we have assumed the dark energy equation of state, \(p_r=\omega \rho ;~\omega <-1\), and hence the NEC, \(p_r +\rho < 0\), is automatically satisfied. Thus, it is an overall observation that present models successfully describe the wormhole features against the background of the Finslerian spacetime.