Slow-roll inflation and BB-mode angular power spectrum of CMB

Abstract

The BB-mode correlation angular power spectrum of CMB is obtained by considering the primordial gravitational waves in the squeezed vacuum state for various inflationary models and results are compared with the joint analysis of the BICEP2/Keck Array and Planck 353 GHz data. The present results may constrain several models of inflation.

1 Introduction

Cosmic inflation is the most widely known scenario proposed for resolving several problems associated with the standard model of cosmology [1, 2]. A number of inflationary models have been proposed over several decades [1–8]. The recent observations on the cosmic microwave background (CMB) anisotropy data may constrain many of the inflationary models [9–13]. It is believed that inflation seeded the formation of the large scale structures in the universe. Inflation also predicts a nearly scale invariant spectrum for the scalar and tensor perturbations which occurred in the early universe. The tensor perturbations of cosmological origin are known as primordial gravitational waves (GWs).

It is believed that the primordial gravitational waves have left an imprint on the cosmic microwave background. The primordial GWs can be studied with the aid of CMB anisotropy and polarization. The CMB is polarized in the early universe due to the Thomson scattering. The density (scalar) fluctuations generate the E-mode polarization of the CMB, while the gravitational waves generate both E-mode and B-mode polarizations [14–17]. The primordial gravitational waves are a unique source of B-mode of CMB and its detection will help in understanding the inflation as well as the primordial gravitational waves itself.

The gravitational waves were generated during the inflation period due to the zero-point quantum oscillations [18]. An initial vacuum state (no graviton) can evolve into a multi-particle quantum state known as the squeezed vacuum state [19], which is a well-known state in the context of quantum optics [20–22]. The primordial gravitational waves are believed to exist in the squeezed vacuum state [23–25]. The primordial gravitational waves are placed in the squeezed vacuum state and its effect on the BB-mode correlation angular power spectrum of CMB is studied with WMAP data [26]. Recently, it is shown that the BB-mode angular power spectrum gets enhanced at its lower multipoles by considering the primordial gravitational waves in thermal state [27]. These studies show that the primordial gravitational waves may exhibit both the squeezing and the thermal features and hence it is worthwhile to examine their combined effects on the BB-mode correlation angular power spectrum in light of the recent joint BICEP2/Keck Array and Planck data.

The aim of the present work is to study effect of primordial gravitational waves in the squeezed vacuum state on the BB-mode correlation angular power spectrum of CMB for various slow-roll inflationary models. Thus the obtained BB-mode correlation angular power spectrum of CMB for the squeezed vacuum as well as the joint effect of squeezing and thermal cases are compared with the joint BICEP2/Keck Array and Planck data.

2 Tensor power spectrum in squeezed state

The perturbed metric for a flat Friedmann–Lemaître–Robertson–Walker universe can be written as

$$\begin{aligned} \mathrm{d}s^2 = R^2(\tau )[-\mathrm{d}\tau ^2 + (\delta _{ij}+h_{ij})\mathrm{d}x^i\mathrm{d}x^j], \end{aligned}$$

(1)

where $\delta _{ij}$ is the flat space metric and $h_{ij}$ is the tensor perturbation, $|h_{ij}|\ll \delta _{ij}$, $\partial _ih^{ij} = 0,\delta ^{ij}h_{ij}=0$, and $\mathrm{d}\tau = \frac{\mathrm{d}t }{R}$ is the conformal time.

In quantum theory, the field $h_{ij}(\mathbf x ,\tau )$ can be written in the Fourier mode as

$$\begin{aligned} h_{ij}(\mathbf x ,\tau )= & {} \frac{D}{(2\pi )^\frac{3}{2}}\int _{-\infty }^{+\infty }\frac{d^3\mathbf k }{\sqrt{2k}}\sum _{p=1}^2 \left[ h_k^{(p)}(\tau ) b_k^{(p)}e^{i\mathbf k .\mathbf x }\varepsilon _{ij}^{(p)}(\mathbf k ) \right. \nonumber \\&\left. + h_k^{(p) *}(\tau )b_k^{(p) \dagger }e^{-i\mathbf k .\mathbf x }\varepsilon _{ij}^{(p) *}(\mathbf k ) \right] , \end{aligned}$$

(2)

where $D=\sqrt{16\pi }l_\mathrm{pl}$ is the normalization constant, $l_{\mathrm{pl}}=\sqrt{G}$ is the Planck length and $\mathbf k$ is the wave vector. The wave number is $k=(\delta _{ij}k^ik^j)^\frac{1}{2}$ and is related to wavelength, $\lambda = \frac{2\pi R}{k}$. The two polarization states $\varepsilon _{ij}^{(p)}$, $p=1,2$ satisfy the conditions $\varepsilon _{ij}^{(p)}\delta ^{ij}=0, ~\varepsilon _{ij}^{(p)}k^i=0, ~\varepsilon _{ij}^{(p)}\varepsilon ^{(p') ij} = 2\delta _{pp'}, ~\varepsilon _{ij}^{(p)}(-\mathbf k )=\varepsilon _{ij}^{(p)}(\mathbf k ).$ These linear polarizations are, respectively, known as plus $(+)$ polarization and cross $(\times )$ polarization.

The creation ($b_k^{(p) \dagger }$) and annihilation ($b_k^{(p)}$) operators satisfy the relationships $[b_k^{(p)},b_{k'}^{(p') \dagger }]\,=\,$   $\delta _{pp'}\delta ^3(k-k')$ and $[b_k^{(p)},b_{k'}^{(p')}]\,=\,$ $[b_k^{(p) \dagger },b_{k'}^{(p') \dagger }]=0.$ The evolution of these operators are governed by the Heisenberg equations of motion,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}{\tau }}b_{k}^{\dagger }(\tau ) = -i[b_k^{\dagger }(\tau ),H], \quad \frac{\mathrm{d}}{\mathrm{d}{\tau }}b_{k}(\tau ) = -i[b_k(\tau ),H].\nonumber \\ \end{aligned}$$

(3)

The initial vacuum state $|0\rangle$ is defined as

$$\begin{aligned} b_k^{(p)} |0\rangle = 0. \end{aligned}$$

Under the Bogoliubov transformation, the creation and annihilation operators become

$$\begin{aligned} b_{k}^{\dagger }(\tau ) = u_k^{*}(\tau )b_{k}^{\dagger }(0) + v_k^{*}(\tau )b_{k}(0), \end{aligned}$$

(4)

$$\begin{aligned} b_{k}(\tau ) = u_{k}(\tau )b_{k}(0) + v_{k}(\tau )b_{k}^{\dagger }(0), \end{aligned}$$

(5)

where $b_{k}^{\dagger }(0)$ and $b_{k}(0)$ are the initial values of the operators, $u_k(\tau )$ and $v_k(\tau )$ are complex functions and they satisfy the condition

$$\begin{aligned} |u_k|^2-|v_k|^2=1. \end{aligned}$$

The coupling of the mode functions $h_k (\tau )$ with $R(\tau )$ gives

$$\begin{aligned} h_k^{(p)}=\frac{\chi _k^{(p)}}{R}, \end{aligned}$$

(6)

where $\chi _k^{(p)}$ can have the following form¹:

$$\begin{aligned} \chi _k(\tau ) = u_k(\tau ) + v_k^{*}(\tau ), \end{aligned}$$

(7)

which satisfies the equation of motion

$$\begin{aligned} \chi _k'' + \left( k^2-\frac{R''}{R}\right) \chi _k = 0, \end{aligned}$$

(8)

where prime indicates the derivative with respect to the conformal time $\tau$.

Two-point correlation function of the tensor perturbation is given by:

$$\begin{aligned} \langle h_k h^{*}_{k'}\rangle = \frac{2\pi ^2}{k^3}P_T(k)\delta ^3(\mathbf k -\mathbf k '), \end{aligned}$$

(9)

where the angle bracket denotes ensemble average and $P_T$ is known as the tensor power spectrum.

Using Eqs. (2) and (6), taking the contribution from each polarization to be the same,

$$\begin{aligned} h(\mathbf x ,\tau ) = \frac{D}{R(\tau )(2\pi )^\frac{3}{2}}\int _{-\infty }^{+\infty }d^3\mathbf k [\chi _k(\tau ) b_k + \chi _k^{*}(\tau )b_k^{\dagger }]e^{i\mathbf k .\mathbf x }. \end{aligned}$$

(10)

The primordial gravitational waves are created due to the zero-point quantum oscillations in the early universe [18, 28]. The initial vacuum state with no graviton evolves into multi-particle quantum state through parametric amplification. Hence the primordial GWs are possible to be considered in the squeezed vacuum state [23, 29, 30].

The squeezed vacuum state is defined as [20, 31]

$$\begin{aligned} |\zeta \rangle = Z(\zeta )|0\rangle , \end{aligned}$$

(11)

where $Z(\zeta )$ is the single mode squeezing operator and is given by

$$\begin{aligned} Z(\zeta ) = \exp \left[ \frac{1}{2} \zeta ^{*} d^2 - \frac{1}{2} \zeta d^{\dagger 2}\right] , \end{aligned}$$

(12)

where $\zeta =r_s e^{i \gamma }$ is a complex number, $r_s$ is the squeezing parameter and $\gamma$ is the squeezing angle. The unitary transformations of the squeezing operator Z on the annihilation and creation operators lead to:

$$\begin{aligned}&Z^{\dagger }(\zeta ) \, d \,Z(\zeta ) = d \cosh r_s -d^{\dagger } e^{i\gamma } \sinh r_s, \nonumber \\&Z^{\dagger }(\zeta ) \, d^{\dagger } \, Z(\zeta ) = d^{\dagger }\cosh r_s -d e^{-i\gamma } \sinh r_s. \end{aligned}$$

(13)

Using Eqs. (2) and (13), the two-point correlation for the tensor perturbation in the squeezed vacuum is obtained:

$$\begin{aligned} \langle h_kh_{k'}^{*} \rangle= & {} \frac{D^2}{R^2} \left[ (1+ 2\sinh ^2 r_s)|\chi _k|^2 \right. \nonumber \\&\left. +\frac{1}{2} \sinh 2r_s (\chi _k^2 e^{i\gamma } + \chi _k^{*2}e^{-i\gamma }) \right] \delta ^3 (\mathbf k -\mathbf k ').\nonumber \\ \end{aligned}$$

(14)

Thus from Eqs. (9) and (14), we get the tensor power spectrum in the squeezed vacuum state as

$$\begin{aligned} P_T(k)= & {} \frac{k^3}{2\pi ^2} \frac{D^2}{R^2} \left[ (1+ 2\sinh ^2 r_s)|\chi _k|^2\right. \nonumber \\&\left. +\frac{1}{2} \sinh 2r_s (\chi _k^2 e^{i\gamma } + \chi _k^{*2}e^{-i\gamma })\right] . \end{aligned}$$

(15)

In the case of a quasi-de Sitter universe during inflation, $R(\tau )=\frac{-1}{H\tau (1-\varepsilon )}$, where the slow-roll parameter $\varepsilon$ is related to the scalar field potential V and is given by $\varepsilon = \frac{m_{\mathrm{pl}}^2}{2}\left( \frac{V'}{V}\right) ^2$. For small $\varepsilon$, $\vartheta = \frac{3}{2}+\varepsilon$, and $n_T = -2\varepsilon = 3-2\vartheta$.

If the slow-roll parameter $\varepsilon$ is considered as constant, then Eq. (8) gets modified as

$$\begin{aligned} \chi ''_k + \left[ k^2 -\frac{1}{\tau ^2}\left( \vartheta ^2 - \frac{1}{4}\right) \right] \chi _k =0. \end{aligned}$$

(16)

The general solution for Eq. (16) is given by

$$\begin{aligned} \chi _k(\tau ) = \sqrt{-\tau }[C_1 (k)H^{(1)}_{\vartheta }(-k\tau )+C_2 (k)H^{(2)}_{\vartheta }(-k\tau )],\nonumber \\ \end{aligned}$$

(17)

where $H^{(1)}_{\vartheta }$ and $H^{(2)}_{\vartheta }$ are respectively the Hankel functions of the first and second kind, and $C_1$ and $C_2$ are the constants of integration. Within the horizon ($k>>RH$), the approximate solution is given by

$$\begin{aligned} \chi _k(\tau )=\frac{1}{\sqrt{2k}}e^{-ik\tau }. \end{aligned}$$

Using the above approximate solution, one can obtain

$$\begin{aligned} C_1(k)=\frac{\sqrt{\pi }}{2}\exp \left[ i\left( \vartheta +\frac{1}{2}\right) \left( \frac{\pi }{2}\right) \right] , \quad C_2(k)=0. \end{aligned}$$

(18)

Therefore, for long wavelength limit ($k<<RH$), Eq. (17) leads to

$$\begin{aligned} \chi _k(\tau )=e^{i\left( \vartheta -\frac{1}{2}\right) \left( \frac{\pi }{2}\right) }2^{\vartheta -\frac{3}{2}}\frac{\Gamma (\vartheta )}{\Gamma {\left( \frac{3}{2})\right) }}\frac{1}{\sqrt{2k}}(-k\tau )^{\frac{1}{2}-\vartheta }. \end{aligned}$$

(19)

Using Eq. (19) in Eq. (15), the tensor power spectrum in the superhorizon limit ($k<<RH$) is obtained:

$$\begin{aligned} P_T(k)= & {} A_T(k_0) \left( \frac{k}{k_0}\right) ^{n_T} \left[ 1+2\sinh ^2 r_s \right. \nonumber \\&\left. + \sinh 2r_s \cos \left( \gamma + (2-n_T)\frac{\pi }{2} \right) \right] , \end{aligned}$$

(20)

where $A_T(k_0) = D^2 \left( \frac{H_{k0}}{2\pi }\right) ^2$ is the normalization constant and $H_{k0}$ is the Hubble parameter at $RH=k_0$ during the inflation, $k_0$ being the pivot wavenumber.

Fig. 1

BB-mode angular spectra for quadratic chaotic inflation model for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 2

BB-mode angular spectra for quadratic chaotic inflation model with thermal effect for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 3

BB-mode angular spectra for quartic chaotic inflation model for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 4

BB-mode angular spectra for quartic chaotic inflation model with thermal effect for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 5

BB-mode angular spectra for new inflation model for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 6

BB-mode angular spectra for new inflation model with thermal effect for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 7

BB-mode angular spectra for hybrid inflation model for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 8

BB-mode angular spectra for hybrid inflation model with thermal effect for unlensing (top panel) and lensing (bottom panel) effects for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

Fig. 9

BB-mode angular spectra for hybrid inflation model for nonthermal (top panel) and thermal (bottom panel) effects with lensing for various values of squeezing parameter and angle with BICEP2/Keck and Planck joint analysis result

3 Inflationary models and tensor power spectrum

In most models of inflation [3], a homogeneous scalar field, called inflaton, is considered as candidate for the inflation. The inflaton field $\phi$ is governed by the equation of motion given by

$$\begin{aligned} \ddot{\phi } + 3H \dot{\phi } + V' =0, \end{aligned}$$

(21)

where dot and prime indicate derivatives with respect to time (t) and the field ($\phi$), respectively. The Hubble parameter H is determined by the energy density of the inflaton field,

$$\begin{aligned} \rho _{\phi } = \frac{\dot{\phi }^2}{2}+V,\end{aligned}$$

thus the Friedmann equation can be written as

$$\begin{aligned} H^2 = \frac{1}{3 m^2_{\mathrm{pl}}}\left( \frac{1}{2} \dot{\phi }^2 + V(\phi )\right) . \end{aligned}$$

(22)

In the slow-roll limit, the energy density of the inflaton field is dominated by its potential, $\frac{\dot{\phi }^2}{2} \ll V$. From Eq. (22), the Hubble parameter and the inflaton potential are related by

$$\begin{aligned} H^2 \simeq \frac{V}{3m^2_{\mathrm{pl}}}. \end{aligned}$$

(23)

This condition is characterized by the slow-roll parameters which are defined in terms of the inflaton potential V and its derivatives as [4, 32–34]

$$\begin{aligned} \begin{aligned}&\varepsilon \equiv \frac{m_{\mathrm{pl}}^2}{2}\left( \frac{V'}{V}\right) ^2, \\&\eta \equiv m^2_{\mathrm{pl}}\left( \frac{V''}{V}\right) ,\\&\xi ^2 \equiv m^4_{\mathrm{pl}} \frac{V' V^{'''}}{V^2}, \\&\sigma ^3 \equiv m^6_{\mathrm{pl}} \frac{V'' V^{''''}}{V^3}, \end{aligned} \end{aligned}$$

(24)

and so on. Inflation lasts as long as the slow-roll conditions are satisfied, i.e., $\varepsilon \ll 1$ and $|\eta |\ll 1$. The duration of inflation is characterized by the e-fold number, N, which can be written in terms of the inflaton potential,

$$\begin{aligned} N \simeq \frac{1}{m^2_{\mathrm{pl}}} \int ^{\phi }_{\phi _\mathrm{end}} \frac{V}{V'} \mathrm{d}\phi . \end{aligned}$$

(25)

In the slow-roll approximation, the power spectrum of the scalar perturbations ($P_S$) and the tensor perturbations ($P_T$) generated outside the horizon are, respectively, given in terms of the potential [35, 36]

$$\begin{aligned} P_S\simeq & {} \frac{1}{12 \pi ^2 m^6_{\mathrm{pl}}}\frac{V^3}{V'^2} |_{k=RH},\end{aligned}$$

(26)

$$\begin{aligned} P_T\simeq & {} \frac{1}{3 \pi ^2 m^4_{\mathrm{pl}}}V |_{k=RH}, \end{aligned}$$

(27)

where $k=RH$ indicates that H and hence, V is evaluated at the time when the mode with wave number k crosses the horizon. For all calculations, we take the scalar power spectrum to be $P_S= 2.43 \times 10^{-9}$.

The tensor-to-scalar ratio can be written in terms of the parameter $\varepsilon$ as [37–39]

$$\begin{aligned} r \equiv \frac{P_T (k)}{P_S (k)} \simeq 16\varepsilon . \end{aligned}$$

(28)

This parameter is often used to characterize the amplitude of the tensor perturbation at the CMB scale. Physically, r is a measure of the slope (of the quantum hill) down which the scalar field is rolling. Since inflation predicts a nearly scale invariant spectrum, the slope is small but not flat. Hence, r is small and can differentiate between the many inflation models.

Next, we obtain the slow-roll parameter and tensor spectral index corresponding to various slow-roll inflation models given below. For this purpose, we use the e-fold number $N = 60$ for all the inflationary models under the present work [40].

3.1 Quadratic chaotic inflation

The chaotic inflation model assumes that the scalar field rolls down its potential and rests at its vacuum state for a while, then after getting displaced due to some fluctuations, rolls back to its true vacuum state and the same mechanism repeats itself. For quadratic chaotic inflation, the scalar field has the potential given by [4]

$$\begin{aligned} V(\phi ) = \frac{1}{2}m^2 \phi ^2, \end{aligned}$$

(29)

where m is the mass of the inflaton field and is taken to be $m= 1.53 \times 10^{13}$ GeV.

Using Eqs. (25) and (29), the slow-roll parameter and index of the tensor power spectrum for the quadratic chaotic inflationary model are obtained:

$$\begin{aligned}&\varepsilon = 8.26 \times 10^{-3},\nonumber \\&n_{T} \simeq -1.65 \times 10^{-2}. \end{aligned}$$

(30)

The corresponding tensor-to-scalar ratio is obtained as, $r=0.132$.

3.2 Quartic chaotic inflation

The quartic chaotic inflation model suggests the existence of the curvaton which generates the curvature fluctuations during inflation after the inflaton field has decayed, while it does not drive the inflation itself. The model has the potential given by [5]

$$\begin{aligned} V(\phi )=\frac{1}{4} \lambda \phi ^4, \end{aligned}$$

(31)

where normalization gives the self-coupling of the scalar field ($\phi$) as $\lambda =5.94 \times 10^{-14}$ GeV, and hence

$$\begin{aligned}&\varepsilon = 1.626 \times 10^{-2},\nonumber \\&n_{T} \simeq -3.25 \times 10^{-2}. \end{aligned}$$

(32)

The tensor-to-scalar ratio for this model is found as $r=0.26$.

3.3 New inflation

The new inflation model [6] is based on the Coleman–Weinberg potential [41, 42],

$$\begin{aligned} V(\phi ) = \frac{1}{4} \lambda \phi ^4 \left( \ln \frac{\phi }{\sigma }-\frac{1}{4}\right) + \frac{\lambda \sigma ^4}{16}. \end{aligned}$$

(33)

In this model, the parameters are taken to be $\sigma =10m_{\mathrm{pl}}$, where $m_{\mathrm{pl}}$ is Planck’s mass, and $\lambda = 2.36 \times 10^{-14}$ GeV. $\sigma$ is the vacuum expectation value of the scalar field at minimum and $\lambda$ is the quadratic self coupling of the field. Therefore we get

$$\begin{aligned}&\varepsilon = 1.16 \times 10^{-2},\nonumber \\&n_{T} \simeq -2.32 \times 10^{-2}. \end{aligned}$$

(34)

The tensor-to-scalar ratio in this case is obtained: $r=0.186$.

3.4 Hybrid inflation

In this model, the inflation is driven by two scalar fields, in which one of the fields ($\phi$) is responsible for the normal slow-roll inflation while the other field ($\sigma$) triggers the end of inflation. The potential for this model is [7, 8]

$$\begin{aligned} V(\phi )=\frac{1}{4\lambda }(M^2 - \lambda \sigma ^2)^2+ \frac{1}{2}m^2\phi ^2 + \frac{1}{2}g^2\phi ^2\sigma ^2, \end{aligned}$$

(35)

where the parameters are taken to be as follows: $g=8 \times 10^{-4}$, $\lambda =1$ are the self-coupling constants of the inflaton field and the trigger field, respectively, and the masses of the fields are $m=1.5 \times 10^{-7} m_{\mathrm{pl}}$, $M =1.21 \times 10^{16}$ GeV, respectively.

The $\phi$ field drives the inflation, thus determining the period of inflation while the $\sigma$ field determines the rate of inflation. Therefore we get

$$\begin{aligned}&\varepsilon = 2.65 \times 10^{-4}, \nonumber \\&n_{T} \simeq -5.3 \times 10^{-4}. \end{aligned}$$

(36)

The tensor-to-scalar ratio in this case is found as $r=4.24 \times 10^{-3}$.

4 BB-mode angular power spectrum of CMB

The CMB radiation can be polarized due to the gravitational waves called the B-mode of CMB [43–45].

The angular power spectrum of the B-mode of CMB is given by [46, 47]

$$\begin{aligned} \frac{C_l^{BB}}{(4\pi )^2}= & {} \int \mathrm{d}k \, k^2 \, P_T(k) \nonumber \\&\times \left| \int _0^{\tau _0} \mathrm{d}\tau g(\tau ) h_k(\tau ) \left[ 2j'_l(x) +\frac{4j_l(x)}{x}\right] \right| ^2, \end{aligned}$$

(37)

where $g(\tau )=\kappa e^{-\kappa }$ is the visibility function, $\kappa$ is the differential optical depth for the Thomson scattering, $x=k(\tau _0 -\tau )$ and $j_l$ is the spherical Bessel function.

The BB-mode correlation angular spectrum of CMB is obtained for the gravitational waves in the squeezed vacuum and thermal vacuum states for the quadratic chaotic, quartic chaotic, new inflation and hybrid inflationary models. The angular power spectra for the different inflation models are generated using the CAMB code with the tensor spectral index $n_T$ corresponding to each inflationary model. For all the cases, the optical depth is taken as $\kappa = 0.08$, the pivot wave number for tensor modes is taken as $k_0 =0.002$ Mpc$^{-1}$ and that for scalar mode is $k_0 =0.05$ Mpc$^{-1}$. The tensor-to-scalar ratio used for each inflationary model is taken from the previous section where their values are computed. The obtained BB-mode angular power spectrum for various values of the squeezing parameter and temperature are compared with the limit of the BICEP2/Keck Array and Planck 353 GHz joint analysis data. The implemented limit (BK $\times$ BK $- \, \alpha$ BK $\times$ P)/(1 $-\, \alpha$) at $\alpha = \alpha _{fid} = 0.04$ is evaluated [48] from the auto-spectra and cross-spectra of the combined BICEP2/Keck 150 GHz maps and Planck 353 GHz maps to clean out the dust contribution, BK $\times$ BK indicates the BICEP2/Keck auto-spectra at 150 GHz and BK $\times$ P indicates the cross-spectra of BICEP2/Keck maps at 150 GHz and Planck maps at 353 GHz. This combination is taken after the subtraction of the dust contribution which is 0.04 times as much in the BICEP2 band as it is in the Planck 353 GHz band (see Ref. [48] for details).

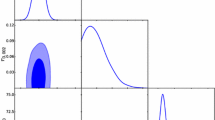
The BB-mode correlation angular spectra for the different inflation models for zero squeezing with nonthermal and thermal effect for unlensing and lensing effects are obtained and their corresponding plots are given in Figs. 1, 2, 3, 4, 5, 6, 7, 8, and 9. The BB-mode angular spectrum for the hybrid inflationary model for squeezing, thermal and their combined effects with lensed and unlensed cases are given up to l=160 to highlight their effects on the angular power spectrum (Fig. 9). It can be seen that for various values of the squeezing parameter and squeezing angle, the quadratic chaotic, quartic chaotic and new inflation models are out of the limit of BICEP2/Keck Array and Planck 353 GHz joint data. For the thermal effect with various values of the squeezing parameter and squeezing angle, the quadratic chaotic, quartic chaotic and new inflation models are also not found within the limit of BICEP2/Keck Array and Planck 353 GHz joint data.

It can be observed that the BB-mode correlation angular power spectrum corresponding to the hybrid inflation model for various values of squeezing parameter and squeezing angle is found within the limit of the BICEP2/Keck and Planck joint analysis data at $l \simeq 145$, even though the squeezing and thermal effects enhance the angular power spectrum. Thus the analysis of the present results show that the hybrid inflation model is most favorable by considering the primordial gravitational waves in the presence of squeezing and thermal effects.

5 Conclusion

The primordial gravitational waves are very important in cosmology. It is believed that the origin of the primordial gravitational waves are due to inflation mechanism. Thus the primordial gravitational waves are placed in a special quantum state called the squeezed vacuum state, a well-known state in quantum optics. The primordial gravitational waves have not been detected directly yet but their effect is expected to be observed through the B-mode of CMB. If this is the case, then the role of squeezing effect is also expected to reflect on the BB-mode correlation angular power spectrum of CMB.

The BB-mode correlation angular power spectrum for various slow-roll inflationary models are studied by considering the primordial gravitational waves in the squeezed vacuum state. The obtained angular spectrum for the squeezing, thermal as well as their combined effects are compared with the BICEP2/Keck Array and Planck 353 GHz joint analysis data. The comparative study of the BB-mode angular spectrum obtained for the various inflationary models with the BICEP2/Keck Array and Planck 353 GHz joint analysis data show that the hybrid inflation model is most favorable with the primordial GWs in the squeezed vacuum state. The BB-mode correlation angular power spectrum can be obtained even with higher or lower values of the squeezing parameters and thermal parameter but the results do not alter the present conclusions. Note that the BB-mode correlation angular power spectrum for the vacuum case can be recovered in the absence of squeezing and thermal effects.

Further, the result of the joint analysis data does not rule out the existence of gravitational waves in the squeezed vacuum or thermal squeezed vacuum states which are in agreement with previous studies.

Appendix A: Thermal effect on GWs spectrum

After the Big Bang, the universe was in the form of plasma of hot and dense matter. During this stage, the light particles like free electrons, due to Thomson scattering, acted as scattering centers for the surrounding radiation, keeping the universe at that time thermalized and opaque to radiations. Among these particles and radiations which got thermalized and escaped after the recombination are the decoupled gravitons which left an imprint on the CMB anisotropy. Due to these thermalized gravitons, the gravitational waves are believed to be amplified by stimulated emission into the existing thermal background of gravitational waves which changes the spectrum of the waves by temperature-dependent factor [27].

Assuming a vacuum state initially, the Fourier coefficients in Eq. (2) satisfy the relations

$$\begin{aligned} \langle b_k^{\dagger }b_{k'}\rangle= & {} \delta ^3 (\mathbf k -\mathbf k '), \end{aligned}$$

(A.1)

$$\begin{aligned} \langle b_k b_{k'} \rangle= & {} \langle b_k^{\dagger }b_{k'}^{\dagger } \rangle =0. \end{aligned}$$

(A.2)

The time-dependent thermal state is defined as [49, 50]

$$\begin{aligned} |0 (\beta ),\tau \rangle = \tilde{T }(\theta _k) |0,\tau \rangle , \end{aligned}$$

(A.3)

where $\tilde{T }(\theta _k) = exp [-\theta _k(\beta ) \{\tilde{b}_k(\tau ) b_k (\tau ) -b_k^{\dagger }(\tau ) \tilde{b}_k^{\dagger }(\tau )\}]$.

The temperature-dependent parameter $\theta (\beta )$ is defined by

$$\begin{aligned} \cosh \theta _k (\beta ) = (1 - e^{-\beta k})^{-\frac{1}{2}}, \sinh \theta _k (\beta ) = e^{-\frac{\beta k}{2}} (1 - e^{-\beta k})^{-\frac{1}{2}}, \end{aligned}$$

where $\beta = \frac{1}{T}$, T is the temperature.

Then the time- and temperature-dependent annihilation and creation operators through the Bogoliubov transformation become

$$\begin{aligned} b_k(\beta , \tau )= & {} \tilde{{T}} (\theta ) b_k \tilde{{T}}^{\dagger } (\theta ) \nonumber \\= & {} \cosh \theta _k (\beta )b_k(\tau )- \sinh \theta _k (\beta )\tilde{b}_{-k}^{\dagger } (\tau ), \end{aligned}$$

(A.4)

$$\begin{aligned} \tilde{b}_k(\beta , \tau )= & {} \tilde{{T}} (\theta ) \tilde{b}_k \tilde{{T}}^{\dagger } (\theta )\nonumber \\= & {} \cosh \theta _k (\beta )\tilde{b}_k(\tau )- \sinh \theta _k (\beta )b_{-k}^{\dagger } (\tau ). \end{aligned}$$

(A.5)

The Hermitian conjugate of the above equations give rise to similar equations for $b_k^{\dagger }(\beta , \tau )$ and $\tilde{b}_k^{\dagger } (\beta , \tau )$.

Thus, Eq. (A.1) modifies to [40]

$$\begin{aligned} \langle b_k^{\dagger }b_{k'}\rangle = \left( 1 + \frac{2}{e^{\frac{k_B}{T}}-1} \right) \delta ^3 (\mathbf k -\mathbf k '). \end{aligned}$$

(A.6)

The power spectrum for gravitational waves in the presence of thermal effect can then be written as

$$\begin{aligned} P_T(k)=A_T(k_0) \left( \frac{k}{k_0}\right) ^{n_T} \coth \left[ \frac{k}{2T}\right] . \end{aligned}$$

(A.7)

This can be used to compute the BB-mode correlation angular power spectrum of CMB in the thermal state.