1 Introduction

The three-meson vertices are important quantities in the phenomenological theories of hadron physics. Knowledge of the mesons’ coupling constants or form factors plays an important role in understanding the mesons’ interactions, meson decays, structure of the exotic mesons, and so on. The form factors depend on the momentum as \(Q^2\) and some input parameters. In the last years the meson form factors of \(D^*D\pi \) [1], \(D^*D\rho \) [2], \(D^*DJ/\psi \) [3], \(D^*_sD_sJ/\psi \) [4], \(B^*_sBK\) [5], \(B^*_sB_s\eta ^{(')}\) [6], \(B^*_cB_c\Upsilon \) [7], \(B^*_cB_cJ/\psi \) [8] and other vertices were widely discussed in the literature (for detailed information see [8] and [9]). Moreover, many new heavy meson states have been observed and investigated in the recent years. The investigation of the strong interaction of heavy hadrons among themselves has received increasing attention and this situation motivates us to investigate the bottom mesons interactions.

On the other hand, beginning from the CERN-SPS data analyses of heavy-ion collisions, the Quark–Gluon Plasma (QGP) phase has taken many physicists’ attention. These days, new experimental results pointing to a QGP phase in p–Pb collisions at the LHC have been announced [10]. The understanding of the thermal meson properties before the phase transition requires one to study the temperature dependencies of the meson form factors. The knowledge of the temperature dependence of the form factors is very important for the interpretation of heavy-ion collision experiments and understanding the QCD vacuum. For instance, comparing to its value in vacuum, we see that the value of the form factor decreases suddenly around the deconfinement temperature. We consider this as a sign of a possible phase transition. The aim of extending the sum rules to finite temperature is to understand the thermal properties of the hadrons. Understanding the thermal properties of QCD vacuum allows us to clarify the properties of the observable universe. Moreover, theoretical studies on QCD at finite temperature is necessary to explain the experimental results obtained from the heavy-ion collisions. It is assumed that the increase of density and temperature of the media where the hadrons are formed rearrange physical properties of hadrons such as decay widths and masses. Also, it is well known that heavy mesons have different behaviors when the temperature of the medium increases (see [11] and references therein). This motivated us to investigate the thermal properties of mesons.

It is not possible to calculate form factors at vertices of three heavy mesons at low energies using perturbative approaches. The QCD sum rules method is one of the most effective tools considering the non-perturbative nature of hadronic properties [12], since it does not have any model dependencies. The extending of QCD sum rules method to finite temperature has been made in Ref. [13]. This extension is based on two basic assumptions: that the Operator Product Expansion (OPE) and the notion of quark–hadron duality remain valid at finite temperature, but the vacuum condensates must be replaced by their thermal expectation values [14–17]. The thermal QCD sum rules approach has been extensively used for studying the masses and decay constants of both light and heavy mesons as a reliable and well-established method [14–27]. But in the literature there are few theoretical works devoted to the analysis of the hadron vertex form factors at finite temperature.

The aim of this paper is to investigate the strong form factor \(B_{c} B_{c}J/\psi \) vertex in the framework of the QCD sum rules method at finite temperature. The key concepts of the strong form factor calculations in sum rules are the three-point correlation functions. In order to calculate the form factors, one must have the temperature dependencies of the masses and decay constants of the hadrons in the vertex. Since we aim to extend the strong form factors to finite temperatures, in this study, we choose mesons whose masses and leptonic decay constants have been investigated in a thermal QCD sum rules approach [26, 27].

The outline of this paper is as follows: in the next section, the QCD sum rules for the form factors of the related mesons are obtained in the framework of the QCD sum rules at finite temperature. In Section III, our numerical predictions for the strong coupling constant and a comparison of the results with the existing predictions of the other studies are presented.

2 QCD sum rules for the strong form factors

In this section, we obtain the sum rules for the strong form factor of \(B_{c} B_{c} J/\Psi \) vertex in the QCD sum rules framework at finite temperature. We evaluate the temperature-dependent version of the three-point correlation function,

$$\begin{aligned} \Pi _{\mu }(q,T) =i^2\int \mathrm{d}^{4}x \mathrm{d}^{4}y \mathrm{e}^{ip' \cdot x}\mathrm{e}^{iq \cdot y}{\langle } \mathcal{T}[J^{B_{c}} (x) J_{\mu }^{J/\psi } (y) J^{B_{c} \dagger }(0)]{\rangle },\nonumber \\ \end{aligned}$$
(1)

where \(\mathcal T\) is the time ordering product in the correlation function and T is the temperature; \(J^{B_{c}}(x)=\overline{c}(x)\gamma _{5}b(x)\) and \(J_{\mu }^{J/\psi }(x)=\overline{c}(x)\gamma _{\mu }c(x)\) are the interpolating currents of the related mesons. The thermal average of any operator A is expressed as

$$\begin{aligned} {\langle }A {\rangle }=\frac{\mathrm{Tr}(\mathrm{e}^{-\beta H} A)}{\mathrm{Tr} \mathrm{e}^{-\beta H}}, \end{aligned}$$
(2)

where H is the QCD Hamiltonian and \(\beta =1/T\) is the inverse temperature.

The correlation function is calculated in two different ways: first, in the hadronic language which is from the physical side; and second, by using the QCD terms, which is from the OPE side. After equating these two different representations of correlation functions, we acquire the QCD sum rules for the strong form factors. In order to suppress the higher state contributions and continuum contributions we apply a double Borel transformation with respect to the variables \(p^2\) and \(p'^2\) to the physical side and the OPE side.

On the phenomenological side, a complete set of intermediate states with the same quantum numbers as the current J(x) are inserted between the currents in Eq. (1) and the integral is performed. As a result, we obtain

$$\begin{aligned}&\Pi _{\mu }^{\mathrm{phen}}(q^2,0)=\frac{\langle 0\mid J^{B_{c}}(0) \mid B_{c}(p')\rangle \langle 0\mid J^{J/\psi }_\mu (q) \mid J/\psi (q)\rangle \langle B_{c}(p') J/\psi (q) \mid B_{c}(p)\rangle \langle B_{c}(p) \mid J^{B_{c}}(0)\mid 0\rangle }{(q^2-m^{2}_{J/\psi }) (p^2-m^{2}_{B_{c}}) (p'^2-m^{2}_{B_{c}})} + \cdots , \end{aligned}$$
(3)

where (\(\cdots \)) represents the higher states and continuum contributions. The creation of the pseudoscalar and vector mesons from the vacuum can be represented in terms of the leptonic decay constants of the mesons, \(f_{M}\):

$$\begin{aligned}&\langle 0\mid J^{B_{c}}(0) \mid B_{c}(p')\rangle =\frac{f_{B_{c}} m^{2}_{B_{c}}}{m_{b}+m_{c}}, \end{aligned}$$
(4)
$$\begin{aligned}&\langle 0\mid J^{J/\psi }_\mu (q) \mid J/\psi (q)\rangle =f_{J/\psi } m_{J/\psi } \epsilon _{\mu }, \end{aligned}$$
(5)
$$\begin{aligned}&\langle B_{c}(p') J/\psi (q) \mid B_{c}(p)\rangle =g_{B_{c}B_{c}J/\psi }(p'-q)\cdot \epsilon , \end{aligned}$$
(6)

where \(m_{M}\) and \(f_{M}\) are the mass and decay constant of the related meson, respectively. Note that Eqs. (4)–(6) are valid also at finite temperature, hence, the final representation for the physical side can be written in terms of the temperature-dependent mass and decay constants as

$$\begin{aligned}&\Pi _{\mu }^{\mathrm{phen}}(q^{2},T) \nonumber \\&\quad =\frac{g_{B_{c}B_{c}J/\psi }(q^{2},T) m^{4}_{B_{c}}(T) m_{J/\psi }(T) f_{B_{c}}^2(T) f_{J/\psi }(T)}{(m_{b}(T)+m_{c}(T))(q^2-m^{2}_{J/\psi }(T)) (p^2-m^{2}_{B_{c}}(T)) (p'^2-m^{2}_{B_{c}}(T))} \nonumber \\&\qquad \times \left[ -2p'_{\mu }+\left( \frac{m^2_{B_{c}}(T)-q^2}{m^2_{J/\psi }(T)}\right) p_{\mu }\right] +\cdots , \end{aligned}$$
(7)

where \(f_M(T)\) and \(m_M(T)\) are temperature-dependent parameters.

On the QCD side, the correlation function is calculated in the deep Euclidean region, \(q^2\ll -\Lambda ^{2}_{\mathrm{QCD}}\), by using an operator product expansion (OPE) where the short and long distance effects are separated:

$$\begin{aligned} \Pi _{\mu }^{\mathrm{QCD}}(q^2,T) =\Pi _{\mu }^{\mathrm{pert}}(q^2,T)+\Pi _{\mu }^{\mathrm{nonpert}}(q^2,T). \end{aligned}$$
(8)
Fig. 1
figure 1

Bare loop diagram

Full size image
Fig. 2
figure 2

Diagrams corresponding to two-gluon condensates

Full size image

The short distance contributions are calculated by using the perturbation theory, contrary to the long distance effects which are represented in terms of the vacuum expectation values of some operators having different mass dimensions. Moreover, we choose \(p_{\mu }\) as the structure and write the terms which are proportional to \(p_{\mu }\). Concluding, by using the dispersion integral representation, the equation above can be written as

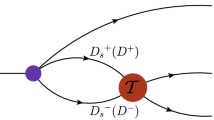
$$\begin{aligned} \Pi ^{\mathrm{QCD}}(q^2,T)= & {} \int \mathrm{d}s \int \mathrm{d}s' \frac{\rho (s,s',q^2,T)}{(s-p^2)(s'-p'^2)} \nonumber \\&+\Pi ^{\mathrm{nonpert}}(q^2,T), \end{aligned}$$
(9)

where \(\rho (s,s',q^2,T)\) is called the spectral density. To obtain the spectral density, the Feynman diagram in Fig. 1, which is called the bare loop diagram, is used. After straightforward calculations, the spectral density is obtained:

$$\begin{aligned}&\rho (s,s',q^2,T) \nonumber \\&\quad =\frac{-N_{c}}{\sqrt{(s+s'-q^{2})-4ss'}} \frac{1}{-q^{4}+(s-s')^{2}-q^{2}(s+s')} \nonumber \\&\qquad \times [ 2m_{c}^{3}(m_{b}-m_{c})s'+(m_{b}^{4}-m_{b}^{3}m_{c})(q^{2}-s+s')\nonumber \\&\qquad +ss'(-2m_{c}^{2}+q^{2}-s+s')m_{b}^{2}(q^{2}-s-s')(-m_{c}^{2}\nonumber \\&\qquad +q^{2}-s+s')+m_{c}^{2}s'(-2m_{b}^{2}+2m_{b}m_{c}-q^{2}+s+s')\nonumber \\&\qquad - m_{c}(m_{b}-m_{c})((q^{2}+s-s')s'+m_{b}^{3}(q^{2}-s+s')\nonumber \\&\qquad +m_{c}^{2}(-q^{2}+s+s')+ m_{b}m_{c} (-q^{4}+m_{c}^{2}(-q^{2}-s-s')\nonumber \\&\qquad +s(-s+s')+q^{2}(2s+s') ) ) ]. \end{aligned}$$
(10)

As regards the non-perturbative part, the main contribution comes from the two gluon condensates since the heavy quark condensates can be safely neglected. They are suppressed by inverse powers of the quark masses. The two-gluon condensate diagrams are shown in Fig. 2. While calculating the non-perturbative contributions, the Fock–Schwinger gauge \(x^{\mu }A^{a}_{\mu }(x)=0\) is used. The vacuum gluon field in momentum space and the quark–gluon–quark vertices used in the calculations are given by

$$\begin{aligned}&A^{a}_{\mu }(k)=-\frac{i}{2}(2 \pi )^4 G^{a}_{\rho \mu }(0)\frac{\partial }{\partial k_{\rho }}\delta ^{(4)}(k), \end{aligned}$$
(11)
$$\begin{aligned}&\Gamma =ig \frac{\lambda ^{a}}{2}\gamma _{\mu }A^{a}_{\mu }(k), \end{aligned}$$
(12)

where k is the gluon momentum.

In order to calculate non-perturbative contributions, \({\langle }\mathrm{Tr}^{c}G_{\alpha \beta }G_{\mu \nu }{\rangle }\) must be known. By using Lorentz invariance at finite temperature, this expectation value is expressed by

$$\begin{aligned}&{\langle } \mathrm{Tr}^{c}G_{\alpha \beta }G_{\mu \nu } {\rangle }=\frac{1}{24}(g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }){\langle } G^{a}_{\lambda \sigma }G^{a\lambda \sigma } {\rangle }\nonumber \\&\quad +\frac{1}{6}[g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }-2(u_{\alpha }u_{\mu }g_{\beta \nu }-u_{\alpha }u_{\nu }g_{\beta \mu }\nonumber \\&\quad -u_{\beta }u_{\mu }g_{\alpha \nu }+u_{\beta }u_{\nu }g_{\alpha \mu })]{\langle } u^{\lambda }\Theta _{\lambda \sigma }^{g}u^{\sigma } {\rangle }. \end{aligned}$$
(13)

The Borel transformed phenomenological part of the correlation function is obtained:

$$\begin{aligned}&\hat{B}\Pi ^{\mathrm{phen}}(q^2,T)\nonumber \\&\quad = \frac{g_{B_{c}B_{c}J/\psi }(q,T) m_{B_c}^{4}(T) m_{J/\psi }(T) f_{B_c}^{2}(T) f_{J/\psi }(T)}{(m_{b}(T) +m_{c}(T))(q^2-m_{J/\psi }^{2} (T))}\nonumber \\&\qquad \times \left( \frac{m_{B_c}^{2}(T)-q^2}{m_{J/\psi }^{2}(T)}\right) \mathrm{exp}\left[ \frac{-m_{B_c}^{2}(T)}{M^2}\right] \mathrm{exp}\left[ \frac{-m_{B_c}^{2}(T)}{M'^2}\right] .\nonumber \\ \end{aligned}$$
(14)
Table 1 Coefficients of the temperature-dependent mass and decay constant functions [26, 27]
Full size table

The non-perturbative part of the QCD side in the Borel transformed scheme is given by

$$\begin{aligned}&\hat{B}\Pi ^{\mathrm{nonpert}}(q,T) \nonumber \\&\quad =\int _{0}^{1} \mathrm{d}x \int _{0}^{1-x} \mathrm{d}y \langle \alpha _{s} G^2\rangle F(m_q,M^2,M'^2,T), \end{aligned}$$
(15)
Fig. 3
figure 3

The dependence of the form factor on \(M^{2}\)

Full size image
Fig. 4
figure 4

The dependence of the form factor on \(M'^{2}\)

Full size image
Fig. 5
figure 5

The plateau of the Borel mass parameters

Full size image

where the F function is dependent on the quark masses, the Borel parameters, and also the temperature. After the required calculations of the gluon condensate contributions, choosing coefficients which are proportional to \(p_{\mu }\), and matching the QCD and the phenomenological sides of the correlation function, we obtain the following sum rule for the strong form factor as a function of \(Q^2=-q^2\) and temperature T:

$$\begin{aligned}&g_{B_{c}B_{c}J/\psi }(Q^2,T)\nonumber \\&\quad =\bigg \{ \int _{s=(m_{c}+m_{b})^2}^{s_{0}(T)} \mathrm{d}s ~ \int _{s'=(m_{c}+m_{b})^2}^{s'_{0}(T)} \mathrm{d}s' ~\rho (s,s',Q^2,T)~\mathrm{exp}\left( -\frac{s}{M^{2}}\right) \nonumber \\&\qquad +~\mathrm{exp}\left( -\frac{s}{M'^{2}}\right) \hat{B}\Pi ^{\mathrm{nonpert}}\bigg \}\nonumber \\&\qquad \times \frac{m^2_{J/\psi }(T) (m_{c}+m_{b})^2 (-Q^2-m^2_{J/\psi }(T))}{m^4_{B_{c}}(T)m_{J/\psi }(T)(m^2_{B_{c}}(T)+Q^2)f^2_{B_{c}}(T)f_{J/\psi }(T)}\nonumber \\&\qquad \times \mathrm{exp}\left( \frac{m^2_{B_{c}}(T)}{M^2}\right) \mathrm{exp}\left( \frac{m^2_{B_c}(T)}{M'^2}\right) , \end{aligned}$$
(16)

where \(M^2\) and \(M'^2\) are the Borel mass parameters, and \(s_{0}\) and \(s'_{0}\) are continuum thresholds. The temperature-dependent expressions of the continuum thresholds are obtained [28, 29]:

$$\begin{aligned} s_{0}(T)=s_{0}\left[ 1- \left( \frac{T}{T_{c}^*}\right) ^{8} \right] +(m_{c}+m_{b})^2\left( \frac{T}{T_{c}^*}\right) ^{8}, \end{aligned}$$
(17)
$$\begin{aligned} s'_{0}(T)=s'_{0}\left[ 1- \left( \frac{T}{T_{c}^*}\right) ^{8} \right] +(m_{c}+m_{b})^2\left( \frac{T}{T_{c}^*}\right) ^{8}, \end{aligned}$$
(18)

where the critical temperature value is given as \(T_c=0.176~\mathrm{GeV}\) and \(T_c^*=1.1 \times T_c\) [28, 29].

3 Numerical analysis

This section presents the numerical analysis of the sum rules for the form factor of the heavy mesons based on thermal considerations. In the analysis, we use the following input parameters: \(m_c=(1.28\pm 0.05)\, \mathrm{GeV}\), \(m_b=(4.18\pm 0.1)\,\mathrm{GeV}\) [30], and \({\langle }0\mid \alpha _s G^2 \mid 0 {\rangle }=0.038\,\mathrm{GeV}^4\) [12]. In the calculations, thermal versions of some parameters such as the continuum thresholds and the vacuum condensates are used. Temperature-dependent masses and decay constants are obtained in [26, 27] by using the thermal QCD sum rules approach. The values of the masses at \(T=0\) are calculated as \(m_{J/\psi }=(3.05\pm 0.08)\) and \(m_{B_c}=(6.37\pm 0.05)\,\mathrm{GeV}\), which values are in very good agreement with the experimental data. The temperature-dependent expressions of the masses and decay constants are (Table 1)

$$\begin{aligned}&m_{B_{c}[J/\psi ]}(T)=A+B ~ \mathrm{exp}\left[ \frac{T}{C}\right] , \end{aligned}$$
(19)
$$\begin{aligned}&f_{B_{c}[J/\psi ]}(T)=D+E~ \mathrm{exp}\left[ \frac{T}{F}\right] . \end{aligned}$$
(20)

The sum rules expression for the form factor contains four other parameters, which are continuum thresholds \(s_0\) and \(s'_0\), and the Borel masses \(M^2\) and \(M'^2\). According to the QCD sum rules standard, the physical quantities should be independent from the Borel parameters. Hence, the Borel mass intervals should be as stable as possible. The working region for the Borel mass parameters is determined requiring that not only the higher state and continuum contributions are suppressed, but also the contribution of the highest order operator should be small. As a result, the working region for the Borel parameters is to be \( 18~ \mathrm{GeV}^2 \le M^{(')2} \le 22~ \mathrm{GeV}^2 \). The continuum thresholds are related to the energy of the first excited states of the mesons with the same quantum numbers of the mesons in the vertex. Continuum thresholds may depend on the Borel mass parameters [31]. We choose the intervals \(s_0=s'_0=(41\)–\(43)~\mathrm{GeV}^2\) for the continuum thresholds.

In the calculation we use the rest frame. In this frame, \(u^{\alpha }\) is defined as \(u^{\alpha }=(1,~0,~0,~0)\). \(\Theta ^{g}\) is the gluonic part of the energy density and described in [21, 28, 29]. We use the lattice results which can be summarized as follows:

$$\begin{aligned} \langle \Theta ^{g}_{00}\rangle \!=\!T^4~ \mathrm{exp}[113,87T^2-12,2T]-10,14T^5\,(\mathrm{GeV}^4).\nonumber \\ \end{aligned}$$
(21)

Here, the temperature is in units of GeV and \(0.1\le T \le 0.197~\mathrm{GeV}\). In [28, 29], \(\langle G^2\rangle \) is parameterized by

$$\begin{aligned} \langle G^2\rangle \!=\!\langle 0|G^2|0\rangle \left[ 1-1.65\left( \frac{T}{T_{c}}\right) ^{8.735}\!+\!0.05\left( \frac{T}{T_{c}}\right) ^{0.72}\right] .\nonumber \\ \end{aligned}$$
(22)

After determining the working regions of the auxiliary parameters, the dependencies of the strong form factor under consideration at \(Q^2=-q^2=1\,\mathrm{GeV}^2\) on the Borel mass parameters \(M^2\) and \(M'^2\) are presented in Figs. 3, 4 and 5. We see from these figures that the strong form factor has good stability with respect to the \(M^2\) and \(M'^2\) variations. By using other input parameters, we see that the strong form factor is fitted to the following polynomial function:

$$\begin{aligned} g(Q^2)=\sum _i C_i Q^{2i}, \end{aligned}$$
(23)
Table 2 Fit function coefficients for the strong form factor
Full size table
Fig. 6
figure 6

The dependence of the form factor on \(Q^2\) at \(T=0~\mathrm{GeV}\) (red dots) and the fitted curve

Full size image
Fig. 7
figure 7

The dependence of the form factor on the temperature, for different continuum thresholds

Full size image

for \(i=0,1,2,\) and 3 (Table 2). The strong coupling constants are determined as the values of the form factors at \(Q^2 = -m_{\mathrm{offshell}}^2 = -9.3\,\mathrm{GeV}^2\) in the case of vacuum. Here, the off-shell meson mass is the mass of \(m_{J/\psi }\) given above. The obtained coupling constant in the framework of thermal QCD sum rules is \(g_{B_c B_c J/\psi }=5.4\pm 1.5\), which is consistent with previous theoretical calculations in the framework of the sum rules in the case of vacuum [8].

The dependence of the form factor of the vertex in the case of vacuum is presented in Fig. 6. Our result for the coupling constant in the case of vacuum can be verified in future experiments. The dependency of the form factor on the temperature is presented in Figs. 7 and 8 for different values of \(Q^2\). The form factor does not change up to \(T\simeq 100~\mathrm{MeV}\) but slightly increases up to \(T\simeq 160~\mathrm{MeV}\); then it suddenly decreases after this point.

4 Conclusion

The knowledge on the temperature dependence of the form factors is very important for the interpretation of heavy-ion collision experiments and understanding the QCD vacuum. In this article, we study the temperature dependence of the strong form factor of the \(B_cB_cJ/\psi \) vertex using the three-point QCD sum rules method. We also obtain the momentum dependence of the form factor at \(T=0\), fit it into an analytic function, and extrapolate into the deep time-like region in order to obtain a strong coupling constant of the vertex. The result is consistent with previous calculations [8]. The coupling constant also can be used as a fundamental input parameter in research of the heavy meson absorptions in hadronic matter. Besides, the behavior of the temperature dependency of the form factor can be checked in future experiments.

Fig. 8
figure 8

The dependence of the form factor on the temperature, for different \(Q^2\) values (\(s_0=42\,\mathrm{GeV}^2\))

Full size image