The top quark right coupling in the tbW-vertex

Abstract

The most general parametrization of the tbW vertex includes a right coupling $V_R$ that is zero at tree level in the standard model. This quantity may be measured at the Large Hadron Collider where the physics of the top decay is currently investigated. This coupling is present in new physics models at tree level and/or through radiative corrections, so its measurement can be sensitive to non-standard physics. In this paper we compute the leading electroweak and QCD contributions to the top $V_R$ coupling in the standard model. This value is the starting point in order to separate the standard model effects and, then, search for new physics. We also propose observables that can be addressed at the LHC in order to measure this coupling. These observables are defined in such a way that they do not receive tree level contributions from the standard model and are directly proportional to the right coupling. Bounds on new physics models can be obtained through the measurements of these observables.

1 Introduction

Top quark physics is now a high statistics physics, mainly due to the huge amounts of data coming from the large hadron collider (LHC) run I and, now, run II [1, 2]. It is strongly believed that, due to its very high mass, the top quark will be a window to new physics [3]. This can easily be understood in the effective lagrangian approach, where the new physics contributions can be parametrized in a series expansion in terms of the parameter $m_t/\Lambda$, where $m_t$ is the top quarks mass and $\Lambda$ is the new physics scale. Besides, most of the top quark properties and couplings are known with a precision far lower than the other quarks and than the other standard model (SM) particles. It is the only quark that weakly decays before hadronization but, up to now, only one decay mode, $t \rightarrow b W^+$, is known. For instance, many extensions of the SM predict new decay modes that may be accessible at LHC. The top quark was detected for the first time at TEVATRON [4, 5], where many of its physical properties where measured and some bound on the anomalous Wtb couplings were set [6–8]. Nowadays, top physics is intensively investigated in theoretical research [3] and at the LHC [1, 2, 9], as the reader can verified in the ATLAS and CMS web pages. In particular, the measurements of the different helicity components of the W in the top decay allows one to study the tbW Lorentz vertex structure [10]. These studies were extended in recent years [11–15]. In these references the longitudinal and transverse helicities of the W coming from the top decay were investigated and they show that a precise determination of the Lorentz form factors of the vertex can be done with a suitable choice of observables. The most general parametrization of the on-shell vertex needs four couplings, but in the SM three of them are zero at tree level while only the usual left coupling $V_L$ is not zero and has a value close to one [16]. This is not the case in extended models where, in addition, some of these couplings can also be sensitive to new CP-violation mechanisms.

The right top coupling is largely unknown and deserves a careful study. The other two couplings, usually called tensorial couplings, were investigated at the LHC [17] and will not be considered here. The predictions for the SM, for the two-Higgs-doublet model (2HDM) and other extended models where recently considered in Refs. [18–20]. In this paper we first compute the right coupling $V_R$ in the SM at leading order, and define appropriate observables in order to have direct access to it. The former one-loop calculation is needed in order to disentangle SM and new physics effects in the observables. Next, we will introduce a set of observables that allows one to perform a precise search of the $V_R$ coupling. We obtain a combination of observables directly proportional to it in such a way that they are not dominated by the leading tree level SM contribution $V_L$. These observables can be an important tool in order to measure new physics contributions to $V_R$.

This paper is organized as follows. In the next section we introduce a precise definition of the right coupling and compute the first order QCD and electroweak (EW) contributions. In Sect. 3 we present and discuss a set of observables that can be measured with LHC data, both in the polarization matrix and in the spin correlations. Finally, we discuss the results and present our conclusions in Sect. 4.

2 Right top tbW coupling in the SM

Considering the most general Lorentz structure for on-shell particles, the $\mathcal {M}_{tbW}$ amplitude for the $t(p)\rightarrow b(p') W^{+}(q)$ decay can be written in the following way:

$$\begin{aligned} \mathcal {M}_{tbW}= & {} - \frac{e}{\sin \theta _{w}\sqrt{2}}\epsilon ^{\mu *} \overline{u}_{b}(p')\left[ \gamma _{\mu }(V_{L} P_{L}+V_{R} P_{R})\right. \nonumber \\&\left. + \frac{i \sigma _{\mu \nu }q^{\nu }}{M_{W}}( g^{}_{L} P_{L}+ g^{}_{R} P_{R})\right] u_{t}(p), \end{aligned}$$

(1)

where the outgoing $W^{+}$ momentum, mass and polarization vector are $q=p-p'$, $M_{W}$, and $\epsilon ^{\mu }$, respectively. The form factors $V_{L}$ and $V_{R}$ are the left and right couplings, respectively, while $g^{}_{L}$ and $g^{}_{R}$ are the so called tensorial or anomalous couplings.

The expression (1) is the most general model independent parametrization for the $tbW^{+}$ vertex. Within the SM, the W couples only to left particles then, at tree level, all the couplings are zero except for $V_L$, which is given by the Kobayashi–Maskawa matix element $V_L=V_{tb} \simeq 1$ [16]. At one loop all of these couplings receive contributions from the SM. For example, the real and imaginary parts of the $g_L$ and $g_R$ couplings were calculated in the SM [18] and in a general alligned-2HDM [19].

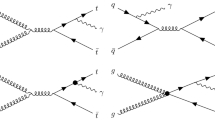
The one-loop electroweak and QCD contributions to the $V_R$ coupling can be calculated just by considering the vertex corrections shown in Fig. 1 and extracting from them the Lorentz structure corresponding to the $V_R$ coupling. Note that this Lorentz structure is not present in the SM lagrangian so, at one loop, there is no need for any counter-term for this contribution. For this reason, the SM one-loop contribution to the $V_R$ coupling is finite. This is similar to what happens for the top $g_{L,R}$ couplings [18, 19].

Fig. 1

One-loop contributions to the $V_R$ coupling in the $t\rightarrow b W^+$ decay

We will denote each diagram by the label ABC according with the particles running in the loop. In addition to the usual notation for the SM particles we use the symbols $w_0$ and w for the neutral and charge would-be Goldstone bosons, respectively, and H for the SM Higgs. There are 18 diagrams that have to be considered and the one-loop $V_R$ value one gets from them is finite, without the need of renormalization as already stated. In particular, the one-loop contributions from diagrams $tw_0w$, tHw, $bww_0$, bwH, $w_0tb$ and Htb are ultraviolet (UV) divergent. However, when summing them up by pairs (i.e. $tw_0w + tHw$, $bww_0 + bwH$, and $w_0tb + Htb$), the result is finite. The electroweak contributions of all the diagrams are given in Appendix A in terms of parametric integrals. For the UV divergent diagrams we present the sum of the two diagrams that cancels the divergence, as can be seen in Eqs. (46), (52), and (57). There, the first (second) term, in each of these expressions, corresponds to the UV safe sector of the first (second) diagram, while the third one corresponds to the sum of the UV divergent part of the two diagrams, which results in a finite contribution, as it should.

All the contributions can be written as

$$\begin{aligned} V_R^{ABC} = \alpha \; V_{tb}\; r_b\, I^{ABC}, \end{aligned}$$

(2)

where $r_b=m_b/m_t$ and $I^{ABC}$ is an integral shown in Appendix A for all the diagrams that contribute to $V_R$. As expected, all the contributions are proportional to the bottom mass through $r_b$.

When one of the particles circulating in the loop is a photon the integral can be performed analytically. Then the contribution can be written as

$$\begin{aligned} V_R^{ABC}= \frac{\alpha }{8 \pi }V_{tb}\, Q_A\, I_0^{ABC}, \end{aligned}$$

(3)

with $Q_A$ being the charge of the A-quark circulating in the loop in units of |e| (for the $\gamma tb$ diagram, $Q_A=Q_t\cdot Q_b$). The $I_0^{ABC}$ analytical expressions, as well as their limits for $r_b \rightarrow 0$, are shown in Appendix B. All these expressions were used as a check of our computations.

The leading QCD contribution can easily be obtained from Eq. (56) just by substituting the couplings of the photon by the gluon ones, so we get

$$\begin{aligned} V_R^{gtb}= -\frac{\alpha _s}{8\pi }\, C_F\, V_{tb} I_0^{\gamma tb}, \end{aligned}$$

(4)

with $I^{\gamma tb}$ given in Eqs. (62) and (67), and $C_F=4/3$ is the color factor.

With the set of values of Ref. [16], the numerical values for the contribution to $V_R$ of each diagram and the complete one-loop SM value are given in Table 1, for $V_{tb}=1$.

Table 1 Contribution to $V_R$ from the different diagrams

In this table the contributions from the UV divergent diagrams are summed up to get a finite result; the first (second) quantity between brackets corresponds to the finite contribution of the first (second) diagram, and the third one (which is logarithmic) is the finite sum of the two UV divergent parts.

As can be seen in Table 1, even though the contribution of most of the diagrams is of the order of $10^{-5}$ for the real part of the $V_R$ coupling, the total EW contribution is, at the end, two orders of magnitude smaller due to the accidental cancellations among the diagrams. The QCD contribution is real and four orders of magnitude bigger than the real EW one so that the real part of the $V_R$ coupling is dominated by the former. The imaginary part, instead, remains of order $10^{-5}$, and it is purely EW.

3 Observables

In general, the LHC observables considered in the literature are not very sensitive to the right coupling $V_R$. This is due to the fact that this coupling comes from a lagrangian term that has the same parity and chirality properties than the leading coupling $V_L$ so that the observables receive contributions from both terms. These observables are the angular asymmetries in the W rest frame [10, 11, 21, 22], angular asymmetries in the top rest frame [11, 22–24] and spin correlations [11, 22, 25, 26]. Our strategy will be to define observables directly proportional to $V_R$ considering the dependencies on the coupling terms. Similar ideas were widely applied when investigating tau physics dipole moments [27, 28]. For top decays, one way to suppress the $V_L$ contribution is to define observables where only right polarized quarks contribute, but this polarization is not accessible to the present facilities and experiments. Given the results shown in the previous section, from now on we always assume that the imaginary part of the $V_R$ coupling is negligible.

3.1 Observables in the W rest frame

Top properties were studied in previous works by means of the observables that we just mentioned. One of the first possibilities are the angular asymmetries for the $t\rightarrow W^+\, b$ decay, with the $W^+$ decaying leptonically. The normalized charged lepton angular distribution in the W rest frame can be written as

$$\begin{aligned} \frac{1}{\Gamma }\frac{\mathrm{d}\Gamma }{\mathrm{d}\cos \theta _l}= & {} \frac{3}{8}\Big (1+\cos \theta _l \Big )^2F_++\frac{3}{8} \Big (1-\cos \theta _l \Big )^2F_-\nonumber \\&+\frac{3}{4}\sin ^2\theta _l\, F_0, \end{aligned}$$

(5)

where $F_0, F_\pm$ are the normalized partial widths of the top decay into the W helicity states, and $\theta _l$ is the angle between the charged lepton momentum in the W rest frame and the W momentum in the t rest frame. Then the asymmetries are defined, in terms of a new parameter z, as follows [10, 21]:

$$\begin{aligned} A_z=\frac{N(\cos \theta _l >z)-N(\cos \theta _l <z)}{N(\cos \theta _l >z)+N(\cos \theta _l <z)}. \end{aligned}$$

(6)

The z parameter allows one to separate the helicity fractions $F_0, F_\pm$. The value $z=0$ gives the usual forward–backward asymmetry while $z=\pm (2^{2/3}-1)$ defines the $A_\mp$ asymmetries, respectively. The first one, $A_0$ depends only on the $F_\pm$ helicity fractions while $A_{\pm }$ depends on both $F_0$ and $F_\pm$.

The helicity fractions, $F_0$ and $F_\pm$, can be computed in terms of the tbW couplings given in Eq. (1), and they can be found, for example, in Ref. [22]. Performing the $\theta _l$ integration of Eq. (6) for a given value of z, the numerator of the asymmetry $A_z$ in terms of $V_{L}$ and $V_R$ is

$$\begin{aligned}&V_L^2 \left( 2.48 z^3 + 2.00 z^2 - 11.45 z- 2.00 \right) + 0.56 z V_L V_R \nonumber \\&\quad + V_R^2 \left( 2.48 z^3 - 2.00 z^2 - 11.45 z + 2.00 \right) . \end{aligned}$$

(7)

One can now choose the value of the z parameter, within the range $(-1,1)$, to make zero the leading $V_L$ contribution. In this way we get the maximum sensitivity to $V_R$. The coefficients of $V_L^2$ and $V_R^2$ from Eq. (7) are plotted in Fig. 2.

Fig. 2

Plot of the coefficients of $V_L^2$ and $V_R^2$ from Eq. (7) in terms of z

Fig. 3

Dependence on the $V_R$ coupling for $A_R$ (blue-solid), Eq. (8), and for the usual $A_+$ (purple-dashed) and $A_-$ (black-dot-dashed) asymmetries, Eq. (6)

There, it can be seen that for $z = \displaystyle z_R = -0.17$ the coefficient of $V_L^2$ cancels, leaving the $V_R$ term, in Eq. (7), as the leading one. For this $z_R$ the new asymmetry $A_R\equiv A_Z(z=z_R)$ is proportional to $V_R$ and has the form

$$\begin{aligned} A_R(V_L,V_R)=\frac{-0.01 V_L V_R + 0.48 V_R^2}{1.12 \left( V_L^2 + V_R^2\right) - 0.07 V_L V_R} \simeq - 0.01 V_R, \end{aligned}$$

(8)

where the last expression is the value of the asymmetry taking $V_L=1$ and assuming $|V_R|<<1$. As can be seen this asymmetry is directly proportional to $V_R$ so that a non-zero measurement of it is a direct test of $V_R \ne 0$.

Note that the leading contribution to the usual $A_\pm$ asymmetries comes from $V_L^2$ so that in order to be sensitive to $V_R$ one needs to subtract this SM central value. In Fig. 3 we show the $V_R$ dependence of $A_R$ and also, for comparison, the dependence of $A_\pm$, with the $V_L^2$ leading contribution subtracted. As can be seen there $A_R$ may allow more precise bounds on $V_R$. Besides, it is directly proportional to $V_R$ and eliminates other uncertainties that the $V_L$ dependence in $A_\pm$ may introduce.

For polarized top it is possible to define asymmetries with respect to the normal and transverse spin directions. These were studied in Ref. [11], but they are not sensitive to the $V_R$ coupling so we are not going to consider them in our analysis.

3.2 Observables in the top rest frame

The angular distribution of the decay products for the weak process $t\rightarrow W^+ b$ carries information as regards the spin of the decaying top. Then angular asymmetries can be built to test the Lorentz structure of the vertex. We will follow the same procedures as described previously, in order to optimize the sensitivity of the observables to $V_R$ but, in this case, for the asymmetries in the top rest frame.

For the top decay $t\rightarrow W^+\, b\rightarrow l^+\nu b,q\bar{q}'b$, the angular distribution of the product $X = l^+,\nu ,q,\bar{q}',W^+,b$, in the top rest frame, is given by

$$\begin{aligned} \frac{1}{\Gamma }\frac{\mathrm{d}\Gamma }{\mathrm{d}\cos \theta _X}=\frac{1}{2}\Big (1+\alpha _X\, \cos \theta _X\Big ), \end{aligned}$$

(9)

where $\theta _X$ is the angle between the momentum of X and the top spin direction, and $\alpha _X$ are the spin-analyzer powers, given in Refs. [11, 22–24, 29] in terms of the couplings shown in Eq. (1). Then an asymmetry can be defined by

$$\begin{aligned} A_X^z\equiv & {} \frac{N(\cos \theta _X >z)-N(\cos \theta _X <z)}{N(\cos \theta _X >z)+N(\cos \theta _X <z)}\nonumber \\= & {} \frac{1}{2}\left[ \alpha _X(1-z^2)-2z\right] . \end{aligned}$$

(10)

For $z=0$, one gets the usual forward–backward asymmetry:

$$\begin{aligned} A_X\equiv \frac{N(\cos \theta _X >0)-N(\cos \theta _X <0)}{N(\cos \theta _X >0)+N(\cos \theta _X <0)}=\frac{\alpha _X}{2}. \end{aligned}$$

(11)

Sensitivities to $V_R$ and $V_L$ for this asymmetry have already been given for $X=l^+,\; b,\; \nu$ in the t-channel single top production in Refs. [11, 30]. In order to define a new asymmetry directly proportional to the $V_R$ coupling one can again extract the SM leading contribution, given by the $V_L^2$ term in the $A_X^z$ asymmetry, and make it zero. For the $X=$ l, $\nu$, b cases, Eq. (10) is

$$\begin{aligned} A_l^z= & {} \frac{-1}{2\left( V_L^2+ V_R^2-0.06 V_L V_R\right) }\Bigg [V_L^2\left( -\frac{1}{2} z^2-z+\frac{1}{2}\right) \nonumber \\&+\,V_R^2 \left( -0.16 z^2-z+0.16\right) \nonumber \\&+ \, 0.06V_L V_R \left( \frac{1}{2}z^2+z-\frac{1}{2}\right) \Bigg ], \end{aligned}$$

(12)

$$\begin{aligned} A_b^z= & {} \frac{0.20}{V_L^2+V_R^2-0.06 V_L V_R}\times \big [V_L^2\left( z^2-4.93 z-1\right) \nonumber \\&+ \, V_R^2\left( -z^2-4.93 z+1\right) +0.31z V_L V_R \big ], \end{aligned}$$

(13)

$$\begin{aligned} A_\nu ^z= & {} \frac{0.16}{V_L^2+V_R^2-0.06 V_L V_R}\times \big [V_L^2\left( z^2-6.30 z-1\right) \nonumber \\&+ \, V_R^2\left( 3.15 z^2-6.30 z-3.15\right) \nonumber \\&+\, V_L V_R\left( -0.19z^2+0.39 z+0.19\right) \big ]. \end{aligned}$$

(14)

Fig. 4

Plot of the coefficients of $V_L^2$, in terms of z, from Eqs. (12), (13), and (14)

Figure 4 shows the behavior of the $V_L^2$ coefficient from the $A_l$, $A_b$, and $A_\nu$ asymmetries. We can choose z in order to make the leading coefficients of Eqs. (12), (13), and (14) zero. These z values are

$$\begin{aligned} z_l=\sqrt{2}-1,\quad z_b=-0.20,\quad z_\nu =-0.16, \end{aligned}$$

(15)

and then the new asymmetries are

$$\begin{aligned} A_l^{z_l}= & {} \frac{-0.28 V_R^2}{V_L^2+ V_R^2-0.06 V_L V_R} \simeq -0.28 V_R^2, \end{aligned}$$

(16)

$$\begin{aligned} A_b^{z_b}= & {} \frac{0.39 V_R^2-0.01 V_L V_R}{V_L^2+ V_R^2-0.06 V_L V_R} \simeq -0.01 V_R, \end{aligned}$$

(17)

$$\begin{aligned} A_\nu ^{z_\nu }= & {} \frac{0.02 V_L V_R-0.33 V_R^2}{V_L^2+ V_R^2-0.06 V_L V_R} \simeq 0.02 V_R, \end{aligned}$$

(18)

where in the last expression we show the value of the asymmetries for $V_L=1$ and assuming $|V_R|<<1$. From Eq. (12) one can see that, unfortunately, for the $A_l$ asymmetry the same value of z as the one that cancels the coefficient of $V_L^2$ also cancels the $V_L V_R$ term, in such a way that a poorer sensitivity to the coupling will be expected from this observable because the surviving term is $V_R^2$ instead of $V_L V_R$.

Fig. 5

Dependence on the $V_R$ coupling for the $A_l^{z_l}$ asymmetry, Eq. (16)

Fig. 6

Dependence on the $V_R$ coupling for the $A_b^{z_b}$ asymmetry, Eq. (17)

Fig. 7

Dependence on the $V_R$ coupling for the $A_\nu ^{z_\nu }$ asymmetry, Eq. (18)

In Figs. 5, 6 and 7 we show the dependence on $V_R$ for the new $A_l^{z_l}$, $A_b^{z_b}$, and $A_\nu ^{z_\nu }$ observables. We have explicitly checked that the usual forward–backward asymmetries for the same decay product have a very similar behavior as the ones shown in the figures, once the leading $V_L^2$ contribution is removed. However, the new observables again have the advantage that are proportional to $V_R$ so that their measurement may provide a direct bound or measurement of the $V_R$ coupling with no assumption on the value of the $V_L^2$ leading term.

3.3 Spin correlations in $t\bar{t}$ production

The top–antitop spin correlations depend on the Lorentz structure of the tbW vertex. This structure can be studied through the measurement of the angular distributions of the decay products for the $t\rightarrow W^+b$ and $\bar{t}\rightarrow W^-\bar{b}$ processes, which carry information on the top and antitop spin correlation terms. In particular, using the notation of previous section, the double angular distribution—of the decay products X, from top, and $\bar{X}'$, from antitop—can be written as [25, 26]:

$$\begin{aligned} \frac{1}{\sigma }\frac{\mathrm{d}\sigma }{\mathrm{d}\cos \theta _X\; \mathrm{d}\cos \theta _{\bar{X}'}}=\frac{1}{4}\left( 1+C\,\alpha _X\, \alpha _{\bar{X}'}\,\cos \theta _X\, \cos \theta _{\bar{X}'}\right) , \end{aligned}$$

(19)

where $\theta _X$ ($\theta _{\bar{X}'}$) is the angle between the momentum of the decay product X ($\bar{X}'$) and the momentum of the top (antitop) quark in the $t\bar{t}$ center-of-mass frame, $\alpha _X$ and $\alpha _{\bar{X}'}$ are the spin-analyzer powers of particles X and $\bar{X}'$, respectively. C is a coefficient that weights the spin correlation between the quark and the antiquark. Then one can define the asymmetry

$$\begin{aligned} A_{X\bar{X}'}^{z_1 z_2}\equiv & {} \frac{1}{\sigma }\Bigg [ \int _{z_1}^1\mathrm{d}(\cos \theta _X)\int _{z_2}^1\mathrm{d}(\cos \theta _{\bar{X}'})\,\frac{\mathrm{d}\sigma }{\mathrm{d}\cos \theta _X\; \mathrm{d}\cos \theta _{\bar{X}'}}\nonumber \\&+ \int _{-1}^{z_1}\mathrm{d}(\cos \theta _X)\int _{-1}^{z_2}\mathrm{d}(\cos \theta _{\bar{X}'})\, \frac{\mathrm{d}\sigma }{\mathrm{d}\cos \theta _X\; \mathrm{d}\cos \theta _{\bar{X}'}}\nonumber \\&- \int _{-1}^{z_1}\mathrm{d}(\cos \theta _X)\int _{z_2}^1\mathrm{d}(\cos \theta _{\bar{X}'})\,\frac{\mathrm{d}\sigma }{\mathrm{d}\cos \theta _X\; \mathrm{d}\cos \theta _{\bar{X}'}}\nonumber \\&- \int _{z_1}^1\mathrm{d}(\cos \theta _X)\int _{-1}^{z_2}\mathrm{d}(\cos \theta _{\bar{X}'})\, \frac{\mathrm{d}\sigma }{\mathrm{d}\cos \theta _X\; \mathrm{d}\cos \theta _{\bar{X}'}}\Bigg ].\nonumber \\ \end{aligned}$$

(20)

The different regions of integration for this asymmetry are plotted in Fig. 8. There, the number of events on each of the regions is collected and the sign of their contribution to the asymmetry is also indicated. The particular case $z_1=z_2=0$ corresponds to the usual spin correlation asymmetry:

$$\begin{aligned} A_{X\, \bar{X}'}{=}\frac{N\left( \cos \theta _X\,\cos \theta _{\bar{X}'}>0\right) - N\left( \cos \theta _X\,\cos \theta _{\bar{X}'}<0\right) }{N\left( \cos \theta _X\,\cos \theta _{\bar{X}'}>0\right) + N\left( \cos \theta _X\,\cos \theta _{\bar{X}'}<0\right) }. \end{aligned}$$

(21)

For the $A_{X\bar{X}'}^{z_1 z_2}$ asymmetry, Eq. (20), there is a range of values of $z_1$ and $z_2$ that cancel the leading $V_L^4$ contribution, in such a way that the observable becomes proportional to the $V_R$ coupling. For the $X=l$, $\bar{X}'=l'$ case, these values satisfy the relation

$$\begin{aligned} z_2^\pm =\frac{-2z_1\pm \sqrt{C^2 (1-z_1^2)^2+4z_1^2}}{C (1-z_1^2)}. \end{aligned}$$

(22)

Fig. 8

Regions of integration and sign of the contribution to the spin correlation asymmetry $A_{X\,\bar{X}'}^{z_1\, z_2}$ defined in Eq. (20), depending on the point $(z_1,z_2$)

Fig. 9

Values of $z_1$ and $z_2$ that make zero the $V_L$ leading terms of the $A_{ll'}^{z_1z_2}$ asymmetry, Eq. (22), for different values of the spin correlation coefficient C

Similarly to what happened for $A_l^z$, in Eq. (12), for values of $z_1$ and $z_2$ satisfying the previous equation, the coefficient of $V_L^3 V_R$ in the asymmetry also accidentally cancels. Then there remains the $V_R^2$ coupling as the leading contribution. Solutions to Eq. (22) are plotted in Fig. 9, where it can be seen that the values of $z_1$ and $z_2$ are restricted to the first quadrant (for the $z_2^+$ solution) or to the third one (for the $z_1^-$ solution). In addition to the trivial solutions of Eq. (22), i.e. $z_1=\pm 1,z_2=0$, which reproduces the usual $A_{ll'}$ asymmetry, one can improve the computation by finding the values of $z_1$ and $z_2$ that, satisfying Eq. (22), also maximize the coefficient of the leading $V_R^2$ term in Eq. (20), namely:

$$\begin{aligned} 2.00\, V_R^2 \left[ z_1 z_2 +0.08\, C \left( z_1^2 \left( 1- z_2^2\right) + z_2^2-1\right) \right] . \end{aligned}$$

(23)

This can be trivially done and the result is

$$\begin{aligned} z_1=z_2=z_{ll'}\equiv \pm \sqrt{1+\frac{2}{C}-\frac{2}{C}\sqrt{1+C}}, \end{aligned}$$

(24)

which corresponds to the intersection of the curves of Fig. 9 with the diagonal line of the first and third quadrants.

Fig. 10

Dependence on $V_R$ coupling for $A_{ll'}^{z_1z_2}$ in Eq. (20), for $C=0.4$ and $z_1=z_2=z_{ll'}=0.29$

These values of $z_1$, $z_2$ give a maximum sensitivity of the $A_{ll'}^{z_1z_2}$ asymmetry to the $V_R$ coupling.

In Fig. 10 we show the dependence on the $V_R$ coupling for the $A_{ll'}^{z_1z_2}$ asymmetry in Eq. (20), for $C=0.4$ [11], and $z_1=z_2=z_{ll'}=0.29$, given by Eq. (24).

The same procedure followed here can be used for other decay products of the $W^\pm$. For $t\bar{t} \rightarrow l\,\nu \, b\, \bar{\nu }\, l'\,\bar{b}$ final state, the values of $z_1$ and $z_2$ that cancel the coefficient of the leading $V_L^4$ term in the $A_{\nu l'}^{z_1 z_2}$ asymmetry ($X=\nu$, $\bar{X}'=l'$ in Eq. (20)) satisfy a quadratic equation,

$$\begin{aligned} z_1z_2=-\beta (1-z_1^2)(1-z_2^2),\quad \beta =0.08C, \end{aligned}$$

(25)

and the solution is

$$\begin{aligned} z_2^\pm =\frac{1}{2\beta (1-z_1^2)}\left[ z_1\pm \sqrt{z_1+4\beta ^2(1-z_1)^2}\right] . \end{aligned}$$

(26)

Here, $-1\le z_1\le 0$ for the $z_2^+$ solution and $0\le z_1\le 1$ for the $z_2^-$ solution of Eq. (26), in order to satisfy $|z_2^\pm |<1$. In that case, these $z_{1,2}$ values do not cancel the $V_R$ term of the asymmetry, which remains as the leading one:

$$\begin{aligned} -0.12\left[ z_1 z_2-\frac{C}{4}(1-z_1^2)(1-z_2^2)\right] V_R. \end{aligned}$$

(27)

Fig. 11

Dependence on the $V_R$ coupling for $A_{\nu l'}^{z_1z_2}$, Eq. (20), for $C=0.4$ and $z_1=-z_2=z_{\nu l'}=0.17$

One can easily find the values that maximize this coefficient and simultaneously verify Eq. (26):

$$\begin{aligned} z_1=-z_2=z_{\nu l'}\equiv \pm \sqrt{1+\frac{1}{2\beta }-\frac{1}{2\beta }\sqrt{1+2\beta }} \end{aligned}$$

(28)

In Fig. 11 we show the dependence of the spin correlation asymmetry $A_{\nu l'}^{z_{\nu l'}z_{\nu l'}}$ on $V_R$, for $z_1$, $z_2$ given by Eq. (28) with $C=0.4$. Note that the sensitivity of both asymmetries shown in Figs. 10 and 11 is rather similar.

Another spin correlation considered in the literature is the angular distribution of the top (antitop) decay products defined as [31]:

$$\begin{aligned} \frac{1}{\sigma }\frac{\mathrm{d}\sigma }{\mathrm{d}\cos \varphi _{X\bar{X}'}}=\frac{1}{4}\left( 1+D\,\alpha _X\, \alpha _{\bar{X}'}\, \cos \varphi _{X\bar{X}'}\right) , \end{aligned}$$

(29)

where $\varphi _{X\bar{X}'}$ is the angle between the momentum of the X particle in the t rest frame, and that of the $X'$ one, in the $\bar{t}$ rest frame. D is the spin correlation coefficient. Then one can construct the following asymmetry:

$$\begin{aligned} \tilde{A}_{X\bar{X}'}^z\equiv & {} \frac{N(\cos \varphi _{X\bar{X}'}>z)-N(\cos \varphi _{X\bar{X}'}<z)}{N(\cos \varphi _{X\bar{X}'}>z)+N(\cos \varphi _{X\bar{X}'}<z)}\nonumber \\= & {} \frac{1}{2}\left( \alpha _X\, \alpha _{\bar{X}'}(1-z^2)-2z\right) . \end{aligned}$$

(30)

For $z=0$ one gets the usual forward–backward spin correlation asymmetry

$$\begin{aligned} \tilde{A}_{X\bar{X}'}=\frac{1}{2}D\, \alpha _X\, \alpha _{\bar{X}'}. \end{aligned}$$

(31)

For both $W^\pm$ leptonic decays, $X=l$ and $\bar{X}'=l'$, and following similar procedures to the previous sections, we can find the value of z that cancels the $V_L^4$ leading term in Eq. (30):

$$\begin{aligned} z=\tilde{z}_{ll'}\equiv \frac{1}{D}\left( 1-\sqrt{1+D^2}\right) . \end{aligned}$$

(32)

This value also cancels the $V_R$ term, so that the $V_R^2$ contribution is the dominant one. Then, for $D=-0.29$ [11], the $\tilde{A}_{ll'}^z$ asymmetry is

$$\begin{aligned} \tilde{A}_{ll'}^{\tilde{z}_{ll'}}=\frac{-0.19 V_L^2 V_R^2+0.01 V_L V_R^3-0.13 V_R^4}{\left( V_L^2-0.06 V_L V_R+V_R^2\right) ^2} \simeq -0.19 V_R^2 \end{aligned}$$

(33)

where again, in the last term, we show the asymmetry for $V_L=1$ and $|V_R|<<1$. This asymmetry can be seen in Fig. 12.

Fig. 12

Dependence on the $V_R$ coupling for the $\tilde{A}_{ll'}^{z}$ asymmetry, Eq. (33), for $D=-0.29$ and $z=\tilde{z}_{ll'}$ given by Eq. (32)

Fig. 13

Dependence on the $V_R$ coupling for the $\tilde{A}_{\nu l'}^{z}$ asymmetry, Eq. (35), for $D=-0.29$ and $z=z=\tilde{z}_{\nu l'}$ given by Eq. (34)

Analogously, for W leptonic decays with a neutrino–lepton final state, $X=\nu$, $\bar{X}'=l'$, the z value that cancels the $V_L^4$ term in Eq. (30) is

$$\begin{aligned} z=\tilde{z}_{\nu l'}=-\frac{3.15}{D}\left( 1-\sqrt{1+\left( \frac{D}{3.15}\right) ^2}\right) , \end{aligned}$$

(34)

and then the $\tilde{A}_{\nu l'}^z$ asymmetry, for $D=-0.29$, is

$$\begin{aligned} \tilde{A}_{\nu l'}^{\tilde{z}_{\nu l'}}= & {} \frac{0.006 V_L^3 V_R-0.068 V_L^2 V_R^2+0.006 V_L V_R^3}{(V_L^2 - 0.062 V_L V_R + V_R^2)^2}\nonumber \\\simeq & {} 0.006 V_R. \end{aligned}$$

(35)

The last term in this equation is given for $V_L=1$ and $|V_R|<<1$. This asymmetry is depicted in Fig. 13. Note that in this case the sensitivity to $V_R$ is lower than the one obtained in some of the previous observables due to the small coefficients in the numerator of Eq. (35).

We checked that the expressions of the observables defined for the $V_R$ coupling in this section show a behavior comparable to the one obtained from the expressions of the observables defined in the literature, once the $V_L$ leading contribution is removed. Moreover, the observables defined here have the advantage of being directly proportional to the $V_R$ term that we want to test.

4 Conclusions

We computed the SM one-loop QCD and electroweak contribution to $V_R$. Due to accidental cancellations between the diagrams, the leading contribution is mainly coming from QCD, it is real and of the order of $10^{-3}$. Any measurement of observables that may lead to $V_R$ higher than $10^{-3}$ should be interpreted as new physics effects.

We also have proposed new observables that may provide a direct measurement of the right coupling. We found that for several angular asymmetries considered in the literature it is possible to define new observables, with an optimal choice of parameters, in such a way that they become a direct probe of $V_R$. These observables include angular asymmetries in the W rest frame, angular asymmetries in the top rest frame and also spin correlations. All the new observables defined in this paper are proportional to $V_R$ and thus suitable for a direct determination of this coupling. In some cases the behavior shown by the expressions for our observables, presents a better sensitivity to $V_R$ (like it is shown in Fig. 3). While the asymmetries usually considered in the literature have leading contributions from $V_L$, the new asymmetries that we have studied here have as a leading term the $V_R$ right coupling we are interested in. These asymmetries can be measured with LHC data, where a huge number of top events are being collected, in order to obtain a direct measurement on the standard model contribution to the right top quark.

Appendices

Appendix A Diagram contributions

Using the following definitions for the denominators:

$$\begin{aligned}&A_Z= x^2 \left[ \left( (y-1) r_b^2+1\right) y- r_w^2 (y-1)\right] \nonumber \\&\qquad - \, r_z^2 (x-1), \end{aligned}$$

(36)

$$\begin{aligned}&B_Z= x \left\{ \left[ \left( x (y-1)+1\right) r_b^2+x-1\right] y -r_z^2 (y-1)\right\} \nonumber \\&\qquad - \, r_w^2 (x-1) \left[ x (y-1)+1\right] , \end{aligned}$$

(37)

$$\begin{aligned}&C_Z= (x-1) (x y-1) r_b^2-r_w^2 (x-1) x (y-1)\ \nonumber \\&\qquad + \, r_z^2 xy+x (y-1) (x y-1),\end{aligned}$$

(38)

$$\begin{aligned}&\left\{ A_\gamma ,B_\gamma ,C_\gamma \right\} =\left\{ A_Z,B_Z,C_Z\right\} (r_z\rightarrow 0),\end{aligned}$$

(39)

$$\begin{aligned}&\left\{ A_H,B_H,C_H\right\} =\left\{ A_Z,B_Z,C_Z\right\} (r_z\rightarrow r_h). \end{aligned}$$

(40)

with

$$\begin{aligned} r_x\equiv \frac{m_x}{m_t} \end{aligned}$$

(41)

and taking the usual definition for the SM couplings

$$\begin{aligned} a_t=-a_b=1, \quad v_b=-1+\frac{4s_w^2}{3} \quad \text{ and } \quad v_t=1-\frac{8s_w^2}{3}, \end{aligned}$$

(42)

the expression for the contribution of each diagram is given by

$$\begin{aligned}&I^{tZW}= -\frac{1}{32 \pi s_w^2}\times \int _0^1\mathrm{d}x\nonumber \\&\quad \times \,\int _0^1\mathrm{d}y\; \frac{2x^2y\left[ v_t(1+2xy)-a_t(5-2xy)\right] }{A_Z}, \end{aligned}$$

(43)

$$\begin{aligned} I^{t \gamma W}= -\frac{1}{8 \pi }\, Q_t \times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; \frac{2 x^2y(1+2xy)}{A_\gamma },\end{aligned}$$

(44)

$$\begin{aligned} I^{t H W} = 0, \end{aligned}$$

(45)

$$\begin{aligned} I^{t w_0 w}+ I^{t H w}= & {} \frac{1}{16 \pi s_w^2}\frac{1}{r_w^2}\int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\nonumber \\&\times \Bigg \{ -\frac{x^3 y\left[ 1+y-r_b^2(1-y)\right] }{A_Z}\nonumber \\&+\, (1-rb^2)\; \frac{x^3y (1-y)}{A_H}+x\log \frac{A_H}{A_Z}\Bigg \},\nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned} I^{t Z w}= \frac{1}{32\pi c_w^2} \times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; \frac{2x^2y(a_t-v_t)}{A_Z}, \end{aligned}$$

(47)

$$\begin{aligned} I^{t \gamma w}= -\frac{1 }{8 \pi }\,Q_t \times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; \frac{2 x^2 y}{A_\gamma }, \end{aligned}$$

(48)

$$\begin{aligned} I^{b W Z}= & {} \frac{1}{32 \pi s_w^2} \times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\nonumber \\&\times \frac{2 x^2y\left[ v_b(1+2xy)-a_b(5-2xy)\right] }{B_Z}, \end{aligned}$$

(49)

$$\begin{aligned} I^{b W \gamma }= \frac{1}{8 \pi }\,Q_b \times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; \frac{2 x^2y(1+2xy)}{B_\gamma }, \end{aligned}$$

(50)

$$\begin{aligned} I^{b W H}= 0, \end{aligned}$$

(51)

$$\begin{aligned} I^{b w w_0}+I^{b w H}= & {} \frac{1}{16 \pi s_w^2}\frac{1}{r_w^2}\int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\nonumber \\&\times \Bigg \{\frac{ x^2 y\left[ 1-x-r_b^2\left( 1-x(1-2y)\right) \right] }{B_Z}\nonumber \\&- (1-r_b^2) \frac{x^2 y(1-x)}{B_H}{+} x\log \frac{B_H}{B_Z}\Bigg \}, \end{aligned}$$

(52)

$$\begin{aligned} I^{b w Z}= \frac{1}{32\pi c_w^2}\times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; \frac{2x^2y(v_b-a_b)}{B_Z}, \end{aligned}$$

(53)

$$\begin{aligned} I^{b w\gamma }= -\frac{1}{8 \pi }\,Q_b\times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; \frac{2 x^2 y}{B_\gamma }, \end{aligned}$$

(54)

$$\begin{aligned} I^{Z t b}= & {} \frac{1}{32 \pi c_w^2 s_w^2}\int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\nonumber \\&\times \frac{x\left[ a_b(1+xy)-v_b(1-xy)\right] \left[ a_t(1+xy)-v_t(1-xy)\right] }{C_Z},\nonumber \\ \end{aligned}$$

(55)

$$\begin{aligned} I^{\gamma t b}= \frac{1}{2 \pi }\, Q_b\, Q_t \times \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; \frac{x(1-xy)^2}{C_\gamma }, \end{aligned}$$

(56)

$$\begin{aligned} I^{w_0 t b}+I^{Htb}= & {} \frac{1}{16 \pi s_w^2} \int _0^1\mathrm{d}x \int _0^1\mathrm{d}y\; x^2(1-x)(1-y)\nonumber \\&\times \Bigg \{ \frac{-1}{C_Z}+\frac{1}{C_H}+\frac{x}{r_w^2}\log \frac{C_Z}{C_H}\Bigg \}. \end{aligned}$$

(57)

Appendix B Contribution of diagrams with a photon

$$\begin{aligned} I_0^{t\gamma W}= & {} \frac{-2}{r_b}\Bigg \{1+\Bigg [\frac{(1-r_w^2-r_b^2-\Delta )(1-r_w^2-3r_b^2-\Delta )}{4r_b^2\, \Delta }\log \left( \frac{r_w^2}{1-r_w^2}\right) \Bigg ] \nonumber \\&+\, \Bigg [\Delta \rightarrow -\Delta \Bigg ]\Bigg \}, \end{aligned}$$

(58)

$$\begin{aligned} I_0^{t\gamma w}= & {} \Bigg [\frac{-1}{r_b\, \Delta }(1-r_b^2-r_w^2-\Delta )\log \left( \frac{1+r_w^2-r_b^2+\Delta }{2r_w}\right) \Bigg ]\nonumber \\&+\Bigg [\Delta \rightarrow -\Delta \Bigg ], \end{aligned}$$

(59)

$$\begin{aligned} I_0^{bW\gamma }= & {} \frac{2}{ r_b}+\Bigg \{\frac{ -2\left( 1-r_b^2-r_w^2+\Delta \right) }{r_b\Delta (1+r_b^2-r_w^2+\Delta )^2}\;\Bigg [(1-r_w^2)^2\nonumber \\&-r_b^2(1+r_w^2)+\Delta (1-r_w^2)\nonumber \\&- 2r_b^2(1-r_w^2+\Delta )\log \left( \frac{2r_b^2}{1-r_w^2-r_b^2+\Delta }\right) \Bigg ]\Bigg \}\nonumber \\&+\Bigg \{\Delta \rightarrow -\Delta \Bigg \} \nonumber \\&+ \,\Bigg [ 4\pi \, i\; r_b\; \frac{(1-r_w^2-r_b^2+\Delta )(1-r_w^2+\Delta )}{(1-r_w^2+r_b^2+\Delta )^2\Delta }\Bigg ]\nonumber \\&-\Bigg [\Delta \rightarrow -\Delta \Bigg ], \end{aligned}$$

(60)

$$\begin{aligned} I_0^{bw\gamma }= & {} -2\; r_b \;\Bigg \{ \Bigg (\pi \,i \;\frac{1-r_b^2-r_w^2+\Delta }{\Delta (1+r_b^2-r_w^2+\Delta ) }\Bigg ) -\Bigg (\Delta \rightarrow -\Delta \Bigg ) \nonumber \\&+\, \Bigg [\frac{1-r_b^2-r_w^2+\Delta }{\Delta (1+r_b^2-r_w^2+\Delta )} \log \left( \frac{2 r_b^2}{1-r_b^2-r_w^2+\Delta }\right) \Bigg ] \nonumber \\&+\Bigg [\Delta \rightarrow -\Delta \Bigg ]\Bigg \}, \end{aligned}$$

(61)

$$\begin{aligned} I_0^{\gamma tb}=\frac{2\; r_b}{\Delta }\log \left( \frac{1-r_w^2+r_b^2+\Delta }{1-r_w^2+r_b^2-\Delta }\right) , \end{aligned}$$

(62)

with

$$\begin{aligned} \Delta =\sqrt{(1-r_w^2)^2+r_b^4-2r_b^2(1-r_w^2)}. \end{aligned}$$

In the limit $r_b \rightarrow 0$, the formulas get the simplest expression:

$$\begin{aligned}&I_0^{t\gamma W}\xrightarrow {\ \ r_b\rightarrow 0\ \ } -\frac{r_b}{(1-r_w^2)^3}\nonumber \\&\quad \times \left[ (3-8r_w^2+5r_w^4)+4r_w^2(1-2r_w^2)\log (r_w)\right] , \end{aligned}$$

(63)

$$\begin{aligned} I_0^{t\gamma w}\xrightarrow {\ \ r_b\rightarrow 0\ \ } \frac{2\; r_b}{(1-r_w^2)^2}\left[ 1-r_w^2+r_w^2\,\log (r_w^2)\right] , \end{aligned}$$

(64)

$$\begin{aligned}&I_0^{bW\gamma } \xrightarrow {\ \ r_b\rightarrow 0\ \ } 2\;r_b\; \Bigg [\pi i\, \frac{\left( 2+r_w^2+r_w^4\right) }{1-r_w^2}\nonumber \\&\quad + \frac{2\,r_w^2\left( 1-2r_w^2+2r_w^6-r_w^8\right) }{(1-r_w^2)^4}\log (r_w)+\,1\nonumber \\&\quad -\frac{2-r_w^2(5-4r_w^2+2r_w^2-2r_w+r_w^8)}{(1-r_w^2)^4}\log (1-r_w^2)\Bigg ], \end{aligned}$$

(65)

$$\begin{aligned}&I_0^{bw\gamma } \xrightarrow {\ \ r_b\rightarrow 0\ \ } \frac{-r_b}{1-r_w^2}\Bigg [2\pi \, i\,(1+r_w^2) +\log \left( \frac{r_b^2}{1-r_w^2}\right) \nonumber \\&\quad +r_w^2\log \left( \frac{r_w^2}{1-r_w^2}\right) \Bigg ], \end{aligned}$$

(66)

$$\begin{aligned} I_0^{\gamma tb}\xrightarrow {\ \ r_b\rightarrow 0\ \ } -\frac{4\; r_b}{1-r_w^2}\log \left( \frac{r_b}{1-r_w^2}\right) , \end{aligned}$$

(67)