Black hole remnant in asymptotic anti-de Sitter space

Abstract

The solution of a remnant was suggested for the black hole ground state after surface gravity is corrected for the loop quantum effect. On the other hand, a Schwarzschild black hole in asymptotic anti-de Sitter space would tunnel into the thermal soliton solution known as the Hawking–Page phase transition. In this letter, we investigate the low temperature phase of a three-dimensional Banados–Teitelboim–Zanelli (BTZ) black hole and four-dimensional AdS Schwarzschild black hole. We find that the thermal soliton is energetically favored rather than the remnant solution at low temperature in three dimensions, while a Planck-size remnant is still possible in four dimensions. Though the BTZ remnant seems energetically disfavored, we argue that it is still possible to find in the overcooled phase if strings were present, and its implication is discussed.

1 Introduction

It was shown that for a Schwarzschild black hole evaporating by massless particles, the Hawking–Bekenstein area law [1] receives a logarithmic correction, $S = 4\pi M^2 - 4\pi \sigma \log (M+\sigma )$ for one-loop corrected temperature $T=(8\pi M)^{-1}(1+\sigma ( M^2)^{-1} )$, where $\sigma$ is the conformal anomaly. In particular, a Planck-size remnant is implied for $\sigma <0$ [2]. There were complaints about remnants such as the one in [3], mainly due to the extraordinary large amount of entropy confined within a tiny volume. Nevertheless, if the Hawking radiation were not exactly thermal, the retained information would have been released through the evaporation process. One could have expected the existence of a remnant with a zero or small amount of residual entropy. In this case, instead of helping to resolve the information loss paradox, the remnant solution might still answer the call for the hypothetically fundamental Planck scale. In general, remnant solutions can be easily found in those theories such as noncommutative geometry, doubly special relativity, or the generalized uncertainty principle (GUP). Readers are referred for a recent review to [4] for instance.

On the other hand, it is well known that a Schwarzschild black hole in asymptotic anti-de Sitter space would tunnel into the thermal AdS solution known as the Hawking–Page phase transition [5, 6]. In particular, the three-dimensional Banados–Teitelboim–Zanelli (BTZ) black hole system [7] has two distinct phases: the black hole with mass $M>0$ and thermal AdS with $M=-1$ [8]. It is unclear for us whether this thermal AdS phase is still energetically favored at low temperatures after the BTZ or AdS black hole receives a loop quantum correction. In other words, there might be a possibility that the black hole would have already stopped evaporating and stayed as a warm remnant before it enters the soliton phase.

To proceed our discussion, one needs to assume that both the first law of thermodynamics and the logarithmic correction to the black hole entropy are valid within the energy range in our discussion. The extrapolation of both relations to the limit of the Planck size may be too naive, especially as regards our ignorance of a complete theory of quantum gravity. However, our strategy is to compare the free energy of the remnant and that of the thermal AdS around the Hawking–Page temperature $T_{HP}=1/2\pi l$. This corresponds to the energy scale $\mathcal{O}(l^{-1})$, which is still far from the Planck or string scale; it should be reasonable to assume that the laws of thermodynamics are valid and the black hole size around $\mathcal{O}(l)$ can be treated as a classical and static background.

Finally, we comment that the logarithmic correction retains a similar form as long as, on the dual CFT side, the number of states reads [9]

$$\begin{aligned} \rho \sim c^{\gamma }e^{S}, \end{aligned}$$

(1)

where c is the central charge, $\gamma$ is some rational power, and S is the entropy to be identified with the Bekenstein–Hawking entropy on the black hole side. We do not expect this Cardy formula to be abruptly modified for large or small BTZ black holes. Another supportive though hand-waving argument comes from the GUP modified Schwarzschild black hole entropy [10]:

$$\begin{aligned} S_\mathrm{GUP} = 4\pi f(M^2)M^2-\log (M+\sqrt{M^2-1}), \end{aligned}$$

(2)

where the black hole mass M is measured in units of the Planck mass, and the function $f(M^2)$ interpolates between 0 and 1 for $0\le M<\infty$. It is obvious that the logarithmically corrected form survives for all $M>1$.

This letter is organized as follows. We review the Hawking–Page phase transition between BTZ black hole and thermal AdS$_3$ in Sect. 2. In Sect. 3, we compute the up to two loops corrected entropy and free energy for the BTZ black hole and discuss its phase transition to thermal AdS. In Sect. 4, we calculate the one-loop corrected entropy and free energy for an AdS$_4$ black hole and discuss its phase transition. In Sect. 5, we discuss a new scale set by the AdS remnant and its effect on the Hawking–Page phase transition. Finally, we discuss possible scenarios around the phase transition if a stringy excitation is considered.

2 BTZ black hole and Hawking–Page phase transition

To justify which phase is energetically favored at a specific temperature, we would like to compare the free energy of a BTZ and that of vacuum. Since we expect a vacuum without nonzero angular momentum, we will only consider a nonrotating BTZ black hole. Having said this, we will not inspect solutions such as an extremal BTZ solution or exotic BTZ [11]. Although the phase diagram would become rich and interesting by including those solutions, they cannot tunnel into the AdS vacuum as long as the conservation of angular momentum is respected. The nonrotating BTZ solution has the metric

$$\begin{aligned} \text {d}s^{2}=-\left( -M+\frac{r^2}{l^2}\right) \text {d}t^2+\left( -M+\frac{r^2}{l^2}\right) ^{-1}\text {d}r^2+r^2 \text {d}\phi ^2 \end{aligned}$$

(3)

with horizon $r_+=l \sqrt{M}$. The thermal quantities, such as the Hawking temperature $T_{H}$, the Bekenstein–Hawking entropy $S_{BH}$, the internal energy E, and the free energy $F_{BH}$ are given by

$$\begin{aligned}&T_{H}=\frac{\kappa }{2\pi }=\frac{\sqrt{M}}{2\pi l},\end{aligned}$$

(4)

$$\begin{aligned}&S_{BH} = \frac{A_H}{4G}=\frac{\pi l \sqrt{M}}{2G},\end{aligned}$$

(5)

$$\begin{aligned}&E=\frac{M}{8G},\end{aligned}$$

(6)

$$\begin{aligned}&F_{BH}= E-T_H S_{BH} = -\frac{M}{8G}. \end{aligned}$$

(7)

There also exists a thermal AdS solution with on-shell action I and free energy $F_\mathrm{AdS}$:

$$\begin{aligned} \begin{aligned} I&= -\frac{\beta }{8G},\\ F_\mathrm{AdS}&= -\frac{1}{8G}, \end{aligned} \end{aligned}$$

(8)

and the phase transition occurs at temperature $T=1/(2\pi l)$, when the free energy of the nonrotating BTZ becomes higher than that of the thermal vacuum.

3 Quantum correction to surface gravity and the emergence of the remnant

The quantum correction to the Hawking temperature has the following form [12]:

$$\begin{aligned} T^{q}_{H} = T_{H} \big /\left( 1+\sum _i\alpha _i\frac{\hbar ^i}{r_+^i}\right) . \end{aligned}$$

(9)

In general, the coefficients $\alpha _i$ will depend on a species of particles included in the ith loop perturbative correction [2]. Following the first law of thermodynamics, the entropy receives a corresponding correction as follows:

$$\begin{aligned}&S^{q\prime }_{BH}= \int {\frac{\text {d}M}{T^q_{H}}}=\frac{\pi r_+}{2G} + \alpha _1\hbar \frac{\pi }{2G}\ln r_+\nonumber \\&\qquad \quad - \alpha _2 \hbar ^2 \frac{\pi }{2G r_+} +-\cdots \end{aligned}$$

(10)

The conformal field theory (CFT) calculation also implies a similar logarithmic correction with coefficient $\alpha _1=-\frac{3G}{\pi \hbar }$ in the above expression [9]. However, we remark that the temperature in the CFT computation was not modified according to (9). Therefore, it is more appropriate to think of the logarithmic correction we will discuss here as to come from a different origin and therefore $\alpha _1$ could be negative but varied for different models of quantum gravity. Nevertheless, Eq. (10) is not UV complete, for it suffers from the divergence as $M\rightarrow 0$. Without knowing much about gravity at the Planck scale, we would like to assume that the entropy takes the same expression as (10) for simplicity. Therefore, one can regard the undetermined integral constants as counterterms, such that the expression (10) can be regularized in each loop computation. Moreover, the uniqueness of the ground state implies that the would-be regularized $S^q_{BH}$ must vanish at some critical mass $m_c$, which can be regarded as the remnant mass. Finally, the finite expression suggests that

$$\begin{aligned} S^{q}_{BH}= & {} \frac{\pi l \sqrt{M}}{2G} -\frac{\pi l \sqrt{m_c}}{2G} + \alpha _1\hbar \frac{\pi }{4G}\ln (M/m_c)\nonumber \\&- \alpha _2 \hbar ^2 \frac{\pi }{2G l \sqrt{M}}+ \alpha _2 \hbar ^2 \frac{\pi }{2Gl \sqrt{m_c}} +-\cdots \end{aligned}$$

(11)

In Fig. 1, we plot the entropy versus mass for a BTZ black hole and its quantum correction. Though there is no constraint on the coefficient of the second loop $\alpha _2$, the numerical result indicates that there is a small region with negative entropy for the case $\alpha _2<0$. This unphysical region should be excluded and the remnant mass is redefined as the larger positive root to the equation $S^{q}_{BH}=0$ in the case $\alpha _2<0$.

Fig. 1

A numerical simulation of entropy for BTZ black hole (black solid), one-loop corrected remnant (red dash), two-loop corrected remnant with $\alpha _2>0$ (blue dot), and two-loop corrected remnant with $\alpha _2<0$ (blue dot-dash). The inset zoom-in graph shows some exotic behavior near the critical remnant mass for $\alpha _2<0$. This unphysical region of negative entropy should be excluded and the remnant mass is chosen to be the larger root to the equation $S^{q}_{BH}=0$

Finally, the quantum-corrected free energy can be computed as

$$\begin{aligned} F^q_{BH} = E - T^q_{H} S^{q}_{BH}. \end{aligned}$$

(12)

We simulate the free energy of quantum-corrected solutions and plot them in Fig. 2. We find that with a quantum correction, the Hawking–Page transition happens at slightly larger M and the black hole turns into the AdS thermal vacuum before a remnant could possibly form. This result can be partially understood by absorbing those quantum corrections in (9) into a definition of an effective horizon size $r_+^{eff} \equiv r_+ - \alpha _1\hbar - \cdots$ for $r_+ \gg l_p$. That is, the quantum fluctuation makes the horizon look smaller than its classical value, therefore less stable (for a small black hole). However, unless the quantum-corrected black hole stops the radiation before it hits the Hawking–Page temperature, it eventually becomes energetically disfavored and decays into the thermal vacuum. This is what happen to the BTZ case. In the following, we will examine a phase transition of the Schwarzschild black hole in AdS$_4$.

Fig. 2

A numerical simulation of free energy for BTZ black hole (black dash), one-loop corrected remnant (blue dot), two-loop corrected remnant (red dot-dash), and thermal soliton (black solid)

4 Schwarzschild–AdS$_4$ black hole

In this section, we would like to compute the free energy of Schawarzschild black hole in AdS$_4$. The following black hole metrics are given:

$$\begin{aligned} \text {d}s^2= & {} -V(r) \text {d}t^2 + V(r)^{-1}\text {d}r^2 + r^2 \text {d}\Omega _2^2,\nonumber \\ V(r)= & {} 1-\frac{2GM}{r}+\frac{r^2}{l^2}. \end{aligned}$$

(13)

The thermal quantities read

$$\begin{aligned} T_H= & {} \frac{l^2+3r_+^2}{4\pi l^2 r_+} ,\end{aligned}$$

(14)

$$\begin{aligned} S_{BH}= & {} \pi r_+^2,\end{aligned}$$

(15)

$$\begin{aligned} F_{BH}= & {} -\frac{r_+(r_+^2-l^2)}{4l^2}, \end{aligned}$$

(16)

where $V(r_+)=0$ is satisfied. The free energy is defined with respect to the AdS soliton, that is, $F_\mathrm{AdS}=0$. The Hawking–Page phase transition happens at $T_{HP}=1/(\pi l)$, where $r_+=l$.

The loop-corrected thermal quantities after regularization are given by [13]

$$\begin{aligned} T_H^q= & {} T_H \left( 1+\frac{\alpha }{M^2}\right) ^{-1},\end{aligned}$$

(17)

$$\begin{aligned} S_{BH}^q= & {} \int {\frac{\text {d}M}{T_H^q}}=S_{BH}-\pi r_c^2 +4\pi \alpha \frac{l^2(r_c^2-r_+^2)}{(l^2+r_+^2)(l^2+r_c^2)}\nonumber \\&-4\pi \alpha \ln \frac{r_c^2(r_+^2+l^2)}{r_+^2(r_c^2+l^2)},\end{aligned}$$

(18)

$$\begin{aligned} F_{BH}^q= & {} E -T^q_H S_{BH}^q. \end{aligned}$$

(19)

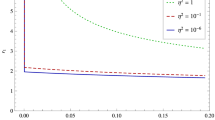
In Fig. 3, we plot the entropy versus horizon radius for the AdS black hole and its quantum correction. The unphysical region of a negative entropy should be excluded in the case $\alpha >0$ and the remnant mass is chosen to be the larger root to the equation $S_{BH}^q=0$. On the other hand, the case of a negative $\alpha$ is consistent with the previous observation from the AdS–CFT correspondence [9] and an argument based on the remnant [14, 15].

Fig. 3

A numerical simulation of the entropy for an AdS black hole (black solid), one-loop corrected remnant (blue dash) with $\alpha <0$, and one-loop corrected remnant with $\alpha >0$ (red dot). The inset zoom-in graph shows some exotic behavior for $\alpha >0$ near the remnant critical mass, where the unphysical region of a negative entropy should be excluded. We has used the unit $l=1$ in the plot

In Fig. 4, we plot the free energy versus the horizon radius for an AdS black hole and its quantum correction. It shows that below some critical size, the thermal AdS soliton is energetically favored rather than the AdS black hole and its one-loop corrected remnant with positive $\alpha$. Nevertheless the one-loop corrected remnant with negative $\alpha$ seems to survive all the way to the Planck size.

Fig. 4

A numerical simulation of free energy for an AdS black hole (black dash), one-loop corrected remnant (blue dash) with $\alpha <0$, one-loop corrected remnant with $\alpha >0$ (red dot), and thermal soliton (black solid or x-axis). The inset zoom-in graph shows that the AdS soliton is energetically favored rather than a black hole below the critical size $r_+=l$; nevertheless a one-loop corrected remnant phase is favored for $\alpha <0$. We have used the unit $l=1$ in the plot

5 Implication of AdS remnant

The partition functions of thermal AdS$_3$ and BTZ black hole are related by a modular transformation [16],

$$\begin{aligned} Z_\mathrm{BTZ}(T_\mathrm{BTZ},\Omega )= & {} Z_\mathrm{AdS}(T_\mathrm{AdS},\Omega ), \nonumber \\ T_\mathrm{AdS}= & {} \frac{1-\Omega ^2l^2}{4\pi ^2 T_\mathrm{BTZ}l^2} \end{aligned}$$

(20)

where $\Omega =\frac{r_-}{r_+l}$ is the chemical potential conjugated to the angular momentum of BTZ. In the nonrotating case, the Hawking–Page transition temperature is defined as $T_\mathrm{AdS}=T_\mathrm{BTZ}=(2\pi l)^{-1}$. Since the loop correction does not modify the metric, this discrete symmetry is believed to persist. Therefore, the remnant temperature implies a cutoff temperature in the thermal AdS phase, that is,

$$\begin{aligned} T^c_\mathrm{AdS} = \frac{1}{2\pi l \sqrt{m_c}}. \end{aligned}$$

(21)

A geometric picture is available to explain this relation [17]: that one can view the Euclidean BTZ or thermal AdS as a hyperbolic three-manifold with a two-torus as its boundary. The choice of one cycle gives the description of temperature in either BTZ or thermal AdS$_3$ and the modular transformation (20) simply swaps the cycle. While the loop correction to the Hawking temperature obstructs the unlimited expansion of the Euclidean time cycle of BTZ, it also creates a lower bound such that the period of the Euclidean time cycle of an AdS cannot be less than $1/T^c_\mathrm{AdS}$.

On the other hand, if the black hole stops radiation at the temperature of remnant, it also implies a minimum length scale $\tau _2^c$ associating to the remnant size, such that the periodicity of cycle $\tau _2 \ge \tau _2^{c}$. Using the same method to determine the Hagedorn temperature $\beta _H^{-1}$, now the partition function for lowest excitation modes becomes [18]

$$\begin{aligned} Z \sim e^{-\frac{1}{4\pi \tau _2^c}(\beta ^2-\beta _H^2)}. \end{aligned}$$

(22)

The available states above the Hagedorn temperature ($\beta <\beta _H$) still grow exponentially but may not be as sharp as that of the usual BTZ where the point-like string limit $\tau _2\rightarrow 0$ can be taken. That is, the existence of a BTZ remnant may also smooth out the phase transition for its slower growth of partition function.

6 Stringy point of view

Earlier it has been shown that a BTZ remnant (up to two-loop correction) is not energetically favored below the critical temperature, nevertheless we would like to argue that it may still survive as a metastable state during the overcooling phase. First we have learned that if there is a stringy excitation, there would appear two Hagedorn temperatures $T_{H/L}$, which are different from the Hawking–Page transition temperature by [18]

$$\begin{aligned} T_{L}= & {} T_{HP}\frac{1}{\sqrt{k}}\left( 4-\frac{1}{k-2}\right) ^{1/2}=\frac{4\pi ^2l^2}{T_{H}}, \nonumber \\ T_{HP}= & {} \frac{1}{2\pi } \end{aligned}$$

(23)

where strings propagating in the AdS$_3$ space are described by the SL(2, R) WZW model at level k. The BTZ could be overcooled between $T_L$ and $T_{HP}$, while a thermal AdS could be overheated between $T_{HP}$ and $T_H$. If the critical remnant mass locates in the following range:

$$\begin{aligned} 1>m_c>\frac{1}{k}\left( 4-\frac{1}{k-2}\right) , \end{aligned}$$

(24)

then the remnant is still likely to be observed as a metastable state in this overcooled phase. To further illustrate this possibility, we recall that while the higher Hagedorn temperature $T_H$ can be understood as the appearance of the Atick–Witten tachyon winding mode [19], the lower temperature $T_L$ can also be understood as the appearance of the tachyonic momentum mode as shown in Fig. 5. The previously mentioned obstruction of an unlimited expansion of the Euclidean time cycle of BTZ can be understood as the appearance of a winding mode to stabilize this tachyon. To illustrate this point, let us consider a toy model of a string with compactified time dimension of circumference $\beta$, that is,

$$\begin{aligned} X^0(\sigma ,\tau )=x^0 + \frac{2\pi m \tau }{\beta }+\frac{n\beta \sigma }{\pi }+\cdots , \end{aligned}$$

(25)

with mass shell condition

$$\begin{aligned} \frac{M^2}{4}= & {} N+\frac{1}{2}\left( \frac{m\pi }{\beta }+\frac{n\beta }{2\pi }\right) ^2-1 \nonumber \\&+ \tilde{N} +\frac{1}{2}\left( \frac{m\pi }{\beta }-\frac{n\beta }{2\pi }\right) ^2-1, \end{aligned}$$

(26)

satisfying the level matching constraint $N-\tilde{N}=mn$. In Fig. 5, we show that for a pure momentum mode $(m,n)=(\pm 1,0)$, the state becomes tachyonic for large enough $\beta$ (such that the temperature is lower than $T_L$), however, this tachyonic state could be stabilized if at the same time a winding mode associated with a remnant is present, say $(m,n)=(\pm 1,\pm 1)$. This metastable remnant solution could be understood from the partition function (22) as well. If the scale $\tau _2^c \sim \mathcal{O}(1/T_L)$, then the phase transition would be too mild to happen, or the difference between two phases is hard to distinguish. In the former case, the BTZ phase remains (as a remnant); while in the latter case, it could be a coexistent phase for both thermal AdS and BTZ.

Fig. 5

Stringy states of pure momentum mode $(m,n)=(\pm 1,0)$ (black solid) become tachyonic for $M^2<0$ at small temperature. They can be stabilized if nonzero winding modes (for the non-contractable Euclidean time cycle of the remnant) are also present. We plot the states of $(\pm 1,\pm 1)$ (blue dotted), and $(\pm 1,\mp 1)$ (red dashed)

7 Summary

In this letter, we investigated the low temperature phase of the three-dimensional BTZ black hole and the four-dimensional AdS Schwarzschild black hole. We found that the thermal AdS is energetically favored rather than the remnant solution at low temperature in three dimensions, while a Planck-size remnant is still possible in four dimensions for a negative one-loop coefficient. Though the BTZ remnant seems energetically disfavored, we argue that it is still possible to find in the overcooled phase if strings were present. Finally, we showed that the existence of a BTZ remnant scale might have the effect to smooth the change of degrees of freedom during a Hawking–Page transition. In order to justify our conclusions derived from black hole thermodynamics and the loop-corrected Hawking temperature, one may need to study possible candidates for microstates, which are responsible to the thermal properties of BTZ remnant. In other words, one would ask, whether after introducing a loop quantum correction a new mechanism for a phase transition between BTZ and remnant could exist in the dual CFT description. We will leave this for a future study.