1 Introduction

In the framework of general relativity (GR), the gravitational force is explained in terms of the space-time curvature so that the field equations connect the space-time geometry to the matter content. More technically, GR exhibits a universe modeled by space-time with a mathematical structure formed by a four dimensional differentiable manifold [1]. It is commonly believed that a unique mathematical framework to reconcile quantum mechanics (QM) with GR is highly dependent on our understanding of the space-time geometry. In other words, there is comprehensive agreement that the geometry of space-time is fundamentally to be explained by a quantum theory. It is assumed that the Planck energy \(\epsilon _\mathrm{pl}\) corresponds to the critical energy scale of the transition from classical GR to quantum gravity (QG), a theory which is supposed to challenge the most fundamental and long standing issues of modern physics. Despite the lack of a complete theory of QG, it seems a semi-classical or effective phenomenological approach of QG may guide us to disclose the mysterious nature of QG [2–18]. It is important to understand how to extract the testable predictions from this fundamental theory. Interestingly, all semi-classical approaches offered so far unanimously insist on the existence of a minimal measurement length in the nature, known as the Planck length \(l_\mathrm{p}\). Besides, it is believed that the modified mass-shell condition (or dispersion relations) arising from the deviation of Lorentz invariance in effective phenomenological approaches [9–18] may justify some of the phenomena taking place on an astronomical and a cosmological scale, like the threshold anomalies of ultra high energy cosmic rays and TeV photons [19–25]. It is noticeable that such Lorentz invariance violation is already predicted in the context of other approaches to QG such as: non-commutative geometry [23–25], spin network in loop quantum gravity [26], and string field theory [27]. Throughout the present work, our attention specifically is focused on a semi-classical formalism known as “gravity’s rainbow”, which has been designed by Magueijo and Smolin [28]. In fact, it can be said that rainbow gravity is nothing but doubly special relativity (DSR) [9–14] in the presence of curved space-time which is known as “doubly general relativity” (DGR). In this formalism, there is no single fixed space-time background, namely the space-time background appears as a geometric spectrum in terms of the energy scale of the particle probe. Therefore, in the cosmological setting, we are dealing with the rainbow modified metric by introducing a function in the Friedmann–Robertson–Walker (FWR) metric which depends on such a variable energy scale. The formation of the rainbow metric proposal involves various motivations such as the lack of a trivial definition of the dual position space in DSR [28]. However, this approach to QG is not free from problems and a considerable number of works have been focused on its various aspects [29–41]. Somehow, the proposal of gravity’s rainbow is similar to the idea of “running coupling constants” in particle physics and field theory, in the sense that at very small distances (high energy) the space-time geometry is related to the energy scale of the particle probe [42–44]. It is worth mentioning that, apart from the effective approaches to QG like DSR and DGR, it has been argued that if the physical space-time of the standard GR theory is emergent, then it is expected that we are faced with a radical picture of the universe at fundamental quantum scale [42–44]. The basic idea of an “emergent universe” dates back to the work of Eddington [45], inspired by the proposal of the Einstein static universe (ESU). In simple words, ESU suggests that the content of the universe as a closed system is made up of at least a cosmological constant and normal matter. While ESU in the context of GR is not stable versus spatially homogeneous perturbations, it predicts that the universe in the past might have emerged as a static initial state [46]. We know that the data obtained by cosmic microwave background (CMB) observations generally supports the inflationary scenario. Also, by the implementation of some singularity theorems with the geometrical assumptions that \(K<0\) or \(K=0\), it has been shown that despite the occurrence of inflation, the universe had a violent beginning in the past [47–51]. Hence, one of the most important motivations for studying QG is to avoid the singularity at the beginning of the universe. Recovery of ESU in the framework of an inflationary universe by Ellise and Maartens, known as a modern version of the Eddington emergent universe, was in this direction of research interest [52]. According to modern standard cosmology, the inflationary expansion of the universe has quickly eliminated any original spatial curvature. On the other hand, the CMB observations imply \(\Omega _{0}\gtrsim 1\) (\(1.02\pm 0.02\)) for the total density parameter. This means that the geometry of the universe is not exactly flat, rather it could have a non-zero spatial curvature at the beginning, resulting in negligible late-time effects. In this sense, the emergent universe scenario allowed for the existence of a positive curvature universe that emanates asymptotically as a static initial state known as ESU which afterwards experienced inflation. The stable ESU addresses the existence of a fixed point around which our universe in the early times was eternally fluctuating. In the case of the universe filled with a massless scalar field \(\phi \) with a suitable inflaton potential, these fluctuations had disappeared and the stable state of the universe had turned into an inflationary phase. Within the context of standard cosmology, the prerequisites of one or more flat wings (of course with a little positive gradient) in the inflaton potential can make an emergent universe. This transmission from a stable ESU to an inflationary phase takes place around the different values of e-folds. For instance, in [46] by analyzing the spectrum of inflationary perturbations of some stable cosmological models in the context of GR, it has been demonstrated that the transmission occurs in over 60 e-folds. Also, it should be noted that while these inflationary emergence GR-based models respect the CMB constraints, they suffer from a fine-tuning problem. This problem can be resolved in the context of modified emergence models of GR. However, recently in [53] some arguments were presented by which one tries to show that the emergent cosmological scenario cannot really be past-eternal. As a prominent feature of emergent universe scenario, one can point to the removal of the initial singularity and also the horizon problem. This is a strong motivation to study the ESU models along with their stability conditions in the presence of high energy corrections of GR. For instance, one can point to the works done in the context of massive gravity [54–56], the Hořava–Lifshitz model of gravity [57–59], braneworld scenarios [60–64], induced matter theory [65], loop quantum cosmology [66–68], f(R), f(T), and f(G) gravity [69–75]. As discussed at the beginning of this section, gravity’s rainbow or DGR is also considered as an alternative of GR with high energy corrections. Besides, it has been shown that in the study of FRW cosmology and an isotropic quantum cosmological perfect fluid model in the rainbow gravity setup, some conditions are derived which prevent the initial singularity [77]. Inspired by this introduction, our main goal in this paper is to study the stability of ESU against the homogeneous scalar, vector, and tensor perturbations in the presence of a rainbow’s gravity setup as a QG modification of GR. But before doing this, by following the phase space method we will analyze the status of the Big-Bang singularity in the framework of a flat rainbow FRW universe model.

The present paper is arranged as follows: In Sect. 2, we have derived the rainbow modified Friedman equations in detail for a general non-flat universe. In Sect. 3, by introducing two different forms of the rainbow functions depending on the energy density, first of all in the absence of the cosmological constant, we obtain the stability conditions of ESU against the homogeneous linear scalar perturbations. In the following of this section, we pursue our goal in the presence of a cosmological constant related to the energy density via introducing a new rainbow function. In Sect. 4, we analyze the stability against vector and tensor perturbations. Finally in Sect. 5, we give the summary and conclusions.

2 Gravity’s rainbow modified FRW universe

In this section, first of all we have a quick review on the gravity’s rainbow theory, known also as DGR. Then, noting the importance of spatial curvature in the emergent universe scenario, we derive the modified Friedman equations for general non-flat universes. In DSR, the modified dispersion relations of a massive particle with mass m read

$$\begin{aligned} \epsilon ^{2}f^{2}(\epsilon /\epsilon _{p},\eta )-p^{2}g^{2}(\epsilon /\epsilon _{p},\eta )=m^{2}, \end{aligned}$$
(1)

where \(f(\epsilon /\epsilon _{p},\eta )\) and \(g(\epsilon /\epsilon _{p},\eta )\) are the well-known energy-dependent rainbow functions and \(\eta \) is a dimensionless parameter. In the low energy limit, the modified dispersion relation (1) reduces to the relativistic dispersion relations. So, the rainbow functions \(f(\epsilon / \epsilon _{p},\eta )\) and \(g(\epsilon /\epsilon _{p},\eta )\) satisfy the following conditions:

$$\begin{aligned} \lim _{\epsilon /\epsilon _{p}\rightarrow 0} f(\epsilon /\epsilon _{p},\eta )=1,\quad \lim _{\epsilon /\epsilon _{p}\rightarrow 0}g(\epsilon /\epsilon _{p},\eta )=1. \end{aligned}$$
(2)

Indeed, the condition (2) points to the correspondence principle. Based on the discussion presented in [78], for established position space in DSR, theories including free fields must also lead to the plane wave solutions in flat space-time, despite satisfying the modified dispersion relations (1). For this reason, the contraction between infinitesimal displacement \(\mathrm{d}x^{a}\) and momentum \(p_{a}\), must be linearly invariant, i.e

$$\begin{aligned} \mathrm{d}x^{a}p_{a}=\mathrm{d}t\epsilon +\mathrm{d}x^{i}p_{i}. \end{aligned}$$
(3)

In fact, the linear contraction (3) guarantees the existence of the plane wave solutions. The rainbow metric generally has the form of

$$\begin{aligned} \mathrm{d}s^{2}=\frac{-1}{f^{2}(\epsilon /\epsilon _{p},\eta )}\mathrm{d}t^{2}+\frac{1}{g^{2} (\epsilon /\epsilon _{p},\eta )}\mathrm{d}x^{2}. \end{aligned}$$
(4)

Using a one parameter family of energy-momentum tensors, the gravity’s rainbow modified Einstein equations will be written as

$$\begin{aligned} G_{\alpha \beta }(\epsilon /\epsilon _{p})=8\pi G(\epsilon /\epsilon _{p})T_{\alpha \beta } (\epsilon /\epsilon _{p})+g_{\alpha \beta }(\epsilon /\epsilon _{p})\Lambda (\epsilon / \epsilon _{p}), \end{aligned}$$
(5)

so that \(G(\epsilon /\epsilon _{p})=h_{1}(\epsilon /\epsilon _{p})G\) and \(\Lambda (\epsilon / \epsilon _{p})=h_{2}(\epsilon /\epsilon _{p})\Lambda \) where \(h_{1}(\epsilon /\epsilon _{p})\) and \(h_{2}(\epsilon /\epsilon _{p})\) are energy-dependent rainbow functions. This means that in the DGR setup, the Newtonian gravitational constant and the cosmological constants are energy dependent such that in the low energy limit, we recover \( G(\epsilon /\epsilon _{p})=G\) and \(\Lambda (\epsilon /\epsilon _{p})=\Lambda \). In order to achieve our main goal, in this section we will set \(\Lambda =0\) for simplicity, and begin with the following modified FRW metric of a homogeneous and isotropic universe:

$$\begin{aligned} \mathrm{d}s^{2}=-\frac{N(t)^{2}}{f^{2}(\epsilon /\epsilon _{p},\eta )}\mathrm{d}t^{2}+\frac{1}{g^{2} (\epsilon /\epsilon _{p},\eta )}a^{2}(t)h_{ij}\mathrm{d}x^{i}\mathrm{d}x^{j}, \end{aligned}$$
(6)

where \(h_{ij}\) represents the spatial part of the metric. Commonly, it is assumed that the energy \(\epsilon \) of the particle probe for each measurement is constant and independent of space-time coordinates. Nevertheless, such an assumption for the measurements at early universe seems to be far from reality. Therefore, it is expected that the background metric of space-time throughout its evolution is affected by the energy \(\epsilon \) of the particle probe. Then, it is reasonable to consider the evolution of the energy \(\epsilon \) with the cosmological time, denoted as \(\epsilon (t)\). In this regard, we will derive the modified FRW equations. In doing so, the following ansatz is usually suggested [79, 80]:

$$\begin{aligned} \eta =1,\quad g^{2}(\epsilon ,\eta )=1, \end{aligned}$$
(7)

where f has the form of \(f(\epsilon /\epsilon _{p})\). Therefore, the modified Einstein field equation can be written as

$$\begin{aligned} R_{\alpha \beta }=-8\pi G(\epsilon )S_{\alpha \beta }(\epsilon ), \end{aligned}$$
(8)

where \(R_{\alpha \beta }\) is the Ricci tensor, defined as follows:

$$\begin{aligned} R_{\alpha \beta }=\frac{\partial \Gamma ^{\lambda }_{\lambda \alpha }}{\partial x^{\beta }}- \frac{\partial \Gamma ^{\lambda }_{\alpha \beta }}{\partial x^{\lambda }}+\Gamma ^{\lambda }_ {\alpha \mu }\Gamma ^{\mu }_{\beta \lambda }-\Gamma ^{\lambda }_{\alpha \beta } \Gamma ^{\mu }_{\lambda \mu },\quad \alpha ,\beta {=}0,1,2,3, \end{aligned}$$
(9)

and \(S_{\alpha \beta }(\epsilon )\) is written in terms of the energy momentum tensor \(T_{\alpha \beta } (\epsilon )\) as

$$\begin{aligned} S_{\alpha \beta }(\epsilon )=T_{\alpha \beta }(\epsilon )-\frac{1}{2}g_{\alpha \beta }T^{\mu }_{\mu } (\epsilon ). \end{aligned}$$
(10)

To continue our calculations, we need the non-zero components of the affine connection [79, 80]:

$$\begin{aligned} \Gamma ^{0}_{00}=-\frac{\dot{f}}{f},\quad \Gamma ^{0}_{ij}=f^{2}\dot{a}a\delta _{ij}, \quad \Gamma ^{i}_{0j}=\delta ^{i}_{j}\frac{\dot{a}}{a}\quad i,j=1,2,3. \end{aligned}$$
(11)

It is seen that unlike the usual FRW metric, for the modified FRW metric (6), the components of the affine connection with two time indices remain non-zero. By putting (11) into (9) and after a straightforward calculation, we obtain

$$\begin{aligned} R_{00}=3\frac{\ddot{a}}{a}+3\frac{\dot{a}}{a}\frac{\dot{f}}{f}\; \end{aligned}$$
(12)

and

$$\begin{aligned} R_{ij}=\tilde{R}_{ij}-\left( (a\ddot{a}+2\dot{a}^{2})f^{2}-f\dot{f}\dot{a}a\right) \delta _{ij}, \end{aligned}$$
(13)

where \(\tilde{R}_{ij}\) denotes the purely spatial Ricci tensor defined as

$$\begin{aligned} \tilde{R}_{ij}=\frac{\partial \Gamma ^{n}_{ni}}{\partial x^{j}}- \frac{\partial \Gamma ^{n}_{ij}}{\partial x^{n}}+\Gamma ^{m}_{in} \Gamma ^{m}_{jm}-\Gamma ^{m}_{ij} \Gamma ^{n}_{nl}. \end{aligned}$$
(14)

The spatial components \(\Gamma ^{i}_{jk}\) of the four dimensional affine connection are identical with those of the affine connection computed in three dimensions from the spatial three-metric \(h_{ij}\), i.e.

$$\begin{aligned} \Gamma ^{i}_{jk}=\frac{1}{2}h^{in}\left( \frac{\partial h_{jn}}{\partial x^{k}} +\frac{\partial h_{kn}}{\partial x^{j}}-\frac{\partial h_{jk}}{\partial x^{n}} \right) \equiv \tilde{\Gamma }^{i}_{jk}, \end{aligned}$$
(15)

where \(\tilde{\Gamma }^{i}_{jk}\) denotes the purely spatial affine connection and \(h^{ij}\) is the inverse of the \(3\times 3\) matrix \(h_{ij}\). Therefore, we have \(\Gamma ^{n}_{ij}=kx^{n} h_{ij}\), which results in

$$\begin{aligned} \tilde{R}_{ij}=-2kh_{ij}. \end{aligned}$$
(16)

Here, k has a geometrical interpretation. Indeed, it measures the spatial curvature with zero, negative, and positive k values corresponding to flat, open, and closed universes, respectively [81]. The Ricci tensor expression (13) can be rewritten as

$$\begin{aligned} R_{ij}=-\left( (a\ddot{a}+2\dot{a}^{2})f^{2}-f\dot{f}\dot{a}a+2k\right) h_{ij}. \end{aligned}$$
(17)

Now, for obtaining the components of \(S_{\alpha \beta }\), we consider the perfect fluid with the energy-momentum tensor as

$$\begin{aligned} T_{\alpha \beta }=(\rho +p)u_{\alpha }u_{\beta }+pg_{\alpha \beta }, \end{aligned}$$
(18)

so that \(\rho \) and p represent the energy density and the pressure, respectively. Also, \(u_{\alpha }\) is the velocity four vector defined by \(u_{\alpha }=(f^{-1},0,0,0)\), with the norm of \(g^{\alpha \beta } u_{\alpha }u_{\beta }=-1\). We should note that the diagonal components of the modified FRW metric tensor \(g_{\alpha \beta }\) are \((-f^{-2},h_{ii})\) with the signature \((-,+,+,+)\) so that the components of the spatial tensor \(h_{ii}\) are independent of the rainbow function f. Using Eq. (10), one can decompose the time and spatial components of \(S_{\alpha \beta }\) tensor as follows:

$$\begin{aligned} S_{tt}=T_{tt}+\frac{1}{2}g_{tt}T,\quad S_{ij}=T_{ij}-\frac{1}{2}h _{ij}a^{2}T, \end{aligned}$$
(19)

where

$$\begin{aligned} T_{tt}=\rho f^{-2},\quad T_{ij}=h_{ij}a^{2}p, \end{aligned}$$
(20)

and

$$\begin{aligned} T=g^{\alpha \beta }T_{\alpha \beta }=(-\rho +3p). \end{aligned}$$
(21)

By substituting Eqs. (20) and (21) into (19), we have

$$\begin{aligned} S_{tt}=\frac{1}{2f^{2}}(\rho +3p),\quad S_{ij}=\frac{1}{2}(\rho -p)a^{2}h_{ij}. \end{aligned}$$
(22)

Ultimately, the first and second rainbow modified Friedman equations for the metric, parameterized by the varying energy probe (6), takes the form of

$$\begin{aligned}&\left( \frac{\dot{a}}{a}\right) ^{2}+\frac{k}{a^{2}}\frac{1}{f^{2}}=\frac{8\pi G\rho }{3}\frac{1}{f^{2}} ,\end{aligned}$$
(23)
$$\begin{aligned}&\frac{\ddot{a}}{a}=-\frac{4\pi G\rho (1+3\omega )}{3}\frac{1}{f^{2}}-\frac{\dot{a}}{a}\frac{\dot{f}}{f}. \end{aligned}$$
(24)

Here, also for simplicity, it is assumed that the gravitational constant G is independent of the energy \(\epsilon \). It should be noted that the existence of the \(\dot{f}\) term in the second rainbow modified Friedman equations does not mean the explicit dependence of the rainbow function to the time, i.e. f(t), at all. As explained above, f is an explicit function of the energy of the test particles which are probing the geometry of space-time in the early universe. Given the fact that \(\epsilon \) can vary with respect to the evolution of the universe, f can be an implicit function of cosmic time and not explicit. We note that the explicit dependence of f on the time maybe leads to this wrong result from Eqs. (23) and (24): that they are nothing but the usual Friedman equations of GR so that the rainbow function f in this case is merely the gauge parameter determining the choice of time. Hence, based on the gauge freedom, one may choose the gauge of \(f=1\). In contrast to this misconception, the gravity’s rainbow theory is a high energy modified theory of GR in which according to the correspondence principle, for the case of the low energy limit, i.e. \(\frac{\epsilon }{\epsilon _\mathrm{pl}}\rightarrow 0\) (\(f\rightarrow 1\)), the modified Friedman equations (23) and (24) reduce to the standard equations for the FRW universe. Also, we mention that due to the existence of the rainbow functions, t may play the role of proper time based on the gauge choice, \( N=\frac{f_{1}(\varepsilon )}{f_2^{3\omega } (\varepsilon )}a^{3\omega }\) [77]. As expected, in the limit of GR, t represents the proper time indicated by the choice of \(N=a^{3\omega }\). Also, by combining the modified Friedman equations (23) and (24), we get the following energy conservation equation:

$$\begin{aligned} \dot{\rho }+3\frac{\dot{a}}{a}\rho (1+\omega )=0. \end{aligned}$$
(25)

It can be mentioned that in the framework of DGR, the form of the equation of state (EOS), \(p=\omega \rho \), remains unchanged for massless probe particles such as photons, while for the massive ones, this equation of state will be modified; see [28, 82] for more discussion.

3 Einstein static universe and scalar perturbations

3.1 In the absence of cosmological constant \(\Lambda \)

In this section, we plan to apply the linear homogeneous scalar perturbations in the vicinity of the Einstein static universe and explore its stability against these perturbations. To achieve our goal, we need to fix the rainbow function f. To this end, using the dispersion relation presented in [83], we introduce the rainbow function as follows:

$$\begin{aligned} f(\epsilon )=\left( 1-\frac{\epsilon }{\epsilon _\mathrm{pl}}\right) ^{-1}, \end{aligned}$$
(26)

where via suggesting the average energy \(\bar{\epsilon }=\frac{4c}{3}\rho ^{\frac{1}{4}}\) (c is some constant) [84], this rainbow function will be rewritten as

$$\begin{aligned} f(\rho )=\left( 1-\frac{4}{3}\xi \rho ^{\frac{1}{4}}\right) ^{-1}, \end{aligned}$$
(27)

where \(\xi =\frac{c}{\epsilon _\mathrm{pl}}\). The authors of [84], to reach the above relation, considered a large ensemble of probe photons which are in thermal equilibrium. This assumption is reasonable since, based on the standard model of cosmology, the early universe passed a radiation dominated era with \(p=\frac{1}{3}\rho \). One may ask the question of why the identification \(\epsilon \sim \bar{\epsilon }\) is used to obtain the rainbow function (27). The answer is that we deal with the energy of a probe particle in the rainbow metric as the statistical mean value of all probe photons in radiation domination. Indeed, we deal with the average effect of photon particles in the radiation dominated era and not with a special elected photon from the radiation [79, 80]. It is worthwhile to recall that the form of \(\bar{\epsilon }\) in terms of \(\rho \) is independent of the modified dispersion relation picked for a specific model [76]. We also mention that the above rainbow function is valuable from the theoretical viewpoint; in [83] it is shown that in the absence of the varying speed of light (VSL) proposal, it can remove the horizon problem in the early universe. Moreover, it is seen that when \(\rho \) or \(\bar{\epsilon }\) get their largest values, then \(f(\rho )\) or \(f(\bar{\epsilon })\) becomes infinite, which causes the timelike component of the rainbow metric to vanish This means that the FRW metric, which is modified with a rainbow function (27) becomes degenerate at that time and has no inverse. Indeed, a degenerate metric addresses the existence of another distinct possibility for lightlike dimension (other than timelike and spacelike dimensions). Also, recall that in the Palatini formulation of standard GR, a degenerate metric also appears. One of the consequences of the degenerate metric is that the curvature remains bounded and the topology of space-time can change. Overall, it is believed that singularities arisen from a degenerate metric have a milder nature than other types of singularities and seem appropriate for a QG proposal [85]. Here, it is necessary to review the finite time singularity issue, including the Big-Bang singularity, in the presence of the rainbow function (27). Indeed, we want to investigate whether the presence of a rainbow function (27) in this system will lead to a resolution of the singularity problem. Inspired by the idea proposed in [84, 86], we want to resolve this problem by finding an upper bound on the density of the energy \(\rho \). In other words, according to [84, 86] the finite time singularity issue will be eliminated via the presentation of a fixed point as \(\rho _\mathrm{f}\) for the energy density \(\rho \), which is reached at an infinite time. More exactly, the author of [84], by following the terminology used for stability analyzing the dynamical systems in [86], demonstrated that for any first order system as \(\dot{\rho }=O(\rho )\), the finite time singularity will be solved through the fulfillment of either of the following conditions: (1) The function \(O(\rho )\) should be continuous and differentiable on a range enclosed by zeros of the function \(O(\rho )\). (2) Asymptotically, the function \(O(\rho )\) growths like a linear function as \(K(\rho )\) or slower than it, i.e. \(K(\rho )\ge O(\rho )\). Therefore, for cancellation of the finite time singularity, it is sufficient that one of these conditions is satisfied. We begin our analysis in this way by substituting the rainbow function (27) into the energy conservation equation (25) and the modified first Friedmann equation (23) (for the case \(k=0\)) to obtain the ordinary differential equation (ODE) \(\dot{\rho }=O(\rho )\) where

$$\begin{aligned} O(\rho )=-4\rho (1-\xi \rho ^{\frac{1}{4}})\left( \frac{8\pi G}{3}\rho \right) ^{1/2}. \end{aligned}$$
(28)

The advantage of the dynamical system analysis method followed in [84, 86] is that by having fixed points and regarding the asymptotic behavior of \(O(\rho )\), one is able to predict the demeanor of the system without the need of the detailed form of the solutions. Hence, by setting \(\omega =\frac{1}{3}\) (since our attention is on radiation dominated state in order to study the initial singularity), Eq. (28) results in the following two fixed points:

$$\begin{aligned} \rho _{f_{1}}=0, \quad \rho _{f_{2}}=\left( \frac{\epsilon _\mathrm{pl}}{c}\right) ^{4}. \end{aligned}$$
(29)

However, to understand the qualitative manner of a solution, we should know how long it takes to get a fixed point. By a straightforward calculation, one can show that the time required to reach these fixed points can be obtained:

$$\begin{aligned} t=-\int _{\rho ^{*}}^{\rho _\mathrm{f}}\frac{\mathrm{d}\rho }{\left( \frac{8\pi G}{3}\rho \right) ^{1/2}\left( 4\rho -\frac{16\xi }{3} \rho ^{5/4}\right) }, \end{aligned}$$
(30)
Fig. 1
figure 1

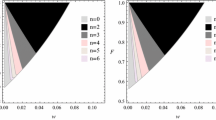
The behavior of \(O(\rho )\) (28) in terms of \(\rho \) for a flat rainbow FRW universe model. To simplify, we set \(\epsilon _\mathrm{pl}=c\) and \(8\pi G=3\). Fixed points are located in \(\rho _{f_{1}}=0\) and \(\rho _{f_{2}}=1\)

Full size image

where \(\rho ^{*}\) represents an arbitrary initial finite value for the density which lies in the intervals between the fixed points. The negative sign in the back of the integral relation denotes a backward in direction of time. We find that for the case of \(\rho _{f_{1}}=0\), the integral (30) does not converge, i.e. \(|t|\rightarrow \infty \), while for the fixed point \(\rho _{f_{2}}=(\frac{\epsilon _\mathrm{pl}}{c})^{4}\) the integral (30) is not solvable and its numerical values fail to converge. At this point, let us to draw the plot \(O(\rho )-\rho \) (or \(\dot{\rho }-\rho )\) in Fig. 1, in order to get a qualitative analysis of the situation. As is seen from Fig. 1, \(O(\rho )\) has two fixed points \(\rho _{f_{1}}=0\) and \(\rho _{f_{2}}=1\). In fact, any of these fixed points are equivalent to a de Sitter space since in these points we are dealing with the constant solution (\(\dot{\rho }=0\)). The first, \(\rho _{f_{1}}\), is a future fixed point because for the case \(\rho ^{*}>0\) we have \(O(\rho )<0\), while the second, \(\rho _{f_{2}}\), is an early (or past) fixed point since for the case of \(\rho ^{*}<1\) and \(\rho ^{*}>1\) we have \(O(\rho )<0\) and \(O(\rho )>0\), respectively. It is noteworthy that for distinction between the types of these singularities, we follow Ref. [84]. These fixed points classify the possible solutions into two classes: (1) a solution belongs to interval \(\rho \in [0,1]\), if \(\rho _{f_{1}}<\rho ^{*}<\rho _{f_{2}}\), and (2) a solution belongs to interval \(\rho \in [1,\infty ) \), if \(\rho ^{*}>\rho _{f_{2}}\). Then, to get the fixed point \(\rho _{f_{1}}\) by beginning from some initial value as \(\rho ^{*}\) and also from \(\rho _{f_{2}}\) to \(\rho ^{*}\), the time required is infinite. In this interval, \(O(\rho )\) is continuous and differentiable. Then, according to the approach in [84] by pursuing the terminology of [86], one can say that the first solution is free from a physical singularity so that it interpolates steadily from \(\rho _{f_{1}}\) to \(\rho _{f_{2}}\). It is clear that the first condition already is not usable for the second solution, which represents a clear violation of the second condition. On the other hand, for the case \(\rho ^{*}>\rho _{f_{2}}\), the function (28) is growing quicker than a linear function. So, we conclude that the second solution is not free from a finite time singularity. Because we are interested in studying the initial singularity problem, let us mention the stability status of the early fixed point \(\rho _{f_{2}}\). A fixed point is stable if, by putting a neighboring initial value, the trajectory of the solution remains always close to the fixed point. Equivalently, a fixed point is unstable if for any point in the vicinity of the fixed point, one can find some solution that starts near the fixed point but goes away from it in a finite time. The fixed point \(\rho _{f_{2}}\) is an unstable point because \(\frac{\mathrm{d}O(\rho )}{\mathrm{d}\rho }|_{\rho =\rho _{f_{2}}}>0\).Footnote 1 Then, although it takes an infinite time to get a fixed point, the issue of the avoidance of finite time singularities remains unsolved and eventually this fixed point will collapse.

Now, we investigate the DGR theory form the emergent universe point of view in which there is no beginning of time and consequently, there is no big bang singularity in the early universe. In this scenario, the universe was not born from a Big-Bang singularity in a past finite time and rather it possesses an eternal Einstein static state. In this context, the key point is the required conditions for the stability of the existing ESU, which we will explore in the following of the present paper. The ESU in the DGR scenario with rainbow functions varying with cosmological time can be obtained by the conditions \(\ddot{a}=\dot{a}=0\) through Eqs. (23) and (24) as

$$\begin{aligned} \frac{k}{a_{0}^{2}}=\frac{8\pi G\rho _{0}}{3}\; \end{aligned}$$
(31)

and

$$\begin{aligned} -\frac{4\pi G\rho _{0}(1+3\omega )}{3f(\rho _{0})^{2}}=0, \end{aligned}$$
(32)

where \(a_0\), \(\rho _0\), and \(\omega \) denote the scale factor, the energy density of the Einstein static universe, and the barotropic equation of state parameter (\(p=\omega \rho \)), respectively. Considering the positive energy condition \(\rho _0>0\) through Eq. (31), it is seen that for the Einstein static universe, the spatial curvature of the universe should be positive, \(k>0\). Also, Eq. (32) shows that, for the Einstein static universe in the framework of rainbow gravity, we need to have \(\omega =-\frac{1}{3}\) or \(f(\rho _{0})\rightarrow \infty \) corresponding to \(\rho _{0}=\left( \frac{4}{3}\xi \right) ^{-4}\). The perturbations in the cosmic scale factor a(t) and the energy density \(\rho (t)\) can be written as

$$\begin{aligned}&a(t)\rightarrow a_{0}(1+\delta a(t)),\nonumber \\&\rho (t)\rightarrow \rho _{0}(1+\delta \rho (t)). \end{aligned}$$
(33)

Substituting (33) into Eq. (23) after linearizing the perturbation terms, we obtain the following equation:

$$\begin{aligned} -\frac{2k}{a_{0}^{2}}\delta a= \frac{8\pi G}{3}\rho _{0}\delta \rho . \end{aligned}$$
(34)

This indicates, with respect to the positiveness of k, that the sign of the variation of the scale factor must be opposite to the sign of the variation of the matter density. We must also apply the same method on Eq. (24), however, before doing this let us introduce the following replacement due to the perturbation in the rainbow function \(f(\rho )\):

$$\begin{aligned} f^{-2}(\rho )\rightarrow \left( f^{-2}(\rho _{0})-\frac{2}{3}\xi \rho _{0}^{\frac{1}{4}} \delta \rho \right) , \end{aligned}$$
(35)

such that

$$\begin{aligned} f^{-2}(\rho _{0})=1-\frac{8}{3}\xi \rho _{0}^{\frac{1}{4}}. \end{aligned}$$
(36)

Also, by combining the energy conservation equation (25) with the first rainbow modified FRW equation (23), we obtain

$$\begin{aligned} -\frac{\dot{a}}{a}\frac{\dot{f}}{f}=-\frac{\dot{a}}{a}\frac{df}{\mathrm{d}\rho }.\frac{\dot{\rho }}{f}=\frac{3(1+3\omega )}{4}\xi f^{-1}\rho ^{\frac{1}{4}} \left( \frac{8\pi G}{3}\rho -\frac{k}{a^{2}}\right) . \end{aligned}$$
(37)

Then, after applying the perturbation (33), we have

$$\begin{aligned} -\frac{\dot{a}}{a}\frac{\dot{f}}{f}= & {} \frac{3(1+3\omega )}{4}\xi \rho _{0}^{\frac{1}{4}}\left( 1+\frac{1}{4}\delta \rho \right) \nonumber \\&\times \left( f^{-1}(\rho _{0})-\frac{\xi }{3}\rho _{0}^{\frac{1}{4}}\delta \rho \right) \nonumber \\&\times \left( \frac{8\pi G}{3}\rho _{0}(1+\delta \rho ) -\frac{k}{a_{0}^{2}} (1-2\delta a)\right) . \end{aligned}$$
(38)

By substituting (31) and (34) into the above expression, one finds that \(-\frac{\dot{a}}{a}\frac{\dot{f}}{f}=0\). It seems that this result is independent of any specific form of the rainbow function f. Therefore, it can be seen that the last term of the second rainbow modified FRW equation (24) does not contribute in the derivation of the stability conditions of the Einstein static universe in the framework of the DGR scenario. Now, using the perturbation equations (33) in (24) and using (35), we get

$$\begin{aligned} \delta \ddot{a}=-\frac{4\pi G}{3}(1+3\omega )\left( f^{-2}_{0}(\rho _{0})-\frac{2}{3}\xi \rho _{0}^{\frac{1}{4}}\right) \rho _{0}\delta \rho , \end{aligned}$$
(39)

where inserting Eq. (34) into (39) and neglecting the non-linear perturbation terms result in the following differential equation:

$$\begin{aligned} \delta \ddot{a}-\frac{k}{a^{2}_{0}}(1+3\omega )\left( 1-\frac{10}{3}\xi \rho _{0}^ {\frac{1}{4}}\right) \delta a=0. \end{aligned}$$
(40)

It is obvious that, for the cases \(\xi \rightarrow 0\), i.e. \(\epsilon _\mathrm{pl}\rightarrow \infty \), Eq. (40) will take the following form:

$$\begin{aligned} \delta \ddot{a}-\frac{k}{a_{0}^{2}}(1+3\omega )\delta a=0, \end{aligned}$$
(41)

which refers to the oscillatory modes of ESU in the framework of standard GR for \(\omega <-1/3\). In order to have the general oscillating perturbation modes in the framework of the DGR scenario, the following condition should be satisfied:

$$\begin{aligned} -\frac{k}{a^{2}_{0}}(1+3\omega )\left( 1-\frac{10}{3}\xi \rho _{0}^ {\frac{1}{4}}\right) >0, \end{aligned}$$
(42)

which results in the following solution for Eq. (40):

$$\begin{aligned} \delta a=\alpha _{1}\mathrm{e}^{i\gamma _{0} t}+\alpha _{2}\mathrm{e}^{-i\gamma _{0} t}, \end{aligned}$$
(43)

where \(\alpha _1\) and \(\alpha _2\) are integration constants and \(\gamma _{0}\) refers to the frequency of oscillation around the stable ESU as

$$\begin{aligned} \gamma _{0}=\left( -\frac{k}{a^{2}_{0}}(1+3\omega )\left( 1-\frac{10}{3}\xi \rho _{0}^ {\frac{1}{4}}\right) \right) ^{\frac{1}{2}}. \end{aligned}$$
(44)

Now, we can analyze the stability condition (42). Equations (31) and (32) will play the role of two fundamental constraints to achieve our goal. There are two possibilities in order to satisfy Eq. (32); the first one is that \(\omega =-\frac{1}{3}\), and the second one is that the matter density of the ESU is \(\rho _{0}=\left( \frac{4}{3}\xi \right) ^{-4}\). If we set \(\omega =-\frac{1}{3}\), then the condition (42) is automatically violated and we obtain \(\delta \ddot{a}=0\) implying that there is no stable ESU against the linear scalar perturbations in the form of Eq. (33). As is clear from Eq. (41), in the framework of the standard GR for \(\omega =-\frac{1}{3}\), there is no stable ESU. For the second possibility as \(\rho _{0}=\left( \frac{4}{3}\xi \right) ^{-4}\), with respect to the positivity of the spatial curvature, due to the positive energy condition through Eq. (31), we need that the barotropic EOS parameter satisfies \(\omega >-1/3\). Overall, one can find that there is a stable ESU versus homogeneous and linear scalar perturbations in the context of the gravity’s rainbow scenario with choosing the rainbow function (27). In this case, we need two bounds, of which the first one is on EOS parameter, \(\omega >-1/3\), and the second one is on the energy density of ESU, \(\rho _{0}<\epsilon _\mathrm{pl}^{4}\). There are no similar results in the framework of the standard GR theory. Unlike GR, here there is a stable solution against small scalar perturbations for a closed universe filled by the matter fields respecting the energy conditions. Also, within standard GR theory and even in many of the modified gravity theories, there is no such upper bound on the energy density of ESU \(\rho _{0}\). In the following, we want to investigate the stability conditions of the Einstein static universe against the linear homogeneous scalar perturbations in the context of DGR, in terms of another rainbow function proposed by Ling et al. in [87], which evolves with cosmic time as

$$\begin{aligned} f=\sqrt{1-l^{2}_{p}\bar{\epsilon }^{2}}. \end{aligned}$$
(45)

Considering the previous arguments after writing the average energy \(\bar{\epsilon }=\frac{4}{3}c \rho ^{\frac{1}{4}}\) [84], it can be rewritten in terms of the energy density \(\rho \) as

$$\begin{aligned} f(\rho )=\sqrt{1-\frac{16}{9}\chi \rho ^{\frac{1}{2}}}, \end{aligned}$$
(46)

where \(\chi =l^{2}_{p} c^{2}\) is a constant. Let us point out that the rainbow function (46) has an application in the framework of black hole physics, leading to valuable phenomenological outcomes, e.g. see [87, 88]. Moreover, it also, like the previous rainbow function, has a theoretical trait. As the energy density \(\rho \) or \(\bar{\epsilon }\) reaches its largest value, \(f(\rho )\) in (46) becomes zero, which leads to vanishing spatial-like components of the rainbow metric. This means that the FRW metric, modified by (46) or (45), is a smooth and differentiable metric but is not invertible. Moreover, by applying the rainbow functions (45) or (46), we will be faced with a degenerate metric at energy levels close to the Planck energy scale. Also, based on the fact that there is no observational evidence for a lightlike dimension in nature, there might be a suppression mechanism for the appearance of a lightlike dimension at the quantum level of the universe [85].

As before, we first examine the Big-Bang singularity problem for such a choice of the rainbow function within a flat rainbow FRW model. In the same way, for the rainbow function (46), we get

$$\begin{aligned} \dot{\rho }=-4\sqrt{\frac{8\pi G\rho ^{3}}{3-\frac{16}{3}\chi \rho \frac{1}{2}}}, \end{aligned}$$
(47)

which has only one fixed point \(\rho _{f_{1}}=0\) and is not bounded; see Fig. 2. As is seen in the figure, the function \(O(\rho )\) begins from the fixed point \(\rho _{f_{1}}\) and ends with a singularity. So we must separately calculate the time needed from an infinite to a finite value \(\rho ^{*}\) as well as the time needed from \(\rho ^{*}\) to the fixed point \(\rho _{f_{1}}=0\), i.e.,

$$\begin{aligned} t= -\frac{1}{4}\int _{\infty } ^{\rho ^{*}} \mathrm{d}\rho \sqrt{\frac{3-\frac{16}{3}\chi \rho ^{\frac{1}{2}}}{8\pi G\rho ^{3}}} \end{aligned}$$
(48)

and

$$\begin{aligned} t= -\frac{1}{4}\int _{\rho ^{*}} ^{0} \mathrm{d}\rho \sqrt{\frac{3-\frac{16}{3}\chi \rho ^{\frac{1}{2}}}{8\pi G\rho ^{3}}}. \end{aligned}$$
(49)

Here, we are dealing with a different situation compared to the previous one. We found that the integral (48) converges which leads to \(\rho ^*\ge \frac{81}{256\chi ^2}\), while the integral (49) does not converge in any way on the given interval. This means that from \(\rho ^{*}\) to the fixed point \(\rho _{f_{1}}=0\) an infinite time is needed, i.e. \(|t|\rightarrow \infty , \) while to get from an infinite to a finite value \(\rho ^{*}\) it takes a finite time. Because the rainbow FRW metric includes a natural cutoff, the Planck energy, the constraint obtained for the integral (48) should lie in the interval \(\frac{81}{256\chi ^2}\le \rho ^*\le \frac{1}{\chi ^2}\). Then the solution derived from the rainbow function (46) for the flat rainbow universe model cannot be free from a finite time singularity. We conclude that even assuming that the integral (48) results in an infinite time, the Big-Bang singularity issue is not canceled, yet. According to the discussion given in the previous case, one can realize that \(\rho _{f_{1}}\) is a future fixed point and not a past one.

Fig. 2
figure 2

The behavior of \(O(\rho )\) (47) in terms of \(\rho \) for the flat rainbow FRW universe model. To simplify, we set \(8\pi G=3\) and \(\chi =1/2\)

Full size image

In the following, we study the DGR theory from the emergent universe point of view and investigate the required conditions for the stability of an ESU with respect to scalar perturbations, in the presence of the rainbow function (46). By applying the scalar perturbation terms on the rainbow function (46), it takes the form

$$\begin{aligned} f^{-2}(\rho )\rightarrow f^{-2}(\rho _{0})+\frac{8}{9}\chi \rho ^{\frac{1}{2}}_{0}\delta \rho , \end{aligned}$$
(50)

where

$$\begin{aligned} f^{-2}(\rho _{0})=1+\frac{16}{9}\chi \rho ^{\frac{1}{2}}_{0} . \end{aligned}$$
(51)

Now, inserting Eqs. (50), (51), and the perturbation equations (33) into the second rainbow modified Friedmann equation (24), we have

$$\begin{aligned} \delta \ddot{a}=-\frac{4\pi G}{3}(1+3\omega )\left( (\rho _{0}+1)f^{-2}(\rho _{0}) +\frac{8}{9}\chi \rho ^{\frac{1}{2}}_{0}\right) \rho _{0}\delta \rho , \end{aligned}$$
(52)

where, similar to the previous analysis, we neglected non-linear terms. Finally, by applying Eqs. (32) and (34), the above differential equation takes the following form:

$$\begin{aligned} \delta \ddot{a}-\frac{k}{a^{2}_{0}}(1+3\omega )\left( 1+\frac{8}{3} \chi \rho ^{\frac{1}{2}}_{0}\right) \delta a=0. \end{aligned}$$
(53)

As can be seen, for the limit \(\chi \rightarrow 0\), the above equation reduces to the oscillatory modes (41). Then, in order to have a stable ESU in the framework of the DGR scenario, the following condition should be satisfied:

$$\begin{aligned} -\frac{k}{a^{2}_{0}}(1+3\omega )\left( 1+\frac{8}{3} \chi \rho ^{\frac{1}{2}}_{0}\right) >0, \end{aligned}$$
(54)

where the frequency of the oscillatory modes \(\gamma _{0}\) for the rainbow function (46) reads

$$\begin{aligned} \gamma _{0}^{2}=-\frac{k}{a^{2}_{0}}(1+3\omega )\left( 1+\frac{8}{3} \chi \rho ^{\frac{1}{2}}_{0}\right) . \end{aligned}$$
(55)

It is seen that for \(\omega =-\frac{1}{3}\), the condition (54) is automatically violated and we get \(\delta \ddot{a}=0\) through Eq. (53), which indicates that there is no stable ESU against the linear scalar perturbations for this rainbow function. For the second possibility, \(\rho _{0}=\left( \frac{16}{9}\chi \right) ^{-2}\), with respect to the positivity of the spatial curvature due to the positive energy condition through Eq. (31), the barotropic EOS parameter \(\omega \) needs to satisfy the condition \(\omega <-1/3\). Therefore, here we have a stable ESU for the barotropic EOS parameter \(\omega <-1/3\), denoting the phantom matter fields, with the bounded energy density of ESU \(\rho _{0}\) as \(\rho _{0}< l_\mathrm{pl}^{-4}\). As mentioned before, the existence of such a constraint on the energy density of ESU may be absent in other modified gravity theories. Here, such a bound on the initial density \(\rho _{0}\) is arising from the energy-dependent metric in gravity’s rainbow proposal, which is one of the common cut offs of quantum gravity theories. Finally, it should be mentioned that choosing the rainbow function (46) leads to the same result as GR so that a closed universe filled by the usual non-relativistic matter fields is not stable against small linear scalar perturbations.

3.2 In the presence of cosmological constant \(\Lambda \)

In this subsection, we want to consider the possible modification by the cosmological constant \(\Lambda (\epsilon )\) and investigate its effects on the stability condition of an ESU. In the presence of a cosmological constant \(\Lambda (\epsilon )\), the second modified FRW equation (24) remains without change. But the first modified FRW equation (23) and the conservation law (25) take the form of

$$\begin{aligned} \left( \frac{\dot{a}}{a}\right) ^{2}+\frac{k}{a^{2}}\frac{1}{f^{2}}=\frac{8\pi G\rho }{3}\frac{1}{f^{2}}+\frac{\Lambda (\epsilon )}{3f^{2}}\; \end{aligned}$$
(56)

and

$$\begin{aligned} \dot{\rho }+3\rho \frac{\dot{a}}{a}(1+\omega )=-\frac{\dot{\Lambda }(\epsilon )}{8\pi G}. \end{aligned}$$
(57)

One may consider another rainbow function \(h(\epsilon )\) so that \(\Lambda (\epsilon )=h(\epsilon )^{2}\Lambda \) where \(\Lambda \) is the usual cosmological constant. By this consideration, the modified FRW equation (56) will be

$$\begin{aligned} \left( \frac{\dot{a}}{a}\right) ^{2}+\frac{k}{a^{2}}\frac{1}{f^{2}}=\frac{8\pi G\rho }{3} \frac{1}{f^{2}}+\frac{h(\epsilon )^{2}\Lambda }{3f^{2}}. \end{aligned}$$
(58)

By setting this new rainbow function as \(h(\epsilon )^{2}=(1+\lambda \rho )\), see [80], for the ESU described by \(\dot{a}=\ddot{a}=0\), we get the following equation from Eq. (56):

$$\begin{aligned} \frac{k}{a_{0}^{2}}=\frac{8\pi G\rho _{0}}{3}+\frac{\Lambda }{3}(1+\lambda \rho _{0}), \end{aligned}$$
(59)

where \(\lambda \) is a dimensional parameter. By keeping the positive energy condition, the above equation implies that a positive spatial curvature \(k>0\), for the two cases \(\Lambda >0\) and \(\Lambda <0\), is guaranteed only under the following constraints, respectively:

$$\begin{aligned} \lambda >-\frac{1}{\rho _{\Lambda }}-\frac{1}{\rho _{0}}\; \end{aligned}$$
(60)

and

$$\begin{aligned} \lambda <\frac{1}{|\rho _{\Lambda }|}-\frac{1}{\rho _{0}}, \end{aligned}$$
(61)

so that \(\rho _{\Lambda }\equiv \frac{\Lambda }{8\pi G}\) and \(|\rho _{\Lambda }|\equiv \frac{|\Lambda |}{8\pi G}\). Noting our previous result on the upper bounds on the energy density of ESU, \(\rho _{0}<l_\mathrm{pl}^{-4}\), the above constraints read as follows:

$$\begin{aligned} \lambda >-\frac{1}{\rho _{\Lambda }}-l_\mathrm{pl}^{4}\; \end{aligned}$$
(62)

and

$$\begin{aligned} \lambda <\frac{1}{|\rho _{\Lambda }|}-l_\mathrm{pl}^{4}. \end{aligned}$$
(63)

In the DGR formalism of gravity, it is expected that the parameter \(\lambda \) has the order of magnitude \(|\lambda |\sim l_\mathrm{pl}^{4}\). It seems that this value of \(\lambda \) is satisfied by both the above constraints. Also, in the presence of a cosmological constant, we recover Eq. (32) from the second modified FRW equation (24). Similar to the previous analysis, by inserting Eq. (33) into Eq. (56) and neglecting the non-linear perturbation terms, we get

$$\begin{aligned} -\frac{2k}{a_{0}^{2}}\delta a= \left( \frac{8\pi G}{3}+\frac{\Lambda }{3}\lambda \right) \rho _{0}\delta \rho . \end{aligned}$$
(64)

It is seen that for the case of a positive spatial curvature \(k>0\), the sign of the variation of the scale factor \(\delta a\) is in contrast to the variation of matter density \(\delta \rho \), provided that

$$\begin{aligned} \lambda >-\frac{1}{\rho _{\Lambda }}\; \end{aligned}$$
(65)

and

$$\begin{aligned} \lambda <\frac{1}{|\rho _{\Lambda }|}, \end{aligned}$$
(66)

which are related to the cases \(\Lambda >0\) and \(\Lambda <0\), respectively. For the case of a positive cosmological constant, \(\Lambda >0\), by comparing the constraints (60) and (65), one realizes that the constraint (60) can be satisfied via the constraint (65), while its inverse is not true, and so Eq. (65) will be a tighter constraint. For the same reason, one can say that for the case of a negative cosmological constant, \(\Lambda <0\), the constraint (61) is tighter than (66). Finally, by using Eq. (64) and considering Eq. (33) combined with the second modified FRW equation (24), after neglecting the non-linear perturbation terms, we arrive at the following differential equation:

$$\begin{aligned} \delta \ddot{a}-\frac{k}{a^{2}_{0}}\left( \frac{1}{1+\lambda \rho _{\Lambda }}\right) \left( 1-\frac{10}{3}\xi \rho _{0}^ {\frac{1}{4}}\right) (1+3\omega )\delta a=0. \end{aligned}$$
(67)

By putting \(\rho _{0}=\left( \frac{4}{3}\xi \right) ^{-4}\), the above differential equation takes the form of

$$\begin{aligned} \delta \ddot{a}+\frac{3k}{2a^{2}_{0}}\left( \frac{1}{1+\lambda \rho _{\Lambda }}\right) (1+3\omega )\delta a=0. \end{aligned}$$
(68)

In order to have a stable ESU against homogeneous and linear scalar perturbation described by the oscillatory modes, we have two possibilities:

  • For the case of \(\Lambda >0\)

    $$\begin{aligned} \omega >-\frac{1}{3},\quad \lambda >-\frac{1}{\rho _{\Lambda }}, \quad \text{ or } \quad \omega <-\frac{1}{3},\quad \lambda <-\frac{1}{\rho _{\Lambda }}. \end{aligned}$$
    (69)

  • For the case of \(\Lambda <0\)

    $$\begin{aligned} \omega >-\frac{1}{3},\quad \lambda <\frac{1}{|\rho _{\Lambda }|}, \quad \text{ or } \quad \omega <-\frac{1}{3},\quad \lambda >\frac{1}{|\rho _{\Lambda }|}. \end{aligned}$$
    (70)

    Now, in the same way as above by using the rainbow function (27), by choosing the rainbow function (46), we obtain the following differential equation:

    $$\begin{aligned} \delta \ddot{a}-\frac{k}{a^{2}_{0}}\left( \frac{1}{1+\lambda \rho _{\Lambda }}\right) \left( 1+\frac{8}{3}\chi \rho ^{\frac{1}{2}}_{0}\right) (1+3\omega )\delta a=0, \end{aligned}$$
    (71)

    where, by inserting \(\rho _{0}=\left( \frac{16}{9}\chi \right) ^{-2}\), coming from the constraint (32) for the rainbow function (46), it can be rewritten

    $$\begin{aligned} \delta \ddot{a}-\frac{5k}{2a^{2}_{0}}\left( \frac{1}{1+\lambda \rho _{\Lambda }}\right) (1+3\omega )\delta a=0. \end{aligned}$$
    (72)

    This differential equation possesses the stable oscillatory modes under the following possibilities:

  • The case of \(\Lambda >0\):

    $$\begin{aligned} \omega >-\frac{1}{3},\quad \lambda <-\frac{1}{\rho _{\Lambda }}, \quad \text{ or } \quad \omega <-\frac{1}{3},\quad \lambda >-\frac{1}{\rho _{\Lambda }}. \end{aligned}$$
    (73)

  • The case of \(\Lambda <0\):

    $$\begin{aligned} \omega >-\frac{1}{3},\quad \lambda >\frac{1}{|\rho _{\Lambda }|}, \quad \text{ or } \quad \omega <-\frac{1}{3},\quad \lambda <\frac{1}{|\rho _{\Lambda }|}. \end{aligned}$$
    (74)

We note that since the cosmological constant does not appear in the constraint equation (32), the energy density of the ESU is bounded as \(\rho _{0}<\epsilon _\mathrm{pl}^{4}\) or \( \rho _{0}< l_\mathrm{pl}^{-4}\), for the two rainbow functions (27) and (46). It is found that in order to have stable solutions for an ESU in the presence of a cosmological constant, beside the cutoff on the energy density \(\rho _{0}\), the conditions (69), (70) and (73), (74), for each of the rainbow functions (27) and (46), should also be satisfied, respectively. For the case of a positive cosmological constant \(\Lambda >0\), by comparing the conditions mentioned in (69) and (73) with the constraint (65), one realizes that with the choice of the rainbow functions (27) and (46), the solutions with \(\omega >-\frac{1}{3},\ \lambda >-\frac{1}{\rho _{\Lambda }}\) and \(\omega <-\frac{1}{3},\ \lambda >-\frac{1}{\rho _{\Lambda }}\) are allowed, respectively. For the case of a negative cosmological constant \(\Lambda <0\), the constraint (61) is tighter than (66). In fact, we recall that the constraint (61) is important in the sense that, with respect to the physical energy condition in the quantum gravity regimes, it ensures that \(k>0\). So, it is clear that all the constraints on the parameter \(\lambda \) in (70) and (74) violate the constraint (61). Overall, this means that in the presence of quantum gravity modifications such as by gravity’s rainbow, with respect to the positive energy condition and the positive spatial curvature \(k>0,\) which is one of the basic assumptions in modern version of emergent universe scenario, for the cosmological models possessing a negative cosmological constant, there is no stability for an ESU.

4 Einstein static universe, vector and tensor perturbations

In the cosmological context, the vector perturbations of a perfect fluid having energy density \(\rho \) and barotropic pressure \(p=\omega \rho \) are governed by the co-moving dimensionless vorticity defined as \({\varpi }_a=a{\varpi }\). The vorticity modes satisfy the following propagation equation [89–92]:

$$\begin{aligned} \dot{\varpi }_{\kappa }+(1-3c_s^2)H{\varpi }_{\kappa }=0, \end{aligned}$$
(75)

where \(c_s^2=\mathrm{d}p/\mathrm{d}\rho \) and H are the sound speed and the Hubble parameter, respectively. This equation is valid in our treatment of Einstein static universe in the framework of the rainbow’s gravity through the modified Friedmann equations (23) and (24). For the Einstein static universe with \(H=0\), Eq. (75) reduces to

$$\begin{aligned} \dot{\varpi }_{\kappa }=0, \end{aligned}$$
(76)

indicating that the initial vector perturbations remain frozen and consequently we have neutral stability against the vector perturbations. Tensor perturbations, namely gravitational-wave perturbations, of a perfect fluid are described by the co-moving dimensionless transverse-traceless shear tensor \(\Sigma _{ab} =a\sigma _{ab}\), whose modes satisfy the following equation:

$$\begin{aligned} \ddot{\Sigma }_{\kappa }+3H\dot{\Sigma }_{\kappa }+\left[ \frac{\mathcal {K}^2}{a^2} +\frac{2k}{a^2}-\frac{(1+3\omega )\rho -2\Lambda (\epsilon )}{3}\right] \Sigma _{\kappa }=0, \end{aligned}$$
(77)

where \(\mathcal {K}\) is the co-moving index (\(D^2\rightarrow -\mathcal {K}^2/a^2\) in which \(D^2\) is the covariant spatial Laplacian) [89–92]. For the Einstein static universe \((H=0)\), this equation reduces to

$$\begin{aligned} \ddot{\Sigma }_{\kappa }+\left[ \frac{\mathcal {K}^{2}}{ a_0^2} +\frac{2k}{a_{0}^2}-\frac{(1+3\omega )\rho _{0}- 2\Lambda (1+\lambda \rho _0)}{3}\right] \Sigma _{\kappa }=0. \end{aligned}$$
(78)

Note that in the general tensor perturbation equation (77), the Hubble parameter H contains the rainbow function f through Eq. (23). But, because for the Einstein static universe we have \(H=0\), the rainbow function f did not appear in Eq. (78). Then, in order to have stable modes against the tensor perturbations, the following inequality should be satisfied:

$$\begin{aligned} \frac{\mathcal {K}^{2}}{ a_0^2} +\frac{2k}{a_{0}^2}>\frac{(1+3\omega )\rho _{0}- 2\Lambda (1+\lambda \rho _0)}{3}. \end{aligned}$$
(79)

Here, for a closed universe with \(k=1\), considering the eigenvalue spectra \(\mathcal {K}^2=n(n+2)\) with \(n=1,2,3,\ldots \) [93], it will take the form of

$$\begin{aligned} \frac{n^2 +2n +2}{a_{0}^2}>\frac{(1+3\omega )\rho _{0}- 2\Lambda (1+\lambda \rho _0)}{3}. \end{aligned}$$
(80)

This inequality gives a restriction on the scale factor of an ESU in terms of its matter density and background cosmological constant. Even though the existence of open and flat solutions is possible in some modified gravity models, in the present modified gravity model it is forbidden by regarding the weak energy condition. Therefore, the stability analysis in the present model is restricted to the physically viable closed cosmological model. For the eigenvalue spectra \(\mathcal {K}^2\) for open and flat models, one is referred to [93].

5 Summery and conclusion

According to a modern version of the emergent cosmological scenario proposed by Ellis and Maartens [52], the early universe before passing to the inflationary phase has experienced an eternal Einstein static state rather than a Big-Bang singularity. More exactly, it refers to a static closed space in the asymptotic past (before entering the universe to the period of inflation) known as “Einstein static universe” (ESU). The initial conditions, the quantum gravity effects in the early high energy universe, will influence the stability of this static state. For this reason, in the present work, we have examined the effects of an effective approach to quantum gravity proposed by Magueijo and Smolin [28], known as “gravity’s rainbow” or “doubly general relativity (DGR)”, on the stability of the Einstein static state against the linear homogeneous scalar, vector, and tensor perturbations. In order to follow our aim in the framework of DGR, we needed to introduce appropriate rainbow functions. Then, we have considered two appropriate well-known rainbow functions; see Eqs. (27) and (46). First, by following the phase space mechanism represented in [84], we have investigated the fixed points belonging to a flat FRW model which is modified by the presence of the rainbow function (27). Indeed, these fixed points are de Sitter space solutions of a typical flat rainbow FRW model. Our results indicate that although the needed time to get a fixed point is infinite, it may not lead to the elimination of the initial finite time singularities (Big Bang). This is because of the fact that the fixed points corresponding to past singularities (Big Bang) are unstable and maybe collapse. Then, we studied the DGR theory in the context of the emergent universe scenario and tried to find its stable Einstein static universe with the required conditions. In order to find a stable ESU, as a first result, we realized that similar to the standard GR scenario and independent of the choice of the rainbow function, the positive spatial curvature, \(k>0\), is the only option respecting the positive energy condition \(\rho _{0}>0\) for an ESU in the framework of the DGR theory. For the case of a zero cosmological constant \(\Lambda =0\), we found that in order to achieve a stable ESU against homogeneous and linear scalar perturbations, we need the conditions on the energy density of ESU and the barotropic equation of state \(\rho _{0}=\left( \frac{4}{3}\xi \right) ^{-4}\) and \(\omega >-\frac{1}{3}\), respectively. Similarly, for the rainbow function (46), we also verified that the Big-Bang singularity can still exist. Unlike the previous case, the time needed to get the fixed point is not infinite in this case. Furthermore, the only fixed point which is revealed in the presence of the rainbow function (46) is a future fixed point and is not a past fixed point. Then, by looking at the DGR theory from the emergent universe point of view, we studied the stability of the Einstein static universe and the conditions it required. For this case, a stable solution for ESU is guaranteed under these conditions, \(\rho _{0}=\left( \frac{16}{9} \chi \right) ^{-2}\) and \(\omega <-\frac{1}{3}\), describing exotic matter fields. As is seen, the stability conditions \(\rho _{0}=\left( \frac{4}{3}\xi \right) ^{-4}\) and \(\rho _{0}=\left( \frac{16}{9}\chi \right) ^{-2}\) are direct results from the idea of an energy-dependent metric in the framework of a gravity’s rainbow scenario. These results are equivalent to an explicit cutoff on the energy density of an ESU as \(\rho _{0}<\epsilon _\mathrm{pl}^{4}\) and \(\rho _{0}<l_\mathrm{pl}^{4}\), respectively. Given that, ESU hints to an initial static state (or static closed space) of the universe before getting into an inflationary phase, so the existence of such an explicit cutoff (or upper bounds) on \(\rho _{0}\) could be interpreted as a result of initial dominant quantum gravity effects such as “gravity’s rainbow”. In the following of our analysis, we take an energy-dependent cosmological constant via the introduction of a new rainbow function, \(h(\epsilon )^{2}=(1+\lambda \rho )\). It is seen that the positive spatial curvature, \(k>0,\) dictates an opposite sign for \(\delta a\) relative to energy density \(\delta \rho \) through Eq. (64). We find that in order to have stable solutions for an ESU, beside the cutoff on the energy density \(\rho _{0}\), the conditions (69), (70) and (73), (74) for each of the rainbow functions (27) and (46) should also be satisfied, respectively. In particular, for the case of a positive cosmological constant, \(\Lambda >0\), by comparing the conditions mentioned in (69) and (73) with the constraint (65), one realizes that with the choice of the rainbow functions (27) and (46), the solutions with \(\omega >-\frac{1}{3},\ \lambda >-\frac{1}{\rho _{\Lambda }}\) and \(\omega <-\frac{1}{3},\ \lambda >-\frac{1}{\rho _{\Lambda }}\) are allowed, respectively. For the case of negative cosmological constant \(\Lambda <0\), the constraint (61), is tighter than (66). In fact, we recall that the constraint (61) is important in the sense that, with respect to the physical energy condition in quantum gravity regimes, it ensures that \(k>0\). So, it is clear that all the constraints on the parameter \(\lambda \) in (70) and (74) violate the constraint (61). Overall, this means that in the presence of quantum gravity modifications such as by gravity’s rainbow, with respect to a positive energy condition and a positive spatial curvature \(k>0,\) which is one of the basic assumptions in modern version of emergent universe scenario, for cosmological models with a negative cosmological constant, there is no stability for an ESU. Finally, we investigated the stability of an ESU in the framework of DGR versus vector and tensor perturbations. It is found that there is neutral stability against the vector perturbations. In order to have stability against the tensor perturbations, the scale factor of an ESU is restricted by its matter density and background cosmological constant.