1 Introduction

One of the important signatures of the quark gluon plasma (QGP) produced by heavy ion collision experiments at the RHIC and the LHC is the suppression of \(J/\psi \) mesons, the \(c\bar{c}\)-pair, production. This phenomenon is understood qualitatively when the temperature of the QGP is larger than the Hagedorn temperature such that the potential interaction between quarks in the \(c\bar{c}\)-pair would not be able to bind them anymore and thus the \(J/\psi \) mesons will be dissociated and screened inside the QGP [1]. The screening potential of the \(c\bar{c}\)-pair depends on a maximum value of the separation length L between the c and \(\bar{c}\) quarks, called the screening length \(L_{\mathrm{max}}\), the screening potential becoming flat beyond this value.

In the string theory prescription of the AdS/CFT correspondence, a heavy quark–antiquark pair, described by a Wilson loop in the gauge theory, is defined as a fundamental string which has both ends attached on the probe brane at the boundary; different orientation of electric fields on both ends of the string represents a source for the quark–antiquark pair [2]. Evaluating the Wilson loop will tell us information as regards the dependence of the screening potential on the screening length. The procedure to evaluate the Wilson loop goes by extremizing the corresponding gravity dual action, as shown in [3, 4] for the zero-temperature case and in [5, 6] for the finite-temperature case.

The screening length calculation of a moving quark–antiquark pair in the four-dimensional \(\mathcal {N}=4\) supersymmetric Yang–Mills theory at finite-temperature was done first in [7] using the AdS/CFT correspondence. It was then generalized to arbitrary dimension of conformal and non-conformal theories (CFT and non-CFT) in [8]. The calculations there were done in the reference frame of a moving quark–antiquark pair, or explicitly by boosting the background metric in the direction of quark–antiquark pair’s velocity. A different approach was done in [9] by going to the reference frame of the plasma and furthermore they also compared the total energy of the quak-antiquark pair in both reference frames. It was found that the screening length is scaled by some power of \((1-v^2)\), where v is velocity of the plasma, depending on the dimension of the black hole backgrounds [8]. However, the computation of the scaling factor is only valid in the ultra-relativistic limit and disagrees with the numerical fitting found in [9]. For the case considered in this article, both scaling factors may coincide in which the background metric is the four-dimensional Schwarzschild–AdS black hole.Footnote 1

Most of the calculations about the screening length in the literature were done for the case of non-rotating plasma. However, in a more realistic scenario, the plasma might have some angular momentum, such as the QGP produced by heavy ion collisions at the RHIC and the LHC. It is natural to think that the peripheral collisions of two nuclei would produce angular momentum to the plasma [10, 11]. Although the amount of angular momentum left to the resulting plasma is small compared to the initial angular momentum of the two nuclei, it is expected that the angular momentum fraction increases when the collision energy is increased; as such, the effect of the angular momentum would be significant. Phenomenologically, the angular momentum might be present in the form of rotation or shearing in the plasma [12, 13]. Holographically, this can be realized by considering asymptotically AdS rotating black holes where the topology of the event horizon is spherical or planar, respectively. In this article, we consider a rotating plasma where the corresponding black hole background is the four-dimensional Kerr–AdS black hole, where the event horizon is a two sphere \(S^2\), which is more advantageous for improving the chemical potential calculation in the plasma compared to the case of a planar event horizon [14].

The screening length calculation in the four-dimensional Kerr–AdS black hole background is tedious because we have written the metric in asymptotically “canonical” AdS (AAdS) coordinates which is very complicated [15]. As we have learned from the non-rotating case, we could also compute the screening length by going to the reference frame of the rotating black hole in which the background metric would be the four-dimensional Schwarzschild–AdS black hole. Therefore we will start from the screening length calculation in the Schwarzschild–AdS black hole and then compare it with the calculation in the Kerr–AdS black hole which turns out to be a special case.

In more detail, we first compute the screening length of a heavy quark–antiquark pair moving in the plasma whose corresponding background metric is the four-dimensional Schwarzschild–AdS black hole in the global coordinates. We then compare it with the computation in the reference frame of the moving quark–antiquark pair in which the plasma is rotating; here, the background metric is a rotating black hole. Unlike the Poincaré coordinate case, in general, the rotating AdS black holes in global coordinates cannot be obtained simply by a boosting procedure as described in [8]. However, the solution for rotating black holes in the global coordinates, by a different procedure, is available and it is known as a Kerr–AdS black hole. For the particular case in this article, the boosting procedure is doable and we can obtain a black hole solution called a “Boost-AdS” black hole. We will compare the screening length computed using both black holes by finding a relation between their parameters.

In the Poincaré coordinate case, we can compute the screening length for arbitrary angle between the separation length of the quark–antiquark pair and its velocity direction, or the hot wind plasma direction [16]. Unfortunately, the situation is quite restricted in the global coordinate case. The main reason is that the geodesic of heavy quarks at the boundary must follow the great circle solutions. If we want to keep the screening length to be fixed, then both the quark and the antiquark must stay on the same great circle plane for stationary motion. Therefore the only possible angle is when the separation length of a quark–antiquark pair is parallel to its angular velocity direction. Furthermore, using \(\mathrm{SO}(3)\) symmetry, we can rotate an arbitrary great circle plane to the equatorial plane. This turns out to be an advantage in the screening length calculation of the Kerr–AdS black hole in which the explicit expression of the background metric in the AAdS coordinates is simple.

In Sect. 2, we will compute the separation length of the heavy quark–antiquark pair in the reference frame of the plasma. We plot numerically the separation length, for various fixed angular velocities \(\omega \), as a function of the momentum transfer of angular coordinate \(\phi \) along the string \(\pi ^\sigma _\phi \propto P\). We also compute the total energy H as a function the separation length. In Sect. 3, we proceed with the computation in the reference frame of the moving quark–antiquark pair. Unlike in the Poincaré case, we have more than one background metrics which are the “Boost-AdS” black hole and Kerr–AdS black hole. We will try to compare the results by finding relations between the parameters of these black holes. Therefore we can plot numerically the screening length as a function of the angular velocity parameter for these black holes using the aforementioned relations. Section 4 contains a discussion and the conclusion of the results from the previous sections.

2 Screening length in plasma reference frame

In the reference fame of the plasma, the background metric is static and is given by the four-dimensional Schwarzschild–AdS black hole in the global coordinates as follows:

$$\begin{aligned}&\mathrm{d}s^2=-r^2 h(r) \mathrm{d}t^2 + {1\over r^2 h(r)}\mathrm{d}r^2+r^2\left( \mathrm{d}\theta ^2 +\sin ^2\theta ~ \mathrm{d}\phi ^2\right) ,\nonumber \\&h(r)=l^2+{1\over r^2}-{2 M_{\mathrm{Sch}} \over r^3},\ T_{\mathrm{Sch}}={1\over 4\pi }\left( {1\over r_\mathrm{H}}+3 r_\mathrm{H} l^2\right) , \end{aligned}$$
(1)

where \(r_\mathrm{H}\le r< \infty \), \(0\le \theta \le \pi \), and \(0\le \phi <2\pi \). Here, l is the curvature radius of the AdS space, \(M_{\mathrm{Sch}}\) is proportional to the mass of the Schwarzschild–AdS black hole, \(T_{\mathrm{Sch}}\) is the Hawking temperature, and \(r_\mathrm{H}\) is the event horizon defined as the most positive real root of h(r); \(h(r_\mathrm{H})=0\). This Schwarzschild–AdS black hole has a minimum temperature and two branches of high temperature region. We choose the branch where \(r_\mathrm{H} l>1/\sqrt{3}\), or \(M_{\mathrm{Sch}}l>{2\over 3\sqrt{3}}\), which is favored thermodynamically [17]. In this metric, the corresponding plasma lives in the boundary of \(\mathrm{AdS}_4\), that is, the three-dimensional Einstein’s static universe, in which the spatial manifold is a two sphere, \(S^2\).

The classical solution of a string is obtained by solving the equation of motion derived from the Nambu–Goto action,

$$\begin{aligned}&S=- T_0\int \mathrm{d}\sigma ^2 \sqrt{-\det g_{\alpha \beta }}, \nonumber \\&g_{\alpha \beta }\equiv G_{\mu \nu }\partial _{\alpha }X^\mu \partial _{\beta }X^\nu ,\quad T_0={1\over 2\pi \alpha '}, \end{aligned}$$
(2)

where \(\sigma ^{\alpha }\equiv (\tau ,\sigma )\) is the worldsheet coordinates, \(X^\mu (\sigma ^\alpha )\) are the spacetime coordinates where the string worldsheet is embedded, and \(G_{\mu \nu }\) is the background metric (1). The equation of motion derived from the action (2) is simply written as

$$\begin{aligned} \nabla _\alpha P^\alpha _\mu&=0,\quad P^\alpha _\mu \equiv {\pi ^\alpha _\mu \over \sqrt{-g}},\quad \pi ^\alpha _\mu \equiv {\delta S \over \delta \partial _\alpha X^\mu }, \end{aligned}$$
(3)

where \(\pi ^\alpha _\mu \) is the canonical worldsheet momentum, and \(g=\det g_{\alpha \beta }\).

In deriving the equation of motion, we choose a gauge \(\tau =t\) while the gauge for \(\sigma \) will be determined later for convenience. As explained in the Introduction, we will consider solutions of (3) in the equatorial plane, \(\theta =\pi /2\). Taking the ansatz

$$\begin{aligned} \phi (\sigma ^\alpha )&\equiv \omega \tau +\phi (\sigma ),\end{aligned}$$
(4)
$$\begin{aligned} r(\sigma ^\alpha )&\equiv r(\sigma ), \end{aligned}$$
(5)

for a moving quark–antiquark pair with a constant angular velocity, the equations of motion are given by

$$\begin{aligned}&\phi '^2(r^4h)'+r'^2\left( 1-{\omega ^2\over h}\right) '-{2r'\sqrt{-g}}{\partial \over \partial \sigma }\left[ {r'(h-\omega ^2) \over h\sqrt{-g}}\right] =0,\end{aligned}$$
(6)
$$\begin{aligned}&\partial _\sigma \pi ^\sigma _\phi \equiv {\partial \over \partial \sigma }\left[ {r^4h\over \sqrt{-g}} \phi '\right] =0, \end{aligned}$$
(7)

where \(\pi ^\sigma _\phi \) is constant and \('\equiv {\partial \over \partial \sigma }\). There are two ways to define the gauge for \(\sigma \). The first one is \(\sigma =\phi \), which is actually nice in the quark–antiquark configuration, since \(r(\phi )\) will be a single valued function. However, the equation of motion given by Eq. (6) is not simple. The other choice of gauge is \(\sigma =r\) in which the equation of motion is given by Eq. (7). This equation has an additional reflection symmetry in \(\phi \). It implies that if \(\phi (r)\) is a solution then \(-\phi (r)\) is also a solution. In the quark–antiquark configuration, in which the string takes a \(\cup \)-shape in the r–\(\phi \) plane, \(\phi (r)\) is a double valued function which consists of two solutions of (7) related by the reflection symmetry. The advantage of using the gauge \(\sigma =r\) is that Eq. (7) is rather simpler than Eq. (6). Another advantage is that there is a conserved momentum transfer \(\pi ^\sigma _\phi \), which can be useful in the discussion of the physical properties of the string configuration. For those reasons, we are going to use the gauge \(\sigma =r\) from now on.Footnote 2

For the quark–antiquark pair, following [9], we take a solution of (7) which satisfies the conditions

$$\begin{aligned} \phi (r\rightarrow \infty )=L/2,\quad \phi '(r_p)=\infty , \end{aligned}$$
(8)

where L is defined to be a dimensionless separation length of the quark–antiquark pair, and \(r_p\) is the turning point at which the string reaches a minimum value in r, with \(r_p> r_\mathrm{H}\). Using reflection symmetry, \(\phi \rightarrow -\phi \), we can get the other solution and set the turning point in the middle such that \(\phi (r_p)=0\). In the holographic prescription, the quark/antiquark is located at the boundary \(\phi (r\rightarrow \infty )=\pm L/2\). This could be the source of the divergence in the calculation of the total energy of the string. However, we will see later that this divergence can be removed by subtracting the energy of each quark and antiquark of the corresponding string configuration. In our definition above, the separation length is finite although the string length, given by the formula \(L_{\mathrm{string}}=2\int ^\infty _{r_p} \mathrm{d}r\sqrt{{1\over r^2 h}+r^2\phi '^2}\), is infinite. Since the length of a string is not of interest here, we do not have to put a UV cut-off to regularize the results. We carefully choose the values of the parameters so that the computed L is smaller than the range of the coordinate \(\phi \) since the coordinate \(\phi \) is periodic with length \(2\pi \), \(-\pi \le \phi <\pi \). Throughout this paper, all numerical calculations will be expressed in terms of dimensionless quantities in which the conversion is carried out using the AdS curvature l, which has dimension \([\text{ length }]\), e.g. the angular velocity \(\omega \), with dimension \([\text{ length }]^{-1}\), in dimensionless form is written as \(\omega /l\).

Solutions to Eq. (7) are given by

$$\begin{aligned} \phi '=\pm {P\over r^2 h}\sqrt{h -\omega ^2\over r^4h-P^2}, \end{aligned}$$
(9)

where now \('\equiv {\partial \over \partial r}\), and \(P\propto \pi ^\sigma _\phi \) is a constant denoting the amount of \(\phi \)-component of momentum transfer on the string. In our convention \(P>0\). The positive sign in (9) corresponds to the configuration in which the energy flows from the boundary down to \(r=r_p\), while the negative sign is the opposite. At \(P=0\), it would correspond to a straight string configuration. The quark–antiquark pair can be built out of these two solutions, corresponding to configurations (a) and (b) as shown in Fig. 1. The negative sign solution may seem to be unphysical according to the drag force analysis [18, 19]. However, this is not the case here, since the energy transferred is not coming from the horizon, but from the turning point \(r_p>r_h\). It is necessary to take these two configurations in order for the string of the quark–antiquark pair to join up at \(r=r_p\) such that the energy transfer, \({\mathrm{d}E\over \mathrm{d}t}\equiv -\pi ^\sigma _t=-T_0P\omega \), is coming from one end of the string at the boundary down to the turning point and then back again to the other end of the string at the boundary. The energy flow is in the opposite direction of the angular velocity as depicted in Fig. 1. Unlike the perpendicular case in [9], the constant force, \({\mathrm{d}p_\phi \over \mathrm{d}t}=\pi ^\sigma _\phi =-T_0P\), is non-vanishing by the non-zero force at the turning point since the string is parallel to the \(\phi \)-axis. In more detail, the double valued function \(\phi \) in our setup is defined as follows:

$$\begin{aligned} {\mathrm{d}\phi \over \mathrm{d}r}=\left\{ \begin{array}{ll} {P \over r^2 h}\sqrt{h -\omega ^2 \over r^4h-P^2} ,&{}\quad 0\le \phi \le L/2 ,\\ -{P \over r^2 h}\sqrt{h -\omega ^2 \over r^4h-P^2} ,&{}\quad -L/2\le \phi \le 0, \end{array} \right. \end{aligned}$$
(10)

where the radius r takes values \(r_p\le r<\infty \).

Fig. 1
figure 1

Two different configurations determined by the sign in P. The positive and negative sign solutions are shown by diagrams b and a, respectively

Full size image

We solve Eq. (9) for a positive sign and the other solution can be obtained by changing \(P\rightarrow -P\). At \(r=r_p\), we must have \(r_p^4 h(r_p)-P^2=0\), which implies that \(h(r_p)>0\), or \(r_p>r_\mathrm{H}\). There is a critical radius \(r_c\) defined by \(h(r_c)=\omega ^2\), which also implies \(r_c>r_\mathrm{H}\) for \(\omega \ne 0\). Solving Eq. (9) in terms of the integral formula, for \(r_p>r_c\), the integral in coordinate r is bounded from below at \(r=r_p\) and thus the string configuration for the quark–antiquark pair is formed. On the other hand, if \(r_p<r_c\) the integral is also bounded from below at \(r=r_c\). However, this solution requires \(P=0\) at \(r=r_c\), since the string there is perpendicular to the \(\phi \)-axis, which is a similar situation to the one considered in [9], and so the physical configuration is given by a straight string. We may ignore the configuration for \(r_p=r_c\), in which the condition (8) could not be satisfied, which is physically similar to the drag force configuration; a moving curved string. Therefore the string configuration for the quark–antiquark pair requires \(r_p>r_c\) or equivalently \(P^2>P_c^2=\omega ^2 r_c^4\). Notice that \(r_c\) equals \(r_{\mathrm{Sch}}\), derived in the drag force computation [20, 21], in which the constant \(\pi ^\sigma _\phi \) is proportional to \(P_c\) because both are given by the same formula, (7), at \(r_p=r_c\). So, for some fixed angular velocity, the string configuration is characterized by the amount of momentum transfer on the string, with \(P^2\ge P_c^2\). At \(P^2=P_c^2\), the string tends to represent a single quark and if we increase the momentum transfer P then it is starting to form the quark–antiquark pair. Figure 2 shows the schematic pictures of the string configuration describing the quark–antiquark pair and the drag force of a single quark/antiquark.

Fig. 2
figure 2

The picture on the left shows the string configuration of a single quark at critical momentum transfer \(P^2=P_c^2=\omega ^2 r_c^4\). Increasing the \(P^2>\omega ^2 r_c^4\), the string configuration turns into the quark–antiquark pair as shown by the picture on the right

Full size image

From Eq. (9), we obtain an integral formulaFootnote 3:

$$\begin{aligned} \int _0^{L/2} \mathrm{d}\phi ={L\over 2}=\int _{r_p}^\infty \mathrm{d}r {P\over r^2 h}\sqrt{h-\omega ^2 \over r^4 h-P^2}. \end{aligned}$$
(11)

The integral above is very difficult to solve analytically and so we are going to plot the integral numerically. The numerical solution of the separation length for various values of \(\omega /l\) is shown in Fig. 3.

Fig. 3
figure 3

Plots of the dimensionless separation length for various \(\omega / l=0,0.25,0.45,0.75,0.95\), with fixed \(M_{\mathrm{Sch}}l=10\), as functions of Pl where the corresponding colors are black, blue, green, brown, and red. The dashed black line is the plot of lower bound momentum transfer, for each \(\omega \), obtained by substituting \(\omega ^2= P^2/r_p^4\) into Eq. (11)

Full size image

As one can see, we produce a similar profile of the separation length as in the Poincaré case of [9], except that the momentum transfer is bounded from below at \(P^2=P_c^2\equiv \omega ^2 r_c^4\), for each \(\omega \). The lower bound of the momentum transfer, for each \(\omega \), is given by the dashed black line in Fig. 3. In this line, the quark–antiquark pair cannot be formed and the string becomes a moving quark or we have the drag force configuration. Therefore our plots in general do not start from \(P=0\), which is different from the plots produced in [9], but instead we start from \(P=P_c\). Similar to the perpendicular case, the separation length in Fig. 3 consists of two regions separated by the maximum value \(L_{\mathrm{max}}\), called the screening length, at the point \(P=P_{\mathrm{max}}\). For \(P_c<P<P_{\mathrm{max}}\), the string configuration is metastable, while for \(P\ge P_{\mathrm{max}}\) it is mostly stable and it depends on the total energy of the quark–antiquark pair which we will compute in the next section; a detailed discussion as regards this subject can be found in [7, 9]. We exclude \(P=P_c\) as a string configuration of the quark–antiquark pair since the string geometry is not bounded from below at \(r_p\) but instead it can be continued down to \(r_\mathrm{H}\) and thus the integral (11) should be taken from \(r=r_\mathrm{H}\) to \(r\rightarrow \infty \). However, the separation length in this case will be infinite because the integrand in (11) is divergent near \(r\rightarrow r_\mathrm{H}\). Therefore this supports our statement above that the string configuration of quark–antiquark pair, at this value of momentum transfer, is dissociated into a single quark and antiquark due to an infinitely large separation length.

2.1 Drag force

As we mentioned previously, the amount of momentum transfer is proportional to the constant P and the total force is given by

$$\begin{aligned} {\mathrm{d}p_\phi \over \mathrm{d}t}=-T_0 P, \quad P>0. \end{aligned}$$
(12)

This denotes the amount of drag force experienced by the quark–antiquark pair moving in the plasma. The amount of momentum transfer P, with fixed separation length L, is actually dependent on the angular velocity \(\omega \) as we can infer from Fig. 3. The negative sign shows that this drag force tends to decrease the angular momentum, or the angular velocity, of the quark–antiquark pair. To have the quark–antiquark pair move with a constant angular velocity, and a fixed separation length, we must supply an external force at the boundary that would overcome the drag force. To see this, notice that the equations of motion (6) and (7) are subject to the boundary terms

$$\begin{aligned} \delta S_{bd}=\int \mathrm{d}\tau \left. [\pi ^\sigma _\phi \delta \phi +\pi ^\sigma _r \delta r]\right| ^{L_{\mathrm{string}}/2}_{\sigma =-L_{\mathrm{string}}/2.} \end{aligned}$$
(13)

For an open string, where both ends are fixed at the boundary \(r\rightarrow \infty \), we have \(\delta r({\pm L_{\mathrm{string}}\over 2})=0\). In the case when the separation length is fixed, \(\delta \phi ({L_{\mathrm{string}}\over 2})=\delta \phi (-{L_{\mathrm{string}}\over 2})\), the boundary term is non-zero, \(\delta S_{bd}\propto -T_0P\), and so we need to impose an external force at the boundary to overcome this non-zero boundary term.

2.2 Total energy

In this section, we are going to compute the total energy H of the quark–antiquark pair. The bounded energy density of the quark–antiquark pair is given by [19]

$$\begin{aligned} \mathcal {H}_{\mathrm{bound}}=2 T_0 {r^4h^2-P^2\omega ^2 \over r^2h\sqrt{(h-\omega ^2)(r^4h-P^2)}}, \end{aligned}$$
(14)

where r takes a value in \(r_p\le r<\infty \). The bounded energy density is linearly divergent near the boundary. As usual, we must subtract it with the unbounded energy density of independent quark and antiquark moving with a constant \(\omega \), see [20],

$$\begin{aligned} \mathcal {H}_{\mathrm{unbound}}=2 T_0 {r^4h^2-P_c^2\omega ^2 \over r^2h\sqrt{(h-\omega ^2)(r^4h-P_c^2)}}. \end{aligned}$$
(15)

Here, r can takes value in \(r_\mathrm{H}\le r<\infty \). This unbounded energy will cancel the divergence of the bounded energy at the boundary with a cost of producing a new divergence at the horizon. As explained in [9], and also in [19], this source of divergence is coming from the unbounded energy density because there is an infinite amount of energy flowing down from boundary, supplied by the external force, to the horizon in order to keep the quark and antiquark move with a constant \(\omega \). Furthermore, this also produces some ambiguity in removing this divergence at the horizon.

Following [9], as a resolution, we need to compute the bounded and unbounded energy density in the rest frame of the quark–antiquark pair, or the moving string. This can be done, using a symmetry of the three-dimensional Einstein’s static universe, by the following boost transformation:

$$\begin{aligned} t\rightarrow \gamma \left( t-{\omega \over l^2} \phi \right) ,\ \phi \rightarrow \gamma \left( \phi -\omega t\right) ,\ \gamma =(1-{\omega ^2 l^{-2}})^{-1/2}, \end{aligned}$$
(16)

where \(\gamma \) is the boost factor. The resulting effective three-dimensional “Boost-AdS” black hole is

$$\begin{aligned} \mathrm{d}s^2&=-r^2 h(r) \gamma ^2\left( \mathrm{d}t-{\omega \over l^2} \mathrm{d}\phi \right) ^2 + {1\over r^2 h(r)}\mathrm{d}r^2\nonumber \\&\quad +r^2 \gamma ^2\left( \mathrm{d}\phi -\omega \mathrm{d}t\right) ^2, \end{aligned}$$
(17)

where the Hawking temperature is now \(T_{\mathrm{Boost}}=T_{\mathrm{Sch}}/\gamma \). One can check that by applying this transformation to the four-dimensional Schwarzschild–AdS black hole, the resulting metric still satisfies the Einstein equation with a negative cosmological constant; \(R_{\mu \nu }=-3 l^2 g_{\mu \nu }\). A more general boost factor should also depend on the \(\theta \)-coordinate and it is given by \(\gamma =(1-{\omega ^2 l^{-2}}\sin ^2\theta )^{-1/2}\). Unfortunately, applying the same boost transformation (17), using this general boost factor for the four-dimensional Schwarzschild–AdS black hole does not give us a solution to the Einstein’s equation with a negative cosmological constant.

Taking the same gauge as before, \(\tau =t\) and \(\sigma =r\), the solutions for \(\phi (r)\) are given by

$$\begin{aligned} \phi '=\pm {P \gamma \over r^2 h}\sqrt{h -\omega ^2 \over r^4 h-P^2}, \end{aligned}$$
(18)

where P is again the same \(\phi \)-component of momentum transfer defined in the previous static black hole case. One can immediately see from (18) that the separation length is scaled by \(\gamma \) compared to the static case and hence the screening length as well; \(L_{\mathrm{Boost}}=\gamma L_{\mathrm{Sch}}\). In this “Boost-AdS” black hole, the bounded energy density can be simply written as

$$\begin{aligned} \mathcal {H}_{\mathrm{bound}}= 2\gamma T_0 r^2\sqrt{h-\omega ^2 \over r^4 h-P^2},\quad P^2>\omega ^2 r_c^4, \end{aligned}$$
(19)

and so the corresponding unbounded energy density is

$$\begin{aligned} \mathcal {H}_{\mathrm{unbound}}= 2\gamma T_0 r^2\sqrt{h-\omega ^2 \over r^4 h-P_c^2},\quad P_c^2=\omega ^2 r_c^4. \end{aligned}$$
(20)

As we can see, the cancellation of the divergence, at the boundary, in the bounded energy by the unbounded energy is done without producing a divergence at the horizon. So, we can define the total energy of the quark–antiquark pair as follows:

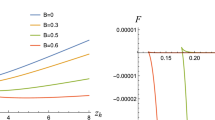
$$\begin{aligned} H=\int ^\infty _{r_p} \mathrm{d}r~ \mathcal {H}_{\mathrm{bound}}-\int ^\infty _{r_\mathrm{H}} \mathrm{d}r~ \mathcal {H}_{\mathrm{unbound}}. \end{aligned}$$
(21)

Rewriting the total energy as a function of L, instead of P, by using Eq. (11), we plot numerically the total energy for various values of \(\omega \) as shown in Fig. 4. In the plots (a)–(c) of Fig. 4, the separation length of the stable configuration (blue line) does not reach its screening length, at the tip of the curve. This behavior of the total energy is similar to the one in [9], except that here the separation length of the metastable configuration (red line) for each value of \(\omega \) is bounded from below by the dashed black line. This dashed black line is defined by the saturated energy with the following function:

$$\begin{aligned} H_{\mathrm{sat}}=-\int ^{r_c}_{r_\mathrm{H}} \mathrm{d}r~ \mathcal {H}_{\mathrm{unbound}}. \end{aligned}$$
(22)
Fig. 4
figure 4

Plots of the total energy for the quark–antiquark pair as a function of L for various \(\omega /l\), with fixed \(M_{\mathrm{Sch}}l=10\). The metastable configuration is the red line, while the stable configuration is the blue line. The dashed black line is the saturated energy; all possible energies inside the area bordered by this line and the vertical axis are forbidden for the quark–antiquark pair

Full size image

3 Screening length in quark–antiquark reference frame

A different way of computing the screening length holographically is by going to the reference frame of the moving quark–antiquark pair. In this case, the plasma will be seen as it is rotating with angular velocity proportional to the angular velocity of the quark–antiquark pair. This corresponds to the configuration of a static string under the background metric of a rotating black hole. In the Poincaré coordinate case, this metric is obtained by boosting the static metric as described in [23]. However, this procedure cannot be done in the global coordinate case in general, as we explained previously. Fortunately, the corresponding rotating black hole, known as the Kerr–AdS black hole, is available in [24, 25]. The procedure to construct the rotating metric from the static metric in the global coordinate case was first done in [26] for the three-dimensional Schwarzschild–AdS black hole, and one obtained the well-known BTZ black hole, using the Newman–Janis procedure [27]. Unfortunately, we have not found an application of this to the four-dimensional Schwarzschild–AdS black hole in the literature so far. A different procedure for constructing the rotating metric in the global coordinate case for arbitrary dimensions was given in [28]. As mentioned in the previous section, the string is rotating in the equatorial plane of the four-dimensional Schwarzschild–AdS black hole. Switching the reference frame to the moving string, the string would still stay in the equatorial plane of the rotating black hole. Therefore the rotating black hole could also be the “Boost-AdS” black hole. For this reason, we will consider the “Boost-AdS” black hole and the Kerr–AdS black hole in the screening length calculation and later we will compare their results.

3.1 Kerr–AdS black hole in Boyer–Linquist coordinates

There are many coordinate representations of the Kerr–AdS black holes [28]. The simplest one is using the Boyer–Linquist coordinate system. We identify the equatorial plane of the Kerr–AdS black hole and the “Boost-AdS” black hole by means of taking the \(\theta \) coordinates of both black holes to be \(\theta =\pi /2\). The four-dimensional Kerr–AdS black hole metric in the Boyer–Linquist coordinates at the equator can be written as [24, 25]

$$\begin{aligned} \mathrm{d}s^2= & {} -{\Delta _r \over r^2}\left( \mathrm{d}t-{a\over \Xi }\mathrm{d}\tilde{\phi }\right) ^2+{r^2 \over \Delta _r}\mathrm{d}r^2\nonumber \\&+{1\over r^2}\left( a \mathrm{d}t-{r^2+a^2 \over \Xi }\mathrm{d}\tilde{\phi }\right) ^2,\nonumber \\ \Delta _r= & {} (r^2+a^2)(1+l^2r^2)-2M_{\mathrm{Kerr}}r,\quad \Xi =1-a^2l^2,\nonumber \\ \end{aligned}$$
(23)

where a is the angular momentum parameter of the black hole. The Hawking temperature is written as

$$\begin{aligned} T_{\mathrm{Kerr}}={r_K(3l^2r_K^2+1+a^2l^2-a^2r_K^{-2}) \over 4\pi (r_K^2+a^2)}, \end{aligned}$$
(24)

where the event horizon \(r_K\) is the largest positive root of \(\Delta _r\). Using the gauge, \(\tau =t\) and \(\sigma =r\), the solutions for \(\tilde{\phi }(r)\) are now given byFootnote 4

$$\begin{aligned} \tilde{\phi }'= \pm {P\Xi ^2 \over \Delta _r }\sqrt{\Delta _r -a^2 \over \Delta _r-P^2\Xi ^2}, \end{aligned}$$
(25)

where we have used the same constant P for the definition of the momentum transfer. Obviously, the momentum transfer here has a different formula compared to the one in the “Boost-AdS” black hole case and it can be extracted from Eq. (25). Unfortunately, the resulting metric (23) is not asymptotically \(\mathrm{AdS}_3\) near the boundary which is different from the “Boost-AdS” black hole. This might give a different CFT theory, or plasma, at the boundary in the context of the AdS/CFT correspondence. Therefore we need to use a more adequate coordinate system as we will discuss in the next section.

3.2 Kerr–AdS black hole in asymptotically-AdS coordinates

Another representation of the Kerr–AdS metric is by using the AAdS (asymptotically-AdS) coordinate system. The Kerr–AdS metric in an AAdS coordinate system is asymptotically \(\mathrm{AdS}_3\) near the boundary, \(Y\rightarrow \infty \), and thus it is preferred by the AdS/CFT correspondence prescription [29, 30]. In general, to get the full geometry in the AAdS coordinate system is quite involved. However, it is still possible to write down the Kerr–AdS metric for particular cases, such as at the equator. The four-dimensional Kerr–AdS metric in the AAdS coordinates at the equator can be obtained by using the following coordinate transformation [15, 25]:

$$\begin{aligned} \Xi Y^2=r^2+a^2,\quad \Phi =\tilde{\phi }-al^2 t. \end{aligned}$$
(26)

The resulting metric is given by

$$\begin{aligned} \mathrm{d}s^2= & {} -{\Delta _Y \over \Xi ^2(\Xi Y^2-a^2)}\left( \mathrm{d}t-a \mathrm{d}\Phi \right) ^2+{\Xi ^2 Y^2 \over \Delta _Y}\mathrm{d}Y^2\nonumber \\&+{1\over \Xi Y^2-a^2}(a(1+l^2Y^2) \mathrm{d}t-Y^2 \mathrm{d}\Phi )^2,\nonumber \\ \Delta _Y= & {} Y^2\Xi ^2(1+l^2Y^2)-2M_{\mathrm{Kerr}}\sqrt{\Xi Y^2-a^2},\nonumber \\ \Xi= & {} 1-a^2l^2. \end{aligned}$$
(27)

The Hawking temperature is rewritten as

$$\begin{aligned} T_{\mathrm{Kerr}}= {Y_K^2+ 3l^2 Y_K^4-a^2(2+5l^2 Y_K^2+3l^4 Y_K^4)\over 4\pi Y_K^2\sqrt{Y_K^2-a^2(1+l^2 Y_K^2)}}, \end{aligned}$$
(28)

where the even horizon \(Y_K\) is the largest positive root of \(\Delta _Y\). Using a gauge, \(\tau =t\) and \(\sigma =Y\), the solutions for \(\Phi (Y)\) is given by

$$\begin{aligned} \Phi '= \pm {P\Xi ^2 \over \Delta _Y}{\sqrt{Y \over \Xi Y^2-a^2}}\sqrt{\Delta _Y -a^2\Xi ^2(1+l^2Y^2)^2 \over \Delta _Y-P^2\Xi ^2}. \end{aligned}$$
(29)

Here, again we use the same constant momentum transfer P whose explicit formula can be extracted from Eq. (29).

In these AAdS coordinates, the metric (27) has a conformal boundary metric,

$$\begin{aligned} \mathrm{d}\bar{s}^2= -\mathrm{d}t^2+{1\over l^2}\mathrm{d}\varPhi ^2, \end{aligned}$$
(30)

with conformal factor \(Y^2l^2\). On the other hand, the Boyer–Linquist coordinates of the metric (23) have a conformal boundary metric

$$\begin{aligned} \mathrm{d}\bar{s}'^2= -\mathrm{d}t^2+2{a\over \Xi }\mathrm{d}t \mathrm{d}\tilde{\phi }+{1\over \Xi l^2}\mathrm{d}\tilde{\phi }^2, \end{aligned}$$
(31)

with the conformal factor \(r^2 l^2\). Both conformal boundary metrics are related by a coordinate transformation,

$$\begin{aligned} \Phi =\tilde{\phi }-al^2 t \end{aligned}$$
(32)

such that

$$\begin{aligned} \mathrm{d}\bar{s}'^2={1\over \Xi }\mathrm{d}\bar{s}^2. \end{aligned}$$
(33)

It shows that if the CFT theory in (30) is in a thermal equilibrium at \(T_0\), then it is related, by Tolman’s redshifting law [31], to the CFT theory in (31) with a thermal equilibrium \(T(a)=\Xi ^{1/2} T_0\). Furthermore, if we consider the full four-dimensional metric, then the temperature of the CFT theory at the boundary of (23) will depend spatially on the \(\theta \)-coordinate in which it could give different thermodynamical properties of the CFT theory. For more details of this issue, we refer the reader to [15].

3.3 Plots of screening length

Now, we are going to compute numerically and plot the screening length for all background metrics: (17), (23), and (27), as functions of \(\omega \), or a. Since we only want to compute the screening length, or the maximum of separation length which is supposed to be the same in any coordinate representations, it is tempting to expect the plot of the Kerr–AdS black hole in AAdS coordinates to be similar to the plot of the “Boost-AdS” black hole. The main reason is that both metrics are asymptotically \(\mathrm{AdS}_3\) near the boundary besides that their full four-dimensional metrics are also solutions to the four-dimensional Einstein’s equation, with a negative cosmological constant. To make a suitable comparison of the plots, we need to find relations between all the black hole parameters: the AdS curvature l, the string angular velocity \(\omega \), the black hole angular velocity a, and the black hole mass parameters (\(M_{\mathrm{Sch}}\) and \(M_{\mathrm{Kerr}}\)).

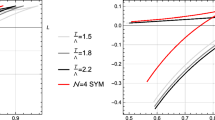
We can immediately see that both metrics have the same cosmological constant, which is given by \(\Lambda =-3l^2\), and thus all the black holes share the same AdS curvature l. The angular velocity \(\omega \) in the metric (17) is bounded from above at the boundary by \(l^2\ge \omega ^2\), while a is also bounded by \(a^2 l^2\le 1\). So, it is natural to identify \(\omega ^2=a^2 l^4\). The remaining parameters that need to be related are the mass parameters. There is no clear relation between the mass parameter of the Schwarzschild–AdS black hole, \(M_{\mathrm{Sch}}\), and the mass parameter of the Kerr–AdS black hole \(M_{\mathrm{Kerr}}\). One may naively identify \(M_{\mathrm{Sch}}=M_{\mathrm{Kerr}}\) and try to see if this could gives a similar physical picture, or if the plots are relatively similar. As we can see from the “naive” plots in Fig. 5, the screening lengths of the Kerr–AdS black holes in Boyer–Linquist and AAdS coordinates are much closer to the screening length of the Schwarzschild–AdS black hole, rather than to the screening length of the “Boost-AdS” black hole. Therefore it is unlikely that \(M_{\mathrm{Sch}}= M_{\mathrm{Kerr}}\), since we expect that computation of the screening length under all metrics (“Boost-AdS”, Boyer–Linquist, and asymptotically-AdS) in the rest frame of the string must give relatively similar plots.

Fig. 5
figure 5

Plots of the screening length as a function of al, with fixed \(M_{\mathrm{Sch}}=M_{\mathrm{Kerr}}=30/l\), for different black holes: Schwarzschild–AdS (black), “Boost-AdS” (red), Boyer–Linquist (blue), and asymptotically-AdS (green)

Full size image

Normally, we would expect the mass parameter of a rotating black hole in the rest frame of the static string to be related to the mass parameter of a static black hole, in which the string is rotating, by some power of the boost factor

$$\begin{aligned} \gamma ={1\over \sqrt{1-{\omega ^2\over l^2}}}\equiv {1\over \sqrt{1-a^2 l^2}}. \end{aligned}$$
(34)

Recall that in the Schwarzschild–AdS black hole the spacetime is static, while in the Kerr–AdS black hole the spacetime is stationary. In the rest frame of a Schwarzschild–AdS black hole, the mass of the black hole is in its rest mass. Switching the reference frame to a moving string, the black hole will be rotating around the string, and thus the mass of the black hole now is in its relativistic mass. Therefore we may identify the mass parameter \(M_{\mathrm{Sch}}\) in the “Boost-AdS” black hole to be related to the relativistic mass of the black hole in the view of the static string.

On the other hand, based on the plots in Fig. 5, we could guess that the mass parameter \(M_{\mathrm{Kerr}}\) of the Kerr–AdS black hole is related to the rest mass of the black hole. It is natural to expect the usual relativistic effect such that the mass parameters are related by \(M_{\mathrm{Sch}}=\gamma M_{\mathrm{Kerr}}\) in which the plots are shown in Fig. 6. One can see that the plots of the Kerr–AdS black hole, in Boyer–Linquist and asymptotically-AdS coordinate systems, bend a little bit towards the expected “Boost-AdS” black hole, though they are still much closer to the Schwarzschild–AdS black hole.

Fig. 6
figure 6

Taking \(M_{\mathrm{Sch}}=\gamma M_{\mathrm{Kerr}}\), we plot the screening length for different black holes: Schwarzschild–AdS (black), “Boost-AdS” (red), Boyer–Linquist (blue), and asymptotically-AdS (green)

Full size image

Using the fact that both “Boost-AdS” black hole and Kerr–AdS black hole, in an asymptotically-AdS coordinate system, are asymptotic to \(\mathrm{AdS}_3\), we may expect that their string equations of motion should be the same near the boundary, or equivalently, the quark–antiquark pair motion. As such, the formula of the separation length of both coordinate systems near the boundary should also be the same. Now, suppose that Y is very large, \(l^2Y^2\gg 1\), such that \(1+l^2Y^2\approx l^2Y^2\). Equation (29) now becomes

$$\begin{aligned} \Phi '&\approx {P\Xi ^{-1/2} \over l^2Y^4-2M_{\mathrm{Kerr}}\Xi ^{-3/2}Y}\nonumber \\&\quad \times \sqrt{l^2Y^4-2M_{\mathrm{Kerr}}\Xi ^{-3/2}Y -a^2 l^4 Y^4 \over l^2Y^4-2M_{\mathrm{Kerr}}\Xi ^{-3/2}Y-P^2}. \end{aligned}$$
(35)

Taking the same condition for large r in Eq. (18), \(l^2r^2\gg 1\), we obtain the separation length formula for the “Boost-AdS” black hole as follows:

$$\begin{aligned} \phi '\approx {P\gamma \over l^2r^4-2M_{\mathrm{Sch}}r}\sqrt{l^2r^4-2M_{\mathrm{Sch}}r -a^2 l^4 r^4 \over l^2r^4-2M_{\mathrm{Sch}}r-P^2}. \end{aligned}$$
(36)

Here, we have identified \(\omega ^2=a^2 l^4\). Near the boundary, we can identify \(r=Y\) and compare both formulas (35) and (36). It turns out that both separation lengths can be equal if we identify

$$\begin{aligned} M_{\mathrm{Kerr}}=M_{\mathrm{Sch}}(1-a^2l^2)^{3/2}. \end{aligned}$$
(37)

We cheat a little bit on the conditions for large r and Y in the computation of separation length formula above. Since we want to keep the mass parameters in the separation formula for large r and Y, it is a necessary condition to take the mass parameters also very large such that \(2M_{\mathrm{Sch}}/r\gg 1\) and \(2M_{\mathrm{Kerr}}/Y\gg \Xi ^{3/2}\). This means that we are considering the plasma at very high temperature. Using the relation (37), we obtain the numerical plots shown in Fig. 7 in which the plots of the Kerr–AdS black hole, in Boyer–Linquist and asymptotically-AdS coordinates, are now much closer to the plot of the “Boost-AdS” black hole, which is in accordance with the physical picture as we expected before.

Fig. 7
figure 7

Plots of screening length, with fixed \(M_{\mathrm{Sch}}=\Xi ^{-3/2} M_{\mathrm{Kerr}}=30/l\), for different black holes: Schwarzschild–AdS (black), “Boost-AdS” (red), Boyer–Linquist (blue), and asymptotically-AdS (green)

Full size image

The mass relation (37) is a bit puzzling, since it was obtained near the boundary of both “Boost-AdS” black hole and Kerr–AdS black hole, in AAdS coordinates. A priori there is no relation between the radial coordinate of the “Boost-AdS” black hole and the radial coordinate of the Kerr–AdS black hole, in AAdS coordinates, near the boundary. One may ask if the mass relation (37) could also lead to the same other physical quantities of both black holes. One of the important physical quantities is the Hawking temperature, which is interpreted as temperature of the plasma at the boundary in the AdS/CFT correspondence prescription. Since the Killing vector of the metric (27) is \(k=\partial _t+\Omega _K\partial _\Phi \), where \(\Omega _K=a(1+l^2Y_K^2)Y_K^{-2}\) is the angular velocity of the black hole relative to the rotating observer at the boundary, the Hawking temperature of the Kerr–AdS black hole can be rewritten as

$$\begin{aligned} T_{\mathrm{Kerr}}={\Xi (1+2l^2Y_K^2)\sqrt{\Xi Y_K^2-a^2}-M_{\mathrm{Kerr}} \over 2\pi \Xi Y_K^2}. \end{aligned}$$
(38)

The mass parameter of the Kerr–AdS black hole is related to the event horizon by the equation \(Y_K^2\Xi ^2(1+l^2Y_K^2)-2M_{\mathrm{Kerr}}\sqrt{\Xi Y_K^2-a^2}=0\). Using the mass relation (37), that equation can be simplified to

$$\begin{aligned} l^2+{1\over Y_K^2}- {2 M_{\mathrm{Sch}} \over Y_K^3}\sqrt{1-{a^2\over \Xi Y_K^2}}=0. \end{aligned}$$
(39)

Now, recall that the event horizon of the Kerr–AdS black hole in the Boyer–Linquist coordinates is related to the event horizon of the Kerr–AdS black hole in the AAdS coordinates by \(r_K=\sqrt{\Xi Y_K^2 -a^2}\). At very high Hawking temperature, it gives the condition \(\Xi Y_K^2\gg a^2\), and thus the above equation can be approximated to

$$\begin{aligned} l^2+{1\over Y_K^2}- {2 M_{\mathrm{Sch}} \over Y_K^3}\approx 0. \end{aligned}$$
(40)

This is the same equation for the event horizon in the Schwarzschild–AdS, or “Boost-AdS”, black hole by taking both event horizons of the Schwarzschild–AdS black hole and the Kerr–AdS black hole in AAdS coordinates to be equal, \(Y_K=r_\mathrm{H}\). Furthermore, substituting the above equation into the Hawking temperature formula of the Kerr–AdS black hole at the high temperature will give us

$$\begin{aligned} T_{\mathrm{Kerr}}=\Xi ^{1/2}{1+3l^2Y_K^2 \over 4\pi Y_K}, \end{aligned}$$
(41)

which is equal to the Hawking temperature of the “Boost-AdS” black hole upon identifying \(\omega ^2= a^2 l^4\). This means that in both CFT theories of the Schwarzschild–AdS black hole and the Kerr–AdS black hole in AAdS coordinates indeed have the same temperature and hence this supports the mass relation (37).

4 Conclusion and discussion

We have computed the separation length as a function of momentum transfer and plotted it for various values of angular velocity. In the plots of Fig. 3, for each fixed \(\omega \), there is a lower bound in the momentum transfer, which is given by the drag force momentum transfer, \(P_c=\omega r_c^2\). At this value of the momentum transfer, the drag force configuration is preferred, while below this value there is no physical solution for the string configuration of the quark–antiquark pair. The appearance of this lower bound implies that not all separation lengths below its screening length are double valued, for each fixed \(\omega \ne 0\). Moreover, the separation length can be divided into two regions identified by \(P_c<P<P_{\mathrm{max}}\) and \(P\ge P_{\mathrm{max}}\), in which the latter is favored due to its Coulomb potential [7].

An interesting black dashed line shown in Fig. 3 is the plot of the bounded momentum transfer, \(P=P_c\). The profile of this plot is mimicking the profile of the separation length with its maximum “separation length” being \(L=0.104309\), at \(P_c=3.98557\), which coincides with the lower bound momentum transfer of the plot \(\omega /l\approx 0.5\). We have no physical intuition about these values and why it is so, but if we plot the normalized energy of quark–antiquark pair at angular momentum \(\omega =0.5\), as shown in Fig. 8, the separation length in the stable region is just about reaching its maximum value, or the screening length. Therefore we may say that this is the minimum angular velocity at which the stable quark–antiquark pair could reach its screening length.

Fig. 8
figure 8

The plot of total energy, for fixed \(\omega =0.5\), in which the quark–antiquark pair reaches its screening length at the tip of the plot

Full size image

Our result and analysis here can be extended to the Poincaré coordinate case, in which the angle between the separation length of the quark–antiquark pair and its velocity, or the plasma wind, can be arbitrary. In [8, 16], this angle is parametrized by the variable \(\theta \), which can take any value from \(\theta =0\) (parallel) to \(\theta =\pi /2\) (perpendicular). One can try to compare the plots of the separation length between the parallel and the perpendicular motion of the quark–antiquark pair, and ask if the perpendicular plot can be obtained from the parallel plot by shifting vertically all plots, for each fixed \(\omega \), so that the plot of bounded momentum transfer coincides with the horizontal axis, at \(L=0\). The full parallel plot, including lines below the plot of bounded momentum transfer, was computed in [22] for the five-dimensional Schwarzschild–AdS black hole in the Poincaré coordinate case. The lines below the plot of bounded momentum transfer, in [22], are related to the deformation of the plot of bounded momentum transfer for \(\theta >0\). To understand this intuitively, we can assume that there is a continuous deformation of separation length in terms of \(\theta \), still keeping the profile the same, for fixed velocity. We may then consider the plot of bounded momentum transfer in the perpendicular plot to be the point at the origin such that all plots have a lower bound in the momentum transfer at \(P=0\). We would expect to see a slow deformation of the plot of bounded momentum transfer from a point, at the origin, in the perpendicular plot to the dashed black line in the parallel plot. Decreasing \(\theta \), the plots of the separation lengths will be shifted up from its corresponding perpendicular plots. As a result, the screening length for each fixed velocity at any value of \(\theta \) is always bigger than the corresponding screening length in the perpendicular plot, except for the zero velocity plot, which is unchanged. Indeed, it was shown in [16] that, for fixed velocity, the parallel plot has a higher screening length than the perpendicular plot. However, there are no corresponding lines below the plot of bounded momentum transfer in the global coordinate case because there is no physical configuration of the quark–antiquark pair as discussed in Sect. 2, and also there is no perpendicular plot in this case.

The existence of bounded momentum transfer is a bit puzzling. One could ask if there is a continuous transformation from the quark–antiquark configuration to the drag force configuration. As one can see from Fig. 3, close to the \(P_c\), the whole separation length is below its screening length. However, at \(P=P_c\), there is a sudden jump in the distance between the quark and the antiquark of the pair. Each of them is considered to be in the drag force configuration, in which the separation length is infinite, as shown in Fig. 2, and followed by the discussion before Sect. 2.1. Fortunately, we could simply avoid this problem since this possible continuous transformation only happens in the metastable region of the plots in Fig. 3, which is not physical.

Unlike the perpendicular case, there is a drag force experienced by the quark–antiquark pair as discussed in Sect. 2.1. As shown in Fig. 3, we would expect the drag force in the metastable region to be similar to the one derived in [20] at least in the non-relativistic limit. This is likely to be true for the metastable region, but not for the stable region, because the tip of the string configuration is closer to the horizon compared to the stable region, and hence it still feels the presence of the black hole or plasma. Another reason is that the string configuration in the metastable region is also close to the drag force configuration for \(P\gtrsim P_c\). Therefore it is expected that \(P\approx \gamma ~p_\phi \), where \(\gamma \) is a constant. In the stable region, the plots in the non-relativistic limit are very dense, and thus the momentum transfer, though very large, may not depend on the angular velocity. Therefore it cannot be interpreted as a drag force.

We also computed the bounded energy density of the quark–antiquark pair. The bounded energy density is divergent at the boundary. This divergence can be removed by subtracting the individual quark and antiquark energy densities. However, it introduces a new divergence at the horizon and to resolve this problem we need to go to the reference frame of the moving quark–antiquark pair in which the background metric is a “Boost-AdS” black hole. We also found that the separation length, in the metastable region of the plots in Fig. 4, is bounded from below, which is given by a dashed line.

The necessity of going to the reference frame of the quark–antiquark pair, using the boost transformation (17), produced a “Boost-AdS” black hole. However, there is another well-known stationary solution of the AdS black hole, called a Kerr–AdS black hole. A priori there is no relation between the parameters of Kerr–AdS black hole and “Boost-AdS” black hole. In Sect. 3, we argued that yet some of these parameters are related. In particular, we computed the screening length of the static quark–antiquark pair under these black holes and compared with the previous calculation of the Schwarzschild–AdS black hole. We concluded that \(M_{\mathrm{Kerr}}=M_{\mathrm{Sch}}(1-a^2l^2)^{3/2}\) is more suitable with our physical picture especially for a very high temperature plasma. In fact, at very high temperature, \(\Xi Y^2\gg a^2\) is satisfied for any Y within the range of the radial coordinate in AAdS coordinates \(0<Y_K\le Y<\infty \). Using this, the metric of a “Boost-AdS” black hole (17) is equal to the metric of a Kerr–AdS black hole (27), provided that we identify the two radius coordinates to be the same, and that we use all relations of the black hole parameters given previously. This means that the equilibrium rotating plasma of the CFT theory is effectively the same at the equator of both metrics: “Boost-AdS” black hole (17) or the Kerr–AdS black hole (27). However, this is only valid at the equator and one could ask whether this is also valid in general for arbitrary \(\theta \)-coordinate.

Recall that transforming the four-dimensional Schwarzschild–AdS black hole, using the transformation (16), gives a metric that is still the solution of the four-dimensional Einstein equation with a negative cosmological constant, with the Hawking temperature equal to \(T_{\mathrm{Boost}}\). It would be interesting to study the thermodynamical properties of this metric compared to the Kerr–AdS black hole. If all thermodynamical properties are equal, then it is better to work in the “Boost-AdS” black hole metric rather than working in the full AAdS coordinates of the Kerr–AdS black hole, which is very complicated. If not, we would expect that there might be some coordinate transformation that depends on the \(\theta \)-coordinate, which is also a symmetry of the three-dimensional Einstein universe. Applying this to the Schwarzschild–AdS black hole might give a metric that could still be a solution of the four-dimensional Einstein equation with a negative cosmological constant. The thermodynamical properties of this metric might be comparable to the Kerr–AdS black hole, although the metric might not be simple.

In the literature, we have not found so far the relation between the mass parameter of the Schwarzschild–AdS black hole, \(M_{\mathrm{Sch}}\), and the mass parameter of the Kerr–AdS black hole, \(M_{\mathrm{Kerr}}\). A general procedure for constructing the metric of Kerr–AdS black holes in [28] is by adding the AdS metric with an additional term, scaled with the mass parameter of the Kerr–AdS black hole, in the Kerr–Schild form. In that sense the mass parameter is added by hand, and thus it has no clear direct connection with the mass parameter of Schwarzschild–AdS black hole. It would be interesting to construct the Kerr–AdS black hole directly from the Schwarzschild–AdS black hole, e.g. by following the Newman–Janis procedure [27], and then verify if the mass relation obtained in this article is satisfied.