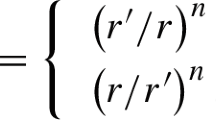1 Introduction

In the last few years the interest in alternative theories of gravity was significantly increased. Major role for this has the experimental confirmation of the accelerated expansion of the universe and the fact that it does not fit in the predictions of general relativity (GR) without the introduction of the so-called dark energy, a matter with exotic properties which interacts with the visible matter only gravitationally. A class of viable alternative theories of gravity are the so-called f(R) theories. In this case we exchange the Lagrangian of the general relativistic Einstein–Hilbert action, namely the Ricci scalar, with a more general one, a function of the Ricci scalar, hence f(R) theories [1–4]. These theories allow us to resolve the problem with the accelerating universe without the necessity of introducing such an exotic matter. However, the theory should be tested not only on cosmological but on astrophysical scales too. The predictions, concerning astrophysical effects, should be very close to the GR ones in the weak field regime, but it is expected to deviate for strong fields. As a source of strong gravitational fields neutron stars (NS) and black holes (BH) are natural laboratories for testing alternative theories of gravity. In this work we are concentrating our efforts on the former.

Future X-ray timing observatories with large collecting area like SKA [5], NICER [6], LOFT [7], and AXTAR [8] may give us a chance to test gravity in strong field regime. A promising way to do that around compact objects are the so-called quasi-periodic oscillations (QPOs). QPOs are Hz to kHz oscillations in the X-ray flux of pulsars or black hole candidates. The latter QPOs are supposed to occur only in the presence of strong gravitational fields, with their origin in the inner edge of the accretion disc, deep into the gravitational field of the star. However, the exact source of these oscillations is unknown so there are different models for their explanation. In the beat frequency models, some connection between the orbital frequency and the spin frequency of the central compact object is suggested. These models require some azimuthally non-uniform structure co-rotating with the central object. In the relativistic resonance models a resonance may occur at a particular radii of the disc at which the orbital and the epicyclic frequencies have integer ratios. It is suggested that some form of resonance may occur due to the interaction between the accretion disc and the central body too. The preferred radii models suggest that a mechanism that chooses some radii exists. The relativistic precession models, investigated in some recent papers [9–13], are based on the assumption that the QPOs are directly related to the orbital (Kepler) \(\varOmega _p\) and to the epicyclic frequencies. In the above-mentioned models all these frequencies or some of them are involved. The radial \(\nu _r\) and the vertical \(\nu _{\theta }\) epicyclic frequencies occur if a particle on a stable circular orbit is perturbed. It will start to oscillate in a radial and in a vertical direction with some stable frequencies. This frequencies are the radial and the vertical epicyclic ones. A review of these models can be found in [14]. In some papers QPOs models concerning oscillations of the accretion disk itself are examined too [15–17].

The epicyclic frequencies of rapidly rotating strange stars are examined in the recent paper [18]. Some of the above-mentioned models were examined in alternative theories of gravity through the years [12, 19–21]. The observed deviations from GR in these papers were quite low, except for the case of rapidly rotating neutron stars in scalar–tensor theories [21].

The structure of this paper is as follows: In Sect. 2 we present the basic steps for deriving the radius of the innermost stable circular orbit (ISCO), the orbital frequency and the radial and the vertical epicyclic frequencies. In Sect. 3 we present and discus the results for neutron and strange stars. The paper ends with conclusions.

2 The epicyclic frequencies of a rotating neutron star

In this section we briefly present the basic steps in the derivation of the equations for the radius of the innermost stable circular orbit (ISCO), the equations for the radial and for the vertical epicyclic frequencies and for the orbital frequency [12, 22–24]. The equations describing stable stationary neutron star models and additional mathematical details concerning \(R^2\) gravity can be found in [25–27].

We are considering a stationary and axisymmetric spacetime with a metric

$$\begin{aligned} \mathrm{d}s^2 = g _{tt}\mathrm{d}t^2 + g_{rr}\mathrm{d}r^2 + g_{\theta \theta }\mathrm{d}\theta ^2 + 2g_{t\varphi }\mathrm{d}t\mathrm{d}\varphi + g_{\varphi \varphi }\mathrm{d}\varphi ^2,\nonumber \\ \end{aligned}$$
(1)

where all the metric functions depend only on the coordinates r and \(\theta \). The massive particles subject to the gravitational force only move on timelike geodesics of the metric (1). The stationary and axial Killing symmetries of the metric, generated by the Killing vectors \(\frac{\partial }{\partial t}\) and \(\frac{\partial }{\partial \varphi }\), give rise to two constants of motion, namely \(E=-u_t\) and \(L=u_{\varphi }\). The first one corresponds to the energy per unit mass and the second one to the angular momentum along the axis of symmetry, and \(u^{\mu }={\dot{x}}^{\mu }=\mathrm{d}x^{\mu }/\mathrm{d}\tau \) is the four-velocity of the particle. It is not difficult to show that the two conservation laws can be cast in the form

$$\begin{aligned}&\frac{\mathrm{d}t}{\mathrm{d}\tau } = \frac{Eg_{\varphi \varphi } + Lg_{t\varphi }}{g2}, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\mathrm{d}\varphi }{\mathrm{d}\tau } = -\frac{Eg_{t\varphi } + Lg_{tt}}{g2}, \end{aligned}$$
(3)

where we defined \(g2 = g_{t\varphi }^2 - g_{tt}g_{\varphi \varphi }\) for simplicity. Here t denotes the coordinate time, and \(\tau \) the proper time. From the normalization condition \(g^{\mu \nu } u_{\mu }u_{\nu } = -1\), we also have

$$\begin{aligned} g_{rr}{\dot{r}}^2 + g_{\theta \theta }{\dot{\theta }}^2 + E^2U(r,\theta ) = -1 \end{aligned}$$
(4)

with

$$\begin{aligned} U(r,\theta )= \frac{g_{\varphi \varphi } + 2l g_{t\varphi } + l^2 g_{tt}}{g2} \end{aligned}$$
(5)

and \(l=L/E\) being the proper angular momentum. The derivatives in the above equations are with respect to the proper time \(\tau \).

For \(\theta =\frac{\pi }{2}\) the problem reduces to an effective one dimensional problem

$$\begin{aligned} {\dot{r}}^2 = V(r), \end{aligned}$$
(6)

with an effective potential

$$\begin{aligned} V(r)=g_{rr}^{-1}\left[ -1 - E^2 U\left( r,\theta =\frac{\pi }{2}\right) \right] . \end{aligned}$$
(7)

The stable circular orbit with a radius \({\bar{r}}\) is determined by the conditions \(V(r_c)= 0 = V^{\prime }(r_c)\) and \(V^{\prime \prime }(r_c)>0\), where with prime we denote the derivative with respect to r. The condition \(V^{\prime \prime }(r_c)=0\) gives the ISCO radius. The angular velocity \(\varOmega _p\) of a particle moving on a circular equatorial orbit can be found from the geodesic equations in the following way. We write down the geodesic equations in the form

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau }\left( g_{\mu \nu }\frac{\mathrm{d}x^\nu }{\mathrm{d}\tau }\right) = \frac{1}{2}\partial _{\mu }g_{\nu \sigma } \frac{\mathrm{d}x^\nu }{\mathrm{d}\tau } \frac{\mathrm{d}x^\sigma }{\mathrm{d}\tau }, \end{aligned}$$
(8)

which for the radial coordinate gives

$$\begin{aligned} \partial _{r}g_{tt} \left( \frac{\mathrm{d}t}{\mathrm{d}\tau }\right) ^2 + 2 \partial _{r}g_{t\varphi } \frac{\mathrm{d}t}{\mathrm{d}\tau } \frac{\mathrm{d}\varphi }{\mathrm{d}\tau } + \partial _{r}g_{\varphi \varphi }\left( \frac{\mathrm{d}\varphi }{\mathrm{d}\tau }\right) ^2=0. \end{aligned}$$
(9)

Taking into account that the angular velocity is defined by \(\varOmega _{p}=\frac{u^\varphi }{u^{t}}=\frac{\mathrm{d}\varphi }{\mathrm{d}t}\) we obtain from the above equation

$$\begin{aligned} \varOmega _p=\frac{\mathrm{d}\varphi }{\mathrm{d}t} = \frac{-\partial _{r} g_{t\varphi } \pm \sqrt{(\partial _{r}g_{t\varphi })^2 - \partial _{r}g_{tt}\partial _{r}g_{\varphi \varphi }}}{\partial _{r}g_{rr}}. \end{aligned}$$
(10)

To derive the epicyclic frequencies we should investigate small perturbations of a stable circular orbit. The perturbations are written in the form

$$\begin{aligned} r(t) = {\bar{r}} + \delta r(t), \quad \theta (t) = \frac{\pi }{2} + \delta \theta (t), \end{aligned}$$
(11)

where \(\delta r(t)\) and \(\delta \theta (t)\) are perturbations to the stable circular orbit with coordinate radius \({\bar{r}}\) in the equatorial plane. The perturbations could be written explicitly in the form \(\delta r(t) \sim \mathrm{e}^{2\pi i \nu _{r}t} \) and \(\delta \theta (t) \sim \mathrm{e}^{2\pi i \nu _{\theta }t}\). Substituting (11) in Eq. (4) and after some calculations, and a change of the proper time \(\tau \) with the coordinate one t, we obtain the expressions for the radial and the vertical epicyclic frequencies:

$$\begin{aligned}&\nu _{r}^{2} = \frac{\left( g_{tt} + \varOmega _p g_{t\varphi }\right) ^2}{2\left( 2\pi \right) ^2 g_{rr}} \partial _{r}^{2} U\left( {\bar{r}},\frac{\pi }{2}\right) , \end{aligned}$$
(12)
$$\begin{aligned}&\nu _{\theta }^{2} = \frac{\left( g_{tt} + \varOmega _p g_{t\varphi }\right) ^2}{2\left( 2\pi \right) ^2 g_{\theta \theta }} \partial _{\theta }^{2} U\left( {\bar{r}},\frac{\pi }{2}\right) . \end{aligned}$$
(13)

For the case of static neutron stars the orbital frequency and the vertical epicyclic frequency coincide, i.e. \(\nu _{\theta } = \nu _p\), for \(f = 0\), where f is the rotational frequency of the star (\(f = \frac{\varOmega }{2 \pi }\)). At the ISCO the square of the radial epicyclic frequency is equal to zero, and for smaller radius it is negative, which shows a radial instabilities for orbits with radius smaller than the ISCO.

For simple accretion disc models the inner edge of the disc is defined by the ISCO. For models with smaller masses the ISCO is in the interior of the star and for massive ones the radius of the ISCO is bigger than the radius of the star itself. The inner edge of the accretion disc, therefore, can reach down to the surface of the star in the former case and to the ISCO in the latter one.

3 Numerical results

We investigate what are the changes in the radius of the ISCO and in the orbital and epicyclic frequencies in f(R) gravity with Lagrangian \(f(R) = R + aR^2\), the so-called \(R^2 \) gravity. The results are compared to pure GR. Deviations due to rotation, in slow rotation approximation, are examined too. We consider two hadronic equations of state (EOS) and a quark one. For the hadronic EOS we are using piecewise polytropic approximation [28]. The ones we choose are APR4 and MS1. APR4 has maximal mass not much bigger than the observational limit of two solar masses (medium stiffness), and MS1 is a stiffer one with higher masses and radii. We examined a soft EOS too but the results are qualitatively the same, and, therefore, graphs are not presented. The quark EOS has the analytical form

$$\begin{aligned} p = b(\rho - \rho _0), \end{aligned}$$
(14)

where the constants b and \(\rho _0\) are taken from [29] for EOS SQS B60. This EOS leads to maximal masses slightly below two solar masses, but we find it to be a good representative.

In this section we examine static, \(f = 0\) Hz, and slowly rotating, \(f = 80\) Hz and \( f = 160\) Hz, models of neutron and strange stars. First we will discus the deviations from pure GR due to \(R^2\) gravity and as a next step we will examine the differences of the results for different rotational frequencies. The presented results in all figures are up to the maximal mass. For the presented results in \(R^2\) gravity, the maximal deviation from GR is for the maximal adopted value of the parameter \(a = 10^4\). This number is close to the maximal values allowed by the observations \(a \sim 10^5\) or in dimensional units—\(a \lesssim 5 \times 10^{11}~\hbox {m}^2\) [30].

In Fig. 1 sequences of models, representing the radius of the ISCO as a function of the stellar mass are plotted. A wide range of values for the parameter a is examined. In the left panel the results for EOS APR4 are plotted, in the middle one for EOS MS1, and in the right one for EOS SQS B60. If the ISCO is in the interior of the star, which happens for models with low masses, we are plotting the radius of the star instead. The points in the different sequences of models, where the radius of the ISCO gets equal to the radius of the star are marked with an asterisk. For all examined EOS the results are qualitatively the same. For models with maximal masses the largest deviation is for the maximal values of the parameter a. It is around 10 % and decreases with the decrease of a. In the limiting case of \(a \rightarrow 0 \) the solutions converge to the GR ones.

Fig. 1
figure 1

The radius of the ISCO in km as a function of the stellar mass for different values of the parameter a. In the left panel the results for EOS APR4 are plotted, in the middle one for EOS MS1, and in the right one for SQS B60. The results are for static neutron stars \((f = 0~\hbox {Hz})\)

Full size image

At this point a comment concerning the presented results should be made. In Fig. 1, in the present paper, the following behavior for the models for which the radius of the ISCO gets bigger than the radius of the star can be observed. Let us start the discussion with the models marked with an asterisk. For small values of the parameter a they have smaller radius and lower mass than the GR case. The \(a = 10\) models have parameters which are close to the GR ones and for high values of a the radii and the masses are higher compared to the GR case. When the ISCO is outside the star its radius is bigger compared to the GR case for models with equal masses and small values of a. For \(a = 10\) the results are comparable to the GR ones. For bigger values of a the radius of the ISCO is smaller than the GR one. The explanation of this behavior we find in the non-monotonous behavior of some stellar parameters as a function of a. This is demonstrated, for example, in Fig. 3 in [25] for the maximal mass. It was shown that for small values of a the mass decreases compared the GR one. At some value of the parameter a there is a turning point and the mass starts to increase, reaching maximal masses higher than the GR one. Our investigations show that this is the case for neutron stars as well as for strange stars. Such a behavior can be observed also for other stellar parameters, although in the different cases the minimum will be shifted to some other values of the parameter a. If one, for example, calculates the mass and the radius for models with fixed central energy density in GR and in \(R^2\) gravity, the same pattern can be found. It is not hard to see that there is a similar dependence for the models marked with an asterisk as well as for the case when the ISCO is outside the star. This leads us to the conclusion that this behavior is characteristic one for the theory. Naturally, similar patterns can be found in the other graphs presented below.

In Fig. 2 we plot the orbital frequency \(\nu _p = \varOmega _p/2\pi \), in kHz, at the ISCO as a function of the stellar mass. If the ISCO is in the interior of the star, we calculated \(\nu _p\) at the surface of the star. For all EOS we see qualitatively the same results. The deviations from GR for models with \(a = 10^4\) is in average around 15 % and it does not change significantly with the mass. For models with small value of a the deviation from GR, when the radius of the ISCO get bigger than the radius of the star, is close to the maximal one, but it rapidly decreases with the increase of the mass and converges to GR for maximal masses.

Fig. 2
figure 2

The orbital frequency of a particle on a circular orbit in kHz as a function of the mass of the star for different values of the parameter a. In the left panel the results for EOS APR4 are plotted, in the middle one for EOS MS1, and in the right one for SQS B60. The results are for static neutron stars (\(f = 0\) Hz)

Full size image

In Fig. 3 we plot the maximal value of the radial epicyclic frequency, in kHz, as a function of the stellar mass. If the ISCO is in the interior of the star, we take the maximal value on the surface or outside the star. In the examined interval of masses the frequency monotonically decreases. For higher values of the parameter a the maximal radial epicyclic frequency is higher, compared to the GR one. For small values of a the frequencies are lower than the GR ones. For smaller masses there are higher deviations, but for maximal masses the plots converge to GR.

Fig. 3
figure 3

The maximal value of the radial epicyclic frequency in kHz as a function of the stellar mass for different values of the parameter a. In the left panel the results for EOS APR4 are plotted, in the middle one for EOS MS1, and in the right one for SQS B60. The results are for static neutron stars (\(f = 0\) Hz)

Full size image

The deviations due to rotation are qualitatively and quantitatively the same for the hadronic and for the quark EOS. This, combined with the small magnitude of the deviations, is the reason why we choose to include only the favored by the observations hadronic EOS in the following graphs.

Fig. 4
figure 4

The difference between the orbital and the vertical epicyclic frequency at the ISCO. The plots are for different rotational rates for GR and for \(R^2\) gravity with \(a = 0.3\) and \(a = 10^4\). ln the left panel the results for EOS APR4 are plotted, and in the right one for EOS MS1

Full size image

In Fig. 4 we plot the difference between the orbital frequency \(\nu _p\) and the vertical epicyclic frequency \(\nu _{\theta }\), i.e. the nodal precession frequency \(\nu _n\), as a function of the mass. In the left panel we plot the results for EOS APR4 and in the right panel for EOS MS1. The plots are for three different rotational rates: \(f = 0 \) Hz (the static case), \(f = 80\) Hz, and \(f = 160\) Hz. In black continuous lines are the results for GR, and in color dashed line the results for \(a = 0.3\) and \(a = 10^4\). As we said before, \(\nu _p \) and \( \nu _{\theta }\) coincide in the static case. With the increase of the rotational frequency of the star the differences between the two frequencies increase. The difference is calculated on the surface of the star if the ISCO is inside the star, and at the ISCO in the opposite case. The transition models are marked with asterisks, in consistence with the previous graphs. The nodal precession frequency tends to decrease with the increase of the mass for models having ISCO in the interior of the star. It increases with the increase of the mass for models having ISCO outside the star. In the case of \(R^2\) gravity we plot the results for \(a = 10^4\) and \(a = 0.3\). The former value of the parameter gives the maximal deviation from GR, and the latter we choose because of the interesting behavior demonstrated in the graphs above. If the ISCO is in the interior of the star, the results are the same for all rotational rates. In the opposite case, when the ISCO is outside the star, the behavior is the following. For \(a = 0.3\), \(\nu _n\) is slightly higher than the GR case, and rapidly converge to GR with the increase of the mass. For \(a = 10^4\), \(\nu _n\) has lower values than the GR one. The deviation from GR is more or less constant with the increase of the mass, and it is about 4 %.

Fig. 5
figure 5

The radius of the ISCO, in km, as a function of the stellar mass. The plots are for GR and for \(R^2\) gravity with \(a = 10^4\) and for stars rotating with \(f = 0\) Hz, \(f = 80\) Hz, and \(f = 160 \) Hz. In the left panel the results for EOS APR4 are plotted, and in the right one for EOS MS1

Full size image
Fig. 6
figure 6

The orbital frequency at the ISCO, in kHz, as a function of the stellar mass. The plots are for GR and for \(R^2\) gravity with \(a = 10^4\) for stars rotating with \(f = 0\) Hz, \(f = 80\) Hz, and \(f = 160 \) Hz. In the left panel the results for EOS APR4 are plotted, and in the right one for EOS MS1

Full size image
Fig. 7
figure 7

The maximal radial epicyclic frequency as a function of the stellar mass. The plots are for GR and for \(R^2\) gravity with \(a = 10^4\) for stars rotating with \(f = 0\) Hz, \(f = 80\) Hz, and \(f = 160 \) Hz. In the left panel the results for EOS APR4 are plotted, and in the right one for EOS MS1

Full size image

In Figs. 5, 6, and 7 we plot the radius of the ISCO, the orbital frequency and the maximal radial epicyclic frequency as a function of the mass in the case of GR and the maximal deviation in \(R^2\) gravity (\(a = 10^4\)) for the aforementioned values of f. The rotation have the same effect for all these quantities in GR and in \(R^2\) gravity. The reason why we are skipping the interestingly behaving case of \(a=0.3\) is the following. The changes of the ISCO and the examined frequencies for different rotational rates causes the graphs for \(a = 0.3\) and \(a = 1\) to overlap with the GR ones. We find that case to be quite uninformative so only the maximal deviation is presented, namely \(a = 10^4\). Due to rotation the radius of the ISCO decreases with about 4 %, and the frequencies increase with the same magnitude. The percentage deviations are the same for GR and for \(R^2\) gravity.

4 Conclusions

In this paper we examine the orbital and the epicyclic frequencies of particles moving in circular orbits around neutron and strange stars. Various models relate all these frequencies or some of them to QPOs. Taking into consideration the new generation observatories for timing of X-ray pulsars with large collective area which are under construction now, QPOs are expected to play a major role in testing the strong field regime of gravity.

\( R^2\) gravity is a viable alternative to GR. We examined how changing the parameter of the theory effects the radius of the ISCO, the orbital and the epicyclic frequencies. Most of the observed neutron stars are slowly rotating, so we concentrated our efforts on the static and slowly rotating solutions. We investigated the deviations of the slow rotating solutions from the static case too.

We concerned two hadronic and one quark equations of state and for both cases we observed qualitatively the same behavior with the change of the parameter of the theory. The largest deviations from GR occurs for the maximal adopted value of the parameter a. The radius of the ISCO decreases with about 10 % and the orbital and the maximal radial epicyclic frequencies increases with 15–20 %. However, the effect due to slow rotation is expectedly small. For the highest examined rotational frequency (\(f = 160\) Hz) the deviation from the static case is about 4 % for all examined quantities.

The deviations for slowly rotating stars, up to 160 Hz, are much smaller than the deviations due to the \(R^2\) gravity. Because of that static theoretical and numerical models can be used for comparison with observational data even for slowly rotating stars.

The frequencies examined in this paper provide us with an opportunity to test GR in strong field regime, as well as alternative theories. Results from the numerical models could be compared to the observational data expected from the new generation X-Ray timing observatories. However, even if the observational data do not provide a concrete information about the correct gravitational theory, it will provide us with an unique opportunity to restrict the wide range of possible values for the free parameter of the theory.