Thermodynamics of charged rotating dilaton black branes with power-law Maxwell field

Abstract

In this paper, we construct a new class of charged rotating dilaton black brane solutions, with a complete set of rotation parameters, which is coupled to a nonlinear Maxwell field. The Lagrangian of the matter field has the form of the power-law Maxwell field. We study the causal structure of the spacetime and its physical properties in ample details. We also compute thermodynamic and conserved quantities of the spacetime, such as the temperature, entropy, mass, charge, and angular momentum. We find a Smarr-formula for the mass and verify the validity of the first law of thermodynamics on the black brane horizon. Finally, we investigate the thermal stability of solutions in both the canonical and the grand-canonical ensembles and disclose the effects of dilaton field and nonlinearity of the Maxwell field on the thermal stability of the solutions. We find that, for $\alpha \le 1$, charged rotating black brane solutions are thermally stable independent of the values of the other parameters. For $\alpha >1$, the solutions can encounter an unstable phase depending on the metric parameters.

1 Introduction

Historically, the presence of a scalar field in the context of general relativity dates back to Kaluza–Klein theory [1–3]. Kaluza–Klein theory was presented in order to give a unified theory describing gravity and electromagnetic. It may be considered as a pioneering theory from the viewpoint of string theory. Afterwards, in Brans–Dicke (BD) theory, the notion was seriously taken into account [4]. The root of this theory can be traced back to Mach’s principle encoded by a varying gravitational constant in BD theory. The variability of the gravitational constant is indicated in this theory by considering a scalar field nonminimally coupled to gravity. BD theory is known as a nonquantum scalar-tensor theory [5]. From a quantum viewpoint, the scalar field called the dilaton field emerged in the low energy limit of string theory [6].

On the other side, there is strong evidence on the observational side that our Universe is currently experiencing a phase of accelerating expansion [7–13]. This acceleration phase cannot be explained through the standard model of cosmology, which is based on the Einstein theory of general relativity. One way of explanation of such an acceleration is to add a new unknown component of the energy, usually called “dark energy”. Another way is to modify the Einstein theory of gravity. In this regard, some physicists have become convinced that the Einstein theory of gravitation cannot give a complete description of what really occurs in our Universe and one needs an alternative theory. As we mentioned above, string theory, in its low energy limit, suggests a scalar field which is nonminimally coupled to gravity and other fields, called the dilaton field [6]. Consequently, dilaton gravity as one of the alternatives of Einstein theory has encountered much interest in recent years. String theory also suggests the dimensions of spacetime to be higher than four dimensions. It seemed for a while that dimensions higher than four should be of Planck scale, but recent theories express that our three-dimensional brane can be embedded in a relatively large higher-dimensional bulk, which is still unobservable [14–17]. In such a scenario, all gravitational objects including black objects are higher dimensional. The action of dilaton gravity usually includes one or more Liouville-type potentials, which can be justified as a trace of supersymmetry breaking of spacetime in ten dimensions.

Many authors have explored exact charged black solutions in the context of Einstein dilaton gravity. For instance, asymptotically flat black hole solutions in the absence of the dilaton potential were studied in Refs. [18–27]. In recent years, AdS/CFT correspondence have made asymptotically nonflat solutions more valuable. On the other hand, the study of asymptotically nonflat and non-AdS solutions extends the validity range of tools already applied and tested in the cases of asymptotically flat or AdS spacetimes. Many efforts have been made to find and study static and rotating nonflat exact solutions in the literature. Static asymptotically nonflat and non-AdS solutions and their thermodynamics were explored in [24–37]. Different aspects of exact rotating nonflat solutions have also been studied in [38–48].

In the present paper we extend the study on the dilaton gravity to include the power-law Maxwell field term in the action. The motivation for this study comes from the fact that, as in the case of the scalar field, it has been shown that a particular power of the massless Klein–Gordon Lagrangian shows conformal invariance in arbitrary dimensions [49], and one can have a conformally electrodynamic Lagrangian in higher dimensions. It is worth mentioning that the Maxwell Lagrangian, $F_{\mu \nu }F^{\mu \nu }$, is conformally invariant only in four dimensions, while it was shown that the Lagrangian $(F_{\mu \nu }F^{\mu \nu })^{(n+1)/4}$ is conformally invariant in $(n+1)$-dimensions [49]. In other words, this Lagrangian is invariant under the conformal transformation $g_{\mu \nu }\rightarrow \Omega ^{2}g_{\mu \nu }$ and $A_{\mu }\rightarrow A_{\mu }$. The studies on the black object solutions coupled to a conformally invariant Maxwell field have got a lot of attention in the past decades [50–61]. The thermodynamics of higher-dimensional Ricci flat rotating black branes with a conformally invariant power-law Maxwell source in the absence of a dilaton field was studied in [60]. Recently, we explored exact topological black hole solutions in the presence of a nonlinear power-law Maxwell source as well as a dilaton field [61]. Since these solutions [61] are static, it is worthwhile to construct the rotating version of the solutions. Charged rotating dilaton black branes in dilaton gravity and their thermodynamics in the presence of a linear Maxwell field and nonlinear Born–Infeld electrodynamics have been studied in [48] and [62], respectively. Till now, charged rotating dilaton black objects coupled to a power-law Maxwell field have not been constructed. In this paper, we intend to construct a new class of $(n+1)$-dimensional rotating dilaton black branes in the presence of power-law Maxwell field, where we relax the conformally invariant issue for generality. Of course, the solutions do exist for the case of a conformally invariant source. We find that the solutions exist provided one takes Liouville-type potentials with two terms. In the limiting case of the Maxwell field, one of the Liouville potentials vanishes. We shall investigate the thermodynamics as well as the thermal stability of our rotating black brane solutions and explore the effects of the dilaton and power-law Maxwell fields on the thermodynamics and thermal stability of these black branes.

The outline of this paper is as follows. In the next section, we present the basic field equations of Einstein dilaton gravity with a power-law Maxwell field and find a new class of charged rotating black brane solutions of this theory and investigate their properties. In Sect. 3, we obtain the conserved and thermodynamic quantities of the solutions and verify the validity of the first law of black hole thermodynamics. In Sect. 4, we study the thermal stability of the solutions in both canonical and grand-canonical ensembles. We finish our paper with closing remarks in the last section.

2 Field equations and rotating solutions

We consider an $(n+1)$-dimensional ($n\ge 3$) action of Einstein gravity which is coupled to dilaton and power-law Maxwell field,

$$\begin{aligned} I= & {} -\frac{1}{16\pi }\int _{{\mathcal {M}}}\mathrm{d}^{n+1}x\sqrt{-g}\left\{ {\mathcal {R}} -\frac{4}{n-1}(\nabla \Phi )^{2}-V(\Phi )\right. \nonumber \\&\left. +\,( -\mathrm{e}^{-4\alpha \Phi /(n-1)}{\mathcal {F}}) ^{p}\right\} -\frac{1}{8\pi }\int _{\partial {\mathcal {M}}}\mathrm{d}^{n}x\sqrt{-\gamma }\Theta (\gamma ),\nonumber \\ \end{aligned}$$

(1)

where ${\mathcal {R}}$ is the Ricci scalar, $\Phi$ is the dilaton field and $V(\Phi )$ is the dilaton potential. Here ${\mathcal {F}}=F^{\mu \nu }F_{\mu \nu }$ where $F_{\mu \nu }=\partial _{[\mu }A_{\nu ]}$ is the electromagnetic field tensor and $A_{\mu }$ is the electromagnetic potential, while p and $\alpha$ are two constants that determine nonlinearity of electromagnetic field and coupling strength of the dilaton and electromagnetic fields, respectively. The well-known Einstein–Maxwell dilaton theory corresponds to the case $p=1$. The last term in (1) is the Gibbons–Hawking boundary term, which is added to the action in order to make the variational principle well defined. We denote the metric of manifold ${\mathcal {M}}$ by $g_{\mu \nu }$, with covariant derivative $\nabla _{\mu }$. The metric of the boundary $\partial {\mathcal {M}}$ is $\gamma _{ab}$ and $\Theta =\gamma _{ab}\Theta ^{ab}$ is the trace of the extrinsic curvature of the boundary $\Theta ^{ab}$. By varying the action (1) with respect to the gravitational field $g_{\mu \nu }$, the dilaton field $\Phi$, and the gauge field $A_{\mu }$, one can obtain the equations of motion as

$$\begin{aligned}&{\mathcal {R}}_{\mu \nu }=g_{\mu \nu }\left\{ \frac{V(\Phi )}{n-1}+ \frac{(2p-1)}{n-1}(-{\mathcal {F}}\mathrm{e}^{-4\alpha \Phi /(n-1)})^{p}\right\} \nonumber \\&\qquad \qquad +\frac{4\left( \partial _{\mu }\Phi \partial _{\nu }\Phi \right) }{n-1}+2pe^{- {4\alpha p\Phi }/({n-1})}(-{\mathcal {F}})^{p-1}F_{\mu \lambda }F_{\nu }^{\ \lambda }, \nonumber \\ \end{aligned}$$

(2)

$$\begin{aligned}&\nabla ^{2}\Phi =\frac{n-1}{8}\frac{\partial V}{\partial \Phi }+\frac{ p\alpha }{2}\mathrm{e}^{-{4\alpha p\Phi }/({n-1})}(-{\mathcal {F}})^{p}, \end{aligned}$$

(3)

$$\begin{aligned}&\nabla _{\mu }(\mathrm{e}^{-{4\alpha p\Phi }/({n-1})}(-{\mathcal {F}} )^{p-1}F^{\mu \nu })=0. \end{aligned}$$

(4)

Here we seek higher-dimensional rotating solutions of the field equations (2)–(4). We know that the rotation group in $(n+1)$-dimensions is SO(n). Thus the number of independent rotation parameters for a localized object is $k\equiv [n/2]$ where [x] is the integer part of x. Note that k is equal to number of Casimir operators. Therefore, the metric of a $(n+1)$-dimensional rotating solution with cylindrical or toroidal horizons and complete set of rotation parameters can be written as [63]

$$\begin{aligned} \mathrm{d}s^{2}= & {} -f(r)\left( \Xi \mathrm{d}t-{{\sum _{i=1}^{k}}}a_{i}\mathrm{d}\phi _{i}\right) ^{2}\nonumber \\&+\frac{r^{2}}{l^{4}}R^{2}(r){{\sum _{i=1}^{k}}}(a_{i}\mathrm{d}t-\Xi l^{2}\mathrm{d}\phi _{i})^{2} \nonumber \\&-\frac{r^{2}}{l^{2}}R^{2}(r){\sum _{i<j}^{k}}(a_{i}\mathrm{d}\phi _{j}-a_{j}\mathrm{d}\phi _{i})^{2}+\frac{\mathrm{d}r^{2}}{f(r)}+\frac{r^{2}}{l^{2}}R^{2}(r)\mathrm{d}X^{2}, \nonumber \\ \Xi ^{2}= & {} 1+\sum _{i=1}^{k}\frac{a_{i}^{2}}{l^{2}}, \end{aligned}$$

(5)

where the $a_{i}$ are k rotation parameters and l has the dimension of length, which is related to the cosmological constant $\Lambda$ for the case of Liouville-type potential with constant $\Phi$. The angular coordinates are in the range $0\le \phi _{i}\le 2\pi$ and $\mathrm{d}X^{2}$ is the Euclidean metric on the $(n-k-1)$-dimensional submanifold with volume $\Sigma _{n-k-1}$. Integrating the Maxwell equation (4) leads to

$$\begin{aligned} F_{tr}=\frac{q\Xi \mathrm{e}^{{{\frac{4\alpha \,p\Phi (r) }{(n-1) ( 2\,p-1)}}}}}{( rR)^{{\frac{n-1}{2\,p-1}} }},\quad F_{\phi _{i}r}=-\frac{a_{i}}{\Xi }F_{tr}, \end{aligned}$$

(6)

where q is an integration constant related to the electric charge of the brane. Substituting (5) and (6) in the field equations (2) and (3), we find the following differential equations:

$$\begin{aligned}&-\frac{{\Xi }^{2}f^{\prime \prime }}{2}-\frac{(n-1) }{2}\left( {\frac{f^{\prime }R^{\prime }}{R}}+{\frac{f^{\prime }}{r}}\right) \nonumber \\&\quad +( {\Xi }^{2}-1) \left[ {\frac{2(n-1) fR^{\prime }}{rR}+} ( n-2) \left( {\frac{f}{{r}^{2}}}+{\frac{fR^{\prime 2}}{R^{2}}} \right) \right. \nonumber \\&\quad \left. -\,\frac{(n-3)}{2}\left( {\frac{f^{\prime }R^{\prime }}{R}}+{\frac{f^{\prime }}{r}}\right) +{\frac{fR^{\prime \prime } }{R}}\right] -{\frac{V(\Phi )}{n-1}}\nonumber \\&\quad -\frac{{2}^{p}{q}^{2\,p}\mathrm{e}^{{\,{\frac{ 4\alpha \,p\Phi }{(n-1) (2\,p-1)}}}}}{\left( rR\right) ^{{\frac{2p\left( n-1\right) }{2\,p-1}}}}\left( {\frac{2p-1}{n-1}} -p{\Xi }^{2}\right) =0, \end{aligned}$$

(7)

$$\begin{aligned}&-{\frac{f^{\prime \prime }}{2}}-\,{\frac{\left( n-1\right) f^{\prime }R^{\prime }}{2R}}-\,{\frac{\left( n-1\right) f^{\prime }}{2r}}-{\frac{ 4f\Phi ^{\prime 2}}{n-1}}\nonumber \\&\quad -{\frac{2\left( n-1\right) fR^{\prime }}{rR}}-{ \frac{\left( n-1\right) fR^{\prime \prime }}{R}}-{\frac{V(\Phi )}{n-1}} \nonumber \\&\quad \left. +\frac{{2}^{p}{q}^{2\,p}\mathrm{e}^{{{\frac{4\alpha \,p\Phi }{\left( n-1\right) \left( 2\,p-1\right) }}}}}{\left( rR\right) ^{{ \frac{2p\left( n-1\right) }{2\,p-1}}}}\left( {\frac{1+p\left( n-3\right) }{ n-1}}\right) =0,\right. \end{aligned}$$

(8)

$$\begin{aligned}&{\frac{f^{\prime \prime }}{2}}-\,{\frac{2\left( n-1\right) fR^{\prime }}{rR}} -{\frac{fR^{\prime \prime }}{R}}+\frac{n-3}{2}\,\left( {\frac{f^{\prime }}{r} }+{\frac{R^{\prime }f^{\prime }}{R}}\right) \nonumber \\&\quad -\left( n-2\right) \left( {\frac{ f}{{r}^{2}}}+{\frac{fR^{\prime 2}}{R^{2}}}\right) -\frac{{2}^{p}p{q}^{2\,p}\mathrm{e}^{ {{\frac{4\alpha \,p\Phi }{\left( n-1\right) \left( 2\,p-1\right) }}}}}{ \left( rR\right) ^{{\frac{2p\left( n-1\right) }{2\,p-1}}}}=0,\nonumber \\\end{aligned}$$

(9)

$$\begin{aligned}&{\frac{a_{i}^{2}f^{\prime \prime }}{2{l}^{2}}+}\left( 1+{\frac{a_{i}^{2}}{{ l}^{2}}}\right) \left[ -2\,\left( n-1\right) \frac{fR^{\prime }}{{r}R}-\frac{ fR^{\prime \prime }}{R}\right. \nonumber \\&\quad \left. -\left( n-2\right) \left( \frac{f}{{r}^{2}}+\frac{ fR^{\prime 2}}{R^{2}}\right) \right] +\left( \frac{\,\left( n-3\right) a_{i}^{2}}{2{l}^{2} }-1\right) \nonumber \\&\quad \times \left( {\frac{f^{\prime }}{r}}+{\frac{R^{\prime }f^{\prime }}{R}} \right) -{\frac{V(\Phi )}{n-1}}\nonumber \\&\quad -\frac{{2}^{p}{q}^{2\,p}\mathrm{e}^{{{\frac{4\alpha \,p\Phi }{\left( n-1\right) \left( 2\,p-1\right) }}}}}{\left( rR\right) ^{{ \frac{2p\left( n-1\right) }{2\,p-1}}}}\left( {\frac{2p-1}{n-1}}+{\frac{ pa_{i}^{2}}{{l}^{2}}}\right) =0, \end{aligned}$$

(10)

$$\begin{aligned}&-\left( n-2\right) f\left( \frac{1}{{r}^{2}}+{\frac{R^{\prime 2}}{R^{2}}} \right) -{\frac{2\left( n-1\right) fR^{\prime }}{rR}}-{\frac{f^{\prime }}{r}}\nonumber \\&\quad -{\frac{R^{\prime }f^{\prime }}{R}}-{\frac{fR^{\prime \prime }}{R}} -{\frac{V(\Phi )}{n-1}}\nonumber \\&\quad -\frac{{2}^{p}{q}^{2\,p}\mathrm{e}^{{{\frac{4\alpha \,p\Phi }{\left( n-1\right) \left( 2\,p-1\right) }}}}}{\left( rR\right) ^{{\frac{2p\left( n-1\right) }{2\,p-1}}}}\left( {\frac{2p-1}{n-1}}\right) =0,\end{aligned}$$

(11)

$$\begin{aligned}&f\Phi ^{\prime \prime }+\left( n-1\right) f\Phi ^{\prime }\left( \frac{1}{r}+ {\frac{R^{\prime }}{R}}\right) +f^{\prime }\Phi ^{\prime }-\frac{\left( n-1\right) }{8}\frac{\mathrm{d}V(\Phi )}{\mathrm{d}\Phi }\nonumber \\&\quad -\frac{{2}^{p-1}p\alpha \,{q}^{2\,p}\mathrm{e}^{ {{\frac{4\alpha \,p\Phi }{\left( n-1\right) \left( 2\,p-1\right) }}}}}{ \left( rR\right) ^{{\frac{2p\left( n-1\right) }{2\,p-1}}}}=0,\end{aligned}$$

(12)

$$\begin{aligned}&{\frac{f^{\prime \prime }}{2}}-\left( n-2\right) f\left( \frac{1}{{r}^{2}}+{ \frac{R^{\prime 2}}{R^{2}}}\right) +\frac{\,\left( n-3\right) }{2}\left( { \frac{f^{\prime }}{r}}+{\frac{R^{\prime }f^{\prime }}{R}}\right) \nonumber \\&\quad -{\frac{fR^{\prime \prime }}{R}}-{\frac{2\left( n-1\right) fR^{\prime }}{rR}}-\frac{{ 2}^{p}p{q}^{2\,p}\mathrm{e}^{{{\frac{4\alpha \,p\Phi }{\left( n-1\right) \left( 2\,p-1\right) }}}}}{\left( rR\right) ^{{\frac{2p\left( n-1\right) }{2\,p-1}}} }=0, \nonumber \\ \end{aligned}$$

(13)

where the prime denotes the derivative with respect to r. In order to construct exact rotating solutions of the theory given by action (1), the functions f(r), R(r), and $\Phi (r)$ should be determined so that the system of Eqs. (7)–(13) are satisfied. To do that, we make the ansatz [48]

$$\begin{aligned} R(r)=\mathrm{e}^{2\alpha \Phi (r)/(n-1)} \end{aligned}$$

(14)

and take the potential of the Liouville-type with two terms, namely

$$\begin{aligned} V(\Phi )=2\,\Lambda _{1}\mathrm{e}^{{2\zeta _{1}\,\Phi }}+2\,\Lambda \mathrm{e}^{{2\zeta _{2}\,\Phi }}, \end{aligned}$$

(15)

where $\Lambda _{1}$, $\Lambda$, $\zeta _{1}$, and $\zeta _{2}$ are constants. Using (14) and (15), one can easily show that Eqs. (7)–(13) have solutions of the form

$$\begin{aligned} f(r)= & {} -\frac{2\Lambda {b}^{2\gamma }(1+\alpha ^{2})^{2}{r}^{2(1-\gamma )}}{ \left( n-1\right) \left( n-{\alpha }^{2}\right) }-\frac{m}{{r} ^{(n-1)(1-\gamma )-1}}\nonumber \\&+\frac{2^{p}p(1+\alpha ^{2})\left( 2p-1\right) {q} ^{2\,p}\,}{\Pi \Upsilon {b}^{{2\left( n-2\right) p\gamma /}\left( 2\,p-1\right) }{r}^{\Upsilon +(n-1)(1-\gamma )-1}}, \end{aligned}$$

(16)

$$\begin{aligned} \Phi (r)= & {} \frac{(n-1)\alpha }{2(1+\alpha ^{2})}\ln \left( \frac{b}{r}\right) , \end{aligned}$$

(17)

where b and m are arbitrary constants, $\gamma =\alpha ^{2}/(\alpha ^{2}+1)$, $\Upsilon =(n-2p+\alpha ^{2})/(2p-1)(1+\alpha ^{2})$, and $\Pi =\alpha ^{2}+( n-1-{\alpha }^{2}) p$. The above solutions will fully satisfy the system of equations, provided

$$\begin{aligned}&\zeta _{1}={\frac{2p\left( n-1+{\alpha }^{2}\right) }{\left( n-1\right) \left( 2\,p-1\right) \alpha }},\quad \zeta _{2}={\frac{2\alpha }{n-1}}, \\&\Lambda _{1}=\frac{2^{p-1}\left( 2\,p-1\right) \left( p-1\right) {\alpha }^{2}\,{q}^{2\,p}}{\Pi {b}^{{\frac{2\left( n-1\right) p}{ 2\,p-1}}}}. \end{aligned}$$

It is worthwhile to note that the necessity of the existence of the term $2\Lambda _{1}\mathrm{e}^{2\zeta _{1}\,\Phi }$ in the scalar field potential is due to the nonlinearity of the Maxwell field and this term vanishes for the case of a linear Maxwell field where $p=1$ [48]. Note that in our solutions $\Lambda$ remains as a free parameter which plays the role of the cosmological constant. Another thing to notice is that, although these rotating solutions are locally the same as those found in [61] with flat horizon ($k=0$), they are not the same globally. One may also note that in the particular case $p=1$ these solutions reduce to the $(n+1)$-dimensional charged rotating dilaton black branes presented in [48]. The parameter m in Eq. (16) is the integration constant, which is known as the geometrical mass and can be written in terms of the radius of the horizon as

$$\begin{aligned} m(r_{+})= & {} \frac{2^{p}p\,\left( 2p-1\right) {q}^{2\,p}}{(1-\gamma )\Upsilon \Pi {b}^{{2\left( n-2\right) \gamma p/}\left( 2\,p-1\right) }{r} _{+}^{\Upsilon }}\nonumber \\&+\frac{{b}^{2\gamma \,}n{r}_{+}^{(1-\gamma )({n+1)-1}}}{ l^{2}(1-\gamma )^{2}(n-{\alpha }^{2})}, \end{aligned}$$

(18)

where $r_{+}$ is the positive real root of $f(r_{+})=0$. One can easily show that the vector potential $A_{\mu }$ corresponding to the electromagnetic tensor (6) can be written as

$$\begin{aligned} A_{\mu }=\frac{q{b}^{{\frac{\left( 2\,p+1-n\right) \gamma }{\left( 2\,p-1\right) }}}}{\Upsilon {r}^{\Upsilon }}(\Xi \delta _{\mu }^{t}-a_{i}\delta _{\mu }^{i}) \quad (\text {no sum on }i). \end{aligned}$$

(19)

Here we pause to make some remarks about the value of $A_{\mu }$ at infinity applying some restrictions on the value of p and $\alpha$. This discussion is given here because it is necessary to know these restrictions for the following studies. In Sect. 3, we will show that the mass of solutions is dependent on the value of $A_{\mu }$ at infinity. Thus, the value of electromagnetic vector potential should be finite at infinity, so that we have finite mass. In order to guarantee this behavior $\Upsilon$ should be positive i.e.

$$\begin{aligned} \frac{{n-2p+}\alpha ^{2}}{({2p-1)(1+}\alpha ^{2})}>0. \end{aligned}$$

(20)

The above equation leads to the following restriction on the range of p:

$$\begin{aligned} \frac{1}{2}<p<\frac{n+\alpha ^{2}}{2}. \end{aligned}$$

(21)

On the other hand, the effect of m in the metric function should vanish at spatial infinity. This fact leads to a restriction on $\alpha$,

$$\begin{aligned} \alpha ^{2}<n-2. \end{aligned}$$

(22)

Therefore, one can sum up the constraints (21) and (22) as follows:

$$\begin{aligned}&\text {for }\frac{1}{2}<p<\frac{n}{2},\quad 0\le \alpha ^{2}<n-2, \end{aligned}$$

(23)

$$\begin{aligned}&\text {for }\frac{n}{2}<p<n-1,\quad 2p-n<\alpha ^{2}<n-2. \end{aligned}$$

(24)

It is worth mentioning that the solution is always well defined in the above allowed ranges of $\alpha$ and p. To continue this section we discuss the properties and asymptotic behaviors of the solutions in the allowed ranges of p and $\alpha$.

2.1 Asymptotic behaviors and properties of the solutions

Now, by considering the restrictions (23) and (24) on p and $\alpha$, we are ready to discuss the behavior of our solutions both in the vicinity of $r=0$ and infinity. First, one should note that in the allowed ranges of p and $\alpha$, the charge term in the metric function disappears at infinity as the mass term does. This behavior is also seen in the special cases of $p=1$ or $\alpha =0$. Therefore, the first term in f(r) (16) determines the behavior of it at infinity. Since we are interested in the solutions that go to infinity as $r\rightarrow \infty$, we assume $\Lambda <0$ and take it in the standard form $\Lambda =-n(n-1)/2l^{2}$. It is also notable that the spacetime is neither asymptotically flat nor AdS due to the existence of a dilaton field. About $r=0$, the term including q in the metric function is dominant. This term is always positive in the permitted ranges of p and $\alpha$ because $\Pi ,\Upsilon >0$ in these ranges. Therefore as in the case of Reissner–Nordstrom black holes, we have a timelike singularity and there are no Schwarzschild-type black hole solutions.

We continue our discussions as regards the properties of the solutions by looking for curvature singularities. Since essential singularities are located at divergencies of the Kretschmann scalar, we seek these for our solutions. It is easy to show that the Kretschmann scalar $R_{\mu \nu \lambda \kappa }R^{\mu \nu \lambda \kappa }$ diverges at $r=0$, while it is finite for $r\ne 0$ and goes to zero as $r\rightarrow \infty$; and therefore there is an essential singularity located at $r=0$. Although the location of the event horizon cannot be determined analytically by using f(r), fortunately we can get more insight in the solutions by calculating the temperature corresponding to the event horizon. The temperature and angular velocity of the horizon can be obtained by analytic continuation of the metric. The analytical continuation of the Lorentzian metric by $t\rightarrow i\tau$ and $a\rightarrow ia$ yields the Euclidean section. In order for the Euclidean metric to be regular at $r=r_{+}$, one should identify $\tau \sim \tau +\beta _{+}$ and $\phi _{i}\sim \phi _{i}+\beta _{+}\Omega _{i}$, where $\beta _{+}$ and $\Omega _{i}$s are the inverse Hawking temperature and the ith component of angular velocity of the horizon. Then the temperature and the ith component of angular velocity can be computed as

$$\begin{aligned} T_{+}= & {} \frac{f^{\prime }(r_{+})}{4\pi \Xi }=\frac{(1+\alpha ^{2})}{4\pi \Xi }\left\{ \frac{nb^{2\gamma }r_{+}^{1-2\gamma }}{l^{2}}\right. \nonumber \\&\left. -\frac{2^{p}p\left( 2p-1\right) {q}^{2\,p}}{\Pi {b}^{\,{2\left( n-2\right) \gamma p/ }\left( 2\,p-1\right) }{r}_{+}^{\Upsilon +(1-\gamma )\left( n-1\right) }} \right\} , \end{aligned}$$

(25)

$$\begin{aligned} \Omega _{i}= & {} \frac{a_{i}}{\Xi l^{2}}. \end{aligned}$$

(26)

Numerical calculations show that the temperature vanishes at the event horizon for extreme black brane solutions. Therefore, one can see from Eq. (25) that we have an extreme black brane if

$$\begin{aligned} m_{\mathrm {ext}}=\frac{(\alpha ^{2}+1)n{b}^{2\gamma \,}}{\Upsilon l^{2}} \left[ 1+\frac{(1+\alpha ^{2})\Upsilon }{\left( n-{\alpha }^{2}\right) } \right] \,{r}_{\mathrm {ext}}^{{(1-\gamma )}(n+1{)-1}}\nonumber \\ \end{aligned}$$

(27)

or

$$\begin{aligned} {q}_{\mathrm {ext}}^{2p}=\frac{\Pi nb^{2\gamma \left( np-1\right) /(2p-1)}}{ 2^{p}p\left( 2p-1\right) l^{2}}{r}_{\mathrm {ext}}^{\Upsilon +(1-\gamma )(n+1)-1}. \end{aligned}$$

(28)

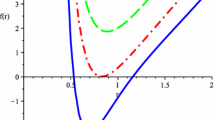
The solutions have two inner and outer horizons located at $r_{-}$ and $r_{+}$, provided the charge parameter q is lower than $q_{\mathrm {ext}}$ or m is greater than $m_{\mathrm {ext}}$ and a naked singularity if $q>q_{ \mathrm {ext}}$ or $m<m_{\mathrm {ext}}$ (see Fig. 1). Note that there is a relation between $m_{\mathrm {ext}}$ and $q_{\mathrm {ext}}$:

$$\begin{aligned} m_{\mathrm {ext}}= & {} \left( \frac{(\alpha ^{2}+1)n{b}^{2\gamma \,}(( n-{\alpha }^{2}) +(1+\alpha ^{2})\Upsilon ) }{\Upsilon l^{2}( n-{\alpha }^{2}) }\right) \nonumber \\&\times \left( \frac{2^{p}p( 2p-1) l^{2}}{\Pi nb^{2\gamma (np-1)/(2p-1)}}{q}_{\mathrm { ext}}^{2p}\right) ^{\frac{{(1-\gamma )}(n+1{)-1}}{\Upsilon +(1-\gamma )(n+1)-1}}, \end{aligned}$$

(29)

which reduces to the extremal mass obtained in [48] for a linear Maxwell field ($p=1$) and to one obtained in [80, 81] in the absence of a dilaton field ${\alpha =}\,\, \gamma =0$ and with a linear Maxwell field. Finally, it is noticeable that there is a Killing horizon in addition to an event horizon for rotating solutions in our Einstein dilaton gravity as in the case of rotating black solutions of the Einstein gravity. It is easy to show that the Killing vector field,

$$\begin{aligned}&\tilde{\chi }=C\chi , \nonumber \\&\chi =\partial _{t}+{{{\sum _{i=1}^{k}}}}\Omega _{i}\partial _{\phi _{i}}, \end{aligned}$$

(30)

is the null generator of the event horizon, where k denotes the number of rotation parameters [64] and C is a constant that we will fix in in next section. The Killing horizon is a null surface whose null generators are tangent to a Killing field.

Fig. 1

The behavior of f(r) versus r with $l=b=1$, $q=0.5$, $\alpha =\sqrt{2}$, $n=5$, $p=2$, $r_{\mathrm {ext}}=1$. In this case $m_{\mathrm {ext}}=60.00$ and $q_{\mathrm {ext}}=1.06$

3 Thermodynamics of black branes

In this section, we discuss the thermodynamics of rotating black brane solutions in the presence of a power-law Maxwell field. Since the discussion of the thermodynamics of these solutions depends on the calculation of the mass and other conserved charges of the spacetime, we first compute these conserved quantities. The way we proceed with calculating the conserved quantities is by the counterterm method. This method is a well-known method for asymptotically AdS solutions to avoid divergencies in calculation of conserved quantities, which is inspired by the AdS/CFT correspondence [65–68]. This method can also be used for dilaton gravity and in the presence of a Liouville-type potential where the spacetime is not asymptotically AdS [42, 43, 48, 69]. Since the boundary curvature of our spacetime is zero ($R_{abcd}(\gamma )=0$), the counterterm for the stress-energy tensor should be proportional to $\gamma ^{ab}$. We find the finite stress-energy tensor in $(n+1)$-dimensional Einstein dilaton gravity with Liouville-type potential as

$$\begin{aligned} T^{ab}=\frac{1}{8\pi }\left[ \Theta ^{ab}-\Theta \gamma ^{ab}+\frac{n-1}{l_{ \mathrm {eff}}}\gamma ^{ab}\right] , \end{aligned}$$

(31)

where $l_{\mathrm {eff}}$ is given by

$$\begin{aligned} l_{\mathrm {eff}}^{2}=\frac{(n-1)(\alpha ^{2}-n)}{V(\Phi )}. \end{aligned}$$

(32)

The first two terms in (31) are the variation of the action (1) with respect to $\gamma _{ab}$, and the last term is the counterterm, which removes the divergences. Note that in the absence of the dilaton field ($\alpha =0$), we have $V(\Phi )=2\Lambda$, and the effective $l_{\mathrm { eff}}^{2}$ of Eq. (32) reduces to $l^{2}=-n(n-1)/2\Lambda$ of the AdS spacetimes. In order to compute the conserved charges of the spacetime, one should first choose a spacelike surface ${\mathcal {B}}$ in $\partial {\mathcal {M}}$ with metric $\sigma _{ij}$, and one should write the boundary metric in ADM (Arnowitt–Deser–Misner) form:

$$\begin{aligned} \gamma _{ab}\mathrm{d}x^{a}\mathrm{d}x^{a}=-N^{2}\mathrm{d}t^{2}+\sigma _{ij}(\mathrm{d}\varphi ^{i}+V^{i}\mathrm{d}t)(\mathrm{d}\varphi ^{j}+V^{j}\mathrm{d}t), \end{aligned}$$

where the coordinates $\varphi ^{i}$ are the angular variables parameterizing the hypersurface of constant r around the origin, and N and $V^{i}$ are the lapse and shift functions, respectively. Then the quasilocal conserved quantities associated with the stress tensors of Eq. (31) can be written as

$$\begin{aligned} Q(\xi )=\int _{{\mathcal {B}}}\mathrm{d}^{n-1}\varphi \sqrt{\sigma }T_{ab}n^{a}{\xi }^{b}, \end{aligned}$$

(33)

where $\sigma$ is the determinant of the metric $\sigma _{ij}$, and $\xi$ and $n^{a}$ are the Killing vector field and the unit normal vector on the boundary ${\mathcal {B}}$. In order to calculate the quasilocal mass and angular momentum, one should choose boundaries with timelike ($\xi =\partial /\partial t$) and rotational ($\varsigma =\partial /\partial \varphi$) Killing vector fields, i.e.

$$\begin{aligned} M=\int _{{\mathcal {B}}}\mathrm{d}^{n-1}\varphi \sqrt{\sigma }T_{ab}n^{a}\xi ^{b} \end{aligned}$$

(34)

and

$$\begin{aligned} J=\int _{{\mathcal {B}}}\mathrm{d}^{n-1}\varphi \sqrt{\sigma }T_{ab}n^{a}\varsigma ^{b}, \end{aligned}$$

(35)

provided the surface ${\mathcal {B}}$ contains the orbits of $\varsigma$. Equations (34) and (35) are the conserved mass and angular momenta of the black hole surrounded by the boundary ${\mathcal {B}}$. It is remarkable that, although mass and angular momenta do not depend on the specific choice of the foliation ${\mathcal {B}}$ within the hypersurface $\partial {\mathcal {M}}$, they are dependent on the location of the boundary ${\mathcal {B}}$ in the spacetime. Taking into account the cylindrical symmetry of the rotating black brane with k rotation parameters along the angular coordinates $0\le \phi _{i}\le 2\pi$, we denote the volume of the hypersurface boundary at constant t and r by $V_{n-1}$. Then the mass and angular momentum per unit volume $V_{n-1}$ of the black branes can be calculated through the use of Eqs. (34) and (35). We find

$$\begin{aligned} {M}= & {} \frac{b^{(n-1)\gamma }}{16\pi l^{n-2}}\left( \frac{(n-\alpha ^{2})\Xi ^{2}+\alpha ^{2}-1}{1+\alpha ^{2}}\right) m, \end{aligned}$$

(36)

$$\begin{aligned} J_{i}= & {} \frac{b^{(n-1)\gamma }}{16\pi l^{n-2}}\left( \frac{n-\alpha ^{2}}{ 1+\alpha ^{2}}\right) \Xi ma_{i}. \end{aligned}$$

(37)

As one can see from (37), the angular momentum per unit volume is proportional to $a_{i}$s and therefore it vanishes if $a_{i}=0$ ($\Xi =1$). Thus, it is physically reasonable to consider the $a_{i}$ as rotational parameters of the spacetime. The last conserved quantity of our solutions is the electric charge. The electric charge can be obtained by calculating the flux of the electric field at infinity. By projecting the electromagnetic field tensor on the specific hypersurfaces, we can find the electric field as $E^{\mu }=g^{\mu \rho }\mathrm{e}^{-4\alpha p\Phi /(n-1)}\left( -F\right) ^{p-1}F_{\rho \nu }u^{\nu }$ where $u^{\nu }$ is normal to such hypersurfaces. The components of $u^{\nu }$ are

$$\begin{aligned} u^{0}=\frac{1}{N},\quad u^{r}=0,\quad u^{i}=-\frac{V^{i}}{N}, \end{aligned}$$

(38)

where N and $V^{i}$ are the lapse function and the shift vector. Eventually, the electric charge per unit volume $V_{n-1}$ can be calculated as

$$\begin{aligned} {Q}= & {} \frac{\Xi \tilde{q}}{4\pi l^{n-2}}, \nonumber \\ {\tilde{q}}= & {} {2^{p-1}{q}^{2\,p-1}.} \end{aligned}$$

(39)

One may note that $\tilde{q}=q$ for $p=1$ [48].

Now we calculate the thermodynamic quantities entropy S and electric potential U. The entropy of almost all black solutions including the ones in Einstein gravity typically obeys the so-called area law [70–76]. Dilaton black solutions are not exceptions (see for instance [48, 61]). Thus, we can calculate the entropy per unit volume $V_{n-1}$ of our rotating black brane as

$$\begin{aligned} {S}=\frac{\Xi b^{(n-1)\gamma }r_{+}^{(n-1)(1-\gamma )}}{4l^{n-2}}. \end{aligned}$$

(40)

The electric potential U can be calculated through the definition [77, 78]

$$\begin{aligned} U=A_{\mu }\tilde{\chi }^{\mu }\left| _{r\rightarrow \infty }-A_{\mu } \tilde{\chi }^{\mu }\right| _{r=r_{+}}, \end{aligned}$$

(41)

where $\tilde{\chi }$ is the null generator of the event horizon given by Eq. (30). Therefore, the electric potential may be obtained as

$$\begin{aligned} U=\frac{Cq{b}^{{\frac{\left( 2\,p+1-n\right) \gamma }{\left( 2\,p-1\right) }} }}{\Xi \Upsilon {r}^{\Upsilon }}. \end{aligned}$$

(42)

We are ready to see the satisfaction of the thermodynamics first law. First, we should obtain the mass M in terms of the extensive quantities S, Q , and ${\mathbf {J}}$. Using Eqs. (36)–(39) and the fact that $f(r_{+})=0$, we obtain

$$\begin{aligned} M(S,Q,{\mathbf {J}})=\frac{((n-\alpha ^{2})Z+\alpha ^{2}-1) {\mathbf {J}}}{(n-\alpha ^{2})l\sqrt{Z(Z-1)}}, \end{aligned}$$

(43)

where $\mathbf {J=}\,\,\sqrt{\sum _{i}^{k}{J_{i}}^{2}}$ and $Z=\Xi ^{2}$, which is the positive real root of the following equation:

$$\begin{aligned}&({\alpha }^{2}+1)\sqrt{Z-1}\left( n-{\alpha }^{2}\right) p\left( 2p-1\right) ^{2}\nonumber \\&\quad \times \left[ \frac{\left( 3{2\pi }^{2}Q^{2}\right) ^{{p}}{l }^{n+4(p-1)}{b}^{{{\alpha }^{2}}}}{\sqrt{Z}^{\left( \alpha ^{2}+2n-2p-1\right) /\left( n-1\right) }}\right. \nonumber \\&\quad \left. \times \left( \frac{4l^{n-2}{S}}{Z}\right) ^{(n-2\,p+{\alpha }^{2})/\left( 1-n\right) }\right] ^{1/(2p-1)} \nonumber \\&\quad +\left( n-2p+\alpha ^{2}\right) \Pi \nonumber \\&\quad \times \left[ -\frac{\left( {\alpha } ^{2}+1\right) \sqrt{Z-1}{b}^{{\alpha }^{2}}n}{{l}^{n-2}\sqrt{Z}^{{({\alpha } ^{2}-2n+1)/(n-1)}}}\left( \frac{4l^{n-2}{S}}{Z}\right) ^{{(n-{\alpha } ^{2})/(n-1)}}\right. \nonumber \\&\quad \left. +16\,\pi \,l{\mathbf {J}}\right] =0. \end{aligned}$$

(44)

Considering S, Q, and ${\mathbf {J}}$ as a complete set of extensive quantities for the mass $M(S,Q,{\mathbf {J}})$, we should define conjugate intensive quantities to them. These quantities are the temperature, the angular velocities, and the electric potential,

$$\begin{aligned} T=\left( \frac{\partial {M}}{\partial {S}}\right) _{{\mathbf {J}},Q},\Omega _{i}=\left( \frac{\partial {M}}{\partial {J_{i}}}\right) _{S,Q},U=\left( \frac{\partial {M}}{\partial {Q}}\right) _{S,{\mathbf {J}}}. \end{aligned}$$

(45)

One can check numerically that the quantities defined by Eq. (45) coincide with Eqs. (25), (26), and (42), provided C is chosen as $C=\left( n-1\right) p^{2}/\Pi$. Note that in the case of a linear Maxwell field ($p=1$), C reduces to 1 as we expect [48]. Therefore one can conclude that the first law of thermodynamics,

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+{{{\sum _{i=1}^{k}}}}\Omega _{i}\mathrm{d}{J}_{i}+U\mathrm{d}{Q}, \end{aligned}$$

(46)

is satisfied. As one can see from (41), U is proportional to the value of $A_{\mu }$ at infinity and therefore U diverges if $A_{\mu }$ diverges at infinity. On the other hand, it is obvious from the first law of thermodynamics that M is dependent on the value of U. Therefore, as we mentioned in Sect. 2, $A_{\mu }$ should be finite at infinity in order to have a finite mass. We took this fact into account for finding constraints on p and $\alpha$ (see Eq. (20)).

4 Stability in canonical and grand-canonical ensembles

In this section, we are going to study the thermal stability of rotating black branes in the presence of a power-law Maxwell field in the canonical and grand-canonical ensembles. It is necessary for a thermodynamic system to discuss its thermal stability. The thermal stability is investigated to ensure that the entropy of system is at local maximum or equivalently the internal energy of the system is at local minimum. Therefore, the stability of a rotating black brane as a thermodynamic system can be studied in terms of the entropy $S(M,Q,{\mathbf {J}})$ or its Legendre transformation $M(S,Q,{\mathbf {J}})$. In terms of the mass $M(S,Q,{\mathbf {J}})$, the local stability in any ensemble implies that $M(S,Q,{\mathbf {J}})$ is a convex function of its extensive variables. Typically, this behavior is studied by calculating the determinant of the Hessian matrix of $M(S,Q,{\mathbf {J}})$ with respect to its extensive variables $X_{i}$, ${\mathbf {H}}_{X_{i}X_{j}}^{M}=\left[ \partial ^{2}M/\partial X_{i}\partial X_{j}\right]$ [77–79]. ${\mathbf {H}}_{X_{i}X_{j}}^{M}\ge 0$ guarantees that the system is thermally stable. The number of thermodynamic variables is ensemble dependent. In the canonical ensemble, the charge and angular momenta are fixed parameters and consequently the determinant of Hessian matrix ${\mathbf {H}}_{X_{i}X_{j}}^{M}$ reduces to $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$. Therefore, in order to find the ranges where the system is at thermal stability, it is sufficient to find the ranges of positivity of $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ where the temperature T is positive as well. In the grand-canonical ensemble Q and ${\mathbf {J}}$ are not fixed parameters.

We discuss thermal stability for the uncharged and charged cases separately. First we discuss the uncharged case. It is notable that in the case of uncharged rotating black branes $(\partial ^{2}M/\partial S^{2})_{ {\mathbf {J}}}$ is exactly the one which is obtained in [48]:

$$\begin{aligned} \left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{{\mathbf {J}}}= & {} \frac{ n( {\alpha }^{2}+1) \left[ ({\Xi }^{2}-1)(n+1-2{\alpha }^{2})+{ \Xi }^{2}(1-{\alpha }^{2}) \right] }{{\pi \Xi }^{2}{l}^{4-n}{b}^{ {( n-3) \gamma }}\left[ ({\alpha }^{2}+n-2){\Xi }^{2}+1-{\alpha } ^{2}\right] }\nonumber \\&\times {r}_{+}^{{(2-n-{\alpha }^{2})/(\alpha }^{2}+1)}. \end{aligned}$$

(47)

Therefore, in the canonical ensemble we just briefly review these results. Since $\Xi ^{2}\ge 1$, (47) is positive provided $\alpha \le 1$. Therefore uncharged rotating black branes are stable in the canonical ensemble for $\alpha \le 1$. Note that for the uncharged case the temperature is always positive (see Eq. (25)). In the grand-canonical ensemble ${\mathbf {H}}_{S {\mathbf {J}}}^{M}$ can be calculated as

$$\begin{aligned} {\mathbf {H}}_{S{\mathbf {J}}}^{M}=\frac{16\left( 1-\,{\alpha }^{2}\right) {l} ^{2(n-3)}{r}_{+}^{2{(1-\,n)/(\alpha }^{2}+1)}}{{b}^{{2(n-1) \gamma }}{\Xi }^{4}[({\alpha }^{2}+n-2) {\Xi }^{2}+1-{ \alpha }^{2}]}. \end{aligned}$$

(48)

From Eq. (48) it is obvious that ${\mathbf {H}}_{S{\mathbf {J}}}^{M}\ge 0$ provided $\alpha \le 1$, which is similar to the case of the canonical ensemble. From the above arguments we conclude that the uncharged rotating black branes are thermally stable provided $\alpha \le 1$ in both canonical and grand-canonical ensembles.

For the charged case, we discuss the stability for $\alpha \le 1$ and $\alpha >1$ separately. Since the charge does not change the stable solutions to unstable ones [80, 81], for $\alpha \le 1$ we have thermally stable charged rotating black branes. This fact is shown in Figs. 2, 3, 5, 6, 8, and 9. Figures 2 and 3 show that for $\alpha \le 1$, the obtained solutions are always stable in the canonical and grand-canonical ensembles for any value of $r_{+}$, as we expect. Since $T>0$ guarantees that we have black branes for our choices, one should choose $q<q_{\mathrm {ext}}$. The behavior of the temperature is depicted in Fig. 4 with the same constants as Figs.  and 3. The behaviors of $(\partial ^{2}M/\partial S^{2})_{Q, {\mathbf {J}}}$ and ${\mathbf {H}}_{SQ{\mathbf {J}}}^{M}$ with respect to $\alpha \le 1$ for different choices of the charge q are plotted in Figs. 5 and 6. These figures once again show that the charge cannot change stable solutions to unstable ones and therefore we have stable charged rotating solutions for $\alpha \le 1$, as we had in uncharged case. Figure 7 shows the positivity of the temperature T for solutions where their thermal stabilities have been depicted in Figs. 5 and 6. Figures 8 and 9 depict the stability of the solutions for $\alpha \le 1$ for different values of p in the canonical and grand-canonical ensembles, respectively. The behavior of the temperature for the latter case is illustrated in Fig. 10. For $\alpha >1$, one can understand from Fig. 11 that the radius of the event horizon of stable black branes encounter an upper limit $r_{+\max }$ in both the canonical and the grand-canonical ensembles. The value of this upper limit is greater in the canonical ensemble than in the grand-canonical ensemble. The effects of $\alpha$ on the stability of the solutions in both canonical and grand-canonical ensembles are depicted in Fig. 12. There is again an ensemble-dependent upper limit, this time on $\alpha$ such that, for values greater than it, the solutions are no longer stable. The value of $\alpha _{\max }$ is smaller in the grand-canonical ensemble. In terms of $1/2<p<n/2$, the stability is shown in Fig. 13. In contrast with $r_{+}$ and $\alpha$, there is a lower limit for p i.e. for $p>p_{\min }$, and we have stable solutions. $p_{\min }$ is again ensemble dependent as well as $r_{+\max }$ and $\alpha _{\max }$. For $n/2<p<n-1$, where $\alpha$ has a p -dependent lower limit, numerical analyses confirm the result of the investigation for $1/2<p<n/2$, i.e. there is again a lower limit $p_{\min }$ such that, for values lower than it, the solutions are unstable. The stability in terms of charge is depicted in Fig. 14. In this case there is an ensemble-dependent $q_{\min }$ in each of the ensembles such that for q greater than it the black branes are stable. The value of $q_{\min }$ is greater in the grand-canonical ensemble.

Fig. 2

The behavior of $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ versus $\alpha \le 1$ with $l=b=1$, $q=0.8$, $\Xi =1.25$, $n=5$, and $p=2$

Fig. 3

The behavior of ${\mathbf {H}}_{SQ{\mathbf {J}}}^{M}$ versus $\alpha \le 1$ with $l=b=1$, $q=0.8$, $\Xi =1.25$, $n=5$, and $p=2$. Note that the curve corresponding to $r_{+}=1$ has been divided by 10

Fig. 4

The behavior of T versus $\alpha \le 1$ with $l=b=1$, $q=0.8$, $\Xi =1.25$, $n=5$, and $p=2$

Fig. 5

The behavior of $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ versus $\alpha \le 1$ with $l=b=1$, $r_{+}=1.5$, $\Xi =1.25$, $n=5$ and $p=2$

Fig. 6

The behavior of ${\mathbf {H}}_{SQ{\mathbf {J}}}^{M}$ versus $\alpha \le 1$ with $l=b=1$, $r_{+}=1.5$, $\Xi =1.25$, $n=5$, and $p=2$. Note that the curve corresponding to $q=0.3$ has been divided by 10

Fig. 7

The behavior of T versus $\alpha \le 1$ with $l=b=1$, $r_{+}=1.5$, $\Xi =1.25$, $n=5$, and $p=2$

Fig. 8

The behavior of $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ versus $\alpha \le 1$ with $l=b=1$, $r_{+}=1.5$, $\Xi =1.25$, $n=5$ and $q=0.8$. Note that the curve corresponding to $p=0.75$ has been rescaled by the factor 1.5

Fig. 9

The behavior of ${\mathbf {H}}_{SQ{\mathbf {J}}}^{M}$ versus $\alpha \le 1$ with $l=b=1$, $r_{+}=1.5$, $\Xi =1.25$, $n=5$, and $q=0.8$. Note that curves corresponding to $p=0.75$ and $p=2$ have been rescaled by the factors 10 and $10^{-1}$, respectively

Fig. 10

The behavior of T versus $\alpha \le 1$ with $l=b=1$, $r_{+}=1.5$, $\Xi =1.25$, $n=5$, and $q=0.8$. Note that the curve corresponding to $p=0.75$ has been rescaled by the factor 1.5

Fig. 11

The behavior of T (solid curve), $10(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ (dashed curve) and $10^{-3}{\mathbf {H}}_{SQ{\mathbf {J}} }^{M}$ (dash-dotted curve) versus $r_{+}$ with $l=b=1$, $q=0.5$, $\alpha =1.35$, $\Xi =1.25$, $n=5$, and $p=2$

Fig. 12

The behavior of T (solid curve), $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ (dashed curve) and ${\mathbf {H}}_{SQ{\mathbf {J}}}^{M}$ (dash-dotted curve) versus $\alpha$ with $l=b=1$, $q=0.8$, $r_{+}=1.5$, $\Xi =1.25$, $n=5$, and $p=2$

Fig. 13

The behavior of T (solid curve), $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ (dashed curve) and $10^{-1}{\mathbf {H}}_{SQ{\mathbf {J}} }^{M}$ (dash-dotted curve) versus p with $l=b=1$, $q=0.9$, $r_{+}=1.1$, $\Xi =1.25$, $\alpha =1.45$, and $n=5$

Fig. 14

The behavior of T (solid curve), $(\partial ^{2}M/\partial S^{2})_{Q,{\mathbf {J}}}$ (dashed curve) and $10^{-2}{\mathbf {H}}_{SQ{\mathbf {J}} }^{M}$ (dash-dotted curve) versus q with $l=b=1$, $p=4$, $r_{+}=0.9$, $\Xi =1.25$, $\alpha =1.5$, and $n=6$

5 Closing remarks

In this paper, we constructed a new class of higher-dimensional nonlinear charged rotating black brane solutions in Einstein dilaton gravity with a complete set of rotation parameters. The nonlinear electromagnetic source was considered in the form of the power-law Maxwell field, which guarantees conformal invariance of the electromagnetic Lagrangian in arbitrary dimensions for specific choices of the power. Due to the presence of the dilaton field, our solutions are neither asymptotically flat nor (A)dS. We showed that in the case of a power-law Maxwell field, one needs two Liouville-type potentials in order to have a rotating black brane solution, while in the case of a linear Maxwell source just one term is needed [48]. The extra dilaton potential term disappears for $p=1$. All our results reproduce the results of [48] in the case of linear charged rotating solutions where $p=1$.

Requiring from one side that the value of the total mass should be finite and from the other side that the effect of the mass term in the metric function should disappear at infinity, we found some restrictions on p and $\alpha$. The allowed ranges of these two parameters are as follows. For $1/2<p<n/2$, we have $0\le \alpha ^{2}<n-2$, while for $n/2<p<n-1$, we have $2p-n<\alpha ^{2}<n-2$. For these permitted ranges, our solutions are always well defined. Also, in these ranges of p and $\alpha$, the charge term in the metric function f(r) is always positive and dominant in the vicinity of $r=0$. Therefore, Schwarzschild-like solutions are ruled out. However, solutions with two inner and outer horizons, extreme solutions, and naked singularities are allowed.

In order to study the thermodynamics of charged rotating black branes, we calculated the mass, charge, temperature, entropy, electric potential energy, and angular momentum. Using these quantities we obtained a Smarr-type formula for the mass $M(S,Q,{\mathbf {J}})$ and showed that the first law of thermodynamics is satisfied. Next, we analyzed the thermal stability of the solutions in both the canonical and the grand-canonical ensembles. These investigations showed that, for $\alpha \le 1$, charged rotating black brane solutions are always stable with any value of the charge parameter. For $\alpha >1$, there is a $r_{+\max }$ in each of ensembles such that we have stable solutions provided their radii are smaller than $r_{+\max }$. In terms of $\alpha ({>}1)$, the solutions changed from stable ones to unstable ones when they meet an $\alpha _{\max }$. As regards p and q, we showed that the solutions encounter $p_{\min }$ and $q_{\min }$, respectively, so that the solutions with q and p parameters lower than them are unstable for $\alpha >1$. All $r_{+\max }$, $\alpha _{\max }$, $q_{\min }$, and $p_{\min }$ values depend on the ensemble.

It is worth noting that the higher-dimensional charged rotating solutions obtained here have a flat horizon. One may be interested in studying the rotating solutions with a curved horizon. Specially the case of a spherical horizon will be a good extension of the Kerr–Newman solution. It seems that the study of the general case is a difficult problem. However, it is possible to seek slowly rotating nonlinear charged solutions with a curved horizon. The latter study is in progress.